Lý thuyết 3 cách tính thể tích trong môn thí nghiệm vật lý 1 | Trường Đại học sư phạm kỹ thuật TP Hồ Chí Minh- Khoa khoa học cơ bản
Phương pháp đĩa (The Disk Method): Để xác định thể tích của một khối tròn xoay và để xây dựng một phương pháp để tính toán nó, chúng ta xét khối tròn xoay S được tạo ra bởi vùng R như được hiển thị ở Hình 1. Cho P = {x , x , …, x } là một phân vùng đều của đoạn [a,b], với x = a và x = b. Phân vùng này chia vùng R thành n vùng con không giao nhau R , R , …, R . Khi các vùng này được quay quanh trục, Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
Môn: Thí nghiệm vật lý 1 (PHYS111202)
Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Thí nghiệm vật lý 1 (PHYS111202)
Trường:
Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
Phương pháp đĩa (The Disk Method):
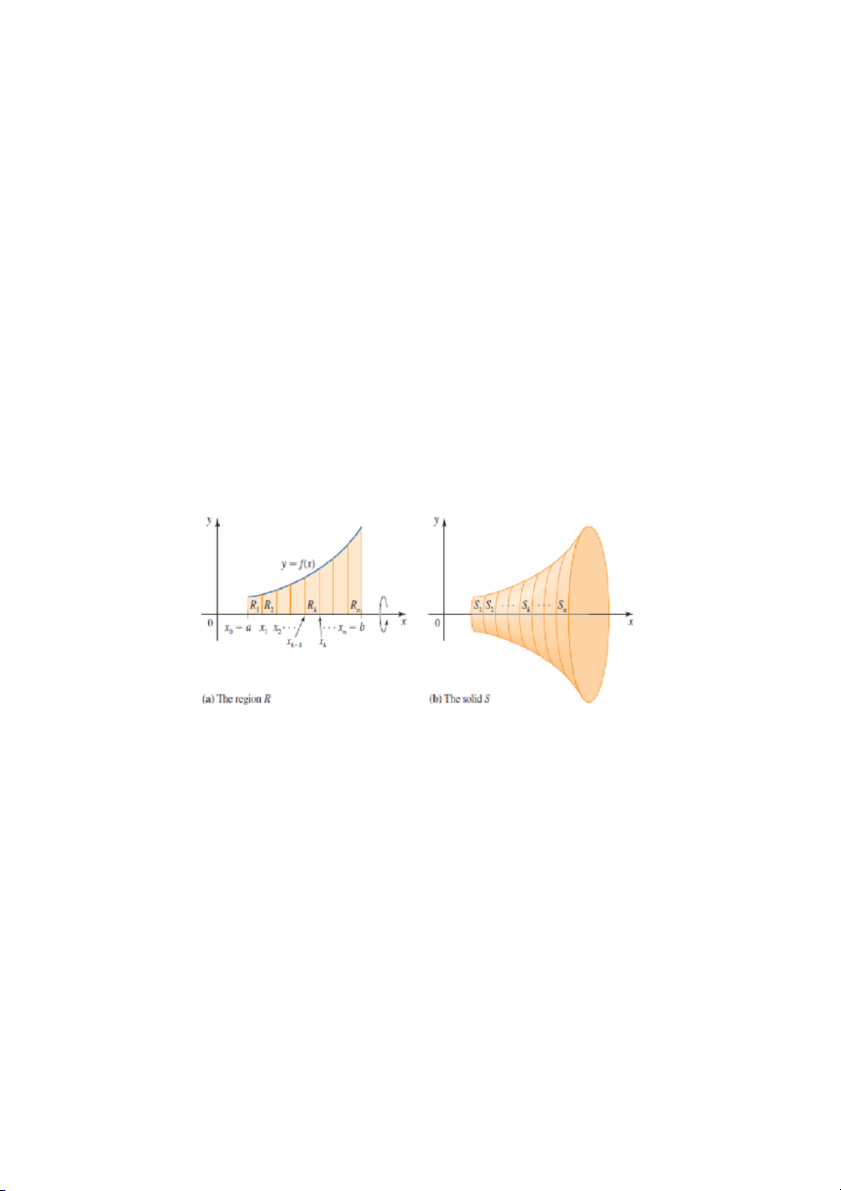
Để xác định thể tích của một khối tròn xoay và để xây dựng một phương
pháp để tính toán nó, chúng ta xét khối tròn xoay S được tạo ra bởi vùng R
như được hiển thị ở Hình 1. Cho P = {x0, x1, …, xn} là một phân vùng đều của
đoạn [a,b], với x0 = a và xn = b. Phân vùng này chia vùng R thành n vùng
con không giao nhau R1, R2, …, Rn. Khi các vùng này được quay quanh trục
x, chúng tạo ra n khối tròn xoay không giao nhau S1, S2, …, Sn, với hợp của chúng là S.
Hình 1: Một phân vùng của [a, b] tạo ra n phân vùng con R , R 1 , …, R 2 được quay quanh trục x n
để thu được n khối tròn xoay S , S 1 , …, 2
S tạo thành khối S (Ở đây cho n = 8). ( a.Vùng R; b. n Khối tròn xoay S)
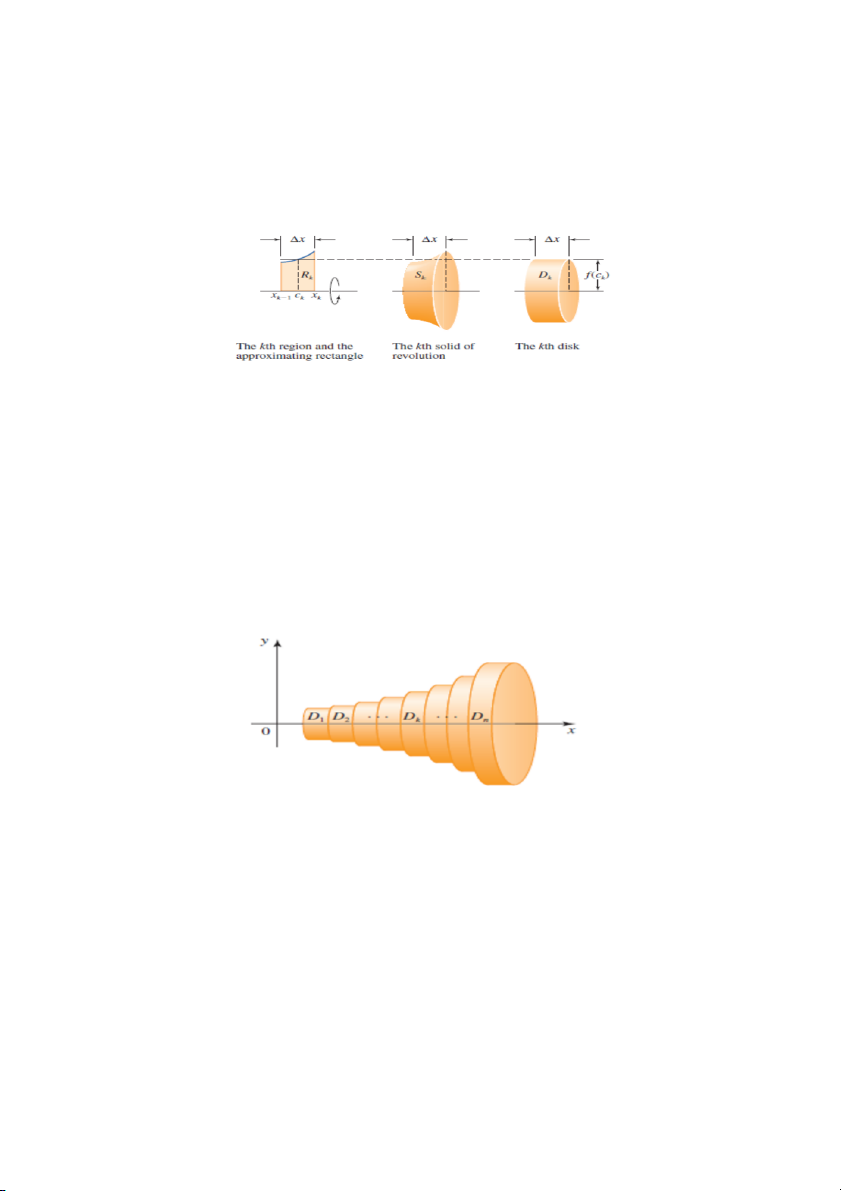
Hãy tập trung vào phần của khối tròn xoay được tạo bởi vùng Rk dưới đồ
thị của hàm f(x) trên đoạn [xk-1, xk]. Vùng này được phóng to để có thể
quan sát rõ hơn trong Hình 2. Nếu có ck là một điểm đánh giá trong đoạn
[xk-1, xk], thì diện tích của Rk được xấp xỉ bằng hình chữ nhật với chiều
cao f(ck) và chiều rộng Δx = (b – a)/n. Nếu hình chữ nhật này được xoay
quanh trục x, nó tạo nên một đĩa Dk với bán kính f(ck) và chiều rộng Δx;
do đó, thể tích của nó là: ΔV 2 2
k = π [f(ck) ] Δx ( π(bán kính) • độ dày )
Hình 2: Vùng R (vùng được tô màu), được xấp xỉ bởi hình chữ nhật. k
Thể tích của khối S được k
tính xấp xỉ bởi thể tích của đĩa D k
Thể tích của Dk cung cấp cho chúng ta thể tích xấp xỉ của Sk. Do đó,
bằng cách xấp xỉ thể tích của từng khối tròn xoay S1, S2, …, Sn với thể
tích của các đĩa D1, D2, …, Dn, chúng ta thấy rằng thể tích V của S được
tính xấp xỉ bởi tổng các thể tích của các đĩa sau (Xem Hình 3). Do đó, V 2 = π [f(ck) ] Δx
Hình 3: Thể tích V của khối tròn xoay S được xấp xỉ bằng tổng các thể tích của n đĩa D , …, D 1 n
Nhận thấy rằng tổng trên cũng là tổng Riemann của hàm πf2 trên đoạn [a, b], ta thấy rằng
Định nghĩa: Thể tích của một khối tròn xoay (Vùng quay quanh trục x)
Cho f là một hàm số liên tục và không âm trên [a, b], và để R là vùng
nằm dưới đồ thị của f trên đoạn [a, b]. Thể tích của khối tròn xoay được
tạo thành bởi việc quay R quanh trục x là V = (1)
Chúng ta có thể nhớ lại công thức tính diện tích của phần bên dưới của
một đường cong bằng cách nhìn vào phần diện tích của một hình chữ
nhật đại diện, vì vậy chúng ta có thể nhớ lại công thức (1) bằng cách
nhìn vào thể tích của phần đĩa thu được thông qua việc quay hình chữ
nhật đại diện đó quanh trục x
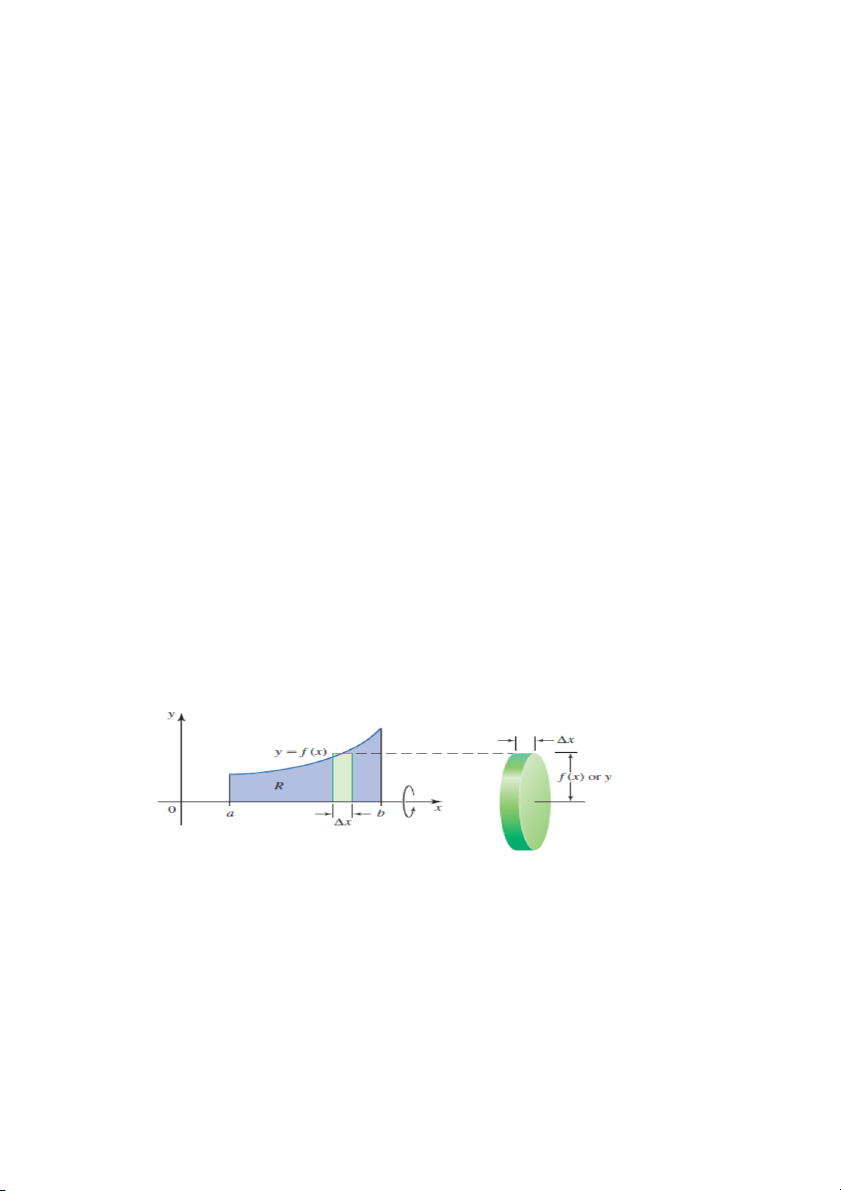
Chúng ta tiến hành như sau: Sau khi vẽ một phác thảo của vùng R bên
dưới đồ thị của hàm y = f(x) trên [a, b], ta vẽ một hình chữ nhật đứng đại
diện có chiều cao f(x) ( hoặc y) tương ứng với giá trị của x trong [a, b],
và chiều rộng Δx. (Xem Hình??) Chúng ta có thể coi phần đĩa này có thể tích ΔV 2 2 2
k = π [f(x) ] Δx = πy Δx ( π(bán kính) • chiều rộng )
là đại diện cho một phần thể tích của một khối.
Hình 4: Nếu một hình chữ nhật đứng đại diện được quay quanh trục x, nó hình thành nên một đĩa
có bán kính f(x) (hoặc y), và chiều rộng Δx
Thể tích tính bằng phương pháp đĩa (Vùng quay quanh trục x) được cho như sau:
Thể tích tính bằng phương pháp đĩa (Vùng quay quanh trục y) được tính như sau: Phương pháp Washer
Gọi R là vùng nằm giữa đồ thị của các hàm f(x), g(x) và các đường thẳng x =
a, x = b, nơi mà f(x) ≥ g(x) ≥ 0 trên đoạn [ ]. Nếu xoay a, b R quanh trục
hoành, ta được một khối tròn xoay có lỗ ở giữa. (Xem Hình 11.) Quan sát
thấy nếu lấy một hình chữ nhật thẳng đứng trong R và xoay nó quanh trục
hoành, ta được một phần thể tích của khối tròn có hình dạng của một vòng
đệm (washer) với bán kính ngoài f(x) và bán kính trong g(x). Do đó, thể tích của phần này là
π(bán kính ngoài)2 × độ dày - π(bán kính trong)2 ×độ dày
HÌNH 11: Khi một hình chữ nhật đứng được xoay quanh trục hoành, nó tạo ra một vòng đệm
(washer) có bán kính ngoài f(x), bán kính trong (x) và chiều rộng g Δx
Tổng thể tích của các vòng đệm và lấy giới hạn, ta thấy thể tích của khối tròn được tính như sau.
Thể tích khối tròn theo phương pháp Washer-vòng đệm (vùng xoay quanh trục hoành)
V = π f ≥ g≥0
Phương pháp mặt cắt ngang
Bây giờ chúng ta chuyển sang bài toán tổng quát hơn là xác định thể tích của một
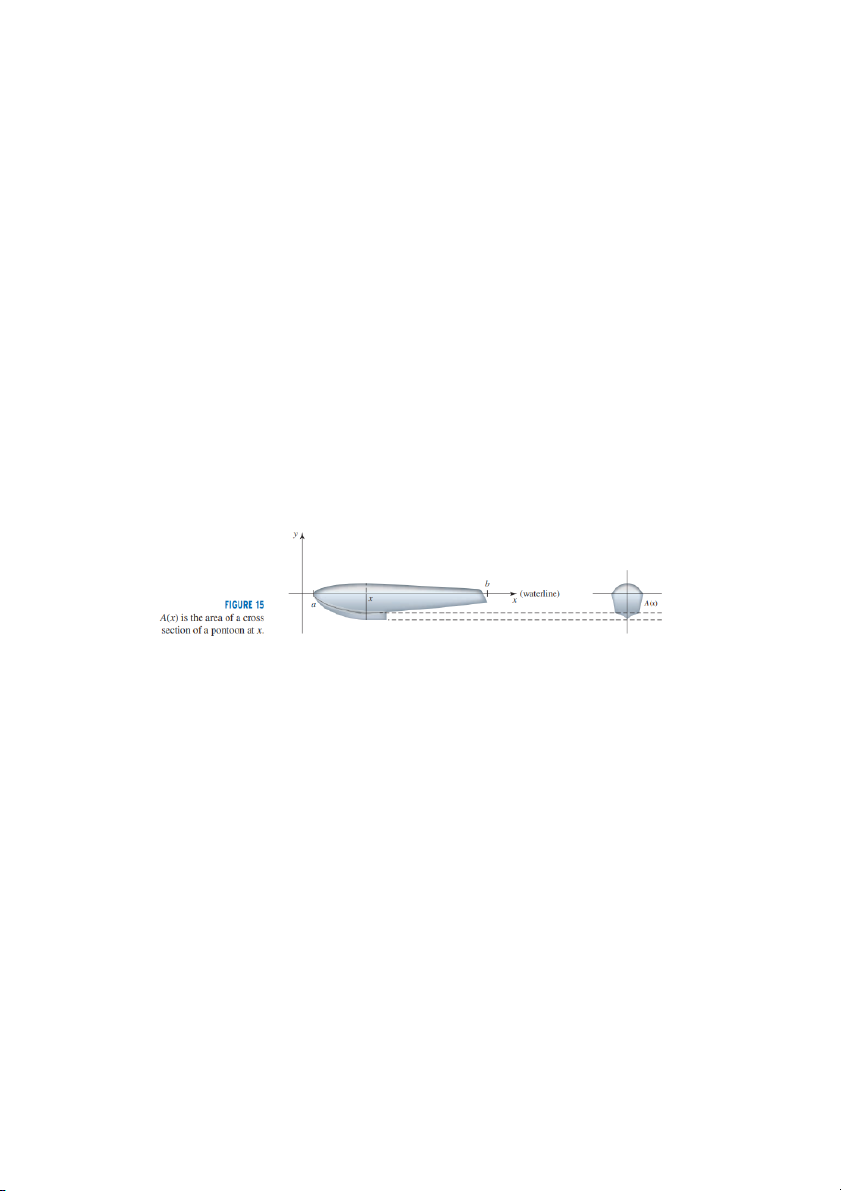
vật có hình dạng không đều. Ví dụ, hãy xem xét vật rắn là một phần của chiếc
phao nằm bên dưới mực nước. Hình nhìn từ bên của một chiếc cầu phao như vậy
được thể hiện trên Hình 15. Mặt cắt ngang của cầu phao (theo mặt phẳng vuông
góc với trục x) tại điểm x được thể hiện bên phải.
Để tìm thể tích của chiếc phao, hãy lấy một phân vùng thông thường P 5 {x
0, x 1, p , x n} trong khoảng [a, b]. Các mặt phẳng vuông góc với trục tại
vách ngăn điểm sẽ cắt chiếc phao thành “tấm” giống như cách người ta cắt
một ổ bánh mì. Thể tích V của tấm thứ k giữa x=x(k-1) và x=xk xấp xỉ
bằng thể tích của hình trụ có tiết diện không đổi A(ck) và chiều cao x,
trong đó ck nằm trong (xem hình 16). Như vậy
Nếu cộng n số hạng này lại, chúng ta sẽ có được thể tích gần đúng V của chiếc
phao. Chúng ta có thể kỳ vọng các giá trị gần đúng sẽ ngày càng tốt hơn khi n ->
∞. Thừa nhận tổng này là tổng Riemann của hàm A(x) trên khoảng [a,b], chúng ta
được dẫn đến định nghĩa sau. ĐỊNH NGHĨA
Thể tích của vật rắn có tiết diện đã biết
Cho S là một vật rắn giới hạn bởi các mặt phẳng vuông góc với trục x tại x=a và
x=b. Nếu diện tích mặt cắt ngang của S tại bất kỳ điểm x nào trong [a,b] là A(x),
trong đó A liên tục trên [a,b] thì thể tích của S là: ≈