lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức
Phần 1. ĐẠI SỐ TUYẾN TÍNH Gv: Phan Ngô Tuấn Anh
Khoa Toán – Thống Kê, UEH
Chương 1. Ma trận & ịnh thức I. Ma trận 1.1 Định nghĩa
Một ma trận (matrix) A cấp m n là một bảng số gồm có m dòng, n cột. Các phần tử của A là những số thực tùy ý. a11 a12 a1n A a21 a22 a2n am1 am2 amn
Trong ma trận A ở trên thì aij
là phần tử thuộc dòng i, cột j của A. Ta ký hiệu ma trận A là A (aij m n) 3 4 2 Ví dụ: A 1 0 7 (ma trận cấp 2 3)
Ma trận cấp n n ược gọi là ma trận vuông cấp n. Ví dụ: 2 3 A 5 1 (ma trận vuông cấp 2) 2 3 0 A 1 1 4 (ma trận vuông cấp 3) 1 6 5 Trang | 1 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức
Đối với ma trận A (aij n n) vuông cấp n thì các phần tử a ,a11 22, ,ann (có chỉ số dòng bằng chỉ số cột)
tạo thành ường chéo chính của A: a11 x x A x a 22 x x x ann 1 4 5 Ví dụ: Với ma trận A 6 2 7
thì ường chéo chính gồm các phần tử là 1,2,3 8 9 3
Ma trận mà mọi phần tử của nó ều bằng 0 ược gọi là ma trận không (ma trận zero), ký hiệu là Om n
(hoặc ký hiệu là O, nếu cấp của ma trận ược hiểu ngầm). 0 0 0 0 0 Ví dụ: O2 3 0 0 0 ; O2 2 0 0
Ma trận ơn vị cấp n, ký hiệu là I (Identity matrix), là ma trận vuông cấp n có dạng: n 1 0 0 0 0 1 0 0 In 0 0 1 0 0 0 0 1
(các phần tử thuộc ường chéo chính ều bằng 1, các phần tử còn lại ều bằng 0) Ví dụ: 1 0 I2 0 1 (ma trận ơn vị cấp 2) 1 0 0 I3 0 1 0 (ma trận ơn vị cấp 3) Trang | 2 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức 0 0 1
Cho A (aij n n) là ma trận vuông cấp n. Ta nói: -
Ma trận A có dạng tam giác trên (upper triangular matrix) nếu mọi phần tử nằm phía dưới
ường chéo chính của A ều bằng 0: a11 a12 a13 a1n 0 a22 a23 a2n A 0 0
a33 a3n (ma trận tam giác trên) 0 0 0 0 ann 1 2 1 Ví dụ: A 0 4 3 (ma trận tam giác trên) 0 0 5 -
Ma trận A có dạng tam giác dưới (lower triangular matrix) nếu mọi phần tử nằm phía trên
ường chéo chính của A ều bằng 0: a11 0 0 0 a21 a22 0 0 A a31 a32 a33
0 (ma trận tam giác dưới) an1 an2 an3 ann 1 0 0 Ví dụ: A 2 3 0
(ma trận tam giác dưới) 4 5 6
Nhận xét: Ma trận ơn vị I là ma trận tam giác trên và cũng là ma trận tam giác dưới. n
Ta quy ước hai ma trận A và B là bằng nhau nếu chúng có cùng cấp (kích thước) và có số liệu hoàn
toàn giống nhau, ký hiệu là A B Trang | 3 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức
1.2 Các phép toán ma trận
a) Phép cộng ma trận (addition)
Cho A và B là hai ma trận có cùng cấp m n , khi ó ma trận tổng A B có ược bằng cách cộng các phần
tử tương ứng của A và B. 1 2 1 3 1 5 4 3 6 Ví dụ: A 3 5 4 ; B 1 2 1 A B 4 7 5
b) Phép nhân vô hướng (scalar multiplication)
Cho A là ma trận cấp m n và là một số thực, khi ó ma trận tích Acó ược bằng cách nhân số vào
tất cả các phần tử của A. 1 1 Ví dụ: A 16 5204 ; 2 A 12 A 32 15 02 2
Mệnh ề. Cho A,B,C là các ma trận cấp m n và , là các số thực. Ta có: • (A B) C A (B
C) (tính kết hợp của phép cộng) • A B B
A (tính giao hoán của phép cộng) • A Om n A
• A ( 1)A Om n (ma trận ( 1) A ược gọi là ma trận ối của A, ký hiệu là A ) • 0.A Om n và 1.A A (A B) A B ( )A A A ( A) ( )A ( A)
c) Phép chuyển vị (Transpose)
Cho A là ma trận cấp m n , khi ó ma trận chuyển vị AT có ược từ A bằng cách xoay các dòng của A
thành các cột tương ứng của A . Ma trận T A có cấp là T n m 1 4 1 2 3 T 2 5 Ví dụ: A 4 5 6 A 3 6 1 2 3 1 4 7 Trang | 4 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức Ví dụ: A 4 5 6 AT 2 5 8 7 8 9 3 6 9
Do phép chuyển vị là xoay dòng thành cột nên ta có:
Mệnh ề. Cho A,B là các ma trận cấp m n và là số thực. Ta có: • AT T A • (A B)T AT BT • ( A)T AT Ví dụ: (2A 3B)T 2AT 3BT
d) Phép nhân ma trận (matrix product)
Cho các ma trận A (aij m) p và B (bij)p n (số cột của A phải bằng với số dòng của B).
Khi ó, ma trận tích AB có cấp là m n
Để tính các phần tử của ma trận AB, chẳng hạn muốn tính phần tử (AB)ij thì ta:
• quan sát dòng thứ i của A và cột thứ j của B (là những véc tơ gồm p tọa ộ): - dòng i của A là ai1 ai2 aip b1j b2j - cột j của B là bpj
• nhân từng cặp tọa ộ tương ứng của hai véc tơ này với nhau, rồi cộng lại: (AB)ij a bi1 1j a bi2 2j a bip pj
Nói cách khác, phần tử (AB)ij là tích vô hướng của véc tơ dòng i của A với véc tơ cột j của B 2 1 3 1 1 2 1 4 5 0 3 Ví dụ: Cho A 3 0 2 2 3 ; B 3 5 1 6 3 4 Trang | 5 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức
Ma trận A có cấp 2 3, ma trận B có cấp 3 4 nên ma trận AB có cấp 2 4 c11 c12 c13 c14 AB c21 c22 c23 c24 2 4
Ta tính các phần tử của AB như sau:
Phần tử c thuộc dòng 1, cột 1 của AB nên ta quan sát: 11
• véc tơ dòng 1 của A: 1 2 1 • véc tơ cột 1 của B: 2
• nhân từng cặp tọa 4 ộ
của hai véc tơ này rồi cộng lại: 3 c11 1 2 2 4 1 3 13
Phần tử c12 thuộc dòng 1, cột 2 của AB nên ta quan sát:
• véc tơ dòng 1 của A: 1 2 1 1
• véc tơ cột 2 của B: 5
• nhân từng cặp tọa 5 ộ
của hai véc tơ này rồi cộng lại: c12 1 1 2 51 5 16
Phần tử c thuộc dòng 1, cột 3 của AB nên ta quan sát: 13
• véc tơ dòng 1 của A: 1 2 1 3
• véc tơ cột 3 của B: 0 1
• nhân từng cặp tọa ộ của hai véc tơ này rồi cộng lại: c13 1 3 2 0 1 1 4
Phần tử c14 thuộc dòng 1, cột 4 của AB nên ta quan sát: Trang | 6 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức
• véc tơ dòng 1 của A: 1 2 1 véc tơ cột 4 của B: 1 3 • nhân từng cặp tọa
ộ của hai véc tơ này rồi cộng lại: 6 c14 1 1 2 3 1 6 13
Các phần tử của dòng 2 ược tính tương tự và sau khi tính, ta ược: 13 16 4 13 AB 12 13 11 15 2 4
Chú ý rằng, trong ví dụ này thì ma trận BA không tồn tại vì số cột của B khác số dòng của A. 7 1 2 3 8 Ví dụ: Cho A 4 56 2 3 ; B 9 3 1
Ma trận A có cấp 2 3, ma trận B có cấp 3 1 nên ma trận AB có cấp 2 1 c11 AB c21 2 1
Phần tử c thuộc dòng 1, cột 1 của AB nên ta quan sát: 11
• véc tơ dòng 1 của 7 A: 1 2 3
• véc tơ cột 1 của B: 8 9
• nhân từng cặp tọa ộ của hai véc tơ này rồi cộng lại: c11 1 7 2 8 3 9 50
Phần tử c21 thuộc dòng 2, cột 1 của AB nên ta quan sát:
• véc tơ dòng 2 của A: 4 5 6 7 8
• véc tơ cột 1 của B: 9 Trang | 7 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức
• nhân từng cặp tọa ộ của hai véc tơ này rồi cộng lại: c21 4 7 5 8 6 9 122 50 Vậy AB 122 2 1
Chú ý rằng, trong ví dụ này thì ma trận BA không tồn tại vì số cột của B khác số dòng của A. 1 2 3 2 1 Ví dụ: Cho A 4 5 6 và B 3 2 7 8 9 3 3 4 3 3 2
Ma trận A có cấp 3 3, ma trận B có cấp 3 2 nên ma trận AB có cấp 3 2 c11 c12 AB c21 c22 c31 c32 3 2
Lập luận tương tự các ví dụ trên, ta có: c11 1 2 2 3 3
4 20 (quan sát dòng 1 của A và cột 1 của B) c12
1 ( 1) 2 ( 2) 3 ( 3) 14 (quan sát dòng 1 của A và cột 2 của B) c21 4 2 5 3
6 4 47 (quan sát dòng 2 của A và cột 1 của B) c22 4 (
1) 5 ( 2) 6 ( 3) 32 (quan sát dòng 2 của A và cột 2 của B) c31 7 2 8 3 9
4 74 (quan sát dòng 3 của A và cột 1 của B) c32 7 ( 1) 8
( 2) 9 ( 3) 50 (quan sát dòng 3 của A và cột 2 của B) Vậy, 20 14 AB 47 32 74 50 3 2 Trang | 8 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức
Trong ví dụ này thì ma trận BA cũng không tồn tại vì số cột của B khác số dòng của A. 1 2 5 6 Ví dụ: Cho A 3 4 2 2 và B 7 8
2 2 thì AB và BA ều có cấp 2 2 1 2 5 6 19 22 AB 3 4 78 4350 5 6 1 2 23 34 BA 7 8 34 3146
(tích của hai ma trận vuông cấp 2 là một ma trận vuông cấp 2) Ta thấy AB BA 1 2 Ví dụ: Cho A 3 4 2 2 thì 1 2 1 3 5 11 AAT 3 4 2 4 11 25 1 3 1 2 14 A AT 2 1 0 4 3 20 4 14 Ta lại thấy AAT A AT
Nhận xét: Phép nhân ma trận, nói chung, không có tính giao hoán. Do ó, khi nhân các ma trận thì ta
không ược phép ảo thứ tự của các ma trận. 1 1 1 1 0 0 Ví dụ: Cho A 1 1 và B 1 1 thì AB 0 0 O2 2 (ma trận không)
Nhưng cả A và B ều khác ma trận không.
Nhận xét: Nếu A và B là các ma trận thì từ ẳng thức AB O (ma trận không) ta không thể suy ra
A O hay B O (trong hệ thống số thực thì xy 0 x 0 hay y 0 )
Ví dụ: Tìm các ma trận A, B vuông cấp 2 thỏa AB O2 2 nhưng BA O2 2 1 2 2 2 Trang | 9 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức Lấy A 2 4 và B 1 1 thì 1 2 2 2 0 0 AB 2 4 1 1 00 O2 2 Nhưng 2 2 1 2 6 12 BA 1 1 24 3 6 O2 2
Đối với số thực, nếu ab ac với a 0 thì suy ra b c, nhưng ối với ma trận thì iều này không còn úng nữa. Hãy xem ví dụ sau:
Ví dụ: Tìm các ma trận A,B,C vuông cấp 2, khác không thỏa AB AC nhưng B C 1 1 1 1 2 2 Lấy A 1 ; B 1 và C thì 1 1 2 2 1 1 1 1 0 0 AB 1 1 1 0 0 1 1 1 2 2 0 0 AC 1 2 2 0 0 1
Vậy AB AC nhưng rõ ràng B C a11 a12 a1n 1 Ví dụ: Cho A a21 a22 a2n và B
0 (B là véc tơ ơn vị thứ nhất) an1 an2 ann n n 0 n 1
Ma trận A có cấp n n , ma trận B có cấp n 1 nên ma trận AB có cấp n 1 Trang | 10 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức a11 a12 a1n 1 a11 a2n 0 a21 : cột 1 a a 21 22 của A AB an2 ann 0 an1 an1
Tổng quát, nếu lấy A nhân với véc tơ ơn vị thứ i thì ta ược cột thứ i của A.
(nhắc lại, véc tơ ơn vị thứ i có tính chất: riêng thành phần thứ i thì bằng 1, các thành phần còn lại ều bằng 0).
Ví dụ: Cho A là ma trận vuông cấp 3 thỏa AAT O3 3 . Chứng minh rằng A O3 3 a1 a2 a3 a1 b1 c1 Đặt A b1 b2 b3 thì AT a2 b2 c2 c1 c2 c3 a3 b3 c3
Các phần tử thuộc ường chéo chính của AA là: T (AAT )11 (a1)2 (a2 )2 (a3)2 (AAT )22 (b1)2 (b2)2 (b3)2 (AAT )33 (c1)2 (c2)2 (c3)2
Do AAT O3 3 nên suy ra các phần tử thuộc ường chéo chính của AAT bằng 0, nghĩa là: (AAT )11 (a1)2 (a2 )2 (a3)2 0 (AAT )22 (b1)2 (b2)2 (b3)2 0 (AAT )33 (c1)2 (c2)2 (c3)2 0 Vậy a1 a2 a3 0 b2 b3 0 A O3 3 b1 c1 c2 c3 0
Phép nhân ma trận, tuy mất i tính giao hoán, nhưng vẫn còn giữ lại ược một số tính chất quen thuộc, cụ thể là: Trang | 11 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức Mệnh ề.
• Nếu A là ma trận cấp m p , B là ma trận cấp p q , C là ma trận cấp q n thì
(AB)C A(BC) (tính kết hợp của phép nhân)
• Nếu A là ma trận cấp m n thì A.On q Om q và Op m .A Op n
• Nếu A là ma trận cấp m n thì A.In Avà I .Am A
Đặc biệt, nếu A là ma trận vuông cấp n thì A.In A I .An
Tính chất này nói rằng, trong phép nhân ma trận thì ma trận In óng vai trò giống như số 1
trong phép nhân số thực (nghĩa là a.1 a
1.a ). Do ó, từ nay trở i, ta sẽ gọi ma trận I là n
phần tử ơn vị trong phép nhân ma trận.
• Nếu A là là ma trận cấp m p , B và C là các ma trận cấp p n thì A(B C)
AB AC (tính phân phối của phép nhân ối với phép cộng)
• Nếu A và B là các ma trận cấp m p , C là ma trận cấp p n thì
(A B)C AC BC (tính phân phối của phép nhân ối với phép cộng)
• Nếu A là ma trận cấp m p , B là ma trận cấp p n và là số thực thì A( B) (AB) ( A)B
• Nếu A là ma trận cấp m p và B là ma trận cấp p n thì (AB)T B AT T
(ta có thể mở rộng: (ABC)T C B AT T T )
Nhận xét: Do tính kết hợp của phép nhân ma trận nên với A,B,C,D là các ma trận thì ta có thể viết: ABCD (ABC)D (AB)(CD) A(BC)D A(BCD)
nhưng phải chú ý giữ nguyên thứ tự của các ma trận trong mỗi cách kết hợp vì phép nhân ma trận không có tính giao hoán.
e) Lũy thừa ma trận (powers of matrix)
Cho A là ma trận vuông cấp n và k là số nguyên dương. Ta ịnh nghĩa: Trang | 12 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức A1 A A2 A.A Ak A.A A Ak 1 .A k
Ta quy ước A0 In (phần tử ơn vị) 1 2 Ví dụ: Cho A 3 4 thì 2 1 2 1 2 7 10 A A.A 3 4 34 1522 0 a 1 Ví dụ: Cho A 0 0 a
, tìm biểu thức của A (với n là số nguyên dương). n 0 0 0 Với n 1 thì A1 A Với n 2 thì A2 A.A 0 1 0 a 1 0 a 0 a 0 0 a 0 0 0 0 0 0 a2 0 0 0 0 0 0 0 0 Với n 3 thì Trang | 13 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức A3 A .A2 a2 0 a 1 0 0 0 0 a 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 O3 3
Suy ra An O3 3 (ma trận không) khi n 3 cos sin Ví dụ: Tính A với n A sin cos cos sin Với n 1 thì A1 A sin cos Với n 2 thì A2 A.A cos sin cos sin sin cos sin cos cos2 sin2 2sin cos 2 2 2sin cos sin cos cos2 sin2 sin2 cos2 Ta sẽ chứng minh n cosn sinn A sinn cosn n 1 ( ) Trang | 14 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức
bằng phương pháp quy nạp.
Với n 1 thì hiển nhiên ( ) úng.
Giả sử ( ) úng với số nguyên n k , nghĩa là ta có: k cosk sink A sink cosk ( )
Ta sẽ chứng minh ( ) cũng úng với số nguyên n k 1, nghĩa là chứng minh: cos(k 1) Ak sin(k 1) cos(k 1 sin(k 1) 1) Ta có: Ak 1 A .Ak cosk sink cos sin cos (do sink cosk sin ( )) cosk cos sink sin cosk sin sink cos sink cos cosk sin sink sin cosk cos
Dùng công thức lượng giác:
cosacosb sinasinb cos(a b) sinacosb sinbcosa sin(a b) thì ta ược: cosk cos sink sin cos(k ) cos(k 1) sink cos cosk sin sin(k ) sin(k 1) Vậy k 1 sin(kcos(k 1) 1) cos(ksin(k 1)1) A
nghĩa là ( ) úng với số nguyên n k 1
Theo nguyên lý quy nạp, ( ) úng với mọi n 1 Trang | 15 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức Nhận xét: I2n I .In
n In (lũy thừa của phần tử ơn vị là phần tử ơn vị)
Ghi chú. Trong hệ thống số thực thì ta có những hằng ẳng thức quen thuộc, chẳng hạn:
(a b)2 a2 2ab b2 ; (a b)(a b) a2 b2 ; (a b)3 a3 3a b2 3ab2 b3
Các ẳng thức này là úng vì phép nhân số thực có tính giao hoán, nghĩa là ab ba . Tuy nhiên, phép
nhân ma trận lại không có tính giao hoán, nghĩa là nói chung thì AB BA . Do ó, nói chung thì các
hằng ẳng thức trên không còn úng ối với ma trận.
Nếu hai ma trận vuông A và B thỏa AB BA (giao hoán với nhau) thì các hằng ẳng thức trên vẫn áp
dụng ược cho ma trận, cụ thể là: (A B)2 A2 2AB B2 (A B)(A B) A2 B2 Thật vậy, ta có (A B)2 (A B)(A B) C AC BC A(A B) B(A B) A2 AB BA B2
Do ó, với giả thiết AB BA thì
(A B)2 A2 AB BA B2 A2 AB AB B2 A2 2AB B2
Đẳng thức (A B)(A B) A2 B2 ược chứng minh tương tự.
Nhận xét: Ta có nhận xét là A.In I .An (vì cùng bằng A), nghĩa là các ma trận A và I giao hoán n với
nhau ối với phép toán nhân ma trận. Vì thế, ta có thể áp dụng các hằng ẳng thức quen thuộc cho hai
ma trận này, chằng hạn: (I 2 n A)(In A) In A2 In A2
(dùng hằng ẳng thức (a b)(a b) a2 b2 ) Hoặc I 3 2 n A3 (InA)(In I .An A )2 In A3 (In A)(In A A )2
(dùng hằng ẳng thức a3 b3 (a b)(a2 ab b )2 )
Ví dụ: Cho A và B là các ma trận vuông cấp n thỏa AB BA . Chứng minh rằng A Bk BA kk rồi suy ra A Bk l B A k,ll k Trang | 16 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức
Ta dùng quy nạp ể chứng minh A Bk BA kk ( )
Với k 1 thì ( ) là hiển nhiên. Giả sử ( ) úng với số nguyên k, nghĩa là: A Bk BA k ( ) Khi ó, do ( ) Ak 1 B (AA )Bk A(A B)k A(BA )k (AB)Ak (BA)Ak BAk 1
Vậy, ( ) cũng úng với số nguyên k 1
Theo nguyên lý quy nạp thì ( ) úng với mọi k.
Đổi vai trò giữa A và B thì ta có ABl B A ll , nghĩa là A giao hoán với B . Áp dụng lại l ( ) với B ược
thay bởi Bl thì ta ược A Bk l B A k,ll k
Ví dụ: Cho A và B là các ma trận vuông cấp n thỏa AB BA . Chứng minh rằng (AB)k A B kk k
Ta dùng quy nạp ể chứng minh (AB)k A B k k k ( )
Với k 1 thì ( ) là hiển nhiên. Giả sử ( ) úng với số nguyên k, nghĩa là: (AB)k A Bk k ( ) Khi ó, do ( ) (AB)k 1 (AB)(AB)k (AB)(A Bk k )
Do AB BA nên theo ví dụ trên (lấy l k) thì A Bk k B Ak k . Do ó, do ( ) (AB)k 1 (AB)(AB)k (AB)(A Bk
k ) (AB)(B Ak k ) A(BB )Ak k ABk 1 Ak
Cũng do AB BA nên theo ví dụ trên thì Bk 1 Ak A Bk k 1 Vậy,
(AB)k 1 ABk 1 Ak AA Bk k 1 Ak 1 Bk 1 Vậy
ẳng thức ( ) cũng úng với số nguyên k 1 Theo nguyên lý quy nạp thì ( ) úng với mọi k.
Ghi chú: Nếu AB BA thì ẳng thức (AB)k A Bk k là sai 1 2 1 1
Thật vậy, nếu chọn A 3 4 và B 1 1 và lấy k 2 thì 1 2 1 1 3 3 AB 34 1 1 7 7 Trang | 17 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức (AB) 2 7373 7373 3070 7030 Trong khi ó, A 2 1 2 1 23 4 3 4 15 227 10 B 2 1 1 1 11 1 1 1 2 22 2 A B 22 15 22 2 27 10 2 2 34 3474 74 Vậy (AB)2 A B2 2
Ví dụ: Cho A và B là các ma trận vuông cấp n. Chứng minh rằng (AB)T A BT T AB BA Giả sử (AB)T A BT
T , lấy chuyển vị 2 vế ta ược: (AB)T T A BT T T AB (B ) .(AT T T )T BA
Ngược lại, nếu AB BA thì lấy chuyển vị 2 vế sẽ ược (AB)T (BA)T A BT T
Ví dụ: Cho A và B là các ma trận vuông cấp n thỏa BA On n (ma trận không). Chứng minh rằng (AB)2 On n và B A2 2 On n
Ta có: (AB)2 (AB)(AB) A(BA)B On n và B A2 2 (BB)(AA) B(BA)A On n On n On n
Chú ý: Ta không thể viết B A2
2 (BA)2 vì không có giả thiết AB BA BÀI TẬP 4 7 3 8 1. Cho A 1 2 1 3 và B 5 Trang | 18 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức 6 9 3 2
Tính AB, ma trận BA có tồn tại không? 1 1 2 T 2. Cho A 4 3 5 2 3 , hãy tính AA
3. Có 3 mặt hàng tên là A, B, C ược bán trong 2 ngày liên tiếp. Giá (price) của 3 mặt hàng ược cho bởi ma trận P 23 15
30 1 3 (tính bằng ơn vị tiền). Lượng hàng (quantity) ược bán ra trong
2 ngày này ược cho bởi 2 cột tương ứng của của ma trận: 210 200 Q 450 480
(tính bằng ơn vị sản phẩm) 135 160 3 2
(mỗi cột của Q thể hiện lượng hàng ược bán ra trong ngày tương ứng)
Tính ma trận tích PQvà nêu ý nghĩa các phần tử của ma trận này. Tính tổng doanh thu bán hàng trong 2 ngày này.
HD: Ma trận P có cấp 1 3, ma trận Q có cấp 3 2 nên ma trận PQ có cấp 1 2 PQ c11 c12
Phần tử c thuộc dòng 1, cột 1 nên ta quan sát: 11
• véc tơ dòng 1 của P: 23 15 30 véc tơ cột 1 của Q: 210 450 • nhân từng cặp tọa
ộ của hai véc tơ này rồi cộng lại: 135 c11 23 210 15 450 30 135 15630
Phần tử c12 thuộc dòng 1, cột 2 nên ta quan sát:
• véc tơ dòng 1 của P: 23 15 30 200
• véc tơ cột 2 của Q: 480 160
• nhân từng cặp tọa ộ của hai véc tơ này rồi cộng lại: Trang | 19 lOMoAR cPSD| 47305584
Chương 1: Ma trận & ịnh thức c12 23 200 15 480 30 160 16600 Vậy PQ 15630 16600
Các phần tử của PQ chính là tổng doanh thu 3 mặt hàng trong ngày thứ nhất, ngày thứ hai. 1 1 1 4. Cho A 2 1 3 , hãy tính A 2 0 3 4
5. Cho A là ma trận cấp m n thỏa AX On 1 với mọi ma trận X cấp n 1 . Chứng minh rằng A Om n
HD: Lấy X là véc tơ ơn vị cột thứ i (thành phần thứ i bằng 1, các thành phần khác bằng 0) thì AX chính
là cột thứ i của A. Do AX On 1 nên suy ra cột thứ i của A bằng On 1
Vậy mọi cột của A ều bằng On 1 , nghĩa là A Om n
II. Định thức (determinant) 2.1 Định nghĩa
Cho A (aij n n) là ma trận vuông cấp n.
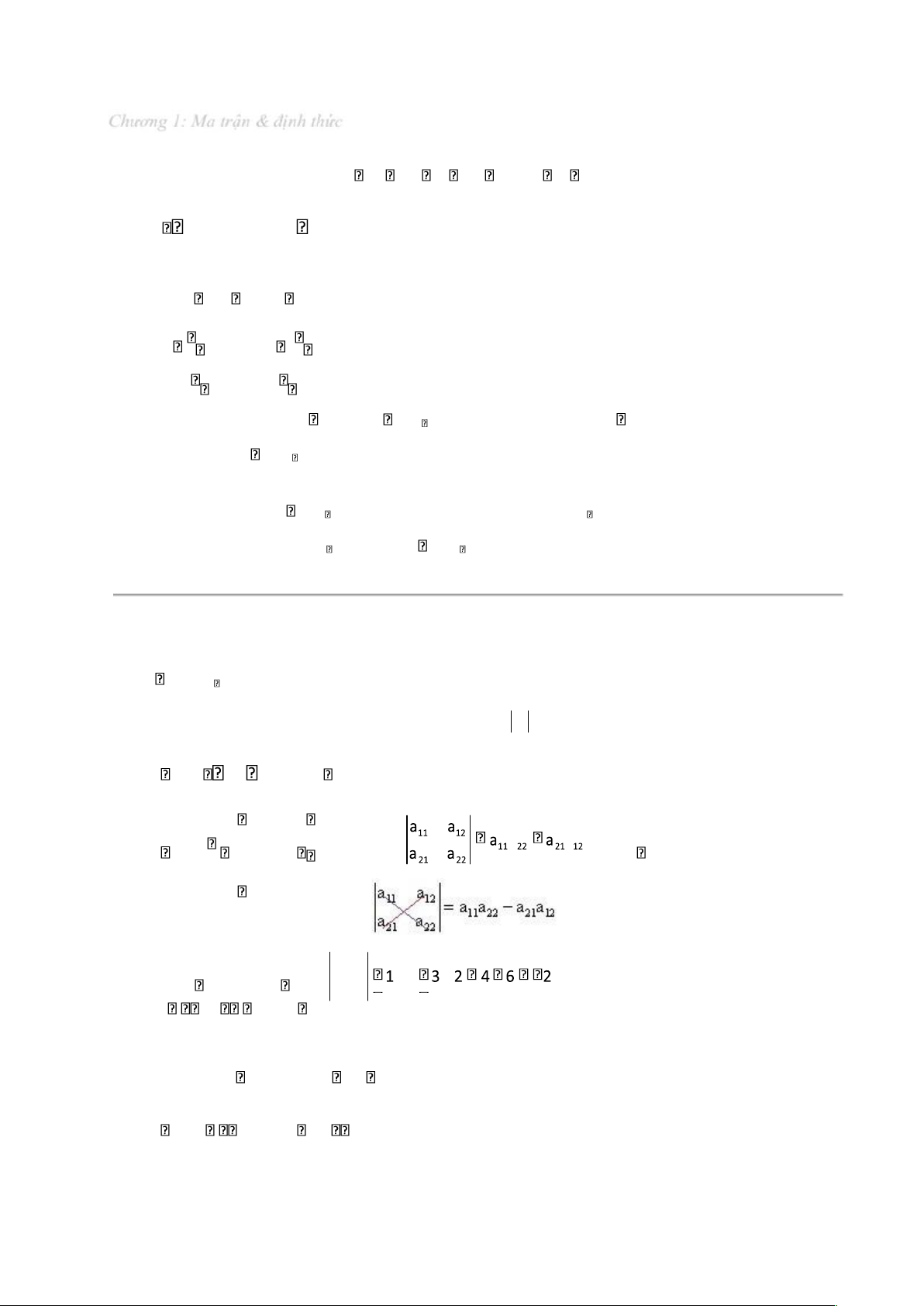
Định thức của A là một số thực, ký hiệu là detA hoặc A , ược ịnh nghĩa như sau: - Với n 1: A
a11 thì detA a11 (chính là phần tử duy nhất của A) a11 a12 - Với n 2: A a21 a22 thì detA 1 2 1 2 Ví dụ: A 3 4 det A 3 4 a11 a12 a1n - Với n 3: A a21 a22 a2n Trang | 20