lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức
Phần 1. ĐẠI SỐ TUYẾN TÍNH
Gv: Phan Ngô Tuấn Anh
Khoa Toán – Thống Kê, UEH
Chương 1. Ma trận & ịnh thức I. Ma trận 1.1 Định nghĩa
Một ma trận (matrix) A cấp m n là một bảng số gồm có m dòng, n cột. Các phần tử của A là những số thực tùy ý. a11 a12 a1n A a21 a22 a2n     am1 am2 amn
Trong ma trận A ở trên thì aij  là phần tử thuộc dòng i, cột j của A. Ta ký hiệu ma trận A là A (aij m n) 3 4 2 Ví dụ: A 1 0 7 (ma trận cấp 2 3)
Ma trận cấp n n ược gọi là ma trận vuông cấp n. Ví dụ: 2 3 A 5 1 (ma trận vuông cấp 2) 2 3 0 A 1 1 4 (ma trận vuông cấp 3) 1 6 5 Trang | 1 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức
Đối với ma trận A (aij n n) vuông cấp n thì các phần tử a ,a11 22,,ann (có chỉ số dòng bằng chỉ số
cột) tạo thành ường chéo chính của A: a11 x  x A x a 22  x     x x ann 1 4 5
Ví dụ: Với ma trận A 6 2 7
thì ường chéo chính gồm các phần tử là 1,2,3 8 9 3
Ma trận mà mọi phần tử của nó ều bằng 0 ược gọi là ma trận không (ma trận zero), ký hiệu là Om n
(hoặc ký hiệu là O, nếu cấp của ma trận ược hiểu ngầm). 0 0 0 0 0 Ví dụ: O2 3 0 0 0 ; O2 2 00
Ma trận ơn vị cấp n, ký hiệu là I (Identity matrix), là ma trn ận vuông cấp n có dạng: 1 0 0 0 0 1 0 0 In 0 0 1 0    0 0 0 1
(các phần tử thuộc ường chéo chính ều bằng 1, các phần tử còn lại ều bằng 0) Ví dụ: 1 0 I2 0 1 (ma trận ơn vị cấp 2) 1 0 0 I3 0 1 0 (ma trận ơn vị cấp 3) Trang | 2 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức 0 0 1
Cho A (aij n n) là ma trận vuông cấp n. Ta nói: -
Ma trận A có dạng tam giác trên (upper triangle matrix) nếu mọi phần tử nằm phía dưới ường
chéo chính của A ều bằng 0: a11 a12 a13 a1n 0 a22 a23 a2n A 0 0
a33 a3n (ma trận tam giác trên)      0 0 0 0 ann 1 2 1 Ví dụ: A 0 4 3 (ma trận tam giác trên) 0 0 5 -
Ma trận A có dạng tam giác dưới (lower triangle matrix) nếu mọi phần tử nằm phía trên ường
chéo chính của A ều bằng 0: a11 0 0  0 a21 a 0 22  0 A a31 a a 32
33  0 (ma trận tam giác dưới)      an1 a n2 an3 ann 1 0 0 Ví dụ: A 2 3 0
(ma trận tam giác dưới) 4 5 6
Nhận xét: Ma trận ơn vị I là ma trn
ận tam giác trên và cũng là ma trận tam giác dưới.
Ta quy ước hai ma trận A và B là bằng nhau nếu chúng có cùng cấp (kích thước) và có số liệu hoàn
toàn giống nhau, ký hiệu là A B Trang | 3 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức
1.2 Các phép toán ma trận a) Phép cộng ma trận (addition)
Cho A và B là hai ma trận có cùng cấp m n , khi ó ma trận tổng A B có ược bằng cách cộng các
phần tử tương ứng của A và B. 1 2 1 3 1 5 4 3 6 Ví dụ: A 3 5 4 ; B 1 2 1 A B 4 7 5
b) Phép nhân vô hướng (scalar multiplication)
Cho A là ma trận cấp m n và là một số thực, khi ó ma trận tích Acó ược bằng cách nhân số vào
tất cả các phần tử của A. 1 1 2 0 1 1 2 1 0 Ví dụ: A 6 54 ; 2 A 2 A 3 5 2 2
Mệnh ề. Cho A,B,C là các ma trận cấp m n và , là các số thực. Ta có: • (A B) C A (B
C) (tính kết hợp của phép cộng) • A B B
A (tính giao hoán của phép cộng) • A Om n A
• A ( 1)A Om n (ma trận ( 1) A ược gọi là ma trận ối của A, ký hiệu là A ) • 0.A Om n và 1.A A (A B) A B ( )A A A ( A) ( )A ( A)
c) Phép chuyển vị (Transpose)
Cho A là ma trận cấp m n , khi ó ma trận chuyển vị AT có ược từ A bằng cách xoay các dòng của A
thành các cột tương ứng của AT . Ma trận AT có cấp là n m 1 4 Ví dụ: A 14 5263 AT 23 56 1 2 3 1 4 7 Trang | 4 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức Ví dụ: A 4 5 6 AT 2 5 8 7 8 9 3 6 9
Do phép chuyển vị là xoay dòng thành cột nên ta có:
Mệnh ề. Cho A,B là các ma trận cấp m n và là số thực. Ta có: • AT T A • (A B)T AT BT • ( A)T AT
Ví dụ: (2A 3B)T 2AT 3BT
d) Phép nhân ma trận (matrix product)
Cho các ma trận A (aij m) p và B (bij)p n (số cột của A phải bằng với số dòng của B).
Khi ó, ma trận tích AB có cấp là m n
Để tính các phần tử của ma trận AB, chẳng hạn muốn tính phần tử (AB)ij thì ta:
• quan sát dòng thứ i của A và cột thứ j của B (là những véc tơ gồm p tọa ộ): - dòng i của A là ai1 a i2 a ip b1j b2j
- cột j của B là bpj
• nhân từng cặp tọa ộ tương ứng của hai véc tơ này với nhau, rồi cộng lại:
(AB)ij a bi1 1j a bi22j a bip pj
Nói cách khác, phần tử (AB)ij là tích vô hướng của véc tơ dòng i của A với véc tơ cột j của B 7 1 2 3 2 3 8thì AB 1 74 7 2 85 8 3 96 9 2 1 12250 2 1 Ví dụ: Cho A 4 56 ;B 9 3 1 Trang | 5 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức
Chú ý rằng, trong ví dụ này thì ma trận BA không tồn tại vì số cột của B khác số dòng của A. 1 2 3 2 1 c11 c 12 Ví dụ: Cho A 4 5 6 và B 3 2 , ta ặt AB c21 c 22 thì: 7 8 9 3 3 4 3 3 2 c31 c32 3 2 c11 1 2 2 3 3 4 20 c12 1 ( 1) 2 ( 2) 3 ( 3) 14 c21 4 2 5 3 6 4 47 c22 4 ( 1) 5 ( 2) 6 ( 3) 32 c31 7 2 8 3 9 4 74 c32 7 ( 1) 8 ( 2) 9 ( 3) 50 Vậy, 20 14 AB 47 32 74 50 3 2
Trong ví dụ này thì ma trận BA cũng không tồn tại vì số cột của B khác số dòng của A. 1 2 5 6 Ví dụ: Cho A 3 4 2 2 và B 78 2 2 thì 1 2 5 6 19 22 AB 34 78 43 50 5 6 1 2 23 34 BA 78 34 31 46 Trang | 6 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức
(tích của hai ma trận vuông cấp 2 là một ma trận vuông cấp 2) Ta thấy AB BA 1 2 Ví dụ: Cho A 3 4 2 2 thì 1 2 1 3 5 11 AAT 3 4 2 4 11 25 1 3 1 2 14 A AT 2 10 4 3 20 4 14 Ta lại thấy AAT A AT
Nhận xét: Phép nhân ma trận, nói chung, không có tính giao hoán. Do ó, khi nhân các ma trận thì ta
không ược phép ảo thứ tự của các ma trận. 1 1 1 1 0 0 Ví dụ: Cho A 11 và B 11 thì AB 00 O2 2 (ma trận không)
Nhưng cả A và B ều khác ma trận không.
Nhận xét: Nếu A và B là các ma trận thì từ ẳng thức AB O (ma trận không) ta không thể suy ra
A O hay B O (trong hệ thống số thực thì xy 0 x 0 hay y 0 )
Ví dụ: Tìm các ma trận A,B,C vuông cấp 2, khác không thỏa AB AC nhưng B C 1 1 1 1 2 2 HD: Lấy A 1 1 ; B 1 1 và C 22
Phép nhân ma trận, tuy mất i tính giao hoán, nhưng vẫn còn giữ lại ược một số tính chất quen thuộc, cụ thể là: Mệnh ề.
• Nếu A là ma trận cấp m p , B là ma trận cấp p q , C là ma trận cấp q n thì
(AB)C A(BC) (tính kết hợp của phép nhân)
• Nếu A là ma trận cấp m n thì A.On q Om q và Op m .A Op n Trang | 7 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức
• Nếu A là ma trận cấp m n thì A.In Avà I .Am A
Đặc biệt, nếu A là ma trận vuông cấp n thì A.In A I .An
Tính chất này nói rằng, trong phép nhân ma trận thì ma trận In óng vai trò giống như số 1 trong
phép nhân số thực (nghĩa là a.1 a 1.a ). Do ó, từ nay trở i, ta sẽ gọi ma trận I là n phần tử
ơn vị trong phép nhân ma trận.
• Nếu A là là ma trận cấp m p , B và C là các ma trận cấp p n thì
A(B C) AB AC (tính phân phối của phép nhân ối với phép cộng)
• Nếu A và B là các ma trận cấp m p , C là ma trận cấp p n thì
(A B)C AC BC (tính phân phối của phép nhân ối với phép cộng)
• Nếu A là ma trận cấp m p , B là ma trận cấp p n và là số thực thì A( B) (AB) ( A)B
Nếu A là ma trận cấp m p và B là ma trận cấp p n thì (AB)T B AT T
(ta có thể mở rộng: (ABC)T C B AT T T )
Nhận xét: Do tính kết hợp của phép nhân ma trận nên với A,B,C,D là các ma trận thì ta có thể viết: ABCD (ABC)D (AB)(CD) A(BC)D A(BCD)
nhưng phải chú ý giữ nguyên thứ tự của các ma trận trong mỗi cách kết hợp vì phép nhân ma trận không có tính giao hoán.
e) Lũy thừa ma trận (powers of matrix)
Cho A là ma trận vuông cấp n và k là số nguyên dương. Ta ịnh nghĩa: A1 A A2 A.A  
Ak A.AA Ak 1 .A k Trang | 8 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức Ta quy ước A0 In 0 a 1 Ví dụ: Cho A 0 0 a
, tìm biểu thức của A (vn ới n là số nguyên dương). 0 0 0 Với n 1 thì A1 A Với n 2 thì A2 A.A 0 a 1 0 a 1 0 0a 0 0 a 0 0 0 0 0 0 0 0 a2 0 0 0 0 0 0 Với n 3 thì A3 A .A2 0 0 a2 0 a 1 0 0 0 0 0 a 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 O3 3
Suy ra An O3 3 (ma trận không) khi n 3.
Ghi chú. Trong hệ thống số thực  thì ta có những hằng ẳng thức quen thuộc, chẳng hạn: Trang | 9 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức
(a b)2 a2 2ab b2 ; (a b)(a b) a2 b2 ; (a b)3 a3 3a b3 3ab2 b3
Các ẳng thức này là úng vì phép nhân số thực có tính giao hoán, nghĩa là ab ba . Tuy nhiên, phép
nhân ma trận lại không có tính giao hoán, nghĩa là nói chung thì AB BA. Do ó, nói chung thì các
hằng ẳng thức trên không còn úng ối với ma trận. Nếu hai ma trận vuông A và B thỏa AB BA thì
các hằng ẳng thức trên áp dụng ược cho ma trận, cụ thể là: (A B )2 A2 2AB B 2 AB BA (A B)(A B ) A2 B2 AB BA Thật vậy, ta có (A B)2 (A B)(A B) A(A B) B(A B) A2 AB BA B2 Do ó, (A B)2 A2 2AB B2 A2 AB BA B2 A2 2AB B2 BA AB
Ví dụ: Cho A và B là các ma trận vuông cấp n thỏa AB BA . Chứng minh rằng A Bk BA kk rồi suy ra A Bk l B A k,ll k
Ta dùng quy nạp ể chứng minh A Bk BA kk ( )
Với k 1 thì ( ) là hiển nhiên. Giả sử ( ) úng với số nguyên k, nghĩa là: A Bk BA k ( ) Khi ó, do ( ) Ak 1 B (AA )Bk A(A B)k A(BA )k (AB)Ak (BA)Ak BAk 1
Vậy, ( ) cũng úng với k 1
Theo nguyên lý quy nạp thì ( ) úng với mọi k.
Đổi vai trò giữa A và B thì ta có ABl B A ll
, nghĩa là A giao hoán với Bl . Áp dụng lại ( ) với B
ược thay bởi B thì ta l ược A Bk l B A k,ll k
Ví dụ: Cho A và B là các ma trận vuông cấp n thỏa AB BA . Chứng minh rằng (AB)k A B kk k
Ta dùng quy nạp ể chứng minh (AB)k A B k k k ( ) Trang | 10 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức
Với k 1 thì ( ) là hiển nhiên. Giả sử ( ) úng với số nguyên k, nghĩa là: (AB)k A B k k k ( ) Khi ó, do ( )
(AB)k 1 (AB)(AB)k (AB)(A Bk k )
Do AB BA nên theo ví dụ trên (lấy l k) thì A Bk k B Ak k . Do ó, do ( )
(AB)k 1 (AB)(AB)k (AB)(A Bk k ) (AB)(B Akk ) A(BB )Akk ABk 1 Ak
Cũng do AB BA nên theo ví dụ trên thì Bk 1 Ak A Bkk 1 Vậy,
(AB)k 1 ABk 1 Ak AA Bkk 1 Ak 1 Bk 1
Theo nguyên lý quy nạp thì ( ) úng với mọi k.
Ghi chú: Nếu AB BA thì ẳng thức (AB)k A Bk k là sai
Ví dụ: Cho A và B là các ma trận vuông cấp n. Chứng minh rằng (AB)T A BT T AB BA
Giả sử (AB)T A BT T , lấy chuyển vị 2 vế ta ược:
(AB)T T A BTT T AB (B ) .(AT T T )T BA
Ngược lại, nếu AB BA thì lấy chuyển vị 2 vế sẽ ược (AB)T (BA)T A BT T
Ví dụ: Cho A và B là các ma trận vuông cấp n thỏa BA On n (ma trận không). Chứng minh rằng (AB)2 On n và B A2 2 On n
Ta có: (AB)2 (AB)(AB) A(BA)B On n và B A22 (BB)(AA) B(BA)A On n On n On n
Chú ý: Ta không thể viết B A2
2 (BA)2 vì không có giả thiết AB BA BÀI TẬP 4 7 3 8 1. Cho A 1 2 1 3 và B 5 Trang | 11 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức 6 9 3 2
Tính AB, ma trận BA có tồn tại không? 1 1 2 T 2. Cho A 4 3 5 2 3 , hãy tính AA
3. Có 3 mặt hàng tên là A, B, C ược bán trong 2 ngày liên tiếp. Giá (price) của 3 mặt hàng ược cho bởi ma trận P 23 15
30 1 3 (tính bằng ơn vị tiền). Lượng hàng (quantity) ược bán ra trong
2 ngày này ược cho bởi 2 cột tương ứng của của ma trận: 210 200 Q 450 480
(tính bằng ơn vị sản phẩm) 135 160 3 2
(mỗi cột của Q thể hiện lượng hàng ược bán ra trong ngày tương ứng)
Tính ma trận tích PQvà nêu ý nghĩa các phần tử của ma trận này. Tính tổng doanh thu bán hàng trong 2 ngày này. 1 1 1 4. Cho A 2 1 3 , hãy tính A 2 0 3 4
II. Định thức (determinant) 2.1 Định nghĩa
Cho A (aij n n) là ma trận vuông cấp n.
Định thức của A là một số thực, ký hiệu là det A hoặc A , ược ịnh nghĩa như sau: - Với n 1: A
a11 thì detA a11 (chính là phần tử duy nhất của A) a11 a12 - Với n 2: A a21 a22 thì detA a a11 22 a a21 12 Trang | 12 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức 1 2 1 Ví dụ: A 3 4 detA 3 2 1.4 3.2 4 6 2 4 a a  11 12 a1n  a a 21 22  a2n - Với n 3: A     an2 a ann n1
Định thức của A ược gọi là ịnh thức cấp n và ịnh thức cấp n này sẽ ược tính thông qua những ịnh thức con cấp n 1 như sau:
Với mỗi i và với mỗi j, ta gọi Mij là ịnh thức của một ma trận có ược từ A bằng cách xóa dòng i và cột j. 3 1 4 Ví dụ: Cho A 5 0 2 thì ta có 6 8 7 0 2 M11
0.7 8.2 16 (xóa dòng 1, cột 1) 8 7 3 1 M23
3.8 6.1 18 (xóa dòng 2, cột 3) 6 8 1 4 M31
1.2 0.4 2 (xóa dòng 3, cột 1) 0 2
Trong ví dụ này, ta thấy A là ma trận vuông cấp 3 và mỗi ịnh thức con M , M , M 11 23 31 là ịnh
thức cấp 2 (nhỏ hơn cấp của A một bậc).
Mỗi ịnh thức con Mij ược gọi là ịnh thức con bù hoặc ược gọi là phần phụ ại số (Minors) của ma trận
A và là ịnh thức cấp n 1
Định thức của A sẽ tính theo các ịnh con bù bởi quy tắc khai triển theo dòng hoặc khai triển theo cột như sau: Trang | 13 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức
a) Khai triển theo dòng: chọn một dòng bất kỳ của A, chẳng hạn ta chọn dòng i ai1 ai2 ain
Duyệt các phần tử của dòng i này từ trái qua phải, ta có:
detA ( 1)i 1 a Mi1i1 ( 1)i 2 a Mi2i2 ( 1)i n a Min in
Trong ó, Mij là ịnh thức của có ược từ A bằng cách xóa dòng i và cột j. 3 2 5 Ví dụ: Cho A 1 4 7 6 2 3
Khai triển theo dòng 1, ta ược:
1 1 . .3 4 7 ( 1)1 2 . .2 16 73 (
1)1 3 . .5 16 42 detA ( 1) 2 3 1  1  1  2 39 22 6 78 110 38
Nếu khai triển theo dòng 2 thì ta ược: 3 2 5 detA 1 4 7 6 2 3 2 5 3 5 3 2 ( 1)
2 1 . .1 2 3 ( 1)2 2 . .4 6 3 ( 1)2 3 . .7 6 2 1 1  1  4 21 6 4 84 42 38
Ta thấy kết quả không phụ thuộc vào dòng khai triển. Trang | 14 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức
Cũng áp dụng quy tắc này, nhưng thay vì duyệt phần tử trên dòng, ta duyệt phần tử trên cột thì ta có
công thức khai triển theo cột:
b) Khai triển theo cột: chọn một cột bất kỳ của A, chẳng hạn ta chọn cột j a1j a2j anj
Duyệt các phần tử của cột j này từ trên xuống dưới, ta có:
det A ( 1)1 ja M1j1j ( 1)2 ja M2j2j ( 1)n j a Mnj nj
Trong ó, Mij là ịnh thức của có ược từ A bằng cách xóa dòng i và cột j. Ví dụ: Vẫn với ma trận trên 3 2 5 A 1 4 7 6 2 3 Khai
triển theo cột 3, ta ược: 1 3 2 3 1 . .5 14 ( 1) 1
. .7 6322 ( 1)3 3 . .3 13 24 detA ( 1) 6 2  1 22 6 10 110 42 30 38
Ta thấy kết quả không phụ thuộc vào cột khai triển. Thật vậy, ta có:
Mệnh ề. Định thức không phụ thuộc vào dòng hoặc cột khai triển, nghĩa là xác ịnh duy nhất.
Hệ quả. Nếu trong ịnh thức có chứa một dòng (cột) nào ó bằng 0 thì ịnh thức sẽ bằng 0. Trang | 15 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức 0 0 0 Ví dụ: a b c 0 (dòng 1 bằng 0) x y z a 0 x b 0 y 0 (cột 2 bằng 0) c 0 z
Đối với ma trận tam giác (trên hoặc dưới) thì việc tính ịnh thức rất ơn giản: Mệnh
ề. Định thức của ma trận tam giác thì bằng tích của các phần tử thuộc ường chéo chính. 2 a b Ví dụ: 0
3 c 2.3.4 24 (có dạng tam giác trên) 0 0 4 3 0 0 x 2
0 3.2.5 30 (có dạng tam giác dưới) y z 5
Ví dụ: Với I là ma trn ận ơn vị cấp n 1 0 0 0 0 1 0 0 In 0 0 1 0    0 0 0 1
thì do I là ma trnận tam giác nên det In 1.11 1n 1 n Quy tắc Sarrus
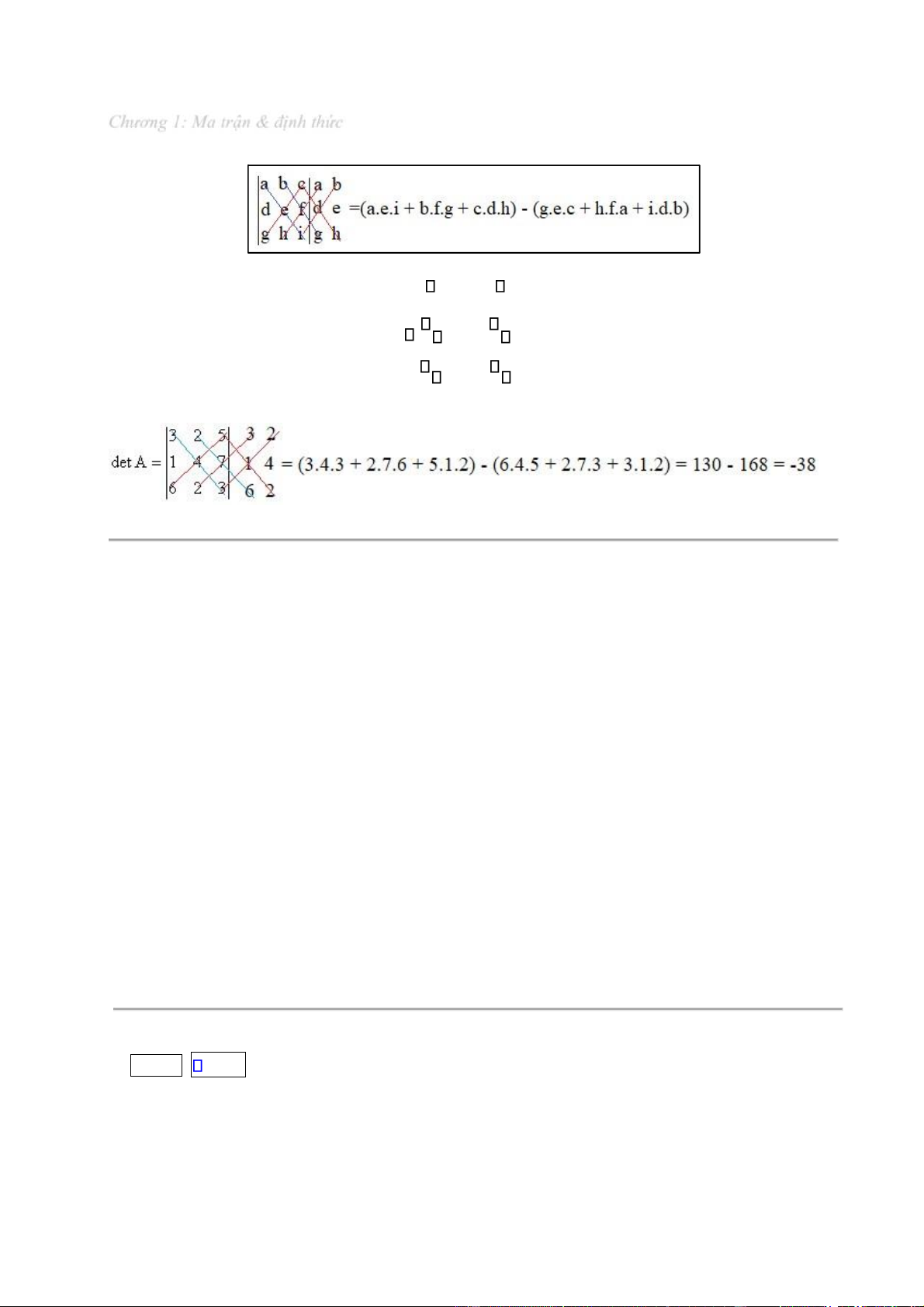
Khi tính ịnh thức cấp 3, ngoài cách khai triển theo dòng (cột) thì ta có thể dùng sơ ồ sau ây, còn ược
gọi là quy tắc Sarrus: Trang | 16 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức 3 2 5
Ví dụ: Lấy lại ma trận trong ví dụ trên A 1 4 7 6 2 3
Dùng quy t ắ c Sarrus, ta có:
Tính ịnh thức trên máy tính Casio FX-570 ES PLUS
Để tính ịnh thức (det) của ma trận vuông cấp 3 trên Casio FX-570 ES PLUS, ta nhớ sẽ có 2 giai oạn:
Giai oạn 1: Nhập ma trận và lưu vào bộ nhớ của máy tính
➢ Bấm phím MODE (SETUP)
➢ Chọn mục MATRIX ➢ Chọn mục MatA
➢ Chọn mục 3×3 (là cấp của ma trận MatA)
➢ Nhập số liệu vào ma trận MatA
➢ Bấm phím AC ể lưu vào bộ nhớ (sau ộng tác này thì màn hình sẽ bị xóa trắng)
Như thế, trong bộ nhớ của máy tính ã lưu một ma trận có tên là MatA và có số liệu như ta ã nhập vào.
Giai oạn 2: Gọi chức năng tính ịnh thức (det) ể tính ịnh thức của ma trận ã lưu trong bộ nhớ
➢ Bấm tổ hợp phím Shift-4 (bấm phím Shift, rồi bấm phím số 4) ➢ Chọn mục det
➢ Lại bấm tổ hợp phím Shift-4
➢ Chọn mục MatA và lúc này, trên màn hình sẽ hiển thị det(MatA ➢ Bấm dấu =
2.2 Tính chất của ịnh thức a) det(A )T det A Trang | 17 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức a1 a2 a 3a1 b1 c1 Ví
dụ: b1 b2 b3 a2 b2 c2 c1 c2 c3a3 b3 c3
 A AT
b) Khi ổi chỗ 2 dòng (cột) của ịnh thức thì chỉ làm ịnh thức ổi dấu mà thôi. a1 a2 a 3d1 d2b1 b2 b 3 Ví dụ: b1 b 2 b a a 3 a1 2 3 ( ổi chỗ dòng 1 và dòng 2) c1 c2 c3c1 c2 c3
Suy ra, nếu trong ịnh thức có 2 dòng giống nhau (hoặc có 2 cột giống nhau) thì ịnh thức sẽ bằng 0 a b c Ví dụ: a b c 0 (dòng 1 và dòng 2 giống nhau) x y z a x a b y b 0 (cột 1 và cột 3 giống nhau) c z c
c) Nếu trên một dòng (cột) của ịnh thức có thừa số chung thì ta có thể mang thừa số chung này ra trước dấu ịnh thức. a a 1 3 3 a a a 2 a1 2 Ví dụ: b b .b 1 3 3 b b b (dòng 1 21 2 c c có thừa 3 3 số chung) c1 c2 c1 a1 c2 .b 1 a c 1 a2 1 a 3a2 a 3 b1 b b b 2 3b2
3 (cột 1 có thừa số chung) c1 c2 c3c2 c3
Suy ra, nếu A là ma trận vuông cấp n thì det( A) n detA 0.3 0.2 0.5 0.4 Chẳng hạn, cho A 0.1 0.2 Trang | 18 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức 0.6
0.7 là ma trận vuông cấp 3 thì 0.3 0.3 0.2 0.53 2 5 det A 0.1 0.4 0.7 (0.1) . 1347 (0.1) .( 38)3 0.038 0.6 0.2 0.36 2 3  38 2 4 1 62 3 Ví dụ: 3 6 9 2.3. 1 2 3 6.0 0 ( ịnh thức có 2 dòng giố x ng nhau thì bằng 0) x y zy z  0
d) Nếu lấy một dòng cộng (hoặc trừ) với lần dòng khác thì ịnh thức không thay ổi giá trị (tương tự ối với cột) m 1 1
Ví dụ: Tính ịnh thức 1 m 1 với m là tham số 1 1 m
Ý tưởng là, ta sẽ dùng các tính chất của ịnh thức ở trên ể biến ổi ịnh thức này về dạng tam giác, khi ó
ịnh thức dạng tam giác sẽ bằng tích của các phần tử thuộc ường chéo chính. Ta biến ổi như sau: m 1 1m 2 m 2 m 2 d d d1 2 3 1 m 1 1 m 1 1 1 m1 1 m m 2 0 0 c c2 1 1 m 1 0 (m 2)(m 1 )2 c c3 1 1 0 m 1
Trong ví dụ này, ta dùng tính chất: ịnh thức không thay ổi khi lấy một dòng cộng với dòng khác, hoặc
khi lấy một cột trừ i cột khác. 1 a a2
Ví dụ: Tính ịnh thức 1 b b2
với a,b,c là các tham số 1 c c2 Trang | 19 lOMoAR cPSD| 49519085
Chương 1: Ma trận & ịnh thức
Cũng như ví dụ trên, ta sẽ biến ổi ịnh thức này về dạng tam giác như sau: 1 a a21 a a21 a a2 d2 d1 b2 0 b a b2 a2 1 b (b a)(c a) 0 1 b a d3 d1 1 c c20 c a c2 a20 1 c a 1 a a2 d3 d2 (b a)(c a) 0 1 b a 0 0 c b  c b (b a)(c a)(c b) a b c 1
Ví dụ: Không khai triển ịnh thức, hãy chứng minh b c a
1 0 (với a,b,c là tham số) c a b 1 Ta có: a b c 1a b c b c 11 b c 1 1 c c 2 b c a 1 b c a c a 1 (a b c)1 c a 1 0 (có 2 cột giống nhau) c a b 1c a b a b 11 a b 1  0
e) Nếu A và B là các ma trận vuông cùng cấp thì det(AB) detAdetB
(suy ra det(AB) det(BA) detA.detB)
Ví dụ: Nếu A là ma trận vuông thì ể tính ịnh thức của ma trận AAT cho nhanh, ta dùng tính chất trên
det(AA )T detA.det(A )T detA.detA (detA)2
Tương tự, ta có det(A )2 det(A.A) detA.detA (detA)2
Tổng quát, det(A )k (detA) kk Trang | 20