lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief
Phần 1. ĐẠI SỐ TUYẾN TÍNH
Gv: Phan Ngô Tuấn Anh
Khoa Toán – Thống Kê, UEH
Chương 3. Mô hình input-output Leontief
I. Giới thiệu mô hình
Trong nền kinh tế của một quốc gia, ta xét n ngành kinh tế ( iện lực, dầu khí, nông nghiệp, xây
dựng…). Các ngành này có mối quan hệ hữu cơ với nhau: ầu ra (output) của một ngành lại ược những
ngành khác sử dụng như là nguyên liệu ầu vào (input).
Chẳng hạn, ầu ra của ngành iện lực là iện năng ược các ngành kinh tế khác sử dụng ể sản xuất. Hơn
nữa, bản thân ngành iện lực cũng tiêu thụ một phần iện năng do nó tạo ra. Vậy, ầu ra của một ngành
lại là ầu vào của ngành khác và cũng có thể là ầu vào của chính ngành này. Các ngành kinh tế tạo
thành một hệ thống “nuôi sống lẫn nhau”, giống như các bộ phận trong cơ thể con người.
Xét 2 ngành bất kỳ, chẳng hạn ngành i và ngành j. Ta gọi aij là giá trị sản lượng của ngành i (tính bằng
ơn vị tiền) cung cấp cho ngành j (trong một năm) ể ngành j tạo ra sản lượng trị giá 1 ơn vị tiền. aij ngành i ngành j
Chẳng hạn, aij 0.1 cho ta biết, ể ngành j tạo ra sản lượng trị giá 1 ơn vị tiền thì ngành i cần cung cấp
cho ngành j lượng nguyên liệu trị giá 0.1 ơn vị tiền.
Do ý nghĩa kinh tế nên 0 aij 1 (nếu a ij
1 thì mâu thuẫn với ịnh nghĩa của aij ).
Nếu aij 0 thì ngành j không sử dụng nguyên liệu do ngành i cung cấp, chẳng hạn ngành xây dựng
không sử dụng sản phẩm của ngành nông nghiệp ể làm nguyên liệu sản xuất.
Các hệ số aij ược thành lập như thế nào, ta hãy xem một ví dụ sau. Giả sử trong năm vừa qua:
• Tổng sản lượng của ngành j là 3000 ( ơn vị tiền)
• Ngành i ã cung cấp cho ngành j lượng nguyên liệu là 200 ( ơn vị tiền)
Ta thấy, ể ngành j tạo ra sản lượng là 3000 ( ơn vị tiền) thì nó ã sử dụng lượng nguyên liệu của ngành
i là 200 ( ơn vị tiền). Vậy, ể ngành j tạo ra sản lượng là 1 ( ơn vị tiền) thì nó cần sử dụng lượng
nguyên liệu của ngành i là
0.067(ơn vị tiền). Do ó, ta ặt aij 0.067
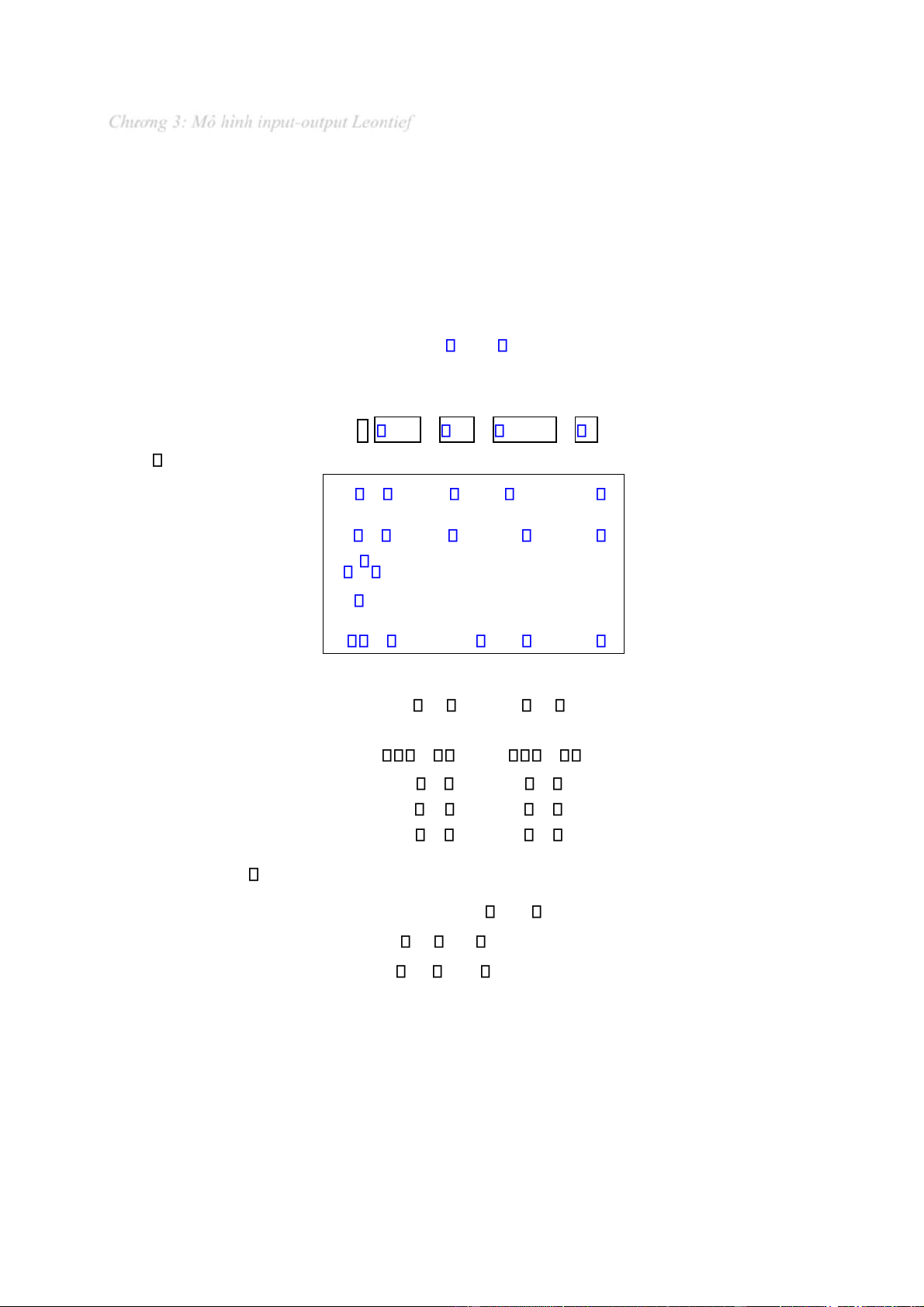
Khi ã có các hệ số aij , ta thành lập ma trận hệ số ầu vào (hoặc ma trận Leontief) của n ngành: Trang | 1 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief a11 a12 a1n A a21 a22 a2n    an1 an2 ann n n
Các phần tử trên một cột nào ó của A, chẳng hạn trên cột thứ j , cho ta biết lượng nguyên liệu ầu vào
của ngành j ược cung cấp bởi n ngành ể ngành j tạo ra sản lượng trị giá 1 ơn vị tiền. ngành j ngành 1 a1j ngành 2 a2j    ng n nà h anj
Tổng các phần tử trên cột j (là a1j a2j anj ) là tổng giá trị nguyên liệu ầu vào của ngành j
( ược cung cấp bởi n ngành) ể ngành j tạo ra sản lượng trị giá 1 ơn vị tiền. Do ó, tổng này không vượt quá 1: a1j a2j anj 1
Đây là tính chất quan trọng của ma trận hệ số ầu vào:
Tổng các phần tử trên một cột bất kỳ luôn nhỏ hơn hay bằng 1
Giả sử người tiêu dùng ( ược gọi là ngành kinh tế mở hoặc ầu cuối) ặt ra yêu cầu òi hỏi n ngành phải
áp ứng, cụ thể là n ngành cần cung cấp cho người tiêu dùng lượng sản phẩm là d ,d ,1 2 ,dn (các giá
trị yêu cầu này ược cho trước).
Bài toán ặt ra cho n ngành là: cần xác ịnh mức sản lượng x ,x ,1
2 ,xn của n ngành ể áp ứng
ược yêu cầu của người tiêu dùng. Đây chính là dạng rút gọn của mô hình input-output mở Leontief.
II. Thiết lập mô hình
Ý tưởng chính trong cách thành lập hệ phương trình cho bài toán này là, sản lượng của mỗi ngành sẽ ược tách thành 2 phần:
• Phần thứ nhất dùng ể cung cấp cho hệ thống nội bộ gồm n ngành ( áp ứng yêu cầu bên trong) Trang | 2 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief
• Phần thứ hai dùng ể cung cấp cho ngành kinh tế mở ( áp ứng yêu cầu bên ngoài) Xét ngành
kinh tế thứ i trong hệ thống. Sản lượng của ngành này là xi ược dùng ể:
• Cung cấp cho n ngành: ể ngành 1, ngành 2,..., ngành n tạo ra sản lượng là x ,x ,1 2 ,xn thì
ngành i cần cung cấp lượng nguyên liệu tương ứng cho từng ngành là a x , a x ,i1 1 i2 2 , a xin
n . Vậy, tổng lượng nguyên liệu mà ngành i cần cung cấp cho hệ thống là: a xi1 1 a xi2 2 a xin n
• Cung cấp cho ngành kinh tế mở: di ( ược cho trước) Vậy, ta có phương trình của ngành i là:
xi (a xi1 1 a xi2 2 a x )in n di
Cho i 1,2,,n thì ta có hệ phương trình:
x1 (a x11 1 a x12 2 a x )1n n d1 x2 (a x21 1 a x22 2 a2nx )n d2 ( )   xn (a xn1 1 an2x2 annx )n dn Đặt x1 d1 X x2 và D d2   xn dn
Hệ phương trình ( ) trở thành: X AX D X AX D (In A)X D
Vậy, ta có phương trình liên hệ giữa X và D: Trang | 3 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief (In A)X D
Trong phương trình cuối (In A)X D, nếu ma trận In A là khả ảo thì phương trình này (chính là hệ
( ) ) sẽ có nghiệp duy nhất: X (InA) .D 1
Mệnh ề. Nếu tổng các phần tử trên một cột bất kỳ của A luôn nhỏ hơn 1 thì ma trận In A khả ảo
Như ã nói trong phần giới thiệu, trong ma trận A, tổng các phần tử trên một cột luôn nhỏ hơn hay
bằng 1. Trong mô hình input-output có ngành kinh tế mở thì ể các ngành áp ứng ược yêu cầu của
ngành kinh tế mở, mỗi ngành ngoài việc phải cung cấp ủ nguyên liệu cho hệ thống nội bộ thì còn phải
tạo ra thặng dư ể cung cấp cho ngành kinh tế mở.
Vì thế, trong mô hình input-output mở, tổng các phần tử trên một cột bất kỳ luôn nhỏ hơn hẳn 1, và
như thế, theo mệnh ề trên, ma trận In A khả ảo, hệ phương trình ( ) có nghiệm duy nhất: X (InA) .D 1 Ghi chú:
• Mọi phần tử của (In A) 1ều dương và det(In A) 0
• Nghiệm của hệ ( ) luôn dương
• Nếu yêu cầu của ngành kinh tế mở thay ổi (tăng hoặc giảm) một lượng là D thì sản lượng
của n ngành thay ổi (tăng hoặc giảm) một lượng tương ứng là: X (In A) 1 D
• Suy ra, nếu yêu cầu của ngành kinh tế mở ối với riêng ngành j tăng thêm 1 ơn vị thì mức tăng
sản lượng của n ngành là cột thứ j của ma trận (In A) 1
Thật vậy, nếu yêu cầu của ngành kinh tế mở ối với riêng ngành j tăng thêm 1 ơn vị thì 0  D
1 (tọa ộ thứ j bằng 1, các tọa ộ khác ều bằng 0)  0 Trang | 4 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief Do ó, 0 
X (In A) 1 D (In A) . 1 1 cột j của (In A) 1  0
Ví dụ: Trong mô hình input-output Leontief gồm 3 ngành kinh tế, cho ma trận hệ số ầu vào: 0.1 0.3 0.2 A 0.4 0.2 0.3 0.2 0.3 0.1
a) Nêu ý nghĩa của con số 0.4 trong ma trận A
Ta thấy 0.4 là phần tử thuộc dòng 2, cột 1 của A, nghĩa là 0.4 a21
Theo ịnh nghĩa của a21 thì a21 0.4 cho ta biết, ể ngành 1 tạo ra sản lượng trị giá 1 ơn vị tiền thì ngành
2 cần cung cấp cho ngành 1 lượng nguyên liệu trị giá 0.4 ơn vị tiền.
Nói cách khác, ể ngành 1 tạo ra sản lượng trị giá 1 ơn vị tiền thì nó cần sử dụng lượng nguyên liệu
của ngành 2 trị giá 0.4 ơn vị tiền.
b) Nếu ngành 3 muốn tạo ra sản lượng trị giá là 150 ( ơn vị tiền) thì tổng lượng nguyên liệu ầu vào
của ngành 3 là bao nhiêu?
Trong câu hỏi này, ngành 3 là ối tượng nhận, còn ối tượng cho là ngành 1, ngành 2, ngành 3.
• Lượng nguyên liệu của ngành 1 cần cung cấp cho ngành 3 là: a13 150 0.2 150 30
• Lượng nguyên liệu của ngành 2 cần cung cấp cho ngành 3 là: a23 150 0.3 150 45
• Lượng nguyên liệu của ngành 3 cần cung cấp cho ngành 3 là: a33 150 0.1 150 15
Vậy, tổng lượng nguyên liệu ầu vào của ngành 3 (nhận từ 3 ngành) là: 30 45 15 90 ( ơn vị tiền).
c) Nếu 3 ngành muốn tạo ra sản lượng trị giá (120,100,150) thì ngành 1 cần cung cấp cho 3 ngành
lượng nguyên liệu tổng cộng là bao nhiêu?
Trong câu hỏi này, ngành 1 là ối tượng cho, còn ối tượng nhận là ngành 1, ngành 2, ngành 3. Trang | 5 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief
• Lượng nguyên liệu của ngành 1 cần cung cấp cho ngành 1 là: a11 120 0.1 120 12
• Lượng nguyên liệu của ngành 1 cần cung cấp cho ngành 2 là: a12 100 0.3 100 30
• Lượng nguyên liệu của ngành 1 cần cung cấp cho ngành 3 là: a13 150 0.2 150 30
Vậy, tổng lượng nguyên liệu của ngành 1 cung cấp cho cả 3 ngành là: 12 30 30 72 ( ơn vị tiền)
d) Để áp ứng yêu cầu của ngành kinh tế mở, các ngành tạo ra sản lượng là (100,100,100) . Tìm yêu
cầu của ngành kinh tế mở. d1 Gọi (d ,d ,d ) là yêu c1
ầu của ngành kinh tế mở ối với 3 ngành 2 3 và ặt D d2 d3 x1 100
Ma trận sản lượng của 3 ngành là X x2 100 x3 100
Ta có công thức: D (I3 A)X, trong ó 1 0 0 0.1 0.3 0.2 0.9 0.3 0.2 I3 A 0 10 0.40.20.3 0.40.8 0.3 0 0 1 0.2 0.3 0.1 0.2 0.3 0.9
 I3 A Vậy, 0.9 0.3 0.2 100 40 D (I3 A)X 0.4 0.8 0.3 100 10 0.2 0.3 0.9 100 40
Do ó, yêu cầu của ngành kinh tế mở ối với 3 ngành là d1 40,d2 10,d3 40 (với yêu cầu này của
ngành kinh tế mở thì 3 ngành sẽ tạo ra sản lượng tương ứng là x1 100,x2 100,x3 100) Trang | 6 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief
e) Tìm mức sản lượng của 3 ngành khi biết yêu cầu của ngành kinh tế mở ối với 3 ngành là (118,52,96)
Giả thiết cho ta yêu cầu của ngành kinh tế mở ối với 3 ngành là d1 118,d2 52,d3 96
Ta cần tìm mức sản lượng của 3 ngành là (x ,x ,x ). Có 2 cách tính: 1 2 3
Cách 1 (ngắn gọn): Gọi (x ,x ,x ) là s1 ản lượng của 3 ngành 2 3
thì ta có hệ phương trình x1 (0.1x1 0.3x2 0.2x )3 118 ( ) x2 (0.4x1 0.2x2 0.3x )3 52 x3 (0.2x1 0.3x2 0.1x )3 96 (hệ số của x ,x ,x 1 2
3 ở vế phải có ược từ ma trận A) Chuyển vế: x1 (0.1x1 0.3x2 0.2x )3 118 0.9x1 0.3x2 0.2x3 118 x2 (0.4x1 0.2x2 0.3x )3 52 0.4x1 0.8x2 0.3x3 52 x3 (0.2x1 0.3x2 0.1x )3 96 0.2x1 0 3. x2 0.9x3 96
Ta giải hệ bằng phương pháp Cramer (xem lại phần quy tắc Cramer) Tính các ịnh thức: 0.9 0.3 0.2 D 0.4 Casio 0.8 0.3 0.2 0.3 0.385 0.9 Trang | 7 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief 118 0.3 0.2 Casio D1 52 0.8
0.3 115.5 (thay cột 1 bởi cột hệ số tự do) 96 0.3 0.9 0.9 118 0.2 Casio D2 0.4 52
0.3 123.2 (thay cột 2 bởi cột hệ số tự do) 0.2 96 0.9 0.9 0.3 118 Casio D3 0.4 0.8
52 107.8 (thay cột 3 bởi cột hệ số tự do) 0.2 0.3 96
Sản lượng của 3 ngành là: x1 D1 115.5 300 D 0.385
2 D2 123.2 320 ( ơn vị tiền) x D 0.385 D3 107.8 x3 D 0.385 280
Cách 2: Dùng công thức X (I3 A) .D 1 Gọi (x ,x ,x ) là s1 ản lượng của 3 2 3 ngành, ặt: x1 d1 118 x3 d3 96 thì X (I3A) .D 1 Trong ó, Trang | 8 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief 0 0.1 0.2 0.9 0.3 0.2 1 0 0.3 1 0.2 0.3 I 0 0.4 0.3 0.4 0.8 3 A 0 B 0 0 1 0.2 0.3 0.1 0.2 0.3 0.9 X x2 ; D d2 52
 I3 A B (I3 A) 1 B 1 với B11 B12 B13 T B B B B 1 1 21 22 23 detB B31 B32 B33 0.9 det B sio 0.4 0.2 0.8 0.3 0.385 0.3 0.3 0.9 0.2 C a 0.8 0.3 B11 ( 1)1 1 .M11 0.30.9 0.63 1 1 2 .M12 0.40.2 0.90.3 0.42 B12 ( 1) 1 0.42 Trang | 9 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief 1 3 .M13 0.40.2 0.80.3 0.28 B13 ( 1) 1 2 1 .M21 0.30.3 0.20.9 0.33 B21 ( 1) 1 0.33 2 2 .M22 0.90.2 0.20.9 0.77 B22 ( 1) 1 2 3 .M23 0.90.2 0.30.3 0.33 B23 ( 1) 1 0.33 3 1 .M31 0.3 0.20.3 0.25 B31 ( 1)0.8 1 3 2 .M32 0.90.4 0.20.3 0.35 B32 ( 1) 1 0.35 3 3 .M33 0.90.4 0.80.3 0.60 B33 ( 1) 1 Thay vào, ta ược: Trang | 10 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief (I3 A) 1 B 1 0.63 0.42 0.28 T 1
(nhớ là có chuyển vị) 0.33 0.77 0.33 0.385 0.25 0.35 0.60 0.63 0.33 0.25 1 0.42 0.77 0.35 0.385 0.28 0.33 0.60
Vậy, sản lượng của 3 ngành là: X (I3 A) .D 1 0.63 0.33 0.25 118 1 0.42 0.77 0.35 52 0.385 0.28 0.33 0.60 96 115.5 300 x 300 1 123.2 320 x12 320 0.385 107.8 280 x3 280
(cách này dài, chỉ nên dùng khi ề bài yêu cầu tìm ma trận (I3 A) 1)
Ghi chú: Ta có thể tính (I3 A) 1 bằng cách ặt 9 3 2 8 3 C 10(I 3 3 A) 4 Trang | 11 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief 2 9
(ma trận C chứa toàn số nguyên nên dễ tính toán) Khi ó,
C 1 [10(I3 A)] 1 1 (I3 A) 1 (I3 A) 1 10C 1 10
Đến ây, ta tìm C 1 theo công thức C11 C12 C13 T 1 C 1 detC CC3121 CC CC 3222 3323 (nhớ là có chuyển vị) rồi suy ra (I3 A) 1 10C 1
Ví dụ: Trong mô hình input-output Leontief gồm 3 ngành kinh tế, cho ma trận hệ số ầu vào: 0.2 0.2 0.1 A 0.3 0.1 0.2 0.2 0.2 0.3
Tìm mức sản lượng của 3 ngành khi biết yêu cầu của ngành kinh tế mở ối với 3 ngành là D (50,240,90)
Theo giả thiết thì yêu cầu của ngành kinh tế mở ối với 3 ngành là d1 50,d2 240,d3 90 Gọi (x ,x ,x ) là s1
ản lượng của 3 ngành thì ta có hệ phương trình: 2 3 x1 (0.2x1 0.2x2 0.1x )3 50 ( ) x2 (0.3x1 0.1x2 0.2x )3 240 Trang | 12 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief x3 (0.2x1 0.2x2 0.3x )3 90 (hệ số của x ,x ,x1 2
3 ở vế phải có ược ma trận A) Chuyển vế: x1 (0.2x1 0.2x2 0.1x )3 50 0.8x1 0.2x2 0.1x3 50 x2 (0.3x1 0.1x2 0.2x )3 240 0.3x1 0.9x2 0.2x3 240 x3 (0.2x1 0.2x2 0.3x )3 90 0.2x1 0.2x2 0 7. x3 90
Ta giải hệ bằng phương pháp Cramer (xem lại phần quy tắc Cramer) Tính các ịnh thức: 0.8 0.2 0.1 Casio D 0.3 0.9 0.2 0.398 0.2 0.2 0.7 50 0.2 0.1 Casio D1 240 0.9
0.2 79.6 (thay cột 1 bởi cột hệ số tự do) 90 0.2 0.7 0.8 50 0.1 Casio D2 0.3 240
0.2 159.2 (thay cột 2 bởi cột hệ số tự do) 0.2 90 0.7 0.8 0.2 50 Casio D3 0.3 0.9
240 119.4 (thay cột 3 bởi cột hệ số tự do) 0.2 0.2 90
Sản lượng của 3 ngành là: x1 DD1 0.39879.6 200 Trang | 13 lOMoAR cPSD| 49519085
Chương 3: Mô hình input-output Leontief
x2 D2 159.2 400 ( ơn vị tiền) D 0.398 D3 119.4 x3 D 0.398 300 BÀI TẬP
Trong mô hình input-output Leontief gồm 3 ngành kinh tế, cho ma trận hệ số ầu vào: 0.1 0.1 0.2 0.2 A 0.1 0.3 0.3 0.2 0.2
Tìm mức sản lượng của 3 ngành khi biết yêu cầu của ngành kinh tế mở ối với 3 ngành là D (50,240,90) HẾT CHƯƠNG 3 Trang | 14