Lý thuyết thống kê và quyết định dựa trên dữ liệu - Chương 3 & 4 môn Lý thuyết thống kê | Đại học Kinh tế Thành phố Hồ Chí Minh

Intuition-based decision: Quyết sách dựa trên những phán đoán chủ quan
Scientific evidence-based decision: suy luận dựa trên xác suât
- Business analytics is a science dealing with the collection, analysis, interpretation,and presentation of
numerical data. (The use of statistics to analyze data) to provide useful information and evidence for
business decisions. - Quyết sách đưa ra nhằm: Giải quyết vấn đề • Nâng cao hiệu quả •
Tìm ra cơ hội phát triển
- Cơ sở ptkd: Dữ liệu và pp ptich dữ liệu
- Tổng thể: Bao gồm tất cả đối tượng nghiên cứu
- Mẫu (Sample): 1 phần nhỏ của tổng thể- Census: Khảo sát toàn diện
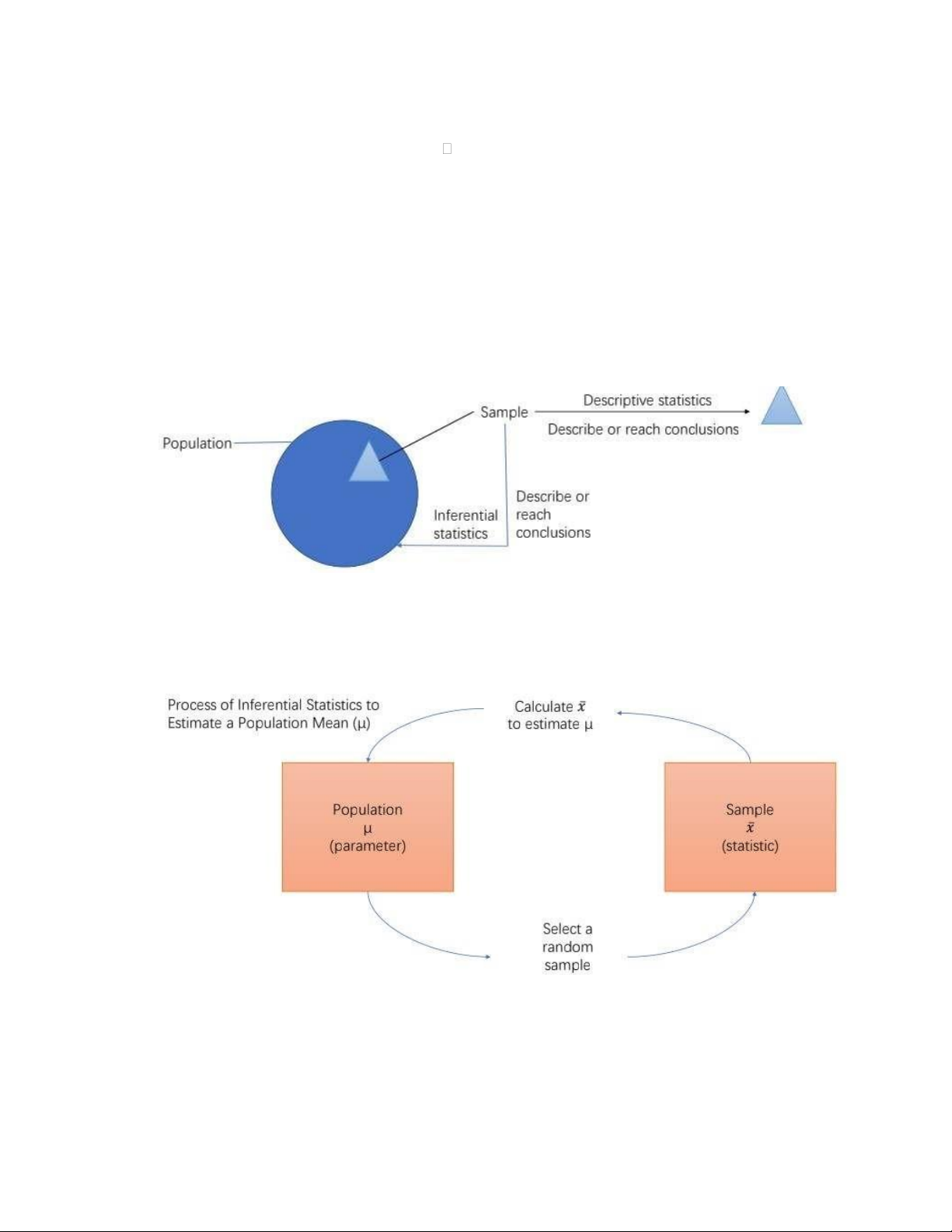
- Thống kê mô tả (Descriptive statistics): Khi một nhà phân tích kinh doanh sử dụng dữ liệu thu thập
được từ một nhóm để mô tả hoặc đưa ra kết luận về chính nhóm đó, các thống kê này gọi là thống kê mô tả.
- Thống kê suy diễn (Inferential statistics): Khi một nhà nghiên cứu thu thập dữ liệu từ một mẫu và sử
dụng các thống kê được tạo ra để rút ra kết luận về quần thể từ đó mẫu được lấy, các thống kê này gọi là thống kê suy diễn.
- Tham số (Parameter): Là một phép đo mô tả cho quần thể. Các tham số thường được ký hiệu bằng các
chữ cái Hy Lạp. Ví dụ: trung bình quần thể (μ), phương sai quần thể (σ²), và độ lệch chuẩn quần thể (σ).
- Thống kê (Statistic): Là một phép đo mô tả cho mẫu. Các thống kê thường được ký hiệu bằng các chữ cái La
Tinh. Ví dụ: trung bình mẫu ( ), phương sai mẫu (s²), và độ lệch chuẩn mẫu (s).x̄
Bốn cấp độ phổ biến của đo lường dữ liệu:
1. Danh nghĩa (Nominal): Đây là cấp độ cơ bản nhất, trong đó dữ liệu được phân loại vào các nhóm
hoặc danh mục mà không có thứ tự hay giá trị số học. Ví dụ: màu sắc, giới tính, quốc gia.
2. Thứ tự (Ordinal): Dữ liệu ở cấp độ này có thể được sắp xếp theo thứ tự hoặc cấp bậc, nhưng
khoảng cách giữa các cấp bậc không nhất thiết phải đồng đều. Ví dụ: xếp hạng (1 sao, 2 sao, 3 sao),
mức độ hài lòng (rất không hài lòng, không hài lòng, hài lòng, rất hài lòng).
=> Bởi vì dữ liệu danh nghĩa và dữ liệu thứ tự thường được thu thập từ các phép đo không chính xác như
các câu hỏi nhân khẩu học, phân loại người hoặc vật thể, hoặc xếp hạng các mục, dữ liệu danh nghĩa và dữ
liệu thứ tự là dữ liệu không định lượng và đôi khi được gọi là dữ liệu định tính.
3. Khoảng (Interval): Dữ liệu ở cấp độ này có các khoảng cách đồng đều giữa các giá trị, nhưng
không có điểm gốc tuyệt đối. Ví dụ: nhiệt độ theo độ Celsius hoặc Fahrenheit, năm trong lịch.
4. Tỉ lệ (Ratio): Đây là cấp độ đo lường cao nhất, trong đó dữ liệu có các khoảng cách đồng đều giữa
các giá trị và có điểm gốc tuyệt đối (zero tuyệt đối), cho phép thực hiện các phép toán như nhân và
chia. Ví dụ: chiều cao, cân nặng, doanh thu.
=> Bởi vì dữ liệu cấp độ khoảng và tỷ lệ thường được thu thập bằng các công cụ chính xác thường sử dụng
trong các quy trình sản xuất và kỹ thuật, trong các bài kiểm tra tiêu chuẩn quốc gia, hoặc trong các quy
trình kế toán chuẩn, chúng được gọi là dữ liệu định lượng và đôi khi được gọi là dữ liệu định lượng.
_________________________________________
CHAPTER 3: DESCRIPTIVE STATISTICS
Đặc tính dữ liệu:
- Độ tập trung của dữ liệu
- Độ phân tán của dữ liệu
- Hình dạng dữ liệu (Sự phân bố của dữ liệu) 1. Độ tập trung của dữ liệu:
- Các chỉ số trung tâm cung cấp thông tin về trung tâm, hoặc phần giữa, của một tập hợp các số.
- Các thông số đo lường: Mode (mode), Median (trung vị), Mean (trung bình), Percentiles (phân vị), và Quartiles(tứ phân vị). 1.1. Mode:
- Mode (mode): là giá trị xuất hiện nhiều nhất trong một tập hợp dữ liệu. Dữ liệu có hai mode được gọi
làbimodal. Dữ liệu có nhiều hơn hai mode được gọi là multimodal. - Cách tìm mode:
Sắp xếp dữ liệu thu thập được từ min
tới max. Xác định giá trị nào xuất hiện nhiều nhất. 1.2. Median:
- Median (Trung vị): Là giá trị ở giữa trong một dãy số được sắp xếp theo thứ tự. - Cách tìm median: •
Sắp xếp các quan sát trong một dãy số theo thứ tự. •
Tính giá trị (n+1)/2, trong đó n là số lượng quan sát. •
Đối với số lượng quan sát là số nguyên, tìm giá trị ở vị trí giữa của dãy đã sắp xếp. Đây chính là trung vị. •
Đối với số lượng quan sát không là số nguyên, tìm trung bình cộng của hai giá trị ở giữa
của dãy đã sắp xếp. Trung bình cộng này chính là trung vị. 1.3. Mean
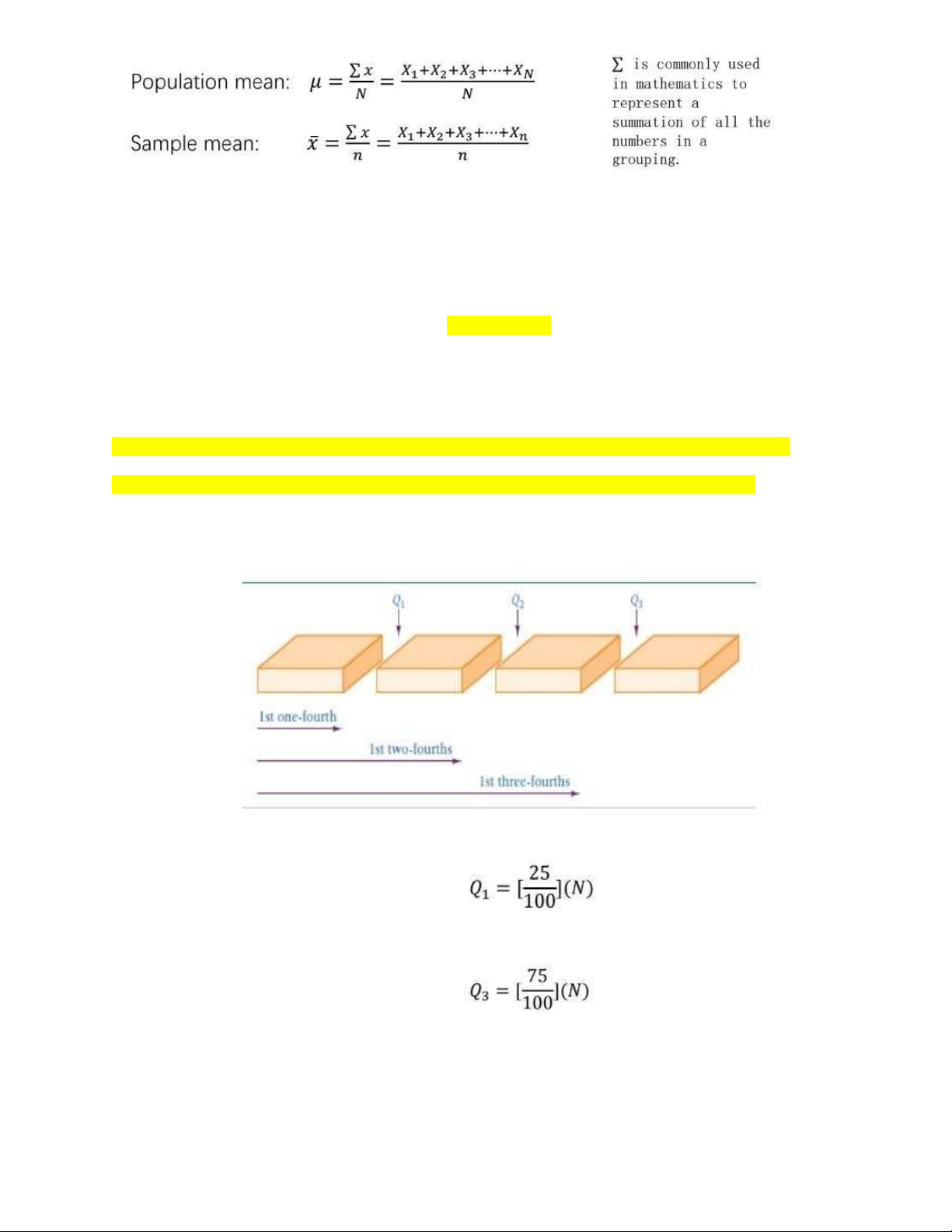
- Mean (Trung bình): Giá trị trung bình của 1 nhóm các giá trị/ bộ dữ liệu.- Công thức:
1.4. Percentiles
- Percentiles (phân vị): Là các chỉ số trung tâm phân chia một tập hợp dữ liệu thành 100 phần. Có 99
percentilesvì cần 99 điểm phân chia để chia một tập hợp dữ liệu thành 100 phần. Percentile thứ n là giá
trị sao cho ít nhất n % dữ liệu nằm dưới giá trị đó và tối đa (100 - n)% dữ liệu nằm trên giá trị đó. - Cách tìm percentile: •
Sắp xếp các số trong một dãy số theo thứ tự tăng dần. •
Tính vị trí percentile (i) bằng công thức: i = (p/100) × N, trong đó: • i = vị trí percentile, • p = percentile quan tâm, •
N = số lượng dữ liệu trong tập hợp. •
Xác định giá trị percentile dựa vào i bằng cách (a) hoặc (b):
a. Nếu i là số nguyên, percentile p là trung bình cộng của giá trị tại vị trí i và giá trị tại vị trí (i + 1).
b. Nếu i không phải là số nguyên, giá trị percentile p nằm ở vị trí của phần nguyên của (i + 1). 1.5. Quartiles:
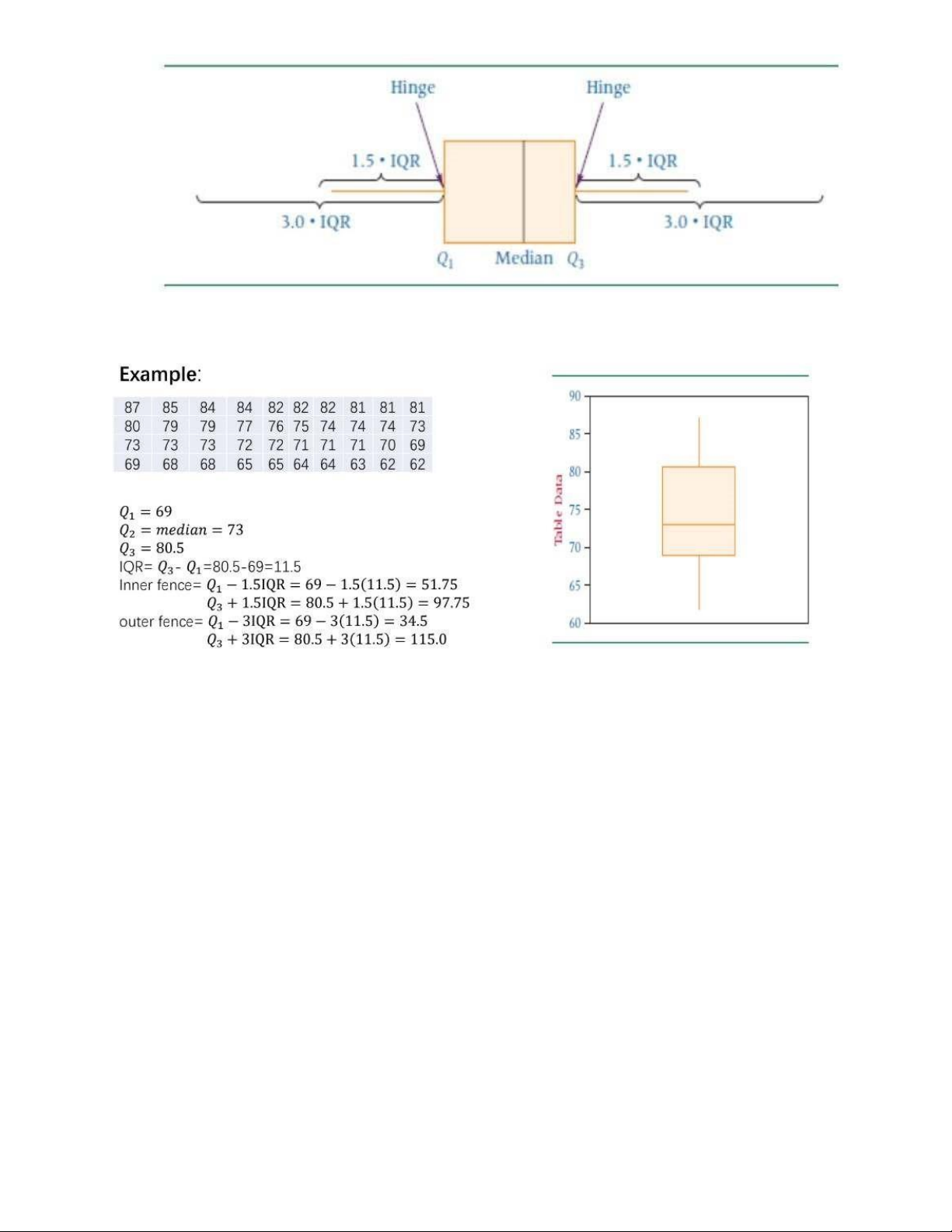
- Quartiles (tứ phân vị): Là các chỉ số trung tâm phân chia một tập hợp dữ liệu thành bốn phần. •
Giá trị của Q1 (Tứ phân vị thứ nhất): Được tìm thấy tại percentile thứ 25, tức là giá trị tại 25% của dữ liệu. •
Giá trị của Q3 (Tứ phân vị thứ ba): Được tìm thấy tại percentile thứ 75, tức là giá trị tại 75% của dữ liệu. •
Giá trị của Q2 (Tứ phân vị thứ hai): Bằng với trung vị (median), tức là giá trị ở giữa của tập hợp dữ liệu. - Ví dụ:
2. Độ phân tán của dữ liệu:
- Các biện pháp đo lường sự biến thiên: mô tả sự phân tán hoặc độ rải của một tập dữ liệu.
- Bảy biện pháp đo lường sự biến thiên cho dữ liệu không phân nhóm: khoảng biến thiên, khoảng phân vị,
độ lệch tuyệt đối trung bình, phương sai, độ lệch chuẩn, điểm z và hệ số biến thiên. 2.1. Range
- Range (Khoảng biến thiên): là sự chênh lệch giữa giá trị lớn nhất và giá trị nhỏ nhất của một tập dữ liệu.
2.2. Interquartile Range:
- Interquartile Range (Khoảng phân vị): là khoảng giá trị nằm giữa phân vị thứ nhất (Q1) và phân vị thứ ba
(Q3) của dữ liệu. Khoảng phân vị cung cấp thông tin về sự phân tán của 50% dữ liệu ở giữa và ít bị ảnh
hưởng bởi các giá trị ngoại lệ (outliers). 2.3. Variance
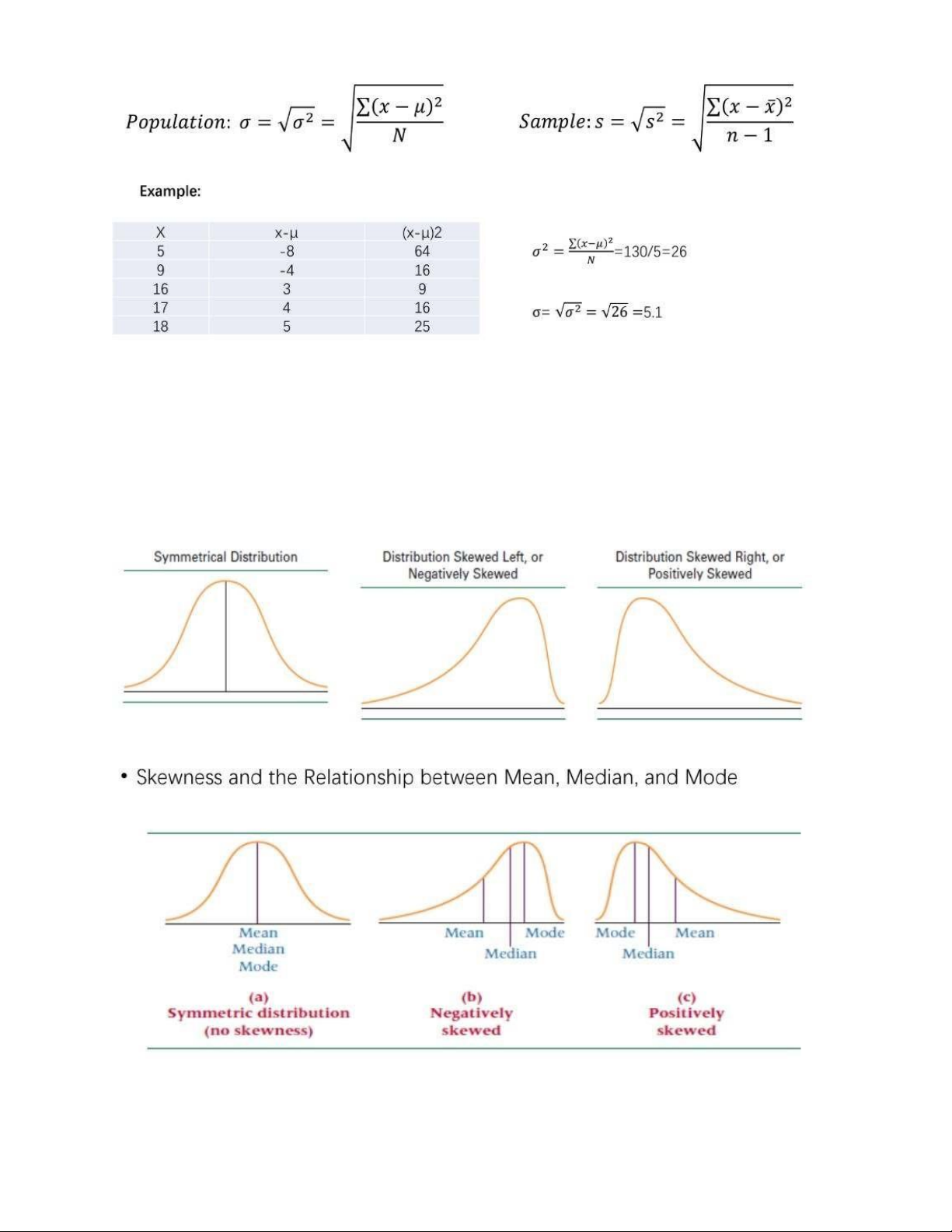
- Variance (Phương sai): là giá trị trung bình của các độ lệch bình phương so với giá trị trung bình của một
tậphợp số liệu. Phương sai đo lường mức độ phân tán của các giá trị trong dữ liệu xung quanh giá trị trung bình. •
u: bình quân (xem lại công thức ở mục 1.3 (= x ngang) •
x - u: Khoảng cách từ các điểm dữ liệu đến bình quân •
N: số giá trị của bộ dữ liệu
2.4 Standard deviation
- Standard deviation (Độ lệch chuẩn): khai căn của phương sai
3. Hình dạng dữ liệu
- Measures of shape: là các công cụ có thể được sử dụng để mô tả hình dạng của phân phối dữ liệu. 3.1. Skewness
- Skewness (Độ lệch): là khi một phân phối không đối xứng hoặc thiếu sự đối xứng. Phần lệch là phần dài
vàmỏng của đường cong.
3.2. Coefficient of skewness:
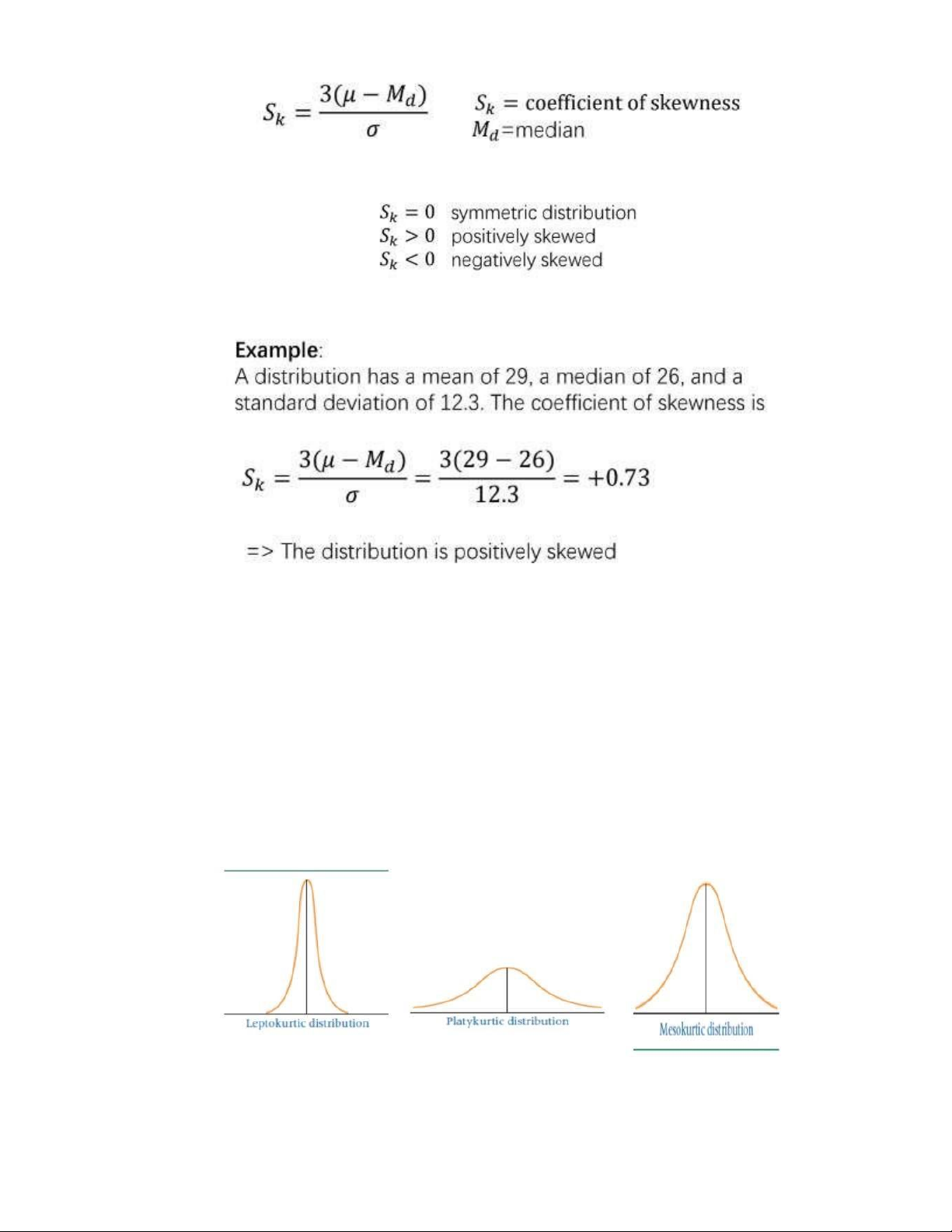
- Coefficient of skewness (Hệ số độ lệch): là một chỉ số thống kê dùng để đo lường mức độ và hướng của
sựkhông đối xứng trong phân phối dữ liệu. Hệ số này cho biết liệu phân phối dữ liệu có bị lệch về phía
bên trái hay bên phải so với giá trị trung bình. * Lưu ý: •
Sk thuộc [-1;1] => nearly normal distribution •
Sk > 1 => positively skewed •
Sk < 1 => negatively skewed 3.3. Kurtosis
- Kurtosis: là một đại lượng thống kê mô tả mức độ nhọn của đỉnh phân phối dữ liệu. Nó cho biết sự phân
bố củadữ liệu xung quanh giá trị trung bình có tập trung vào trung tâm (nhọn) hay phân tán ra ngoài (phẳng).
- Các loại phân bố dữ liệu:
3.4 Box-and-Whisker Plots (Box plot):
- Biểu đồ Box-and-Whisker (biểu đồ hộp): là một sơ đồ sử dụng các phần tư trên cùng và dưới cùng cùng
với giátrị trung vị và hai giá trị cực trị nhất để miêu tả phân phối một cách trực quan. - Ví dụ:
_________________________________________
CHAPTER 4: SAMPLING AND SAMPLING DISTRIBUTION 1. Normal distribution
- Đặc tính của phân bố chuẩn: • Phân bố liên tục •
Phân bố đối xứng xung quanh giá trị trung bình của nó •
Tiếp cận trục hoành nhưng không chạm vào •
Chỉ có một đỉnh duy nhất •
Có một tổ hợp của những đường phân phối •
Diện tích dưới đường cong bằng 1
- Ví dụ: Nhiều đặc điểm của con người, chẳng hạn như chiều cao, cân nặng, độ dài, tốc độ, chỉ số IQ, thành
tíchhọc tập và số năm kỳ vọng sống, thường được phân phối theo phân phối chuẩn.
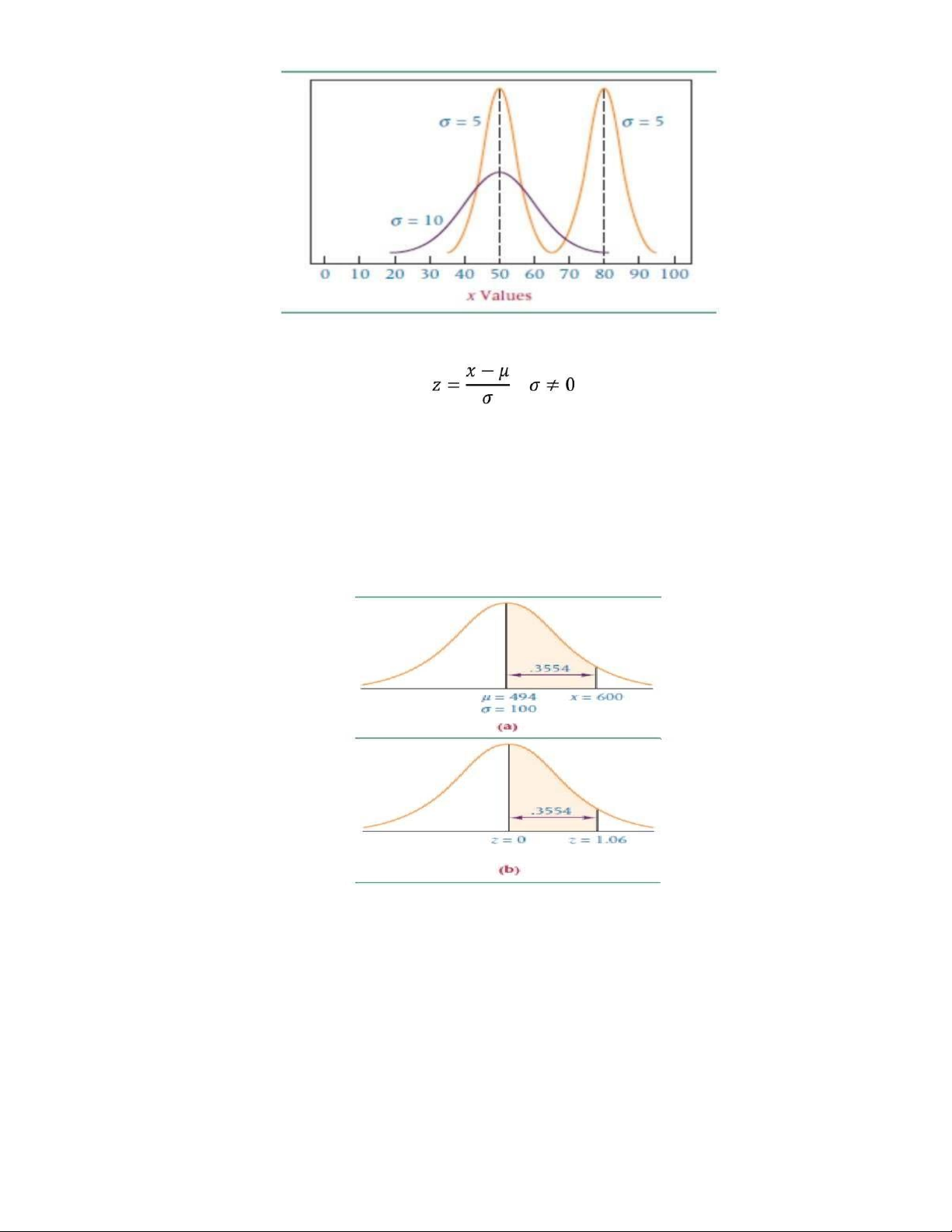
- Mỗi cặp giá trị μ (trung bình) và σ (độ lệch chuẩn) xác định một phân phối chuẩn khác nhau => Mỗi sự
thay đổitrong một tham số (μ hoặc σ) xác định một phân phối chuẩn khác nhau => Chuyển đổi phân phối
chuẩn thành phân phối chuẩn hóa (phân phối Z).
- Công thức tiêu chuẩn hóa phân phối: Trong đó: •
X là giá trị của biến trong phân phối chuẩn. •
μ là trung bình của phân phối chuẩn. •
σ là độ lệch chuẩn của phân phối chuẩn.
- Phân phối chuẩn hóa: Phân phối Z là một phân phối chuẩn với trung bình μ=0 và độ lệch chuẩn σ=1. 2. Sampling - Lý do chọn mẫu: •
Tiết kiệm chi phí: Chọn mẫu có thể tiết kiệm chi phí so với việc thực hiện điều tra toàn bộ dân số,
vì nó liên quan đến việc nghiên cứu một tập hợp nhỏ hơn của dân số. •
Tiết kiệm thời gian: Thu thập dữ liệu từ một mẫu thường nhanh hơn so với việc thu thập dữ liệu từ toàn bộ dân số. •
Mở rộng phạm vi nghiên cứu: Với nguồn lực hạn chế, việc chọn mẫu cho phép mở rộng phạm vi
nghiên cứu, giúp nghiên cứu nhiều biến số hơn hoặc các khía cạnh khác nhau của nghiên cứu. •
Nghiên cứu phá hủy: Trong các trường hợp nghiên cứu có thể gây hư hỏng (ví dụ, thử nghiệm sản
phẩm), việc chọn mẫu giúp bảo tồn các sản phẩm hoặc đối tượng còn lại. •
Khó tiếp cận: Nếu không thể hoặc không thực tế để tiếp cận toàn bộ dân số, chọn mẫu trở thành phương án duy nhất. - Lý do chọn tổng thể: •
Loại bỏ khả năng mẫu ngẫu nhiên không đại diện: Để loại bỏ khả năng mẫu ngẫu nhiên chọn được
không đại diện cho toàn bộ dân số. •
Đảm bảo an toàn cho người tiêu dùng: Để đảm bảo rằng các thông tin thu được là chính xác và
bảo vệ quyền lợi của người tiêu dùng.
- Khung mẫu (Frame): là danh sách của dân số mục tiêu bao gồm các cá nhân, tổ chức hoặc thực thể là
đối tượng của cuộc điều tra.
- Ví dụ: danh sách trường học, danh sách các hiệp hội thương mại, danh sách công ty. •
Về lý thuyết, dân số mục tiêu và khung mẫu là giống nhau. Trong thực tế, khung mẫu và dân số
mục tiêu thường khác nhau. •
Khung mẫu có sự đăng ký thừa: bao gồm các đơn vị của dân số mục tiêu cộng với một số đơn vị bổ sung.
Khung mẫu có sự đăng ký thiếu: chứa ít đơn vị hơn so với dân số mục tiêu. - Có 2 cách chọn mầu: •
Lấy mẫu ngẫu nhiên (probability sampling): Mỗi đơn vị trong dân số có xác suất như nhau để được chọn vào mẫu. •
Lấy mẫu ngẫu nhiên đơn giản (Simple Random Sampling): Mỗi đơn vị trong dân số có cơ hội như
nhau để được chọn vào mẫu. •
Lấy mẫu phân tầng ngẫu nhiên (Stratified Random Sampling): Dân số mục tiêu được chia thành
các nhóm (tầng) đồng nhất về một hoặc nhiều đặc điểm, và mẫu được lấy ngẫu nhiên từ mỗi tầng. •
Lấy mẫu hệ thống ngẫu nhiên (Systematic Random Sampling): Chọn mỗi đơn vị thứ k từ danh sách
sắp xếp của dân số mục tiêu, sau khi chọn ngẫu nhiên một điểm khởi đầu. •
Lấy mẫu cụm ngẫu nhiên (Cluster Random Sampling): Dân số được chia thành các cụm hoặc nhóm,
chọn ngẫu nhiên một số cụm, và sau đó lấy mẫu từ tất cả các đơn vị trong các cụm được chọn. •
Lấy mẫu không ngẫu nhiên (nonprobability sampling): Không phải mọi đơn vị trong dân số đều
có xác suất như nhau để được chọn vào mẫu. •
Lấy mẫu thuận tiện (Convenience Sampling): Chọn các đơn vị dễ tiếp cận nhất. •
Lấy mẫu theo đánh giá (Judgement Sampling): Chọn các đơn vị dựa trên sự đánh giá chủ quan của
nhà nghiên cứu về những đơn vị có thể cung cấp thông tin hữu ích nhất. •
Lấy mẫu theo chỉ tiêu (Quota Sampling): Chia dân số thành các nhóm và chọn mẫu từ mỗi nhóm
cho đến khi đạt được số lượng đơn vị cần thiết trong mỗi nhóm. •
Lấy mẫu dây chuyền (Snowball Sampling): Ban đầu chọn một số đơn vị nghiên cứu, sau đó yêu cầu
họ giới thiệu thêm những người khác. Phương pháp này thường được sử dụng để nghiên cứu các nhóm khó tiếp cận. * Random Sampling:
- Simple Random Sampling: •
Bước 1: Mỗi đơn vị trong khung mẫu được đánh số từ 1 đến N (trong đó N là kích thước của dân số). •
Bước 2: Sử dụng bảng số ngẫu nhiên để chọn n đơn vị vào mẫu. •
Ưu điểm: Dễ thực hiện đối với các dân số nhỏ. •
Nhược điểm: Việc chọn mẫu có thể trở nên khó khăn và phức tạp đối với các dân số lớn.
- Stratified Random Sampling: •
Bước 1: Dân số được chia thành các phân nhóm không chồng chéo, gọi là các tầng (strata). •
Bước 2: Lấy mẫu ngẫu nhiên từ từng phân nhóm. •
Lấy mẫu phân tầng tỷ lệ (Proportionate Stratified Random Sampling): Khi tỷ lệ mẫu lấy từ mỗi
tầng tương ứng với tỷ lệ của từng tầng trong toàn bộ dân số. •
Lấy mẫu phân tầng không tỷ lệ (Disproportionate Stratified Random Sampling): Khi tỷ lệ của các
tầng trong mẫu khác với tỷ lệ của các tầng trong dân số. •
Ưu điểm: Giảm sai số mẫu (sampling error) •
Nhược điểm: Tốn kém hơn so với lấy mẫu ngẫu nhiên đơn giản.
- Systematic Random Sampling: •
Bước 1: Đánh số mỗi đơn vị trong khung mẫu từ 1 đến N (trong đó N là kích thước của dân số).
Bước 2: Tính toán: • n = kích thước mẫu • N = kích thước dân số •
k = kích thước khoảng cách chọn (interval size) •
Bước 3: Chọn mỗi đơn vị thứ k vào mẫu. (Cách 4 đơn vị lấy 1 mẫu) •
Ví dụ: Giả sử dân số có 1000 đơn vị, bạn muốn lấy một mẫu gồm 100 đơn vị. • Tính k = 1000/100 = 10 •
Nếu bạn chọn một điểm khởi đầu ngẫu nhiên từ 1 đến 10, chẳng hạn là số 7, thì bạn sẽ chọn các
đơn vị ở các vị trí 7, 17, 27, 37, và cứ thế tiếp tục chọn mỗi đơn vị thứ 10 cho đến khi đủ kích thước mẫu. •
Ưu điểm: Tiện lợi và dễ thực hiện. •
Nhược điểm: Vấn đề với lấy mẫu hệ thống:
1. Vấn đề với Mẫu Định kỳ:
o Nếu có chu kỳ trong dân số tương ứng với khoảng cách chọn kkk, thì mẫu có thể bị thiên
lệch. Ví dụ, nếu dân số có một chu kỳ nào đó (như có sự thay đổi theo tháng hoặc theo
mùa), khoảng cách chọn cố định có thể dẫn đến việc chọn các đơn vị không đại diện.
2. Thiếu Độ Ngẫu Nhiên:
o Nếu điểm khởi đầu không được chọn hoàn toàn ngẫu nhiên, thì mẫu có thể không phản
ánh chính xác dân số. Ví dụ, nếu điểm khởi đầu được chọn dựa trên một tiêu chí không
ngẫu nhiên, các đơn vị được chọn có thể không đủ đại diện cho dân số.
3. Khó Kiểm Soát Đối Tượng Đặc Thù:
o Nếu dân số có sự phân bố đặc thù hoặc có các nhóm đơn vị quan trọng nhưng không
đồng đều, việc chọn mẫu theo hệ thống có thể bỏ sót hoặc không đủ đại diện cho những nhóm này.
- Cluster (Area) Sampling: •
Bước 1: Chia dân số thành các khu vực không chồng chéo, hoặc các cụm (clusters) (các vùng địa lý). •
Bước 2: Chọn ngẫu nhiên các cụm từ dân số. Sau đó, có thể thực hiện một trong hai phương pháp: •
Chọn tất cả các đơn vị trong các cụm được chọn. •
Hoặc, chọn ngẫu nhiên các đơn vị từ các cụm được chọn để đưa vào mẫu. Ưu điểm: Tiện
lợi và tiết kiệm chi phí. • Nhược điểm:
1. Hiệu quả thống kê kém hơn:
o Nếu các đơn vị trong một cụm tương đối giống nhau (có tính đồng nhất cao), thì lấy mẫu
cụm có thể ít hiệu quả hơn về mặt thống kê so với lấy mẫu ngẫu nhiên đơn giản. Điều này
là vì sự khác biệt giữa các cụm có thể lớn hơn sự khác biệt trong các đơn vị của cùng một cụm.
2. Vấn đề phân tích thống kê:
o Các vấn đề trong phân tích thống kê có thể phức tạp hơn với lấy mẫu cụm so với lấy mẫu
ngẫu nhiên đơn giản. Việc phân tích dữ liệu từ các cụm có thể đòi hỏi các kỹ thuật phức
tạp hơn để điều chỉnh cho sự tương đồng giữa các đơn vị trong cụm. * Nonrandom Sampling: •
Lấy mẫu thuận tiện: Các đơn vị trong mẫu được chọn dựa trên sự tiện lợi của nhà nghiên cứu. Ví
dụ, nhà nghiên cứu chọn những người dễ tiếp cận như bạn bè, đồng nghiệp, hoặc người qua lại gần nơi nghiên cứu. •
Lấy mẫu theo đánh giá/ phán đoán chủ quan: Các đơn vị trong mẫu được chọn dựa trên sự đánh
giá của nhà nghiên cứu về những đơn vị có khả năng cung cấp thông tin hữu ích nhất. Ví dụ, nhà
nghiên cứu có thể chọn các chuyên gia trong một lĩnh vực cụ thể để thu thập dữ liệu. •
Lấy mẫu theo chỉ tiêu: Dân số được chia thành các phân nhóm không chồng chéo (tầng). Thay vì
lấy mẫu ngẫu nhiên từ mỗi tầng, nhà nghiên cứu sử dụng phương pháp lấy mẫu không ngẫu nhiên
để thu thập dữ liệu từ từng tầng cho đến khi đạt được số lượng mẫu cần thiết cho mỗi tầng. Ví dụ,
nhà nghiên cứu có thể tiếp cận một số lượng nhất định từ mỗi nhóm tuổi hoặc giới tính. •
Lấy mẫu dây chuyền: Các đối tượng khảo sát được chọn dựa trên sự giới thiệu từ những người đã
tham gia khảo sát. Ví dụ, một người tham gia khảo sát được yêu cầu giới thiệu những người khác
mà họ biết để tham gia nghiên cứu. •
Lỗi mẫu: Xảy ra khi mẫu không đại diện cho toàn bộ dân số. Ví dụ, nếu mẫu chọn không đủ đa
dạng hoặc không phản ánh đúng cấu trúc của dân số, kết quả nghiên cứu có thể bị sai lệch. •
Lỗi không phải mẫu: Tất cả các lỗi khác ngoài lỗi mẫu. Ví dụ bao gồm lỗi trong quá trình thu thập
dữ liệu, lỗi trong xử lý dữ liệu, hoặc lỗi từ việc các đối tượng khảo sát không cung cấp thông tin chính xác.
3. Phân phối mẫu của trung bình mẫu (Sampling Distribution of Sample Mean):
- Định lý Giới hạn Trung tâm (Central Limit Theorem - CLT): •
Định nghĩa: Nếu các mẫu có kích thước n được chọn ngẫu nhiên từ một dân số có trung bình μ và
độ lệch chuẩn σ, thì phân phối của các trung bình mẫu (xˉ) sẽ xấp xỉ phân phối chuẩn (normal
distribution) khi kích thước mẫu đủ lớn (thường là n ≥ 30), bất kể hình dạng của phân phối dân số. •
Trường hợp dân số phân phối chuẩn: Nếu dân số đã có phân phối chuẩn, thì phân phối của các
trung bình mẫu sẽ là phân phối chuẩn cho bất kỳ kích thước mẫu nào, không cần kích thước mẫu phải lớn. - Giải thích: •
Kích thước mẫu lớn: Khi kích thước mẫu n lớn (thường là n ≥ 30), phân phối của trung bình mẫu
sẽ trở nên gần với phân phối chuẩn, ngay cả khi dân số gốc không có phân phối chuẩn. Điều này là
do định lý giới hạn trung tâm. •
Dân số phân phối chuẩn: Nếu dân số gốc đã phân phối chuẩn, thì phân phối của trung bình mẫu sẽ
luôn là phân phối chuẩn, bất kể kích thước mẫu là bao nhiêu. - Ứng dụng: •
Dự đoán và ước lượng: Định lý giới hạn trung tâm cho phép các nhà nghiên cứu và thống kê sử
dụng phân phối chuẩn để thực hiện ước lượng và kiểm định giả thuyết về trung bình dân số, ngay
cả khi dân số gốc không phân phối chuẩn, miễn là kích thước mẫu đủ lớn. •
Tính toán khoảng tin cậy và kiểm định giả thuyết: Với sự hiểu biết về phân phối của trung bình
mẫu, các nhà nghiên cứu có thể tính toán khoảng tin cậy cho trung bình dân số và thực hiện các
kiểm định giả thuyết để đưa ra các kết luận từ dữ liệu mẫu.
_________________________________________
CHAPTER 5: ESTIMATION AND HYPOTHESIS TESTING FOR SINGLE POPULATIONS
1. Estimation for single population
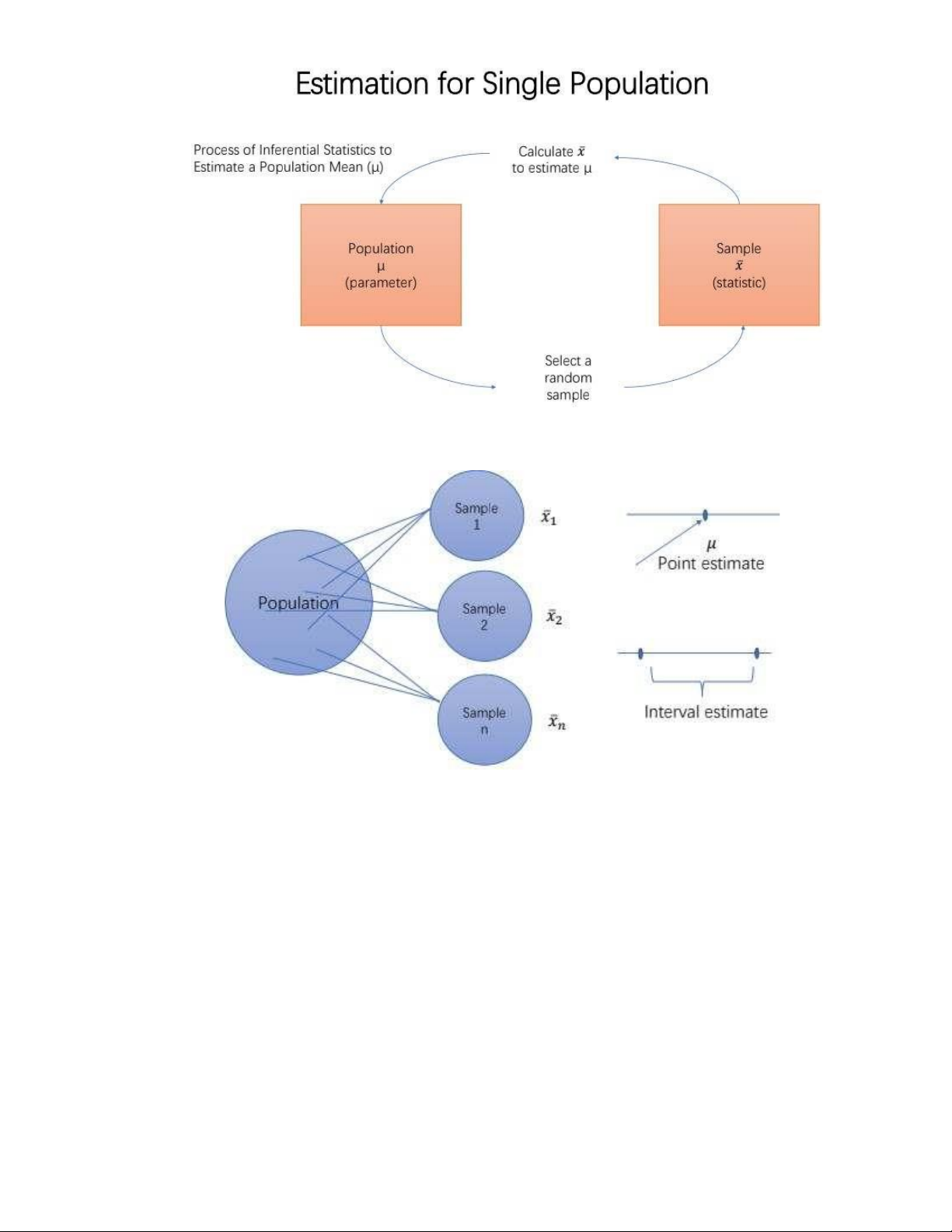
- Điểm ước lượng (A point estimate): là một thống kê được lấy từ mẫu để ước tính tham số của tổng thể. -
Khoảng ước lượng (Interval estimate, or confidence interval): là một phạm vi giá trị trong đó nhà phân
tích có thể tuyên bố, với một mức độ tin cậy nhất định, tham số của tổng thể nằm trong đó.
2. Ước Lượng Trung Bình Dân Số Sử Dụng Thống Kê t (Phương Sai Dân Số Không Được Biết) -
Phân Phối t: được sử dụng thay vì phân phối z để thực hiện các phân tích suy diễn về trung bình
dân số khi phương sai dân số không được biết và dân số phân phối theo phân phối chuẩn. -
Các Đặc Điểm của Phân Phối t: Giống như đường cong phân phối chuẩn, các phân phối t đối
xứng, đơn cực và là một tập hợp các đường cong. Các phân phối t có phần giữa phẳng hơn và có nhiều diện
tích hơn ở phần đuôi so với phân phối chuẩn. -
Đọc Phân Phối t: Để tìm giá trị trong bảng phân phối t, bạn cần biết số bậc tự do. Mỗi giá trị khác
nhau của số bậc tự do tương ứng với một phân phối t khác nhau. -
Số bậc tự do (Degrees of freedom): Ám chỉ số quan sát độc lập cho một nguồn biến động trừ đi số
lượng tham số độc lập được ước lượng trong việc tính toán biến động. Công thức tính số bậc tự do là bậc
tự do = n−1, trong đó n là kích thước mẫu. -
Khoảng Tin Cậy Để Ước Lượng Trung Bình Dân Số (μ): Khi ước lượng trung bình dân số (μ)
với một mẫu, chúng ta thường sử dụng khoảng tin cậy để đưa ra một khoảng giá trị mà chúng ta tin rằng
trung bình dân số thực sự nằm trong đó với một mức độ tin cậy nhất định. Trong đó:
3. Kiểm định giả thuyết:
- Giả Thuyết: Là các giải thích tạm thời về một nguyên tắc hoạt động trong tự nhiên. Giả thuyết được xây
dựng dựa trên quan sát, lý thuyết hoặc sự hiểu biết hiện tại và thường là điểm khởi đầu để nghiên cứu và
kiểm định. - Hai Loại Giả Thuyết Chính: •
Giả Thuyết Nghiên Cứu (Research Hypothesis): Là giả thuyết mà các nhà nghiên cứu dự đoán sẽ
có sự khác biệt hoặc mối quan hệ giữa các biến. Nó thường dựa trên lý thuyết hoặc quan sát và
cung cấp hướng đi cho nghiên cứu. •
Giả Thuyết Thống Kê (Statistical Hypothesis): Là các tuyên bố cụ thể về một hoặc nhiều tham số
của một phân phối thống kê. Trong kiểm định giả thuyết thống kê, bạn so sánh dữ liệu thực tế với
dự đoán của giả thuyết để xác định xem giả thuyết đó có thể bị bác bỏ hay không.
* Research Hypothesis:
- Khái niệm: là một tuyên bố về những gì nhà nghiên cứu tin tưởng sẽ là kết quả của một thí nghiệm hoặc
nghiên cứu. Nó thường được xây dựng dựa trên lý thuyết, quan sát hoặc kinh nghiệm và hướng dẫn các
nhà nghiên cứu trong việc thu thập và phân tích dữ liệu. - Ví dụ:
_________________________________________
CHAPTER 6: STATISTICAL INFERENCES ABOUT TWO POPULATIONS
1. Kiểm định giả thuyết và khoảng tin cậy về hai trung bình quần thể (Mẫu độc lập, σ2 chưa biết, thống kê t)
- Công thức 1 (phương sai của 2 tổng thể bằng nhau):
- Công thức 2 (phương sai của 2 tổng thể khác nhau): - Khoảng tin cậy:
Lớn hơn 3 ngưỡng => Chấp nhận H0
Nhỏ hơn 1 trong 3 ngưỡng => Chấp nhận Ha
_________________________________________
CHAPTER 8: ANALYSIS OF VARIANCE AND DESIGN OF EXPERIMENTS
Kết luận: Ít nhất 1 nhóm khác với các nhóm còn lại
_________________________________________
CHAPTER 9: REGRESSION ANALYSIS
1. PHÂN TÍCH MỐI TƯƠNG QUAN
2. PHÂN TÍCH HỒI QUY ĐƠN BIẾN
- Các mối quan hệ chức năng giữa hai biến:
+ Nếu X là biến độc lập và Y là biến phụ thuộc, mối quan hệ chức năng có dạng: Y=f(X)
+ Ví dụ: Mối quan hệ giữa doanh số bán hàng bằng đô la (Y) của một sản phẩm bán với giá cố định là 2 đô
la và số lượng đơn vị bán được (X). Mối quan hệ là: Y=2X
- Mối quan hệ thống kê giữa hai biến: Đánh giá hiệu suất của 10 nhân viên. Đánh giá vào cuối năm được
xem làbiến phụ thuộc YYY, và đánh giá giữa năm là biến độc lập XXX. Mối quan hệ giữa chúng được
thể hiện qua các biểu đồ phân tán sau đây.
- Phân tích hồi quy: là một phương pháp thống kê phân tích mối quan hệ thống kê giữa hai hay nhiều biến,
nhằmdự đoán biến phụ thuộc từ các biến độc lập khác.
- Mô hình hồi quy đơn giản: •
Yi là biến phụ thuộc trong thử nghiệm thứ iii (biến kết quả, biến phản hồi). •
Xi là biến độc lập trong thử nghiệm thứ iii (biến dự đoán, biến khám phá). •
β0 và β1 là các tham số. β0 là hệ số chặn hay hằng số (khi X = 0, nó cung cấp giá trị trung bình của
phân phối xác suất của Y tại X = 0; khi X # 0, nó không có ý nghĩa rõ ràng). β1 là hệ số hồi quy
hay sự thay đổi trong giá trị trung bình của phân phối xác suất của Y cho mỗi đơn vị tăng của X
(hay nói cách khác, β1 là hệ số đo lường ảnh hưởng của biến độc lập lên biến phụ thuộc) •
β1 > 0 => tác động tích cực •
β1 < 0 => tác động tiêu cực ϵi là sai số ngẫu nhiên.
Mô hình này được gọi là đơn giản, tuyến tính theo các tham số, và tuyến tính theo các biến dự đoán.
- Ước lượng hàm hồi quy:
2. PHÂN TÍCH HỒI QUY ĐA BIẾN
_________________________________________
CHAPTER 7: ANALYSIS OF CATEGORICAL DATA
1. Contingency Analysis: Chi-Square Test of Independence
- Kiểm định Chi-square về sự độc lập có thể được sử dụng để phân tích tần suất của hai biến với nhiều loại
khác nhau nhằm xác định xem hai biến có độc lập với nhau hay không. •
H0: Hai biến không liên quan • Ha: Hai biến liên quan •
f0: observed frequency (tần suất quan sát) •
fe: expected frequency (tần suất kỳ vọng)