Lý thuyết Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số
Tóm tắt lý thuyết TOÁN 12 chương 1: Sự đồng biến nghịch biến của hàm số. Tài liệu được biên soạn dưới dạng file PDF gồm 5 trang giúp bạn củng cố kiến thức, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!
Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Môn:
Tác giả:
Tài liệu liên quan:
Preview text:
Lý thuyết Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số
A. Sự đồng biến, nghịch biến của hàm số
1. Tính đơn điệu của hàm số
- Cho K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói
+ Hàm số đồng biến (tăng) trên K nếu mọi cặp x1,x2 thuộc K mà x1 nhỏ hơn x2 thì
f(x1) nhỏ hơn f(x2), tức là x1 < x2 => f(x1) < f(x2)
+ Hàm số nghịch biến (giảm) trên K nếu với mọi cặp x1,x2 thuộc K mà x1 < x2 thì
f(x1) nhỏ hơn f(x2), tức là x1 < x2 => f(x1) > f(x2)
- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K, K
được gọi chung là khoảng đơn điệu của hàm số.
Nhận xét: Hàm số đồng biến trên K thì đồ thị hàm số đi lên từ trái sang phải. Hàm
số nghịch biến trên K thì đồ thị hàm số đi xuống từ trái sang phải.
2. Tính đơn điệu và dấu của đạo hàm
- Giả sử hàm số y = f(x) có đạo hàm trên khoảng (a;b). Khi đó:
+ Nếu f'(x) ≥ 0, ∀x ∈ (a; b) và f'(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên (a;b).
+ Nếu f'(x) ≤ 0, ∀x ∈ (a; b) và f'(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số nghịch biến trên (a;b).
Ghi chú: Dấu bằng xảy ra chỉ tại một số hữu hạn điểm.
B. Các dạng bài tập xét tính đơn điệu của hàm số
Dạng 1: Xét tính đơn điệu của hàm số lớp 12
Bài toán xét tính đơn điệu của hàm số không hề phức tạp. Học sinh chỉ cần hiểu rõ
kiến thức là có thể làm được bài. Vì vậy, trước khi đi sâu vào phương pháp, công
thức giải nhanh dạng bài tập này, VnDoc sẽ điểm qua một số kiến thức trọng tâm.
Hàm số y = f(x) xác định trên I, I là một khoảng, một đoạn hay một nửa khoảng.
– Hàm số y = f(x) được gọi là đồng biến trên I nếu:
∀ x1, x2 ∈ I: x1 < x2 ⇔ f(x1) < f(x2).
– Hàm số y = f (x) được gọi là nghịch biến trên I nếu:
∀ x1, x2 ∈ I: x1 < x2 ⇔ f(x1) > f(x2).
Hàm số đồng biến, nghịch biến được gọi chung là hàm số đơn điệu trên I.
Phương pháp giải dạng bài xét tính đơn điệu của hàm số lớp 12
Để giải dạng bài tập này, các bạn cần thực hiện đủ các bước sau:
– Tìm tập xác định D.
– Tìm f'(x). Tìm các điểm mà f'(xi)=0 và f'(xi) không xác định.
– Lập bảng biến thiên.
– Kết luật khoảng đồng biến, nghịch biến.
Ví dụ: Xét hàm số y = f(x) = x³ – 3x + 1. Tập xác định D = R
Ta có f'(x) = 3x² -3. f'(x) = 0 ⇔ x= 1; hoặc x= -1. Thay x = -2, f'(x) = 9 >0.
Thay x = 0. f'(x) = -3 < 0.
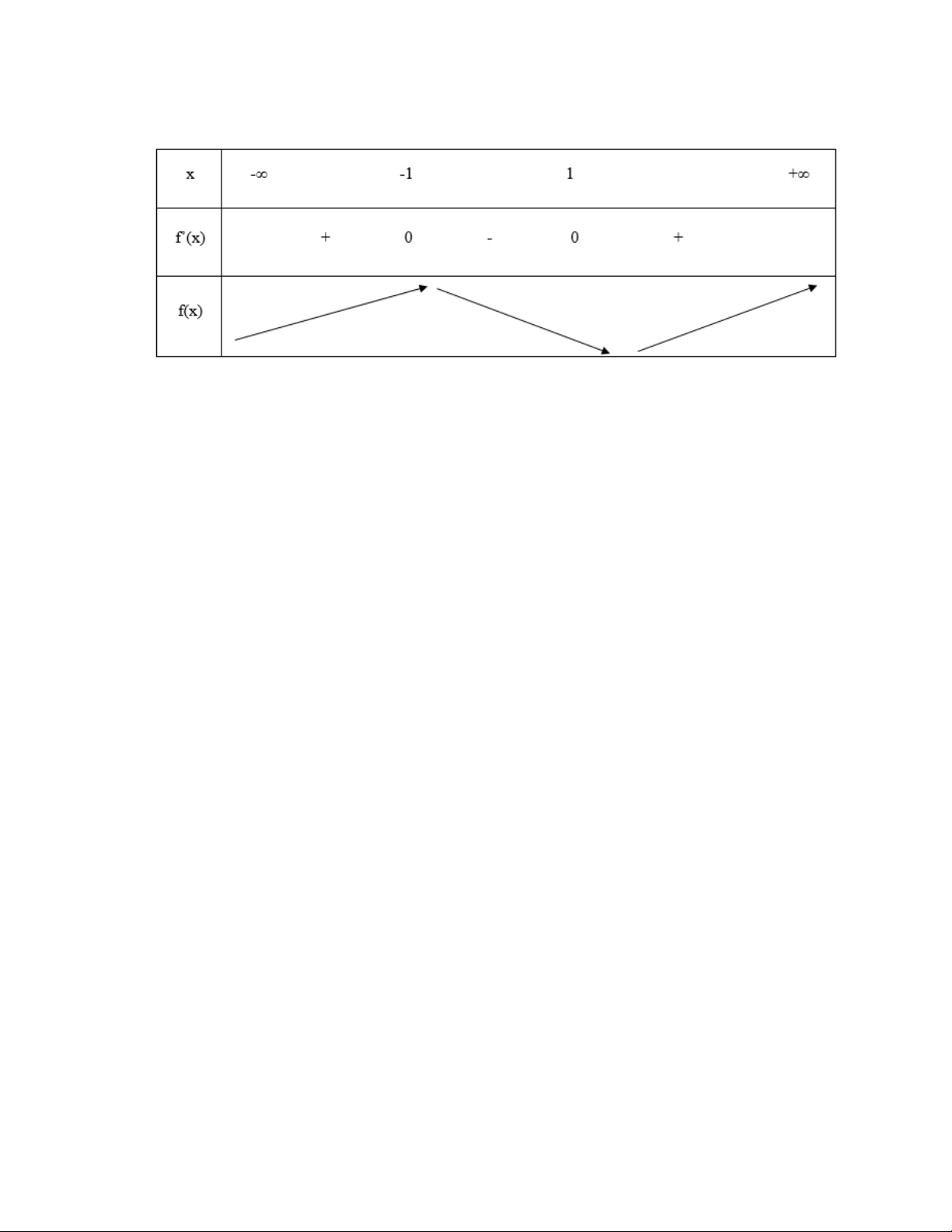
Ta có bảng biến thiên sau:
Bảng biến thiên của hàm số
Từ bảng biến thiên kết luận:
– Hàm số đồng biến trên khoảng (- ∞; -1) và (1;+∞)
– Hàm số nghịch biến trên khoảng (-1;1).
Giải bài toán xét tính đơn điệu của hàm số bằng máy tính cầm tay:
Ngoài cách sử dụng bảng biến thiên để giải bài tập xét tính đơn điệu của hàm số
lớp 12, học sinh cũng có thể dùng chiếc casio của mình để giải.
Ví dụ: Cho hàm số y = x4 -2x2 + 4. Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên khoảng (- ∞; -1).
B. Hàm số nghịch biến trên khoảng (- ∞; -1) và (1;+∞).
C. Hàm số nghịch biến trên khoảng (- ∞; -1) và ( 0;1).
D. Hàm số đồng biến trên khoảng (-1;1).
Chúng ta có thể dùng máy tính để xét tính đơn điệu như nhau:
Nhập MODE 7, nhập f(x) = x4 -2x2 + 4 Start?-5 → End?5→ Step?1. Khi đó ta
nhận được bảng giá trị. x F(x) x F(x) -5 579 0 4 -4 228 1 -3 -3 67 2 12 -2 12 3 67 -1 -3 4 228 5 579
Từ bảng giá trị ta thấy hàm số nghịch biến trên (- ∞; -1) và (0;1).
Trên đây là ví dụ cơ bản nhất về bài tập xét tính đơn điệu của hàm số lớp 12. Từ
phương pháp giải dạng bài tập trên, các em có thể vận dụng giải nhiều bài tập khác.
Dạng 2: Tìm điều kiện của tham số để hàm số đơn điệu
Điều kiện cần để hàm số đơn điệu:
Giả sử hàm số y = f (x) có đạo hàm trên I. Khi đó:
– Nếu hàm số y = f(x) đồng biến trên I thì f'(x) ≥ 0, ∀ x ∈ I.
– Nếu hàm số y = f(x) nghịch biến trên I thì f'(x) ≤ 0, ∀ x ∈ I.
Điều kiện đủ để hàm số đơn điệu:
– Nếu f'(x) > 0 , ∀ x ∈ I thì hàm số f(x) đồng biến trên I.
– Nếu f'(x) < 0 , ∀ x ∈ I thì hàm số f(x) nghịch biến trên I.
– Nếu f'(x) = 0 , ∀ x ∈ I thì hàm số f(x) không đỏi trên khoảng I. Phương pháp giải:
Hàm số y = ax³ + bx² + cx + d. Tập xác định: D= R y’ = 3ax² + 2bx + c
– Để hàm số đồng biến trên R thì y’ ≥ 0, ∀ x ∈ R. Khi đó: a > 0; Δ ≤ 0.
– Để hàm số nghịch biến trên R thì y’ ≤ 0, ∀ x ∈ R. Khi đó: a <0; Δ ≤ 0
Hàm số đồng biến trên các khoảng xác định khi và chỉ khi:
y’ >0, ∀ x ∈ D ⇒ ad-bc > 0
Hàm số nghịch biến trên các khoảng xác định khi và chỉ khi.
y’ < 0, ∀ x ∈ D ⇒ ad-bc < 0. Ví dụ:
Cho hàm số y = mx³ + x +1. Tập xác định d = R. y’ = 3mx² +1.
Để hàm số đồng biến trên R thì:
y’≥ 0, ∀ x ∈ R ⇔ 3mx² +1 ≥ 0; ∀ x ∈ R.
⇔ 3m > 0; Δ= -12m ≤ 0 ⇔ m > 0.
Hàm số nghịch biến trên R thì:
y’ ≤ 0, ∀ x ∈ R ⇔ 3mx² +1 ≤ 0; ∀ x ∈ R.
Khi đó a <0; Δ ≤ 0 ⇔ 3m < 0; -12m ≤ 0 ⇔ m ∈ Ø.
Như vậy, VnDoc đã tổng hợp 2 dạng bài tập xét tính đơn điệu của hàm số lớp 12
quan trọng nhất. Các em học sinh cần nắm chắc những kiến thức trên và vận dụng
làm bài tập để ghi nhớ.