-
Thông tin
-
Quiz
Lý Thuyết xác suất thống kê - Toán Kinh Tế | Trường Đại học Tôn Đức Thắng
Hoán vị của n phần tử chính là một chỉnh hợp chập n của n phần tử đó. Hay hoán vị của n phần tử là một cách sắp có thứ tự gồm đủ mặt n phần tử đã cho. Số hoán vị của n phần tử được ký hiệu là Pn. Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Toán Kinh Tế (C01120) 73 tài liệu
Đại học Tôn Đức Thắng 3.5 K tài liệu
Lý Thuyết xác suất thống kê - Toán Kinh Tế | Trường Đại học Tôn Đức Thắng
Hoán vị của n phần tử chính là một chỉnh hợp chập n của n phần tử đó. Hay hoán vị của n phần tử là một cách sắp có thứ tự gồm đủ mặt n phần tử đã cho. Số hoán vị của n phần tử được ký hiệu là Pn. Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Toán Kinh Tế (C01120) 73 tài liệu
Trường: Đại học Tôn Đức Thắng 3.5 K tài liệu
Thông tin:
Tác giả:
Preview text:
Chương 1
XÁC SUẤT VÀ CÔNG THỨC TÍNH XÁC SUẤT
Chương này giới thiệu các khái niệm liên quan đến phép thử, biến cố, định
nghĩa và các công thức tính xác suất. Đây là những vấn đề cơ bản ban đầu mà người
đọc cần nắm vững để có thể hiểu được những kiến thức liên quan khác của xác suất.
§ 1. QUY TẮC ĐẾM 1.1 Qui tắc nhân
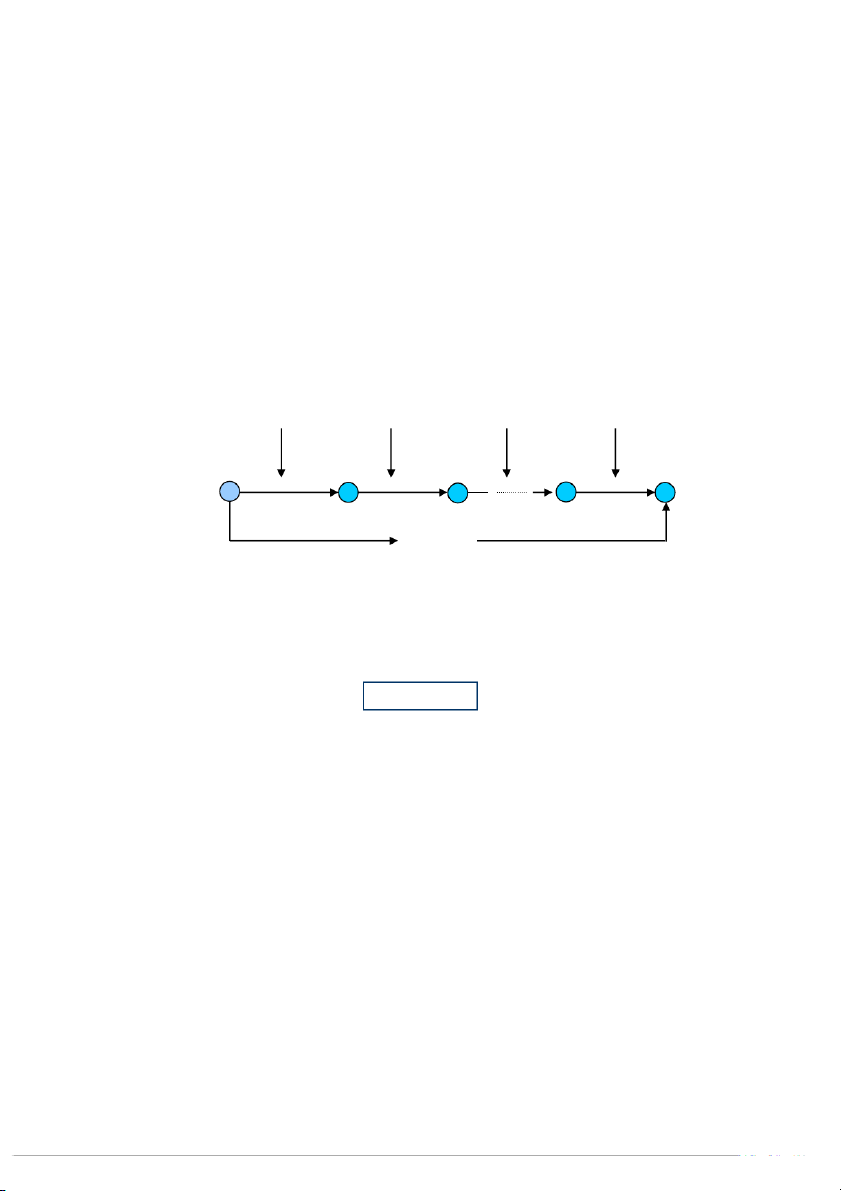
Giả sử một công việc nào đó được thực hiện qua k giai đoạn:
Giai đoạn 1 Giai đoạn 2 Giai đoạn i Giai đoạn k Công việc Giai đoạn 1: Có 1
n cách thực hiện, Giai đoạn 2: Có cách thực hiện, 2 n . . . . . . . .
Giai đoạn k: Có n cách thực hiện. k
Khi đó số cách để thực hiện cả công việc là
n n .n ...n 1 2 k (1.1)
■ Ví dụ 1.1. Có 3 sinh viên trường A và 6 sinh viên trường B.
a) Chọn ngẫu nhiên 2 sinh viên trường A và 1 sinh viên trường B, hỏi có bao nhiêu cách thực hiện?
b) Chọn ngẫu nhiên 1 sinh viên trường A và 1 sinh viên trường B, cử đi học 2
nước khác nhau, hỏi có bao nhiêu cách thực hiện? Giải
a) Việc thực hiện công việc này được chia thành 2 giai đoạn:
Chọn 2 sinh viên trường A: Có 3 cách thực hiện.
Chọn 1 sinh viên trường B: Có 6 cách thực hiện.
Vậy ta có 3.6 = 18 cách thực hiện.
b) Việc thực hiện công việc này được chia thành 3 giai đoạn:
Chọn 1 sinh viên trường A: Có 3 cách thực hiện.
Chọn 1 sinh viên trường B: Có 6 cách thực hiện.
Cử 2 sinh viên đã chọn đi học ở 2 nước khác nhau: Có 2 cách.
Vậy ta có 3.6.2 = 36 cách thực hiện. 1
1.2 Qui tắc cộng
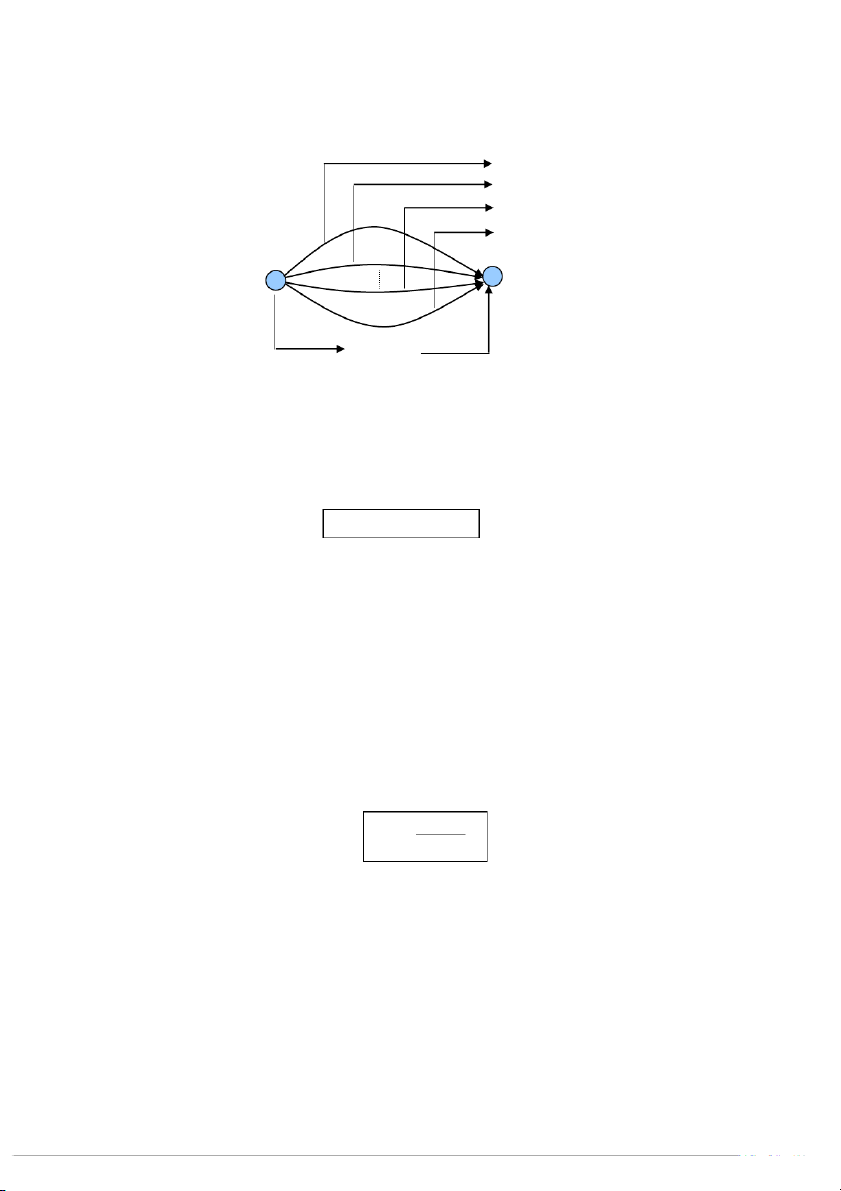
Giả sử thực hiện một công việc nào đó có k trường hợp xảy ra: Trường hợp 1 Trường hợp 2 Trường hợp i Trường hợp k Công việc Trường hợp 1: Có cách thực hiện, 1 n Trường hợp 2: Có 2
n cách thực hiện, . . . . . . . . . .
Trường hợp k: Có n cách thực hiện. k
Khi đó số cách để thực hiện cả công việc là
n n n ... n (1.2) 1 2 k
■ Ví dụ 1.2. Một lọ đựng 2 viên thuốc tốt và 3 viên thuốc xấu. Chọn ngẫu nhiên 2 viên
thuốc từ lọ này. Tính số cách để chọn được ít nhất 1 viên thuốc xấu. Giải
Chọn thỏa yêu cầu bài toán có 2 trường hợp xảy ra:
Trường hợp 1: Chọn được 1 viên thuốc xấu, 1 viên thuốc tốt: Có 3.2 = 6 cách.
Trường hợp 2: Chọn được 2 viên thuốc xấu: Có 3 cách.
Vậy số cách chọn thỏa yêu cầu bài toán là 6 + 3 = 9.
1.3 Chỉnh hợp
Chỉnh hợp chập k của n phần tử là một tập gồm k phần tử khác nhau, có quan
tâm đến thứ tự sắp xếp các phần tử trong tập đó, được chọn từ n phần tử đã cho.
Số chỉnh hợp chập k của n phần tử được ký hiệu là k A n . ▼ Công thức: ! n Ak (1.3) n (n k)!
■ Ví dụ 1.3. Từ các số {1, 2, 3, 4, 5, 6,7}, có thể thành lập được bao nhiêu số trong các trường hợp sau:
a) Số có 3 chữ số đôi một khác nhau.
b) Số có 4 chữ số đôi một khác nhau, trong đó có chữ số 1. Giải
a) Mỗi cách thực hiện là việc chọn 3 số từ 7 số. Sự sắp xếp các số chọn ra khác
nhau sẽ tạo ra những số khác nhau vì vậy số có 3 chữ số được thành lập là số
chỉnh hợp chập 3 của 7: 2 3 ! 7 A 5 . 6 . 7 210 7 (7 ) 3 !
b) Việc thành lập được chia thành 2 giai đoạn:
Chọn số 1 đặt vào 1 trong 4 vị trí: Có 4 cách. 3 ! 6
Chọn 3 số còn lại khác nhau từ 6 số: Có A 6 4 . 5 . 6 120 cách. (6 ) 3 !
Vậy ta có thể thành lập được 4.120 = 480 số. 1.4 Hoán v ị
Hoán vị của n phần tử chính là một chỉnh hợp chập n của n phần tử đó. Hay
hoán vị của n phần tử là một cách sắp có thứ tự gồm đủ mặt n phần tử đã cho.
Số hoán vị của n phần tử được ký hiệu là Pn. ▼ Công thức: Pn = n! (1.4)
■ Ví dụ 1.4. Xếp 10 sinh viên, trong đó có 5 nam và 5 nữ vào 2 dãy bàn dài. Hỏi có
bao nhiêu cách xếp sao cho nam ngồi 1 dãy, nữ ngồi 1 dãy. Giải
Việc xếp các sinh viên theo yêu cầu được chia thành các giai đoạn:
Chọn dãy để xếp sinh viên nam và nữ có 2 cách.
Xếp 5 sinh viên nữ vào dãy dành cho nữ có 5! = 120 cách.
Xếp 5 sinh viên nam vào dãy dành cho nam có 5! = 120 cách.
Vậy số cách xếp 10 sinh viên thỏa bài toán là 2.120.120 = 28800.
1.5 Chỉnh hợp lặp
Chỉnh hợp lặp chập k của n phần tử là một tập gồm k phần tử có thể lặp lại, có
quan tâm đến thứ tự sắp xếp các phần tử trong tập đó, được chọn từ n phần tử đã cho.
Số chỉnh hợp lặp chập k của n phần tử được ký hiệu là k B n . ▼ Công thức: k k B n (1.5) n
■ Ví dụ 1.5. Trong một đợt xổ số, người ta phát hành trên mỗi tờ vé số có 5 chữ số.
Trong một đợt xổ số khác người ta phát hành trên mỗi tờ vé số có 6 chữ số, khi đó số
vé số tăng cho việc phát hành tăng thêm một chữ số là bao nhiêu? Giải
Các chữ số trong mỗi vé số được hình thành từ các số tự nhiên: 0, 1, 2, .., 9 (10 số).
Muốn hình thành một vé số gồm k chữ số, ta chọn ra k số từ 10 số. Ta có
k số này có thể giống nhau và thứ tự sắp xếp của chúng là quan trọng. Vậy việc
hình thành mỗi vé số có k chữ số là một chỉnh hợp lặp chập k của 10 phần tử.
Với 5 chữ số trên mỗi vé số ta có thể thành lập được 5 B = 105 vé số 10 khác nhau.
Với 6 chữ số trên mỗi vé số ta có thể thành lập được 6 B = 106 vé số 10 khác nhau. 3
Vậy số vé số tăng có thể cho việc gia tăng này là 1000000 – 100000 = 900000. 1.6 Tổ hợp
Tổ hợp chập k của n phần tử là một tập gồm k phần tử khác nhau, không quan
tâm đến thứ tự sắp xếp các phần tử trong tập đó, được chọn từ n phần tử đã cho.
Số tổ hợp chập k của n phần tử được ký hiệu k C . n ▼ Công thức: ! n C k = (1.6) n k ( ! n k )!
■ Ví dụ 1.6. Có 8 người, mỗi người bắt tay một lần với những người khác. Hỏi:
a) Có bao nhiêu cái bắt tay?
b) Nếu trong họ có 3 người không bắt tay lẫn nhau thì còn lại bao nhiêu cái bắt tay? Giải
Cứ 2 người tạo thành một cái bắt tay. Vì người A bắt tay với người B
cũng chính là cái bắt tay của người B với người A, do đó mỗi cái bắt tay trong n
người chính là việc chọn 2 phần tử khác nhau không thứ tự từ n phần tử. Vì vậy
nếu có n người bắt tay lẫn nhau một lần thì mỗi cái bắt tay là một tổ hợp chập 2 của n. Vậy:
a) Nếu có 8 người, mỗi người bắt tay lẫn nhau một lần thì số cái bắt tay là C 2 = 28. 8 b) Ta có
Số cái bắt tay lẫn nhau giữa 8 người là 2 C 2 . 8 8
Số cái bắt tay lẫn nhau giữa 3 người là 2 C . 3 3
Vậy nếu trong 8 người có 3 người không bắt tay lẫn nhau thì số cái bắt tay sẽ là 28 – 3 = 25.
§ 2. PHÉP THỬ VÀ BIẾN CỐ
2.1 Khái niệm phép thử và biến cố
Hai khái niệm được xem là cơ bản nhất trong lý thuyết xác suất đó là khái niệm phép thử và biến cố.
Phép thử là việc thực hiện một hoạt động tác động lên đối tượng theo qui tắc
định trước và ghi nhận kết quả của nó.
Biến cố là những kết quả liên quan (kết quả có thể xảy ra hoặc có thể không xảy
ra) thu được khi thực hiện phép thử. ■ Ví dụ 1.7.
* Từ một mẫu gồm có người bệnh và cả người không bệnh, chọn ngẫu nhiên
một người để kiểm tra là một phép thử. Chọn được người bệnh hay người không bệnh là biến cố. 4
* Bắn một viên đạn vào một mục tiêu là một phép thử. Viên đạn bắn trúng hay
bắn trật là một biến cố.
Chúng ta hiểu biến cố như là sự kiện hay sự việc xảy ra trong tự nhiên, trong
khoa học kỹ thuật, trong đời sống kinh tế xã hội, . . , còn phép thử là một bộ các điều
kiện xác định cho sự xuất hiện biến cố. Nó đơn giản là một hoạt động như quan sát
một hiện tượng nào đó có xảy ra hay không, hoặc thực hiện một hành động như rút
ngẫu nhiên một sản phẩm từ lô hàng; hoặc phức tạp hơn là sự phối hợp nhiều hoạt
động, nhiều giai đoạn như: chọn một sản phẩm từ lô hàng thứ nhất bỏ vào lô hàng thứ
hai, rồi rút một sản phẩm từ lô hàng thứ hai, . . .
2.2 Phân loại biến cố
Một biến cố bất kỳ sẽ được xếp vào một trong ba loại sau:
Biến cố chắc chắn: Là biến cố luôn luôn xảy ra khi ta thực hiện phép thử. Kí hiệu: .
Biến cố không thể: Là biến cố không bao giờ xảy ra khi ta thực hiện phép thử. Kí hiệu: .
Biến cố ngẫu nhiên: Là biến cố có thể xảy ra hoặc có thể không xảy ra khi ta thực hiện phép thử.
Kí hiệu: A, B, C, …, hoặc A1, A2, A3, …
■ Ví dụ 1.8. Tung một con xúc xắc cân đối và đồng chất. Ta có
* Biến cố con xúc xắc xuất hiện có số chấm nhỏ hơn hoặc bằng 6 là biến cố chắc chắn.
* Biến cố con xúc xắc xuất hiện có số chấm lớn hơn 6 là biến cố không thể.
* Biến cố con xúc xắc xuất hiện có số chấm chẵn là biến cố ngẫu nhiên.
2.3 Mối quan hệ giữa các biến cố
a) Biến cố thuận lợi
Biến cố A được gọi là thuận lợi cho biến cố B nếu A xảy ra thì B xảy ra.
Kí hiệu: A B.
■ Ví dụ 1.9. Tung một con xúc xắc cân đối và đồng chất. Gọi:
A là biến cố con xúc xắc xuất hiện số chấm lẻ.
Ai là biến cố con xúc xắc xuất hiện có số chấm là i (i = 6 , 1 ).
Ta có A1 A; A3 A; A5 A.
b) Biến cố tương đương
Hai biến cố A và B được gọi là tương đương với nhau nếu biến cố A xảy ra thì biến
cố B phải xảy ra và ngược lại. Kí hiệu: A = B.
■ Ví dụ 1.10. Có 3 xạ thủ, mỗi người bắn 1 viên đạn vào một mục tiêu. Gọi:
A là biến cố có đúng một người bắn trúng,
B là biến cố có ít nhất một người bắn trúng,
C là biến cố có số người bắn trúng lớn hơn hoặc bằng 1.
Khi đó, ta có A B và B = C. 5 c) Biến cố tổng
Biến cố C được gọi là biến cố tổng của hai biến cố A và B nếu C xảy ra khi và
chỉ khi ít nhất một trong hai biến cố A hoặc B xảy ra.
Kí hiệu: C = A + B.
Biến cố tổng có thể mở rộng cho n biến cố: Biến cố A được gọi là tổng của n
biến cố A1, A2, …, An nếu A xảy ra khi và chỉ khi có ít nhất một trong n biến cố đó xảy ra.
Kí hiệu: A = A1 + A2 + …+ An.
■ Ví dụ 1.11. Chúng ta biết rằng một người có huyết áp bị hạ sẽ có triệu chứng là tim
đập yếu hoặc giãn mạch hoặc cả hai triệu chứng đó. Vì vậy, nếu ta gọi:
A là biến cố huyết áp bị hạ,
B là biến cố tim đập yếu ,
C là biến cố giãn mạch .
Thì ta sẽ có sự biểu diễn của biến cố A thông qua biến cố B và C là A = B + C.
d) Biến cố hiệu và hiệu đối xứng của hai biến cố
Biến cố C được gọi là hiệu của hai biến cố A và B nếu C xảy thì A xảy ra nhưng B không xảy ra.
Kí hiệu: C = A \ B.
Hiệu đối xứng của hai biến cố A và B (kí hiệu AB ) là biến cố được định nghĩa bởi: A B (A\ ) B (B \ ) A e) Biến cố tích
Biến cố C được gọi là tích của 2 biến cố A và B nếu C xảy ra khi và chỉ khi cả A
và B đồng thời xảy ra. Kí hiệu: C = A.B.
Khái niệm biến cố tích cũng được mở rộng cho nhiều biến cố: Biến cố A được
gọi là tích của n biến cố A1, A2, …, An nếu A xảy ra khi và chỉ khi cả n biến cố ấy đồng thời xảy ra.
Kí hiệu: A = A1.A2…An.
■ Ví dụ 1.12. Một kỹ sư nông nghiệp trồng thí điểm một loại giống lúa mới ở 5 địa điểm khác nhau. Gọi:
Ai là biến cố địa điểm thứ i thành công (i = 5 , 1 ).
Ai là biến cố địa điểm thứ i không thành công.
A là biến cố cả 5 địa điểm thành công.
B là biến cố có đúng 1 địa điểm không thành công. Khi đó ta có
A = A1. A2. A3. A4. A5.
B = A 1.A2.A3.A4.A5 + A1. A 2.A3.A4.A5 + A1.A2. A 3.A4. A5
+ A1.A2.A3. A 4.A5 + A1.A2.A3.A4. A 5.
f) Biến cố xung khắc
Hai biến cố A và B được gọi là xung khắc nhau nếu chúng không đồng thời xảy ra trong một phép thử.
Vậy khi A và B xung khắc nhau thì A.B = . 6
Chúng ta có thêm một khái niệm mở rộng: Nhóm biến cố A1, A2, …, An được gọi là
nhóm biến cố đầy đủ nếu tổng của chúng là một biến cố chắc chắn và bất kỳ hai biến
cố nào trong chúng cũng xung khắc nhau.
■ Ví dụ 1.13. Một kho hàng chứa những sản phẩm do 3 nhà máy sản xuất. Chọn ngẫu
nhiên một sản phẩm từ kho hàng này.
Gọi Ai là biến cố chọn được sản phẩm do nhà máy thứ i, i =1, 2, 3 sản xuất.
Khi đó, ta có {A1, A2, A3} là nhóm biến cố đầy đủ và xung khắc từng đôi vì
A1 + A2 + A3 = và với i j thì Ai.Aj = ; i, j {1, 2, 3}.
g) Biến cố đối lập
Biến cố không xảy ra của biến cố A được gọi là biến cố đối lập của biến cố A. Kí hiệu: A .
Theo định nghĩa này ta dễ dàng có A và A sẽ tạo nên biến cố đầy đủ và xung
khắc, nhưng chú ý rằng hai biến cố xung khắc thì chưa chắc là hai biến cố đối lập.
■ Ví dụ 1.14. Kiểm tra 5 sản phẩm từ một cơ sở sản xuất Gọi:
A là biến cố có ít nhất 1 phế phẩm,
B là biến cố không có phế phẩm nào.
Ta có A và B là hai biến cố đối lập nha : u A = B , B = A .
h) Biến cố độc lập
Hai biến cố được gọi là độc lập nhau nếu biến cố này xảy ra hay không xảy ra
đều không ảnh hưởng đến khả năng xảy ra hay không xảy ra của biến cố kia và ngược lại.
Cần lưu ý rằng nếu A và B là hai biến cố độc lập nhau, thì A và B ; B và A ; A
và B cũng độc lập với nhau.
Chúng ta có một khái niệm mở rộng: Nhóm biến cố A1, A2, …, An được gọi là
độc lập toàn phần nếu mỗi biến cố trong nhóm độc lập với tích của một tổ hợp bất kỳ
các biến cố còn lại.
■ Ví dụ 1.15. Có 4 lọ thuốc, mỗi lọ đều chứa những viên thuốc tốt và thuốc xấu.
Chọn ngẫu nhiên 1 viên thuốc từ mỗi lọ. Gọi Ai là biến cố chọn được viên thuốc tốt từ
lọ thứ i (i = 1, 2, 3, 4). Ta có {A1, A2, A3, A4} là nhóm biến cố độc lập toàn phần.
★ Chú ý: Khi tính xác suất của một biến cố không đơn giản, vấn đề quan trọng là
phải biết cách phân tích biến cố đó thành biến cố tương đương. Biến cố tương đương
này thường là tổng và tích của những biến cố khác đơn giản hơn mà chúng ta có thể
dễ dàng tính được xác suất của chúng.
■ Ví dụ 1.16. Có 3 hộp đựng sản phẩm. Chọn từ mỗi hộp 1 sản phẩm, gọi Ai là biến
cố chọn được phế phẩm ở hộp thứ i, (i = 1, 2, 3). Hãy biểu diễn các biến cố sau qua các biến cố Ai:
a) A: Chọn được 3 phế phẩm.
b) B: Chọn được đúng 1 phế phẩm.
c) C: Chọn được ít nhất 2 phế phẩm.
d) D: Chọn được đúng 2 phế phẩm, biết hộp thứ nhất đã chọn được phế phẩm. Giải 7 Ta có
a) A = A1.A2.A3
b) B = A1. A 2 . A 3 + A 1.A2. A 3 + A1. A 2.A3
c) C = A1. A2. A 3 + A1. A2. A3 + A 1. A2. A3 + A1. A2. A3
d) D = A1. A2. A 3 + A1.A 2. A3
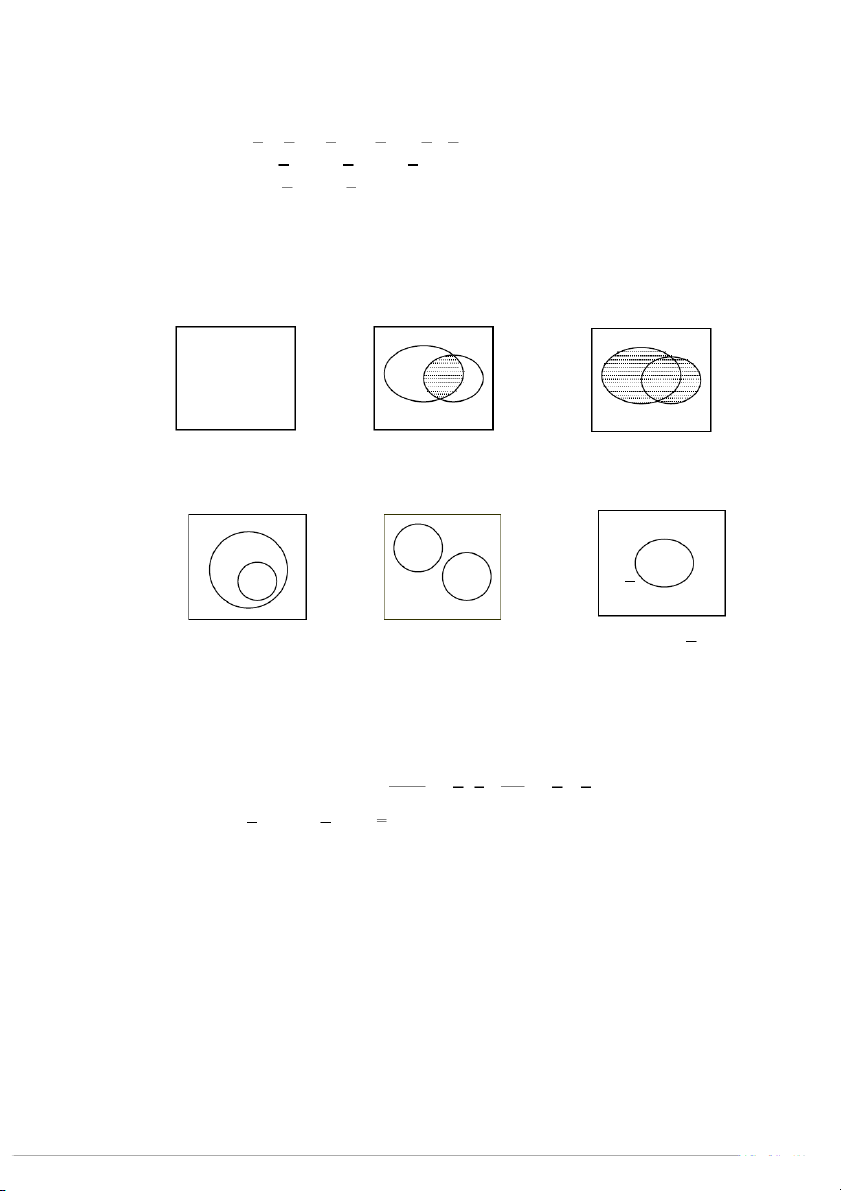
► Nhận xét: Qua các khái niệm trên ta thấy biến cố tổng, tích, đối lập, thuận lợi
tương ứng với khái niệm hội, giao, phần bù và tập con trong lý thuyết tập hợp.
Do đó ta có thể sử dụng các tính chất đã biết trong lý thuyết tập hợp cho các
phép toán trên các biến cố. Cụ thể chúng ta có thể sử dụng các tính chất sau: A B A B
Biến cố chắc chắn A.B A + B A A
B A B A
A B A, B xung khắc B = A
Hình 1.1. Minh họa mối quan hệ giữa các biến cố
i) Giao hoán: A+B=B+A; A.B=B.A.
ii) Kết hợp: (A+B)+C=A+(B+C); (A.B).C=A.(B.C).
iii) Phân phối: A(B+C)=A.B+A.C.
iv) Luật đối ngẫu De Morgan: A B = A. B ; A B . = A +B .
v) Nếu A = B B = A hay A = A. 8
§ 3. ĐỊNH NGHĨA XÁC SUẤT
3.1 Định nghĩa xác suất cổ điển
Giả sử khi thực hiện một phép thử ta có n trường hợp đồng khả năng có thể xảy
ra, trong đó có m trường hợp thuận lợi cho biến cố A. Khi đó, xác suất của biến cố A m là . n
Số trường hợp thuận lợi cho biến cố A ( ) m P A n
Số trường hợp đồng khả năng của phép
Hình 1.2. Hình vẽ về con xúc xắc
■ Ví dụ 1.17. Một danh sách có 10 sinh viên, trong đó có 4 sinh viên khoa X và 6 sinh
viên khoa Y. Chọn ngẫu nhiên từ danh sách 4 sinh viên. Tính xác suất trong các trường hợp sau:
a) Chọn được số sinh viên khoa X bằng số sinh viên khoa Y.
b) Chọn được ít nhất một sinh viên khoa X. Giải
Gọi A là biến cố chọn được số sinh viên khoa X bằng số sinh viên khoa Y.
Gọi B là biến cố chọn được ít nhất một sinh viên khoa X.
Số trường hợp có thể của phép thử là 4 C = 210. 10
a) Số trường hợp thuận lợi cho biến cố A là 2 C . 2 C = 90. 4 6 Vậy 3 P( ) A . 7
b) Ta có B là biến cố không chọn được sinh viên khoa X.
Số trường hợp thuận lợi cho biến cố B là 46 C .
Do đó số trường hợp thuận lợi cho biến cố B là 41 C - 4 0 6 C =195. Vậy 13 ( P ) B . 14
3.2 Định nghĩa xác suất theo quan điểm thống kê
Để tính xác suất của một biến cố theo định nghĩa cổ điển thì phép thử phải được
phân tích thành những kết cục đồng khả năng. Tuy nhiên, trong thực tế đa số phép thử
mà chúng ta gặp đều không thể phân tích thành các kết cục đồng khả năng. Để khắc
phục hạn chế này của định nghĩa xác suất theo cổ điển người ta xây dựng định nghĩa
xác suất bằng thống kê:
Giả sử ta thực hiện một phép thử nào đó n lần độc lập và giống nhau. Biến cố m
A xuất hiện m lần. Khi đó ta gọi m là tần số của biến cố A và tỷ số
được gọi là tần n
suất xuất hiện biến cố A trong phép thử. Cho phép thử tăng lên vô hạn, tần suất xuất 9
hiện biến cố A dần về một giá trị hữu hạn, giá trị này được định nghĩa là xác suất của biến cố A. m
P(A)= lim (1.7) n n
Trong thực tế ta không thể thực hiện vô hạn phép thử, vì vậy xác suất của một
biến cố trong thực tế được lấy bằng tần suất khi số phép thử đủ lớn.
■ Ví dụ 1.18. Để nghiên cứu khả năng xuất hiện mặt sấp khi tung một đồng xu cân đối
đồng chất, các nhà bác học đã tiến hành tung đồng xu nhiều lần và được kết quả cho ở bảng sau: Người làm thí Số lần tung Số lần xuất hiện
Tần suất f(A) nghiệm mặt sấp Buyffon 4040 2048 0,5064 Pearson 12000 6019 0,5016 Pearson 24000 12012 0,5005
Từ thí nghiệm trên ta thấy khi số phép thử tăng lên thì tần suất xuất hiện mặt
sấp của đồng xu tiến dần đến 0,5. Trong trường hợp này ta có thể kết luận xác suất
xuất hiện mặt sấp của đồng xu khi tung là 0,49.
■ Ví dụ 1.19. Chúng ta thường nói khi một bà mẹ sinh một đứa con thì khả năng sinh
được con trai và con gái là như nhau và bằng 0,5. Chúng ta xem điều này có đúng
không qua các sự kiện thống kê sau:
* Người Trung Hoa từ năm 2228 trước công nguyên đã thống kê qua kinh
nghiệm đưa ra tỉ số sinh con gái là 0,5.
* Laplace nghiên cứu sinh đẻ ở Luân Đôn, Petecbua và Berlin trong 10 năm 21
và đưa ra tỉ số con gái là . 43
* Dacnon nghiên cứu sinh đẻ ở Pháp cho các số liệu: Năm 1086 1816 1836 1856 1913 1920 Tần suất sinh con gái 0,485 0,484 0,485 0,487 0,488 0,489
Từ số liệu thống kê này ta có thể nói khi đi sinh trong hoàn cảnh tự nhiên thì xác
suất sinh con gái của bà mẹ là 0,49.
3.3 Định nghĩa xác suất bằng hình học
Khi tính xác suất của một biến cố theo lối cổ điển ta cần phải tính được số
trường hợp có thể của phép thử và số trường hợp thuận lợi của biến cố bằng những con
số cụ thể. Trong thực tế có nhiều bài toán số trường hợp có thể của phép thử và số
trường hợp thuận lợi của biến cố là vô hạn, không tính được cụ thể, khi đó ta có thể
giải quyết bài toán dựa vào định nghĩa xác suất bằng hình học:
Giả sử khi ta thực hiện một phép thử, các trường hợp có thể của nó được biểu
diễn bằng miền hình học W có độ đo (độ dài, diện tích, thể tích) hữu hạn khác không.
Biến cố A được biểu diễn bằng miền hình học A trong miền hình học W. Khi đó, xác
suất của biến cố A là 10
Độ đo của miền A (1.8) P(A) =
Độ đo của miền
Định nghĩa xác suất bằng hình học có thể xem là sự mở rộng của định nghĩa
xác suất theo cổ điển trong trường hợp số khả năng có thể xảy ra là vô hạn.
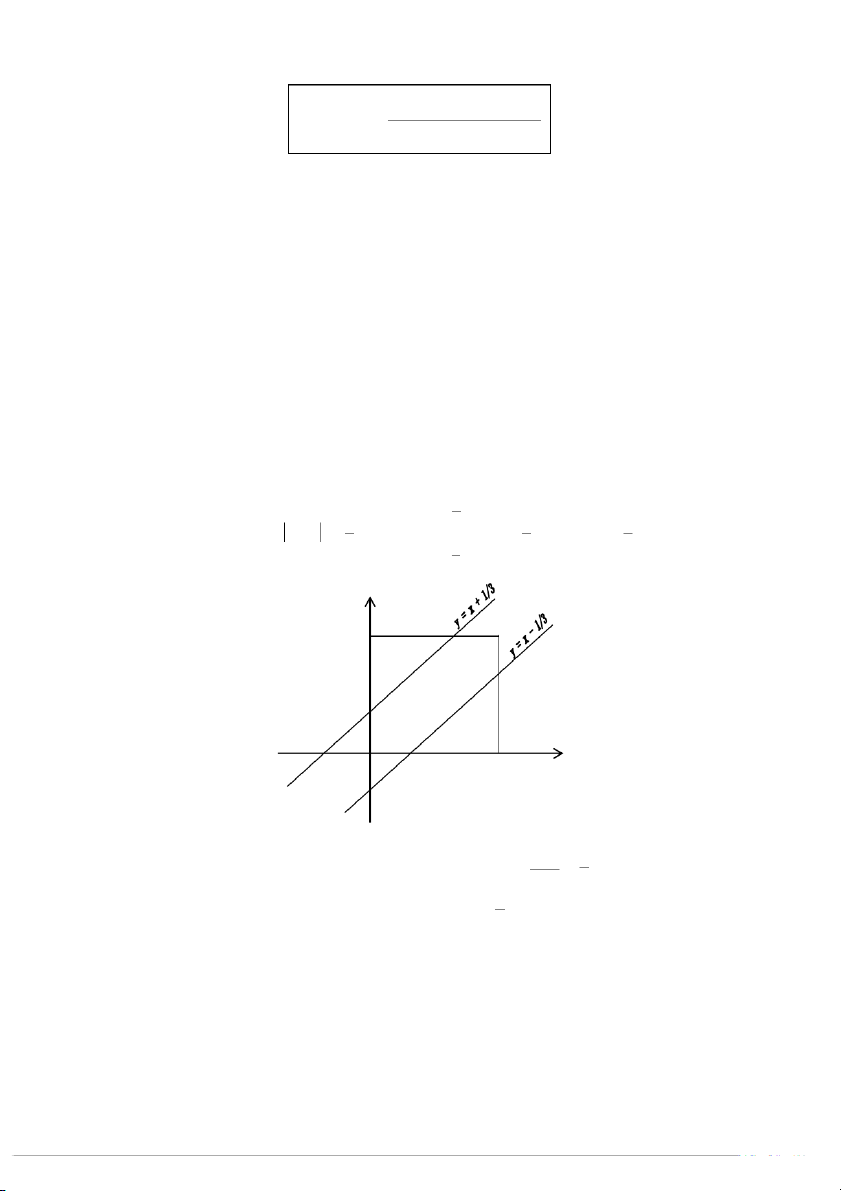
■ Ví dụ 1.20. (Bài toán hai người gặp nhau)
Hai người hẹn gặp nhau trong khoảng thời gian từ 7h đến 8h tại một địa điểm
nào đó. Họ quy ước rằng nếu người này đến điểm hẹn không gặp người kia sẽ đợi 20
phút. Tính xác suất để 2 người hẹn gặp nhau trong cuộc hẹn này. Giải
Gọi A là biến hai người gặp nhau.
Gọi x là thời gian đến điểm hẹn của người thứ nhất.
Gọi y là thời gian đến điểm hẹn của người thứ hai.
Biểu diễn x, y lên hệ trục tọa độ Decac Oxy. Chọn góc thời gian lúc 7h. 0 x 1
Trường hợp có thể của phép thử: 0 y 1
được biểu diễn bằng hình vuông OABC có diện tích là 1.
Trường hợp thuận lợi cho biến cố A: 1 y x 1 3 1 1
x y
x - y x + 3 1 3 3 y x 3 y
A 1 N B P M 1/3 0 Q C x -1/3 1/3 1
được biểu diễn bằng hình 5
OMNBPQ có diện tích là 1 – 2. . 2 . 1 2 = . . 2 3 . 3 9
Vậy xác suất để hai người gặp nhau là 5 P(A) = . 9
3.4 Ý nghĩa và tính chất a) Ý nghĩa
Xác suất của một biến cố là con số đặc trưng cho khả năng xảy ra ít hay nhiều
của biến cố đó. Biến cố có xác suất càng lớn thì càng dễ xảy ra và ngược lại. 11
Thực tế xác suất của một biến cố là trị số trung bình khả năng của một sự kiện
được lặp lại nhiều lần. b) Tính chất
Dựa vào định nghĩa xác suất ta dễ dàng rút ra những tính chất sau:
i) 0 P(A) 1 với A là một biến cố bất kỳ.
ii) Nếu A là biến cố chắc chắn thì P(A) = 1.
iii) Nếu A là biến cố không thể thì P(A) = 0.
iv) P(A) = 1 – P( A ).
v) A B P(A) P(B). ★ Chú ý:
i) Mệnh đề đảo của ii) và iii) chưa chắc đúng. Chẳng hạn, theo định nghĩa xác
suất bằng thống kê P(A) là giới hạn của tần suất xuất hiện biến cố A khi
phép thử dần ra vô hạn nên nếu P(A) = 1 chưa chắc A là biến cố chắn chắc;
tương tự P(B) = 0 chưa chắc B là biến cố không thể.
ii) Áp dụng tính chất iv) nhiều bài toán ta giải quyết nhanh gọn hơn khi tính một cách trực tiếp.
■ Ví dụ 1.21. Tỷ lệ phế phẩm của một nhà máy là 10%.
a) Chọn ngẫu nhiên 100 sản phẩm của nhà máy, tính xác suất để chọn được ít nhất một phế phẩm.
b) Phải chọn ít nhất bao nhiêu sản phẩm để có xác suất chọn được ít nhất 1
phế phẩm không bé hơn 0,95. Giải
a) Gọi A là biến cố khám được ít nhất 1 phế phẩm A là biến cố không chọn được phế phẩm nào.
Ta có: P( A ) = (0,9)100 P(A) = 1 – P( A ) = 1 - (0,9)100.
b) Gọi n là số sản phẩm cần phải chọn.
Gọi B là biến cố chọn được ít nhất 1 phế phẩm B là biến cố không chọn được phế phẩm nào. Ta có
P(B ) = (0,9)n P(B) = 1 – P( B ) = 1- (0,9)n.
P(B) 0,95 1 - (0,9)n 0,95 (0,9)n 0,05 ln 0 , 0 5 Do đó n = 28,43. ln 9 , 0
Vậy để thỏa điều kiện bài toán thì ta phải chọn ít nhất 29 người.
§ 4. CÔNG THỨC TÍNH XÁC SUẤT
4.1 Công thức cộng
a) Công thức cộng với hai bi n ế cố
Cho A1, A2 là hai biến cố tùy ý, ta c ó
P(A1 + A2)=P(A1) + P(A2) – P(A1A2) (1.9) 12
Khi A1 và A2 xung khắc nhau, vì P(A1A2) = 0 nên
P(A1 + A2)=P(A1) + P(A2) (1.10)
b) Công thức cộng tổng quát
Cho A1, A2, …, An là các biến cố t ùy ý, ta có n
P(A1+ A2+ …+ An) = P(A ) - P(A .A )+ P(A A A ) (1.11) i i j i j k i 1 i j i jk
+ …+ (-1)n-1P(A1A2… An)
Khi A1, A2, …, An là các biến cố xung khắc từng ô đ i thì
P(A1+ A2 + …+ An) = P(A1) + P(A2 ) + …+ P(An) (1.12)
■ Ví dụ 1.22. Một lớp có 100 sinh viên, trong đó có 50 sinh viên giỏi toán, 50 sinh
viên giỏi văn và trong số này có 15 sinh viên vừa giỏi toán vừa giỏi văn. Chọn ngẫu
nhiên 1 sinh viên của lớp. Tính xác suất để chọn được sinh viên giỏi ít nhất 1 trong 2 môn trên. Giải
Gọi A là biến cố chọn được sinh viên giỏi ít nhất một trong 2 môn.
Gọi T là biến cố chọn được sinh viên giỏi toán.
Gọi V là biến cố chọn được sinh viên giỏi văn. Ta có A = T + V.
Vì T và V là hai biến cố không xung khắc nên: 50 50 15 85
P(A) = P(T) + P(V) – P(TV) = + - = . 100 100 100 100
Như vậy xác suất để chọn được sinh viên giỏi ít nhất một trong 2 môn là 85%.
■ Ví dụ 1.23. Một mẫu có 10 người, trong đó có 6 người bị bệnh. Chọn ngẫu nhiên 6
người, tính xác suất để chọn được số người bị bệnh nhiều hơn số người không bị bệnh. Giải
Gọi A là biến cố chọn được số người bị bệnh nhiều hơn số người không bị bệnh.
Gọi Ai là biến cố chọn được i người bị bệnh (i = 0 6 , ).
Ta có A = A4 + A5 + A6
Vì A4, A5, A6 xung khắc từng đôi nên
P(A) = P(A4 + A5 + A6)
= P(A4) + P(A5) + P(A6) 4 2 C . 5 1 C . 6 = 6 4
C + 6 C4 + C6 6 C 6 6 10 1 C 0 1 C 0 = 23 . 42
■ Ví dụ 1.24. Bỏ ngẫu nhiên 4 lá thư vào 4 phong bì tương ứng đã ghi sẵn địa chỉ.
Tính xác suất sao cho có ít nhất một lá thư bỏ đúng phong bì của nó. Giải
Gọi A là biến cố cần tính xác suất. 13
Ai là biến cố lá thư thứ i bỏ đúng phong bì.
Ta có A = A1 + A2 + A3 + A4 P( ) A [ ( P A ) ( P A ) ( P A ) ( P A )] [ ( P A A ) ( P A A ) ( P A A ) 1 2 3 4 1 2 1 3 1 4 + P(A A ) (
P A A ) P( A A )] [ (
P A A A P(A A A ) 2 3 2 4 3 4 1 2 3 1 2 4
+ P(A A A ) P(A A A )] P(A A A A ) 1 3 4 2 3 4 1 2 3 4 ! 3 ! 2 1 1 4 6 4 , 0 625. ! 4 ! 4 ! 4 ! 4
4.2 Công thức nhân
a) Công thức nhân với hai biên cố
Giả sử A1, A2 là hai biến cố tùy ý, ta có
P(A1.A2) =P(A1)P(A2|A1) (1.13)
Trong đó P(A2|A1) là xác suất của biến cố A2 trong điều kiện biến cố A1 đã xảy ra.
Khi hai biến cố A1 và A2 độc lập nhau thì P(A2|A1) = P(A1) nên công thức trên trở thành
P(A1.A2) = P(A1)P(A2) (1.14)
b) Công thức nhân tổng quát
Cho A1, A2, …, An là n biến cố tùy ý, ta có
P(A1.A2…An) = P(A1)P(A2 |A1)… (
P An |A1A2…An - 1) (1.15)
Khi A1, A2, …, An độc lập toàn phần thì
P(A1.A2…An) = P(A1)P(A2)…P(An) (1.16)
■ Ví dụ 1.25. Một sinh viên đã để lẫn lộn một mẫu hóa chất xấu trong 4 mẫu hóa chất
tốt. Sinh viên này cần kiểm tra lần lượt từng mẫu cho đến khi phát hiện được mẫu hóa
chất xấu thì dừng lại. Tính xác suất để việc kiểm tra dừng lại ở lần lấy thứ tư. Giải
Gọi A là biến cố để việc kiểm tra dừng lại ở lần lấy thứ 4.
Gọi Ai là biến cố sinh viên chọn được mẫu hóa chất tốt thứ i (i = 0..4).
Ta có A = A1. A2. A3. A . 4
P(A) = P (A1. A2. A3. A ) 4
= P(A1) P(A2 | A1). P(A3|A1.A2). P( A4 | A1. A2. A3) 4 3 2 1 1 = = = 0,2. 5 4 3 2 5
Vậy xác suất để việc kiểm tra dừng lại ở lần lấy thứ 4 là 0,2.
■ Ví dụ 126. Để dập tắt nạn dịch sâu bệnh hại lúa, đội bảo vệ thực vật đã tiến hành
phun thuốc 3 lần liên tiếp trong 1 tuần. Xác suất sâu bị chết sau lần phun nhất là 0,5.
Nếu sống sót ở lần phun thứ nhất thì khả năng sâu bị chết ở lần phun thứ hai là 0,7. 14
Nếu sống sót ở lần phun thứ hai thì khả năng sâu bị chết ở lần phun thứ ba là 0,9. Tính
xác suất sâu bị chết sau đợt phun thuốc. Giải
Gọi A là biến cố sâu bị chết sau đợt phun thuốc.
Ai là biến cố sâu bị chết sau lần phun thứ i, i = 1, 2, 3.
Ta có A1, A2, A3 là 3 biến cố phụ thuộc v à
A = A1 + A A2 + A A A 1 1 2 3
P(A) = P(A1) + P(
P(A1) P(A P A 1
A )P(A2| 1 A ) + 2| 1 A ) ( 3| 1 A A ) 2
= 0,5 + 0,5.0,7 + 0,5.0,3.0,9 = 0,985
Vậy xác suất sâu bị chết sau đợt phun là 98,5%. ◘ Áp dụng:
i) Xác suất của biến cố tích bao giờ cũng không lớn hơn mỗi biến cố trong tích đó.
Vì vậy trong y học, trong chăn nuôi, trong bảo vệ thực vật người ta có xu hướng phối
hợp nhiều thuốc kháng sinh trong điều trị để hạn chế khả năng kháng thuốc của vi
khuẩn của bệnh. Chẳng hạn trong điều trị bệnh lao ta có:
Khả năng kháng INT của vi khuẩn lao là 20%.
Khả năng kháng PAS của vi khuẩn lao là 40%.
Khả năng kháng Streptomycin của vi khuẩn lao là 30%.
Nếu ta dùng phối hợp 3 kháng sinh trên thì xác suất kháng thuốc của vi khuẩn lao lúc
này sẽ là 0,2.0,3.0,4 = 0,024.
ii) Xác suất của biến cố tổng bao giờ cũng không bé hơn xác suất của các biến cố
thành phần. Chính vì vậy trong y học, trong chăn nuôi thú y, trong bảo vệ thực vật để
chẩn đoán một loại bệnh người ta thường có xu hướng phối hợp nhiều phương pháp
chẩn đoán để xác suất chọn đúng được nâng cao. Chẳng hạn, trong chẩn đoán bệnh
M, nếu dùng phương pháp A thì khả năng đúng là 80%, dùng phương pháp B thì khả
năng đúng là 70%, dùng phương pháp C thì khả năng đúng là 60%. Nếu ta phối hợp
cả 3 phương pháp (giả sử các phương pháp không có sự tương tác) thì khả năng chẩn
đoán đúng là 97,6%. Vấn đề nêu trên chỉ mang tính khái quát vì trong thực tế sinh
học vấn đề còn phức tạp hơn nhiều: sự tương tác của các phương pháp, các loại
thuốc, liều lượng dùng, cơ địa của từng đối phương áp dụng,… Tuy nhiên nếu phối
hợp đúng cách thì có khả năng nâng cao rõ rệt hiệu lực chẩn đoán và điều trị.
4. 3 Công thức xác suất toàn phần và công thức Bayes
a) Công thức xác suất toàn phần
Giả sử A1, A2, …, An là nhóm biến cố đầy đủ, A là biến cố tùy ý, ta có n
P(A) = P(A ) P
. (A | A ) (1.17) i i i 1
Khi vận dụng công thức toàn phần vào việc giải những bài toán cụ thể. Vấn đề quan
trọng là việc chỉ ra nhóm biến cố đầy đủ và xung khắc từng đôi. Biến cố đầy đủ và
xung khắc từng đôi này thường được chỉ ra trong 2 trường hợp sau:
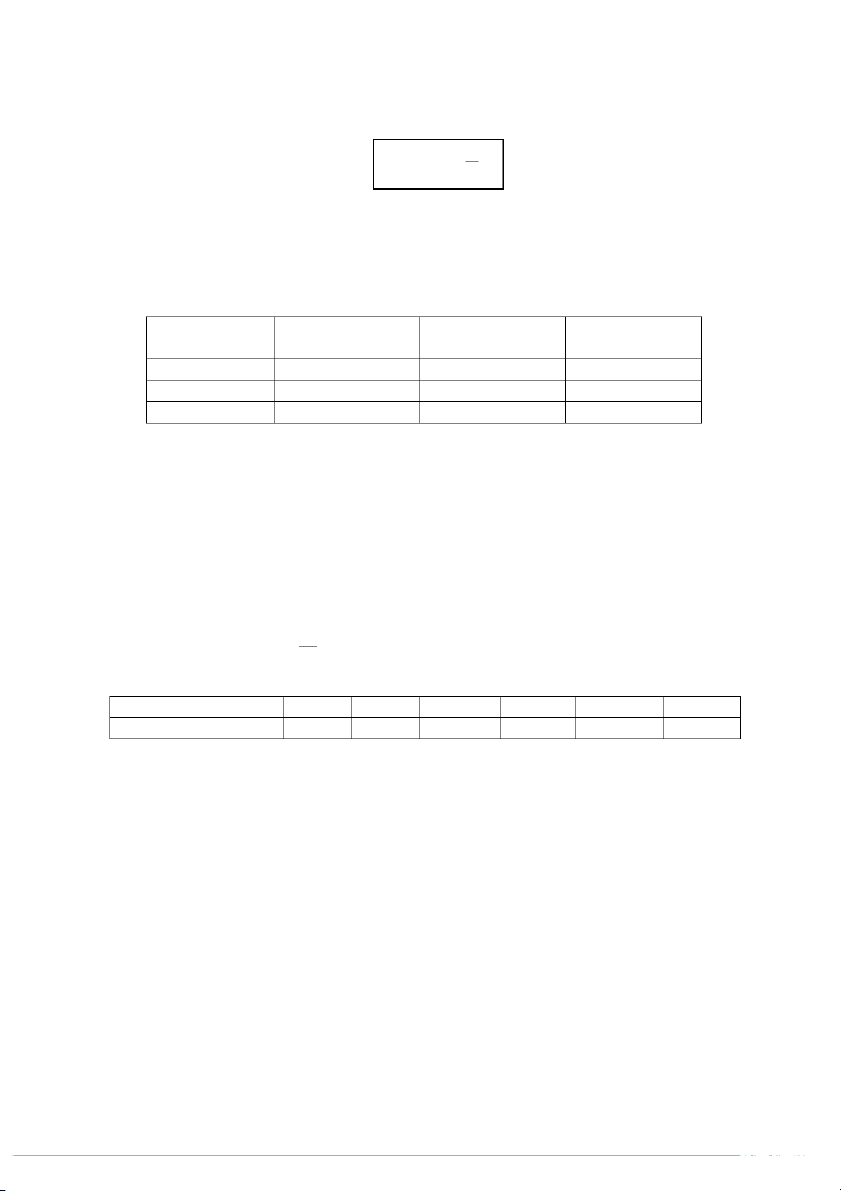
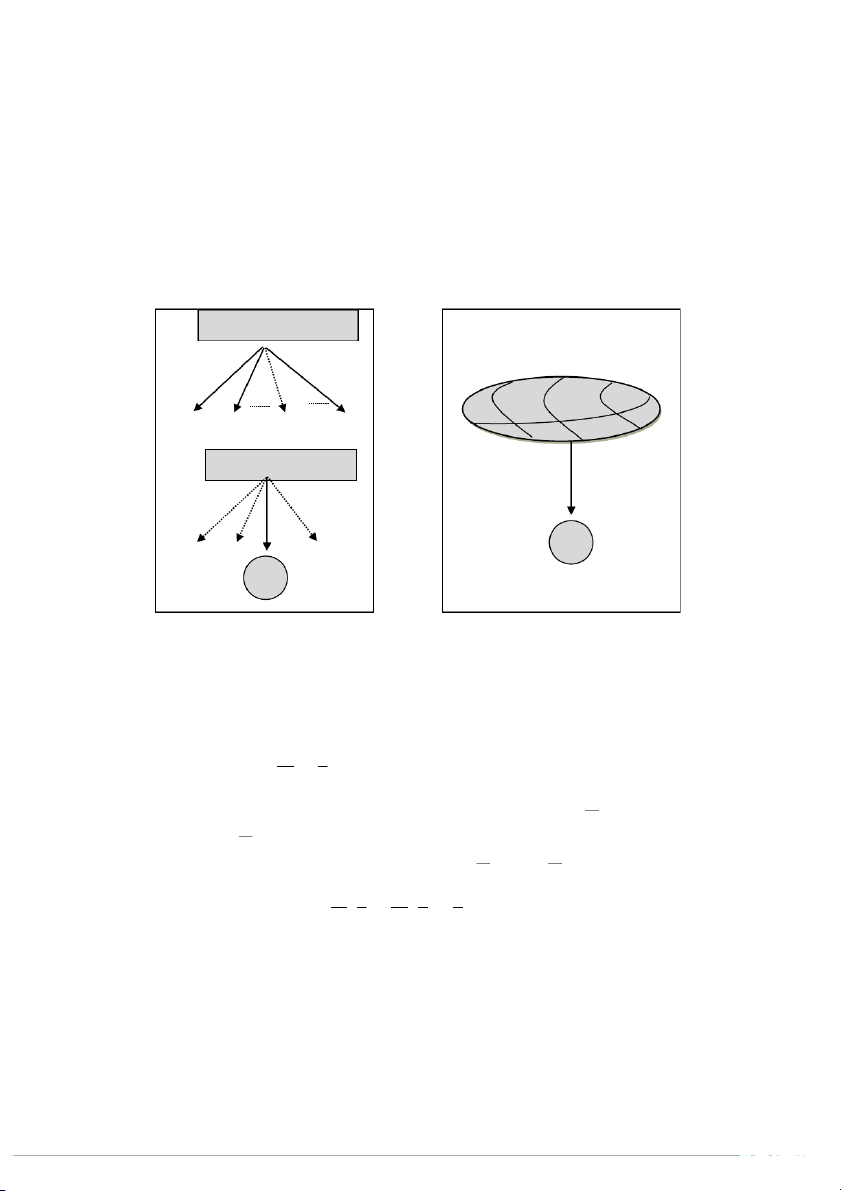
Trường hợp 1: Giả sử ta thực hiện 2 phép thử. Khi thực hiện phép thử thứ nhất, một
trong n biến cố xảy ra. Thực hiện tiếp phép thử thứ hai có nhiều biến cố xảy ra, nhưng 15
chúng ta đang quan tâm đến biến cố A. Biến cố A khi đó được tính theo công thức xác
suất toàn phần, với nhóm biến cố đầy đủ và xung khắc từng đôi là A1, A2, …, An.
Trường hợp 2: Một tập hợp được chia thành n nhóm. Nhóm thứ i đều có những phần
tử có tính chất A với tỷ lệ pi nào đó. Chọn ngẫu nhiên 1 phần tử của tập hợp. Tính xác
suất để chọn được phần tử có tính chất A. Khi đó, nếu gọi Ai là biến cố chọn được
phần tử thuộc nhóm i thì biến cố A được tính theo công thức xác suất toàn phần, với
mẫu biến cố đầy đủ và xung khắc từng đôi là các biến cố Ai.
TRƯỜNG HỢP 1 TRƯỜNG HỢP 2 Phép thử thứ nhất A A n A1 A2 Ai An A1 A2 Ai An Phép thử thứ hai 1 phần tử A A
■ Ví dụ 1.27. Một lô hàng có 10 sản phẩm, trong đó có 6 sản phẩm tốt. Hai người
khách hàng lần lượt đến mua mỗi người một sản phẩm. Hỏi khả năng mua được sản
phẩm tốt của mỗi người có giống nhau không, tại sao? Giải
Gọi Ai là biến cố chọn được sản phẩm tốt của người thứ i. Ta có 6 3 P(A1) = = . 10 5
Người thứ 2 mua hàng khi người thứ nhất đã mua 1 sản phẩm. Sản phẩm này có
thể là sản phẩm tốt hoặc không. Nghĩa là biến cố A1 hoặc 1 A đã xảy ra. Vì A1 và
là mẫu biến cố đầy đủ và xung khắc từng đôi, nên 1 A
P(A2) = P(A1) P(A2| A1) + P( 1
A ) P(A2| 1 A ) 6 5 4 6 3 = + = . 10 9 10 9 5
Vì P(A1) = P(A2) nên ta nói rằng khả năng mua được sản phẩm tốt của hai người là như nhau.
■ Ví dụ 1.28. Có hai chuồng nuôi chuột. Chuồng I có 4 con chuột trắng và 3 con chuột
đen, chuồng II có 2 chuột trắng và 5 chuột đen. Chọn ngẫu nhiên 2 con từ chuồng I bỏ 16
vào chuồng II, rồi từ chuồng II chọn ngẫu nhiên 1 con. Tính xác suất để con chuột
chọn từ chuồng II có màu trắng. Giải
Gọi Ai là biến cố chọn được i con chuột trắng từ chuồng I (i = 1, 2).
B là biến cố chọn được con chuột trắng từ chuồng II. Ta có 2 1 1 2 C 3 C C 12 C 6 P(A 3 4 3 4 0) = =
; P(A1) = =
; P(A2) = = . 2 C 2 2 7 21 C7 21 7 C 21
Trước khi thực hiện phép thử thứ hai: Chọn ngẫu nhiên 1 con chuột từ chuồng
II, ta có phép thử thứ nhất: Chọn ngẫu nhiên 2 con chuột từ chuồng I. Khi thực
hiện phép thử này ta có 1 trong 3 khả năng xảy ra: Hoặc biến cố A0, hoặc biến
cố A1, hoặc biến cố A2 xảy ra.
Các biến cố A0, A1, A2 là mẫu biến cố đầy đủ và xung khắc từng đôi nên
P(B) = P(A0).P(B|A0) + P(A1).P(B|A1) + P(A2).P(B|A2) 3 2 12 3 6 4 66 = . . . . 21 9 21 9 21 9 189
Vậy khả năng chọn được con chuột trắng từ chuồng II là 66 . 189
■ Ví dụ 1.29. Một kho hàng chứa cùng một loại sản phẩm do ba nhà máy sản xuất,
biết số sản phẩm của nhà máy I chiếm 2/3 số sản phẩm của kho hàng, số sản phẩm của
nhà máy II chiếm 1/4 số sản phẩm của kho hàng, số sản phẩm còn lại của nhà máy III.
Tỷ lệ sản phẩm tốt của mỗi nhà máy lần lượt là 80%, 60% và 40%. Hỏi tỷ lệ sản phẩm
tốt của nhà máy là bao nhiêu? Giải
Gọi A là biến cố chọn được sản phẩm tốt khi chọn ngẫu nhiên 1 sản phẩm từ kho hàng.
Gọi Ai là biến cố chọn được sản phẩm do nhà máy thứ i sản suất, i = 1, 2, 3.
Ta có A1, A2, A3 là biến cố đầy đủ và xung khắc từng đôi nên
P(A) = P(A1) P(A|A1) + P(A2) P(A|A2) + P(A3) P(A|A3) 2 1 1 = 0,8 + 0,6 + 0,4 = 0,72. 3 4 12
Vậy tỷ lệ nảy sản phẩm tốt của kho hàng là 72%. b) Công thức Bayes
Giả sử A1, A2, …, An là nhóm biến cố đầy đủ, A là biến cố đã xảy ra cùng với một
trong các biến cố Ai. Khi đó, ta có ( . )
P(A )P(A | A ) P A A P(A i i |A) = = i i (1.18) n ( P )
P( A ).P( A| A ) A i i i 1
■ Ví dụ 1.30. Một mạch điện gồm 2 bộ phận độc lập được mắc nối tiếp, với xác suất
bị hỏng trong thời gian nào đó của mỗi bộ phận lần lượt là 0,01 và 0,015. Tại một thời
điểm người ta thấy mạch điện bị ngừng làm việc (do ít nhất một bộ phận nào đó bị
hỏng). Tìm xác suất để để bộ phận thứ nhất hỏng. 17 Giải
Gọi Ai là biến cố bộ phận thứ i bị hỏng, i = 1, 2.
A là biến cố mạch điện không làm việc.
Đặt B A A , B A A , B A A , 0 1 2 1 1 2 2 1 2 B A A 3 1 2 Ta có P( )
A P(B ) (
P A | B ) P(B )P( A | B ) P(B ) ( P A | B ) 0 0 1 1 2 2 trong đó P(B ) 0 , 0 99 9 , 0 . 85 9 ,
0 7515 , P(B ) 0 , 0 0985 , 0 1 P(B ) 0 ,
0 1485 , P(B ) 0 , 0 0015 . 2 3
Xác suất để bộ phận thứ nhất hỏng là
P(B )P(A | B ) , 0 00985 ( P B A 1 | ) 1 1 , 0 396378. P( ) A , 0 00985 0 , 0 1485 , 0 00015
■ Ví dụ 1.31. Qua thống kê thực tế người ta thấy rằng: Tỷ lệ người bị viêm họng trong
số người nghiện thuốc lá là 60% và trong số người không hút thuốc lá là 40%. Giả sử
một vùng dân cư hiện có 30% người nghiện thuốc.
a) Tính tỷ lệ người bị viêm họng của vùng dân cư này?
b) Nếu chọn được người không bị viêm họng từ vùng này, tính xác suất để
người này là người nghiện thuốc lá. Giải
Gọi V là biến cố chọn được người bị viêm họng khi chọn từ vùng dân cư 1 người.
Gọi N là biến cố chọn được người nghiện thuốc lá khi chọn từ vùng dân cư 1 người. a) Ta có:
P(V) = P(N) P(V|N) + P( N )P(V| N ) = 0,3.0,6 + 0,7.0,4 = 0,46.
Vậy tỷ lệ người bị viêm họng của vùng dân cư này là 46%.
b) Ta cần tính xác suất P(N|V ).
Ta có P(V )= 0,54; P(V |N) = 0,4, do đó theo công thức Bayes ta có
P(N )P(V | N ) , 0 . 3 , 0 4
P(N|V ) = = = 0,222%. P (V ) 5 , 0 4
Vậy khả năng người này nghiện thuốc là 22,2%.
4.4 Công thức Bernoulli
Giả sử ta thực hiện một phép thử nào đó n lần độc lập và giống nhau. Trong
mỗi phép thử chỉ có một trong hai khả năng xảy ra. Biến cố A xảy ra với xác suất là p,
hoặc biến cố A không xảy ra với xác suất là q = 1- p. Khi đó, xác suất để trong n lần
thực hiện phép thử biến cố A xảy ra k lần là
Pp(n, k) = C k pkqn-k (1.19) n
■ Ví dụ 1.32. Người ta thống kê tỷ lệ sâu răng ở hai trường tiểu học A và B trong một
huyện lần lượt là 20% và 30%. Chọn ngẫu nhiên từ mỗi trường 1 học sinh. Tính xác
suất để chọn được đúng 1 học sinh bị sâu răng. 18 Giải
Gọi A là biến cố chọn được đúng 1 học sinh bị sâu răng.
Gọi Ai là biến cố chọn được i học sinh bị sâu răng từ trường A.
Gọi Bi là biến cố chọn được i học sinh bị sâu răng từ trường B.
Để chọn được 1 học sinh bị sâu răng thì có 2 trường hợp xảy ra: Chọn được 1
học sinh bị sâu răng từ trường A, 0 học sinh bị sâu răng từ trường B hoặc chọn
được 1 học sinh bị sâu răng từ trường B, 0 học sinh bị sâu răng từ trường A. Do đó ta có
A = A1.B0 + A0.B1.
P(A) = P(A1)P(B0) + P(A0)P(B1). = 1 C (0,2)1.(0,8)1 0 C (0,3)0.(0,7)2 + 0 C (0,2)0.(0,8)2 1 C (0,3)1.(0,7)1. 2 2 2 2 = 0,362.
Vậy khả năng chọn đúng một học sinh bị sâu răng là 0,362. BÀI TẬP CHƯƠNG 1 A. TỰ LUẬN
1. Trong một lớp có 20 học sinh nam và 15 học sinh nữ. Giáo viên cần chọn 7 học
sinh đi tham gia chiến dịch “Mùa hè xanh” của Đoàn TNCS Hồ Chí Minh. Hỏi
giáo viên có bao nhiêu cách chọn sao cho:
a) Có 2 nam trong số sinh viên được chọn.
b) Có ít nhất một sinh viên nam được chọn.
c) Có nhiều nhất 2 nam trong số được chọn.
d) Không có sinh viên nam nào được chọn.
2. Cần xếp 3 nam và 2 nữ vào 1 hàng ghế có 5 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho:
a) 3 nam ngồi kề nhau và 2 nữ ngồi kề nhau.
b) 2 bạn nữ không ngồi kề nhau.
3. Từ các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số trong các trường hợp sau:
a) Có 6 chữ số khác nhau.
b) Số chẵn có 4 chữ số khác nhau.
c) Số 3 chữ số trong đó chữ số đứng sau nhỏ hơn chữ số đứng trước.
d) Số có 3 chữ số khác nhau lớn hơn 300.
e) Số có 7 chữ số, trong đó chữ số 1 xuất hiện 2 lần, các chữ số khác xuất hiện 1 lần.
4. Có 10 quyển sách khác nhau, trong đó có 5 quyển sách toán và 5 quyển sách văn.
Xếp liên tiếp các quyển sách này lên một kệ sách, tính xác suất trong các trường hợp sau:
a) 2 quyển sách ở hai đầu cùng thể loại.
b) 2 quyển sách toán bất kỳ không xếp kề nhau.
5. Xếp ngẫu nhiên 12 hành khách lên 4 toa tàu hỏa. Tính xác suất để
a) Toa đầu có 3 hành khách.
b) Toa đầu có 6 hành khách, toa thứ hai có 4 hành khách, 2 toa còn lại mỗi toa có 1 hành khách.
c) 1 toa có 5 hành khách và 1 toa khác có 4 hành khách. 19