Marginal benefits | Microeconomics | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

Table 1: consumption of glass of beer Q TB MB TC MC NB 0 0 0 0 1 50 50 1st glass 20 20 30 2 80 30 2nd glass 40 20 40 3 100 20 3rd glass 60 20 40 4 110 10 4th glass 80 20 30
*: NB ( net benefit ) = TB( total benefit) – TC ( total cost )
* MB(Q)>MC(Q): you are consuming the amount that the last unit
generates higher benefit than its cost -> still have the way to increase
NB by consuming more product -> increase Q it’s logical, therefore we should increase the quantity consumed
o MB(Q)-> have a way to increase NB by do not consume it -> decrease Q, it is illogical, therefore we
should decrease the quantity consumed
Figure 1: marginal benefit formula.
Example 1: the marginal benefit of drinking 1st glass of beer: Table 2 Quantity of Tea Total Utility 1 300 2 540 3 670 4 780 5 880
2nd cup of tea: (540-300)/(2-1) =240
3rd cup of tea: (670-540)/(3-2) =130 4th cup of tea:110 5th cup of tea: 100
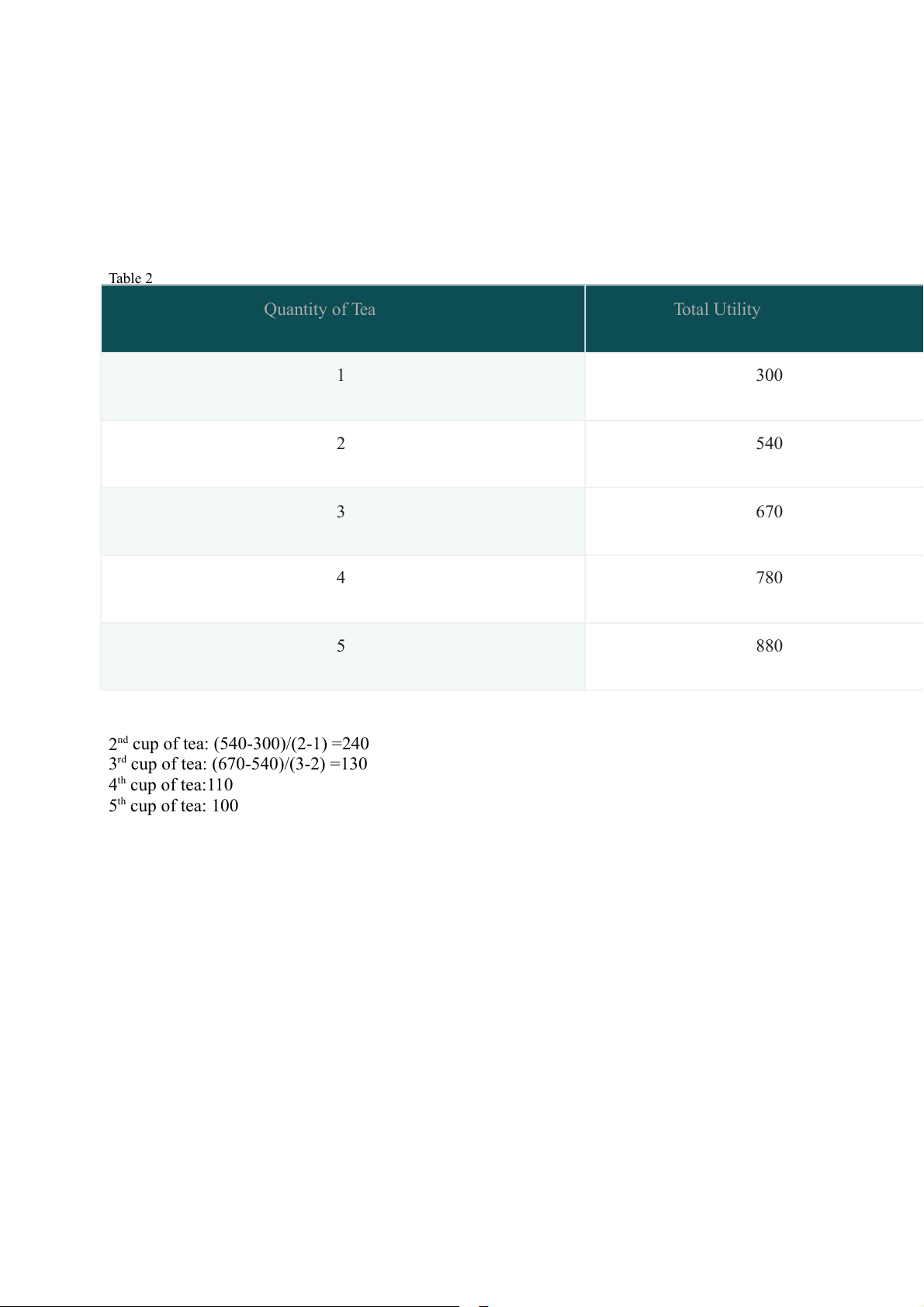
Table 3 : total cost and total benefit of drinking beer Q TB TC NB 0 0 0 0 1 50 20 30 2 80 40 40 3 100 60 40 4 110 80 30 Figure 2 : graph illustration
-The total cost graph is linear
- The total benefit grah face diminishing returns
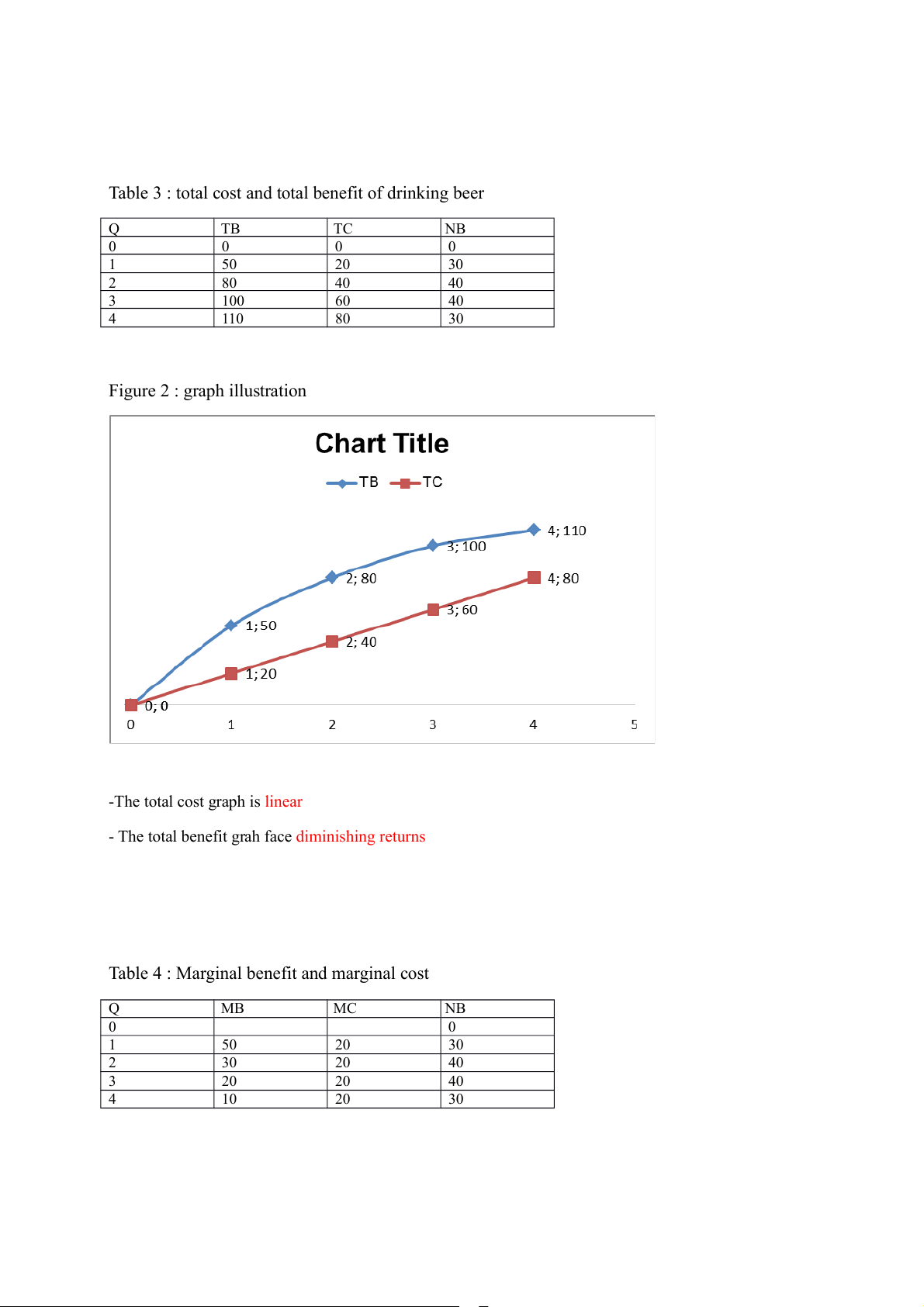
Table 4 : Marginal benefit and marginal cost Q MB MC NB 0 0 1 50 20 30 2 30 20 40 3 20 20 40 4 10 20 30
YQur car needs to be repaired. You have already paid $500 to have the transmission
fixed, but it still doesn't work properly.You can sell your car "as is" for $2,000. Ifyour
car were fixed, you could sell'it for $2,500.Your car can be fixed with a guarantee for
another $300, Should you repair your car? Why?
Yes we should, as the marginal benefit (2500$) is greater than marginal cost ( 300$)
You have spent $1,000 building a hot-dog stand based on estimates of sales of$2,000.~·
The hot-dog stand is nearly completed, but now you estimate total sales to be only
$800.You can complete the hot-dog stand for another $300. Should you complete the
hot-dog stand? (Assume that the hot dogs cost you nothing.)