













Preview text:
Economics Honors Exam Review (Micro) Mar. 2017
Based on Zhaoning Wang’s final review packet for Ec 1010a, Fall 2013
1. The inverse demand function for apples is defined by the equation p = 214 − 5q, where q
is the number of units sold. The inverse supply function is defined by p = 7 + 4q.
(a) How many apples will be sold in equilibrium? Solutions:
To find the number of apples sold, we equate the price paid by the buyers (pD) and
the pice received by the suppliers (pS): 214 − 5q = 7 + 4q =⇒ 207 = 9q =⇒ q = 23.
(b) A tax of $36 is imposed on suppliers for each unit of apples that they sell. How
many apples will be sold after the tax is imposed? Solutions:
In this case, the price received by the suppliers is $36 lower than the price paid by the consumers so that we have pS = pD − 36 =⇒ 214 − 5q = 7 + 4q + 36 =⇒ 171 = 9q =⇒ q = 19.
(c) A tax of $36 is imposed on consumers for each unit of apples that they buy. How
many apples will be sold after the tax is imposed? Solutions:
In this case, the price paid by the consumers is $36 higher than the price received
by the suppliers so that we have pD = pS + 36 =⇒ 214 − 5q = 7 + 4q + 36 =⇒ 171 = 9q =⇒ q = 19.
2. On a tropical island there are 100 potential boat builders, numbered 1 through 100. Each
can build up to 20 boats a year, but anyone who goes into the boat-building business has 1
to pay a fixed cost of $19. Marginal costs differ from person to person. Where y denotes
the number of boats built per year, boat builder 1 has a total cost function c(y) = 19 + y.
Boat builder 2 has a total cost function c(y) = 19 + 2y, and more generally, for each i,
from 1 to 100, boat builder i has a cost function c(y) = 19 + iy. If the price of boats is
25, how many boats will be built per year? Solution:
A builder will enter the market if it makes at least $0 profit. That happens when its
average cost is lower than the price.
For builder i to produce y units, its average cost is: ci(y) 19 ACi(y) = = + i. y y
We notice two things about the average cost function: it is decreasing in y, and it is increasing in i.
The first feature means that if a builder is to produce anything, he will produce the
maximum number of units, which is 20, since producing more makes the average cost
lower. The second feature means that if builder i is producing, then builder j with j is also producing, since j has a lower average cost.
Hence we just need to find the highest i a boat builder produces, and the total supply is 20i.We need to have 19 + i ≤ 25 20 1 i ≤ 24 . 20
Hence the highest i is 24. The total supply is 20 × 24 = 480.
3. A monopolist is able to practice third-degree price discrimination between two markets,
so it can charge different prices in the two markets and prevent resale. The demand
function in the first market is q = 500 − 2p and the demand function in the second
market is q = 1, 500 − 6p. The marginal cost is constant at c per unit of output. To
maximize his profits, should he charge a higher price in the first market or the second market? Solution: 2
The monopolist will charge a price such that the marginal revenue is the same as the marginal cost in each market. For market 1, q p 1 1 = 250 − 2 q1 = 500 − 2p1 TR1 = p1q1 q = (250 − 1 )q 2 1 dTR MR 1 1 = dq1 = 250 − q1 = 250 − 500 + 2p1 = 2p1 − 250. For market 2, q p 2 2 = 250 − 6 q2 = 1500 − 6p2 TR1 = p1q1 q = (250 − 2 )q 6 2 dTR MR 1 1 = dq1 q = 250 − 23 = 250 − 500 + 2p2 = 2p2 − 250.
To maximize profit in both markets, we need to have MR1 = MR2 = c 2p1 − 250 = 2p2 − 250 p1 = p2.
Hence, the monopolist needs to set the same price in both market.
4. Tina consumes apples (a) and butter (b). Apples cost pa and butter costs pb. Tina’s 3
income is M. Her utility is given by u(a,b) = 2 ln a + ln b.
(a) What is Tina’s marginal rate of substitution between apples and butter? Solution:
Tina’s marginal rate of substitution between apples and butter is 2 2b MRS= a 1 = . a b
(b) Find Tina’s optimal consumption bundle as a function of prices and income. Solution: Tina’ budget constraint is paa + pbb = M. (1)
Her optimal consumption bundle must satisfy 2b p MRS= = a . (2) a pb Solve (5) and (6), we have 2M a = 3pa M b = . 3pb
(c) For apples, calculate Tina’s price elasticity of demand. Solution:
Tina’s price elasticity of demand is 2M 3p2 ε a p = − · 3p2 = −1. a 2M
(d) What happens to Tina’s demand for butter if pa doubles? Solution:
When pa doubles, Tina’ budget constraint is 2paa + pbb = M. (3) 4
Her optimal consumption bundle must satisfy 2b 2p MRS= = a . (4) a pb Solve (5) and (6), we have M a = 3pa M b = . 3pb
Hence, TIna’s demand for butter stays the same.
(e) Now imagine that Tina is trapped on an island, with an allocation of 7 apples and
3 lumps of butter. From now on, we assume that the price of apples is 1. The
only income that Tina now gets is from selling her allocation of apples and butter.
Calculate Tina’s demand for butter as a function of pb. Solution: In this case, M = 7 + 3pb.
Hence, Tina’s demand for butter is 7 + 3p b b T = 3pb
(f) Also on the island is Stanley. He has exactly the same preferences as Tina, but
has 8 lumps of butter and 2 apples. Draw an Edgeworth box for this economy,
and sketch both Tina and Stanley’s indifference curves that pass through their ini-
tial endowment. (You need to label the axes, label the curves, and mark important points.) Solution: (omitted)
(g) Write down Stanley’s demand for butter as a function of pb. Solution:
Stanley’s income is 2 + 8pb. Hence, Stanley’s demand for butter is 2 + 8p b b S = 3pb
(h) What is the equilibrium price of butter in this economy? What are the equilibrium
allocations for Tina and Stanley? 5 Solution:
Tina and Stanley’s demand for apples and butter are 2(7 + 3p a b) T = 3 2(2 + 8p a b) S = 3 7 + 3p b b T = 3pb 2 + 8p b b S = . 3pb
Using the market-clearing condition, we have
2(7 + 3pb) 2(2 + 8pb) 2(9 + 11pb) + = = 9. 3 3 3 Hence, we have 9 pb = 22 181 aT = 33 116 aS = 33 181 bT = 27 116 bS = . 27
5. Henry can work as many hours as he likes within a day at a wage rate of $40 per hour.
Henry likes both consumption (C) and leisure (L), and leisure is defined as the hours
within a day that he does not have to work. His utility function is given by: U(C,L) = C · L
The price of consumption is $1 and a day has 24 hours.
(a) Suppose Henry has no other sources of income. Write down his budget constraint.
Sketch his budget constraint, with leisure on the horizontal axis and consumption on the vertical axis. 6
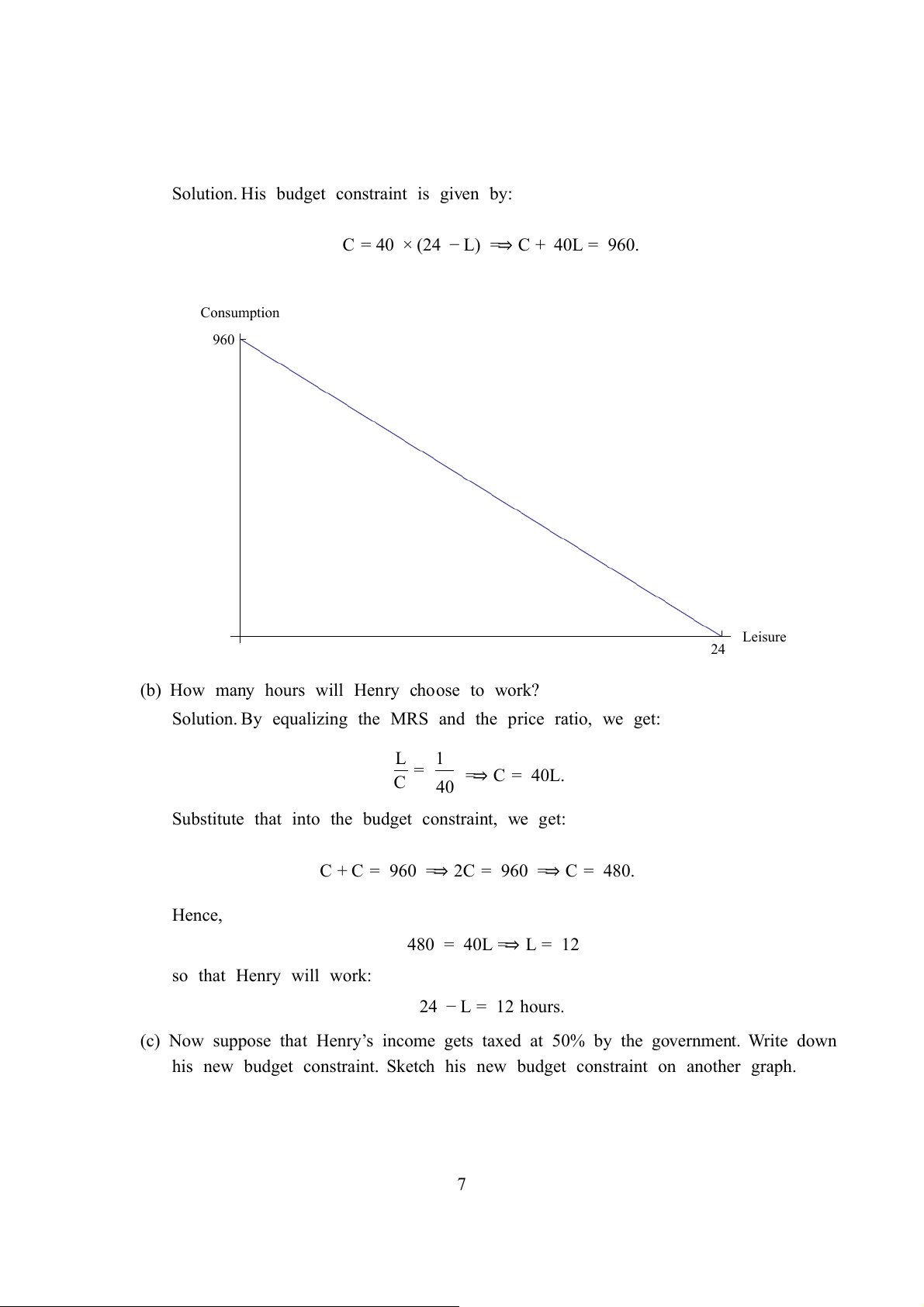
Solution. His budget constraint is given by:
C = 40 × (24 − L) =⇒ C + 40L = 960. Consumption 960 Leisure 24
(b) How many hours will Henry choose to work?
Solution. By equalizing the MRS and the price ratio, we get: L 1 = C =⇒ C = 40L. 40
Substitute that into the budget constraint, we get:
C + C = 960 =⇒ 2C = 960 =⇒ C = 480. Hence, 480 = 40L =⇒ L = 12 so that Henry will work: 24 − L = 12 hours.
(c) Now suppose that Henry’s income gets taxed at 50% by the government. Write down
his new budget constraint. Sketch his new budget constraint on another graph. 7
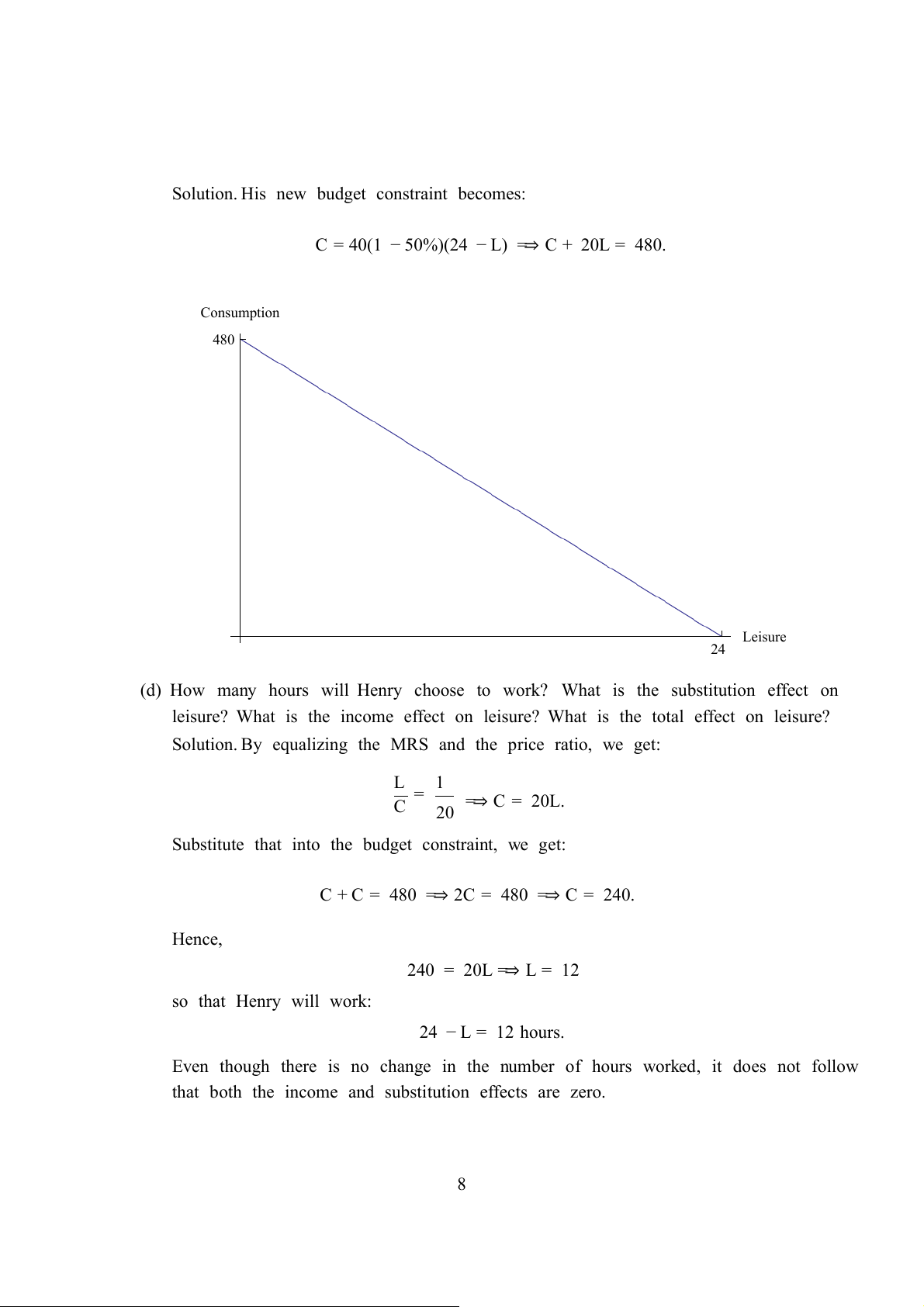
Solution. His new budget constraint becomes:
C = 40(1 − 50%)(24 − L) =⇒ C + 20L = 480. Consumption 480 Leisure 24
(d) How many hours will Henry choose to work? What is the substitution effect on
leisure? What is the income effect on leisure? What is the total effect on leisure?
Solution. By equalizing the MRS and the price ratio, we get: L 1 = C =⇒ C = 20L. 20
Substitute that into the budget constraint, we get:
C + C = 480 =⇒ 2C = 480 =⇒ C = 240. Hence, 240 = 20L =⇒ L = 12 so that Henry will work: 24 − L = 12 hours.
Even though there is no change in the number of hours worked, it does not follow
that both the income and substitution effects are zero. 8
If we want to make the old bundle (12, 480) affordable, his “income” needs to be: 20 × 12 + 480 = 720.
At this compensated income, his budget constraint is: C + 20L = 720.
By equalizing the MRS and the price ratio, we get:
C = 20L =⇒ C + C = 720 =⇒ C = 360,L = 18
Hence the substitution effect increases L from 12 to 18, a change of 6 hours (since
price for leisure goes down, he demands more leisure). In other words, the substi-
tution effect DECREASES the number of hours worked by 6, and the income effect
INCREASES the number of hours worked by 6 to get back to 12 hours.
6. Jennifer will earn income this period and next period and she needs to decide how much
to consume this period and next period. She earns $200 in period 1 and $410 in period
2. The interest rate is constant at 10%. Her utility function is given by: 1 u(c1,c2) = ln c1 + ln c 1.10 2,
where c1 and c2 are her consumptions in period 1 and period 2, respectively.
(a) Suppose Jennifer can save and borrow at the interest rate, 10%. What is Jennifer’s
intertemporal budget constraint? You do not have to simplify the expression. Solution:
Jennifer’s budget constraint is given by c m c 410 c 2 2 2 1 + = m =⇒ c = 200 + . 1 + r 1 + 1 + r 1 + 1.1 1.1
(b) What is the optimal c1, Jennifer’s consumption in period 1? What about the optimal c2, consumption in period 2? Solution: MRS Rule Approach: 9
Setting MRS equal to the price ratio, we have MUc 1.1c 1.1 1 = 2 = MU =⇒ c1 = c2. (5) c c 2 1 1
Plugging (5) into the budget constraint, c 410 c 2 2 + = 200 + 1.1 1.1 we can solve for c2: 410 200 + 630 c 1.1 1.1 × 200 + 410 2 = = 300. (6) 1 = = 2.1 1 + 1.1 + 1 1.1
Plugging (6) into the budget constraint: c 410 300 410 c 2 1 + = 200 + =⇒ c = 200 + 1.1 1.1 1 + 1.1 1.1 so that
1.1c1 + 300 = 1.1 × 200 + 410 =⇒ 1.1c1 = 330 =⇒ c1 = 300. Substitution Approach: From budget constraint, c2 = (200 − c1)1.1 + 410.
Plugging (7) into utility function, 1 u(c1) = ln c1 + ln [(200 − c 1.1 1)1.1 + 410] . 10
Then, take the first order condition (take the derivative and set to zero), ∂u 1 1 = + −1.1 = 0 ∂c1 c1 1.1 (200 − c1)1.1 + 410 1 1 =⇒ = c1 (200 − c1)1.1 + 410 =⇒ c1 = (200 − c1)1.1 + 410 =⇒ 2.1c1 = 200(1.1) + 410 = 630 =⇒ c1 = 300
and plugging into the budget constraint, we also get
c2 = (200 − c1)1.1 + 410 = (200 − 300)1.1 + 410 = 300.
(c) Now suppose that Jennifer cannot borrow money from the future because no one is
willing to lend her money. However, she is still free to save at an interest rate of
10%. What are the optimal choices for c1 and c2 now? Solution:
Since Jennifer cannot borrow, we have the new constraint: c1 ≤ m1 = 200.
And since the answer we found in part (b), c1 = 300, was the only allocation that
satisfied the first order condition and this allocation violates the new constraint,
we know that our new constrained optimal bundle cannot satisfy the first order
condition and hence has to be a corner solution. All we have to do is check the
marginal utility with respect to c1 at the corner (c1 = 200). From before we had: ∂u 1 1 = + −1.1 . ∂c1 c1 1.1 (200 − c1)1.1 + 410
and plugging in c1 = 200 we have ∂u 1 = −1 > 0. ∂c + 1 200 410
So Jennifer would have more utility if she could consume marginally more c1 than
200, but she cannot because she is credit constrained. However, this proves that
setting c1 = 200 is the best she can do and that leaves c2 = 410. 11 √
7. Noah’s utility function for money is given by u(x) = x.
(a) What utility would Noah get if he received $100 for sure? What about if he had a
lottery ticket that gave him $50 with a probability 2and $200 with probability 1? Is 3 3
Noah risk averse or risk loving? Solution: Noah’s utility will be ¯
u = 10 if he gets 100 for sure. For the lottery ticket, his expected utility is 2 E(u) = √ 1 √ 4 √ 20 √ 50 + 200 = 50 = 2 3 3 3 3
Note that the expected value of the lottery is $100, but 20√2 < 10 3 so Noah is risk-averse.
(b) What is the variance of the outcomes of the lottery described in part (a)? Solution: The variance is 2 1 (100 − 50)2 + 3 (200 − 100)2 = 5000. 3
(c) Noah’s wealth is $90,000. However, he lives in Alaska, and there is a 1 probability 6
that his house will be destroyed by a moose, which will cost his $50,000. Alternatively,
he can buy insurance for an amount F , which will pay him $50,000 in the case of a
moose destroying his house. What is the maximum amount (denoted by Fmax) that Noah would pay for insurance? Solution:
In order to solve for Fmax, we use Noah’s indifference condition: 5 √ 1 × 90000 + √ p 6
× 90000 − 50000 = 90000 − F 6 max. Hence, we have 87500 . 850 2 = 9 Fmax = 90000 − 3 12
(d) Following part (c), would the insurance company make positive or negative expected
profit if it sold insurance at price Fmax? What is the least amount (denoted by Fmin)
that the insurance company would be willing to sell the insurance for (such that they make a non-zero profit)? Solution: The expected profit is 1 87500 12500 − × 50000 + = > 0. 6 9 9
The least amount that the insurance company would be willing to sell the insurance for is given by 1 50000 − × 50000 + F . 6 min = 0 =⇒ Fmin = 6
8. A small coffee company roasts coffee beans in its shop. The unroasted beans cost the
company $2 per pound. The marginal cost of roasting coffee beans is $(150−10q+q2)/100
per pound when q pounds are roasted. The smell of roasting beans imposes costs on the
company’s neighbors. The total amount that neighbors would be willing to pay to have
the shop stop roasting altogether is q2, where q is the number of pounds being roasted. 20
The company sells its output in a competitive market at $4.50 per pound. Assuming the
coffee company owns the right to roast as much as they want, how much coffee will the
company roast? What is the socially efficient amount of coffee for the company to roast? Solution:
If the coffee company owns the right to roast as much as they want, they would roast to the point where MC= MR= p. We must have 150 − 10q + q2 + 2 = 4.5 100 q2 − 10q − 100 = 0 q = 16.18
(we discard the negative root above)
In order to be socially efficient, we need to take into account the social marginal cost,
which is the sum of the private marginal cost and the externality marginal cost, which is 13 given by: d q2 q 10 = dq 20 Hence, we need 150 − 10q + q2 q + + 2 = 4.5 100 10 q2 = 100 q = 10
(again, we discard the negative root)
9. Consider the market of used cars. p fraction of all used cars in the market are “peaches”
and 1 − p of them are “lemon.” Both sellers and buyers know the fraction p. There exists
asymmetry in information on quality of cars: each seller knows the quality of the car
which he sells, but buyers can not observe the quality of each used car. Assume that the
value of a peach is $2000 for a seller and $2500 for a buyer and the value of a lemon is
$1000 for a seller and $1500 for a buyer.
(a) Derive the maximum price which a buyer will pay for a used car as a function of p. Solution:
The expected value of a used car is
2500p + 1500(1 − p) = 1500 + 1000p.
This is the maximum price which a buyer will pay for a used car.
(b) Derive the condition of p with which peaches will be sold in the market. Solution:
Owners of peaches would be willing to sell their cars if 1
1500 + 1000p ≥ 2000 =⇒ p ≥ . 2
(c) Describe the market situation clearly when the actual p does not satisfy the condition in (b). Solution: 14
If more than half of the cars in the market are lemons, that is, if p,< 1 then owners 2
of peaches will not be willing to sell their cars so that the condition in (b) fails.
(d) Now a seller of a peach offers a warranty which promises to pay the buyer some
agreed upon amount if the car turned out to be a lemon. Explain how this warranty
works as a signal. What is the equilibrium behavior of buyers and sellers given that
the promised refund (if a car turns out to be a lemon) is sufficiently large? Solution:
By offering the warranty, sellers of peaches are able to distinguish themselves from
sellers of lemons. As long as the promised refund is sufficiently large, sellers of lemons
will not be willing to offer this warranty because they would have paid the refund
for each car they sell. In this way, since buyers know that only sellers of peaches
are willing to offer this warranty, they are willing to pay a higher price. In the
equilibrium, buyers are willing to pay $2500 if the seller offers a warranty, and only
$1500 if the seller does not offer a warranty. In other words, sellers of peaches are
able to signal their type by offering the warranty.
10. (Battle of the sexes) A couple can attend either a basketball game (B) or an opera
performance (O) this evening. The husband would prefer basketball, while the wife
would prefer opera. Both would prefer to go to the same place rather than different ones.
If one goes to one’s preferred place, he/she gets a payoff of 3 while the other gets 2; if
they can’t agree, then they are going nowhere and both get 0. (a) Draw the payoff matrix. Solution: The payoff matrix is: Wife Basketball Opera Husband Basketball 3,2 0,0 Opera 0,0 2,3
(b) Identify all pure strategy equilibria, if any exists. Solution:
The pure strategy (Nash) equilibria are (B,B) and (O, O). If either of the players
changes behavior, he/she will get a lower payoff.
(c) Identify all mixed strategy equilibria, if any exists. Solution: 15
We find the mixed strategy equilibrium by doing the following: for the husband, we
let him play B with probability p and O with probability (1 − p), so the wife will
always get the same expected payoff regardless of what the husband does. The wife
does so likewise. This will be a mixed strategy equilibrium, since given that the other
player mixes the strategies in a way that it does not profit one player to change his
strategy, he will not change his current strategy.
From husband’s point of view, what he needs is a p such that: 2p = 3(1 − p) p = 0.6
The first equation needs a bit more elaboration. Given that the husband chooses B
with probability p, if the wife chooses B, her expected payoff is 2p +0(1-p) = 2p,
which is the LHS; if the wife chooses O, her expected payoff is 0p+3(1−p) = 3(1−p), which is the RHS. 16




