16 trang 39 lượt tải

Một số bài toán chọn lọc về tích phân Toán 12

77

Tài liệu gồm 16 trang, trình bày lý thuyết trọng tâm, các dạng toán trọng tâm kèm phương pháp giải và bài tập trắc nghiệm tự luyện chuyên đề một số bài toán chọn lọc về tích phân, có đáp án và lời giải chi tiết; hỗ trợ học sinh lớp 12 trong quá trình học tập chương trình Toán 12 phần Giải tích chương 3.

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Profile

Mai Nguyệt

1 năm trước
Danh sách Quiz
/16
CHỦ ĐỀ 15: MỘT SỐ BÀI TOÁN CHỌN LỌC VỀ TÍCH PHÂN
Ví dụ 1: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[ ]
1; 2
thỏ
a mãn
(
)
( )
( )
2
. .1
f x xf x xf x
′
+= +


. Biết
( )
12f = −
, tính
( )
2f
A.
(
)
1
2.
2
f
−
=
B.
(
)
1
2.
2
f =
C.
D.
(
)
3
2.
4
f
−
=
Lời giải:
Ta có
( ) ( ) (
)
(
)
( )
( )
( )
( )
2
22
.
.
. .1 1 1
.1 .1
xf x
f x xf x
f x xf x xf x
xf x xf x
′

′
+

′
+ = +⇔ =⇔ =


++


Lấy nguyên hàm 2 vế ta được:
(
)
1
.1
xC
xf x
−
= +
+
Thay
( ) ( )
2
1 11 3
110 2
21 4
x C C fx f
x
x
−−
=⇒ =+⇒=⇒ = −⇒ =−
−+
. Chọn D.
Ví dụ 2: Cho hàm số
(
)
y fx
=
xác định và liên tục trên đoạn
[ ]
1; 3
và thỏa mãn
( )
( )
(
)
[ ]
( )
2
23
. . . 1 1; 3xfx xf x xfx x
′
+ = + ∀∈


và
( )
2
1
3
f
−
=
. Khi đó:
A.
( )
0 3 1.f
<<
B.
( )
1 3 3.
f<<
C.
( )
3 3.
f >
D.
( )
3 0.
f <
Lời giải:
Ta có:
( ) ( ) ( ) ( ) ( ) ( )
22
23 2
.. 1 . 1xfx xf x xfx x fx xf x xfx
′′
+ = +⇔ + = +
 
 
( ) ( )
( )
( )
( )
2 2 22
.
.
11
11
xf x
f x xf x
xx
xf x xf x
′

′
+

⇔ =⇔=
++
 
 
Lấy nguyên hàm 2 vế ta được:
( )
( )
( )
22
1
1 11
1
1
d xf x
dx C
xf x x
x
xf x
+

−−

=⇒=+
+
+


∫∫
Lại có:
(
)
( )
21 1
1 1 12
2
3 1. 1 1
1
3
f CC
f
−− −
= ⇒ =−+ ⇒ = +=−
−
+
+
Do đó
( )
11
2
.1xf x x
= +
+
, thay
(
)
(
)
11 4
3 23
3. 3 1 3 21
xf
f
−
=⇒ =+⇒ =
+
. Chọn D.
Ví dụ 3: Cho hàm số
( )
y fx=
đồng biến và luôn dương trên đoạn
[ ]
1; 3
đồng thời thỏa mãn
( )
( )
( )
2
42
3f x x x fx
′
= +


, biết
( )
14f =
. Khi đó
A.
( )
0 2 3.
f<<
B.
( )
3 2 5.f<<
C.
( )
5 2 9.f<<
D.
( )
2 9.f >
Lời giải:
Ta có:
( )
( )
( )
( )
( )
( )
2
2
4 2 22
33
fx
f x x x fx x x
fx
′


′
=+⇒=+


( )
( )
2
3
fx
xx
fx
′
⇔=+
(do
( )
[ ]
0 1; 2fx x> ∀∈
)
Lấy nguyên hàm 2 vế ta được:
(
)
(
)
( )
( )
2 22
1
32 3 3
2
dfx
x x dx f x x dx x
fx


= +⇔ = + +
∫∫ ∫
(
)
( )
( )
33
22
12 1
.3 3
43 6
fx xCxC
⇔ = ++= ++
Do
( )
( )
( )
3
2
3
82 2
142 .
6 3 63
x
f C C fx
+
=⇒=+⇒ =⇒ = +
( )
( )
( )
2
3
2
3
2
2 14,1
63
x
fx f

+

⇒ = +⇒ ≈



. Chọn D.
Ví dụ 4: Cho hàm số
( )
fx
có đạo hàm xác định, liên tục
[ ]
0;1
đồng thời thỏa mãn các điều kiện
( )
01f
′
= −
và
(
)
( )
2
fx f x
′ ′′
=


. Đặt
( ) ( )
10Tf f= −
, hãy chọn khẳng định đúng?
A.
2 1.T− ≤ <−
B.
1 0.T−≤ <
C.
0 1.T≤<
D.
1 2.T≤<
Lời giải:
Ta có:
( ) ( )
( )
( )
2
2
1
fx
fx f x
fx
′′
′ ′′
=⇒=


′


Lấy nguyên hàm 2 vế ta có:
(
)
( )
( )
( )
2
11
df x
dx x C f x
fx xC
fx
′

−−

′
= ⇔ =+⇒ =
′
+
′


∫∫
Do
( )
01 1fC
′
=−⇒ =
Suy ra
( ) ( ) ( )
11
00
1
1 0 ln 2
1
f x dx dx f f
x
−
′
= ⇔− =−
+
∫∫
. Chọn B.
Ví dụ 5: Cho hàm số
( )
fx
liên tục và đồng biến trên đoạn
[ ]
0;1
, biết
( )
01f =
và
( ) (
)
[ ]
2
3
2 9 9 . 0;1f x x x xf x x
′
+ = + ∀∈


. Mệnh đề nào dưới đây đúng
A.
( )
1 3.f =
B.
( )
1 5.f =
C.
(
)
1 6.
f
=
D.
(
)
1 4.
f
=
Lời giải:
Ta có:
(
) ( )
( )
( )
( )
( )
2
2
3
2
2
2
2
2 9 9. 9 3
fx x
fx x
f x x x xf x x x
fx x
fx x
′
+

′
+

′
+=+ ⇔ =⇔ =


+
+
Lấy nguyên hàm 2 vế ta được
( )
( )
2
2
3
dfx x
xdx
fx x

+

=
+
∫∫
( ) (
)
2 3 23
2 22fx x x C fx x x C⇔ += + ⇔ += +
Thay
(
)
23
0 1 1.x C fx x x=⇒=⇒ + = +
Suy ra
( )
(
)
( )
2
32
1 1 3.fx x x f= + −⇒ =
Chọn A.
Ví dụ 6: Cho hàm số
( )
fx
liên tục thỏa mãn
( )
( )
(
) ( )
2
4
. 15 12 ,f x fxf x x x x
′ ′′
+ = + ∀∈
và
( ) ( )
0 01
ff
′
= =
. Giá trị của
( )
2
1f
bằng
A. 8. B.
9
.
2
C. 10. D.
5
.
2
Lời giải:
Ta có:
( ) (
) ( ) ( ) ( )
2
4
. . 15 12fxf x f x fxf x x x
′
′ ′ ′′
=+=+


Nguyên hàm 2 vế ta được
( ) ( )
5
2 52
15
. 6 36
5
x
fxfx xC x xC
′
= ++=++
Do
( ) ( )
0 01 1ff C
′
= =⇒=
Tiếp tục nguyên hàm 2 vế ta được:
( )
( )
( )
52
361
f x df x x x dx
= ++
∫∫
(
)
2
63
63
36 1
2
2 63 2
fx
xx
xD x x xD
⇒ = + ++ = + ++
. Do
( )
( )
2
1
01 18
2
f Df=⇒=⇒ =
. Chọn A.
Ví dụ 7:
Cho hàm số
( )
y fx=
có đạo hàm liên tục và luôn dương trên đoạn
[ ]
1; 3
thỏa mãn
( ) ( )
1 11ff
′
= =
và
( )
( )
( )
( )
2 22
..f xfx f x xf x
′′ ′
= −
. Giá trị của
( )
ln 3f


thuộc khoảng nào trong các
khoảng sau:
A.
( )
1; 6 .
B.
( )
7;12 .
C.
( )
0;1 .
D.
( )
12;15 .
Lời giải:
Ta có:
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 22
. ..f xfx f x xf x f xfx f x xf x
′′ ′ ′′ ′
=− ⇔ −=
( ) ( ) ( )
(
)
( )
2
2
2
.f xfx f x
x
fx
′′ ′
−
⇔=∗
Mặt khác
( )
( )
( )
(
) (
)
(
)
2
2
.f x f xfx f x
fx
fx
′
′ ′′ ′

−
=


, lấy nguyên hàm 2 vế của
( )
∗
ta được:
( )
( )
3
3
fx
x
C
fx
′
= +
Do
( ) (
)
2
1 11
3
ff C
′
= =⇒=
. Tiếp tục nguyên hàm 2 vế ta được:
( )
4
2
ln
12 3
xx
fx D

=++


Do
( ) (
)
( )
4
3 23
1 1 ln ln 3 8
4 12 3 4
xx
f D fx f=⇒ =−⇒ = + −⇒ =


. Chọn B.
Ví dụ 8: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
(
) (
)
1
2
0
9
1 1,
5
f f x dx
′
= =


∫
và
(
)
1
0
2
5
f x dx =
∫
. Tính tích phân
( )
1
0
I f x dx=
∫
.
A.
3
.
5
I
=
B.
1
.
4
I
=
C.
3
.
4
I =
D.
1
.
5
I =
Lời giải:
Đặt
2
2
t x t x dx tdt= ⇔=⇔ =
và
00
.
11
xt
xt
=⇒=
=⇒=
Khi đó:
( )
( ) ( ) ( )
11 1 1
00 0 0
21
2. 2 . . .
55
f x dx t f t dt x f x dx x f x dx== =⇔=
∫∫ ∫ ∫
Đặt
( )
( )
( )
( )
(
) ( )
1
2
1 11
22
2
0 00
0
.
13
. . ..
22 5
2
du f x dx
u fx
xfx
x f x dx x f x dx x f x dx
x
dv xdx
v
′
=
=

′′
⇔ ⇒=− ⇒ =

=
=
∫ ∫∫
Xét
( ) ( ) ( )
2
1 1 11
2
2 2 24 2
0 0 00
96 1
2 . 0 3.
55 5
f x kx dx f x dx k x f x dx k x dx k k k
′ ′′

+ = + + =+ + =⇔=−



∫ ∫ ∫∫
Do đó
( ) ( ) ( ) ( )
22 3
30 3fx x fx x fx fxdxx C
′′ ′
−=⇔ =⇒ = =+
∫
mà
( )
1 1 0.
fC=⇒=
Vậy
( )
1
1
4
33
0
0
1
44
x
f x x I x dx= → = = =
∫
. Chọn B.
Ví dụ 9: Cho hàm số
( )
y fx
=
có đạo hàm liên tục trên đoạn
[ ]
0;1
và
( ) ( )
0 10ff+=
. Biết rằng tích
phân
(
)
( )
11
2
00
1
, .cos
22
f x dx f x xdx
π
π
′
= =
∫∫
. Tính tích phân
( )
1
0
f x dx
∫
?
A.
3
.
2
π
B.
2
.
π
C.
.
π
D.
1
.
π
Lời giải:
Ta có
(
)
(
)
( )
( )
(
)
(
)
11 1
1
0
00 0
.cos cos .cos . cosf x xdx xdfx fx x fx xdx
ππ π π
′
′
= = −
∫∫ ∫
( )
(
) (
)
(
)
11
00
1
1 0 .sin .sin .
22
f f f x xdx f x xdx
π
ππ π
=−+ + =⇒ =


∫∫
Xét
(
) ( ) ( ) (
)
1 11 1
2
2 22
0 00 0
.sin 0 2 . .sin . sin 0
f x k x dx f x dx k f x xdx k x dx
π ππ
+ =⇔+ + =


∫ ∫∫ ∫
( )
2
2
1 11
2 . 0 1 0 1.
2 22
kk k k⇔ + +=⇔ + =⇔=−
Suy ra
( )
1
2
0
sin 0.f x x dx
π
−=


∫
Vậy
( ) ( )
11
00
2
sin sinf x x f x dx xdx
ππ
π
=⇒==
∫∫
. Chọn B.
Ví dụ 10: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[
]
0;1
,
( )
fx
và
( )
fx
′
luôn nhận giá trị dương
trên đoạn
[ ]
0;1
và thỏa mãn
( )
01f =
;
( ) ( ) (
) (
)
11
2
22
00
4.
f x f x x dx x f x f x dx

′′
+=

∫∫
. Tính
( )
1
f
?
A.
( )
3
1 4.f =
B.
( )
1 2.f =
C.
( )
1 1.f =
D.
( )
1 4.f =
Lời giải:
Giả thuyết tương đương với
( ) (
)
1
2
2
0
'0f x f x x dx

−=

∫
( ) ( ) ( ) ( ) ( ) ( )
22
' 0' .f xfx x f xfx x f x fx x
′
⇔ −=⇔ =⇔ =
Nguyên hàm 2 vế ta được:
( )
33
22
33
fx x C
= +
Mặt khác
( ) ( )
33
2
01 1
3
f C fx x=⇒=⇒ = +
Vậy
( )
3
1 4.f =
Chọn A.
Ví dụ 11: Cho hàm số
( )
fx
xác định trên
1
\
2



thỏa mãn
(
) ( )
2
, 01
21
fx f
x
′
= =
−
và
( )
12f =
. Giá
trị của biểu thức
( ) ( )
13ff−+
bằng
A.
4 ln 5.+
B.
2 ln15.+
C.
3 ln15.+
D.
ln15.
Lời giải:
Ta có
( )
(
)
( )
1
2
1
ln 2 1 khi
2
ln 2 1 .
1
ln 1 2 khi
2
x Cx
f x dx x C
xC x
−+ >
′
= −+=
−+ <
∫
Do
(
)
01f
=
và
( ) ( )
( )
1
12
2
1
1 2 1 3 ln 3 ln 5 3 ln15
2
C
f f f CC
C
=
=⇒ ⇒ −+ = + + + =+
=
. Chọn C.
Ví dụ 12: Cho hàm số
( )
fx
xác định trên
{ }
\ 2; 2−
và thỏa mãn
( )
2
4
4
fx
x
′
=
−
;
( )
30f −=
;
( )
01f =
và
( )
32f =
. Tính giá trị biểu thức
( ) ( ) ( )
4 14Pf f f
= −+ −+
.
A.
3
3 ln
25
P = +
B.
3 ln 3P = +
C.
5
2 ln
3
P = +
D.
5
2 ln
3
P
= −
Lời giải:
Ta có:
(
)
(
)
( )(
)
22
4 4 4 11
22 2 2
44
dx dx
f x f x dx dx
xx x x
xx

′′
=⇒== =−

−+ − +
−−

∫ ∫∫ ∫
( )
1
2
3
2
ln khi 2
2
22
ln ln khi 2 2.
22
2
ln khi 2
2
x
Cx
x
xx
fx C C x
xx
x
Cx
x
−
+>
+
−−

⇒ = + = + −<<

++

−
+ <−
+
Lại có:
( )
3
3 0 ln 5fC−=⇒ =−
;
( )
2
01 1fC=⇒=
;
(
)
1
1
3 2 2 ln
5
fC=⇒=−
.
Do đó
( ) ( ) ( )
123
1
4 1 4 ln 3 ln 3 ln 3 ln 3
3
Pf f f CC C= −+ −+ = + + + + + =+
. Chọn B.
Ví dụ 13: Cho hàm số
( )
fx
xác định trên
{ }
\1±
thỏa mãn
( )
2
1
1
fx
x
′
=
−
. Biết
( ) ( )
3 30
ff−+ =
và
11
2
22
ff

−+ =


. Giá trị
( ) ( ) ( )
204
Tf f f= −+ +
bằng
A.
15
2 ln .
29
T = +
B.
19
1 ln .
25
T = +
C.
19
3 ln .
25
T = +
D.
19
ln .
25
T =
Lời giải:
Ta có:
( ) ( )
( )( )
22
1 11 1
1 12 1 1
11
dx dx
f x f x dx dx
xx x x
xx

′′
=⇒== =−

−+ − +
−−

∫ ∫∫ ∫
( )
1
2
3
11
ln khi 1
21
1 1 11
ln ln khi 1 1.
21 2 1
11
ln khi 1
21
x
Cx
x
xx
fx C C x
xx
x
Cx
x
−
+>
+
−−

⇒ = + = + −< <

++

−
+ <−
+
Theo bài ra ta có:
(
)
( )
13
22
3 30
0
11
22 1
2
22
ff
CC
CC
ff
−+ =
+=
⇔


=⇒=
−+ =


Do đó
( ) ( ) ( ) ( ) ( ) ( )
204 24 0Tffffff= −+ + = −+ +


1 32
1 13 19
ln 3 ln 1 ln
2 25 25
C CC= ++ ++ =+
. Chọn B.
Ví dụ 14: Cho hàm số
( )
fx
liên tục trên
( )
0;
+∞
và thỏa
( )
2
0
.cos
x
f t dt x x
π
=
∫
. Tính
( )
4f
.
A.
( )
1
4.
2
f =
B.
( )
1
4.
4
f =
C.
( )
3
4.
4
f =
D.
( )
3
4 12.
f =
Lời giải:
Ta có
( ) ( )
( ) ( )
2
22
0
.cos . cos .sin
x
f t dt x x x f x x x x
π ππ π
′

′
′
=⇔=−



∫
( )
2
2 . cos .sin .xf x x x x
ππ π
⇔=−
Thay
2x =
vào 2 vế, ta được
( ) ( )
1
441 4
4
ff=⇔=
. Chọn B.
Ví dụ 15: Cho hàm số
( ) ( )
2
0
cos 0
x
G x tdt x= >
∫
. Tính
( )
Gx
′
.
A.
( )
2
.cos .Gx x x
′
=
B.
( )
2 .cos .Gx x x
′
=
C.
( )
cos .Gx x
′
=
D.
( )
cos 1.Gx x
′
= −
Lời giải:
Gọi
( )
Ft
là nguyên hàm của hàm số
( )
cos .ft t=
Ta có
( )
( )
( ) ( )
( ) ( ) ( )
2
2 2 22
0
cos 0 2. 2. .
x
Gx tdt Fx F G x Fx xF x xf x
′

′′
= = − → = = =

∫
Lại có
(
)
22
cos cosfx x x= =
nên suy ra
( )
2 .cos .Gx x x
′
=
Chọn B.
BÀI TẬP TỰ LUYỆN
Câu 1: Cho hàm số
( )
fx
xác định trên
{ }
\1
thỏa mãn
(
)
1
1
fx
x
′
=
−
,
( )
0 2017f =
,
( )
2 2018f =
. Tính
(
)
( )
31Sf f= −−
.
A.
1.S =
B.
ln 2.
S
=
C.
ln 4035.
S
=
D.
4.S =
Câu 2: Cho hàm số
( )
fx
xác định trên
thỏa mãn
( )
21fx x
′
= +
và
( )
15f =
. Phương trình
( )
5fx=
có hai nghiệm
12
,xx
. Tính tổng
21 22
log log
Sx x= +
.
A.
1.S =
B.
2.
S
=
C.
0.
S
=
D.
4.S =
Câu 3: Cho hàm số
( )
fx
xác định trên
1
\
3



thỏa mãn
( )
3
31
fx
x
′
=
−
,
( )
01f =
và
2
2
3
f

=


. Giá trị
của biểu thức
( ) (
)
13
ff−+
bằng
A.
3 5 ln 2.+
B.
2 5 ln 2.−+
C.
4 5 ln 2.+
D.
2 5 ln 2.+
Câu 4: Cho hàm số
( )
fx
xác định trên
{ }
\ 2;1−
thỏa mãn
(
)
2
1
2
fx
xx
′
=
+−
;
( ) ( )
3 30ff−− =
và
(
)
1
0
3
f =
. Giá trị của biểu thức
( ) (
) ( )
414
f ff−+ −
bằng
A.
11
ln 2.
33
+
B.
1 ln 80.+
C.
14
1 ln 2 ln .
35
++
D.
18
1 ln .
35
+
Câu 5: Cho hàm số
( )
fx
nhận giá trị dương, có đạo hàm liên tục trên
(
)
0;
+∞
thỏa mãn
( )
1
2
15
f =
và
( ) ( ) ( )
2
24 0fx x f x
′
++ =
. Tính
( ) ( ) ( )
123ff f++
.
A.
7
.
15
B.
11
.
15
C.
11
.
30
D.
7
.
30
Câu 6: Cho hàm số
( )
fx
xác định và liên tục trên
. Biết
( ) ( )
6
. 12 13f xf x x
′
= +
và
( )
02f
=
. Khi đó
phương trình
( )
3fx=
có bao nhiêu nghiệm?
A. 2. B. 3. C. 7. D. 1.
Câu 7: Cho hàm số
( )
fx
có đạo hàm liên tục trên
và thỏa mãn
( )
0,fx x> ∀∈
. Biết
( )
01f =
và
( )
( )
22
fx
x
fx
′
= −
. Tìm các giá trị thực của tham số m để phương trình
( )
fx m=
có hai nghiệm thực phân
biệt.
A.
.me>
B.
0 1.m<≤
C.
0.me<<
D.
1.me<<
Câu 8: Cho hàm số
( )
fx
liên tục trên
và
( )
0fx≠
với mọi
x ∈
;
( ) ( ) (
)
2
21fx x f x
′
= +
và
( )
1 0,5f = −
. Biết rằng tổng
( ) ( ) (
)
( )
1 2 3 ... 2017
a
ff f f
b
+ + ++ =
;
( )
,ab∈∈
với
a
b
tối giản. Mệnh
đề nào dưới đây đúng?
A.
1.ab
+=−
B.
( )
2017;2017 .a ∈−
C.
1.
a
b
<−
D.
4035.ba−=
Câu 9: Cho hàm số
( )
0fx≠
thỏa điều kiện
( ) ( )
(
)
2
2 3.fx x f x
′
= +
và
(
)
1
0
2
f
−
=
. Biết tổng
( ) ( ) ( ) (
)
1 2 ... 2017 2018
a
ff f f
b
+ ++ + =
với
,ab
∗
∈∈
và
a
b
là phân số tối giản. Mệnh đề nào sau
đây đúng?
A.
1.
a
b
<−
B.
1.
a
b
>
C.
1010.ab+=
D.
3029.
ba
−=
Câu 10: Cho hàm số
( )
,0y fx x= ∀≥
, thỏa mãn
( )
( ) (
) ( )
( ) (
)
2
3
.2 0
0 0; 0 1
f x f x f x xf x
ff
′′ ′
− +=


′
= =
. Tính
( )
1f
.
A.
2
.
3
B.
3
.
2
C.
6
.
7
D.
7
.
6
Câu 11: Cho hàm số
(
)
y fx=
đồng biến trên
( )
0; +∞
;
( )
y fx=
liên tục, nhận giá trị dương trên
(
)
0;
+∞
và thỏa mãn
( )
2
3
3
f
=
và
( ) ( ) ( )
2
1.f x x fx
′
= +


. Mệnh đề nào dưới đây đúng?
A.
( )
2
2613 8 2614.f<<
B.
( )
2
2614 8 2615.f<<
C.
(
)
2
2618 8 2619.
f<<
D.
(
)
2
2616 8 2617.
f<<
Câu 12: Giả sử hàm số
( )
y fx=
liên tục, nhận giá trị dương trên
( )
0;
+∞
và thỏa mãn
( )
11f =
,
( )
(
)
31
fx f x x
′
= +
, với mọi x > 0. Mệnh đề nào sau đây đúng?
A.
( )
4 5 5.f<<
B.
( )
2 5 3.f<<
C.
( )
3 5 4.f<<
D.
( )
1 5 2.f<<
Câu 13: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( ) ( )
1 2 13
5
1
fx x
dx C
x
x
+ ++
= +
+
+
∫
. Nguyên hàm
của hàm số
( )
2fx
trên tập
+
là:
A.
( )
2
3
.
24
x
C
x
+
+
+
B.
2
3
.
4
x
C
x
+
+
+
C.
( )
2
23
.
41
x
C
x
+
+
+
D.
( )
2
23
.
81
x
C
x
+
+
+
Câu 14: Cho hàm số
( )
fx
thỏa mãn
( )
2
0
cos
fx
t dt x x
π
=
∫
. Tính
( )
4f
.
A.
(
)
4 2 3.
f
=
B.
( )
4 1.f = −
C.
( )
1
4.
2
f =
D.
( )
3
4 12.f
=
Câu 15: Cho hàm số
( )
fx
có đạo hàm xác định, liên tục trên đoạn
[ ]
0;1
đồng thời thỏa mãn các điều kiện
( )
01f
′
= −
và
( )
( )
2
fx f x
′ ′′
=


. Đặt
( ) ( )
10Tf f= −
. Hãy chọn khẳng định đúng?
A.
2 1.T− ≤ <−
B.
1 0.
T−≤ <
C.
0 1.T
≤<
D.
1 2.T≤<
Câu 16: Cho hàm số
( )
2
1
1
x
G x t dt= +
∫
. Tính
(
)
Gx
′
.
A.
2
.
1
x
x+
B.
2
1.x+
C.
2
1
.
1 x+
D.
( )
22
1 1.
xx++
Câu 17: Cho hàm số
( ) ( )
2
1
sin 0
x
G x t dt x
= >
∫
. Tính
( )
Gx
′
.
A.
sin .x
B.
sin
.
2
x
x
C.
2sin
.
x
x
D.
sin .x
Câu 18: Tính đạo hàm của
( )
fx
, biết
( )
fx
thỏa
(
)
( )
0
.
x
ft fx
te e=
∫
.
A.
( )
.fx x
′
=
B.
( )
2
1.fx x
′
= +
C.
( )
1
.
fx
x
′
=
D.
( )
1
.
1
fx
x
′
=
−
Câu 19: Cho hàm số
( )
y fx=
liên tục trên
[
)
0; +∞
và
( ) ( )
2
0
sin
x
f t dt x x
π
=
∫
. Tính
( )
4f
.
A.
(
)
1
.
4
f
π
π
−
=
B.
(
)
.
2
f
π
π
=
C.
(
)
.
4
f
π
π
=
D.
( )
1
.
2
f
π
=
Câu 20: Cho hàm số
( )
fx
xác định trên
{ }
\0
, thỏa mãn
(
)
(
)
35
1
,1fx f a
xx
′
= =
+
và
( )
2.fb−=
Tính
( ) ( )
12ff−+
.
A.
( ) (
)
12 .f f ab− + =−−
B.
( ) ( )
12 .f f ab−+ =−
C.
( ) ( )
12 .f f ab−+ =+
D.
( ) ( )
12 .f f ba−+ =−
Câu 21: Cho hàm số
( )
y fx=
xác định và liên tục trên
thỏa mãn đồng thời các điều kiện
( ) ( ) (
)
2
0, ; ,
x
f x x f x ef x x
′
> ∀∈ =− ∀∈
và
( )
1
0
2
f
=
. Tính giá trị của
( )
ln 2f
.
A. 1. B.
4
.
3
C.
1
.
3
D.
2
.
3
Câu 22: Cho hàm số
( )
y fx=
có đồ thị (C), xác định và liên tục trên
thỏa mãn đồng thời các điều kiện
( )
( ) ( )
( )
2
0, , . ,fx x f x xfx x
′
> ∀∈ = ∀∈
và
( )
02f =
. Phương trình tiếp tuyến tại điểm có hoành độ
1
x =
của đồ thị (C) là
A.
6 30.yx= +
B.
6 30.yx
=−+
C.
36 30.yx
= −
D.
36 42.
yx=−+
Câu 23: Cho hàm số
( )
0
y fx= >
xác định, có đạo hàm trên đoạn
[ ]
0;1
và thỏa mãn:
( )
(
)
0
1 2018
x
g x f t dt
= +
∫
,
( ) ( )
2
gx f x=
. Tính
( )
1
0
g x dx
∫
.
A.
1011
.
2
B.
1009
.
2
C.
2019
.
2
D.
505.
Câu 24: Cho hàm số
( )
fx
có đạo hàm xác định, liên tục trên đoạn
[ ]
0;1
đồng thời thỏa mãn các điều kiện
( )
01f
′
= −
và
( ) ( )
2
fx f x
′ ′′
=


. Đặt
( ) ( )
10Tf f= −
. Hãy chọn khẳng định đúng?
A.
2 1.T− ≤ <−
B.
1 0.
T
−≤ <
C.
0 1.T≤<
D.
1 2.T≤<
LỜI GIẢI CHI TIẾT
Câu 1:
( ) (
)
( )
( )
1
2
ln 1 khi 1
1
ln 1 .
11
ln 1 khi 1
xC x
dx
f x fx x C
xx
xC x
−+ >
′
= ⇒ = = −+ =
−−
−+ <
∫
Do
( )
2
0 2017 2017fC
= ⇒=
;
( )
1
2 2018 2018fC= ⇒=
Suy ra
(
)
ln 2 2018 ln 2017 1S
= + −+ =
. Chọn A.
Câu 2:
(
)
( )
2
21f x x fx x x C
′
= +⇒ = + +
Do
( ) ( )
2
15 3 3f C fx x x=⇒ =⇒ = ++
Khi đó
( )
2
21 22
1
5 2 0 log log 1
2
x
fx x x S x x
x
=
=⇔ +−=⇔ ⇒ = + =
= −
. Chọn A.
Câu 3:
( ) (
)
( )
( )
1
2
1
ln 3 1 khi
33
3
ln 3 1 .
1
31 31
ln 1 3 khi
3
xC x
dx
f x fx x C
xx
xC x
−+ >
′
= ⇒ = = −+ =
−−
−+ <
∫
Do
( )
2
01 1fC=⇒=
;
1
2
22
3
fC

=⇒=


Khi đó
( ) ( )
1 3 ln 4 1 ln 8 2 3 5 ln 2ff− + = ++ + = +
. Chọn A.
Câu 4:
( )
2
11 1 1 2
ln .
232131
dx x
f x dx C
xx x x x
−

= = −= +

+− − + +

∫∫
( )
1
2
3
12
ln khi 2
31
1 2 12
ln ln khi -1< 2.
31 3 1
12
ln khi 1
31
x
Cx
x
xx
fx C C x
xx
x
Cx
x
−
+>
+
−−

⇒ = += + <

++

−
+ <−
+
Khi đó:
( ) ( )
15
3 4 ln
34
ff−− −=
;
( ) ( )
18
4 3 ln
35
ff
−=
( )
( ) ( )
( ) (
) ( )
1
3 4 4 3 ln 2 4 4 ln 2
3
f f ff f f−− −+ − = ⇒ −− =−
Mặt khác
( ) ( ) ( )
11 111
1 0 ln 1 ln
34 334
ff f−= ⇒=+
Do đó
( )
( ) ( )
18
4 1 4 1 ln
35
f ff
−+ − =+
. Chọn D.
Câu 5:
( ) ( ) ( )
( )
( )
( )
( )
( )
2
22
''
' 24 0 24 24.
fx fx
f x x f x x dx x dx
fx fx
−−
+ + =⇔ = +⇔ = +
∫∫
( )
( )
( )
(
)
(
)
22
22
11
44
4
dfx
x xC x xC fx
fx
f x x xC
⇔− = + +⇔ = + +⇔ =
++
∫
Mặt khác
( ) (
)
2
11 1
23
12 15
43
f C fx
C
xx
= = ⇒=⇒ =
+
++
Suy ra
(
) (
)
( )
7
123
30
ff f++=
. Chọn D.
Câu 6: Ta có
( )
( )
( ) ( ) ( )
6 62
12 13 6 13f x f x dx x dx f x df x x x C
′
= + ⇔ =++
∫ ∫∫
( )
7
2
6 13
7
fx
x xC⇒ =++
Lại có
( )
02f =
nên
7
2 222
24 26
77
CC
= + +⇒=−
Suy ra
( )
2
7
222
7 6 13
7
fx x x

= +−


do đó
( )
3fx=
có 2 nghiệm phân biệt. Chọn A.
Câu 7: Lấy nguyên hàm 2 vế của biểu thức
( )
( )
22
fx
x
fx
′
= −
ta được:
( )
( )
( )
( )
( )
( ) ( )
( )
22
2 2 2 ln 2 0
dfx
fx
dx x dx x x C f x x x C Do f x
fx fx

′

= − ⇔ = −+⇔ = −+ >


∫∫ ∫
Do
( ) ( ) ( )
2
2
0 1 ln 0 0 .
xx
f f C C fx e
−
=⇒ =⇔=⇒ =


Lại có:
( ) ( )
2
2
22. 0 1
xx
f x xe x
−
′
= − =⇔=
(
) ( )
lim lim 0
xx
fx fx
→−∞ →+∞
= =
và
( )
1fe=
Suy ra phương trình
( )
fx m
=
có 2 nghiệm thực phân biệt khi
0 me<<
. Chọn C.
Câu 8:
( ) (
) ( )
( )
( )
( )
( )
( )
2
22
''
' 21 21 21.
fx fx
f x x f x x dx x dx
fx fx
= + ⇔ = +⇔ = +
∫∫
( )
(
)
( )
( )
(
)
22
22
11
dfx
x xC x xC fx
fx
f x x xC
−−
⇔ = ++ ⇔ = ++ ⇔ =
++
∫
mà
( )
1
10
2
fC
−
= ⇒=
Khi đó
(
)
( ) ( )
2
1 11 1 1 1
1 1 ;...; 2017 .
1 2 2017 2018
fx f f
xx
xx
−= =−⇒=− = −
+
+
Vậy
504
1 1 1 1 1 1 504
P ...
1009
2 3 3 4 2017 2018 1009
a
b
= −
−

=− −+−++ − = ⇒

=

. Chọn B.
Câu 9:
( ) ( ) ( )
( )
( )
( )
( )
( )
2
22
''
' 23 23 23.
fx fx
f x x f x x dx x dx
fx fx
= + ⇔ = +⇔ = +
∫∫
(
)
( )
( )
( )
( )
22
22
11
33
3
dfx
x xC x xC fx
fx
f x x xC
−−
⇔ = + +⇔ = + +⇔ =
++
∫
mà
( )
1
0 2.
2
fC
−
= ⇒=
Khi đó
( ) ( )
( )
2
1 1 1 11 1 1
1 ;...; 2018 .
1 2 2 3 2019 2020
32
fx f f
xx
xx
− = = − ⇒− = − − = −
++
++
Vậy
1 1 1 1 1 1 1009
P ...
2 3 3 4 2019 2020 2020
−

=− −+−++ − =


. Chọn D.
Câu 10:
( ) ( ) ( )
( )
( ) ( ) ( )
( )
( )
2
2
3
3
.2
.2 0
f xfx f x
f x f x f x xf x x
fx
′′ ′
−


′′ ′
− + =⇔ =−∗


Lại có:
( )
( )
( ) ( ) ( ) ( )
(
)
( ) ( ) ( )
( )
22
2
24 3
. 2. . 2f xf x fx f x f xfx f x
fx
fx fx fx
′
′′ ′ ′′ ′
−−
 
′

 
= =



Do đó lấy nguyên hàm 2 vế của
( )
∗
ta được:
( )
( )
( )
( )
( )
22
22
22
dfx
f x dx
xx
CC
fx fx
′
−−
= +⇔ = +
∫∫
( )
2
1
2
x
C
fx
−−
⇔=+
. Do
( )
( )
( )
22
2
1 22
01 1 1 .
22
2
xx
f C fx
fx
x
− − −−
= ⇒− = ⇒ = − = ⇒ =
+
Do đó
( )
2
1
3
f =
. Chọn A.
Câu 11:
( )
( )
( ) (
) (
) (
)
( )
( )
(
)
2
1 1 1 .
fx
f x x fx f x x fx x
fx
′
′′
=+ ⇔=+ ⇔ =+ ∗


Lấy nguyên hàm hai vế của
(
)
,
∗
ta được:
(
)
( )
( )
(
)
( )
( )
3
2
1 2. 1
3
2
dfx
fx
dx x dx dx x C
fx fx
′
= + ⇔ = ++
∫∫ ∫
(
)
( )
3
2
21
3
fx x C⇔ = ++
mà
( ) ( )
2
2 2 2 6 16
3 23 4 .
33 3
f f CC
−
=⇒ = +⇒=
Do đó
( ) (
) ( )
( )
2
33
1 68 1 68
1 1.
33 33
fx x fx x

−−
= ++ ⇒ = ++


Vậy
( )
2
2613 8 2614f<<
. Chọn A.
Câu 12:
( )
( )
( )
( )
1
31
31
fx
fx f x x
fx
x
′
′
= +⇒ =
+
Lấy nguyên hàm 2 vế ta được
( )
( )
( )
( )
31
22
ln 3 1
33
31 231
dfx
dx
dx
fx x C
fx
xx

+

= = ⇔ = ++
++
∫∫∫
Thay
44
1 ln1
33
x CC=⇒ =+⇒=−
Thay
( )
( )
4
3
84 4
5 ln 5 5 3, 8
33 3
x f fe
=⇒ =−=⇒ = ≈
. Chọn C.
Câu 13: Đặt
2
11t x xt= +⇒ = −
. Khi đó
( ) ( )
1 2 13
5
1
fx x
dx C
x
x
+ ++
= +
+
+
∫
( )
( )
( )
(
)
(
)
(
)
2
2 22
23 23
3
12
4 44
ft t t
t
d t C f t dt C f t dt C
t
t tt
++
+
⇒ −= +⇔ = +⇔ = +
+ ++
∫ ∫∫
Do đó
( ) ( ) ( )
( )
2
2
23 23
22 2
44
81
xx
f xd x C f xdx C
x
x
++
= +⇒ = +
+
+
∫∫
. Chọn D.
Câu 14: Ta có
(
)
( )
(
)
( )
3
3
2
0
0
cos .cos .cos .
33
fx
fx
fx
t
tdtxx xx xx
ππ π
= ⇔= ⇔ = ∗
∫
Thay
4x
=
vào biểu thức
(
)
∗
, ta được
( )
( ) ( )
3
3
3
4
4 4 12 4 12
3
f
ff=⇔ =⇔=
. Chọn D.
Câu 15: Ta có
( ) ( )
( )
( )
( )
( )
2
22
'1
''
fx fx
f x f x dx dx x C
fx fx
′′ ′′
′′
=⇔=⇔ ==+


 
 
∫∫
( )
( )
11
'
'
xC f x
fx xC
⇔− = + ⇔ =−
+
mà
( )
'0 1 1
fC= − → =
Do đó
( )
( )
( )
( )
11
00
11
' ' 1 0 0,693
11
f x f x dx f f dx
xx
=− ⇔ = − = − ≈−
++
∫∫
. Chọn B.
Câu 16: Gọi
( )
Ft
là nguyên hàm của hàm số
(
)
2
1.ft t
= +
Ta có
( ) ( ) ( ) ( )
( ) ( ) ( )
2
0
10 .
x
Gx tdt Fx F G x Fx F x f x
′
′′
= + = − → = = =


∫
Lại có
( )
2
1fx x= +
nên suy ra
( )
2
1Gx x
′
= +
. Chọn B.
Câu 17: Gọi
( )
Ft
là nguyên hàm của hàm số
( )
2
sinft t=
.
Ta có
( )
( )
( )
( )
( )
( )
(
)
2
0
'
sin 0 .
22
x
F x fx
Gx tdtFxF Gx Fx
xx
′

′
= = − → = = =

∫
Lại có
( ) ( )
2
sin sinfx x x= =
nên suy ra
( )
sin
.
2
x
Gx
x
′
=
Chọn B.
Câu 18: Ta có
( ) ( ) ( )
(
)
( )
( )
0
. .. .
x
ft fx fx fx
te dt e xe fxe fx x
′′
=⇔= ⇔=
∫
Chọn A.
Câu 19: Ta có
( ) ( )
( ) ( )
2
22
0
.sin . sin .cos
x
f t dt x x x f x x x x
π ππ π
′

′
′
=⇔=+



∫
( )
2
2 . sin .cos .xf x x x x
ππ π
⇔=+
Thay
4x =
vào hai vế, ta được
( ) ( )
44 4
4
ff
π
π
=⇔=
. Chọn C.
Câu 20: Ta có
(
)
( )
(
)
1
2
12f f f x dx
−
−
′
−− − =
∫
và
( )
(
) ( )
2
1
21 .
f f f x dx
′
−=
∫
(
) ( ) ( ) (
) (
)
( )
12
21
12 21f f f x dx f x dx f f a b
−
−
′′
⇒ −+ = + + −+ =+
∫∫
. Chọn C.
Câu 21:
( ) (
)
( )
( )
( )
( )
2
22
..
x xx
fx fx
f x e f x e dx e dx
fx fx
′′
′
=− ⇔− = ⇔ − =
∫∫
( )
( )
11
x
x
e C fx
fx
eC
⇔ = +⇔ =
+
mà
( )
1
0 1.
2
fC= → =
Do đó
(
)
( )
ln 2
1 1 11
ln 2
1 1 21 3
x
fx f
ee
= → = = =
+ ++
. Chọn C.
Câu 22:
( )
( )
(
)
(
)
(
)
(
)
22 2 2
22
.
fx fx
f x x f x x dx x dx
fx fx
′′
′
= ⇔=⇔ =
∫∫
( )
(
)
3
3
11
3
3
x
C fx
fx
x
C
⇔− = + ⇔ =−
+
mà
(
)
1
02
2
fC=⇒=−
.
Do đó
( )
( )
( )
3
1 36
1
1
16
32
f
fx
x
f
′
=
=−→
=
−
nên phương trình tiếp tuyến là
36 30yx= −
. Chọn C.
Câu 23: Ta có
( )
01g =
và
( ) ( ) ( ) (
) ( )
1
1 2018 2018 2018
x
gx ftdt g x f x gx
′
=+ ⇒= =
∫
( )
( )
(
)
( )
( )
00
2018 2018 2 1 2018
tt
gx gx
dx dx g t t
gx gx
′′

⇒ = ⇔ = ⇒ −=

∫∫
( )
1009 1.gt t⇒=+
Vậy
( )
1
0
1011
2
g t dt =
∫
. Chọn A.

Tài liệu khác của Toán 12

Preview text:

CHỦ ĐỀ 15: MỘT SỐ BÀI TOÁN CHỌN LỌC VỀ TÍCH PHÂN
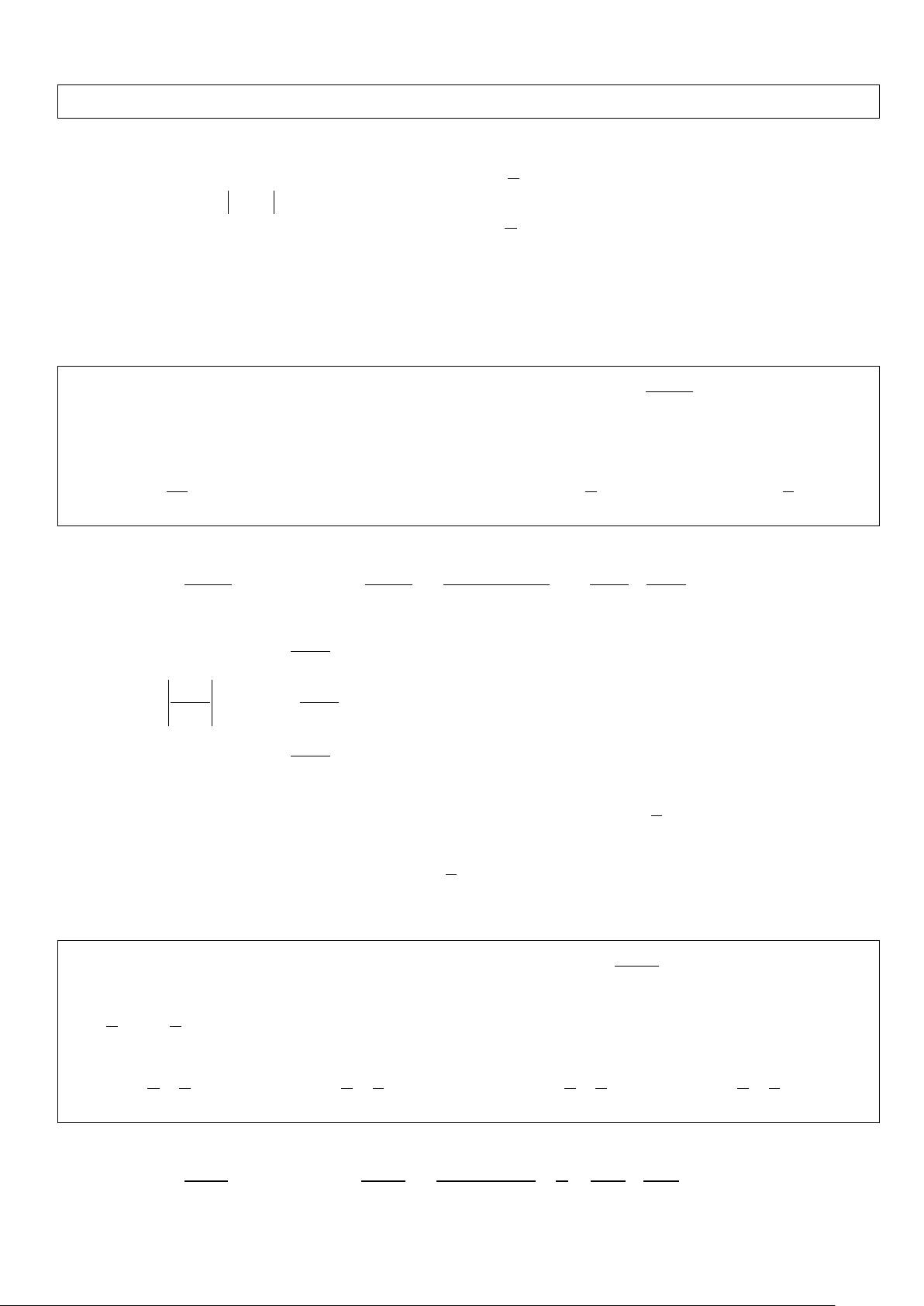
Ví dụ 1: Cho hàm số y = f (x) có đạo hàm liên tục trên đoạn [1;2] thỏa mãn
f (x) + x f ′(x) = x f (x) 2 . . +1   . Biết f ( ) 1 = 2 − , tính f (2) A. f ( ) 1 2 − − − = . B. f ( ) 1 2 = . C. f ( ) 3 2 = . D. f ( ) 3 2 = . 2 2 2 4 Lời giải: ′ 2 f x + . x f ′ x  . x f  (x)
Ta có f (x) + .x f (x) =  .x f  (x) ( ) ( ) +1 ⇔ = 1  ′ ⇔ = 1   . x f (x) 2 +1  . x f (x) 2 +1    
Lấy nguyên hàm 2 vế ta được: 1 − = x + C .x f (x) +1 Thay 1 x − = ⇒
= + C ⇒ C = ⇒ f (x) 1 − 1 = − ⇒ f ( ) 3 1 1 0 2 = − . Chọn D. 2 2 − +1 x x 4
Ví dụ 2: Cho hàm số y = f (x) xác định và liên tục trên đoạn [1; ] 3 và thỏa mãn −
x f (x) + x f ′(x) = x f (x) 2 2 3 . . . +1   ( x ∀ ∈[1; ] 3 ) và f ( ) 2 1 = . Khi đó: 3
A. 0 < f (3) < 1.
B. 1 < f (3) < 3.
C. f (3) > 3.
D. f (3) < 0. Lời giải:
Ta có: x f (x) + x f ′(x) = xf (x) 2
+  ⇔ x f (x) + x f ′(x) = xf (x) 2 2 3 2 . . 1 . +1      
f (x) + .x f ′(x) 1 .x f  (x) ′   1 ⇔ = ⇔ = xf  ( x) 2 2 +1 xxf   ( x) 2 2 +1 xd xf  ( x) +1
Lấy nguyên hàm 2 vế ta được:  1 1 − 1 = dx − ⇒ = + C ∫ ∫ xf  ( x) 2 2 +1 x xf (x) +1 x  Lại có: f ( ) 2 − 1 − 1 1 C C − = ⇒ = − + ⇒ = + = − 3 1. f ( ) 1 1 2 1 +1 2 − +1 3 Do đó 1 1 − = + , thay 1 1 4 x = 3 ⇒ = + 2 ⇒ f 3 = . Chọn D. x f (x) 2 . +1 x 3. f (3) ( ) +1 3 21
Ví dụ 3: Cho hàm số y = f (x) đồng biến và luôn dương trên đoạn [1; ] 3 đồng thời thỏa mãn  f ′  ( x) 2  =  ( 4 2
x + 3x ) f (x), biết f ( ) 1 = 4. Khi đó
A. 0 < f (2) < 3.
B. 3 < f (2) < 5.
C. 5 < f (2) < 9.
D. f (2) > 9. Lời giải: 2  f ′  ( x) 2  Ta có:  f ′  ( x) =  ( 4 2
x + x ) f (x)  2 ⇒ = x ( 2 3 x + 3) f (x) f ′(x) 2 ⇔
= x x + 3 (do f (x) > 0 x ∀ ∈[1;2]) f (x) d f  ( x)
Lấy nguyên hàm 2 vế ta được:  2
= x x + 3dx ⇔ 2 f ∫ ∫ (x) 1 2 = x + 3dx ∫ ( 2x +3) f (x) 2 ⇔ f (x) 1 2 = (x + )3 1 . 3 + C = (x +3)3 2 2 + C 4 3 6 8 2 (x + )3 2 3
Do f ( ) = ⇒ = + C ⇒ C = ⇒ f (x) 2 1 4 2 = + . 6 3 6 3   ( x ) 2 3 2 3  + f (x) 2 ⇒ = + ⇒ f (2) ≈ 14,1  . Chọn D. 6 3    
Ví dụ 4: Cho hàm số f (x) có đạo hàm xác định, liên tục [0; ]
1 đồng thời thỏa mãn các điều kiện f ′(0) = 1 − và  ′  ( ) 2
f x  = f ′′ 
(x). Đặt T = f ( )
1 − f (0) , hãy chọn khẳng định đúng? A. 2 − ≤ T < 1. − B. 1 − ≤ T < 0.
C. 0 ≤ T < 1.
D. 1 ≤ T < 2. Lời giải: f ′′ x Ta có:  f ′  ( x) 2  = f ′′  (x) ( ) ⇒ = 1  f ′(x) 2    d f ′  ( x)
Lấy nguyên hàm 2 vế ta có:  1 − 1 = dx ⇔
= x + C ⇒ f ′ x − = ∫ ∫  f ′  ( x) f ′(x) ( ) 2 x + C  Do f ′(0) = 1 − ⇒ C = 1 1 1 Suy ra f ∫ (x) 1 dx − ′ = dx ⇔ f ∫ ( )
1 − f (0) = −ln 2 . Chọn B. x +1 0 0
Ví dụ 5: Cho hàm số f (x) liên tục và đồng biến trên đoạn [0; ]
1 , biết f (0) = 1 và  f ′  ( x) 2 3
+ 2x = 9x + 9 . x f  (x) x ∀ ∈[0; ]
1 . Mệnh đề nào dưới đây đúng A. f ( ) 1 = 3. B. f ( ) 1 = 5. C. f ( ) 1 = 6. D. f ( ) 1 = 4. Lời giải: 2 2
f ′ x + 2xf ′ x +   2x 3 ( ) Ta có:  f ′
 ( x) + 2x = 9x + 9 . x f  (x) ( ) ⇔ = ⇔ = f (x) 9x 3 x 2 + x f (x) 2 + x
d f (x) 2 + x
Lấy nguyên hàm 2 vế ta được   = 3 xdx ∫ ∫ f (x) 2 + x ⇔ f (x) 2 3 + x =
x + C ⇔ f (x) 2 3 2 2 2
+ x = x + C
Thay x = ⇒ C = ⇒ f (x) 2 3 0 1 + x = x +1. 2
Suy ra f (x) = ( 3x + ) 2
1 − x ⇒ f ( ) 1 = 3. Chọn A.
Ví dụ 6: Cho hàm số f (x) liên tục thỏa mãn ( f ′(x))2 + f (x) f ′′(x) 4 .
= 15x +12x, x ∀ ∈  và
f (0) = f ′(0) = 1. Giá trị của 2 f ( ) 1 bằng A. 8. B. 9 . C. 10. D. 5 . 2 2 Lời giải: Ta có:  f
 ( x) f ( x) ′ ′  =  f ′   ( x) 2  + f
(x) f ′′(x) 4 . . = 15x +12x 5
Nguyên hàm 2 vế ta được f (x). f ′(x) 15x 2 5 2 =
+ 6x + C = 3x + 6x + C 5
Do f (0) = f ′(0) = 1 ⇒ C = 1
Tiếp tục nguyên hàm 2 vế ta được: f (x)df (x) = ( 5 2 3x + 6x + ∫ ∫ )1dx 2 f (x) 6 3 3x 6x 1 6 3 ⇒ = +
+ x + D = x + 2x + x + D . Do f (0) 1 2
= 1 ⇒ D = ⇒ f ( ) 1 = 8 . Chọn A. 2 6 3 2 2
Ví dụ 7: Cho hàm số y = f (x) có đạo hàm liên tục và luôn dương trên đoạn [1; ] 3 thỏa mãn f ( ) 1 = f ′( )
1 = 1và f ′′(x) f (x) 2 = f ′ (x) 2 2 .
− x . f (x) . Giá trị của ln  f (3) 
 thuộc khoảng nào trong các khoảng sau: A. (1;6). B. (7;12). C. (0; ) 1 . D. (12;15). Lời giải:
Ta có: f ′′(x) f (x) 2 = f ′ (x) 2 2
− x f (x) ⇔ f ′′(x) f (x) 2 − f ′ (x) 2 2 . . . = x f (x)
f ′′(x). f (x) 2 − f ′ (x) 2 ⇔ = x ∗ 2 f (x) ( )  f (x) ′ ′ 
f ′′(x). f (x) 2 − f ′ (x) Mặt khác   =
, lấy nguyên hàm 2 vế của (∗) ta được: f  ( x) 2  f (x) f ′(x) 3 x ( ) = + C f x 3 4   Do f ( ) x 2 = f ′( ) 2 1
1 = 1 ⇒ C = . Tiếp tục nguyên hàm 2 vế ta được: ln ( ) x f x =  +  + D 3  12 3  4 Do f ( ) 3 = ⇒ D = − ⇒ f (x) x 2x 3 1 1 ln = + − ⇒ ln  f  (3) = 8 4 12 3 4  . Chọn B.
Ví dụ 8: Cho hàm số f (x) có đạo hàm liên tục trên đoạn [0; ] 1 thỏa mãn 1 1 1 f ( ) =  f ′ ∫ 2  ( x) 2 9 1 1,  dx =  và f
∫ ( x)dx = . Tính tích phân I = f ∫ (x)dx . 5 5 0 0 0 A. 3 I = . B. 1 I = . C. 3 I = . D. 1 I = . 5 4 4 5 Lời giải:
x = 0 ⇒ t = 0 Đặt 2
t = x ⇔ t = x ⇔ dx = 2tdt và  .
x = 1 ⇒ t = 1 1 1 1 1 Khi đó: f
∫ ( x)dx = t f ∫
(t)dt = x f ∫ (x) 2 dx = ⇔ x f ∫ (x) 1 2 . 2 . . dx = . 5 5 0 0 0 0  = ′ u  = f (x)
du f (x)dx 1 1 2 1 1  x . f x Đặt  ⇔  ⇒ .x f ∫ (x) ( ) 1 2 dx = − x . f ′ ∫ (x) 2 3 2
dx ⇒ x . f ′ ∫ (x)dx = . x dv = xdxv = 2 2 5 0 0 0 0  2 2 1 1 1 1 Xét  f ′
∫ (x) + kx dx =  f ′   ∫ (x) 2 2 2
dx + 2k x . f ′  ∫ (x) 2 4 9 6 1 2
dx + k x dx = + k + k = 0 ⇔ k = 3. − ∫ 5 5 5 0 0 0 0 Do đó f ′(x) 2
− x = ⇔ f ′(x) 2
= x ⇒ f (x) = f ′ ∫ (x) 3 3 0 3
dx = x + C mà f ( ) 1 = 1 ⇒ C = 0. 1 1 4 Vậy f (x) 3 3 x 1 = x  → I = x dx = = ∫ . Chọn B. 4 4 0 0
Ví dụ 9: Cho hàm số y = f (x) có đạo hàm liên tục trên đoạn [0; ]
1 và f (0) + f ( ) 1 = 0 . Biết rằng tích 1 1 1 phân 2 π f (x) 1 dx = , f ′
∫ (x).cosπ xdx = ∫ . Tính tích phân f ∫ (x)dx? 2 2 0 0 0 A. 3π . B. 2 . C. π. D. 1 . 2 π π Lời giải: 1 1 1 Ta có f
∫ (x).cosπ xdx cosπ xd ∫
( f (x)) f (x) 1 .cosπ x f
∫ (x).(cosπ x)′ ′ = = − dx 0 0 0 0 1 1 π = −  f
 ( ) + f ( ) + π f
∫ (x) π xdx = ⇒ f ∫ (x) 1 1 0 .sin .sinπ xdx = . 2 2 0 0 1 1 1 1 Xét  f ∫ (x) 2 2
+ k.sinπ xdx = 0 ⇔ f
∫ (x)dx + 2k. f ∫ (x) 2 2
.sinπ xdx + k . sin ∫ (π x)dx = 0 0 0 0 0 1 1 2 1 1
⇔ k + 2k. + = 0 ⇔ (k + )2 1 = 0 ⇔ k = 1. − Suy ra  f ∫ (x) 2
− sinπ xdx = 0. 2 2 2  0 1 1 Vậy f (x) =
π x ⇒ f (x) 2 sin dx = sinπ xdx = ∫ ∫ . Chọn B. π 0 0
Ví dụ 10: Cho hàm số f (x) có đạo hàm liên tục trên đoạn [0; ]
1 , f (x) và f ′(x) luôn nhận giá trị dương 1 1 2 trên đoạn [0; ]
1 và thỏa mãn f (0) = 1;  2 f ′ ∫
(x) f (x)  2 + x dx = 4 . x f ′ ∫
(x) f (x)dx   . Tính f ( ) 1 ? 0 0 A. f ( ) 3 1 = 4. B. f ( ) 1 = 2. C. f ( ) 1 = 1. D. f ( ) 1 = 4. Lời giải: 1
Giả thuyết tương đương với  f ' ∫ (x) f (x) 2 2 − xdx = 0   0 2
⇔ f (x) f (x) 2 '
− x = 0 ⇔ f '(x) f (x) = x ⇔ f ′(x). f (x) = x
Nguyên hàm 2 vế ta được: 2 3 f (x) 2 3 = x + C 3 3 Mặt khác f (0) 2 3
= 1 ⇒ C = ⇒ f (x) 3 = x +1 3 Vậy f ( ) 3 1 = 4. Chọn A.
Ví dụ 11: Cho hàm số f (x) xác định trên 1 2  \  
thỏa mãn f ′(x) =
, f (0) =1 và f ( ) 1 = 2. Giá 2   2x −1
trị của biểu thức f (− ) 1 + f (3) bằng A. 4 + ln 5. B. 2 + ln15. C. 3+ ln15. D. ln15. Lời giải:  ( x − ) 1 ln 2
1 + C khi x >  1 Ta có f ′ ∫ (x)  2
dx = ln 2x −1 C + =  .  ( − x) 1
ln 1 2 + C khi x < 2  2 C  = 1
Do f (0) = 1 và f ( ) 1 1 = 2 ⇒  ⇒ f (− )
1 + f (3) = ln 3 + ln 5 + C + C = 3 + ln15. Chọn C. 1 2 C =  2 2
Ví dụ 12: Cho hàm số f (x) xác định trên 4  \ { 2; − }
2 và thỏa mãn f ′(x) = ; f ( 3 − ) = 0 ; f (0) = 1 2 x − 4
và f (3) = 2 . Tính giá trị biểu thức P = f ( 4 − ) + f (− ) 1 + f (4) . A. 3 P = 3 + ln B. P = 3 + ln 3 C. 5 P = 2 + ln D. 5 P = 2 − ln 25 3 3 Lời giải: Ta có: f (x) 4 = ⇒ f ∫ (x) 4dx 4dx  1 1 dx = = = − ∫ ∫ ∫ dx  ′ ′ 2 2 x − 4 x − 4 (x 2)(x 2)  x 2 x 2  − + − +   x − 2 ln
+ C khi x > 2  1 x + 2  ( ) x − 2   2 ln ln − x f x C  ⇒ = + = + 
C khi − 2 < x < 2. 2 x + 2   x + 2   x − 2 ln
+ C khi x < 2 − 3  x + 2 Lại có: f ( 3
− ) = 0 ⇒ C = −ln 5; f (0) = 1 ⇒ C = 1; f ( ) 1
3 = 2 ⇒ C = 2 − ln . 3 2 1 5
Do đó P = f (− ) + f (− ) + f ( ) 1 4 1
4 = ln 3 + ln 3 + ln + C + C + C = 3 + ln 3. Chọn B. 1 2 3 3
Ví dụ 13: Cho hàm số f (x) xác định trên 1  \ { } 1
± thỏa mãn f ′(x) = . Biết f ( 3 − ) + f (3) = 0 và 2 x −1  1   1 f f  − + =  
  2 . Giá trị T = f ( 2
− ) + f (0) + f (4) bằng  2   2  A. 1 5 T = 2 + ln . B. 1 9 T =1+ ln . C. 1 9 T = 3+ ln . D. 1 9 T = ln . 2 9 2 5 2 5 2 5 Lời giải: Ta có: f (x) 1 = ⇒ f ∫ (x) dx dx 1  1 1 dx = = = − ∫ ∫ ∫ dx  ′ ′ 2 2 x −1 x −1 (x ) 1 (x ) 1 2  x 1 x 1 − + − +  1 x −1 ln
+ C khi x >1  1 2 x +1  ( ) 1 x −1 1 1 ln  ln − x f x C  ⇒ = + = + 
C khi −1 < x < 1. 2 2 x +1 2   x +1 1 x −1  ln
+ C khi x < 1 − 3 2 x +1  f ( 3 − ) + f (3) = 0  C  + C = 0 Theo bài ra ta có: 1 3   1   1 ⇔    f − +   f =   2
2C = 2 ⇒ C = 1 2 2   2   2 
Do đó T = f ( 2
− ) + f (0) + f (4) =  f  ( 2
− ) + f (4) + f  (0) 1 1 3 1 9
= ln 3 + C + ln + C + C = 1+ ln . Chọn B. 1 3 2 2 2 5 2 5 2 x
Ví dụ 14: Cho hàm số f (x) liên tục trên (0;+∞) và thỏa f
∫ (t)dt = .xcosπ x . Tính f (4). 0 A. f ( ) 1 4 = . B. f ( ) 1 4 = . C. f ( ) 3 4 = . D. f ( ) 3 4 = 12. 2 4 4 Lời giải: 2 x ′   Ta có  f
∫ (t)dt ( .xcosπ x)′ = ⇔ ( 2 x )′ . f ( 2
x ) = cosπ x −π .xsinπ x    0  ⇔ x f ( 2
2 . x ) = cosπ x −π .xsinπ .x Thay x = 2 vào 2 vế, ta được f ( ) = ⇔ f ( ) 1 4 4 1 4 = . Chọn B. 4 2 x
Ví dụ 15: Cho hàm số G(x) = cos tdt ∫
(x > 0) . Tính G′(x). 0
A. G′(x) 2 = x .cos . x
B. G′(x) = 2 .xcos .x
C. G′(x) = cos .x
D. G′(x) = cos x −1. Lời giải:
Gọi F (t) là nguyên hàm của hàm số f (t) = cos t. 2 x
Ta có G (x) = cos tdt = F ∫
( 2x)− F (0)→G′(x) = F  ( 2 x ) ′   = 2 .xF′ 
( 2x) = 2 .xf ( 2x). 0 Lại có f ( 2 x ) 2
= cos x = cos x nên suy ra G′(x) = 2 .xcos .x Chọn B.
BÀI TẬP TỰ LUYỆN
Câu 1: Cho hàm số f (x) xác định trên  \ { }
1 thỏa mãn f ′(x) 1 =
, f (0) = 2017 , f (2) = 2018. Tính x −1
S = f (3) − f (− ) 1 . A. S =1. B. S = ln 2. C. S = ln 4035. D. S = 4.
Câu 2: Cho hàm số f (x) xác định trên thỏa mãn f ′(x) = 2x +1 và f ( )
1 = 5 . Phương trình f (x) = 5
có hai nghiệm x , x . Tính tổng S = log x + log x . 1 2 2 1 2 2 A. S =1. B. S = 2. C. S = 0. D. S = 4.
Câu 3: Cho hàm số f (x) xác định trên 1  \  
thỏa mãn f ′(x) 3 = , f (0) = 1 và 2 f   =   2 . Giá trị 3   3x −1  3 
của biểu thức f (− ) 1 + f (3) bằng A. 3+ 5ln 2. B. 2 − + 5ln 2. C. 4 + 5ln 2. D. 2 + 5ln 2.
Câu 4: Cho hàm số f (x) xác định trên 1  \ { 2; − }
1 thỏa mãn f ′(x) = ; f ( 3
− ) − f (3) = 0 và 2 x + x − 2 f ( ) 1
0 = . Giá trị của biểu thức f ( 4 − ) + f ( ) 1 − f (4) bằng 3 A. 1 1 + ln 2. B. 1+ ln80. C. 1 4 1+ ln 2 + ln . D. 1 8 1+ ln . 3 3 3 5 3 5
Câu 5: Cho hàm số f (x) nhận giá trị dương, có đạo hàm liên tục trên (0;+∞) thỏa mãn f ( ) 1 2 = và 15
f ′(x) + ( x + ) 2 2
4 f (x) = 0. Tính f ( )
1 + f (2) + f (3) . A. 7 . B. 11. C. 11 . D. 7 . 15 15 30 30
Câu 6: Cho hàm số f (x) xác định và liên tục trên  . Biết 6
f (x). f ′(x) = 12x +13 và f (0) = 2. Khi đó
phương trình f (x) = 3 có bao nhiêu nghiệm? A. 2. B. 3. C. 7. D. 1.
Câu 7: Cho hàm số f (x) có đạo hàm liên tục trên  và thỏa mãn f (x) > 0, x
∀ ∈  . Biết f (0) = 1 và f ′(x)
( ) = 2 − 2x. Tìm các giá trị thực của tham số m để phương trình f (x) = m có hai nghiệm thực phân f x biệt.
A. m > .e
B. 0 < m ≤1.
C. 0 < m < .e
D. 1< m < .e
Câu 8: Cho hàm số f (x) liên tục trên  và f (x) ≠ 0 với mọi x ∈  ; f ′(x) = ( x + ) 2 2 1 f (x) và f ( ) 1 = 0,
− 5 . Biết rằng tổng ( )
1 + (2) + (3) + ... + (2017) a f f f f
= ; (a ∈, b∈) với a tối giản. Mệnh b b
đề nào dưới đây đúng?
A. a + b = 1. − B. a ∈( 2017 − ;2017). C. a < 1. −
D. b − a = 4035. b
Câu 9: Cho hàm số f (x) −
≠ 0 thỏa điều kiện f ′(x) = ( x + ) 2 2
3 . f (x) và f ( ) 1 0 = . Biết tổng 2 ( )
1 + (2) + ... + (2017) + (2018) a f f f f = với a , b ∗ ∈
∈  và a là phân số tối giản. Mệnh đề nào sau b b đây đúng? A. a < 1. − B. a >1.
C. a + b =1010.
D. b − a = 3029. b b
 f ′′(x) f (x) −  f ′  ( x) 2 3 . 2  + xf  (x) = 0
Câu 10: Cho hàm số y = f (x), x ∀ ≥ 0, thỏa mãn  . Tính f ( ) 1 .  f ′  (0) = 0; f (0) = 1 A. 2 . B. 3 . C. 6 . D. 7 . 3 2 7 6
Câu 11: Cho hàm số y = f (x) đồng biến trên (0;+∞); y = f (x) liên tục, nhận giá trị dương trên (0;+∞) và thỏa mãn f ( ) 2 3 = và  f ′  ( x) 2  =  (x + )
1 . f (x). Mệnh đề nào dưới đây đúng? 3 A. 2
2613 < f (8) < 2614. B. 2
2614 < f (8) < 2615. C. 2
2618 < f (8) < 2619. D. 2
2616 < f (8) < 2617.
Câu 12: Giả sử hàm số y = f (x) liên tục, nhận giá trị dương trên (0;+∞) và thỏa mãn f ( ) 1 = 1,
f (x) = f ′(x) 3x +1, với mọi x > 0. Mệnh đề nào sau đây đúng?
A. 4 < f (5) < 5.
B. 2 < f (5) < 3.
C. 3 < f (5) < 4.
D. 1< f (5) < 2. f ( x +1) 2( x +1 + 3)
Câu 13: Cho hàm số f (x) liên tục trên  và thỏa mãn dx = + C ∫ . Nguyên hàm x +1 x + 5
của hàm số f (2x) trên tập +  là: A. x + 3 + + + + C
B. x 3 + C.
C. 2x 3 + C.
D. 2x 3 + C. 2( . 2 x + 4) 2 x + 4 4( 2 x + ) 1 8( 2 x + ) 1 f (x)
Câu 14: Cho hàm số f (x) thỏa mãn 2
t dt = x cosπ x ∫ . Tính f (4) . 0 A. f (4) = 2 3. B. f (4) = 1. − C. f ( ) 1 4 = . D. f ( ) 3 4 = 12. 2
Câu 15: Cho hàm số f (x) có đạo hàm xác định, liên tục trên đoạn [0; ]
1 đồng thời thỏa mãn các điều kiện f ′(0) = 1 − và  ′  ( ) 2
f x  = f ′′ 
(x). Đặt T = f ( )
1 − f (0) . Hãy chọn khẳng định đúng? A. 2 − ≤ T < 1. − B. 1 − ≤ T < 0.
C. 0 ≤ T < 1.
D. 1 ≤ T < 2. x
Câu 16: Cho hàm số G(x) 2 = 1+ t dt ∫
. Tính G′(x). 1 A. x . B. 2 1+ x . C. 1 . D. ( 2 x + ) 2 1 x +1. 2 1+ x 2 1+ x x
Câu 17: Cho hàm số G(x) 2 = sin t dt ∫
(x > 0) . Tính G′(x). 1 A. sin .x B. sin x . C. 2sin x . D. sin x. 2 x x x
Câu 18: Tính đạo hàm của f (x) , biết f (x) thỏa f (t) f (x) t.e = e ∫ . 0
A. f ′(x) = .x
B. f ′(x) 2 = x +1.
C. f ′(x) 1 = .
D. f ′(x) 1 = . x 1− x 2 x
Câu 19: Cho hàm số y = f (x) liên tục trên [0;+∞) và f
∫ (t)dt = xsin(π x). Tính f (4). 0 A. π π π f (π ) −1 = . B. f (π ) = . C. f (π ) = . D. f (π ) 1 = . 4 2 4 2
Câu 20: Cho hàm số f (x) xác định trên 1  \ { }
0 , thỏa mãn f ′(x) =
, f 1 = a và f ( 2 − ) = . b Tính 3 5 ( ) x + x f (− ) 1 + f (2) . A. f (− )
1 + f (2) = −a − . b B. f (− )
1 + f (2) = a − . b C. f (− )
1 + f (2) = a + . b D. f (− )
1 + f (2) = b − . a
Câu 21: Cho hàm số y = f (x) xác định và liên tục trên  thỏa mãn đồng thời các điều kiện f (x) > x
∀ ∈  f ′(x) x 2 0, ;
= −e f (x), x ∀ ∈  và f ( ) 1
0 = . Tính giá trị của f (ln 2) . 2 A. 1. B. 4 . C. 1. D. 2 . 3 3 3
Câu 22: Cho hàm số y = f (x) có đồ thị (C), xác định và liên tục trên  thỏa mãn đồng thời các điều kiện f (x) > x
∀ ∈  f ′(x) = (x f (x))2 0, , . , x
∀ ∈  và f (0) = 2. Phương trình tiếp tuyến tại điểm có hoành độ
x =1 của đồ thị (C) là
A. y = 6x + 30. B. y = 6 − x + 30.
C. y = 36x − 30. D. y = 36 − x + 42.
Câu 23: Cho hàm số y = f (x) > 0 xác định, có đạo hàm trên đoạn [0; ] 1 và thỏa mãn: x 1
g (x) = 1+ 2018 f
∫ (t)dt , ( ) 2
g x = f (x) . Tính g (x)dx ∫ . 0 0 A. 1011. B. 1009 . C. 2019 . D. 505. 2 2 2
Câu 24: Cho hàm số f (x) có đạo hàm xác định, liên tục trên đoạn [0; ]
1 đồng thời thỏa mãn các điều kiện f ′(0) = 1 − và  ′  ( ) 2
f x  = f ′′ 
(x). Đặt T = f ( )
1 − f (0) . Hãy chọn khẳng định đúng? A. 2 − ≤ T < 1. − B. 1 − ≤ T < 0.
C. 0 ≤ T < 1.
D. 1 ≤ T < 2.
LỜI GIẢI CHI TIẾT 1 dx ln(x − )
1 + C khi x > 1
Câu 1: f ′(x) = ⇒ f (x) 1 =
= ln x −1 + C = x ∫ x  − −  ( − x) . 1 1 ln 1
+ C khi x < 1 2
Do f (0) = 2017 ⇒ C 2017 =
; f (2) = 2018 ⇒ C = 2018 2 1
Suy ra S = ln 2 + 2018 − (ln+ 2017) = 1. Chọn A.
Câu 2: f ′(x) = x + ⇒ f (x) 2 2 1
= x + x + C
Do f ( ) = ⇒ C = ⇒ f (x) 2 1 5 3 = x + x + 3 x = 1 Khi đó f (x) 2
= 5 ⇔ x + x − 2 = 0 ⇔
⇒ S = log x + log x =  1. Chọn A. 2 1 2 2 x = 2 −  ( x − ) 1
ln 3 1 + C khi x >  1
Câu 3: f ′(x) 3 = ⇒ f (x) 3dx  3 =
= ln 3x −1 + C = ∫  . 3x −1 3x −1 ln(1− 3x) 1 + C khi x < 2  3
Do f (0) =1⇒ C =1;  2 f  = 2 ⇒ C =   2 2 1  3  Khi đó f (− )
1 + f (3) = ln 4 +1+ ln8 + 2 = 3 + 5ln 2 . Chọn A.
Câu 4: f (x) dx 1  1 1  1 x − 2 = = − dx = ln + ∫ ∫  C. 2
x + x − 2 3  x − 2 x +1 3 x +1 1 x − 2 ln
+ C khi x > 2  1 3 x +1  ( ) 1 x − 2 1  2 ln  ln − x f x C  ⇒ = + = + 
C khi -1< x < 2. 2 3 x +1 3   x +1  1 x − 2  ln
+ C khi x < 1 − 3 3 x +1
Khi đó: f (− ) − f (− ) 1 5 3
4 = ln ; f ( ) − f ( ) 1 8 4 3 = ln 3 4 3 5
f (− ) − f (− ) + f ( ) − f ( ) =
⇒ f (− ) − f ( ) 1 3 4 4 3 ln 2 4 4 = − ln 2 3
Mặt khác f ( ) − f ( ) 1 1 = ⇒ f ( ) 1 1 1 1 0 ln 1 = + ln 3 4 3 3 4
Do đó f (− ) + f ( ) − f ( ) 1 8 4 1 4 = 1+ ln . Chọn D. 3 5 − f ' x − f ' x 2 ( )
Câu 5: f '(x) + (2x + 4) f (x) ( ) = 0 ⇔ = 2x + 4 ⇔ dx = 2x + 4 . dx 2 f (x) ∫ 2f(x) ∫( )
d ( f (x)) 2 1 2 1 ⇔ −
= x + 4x + C ⇔
= x + 4x + C ⇔ f x = ∫ 2 f (x) f (x) ( ) 2
x + 4x + C Mặt khác f ( ) 1 1 = =
⇒ C = ⇒ f (x) 1 2 3 = 2 12 + C 15 x + 4x + 3
Suy ra f ( ) + f ( ) + f ( ) 7 1 2 3 = . Chọn D. 30 Câu 6: Ta có 6 f
∫ (x) f ′(x)dx = ∫( x+ ) 6 dx ⇔ f
∫ (x)df (x) 2 12 13
= 6x +13x + C 7 f (x) 2 ⇒
= 6x +13x + C 7 7
Lại có f (0) = 2 nên 2 222
= 24 + 26 + C ⇒ C = − 7 7 Suy ra f (x)  2 222 
= 7 7 6x +13x − 
do đó f (x) = 3 có 2 nghiệm phân biệt. Chọn A. 7    f ′(x)
Câu 7: Lấy nguyên hàm 2 vế của biểu thức ( ) = 2−2x ta được: f x f ′(x) d f x    2 2
dx = 2 − 2x dx ⇔
= 2x − x + C ⇔ ln  f x  = 2x − x + C ∫ ∫ ∫   (Do 0 f x > ) f (x) ( ) ( ) f (x) ( ) ( ) Do ( )  ( )   ( ) 2 2 0 1 ln 0 0 x x f f C C f x e − = ⇒ = ⇔ = ⇒ = . Lại có: ′( ) = ( − ) 2 2 2 2 . x−x f x x e = 0 ⇔ x = 1
lim f (x) = lim f (x) = 0 và f ( ) 1 = e x→−∞ x→+∞
Suy ra phương trình f (x) = m có 2 nghiệm thực phân biệt khi 0 < m < e . Chọn C. f ' x f ' x 2 ( )
Câu 8: f '(x) = (2x + ) 1 f (x) ( ) ⇔ = 2x +1 ⇔ dx = 2x +1 . dx 2 ∫ ∫ f (x) 2 f (x) ( )
d ( f (x)) 2 1 − 2 1 x x C x x C f x − − ⇔ = + + ⇔ = + + ⇔ = ∫ mà f ( ) 1 1 = ⇒ C = 0 2 f (x) f (x) ( ) 2 x + x + C 2
Khi đó − f (x) 1 1 1 = = − ⇒ f ( ) 1 = − f ( ) 1 1 1 1 ;...; 2017 = − . 2 x + x x x +1 2 2017 2018  1 1 1 1 1 1  504 − a = 504 − Vậy P = − − + − +  ... + − = ⇒ . Chọn B.  2 3 3 4 2017 2018  1009 b   = 1009 f ' x f ' x 2 ( )
Câu 9: f '(x) = (2x + 3) f (x) ( ) ⇔ = 2x + 3 ⇔ dx = 2x + 3 . dx 2 ∫ ∫ f (x) 2 f (x) ( )
d ( f (x)) 2 1 − 2 1 x 3x C x 3x C f x − − ⇔ = + + ⇔ = + + ⇔ = ∫ mà f ( ) 1 0 = ⇒ C = 2. 2 f (x) f (x) ( ) 2
x + 3x + C 2
Khi đó − f (x) 1 1 1 = = − ⇒ − f ( ) 1 1 = − − f ( ) 1 1 1 ;...; 2018 = − . 2
x + 3x + 2 x +1 x + 2 2 3 2019 2020 Vậy  1 1 1 1 1 1  1009 P = − − + − + ... − + − =  . Chọn D. 2 3 3 4 2019 2020    2020 2
f ′′ x . f x − 2  f ′ x
Câu 10: f (x). f (x) − 2 f  ( x) 2 3  + xf  (x) ( ) ( )  ( ) = 0  ′′ ′ ⇔ = −x ∗ 3 f (x) ( )
f ′(x) ′
f ′′(x). f (x) − 2 f (x). f ′  ( x) 2  f ′′ 
(x).f (x) − 2 f ′  ( x) 2 2  Lại có:    = = 2  f  (x) 4  f  (x) 3 f (x) f ′(x) 2 dx −x
d ( f (x)) 2
Do đó lấy nguyên hàm 2 vế của ( − ∗) ta được: x = + C ⇔ = + C ∫ 2 ∫ f (x) 2 2 f (x) 2 2 1 − −x 2 2 − − − − ⇔ 1 x x 2 2 ( ) =
+ C . Do f (0) = 1 ⇒ 1 − = C ⇒ = −1 = ⇒ f x = . f x 2 f (x) ( ) 2 2 2 x + 2 Do đó f ( ) 2 1 = . Chọn A. 3 f ′ x
Câu 11:f ′  ( x) 2  = 
(x + )1 f (x) ⇔ f ′(x) = (x + )1 f (x) ( ) ⇔ = x +1 (∗). f (x)
Lấy nguyên hàm hai vế của (∗), ta được: f ′(x)
d ( f (x)) 2 dx = x +1dx ⇔ 2. dx = ∫ ∫ ∫ (x + )3 1 + C f (x) 2 f (x) 3 ⇔ f (x) 2 2 = (x + )3
1 + C mà f ( ) 2 f ( ) 2 2 2 6 16 3 2 3 4 C C − = ⇒ = + ⇒ = . 3 3 3 3 2 −  −  Do đó f (x) 1 = (x + )3 6 8 + ⇒ f (x) 1 =  (x + )3 6 8 1 1 +  . 3 3 3 3   Vậy 2
2613 < f (8) < 2614. Chọn A. f ′ x
Câu 12: f (x) = f ′(x) ( ) 1 3x +1 ⇒ = f (x) 3x +1
d f (x) dx 2 d (3x +   )1
Lấy nguyên hàm 2 vế ta được 2 ∫ ( ) = = ⇔ ln f ∫ ∫ (x) = 3x +1 + C f x 3x +1 3 2 3x +1 3 Thay 4 4
x = 1 ⇒ ln1 = + C ⇒ C = − 3 3 4 Thay x = ⇒ f ( ) 8 4 4 5 ln 5 = − = ⇒ f (5) 3
= e ≈ 3,8. Chọn C. 3 3 3 f ( x +1) 2( x +1 + 3) Câu 13: Đặt 2
t = x +1 ⇒ x = t −1. Khi đó dx = + C ∫ x +1 x + 5 f (t) + + ⇒ d ∫ ( 2 t 3 2 t 3 2 t − ) ( ) = + C ⇔ f ∫ (t) ( ) dt = + C ⇔ f ∫ (t) t + 3 1 2 dt = + C 2 2 2 t t + 4 t + 4 t + 4 Do đó f
∫ ( x)d ( x) 2x + 3 = + C ⇒ f ∫ ( x) 2x + 3 2 2 2 dx = + C . Chọn D. 2 4x + 4 8( 2 x + ) 1 f (x) f (x) 3 3 t f x 2 ( ) Câu 14: Ta có
t dt = x cosπ x ⇔ = . x cosπ x ⇔ = . x cosπ x (∗ ∫ ). 3 3 0 0 3 f (4)
Thay x = 4 vào biểu thức (∗) , ta được 3
= 4 ⇔ f (4) = 12 ⇔ f (4) 3 = 12 . Chọn D. 3 2 f ′′ x f ′′(x)
Câu 15: Ta có  f '
 ( x) = f ′′  (x) ( ) ⇔ = 1 ⇔
dx = dx = x + C ∫ ∫  f '(x) 2   f '(x) 2      1 1 ⇔ −
= x + C ⇔ f x = − mà f '(0) = 1 −  → C =1 f '(x) '( ) x + C 1 1 Do đó f (x) 1 = − ⇔ f
∫ (x)dx = f ( ) − f ( ) 1 ' ' 1 0 = − dx ≈ 0 − ,693 x ∫ . Chọn B. +1 x +1 0 0
Câu 16: Gọi F (t) là nguyên hàm của hàm số f (t) 2 = 1+ t . x Ta có G (x) 2 = 1+ t dt = F ∫
(x)− F (0) → G (x) = F  ( x) ′ ′  = F′ 
(x) = f (x). 0 Lại có f (x) 2
= 1+ x nên suy ra G′(x) 2
= 1+ x . Chọn B.
Câu 17: Gọi F (t) là nguyên hàm của hàm số f (t) 2 = sin t . x ′ F ' x f x Ta có G (x) 2 = sin t dt = F ∫
( x)−F(0) → G′(x) = F( x) ( ) ( )  = = .  0 2 x 2 x
Lại có f ( x) = ( x)2 sin
= sin x nên suy ra ′( ) sin x G x = . Chọn B. 2 x x Câu 18: Ta có f (t) f (x) f (x)
t.e dt = e ⇔ . x e = f ′ ∫ (x) f(x) .e
⇔ f ′(x) = .x Chọn A. 0 2 x ′  
Câu 19: Ta có  f
∫ (t)dt ( .xsinπ x)′ = ⇔ ( 2 x )′ . f ( 2
x ) = sinπ x + π .xcosπ x    0  ⇔ x f ( 2
2 . x ) = sinπ x + π .xcosπ .x Thay π
x = 4 vào hai vế, ta được 4 f (4) = π ⇔ f (4) = . Chọn C. 4 1 − 2
Câu 20: Ta có f (− ) 1 − f ( 2 − ) = f ′
∫ (x)dx và f (2) − f ( )1 = f ′ ∫ (x) . dx 2 − 1 1 − 2 ⇒ f (− )
1 + f (2) = f ′
∫ (x)dx + f ′
∫ (x)dx + f ( 2 − ) + f ( )
1 = a + b . Chọn C. 2 − 1 f ′ x f ′ x x 2 x ( )
Câu 21: f ′(x) = −e . f (x) ( ) x ⇔ − = e ⇔ −
dx = e .dx 2 ∫ ∫ f (x) 2 f (x) 1 x 1 ⇔ = + ⇔ = mà f ( ) 1 0 =  → C =1. f (x) e C f (x) x e + C 2 Do đó f (x) 1 =  → f = = = . Chọn C. x ( ) 1 1 1 ln 2 ln 2 e +1 e +1 2 +1 3 f ′ x f ′ x 2 2 2 ( )
Câu 22: f ′(x) = x . f (x) ( ) 2 ⇔ = x ⇔ dx = x dx 2 f (x) ∫ 2f(x) ∫ 3 1 x 1 ⇔ − = + ⇔ = − mà f ( ) 1 0 = 2 ⇒ C = − . f (x) C f (x) 3 3 x 2 + C 3 1  f ′( ) 1 = 36
Do đó f (x) = − →
nên phương trình tiếp tuyến là y = 36x − 30. Chọn C. 3 x 1   f −  ( ) 1 = 6 3 2 x
Câu 23: Ta có g (0) = 1 và g (x) = 1+ 2018 f
∫ (t)dt ⇒ g′(x) = 2018 f (x) = 2018 g(x) 1 ′( ) t ′( ) t g x g x ⇒ = 2018 ⇔
dx = 2018 dx ⇒ 2  g ∫ ∫
(t) −1 = 2018t g (x)   0 g (x) 0 1
⇒ g (t) = 1009t +1. Vậy g (t) 1011 dt = ∫ . Chọn A. 2 0
Document Outline

  • ITMTTL~1
  • IIBITP~1
  • IIILIG~1

Tài liệu liên quan: