
2
MỘT SỐ CHUYÊN ĐỀ
BỒI DƯỠNG HỌC SINH GIỎI TOÁN 8
Lời nói đầu 1
Chủ đề 1. Hằng đẳng thức 3
Chuyên đề 2: Phân tích đa thức thành nhân tử 19
Chuyên đề 3: Giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 58
Chuyên đề 4: Phương trình đại số 111
Chuyên đề 5: Đồng nhất thức 131
Chuyên đề 6: Bất đẳng thức 157
Chuyên đề 7: Đa thức 175
Chuyên đề 8: Hình học 186
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

3
CHUYÊN ĐỀ 1: HẲNG ĐẲNG THỨC
A. CÁC HẰNG ĐẲNG THỨC CƠ BẢN
1.
22 22 2 2
( ) 2 2 4 ( )4a b a ab b a ab b ab a b ab+ =+ +=− ++ =− +
2.
22 22 2 2
( ) 2 2 4 ( )4a b a ab b a ab b ab a b ab− =− +=+ +− =+ −
3.
22
( )( )a b a ba b−=− +
4.
3 3 2 23 33 33 3
() 3 3 3() ()3()ab a ab ab b a b abab a b ab abab+ =+ + +=++ +⇒+=+ − +
5.
3 3 2 23 33 33 3
() 3 3 3() ()3()a b a a b ab b a b ab a b a b a b ab a b− =− + −=−− +⇒−=− + −
6.
33 2 2
( )( )a b aba abb−=− ++
7.
33 2 2
( )( )a b a b a ab b+=+ −+
Bài 1:
a) Tính
2222 22
100 99 98 97 ... 2 1A = −+−++−
b) Tính
( )
2222 2
1 2 3 4 .... 1 .
n
Bn=−+−+−+−
Lời giải
a) Ta có:
2 2 2 2 22
101.100
100 99 98 97 ... 2 1 (100 99)(100 99) ... (2 1)(2 1) 100 ... 1 5050
2
A = − + − ++ −= − + ++ − += ++= =
b) Ta xét hai trường hợp
- TH1: Nếu n chẵn thì
( ) ( )
( ) ( )
( )
2
22 2 2 2
1
2 1 4 3 ... 1 1 2 3 4 ... 1
2
nn
B nn n
n
+
= − + − + + − − =+++++ − +=
- TH1: Nếu n lẻ thì
( ) ( )
( ) ( ) ( )
( )
22
22 2 2 2 2
1
2 1 4 3 ... 1 2 1 2 3 4 ... 1
2
nn
B n
n n nn
+
= − + − + + − − − − =+++++ − − =−
⇒
Hai kết quả trên có thể dùng công thức:
( )
( )
1
1.
2
n
nn+
−
Bài 2: So sánh
19999.39999A =
và
2
29999B =
Lời giải
Ta có:
22 2
19999.39999 (29999 10000)(29999 10000) 29999 10000 29999 AB= − + = − < ⇒<
Bài 3: Rút gọn các biểu thức sau
a.
2 64
(2 1)(2 1)...(2 1) 1A = + + ++
b.
2 64
(3 1)(3 1)...(3 1) 1B = + + ++
c.
2 22
( ) ( ) 2( )C abc abc ab= ++ + +− − +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

4
Lời giải
a.
2 64 2 64 128 128
(2 1)(2 1)...(2 1) 1 (2 1)(2 1)(2 1)...(2 1) 1 2 1 1 2A = + + + += − + + + += −+=
b.
128
2 64 2 64 128
1 1 31
(3 1)(3 1)...(3 1) 1 (3 1)(3 1)(3 1)...(3 1) 1 (3 1) 1
2 22
B
+
= + + + += − + + + += − +=
c. Ta có:
2 22 2 2
()()2()()2()()()2()()C abc abc ab abc abcabc abc abcabc= ++ + +− − + = ++ − ++ +− + +− − ++ +−
( ) ( )
22
2 2 2 2
2 2 22
2( ) ( ) 2 -2 4( ) 2( ) 2 2( ) 2ab abcabc ab c ab ab ab c ab c
− + = ++++− − + − + = + − + + − + =
Bài 4: Chứng minh rằng
a.
( )
2
2 22 2 2
( )( ) ( )a b x y bx ay ax by+ +=− ++
b.
( )
2
2222 22 2
2 2
( )( ) ( )( )( )a b c x y z ax by cz bx ay cy bz az cx++ ++ − ++ = − + − + −
Lời giải
a. Ta có: VT =
222 2 22222222 2 2 2 2
( )( ) ()()(ax)()a b x y a x a y b x b y bx ay by+ += + + + = + + +
( )
2
2 2 22
2
() 2. () 2. (ax) () ( ) ( )bx bx ay ay bx ay by bx ay ax by dpcm= − + + + + =− ++
b. VT =
( ) ( ) ( )
22
222 2 22222 22
()()()( ) 2 zza b x y a b z c x y z ax by ax by c c
+ ++++++−+++ +
( ) ( )
22
222222 2
= ( )()()()()() ()2. 2.ax by bx ay az bz cx cy cz ax by cz ax cz by cz++−+ + + + + −+− − −
2 2 222 2 2 2
( )[(cy)2. ()]+(az)()2. ( )( )( )bx ay by cz bz cx az cx bx ay cy bz az cx=−+ − + + − =−+−+−
Nhận xét: Đây là bất đẳng thức Bunhicopski.
Bài 5: Cho
2 22
.= +xyz
Chứng minh rằng:
2
(5 3 4 )(5 3 4 ) (3 5 )−+ −− = −xyzxyz xy
Lời giải
VT =
22 2 22
(5 3 ) 16 25 30 9 16x y z x xy y z− − = − +−
Mà:
222 2 2 22 2 2 2
25 30 9 16( ) 9 30 25 (3 5 ) ( )z x y VT x xy y x y x xy y x y dpcm=−⇒=−−− −=−+=−
Bài 6: Cho
()()()()abcdabcd abcdabcd+++ −−+ = −+− +−−
. Chứng minh rằng: ad = bc
Lời giải
VT =
(
) ( ) ( ) ( ) ( )
2
2 2 2 22
= () 2 2ad bc ad bc ad bc a d adb c bc+++ +−+ + −+ =++ −−−
VP =
22 2222 22
[(a-d)+(c-b)][(a-d)-(c-b)]=(a-d) ( ) ( ) ( ) 2 2c b a d c b a d ad c b bc−− =− −− = + − −−+
VT = VP
22 22 44 ( )ad bc ad bc ad bc ad bc dpcm⇒ − =− + ⇔ = ⇔=
Bài 7: Chứng minh rằng, nếu:
a. a + b + c = 0 thì
32 2 3
0a a c abc b c b+ − + +=
b.
222 222
( )( )( )( 2)( 2)( 2)yz zx xy yz x zx y yx z− + − + − = +− + +− + +−
thì x = y = z
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

5
a. Ta có :
33 2 2
33 2 2 2 2 332 2
( )( )
() 0
a b a b a ab b
a b c a ab b a c abc b c a b a c abc b c
abc ab c
+=+ −+
⇒+=− −+ =− + − ⇒++ − + =
++⇒+=−
b. Đặt :
;; 0yzazxbxyc abc−= −= − =⇒++=
và
2 ( )( )
2
2
yz x yx zx bc
zx yca
xy z ab
+− = − + − =−
+− =−
+− =−
Từ giả thiết ta có :
222 2 2 2 222 2 22 22 2
( )( )( ) 2 2 2abc bc ca ab abcb bccc acaa abb++=− +− +− ⇔ ++=− ++− ++− +
222 222 222
2 2 2 0 2( ) ( 2 2 2 ) 0abc abbcca abc abc abbcca⇔++− − − =⇔ ++ − +++ + + =
222 2
2( ) ( ) 0a b c abc⇔ + + − ++ =
222
0
xy
a b c abc yz xyz
zx
=
⇔ + + =⇔==⇒ =⇒==
=
Bài 8: Chứng minh rằng không tồn tại các số thực x, y, z thỏa mãn:
a.
22
5 10 6 4 2 3 0x y xy x y+ − − − +=
b.
2 22
4 2 6 8 15 0x yz xzy+ +−−++=
Lời giải
a.
2 22
(3)(21)(1)1( )=− + −+− ≥VT x y x y dpcm
b.
2 22
( 1) 4( 1) ( 3) 1 1 ( )= − + + + − +≥VT x y z dpcm
Bài 9: Tìm x, y thỏa mãn
a.
22
8 9 4 ( 3)x y yx+ += +
b.
22
9 8 8 28 28 0x xy y x− + − +=
c.
2 22
2 5 1 2( 2 )x y z xy yz z+ + += + +
Lời giải
a. Ta có:
22 2 2
3
8 9 4 ( 3) ( 2 ) (2 3) 0 3;
2
x y yx x y y x
+ += + ⇔ − + − =⇔∈
b. Ta có:
22 2 22
22
9 8 8 28 28 0 (7 28 28) (2 8 8 ) 0
2
7( 2) 2( 2 ) 0
1
−+−+=⇔ −++ −+ =
=
⇔ −+− =⇔
=
x xy y x x
x x xy y
x
x xy
y
c. Ta có:
2 22 2 2 2
2 5 12( 2 ) ( )( 2)(1)0 ; 2; 1x y z xy yz z x y y z z x y z+ + += + + ⇔ − + − + − = ⇔ = = =
Bài 10: Chứng minh rằng biểu thức sau viết được dưới dạng tổng các bình phương của hai
biểu thức:
( ) ( ) ( )
222
2
213243xx x x++++++
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

6
Ta có:
( ) ( ) ( )
( ) ( ) ( )
222
2 22 2 2
213243 2 213 444 69x x x x x xx xx xx+ ++ + + + =+ +++ +++ ++
( ) ( )
22
2
10 40 50 5 3 5x x x x dpcm= + +=+ + + ⇒
Bài 11: Cho
2
1ax x= ++
. Tính theo a giá trị của biểu thức
432
2 5 44Axxxx=+ + ++
Lời giải
Ta có:
( )
432 42 32 2
2 5 44 12 2 22 23Axxxx xx xxxxx=+ + ++= +++ + ++ ++
( ) ( )
( )
2
22 2 2
1 2 1 1 2a 1 1Axx xx Aa a⇒ = ++ + ++ +⇒ = + += +
Bài 12: Chứng minh
( )( )( )
4
2axxaxax a− + ++
là bình phương của một đa thức
Lời giải
Ta có:
( )( )
2 2 24
2aA x ax x ax a= + +− +
Đặt
( ) ( ) ( )
22
2 2
42 24 2 2 2
2a 2t x ax A t t a t ta a t a A x ax a dpcm=+⇒= − +=− +=− ⇔= +− ⇒
Bài 13:
a) Cho a, b, c thỏa mãn
2010 2010 2010 1005 1005 1005 1005 1005 1005
a b c ab bc ca++= + +
. Tính giá trị của biểu
thức sau
( ) ( ) ( )
20 11 2010
A ab bc ca=− +− +−
b) Cho
,,,abcd Z∈
thỏa mãn
.abcd+=+
Chứng minh rằng
222 2
abcd+++
luôn là tổng
của ba số chính phương
c) Chứng minh rằng: Nếu p và q là hai số nguyên tố thỏa mãn
22
32pq pq−=−+
thì
22
pq+
cũng là số nguyên tố
Lời giải
a) Ta có:
2010 2010 2010 1005 1005 1005 1005 1005 1005 2010 2010 2010 1005 1005 1005 1005 1005 1005
2222 2 2 0a b c ab bc ca a b c ab bc ca++= + + ⇔ + + − − − =
( ) ( ) ( )
222
1005 1005 1005 1005 1005 1005 1005
1005 1005 1005 1005 1005
0ab bc ca abbcca abc⇔ − + − + − =⇔ − = − = − ⇔==
Vậy
( ) ( ) ( )
20 11 2010
0A aa bb cc A= − +− +− ⇒=
b) Ta có:
( ) ( ) ( )
22
222 2 22 2 222 2
;2abcd acdba b c d cdb b c d cd cdbb b c d+=+⇒=+− +++ =+− +++ =+ − + ++++
( ) ( ) ( ) ( )
2 22 2
222 2
22c d bc bd b b c d c d b c b d=+ − − ++++ =+ +− +−
c) Ta có:
( ) ( )
22
22 2 2 2 2
324 4 41284 414 129 21 23pq pq p q p q p p q q p q−=−+⇒ −=−+⇒ −+=−+⇒ −=−
mà
2 10p −>
( p nguyên tố );
2 30q −>
(q nguyên tố ). Do đó
2 12 3 1p q qp−= −⇔ = +
Ta có:
( )
32qp q≥ ≥⇒
lẻ, do đó p chẵn
22
2 3 13p q pq⇒=⇒=⇒ + =
là số nguyên tố
Bài 14: [ HSG – năm 2015 ]
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

7
Cho a, b, c thỏa mãn:
222 2 2 2
2; 2. : ( 1)( 1)( 1)a b c abc CMRM a b c+ + = ++= = + + +
viết được
dưới dạng bình phương của một biểu thức
Lời giải:
Cách 1:
2 2 2 222 22 22 22 2 2 2
( 1)( 1)( 1) 1(*)M a b c abc ab ac bc a b c= + + += + + + + + + +
Có:
222 2222 2
2 ( )( )a b c abc a b c abc+ + ==++⇒ + + = ++
Có:
2 2 2 2 22 22 22 2 2 2
( ) 2( ) 4 1 2( ) 1a b c a b c ab bc ca ab bc ca a b a c b c acb a bc c ab++ =+++ ++ =⇒++=⇒ + + + + + =
22 22 22 2 2 2 2 2 2 2
1 2( ) ( ) 2 ( ) 1 1a b a c b c acb a bc abc M abc abc a b c a b c⇒ + + =− + + ⇒ = − + + ++ + + +
( )
2
22
()2()() ()M abc abc a b c a b c abc a b c dpcm
= − ++ + ++ = − ++
Cách 2: Ta có:
22 2 2 2
1 ( )( ); 1 ( )( ); 1 ( )( ) [(a+b)(b+c)(c+a)]a a abbcca abacb abbcc accb M+= + + + = + + += + + += + + ⇒ =
HẰNG ĐẲNG THỨC BẬC BA
1.
3 3 2 23 33 33 3
() 3 3 3() ()3()ab a ab ab b a b abab a b ab abab+ =+ + +=++ +⇒+=+ − +
2.
3 3 2 23 33 33 3
() 3 3 3() ()3()a b a a b ab b a b ab a b a b a b ab a b− =− + −=−− +⇒−=− + −
Bài 1: Cho
2
10xx−=
. Tính
6543 2
3432 1Ax x x x x x=−+−+−+
Lời giải
6543 2 6543 432 2
23222
3 4 3 2 1( 3 3 )( 2 )( 1)
( ) ( ) ( ) 1 1111
Ax x x x xx x x xx x xx xx
xx xx xx
=−+ −+ −+=−+−+−++−+
=−+−+−+=
Bài 2: Tính
33 3
33 3
(2 1)(3 1)...(100 1)
(2 1)(3 1)....(100 1)
A
++ +
=
−− −
Lời giải
Ta có:
32
32
( 1) 1 ( 2)[(k+1) -(k+1)+1] 2
1 (k-1)(k 1) 1
kk k
k k
k
++ + +
= =
− ++
−
Cho k chạy từ 2 đến 100, ta thu được:
33 3
3
33 3 3 2
3 1 4 1 100 1 1 4 5 101 1
(2 1). . ..... . 9. . .... .
2 1 3 1 99 1 100 1 1 2 98 99(100 100 1)
A
++ +
=+=
− − − − ++
99.100.101 9.99.100.101 30300
9.
1.2.3...10101 6.99.10101 20202
A = = =
Bài 3: Cho
22
1xy+=
. Chứng minh rằng biểu thức sau không phụ thuộc vào x, y.
( ) ( )
66 44
23A xy xy= +− +
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

8
Ta có:
( ) ( ) ( ) ( )( ) ( )
33
2 2 44 224224 44 4 22 4 4 4
1
2 32 322233A x y xy xyxxyy xy x xy y x y
= + − += + − +− +=− +−−
( ) ( )
2
4 224 22
21x x y y x y dpcm=−+ + =−+ =−⇒
Bài 4: Cho
3232
3 2; 3 11.a ab b a b−=−=−
. Tính
22
ab+
Lời giải
Ta có:
( ) ( )
( )
22
2
3 2 3 2 2 6
42 24 6 24 42
3 3 2 11 6a 9 6 9 4 121a ab b ab a b ab b ab ab− +− =+−⇒−++−+=+
( )
3
6 42 24 6 2
2 3 2 2
3 3 125 5 5a ab ab b a b a b⇒+++=⇒+=⇒+=
Bài 5: Phân tích đa thức sau thành nhân tử:
333
3A a b c abc=++−
Lời giải
333 3 3
3 ()3() 3A a b c abc a b ab a b c abc=++− =+ − ++−
( ) ( ) ( )
33
3
-3 = 3().()3()A ab c ababc abc abcabc ababc
= + + ++ ++ − + ++ − ++
( )
2
( ) 3( ) 3A abc abc abc ab
= ++ ++ − + −
222
( )( )a b c a b c ab bc ca= ++ + + − − −
Bài 6: Cho a + b + c = 0, Chứng minh rằng:
333
3a b c abc++=
Áp dụng tính
2 23 2 23 2 23
333
( )( )( )
( )( )( )
ab bc ca
B
ab bc ca
− +− +−
=
− +− +−
Lời giải
Từ giả thiết
333 33 3
() ()3()3c a b a b c a b a b ab a b abc⇒=−+⇒++=+−+ =− +=
+)
222222
2 22 22 2
0
3( )( )( )
( )( )( )
3( )( )( )
0
abbcca
abbcca
B ab
bcca
abbcca
abbcca
−+−+−=
−−−
⇒= =+ + +
−−−
−+−+−=
Bài 7: Cho a, b, c thỏa mãn:
2 222
() .++ = + +abc a b c
Chứng minh rằng:
333
111 3
++=
a b c abc
Lời giải
Ta có:
2 222
333
1 1 1 1 1 1 111 3
( ) 0 0 3.
. .a b c a b c ab bc ca
a b c a b c a b c abc
++ =++⇒ ++=⇔++=⇒ ++ = =
Bài 8: Cho a, b, c thỏa mãn:
111
0
abc
++=
. Tính
222
bc ca ab
A
abc
=++
Lời giải
Đặt
3 33
333
1 1 1 111 3
;; 0
3x y z x y z x y z xyz
a b c a
b c abc
= = =⇒++=⇒ + + = ⇔ + + =
3 3 3 333
111 3
( ). 3
abc abc abc
A abc abc
a b c a b c abc
⇒= + + = + + = =
Bài 9: Cho
2 2 22
;.x y a bx y a b+=+ + = +
Chứng minh rằng
33 3 3
xy ab+=+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

9
Lời giải
Ta có:
( )
( )
( ) ( )
22
33 2
2 2 2 2 2
; 22x y xyx xyy xyab xy ab x xyy a abb+ = + + + +=+⇒ + = + ⇔ + + = + +
Do
2 222
22x y a b xy ab xy ab+ =+⇒ = ⇒ =
Thay các kết quả vào ta được:
( )
( )
( )
( )
33 2 2 2 2 3 3
x y x y x xy y a b a ab b a b dpcm+=+ ++ =+ ++ =+⇒
Bài 10: Cho
;.abmabn+= −=
Tính
33
;ab a b−
theo m và n
Lời giải
Cách 1: Từ
22
;. , .
2 2 22 4
mn mn mnmn m n
abmabn b a ab
− + −+ −
+= −= ⇒= = ⇒ = =
( ) ( )
33
33
23
33
3
22 8 4
mn mn
m n m n mn
n
ab
+ −−
+− +
−= − = =
Cách 2: Ta có:
( ) ( )
22
22
22
4a
4
mn
b a b a b m n ab
−
=+ −− = −⇒ =
Lại có:
( )
( )
( ) ( )
22
2
33 2
2 2
4
mn
a b aba abb ab ab ab nm
−
−=− ++ =− + − = −
( )
22
23
3
3
44
nm n
mn n
+
+
= =
Bài 11: Cho
22 2
.abc m++=
Tính giá trị biểu thức sau theo m
( ) ( ) ( )
222
22 22 22A a bc b ca c ab= +− + +− + +−
Lời giải
Ta có:
( ) ( ) ( )
222
2223 2223a 2223A abcc bca cabb= ++− + ++− + ++−
Đặt
( ) ( ) ( ) ( )
( )
222
2 2
22
23 23 23 12 12 9xabc A x c x a x b x xabc a b c=++⇒ = − + − + − = − ++ + + +
( )
2 2 222
12 12 9 9x x abc m= − + ++ =
HẰNG ĐẲNG THỨC: (a + b + c)
3
Ta có:
( )
3
3 3 2 23
2 22 22 2
( ) ()3()3()
3( )
++=++=+++ ++ +
= + +++++ +
abc ab c ab abc abc c
a b ab a c ac b c bc abc abc
( )( )( )
2 2 2 2 2 2 2 333
3( )( )( )( )=3 +a b ab a c ac ac bc b c abc a b b c c a a b c
= +++++++ +++ ++
3 333
( ) 3( )( )( )abc a b c abbcca⇒ ++ = + + + + + +
Bài 1: Cho a, b, c thỏa mãn: abc =1 . Tính:
3333
( )( )( )( )A abc bca cab abc= ++ − +− − +− − +−
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

10
Đặt
2
2;
2
xbca xy c
ycab yz axyzabc
z abc zx c
=+− + =
=+−⇒ += ++=++
=+− +=
33 33
( ) 3( )( )( ) 3.2 .2 .2 24 24A x y z x y z x y y z z x c b a abc⇒ = ++ − − − = + + + = = =
Bài 2: Phân tích thành nhân tử
a.
3333
8( ) (2 ) (2 ) (2 )A abc abc bca cab= ++ − +− − +− − +−
b.
3333
27( ) (2 3 2 ) (2 3 2 ) (2 3 2 )B abc a b c b c a c a b= ++ − + − − + − − + −
Lời giải
a. Đặt
33 33
23
2 3 2( )
23
( ) 3
( )( )( ) 3( 3 )( 3 )( 3 )
+−= + =+
+−=⇒ +=+ ⇒++= ++
+−= +=+
⇒ = ++ − − − = + + + = + + +
abc x xy a b
bca y yzb c xyz abc
cab z zxc a
A xyz x y z xyyzzx a bb cc a
b. Ta có:
3333
27( ) (2 3 2 ) (2 3 2 ) (2 3 2 ) 3(5 )(5 )(5 )B abc a b c b c a c a b ab bc ca= ++ − + − − + − − + − = + + +
Bài 3: Cho a, b, c thỏa mãn : a + b + c = a
3
+ b
3
+ c
3
= 1
Tính
nnn
Aabc=++
( n là số tự nhiên lẻ )
Lời giải
Ta có:
3 333
0
( ) 1 3( )( )( ) 0 0
0
ab
abc a b c abbcca bc
ca
+=
++ ==++⇒ + + +=⇒+=
+=
+) TH1:
011
nnn
ab a bc abc+ = ⇒ =−⇒ =⇒ + + =
+) Tương tự ta có: A = 1.
Bài 4: Giải các phương trình sau
a.
33 3
27 ( 5) 64 (4 1)xx x+− + = −
b.
2 3 3 2 32 3
(2 2 1) (2 1) ( 1) ( 3)x x x xx xx− − + − = −+ + +−
c.
2 33 3 3
( 2 2) ( 1)( 2)x x xx x−+ =+ − −
d.
2 32 3 2 3
( 3 3) ( 1) ( 2 2 1) 1
ab c
x x xx x x+ + + − − +− − − =
Lời giải
a. Ta có:
( )
3
33 333
27 ( 5) 64 (4 1) (3 ) ( 5) 64 3 5 4 3(3 5)( 5 4)(4 3 ) 0x x x x x x x xx x x+− + = − ⇔ +− + =+−+⇒ +− −+ + =
54
;1;
43
x
−
⇒∈
b.
2 3 3 2 32 3
(2 2 1) (2 1) ( 1) ( 3)x x x xx xx− − + − = −+ + +−
2 3 3 23 2 3
(2 2 1) (2 1) ( 1) ( 3)x x x xx x x⇔ −−+ −+−−= +−
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

11
Đặt
2
2
2 2 3
33 3
2
2
22
32
2 21;21; 1 (
)
2
3
ab x
bc xx
x x ax bxx c a
b c abc
ca x x
abc x x
+= −
+= − −
− −= −= − −= ⇒ ⇒
+ + = ++
+= −−
++= +−
{ }
2
2
2
2 20
00
3( )( )( ) 0 0 0 3 2 0 1;1; 2
00
0
x
ab ab
abbcca bc bc xx x
ca ca
xx
−=
+= +=
⇔ + + + =⇔ += ⇔ += ⇔ − −=⇒∈−
+= +=
−=
c.
2 33 3 3
( 2 2) ( 1)( 2)x x xx x−+ =+ − −
2 3 33 3 3 2 2 2
( 2 2) ( 2) (2 ) 3( 2 )( 2 2 )(2 ) 0xx xxx x xxxxx x xx⇔ − + = + − + − ⇔ + − − +− −+ =
{ }
22
6( )( 3 2) 0 0;1;2x xx x x⇔ − − + =⇔∈
Bài 5: Cho
0; 0x y z xyz++= ≠
. Tính
222
xyz
A
yz xz xy
=++
Lời giải
2 2 2 3 33
x y z xyz
A
yz xz xy xyz
++
=++=
Cách 1: Nếu
3 33
0 33++=⇒ + + = ⇒ =x y z x y z xyz A
Cách 2:
3 333 3 33 3
0
( ) 3( )( )( ) ( ) 3( )( )( ) 3xyz x y z xyyzzx x y z xyz xyyzzx A
=
++ = + + + + + + → + + = ++ − + + + → =
Bài 6: Giải các phương trình sau:
2 32 3 2 3
( 3 3) ( 1) ( 2 2 1) 1(*)
ab c
x x xx x x+ + + − − +− − − =
Lời giải
{ }
2
2
2
2 22
32
(*) 3(
)( )( ) 0 2; 2; 1
2
1
ab x x
bc x x
abbcca x
ca x x
abc
+= + +
+=− − −
⇒ ⇒ + + + =⇒∈ −−
+=− ++
++=
Bài 7: Rút gọn
333 3
( )( )( )( )A xyz xyz xyz xyz= ++ − +− − −+ −−++
Lời giải
Đặt
24
+−=
−+=⇒++=++⇒ =
++=
xyza
x y z b a b c x y z A xyz
xyzc
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

12
HẰNG ĐẲNG THỨC: a
3
+ b
3
+ c
3
-3abc = (a + b + c)(a
2
+ b
2
+ c
2
– ab – bc - ca)
Nhận xét
- Nếu
333
0
30
++=
++− =⇒
= =
abc
a b c abc
abc
- Nếu
333
0
30
++=
⇒++− =
= =
abc
a b c abc
abc
Áp dụng:
Bài 1: Cho các số thực a, b, c khác 0 thỏa mãn:
333
3a b c abc++−
. Tính giá trị của biểu thức
111
=+++
abc
M
bca
Lời giải
Vì:
333
0
30
abc
a b c abc
abc
++=
++− =→
= =
+) Nếu
0 . . .. 1
+ + + −−−
++=⇒ = =
=−
abbcca c a b
abc M
b c a bca
+) Nếu
(1 1)(1 1)(1 1) 8==⇒=+++=abc M
Bài 2: Giải hệ phương trình sau:
33
68
21
x y xy
xy
+= −
+=
Lời giải
Ta có:
33 333
20
6 8 2
3. . .2 0
2
++=
+ = −⇔ + + − =⇔
= =
xy
xy xy xy xy
xy
+) Nếu
20 3
20
21 5
++= =
++=⇒ ⇔
+= =−
xy x
xy
xy y
+) Nếu
2xy= =
( khôn thỏa mãn )
Vậy hệ phương trình có nghiệm (x; y) = (3; -5)
Bài 3: Giải phương trình sau:
3 33
27( 3) 8( 2) ( 5)x xx− = − +−
Lời giải
3 33 3 33
27( 3) 8( 2) ( 5) (3 9) (4 2 ) (5 ) 0 (1)−=−+−⇔−+− +−=x xx x xx
Ta có:
(3 9) (4 2 ) (5 ) 0 (2)−+− +−=x xx
Từ (1), (2) suy ra:
{ }
3
3(3 9)(4 2 )(5 ) 0 2 2;3;5
5
=
− − − =⇔ =⇒=
=
x
x xx x S
x
Bài 4: Cho các số thực phân biệt a, b, c khác 0 và thỏa mãn:
0abc++=
.
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

13
Tính giá trị của biểu thức:
−− −
= ++ ++
−− −
bc ca ab a b c
P
a b c bc ca ab
Lời giải
Ta đặt
2 223
22
.1 1.
1 1
−−− −
− −+−
= + + → =+ + =+ =
+=+
−− −
bc ca ab a a ca ab a c cabab a a
MM
a b c b c b c b c b c bc bc
bc
Tương tự ta có:
33
22
. 1 ;. 1
b bc c
MM
c a abc a b abc
=+=+
−−
333
2( ) 2.
3 3
( : 0) 9 9
++
⇒=+ =+ ++= =⇒=
a b c abc
P doabc P
abc abc
Bài 5
*
: Giả sử bộ ba số
;;
abc
b ca ca b
−−−
là nghiệm của phương trình
222
3
xyz
yz zx xy
++=
.
Chứng minh rằng bộ ba số
222
;;
( )( )( )
abc
bc ca ab−− −
cũng là nghiệm của phương trình đó
Lời giải
Ta có:
222
3 33
3 30
0
= =
+ + =⇔++− =⇒
++=
xyz
xyz
x y z xyz
xyz
yz xz xy
Vì nghiệm của phương trình là bộ ba số khác 0 nên các số a, b, c là ba số khác nhau và
khác 0
+) Nếu:
0 ( ); ( ); ( ) 0= = = ≠⇒ = − = − = − ⇒++=⇔+=−
−− −
abc
k akbcbkcackab abc ab c
bc ca ab
Từ:
222
( ) 0 0 0( )= ⇔ = ⇔ + + + =⇔==⇒===
− − + + −−−
ab a b
ab a b ab abc loai
bc ca bab aba
+) Nếu:
22
2
( )( )
0 (1)
( )( ) ( ) ( )( )( )
−+ − −+−
++=⇒=+= ⇒ =
− − − − − − − − − −−−
a b c a b c bba cac a b bacac
bc ca ab bc ac ba caab bc abbcca
Tương tự ta có:
2 2 22
22
(2); (3)
( ) ( )( )( ) ( ) ( )( )( )
−+− −
+−
= =
− −−− − −−−
b c cb ab a c a ac bc b
ca abbcca ab abbcca
Từ (1), (2), (3) suy ra:
222
0
( )( )( )
++=
−− −
abc
bc ca ab
Đặt
22 2
;;
() () ()
= = =
−− −
ab c
mn p
bc ca ab
22 2
33 3
03 3++ =⇒ + + = ⇒ + + =
mn p
m n p m n p mnp
np mp mn
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

14
Vậy bộ ba số
222
;;
( )( )( )
abc
bc ca ab−− −
cũng là nghiệm của phương trình đã cho.
BÀI TẬP TỰ LUYỆN:
Bài 1: Tính giá trị của biểu thức
a)
( )
3
333
abc
M
abc
++
=
++
với a, b, c là các số thực thỏa mãn:
333
3a 0
0
abc bc
abc
++− =
++≠
b)
111
abc
N
bca
=+++
với a, b, c là các số thực khác 0 thỏa mãn:
33 33 33 222
3ab bc ca abc++=
Bài 2: Cho
111
0.
xy yz zx
++=
+ ++
Tính giá trị của biểu thức
( )( )
( )
( )( )
( )
( )( )
( )
222
yzzx xyzx yxyz
P
xy yz xz
++ ++ ++
=++
+++
Bài 3: Cho a, b, c là các số nguyên thỏa mãn
( )( )( )
.abc abbcca++= − − −
Chứng minh
rằng
( ) ( ) ( )
333
ab bc ca− +− +−
chia hết cho 81
Bài 4: Giải các hệ phương trình sau
a)
33
27 27 27
4
x y xy
xy
+=−
−=
b)
2 22
3 33
0
6
6
xyz
xyz
xyz
++=
++=
++=
CÁC HẰNG ĐẲNG THỨC MỞ RỘNG HAY SỬ DỤNG
1.
2 222
( ) 222a b c a b c ab bc ca++ = + + + + +
2.
2 222
( ) 222a b c a b c ab bc ca−+ = + + − − +
3.
2 22 2
1 2 3 1
2 12 23 1
( .... ) ... 2( .... )
n n nn
aaaaaaaaaaaaa
−
++++ =++++ + ++
Áp dụng:
Bài 1: Chứng minh rằng:
222222
(2 2 ) (2 2 ) (2 2 ) 9( )a bc b ca c ab a b c+− + +− + + − = ++
Lời giải
Ta có:
( )
( )
( )
2
2 22
2
2 22
2
2 22
22 4 4 8 4 4
22 4 4 8 4 4
22 4 4 8 4 4
+−=+++−−
+− = + ++ − −
+− = + ++ − −
a b c a b c ab ac bc
b c a b c a bc ab ac
c a b c a b ac bc ab
Cộng theo vế 3 đẳng thức trên ta được:
222222
(2 2 ) (2 2 ) (2 2 ) 9( )a bc b ca c ab a b c+− + +− + + − = ++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

15
Bài toán được chứng minh.
Bài 2: Cho a, b, c, d thỏa mãn: a
2
+ b
2
+ c
2
+ d
2
= 1. Tính giá trị của biểu thức
2222
( )( )( )( )A abcd abcd abcd abcd=+++ ++−− +−+− +−−+
Lời giải
Ta có
2 2 22
( ) ( ) 2( )xy xy x y+ +− = +
Áp dụng ta được:
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
2 22
A ab cd ab cd ab cd ab cd=+++ ++−++−+− +−−−
( ) ( ) ( ) ( )
2 2 22
2 2 22
2 ()2 ()2 2()()A ab cd ab cd ab ab cd cd
= + ++ + − +− = + +− + + +−
( )
22 2 2
4 4( ) 4A ab cd= ++ + =
Bài 3: Phân tích các đa thức sau thành nhân tử
a.
222
4 5 4 12 6a b c ab bc ac+++ + +
b.
444222222
2( )a b c a b b c c a abc a b c+ + + + + − ++
c.
222
34484a b c ab bc ac+++ ++
Lời giải
a.
222 2 2
4 5 4 12 6 (23)(2)(2 )(25)a b c ab bc ac a b c c a b c a b c+ + + + + =++ − =++ ++
b.
444222222
2( )a b c a b b c c a abc a b c+ + + + + − ++
2222 2 222 222
( ) ( ) ( )( )a b c ab bc ca a b c ab bc ca a b c ab bc ac= ++ − ++ = +++++ ++−−−
c.
2 2 2 22
3 4 4 8 4 ( 2 2) ( 2)( 3 2)a b c abbcacabc b abcabc+ + + + + = + + − = ++ + +
Bài 4: Tìm x, y, z thỏa mãn
a.
2 22
5 5 8 4 4 2 2 20x y z xy yz zx x y++++++−+=
b.
22 2
2 2 2 10x y z xy yz zx x y+ + + + + ++ +=
c.
2 22
2 5 8 6 8 4 4 10x y z xy yz zx z+ + − − + − +=
d.
222
5 11 28 14 16 8 20 5 0x y z xy yz zx z++−−+−+=
e.
22 2
3 8 23 6 22 12 12 6 0x y z xy yz zx z+ + + − − − +=
Lời giải
a.
2 22
5 5 8 4 4 2 2 20x y z xy yz zx x y++++++−+=
22 2
( 1) ( 1) (2 2 ) 0 ( ; ; ) ( 1;1; 0)x y x y z xyz⇔+ +−+ + + =⇔ =−
b.
22 2
2 2 2 10x y z xy yz zx x y+ + + + + ++ +=
2 22 2 2 2
2 2 4 2 4 4 2 2 2 0 ( 1) ( 1) ( 2 ) 0 ( 1; 1;1)x y z xy yz zx x y x y x y z⇔ + + + + + +++=⇔++++++ =⇔−−
c.
2 22
2 5 8 6 8 4 4 10x y z xy yz zx z+ + − − + − +=
2 222 2 2 2
(4 4 1) 2 5 4 6 8 4 0 (2 1) ( ) ( 2 2 ) 0z z x y z xy yz zx z x y x y z⇔ −++ + + − − + =⇔ − +− +− + =
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
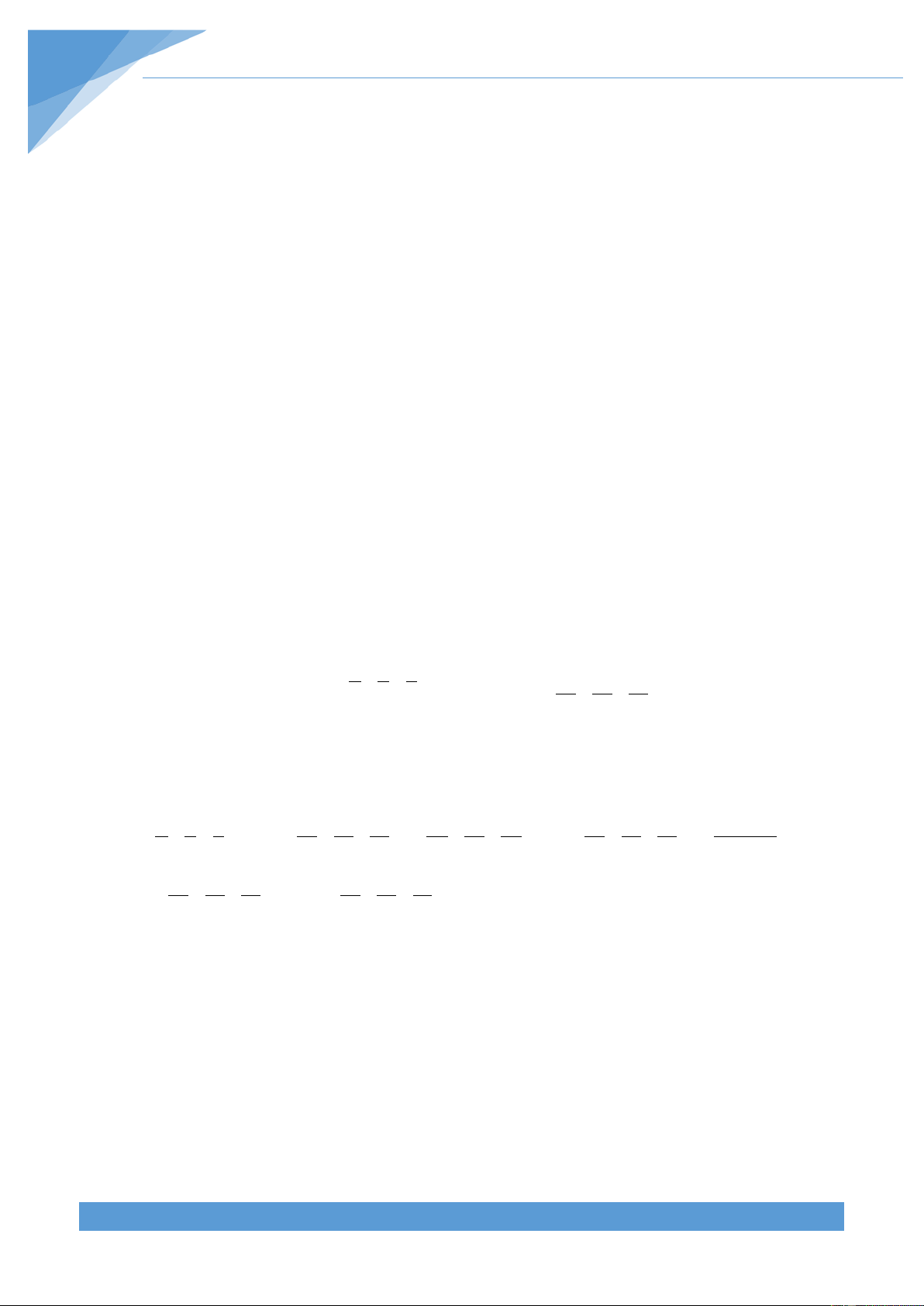
16
d.
222
5 11 28 14 16 8 20 5 0x y z xy yz zx z++−−+−+=
2 2 22 2 2 2
5(4 4 1) 5 11 8 14 16 8 0 5(2 1) 3( ) 2( 2 2 ) 0 (1;1;1)z z x y z xy yz zx z x y x y z− ++ + + − − + =⇔ − + − + − + =⇔
e.
22 2
3 8 23 6 22 12 12 6 0x y z xy yz zx z+ + + − − − +=
2 22
3( 2 ) 5( ) 6( 1) 0 ( ; ; ) (1;1;1)x y z y z z xyz⇔ +− + − + − =⇔ =
Bài 5: Chứng minh rằng không tồn tại số thực x, y, z thỏa mãn:
a.
22
26 10 14 76 59 0x y xy x y+ − + − +=
b.
22
5 2 4 10 14 0x y x xy y++−−+=
Lời giải
a. Ta có:
2 2 2 2 22
( 10 25 ) 14 76 59 ( 5 ) 2.7.( 5 ) 6 7 10= − + ++ − +=− + − −+++VTx xy y y x y xy xy yy
2 22 22
( 5 ) 2.7.( 5 ) 7 ( 3) 1 ( 5 7) ( 3) 1 1 ( )=− + − ++− +=−+ +− +≥xy xy y xy y dpcm
b.
22
( 2 1) ( 3) 4 4( )VT x y y dpcm= − + + − +≥
Bài 6: Cho a + b + c = 0 và a
2
+ b
2
+ c
2
= 2. Tính a
4
+ b
4
+ c
4
Lời giải
Ta có:
2 222
( ) 0 2( ) 0 2 2( ) 0 1 (1)++ =⇔+++ ++ =⇔+ ++ =⇒++=−a b c a b c ab bc ca ab
bc ca ab bc ca
Có:
2222 444 222222
( ) 2 2( ) 4 (2)++ =⇔+++ + + =abc abc abbcca
Từ (1) suy ra:
22 22 22 2 2 2 22 22 22
2221 1+++ + + =⇔ ++=ab bc ca abc abc abc ab bc ca
Thay vào (2) ta được:
444
422+ + =−=abc
Bài 7: Chứng minh rằng, nếu:
111
2 (1)
(2)
++=
++=
abc
a b c abc
thì
222
111
2
abc
++=
Lời giải
Từ (1) suy ra:
2
222 2
22
111 111 111 111
4 2 4 24
++
++ =⇔+++ ++ =⇒+++ =
abc
a b c a b c ab bc ca a b c abc
222 222
111 111
2 4 2.
abc abc
⇒+++=⇒++=
HẰNG ĐẲNG THỨC MỞ RỘNG ( tiếp )
1.
33 2 2
( )( )a b a b a ab b+=+ −+
2.
5 5 4 3 22 3 4
( )( )a b a b a a b a b ab b+=+ − + − +
3.
1 2 32 2 1
( )( .... )
nn n n n n n
a b a b a a b a b ab b
−− − − −
+=+ − + −− +
4.
5 5 4 3 22 3 4
( )( )a b a b a a b a b ab b−=− + + + +
5.
1 2 32 2 1
( )( .... )
nn n n n n n
a b a b a a b a b ab b
−− − −−
−=− + + ++ +
( với n lẻ )
Áp dụng:
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

17
Bài 1: Giải hệ phương trình sau
a.
4
44 2 2
( 1)
( ) 31
x yy
x y xy x xy y
= +
++ ++ =
b.
4224 42 3
2
()
xy
x xy y xx xy y
+=
+ += + +
c.
5
4 22 4 2 2
2
( )1
xy x
x x y y xy x y
+=
+ += + +
Lời giải
a. Ta có:
5 5 443223 555 55 5 5
5
( )( ) 31 31 32 (2 )
0 0( )
1
22 1
2
1
12
= +⇒−= ⇒ − + + + + = ⇔ − = ⇔ = =
= =
=
⇔= ⇒ −= ⇔ = ⇒ = ⇒
= −
=−=−
xy y xyy xyx y xyxy xy y x y y x y y
y x loai
y
x y yyy y x
y
yx
b. Ta có:
4 22 4 5 3 3 4 3 22 3 4 5 4 3 22 3 4 5
55555
( )( ) 2
21
x x y y x x y xy x x y x y xy y x x y x x y x y xy y x
x y x x y xy xy
++=++⇔−+−+=⇒+ −+−+=
⇔ + = ⇔ = ⇔=⇒==
c. Ta có:
4 3 22 3 4 5 5 5
12 1x x y x y xy y x x y x y− + − + =⇔ = + ⇒==
Bài 2: Chứng minh rằng :
9 99
2 2 100 4.25+=
Lời giải
Ta có:
9 99 9 90 9 10 9 9 9 9 8 7 6
4
25
2 2 2 (1 2 ) 2 [(2 ) 1] 2 (1024 1) 2 .(1024 1)(1024 1024 1024 .... 1) 100A+ = + = += += + − + − +⇒
Bài 3: Chứng minh rằng: Ta có:
*
20 16 3 1 323
n nn
A nN= + − − ∀∈
, n chẵn
Lời giải
Vì n chẵn, đặt n = 2k ( k thuộc N
*
), ta có: 323 = 17.19
222 2122 22 21
17 17
(20 3 ) (16 1) (20 3)(20 20 .3 ... 3 ) (16 1)[(16 ) ... 1] 17(1)
kk k k k k k
AA
−− −
= − + −= − + ++ + − ++⇒
2 2 2 21 2 2 21 21
19 19
(20 1) (16 3 ) (20 1).(20 ... 1) (16 3 )[(16 ) ... (3 ) ] A 19(2)
k kk k k k
A
− −−
= −+ − = − +++ − ++ ⇒
Từ (1) và (2)
323A⇒
Bài 4: Tìm n thuộc N
*
để
100 2
1An n= ++
là số nguyên tố
Lời giải
Ta có
100 2 99 2 3 33 2
( ) ( 1) ( 1) ( 1) [(n ) 1] ( 1)An n nn nn nn n nn= −+−+= −+++= −+++
{ }
3 3 32 3 31 2 2 2
( 1)[(n ) ( ) ... 1] ( 1) ( 1) ( 1).[...]+1 1nn n nn nn nn nn= − + +++ ++ = ++ − ++
+) Nếu n > 1 thì A > n
2
+ n + 1 suy ra A là hợp số
+) Nếu n = 1 thì A = 3 ( thỏa mãn ). Vậy n = 1
Bài 5: Chứng minh rằng số
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

18
a.
100
1000.09A =
là hợp số b.
10000000099B =
là hợp số
Lời giải
a. Ta có:
101 101 2 2 2 3 33 2
100
1000......09 10 10 1 (10 10 ) (10 10 1) 10 [(10 ) 1] (10 10 1)A = = +−= + − −+= +− −+
2 3 3 32 3 31 2 2 2 2
10 (10 1)[(10 ) (10 ) ... 1] (10 10 1) 10 (10 1)(10 10 1).[...]-(10 10 1)= + − ++− −+= + −+ −+
2
10 10 1 91 7.13 7, 13A AA⇒ − += = ⇒ ⇒
Là hợp sô
b.
10 5 5 2 3 2
10000000099 10 99 100 99 100 100 1 100 (100 1) (100 100 1)B = = += += + −= +− − +
2
100 100 1B⇒ −+
và B >
2
100 100 1B⇒ −+
nên B là hợp số.
Bài 6: Chứng minh rằng
2 21 *
10 11 111
nn
A nN
++
= + ∀∈
Lời giải
Ta có 111 = 37 . 3 = 10
2
+ 10 + 1
21 21 42 2 21 21 2 3
(11 100 ) (10 10 ) (11 100 ) 10 (10 1)
nn nn nnnn
A
++ ++ +++
=+−−=+− −
2 3 31 32
(....) 10 .(10 1) (10 ) (10 ) ... 1
n nn
A
+ −−
⇒= − − + ++
{ }
2n 2 1 2 n+2 3 n+2
(11 100) 11 11 .100 ... 100 -10 (10 1).[...]=111 [...]-10 ...[...] 111
nn
A
−
⇒= + − ++ −
Bài 7: Chứng minh rằng
*
2903 803 464 261 1897
nnnn
A nN= − − + ∀∈
Lời giải
Ta có:
(2903 803 ) (2903 803) 2100 7.300 2903 464 2439 271.9
7; 271
(464 261 ) :(464 261) 203 7.29 803 261 542 2.271
nn nn
nn nn
AA
− −= = − =
⇒⇒
− −== − =
Vậy A chia hết cho 7. 271 = 1897.
Bài 8: Chứng minh rằng
2 21 *
(11 12 ) 133
nn
A nN
++
= + ∀∈
Lời giải
Ta có 133 = 11
2
+ 11 +1
21 21 2 3 2 21 2 2 3 n-1 2
133
(12 121 ) 11 (11 1) (12 121)(12 12 .121 ... 121 ) 11 (11 1)[11 11 ... 1]
n n n n nn nn n
A
+ ++ − + −
= + − −= + − ++ − − + ++
Vậy
133 ( )A dpcm
Bài 9: Cho a, b, c thỏa mãn a
2
+ b
2
+ c
2
= 1. Tính giá trị của biểu thức
2 222
( )( )( )( )A abc abc abc abc= ++ +−++ + −+ + +−
Lời giải
Khai triển và rút gọn ta được:
222
4( ) 4A abc= ++ =
Bài 10: Phân tích đa thức sau thành tích của 2 đa thức
222
34484A a b c ab bc ca=+++ ++
Lời giải
Ta có:
2 2 2 22
3 4 4 8 4 ( 2 2) ( 2)( 3 2)Aa b c abbccaabc b abcabc=+++++=++ −=++ ++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

19
Bài 11: Tìm x, y, z thỏa mãn
a.
2 22
52 4242220x y z xy yz zx x y+ + + − − − − +=
b.
22 2
3 8 23 6 22 12 12 6 0x y z xy yz xz z+ + + − − − +=
Lời giải
a.
2 22 2 2 2
5 2 4 2 4 2 2 2 0 (2 ) ( 1) ( 1) 0x y z xy yz zx x y x y z x y+ + + − − − − +=⇔ +− + − + − =
b.
22 2 2 2 2
3 8 23 6 22 12 12 6 0 3( 2 ) 5( ) 6( 1) 0x y z xy yz xz z x y z y z z+ + + − − − +=⇔ +− + − + − =
CHUYÊN ĐỀ 2: PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
A
. PHƯƠNG PHÁP TÁCH HẠNG TỬ
Phương pháp:
- Đa thức f(x) có nghiệm hữu tỉ thì có dạng
p
q
trong đó p là ước của hệ số tự do, q kà ước
dương của hệ số cao nhất
- Nếu f(x) có tổng các hệ số bằng 0 thì f(x) có một nhân tử là: x – 1
- Nếu f(x) có tổng các hệ số của các hạng tử bậc chẵn bằng tổng các hệ số của các hạng tử
bậc lẻ thì f(x) có một nhân tử là: x + 1
- Nếu a là nghiệm nguyên của f(x) và
(1) ( 1)
(1) 0; ( 1) 0 ;
11
ff
ff
aa
−
≠ −≠⇒
−+
đều là số nguyên.
Để nhanh chóng loại trừ nghiệm là ước của hệ số tự do.
1. Đối với đa thức bậc hai : ax
2
+ bx + c
Cách 1: Tách hạng tử bậc nhất bx
- Tính a.c rồi phân tích a.c ra tích của hai thừa số ac = a1c1 = a2c2 = .....
- Chọn ra hai thừa số có tổng bằng b , chẳng hạn : ac = a1c1 với a1 + c1 = b
- Tách bx = a1x + c1x
- Dùng phương pháp nhóm số hạng để phân tích tiếp
Bài 1: Phân tích các đa thức sau thành nhân tử
a.
2
3 84xx++
b.
2
3 84xx−+
c.
2
11 8xx−+
d.
2
5 24xx+−
e.
2
54xx−+
Lời giải
a) Ta có: 3.4 = 12 = 2.6 , mà 2 + 6 = 8 nên ta được:
( )( )
22
3 843 62432 2x x x xx x x+ += + + += + +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

20
b) Cách 1: Tách hạng tử thứ 2:
( ) ( ) ( )( )
22
3 8 43 6 2 43 2 2 2 23 2xxxxxxx x xx− += − − += − − − = − −
Cách 2: Tách hạng tử thứ nhất:
( )
( )( )
2 22
3 844 84 232xx xx xx x−+= −+−=− −
c)
( )( )
2
11 28 4 7xx xx− +=− −
d)
( )( )
2
5 24 8 3xx x x+−=+ −
e)
( )( )
2
54 1 4xx x x− += − −
Cách 2: Tách hạng tử bậc ax
2
- Ta thường làm làm xuất hiện hằng đẳng thức:
( )( )
22
a b abab−=− +
Bài 2: Phân tích đa thức sau thành nhân tử :
2
3 84xx++
Lời giải
Ta có:
( )
( ) ( )( )
2
2 22 2
3 844 84 22 232xx xx x x xx x++= ++−= + −=+ +
Cách 3: Tách hạng tử tự do c
- Ta tách c thành c1 và c2 để dùng phương pháp nhóm hạng tử hoặc tạo ra hằng đẳng thức
bằng cách c1 nhóm với ax
2
còn c2 nhóm với bx
Bài 3: Phân tích các đa thức sau thành nhân tử
a.
2
3 84xx++
b)
2
4 43xx−−
c)
2
9 12 5xx+−
Lời giải
a.
( )
( ) ( )( )
22
3 8 16 12 3 12 16 2 3 2xx x x x x++−= − ++ =+ +
b.
( )
( ) ( )( )
2
22 2
4 434 41421 2 2123xx xx x x x−−= −+−= −−= + −
c.
( )
( ) ( )( )
2 2 22
9 12 5 9 12 4 9 3 2 3 3 5 3 1xx xx x x x+−= ++−=+−=+ −
2. Đối với đa thức bậc ba trở lên ( dùng phương pháp nhẩm nghiệm )
Cơ sở để phân tích: Xét đa thức
1
1 10 0
( ) ... ( ... , 1)
nn
n nn n
P x a x a x ax a a a Z n
−
−
= + ++ + ∈ ≥
+) Nếu x = a là nghiệm của P(x) thì P(a) = 0
Hệ Quả : Nếu Pn(x) = 0 có nghiệm nguyên thì nghiệm đó là ước của a0
+) Định lý Bezut: Nếu Pn(x) = 0 có nghiệm x = a thì Pn(x) = (x - a). H(x) bậc (n - 1)
Bài 4: Phân tích các đa thức sau thành nhân tử:
32
4xx−−
Lời giải
Ta nhận thấy nghiệm của f(x) nếu có thì
1, 2 4.x =±±±
Chỉ có f(2) = 0 nên x = 2 là nghiệm
của f(x) nên f(x) có một nhận tử là x – 2. Do đó ta tách f(x) thành các nhóm có xuất hiện
một nhân tử là x – 2
Cách 1:
( ) ( )
( ) ( )
( )
32 3 2 2 2
4 2 2 24 2 2xx x x x x x x xx− −= − + − + − = − + +
Cách 2:
( ) ( )
( )
( )
32 3 2 3 2 2
4 84 8 4 2 2xx x x x x x xx− −= −− += − − − = − + +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

21
Bài 5: Phân tích các đa thức sau thành nhân tử
a.
32
4xx++
b.
32
5 84xxx− +−
Lời giải
a. Ta có các ước của 4 là:
1;2;4±±±
Nhận thấy x = -2 là nghiệm của đa thức vậy đa thức có 1 nhân tử là: x – (-2) = x + 2
3 22 2
0
2 4 ( 2)( 2)x xx x xx
>
⇒ + − += + −+
Hoặc:
32 2
( 8) ( 4) ( 2)( 2)x x x xx= + + − = + −+
b. Nhận thấy x = -1 là nghiệm của đa thức nên có 1 nhân tử là: x + 1
32
5 84xxx− +−
32 2 2
( ) (4 4 ) (4 4) ( 1)( 2)xx x x x x x= − − − + −=− −
*) Chú ý:
+ Nếu f(x) có tổng các hệ số bằng 0 thì f(x) có một nhân tử là x – 1
+ Nếu f(x) có tổng các hệ số của các hạng tử bậc chẵn bằng tổng các hệ số của các hạng tử
bậc lẻ thì f(x) có một nhân tử là x + 1
Bài 6: Phân tích các đa thức sau thành nhân tử
a.
2
2 75xx++
b.
43
1xxx+ −−
c.
3
19 30xx−−
d.
32
4 7 10xxx+ −−
e.
432
25553xxxx− − ++
Lời giải
a. Ta có: 2 + 5 = 7 nên đa thức có 1 nhân tử là x + 1.
2
2 7 5 ( 1)(6 5)xx x x+ += + +
b. Ta có tổng các hệ số bằng 0 và tổng chẵn cũng bằng tổng lẻ nên có nhân tử x
2
-1
43 4 3 2
1 ( 1) ( ) ( 1)( 1)( 1)xxx x xx x x xx+ − −= − + − = − + + +
43 43 2
1 ( ) ( 1) ( 1)( 1)( 1)xxx xx x x x xx+ − −= + − − = − + + +
c. Ta có x = -3 là nghiệm nên có nhân tử là x + 3
3 322 2
19 30 3 3 9 10 30 ( 3)( 3 10) ( 3)( 2)( 5)x x xxxxx x xx x x x− −=+ − −− −=+ −− =+ + −
d. Ta có: x = -1 là nghiệm của đa thức nên có nhân tử là: x + 1
3 2 32 2
4 7 10 3 3 10 10 ( 1)( 2)( 5)xxx xxxxx xx x+ −−=++ +− −=+ − +
e. Ta có tổng chẵn bằng tổng lẻ nên có nhân tử: x + 1, sau đó lại tổng chẵn bằng tổng lẻ.
432
2 5 5 5 3 ( 1)( 1)( 3)(2 1)xxxx xxx x− − + += − + − +
Bài 7: Phân tích đa thức thành nhân tử:
32
6 11 6xx x+++
Lời giải
Bấm máy ta thấy đa thức có ba nghiệm nguyên là -1, -2, -3, nên ta phân tích :
( )( )( )
32
6 11 6 1 2 3xx x x x x+ + += + + +
Bài 8: Phân tích đa thức thành nhân tử:
32
4 29 24aa a+−+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

22
Lời giải
Bấm máy nhận thấy đa thức có ba nghiệm là 1,3 và -8, nên sẽ có chứa các nhân tử
(a - 1), (a - 3) và (a + 8),
Ta có:
( ) ( )
( )
3 2 32 2
4 29 24 5 5 24 24a a a aa a a a+ − + = − + − +− +
( ) ( ) ( ) ( )
( )
22
1 5 1 24 1 1 5 24a a aa a a a a−+ −− −= − + −
=
( )( )( )
138aaa−−+
Bài 9: Phân tích đa thức thành nhân tử:
32
5 84xxx+ ++
Lời giải
Nhận xét : Tổng các hệ số của hạng tử bậc chẵn bằng tổng các hệ số của hạng tử bậc lẻ nên
đa thức có một nhân tử là: x + 1
Như vậy ta có :
( ) ( )
( ) ( )( )
2
3 2 32
2
5 84 4 4 44 1 2x x x xx x x x x x+ + += + + + + + = + +
Bài 10: Phân tích đa thức thành nhân tử:
43 2
6 7 37 8 12aa aa+ − −+
Lời giải
Nhẩm thấy đa thức có nghiệm là x = 2, hay có 1 nhân tử là: x - 2
Ta có:
( )
( )
43 2 4 3 3 2 2
6 7 37 8 12 (6 12 ) (19a 38 ) 2 6 12aa aa a a a aa a+ − −+= − + − + − − −
( ) ( ) ( ) ( ) ( )
( )
3 2 32
6 2 19 2 2 6 2 2 6 19 6a a a a aa a a a a a−+ −+ −− −=− + +−
=
( )( )( )( )
2 32 13 2aa a a−+ − +
Bài 11: Phân tích đa thức thành nhân tử:
43 2
6 13 12 4xx x x++ ++
Lời giải
Thấy tổng các hệ số bậc chẵn bằng tổng hệ số bậc lẻ, nên đa thức có 1 nghiệm bằng -1
Ta có:
( ) ( ) ( )
( )
4 3 2 43 3 2 2
6 13 12 4 5 5 8 8 4 4x x x x xx x x x x x+ + + += + + + + + + +
=
( ) ( ) ( ) ( ) ( )
( )
3 2 32
15 18 14 1 1 5 8 4x x x x xx x x x x x++ ++ ++ += + + + +
=
( ) ( )
22
12xx++
*) Trường hợp đặc biệt: Đa thức không có nghiệm nguyên.
Xét đa thức
1
1 10 0
( ) ... ( ... , 1)
nn
n nn n
P x a x a x ax a a a Z n
−
−
= + ++ + ∈ ≥
+) Nếu Pn(x) = 0 có nghiệm
n
0
a
[(p;q)=1]
q
p
x
ap
q
= ⇒
Bài 12: Phân tích các đa thức sau thành nhân tử
a.
32
3 7 17 5xx x−+−
b.
43 2
9 15 43 22 40xxxx+ + +−
c.
43 2
6 19 31 30xx x x++ − −
Lời giải
a. Các ước của 5 là:
1; 5±±
. Nhận thấy đa thức không có nghiệm nguyên, ta đi tìm nghiệm
hữu tỷ của đa thức
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

23
( 5)
(3)
pU
p
x
qU
q
∈−
= ⇔
∈
ta thấy nghiệm của đa thức là
1
3
x =
nên có nhân tử
1
3
x −
hay 3x -1
Vậy:
3 2 32 2 2
3 7 17 5 3 6 2 15 5 (3 1)( 2 5)x x x xx x x x x x x− + −= − − + + −= − − +
b. Ta thấy đa thức có 1 nhân tử là:
2
32
3
xx−⇔ −
4 3 2 32
9 15 43 22 40 (3 2)(3 7 19 20)x x x x x xx x+ + + −= − + + +
Lại có nhân tử là: 3x + 4
32 2
(3 2)(3 7 19 20) (3 2)(3 4)( 5)xxxx xxxx⇒ − + + + = − + ++
c.
43 2 2
6 19 31 30 (2 3)(3 2)( 5)xx x x x x xx+ + − − = − + ++
BÀI TẬP TỰ LUYỆN
Bài 13: Phân tích đa thức sau thành nhân tử:
5432
2342xxxx−+−+
Lời giải
Nhận xét: Tổng các hệ số bằng 0 nên đa thức có một nhân tử là: x – 1, chia đa thức cho x –
1 ta được:
( )
( )
5 4 3 2 43 2
2 3 4 2 1 2 22x x x x x xx x x−+−+=− −+−−
Vì
( )
43 2
2 22xx x x−+ − −
không có nghiệm nguyên cũng không có nghiệm hữu tỷ nên
không phân tích được nữa
Vậy
( )
( )
5 4 3 2 43 2
2 3 4 2 1 2 22x x x x x xx x x−+−+=− −+−−
Bài 14: Phân tích đa thức sau thành nhân tử:
42
2017 2016 2017xxx+ ++
Lời giải
Cách 1:
( ) ( ) ( )( )
4 2 42 2 2 2
2017 2016 2017 1 2016 2016 2016 1 2017x x x xx x x xx xx+ ++=+++ ++=++−+
Cách 2:
( ) ( ) ( )( )
42 4 2 2 2
2017 2016 2017 2017 2017 2017 1 2017x x x xx x x xx xx+ + + = − + + + = ++ −+
Bài 15: Phân tích đa thức sau thành nhân tử:
2
2017.2018xx−+
Lời giải
Ta có:
( )( )
22
2017.2018 2017 2018 2017.2018 2017 2018xx x x x x x−+=+−+=+−
Bài 16: Phân tích đa thức thành nhân tử:
432
6 7 61xxxx+ + −+
Lời giải
Nhận thấy đa thức bậc 4 này không dùng được máy tính
Và đa thức không có hai nghiệm là 1 và -1
Tuy nhiên đa thức lại có hệ số cân xứng nhau:
Nên ta làm như sau:
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

24
4 3 2 22 22
22
61 1 1
6 7 61 67 6
7x x x x xx x xx
x
xx x x
−
+ + − += + ++ + = + + − +
Đặt
22
2
11
2x tx t
xx
−==> + =+
Đa thức trở thành :
( ) ( )
( )
2
22 22 2
26 7 6 9 3xt t xt t xt+++= ++= +
Thay t trở lại ta được :
2
2
2
2 2 22
1 13
3 ( 3 1)
xx
xx x x x
xx
−+
−+ = = + −
Vậy
( )
2
432 2
6 7 61 31xxxx xx+ + − += + −
Bài 17: Phân tích đa thức thành nhân tử:
32
6 11 6xx x+++
Lời giải
Bấm máy ta thấy đa thức có ba nghiệm nguyên là -1, -2, -3, nên ta phân tích :
( )( )( )
32
6 11 6 1 2 3xx x x x x+ + += + + +
Bài 18: Phân tích đa thức thành nhân tử:
( )( )( )( )
1 3 5 7 15xxxx+ + + ++
Lời giải
Với dạng này, ta chỉ việc lấy số nhỏ nhất nhân với số lớn nhất, để tạo ra những số hạng
giống nhau :
( )( )( )( )
( )( )
22
1 7 3 5 15 8 7 8 15 15x x x x xx xx+ + + ++= ++ ++ +
Đặt
( )( )
2 22
8 7 15 15 22 105 15 22 120xxttt tt tt+==>+ + +=+ + +=+ +
( )( )
( )( )
22
10 12 8 10 8 12t t xx xx=+ + = ++ ++
=
( )
( )( )
2
8 10 6 2xx x x++ + +
Bài 19: Phân tích đa thức thành nhân tử:
32
3 7 17 5xx x−+−
Lời giải
Bấm máy tính cho ta có nghiệm là
1
3
x =
, nên có nhân tử là : (3x - 1)
nên ta có :
3 2 32 2
3 7 17 5 3 6 2 15 5x x x xx x x x− + −= − − + + −
( ) ( ) ( ) ( )
( )
22
31231531 31 25x x xx x x x x= −− −+ −= − − +
Bài 20: Phân tích đa thức thành nhân tử:
32
2 5 83xxx− +−
Lời giải
Bấm máy tính cho ta có nghiệm là
1
2
x =
, nên có nhân tử là : (2x - 1)
Nên ta có :
3 2 32 2
2 5 8 32 4 2 6 3x x x xx x xx− + −= − − + + −
( ) ( ) ( ) ( )
( )
22
21221321 21 23x x xx x x x x= −− −+ −= − − +
Bài 21: Phân tích đa thức thành nhân tử:
32
3 14 4 3x xx− ++
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

25
Bấm máy tính cho ta nghiệm là :
1
3
x
−
=
nên có 1 nhân tử là : (3x + 1)
Ta có :
3 2 32 2
3 14 4 3 3 15 5 9 3x x x xx x xx− + += + − − + +
( ) ( ) ( ) ( )
( )
22
31531331 31 53x x xx x x x x+− ++ += + − +
Bài 22: Phân tích đa thức thành nhân tử:
32
5 84xxx+ ++
Lời giải
Bấm máy tính cho ta nghiệm là : x= -1 và x= -2
Như vậy ta có :
( )( )
2
32
5 84 1 2xxx x x+ + += + +
Bài 23: Phân tích đa thức thành nhân tử:
42
1997 1996 1997xxx+ ++
Lời giải
Ta có:
( ) ( ) ( )( ) ( )
42 2 2 2 2
1 1996 1996 1996 1 1 1996 1xx x x xx xx xx+ + + + + = ++ −+ + ++
( )( )
22
1 1997xx xx= ++ −+
Bài 24: Phân tích thành nhân tử:
42
2004 2003 2004xxx+ ++
Lời giải
42
2004 2004 2004x x xx= + + −+
( ) ( )
42
2004 1xx xx= − + ++
( ) ( )
( )
( ) ( )
32 2 2
1 2004 1 1 1 2004 1xx xx xx xx xx= − + ++ = − ++ + ++
( )( )
22
1 2004xx xx= ++ −+
Bài 25: Phân tích đa thức thành nhân tử:
2
2001.2002xx−−
Lời giải
Ta có:
( )
( )
( )
2 2 2 22
2001 2001 1 2001 2001 2001 2001xx xx x
x−− + = −+ − = − − +
( )( ) ( ) ( )( )
2011 2011 2011 2011 2012xx x xx− + −+ =+ −
Bài 26: Phân tích đa thức thành nhân tử:
43 2
6 7 37 8 12aa aa+ − −+
Lời giải
Nhẩm thấy đa thức có nghiệm là x = 2, hay có 1 nhân tử là x - 2
Ta có :
( )
( )
43 2 4 3 3 2 2
6 7 37 8 12 (6 12 ) (19a 38 ) 2 6 12aa aa a a a aa a+ − −+= − + − + − − −
( ) ( ) ( ) ( ) ( )
( )
3 2 32
6 2 19 2 2 6 2 2 6 19 6a a a a aa a a a a a−+ −+ −− −=− + +−
=
( )( )( )( )
2 32 13 2aa a a−+ − +
Bài 27: Phân tích đa thức thành nhân tử:
43 2
6 13 12 4xx x x++ ++
Lời giải
Thấy tổng các hệ số bậc chẵn bằng tổng hệ số bậc lẻ, nên đa thức có 1 nghiệm bằng -1
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

26
Ta có :
( ) ( ) ( )
( )
4 3 2 43 3 2 2
6 13 12 4 5 5 8 8 4 4x x x x xx x x x x x+ + + += + + + + + + +
=
( ) ( ) ( ) ( ) ( )
( )
3 2 32
15 18 14 1 1 5 8 4x x x x xx x x x x x++ ++ ++ += + + + +
=
( ) ( )
22
12xx++
3. Đối với đa thức nhiều biến
Tương tự như phân tích đa thức dạng:
2
ax bx c++
Bài 28: Phân tích các đa thức sau thành nhân tử
a.
22
252x xy y−+
b.
22
253x xy y−−
c.
22
2 221a ab b a b+ +−−+
d.
2 22
()()( )xyz yzx zxy−+ −+ −
Lời giải
a.
2 22 2
2 5 2 (2 4 ) ( 2 ) ( 2 )(2 )x xy y x xy xy y x y x y−+ = − −− =− −
b.
2 22 2
2 5 3 2 2 3 3 ( 3 )(2 )x xy y x xy xy y x y x y−−=−−−=− +
c.
22 2 2
2 2 2 1( ) 2( )1( 1)a abb a b ab ab ab+ + − − += + − + += +−
d. Ta có:
2 2 2 2 2 2 2 2 2 22
()()()() ()()( )xyz yzx zxy zxy xyxzyzyxzxy xyxy zx y−+ −+ −= −+ − + − = −+ −− −
( )( )( )x yy zz x=− −−
B. PHƯƠNG PHÁP NHÓM HẠNG TỬ
– Kết hợp các hạng tử thích hợp thành từng nhóm.
– Áp dụng liên tiếp các phương pháp đặt nhân tử chung hoặc dùng hằng đẳng thức.
Bài 1: Phân tích thành nhân tử
22 22 22
( ) ( ) ( )2A a b c b c a c a b abc= ++ ++ ++
Lời giải:
22 22 22 2 2 22 2 2
( ) ( ) ( )2 ( 2 )( )( )A a b c b c a c a b abc a a ab b ab a b ac bc= ++ ++ ++ = + ++ + + +
22
() ()()()()()cab abab cab abbcca= + + ++ +=+ + +
Bài 2: Phân tích thành nhân tử:
22 22 22
( ) ( ) ( )3A a b c b c a c a b abc= ++ ++ ++
Lời giải:
22 22 22
( )( )( )( )( )A ab a b abc ac a c abc bc b c abc a b c ab bc ca=++++++++=++ ++
Bài 3: Phân tích thành nhân tử:
() 1A abc ab bc ca a b c= − + + +++−
Lời giải
( ) ( ) ( ) ( 1) ( 1)( 1)( 1)A abc bc ab b ac c a a b c= − − −− −+ −= − − −
Bài 4: Phân tích thành nhân tử:
8 4( ) 2( ) 1A abc ab bc ca a b c= + + + + ++ +
Lời giải
(8 4 ) (4 2 ) (4 2 ) (2 1) (2 1)(2 1)(2 1)A ab bc ab b ac c a a b c= + + + + + + += + + +
Bài 5: Phân tích thành nhân tử:
33 33 33
( )( )( ) ( )A a b c b c a c a b abc a b c= + + + + + + ++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

27
Lời giải
Ta có:
222
( )( )A a b c ab bc ca= ++ ++
C. PHƯƠNG PHÁP DÙNG HẰNG ĐẲNG THỨC
Cần nắm chắc cách biến đổi các hằng đẳng thức sau:
1)
( ) ( )
22
22
24a b a b ab a b ab+ =++ =− +
2)
( ) ( )
22
22
24a b a b ab a b ab− =+− =+ −
3)
( ) ( )
22
22
22a b a b ab a b ab+=+ − =− +
4)
( )
( )
( ) ( )
3
33 2 2
3a b aba abb ab abab+=+ −+ =+ − +
5)
( )
( )
( ) ( )
3
33 2 2
3a b aba abb ab abab−=− ++ =− + −
6,
( )
( ) ( )
22
22
2 a b ab ab+ =+ +−
7)
( ) ( )
22
4a b a b ab+ −− =
8)
( )( ) ( )
2
44
2a b abab ab ab
+=+ − + −
9)
( ) ( )
2
22
44
22a b a b ab ab
+= + − −
.
10)
( )
( )
333 222
3a b c abc a b c a b c ab bc ca+ + − = ++ + + − − −
.
11)
( )( )
4 22 4 2 2 2 2
a a b b a ab b a ab b+ += ++ −+
.
12)
( )( )
42 2 2
1 11aa aa aa+ += + + − +
.
13)
2 222
( ) 222a b c a b c ab bc ca++ = + + + + +
Bài 1: Phân tích thành nhân tử
a.
36
8 27ab−
b.
22
10 6 16xy xy−+ −+
c.
333
3a b c abc++−
d.
3333
()abc a b c++ − − −
Lời giải
a.
36 3 23 2 2 2 4
8 27 2 (3 ) (2 3 )(4 6 9 )a b ab ab ab a b− =− =− ++
b.
22 2 2
10 6 16 ( 5) ( 3) ( 8)( 2)x y x y x y xy xy− + − + = + − + = ++ −+
c. Ta có:
( )
2
3 2 23 2 23 33 2
3 3 3 3 3 () 3( )( ) ()a ab ab b ab ab c abc ab c ababc abc ab abcc
= + + + − − + − = + + − ++ = ++ + − + +
( ) ( ) ( )
2
2 2
22
3 ( ) 3 ( )( )ababc abc ab abcc ab abca b c abbcca
− ++ = ++ + − + + − = ++ + + − − −
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

28
d.
( )
3
333 3 2 2
3 33 3
()3()3() ( )ab c a b c ab abc abc c a b c= ++−−−=+++ ++ +−+−
( )
( )
( )( )( )
2 2 22 2 2
= 2 333 3 3a b a ab b ac bc c a ab b ab ac bc c a b b c c a
+ + ++ + + −+− = +++ = + + +
Bài 2: Phân tích thành nhân tử
a.
33
31x y xy+− +
b.
22
4 9 12 4 6 3x y xyxy+ − +−+
c.
222222 444
2( ) ( )ab bc ca a b c+ + − ++
Lời giải
a. Ta có:
33 3 2 2
3 ( ) 3 ( ) 3 1 ( ) 1 3 ( 1) ( 1)( 1)x y xy x y xy x y xy x y xy x y x y x xy y x y+ + + − + − += + +− ++= ++ − + −−+
b. Ta có:
22
4 9 12 4 6 3x y xyxy+ − +−+
2 2 22
(2 ) (3 ) 2.2 .3 2(2 3 ) 1 4 (2 3 ) 2 (2 3 1)(2 3 3)x y xy xy xy xy xy= + − + − +−= − −= −− −+
c. Ta có:
22 4 4 4 22 22 22 2 2 2 22
4 ( 2 2 2 ) (2 ) ( ) ( )( )( )( )bc a b c bc ab ca bc b c a bcabcaabcabc− + + + − − = − + − = +− ++ −+ +−
Bài 3: Cho biểu thức:
( )
2
2 2 2 22
4A b c a bc= +− −
a) Phân tích A thành nhân tử
b) Chứng minh rằng: Nếu a, b, c là độ dài các cạnh của 1 tam giác thì A< 0
Lời giải
a) Ta có:
( ) ( )
( )
22
2
222 22 222
42Abca bc bca bc= +− − = +− −
( )( )
( )( )( )( )
222 222
22b c a bcb c a bc bcabcabcabca= + − − + − + = +− ++ −− −+
b) Vì a, b, c là độ dài ba cạnh của 1 tam giác nên:
0, 0, 0, 0 0bca bca bca bca A+−>++>−−<−+>=><
Bài 4: Phân tích đa thức thành nhân tử:
42
2010 2009 2010xxx+ ++
Lời giải
( )( ) ( )
42 2 2 2 2
1 2009 2009 2009 1 1 2009 1xx x x xx xx xx+ ++ + + = ++ −+ + ++
( )( )
22
1 2010xx xx= ++ −+
BÀI TẬP VỀ NHÀ
Bài 1: Phân tích các đa thức sau thành nhân tử ( Sử dụng tách hạng tử )
a.
3
76xx−+
b.
32
5 84xxx+ ++
c.
32
9 6 16xxx− ++
d.
42
30 31 30xxx− +−
e.
42
2010 2009 2010xxx+ ++
Lời giải
a.
3
7 6 ( 1)( 2)( 3)xx xx x− += − − +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

29
b.
32 2
5 8 4 ( 1)( 2)xxx xx+ + += + +
c.
32
9 6 16 ( 1)( 2)( 8)xxx xx x− ++=+ − −
d.
42 2
30 31 30 ( 5)( 6)( 1)x x x x x xx− + − = − + −+
e.
424222
2010 2009 2010 ( ) 2010 2010 2010 ( 1)( 2010)xxx xxxx xxxx+ + +=−+ + +=++−+
Bài 2: Phân tích thành nhân tử:
2( ) 4( ) 8A abc ab bc ca a b c= − + + + ++ −
Lời giải
2( ) 4( ) 8 ( 2)( 2)( 2)A abc ab bc ca a b c a b c= − + + + ++ −= − − −
Bài 3: Phân tích thành nhân tử:
322
2 22A x x y x x xy y= − + +− −
Lời giải
322 2
2 2 2 ( 2 )( 1)Ax xyxxxyyxyxx= − + +− − = − ++
Bài 4: Phân tích thành nhân tử:
3 3 33 3 3
A ab bc ca a b b c c a=++−−−
Lời giải
3 3 33 3 3
( )( )( )( )A ab bc ca a b b c c a a b b c c a a b c=++−−−=− − − ++
Bài 5: Phân tích các đa thức sau thành nhân tử ( dùng hằng đẳng thức )
a.
22
4 4 6 12 5x y xy x y+++++
b.
84
34xx++
Lời giải
a.
22
4 4 6125(21)(25)x y xyx y xy xy+ + ++ +=++ ++
b.
8 4 42 42
3 4 ( 2)( 2)x x xx xx+ += + + − +
D. PHƯƠNG PHÁP THÊM, BỚT CÙNG MỘT HẠNG TỬ
- Các đa thức không thể sử dụng các phương pháp như đặt nhân tử chung, nhóm hạng tử
và sủ dụng hằng đẳng thức cũng như đoán nghiệm,
- Trong các thành phần của đa thức có chứa các hạng tử bậc 4, ta sẽ thêm bớt để đưa về
hằng đẳng thức số 3:
( )( )
22
a b abab−=− +
- Đôi khi thêm, bớt hạng tử để làm xuất hiện nhân tử chung
1. Thêm, bớt cùng một hạng tử làm xuất hiện hằng đẳng thức: a
2
– b
2
Bài 1: Phân tích các đa thức sau thành nhân tử
a.
4
4a +
b.
44
4 81xy+
c.
84
98 1xx++
d.
3
216 125x−
e.
66
64xy−
f.
42
34aa++
Lời giải
a.
4 42 2 222 22 2
4 2 2. .2 2.2. ( 2) (2 ) ( 2 2)( 2 2)a a a aa a aa aa+= + + − = + − = − + + +
b.
2 2 22 22
(2 9 ) (6 ) (2 9 6 )(2 9 6 )x y xy x y xy x y xy=+ − = +− ++
c.
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

30
8 4 8 4 4 4 2 24 4 2 4 4
4 2224 242232
98 1 ( 2 1) 96 ( 1) 16 ( 1) 64 16 ( 1) 32
( 1 8 ) 16 ( 1 2 ) ( 8 1) (4 4 ) ...
x x x x x x xx x xx x
x x xx x x x x x
+ += + ++ = + + ++ − ++
= ++ − +− = + + − − =
e.
6 6 32 32
64 ( ) (8 )x yx y−=−
f.
42 2222 2
3 4 ( 2) ( 2)( 2)aa a aaa aa+ += + − = −+ ++
2. Thêm, bớt cùng một hạng tử làm xuất hiện nhân tử chung
Bài 2: Phân tích các đa thức sau thành nhân tử
a.
54
1xx++
b.
87
1xx++
c.
84
1xx++
Lời giải
a.
54 543 3 32 2 2 3
1 1 ( 1) ( 1)( 1) ( 1)( 1)xx xxx xxxx x xx xx xx+ += + + +− = ++ − − ++ = ++ −+
b.
87 8766 2 6 3 2 643
1 1 ( 1)[x ( 1( 1)]=(x 1)( 1)xx xxxx xx x x x xxxx+ += + + − += ++ − − + + + − + −+
c.
8 4 4 2 22 4 2 2 2
1 ( 1) ( ) ( 1)( 1)( 1)xx x x xx xx xx++=+− =−+−+++
Bài 3: Phân tích các đa thức sau thành nhân tử
a.
8
1xx++
b.
5
1xx+−
c.
42
1xx++
d.
75
1xx++
Lời giải
a.
8 8 2 2 26 2 2 2 3 2
1 1 ( 1) ( 1) ( 1)[x ( 1)( 1) ( 1)]xx xxxx xx xx xx x x xx++= − + ++= −+ ++ = ++ − ++ ++
b.
5 5434322 32 22 2
1 1 ( 1) ( 1) ( 1)xx xxxxxxxx xxx xxx xx+−= − + + − + − +−= −+ − −+ − −+
2 32
( 1)( 1)xx xx= −+ − −
Hoặc:
5 5 2 2 23 2 2 3 2
1 1 ( 1) 1 ( 1)( 1)xx xxxx xx xx xx xx+ −= + − + −= + − + −= −+ − −
c) Cách 1:
( ) ( ) ( )( )
2
42 4 2 2 2 2 2 2
1 21 1 1 1xx x x x x x xx xx++= + +−= +−= −+ ++
Cách 2:
( )
( )
( ) ( )( )
42 4323 22 2 2 2
1 1 11 1 1 1xx xxxx xxx x xx xx xx+ += − + + += −+ + + −+ = −+ ++
Cách 3:
( ) ( )
( )
( ) ( )( )
42 432 3 22 2 2 2
1 1 11 1 1 1xx xxx x xxx x xx xx xx+ += + + − − = ++ + − ++ = ++ +−
d) Ta có:
( ) ( ) ( ) ( )( ) (
) ( )
7 5 7 5 2 2 3 3 23 2
1 1 11 1 1xx xx xx xx xx x xx xx+ += − + − + ++ = − + + − + ++
( ) ( ) ( ) ( )( )
2 542 32 2 542
1 11 1xx xxxx xx xx xxxx
= ++ − + − + − + = ++ − + −+
BÀI TẬP ÁP DỤNG
Bài 4: Phân tích đa thức thành nhân tử:
a)
4
4 81x +
b)
44
64xy+
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

31
a) Ta có :
( ) ( )
22
4 22 2 2 2 2
4 81 2 9 2.2 .9 2.2 .9 2 9 36x x x xx x+= ++ − = + −
( )
( )
( )( )
2
2
2 22
2 9 6 2 692 69x x xx xx= + − = ++ −+
b) Ta có :
( ) ( ) ( )
22 2
4 4 2 2 22 22 2 2 22
64 8 2.8 . 2.8 . 8 16x y x y xy xy x y xy+= + + − = + −
( )
( )
( )( )
2
2
22 2
2 2 2
8 4 84 84x y xy x xy y x xy y= + − = ++ −+
Bài 5: Phân tích đa thức thành nhân tử:
a)
44
4xy+
b)
8
41x +
c)
44
4xy+
Lời giải
a) Ta có :
( ) ( ) ( ) ( )
22 22
4422 22 2222
4 2 2 2.2 . 4xyxy xy xyxy+= + = + + −
( )
( )
2
2
22
22x y xy=+−
( )( )
22 22
2 22 2x y xy x y xy= ++ +−
b) Ta có :
( )
2
8 4 44
4 1 2 1 2.2 .1 4x x xx+= ++ −
( ) ( ) ( )( )
22
4 2 42 42
21 2 221221x x xx xx= +− = + + − +
c) Ta có :
( ) ( )
22
44 22 2 22 2 2 2 22
4 2 2 2. . .2 4xy xy xy x y xy+= + = + + −
( )
( )
( )( )
2
2
22 22 22
2 2 22 22x y xy x y xy x y xy= +− = − + + +
Bài 6: Phân tích đa thức thành nhân tử:
a)
84
1xx++
b)
75
1xx++
Lời giải
a) Ta có:
84 844 4 8 4 4
1 1 21xx xxx xx x x++=+++−=+ +−
( ) ( ) ( )( )
22
4 2 42 42
1 11x x xx xx= + − = ++ −+
b) Ta có:
( ) ( ) ( )
75 75 2 2 7 52 2
1 ( )1 1xx xx xx xxxx xx xx++=++ ++−−= −+ − + ++
( ) ( ) ( ) ( )( ) ( ) ( )
6 23 2 3 3 23 2
11 1111 1xx x x x x xx x x x x x= −+ −+ ++= + −+ −+ ++
=
( )
( )
( ) ( ) ( )
3 2 23 2
11 1 1 1xx x xx xx xx+ − ++ + − + ++
( )( ) ( )( ) ( )
2 542 322 2
1 11xx xxxx xxxx xx= ++ − + − + − ++ + ++
=
( )( )
2 542 32
11xx xxxxxx++ −+−+−+
( )( )
2 543 2
1 21xx xxx xx= ++ − + − −+
Bài 7: Phân tích đa thức thành nhân tử:
a)
72
1xx++
b)
5
1xx+−
c)
8
1xx++
Lời giải
a) Ta có:
( ) ( ) ( ) ( )
72 7 2 6 2
1 11 1xx xx xx xx xx+ += − + ++ = − + ++
( )( ) ( )
( )
( )( ) ( )
332 2 32
11 1 1 11 1xx x xx xx xx x xx= − + + ++ = − ++ + + ++
( )( )
2 542
11xx xxxx++ − + −+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

32
b) Ta có:
( ) ( ) ( ) ( )
5 5 2 2 23 2
1 11 1xx xx xx xx xx+−= + +− +− = + − −+
=
( )
( ) ( ) ( )( )
2 2 2 2 32
11 1 1 1xx xx xx xx xx+ −+ − −+ = −+ + −
c) Ta có:
( ) ( ) ( ) ( )
8 8 2 2 26 2
1 11 1xx xx xx xx xx++= − + ++ = − + ++
( )
( )
( ) ( ) ( )( )
23 2 2 2 6532
11 1 1 1 1xx x xx xx xx xxxx= + − ++ + ++ = ++ − + − +
Bài 8: Phân tích đa thức thành nhân tử:
a)
44
64xy+
b)
44
4xy+
c)
4
324x +
Lời giải
a) Ta có:
( ) ( ) ( )
( )
22 2
2
44 2 2 22 22 22
64 8 2.8 16 . 8 4xy x y xy xy xy xy+= + + − = + −
( )( )
22 22
8 48 4x y xy x y xy= +− ++
b) Ta có:
( ) ( ) ( ) ( )
22 22
4422 22 2222
4 2 2 2.2 . 4xyxy xy xyxy+= + = + + −
( )
( )
( )( )
2
2
22 22
22
2 2 2 22 2x y xy x y xy x y xy= + − = +− ++
c) Ta có:
( )
( )
( )
( )
22
22
4 2 2 22
324 18 18 2. .18 36x x x xx+= + = + + −
( )
( )
( )( )
2
2
2 22
18 6 18 6 18 6x x x xx x= + − = ++ +−
Bài 9: Phân tích đa thức thành nhân tử:
a)
4
64x +
b)
44
81 4xy+
c)
44
4xy+
Lời giải
a) Ta có:
( ) ( )
22
4 22222 2
64 8 8 2. .8 16x x x xx+ = += ++ −
( )
( )
( )( )
2
2
2 22
8 4 84 84x x x xx x= + − = +− ++
b) Ta có:
( ) ( ) ( ) ( )
2222
442222 2222
81 4 9 2 9 2 2.9 .2 36xyxyxy xyxy+= + = + + −
( )
( )
( )( )
2
22 22 22
92 6 926926x y xy x y xy x y xy+ − = +− ++
c) Ta có:
( ) ( ) ( ) ( )
2222
4422222222
4 2 2 2. .2 4xyxyxyxyxy+= + = + + −
( )
( )
( )( )
2
2
22 22
22
2 2 22 22x y xy x y xy x y xy=+ − =++ +−
Bài 10: Phân tích đa thức thành nhân tử:
a)
44
4xy+
b)
44
41xy+
c)
4
4 81x +
Lời giải
a) Ta có:
( ) ( )
22
44 22 2 22 2 22 2 2
4 2 2 2. .2 4 .xy xy xy xy x y+= + = + + −
( )
( )
( )( )
2
2
22 22 22
2 2 22 22x y xy x y xy x y xy+− = − + + +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

33
b) Ta có:
( ) ( )
22
44 22 22 22
22
4 1 2 1 2 1 2.2 4xy xy xy xy xy+= += ++ −
( )
( )
( )( )
2
2
22 22 22
212 212212x y xy x y xy x y xy+ − = ++ +−
c) Ta có:
( ) ( )
22
4 22 22 2 2
4 81 2 9 2 9 2.2 .9 36x x x xx+= += ++ −
( )
( )
( )( )
2
2
2 22
29 6 296296x x x xx x= + − = ++ +−
Bài 11: Phân tích đa thức thành nhân tử:
a)
44
64xy+
b)
4
64a +
c)
42
4ab+
Lời giải
a) Ta có:
( ) ( ) ( ) ( )
22 22
4422 22 2222
64 8 8 2.8 . 16xyxy xy xyxy+= + = + + −
=
( )
( )
( )( )
2
2
22 22 22
8 4 8 48 4x y xy x y xy x y xy+ − = ++ +−
b) Ta có:
( ) ( )
22
4 22222 2
64 8 8 2. .8 16a a a aa+ = += ++ −
=
( )
( )
( )( )
2
2
2 22
8 4 84 84a a a aa a+ − = ++ +−
c) Ta có:
( ) ( )
22
4 4 2 2 2 2 22
4 2 2. .2 4 .aba b abab+= + + −
=
( )
( )
( )( )
2
2
22 2
2 22
2 2 22 22a b ab a b ab a b ab− − =−+ −−
Bài 12: Phân tích đa thức thành nhân tử:
a)
4
4x +
b)
8
41x +
Lời giải
a) Ta có:
( ) ( )
( )
22
2
4 2 2 2 22
4 2 2. .2 4 2 2x x x xx x+= + + − = + −
=
( )( )
22
22 22x xx x+− ++
b) Ta có:
( ) ( ) ( )
2 22
8 42 4 4 4 2
4 1 2 1 2.2 .1 4 2 1 2x x xxx x+= + + − = + −
=
( )( )
4 24 2
212212x xx x+− ++
Bài 13: Phân tích đa thức thành nhân tử:
a)
64 32
1xx++
b)
10 5
1aa++
c)
54
1xx−−
Lời giải
a) Ta có:
( )
2
64 32 64 32 32 32 32
1 2. 1 1xx x x x x x+ += + +− = + −
( )( )
32 16 32 16
11x xx x= ++ +−
b) Ta có:
( ) ( ) ( ) ( ) ( ) ( )
10 5 10 5 2 2 9 2 3 2
1 11 1 1a a a a aa aa aa aa aa+ += − + − + ++ = − + − + ++
=
( ) ( ) ( ) ( )( ) ( ) ( )
33 23 2 3 6 3 23 2
()11 11211 1aa aa a a aa a a aa a a−+ −+ ++= − + ++ −+ ++
=
( )
( )
( )
( )
( ) ( )
74 2 2 2 2
2 1111 1a aaa aa aa aa aa+ + − ++ + − ++ + ++
=
( ) ( )
( )
( )
2 7 4 32
12 1 1aa a aaa aa
++ + + − + − +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

34
c) Ta có:
( ) ( ) ( )
( )
( )
54 543 3 32 2
1 1 11 1xx xxx x xxx x xx− −= − + − + = −+ − + −+
( )( )
23
11xx xx= −+ −−
E. PHƯƠNG PHÁP ĐỔI BIẾN
1. Dạng P(x) = ax
4
+ bx
2
+ c ( a ≠ 0)
Đặt t = x
2
, ta được G(t) = at
2
+ bt + c. Sau đó dùng phương pháp tách hạng tử
Bài 1: Phân tích đa thức sau thành nhân tử:
42
54xx−+
Lời giải
Đặt
2
tx=
, ta được:
( )( ) ( )( )( )( )
2
54 1 4 1 1 2 2tt t t x x x x− += − − = − + − +
2. Dạng A(x) = (x + a)(x + b)(x + c)(x + d) + e mà a + b = c + d
Cách giải:
22
( ) ( )( )( )( ) [x ( ) ][x ( ) ]Ax xaxbxcxd e abxab cdxcd e= + + + + += + + + + + + +
Đặt
2
()=++ +t x a b x ab
ta có:
22
( ) () ( ) ( )++ +=−+⇒ =−+ +=+ − +x c d x cd t ab cd G t t t ab cd e t cd ab t e
Bài 2: Phân tích đa thức thành nhân tử:
( )( )( )( )
12341aa aa+ + + ++
Lời giải
Ta có :
( )( )( )( )
( )( )
22
1 4 2 31 5 4 5 61a a a a aa aa+ + + ++= ++ +++
Đặt
2
55aa t+ +=
, Khi đó đa thức trở thành :
( )( )
( )
2
22
1 11 5 5t t taa− + += = + +
Bài 3: Phân tích đa thức thành nhân tử:
( )( )( )( )
234524xxxx++++−
Lời giải
Ta có :
( )( )( )( )
( )( )
22
2 5 3 4 24 7 10 7 12 24x x x x xx xx+ + + +−= ++ ++ −
Đặt :
2
7 11xx t+ +=
, Khi đó đa thức trở thành
( )( ) ( )( )
( )( )
( )( )
( )
2 22 2
1 1 24 25 5 5 7 6 7 16 1 6 7 16t t t t t xx xx x x xx− +−=−=− += ++ ++ =+ + ++
Bài 4: Phân tích đa thức thành nhân tử:
( )( )( )( )
4 5 6 7 1680xxxx− − − −−
Lời giải
( )( )( )( )
( )( )
22
4 7 5 6 1689 11 28 11 30 1680xxxx xx xx− − − −− =−+ −+−
Đặt
2
11 29xx t− +=
, Khi đó đa thức trở thành :
( )( ) ( )( )
2
1 1 1680 1681 41 41tt t t t− +− =− =− +
Bài 5: Phân tích đa thức thành nhân tử:
( )( )
22
3 4 6 24x x xx+ − +− −
Lời giải
Ta có :
( )( )
( )( )( )( )
22
3 4 6 24 1 4 2 3 24x x xx x x x x+ − +− − = − + − + −
( )( )( )( )
( )( )
22
2 4 1 3 24 2 8 2 3 24x x x x xx xx− + − +−= +− +−−
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

35
Đặt :
2
2x xt+=
, khi đó đa thức trở thành :
( )( ) ( )
2
8 3 24 11 11t t t t tt− −− =− = −
Thay t trở lại ta được :
( )( )
( )
( )
22 2
2 2 11 2 2 11xxxx xx xx+ +− = + +−
Bài 6: Phân tích các đa thức sau thành nhân tử:
( )( )( )
4 6 10 128xx x x+ + ++
Lời giải
Ta có:
( )( )( ) ( ) ( )( )
( )( )
22
4 6 10 128 10 4 6 128 10 10 24 128xx x x xx x x x x x x+ + ++= + + ++=+ +++
Đặt
( )( ) ( )( )
2 22
10 12 12 12 128 144 128 16 4 4x x yy y y y y y++=⇒− ++=−+=−=+ −
( )( )
( )( )
( )
22 2
10 8 10 16 2 8 10 8xxxx xxxx=++ ++=+ + ++
Bài 7: Phân tích các đa thức sau thành nhân tử
a.
( 1)( 2)( 3)( 4) 3xx xx− − − −−
b.
4
( )( 2 )( 3 )( 4 )x yx yx yx y y+ + + ++
Lời giải
a)
22 2
2
( 1)( 2)( 3)( 4) 3 ( 5 4).( 5 6) 3 2 3 ( 1)( 3)
tt
xx x x xx xx tt tt
+
− − − − −= − + − + −= + −= − +
22
(53)(57)xx xx= −+ −+
b)
4 2 22
( )( 2 )( 3 )( 4 ) ( 5 5 )x yx yx yx y y x xy y+ + + ++=++
Bài 8: Phân tích các đa thức sau thành nhân tử
a)
22 2
4( 15 50)( 18 72) 3xx xx x++ ++−
b)
(2 1)( 1)( 3)(2 3) 9xxx x−−− ++
Lời giải
a)
22 2 2
4( 15 50)( 18 72) 3 4( 5)( 10)( 6)( 12) 3xx xx xxx xx x++ ++−=+ + + +−
22 2
4( 17 60)( 16 60) 3xx xx x= ++ ++−
Đặt
2 2 22 2 2 2
16 60 17 60 4[( ). ]-3x 4 4 3 (2 ) (2 )tx x x x tx txt t tx x tx x= + + ⇒ + + =+⇒ + = + − = + −
22 2
(2 )(2 3 ) (2 31 120)(2 25 120) ( 8)(2 15)(2 35 120)tx t x x x x x x x x x=− += ++ ++ =+ + ++
b) Ta có:
22 2 2
(2 1)( 1)( 3)(2 3) 9 (2 3 1)(2 3 9) 9 10 9 (2 3)(2 3 8)xxx x xx xx t t xx xx− − − + += − + − − += − += − − −
3. Dạng: (x + a)
4
+ (x + b)
4
Đặt
2
+
= +
ab
tx
ta có:
4 4 44
()
2 2 2 22
+ + + −−
=− ⇒ =− + +− + =− ++
ab ab
ab ba ba
x t Gt t a t b t t
42
.... ct dt e==++
( Dạng 1)
Bài 9: Phân tích các đa thức sau thành nhân tử
a.
44
(3)(5)2xx+ ++ −
b.
44
( 3) ( 1) 16xx+ ++ −
c.
44
(3)(5)16xx+ ++ −
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
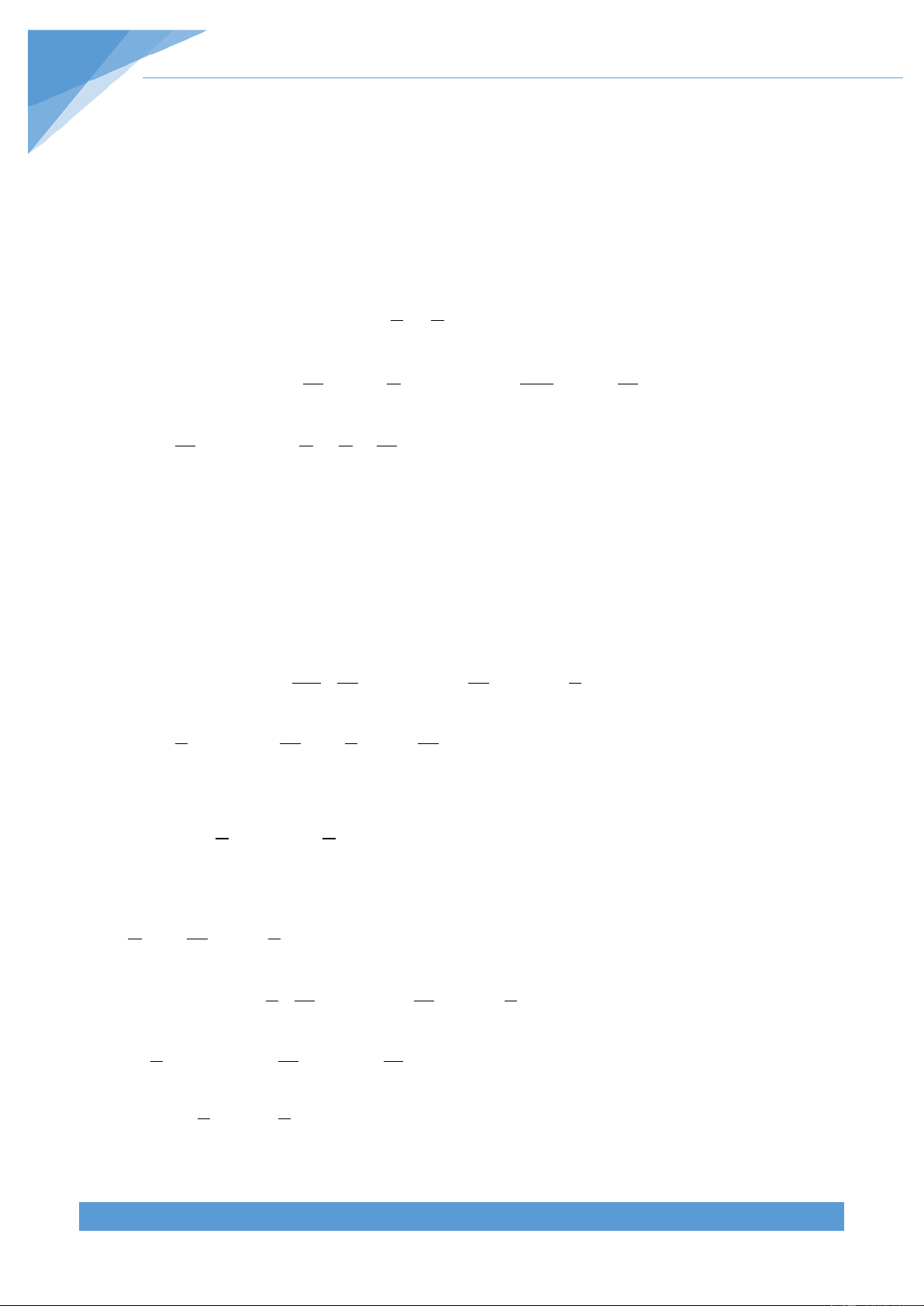
36
Lời giải
a. Đặt
44
4 4 ( 1) ( 1) 2tx xt t t=+⇒=−⇒ − ++ −
( ) ( ) ( )
2
22 2
4 2 22 2
1 1 2 2 12 2 ( 6) 2( 4) 4 6t t t t tt x x
= − + + −= + = + = + + +
b. Đặt
4 4 42 2 2
2 ( 1) ( 1) 16 2( 6 7) 2( 6 7)( ) ...tx t t t t y y yt=+⇒ + + − − = + − = + − = =
c.
( )
2
44
(3)(5)162(3)(5) 4 7x x xx x
+ ++ −= + + + +
4. Dạng
2
432
( ) ax (a 0)
= + + ++ = ≠
ed
P x bx cx dx e
ab
Cách giải:
22 22
22
( ) [(ax ) ( ) ]=x [a(x ) ( ) ]
.
ed e d
P x x bx c b x c
x x a
x bx
= + + ++ + + + +
Đặt
2
22
2
1
2 . ...
=+ ⇒= + + =
d dd
tx t x
bx b
b x
Bài 10: Phân tích các đa thức sau thành nhân tử
a.
432
( ) 2 21 30 105 50Px x x x x=−−−+
b.
4 32
3 6 31x xx x− − ++
c.
432
6 7 6 1( 0)x x x xx+ + −+ ≠
Lời giải
a.
432
( ) 2 21 30 105 50Px x x x x=−−−+
22 2 2
22
105 50 25 5
( ) 2 30 21 2
x 21 30
= −− − + = + − + −
Px x x x x x
xx x
x
Đặt
22 2 2
22
5 25 5 25
2. . 10tx t x x x t
x xx x
=+⇒ = + + ⇒ + =−
22
( ) 2( 10) 21 30 2 21 50 ( 2)(2 25)Gt t t t t t t= − − −= − −=+ −
2 22
55
( ) 2 x+ 25 x+ 2 (2 25 10)(2 2 5)
xx
= − += − + ++
Px x x x x x
b.
4 32
3 6 31− − ++x xx x
Có
22
3
1
3
= = =
−
de
ba
22 2 2
22
31 1 1
() 3 6 x 3 6
= − −+ + = + − − −
Px x x x x x
xx x x
Đặt
22 2 2
22
1 11
22x ttx x t
x xx
− =⇒ = + −⇒ + = +
;
22
( ) 2 3 6 3 4 ( 1)( 4)Gt t t t t t t=+−−=−−=+ −
2 22
11
( ) 1 4 ( 1)( 4 1)
= −+ −− = +− − −
Px x x x x x x x
xx
c.
432
6 7 6 1 ( 0)+ + −+ ≠xxxx x
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
37
4 3 2 22 2 2
22
61 1 1
6 7 61 67 6
7xxxx xxx xx x
xx x x
+ + − += + +− + = + + − +
Đặt
( )
( ) ( )
22
2 2 22 2
2
11
2 26
7 3 3yxx yAxyyxy xyx
xx
=− ⇒ + = +⇒ = ++ + = + = +
( )
2
2
2
1
3 31xx x x x
x
= − + = +−
Bài 11: Phân tích đa thức thành nhân tử:
43 2
6 11 6 1xx xx+ − ++
Lời giải
Nhận thấy đa thức bậc 4 này không dùng được máy tính
và đa thức không có hai nghiệm là 1 và -1
Tuy nhiên đa thức lại có hệ số cân xứng nhau, nên ta làm như sau:
4 3 2 22 22
22
61 1 1
6 7 61 67 6 7xxxx xxx xx x
xx x x
+ + ++= ++++ = ++ + +
Đặt
22
2
11
2x tx t
xx
+==> + =−
. Đa thức trở thành :
( ) ( )
( )( )
22 22 2
26 7 6 5 1 5xt t xt t xt t−++= ++= + +
Thay t trở lại ta được :
( )( )
22
2 2 22
1 1 1 15
1 5 1 51
x xx x
xx x x x x x x
xx x x
++ ++
++ ++ = = ++ + +
Vậy
( )( )
432 2 2
6 7 61 1 51x x x x xx x x+ + − += + + + +
Bài 12: Phân tích đa thức thành nhân tử:
43 2
10 26 10 1xxxx+ + ++
Lời giải
4 3 2 22 22
22
10 1 1 1
10 26 10 1 10 26 10 26xxxxxxx xx x
xx x x
+ + ++= ++++ = ++ −+
Đặt
22
2
11
2x tx t
xx
+==> + =−
đa thức trở thành :
( ) ( )
( )( )
22 22 2
2 10 26 10 24 4 6xt t xt t xt t−++ = ++ = + +
Thay t trở lại ta được :
( )( )
22
2 2 22
1 1 41 61
4 6 4
1 61
xx xx
xx x x x
x x x
xx x x
++ ++
++ ++ = =
+ + + +
Vậy
( )( )
43 2 2 2
10 26 10 1 4 1 6 1xxxx xxxx+ + + += + + + +
Bài 13: Phân tích đa thức thành nhân tử:
43 2
7 14 7 1xx xx− + −+
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

38
4 3 2 22 22
22
71 1 1
7 14 7 1 7 14 7
14xx xx xxx x
x x
xx x x
−
− + −+= −++ + = +− + +
Đặt
22
2
11
2x tx t
xx
+==> + =−
đa thức trở thành :
( ) ( )
( )( )
22 22 2
2 7 14 7 12 3 4xt t xt t xt t−−+ = −+ = − −
Thay t trở lại ta được :
( ) ( )
22
2 2 22
1 1 31 41
3 4 3 1. 4 1
xx xx
xx x x x x x x
xx x x
−+ −+
+− +− = = − + − +
Vậy
( )( )
43 2 2 2
7 14 7 1 3 1 4 1xx xx xx xx− + −+= −+ −+
Bài 14: Phân tích đa thức thành nhân tử:
43 2
41xx xx+ − ++
Lời giải
4 3 2 22 22
22
11 1 1
41 4 4xx xx xxx xx x
xx x x
+ − ++= +−+ + = + + + −
Đặt
22
2
11
2x tx t
xx
+==> + =−
đa thức trở thành :
( ) ( )
( )( )
22 22 2
24 6 23xt t xt t xt t− +− = +− = − +
Thay t trở lại ta được :
( )
( )
22
2
22 2
1 1 21 31
2 3 1. 3 1
xx xx
xx x x x x x
xx x x
−+ ++
+− ++ = = − + +
Vậy
( )
( )
2
43 2 2
4 1 1 31xx xx x x x+ − ++= − + +
Bài 15: Phân tích đa thức thành nhân tử:
( )( )( )( )
2
4 5 6 10 12 3xxx x x+ + + +−
Lời giải
Ta có :
( )( )( )( )
( )( )
22 2 2
4 5 12 6 10 3 4 17 60 16 60 3xx xx x xx xx x+ + + +− = + + + +−
2
60 60
4 17 16 3xx x
xx
++ ++ −
, Đặt :
60
xt
x
+=
, Khi đó đa thức trở thành :
( )( )
( )
( )( )
2 22 2
4 17 16 3 4 132 1085 2 31 2 35x t t xt t xt t+ + −= + + = + +
( )( )
2 22
120 120
2 31 2 35 2 31 120 2 35 120xx x x x x x
xx
= ++ ++= ++ ++
Bài 16: Phân tích đa thức thành nhân tử:
432
6 7 61xxxx+ + −+
Lời giải
Nhận thấy đa thức bậc 4 này không dùng được máy tính và đa thức không có hai nghiệm
là 1 và -1. Tuy nhiên đa thức lại có hệ số cân xứng nhau: nên ta làm như sau:
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

39
4 3 2 22 22
22
61 1 1
6 7 61 67 6
7x x x x xx x xx
x
xx x x
−
+ + − += + ++ + = + + − +
Đặt
22
2
11
2x tx t
xx
−==> + =+
Đa thức trở thành :
( ) ( )
( )
2
22 22 2
26 7 6 9 3xt t xt t xt+++= ++= +
Thay t trở lại ta được :
2
2
2
2 2 22
1 13
3 ( 3 1)
xx
xx x x x
xx
−+
−+ = = + −
Vậy
( )
2
432 2
6 7 61 31xxxx xx+ + − += + −
BÀI TẬP VỀ NHÀ
Bài 1: Phân tích đa thức thành nhân tử:
( )( )
22
1 2 12xx xx++ ++ −
Lời giải
Đặt
2
x xt+=
khi đó đa thức trở thành :
( )( ) ( )( )
2
1 2 12 3 10 2 5t t tt t t+ +−=+−=− +
Thay t trở lại đa thức ta được :
( )( )
( )( )
( )
22 2
2 5 12 5xx xx x x xx+− ++ = − + ++
Bài 2: Phân tích đa thức thành nhân tử:
( )( )
22
4 10 72xx− −−
Lời giải
Đặt
2
4xt−=
khi đó đa thức trở thành :
( ) ( )( )
( )( )
( )( )
( )
2 22 2
6 72 6 72 12 6 16 2 4 4 2tt t t t t x x x x x−−=−−=− += − +=− + +
Bài 3: Phân tích đa thức thành nhân tử:
( )( )( )( )
4 1 12 1 3 2 1 4x x xx+ − + +−
Lời giải
( )( )( )( )
( )( )
22
4 1 3 2 12 1 1 4 12 11 2 12 11 1 4x x xx xx xx+ + − +−= ++ +−−
Đặt
2
12 11x xt+=
, Khi đó đa thức trở thành :
( )( ) ( )( )
2
2 14 6 2 3t t tt t t+ − − = +− = − +
( )( )
22
12 11 2 12 11 3xx xx+− ++
Bài 4: Phân tích đa thức thành nhân tử:
( )( )
22
31 3 35xx xx++ +−−
Lời giải
Đặt :
2
3x xt+=
, Khi đó đa thức trở thành :
( )( ) ( )( )
( )( )
( )( )( )( )
2 22
135 28 24 32 34 1214+ −−=−−=+ −= ++ +−=+ + − +t t tt t t xx xx x x x x
Bài 5: Phân tích đa thức thành nhân tử:
( )
2
2 32
4 8 3 14 24xx x x x++ + + +
Lời giải
( ) ( )
2
2 22
48 3 482xx xxx x++ + +++
, Đặt:
( )
2 22
48 3 2x x y y xy x+ +==> + +
=>
( )( )
2yxy x++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

40
Bài 6: Phân tích đa thức thành nhân tử:
( ) ( )( )
2 22
27 24 23xx xx xx++− ++ ++
Lời giải
Đặt :
2
2x xt+=
, khi đó đa thức trở thành :
( ) ( )( ) ( )( )
22
7 4 3 7 7 12 6 5 1 5t t t t tt tt t t+ − + + =+− − − =−− −=− + +
, thay t trở lại ta được :
( )( )
( )
( )
2
22 2
21 25 1 25xx xx x xx− ++ ++=−+ ++
Thay t trở lại đa thức ta được :
( )( )
( )( )
( )
22 2
11 12 11 70 12 1 11 70xx xx x xxx−− −+=− + −+
Bài 7: Phân tích đa thức thành nhân tử:
( )
( ) ( )
22
2 22
A x y z x y z xy yz zx= + + ++ + + +
Lời giải
Ta có :
( )
( ) ( )
( )
( )
( )
( )
22
2 22
2
2 22 2
22
2
= + + ++ + + +
= ++ + ++ ++ + ++
A x y z x y z xy yz zx
x y z xy yz zx x y z xy yz zx
Đặt
( )
( )
2
2
2 22 2 22
;x y z a xy yz zx b A a b x y z xy yz zx++= ++=⇒=+ = +++++
Bài 8: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
( ) ( )
2
24
4 44 2 22 222
22A xyz xyz xyzxyz xyz= ++ − ++ − ++ ++ +++
Lời giải
Đặt
4 44 2 22
;;xyzaxyzbxyzc++= ++= ++=
ta được :
( )
( )
2
2
2 24 22 24 2
222222A ab bc c a b b bc c ab bc= −− += − +− += − +−
Lại có :
( )
( )
2 2 2 22 22 2
2 ;2a b x y y z z x b c xy yz zx−=− + + −=− ++
Do đó :
( )
( )
( )
2
2 2 22 22
2 2 22 22 2 2 22 22 2 2 2
44
444444888
8
=− + + + ++
=−−−+ + ++++
= ++
A x y y z z x xy yz zx
x y y z z x x y y z z x x yz xy z xyz
xyz x y z
Bài 9: Phân tích đa thức thành nhân tử:
( )
( )
3
333
4 12A a b c a b c abc= ++ − + + −
Lời giải
Đặt
( ) ( )
22
2
2 233 2
,4;
4
mn
abmabn abm nab ab ab ab mn
−
+= −=⇒ = − + = + − + = +
( )
( ) ( )
32
3
3 22 3 2 2 2
3
4. 4
3 3
4
m mn
A m c c c m n c mc mn cn
+
⇒= + − − − − = −+ − +
( )( )( ) ( )( )( )
33mccncn abccabcab= − − + = ++ +− −+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

41
F. Đối với đa thức bậc cao có dạng
31 32
1
mm
xx
++
++
luôn luôn có nhân tử chung là bình
phương thiếu của tổng hoặc hiệu, nên ta thêm bớt để làm cuất hiện bình phương thiếu của
tổng hoặc hiệu:
Bài 1: Phân tích đa thức thành nhân tử:
75432
1xxxxx+++++
Lời giải
Ta có:
( ) ( ) ( ) ( )
753 42 342 42
1 11xxx xx xxx xx++ + ++= +++ ++
=
( )( ) ( )( )
( )
( )
42 3 2 2 2
1 1 1 11 1xx x xx xx x xx+ + + = ++ −+ + −+
=
( )
( )
( )
2
22
11 1xx x xx−++++
Bài 2: Phân tích đa thức thành nhân tử:
11 10 9 2
... 1x x x xx+ + ++ ++
Lời giải
Ta có:
11 10 9 2
... 1x x x xx+ + + + ++
( ) ( ) ( )
11 10 9 8 7 6 2
... 1x x x xxx xx= + + + + + ++ ++
( ) ( ) ( )
92 62 2
1 1 ... 1xxx xxx xx= ++ + ++ ++ ++
( )( )
2 963
11xx xxx++ + + +
( )
( )( )( )( )
2422 2
11 1 1 1x x xx xx xx=++−+−+++
Bài 3: Phân tích đa thức thành nhân tử:
84
14 1xx++
Lời giải
Ta có:
( ) ( ) ( ) ( )
22
84 44 44 4 2424 4
2 1 12 1 12 1 2. 1 .2 4 4 1 8xx xx xx x xxxx x+ ++ = ++ = ++ + + − ++
=
( ) ( )
22
423
12 2 2x x xx++ − −
( )( )
423 423
12 2 2 12 2 2xxxxxxxx= ++ − + ++ + −
Bài 4: Phân tích đa thức thành nhân tử:
84
98 1xx++
Lời giải
Ta có:
( ) ( ) ( )
22
4 4 2 4 24 4
1 2 1 .8 64 16 1 32x x x x xx x+ + + + − ++
=
( ) ( ) ( ) ( )
2 22
42 24 2 42 3
8116 12 81 44xx xx x xx xx+ +− +− = + +− −
Bài 5: Phân tích đa thức thành nhân tử:
5432
23683xxxx−+−+
Lời giải
Ta có:
5 4 3 2 5 443 3 2 2
2368322 5533x x x x x xxx x x x−+−+=−−++−−+
( ) ( ) ( )
( )
43 2 2
2 1 15 13 1xx xx xx x= −− −+ −− −
=
( )
( )
( )
2
2
1 32 1xx x− ++
G. ĐỐI VỚI ĐA THỨC ĐA ẨN
Bài 1: Phân tích đa thức thành nhân tử:
2 22
2 21x y z xy z+−+ −−
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

42
Lời giải
Ta có:
( ) ( )
( ) ( )
22
2 22 2
2 2
2 21 2 21 1x y z xy z x xy y z z x y z+−+−−=++−++=+−+
( )( )
11xyz xyz= +++ +−−
Bài 2: Phân tích đa thức thành nhân tử:
222
2 21x y z xz y−+− + −
Lời giải
Ta có:
( ) ( )
( ) ( )
22
222 2
2 2
2 21 2 21 1x y z xz y x xz z y y x z y−+−+−=−+−−+=−−−
( )( )
11xzy xzy−+− −−+
Bài 3: Phân tích đa thức thành nhân tử:
6 4 33 3
22x x x y xy−− +
Lời giải
Ta có:
6 4 33 3
22x x x y xy−− + =
( )
5 3 23 3
22xx x xy y−− +
=
( ) ( ) ( )( )
32 32 3 3 2
22 2xx x y x xx y x
−− − = − −
=
( )
( )( )
22 2
2x x y x x xy y− − ++
Bài 4: Phân tích đa thức thành nhân tử:
64 3 2
99xx x x−− +
Lời giải
Ta có:
64 3 2
99xx x x−− +
=
( )
24 2
99xx x x−−+
=
( )
( ) ( )( ) ( )
222 22
191 1 191xxx x xxx x x
−−−= − +−−
=
( )
( )
2 32
19xx x x− +−
Bài 5: Phân tích đa thức thành nhân tử:
( ) ( )
22
2
4abc abc b+++−+−
Lời giải
Ta có:
( ) ( )
222 222 2
222 222 4a b c ab bc ca a b c ab bc ac b+++ + + + ++− − + −
( ) ( )
( )
2
2 2 2 2 22 2
2224 2 2 2a c b ac a ac c b a c b
= + − + = + +− = + −
( )( )
2 acbacb= ++ +−
Bài 6: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
22 22 22
ab c bc a ca b−− −+ −
Lời giải
Ta có:
( ) ( ) ( )
222222 2 2 2
ab ac bc a b a c b c a b c b a c c a b−−++−= ++ −− +
=
( ) ( ) ( ) ( )
22 2
abc b ab bc cab++ +−+ − +
=
( ) ( ) ( ) ( )
22 22
abc bab bbc cab++ +− +− +
=
( )
( )
( )
( )
( )( )( ) ( )( )( )
22 22
bca b abb c bcabab abbcbc+ − ++ − =+ − +++ − +
=
( )( )( ) ( )( )( )
abbcabbc abbcac++−+−=++−
Bài 7: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
3xy x y yz y z zx x z xyz++ ++ ++
Lời giải
Ta có:=
( ) ( ) ( )
xy x y xyz yz y z xyz zx z x xyz+++ +++ ++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

43
=
( ) ( ) ( ) ( )( )
xy x y z yz x y z zx x y z x y z xy yz zx++ + ++ + ++ = ++ + +
Bài 8: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
xy x y yz y z zx z x+− +− −
Lời giải
Ta có: =
( ) ( ) ( ) ( )
xy x y yz y z zx y z x y+− +− +−+
=
( ) ( ) ( ) ( )
xy x y yz y z zx y z zx x y+− +− ++ +
=
( )( ) ( )( ) ( )( )( )
xxyyz zyzxy xyyzxz+ +−++=+ +−
Bài 9: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
4 44
xyz yzx zxy−+ −+ −
Lời giải
Ta có:
( ) ( ) ( ) ( )
44 4
xyz y yz xy zxy−+ −−−− + −
=
( ) ( ) ( ) ( )
4444
xyz yyz yxy zxy−− −− −+ −
=
( )
( )
( )
( )
4 4 44
yzx y xyy z− − −− −
=
( )( )( )
( )
( )( )( )
( )
2 2 22
yzxyxyx y xyyzyzy z− − + + −− − + +
=
( )( ) ( )
( )
( )
( )
2 2 22
xyyz xyx y yzy z
− − + + −+ +
=
( )( )
( )
3 22 33 22 3
x y y z x xy x y y y yz y z z− − + + +−− − −
=
( )( ) ( )
( )
( )
33 2 22
x y y z x z y x z yx z− − −+ −+ −
=
( )( ) ( )
( )
( ) ( )( )
2 22
xyyz xzx xzz yxz yxzxz
− − − ++ + −+ − +
=
( )( )( )
( )
2 22
x y y z x z x xz z y xy yz− − − +++++
Bài 10: Phân tích đa thức thành nhân tử:
( )( )
a b c ab bc ca abc++ + + −
Lời giải
Ta có:
2 2 22 2 2
a b abc a c ab b c abc abc bc ac abc++++++++−
=
( ) ( )
2 2 22 22
a b ab abc b c bc abc a c ca+++++++
=
( ) ( ) ( )
ababc bcabc acac++ + ++ + +
=
( )( ) ( )
babcac acac++ + + +
=
( )
( )
( )( )( )
2
a c ab b bc ac a c b c a b+ +++ =+ + +
Bài 11: Phân tích đa thức thành nhân tử:
( ) ( ) ( ) ( )
3333
abc abc bca cab++ − +− − +− − +−
Lời giải
Ta có:
( ) ( ) ( ) ( )
3 333
abc abc bca cab
++ − +− + +− + +−
xabc
ybca xyz abc
zcab
=+−
=+−=>++=++
=+−
=
( )
( )
( )( )( )
3
3 33 333 3
33
3xyz x y z x y z xyyzzx x y z++ − ++ =+++ + + +−−−
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

44
=
( )( )( )
3 3.2 .2 .2 24x y y z z x a b c abc+ + += =
Bài 12: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
222
abc bca cab−+ −+ −
Lời giải
Ta có:
( ) ( ) ( ) ( )
22 2
abc b bc ab cab−+ −−−− + −
=
( ) ( ) ( ) ( )
2222
abc bbc bab cab−− −− −+ −
=
( )( )( ) ( )( )( )
bcabab abbcbc− − +−− − +
=
( )( )( ) ( )( )( )
bcababbc abbcac−−+−−=−−−
Bài 13: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
33 33 3 3
xy z yz x zx y−+ −+ −
Lời giải
Ta có:
3 3 33 3 3
xy xz yz x y x z y z−+−+−
=
( ) ( ) ( )
3 33
xzy yxz zyx−+ −+ −
=
( ) ( ) ( ) ( )
33 3
xzy y zy yx zyx−+ −−−− + −
=
( ) ( ) ( ) ( )
3333
xzy yzy yyx zyx−− −− −+ −
=
( )
( )
( )
( )
33 33
zyx y yxz y− − +− −
=
( )( )
( )
( )( )
( )
22 22
z y x y x xy y y x z y z yz y− − ++ +− − ++
=
( )( )
( )
2 22 2
z y x y x xy y z yz y− − ++−−−
=
( )( )
( )
( )( )( )( )
22
zyxyx z xyyz zyxyxzxyz−− −+−=−−−++
Bài 14: Phân tích đa thức thành nhân tử:
( )
( ) ( )
22
2 22
x y z x y z xy yz zx+ + ++ + + +
Lời giải
Ta có:
( ) ( )
( ) ( )
2
2 22 2 22
2x y z x y z xy yz zx xy yz zx
++ ++ + ++ + ++
Đặt:
2 22
,x y z a xy yz zx b++= ++=
khi đó đa thức:
( )
2
2aa b b++
( )
( )
2
2
2 2 2
22
2a ab b a b x y z xy yz zx=+ +=+ = +++++
Bài 15: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
( ) ( )
2
24
4 44 2 22 222
22xyz xyz xyzxyz xyz++ − ++ − ++ ++ +++
Lời giải
Đặt:
4 44 2 22
,,xyzaxyzbxyzc++= ++= ++=
,
Khi đó ta có:
( ) ( )
2
2 24 22 24 2 2
222222ab bc c a b b bc c ab bc−− += − +− += − +−
,
Lại có :
( )
2 22 22 22
2a b xy yz zx−=− + +
và
( )
2
2b c xy yz zx−=− ++
,
Thay vào ta được :
( )
( ) ( )
2
2 2 22 22
4 48x y y z z x xy yz zx xyz x y z− + + + + + = ++
Bài 16: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
222
cab bac abc− −+ −− −
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

45
Ta có :
( ) ( ) ( ) ( )
22 2
cab b ab bc abc− −+ −+− − −
=
( ) ( ) ( ) ( )
2222
cab bab bbc abc− −+ −+ −− −
=
( )( )( ) ( )( )( )
abbcbc bcbaba−−++−−+
=
( )( )( ) ( )( )( )
abbcbcab abbcca−−+−−=−−−
Bài 17: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
333
x yz y zx z xy− +− +−
Lời giải
Ta có :
( ) ( ) ( ) ( )
33 3
zxy x xy zx yzx−+ −−−− + −
=
( ) ( ) ( ) ( )
3 3 33
zxy xxy yzx xzx−− −+ −− −
=
( )
( )
( )
( )
33 33
xyz x zxy x− − +− −
=
( )( )
( )
( )( )
( )
22 22
xyzxz zxx zxyxy xyx− − ++ +− − ++
=
( )( )
( )
( )( )( )( )
2 22 2
xyzxz zxx y xyx xyzxzyzyx−− ++−−−=−−−+−
Bài 18: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
ab a b bc b c ac c a+−+−−
Lời giải
Ta có :
( ) ( ) ( ) ( )
ab a b bc a b c a ac c a+− ++− − −
=
( ) ( ) ( ) ( )
ab a b bc a b bc c a ac c a+− +− −− −
=
( )( ) ( )( ) ( )( )( )
babac ccaba abbcac+ −− − + =+ + −
Bài 19: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
33
11xy x y y x−− −+ −
Lời giải
Ta có :
( ) ( ) ( ) ( )
33
11xy x xy x y x−− −+− + −
=
( ) ( ) ( ) ( )
3 33
11xy xxy x x y x−− −− −+ −
=
( )
( )
( )
( )
3 33
11xy x xx y− − −− −
=
( )( )
( )
( )( )
( )
2 22
11 1xy x xx xxyx xyy− − ++ − − − + +
=
( )( )
( )
( )( )( )( )
22 2
11 11 1xy x xx x xyy xy x yxy−−++−−−=−−− ++
Bài 20: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
22 22 22
42 42ab a b bc c b ca a c++ −− +
Lời giải
Ta có :
( ) ( ) ( ) ( )
22 22 2 2
42 2 2 42ab a b bc a c a b ca a c++ +− + − +
=
( ) ( ) ( ) ( )
22 22 22 22
42 2 2 42ab a b bc a c bc a b ca a c++ +− +− +
=
( )
( )
( )
( )
2 22 2 2 2
24 2 4b ab a c c acb a+ −+ + −
=
( )( )( ) ( )( )( )
22
222 222b ab ac ac c ac ab ab+ − +− + − +
=
( )( )
( )
22 2 2
222 2a c a b ab b c ac bc+ + −− +
=
( )( )( )( )
2 2 22a c a b b c ab ac bc+ + − +−
Bài 21: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
3 33
xyz yzx zxy−+ −+ −
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

46
Ta có :
( ) ( ) ( ) ( )
33 3
zxy x xy zx yzx−+ −−−− + −
=
( ) ( ) ( ) ( )
3 3 33
zxy xxy yzx xzx−− −+ −− −
=
( )
( )
( )
( )
33 33
xyz x zxy x− − +− −
=
( )( )
( )
( )( )
( )
22 22
xyzxz zxx zxyxy xyx− − ++ +− − ++
=
( )( )
( )
( )( )( )( )
2 22 2
xyzxz zxx y xyx xyzxzyzyx−− ++−−−=−−−+−
Bài 22: Phân tích đa thức thành nhân tử:
( )( ) ( )( ) ( )( )
bc a d b c ac b d a c ab c d a b+ −− + −+ + −
Lời giải
Ta có :
( ) ( ) ( )
bc ab ac bd dc ac ab bc ad dc ab ac bc ad bd−+ − − −+ − + −+ −
=
( ) ( ) ( ) ( )
bc ab ac bd dc ac ab ac bd dc ac bc ad bd ab ac bc ad bd−+ − − −+ − + −+ − + −+ −
=
( )( ) ( )( )
ab ac bd dc bc ac ac bc ad bd ac ab−+− −−−+− −
=
( )( ) ( ) ( )( ) ( )
a d b ccb a c d a bac b+ − −−+ − −
=
( )( )( ) ( )( )( )
.b c b a ac dc ca ad b c b a c a d−− +−−=−−−
Bài 23: Phân tích đa thức thành nhân tử:
( ) ( ) ( )
333
a xy a yx x ya− −− +−
Lời giải
Ta có :
( ) ( ) ( ) ( )
33 3
yax x ax xy axy−− −+− + −
=
( ) ( ) ( ) ( )
3333
yax xax xxy axy−− −− −+ −
=
( )
( )
( )
( )
33 33
axy x xyx a−−−−−
=
( )( )
( )
( )( )
( )
22 22
x a x y x xy y x y x a x xa a− − ++ −− − ++
=
( )( )
( )
2 22 2
x a x y x xy y x xa a− − ++−−−
=
( )( )( )( )
xaxyyayax− − − ++
Bài 24: Phân tích thành nhân tử:
2 22222
2x y xy xz yz x z y z xyz++++++
Lời giải
Ta có:
( ) ( ) ( ) ( )
( )
2
22
xy x y z x y z x y x y xy z xz yz= ++ ++ + =+ +++
( )( )( )
xyyzzx=+++
F. PHƯƠNG PHÁP HỆ SỐ BẤT ĐỊNH
- Chú ý: Hai đa thức bằng nhau khi hệ số của mỗi lũy thừa tương ứng trong hai đa thức
bằng nhau
- Phương pháp này dùng cho đa thức không có nghiệm nguyên cũng không có nghiệm
hữu tỷ
Bài 1: Phân tích các đa thức sau thành nhân tử
a.
43 2
( ) 6 12 14 3fx x x x x=−+ −+
b.
432
() 2 3 7 6 8Qx x x x x= − − ++
c.
43 2
( ) 2 7 17 20 14Px x x x x=−+ −+
d.
432
() 4 4 5 2 1Rxxxxx= + + ++
e.
22
( , ) 12 5 12 12 10 3H x y x x y y xy= +− + − −
f.
22
( , ) 2 7 6 9 13 5Txyxxyyxy= − + +− −
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

47
Lời giải
a. Ta nhận thấy đa thức không có nghiệm nguyên cũng không có nghiệm hữu tỷ
Giả sử
2 2 43 2
( ) ( ax+b)(x ) ( ) ( ) ( )f x x c
x d x a c x ac b d x ad bc x bd= + + + = + + + ++ + + +
Đồng nhất các hệ số ta được:
{ }
6
14
14
3 1; 3
ac
ac b d
ad bc
bd b
+=−
++ =−
+=−
= ⇒ ∈± ±
+)
22
6
3 8 4; 2( ) ( ) ( 2 3)( 4 1)
3 14
ac
b ac c a tmfxxx xx
ac
+=−
=⇒ = ⇒=− =− ⇒ = −+ −+
+=−
b. Cách 1: Ta nhận thấy đa thức có 1 nhân tử là x + 1
432 32 4 3 2
()2 3 7 6 8( 1)(2 ax )2 ( 2) ( ) ( )Qx x x x x x x bxc x a x abx bcxc= − − ++=+ + ++= ++ ++ ++ +
2
23
5
7
2 ( ) ( 1)( 2)(2 4)
6
8
8
a
a
ab
b Qx x x x x
bc
c
c
+=−
= −
+=−
⇒ =−⇒ = + − −−
+=
=
=
Cách 2: Giả sử
22 4 3 2
( ) (2 + +b)(x ) 2 (2 ) (2 ) ( )Q x x ax cx d x c a x d ac b x ad bc x bd= ++= + + + ++ + + +
Đồng nhất các hệ số:
2
23
2
27
4 ( ) (2 4)( 1)( 2)
6
1
8
ca
b
d ac b
d Qx x x x x
ad bc
ac
bd
+=−
= −
+ +=−
⇔ =− ⇒ = −− + −
+=
= = −
=
c.
27
2 17
20
14 2; 7( ) 2; 3
bn
c p bn
cn bp
cp c p tm b n
+=−
++ =
+=−
= ⇒= = ⇒=− =−
d.
22
(2 1)xx= ++
e. Giả sử
( )( ) ( )
22
(, ) ( ) ( )H x y ax by c dx ey f adx af cd x bey ce bf y cf bd ac xy= ++ ++ = + + + + + ++ +
12
5
12 (;) (3 2 1)(4 6 3)
12
3 1; 3 3; 4; 2; 6
ad
af cd
be H
xy xy xy
ce bf
cf cf adbe
=
+=
=− ⇒
=−− +−+ −
+=
=−⇒ = =−⇒ =− =− =− =
f.
( )( )
( , ) 2 2, 3, 1, 5T x y x by c x ny p n b c p= + + + + ⇒=− =− =− =
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

48
Bài 2: Phân tích đa thức thành nhân tử:
( )
2
2 2 22 22 22
xyxy xyyzzx
++ − − −
Lời giải
( )
2
2 2 22
22 22 4 4 22 22 3 3 22 22 22
2 22x y xy xy yz zx x y xy xy xy xy xy yz zx++−−−=+++ ++−−−
=
( ) ( )
44 22 22 222
22xy xy xyxy zxy++ + + − +
=
( ) ( ) ( )
2
22 22 222
2xy xyxy zxy+ + +− +
=
( )( ) ( ) ( )
2222 2 22 2 2
2xyxy xyz xy xy z
+ ++ − = + + −
=
( )
( )( )
22
x y xyzxyz+ ++ +−
Bài 3: Phân tích đa thức thành nhân tử:
( )
42 2 2 2
81xz y z y− −+
Lời giải
Ta có:
( ) ( ) ( )
422 22 422 22
81 81xzy zy xzy zy−−+= −−−
=
( )( )
( )( )
( )( )
22 4 2 2
81 1 9 1 9 1z y x zyzy x x− −= − + − +
=
( )( )( )( )
( )
2
3 13 19 1zyzy x x x−+ + − +
Bài 4: Phân tích đa thức thành nhân tử:
642246
x x xy y y++ +−
Lời giải
Ta có:
642246
x x xy y y++ +−
=
( ) ( ) ( )
22 2
6 6 4 22 4 22 3 3 2 2 22
2x y x xy y xy x y x y xy−++ +− = − + + −
=
( )( ) ( )( )
3333 22 22
x y x y x y xy x y xy− + + +− ++
=
( )
( )
( )
( ) ( )( )
2 2 2 2 22 22
x y x xy y x y x xy y x y xy x y xy− ++ + −+ + +− ++
=
( )( )( )
22 22 22
1x y xy x y xy x y++ +− −+
Bài 5: Phân tích đa thức thành nhân tử:
4
8 63xx++
Lời giải
Ta có:
( )( )
4 22
8 63x x x ax b x cx d++= ++ ++
Đồng nhất hệ số ta có:
4
8 63xx++=
( )( )
22
47 49xx xx−+ ++
Bài 6: Phân tích đa thức thành nhân tử:
( )
( )
2
4
2
11x xx+ + ++
Lời giải
Ta có:
( )
( )
( ) ( )
2
2
44
2
1 1 1 11x x x x xx++ ++=++ ++
=
( ) ( ) ( )
42
2
1 1 2 11x x x xx++ ++ ++
=
( ) ( )
( )
22
22
1 1 2 21x x x xx
+ ++ + ++
=
( )
( )
2
2
2 21 1 1xx x
++ ++
=
( )( )
22
2 22 2 1xx xx++ ++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

49
BÀI TẬP VỀ NHÀ
Bài 1: Phân tích các đa thức sau thành nhân tử
a.
75
1xx++
b.
72
1xx++
c.
42
8 15
nn
xx++
Lời giải
a. Ta có:
7 5 7 6 5 6 52 3 3 52 2 3
1 1 ( 1) ( 1)( 1) ( 1) ( 1)( 1)( 1)xx xxxx xxx x x xxx x xx x+ += + + − += ++ − − + = ++ − − ++ +
253
( 1) ( 1)( 1)xx x x x
= ++ − − +
b.
72 7 2 2 542
1 ( ) ( 1) ( 1)( 1)xx xx xx xx xxxx+ += − + ++ = ++ − + −+
c.
42 2 2 2 2
8 15 8 15( ) ( 3)( 5) ( 3)( 5)
nn n n n
x x aa xaa a x x+ += ++ ==+ += + +
Bài 2: Phân tích các đa thức sau thành nhân tử
a.
2 22 2 2
( )( ) 3( )x y z x y z xy yz zx+ + ++ − + +
b.
333
( )( )( )xy yz zx− +− +−
c.
3 33 3 33 3 33
( )( )( )xy yz zx− ++ −+
d.
333 3
( )( )( )8( )ab bc ca abc+ + + + + − ++
e.
3333
( )( )( )( )abc abc bca cab++ − +− − +− − +−
Lời giải
a. Ta có
2 222
( ) 2( )x y z x y z xy yz zx++ = + + + + +
Đặt
2 22
22 2
( 2 ).3 2 3 ( )( 3 )
xyza
A a a b b a ab b a b a b
xy yz zx b
++=
⇒= + = + − =− +
++=
2 22 222
( )[(x 3( )]A x y z xy yz zx y z xy yz zx⇒= ++−−− ++++ ++
b. Ta đã biết: Nếu
333
03a b c a b c abc++=⇒ + + =
Đặt
333
0 3 3( )( )( )
xya
y z b a b c B a b c B abc x y y z z x
zxc
−=
−=⇒++=⇒= ++⇒= = − − −
−=
c. Tương tự câu b.
33
33 333 3333 33
33
0 3 3( )( )( )
xya
y z b a b c B a b c B abc x y y z z x
xzc
−=
+ = ⇒++=⇒= ++⇒= = − + −−
−− =
d. Đặt
33
2()()8()
ab x
bc y xyz abc xyz abc
ca z
+=
+= ⇒++= ++ ⇒ ++ = ++
+=
;
3 33 3
()Dx y z xyz= + + − ++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

50
Ta có:
3 333
( ) 3( )( )( ) 3( )( )( ) 3....xyz x y z xyyzzx D xyyzzx++ =+++ + + +⇒=− + + +=−
e. Đặt
=+−
=+−
=+−
mabc
nbca
pcab
thì:
3 33 3
( ) 3( )( )( )++= ++ ⇒ = ++ − − − = + + +abcmnp E mnp m n p mnnppm
3.2 .2 .2 24E b c a abc⇒= =
Bài 3: Cho x, y, z thuộc Z. Chứng minh rằng:
( )( )( )( )
4
234S xyx yx yx y y=+ + + ++
là số
chính phương
Lời giải
Ta có:
4 2 22 2 4
( )( 4 )( 2 )( 3 ) ( 5 4 )( 5 6 )S x yx yx yx y y x xy y x xy y y=+ + + ++=++ ++ +
2 4 22 2 22
( 2 ) ( ) ( 5 5 )( )
t
S t t y y t y x xy y dpcm=+ +=+ = + +
Bài 4: Phân tích các đa thức sau thành nhân tử
a.
432
4 8 3 84xxxx− + −+
b.
43 2
2 15 35 30 8xxxx− + −+
c.
3 22 2 3
2 3 ( 1) ( 1)x xxx xx− −+ + −+
d.
432
4 4 7 44xxxx− − −+
Lời giải
a. Ta có:
432 4 2222222 2
4 8 3 8 4 4( 1) 8 ( 1) 3 4( 1) 8 ( 1) 5 4 8 5x x x x x xx x x xx x y xy x− + − += +− ++ = + − +− = − −
2 2 22 2
4 2 10 5 (2 )(2 5 ) (2 2)(2 5 2) (2 2)( 2)(2 1)y xy xy x y x y x x x x x x x x x= + − − = + − = ++ − + = ++ − −
b. Ta có:
4 3 2 4 2 2 22 2 2 2 2
2 15 35 30 8 2( 4) 15 ( 2) 35 2( ) 15( 2) 27 2 15 27xxxx x xx xxx x xyyx− + − += +− ++ = + − ++ = − +
22
( 3 )(2 9 ) ( 3 2)(2 9 4) ( 1)( 2)( 4)(2 1)yxyx x x x x x x x x=− − = −+ −+=− − − −
c. Ta có:
322 2 3 32 3 2 22
23( 1)( 1)23 2()()()()(2 )x xx x x x x xyy xxy yxyxy xy x y xy− −+ + −+ = − + = − − − + = − − −
2
()()(2)()(2)xyxy xy xy xy=− − +=− +
d. Ta có:
432 2
4 4 7 4 4 ( 2)(2 1)(2 3 2)xxxx x x xx− − − += − − + +
Bài 5: Phân tích các đa thức sau thành nhân tử
a.
43 2
( ) 2 19 2002 9779 11670Ax x x x x=−+ − +
b.
65 4 32
( ) 3 10 34 47 52 8 40Bx x x x x x x=−+−++−
Lời giải
a. Ta nhận thấy đa thức có hai nhân tử là x - 2 và x - 3
22
( ) ( 2)( 3)(ax ) 2; 1945; 9 ( ) ( 2)( 3)(2 9 1945)Ax x x bx c a c b Ax x x x x=−− ++⇒== =−⇒ =−− −+
b. Nhận thấy đa thức có 2 nhân tử là: x – 1 và 3x + 2
43 2 2 2
( ) ( 1)(3 2)( 3 11 14 20) ( 1)(3 2)( 2 4)( 5)Bxx xxxxx x xxxxx=−+−+−+=−+−+−+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

51
Bài 6: Phân tích các đa thức sau thành nhân tử
a.
()()()A ab a b bc b c ca c a= −+ −+ −
b.
333
( )( )( )B ab bc ca= − +− +−
c.
333
()()( )C ab c bc a ca b= −+ −+ −
d.
555
( )( )( )D ab bc ca=− +− +−
Lời giải
Đặt
;xabybc xy ac=− =−→+ =−
a.
( ) ( ) ( ) ( ) ( )( )( )A abx bcy ca x y ax b c cy a b axy cxy xy a c a b b c c a=+− += −− −=−= −=− − −
b.
33 3333 3
() 3() 3()3()()()Bx y xy x y x xyxy y xyxy abbcca=+−+ =+−− +−=− += − − −
c. Ta có:
3 3 3 3 33 3 3 3
33 2
2
() 3() ()()3()
3()( )3()()( 3)()( 3)
( )( ) ( )( )( )( )
C ay b x y cx ay b x y xy x y cx y a b x b c bxy x y
xy x y bxy x y xy y x bxy x y xy x y y x b xy x y b c a b b
xyxyabc abbccaabc
=−++=− ++ ++= −− −− +
= − − += − − += + −− = + −−+−
=− + ++ = − − − ++
d. Ta có:
5 4 2 2 2 4 22 4 3 3 22
()()()()(2 )()(4 4 4 2)xy xyxy xyx xyy xyx xy y xy xy xy+=++=+++=++ ++++
4 4 3 22 3 5 5 3 3 2 2
( )( ) ( )(4 6 4 ) ( ) ( )(4 6 4 )x y x y x y x y x y xy x y xy x y xy x y x xy y=+ + ++ + + =++ + + + + +
55 2 2 55 2 2
( )(5 5 5 ) 5 ( )( )x y xy x y x xy y x y xy x y x xy y=++ + + + =++ + ++
55 555 55 2 2 2 2
() 5()( )5()( )
⇒=+−+ =+− ++ + ++ =− + ++
D x y x y x y x y xy x y x xy y xy x y x xy y
2 2 222
5( )( )( ) ( ) ( )( ) ( ) 5( )( )( )( )abbcca ab abbc bc abbccaa b c abbcca
=−−− −+−−+−=−−− ++−−−
Bài 7: Phân tích các đa thức sau thành nhân tử
a.
33 33 33
( )( )( )A ab c bc a ca b= −+ −+ −
b.
32 2 32 2 32 2
( )( )( )B ab c bc a ca b= −+ −+ −
Lời giải
a. Đặt
33 33 33
; ( ) ( )( )=− =−⇒+=−⇒= − ++= −− −xa byb c xya c Aaybxy cxyab xbc
33 33 2 2 2 2
22
( )( ) ( )( ) ( )( )( )
( )( )( )
( )( )( )( )
= − −− − −=− − ++− − −
=−− −+−=−−−++
b c ab a b bc bcabb bcc a abb
bcabbcabc a bcabcaabc
b. Đặt
22 22 22
;= − = − ⇒+= −xa byb c xya c
3 3 3 33 33 2233 2233
2 2 22
2 22 2 2 2 2 2
2
( ) ( ) ( ) ( )( ) ( )( )
( )( ) ( )( ) ( )( )
( )( )
()( ) ()()()(
= − ++ = −− −=− −−− −
=− − + + + −+ ++
= ++−−− + + + − − −
= − ++ + − − − = −
Baybxycxyab xbc bcab abbc
bcab bca abb abb bcc
b a ab b b bc c a c abc b c ab abc ac
bacabc acac bac aca
22
) ( )( )
( )( )( )( )
+++− =− ++
⇒=− − − + +
b b bc ac b a c ab bc ca
B abbcacabbcca
Bài 8: Phân tích các đa thức sau thành nhân tử
a.
3 33 3
()A abc a b c= ++ − − −
b.
33
( 2) ( 2)B xx y yy x=+ −+
c.
4 44
()Cx xy y=++ +
d.
444 222222
2( )D a b c ab bc ca= ++− + +
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

52
a. Đặt
=++mabc
suy ra:
[ ]
33 3 3 2 2 2 2
2 22 2 22 22
( ) ( )( ) ( )( )
( )( )( )( )( )( )
( ) ( )( ) ( )( ) ( )( ) ( )( )( )
3( )( )( )
= −− + = − + + −+ − +
=+ + +−+− =+ − + − + +
= + − + + − + + + + = + + ++−++
=++ +
A m a b c m a m ma a b c b bc c
bcm maa b bca bc m b a c mabc
bc mbmb acac abac bcacmbacab
bccaab
b. Đặt
mxy= +
3 33 3 3 3
3 22 3
2 2 33
()() 3() 3()
( ) ( )3 ( )( )( ( )3 )
()(4)()()4 ()()()
B x m y y m x x m my m y y y m mx m x x
m x y xy x y mxy m x m y x y m xy x y mxy
mxym xy mxy xy xy mxy xyxy
= +− += + ++− + ++
= − − − − +− − = − − + −
= − − = − +− = −=+ −
c. Đặt
mxy= +
444 4 3 22 34 44 4 224 22 22
2
22 2 22 2 22
( ) 4 6 4 2( 2 ) 4 ( ) 2
2( ) 2 ( ) ( ) 2( )
C m y m y m my my my y m y m my y mym y my
m y my xy y xyy x xyy
=− ++=− + − +++= + + − + +
= +− = + +−+ = ++
d. Đặt
222
mabc=++
2 2 22 22 22 22 2 2 2 2 22 2 2 2 22
22 2 2 2 222 2 222 2
22 22
( )4( ) 4( ) 4( )
( 2) (2) ( 2 2)( 2 2)( 2 2)( 2 2)
( ) ( ) ( )( )(
D a b c ab bc ca m b a c ca m b m b ca
m b ca m b ca m b ca a b c b ca a b c b ca
ac b ac b acbacbacb
= ++ − + + = − + + = − − +
=− − =−− −+ =++−− ++−+
= − − + − = −− −+ +−
)( )abc++
Bài 9: Phân tích các đa thức sau thành nhân tử
a.
222
()()()()()()Aabca bcab cabc bcacababc= +− + +− + +− + +− +− +−
b.
3333
( )( )( )( )B abc abc bca cab= ++ − +− − +− − +−
c.
333
()()() 2C ab a b b b c ca c a a b c abc= ++ ++ +−−−−
Lời giải
a. Đặt
; ; ; 2 ;2 ;2=++ +−= +−= +−=⇒ =+ =+ =+m xyzabc xbca ycab z a yzb zxc xy
222
2()()()2 ()()()2
( ) ( ) ( ) 2 ( ) ( )( )( ) 8 4
A y z x x z y y x z xyz xy x y yz y z zx z x xyz
xy m z yz m x zx m y xyz m xy yz zx xyz x y y z z x abc A abc
=+ ++ ++ + = ++ ++ ++
= −+ −+ −+ = + + − =+ + += ⇒=
b. Đặt
;;abc zbca xcab y xyz abc+−= +−= +−= →++=++
33 33
( ) 3( )( )( ) 3.2 .2 .2 24B x y z x y z x y y z z x c a b abc= ++ − − − = + + + = =
c. Đặt
; ; 2 ;2 ;2+−= +−= +−=⇒ =+ =+ =+abc zbca xcab y a yzb xzc xy
Ta có:
222
22 2
44()4()4()8
( ) ( ) ( ) ( )( )( )
= +− + +− + +− −
=+ ++ ++ −+ + +
C a b c a b c a b c a b c abc
yzx zxy xyz xyyzzx
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

53
2
2
( ) ( ) ( ) ( )( )( ) 6
()()()()()()()4
( )( ) ( )( )( ) 4
( )( )( ) ( )( )( ) 4
4
( )(
= ++ ++ +−+ + ++
= ++ ++ ++ +−+ + ++
=+ + ++ −+ + ++
=+ + +−+ + ++
=
⇒ = = +− +−
xy x y yz y z zx z x x y y z z x xyz
xyxy yzxy zxxy zxy xyyzzx xyz
x y xy yz zx z x y y z z x xyz
x y y z z x x y y z z x xyz
xyz
C xyz b c a c a b)( )+−abc
CÁC ỨNG DỤNG CỦA PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
A. Ứng dụng 1: Dùng để rút gọn biểu thức
Bài 1: Cho a + b + c = 0 , Rút gọn
33 22
()A a b c a b abc=++ + −
Lời giải
Ta có:
33 22 332 2
32 32 2
2
()
( )( ) ( ) ( )
=++ + − =++ + −
= + + + − = ++ +−
A a b c a b abc a b a c b c abc
a a c b b c abc a a c b b c abc
Vì
22
0 ( ) ( ) ( ) 0.
ac b
abc Aa b b a abc ababc
bc a
+=−
++=⇒ ⇒ = − + − − =− ++ =
+=−
B. Ứng dụng 2: Dùng để chứng minh
Bài 2: Cho
22 2 2
1; 1, 0.+= += + =a b c d ac bd
Chứng minh rằng:
0+=ab cd
Lời giải
Ta có:
2 2 22 2 22 2 22 22
.1 .1 ( ) ( ) ( ) ( )ab cd ab cd ab c d cd a b abc abd a cd b cd abc a cd abd b cd+= + = + + + = + + + = + + +
()()()()0( 0)ac bc ad bd ad bc ad bc ac bd ac bd= + + + = + + = +=
Bài 3: Chứng minh rằng tích của bốn số tự nhiên liên tiếp cộng thêm 1 là 1 số chính
phương.
Lời giải
Gọi 4 số tự nhiên liên tiếp là: n ; n + 1 ; n + 2 ; n + 3 ( n thuộc N
*
)
Theo bài ra ta có:
2 2 22 2
( 1)( 2)( 3) 1 ( 3 )( 3 2) 1 ( 1)( 1) 1 ( 3 1) ( )nnn n nnnn k k knn dpcm+ + + += + + + += − + += = + +
Bài 4: Chứng minh rằng số
44
( 1) 1An n=+++
chia hết cho 1 SCP khác 1 với mọi n nguyên
dương.
Lời giải
Ta có:
224 2 22 42 2 2 42
[(n+1) ] 1 ( 2 1) ( 1) ( 3 1)( 1) ( 1)A n n n n nn n n nn nn= ++= ++−+ ++= ++ +++ ++
2 2 2 2 2 2 22
( 3 1)( 1) ( 1)( 1) ( 1)(2 2 1) 2( 1) ( )n n nn nn nn nn n n nn dpcm= + + ++ + ++ −+ = ++ + + = ++
Bài 5: Chứng minh rằng với mọi số nguyên x, ta có:
(x+1)(x+3)(x+5)(x+7)+15 (x+6)
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

54
Lời giải
Dùng phương pháp đặt ẩn phụ ta được:
2
(x+1)(x+3)(x+5)(x+7)+15 (x+6)=(x 8 10)( 2)( 6)x xx++ + +
Bài 6: Chứng minh rằng với mọi số nguyên n, biểu thức:
23
33 6
nn n
A =++
là số nguyên
Lời giải
Ta có:
233 2
3 2 ( 1)( 2)
33 6 6 6
n n n n n n nn n
A nZ
++ ++
= + + = = ∀∈
MỘT SỐ BÀI TOÁN TỔNG HỢP PHÂN TÍCH
ĐA THỨC THÀNH NHÂN TỬ
Bài 1: Phân tích các đa thức sau thành nhân tử
a.
22 22 22
() () ()ab a b cb c b ac c a−− −+ −
b.
2 ( 2) 2 ( 2) 2 ( 2) 7bc b c ac c a ab a b abc++ −− +−
c.
()()()ab b a bc b c ac c a−−−−−
d.
3 (3 ) 3 (3 ) 3 (3 ) 28bc b c ac c a ab a b abc−− −− ++
e
*
.
22 2 2 22 333
( ) ( ) ( )2a b c b c a c a b abc a b c+ + + + + − −−−
Lời giải
a. Ta nhận thấy nếu b = c thì A = 0. Vậy đa thức có 1 nhân tử là b – c
22 22 22 22 22 22
() () () ( ) () ()abab cbcb acca abaccb cbcb acca−− −+ −= −+−− −+ −
22 22 22 22 2 2 2 2
() () () ()()()()()( )abac abcb cbcb acca cbbacac aacb c= −+ −− −+ −=− − ++ − −
( )( )
2 2 2222
( )( ) ( ) ( ) (ab )
( )( )( )( )( )
=− − +− + = − − − + −
=− − − −−−−
accbbac abc accb abbcac
a b c b a c a b ab bc ca
b. Nhận thấy nếu c = 2a thì B = 0. Vậy đa thức có nhân tử là c – 2a
( )
( ) ( ) ( )
2 22 2
22
2 ( 2) 2 ( 2) 2 ( 2) 7 2 2 2 4 2 4 7
2 22 24 28 2 7
++ −− +− = −++−−−
= −+ −+ −+ − −
bc b c ac c a ab a b abc ac c a b c bc a b ab abc
ac c a b c a bc c a abc a b abc
( ) ( ) ( )
( ) ( ) ( ) ( )
22
2
2 22 24 28 2 7
2 22 24 2 2
= −+ −+ −+ − −
= −+ −+ −+ −
ac c a b c a bc c a abc a b abc
acca bca bccaabca
( )
( )
( ) ( ) ( ) ( )( )( )
2
22 2 4 22 2 2 2 2 2caacb bcab caaabbabcaabbc=− +++=− ++ + − + +
c. Nhận thấy a = b nên có nhân tử a – b
2 2 22 22 2
()()()() ()( )()ab b a bc b c ac c a ab b a b c bc ac a c ab b a c b a c b a−− −− −= −− + − + = −− − + −
2
( )( ) ( )( )( )baabcbcac baacbc=− −−+ =− − −
d. Dự đoán c = 3b, vậy đa thức có nhân tử là 3b – c
3 (3 ) 3 (3 ) 3 (3 ) 28bc b c ac c a ab a b abc−− −− ++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

55
( )
( ) ( ) ( )
22 2 2
22
3 3 9 3 9 3 28
3 3 9 3 27 3 3 3 28
= −− + − − +
= −+ −− − −− +
bc b c ac a c a b ab abc
bc b c ac b c abc a b c ab abc
( ) ( ) ( ) ( ) ( )
( )
( )( )( )
22
33 93 33 3 3 3 9 3
333
= −+ −− −− −= − + − −
=−+−
bc b c ac b c a b c abc b c b c bc ac a ab
bc ab ca
e. Ta không nhẩm được nghiệm của đa thức
22 2 2 22 333
( ) ( ) ( )2a b c b c a c a b abc a b c+ + + + + − −−−
22 2 2 22 222
22 2 2 2 222
(2)()()
( ) +b(c 2 ) ( 2
)
= +− − + +− + +−
= − − +− − + +−+
ab c bc a bc a b ca b c
a b c a a ac b c a b c ab
( ) ( )
22
22 2 2
() + +abcabcabcabc
= −− −− +−
( )( ) ( )( ) ( )( )
+abcabca bcabcab cabcabc= −− −+ −− −+ + +− ++
( )( ) ( ) ( ) ( )
22
=( )abcabcacab cabc abc acab bcabb acbcc
+− −− −+ + ++ = ++ − +− − + − + + +
( ) ( ) ( ) ( ) ( )( )( )
abc aacb bacb cacb abcacbbca= +− − +− + +− + +− = +− +− +−
Bài 2: [ HSG – BG – 30/03/2013 ]
3 2 2 3 33
2 7 7 2 2( ) 7 ( ) ( )(2 )( 2 )A a ab ab b a b abab ab aba b= + + + = + + +=+ + +
Bài 3: [ HSG – Long Biên – Hà Nội – 2015 ]
a. Phân tích:
32 2
( 7) 36xx x−−
b. Dựa vào kết quả hãy chứng minh:
32 2
( 7) 36 210A nn n n N= − − ∀∈
Lời giải
a.
32 2 3 3
( 7) 36 ( 7 6)( 7 6) ( 1)( 2)( 3)( 1)( 2)( 3)x x x xx x x x xx x x x x x− − = −+ −−= + + − − − +
b. A là tích của 7 số tự nhiên liên tiếp
2,3,5,7 210AA⇒⇒
Bài 4: [ Bắc Giang 2013 ]
a.
42
2013 2012 2013xxx+ ++
b.
( )( )( )x y y z z x xyz+ + ++
Lời giải
a.
42 4 2 2 2
2013 2012 2013 ( ) 2013( 1) ( 1)( 2013)x x x xx xx xx xx+ + + = − + ++ = ++ −+
b.
2 2 2 22 22
( )( ) ( )( )( )xy xz y yz x z xyz xyz x y x z xyz xz yz xyz xy zy=+++ ++=++++++++
()()()()()x xy yz zx z xy yz zx y xy yz zx x y z xy yz zx= ++ + ++ + ++ =++ ++
Bài 5: [ Bắc Giang – 2014 ]
a.
2
( 2)( 2 2) 1xx x x+ + ++
b.
22
2 445x xy y x y− ++−−
c.
32
6 13 4 3x xx+ +−
Lời giải
a.
2 22 224
( 2)( 2 2) 1 ( 2 )[(x 2 ) 2] 1 ( 2 1) ( 1)xx xx xx x xx x+ + + += + + + += + + = +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

56
b.
22
2 445x xy y x y− ++−−
22
( ) 4( ) 4 9 ( 2) 9 ( 5)( 1)xy xy xy xy xy= − + − +−= −+ −= −+ −−
c.
32
6 13 4 3x xx+ +−
322
6 6 7 733= + + +−−xxxxx
22
6 ( 1) 7 ( 1) 3( 1) ( 1)(6 7 3) ( 1)(3 1)(2 3)= ++ +− += + + − = + − +xx xx x xxx xxx
CÔNG THỨC KHAI TRIỂN NHỊ THỨC NEWTON
A. Công thức
0 1 1 2 22 1 1
( ) ...
n n n n n n nn
nn n n n
a b C a C a b C a b C ab C b
− − −−
+ = + + ++ +
Trong đó:
!
( 0,1,... 0, ); ! 1.2.3...
!( )!
k
n
n
C k
n k nn n
knk
= = ⇔= =
−
+) Quy ước: 0!=1
+)
0 11
!! ! ! !
1; 1; ;
0!( 0)! ! !( )! 1!( 1)! ( 1)!( 1)!
nn
n n nn
nn n n n
C C C nC n
n n nnn n n
nn
−
= = = = = = = = =
− − − −
−+
+) Bảng tam giác Pascal
n = 2 1 2 1
n = 3 1 3 3 1
n = 4 1 4 6 4 1
n = 5 1 5 10 10 5 1
n = 6 1 6 15 20 15 6
n = .....
B. Bài tập áp dụng
Bài 1: Phân tích thành nhân tử:
555
()A ab a b=+ −−
Lời giải
5 4 32 23 4 5 5 5 4 32 23 4 3 2 2 3
5 10 10 5 5 10 10 5 5 ( 2 2 )A a ab ab ab ab b a b ab ab ab ab aba ab ab b=+++++−−=+++=+++
3 2 23 2 2 3
2 22
5 [( 3 3 ) ( )]=5ab[(a+b) ( )]
=5ab(a+b)[(a+b) ] 5 ( )( )
= + + +− + − +
− = + ++
ab a a b ab b a b ab ab
a b
ab ab a b a ab b
Bài 2: Cho
0.++=abc
Chứng minh rằng:
555
5( )++=− ++a b c abc ab bc ca
Lời giải
Từ:
0 ()++=⇒=− +abc c ab
55 5 2
( ) 5 ( )[(a+b) ] 5 ( )[(a+b)c-ab]=+−+ =− + − =− −VP a b a b ab a b ab ab c
5( ) ( )abc ab bc ca VP dpcm=− ++ =
Bài 3: Cho
0.++=abc
Chứng minh rằng:
2 2 23 3 3 5 5 5
.
23 5
++ ++ ++
=
abcabc abc
Lời giải
Ta có:
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

57
333
5( )
( ) (1);
5
3
33
− ++
= =
− ++
++
= =
abc ab bc ca
VP abc ab bc ca
a b c abc
abc
Lại có:
222
2 222
()0 2() ()
2
abc
a b c a b c ab bc ca ab bc ca
++
++ =⇔++=− ++ ⇒ =− ++
( )(2).(1)(2)VT abc ab bc ca VT VP=− ++ ⇒ =
Bài 4:
2 2 23 3 3 5 5 5
()()()()()()()()()
:.
23 5
ab bc ca ab bc ca ab bc ca
CMR
− +− +− − +− +− − +− +−
=
Lời giải
Ta có:
( )( )( )0ab bc ca−+−+− =
Đặt
;; 0xabybczca xyz=− =− =−⇒++=
Ta cần chứng minh:
2 2 23 3 3 5 5 5
.
23 5
x y zx y z x y z++ ++ ++
=
Bài 5: Cho a,b là các số nguyên. CMR số sau là số chính phương
444
()A ab a b=+ ++
Lời giải
4 3 22 3444 44 22 22 222 2 22
22 2
464 32()()()2()
( )( )
Aa abab abbabab ab abab ab ab abab
a b ab dpcm
=+ + + +++=++ + + = + + + +
= ++
Bài 6: Giải phương trình:
6 66
( 2) ( 2) 2 128(*)xx x+ +− = +
Lời giải
Ta có:
66 5 42 33 24 566 5 4 3 2
( 2) 6 .2 15 .2 20 .2 15 2 6 .2 2 12 60 160 240 192 64x xx x x xx xxxxxx+=++ + + ++=+++ + ++
6 66 5 4 3 2
( 2) [x+(-2)] 12 60 160 240 192 64x xxxxxx−= =− + − + − +
64 2 4 2
2 120 480 128 (*) 120 480 0 0VTxxx xx x= + + + ⇒ ⇔ + =⇔=
Bài 7: Cho a, b, c là các số nguyên, CMR:
777
() 7ab a b+ −−
Lời giải
7 7 6 55 43 34 25 6 7
7 7 7 6 52 43 34 25 6
( ) 7 21 35 35 21 7
() 7(3553 )7()
+=+++++++
⇒+−−=+++++
a b a ab ab ab ab ab ab b
a b a b a b a b a b a b a b ab dpcm
Bài 8: Chứng minh rằng:
16 15 1 225= − − ∀∈
n
A n nN
Lời giải
+)
02
0 16 15.0 1 0 225 15n = ⇒ − −= =
+)
2
1 0 225 15nA=⇒= =
+)
2
2 225 225 15nA=⇒= =
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

58
0 11
) 3 16 (15 1) .1 .1 ... 15 (1 15 (225) (16 15 1) (225) 225
−
+ ≥⇒ = + = + + = + + ⇒ − − = ∀
n n n n nn n
nn n
n C C C n BS n BS n
Bài 9: Chứng minh rằng:
2
22 3 *
( 1) ( 1)= + − + ∀∈
n
A n n n nN
Lời giải
+) n = 1 ; n = 2 thì thỏa mãn
+)
2 2 0 12 24 2 3 3
3 ( 1) (1 ) .1 . . ... . 1 ( ) (1)≥⇒ + = + = + + + + =+ +
n n n nn
nnn n
n n n C C n C n C n n BS n
Lại có:
( )
22
22 2 2
22
0 1 22 3 2
3
2
33 3 3
( 1)
(1 ) .
. ... 1 . ( )
2
( 1)
1 . ()
1 () 2
2
−
+ = + + + =++ +
−
=++ + =+
nn
nn n n
nn
n C CnCn C n n BSn
nn
n n B
S n BS n
Từ (1), (2) ta có điều phải chứng minh.
CHUYÊN ĐỀ 3: GIÁ TRỊ LỚN NHẤT,
GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC
A. Giá trị lớn nhất, giá trị nhỏ nhất của một biểu thức
Khái niệm: Nếu với mọi giá trị của biến thuộc một khoảng xác định nào đó mà giá trị của
biểu thức A luôn luôn lớn hơn hoặc bằng (nhỏ hơn hoặc bằng) một hằng số k và tồn tại
một giá trị của biến để A có giá trị bằng k thì k gọi là giá trị nhỏ nhất (giá trị lớn nhất) của
biểu thức A ứng với các giá trị của biểu thức thuộc khoảng xác định nói trên
Xét biểu thức
()Ax
+) Ta nói
()Ax
có giá trị lớn nhất là M, nếu
()Ax M x≤∀
và có giá trị x0 sao cho
0
()Ax M=
(Chỉ ra 1 giá trị là được)
+) Ta nói
()Ax
có giá trị nhỏ nhất là m, nếu
()Ax m x≥∀
và có giá trị x0 sao cho
0
()Ax m=
(Chỉ ra 1 giá trị là được)
Như vậy :
a) Để tìm giá trị nhỏ nhất của A, ta cần :
- Chứng minh
Ak≥
với k là hằng số
- Chỉ ra dấu “ = ” có thể xảy ra với giá trị nào đó của biến
b) Để tìm giá trị lớn nhất của A, ta cần :
- Chứng minh
Ak≤
với k là hằng số
- Chỉ ra dấu “ = ” có thể xảy ra với giá trị nào đó của biến
Ký hiệu: Min A là giá trị nhỏ nhất của A và Max A là giá trị lớn nhất của A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

59
Ví dụ: Sai lầm
2 22
( ) 2 2 3 ( 1) 2 2 2A x x x x x GTNN= − += + − +≥⇒ =
( Không chỉ ra được dấu = )
Đáp án đúng là :
2
1 55 5 1
() 2
2 22 2 2
= − +≥⇒ =⇔=
A x x GTNN x
B. Các dạng toán
Dạng 1: Tìm GTLN, GTNN của tam thức bậc hai
2
ax bx c++
Phương pháp: Áp dụng hằng đẳng thức số 1 và số 2
Bài 1: Tìm GTNN của các biểu thức sau
a.
2
( ) 4 24Ax x x=−+
b.
2
() 2 8 1Bx x x= −+
c.
2
() 3 1Cx x x= +−
Lời giải
a.
22
( ) 4 24 ( 2) 20 20 min ( ) 20 2Ax x x x x Ax x= − + = − + ≥ ∀⇒ = ⇔ =
b.
22 2
( ) 2 8 1 2( 4 4) 7 2( 2) 7 7 minB 7 2Bx x x x x x x= − + = − + − = − − ≥− ⇒ =− ⇔ =
c.
2
2
1 13 13 1
() 3 1 3
6 12 12 6
−−
= + −= + − ≥ ⇔ =
Cx x x x x
Bài 2: Tìm GTLN của các biểu thức sau
a.
2
() 5 4 1Ax x x=− −+
b.
2
() 3 1Bx x x=− ++
Lời giải
a.
2
22
4 1 2 99 2
() 5 4 1 5 5
5 5 5 55 5
−
=− − +=− + − =− + + ≤ ⇔ =
Ax x x x x x x
b.
2
2
1 13 13 1
() 3 1 3
6 12 12 6
=− + +=− − + ≤ ⇔ =
Bx x x x x
Dạng 2: Tìm GTLN, GTNN của đa thức có bậc cao hơn 2
Phương pháp: Ta đưa về dạng tổng bình phương
Bài 1: Tìm GTNN của các biểu thức sau
a.
43 2
( ) 6 10 6 9Axxx xx=− + −+
b.
43 2
( ) 10 26 10 30Bxxxxx=− + −+
c.
432
( ) 2 3 4 2017Cxxxxx=− + −+
d.
42
() 2 7Dx x x x=−++
e.
432
( ) 4 9 20 22Ex x x x x=−+−+
f.
( ) ( 3)( 4)( 7)Fx xx x x=−−−
g.
( ) ( 1)( 2)( 3)( 6) 2006Gx x x x x=− + + +−
Lời giải
a.
43 2 432 2 2 2 2
( ) 6 10 6 9 ( 6 9 ) ( 6 9) ( 3 ) ( 3) 0Axxx xx xxx xx xx x x=− + −+= − + + −+= − +− ≥∀
2
30
min ( ) 0 3
30
xx
Ax x
x
−=
⇒ =⇔ ⇔=
−=
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

60
b.
2
43 2 22
2
50
( ) 10 26 10 30 ( 5 ) ( 5) 5 5 5
50
xx
Bxxxxx xxx x
x
−=
= − + − + = − + − +≥⇔ ⇔ =
−=
c.
22 2 2 2 2
( ) ( 2) 2 ( 2) ( 2) 2015 ( 2)( 1) 2015 2015 1Cx x x xx x x x x= +− ++ ++ = + − + ≥ ⇔=
d.
4 2 2 22 2
( ) 2 1 2 1 5 ( 1) ( 1) 5 5 1Dx x x x x x x x= − ++ + ++ = − + + + ≥ ⇔ =−
e. Ta có :
432 432 2 2 2 2
( ) 4 9 20 22 ( 4 4 ) 5( 4 4) 2 ( 2 ) 5( 2) 2 2 2Exxxx x xxx xx xx x x=−+−+=−+ + −++=− +−+≥⇔=
f.
22 2
1
( ) ( 3)( 4)( 7) ( 7 )( 7 12) 36 36 0
6
x
Fxxx x x xxxx y y
x
=
= − − − = − − + = − ≥− ⇔ = ↔
=
g.
2 2 22
0
( ) ( 5 6)( 5 6) 2006 ( 5 ) 2042 2042
5
x
Gxxx xx xx
x
=
= +− ++− = + − ≥− ⇔
= −
Dạng 3 : Đa thức có từ 2 biến trở lên
Phương pháp: Đa số các biểu thức có dạng
( ) ( )( )
22
; .. 0 1F x y ax by cxy dx ey h a b c= + + +++ ≠
- Ta đưa dần các biến vào trong hằng đẳng thức
( )
( )
2
22
2a ab b a b± +=±
như sau
( )
[ ] [ ]
( )
22
;; 2F xy mKxy nGy r= ++
hoặc
( )
[ ] [ ]
( )
22
;; 3F xy mKxy nH x r= ++
Trong đó
[ ] [ ]
,Gy Hx
là biểu thức bậc nhất đối với biến, còn
[ ]
;K x y px qy k= ++
cũng là
biểu thức bậc nhất đối với cả hai biến x và y
Cụ thể:
Ta biến đổi (1) để chuyển về dạng (2) như sau với
2
0;4 0a ac b≠ −≠
Ta có
( )
22 2 22 22 2
4.;4 4 4 4444 4 42a F x y a x abxy acy adx aey ah a x b y d abxy adx bdy= + + +++= +++ ++
( )
( )
22 2
4 22 4ac b y y ae bd ah d− + −+−
( )
( )
2
2
22
22
22
24 4
44
ae bd ae bd
ax by d ac b y ah d
ac b ac b
−−
= ++ + − + + −−
−−
Vậy có (2) với
( )
( )
( )
2
22
2
2
2
1 42
. ; 2 ; ;
( ) ;r h
4 4
44
44
ae bd
b ac ae
bd d
m F x y ax by d n G
y y
a a ac
b a
a ac b
−
−−
= = ++ =− =+ =− −
−
−
+) Nếu
( ) ( ) ( )
2
0;4 0 0, 0 2 : ; *a ac b m n F x y r> − >⇒ > >⇒ ≥
+) Nếu
( ) ( ) ( )
2
0;4 0 0, 0 2 : ; **a ac b m n F x y r< − >⇒ < <⇒ ≤
+) Nếu m > 0, n > 0 thì ta tìm được giá trị nhỏ nhất
+) Nếu m < 0, n <0 thì ta tìm được giá trị lớn nhất
Dễ thấy rằng luôn tồn tại (x; y) để có dấu của đẳng thức, như vậy ta sẽ tìm được cực trị
của đa thức đã cho
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

61
Trong cả hai trường hợp trên:
- Nếu r = 0 thì phương trình F(x; y) = 0 có nghiệm
- Nếu
( )
;0F xy r≥>
hoặc
( )
;0F xy r≤<
thì không có
( )
;xy
nào thảo mãn F(x; y) = 0
+) Nếu
( ) ( )
2
0;4 0; 0 2 : ;a ac b r F x y> −< =⇒
phân tích được tích của hai nhân tử, giúp ta
giải được các bài toán khác
Bài 1: Tìm giá trị nhỏ nhất của
a.
22
2 2 45A x y xy y=+ − −+
b.
222
2255Bx y y=−++
Lời giải
a) Ta có
( ) ( )
( ) ( )
22
22 2
2 2
() 2 2 4 5 2 4 4 1 2 1A x x y xy y x xy y y y x y y=+ − −+= − + + −++=− +− +
0
1 , "" 2
20
−=
⇒ ≥ ∀ ∈ ⇒=⇔ ⇔ = =
−=
xy
A xy R x
y
y
Vậy
min 1 2A xy=⇔==
b)
( ) ( )
( ) ( )
22
2 22 2 2 2 22
2 2 5 5 4 4 2 5 2 55B x y y x xy y x xy y y x y x y= − + += − + + + + + += − + + +≥
20
0
0
xy
xy
xy
−=
⇒==
+=
Bài 2: Tìm giá trị nhỏ nhất của
a.
22
() 2 2 2 3A x x y xy x= +− −+
b.
22
() 3 3B x x xy y x y=++−−
c.
22
( ) 2 3 4 8 2 18C x x y xy x y= + + −−+
d.
222
( ) 2 3 4 2( ) 2Dx x y z x y z= + + − ++ +
e.
22
( ) 2 8 11 4 2 6E x x xy y x y= + + −−+
f.
2 22
()265682242F x x y z xy yz xz y z=++−+−+++
g.
2 22
()22 22224G x x y z xy xz yz x y= + ++ − − −−
h.
22
() 1H x x y xy x y= + − −++
Lời giải
a. Ta có :
22 2 2 2 2 2
( ) 2 2 2 3 ( 2 ) ( 2 1) 2 ( ) ( 1) 2 2 1A x x y xy x x xy y x x x y x x y= +− −+= − + + −++=− +−+≥⇔==
b.
2 2 22
( ) ( 2 1) ( 2 1) ( 1) ( 1) 3 ( 1) ( 1) ( 1)( 1) 3Bx x x y y xy y x y x y= − ++ − ++ −− −−= − + − + − −−
22 2
2
2 22
1 1 1 1 21
( 1) 2( 1). .( 1) (
1) 3 1 2 1 3
2 22 2
4
− − −
−+
=−+ − −+ − +−−=−+ − +−+−
y y y yy
x x y y
x yy
2
2
1
1
10
1 3( 1)
1 33
2
1
24
10
y
x
x
yy
x
y
y
−
=
−+ =
−−
= − + + − ≥− ⇔ ⇔
=
−=
c.
2 22 2 2
( ) 2 4 2 8 2 18 2 ( ) 2( )2 4 ( 6 9) 1Cx x xy y y x y xy xy y y
= + + +−−+= + − + ++ +++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
62
22
2( 2) ( 3) 1 1 min 1 3; 5xy y A y x= + − + + +≥⇒ =⇔ =− =
d.
222 2 2 2
( ) 2 3 4 2( ) 2 2( ) (3 2 ) (4 2 ) 2Dx x y z x y z x x y y z z= + + − ++ += − + − + − +
22 2
1 2 1 1 111
2 3 (2
) 2 2
4 3 9 4 234
= −+ + − + + − + +−−−
xx y y z z
222
1 1 1 11 11 1 1 1
2 3 2 (,
,) ; ;
2 3 2 2 2 234
=−+−+−+≥⇒ =
x y z x
yz
e.
2 22 2 2
( ) 2( 4 4 ) 3 4 2 6 2( 2 ) 4( 2 ) 2 3 6 4Ex x xyy y xy xy xy y y
= + + + −−+= + − + ++ ++
22
2 10 3
2( 2 1) 3( 1) 1 1
10 1
xy x
xy y
yy
+ −= =
= + − + + +≥⇔ ⇔
+= =−
f.
2 22
()265682242()F x x y z xy yz xz y z kho=++−+−+++
22
2 22
33
( ) 2 2 (3 ) 2 6 5 8 2 4 2
22
++
= − ++ + + + − + + +
yz yz
F x x x y z y z yz y z
2
2 22
3 3 10 25 1
2 242
2 2 39 3
+
= − + + + + +++
yz
x y yz z z y z
22
2
3 3 5 5 2 1 21
22 1
2 2 3 3 3 3 33
+
= − + + + + ++ + ++
yz
x yz
yz z z
2
2
3
0
2
1
3 3 52 1 52
2 x ( 1) 1 1 0 1 min 1
2 2 33 3 33
1
10
+
−=
=
+
= − + ++ + ++≥⇔++=⇔=⇒ =
= −
+=
yz
x
x
yz
yz x yz y A
z
z
g. Ta có :
2 22 2 2 2
()2 2 2 2 2 24 (1)( 2)( )55 1; 2; 3G x x y z xy xz yz x y x y x y z x y z= + + + − − − − = − + − + + − − ≥− ⇔ = = =
h.Ta có :
22 2 2 2
( ) 1 4 ( ) (2 ) 2.2 . 3 4 4 4Hx x y xy x y Hx x xy y y x y=+−−++⇒ = − ++ −++
22 2 2
2 1 88
(2 ) 2(2 ) 3 2 3 1 (2 1) 3( 1) (2 1) 3( )
3 2
33
xy xy y y xy y y xy y= − − − + + ++= −−+ + += −−+ + +≥
8 21 2
min 4 ; min
3 33 3
A xy A
−
⇒ =⇔= = ⇒ =
Bài 3: Tìm GTLN của các biểu thức sau
a.
22
4 5 8 10 12A x y xy y=−−++ +
b.
22
22x y xy x y−−++ +
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

63
a. Ta có:
2 2 2 22 2 2
4 5 8 10 12 4 8 4 10 25 37 4( ) ( 5) 37 37A x y xy y x xy y y y x y y=−−++ +=−+ − −+ −+=−−−−+≤
5
5
x
y
=
⇔
=
b.
22 2 2
22 4 4 4 4 88A x y xy x y A x y xy x y=−−++ + ⇒ =− − + + +
2 2 22
4 4 ( 2) ( 2) ( 2) 4 8A xxy y y yy=−+ +−+++− +
22 2 2
2 20 2
(2 2) 3( 4 ) 4 (2 2) 3( 2) 16 16 4
20 2
xy x
xy y y xy y A
yy
−−= =
=− −− − − +=− −− − − + ≤ ⇒ ≤⇔ ⇔
−= =
Bài 4: Tìm GTNN của các biểu thức sau
a.
22
5 9 12 24 48 82Axy xyxy=+− +− +
b.
2 22
3 3 5 3 3 223B x y z xy yz xz x y= + ++ − − − − +
Lời giải
a.
2 2 2 2 22
5 9 12 24 48 82 9 12 ( 4) 4( 4) 4( 4) 5 24 82Axy xyxy y yx x x x x= + − + − += − +++−++ + +
[ ]
2
2
16
3 2( 4) ( 4) 2 2 , 4
;
3
y x x xy
R x y= − + + − + ≥∀ ∈ ⇔ = =
b.
22
2
3 3 42
( ) (
2) 1 1
2 4 33 3
= − + + + − + − +≥
y
B z xy x y
Bài 5: Tìm GTLN của
2 22
( 2 4)Axyz x y z=++− + +
Lời giải
2 22
1 1 1 77 7 1 1 1
2 2 ;;
2 4 4 16 16 16 2 4 8
−−
−=−+−+−−≥⇒≤⇔= = =
Ax y z A x y z
Bài 6: [ HSG – Yên Dũng – Bắc Giang ] .
Tìm GTNN của
22
2 2 2 4 2013A x y xy x y=+ + +−+
Lời giải
22 2 2 2
2 2 2 4 2013 2 ( 1) ( 1) ( 3) 2003 2003 4; 3A x y xy x y x x y y y x y=+ + +− + =+ +++ +− + ≥ ⇔=− =
BÀI TẬP TỰ LUYỆN
Bài 1: Tìm GTNN của:
22
2 2 2 10 17A x xy y x y=−++−+
Hướng dẫn
( )
22
2 1 2 10 17A x xy y y= − −+ − +
( ) ( ) ( )
22
22
2 1 1 2 10 17 1x xy y y y y
=− −+− + − +−−
( )
( )
2
2
1 8 16xy y y= −+ + − +
Bài 2: Tìm min của:
22
22B x xy y x y=−+−−
Hướng dẫn
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

64
( )
22
2 22 2
2 44
2 2 2. . 2
1
24 4
y yy y
Bxxy yyx x yy y
+ ++
=− ++− = − + +−− −−
( )
2
22
4 2 4 8 44B xy y yy y= −− + − − − −
Bài 3: Tìm min của:
22
33C x xy y x y=++−−
Hướng dẫn
( )
22
2 22 2
3 69 69
3 3 2. . 3
24 4
y yy yy
Cxxy yyx x yy
− −+ −+
=+ −+−= + + +−−
( )
2
22
4 3 4 12 6 9C xy y yy y
= +− + − − + −
Bài 4: Tìm min của:
22
2 6 12 2 45Dx xyy xy=− + − ++
Hướng dẫn
( ) ( ) ( )
( )
2
2 22 2
2
2 6 6 2 45 2 . 6 6 6 2 45 12 36Dxxy yy xxy y yy y y=− ++ ++=− +++ + ++− + +
( )
2
2
6 5 10 9xy y y= −− + − +
Bài 5: Tìm min của:
22
3 2 10 20E x xy y x y=−+ −− +
Hướng dẫn
( )
22
2 22 2
2 44 44
2 3 10 20 2 . 3
10 20
24 4
y yy yy
Exxy yy xx yy
− −+ −
+
=− −+−+=− + +−+−
( )
( ) ( )
2
22
4 2 12 40 80 4 4E xy y y y y= −+ + − + − − +
( )
( )
2
2
2 11 36 76xy y y= −+ + − +
Bài 6: Tìm max của:
22
2 4 2 10 3F x xy y x y=−+−++−
Hướng dẫn
( )
22 2 2
2 4 2 10 3 2 1 4 10 3Fxxyyxy xxy y y−=−+−−+=− ++−+
( ) ( ) ( )
22
22
2 1 1 4 10 3 1F x xy y y y y−= − + + + + − +− +
Bài 7: Tìm min của:
( ) ( )
2
22
6 16 8 2 8 10G x ay x ay x y ay x y=− + − ++ − +−+
Hướng dẫn
( ) ( )
( )
2
22
6 9 2 1 16 8 8G x ay x ay x x y ay y
= − + − + + + ++ − −
( ) ( ) ( ) ( ) ( )
22 22
2
3 1 16 8 1 1 1G x ay x y y a a a=−++++ − +++−+
( ) ( ) ( ) ( ) ( )
22 22 2
3 14 1 1 1G x ay x y a a a= − + + + + − − − + ≥− +
Bài 8: Tìm max của:
22
2 4 11H x xy y x y=−+ − − + +
Hướng dẫn
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

65
( )
22 2 2
2 4 11 2 4 11Hxxyy xy xxy y y−=−++ −−=− −+−−
( )
2
2
22
2
2 44
2 . 4
11
24 4
y
y yy
Hx x y y
−
− −+
−= − + + − − −
( )
( )
⇒−=−++ − −−−+
2
22
4 2 4 16 44 4 4H xy y y y y
Bài 9: Tìm min của:
22
4 5 6 11I x xy y y=+ + −+
Hướng dẫn
( )
2 22
4 4 6 11I x xy y y y= + + +−+
Bài 10: Tìm min của:
22
3 3 20K x y xy x y=+−+++
Hướng dẫn
( ) ( ) ( )
22
22 2 2
4 4 4 4 12 12 80 4 4 3 3 4 12 80 3K x y xy x y x x y y y y y
=+−+++= − −+− + ++−−
( )
2
2
4 2 3 3 18 71K xy y y= −+ + + +
Bài 11: Tìm min của:
22
2 2 21M x xy y y=− + −+
Hướng dẫn
( ) ( )
2 22
2 21M x xy y y y= − + + −+
Bài 12: Tìm min của:
22
22N x xy y x=−+−
Hướng dẫn
( )
( )
( )
22
2 22 2
21 21
21
2 1 2 2. 2
24 4
yy
y
Nx xy y x x y
++
+
= − ++ = − + + −
( )
( )
2
22
4 21 8 4 41Nxy y y y=−−+ − ++
Bài 13: Tìm min của:
22
2 3 2 1997=− + −+A x xy y x
Hướng dẫn
( ) ( ) ( )
( )
2
2 22 2 2
2 1 3 1997 2 1 1 3 1997 2 1A x xy y x xy y y y y=− +++ =− −+−++ −++
Bài 14: Tìm min của:
22
2 2 2 10Q x y xy x y=+ − +−
Hướng dẫn
( ) ( ) ( )
( )
2
2 22 2
2
2 1 2 10 2 1 1 2 10 2 1Q x xy y y x xy y y y y y= − −+ − = − −+ − + − − − +
Bài 15: Tìm min của:
22
222R x y xy y=++−
Hướng dẫn
2 2 2 22
2 2 2 2 2 11R x y xy y x xy y y y=+ + − =+ ++−+−
( ) ( )
22
111xy y= + + − − ≥−
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

66
Bài 16: Tìm min của:
22
4 5 4 16 32Axyxyy=+−−+
Hướng dẫn
( ) ( )
22 2 2 2
4 5 4 16 32 4 4 4 16 32A x y xy y x xy y y y=+−−+= −++ −+
Bài 17: Tìm min của:
2 22
5544412B x y z xy yz z=++−−−+
Hướng dẫn
( ) ( ) ( )
2 22 22
4 4 4 4 448B x xy y y yz z z z= − + + − + + −++
( ) ( ) ( )
2 22
2 2 2 88xy yz z= − + − + − +≥
Bài 18: Tìm min của:
22
5 12 9 4 4C x xy y x= − + −+
Hướng dẫn
( ) ( )
( ) ( )
22
2 22
4 2.2 .3 9 4 4 2 3 2 0C x xy y x x x y x= − + +−+= − +−≥
Bài 19: Tìm max của:
22
22D x y xy x y=−− + + +
Hướng dẫn
( )
22 2 2
22 2 2D x y xy x y x x y y y−=+−−− =− ++−
( )
2
2
22
2
2 44
2. 2
24 4
y
y yy
Dx x y
y
+
+ ++
−= − + + − −
Bài 20: Tìm min của:
22
5 4 23Exyxyy=+ − +−
Hướng dẫn
( ) ( )
22
2 22
4 4 2 14 2 1 4 4E x xy y y y x y y= − + + + + − = − + + − ≥−
Bài 21: Tìm GTNN của
22
333A a ab b a b=++−−+
Hướng dẫn
Ta có:
( )
2 2 22
4 2 3 42 4 4P a ab b a b ab a b= − + + + ++ − −
( ) ( )
22
3 20ab ab= − + +− ≥
Bài 22: Tìm min của:
( )
22
33G x xy y x y=++− ++
Hướng dẫn
22
4 4 4 4 12 12 12G x xy y x y=++−−+
( ) ( )
( ) ( )
2
2 22
4 4 4 3 3 4 12 12 6 9G x xy y y y y y= + −+− + − + − − +
( ) ( ) ( )
2 22
2
4 2 33632 3310G xy y y xy y= +− + − += +− + − ≥
Bài 23: CMR không có giá trị x, y, z thỏa mãn:
2 22
4 2 8 6 15 0x yz xyz+ +−+−+=
Hướng dẫn
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

67
( ) ( ) ( )
2 22
2 1 4 8 4 6 9 11xx yy zz− + + + + + − + +≥
Bài 24: Tìm min của:
22
2 2 23A x y xy x= +− −+
Hướng dẫn
( ) ( )
22
2 22
2 2 12 1 2 2Axxyyxx xy x= − + + − ++ = − + − + ≥
Bài 25: Tìm min của:
22
2 2 2 10 17B x xy y x y=−++−+
Hướng dẫn
( ) ( )
( )
2
2 22
2 1 1 2 10 17 2 1B x xy y y y y y=− −+− + − +− −+
( )
( )
2
2
1 8 16xy y y= −+ + − +
Bài 26: Tìm min của:
22
2 2 5 8 22D x xy y x y= + + −−
Hướng dẫn
( )
22 2 2
2 4 4 10 16 44 4 4 4 10 44Dxxyy xyxxy y y=++−−=+ −+−
( ) ( )
2
2 22
2 4 2.2 4 4 10 44 8 16D x xy y y y y y= + −+− + − −+−
Bài 27: Tìm min của:
22
2 9 6 6 12 2004E x y xy x y= + − −− +
Hướng dẫn
22
2 4 18 12 12 24 4008Exyxyxy=+ − −−+
( ) ( )
( )
2
2 22
2 4 12 1 9 1 18 24 4008 9 2 1E x xy y y y y y= − ++ + + − + − + +
( )
2
2
2 2 1 9 42 3999E xy y y= −− + − +
Bài 28: Tìm min của:
22
2 6 12 12 45F x xy y x y=−+−++
Hướng dẫn
( ) ( )
( )
2
2 22
2 6 6 6 12 45 12 36Fxxy y yy yy=− ++++++−++
( )
2
2
6 5 99xy y= −− + +≥
Bài 29: Tìm GTNN của biểu thức :
22
333a ab b a b++−−+
Hướng dẫn
( ) ( )
22
22
333 4 3 2 0Pa abb a b P ab ab= + + − − +=> = − + +− ≥
Bài 30: Tìm min của:
22 2
6 14 8 6 4A x y z yz zx xy=++ −+−
Hướng dẫn
( )
2 22
2 2 3 6 14Ax xy z y z=− ++ −
( ) ( )
( )
⇒= − + + + + − − + +
2
2 222 2
2 2 3 2 3 6 14 4 12 9Ax xyz yz y z y yzz
( )
⇒= − − + − −
2
22
2 3 2 12 23A x y z y yz z
Bài 31: Tìm min của:
2 22
2 3 2 2 2 2 8 2000B x y z xy xz x y z=+ + − + −− −+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

68
Hướng dẫn
( )
2 22
2 1 2 3 2 8 2000B x xy z y z y z= − −+ + + − − +
( ) ( )
( )
2
2 2
2 22
2 1 1 2 3 2 2 2000 1 2 2 2x xyz yz y z y z y z yz z y= − −+ + −+ + + − − + − + +− − +
( )
( )
2
22
1 2 4 2 1999x y z y z y yz= −+− + + − + +
( ) ( ) ( )
( )
22
2 22
1 2 2 2 2 4 4 1999x y z y yz z z z z
= −+− + − + + + + − + + +
( ) ( )
( )
22
2
1 2 4 1995xyz yz z z= −+− + −− + − +
Dạng 4: Tìm GTLN, GTNN của biểu thức có quan hệ ràng buộc giữa các biến
Phương pháp :
- Dồn biến từ điều kiền rồi thay vào biểu thức.
- Biến đổi biểu thức thành các thành phần có chứa điều kiện để thay thế.
- Sử dụng thêm một số bất đẳng thức phụ :
+
2a b ab+≥
( Dấu = khi a = b, với a, b không âm)
+
22
2a b ab+≥
( Dấu “=” khi a = b)
+
1
2a
a
+≥
( Dấu “=” khi a = 1)
Bài 1: Tìm GTNN của các biểu thức sau
a.
33
;1A x y xy x y= + + +=
b.
22
5; 1B x yxy= + +=
c.
22
2; 2 1C x yx y=+ +=
d.
22
2 5 ;4 3 7D x yxy= + −=
Lời giải
a.
2 2 22
( )( )A x y x xy y xy x y=+ −+ +=+
Có :
2
22 2 2
1 11 1 11
1 1 (1 ) 2 2 12 .2 12
2 44 2 22
+ =⇒ =− ⇒ = − + = − += − + − += − + ≥
xy x y A y y y y y y y
Dấu bằng xảy ra
11
;
22
xy= =
b. Có
2
2 22 2
1 1 1 55 1 5
1 1 5 (1)6 216 6 ;
3 6 6 66 6 6
+=⇒=−⇒= +− = − += − + = − +≥⇔= =
xy y x B x x x x x x x x
y
c.
22 2
11
2 6 4 1 min
33
Cxyyy C yx= + = − +⇒ = ⇔ = =
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

69
d. Ta có :
22 2 2
47 47
4 3 7 2 5( ) 9 98 280 245 2(7 10) 45 45
33
xx
xy y Dx D x x x
−−
− =⇒= ⇒ = + ⇒ = − + = − + ≥
10 3
min 5 ;
77
D xy
−
⇒ =⇔= =
Bài 2: [ HSG – BG – 2011 ]
Cho a + b = 1. Tìm GTNN của
22
( 2) ( )A aa b bb a= ++ −
Lời giải
Có a + b = 1
2 2 3 3 33 3 3 2
1 ( 2)( ) 2 (1) (1)2 21b a A a a b b b a a ab b ab a b ab a a a a a a⇒=−⇒= + + −=+ +− =++ =+− + −= − +
2
2
1 1 11 1
22
2 2 22 2
= −+ = − + ≥ ∀⇔ = =
a a a a ab
Bài 3: [ HSG – HN – 2006 - 2007 ]
Cho các số thực x, y thỏa mãn: x + y = 2. Tìm GTNN của
33
2A x y xy=++
Lời giải
33 3
2()3()2A x y xy x y xy x y xy=++ =+ − ++
Theo giả thiết
3 22
2 2 2 6 (2 ) 2 (2 ) 4 8 8 4( 1) 4 4 1xy y xA xxxxxx x Rxy+ = ⇒ = − ⇒ = − − + − = − + = − + ≥ ∀∈ ⇔ = =
Bài 4: Cho các số thực x, y thỏa mãn : x + y + 4 = 0. Tìm giá trị nhỏ nhất của :
33 22
2( ) 3( ) 10A x y x y xy= ++ ++
Lời giải
Ta có :
33 22 3 2
2( ) 3( ) 10 2( ) 6 ( ) 3( ) 6 10A x y x y xy x y xy x y x y xy xy= ++ ++ =+− +++− +
22
28 80 28 ( 4 ) 80 28( 4 4) 32 28( 2) 32 32 2 2= −= −−−=− +++⇒=− + +≤⇔=−⇒=−xy x x x x A x x y
Bài 5: [ HSG – HN – 1996 - 1997 ]
Cho các số thực x, y thỏa mãn:
22
4x y xy+−=
. Tìm GTLN, GTNN của
22
Px y= +
Lời giải
Ta có:
22 2222 22 222
22
0
48 2
( ) 8
4
xy
xyxy xyxy xyxy xy xy P
x y xy
−=
+−=⇒=+++− =++− ≥+⇒≤⇔
+−=
2xy⇔==±
Vậy GTLN của P = -2
2
2
xy
xy
= =
⇔
= = −
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

70
Mặt khác:
22 22 2 22
22
2
0
8
3
82()23()()3()
2
3
4
3
xy
xy
xy xy xy xy xy P
x y xy
xy
=−=
+=
= +− = +−−≤ +⇒≥⇔ ⇔
−
+−=
=−=
Vậy GTNN của P =
22
;
8
33
22
3
;
33
xy
xy
−
= =
⇔
−
= =
Bài 6: Cho các số thực x, y, z thỏa mãn:
22 4x yz+ +=
. Tìm GTLN của biểu thức
2A xy yz zx= ++
Lời giải
Từ giả thiết:
2 2 4 42 2 2 (42 2) (42 2)xyz z xyAxyy xyx xy++=⇒=−−⇒= + −− + −−
22 22 2 2 22
2 2 2 4 4 2 4 4 4 8 8 4 4 ( 2) ( 2) ( 2) 4 8xyxyxyA xyxyxy xxy y y yy=−− − ++⇒=−− − ++=−− +−−+−− +
2
2
2
4 2
16 16 16 4
3
(2 2) 3 4
(2 2) 3
2
3 3
33 3 3
3
=
=− +− − − +=− +− − − + ≤ ⇒ ≤ ⇔ ⇒=
=
x
xy y y xy y A z
y
Bài 7: Cho các số thực x, y, z thỏa mãn: x + y + z = 6. Tìm GTLN của
23A xy yz xz=++
Lời giải
Từ giả thiết
22
6 (2 3 ) (6 )(2 3 ) 3 2 4 18 12z x y A xy z y x xy x y y x x y xy x y⇒=−−⇒ = + + = + −− + =− − − + +
22 2 2 22
3 9 6 12 54 36 9 6 (2 9) 6 36 (3 2 9) 2 81 81A x y xy x y x x y y y x y y⇒=−− − + + =−− −− + =−+−− +≤
3 2 90 3
27 3
00
xy x
Az
yy
+ −= =
⇒ ≤ ⇔ ⇔ ⇒=
= =
Bài 8: Cho các số thực x, y thỏa mãn:
22
2 7( ) 2 10 0x xy x y y+ + ++ +=
. Tìm giá trị nhỏ nhất
của:
3Axy=++
Lời giải
Từ giả thiết
2 2 2 2 22
2 7( ) 2 10 0 4 8 28 28 8 40 0 (2 2 7) 4 9x xy x y y x xy x y y x y y+ + ++ +=⇒ + + + + + =⇔ + + + =
2
(227)92273 32273 5 2 2 1xy xy xy xy A⇒ + + ≤⇒ + + ≤⇒−≤ + +≤⇔−≤+≤−⇔−≤ ≤
+)
1 2; 0A xy=⇔=− =
+)
2 5; 0A xy=−⇔ =− =
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
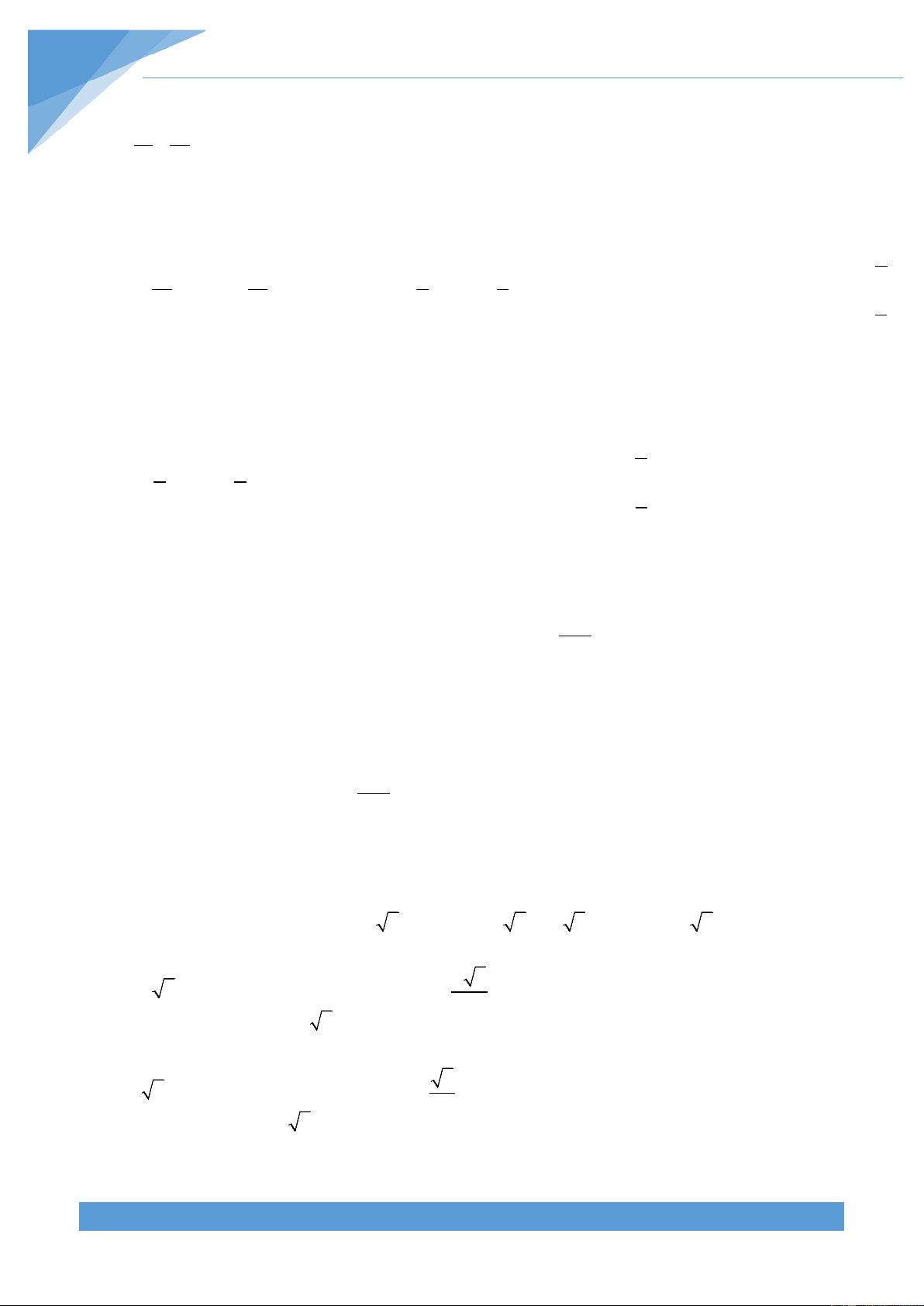
71
Bài 9: Tìm GTLN, GTNN của
2009S ab= +
, với a, b, là hai số thực khác 0 và
2
2
2
1
24
4
b
a
a
++=
Lời giải
Ta có:
22
2
22
2
1
0
11
4 2 2 2 2 2011
42
0
2
−=
= + −+ + − + −= − + − + +≥ +⇒ ≤⇒≤ ⇔
−=
a
bb
a
a a ab ab a a ab a ab ab S
b
aa
a
1; 2
1; 2
ab
ab
=−=−
⇔
= =
Ta lại có:
22
1
0
1; 2
1
4 2 2 2 2007
1; 2
2
0
2
−=
= = −
= − + + − + ≥− + ⇒ ≥− ⇒ ≥ ⇔ ⇔
=−=
+=
a
ab
b
a
a a ab ab ab S
ab
b
a
a
Vậy GTNN của S = 2007
( , ) ( 1; 2)ab⇔ =±±
Bài 10: [ Tuyển sinh vào 10 – TH – 2009 – 2010 ]
Cho các số thực m, n, p thỏa mãn:
2
22
3
1
2
m
n np p++=−
. Tìm GTNN, GTLN của
Amnp= ++
Lời giải
Theo giả thiết có:
2
22
2 22
22 2 2
2 2 2
22 2
2
3
1
2
2223 2
2 22 2 2 2
( )( )( )2
()22222
++=−
⇔+++ =
⇔ +++ + + + − ++ − + =
⇔++ +− +− =
⇒ ++ ≤⇒− ≤ ++ ≤ ⇒− ≤ ++ ≤
m
n np p
n np p m
m n p mn np mp m mn n m np p
mnp mn mp
mnp mn
p mnp
+)
0
2
20
3
2
mn
A mp mnp
mnp
−=
−
=− ⇔ −= ⇔ ===
++ =−
+)
0
2
20
3
2
mn
A mp mnp
mnp
−=
= ⇔ −= ⇔ ===
++ =
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

72
Bài 11: Cho x, y, z là các số thực thỏa mãn :
2 22
3xyz++=
. Tìm GTLN, GTNN
2Axy z=++
Lời giải
Từ
222222 2222
36 6 6 18 ( 2)( )(2 )(2 )18x y z x y z xy z xy xz yz+ + =⇔ + + = ⇔ ++ + − + − + − =
2 18 32 32xy z A⇒ + + ≤ ⇒− ≤ ≤
+)
0
2
20
32
2
20
2
20
xy
xz
xy
A
yz
z
xy z
−=
−
−=
= =
=−⇔ ⇔
−=
= −
++ =
+)
2
32 ; 2
2
A xy z= ⇔== =
Bài 12: Cho các số thực m, n, p thỏa mãn :
2 22
3
2 2 4 3 2 (1
)
2
+ + + ++ =m n p mn mp np
Tìm GTLN, GTNN của biểu thức
Amnp= ++
Lời giải
222
22 2 2 2
2 2
2 22
2
(1) 4 4 8 6 2 4 3
3( 2 2 2 )( 4 4 )( 2 )3
3( )( 2)( )3
3( ) 3 1 1
⇔ +++ + + =
⇔ +++++ +−+ +−+=
⇔ ++ + − + − =
⇒ ++ ≤⇒−≤ ++ ≤
m n p mn mp np
m n p mn np pm m mp p n np p
mnpmpnp
mnp mnp
+)
20
11
10 ;
24
1
mp
A np m np
mnp
−=
−−
=−⇔ − = ⇔ = = =
++ =−
+)
20
11
10 ;
24
1
mp
A np m np
mnp
−=
=⇔ −= ⇔ = ==
++ =
Bài 13: Cho x + y = z = 3 ;
2 22
;A x y z B xy yz zx=++ =++
a. Chứng minh
AB≥
b. Tìm GTNN của A
c. Tìm GTLN của B d. Tìm GTNN của A + B
Lời giải
a. Xét
222
1
( )( )( ) 0
2
AB xy xz yz AB x y z
− = − + − + − ≥⇒ ≥ ⇔==
b. Ta có :
2 22
2 2
22 222
2 22
2( ) 0
( ) 9 9 2
( ) 3( )
x y z xy yz zx
x y z x y z xy yz zx x y z
x y z xy yz zx
+++ ++ =
++ =⇔ ⇒
=+++ ++ ≤ ++
++≥++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

73
93 3 1A A xyz⇔≤ ⇒ ≥⇔= ==
c.
2 22
9()2()3()33 1x y z xy yz zx xy yz zx B B x y z= ++ + ++ ≥ ++ = ⇒≤⇔===
d. Có:
29
96 1
3
AB
AB B x y z
B
+=
⇒+=−≥⇔===
≤
Bài 14: Cho
[ ]
, , 1; 2abc∈−
thỏa mãn:
0abc++=
. Tìm GTLN của
222
Pabc=++
Lời giải
Với
[ ]
1, 2x∈−
, ta có:
22
1; 2 ( 1)( 2) 0 2 0 2x x x x xx xx≥− ≤⇒ + − ≤⇒ −−≤⇔ ≤+
Áp dụng :
222
2 2 2 6 6 ( , , ) ( 1, 1, 2) 6P a b c a b c a b c a b c G
TLN= + + ≤+++++=+++=⇒ =−− ⇒ =
Bài 15: Cho
[ ]
, , 1; 2abc∈−
thỏa mãn
1abc++=
. Tìm GTLN của
222
Pabc=++
Lời giải
Ta có :
( 1)( 1)( 1) 0 1 0a b c abc ab bc ca a b c+ + + ≥ ⇒ + + + + +++≥
(2 )(2 )(2 ) 0 8 4( ) 2( ) 0 3( ) 9 3( ) 0a b c a b c ab bc ca abc ab bc ca a b c− − − ≥⇒− ++ + + + − ≥⇒ + + +− ++ ≥
2
3()6 2()2()12()5ab bc ca ab bc ca P a b c ab bc ca ab bc ca⇔ ++ ≥−⇔ ++≥−⇒=++ − ++ =− ++ ≤
Dấu ‘ = ’’ xảy ra
( , , ) ( 1,0,2) axP=5abc m⇔ =−⇒
BÀI TẬP TỰ LUYỆN
Bài 1: Tìm min của:
22
3Axy= +
biết
31xy+=
Hướng dẫn
Từ
31xy+==>
( )
2
2
13 3 13y xAx x=− ⇒= +−
22
12 6 1xx= −+
Bài 2: Tìm min của:
A xy=
biết
31xy+=
Hướng dẫn
Ta có
31xy+=⇒
( )
2
13 13 3y x Ax x x x=− =>= − =− +
Bài 3: Tìm min của:
33
A a b ab=−−
biết: a – b =1
Hướng dẫn
Ta có:
( ) ( )
3
3
11 1ab A b b b b= +=> = + − − +
=
2
2 21bb++
Bài 4: Tìm max của:
.B ab=
biết:
3512ab+=
Hướng dẫn
Từ giả thiết ta có:
12 5
3
b
a
−
=
, thay vào
2
12 5 5 12
3 33
b
Bb b b
−−
= = +
Bài 5: Tìm min của:
33
C x y xy=++
biết:
1xy+=
Hướng dẫn
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
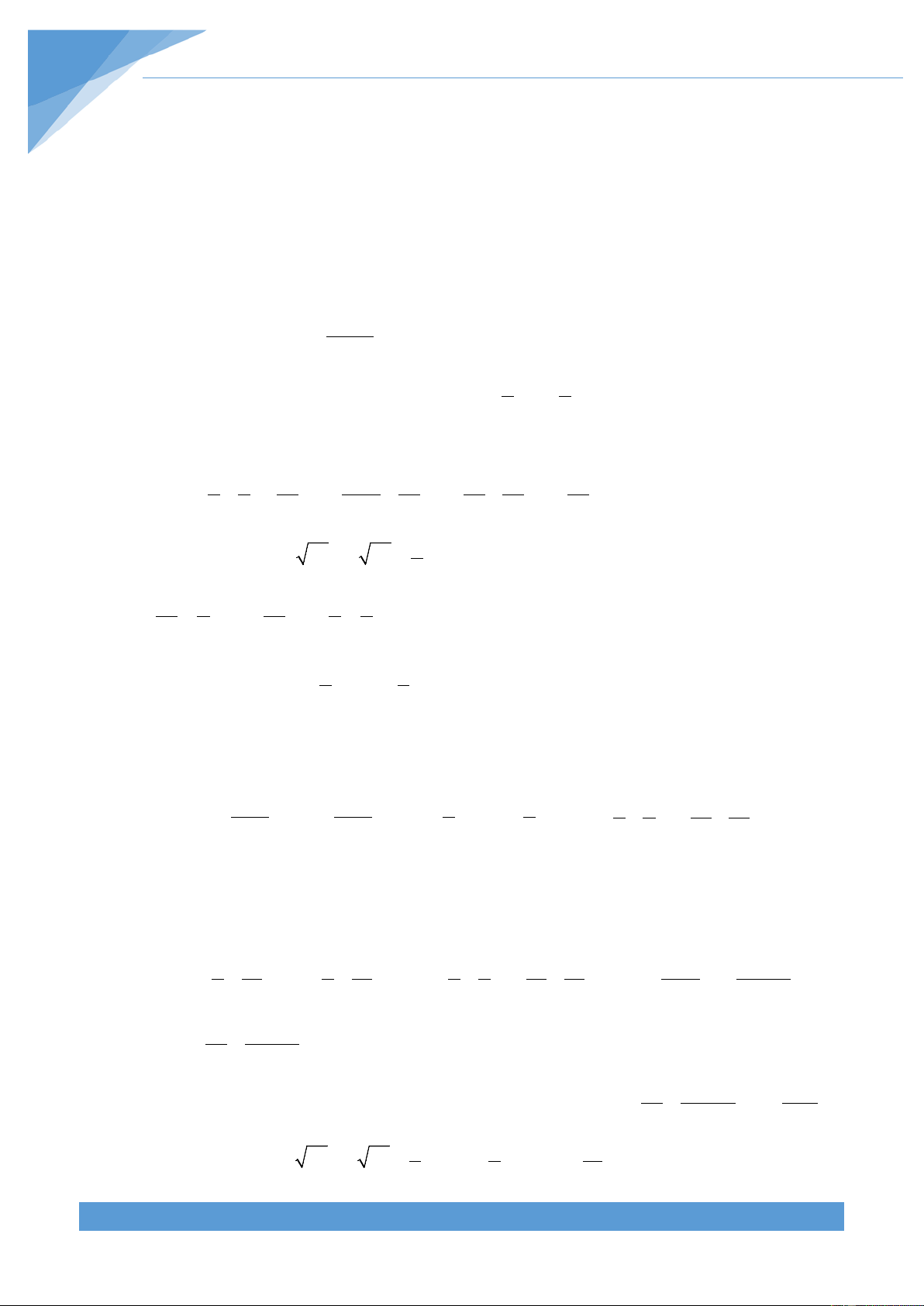
74
Từ giả thiết =>
1yx= −
thay vào C ta được:
( )
3
32
1 2 21C x x xy x x= +− + = − +
Bài 6: Tìm min của:
22
2Dx y= +
biết:
21xy+=
Hướng dẫn
Từ giả thiết suy ra
12xy= −
thay vào
( )
2
2
12 2D yy=−+
Bài 7: Tìm min của:
22
25Ex y= +
biết:
43 7xy−=
Hướng dẫn
Từ giả thiết suy ra
47
3
x
y
−
=
thay vào E và làm tiếp
Bài 8: Cho a, b>0 và a+b=4, tìm GTLN của
11
11P
ab
=−−
Hướng dẫn
Ta có:
11 1 1 4 1 3
1 1 11
ab
P
a b ab ab ab ab ab ab
+
=−++=− +=−+=−
Do
4
, 0 42 2
4
2
a b a b ab ab ab>=>+=≥ => ≤ ==> ≤
Khi đó:
3 3 3 31
11
4 44ab ab
≥ =>− ≤− =
, dấu = xày ra khi
4
2
ab
ab
ab
+=
<=> = =
=
Bài 9: Tìm min của:
22
11
11F
ab
=+ ++
, biết: a + b = 1 và a,b > 0
Hướng dẫn
Cách 1:
Ta có:
2 2 22
1 1 22
ab ab b a
a b ab
++
+ ++ = + + +
=
22
22
84
ab a b
ba b a
+ ++ +
8 4.2 2 18≥+ +=
Cách 2:
Ta có:
22
2 2 2 2 22
2 1 2 1 11 1 1
1 1 22 22
ab a b
F
a b a b ab
a b a b ab
++
=+++++=+ +++=+ +
22
22
2
2
ab
F
ab
ab
+
=++
(1)
Mà
22
1 12a b a b ab+==> + =−
thay vào (1) ta được:
22 22
2 12 1
22
ab
F
ab
ab ab
−
=++ =+
Lại có:
22
11 1
12
2 4 16
a b ab ab ab a b+=≥ => ≤ => ≤ => ≤
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
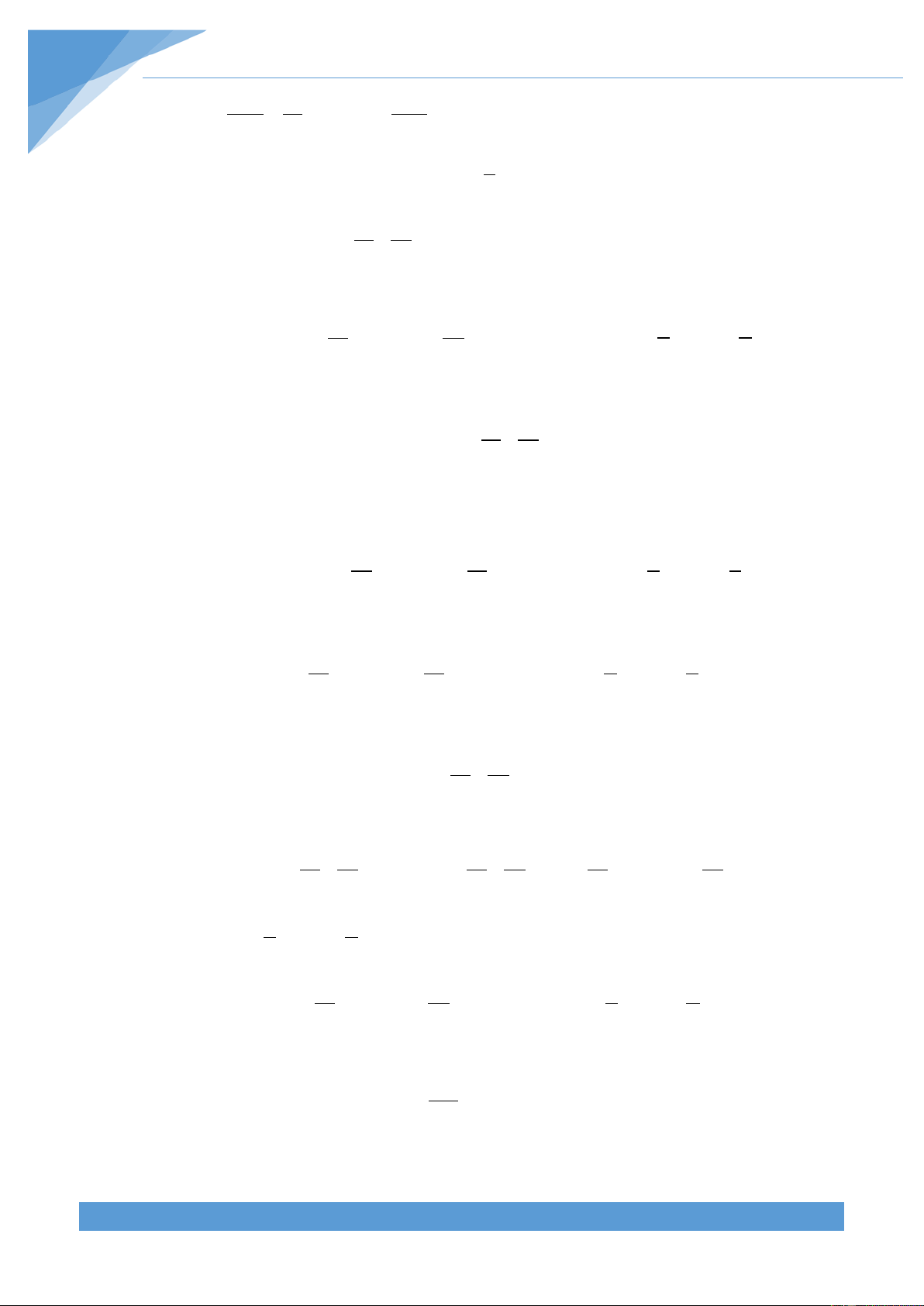
75
22 22
1 16 1
2 2 16 18F
ab ab
=> ≥ => =+ ≥+ =
Dấu = khi và chỉ khi
1
1
2
ab
ab
ab
+=
<=> = =
=
Bài 10: Cho x, y thỏa mãn:
2
2
2
1
24
4
y
x
x
++=
, tìm Max của: A= x.y
Hướng dẫn
Từ giả thiết ta có :
2
22
2
1
42 2
4
y
x x xy xy
x
= +−+ + − ++
=>
22
1
42
2
y
x x xy
x
=− +− ++
=>
24 2xy xy+≤=> ≤
Bài 11: Cho hai số thực a,b
≠
0, thỏa mãn:
2
2
2
1
24
4
b
a
a
++=
, Tìm min, max của:
2017S ab= +
Hướng dẫn
Từ giả thiết ta có :
22
2
22
2
11
42 2 2
42
bb
a a ab ab a a ab
aa
= +−+ +− ++=− +− ++
=>
2 4 2017 2019 2019ab ab S+≤=> + ≤ => ≤
Mặt khác :
22
2
22
2
11
42 2 2
42
bb
a a
ab ab a a ab
aa
= +−+ ++ −+=− +− −+
=>
2 4 2 2017 2015ab ab ab− + ≤ => ≥− => + ≥
=>
2015S ≥
Bài 12: Cho hai số x,y khác 0 thỏa mãn:
2
2
2
8
8
8
y
x
x
++=
, Tìm min, max của:
2024A xy= +
Hướng dẫn
Từ gt ta có :
22 2
2 2 22
2 22
8 16 16
8 16
2 8 8
84 4
yy y
x x x x xy xy
x xx
=++=>= ++= +−+ ++ −+
=>
22
4
8 8
8 16 8 2024 2016
2
y
x x xy xy xy A xy
x
= − + + − + =>− + ≤ => ≥− => = + ≥
Mặt khác :
22
2
22
2
16 4
16 8 8 8
42
yy
x x
xy xy x x xy
xx
= +−+ + − ++=− +− +−
=>
8 16 8 2024 2032xy xy S xy−≤ => ≤=> = + ≤
Bài 13: Cho x, y
∈
R khác 0 biết:
22
2
1
84
4
xy
x
++ =
, Tìm x, y để
.B xy=
đạt min và đạt max
Hướng dẫn
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

76
Ta có :
( )
22 2 22
22
11
48 4 2 4 4 4 2
44
x y x x y xy xy
xx
= ++ = + −+ +− + +
4 =
( )
2
2
11
2 2 42424
22
x x y xy xy B xy
x
− + − + +=> +≤=> = ≤
Mặt khác :
( )
2
2
11
42 2 42 424
22
x x y xy xy B xy
x
−
= − + + − + =>− + ≤ => = ≥
Bài 14: Cho x, y > 0 thỏa mãn: x + y = 1, Tìm min của:
( )( )
22
4 3 4 3 25A x y y x xy= + ++
Hướng dẫn
Ta có :
( )
2 3 3 22 3 3
16( ) 12 12 9 25 6 12 34A xy x y xy xy x y x y xy= + + ++ = + ++
Vì x + y = 1 nên
( )
( )
( )
2
33 2
2
3 13x y x y x xy y x y xy xy+=+ −+ =+ − =−
, thay vào A
( )
22
6 12 1 3 34A x y xy xy= +−+
, Đặt xy = t khi đó:
2
6 2 12At t= −+
Bài 15: Cho x, y là các số thực thỏa mãn:
1xy+=
Tìm min của biểu thức:
( )( )
22
4 48C x y y x xy=+ ++
Hướng dẫn
Ta có :
( )( ) ( )
2 2 22 3 3 22 3 3
4 4 8 4 4 16 8 4 24C x y y x xy x y x y xy xy x y x y xy=+ ++= +++ += + ++
Do
( ) ( )
3
33
1 3 13xy x y xy xyxy xy+==> + = + − + =−
Thay vào C ta được :
( )
( )
( )
2
22 22 22
4 1 3 24 12 4 2 .6 36 32 6 32 32C x y xy xy x y xy x y xy xy= + − + = + + = + + − = + − ≥−
32MinC = −
, Dấu = xảy ra khi và chỉ khi
13
62
xy x
xy y
+= =
=>
=−=−
hoặc
2
3
x
y
= −
=
Bài 16: Cho x, y là hai số thực thỏa mãn: x + 2y = 3 tìm min của:
22
2Ax y= +
Hướng dẫn
Từ gt ta có:
32xy= −
thay vào
( )
2
22
3 2 2 6 12 9A y yy y=− +=−+
Bài 17: Cho x, y là hai số thực thỏa mãn:
22
4x y xy+−=
, Tìm min và max của:
22
Ax y= +
Hướng dẫn
Ta có :
( )
2
22 2 2 22
42 2 2 8 8x y xy x y xy x y x y+−==> + − ==>− ++=
22
8xy⇒+≤
hay
8A ≤
Mặt khác :
( )
2
22 22 22
8222 2282 338x y xy x y xy x y x y=+−=>+=+=>+=++
8≥
=>
22
8
3
xy+≥
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

77
Hay
8
3
A ≥
Bài 18: Cho x,y thỏa mãn: x+ y =2, Tìm min của:
33
2A x y xy=++
Hướng dẫn
Từ gt ta có :
2yx= −
thay vào A ta được :
( ) ( )
3
3
2 22Ax x x x=+− + −
Bài 19: Cho các số thực x, y thỏa mãn:
40xy++=
, Tìm max của:
( ) ( )
33 22
2 3 10Axyxyxy= ++ ++
Hướng dẫn
Ta có:
4xy+=−
, nên
( ) ( )
3
33
3 64 12x y x y xy x y xy+ = + − + =−+
,
( )
2
22
2 16 2x y x y xy xy+=+ − =−
thay vào
( ) ( )
2 64 12 3 16 2 10A xy xy xy=−+ + − +
Bài 20: Cho x, y, z
∈
R, thỏa mãn:
22 4x yz+ +=
, tìm max của:
2A xy yz zx= ++
Hướng dẫn
Từ giả thiết
42 2z xy⇒=− −
thay vào A ta được :
( ) ( )
22
2 42 2 42 2 2 2 2 4 4A xy y x y x x y x y xy x y= + −− + −− =− − − ++
Bài 21: Cho x, y, z
∈
R thỏa mãn:
6xyz++=
. Tìm max của:
23A xy yz zx=++
Hướng dẫn
Từ gt =>
6z xy=−−
thay vào
( ) ( )
26 36Axy y xy x xy= + −− + −−
Bài 22: Cho x,y
∈
R thỏa mãn:
( )
22
2 7 2 10 0x xy x y y+++++=
. Tìm min và max của:
3Sxy=++
Hướng dẫn
Từ gt ta có:
22
2 7 7 2 10 0x xy x y y+ ++ + +=
( )
2
2
22
27
27 (27)
2 2 7 10 0
24 4
y
yy
xx yy
+
++
⇒+ + + + +− =
2
2
79
0
24
xy y
⇒ ++ + −=
3 73
52
2 22
xy xy⇒− ≤ + + ≤ =>− ≤ + ≤− ⇒
2 31xy−≤ + +≤
Bài 23: Cho các số thực m, n, p thỏa mãn:
2
22
3
1
2
m
n np p++=−
. Tìm min, max của:
Amnp= ++
Hướng dẫn
Từ gt ta có :
2 2 2 22 2
222 23 3 222 2n np p m m n p np++=−=>+++=
=>
( )
22 2 22 2
( 2 2 2)2 2 2 2m n p mn np mp m n p mn mp++ + + + + ++ − − =
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

78
=>
( ) ( ) ( )
2 22
2mnpmpmn++ +− +− ≤
=>
22mnp− ≤ ++ ≤
Bài 24: Cho x, y, z là các số thực thỏa mãn:
2 22
3xyz++=
, Tìm min, max của:
2Pxy z=++
Hướng dẫn
Ta có :
( )
2
2 22 2
2 4244P x y z x y z xy yz xz=++ =+++++
, nên ta nhân 6 vào gt :
( ) ( )
222222 222
18666 4244 552244x y z x y z xy yz zx x y z xy yz zx=++=+++++ + ++−−−
( ) ( ) ( ) ( )
22 2 2
18 2 2 2xy z xy xz yz= ++ + − + − + −
=>
( )
2
2 18xy z++ ≤
18 2 18xy z− ≤++ ≤
Bài 25: Cho các số thực m, n, p thỏa mãn:
22 2
3
2 243 2
2
m n p mn mp np+ + + ++ =
,
Tìm min max của:
Bmnp= ++
Hướng dẫn
Từ gt ta có :
222
4 48 6 2 4 3m n p mn mp np+++ + + =
=>
( ) ( )
22 2 22 2
3 222 542 3m n p mn mp np m n p mp np+++ + + + ++ − − =
=>
( ) ( ) ( )
2 22
32 3mnp pm np++ + − + − =
=>
( )
2
3 31 1mnp mnp++ ≤=>−≤ ++ ≤
Bài 26: Cho x, y, z thỏa mãn:
3xyz++=
, Tìm min max của:
A xy yz zx=++
Hướng dẫn
Từ gt =>
3z xy=−−
thay vào
( ) ( )
33Axyy xy x xy= + −− + −−
=
22
33x y xy x y−−++
Bài 27: Cho x, y, z thỏa mãn: x + y + z = 3, Tìm min max của:
34B xy yz zx=−+ +
Hướng dẫn
Từ gt ta có:
3z xy=−−
=>
( ) ( )
33 43B xy y xy x xy=− + −− + −−
22
4 3 16 9 12B x y xy y x⇒=− − − + +
Bài 28: Cho các số thực x,y,z thỏa mãn:
23 4x yz+ −=
, Tìm min max của
A xy yz zx=−+ +
Hướng dẫn
Từ gt =>
234z xy=+−
thay vào
( ) ( )
234 234Axyyxy xxy=−+ +−+ +−
Bài 29: Cho các số thực x,y,z thỏa mãn:
23 4x yz+ −=
, Tìm min max của:
1234B xy yz zx= −−
Hướng dẫn
Từ gt ta có :
234z xy=+−
thay vào
( ) ( )
12 32344234B xyyxy xxy= − +−− +−
Bài 30: Cho hai số thực x,y thỏa mãn:
2xy+=−
, tìm min của:
( )
33
2 15 7A x y xy= +− +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

79
Hướng dẫn
Từ x + y = -2, ta có:
( ) ( )
3
33
3 86x y x y xy x y xy+ = + − + =−+
thay vào
( )
2 8 6 15 7 3 9A xy xy xy= −+ − + =− −
và y = - 2 - x thay vào
( )
32 9Ax x=− −− −
Bài 31: Cho hai số thực x, y thỏa mãn:
2xy+=−
, Tìm min của
( )
4433 22 22
2 2 13B x y x y x y xy x y xy=+−−+ + + +
Hướng dẫn
( )
4433 22 22
2 2 13B x y x y x y xy x y xy=+−−+ + + +
Từ x + y = - 2, ta có:
( ) ( )
2
22
4 4 22 22
2 2 42 2x y x y xy x y xy x y
+= + − − =− −
33
68x y xy+= −
,
22
42x y xy+=−
, Thay vào b ta được :
( ) ( ) ( )
2
22 22
42 2 6 8 2 2 42 13B xy x y xy x y xy xy xy=− − − −+ + − +
24B xy=−+
, thay
2
22y x Bx x=−− => = +
Bài 32: Cho hai số thực x, y thỏa mãn:
5xy+=
, Tìm max của:
( )
33 22
82A x y x y xy=+− + ++
Hướng dẫn
Vì
5xy+=
nên
33
125 15x y xy+= −
và
22
25 2x y xy+=−
thay vào
( )
125 15 8 25 2 2A xy xy xy= − − − ++
Bài 33: Cho hai số x,y thỏa mãn: x + y = 5, Tìm max của:
( ) ( )
44 33 22 22
4 20 2Bxy xy xy xyxy=+− + − + − +
Hướng dẫn
( ) ( )
44 33 22 22
4 20 2Bxy xy xy xyxy=+− + − + − +
Vì x + y = 5 nên
( )
2
4 4 22
25 2 2x y xy x y+= − −
,
33
125 15x y xy+= −
,
22
25 2x y xy+=−
( ) ( ) ( )
2
22 22
25 2 2 4 125 15 20 25 2 2B xy x y xy xy x y xy=−−−−−−−+
Bài 34: Cho hai số x, y thỏa mãn:
( )
44
7 32x y xy xy+ −= −
, Tìm min max của:
P xy=
Hướng dẫn
Từ giả thiết suy ra:
4 4 22
32 7x y xy x y+− + =
=>
( ) ( )
2
2
4 22 4 22 2 2
3 121
2 4 37 2
4 16
x x y y x y xy x y xy
− ++ −==>− + − =
=>
2
3 121
2
4 16
xy
−≤
Bài 35: Cho các số thực x, y thỏa mãn:
22
7 9 12 4 6 15 0x y xy x y+ + −−−=
, Tìm min max của:
235Axy=++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

80
Hướng dẫn
Từ giả thiết suy ra:
( ) ( )
22
2
2 3 2.2 .3 2.2 2.3 1 3 16x y xyxy x+ + − − ++ =
=>
( )
2
2
2 3 1 3 16xy x+++ =
Bài 36: Cho các số thực x,y,z thỏa mãn:
2 22
3254225x y z xy xz yz+ ++−+ =
, Tìm min max
của:
Pxy= +
Hướng dẫn
Từ gt ta có:
( ) ( )
22 22 2
2 2 5222 5x y xy x y z xy xz yz++ + ++ + − + =
=>
( )
( ) ( )
2
2 22 2 2
222 44 5x y x y z xy yz zx z xz x+++++++ + −+=
=>
( )
2
55 5xy xy+ ≤=>− ≤+≤
Bài 37: Cho các số x, y, z thỏa mãn:
3 21xy z++ =
. Tìm min max của:
2 22
px y z=++
Hướng dẫn
Từ gt ta có:
13 2y xz=−−
=>
2 22
1 9 4 6 12 4y x z x xz z=++−+ −
khi đó :
22
10 5 12 6 4 1P x z xz x z= + + −−+
Bài 38: Cho các số x, y, z thỏa mãn: x + y + z = 1, Tìm max của:
234A xy yz zx=++
Hướng dẫn
Từ gt =>
1z xy=−−
thay vào
( ) ( )
2 31 41A xy y xy x xy= + −− + −−
Bài 39: Cho x, y
∈
R, thỏa mãn: x + 2y = 1, Tìm max của: P = x. y
Hướng dẫn
Từ gt =>
12xy= −
thay vào
( )
12Py y= −
Bài 40: Cho x, y
≥
0, x + y = 1, Tìm min, max của:
22
Ax y= +
Hướng dẫn
Từ gt =>
1yx= −
thay vào
( )
2
2
1Ax x= +−
Bài 41: Tìm min max của:
Pxyz=++
, biết:
22 2
3
1
2
y z yz x++=−
Hướng dẫn
Từ gt =>
22 2 2 22
222 23 3222 2y z yz x x y z yz++=−=>+++=
=>
( ) ( )
2 22 2 22
222 2 22 2x y z xy yz zx x y z xy zx+++ + + + ++− − =
=>
( ) ( ) ( ) ( )
2 22 2
22xyz xy xz xyz++ + − + − ==> ++ ≤
Bài 42: Cho
22
3 2 10 14 18 0x y xy x y+ + − − +=
, Tìm min, max của:
Sxy= +
Hướng dẫn
Từ gt =>
( ) ( )
2
2 22
2 5 5 3 14 18 10 25 0x xy y y y y y+ −+ − + − +− + − =
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

81
=>
( )
( )
( )
22
2
5 2 219 5 9xy y y xy+− + − + ==> +− ≤
=>
3 53xy−≤ + −≤
Bài 43: Cho a, b, c không âm thỏa mãn: 3a + 2c = 51 và c + 5b = 21.
Tìm max của A = a + b + c
Hướng dẫn
Cộng theo vế giả thiết ta được :
( )
3 3 5 72 3 72 2 72a c b abc b+ + = => ++ = − ≤
Do
72
0 24
3
b abc≥=>++≤ =
Bài 44: Cho a, b, c là các số không âm thỏa mãn: 2a + b = 6 - 3c và 3a + 4b = 3c + 4.
Tìm min
234E abc= +−
Hướng dẫn
Cộng theo vế ta được :
4
43
3
2
32 2
3
c
ac
ab
bc
c
≤
= −
+==> =>
= −
≥
do
0
0
a
b
≥
≥
Khi đó:
( ) ( )
24 3 33 2 4 2E c c cc= − + −− =−
Bài 45: Cho
, , 0,2 7 2014,3 5 3031xyz x y x z≥ + = +=
, Tìm GTLN của biểu thức
Axyz=++
Hướng dẫn
Cộng theo vế của gt ta có:
5 5 5 5045 2 5045xyz y++= −≤
do
0y ≥
nên
( )
5 5045 1009xyz xyz++ ≤ =>++≤
Bài 46: Cho
2ab+=
,Tìm max của:
( )
22
A ab a b= +
Hướng dẫn
Ta có:
( )
2 2 22
2 42 42 2 4a b a b ab A ab ab a b ab+==> + =− => = − =− +
( )
22
2 1 22A a b ab=− − ++≤
, Max
2A =
Bài 47: Cho x, y thỏa mãn:
( )( )
11 6 2015 3 0x y xy+ + −+ =
, Tìm min của:
5 2016P xy x=−+
Hướng dẫn
Từ gt ta có :
11 6 2015 0xy++ =
hoặc
30xy−+=
TH1: Ta có :
11 2015
11 6 2015 0
6
x
xy y
+
+ + ==>=
thay vào P
TH2: ta có:
30 3xy yx−+==> =+
thay vào P
Bài 48: Cho 3 số x,y,z thỏa mãn :
3xyz++=
, Tìm GTLN của :
B xy yz zx=++
Hướng dẫn
Ta có :
( ) ( ) ( )
3Bxyzxy xy xy xy= + +=+−+ +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

82
=
( ) ( )
2
22
3 33xy x y x y x y xy x y+ + −+ =−− − + +
=
( )
2
2
33
1 33
24
y
xy
−−
− + + − +≤
Bài 49: Cho
22
35x xy y++ =
, tìm Min hoặc max của biểu thức :
22
22P x xy y=−+
Hướng dẫn
Ta có :
22
22
22
53
P x xy y
x xy y
−+
=
++
Dạng 5: Phương pháp đổi biến số
Phương pháp:
- Phân tích thành các biểu thức tương đồng để đặt ẩn phụ.
- Sử dụng phương pháp nhóm hợp lý làm xuất hiện nhân tử để đặt ẩn phụ.
- Sử dụng các hằng đẳng thức
( ) ( )
22
,ab abc± ++
.
Bài 1: Tìm GTNN của biểu thức
22
( 1) ( 3)Ax x=− +−
Lời giải
Đặt
2 22
2 ( 1) ( 1) 2 2 2 min 2 0 2yx A y y y A
y x=−⇒ = + + − = +≥⇒ =⇔ =⇒=
Bài 2: Tìm GTNN của
( 1)( 4)( 5)( 8)Ax x x x=−− − −
Lời giải
22
( 1)( 4)( 5)( 8) ( 9 8)( 9 20)Axx x x xx xx=− − − −= −+ −+
Đặt
2 22 2
2
9 8 ( 12) 12 ( 6) 36 36 6 9 14 0
7
x
txx Att t tt t
xx
x
=
=−+⇒=+ =+ =+ −≥−⇔=⇔−+=⇔
=
Bài 3: Tìm GTNN của biểu thức
2
2
41
( 0)
−+
= ≠
xx
Ax
x
Lời giải
22
2
41 1 1
1 1 4 ( ) ( 2) 3 3 2
2
A yyy A y y x
xx x
= − + = − + = ⇒ = − − ≥− ⇔ = ⇔ =
Bài 4: Tìm GTNN của:
( )( )( )
347A xx x x=−−−
Lời giải
( )( )( )
( )( )
22
7 3 4 7 7 12Axx x x xxxx= − − −= − −+
, đặt
2
76xx t− +=
, khi đó:
( )( )
2
6 6 36 36At t t= − + = − ≥−
, dấu “ = ” khi
22
1
0 7 60
6
x
t xx
x
=
= <=> − + = <=>
=
Vậy Min A = - 36 khi x = 1 hoặc x = 6
Bài 5: Tìm GTNN của:
( )( )
( )
2
1 3 45Bx x x x=− − −+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

83
Lời giải
( )( )
22
45 45Bxx xx= −+ −+
, Đặt
2
4 40xx− +=
. Khi đó:
( )( )
2
1 1 11Bt t t= − + = − ≥−
, Dấu “ = “ khi
22
0 4 40 2t xx t= <=> − + = <=> =
Bài 6: Tìm min của:
( )( )( )
2 4 68Axxxx=++++
Lời giải
( )( )( )
( )( )
22
6 2 48 6 6 88Axx x x xxxx= + + + += + + + +
, Đặt
2
64xx t+ +=
. Khi đó:
( )( )
22
4 4 8 16 8 8 8At t t t= − + += − += −≥−
, Dấu “ = ” Khi đó:
22
35
0 6 40
35
x
t xx
x
=
−+
= <=> + + = <=>
=−−
Bài 7: Tìm GTNN của:
( )( )( )( )
1234Bx x x x=++ + +
Lời giải
( )( )( )( )
( )( )
22
1 4 2 3 54 56Bx x x x xx xx=+ + + += ++ ++
, Đặt
2
55xx t+ +=
, Khi đó:
( )( )
2
1 1 11Bt t t= − + = − ≥−
, Dấu “ = “ khi
22
55
0 5 50
2
t xx x
−±
= <=> + + = <=> =
Bài 8: Tìm GTNN của:
( )( )
22
62Axx xx= +− ++
Lời giải
Đặt
2
2xx t+−=
. Khi đó:
( )( )
2
4 4 16 16At t t= − + = − ≥−
Dấu “ = “ xảy ra khi:
2
1
0 20
2
x
t xx
x
=
= <=> + − = <=>
= −
Bài 9: Tìm GTNN của :
( )( )( )( )
1236Cx x x x=−+ + +
Lời giải
( )( )( )( )
( )( )
22
1623 56 56Cx x x x xx xx=− + + += +− ++
, Đặt
2
5x xt+=
. Khi đó:
( )( )
2
6 6 36 36Ct t t= − + = − ≥−
, Dấu “ = ” khi
2
0
0 50
5
x
t xx
x
=
= <=> + = <=>
= −
Bài 10: Tìm GTNN của:
( )( )( )( )
2 1 2 32 1Dx x x x=−+ + +
Lời giải
( )( )( )( )
( )( )
22
21 3 221253252Dx x x x xx xx= − + + += +− ++
, Đặt
2
25x xt+=
, Khi đó:
( )( )
2
2
1 25 25
32 6
2 44
Dt t tt t
−
= − + = −− = − − ≥
, Dấu “ = “ khi:
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

84
2
1 1 5 29
25
2 24
t xx x
−±
= <=> + = <=> =
Bài 11: Tìm min của:
( )( )( )( )
1 2 3 4 2011Cx x x x=+ + + ++
Lời giải
( )( )( )( )
1 4 2 3 2011Cx x x x= + + + ++
( )( )
22
5 4 5 6 2011xx xx= ++ +++
, Đặt
2
55xx t+ +=
Khi đó:
( )( )
2
55
1 1 2011 5 5 0
2
Ct t x x x
−±
= − + + <=> + + = <=> =
Bài 12: Tìm max của:
( )( )( )( )
51 2 3 6E xx x x=+−+++
Lời giải
( )( )( )( )
( )( )
22
5 1623 56 565E x x x x xx xx=−− + + +=− +− +++
, đặt
2
5x xt+=
.
Khi đó:
( )( )
( )
22
6 6 5 36 5 41 41Et t t t=−− + +=− − +=−+ ≤
Dấu “ = “ Khi
22
0
0 50
5
x
t xx
x
=
= <=> + = <=>
= −
Bài 13: Tìm GTNN của:
( )( )( )( )
1236Mx x x x=−+ + +
Lời giải
( )( )( )( )
( )( )
22
1 6 2 3 56 56Mx x x x xx xx=− + + == +− ++
, Đặt
2
5x xt+=
.
Khi đó:
( )( )
2
6 6 36 36Mt t t= − + = − ≥−
, Dấu “ = ” khi
2
0
0 50
5
x
t xx
x
=
= <=> + = <=>
= −
Bài 14: Tìm min của:
( )
( )
( )
2
1 4 5 2014Dx x x=+ − ++
Lời giải
( )( )( )( )
( )( )
22
1 2 2 5 2014 3 10 3 2 2014Dx x x x xx xx=+ + − ++ = +− +++
, Đặt
2
34xx t+ −=
Khi đó:
( )( )
2
6 6 2014 1978Dt t t=− ++ =+
, Dấu “= “ xảy ra khi:
22
1
0 3 40
4
x
t xx
x
=
= <=> + − = <=>
= −
Bài 15: Tìm GTNN của:
43 2
6 10 6 9Cxx xx=− + −+
Lời giải
( ) ( ) ( )
( )
2
2
4 2 22 2
2.3 . 9 6 9 3 3 0C x xx x x x x x x= − + + −+= − +− ≥
Bài 16: Tìm GTNN của:
( ) ( )
44
86Dx x=+ ++
Lời giải
Đặt:
( ) ( )
44
42
7 1 1 2 12 2 2x yDy y y y+= => = + + − = + +≥
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

85
Bài 17: Tìm max của:
( ) ( )
44
23 1 3 5Fx x=−+−−
Lời giải
Đặt
( ) ( )
44
2 23 3 3 3x tF t t−==>=−+−−
( ) ( ) ( )
22
2 2 4
2 42
3 6 9 3 6 9 2 6 324 484 6 54 484F tt tt t t t t−= +++ −+−=+ + = + +
( )
2
2
6 27 3890 3890Ft=−+ + ≤
Bài 18: Tìm min của:
( ) ( )
44
37Gx x=+ +−
Lời giải
Đặt
( ) ( )
( ) ( )
22
44
22
2 5 5 10 25 10 25x t Gt t t t t t−==> = + + − = + + + − +
( ) ( )
2
4 2 4 2 42 4 4
2 300 1250 2 2.75 5625 10 2 75 10 10Gt t t t t= + + = + + − = + − ≥−
Bài 19: Tìm min của:
43 2
6 11 12 20Ix x x x=−+ ++
Lời giải
( )
4 3 2 22 2
6 11 12 20 6 9 2 12 20Ixxxx xxx xx=−+ −+= −++−+
( )
( )
( ) ( )
2 22
22 2
32 692 32 322I xx x x xx x= −+ −++= −+ −+≥
Bài 20: Tìm số nguyên m lớn nhất sao cho BĐT luôn đúng với mọi x:
( )( ) ( )
2
12 3xx x m+ + +≥
Lời giải
( )( )( )
( )( )
2
22
1 3 2 43 44VTx x x xx xx=+ + + = ++ ++
, Đặt
2
4x xt+=
, Khi đó:
( )( )
2
22
7 49 49 7 1 1
3 4 7 12 2. . 12
24 4 2 44
VT t t t t t t t
−
=+ + =++ =+ + + − = + −≥
Dạng 6 : Sử dụng bất đẳng thức có chứa dấu giá trị tuyệt đối
a. Định nghĩa:
0
0
AA A
A AA
=⇔≥
=−⇔ ≤
b. Tính chất
+)
0;AR A A A∀∈ ⇒ ≥ ≥
+)
,0x y R x y x y xy∀ ∈⇒+≤ + ⇔ ≥
+)
, ( ). 0xyR xy x y xyy∀ ∈⇒−≥ − ⇔ − ≥
Bài 1: Tìm GTNN của các biểu thức sau
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

86
a.
37Ax x=−+−
b.
123Bx x x=−+−+−
c.
1234Cx x x x=−+−+−+−
d.
5278Dx x x x=++++−+−
e.
123456Exxxxxx=+++++++++++
Lời giải
a.
3 7 3 7 3 7 4 4 4 ( 3)(7 ) 0 3 7Ax x x x x x A x x x=−+−=−+− ≥ −+− = =⇒ ≥⇔ − − ≥⇔≤≤
b.
123Bx x x=−+−+−
Ta có :
1 3 1 3 2(1) ( 1)(3 ) 0 1 3Bx x x x x x x= −+ − = −+ − ≥ ⇔ − − ≥ ⇔≤≤
Mà :
2 0 2(2) 2 2x x Cx−≥⇔= ⇒ ≥⇔=
c.
1234Cx x x x=−+−+−+−
Ta có :
1 3 1 3 2 1 3; 2 4 2 4 2 2 4x x x x xx x x x x−+−=−+−≥⇔≤≤ −+−=−+−≥⇔≤≤
4 min 4 2 4CCx⇒ ≥⇒ =⇔≤≤
d.
5278Dx x x x=++++−+−
Áp dụng bất đẳng thức
M MM R≥∀∈
Ta có :
5 2 7 8 5 2 7 8 22D x x x x x x x x xR= ++ + + − +− ≥++++−+−= ∀∈
50 5
20 2
min 22 2 7
70 7
80 8
xx
xx
Dx
xx
xx
+ ≥ ≥−
+ ≥ ≥−
⇒ = ⇔ ⇔ ⇔− ≤ ≤
−≥ ≤
−≥ ≤
e. Ta có :
123456 1 2 3456Exxxxxx x x xxxx=+++++++++++=−−+−−+−−++++++
1234569 min94 3E x x x x x x xR E x⇒ ≥−−−−−−++++++=∀∈⇒ =⇔−≤≤−
Bài 2: Cho số thực x. Tìm GTNN của các biểu thức sau
a.
325Ax x x=++−+−
b.
23456Bxxxxx=−+−+−+−+−
Lời giải
a.
32532535 358Axxxxxxx xx xxR=++−+−=++−+−≥++−≥++−=∀∈
Dấu ‘ = ’
30 3
20 2 2
50 5
xx
x xx
xx
+ ≥ ≥−
⇔ −=⇔ = ⇔=
−≥ ≤
b.
2345623456Bxxxxxxxx xx=−+−+−+−+−=−+−+−+−+−
2 35 6 23566 4x x x x x x x x xR x≥ − + −+− + − ≥−+−+−+−=∀∈ ⇔ =
Bài 3: Cho số thực x. Tìm GTLN của các biểu thức sau
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

87
a.
52Ax x=+−−
b.
23 5 4Bx x x=−− −−−
Lời giải
a.
52Ax x=+−−
Áp dụng bất đẳng thức :
, ( )0x y xyxyR yxy− ≤−∀ ∈⇔ − ≥
5 2 5 ( 2) 7 max 7 ( 2)( 5 2) 0 2Axxxx xRAxxx x= + − − ≤ +− − =∀∈ ⇒ = ⇔ − +−+ ≥ ⇔ ≥
b.
23 5 4Bx x x=−− −−−
Vì
50 5
50 2 4 2 42 5
( 4)( 2 4) 0 4
xx
x Bx x x x x
xx x x
−= =
−−≤⇒≤−−−≤−−+=⇔ ⇔ ⇔=
− −−+ ≥ ≥
Bài 4:[ Chuyên LHP – 2003 ] Cho số thực x. Tìm GTNN của
12 2 76 2Ax x x x= −− − + + − +
Lời giải
Đặt
2 2 2 2 22
2( 0) 2 2 2 1 6 9 ( 1) ( 3)t x t t x xt A t t t t t t= − ≥ ⇒ =−⇒= −⇒ = − ++ − += − + −
10
1 3 1 3 2 1
3 1 2 3 3 11
30
t
t tt t t x x
t
−≥
= −+ − ≥−+−= ⇔ ⇔≤≤ ⇔≤ − ≤ ⇔ ≤ ≤
−≥
Bài 5: Cho số thực x. Tìm GTNN của các biểu thức sau
a.
425 145(5)Ax x x x x= − + − + −− − ≥
b.
215341 861(1)Bxxxxxxx= − −+ +− −+ +− − ≥
Lời giải
a. Đặt
2 22
5( 0) 5 ( 1) (2 ) 1 2 1 2 1 2 3t x t xt A t t t t t t t t= − ≥ ⇒ = + ⇒ = + + − = + + − =++ − ≥++ −=
32 0 2 525 9A tt x x=⇔−≥⇔≤⇔ −≤⇔≤≤
b. Đặt
2 2 22
1( 0) 1 ( 1) 5 ( 2) ( 3) 1 5 2 3t x t xt A t t t t t t=−≥⇒=−⇒=−+ −+−=−+−+−
10
13 132 2 2 125min25
3
t
t tt t t t x x A x
t
−≥
≥ −+ − ≥−+−= ⇔ = ⇔= ⇔ −= ⇔ = ⇒ = ⇔ =
≤
Bài 6: (HSG Tỉnh Sóc Trăng năm 2014 – 2015)
Tìm GTNN của
3 2 2012Ax x=++−+
Lời giải
Ta có
3 2 2012 3 2 2012Ax x x x=++−+ =++−+
Lại có :
33 3xx x+ ≥ + ⇔ ≥−
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

88
Mà
2 2 2 3 2 2012 3 2 2012 2017x x x Ax x x x− ≥−⇔≤⇒ = ++ − + ≥++−+ =
Vậy
2017 3 2MinA x= ⇔− ≤ ≤
Bài 7: (HSG Tỉnh Quảng Ngãi năm 2015 – 2016)
Tìm GTNN của
3 1 43Ax x x=++−+−−
Lời giải
Ta có
31433143Axxx xx x=++−+−−=++−+−−
Lại có
1 0 1; 3 3 3; 4 4 4 3 0 4 3 4x x x x x x x x Ax x−≥⇔ = + ≥+⇔ ≥− − ≥−⇔ ≤⇒ ≥+++−−=
Vậy
41MinA x=⇔=
Bài 8: (Tạp chí Toán học và tuổi trẻ số 420) Tìm GTNN của
( )
1 2 12
.... 2017 ...
nn
A xa xa xa a a a=− +− + +− + < <<
Lời giải
- Trường hợp
12 1 2 2
2 ... ... 2017
kk k k
n k A xa xa xa a x a x a x
++
= ⇒=− +− ++− + −+ −++ −+
Ta có
1
1, ; 1,
i i i k kj kj
xa xa xai ka x a x xa j k
++ +
− ≥− ⇔≥∀= − ≥ −⇔≤ ∀=
( )
1 2 1 2 2 12 2
... ... 2017 ...
kk k k k k k
Axa xa xa a xa x a x a a a
+ + ++
⇒ ≥− +− + +− + −+ −++ −+ = + + + −
( )
12 1
... 2017
k kk
a a a a xa
+
+ ++ + ⇔ ≤≤
- Trường hợp
1 2 12 3 2
2 1 .. ... 2017
k kk k k
n k A xa xa xa xa a x a x a x
++ +
= +⇒=− +− ++− +− + −+ −++ −+
Ta có:
111
0 ; 1,
k k kj k kj
xa xa a x a x xa j k
+ ++ + +
− ≥ ⇔ = − ≥ − ⇔ ≤ ∀=
Lại có
1, ; 1,
i i kj kj kj
xa xa xai ka x a x xa j k
++ +
− ≥− ⇔≥∀= −≥ −⇔≤ ∀=
1
Axa x⇒ =− +−
Bài 9: (HSG Tỉnh Yên Bái năm 2015 – 2016) Tìm GTNN của
5323 1Ax x x= ++ −−+
Lời giải
Ta có
33
5323 12 3 23 1
55
Ax xx x x xx= ++ −−+= + + + + −−+
Mặt khác
3 33 3 3
2 0 ;3 3
5 55 5 5
x xx xx
−−
+≥⇔= +≥ + ⇔≥
Lại có
3 3 29 29 3
32 32 03 32 1
2 5 5 55
x x x B x x MinB x
−
− ≥− ⇔ ≤ ⇒ ≥ + + +− += ⇒ = ⇔ =
BÀI TẬP TỰ LUYỆN
( ) ( ) ( )
12 2 3 21 12 1
... 2017 ... ... 2017
k kk k k k
aa a MinB a a a aa a xa
++ + +
++ + ⇒ = + ++ − ++ + ⇔=
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
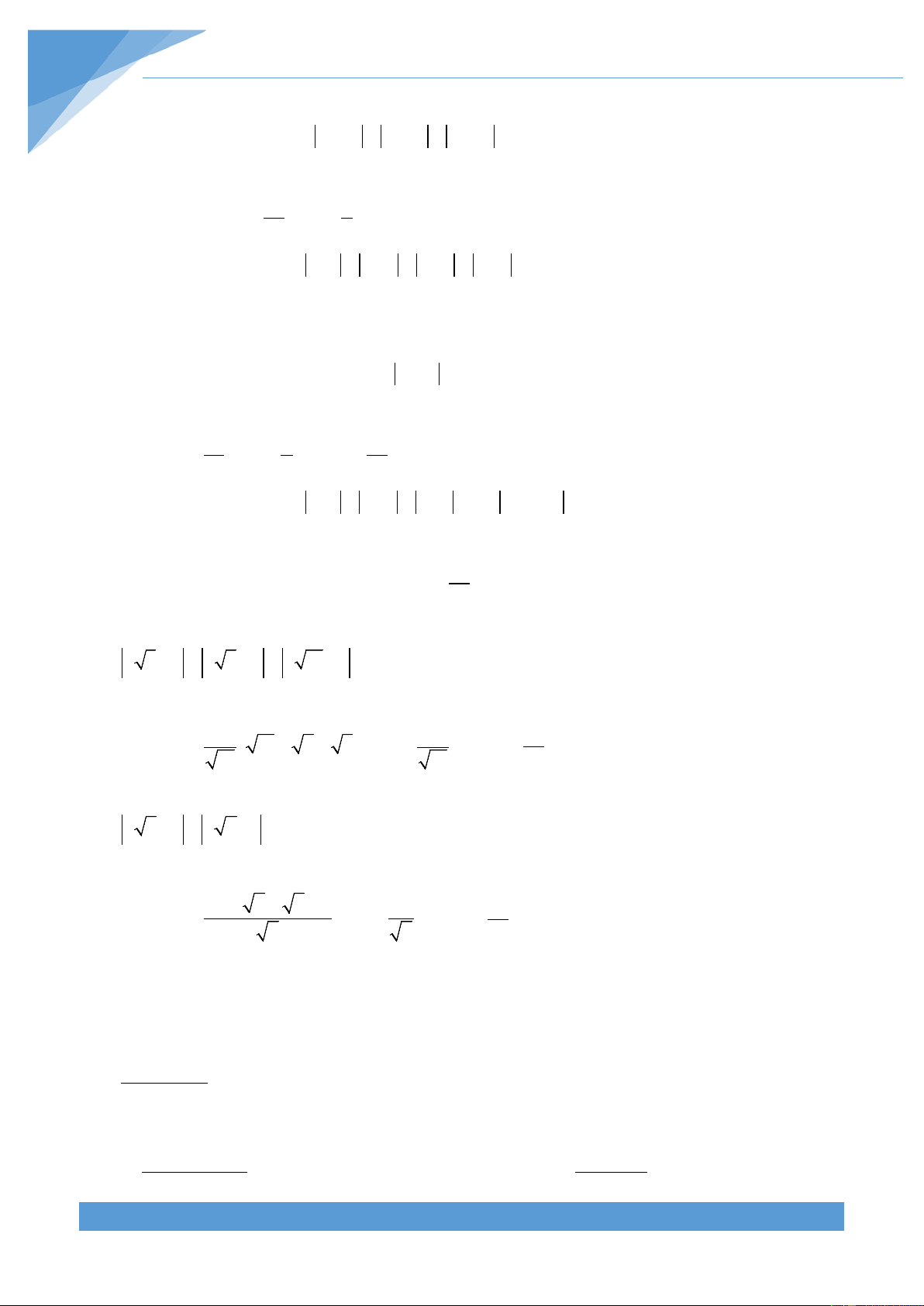
89
Bài 1: (Chuyên Toán Quảng Ngãi năm 2014 – 2015)
Tìm GTNN của
43572915Ax x x= ++ −+ −−
Lời giải
Ta có
17
55
MinA x
−
= ⇔=
Bài 2: Tìm GTNN của
1234Ax x x x=−+−+−+−
Lời giải
Ta có
42 3MinA x=⇔≤≤
Bài 3: Tìm GTNN của
( )
2
21 3212Ax x= − − −+
Lời giải
Ta có
15
.
44
Min A x
−
= ⇔=
hay
1
4
x
−
=
Bài 4: Tìm GTNN của
1 2 3 ... 1998Ax x x x=−+−+−++−
Lời giải
Ta có
2
. 999 999 1000Min A x= ⇔ ≤≤
hay
1
4
x
−
=
Bài 5: (Chuyên Toán Quảng Ngãi năm 2015 – 2016) Tìm GTNN của
3 2 5 7 11 9Axxx= ++ −+ −
Lời giải
Ta có
( )
99
. 11 5 3
11 11
Min A x= − + ⇔=
hay
1
4
x
−
=
Bài 6: (Chuyên Toán Quảng Trị năm 2015 – 2016) Tìm GTNN của
5 6 2 1 2 2017Ax x x= − + ++ +
Lời giải
Ta có
2018 2 5 2 1
.
22
Min A x
+− −
= ⇔=
hay
1
4
x
−
=
Dạng 7: Dạng phân thức
A. Phân thức có tử là hằng số, mẫu là tam thức bậc hai
Phương pháp: Biểu thức dạng này đạt giá trị nhỏ nhất khi mẫu đạt giá trị lớn nhất
2
min a
x
2
()
m
m
A A
ax bc c
ax bc c
= ⇒ ⇔ ++
++
Bài 1: Tìm GTLN hoặc GTNN của các biểu thức sau
a)
2
1
9 12 10
A
xx
=
−+
b)
2
2
4
B
xx
=
++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

90
c)
2
22
( 0)
9 12 5
y
Cx
x xy y
= ≠
−+
Lời giải
a.
ax
22
1 11 12
9 12 10 (3 2) 6 6 6 3
m
A Ax
xx x
= = ≤⇒ =⇔=
− + −+
b.
ax
2
2
2 2 28 8 1
1 15
4 15
15 2
()
24
m
B Bx
xx
x
−
= = ≤ = ⇒ = ⇔=
++
+
c.
2
22
( 0)
9 12 5
y
Cx
x xy y
= ≠
−+
+)
00yA=⇒=
+)
2
22
2
1 1 1 22
0 () 1
9 12 5 (3 2) 1 3 3
9 12 5
x
y A t t xy
xx
tt yt
yy
≠ ⇒ = = = = ≤⇔= ⇔ =
−+ −+
−+
Bài 2: Tìm GTNN hoặc GTLN của biểu thức sau
a)
2
1
1
y
xx
=
++
b)
2
2
6 59
y
xx
=
−−
c)
2
22
3
( 0)
25 20 5
= ≠
−+ −
y
Ax
x xy y
Lời giải
a) Ta có thể viết:
2
2
11
1
13
24
y
xx
x
= =
++
++
Vì
2
1 33 4 1
2 44 3 2
x yx
−
+ +≥⇒≤⇔=
Vậy GTLN của
4
3
y =
tại
1
2
x
−
=
b) Ta có:
2
22 2 2
2 2 1 1 2 21 1
; (3 1) 4 4
6 5 9 (3 1) 4 (
3 1) 4 4 (3 1) 4 4 2 3
y xx x
x xx x x
− −
−−
== −+≥∀⇒≤⇒≥=⇔=
−− −+ −+
−+
c)
00yA=⇒=
+)
2
22
2
3 33
0
25 20 5 (5 2) 1
25 20 5
yA
xx
tt t
yy
−
≠⇒ = = =
− +− −+
− +−
Vì
2
2
1 22
(5 2) 0 1
3
(5 2) 1 5
5
t A
t xy
t
− ≥ ⇒ ≤ ⇒ ≥− ⇔ = ⇔ =
−+
Bài 3: Tìm GTLN của biểu thức sau
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

91
a)
2
5
25
A
xx
=
−−
b)
2
1
4 11
B
xx
=
−+
Lời giải
a)
( )
2
2
55 5
1
25 6
16
A m
axA x
xx
x
−
= = ⇒ = ⇔=
−−
−−
b)
2
11
2
4 11 7
Bx
xx
= ≤⇔=
−+
Bài 4: Tìm min của:
2
1
49
B
xx
=
−+
Lời giải
Ta có :
( )
2
2
4 9 2 55xx x− += − +≥
( )
22
1 11
5
49
25
B
xx
x
=>= = ≤
−+
−+
, Dấu “ = “ khi x=2
Bài 5: Tìm max của:
2
3
51
C
xx
−
=
−+
Lời giải
Ta có :
2
2
2
5 21 21 3 12 4
51
2 4 4 21 7
51
xx x C
xx
−−
− += − − ≥ => = ≤ =
−+
, dấu “ = ’’ khi
5
2
x =
Bài 6: Tìm min hoặc max của:
2
6
23
D
xx
=
−+ −
Lời giải
Ta có :
( )
( )
2
22
23 23 1 22xx xx x− + − =− − + =− − − ≤−
2
66
3
2
23xx
=> ≥=−
−
−+ −
Bài 7: Tìm min hoặc max của:
2
2
8
K
x
=
+
Lời giải
Ta có :
2
2
2 21
88
84
8
x
x
+≥=> ≤ =
+
Bài 8: Tìm min hoặc max của:
2
4
1
M
xx
=
++
Lời giải
Ta có :
2
2
2
1 3 3 4 16
1
2 44 3
1
xx x
xx
++= + + ≥ => ≤
++
B. Phân thức có mẫu là bình phương của 1 nhị thức
Cách 1: Tách tử thành các nhóm có nhân tử chung với mẫu
Cách 2: Viết biểu thức A thành tổng của một số với một phân thức không âm
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

92
⇒
Ta đưa về dạng:
0
=+≥
CC
Am
DD
Bài 1: Tìm GTNN của các biểu thức sau
a.
2
2
3 86
( 1)
21
−+
= ≠
−+
xx
Ax
xx
b.
2
2
1
( 1)
( 1)
−+
= ≠
−
xx
Bx
x
c.
2
2
4 61
( 2)
( 2)
−+
= ≠
−
xx
Cx
x
d.
2
2
2 16 41
()
8 22
−+
= ∈
−+
xx
D xR
xx
e.
42
22
41
( 1)
xx
E
x
−−
=
+
f.
2
2
3 12 10
45
xx
F
xx
−+
=
−+
Lời giải
a.
2 22 2
2 22 2
3 8 6 2( 2 1) ( 4 4) ( 2)
( 1) 2 2 2
2 1 ( 1) ( 1) ( 1)
−+ −+ −+ −
= ≠ = + =+ ≥⇔=
−+ − − −
xx xx xx x
Ax x
xx x x x
Cách khác:
( )
( )
2
2
2
22
3( 2 1) 2 1 1
3 86 2
1
2 1 (
1) 1
1
− +− −+
−+
= = =
+
−+ − −
−
xx x
xx
A
xx x x
x
Đặt
( )
2
2
11
3 2 1
2 2 min 2 1 1 2
11
y A yy y A y x
xx
= ⇒ =− + = − +≥⇒ =⇔ =⇔ =⇔=
−−
b.
2 22 2 2
2 2 2 22
1 4 4 4 2 1 3 6 3 ( 1) 3 3
( 1) 1
( 1) 4( 1) 4( 1) 4( 1) 4( 1) 4 4
xx x x x x x x x
Bx x
x x x xx
−+ − + + + − + +
= ≠ = = + = +≥⇔=−
− − − −−
c. Đặt
11
2
2
= ⇒=+
−
tx
xt
khi đó:
2
2 2
22
11
4 2 6 2 1 4(2 1) 6 (2 1) 5( 1) 1 1
= + − ++= +− ++=+−≥−
At t
tt t t
tt
11tx⇔ =−⇔ =
d.
22
222
2 16 41 2( 8 22) 3 3
() 2
8 22 8
22 ( 4) 6
x x xx
D xR
xx xx x
− + −+
−
= ∈= =
−
−+ −+
− +
Vì
22
2
3 31
( 4) 0 ( 4) 6 6
( 4) 6 6 2
xx
x
− ≥⇒ − +≥⇒ ≤ =
−+
2
min
2
3 13 3
2 2 (
4) 0 4
( 4) 6 2 2 2
D Ax
x
x
=− ≥− = ⇒ = ⇔ − =⇔=
−+
e.
42 4 2 2
2
22 22 2 22 2
4 1 4( 2 1) 9( 1) 4 9 4 1
4 4 94
( 1) ( 1) 1 ( 1) 1
− − + +− ++
= = =− + = −+ =
+ + ++ +
xx x x x
E tt t
x x xx x
2
9 81
24
4 16
= − −+
Et
Ta có:
2
9 9 1 9 1 1 17
12 2 2 1 1 0
4 4 4 4 16 16 16
−
≤⇒ − ≤ − = ⇒ − ≥ ⇒ ≥ − =−⇔ =⇔ =
t t t A tx
Lời giải ngắn gọn hơn
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

93
42
22
5
1 0 10
( 1)
xx
E Ax
x
+
+ = ≥ ⇒ ≥− ⇔ =
+
Cách khác:
42
22 22
41
01 1 0
( 1) ( 1)
xx
Ex
xx
+
= − ≥ −=−⇔ =
++
f.
2
22 2
3 12 10 5 5
33352
45 45 (2)1
xx
F
xx xx x
−+
= =−=−≥−=−
−+ −+ − +
Do
2
2
5
( 2) 1 1 5
2
( 2) 1
xx
x
−
− +≥⇒ ≥−⇔ =
−+
Bài 2: Tìm GTLN của các biểu thức sau
a.
2
2
3 6 10
( 1)
23
xx
Ax
xx
++
= ≠
++
b.
2
2
11
( 1)
21
xx
Bx
xx
− +−
= ≠
−+
c.
2
( 5)
10 25
x
Cx
xx
= ≠−
++
d.
2
2
4 14
( 1)
21
xx
Dx
xx
+−
= ≠
−+
Lời giải
a.
22
22 2 2
3 6 10 3( 2 3) 1 1
3
2 3 2 3 ( 1) 2 ( 1) 2
xx xx
A
xx xx x x
++ ++
= = +=+
++ ++ ++ ++
Có:
22
ax
2
1 1 17 7
( 1) 0 ( 1) 2 2 3 1
( 1) 2 2 2 2 2
m
x x A Ax
x
+ ≥⇒ + +≥⇒ ≤ ⇒ =+ = ⇒ = ⇔=−
++
b.
22 2
2 22 2
11 2 1 1 11 ( 1) ( 1) 11 1 11
1
2 1 ( 1) ( 1) 1 ( 1)
xx x x x x x
B
xx x x x x
−+− −+ −−+− −− −−−
= = = =−− −
−+ − − − −
Đặt
22 2
22
1 11 11
1 11 (11 1) 11 2. .
1 22
22 22 11
= ⇒ =−− − =− + + =− + + − +
−
yA y y yy y y
x
22
1 43 43 1 43 1
11 11 21
22 44 44 22 44 22
− −−
=− + + = − + ≤ ⇔= ⇔=−
y y
yx
c.
2
2 22
2
( 5) 5 1 5 1
( 5) 5
10 25 (
5) ( 5) 5 ( 5) 5
+−
= ≠−
= = = − = − =
++ +
+ + + +
x xx
C x tt
t
xx x
x x x x
2
2
1 11 1 1 11
55 5
10 20 20 20 10 5 10
−
⇒− = − = − − ≥ ⇒ ≤ ⇔ = ⇔ = ⇔ =
+
Att t A t x
x
d.
2
2
4 14
( 1)
21
xx
Dx
xx
+−
= ≠
−+
. Đặt
11
1
1
= ⇒=+
−
tx
xt
2
2 2
22
11
1 4 1 14 ( 1) 4 ( 1) 14 (3 1) 2 2
= + + + − = + + +− =− − +≤
A t t
tt t t
tt
1
24
3
Dt x= ⇔= ⇔ =
Bài 3: Tìm GTNN, GTLN của
2
22
74
22
y xy
A
x xy y
−
=
−+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

94
Lời giải
Điều kiện
( , ) (0,0)xy≠
+)
22 2
22 2 2
6 9 ( 3)
1 0
1 30
() ()
x xy y x y
A A xy
xy y xy y
−+ −
+ = = ≥ ⇒ ≥− ⇔ = ≠
−+ −+
+)
22 2
22 22
( 4 4 ) (2 )
4 0 4 1; 2
() ()
y xy x x y
A A xy
xy y xy y
−+ − −−
−= = ≤⇒ ≤⇔= =
−+ −+
Bài 4: Tìm GTNN của biểu thức
( ) ( )
22
22
1 33
1; 1
( 1) (
1)
++ −
+
= ≠−
= ≠
+−
xx x
x
A xB x
xx
Lời giải
22
2
22 2
1 ( 2 1) 1 1 1 1 1
11
( 1) ( 1) 1
( 1) 1
+ + + + − −+
= = =
− + =−+ =
+ + ++ +
xx x x x
A yy
y
x x xx x
2
min
1 33 3 1
1
2 44 4 2
= − +≥⇒ =⇔=⇔=
Ay A
y x
+)
22
2
22 2
3 3 ( 2 1) 1 1 1 1 1
11
( 1) ( 1) 1 ( 1) 1
− + − + − ++
= = =− + = −+ =
− − −− −
xx xx x
B yy y
x x xx x
2
1 33 1
3
2 44 2
= − +≥⇔=⇔=
By y
x
Bài 5: Tìm GTNN của biểu thức
22
22
2
xy
A
x xy y
+
=
++
Lời giải
Ta có:
( ) ( )
( )
( )
( )
22
2
22
22
22
1
11 1 1
2
.
2 22
2 2
xy xy
xy
xy
A mi
nA x y
x xy y
xy xy
+ +−
−
+
= = =
+ ≥⇒ =⇔=
++
++
Bài 6: Tìm GTNN của biểu thức
( )
2
2
2 10 1
1
21
−−
= ≠
−+
xx
Ax
xx
Lời giải
Ta có:
( )
( )
( )
( )
2
2
2
22
2
2 2 16 19
2 10 1 6
9 3
2 1
33
21 1 1
11
xx x
xx
A
xx x x
xx
− +− −−
−−
= = =
+ − =− + +≤
−+ − −
−−
Vì
2
33
1 0 1 3 10 2
11
− + ≤ ∀≠⇒ = ⇔ += ⇔ =−
−−
x maxA x
xx
Bài 7: Tìm min hoặc max của:
2
2
41xx
G
x
−+
=
Lời giải
2
41
1G
x
x
=−+
, đặt
( )
2
2
1
41 2 3 3t Gt t t
x
= => = − + = − − ≥−
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

95
Bài 8: Tìm min hoặc max của:
2
2
3 86
21
xx
E
xx
−+
=
−+
Lời giải
Đặt
22
1 1 21x t xt x t t−==> =+=> = + +
( )
( )
2
2
2 22
3 218 16
3 21 21
3
tt t
tt
E
t
t tt
++− ++
−+
= =
=−+
,
Đặt :
( )
2
2
1
2 3 1 22a Ea a a
t
==> = − += − +≥
Bài 9: Tìm min hoặc max của:
( )
2
2
4 61
21
xx
F
x
−+
=
+
Lời giải
Đặt
2
2
1 21
21
24
t tt
x tx x
− −+
+==> = => =
, khi đó:
( )
2
2
2 22
2 13 1 1
55 55
1
tt t
tt
F
t
t tt
− +− − +
−+
= = =−+
, đặt
2
1
15 5a F aa
t
==>=− +
Bài 10: Tìm min hoặc max của:
( )
2
10
x
H
x
=
+
Lời giải
Đặt
22
10 1 10
10 10
t
x t xt H
t
tt
−
+ ==>=− => = =−
, đặt
2
1
10a H aa
t
==>=− +
Bài 11: Tìm min hoặc max của:
( )
2
2016
x
I
x
=
+
Lời giải
Đặt
22
2016 1 2016
2016 2016
t
x t xt I
t
tt
−
+ ==>=− =>= =−
, Đặt
2
1
2016a Ia a
t
==>=−
Bài 12: Tìm min hoặc max của:
2
2
2 2000xx
D
x
−+
=
Lời giải
Ta có :
2
2 2000
1D
x
x
=−+
, Đặt
2
1
1 2 2000aD a a
x
==>=− +
Bài 13: Tìm min hoặc max của:
2
2
2 2015
2015
xx
E
x
−+
=
Lời giải
Ta có :
2
22
2 2015 2 2015
2015 1
xx
E
x
xx
−+
= =
−+
, đặt
2
1
2015 1 2 2015a Eaa
x
==> =−+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

96
2
21
.
2015 2015
Ea a=>= − +
Bài 14: Tìm min hoặc max của:
( )
2
2000
x
F
x
=
+
Lời giải
Đặt
22
2000 1 2000
2000
t
x tF
t
tt
−
+ ==>= =−
, Đặt
2
1
2000a Fa a
t
==>=−
Bài 15: Tìm min hoặc max của:
( )
2
2
1
21
xx
B
xx
−+
=
++
Lời giải
( )
2
2
1
1
xx
B
x
−+
=
+
,Đặt
2
1 1 21x t xt x t+==> =−=> − +
2
22
33 33
1
tt
B
t
tt
−+
=> = =−+
, Đặt
2
1
3 31aBa a
t
==>= − +
Bài 16: Tìm min hoặc max của:
2
2
2 44xx
A
x
++
=
Lời giải
2
44
2A
x
x
=++
, Đặt
2
1
4 42aAa a
x
==>= + +
Bài 17: Tìm min hoặc max của:
2
2
2 2012xx
B
x
−+
=
Lời giải
2
2 2012
1B
x
x
=−+
, Đặt
2
1
2012 2 1aB a a
x
==>= − +
C. Tìm GTLN, GTNN của phân thức có dạng khác
Cách 1: Tách tử thành các nhóm có nhân tử chung với mẫu
Cách 2: Viết biểu thức A thành tổng của một số với một phân thức không âm
1. Bậc của tử nhỏ hơn bậc của mẫu
Bài 1: Tìm GTNN của các biểu thức sau
a.
2
8 12
4
x
A
x
+
=
+
b.
2
42
2
x
B
x
+
=
+
c.
( 2)( 8)
( 0)
++
= >
xx
Cx
x
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

97
a.
22 2
22 2
8 12 8 16 4 ( 4)
1 14
44 4
x xx x x
Ax
xx x
+ ++−− +
= = =− + ≥− ⇔ =−
++ +
b.
22 2
22 2
4 2 ( 4 4) ( 2) ( 2)
11 2
22 2
x xx x x
Bx
xx x
+ + +− + +
= = =
− ≥− ⇔ =−
++ +
c.
2
( 2)( 8) ( 4)
( 0) 18 18 4
xx x
Cx x
xx
++ −
= > = + ≥ ⇔=
Bài 2: Tìm GTNN, GTLN của các biểu thức sau
a. [ HSG – Thanh Chương – 2011]
2
34
1
x
A
x
−
=
+
b.
2
21
2
x
B
x
+
=
+
c.
2
43
1
x
C
x
+
=
+
d.
2
83
41
x
D
x
+
=
+
e.
2
4
41
x
E
x
=
+
Lời giải
a. [ HSG – Thanh Chương – 2011]
22 2
22 2
3 4 4 4 1 ( 2)
1 1 20 2
11 1
xx x x x
A xx
xx x
− − +− − −
= = = − ≥− ⇔ − = ⇔ =
++ +
+)
22 2
ax
22 2
3 4 4 4 4 4 1 (2 1) 1
4 44
11 1 2
m
xx xx x
A Ax
xx x
− +− − − + −
= = =
− ≤⇒ =⇔=
++ +
Cách khác:
Nháp để nhẩm GTLN và GTNN nếu có :
22
2
34
34 . 4 30
1
x
a ax a x a x x a
x
−
= = +=− => + +−=
+
,
Xét
2
1
16 4 12 0
4
a
aa
a
= −
∆= − + = =>
=
Khi đó ta có :
2
22
34 4 4
11 1 1
11
x xx
K
xx
− ++
= + − = − ≥−
++
, Dấu = khi
2x = −
Mặt khác :
2
22
34 4 4 1
4 4 44
11
x xx
K
xx
− − −−
= − += +≤
++
, Dấu = khí
1
2
x
−
=
b.
22
21 42
2 2( 2)
xx
B
xx
++
= =
++
+)
22 2
min
22 2 2
2 1 4 2 ( 4 4) ( 2) ( 2) 1 1 1
2
2 2( 2) 2( 2) 2( 2) 2 2 2
x x xx x x
B Ax
xx x x
+ + + +− + + − −
= = = = −≥ ⇒ = ⇔=−
++ + +
+)
22 2
ax
2 2 2 22
2 1 4 2 2 1 2 ( 1)
11 1 1
2 2( 2) 2 2 2
m
x x xx x x
B Ax
x x x xx
+ + −+ − + −−
= = = + = +≤⇒ =⇔ =
+ + + ++
c.
22 2
22 2
4 3 4 4 1 ( 2)
11 2
11 1
x xx x x
Cx
xx x
+ + +− − +
= = =
− ≥− ⇔ =−
++ +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

98
+)
22 2
22 2
43 4 414 4 (21) 1
44
11 1 2
x xx x x
Cx
xx x
+ − + −+ + − −
= = = +≤⇔=
++ +
d.
22 2
22 2
8 3 (4 8 4) (4 1) (2 2)
1 11
41 41 41
x xx x x
Dx
xx x
+ ++− + +
= = =−
+ ≥− ⇔ =−
++ +
+)
22 2
22 2
8 3 16 4 (16 8 1) (4 1) 1
44
41 41 41 4
x x xx x
Dx
xx x
+ +− − + −
= = =
− ≤⇔=
++ +
e.
22 2
22 2
4 4 1 4 1 4 (2 1) 1
11
41 41 41 2
xxxx x
Ex
xx x
+− −+ −
= = =
− ≤⇔ =
++ +
+)
22 2
22 2
4 (4 1) (4 4 1) (2 1) 1
11
41 41 41 2
x x xx x
Ex
xx x
− ++ + + + −
= = =− + ≥− ⇔ =
++ +
Bài 3: [ HSG – Yên Phong – 14/04/2014 ]
Tìm GTLN của biểu thức
32
3( 1)
1
x
A
xxx
+
=
+ ++
Lời giải
ax
32 2
3( 1) 3
30 30
11
m
x
A x
A x
xxx x
+
= = ≤⇔=⇒ =⇔=
+ ++ +
Bài 4: [ HSG – Yên Phong – 2016 – 2017 ]
Tìm GTNN của các biểu thức sau
2
2010 2680
()
1
+
= ∈
+
x
D xR
x
Lời giải
22 2
2 222
2010 2680 335(6 8) 335( 6 9 1) 335( 3)
( ) 335
335 3
1 111
x x
xx x x
D xR x
x xxx
+ + + +− − +
= ∈
= = = − ≥− ⇔ =−
+ +++
Bài 5: Tìm GTNN của biểu thức sau
( )
2
15 16
3
+
++
= ∈
xx
A xR
x
Lời giải
Ta có:
( )
( )
2
2
4
15 16 23
23 23
4
3 3
33 3
x
xx
A x
R minA x
xx
+
−
++
= ∈ = + ≥ ⇒ = ⇔=
Bài 6: Tìm GTLN của biểu thức sau
( )
( )
2 22
24 4 2
1
,
22
+ −+
= ∈
+ ++
xy y y x
A xy
R
xy y x
Lời giải
Ta có:
( )
( )
( )( )
2 22
4
24 4 2
42
1
1
,
22
12
+ −+
+
= ∈=
+ ++
++
xy y y x
y
A xy
R
xy y x
yx
Vì
4
10+≠ ∀yx
nên chia cả tử và mẫu cho
4
1y +
ta được:
2
1
2
A
x
=
+
Vì
22
2
11
0 2 2 0;
22
≥ ∀⇒ + ≥ ∀⇒ = ≤ ⇔ = ∈
+
x x x x A x yR
x
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
99
Bài 7: Tìm GTLN của biểu thức sau
2
42
1
x
A
xx
=
++
Lời giải
+) Xét
00xA=⇒=
giá trị này không phải giá trị lớn nhất của A vì với
00xA≠⇒ >
+) Xét
0x ≠
đặt
1
max min
P AP
A
=⇒⇔
Ta có
( )
42
22
2 22
11 1
1; 2 2 1 3 3 1
min
xx
P x x Cosi P P x
x xx
++
= = + + + ≥ ⇒ ≥ += ⇒ = ⇔ =±
Bài 8: Tìm min hoặc max của:
2
27 12
9
x
M
x
−
=
+
Lời giải
Nháp :
22
2
27 12
. 9 27 12 . 12 9 27 0
9
x
a ax a x ax x a
x
−
= =>+=−=>++−=
+
Có
( )
4
' 36 9 27 0
1
a
aa
a
=
∆= − − = =>
= −
Khi đó ta có :
( )
2
2
2 22
23
27 12 4
12 9
4 4 4 44
9 99
x
x xx
M
x xx
−−
− −− −
= − += +=
+≤
+ ++
Mặt khác :
( )
2
2
2 22
6
27 12 12 36
11 1 1 1
9 99
x
x xx
M
x xx
−
− −+
= + −= −= −≥−
+ ++
Bài 9: Tìm min hoặc max của:
2
83
41
x
P
x
+
=
+
Lời giải
Nháp :
22
2
83
4. 8 3 4. 8 3 0
41
x
a ax
a x ax x a
x
+
= =>+=+=>−+−=
+
Có
( )
' 16 4 3 4; 1aa a a∆= − − => = =−
Khi đó :
( )
2
2
2 22
41
8 3 16
8 1
4 4 4 44
41 41 41
x
x xx
P
x xx
−−
+ − +−
= − += +=
+≤
+ ++
Mặt khác :
( )
2
2
2 22
41
83 4 84
11 1
1 1
41 41 41
x
x xx
P
x xx
+
+ ++
= + −= −= −≥−
+ ++
Bài 10: Tìm min hoặc max của:
2
21
2
x
D
x
+
=
+
Lời giải
Nháp :
2
2
21
. 2 2 10
2
x
a ax x a
x
+
= => − + −=
+
, có
( )
1
' 1 2 1 0 1;
2
aa a a
−
∆= − − = => = =
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

100
Khi đó :
( )
2
2
2 22
1
21 21
1 1 1 11
1 22
x
x xx
D
x xx
−−
+ −+ −
= − += += +≤
+ ++
Mặt khác :
( )
2
2
2
2 11 1 4 41 1
22 22
2
22
x xx
D
x
x
+ ++
−
= + −= −≥
+
+
Bài 11: Tìm min hoặc max của:
2
21x
E
x
+
=
Lời giải
2
21
E
x
x
= +
, Đặt
2
1
2a Ea a
x
==>= +
Bài 12: Tìm min hoặc max của:
2
21
2
x
F
x
−
=
+
Lời giải
Nháp :
2
2
21
. 2 2 10
2
x
a ax x a
x
−
= => − + +=
+
, có
( )
2
1
'1 2 1 12 ; 1
2
aa a a a a∆= − + = − − => = =−
Khi đó :
( )
( )
( )
2
2
2
22
2
2 11 1 4 41 11
2 2 2 22
2
22 22
x
x xx
F
x
xx
−−
− −+ −
= − += += +≤
+
++
Mặt khác :
( )
2
2
2 22
1
21 21
11 1 1 1
2 22
x
x xx
F
x xx
+
− ++
= + −= −= −≥−
+ ++
Bài 13: Tìm min hoặc max của:
2
68
1
x
G
x
−
=
+
Lời giải
Nháp :
2
2
68
. 6 80
1
x
a ax x a
x
−
= => − ++=
+
, có :
( )
2
' 9 8 8 9 0 1; 9aa a a a a∆= − + =− − + = => = =−
Khi đó :
( )
2
2
2 22
3
68 6
9
1 1 1
11
1 11
x
x xx
G
x xx
−−
− −+ −
= − += += +≤
+ ++
Mặt khác :
( )
2
2
2 22
31
68 9 61
99 9 9 9
1 11
x
x xx
G
x xx
+
− ++
= + −= −= −≥−
+ ++
Bài 14: Tìm min hoặc max của:
6
432
27
3 6 99
x
A
xxxx
+
=
− + −+
Lời giải
Hạ phép chia ta được :
2
33Ax x=++
Bài 15: Tìm min hoặc max của:
6
2
512
8
x
B
x
+
=
+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

101
Lời giải
Hạ phép chia ta được :
( )
2
42 2
8 64 4 48 48Bx x x=− += − +≥
Bài 16: Tìm min hoặc max của:
432
2
4 16 56 80 356
25
xxxx
G
xx
+ + ++
=
++
Lời giải
Hạ phép chia ta được:
( )
2
2
256
4 25
25
G xx
xx
= + ++
++
, Đặt
2
256
25 4x x tGt
t
+ +==> = +
Sau đó sử dụng co si là ra.
Bài 17: Tìm min hoặc max của:
2
8
32
I
x
−
=
+
Lời giải
Ta có :
2
2
88
3 22 4
2
32
x
x
+≥=> ≤ =
+
Bài 18: Tìm min hoặc max của:
2
21
2
x
B
x
+
=
+
Lời giải
Nháp :
2
2
21
. 2 2 10
2
x
a ax x a
x
+
= => − + −=
+
, có
( )
1
' 1 2 1 0 1;
2
aa a a
−
∆= − − = => = =
Khi đó ;
( )
2
2
2 22
1
21 2
1
1 1 11
1
2 22
x
x xx
B
x xx
−
+ −+ −
= − += +=− ≤
+ ++
Mặt khác :
( )
( )
( )
2
2
2
22
2
2 11 1 4 41 1 1
22 2 22
2
22 22
x
x xx
B
x
xx
+
+ ++ −
= + −= −= −≥
+
++
Bài 19: Tìm min hoặc max của:
( )
2 22
4 42 2
1
22
xy x x y
G
x xy y
+ −+
=
+ ++
Lời giải
Ta có :
( ) ( )
2 42 4
4 42 2 2
4 24
1 11
22 2
21 1
xy x xy x
G
x xy y y
x yx
+− + +
= = =
+ ++ +
++ +
Bài 20: Tìm min hoặc max của:
( )
4
2
2
1
1
x
H
x
+
=
+
Lời giải
Đặt
2 2 42
1 1 21x t xt xt t+==> =−=> = − +
, khi đó
2
22
2 11 2 2
1
tt
H
t
tt
− ++
= =−+
Đặt
2
1
2 21aHa a
t
==>= −+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
102
Bài 21: Tìm min hoặc max của:
2
2
2 16 71
8 22
xx
I
xx
−+
=
−+
Lời giải
Hạ phép chia ta được :
2
27
2
8 22
I
xx
= +
−+
, mà
( )
2
2
8 22 4 6 6xx x− + = − +≥
Bài 22: Tìm min hoặc max của:
2
4
1
x
P
x
=
+
Lời giải
Nháp : Đặt
22
2
1
0
2
1
t
x t a at t a a
t
==>= => −+==>=±
+
Khi đó :
( )
( )
( )
2
2
2 42
4
44
1
1 1 2 11 1 1
22 2
22
1
21 21
x
x xx
P
x
xx
+
++ −
= + −= −= −≥
+
++
, Không xảy ra dấu bằng
Mặt khác :
( )
( )
( )
2
2
2 42
4
44
1
1 1 2 11 1 1
2 2 2 22
1
21 21
x
x xx
P
x
xx
−−
−+ −
= − += += +≤
+
++
Bài 23: Tìm min hoặc max của:
( )
4
2
2
1
1
x
G
x
+
=
+
Lời giải
Đặt
2 2 42
1 1 21x t xt xt t+==> =−=> = − +
Khi đó :
2
22
22 22
1
tt
G
t
tt
−+
= =−+
, đặt
2
1
2 21aGa a
t
==>= − +
Bài 24: Tìm min
( )
2
22 1
2
x
P
x
+
=
+
Lời giải
Nháp :
2
2
42
. 4 2 20
2
x
a ax
x a
x
+
= => − + −=
+
, có
( )
' 4 2 2 0 2; 1aa a a∆= − − = => = =−
Khi đó :
( )
2
2
2 22
21
42 2 42
2 2 2 22
2 22
x
x xx
P
x xx
−−
+ − +−
= − += +=
+≤
+ ++
Mặt khác :
2
22
42 44
11 1 1
22
x xx
P
xx
+ ++
= + − = − ≥−
++
Bài 25: Tìm min hoặc max của:
2
2
2
2
x
K
xx
+
=
++
Lời giải
Ta có :
2
1
2
x
K
xx
= −
++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

103
Nháp :
2
2
. . 20
2
x
a ax ax x a
xx
−
= => + ++ =
++
, có :
( )
2
1 22
1 4 .2 0
7
a aa a
±
∆= + − = => =
Bài 26: Tìm min hoặc max của:
2
41
3
x
M
x
+
=
+
Lời giải
Nháp :
2
2
41
. 4 3 10
3
x
a ax x a
x
+
= => − + −=
+
, có
( )
4
' 4 3 1 0 1;
3
aa a a∆= − − = => =− =
Bài 27: Tìm min hoặc max của:
2
12 13
23
x
P
xx
+
=
++
Lời giải
Nháp :
2
2
12 13
. 2 . 3 12 13 0
23
x
a ax ax a x
xx
+
= => + +− −=
++
,
Có
( ) ( )
2
9
' 6 3 13 0 4;
2
a aa a a∆= − − − = => =− =
Bài 28: Tìm GTLN của biểu thức:
2
42
1
x
xx++
, GTLN đó đạt được tại giá trị nào của x
Lời giải
Ta có :
2
42
()
1
x
Px
xx
=
++
=
2
2
11
13
()
x
Px x
= + +≥
Bài 29: Tìm GTNN của biểu thức:
2
2
1
( 1)
21
++
= ≠−
++
xx
Mx
xx
Lời giải
Ta có :
( )
( )
2
2
2
2 1 11
11
1
21 1
1
xx x
M
xx x
x
+ +− + +
= =
−+
++ +
+
Đặt
1
1
t
x
=
+
, ta có:
2
2
1 33
1
2 44
Mt t t
= −+= − + ≥
Bài 30: Tìm giá trị lớn nhất của biểu thức:
( )
32
31
1
x
B
xxx
+
=
+ ++
Lời giải
Ta có:
( ) ( )
( )
( )
( )
( )
32 2 2
2
31 31 31
3
1 11 1
11
xxx
B
x x x xx x x
xx
+++
= = = =
+ ++ + ++ +
++
Do
2
2
3
10 3
1
xB
x
+> => = ≤
+
, Dấu bằng khi và chỉ khi x=0
2. Bậc của tử bằng bậc của mẫu
Bài 1: Tìm GTN N của các biểu thức sau
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

104
a.
2
2
23
( 0)
xx
Ax
x
−+
= ≠
b.
2
2
1
( 1)
( 1)
xx
Bx
x
−+
= ≠
−
c.
2
2
23
2
xx
C
x
++
=
+
d.
2
2
2 2016xx
D
x
−+
=
Lời giải
a.
2 22
min
2 22
2 3 3( 2 3) ( 3) 2 2 2
( 0) 3 3
3 3 33 3
xx xx x
A x xA
x
x xx
−+ −+
−
= ≠ = = +≥⇔=⇒ =⇔=
b.
2 22 2 2
2 2 2 22
1 4 4 4 2 1 3 6 3 ( 1) 3 3
( 1) 1
( 1) 4( 1) 4( 1) 4( 1) 4( 1) 4 4
xx x x x x x x x
Bx x
x x x xx
−+ − + + + − + +
= ≠ = = + = +≥⇔=−
− − − −−
c.
22 2 2
2 22 2
2( 2 3) 4 4 2 1 ( 2) 1
2
2( 2) 2( 2) 2( 2) 2 2( 2) 2
xx xx x x
Cx
x xx x
++ ++ + +
= = + =+ ≥⇔=−
+ ++ +
d.
22 2
2 22
2 2016 2016 2 .2016 2016 ( 2016) 2015 2015
2016
2016 2016
2016
xx xx x
Dx
x xx
−+ −
+ −
= = =
+ ≥ ⇔=
Bài 2: Tìm GTLN của các biểu thức sau
a.
2
2
6 2 19
37
xx
A
xx
++
=
++
b.
2
2
23
2
xx
B
x
++
=
+
Lời giải
a.
22
22 2
6 2 19 2(3 7) 5 5
2
3737 37
x x xx
A
xx xx xx
+ + ++ +
= = =
+
++ ++ ++
2
2
ax min ax
1 83 83 1 5 60 1
3 73 2
2
83
6 12 12 6 83
6
12
−−
= ++= + + ≥ ⇔= ⇒ = ⇒ =+ = ⇔=
mm
M xx x x A M A x
b.
2 22 2 2 2
22 2 2
232 232( 2)4 23 (1)
2 21
22 2 2
xx xxx x xx x
Bx
xx x x
++ −++ +−−++ −
= = = =
− ≤⇔=
++ + +
Bài 3: Tìm GTLN, GTNN của các biểu thức sau
a.
2
2
3 23
1
xx
A
x
++
=
+
b.
2
2
22
1
xx
B
xx
−−
=
++
Lời giải
a.
2 222
2 22 2
3 2 3 2( 1) ( 1) ( 1)
2 21
1 11 1
xx x x x
Ax
x xx x
++ + + +
= = + =+ ≥⇔=−
+ ++ +
+)
2 22 2
222 2
3 2 3 4 4 ( 2 1) ( 1)
4 41
111 1
xx x xx x
Ax
xxx x
++ + −+ −
= = − =− ≤⇔=
+++ +
b.
2 22 2
2 22
2 2 3 (2 2 2) 3
22 0
1 11
xx x xx x
Bx
xx xx xx
−− − ++
= = =
− ≤− ⇔ =
++ ++ ++
+) Với
2
2
2
33
0 22
11
1
1
x
xA
xx
xx
≠⇒ = −= −
++
++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

105
Ta lại có:
2
2
1 1 3 11 3 3 1 1
1 22 2
3
42 4 2
4
−
++ =+ + ≥⇒≥−=⇒= ⇔=−
Ax
xx x x
Bài 4: Tìm GTLN của
2
2
3 6 10
23
xx
A
xx
++
=
++
Lời giải
22
ax mi
n
22 2
max
11 1
3 3 [
( 1) 2] ( 1) 2 2 1
2 3 ( 1) 2 (
1) 2
=+ =+ ⇒ ⇔ ⇔
++ ⇔++=⇔=−
++ ++ +
+
m
A A x xx
xx x x
ax
2
11 7
11
( 1) 2 2 2
m
xA x
x
⇒ ≤⇔=−⇒ =⇔=−
++
Bài 5: Tìm GTLN của biểu thức sau
( )
2
2
3 6 10
23
++
= ∈
++
xx
A xR
xx
Lời giải
Ta có:
( )
2
2
2
3 6 10 1 1 7
33 1
2 3 22
12
xx
Ax
xx
x
++
= =+ ≤+ = ⇔ =−
++
++
Bài 6: Tìm min hoặc max của:
( )
2
2
21
1
xx
C
x
++
=
+
Lời giải
2
2
2
1
x
C
x
= +
+
, Nháp :
2
2
2
. 20
1
x
a ax a x
x
= => +− =
+
, có
2
44 0 1aa∆= − = => =±
Khi đó :
2
22
2 21
1 12 11
11
x xx
C
xx
++
= + −+ = +≥
++
Mặt khác :
( )
2
2
2 22
1
2 2
1
1 12 3
33
1 11
x
x xx
C
x xx
−−
−+ −
= − ++ = + = +≤
+ ++
Bài 7: Tìm min hoặc max của:
2
2
1
1
xx
N
x
++
=
+
Lời giải
2
1
1
x
N
x
= +
+
, Nháp :
2
2
.0
1
x
a ax x a
x
= = −+=
+
, có :
2
1
14 0
2
aa∆= − = => =±
Khi đó ta có :
( )
2
2
2
1 1 2 11 1
1
2 2 22
1
21
x xx
N
x
x
++
= + +− = + ≥
+
+
Mặt khác :
( )
( )
( )
2
2
2
22
1
1 1 2 13 33
1
2 2 2 22
1
21 21
x
x xx
N
x
xx
−−
−+ −
= − ++= += +≤
+
++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

106
Bài 8: Tìm min hoặc max của:
2
2
3 6 17
25
xx
Q
xx
−+
=
−+
Lời giải
Ta có :
2
2
3
25
Q
xx
= +
−+
, mà
( )
2
2
2
2 21
2 5 1 44
42
25
xx x
xx
− += − +≥=> ≤ =
−+
Bài 9: Tìm min hoặc max của:
2
2
2 16 41
8 22
xx
R
xx
−+
=
−+
Lời giải
Ta có :
2
22
2 16 44 3 3
2
8 22 8 22
xx
R
xx xx
− +−
= = −
−+ −+
,
Mà
( )
( )
( )
2
2
22
3 31 3 1
8 22 4 6 6
62 2
46 46
xx x
xx
−−
−+=−+≥=>≤
==>≥
−+ −+
Bài 10: Tìm min hoặc max của:
2
2
2 2010
x
P
xx
=
−+
Lời giải
Hạ phép chia ta được :
2
2 2010
1
2 2010
x
P
xx
−
= +
−+
,
Nháp :
2
2
2 2010
. 2 . 2010 2 2010 0
2 2010
x
a ax
ax a x
xx
−
= =
> − + −+ =
−+
Có
( ) ( )
2
1
' 1 2010 2010 0 1;
2009
a a a aa∆= + − + = => =− =
Làm tương tự như các bài trên .
Bài 11: Tìm min hoặc max của:
2
2
2 65
21
xx
Q
xx
−+
=
−+
Lời giải
Hạ phép chia ta được :
2
23
2
21
x
Q
xx
−+
= +
−+
, Đặt
1xt−=
, khi đó ta có :
( )
2
22 2
32 1
2 21 21
22
t
tt
Q
t
tt t
−+
−+
=+ = =−+
, Đặt
1
a
t
=
2
22Qa a=>= − +
Bài 12: Tìm min hoặc max của:
2
2
2 44xx
A
x
++
=
Lời giải
2
44
2A
x
x
=++
, Đặt
2
1
4 42t At t
x
==>= ++
Bài 13: Tìm min hoặc max của:
2
2
3 6 17
35
xx
H
xx
−+
=
−+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

107
Lời giải
Hạ phép chia ta được :
2
32
3
35
x
H
xx
+
= +
−+
Nháp :
2
2
32
. 3. 3 5 2 0
35
x
a ax ax x a
xx
+
= => − − + −=
−+
, có :
( ) ( )
2
2
13 2 67
9 1 4 5 2 11 26 9 0
11
x aa a a a
±
∆= + − − =− + + = => =
,
Bài 14: Tìm min hoặc max của:
2
2
41xx
K
x
−+
=
Lời giải
2
41
1K
x
x
=−+
, đặt
( )
2
2
1
41 2 3 3t Kt t t
x
= => = − + = − − ≥−
Bài 15: Tìm min hoặc max của:
2
2
2 49
24
xx
N
xx
++
=
++
Lời giải
Hạ phép chia ta được :
2
1
2
24
N
xx
= +
++
, mà
( )
2
2
2 4 1 33xx x+ += + +≥
Bài 16: Tìm min hoặc max của:
23
2 22
2 1999
:
32 3 2
xx x
Q
xx xxx
−+
=
−+ − +
Lời giải
Thực hiện phép tính ta được :
2
22
2 1999 2 1999
1
xx
Q
x
xx
−+
= =−+
,
Đặt
2
1
1999 2 1tQ t t
x
==>= −+
Bài 17: Tìm min hoặc max của:
2
2
2 49
24
xx
D
xx
++
=
++
Lời giải
2
1
2
24
D
xx
= +
++
, mà
( )
2
2
2 4 1 33
xx x+ += + +≥
Bài 18: Tìm min hoặc max của:
2
2
22
22
xx
F
xx
−+
=
++
Lời giải
2
4
1
22
x
F
xx
−
= +
++
Nháp :
2
2
4
. 2. 4 2 0
22
x
a ax ax a a
xx
−
= => + ++=
++
, có
( )
2
' 2 .2 0 2 2 2a aa a∆= + − = => = ±
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
108
Bài 19: Tìm min hoặc max của:
22
22
229
25
x xy y
H
x xy y
−+
=
++
Lời giải
Với y = 0 ta được H = 2
Với y ≠ 0. Chia cá tử và mẫu cho
2
y
ta được:
2
2
2
2
2. 2. 9
2. 5
xx
y
y
H
xx
y
y
−+
=
++
, đặt
2
22
2 29 61
2
25 25
x tt t
tH
y
tt tt
−+ +
==>= =−
++ ++
Nháp :
2
2
61
2 5 6 10
25
t
a at at a t
tt
+
=− => + + + +=
++
,
Có :
( ) ( )
2
9
' 3 5 1 0 1;
4
a aa a a∆= + − + = => =− =
, làm giống các bài trên
Bài 20: Tìm min hoặc max của:
2
2
1
1
x
J
xx
+
=
−+
Lời giải
Ta có :
2
1
1
x
J
xx
= +
−+
Nháp :
2
2
.. 0
1
x
a ax
ax x a
xx
= => − −+=
−+
, có
( )
2
1
1 4 . 0 1;
3
a aa a a
−
∆= + − = => = =
Khi đó :
( )
2
2
2 2
2
1
21
1 1
12 2 2
1 11
x
x xx
J
xx xx
xx
−
−+ −
=+ − +=+ =
− ≤
−+ −
+ −+
Mặt khác :
( )
2
2
2
1 12 2 1 2
1
3 33 3
1
31
x xx
J
xx
xx
++
=+ + −=+ ≥
−+
−+
Bài 21: Tìm min hoặc max của:
2
22
53
34
y xy
Q
x xy y
−
=
−+
Lời giải
Chia cả tử và mẫu cho
2
y
ta được:
2
2
5 3.
3. 4
x
y
Q
xx
y
y
−
=
−+
, đặt
2
53
34
xt
tQ
y
tt
−
==>=
−+
Nháp :
2
2
53
3 4 3 50
34
t
a at
at a t
tt
−
= => − + + −=
−+
, có :
( ) ( )
2
9 1 44 5 0a aa
∆= − − − =
=>
9
1;
7
aa=−=
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
109
Bài 22: Tìm min hoặc max của:
22
22
4
345
xy
R
x xy y
−
=
−+
Lời giải
Chia cả tử và mẫu cho
2
y
ta được:
2
2
2
2
4
3. 4. 5
x
y
R
xx
y
y
−
=
−+
, Đặt
2
2
4
3 45
xt
tR
y
tt
−
==>=
−+
Nháp :
2
22
2
4
3 4 5 40
3 45
t
a at at a t
tt
−
= => − + − +=
−+
,
Có
( )( )
2
4
' 4 3 1 5 4 0 1;
11
aa a a a∆= − − + = => =− =
Bài 23: Tìm min hoặc max của:
2
2
6 23
6 10
xx
A
xx
−+
=
−+
Lời giải
2
13
1
6 10
A
xx
= +
−+
Bài 24: Tìm min hoặc max của:
2
22
9 12 5
y
B
x xy y
=
−+
Lời giải
Chia cả tử và mẫu cho
2
y
ta được:
2
2
1
9 12 5
B
xx
y
y
=
−+
, Đặt
2
1
9 12 5
x
tB
y
tt
==>=
−+
Bài 25: Tìm min hoặc max của:
2
22
3
25 20 5
y
D
x xy y
=
−+ −
Lời giải
Chia cả tử và mấu cho
2
y
ta được:
2
2
3
25 20 5
D
xx
y
y
=
− +−
, Đặt
2
3
25 20 5
x
tD
t
tt
==>=
− +−
Bài 26: Tìm min hoặc max của:
( )
2
2
4 61
2
xx
E
x
−+
=
−
Lời giải
Đặt
22
2 44x t xt t−==> = + +
, khi đó :
2
22
4 10 5 10 5
4
tt
E
t
tt
++
= =++
,
Đặt
2
1
5 10 4aEa a
t
==>= + +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

110
Bài 27: Tìm min hoặc max của:
2
2
4 14
21
xx
F
xx
+−
=
−+
Lời giải
Đặt
22
1 21x t xt t−==> = + +
, Khi đó :
2
22
69 69
1
tt
F
t
tt
+−
= =+−
Đặt
2
1
9 61aF a a
t
==>=− + +
Bài 28: Tìm min hoặc max của:
2
2
4 63
2 32
xx
G
xx
−+
=
−+
Lời giải
Hạ phép chia ta được :
2
1
2
2 32
G
xx
−
= +
−+
Bài 29: Tìm min hoặc max của:
22
22
32
962
x xy y
H
x xy y
−+
=
−+
Lời giải
Chia cả tử và mẫu cho
2
y
ta được:
2
2
2
2
3 2. 1
9 62
xx
y
y
H
xx
y
y
−+
=
−+
, Đặt
2
2
3 21
9 62
x tt
tH
y
tt
−+
==>=
−+
Nháp:
2
22
2
3 21
9 6 2 3 2 10
9 62
tt
a at
at a t t
tt
−+
= => − + − + −=
−+
,
có :
( ) ( )( )
2
12
' 3 1 9 32 1 0 ;
33
a a a aa∆= − − − − = => = =
Bài 30: Tìm min hoặc max của:
2
2
4 22 19
44
xx
I
xx
++
=
++
Lời giải
( )
2
63
4
2
x
I
x
+
= +
+
, Đặt
( )
22
6 23
69
24 4
t
x tI
t
tt
−+
+==>=+ =+−
Đặt
2
1
9 64aI a a
t
==>=− + +
Bài 31: Tìm min hoặc max của:
2
2
9 30 7
9 61
xx
K
xx
+−
=
++
Lời giải
( )
2
24 8
1
31
x
K
x
−
= +
+
, đặt
22
3 3 8 3 11
31 3 1 1 1
t
x t xt K
t
tt
−−
+==> =−=> =+ =+ −
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
111
Đặt
2
1
11 3 1aK a a
t
==>=− ++
Bài 32: Tìm min hoặc max của:
22
22
52
2 10 7
x xy y
M
x xy y
−+
=
−+
Lời giải
Với y = 0 thì M =
=
2
2
1
2
2
x
x
Với y ≠ 0 chia cả tử và mẫu cho
2
y
ta được:
2
2
2
2
52
2 10 7
xx
y
y
M
xx
y
y
−+
=
−+
,
Đặt
2
2
52
2 10 7
x tt
tM
y
tt
−+
==>=
−+
Nháp
2
22
2
52
2 10 7 5 2
2 10 7
tt
a at at a t t
tt
−+
= => − + −+−
−+
, có :
( ) ( )( )
2
2521 42172a aa∆= − − − −
1 17
0;
2 22
aa∆= => = =
Bài 33: Tìm min hoặc max của:
22
22
22 58 73
44
x xy y
N
x xy y
−+
=
−+
Lời giải
Chia cả tử và mấu cho
2
y
ta được:
2
2
2
2
22 58 73
44
xx
y
y
N
xx
y
y
−+
=
−+
, Đặt
2
2
22 58 73
44
x tt
tN
y
tt
−+
==>=
−+
( )
2
30 15
22
2
t
N
t
−
= +
−
, Đặt
( )
2 22
30 2 15
30 45 30 45
2 22 22 22
a
a
t aN
a
a aa
+−
+
−==> = + =
+ = + +
Đặt
2
1
22 30 45bN b b
a
==>= + +
Bài 34: Tìm min hoặc max của:
2
22
86x xy
P
xy
+
=
+
Lời giải
Chia cả tử và mẫu cho
2
y
ta được:
2
2
2
2
86
1
xx
y
y
P
x
y
+
=
+
, Đặt
2
22
8 6 68
8
11
x tt t
tP
y
tt
+−
==>= =+
++
Nháp:
2
2
68
6 80
1
t
a at a t
t
−
= => +− +=
+
, có
( )
' 9 8 0 1; 9aa a a∆= − + = => = =−
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

112
Bài 35: Tìm min hoặc max của:
2
2
33
21
xx
Q
xx
−+
=
−+
Lời giải
( )
2
2
1
1
x
Q
x
−+
= +
−
, Đặt
11x t xt−==> =+
Khi đó :
22
1 11
11
t
Q
t
tt
−+
=+ =−+
Đặt
2
1
1a Qa a
t
==> = −+
Bài 36: Tìm min hoặc max của:
22
22
x xy y
R
x xy y
++
=
−+
Lời giải
Với y = 0 thì R = 1
Với y ≠ 0. Chia cả tử và mẫu cho
2
y
ta được:
2
2
2
2
1
1
xx
y
y
R
xx
y
y
++
=
−+
,
Đặt
2
22
12
1
11
x tt t
tR
y
tt tt
++
==>= =+
−+ −+
Nháp :
2
2
2
20
1
t
a at at a t
tt
= => − +− =
−+
, có
( )
2
2
2 4 . 0 2;
3
a aa a a
−
∆= + − = => = =
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

113
CHUYÊN ĐỀ 4:
PHƯƠNG TRÌNH ĐẠI SỐ
- Là phương trình có dạng: ax = b phụ thuộc vào tham số m
+) Nếu
0≠⇒=
b
ax
a
+) Nếu
( )
000
00
0
=⇔=
=⇔=→
≠
bx
a xb
b PTVN
Bài 1: Giải và biện luận số nghiệm của phương trình sau
a.
2
( 4) 3 6m xm−=−
b.
(2 1) 2 3 2m xmx+−=−
c.
( 2) 3 1mx x−=+
d.
2
( 2) 2 3m x mx+−=−
Lời giải
a.
2
( 4) 3 6m xm−=−
+) Nếu
2
2
36 3
( 4) 0 2
42
−
− ≠ ⇔ ≠± ⇒ = =
−+
m
m mx
mm
+) Nếu
2
00
2
( 4) 0
2
0 12
=
=
−=⇔ ⇒
= −
= −
x
m
m
m
x
b.
(2 1) 2 3 2 (2 2) 2 2+ − = −⇔ − = −m xmx m xm
+) Nếu
22
2 20 1
22
−
−≠⇒= =
−
m
mx
m
+) Nếu
2 20 1 0 0− = ⇔ =−⇒ =m mx
(vô số nghiệm)
Vậy nếu:
+) Nếu
1m ≠
phương trình có vô số nghiệm
+) Nếu m = 1 phương trình vô nghiệm
c.
( 2) 3 1 ( 3) 2 1− = +⇔ − = +mx x m x m
+)
21
30 3
3
+
−≠⇔ ≠⇒ =
−
m
m mx
m
+)
30 3 0 7−=⇔ =⇒ =m mx
(vô nghiệm)
d.
22
( 2) 2 3 ( 1) 2 3+ − =−⇒ + = −m x mx m x m
Ta có:
2
1) 0+>∀mm
suy ra phương trình luôn có nghiệm
2
23
1
m
x
m
−
=
+
Bài 2: Cho phương trình
2
( 1)( 2) 1mx m− + +=
(Vô số nghiệm)
(Vô số nghiệm)
(Vô nghiệm)
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

114
a. Tìm m để x = 3 là nghiệm của phương trình
b. Tìm m để phương trình có nghiệm
c. Tìm m để phương trình có nghiệm duy nhất x = 3
Lời giải
a. Thay x = 3 vào phương trình, ta được:
22
4
5( 1) 1 5 4 0 1;
5
−
− += ⇔ − − = ⇔ ∈
m m mm m
b.
2 22
( 1)( 2) 1 ( 1) 2 1− + += ⇔ − =− + +m x m m x mm
Để phương trình có nghiệm thì xảy ra 2 trường hợp
+) Phương trình có nghiệm duy nhất khi
2
10 1− ≠ ⇔ ≠±mm
+) Phương trình có vô số nghiệm
2
2
10
1
2 10
−=
⇔=
− + +=
m
m
mm
Vậy
1m ≠−
thì phương trình luôn có nghiệm
c. Để phương trình có nghiệm duy nhất thì
2
2
1
1
4
1
21
5
3
4
1
5
≠±
≠±
−
=
⇔ ⇔=
− ++
=
−
=
−
m
m
m
m
mm
m
m
Vậy
4
5
m
−
=
Bài 3: Cho phương trình
2
( 1) 2 4.mx x m m+− = +−
Tìm m sao cho
a. Phương trình nhận 1 là nghiệm
b. Phương trình có nghiệm
c. Phương trình vô nghiệm
Lời giải
a. Thay x = 1 vào phương trình ta được
{ }
1; 2∈−m
b. Phương trình có nghiệm xảy ra 2 trường hợp là có nghiệm duy nhất hoặc có vô số
nghiệm
22
( 1) 2 4 ( 2) 4+− = + −⇔ − = −mx xm m m xm
+) Phương trình có nghiệm duy nhất khi
20 2−≠⇔ ≠mm
+) Phương trình có vô số nghiệm
2
20
2
40
−=
⇔ ⇔=
−=
m
m
m
Vậy phương trình có nghiệm với mọi m
c. Phương trình vô nghiệm
2
20
40
−=
⇔ ⇔ ∈∅
−≠
m
m
m
Bài 4: Tìm
aZ∈
để phương trình
3( 2) 4x ax+=+
có nghiệm nguyên
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

115
3( 2) 4 (3 ) 2+ = +⇔ − =−x ax a x
+) Nếu
30 3−=⇔=aa
thì phương trình vô nghiệm.
+) Nếu
{ } { }
2
3 0 3
( 2) 1; 2 1; 2; 4; 5
3
−
−≠⇒= ∈⇔−∈ − =±± ⇔∈
−
a x Z aU a
a
Bài 5: Giải và biện luận các phương trình sau
a.
( 2) 3
21
1
mx
m
x
−+
= −
+
b.
21
2
2
a
a
x
−
= −
−
c.
1
1
1
mx
x
+
=
−
d.
( 1) 2
3
m xm
m
x
+ +−
=
+
Lời giải
a. Điều kiện:
1 ( 2) 3 (2 1)( 1) ( 1) 2 4≠− ⇒ − + = − + ⇔ − − = −x m x m x mxm
+)
24
10 1
1
−
− − ≠ ⇔ ≠− ⇒ =
−−
m
m mx
m
nghiệm này phải khác -1
24 24
1 10 2 4 10 5
11
−−
⇔ ≠−⇔ +≠⇔ −−−≠⇔ ≠
−− −−
mm
mm m
mm
Vậy với
24
1; 5
1
−
≠− ≠ ⇒ =
−−
m
mm x
m
Với m = 5 phương trình vô nghiệm
+)
10 1− −= ⇔ =−mm
khi đó phương trình trở thành 0x = -5 (vô nghiệm)
b. Điều kiện xác định:
20 2−≠⇔≠xx
21
2 ( 2) 4 5
2
−
=−⇔ − = −
−
a
a a xa
x
+)
45
20 2
2
−
−≠⇔≠⇒=
−
a
a ax
a
. Xét
45 3
2 4 5 2( 2)
22
−
≠⇔ −≠ − ⇔ ≠
−
a
aaa
a
+)
200 2 0 3− ⇔=⇔ =a ax
(vô nghiệm). Xét
45 3
2 4 5 2( 2)
22
a
aaa
a
−
≠↔ −≠ − ↔ ≠
−
Vậy
3
2;
2
= =aa
thì phương trình vô nghiệm
3
2;
2
≠≠aa
suy ra phương trình có nghiệm
45
2
a
x
a
−
=
−
c. Điều kiện
1x ≠
1
1 1 1 ( 1) 2
1
+
=⇔ += −⇔ − =−
−
mx
mx x m x
x
+)
10 1−= ⇔ =mm
phương trình vô nghiệm
+)
2 2 21 1
10 1 1 10 0
0 1
11 1 1
− − −− + − −
−≠⇔ ≠⇒= ≠⇔ −≠⇔ ≠⇔ ≠⇔ ≠−
−− − −
mm
m mx m
mm m m
Vậy
1; 1≠− mm
thì phương trình có nghiệm
2
1
x
m
−
=
−
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

116
Vậy
1; 1mm= = −
phương trình vô nghiệm
d. Điều kiện
3x ≠−
( 1) 2
(1)2(3)22
3
+ +−
= ⇔ + + −= + ⇔= +
+
m xm
m m x m mx x m
x
Xét
5
223
2
−
+ ≠− ⇔ ≠mm
Vậy
5
2
m
−
=
phương trình có nghiệm
22xm= +
BÀI TẬP VỀ NHÀ:
Bài 1: Giải và biện luận số nghiệm của phương trình sau
a.
( ) ( 2)mx m x m−=+−
b.
2
( 1) 1 (2 )m x mx+ −= −
c.
2
64 3mx x m+= +
d.
2
( 1) (3 2)mx m xm−+= −
Bài 2: Tìm m để mỗi phương trình sau có 1 nghiệm
a.
( )( 1) 0xmx− −=
b.
2
( 1) 1mm x m−=−
Hướng dẫn
a.
1
( )( 1) 0 1
=
− −=⇔ ⇒ =
=
x
xmx m
xm
b.
2
0
( 1) 1 ( 1) 0
1
≠
− = −⇔ − ≠ ⇔
≠
m
mm x m mm
m
.
Vậy
0; 1mm≠≠
thì phương trình có 1 nghiệm
Bài 3: Tìm m để phương trình sau vô nghiệm :
( 1) ( 2) 0m xx+ −+=
Hướng dẫn
( 1) ( 2) 0 2 0+ − + =⇔ −=m x x mx
Để phương trình vô nghiệm thì
0
0
20
=
⇔=
−≠
m
m
Bài 4: Tìm m để phương trình sau có vô số nghiệm :
2
4 2 (1)−= −mx m x
Lời giải
2
(1) ( 4) 2⇔ −=−m xm
có vô số nghiệm
2
40
2
20
−=
⇔ ⇔=
−=
m
m
m
Bài 5: Với giá trị nào của m thì:
a.
2 15 4xa−= +
có nghiệm dương b.
3( 2) 4x ax+=+
có nghiệm lớn hơn -1
c.
2
( 3 2) 3 3aax a− + +=
có nghiệm duy nhất
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
117
a.
5( 1)
2 15 4 2 5 5 0 1
2
+
− = + ⇔ = + ⇔ = > ⇔ >−
a
x a xa x a
b.
3( 2) 4 (3 ) 2+ = +⇔ − =−x ax a x
+)
30 3−=⇔=aa
thay vào phương trình vô nghiệm
+)
3
22 2 1
3 0 3 1
10 0
1
33 3 3
>
−−
−≠⇔≠⇒= = >−⇔ +>⇔ >⇔
<
−− − −
a
a
aax
a
aa a a
c.
22
( 3 2) 3 3 ( 3 2) 3 3−+ +=⇔ −+ =−aax aaaxa
có nghiệm duy nhất
2
1
3 20
2
≠
⇔ − +≠⇔
≠
a
aa
a
Bài 6: Tìm a để phương trình có nghiệm nguyên:
2 3 ( 2)xa x a+−= +
Lời giải
3 25 5
2 3 ( 2) 1
22 2
+ −+
+ − = + ⇔ = = =−+
−− −
aa
xa x a x
aa a
Để
55 55
( 0) 2 2
( ; 0)
22
∈⇒ ∈⇒ =∈ ≠ ⇒−=⇒=− ∈ ≠
−−
x Z Z k zk a a k Zk
aa kk
( Vì a có thể không nguyên )
+) Nếu a nguyên
5
5 1; 5⇒∈⇒ ⇒=± =±Z kk k
k
Bài 7: Cho phương trình:
23
1 (1)
2
−
= +
−
m
m
x
. Tìm m để phương trình có nghiệm duy nhất
Lời giải
Điều kiện:
2x ≠
23
1 2 3 ( 1)(2 ) ( 1) 5
2
−
= +⇔ − = + − ⇔ + =
−
m
m mm x m xm
x
+)
5
10 1
1
+ ≠ ⇔ ≠− ⇒ =
+
m
m mx
m
. Vì
11
2
52
2
13
≠− ≠−
≠⇒ ⇒
≠≠
+
mm
x
m
m
m
Bài 8: Cho phương trình:
21 3
21
xx
xm x
++
=
−−
. Tìm m để phương trình vô nghiệm
Lời giải
Điều kiện:
1;
2
m
xx≠≠
21 3
(2 1)( 1) ( 3)(2 ) ( 7) 1 3 (1)
21
++
= ⇔ + −= + − ⇔ − =−
−−
xx
x x x xm m x m
xm x
+) TH1: m ≠ -7 thì
13
(1)
7
−
⇔=
−
m
x
m
. Vì
;1
2
m
xx≠≠
nên ta có các trường hợp sau:
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

118
Với
2
1
13
26 7
2
2 72
= −
−
= ⇔ = ⇔− = −⇔
=
−
m
m mm
x mm
m
m
Với
13
1 1 13 7 2
7
−
=⇔ =⇔− = − ⇔ =
−
m
x mm
m
m
Vậy phương trình vô nghiệm khi
{ }
1; 2; 7∈−m
Bài 9: Giải và biện luận phương trình sau:
2
22
3 43 1m mm
xm m x xm
−+
+=
− −+
Lời giải
Điều kiện xác định:
≠±xm
2
22
2
2
3 43 1
3 43 1
( )( )
( )3 4 3
( 1) ( 1)(2 3)
−+
+=
− −+
−+
⇔− =
− −+ +
⇔ + − + +=−
⇔−=− −
m mm
xm m x xm
m mm
xm xmxm xm
mx m m m x m
m xm m
) 1 0 1 0. 0+ −= ⇔ =⇒ =m mx
Vì
11≠± ⇒ ≠± ⇒ =x mx m
phương trình nghiệm đúng với mọi
1x ≠±
Hay
{ }
/1S x Rx= ∈ ≠±
+)
10 1 2 3−≠ ⇔ ≠⇒ = −m m xm
vì điều kiện
≠±xm
+)
23 3≠⇔ −≠⇔≠xm m m m
+)
23 1≠− ⇔ − ≠− ⇔ ≠xm m mm
Vậy
1; 3mm≠≠
phương trình đã cho có nghiệm
23xm= −
B. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Dạng tổng quát:
0
0
0
−
>⇔≥
+ ≥ ⇔ ≥− ⇔
−
<⇔≤
b
ax
a
ax b ax b
b
ax
a
Ví dụ 1: Giải các bất phương trình sau
a.
41 32
23
xx
x
−−
+≥
b.
10 3 6 5
1
48
xx+−
<+
c.
0+≥ax b
Lời giải
4 1 3 2 1 2 12 1
. 22
2 3 2 3 23 8
−−
+≥ ⇔ −+≥−⇔ ≥ − ⇔≥−
xx
a x x xx x x
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
119
b.
10 3 6 5 5 5 3 3 25 8
1 11
4 8 2 8 4 4 8 25
+−
<+ ⇔ + <+ − ⇔ <⇔ <
x x xx x
x
c.
0 (1)+ ≥ ⇔ ≥−ax b ax b
+) Nếu
0a ≠
+)
0 (1)
−
>⇒ ⇔≥
b
ax
a
+)
0 (1)
−
<⇒ ⇔≤
b
ax
a
+) Nếu
00= ⇔ ≥−a xb
+)
0−≤b
thì bất phương trình vô số nghiệm
+)
0−>b
thì bất phương trìn vô nghiệm
Ví dụ 2: Giải các hệ bất phương trình sau
a.
32 7
2
53
1 (3 1)
5
22
x
x
x
x
−
− +>
−
−<
b.
3 13 12 1
2343
21 4
3
53
x xx x
x
x
+− + −
−≤−
+
− >+
c.
1
15 2 3
3
3 14
2( 4)
2
xx
x
x
−> +
−
−<
d.
22
21 5
(1 2 ) (2 3)
xx
xx
−> −
+ ≤−
Hướng dẫn
a.
11
32 7
2
4 11
10
53
4
1 (3 1)
13 10
5
13
22
−
<
− +>
⇔ ⇔ <<
−
>
−<
x
x
x
x
x
x
x
b.
3 13 12 1
13
13
2343
27
21 4
22
27
3
53
21
+− + −
−≤−
≤
⇔ ⇔≤
+
− >+
<
x xx x
x
x
x
x
x
*) Giải và biện luận bất phương trình
0 (1)+ ≥ ⇔ ≥−ax b ax b
+) Nếu
0a ≠
+)
0 (1)
−
>⇒ ⇔≥
b
ax
a
+)
0 (1)
−
<⇒ ⇔≤
b
ax
a
+) Nếu
00= ⇔ ≥−a xb
+)
0−≤b
thì bất phương trình vô số nghiệm
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

120
+)
0−>b
thì bất phương trìn vô nghiệm
Bài 1: Giải và biện luận các bất phương trình sau
a.
( )3 9mx m x−≥−
b.
62 3mx x m+< +
c.
( ) 34x mm x x+ +> +
d.
3
3( ) ( 1) 1x m m mx+ − + ≥− −
Lời giải
a.
2
( ) 3 9 ( 3) 9 (1)− ≥ −⇔ − ≥ −mx m x m x m
+)
30 3−>⇔ >mm
thì
2
9
(1) 3
3
−
⇔≥ = +
−
m
xm
m
+)
3 0 3 (1) 3−<⇔ <⇒ ⇔ ≤ +m m xm
+)
3 0 3 (1) 0 0−=⇔ =⇒ ⇔ ≥mm x
( vô số nghiệm )
b.
6 2 3 ( 2) 3 6 (1)+< + ⇔ − < −mx x m m x m
+)
36
2 0 2 (1) 3
2
−
−>⇔ >⇒ ⇔< =
−
m
mm x
m
+)
2 0 2 (1) 3−<⇔ <⇒ ⇔>mm x
+)
2 0 2 (1) 0 0−=⇔ =⇒ ⇔ <mm x
vô nghiệm
c.
2
( ) 3 4 ( 2) 4 (1)+ + > + ↔ − >− +x mm x x m x m
+)
2
4
2 0 2 (1) 2
2
−+
−>⇔ >⇒ ⇔> =−−
−
m
mm x m
m
+)
2 0 2 (1) 2−<⇔ <⇒ ⇔<−−m m xm
+)
2 0 2 (1) 0 0−=⇔ =⇒ ⇔ >mm x
suy ra phương trình vô nghiệm
d.
3 32
3( ) ( 1) 1 ( 3) 3 (1)+ − + ≥− − ⇔ + ≥ +x m m mx m x m m
+)
2
3 0 3 (1)+ > ⇔ >− ⇒ ⇔ ≥m m xm
+)
2
3 0 3 (1)+ < ⇔ <− ⇒ ⇔ ≤m m xm
+)
3 0 3 (1) 0 0+ = ⇔ =−⇒ ⇔ ≥mm x
vô số nghiệm.
PHƯƠNG TRÌNH BẬC CAO
A. Phương trình bậc cao đưa về dạng tích
1. Phương trình bậc cao đưa về phương trình tích
- Dùng phương pháp nhẩm nghiệm
- Dùng định lý Bezut: Nếu f(x) = 0 có nghiệm x = a thì
() ( ).()f x x a hx= −
-
1
10
( ) ... 0
nn
nn
f x ax a x a
−
−
= + ++ =
Nếu f(x) có nghiệm hữu tỷ
0
()
()
∈
= ⇒
∈
n
p Ua
p
x
q Ua
q
- Nếu tổng các hệ số của đa thức bằng 1 thì có nghiệm x = 1
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

121
- Nếu tổng các hệ số của hạng tử bậc chẵn bằng tổng các hệ số của hạng tử bậc lẻ thì ó
nghiệm x = 1
- Có thể sử dụng lược đồ Hoocne
VD:
432 2
2
2 3 3 5 6 0 ( 2)(2 3)( 1) 0
3
2
=
− − + −=⇔ − + −+ =⇔
−
=
x
x x x x x x xx
x
Bài 1: Giải các phương trình sau
a.
2
4 30xx− +=
b.
2
4 10xx− +=
c.
32
2 9 18 0xx x+ −−=
d.
32
2 3 60x xx− ++=
e.
32
2 3 3 10xxx− + −=
f.
42
2 3 20x xx− − −=
Lời giải
a.
2
1
4 3 0 ( 1)( 3) 0
3
=
− +=⇔ − − =⇔
=
x
xx x x
x
b.
( )
2
2 22
23
4 1 0 ( 2) 3 0 ( 2) 3 0
23
= +
−+=⇔− −=⇔− − =⇔
= −
x
xx x x
x
c. Ta có:
{ }
32 3 2 2 2
2 9 18 0 ( 3 ) (5 15 ) (6 18) 0 ( 3)( 5 6) 0 3; 2+ −−=⇔ − + − + − =⇔− ++=⇔∈±−xxx xx x x x x xx x
d.
2
32 2
5 23
2 3 6 0 ( 1)(2 5 6) 0 ( 1) 0
1
4 16
− ++=⇔+ −+=⇔+ − + =⇔=−
x xx x x x x x x
e.
32 2
1
2 3 3 1 0 (2 1)( 1)
2
− + −= ⇔ − − + ⇔ =x x x x xx x
f.
{ }
4 2 32 2
2 3 2 0 ( 1)( 2) 0 ( 1)( 2)( 1) 0 1; 2− −−=⇔+ −−−=⇔+ − ++=⇔∈−xxx xxxx xx xx x
Bài 2: (HSG – Đông Anh – 2003)
Giải các phương trình sau
a.
2
4 30xx− +=
b.
32
2 3 10 0xx x− −+=
Lời giải
a.
2 22
3/2
4 3 0 (2 1) 2 0
1/2
= −
− −=⇔ + − =⇔
=
x
xx x
x
b.
32 2
2 3 10 0 ( 2)( 4 5) 0 2− −+=⇔+ +−=⇔=−xx x x x x x
Bài 3: Giải các phương trình sau
a.
42
6 80xx x+ + −=
b.
3 33
( 1) (3 3) 27 8xx x−+ + = +
c.
22
( 1) ( 2) ( 1) ( 2) 12xx xx+ ++− −=
d.
222
( 5 ) 2( 5 ) 24xx x x+ − +=
e.
2 2 42
( 1) 3( 1)x x xx++ = + +
f.
5432
2xxxxx= + + ++
Lời giải
a. Ta có tổng các hệ số = 0 nên có nhân tử là x – 1
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

122
{ }
4 2 4 3 32 2
32 2
6 80 ( )( )(2 2)(8 8)0
( 1)( 2 8) 0 ( 1)( 2)( 4) 0 1; 2
+ + −=⇔ − + − + − + − =
⇔− +++=⇔− + −+=⇔∈−
xxx xx xx xx x
xxxx xx xx x
b. Ta có:
3 3 3 32 32 2
2
( 1) (3 3) 27 8 6 11 19 6 0 (6 18 ) (7 21 ) (2 6) 0
12
( 3)(6 7 2) 0 ( 3)(2 1)(3 2) 0 3; ;
23
− + + = +⇔ − − −=⇔ − + − + − =
−−
⇔− ++=⇔− + +=⇔∈
x x x xxx xx x xx
x xx x x x x
c.
22 3 2
( 1) ( 2) ( 1) ( 2) 12 2 10 12 0 ( 1)( 6) 0 1+ ++− −=⇔ + −=⇔− ++=⇔=x x x x x x x xx x
d. Ta có:
{ }
2 2 2 2 2 2 2 22
( 5 ) 2( 5 ) 24 ( 5 ) 2( 5 ) 1 25 0 ( 5 1) 5 0
( 1)( 4) ( 1)( 6) 0 1; 4;1; 6
+ − + = ⇔ + − + +− =⇔ + − − =
⇔+ +⇔− +=⇔∈−− −
xx xx xx xx x
x
xx xx x
e. Ta có:
2242 2 242 222 2
( 1) 3( 1) ( 1) 3( 1) 0 ( 1) 3( 1)( 1) 0++ = + + ⇔ ++ − + + =⇔ ++ − ++ −+ =xx xx xx xx xx xx xx
22 2 2 2
( 1) 1 3( 1) 0 ( 1)( 1) 0 1
⇔ ++ ++− −+ =⇔ ++ − =⇔=
xx xx xx xx x x
f. Ta có:
5432 5432 5 4 32
432 432 4
32
432
2 2 0 ( 1) ( 1) 0
( 1)( 1)
( 1) 0 ( 2)( 1) 0
2
1 0(*)
= + + ++⇔ − − − −−=⇔ −− + + ++ =
⇔ − + + ++− + + ++ =⇔ − + + ++ =
=
⇔
+ + ++=
x xxxx xxxxx x xxxx
x xxxx xxxx x xxxx
x
xxxx
( )
4 3 2 3 2 22 2
(*) ( ) ( 1) 0 ( 1)( 1) 0 ( 1) ( 1) 0⇔ + + ++ =⇔ + ++ =⇔ + −++ =xxxx xx x xxxx VN
Bài 4: Dùng cách đặt ẩn phụ giải các phương trình sau
a.
23 2 2 2
( 1) (1 3 ) ( 3 2) (1)x x xx+ +− = − +
b.
2 32 3 2 3
( 34)(2 53)(3 21)xx x x x x+− + − + = − −
c.
42
2 30xx− + +=
d.
43 2
8 15 4 2 0xx x x+ + − −=
e.
2
2 2 120x xx+ + +−=
f.
2
( 2)( 2)( 10) 72xxx− + −=
g.
333
(2 5) ( 2) ( 3)xx x− −− =−
Lời giải
Đặt
2
1; 1 3=+=−ax b x
khi đó:
33 3 33 3 2 23
() 3 3 3()0+=+ ⇔+=+ + +⇔ +=a b a b a b a a b ab b ab a b
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

123
( )
2
2
10
0
1 3 1 (*)
01
3
+=
=
⇔ =−⇔ += −
=
=
x VN
a
ab x x
b
x
{ }
2
1
(*) 3 2 0 1; 2 1; 2;
3
⇔ − +=⇔∈ ⇒∈
xx x x
b.
2 32 3 2 3
( 34)(2 53)(3 21)xx x x x x+− + − + = − −
Đặt
22
34; 2 53=+− = − +ax x b x x
khi đó:
{ }
2 33 3
321 () ()0
1; 4
0
13
0 1; 3 / 2 4
;1; ;
32
1; 1 / 3
+ = − −⇒ + = + ⇔ + =
∈−
=
−
⇔ = ⇒
∈−
=−−
ab x x a b ab abab
x
a
bx
ab
c. Đặt
22 2
1( )
( 0) 2 3 0 3 3
3 ()
= −
= ≥ ⇒− + + = ⇔ ⇒ = ⇔ =±
=
t loai
t xt t t x x
t tm
d.
43 2 43 22 2 2 2
8 15 4 20 8 16 4 20 ( 4) ( 4)20+ + − −=⇔ + + − − −=⇔ + − + −=xx x x xx xxx x x x x
Đặt
22
22
22
1 4 1 0 ( 2) 3 2 3
4 20
2
4 2 0 ( 2) 6
26
=− + += + = =−±
= + ⇒ −− = ⇔ ⇔ ⇔ ⇔
=
+ −= + =
=−±
t xx x x
tx x tt
t
xx x
x
e.
22 2
2 2 120 2 12 130 2 30( 1; 0)+ + +−=⇔ + ++ +−=⇔ + −= = + ≥xxx xx x yy yxy
10
11
32
= =
⇔ ⇒ +=⇒
=−=−
yx
x
yx
f. Ta có:
( )
2 22
16
( 2)( 2)( 10) 72 ( 4)( 10) 72 , 0 14 32 0 4
2
=
− + −=⇒− −= = ≥⇔− −=⇔ ⇒=±
= −
y
x x x y y y xy y y x
y
g. Đặt
25;2−= −=x ax b
khi đó:
33 3
5
3 ()3()0 0 3;2;
2
0
=
−=−⇒ − = − ⇔ − = ⇔ =⇔∈
=
ab
ab x a b ab abab a x
b
B. Phương trình dạng:
( )( )( )( ) (1) ( )+ + + + = +=+xaxbxcxd m adbc
22
(1) ( )( )( )( ) ( ) ( )
⇔+ + + +=⇔ ++ + ++ + =
xaxdxbxc m x adxad x bcxbc m
Đặt
2
( ) ( )( ) 0 ... ...= + + ⇒ + + = ⇒= ⇒ =t x a d x t ad t bc t x
Bài 1: Giải các phương trình sau
a.
( 1)( 1)( 2) 24 (1)+ − +=xx x x
b.
( 2)( 3)( 5)( 6) 180xxxx++−−=
c.
( 4)( 5)( 6)( 7) 1680xxxx− − − −=
d.
2
(4 3) (2 1)( 1) 75x xx+ + +=
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
124
e.
2
2 (8 1) (4 1) 9xx x− −=
f.
2
(12 7) (3 2)(2 1) 3x xx+ + +=
Lời giải
a. Ta có:
{ }
22 2
2
2
6
( 1)( 1)( 2) 24 ( )( 2) 24 ( 2) 24 2 24 0
4
60
2; 3
40
=
+ − += ⇔ + +−= ⇔ −= ⇔−− =⇔
= −
+−=
⇔ ⇔∈ −
++=
t
xx x x xxxx tt t t
t
xx
x
xx
b.
{ }
2
( 2)( 3)( 5)( 6) 180 3 14 14 7;3;0; 4+ + − −= ⇔−−=±⇔∈ −xxxx xx x
c. Ta có:
22
( 4)( 5)( 6)( 7) 1680 ( 11 28)( 11 30) 1680 ( 1)( 1) 1680 41− − − −= ⇔−+ −+= ⇔+ −= ⇔=±xxxx xx xx yy y
+)
{ }
2
41 11 12 0 1; 12= ⇒ − − =⇔∈ −y xx x
+)
2
41 11 70 0=−⇒ − + =y xx
(vô nghiệm)
d.
2
(4 3) (2 1)( 1) 75 (4 3)(4 3)(4 2)(4 4) 8.75 24.25+ ++=⇔++++==x xx xxxx
Đặt
2
(4 3)= +tx
ta được:
2 22
2
(4 2)(4 4) (4 3) 1 1 ( 1) 24.25 25 25 ( 25)( 24) 0
4 35 2
25( 0) (4 3) 25
435 2
+ + = + −=−⇒ − = ⇔ −= − ⇔ − + =
+= =
⇔= ≥ ⇔ + = ⇔ ⇔
+=− =−
x x x t tt t
t t t
xx
tt x
xx
e. Nhân với 8 ta được:
8 (8 1)(8 1)(8 2) 72xxxx−−−=
Đặt
81−=xy
ta được:
2 22 4 2 2 2 2
1
2
( 1). .( 1) 72 ( 1) 72 72
0 ( 9)( 8) 0 9
1
4
=
+ −= ⇔ −= ⇔ − − =⇔ − + =⇔ =⇔
−
=
x
y y y yy y y y y y
x
f.
2
(12 7) (3 2)(2 1) 3+ + +=x xx
Nhân hai vế với 24 ta được:
2
(12 7) (2 8)(12 6) 72+ + +=xxx
Đặt
12 7+=xy
ta được:
2
42
2
1
9
3
( 1). . ( 1) 72 72 0
5
8
6
−
=
=
− += ⇔ − − =⇔ ⇔
−
= −
=
x
y
y yy y y y
y
x
Bài 2: Giải các phương trình sau
a.
22
( 3 )( 7 10) 216x xx x− ++ =
b.
22
(2 7 3)(2 3) 9 0x x xx− + +− +=
Lời giải
a. Ta có:
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

125
22 2 2
2
2
2
( 3 )( 7 10) 216 ( 3)( 2)( 5) 216 ( 2 )( 2 15) 216
( 15) 216 0 15 216 0 ( 24)( 9) 0
24 2 24 0 6
94
2 90 ( )
− ++ = ⇔ − + += ⇔ + + − =
⇔−−=⇔−−=⇔− +=
= +−= =
−
⇔⇔ ⇔
=−=
+ +=
x xx x x
x x x x xx x
yy y
y y y
y xx x
yx
x x vo nghiem
b. Ta có:
2 2 22
(2 7 3)(2 3) 9 0 ( 3)(2 1)(2 3)( 1) 9 0 (2 3 1)(2 3 9) 9 0− + +− +=⇔ − − + −+=⇔ − + − − +=xx xx x x x x xx xx
2
2
1 2 3 8 0 ....
( 10) 9 0
9 .....
2 30
=− − −=
⇔ + +=⇔ ⇔ ⇔
= −
−=
t xx
tt
t
xx
Bài 3: HSG Bắc Giang 30/03/2013.
Giải phương trình sau:
2 ( 1)( 1)( 2) 4xxxx− − + +=
Lời giải
+) Nếu x ≥ 2 thì:
2 2 42
0( )
( 2)( 1)( 1)( 2) 4 ( 1)( 4) 4 5 0 5 ( )
5( )
=
− − + +=⇔ − −=⇒− =⇔ =
= −
x loai
x x x x x
x x x x tm
x loai
+) Nếu x < 2 thì:
22
42 2 2
(2 )( 1)( 1)( 2) 4 ( 2)( 1)( 1)( 2) 4 ( 1)( 4) 4
57
5 8 0 0( )
24
− − + +=⇔− − + +=−⇔ − −=−
⇔ − +=⇔ − + =
xxxx x xxx x x
x x x vo nghiem
Vậy phương trình có nghiệm
5=x
C. Phương trình dạng:
2
( )( )( )( ) ( )+ + + += =x a x b x c x d mx ad bc
Cách 1: Đặt
( )( )t x axb=++
Ví dụ 1: Giải phương trình sau:
a.
2
( 2)( 3)( 4)( 6) 30++++=xxxx x
b.
2
( 2)( 3)( 6)( 9) 80+ + + +=xxxx x
Lời giải
a. Đặt
22
7 12 8 12=++⇒++=+tx x x x tx
ta được:
22 2 2 2
(1) ( ) 30 30 0 ( 5 ) (6 30 ) 0⇔+ = ⇔+− =⇔ − + − =t x t x t tx x t tx tx x
2
2
5 2 12 0 ( ) 1
( 5 )( 6 ) 0
6 12
13 12 0
= ++= =
−
⇔− + =⇔ ⇔ ⇔
=−=−
+ +=
t x x x vo nghiem x
t xt x
tx x
xx
b.
{ }
22 2 2
( 2)( 3)( 6)( 9) 80 ( 11 18)( 9 18) 80 1; 8+ + + + = ⇔ + + + + = ⇔ ∈− −x x x x x x x xx xx
Cách 2:
+) Kiểm tra xem x = 0 có là nghiệm hay không?
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
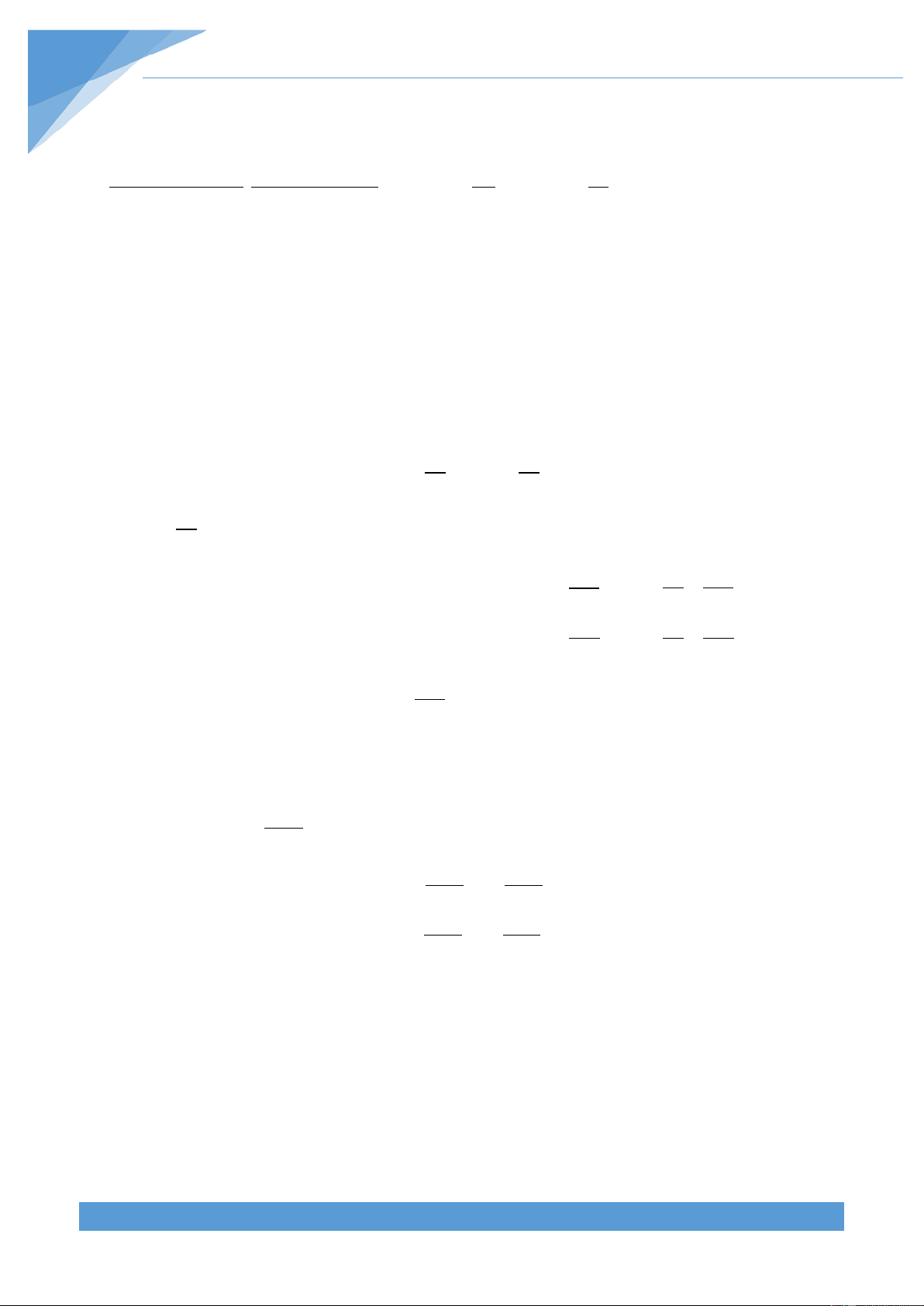
126
+) Xét
22 2
0 ( ) ()
≠⇒ ⇔ + + + + + + =
x pt x a d x ad x b c x bc mx
Chia cả hai vế cho x
2
ta được:
22
( ) ()
. ( )( )
( )( ) ... ...
++ + ++ +
= ⇔ + ++ + ++ =
⇔ + + ++ = ⇒= ⇒ =
x a d x ad x b c x bc ad bc
m x adx bc m
x x xx
t d at b c m t x
Ví dụ 2: Giải phương trình sau:
2
4( 5)( 6)( 10)( 12) 3xxx x x+ + + +=
Lời giải
2
2
22 2
4( 5)( 6)( 10)( 12) 3
4( 5)( 12)( 6)( 10) 3
4( 17 60)( 10 60) 3
+ + + +=
⇔ + + + +=
⇔ ++ ++=
xxx x x
xx xx x
xx xx x
Do x = 0 không thỏa mãn phương trình nên ta chia cả hai vế cho x
2
, được:
60 60
4( 17 )( 16 ) 3++ ++ =xx
xx
Đặt
60
= +tx
x
ta được:
2
60 31
31
2
2
4( 17)( 16) 3 4 132 1085 0
35 60 35
22
−
−
+=
=
+ +=⇔+ + =⇔ ⇔
−−
= +=
x
t
x
tt t t
tx
x
{ }
2
2
15
8;
2 31 120 0
2
2 35 120 0
....
x
xx
xx
x
−
∈−
++=
⇔↔
++=
∈
D. Phương trình dạng:
44
( )( )+ ++ =xa xb m
Cách giải: Đặt
2
+
= +
ab
tx
ta được:
;
22
22
α
α
+−
+=+−=+=+
+−
+=+− =− =−
ab ab
xata t t
ab ab
xbtb t t
44 44
( ) ( ) ( ) ( ) ..... .....
αα
+ + + = ⇔ + + − = ⇒= ⇒ =xa xb m t t m t x
Bài 1: Giải các phương trình sau
a.
44
( 2) ( 4) 16xx− +− =
b.
44
( 1) ( 3) 16xx+ ++ =
c.
55
(4 ) ( 2) 32xx− +− =
d.
44 4
( 7) ( 8) (15 2 )xx x−+−=−
e.
44
( 6) ( 8) 272xx+ ++ =
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

127
a. Đặt t = x – 3 ta được:
2
4 4 42
2
14
( 1) ( 1) 16 6 7 0
2
7( )
= =
+ +− = ⇔ + −=⇔ ⇔
=
= −
tx
t t tt
x
t loai
b. Đặt t = x + 2 ta được:
44
11
( 1) ( 1) 16
13
= = −
− ++ = ⇔ ⇔
=−=−
tx
tt
tx
c.
55 55
(4 ) ( 2) 32 ( 2) ( 4) 32−+−=⇔−−−=xx x x
Đặt y = x – 3 suy ra:
2 1; 4 1−=+ −=−xyxy
ta được:
5 5 5432
54 3 2 42
( 1) ( 1) 32 5 10 10 5 1
4
( 5 10 10 5 1) 32 0 2 3 0 1
2
+ −− = ⇔ + + + ++
=
− − + − + − − = ⇔ + − = ⇔ =±⇒
=
y y yy y yy
x
yy y yy yy y
x
d. Đặt
7
8 2 15
15 2
−=
− = ⇒− = − ⇒ + =−
−=
xa
x b c x ab c
xc
ta được:
4 4 4 444 444 44 4
2
22 2
(7)(8)(152) 0 ( )0
3 37
4 04 0
0
2 4
16
− +− = − ⇔+=⇔+−=⇔+−+ =
⇔ + + =⇔ + + =⇔=
x x x abc abc ab ab
ab
ab a b ab a b b ab
( do
22
37
0
4 16
++≥
ab b
nhưng không xảy ra dấu “ = “)
{ }
( 7)( 8) 0 7;8− − =⇔∈xx x
e.
{ }
4; 10x∈− −
E. Phương trình dạng: ax
4
+ bx
3
+ cx + a = 0 ( phương trình đối xứng )
Cách giải:
432 4 2 2
0 ( 1) ( 1) 0ax bx cx bx a a x bx x cx+ + + +=↔ ++ ++ =
Đặt
2
1tx= +
hoặc
1
tx
x
= +
Ví dụ: Giải phương trình sau
4 32
2 3 3 20xxxx− − − +=
Lời giải
4 32 4 2 2 2 2 2 2
2 3 3 2 0 2( 1) 3 ( 1) 0 2( 1) 3 ( 1) 5 0− − − +=⇔ +− +− =↔ + − +− =x x x x x xx x x xx x
Đặt
2
1= +tx
ta được:
2
22
0
1 0( )
1
2 3 5 0 ( )(2 5 ) 0 2;
25 0
2
25 0
+=
++=
− − =⇔ − − =⇔ ⇔ ⇔∈
−=
−=
tx
x x vo nghiem
t tx x t x t x x
tx
tx
F. Phương trình dạng: ax
5
+ bx
4
+ cx
3
+ bx + a = 0 ( phương trình đối xứng )
- Nhận thấy x = -1 là nghiệm của phương trình vậy vế trái của phương trình có 1 nhân tử
là x + 1
Sau đó phương trình quay trở về dạng E
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

128
Ví dụ: Giải các phương trình sau
a.
543 2
2 4 4 20xx x xx− − − −+=
b.
543 2
6 11 15 15 11 6 0xx xxx−−−−+=
c.
5432
3 3 10xx x xx− + + −+=
Lời giải
a.
5 4 3 2 4 32
1
2 4 4 2 0 ( 1) (2 3 3 2) 0 1; 2;
2
− − − − + = ⇔ + − − − + = ⇔ ∈−
dang E
xxxxx x xxxx x
b. Ta có:
5 4 3 2 54 4 3 3 2 2
6 11 15 15 11 6 0 (6 6 ) (17 17 ) (2 2 ) (17 17 ) 6 6 0− − − − +=⇔ + − + + + − + + +=xxxxx xxxxxxxxx
4 32
4 32
1
( 1)(6 17 2 17 6) 0
6 17 2 17 6 0 (*)
= −
⇔+ − + − +=⇔
− + − +=
x
x xxxx
xxxx
22 2 2
(*) 6( 1) 17( 1) 10 0⇔ + − +− =x xx
Đặt
2
1= +tx
ta được:
2
2 22 2
2
2 20
6 17 10 0 6 3 20 10 0 (2 )(3 10 ) 0
3 10 3 0
++=
− − =⇔ +− − =⇔+ − =⇔
− +=
xx
t tx x t tx tx x t x t x
xx
2
3
1
3 9 3 0 3 ( 3) ( 3) 0 1
;3;
1
3
3
=
⇔ − −+=⇔ − − + =⇔ ⇒ =−
=
x
x x x xx x S
x
c. Ta có:
5432 432
432
1
3 3 1 0 ( 1)( 2 5 2 1) 0
2 5 2 1 0 (*)
= −
− + + −+= ⇔ + − + − + = ⇔
− + − +=
x
xx x xx x x x x x
xxxx
Giải (*):
Với x = 0 phương trình vô nghiệm.
Với x ≠ 0 ta có:
( )
2
2
2
2
11 1 1 1
(*) 250 230 120
⇔ + − ++=⇔+ − ++=⇔+−+=
x x x x x VN
xx yx x
Vậy phương trình có tập nghiệm
{ }
1S = −
G. Phương trình dạng:
2
432
0
+ + + += =
ed
ax bx cx dx e
ab
- Phương trình ở trường hợp 4 là trường hợp đặc biệt của phương trình này
- Cách giải:
+) Đặt
2
1tx= +
+) Xét
0x ≠
, chia cả hai vế cho
22 2
22
00
⇒ + ++ + =⇔ + + + +=
de e
d
x ax bx c ax
bx c
xx x
x
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

129
Đặt
2
22
2
2=+⇒=+ + ⇒
mm
tx t x m
xx
phương trình bậc hai
⇒⇒tx
Ví dụ: Giải các phương trình sau
a.
432
8 21 24 9 0xx x x− + − +=
b.
432
2 21 74 105 50 0xxx x− + − +=
c.
43 2
2 3 27 6 8 0xx x x+ − + +=
d. [ HSG Nam Trực – 2015 ]
43 2
3 4 3 10xx xx+ + + +=
e.
43 2
6 25 12 25 6 0xxx x+ + − +=
Lời giải
a. Do x = 0 không thỏa mãn phương trình nên ta chia cả hai vế cho x
2
, được:
432 2
2
2
2
2
24 9
8 21 24 9 0 8 21 0
93 3 3
8 21 0 8 15 0
− + − +=⇔ − + − + =
⇔ + − ++=⇔+ − ++=
xx x x xx
xx
x x xx
xx xx
2
2
3
3
3 3 0( )
5 13
x
3
2
5 30
5
+=
− +=
±
⇔ ⇔ ⇔=
− +=
+=
x
x x vo nghiem
x
xx
x
x
b. Ta có:
2
432 2
2
6
6 50
5
2 21 74 105 50 0 2 21 54 0 1
;2;5;
9
2
2 9 10 0
2
=
− +=
− + − +=⇔ − +=⇔ ⇔ ⇔
∈
=
−+=
t
xx
xxx x t t x
t
xx
c. Ta có:
2
43 2
2
2
27
22
2
2 3 27 6 8 0 2 3 35 0
2
5
7 40
7 33 5 17
;
22
5 20
+=
+ − + +=⇔ + + + − =⇔
+=−
− +=
± −±
⇔ ⇔∈
+ +=
x
x
xx x x x x
xx
x
x
xx
x
xx
d. Ta có:
43 2 2 2
2
11
3 4 3 10 3
40 3 20
1
1( )
1
1
21
2
+ + + +=⇔ + + + +=⇔ + +=
+=−
= −
⇔ ⇔ ⇔=
−
= −
+=−
xx xx x x y y
xx
x vo nghiem
y
x
x
y
x
x
Vậy phương trình có tập nghiệm
{ }
1S = −
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

130
e. +) Với x = 0 không là nghiệm của phương trình
+) Với x ≠ 0 chia cả hai vế cho x
2
ta được:
2
2
11
6 25 12 0
+ + − +=
xx
xx
Đặt
22
2
11
2=−⇒ + = +yx x y
xx
ta được:
22
13
2
6 25 24 0 6 9 16 24 0 (2 3)(3 8) 0
18
3
−
−=
+ +=⇔ ++ +=⇔ + +=⇔
−
−=
x
x
y y yy y y y
x
x
2
2
1
2;
2 23
11
2
2; ; 3;
1
23
3 38
3;
3
=−=
−=−
⇔ ⇔ ⇒=− −
−=−
=−=
xx
xx
S
xx
xx
BÀI TẬP VỀ NHÀ BÀI
Bài 1: Giải các phương trình sau
a.
22
1 1 13
( 29) ( 30) 36xx
+=
++
b.
65432
3 6 7 6 3 10xx x x x x−+−+−+=
Lời giải
a. Điều kiện: x ≠ -29, x ≠ -30
22 22
1 1 13 1 1 2 2 13
( 29) ( 30) 36 ( 29) ( 30) ( 29)( 30) ( 29)( 30) 36
+=⇔+− + =
+ + + + ++ ++x x x x xx xx
2
2
1 1 2 13 1 2 13
( ) 11
29 30 ( 29)( 30) 36 ( 29)( 30) ( 29)( 30) 36
⇔ − + =
⇔ + += +
+ + ++ ++ ++
x x xx xx xx
2
2
17
1
( 29)( 30) 6
⇔ +
=
++
xx
+)
{ }
2
1 71
1 ( 29)( 30) 6 0 59 864 0 27; 32
( 29)( 30) 6 6
=−=⇔+ +−=⇔+−=⇔∈−−
++
x x xx x
xx
22
2
1 13 6 59 6 59
) 59
870 0 870 0 ( )
( 29)( 30) 6 13 2
13 2
−
+ =
⇔+++=⇔+ ++− =
++
x x x v
o nghiem
xx
Vậy phương trình có tập nghiệm
{ }
27; 32S =−−
b.
65432
3 6 7 6 3 10xx x x x x−+−+−+=
+) x = 0 không là nghiệm của phương trình
+) Chia cả hai vế cuả phương trình cho x
3
ta được:
32 3 2
23 3 2
63 1 1 1 1
3 6 7 0
( ) 3( ) 6( ) 7 0− +−+−+=⇔ + − + + +−=xxx x x x
xx x x x x
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

131
Đặt
2 23 3 3
23
1 1 1 1 11
2; 3
. 3
=+⇒ + =− + = + − + =−
tx x t x x x x t t
x x x x xx
Thay vào phương trình ta được:
( )
32 3
2
2
3 3( 2) 6 7 0 ( 1) 0 1
1 13
1 10 0
24
− − − + −= ⇔ − = ⇔=
⇔ + =⇔ −+= ⇔ − + =
ttt t t t
x x x x VN
x
CHUYÊN ĐỀ 5: ĐỒNG NHẤT THỨC
A. Các bài toán về biểu thức nguyên
1.
2 222
( ) 2( )a b c a b c ab bc ca++ = + + + + +
2.
1 2 32 1
( )( ... )
nn n n n n
a b a ba a b a b b
−− − −
− = − + + ++
3.
2 2 21 22 232 21
( )( ... )
nn n n n n
a b a ba a b a b b
−− − −
− = + − + −−
4.
1 2 32 1
( )( ... )
nn n n n n
a b a ba a b a b b
−− − −
+ = + − + −+
5. Nhị thức Newton:
1 22
( 1)
( ) . . ...
2
nn n n n
nn
a b a na b a b b
−−
−
+ = + + ++
Bài 1: Cho a + b + c = 0 và a
2
+ b
2
+ c
2
= 14. Tính A = a
4
+ b
4
+ c
4
Lời giải:
Ta có:
2 222
0( )0 2 2 2 0++=⇒ ++ =⇒ + + + + + =abc abc a b c ab bc ca
14 2( ) 7 (1)⇔=− ++ ⇒++=−ab bc ca ab bc ca
Lại có:
2 2 2 4 4 4 22 22 22 2
14 2 2 2 14 169 (2)++=⇒+++ + + = =abc abc ab ac bc
Từ (1) suy ra:
22 22 22 2 2 2 22 22 22
2 2 2 49 2 ( ) 49+++ + + =⇔ +++ ++=a b b c c a ab c a bc abc a b b c c a abc a b c
222222 444 2
49 (2): 14 2.49 98ab bc ca a
b c⇒ + + = ⇒ ++= − =
Bài 2: Cho x + y + z = 0 và xy + yz + xz = 0. Tính
2019 2020 2021
( 1) ( 1)Ax y z=− + ++
Lời giải
Từ :
2 22 222
0 2( ) 0 0 0x y z x y z xy yz zx x y z x y z++=⇒+++ ++ =⇒++=⇒===
2019 2020 2021
1010A⇒=− + + =
Bài 3 : Cho x + y + z = 0 , chứng minh rằng
a.
2 222 4 44
()2()xyz xyz++ = ++
b.
3 3 32 2 2 5 5 5
5( )( ) 6( )xyzxyz xyz++ ++ = ++
c.
5 55 2 22
2( ) 5 ( )x y z xyz x y z++ = ++
Lời giải:
a.
2 222 444 22 2222
( ) 2( ) (1)++ =+++ + +xyz xyz xyyzzx
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

132
2 22 2 222 2
0 2( ) ( ) 4( ) (2)++=⇒++=− ++ ⇒ ++ = ++x y z x y z xy yz zx x y z xy yz zx
Từ (1), (2) suy ra :
4 44 22 2222 22 2222 2 2 2
2( ) 4( 2 2 2 )+++ ++ = +++ + +x y z x y y z z x x y y z z x xy z x yz xyz
222222 22 2222 4 44 22 2222
=0
4[ 2( )]=4(x ) 2( )xy yz zx x y z y yz zx x y z xy yz zx= +++++ ++ ⇒++= ++
Thay vào (1), ta được :
2 222 4 44
()2()xyz xyz++ = ++
b.
5 5 5 2 2 22 22
1
() () ()
5
VT x y z x y x y x z x z y z y z=+++ ++ ++ +
Từ x + y + z = 0 suy ra :
5 55
1
; ; (
) (1)
5
+=− +=− +=−⇒ = + + − + +x y z x z y y z x VT x y z xyz xy yz zx
2 22
2 2 22
0 ( ) 0 2( )
2
xyz
x y z x y z x y z xy yz zx xy yz zx
++
++=⇒ ++ =⇒ + + =− + + ⇒ + + =
−
Theo câu a, ta có :
3 33
3x y z xyz++=
khi x + y + z = 0
2 2 23 3 3
( ). . (2)
23
++ ++
⇒− + + =
x y zx y z
xy yz zx xyz
Thay vào (1), ta được :
3 3 32 2 2 5 5 5
5( )( ) 6( ) (*)++ ++ = ++xyzxyz xyz
c. Ta có :
3 33
3x y z xyz++=
, thay vào (*), ta được :
2 22 5 55 2 22 5 55
5.3 ( ) 6( ) 5 ( ) 2( ) ( )++ = ++ ⇒ ++ = ++xyz x y z x y z xyz x y z x y z dpcm
Bài 4 : Chứng minh rằng
a.
333 2 2 2
2( 3)( )( )( )( )a b c abc a b c a b b c c a
+ + − = ++ − + − + −
b.
222
( )( )( ) 4 ( ) ( ) ( )abbcca abccab abc bca+ + ++ = + + + + +
Lời giải
a.
222
( )( )VP a b c a b c ab bc ca= ++ + + − − −
333 33 33
1
3 () 3()3 () 3( )
2
VT a b c abc a b c ab a b abc a b c ab a b c=++− =+ +− +− =+ +− ++
2 2 222
( )[(a+b) ( ) 3 ] ( )( )abc abcc ab abca b c abbcca VTVP= ++ − + + − = ++ + + − − − ⇒ =
b.
2 2 22 22
6VT abc ca ac ab a b bc b c= ++++++
2 2 22 22
6VP abc ca ac ab a b bc b c VT= ++++++=
Bài 5 : Cho a + b + c = 4m. Chứng minh rằng
a.
2 22 2
2 16 8ab b a c m mc++−= −
b.
22 2
222 2
4
22 2
+− +− −++
+ + =++−
abc acb abc
abc m
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

133
Lời giải:
a.
22 22 2
( ) (4 ) 16 8VT a b c m c c m mc VP=+ −= − −= − =
b. Từ
4 42 2
2
abc
abc m abc m c m
c
+−
++= ⇒+−= − ⇒ = −
Tương tự:
2 2 2 222 2 222 2
(2 ) (2 ) (2 ) 12 4 ( ) 4VT mc mb ma abc m mabcabc mVP= − + − + − =+++ − ++=++− =
Bài 6:
a. Cho
( )( ) (*)++ + + =x y z xy yz zx xyz
Chứng minh rằng:
2019 2019 2019 2019
()+ + = ++x y z xyz
b. Nếu
6++xyz
. Chứng minh rằng:
( )( )( ) 2 6=+ + +− A x y y z z x xyz
Lời giải
a. Theo (*)
( )( ) 0⇔ ++ + + − =x y z xy yz zx xyz
22 2 2 2 2
0⇔++++++++−=xy x y xyz xyz y z z y x z xz xyz xyz
22
()()()()0()( )0
0
( )( )( ) 0 0
0
xy x y yz x y z x y xz x y x y xy yz z xz
xy x y
xyyzzx yz y z
zx z x
⇔ ++ ++ ++ +=⇔+ +++ =
+= =−
⇔ + + + =⇔ +=⇔ =−
+= =−
Giả sử:
2013 2013 2013 2013 2013 2013 2013 2013
;( )x y x y x y z z x y z z dpcm=−⇒ =− ⇒ + + = + + = ⇒
b. Theo câu a, ta có:
( )( )
( )( )( ) ( )( )
3
x y z xy yz zx
x y y z z x x y z xy yz zx xyz A x
yz
++ + +
+ + + = ++ + + − ⇒ = −
Vì
6xyz xyz++ ⇒++
là số chẵn
⇒
1 trong 3 số x, y, z là số chẵn
36 6xyz A⇒⇒
Bài 7 : Cho
222 357
1abcabc++=++=
. Tính
2 9 1945
Aa b c=++
Lời giải
Ta có :
222 2
1 0 1 1 1 1; 1 , 1abc a a a bc+ + =⇒ ≤ ≤ ⇔ ≤ ⇔−≤ ≤ −≤ ≤
2 23
0
1 1 (1 ) 0 ,'' ''
1
a
a a a aa
a
=
−≤ ≤⇒ − ≥ ⇒ ≥ =⇔
=
3 32 2 5
1 1 1 (1 ). 0−≤ ≤⇒ ≤⇒ − ≥ ⇒ ≥b b bb b b
Dấu « = » xảy ra khi b = 0 hoặc b = 1.
Tương tự :
27
≥cc
. Dấu « = » xảy ra khi c = 0 và c = 1.
Mặt khác ta lại có :
222357 232527
1 ; ; ,,a b c a b c a a b b c c abc++=++=⇒ = = =⇒
có 1 số bằng 1 và 2 số bằng 0
1A⇒=
Bài 8 : Tìm các số a, b, c sao cho :
32
ax ( )( )( )x bxc xaxbxc xR− + − = − − − ∀∈
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

134
Lời giải:
Ta có:
2 33 2
( )( )( ) ( ) ( ) axx a x b x c a b c x ab bc ac x abc x x bx c− − −=++ + ++ − +=− +−
0
0,
()
1; 1
(1 ) 0
abca bc
bc a
ab bc ca b a b c bc b bc b
ab c
abc c c
ab
++= +=
= = ∀
⇒ + + = ⇒⇒ + + = ⇒ = ⇒
==−=
= −
=
Bài 9: Cho a, b thỏa mãn:
32 32
3 5 17 0; 3 5 11 0.− + −= − ++=aaa bbb
Tính A = a + b
Lời giải:
33 22
32
( ) 3( ) 5( ) 6 0
()3()3[()2]5()60
+ − + + + −=
⇔+ − +− + − + +−=
a b a b ab
ab abab ab ab ab
32
()3()5()63()60ab ab ab abab ab⇔+ − + + +−− ++ =
32
()3()5()63( 2)0⇔ + − + + + −− +− =ab ab ab abab
3 22
()2()()2()3()63( 2)0ab ab ab ab ab abab⇔+ − + −+ + ++ +−− +−=
2
( ) ( 2) ( )( 2) 3( 2) 3 ( 2) 0ab ab abab ab abab⇔ + +− − + +− + +− − +− =
( ) ( ) (
) ( )
2
2
22 2
2
222
20
( 2)[(a+b) ( ) 3 3 ] 0
()()330
22
30 2 2 2 2 2 60
2
2
1 1 40
+−=
⇔ +− − + +− = ⇔
+ − + +− =
= =
⇔⇔
− + −−+= − + − − +=
=
⇔ ⇔=
− +−+−+=
ab
ab ab ab
ab ab ab
AA
a ab b a b a
ab b a b
A
A
a b a b VN
Vậy A = 2.
Bài 10: Chứng minh rằng
8753
10Ax x x x= − + − +>
Lời giải
+) Xét
7 8 732 5 3
1 ( 1) 0 ; ( 1) 0 1 0x xx x xxx x x A≥⇒ −≥⇒ ≥ −≥⇒ ≥ ⇒ ≥>
3 5 2 35 7 8 3 5 7
) 0 1 1 0; (1 ) 0 1 ; 1 0 0+ ≤≤⇒− ≥ − ≥⇒≥ ≥ ⇒ = +− + − ≥⇒ >x x x x xx x A x x x x A
Với
7
3
0
0
0
−>
<⇒
−>
x
x
x
Với
53 8 5
1 ( 1) 0 0 1≤−⇒ + ≥⇒ + ≥⇒ ≥x xx x x A
Với
5
1 01 0 0x xA−≤<⇒+ >⇒ >
Vậy A > 0 với mọi x.
BÀI TẬP VỀ NHÀ
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

135
Bài 1: Tìm các số a, b, c, d sao cho:
432
( ) ax 8 4A x x bx x=+ + −+
là bình phương của đa
thức
2
()B x x cx d=++
Lời giải:
2
2 2 24 3 2 2 2 2
2
2
2
[()] ( ) 2 ( 2) 2 () ()
28
4
ca
c db
B x x cx d x cx c d x cdx d A x B x
cd
d
=
+=
= ++ =+ + + + + ⇒ = ⇔
= −
=
+)
2 2; 4; 8d cad=⇒=− =− =
+)
2 2, 4, 0d cab=−⇒ = = =
Bài 2: Cho
3 2 32
3 19; 3 98.a ab b a b−= −=
Tính
22
Ea b= +
Lời giải:
Ta có:
3 22 2 6 42 24 2 3 2 6 42 42
( 3 ) 19 6 9 ;98 ( 3 ) 6 9a ab a ab ab b ab b ba ab− ==−+ =−=−+
2 2 6 6 42 24 2 23 2 2
3
19 98 3 3 ( ) 9965a b ab ab a b a b+ =++ + = + ⇒+=
Bài 3: Chứng minh rằng:
12 9 4
10= − + − + > ∀∈Ax x x x xR
Lời giải
+) Với
93
3
( 1) 0
1 10
( 1) 0
−≥
≥ ⇒ ⇒
≥ > ∀∈
−≥
xx
x A
xR
xx
+) Với
9
0
00
0
−>
<⇒ ⇒ >
−>
x
xA
x
+) Với
49 4 5
10
01 0
(1 ) 0
−≥
≤ ≤⇒ ⇒
>
−= − ≥
x
xA
xxx x
Bài toán được chứng minh
Bài 4: Chứng minh rằng
a. Nếu a + b + c ≥ 0 thì
333
3 0 (,, )++− ≥ ∈a b c abc a b c R
b.
444 4
4 0 ,,,+++ − ≥ ∀ ∈a b c d abcd a b c d R
Lời giải
a. Có:
333 222
3 ( )( )a b c abc a b c a b c ab bc ca+ + − = ++ + + − − −
mà
2
0 ( ); ( ) 0++≥ − ≥abc gt ab
nên:
2 2 22
2 0 2.− +≥⇒+≥a ab b a b ab
Tương tự:
22 22
2; 2+≥ +≥a c ac b c bc
222 222
0a b c ab bc ca a b c ab bc ca⇒++≥ ++⇒++−−−≥
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

136
b.
4 4 4 4 4 4 22 4 4 2 2 22 2 2
4 2 2224a b c d abcd a b a b c d c d a b c d abcd+++ − =+− ++ − + + −
2 22 2 22 2
( ) ( ) 2( ) , , ,=− +− + − ∀ ∈a b c d ab cd abcd R
CÁC DẠNG TOÁN VỀ PHÂN THỨC ĐẠI SỐ
A. Rút gọn, tính giá trị của biểu thức thỏa mãn điều kiện cho trước
Bài 1: a. Cho a – 2b = 5. Tính giá trị biểu thức
323
25 5
a b ba
A
ab
−−
= +
+−
b. Biết 2a – b = 7. Tính
5 32
3727
ab b a
B
ab
−−
= +
+−
c. Biết
2 2 22
10 3 5 0;9 0a b ab a b− + = −≠
. Tính
25
33
ab ba
C
ab ab
−−
= +
−+
d. Cho
22
3 3 10a b ab+=
và
0.ba>>
Tính
ab
D
ab
−
=
+
e. Biết
22
94 2 3x y xy xy x+ − = −−
. Tính
2
32 2
25 2
:
10 25 2
xy
E
x x xy y
−−
=
− + −−
Lời giải
a) Ta có:
3(2 5) 2 3 (2 5) 4 15 5
25 25 2
2(2 5) 5 5 4 15 5
+− − + + −
− =⇒ = +⇒ = +
= + =
++ − + −
b bb b b b
ab ab A
b b bb
b) Ta có : 2a – b = 7 thì b = 2a – 7 do đó :
( ) ( )
( )
5 273272
5 3 2 3
7 4 21
2
3727 37 227737421
− − −−
−− +
−
=+= + =+=
+ − + −− + −
aa a a
ab b a a
a
B
a b a a aa
c) Ta có:
22
22
(2 )(3 ) (5 )(3 ) 3 15 6
(1)
(3 )(3 ) 9
− ++ − − + −
= =
−+ −
ab ab ba ab a ab b
C
ab ab a
b
Từ giải thiết:
2 2 2 2 22
22 2
2
22 22
3 3(3 10 ) 6 27 3
10 3 5 0 5 3 10 3
99
a b a b ab
a b ab ab b a A
ab ab
+ − − −+
− + =⇒ = − ⇒= =
=−
−−
d) Ta có:
Cách 1: Ta có:
22 22
3
3 3 10 3 3 10 0 (3 )( 3 ) 0
3( )
31
32
=
+= ⇒+− =⇔− −=⇔
=
− −−
⇒= = =
++
ba
a b ab a b ab a b a b
a b loai
ab a a
D
ab a a
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

137
Cách 2:
22 2 2 2
2
22 2 2 2
( ) 2 336 1 1
( ) 2 336 4 2
− − + +− ±
= = = =
⇒=
+ + + ++
a b a ab b a b ab
DA
a b a ab b a b ab
Do
0
1
0
0
2
−<
−
>⇒ ⇒ <⇒ =
+>
ab
ba D
D
ab
e) Ta có:
22 2
30 3
8
9 4 2 3 ( 3) 3 0
30 1
3
xy x
x y xy xy x x y x A
xy
−= =
−
+ − = −−⇔ − +−=⇔ ⇔ ⇒ =
−= =
Bài 2: Cho
1
3x
x
+=
. Tính giá trị của các biểu thức sau:
a.
2
2
1
Ax
x
= +
b.
3
3
1
Bx
x
= +
c.
4
4
1
Cx
x
= +
d.
5
5
1
Dx
x
= +
Lời giải
a.
2
2
2
11 1
2. . 2 2
7
= + + −= + −=
Ax x x
xx x
b.
3
32
2
11 1
1 3.6 18
= + = + −+ = =
Bx x x
xx x
c.
4 4 2 22
442 2
111 1
2. . 2 2
47
= + = + + − = + −=
Cx x x x
xxx x
d.
5
5 43
2 4 2
2 34 4 2
1 1 1 1 11 1 1 1
... 1
=+ =+ −+ −+=+ +−+−
Dx xxxxx xx x
x x x x xx x x x
3.(47 7 1) 123= −+ =
Cách 2:
23 5
23 5
1 1 11
( )( ) 123x x xx
x x xx
+ + = ++ + =
Bài 3: Cho
2
4 10xx− +=
. Tính
5
5
1
Ax
x
= +
và
7
7
1
Bx
x
= +
Lời giải
Có:
22
4 10 14 0x x x xx− += ⇔ += ⇒ ≠
Chia cả hai vế cho x ta được:
1
4x
x
+=
Ta có:
2
22
22
11 1
2 16 14
+ =++=⇒+=
xx x
xx x
3
3 3 33
3 33
1 1 11 1 1
3. . . 3.4 4 52
+ =++ + =++ =⇒+=
x x xx x x
x x xx x x
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

138
23 5 5
23 5
5
5 23
5 23
1 1 11 1
4
1 11
4 14.52 4 724
⇒ + + = + ++ =+ +
⇒ + = + + −= −=
x x xx x
x x xx x
x xx
x xx
Bài 4: Cho
2
2008
1
x
xx
=
−+
. Tính
2
42
1
x
M
xx
=
++
và
2
42
1
x
N
xx
=
−+
Lời giải
Có:
42 2 2 2
1 ( 1)( 1); 2008( 1) (1)+ += −+ ++ = −+xx xx xx x xx
Ta có:
2
2
22
2008 2008( 1) 2008
1
2009 2008( 1) 2009 2008 2008( 1)
= ⇒= +−
−+
⇒ = + ⇒ + = ++
x
xx x
xx
xx xxxx
2
4017 2008( 1) (2)⇔ = ++x xx
Lấy (1).(2) được:
22
2 24 2 2 2
42
4017 2008
4017 2008 ( 1) (*) 2008
4017. 2008
1 4017
= ++ ⇔ = ⇔ = ⇒ =
++
x
x xx M
M
xx
2
2 42 42
2 42 2 2 42 2
2008
(*) ( 1) ( 1)
4017
(12) (1)2
⇒= ++= ++
⇔= −++ ⇒= −++
x xx Mxx
x Mx x x x Mx x Mx
2
2 42
42
(1 2 )
(1 2 ) ( 1) (1
2 ).
1 12
Mx M
Mx Mx x M
M N M N
xx M
−
⇒− = − +⇒ = ⇒− = ⇒ =
−+ −
Bài 5: Cho
0 (1); 2 (2)++= ++=
xyz abc
abc xyz
. Tính
2
22
=++
abc
A
xyz
Lời giải
Ta có:
0 0 0 (3)
++
++=⇒ =⇒ + + =
x y z bcx acy abz
bcz acy abx
a b c abc
Từ (2) ta có:
22
22
2 4 24
++=⇒ ++ =⇔ + + + + + =
a b c a b c a b c ab ac bc
x y z x y z x y z xy xz yz
2
22
2 4 (4)
++
⇔+++ =
a b c abz acy bcx
x y z x
yz
Thay (3) vào (4), ta được:
2
22
4
=++=
abc
A
xyz
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

139
Bài 6: Biết
333
3a b c abc++=
và
0abc++≠
. Tính
222
2
()
abc
A
abc
++
=
++
Lời giải
Ta có:
333 222 222
3 ( )( ) 0a b c abc a b c a b c ab bc ca a b c ab bc ca++− =++ ++− −− ⇒++−−−=
2
222
2
31
( )( )( )0
(3 ) 3
a
ab bc ca abc A
a
⇔ − + − + − =⇒==⇒ = =
Bài 7: Tính
22 2
2 22
() () ()bc y z ac z x ab x y
A
ax by cz
−+ −+ −
=
++
, biết
0
25
ax by cz
abc
++=
++=
Lời giải
Ta có:
2 2 22 2 2
()()() ()()()2( )M bc y z ac z x ab x y by a c cz a b ax b c bcyz acxz abxy= − + − + − = ++ ++ +− + +
Ta phải tạo ra nhân tử: a + b + c
2 2 2 2 2 22 22
()()()2( )
= ++ + ++ + ++ − + + − − −M by a b c cz a b c ax a b c bcyz acxz abxy b y c z a x
2 2 2 2 2 22 22
( )( ) 2( ) ( )= ++ + + − + + − + +a b c by cz ax bcyz acxz abxy b y c z a x
Lại có :
2 22 2 2 22 2 2 2
( ) 0 2( ) 0 ( )( )ax by cz a x b y c z abxy acxz bcyz M a b c by cz ax+ + =⇒ + + + + + =⇒ = ++ + +
25Aabc⇒ =++=
Bài 8: Cho a.b.c = 2, rút gọn :
2
2 1 22
ab c
A
ab a bc b ac c
= ++
++ ++ + +
Lời giải
2
2 1 22
2
22
2
22 2
2
2
1
= ++
++ ++ + +
=++
++ + + + +
=++
++ + + ++
++
=
++
=
ab c
A
ab a bc b ac c
a ab c
ab a abc ab a ac c abc
a ab
ab a ab a a ab
a ab
a ab
Bài 9: Cho a + b + c = 0, rút gọn :
222
222 222 222
abc
A
abc bca cba
=++
−− −− −−
Lời giải
Từ:
2 22 222
0 () 2 2abc a bc a b c bc a b c bc++=⇒ =− + ⇒ = + + ⇒ − − =
Tương tự:
2 2 2 333
222 222
2 ; 2 (*)
222 2
++
−−= −−= ⇒= + + =
a b c abc
b a c ac c a b ab B
bc ac ab abc
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

140
Ta có:
3 3 3 33 33
332
0 () 3() 3
3
++=⇒+=−⇒ + =− ⇒− = + + + = + −
⇒++=
abc bc a bc a a b c bcbc b c abc
a b c abc
Do đó:
333
33
2 22
++
= = =
a b c abc
B
abc abc
Bài 10: Cho ba số a, b, c khác 0 thỏa mãn:
111
2019 ; 0++= + + =abc
abc
.
Tính
222
Aabc=++
Lời giải
Từ:
2 222
2019 ( ) 2019 2( ) 2019abc abc a b c abbcca++= ⇒ ++ = ⇒ + + + + + =
Mặt khác:
111
0 0 0
( 0) 2019
++
++=⇔ =⇒ + + = ≠ ⇒=
bc ca ab
bc ca ab abc A
a b c abc
Bài 11: [ HSG Yên Phong – 2015 ]
Cho a, b, c thỏa mãn:
2 2 2 2013 2013 2013
( )( ) ( )4; 1+++ + + = + + =a b c b c a c a b abc a b c
.
Tính
2015 2015 2015
111
A
abc
=++
Lời giải
Ta có:
22 2
2 22 2
2 2
( ) ( ) ( )4 0
2 2 2 40
+++ + +− =
⇔++++++++−=
a b c b c a c a b abc
ab abc ac bc abc ba ca abc cb abc
2 22222
22 2
20
( ) ( )( ) 2 0
⇔ + +++++=
⇔ + ++ + + =
ab abc ac ba bc ca cb
a b c b c a bc abc
22 2
2
( 2 ) ( )( ) 0
( )( ) 0
( )( )( ) 0
⇔ ++ ++ + =
⇔+ +++ =
⇔+ + +=
a b c bc b c a bc
b c ab ac bc a
abbcca
2013 2013 2015 2015
0 ;1
01
01
ab a b a b a b M
bc b c M
ca c a M
+ = =−⇒ =− =− ⇒ =
⇔ + = ⇔ =−⇒ =
+ = =−⇒ =
Vậy M = 1 với a = b = c = 1.
Bài 12: Cho ba số a, b, c khác 0 và thỏa mãn: a + b + c = 0.
Tính
222 222 222
111
A
abc bca cab
=++
+− +− +−
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

141
Từ:
222
2 2 222
222
2
0 () () 2
2
a b c ab
abc a bc ab c ab c b c a bc
c a b ac
+−=−
+ + = ⇒ =− + ⇒ + =−⇒ + = ⇒ + − =−
+−=−
Do đó:
111 ( )
0
222 2
− ++
= + + ⇒= =
−−−
abc
AA
ab bc ac abc
Bài 13: Cho x, y, z đôi một khác nhau và Từ:
111
0
xyz
++=
.
Tính
2 22
222
yz xz xy
A
x yz y xz z xy
=++
+++
Lời giải
Từ :
111
000
xy yz zx
xy yz zx yz xy xz
x y z xyz
++
++=⇒ =⇒ + + =⇒ =−−
Có :
22
2 ( ) ( )( );+ = + +− − = − −x yz x yz xy xz x y x z
Tương tự:
22
2 ( )( ); 2 ( )( )+=− − +=− −y xz y x y z z xy z x z y
()()( )
( )( ) ( )( ) ( )( ) ( )( )( )
yz xz xy yz y z xz z x xy x y
A
xyxz yxyz zxzy xyyzzx
− −− −− −
⇒= + + =
−− −− −− −−−
Tử số của A
22 2 2 22
2 22
2
()( )()
( )( ) ( )( )
−−−+−
= −+ − + −
=− ++− +
yz y z xz xz xy x y
zyx zx y xyyx
y x z xy z x y x y
2
( ) ( ) ( )( )( ) 1xyzxy z xy xyyzzx A
=− + −− = − − −⇒=
Bài 14: Tính
3 33
111 ;,,0; 3
=+++ ≠ ++=
xyz
A x y z x y z xyz
yzx
Lời giải
( ) ( )
( ) ( )( ) ( )
( ) ( )( )
( ) ( ) ( )
3 33
3
3
3
3
2
2 22
3
3 30
3 30
30
30
( )( )
0
++=
⇔+ +− +− =
⇔ ++ − + ++ − ++ =
⇔ ++ − ++ + + =
⇔ ++ ++ − + + =
⇔ ++ + + − − − =
x y z xyz
x y z xy x y xyz
xyz zxyxyz xyxyz
x y z x y z xy yz zx
x y z x y z xy yz zx
x y z x y z xy yz zx
2 22
0
0
++=
⇔
++−−−=
xyz
x y z xy yz zx
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

142
+) Trường hợp:
0 ;;++=⇒+=− +=− +=−xyz xy zxz yyz x
Do đó:
.. 1
+ ++−
= = = −
x y y z x z xyz
A
y y x xyz
+) Trường hợp
2 22
0++−−−=x y z xy yz zx
ta có:
222
0
( )( )( )0 0 8
0
−=
− + − + − =⇔ −=⇔= =⇒ =
−=
xy
xy xz yz yz x yz A
zx
BÀI TẬP VỀ NHÀ
Bài 1: Cho ba số a, b, c khác 0 và thỏa mãn: a + b + c = 0.
Tính
222
222 222 222
a bc b ac c ab
A
abc bca cab
+++
=++
−− −− −−
Lời giải
Từ :
2 2 2 222
02 2abc bc a b bcc a a b c bc++=⇒+=−⇒ + + = ⇒ − − =
Tương tự :
2 2 2 222
222 222
3
2; 2
2 2 2 2222
a bc b ca c ab a b c
b c a ac c a b ab S
bc ac ab bc ac ab
+++
− − = − − = ⇒= + + = + + +
333
33 3
3
2 22 2
a b c abc
abc abc
++
= += +=
Bài 2*: Biết a + b + c = 0. Tính giá trị của biểu thức sau,
−−−
= ++ ++
−−−
ab bc ca c a b
A
c a b ab bc ac
Lời giải
Đặt
ab bc ca
M
cab
−−−
=++
Ta có:
22
()()()
. 1 ( )1
. 1
c c b bcaca c abcab ccab
M
a b a b ab a
b ab ab
− + − −
−− −−
=+
=+=+
−− −
[ ]
2
()
.2 2
1 11
cc a b
cc c
ab ab ab
−−
=+ =+=+
Tương tự:
2 2 2 2 2 333
22
. 1 ; . 1 32 32
++
=+ =+ ⇒=+ + + =+
−−
a a b b c a b abc
MM A
b c bc a c bc ab
bc ac abc
Ta có:
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

143
333 3 3 33
22
()3() () 3()
( )()() 3
++=+ − ++= + + − −
= ++ + − + + +
a b c ab abab c ab c abc
abc ab abcc abc
3 3 3.2 9abc A= ⇒=+ =
B. Chứng minh đẳng thức thỏa mãn điều kiện của biến
Bài 1: Cho
222
111 1 1 1
2 (1); 2 (2)++= + + =
abc a b c
. Chứng minh rằng:
a b c abc++=
Lời giải
Từ (1) suy ra:
2
222
111 1 1 1 1 1 1
4 24
111
11
++ =⇔ + + + + + =
++
⇒ + + =⇔ =⇔++=
a b c a b c ab bc ca
abc
a b c abc
ab bc ca abc
Bài 2: Cho
, , 0; 0abc a b c≠ ++≠
, thỏa mãn
111 1
abc abc
++=
++
Chứng minh rằng:
2019 2019 2019 2019 2019 2019
111 1
abc abc
++=
++
Lời giải
Ta có:
111 1 111 1
0
11
0( ) 0
() ()
++= ⇒++− =
++ +
+
+ ++−
⇔ + =⇔+ + =
++ +
+
abc abc a bc abc
ab abcc
ab
ab cabc abcabc
2
( )( )( )
() 0 0
() ()
( )( )( ) 0
+++ + + +
⇔+ =
⇔ =
++ +
+
⇔+ + +=
ca cb c ab a b a c c b
ab
abc a b c abc
a b c
abbcca
+)
2019 2019
0 ()a b a b a b VT VP+ = ⇒ =−⇒ =− ⇒ =
Chứng minh tương tự, ta có điều phải chứng minh.
Bài 3: Cho
1
abc
bc ac ab
++=
+++
. Chứng minh rằng
222
0
abc
bc ac ab
++=
+++
Lời giải
Để xuất hiện a
2
, b
2
, c
2
ta nhân với a + b + c ta có:
1 ()
+ + =⇒ + + ++ =++
+++ +++
abc abc
abc abc
bc ac ab bc ac ab
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

144
2 2 2 222
0( )⇔ ++ ++ +=++⇒ + + =
+ + + ++
+
a b c ab
c
a b c a b c dpc
m
bc ac ab bc
ac ab
Bài 4: Cho a + b + c = x + y + z = 0 và
0
abc
xyz
++=
. Chứng minh rằng :
2 22
0ax by cz++=
Lời giải
Cách 1:
Ta có :
00
11 11
00
−−
+ + = ⇒ =−−⇒ + + =
−−
⇒ −+ −=⇒ + =
bc b c
abc a bc
x yz
xy xz
bc bc
y x z x xy xz
( )
( ). ( ).
0
( ) ( ) 01
− +−
⇒=
⇒−+− =
bx y z cz x y
xyz
bx yz cz xy
Ta có :
2 22 2 22
22 22
()
( ) ( ) ( )( ) ( )( )
++=−− ++
= − + − = − ++ − +
ax by cz b c x by cz
by x cz x by z y x cz x z x
( )
( )
2 22
( )( ) ( )( ) ( ) ( ) 0 1
0
= −−+ −−= − + − =
⇒++=
by x z cz x y bx yz cx zy theo
ax by cz
Cách 2 : Ta có
2 2 2 22 2
0 ( ); ( ); ( )xyz x yz y xz z xy++=⇒ = + = + = +
Do đó :
2 22 2 2 2
2 22 22 2
( )()( )
(2 )(2 )(2 )
++= +++++
= + ++ + ++ + +
ax by cz a y z b x z c x y
a y yz z b x xz z c x yx y
222
( ) ( ) ( ) 2( ) (*)= ++ ++ ++ + +x b c y a c z a b ayz bxz cxy
Từ
0;++=⇒+=−abc bc a
Tương tự:
;+=− +=−a c ba b c
Có:
2 2 22 2 2
000
(*) : (
) ( ) ( )
++
++=⇒ =
⇒ + + =
⇒ + + = −+ −+ −
a b c ayz bxz cxy
ayz bxz cxy
x y z x
yz
ax by cz x a y b z c
2 22 2 22
2( ) 0 0ax by cz ax by cz⇒ ++ =⇒++=
Bài 5: [ GVG- Yên Phong – 2014]
Cho a, b, c là các số thực thỏa mãn :
111
1
abc
++=
và a + b + c = 1.
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

145
Chứng minh rằng :
( 1)( 1)( 1) 0abc− − −=
Lời giải
Ta có :
111
11
bc ac ab
bc ac ab abc
a b c abc
++
++=⇒ =⇒ + + =
Có :
( 1)( 1)( 1) 1 ( ) ( ) 1 0a b c abc ab ac a bc b c abc ab ac bc a b c− − − = − − + − ++−= − + + + + + −=
Bài 6: Cho
111xy yz xz
yzx
+++
= =
. Chứng minh rằng :
xyz= =
hoặc
2 22
1xyz =
Lời giải
Từ :
1 1 1 1 1 1 11 11
;
xy yz xz y z z x
x y z xy yz
y z x y z x z y yz x z zx
+++ − −
= = ⇒+ =+ =+⇒−= − = −= −=
2 22
2 22
1 1 ( )( )( )
( )( )( ) (
)( )( )( 1)
xy xy
yzzx
zx x
yyzzx xyyzzxxyz
y x xy x
y z
− −
−−
−=−= ⇒− − −= ⇒
− − − −=
2 22
2 22
( )( )( ) 0
1
1
xy
yz xyz
x yy zz x
zx
xyz
xyz
=
=⇒==
− − −=
⇔⇔
=
=
=
Bài 7: Cho
0
abc
bc ca ab
++=
−− −
. Chứng minh rằng:
222
0
( )( )( )
abc
bc ca ab
++=
−− −
Lời giải
Từ :
2222
0
( )( ) ( )( )
a b c a b c b ab ac c b ab ac c
bc ca ab bc ac ba acba abca
−+− −+−
++=⇒=+= =
− − − − − − −− −−
22
2
(1)
( ) ( )( )( )
−+−
⇒=
− −−−
a b ab ac c
bc abbcca
nhân với
1
bc−
Tương tự :
2 2 22
22
(2); (3)
( ) ( )( )( ) ( ) ( )( )( )
b c bc ab a c a ac bc b
ca bcacab ab abbcca
−+− −
+−
= =
− −−− − −−−
222
(1) (2) (3) : 0( )
( )( )( )
abc
dpcm
bc ca ab
++ + + =
−− −
Bài 8: Cho x, y, a, b là những số thực thỏa mãn :
4 4 22
xy xy
a b ab
+
+=
+
và
22
1xy+=
Chứng minh rằng :
2006 2006
1003 1003 1003
2
()
xy
a b ab
+=
+
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

146
Nếu
22
2013 2013
2013
1
() ()
()
xy
a b ab
±= ⇒
+
xong
Ta có :
4 4 22 222 4 4 222
4 4 2
22
() ()
( )( ) ( )
xy xy xy bxay xy
bx ay a b ab x y
a b ab ab ab ab
++ + +
+ = = ⇔ = ⇔ + += +
++ +
4 24 24 4 4 22 4 24 22 24
2 20abx b x a y aby abx abx y aby b x abx y a y⇔+++=+ +⇔− +=
2 2 22
2 22 2
2
2003 2003
22
2003
1
( )0
1
()
()
+
⇔ − =⇔ = ⇔== =
++
⇔==
+
x y xy
bx ay bx ay
a b ab ab
xy
dpcm
a b ab
Bài 9 : [ HSG Quảng Xương – 20/04/2015]
Cho ba số a, b, c khác 0, thỏa mãn:
2 222
()abc a b c++ = + +
.
Chứng minh rằng:
222
222
1
222
abc
a bc b ac c ab
++=
+++
Lời giải
Từ
2 222
()++ = + +abc a b c
ta có :
22
0 () 2 ()()()++=⇒=− + ⇒+ =+− + =− −ab bc ca bc ab ac a bc a bc ab ac a b a c
Tương tự:
22
2 ( )( ); 2 ( )( )+=−− +=−−b ac b c b a c ab c a c b
222
222
222
⇒= + +
+++
abc
A
a bc b ac c ab
222
( ) ( ) ( ) ( )( )( )
1
( )( )( ) ( )9 )( )
abc bca cab abbcca
A
abbcca abbcca
− −+ −+ − − − −
= = =
−−− − −−
Bài 10: Cho
111
0
abc
++=
với
,, 0abc≠
và
22 22 22
bc ac ab
M
abc
=++
.
Chứng minh rằng:
3M abc=
Lời giải
Đặt
111
;; 0x y z xyz
abc
= = =⇒++=
22 22 22
222 22
2 3 3 3
333
111
( )( )
bc ac ab
M abc abc
x y z
a b c abc
= + + = ++ = ++
Từ x + y + z = 0 suy ra:
3 3 33 3 333
() 3() 3+=−⇒ + =−⇒ + + + =−⇒ + + =x y z x y z x y xy x y z x y z xyz
222 222
111
.3 .3. . . 3M abc xyz abc a
bc
abc
⇒= = =
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

147
Bài 11: Cho
0
xyz
abc
++=
và
2
abc
xyz
++=
Chứng minh rằng:
222
4abc
bcx acy abz abc
++=
Lời giải
Có
2
0 0; 2 ( ) 4
xyz ab
c abc
bcx acy abz
abc x
yz xyz
++=⇔ + + = ++=⇒ ++ =
222 222 222
2 22 2
22 2 22
24 2 4 4
++
⇔+++ ++ =⇔+++ =⇒++=
a b c ab bc ac a b c abz bcx acy a b c
x y z xy yz xz x y z x
yz x y z
Chia cả hai vế cho abc
222
4abc
bcx acy abz abc
⇒++=
Bài 12: Cho
1xy+=
và
0xy ≠
. Chứng minh rằng:
3 3 22
2( )
0
11 3
x y xy
yxxy
−
−+ =
−− +
Lời giải
Ta có:
4 4 44
3 3 33 2 2
( )( )
1 1 ( 1)( 1) ( 1)( 1)( 1)( 1)
x y x xy y x y xy
y x y x y yy x xx
−− + − − −
−= =
− − − − − ++ − ++
Theo đầu bài:
1 1; 1x y x yy x+=⇒=− =−
22 22
2 2 22
2 2 2 2
( )( )( ) ( ) ( )( 1)
( 1)( 1) ( 1)
x yx yx y x y x yx y
xy x x y y xy x y x y x xy xy x y y
− + + −− −
+ −
= =
++ ++ +
+ + + ++ ++
[ ]
22 22
22
22 2
2 22 2
( ) ( 1) ( 1)
( )( 1) (
)( 1)
( 3)
() 2 ()2
x y xx yy
x yx y x yx y
xy x y
xy x y xy x y x y xy xy x y x y
− −+ −
− +− − +−
= = =
+
+ +++ ++ ++ +
[ ]
22 22 22
( )( ) ( )
()(2)2()
( 3) ( 3) 3
xyx y y x
xy xy xy
dpcm
xyxy x
yxy xy
− −+−
−− −−
= = =
⇒
+ ++
RÚT GỌN BIỂU THỨC
Bài 1: Rút gọn
222 2
2
( )( ) ( )
( )( )
a b c a b c ab bc ca
A
a b c ab bc ca
+ + ++ + + +
=
++ − + +
Lời giải
Ta có:
2 2 22 2 2 2
( )( )a b c ab bc ca a b c ab bc ca MS a b c ab bc ca++ − ++ =+++++⇒ =+++++
222222 2
222 2
222 222 2
( )( 2 2 2 ) ( )
( )( )
( )
( ). ( )( ) ( )
= ++ +++ + + + ++
= ++ +++ + ++
= ++ + ++ ++ + ++
TS a b c a b c ab bc ac ab bc ca
a b c MS ab bc ca ab bc ca
a b c MS a b c ab bc ca ab bc ca
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

148
222 222
222
2
( ). ( )( )
.( )
= ++ + ++ +++++
= ++++ +
=
a b c MS ab ac bc a b c ab bc ca
MS a b c ab bc ca
MS
2
TS MS
A MS
MS MS
⇒= = =
Bài 2: Rút gọn các biểu thức sau
a.
2 22
111
x yz y zx z xy
A
yz zx xy
xyz
−−=
=++
+++
+++
b.
2 22
()()()()()()
() () ()
111
( )( ) ( )( ) ( )( )
aa b aa c bb c bb a cc a cc b
ab ac bc ba ca cb
B
bc c
a ab
abac bcba cacb
++ ++ ++
+++
−− −− −−
= ++
−−−
+++
−− −− −−
Lời giải
a) Ta có:
222222333
( )( )( ) 3
111
x yz y zx z xy x x yz y y yz z z xy x y z xyz
A
yz zx xy
xyz xyz xyz xyz
xyz
− − = − − − ++−
=++ = + + =
+++
++ ++ ++ ++
+++
2 22
2 22
( )( )x y z x y z xy yz zx
A x y z xy yz zx
xyz
++ + + − − −
= =++−−−
++
b) Đặt
1 23
2 22
()() ()() ()()
;;
() (
) ()
1 11
( )( ) ( )( ) ( )( )
aa b aa c bb c bb a cc a cc b
ab ac bc ba ca cb
BBB
bc c
a ab
abac bcba cacb
++ ++ ++
+++
−− −− −−
= = =
−−−
+ ++
−− −− −−
Tử số
22
2
1
( )( ) ( )( ) (2 2 )
( )( ) (
)( ) ( )( )
a a ab ac bc a ab ac bc
aa b a c aa c a b a
a bc
B
a ba c a
ba c a ba c
+−−+−+−
+ −+ + − −
= = =
−− −
− −−
Mẫu số
2 2 222
1
() ()()()
1
( )( ) ( )( ) (
)( )
bc abac bc a b c abbcca
B
a ba c a ba c a
ba c
− − −+− ++− −−
=+
= =
−− −− −
−
3
1
222
22a abc
B
a b c ab bc ca
−
⇒=
++−−−
Tuơng tự:
33
23
222 2
22
22 22
;
b abc c abc
BB
a b c ab bc ca a b c ab bc ca
−−
⇒= =
++−−− ++−−−
333
222
2( 3 )
2( )
a b c abc
B abc
a b c ab bc ca
++−
⇒ = =
++
++−−−
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

149
Bài 3: Rút gọn
3 3 4 22 4
3 3
4 22 4
( 2) ( 2) 3 7 4
:
(2 ) (2 ) 4 7 3
a b a b a ab b
A
a b a b a ab b
+ −− + +
=
+− − + +
Lời giải
+)
[ ]
33 2 2
2 22
22 2 2 2
( 2) ( 2) ( 2) ( 2) ( 2) ( 2)( 2) ( 2)
4( 4 4 4 4 4 ) 4(3 4 )
ab ab ab ab ab abab ab
b a ab b a b a ab b b a b
+ −− = + −− + ++ − +−
= + + +− +− + = +
+)
3 3 22
(2 ) (2 ) 2 (12 )ab ab b a b+− −= +
+)
4 22 4 2 2 2 2 4 22 4 2 2 2 2
3 7 4 ( )(3 4 );4 7 3 ( )(4 3 ) 2a ab b a b a b a ab b a b a b A++=+ + ++=+ +⇒=
Bài 4: Thực hiện phép tính sau
33 3
33 2 2 33 2 2 33 2 2
222
( ) ( )( ) ( ) ( )( ) ( ) ( )( )
ab c bc
a ca b
A
ab cacb bc abac ca babc
a b a ab b b c b bc c c a c ca a
+− +− +
−
=++
− −− − −− − −−
+++
− ++ − ++ − ++
Lời giải
Đặt
1
3
33 2 2
2
( ) ( )( )
ab c
A
a b c ac b
a b a ab b
+−
=
− −−
+
− ++
MS:
3 2 22
11
3322 22 222
( ) ( )( ) ( ) ( )( ) ( 2 )( )a b c ac b a b c ac b a b ca ab b
AA
a b a ab b a ab b a b c ab bc ca
− −− −+−− +− ++
= + = ⇒=
− ++ ++ ++−−−
Tương tự:
22 22
23
222 2
22
( 2 )( ) ( 2 )( )
;
b c ab bc c c a bc ca a
AA
a b c ab bc ca a b c ab bc ca
+− + + +− + +
= =
++−−− ++−−−
Tử số của
[ ] [ ] [ ]
2 2 22 2 2
( ) ( )( ) ( ) ( )( ) ( ) ( )( )A a c b c a ab b b a c a b bc c c b a b c ca a= −+− + + + −+− + + + −+− + +
( )
( )
( )
( )
( )
( )
( )
( )
2 2 2 2 22 22
22 22
( )( ) ( )( )=− ++ +− ++ +− ++ +− ++
+− ++ +− ++
a c a ab b b c a ab b b a b bc c c a b bc c
c a c ca a a b c ca a
2222 2222
2 22 2
( )( ) ( )( )
( )( )
=− ++−−− +− ++−−−
+− + + − − −
a c a ab b b bc c b c a ab b c ca a
babbccccaa
( )( )( ) ( )( )( ) ( )( )( )acacabc bcbcabc babaabc= − − ++ + − − ++ + − − ++
22 2
222
( )( )( )( )
( ).2.( ) 2( )
=++ −+−+−
= ++ + + − − − ⇒ = = ++
MS
abc ac bc ca
TS
abc a b c abbcca A abc
MS
Bài 5: Cho a, b, c là ba số phân biệt. Chứng minh rằng giá trị của biểu thức sau không phụ
thuộc vào giá trị x :
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

150
( )( ) ( )( ) ( )( )
( )( ) ( )( ) ( )( )
x
xaxb xbxc xcxa
S
cacb abac bcba
−− −− −−
=++
−− −− −−
Lời giải
2 22
() () ()
( )( ) ( )( ) ( )( )
x
x a b x ab x b c x bc x a c x ac
S
cacb abac bcba
−+ + −+ + −+ +
= ++
−− −− −−
2
111
( )( ) ( )( ) ( )( )
() () ()
( )( ) ( )( ) ( )( )
= ++
−− −− −−
−+ + +
+ −−
−− −− −−
x
Sx
cacb abac bcba
ab bc ac
x
cacb abac bcba
2
.
( )( ) ( )( ) ( )( )
x
ab bc ac
S A x Bx C
cacb abac bcba
+ + + ⇒= ++
−− −− −−
+)
111
0
( )( ) ( )( ) ( )( ) ( )( )( )
abbcca
A
cacb abac bcba abacbc
−+−+−
=++= =
−− −− −− −−−
+)
()
0
( )( ) ( )( ) ( )( )
ab bc ac
B
cacb abac bcba
−+ + +
=−−=
−− −− −−
( )( ) ( )( ) ( )( )
x
ab bc ac
SC
cacb abac bcba
⇒== + +
−− −− −−
Bài 6: Cho a, b, c đôi một khác nhau. Chứng minh rằng giá trị các biểu thức sau không phụ
thuộc vào a, b, c
a.
2 22
210
23 23 23
23
( )( ) ( )( ) ( )( )
a a bb c c
S S
SS
abac bcba cacb
+ + ++ + +
= + + =++
−− −− −−
+)
2 2 22 2 2
2
()()()
1
( )( ) ( )( ) ( )( ) ( )( )( )
a b c acb bac cba
S
abbc bcba cacb abbcca
−+ −+ −
=++= =
−− −− −− −−−
+)
0
111
0
( )( ) ( )( ) ( )( ) ( )( )( )
cbacba
S
abac bcba cacb abbcca
−+−+−
=++= =
−− −− −− −−−
1
( )( )( )
) 01
( )( ) ( )( ) ( )( ) ( )( )( )
−+ −+ −
+ = + + = =
⇒=
−− −− −− −−−
a b c
ac b ba c cb a
SS
abbc bcba cacb abbcca
b.
222
0
( )( ) ( )( ) ( )( )
a bc b ca c ab
AA
abac bcba cacb
−−−
= + + ⇒=
−− −− −−
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

151
C. Chứng minh phân số tối giản
- Có hai cách cơ bản chứng minh tử số và mẫu số có ƯCLN bằng 1
+) Cách 1: Giả sử d = (a,b), sau đó chỉ ra d = 1
+) Giải sử d ± 1 ( d ≥2)
- Gọi p là ước nguyên tố của d
- Chỉ ra rằng p = 1 ( Vô lý)
- Kết luận d = 1
Bài 1: Chứng minh rằng phân số
31
52
n
n
+
+
là phân số tối giản
nN∀∈
Lời giải
Giải sử
*
(3 1, 5 2) ( )+ += ∈n n dd N
suy ra:
31 5(31) 155
11
5 2 3(5 2) 15 6
+++
⇒ ⇒ ⇒ ⇒=
+++
nd n d nd
dd
nd n d nd
Vậy phân số
31
52
n
n
+
+
là phân số tối giản
nN∀∈
Bài 2: Chứng minh rằng phân số
12 1
30 2
n
n
+
+
là phân số tối giản
nN∀∈
Lời giải
Gọi
*
12 1 : 5(12 1)
(12 1,30 2) ( ) 1
1
30 2 2(
30 2)
+⇒ +
+ + = ∈ ⇒ ⇒ ⇒
⇒=
++
n d d le n d
n n dd N d d
nd n
d
Bài 3: Chứng minh rằng phân số
2
21
21
n
n
+
−
là phân số tối giản
nN∀∈
Lời giải
Gọi
2*
(2 1, 2 1) ( )+ −= ∈n n dd N
ta có:
2
22
(2 1) (2 1) 1 1
1
21
+
+− − ⇒+ ⇒ ⇒ ⇒ =
+
nd
nn n dnd dd
nd
Bài 4: Chứng minh rằng phân số
3
42
2
31
nn
nn
+
++
là phân số tối giản
nN∀∈
Lời giải
Gọi
3 42 *
( 2 , 3 1) ( )+ + += ∈n nn n dd N
ta có:
33
3 42
42 42
2 ( 2)
( 2 ) ( 3 1)
31 31
++
⇒ ⇒ +−++
++ ++
nnd nnnd
nn n n n d
nn d nn d
22
( 1) 1n dn d⇒− − ⇒ +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

152
Ta có:
2 4 42
3
2 2 42
( 1) 3
2 11
1 33
nn nd nd n nd
n n nd d d
n d nd n n d
++ +
+ = ⇒ ⇒ ⇒ ⇒ ⇒=
+ ++
Bài 5: Cho
32
32
21
2 21
nn
A
nnn
+−
=
+ ++
a. Rút gọn A
b. Chứng minh rằng nếu
nZ∈
thì giá trị tìm được ở câu a là phân số tối giản
Lời giải
a.
32 2 2
32 2
2
2 1 ( 1)( 1) 1
2 2 1 ( 1)( 1) 1
n n n nn nn
A
n n n n nn nn
+ − + +− +−
= = =
+ + + + ++ ++
b. Gọi
2
22 *
2
1
( 1, 1) ( ) 2 1; 2
1
nn d
nn nn ddN d d d
nn d
+−
+− ++ = ∈ ⇒ ⇒− ⇒ = =
++
Lại có:
2
2
1 ( 1) 1 ( ) 2 1++= ++ ⇒≠⇒=
n n n n le d d
Bài 6: Cho phân số
2
4
()
5
n
A nN
n
+
= ∈
+
. Có bao nhiêu số tự nhiên nhỏ hơn 2009 sao cho
phân số A chưa tối giản
Lời giải
22
4 25 29 29
5
55 5
nn
An
nn n
+ −+
= = =−+
++ +
Để A là phân số chưa tối giản thì
29
5n +
là phân số chưa tối giản
5 29 29 5n nk⇒+ ⇒= −
Ta có:
5 2014
0 29 5 2009 1 69
29 29
≤ −≤ ⇒ ≤≤ ⇒≤≤k kk
Vậy có 69 giá trị
D. Các bài toán về biểu thức hữu tỷ
Các bước rút gọn biểu thức hữu tỷ
- Tìm điều kiện xác định: Phân tích tử và mẫu thành nhân tử, cho tất cả các nhân tử khác 0
- Phân tích tử và mẫu thành nhân tử rồi chia cả tử và mẫu cho nhân tử chung
Bài 1: Cho biểu thức
42
42
54
10 9
xx
A
xx
−+
=
−+
a. Rút gọn A b. Tìm x để A = 0
c. Tìm giá trị của A khi
2 17x −=
Lời giải
a. ĐKXĐ:
42 2 2
10 9 0 ( 1)( 9) 0 1; 3xx xx xx− + ≠ ⇔ − − ≠ ⇔ ≠± ≠±
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

153
42
42
5 4 ( 1)( 1)( 2)( 2) ( 2)( 2)
10 9 ( 1)( 1)( 3)( 3) ( 3)( 3)
xx xxx x x x
A
x x xxxx xx
−+ −++ − − +
= = =
− + −+−+ −+
b.
2
2
4
0 02
9
x
Ax
x
−
=⇔ =⇔=±
−
c.
12
4( )
2 17
7
3( )
= ⇒=
−=⇒
= −
x tm A
x
x loai
Bài 2: Cho biểu thức
32
2
2
24
xx x
A
xx x
+−
=
+− +
a. Rút gọn A b. Tìm x nguyên để A có giá trị nguyên
c. Tìm giá trị của A khi x = 6
Lời giải
a. Nếu x + 2 > 0 ta có:
32
2
2 ( 1)( 2) ( 1)
2 22
( 2) 4 2( 2) 2
+− − + −
>− ⇒ + = + ⇒ = = =
+−+ +
x x x xx x xx
x xx A
xx x x
Nếu
32
2
2
2 0 2 2 ( 2)
( 2) 4 2
xx x x
x x x xA
xx x
+− −
+ < ⇔ <− ⇒ + =− + ⇒ = =
− +−+
Nếu
2xA=−⇒
không xác định
b. Để A nguyên thì
( 1)
2
xx−
hoặc
2
x−
có giá trị nguyên
+)
( 1)
2
xx−
có giá trị nguyên
( 1) 2
2
xx
x
−
⇔
>−
Ta có:
( 1) 2 2xx x− ∀ >−
+)
2
x−
có giá trị nguyên
2
2 ( , 1)
2
x
x kk Zk
x
⇔ ⇔ = ∈ <−
<−
Ta có:
( 1) 2 2xx x− ∀ >−
c.
2
6 2 15
2
xx
xx A
−
= ⇒ >− ⇒ = =
Bài 3 : [ HSG – Yên Phong – 2015]
Cho biểu thức
22
2 2 22
. ( 0, 0, )
+
= − ≠ ≠ ≠−
−− −
y x x y xy
A x y xy
x xy xy y x y
a. Rút gọn A
b. Tính giá trị của A khi x > y > 0 và thỏa mãn :
22
225x y xy+=
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

154
a.
()xy
A
xy
−+
=
−
b. Ta có
22 2 2
2 0( )
2 2 5 (2 ) (2 4 ) 0 (2 )( 2 ) 0
2 0 ()
−=
+ = ⇔ −+ − =⇔− − =⇔
−=
x y loai
x y xy x xy y xy x y x y
x y tm
Thay x = 2y vào A, ta được :
(2 )
3
2
yy
A
yy
−+
= = −
−
Bài 4: Cho
2
32 32 2
3( 2) 2 10 5 3 3
:
2( 1)
2( 1) 1 2( 1) 2( 1)
x xx
A
xxx xxx x x x
+ −
−
= + +−
+ ++ − +− + + −
a. Rút gọn A
b. Tính giá trị của A khi
2 11x −=
c. Tìm x để A > 0
d. Tìm x để A nhận giá trị nguyên dương
Lời giải
a. Ta có:
32 2 32 2
1 ( 1)( 2); 1 ( 1)( 1)xxx x x xxx x x+ ++= + + − +−= − +
2
44
( 2) ( 2) 2( 2)( 2) 2
; :
( 1; 2)
2( 1) 1 2
+ − +− +
= = ⇒
= = ≠± ≠±
−−
x x xx x
M N A
MN x x
xx
b.
1( )
2 11
0() 1
=
−=⇒
= ⇒=
x loai
x
x tm A
c.
2
0 20
1; 2
x
Ax
xx
>−
>⇔+>⇔
≠± ≠±
d. A nguyên dương:
*
2
( 2) 2 2 2 ( ; 0; 2) 2 2 2( 1)( ; 2)
2
x
Z x x kkZk k x k k kZk
+
⇔ ∈ ⇔ + ⇔+= ∈ ≠ ≠ ⇔= −= − ∈ ≠
Bài 5: [ HSG – Long Biên – 2014 ]
Cho
2
2 2 24 3 1
( 3)
:
3 1 13
x x
x x
A
xx x x
+ − +−
= +− −
++
a. Rút gọn A
b. Tính giá trị của A khi
2014 2 1 2013x− −=
c. Tìm x để A < 0
d. Tìm các giá trị nguyên của x để A có giá trị là số nguyên
Lời giải
a. ĐKXĐ:
11
1; 0;
23
x
x xx A
−
≠− ≠ ≠ ⇒ =
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

155
b.
10
2014 2 1 2013
0( )
=⇒=
− −= ⇒
=
xA
x
x loai
c.
1
0 10
1
0, 1,
2
x
Ax
xx x
<
< ⇒ −< ⇔
≠ ≠− ≠
d. A có giá trị nguyên
( 1) 3 3 1 ( )⇒ − ⇒= + ∈x x k kZ
BIỂU THỨC CÓ TÍNH QUY LUẬT
Bài 1: Tính
a.
[ ]
2
22
3 5 21
...
(1.3) (2.3)
( 1)
n
nn
+
+ ++
+
b.
22 2
11 1
(1 )(1 )...(1 )
23 n
−− −
Lời giải
a. Ta có:
[ ]
2
2222 222222 2
21 21 1 1 11 11 1 1 (1)
...
( 1) ( 1) 1 2 2 3 ( 1) ( 1)
( 1)
n n nn
A
nn nn nn n
nn
++ +
= = − ⇒ = − + − ++ − =
+ + ++
+
b. Ta có:
22 2 2 2
1 ( 1)( 1) (2 1)(2 1) (3 1)(3 1) ( 1)( 1)
1 . ...
23
nn n
n
B
nn n
−+ −+ −+ +−
− = ⇒=
2 2 2 2 222 2
1.3 2.4 3.5 ( 1)( 1) 1.3.2.4.3.5...( 1)( 1) 1.2.3...( 1) 3.4.5...( 1)
. . .... .
2 3 4 2
.3 .4 .... 2.3.4..( 1). 2.3.4...( 1).
nn nn
n n
n n nn
nn
−+ −+
− +
= = =
−−
11 1
.
22
nn
nn
++
= =
Bài 2: Cho
9998 2 1 111 1
... ; ...
1 2 98 99 2 3 4 100
AB= + ++ + =++++
. Tính A. B
Lời giải
99 98 2 1 100 100 100
99 ( 1) ( 1) ... ( 1) ( 1) 100 ...
1 2 98 99 2
98 99
A+ = ++ +++ ++ += + ++ +
11 11 11 1
100 100( ... ) 1 100( ... ) 100.( ... ) : 100
2 99 2
99 2 3 100
A AB= + ++ ⇒=+ ++ = +++ ⇒ =
Bài 3: Cho
111 1 1 1 1 1 1
... ; ...
1 3 5 99 1.99 3.97 5.95 97.3 99.1
AB=++++ = + + ++ +
. Tính A : B
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

156
99 1 97 3 5 95 97 3 99 1 1 1 1 1 1 1 1 1
100. ... 1 ... 1
1.99 97.3 5.95 97.3 99.1 99 3 97 5 95 97 3 99
B
+ ++ + +
= + + ++ + =+ ++ ++ ++ ++ +
111 1 1 1 11
( ... ) ( ... ) 2 : 50
1 3 5 99 99 97 3 1
A A A AB= ++++ + + +++ =+= ⇒ =
Bài 4: Chứng minh rằng:
111 1 1 1 1
... ...
1.2 3.4 5.6 (2 1).2 1 2 2n nn n n
+ + ++ = + ++
− ++
Lời giải
11111 1 1 111 1 111 1
1 ... (
... ) ( ... )
23456 2 12 135 2 1 246 2
VT
nn n n
=−+−+−++ − = ++++ − ++++
−−
111 1 1 111 1 11 1 11 1
( ... )
2( ... ) ( ... ) (1 ... )
123 2 12 246 2 12 2 23nn n
n n
= ++++ + − ++++ = +++ −++++
−
11 1
...
12 2
VT VP
nn n
= + ++ ⇒ =
++
Bài 5:
a. Chứng minh rằng:
*
123
123
... 2
222 2
n
n
nN+ + + + <∀∈
b.
123
123 3
...
333 3 4
n
n
S nZ
+
= + + + + < ∀∈
Lời giải
2121
23 1
23 3
2. 1 ... 2 ...
222 22
11 1 1
2 1 ...
22 2 2 2 2
−−
−
=++ ++ =+ ++
⇒ − = =++ + ++ − =−
nn
nn n
nn
VT
nn
VT VT VT A
Trong đó:
12 1 2 1
*
1
11 1 1 1 1
1 ... 2 2 1 ... 2 2
22 2 2 2 2
1
22
22
− −−
−
=+ + ++ ⇒ =++++ ⇒ −==−
⇒ = − − < ∀∈
n nn
nn
A A AAA
n
VT n N
b) Ta có:
1
123 1 12 1
234 11 1
3 1 ... 2 1 .... 2
333 3 33 3 3 3
n nn n
n nn
S S SS
−−
=+++++ ⇒ =++++ − ⇒ =−
1 1 11
23 1 12
2 1 1
111 1 11 1 1 3 1
1 ...
3 3 1 ... 2 3
3 3 3 3 3
3 3 3 2 2.3
n n nn n
S S SS
− −− −
=+ + + ++ ⇒ =++ + ++ ⇒ =− ⇒ =−
1
31 3
()
4 4.3 2.3 4
−
⇒=− − <
nn
n
S dpc
m
Bài 6: Chứng minh rằng:
*
123
1.2! 2.3! 3.4! ( 1)! ( 2)!
... 2
222 2 2
++
++++ = −∀∈
nn
nn n
nN
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

157
Cách 1: Chứng minh bằng quy nạp toán học
+) Với n = 1, ta có:
1.2! 3!
1; 2 1
2! 2
VT VP VT
VP= = = −=⇒ =
+) Giả sử đúng với n = k, tức là :
*
123
1.2! 2.3! 3.4! ( 1)! ( 2)!
... 2
222 2 2
++
++++ = −∀∈
kk
kk k
kN
Ta sẽ chứng minh đúng với n = k + 1, tức là :
*
123 1
1
1.2! 2.3! 3.4! ( 1)! ( 1)( 2)! ( 3)!
... 2
(**)
222 2 2 2
++
+ ++ +
++++ + = −∀∈
kk k
kk k k k
kN
Thật vậy :
11 1
11
( 2)! ( 1)( 2)! 2( 2) ( 1)( 2)
(**) 2 2
2 22 2
( 2)!( 3) ( 3)!
2 (**)
22
++ +
++
+ ++ + ++
= −+ =
−+
++ +
= =
−=
k kk k
kk
k kk k kk
VT
kk k
VP
Cách 2: Xét số hạng tổng quát
1
( 1)! ( 2 2)( 1)! ( 2)! 2( 1)! ( 2)! ( 1)!
2 2 2 22
k k k kk
kkkkk kkk
−
++−++−+++
= = = −
Áp dụng cho k chạy từ 1 đến n, ta được :
102132 1 0
3! 2! 4! 3! 5! 4! ( 2)! ( 1)! ( 2)! 2! ( 2)!
... 2 ( )
222222 2 2 2 2 2
−
+++ +
= − + − + − ++ − = − = −=
nn n n
nnn n
VT VP dpcm
CHUYÊN ĐỀ 6: BẤT ĐẲNG THỨC
I. Các kiến thức cơ bản
1. Định nghĩa: Ta gọi hệ thức dạng a > b (
;;ababab<≥≤
) là một bất đẳng thức
0
0
≥⇔−≥
≤⇔−≤
AB AB
AB AB
2. Các tính chất
a. Bắc cầu:
>
⇒>
>
ab
ac
bc
b. Cộng hai vế của bất đẳng thức với cùng một số:
>⇒+>+ab acbc
Hệ quả 1:
>⇒−>−ab acbc
c. Cộng, trừ từng vế của bất đẳng thức cùng chiều được bđt cùng chiều với bđt đã cho
>
⇒+>+
>
ab
acbd
cd
( lưu ý: không có tính chất trừ vế với vế )
d. Nhân cả hai vế của bddt với cùng một số
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

158
;0 . .
;0 . .
> >⇒ >
> <⇒ <
a b c ac bc
a b c ac bc
Hệ quả:
( 0)
( 0)
> ⇒− <−
>>
>⇒
<<
ab a b
ab
c
cc
ab
ab
c
cc
e. Trừ từng vế của bđt ngược chiều:
>
⇒−>−
<
ab
acbd
cd
f. Nhân từng vế hai bất đẳng thức cùng chiều mà hai vế không âm:
0; 0>≥ > ≥⇒ ≥a b c d ac bd
g. Nâng lên lũy thừa bậc nguyên dương hai vế của bất đẳng thức:
0>>⇒ >
nn
ab a b
>⇒ >
nn
ab a b
(n lẻ)
>⇔ >
nn
ab ab
(n chẵn)
h. Lấy căn
*
0,>> ∈ ⇒ >
nn
ab nN a b
Hệ quả: a, b > 0 có
22 22
;, 0>⇔ > ≥⇒≥⇔ ≥ababab abab
i. Lấy nghịch đảo hai vế và đổi chiều bđt nếu hai vế cùng dấu
Với
11
00>>⇒< <ab
ab
11
,0> >⇒ <a b ab
ab
II. Các hằng đẳng thức
1.
22
0; 0aa≥− ≤
2.
00≤⇔=aa
3.
0=⇔≥aa a
4.
0+= + ⇔ ≥a b a b ab
III. Các bổ đề hay sử dụng
1.
22
2a b ab+≥
2.
2
2
( ) 4 (AM GM )
2
+
≥ ⇔+ ≥ −
ab
ab a b ab
3.
11 4
( , 0)+≥ >
+
ab
ab ab
4.
2 ( , 0)+≥ >
ab
ab
ba
5.
2 22 2 2
( )( ) ( ) ( )+ + ≥ + − −− −a b x y ax by bu nhi a cop ski
IV. Các dạng toán
Dạng 1: Dùng định nghĩa và các phép biến đổi tương đương
- Để chứng minh:
AB≥
ta xét A – B và chứng minh
0AB−≥
Bài 1: Cho ba số a, b, c bất kỳ, chứng minh bất đẳng thức sau:
222
(1)++≥ ++a b c ab bc ca
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

159
Lời giải
222 2 2 2
(1) 2 2 2 2 2 2 ( )( )( )0⇔ + + ≥ + + ⇔ − +− +− ≥a b c ab bc ca a b b c c a
(luôn đúng)
Dấu “ = ” xảy ra
abc↔==
Bài 2: Cho ba số a, b, c bất kỳ, chứng minh rằng:
2
( ) 3 ( )(1)ab bc ca abc a b c+ + ≥ ++
Lời giải
( ) ( )
22 22 22 2 2 2
22 22 22 2 2 2
22 2 22 22 2 22 22 2 22
222
(1) 0
0
(ab 2abc bc) 2 2 0
( )( )( )0
⇔++−−−≥
⇔++−−−≥
⇔−++− ++− +≥
⇔ − +− +− ≥
a b b c c a a bc ab c abc
a b b c c a a bc ab c abc
b c abc c a a c a bc a b
ab bc bc ca ca ba
Bất đẳng thức cuối cùng đúng các phép biến đổi là tương đường nên bài toán được chứng
minh.
Dấu “ = ” xảy ra
;;⇔ = = = ⇔==ab bc bc ca ca ab a b c
Bài 3: Chứng minh rằng:
222 22
( ) ,,,,++++≥ +++ ∀ ∈a b c d e ab c d e abcde R
Lời giải
Ta có:
222 22
222 2
22 2 2
()
0
444 4
++++≥ +++
⇔−++−++−++−+≥
abcdeabcde
aaa a
ab b ac c ad d ae e
22 22
0
222 2
⇔− +− +− +− ≥
aaa a
bcde
Bất đẳng thức cuối cùng đúng các phép biến đổi là tương đương nên bài toán được
chứng minh.
Dấu “=” xảy ra khi:
2
= = =
a
bcd
Bài 4: Cho ba số a, b, c thỏa mãn:
0 <≤≤abc
. Chứng minh rằng:
++≤++
abcbac
bcaacb
Lời giải
Xét hiệu:
2 2 22 2 2
222222
1
()
1
( )( )( )
++−−−
= + +−−−
= −+−+−
abcbac
bcaacb
a c ab bc b c ba ac
abc
ac bc ba ab cb ac
abc
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

160
( )
( )
( ) ( ) ( )
( )
( )( )
2
2
1
()()()()
1
1
1
( ) 0 ( :0 )
= − +− −− −
= − +−−
= − −+ −
= − − − ≤ <≤≤
cabab abab cab
abc
a b ac bc ab c
abc
a b ca c bc a
abc
abaccb do abc
abc
Vậy bất đẳng thức được chứng minh.
Bài 5: Chứng minh rằng:
111
2
+ + ≥ ++
abc
bc ac ab a b c
với a, b, c > 0
Lời giải
Xét hiệu:
222
2
111
2
20
222 0
( )0
+ + ≥ ++
⇔++− + + ≥
⇔ ++− − − ≥
⇔ +− ≥
abc
bc ac ab a b c
a b c bc ac ab
bc ac ab abc abc abc
a b c bc ca ab
abc
Bất đẳng thức cuối cùng đúng các phép biến đổi là tương đương nên bài toán được
chứng minh.
Dấu “=” xảy ra khi:
+=abc
Bài 6: Chứng minh rằng nếu
2ab+≥
thì
3 3 44
a b ab+≤+
Lời giải
Xét hiệu:
44 3 3 3 3 3 3
( 1) ( 1) ( 1) ( 1) ( 1) ( 1) ( 1) ( 1)a b a b aa bb aa a a bb b b+− − = −+ −= −− −+ −+ −− −+ −
3 3 22 22
( 1)( 1) ( 1)( 1) 2 ( 1) ( 1) ( 1) ( 1) 2 0 0 0 0a a b b ab a a a b b b ab= − −+ − −++−= − +++ − ++++−≥++=
Vậy bất đẳng thức được chứng minh. Dấu “=” xảy ra khi a = b = 1.
Bài 7: Chứng minh rằng nếu
,,abc∀
ta luôn có:
44 4
()a b c abc a b c+ + ≥ ++
Lời giải
Xét hiệu:
444 444222 4442 2 2
1
( ) (2
2 2 2 2 2 )
2
a b c abc a b c a b c a bc b ac c ab a b c a bc b ac c ab+ + − ++ = + + − − − = + + − − −
4 22 4 22 4 22 4 22 4 22 4 22 2 2 2
1
( 2 )2 ( 2 )2 ( 2 )2
2
a ab b ab a ac c ac b bc c bc abc bac cab
= − ++ +− ++ +− ++ − − −
2 22 2 22 2 22 22 22 2 22 2 2 2 22 2 2 2
1
( )( )( )( 2 )( 2 )( 2 )
2
a b a c b c ab bc abc bc ca abc ab ca abc
= −+−+−+ +− + + − + +−
2 22 2 22 2 22 2 2 2
1
( )( )( )( )( )( ) 0 ,,
2
= − +− +− +− +− +− ≥∀
a b b c c a ab bc bc ca ab ac a b c
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

161
Bất đẳng thức cuối cùng đúng nên bài toán được chứng minh.
Dạng 2: Dùng các phép biến đổi tương đương
- Ta biến đổi các bất đẳng thức cần chứng minh tương đường với BĐT đúng hoặc BĐT đã
được chứng minh là đúng
- Nếu
<⇔<AB CD
, với C < D luôn đúng
Bài 1: Cho a, b, c, d, e là các số thực, Chứng minh rằng:
a.
2
2
4
b
a ab+≥
b.
22
1a b ab a b+ +≥ + +
c.
222
44448a b c ab ac bc++≥ −+
d.
2
222
33
+ + ++
≥
a b c abc
Lời giải
a.
22
2 2 22 2
0 4 4 (2 ) 0
44
+ ≥ ⇔ + − ≥⇔ + ≥ ⇔ − ≥
bb
a ab a ab a b ab a b
(đúng)
22 22 2 2 2
. 1 2( 1) 2( ) ( ) ( 1) ( 1) 0 1+ +≥ ++⇔ + + ≥ ++ ⇔ − + − + − ≥⇔==b a b ab a b a b ab a b a b a b a b
c.
222 2 2 2
4 4 4 4 8 ( 4 4 ) 4 (4 ) 0++≥ − + ⇔− + ++ −≥a b c ab ac bc a ab b c ac bc
2 22
(2)2(2).2(2)0(22)0⇔− + − + ≥⇔−+ ≥ab abc c abc
(luôn đúng)
d.
2
222
222 2
222
3( ) ( ) 2 2 2
33
+ + ++
≥ ⇔ ++ ≥++ =+++ + +
a b c abc
abc abc abc abbcca
222
( )( )( )0⇔ − +− +− ≥ab bc ca
(luôn đúng)
Bài 2: Cho ba số
,,abc R∈
thỏa mãn: abc = 1 và
111
abc
abc
++> + +
a. Chứng minh rằng:
( 1)( 1)( 1) 0abc− − −>
b. Chứng minh răng luôn tồn tại 1 trong ba số a, b, c nhỏ hơn 1
Lời giải
a. Ta có:
( 1)( 1)( 1) 0
0
( )( )0
1 ( ) ( ) 0 (1)
− − −>
⇔ − − − +++>
⇔ + ++ − + + >
⇔+ ++ − + + >
abc
abc ab bc ca a b c
abc a b c ab bc ca
a b c ab bc ca
và
111
(2)
++
++> + + ⇔++> ⇔++> + +
ab bc ca
abc abc abc
abbcca
a b c abc
Từ (1), (2) ta có điều phải chứng minh.
b. Giả sử tồn tại cả ba số a, b, c lớn hơn 1
1⇔>abc
( mâu thuẫn với giả thiết )
Vậy luôn tồn tại 1 số nhỏ hơn 1.
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

162
Bài 3: Chứng minh bất đẳng thức sau:
10 10 2 2 8 8 4 4
( )( ) ( )( ) (1)+ +≥+ +a bab abab
Lời giải
10 10 2 2 8 8 4 4 12 10 2 2 10 12 12 8 4 8 12
(1) ( )( ) ( )( ) 0 0⇔ + +−+ +≥⇔+ + +−− − −≥a b a b a b a b a a b ab b a ab ab b
102 84 210 48 82 2 2 28 2 2 2 22 22 4 22 4
( )( )0 ( ) ( )0 ( ) ( )0⇔ − + − ≥⇔ − − − ≥⇔ − + + ≥a b ab ab ab ab a b ab a b a b ab a ab b
Bài 4: Chứng minh rằng:
1 2 ( , , 0)<++< >
+++
abc
abc
abbc ca
Lời giải
Ta có:
11
+<++⇒ > ⇒ >
+ ++ + ++
aa
ababc
ab abc ab abc
Tương tự:
;
b bc c
bc abcac abc
>>
+ ++ + ++
. Vậy
1 (*)++>
+++
abc
abbc ca
Lại có:
;;
+++
<+⇒ < < <
+ ++ + ++ + ++
a ac b ab c cb
aab
ab abcbc abcca abc
Cộng vế với vế ba bất đẳng thức ta được:
2 (**)++<
+++
abc
abbc ca
Do đó bài toán được chứng minh.
Bài 5: [ Vào 10, ĐHSP TPHCM năm 2007 – 2008 ].
Cho a, b, c > 0. Chứng minh rằng:
32 32 32 23 23 2 3
ab bc ca ab bc ca++>++
Lời giải
32 32 32 23 23 23 32 23 32 23 32 23
0++>++⇔ −+−+−>ab bc ca ab bc ca ab ab bc ca ca bc
22 2 3 3 3 2 2 22 2 2 2 3
( )( )( )0( ) ( )( )0
⇔ −+ −+ −>⇔− − +++ +>
ab a b c b a c a b a b ab c b ab a c a b
( )( )( )( ) 0− − − ++ >abbccaabbcca
(luôn đúng)
Bài 6: [ Vào 10 Thanh Hóa, năm 2007 – 2008 ].
Chứng minh rằng với a > 0 thì:
2
2
5( 1) 11
12 2
aa
aa
+
+≥
+
Lời giải
( )
( ) ( )
( )
( )
( )
22
22
22 2 2
2
2
2
22
2
2
2
2
2
2
5( 1) 11 1 5( 1)
50
1 2 2 12 2
( 1) 5 10 5 ( 1) 5( 1)
00
2( 1) 2 2
21
1 51 1 5 5
1 01 0
2 12
1
1 19
4
1
24
10
2
1
++
+ ≥ ⇔ − + −≥
++
−− − + −− −
⇔ + ≥⇔ + ≥
+
+
−+
⇔− − ≥⇔− ≥
+
+
−++
⇔− ≥
+
aa a a
aa a a
a aa a a
aa a
a
aa
aa
aa
aa
aa
a
aa
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

163
Bất đẳng thức cuối đúng với mọi a > 0 nên bài toán được chứng minh.
Dấu “=” xảy ra khi a = 0
Bài 7: [ HSG – 1994 - 1995 ]
Chứng minh rằng với mọi số thực
,0xy≠
ta có
22
22
4 3 (1)
+ +≥ +
x y xy
y x yx
Lời giải
2
22
22
22 2
22
22 2 2
2 2
22 22
(1) 4 3 0 2 2 0
( )( )
2 10 0
2( )( ) ( )(2 2 2 )
00
⇔++− +≥⇔+ − +−++≥
− −+
⇔ +− +−≥⇔ ≥
− −+ − − +
⇔ ≥
⇔ ≥
x y xy xy xy xy
y x yx yx yx yx
xy xy xyx xyy
yx yx x
y
x y x xy y x y x xy y
xy x
y
22 2 2
22
( )( ( ))
0
− + +−
⇔≥
xy x y xy
xy
Bất đẳng thức cuối cùng luôn đúng các phép biến đổi là tương đương nên bài toán được
chứngminh.
Dấu “=” xảy ra khi x = y.
Bài 8: [ Chuyên An Giang năm 2010 - 2011 ]
Cho
4, 4≥≥ab
. Chứng minh rằng:
22
6( )++≥ +a b ab a b
Lời giải
Do
4, 4 40; 40≥ ≥⇒−≥ −≥ab a b
Đặt
4 ( 0); 4( 0)=− ≥ =−≥xa x yb y
ta có:
22
(1) ( 4) ( 4) ( 4)( 4) 6( 8)⇔+++++ +≥ ++x y x y xy
( )
22
2
2
6( ) 0
3
60
24
⇔+++ +≥
⇔+ + + +≥
x y xy x y
yy
x xy
Bất đẳng thức đúng với mọi x, y ≥ 0 do đó bài toán được chứng minh
Dấu “=” xảy ra khi x = y = 0 hay a = b = 4.
Bài 9: [ Vào 10 chuyên KHTN, ĐHQGHN, năm 2000 – 2001 ]
Cho hai số thực x, y ≠ 0. Chứng minh rằng:
22 2 2
2 22 2 2
4
3 (1)
()
++≥
+
xy x y
xy yx
Lời giải
Ta có:
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

164
22 2 2 22 2 22 4 4 22
2 22 2 2 2 22 2 2
2 22 2 22
2 22
2 22 2 2 2 2 2 22
2 22 22 4 4 22
2 22 2 22
2 2 2 22 2
4 4() 2
(1) 1 2 0 0
() ()
()() 1 1
0 ( ). 0
() ()
()
( ). 0 ( ).
()
− + +−
⇔ −++−≥⇔ + ≥
++
−− −
⇔ + ≥⇔ − − ≥
++
+ − ++
⇔− ≥⇔−
+
xy x y xy x y x y xy
xy yx xy xy
xy xy
xy
x y xy xy x y
x y xy x y xy
xy xy
xy x y xy
2 2 22
0
()
≥
+xy
Bất đẳng thức cuối cùng đúng các phép biến đổi là tương đương nên bài toán được chứng
minh.
Dấu “=” xảy ra khi
= ±xy
Bài 10: Cho các số thực a,b. Chứng minh rằng:
22
2
(1)
22
++
+ ≥+
+
a a b ab
ab
ab
Lời giải
Ta có:
22
2 22 2
22
22
2 () ()
2
;
2 2( ) 2
2
2
2
+
−
+ −+ −
− = −
= =
++
+
+
+
+
ab
ab
ab a ab a b ab
ab
ab ab
ab
ab
ab
ab
2
2 22
22
() 1 1
(1) 0 ( ) 2 2 2( ) 2 0
2
2
−
⇔ − ≥⇔ − + − + − ≥
+
+
+
ab
a b a b a b ab
ab
ab
ab
22
2 2 2( ) 2 0 (*)⇔+− + − ≥a b a b ab
Ta có:
22
2 22
2
22
() ()
2 ( ) ;
2( )
()
2( ) ( )
− −
−
+− = − = +−
+ =
+
+ ++
ab ab
ab ab a b ab
a b
ab
a b ab
2 2 22 2
2
22
11
(*)() 0
()2( ) ( )0
()
2( ) ( )
⇔− − ≥
⇔− + ++− + ≥
+
+
++
ab ab
a b ab a b
ab
a b ab
22
2 22 2
22
4
22
2( ) 4
()2( )2 0(). 0
2( ) 2
2( )
0
2( ) 2
+−
⇔− + − ≥⇔− ≥
++
−
⇔≥
++
a b ab
ab a b ab ab
a b ab
ab
a b ab
Bất đẳng thức cuối cùng đúng nên bài toán được chứng minh.
Dấu “=” xảy rakhi a = b.
Dạng 3: Bất đẳng thức dạng nghịch đảo ( Cô si cộng mẫu )
*)
11 4
ab ab
+≥
+
*)
111 9
ab c abc
++≥
++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

165
*)
2
12 1
1 2 12
11 1
... ...
, ,....., 0
...
+ ++ ≥ ⇔ = == ∀ >
+ ++
nn
nn
n
a a a aa a
aa a aa a
Bài 1: Cho a, b, c > 0. Chứng minh rằng:
111 3 3 3
222abca bb cc a
++≥ + +
+++
Lời giải
Áp dụng bất đẳng thức dạng:
111 9
ab c abc
++≥
++
( tự chứng minh bđt)
111 9 111 9 111 9
;;
222abba bbccb ccaac a
++≥ ++≥ ++≥
+++
Cộng vế các bất đẳng thức trên ta được:
111 3 3 3
222abca bb cc a
++≥ + +
+++
Vậy bài toán được chứng minh.
Dấu “=” xảy ra khi a = b = c.
Bài 2: Cho a, b, c > 0. Chứng minh rằng:
2 3 4 567
4
+ + ≤++
+++
abcabc abc
Lời giải
Áp dụng bất đẳng thức dạng:
4 11 4 11 4 11
2. 2 ;
≤+⇒ ≤+⇒ ≤ +
++ +
xy x y ab a b ab ab
Tương tự:
4 11 4 11 4 11 4 11
3. 3. ; 4. 4
≤+⇒ ≤ + ≤+⇒ ≤ +
++ ++
ca c a ac c a bc b c bc bc
Cộng vế ba bất đẳng thức trên ta được:
2 3 4 567
4
+ + ≤++
+++
abcabc abc
Bất đẳng thức được chứng minh. Dấu “=” xảy ra khi a = b = c
Bài 3: Cho a, b, c > 0. Chứng minh rằng:
1
(1)
44 44 44 3
++≥
++ ++ ++
abc
abcbcacab
Lời giải
333
(1) 1
44 44 44
333
1 1 14
44 44 44
⇔++≥
++ ++ ++
⇔ ++ ++ +≥
++ ++ ++
abc
abcbcacab
abc
abc bca aab
111
4( ) 4
44 44 44
1111
(2)
44 44 44
⇔ ++ +
+ ≥
++ ++ ++
⇔++≥
+ + + + + + ++
abc
abcbcacab
abcbcacababc
Áp dụng bất đẳng thức:
111 9
x y z xyz
++≥
++
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

166
Ta được:
91
(2) .
9( )
≥=
++ ++
VT
abc abc
(đpcm)
Bài 4: Cho a, b, c > 0 thỏa mãn:
3.abc++=
Tìm GTLN của
12 12 12
abc
A
abc
=++
+++
Lời giải
Cách 1:
222 1 1 1
2 111 3
12 12 12 12 12 12
abc
AB
abc a b c
= + + =− +− +− = −
+++ + + +
111 9
1
12 12 12 32( )
B
a b c abc
=++≥ =
+ + + + ++
23 2 1=− ≤ ⇒ ≤⇔ = =A B A abc
Cách 2: Áp dụng bất đẳng thức:
9 111 9 111 1 1 2 2
1
1 1 12 9 12 9 9
≤++⇒ ≤++⇒ ≤ + ⇒ ≤+
++ ++ + +
aa
xyz x y z aa aa a a a
Tương tự:
22
;
12 9 9 12 9 9
≤+ ≤+
++
bb cc
bc
Cộng ba vế của bất đẳng thức ta được:
6
1
99
++
≤ +=⇔==
abc
A abc
Bài 5: Cho a, b, c > 0. Chứng minh rằng
2 2 24
ab bc ca a b c
ab c bc a ca b
++
++≤
++ ++ ++
Lời giải
Áp dụng bất đẳng thức:
4 11
xy xy
≤+
+
( ) ( )
( ) ( )
111
.. .
( )( )
1 1 11 1 11 1 1
.
444
=++
+++ +++ +++
≤+++++
++ ++ ++
VT ab bc ca
ac bc ba ca cb ab
ab bc ca
ac bc ba ca cb ab
1
44
+ + + ++
= ++ =
+++
bc ca ab bc ab bc a b c
ab bc ac
Bài 6: Cho a, b, c > 0 thỏa mãn: a + b + c = 1. Tìm GTNN:
222
11
A
abc a b c
= +
++
Lời giải
222 2
1 111 9 1 1 1 9
;9
()
++
= =++≤ +
+ ≥ =
++ ++ ++ ++ ++
abc
abc abc ab bc ca ab bc ca a b c ab bc ca ab bc ca a b c
Lại có:
2
17
3( ) ( ) 1 3 2
1++≤++=⇒≥⇒≥
++ ++
ab bc ca a b c
ab bc ca ab bc ca
Cộng theo vế ba bất đẳng thức:
99 1
30 30
3
+≥+⇒≥⇔===
++ ++
A A
abc
ab cb ca ab bc ca
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

167
BÀI TẬP VẬN DỤNG:
Bài 1: Cho a, b, c > 0 . Chứng minh rằng:
111444
222a bc ab cbc a ca b
++≥ + +
++ ++ ++
Lời giải
Ta có:
4 11
( )( )
≤+
++ + +acbc acbc
Tương tự:
4 11 4 11
;
22
≤+ ≤+
++ + + ++ + +bc a ba ca ca b cbab
Cộng theo vế ta được:
( )
444 111
21
222
+ + ≤ ++
++ ++ ++ + + +
ab c bc a ca b abbc ca
Lại có:
1 11 1 1 11 1 1 11 1
;;
4 44
≤+ ≤+ ≤+
+ ++
ac a c bc b c ab a b
Cộng theo vế ta được:
Cộng theo vế ta được:
( )
1 1 1 11 1 1
2
2
+ + ≤ ++
+++
abbc ca abc
Từ (1) và (2) nên:
111444
222a bc ab cbc a ca b
++≥ + +
++ ++ ++
Vậy bài toán được chứng minh , Dấu “=” xảy ra khi a = b = c
Bài 2: Cho a, b, c > 0 . Chứng minh rằng:
747 1 2 3
9
222
++≥ + +
+++
abc abbcca
Lời giải
Ta có:
9 111 9 111 9 222
; 2.≤++ ≤++⇒ ≤++
++ ++ ++abb a bcbcc b cc bcc b c c
9 111 9 333
3.≤++⇒ ≤++
++ +
+acccaa caacaa
Cộng vế với vế các bất đẳng thức ta được đpcm
Bài 3: Cho a, b, c > 0 . Chứng minh rằng:
1
(1)
255 255 255 4
++≥
++ ++ ++
abc
abc bca cab
Lời giải
3 15
(1) 3. 3. 3
44
⇔ ≥ ⇔ +≥VT VT
Thật vậy:
1 1 1 9 45 15
3. 3 (5 5 5 ) 5(
).
2 5 5 2 5 5 2 5 5 12(
) 12 4
⇒ += + + +
+ ≥ ++ = =
+ + + + + + ++
VT a b c abc
abc bca cab a
bc
Bài toán được chứng minh. Dấu “=” xảy ra khi a = b = c.
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

168
Dạng 4: Dùng các bất đẳng thức phụ
Các bất đẳng thức phụ thường sử dụng:
22
2x y xy+≥
22
22+≥ ≥x y xy xy
2 2 22
( )4;( )2( )
+≥ +≤ +xy xy xy x y
2
ab
ba
+≥
33
()x y xy x y+≥ +
( )( )( ) 8x y y z z x xyz+ + +≥
Bài 1: Cho hai số a và b thỏa mãn: a + b = 1 . Chứng minh rằng:
33
1
4
+≥ab
Lời giải
Ta có:
33 2222
( )( )a b a b a ab b a ab b+=+ −+ =−+
Từ:
2 2 22 2
1 2 1; ( ) 0 2 0+=⇒ + + = − ≥⇔ − + ≥ab a abb ab a abb
2 2 22
1
2 2 1 (1)
2
⇒ + ≥⇔ + ≥a b ab
Lại có:
22
2 2 22
2 0 2 (2)
2
+
− + ≥⇒ + ≥ ⇒ ≤
ab
a ab b a b ab ab
Từ (1), (2) ta có:
22
1 1 111
4 4 24
4
−
≤⇒− ≥ ⇒ +− ≥−=ab ab a b ab
Vậy bài toán được chứng minh. Dấu “=” xảy ra khi a = b.
Bài 2: Cho a + b > 1 . Chứng minh rằng:
44
1
8
ab+>
Lời giải
Từ
222 222
1 ( ) 1 2 1; ( ) 0 2 0+ >⇒ + >⇔ + + > − ≥ ⇔ + − ≥a b a b a ab b a b a b ab
22 222 44 22
11 1
( ) 2 (1
)
24 4
⇒ + ≥⇒ + ≥⇔ + + ≥ab ab ab ab
Có tiếp:
2 22 4 4 22
( ) 0 2 0 (2)− ≥⇒ + − ≥a b a b ab
Cộng theo vế của (1) và (2) ta được:
( )
44 44
11
2
48
+ ≥⇒ + ≥ab ab
Vậy bài toán được chứng minh. Dấu “=” xảy ra khi a = b
Bài 3: Chứng minh rằng:
222
22 2
a b c cba
b c a bac
+ + ≥++
Lời giải
Ta có:
2 22
( )0 2− ≥⇒ + ≥x y x y xy
Dấu “=” xảy ra khi x = y
Áp dụng:
22 22 22
22 2
2 2 2
2 . 2 ; 2. ; 2.+≥ = +≥ +≥
a b ab a b c b a c b
bcbcccaabac
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

169
22
⇔ ≥ ++ ⇒ ≥
abc
VT V
T VP
cab
Vậy bài toán được chứng minh. Dấu “=” xảy ra khi a = b
Bài 4: Cho a, b, c, d, > 0 và abcd = 1. Chứng minh rằng:
222 2
( ) ( ) ( ) 10a b c d ab c bc d dc a+++ + ++ + + +≥
Lời giải
Ta có:
22 22 222 2
2 ; 2 2( )+≥ +≥ ⇒+++ ≥ +ab abcd cd abcd abcd
Từ :
1111111
1 ;;;;;;=⇒= = = = = = =abcd ab ac ad bc bd cd ad
cd bd bc ad ac ab bc
Có:
2
1 11
2( ) 2 2.2.
4 : 0 2
1
+ = + ≥ = + ≥⇔ + ≥
ab
ad bc ab do ab
ab ab ab
Vậy
222 2
4abcd+++ ≥
Lại có:
()()()+++++= +++ ++ab ac bc bd cd ad ad bc ac bd bc ad
222
111
( )( )( )6 10
≥≥≥
=+ ++ ++ =⇒≥
ab ac bc VT
ab ac bc
Bài 5: Cho
,, 0xyz≥
. Chứng minh rằng:
( )( )( ) 8 (1)+ + +≥x y y z z x xyz
Lời giải
Ta có:
2 2 2 222
(1) ( )( )( ) 64⇔+ + + ≥x y y z z x xyz
Lại có:
222
2 2 2 2 22
( )4;( )4;( )4
( )( )( ) 64
+≥ +≥ +≥
⇒+ + + ≥
x y xy y z yz z x xz
x y y z z x xyz
Vậy bài toán được chứng minh. Dấu “=” xảy ra khi a = b
Bài 6: Cho
, , 0; 1a b c abc>=
. Chứng minh rằng:
( 1)( 1)( 1) 8abc+ + +≥
Lời giải
Ta có:
[ ]
2
222 2
( 1) 4 ; ( 1) 4 ; ( 1) 4 ( 1)( 1)( 1) (8 ) ( 1)( 1)( 1) 8+≥ +≥ +≥⇒+ + + ≥ ⇒+ + +≥a a b b c c a b c abc a b c abc
Vậy bài toán được chứng minh. Dấu “=” xảy ra khi a = b = c.
Bài 7: Cho
, , , 0; 1a b c d abcd>=
. Chứn minh rằng:
222 2
6abcdabcd+++ ++ ≥
Lời giải
Có:
222 2
2 2 3( )a b c d ab cd ab cd ab cd ab cd+++++≥ + ++= +
Lại có:
1
3( ) 3 3.2
6
+= + ≥=
ab cd ab
ab
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

170
Vậy bài toán được chứng minh. Dấu “=” xảy ra khi a = b = c = d.
Bài 8: Cho
1xyz++=
. Chứng minh rằng:
a.
2 22
1
3
xyz++≥
b.
1
3
xy yz zx++≤
Lời giải
a. Ta có:
2 22
( ) 0 , 2.− ≥∀ ⇒ + ≥x y x y x y xy
Tương tự:
22 22
2; 2+≥ +≥y z yz x z xz
Cộng theo vế ta được:
( )
( )
( )
( )
( )
( )
2 22 2 22 2 22
2
2 22 2 22
22 3 2
1
31
3
++ ≥ ++ ⇒ ++ ≥+++ ++
⇒ ++ ≥++ =⇒++≥
x y z xy yz zx x y z x y z xy yz zx
xyz xyz xyz
Vậy bài toán được chứng minh. Dấu “=” xảy ra khi x = y = z.
b. Theo chứng minh trên:
2 2 2 2 22
2
2222( )
( ) 3( ) 1 3( )
+ + ≥ ++ ⇒++≥++
⇒++≥ ++ ⇔≥ ++
x y z xy yz zx x y z xy yz zx
x y xy yz zx xy yz zx
1
3
⇒++≤xy yz zx
Vậy bài toán được chứng minh. Dấu “=” xảy ra khi x = y = z.
Bài 9: Cho
,, 0abc≥
thỏa mãn:
1abc++=
. Chứng minh rằng:
2 4(1 )(1 )(1 )abc abc++ ≥ − − −
Lời giải
Ta có:
22
()4 4()+ ≥ ⇔ ≤+x y xy xy x y
Áp dụng ta được:
22 2 2
0 , , 1 1 0 4(1 )(1 ) (1 1 ) (1 ) (1 ) (1 ) (1 )(1 ) 1≤ ≤⇒−≥ ⇒ − − ≤ − +− = + ⇒ ≤ + − = − + ≤+abc c a b a b c VP c c c c c
Mà:
1
12
2
0
= =
=++⇒ ≤++ ⇔
=
ab
abc VPab c
c
Bài 10: Cho
,, 0abc>
thỏa mãn:
1abc =
. Chứng minh rằng:
33 33 3 3
11 1
1
11 1ab bc ca
++ ≤
++ ++ ++
Lời giải
Ta có:
33 2
()()()0 ,0+ ≥ +⇔+ − ≥ ∀ >x y xyxy xyxy xy
Áp dụng ta có:
33
33
11
1() ( )
1()()
++≥ ++ = ++⇒ ≤ = =
+ + ++ ++ ++
abc c
a b ab a b abc ab a b c
a b ababc ababc abc
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

171
Tương tự:
33 3 3
11
;
11
ab
b c abcc a abc
≤≤
+ + ++ + + ++
Cộng vế các bất đẳng thức trên ta được điều phải chứng minh.
Dấu “=” xảy ra khi a = b = 1.
Bài 11: Cho
,, 1abc≥
. Chứng minh rằng:
22 2
11 1 3
11 1 1a b c abc
++ ≥
++ + +
Lời giải
Chứng minh:
22
22 2 2
22 22 22
11 2
, 0; 1
11 1
(2 )(1 ) 2(1 )(1 )
2() 2
+ ≥ ∀> ≥
++ +
⇔++ + ≥ + +
⇔ + + ≥++
x y xy
x y xy
x y xy x y
xy xy x y x y x y
2
( ) ( 1) 0 ( : 1)⇔ − −≥ ≥x y xy do xy
Áp dụng:
22 2 2 2 2
11 2 2 1 1 21 1 2
;;
11 1 1 1 1 1 11 1
+≥ ≥ + ≥ + ≥
++ + + + + + ++ +a b ab abc b c abc c a abc
Cộng vế các bất đẳng thức thức ta được điều phải chứng minh.
Bài 12: Cho
, , 0; 1xyz x y z> ++=
. Tìm GTNN:
2 22
( ) ( )( )xyz yzx zxy
A
yz zx xy
+ ++
=++
Lời giải
Ta có:
222222
=+++++
xyxzyz
A
yxzxzy
Dễ chứng minh:
33
( ) ,0+≥+ ∀ >a b a b ab a b
Thật vậy
22 2
()( )()0()()0 ,0⇔+ −+ −+ ≥⇔+ − ≥ ∀ ≥aba abb abab abab ab
Hoặc:
22 2 2 33
, ()( )() ()+−≥∀⇔+ −+≥+⇔+≥+a b ab ab a b a b a ab b ab a b a b ab a b
Áp dụng:
2 2 33
, 0;
+
+ = ≥+ ∀ >
x y xy
x y xy
y x xy
Tương tự:
22 22
;+ ≥+ + ≥+
yz zx
yz xz
zy xz
Cộng vế ba bất đẳng thức ta được:
1
2( 0 2 min 2
3
A xyz A xyz≥ ++ =→ =↔===
Bài 13: Cho
2 22
, , 0; 1xyz x y z> ++=
. Tìm GTNN:
xy yz xz
A
zxy
=++
Lời giải
Ta có:
2 2 22 22
2
222
2=+++
xy yz xz
A
zxy
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

172
Mà:
22
2a b ab+≥
Áp dụng:
2 2 22 22 22 2 2 22
22 2
22 22 22
2 ; 2; 2+≥ +≥ +≥
xy yz yz xz xy xz
yzx
zx xy zy
Cộng theo vế ta được:
( )
2 2 22 22 2 2 22 22
2 22
222 222
2 22 1
++ ≥++=⇒++≥
xy yz xz xy yz xz
xyz
zxy zxy
Do đó:
2
3
3 mi
n 3
3
≥⇔= == ⇒ =A xyz A
DẠNG 5: PHƯƠNG PHÁP PHẢN CHỨNG
- Muốn chứng minh bất đẳng thức
AB≥
đúng, ta giả sử
AB≥
là sai, tức là A < B là đúng
- Sau đó chứng minh A < B là sai
⇒≥AB
là đúng
Bài 1: Cho
22
2ab+≤
. Chứng minh rằng:
2ab
+≤
Lời giải
Giả sử
2ab+>
, bình phương hai vế ta được:
22 2
( ) 4 2 4 (1)+ >⇔ + + >a b a ab b
Mặt khác ta lại có:
22 2 2 2
2 2( ) ( )+≥ ⇒ + ≥+a b ab a b a b
Theo giải thiết:
22 2
2( ) 4 ( ) 4+ ≤⇒ + ≤a b ab
Điều này mâu thuẫn với (1) nên suy ra
2+≤ab
Bài 2: Với mọi số thực a, b, c hãy chứng tỏ:
2
22
( )( )
4
a
b c ba c ca b++≥ −+ −
.
Lời giải
Giả sử:
22
22 22
( )( ) 0
44
++< −+ −⇔ ++− + − + <
aa
b c b a c c a b b c ab bc ac bc
2
22
20
4
⇔ ++− − + <
a
b c ab ac bc
2
0
2
⇔ −− <
a
bc
Vậy điều giả sử là sai suy ra:
2
22
( )( )
4
++≥ −+ −
a
b c ba c ca b
Bài 3: Cho
33
2+=ab
. Chứng minh rằng:
2+≤ab
.
Lời giải
Giả sử a + b > 2. Ta có:
3 33
33
22 2
()8 3()83()6
()2 ()
0()( )()0()()
+ >⇔ + + + >⇔ + >
⇔ +>⇔ +>+
⇔> + − + − + ⇔> + −
ab a b abab abab
ab a b ab a b a b
aba abb abab abab
Bất đẳng thức cuối cùng sai nên
2+≤ab
.
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

173
Bài 4: Cho các số thực
, , (0;2).∈abc
Chứng minh rằng có ít nhất 1 trong ba bất đẳng thức
sau là sai
(2 ) 1; (2 ) 1; (2 ) 1ab bc ca−> −> −>
Lời giải
Giả sử cả ba bất đẳng thức trên đều đúng, nhân chúng với nhau theo vế, ta được:
(2 ). (2 ). (2 ) 1 (2 ). (2 ). (2 ) 1− − − >⇔ − − − >a bb cc a a ab bc c
Mặt khác, do
(0; 2)a∈
nên a và
2
2 0 0 .(2 ) 1 ( 1) 1−>⇒< − =− − ≤a aa a
Tương tự:
0 .(2 ) 1;0 (2 ) 1bb cc< −≤ < −≤
Do đó:
(2 ). (2 ). (2 ) 1a ab bc c− − −≤
( mâu thuẫn ). Vậy ta có bài toán được chứng minh.
Bài 5: [ Chuyên Thái Bình: năm 2007 – 2008 ]
Cho các số thực a, b, c thỏa mãn
22
0++++ <a b ab bc ca
. Chứng minh rằng:
222
+<abc
Lời giải
Giả sử
22 2
,ab c+≥
khi đó:
22 22 222 22 2
2( ) 2( ) 2( ) ( )++ ++ ++≥+++ ++ ⇔ ++++ ≥++a b ab bc ca a b a b c ab bc ca a b ab bc ca a b c
Kết hợp với gỉa thiết:
22 2 2
02( )()()0> + + + + ≥ ++ ⇒ ++ <a b abbcca abc abc
( mâu thuẫn )
Bài 6: [ Chuyên Lam Sơn Thanh Hóa: năm 2007 – 2008 ]
Cho các số thực a, b, c thỏa mãn:
0; 0; 0a b c ab bc ca abc++> + + > >
Chứng minh rằng cả ba số a, b, c đều dương
Lời giải
Giả sử ba số a, b, c có 1 số không dương. Không mất tính tổng quát, ta giả sử:
0a ≤
Mà lại có:
000>⇒≠⇒<abc a a
Lại có:
0 0 ( )0++>⇒+>⇒ + <abc bc abc
Từ giả thiết thứ hai: ab + bc + ca > 0, ta có:
() 0 0+ + >⇒ >a b c bc bc
Vì thế abc < 0 ( mâu thuẫn ).
Vậy bài toán được chứng minh.
Bài 7: Cho ba số a, b, c đôi một khác nhau. Chứng minh rằng: Tồn tại một trong các số 9ab,
9bc, 9ca nhỏ hơn
2
()abc++
Lời giải
Giả sử:
222
9();9();9()≥ ++ ≥ ++ ≥ ++ab abc bc abc ca abc
22
3( ) 9( ) ( ) 3( )⇒ ++ ≤ + + ⇔ ++ ≤ + +a b c ab bc ca a b c ab bc ca
22 2 2 2 2
( )( )( ) 0(1)++ ≤ + + ⇔ − +− +− ≤a b c abbcca ab bc ca
Theo đầu bài: a, b, c đôi một khác nhau nên:
22 2
( )( )( ) 0 (2)− +− +− >ab bc ca
Từ (1), (2) ta thấy mâu thuẫn nên bài toán được chứng minh.
Bài 8: [ Chuyên HCM năm 2006 – 200 7 ] .
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

174
Cho hai số dương x, y thỏa mãn:
33
+=−x y xy
. Chứng minh rằng:
22
1+<xy
Lời giải
Do x, y dương nên
,0>xy
mà
33
+=−x y xy
nên x > y
Giả sử:
22
1+≥xy
33 22 3332 23 2 2 3 2 2
( )( ) 2 0 ( 2 ) 0 (*)⇒+≤ + −⇔+≤+ − −⇔ − − ≥⇔ −− ≥x y x y x y x y x x y yx y xy yx y y xy x y
2
0
( )2 0
<
⇔ −− ≥
y xy x y
do
0>⇒−<xy yx
Do đó (*) không thể xảy ra
22
1+<xy
Bài 9: Cho cặp số (x; y) thỏa mãn các điều kiện sau:
1 1 (1)
1 1 (2)
−≤ + ≤
−≤ + + ≤
xy
x y xy
Chứng minh rằng:
2; 2≤≤xy
Lời giải
Ta đi chứng minh:
2x <
Giả sử
2x >
, khi đó
22−< <x
+)
2, (1) 1 1 2> ⇒ ≤ − <− ⇒ <−x y x xy
+)
2, (1) 1 1 2<− ⇒ ≥− − > ⇒ <−x y x xy
Do đó nếu
22> ⇒ <−x xy
. Mà
11+ ≤ ⇒ + + <−xy xyxy
( mâu thuẫn với 2)
Suy ra:
2≤x
Ta đi chứng minh
2y <
( tương tự chứng minh
2x <
)
Bài 10: [ Olympic Toán Ireland năm 1997 ]
Cho
, , 0;≥ ++≥a b c a b c abc
. Chứng minh rằng:
222
++≥a b c abc
Lời giải
+) Nếu 1 trong ba số bằng 0 thì bất đẳng thức được chứng minh
Ta xét: a, b, c > 0
Giả sử ngược lại:
222 222 2
++< ⇒ >++> ⇒<a b c abc abc a b c a a bc
Tương tự ta có:
; (1)< < ⇒++< + +b ac c ab a b c ab bc ca
Lại có:
222 222
(2)++≥++⇒ >++≥++⇒ >++a b c ab bc ca abc a b c ab bc ca abc ab bc ca
Từ (1), (2) suy ra:
>++abc a b c
( mâu thuẫn với giả thiết ) nên điều giả sử là sai.
Bài 11: Cho a, b, c là các số thực dương thỏa mãn
a b c abc++≥
. Chứng minh rằng có ít
nhất hai trong số các bất đẳng thức sau đúng:
236 236 236
6; 6; 6++≥ ++≥ ++≥
abc bca cab
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

175
Ta có:
111
1 ( : 0)++≥ ⇔ + + ≥ >a b c abc do
abc
bc ca ab
Đặt
111
; ; , , 0; 1= = =⇒ > ++≥x y z x y z xy yz xz
abc
Ta phải chứng minh có ít nhất hai trong ba bất đẳng thức sau đúng:
2 3 6 6; 2 3 6 6; 2 3 6 6++≥ ++≥ ++ ≥xyz yzx xzy
Giả sử có ít nhất 2 trong 3 bất đẳng thức sau là sai, chẳng hạn:
2 3 6 6; 2 3 6 6++< ++<xyz yzx
Cộng vế hai bất đẳng thức:
85912xyz++<
Từ giả thiết:
1
1 ( )1
−
+ + ≥⇒ + ≥− ⇒ ≥
+
yz
xy yz zx x y z yz x
yz
Do đó:
1
12 8. 5 9 12( ) 8(1 ) (5 9 )( )
−
> + + ⇔ +> − + + +
+
yz
y z yz yz y zyz
yz
22 2 2 2
5 6 9 12 12 8 0 2 (3 2) 9 12 4 4 8 4 0⇔ ++−−+<⇔+ −+−++ −+<y yz z y z y y z z z y y
22
( 3 2) 4( 1) 0⇔+− + − <yz y
Bất đẳng thức cuối cùng vô lý nên bài toán được chứng minh.
Bài 12: Cho bốn số a, b, c, d thỏa mãn điều kiện:
2( )ac b d≥+
. Chứng minh rằng có ít nhất
một trong các bđt sau là sai:
22
4; 4a bc d<<
Lời giải
Giả sử hai bđt trên đều đúng
22
4( ) (1)+< +a c bd
Theo giả thiết:
2( ) 2 4( ) (2)≥+⇔ ≥+ac b d ac b d
Từ (1) và (2) suy ra:
( )
2
22
20+< ⇔− <a c ac a c
Bất đẳng thức cuối cùng vô lý nên bài toán được chứng minh.
CHUYÊN ĐỂ 7: ĐA THỨC
Bài 1: TÍNH CHIA HẾT CỦA ĐA THỨC
A. Các kiến thức cần nhớ
Giả sử f(x) và g(x) là các đa thức và bậc của f(x) lớn hơn hoặc bằng bậc của g(x). Khi đó
luôn tồn tại duy nhất các đa thức q(x) và r(x), thỏa mãn:
f(x) = g(x) . q(x) + r(x)
Trong đó: Bậc của r(x) nhỏ hơn bậc của g(x)
Nếu r(x)
≡
0 thì ta nói f(x) chia hết cho g(x)
Xét phép chia đa thức f(x) cho đa thức bậc nhất x – a
f(x) = (x-a) . q(x) + r . Cho x = a
⇒
f(a) = r
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

176
- Kết luận: Phần dư trong phép chia đa thức f(x) cho x – a là một số bằng f(a)
- Nếu f(a) = 0 hay x = a là nghiệm của đa thức f(x) thì f(x) chia hết cho x – a
- Định lý Bơ Du:
Số dư trong phép chia đa thức f(x) cho nhị thức x – a bằng giá trị của f(x) tại x = a
()( ) () 0fx x a fa⇒ −⇔ =
Ví dụ: Không đặt tính chia, hãy xét xem đa thức A = x
3
– 9x
2
+ 6x + 16 có chia hết cho x + 1;
x – 3 hay không?
Lời giải
Ta có: f(-1) = 0 suy ra A chia hết cho B
f(3) = -20 ≠ 0 nên A không chia hết cho C
- Chú ý:
+) Nếu f(x) có tổng các hệ số bằng 0 thì chia hết cho x – 1
+) Nếu f(x) có tổng các hệ số của hạng tử bậc chẵn bằng tổng các hệ số của các hạng tử bậc
lẻ thì chia hết cho x + 1
+) a
n
– b
n
chia hết cho a – b (a
≠
-b)
+) a
n
+ b
n
( n lẻ) chia hết cho a + b (a
≠
-b)
+)
1 2 32 2 1
( )( .... )
nn n n n n n
a b a b a a b a b ab b
−− − −−
−=− + + ++ +
+)
1 2 32 2 1
( )( .... )
nn n n n n n
a b a b a a b a b ab b
−− − − −
+=+ − + −− +
B. Bài tập và các dạng toán
Dạng 1: Chứng minh một đa thức chia hết cho một đa thức (Xét các đa thức một biến)
Cách 1: Phân tích đa thức bị chia thành nhân tử có một thừa số là đa thức chia
Nếu
() ()
() ().()
() ()
fx gx
f x gx hx
f x hx
= ⇒
Bài 1: Chứng minh rằng
a.
98 2
() 8 9 1 () ( 1)f x x x gx x=−+ =−
b.
9998 432
( ) ... 1; ( ) 1fxx x x gxxxxx= + +++ = + + ++
c.
84 2
() 1; () 1
n n nn
fxx x gxx x= + + = ++
d.
100 20 40 20
() 1; () 1fxx x gxx x= ++ =++
e.
10 2
() 10 9; () ( 1)f x x x gx x=−+ =−
Lời giải:
a. Ta có:
98 9 8
9 8 87 765
() 8 9 1 8 8 9 9
8( 1) 9( 1) 8( 1)( ... 1) 9( 1)( ... 1)
=−+=−−+
= −− −= − + ++− − + + ++
fx x x x x
x x xxx xxxx
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

177
87
( 1)(8 ..... 1)x xx x= − − − −−
Cách 1: Ta có
87
8 ..... 1xx x− − −−
có tổng các hệ số = 0
2
( 1) ( ) ( 1)x fx x⇒ −⇒ −
Cách 2: Ta có:
9 8 87
87 76
27 6 2
( ) 8 9 1 ( 1)(8 ..... 1)
( 1)(8 8 7 7 ..... 1)
( 1) (8 7 ... 2 1) ( 1)
= − += − − − −−
= − − + − + +−
= − + ++ + −
fx x x x x x x
x xxxx x
x xx x x
b. Ta có:
99 98 99 95 4 3 4 95 90 5
( ) ... 1 ( ... ) ...( ... 1) ( ... 1)( ... 1) ( )fxxxxxxxxxx xxxgx= + +++= ++ + + +++= ++ + ++ +
Cách 2: Ta có
100 5 20 5
( 1). ( ) 1 [( ) 1] (x 1) ( 1). ( ) ( ) ( )x fx x x x gx f x gx− = −= − − = − ⇒
c. Ta có
8 4 42 4 4 4 2 22 4 2 4 2
( ) 1 ( ) 2. 1 ( 1) ( ) ( 1)( 1)
nn n n n n n nn nn
fx x x x x x x x x x x x=++= + +−= +− = ++ −+
Lại có:
42 2 2
1 ( 1)( 1) ( ) ( )
n n nn nn
xx xx xx fxgx+ += − + + + ⇒
d. Đặt
20 5 2
() 1; () 1tx fttt gttt= ⇒ = ++ = ++
Ta có:
5 2 2 23 2 2 3 2
( ) 1 ( 1) ( 1) ( 1)( 1) ( ) ( )fttttt tt tt tt tt fxgx= − + ++= − + ++ = ++ − + ⇒
e.Ta có:
10 9 8 9
28 7
( ) ( 1) (10 10) ( 1)( ... 1 10) ( 1)[(x 1) ... ( 1)]
=(x-1) ( 2 ... 8 9) ( ) ( )
fx x x x x x x x x
x x x fx gx
= −− − = − + +++− = − −++ −
+ ++ + ⇒
Cách 2: Biến đổi đa thức bị chia thành một tổng các đa thức chia hết cho đa thức chia
Nếu f(x) = g(x) + h(x) + k(x), mà
() ()
() () () ()
() ()
gx qx
hx qx f x qx
kx qx
⇒
Bài 2: Chứng minh rằng
a.
50 10 20 10
() 1 () 1fxx x gxx x=++ =++
b.
199 27 2 2
() () 1fxx x xgxxx= + − = −+
c.
99 88 11 9 8
( ) .. 1; ( ) ... 1fxx x x gxxx x= + ++ + = + + ++
d.
31 32 2
() 1; () 1
++
= + + = + + ∀∈
mm
fxx x gxxx nN
e.
6 4 62 2
() 1; () 1 .
++
= + + = −+ ∀ ∈
mn
fxx x gxxx mnN
Lời giải
a.
50 10 50 20 20 10
( ) 1 ( ) ( 1)fx x x x x x x=++= − + ++
Lại có:
50 20 20 30 20 10 3 20 10 20 10
( 1) [(x ) 1] ( 1)( 1) ( ) ( )x x xx x xx x x fxgx− = −= −= − + +⇒
b. Ta có:
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

178
199 27 2 199 27 2
199 27 2 1998 27
() 1 1
1 ( 1) ( 1) ( 1) ( )
= +−= −++−+−
= −+ +− −+ = − + + −
fx x x x x x x x x
xxxxxxx xgx
999 3 3
999 2 3 9 999 999 3 9
11 1
[(x ) 1] ( ) 1 () ( 1)( 1) ( ) 1 () () ()
xx x
x x gx xx x x gx f x gx
+⇒ + +
= − + +− = − + + +− ⇒
c. Ta có:
10
( 1). ( ) 1x gx x−=−
99 88 11 99 9 88 11 9 8
( ) .. 1 ( ) ( 8) ...( ) ... 1fx x x x x x x x x x x x= + ++ += − + − + − + + + + +
10 10 10
9 90 8 80 10
9 10 9 8
10 8 10
11 1
( 1) ( 1) ... ( 1) ( )
[(x ) 1] [(x ) 1] ... ( 1) ( ) ( ) ( )
−− −
= −+ −++ −+
= −+ −++ −+ ⇒
xx x
x x x x xx gx
x x x
x gx f x gx
d. Ta có
31 32 31 32 2 2
() 1( )( )( 1)
mm m m
fx x x x x x x x x
++ + +
= + += − + − + + +
31 3 3 3 2
( 1) [(x ) 1] 1 ( 1)( 1)
mm m
x x xx x x x x x
+
− = − = − −= − + +
32 2 2 3 2 3 3 2
( 1) [(x ) 1] 1 ( 1)( 1)
m mm
x x xx x x x x x
+
− = − = − −= − + +
() ()fx gx⇒
e. Ta có:
66
6462 64462242 46 26 42
11
( ) 1 1 [(x ) 1] [(x ) 1] ( 1)
mn m n m n
xx
fxx x x xx xxx x x xx
++ + +
−−
= + += −+ −+++= −+ −+ ++
22
63233422 2
11
1 ( ) 1 ( 1)( 1) ; 1 ( 1)( 1) ( ) ( )
xx xx
x x x x xx xx xx fxgx
−+ −+
−= −= − + + += + + − + ⇒
Cách 3: Sử dụng các phép biến đổi tương đương
Muốn chứng minh f(x) chia hết cho g(x) ta đi chứng minh
() () ()
() ()
() () ()
fx gx gx
fx gx
fx gx gx
+
⇒
−
Bài 3: Chứng minh rằng
99 88 11 9 8
( ) ... 1 ( ) ... 1fxx x x gxxx x= + ++ + = + +++
Lời giải
Ta có:
10 10 10
99 90 8 80 10
11 1
( ) ( ) ( 1) ( 1) ... ( 1)
xx x
f x gx x x x x xx
−− −
− = −+ −++ −
Mà
10 9 8 7
1 ( 1)( ... 1) () () ()x x x x x x f x gx gx−= − + + + + + ⇒ −
Lại có:
() () () ()gx gx f x gx⇒
Cách 4: Chứng tỏ rằng mọi nghiệm của đa thức chia đều là nghiệm của đa thức bị chia
- Cách này áp dụng với những bài toán mà đa thức chia dễ tìm được nghiệm
Bài 4: Chứng minh rằng
a.
2 10 2 10 2
[ ( ) ( 1) ( 1) 2] ( )fx xx xx gxxx= +− + −+ − = −
b.
22
( ) ( 1) 2 1; ( ) ( 1)(2 1)= + − − − = + + ∀∈
nn
f x x x x gx xx x n N
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

179
c.
22 2 *
() ( 2) ( 3) 1 () 5 6= − + − − = − + ∀∈
nn
fx x x gx x x n N
d.
2 9 1945 2
() () 1fxxxx gxxx= − − = −+
Lời giải
a.
2
0
() 0 0
2
x
gx x x
x
=
=⇔ −=⇔
=
, Vậy g(x) có hai nghiệm là x = 0 ; x = 2
(1) 0; (0) 0 ( ) ( 1); ( )f f fx x fx x
==⇒−
, mà x và x -1 không chứa nhân tử chung.
Vậy
2 10 2 10 2
[ ( ) ( 1) ( 1) 2] ( )fx xx xx gxxx= +− + −+ − = −
b.
11
( ) 0 0; 1; ; (0) 0; ( 1) 0; 0 ( ) ( )
22
−−
=⇔∈ − = −= =⇒
gx x f
f f f x gx
c.
{ }
() 0 2;3; (2) (3) 0 () ()gx x f f f x gx=⇔∈ = =⇒
d. Ta có:
2 9 1945 2 9 1945
( ) 1 ( 1) ( )fxxxx xx x x x= − − = − +− + − −
( )
2 2 9 3 3 3 2 1945 1944 3
1 1 (1); 1 [( ) 1] ( 1) 1 (2); ( 1) 1 (3)−+ −+ += + + −+ −= − + xx xx x x x xx x xxx x
Từ (1), (2), (3) ta có f(x) chia hết cho g(x).
CHUYÊN ĐỂ 3: ĐA THỨC
Bài 2: PHẦN DƯ TRONG PHÉP CHIA ĐA THỨC
A. Tìm dư của phép chia đa thức mà không thực hiện phép chia
1. Cách 1: Tách đa thức bị chia thành tổng các đa thức chia hết cho đa thức chia và còn dư
Bài 1: Tìm dư trong phép chia
a.
753 2
() 1; () 1fxxxx gxx=+++ =−
b.
27 9 3 2
() ; () 1fxx xxxgxx= +++ =−
c.
41 2
() ; () 1fxxgxx= = +
d.
43 2
() ; () 1fxxgxx= = +
e.
100 99 2
( ) ... 1; ( ) 1fxx x x gxxx= + +++ = ++
f.
100 90 10 2
( ) ... 1; ( ) 1fxx x x gxxx= + ++ + = −+
g.
100 99 2
( ) ... 1; ( ) ( 1)( 1)fx x x x gx x x= + +++ = + +
h.
10 9 2
( ) ... 1; ( ) 1fxx x x gxxx= + + ++ = −−
Lời giải:
a.
7 5 5 3 3 52 32 2
( ) ( ) (2 2 ) (3 3 ) (3 1) ( 1) 2 ( 1) 3 ( 1) 3 1fxxxxxxxxxxxxxxx= − + − + − + += −+ −+ −+ +
Vậy đa thức dư là: 3x + 1
b.
27 9 3 2 13 2 4 2
( ) ( ) ( ) ( ) 4 [(x ) 1] [(x ) 1] ( 1) 4fxxxxxxx xx x xx x= −+ −+ −+ = −+ −+ −+
, dư là : 4x
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

180
c.
42
41 41 4 10
11
( ) ( ) [(x ) 1]
xx
fx x x x x x x
−⇒ +
= = − += −+
, Vậy dư là : x
d.
2
43 43 2 21
1
( ) ( ) [(x ) 1]
x
fx x x x x x x
+
= = + −= +−
, Vậy dư là : -x
e.
2
100 99 100 99 98 2 98 95 2
u
( 1)
( ) ... 1 ( ) ...( 1) ( 1)( ... ) 1
d
xx
fxxx x xxx x xxxx xx
++
= + +++= + + + + = ++ + ++ ++
f.Ta có:
( )
100 90 10
100 90 80
2 70 60 50 2 40 30
20 2 10 2
3 33 6
15 2 6 13 3 33 2
( ) ... 1
( )( 1)( )( )( 1)( )( )( 1)
( )( )3 4 4
[(x ) 1] [(x ) 1] [(x ) 1] [(x ) 1] .... 3( 1) 1
= + ++ +
= + + −+ − + + + −+ − + + + −+
− + ++ − +
= ++ −+ −+ ++ + −+− −
du
fx x x x
x xx xx xxx xx xxx
xx xxx x
x x
x xx x
g. g(x) có 101 số hạng, nhóm 4 số hạng 1 nhóm, dư là : 1
h. Ta có:
10 9
109
82765243
( ) ... 1
( )( 1)( )( )( 1)( )( )( 1) 1
= + +++
= + + ++ − + − + ++ + + + + +−−
du
fx x x x
xxx xx xxx xx xxx x
Bài 2: Tìm số dư trong phép chia
( )( )( )( ) ( )
2
( ) 2 4 6 8 2008; 10 21=+++++ =++fxxxxx gxxx
Lời giải:
Ta có:
( )( )( )( )
( )( )
22
( ) 2 4 6 8 2008 `10 16 10 24 2008=+++++ =++ +++fxxxxx xx xx
Đặt
22
10 21 ( 3; 7) ( ) 2 1993= + + ≠− ≠− ⇒ = − +
du
t x x t t Pt t t
2. Cách 2: Xét giá trị riêng ( phép chia ảo )
Bài 3: Tìm số dư của f(x) cho g(x), biết rằng
a.
753 2
() 1; () 1fxxxx gxx=+++ =−
b.
10 8 2
( ) ... 1; ( ) 2fxx x x gxxx= + + + = −−
c.
2
( ) ( 1)( 3)( 5)( 7) 1999; ( ) 8 12f x x x x x gx x x=+ + + ++ = ++
Lời giải
a. Gọi thương phép chia là q(x) và dư là: ax + b , ta có:
753 2
1 ( 1). ( ) ax+b x+ + += − + ∀x x x x qx
Vì đẳng thức đúng với mọi x nên ta chọn x = 1 và x = -1, được:
14 3
:3 1
12 1
x ab a
du x
x ab b
=⇒=+ =
⇒⇒+
=−⇒−=−+ =
b. Ta có :
2
( ) 2 ( 1)( 2)gx x x x x= −−= + −
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

181
Thực hiện phép chia f(x) cho g(x) ta được:
( ) ( 1)( 2). ( ) ax+bf x x x qx=+− +
Cho
1 1 682
:682 683
2 2047 2 683
x ab a
du x
x ab
b
=−⇒ =−+ =
⇒⇒+
=⇒=+ =
c. Cách 1:
432
( ) ( 1)( 7)( 3)( 5) 1999 16 86 176 2014 ( 2)( 6). ( ) ax+bfxxxxx xx x x xxqx=+++++ =++ + + =++ +
Cho
2 1984 2 0
:1984
6 1984 6 1984
x ba a
du
x ba b
=−⇒ = − =
⇒⇒
=−⇒ = − =
Cách 2: Đặt
22
8 7 ( ) ( 8) 1999 ( 8 15) 1984 ( 3)( 5) 1984
du
t x x f t tt t t t t=++⇒=++=+++=+++
Bài 4: Tìm đa thức f(x) biết rằng :
a. f(x) chia cho x – 3 thì dư 7, chia cho x – 2 thì dư 5, chia cho (x-2)(x-3) thì được thương là
3x và còn dư.
b. f(x) chia cho x – 2 thì dư 5, chia cho x – 3 thì dư 7, chia cho (x-2)(x-3) thì được thương là
x
2
- 1 và còn dư.
c. f(x) chia cho x + 3 thì dư -5, chia cho x – 2 thì dư 5, chia cho x
2
+ x - 6 thì được thương là
x
2
+ 2 và còn dư.
Lời giải
a.Ta có:
( ) ( 3). ( ) 7 (1);
( ) ( 2). ( ) 5 (2);
( ) ( 2)( 3) ax+b (3)
=−+
=−+
=− −+
fx x gx
f x x hx
fx x x
Cho x = 2
(2) (2) 5
2 5 (*)
(3) (2) 2
⇒=
⇒ +=
⇒=+
f
ab
f ab
Cho x = 2
(2) (3) 7
3 7 (**).
(3) (3) 3
⇒=
⇒ +=
⇒=+
f
ab
f ab
Từ (*) và (**) suy ra: a = 2 và b = 1 suy ra
( ) ( 2)( 3) 2x+1= − −+fx x x
b.
432
() 5 5 5 6fx x x x x=−+ − − +
c.
22 2
( ) ( 6)( 2) ax +b= (x + 3)(x - 2)(x 2) ax + b= +− ++ +
+fx x x x
Cho x = 2, 3
43 2
(2) 2 5; ( 3) 3 5 2; 1 ( ) 4 4 11f ab f ab a b fx x x x x⇒ = += −=− +=−⇒= =⇒ = + − + −
Bài 5: Giả sử đa thức f(x) chia x – 2 dư 11, chia x
2
– x + 1 dư 3x + 2. Tìm phần dư khi chi f(x)
cho g(x) = x
3
– 3x
2
+ 3x -2
Lời giải
g(x) = x
3
– 3x
2
+ 3x -2 = ( x – 2 )( x
2
– x + 1);
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

182
Thực hiện phép chia f(x) cho g(x) ta được:
22
( ) ( 2)( 1) axf x x x x bx c= − −+ + + +
( ) ( 2). ( ) 11f x x hx=−+
.
Cho x = 2
(2) 4 2 11 (1)⇒ = + +=f a bc
Mặt khác:
22 2
32
( ) ( 2)( 1) a( 1) ( ) ( 2 )( 1) ( )
2 (2)
.
3 (3)
= +
= − −+ + −+ + + +−= −+ −+ + + +−
−=
⇒
+=
du x
fx x x x x x abxca x ax x abxca
ca
ab
Từ (1), (2) và (3) suy ra (a, b, c) = (1; 2; 3) . Do đó phần dư là x
2
+ 2x + 3
Bài 6: Giả sử f(x) chia cho x + 2 dư 4 và chia cho x
2
+ 1 dư 2x + 3. Tìm phần dư trong phép
chia f(x) cho ( x + 2 )( x
2
+ 1).
Lời giải
Ta có:
22
( ) ( 2)( 1) axf x x x bx c= + ++ + +
+)
( 2) 4 4 2 4(1)f a bc− =⇒ − +=
+)
22 2
2(2)
( ) ( 2)( 1) a(x 1) (
, , ) (1, 2, 4) : 2 4
3(3)
du
b
f x x x bx
c a a b c du x x
ca
=
= + ++ ++ +−⇒ ⇒ = ⇒ + +
−=
Do đó phần dư là x
2
+ 2x + 4
BÀI TẬP VỀ NHÀ
Bài 1: Chứng minh rằng
a.
42 21 2
2. 1 ( 1)
nn
x x x nN
++
+ + − ∀∈
b.
42 42 2
( 1) ( 1) 1
nn
x x x nN
++
+ + − +∀∈
Bài 2: Chứng minh đa thức
a.
95 94 2 31 30 2
( ) ... 1 ( ) ... 1fxx x xx gxx x xx= + + ++ = + ++ ++
b.
124 123 2 24 23 2
( ) .... 1 ( ) ... 1fxx x xx gxx x xx= + + + ++ = + ++ ++
Bài 3: Chứng minh rằng
19 18 2
( ) ... 1 ( ) ( 1)( 1)f x x x x gx x x= + +++ = + +
Bài 4: Chứng minh rằng
24 18 12 6 4 3 2
() 1 () 1fxx x x x gxxxxx= + + + + = + + ++
Lời giải
Bài 1:
42 21 21 2
2. 1 ( 1)
nn n
xx x
++ +
+ += +
Lại có:
21 21 2 2
1 ( 1) ( 1) ( 1)
nn
xxx x
++
+ +⇒ + +
Bài 2: Ta có
96 32 3 32
( 1). ( ) 1 [(x ) 1] ( 1) ( 1). ( ) ( ) ( )x fx x x x gx fxqx− = −= − − = − ⇒
Bài 3:
19 16 3 3 16 12 8 4 2
( ) ( ... ) ...( ... 1) ( ... 1)( 1) ( 1)( 1)fxx x x x xxxx x x= + + ++= ++ + + + + + +
Bài 4:
4 20 3 15 2 10 5
( ) ( 1) ( 1) ( 1) ( 1) ( )fx xx xx xx xx gx= −+ −+ −+ −+
5 5 55
4 54 3 53 2 52 5
1 1 11
([(x ) 1] [(x ) 1] [(x ) 1] ( 1) ( )
x x xx
x x x xx gx
− − −−
= −+ −+ −+ −+
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

183
Bài 5: Chứng minh rằng
80 70 20 10
() 1 () 1fxx x gxx x=++ =++
Lời giải
Đặt
10 8 7 2
() 1; () 1
tx fttt gttt= ⇒ = + + = ++
8 2 7 2 2 32 32 2 2
( ) ( ) ( ) 1 [(t ) 1] [(t ) 1] ( 1) 1ft tt tttt t t tt tt= − + − + ++= − + − + ++ ++
Bài 6: Tìm số a để đa thức
10 2
( ) ax 3 2 2fx x x x= − ++ +
Lời giải
Ta có
( ) 2 ( 2) 0 1024 4 6 2 0 255.fx x f a a+⇔ − =⇔ − −+=⇔=
CHUYÊN ĐỂ 3: ĐA THỨC
Bài 3:
DÙNG PHƯƠNG PHÁP XÉT GIÁ TRỊ RIÊNG ĐỂ TÌM HỆ SỐ CỦA MỘT ĐA THỨC
A. Kiến thức cần nhớ
Giả sử f(x) và g(x) là các đa thức và bậc của f(x) lớn hơn hoặc bằng bậc của g(x). Khi đó
luôn tồn tại duy nhất các đa thức q(x) và r(x), thỏa mãn:
f(x) = g(x) . q(x) + r(x)
Trong đó: Bậc của r(x) nhỏ hơn bậc của g(x)
Nếu r(x)
≡
0 thì ta nói f(x) chia hết cho g(x)
Xét phép chia đa thức f(x) cho đa thức bậc nhất x – a
f(x) = (x-a) . q(x) + r . Cho x = a
⇒
f(a) = r
- Kết luận: Phần dư trong phép chia đa thức f(x) cho x – a là một số bằng f(a)
- Nếu f(a) = 0 hay x = a là nghiệm của đa thức f(x) thì f(x) chia hết cho x – a
- Định lý Bơ Du:
Số dư trong phép chia đa thức f(x) cho nhị thức x – a bằng giá trị của f(x) tại x = a
()( ) () 0fx x a fa⇒ −⇔ =
Bài 1: Xác định các hằng số a, b, c sao cho
a.
32
( ) ax 5 50 ( ) ( 5)( 2)f x bx x g x x x= + +− =+ −
b.
42
( ) axf x x bx c=+ ++
chia cho x – 2 thì dư 9, chia cho x
2
– 1 thì dư 2x - 1
c.
4 32 2
() 2 3 +5x () 2 3f x x x ax bgx x x= + ++ =++
d.
32
( ) ax ( 2)f x bx c x=++ +
và chia x
2
– 1 dư x + 5.
e.
32
() xf x ax bx c=+ ++
chia hết cho x – 2 và chia x
2
– a dư 2x
Lời giải
a. Gọi q(x) là thương của phép chia f(x) cho g(x)
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

184
Ta có:
32
ax 5 50 ( 5)( 2). ( )bx x x x q x+ +−=+ −
Xét các giá trị riêng x = -5 ; x = 2 , ta được:
5 12 25 75 1
2 8 4 40 8
x ab a
x ab b
=− ⇒− + = =
⇒
=⇒+= =
b.
2
() ( 1).() 2 1f x x qx x= − +−
Cho
1 0 (1)
1 4 (2)
=⇒++=
=−⇒ − + =−
x abc
x abc
Mặt khác: f(x) chia cho x - 2 dư 9
(2) 9 4 2 7 (3)⇒ =⇒ + +=−f a bc
Từ (1), (2) và (3)
( , , ) ( 3, 2,1)abc⇒=−
c. Ta có:
( ) ( 1)( 2). ( ) 1; 3fxxxqxa b= + + ⇒=− =
d. Ta có
( ) ( 2). ( ) ( 2) 0 8 4 0 (1)= + ⇒ − = ⇔− + + =f x x px f a b c
(1) 6 (2)
( ) ( 1)( 1). ( ) 5 .
( 1) 4
(3)
(1)(2)(3) ( , , ) (1,1,4)
=++=
= − + ++⇒
− =−++=
⇒=
f abc
f x x x qx x
f abc
abc
e.
10 10
( , , ) ;1;
33
−
=
abc
Bài 2: Đa thức P(x) có bậc 4, có hệ số bậc cao nhất là 1. Biết P(1) = 0, P(3) = 0; P(5) = 0. Tính
Q = P(-2) + 7.P(6)
Lời giải
Ta có P(x) chia hết cho x – 1: x – 3 ; x – 5 và bậc của P(x) là 4 nên P(x) có dạng:
( ) ( 1)( 2)( 3)( )Px x x x x a=−− −−
( 2) 7 (6) ( 3)( 5)( 7)( 2 ) 7.5.3.1( 6) 105( 2) 105( 6) 840Pp a
a a a−+ =−−−−++ +=− −+ +=
Bài 3: [GVG Tỉnh – Bắc Ninh : 09/12/2016 ]
Tìm đa thức f(x), biết f(x) chia cho x – 2 dư 5, f(x) chia cho x – 3 dư 7, chia cho (9x-2)(x-3)
được thương là x
2
– 1 và đa thức dư bậc nhất đối với x.
Lời giải
Gọi dư trong phép chia f(x) cho (x-2)(x-3) là ax + b
Ta có:
2
( ) ( 2)( 3)( 1) ax+bfx x x x= − − −+
Theo bài ra ta có:
(2) 5 2 5 2
(3) 7 3 7 1
f ab a
f ab b
=⇒ += =
⇒
=⇒ += =
Bài 4: Tìm f(x), biết f(x) chia cho x – 1 và x – 3 đều dư 2 và f(x) chia cho x
2
– 4x + 3 được
thương là x + 1 và còn dư.
Lời giải
f(x) chia cho x – 1 dư 2
( ) ( 1). ( ) 2(1)f x x gx⇒=− +
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

185
f(x) chia cho x – 3 dư 2
( ) ( 3). ( ) 2(2)f x x hx⇒=− +
f(x) chia cho x
2
– 4x + 3 được x + 1 và dư
2
( ) ( 4 3)( 1) ax+b(3)fx x x x⇒ = − + ++
Từ (1), cho x = 1
2(4)ab⇒+=
Từ (2)(3) cho x = 3
3 2(5)ab⇒ +=−
Từ (4)(5)
2
0; 2 ( ) ( 4 3)( 1) 2a b fx x x x= =⇒ = − + −+
Bài 4: ĐẶT PHÉP CHIA ĐỂ TÌM HỆ SỐ
Bài 1: Tìm a, b sao cho
4 3 22 3 2 2 2
() axy () 2 3fxxxyxy bygxx xyy=−− + + =−+
Lời giải
Đặt phép chia
22 3 4
( ) ( ).( 2 ) ( 7) ( 6)f x g x x xy y a xy b y= +− +− ++
Để phép chia hết thì dư phải bằng 0
70 7
60 6
aa
bb
−= =
⇒⇒
+= =−
Bài 2: Với giá trị nào của a, b thì đa thức ax
4
+ bx
3
+ 1 chia hết cho (x -1)
2
.
Lời giải
Ta có:
4 3 22
ax 1 ( 1) [ax ( 2 ) 3 2 ] ( 2 6 4 ). 1 3 2bx x baxab baabx ab+ +=− ++ ++ +−−++ +−−
Để phép chia hết thì dư phải bằng 0
2640 3
13 2 0 4
baab a
ab b
−−++= =
⇒⇔
−− − = =−
Bài 3: Tìm các số a, b sao cho :
5 4 3 22 4 5 3 2 3
3 3 4 3 axy 3 2x xy xy xy by x xy y−++ −− −+
Lời giải
Thực hiện phép chia ta được thương: x
2
– xy + y
2
và dư: -(a-5)xy
4
– (b+2)y
5
Để phép chia hết thì dư phải bằng 0
( 5) 0 5
20 2
aa
bb
−−= =
⇔⇔
+= =−
Bài 4
*
: Tìm các số a, b, c sao cho:
42
4 81 axx bx c+ ++
Lời giải
Ta có:
44 222 2 2 2
4 3 (2 3 ) (6 ) (2 6 9)(2 6 9)x x x xx xx+= + − = −+ ++
Chia hết cho
22
2
22
ax (2 6 9) ( 0)
ax
ax (
2 6 9) ( 0)
+ += − + ≠
+ +⇔
+ += + + ≠
bx c k x x k
bx c
bx c h x x h
0 ( 0)
2; 6; 9
2 69
2; 6; 9
0 ( 0)
269
==≠≠
= =−=
−
⇔⇔
= = =
==≠≠
abc
k
a kb kc k
a hb hc h a b c
h
Bài 5: Tìm các số nguyên a, b sao cho
43 2
( ) 4 ax+b g(x) = x 3 4=− + −+fx x x x
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
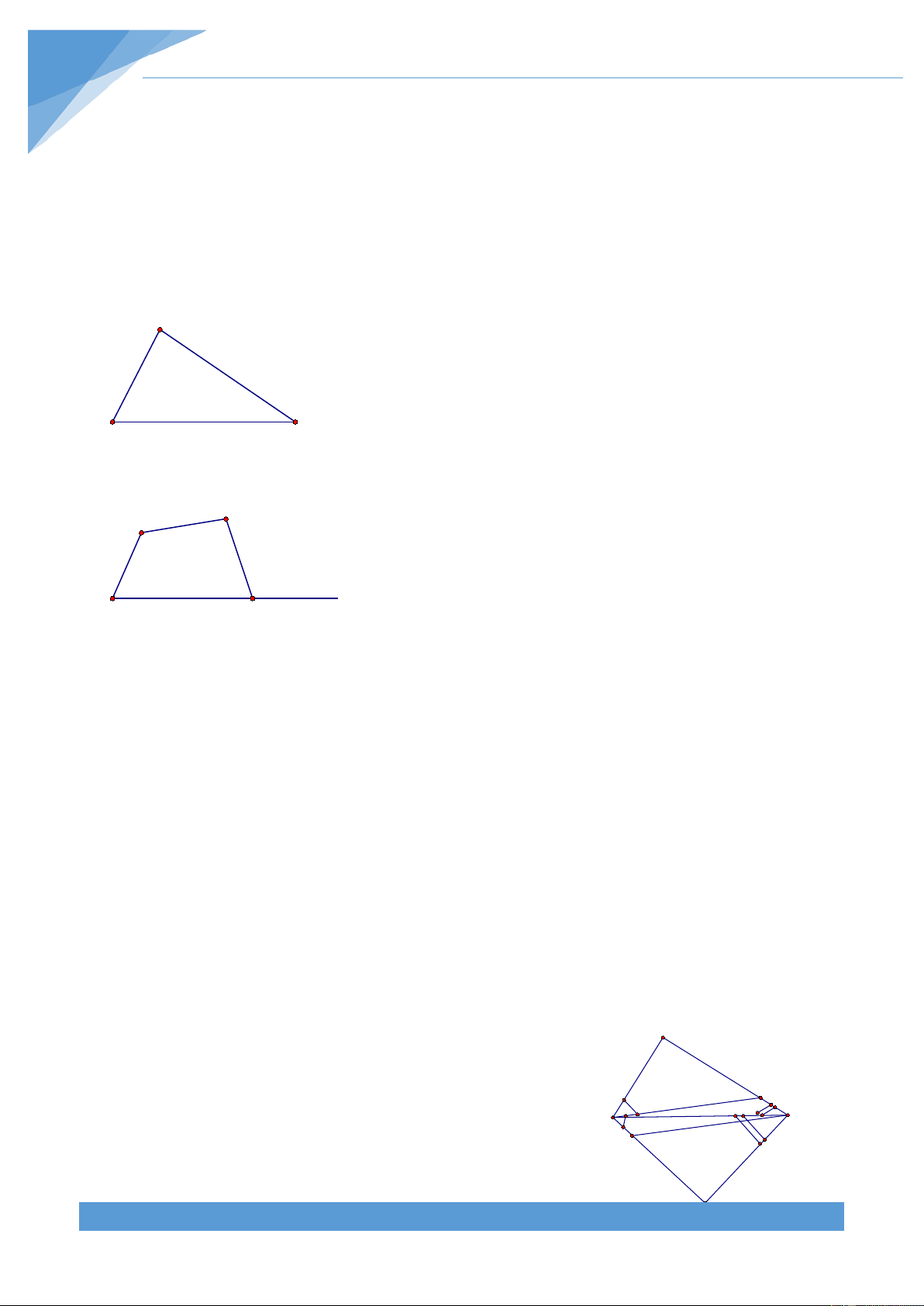
186
2
4
() ().( 1) ( 3) 4
4
a
fx gx x a x b
b
=
= − + − ++⇒
= −
CHUYÊN ĐỀ 8: HÌNH HỌC
A. Kiến thức
1. Tam giác
-
0
ˆˆ
ˆ
A + B + C = 180
( Tổng 3 góc trong 1 tam giác )
-
AB AC BC+>
( Bất đẳng thức tam giác)
-
AB AC BC−<
( Bất đẳng thức tam giác)
2. Tứ giác
a. Định nghĩa: Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó bất kỳ 2
đoạn thẳng nào cũng không cùng nằm trên 1 đường thẳng
b. Tứ giác lồi: Là tứ giác luôn nằm trong 1 nửa mặt phẳng có bờ là đường thẳng chứa bất
kỳ cạnh nào của tứ giác
c. Chú ý: Khi nói đến tứ giác mà không chú thích gì them, ta hiểu đó là tứ giác lồi
3. Tổng các góc của 1 tứ giác
- Định lý: Tổng các góc cảu một tứ giác bằng 360
0
ˆˆ
ˆˆ
0
A + B + C + D = 360⇒
- Chú ý: Để bốn góc cho trước thỏa mãn là bốn góc của một tứ giác khi bốn góc đó có tổng
bằng
0
360
- Bất đẳng thức đường gấp khúc:
AB + BC + CD > DA
- Mở rộng: Tổng bốn góc ngoài ở bốn đỉnh của một tứ giác
bằng 360
0
.
4. Góc ngoài của tứ giác: Góc kề bù với 1 góc trong của tứ
giác gọi là góc ngoài của tứ giác
- Ta có
1
ˆ
B
là góc ngoài tại đỉnh B.
B. Bài tập
β
α
1
E
D
C
B
A
C
B
A
1
D
C
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
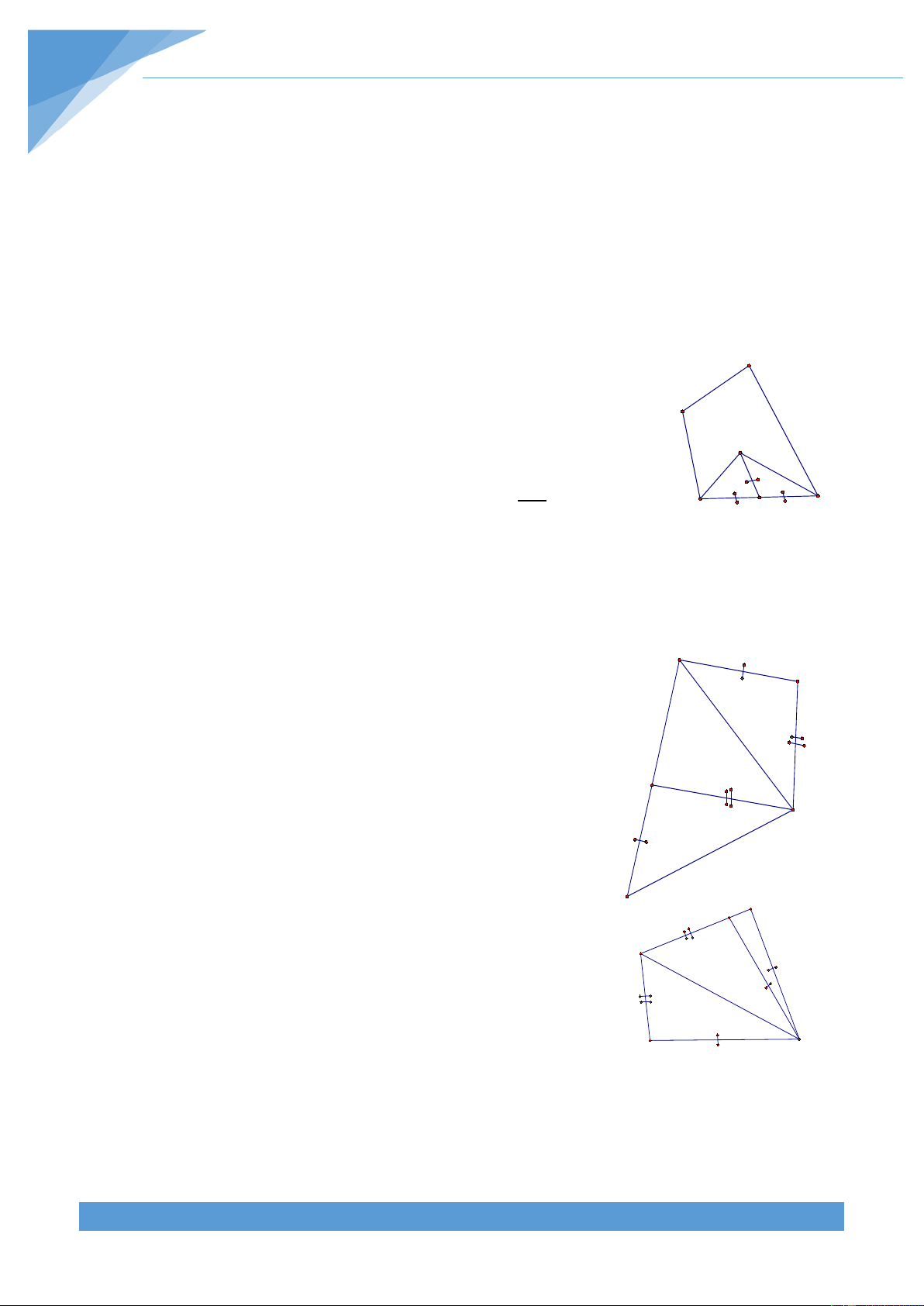
187
Bài 1: Cho tứ giác ABCD có:
0
ˆˆ
90BAD BCD= =
, phân giác trong của góc ABC cắt AD tại E.
phân giác trong của góc ADC cắt BC tại F. Chứng minh BE // DF
Lời giải
+)
0
180ABC ADC+=⇒
0
90 (1)
αβ
+=
+) Xét tam giác ABE, có:
0
1
90 (2)E
α
+=
+) Từ (1), (2)suy ra
1
β
=
E
và hai góc này ở vị trí đồng vị nên
//BE DF
Bài 2: Cho tứ giác ABCD có:
0
D 180ABC BA+=
. Phân giác trong của các góc BCD và CDA
cắt nhau tại E, biết rằng CD = 2 DE . Chứng minh rằng :
2ADC BCD=
Lời giải
+) Ta có:
00 0
11
ˆˆ
ˆˆ
180 180 90
90
o
A B C D C D DEC+= ⇒+= ⇒ + = ⇒ =
+) Gọi M là trung điểm của CD
2
CD
EM MC MD⇒===
DEM⇒∆
đều
00
11
60 30 2 ( )D C D C dpcm= ⇒ = ⇒=
Bài 3: Cho tứ giác ABCD , có:
0
2 180 ,BAD BCD+=
DA DC=
. chứng minh rằng BD là phân
giác
ABC
Lời giải:
+) Trên tia đối của tia AB lấy điểm E sao cho AE = BC
+)
11
(1)
()
BE
BCD EAD cgc BED
DB DE
=
∆ =∆ ⇒ ⇒∆
=
cân tại D
12
(2)EB⇒=
Từ (1)(2)
12
()B B dpcm⇒=
Bài 4: Cho tứ giác ABCD có BD là phân giác của góc ABC ,
AD = CD , AB < BC . Chứng minh rằng :
0
180BAD BCD+=
Lời giải
+) Trên cạnh BC lấy điểm E sao cho BE = BA
+)
11
(1)
()
AE
BED BAD cgc ED CD ECD
AD ED
ED DA
=
∆ =∆ ⇒ ⇒ = ⇒∆
=
=
cân tại
D
21
(2)EC⇒=
. Từ (1)(2)
0
1 11 2
180AC EE+=+=
Bài 5: Cho tứ giác ABCD có:
ˆˆ
ˆˆ
: : : 5:8:13:10ABCD=
1
1
M
E
D
C
B
A
1
1
1
2
1
E
D
C
B
A
1
2
1
E
D
C
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
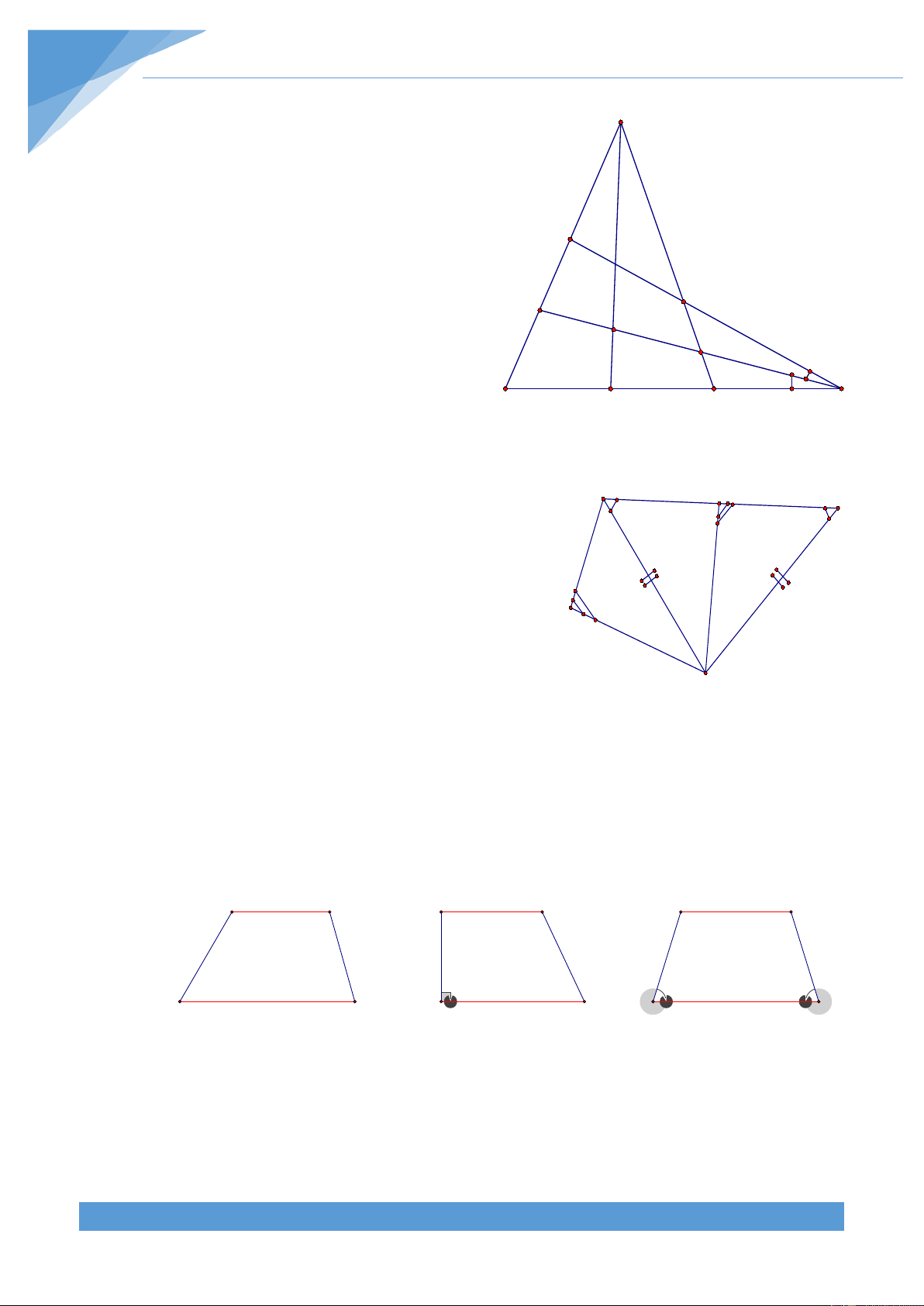
188
a. Tính các góc của tứ giác ABCD
b. AB cắt CD tại E, AD cắt BC tại F. Phân giác
góc AED và góc AFB cắt nhau tại O, phân giác
góc AFB cắt CD và AB tại M và N. Chứng
minh rằng O là trung điểm của MN
Lời giải
a.
00 0 0
ˆˆ
ˆˆ
50 , 80 , 130 , 100ABC D= = = =
b.
0 00 0
ˆˆ
ˆ ˆˆ ˆ
180 30 ; 180 50AED A D AFB A B= −− = = −−=
0 0 000 0
11
ˆ ˆˆ ˆ
180 75 ; 180 75 30 75EMN F B ENM= −−= = − − =
EMN⇒∆
cân
O⇒
là trung điểm của MN
Bài 6: Cho tứ giác ABCD có
0
ˆˆ
180BD+=
, AC là phân
giác của góc A.
Chứng minh rằng: CB = CD
Lời giải
Dựng tam giác ACE cân tại C
CA CE⇒=
Theo gt:
0
2
11
0
21
ˆˆ
180
ˆˆ
ˆˆ
180
BD
DB
BB
+=
⇒=
+=
Có:
11
12
12
ˆ
ˆ
ˆ
ˆ
ˆˆ
AE
EA
AA
=
⇒
=
=
CEB∆
và
CAD∆
có:
21
12
11
ˆ
ˆ
ˆˆ
( .. )
ˆˆ
=
⇒ = ⇒∆ =∆ ⇒ =
=
AE
C C CEB CAD g c g CB CD
DB
HÌNH THANG, HÌNH THANG CÂN
A. HÌNH THANG
1. Định nghĩa: Hình thang là tứ giác có hai cạnh đối song song.
ABCD◊
Là hình thang ( đáy AB, CD )
//
ABCDla
AB CD
◊
⇔
+) AB: đáy nhỏ +) CD: đáy lớn +) AD, BC: cạnh bên
75
°
1
O
2
1
1
D
N
F
C
E
B
M
A
1
2
1
1
2
2
1
1
D
C
E
B
A
H3. THANG CÂN
H2. THANG VUÔNG
H1. HÌNH THANG
C
A
A
B
D
B
C
C
D
A
B
D
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
189
Nhận xét
- Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau
- Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau
Dựa vào nhận xét ta có
Hình thang ABCD ( AB // CD ), có:
+)
// ;AD BC AD BC AB CD⇒= =
+)
// ;AB CD AD BC AD BC=⇒=
2. Hình thang vuông là hình thang có 1 góc vuông
B. HÌNH THANG CÂN
1. Định nghĩa
Hình thang cân là hình thang có hai góc kề 1 đáy bằng nhau
ABCD là hình thang cân ( đáy AB, CD )
( à hinh thang )
ˆˆ
ˆˆ
C=D hoac A=B
⇔
ABCD l
2. Tính chất: Trong hình thang cân
- Hai cạnh bên bằng nhau
- Hai đường chéo bằng nhau
3. Dấu hiệu nhận biết
- Hình thang có 2 góc kề 1 đáy bằng nhau là hình thang cân
- Hình thang có hai đường chéo bằng nhau là hình thang cân
4. Chú ý: Hình thang có hai cạnh bên bằng nhau chưa chắc đã là hình thang cân ( Hình
bình hành )
C. BÀI TẬP ÁP DỤNG
Bài 1: Cho tam giác ABC và đường thẳng d đi
qua trọng tâm G của tam giác ABC và cắt các
đoạn AB, AC. Chứng minh rằng tổng khoảng
cách từ B và C tới d bằng khoảng cách từ A tới d
Lời giải
Ta có tứ giác BEFC là hình thang ( BE // CF )
P
M
D
G
N
K
C
F
B
E
A
H3. THANG CÂN
H2. THANG VUÔNG
H1. HÌNH THANG
C
A
A
B
D
B
C
C
D
A
B
D
D
C
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
190
Gọi N là trung điểm của EF, M là trung điểm của BC
2 (1)
2
BE CF MN
BE CF
MN
MN d
+=
+
⇒= ⇒
⊥
+) Lấy P thuộc tia đối của MG sao cho MP = MG
GP GA⇒=
+) Lấy K thuộc d sao cho NG = NK
1
2
MN PK
PK D
=
⇒
⊥
1
( ) (2)
2
ADG PKG ch gn PK DA MN AD AD BE CF∆ =∆ −⇒=⇒ = ⇒=+
Bài 2: Cho tam giác ABC có trọng tâm G và đường thẳng d nằm ngoài tam giác. Gọi D, E,
F, H lần lượt là hình chiếu của A, B, C, D lên đường thẳng d. Chứng minh rằng: AD + BE +
CF = 3GH
Lời giải
+) Gọi M là trung điểm của BC
+) P là trung điểm của AG
+) K là hình chiếu của M lên d
Ta có : BE + CF = 2MK
AD + GH = 2PQ; MK + PQ = 2GH
2( MK + PQ ) = 4GH; BE + AD + CF =
3GH (dpcm)
Bài 3: Cho hình thang ABCD ( AB // CD ), trong đó CD = BC + AD. Hai đường phân giác
của hai góc A và B cắt nhau tại K. Chứng minh rằng C, D, K thẳng hàng.
Lời giải
Trên CD lấy điểm E sao cho CE = CB
AD DE CBE⇒ = ⇒∆
cân tại C
11
ˆˆ
EB⇒=
Mặt khác
12 12
ˆˆ ˆˆ
()E B slt B B= ⇒=
ADE∆
cân tại D
12
ˆ
ˆ
AE⇒=
mà
2 2 12
ˆ ˆˆ
ˆ
()E A slt A A⇒= ⇒=
,EA EB⇒
là phân giác của
ˆ
ˆ
,AB⇒
giao điểm của hai đường phân giác góc A và B cắt nhau
tại E thuộc BC
,,E K DKC⇒≡⇒
thẳng hàng.
Bài 4: Cho hình thang cân ABCD ( AB // CD ) có đường chéo BD vuông góc với cạnh bên
BC và đồng thời DB là tia phân giác của
ˆ
ADC
a. Tính các góc của hình thang cân ABCD
b. Biết BC = 6cm, tính chu vi và diện tích của hình thang cân ABCD
M
G
P
E
D
Q
H
K
F
B
C
A
2
1
2
1
1
2
E
C
B
D
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
191
Lời giải
a)
0
ˆ
( 90 )DBC B∆=
có
00
ˆ ˆˆ
ˆˆ ˆ
2 60 ; 120BCD BDC ADC BCD DAB CBA= ⇒== ==
b) Tính được DC = 2.BC
30
ABCD
P cm=
Hạ đường cao BK, ta có
2
3 3 27 3( )
ABCD
BK cm S cm= ⇒=
Bài 5: Cho tam giác đều ABC. Từ 1 điểm M nằm bên trong tam giác ta vẽ các tia gốc M
song song với BC cắt AB ở D, song song với AC cắt BC tại E, song song với AB cắt AC tại
F. Chứng minh rằng chu vi tam giác DEF bằng tổng các khoảng cách từ M đến ba đỉnh của
tam giác.
Lời giải
Chu vi tam giác ABC là : DE + DF + EF
Khoảng cách từ M đến 3 đỉnh là : MA + MB + MC
Ta cần chứng minh : DE + DF + EF = MA + MB + MC
+) Ta có hình thang BDME là hình thang cân (
0
ˆ
ˆˆ
// , 60 )MD BE B E C= = =
DE MB⇒=
Chứng minh tương tự ta có : DF= MA, EF = MC
⇒
DE + DF + EF = MA + MB + MC ( đpcm)
Bài 6: Cho tam giác ABC cân tại A, điểm I thuộc đường cao AH, BI giao với AC tại D, CI
giao với AB tại E
a. Chứng minh rằng: AD = AE b. Xác định dạng của tứ giác BEDC
c. Xác định I sao cho: BE = ED = DC
Lời giải
a. Ta có:
11
ˆ
ˆ
(. .) (
.. )∆ =∆ ⇒ = ⇒∆ =∆ ⇒ =AIC AIB c g c C B ACE ABD g c g AE AD
b.
,ADE ACB∆∆
cân tại A có chung góc A
0
ˆ
//
180
ˆ
ˆˆ ˆ
ˆ
ˆ
2
DE BC
A
ADE AED ACB ABC d
pcm
CB
−
⇒==== ⇒ ⇒
=
c.
22
ˆˆ
//DE BC B D⇒=
. Để BE = ED
BED⇒∆
cân tại E
12
12
22
ˆˆ
ˆˆ
ˆˆ
BD
BB
BD
=
⇒ ⇒=
=
2
2
1
2
1
2
1
H
I
D
E
B
C
A
K
D
C
B
A
M
D
B
E
C
F
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
192
Chứng minh tương tự:
12
ˆˆ
CC=
Vậy CE và BD là giao điểm của góc C và B
Vậy I là giao điểm của 3 đường phân giác của tam giác ABC.
Bài 7: Cho hình thang ABCD ( AB // CD) tia phân giác góc C đi qua trung điểm M của AD.
CMR:
a)
0
90BMC =
b) BC = AB + CD
Lời giải
a) Giả sử MC cắt AB tại E
Khi đó
( )
.. ; D ECMD EMA g c g CM EM A A∆ =∆ ⇒= =
Xét
∆
BEC có:
21
EC C= =
=>
∆
BEC cân
Mà BM là đường trung tuyến
=> BM là đường cao
Vậy BM
⊥
EC
b) Vì
∆
BEC cân nên EB = BC => BC = EA + AB = DC + AB
Bài 8: Cho hình thang ABCD ( AB // CD), có
0
60C =
, DB là phân giác của góc
D
, Biết chu
vi của hình thang là 20cm, Tính mỗi cạnh của hình thang
Lời giải
Đặt BC= a, ta có ngay: AD = AB = BC = a
Mà:
00 0
2
60 30 90C D DBC= ⇒= ⇒ =
Xét
∆
BDC có
00
2
30 , 60 2D C DC a= =⇒=
Mà Chu vi hình thang là 20 cm nên ta có:
a + a + a + 2a = 20 => a = 4
2
2
1
2
1
E
M
B
A
D
C
a
1
1
2
1
A
B
D
C
E
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
193
ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC, HÌNH THANG
A. ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
1. Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của
tam giác.
2. Các định lý
a. Định lý 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh
thứ hai thì đi qua trung điểm của cạnh thứ ba
, ,/ABC AM MB MN BC AN NC∆ = ⇒=
b. Định lý 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa
cạnh ấy:
1
// ;
2
MN BC MN BC=
B. ĐƯỜNG TRUNG BÌNH CỦA HÌNH THANG
1. Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh
bên của hình thang
2. Các định lý
a. Định lý 1: Đường thẳng đi qua trung điểm 1 cạnh bên của hình thang và song song với
hai đáy thì đi qua trung điểm của cạnh bên thứ hai
Nếu EA = ED và EF // AB // CD thì FB = FC
b. Định lý 2: Đường trung bình của hình thang song song với hai đáy và bằng nửa tổng
hai đáy
H5. ĐƯỜNG TRUNG BÌNH HÌNH THANG
H4.ĐƯỜNG TRUNG BÌNH TAM GIÁC
N
M
N
M
A
B
C
A
B
D
C
H5. ĐƯỜNG TRUNG BÌNH HÌNH THANG
H4.ĐƯỜNG TRUNG BÌNH TAM GIÁC
N
M
N
M
A
B
C
A
B
D
C
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
194
Ta có: EF // AB // CD và
1
EF= ( )
2
AB CD+
3. Mở rộng
- Trong hình thang có hai cạnh bên không song song, đoạn thẳng nối trung điểm của hai
đường chéo thì song song với hai đáy và bằng một nửa hiệu hai đáy
Ta có:
// //MN AB CD
và
2
CD AB
MN
−
=
C. BÀI TẬP VẬN DỤNG
Bài 1: Cho tứ giác ABCD. Gọi E, K, F lần lượt là trung điểm của AD, BC, AC
a. Chứng minh EK // CD, FK // AB
b. So sánh EF và
1
()
2
AB CD+
c. Tìm điều kiện của tứ giác ABCD để 3 điểm E, F, K thẳng hàng, chứng minh
1
EF = ( )
2
AB CD+
Lời giải
b. Xét
EFK∆
,có:
11
()
22
1
EF EK+KF= CD AB AB CD
2
≤ += +
c. Để E, F, K thẳng hàng, khi đó EF đồng thời song song
với AB, CD. Tức là tứ giác ABCD là hình thang ( AB //
CD )
( )
1
D
2
EF AB C⇒= +
Bài 2: Tính độ dài đường trung bình của một hình thang cân biết rằng các đường chéo của
nó vuông góc và chiều cao = 10cm
Lời giải
+)
11 11
ˆˆ
ˆˆ
()ABC BAD ccc A B D C∆ =∆ ⇒=⇒=
+)
0
111 1
ˆˆ
ˆˆ
45AC BD A B C D⊥ ⇒====
I
1
1
M
N
H
1
1
D
C
B
A
K
F
E
D
C
B
A
M
N
A
B
D
C
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
195
,IAB ICD⇒∆ ∆
vuông cân tại I
;
22 2
AB CD A
B CD
MI NI MI NI
+
⇒ = = ⇒+= =
đường trung bình của tam giác = 10cm.
Bài 3: Cho tam giác ABC có AB = c, BC = a, AC = b. Qua A kẻ đường thẳng song song với
BC cắt tia phân giác góc B và C tại D và E. Từ A kẻ AP vuông góc với BD; AQ vuông góc
với CE. PQ lần lượt cắt EB, CD tại M, N. Tính MN, PQ theo a, b, c
Lời giải
+)
112
ˆˆ
ˆ
()E C C slt EAC= = ⇒∆
cân tại A
;AE AC AQ EC AQ⇒= ⊥⇒
là đường cao, phân giác,
trung trực, đường trung tuyến
QE QC⇒=
+) Tương tự
ABD∆
cân tại A và
BP PD=
+)
ABH∆
có BP là phân giác và đường cao
ABH⇒∆
cân tại B
P⇒
là trung điểm của AH
Tương tự: Q là trung điểm của AF
1
2
PQ FH⇒=
+)
//MQ BC M⇒
là trung điểm của BE ; +) N là trung điểm của BE
+)
11 1
( )( )( )
22 2
MN ED BC EA AD BC AC AB BC= += ++= ++
11 1 1 1 1
( )( )( ( ))( )( )
22 2 2 2 2
PQ HF FC HC AC HC AC BC BH AC BC BA b a c= = −= −= −= = −+=−+
Bài 4: Cho hình thang ABCD ( AB // CD), Gọi E là giao điểm của AD và BC, Gọi M, N, P, Q
lần lượt là trung điểm của AE, BE, AC, BD. CMR: MNPQ là hình thang
Lời giải
Dễ dạng chứng minh được MN // AB
- Gọi R là trung điểm của AD khi đó ta có: RQ // AB
RP // DC // AB
Nên RP // AB => R, Q, P thẳng hàng => PQ // AB
Vậy MNPQ là hình thang
1
2
1
P
Q
M
E
D
N
H
F
C
B
A
R
P
Q
N
M
B
E
D
C
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
196
Bài 5: Cho tam giác ABC vuông tại A, Vẽ AH vuông góc với BC tại H, Gọi M, N lần lượt là
trung điểm của các đoạn thẳng AH CH, CMR :
MN vuông góc với AB và BM vuông góc với AN
Lời giải
Vì MN là đường trung bình
=> MN // AC mà AC
⊥
AB
=> MN
⊥
AB => M là trực tâm của
∆
ABN
∆
ABN có M là trực tâm => BM
⊥
AN
Bài 6: Cho đoạn thẳng AB và trung điểm O của nó, trên cùng 1 nửa mặt phẳng có bờ AB,
vẽ hai tia Ax và By vuông góc với AB, Một góc vuông đỉnh O cắt Ax tại C, cắt By tại D
a) AC + BD = CD b) CO là tia phân giác của
ACD
Lời giải
a) Gọi I là trung điểm của CD
AC // BD => OI là trung bình của hình thang ABCD
=>
2
AC BD
OI
+
=
=>
2.AC BD OI+=
Lại có
∆
COD vuông => OI là đường trung tuyến
=> OI = CI = ID => 2OI = IC + ID = CD
b) Ta có
∆
OCD vuông tại O có OI là đường trung tuyến nên OI = IC
=>
OIC⇒∆
cân tại I
21
CO⇒=
Mà:
11
OC=
Nên
12
CC⇒=
Vậy OC là tia phân giác góc
ACD
Bài 7: Cho tứ giác ABCD có AD = BC, đường thẳng đi qua trung điểm M và N của các
cạnh AB và CD cắt AD và BC lần lượt ở E và F, CMR :
AEM MFB=
Lời giải
Gọi I là trung điểm của BD
Ta có: MI, NI lần lượt là đường trung bình
22
AD BC
MI IN
IMN⇒ = = = ⇒∆
cân
ME⇒=
( đồng vị )
và
NF=
( so le trong)
Vậy
EF=
M
N
H
B
C
A
1
2
1
I
D
O
A
B
C
?
?
I
F
E
M
N
D
C
A
B
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
197
Bài 8: Cho tam giác ABC, AM là đường trung tuyến, vẽ đường thẳng (d) đi qua trung
điểm I của AM cắt các cạnh AB, AC, Gọi A’, B’, C’ lần lượt là hình chiếu của A, B, C trên
đường thẳng (d). CMR:
''
AA'
2
BB CC+
=
Lời giải
Gọi H, K lần lượt là giao của (d) với AB và AC
Lấy N là hình chiếu của M trên đường thẳng (d)
=>
∆
AA’I =
∆
MNI ( cạnh huyền - góc nhọn)
=> AA’ = MN
Hình thang BB’C’C có MN là đường trung bình nên:
''
'
2
BB CC
MN AA
+
= =
Bài 9: Cho tam giác ABC có 3 góc nhọn, các đường cao BD và CE, gọi I và K theo thứ tự là
hình chiếu của B và C trên đường thẳng ED, CMR: IE = DK
Lời giải
Gọi M là trung điểm của BC, kẻ MN
⊥
ED
Tứ giác BIKC là hình thang => NI = NK (1)
∆
BEC vuông có EM =
1
2
BC
∆
BDC vuông có DM =
1
2
BC => EM = DM
=>
∆
EDM cân có MN đường cao và là trung tuyến
=> NE = ND (2)
Từ (1) và (2) => IE = DK
Bài 10: Cho tam giác ABC có G là trọng tâm, đường thẳng (d) không cắt các cạnh của tam
giác ABC, Gọi A’, B’, C’, G’ lần lượt là hình chiếu của A, B, C, G trên đường thẳng (d).
CMR:
'''
'
3
AA BB CC
GG
++
=
Lời giải
Gọi M là trung điểm của AC, và D đối xứng với G qua M,
M’ là hình chiếu của M trên (d), Khi đó ta có :
2
BG
GM DM= =
=> G là trung điểm của BD
=> GG’ là đường trung bình của hình thang BB’D’D
d
C'
M'
A'
B'
I
M
B
C
A
d
M'
C'
D'
G'
A'
B'
D
G
M
A
B
C
K
N
I
M
D
E
B
C
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
198
=> MM’ là đường trung bình của hình thang GG’D’D
Nên:
''
'
2
BB DD
GG
+
=
(1)
' CC' ' '
' ;'
22
AA DD GG
MM MM
++
= =
=> DD’ + GG’ = AA’ + CC’ => DD’ = AA’ + CC’ - GG’
Thay (1) vào ta được: 2GG’ = BB’ + AA’ + CC’ - GG’
=> 3GG’ = AA’ + BB’ + CC’ => ĐPCM
Bài 11: Cho tam giác ABC có trọng tâm G ( G nằm bên trong tam giác), Vẽ đường thẳng
(d) đi qua G, cắt AB, AC, Gọi A’, B’, C’ là hình chiếu của A, B, C trên (d), khi đó AA’, BB,
CC’ có mỗi quan hệ gì?
Lời giải
Gọi I trên AG sao cho AI = IG
Kẻ MM’
⊥
(d)
Khi đó ta có:
∆
GII’ =
∆
GMM’ (cạnh huyền = góc nhọn)
=> II’ = MM’ mà II’ =
1
2
AA’ => AA’ = 2. MM’
Hình thang BB’C’C có MM’ là đường trung bình
Nên ta có: 2. MM’ = BB’ + CC’
Nên ta có: AA’ = BB’ + CC’
Bài 12: Cho tam giác ABC, Gọi D là trung điểm cạnh AB, trên BC lấy các điểm E, F sao cho
BE = EF = FC, trên tia đối của tia BA lấy điểm G sao cho BG = BD
CMR: AF, CD, GE đồng quy
Lời giải
Gọi I là giao điểm của CD và GE
=> E là trọng tâm của
∆
DGC => DI = IC
∆
DEC có IF là đường trung bình nên IF // DE
Lại có: DE là đường trung bình
∆
ABF => DE // AF
Khi đó A, I, F thẳng hàng hay AF có đi qua I
Bài 13: Cho tam giác ABC có BC = a, các đường trung tuyến BD, CE, lấy các điểm M, N
trên các cạnh BC sao cho BM = MN = NC, gọi I là giao điểm của AM và BD, K là giao điểm
của AN và CE. Tính IK
C'
M'
I'
A'
B'
I
G
M
A
B
C
I
G
C
F
D
B
A
E
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
199
Lời giải
Vì DN là đường trung bình của
∆
ACM => DN // AM
∆
BDN có:
//
BM MN
AM DN
=
=> I là trung điểm của BD
Chứng minh tương tự =>
K là trung điểm của EC
Kéo dài IK cắt AB và AC lần lượt tại G và H
Khi đó
∆
BED có GI đi qua trung điểm I của BD
và // ED nên GE = GB
∆
CED có KH đi qua trung điểm K của EC và // ED
Nên HD = HC
Khi đó ta có:
11 11
,
24 24
GI ED a KH ED a= = = =
Còn
13 3
2
22 4
aa
GH a a GH=+==> =
Nên IK= GH - GI - HK=
311
44 4 4
aa
aa−−=
Vậy
4
a
IK =
Bài 14: Cho hình thang ABCD có
1, 2 2A B v BC AB AD= = = =
, Gọi M là 1 điểm nằm trên
đáy nhỏ AD, kẻ Mx vuông góc với BM và Mx cắt CD tại N. CMR: MB = MN
Lời giải
Kẻ DK //AB, chứng minh
∆
BDC vuông tại D
00 0
90 45 135ADC⇒ =+=
Gọi H là trung điểm của BN,
Chứng minh MH
⊥
BN vì
∆
BMN vuông
11
,
22
MH BN DH BN MH DH= = =>=
HMD HDM=
mà
HDM ABH DMN MBH= = +
(1)
Và
HMD HMN DMN= +
(2)
Từ (1) và (2) =>
MBH HMN=
Mà:
00
90 90MBH MNH HMN MNH+==>+=
Bài 15: Cho tam giác ABC nhọn, trực tâm H, M là trung điểm của BC, qua H kẻ đường
thẳng vuông góc với HM, cắt AB, AC theo thứ tự tại E và F
H
G
K
I
D
C
N
E
B
A
M
2
2
1
1
3
2
1
K
H
N
C
B
A
D
M
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
200
a) Trên Tia đối tia HC, lấy điểm D sao cho HD = HC, CMR E là trực tâm của tam giác DBH
b) CMR: HE = HF
Lời giải
a) Ta có MH là đường trung bình
∆
BCD
=> MH// BD
Mà EF // MH => EF
⊥
BD
Ta lại có: BA
⊥
DH =>
∆
BDH có E là trực tâm
b) Gọi G là giao điểm của DE và BH
=> K là giao điểm BH và AC
=>
∆
DHG =
∆
CHK ( cạnh huyền - góc nhọn)
=> HG = HK =>
∆
HE =
∆
HKF ( c. g. c) => HE = HF
Bài 16: Cho hình thang ABCD (AB // CD), Gọi E và F theo thứ tự là trung điểm của BD và
AC, vẽ đường thẳng đi qua E và vuông góc với AD và đường thẳng qua F vuông góc với
BC, cắt nhau tại I, CMR: IC = ID
Lời giải
Gọi N là trung điểm của DC
=> FN là đường trung bình của
∆
ADC
=>
//FN AD
PE FN EI FN
PE AD
=> ⊥ =>⊥
⊥
Chứng minh tương tự:
FQ EN FI EN⊥ =>⊥
=> I là trực tâm
=> IN
⊥
EF, mà EF // DC => IN
⊥
DC
∆
IDC có IN vừa trung tuyến vừa đường cao
=>
∆
IDC cân => ID = IC
Bài 17: Cho hình thang ABCD, (AB<CD), Gọi M, N, P lần lượt là trung điểm của AB, BD,
AC, đường thẳng vuông góc với MN tại N và đường thẳng vuông góc với MP tại P cắt
nhau tại E, CMR: EC = ED
Lời giải
Gọi Q là trung điểm của CD
MN là đường trung bình
1
, //
2
MN AD MN AD⇒=
K
P
I
F
E
N
A
B
D
C
G
D
F
E
H
M
K
B
C
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
201
PQ là đường trung bình
1
, //
2
PQ AD PQ AD⇒=
Bài 18: Cho 3 điểm A, B, C theo thứ tự nằm trên đường thẳng d, ( AB > BC), Trên cùng 1
nửa mặt phẳng bờ là đường thẳng d, vẽ các
,ADB BEC∆∆
đều, Gọi M, N, P, Q, I theo thứ
tự là Trung điểm của các đoạn thẳng BD, AE, BE, CD, DE
a) CMR: 3 điểm I, M, N thẳng hàng b) CMR: 3 điểm I, Q, P thẳng hàng
c) CMR: MNPQ là thình thang cân d)
1
2
NQ DE=
Lời giải
a) Dễ thấy AD // BE
IN là đường trung bình
∆
ADE => IN // AD
IM là đường trung bình
∆
DBE => IM // BE // AD
=> 3 điểm I, M, N thẳng hàng
b) Chứng minh tương tự
c) Trong
∆
AEB có NP là đường trung bình
=> NP // (d)
Tương tự MQ // (d) => MQ // NP
=>
11
0
22
60
NA
NA
NA
=
⇒ ⇒==
=
,
Chứng minh tương tự ta có:
11
000 0
22
180 60 60 60
DB
QPN
PB
=
=> = −−=
=
d) Vì MNPQ thang cân => NQ = MP, Mà MP là đường trung bình
∆
BED nên:
11
22
MP DE NQ MP DE= =>==
Bài 19: Cho
ABC∆
đều, Trên tia đối của tian AB, lấy D, trên tia đối của tia AC lấy điểm E
sao cho AD=AE, Gọi M, N, P, Q theo thứ tự là các trung điểm của BE, AD, AC, AB, CMR:
a) Tứ giác BCDE là hình thang cân b) Tứ giác CNEQ là hình
thang
c)
MNP∆
là tam giác đều
E
Q
P
N
M
A
B
D
C
2
2
2
1
1
1
2
1
Q
P
N
M
I
E
D
A
B
C
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
202
Lời giải
a)
∆
AED đều =>
0
60 / /D B ED BC= = =>
Lại có 2 đường chéo bằng nhau => là hình thang cân
b)
∆
ABC đều => CQ
⊥
AD
∆
AED đều => EN
⊥
AD => CQ // EN => là hình thang
c) Ta có: NP là đường trung bình =>
1
2
NP DC=
Xét
∆
BEP có
0
90P =
, MP là đường trung tuyến
=>
11
22
MP BE DC= =
Xét
∆
ENB có
0
90N =
và MN là đường trung tuyên
=>
11
22
MN BE DC= =
Vậy
∆
NMP có 3 cạnh bằng nhau nên là tam giác đều
Bài 20: Cho tứ giác ABCD, Gọi P, Q theo thứu tự là trung điểm của AD và BC
a) CMR:
2
AB CD
PQ
+
≤
b) Tứ giác ABCD là hình thang khi và chỉ khi
2
AB CD
PQ
+
=
Lời giải
b) Ta chứng minh ABCD là hình thang
2
AB CD
PQ
+
⇒=
Thật vậy :
∆
ADC có pR là đường trung bình
1
2
PR DC⇒=
(1)
RQ là đường trung bình
∆
ABC
1
2
RQ AB⇒=
(2)
Cộng theo vế (1) và (2) ta được :
2
AB CD
PQ RQ
+
+=
Ngược lại :
2
AB CD
PQ P
Q PR RQ
+
= =>=+⇒
3 điểm P, Q, R thẳng hàng,
Mà : PQ // DC và RQ // AB => AB // CD => ABCD là hình thang
1
Q
P
N
M
E
A
B
C
D
R
Q
P
A
B
C
D
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
203
ĐỐI XỨNG TRỤC, DỐI XỨNG TÂM
A. LÝ THUYẾT
1. Định nghĩa:
- Hai điểm A và A’ được gọi là đối xứng với nhau qua đường thẳng d, nếu d là đường
trung trực của đoạn thẳng AA’. (H1)
- Hai điểm A và A’ được gọi là đối xứng với nhau qua điểm O, nếu O là trung điểm của
AA’.(H2)
2. Tính chất:
-. Mọi điểm nằm trên đường thẳng (d) đều cách đều hai đầu mút A và A’.
3. Quy ước:
-. Điểm nằm trên trục đối xứng (d) thì điểm đối xứng với nó qua (d) là chính nó.
- Điểm đối xứng với điểm O qua tâm O chính là điểm O.
B. Bài tập
Bài 1: Cho
∆
ABC có
0
60A =
, các đường phân giác BD và CE cắt nhau tại I, qua E kẻ
đường thẳng vuông góc với BD cắt BC ở F, CMR:
a, E và F đối xứng nhau qua BD b, IF là phân giác
BIC
c, D và F đối xứng nhau qua IC
Lời giải
a)
∆
EBF cân tại B, BD là tia phân giác góc
B
,
nên BD là đường trung trực EF.
Vậy E, F đối xứng với nhau qua BD
b) Tính
0
120BIC =
nên
000
123
60 , 60 , 60 ,III= = =
vậy IF là tia phân giác
BIC
c)
∆
IDC =
∆
IFC (g.c.g) => IF =ID, CF= CD
Do đó: CI là đường trung trực của DF
Vậy D, F đối xứng với nhau qua CI
Bài 2: Cho
∆
ABC nhọn, trong đó
0
60A =
, Lấy D là điểm bất kì trên BC, gọi E, F lần lượt là
điểm đối xứng của D qua cạnh AB, AC. EF cắt AB, AC lần lượt tại M, N
H2
H1
( d )
O
A
A'
A
A'
60
4
3
2
1
F
D
E
I
B
A
C
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
204
a, CMR: AE=AF và Tính
EAF
b, CMR: AD là tia phân giác
∆
DMN
Lời giải
a) Ta có: D và E đối xứng với nhau qua AB
nên AB là đường trung trực của ED => AE = AD
Tương tự AD = AF
khi đó AE=AF, Ta có:
2.
2.
EAD MAD
DAF DAM
=
=
=>
( )
0
2 2. 120EAF MAD DAM A= +==
b) Do đối xứng nên ta có:
AEM ADM
AFN ADN
=
=
và
∆
AEF cân tại A nên
AEM AFN ADM ADN==>=
Vậy AD là phân giác góc
MDN
Bài 3: Cho tứ giác ABCD, có các đường chéo AC và BD cắt nhau tại O, AD vuông góc AC,
BD vuông góc với CB, Gọi E là giao điểm của AD và BC, d là đường thẳng đi qua các
trung điểm của EO và CD
a) CMR: A và B đối xứng nhau qua đường thẳng d
b) Tứ giác ABCD sẽ như thế nào nếu D trùng EO
Lời giải
a, Ta có: Gọi I, K lần lượt là trung điểm của OE và BC
∆
AOE vuông tại A có AI là trung tuyến
Nên AI = IE = IO (1)
∆
BOE vuông tại B có BI là đường trung tuyến
Nên BI = EI = IO (2)
Từ (1) và (2) ta có: IA = IB
Tương tự
∆
ADC vuông tại A có AK là đường trung tuyến
=> AK = DK = CK
∆
BDC có BK là đường trung tuyến của tam giác vuông
nên BK = KD = KC
Nên KA = KB hay K nằm trên đường trung trực AB
Vậy IK là trung trực của AB hay A và B đối cứng với nhau qua (d)
b, Ta thấy EO là đường thẳng chứa đường cao của
∆
EDC
Nếu d trùng với EO thì d vừa là đường trung trực AB và CD nên ABCD là hình thang cân
N
M
F
E
B
A
C
D
I
O
E
K
D
C
A
B
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
205
Bài 4: Cho
∆
ABC, kẻ các đường cao BD và CJ, Gọi H là trực tâm của
∆
, E là trung điểm
của AH, D là trung điểm của BC, Chứng minh rằng: I và J đối xứng với nhau qua ED
Lời giải
∆
BIC vuông tại I có ID là trung tuyến ứng với cạnh huyền BC
=>
2
BC
ID =
Chứng minh tương tự:
2
BC
JD ID JD= =>=
Chứng minh tương tự: JE = EI
=> ED là đường trung trực của IJ
=> IJ đối xứng nhau qua ED
Bài 5: Cho
∆
ABC, kẻ đường cao AH, Gọi D và E theo thứ tự là các điểm đối xứng với H
qua AB và AC, đường thẳng DE cắt AB, AC lần lượt tại M, N
a) CMR:
∆
DAE cân b) CMR: HA là phân giác
MHN
c) CME : 3 đường thẳng BN, CM, AH thẳng hàng
d) CMR : BN, CM là các đường cao của
∆
ABC
Lời giải
b, Do Tính chất đối xứng ta => AB là phân giác
DMH
Kẻ
AI HM
AI AJ
AJ DM
⊥
=>=
⊥
(1)
AC là phân giác
ENH
,
Kẻ AK
⊥
HN=> AK= AJ (2)
Từ (1) và (2) ta có: AI = AK
Vậy A cách đều 2 cạnh góc
MHN
=> HA là phân giác góc
MHN
c, Chứng minh tương tự ta cũng có:
CM là tia phân giác
HMN
BN là tia phân giác góc
MNH
Trong
∆
MHN các đường phân giác trong HA, MC, NB cùng đồng quy tại 1 điểm
d, AB là phân giác góc
DMH
MC là phân giác góc
MHN
, mà 2 góc
,DMH MHN
kề bù => MC
⊥
AB => MC là đường cao
∆
ABC
Chứng minh tương tự BN là đường cao của
∆
ABC
E
D
H
I
J
B
C
A
J
K
I
N
M
E
D
H
B
C
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
206
Bài 6: Cho hình thang vuông ABCD, (AB//CD). Gọi E , F theo thứ tự là các điểm đối xứng
của B và điểm A qua đường thẳng DC, G, H theo thứ tự là các điểm đối xứng của C và E
qua AD
a, CMR: D là trung điểm của BH b, CMR: AH // BF, CH // BG
Lời giải
a, Gọi I là giao BE và DC, do tính chất đối xứng ta có:
BI = IE, Mà DF = AD và AD = BI => DF = BI
Ta cũng có: DI = HF
Hai tam giác vuông
∆
BID và
∆
DFH bằng nhau
cho ta DB = DH (1)
Và
0 00 0
1 1 1 2 3 11
90 90 90 180BD DDD DB==>++=++=+=
=> H, B, D thẳng hàng (2)
Từ (1) và (2) => D là trung điểm BH
b, Dễ dạng chứng minh được
∆
ADH =
∆
FDB =>
11
//A F AH BF= =>
Dễ chứng minh được
∆
BDG =
∆
HDC =>
11
//C G CH GB= =>
HÌNH BÌNH HÀNH
A. LÝ THUYẾT
1. Định nghĩa: Hình bình hành là tứ giác có các cặp cạnh
đối song song
ABCD◊
là hình hình hành
// , //
ABCD
AB CD AD BC
◊
⇔
- Chú ý: Hình bình hành là hình thang đặc biệt có hai cạnh bên song song
2. Tính chất: Trong hình bình hành
- Tính chất về cạnh: Các cạnh đối bằng nhau
- Tính chất về góc: Các góc đối bằng nhau
- Tính chất về đường chéo: Hai đường chéo cắt nhau tại trung điểm của mỗi đường
3. Dấu hiệu nhận biết
- Tứ giác có các cạnh đối song song là hình bình hành
- Tứ giác có các cạnh đối bằng nhau là hình bình hành
- Tứ giác có hai cạnh đối vừa song song vừa bằng nhau là hình bình hành
- Tứ giác có các góc đối bằng nhau là hình bình hành
H1
A
B
D
C
1
1
1
1
3
2
1
G
H
F
E
I
A
B
D
C
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
207
- Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành
4. Mở rộng
- Hai hình bình hành có một đường chéo chung thì các đường chéo của chúng đồng quy
tại trung điểm của đường chéo chung.
B. BÀI TẬP
Bài 1: Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD. Gọi M, N, P, Q lần
lượt là trung điểm của AF, CE, BF, DE. CMR: Tứ giác MNPQ là hình bình hành
Lời giải
Ta có : QF, NF là đường trung bình của tam giác DEC
// //
;
// //
QF EC QF NE
NF DE QE NF
⇒
QFNE⇒◊
là hình bình hành
,QN FE⇒
Cắt nhau tại trung điểm của mỗi đường
Gọi I là trung điểm của EF
I⇒
là trung điểm của QN
Chứng minh tương tự: Tứ giác MEPF là hình bình hành
I⇒
là trung điểm của MP
dpcm⇒
Bài 2: Cho tứ giác ABCD và điểm I thuộc miền trong tứ giác. Gọi M, N, P, Q lần lượt là các
điểm đối xứng với I qua trung điểm của các cạnh AB, BC, CD, DA. CMR: MNPQ là hình
bình hành
Lời giải
// ; 2 ; // ; 2 ; //
11
;//;
22
MN FE MN FE PQ GH PQ GH HG AC
HG AC FE AC FE AC
= =
= =
I
P
N
M
Q
D
F
C
B
E
A
I
Q
A
H
D
G
P
C
F
N
E
B
M
O
H
A
B
D
C
K
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
208
Bài 3: Cho tam giác ABC và một điểm I thuộc miền trong của tam giác. Gọi M, N, P lần
lượt là trung điểm của BC, CA, AB. Gọi D, E, F lần lượt là các điểm đối xứng với I qua M,
N, P. Chứng minh rằng các đường thẳng AD, BE, CF đồng quy
Lời giải
+) Tứ giác FAIB là hình bình hành ( hai
đường chéo cắt nhau tại trung điểm
của mỗi đường )
// (1)FA BI⇒=
+) Tứ giác BICD là hình bình hành
// (2)BI CD⇒=
Từ (1)(2)
/ / (1)FA CD FACD⇒ = ⇒◊
là
hình bình hành
,AD CF⇒
cắt nhau tại
trung điểm của mỗi đường (3)
Tương tự: ABDE là hình bình hành
,AD BE⇒
cắt nhau tại trung điểm của
mỗi đường (4)
Từ (3), (4) ta có điều phải chứng minh
Bài 4: Cho
ABC∆
, O là 1 điểm thuộc miền trong tam giác. D, E, F là trung điểm của AD,
BC, CA. L, M, N lần lượt là trung điểm của
OA, OB, OC. CMR: EL, FM, DN đồng quy
Lời giải
+) DMFN là hình bình hành, do:
1
2
// //
DF MN BC
DF MN BC
= =
,DN FM⇒
cắt nhau tại trung điểm của mỗi
đường
Tương tự:
:
:
MLFE hbh
DLNE hbh
Bài 5: Cho hình bình hành ABCD,
0
ˆ
75ADC =
. O là giao điểm hai đường chéo. Từ D hạ
DE, DF lần lượt vuông góc với AB và BC (
,E AB F AC∈∈
). Tính
ˆ
FOE
B
I
M
D
C
E
N
P
F
A
O
L
D
M
N
B
E
C
F
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
209
Lời giải
+) Gọi O là giao điểm của AC và
BD
Vậy O là trung điểm của AC, BD
0
ˆˆ
75ABC ADC= =
Xét tam giác vuông DEB, có:
11
ˆˆ
2
BD
AO OD OB E B= = = ⇒=
+)
11 1
ˆˆ ˆ
2( )EOD B E B Gocngoai=+= ∆
+)
21 2
1
ˆ
ˆˆ ˆ
00 2
2
FO BD B D B F FOD B= = = →=→ =
Tương tự:
0
12
ˆˆˆ
ˆˆ ˆ
2( ) 2 150FOE EOD FOD B B ABC= + = += =
Bài 6: Cho
ABC∆
, có các trung tuyến AD, BE, CF. Biết rằng
BE CF⊥
. CMR:
222
AD BE CF= +
Sử dụng phương pháp dịch chuyển tức thời
Lời giải
Dựng hình bình hành BEMC
// ( )
=
⇒
→⊥ ⊥
MC BE
MC BE MC CF BE CF
//
// ( )
⇒
∆
ME BC
FE CB duongTB
Vậy M, E, F thẳng hàng
+)
1
2
FE BC=
13
(1)
22
= +=+ =FM ME FE BC BC BC
Mặt khác:
3
3
(2)
1
2
:
2
=
⇒=
∆=
AD GD
AD BC
BGC GD BC
Từ (1) và (2) ta có:
22
2 22
22 2
()
:
MF AD MF AD
AD FC BE dpcm
Pytago FM FC MC
=→=
⇒=+
= +
1
1
2
1
O
F
C
B
D
A
E
G
C
M
D
B
F
E
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
210
Bài 7: Cho hình bình hành ABCD. Về phía trong hình bình hành dựng các tia Ax, By, Cz,
Dt lần lượt tạo với AB, BC, CD, DA các góc bằng nhau và bằng
∝
. Các tia này cắt nhau tạo
thành tứ giác MNPQ. Chứng minh rằng: AC, BD, MP, NQ đồng quy
Lời giải
+) Đi chứng minh tứ giác MNPQ là hình bình hành
1,2 1,2
22
11
ˆˆ
ˆ
ˆˆ
/ / (1)
ˆˆ
=
⇒=⇒
=
AC
C A MN PQ
AC
Tương tự:
22
ˆˆ
/ / (2) := ⇒ ⇒◊B D MQ NP MNPQ hinhbinhhanh
+) Thêm: AMCP là hình bình hành
()
//
AM CP
ADM CBP gcg HBH dpcm
AM CP
=
∆=∆ ⇒ ⇒⇒
Bài 8: Cho tứ giác ABCD, E là trung điểm của AD, F là trung điểm của BC. G là đỉnh của
hình bình hành CADG và H là đỉnh của hình bình hành CABH
a. Chứng minh BD // GH b. HD = 2EF
Lời giải
a. Có DG // BH và DG = BH nên tứ giác BDGH là hình bình hành
()BD GH dpcm→=
b. Gọi I là trung điểm của BD, J là trung điểm của BH
1
(1)
2
JI DH→=
2
1
2
1
2
1
2
1
P
N
M
Q
D
C
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

211
1
2
1
//
2
EI A
EI JF
JE CH
EI JF
AB CH
=
=
= ⇒
=
:EIJF hinhbinhhanh⇒◊
(2) 2 ( )JI FE HD FE dpcm⇒= ⇒ =
Bài 9: Cho tam giác ABC. Gọi A’ đối xứng với A qua C, B’ đối xứng với B qua A, C’ đối
xứng với C qua B. Gọi BM là trung tuyến của tam giác ABC, B’M’ là trung tuyến của tam
giác A’B’C’
a. Chứng minh tứ giác ABM’M là hình bình hành
b. G là giao điểm của BM và B’M’. Chứng minh rằng G là trọng tâm tam giác ABC và
A’B’C’
Lời giải
a.
11
' // ' ' // '
:
22
BM A C BM AC AM ABMM hinhbinhhanh= → = = →◊
b. Gọi I là trung điểm của B’G, J là trung điểm của BG
Suy ra IJ là đường trung bình của tam giác GBB’
//
1
// '
// ' ':
2
JI AB
JI BB
JI AB JI MM JIMM hinhbinhhanh
⇒= ⇒
=→= →
Suy ra G là trung điểm của IM’ ; MJ
''
..................... , ' ' '
GM GI IB
G A
BC A B C
GM GJ JB
= =
⇒ ⇒ ∆∆
= =
F
I
C
G
H
J
B
A
E
D
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
212
Bài 10
*
: Cho tam giác đều ABC, một đường thẳng song song với BC cắt AB, AC tại D và E.
Gọi G là trọng tâm của tam giác ADE, I là trung điểm của CD. Tính số đo các góc tam giác
GIB
Lời giải
+) Qua C kẻ đường thẳng song song với BD cắt ED tại K
+)
CBDK◊
là hình bình hành. Nên KB cắt CD tại I
+) GD = GE
+)
0
ˆˆ
150GDK GDB= =
+)
KEC∆
đều
( ) : ân
KC KE
KE BD GEK GDB cgc GK GB GBK c
KC DB
=
⇒ ⇒ = →∆ =∆ → = →∆
=
Suy ra GI là trung tuyến, đường cao
00
ˆ
ˆˆ
90 ; 120
( : , : )GI BK GIB KGB EDG AED deu G trongtam⇒⊥ → = = = ∆
00
ˆ
30 ( : ) 60GBK GKB GKB cantaiG IGB⇒ = =∆ ⇒=
I
M
G
J
B
C
A'
M'
C'
A
B'
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
213
Bài 11
*
: Cho tam giác ABC, H là trực tâm, I là giao điểm các đường trung trực, K là điểm
đối xứng với H qua trung điểm BC. CMR: K đối xứng với A qua I
Lời giải
M là trung điểm của BC và HK
BHCK⇒◊
Là hình bình hành
//
;
//
BH CK
BH AC CK AC
CH BK
⇒ ⊥→⊥
//BK CH
AB BK
CH AB
→⊥
⊥
Gọi I’ là trung điểm của AK
'IN→
là đường trung bình của
tam giác ACK
' // ' 'IN CKIN AC⇒⊥
Goi P là trung điểm của AB
'IP⇒
là đường trung bình của tam giác ABK
' // 'I P BK I P AB⇒ →⊥
Có:
': :
'
' ': :
I N trungtruc AC
II K
I P AB I P trungtruc AB
→≡ →
⊥→
đối xứng với A qua I.
Bài 12
*
: Cho
ABC∆
, về phía ngoài tam giác vẽ các tam giác đều ABD, ACE. Gọi I, M, N lần
lượt là trung điểm của DE, AB, AC. CMR:
IMN∆
đều
I'
P
B
H
I
M
K
C
N
A
G
E
K
C
I
B
D
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
214
Lời giải
Dùng phương pháp phóng to tam giác IMN
Gọi F là điểm đối xứng với A qua I
ADFE⇒◊
là hình bình hành
FE AD BD
DF AE CE
= =
⇒
= =
+)
0
11
11
ˆ ˆ ˆˆ ˆ
( 60 ) ( )
ˆˆ
=
= → = = − ⇒∆ = ⇒
=
BF FC
ADF AEF D E ADF FEC BDF cgc
FB
0 0 00 0
1
ˆ ˆˆˆ ˆˆˆ ˆ ˆ
) 360 360 360 (180 ) (180 )+ =−−−=−−−=− − − −BFC F BFD DFE DBF BFD DFE BDF ADF
0
ˆˆˆ
60BDF ADF ADB BFC= + = = ⇒∆
đều
+)
11 1
;;
22 2
MI BF NI FC MN BC MI NI MN MNI= = = ⇒ = = ⇒∆
đều
Bài 13: Cho HBH ABCD, Gọi E, F lần lượt là trung điểm của AD, BC, đường chéo AC cắt
BE, DF lần lượt tại P và Q, gọi R là trung điểm của đoạn thẳng BP, CMR:
a) AP = PQ = QC b) Tứ giác ARQE là hình bình hành
Lời giải
a, Trong
∆
BDC có CO và DF là hai đường trung tuyến
nên Q là trọng tâm
11
23
OQ QC OC⇒= =
Tương tự
∆
ABD có P là trọng tâm
1
1
1
N
I
F
M
D
B
C
E
A
O
R
P
Q
E
D
A
B
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
215
11
23
OP AP AO⇒= =
Từ (1) và (2) ta có AP= QC
Ta lại có :
( )
22
2
3 33
AC
PQ AC AP QC AC AP AC AO AC AC AP= −− = − = − = − = =
Vậy AP = PQ = QC
b, Vì P là trọng tâm
∆
ABD nên
1
2
EP PB PR= =
Tứ giác ARQE có hai đường chéo cắt nhau tịa trung điểm mỗi đường nên là HBH
Bài 14: Cho HBH ABCD có
0
120A =
, Tia phân giác góc D đi qua trung điểm I của AB, Kẻ
AH vuông góc với DC, CMR:
a) AB = 2AD b) DI = 2AH c) AC vuông góc AD
Lời giải
a)
∆
DAI cân đỉnh A
=> AD = AI=
1
2
AD AI AB⇒==
b) Kẻ AH
⊥
DC, AM
⊥
DI
=>
∆
ADM =
∆
ADH => AH= DM =
1
2
DI
c,
∆
ADC có
0
60 2.D CD AD ADC= => = =>∆
vuông tại A
Bài 15: Cho HBH ABCD, lấy hai điểm E, F trên BD sao cho
2
BD
BE DF= <
a) CMR: AECF là HBH
b) Gọi K là giao điểm của CE và AB, I là trung điểm của AK, xác định vị trí điểm E sao cho
AI = IK = KB
Lời giải
a) Xét
∆
ABE và
∆
CDF ta có:
AB = CD,
11
BD=
và BE = CF
=>
∆
ABE=
∆
CDF (c. g.c) => AE= CF
Chứng minh tương tự AF = CE
=> AECF là hình bình hành
b) Ta có:
//
OA OC
OI CK
AI KI
=
=>
=
, khi đó:
//
BK IK
KE IO
=
⇒
E là trung điểm OB
M
H
C
B
D
A
I
1
1
I
K
O
E
A
D
C
B
F
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
216
Bài 16: Cho tam giác ABC, trên tia đối của tia BC, lấy điểm D, trên tia đối của tia CB lấy
điểm E sao cho BD=BC=CE, Qua D kẻ đường thẳng // với AB cắt AC ở H, qua E kẻ đường
thẳng // với AC cắt AB ở k, chúng cắt nhau ở I
a) Tứ giác BHKC là hình gì? b) Tia IA cắt BC tại M, CMR :
MB=MC
c) Tìm điều kiện của
∆
ABC để tứ giác DHKE là hình thang cân
Lời giải
a, Tứ giác BHKC là hình bình hành vì
có 2 đường chéo BK và HC cắt nhau tại trung điểm
của mỗi đường
b, Tứ giác AHIK cũng là hình bình hành
nên AK// IH và AK= IH
AB // IH và AB = IH
=> ABHI là hình bình hành
=> IA // HB => AM là đường trung bình của
⊥
HBC
=> BM = MC
c, Tứ giác DHKE là hình thang vì HK // DE,
để là hình thang cân
DE⇒=
Hay
B C ABC= ⇒∆
cân tại A
Bài 17: Cho hình thang vuông ABCD
( )
0
90AD= =
, có CD= 2AB, gọi H là hình chiếu của
D trên AC, M là trung điểm của HC, Chứng minh rằng:
0
90BMD =
Lời giải
Gọi N là trung điểm của HD, ta có: MN là đường trung bình
1
, //
2
MN DC MN DC⇒=
Mà:
1
// ,
2
AB DC AB DC=
nên AB // MN và AB = MN => ABMN là hình bình hành
=> AN // BM
∆
ADM có DH
⊥
AM, MN
⊥
AD, AN
⊥
DM
Khi đó
0
90BMD =
Bài 18: Cho hình thang vuông ABCD,
0
90AD= =
, CD = 2AB = 2AD, Gọi H là hình chiếu
của D lên AC. Gọi M, P, Q lần lượt là trung điểm của CD, HC và HD
N
M
H
A
D
C
B
K
H
M
I
E
D
A
B
C
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
217
a) CMR: Tứ giác ABMD là hình vuông và tam giác BDC là tam giác vuông cân
b) CMR: DMPQ là hình bình hành
c) CMR: AQ vuông góc với DP
Lời giải
a) Chứng minh tứ giác ABMD có 4 cạnh bằng nhau,
lại có
0
90A =
nên ABMD là hình vuông
∆
BCD có MB = MC = MD nên là tam giác vuông ,
lại có
0
45BDC =
Do đó:
∆
BDC là tam giác vuông cân ở B
b) Tứ giác DMPQ là hình bình hành vì có PQ// DM
và PQ = DM
c) Chứng minh Q là trực tâm của
∆
ADP
Bài 19: Cho tam giác ABC có góc A tù, AC > AB, H là chân đường cao hạ từ A, về phía
trong góc
BAC
, dựng D và E sao cho AD vuông góc với AB, AD = AB, AE vuông góc với
AC và AE = AC, M là trung điểm DE. CMR: A, H, M thẳng hàng
Lời giải
Dựng hình bình hành DAEF
⇒
M là trung điểm A
⇒
AE = DF
Mà AE
⊥
AC => DF
⊥
AC
Ta có:
00 0
90 90 180DAE BAC DAE BAD DAC+ = + + =+=
Mà:
0
180DAE ADF BAC ADF+==>=
∆
ADF =
∆
ABC (c.g.c)
B DAF⇒=
và
CF=
Gọi FD cắt BC tại I, cắt AC tại N và AF cắt BC tại H’
⇒
( )
2
0
'
' 90
H IF NIC d
IH F N
CF
=
⇒==
=
,
Hay AF
⊥
BC tại H
⇒
A, F, H thẳng hàng
⇒
A, H, M thẳng hàng
Bài 20: Cho HBH ABCD có AB và BD cắt nhau tại O, Gọi (d) là đường thẳng đi qua A và
không cắt đoạn BD, gọi BB’, CC’, DD’ là khoảng cách từ B, C, D đến đường thẳng (d), ( B’,
C’, D’ nằm trên (d) ). CMR: BB’ + DD’ = CC’
Lời giải
Vẽ OO’
⊥
(d) (O’
∈
(d) )
Khi đó ta có: BB’D’D là hình thang
có OO’ là đường trung bình nên:
I
H
N
F
M
E
D
B
C
A
Q
P
H
C
M
D
A
B
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
218
2.OO’= BB’ + DD’ (1)
Tương tự
∆
ACC’ có OO’ là đường trung bình nên:
2.OO’ = CC’ (2)
Từ (1) và (2)
⇒
BB’ + DD’ = CC’
Bài 21: Cho HBH ABCD và đường thẳng (d) nằm bên ngoài HBH, Gọi A’, B’, C’, D’ lần
lượt là hình chiếu của A, B, C, D trên (d). Chứng minh: AA’+ CC’ = BB’ + DD’
Lời giải
Vì ABCD là hình bình hành
Nên hai đường chéo cắt nhau tại trung điểm mỗi đường
Gọi O là giao của hai đường chéo AC và BD
O’ là hình chiếu của O xuống (d)
Khi đó ta có: OO’ là đường trung bình của
hình thang AA’C’C nên: 2OO’ = AA’ + CC’ (1)
Tương tự OO’ là đường trung bình của hình thang DD’B’B
Nên: 2.OO’ = DD’ + BB’ (2)
Từ (1) và (2) => AA’ + CC’ = BB’ + DD’
Vậy HM
⊥
BN =>
∆
BMN có MH vừa là đường cao
vừa là trung tuyến nên MB = MN
Bài 22: Cho
∆
ABC có ba góc nhọn (AB<AC), gọi H là trực tâm, O là giao điểm của 3
đường trung trực của tam giác, D là điểm đối xứng của A qua O
a) CMR: Tứ giác BHCD là HBH
b) Gọi M là trung điểm của BC, CMR : AH = 2.MO
Lời giải
a) Từ AO= OC = OD
⇒
Chứng minh
0
90ACD =
,
ta có: DC
⊥
AC, BH
⊥
AC ( H là trực tâm của
∆
ABC)
⇒
BH // DC
Chứng minh tương tự ta cũng có: CH// DB
Vậy BHCD là Hình bình hành
D'
C'
O'
O
B'
A
B
D
C
d
C'
B'
O'
D'
A'
O
A
B
D
C
D
O
M
H
B
C
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
219
b, M là trung điểm của BC
⇒
M là trung điểm của HD
Mà O là trung điểm của AD
⇒
OM là đường trung bình của
∆
AHD
⇒
OM =
1
2
AH
⇒
AH = 2OM
Bài 23: Cho HBH ABCD, Các đường cao AE và AF, biết AC = 25cm, EF = 24cm, Tính
khoảng cách từ A đến trực tâm H của
∆
AEF
Lời giải
Kẻ CN vuông góc với AB,
Tứ giác EHFC có EH // CF, HF // FC
nên EHFC là hình binh hành
⇒
AN = HF (= EC)
Tứ giác ANFH có AN = HF, AN // HF
nên là hình bình hành
⇒
AH + NF, AH// NF
Lại có AH
⊥
EF nên NF
⊥
EF
∆
EFN vuông tại F có EF = 24cm, NE = AC = 25cm nên
2 2 2 22
25 24 49 7 7NF NE EF NF AH cm= − =−==>==> =
Bài 24: Cho tam giác ABC đều, một đường thẳng // với BC cắt AB, AC ở D và E, Gọi D là
trọng tâm của tam giác ADE, I là trung điểm của CD, Tính số đo các góc của tam giác GIB
Lời giải
Qua C vẽ đường thẳng song song với BD, cắt DE tại K
Ta có: BDKC là hình bình hành => B, I, K thẳng hàng
Chứng minh
∆
GDB=
∆
GEK (c.g.c)
Để
∆
GBK cân tại G có
0
120BGK =
,
do đó các góc của
∆
GBI lần lượt là
000
90 ,60 ,30
Bài 25: Cho
∆
ABC, D trên AB, E trên AC sao cho BD = CE, Gọi M, N là trung điểm của
BC, DE, Vẽ các hình bình hành BDNI và CENK
a) CMR: I, M, K thẳng hàng
b) MN cắt AC tại Q, cắt BA tại P, CMR:
∆
APQ cân
Lời giải
a, Tứ giác BDNI là hình bình hành
//
//
BI DN
BI DE
BI DN
⇒⇒
=
N
H
F
E
A
B
D
C
G
I
K
E
A
B
C
D
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
220
Tứ giác NECK là hình bình hành
//
//
KC NE
KC DE
KC NE
⇒⇒
=
Từ đó ta có KC // DE và BI = KC
=> Tứ giác BICK là hình bình hành
có M là trung điểm của BC
=> M đi qua trung điểm IK => I, K, M thẳng hàng
b, Ta có: NI = DB, NK = CE mà BD = CE => NI = NK
=>
∆
NIK cân tại N
Mà MN là đường trung tuyến => NM là phân giác
12
NN⇒=
Lại có: NK // QC
22
NQ⇒=
( đồng vị)
và NI // BD
1
NP⇒=
( đồng vị )
2 12
Q P QQ⇒==>=
( đối đỉnh)
1
PQ⇒=
. Vậy
∆
APQ cân tại A
ÔN TẬP HÌNH CHỮ NHẬT
A. Tóm tắt lý thuyết
1. Định nghĩa: Hình chữ nhật là tứ giác có bốn góc
vuông
ABCD◊
là hình chữ nhật
ˆˆ
ˆˆ
ABCD
ABCD
◊
⇔
= = =
- Nhận xét: Hình chữ nhật cũng là 1 hình bình hành, 1 hình thang cân
2. Tính chất: Hình chữ nhật có tất cả các tính chất của hình bình hành và hình thang cân
- Tính chất về cạnh: Các cạnh đối bằng nhau, song song với nhau
- Tính chất về góc: Bốn góc bằng nhau
- Tính chất về đường chéo: Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi
đường
3. Dấu hiệu nhận biết
- Tứ giác có ba góc vuông là hình chữ nhật
- Hình thang cân có 1 góc vuông là hình chữ nhật
- Hình bình hành có 1 góc vuông là hình chữ nhật
- Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật
4. Ứng dụng vào tam giác vuông
2
1
2
1
Q
P
K
I
M
N
E
B
C
A
D
H1
C
A
B
D
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
221
- Trong tam giác vuông, đường trung tuyến ứng với cạnh
huyền bằng nửa cạnh huyền, ta có:
1
2
BM AC=
- Nếu một tam giác có đường trung tuyến ứng với 1 cạnh
bằng nửa cạnh ấy thì tam giác đó là tam giác vuông:
1
2
BM AC ABC= ⇒∆
vuông
B. Bài tập
Bài 1: Cho hình chữ nhật ABCD. Gọi H là hình chiếu của B lên AC. Trên tia đối của tia BM
lấy điểm E sao cho BE = AC. Chứng minh rằng:
0
ˆ
45ADE =
Lời giải
+) Ta có ABCD là hình chữ nhật
AC BD BE BED→ = = →∆
Cân tại B
1
ˆˆ
DE→=
Mặt khác
ˆ
ˆ
OC OD OCD ODC=→=
+)
11
ˆ
ˆˆˆ ˆ
22
ADE EDB BDC OBH BOH=+= +
( góc ngoài
tam giác )
00
1
.90 45
2
= =
Bài 2: Cho hình chữ nhật ABCD. Trên các đoạn AB, BC, CD, DA lần lượt lấy các điểm M,
N, P, Q. Chứng minh rằng:
2MN NP PQ QM AC+++ ≥
Lời giải
Gọi E, F, I lần lượt là trung điểm của MQ, NP,
QN
Vì
,AQN CPN∆∆
là các tam giác vuông
2; 2
2( )
2
11
;
22
= =
⇒ = +++ ≥
= =
MQ AE NP CF
VT AE EI FI FC AC
IE MN FI PQ
Bài 3: Cho hình chữ nhật ABCD và điểm E thuộc đoạn BD, gọi F là điểm đối xứng với A
qua E. Gọi H, K lần lượt là hình chiếu của F lên BC, CD. CMR: E, H, K thẳng hàng
H
2
1
O
E
D
C
B
A
E
Q
D
I
F
N
C
B
M
A
M
C
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
222
Lời giải
Ta có HKCF là hình chữ nhật
,HK FC→
cắt nhau tại trung
điểm của mỗi đường
EI→
là đường trung bình
// (1)CFA EI AC∆→
+) Gọi M là trung điểm của
DK nên EM là đường trung
bình hình thang ADKF
//⇒ ⇒ ⊥ ⇒∆EM FK EM CD DEK
cân tại E
1 11
ˆ
ˆˆ
/ / (2)⇒==⇒D K C EK AC
Từ (1)(2) suy ra:
,, :
,,
⇒
∈
E I K thanghang
EHK
H IK
thẳng hàng
Bài 4: Cho hình chữ nhật ABCD. Gọi H là hình chiếu của A lên BD, gọi M, N lần lượt là
trung điểm của HD, BC. CMR:
AM MN⊥
Lời giải
Gọi e là trung điểm của AH nên ME là đường
trung bình của
11
// ;
22
∆ ⇒ = = = ⇒◊AHD ME AD ME AD BC BN BEMN
Là hình bình hành
// (1)BE MN→
+)
//
⇒⊥
⊥
ME AD
ME AB
AD AB
AMB∆
có E là trực tâm
(2) ( )⇒⊥ ⇒ ⊥BE AM AM MN dpcm
Bài 5: Cho hình chữ nhật ABCD. Qua điểm E thuộc đoạn AC kẻ đường thẳng song song
với BD nó cắt AD, CD ở M và N. Dựng hình chữ nhật NDMF. Chứng minh E là trung
điểm của BF
Lời giải
+)
11 1 1 1
ˆˆ
ˆˆ ˆ
= = = = ⇒∆A P B D C AEP
cân tại E
⇒=AE EP
+) Tương tự:
=⇒=AE EM EM MP
+) BPND là hình bình hành
1
1
I
M
E
H
K
F
O
D
C
B
A
H
M
F
N
D
C
B
A
P
1
1
1
1
E
M
F
N
D
C
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
223
:=
⇒⇒
= =
ND PB PBMF hinhbinhhanh
ND FM EM MP
Vậy E là trung điểm của BF
Bài 6: Cho hình chữ nhật ABCD có AB > AD. Lấy điểm E thuộc đoạn AD, các điểm I, K
thuộc đoạn CD sao cho DI = CK = AE. Đường thẳng qua K và vuông góc với EK cắt đoạn
BC tại M. Chứng minh rằng:
IM IE⊥
Lời giải
+) Gọi N, H là trung điểm của EM, CD
⇒ NH
là đường trng bình hình thang
EDCM
NH CD→⊥
=
+ = + ⇒ = →∆
=
HD HC
DI IH HK KC HI HK NIK
DI KC
Cân tại N
11
1
22
2
=
⇒ ⇒ = ⇒=
=
NI NK
NK NM NI NM
NK EM
⇒∆EIM
vuông tại I
⇒⊥EI MI
Bài 7: Cho hình chữ nhật ABCD, kẻ
BH AC⊥
, gọi M là trung điểm của AH, K là trung
điểm của CD. Chứng minh rằng:
BM MK⊥
Lời giải
Qua M kẻ đường thẳng vuông góc với BC, cắt
BH tại I
Ta có:
// //MI AB CD
M là trung điểm của AH nên MI là đường
trung bình của
1 //
2
1
2
=
∆ ⇒ ⇒ ⇒◊
= =
=
MI CK
MI AB
ABH MICK
MI CK CD
IH IB
là hình bình hành
/ / (1)⇒ MK CI
Trong
MBC∆
có I là trực tâm
(2)⇒⊥ ⇒ ⊥CI MB BM MK
Bài 8: Cho hình chữ nhật ABCD, M là điểm bất kỳ nằm trong hình chữ nhật, vẽ ME
⊥
AB
tại E, MF
⊥
AD tại F, CK
⊥
AM tại K. Chứng minh rằng :
E
K
M
I
N
H
D
C
B
A
H
I
M
K
D
C
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
224
a)
222
ME MF MA+=
b)
2222
MA MC MB MD+=+
c)
0
90BKD =
Lời giải
a) Tứ giác AEMF là hình chữ nhật
2 22 2
MA EF ME MF EF AM⇒=⇒ + = =
b) Gọi G là giao điểm của EM và CD,
H là giao điểm của FM và BC
=> Tứ giác DFMG, GMHC, EBHM là hình chữ nhật,
Do vậy
2 22
MC MH MG= +
222
MB ME MH= +
2 22
MD MG MF= +
=> ĐPCM
c) Gọi O là giao của 2 đường chéo AC và BD
=>
0
90
22
AC BD
KO BK DK BKD= ==>⊥=> =
Bài 9: Cho H là hình chiếu của B trên đường chéo AC của HCN ABCD, M và K theo thứ tự
là trung điểm của AH và CD
a) Gọi I và O theo thứ tự là trung điểm của AB và IC. CMR:
1
2
MO IC=
b) Tính số đo
BMK
?
Lời giải
Ta có: BIKC là Hình chữ nhật nên O là trung
điểm của IC và BK
Xét
∆
IMC vuông, Ta có : MO=
1
2
DC
b,
∆
MBK có MD =
1
2
IC=
1
2
BK, Nên
0
90BMK =
MBK∆
có
0
11
90
22
MD IC BK BMK==⇒=
Bài 10: Cho
∆
ABC vuông cân tại A
có AH là đường cao, Gọi M là 1 điểm
bất kỳ trên cạnh BC, I và K là hình
chiếu vuông góc của M trên AB, AC,
CMR:
∆
IHK vuông cân
Lời giải
Chứng minh AIMK là hình chữ nhật
Vì
∆
ABC vuông cân tại A
O
K
G
H
F
E
C
A
B
M
D
O
I
M
H
C
A
B
D
3
2
1
I
K
A
H
B
C
M
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
225
=> AK= IM = BI
mà BH = HA =>
0
45HBI HAK= =
=>
∆
BHI =
∆
AHK (c. g. c)
=> IH = HK
Mà
00
32 12
90 90HH HH+= =>+=
Bài 11: Cho
∆
ABC vuông tại A (AC > AB), đường cao AH, trên HC lấy HD = HA, đường
⊥
BC tại D cắt AC tại E
a) CMR: AE = AB b) M là TĐ của BE, Tính
AHM
Lời giải
a, Chứng minh AE = AB
Kẻ EF
⊥
AH => tứ giác HDEF là hình chữ nhật
=>
() EHBA FAE gcg AB A⇒∆ =∆ ⇒ =
b,
∆
ABE vuông cân tại A
2
BE
AM⇒=
∆
BDE vuông cân tại D
2
BE
MD⇒=
Từ đó ta có: AM = MD
Xét
()AHM DHM cgc∆=∆
0
12
45HH⇒==
Bài 12: Cho
∆
ABC cân tại A, từ 1 điểm D bất
kỳ trên đáy BC, vẽ đường thẳng vuông góc với BC cắt các đường thẳng AB, AC ở E và F,
Vẽ các HCN BDEH, CDFK, Gọi I, J lần lượt là tâm các HCN BDEH và CDFK, M là trung
điểm của AD
a) CMR: Trung điểm HK là 1 điểm có định không phụ thuộc vào vị trí của D trên BC
b) CMR: 3 điểm I, J, M thẳng hàng và 3 đường thẳng AD, HJ, KI đồng quy
Lời giải
a) Ta có:
11
BD=
mà
11 11
//BCDCIDAC==>==>
Chứng minh tương tự ta có: JD // AB
Khi đó AIDJ là hình bình hành => AJ // ID, AJ =
ID
=> Chứng minh AHIJ là hình bình hành
=> IJ // AH và IJ = AH và IJ // AK và IJ = AK
F
M
E
D
H
B
C
A
1
1
2
1
M
J
I
K
F
H
E
B
C
A
D
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
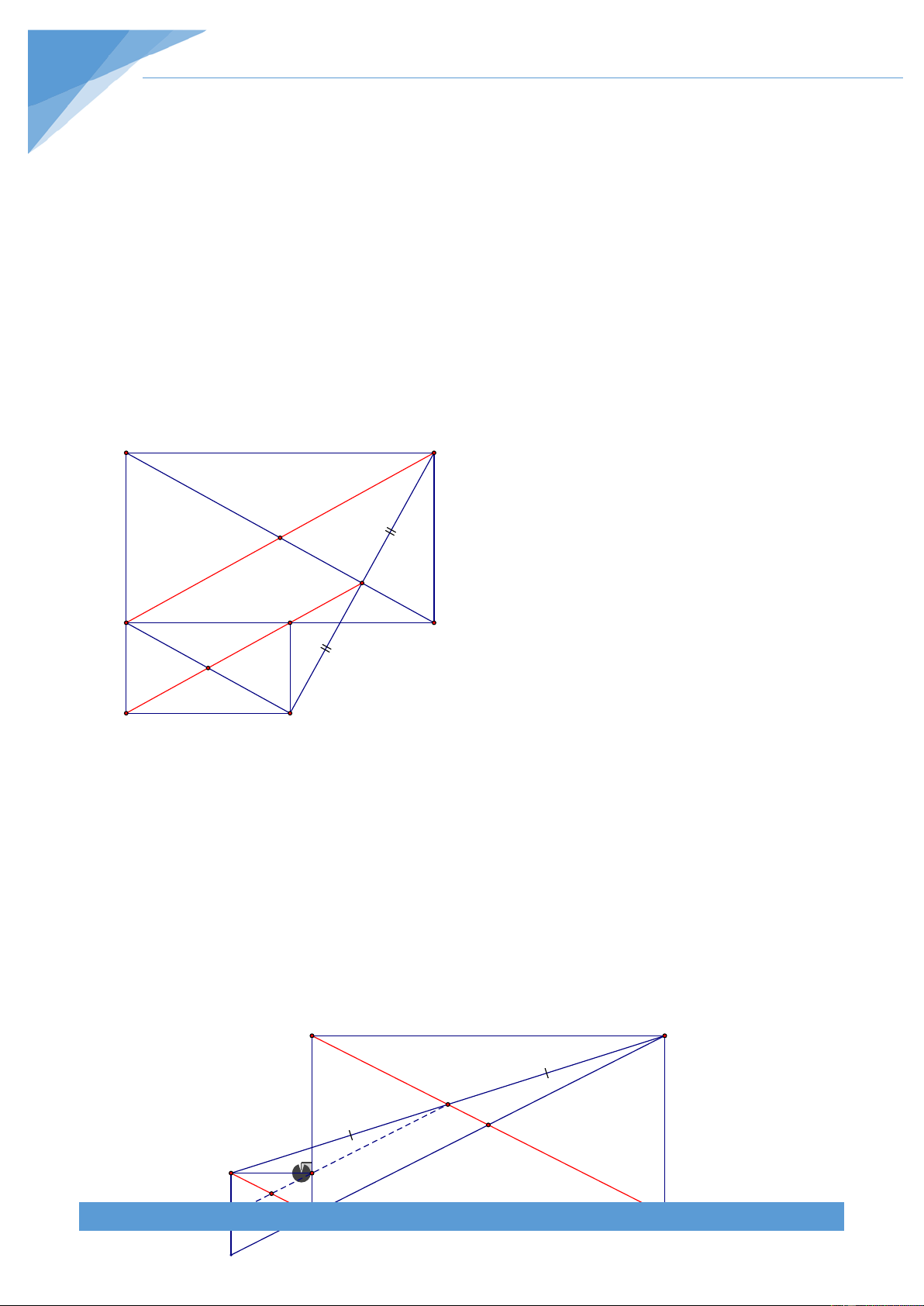
226
Khi đó 3 điểm A, H, K thẳng hàng
và A là trung điểm của HK
b) Tứ giác AIDJ là hình bình hành
=> M là trung điểm của AD,
thì M nằm trên đường chéo của HBH
Bài 13: Cho HCN ABCD và E là điểm nằm trên đường chéo AC, trên tia đối của tia EB lấy
F sao cho EF = BE, Gọi M, N là hình chiếu của F trên 2 đường thẳng AD, DC. CMR:
a) DF // AC và MN // BD b) 3 điểm E, M, N thẳng hàng
Lời giải
a, Dễ thấy OE là đường trung bình của
∆
BDF
=> DF // OE => DF // AC
11
AD⇒=
( Đồng vị )
=>
∆
OAD cân
121
ADD⇒= =
=>
∆
IDM cân
11
DM⇒=
21
DM⇒=
( đồng vị) => MN // DB
b, I là trung điểm DF => IE là trung bình
=> IE // DB mà MN // BD
Vậy M, N, E thẳng hàng
Bài 14: Cho hình chữ nhật ABCD, điểm P thuộc đường chéo BD ( P khác B và D), Gọi M là
điểm đối xứng của C qua P
a) Chứng minh AM song song với BD
b) Gọi E, F lần lượt là hình chiếu của M trên AD và AB. Chứng mỉnh ba điểm E, F, P
thẳng hàng
c) Chứng minh tỉ số độ dài hai đoạn thẳng MF và FA không phụ thuộc vào vị trí của P
Lời giải
1
1
1
2
1
O
I
M
N
F
C
A
B
D
K
I
F
E
O
M
D
B
C
A
P
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
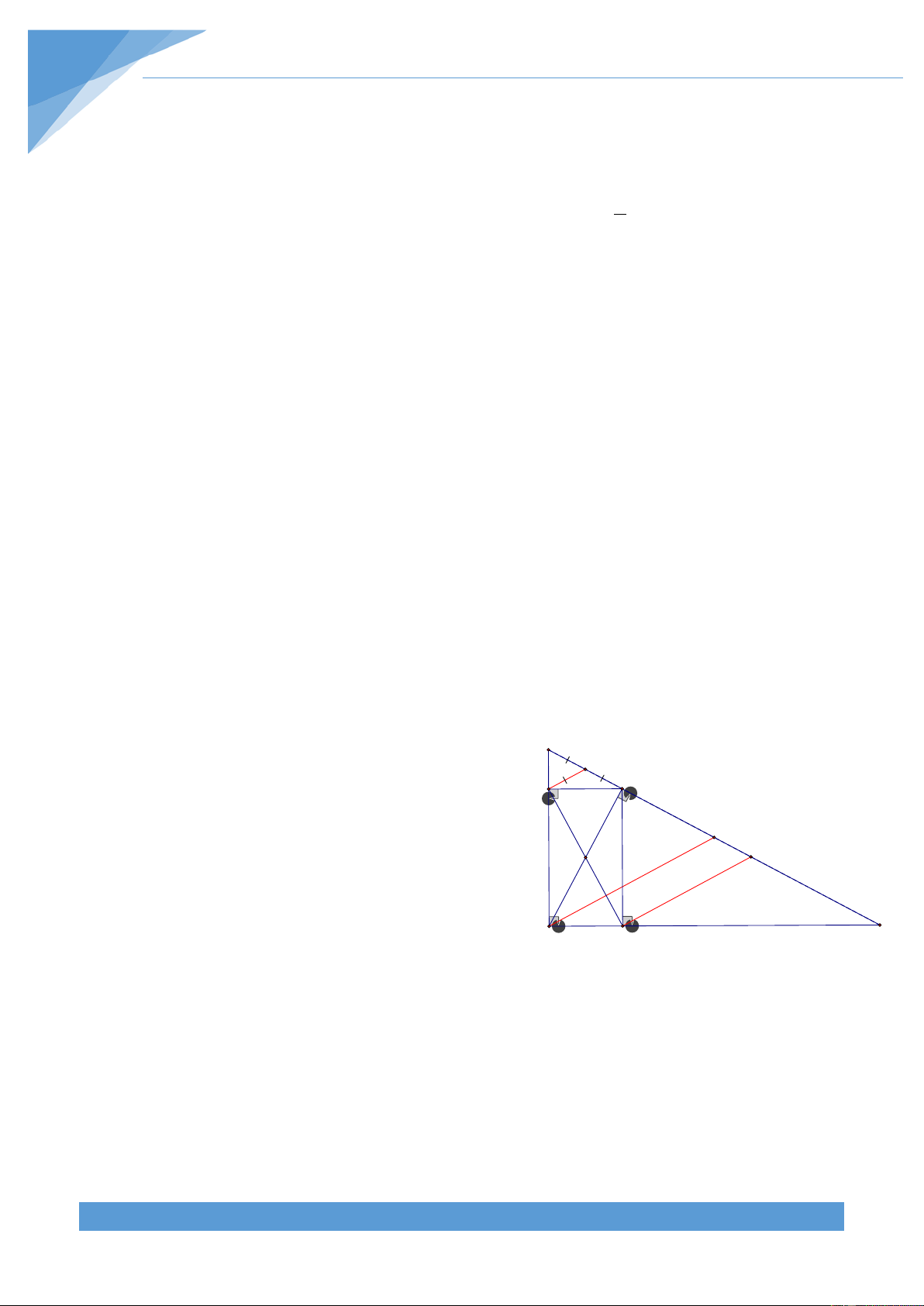
227
a) Ta có: O là trung điểm của AC (ABCD là hình chữ nhật)
P là trung điểm của CM ( Vì M đối xứng với C qua P)
Nên Op là đường trung bình của
∆
ACM, do đó: OP // AM => AM // BD
b) Vì OP là đường trunh bình của
∆
ACM nên OP//AM và OP =
1
2
AM
Do đó: OP // AI và OP = AI => tứ giác AIPO là hình bình hành => PI // AC (1)
Kẻ ME // AB cắt AC tại K, ta có:
KAE EAM=
(
)
KDA=
Nên AE là phân giác
KAM
, mặt khác:
AE KM AKM⊥ =>∆
cân
E là trung điểm của KM,
do đó EI là đường trung bình của
∆
AMK => EI // OA => EI // AC (2)
Ta lại có: E, I, F thẳng hàng (3)
Từ (1), (2) và (3) ta có: E, F, P thẳng hàng.
Bài 15: Cho
∆
ABC vuông tại A, đường cao AH, trung tuyến AM, Gọi D và E theo thứ tự
là chân đường vuông góc kẻ từ H đến AB, AC ,CMR:
a, AH = DE b,
HAB MAC=
c,
AM DE⊥
d, DI // EK, với I là trung điểm của HB, K là trung điểm của HC
Lời giải
a) Tứ giác ADHE có 3 góc vuông nên là HCN => AH = DE
b)
∆
ABC vuông tại A, Có AM là đường trung tuyến => AM = MB = MC
=>
∆
AMC cân tại M =>
MAC C=
Mặt khác
HAB C=
,
Vì cùng phụ với
( )
HAC HAB MAC C=>= =
c) Chứng minh AM
DE⊥
, Ta có:
0
12
90AE+=
, ta có:
0
21 23 21
90EAEAEE+=+=+=
d, Ta có:
∆
HEC có EK = KH = KC =>
∆
EKC cân tại K
=>
31
E CA= =
=> EK // AM => KE
⊥
DE. Chứng minh tương tự =>
//DI DE DI EK⊥=>
Bài 16: Cho
∆
ABC đều có cạnh bằng 4cm, M và N là các điểm lần lượt chuyển động trên
hai cạnh BC và AC sao cho BM= CN
a) Tính diện tích
∆
ABC
b) Xác định vị trí của M, và N để độ dài MN nhỏ nhất . Tìm độ dài nhỏ nhất đó?
1
3
2
1
3
2
1
O
K
I
E
D
M
H
B
A
C
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
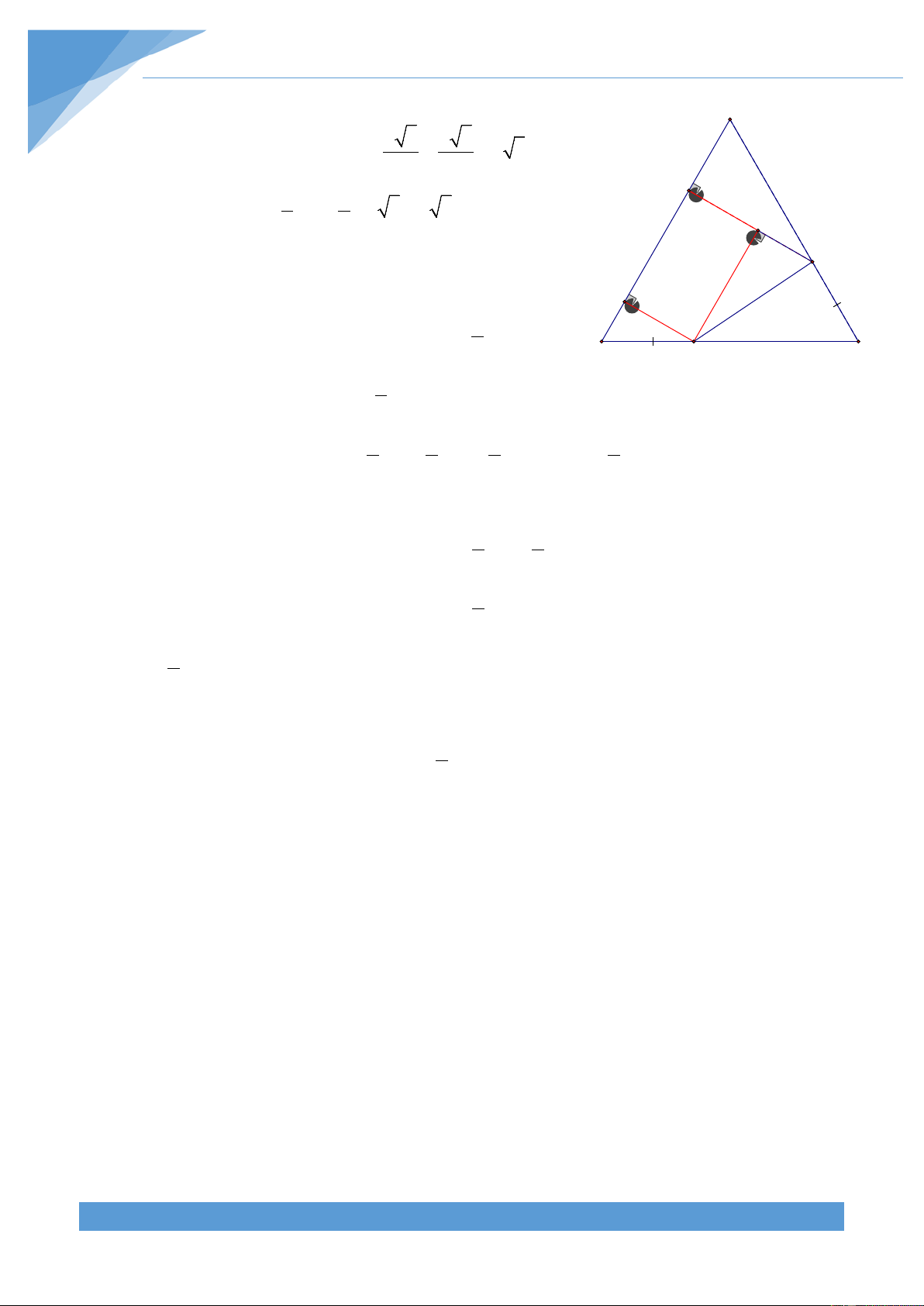
228
Lời giải
a) Tính được độ dài đường cao:
( )
3 43
23
22
a
h c
m= = =
Suy ra diện tích:
2
11
. 4.2 3 4 3( )
22
ABC
S a h cm= = =
b) Gọi P và Q là chân đường vuông góc
kẻ từ M và N xuống AB
Ta có:
∆
ANQ vuông ở Q, có:
0
1
60
2
A AQ AN==>=
Tương tự đối với
∆
MPB có :
1
2
PB BM=
Cộng theo vế ta được :
( )
11 1 1
22 2 2
AQ PB AN BM AN NC AC+= + = + =
Kẻ
⊥MH QN
. Tứ giác MPQH là hình chữ nhật
Ta có:
( )
11
22
MN MH PQ AB AQ BP AB AC AB≥==−+=− =
Như vậy khi M, N di chuyển ta luôn có:
1
2
MN AB≥
Và
1
2
MN AB=
, Khi M, N lần lượt là trung điểm của BC và AC
Suy ra vị trí của M,N cần xác định lần lượt là trung điểm BC và AC,
Khi đó độ dài nhỏ nhất của MN là :
1
2
2
MN AB cm= =
Bài 17: Cho
∆
ABC nhọn, Trực tâm H, giao điểm của các đường trung trực là O, Gọi P, Q,
N theo thứ tự là trung điểm của các đoạn thẳng AB, AH, AC
a) CMR: OPQN là HBH
b)
∆
ABC cần có điều kiện gì để OPQN là HCN
Lời giải
a) Gọi O là giao của 3 đường trung trực nên
,OP AB ON AC⊥⊥
Trong
∆
AHC, QN là đường trung bình nên QN // HC
Và PO // HC ( cùng vuông góc với AB)
Chứng minh tương tự ta có: OPQN là hình bình hành
H
Q
P
N
A
B
C
M
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
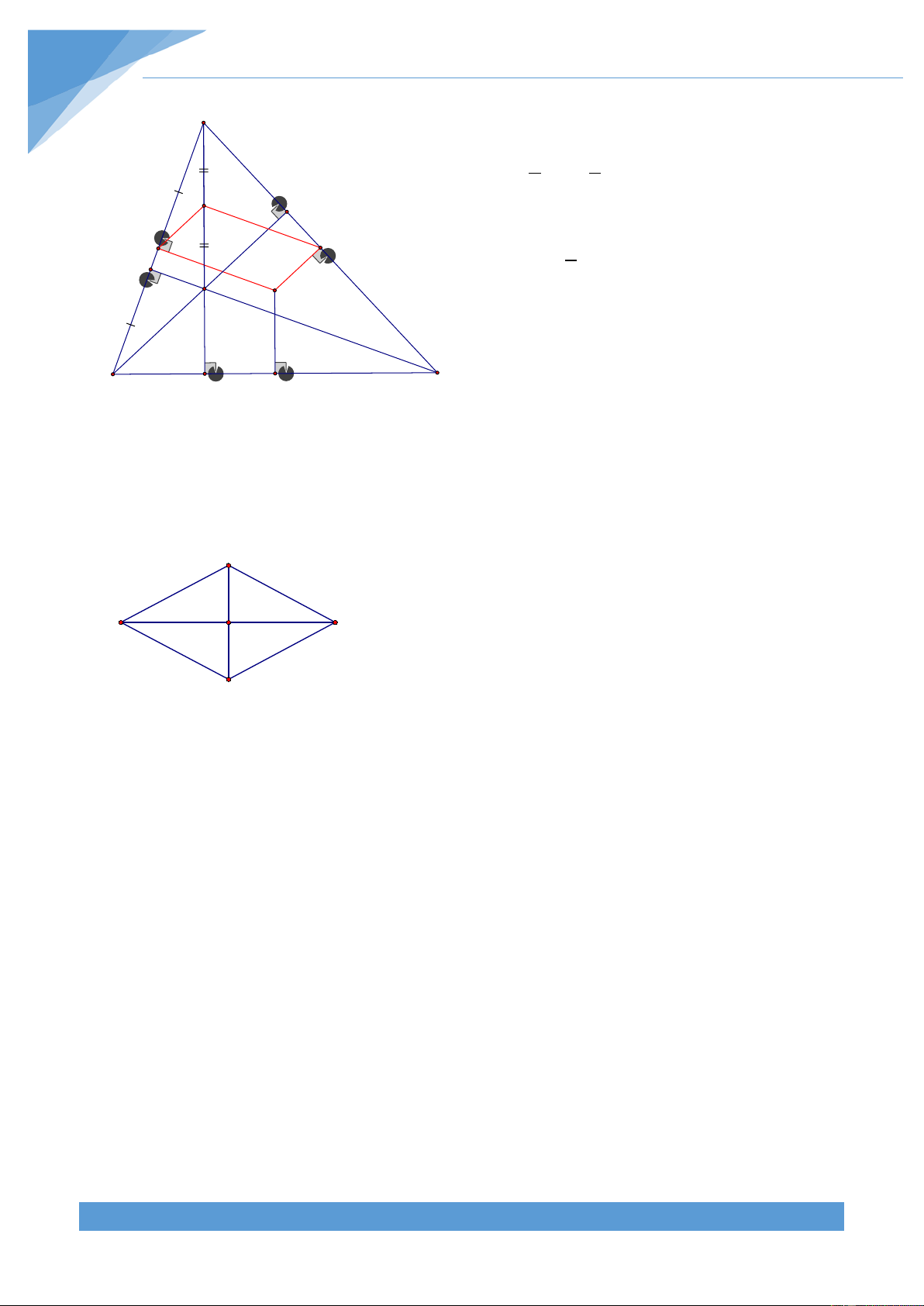
229
b) Tứ giác BCQN là hình chữ nhật có 2
đường chéo là NC và BQ => NC = BQ =>
11
22
MP NC BQ= =
Xét
∆
MQB có MP là đường trung tuyến
nên MP =
1
2
BQ
Nên
∆
MBQ vuông tại M => MB
⊥
MQ
HÌNH THOI
A. Tóm tắt lý thuyết
1. Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng
nhau
ABCD◊
là hình thoi
ABCD
AB BC CD DA
◊
⇔
= = =
2. Tính chất: Hình thoi có tất cả các tính chất của hình
bình hành
- Tính chất về cạnh:
+) Có bốn cạnh bằng nhau +) Các cạnh đối song song
- Tính chất về góc: Các góc đối bằng nhau
- Tính chất về đường chéo:
+) Hai đường chéo cắt nhau tại trung điểm của mỗi đường
+) Hai đường chéo vuông góc với nhau
+)Hai đường chéo là các đường phân giác của các góc ở đỉnh của hình thoi
3. Dấu hiệu nhận biết
- Tứ giác có bốn cạnh bằng nhau là hình thoi
- Hình hình hành có hai cạnh kề bằng nhau là hình thoi
- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi
- Hình bình hành có một đường chéo là đường phân giác của một góc ở đỉnh là hình thoi
4. Chú ý:
- Hình thoi có 1 tâm đối xứng là giao điểm của hai đường chéo
O
D
C
B
A
Q
O
N
P
H
B
C
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
230
- Hình thoi có hai trục đối xứng là các đường chéo của hình thoi
B. Bài tập
Bài 1: Cho hình thoi ABCD và điểm E nằm ngoài hình thoi và không nằm trên đường
thẳng CD sao cho CD = CE. Dựng hình bình hành ACEF. Chứng minh rằng B là trực tâm
DEF∆
Lời giải
Vì ABCD là hình thoi
CB CD→=
Có :
(1)
//
BD AC
BD FE
AC FE
⊥
→⊥
Lấy K đối xứng với E qua C
⇒∆EBK
vuông tại B
( đường trung tuyến bằng nửa cạnh
huyền )
+) Có
KCFA◊
là hình bình hành (
//,CK FE=
)
,⇒ CA FK
cắt nhau tại trung điểm
của mỗi đường
,⇒ BD FK
cắt nhau tại trung điểm của mỗi đường
⇒◊BFDK
là hình hình hành
//
(2)
⇒
⊥
BK DF
EB BK
Từ (1), (2) suy ra
B
là trực tâm
EDF∆
Bài 2: Cho tam giác ABC có AB < AC, phân giác trong AD. Lấy các điểm M, N lần lượt
thuộc các đoạn AB, AC sao cho BM = CN. Gọi
P, Q lần lượt là rung điểm của MC, MB. Chứng
minh rằng
AD PQ⊥
Lời giải
Gọi E, F lần lượt là trung điểm của MN, BC
,,,⇒ EQ QF FP PE
là đường trung bình của các
1
,,, ;
2
1
::
2
∆ ∆ ∆ ∆ ⇒==
= = ⇒◊ ⇒
BMN BNC BMC MNC EQ FP BM
EP FQ NC EPFQ lahinh thoi FE la phan giac
của
1
ˆ ˆˆ ˆ
(1)
2
⇒ = = ⇒⊥QEP FEQ FEP PEQ FE PQ
+) Gọi k là giao điểm của FE và AB
I
B
A
D
K
C
E
F
Q
D
F
P
E
K
A
B
C
N
M
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
231
Vì
ˆˆ
/ / (2)⇒=EQ AB BKF FEQ
mà:
ˆ
ˆ
(3)=QEP BAC
( góc có cạnh tương ứng song song )
Từ (1), (2), (3) suy ra
1
ˆˆ
ˆ
//
2
= = → ⇒⊥BKF BAC BAD FK AD AD PQ
Bài 3: Cho hình thoi ABCD có
0
ˆ
60A =
. Đường thẳng MN cắt AB ở M, cắt BC ở N. Biết BM
+ NB có độ dài bằng 1 cạnh của hình thoi. Chứng minh rằng
MND∆
đều
Lời giải
+)
ABD∆
đều (1)
+)
+=
⇒=
= +
BM BN AB
BN AM
AB BM MA
+)
( . . ) (2)∆ =∆ ⇒=AMD BND c g c DM DN
13
0
23
0
12
ˆˆ
ˆˆ
60 (3) :
ˆˆ
60
=
⇒ + = ⇒∆
+=
DD
D D M
ND deu
DD
Bài 4: Cho hình bình hành ABCD có AB = 2AD,
0
70D =
, vẽ BH vuông góc với AD,
H AD∈
. Gọi M, N theo thứ tự là trung điểm của CD và AB
a) CMR: ANMD là hình thoi b) Tính
HMC
Lời giải
b) Ta có:
0
1
70MD= =
, Tính
2
M
Ta có:
21
MH=
( So le trong)
Mà :
23 13
MH HH==>=
Xét
∆
HAN cân tại N =>
0
13
70HH A+==
=>
00
12
35 35HM==>=
, Vậy
00 0
35 70 105HMC =+=
Bài 5: Cho
∆
ABC nhọn, vẽ các đường cao AD và BE, Tia phân giác Ax của
DAC
cắt BE và
BC lần lượt ở M và N, Tia phân giác By của
EBC
cắt AD và AC lần lượt tại P và Q. CMR:
a) AN
⊥
BQ b) Tứ giác MPNQ là hình
thoi
Lời giải
a) Ta có:
EBC DAC=
( cùng phụ góc C)
1212
AABB⇒===
4
3
2
1
N
M
D
C
B
A
2
1
3
2
1
70
H
M
C
N
A
B
D
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
232
∆
EBQ vuông
00
12
90 90B BQE A BQE⇒+=⇒+=
0
90AOQ AN BQ⇒ =⇒⊥
b)
∆
APQ có AO vừa là đường phân giác vừa là đường
cao
=> AO là đường trung trực
=> MP = MQ, NP = NQ
∆
BMN có BO vừa là đường phân giác vừa là đường cao
=> là đường trung trực ( đpcm)
Bài 6: Cho
∆
ABC đều, đường cao AD, M là điểm nằm giữa B và D, gọi N là Trung điểm
của AM, vẽ ME vuông góc AB tại E, MF vuông góc AC tại F. CMR: DENF là hình thoi
Lời giải
Ta có: MN = EN = DF= FN
1
2
AM
=
0
2. 2 2. 60END ENM MND EAM MAD DAE⇒= + = + = =
DNF MNF MND⇒=−
0
2. 2. 2. 60DNF MAC MAD DAC⇒= − = =
=>
∆
NED đều,
∆
NDF đều
Vậy DENF là hình thoi
Bài 7: Cho tam giác đều ABC, trực tâm H, kẻ đường cao AD, một điểm M thuộc cạnh BC,
từ M kẻ ME vuông góc với AB và MF vuông góc với AC, Gọi I là trung điểm của AM,
CMR:
a) DEIF là hình thoi
b) Đường thẳng HM đi qua tâm đối xứng của hình thoi DEIF
Lời giải
a)
∆
ADM vuông có
1
2
DI AM=
Tương tự:
1
2
EI AM DI EI EID= ⇒ = ⇒∆
cân
EI AI AIE= =>∆
cân có
11
2IA=
Tương tự :
0
2 2 12
2. 60I A EID I I= => =+=
=>
∆
EID đều => EI = ED = IP
2
1
2
1
O
P
N
Q
M
D
E
B
C
A
2
1
2
1
N
F
E
D
A
B
C
M
K
G
J
N
I
F
E
D
H
A
B
C
M
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
233
Chứng minh tương tự: IF = FD = ID
=> Tứ giác EIFD là hình thoi
b) Gọi O là giao điểm của hai đường chéo
của hình thoi DEIF và N là trung điểm AH,
Ta có:
∆
AMH có IN là đường trung bình => IN // MH,
∆
IDN có OH là đường trung bình => OH // IN
Như vậy O, H, M thẳng hàng => MH đi qua giao điểm O của ID và EF
Bài 8: Cho
∆
ABC, trên tia AB ta lấy 1 điểm D, trên tia AC lấy 1 điểm E sao cho BD=CE,
Gọi M, N, P, Q lần lượt là trung điểm của BC, CD, DE, EB
a) CMR: MNPQ là hình thoi
b) CMR: các đường chéo của hình thoi MNPQ song song với các phân giác trong và ngoài
của góc A
Lời giải
b, Vì MNPQ là hình thoi, MP và NQ là hai đường chéo
=> MP
⊥
NQ
Gọi I, J lầ lượt là giao NQ với AB và AC
=> PQ // AD =>
11
IQ=
( so le trong )
Tương tự:
11
NQ=
=>
∆
IAJ cân tại A
=> Phân giác Ax là đường cao
=> Ax
⊥
IJ, Mà MP
⊥
IJ
=> Ax // MP
Dễ dàng chứng minh được NQ // Ay.
Bài 9: Cho hình thoi ABCD, trên tia đối của tia BA, ta lấy điểm M, trên tia đối của tia CB
lấy N, trên tia đối tia DC lấy P, trên tia đối tia AD lấy Q sao cho BM = CN = DP = AQ
a, CMR: MNPQ là hình bình hành
b, CMR : MNPQ là hình thoi và ABCD có cùng tâm đối xứng
c, Hình thoi ABCD phải có ĐK gì để MNPQ là hình vuông
Lời giải
a)
AQM NCP QM PN∆ =∆⇒=
MBN PDQ QP MN∆ =∆ ⇒=
b)
12
ˆˆ
0DOBM N O O∆ =∆ ⇒=
0
1
ˆ ˆˆ ˆˆ ˆ
180
?
POM POB O POB O BOD⇒ = += += =
y
x
J
I
P
Q
N
M
E
A
B
C
D
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
234
=> P, O, M thẳng hàng
Chứng minh tương tự ta có: Q, O, N thẳng
hàng
=> HBH MNPQ có tâm O
c, Để MNPQ là hình thoi thì Hình bình hành
MNPQ
có hai cạnh kề bằng nhau: QM= QD. Thật
vậy:
∆
QAM=
∆
MBN =>
MBN QAM QAM BAD==>=
,
Mà
QAM BAD=
và
00
180 90QAM BAD BAD+==>=
Bài 9: Cho HBH ABCD, các đường chéo cắt nhau ở O, gọi E, F, G, H theo thứ tự là giao
điểm của các đường phân giác của các
∆
OAB,
∆
OBC,
∆
OCD,
∆
OAD
Chứng minh rằng: EFGH là hình thoi
Lời giải
Vì OH , OF là hai tia phân giác của các góc đối đỉnh
nên H, O, F thẳng hàng
Tương tự ta có: G, O, E thẳng hàng
Lại có OH
⊥
OG
( Hai tia phân giác của hai góc kề bù)
Xét
∆
OAE =
∆
OCG (c.g.c) => OG =OE
Chứng minh tương tự : OH= OF
=> EFGH là hình bình hành
có hai đường chéo vuông góc với nhau
=> là hình thoi
HÌNH VUÔNG
A. Tóm tắt lý thuyết
1. Định nghĩa: Hình vuông là tứ giác có bốn góc vuông và bốn
cạnh bằng nhau
ABCD◊
là hình vuông
ˆˆ
ˆˆ
ABCD
AB BC CD DA
= = =
⇔
= = =
2. Nhận xét : Từ định nghĩa hình vuông ta suy ra
- Hình vuông là hình chữ nhật có bốn cạnh bằng nhau
D
C
B
A
2
1
Q
P
N
D
O
A
C
B
M
1
1
2
1
H
G
F
E
O
A
B
D
C
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

235
- Hình vuông là hình thoi có 4 góc vuông
⇒
Hình vuông vừa là hình chữ nhật vừa là hình thoi
3. Tính chất: Hình vuông có tất cả các tính chất của hình bình thoi và hình chữ nhật
- Tính chất về cạnh:
+) Có bốn cạnh bằng nhau
+) Các cạnh đối song song
- Tính chất về góc: Bốn góc bằng nhau
- Tính chất về đường chéo:
+) Hai đường chéo bằng nhau
+) Hai đường chéo cắt nhau tại trung điểm của mỗi đường
+) Hai đường chéo vuông góc với nhau
+) Hai đường chéo là các đường phân giác của các góc ở đỉnh của hình thoi
3. Dấu hiệu nhận biết
- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
- Hình chữ nhật có hai đường chéo vuôn góc với nhau là hình vuông
- Hình chữ nhật có 1 đường chéo là đường phân giác của một góc là hình vuông
- Hình thoi có một góc vuông là hình vuông
- Hình thoi có hai đường chéo bằng nhau là hình vuông
4. Nhận xét: Một tứ giác vừa là hình chữ nhật vừa là hình thoi thì tứ giác đó là hình vuông
5. Tính chất đối xứng của hình vuông
- Hình vuông có 1 tâm đối xứng là giao điểm của hai đường chéo
- Hình vuông có bốn chục đối xứng:
+) 2 đường chéo của hình vuông
+) 2 đường thẳng nối trung điểm các cạnh đối diện của hình vuông
B. Bài tập và các dạng toán
Bài 1: [ HSG – Hà Nội – 2009 ]
Cho hình vuông ABCD và 1 điểm E bất kỳ nằm giữa hai điểm A và B. Trên tia đối của tia
CB lấy điểm F sao cho CF = AE
a. Tính
ˆ
EDF
b. Gọi G là điểm đối xứng với D qua trung điểm I của EF. Tứ giác DEGF là hình gì? Vì sao?
c. Chứng minh ba đường thẳng AC, DG, EF đồng quy tại 1 điểm
Lời giải
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
236
a. Ta có:
0
ˆˆˆˆˆ ˆˆ
90 ( )=+=+= =EDF EDC CDF EDC EDA CDF EDA
b. Xét
DEGF◊
có:
IF, DI = IG DEGFEI = ⇒◊
là
hình bình hành , lại có
0
ˆ
90D DEGF= ⇒◊
là
hình chữ nhật mà
ADE CDF ED FD DEGF∆ = ⇒ = ⇒◊
là hình
vuông ( dấu hiệu nhận biết )
c. Ta có EF giao DG tại I, ta đi chứng minh I
thuộc đường trực của AC
Có:
1
EF I
2
IB ID= = ⇒
thuộc đường trung trực
của BD
I AC⇒∈
( AC là đường trung trực của BD)
Bài 2: Cho hình vuông ABCD. Trên tia đối của tia CB lấy điểm M , trên tia đối của tia DC
lấy điểm N sao cho BM = DN. Vẽ hình bình hành AFMN. Chứng minh rằng
a.
ABM ADN∆=∆
b. Tứ giác AMFN là hình
vuông
c. Kẻ
,FH BM FK CN⊥⊥
, chứng minh rằng :
0
ˆ
90ACF =
d. B, D, O thẳng hàng ( O là trung điểm của FA )
Lời giải
a. Ta có
ˆˆ
()ABM ADN cgc AM AN DAN BAM∆ =∆ ⇒=⇒ =
b. Hình bình hành AMFN, có: AM = AN
AMFN⇒◊
là hình thoi. Lại có
0
90 AMFNMAN MAD DAN MAD MAB= + = + = ⇒◊
là hình vuông
c.
0
ˆˆˆ ˆ
45ACF ACD DCF DCF=+=+
Ta đi chứng minh
0
ˆ
45DCF CHFK= ⇒◊
là
hình vuông
Có:
0 00
1 2 2 2 12 2 1
ˆˆˆˆˆˆˆˆ
90 90 , 90 ( )M M N M N N M N MHF NKF ch gn FH FK+=⇒+= +=⇒=⇒∆ =∆ −⇒ =
CHFK⇒◊
là hình vuông
00
ˆ
ˆ
45 90DCF ACF=⇒=
(đpcm)
d. Ta đi chứng minh 3 điểm B, D, O nằm trên đường trung trực của AC
I
E
G
D
F
C
B
A
2
2
1
2
1
O
K
H
F
N
M
D
C
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
237
Ta có: ABCD là hình vuông
⇒
B, D nằm trên đường trung trực của AC
O là trung điểm của AF
⇒
O là trung điểm của MN
OA OM⇒=
Lại có
1
2
OC OM AC OM OC OA OC O= = ⇒ =⇒=⇒
nằm trên đường trung trực của AC
,,BDO⇒
thẳng hàng.
Bài 3: Cho đoạn thẳng AB và điểm M thuộc đoạn thẳng đó. Vẽ về một phía của AB các
hình vuông AMCD, BMEF
a. Chứng minh
AE BC⊥
b. Gọi H là giao điểm của AE và BC. Chứng minh ba điểm D, H, F thẳng hàng
c. Chứng minh đường thẳng DF luôn đi qua một điểm cố định khi M di chuyển trên đoạn
thẳng cố định AB
Lời giải
a. Có MD // BE ( hai góc đồng vị bằng
nhau )
mà:
MD AC AC BE⊥⇒⊥
. Lại có
EC AB C⊥⇒
là trực tâm tam giác ABE
AE BC⇒⊥
b. Gọi O và O’ lần lượt là tâm của hai hình vuông AMCD và BMEF
Tam giác vuông AHC có OH là đường trung tuyến ứng với cạnh huyền AC
11
22
OH AC DM⇒= =
0
ˆ
( 90 ) (1
)DMH H DH MH⇒∆ = ⇒ ⊥
Chứng minh tương tự, ta được
(2) , ,HF MH D H F⊥⇒
thẳng hàng.
c. Gọi I là giao điểm của AC và DF
Chứng minh được OI là đường trung bình của tam giác DMF, hay I là trung điểm DF
Kẻ IK vuông góc AB ( K thuộc AB )
K⇒
là trung điểm của AB, vậy K cố định
Mặt khác
11
()
22
IK AD BF AB= +=
( Không đổi )
I⇒
cố định. Vậy DE luôn đi qua I cố
định.
Bài 4: Cho hình vuông ABCD và điểm M thuộc đoạn BC. Lấy điểm N thuộc đoạn CD sao
cho
0
ˆ
45MAN =
. Chứng minh rằng:
BM DN MN+=
K
I
H
O'
O
E
F
D
C
M
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
238
Lời giải
Trên tia đối của tia DC lấy điểm E sao cho : DE
= BM
Ta có:
13
ˆˆ
() ;ABM ADE cgc AM AE A A∆ =∆ →= =
00
ˆˆˆˆˆ ˆ
90 90MAE MAD DAE MAD BAM EAN= += + =→=
()EAN MAN cgc EN MN DN BM MN∆ =∆ →= ↔+ =
Bài 5: Cho hình vuông ABCD và điểm M thuộc đoạn BD. Gọi E, F lần lượt là hình chiếu
của M lên AB, AD. Chứng minh rằng: BF, DE, CM
đồng quy.
Lời giải
+) Ta có:
FAEM◊
là hình chữ nhật
+) Ta có:
FDM∆
vuông cân tại F
⇒= =AE FM FD
0
ˆˆ
ˆˆ
( ) 90
ˆ
ˆ
=
⇒∆ =∆ ⇒ = = + =
=
AD DC
EAD FDC cgc EAD FCD EDA EDC
AD
(1)⇒⊥CF DE
Tương tự:
(2)⊥BF CE
+) Gọi K là giao điểm của CM và EF
0
ˆˆ
ˆ ˆˆ ˆ ˆˆˆ
( ) 90 (3)
∆
= == =⇒+=+=⇒⊥
AFK can
doi xung hinh vuong
KMF MCD dvi MAD AFE FEM KFM KMF KFM FEM CM FE
Từ (1), (2) và (3) suy ra ba đường cao trong
CEF∆
Bài 6: Cho hình vuông ABCD, E là điểm bất kỳ trên AB.
Phân giác góc CDE cắt BC tại K. Chứng minh rằng: CK +
EA = DE
Lời giải
+) Trên tia đối của tia CK lấy điểm F sao cho CF = AE
⇒ += +=CK EA CK CF FK
+)
14
ˆˆ
(..) ;∆ =∆ ⇒= =AED CFD c g c DE DF D D
1
2
45
°
M
N
E
D
C
B
A
K
M
E
F
D
C
B
A
4
3
2
1
F
K
E
D
C
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
239
+) Xét
DKF∆
có:
0
1 34
ˆ ˆ ˆˆ ˆˆ
90 ;DFK DEA D FDK D D==−=+
0 00 0
1 34 134
ˆ ˆ ˆ ˆ ˆˆ ˆˆˆ
180 180
(90 ) ( ) 90DFK DEK FDK D D D D D D= − − = − − − + = +−−
0
312 43
ˆ ˆˆ ˆˆ ˆ ˆ
90= − = + = + ⇒ = ⇒∆D D D D D FDK DKF DKF
cân tại F
⇒ ==⇒+=⇒+=DF KF DE CK FC DE AE CK DE
Bài 7: Cho hình vuông ABCD. Gọi E, F lần lượt là trung điểm của AB, BC. M là giao điểm
của CE và DF. Chứng minh rằng : AM = AB
Lời giải
+)
0
1
ˆ
ˆˆ ˆ
90E F F C CE FD=→= = → ⊥
+) Gọi N là trung điểm của CD
+)
AECN◊
là hình bình hành
+)
MCD∆
vuông
MN ND→=
Có :
AN DM⊥→
Chứng minh :
AM AD AB= =
Bài 8: Cho hình vuông ABCD. Gọi M, N là trung điểm của AB, AD. BN và CM cắt nhau
tại P. Chứng minh rằng: DP = AB
Lời giải
+)
ˆ
ˆ
( . . );∆=∆ =BAN CBM c g c ABN BCN
00
12
ˆ
ˆˆ
90 90⇒+= ⇒ =C B BPC
+) Kéo dài BN cắt CD tại E
(..)∆ =∆ ⇒=⇒BAN EDN c g c AB DE D
là
trung điểm của EC
+) Xét
CPE∆
vuông tại P
1
()
2
⇒= ==PD EC CD AB dpcm
Bài 9: Cho
ABC∆
. Về phía ngoài
tam giác dựng các hình vuông
ABDE, ACFG. Chứng minh rằng
đường cao AH của
ABC∆
đi qua
trung điểm của EG
Lời giải
Gọi P, Q là hình chiếu của E, G lên
AH
H
Q
I
P
F
G
E
D
B
C
A
I
M
N
E
F
D
C
B
A
2
1
P
M
N
E
D
C
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
240
0
ˆˆ
90
ˆˆ
ˆ
(: )
=
= = ⇒∆ =∆
=
AE AB
EPA AHB E
AP AHB
EAP ABH phu BAH
(1)⇒=PE AH
Tương tự:
( . ) (2)∆ =∆ ⇒= ⇒=GQA CHA ch gn GQ AH GQ EP
Xét
,EPI GQI∆∆
có:
12
0
ˆˆ
( .. )
ˆ
ˆ
90
=
= ⇒∆ =∆ ⇒ =
= =
EP GQ
I I EPI GQI g c g EI IG
PQ
Bài 10: Cho
ABC∆
, M là trung điểm của BC. Về phía ngoài tam giác dựng các hình vuông
ABDE, ACFG. Gọi P, Q lần lượt là tâm của các hình vuông đó. CMR:
MPQ∆
vuông cân
Lời giải
+) PM và QM là đường trung bình của các
// //
,;
11
22
∆∆⇒
= =
MP EC MQ BG
EBC BGC
MP EC MQ BG
+)
(..)
ˆˆ
=
∆=∆ ⇒
=
EC BG
AEC ABG c g c
AEC ABG
Xét
IHB∆
có:
0
1
ˆˆˆ
180I BH++ =
21
00
12
ˆˆ
ˆˆˆ ˆ ˆ
90 90
ˆˆ
=
⇒+=+= ⇒ =
=
II
I BI E H
BE
⊥
⇒⊥⇒ ⇒∆
=
MP MQ
EC BG MPQ
MP MQ
vuông
cân.
Bài 11: Cho
ABC∆
, về phía ngoài tam giác dựng các hình vuông ABGH, ACEF, BCIJ. Gọi
123
,,OOO
lần lượt tâm các hình vuông, M là trung điểm của BC, D là trung điểm của HF.
CMR:
a.
12
O MO∆
vuông cân b.
12
DO MO◊
là hình vuông
c.
2HF AM=
d.
;AD BC AM HF⊥⊥
e.
12 3
O O AO=
Lời giải
Xét ta giác FAB và tam giác CAH có:
I
H
P
D
E
Q
G
F
C
M
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
241
0
;
;
ˆ ˆˆ
90
=
=
= +=
FA AC
AB AH
FAB A CAH
1 11
ˆˆ
()⇒∆ =∆ ⇒ = ⇒ =FAB CAH cgc FB CH AHJ I BJ
Mà:
00
1 1 1 1 11
ˆˆ ˆˆ
90 90AHJ AJ H I BJ BJ I FB CH+ =⇒ + =⇒⊥
+)
2
OM
là đường trung bình
22
1
// ;
2
∆⇒ =FCB O M FB O M BF
+)
1
OM
là đường trung bình
12
1 2 12
12
1
// ;
2
⊥
∆ ⇒ = ⇒ ⇒∆
=
OM OM
HBC O M HC O M HC O MO
OM OM
vuông cân.
b. +)
2
OD
là đường trung bình
11
1
// ;
2
∆⇒ =FHC O D BF O D BF
+)
1
OD
là đường trung bình
2 2 1 2 1 2 12
1
// ;
2
∆ ⇒ =
⇒ = = = ⇒◊FBH O D HC O D HC O M O M O D O D DO MO
là hình thoi,
0
ˆ
90= ⇒M
là hình vuông
c. Tứ giác
1
ABAC
là hình bình hành
0
11 1
0
1
ˆ
ˆ
; 180 ;
ˆˆ
ˆ
180
⇒= = − ⇒=
= − = ⇒=
BA AC ABA BAC BA FA
ABA BAC FAH BA AH
+)
11
2∆ =∆ ⇒=⇔ =ABA FAH AA HF AM FH
d. Hạ
11
CC AM C⊥≡
AM cắt FH tại D1:
1 11
ˆˆ
ˆ
(..) (
)∆=∆ ⇒ = =HAF BAA c g c HFA AA B CAA slt
Mà:
0 00
11 11 1
ˆˆ ˆ
ˆˆ
90 90
90+ = ⇒ + = ⇒= ⇒ ⊥CAA FAD D FA D AF D AM FH
Bài 12: Cho hình vuông ABCD, các điểm E, F lần lượt trên các cạnh BC, CD sao cho
0
45EAF =
, trên tia đối của tia DC lấy điểm M sao cho DM = BE. CMR:
a)
0
, 45ABE ADM MAF∆=∆ =
b) Chu vu tam giác CEF bằng 1 nửa chu vi tứ giác ABCD
Lời giải
a,
∆
ABE =
∆
ADN ( 2 cạnh góc vuông)
I1
J1
D1
M
O3
O1
O2
E
F
D
H
G
I
J
B
C
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
242
=>
12
AA
=
=>
0 00
90 90 45 45MAE MAF
0
==> =−=
b,
∆
AEF =
∆
AMF (c.g.c)
=> EF = MF, EF = MD + DF = BE + DF
Chu vi
∆
CEF = CE + EF + CF
= CK + BE + DF + CF = BC + CD
=
1
2
chu vi ABCD
Bài 13: Cho tam giác ABC vuông tại A, kẻ đường cao AH và trung tuyến AM, đường phân
giác góc A, cắt đường trung trực BC tại D, Từ D kẻ DE vuông góc với BA và DF vuông góc
với AC
a) CMR: AD là phân giác
HAM
b) 3 điểm E, M, F thẳng hàng
c) Tam giác BDC là tam giác vuông cân
Lời giải
a) Ta có:
11
CA=
( cùng phụ góc B)
Mà AM=
1
2
BC=> AM= MC=>
2 1 1 23 4
,A C A AA A==>= =
=> AD là tia phân giác
b) AH // DM =>
14
DA=
,
mà
43 13
A A D A ADM= => = =>∆
cân
=> AM= MD
Chứng minh Tứ giác AEDF là hình vuông
=> EA = ED => FA = FD
Ta có: M, E, F đều nằm trên đường trung trực của AD
=> Thẳng hàng
c,
∆
BED =
∆
CFD =>
23
DD=
0
32
90BDC BDF D BDF D EDF= += += =
=>
∆
BDC vuông cân
Bài 14: Cho tam giác ABC vuông tại A, và AB<AC, kẻ đường cao AH, trong nửa mặt
phẳng có chưa A bờ BC vẽ hình vuông AHDE
a) CMR: D nằm trên HC
b) Gọi F là giao của DE và AC, đường thẳng qua F và // với AB cắt đường thẳng qua B và
// với AC tại G, CMR: ABGF là hình vuông
2
1
45
F
M
C
D
A
B
E
3
2
1
1
4
3
2
1
F
E
D
H
M
B
C
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
243
c) CMR: AG, BF, HE đồng quy d) DEHG là hình
thang
Lời giải
a) AC > AB =>
BC>
Mà:
B HAC HAC C==>>
=> HC > AH => AH = HD => HC > HD => D nằm giữa H,C
b, Ta có:
00
12 23 1
3
90 , 90AA AA AA+= += =>=
kết hợp với AE= AH =>
∆
AEF =
∆
AHB => AB= AF
Tứ giác ABGF là hìn bình hành có 1 góc vuông => HCN có AB = AF => là hình vuông
c) Gọi M là giao điểm BF, AG,
Khi đó
∆
BDF có DM =
1
2
BF
Tương tự AM=
1
2
BF
=> M nằm trên đường trung trực AD
Ta lại có: AE= ED, HA= HD
=> E, H cũng nằm trên đường trung trực
của AD hay H, M, E thẳng hàng
Bài 15: Cho hình vuông ABCD và 1 điểm E bắt kỳ nằm giữa 2 điểm A và B, trên tia đối của
tia CB lấy 1 điểm F sao cho CF =AE
a) Tính
EDF
b) Gọi G là điểm đối xứng với D qua trung điểm I của EF, tứ giác DEGF là hình gì?
c) CMR: AC, DG, EF đồng quy
Lời giải
a)
∆
AED =
∆
CFD (c.g.c)
=>
ADE CDF EDF EDC CDF EDC ADE==>=+=+
=>
0
90EDF ADC= =
b) Tứ giác DEGF có I là trung điểm của EF (gt)
I là trung điểm của DG
Do đó: DEGF là hình bình hành
lại có:
0
90EDF =
=> Là hình chữ nhật, lại có tiếp DE = DF
=> Là hình vuông
G
I
F
C
D
A
B
E
3
2
1
G
M
F
E
D
H
B
C
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
244
Bài 16: Cho hình vuông ABCD, M là điểm bất kì trên cạnh BC, trong nửa mp bờ AB chứa
C đựng hình vuông AMHN, Qua M dựng đường thẳng d song song với AB, d cắt AH ở E,
Cắt DC ở F. Chứng minh rằng:
a) : B M = ND b) N, D, C thẳng hàng c) EMFN là hình gì?
d) Chứng minh
DF BM FM+=
và chu vi
∆
MFC không đổi khi M thay đổi trên BC
Lời giải
a) Tứ giác ABCD là hình vuông =>
0
1
90A MAD+=
(1)
Vì AMHN là hình vuông
0
2
90A MAD=>+ =
(2)
Từ (1) và (2) ta có:
12
AA=
Ta có :
∆
AND=
∆
AMB (c.g.c)
0
1
90 ,B D BM ND=>= = =
b, ABCD là hình vuông
00
2 1
2
90 180D D D NDC=> = =>+= =
,
Nên N, D, C thẳng hàng
c, Gọi O là giao điểm của hai đường chéo AH và MN
của hình vuông AMHN
=> O là tâm đối xứng của hình vuông AMHN
=> AH là đường trung trực của đoạn MN, mà E, F
∈
AH
=> EN = EM và FM = FN (3)
12
O O EM NF=>==> =
(4)
Từ (3) và (4) => EM = NE = NF = FM => MENF là hình thoi (5)
d, Từ (5) suy ra FM = FN = FD + DN, mà DN = MB (cmt) => MF = DF + BM
Gọi chu vi của
∆
MCF là P và cạnh hình vuông ABCD là a
Ta có :
P MC CF MF MC CF BM DF= ++ = ++ +
, Vì ( MF = DF + MB)
( ) ( )
2MC MB CF FD BC CD a a a= + + + = + =+=
Hình vuông ABCD cho trước => a không đổi => P không đổi
Bài 17: Cho hình vuông ABCD, Gọi E là 1 điểm bất kỳ trên cạnh BC ( E khác B và C), Qua
A kẻ Ax vuông góc với AE, Ax cắt CD tại F, trung tuyến AI của
∆
AEF cắt CD ở K, đường
thẳng kẻ qua E, song song với AB cắt AI ở G
a) Chứng minh AE=AF và tứ giác EGFK là hình thoi
b) Chứng minh
∆
AKF đồng dạng với
∆
CAF và
2
AF .FK FC=
2
2
1
1
3
2
1
d
O
E
F
N
A
B
D
C
M
H
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
245
c) Khi E thay đổi trên BC, chứng minh chu vi của
∆
EKC không đổi
Lời giải
a) Xét
∆
ABE vuông tại B và
∆
ADF vuông tại D có:
AB = AD,
BAE CAF=
=>
∆
ABE =
∆
ADF
=> AE = AF Vì AE = AF và AI là đường trung tuyến
∆
AEF => AI
⊥
EF
Hai
∆
IEG vuông tại I và
∆
IFK vuông tại I có:
IE=IF,
IEG IFK=
,
Nên
∆
IEG =
∆
IFK => EG = FK
Tứ giác EGFK có hai cạnh đối EG và FK song song và
bằng nhau nên là hình bình hành.
Hình bình hành EGFK có hai đường chéo GK và EF
vuông góc nên là hình thoi
b) Xét
∆
AKF và
∆
CAF có:
AFK CFA=
,
0
45KAF A CF= =
2
(.) .
AF FK
AKF CAF g g AF FK FC
FC AF
=> ∆ ∆ => = <=> =
c) Theo câu a ta có:
∆
ABE =
∆
ADF nên EB=FD, Tứ giác EGFK là hình thoi nên EK= KF
Do đó chu vi
∆
EKC là:
2
EKC
C EK KC CE CF CE CD DF CE CD=++=+=++=
( Không đổi)
Bài 18: Cho hình vuông ABCD cạnh a, trên AB lấy
2
3
a
AM =
, trên BC lấy BN sao cho
2
3
a
BN =
a) CMR: AN vuông góc DM
b) Gọi I và J lần lượt là trung điểm của NM, DN và K là giao AN và DN, Tính IK , KJ và IJ
Lời giải
a, Ta chứng minh
∆
ABN =
∆
DAM =>
11
DA=
, Mà :
0
11
90DM+=
=>
00
11
90 90AM K+ = =>=
b, Ta có :
22
4
5
993
a aa
MN =+=
1
5
26
a
KI MN= =
Tương tự ta có :
10
10
36
aa
DN K
J= =>=
x
K
G
I
F
C
A
B
D
E
1
1
1
K
J
I
N
C
D
B
M
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
246
Tương tự
13 13
36
aa
DM IJ= =>=
Bài 19: Cho hình vuông ABCD, Từ điểm M tùy ý trên đường chéo BD, kẻ ME, MF lần lượt
vuông góc với AB và AD, CMR:
a, CF = DE, CF
⊥
DE b, CM = EF, OM
⊥
EF
c, CM, BF, DE đồng quy d, Xác định M để diện tích AEMF lớn nhất
Lời giải
a) BD là đường chéo của hình vuông ABCD
=> BD là phân giác góc D
=>
0
45ADB DFM= =>∆
cân tại F=> DF = FM = AE
∆
CDF =
∆
DAE (c.g.c) => CF = DE và
11
CD=
Mà
0 00
11 11
90 90 90CFDFFOD+= =>+= => =
b, AM = EF, BD là đường trung trực của AC
=> MA = MC => MC = EF
Kéo dài FM cắt BC tại N => Tứ giác BEMN là hình vuông,
=> MN = ME
=>
∆
EMF =
∆
MNC(c. g. c) =>
1
M MEF=
,
Mà
00
12 2
90 90M M MEF M+==> +=
=>
0
90EHM =
=> ĐPCM
c)
∆
EFC có CH
⊥
EF => CM trùng CH là đường cao ứng với cạnh EF
Lại có ED
⊥
CF tại O => ED là đường cao ứng với cạnh CF
Chứng minh tương tự câu a => CE
⊥
BF => BF là đường cao ứng với cạnh CE
=> 3 đường CM, BF, DE đồng quy
1
1
1
2
1
O
H
N
E
F
C
D
A
B
M
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
247
CÁC BÀI TẬP TỔNG HỢP VỀ TỨ GIÁC ĐẶC BIỆT
Bài 1: Cho
ABC∆
, về ra phía ngoài tam giác dựng các hình vuông BCDE, ACIG và hình
bình hành BEQK, CDPE. Chứng minh rằng
APQ∆
vuông cân
Lời giải
11 1 2
( . . ): ; ;
ˆ ˆ ˆˆ
ˆ
( ù: DCF ) CP = AB ; A
∆=∆ = ==
=⇒=
ABC CFP c g c AC CF BC PF CD
C Fb C
Tương tự:
11
(..)
ˆ
ˆ
=
∆=∆ ⇒
=
AC BQ
ABC BKQ c g c
AB
()∆ =∆ ⇒ = ⇒∆ABQ ACP cgc AQ AP APQ
Cân tại A
Ta có:
ˆ ˆˆ ˆ ˆˆ
ˆ
QAP QAB BAC CAP APC FCP CAP=++=++
00 0
180 90 90= −=
( Tổng ba góc tam giác )
⇒∆APQ
vuông cân
Bài 2: [ HSG: 14/04/2014 ]
Cho hình thang ABCD vuông tại A và D, biết CD = 2AB = 2AD và
2BC a=
. Gọi E là
trung điểm của CD
a.
ABED◊
là hình gì? Vì sao b. Tính
ABCD
S
theo a
c. Gọi I là trung điểm của BC, H là chân đường vuông góc kẻ từ D xuống AC. Tính
ˆ
HDI
Lời giải
a. Hình chữ nhật có hai cạnh kề bằng nhau nên là hình vuông
b.
BEC∆
vuông cân vuông cân
2
; 2;
( ). ( 2 ). 3
2 22
⇒== =
++
= =
=
ABCD
AB AD a CD a
AB CD AD a a a a
S
c.
0
ˆˆˆ
ˆˆ
90
HDI HDB BDI
HDB HDA
= +
+=
. Ta đi chứng minh :
ˆ
ˆˆ ˆ
( : ) ()= = ⇐∆
∆BDI ADH ACD phu HDC BDI DCA cgc
Vì :
00
1
ˆˆ ˆ
; 90 .... 45
2
====⇒=
BI AD
B D HDI
BD DC
Bài 3: [ HSG – Yên Dũng – Bắc Giang – 2014 ]
Cho
ABC∆
. Gọi I là 1 điểm di chuyển trên cạnh BC. Qua I kẻ đường thẳng song song với
cạnh AC cắt AB tại M. Qua I kẻ đường thẳng song song với AB cắt AC tại N
1
1
1
2
1
H
K
Q
E
D
P
G
F
C
B
A
a
2
H
I
C
D
E
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
248
a. Gọi O là trung điểm của AI. CMR: M, O, N thẳng hàng
b. Kẻ MH, NK, AD vuông góc với BC lần lượt tại H, K, D.
Chứng minh rằng MH + NK = AD
c. Tìm vị trí của điểm I để MN // BC
Lời giải
a.
//
//
⇒ ⇒∩
AM NI
HBH MN AI
AN MI
tại
trung điểm của mỗi đường
,,MON→
thẳng hàng
b. Kẻ
OE BC⊥
ta đi chứng minh
MHKN là hình thang vuông
Ta có: O là trung điểm của MN, mà :
// // ⇒OE MH NK OE
là đường trung
bình hình thang vuông
2 (1)⇒ +=MNHK MH NK OE
+) Xét
∆⇒ADI OE
là đường trng bình
2 (2) ( )∆⇒= ⇒ +=ADI AD OE MH NK AD dpcm
c. Ta có :
// ⇔MN BC MN
là đường trung bình
ABC∆
, lại có O là trung điểm của AI
mà : MI // AC, M là trung điểm của AB
⇒ I
phải là trung điểm của BC
Bài 4: Cho hình vuông ABCD, M là điểm trên cạnh BC. Trong nửa mặt phẳng bờ AB chứa
điểm C dựng hình vuông AMHN. Qua M dựng đường thẳng d song song với AB, d cắt
AH ở E, cắt DC ở F
a. Chứng minh rằng: BM = ND b. N, D, C thẳng hàng c. FMNE là
hình gì?
d. DF + BM = FM và chu vi
MFC∆
không đổi khi M thay đổi vị trí trên BC
Lời giải
a.
0
1
ˆˆ
( . . ) 90
;∆ =∆ ⇒= = =AND AMB c g c B D BM ND
b.
0
ˆ
180 , ,= ⇒NDC N D C
thẳng hàng
c. Ta có : MN là đường trung trực của AH
, ; ()
=
∈⇒ ∆ =∆ −⇒=
=
EN EM
E F AH EOM FON ch gn FN EM
FM FN
Vậy 4 cạnh bằng nhau nên là hình thoi.
d.
FM FN ND DF BM FD==+= +
+)
MFC
P MC CF FM MC CF BM DF
∆
= ++ = ++ +
o
m
h
d
e
i
n
k
c
b
a
O
2
1
1
2
1
2
1
E
M
F
H
N
D
C
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
249
( )( )2MC MB CF DF AB= + ++ =
( không đổi )
Bài 5: Cho hình vuông ABCD có độ dài cạnh là a. Gọi M và N theo thứ tự là hai điểm trên
cạnh BC và CD sao cho
0
ˆ
45MAN =
. Trên tia đối của tia DC lấy điểm K sao cho DK = BM
a. Chứng minh
ADK ABM∆=∆
b. Chứng minh AN là tia phân giác
ˆ
KAM
c. Tính chu vi
CMN∆
theo a
d. BD cắt AM và AN lần lượt tại E và F. Chứng minh rằng ba đoạn BE, FE, FD lập thành
ba cạnh của 1 tam giác vuông
Lời giải
a.
()ADK ABM c g c∆ =∆ −−
b.
15
ˆˆ
ADK ABM A A∆ =∆ →=
0
1234 5234
ˆ ˆˆˆˆˆˆˆˆ
90KAMAAAAAAAA=+++=+++=
00 0
ˆ ˆ ˆˆ
90 45 45
( )=− =⇒= =KAN NAM KAN MAN dpcm
c.
CMN
P MN NC CM CM CN KN= ++ = ++
() 2ANK AMN CM CN KD DN a∆ =∆ = +++ =
d. Gọi H là chân đường vuông góc kẻ từ A
đến MN
23
0
ˆˆ
()
(..)
ˆˆ
; 45
∆ =∆ − ⇒=
⇒∆ =∆
⇒= = =
AND AMH ch gn A A
FAD FAH c g c
FH FD AHF ADF
0
ˆ
( . . ) ; 45∆ =∆ ⇒= = =AEH AEB c g c EH EB AHE ABE
Ta có:
0
ˆ ˆˆ
90=+=⇒EHF EHA FHA
vuông tại H
Vậy
,,BE DF FE
lập thành ba cạnh của một tam giác vuông
5
4
3
2
1
N
M
H
E
F
K
D
C
B
A
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC

250
Sưu tầm và tổng hợp
TÀI LIỆU TOÁN HỌC
Bấm Tải xuống để xem toàn bộ.




