Một số mẹo phân tích đồ thị hàm bậc 4 trong khảo sát Toán 12
Để biết được một số mẹo phân tích đồ thị hàm bậc 4 trong quá trình làm các bài
toán liên quan khảo sát hàm số thì chúng ta chỉ cần nhớ được dạng đồ thị tổng quát
của hàm bậc 4. Nội dung trong bài giảng này thầy sẽ trình bày một số vấn đề liên
quan tới tính biến thiên và cực trị của hàm số.
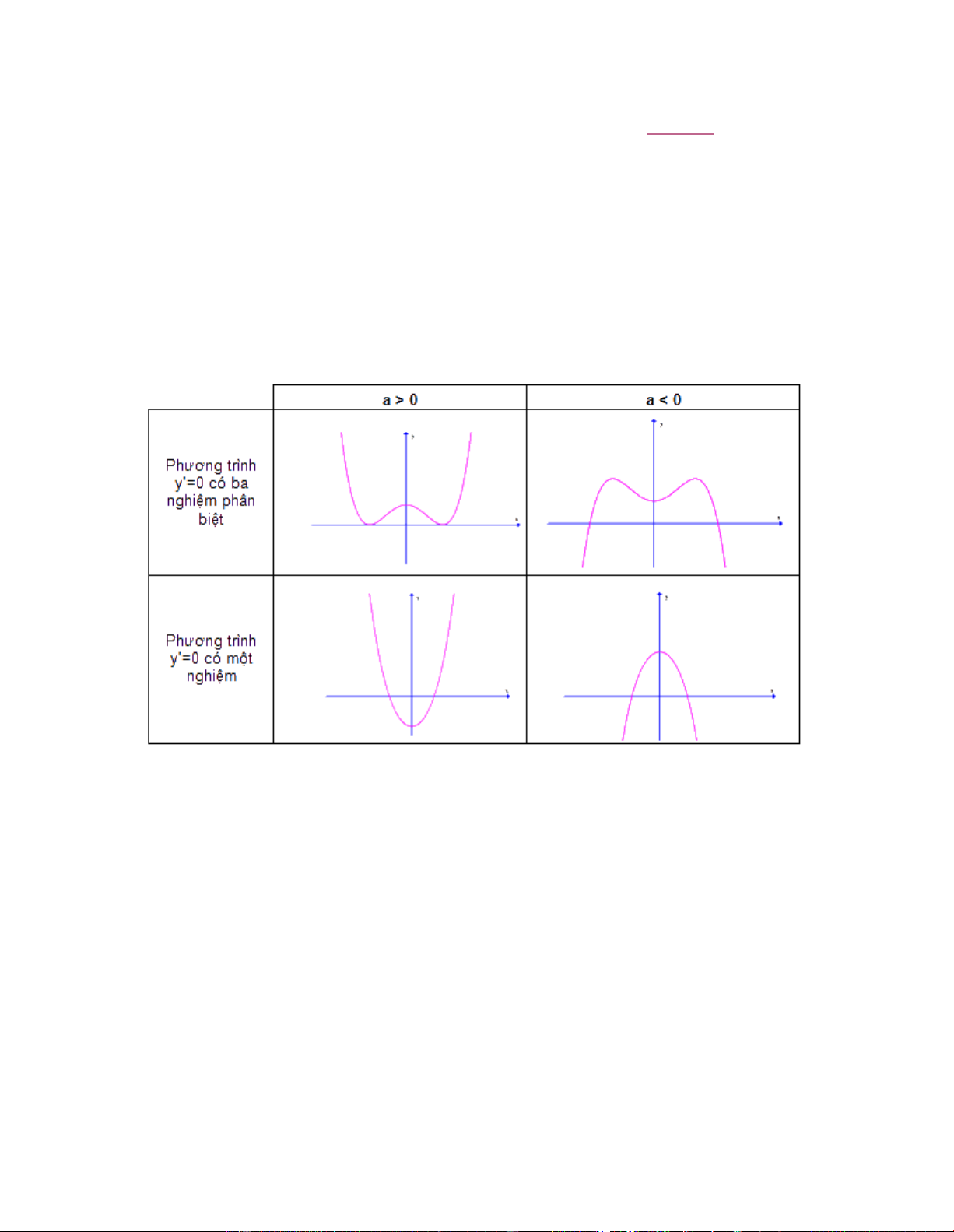
Trước tiên các bạn cần quan sát và nhớ được dạng tổng quát của đồ thị hàm bậc 4
1) Dạng toán về tính đơn điệu của hàm số
* Tìm m để hàm số đồng biến, nghịch biến trên R
Theo các bạn thì đối với hàm bậc 4 cụ thể là hàm trùng phương mà chúng ta vẫn
xét trong chương trình học thì liệu có câu hỏi như trên không? Tức là có bài toán
nào yêu cầu tìm m để hàm số đồng biến, nghịch biến trên R hay không?
Theo quan điểm của riêng thầy thì sẽ không ai hỏi như vậy. Tại vì sao ? Chúng ta
để ý lên đồ thị hàm trùng phương ở trên thì sẽ thấy ngay. Trong 4 cái đồ thị mà các
bạn nhìn thấy thì không có một cái đồ thị nào mà hàm số của chúng ta đồng biến
hay nghịch biến trên R cả. Do đó câu hỏi này có lẽ sẽ không ai cho vào bài toán.
Vậy thì với hàm trùng phương hàm số của chúng ta chỉ có thể đồng biến, nghịch
biến trên từng khoảng hay đoạn bất kì khác R. Nếu gặp bài toán như vậy thì chúng ta sẽ làm như thế nào?
* Tìm m để hàm số đồng biến, nghịch biến trên khoảng (a; b) bất kì
Để giải được bài toán dạng này thì các bạn lại để ý lên đồ thị dạng tổng quát ở
hình phía trên. Trong 4 cái đồ thị của chúng ta thì đều có thể sảy ra trường hợp như
này. Tuy nhiên nếu nhìn vào dạng đồ thị tổng quát ta sẽ biện luận bài toán này theo 2 trường hợp.
Trường hợp 1: Phương trình y' = 0 có 3 nghiệm phân biệt
Với dạng này phương trình y' = 0 bao giờ cũng phân tích được thành dạng: (x −
m)(x2 + ax + b) = 0 với m là hằng số, tức là x = m là 1 nghiệm của phương trình
này rồi. Công việc của chúng ta là tìm điều kiện để phương trình bậc 2 còn lại có 2
nghiệm phân biệt khác m là xong. Sau đó ta lập bảng biến thiên, xét xem khoảng
đồng biến hay nghịch biến bài toán cho phù hợp với khoảng nào của nghiệm.
Trường hợp 2: Phương trình y' = 0 có 1 nghiệm
Với dạng này phương trình y' = 0 cũng phân tích được thành dạng: (x − m)(x2 + ax
+ b) = 0 với m là hằng số, tức là x = m là 1 nghiệm của phương trình này rồi. Công
việc của chúng ta là tìm điều kiện để phương trình bậc 2 còn lại vô nghiệm là xong.
Sau đó ta lập bảng biến thiên, xét xem khoảng đồng biến hay nghịch biến bài toán
cho phù hợp với khoảng nào của nghiệm.
Tuy kiến thức rất đơn giản nhưng không phải bạn nào cũng để ý và suy luận được
từ dạng đồ thị tổng quát này. Do đó thầy cũng có thể gọi đây là mẹo phân tích đồ
thị hàm bậc 4. Với phân tích rất nhỏ như trên thôi nhưng sẽ giúp các bạn rất nhiều
trong quá trình tư duy giải toán.
2) Dạng toán về cực trị của hàm số
Nhìn vào dạng đồ thị của hàm số ta sẽ thấy hàm số này luôn luôn có 1 cực trị hoặc
là 3 cực trị. Do đó trong bài toán thông thường sẽ có câu hỏi: ⚫ Tìm m để hàm số có 1 cực trị ⚫ Tìm m để hàm số có 3 cực trị
Và chắc chắc sẽ chẳng bao giờ ai lại đi hỏi: ⚫ Tìm m để
hàm số không có cực trị ⚫ Tìm m để hàm số có 2 cực trị
Với bài toán hỏi về cực trị ta sẽ làm như sau (các bạn nhìn vào hình vẽ nhé):
Trường hợp 1: Tìm m để hàm số có 3 cực trị
Để hàm số có 3 cực trị ta cần biện luận phương trình y' = 0 có 3 nghiệm phân biệt.
Biện luận cụ thể thế nào thì bên trên về tính biến thiên thầy nói rõ rồi.
Trường hợp 2: Tìm m để hàm số có 1 cực trị
Để hàm số có 1 cực trị ta cần biện luận phương trình y' = 0 có 1 nghiệm. Biện luận
cụ thể thế nào thì bên trên về tính biến thiên thầy cũng lại nói rõ rồi. Trong trường
hợp này có thể bài toán sẽ hỏi thành hai trường hợp như sau:
a. Tìm m để hàm số chỉ có cực tiểu hay có 1 cực tiểu và không có cực đại
Nhìn vào dạng đồ thị tổng quát thì đây là một Parabol quay bề lõm lên trên, do đó
ta cần biện luận phương trình y′ = 0 có 1 nghiệm kết hợp với hệ số a > 0.
b. Tìm m để hàm số chỉ có cực đại hay có 1 cực đại và không có cực tiểu
Nhìn vào dạng đồ thị tổng quát thì đây là một Parabol quay bề lõm xuống dưới, do
đó ta cần biện luận phương trình y′ = 0 có 1 nghiệm kết hợp với hệ số a < 0.
Trường hợp 3: Tìm m để hàm số có 2 cực tiểu và 1 cực đại
Với trường hợp này các bạn nhìn vào 1 trong 4 đồ thị phía trên sẽ thấy được câu
trả lời ngay. Nhìn qua ta có, để thỏa mãn yêu cầu bài toán thì: phương trình y'= 0
có 3 nghiệm phân biệt và hệ số a > 0
Trường hợp 4: Tìm m để hàm số có 1 cực tiểu và 2 cực đại
Tương tự như trường hợp 3 các bạn nhìn vào 1 trong 4 đồ thị phía trên sẽ thấy
được câu trả lời ngay. Nhìn qua ta có, để thỏa mãn yêu cầu bài toán thì: phương
trình y' = 0 có 3 nghiệm phân biệt và hệ số a < 0
Trong 4 cái hình dạng đồ thị như trên thì các bạn để ý giúp thầy 2 dạng đồ thị bên
trên (tức là dạng đồ thị có 3 cực trị), các bạn có thấy 3 điểm cực trị này có gì đặc
biệt không? Nếu chưa để ý thấy thì hãy thử vẽ hình và nối 3 điểm cực trị này lại
với nhau xem có được một cái gì đó hay không?
Sau một thời gian chờ đợi các bạn vẽ hình thì chúng ta sẽ rút ra một nhận xét như sau:
Chú ý: Với hàm bậc 4 (hàm trùng phương) trong trường hợp mà đồ thị hàm số có
3 cực trị thì 3 cực trị này luôn luôn tạo thành 1 tam giác cân với đỉnh là điểm cực trị thuộc trục tung.
Đó là một số mẹo phân tích đồ thị hàm bậc 4 (hàm trùng phương) mà thầy muốn
chia sẻ với các bạn. Đây là kiến thức rất cơ bản và dễ hiểu khi các bạn sử dụng đồ
thị dạng tổng quát. Qua bài viết này các bạn sẽ thấy việc sử dụng đồ thị hay là hình
vẽ trực quan trong quá trình giải toán sẽ giúp chúng ta rất nhiều trong việc tư duy tìm lời giải.