Một số thủ thuật tính tích phân Toán 12

Một số thủ thuật tính tích phân Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

35 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
KÊNH PPT – TIVI – 2020
MỘT SỐ THỦ THUẬT TÍNH TÍCH PHÂN
TRONG ĐỀ MH-BGD NĂM 2020 VÀ CÁC ĐỀ PHÁT TRIỂN
Tổng hợp: Thủy Đinh Ngọc
I. CÁC PP HAY SỬ DỤNG
- PP tự luận
- PP Casio
- PP chọn hàm đại diện….
II. BÀI TẬP
ĐỀ MINH HỌA CỦA BỘ GIÁO DỤC NĂM 2020.
Câu 1. [CÂU 48-MH-BGD-L1] Cho hàm số
f x
liên tục trên
thoả mãn
3 2 10 6
1 2 ,
xf x f x x x x x
. Khi đó
0
1
d
f x x ?
A.
17
20
. B.
13
4
. C.
17
4
. D.
1
.
Câu 2. [CÂU 7-MH-BGD-L1] Nếu
2
1
d 2f x x
và
3
2
d 1f x x
thì
3
1
df x x
bằng
A.
3
. B.
1
. C.
1
. D.
3
.
Câu 3. [CÂU 18-MH-BGD-L2] Nếu
1
0
( )d 4f x x
thì
1
0
2 ( )df x x
bằng
A.
16
. B.
4
. C.
2
. D.
8
.
Câu 4. [CÂU 45-MH-BGD-L2] Cho hàm số
f x
có
0 0f
và
2
cos cos 2 ,f x x x x
. Khi
đó
0
df x x
bằng
A.
1041
.
225
. B.
208
.
225
. C.
242
.
225
. D.
149
.
225
ĐỀ PHÁT TRIỂN
Câu 5. [TRẦN BÌNH TRỌNG–KHÁNH HÒA-2020] Cho hàm số
f x
có
9
3
2
f
và
3 2
2
1
, 1.
1
x x
f x x
x x x
Tính
3
0
I f x dx
.
A.
29
6
I
B.
101
6
I
C.
43
6
I
D.
52
6
I
.
Câu 6. Cho hàm số
y f x
có
ln3 4f
và
, .
1
x
x
e
f x x
e
Khi đó
ln8
ln 3
x
e f x dx
bằng:
A.
2
B.
38
3
C.
76
3
D.
136
3
.
Câu 7. Cho hàm số
y f x
có đạo hàm liên tục trên
thỏa mãn
1 1
f
và
3 7
1 2,xf x f x x x x
. Tính tích phân
1
0
d
I f x x
.
A.
2
3
. B.
5
9
. C.
5
9
. D.
2
3
Câu 8. Cho hàm số
( )
y f x
liên tục trên
và thỏa mãn
2 3
3
4 ( ) 6 (2 ) 4
5
xf x f x x
. Giá trị
4
0
( )d
f x x
bằng
A.
52
25
. B. 52. C.
48
25
. D. 48.
Câu 9. Cho hàm số
f x
liên tục trên
thỏa mãn
2 5 3 2
3 . 2 5 18 45 11 1,f x x f x x x x x x
. Khi đó
3
3
d
f x x
bằng
A.
96
. B.
64
. C.
192
. D.
32
.
Câu 10. Cho hàm số
f x
có đạo hàm liên tục trên
0;1
thỏa mãn
0 1
f
và
2
2 6 4 2
4 6 1 40 44 32 4, 0;1
f x x f x x x x x
. Tích phân
1
0
d
f x x
bằng
A.
23
15
. B.
17
15
. C.
13
15
. D.
7
15
.
Câu 11. [SỞ HÀ NỘI LẦN 1 – CÂU 31 - 2020] Cho hàm số
y f x
có đạo hàm liên tục trên
0;1
,
thỏa mãn
1
0
d 3
f x x
và
1 4
f
. Tích phân
1
0
d
xf x x
có giá trị là
A.
1
2
. B.
1
2
. C.
1
. D.
1
.
Câu 12. [LAM SƠN – THANH HÓA – CÂU 40 - 2020] Cho hàm số
f x
liên tục trên đoạn
0;10
thỏa mãn
10 10
0 2
d 7, d 1
f x x f x x
. Tính
1
0
2 d
P f x x
.
A.
6
P
. B.
6
P
. C.
3
P
. D.
12
P
.
Câu 13. [CHUYÊN SP HÀ NỘI – CÂU 40 - 2020] Cho hàm số
( )
y f x
liên tục trên tập số thực thỏa
mãn
2 3 2
( ) (5 2). 5 4 50 60 23 1,
f x x f x x x x x x R
.
Giá trị của biểu thức
1
0
( )
f x dx
bằng
A.
2
. B.
1
. C.
3
. D.
6
.
Câu 14. [CHUYÊN BIÊN HÒA – HÀ NAM – CÂU 42- 2020] Cho hàm số
f x
liên tục trên
R
và
thỏa mãn
1
5
d 9
f x x
. Tính tích phân
2
0
1 3 9 d
f x x
.
A.
15
. B.
27
. C.
75
. D.
21
.
Câu 15. [CHUYÊN THÁI BÌNH – CÂU 37 - 2020] Biết
1
0
1
f x dx
và
2
1
2 1 3.
f x dx
Tính
3
0
.
f x dx
A.
5.
. B.
2.
. C.
7.
. D.
4.
Câu 16. [CHUYÊN ĐẠI HỌC VINH – CÂU 40 – 2020]
Cho
f x
là hàm số có đạo hàm liên tục trên đoạn
0;1
và
1
1
18
f
,
1
0
1
d
36
xf x x
.
Giá trị của
1
0
d
f x x
bằng
A.
1
12
. B.
1
36
. C.
1
12
. D.
1
36
.
Câu 17. Cho hàm số
f x
liên tục trên đoạn
0;1
thỏa mãn điều kiện
2
2 1 3 6 , 0;1
f x f x x x x
. Tính
1
2
0
1
I f x dx
A.
4
15
I
. B.
1
I
. C.
2
15
I
. D.
2
15
I
.
Câu 18. Cho hàm số có đạo hàm liên tục trên và thỏa mãn và
2
2 2 2;f x f x x x x
. Tích phân bằng
A. . B. . C. . D.
Câu 19. [THTT-L1-2017-2018] Cho hàm số có đạo hàm liên tục và dương trên
0;
a
, thỏa mãn và
. 1; 0;
f x f a x x a
. Tích phân
0
1
1
a
ba
dx
f x c
trong đó
,
b c
là hai số nguyên
dương và
b
c
là phân số tối giản. Khi đó
b c
có giá trị là
A.
3
. B.
4
. C.
5
. D.
6
Câu 20. Cho
f x
là hàm liên tục trên
thỏa
1 1
f
và
1
0
1
dt
3
f t
, tính
2
0
sin 2 . sin d
I x f x x
.
A.
4
3
I
. B.
2
3
I
. C.
1
3
I
. D.
2
3
I
.
Câu 21. Cho hàm số liên tục trên đoạn
0;1
và thỏa điều kiện
1
2
0
21
f x dx
và
1
0
1 7
x f x dx
.
Tính
1
0
x
I e f x dx
.
A.
e
. B.
2
e
. C.
3
e
. D.
4
e
.
Câu 22. Cho
1
2
0
1 d 10
x f x x
. Tính
2
3
0
cos sin d
I xf x x
.
A.
5
I
. B.
10
I
. C.
10
I
. D.
5
I
.
( )
f x
(0) 3
f
2
0
( )d
xf x x
4
3
10
3
2
3
5
3
( )
f x
Câu 23. Cho hàm số liên tục trên đoạn
1
0;
3
và thỏa điều kiện
1
0
3 1 ( ) 2019
x f x dx
và
4 1 0 2020
f f . Tính
1
3
0
3
f x dx
.
A.
1
9
. B.
3
. C.
1
3
. D.
1
.
Câu 24. Cho
4
0
( ) 16
f x dx
. Tính
2
0
(2 )
I f x dx
A.
32
I
. B.
8
I
. C.
16
I
. D.
4
I
Câu 25. Cho
9
4
d 10
f x x
. Tính tích phân
1
0
5 4 dx
J f x
.
A.
2
J
. B.
10
J
. C.
50
J
. D.
4
J
.
Câu 26. Giả sử hàm số
f x
liên tục trên đoạn
0;2
thỏa mãn
2
0
d 6
f x x
. Tính tích phân
2
0
2sin cos d .
I f x x x
A.
3
. B.
3
. C.
6
. D.
6
.
Câu 27. Cho hàm số
f x
thỏa mãn
1
0
1 d 10
x f x x
và
2 1 0 2
f f
. Tính
1
0
d
f x x
.
A.
12
I
. B.
8
I
. C.
1
I
. D.
8
I
Câu 28. Cho hàm số
f x
có đạo hàm
f x
và thỏa mãn
1
0
2 1 d 10
x f x x
,
3 1 0 12
f f
.
Tính
1
0
d
I f x x
.
A.
1
I
. B.
2
I
. C.
2
I
. D.
1
I
.
Câu 29. Biết rằng
2
2
1
8 5
ln 2 ln3 ln 5
6 7 2
x
dx a b c
x x
với a,b,c là các số thực. Tính
2 2
3
P a b c
A. 1. B. 2. C. 3. D. 4.
Câu 30. Biết
6
3
2
2
2 4
d ; , .
2
x a
x a b
b
x
Mệnh đề nào sau đây là đúng?
A.
7.
a b
B.
7.
a b
C.
15.
a b
D.
9.
a b
Câu 31. [CHUYÊN NGUYỄN TRÃI – HẢI DƯƠNG - CÂU 37 - 2020]
Cho
ln ln ln
x
dx a b c
x x
3
2
1
3
2 3 5
3 2
với
, ,
a b c
là các số hữu tỉ. Tính
S a b c
2 2 2
.
A.
S
5
. B.
S
3
. C.
S
4
. D.
S
6
.
Câu 32. Cho với , , . Tính .
A. . B. . C. . D. .
e
1
ln d
I x x x
2
.e
a b
c
a
b
c
T a b c
5
3
4
6
Câu 33. Biết
2
0
2 ln 1 d .ln
x x x a b
, với
*
,a b
,
b
là số nguyên tố. Tính .
A.
33
. B.
25
. C.
42
. D. .
Câu 34. Cho
1
2
0
1
d ln 2 ln 3
3 2
x a b
x x
với
,
a b
là các số nguyên. Mệnh đề nào đúng?
A.
2 0
a b
. B.
2 0
a b
. C.
2
a b
. D.
2
a b
.
Câu 35. Cho biết
e
1
ln 3
d 3
3
x a
x b
x
, với
a
,
b
là các số nguyên. Giá trị của biểu
thức
2
1
log
2
b
a
bằng
A. -1. B.
7
2
. C. 8. D. 6.
Câu 36. Biết
4
2
3
d
ln 2 ln 3 ln 5
x
I a b c
x x
, trong đó
, ,a b c
. Tính giá trị của
T a b c
.
A.
2
T
. B.
3
T
. C.
1
T
. D.
5
T
.
Câu 37. Biết
2
0
2 ln 1 d .ln
x x x a b
, với
*
,a b
,
b
là số nguyên tố. Tính
3 4
a b
.
A.
42
. B.
21
. C.
12
. D.
32
.
Câu 38. Cho
3
2
1
ln
d ln 3 ln 2
1
x a
x c
b
x
với
, , *
a b c
và phân số
a
b
tối giản. Giá trị của
a b c
bằng
A.
8
. B.
7
. C.
6
. D.
9
.
Câu 39. Biết
ln 6
0
e
d ln 2 ln 3
1 e 3
x
x
x a b c
với
a
,
b
,
c
là các số nguyên. Tính
T a b c
.
A.
1
T
. B.
0
T
. C.
2
T
. D.
1
T
.
Câu 40. Cho biết
1
2
0
1d
x x x
2 1
a
b
với
a
,
b
là các số tự nhiên. Giá trị của
2 2
a b
bằng
A.
5
. B. 5. C. 2. D. 7.
--------------Hết--------------
6 7
a b
39
BẢNG ĐÁP ÁN
1.B
2.B
3.D
4.C
5.C
6.C
7.D
8.A
9.A
10.D
11.C
12.C
13.A
14.D
15.A
16.A
17.C
18.B
19.A
20.A
21.C
22.C
23.A
24.B
25.A
26.A
27.D
28.A
29.D
30.A
31.D
32.D
33.D
34.A
35.C
36.A
37.B
38.A
39.B
40.A
HƯỚNG DẪN PHẦN ĐỀ MINH HỌA CỦA BỘ GIÁO DỤC NĂM 2020.
Câu 1. [CÂU 48-MH-BGD-L1] Cho hàm số
f x
liên tục trên
thoả mãn
3 2 10 6
1 2 ,
xf x f x x x x x . Khi đó
0
1
d
f x x
?
A.
17
20
. B.
13
4
. C.
17
4
. D.
1
.
Lời giải
Chọn B
Cách 1: PP tự luận
Ta có
3 2 10 6 2 3 2 11 7 2
1 2 1 2
xf x f x x x x x f x xf x x x x
.
Lấy tích phân hai vế cận từ
0
đến
1
ta được:
1 1 1
2 3 2 11 7 2
0 0 0
1 1 1 0
3 3 2 2
0 0 0 1
1 1 1 1
0 0 0 0
d 1 d 2 d
1 1 5 1 1 5
d 1 d 1 d d
3 2 8 3 2 8
1 1 5 5 5 3
d d d d
3 2 8 6 8 4
x f x x x f x x x x x x
f x x f x x f t t f t t
f t t f t t f t t f t t
.
Suy ra
1
0
3
d
4
f x x
.
Lấy tích phân hai vế cận từ
1
đến
0
ta được:
0 0 0
2 3 2 11 7 2
1 1 1
0 0
3 3 2 2
1 1
0 1 0 1
1 0 1 0
0 1
1 0
d 1 d 2 d
1 1 17
d 1 d 1
3 2 24
1 1 17 1 1 17
d d d d
3 2 24 3 2 24
1 17 1
d d
3 24 2
x f x x x f x x x x x x
f x x f x x
f t t f t t f t t f t t
f t t f t t
0 1 0
1 0 1
1 17 1 17 1 3 13 13
d d . d
3 24 2 24 2 4 12 4
f x x f x x f x x
.
Cách 2: PP chọn hàm đại diện:
Từ đẳng thức
3 2 10 6
1 2 ,
xf x f x x x x x
suy ra chọn đặt hàm số
f x
là hàm
số bậc 3 dạng
3 2
f x ax bx cx d
.
Ta có
3 9 6 3 3 10 7 4
f x ax bx cx d xf x ax bx cx dx
2 6 4 2
3 2 10 7 6 4 2
1 3 3 2
1 3 3 2
f x ax a b x a b c x a b c d
f x f x ax bx ax a b c x a b c x dx a b c d
Đồng nhất thức ta được
1
0
3
2
a
b
c
d
. Suy ra
3
3 2
f x x x
Vậy
0
0
3
1
1
13
3 2
4
f x dx x x
.
Câu 2. [CÂU 7-MH-BGD-L1] Nếu
2
1
d 2
f x x
và
3
2
d 1
f x x
thì
3
1
d
f x x
bằng
A.
3
. B.
1
. C.
1
. D.
3
.
Lời giải
Chọn B
Cách 1: PP tự luận
Áp dụng tính chất
d d d ,
b c b
a a c
f x x f x x f x x a c b
Ta có
3 2 3
1 1 2
d d d 2 1 1
f x x f x x f x x
.
Cách 1: PP chọn hàm đại diện
Gợi ý: Do cho hai điều kiện nên chọn hàm có hai hệ số chưa biết dạng
f x ax b
, cách này
dài hơn tự luận.
Câu 3. [CÂU 18-MH-BGD-L2] Nếu
1
0
( )d 4
f x x
thì
1
0
2 ( )d
f x x
bằng
A.
16
. B.
4
. C.
2
. D.
8
.
Lời giải
Chọn D
Cách 1: PP tự luận
Ta có
1
0
2 ( )d
f x x
1
0
( )d 2.4 8
2 f x x
.
Cách 1: PP chọn hàm đại diện
Gợi ý: Do giả thiết cho một điều kiện nên chọn hàm có dạng
f x a
, cách này dài hơn tự luận.
Câu 4. [CÂU 45-MH-BGD-L2] Cho hàm số
f x
có
0 0
f
và
2
cos cos 2 ,f x x x x
. Khi
đó
0
d
f x x
bằng
A.
1041
.
225
. B.
208
.
225
. C.
242
.
225
. D.
149
.
225
Lời giải
Chọn C
Cách 1: PP tự luận áp dụng tính chất
d
f x f x x
Ta có
2
cos cos 2
f x x x
cos cos3 cos5
2 4 4
x x x
Do đó
cos cos3 cos5
d d
2 4 4
x x x
f x f x x x
sin sin 3 sin 5
( )
2 12 20
x x x
f x C
, vì
(0) 0
f
nên
0
C
0
242
( )
225
I f x dx
Cách 2: PP chọn hằng số C
Để tính
0
d
f x x
ta đặt
u f x du f x dx
dv dx v x C
Khi đó
0
0 0 0
0 .
|
f x dx x C f x x C f x dx f C f C x C f x dx
Chọn
C
Suy ra
2
0 0 0
242
( ) . 2
255
f x dx x f x dx x cosx cos xdx
Bài toán tổng quát cho Câu 4
Cho hàm số
f x
có biết
f a
và
,f x g x x
.
Khi đó
b b
a a
f x dx b x g x dx b a f a
(1*) - công thức tính nhanh.
Chứng minh bằng PP chọn hằng số C
Đặt
u f x du f x dx
dv dx v x C
Khi đó
0
( ) .
|
b b
b
a
a a
f x dx x C f x x C f x dx b C f b a C f a x C f x dx
Chọn
C b
0
b
a
f x dx b x f x dx b a f a
Áp dụng công thức tính nhanh (1*) cho câu 4
2
0
242
cos .cos 2 0 0
255
b b
a a
f x dx b x g x dx b a f a x x xdx
HƯỚNG DẪN PHẦN ĐỀ PHÁT TRIỂN
Câu 5. [TRẦN BÌNH TRỌNG–KHÁNH HÒA-2020] Cho hàm số
f x
có
9
3
2
f
và
3 2
2
1
, 1.
1
x x
f x x
x x x
Tính
3
0
I f x dx
.
A.
29
6
I
B.
101
6
I
C.
43
6
I
D.
52
6
I
.
Lời giải
Chọn C
Cách 1: PP tự luận (chọn hằng số C)
Đặt
u f x du f x dx
dv dx v x C
Khi đó:
3 3 3
3
0
0 0 0
. 3 3 0 .
|
f x dx f x x C x C f x dx f C f C x C f x dx
Chọn
0
C
Suy ra
3
3 2
2
0
9 1 43
.3 .
2 6
1
x x
I x dx
x x x
.
Cách 2: PP tính nhanh
Cho hàm số
f x
có biết
f a
và
,f x g x x
.
Khi đó
b b
a a
f x dx b x g x dx b a f a
(1*) - công thức tính nhanh.
Áp dụng công thức (1*) ta có
3 0 0
0 3 3
3
3 2
2
0
0 0 3 3
1 9 43
3.
2 6
1
f x dx f x dx x f x dx f
x x
x dx
x x x
(Chú ý gt cho
9
3
2
f a f
vậy ta cần đổi cận trên thành cận dưới).
Câu 6. Cho hàm số
y f x
có
ln 3 4
f
và
, .
1
x
x
e
f x x
e
Khi đó
ln8
ln3
x
e f x dx
bằng:
A.
2
B.
38
3
C.
76
3
D.
136
3
.
Lời giải
Chọn C.
Cách 1: PP tự luận
1
, 2 2 1
1 2 1
x
x
x
x x
d e
e
f x x f x f x dx e C
e e
ln 3 4 4 4 0
f C C
ln8 ln8
ln3 ln3
76
2 1
3
x x x
e f x dx e e dx
Cách 2: PP tự luận (chọn hằng số C)
Đặt
x x
u f x du f x dx
dv e dx v e C
Khi đó
ln8 ln8
ln8
ln3
ln3 ln3
|
x x x
e f x dx f x e C e C f x dx
ln8
ln8 ln3
ln3
ln8
ln3
ln8 ln3
ln8 8 ln3 3
x
x
f e C f e C e C f x dx
f C f C e C f x dx
Chọn
8
C
suy ra
ln8 ln8
ln3 ln3
76
4. 3 8 8
3
1
x
x x
x
e
e f x dx e
e
.
Câu 7. Cho hàm số
y f x
có đạo hàm liên tục trên
thỏa mãn
1 1
f
và
3 7
1 2,xf x f x x x x
. Tính tích phân
1
0
d
I f x x
.
A.
2
3
. B.
5
9
. C.
5
9
. D.
2
3
Lời giải
Chọn D
Cách 1: PP tự luận:
Từ
3 7 2 3 8 2
1 2, 1 2 ,xf x f x x x x x f x xf x x x x x
1 1 1
2 3 8 2
0 0 0
1 2
x f x dx xf x dx x x x dx
Đặt
3 2
1 3
t x dt x dx
1 0 1 1
2 3
0 1 0 0
1 1 1
1
3 3 3
x f x dx f t dt f t dt f x dx
Vậy ta có
1 1 1
2 3 8 2
0 0 0
1 2
x f x dx xf x dx x x x dx
1 1
0 0
1 5
3 9
f x dx xf x dx
1 1
1
0
0 0
1 5
|
3 9
f x dx xf x f x dx
1 1
0 0
2 5 5 4 2
1 0. 0 1 0. 0
3 9 9 9 3
f x dx f f f f x dx
Cách 2: PP chọn hàm đại diện
Từ đẳng thức
3 7
1 2,xf x f x x x x
suy ra chọn đặt hàm số
f x
là hàm số bậc
2 dạng
2
( )
f x ax bx c
với , ,a b c
.
Ta có
3 7
1 ( ) 2
xf x f x x x
2
3 3 7
1 1 2 2
x a x b x c ax b x x
1; 2; 0
a b c
.
2
( ) 2
f x x x
thỏa mãn
(1) 1
f
.
Từ đó ta có
2
1 1
0 0
2
d d2
3
I x xf xx x
.
Câu 8. Cho hàm số
( )
y f x
liên tục trên
và thỏa mãn
2 3
3
4 ( ) 6 (2 ) 4
5
xf x f x x
. Giá trị
4
0
( )d
f x x
bằng
A.
52
25
. B. 52. C.
48
25
. D. 48.
Lời giải
Chọn A
Cách 1: PP tự luận
2 2
2 3 2 3
0 0
2 2 4 4
2 2
0 0 0 0
4 4 4 4
0 0 0 0
3 3
4 ( ) 6 (2 ) 4 4 ( ) 6 (2 ) d 4 d
5 5
52 52
2 ( )d( ) 3 (2 )d(2 ) 2 ( )d 3 ( )d
5 5
52 52 52
2 ( )d 3 ( )d 5 ( )d ( )d
5 5 25
xf x f x x xf x f x x x x
f x x f x x f t t f u u
f x x f x x f x x f x x
Cách 2: PP khác (xin đề nghị Quý độc giả đề xuất).
Câu 9. Cho hàm số
f x
liên tục trên
thỏa mãn
2 5 3 2
3 . 2 5 18 45 11 1,f x x f x x x x x x
. Khi đó
3
3
d
f x x
bằng
A.
96
. B.
64
. C.
192
. D.
32
.
Lời giải
Chọn A
Cách 1: PP tự luận
Ta có :
2 5 3 2
3 . 2 5 18 45 11 1 1
f x x f x x x x x
.
Thay
x
bởi
x
vào (1) ta có :
2 5 3 2
3 . 2 5 18 45 11 1 2
f x x f x x x x x .
Cộng (1) và (2) vế với vế ta được:
1 1
2
1 1
3 3 90 2 3 d 3 d 64
f x f x x f x x f x x
.
Xét
1
1
3 d
f x x
. Đặt
3 d 3d
t x t x
.
Đổi cận:
1 3; 1 3
x t x t
.
Khi đó
1 3 3
1 3 3
1 1
3 d d d
3 3
f x x f t t f x x
.
Tương tự ta có
1 3
1 3
1
3 d d
3
f x x f x x
.
Vậy
3 3 3
3 3 3
1 1
d d 64 d 96
3 3
f x x f x x f x x
.
Cách 2: PP khác (xin đề nghị Quý độc giả đề xuất).
Câu 10. Cho hàm số
f x
có đạo hàm liên tục trên
0;1
thỏa mãn
0 1
f
và
2
2 6 4 2
4 6 1 40 44 32 4, 0;1
f x x f x x x x x
. Tích phân
1
0
d
f x x
bằng
A.
23
15
. B.
17
15
. C.
13
15
. D.
7
15
.
Lời giải
Chọn D
Cách 1: PP tự luận
Lấy tích phân hai vế đẳng thức trên đoạn
0;1
ta có:
1 1 1
2
2 6 4 2
0 0 0
376
d 4 6 1 d 40 44 32 4 d
105
f x x x f x x x x x x
.
Theo công thức tích phân từng phần có:
1 1 1
2 3 3 3
0 0 0
1
6 1 d d 2 2 2 d
0
x f x x f x x x x x f x x x f x x
1 1
2 3
0 0
6 1 d 1 2 d
x f x x x x f x x
.
Thay lại đẳng thức trên ta có
1 1
2
3
0 0
376
d 4 1 2 d
105
f x x x x f x x
1 1
2
3
0 0
44
d 4 2 d 0
105
f x x x x f x x
1
2
3
0
2 2 d 0
f x x x x
3
2 2 , 0;1
f x x x x
4 2
f x x x C
.
Mặt khác
1 1
4 2 4 2
0 0
13
1 1 1 1 d 1 d
15
f C f x x x f x x x x x
.
Cách 2: PP chọn hàm đại diện
Từ đẳng thức
2
2 6 4 2
4 6 1 40 44 32 4, 0;1
f x x f x x x x x
suy ra chọn đặt
hàm số
f x
là hàm số bậc 4 trùng phương dạng
4 2
( )
f x ax bx c
với , ,a b c
.
Khi đó ta có
2
3 2 4 2 6 4 2
4 2 4 6 1 40 44 32 4, 0;1
ax bx x ax bx c x x x x
Đồng nhất hai vế ta có
2
40 40
16 24 4 44
1
1
4 24 4 32
4 4
a
ab b a
a c
b
b c b
c
Vậy
1 1
4 2 4 2
0 0
13
1 d 1 d
15
f x x x f x x x x x
Câu 11. [SỞ HÀ NỘI LẦN 1 – CÂU 31 - 2020] Cho hàm số
y f x
có đạo hàm liên tục trên
0;1
,
thỏa mãn
1
0
d 3
f x x
và
1 4
f
. Tích phân
1
0
d
xf x x
có giá trị là
A.
1
2
. B.
1
2
. C.
1
. D.
1
.
Lời giải
Chọn C
Cách 1: PP tự luận:
Đặt
'
u x du dx
dv f x dx v f x C
Khi đó
1 1
1
0
0 0
|
I xf x dx f x C x f x C dx
1 1
0 0
1 4 3 1
I f C f x dx C dx C C
Cách 2: PP chọn hàm đại diện
Ta có hàm số
f x
có hai giả thiết
1
0
d 3
f x x
và
1 4
f
nên dự kiến chọn đặt hàm số là
y f x ax b
1
1 1
2
0 0
0
d 3 d 3 3 3 1
2 2
ax a
f x x ax b x bx b
.
1 4 4 2
f a b
. Từ
1 , 2
suy ra:
2
2
a
b
2 2 ' 2
y f x x f x
.
1 1
0 0
d 2 d 1
xf x x x x
.
Câu 12. [LAM SƠN – THANH HÓA – CÂU 40 - 2020] Cho hàm số
f x
liên tục trên đoạn
0;10
thỏa mãn
10 10
0 2
d 7, d 1
f x x f x x
. Tính
1
0
2 d
P f x x
.
A.
6
P
. B.
6
P
. C.
3
P
. D.
12
P
.
Lời giải
Chọn C
Cách 1: PP tự luận:
Ta có
2
0
d 2 0 10 2 10 0
f x x F F F F F F
10 10
2 0
d d 1 7 6.
f x x f x x
Đổi biến:
2 , d 2d
x t x t
.
Đổi cận:
0 0; 2 1
x t x t
.
Khi đó
2 1 1
0 0 0
6 d 2 2 d 2 d 3
f x x f t t f t t
, hay
1
0
2 d 3
f x x
.
Cách 2: PP chọn hàm đại diện
Giả thiết cho hai điều kiện
10 10
0 2
d 7, d 1
f x x f x x
nên chọn đặt
f x ax b
.
Khi đó
10 10
0 0
d d 50 10 7
f x x ax b x a b
và
10 10
2 2
d d 48 8 1
f x x ax b x a b
.
Suy ra hệ
23
50 10 7
40
48 8 1 143
40
a
a b
a b
b
. Do đó
23 143
40 40
f x x
.
1 1
0 0
23 143
2 d d 3
20 40
P f x x x x
.
Câu 13. [CHUYÊN SP HÀ NỘI – CÂU 40 - 2020] Cho hàm số
( )
y f x
liên tục trên tập số thực thỏa
mãn
2 3 2
( ) (5 2). 5 4 50 60 23 1,
f x x f x x x x x x R
.
Giá trị của biểu thức
1
0
( )
f x dx
bằng
A.
2
. B.
1
. C.
3
. D.
6
.
Lời giải
Chọn A
Cách 1: PP tự luận:
1 1 1 1
3 2 2 2
0 0 0 0
( ) (50 60 23 1) (5 2) (5 4 ) 3 (5 2) (5 4 )
f x dx x x x dx x f x x dx x f x x dx
(1)
Xét tích phân
1
2
0
(5 2) (5 4 )
x f x x dx
:
Đặt
2
5 4
t x x
thì
(5.2 4) 2(5 2)
dt x dx x dx
Khi
1
x
thì
1
t
; Khi
0
x
thì
0
t
Suy ra:
1 1 1
2
0 0 0
1 1
(5 2) (5 4 ) ( ) ( )
2 2
x f x x dx f t dt f x dx
Thay vào (1) ta được:
1 1 1 1
0 0 0 0
1 3
( ) 3 ( ) ( ) 3 ( ) 2
2 2
f x dx f x dx f x dx f x dx
Cách 2: PP chọn hàm đại diện
Từ công thức
2 3 2
( ) (5 2). 5 4 50 60 23 1,f x x f x x x x x x
ta dự đoán hàm số là
bậc nhất dạng ( )
f x ax b
, thay vào điều kiện ta được
2 3 2
2 3 2
3 2 3 2
(5 2) (5 4 ) 50 60 23 1
(5 2)(5 4 ) 50 60 23 1
25 30 (9 5 ) 50 60 23 1
ax b x a x x b x x x
ax b x ax ax b x x x
ax ax a b x b x x x
25 50
30 60 2
(9 5 ) 23 1
1
a
a a
a b b
b
Do vậy
( ) 2 1
f x x
suy ra
1 1
0 0
( ) (2 1) 2
f x dx x dx
.
Câu 14. [CHUYÊN BIÊN HÒA – HÀ NAM – CÂU 42- 2020] Cho hàm số
f x
liên tục trên
R
và
thỏa mãn
1
5
d 9
f x x
. Tính tích phân
2
0
1 3 9 d
f x x
.
A.
15
. B.
27
. C.
75
. D.
21
.
Lời giải
Chọn D
Cách 1: PP tự luận:
Đặt
1 3
t x
d 3d
t x
.
Với
0 1
x t
và
2 5
x t
.
Ta có
2
0
1 3 9 d
f x x
2 2
0 0
1 3 d 9d
f x x x
5
2
0
1
d
9
3
t
f t x
1
5
1
d 18
3
f x x
1
.9 18 21
3
.
Cách 2: PP chọn hàm đại diện
Giả thiết cho một điều kiện
1
5
d 9
f x x
nên dự kiến chọn hàm dạng
f x ax
.
Khi đó
1 1
5 5
3
d d 12 9
4
f x x ax x a a
. Do đó
3
4
f x x
.
Vậy
2 2 2
0 0 0
3 9 33
1 3 9 d 1 3 9 d d 21
4 4 4
f x x x x x x
.
Câu 15. [CHUYÊN THÁI BÌNH – CÂU 37 - 2020] Biết
1
0
1
f x dx
và
2
1
2 1 3.
f x dx
Tính
3
0
.
f x dx
A.
5.
B.
2.
C.
7.
D.
4.
Lời giải
Chọn A
Cách 1: PP tự luận:
Ta đặt :
2 1 2 .
t x dt dx
2 3 3
1 1 1
1
2 1 3 6
2
f x dx f t dt f x dx
Mà
3 1 3
0 0 1
1 6 5.
f x dx f x dx f x dx
Cách 2: PP chọn hàm đại diện
Đặt
f x ax b
.
Khi đó
1 1
0 0
1
2
a
f x dx ax b dx b
và
2 2 2
1 1 1
2 1 2 1 2 2 3
f x dx a x b dx ax a b dx a b
.
Suy ra hệ
8
1
3
2
7
2 3
3
a
a
b
a b
b
. Do đó
8 7
3 3
f x x
.
Vậy
3 3
0 0
5
8 7
3 3
f x dx x dx
.
Câu 16. [CHUYÊN ĐẠI HỌC VINH – CÂU 40 – 2020]
Cho
f x
là hàm số có đạo hàm liên tục trên đoạn
0;1
và
1
1
18
f
,
1
0
1
d
36
xf x x
. Giá
trị của
1
0
d
f x x
bằng
A.
1
12
. B.
1
36
. C.
1
12
. D.
1
36
.
Lời giải
Chọn A
Cách 1: PP tự luận:
Đặt:
u x du dx
dv f x dx v f x
Ta có:
1 1 1
0 0 0
1
. 1
0
xf x dx x f x f x dx f f x dx
.
Theo giả thiết:
1
0
1
36
xf x dx
,
1
1
18
f
1 1
0 0
1 1 1 1 1
18 36 18 36 12
f x dx f x dx
.
Cách 2: PP chọn hàm đại diện
Đặt
f x ax b
.
Khi đó
1
1
18
f a b
và
1
1 1
2
0 0
0
1 1
d d
2 2 36 18
x a
xf x x ax x a a
.
Suy ra hệ
1 1
18 18
1 1
18 9
a b a
a b
. Do đó
1 1
18 9
f x x
.
Vậy
1 1
0 0
1 1 1
d d
18 9 12
f x x x x
.
Câu 17. Cho hàm số
f x
liên tục trên đoạn
0;1
thỏa mãn điều kiện
2
2 1 3 6 , 0;1
f x f x x x x
. Tính
1
2
0
1
I f x dx
A.
4
15
I
. B.
1
I
. C.
2
15
I
. D.
2
15
I
.
Lời giải
Chọn C
Bài toán: Cho hàm số
f x
liên tục trên đoạn
0;
c
thỏa mãn điều kiện
( ), 0;
mf x nf c x g x x c
;
m n
và
2 2
( )
, ( )
mg x ng c x
m n f x
m n
.
Chứng minh
Đặt
t c x x c t
. Do
0;
x c
nên
0;
t c
.
Thay
x c t
vào
( ), 0;
mf x nf c x g x x c
(1*)
ta có
( ) 2 *
mf c t nf t g c t
thay tiếp
t x
vào (2*) ta có
( )
nf x mf c x g c x
(3*)
Từ (1*) và (2*) ta có hệ
2
2
( ) ( ) 4 *
( )
( ) 5*
mf x nf c x g x m f x nmf c x mg x
nf x mf c x g c x
n f x nmf c x ng c x
Trừ tương ứng từng vế của (4*) và (5*) ta có
2 2
( )
m f x n f x mg x ng c x
2 2
( )
( )
mg x ng c x
f x
m n
(công thức tính nhanh).
Cách 1: PP tính nhanh
2
2
2
2
2
2 2
2 1 3 6 , 0;1
3 6 2 3 1 6 1
3 6 6
2 2
3
1 2
f x f x x x x
x x x x
x x
f x x x
Khi đó
2
2 2 2 4 2
1 1 2 1 2 4 1
f x x x x x
Suy ra
1 1
2 4 2
0 0
2
1 4 1
15
I f x dx x x dx
.
Cách 2: PP chọn hàm đại diện
Từ
2
2 1 3 6 , 0;1
f x f x x x x
Ta dự kiến chọn hàm đại diện là
2
f x ax bx c
thì ta có
2
2 2
2 1 2 1 1 3 4 2 2 3 .
f x f x ax bx c a x b x c ax a b x a b c
Đồng nhất thức hệ số ta có
3 3 1
4 6 2 .
2 2 3 0 2
a a
a b b
a b c c
Suy ra
2
2 2
f x x x
.
Dó đó
1 1
2
2 2 2
0 0
2
1 1 2 1 2
15
I f x dx x x dx
.
Cách 3: Tự luận
Đặt
1 , 0;1 0;1
t x x t
.
Ta có
2
2
2 1 3 6 2 1 3 1 3
f x f x x x f x f x x
2 2
1 2 3 3 2 1 3 3
f t f t t f x f x x
Ta có hệ phương trình
2 2
2 2
2
2 2
2 1 3 6 2 1 3 6
2 1 3 3 4 2 1 6 6
3 6 6
3 3 6 6 2 2
3
f x f x x x f x f x x x
f x f x x f x f x x
x x
f x x x f x x x
Khi đó
2
2 2 2 4 2
1 1 2 1 2 4 1
f x x x x x
Suy ra
1 1
2 4 2
0 0
2
1 4 1
15
I f x dx x x dx
.
Câu 18. Cho hàm số có đạo hàm liên tục trên
và thỏa mãn
0 3
f
và
2
2 2 2;f x f x x x x
. Tích phân bằng
( )
f x
2
0
( )d
xf x x
A. . B. . C. . D.
Lời giải
Chọn B
Cách 1: Tự luận
Áp dụng công thức tích phân từng phần, ta có:
2 2
2
0
0 0
|
xf x dx xf x f x dx
.
Từ
2
2 2 2;f x f x x x x
(1*)
Thay
0
x
vào (1*) ta được
0 2 2 2 2 0 2 3 2 1
f f f f f
.
Xét
2
0
I f x dx
. Đặt
1 1
t x x t dx dt
Đổi cận:
0 2; 2 0
x t x t
Khi đó
2 0 2 2
0 2 0 0
1 1 1
I f x dx f t dt f t dt f x dx
Do đó ta có
2 2 2 2 2
2 2
0 0 0 0 0
8 4
2 2 2 2 2 2
3 3
f x f x dx x x f x dx x x f x dx
(2*)
Vậy
2 2
2
0
0 0
4 10
| 2 2 2 1
3 3
xf x dx xf x f f x dx
Bài toán dùng để tính nhanh (2*):
Cho hàm số
f x
liên tục trên đoạn
0;
c
thỏa mãn điều kiện
( ), 0; ; 0
mf x nf c x g x x c m n
; và
0 0
c c
g x
I f x dx dx
m n
.
Chứng minh
Đặt
t c x x c t
. Ta có
0
0 0
c c
c
I f x dx f c t dt f c x dx
0 0 0 0
( ), 0; ; 0
( )
c c c c
mf x nf c x g x x c m n
g x
m n f x dx g x dx I f x dx dx
m n
Áp dụng: Biết
2
2 2 2;f x f x x x x
Áp dụng công thức tính nhanh ta có
2 2
2
0 0
1 1 8 4
2 2 .
2 2 3 3
f x dx x x
(2*)
Cách 2: PP chọn hàm đại diện
Từ
2
2 2 2; *
f x f x x x x
ta dự kiến chọn hàm số
2
f x ax bx c
thay
vào đk (*) ta có
2
2
2 2 2
f x f x ax bx c a x b x c
4
3
10
3
2
3
5
3
2
2 4 4 2 2 .
ax ax a b c
Đồng nhất hệ số ta có
2 1
1
4 2 .
2
0
4 2 2 2
a
a
a
b c
a b c
Do
0 3 3; 3
f c b
. Suy ra
2
1
3 3; ' 3
2
f x x x f x x
.
Vậy
2 2
0 0
10
' 3
3
xf x dx x x dx
.
Cách 3: PP tính nhanh
Do
2
[0;2]: 2 2 2
x f x f x x x
1
m n
Không dùng được công thức tính nhanh sau đây:
2 2
( )
, ( )
mg x ng c x
m n f x
m n
Câu 19. [THTT-L1-2017-2018] Cho hàm số có đạo hàm liên tục và dương trên
0;
e
, thỏa mãn
và
. 1; 0;
f x f e x x e
. Tích phân
0
1
1
e
be
dx
f x c
trong đó
,
b c
là hai số nguyên
dương và
b
c
là phân số tối giản. Khi đó
b c
có giá trị là
A.
3
. B.
4
. C.
5
. D.
6
Lời giải
Chọn A
Cách 1: PP tính nhanh
Bài toán: Cho hàm số có đạo hàm liên tục và dương trên
0;
a
, thỏa mãn và
. 1; 0;
f x f a x x a
thì tích phân
0
1
1 2
a
a
dx
f x
Chứng minh:
Đặt
t a x
ta có
0
0 0 0 0
1 1 1 1 ( )
1
1 1 1 1
1
( )
a a a a
a
f t
dx dt dt dt dt
f x f a t f a t f t
f t
0 0 0 0 0
1
1 1
2
1 1 1 1
a a a a a
f x f x
dx dx dx dx dx a
f x f x f x f x
0
1
*
1 2
a
a
f x
( )
f x
( )
f x
Áp dụng công thức (*) vào bài toán ta có
0
1 1
1 2 2
e
e eb b
f x c c
, do
,
b c
là hai số
nguyên dương và
b
c
là phân số tối giản
2, 1 3
c b b c
.
Cách 2: PP chọn hàm đại diện
Do
. 1; 0;
f x f e x x e
chọn hàm đại diện
f x k
(là hàm hằng)
Ta có
2
. 1; 0; 1 1
f x f e x x e k k
.
Vậy ta chọn hàm đại diện
1
f x
0
1 1
1
1 2 2
e
eb eb e b
dx
c f x c c
, do
,
b c
là hai số nguyên dương và
b
c
là phân số
tối giản
2, 1 3
c b b c
Câu 20. Cho
f x
là hàm liên tục trên
thỏa
1 1
f
và
1
0
1
dt
3
f t
, tính
2
0
sin 2 . sin d
I x f x x
.
A.
4
3
I
. B.
2
3
I
. C.
1
3
I
. D.
2
3
I
.
Lời giải
Chọn A
Cách 1: PP tự luận:
Đặt
sin d cos d
x t t x x
.
Đổi cận: khi
0 0
x t
;
1
2
x t
. Từ đó ta có
1
2 2
0 0 0
sin 2 . sin d 2sin .cos . sin d 2 . d
I x f x x x x f x x t f t t
Đặt:
d d
d d
u t u t
v f t t v f t
.
1
0
1
1 4
2 . d 2 1
0
3 3
I t f t f t t
.
Cách 2: PP chọn hàm đại diện
Phân tích có hai giả thiết, ta tìm hàm
f x
thỏa hai điều kiện, chọn
f x ax b
Khi đó:
1 1 1
f a b
1
1 1 1 1 1
0 0 0 0 0
1 1 1
dt dx dx xdx+ bdx= 2
3 2 3
f t f x ax b a a b
Từ
1 , 2
ta có hệ
4
1
3
1 1
1
2 3
3
a b
a
a b
b
Ta được
4 1 4
; '
3 3 3
f x x f x
, do đó
4
' sin
3
f x
Vậy
2 2
0 0
4 4
sin 2 . sin d sin 2 . d
3 3
I x f x x x x
.
Câu 21. Cho hàm số liên tục trên đoạn
0;1
và thỏa điều kiện
1
2
0
21
f x dx
và
1
0
1 7
x f x dx
. Tính
1
0
x
I e f x dx
.
A.
e
. B.
2
e
. C.
3
e
. D.
4
e
.
Lời giải
Chọn C
Cách 1: PP chọn hàm đại diện
Nhận xét: Giả thiết có 2 điều kiện cho trước là
1
2
0
21
f x dx
và
1
0
1 7
x f x dx
, tìm
hàm số
f x
bằng cách dựa vào tỷ số
2
21
3 1
1 7
f x
f x x
x f x
Ta có
1 1
0 0
3 1 3
x x
I e f x dx e x dx e
Cách 2: PP chọn hàm đại diện
Đặt
f x ax b
dựa vào giả thiết tìm hệ số
;
a b
.
Cách 3: PP chọn hàm đại diện
Nhắc lại bất đẳng thức Holder tích phân như sau:
2
2 2
.
b b b
a a a
f x g x dx f x dx g x dx
Dấu bằng xảy ra khi
. , ; ,f x k g x x a b k
Đặt
( ) 1
g x x
; ta có
1
0
1 7
x f x dx
suy ra
1
0
7
g x f x dx
;
1
2
0
21
f x dx
;
1
2
0
7
1
3
x dx
Vì
2
1 1 1
2 2
0 0 0
.
g x f x dx f x dx g x dx
Dấu bằng xảy ra khi
3 3 1
f x kg x f x g x x
Vậy
1 1
0 0
3 1 3
x x
I e f x dx e x dx e
.
Câu 22. Cho
1
2
0
1 d 10
x f x x
. Tính
2
3
0
cos sin d
I xf x x
.
A.
5
I
. B.
10
I
. C.
10
I
. D.
5
I
.
Lời giải
Chọn C
Cách 1: Tự luận
2 2
3 2
0 0
cos sin d 1 sin . sin .cos d
I xf x x x f x x x
.
Đặt
sin d cos d
t x t x x
và
0 0; 1
2
x t x t
.
Khi đó
1
2
0
1 d 10
I t f t t
.
Cách 2: PP chọn hàm đại diện
Giả thiết cho một điều kiện
1
2
0
1 d 10
x f x x
nên nghĩ đến chọn
f x a
.
Ta có
1 1
2 2
0 0
2 30
1 d 10 1 d 10 10
3 2
x f x x x a x a a
.
Suy ra
30
2
f x
.
Ta có:
2 2
3 3
0 0
30
cos sin d cos d 10
2
I xf x x x x
.
Câu 23. Cho hàm số liên tục trên đoạn
1
0;
3
và thỏa điều kiện
1
0
3 1 ( ) 2019
x f x dx
và
4 1 0 2020
f f . Tính
1
3
0
3
f x dx
.
A.
1
9
. B.
3
. C.
1
3
. D.
1
.
Lời giải
Chọn A
Cách 1: PP tự luận
Áp dụng tích phân từng phần tính
1
0
3 1 ( )
x f x dx
Ta có

1
1 1
3 1 ( ) 3
3 1
0 0
0
x f x dx f x dx
f x x
1 1
0 0
1
2019 4 1 0 3
3
f f f x dx f x dx
Vậy
1
1
3
0 0
1 1 1 1
3 .
3 3 3 9
f x dx f t dt
.
Cách 2: PP chọn hàm đại diện
Giả thiết có 2 điều kiện cho trước là
1
0
3 1 ( ) 2019
x f x dx
và
4 1 0 2020
f f
ta chọn
đặt
f x ax b f x a
.
Ta có
1 1
0 0
4038
3 1 ( ) 2019 3 1 2019
5
x f x dx a x dx a
Mặt khác
2020 4
4 1 0 2020 4 2020 .
3
a
f f a b b b
Vậy
1 1
3 3
0 0
1
3 3
9
f x dx ax b dx
.
Câu 24. Cho
4
0
( ) 16
f x dx
. Tính
2
0
(2 )
I f x dx
A.
32
I
. B.
8
I
. C.
16
I
. D.
4
I
Lời giải
Chọn B
Cách 1: PP tự luận
Đặt
2x =dx
2
dt
t
. Đổi cận
0 2
x t
;
2 4
x t
Khi đó ta có
2
4 4
0 0
0
1 1
(2 ) ( ) ( ) 8
2 2
I f x dx f t dt f x dx
Cách 2: PP casio
Phương pháp casio nhanh:
Nếu có
m
n
M
f x dx
thì
; . , .
f x b dx n a b m a b
M
a
a
Áp dụng
.
Câu 25. Cho
9
4
d 10
f x x
. Tính tích phân
1
0
5 4 dx
J f x
.
A.
2
J
. B.
10
J
. C.
50
J
. D.
4
J
.
Lời giải
Chọn A
Cách 1: PP casio
Phương pháp casio nhanh:
Nếu có
m
n
M
f x dx
thì
; . , .
f x b dx n a b m a b
M
a
a
Áp dụng
.
Câu 26. Giả sử hàm số
f x
liên tục trên đoạn
0;2
thỏa mãn
2
0
d 6
f x x
. Tính tích phân
2
0
2sin cos d .
I f x x x
A.
3
. B.
3
. C.
6
. D.
6
.
Lời giải
Chọn A
Cách 1: PP casio
.
Câu 27. Cho hàm số
f x
thỏa mãn
1
0
1 d 10
x f x x
và
2 1 0 2
f f
. Tính
1
0
d
f x x
.
A.
12
I
. B.
8
I
. C.
1
I
. D.
8
I
Lời giải
Chọn D
Cách 1: PP tự luận
Đặt
1 d d
d d
u x u x
v f x x v f x
. Khi đó
1
1
0
0
1 d
I x f x f x x
Suy ra
1 1
0 0
10 2 1 0 d d 10 2 8
f f f x x f x x
. Vậy
1
0
d 8
f x x
.
Cách 2: PP casio
Phương pháp casio nhanh:
Nếu hàm số
f x
thỏa mãn
d
K
ax b f x x
và
.
P
a b f a b f
thì
d
a
f x
P K
x
.
Áp dụng
.
Câu 28. Cho hàm số
f x
có đạo hàm
f x
và thỏa mãn
1
0
2 1 d 10
x f x x
,
3 1 0 12
f f
.
Tính
1
0
d
I f x x
.
A.
1
I
. B.
2
I
. C.
2
I
. D.
1
I
.
Lời giải
Chọn A
Phương pháp casio nhanh: Nếu hàm số
f x
thỏa mãn
d
K
ax b f x x
và
.
P
a b f a b f
thì
d
a
f x
P K
x
.
Áp dụng:
Câu 29. Biết rằng
2
2
1
8 5
ln 2 ln3 ln 5
6 7 2
x
dx a b c
x x
với a,b,c là các số thực. Tính
2 2
3
P a b c
A. 1. B. 2. C. 3. D. 4.
Lời giải
Chọn D
Cách 1: PP tự luận
Ta có
2
2 2
2
1 1
1
9 5 2(3 2) (2 1) 1 2
ln 2 1 ln 3 2 ln 2 ln 3 ln 5
6 7 2 (2 1)(3 2) 3 3
x x x
dx dx x x
x x x x
Do đó
2 2
2
1; 1; 3 4.
3
a b c P a b c
Cách 2: PP casio
B1: Tính
2
2
1
8 5
6 7 2
x
dx
x x
và gán cho biến A
B2: Ta có
ln 2 ln 3 ln 5 ln 2 .3 .5
a b c
A a b c A
2 .3 .5 2 .3 .5
A a b c nA na nb nc
e e với
*
n
B3. Tính
nA
e
sao cho
nA
e
là 1 số hữu tỉ ( thường n = 1,2,3,4…).
Ta có
3 1 3 2 3
200
200.27 2 .5 .3
27
A
e
(1)
Mà
3 3 3 3
2 .3 .5
A a b c
e (2)
Từ (1) và (2) suy ra
3 3 1
3 3 1
3 2 2
3
a a
b b
c
c
2 2
3 4
P a b c
.
Câu 30. Biết
6
3
2
2
2 4
d ; , .
2
x a
x a b
b
x
Mệnh đề nào sau đây là đúng?
A.
7.
a b
B.
7.
a b
C.
15.
a b
D.
9.
a b
Lời giải
Chọn A
Cách 1: PP tự luận
Tính
6
3
2
2
d
2
x
I x
x
. Đặt
2 2 2
2 2
t x t x tdt xdx
Đổi cận
Suy ra
3 2 2
6 6 2 2
2 2
2 2 2
. 2
2 2
x x x t
I dx dx tdt
t
x x
3
2 2
2 2
2
2
2
4 2 4
2 2
3 3
|
t
I t dt t
Suy ra: a = 4, b = 3. Vậy a + b = 7
Cách 2: PP casio
B1: Tính
6
3
2
2
d
2
x
I x
x
và gán cho biến A
B2:
2 4 2 4
a a
A b
b A
Đặt
x a b F x
B3: Mode 7 (dùng Table)
Nhập
2 4
x
F x
A
Star -9
End 9
Step 1
Ta dò được F(x) = 3 suy ra x = 4
Suy ra: a = 4, b = 3
Vậy a + b = 7.
Câu 31. [CHUYÊN NGUYỄN TRÃI – HẢI DƯƠNG - CÂU 37 - 2020]
Cho
ln ln ln
x
dx a b c
x x
3
2
1
3
2 3 5
3 2
với
, ,
a b c
là các số hữu tỉ. Tính
S a b c
2 2 2
.
A.
S
5
. B.
S
3
. C.
S
4
. D.
S
6
.
Lời giải
Chọn D
Cách 1: PP tự luận
Ta có
ln ln
x x
dx dx dx x x
x x x x x x
3 3 3
2
1 1 1
3
3 3 2 1
2 1 2
1
3 2 1 2 1 2
ln ln ln ln ln ln ln
2 4 5 2 2 3 2 2 3 5
Suy ra ; ;a b c S
2 1 1 6
.
Cách 2: PP casio
Bước 1: Tính tích phân
x
dx
x x
3
2
1
3
3 2
sau đó gán thành biến
A
.
Nhấn SHIFT STO (-) để được
Bước 2: Tính phép toán lũy thừa
kA
e
với
1, 2,3,4,5,...
k
là các số nguyên mục tiêu là ta được
kết quả trên máy là một số hữu tỷ.
Bước 3: Ta dễ dàng phân tích được
2
2 1 1
12 2 .3
2 .3 .5
5 5
do vậy
2 1 1
12
ln ln(2 .3 .5 ) 2ln 2 ln3 ln 5
5
A
suy ra
2, 1, 1
a b c
từ đây
2 2 2
6
a b c
.
Chú ý: Quá trình bấm máy có thể nhanh hơn so với tốc độ ghi tự luận nhiều.
Câu 32. Cho với , , . Tính .
A. . B. . C. . D. .
Lời giải
Chọn D
Cách 1: PP tự luận
Ta có: nên .
.
Vậy .
Cách 2: PP casio
e
1
ln d
I x x x
2
.e
a b
c
a
b
c
T a b c
5
3
4
6
ln
d d
u x
v x x
2
1
d d
2
u x
x
x
v
e
1
ln d
I x x x
e
e
2
1
1
1
ln d
2 2
x
x x x
2
e 1
4
1
1
4
a
b
c
T a b c
6
+ Thử C=1,2,3,4,5,6. giải hệ tìm a,b nguyên.
.
Câu 33. Biết
2
0
2 ln 1 d .ln
x x x a b
, với
*
,a b
,
b
là số nguyên tố. Tính .
A.
33
. B.
25
. C.
42
. D. .
Lời giải
Chọn.D.
Cách 1: PP tự luận
Xét .
Đặt .
Ta có:
.
Vậy , .
Cách 2: PP casio
Ta có
Bước 1.
Bước 2.
.
Bước 3. Bấm Shift + FACT
6 7
a b
39
2
0
2 ln 1 d
I x x x
6
ln 1
d 2 d
u x
v x x
2
1
d d
1
1
u x
x
v x
2
2
2
2
0
0
1
1 ln 1 d
1
x
I x x x
x
2
0
3ln 3 1 d
x x
2
2
0
3ln3 3ln3
2
x
x
3
a
3
b
6 7 39
a b
.ln ln
a
a b b
ln
a a A
A b b e
Vậy ,
6 7 39
a b
.
Câu 34. Cho
1
2
0
1
d ln 2 ln 3
3 2
x a b
x x
với
,
a b
là các số nguyên. Mệnh đề nào đúng?
A.
2 0
a b
. B.
2 0
a b
. C.
2
a b
. D.
2
a b
.
Lời giải
Chọn A
Cách 1: PP casio
.
Câu 35. Cho biết
e
1
ln 3
d 3
3
x a
x b
x
, với
a
,
b
là các số nguyên. Giá trị của biểu
thức
2
1
log
2
b
a
bằng
A. -1. B.
7
2
. C. 8. D. 6.
Lời giải
Chọn C
Cách 1: PP casio
.
:3
3
3
3
a A a
A b b
. Solve nghiệm nguyên:
2
:3
3
1
log
2
A x
x
3
a
3
b
. Thử từ đáp án. Thấy ngay A thỏa mãn vì phương trình có nghiệm nguyên.
Câu 36. Biết
4
2
3
d
ln 2 ln 3 ln 5
x
I a b c
x x
, trong đó
, ,a b c
. Tính giá trị của
T a b c
.
A.
2
T
. B.
3
T
. C.
1
T
. D.
5
T
.
Lời giải
Chọn A
Cách 1: PP casio
.Ta có:
4
2
3
d
ln2 ln3 5ln
e e 2 .3 .5
x
x x
a b c a b c
.
. Nhập
4 1 1
16
2 .3 .5 2 .3 .5 4; 1; 1.
15
a b c
a b c
.
Câu 37. Biết
2
0
2 ln 1 d .ln
x x x a b
, với
*
,a b
,
b
là số nguyên tố. Tính
3 4
a b
.
A.
42
. B.
21
. C.
12
. D.
32
.
Lời giải
Chọn B
Cách 1: PP casio
. Ta có:
2
0
2 ln 1
e
x x dx
a
b
Shift FACT
. Vậy
3
a
,
3
b
3 4 21
a b
.
Câu 38. Cho
3
2
1
ln
d ln 3 ln 2
1
x a
x c
b
x
với
, , *
a b c
và phân số
a
b
tối giản. Giá trị của
a b c
bằng
A.
8
. B.
7
. C.
6
. D.
9
.
Lời giải
Chọn A
Cách 1: PP casio
. Chú ý: c=x,
a
f x
b
, bài toán có điều kiện
, , *
a b c
. Do đó
8
a b c
.
Câu 39. Biết
ln 6
0
e
d ln 2 ln 3
1 e 3
x
x
x a b c
với
a
,
b
,
c
là các số nguyên. Tính
T a b c
.
A.
1
T
. B.
0
T
. C.
2
T
. D.
1
T
.
Lời giải
Chọn B
Cách 1: PP casio
.
ln 2 ln 3 2 .3
A a b c
A a b c e
. Suy ra
2
a
,
4
b
,
2
c
nên
0
T a b c
.
Câu 40. Cho biết
1
2
0
1d
x x x
2 1
a
b
với
a
,
b
là các số tự nhiên. Giá trị của
2 2
a b
bằng
A.
5
. B. 5. C. 2. D. 7.
Lời giải
Chọn A
Cách 1: PP casio
. Với
;
b x a f x
2
a
,
3
b
.
. Vậy
2 2
5
a b
.
| 1/35
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

KÊNH PPT – TIVI – 2020
MỘT SỐ THỦ THUẬT TÍNH TÍCH PHÂN
TRONG ĐỀ MH-BGD NĂM 2020 VÀ CÁC ĐỀ PHÁT TRIỂN
Tổng hợp: Thủy Đinh Ngọc I. CÁC PP HAY SỬ DỤNG - PP tự luận - PP Casio
- PP chọn hàm đại diện…. II. BÀI TẬP
ĐỀ MINH HỌA CỦA BỘ GIÁO DỤC NĂM 2020.
Câu 1. [CÂU 48-MH-BGD-L1] Cho hàm số
f x liên tục trên  thoả mãn 0 xf  3 x   f  2  x  10 6 1  x  x  2 ,
x x . Khi đó  f xdx ? 1 A. 1  7 . B. 1  3 . C. 17 . D. 1  . 20 4 4 2 3 3
Câu 2. [CÂU 7-MH-BGD-L1] Nếu f xdx  2   và f
 xdx 1 thì f xdx  bằng 1 2 1 A. 3  . B. 1  . C. 1. D. 3. 1 1
Câu 3. [CÂU 18-MH-BGD-L2] Nếu f ( ) x dx  4  thì 2 f (x)dx  bằng 0 0 A. 16 . B. 4. C. 2. D. 8.
Câu 4. [CÂU 45-MH-BGD-L2] Cho hàm số f x có f   0  0 và f x 2  cos xcos 2 , x x  . Khi  đó f  xdx bằng 0 A. 1041. . B. 208 . . C. 242 . . D. 149 . 225 225 225 225 ĐỀ PHÁT TRIỂN
Câu 5. [TRẦN BÌNH TRỌNG–KHÁNH HÒA-2020] Cho hàm số f x có f   9 3  và 2 3 2   3 f  x x x 1  , x   1  . Tính I  f  xdx. 2 x  x  x 1 0 A. 29 I   B. 101 I   C. 43 I  D. 52 I  . 6 6 6 6 x e ln 8
Câu 6. Cho hàm số y  f  x có f ln  3  4 và f x  ,x  .  Khi đó x e f  x dx  bằng: x e 1 ln 3 A. 2 B. 38 C. 76 D. 136 . 3 3 3
Câu 7. Cho hàm số y  f  x có đạo hàm liên tục trên  thỏa mãn f   1  1  và 1 xf  3  x   f x 7 1
 x  x  2, x   . Tính tích phân I  f  xdx . 0 A. 2 . B. 5  . C. 5 . D. 2  3 9 9 3 3
Câu 8. Cho hàm số y  f ( x) liên tục trên  và thỏa mãn 2 3 4xf (x )  6 f (2 ) x  x  4. Giá trị 5 4 f ( ) x dx  bằng 0 52 48 A. . B. 52. C. . D. 48. 25 25
Câu 9. Cho hàm số f x liên tục trên  thỏa mãn 3 f  x  x f  2 x   5 3 2 3 .
2  5x 18x  45x 11x 1,x   . Khi đó f  xdx bằng 3 A. 96. B. 64 . C. 192 . D. 32 .
Câu 10. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 thỏa mãn f 0 1 và  1 f  x2   2 x   f x 6 4 2 4 6 1
 40x  44x  32x  4, x  0;  1 . Tích phân f  xdx  bằng 0 A. 23 . B. 17  . C. 13 . D. 7  . 15 15 15 15
Câu 11. [SỞ HÀ NỘI LẦN 1 – CÂU 31 - 2020] Cho hàm số y  f  x có đạo hàm liên tục trên 0;  1 , 1 1 thỏa mãn f
 xdx  3 và f  1  4 . Tích phân xf 
 xdx có giá trị là 0 0 1 1 A.  . B. . C. 1. D. 1. 2 2
Câu 12. [LAM SƠN – THANH HÓA – CÂU 40 - 2020] Cho hàm số f  x liên tục trên đoạn 0;10 10 10 1 thỏa mãn f  xdx  7, f
 xdx 1. Tính P  f  2xdx. 0 2 0 A. P  6 . B. P  6 . C. P  3 . D. P  12 .
Câu 13. [CHUYÊN SP HÀ NỘI – CÂU 40 - 2020] Cho hàm số y  f (x) liên tục trên tập số thực thỏa mãn f x  x  f  2 x  x 3 2 ( ) (5 2). 5
4  50x  60x  23x 1, x   R . 1
Giá trị của biểu thức f (x)dx  bằng 0 A. 2 . B. 1. C. 3 . D. 6 .
Câu 14. [CHUYÊN BIÊN HÒA – HÀ NAM – CÂU 42- 2020] Cho hàm số f x liên tục trên R và 1 2 thỏa mãn f
 xdx  9 . Tính tích phân  f  13x9dx  . 5 0 A. 15 . B. 27 . C. 75 . D. 21. 1 2
Câu 15. [CHUYÊN THÁI BÌNH – CÂU 37 - 2020] Biết f  xdx  1   và f
 2x 1dx  3. Tính 0 1 3 f xd .x  0 A. 5. . B. 2.. C. 7. . D. 4  .
Câu 16. [CHUYÊN ĐẠI HỌC VINH – CÂU 40 – 2020] 1 1
Cho f  x là hàm số có đạo hàm liên tục trên đoạn 0;  1 và f   1 1   , xf  xdx   . 18 36 0 1 Giá trị của f  xdx  bằng 0 1 1 1 1 A.  . B. . C. . D.  . 12 36 12 36
Câu 17. Cho hàm số f  x  liên tục trên đoạn 0;  1 thỏa mãn điều kiện 1 f  x  f   x 2 2 1
 3x  6x,x 0;  1 . Tính I  f   2 1 x dx 0 4 2 2 A. I  . B. I  1. C. I   . D. I  . 15 15 15 Câu 18. Cho hàm số f ( )
x có đạo hàm liên tục trên  và thỏa mãn f (0)  3và 2 f  x  f   x 2 2  x  2x  2; x
   . Tích phân xf (x)dx bằng 0 4 5 A.  10 . B.  2 . C. . D. 3 3 3 3
Câu 19. [THTT-L1-2017-2018] Cho hàm số f ( )
x có đạo hàm liên tục và dương trên0;a, thỏa mãn và a 1 ba
f  x. f a  x  1;x 0;a . Tích phân dx  
trong đó b, c là hai số nguyên 1 f x c 0   b
dương và là phân số tối giản. Khi đó b  c có giá trị là c A. 3 . B. 4 . C. 5 . D. 6  1 1 2
Câu 20. Cho f  x là hàm liên tục trên  thỏa f   1 1 và f tdt   , tính I  sin 2 . x f   sin xdx . 3 0 0 4 2 1 2 A. I  . B. I  . C. I  . D. I   . 3 3 3 3 1 1
Câu 21. Cho hàm số liên tục trên đoạn  2 0; 
1 và thỏa điều kiện  f   x dx21 
và  x 1 f xdx  7. 0 0 1 Tính x I  e f  xdx . 0 A. e . B. 2e . C. 3e . D. 4e .  1 2  2 1 x  f xdx 10 3 I  cos xf  sin xdx Câu 22. Cho 0 . Tính 0 . A. I  5 . B. I  10 . C. I 10 . D. I  5 .  1  1
Câu 23. Cho hàm số liên tục trên đoạn 0; 
và thỏa điều kiện  3x   1 f (  x)dx  2019 và 3   0 1 4 f  
1  f 0  2020 . Tính 3 f 3xdx  . 0 1 1 A. . B. 3 . C. . D. 1. 9 3 4 2 f (x)dx  16  I  f (2x)dx  Câu 24. Cho 0 . Tính 0 A. I 32 . B. I 8 . C. I 1  6 . D. I  4 9 1 Câu 25. Cho f
 xdx 10. Tính tích phân J  f  5x 4dx . 4 0 A. J  2 . B. J  10 . C. J  50 . D. J  4 . 2
Câu 26. Giả sử hàm số f x liên tục trên đoạn 0;2 thỏa mãn f  x . Tính tích phân dx  6 0  2 I  f  2sin xcos d x . x 0 A. 3. B. 3 . C. 6 . D. 6 . 1 1
Câu 27. Cho hàm số f  x thỏa mãn x  
1 f  xdx 10 và 2 f  
1  f 0  2. Tính f xdx  . 0 0 A. I  1  2 . B. I  8 . C. I  1. D. I  8 1
Câu 28. Cho hàm số f  x có đạo hàm f  x và thỏa mãn 2x  1 f xdx 10 , 3f   1  f 0 12. 0 1 Tính I  f  xdx . 0 A. I  1. B. I  2 . C. I  2 . D. I  1 . 2 8x  5 Câu 29. Biết rằng
dx  a ln 2  b ln 3  c ln 5 
với a,b,c là các số thực. Tính 2 2 P  a  b  3c 2 6x  7x  2 1 A. 1. B. 2. C. 3. D. 4. 6 3 x a 2  4 Câu 30. Biết dx  ; a,b  . 
 Mệnh đề nào sau đây là đúng? 2 x  b 2 2 A. a  b  7. B. a  b  7. C. a  b  15. D. a  b  9.
Câu 31. [CHUYÊN NGUYỄN TRÃI – HẢI DƯƠNG - CÂU 37 - 2020] 3 x  3 Cho
dx  a ln 2  b ln 3  c ln  5 với a, ,
b c là các số hữu tỉ. Tính S  a2  b2  c2 . x2  3x  2 1 A. S  5 . B. S  3 . C. S  4 . D. S  6 . e 2 . a e  b Câu 32. Cho I  x ln d x x 
với a , b , c   . Tính T  a  b  c .  c 1 A. 5. B. 3 . C. 4 . D. 6 . 2 Câu 33. Biết 2x ln 
x  1dx  .alnb , với *
a, b   , b là số nguyên tố. Tính 6a  7b . 0 A. 33 . B. 25 . C. 42 . D. 39 . 1  1 Câu 34. Cho  dx  aln 2 bln3 
với a,b là các số nguyên. Mệnh đề nào đúng? 2   x  3x  2  0 A. a  2b  0 . B. a  2b  0 . C. a  b  2 . D. a  b  2 . e ln x  3 a Câu 35. Cho biết dx   b 3 
, với a , b là các số nguyên. Giá trị của biểu x 3 1 1 thức  log a bằng 2 2b 7 A. -1. B. . C. 8. D. 6. 2 4 dx Câu 36. Biết I 
 a ln 2  b ln 3  c ln 5 
, trong đó a,b, c   . Tính giá trị của T  a  b  c . 2 x  x 3 A. T  2 . B. T  3. C. T  1 . D. T  5 . 2 Câu 37. Biết 2x ln 
1 xdx  .aln b , với * ,
a b , b là số nguyên tố. Tính 3a  4b . 0 A. 42 . B. 21 . C. 12 . D. 32 . 3 ln x a a Câu 38. Cho dx   ln 3  c  ln 2  với a, ,
b c  * và phân số tối giản. Giá trị của a  b  c x  2 b b 1 1 bằng A. 8 . B. 7 . C. 6 . D. 9 . ln 6 ex Câu 39. Biết dx  a  b ln 2  c ln 3 
với a , b , c là các số nguyên. Tính T  a  b  c . x 0 1  e  3 A. T  1. B. T  0 . C. T  2 . D. T  1. 1 a 2 1 Câu 40. Cho biết 2 x x 1 dx  
với a , b là các số tự nhiên. Giá trị của 2 2 a  b bằng b 0 A. 5. B. 5. C. 2. D. 7.
--------------Hết-------------- BẢNG ĐÁP ÁN 1.B 2.B 3.D 4.C 5.C 6.C 7.D 8.A 9.A 10.D 11.C 12.C 13.A 14.D 15.A 16.A 17.C 18.B 19.A 20.A 21.C 22.C 23.A 24.B 25.A 26.A 27.D 28.A 29.D 30.A 31.D 32.D 33.D 34.A 35.C 36.A 37.B 38.A 39.B 40.A
HƯỚNG DẪN PHẦN ĐỀ MINH HỌA CỦA BỘ GIÁO DỤC NĂM 2020. Câu 1.
[CÂU 48-MH-BGD-L1] Cho hàm số f  x liên tục trên  thoả mãn 0 xf  3 x   f  2  x  10 6 1  x  x 2 ,
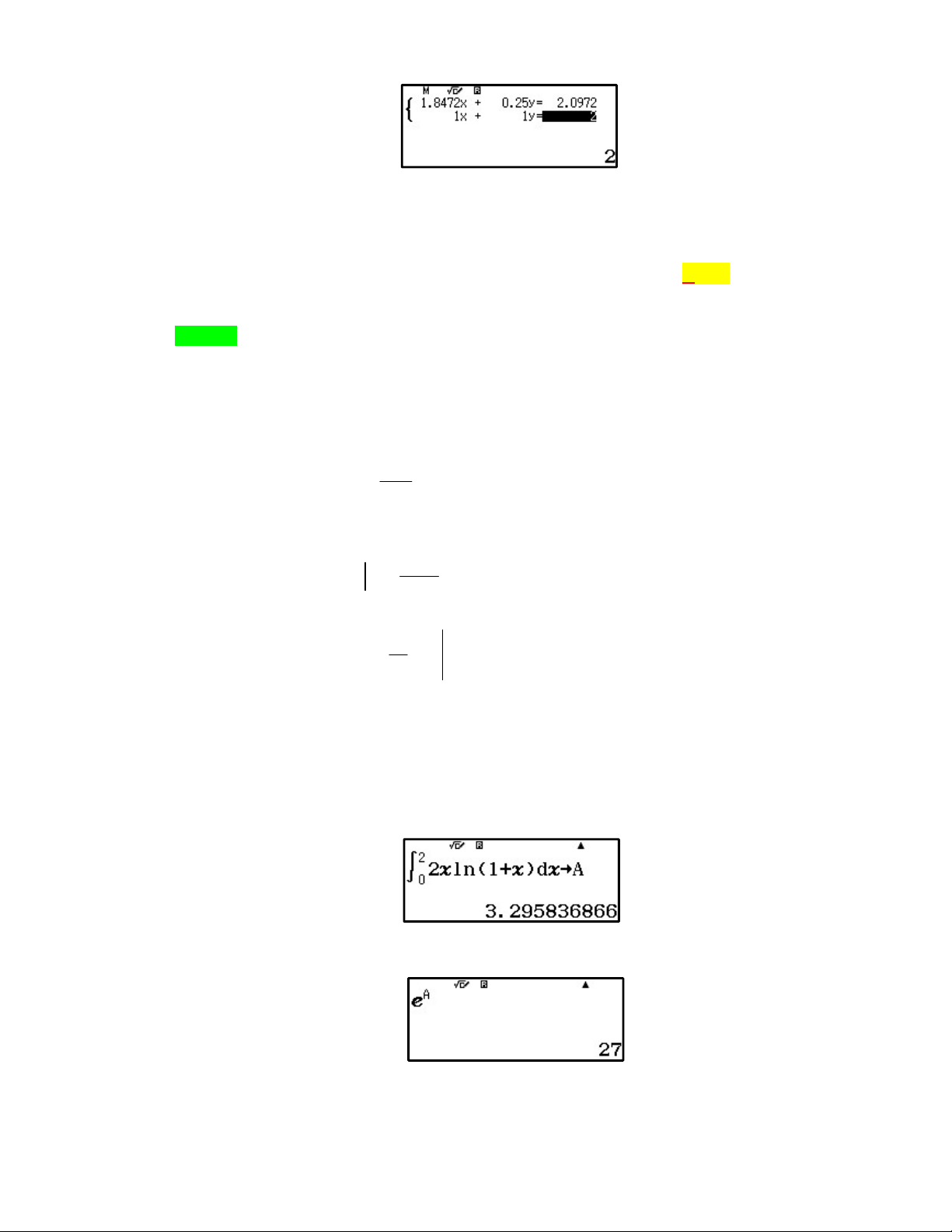
x x . Khi đó  f xdx? 1  17 13 17 A. . B. . C. . D. 1. 20 4 4 Lời giải Chọn B Cách 1: PP tự luận Ta có xf  3 x   f  2  x  10 6 2
 x  x  x  x f  3 x   xf  2  x  11 7 2 1 2 1  x  x  2x .
Lấy tích phân hai vế cận từ 0 đến 1 ta được: 1 x f  x  1 dx  x f  1 x  1 2 3 2 dx   11 7 2 x  x  2x dx 0 0 0 1 1  f  x dx  1 1  f
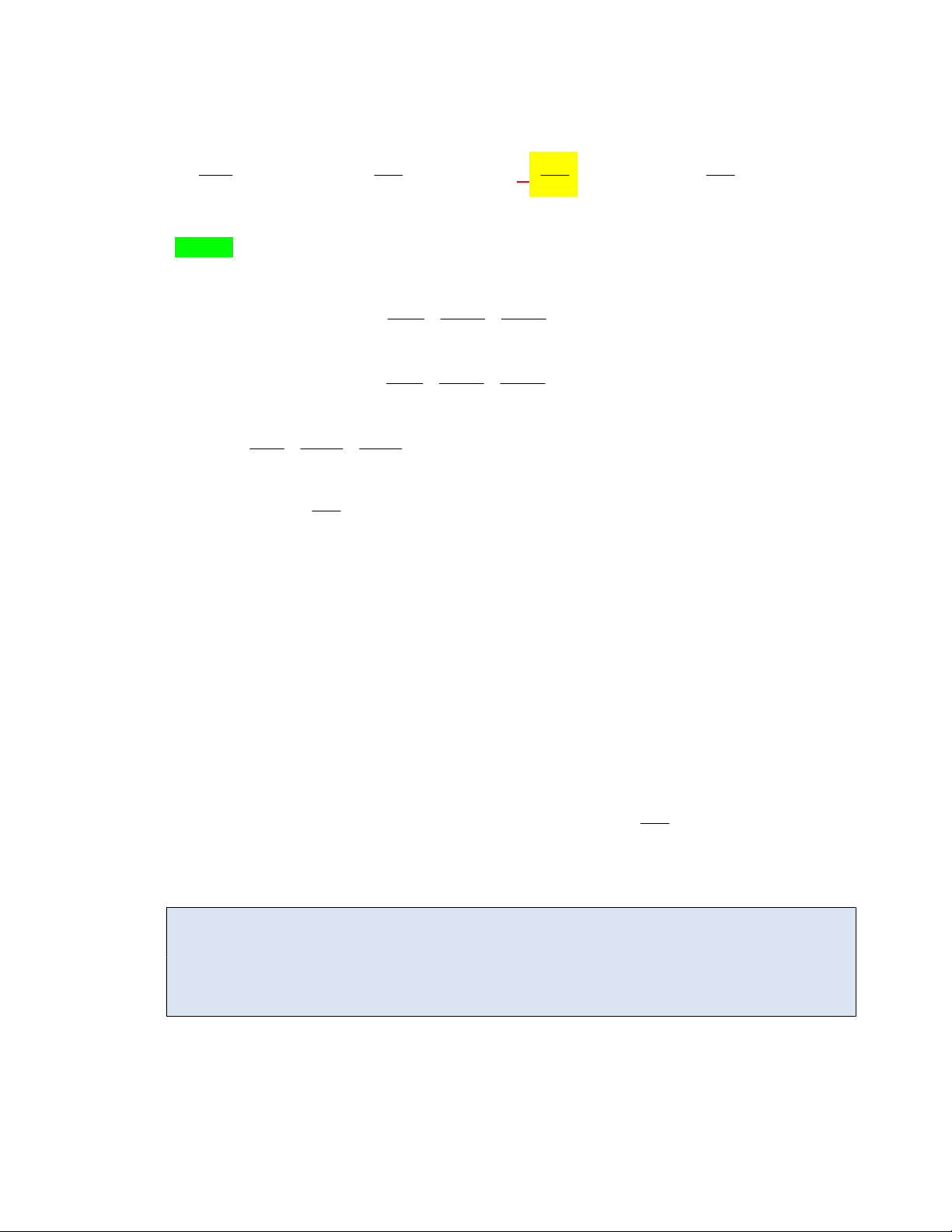
 1 x d1 x  1 0 5 1 1 5 3 3 2 2    f  tdt  f  tdt   . 3 2 8 3 2 8 0 0 0 1 1 1 1 1 1  f  t 1 t  f  t 5 5 t    f  t 5 t    f  t 3 d d d dt   3 2 8 6 8 4 0 0 0 0 1 3 Suy ra  d    f x x . 4 0
Lấy tích phân hai vế cận từ 1 đến 0 ta được: 0 x f  x  0 dx  x f  1 x  0 2 3 2 dx    11 7 2 x  x  2x dx 1 1 1 0 1  f  x dx  0 1 17 3 3  f   2 1 x d 2 1 x    3 2 24 1  1  0 1 0 1 1  f  t 1 t  f  t 17 1 t    f  t 1 t  f  t 17 d d d dt   3 2 24 3 2 24 1 0 1 0 0 1 1  f  t 17 1 dt    f  tdt 3 24 2 1  0 0 1 0 1  f  x 17 1 x   f  x 17 1 3 13 x      f x 1  3 d d . dx     . 3 24 2 24 2 4 12 4 1 0 1
Cách 2: PP chọn hàm đại diện: Từ đẳng thức xf  3 x   f  2  x  10 6 1
 x  x  2x,x   suy ra chọn đặt hàm số f x là hàm số bậc 3 dạng   3 2
f x  ax  bx  cx  d . Ta có  3  9 6 3       3 10 7 4 f x ax bx cx d
xf x  ax  bx  cx  dx f  2 1 x  6  ax  3a  b 4 x  3a  2b  c 2 x  a  b  c  d  f  3 x   f  2 1 x  10 7 6
 ax  bx  ax  3a  b  c 4 x  3a  2b  c 2
x  dx  a  b  c  d a  1  b    0
Đồng nhất thức ta được  . Suy ra f  x 3  x  3x  2 c  3  d  2  0 0 13 Vậy f  xdx   3
x  3x  2      . 1 4 1 2 3 3 Câu 2.
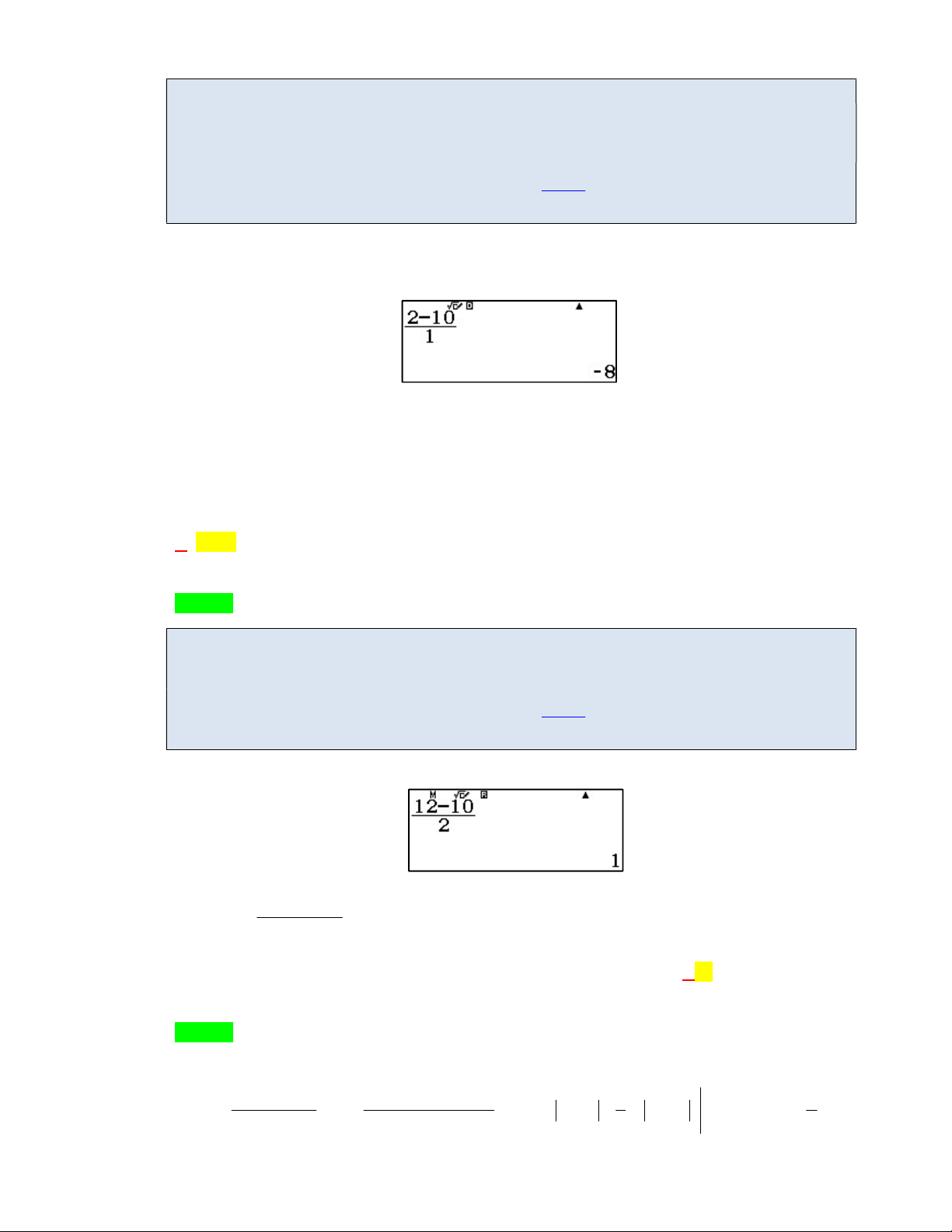
[CÂU 7-MH-BGD-L1] Nếu f  xdx  2   và f
 xdx 1 thì f xdx  bằng 1 2 1 A. 3 . B. 1. C. 1. D. 3 . Lời giải Chọn B Cách 1: PP tự luận b c b Áp dụng tính chất f  xdx  f  xdx f  xdx,a  c  b a a c 3 2 3
Ta có f  xdx  f  xdx  f  xdx  2  1  1     . 1 1 2
Cách 1: PP chọn hàm đại diện
Gợi ý: Do cho hai điều kiện nên chọn hàm có hai hệ số chưa biết dạng f  x  ax  b , cách này dài hơn tự luận. 1 1 Câu 3. [CÂU 18-MH-BGD-L2] Nếu f (x)dx  4  thì 2 f (x)dx  bằng 0 0 A. 16 . B. 4 . C. 2 . D. 8 . Lời giải Chọn D Cách 1: PP tự luận 1 Ta có 2 f (x)dx  1  2 f (x)dx  2.4  8  . 0 0
Cách 1: PP chọn hàm đại diện
Gợi ý: Do giả thiết cho một điều kiện nên chọn hàm có dạng f  x  a , cách này dài hơn tự luận. Câu 4.
[CÂU 45-MH-BGD-L2] Cho hàm số f x có f 0  0 và f  x 2  cos xcos 2 , x x   . Khi  đó f  xdx bằng 0 1041 208 242 149 A. . . B. . . C. . . D. . 225 225 225 225 Lời giải Chọn C
Cách 1: PP tự luận áp dụng tính chất f  x  f   xdx cos x cos 3x cos 5x Ta có f  x 2  cos xcos 2x    2 4 4  x x x  Do đó f  x  f   x cos cos 3 cos 5 dx    dx    2 4 4  sin x sin 3x sin 5x  f (x)   
 C , vì f (0)  0 nên C  0 2 12 20  242  I  f (x)dx   0 225
Cách 2: PP chọn hằng số C  u  f x du  f xdx Để tính f  xdx ta đặt    dv  dx v  x  C 0 Khi đó     f
 xdx  xC f x|  xC f xdx  f   C f 0.C xC f xdx 0 0 0 0 Chọn C       242
Suy ra f  x dx    x   f x 2 dx  (  x)cos . x cos 2xdx     255 0 0 0
Bài toán tổng quát cho Câu 4
Cho hàm số f  x có biết f a và f  x  g  x, x   . b b Khi đó f
 xdx  b xgxdx  ba f a 
 (1*) - công thức tính nhanh. a a
Chứng minh bằng PP chọn hằng số C u  f x du  f xdx Đặt    dv  dx v  x  C Khi đó b b  f  xdx xC b
f (x)|  x C f xdx  bC f ba C.f axC f xdx a a a 0 Chọn C  b b   f
 xdx  b x f xdx b a f a   a 0
Áp dụng công thức tính nhanh (1*) cho câu 4 b b 
f  x dx  b  x g x dx  b  a f a    x 242 2 cos .
x cos 2xdx    00     255 a a 0
HƯỚNG DẪN PHẦN ĐỀ PHÁT TRIỂN Câu 5.
[TRẦN BÌNH TRỌNG–KHÁNH HÒA-2020] Cho hàm số f  x có f   9 3  và 2 3 2   3 f  x x x 1  ,x  1. Tính I  f  xdx . 2 x  x  x 1 0 29 101 43 52 A. I   B. I   C. I  D. I  . 6 6 6 6 Lời giải Chọn C
Cách 1: PP tự luận (chọn hằng số C) u  f x du  f xdx Đặt    dv  dx v  x  C Khi đó: 3 3 3 f
 xdx  f x.xC 3|xC f xdx  f 33C f 0.C x C f xdx 0 0 0 0 Chọn C  0 3 3 2 9 x  x 1 43 Suy ra I  .3  . x dx   . 2 2 x  x  x 1 6 0 Cách 2: PP tính nhanh
Cho hàm số f x có biết f a và f  x  g  x, x   . b b Khi đó f
 xdx  b xgxdx ba f a 
 (1*) - công thức tính nhanh. a a
Áp dụng công thức (1*) ta có 3 0 0   f  xdx   f
 xdx  0 x f xdx03 f 3 0 3  3  3 3 2      x x x 1 9 43 dx  3.  2 x  x  x 1 2 6 0
(Chú ý gt cho f a  f   9
3  vậy ta cần đổi cận trên thành cận dưới). 2 x e ln8 Câu 6.
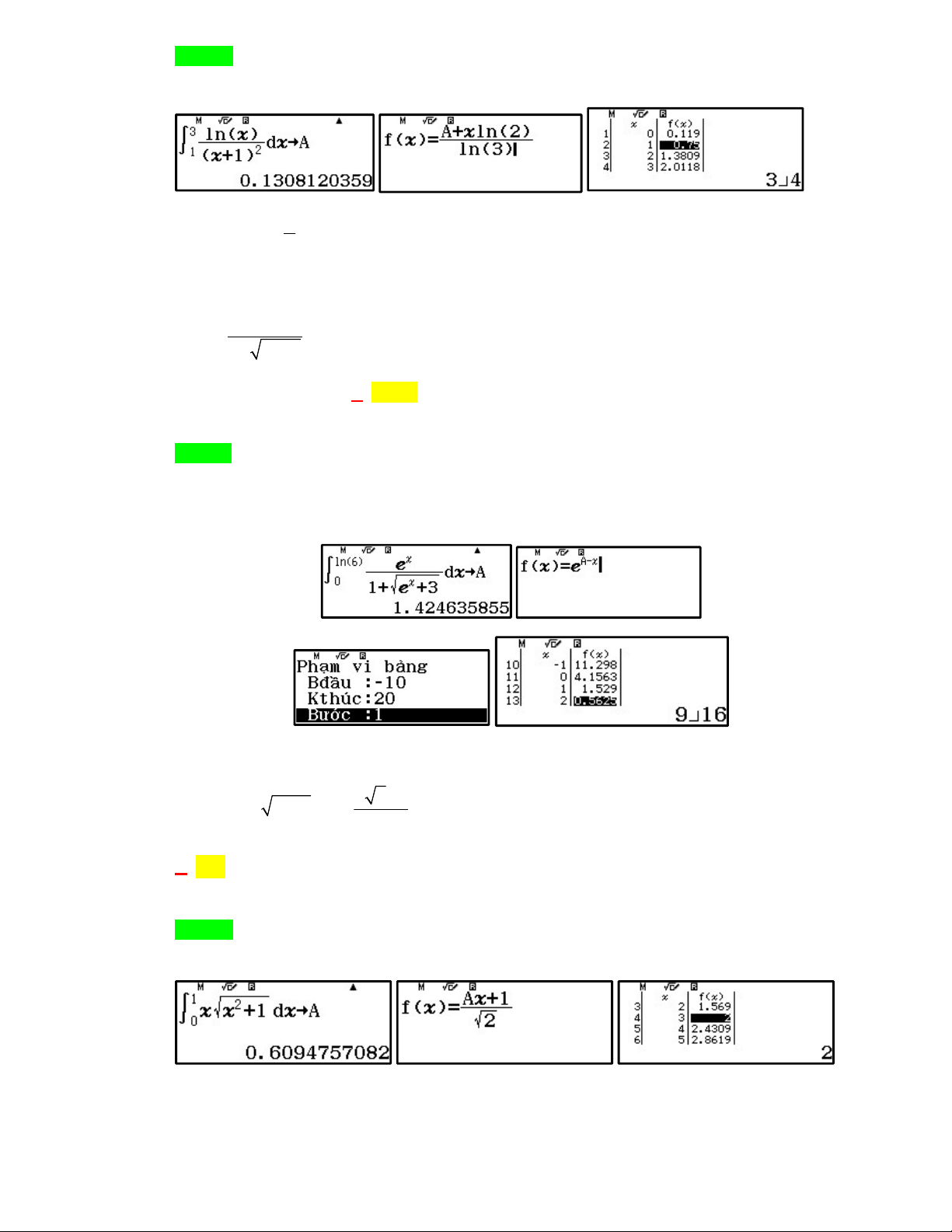
Cho hàm số y  f  x có f ln 3  4 và f  x  , x   .  Khi đó x e f  x dx  bằng: x e 1 ln 3 38 76 136 A. 2 B. C. D. . 3 3 3 Lời giải Chọn C. Cách 1: PP tự luận e d  x x e   f  x 
x    f x  f   x 1 , dx  2  2 x e 1  C  x e 1 2 x e 1
f ln 3  4  4  C  4  C  0 ln8 ln8 x e f  x x x 76 dx  e 2 e 1dx    3 ln 3 ln 3
Cách 2: PP tự luận (chọn hằng số C) u  f x du  f xdx Đặt    x x dv  e dx v  e  C ln8 ln8 ln8 Khi đó x 
     x  |    x e f x dx f x e C e  C  f xdx ln 3 ln 3 ln3 ln8  f ln8 ln8
e  C   f ln 3 ln3
e  C     xe  C f xdx ln3 ln8
 f ln88  C  f ln 33 C    xe C f xdx ln3 ln8 ln8 x e x x 76 Chọn C  8 suy ra e f  xdx  4
 .38   e 8  . x e 1 3 ln 3 ln3 Câu 7.
Cho hàm số y  f  x có đạo hàm liên tục trên  thỏa mãn f   1  1  và 1 xf  3  x   f x 7 1
 x  x  2, x   . Tính tích phân I  f  xdx . 0 2 5  5 2  A. . B. . C. . D. 3 9 9 3 Lời giải Chọn D Cách 1: PP tự luận: Từ xf  3  x   f x 7 2
 x  x  x    x f  3  x   xf x 8 2 1 2, 1  x  x  2x, x   1  x f  1 x  1 1 2 3 dx  xf   xdx   8 2 x  x  2xdx 0 0 0 Đặt 3 2 t  1 x  dt  3  x dx 1  x f  1 x  0 1 1 1 1 1 2 3 dx   f  tdt  f  tdt  f  xdx 3 3 3 0 1 0 0 1 1 1 Vậy ta có 2 x f   3 1 x dx  xf   xdx   8 2 x  x  2x dx 0 0 0 1 1 1  1 1     1 5
f  xdx  xf  x 5 dx     f
 xdxxf x 1|  f x dx    0   3 9 3 9 0 0 0  0  1 1 2    f  x 5
dx     f    f   5
      f   4   f x 2 1 0. 0 1 0. 0 dx    3 9 9 9 3 0 0
Cách 2: PP chọn hàm đại diện Từ đẳng thức xf  3  x   f x 7 1
 x  x  2, x   suy ra chọn đặt hàm số f x là hàm số bậc 2 dạng 2
f (x)  ax  bx  c với a, , b c   . Ta có xf  3  x  7 1
 f (x)  x  x  2  x a    x 2 3  b 3  x   7 1 1
 c  2ax  b  x  x  2        a 1;b 2;c 0 . 2
 f (x)  x  2x thỏa mãn f (1)  1. 1 1 2 
Từ đó ta có I  f  xdx   2 x  2xdx    . 3 0 0 3 Câu 8.
Cho hàm số y  f (x) liên tục trên  và thỏa mãn 2 3
4xf (x )  6 f (2x)  x  4 . Giá trị 5 4 f (x)dx  bằng 0 52 48 A. . B. 52. C. . D. 48. 25 25 Lời giải Chọn A Cách 1: PP tự luận 2 2 3 3 2 3 2 3 
4xf (x )  6 f (2x)  x  4  4xf (x )  6 f (2x) dx  x  4 dx   5   5    0 0 2 2 4 4 2 2 52 52
 2 f (x )d(x )  3 f (2x)d(2x) 
 2 f (t)dt  3 f (u)du      5 5 0 0 0 0 4 4 4 4 52 52 52
 2 f (x)dx  3 f (x)dx   5 f (x)dx   f (x)dx      5 5 25 0 0 0 0
Cách 2: PP khác (xin đề nghị Quý độc giả đề xuất). Câu 9.
Cho hàm số f  x liên tục trên  thỏa mãn 3 f  x  x f  2 x   5 3 2 3 .
2  5x 18x  45x 11x 1, x    . Khi đó f  xdxbằng 3  A. 96 . B. 64 . C. 192 . D. 32 . Lời giải Chọn A Cách 1: PP tự luận
Ta có : f  x  x f  2 x   5 3 2 3 .
2  5x 18x  45x 11x 1   1 . Thay x bởi x
 vào (1) ta có : f  x  x f  2x   5 3 2 3 . 2  5
 x 18x  45x 11x 1 2 .
Cộng (1) và (2) vế với vế ta được: 1 1 f 3x f  3  x 2  90x 2  f  3xdx f  3xdx64. 1  1 1 Xét f
 3xdx. Đặt t 3xdt 3dx. 1 
Đổi cận: x  1 t  3; x  1 t  3 . 1 3 3 1 1 Khi đó f  3xdx f  tdt  f  xdx. 3 3 1  3  3  1 3 1 Tương tự ta có f   3  xdx  f  xdx. 3 1  3  3 3 3 1 1 Vậy f  xdx f  xdx64 f  xdx96. 3 3 3 3  3
Cách 2: PP khác (xin đề nghị Quý độc giả đề xuất).
Câu 10. Cho hàm số f x có đạo hàm liên tục trên 0; 
1 thỏa mãn f 0 1 và  1 f  x2   2 x   f x 6 4 2 4 6 1
 40x  44x  32x  4, x  0;  1 . Tích phân f  xdx  bằng 0 A. 23 . B. 17  . C. 13 . D. 7  . 15 15 15 15 Lời giải Chọn D Cách 1: PP tự luận
Lấy tích phân hai vế đẳng thức trên đoạn 0;  1 ta có: 1  1 1 f  x2 dx  4  376 2 6x   1 f  xdx   6 4 2
40x  44x  32x  4dx     . 105 0 0 0
Theo công thức tích phân từng phần có: 1 6x   1 1 1 2 1 f  xdx  f  xd 3 2x  x   3
2x  x f x   3 2x  x f  xdx 0 0 0 0 1  6x   1 2
1 f  xdx  1  3 2x  x f xdx . 0 0
Thay lại đẳng thức trên ta có 1  1  
f  x2 dx  41  376 3
2x  x f xdx  105 0  0  1 1 2   1
f  x2 dx  4 44 3 2x  x f xdx 
 0   f x 2 3 2x  x dx  0 105 0 0 0  f  x   3 2 2x  x, x  0;  1    4 2 f x  x  x  C . 1 1 13 Mặt khác f  
1  1  C  1  f  x 4 2
 x  x 1  f xdx   4 2 x  x   1 dx    . 15 0 0
Cách 2: PP chọn hàm đại diện
Từ đẳng thức  f  x2   2 x   f x 6 4 2 4 6 1
 40x  44x  32x  4, x  0;  1 suy ra chọn đặt
hàm số f  x là hàm số bậc 4 trùng phương dạng 4 2
f (x)  ax  bx  c với a, , b c   . 2 Khi đó ta có  3 ax  bx   2 x   4 2 ax  bx c 6 4 2 4 2 4 6 1
 40x  44x  32x  4, x  0;  1 40a  40 1 
 6ab  24b  4a  44 a  c  1
Đồng nhất hai vế ta có    2 4b  24c  4b  32 b    1  4  c  4  1 1 13 Vậy f  x 4 2
 x  x 1 f  xdx   4 2 x  x   1 dx    15 0 0
Câu 11. [SỞ HÀ NỘI LẦN 1 – CÂU 31 - 2020] Cho hàm số y  f  x có đạo hàm liên tục trên 0;  1 , 1 1 thỏa mãn f
 xdx  3 và f  1  4 . Tích phân xf 
 xdx có giá trị là 0 0 1 1 A.  . B. . C. 1. D. 1. 2 2 Lời giải Chọn C Cách 1: PP tự luận: u  x  du  dx  Đặt    dv  f '  xdx v  f  x  C 1 1 1 Khi đó I  xf 
 xdx   f xC   |
x   f x Cdx 0 0 0 1 1 I   f    1  C   f
  x dx  C dx  4  C  3  C  1  0 0
Cách 2: PP chọn hàm đại diện 1
Ta có hàm số f  x có hai giả thiết f
 xdx  3 và f  1  4 nên dự kiến chọn đặt hàm số là 0 1 1 1 2  ax  a
y  f  x  ax  b  f
 xdx  3 ax bdx  3  bx  3   b  3     1 .  2  2 0 0 0 a  2 f  
1  4  a  b  4 2 . Từ   1 ,2 suy ra: 
 y  f  x  2x  2  f 'x  2 . b  2 1 1 xf   xdx  2xdx 1  . 0 0
Câu 12. [LAM SƠN – THANH HÓA – CÂU 40 - 2020] Cho hàm số f  x liên tục trên đoạn 0;10 10 10 1 thỏa mãn f  xdx  7, f
 xdx 1. Tính P  f  2xdx. 0 2 0 A. P  6 . B. P  6 . C. P  3 . D. P  12 . Lời giải Chọn C Cách 1: PP tự luận: 2 Ta có f
 xdx  F 2 F 0  F
 10  F 2  F
  10  F 0 0 10 10   f  xdx  f
 xdx  1 7  6. 2 0
Đổi biến: x  2t, dx  2dt .
Đổi cận: x  0 t  0; x  2  t  1. 2 1 1 1 Khi đó 6  f  xdx  2 f  2tdt  f  2tdt  3, hay f  2xdx 3. 0 0 0 0
Cách 2: PP chọn hàm đại diện 10 10
Giả thiết cho hai điều kiện f  xdx  7, f
 xdx 1 nên chọn đặt f x  ax b. 0 2 10 10 Khi đó f
 xdx  axbdx  50a 10b  7 0 0 10 10 và f
 xdx  ax bdx  48a 8b 1. 2 2  2  3 a  5  0a 10b  7   Suy ra hệ 40    . Do đó f  x 23 143  x  . 48a  8b  1 143 40 40 b    40 1 1    P  f   x 23 143 2 dx  x  dx  3   .  20 40  0 0
Câu 13. [CHUYÊN SP HÀ NỘI – CÂU 40 - 2020] Cho hàm số y  f (x) liên tục trên tập số thực thỏa mãn f x  x  f  2 x  x 3 2 ( ) (5 2). 5
4  50x  60x  23x 1, x   R . 1
Giá trị của biểu thức f (x)dx  bằng 0 A. 2 . B. 1. C. 3 . D. 6 . Lời giải Chọn A Cách 1: PP tự luận: 1 1 1 1 3 2 2 2
f (x)dx  (50x  60x  23x 1)dx  (5x  2) f (5x  4x)dx  3  (5x  2) f (5x  4x)dx     (1) 0 0 0 0 1 Xét tích phân 2 (5x  2) f (5x  4x)dx  : 0 Đặt 2
t  5x  4x thì dt  (5.2x  4)dx  2(5x  2)dx
Khi x 1thì t  1; Khi x  0 thì t  0 1 1 1 1 1 Suy ra: 2 (5x  2) f (5x  4x)dx  f (t)dt  f (x)dx    2 2 0 0 0 1 1 1 1 1 3
Thay vào (1) ta được: f (x)dx  3  f (x)dx 
f (x)dx  3  f (x)dx  2     2 2 0 0 0 0
Cách 2: PP chọn hàm đại diện
Từ công thức f x  x  f  2 x  x 3 2 ( ) (5 2). 5
4  50x  60x  23x 1, x
  ta dự đoán hàm số là
bậc nhất dạng f (x)  ax  b , thay vào điều kiện ta được 2 3 2
ax  b  (5x  2) a(5x  4x)  b  50x  60x  23x 1   2 3 2
 ax  b  (5x  2)(5ax  4ax  b)  50x  60x  23x 1 3 2 3 2
 25ax  30ax  (9a  5b)x  b  50x  60x  23x 1 25a  50 3   0a  60 a  2     (9a  5b)  2  3 b   1  b   1  1 1
Do vậy f (x)  2x 1 suy ra f (x)dx  (2x 1)dx  2   . 0 0
Câu 14. [CHUYÊN BIÊN HÒA – HÀ NAM – CÂU 42- 2020] Cho hàm số f  x liên tục trên R và 1 2 thỏa mãn f
 xdx  9 . Tính tích phân  f  13x9dx  . 5 0 A. 15 . B. 27 . C. 75 . D. 21. Lời giải Chọn D Cách 1: PP tự luận:
Đặt t  1 3x  dt  3dx .
Với x  0  t  1 và x  2  t  5 . 2 2 2 Ta có  f  13x9dx   f  13xdx  9dx  0 0 0 5 dt 1 1   f   t 2   9x    f  1
  x dx 18  .9 18  21. 0 3  3  3 1 5
Cách 2: PP chọn hàm đại diện 1
Giả thiết cho một điều kiện f
 xdx  9 nên dự kiến chọn hàm dạng f x  ax . 5 1 1 3  Khi đó f  xdx  a d
x x  12a  9  a     . Do đó f x 3  x . 4 4 5 5  2 2 2  3   9 33 Vậy   f
 13x9dx     13x  9 dx  x  dx  21   . 4   4 4      0 0 0 1 2
Câu 15. [CHUYÊN THÁI BÌNH – CÂU 37 - 2020] Biết f  xdx  1   và f
 2x 1dx  3. Tính 0 1 3 f xd .x  0 A. 5. B. 2. C. 7. D. 4  . Lời giải Chọn A Cách 1: PP tự luận:
Ta đặt : t  2x 1  dt  2d . x 2 f  2x   1 3 1 dx  f  t 3 dt  3  f  xdx  6 1 1 1 2 3 1 3 Mà f  xdx  f  xdx f  xdx  1   6  5. 0 0 1
Cách 2: PP chọn hàm đại diện
Đặt f  x  ax  b . 1 1 a Khi đó f
 xdx   ax bdx  b  1 0 0 2 2 2 2 và f  2x 1dx  a
  2x 1bdx  
 2axabdx  2ab  3. 1 1 1  8  a a    b  1  Suy ra hệ 3  2   . Do đó f  x 8 7  x  . 7  3 3 2a  b  3 b     3 3 3  8 7  Vậy f  xdx  x  dx  5    . 0 0  3 3 
Câu 16. [CHUYÊN ĐẠI HỌC VINH – CÂU 40 – 2020] 1 1
Cho f  x là hàm số có đạo hàm liên tục trên đoạn 0;  1 và f   1 1   , xf  xdx   . Giá 18 36 0 1 trị của f  xdx  bằng 0 1 1 1 1 A.  . B. . C. . D.  . 12 36 12 36 Lời giải Chọn A Cách 1: PP tự luận: u   x  du  dx  Đặt:    dv  f   xdx v   f  x 1 1 1 1 Ta có: xf 
 xdx  .xf x  f
 xdx  f  1 f  xdx . 0 0 0 0 1 1
Theo giả thiết: xf  xdx   , f   1 1   36 18 0 1 1 1    f x 1 dx   f x 1 1 1 dx        . 18 36 18 36 12 0 0
Cách 2: PP chọn hàm đại diện
Đặt f  x  ax  b . 1 1 1 2 x a 1 1 Khi đó f   1 1  a  b   và xf  xdx  a d x x  a    a    . 18 2 2 36 18 0 0 0  1  1 a  b   a      Suy ra hệ 18 18    . Do đó f  x 1 1  x  . 1 1  18 9 a   b    18  9 1 1  1 1  1 Vậy f  xdx  x  dx     . 18 9  12 0 0
Câu 17. Cho hàm số f  x  liên tục trên đoạn 0;  1 thỏa mãn điều kiện 1 f  x  f   x 2 2 1
 3x  6x,x 0;  1 . Tính I  f   2 1 x dx 0 4 2 2 A. I  . B. I  1. C. I   . D. I  . 15 15 15 Lời giải Chọn C
Bài toán: Cho hàm số f  x liên tục trên đoạn 0;c thỏa mãn điều kiện mg(x)  ng c  x
mf  x  nf c  x  g(x),x  0;c ; m  n và , m n    f (x)  . 2 2 m  n Chứng minh
Đặt t  c  x  x  c  t . Do x  0; c nên t 0;c.
Thay x  c t vào mf  x  nf c  x  g(x),x 0;c (1*)
ta có mf c  t   nf t   g(c  t) 2 * thay tiếp t  x vào (2*) ta có
nf  x  mf c  x  g(c  x) (3*)
Từ (1*) và (2*) ta có hệ mf  x  nf c  x 2  g(x) m f 
x  nmf c  x  mg(x) 4*    nf
  x  mf c  x 2  g(c  x) n f 
x  nmf c  x  ng(c  x) 5*
Trừ tương ứng từng vế của (4*) và (5*) ta có 2 m f  x 2
 n f x  mg(x)  ng c  x mg(x)  ng c  x  f (x)  (công thức tính nhanh). 2 2 m  n Cách 1: PP tính nhanh f x  2 f 1 x 2  3x  6 , x x  0;  1
3x 6x231 x2 2  61 x 2       f x 3x 6x 6 2    x  2x  2 2 2 1  2 3  2 Khi đó f  2  x    2  x    2  x  4 2 1 1 2 1  2  x  4x 1 1 1 2 Suy ra I  f  2 1 x dx   4 2 x  4x   1 dx     . 15 0 0
Cách 2: PP chọn hàm đại diện
Từ f  x  f   x 2 2 1
 3x  6x,x 0;  1
Ta dự kiến chọn hàm đại diện là   2
f x  ax  bx  c thì ta có
f  x  f   x  ax  bx  c  a   x2 2  b  x 2 2 1 2 1 1  c  3ax   4
 a  b x  2a  2b  3 .c  
Đồng nhất thức hệ số ta có 3  a  3 a  1   4a  b  6 
 b  2 . Suy ra f  x 2  x  2x  2 .  2a 2b 3c 0     c  2   1 1 2 2 Dó đó I f   2 1 x dx   2 1 x  2 2 1 x  2        dx     . 15 0 0 Cách 3: Tự luận
Đặt t  1  x, x  0;  1  t  0;  1 .
Ta có f  x  f   x  x  x  f  x  f   x    x2 2 2 1 3 6 2 1 3 1 3
 f   t   f t  2
 t   f  x  f   x 2 1 2 3 3 2 1  3x  3 Ta có hệ phương trình  f
  x  2 f 1 x 2  3x  6x  f
  x  2 f 1 x 2  3x  6x    2 f  x  f 1 x 2  3x  3 4 f  x 2 f 1 x 2  6x  6 2 x  x   3 f x 3 6 6 2
 3x  6x  6  f x 2   x  2x  2 3 2 Khi đó f  2  x    2  x    2  x  4 2 1 1 2 1  2  x  4x 1 1 1 2 Suy ra I  f  2 1 x dx   4 2 x  4x   1 dx     . 15 0 0 Câu 18. Cho hàm số f ( )
x có đạo hàm liên tục trên  và thỏa mãn f 0  3và 2 f  x  f   x 2 2  x  2x  2; x
   . Tích phân xf (x)dx bằng 0 4 5 A.  10 . B.  2 . C. . D. 3 3 3 3 Lời giải Chọn B Cách 1: Tự luận 2 2
Áp dụng công thức tích phân từng phần, ta có: xf 
 xdx  xf x 2|  f x dx . 0    0 0
Từ f  x  f   x 2 2  x  2x  2; x    (1*)
Thay x  0vào (1*) ta được f 0  f 2  2  f 2  2  f 0  2  3  f 2  1. 2 Xét I  f
 xdx . Đặt t 1 x  x 1 t  dx  dt 0
Đổi cận: x  0  t  2; x  2  t  0 2 0 2 2 Khi đó I  f  xdx   f  1tdt  f  1tdt  f  1 xdx 0 2 0 0 Do đó ta có 2 2 2 2 2  f
 x  f 2 x dx    8 4 2 x  2x  2  2 f
 xdx   2x  2x  2   f  xdx  (2*) 3 3 0 0 0 0 0 2 2 4 10
Vậy xf  xdx  xf  x 2|  2 f 2  f x dx  2 1     0        3 3 0 0
Bài toán dùng để tính nhanh (2*):
Cho hàm số f  x  liên tục trên đoạn 0;c thỏa mãn điều kiện c c g x
mf  x  nf c  x  g(x),x  0; c; m  n  0 ; và I  f  x   dx  dx  . m  n 0 0 Chứng minh c 0 c
Đặt t  c  x  x  c  t . Ta có I  f  xdx   f  c tdt  f  c  xdx 0 c 0
mf  x  nf c  x  g(x),x  0;c; m  n  0 c c c c g x  (m  n) f  xdx  g  xdx  I  f  x   dx  dx  m  n 0 0 0 0
Áp dụng: Biết f  x  f   x 2 2
 x  2x  2;x   2 2 1 1 8 4
Áp dụng công thức tính nhanh ta có  f  xdx 
 2x  2x  2  .    (2*) 2 2 3 3 0 0
Cách 2: PP chọn hàm đại diện
Từ f  x  f   x 2 2  x  2x  2; x
  * ta dự kiến chọn hàm số   2 f x  ax  bx  c thay
vào đk (*) ta có f x  f   x  ax  bx  c  a   x2 2 2 2  b2  x  c 2
 2ax  4ax  4a  2b  2c. 2a  1  1  a 
Đồng nhất hệ số ta có  4  a  2    2 . 4a  2b  2c  2 b     c  0 1
Do f 0  3  c  3;b  3 . Suy ra f  x 2
 x  3x  3; f 'x  x  3 . 2 2 2 10
Vậy xf ' x dx  x x  3 dx     . 3 0 0 Cách 3: PP tính nhanh Do x  f  x  f   x 2 [0; 2] : 2
 x  2x  2  m  n  1 mg(x)  ng c  x
Không dùng được công thức tính nhanh sau đây: , m n    f (x)  2 2 m  n
Câu 19. [THTT-L1-2017-2018] Cho hàm số f ( )
x có đạo hàm liên tục và dương trên0;e , thỏa mãn e 1 be
và f  x. f e  x  1; x
 0;e . Tích phân dx  
trong đó b, c là hai số nguyên 1 f x c 0   b
dương và là phân số tối giản. Khi đó b  c có giá trị là c A. 3 . B. 4 . C. 5 . D. 6 Lời giải Chọn A Cách 1: PP tính nhanh
Bài toán: Cho hàm số f ( )
x có đạo hàm liên tục và dương trên 0;a, thỏa mãn và a 1 a
f  x. f a  x  1;x 0;a thì tích phân dx   1 f x 2 0   Chứng minh: Đặt t  a  x ta có a 0 a a a 1 1 1 1 f (t) dx   dt  dt  dt  dt      1 f x 1 f a  t 1 f a  t 1 1 f t 0   a   0   0 0   1 f (t) a 1 a 1 a   a 1   a f x f x  2 dx  dx  dx  dx  dx  a      1 f x 1 f x 1 f x 1 f x 0   0   0   0   0 a 1 a    1 f  x * 2 0 e 1 e eb b 1
Áp dụng công thức (*) vào bài toán ta có      , do b, c là hai số 1 f x 2 c c 2 0   b
nguyên dương và là phân số tối giản  c  2,b  1 b  c  3. c
Cách 2: PP chọn hàm đại diện
Do f  x. f e  x  1; x
 0;e chọn hàm đại diện f  x  k (là hàm hằng)
Ta có f  x f e  x  x   e 2 . 1; 0;  k  1  k 1.
Vậy ta chọn hàm đại diện f  x  1 e eb 1 eb e b 1   b dx  1     
, do b, c là hai số nguyên dương và là phân số c 1  f x c 2 c 2 c 0  
tối giản  c  2,b  1 b  c  3  1 1 2
Câu 20. Cho f  x là hàm liên tục trên  thỏa f   1 1 và f tdt   , tính I  sin 2 . x f   sin xdx . 3 0 0 4 2 1 2 A. I  . B. I  . C. I  . D. I   . 3 3 3 3 Lời giải Chọn A Cách 1: PP tự luận:
Đặt sin x  t  dt  cos d x x . 
Đổi cận: khi x  0  t  0 ; x   t  1. Từ đó ta có 2   2 2 1 I  sin 2 . x f  
sin xdx  2sin .xcos .xf   sin xdx  2 t.f   tdt 0 0 0 u  t  du  dt  Đặt:    . dv  f   tdt v  f  t     I   1 t f t 1  f  t 1 4 2 . dt  2 1    . 0    3  3 0
Cách 2: PP chọn hàm đại diện
Phân tích có hai giả thiết, ta tìm hàm f  x thỏa hai điều kiện, chọn f  x  ax  b Khi đó: f   1 1 a  b 1   1 1 1 1 1 1 f t  f  x  ax  b 1 1 1 dt dx
dx  a xdx+ bdx=  a  b       2 3 2 3 0 0 0 0 0  4 a  b  1 a     Từ   1 ,2 ta có hệ 3 1 1   a  b  1 2 3 b    3 4 1 4
Ta được f  x  x  ; f ' x  , do đó f  x 4 ' sin  3 3 3 3   2 2 4 4 Vậy I  sin 2 .
x f sin xdx  sin 2 . x dx    . 3 3 0 0 1
Câu 21. Cho hàm số liên tục trên đoạn  2 0; 
1 và thỏa điều kiện  f   x dx  21  và 0 1   1 x   1 f  x dx  7 . Tính x I  e f  xdx . 0 0 A. e . B. 2e . C. 3e . D. 4e . Lời giải Chọn C
Cách 1: PP chọn hàm đại diện 1 1
Nhận xét: Giả thiết có 2 điều kiện cho trước là  f   x 2 dx  21  và  x   1 f  x dx  7 , tìm 0 0
hàm số f  x bằng cách dựa vào tỷ số  f x 2    21      x   f x f  x 3 x 1 1 7 1 1 Ta có x      3 x I e f x dx e  x 1dx  3e 0 0
Cách 2: PP chọn hàm đại diện
Đặt f  x  ax  b dựa vào giả thiết tìm hệ số ; a b .
Cách 3: PP chọn hàm đại diện
Nhắc lại bất đẳng thức Holder tích phân như sau: 2 b b b    f  xgx 2 dx   f  x 2 d . x g  xdx  a  a a
Dấu bằng xảy ra khi f  x  k.g  x, x   ; a b,k  1
Đặt g(x)  x 1; ta có  x   1 f  x dx  7 0 1 1 1 7 suy ra g
 x f xdx  7;  f  2   x 2  dx  21  ;  x   1 dx   0 0 0 3 2 1 1 2 1 2 Vì  g
 x f xdx   f x  d .x g x  dx       0      0 0
Dấu bằng xảy ra khi f  x  kg  x  f  x  3g  x  3 x   1 1 1 Vậy x      3 x I e f x dx e  x  1dx  3e. 0 0  1 2  2 1 x  f xdx 10 3 I  cos xf  sin xdx Câu 22. Cho 0 . Tính 0 . A. I  5 . B. I  10 . C. I 10 . D. I  5 . Lời giải Chọn C Cách 1: Tự luận   2 2 3 I  cos xf  sin xdx   2
1 sin x. f sin x.cos d x x . 0 0 
Đặt t  sin x  dt  cos d
x x và x  0  t  0; x   t 1. 2 1 Khi đó I   2 1 t  f tdt 10. 0
Cách 2: PP chọn hàm đại diện 1
Giả thiết cho một điều kiện  2
1 x  f xdx 10 nên nghĩ đến chọn f x  a . 0 1 1 2 30 Ta có  2
1 x  f xdx 10   2 1 x  d
a x 10  a 10  a    . 3 2 0 0 Suy ra f  x 30  . 2   2 2 30 Ta có: 3 I  cos xf  sin x 3 dx  cos xdx  10  . 2 0 0  1  1
Câu 23. Cho hàm số liên tục trên đoạn 0; 
và thỏa điều kiện  3x   1 f (  x)dx  2019 và 3   0 1 4 f  
1  f 0  2020 . Tính 3 f 3xdx  . 0 1 1 A. . B. 3 . C. . D. 1. 9 3 Lời giải Chọn A Cách 1: PP tự luận 1
Áp dụng tích phân từng phần tính 3x    1 f (  x)dx 0 1 Ta có 10
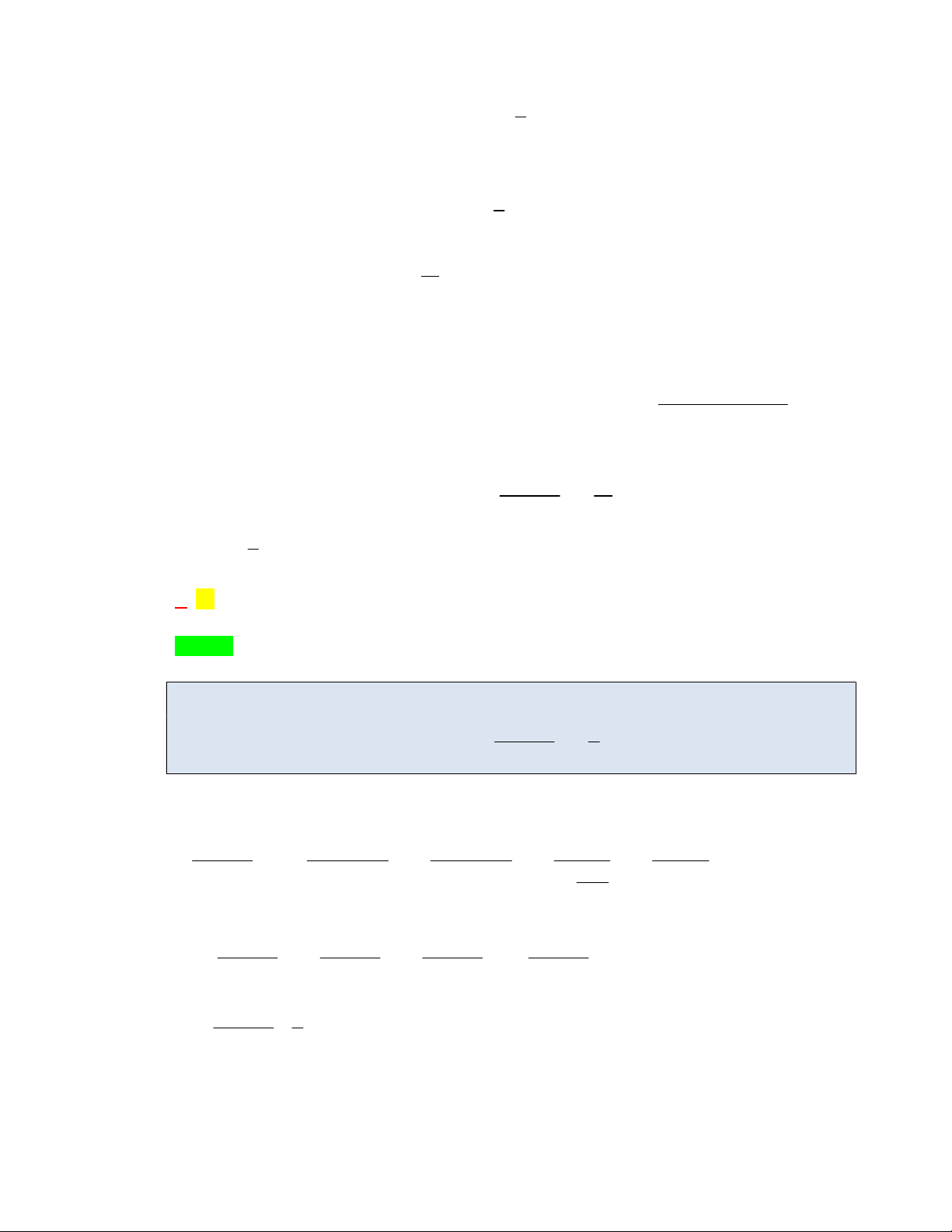
  x   f  x dx  f x3x  1 3 1 ( ) 1  3 0 f xdx 0  f    f   1  f  x 1 dx  f  x 1 2019 4 1 0 3 dx    0 0 3 1 1 1 1 1 1 Vậy 3 f 3x dx  f tdt  .    . 0 0 3 3 3 9
Cách 2: PP chọn hàm đại diện 1
Giả thiết có 2 điều kiện cho trước là  3x   1 f (
 x)dx  2019 và 4 f  
1  f 0  2020 ta chọn 0
đặt f  x  ax  b  f  x  a . 1 1 4038 Ta có 3x   1 f (
 x)dx  2019  a 3x   1 dx  2019  a    0 0 5  a
Mặt khác f    f     a  b 2020 4 4 1 0 2020 4  b  2020  b  . 3 1 1 1 Vậy 3 f 3x 3 dx  3ax bdx    . 0 0 9 4 2 Câu 24. Cho f (x)dx  16  . Tính I  f (2x)dx  0 0 A. I 32 . B. I 8 . C. I 1  6 . D. I  4 Lời giải Chọn B Cách 1: PP tự luận dt Đặt t  2x 
=dx . Đổi cận x  0  t  2 ; x  2  t  4 2 2 1 4 1 4
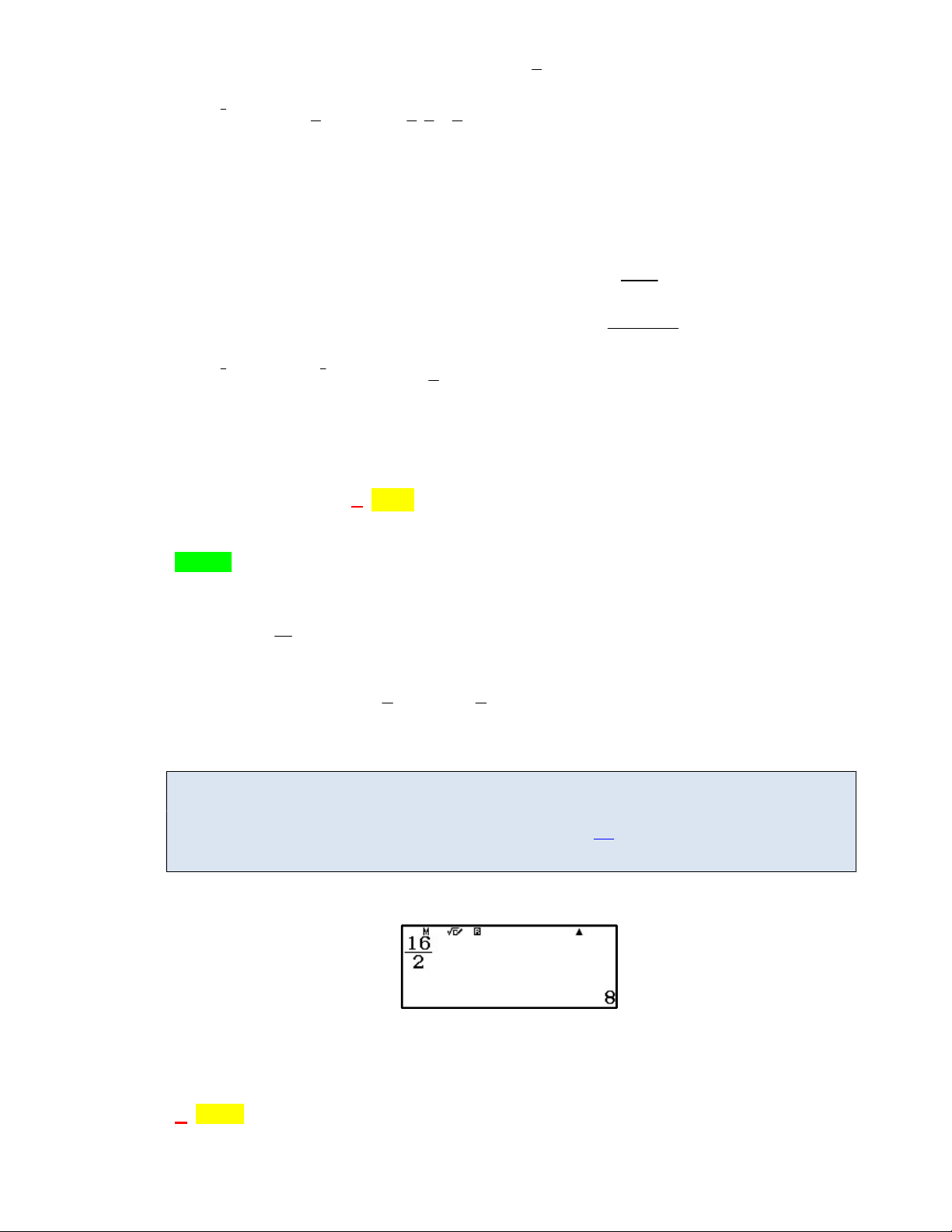
Khi đó ta có I  f (2x)dx  f (t)dt  f (x)dx 8     0 0 2 2 0 Cách 2: PP casio Phương pháp casio nhanh: m  M Nếu có f  xdx  M thì f   x a  bdx  ;n  . a   , b m  . a   b a n  Áp dụng . 9 1 Câu 25. Cho f
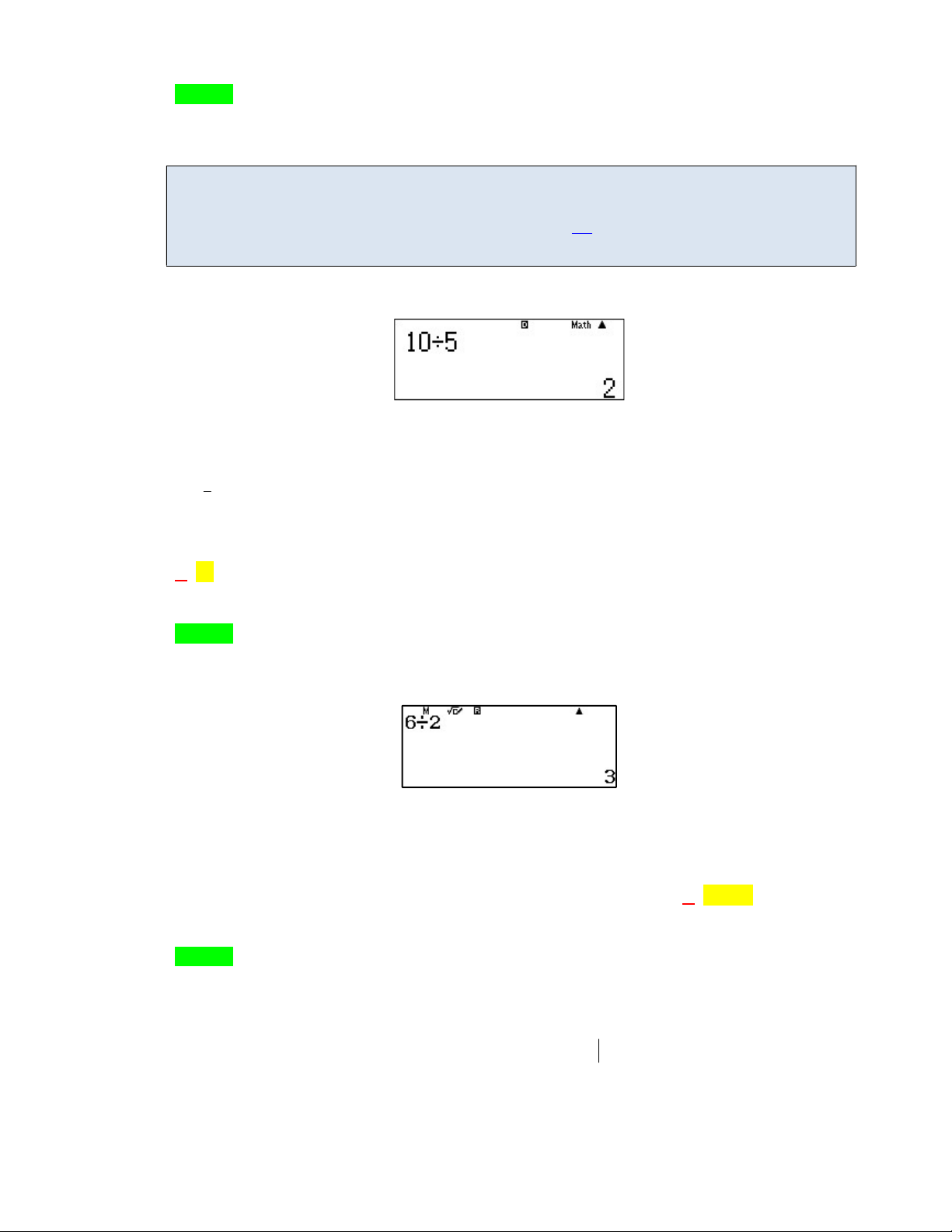
 xdx 10. Tính tích phân J  f  5x 4dx . 4 0 A. J  2 . B. J  10 . C. J  50 . D. J  4 . Lời giải Chọn A Cách 1: PP casio Phương pháp casio nhanh: m  M Nếu có f  xdx  M thì f   x a  bdx  ;n  . a   , b m  . a   b a n  Áp dụng . 2
Câu 26. Giả sử hàm số f  x liên tục trên đoạn 0;2 thỏa mãn f  x . Tính tích phân dx  6 0  2 I  f  2sin xcos d x . x 0 A. 3. B. 3 . C. 6 . D. 6 . Lời giải Chọn A Cách 1: PP casio . 1 1
Câu 27. Cho hàm số f  x thỏa mãn x  
1 f  xdx 10 và 2 f  
1  f 0  2. Tính f xdx  . 0 0 A. I  1  2 . B. I  8 . C. I  1. D. I  8 Lời giải Chọn D Cách 1: PP tự luận u   x 1 du   dx 1 Đặt    . Khi đó I   x   1 f  x1  f  xdx dv  f   xdx v  f  x 0 0 1 1 1 Suy ra 10  2 f   1  f 0  f  xdx  f
 xdx  10 2  8. Vậy f  xdx  8. 0 0 0 Cách 2: PP casio Phương pháp casio nhanh: 
Nếu hàm số f  x thỏa mãn ax b f xdx  K và    P  K
a  b. f   a b f    P thì f  xdx  . a  Áp dụng . 1
Câu 28. Cho hàm số f  x có đạo hàm f  x và thỏa mãn 2x  1 f xdx 10 , 3f   1  f 0 12. 0 1 Tính I  f  xdx . 0 A. I  1. B. I  2 . C. I  2 . D. I  1 . Lời giải Chọn A 
Phương pháp casio nhanh: Nếu hàm số f  x thỏa mãn ax b f xdx  K và    P  K
a  b. f   a b f    P thì f  xdx  . a  Áp dụng: 2 8x  5 Câu 29. Biết rằng
dx  a ln 2  b ln 3  c ln 5 
với a,b,c là các số thực. Tính 2 2 P  a  b  3c 2 6x  7x  2 1 A. 1. B. 2. C. 3. D. 4. Lời giải Chọn D Cách 1: PP tự luận 2 2 2 9x  5 2(3x  2)  (2x 1)  1  2 Ta có dx 
dx  ln 2x 1  ln 3x  2  ln 2  ln 3  ln 5   2   6x  7x  2 (2x 1)(3x  2)  3  3 1 1 1 2 Do đó 2 2
a  1;b  1;c   P  a  b  3c  4. 3 Cách 2: PP casio 2 8x  5 B1: Tính dx  và gán cho biến A 2 1 6x  7x  2
B2: Ta có  ln 2  ln 3  ln 5   ln 2a.3 .b5c A a b c A  A   2a.3 .b5c nA   2n .a3n .b5nc e e với * n  B3. Tính nA e sao cho nA
e là 1 số hữu tỉ ( thường n = 1,2,3,4…). A 200 Ta có 3 1  3 2 3 e 200.27 2 .5 .3    (1) 27 Mà 3A 3a 3b 3 2 .3 .5 c e  (2)  3  a  3 a 1   Từ (1) và (2) suy ra 3  b  3   b   1  2 2
 P  a  b  3c  4 . 3  c 2   2  c   3 6 3 x a 2  4 Câu 30. Biết dx  ; a,b  . 
 Mệnh đề nào sau đây là đúng? 2 x  b 2 2 A. a  b  7. B. a  b  7. C. a  b  15. D. a  b  9. Lời giải Chọn A Cách 1: PP tự luận 6 3 x Tính I  dx  . Đặt 2 2 2
t  x  2  t  x  2  tdt  xdx 2  2 x 2 Đổi cận 3 2 2 6 x 6 x .x 2 2 t  2 Suy ra I  dx  dx  tdt    2 2 2 2 2 x  2 x  2 t  t  4 2  4 I   t  2 3 2 2 2 2 2 dt    2t |  2 2  3  3
Suy ra: a = 4, b = 3. Vậy a + b = 7 Cách 2: PP casio 6 3 x B1: Tính I  dx  và gán cho biến A 2  2 x 2 a 2  4 a 2  4 B2: A   b  b A
Đặt x  a  b  F  x B3: Mode 7 (dùng Table) x  Nhập F x 2 4  A Star -9 End 9 Step 1
Ta dò được F(x) = 3 suy ra x = 4 Suy ra: a = 4, b = 3 Vậy a + b = 7.
Câu 31. [CHUYÊN NGUYỄN TRÃI – HẢI DƯƠNG - CÂU 37 - 2020] 3 x  3 Cho
dx  a ln 2  b ln 3  c ln 
5 với a,b,c là các số hữu tỉ. Tính S  a2  b2  c2 . x2  3x  2 1 A. S  5 . B. S  3 . C. S  4 . D. S  6 . Lời giải Chọn D Cách 1: PP tự luận 3 x  3 3 x  3 3  2 1  3 Ta có dx  dx   dx   2 1 2 2    ln x  ln x     x  3x  2 1 2 1 2 1 1 1  x    x   1  x  x  
 2ln 4  ln 5  2ln 2  ln 3  2ln 2  ln 3  ln 5 Suy ra a  ; 2 b  ; 1 c  1  S  6 . Cách 2: PP casio 3 x  3 Bước 1: Tính tích phân dx 
sau đó gán thành biến A. x2  3x  2 1
Nhấn SHIFT STO (-) để được
Bước 2: Tính phép toán lũy thừa kA
e với k  1, 2,3, 4,5,... là các số nguyên mục tiêu là ta được
kết quả trên máy là một số hữu tỷ. 2 12 2 .3 Bước 3: Ta dễ dàng phân tích được 2 1 1 2 .3 .5   do vậy 5 5 12 2 1 1 A ln ln(2 .3 .5  
)  2 ln 2  ln 3  ln 5 suy ra a  2,b  1,c  1  từ đây 2 2 2 a  b  c  6 . 5
Chú ý: Quá trình bấm máy có thể nhanh hơn so với tốc độ ghi tự luận nhiều. e 2 . a e  b Câu 32. Cho I  x ln d x x 
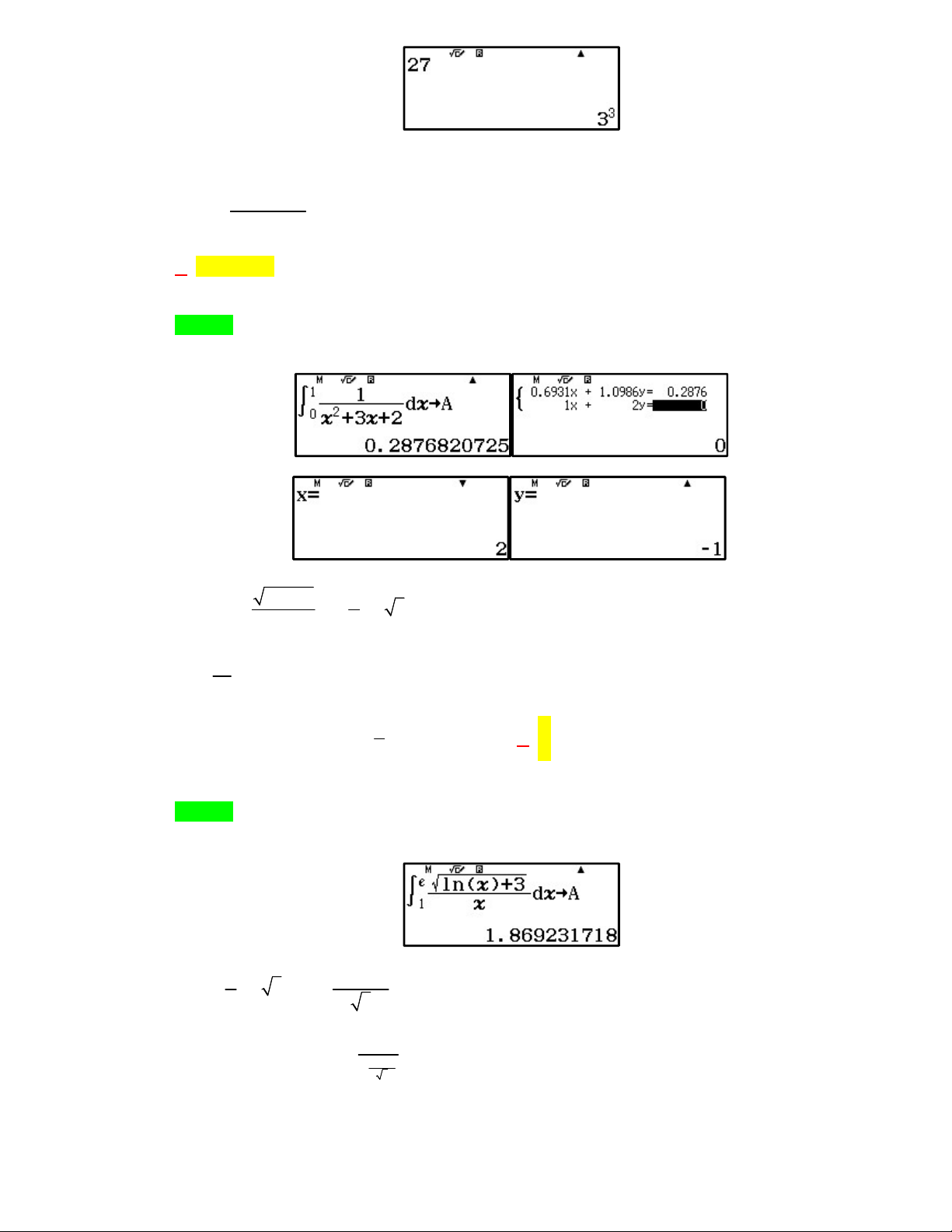
với a , b , c   . Tính T  a  b  c .  c 1 A. 5 . B. 3 . C. 4 . D. 6 . Lời giải Chọn D Cách 1: PP tự luận  1 du  dx u   ln x  x Ta có:  nên  . dv  d x x 2 x v   2 a  1 e e 2 e x 1 2 e  1  I  x ln d x x  ln x  xdx   b   1 .   2 2 4 1 1 1 c  4 
Vậy T  a  b  c  6 . Cách 2: PP casio
+ Thử C=1,2,3,4,5,6. giải hệ tìm a,b nguyên. . 2 Câu 33. Biết 2x ln 
x  1dx  .alnb, với *
a, b   , b là số nguyên tố. Tính 6a  7b . 0 A. 33 . B. 25 . C. 42 . D. 39 . Lời giải Chọn.D. Cách 1: PP tự luận 2 Xét I  2x ln  x    1 dx  6 . 0  1 u   ln x   1 du  dx Đặt    x 1 . dv  2 d x x 2 v  x 1 2 2 2 x 1 Ta có: I   2 x   1 ln  x   1  dx  0 x 1 0 2 2 2    x 3ln 3   x    1 dx  3ln 3   x  3ln 3 .   2 0   0
Vậy a  3, b  3  6a  7b  39 . Cách 2: PP casio Ta có .ln  ln a a b b Bước 1. Bước 2.  ln a a A A b  b  e . Bước 3. Bấm Shift + FACT
Vậy a  3, b  3  6a  7b  39 . 1  1 Câu 34. Cho  dx  aln 2 bln3 
với a,b là các số nguyên. Mệnh đề nào đúng? 2   x  3x  2  0 A. a  2b  0 . B. a  2b  0 . C. a  b  2 . D. a  b  2 . Lời giải Chọn A Cách 1: PP casio . e ln x  3 a Câu 35. Cho biết dx   b 3 
, với a , b là các số nguyên. Giá trị của biểu x 3 1 1 thức  log a bằng 2 2b 7 A. -1. B. . C. 8. D. 6. 2 Lời giải Chọn C Cách 1: PP casio a A  a : 3 . A   b 3  b  3 3 1 . Solve nghiệm nguyên:  log x A x:3 2 3 2
. Thử từ đáp án. Thấy ngay A thỏa mãn vì phương trình có nghiệm nguyên. 4 dx Câu 36. Biết I 
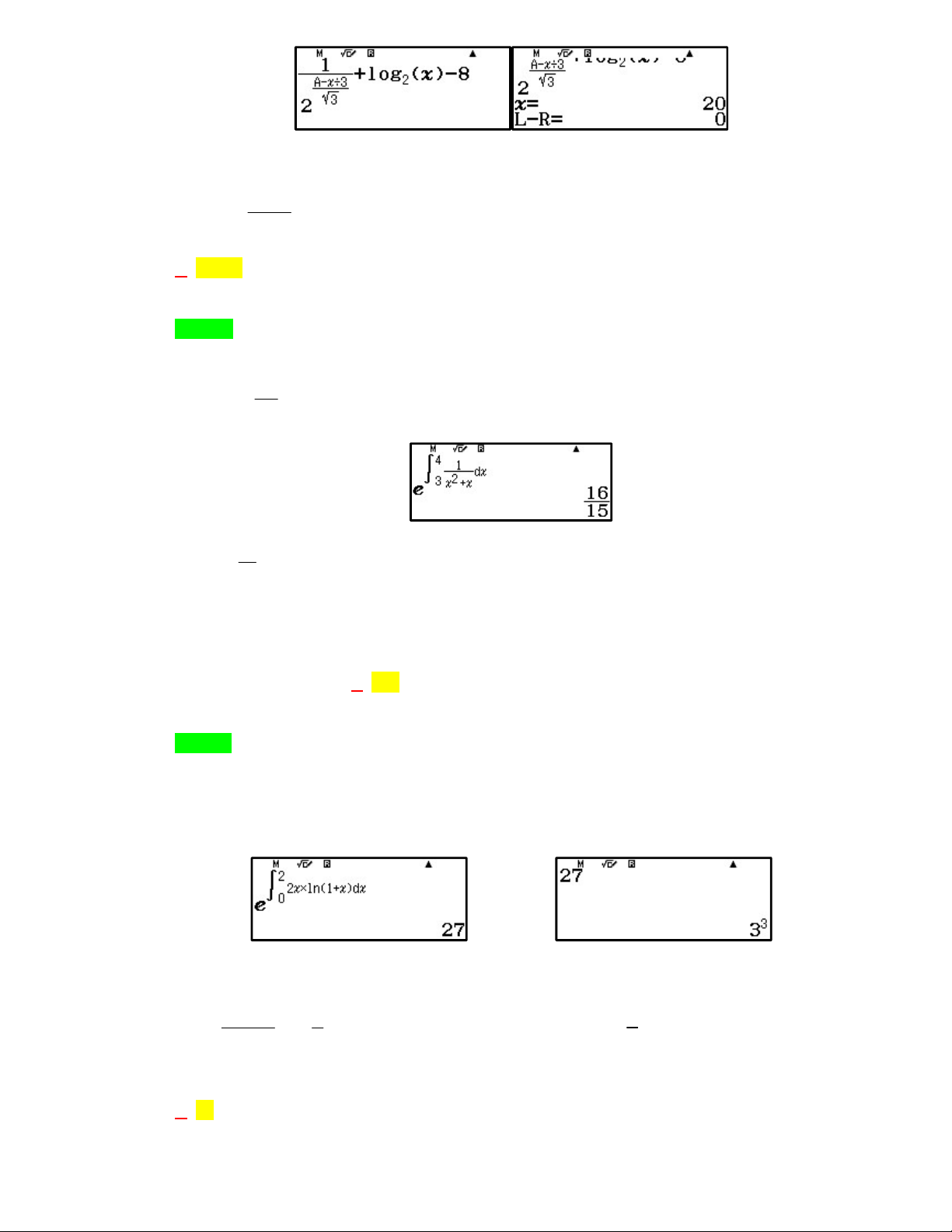
 a ln 2  b ln 3  c ln 5 
, trong đó a,b, c   . Tính giá trị của T  a  b  c . 2 x  x 3 A. T  2 . B. T  3. C. T  1 . D. T  5 . Lời giải Chọn A Cách 1: PP casio 4 dx  2 .Ta có: x x 3 a ln 2bln35ln e  e c  2a.3 .b5c . 16 . Nhập 4 1 1 2 .3 .5 
 2a.3 .b5c  a  4;b  1  ;c  1. . 15 2 Câu 37. Biết 2x ln 
1 xdx  .aln b , với * ,
a b , b là số nguyên tố. Tính 3a  4b . 0 A. 42 . B. 21 . C. 12 . D. 32 . Lời giải Chọn B Cách 1: PP casio 2 2 x ln1xdx  . Ta có: 0 e a  b Shift FACT
. Vậy a  3 , b  3  3a  4b  21 . 3 ln x a a Câu 38. Cho dx   ln 3  c  ln 2  với a, ,
b c * và phân số tối giản. Giá trị của x  2 b b 1 1 a  b  c bằng A. 8 . B. 7 . C. 6 . D. 9 . Lời giải Chọn A Cách 1: PP casio a . Chú ý: c=x,
 f  x , bài toán có điều kiện a, , b c  * b
. Do đó a  b  c  8 . ln 6 ex Câu 39. Biết dx  a  b ln 2  c ln 3 
với a , b , c là các số nguyên. Tính T  a  b  c . x 0 1  e  3 A. T  1. B. T  0 . C. T  2 . D. T  1. Lời giải Chọn B Cách 1: PP casio . ln 2 ln 3 A a 2b.3c A a b c e      
. Suy ra a  2 , b  4 , c  2 nên T  a  b  c  0 . 1 a 2 1 Câu 40. Cho biết 2 x x 1 dx  
với a , b là các số tự nhiên. Giá trị của 2 2 a  b bằng b 0 A. 5. B. 5. C. 2. D. 7. Lời giải Chọn A Cách 1: PP casio
. Với b  x; a  f  x  a  2 , b  3 . . Vậy 2 2 a  b  5  .