Một số ứng dụng khác của tích phân Toán 12

Tài liệu gồm 25 trang, trình bày lý thuyết trọng tâm, các dạng toán trọng tâm kèm phương pháp giải và bài tập trắc nghiệm tự luyện chuyên đề một số ứng dụng khác của tích phân, có đáp án và lời giải chi tiết; hỗ trợ học sinh lớp 12 trong quá trình học tập chương trình Toán 12 phần Giải tích chương 3.

Môn:

Toán 12 3.8 K tài liệu

Thông tin:
25 trang 1 năm trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Một số ứng dụng khác của tích phân Toán 12

Tài liệu gồm 25 trang, trình bày lý thuyết trọng tâm, các dạng toán trọng tâm kèm phương pháp giải và bài tập trắc nghiệm tự luyện chuyên đề một số ứng dụng khác của tích phân, có đáp án và lời giải chi tiết; hỗ trợ học sinh lớp 12 trong quá trình học tập chương trình Toán 12 phần Giải tích chương 3.

62 31 lượt tải Tải xuống

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn: Toán 12 3.8 K tài liệu

Thông tin:

25 trang 1 năm trước

Tác giả:

Profile Mai Nguyệt
Chủ đề 14: MỘT SỐ ỨNG DỤNG KHÁC CỦA TÍCH PHÂN
Dạng 1: Bài toán liên quan đến quãng đường, vận tốc, gia tốc và thời gian
Với bài toán chuyển động giả sử vận tốc tức thời của vật là
(
)
vt
thì
( ) ( )
'vt s t=
Gia tốc tức thời của vật:
( ) ( ) ( )
'"at v t s t
= =
Do đó quãng đường vật đi được từ thời điểm
1
t
đến
2
t
là
(
)
2
1
.
t
t
S v t dt=
∫
Vận tốc tức thời của vật:
( ) ( )
v t a t dt=
∫
Ví dụ 1: Một ô tô đang chạy với vận tốc 20 m/s thì người lái hãm phanh. Sau khi hãm phanh, ô tô chuyển
động chậm dần đều với vận tốc
(m/s) trong đó
t
là khoảng thời gian tính bằng giây kể từ
lúc bắt đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét?
A. 25 m. B. 50 m. C. 10 m. D. 30 m.
Lời giải:
Khi vật dừng hẳn thì
( )
0 4 20 0 5 .v t ts= ⇒− + = ⇔ =
Quãng đường vật đi được trong khoảng thời gian trên là:
( ) ( ) ( )
55
00
4 20 50S t v t dt t dt= = −+ =
∫∫
m.
Chọn A.
Ví dụ 2: Một ô tô xuất phát với vận tốc
( ) ( )
1
2 12 / ,vt t ms= +
sau khi đi được khoảng thời gian
1
t
thì bất
ngờ gặp chướng ngại vật nên tài xế phanh gấp với vận tốc
( ) ( )
2
24 6 / ,v t tms= −
và đi thêm một khoảng
thời gian
2
t
nữa thì dừng lại. Hỏi từ khi xuất phát đến lúc dừng lại thì xe ô tô đã đi được bao nhiêu mét ?
A.
12 .m
B.
156 .m
C.
108 .m
D.
48 .m
Lời giải:
Ta có:
( )
02
24 /v ms=
do đó khi gặp chướng ngại vật vật có vận tốc là
24 /ms
Khi đó
(
) ( )
1
2 12 24 6vt t t s= + = ⇔=
Vật dừng lại khi
( ) ( )
22
24 6 0 4vt t t s= −=⇔=
Quãng đường vật đi được là:
( ) ( ) ( ) ( )
64 6 4
12
00 0 0
2 12 24 6 156 .s v t dt v t dt t dt t dt m= + =+ +− =
∫∫ ∫ ∫
Chọn B.
Ví dụ 3: Một chất điểm đang chuyển động với vận tốc
( )
0
16 /v ms=
thì tăng tốc với gia tốc
(
)
(
)
22
3 /.
at t t m s= +
Tính quãng đường chất điểm đó đi được trong khoảng thời gian
4s
kể từ lúc bắt đầu
tăng tốc.
A.
( )
160
.
3
m
B.
( )
352
.
3
m
C.
( )
400
.
3
m
D.
( )
250
.
3
m
Lời giải:
Ta có:
( ) ( )
( )
32
2
3
3
32
tt
v t a t dt t t dt C= = + =++
∫∫
Khi đó
( ) ( )
32
0
3
0 16 16
32
tt
v v C vt= ==⇒ =++
Khi đó quãng đường đi được bằng:
( ) ( )
44
32
00
3
16
32
tt
s t v t dt dt

= = ++


∫∫
( )
4
43
0
352
16 .
12 2 3
tt
tm

++ =


Chọn B.
Ví dụ 4: Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc
( ) ( )
1
2 /.vt tms=
Đi được 12 giây,
người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc
(
)
2
12 / .
a ms= −
Tính quãng đường
(
)
sm
đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng
hẳn
A.
168 .sm=
B.
166 .sm
=
C.
144 .sm=
D.
152 .sm
=
Lời giải:
Quãng đường xe đi được trong 12 s đầu là:
12
1
0
2 144 .s tdt m
= =
∫
Sau khi đi được 12 s vật đạt vận tốc
24 / ,v ms=
sau đó vận tốc của vật có phương trình
24 12vt= −
Vật dừng hẳn sau
2 s
kể từ khi phanh.
Quãng đường vật đi được từ khi đạp phanh đến khi dừng hẳn là:
( )
2
2
0
24 12 24 .s t dt m
=−=
∫
Vậy tổng quãng đường ô tô đi được là
12
144 24 168 .ss s m=+= + =
Chọn A.
Ví dụ 5: Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang phải) với gia
tốc phụ thuộc thời gian
( )
ts
là
( )
( )
2
27 / .at t m s= −
Biết vận tốc ban đầu bằng
( )
10 / ,ms
hỏi trong 6 giây
đầu tiên, thời điểm nào chất điểm ở xa nhất về phía bên phải?
A.
(
)
5.s
B.
( )
6.s
C.
( )
1.s
D.
( )
2.s
Lời giải:
Vận tốc của vật được tính theo công thức
( ) ( )
2
10 7 / .vt t t m s= +−
Suy ra quãng đường vật đi được tính theo công thức
( )
(
) ( )
3
2
7
10 .
32
t
S t v t dt t t m= =−+
∫
Ta có
( ) (
)
22
2
7 10 0 7 10 0 .
5
t
St t t St t t
t
=
′′
=−+⇒ =⇔−+=⇔
=
Suy ra
( )
(
)
( )
( )
[
]
( ) ( )
0;6
00
26
2
26
6
2.
25
3
5
6
66
S
S
Max S t S
S
S
=
=
⇒==
=
=
Chọn D.
Ví dụ 6: [Đề thi thử Chuyên Đại học Vinh 2017] Tại một nơi không có gió, một chiếc khí cầu đang đứng
yên ở độ cao 162 (mét) so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết
rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật
( )
2
10 ,vt t t= −
trong
đó
t
(phút) là thời gian tính từ lúc bắt đầu chuyển động,
( )
vt
được tính theo đơn vị mét/phút (m/p). Nếu
như vậy thì khi bắt đầu tiếp đất vận tốc
v
của khí cầu là
A.
( )
7 /.v mp=
B.
( )
9 /.v mp=
C.
(
)
5 /.v mp=
D.
( )
3 /.v mp=
Lời giải:
Khi bắt đầu tiếp đất vật chuyển động được quãng đường là
162sm=
Ta có:
( )
0
0
3
3
22
0
0
0
0
10 5 5
33
t
t
t
t
S t t dt t t

=−=−=−


∫
(trong đó
0
t
là thời điểm vật tiếp đất)
Cho
3
2
0
00
5 162 9
3
t
tt−= ⇒=
(Do
( )
2
10 0 10)vt t t t
= − ⇒ ≤≤
Khi đó vận tốc của vật là:
( ) ( )
2
9 10.9 9 9 / .v mp
= −=
Chọn B.
Ví dụ 7: [Đề thi THPT Quốc gia 2018] Một chất điểm
A
xuất phát từ
,O
chuyển động thẳng với vận tốc
biến thiên theo thời gian bởi quy luật
( )
( )
2
1 13
/,
100 30
vt t t m s= +
trong đó
t
(giây) là khoảng thời gian tính
từ lúc
A
bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm
B
cũng xuất phát từ
,O
chuyển độ
ng
thẳng cùng hướng với
A
nhưng chậm hơn 10 giây so với
A
và có gia tốc bằng
( )
2
/ams
(
a
là hằng số).
Sau khi
B
xuất phát được 15 giây thì đuổi kịp
.A
Vận tốc của
B
tại thời điểm đuổi kịp
A
bằng
A.
( )
25 / .ms
B.
(
)
15 / .
ms
C.
( )
9 /.ms
D.
( )
42 / .ms
Lời giải:
Quãng đường chất điểm A đi được cho đến khi hai chất điểm gặp nhau là:
25
2
0
1 13 375
.
100 30 2
S t t dt m

= +=


∫
Vận tốc của chất điểm B tại thời điểm
( )
ts
tính từ lúc B xuất phát là:
( )
.
B
v t at=
Quãng đường chất điểm B đi được cho đến khi 2 chất điểm gặp nhau là:
( )
10
10
2
0
0
225
.
22
at
S atdt a m= = =
∫
Suy ra
225 375 5
22 3
aa= ⇔=
Vậy vận tốc của B tại thời điểm đuổi kịp A là:
( ) ( )
15 15 25 / .
B
v a ms= =
Chọn A.
Ví dụ 8: [Đề thi THPT Quốc gia 2018] Một chất điểm
A
xuất phát từ
,O
chuyển động thẳng với vận tốc
biến thiên theo thời gian bởi quy luật
(
)
2
1 11
180 18
vt t t
= +
(m/s), trong đó
t
(giây) là khoảng thời gian tính
từ lúc
A
bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm
B
cũng xuất phát từ
,O
chuyển độ
ng
thẳng cùng hướng với
A
, nhưng chậm hơn 5 giây so với
A
và có gia tốc bằng
( )
2
/am s
(
a
là hằng số).
Sau khi
B
xuất phát được 10 giây thì đuổi kịp
.A
Vận tốc của
B
tại thời điểm đuổi kịp
A
bằng
A.
22
(m/s). B. 15 (m/s). C. 10 (m/s). D. 7 (m/s).
Lời giải:
Quãng đường chất điểm A đi được cho đến khi hai chất điểm gặp nhau là:
15
2
0
1 11
75 .
180 8
S t t dt m

= +=


∫
Vận tốc của chất điểm B tại thời điểm
( )
ts
tính từ lúc B xuất phát là:
( )
.
B
v t at=
Quãng đường chất điểm B đi được cho đến khi 2 chất điểm gặp nhau là:
( )
10
10
2
0
0
50 .
2
at
S atdt a m= = =
∫
Suy ra
50 75 1,5aa= ⇔=
Vậy vận tốc của B tại thời điểm đuổi kịp A là:
( ) ( )
10 10 15 / .
B
v a ms= =
Chọn B.
Ví dụ 9: Một vật chuyển động trong 4 giờ với vận tốc
(
)
/
v km h
phụ thuộc
thời gian
(
)
th
có đồ thị của vận tốc như hình bên. Trong khoảng thời gian 3
giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol
có đỉnh
( )
2;9I
với trục đối xứng song song với trục tung, khoảng thời gian
còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường
s
mà vật di chuyển được trong 4 giờ đó?
A.
( )
27 .s km=
B.
( )
24 .s km=
C.
( )
28,5 .s km=
D.
( )
26,5 .s km=
Lời giải:
Dựa vào đồ thị ta tính được phương trình vận tốc của vật
Từ 0 đến 3 giây:
( ) ( )
2
1
9
9 /.
4
v t t t km h=−+
Từ 3 giây trở đi:
( )
( )
2
27
/.
4
v t km h=
Suy ra quãng đường vật đi được trong 4 giây sẽ bằng
( )
34
2
03
9 27
9 27 .
44
s t t dt dt km

=−+ + =


∫∫
Chọn A.
Ví dụ 10: [Đề thi THPT Quốc gia 2017] Một người chạy trong thời gian 1
giờ, vận tốc
( )
/v km h
phụ thuộc thời gian
( )
th
có đồ thị là một phần của
đường parabol với đỉnh
1
;8
2
I



và trục đối xứng song song với trục tung
như hình bên. Tính quãng đường
s
người đó chạy được trong khoảng thời
gian 45 phút, kể từ khi bắt đầu chạy.
A.
( )
4,0 .s km=
B.
( )
2,3 .s km=
C.
( )
4,5 .s km=
D.
( )
5,3 .s km=
Lời giải:
Dựa vào đồ thị ta tính được PT vận tốc là
( )
2
1
8
2
vt a x

= −+


Do parabol
( )
P
qua điểm
( ) ( ) ( )
2
1;0 32 32 32 / .a v t t t km h⇒=− ⇒ =− +
Suy ra quãng đường đi được trong 45 phút bằng
( )
0,75 h
là
( )
(
)
0,75
2
0
32 32 4,5 .
S t t dt km
=−+ =
∫
Chọn C.
Dạng 2: So sánh các giá trị của hàm số
Ví dụ 1: Cho hàm số
( )
y fx=
có đồ thị hàm số
( )
y fx
′
=
cắt trục
Ox
tại ba điểm có hoành độ
,,abc
thỏa mãn
abc<<
như hình vẽ. Mệnh đề nào sau đây
đúng?
A.
( ) ( ) ( )
.fa fb fc>>
B.
( ) ( ) ( )
.fa fc fb>>
C.
( ) ( ) ( )
.fc fb fa>>
D.
( ) ( ) (
)
.fc fa fb>>
Lời giải:
Dựa vào đồ thị hàm số
( )
y fx
′
=
ta có BBT của hàm số
( )
y fx
=
như sau:
x
−∞
a
b
c
+∞
( )
fx
′
+ 0
−
0 + 0
−
( )
fx
( )
fa
(
)
fc
−∞
( )
fb
−∞
Lại có:
(
)
(
) ( ) (
)
1
'' ;
bb
aa
S f x dx f x dx f a f b= =−=−
∫∫
tương tự
(
) (
)
2
S fc fb
= −
Dựa vào hình vẽ ta thấy
( )
( ) ( ) (
) ( ) ( )
12
.S S fa fb fc fb fa fc>⇒−>−⇔>
Chọn B.
Ví dụ 2: Cho
(
)
y fx
=
có đồ thị
(
)
y fx
′
=
như hình.
Đặt
(
)
( )
cos .gx f x x
= +
Mệnh đề nào đúng?
A.
( )
(
)
3
0.
4
ggg
π

< π<


B.
( ) ( )
3
0.
4
g gg
π

< <π


C.
(
) (
)
3
0.
3
ggg
π

π< <


D.
( )
( )
3
0.
4
g gg
π

< π<


Lời giải:
Ta có
( ) ( ) ( )
( )
' ' sin ' ' sing x f x x g x dx f x x dx= −⇒ = −


∫∫
Bảng biến thiên của hàm số
( )
y gx=
x
−∞
0
3
4
π
π
+∞
( )
gx
′
+ 0
−
0 + 0
−
(
)
gx
( )
0g
( )
g
π
−∞
3
()
4
g
π
−∞
Đặt
( )
( )
(
)
33
44
1
00
3
sin ' 0
4
S x f x g x dx g g
ππ
π

= −=− =−




∫∫
( )
(
) ( )
2
33
44
3
sin '
4
S f x x g x dx g g
ππ
ππ
π

= − = = π−




∫∫
Dựa vào hình vẽ ta có
( ) ( )
12
0.SS g g>⇒ >π
Do đó
( ) ( )
3
0.
4
g gg
π

< π<


Chọn D.
Ví dụ 3: Cho hàm số
(
)
y fx=
. Đồ thị của hàm số
(
)
y fx
′
=
như hình
bên. Đặt
(
) (
)
( )
2
2 1.
gx f x x
= ++
Mệnh đề nào dưới đây đúng?
A.
( ) ( ) ( )
1 3 3.gg g< <−
B.
( ) ( ) ( )
1 3 3.gg g< −<
C.
( ) ( ) ( )
3 3 1.gg g< −<
D.
( ) ( ) ( )
3 3 1.gg g< −<
Lời giải:
Ta có
( ) ( ) ( ) ( )
' 2' 12' 1gx fx x fx x= + + = −−−


( )
( ) ( )
'
'1
2
gx
dx f x x dx⇒ = −− −


∫∫
Đường thẳng
:1dy x
=−−
đi qua các điểm
( ) ( )
3; 2 ; 1; 2−−
và
( )
3; 4−
Với
3
x >
ta có:
( )
( )
1' ' 0
x f x gx−−> ⇒ <
Ta có BBT của hàm số
( )
gx
x
−∞
3
−
1
3
+∞
( )
gx
′
+ 0
−
0 + 0
−
(
)
gx
( )
3g −
( )
3g
−∞
( )
1g
−∞
Đặt
(
) ( )
( ) ( )
13
12
31
1 ' d; ' 1 d
S x fx xS fx x x
−
= −− − = −−−


∫∫
Dựa vào hình vẽ ta có
( ) ( )
13
12
31
''
dd
22
gx gx
SS x x
−
> ⇒− >
∫∫
Do đó
( ) ( )
( ) ( ) (
) ( )
31 31 3 3.
g ggg g g−− > − ⇒ −>
Chọn A.
Ví dụ 4: Cho hàm số
( )
.
fx
Đồ thị của hàm số
(
)
y fx
′
=
như hình bên.
Đặt
( ) ( )
2
2.hx f x x= −
Mệnh đề nào dưới đây đúng?
A.
( )
( )
(
)
4 2 2.hh h= −>
B.
( ) ( ) ( )
4 2 2.hh h= −<
C.
( ) ( ) ( )
2 2 4.hh h> −>
D.
( ) ( ) ( )
2 4 2.
hhh> >−
Lời giải:
Ta có:
( ) ( )
( )
( )
'
' 2' d ' d
2
hx
hx fx x x fx xx= −⇒ = −
 
 
∫∫
Đường thẳng
yx=
đi qua các điểm
( ) ( ) ( )
2; 2 ; 2; 2 ; 4; 4−−
trên hình vẽ
Với
2x <−
ta có:
( )
'hx x<
suy ra hàm số nghịch biến trên khoảng
( )
;2−∞ −
Ta có bảng biến thiên của hàm số
( )
hx
như sau:
x
−∞
2−
2
4
+∞
( )
hx
′
−
0 + 0
−
0 +
( )
hx
+∞
( )
2h
+∞
( )
2h −
( )
4h
Đặt
( ) ( )
24
12
22
' d; ' dS fx xxS xfx x
−
=−=−
 
 
∫∫
Dựa vào hình vẽ ta có:
( ) ( )
24
12
22
dd
22
hx hx
SS x x
−
−
>⇒ >
∫∫
( )
( ) ( ) ( )
( ) (
)
2 2 2 4 4 2.hh hh h h⇒−−>−⇔>−
Chọn D.
Ví dụ 5: Cho hàm số
( )
.y fx=
Đồ thị hàm số
( )
y fx
′
=
như hình vẽ bên. Đặt
[ ]
( )
2;6
max ,M fx
−
=
.TMm= +
Mệnh đề nào dưới đây
đúng?
A.
( )
( )
0 2.Tf f= +−
B.
( ) ( )
5 2.
Tf f= +−
C.
( ) ( )
5 6.Tf f= +
D.
(
) (
)
0 2.
Tf f= +
Lời giải:
Dựa vào đồ thị hàm số
( )
'y fx
=
ta lập được bảng biến thiên của hàm số
(
)
y fx
=
x
2−
0
2
5
6
y
′
+ 0
−
0 + 0
−
y
Ta đặt:
( )
( )
( )
(
) (
) (
)
05
12
22
'd 0 2; 'd 5 2
fxxS f f fxxS f f==−==−
∫∫
Dựa vào đồ thị ta có:
( ) ( ) ( )
21
50 5SS f f Mf
>⇒>⇒=
(loại A và D).
Ta cần so sánh
( )
2f −
và
(
)
6f
Tương tự ta có:
(
)
( )
( )
( )
(
) (
)
05
34
26
'd 0 2 ; 'd 5 6fxx f f S fxx f f S
−
= − −= = − =
∫∫
Quan sát đồ thị suy ra
( ) (
) ( ) ( ) ( ) ( )
( ) ( )
34
0 2 56 6 2 500SSff ff ff ff> ⇒ − −> − ⇒ − −= − >
Do đó
( ) ( ) ( )
2 6 2.f f mf
−< ⇒= −
Chọn B.
BÀI TẬP TỰ LUYỆN
Câu 1: Một chất điểm đang chuyển động với vận tốc
0
18 /v ms=
thì tăng tốc với gia tốc
(
)
( )
22
5 /.at t tm s
= +
Tính quãng đường chất điểm đó đi được trong khoảng thời gian
3
s
kể từ lúc bắt đầu
tăng tốc.
A.
117
.
4
m
B.
333
.
4
m
C.
63
.
2
m
D.
126 .m
Câu 2: Một vật chuyển động chậm dần với vận tốc
( ) ( )
150 15 / .vt t m s= −
Hỏi rằng trong
5
s
trước khi
dừng hẳn vật di chuyển được bao nhiêu mét?
A.
1125
.
2
m
B.
120 .m
C.
375
.
2
m
D.
750 .
m
Câu 3: Một ô tô đang chạy đều với vận tốc
(
)
/bms
thì người lái xe đạp phanh. Từ thời điểm đó ô tô
chuyển động chậm dần đều với vận tốc
( ) ( )
4 /.vt t b m s=−+
Biết từ khi đạp phanh đến lúc dừng hẳn thì ô
tô di chuyển được
50 .m
Tìm
.b
A.
12, 5 / .ms
B.
15 / .ms
C.
25 / .ms
D.
20 / .ms
Câu 4: Một ô tô xuất phát với vận tốc
( ) (
)
1
2 12 /vt t ms= +
sau khi đi được một khoảng thời gian
1
t
thì bất
ngờ gặp chướng ngại vật nên tài xế phanh gấp với vận tốc
( ) ( )
2
24 6 /c t tms= −
và đi thêm một khoảng thời
gian
2
t
nữa thì dừng lại. Hỏi từ khi xuất phát đến lúc dừng lại thì xe ô tô đã đi được bao nhiêu mét?
A.
156 .
m
B.
108 .
m
C.
48 .
m
D.
112 .m
Câu 5: Một ô tô đang chạy với vận tốc
20 /ms
thì dừng lái đạp phanh. Sau khi đạp phanh, ô tô chuyển
động chậm dần đều với vận tốc
( ) ( )
20 40 / ,vt t m s= −
trong đó
t
là khoảng thời gian tính bằng giây kể từ
lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét?
A.
10 .
m
B.
7.
m
C.
5.m
D.
3.m
Câu 6: Một vật chuyển động với gia tốc
( )
( )
22
3 /.at t t m s= +
Vận tốc ban đầu của vật là
( )
2 /.ms
Hỏi
vận tốc của vật là bao nhiêu sau khi chuyển động với gia tốc đó được
2.s
A.
8 /.ms
B.
12 / .ms
C.
16 / .ms
D.
10 / .ms
Câu 7: Một ô tô đang dừng và bắt đầu chuyển động theo một đường thẳng với gia tốc
( )
( )
2
62 / ,at t m s= −
trong đó
t
là khoảng thời gian tính bằng giây kể từ lúc ô tô bắt đầu chuyển động. Hỏi quãng đường ô tô đi
được kể từ lúc bắt đầu chuyển động đến khi vận tốc của ô tô đạt giá trị lớn nhất là bao nhiêu mét?
A.
45
.
2
m
B.
18 .m
C.
36 .m
D.
27
.
4
m
Câu 8: Một vật chuyển động với vận tốc
(
)
(
)
2
4
1, 2 / .
3
t
vt m s
t
+
= +
+
Tính quãng đường vật đó đi được trong
4 giây đầu (làm tròn kết quả đến chữ số thập phân thứ hai).
A.
1, 64 .m
B.
11,01 .
m
C.
11,81 .m
D.
11,18 .m
Câu 9: Một chất điểm
A
từ trạng thái nghỉ chuyển động với vận tốc nhanh dần đều,
8
s
sau nó đạt đến vận
tốc
6 /.
ms
Từ thời điểm đó nó chuyển động đều. Một chất điểm
B
khác xuất phát từ cùng vị trí với
A
nhưng chậm hơn nó
12 s
với vận tốc nhanh dần đều và đuổi kịp
A
sau
8 s
(kể từ lúc
B
xuất phát). Tìm vận
tốc
B
tại thời điểm đó.
A.
12 / .ms
B.
24 / .ms
C.
18 / .ms
D.
30 / .ms
Câu 10: Một ô tô đang chạy với vận tốc
36 /km h
thì tăng tốc chuyển động nhanh dần với gia tốc
( )
(
)
2
1
1 /.
3
at t m s= +
Tính quãng đường mà ô tô đi được sau 6 giây kể từ khi ôtô bắt đầu tăng tốc.
A.
90 .m
B.
246 .
m
C.
58 .m
D.
102 .m
Câu 11: Một ô tô đang chuyển động đều với vận tốc
12 /
ms
thì người lái đạp phanh; từ thời điểm đó ô tô
chuyển động chậm dần đều với vận tốc
( ) ( )
12 2 /
vt t m s= −
(trong đó
t
là thời gian tính bằng giây, kể từ
lúc đạp phanh). Hỏi trong thời gian 8 giây cuối (tính đến khi xe dừng hẳn) thì ô tô đi được quãng đường
bằng bao nhiêu?
A.
16 .m
B.
60 .m
C.
32 .m
D.
100 .
m
Câu 12: Bạn An ngồi trên máy bay đi du lịch thế giới vận tốc chuyển động của máy bay là
( ) ( )
2
3 5 /.
vt t m s= +
Hỏi quãng đường máy bay đi được từ giây thứ 4 đến giây thứ 10 bằng bao nhiêu?
A.
996 .m
B.
876 .m
C.
966 .m
D.
1086 .m
Câu 13: Một vận động viên đua xe
F
đang chạy với vận tốc
( )
10 /ms
thì anh ta tăng tốc với vận tốc
( )
( )
2
6 /,at t m s=
trong đó
t
là khoảng thời gian tính bằng giây kể từ lúc tăng tốc, hỏi quãng đường xe của
anh ta đi được trong thời gian
10 s
kể từ lúc bắt đầu tăng tốc là bao nhiêu?
A.
1100 .m
B.
100 .
m
C.
1010 .m
D.
1110 .m
Câu 14: Một vật chuyển động chậm dần đều với vận tốc
( ) ( )
30 2 / .vt t m s= −
Hỏi trong
5 s
trước khi
dừng hẳn, vật di chuyển động được bao nhiêu mét?
A.
50 .m
B.
225 .
m
C.
125 .m
D.
25 .
m
Câu 15: Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc
( ) ( )
1
7 /s .vt tm=
Đi được
5 s
người lái
xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc
( )
2
70 / .a ms= −
Tính quãng đường đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
A.
95, 70 .m
B.
96,25 .m
C.
87,50 .m
D.
94,00 .m
Câu 16: Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi công thức
( )
3 2,vt t= +
thời
gian tính theo đơn vị giây, quãng đường vật đi được tính theo đơn vị mét. Biết tại thời điểm
2ts=
thì vật đi
được quãng đường là
10 .m
Hỏi tại thời điểm
30ts=
thì vật đi được quãng đường là bao nhiêu?
A.
240 .m
B.
1140 .m
C.
300 .m
D.
1410 .
m
Câu 17: Một học sinh đi học từ nhà đến trường bằng xe đạp với vận tốc thay đổi theo thời gian được tính
bởi công thức
( )
40 100 ( /vt t m= +
phút). Biết rằng sau khi đi được 1 phút thì quãng đường học sinh đó đi
được là
120 .m
Biết quãng đường từ nhà đến trường là
3.km
Hỏi thời gian học sinh đó đi đến trường là bao
nhiêu phút?
A. 9 phút. B. 15 phút. C. 10 phút. D. 12 phút.
Câu 18: Một vật chuyển động với vận tốc
( )
10 /
ms
thì tăng tốc với gia tốc
( )
( )
22
3 /.at t t m s= +
Tính
quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc.
A.
4000
.
3
m
B.
4350
.
3
m
C.
4300
.
3
m
D.
1433 .m
Câu 19: Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang phải) với gia
tốc phụ thuộc vào thời gian
(
)
ts
là
( )
(
)
2
27 / .at t m s
= −
Biết vận tốc đầu bằng
( )
10 / .ms
Hỏi trong 6 giây
đầu tiên, thời điểm nào chất điểm ở xa nhất về phía bên phải?
A.
5.s
B.
6.s
C.
1.
s
D.
2.s
Câu 20: Một ô tô đang chạy thì người lái đạp phanh, từ thời điểm đó, ô tô chuyển động chậm dần đều với
vận tốc
(
) (
)
12 24 / ,vt t m s=−+
trong đó
t
là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh.
Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
A.
18 .m
B.
15 .m
C.
20 .
m
D.
24 .
m
Câu 21: Một vật chuyển động với vận tốc
( )
vt
( )
/ms
có gia tốc
(
)
( )
2
3
' /.
1
vt ms
t
=
+
Vận tốc ban đầu của
vật là
6 /.ms
Tính vận tốc của vật sau 10 giây, (làm tròn kết quả đến hàng đơn vị).
A.
( )
10 / .ms
B.
( )
8 /.ms
C.
( )
15 / .ms
D.
( )
13 / .ms
Câu 22: Một đám vi sinh trùng tại ngày thứ
t
có số lượng
( )
,Nt
biết rằng
( )
7000
'
2
Nt
t
=
+
và lúc đầu đám vi
trùng có 300000 con. Hỏi sau 10 ngày, đám vi trùng có bao nhiêu con (làm tròn đến hàng đơn vị)?
A. 322542 con. B. 332542 con. C. 302542 con. D. 312542 con.
Câu 23: Khi quan sát một đám vi khuẩn trong phòng thí nghiệm người ta thấy tại ngày thứ
x
có số lượng
( )
Nx
con. Biết rằng
( )
2017
'
1
Nx
x
=
+
và lúc đầu đám vi khuẩn có 30000 con. Hỏi số lượng vi khuẩn sau
đúng một tuần gần với số nào sau đây?
A. 36194. B. 38417. C. 35194. D. 34194.
Câu 24: (Đề thi THPT Quốc gia 2017) Một vật chuyển động trong 3 giờ với vận tốc
( )
km/hv
phụ thuộc thời gian
( )
ht
có đồ thị là một phần của đường parabol có đỉnh
( )
2;9
I
và trục đối xứng song song với trục tung như hình bên. Tính quãng đường
s
mà
vật di chuyển được trong 3 giờ đó.
A.
( )
26,75 km .
s =
B.
( )
25,25 km .s =
C.
( )
24,25 km .s =
D.
( )
24,75 km .s
=
Câu 25: (Đề thi THPT Quốc gia 2017) Một người chạy trong thời gian 1 giờ
với vận tốc
( )
km/hv
phụ thuộc thời gian
( )
ht
có đồ thị là một phần parabol với
đỉnh
1
;8
2
I



và trục đối xứng song song với trục tung như hình bên. Tính quãng
đường
s
mà người đó chạy được trong khoảng thời gian 45 phút kể từ khi chạy.
A.
( )
4 km .s =
B.
(
)
2,3 km .
s =
C.
( )
4,5 km .s =
D.
( )
5,3 km .s =
Câu 26: (Đề thi THPT Quốc gia 2017) Một vật chuyển động trong 4 giờ với
vận tốc
( )
km/hv
phụ thuộc thời gian
( )
ht
có đồ thị vận tốc như hình bên.
Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một
phần của đường parabol có đỉnh
( )
2;9I
với trục đối xứng song song với trục
tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành.
Tính quãng đường
s
mà vật di chuyển được trong 4 giờ đó.
A.
26,5 km.
B.
28,5 km.
C.
27 km.
D.
24 km.
Câu 27: (Đề thi THPT Quốc gia 2017) Một vật chuyển động trong 3 giờ với vận
tốc
( )
km/hv
phụ thuộc vào thời gian
( )
ht
có đồ thị vận tốc như hình vẽ bên.
Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một
phần của đường parabol có đỉnh
( )
2;9I
và trục đối xứng song song với trục tung,
khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính
quãng đường
s
mà vật di chuyển được trong 3 giờ đó (kết quả làm tròn đến hàng
phần trăm).
A.
( )
23, 25 km .s =
B.
( )
21,58 km .s =
C.
( )
15,50 km .s =
D.
( )
13,83 km .s =
Câu 28: Một vật chuyển động trong 3 giờ với vận tốc
( )
km/hv
phụ thuộc vào
thời gian
( )
ht
có đồ thị là một phần của đường parabol có đỉnh
3 25
;
24
I



và
trục đối xứng song song với trục tung như hình vẽ. Tính quãng đường mà vật di
chuyển được trong 3 giờ.
A.
33
km.
2
B.
29
km.
2
C.
31
km.
2
D.
35
km.
2
Câu 29: Một vật chuyển động trong 3 giờ với vận tốc
( )
km/hv
phụ thuộc
vào thời gian
(
)
h
t
có đồ thị vận tốc như hình bên. Trong khoảng thời gian 1
giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có
đỉnh
(
)
2;5I
và trục đối xứng song song với trục tung, khoảng thời gian còn
lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường mà
vật di chuyển được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm).
A.
32
km.
3
B.
15 km.
C.
12 km.
D.
35
km.
3
Câu 30: Hai vật chuyển động ngược chiều nhau trên một quãng đường
AB
dài 30 km. Vật
M
chuyển động từ
A
đến
B
trong 3 giờ với vận tốc
( )
1
km/h
v
phụ thuộc vào thời gian
( )
h,t
trong khoảng thời gian 1 giờ kể
từ khi bắt đầu chuyển động có đồ thị là một phần của parabol có đỉnh
(
)
1
2;5I
và trục đối xứng song song với trục tung, khoảng thời gian còn lại
đồ thị là một đoạn thẳng song song với trục hoành. Vật
N
chuyển động
trong 3 giờ từ
B
đến
A
với vận tốc
( )
2
km/hv
phụ thuộc vào thời gian
( )
ht
với đồ thị là một phần của đường parabol có đỉnh
2
3 13
;
24
I



và trục
đối xứng song song với trục tung. Hỏi sau 3 giờ thì hai vật
, MN
cách
nhau bao nhiêu km?
A.
19
km.
6
B.
37
km.
2
C.
18 km.
D.
45
km.
2
Câu 31: Một vật chuyển động trong 4 giờ với vận tốc
( )
km/hv
phụ thuộc
thời gian
( )
ht
có đồ thị vận tốc như hình bên. Trong khoảng thời gian 2 giờ
kể từ khi bắt đầu chuyển động nhanh dần, đồ thị là một phần của đường
thẳng. Khoảng thời gian còn lại đồ thị là một parabol có đỉnh
( )
3; 7I
và trục
đối xứng song song với trục tung. Tính quãng đường
s
mà vật di chuyển
được trong 210 phút.
A.
( )
15,375 km .s =
B.
( )
16,375 km .s =
C.
( )
17,5 km .s =
D.
( )
18,5 km .s =
Câu 32: Một vật chuyển động trong 2 giờ với vận tốc
( )
km/hv
phụ thuộc
thời gian
(
)
ht
có đồ thị của vận tốc như hình bên. Trong khoảng thời gian
1,5 giờ kể từ khi bắt đầu chuyển động, đồ thị là parabol có đỉnh
( )
1; 9I
và
trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một
đoạn thẳng. Tính quãng đường
s
mà vật di chuyển được trong 2 giờ đó.
A.
13,8 km.
B.
14,8 km.
C.
15,8 km.
D.
16,8 km.
Câu 33: Một vật chuyển động trong 10 giờ với vận tốc
( )
km/h
v
phụ thuộc
thời gian
( )
ht
có đồ thị của vận tốc như hình bên. Tính quãng đường
s
mà vật đi được trong 10 giờ đó.
A.
72 km.
B.
70 km.
C.
74 km.
D.
76 km.
Câu 34: Một vật chuyển động với vận tốc
0
15 m/sv
=
thì tăng tốc với gia
tốc
( )
2
m/sa
phụ thuộc thời gian
( )
ts
có đồ thị là một phần của parabol có
đỉnh
( )
1; 4I −
và trục đối xứng song song với trục tung như hình bên. Tính
quãng đường
s
mà vật di chuyển được trong 3 giây kể từ lúc bắt đầu tăng
tốc.
A.
45, 25 m.
B.
36 m.
C.
50 m.
D.
44, 5 m.
Câu 35: Một vật chuyển động trong 4 giây với gia tốc
( )
2
m/sa
phụ
thuộc thời gian
( )
ts
có đồ thị của gia tốc như hình bên. Trong khoảng
thời gian 3 giây kể từ khi bắt đầu chuyển động, đồ thị là một parabol có
đỉnh
( )
2; 4
I
và trục đối xứng song song với trục tung, khoảng thời gian
còn lại đồ thị là một đoạn thẳng. Tính quãng đường
s
mà vật di chuyển
được trong 4 giây đó. Biết rằng vận tốc của vật tại giây thứ 3 bằng
18 m/s.
A.
55, 9 m.
B.
56, 9 m.
C.
57,9 m.
D.
58, 9 m.
LỜI GIẢI CHI TIẾT
Câu 1: Ta có
( ) ( )
( )
(
)
3
22
5
d 5 d m/s
32
t
vt at t t t t t C= = + =++
∫∫
Do khi bắt đầu tăng tốc
0
18
v =
nên
(
)
( )
3
2
0
5
18 18 18
32
t
t
v C vt t
=
=⇒= ⇒ =+ +
Khi đó quãng đường xe đi được sau 3 giây kể từ khi ô tô bắt đầu tăng tốc bằng
( )
33
32
00
5 333
18 d m.
32 4
tt
S v t dt t

= = ++ =


∫∫
Chọn B.
Câu 2: Khi dừng hẳn
( )
( )
150 15 0 10vt t t s= − = ⇔=
Khi đó trong
5 s
trước khi dừng hẳn vật di chuyển được:
( ) ( )
10 10
55
375
d 150 15 d .
2
S vtt tt m= =−=
∫∫
Chọn C.
Câu 3: Khi dừng hẳn
( ) ( )
40
4
b
vt t b t s=− += ⇔=
Quãng đường xe đi được từ khi đạp phanh đến lúc dừng hẳn là:
( ) ( )
( )
22
44
22
4
0
00
d 4 d 2 50 400 20.
84
bb
b
bb
S v t t t b t t bt b b
−
= = −+ =− + = + = ⇔ = ⇔=
∫∫
Chọn D.
Câu 4: Ta có:
( )
02
24 /v ms=
do đó khi gặp chướng ngại vật vật có vận tốc là
24 /ms
Khi đó
(
) ( )
1
2 12 24 6vt t t s
= + = ⇔=
Vật dừng lại khi
( ) ( )
22
24 6 0 4vt t t s= −=⇔=
Quãng đường vật đi được là:
(
) ( )
( ) ( )
64 6 4
12
00 0 0
d d 2 12 d 24 6 d 156 .s vtt vtt t t tt m= + =+ +− =
∫∫ ∫ ∫
Chọn A.
Câu 5: Khi dừng hẳn
( )
( )
20 40 0 0,5vt t t s= − = ⇔=
Quãng đường xe đi được từ khi đạp phanh đến lúc dừng hẳn là:
(
) ( )
11
22
00
d 20 40 d 5 .
S vtt tt m= =−=
∫∫
Chọn C.
Câu 6: Ta có
( ) ( )
( )
( )
2 32
1
d 3 d m/s
2
vt att tttt tC= = + =++
∫∫
Do khi bắt đầu tăng tốc
0
2v
=
nên
( )
( )
32
0
1
22 2
2
t
v C vt t t
=
=⇒=⇒ =+ +
Vận tốc của vật khi chuyển động với gia tốc đó được
2 s
là
( )
2 12 / .v ms=
Chọn B.
Câu 7: Ta có:
(
) (
)
( ) ( )
2
d 6 2 d 6 m/svt att tt tt C= = − = −+
∫∫
Khi đó
max
3,vt⇔=
do ban đầu ô tô đang dừng nên
( )
0 0 0.vC=⇔=
Quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc của ô tô đạt giá trị lớn nhất là:
( )
3
2
0
6 d 18 .
S tt t m=−=
∫
Chọn B.
Câu 8: Quãng đường vật đó đi được trong 4 giây đầu là:
( )
44
2
CASIO
00
4
d 1, 2 d 11, 81 .
3
t
S vt t t S m
t

+
= = + → ≈

+

∫∫
Chọn C.
Câu 9: Phương trình vận tốc của vật
A
là:
1
v at=
Do
( )
1
33
86
44
v a vt
=⇒=⇒ = ⇒
Quãng đường vật
A
đi được sau
20s
đầu là
8
0
3
d 6.12 96 .
4
tt m+=
∫
Phương trình vận tốc của vật
B
là:
8
2
0
d 96 3
B
v bt S bt t b= ⇒ = = ⇒=
∫
Do đó
2
v bt
= ⇒
vận tốc của vật
B
khi hai vật gặp nhau là
3.8 24 / .
B
v ms= =
Chọn B.
Câu 10: Ta có
( ) (
)
( )
2
1
d 1 d m/s
36
t
vt at t t t t C

= =+ =++


∫∫
Do khi bắt đầu tăng tốc
( ) ( )
0
36 / 10 /v km h m s
= =
nên
( )
( )
2
0
1
10 10 10
6
t
v C vt t t
=
= ⇒= ⇒ =+ +
Khi đó quãng đường xe đi được sau 6 giây kể từ khi ô tô bắt đầu tăng tốc bằng
( )
66
2
00
10 d 90 m.
6
t
S v t dt t t

= = ++ =


∫∫
Chọn A.
Câu 11: Khi dừng hẳn
( ) (
)
12 2 0 6
vt t t s= − = ⇔=
Khi đó trong
8 s
trước khi dừng hẳn vật di chuyển được (bao gồm 2 s trước khi đạp phanh):
( ) ( )
66
00
2.12 d 24 12 2 d 24 36 60 .S vt t t t m
= + =+ − =+=
∫∫
Chọn B.
Câu 12: Quãng đường máy bay đi được từ giây thứ 4 đến giây thứ 10 là:
( )
( )
10 10
2
44
3 5 d 996 .S v t dt t t m
= = +=
∫∫
Chọn C.
Câu 13: Ta có
( ) ( ) ( )
2
d 6td 3 m/svt at t t t C= = = +
∫∫
Do khi bắt đầu tăng tốc
0
10v =
nên
( )
( )
2
0
10 10 3 10
t
v C vt t
=
= ⇒= ⇒ = +
Khi đó quãng đường xe đi được sau 10 giây kể từ khi ô tô bắt đầu tăng tốc bằng
(
)
(
)
10 10
2
00
3 10 d 1100 .S v t dt t t m
= =+=
∫∫
Chọn A.
Câu 14: Khi dừng hẳn
(
)
( )
30 2 0 15
vt t t s= − = ⇔=
Khi đó trong
5
s
trước khi dừng hẳn vật di chuyển được:
(
) (
)
15 15
10 10
d 30 2 d 25 .S vt t t t m
= =−=
∫∫
Chọn D.
Câu 15: Vận tốc vật đạt được sau 5 s là:
0
7.5 35 / .v ms= =
Ta có
( ) ( ) ( )
2
d 70d 70 m/s
v t at t t t C
= =− =−+
∫∫
Do khi bắt đầu tăng tốc
0
35v =
nên
( )
( )
2
0
35 35 70 35
t
v C vt t
=
= ⇒= ⇒ =− +
Vật dừng hẳn khi
( )
( )
22
1
70 35 0 .
2
vt t t s=− + =⇔=
Khi đó quãng đường đi được bằng
( ) ( )
( )
11
55
22
12
0 0 00
d d 7 d 70 35 d 96, 25 .S vtt vtt tt t t m= + = +− + =
∫ ∫ ∫∫
Chọn B.
Câu 16: Quãng đường vật đi được từ thời điểm
2ts
=
đến
30ts=
là:
( ) ( ) ( ) ( ) ( ) ( )
30 30
22
d 3 2 d 1400 30 2 30 2 1400 1410.S vt t t t m S S S S= =+= = −⇒ =+=
∫∫
Cách 2:
( )
( )
30
0
30 3 2 d 1410.
S tt=+=
∫
Chọn D.
Câu 17:
( )
( )
2
d 20 100St vt t t t C= =++
∫
Do
(
)
1 120 120 0
S CC= += ⇒=
Để học sinh đó đến trường thì
( )
2
20 100 3000 10.St t t t= + = ⇔=
Chọn C.
Câu 18:
( ) ( )
( )
( )
3
22
3
d 3 d m/s
32
t
vt at t t t t t C= = + =++
∫∫
Do khi bắt đầu tăng tốc
0
18v =
nên
( )
( )
3
2
0
3
10 10 10
32
t
t
v C vt t
=
= ⇒= ⇒ =+ +
Khi đó quãng đường đi được bằng
( )
10 10
32
00
3 4300
10 d m.
32 3
tt
S v t dt t

= = ++ =


∫∫
Chọn C.
Câu 19: Vận tốc của vật được tính theo công thức
( ) (
)
2
10 7 / .vt t t m s= +−
Suy ra quãng đường vật đi được tính theo công thức
( ) ( ) ( )
3
2
7
d 10 .
32
t
St vt t t t m= =−+
∫
Ta có
(
) ( )
22
2
7 10 0 7 10 0 .
5
t
St t t St t t
t
=
′′
=−+⇒ =⇔−+ =⇔
=
Suy ra
(
)
( )
(
)
(
)
[ ]
( ) (
)
0;6
00
26
2
26
3
2.
25
3
5
6
66
S
S
Max S t S
S
S
=
=
⇒==
=
=
Chọn D.
Câu 20: Khi dừng hẳn
( ) ( )
12 24 0 2vt t t s=− + = ⇔=
Do đó từ lúc đạp phanh đến khi dừng hẳn, ô tô đi được:
( ) ( )
22
00
12 24 d 24 .
S v t dt t t m= =−+ =
∫∫
Chọn D.
Câu 21: Vận tốc của vật là:
( ) ( ) ( )
3d
' d 3ln 1
1
t
vt v t t t C
t
= = = ++
+
∫∫
Do vận tốc ban đầu của vật là
( )
0
6 / 6 3ln1 6 6.
t
ms V C C
=
⇒ =⇒ +=⇒=
Vận tốc của vật sau 10 s là:
( )
10 3ln11 6 13 / .v ms= +≈
Chọn D.
Câu 22:
( ) (
) ( )
7000
' d d 7000ln 2
2
Nt N t t t t C
t
= = = ++
+
∫∫
Do
( )
(
)
0
0 7000ln 2 300000 300000 7000ln 2.
t
NN C C
=
= = += ⇒= −
Sau 10 ngày, đám vi trùng có
( )
10 7000ln12 7000ln 6 300000 312542NC= += + ≈
con. Chọn D.
Câu 23:
(
) ( )
( )
2017
' d d 2017 ln 1
1
Nx N x t t x C
x
= = = ++
+
∫∫
Do
( )
(
)
0
0 2017.ln1 30000 30000.
x
NN C C
=
= = += ⇒=
Sau 1 tuần, đám vi trùng có
( )
7 2017ln8 3000 34194N = +≈
con. Chọn D.
Câu 24: Gọi phương trình parabol là
(
)
2
0.y at bt c a= ++ ≠
Vì
( )
P
có đỉnh
( )
2;9
I
và đi qua
( )
0; 6M
nên
3
6; 2
.
2
4
3; 6
42 9
b
c
a
a
bc
a bc
=−=
= −

⇔


= =
+ +=
Do đó, phương trình parabol là
2
3
3 6.
4
y tt=− ++
Vậy quãng đường mà vật di chuyển là
3
2
0
3
3 6 d 24,75.
4
S tt t

= − ++ =


∫
Chọn D.
Câu 25: Gọi phương trình parabol là
( )
2
0.y at bt c a= ++ ≠
Vì
( )
P
có đỉnh
1
;8
2
I



và đi qua
( )
0; 0O
nên
1
0;
32
22
.
32; 0
8
42
b
c
a
a
bc
ab
c
=−=
= −
⇔

= =
++=
Do đó, phương trình parabol là
2
32 32 .
y tt
=−+
Vậy quãng đường mà vật di chuyển là
( )
3
4
2
0
9
32 32 d .
2
S t tt=−+ =
∫
Chọn C.
Câu 26: Gọi phương trình parabol là
( )
2
0.y at bt c a= ++ ≠
Vì
( )
P
có đỉnh
( )
2;9
I
và đi qua
( )
0; 0
O
nên
9
0; 2
.
2
4
9; 0
42 9
b
c
a
a
bc
a bc
=−=
= −

⇔


= =
+ +=
Do đó, phương trình parabol là
2
9
9.
4
y tt=−+
Với
( )
27
33 .
4
ty=⇒=
Vậy quãng đường mà vật di chuyển là
(
)
3
2
0
9 27
9 d . 4 3 27.
44
S t tt

=− + + −=


∫
Chọn C.
Câu 27: Gọi phương trình parabol là
(
)
2
0.
y at bt c a= ++ ≠
Vì
( )
P
có đỉnh
( )
2;9I
và đi qua
( )
0; 4M
nên
5
4; 2
.
2
4
5; 4
42 9
b
c
a
a
bc
a bc
=−=
= −

⇔


= =
+ +=
Do đó, phương trình parabol là
2
5
5 4.
4
y tt=− ++
Với
( )
31
11.
4
ty=⇒=
Vậy quãng đường mà vật di chuyển là
( )
1
2
0
5 31
5 4 d . 3 1 21,58.
44
S tt t

= − ++ + −=


∫
Chọn B.
Câu 28: Gọi phương trình parabol là
( )
2
0.y at bt c a= ++ ≠
Vì
(
)
P có đỉnh
3 25
;
24
I



và đi qua
( )
0; 4M
nên
3
1
4;
22
3.
9 3 25
4
42 4
b
a
c
a
b
a bc
c
= −
=−=

⇔=


+ +=
=
Do đó, phương trình parabol là
2
3 4.yt t
=−+ +
Vậy quãng đường mà vật di chuyển là
( )
3
2
0
33
3 4d .
2
S tt t= −+ + =
∫
Chọn A.
Câu 29: Gọi phương trình parabol là
( )
2
0.y at bt c a= ++ ≠
Vì
( )
P
có đỉnh
( )
2;5I
và đi qua
( )
0;1M
nên
1
1; 2
4.
2
42 5
1
a
b
c
b
a
a bc
c
= −
=−=

⇔=


+ +=
=
Do đó, phương trình parabol là
2
4 1.yt t=−+ +
Vậy quãng đường mà vật di chuyển là
(
)
(
)
1
2
0
32
4 1 d 4. 3 1 .
3
S tt t
= −+ + + − =
∫
Chọn A.
Câu 30: Ta xét riêng các vật
, :MN
- Xét chiều di chuyển của vật
.M
Gọi phương trình của parabol
( )
P
là
2
y at bt c= ++
Vì
( )
P
có đỉnh
(
)
2;5
I
và đi qua
(
)
0;1M
nên suy ra
1
1; 2
4.
2
42 5
1
a
b
c
b
a
a bc
c
= −
=−=

⇔=


+ +=
=
Do đó, phương trình
( )
P
là
2
41yt t=−+ +
cũng chính là phương trình vận tốc.
Suy ra quãng đường vật
M
đi trong 3 giờ là
( )
(
)
1
2
0
32
4 1 d 4. 3 1 .
3
M
S t t t km
= −+ + + − =
∫
- Xét chiều di chuyển của vật
.N
Gọi phương trình parabol
( )
P
là
2
y at bt c= ++
Vì
( )
P
có đỉnh
3 13
;
24
I



và đi qua
( )
0;1M
nên suy ra
3
1
1;
22
3.
9 3 13
1
42 4
b
a
c
a
b
a bc
c
= −
=−=

⇔=


+ +=
=
Do đó, phương trình
( )
P
là
2
31yt t=−+ +
cũng chính là phương trình vận tốc.
Suy ra quãng đường vật
N
đi trong 3 giờ là
( )
3
2
0
15
3 1d .
2
N
S t t t km
= −+ + =
∫
Vậy sau 3 giờ thì hai vật
, MN
cách nhau một khoảng
32 15 19
.
326
km−=
Chọn A.
Câu 31: Gọi phương trình đường thẳng là
:d y mt n= +
Vì
d
đi qua điểm
( )
0;3M
và
( )
2; 4N
1
3
2
yt → = +
là phương trình vận tốc.
Gọi phương trình của parabol
( )
P
là
2
y at bt c= ++
Vì
( )
P
có đỉnh
( )
3; 7I
và đi qua
( )
2; 4N
nên suy ra
42 4 3
9 3 7 18 .
6 0 20
a bc a
a bc b
ab c
+ += =−


+ += ⇔ =


+= =−

Do đó, phương trình
( )
P
là
2
3 18 20
yt t
=−+ −
cũng chính là phương trình vận tốc.
Vậy quãng đường cần tính là
(
)
7
2
2
2
02
1
3 d 3 18 20 d 16,375.
2
S t t tt t

= + +− + − =


∫∫
Chọn B.
Câu 32: Gọi phương trình của parabol
( )
P
là
2
y at bt c= ++
Vì
( )
P
có đỉnh
( )
1; 9I
và đi qua
( )
0; 0O
nên suy ra
9
0; 1
18 .
2
9
0
a
b
c
b
a
abc
c
= −
=−=

⇔=


++=
=
Do đó, phương trình
(
)
P
là
2
9 18yt t=−+
cũng chính là phương trình vận tốc.
Với
2
3 3 3 3 27
9. 18. .
2 2 2 24
tv
 
= → = − + =
 
 
Gọi phương trình đường thẳng là
:d y mt n
= +
Vì
d
đi qua điểm
3 27
;
24
M



và
(
)
2;12N
21
9.
2
yt → = −
Vậy quãng đường cần tính là
( )
3
2
2
2
3
0
2
21
9 18 d 9 d 14,8 .
2
S t t t t t km

=−+ + − =


∫∫
Chọn B.
Câu 33: Trong 2 giờ đầu, vật chuyển động với vận tốc
( )
2
1
0
3 3 d 6 .
v t t S t t km= → = =
∫
Trong 2 giờ tiếp theo, vật chuyển động với vận tốc
( )
2
6 6.2 12 .v t S km= → = =
Trong 6 giờ cuối, vật chuyển động với vận tốc
( ) ( )
10
3
4
2 2 d 54 .v t t S t t km= + → = + =
∫
Vậy tổng quãng đường vật đi trong 10 giờ là
123
6 12 54 72 .S S S S km=++=++=
Chọn A.
Câu 34: Gọi phương trình của parabol
( )
P
là
2
y at bt c= ++
Vì
( )
P
có đỉnh
( )
1; 4I −
và đi qua
( )
0; 0O
nên suy ra
4
0; 1
8.
2
4
0
a
b
c
b
a
abc
c
=
=−=

⇔=−


++=−
=
Do đó, phương trình
( )
P
là
2
48yt t= −
cũng chính là phương trình gia tốc.
Ta có
( ) ( )
( )
3
2 22
4
48 48d 4
3
t
at ttvt ttt tC= −⇒ = − = − +
∫
Mà
( )
0 15 15.vC=⇒=
Vậy
( )
33
3
2
00
4
d 4 15 d 36 .
3
t
S vt t t t m

= = −+ =


∫∫
Chọn B.
Câu 35: Gọi phương trình của parabol
( )
P
là
2
y at bt c= ++
Vì
( )
P
có đỉnh
( )
2; 4I
và đi qua
(
)
0; 0O
nên suy ra
1
0; 2
4.
2
42 4
0
a
b
c
b
a
a bc
c
= −
=−=

⇔=


+ +=
=
Do đó, phương trình
(
)
P
là
2
4yt t
=−+
cũng chính là phương trình gia tốc.
Suy ra
( ) ( )
( )
3
22
d 4d 2
3
t
vt at t t t t t C= = −+ =− + +
∫∫
mà
( )
3 18 9.vC=⇒=
Với
( )
2
3 3 3 4.3 3.tv
= → = − + =
Gọi phương trình đường thẳng là
:d y mt n= +
Vì
d
đi qua điểm
( )
0; 0O
và
( )
3; 3M
yt
→ =
là phương trình gia tốc
Suy ra
( ) ( )
2
dd
2
t
vt at t tt C= = = +
∫∫
mà
( )
27
3 18 .
2
vC=⇒=
Vậy quãng đường cần tính là
34
3
2
03
27
2 9 d d 57,9 .
32
t
S t t t t km


= −+ + + + =




∫∫
Chọn B.
| 1/25

Tài liệu khác của Toán 12

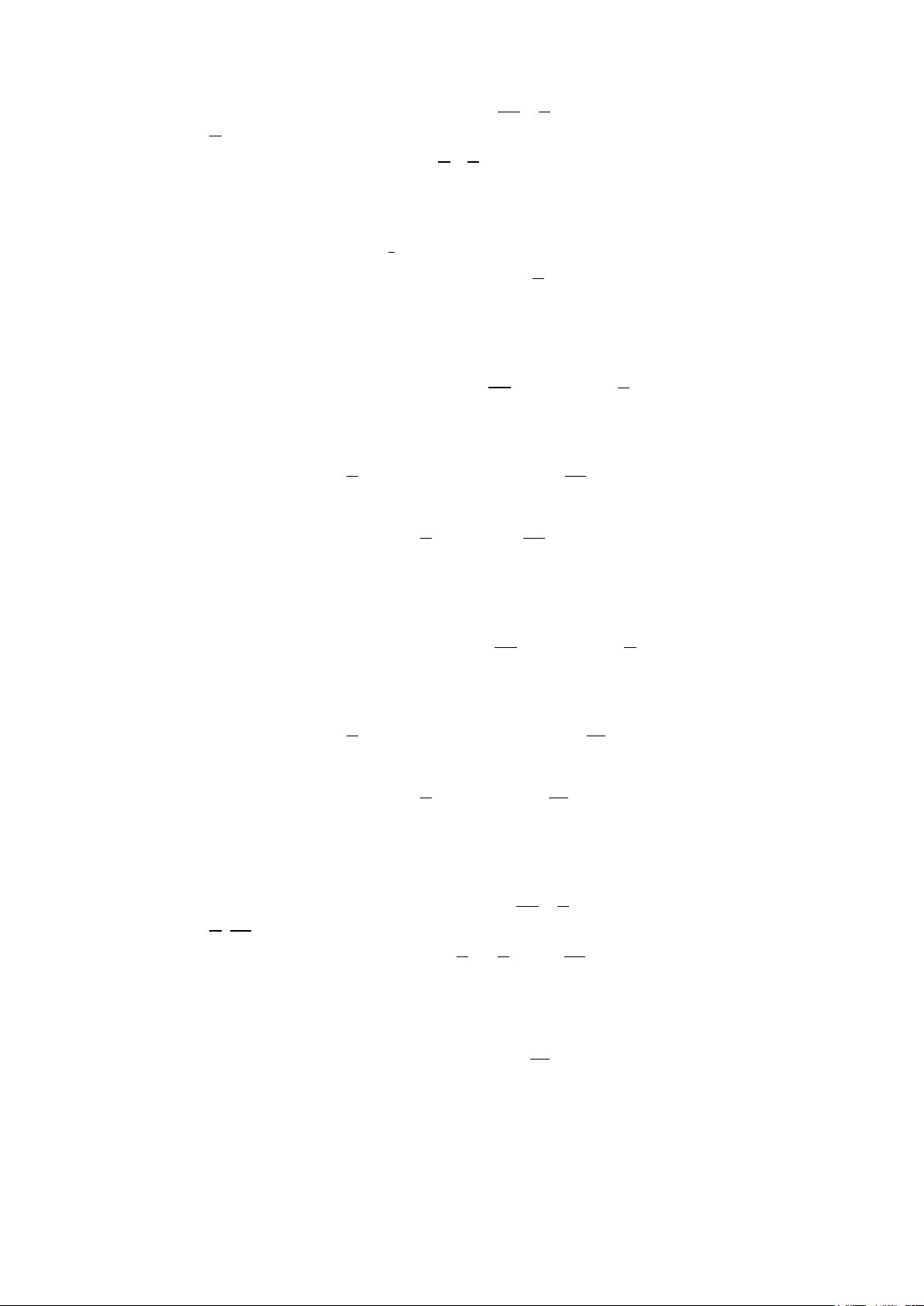
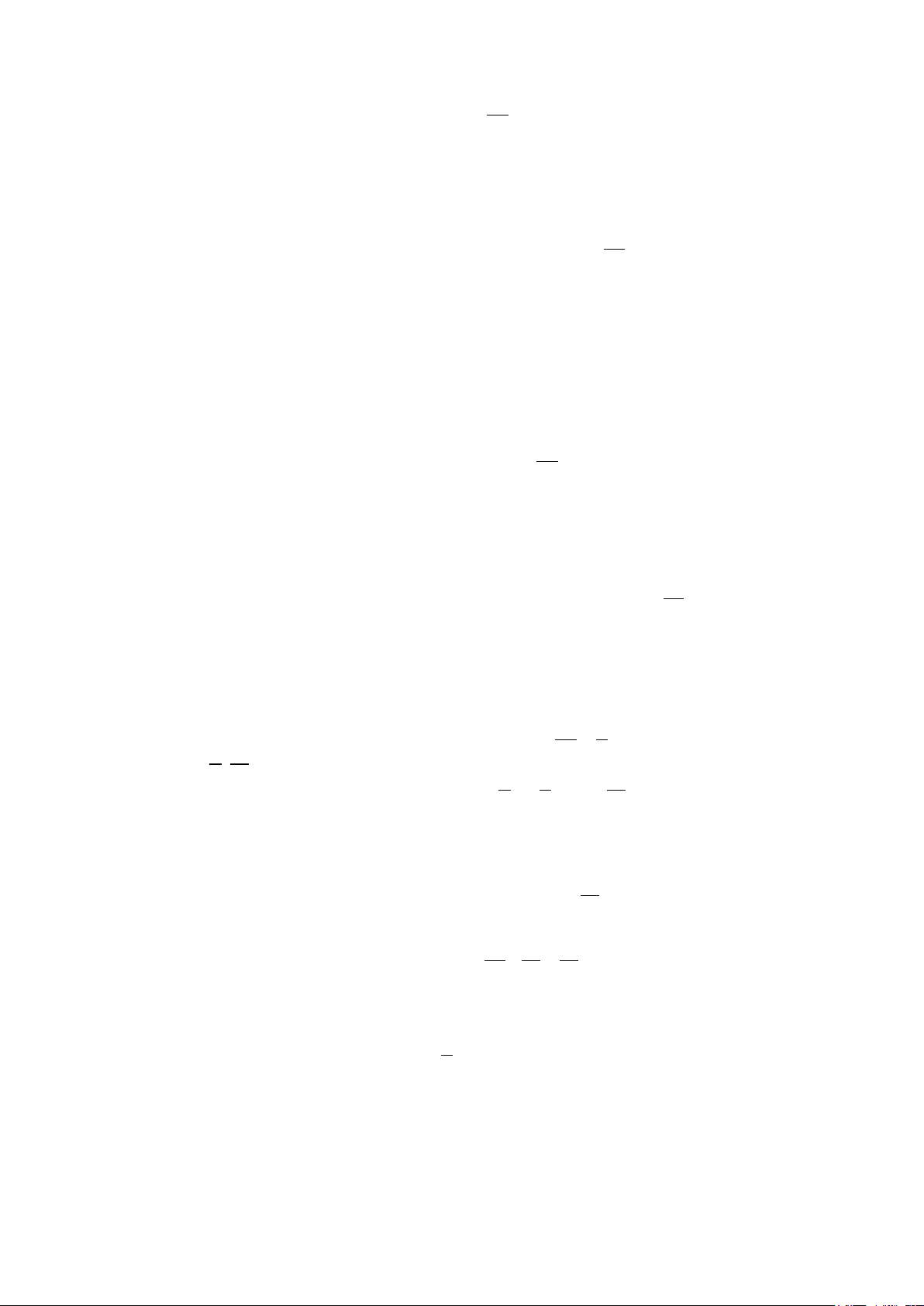
Preview text:

Chủ đề 14: MỘT SỐ ỨNG DỤNG KHÁC CỦA TÍCH PHÂN
Dạng 1: Bài toán liên quan đến quãng đường, vận tốc, gia tốc và thời gian
Với bài toán chuyển động giả sử vận tốc tức thời của vật là v(t) thì v(t) = s '(t)
Gia tốc tức thời của vật: a(t) = v'(t) = s"(t) t2
Do đó quãng đường vật đi được từ thời điểm t đến t là S = v ∫ (t)dt. 1 2 1 t
Vận tốc tức thời của vật: v(t) = a ∫ (t)dt
Ví dụ 1: Một ô tô đang chạy với vận tốc 20 m/s thì người lái hãm phanh. Sau khi hãm phanh, ô tô chuyển
động chậm dần đều với vận tốc v(t) = 4
− t + 20 (m/s) trong đó t là khoảng thời gian tính bằng giây kể từ
lúc bắt đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét? A. 25 m. B. 50 m. C. 10 m. D. 30 m. Lời giải:
Khi vật dừng hẳn thì v = 0 ⇒ 4
− t + 20 = 0 ⇔ t = 5(s). 5 5
Quãng đường vật đi được trong khoảng thời gian trên là: S (t) = v
∫ (t)dt = ∫( 4
− t + 20)dt = 50 m. 0 0 Chọn A.
Ví dụ 2: Một ô tô xuất phát với vận tốc v t = 2t +12 m / s , sau khi đi được khoảng thời gian t thì bất 1 ( ) ( ) 1
ngờ gặp chướng ngại vật nên tài xế phanh gấp với vận tốc v t = 24 − 6t m / s , và đi thêm một khoảng 2 ( ) ( )
thời gian t nữa thì dừng lại. Hỏi từ khi xuất phát đến lúc dừng lại thì xe ô tô đã đi được bao nhiêu mét ? 2 A. 12 . m B. 156 . m C. 108 . m D. 48 . m Lời giải:
Ta có: v = 24 m / s do đó khi gặp chướng ngại vật vật có vận tốc là 24 m / s 02 ( )
Khi đó v t = 2t +12 = 24 ⇔ t = 6 s 1 ( ) ( )
Vật dừng lại khi v t = 24 − 6t = 0 ⇔ t = 4 s 2 ( ) 2 ( ) 6 4 6 4
Quãng đường vật đi được là: s = v t dt + v t dt = 2t +12 dt + 24 − 6t dt =156 . m ∫ 1 ( ) ∫ 2 ( ) ∫( ) ∫( ) 0 0 0 0 Chọn B.
Ví dụ 3: Một chất điểm đang chuyển động với vận tốc v =16 m / s thì tăng tốc với gia tốc 0 ( ) a(t) 2 = t + t ( 2
3 m / s ). Tính quãng đường chất điểm đó đi được trong khoảng thời gian 4s kể từ lúc bắt đầu tăng tốc. A. 160 (m). B. 352 (m). C. 400 (m). D. 250 (m). 3 3 3 3 Lời giải:
Ta có: ( ) = ∫ ( ) = ∫( + ) 3 2 2 t 3 3 t v t a t dt t t dt = + + C 3 2 3 2 Khi đó t 3 = 0 = =16 t v v C ⇒ v t = + +16 0 ( ) ( ) 3 2 4 4 3 2  
Khi đó quãng đường đi được bằng: ( ) = ∫ ( ) t 3t s t
v t dt = ∫ + +16dt  3 2 0 0  4 4 3  t t  352  + +16t  = (m). Chọn B. 12 2  3 0
Ví dụ 4: Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v t = 2t m / s . Đi được 12 giây, 1 ( ) ( )
người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc a = − ( 2
12 m / s ). Tính quãng đường s(m) đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn A. s =168 . m B. s =166 . m C. s =144 . m D. s =152 . m Lời giải: 12
Quãng đường xe đi được trong 12 s đầu là: s = 2tdt =144 . m 1 ∫ 0
Sau khi đi được 12 s vật đạt vận tốc v = 24 m / s, sau đó vận tốc của vật có phương trình v = 24 −12t
Vật dừng hẳn sau 2 s kể từ khi phanh. 2
Quãng đường vật đi được từ khi đạp phanh đến khi dừng hẳn là: s = 24 −12t dt = 24 . m 2 ∫( ) 0
Vậy tổng quãng đường ô tô đi được là s = s + s =144 + 24 =168 . m Chọn A. 1 2
Ví dụ 5: Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang phải) với gia
tốc phụ thuộc thời gian t (s) là a(t) = t − ( 2
2 7 m / s ). Biết vận tốc ban đầu bằng 10 (m / s), hỏi trong 6 giây
đầu tiên, thời điểm nào chất điểm ở xa nhất về phía bên phải? A. 5 (s). B. 6 (s). C. 1 (s). D. 2 (s). Lời giải:
Vận tốc của vật được tính theo công thức v(t) 2
= 10 + t − 7t (m / s). 3
Suy ra quãng đường vật đi được tính theo công thức S (t) = v ∫ (t) t 7 2
dt = − t +10t (m). 3 2 t = 2 Ta có S′(t) 2
= t − 7t +10 ⇒ S′(t) 2
= 0 ⇔ t − 7t +10 = 0 ⇔  . t = 5 S (0) = 0  S ( ) 26 2 = Suy ra  6 
⇒ Max S (t) = S (2) 26 = . Chọn D. S ( ) 25 [0;6] 3 5 =  6 S  (6) = 6
Ví dụ 6: [Đề thi thử Chuyên Đại học Vinh 2017] Tại một nơi không có gió, một chiếc khí cầu đang đứng
yên ở độ cao 162 (mét) so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết
rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật v(t) 2
= 10t − t , trong
đó t (phút) là thời gian tính từ lúc bắt đầu chuyển động, v(t) được tính theo đơn vị mét/phút (m/p). Nếu
như vậy thì khi bắt đầu tiếp đất vận tốc v của khí cầu là
A. v = 7 (m / p).
B. v = 9 (m / p).
C. v = 5 (m / p).
D. v = 3 (m / p). Lời giải:
Khi bắt đầu tiếp đất vật chuyển động được quãng đường là s =162 m 3 t t   Ta có: S = ∫( 2 10t − t ) 0 0 3 t 2 t0
dt = 5t −  = 5t − (trong đó t là thời điểm vật tiếp đất) 0  3  3 0 0 0 3 Cho 2 t0
5t − =162 ⇒ t = 9 (Do v(t) 2
= 10t − t ⇒ 0 ≤ t ≤10) 0 0 3
Khi đó vận tốc của vật là: v( ) 2 9 =10.9 − 9 = 9 ( / m p). Chọn B.
Ví dụ 7: [Đề thi THPT Quốc gia 2018] Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc
biến thiên theo thời gian bởi quy luật v(t) 1 2 13 = t +
t (m / s), trong đó t (giây) là khoảng thời gian tính 100 30
từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động
thẳng cùng hướng với A nhưng chậm hơn 10 giây so với A và có gia tốc bằng a ( 2
m / s ) ( a là hằng số).
Sau khi B xuất phát được 15 giây thì đuổi kịp .
A Vận tốc của B tại thời điểm đuổi kịp A bằng
A. 25 (m / s).
B. 15 (m / s).
C. 9 (m / s).
D. 42 (m / s). Lời giải:
Quãng đường chất điểm A đi được cho đến khi hai chất điểm gặp nhau là: 25  1 2 13  375 S = t + t dt = ∫   . m 100 30  2 0
Vận tốc của chất điểm B tại thời điểm t (s) tính từ lúc B xuất phát là: v t = at B ( ) .
Quãng đường chất điểm B đi được cho đến khi 2 chất điểm gặp nhau là: 10 10 2 at 225 S = atdt = = a ∫ (m). Suy ra 225 375 5 a = ⇔ a = 2 2 2 2 3 0 0
Vậy vận tốc của B tại thời điểm đuổi kịp A là: v = a = m s Chọn A. B (15) 15 25 ( / ).
Ví dụ 8: [Đề thi THPT Quốc gia 2018] Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc
biến thiên theo thời gian bởi quy luật v(t) 1 2 11 =
t + t (m/s), trong đó t (giây) là khoảng thời gian tính 180 18
từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động
thẳng cùng hướng với A , nhưng chậm hơn 5 giây so với A và có gia tốc bằng a( 2
m / s ) ( a là hằng số).
Sau khi B xuất phát được 10 giây thì đuổi kịp .
A Vận tốc của B tại thời điểm đuổi kịp A bằng A. 22 (m/s). B. 15 (m/s). C. 10 (m/s). D. 7 (m/s). Lời giải:
Quãng đường chất điểm A đi được cho đến khi hai chất điểm gặp nhau là: 15  1 2 11 S t t  = + dt = ∫  75 . m 180 8 0 
Vận tốc của chất điểm B tại thời điểm t (s) tính từ lúc B xuất phát là: v t = at B ( ) .
Quãng đường chất điểm B đi được cho đến khi 2 chất điểm gặp nhau là: 10 10 2 at S = atdt = = 50a ∫
(m). Suy ra 50a = 75 ⇔ a =1,5 2 0 0
Vậy vận tốc của B tại thời điểm đuổi kịp A là: v = a = m s Chọn B. B (10) 10 15 ( / ).
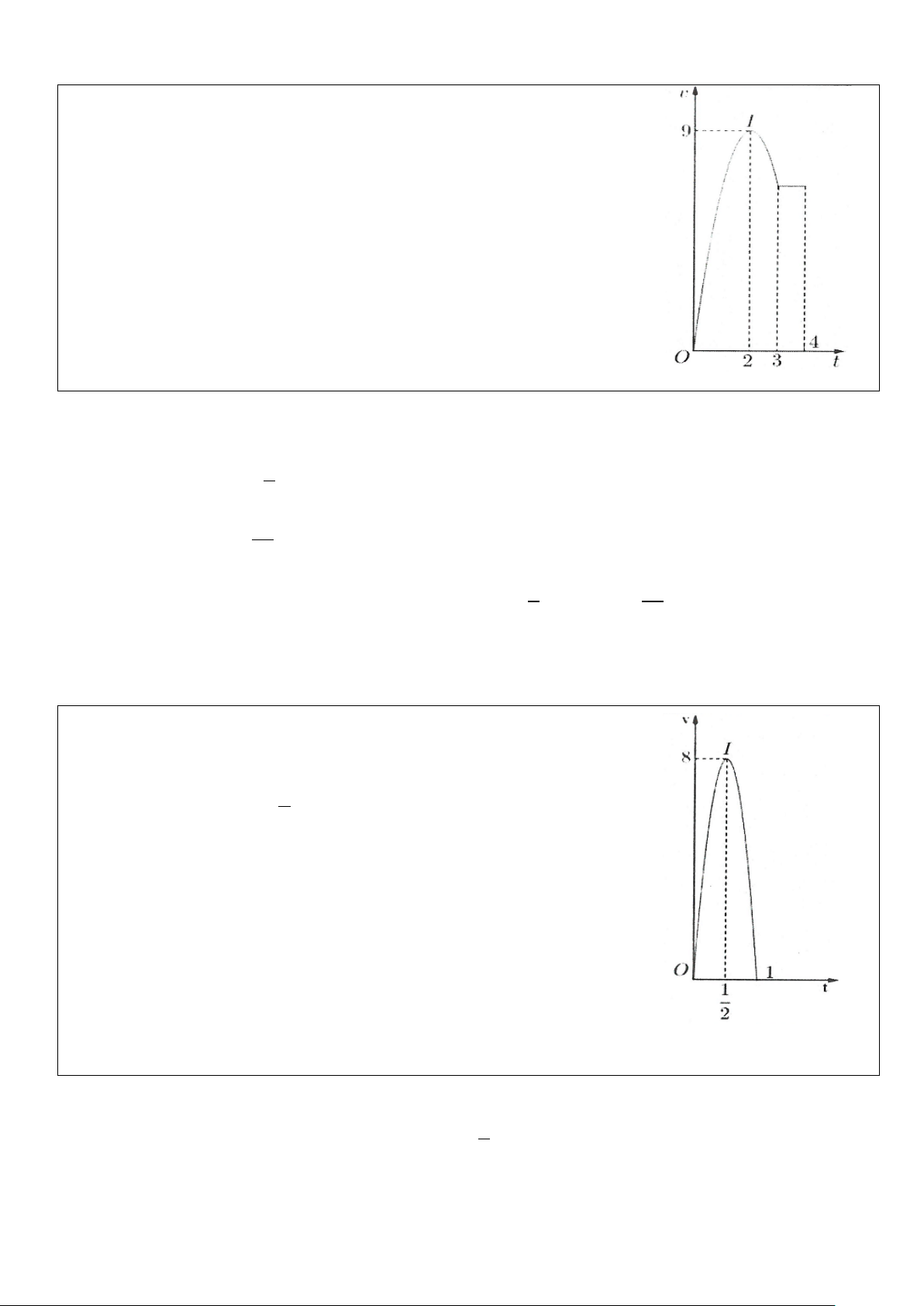
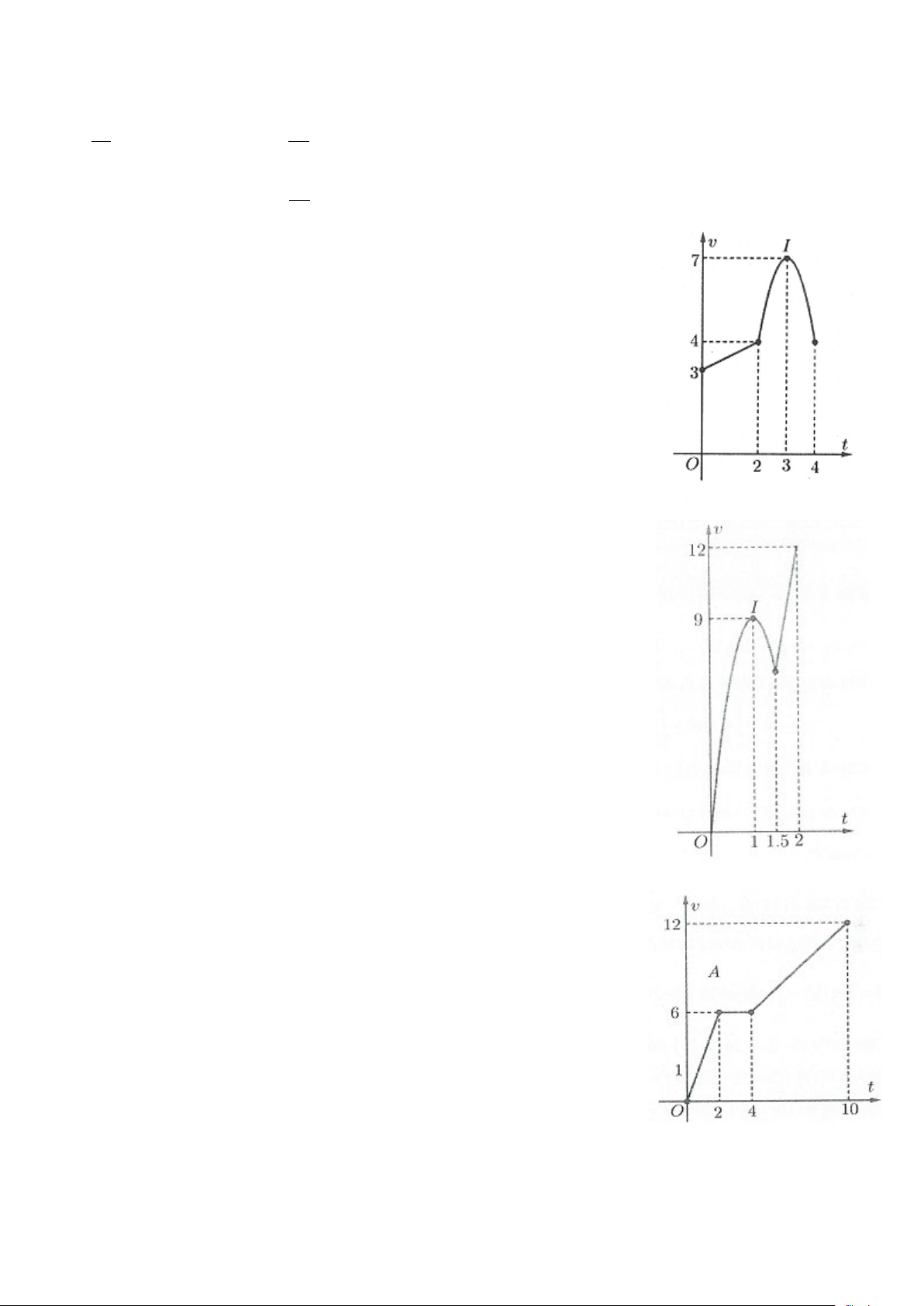
Ví dụ 9: Một vật chuyển động trong 4 giờ với vận tốc v(km / h) phụ thuộc
thời gian t (h) có đồ thị của vận tốc như hình bên. Trong khoảng thời gian 3
giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol
có đỉnh I (2;9) với trục đối xứng song song với trục tung, khoảng thời gian
còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường
s mà vật di chuyển được trong 4 giờ đó?
A. s = 27 (km).
B. s = 24 (km).
C. s = 28,5 (km).
D. s = 26,5 (km). Lời giải:
Dựa vào đồ thị ta tính được phương trình vận tốc của vật
Từ 0 đến 3 giây: v (t) 9 2
= − t + 9t km / h . 1 ( ) 4 Từ 3 giây trở đi: 27 v t = km / h . 2 ( ) ( ) 4 3 4
Suy ra quãng đường vật đi được trong 4 giây sẽ bằng  9 2  27
s = − t + 9t dt + dt = ∫  27 ∫ (km).  4  4 0 3 Chọn A.
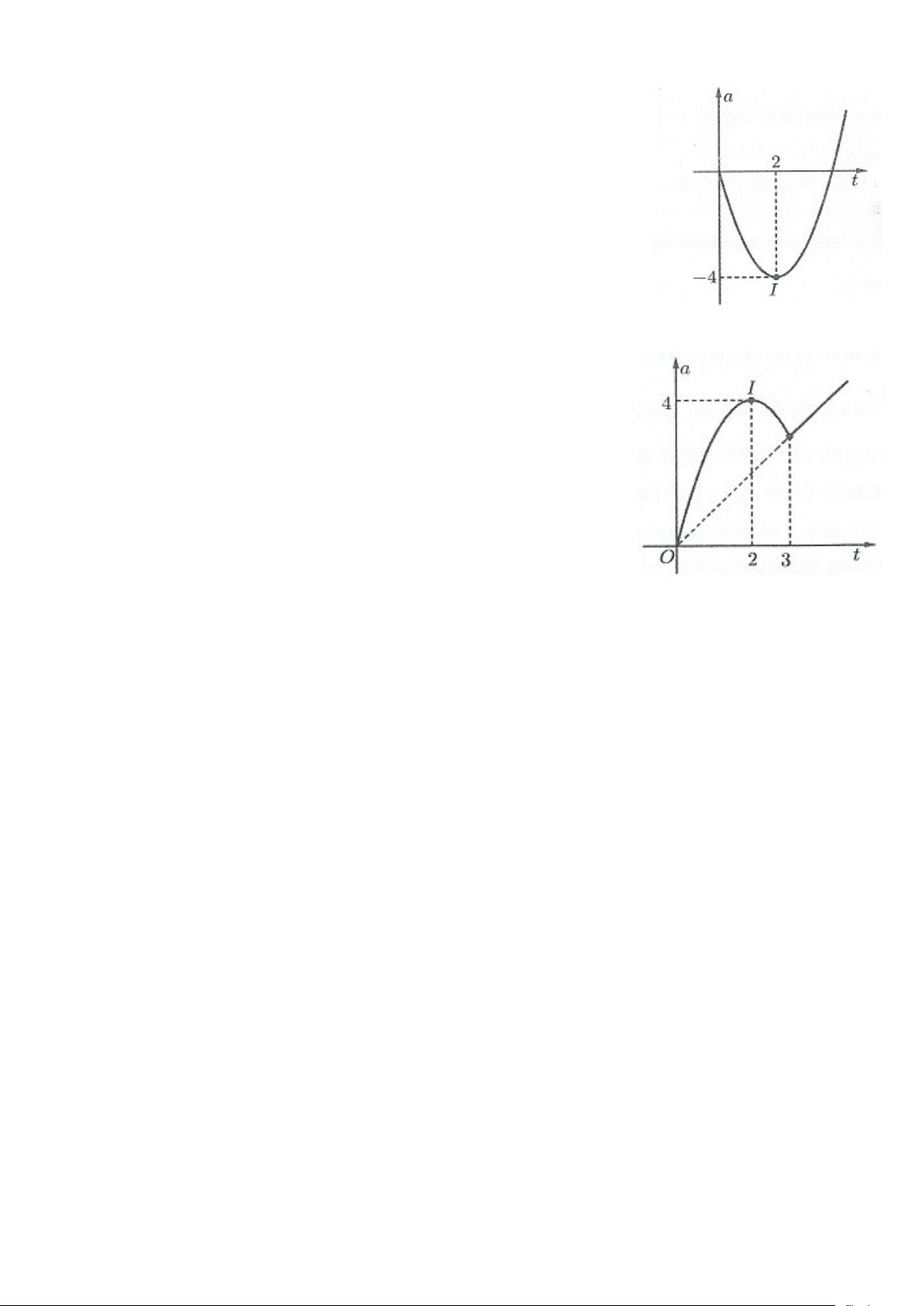
Ví dụ 10: [Đề thi THPT Quốc gia 2017] Một người chạy trong thời gian 1
giờ, vận tốc v(km / h) phụ thuộc thời gian t (h) có đồ thị là một phần của
đường parabol với đỉnh 1 I  ;8 
và trục đối xứng song song với trục tung 2   
như hình bên. Tính quãng đường s người đó chạy được trong khoảng thời
gian 45 phút, kể từ khi bắt đầu chạy.
A. s = 4,0 (km).
B. s = 2,3 (km).
C. s = 4,5 (km).
D. s = 5,3 (km). Lời giải: 2
Dựa vào đồ thị ta tính được PT vận tốc là v(t)  1 a x  = − +   8  2 
Do parabol (P) qua điểm ( ) ⇒ a = − ⇒ v(t) 2 1;0 32 = 32
− t + 32t (km / h). 0,75
Suy ra quãng đường đi được trong 45 phút bằng 0,75 (h) là S = ∫ ( 2 32
− t + 32t)dt = 4,5 (km). 0 Chọn C.
Dạng 2: So sánh các giá trị của hàm số
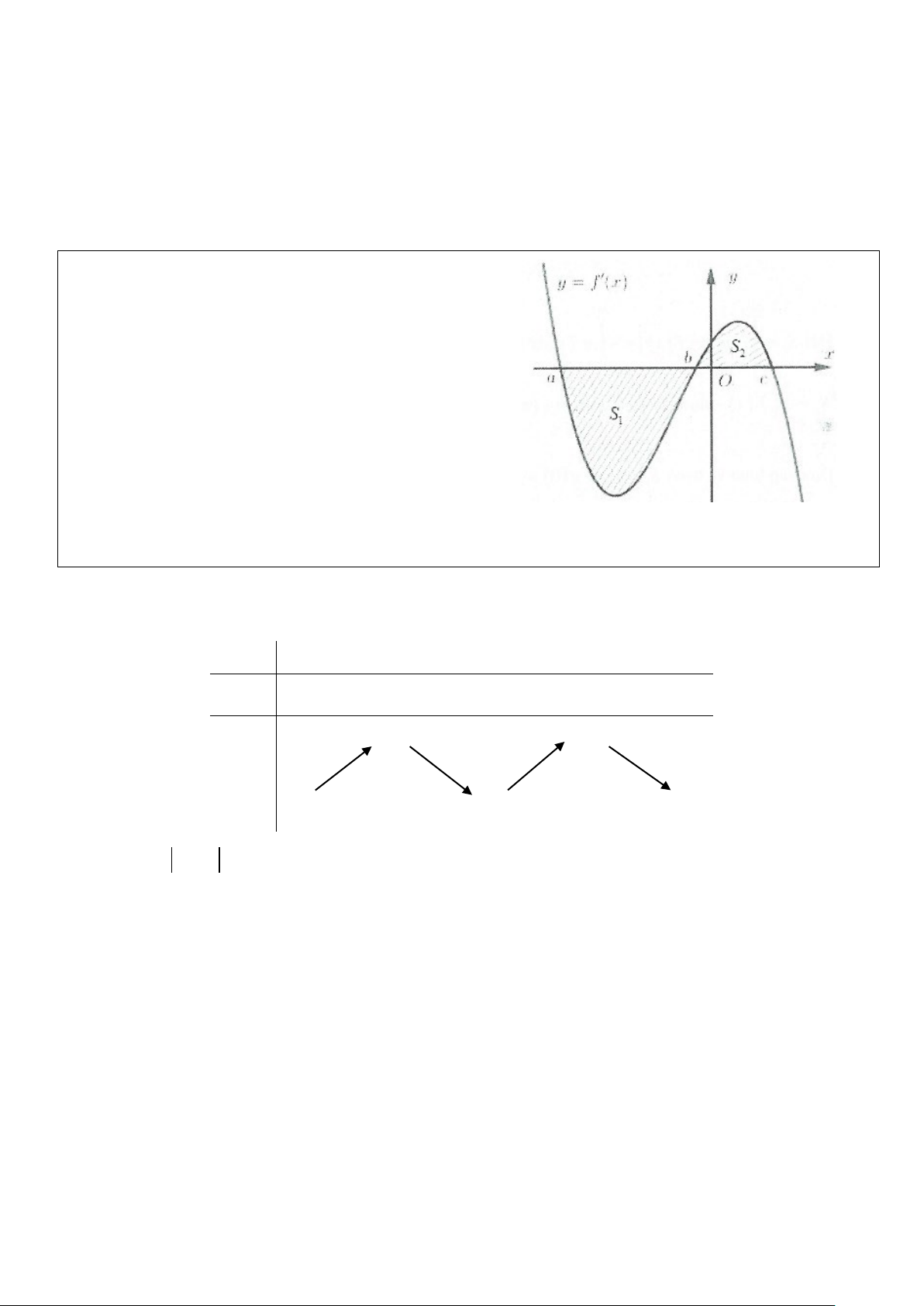
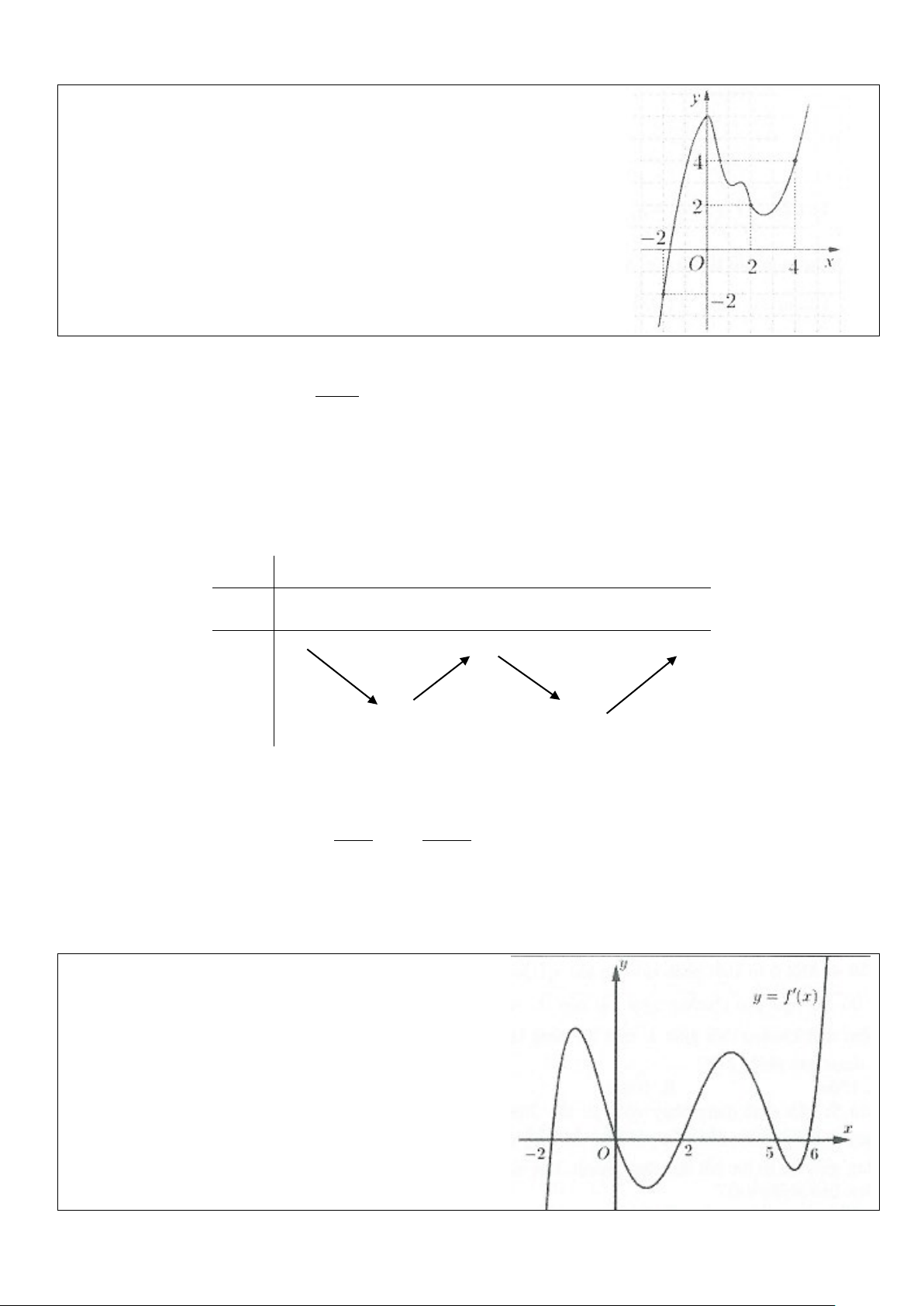
Ví dụ 1: Cho hàm số y = f (x) có đồ thị hàm số
y = f ′(x) cắt trục Ox tại ba điểm có hoành độ a, , b c
thỏa mãn a < b < c như hình vẽ. Mệnh đề nào sau đây đúng?
A. f (a) > f (b) > f (c).
B. f (a) > f (c) > f (b).
C. f (c) > f (b) > f (a).
D. f (c) > f (a) > f (b). Lời giải:
Dựa vào đồ thị hàm số y = f ′(x) ta có BBT của hàm số y = f (x) như sau: x
−∞ a b c +∞
f ′(x) + 0 − 0 + 0 −
f (a) f (c) f (x)
−∞ f (b) −∞ b b
Lại có: S = f ' x dx = − f ' x dx = f a − f b ; tương tự S = f c − f b 2 ( ) ( ) 1 ∫ ( ) ∫ ( ) ( ) ( ) a a
Dựa vào hình vẽ ta thấy S > S ⇒ f a − f b > f c − f b ⇔ f a > f c . Chọn B. 1 2 ( ) ( ) ( ) ( ) ( ) ( )
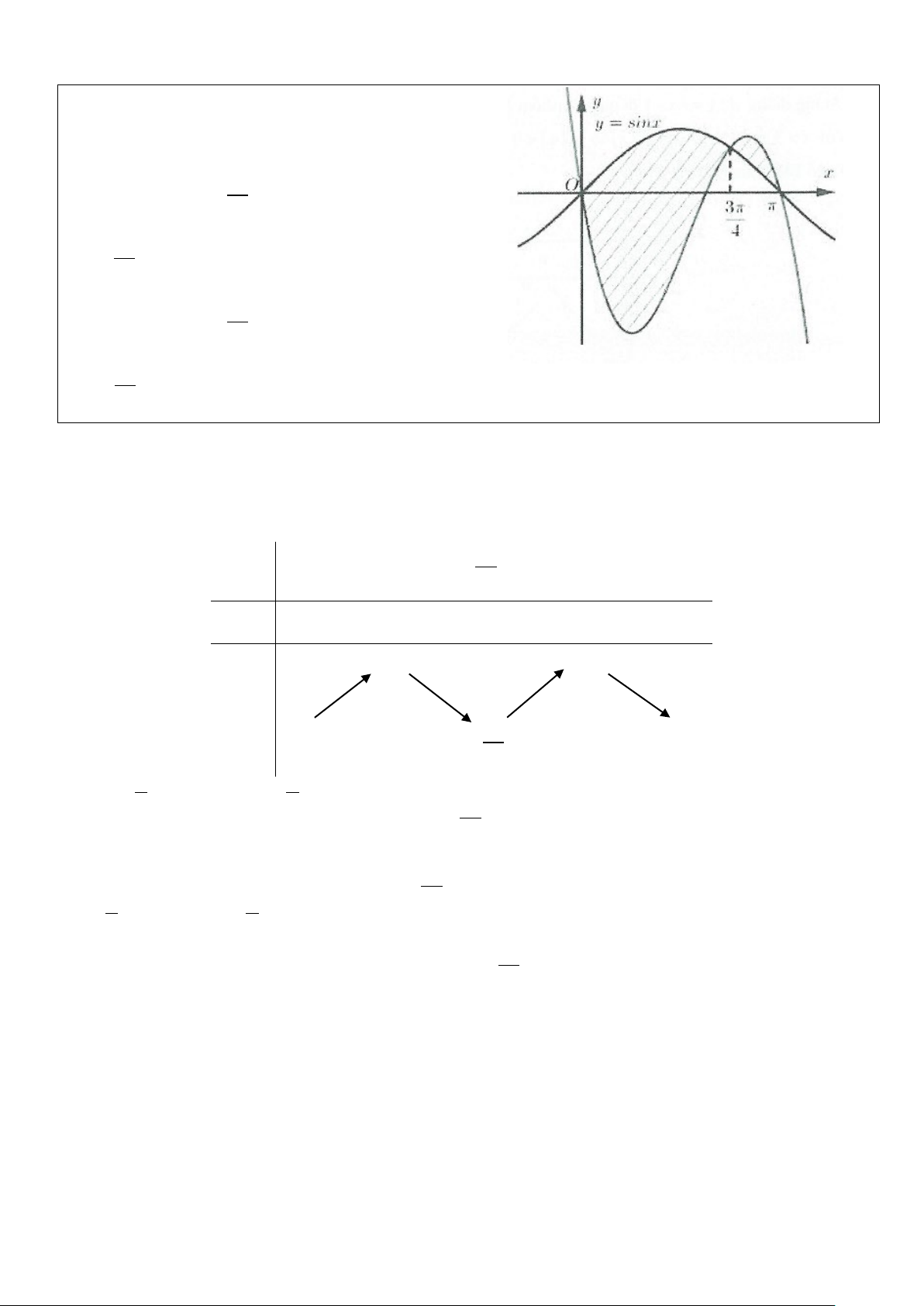
Ví dụ 2: Cho y = f (x) có đồ thị y = f ′(x) như hình.
Đặt g (x) = f (x) + cos .x Mệnh đề nào đúng?
A. g ( ) g ( )  3 0 g π  < π <  .  4  B.  3
g π  < g (0) < g (π   ).  4 
C. g ( ) g ( )  3 0 g π  π < <  .  3  D.  3
g π  < g (π) <   g (0).  4  Lời giải:
Ta có g '(x) = f '(x) −sin x ⇒ g '
∫ (x)dx =  f '
∫ (x)−sin xdx
Bảng biến thiên của hàm số y = g (x) π x −∞ 0 3 π +∞ 4
g′(x) + 0 − 0 + 0 − g (0) g (π ) g (x) π −∞ 3 g( ) −∞ 4 3π 3π 4 4 Đặt  3 S sin x f x
g ' x dx g 0 g π  = − = − = − 1 ∫  ( ) ∫ ( ) ( )  4  0 0  π π  3 Sf x sin xg ' x dx g g π  = − = = π − 2 ∫  ( )  ∫ ( ) ( )   3π 3π  4  4 4
Dựa vào hình vẽ ta có S  π
> S ⇒ g 0 > g π . Do đó 3 g  < g(π) <  
g (0). Chọn D. 1 2 ( ) ( )  4 
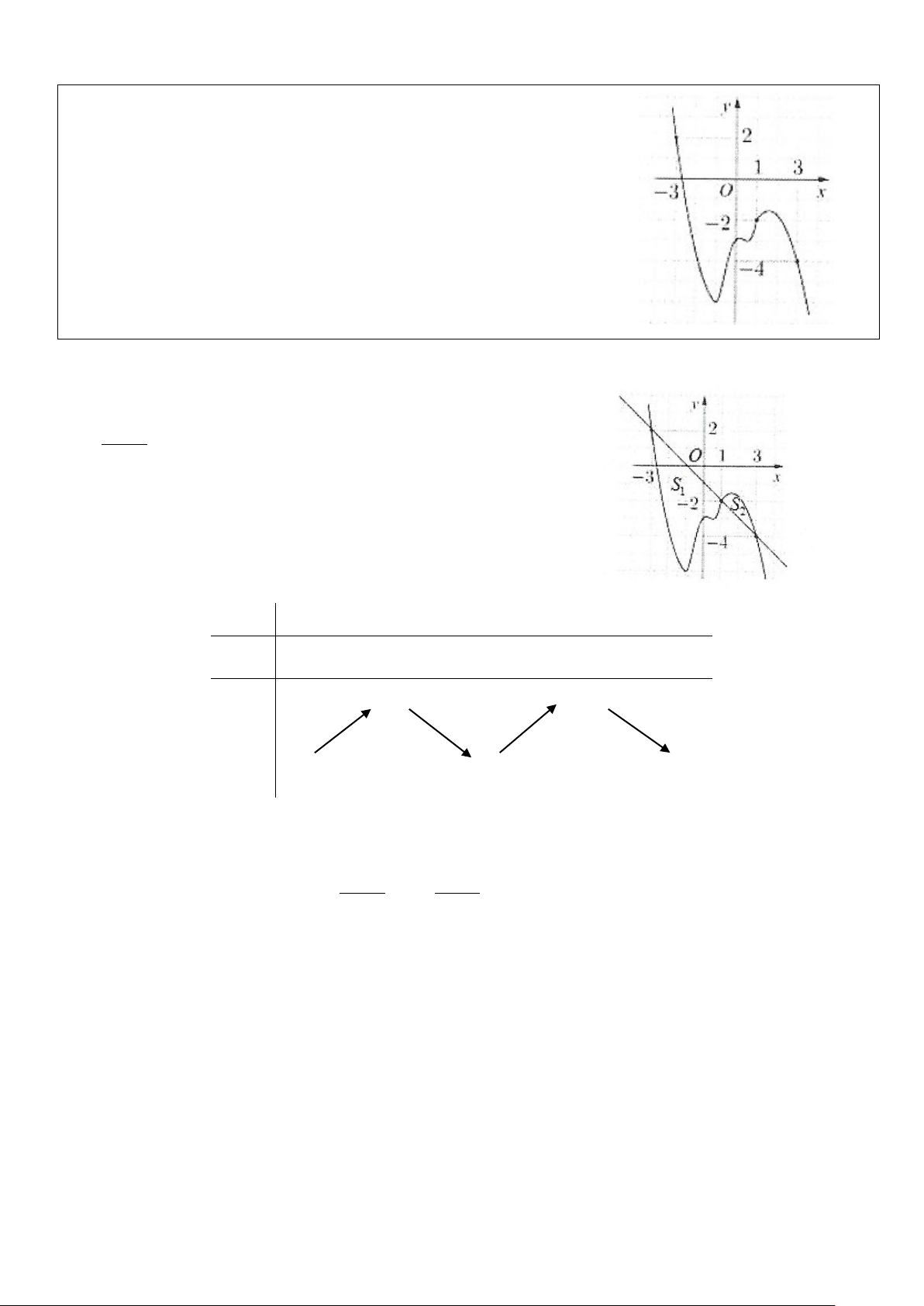
Ví dụ 3: Cho hàm số y = f (x) . Đồ thị của hàm số y = f ′(x) như hình
bên. Đặt g (x) = f (x) + (x + )2 2
1 . Mệnh đề nào dưới đây đúng? A. g ( )
1 < g (3) < g ( 3 − ). B. g ( ) 1 < g ( 3 − ) < g (3).
C. g (3) < g ( 3 − ) < g ( ) 1 .
D. g (3) < g ( 3 − ) < g ( ) 1 . Lời giải:
Ta có g '(x) = 2 f '(x) + x +1 = 2  f '(x) −(−x − ) 1      g '(x) ⇒ dx =  f ' ∫
∫ (x)−(−x− )1dx 2 
Đường thẳng d : y = −x −1 đi qua các điểm ( 3 − ;2);(1; 2 − ) và (3; 4 − )
Với x > 3 ta có: −x −1 > f '(x) ⇒ g '(x) < 0
Ta có BBT của hàm số g (x) x −∞ 3 − 1 3 +∞
g′(x) + 0 − 0 + 0 − g ( 3 − ) g (3) g (x) −∞ g ( ) 1 −∞ 1 3
Đặt S =  −x −1 − f ' x  d ;
x S =  f ' x − −x −1  dx 1 ∫ ( ) ( ) 2 ∫ ( ) ( ) 3 − 1 1 g '(x) 3 g '(x)
Dựa vào hình vẽ ta có S > S ⇒ − dx > dx 1 2 ∫ ∫ − 2 2 3 1 Do đó g ( 3 − ) − g ( )
1 > g (3) − g ( ) 1 ⇒ g ( 3
− ) > g (3). Chọn A.
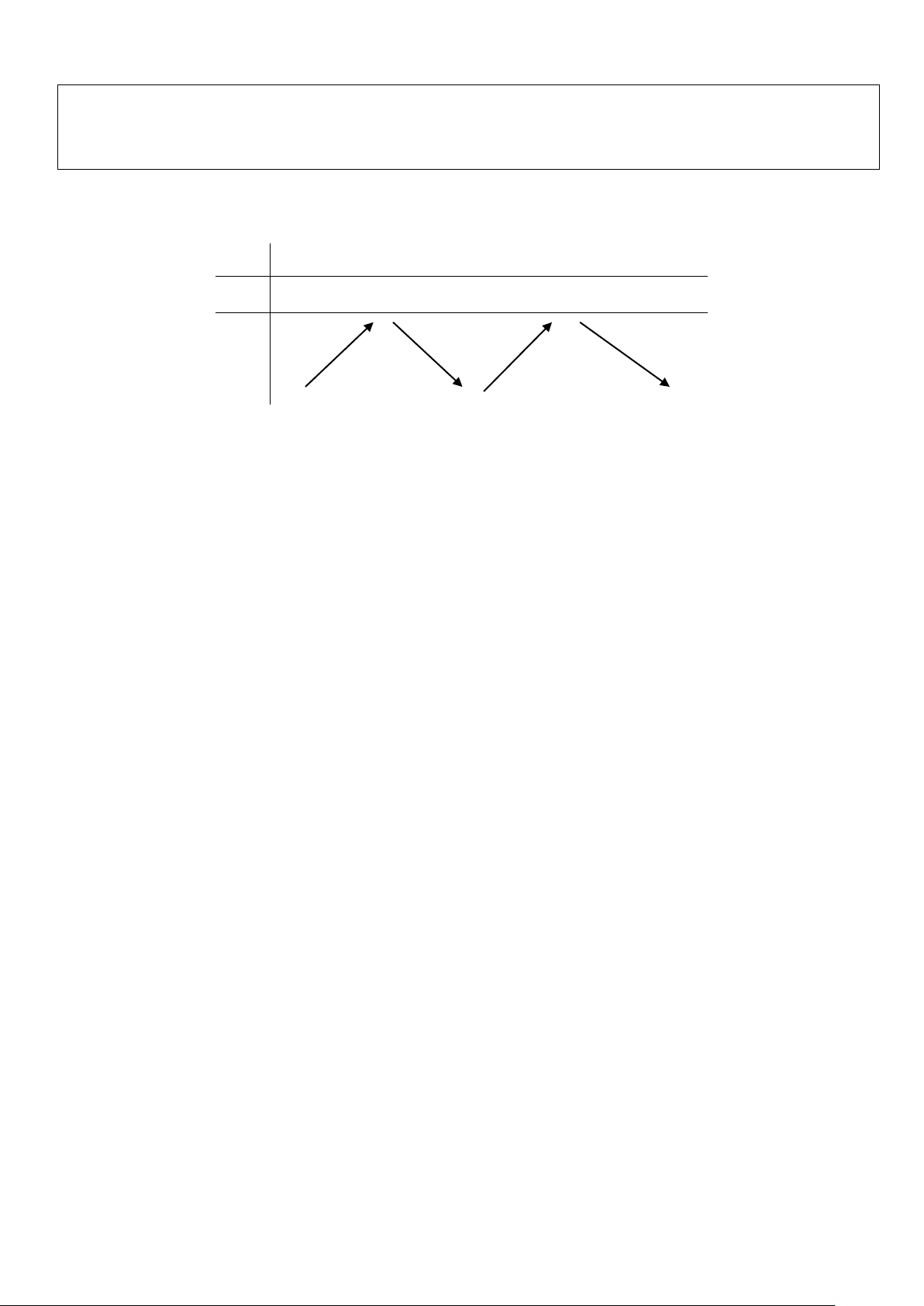
Ví dụ 4: Cho hàm số f (x). Đồ thị của hàm số y = f ′(x) như hình bên.
Đặt h(x) = f (x) 2 2
− x . Mệnh đề nào dưới đây đúng?
A. h(4) = h( 2 − ) > h(2).
B. h(4) = h( 2 − ) < h(2).
C. h(2) > h( 2 − ) > h(4).
D. h(2) > h(4) > h( 2 − ). Lời giải: h' x
Ta có: h'(x) = 2  f '  ( x) ( ) − x ⇒ dx =  f '  ∫
∫ (x)− xdx 2 
Đường thẳng y = x đi qua các điểm ( 2; − 2
− );(2;2);(4;4) trên hình vẽ Với x < 2
− ta có: h'(x) < x suy ra hàm số nghịch biến trên khoảng ( ; −∞ 2 − )
Ta có bảng biến thiên của hàm số h(x) như sau: x −∞ 2 − 2 4 +∞
h′(x) − 0 + 0 − 0 + +∞ h(2) +∞ h(x) h( 2 − ) h(4) 2 4
Đặt S =  f ' x − x d ;
x S = x − f ' x  dx 1 ∫  ( )  2 ∫ ( ) 2 − 2 2 h(x) 4 −h(x)
Dựa vào hình vẽ ta có: S > S ⇒ dx > dx 1 2 ∫ ∫ − 2 2 2 2
⇒ h(2) − h( 2
− ) > h(2) − h(4) ⇔ h(4) > h( 2 − ). Chọn D.
Ví dụ 5: Cho hàm số y = f (x). Đồ thị hàm số
y = f ′(x) như hình vẽ bên. Đặt M = max f (x), [ 2 − ;6]
m = min f (x), T = M + .
m Mệnh đề nào dưới đây [ 2 − ;6] đúng?
A. T = f (0) + f ( 2 − ).
B. T = f (5) + f ( 2 − ).
C. T = f (5) + f (6).
D. T = f (0) + f (2). Lời giải:
Dựa vào đồ thị hàm số y = f '(x) ta lập được bảng biến thiên của hàm số y = f (x) x 2 − 0 2 5 6 y′ + 0 − 0 + 0 − y 0 5 Ta đặt: f '
∫ (x)dx = S = f 0 − f 2 ; f ' x dx = S = f 5 − f 2 1 ( ) ( ) ∫ ( ) 2 ( ) ( ) 2 2
Dựa vào đồ thị ta có: S > S ⇒ f 5 > f 0 ⇒ M = f 5 (loại A và D). 2 1 ( ) ( ) ( ) Ta cần so sánh f ( 2 − ) và f (6) 0 5
Tương tự ta có: f '
∫ (x)dx = f (0)− f ( 2
− ) = S ; f ' x dx = f 5 − f 6 = S 3 ∫ ( ) ( ) ( ) 4 2 − 6
Quan sát đồ thị suy ra S > S ⇒ f 0 − f 2
− > f 5 − f 6 ⇒ f 6 − f 2
− = f 5 − f 0 > 0 3 4 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) Do đó f ( 2
− ) < f (6) ⇒ m = f ( 2 − ). Chọn B.
BÀI TẬP TỰ LUYỆN
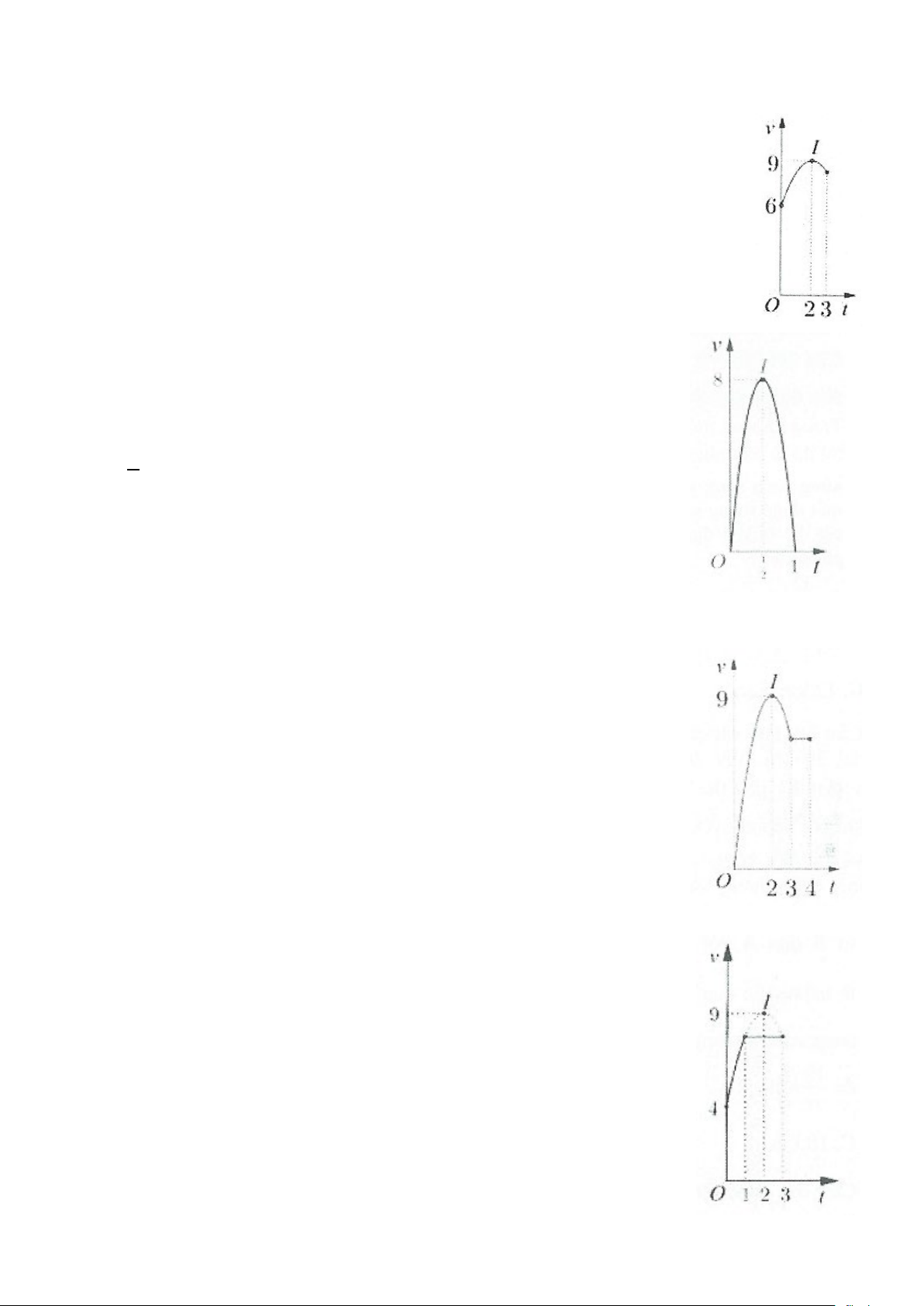
Câu 1: Một chất điểm đang chuyển động với vận tốc v =18 m / s thì tăng tốc với gia tốc 0 a(t) 2 = t + t ( 2
5 m / s ). Tính quãng đường chất điểm đó đi được trong khoảng thời gian 3 s kể từ lúc bắt đầu tăng tốc. A. 117 . m B. 333 . m C. 63 . m D. 126 . m 4 4 2
Câu 2: Một vật chuyển động chậm dần với vận tốc v(t) =150 −15t (m / s). Hỏi rằng trong 5 s trước khi
dừng hẳn vật di chuyển được bao nhiêu mét? A. 1125 . m B. 120 . m C. 375 . m D. 750 . m 2 2
Câu 3: Một ô tô đang chạy đều với vận tốc b (m / s) thì người lái xe đạp phanh. Từ thời điểm đó ô tô
chuyển động chậm dần đều với vận tốc v(t) = 4
− t + b (m / s). Biết từ khi đạp phanh đến lúc dừng hẳn thì ô tô di chuyển được 50 . m Tìm . b
A. 12,5 m / .s
B. 15 m / .s
C. 25 m / .s
D. 20 m / .s
Câu 4: Một ô tô xuất phát với vận tốc v t = 2t +12 m / s sau khi đi được một khoảng thời gian t thì bất 1 ( ) ( ) 1
ngờ gặp chướng ngại vật nên tài xế phanh gấp với vận tốc c t = 24 − 6t m / s và đi thêm một khoảng thời 2 ( ) ( )
gian t nữa thì dừng lại. Hỏi từ khi xuất phát đến lúc dừng lại thì xe ô tô đã đi được bao nhiêu mét? 2 A. 156 . m B. 108 . m C. 48 . m D. 112 . m
Câu 5: Một ô tô đang chạy với vận tốc 20 m / s thì dừng lái đạp phanh. Sau khi đạp phanh, ô tô chuyển
động chậm dần đều với vận tốc v(t) = 20 − 40t (m / s), trong đó t là khoảng thời gian tính bằng giây kể từ
lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét? A. 10 . m B. 7 . m C. 5 . m D. 3 . m
Câu 6: Một vật chuyển động với gia tốc a(t) 2 = t + t ( 2 3
m / s ). Vận tốc ban đầu của vật là 2 (m / s). Hỏi
vận tốc của vật là bao nhiêu sau khi chuyển động với gia tốc đó được 2 .s
A. 8 m / .s
B. 12 m / .s
C. 16 m / .s
D. 10 m / .s
Câu 7: Một ô tô đang dừng và bắt đầu chuyển động theo một đường thẳng với gia tốc a(t) = − t ( 2 6 2 m / s ),
trong đó t là khoảng thời gian tính bằng giây kể từ lúc ô tô bắt đầu chuyển động. Hỏi quãng đường ô tô đi
được kể từ lúc bắt đầu chuyển động đến khi vận tốc của ô tô đạt giá trị lớn nhất là bao nhiêu mét? A. 45 . m B. 18 . m C. 36 . m D. 27 . m 2 4 2
Câu 8: Một vật chuyển động với vận tốc v(t) t + 4 = 1,2 +
(m / s). Tính quãng đường vật đó đi được trong t + 3
4 giây đầu (làm tròn kết quả đến chữ số thập phân thứ hai). A. 1,64 . m B. 11,01 . m C. 11,81 . m D. 11,18 . m
Câu 9: Một chất điểm A từ trạng thái nghỉ chuyển động với vận tốc nhanh dần đều, 8s sau nó đạt đến vận
tốc 6 m / .s Từ thời điểm đó nó chuyển động đều. Một chất điểm B khác xuất phát từ cùng vị trí với A
nhưng chậm hơn nó 12 s với vận tốc nhanh dần đều và đuổi kịp A sau 8s (kể từ lúc B xuất phát). Tìm vận
tốc B tại thời điểm đó.
A. 12 m / .s
B. 24 m / .s
C. 18 m / .s
D. 30 m / .s
Câu 10: Một ô tô đang chạy với vận tốc 36 km / h thì tăng tốc chuyển động nhanh dần với gia tốc a(t) 1 = 1+ t ( 2
m / s ). Tính quãng đường mà ô tô đi được sau 6 giây kể từ khi ôtô bắt đầu tăng tốc. 3 A. 90 . m B. 246 . m C. 58 . m D. 102 . m
Câu 11: Một ô tô đang chuyển động đều với vận tốc 12 m / s thì người lái đạp phanh; từ thời điểm đó ô tô
chuyển động chậm dần đều với vận tốc v(t) =12 − 2t (m / s) (trong đó t là thời gian tính bằng giây, kể từ
lúc đạp phanh). Hỏi trong thời gian 8 giây cuối (tính đến khi xe dừng hẳn) thì ô tô đi được quãng đường bằng bao nhiêu? A. 16 . m B. 60 . m C. 32 . m D. 100 . m
Câu 12: Bạn An ngồi trên máy bay đi du lịch thế giới vận tốc chuyển động của máy bay là v(t) 2
= 3t + 5 (m / s). Hỏi quãng đường máy bay đi được từ giây thứ 4 đến giây thứ 10 bằng bao nhiêu? A. 996 . m B. 876 . m C. 966 . m D. 1086 . m
Câu 13: Một vận động viên đua xe F đang chạy với vận tốc 10 (m / s) thì anh ta tăng tốc với vận tốc
a(t) = t ( 2
6 m / s ), trong đó t là khoảng thời gian tính bằng giây kể từ lúc tăng tốc, hỏi quãng đường xe của
anh ta đi được trong thời gian 10 s kể từ lúc bắt đầu tăng tốc là bao nhiêu? A. 1100 . m B. 100 . m C. 1010 . m D. 1110 . m
Câu 14: Một vật chuyển động chậm dần đều với vận tốc v(t) = 30 − 2t (m / s). Hỏi trong 5 s trước khi
dừng hẳn, vật di chuyển động được bao nhiêu mét? A. 50 . m B. 225 . m C. 125 . m D. 25 . m
Câu 15: Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v t = 7t m / s . Đi được 5 s người lái 1 ( ) ( )
xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc a = − ( 2
70 m / s ). Tính quãng đường đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn. A. 95,70 . m B. 96,25 . m C. 87,50 . m D. 94,00 . m
Câu 16: Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi công thức v(t) = 3t + 2, thời
gian tính theo đơn vị giây, quãng đường vật đi được tính theo đơn vị mét. Biết tại thời điểm t = 2 s thì vật đi
được quãng đường là 10 .
m Hỏi tại thời điểm t = 30 s thì vật đi được quãng đường là bao nhiêu? A. 240 . m B. 1140 . m C. 300 . m D. 1410 . m
Câu 17: Một học sinh đi học từ nhà đến trường bằng xe đạp với vận tốc thay đổi theo thời gian được tính
bởi công thức v(t) = 40t +100 (m / phút). Biết rằng sau khi đi được 1 phút thì quãng đường học sinh đó đi được là 120 .
m Biết quãng đường từ nhà đến trường là 3 k .
m Hỏi thời gian học sinh đó đi đến trường là bao nhiêu phút? A. 9 phút. B. 15 phút. C. 10 phút. D. 12 phút.
Câu 18: Một vật chuyển động với vận tốc 10 (m / s) thì tăng tốc với gia tốc a(t) 2 = t + t ( 2 3 m / s ). Tính
quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc. A. 4000 . m B. 4350 . m C. 4300 . m D. 1433 . m 3 3 3
Câu 19: Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang phải) với gia
tốc phụ thuộc vào thời gian t (s) là a(t) = t − ( 2
2 7 m / s ). Biết vận tốc đầu bằng 10 (m / s). Hỏi trong 6 giây
đầu tiên, thời điểm nào chất điểm ở xa nhất về phía bên phải? A. 5 .s B. 6 .s C. 1 .s D. 2 .s
Câu 20: Một ô tô đang chạy thì người lái đạp phanh, từ thời điểm đó, ô tô chuyển động chậm dần đều với
vận tốc v(t) = 12
− t + 24 (m / s), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh.
Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 18 . m B. 15 . m C. 20 . m D. 24 . m
Câu 21: Một vật chuyển động với vận tốc v(t) (m / s) có gia tốc v (t) 3 ' = ( 2
m / s ). Vận tốc ban đầu của t +1
vật là 6 m / .s Tính vận tốc của vật sau 10 giây, (làm tròn kết quả đến hàng đơn vị).
A. 10(m / s).
B. 8 (m / s).
C. 15 (m / s).
D. 13 (m / s).
Câu 22: Một đám vi sinh trùng tại ngày thứ t có số lượng N (t), biết rằng N (t) 7000 ' = và lúc đầu đám vi t + 2
trùng có 300000 con. Hỏi sau 10 ngày, đám vi trùng có bao nhiêu con (làm tròn đến hàng đơn vị)? A. 322542 con. B. 332542 con. C. 302542 con. D. 312542 con.
Câu 23: Khi quan sát một đám vi khuẩn trong phòng thí nghiệm người ta thấy tại ngày thứ x có số lượng
N (x) con. Biết rằng N (x) 2017 ' =
và lúc đầu đám vi khuẩn có 30000 con. Hỏi số lượng vi khuẩn sau x +1
đúng một tuần gần với số nào sau đây? A. 36194. B. 38417. C. 35194. D. 34194.
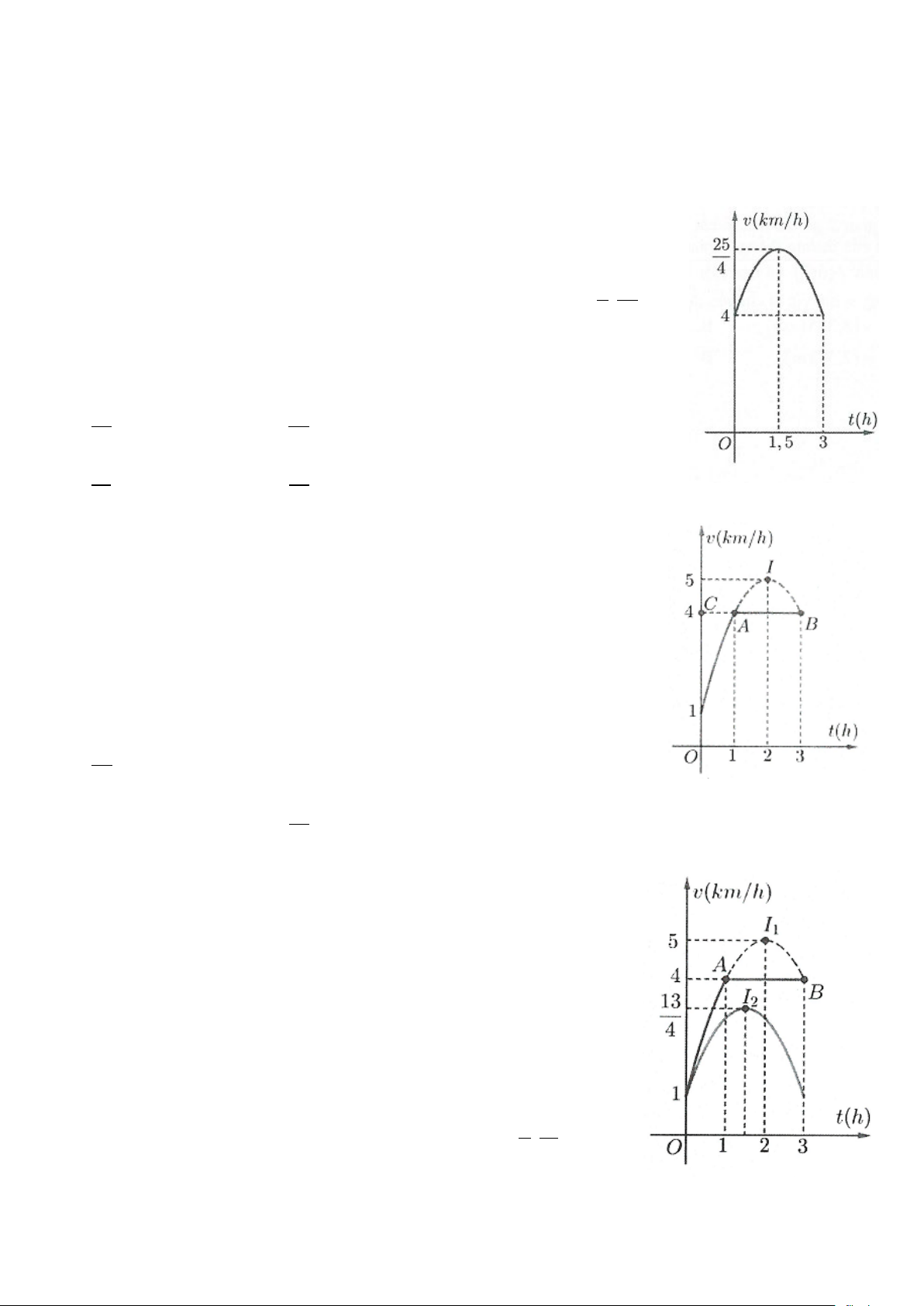
Câu 24: (Đề thi THPT Quốc gia 2017) Một vật chuyển động trong 3 giờ với vận tốc
v (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần của đường parabol có đỉnh
I (2;9) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s mà
vật di chuyển được trong 3 giờ đó.
A. s = 26,75 (km).
B. s = 25,25 (km).
C. s = 24,25 (km).
D. s = 24,75 (km).
Câu 25: (Đề thi THPT Quốc gia 2017) Một người chạy trong thời gian 1 giờ
với vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần parabol với đỉnh 1 I  ;8 
và trục đối xứng song song với trục tung như hình bên. Tính quãng 2   
đường s mà người đó chạy được trong khoảng thời gian 45 phút kể từ khi chạy. A. s = 4 (km).
B. s = 2,3 (km).
C. s = 4,5 (km).
D. s = 5,3 (km).
Câu 26: (Đề thi THPT Quốc gia 2017) Một vật chuyển động trong 4 giờ với
vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị vận tốc như hình bên.
Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một
phần của đường parabol có đỉnh I (2;9) với trục đối xứng song song với trục
tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành.
Tính quãng đường s mà vật di chuyển được trong 4 giờ đó. A. 26,5 km. B. 28,5 km. C. 27 km. D. 24 km.
Câu 27: (Đề thi THPT Quốc gia 2017) Một vật chuyển động trong 3 giờ với vận
tốc v (km/h) phụ thuộc vào thời gian t (h) có đồ thị vận tốc như hình vẽ bên.
Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một
phần của đường parabol có đỉnh I (2;9) và trục đối xứng song song với trục tung,
khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính
quãng đường s mà vật di chuyển được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm).
A. s = 23,25 (km).
B. s = 21,58 (km).
C. s =15,50 (km).
D. s =13,83 (km).
Câu 28: Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc vào
thời gian t (h) có đồ thị là một phần của đường parabol có đỉnh 3 25 I  ;   và 2 4   
trục đối xứng song song với trục tung như hình vẽ. Tính quãng đường mà vật di
chuyển được trong 3 giờ. A. 33 km. B. 29 km. 2 2 C. 31 km. D. 35 km. 2 2
Câu 29: Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc
vào thời gian t (h) có đồ thị vận tốc như hình bên. Trong khoảng thời gian 1
giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có
đỉnh I (2;5) và trục đối xứng song song với trục tung, khoảng thời gian còn
lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường mà
vật di chuyển được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm). A. 32 km. B. 15 km. 3 C. 12 km. D. 35 km. 3
Câu 30: Hai vật chuyển động ngược chiều nhau trên một quãng đường
AB dài 30 km. Vật M chuyển động từ A đến B trong 3 giờ với vận tốc
v km/h phụ thuộc vào thời gian t (h), trong khoảng thời gian 1 giờ kể 1 ( )
từ khi bắt đầu chuyển động có đồ thị là một phần của parabol có đỉnh
I 2;5 và trục đối xứng song song với trục tung, khoảng thời gian còn lại 1 ( )
đồ thị là một đoạn thẳng song song với trục hoành. Vật N chuyển động
trong 3 giờ từ B đến A với vận tốc v km/h phụ thuộc vào thời gian 2 ( )
t (h) với đồ thị là một phần của đường parabol có đỉnh 3 13
I  ;  và trục 2 2 4   
đối xứng song song với trục tung. Hỏi sau 3 giờ thì hai vật M , N cách nhau bao nhiêu km? A. 19 km. B. 37 km. 6 2 C. 18 km. D. 45 km. 2
Câu 31: Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ thuộc
thời gian t (h) có đồ thị vận tốc như hình bên. Trong khoảng thời gian 2 giờ
kể từ khi bắt đầu chuyển động nhanh dần, đồ thị là một phần của đường
thẳng. Khoảng thời gian còn lại đồ thị là một parabol có đỉnh I (3;7) và trục
đối xứng song song với trục tung. Tính quãng đường s mà vật di chuyển được trong 210 phút.
A. s =15,375 (km).
B. s =16,375 (km).
C. s =17,5 (km).
D. s =18,5 (km).
Câu 32: Một vật chuyển động trong 2 giờ với vận tốc v (km/h) phụ thuộc
thời gian t (h) có đồ thị của vận tốc như hình bên. Trong khoảng thời gian
1,5 giờ kể từ khi bắt đầu chuyển động, đồ thị là parabol có đỉnh I (1;9) và
trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một
đoạn thẳng. Tính quãng đường s mà vật di chuyển được trong 2 giờ đó. A. 13,8 km. B. 14,8 km. C. 15,8 km. D. 16,8 km.
Câu 33: Một vật chuyển động trong 10 giờ với vận tốc v (km/h) phụ thuộc
thời gian t (h) có đồ thị của vận tốc như hình bên. Tính quãng đường s
mà vật đi được trong 10 giờ đó. A. 72 km. B. 70 km. C. 74 km. D. 76 km.
Câu 34: Một vật chuyển động với vận tốc v =15 m/s thì tăng tốc với gia 0 tốc a ( 2
m/s ) phụ thuộc thời gian t (s) có đồ thị là một phần của parabol có đỉnh I (1; 4
− ) và trục đối xứng song song với trục tung như hình bên. Tính
quãng đường s mà vật di chuyển được trong 3 giây kể từ lúc bắt đầu tăng tốc. A. 45,25 m. B. 36 m. C. 50 m. D. 44,5 m.
Câu 35: Một vật chuyển động trong 4 giây với gia tốc a ( 2 m/s ) phụ
thuộc thời gian t (s) có đồ thị của gia tốc như hình bên. Trong khoảng
thời gian 3 giây kể từ khi bắt đầu chuyển động, đồ thị là một parabol có
đỉnh I (2;4) và trục đối xứng song song với trục tung, khoảng thời gian
còn lại đồ thị là một đoạn thẳng. Tính quãng đường s mà vật di chuyển
được trong 4 giây đó. Biết rằng vận tốc của vật tại giây thứ 3 bằng 18 m/s. A. 55,9 m. B. 56,9 m. C. 57,9 m. D. 58,9 m.
LỜI GIẢI CHI TIẾT 3
Câu 1: Ta có v(t) = a
∫ (t)dt = ∫( 2t +5t) t 5 2
dt = + t + C ( m/s) 3 2 3
Do khi bắt đầu tăng tốc v =18 nên t 5 v = ⇒ = ⇒ = + + = 18 C 18 v t t 18 t 0 ( ) 2 0 ( ) 3 2
Khi đó quãng đường xe đi được sau 3 giây kể từ khi ô tô bắt đầu tăng tốc bằng 3 3 3 2   S = v ∫ (t) t 5t 333
dt = ∫18+ + dt = m. Chọn B.  3 2  4 0 0
Câu 2: Khi dừng hẳn v(t) =150 −15t = 0 ⇔ t =10 (s) 10 10
Khi đó trong 5 s trước khi dừng hẳn vật di chuyển được: S = v
∫ (t) t = ∫( − t) 375 d 150 15 dt = . m 2 5 5 Chọn C.
Câu 3: Khi dừng hẳn ( ) = 4 − + = 0 b v t t b ⇔ t = (s) 4
Quãng đường xe đi được từ khi đạp phanh đến lúc dừng hẳn là: b b 4 4 b S = v
∫ (t)dt = ∫( 4
− t + b)dt = ( 2 2 − t + bt) 2 2 b − b 4 2 = +
= 50 ⇔ b = 400 ⇔ b = 20. Chọn D. 0 8 4 0 0
Câu 4: Ta có: v = 24 m / s do đó khi gặp chướng ngại vật vật có vận tốc là 24 m / s 02 ( )
Khi đó v t = 2t +12 = 24 ⇔ t = 6 s 1 ( ) ( )
Vật dừng lại khi v t = 24 − 6t = 0 ⇔ t = 4 s 2 ( ) 2 ( ) 6 4 6 4
Quãng đường vật đi được là: s = v t dt + v t dt = 2t +12 dt + 24 − 6t dt =156 . m ∫ 1 ( ) ∫ 2 ( ) ∫( ) ∫( ) 0 0 0 0 Chọn A.
Câu 5: Khi dừng hẳn v(t) = 20 − 40t = 0 ⇔ t = 0,5 (s) 1 1 2 2
Quãng đường xe đi được từ khi đạp phanh đến lúc dừng hẳn là: S = v
∫ (t)dt = ∫(20−40t)dt = 5 . m 0 0 Chọn C.
Câu 6: Ta có v(t) = a
∫ (t)dt = ∫( 2 3t + t) 3 1 2
dt = t + t + C ( m/s) 2
Do khi bắt đầu tăng tốc v = 2 nên 1 v = ⇒ = ⇒ = + + = 2 C 2 v t t t 2 t 0 ( ) 3 2 0 ( ) 2
Vận tốc của vật khi chuyển động với gia tốc đó được 2 s là v(2) =12 m / .s Chọn B.
Câu 7: Ta có: v(t) = a
∫ (t) t = ∫( − t) 2 d
6 2 dt = 6t − t + C ( m/s)
Khi đó v ⇔ t = 3, do ban đầu ô tô đang dừng nên v(0) = 0 ⇔ C = 0. max
Quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc của ô tô đạt giá trị lớn nhất là: 3 S = ∫( 2
6t − t )dt =18 . m Chọn B. 0
Câu 8: Quãng đường vật đó đi được trong 4 giây đầu là: 4 4 2  +  S = v ∫ (t) t 4 CASIO dt = ∫1,2+ d
t → S ≈ 11,81 . m Chọn C. t + 3 0 0 
Câu 9: Phương trình vận tốc của vật A là: v = at 1 Do v( ) 3 3
8 = 6 ⇒ a = ⇒ v = t ⇒ 1 4 4 8
Quãng đường vật A đi được sau 20s đầu là 3 tdt + 6.12 = 96 . m ∫ 4 0 8
Phương trình vận tốc của vật B là: v = bt ⇒ S = bt t = ⇒ b = B d 96 3 2 ∫ 0
Do đó v = bt ⇒ vận tốc của vật B khi hai vật gặp nhau là v = = m s Chọn B. B 3.8 24 / . 2
Câu 10: Ta có v(t) = a ∫ (t)  t  1 2 dt = 1+
dt = t + t + ∫  C ( m/s)  3  6
Do khi bắt đầu tăng tốc v = 36 km / h =10 m / s nên 1 v = ⇒ = ⇒ = + + = 10 C 10 v t t t 10 t 0 ( ) 2 0 ( ) ( ) ( ) 6
Khi đó quãng đường xe đi được sau 6 giây kể từ khi ô tô bắt đầu tăng tốc bằng 6 6 2 = ∫ ( )  tS
v t dt = ∫t + +10dt = 90 m. Chọn A.  6 0 0 
Câu 11: Khi dừng hẳn v(t) =12 − 2t = 0 ⇔ t = 6 (s)
Khi đó trong 8 s trước khi dừng hẳn vật di chuyển được (bao gồm 2 s trước khi đạp phanh): 6 6 S = 2.12 + v
∫ (t)dt = 24+ ∫(12−2t)dt = 24+36 = 60 . m Chọn B. 0 0
Câu 12: Quãng đường máy bay đi được từ giây thứ 4 đến giây thứ 10 là: 10 10 S = v
∫ (t)dt = ∫( 2
3t + 5)dt = 996 . m Chọn C. 4 4
Câu 13: Ta có v(t) = a ∫ (t) 2
dt = 6tdt = 3t + C ∫ ( m/s)
Do khi bắt đầu tăng tốc v =10 nên v = ⇒ = ⇒ = + = 10 C 10 v t 3t 10 t 0 ( ) 2 0 ( )
Khi đó quãng đường xe đi được sau 10 giây kể từ khi ô tô bắt đầu tăng tốc bằng 10 10 S = v
∫ (t)dt = ∫( 2
3t +10)dt =1100 . m Chọn A. 0 0
Câu 14: Khi dừng hẳn v(t) = 30 − 2t = 0 ⇔ t =15 (s)
Khi đó trong 5 s trước khi dừng hẳn vật di chuyển được: 15 15 S = v
∫ (t)dt = ∫(30−2t)dt = 25 . m Chọn D. 10 10
Câu 15: Vận tốc vật đạt được sau 5 s là: v = 7.5 = 35 m / .s 0
Ta có v t = a t dt = 70d − t = 70 − t + C m/s 2 ( ) ∫ ( ) ∫ ( )
Do khi bắt đầu tăng tốc v = 35 nên v = ⇒ = ⇒ = − + = 35 C 35 v t 70t 35 t 0 2 ( ) 0 ( ) Vật dừng hẳn khi 1 v t = 70
− t + 35 = 0 ⇔ t = s . 2 ( ) 2 ( ) 2 1 1 5 2 5 2
Khi đó quãng đường đi được bằng S = v t dt + v t dt = 7tdt + 70
− t + 35 dt = 96,25 . m ∫ 1 ( ) ∫ 2 ( ) ∫ ∫( ) 0 0 0 0 Chọn B.
Câu 16: Quãng đường vật đi được từ thời điểm t = 2 s đến t = 30 s là: 30 30 S = v
∫ (t)dt = ∫ (3t + 2)dt =1400 m = S (30)− S (2) ⇒ S (30) = S (2)+1400 =1410. 2 2 30
Cách 2: S (30) = ∫ (3t + 2)dt =1410. Chọn D. 0
Câu 17: S (t) = v ∫ (t) 2
dt = 20t +100t + C Do S ( )
1 =120 + C =120 ⇒ C = 0
Để học sinh đó đến trường thì S (t) 2
= 20t +100t = 3000 ⇔ t =10. Chọn C. 3
Câu 18: v(t) = a
∫ (t)dt = ∫( 2t +3t) t 3 2
dt = + t + C ( m/s) 3 2 3
Do khi bắt đầu tăng tốc v =18 nên t 3 v = ⇒ = ⇒ = + + = 10 C 10 v t t 10 t 0 ( ) 2 0 ( ) 3 2 10 10 3 2  
Khi đó quãng đường đi được bằng S = v ∫ (t) t 3t 4300
dt = ∫10+ + dt = m. Chọn C.  3 2  3 0 0
Câu 19: Vận tốc của vật được tính theo công thức v(t) 2
= 10 + t − 7t (m / s). 3
Suy ra quãng đường vật đi được tính theo công thức S (t) = v ∫ (t) t 7 2
dt = − t +10t (m). 3 2 t = 2 Ta có S′(t) 2
= t − 7t +10 ⇒ S′(t) 2
= 0 ⇔ t − 7t +10 = 0 ⇔  . t = 5 S (0) = 0  S ( ) 26 2 = Suy ra  3 
⇒ Max S (t) = S (2) 26 = . Chọn D. S ( ) 25 [0;6] 3 5 =  6 S  (6) = 6
Câu 20: Khi dừng hẳn v(t) = 12
− t + 24 = 0 ⇔ t = 2 (s) 2 2
Do đó từ lúc đạp phanh đến khi dừng hẳn, ô tô đi được: S = v
∫ (t)dt = ∫( 12
− t + 24)dt = 24 . m 0 0 Chọn D.
Câu 21: Vận tốc của vật là: ( ) = ∫ ( ) 3d ' d t v t v t t = = 3ln ∫ (t + ) 1 + C t +1
Do vận tốc ban đầu của vật là 6 m / s ⇒ (V = ⇒ + = ⇒ = = 6 3ln1 C 6 C 6. t 0)
Vận tốc của vật sau 10 s là: v(10) = 3ln11+ 6 ≈13 m / .s Chọn D.
Câu 22: N (t) = N ∫ (t) 7000 ' dt = dt = 7000ln ∫ (t + 2)+C t + 2 Do N (0) = N( = + = ⇒ = − = 7000ln 2 C 300000 C 300000 7000ln 2. t 0)
Sau 10 ngày, đám vi trùng có N (10) = 7000ln12 + C = 7000ln 6 + 300000 ≈ 312542 con. Chọn D.
Câu 23: N (x) = N ∫ (x) 2017 ' dt = dt = 2017ln ∫ (x + ) 1 + C x +1 Do N (0) = N( = + = ⇒ = = 2017.ln1 C 30000 C 30000. x 0)
Sau 1 tuần, đám vi trùng có N (7) = 2017ln8 + 3000 ≈ 34194 con. Chọn D.
Câu 24: Gọi phương trình parabol là 2
y = at + bt + c (a ≠ 0).  b  3 c = 6;− = 2 a = −
Vì (P) có đỉnh I (2;9) và đi qua M (0;6) nên  2a ⇔  4 .
4a + 2b + c = 9 b  = 3; c = 6
Do đó, phương trình parabol là 3 2
y = − t + 3t + 6. 4 3
Vậy quãng đường mà vật di chuyển là  3 2 S t 3t 6 = − + + dt = ∫  24,75. Chọn D.  4 0 
Câu 25: Gọi phương trình parabol là 2
y = at + bt + c (a ≠ 0).  b 1 c = 0; − =  2a 2 a = 32 − Vì (P) có đỉnh 1 I  ;8 
và đi qua O(0;0) nên  ⇔  . 2    a b b   = 32; c = 0 + + c = 8 4 2
Do đó, phương trình parabol là 2 y = 32 − t + 32t. 3 4
Vậy quãng đường mà vật di chuyển là S = ∫( 2 − t + t) 9 32
32 dt = . Chọn C. 2 0
Câu 26: Gọi phương trình parabol là 2
y = at + bt + c (a ≠ 0).  b  9 c = 0; − = 2 a = −
Vì (P) có đỉnh I (2;9) và đi qua O(0;0) nên  2a ⇔  4 .
4a + 2b + c = 9 b  = 9; c = 0
Do đó, phương trình parabol là 9 2
y = − t + 9t. Với t = ⇒ y ( ) 27 3 3 = . 4 4 3
Vậy quãng đường mà vật di chuyển là  9 2  27
S = − t + 9t dt + . ∫ (4−3) =   27. Chọn C.  4  4 0
Câu 27: Gọi phương trình parabol là 2
y = at + bt + c (a ≠ 0).  b  5 c = 4; − = 2 a = −
Vì (P) có đỉnh I (2;9) và đi qua M (0;4) nên  2a ⇔  4 .
4a + 2b + c = 9 b  = 5; c = 4
Do đó, phương trình parabol là 5 2
y = − t + 5t + 4. Với t = ⇒ y ( ) 31 1 1 = . 4 4 1
Vậy quãng đường mà vật di chuyển là  5 2  31
S = − t + 5t + 4 dt + . ∫ (3− ) 1 =   21,58. Chọn B.  4  4 0
Câu 28: Gọi phương trình parabol là 2
y = at + bt + c (a ≠ 0).  b 3 c = 4; − = a = 1 − 
Vì (P) có đỉnh 3 25 I  ;   2a 2  
và đi qua M (0;4) nên  ⇔ b  = 3 . 2 4    9 3 25  a b c  + + = c =  4 4 2 4
Do đó, phương trình parabol là 2 y = t − + 3t + 4. 3
Vậy quãng đường mà vật di chuyển là S = ∫( 2t − + t + ) 33 3 4 dt = . Chọn A. 2 0
Câu 29: Gọi phương trình parabol là 2
y = at + bt + c (a ≠ 0).  ba = 1 − c = 1; − = 2
Vì (P) có đỉnh I (2;5) và đi qua M (0; ) 1 nên   2a ⇔ b  = 4 .
4a + 2b + c = 5 c =1
Do đó, phương trình parabol là 2 y = t − + 4t +1. 1
Vậy quãng đường mà vật di chuyển là S = ∫( 2t
− + t + ) t + ( − ) 32 4 1 d 4. 3 1 = . Chọn A. 3 0
Câu 30: Ta xét riêng các vật M , N :
- Xét chiều di chuyển của vật M.
Gọi phương trình của parabol (P) là 2
y = at + bt + cba = 1 − c =1; − = 2
Vì (P) có đỉnh I (2;5) và đi qua M (0; ) 1 nên suy ra   2a ⇔ b  = 4 .
4a + 2b + c = 5 c =1
Do đó, phương trình (P) là 2 y = t
− + 4t +1 cũng chính là phương trình vận tốc. 1
Suy ra quãng đường vật M đi trong 3 giờ là S = t − + t + t + − = km M ∫( 2 ) ( ) 32 4 1 d 4. 3 1 . 3 0
- Xét chiều di chuyển của vật N.
Gọi phương trình parabol (P) là 2
y = at + bt + cb 3 c =1; − = a = 1 − 
Vì (P) có đỉnh 3 13 I  ;   2a 2   và đi qua M (0; ) 1 nên suy ra  ⇔ b  = 3 . 2 4    9 3 13  a b c  + + = c =  1 4 2 4
Do đó, phương trình (P) là 2 y = t
− + 3t +1 cũng chính là phương trình vận tốc. 3
Suy ra quãng đường vật N đi trong 3 giờ là S = t − + t + t = km N ∫( 2 ) 15 3 1 d . 2 0
Vậy sau 3 giờ thì hai vật M , N cách nhau một khoảng 32 15 19 − = k . m Chọn A. 3 2 6
Câu 31: Gọi phương trình đường thẳng là d : y = mt + n
Vì d đi qua điểm M (0;3) và N (2;4) 1 
→ y = t + 3 là phương trình vận tốc. 2
Gọi phương trình của parabol (P) là 2
y = at + bt + c
4a + 2b + c = 4 a = 3 −
Vì (P) có đỉnh I (3;7) và đi qua N (2;4) nên suy ra 9   a 3b c 7 b  + + = ⇔  =18 . 6a b 0  + = c = 20 −  
Do đó, phương trình (P) là 2 y = 3
− t +18t − 20 cũng chính là phương trình vận tốc. 7 2 2
Vậy quãng đường cần tính là  1 S t 3 = + dt + ∫ ∫( 2 3
− t +18t − 20)dt =   16,375. Chọn B.  2 0  2
Câu 32: Gọi phương trình của parabol (P) là 2
y = at + bt + cba = 9 − c = 0; − = 1
Vì (P) có đỉnh I (1;9) và đi qua O(0;0) nên suy ra   2a ⇔ b  = 18 .
a +b + c = 9  c = 0
Do đó, phương trình (P) là 2 y = 9
− t +18t cũng chính là phương trình vận tốc. 2 Với 3 3  3  3 27 t =  →v  = 9. − +18. =     . 2  2   2  2 4
Gọi phương trình đường thẳng là d : y = mt + n Vì d đi qua điểm 3 27 M  ;   và N (2;12) 21  → y = t − 9. 2 4    2 3 2 2
Vậy quãng đường cần tính là S ∫( 2t t)  21 9 18 dt t 9 = − + + − dt = ∫  14,8 . km Chọn B.  2 0 3  2 2
Câu 33: Trong 2 giờ đầu, vật chuyển động với vận tốc v(t) = 3t 
→ S = 3tdt = 6 . km 1 ∫ 0
Trong 2 giờ tiếp theo, vật chuyển động với vận tốc v(t) = 6  → S = 6.2 =12 . km 2 10
Trong 6 giờ cuối, vật chuyển động với vận tốc v(t) = t + 2 
→ S = t + 2 dt = 54 . km 3 ∫( ) 4
Vậy tổng quãng đường vật đi trong 10 giờ là S = S + S + S = 6 +12 + 54 = 72 . km Chọn A. 1 2 3
Câu 34: Gọi phương trình của parabol (P) là 2
y = at + bt + cba = 4 c = 0; − = 1
Vì (P) có đỉnh I (1; 4
− ) và đi qua O(0;0) nên suy ra   2a ⇔ b  = 8. −
a +b + c = 4 −  c = 0
Do đó, phương trình (P) là 2
y = 4t −8t cũng chính là phương trình gia tốc.
Ta có a(t) = 4t −8t ⇒ v(t) = ∫(4t −8t) 3 2 2 4t 2 dt = − 4t + C 3 3 3 3  
Mà v(0) =15 ⇒ C =15. Vậy S = v ∫ (t) 4t 2
dt = ∫ −4t +15dt = 36 . m Chọn B.  3 0 0 
Câu 35: Gọi phương trình của parabol (P) là 2
y = at + bt + cba = 1 − c = 0; − = 2
Vì (P) có đỉnh I (2;4) và đi qua O(0;0) nên suy ra   2a ⇔ b  = 4 .
4a + 2b + c = 4 c = 0
Do đó, phương trình (P) là 2 y = t
− + 4t cũng chính là phương trình gia tốc.
Suy ra v(t) = a
∫ (t) t = ∫( t− + t) 3 2 t 2 d
4 dt = − + 2t + C mà v(3) =18 ⇒ C = 9. 3 Với t =  →v( ) 2 3 3 = 3
− + 4.3 = 3. Gọi phương trình đường thẳng là d : y = mt + n
Vì d đi qua điểm O(0;0) và M (3;3) 
→ y = t là phương trình gia tốc 2
Suy ra ( ) = ∫ ( )d = d t v t a t t t t = + C ∫ mà v( ) 27 3 =18 ⇒ C = . 2 2 3 3 4  
Vậy quãng đường cần tính là t 2  27 S ∫ 2t 9dt ∫t  = − + + + + dt = 57,9 . km Chọn B.  3   2 0 3 
Document Outline

  • ITMTTL~1
  • IIBITP~1
  • IIILIG~1