Một số vấn đề chọn lọc nguyên hàm, tích phân và ứng dụng – Vũ Ngọc Huyền Toán 12

Một số vấn đề chọn lọc nguyên hàm, tích phân và ứng dụng – Vũ Ngọc Huyền Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

110 55 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

NGỌC HUYỀN LB

(facebook.com/huyenvu2405)

Đây là 1 tài liệu nhỏ chị viết gấp gáp để dành tặng

cho các em nhân ngày Valentine 2017. Tuy CHƯA

ĐẦY ĐỦ, nhưng chị tin nó cũng giúp ích cho em

phần nào khó khăn trong quá trình ôn luyện!

NGỌC HUYỀN LB

Tác giả “Bộ đề tinh túy Toán” & “Chắt lọc tinh túy toán”

Một số vấn đề chọn lọc

NGUYÊN HÀM

TÍCH PHÂN

VÀ ỨNG DỤNG

Đời phải trải qua giông tố nhưng không được cúi đầu trước giông tố!

Đã nói là làm – Đã làm là không hời hợt – Đã làm là hết mình – Đã làm là không hối hận!

facebook.com/huyenvu2405

Một số vấn đề chọn lọc Nguyên hàm – Tích phân và Ứng dụng

Đừng bao giờ bỏ cuộc Em nhé!

Chị tin EM sẽ làm được!

__Ngọc Huyền LB__

Nguyên hàm – Tích phân và ứng dụng The best or nothing

The best or nothing | 1

Chủ đề: Nguyên hàm – tích phân và ứng dụng

I. Nguyên hàm và các tính chất cơ bản.

Kí hiệu K là một khoảng, một đoạn hay một nửa khoảng.

Định nghĩa

Cho hàm số f xác định trên K. Hàm số F được gọi là nguyên hàm của hàm số f

trên K nếu

   

'F x f x

với mọi x thuộc K.

Định lý 1

1. Nếu F là một nguyên hàm của f trên K thì với mỗi hằng số C, hàm

   

G x F x C

cũng là một nguyên hàm của hàm f trên K.

2. Đảo lại nếu F và G là hai nguyên hàm của hàm số f trên K thì tồn tại hằng số C

sao cho

   

.F x G x C

Kí hiệu:

   

f x dx F x C



Người ta chứng minh được rằng: “Mọi hàm số liên tục trên K đều có nguyên

hàm trên K.”

Tính chất của nguyên hàm

Định lý 2 sau đây cho ta một số tính chất cơ bản của nguyên hàm

Định lý 2

1. Nếu f, g là hai hàm số liên tục trên K thì

       

f x g x dx f x dx g x dx



  



  

   

af x dx a f x dx



với mọi số thực a khác 0.

 

d f x dx f x dx



Bài toán tìm nguyên hàm là bài toán ngược với bài toán tìm đạo hàm. Việc tìm

nguyên hàm của một hàm số thường được đưa về tìm nguyên hàm của một số

hàm số đơn giản hơn. Dưới đây ta có bảng một số nguyên hàm :

dx x C



   

ax b dx ax b C

   



0a 

 

x a dx C a







      





   

ax b

ax b dx C









     









lndx x a C

  





.ln

ax b C

ax b a

  





e dx e C



ax b ax b

e dx e C







 

, 0, 1

a dx a C a a

   



 

, 0, 1

.ln

px q px q

a dx a C a a



   



sin cosxdx x C  



 

cos

sin , 0

axdx C a



  



cos sinxdx x C



 

sin

cos , 0

axdx C a

  



tan

cos

dx x C





cot

sin

dx x C

  



STUDY TIP:

Từ định nghĩa nguyên

hàm ta có được

 

f x dx ' f x



Quà tặng Valentine Ngọc Huyền LB

Ngọc Huyền LB | 2

II. Hai phương pháp cơ bản để tìm nguyên hàm.

a, Phương pháp đổi biến số.

Định lí 3

Cho hàm số

 

u u x

có đạo hàm liên tục trên K và hàm số

 

y f u

liên tục sao

cho hàm hợp

 

f u x





xác định trên K. Khi đó nếu F là một nguyên hàm của f thì

     

'f u x u x dx F u x C

   



   



Ví dụ 1: Tìm nguyên hàm

 

1x dx



Lời giải

Theo định lý trên thì ta cần viết về dạng

 

f u du



Mà

 

' 1 ' 1ux  

, do vậy

     

10 10

1 1 . 1 'x dx x x dx   



   

 

x d x C



    



Từ ví dụ trên ta có các bước gợi ý để xử lý bài toán tìm nguyên hàm theo

phương pháp đổi biến

1. Đặt

 

u g x

2. Biến đổi x và dx về u và du.

3. Giải bài toán dưới dạng nguyên hàm hàm hợp

 

f u du



, sau đó thay biến x

vào nguyên hàm tìm được và kiểm tra lại kết quả.

Ta đến với ví dụ 2

Ví dụ 2: Tìm

 

1x x dx



Ở bài toán này, ta thấy số mũ 7 khá cao mà lại có biểu thức trong ngoặc phức

tạp hơn là

. Do vậy ta sẽ đặt

 

1 x

để đổi biến, dưới đây là lời giải áp dụng

gợi ý các bước trên.

Lời giải

Đặt

 

1 1 'u x du x dx du dx       

ta có

 

1x x dx



   

 

7 7 8 9

1 . 1 2u u du u u u du      



8 9 10

u u u

C    

     

8 9 10

1 2 1 1

8 9 10

x x x

  

    

b, Phương pháp lấy nguyên hàm từng phần.

Định lý 4

Nếu u và v là hai hàm số có đạo hàm liên tục trên K thì

           

' . 'u x v x dx u x v x v x u x dx



Công thức trên thường được viết gọn dưới dạng

.udv uv vdu



STUDY TIP:

Với phương pháp đổi

biến ta cần chú trọng

công thức mà suy ra từ

định lý như sau:

Nếu

 

u f x

, khi đó

 

du f' x dx

Nguyên hàm – Tích phân và ứng dụng The best or nothing

The best or nothing | 3

Ví dụ 3: Thầy Điệp Châu cho bài toán “ Tìm

sin cosx xdx



” thì ba bạn Huyền,

Lê và Hằng có ba cách giải khác nhau như sau:

Bạn Huyền giải bằng phương

pháp đổi biến số như sau:

“Đặt

sinux

, ta có:

cosdu xdx

Vậy

sin .cosx xdx udu



sin

CC   

”

Bạn Lê giải bằng phương pháp lấy nguyên hàm

từng phần như sau:

“Đặt

cos , ' sinu x v x

Ta có

' sin , cosu x v x   

Công thức nguyên hàm từng phần cho ta

sin cos cos sin cosx xdx x x xdx  



Giả sử F là một nguyên hàm của

sin .cosxx

. Theo đẳng thức trên ta có

   

cosF x x F x C   

Suy ra

 

cos

Fx  

Điều này chứng tỏ

cos



là một nguyên

hàm của

sin .cos .xx

Vậy

cos

sin .cos

x xdx C  



.”

Bạn Hằng chưa học đến hai

phương pháp trên nên làm như

“

sin .cosx xdx



sin2 cos2

dx C   



.”

Kết luận nào sau đây là đúng?

A. Bạn Hằng giải đúng, bạn Lê và Huyền giải sai.

B. Bạn Lê sai, Huyền và Hằng đúng.

C. Ba bạn đều giải sai.

D. Ba bạn đều giải đúng.

Nhận xét: Sau khi soát kĩ cả ba lời giải, ta thấy ba lời giải trên đều không sai ở

bước nào cả, tuy nhiên, tại sao đến cuối cùng đáp án lại khác nhau? Ta xem giải

thích ở lời giải sau:

Lời giải

Cả ba đáp số đều đúng, tức là cả ba hàm số

sin cos

;



và

cos2



đều là

nguyên hàm của

sin .cosxx

do chúng chỉ khác nhau về một hằng số. Thật vậy

sin cos 1

2 2 2



  





;

 

2sin 1 2sin

sin cos2 1

2 4 4 4





   





.

III. Khái niệm và các tính chất cơ bản của tích phân.

a. Định nghĩa

Cho hàm số f liên tục trên K và a, b là hai số bất kì thuộc K. Tích phân của f từ a

đến b, kí hiệu là

 

f x dx



là một số xác định bởi công thức sau

     

f x dx F b F a



trong đó F là nguyên hàm của f trên K.

b. Các tính chất của tích phân.

Định lý 1

Giả sử các hàm số f, g liên tục trên K và a, b, c là ba số bất kì thuộc K. Khi đó ta

có

STUDY TIP:

Bài toán củng cố về

định lý 1 đã nêu ở trên,

và củng cố các cách giải

nguyên hàm cơ bản.

Quà tặng Valentine Ngọc Huyền LB

Ngọc Huyền LB | 4

 

f x dx 



   

f x dx f x dx



     

b c c

a b a

f x dx f x dx f x dx

  

       

b b b

a a a

f x g x dx f x dx g x dx



  



  

     

kf x dx k f x dx k



Định lý 2

Cho f là hàm số xác định trên K và a là một điểm cố định thuộc K. Xét hàm số

 

xác định trên K bởi công thức

   

G x f t dt



Khi đó G là một nguyên hàm của f.

Định lý 3

Tích phân của hàm lẻ và hàm chẵn trên .

1. Nếu f là một hàm số chẵn, khi đó

   

f x dx f x dx







2. Nếu f là một hàm số lẻ, khi đó

 

f x dx







Đọc thêm

Ta vừa đưa ra 3 tính chất của tích phân theo chương trình chuẩn. Dưới đây là

các tính chất bổ sung:

dx 



 

cdx c b a



3. Nếu

 

0fx

,x a b







thì

 

f x dx 



Hệ quả 3: Nếu hai hàm số

 

và

 

liên tục và thỏa mãn

   

,,f x g x x a b



  



thì

   

f x dx g x dx



Chú ý: Nếu

 

liên tục và dương trên

,ab





thì

 

f x dx 



     

f x dx f x dx a b



5. Nếu

 

, , ; ,m f x M x a b m M



   



là các hằng số thì

     

m b a f x dx M b a   



hay

 

m f x dx M







Hàm số chẵn

Hình 3.1

Hàm số lẻ

Hình 3.2

Nguyên hàm – Tích phân và ứng dụng The best or nothing

The best or nothing | 5

IV. Hai phương pháp cơ bản tính tích phân.

a. Phương pháp đổi biến số.

Quy tắc đổi biến số

1. Đặt

 

,u u x

2. Biến đổi

   

f x dx g u du

3. Tìm một nguyên hàm

 

của

 

4. Tính

 

g u du G u b G u a



5. Kết luận

   

 

f x dx G u b G u a



b. Phương pháp tích phân từng phần.

Cho hai hàm số u, v có đạo hàm liên tục trên K và a, b là hai số thuộc K. Khi đó

               

' ' . .

u x v x dx u b v b u a v a u x v x dx  



IV. Ứng dụng hình học của tích phân.

a. Tính diện tích hình phẳng.

Diện tích hình phẳng giới hạn bởi một đường cong và trục hoành.

Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số

 

liên tục, trục

hoành và hai đường thẳng

,x a x b

được tính theo công thức

 

S f x dx



Chú ý: Trong trường hợp dấu của

 

thay đổi trên đoạn

;ab





thì ta phải

chia đoạn

;ab





thành một số đoạn con để trên đó dấu của

 

không đổi, do

đó ta có thể bỏ dấu giá trị tuyệt đối trên đoạn đó.

Diện tích hình phẳng giới hạn bởi hai đường cong.

Cho hai hàm số

 

y f x

và

 

y g x

liên tục trên đoạn

;ab





. Khi đó diện tích

S của hình phẳng giới hạn bởi đồ thị hàm số

   

,y f x y g x

và hai đường

thẳng

,x a x b

là

   

S f x g x dx



Tương tự như chú ý ở trên thì ở bài toán này ta cũng phải xét đoạn mà dấu của

   

f x g x

không đổi.

Ví dụ 4: Tính diện tích hình phẳng ( hình được tô màu) ở biểu diễn ở hình 3.4.

Lời giải

Nhận thấy trên

;ac





và

;db





thì

   

f x f x

; trên

;cd





thì

   

f x f x

Do vậy

       

 

   

 

   

 

1 2 1 2 2 1 1 2

b c d b

a a c d

S f x f x f x f x dx f x f x dx f x f x dx       

   

(Trên đây là cách bỏ dấu giá trị tuyệt đối)

Hình 3.3

Hình 3.4

Quà tặng Valentine Ngọc Huyền LB

Ngọc Huyền LB | 6

Ví dụ 5: Cho hình thang cong

 

giới hạn bởi các đường

y e , 

y, 0

x  0

và

 4x ln .

Đường thẳng

x k k  0( ln4)

chia

 

thành hai phần có diện tích

là

và

như hình vẽ bên.

Tìm k để



2SS



k ln

 2k ln



k ln

 3k ln

( Trích đề minh họa môn Toán lần 2 – Bộ GD&ĐT)

Lời giải

Đáp án D.

Nhìn vào hình vẽ ta có được các công thức sau:

ln4

e dx e dx



ln4



0 ln4

2. 2. 3 9

k k k

e e e e e     

3 ln3

ek   

Ví dụ 6: Ông An có một mảnh vườn hình elip có độ dài trục lớn bằng 16m và

độ dài trục bé bằng 10 m. Ông muốn trồng hoa trên một dải đất rộng 8m và

nhận trục bé của elip làm trục đối xứng (như hình vẽ). Biết kinh phí để trồng

hoa là 100.000 đồng/1

. Hỏi ông An cần bao nhiêu tiền để trồng hoa trên dải

đất đó ? (Số tiền được làm tròn đến hàng nghìn.)

A. 7.862.000 đồng. B.7.653.000 đồng.

C. 7.128.000 đồng. D. 7.826.000 đồng.

( Trích đề minh họa môn Toán lần 2 – Bộ GD&ĐT)

Lời giải

Đáp án B.

Nhận thấy đây là bài toán áp dụng ứng dụng của tích phân vào tính diện tích

hình phẳng. Ta có hình vẽ bên:

Ta thấy, diện tích hình phẳng cần tìm gấp 4 lần diện tích phần gạch chéo, do đó

ta chỉ cần đi tìm diện tích phần gạch chéo.

Ta có phương trình đường elip đã cho là



. Xét trên

0;4





nên

0y 

thì

yx

. Khi đó

cheo

S x dx



, vậy diện tích trồng hoa của ông

An trên mảnh đất là

4. 8 76,5289182

S x dx  



Khi đó số kinh phí phải trả của ông An là

76,5289182.100000 7.653.000

đồng.

b. Tính thể tích vật thể.

Cho H là một vật thể nằm giới hạn giữa hai mặt phẳng

xa

và

xb

. Gọi

 

là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành

tại điểm có hoành độ x

 

a x b

. Giả sử

 

là một hàm liên tục. Khi đó thể

tích V của H là

 

V S x dx



(hình 3.5)

-4

-5

-8

Nguyên hàm – Tích phân và ứng dụng The best or nothing

The best or nothing | 7

Ví dụ 7: Tính thể tích vật thể tạo được khi lấy giao vuông góc hai ống nước

hình trụ có cùng bán kính đáy bằng a. ( hình 3.6)



(Trích sách bộ đề tinh túy ôn thi THPT QG môn Toán)

Ta sẽ gắn hệ trục tọa độ Oxyz vào vật thể này, tức là ta sẽ đi tính thể tích vật thể

V giới hạn bởi hai mặt trụ:



2 2 2

x y a

và



2 2 2

x z a

 

 0a

Hình vẽ trên mô tả một phần tám thứ nhất của vật thể này, với mỗi







0;xa

thiết diện của vật thể (vuông góc với trục Ox ) tại x là một hình vuông có cạnh



y a x

( chính là phần gạch chéo trong hình 3.7). Do đó diện tích thiết

diện sẽ là:

 

    

2 2 2 2 2 2

.S x a x a x a x







0; .xa

Khi đó áp dụng công thức

 

thì thể tích vật thể cần tìm sẽ bằng:

 

  



V S x dx a x dx



  





Ví dụ 8: Tính thể tích của vật thể H biết rằng đáy của H là hình tròn

1xy

và thiết diện cắt bởi mặt phẳng vuông góc với trục hoành luôn là tam giác đều.

Lời giải

S(x)

Hình 3.5

Hình 3.6

Hình 3.7

Quà tặng Valentine Ngọc Huyền LB

Ngọc Huyền LB | 8

Giả sử mặt phẳng vuông góc với trục hoành chứa thiết diện là tam giác đều

ABC tại điểm có hoành độ là

 

11xx  

với AB chứa trong mặt phẳng xOy

(hình 3.8).

Ta có

21AB x

. Do đó

 

3 1 .

S x x  

Vậy

 

31V S x dx x dx



  





  





( đvtt).

c. Tính thể tích khối tròn xoay.

Một hình phẳng quay quanh một trục nào đó tạo nên một khối tròn xoay.

Định lý 4

Cho hàm số

 

y f x

liên tục, không âm trên đoạn

,ab





. Hình phẳng giới hạn

bởi đồ thị hàm số

 

y f x

, trục hoành và hai đường thẳng

,x a x b

quay

quanh trục hoành tạo nên một khối tròn xoay. Thể tích V của khối tròn xoay đó

là

 

V f x dx



Ví dụ 9: Thể tích của khối tròn xoay thu được khi quay hình phẳng được giới

hạn bởi đường cong

sinyx

, trục hoành và hai đường thẳng

0,xx  

(hình

3.10) quanh trục Ox là



(đvtt) B.



(đvtt) C.



(đvtt) D.



(đvtt)

Lời giải

Đáp án B.

Áp dụng công thức ở định lý 4 ta có

 

sin 1 cos2

V xdx x dx





   



sin2 .

2 2 2







  





Tiếp theo dưới đây là một bài toán thường xuất hiện trong các đề thi thử, bài

toán có thể đưa về dạng quen thuộc và tính toán rất nhanh

Ví dụ 10: Tính thể tích khối tròn xoay thu được khi quay hình phẳng được giới

hạn bởi đường cong

y A x

và trục hoành quanh trục hoành.

Lời giải tổng quát

Ta thấy

2 2 2 2 2 2 2 2

y A x y A x x y A       

0Ax

với mọi x, do vậy đây là phương trình nửa đường tròn tâm O,

bán kính

RA

nằm phía trên trục Ox. Khi quay quanh trục Ox thì hình phẳng

sẽ tạo nên một khối cầu tâm O, bán kính

RA

(hình 3.11). Do vậy ta có luôn

VA

Vậy với bài toán dạng này, ta không cần viết công thức tích phân mà kết luận

luôn theo công thức tính thể tích khối cầu.

Hình 3.8

y = f (x)

Hình 3.9

y = sinx

Hình 3.10

-A

Hình 3.11

Nguyên hàm – Tích phân và ứng dụng The best or nothing

The best or nothing | 9

Đọc thêm

Định lý 5

Cho hàm số

 

y f x

liên tục, không âm trên đoạn

,ab





 

0a 

. Hình phẳng

giới hạn bởi đồ thị hàm số

 

y f x

, trục hoành và hai đường thẳng

,x a x b

quay quanh trục tung tạo nên một khối tròn xoay. Thể tích V của

khối tròn xoay đó là

 

V xf x dx



Quà tặng Valentine Ngọc Huyền LB

Ngọc Huyền LB | 10

1. Nguyên hàm – chọn lọc các bài tập về nguyên hàm trong các đề thi thử

Câu 1: Tìm nguyên hàm

 

2 1 .

I x e dx







 

I x e C



   

 

I x e C



   

 

I x e C



   

 

I x e C



   

(Trích đề thi thử THPT chuyên KHTN – Hà Nội)

Câu 2: Tìm nguyên hàm

 

ln 2 1 .I x x dx



 

ln 2 1

I x C





   

 

ln 2 1

I x C



   

 

ln 2 1

I x C





   

 

ln 2 1

I x C



   

(Trích đề thi thử THPT chuyên KHTN – Hà Nội)

Câu 3: Tìm nguyên hàm

 

1 sin2 .I x xdx



 

1 2 cos2 sin2

x x x





 

2 2 cos2 sin2

x x x





 

1 2 cos2 sin2

x x x





 

2 2 cos2 sin2

x x x





(Trích đề thi thử THPT chuyên KHTN – Hà Nội)

Câu 4: Cho

   

,f x g x

là các hàm số liên tục trên

Tìm khẳng định sai trong các khẳng định sau?

   

..k f x dx k f x dx



với

là hằng số

       

f x g x dx f x dx g x dx



  



  

       

..f x g x dx f x dx g x dx







  

       

f x g x dx f x dx g x dx



  



  

(Trích đề thi thử THPT chuyên Kim Thành – Hải Dương)

Câu 5: Họ nguyên hàm của hàm số

 

2017x

f x e





là:

2017





2017x





2017

2017.





2017





(Trích đề thi thử THPT chuyên Hoàng Văn Thụ)

Câu 6: Tìm một nguyên hàm

 

của hàm số

 

cos 3



biết

  







 

tan3

F x x

 

4tan3 3 3F x x

 

tan3

F x x

 

tan3

F x x  

(Trích đề thi thử THPT chuyên Hoàng Văn Thụ)

Câu 7: Tìm nguyên hàm của hàm số

 

.f x x x

 

f x dx x x C



 

f x dx x x C



 

f x dx x x C



 

f x dx x C



(Trích đề thi thử THPT Lương Thế Vinh lần 2)

Câu 8:

lnx



bằng:

 

2 lnxC

 

xC

2 ln



 

xC

(Trích đề thi thử THPT chuyên Lam Sơn)

Câu 9: Cho hàm số

 

sin



Nếu

 

là một

nguyên hàm của hàm số

 

và đồ thị hàm số

 

y F x

đi qua

  





thì

 

là:

cot

x

3 cotx

cot

x

cotxC

(Trích đề thi thử THPT chuyên Lam Sơn)

Câu 10: Cho hàm số

 





Hãy chọn mệnh đê

sai:

Bài tập rèn luyện kỹ năng

Nguyên hàm – Tích phân và ứng dụng The best or nothing

The best or nothing | 11

 

ln 2

dx x C

  





 

ln 3 2x 

là một nguyên hàm của

 

ln 2xC

là họ nguyên hàm của

 

ln 2x 

là một nguyên hàm của

 

(Trích đề thi thử THPT chuyên Lam Sơn)

Câu 11:

xe dx





bằng:



21x

x e C



(Trích đề thi thử THPT chuyên Lam Sơn)

Câu 12:

x



bằng:

 

21x x C   

 

11x x C  

 

11x x C   

 

21x x C  

(Trích đề thi thử THPT chuyên Lam Sơn)

Câu 13: Tìm nguyên hàm của hàm số

   

2 3 .f x x

 

f x dx C







   

23f x dx x C  



 

f x dx C







 

f x dx C







(Trích đề thi thử THPT chuyên Hạ Long)

Câu 14: Tìm nguyên hàm của hàm số

 

3sin3 cos3 .f x x x

 

cos3 sin3f x dx x x C  



 

cos3 sin3f x dx x x C  



 

cos3 sin3

f x dx x x C   



 

cos3 sin3

f x dx x x C   



(Trích đề thi thử THPT chuyên Hạ Long)

Câu 15: Tìm nguyên hàm của hàm số

 

f x e e





 

f x dx e e C



  



 

f x dx e e C



   



 

f x dx e e C



  



 

f x dx e e C



   



(Trích đề thi thử THPT chuyên Hạ Long)

Câu 16: Tìm nguyên hàm

 

của hàm số

 

3 4,f x x

biết

 

0 8.F 

 

1 38

F x x  

   

2 16

3 4 3 4

F x x x   

   

2 56

3 4 3 4

F x x x   

   

3 4 3 4

F x x x   

(Trích đề thi thử THPT chuyên Hạ Long)

Câu 17: Tìm nguyên hàm của hàm số

 





 

f x dx C







 

ln 1f x dx x C  



 

ln 1f x dx x x C  



 

ln 1

f x dx x C  



(Trích đề thi thử THPT chuyên Hạ Long)

Câu 18: Tính nguyên hàm

 

2 1 .

x e dx



 

x e dx C



   



 

x e dx C



   



 

3 2 3

x e dx x x e C   



 

3 2 3

x e dx x x e C   



(Trích đề thi thử THPT chuyên Hạ Long)

Câu 19: Tìm nguyên hàm

I dx



























(Trích đề thi thử THPT chuyên KHTN – Hà Nội)

Câu 20: Hàm số nào sau đây không là nguyên hàm

của hàm số

 







 





 







 







 







(Trích đề thi thử THPT chuyên Hoàng Văn Thụ)

Câu 21:

xx



bằng:

Quà tặng Valentine Ngọc Huyền LB

Ngọc Huyền LB | 12















(Trích đề thi thử THPT chuyên Lam Sơn)

Câu 22: Hàm số

 

ln 2

F x e x

là nguyên hàm

của hàm số nào sau đây?

 

ln 2x



 

ln 2x

f x e

 

ln 2



 

ln 2

f x e

(Trích đề thi thử THPT chuyên Thái Bình lần 2)

Câu 23: Nguyên hàm của hàm số:

2 1 4







là:

 

2 1 4ln 2 1 4F x x x C     

 

2 1 4ln 2 1 4F x x x C     

 

2 1 ln 2 1 4

F x x x C     

 

2 1 4ln 2 1 4F x x x C     

(Trích đề thi thử THPT Triêụ Sơn 2

)

2. Tích phân – chọn lọc các bài tập về tích phân trong các đề thi thử.

Câu 1: Biết tích phân

 

I x e dx a be   



 

;.ab

Khi đó tích

.ab

có giá trị bằng:

A. 1 B.

1

C. 2 D. 3

(Trích đề thi thử THPT chuyên Thái Bình lần 2)

Câu 2: Biết

 

2f x dx 



và

 

là hàm số lẻ. Khi đó

 

I f x dx







có giá trị bằng:

1I 

0I 

2I 

2I 

(Trích đề thi thử THPT chuyên Thái Bình lần 2)

Câu 3: Tích phân

1I x x dx



có giá trị bằng:

2 2 1





I 

(Trích đề thi thử THPT chuyên Thái Bình lần 2)

Câu 4: Cho tích phân

I dx







nếu đặt

1tx

thì

 

I f t dt



trong đó:

 

f t t t

 

22f t t t

 

f t t t

 

22f t t t

(Trích đề thi thử THPT chuyên Thái Bình lần 2)

Câu 5: Tính tích phân

1 sin

sin









3 2 2





3 2 2 2



(Trích đề thi thử THPT Cái Bè)

Câu 6: Cho

cos2x 1

ln3.

1 2sin2 4

I dx









Tìm giá trị của

a là:

A. 3 B. 2 C. 4 D. 6

(Trích đề thi thử THPT Cái Bè)

Câu 7: Tích phân

cos

sin





bằng:

ln 2



ln 2



ln 2



ln 2



(Trích đề thi thử THPT Triệu Sơn 2)

Câu 8: Tích phân

xe dx





bằng:

e 



e 



(Trích đề thi thử THPT Triệu Sơn 2)

Câu 9: Tính tích phân:

x 



ln2



2ln2



4 2 2



ln2



(Trích đề thi thử THPT Nguyễn Đình Chiểu)

Nguyên hàm – Tích phân và ứng dụng The best or nothing

The best or nothing | 11

Câu 10: Giá trị dương a sao cho:

ln3

x x a

dx a



  





là:

A. 5 B. 4 C. 3 D. 2

(Trích đề thi thử THPT Nguyễn Đình Chiểu)

Câu 11: Giả sử

ln .







Giá trị của c là:

A. 9 B. 3 C. 81 D. 8

(Trích đề thi thử THPT Nguyễn Đình Chiểu)

Câu 12: Tích phân

 

I dx







có giá trị là:



(Trích đề thi thử THPT Diệu Hiền)

Câu 13. Giả sử

 

5f t dt







và

 

6f r dr







. Tính

 

I f u du



4I 

3I 

2I 

1I 

(Trích đề thi thử Sở GD – ĐT Phú Thọ)

Câu 14. Tính tích phân

cosI xdx







0I 

1I 

2I 

3I 

(Trích đề thi thử Sở GD – ĐT Phú Thọ)

Câu 15. Cho biết

 

cos( ).

t dt x x



Tính

(4)f

(4) 2 3f 

(4) 1f 

(4)

f 

(4) 12f 

(Trích đề thi thử Sở GD – ĐT Phú Thọ)

Câu 16. Đẳng thức

 

cos sin

x a dx a



xảy ra nếu:

a 

3a 

2a 

(Trích đề thi thử Sở GD – ĐT Phú Thọ)

Câu 17: Tính tích phân

.sin .I x xdx







 3I

 2I

 1I

1I

(Trích đề thi thử THPT Bảo Lâm)

Câu 18. Tính tích phân

1 sin

sin









; B.

3 2 2





. D.

3 2 2 2



(Trích đề thi thử THPT Bảo Lâm)

Câu 19. Nếu

xe dx 



thì giá trị của

bằng:

A. 0 B. 1 C. 2 D.

(Trích đề thi thử THPT chuyên KHTN)

Câu 20. Nếu

sin cos

x xdx







thì

bằng:

A. 3 B. 4 C. 5 D. 6

(Trích đề thi thử THPT chuyên KHTN)

Câu 21. Giá trị của

lim









bằng:

1

B. 1 C.

D. 0

(Trích đề thi thử THPT chuyên KHTN)

Câu 22. Tích phân

4 x xdx



có giá trị bằng

(Trích đề thi thử THPT Phạm Văn Đồng)

Câu 23. Tích phân

cot .x dx





có giá trị bằng

ln 2

B. ln2 C. ln4 D.

ln 2

(Trích đề thi thử THPT Phạm Văn Đồng)

Câu 24. Tích phân

e xdx





có giá trị bằng:

e 



e 



(Trích đề thi thử THPT Phạm Văn Đồng)

Câu 25. Tích phân

 

2 1 ln

I x x dx



bằng:

e 

(Trích đề thi thử THPT Quảng Xương I)

Câu 26: Hàm số nào sau đây không là nguyên hàm

của hàm số

( 2)

()

( 1)



















x 

(Trích đề thi thử THPT Quảng Xương I)

Câu 27: Nếu

( ) 5; ( ) 2

f x dx f x



với

a d b

thì

()

f x dx



bằng:

2

(Trích đề thi thử THPT Quảng Xương I)

Quà tặng Valentine Ngọc Huyền LB

Ngọc Huyền LB | 12

3. Ứng dụng của tích phân trong hình học.

Câu 1: Tính diện tích hình phẳng giới hạn bởi đồ thị

hàm số

2yx

và

3:yx

A. 1 B.

(Trích đề thi thử THPT Nguyễn Đình Chiểu)

Câu 2: Thể tích khối tròn xoay tạo thành khi quay

quanh trục

hình phẳng được giới hạn bởi đồ thị

hàm số

 

y x e

và hai trục tọa độ là:

2 10e 

2 10e 

 

2 10e

 

2 10e

(Trích đề thi thử THPT Nguyễn Đình Chiểu)

Câu 3: Tính diện tích hình phẳng giới hạn bởi đồ thị

hàm số







và các trục tọa độ. Chọn kết quả

đúng nhất?

3ln6

3ln

3ln 2



3ln 1



(Trích đề thi thử THPT Quảng Xương I)

Câu 4. Cho hàm số

( ) 3 2f x x x x  

. Tính diện tích

S của hình phẳng giới hạn bởi đồ thị hàm số

()y f x

trục tung, trục hoành và đường thẳng

3x 

S 

(Trích đề thi thử sở GD&ĐT Phú Thọ)

Câu 5. Tính thể tích của vật thể giới hạn bởi hai mặt

phẳng

0x 

và

3x 

, biết rằng thiết diện của vật thể

bị cắt bởi mặt phẳng vuông góc với trục

tại điểm

có hoành độ

 

03x

là một hình chữ nhật có hai

kích thước là

và

29 x

(Trích đề thi thử sở GD&ĐT Phú Thọ)

Câu 6. Tính diện tích hình phẳng S giới hạn bởi đồ thị

các hàm số

y 

và

3yx

, trục hoành và trục tung.

ln2

S 

2S 

ln2

S 

4S 

(Trích đề thi thử sở GD&ĐT Phú Thọ)

Câu 7. Tính thể tích của tứ diện đều có cạnh bằng a.

V 

(Trích đề thi thử sở GD&ĐT Phú Thọ)

Câu 8: Công thức tính diện tích S của hình thang

cong giới hạn bởi hai đồ thị

   

, , ,y f x y g x x a x b   

 

ab

   

 

S f x g x dx



   

S f x g x dx



   

 

S f x g x dx



   

 

S f x g x dx



(Trích đề thi thử THPT Bảo Lâm)

Câu 9: Diện tích hình phẳng giới hạn bởi đồ thị (C)

của hàm số

25y x x x    

và đồ thị (C’) của

hàm số

5y x x  

bằng:

A. 0 B. 1 C. 2 D. 3

(Trích đề thi thử THPT Bảo Lâm)

Câu 10: Tìm diện tích hình phẳng giới hạn bởi các

đường

 

1 , 1.

y x e y x   

Se

Se

(Trích đề thi thử THPT chuyên KHTN – HN)

Câu 11: Tính diện tích hình phẳng giới hạn bởi đồ thị

hàm số

 

y x e

trục hoành và các đường thẳng

0, 2.xx

4 2 4



4 2 4



4 2 4



4 2 4



(Trích đề thi thử THPT chuyên KHTN – HN)

Câu 12: Tính thể tích khối tròn xoay khi cho hình

phẳng giới hạn bởi đồ thị các hàm số

2y x x

và

yx

quay quanh trục

.Ox



(Trích đề thi thử THPT chuyên KHTN – HN)

Lưu ý: Lời giải chi tiết sẽ được gửi vào 23h ngày 25/02/2017.

Đề nghị các bạn đăng ký tại http://ngochuyenlb.gr8.com/ để

được gửi vào đúng thời gian trên.

Nguyên hàm – Tích phân và ứng dụng The best or nothing

The best or nothing | 13

Bổ sung một số dạng về nguyên hàm – tích phân

1. Tích phân và nguyên hàm một số hàm lượng giác

a. Dạng

sin .cos

x xdx



trong đó

,mn

là các số tự nhiên.

Trường hợp 1: Trong hai số m, n có ít nhất một số lẻ.

Lũy thừa của

cosx

là số lẻ,

21nk

thì đổi biến

sinux

Lũy thừa của

sinx

là số lẻ,

21mk

thì

đổi biến

cosux

 

sin .cos sin cos cos

m n m

x xdx x x xdx



 

sin 1 sin . sin '

x x x dx

 

u u du



 

sin .cos cos sin sin

m n n

x xdx x x xdx



 

cos . 1 cos cos '

x x x dx  



 

u u du  



Ví dụ 1: Tìm

sin .cosx xdx



Lời giải

Vì lũy thừa của

sin x

là số lẻ nên ta đổi biến

cosux

 

5 2 2 2

sin .cos 1 cos .cos . cos 'x xdx x x x dx  



   

2 2 4 2 6

1 . 2u u du u u u du     



5 3 7

uuu

C   

5 3 7

2cos cos cos

5 3 7

x x x

C   

Trường hợp 2: Cả hai số m, n đều là số chẵn: Ta sử dụng công thức hạ bậc để

giảm một nửa số mũ của

sin ;cosxx

, để làm bài toán trở nên đơn giản hơn.

b. Dạng

sin .cosmx nxdx



sin .sinmx nxdx



cos .cosmx nxdx



Ta sử dụng công thức biến đổi tích thành tổng trong lượng giác.

c. Dạng

tan

cos



trong đó

,mn

là các số nguyên.

Lũy thừa của

cosx

là số nguyên dương chẵn,

2nk

thì ta đổi biến

tanux

Lũy thừa của

tan x

là số nguyên dương lẻ,

21mk

thì ta đổi biến

cos



2 2 2

tan tan 1

cos cos cos

dx dx







 

tan

. tan '

cos

x dx







 

tan . 1 tan . tan

x x d x







 

u u du







Khi đó

sin

cos



, do đó

tan tan tan

cos

cos cos

dx dx







sin

cos

cos cos















 

u u du







Đọc thêm

Quà tặng Valentine Ngọc Huyền LB

Ngọc Huyền LB | 14

Ví dụ 2: Tìm nguyên hàm

tan

cos



tan

cos



Lời giải

a.Do lũy thừa của

cosx

là số nguyên dương chẵn nên đặt

tanux

. Từ công

thức tổng quát đã chứng minh ở trên ta có

 

tan

cos

dx u u du





9 7 9 7

tan tan

9 7 9 7

CC     

b. Do lũy thừa của

tan x

là một số lẻ nên ta đặt

cos



, do vậy, từ công thức

tổng quát chứng minh ở trên ta có

 

5 11 9 7

tan 2

11 9 7

cos

x u u u

dx u u du C

     



11 9 7

1 2 1

11cos 9cos cos

x x x

   

2. Đổi biến lượng giác

Khi nguyên hàm, tích phân của các hàm số mà biểu thức của nó có chứa các

dạng

2 2 2 2 2 2

,,x a x a a x  

, thì ta có cách biến đổi lượng giác như sau:

Biểu thức có chứa

Đổi biến

xa

tanx a t

;











Hoặc

 

cos , 0;x a t t  

xa

sin



 

; \ 0











Hoặc

, 0; \

cos 2







  







ax

sinx a t

;











Hoặc

cos , 0;x a t t



  



a x a x







cos2x a t

  

x a b x

 

sin , 0;

x a b a t t





   





3. Nguyên hàm và tích phân của hàm phân thức hữu tỉ

Cho hàm số

 

y f x

có dạng

 



trong đó P và Q là các đa thức, và P

không chia hết cho Q.

Hàm f được gọi là hàm phân thức hữu tỉ thực sự nếu

   

deg degPQ

STUDY TIP: Kí hiệu

 

deg Px

là bậc của

đa thức

 

.Px

Nguyên hàm – Tích phân và ứng dụng The best or nothing

The best or nothing | 15

Trong các bài toán tìm nguyên hàm và tích phân của hàm phân thức hữu tỉ, nếu

 

chưa phải là hàm phân thức hữu tỉ thực sự thì ta thực hiện chia đa thức

tử số cho đa thức mẫu số để được:

 

   

P x R x

f x S x S x h x

Q x Q x

    

Khi đó,

 

sẽ là hàm phân thức hữu tỉ thực sự.

Định lý: Một phân thức thực sự luôn phân tích được thành tổng các phân thức

đơn giản hơn.

Đó là các biểu thức có dạng

 

; ; ;

ax b ax b

x px q











là các

hàm số có thế tìm nguyên hàm một cách dễ dàng.Để tách được phân thức ta

dùng phương pháp hệ số bất định.

a. Trường hợp phương trình

 

0Qx

không có nghiệm phức và các nghiệm

đều là nghiệm đơn.

      

1 1 2 2

...

k k k

Q x a x b a x b a x b   

(Số nhân tử chính bằng bậc của đa thức

 

Trong trường hợp này, g có thể biểu diễn dưới dạng

 

1 1 2 2

...

a x b a x b a x b

    

  

Sau khi biểu diễn được

 

về dạng này, bài toán trở thành bài toán cơ bản.

Ví dụ 3: Họ nguyên hàm của hàm số

 







là

 

4ln 2 ln

F x x C



   



 

4ln 2 ln

F x x C



   



 

4ln 2 ln

F x x C



    



 

4ln 2 ln

F x x C



   



Phân tích

Đáp án B.

Ta có

  

4 3 4 3

x x A B



  





  

Ax A Bx B

  





Khi đó

 

2 4 3A B x A B x    

, đồng nhất hệ số thì ta được

2 3 5

A B A

A B B



   





  



Lời giải

Quà tặng Valentine Ngọc Huyền LB

Ngọc Huyền LB | 16

Ta có

4 3 1 5

ln 1 5.ln 2

dx dx x x C





       











4.ln 2 ln



   



4.ln 2 ln



   



Đáp số bài tập kiểm tra khả năng vận dụng:

x 2x 1 1 1 1

dx .ln x .ln 2x 1 .ln x 2 D

2 10 10

2x 3x 2x



     





Ví dụ 4: Biết

ln2 ln 3 ln5 ln6 ln7

a b c d e



     





I dx

. Khi đó

6 3 6 3 2a b c d e   

có giá trị là

16



Phân tích

Đáp án A.

Ta có

    

1 1 2 2

x x x x





   



1 2 1 2

A B C D

x x x x

   

   

 

   

3 2 2

2 4 1 1 2

4 1 1 2 , *

x A x x B x x

C x x D x x x

       

      

Thay

1x 

vào

 

ta có

A 

Thay

2x 

vào

 

ta có

B 

Thay

1x 

vào

 

ta có

C 

Thay

2x 

vào

 

ta có

D 

Lời giải









 

5 5 5 5

4 4 4 4

1 5 1 1

2 6 2 6 1 2 2

dx dx dx dx

x x x

    

  



   

1 5 1 1

ln 1 ln 2 ln 1 ln 2

2 6 6 2

x x x x



        





5 1 1 1 5 1 1

2 3 6 7 3 2 5 6

6 6 2 2 6 6 2

ln ln ln ln ln ln ln ln



         





11 4 1 1 1

2 3 5 6 7

6 3 6 3 2

ln ln ln ln ln     

Khi đó

6 3 6 3 2 11 4 1 1 1 16a b c d e           

b. Trường hợp

 

0Qx

không có nghiệm phức, nhưng có nghiệm thực là

nghiệm bội.

Nếu phương trình

 

0Qx

có các nghiệm thực

; ;...;

a a a

trong đó

là

nghiệm bội k thì ta phân tích

 



về dạng

Kiểm tra khả năng vận

dụng từ ví dụ 3:

Tìm

x 2x 1

2x 3x 2x





STUDY TIP: đây là

dạng toán tích phân

chống casio đã gặp

trong đề minh họa lần

Nguyên hàm – Tích phân và ứng dụng The best or nothing

The best or nothing | 17

 

   

1 2 1 2

... ...

A A B B

x a x a x a

x a x a



       

  





Trên đây là phần lý thuyết khá phức tạp, ta đến với bài tập ví dụ đơn giản sau:

Ví dụ 5: Họ nguyên hàm của hàm số

 





là

 

F x C

  



 

F x C

  



 

F x C

  



 

F x C

  



Phân tích

Nhận thấy

1x 

là nghiệm bội ba của phương trình

 

10x 

, do đó ta biến

đổi

     

 

3 2 3 3

2 1 1

1 1 1 1

A x x B x C

x A B C

x x x x

    

   



   

 

Ax A B x A B C

     





Từ đây ta có

2 2 2

A B B

A B C C







     





   



Lời giải

Ta có

     

3 2 3

2 2 2

1 1 1

dx dx

x x x











  





 

  



Đáp số bài tập kiểm tra khả năng vận dụng ví dụ 4:

4 2 2

x 2x 4x 1 x 2

dx x ln x 1 ln x 1 C

2 x 1

x x x 1

  

       



  



TỔNG QUÁT: Việc tính nguyên hàm của hàm phân thức hữu tỉ thực sự được

đưa về các dạng nguyên hàm sau:

.ln

dx A x a C

  





   

dx C

x a x a



  







Kiểm tra khả năng vận

dụng từ ví dụ 4:

Tìm

x 2x 4x 1

x x x 1

  

  



Quà tặng Valentine Ngọc Huyền LB

Ngọc Huyền LB | 18

5. Bảng một số nguyên hàm thường gặp

..k dx k x C



x dx C









dx C

  



lndx x C





( ) ( 1)( )

dx C

ax b a n ax b



  

  



.lndx ax b C

ax b a

  





sin cosxdx x C  



cos sinxdx x C

   

sin cosax b dx ax b C

    



10)

   

cos sinax b dx ax b C

   



11)

(1 tan ) tan

cos

dx x dx x C

   



12)

(1 cot ) cot

sin

dx x dx x C

    



13)

tan( )

cos ( )

dx ax b C

ax b

  





14)

cot( )

sin ( )

dx ax b C

ax b

   





15)

e dx e C



16)

e dx e C



  



17)

ax b ax b

e dx e C







18)

 

ax b

ax b dx C n



   





19)

a dx C





20)

arctan

dx x C







21)

1 1 1

dx C











22)

arctan

dx C







23)

dx C











24)

arcsin

dx x C







25)

arcsin

dx C







26)

ln 1

dx x x C

   





27)

lndx x x a C

   





28)

2 2 2 2

arcsin

x a x

a x dx a x C

    



29)

2 2 2 2 2 2

.ln

x a dx x a x x a C      



Nguyên hàm – Tích phân và ứng dụng The best or nothing

The best or nothing | 19

III. Ứng dụng của nguyên hàm, tích phân trong thực tế.

1. Dạng bài toán về chuyển động.

Ví dụ 1: Một ô tô đang chạy với vận tốc 10 m/s thì tài xế đạp phanh; từ thời

điểm đó, ô tô chuyển động chậm dần đều với vận tốc

   

5 10 /v t t m s  

trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi

từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?

A. 0,2 m B. 2 m C. 10 m D. 20 m

(Trích đề minh họa lần I- BGD&ĐT)

Lời giải

Đáp án C.

Nguyên hàm của hàm vận tốc chính là quãng đường

 

mà ô tô đi được sau

quãng đường t giây kể từ lúc tài xế đạp phanh xe.

Vào thời điểm người lái xe bắt đầu đạp phanh ứng với

0t 

Thời điểm ô tô dừng lại ứng với

, khi đó

 

02v t t  

Vậy từ lúc đạp phanh đến khi dừng lại quãng đường ô tô đi được là

 

5 10 10 10

s t dt t t m





     







Ví dụ 2: Một chiếc ô tô đang đi trên đường với vận tốc

   

2 0 30v t t t  

(m/s). Giả sử tại thời điểm

0t 

thì

0s 

. Phương trình thể hiện quãng đường

theo thời gian ô tô đi được là

 

s t m

 

2s t m

 

s t m

 

2s t m

Lời giải

Đáp án A

Tương tự như ở ví dụ 1 thì ta có

 

2 2 2. . .

s t tdt t dt t t   





(m)

Ví dụ 3: Một vật chuyển động với vận tốc đầu bằng 0, vận tốc biến đổi theo

quy luật, và có gia tốc

0,3(m/ s )a 

.Xác định quãng đường vật đó đi được

trong 40 phút đầu tiên.

A. 12000m B. 240m C. 864000m D. 3200m

(Trích đề thi thử THPT Hoàng Diệu)

Phân tích: Nhận thấy bài toán này khác với hai ví dụ trên ở chỗ bài toán cho

biểu thức gia tốc mà không cho biểu thức vận tốc, ở đây ta có thêm một kiến

thức như sau:

Biểu thức gia tốc là đạo hàm của biểu thức vận tốc, đến đây, kết hợp với 2 ví dụ

đầu ta kết luận: “Biểu thức gia tốc là đạo hàm cấp một của biểu thức vận tốc, và

là đạo hàm cấp hai của biểu thức quãng đường”. Từ đây ta có lời giải như sau:

Lời giải

Ta có

 

0,3 0,3v t dt t



(do ban đầu vận tốc của vật bằng 0).

Vậy quãng đường vật đi được trong 40 phút đầu tiên là

40.60

2400

0,3

0,3 .

tdt t



864000m

STUDY TIP:

Hàm số thể hiện quãng

đường vật đi được tính

theo thời gian là biểu

thức nguyên hàm của

hàm số vận tốc.

STUDY TIP:

Biểu thức gia tốc là đạo

hàm cấp một của biểu

thức vận tốc, và là đạo

hàm cấp hai của biểu

thức quãng đường

Quà tặng Valentine Ngọc Huyền LB

Ngọc Huyền LB | 20

Câu 1: Một vật chuyển động với vận tốc thay đổi theo

thời gian được tính bởi công thức

 

3 2,v t t

thời gian

tính theo đơn vị giây, quãng đường vật đi được tính

theo đơn vị

Biết tại thời điểm

2ts

thì vật đi được

quãng đường là

10 .m

Hỏi tại thời điểm

30ts

thì vật

đi được quãng đường là bao nhiêu?

1410m

1140m

300m

240m

(Trích đề thi thử THPT chuyên Hạ Long)

Câu 2: Một tàu lửa đang chạy với vận tốc 200 m/s thì

người lái tàu đạp phanh; từ thời điểm đó, tàu chuyển

động chậm dần đều với vận tốc

 

200 20v t t

(m/s).

Trong đó

là khoảng thời gian tính bằng giây, kể từ

lúc bắt đầu đạp phanh. Hỏi thời gian khi tàu đi được

quãng đường 750 m (kể từ lúc bắt đầu đạp phanh) ít

hơn bao nhiêu giây so với lúc tàu dừng hẳn?

A. 5 s B. 8 s C. 15 s D. 10 s

(Trích đề thi thử THPT Hoàng Văn Thụ)

Câu 3. Giả sử một vật từ trạng thái nghỉ khi

 

0ts

chuyển động thẳng với vận tốc

    

5 / .v t t t m s

Tìm quãng đường vật đi được cho đến khi nó dừng lại.

 

125

 

125

 

125

 

125

(Trích đề thi thử THPT Lương Thế Vinh lần 2)

Câu 4: Một người đi xe đạp dự định trong buổi sáng đi

hết quãng đường 60km. Khi đi được 12 quãng đường,

anh ta thấy vận tốc của mình chỉ bằng 23 vận tốc dự

định, anh ta bèn đạp nhanh hơn vận tốc dự định

3km/h, đến nơi anh ta vẫn chậm mất 45 phút. Hỏi vận

tốc dự định của người đi xe đạp là bao nhiêu?

5/km h

12 /km h

7/km h

18 /km h

(Trích đề thi thử THPT TVB)

Câu 5: Một ôtô đang chạy với vận tốc 10 m/s thì người

lái đạp phanh; từ thời điểm đó, ôtô chuyển động chậm

dần đều với vận tốc

5 15vt  

(m/s), trong đó t là khoảng thời gian tính bằng giây, kể

từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến

khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét?

A. 20m B. 10 m C. 22,5 m D. 5 m

Câu 6: Cho chuyển động thẳng xác định bởi phương

trình

21S t t  

, trong đó t được tính bằng giây và S

được tính bằng mét. Gia tốc của chuyển động khi t = 2s

là:

A. 63m/s

B. 64m/s

C. 23m/s

D. 24m/s

(Trích đề thi thử THPT Ngọc Tộ)

Câu 7: Cho một vật chuyển động có phương trình là:

23st

  

(t được tính bằng giây, S tính bằng mét).

Vận tốc của chuyển động thẳng

2ts

là:

A. 3 B.

C. 12 D.

(Trích đề thi thử THPT Ngọc Tộ)

Câu 8. Cho chuyển động thẳng xác định bởi phương

trình

21S t t  

, trong đó t được tính bằng giây và S

được tính bằng mét. Vận tốc của chuyển động khi t = 1s

là:

A. 24m/s B. 23m/s C. 7m/s D. 8m/s

(Trích đề thi thử THPT Ngọc Tộ)

Câu 9: Một chiếc xe ô tô sẽ chạy trên đường với vận

tốc tăng dần đều với vận tốc v = 10t (m/s) t là khoảng

thời gian tính bằng giây, kể từ lúc bắt đầu chạy. Hỏi

quảng đường xe phải đi là bao nhiêu từ lúc xe bắt đầu

chạy đến khi đạt vận tốc 20 (m/s)?

A. 10m B. 20m C. 30m D. 40m

(Trích đề thi thử THPT Hoàng Diệu)

Bài tập rèn luyện kỹ năng

Lưu ý: Lời giải chi tiết sẽ được gửi vào 23h ngày 25/02/2017. Đề nghị các bạn đăng ký

tại http://ngochuyenlb.gr8.com/ để được gửi vào đúng thời gian trên.

Bấm Tải xuống để xem toàn bộ.

| 1/24

| | Tải xuống

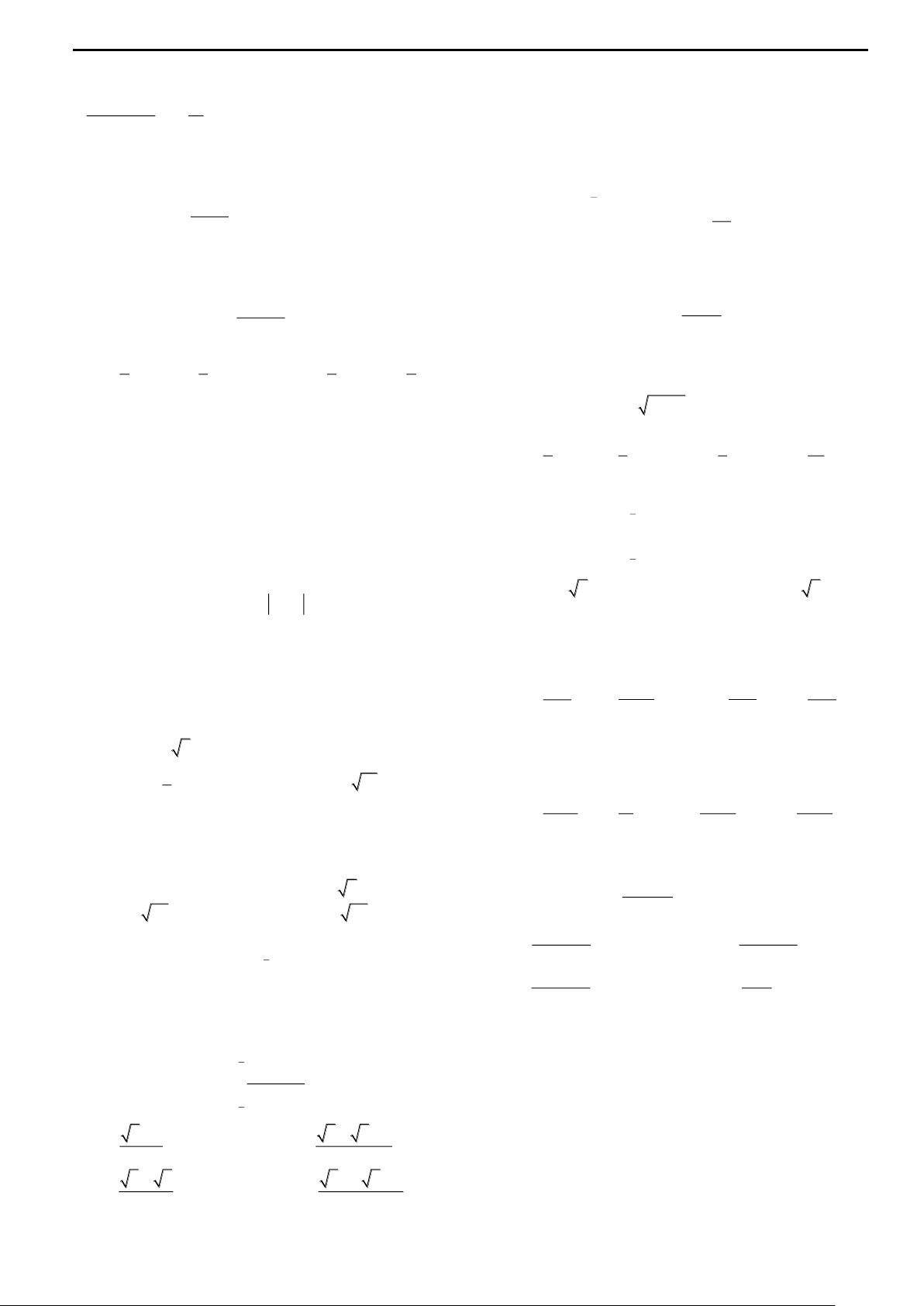
Preview text:

NGỌC HUYỀN LB
(facebook.com/huyenvu2405)
Một số v ấn đề chọn lọc
Đây là 1 tài liệu nhỏ chị viết gấp gáp để dành tặng
cho các em nhân ngày Valentine 2017. Tuy CHƯA NGUYÊN HÀM
ĐẦY ĐỦ, nhưng chị tin nó cũng giúp ích cho em
phần nào khó khăn trong quá trình ôn luyện! TÍCH PHÂN NGỌC HUYỀN LB
Tác giả “Bộ đề tinh túy Toán” & “Chắt lọc tinh túy toán” VÀ ỨNG DỤNG
Một số vấn đề chọn lọc Nguyên hàm – Tích phân và Ứng dụng
Đời phải trải qua giông tố nhưng không được cúi đầu trước giông tố!
Đừng bao giờ bỏ cuộc Em nhé!
Chị tin EM sẽ làm được! __Ngọc Huyền LB__
Đã nói là làm – Đã làm là không hời hợt – Đã làm là hết mình – Đã làm là không hối hận! facebook.com/huyenvu2405
Nguyên hàm – Tích phân và ứng dụng The best or nothing
Chủ đề: Nguyên hàm – tích phân và ứng dụng
I. Nguyên hàm và các tính chất cơ bản.
Kí hiệu K là một khoảng, một đoạn hay một nửa khoảng. Định nghĩa
Cho hàm số f xác định trên K. Hàm số F được gọi là nguyên hàm của hàm số f
trên K nếu F'x  f x với mọi x thuộc K. Định lý 1 STUDY TIP:
1. Nếu F là một nguyên hàm của f trên K thì với mỗi hằng số C, hàm Từ định nghĩa nguyên
Gx  Fx  C cũng là một nguyên hàm của hàm f trên K. hàm ta có được
2. Đảo lại nếu F và G là hai nguyên hàm của hàm số f trên K thì tồn tại hằng số C
 fxdx'fx
sao cho Fx  Gx  . C Kí hiệu: f
 xdx  Fx C .
Người ta chứng minh được rằng: “Mọi hàm số liên tục trên K đều có nguyên hàm trên K.”
Tính chất của nguyên hàm
Định lý 2 sau đây cho ta một số tính chất cơ bản của nguyên hàm Định lý 2
1. Nếu f, g là hai hàm số liên tục trên K thì  f
 x gxdx  f 
 xdx g  xdx af
 xdx  a f
 xdx với mọi số thực a khác 0. 2. d f
 xdx  f xdx
Bài toán tìm nguyên hàm là bài toán ngược với bài toán tìm đạo hàm. Việc tìm
nguyên hàm của một hàm số thường được đưa về tìm nguyên hàm của một số
hàm số đơn giản hơn. Dưới đây ta có bảng một số nguyên hàm :
dx  x  C     1
ax b dx  ax  b  C , a  0 a 1 1         1 ax b x  a x  dx 
 C a  ,   
1  ax  b dx   C,     1   1 a    1  1 dx 1
dx  ln x  a  C 
 .ln ax  b  C  x  a ax  b a x x
e dx  e  C  axb 1 axb e dx  e  C  a x 1 x pxq 1 a dx 
a  C,a  0, a   1 pxq a dx  a
 C,a  0,a   1 ln a . p ln a
sin xdx   cos x  C  cos ax sin axdx   C,  a  0 a
cos xdx  sin x  C  sin ax cos axdx   C,  a  0 a 1 1
dx  tan x  C 
dx   cot x  C  2 cos x 2 sin x
The best or nothing | 1 Quà tặng Valentine Ngọc Huyền LB
II. Hai phương pháp cơ bản để tìm nguyên hàm.
a, Phương pháp đổi biến số. Định lí 3
Cho hàm số u  ux có đạo hàm liên tục trên K và hàm số y  f u liên tục sao
cho hàm hợp f ux 
 xác định trên K. Khi đó nếu F là một nguyên hàm của f thì f u 
  xu'
 xdx  F u
 x C 
Ví dụ 1: Tìm nguyên hàm x   10 1 dx . Lời giải STUDY TIP: Với phương pháp đổi
Theo định lý trên thì ta cần viết về dạng f udu  . biến ta cần chú trọng công thức mà suy ra từ
Mà u'  x   1 '  1 , do vậy định lý như sau:
Nếu u  f x , khi đó du  f'xdx  x 
x  10 dx  x  10 1 1 .x   
1'dx  x   dx    11 10 1 1 1   C . 11
Từ ví dụ trên ta có các bước gợi ý để xử lý bài toán tìm nguyên hàm theo phương pháp đổi biến
1. Đặt u  g x .
2. Biến đổi x và dx về u và du.
3. Giải bài toán dưới dạng nguyên hàm hàm hợp f udu 
, sau đó thay biến x
vào nguyên hàm tìm được và kiểm tra lại kết quả. Ta đến với ví dụ 2
Ví dụ 2: Tìm x    x7 2 1 dx .
Ở bài toán này, ta thấy số mũ 7 khá cao mà lại có biểu thức trong ngoặc phức tạp hơn là 2
x . Do vậy ta sẽ đặt   7
1 x để đổi biến, dưới đây là lời giải áp dụng gợi ý các bước trên. Lời giải
Đặt u  1  x  du  1  x'dx  du  d  x 2 ta có x    x7 2 1
dx    u 7
u  du   7 8 9 1 . 1
u  2u  u du 8 9 10 8 9 10 u 2u u
1 x 21 x 1 x      C      C. 8 9 10 8 9 10
b, Phương pháp lấy nguyên hàm từng phần. Định lý 4
Nếu u và v là hai hàm số có đạo hàm liên tục trên K thì u
 xv'xdx ux.vx v
 xu'xdx .
Công thức trên thường được viết gọn dưới dạng udv  uv  vd . u   Ngọc Huyền LB | 2
Nguyên hàm – Tích phân và ứng dụng The best or nothing
Ví dụ 3: Thầy Điệp Châu cho bài toán “ Tìm sin x cos xdx  ” thì ba bạn Huyền,
Lê và Hằng có ba cách giải khác nhau như sau:
Bạn Huyền giải bằng phương
Bạn Lê giải bằng phương pháp lấy nguyên hàm Bạn Hằng chưa học đến hai
pháp đổi biến số như sau:
từng phần như sau:
phương pháp trên nên làm như
“Đặt u  sin x , ta có:
“Đặt u  cosx,v'  sin x . sau: du  cos xdx
Ta có u'  sin x,v  cosx . “ sin . x cos xdx  Vậy sin .
x cos xdx  udu  
Công thức nguyên hàm từng phần cho ta sin 2x cos2x  dx    C  .” 2 2 u sin x 2      sin xcos xdx cos x sin xcos xdx   2 4 C   C ” 2 2
Giả sử F là một nguyên hàm của sin .
x cosx . Theo đẳng thức trên ta có Fx 2
 cos x  Fx C . x C Suy ra F x 2 cos    . 2 2 2 cos x Điều này chứng tỏ  là một nguyên 2 hàm của sin . x cos . x 2 cos x Vậy sin .
x cos xdx    C  .” 2
Kết luận nào sau đây là đúng?
A. Bạn Hằng giải đúng, bạn Lê và Huyền giải sai.
B. Bạn Lê sai, Huyền và Hằng đúng.
C. Ba bạn đều giải sai.
D. Ba bạn đều giải đúng.
Nhận xét: Sau khi soát kĩ cả ba lời giải, ta thấy ba lời giải trên đều không sai ở STUDY TIP:
bước nào cả, tuy nhiên, tại sao đến cuối cùng đáp án lại khác nhau? Ta xem giải Bài toán củng cố về
thích ở lời giải sau:
định lý 1 đã nêu ở trên, Lời giải
và củng cố các cách giải 2 2 nguyên hàm cơ bản. sin x cos x cos 2x
Cả ba đáp số đều đúng, tức là cả ba hàm số ;  và  đều là 2 2 4 nguyên hàm của sin .
x cos x do chúng chỉ khác nhau về một hằng số. Thật vậy 2 2 sin x  cos x  1     ; 2  2  2 2 x  2 2 2 sin 1 2 sin sin cos 2 x x x      1       . 2  4  4 4
III. Khái niệm và các tính chất cơ bản của tích phân. a. Định nghĩa
Cho hàm số f liên tục trên K và a, b là hai số bất kì thuộc K. Tích phân của f từ a b
đến b, kí hiệu là f
 xdx, là một số xác định bởi công thức sau a b f
 xdx  FbFa trong đó F là nguyên hàm của f trên K. a
b. Các tính chất của tích phân. Định lý 1
Giả sử các hàm số f, g liên tục trên K và a, b, c là ba số bất kì thuộc K. Khi đó ta có
The best or nothing | 3 Quà tặng Valentine Ngọc Huyền LB a 1. f
 xdx  0. a b a 2. f
 xdx   f  xdx . a b b c c 3. f
 xdx f
 xdx  f  xdx . a b a b b b 4.  f
 x gxdx  f 
 xdx g  xdx . a a a b b
5. kf xdx  k f xdx, k     . y a a A Định lý 2 x
Cho f là hàm số xác định trên K và a là một điểm cố định thuộc K. Xét hàm số A O
G x xác định trên K bởi công thức
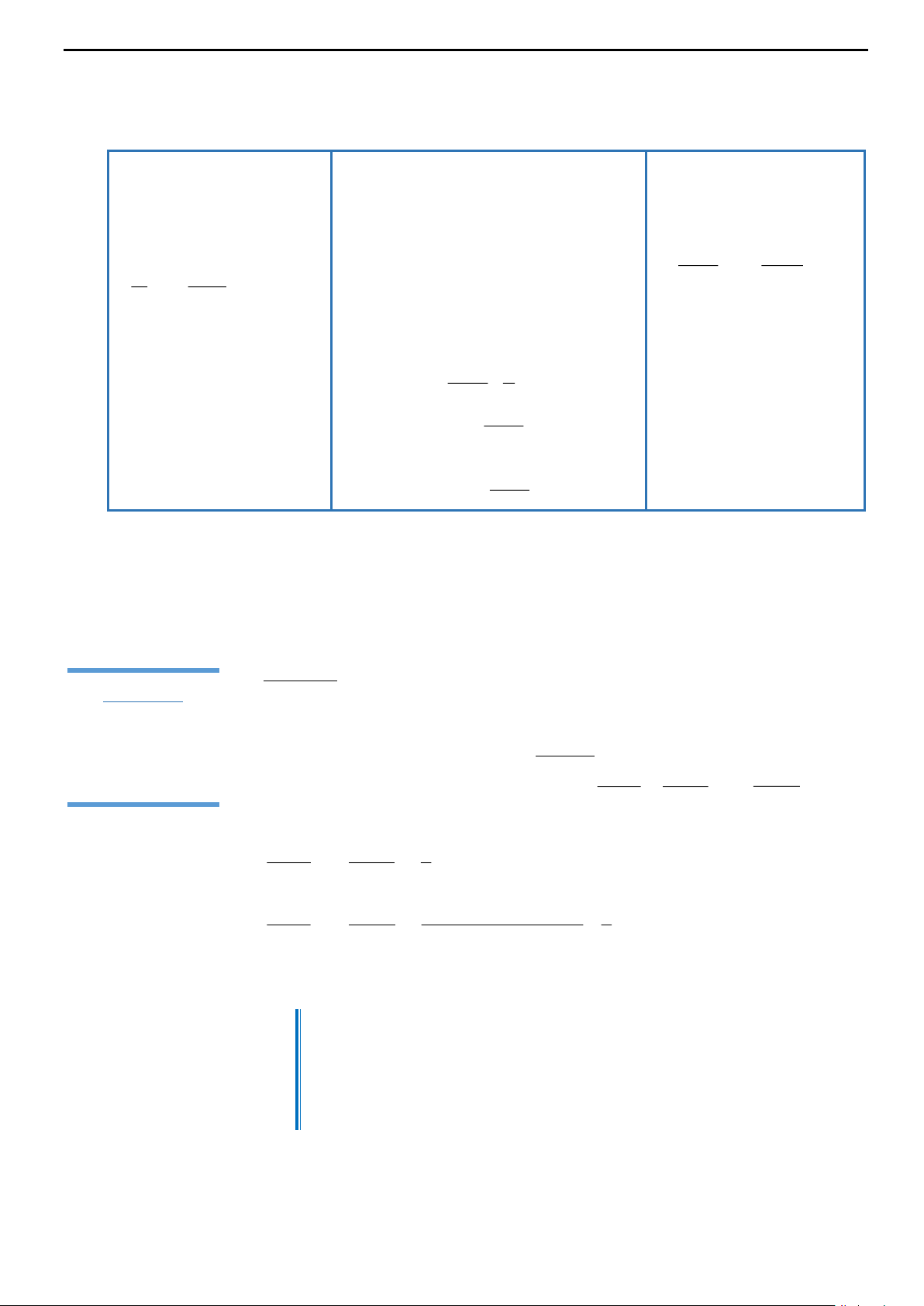
G x x  f  tdt. Hàm số chẵn a
Khi đó G là một nguyên hàm của f. Hình 3.1 Định lý 3
Tích phân của hàm lẻ và hàm chẵn trên . a a y
1. Nếu f là một hàm số chẵn, khi đó f A Hàm số lẻ
 xdx  2 f
 xd .x a 0 a
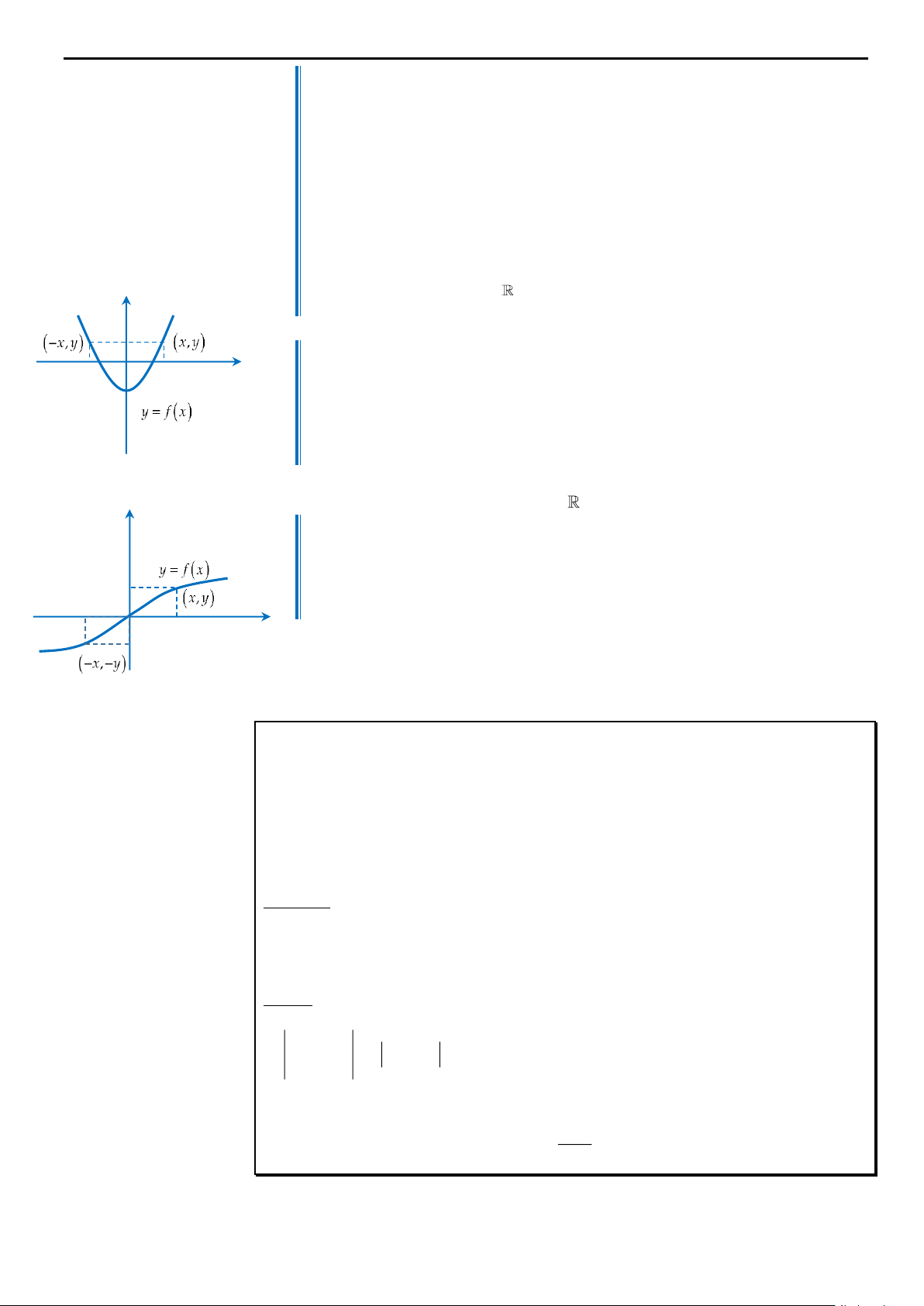
2. Nếu f là một hàm số lẻ, khi đó f
 xdx  0. x a A O 0 Đọc thêm
Ta vừa đưa ra 3 tính chất của tích phân theo chương trình chuẩn. Dưới đây là Hình 3.2 các tính chất bổ sung: b 1. 0dx  0  a b 2. cdx  c  b  a a b
3. Nếu f x  0 , x  a,b   thì f
 xdx  0. a
Hệ quả 3: Nếu hai hàm số f x và g x liên tục và thỏa mãn b b
f x  g x , x  a,b   thì f
 xdx  g
 xd .x a s b
Chú ý: Nếu f x liên tục và dương trên a,b   thì f
 xdx  0 . a b b 4. f
 xdx  f
 xdx ,a  b. a a
5. Nếu m  f x  M, x   a
 ,b ;m,M   là các hằng số thì 1 b
mb  a b  f
 xdx  Mb  ahay m f
 xdx  M . b  a a a Ngọc Huyền LB | 4
Nguyên hàm – Tích phân và ứng dụng The best or nothing
IV. Hai phương pháp cơ bản tính tích phân.
a. Phương pháp đổi biến số.
Quy tắc đổi biến số
1. Đặt u  ux ,
2. Biến đổi f x dx  gu du.
3. Tìm một nguyên hàm G u của g u . ub 4. Tính g
 udu Gub Gua . ua b 5. Kết luận f
 xdx Gub  Gua . a
b. Phương pháp tích phân từng phần.
Cho hai hàm số u, v có đạo hàm liên tục trên K và a, b là hai số thuộc K. Khi đó b u  x b
v' xdx  ub v b  ua v a  u'
 x.vxd .x a a
IV. Ứng dụng hình học của tích phân.
a. Tính diện tích hình phẳng.
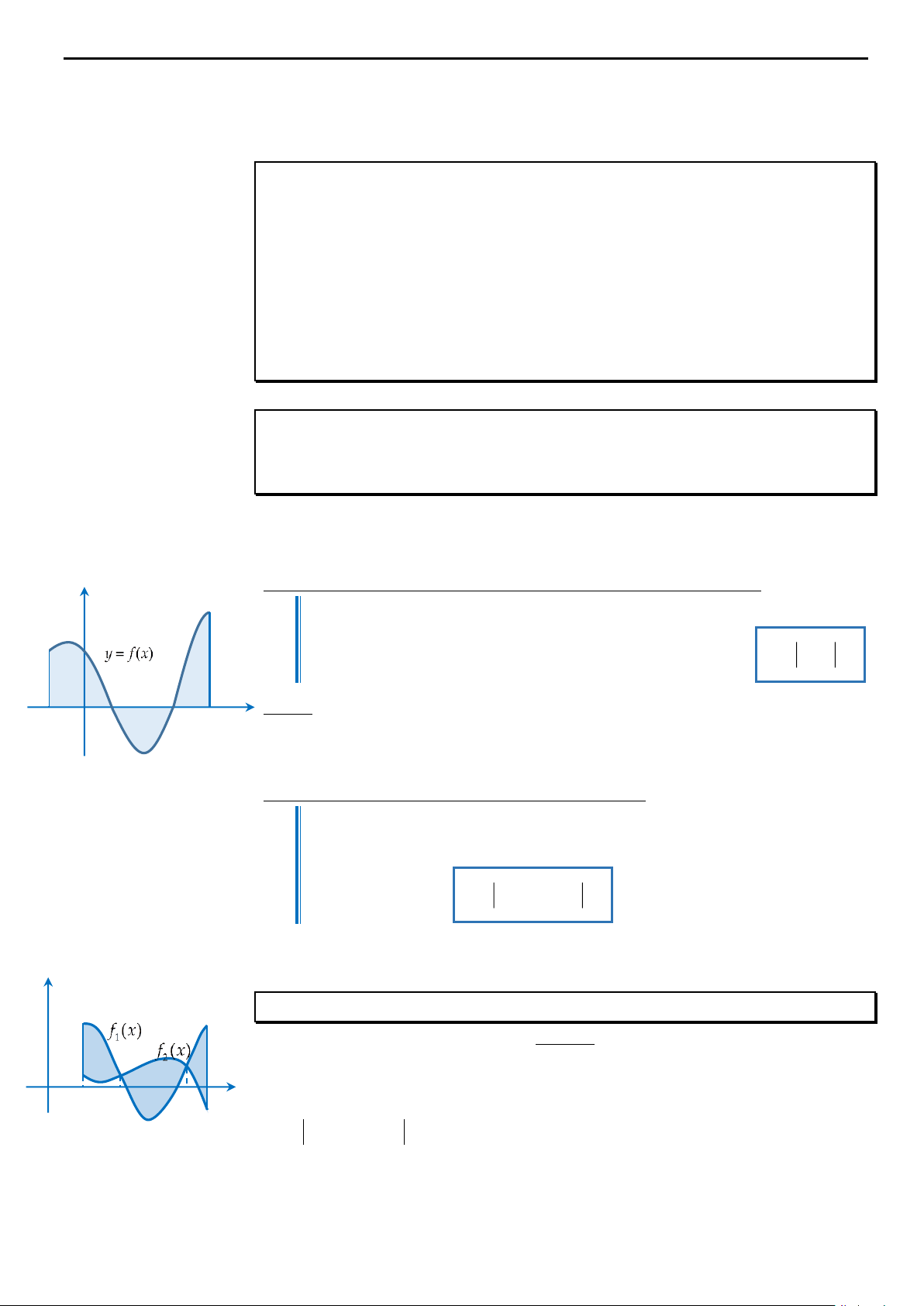
Diện tích hình phẳng giới hạn bởi một đường cong và trục hoành. y
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số f x liên tục, trục b
hoành và hai đường thẳng x  a, x  b được tính theo công thức S  f
 x dx . a x
Chú ý: Trong trường hợp dấu của f x thay đổi trên đoạn a; b   thì ta phải a O b
chia đoạn a; b 
 thành một số đoạn con để trên đó dấu của f x không đổi, do
đó ta có thể bỏ dấu giá trị tuyệt đối trên đoạn đó. Hình 3.3
Diện tích hình phẳng giới hạn bởi hai đường cong.
Cho hai hàm số y  f x và y  g x liên tục trên đoạn a; b   . Khi đó diện tích
S của hình phẳng giới hạn bởi đồ thị hàm số y  f x , y  g x và hai đường b
thẳng x  a, x  b là S  f
 x  gx dx . a
Tương tự như chú ý ở trên thì ở bài toán này ta cũng phải xét đoạn mà dấu của
f x  g x không đổi. y
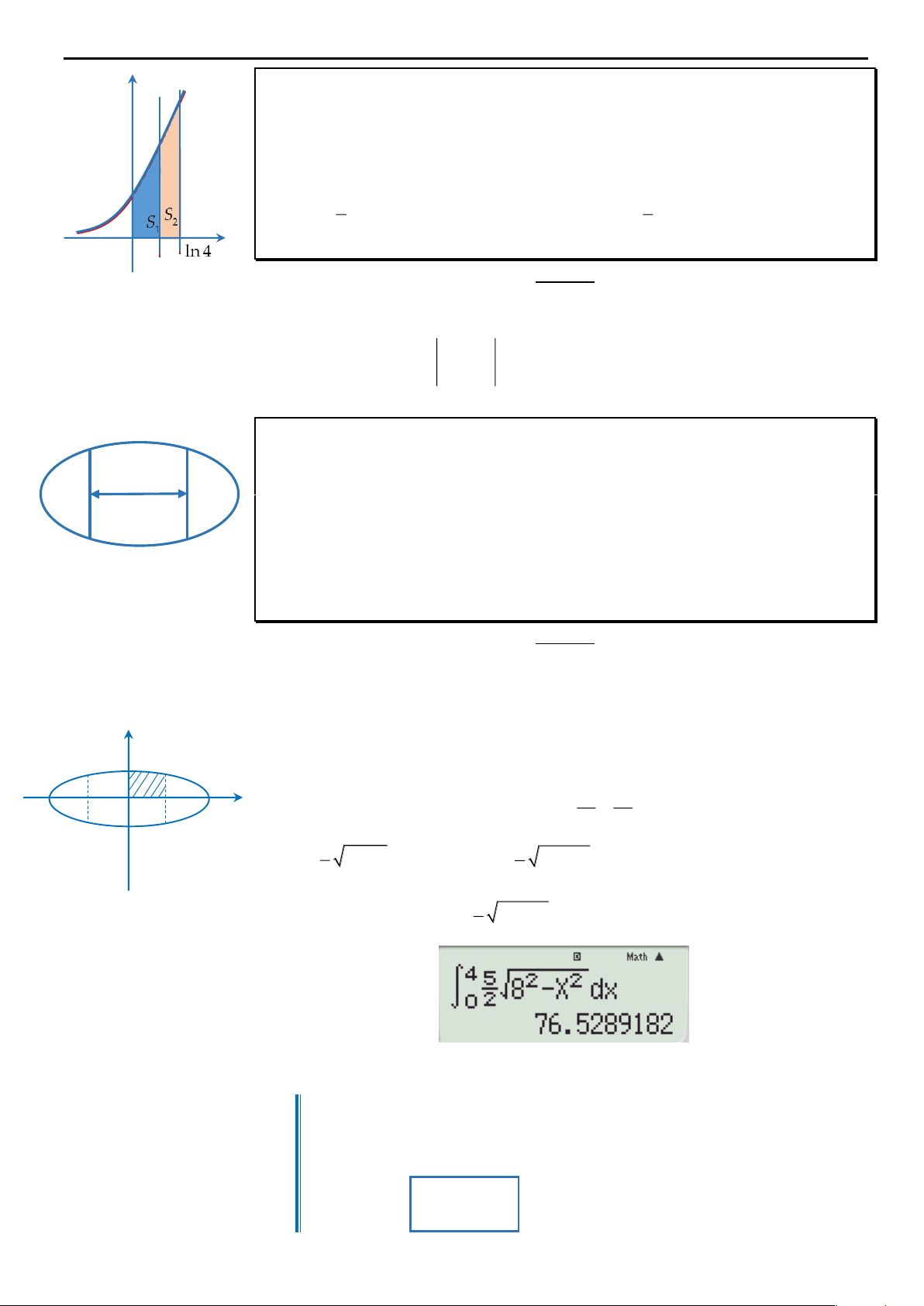
Ví dụ 4: Tính diện tích hình phẳng ( hình được tô màu) ở biểu diễn ở hình 3.4. Lời giải
Nhận thấy trên a; c 
 và d; b 
 thì f x  f x ; trên c; d f x  f x 1   2     thì 1   2   Do vậy O a c d b x b c d b S  f x  f x  f x  f x dx  f x  f x dx  f x  f x dx     1 
 2    1   2    2   1    1   2   Hình 3.4 a a c d
(Trên đây là cách bỏ dấu giá trị tuyệt đối)
The best or nothing | 5 Quà tặng Valentine Ngọc Huyền LB
Ví dụ 5: Cho hình thang cong H giới hạn bởi các đường x
y  e , y  0, x  0 y x
và x  ln4. Đường thẳng x  k(0  k  ln 4) chia H thành hai phần có diện tích
là S và S như hình vẽ bên. 1 2
Tìm k để S  2S . 1 2
A. k  2 ln4
B. k  ln2 C. k  8 ln
D. k  ln3 x 3 3
( Trích đề minh họa môn Toán lần 2 – Bộ GD&ĐT) O k x O Lời giải Đáp án D.
Nhìn vào hình vẽ ta có được các công thức sau: k ln 4 k ln 4 x e dx  2. x e dx   x  e  2. x e k 0 ln4    2.  2. k  3 k e e e e e  9 0 k 0 k k
 e  3  k  ln3 .
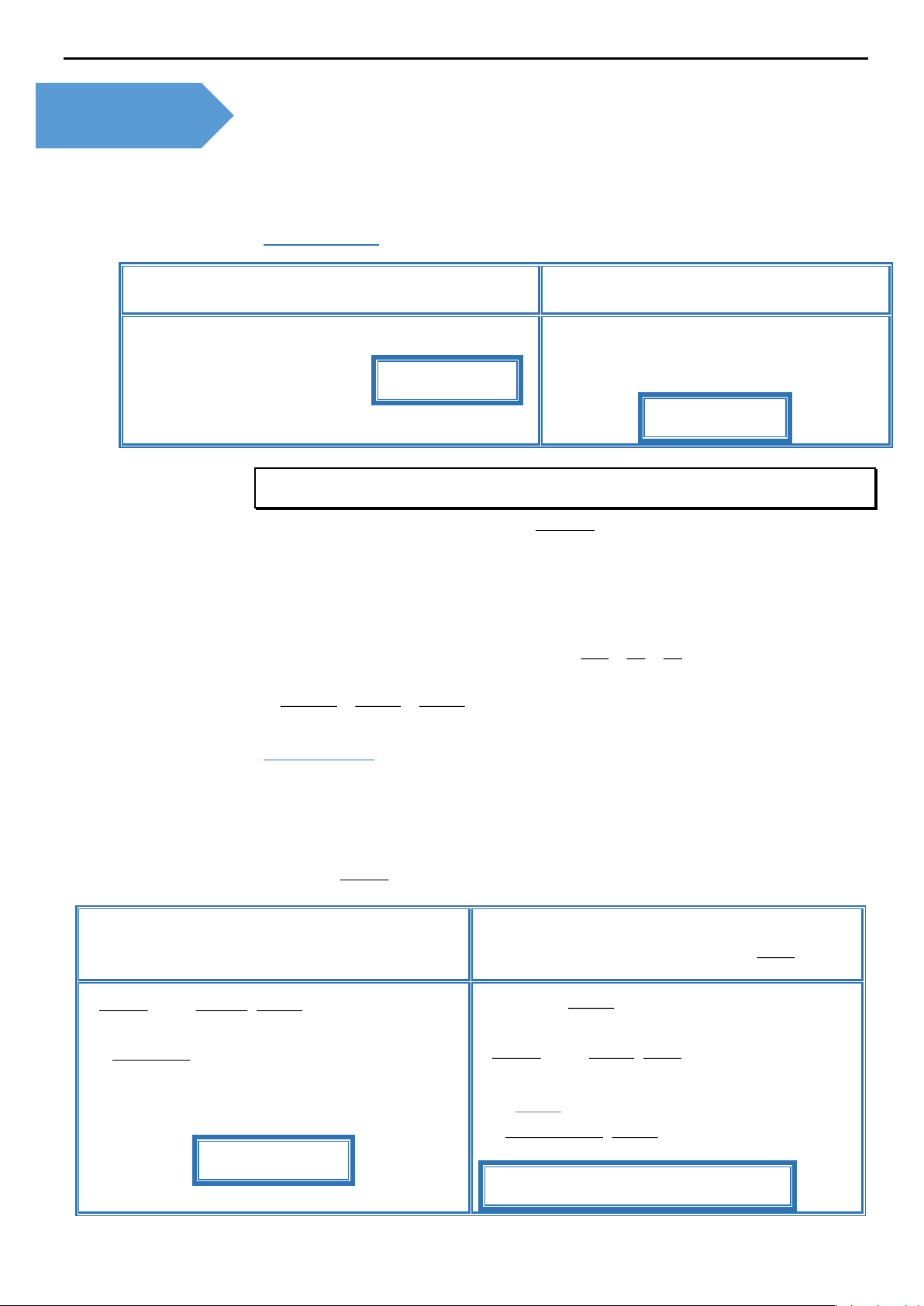
Ví dụ 6: Ông An có một mảnh vườn hình elip có độ dài trục lớn bằng 16m và
độ dài trục bé bằng 10 m. Ông muốn trồng hoa trên một dải đất rộng 8m và 8m
nhận trục bé của elip làm trục đối xứng (như hình vẽ). Biết kinh phí để trồng hoa là 100.000 đồng/1 2
m . Hỏi ông An cần bao nhiêu tiền để trồng hoa trên dải
đất đó ? (Số tiền được làm tròn đến hàng nghìn.)
A. 7.862.000 đồng. B.7.653.000 đồng. C. 7.128.000 đồng. D. 7.826.000 đồng.
( Trích đề minh họa môn Toán lần 2 – Bộ GD&ĐT) Lời giải Đáp án B.
Nhận thấy đây là bài toán áp dụng ứng dụng của tích phân vào tính diện tích
hình phẳng. Ta có hình vẽ bên: y
Ta thấy, diện tích hình phẳng cần tìm gấp 4 lần diện tích phần gạch chéo, do đó 5
ta chỉ cần đi tìm diện tích phần gạch chéo. x 2 2 x y -8 -4 4
Ta có phương trình đường elip đã cho là   1 . Xét trên 0; 4 O 8   nên y  0 2 2 8 5 -5 5 4 5 thì 2 y  8  x . Khi đó 2 2 S  8  x dx 
, vậy diện tích trồng hoa của ông 8 cheo 8 0 4 5 An trên mảnh đất là 2 2 S  4.
8  x dx  76, 5289182  8 0
Khi đó số kinh phí phải trả của ông An là 76, 5289182.100000  7.653.000 đồng.
b. Tính thể tích vật thể.
Cho H là một vật thể nằm giới hạn giữa hai mặt phẳng x  a và x  b . Gọi S x
là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành
tại điểm có hoành độ x a  x  b . Giả sử Sx là một hàm liên tục. Khi đó thể b
tích V của H là V  S
 xd .x (hình 3.5) a Ngọc Huyền LB | 6
Nguyên hàm – Tích phân và ứng dụng The best or nothing P Q S(x) x a x O b Hình 3.5
Ví dụ 7: Tính thể tích vật thể tạo được khi lấy giao vuông góc hai ống nước
hình trụ có cùng bán kính đáy bằng a. ( hình 3.6) 3 3 3 A.  16a 2a 4a V B. V  C. V  D.  3 V a 3 3 3
(Trích sách bộ đề tinh túy ôn thi THPT QG môn Toán)
Ta sẽ gắn hệ trục tọa độ Oxyz vào vật thể này, tức là ta sẽ đi tính thể tích vật thể
V giới hạn bởi hai mặt trụ: 2  2  2 2 2 2 x y
a và x  z  a a  0 . Hình 3.6 z a z y O y a x a x Hình 3.7
Hình vẽ trên mô tả một phần tám thứ nhất của vật thể này, với mỗi x  0; a   ,
thiết diện của vật thể (vuông góc với trục Ox ) tại x là một hình vuông có cạnh  2  2 y a
x ( chính là phần gạch chéo trong hình 3.7). Do đó diện tích thiết diện sẽ là: Sx  2 a  2 2 x a  2 x  2 a  2 .
x x  0; a  .
Khi đó áp dụng công thức * thì thể tích vật thể cần tìm sẽ bằng: a a  3 x  3 a 16a
V  8 Sxdx 8 a  
 2 2x dx  8 2ax    . 3 0 3 0 0  
Ví dụ 8: Tính thể tích của vật thể H biết rằng đáy của H là hình tròn 2 2 x  y  1
và thiết diện cắt bởi mặt phẳng vuông góc với trục hoành luôn là tam giác đều. Lời giải
The best or nothing | 7 Quà tặng Valentine Ngọc Huyền LB
Giả sử mặt phẳng vuông góc với trục hoành chứa thiết diện là tam giác đều y C
ABC tại điểm có hoành độ là x  1   x  
1 với AB chứa trong mặt phẳng xOy (hình 3.8). 2 AB 3 Ta có 2
AB  2 1  x . Do đó S x   3  2 1  x . Vậy 4 B 1 x 3  x  4 3 O x A V  S  x 1 dx  3   2
1  x dx  3  x    ( đvtt).  3  3 1  1  A
c. Tính thể tích khối tròn xoay. Hình 3.8
Một hình phẳng quay quanh một trục nào đó tạo nên một khối tròn xoay. y Định lý 4 y = f (x)
Cho hàm số y  f x liên tục, không âm trên đoạn a,b 
 . Hình phẳng giới hạn
bởi đồ thị hàm số y  f x , trục hoành và hai đường thẳng x  a, x  b quay a O x b x
quanh trục hoành tạo nên một khối tròn xoay. Thể tích V của khối tròn xoay đó b là 2 V   f
 xd .x Hình 3.9 a
Ví dụ 9: Thể tích của khối tròn xoay thu được khi quay hình phẳng được giới
hạn bởi đường cong y  sin x , trục hoành và hai đường thẳng x  0, x   (hình y
3.10) quanh trục Ox là y = sinx  2  A. (đvtt) B. (đvtt) C.  (đvtt) D. 2  (đvtt) 2 2 x O x Lời giải Đáp án B.
Áp dụng công thức ở định lý 4 ta có Hình 3.10    2   1    2
V   sin xdx  
1 cos2xdx  x  sin2x    . 2 2  2  0 2 0 0
Tiếp theo dưới đây là một bài toán thường xuất hiện trong các đề thi thử, bài
toán có thể đưa về dạng quen thuộc và tính toán rất nhanh
Ví dụ 10: Tính thể tích khối tròn xoay thu được khi quay hình phẳng được giới y hạn bởi đường cong 2 2
y  A  x và trục hoành quanh trục hoành.
Lời giải tổng quát O -A A x Ta thấy 2 2 2 2 2 2 2 2
y  A  x  y  A  x  x  y  A Do 2 2
A  x  0 với mọi x, do vậy đây là phương trình nửa đường tròn tâm O,
bán kính R  A nằm phía trên trục Ox. Khi quay quanh trục Ox thì hình phẳng Hình 3.11
sẽ tạo nên một khối cầu tâm O, bán kính R  A (hình 3.11). Do vậy ta có luôn 4 3 V  . .  A 3
Vậy với bài toán dạng này, ta không cần viết công thức tích phân mà kết luận
luôn theo công thức tính thể tích khối cầu. Ngọc Huyền LB | 8
Nguyên hàm – Tích phân và ứng dụng The best or nothing Đọc thêm Định lý 5
Cho hàm số y  f x liên tục, không âm trên đoạn a, b 
 a  0 . Hình phẳng
giới hạn bởi đồ thị hàm số y  f x , trục hoành và hai đường thẳng
x  a, x  b quay quanh trục tung tạo nên một khối tròn xoay. Thể tích V của b
khối tròn xoay đó là V  2 xf
 xd .x a
The best or nothing | 9 Quà tặng Valentine Ngọc Huyền LB
Bài tập rèn luyện kỹ năng
1. Nguyên hàm – chọn lọc các bài tập về nguyên hàm trong các đề thi thử
Câu 1: Tìm nguyên hàm  2   1 x I x e d . x
Câu 6: Tìm một nguyên hàm F x của hàm số A.  2   1 x I x e  C B.  2   1 x I x e  C    f x 4  biết F    3. 2 cos 3x  9 
C.  2  3 x I x e  C
D.  2  3 x I x e  C
(Trích đề thi thử THPT chuyên KHTN – Hà Nội)
A. F x 4 3  tan3x  3 3
Câu 2: Tìm nguyên hàm I  xln2x   1d .x
B. Fx  4tan3x  3 3 2 4x  1 xx   1 A. I  ln 2x  1   C 8 4
C. F x 4 3  tan3x  3 3 2 4x  1 xx   1 B. I  ln 2x  1   C 8 4
D. F x 4 3   tan3x  3 3 2 4x  1 xx   1 C. I  ln 2x  1   C
(Trích đề thi thử THPT chuyên Hoàng Văn Thụ) 8 4
Câu 7: Tìm nguyên hàm của hàm số f x  x x. 2 4x  1 xx   1 D. I  ln 2x  1   C 8 4 2 A. f  x 2 dx  x x  C
(Trích đề thi thử THPT chuyên KHTN – Hà Nội) 5
Câu 3: Tìm nguyên hàm I  x   1sin2xd .x B. f  x 2
dx  x x  C 5
12xcos2xsin2x 1 A. I   C C. f  x 2 dx  x x  C 2 5
22xcos2xsin2x B. I   C D. f  x 3 dx  x  C 2 2
12xcos2xsin2x
(Trích đề thi thử THPT Lương Thế Vinh lần 2) C. I   C 4 ln x  Câu 8: dx  bằng:
2  2xcos2x  sin2x x D. I   C 4 2 A.  32 2 ln x  C B.
lnx3 C
(Trích đề thi thử THPT chuyên KHTN – Hà Nội) 3 1 3
Câu 4: Cho f x,gx là các hàm số liên tục trên . C.  C D.
lnx3 C 2 ln x 2
Tìm khẳng định sai trong các khẳng định sau?
(Trích đề thi thử THPT chuyên Lam Sơn) A. . k f
 xdx  .k f
 xdx với k là hằng số 1
Câu 9: Cho hàm số f x 
. Nếu F x là một 2 B.  f
 xgxdx  f 
 xdx g  xdx sin x
nguyên hàm của hàm số f x và đồ thị hàm số C.  f
 x.gxdx  f 
 xd .x g  xdx    D.  f 
y  F x
 x  gxdx  f 
 xdx g  xdx
đi qua M  ;0 thì Fx là:  3 
(Trích đề thi thử THPT chuyên Kim Thành – Hải Dương) 1 A.  cot x B. 3  cot x
Câu 5: Họ nguyên hàm của hàm số   2017 x f x e  là: 3 1 A. 2017  x e  C B. 2017  x e C 3 C.  cot x
D. cot x  C 2017 3 1  C. 2017 2017.  x  e C D. 2017  x e  C
(Trích đề thi thử THPT chuyên Lam Sơn) 2017
Câu 10: Cho hàm số f x 1  .
(Trích đề thi thử THPT chuyên Hoàng Văn Thụ) x  Hãy chọn mệnh đê 2 sai: Ngọc Huyền LB | 10
Nguyên hàm – Tích phân và ứng dụng The best or nothing 1
Câu 16: Tìm nguyên hàm F x của hàm số A. dx  ln 
x2C x  2
f x  3x  4, biết F0  8.
B. ln3 x  2  là một nguyên hàm của f x   
C. ln x  2  C là họ nguyên hàm của f x
A. Fx 1 38 3x 4 3 3
D. ln x  2 là một nguyên hàm của f x 2 16
B. Fx  3x  4 3x  4  3 3
(Trích đề thi thử THPT chuyên Lam Sơn) 2 56 2     Câu 11: x 1 xe  dx  bằng:
C. Fx 3x 4 3x 4 9 9 2 2 A. 1 2 x e   C B. x 1 e   C 2 8
D. Fx  3x  4 3x  4  3 3 2 2 1 C. 2 x 1 x e   C D. x 1 e   C 2
(Trích đề thi thử THPT chuyên Hạ Long)
(Trích đề thi thử THPT chuyên Lam Sơn) x
Câu 17: Tìm nguyên hàm của hàm số f x 3  . 4 3  3x x 1 Câu 12: dx  bằng: 2 1  x 3x A. f  x 4 dx   C 4 2x  6 A.  2 x   2 2
1 x  C B.  2 x   2 1 1 x  C B. f
 xdx   4 ln x   1  C C.  2 x   2 1
1 x  C D.  2 x   2 2 1 x  C C. f  x 3 dx  x  4 ln x   1  C
(Trích đề thi thử THPT chuyên Lam Sơn) 1
Câu 13: Tìm nguyên hàm của hàm số D. f
 xdx  ln 4x  1C 4
f x   x  2 2 3 .
(Trích đề thi thử THPT chuyên Hạ Long) x x 
Câu 18: Tính nguyên hàm  x    3 2 1 e d . x A. f  x  3 2 3 dx   C 3 2x  1 x e x 2 x e
A. 2x     3 3 3 1 e dx    C B. f
 xdx  x 3 2 3  C 3 9 2x  1 x e x 2 x e x 
B. 2x     3 3 3 1 e dx    C C. f  x  3 2 3 dx   C 3 3 6 3x 1 2 3x     x  C. 2x  1 e dx x xe C D. f  x  3 2 3 dx   C 3 2 D.    3   2   3 2 1 x x x e dx x x e  C
(Trích đề thi thử THPT chuyên Hạ Long)
Câu 14: Tìm nguyên hàm của hàm số
(Trích đề thi thử THPT chuyên Hạ Long) 1
f x  3sin3x  cos3 . x
Câu 19: Tìm nguyên hàm I  d . x  2 4  x A. f
 xdx  cos3xsin3xC 1 x  2 1 x  2 A. I  ln  C B. I  ln  C B. f
 xdx  cos3xsin3xC 2 x  2 2 x  2 1 x  2    1 x 2   C. f  x 1
dx  cos3x  sin3x  C C. I ln C D.  I ln C  3 4 x 2 4 x 2
(Trích đề thi thử THPT chuyên KHTN – Hà Nội) D. f  x 1 1
dx   cos3x  sin3x  C 3 3
Câu 20: Hàm số nào sau đây không là nguyên hàm
(Trích đề thi thử THPT chuyên Hạ Long) x 2  x
của hàm số f x    .
Câu 15: Tìm nguyên hàm của hàm số   x x f x e e   . x 2 1 A.    x x
f x dx  e  e  C x x  x 
A. F x 2   
B. F x 2 1  B.    x x
f x dx  e  e  C x 1 x 1 x  x  x  x  C.    x x
f x dx  e  e  C
C. F x 2 1  F x  x  D.   2 1 1 x  1 D.    x x
f x dx  e  e  C
(Trích đề thi thử THPT chuyên Hoàng Văn Thụ)
(Trích đề thi thử THPT chuyên Hạ Long) 1 Câu 21: dx  bằng: 2 x  x  2
The best or nothing | 11 Quà tặng Valentine Ngọc Huyền LB 1 x  1 1 x  2
(Trích đề thi thử THPT chuyên Thái Bình lần 2) A. ln  C B. ln  C 3 x  2 3 x  1 dx
Câu 23: Nguyên hàm của hàm số: I   là: 1 x  1 x  2 2x  1  4 C. ln  C D. ln  C 3 x  2 x  1
A. Fx  2x  1  4ln 2x 1  4 C
(Trích đề thi thử THPT chuyên Lam Sơn)
B. Fx  2x 1  4ln 2x 1  4 C
Câu 22: Hàm số Fx l  n 2x  e
x  0 là nguyên hàm 7
của hàm số nào sau đây?
C. Fx  2x 1  ln 2x 1  4 C 2 ln2x e
A. f x 
B. f x l  n 2x  e
D. Fx  2x 1  4ln 2x 1  4 C x ln2x e
(Trích đề thi thử THPT Triêụ Sơn 2
C. f x  D.   l  n 2   2 x f x e 2x )
2. Tích phân – chọn lọc các bài tập về tích phân trong các đề thi thử. 1 3  2 3  2  2
Câu 1: Biết tích phân  2   1 x I x
e dx  a  be A. B. 2 2 0
a ;b . Khi đó tích .ab có giá trị bằng: 3  2 3  2 2  2 C. D. 2 2 A. 1 B. 1  C. 2 D. 3
(Trích đề thi thử THPT Cái Bè)
(Trích đề thi thử THPT chuyên Thái Bình lần 2)  1 a cos2x 1 Câu 2: Biết f
 xdx  2 và f x là hàm số lẻ. Khi đó
Câu 6: Cho I  dx  ln 3.  Tìm giá trị của 1  2sin 2x 4 0 0 0 a là: I  f
 xdx có giá trị bằng: A. 3 B. 2 C. 4 D. 6 1 
(Trích đề thi thử THPT Cái Bè) A. I  1 B. I  0 C. I  2  D. I  2 
(Trích đề thi thử THPT chuyên Thái Bình lần 2) 2 3 cos x Câu 7: Tích phân dx  bằng: 1  sin x Câu 3: Tích phân 2
I  x x  1dx  có giá trị bằng: 4 0 1  1   2 2  1 2 A. ln 2 B. ln 2 A. I  B. I  4 4 3 3 1 1 C.  ln 2 D.   ln 2 2 2 2 4 4 C. I  D. I  3 3
(Trích đề thi thử THPT Triệu Sơn 2)
(Trích đề thi thử THPT chuyên Thái Bình lần 2) 1 2 x 3
Câu 8: Tích phân xe dx  bằng: x
Câu 4: Cho tích phân I  dx  nếu đặt 0   0 1 x 1 e  1 e  1 e  1 e  1 A. B. C. D. 2 2 2e 2 2e
t  x  1 thì I  f
 tdt trong đó:
(Trích đề thi thử THPT Triệu Sơn 2) 1 1 A.   2
f t  t  t
B. f t 2  2t  2t x
Câu 9: Tính tích phân: dx  x  C.   2
f t  t  t
D. f t 2  2t  2t 0 1 1  5 
(Trích đề thi thử THPT chuyên Thái Bình lần 2) A. ln 2 B. 2ln 2 6 3  4 3  1  sin x 4 2 2 1 
Câu 5: Tính tích phân dx  C. D. ln 2 2 3 6  sin x 6
(Trích đề thi thử THPT Nguyễn Đình Chiểu) Ngọc Huyền LB | 12
Nguyên hàm – Tích phân và ứng dụng The best or nothing
Câu 10: Giá trị dương a sao cho:
(Trích đề thi thử THPT Bảo Lâm) a 2 2 a x  2x  2 a x dx   a  ln3  là:
Câu 19. Nếu xe dx  1 
thì giá trị của a bằng: x  1 2 0 0 A. 5 B. 4 C. 3 D. 2 A. 0 B. 1 C. 2 D. e
(Trích đề thi thử THPT Nguyễn Đình Chiểu)
(Trích đề thi thử THPT chuyên KHTN)  5 dx 6 Câu 11: Giả sử  ln . c 
Giá trị của c là: n 1  2x  1
Câu 20. Nếu sin x cos xdx  thì n bằng: 1 64 0 A. 9 B. 3 C. 81 D. 8 A. 3 B. 4 C. 5 D. 6
(Trích đề thi thử THPT Nguyễn Đình Chiểu)
(Trích đề thi thử THPT chuyên KHTN)  1 n 1 x 1
Câu 12: Tích phân I  
Câu 21. Giá trị của lim dx  bằng:  có giá trị là: x  x   dx 3 n 1  e 0 1 n A. 1  B. 1 C. e D. 0 1 1 1 1 A. B. C.  D.
(Trích đề thi thử THPT chuyên KHTN) 2 8 8 4 2
(Trích đề thi thử THPT Diệu Hiền) Câu 22. Tích phân 2 4  x xdx  có giá trị bằng 1 3 0 Câu 13. Giả sử f
 tdt  5 và f
 rdr  6. Tính 2 5 8 10 A. B. C. D. 1  1  3 3 3 3 3
(Trích đề thi thử THPT Phạm Văn Đồng) I  f  udu .  1 4 A. I  4 B. I  3 C. I  2 D. I  1
Câu 23. Tích phân cot . x dx  có giá trị bằng 
(Trích đề thi thử Sở GD – ĐT Phú Thọ) 6 
A. ln 2 B. ln2 C. ln4 D. ln 2
Câu 14. Tính tích phân I  cos xdx  .
(Trích đề thi thử THPT Phạm Văn Đồng) 0 1 A. I  0 B. I  1 C. I  2 D. I  3 2 Câu 24. Tích phân x e xdx  có giá trị bằng:
(Trích đề thi thử Sở GD – ĐT Phú Thọ) 0   f x e  1 2e 1 e  1 e 1 A. B. C.  D. Câu 15. Cho biết 2
t dt  xcos( x  ).  Tính f (4) . 2 2e 2 2e 0
(Trích đề thi thử THPT Phạm Văn Đồng)
A. f (4)  2 3 B. f (4)  1  e
Câu 25. Tích phân I  2x
 1lnxdx bằng: 1 C. f (4)  D. 3 f (4)  12 1 2 2 e  1 2 e 2 e  3 2 e  3
(Trích đề thi thử Sở GD – ĐT Phú Thọ) A. B. C. D. 2 2 4 2 a
Câu 16. Đẳng thức cos   2
x  a dx  sina xảy ra nếu:
(Trích đề thi thử THPT Quảng Xương I) 0
Câu 26: Hàm số nào sau đây không là nguyên hàm A. a   B. a   ( x x  2)
của hàm số f (x)  ? 2  C. a  3
D. a  2 (x 1)
(Trích đề thi thử Sở GD – ĐT Phú Thọ) 2 x  x  1 2 x  x  1 A. B.  x  1 x  1 2 2 2
Câu 17: Tính tích phân I  . x sin xd . x  x  x  1 x C. D. 0 x  1 x  1
A. I  3
B. I  2
C. I  1
D. I  1
(Trích đề thi thử THPT Quảng Xương I)
(Trích đề thi thử THPT Bảo Lâm) d d 
Câu 27: Nếu f (x)dx  5; f (x)  2  
với a  d  b thì 4 3 1  sin x a a
Câu 18. Tính tích phân dx  2 b  sin x 6 f (x)dx  bằng: a 3  2 3  2  2 A. ; B. A. 2  B. 7 C. 0 D. 3 2 2 3  2 3  2 2  2
(Trích đề thi thử THPT Quảng Xương I) C. . D. 2 2
The best or nothing | 11 Quà tặng Valentine Ngọc Huyền LB
3. Ứng dụng của tích phân trong hình học.
Câu 1: Tính diện tích hình phẳng giới hạn bởi đồ thị 3 a 3 a 3 A. V  B. V  hàm số 2
y  x  2 và y  3x : 12 4 3 3 1 1 1 a 2 a 2 A. 1 B. C. D. C. V  D. V  4 6 2 12 6
(Trích đề thi thử THPT Nguyễn Đình Chiểu)
(Trích đề thi thử sở GD&ĐT Phú Thọ)
Câu 2: Thể tích khối tròn xoay tạo thành khi quay
Câu 8: Công thức tính diện tích S của hình thang
quanh trục Ox hình phẳng được giới hạn bởi đồ thị
cong giới hạn bởi hai đồ thị x
y  f x,y  gx,x  a,x  b , a  b
hàm số y    x 2 2
e và hai trục tọa độ là: b
A. S    f x  gxdx A. 2 2e  10 B. 2 2e  10 a b C.  2 2e  10 D.  2 2e  10 B. S  f
 xgxdx a
(Trích đề thi thử THPT Nguyễn Đình Chiểu) b
C. S    f x  gx2dx
Câu 3: Tính diện tích hình phẳng giới hạn bởi đồ thị a b x  1
D. S    2 f x 2
 g xdx hàm số y  a
x  và các trục tọa độ. Chọn kết quả 2
(Trích đề thi thử THPT Bảo Lâm) đúng nhất?
Câu 9: Diện tích hình phẳng giới hạn bởi đồ thị (C) 3 A. 3ln6 B. 3ln của hàm số 3 2 y  2
 x  x  x  5 và đồ thị (C’) của 2 3 3 hàm số 2
y  x  x  5 bằng: C. 3ln  2 D. 3ln  1 2 2 A. 0 B. 1 C. 2 D. 3
(Trích đề thi thử THPT Quảng Xương I)
(Trích đề thi thử THPT Bảo Lâm) Câu 4. Cho hàm số 3 2 f ( )
x  x  3x  2x . Tính diện tích
Câu 10: Tìm diện tích hình phẳng giới hạn bởi các
S của hình phẳng giới hạn bởi đồ thị hàm số y  f ( ) x
đường y  x   x 2
1 e ,y  x  1.
trục tung, trục hoành và đường thẳng x  3 8 2
A. S  e 
B. S  e  10 12 3 3 A. S  B. S  4 4 2 8
C. S  e 
D. S  e  11 9 3 3 C. S  D. S  4 4
(Trích đề thi thử THPT chuyên KHTN – HN)
(Trích đề thi thử sở GD&ĐT Phú Thọ)
Câu 11: Tính diện tích hình phẳng giới hạn bởi đồ thị
Câu 5. Tính thể tích của vật thể giới hạn bởi hai mặt hàm số     2 1 x y x
e , trục hoành và các đường thẳng
phẳng x  0 và x  3 , biết rằng thiết diện của vật thể
x  0,x  2.
bị cắt bởi mặt phẳng vuông góc với trục 0x tại điểm 4 2 e e 3 4 2 e e 3
có hoành độ x 0  x  3 là một hình chữ nhật có hai A.   B.   4 2 4 4 2 4
kích thước là x và 2 2 9  x . 4 2 e e 3 4 2 e e 3 C.   D.   A. 18 B. 19 C. 20 D. 21 4 2 4 4 2 4
(Trích đề thi thử sở GD&ĐT Phú Thọ)
(Trích đề thi thử THPT chuyên KHTN – HN)
Câu 6. Tính diện tích hình phẳng S giới hạn bởi đồ thị
Câu 12: Tính thể tích khối tròn xoay khi cho hình các hàm số 2x y 
và y  3  x , trục hoành và trục tung.
phẳng giới hạn bởi đồ thị các hàm số 2
y  x  2x và 1 2
y  x quay quanh trục . Ox A. S  2  B. S  2 ln 2 4 4  1 1 A. B. C. D. C. S  2  D. S  4 3 3 3 3 ln 2
(Trích đề thi thử THPT chuyên KHTN – HN)
(Trích đề thi thử sở GD&ĐT Phú Thọ)
Câu 7. Tính thể tích của tứ diện đều có cạnh bằng a.
Lư u ý: Lời giải chi tiết sẽ được gửi vào 23h ngày 25/02/2017.
Đề nghị các bạn đăng ký tại http://ngochuyenlb.gr8.com/ để
được gửi vào đúng thời gian trên. Ngọc Huyền LB | 12
Nguyên hàm – Tích phân và ứng dụng The best or nothing
Bổ sung một số dạng về nguyên hàm – tích phân Đọc thêm
1. Tích phân và nguyên hàm một số hàm lượng giác
a. Dạng sinm .cosn x xdx 
trong đó m, n là các số tự nhiên.
Trường hợp 1: Trong hai số m, n có ít nhất một số lẻ.
Lũy thừa của cos x là số lẻ, n  2k  1 thì đổi biến
Lũy thừa của sin x là số lẻ, m  2k  1 thì u  sin x
đổi biến u  cos x k x xdx  x    k m n m 2 sin .cos sin
cos x cosxdx m n n x xdx  x    2 sin .cos cos
sin x sinxdx k  k n   x   2 cos
. 1  cos x cos x x  k m 2 sin
1  sin x .sin x' dx m  u   2 1  u  du 'dx    k 2 1    . n u u du Ví dụ 1: Tìm 5 2 sin . x cos xdx  . Lời giải
Vì lũy thừa của sin x là số lẻ nên ta đổi biến u  cos x . x xdx      x2 5 2 2 2 sin .cos 1 cos .cos .
x cos x' dx 5 3 7    2u u u u 2 2 2 u du   4 2 6 1 .
2u  u  u du     C 5 3 7 5 3 7 2 cos x cos x cos x     C . 5 3 7
Trường hợp 2: Cả hai số m, n đều là số chẵn: Ta sử dụng công thức hạ bậc để
giảm một nửa số mũ của sin ;
x cos x , để làm bài toán trở nên đơn giản hơn.
b. Dạng sin m . x cos nxdx  , sin m . x sin nxdx  , cos m . x cos nxdx  .
Ta sử dụng công thức biến đổi tích thành tổng trong lượng giác. tanm x c. Dạng dx 
trong đó m, n là các số nguyên. cosn x
Lũy thừa của cos x là số nguyên dương chẵn,
Lũy thừa của tan x là số nguyên dương lẻ,
n  2k thì ta đổi biến u  tan x 1
m  2k  1 thì ta đổi biến u  cos x tanm x tanm x 1 sin x dx  . dx   Khi đó u'  , do đó n 2k2 2 cos x cos cos x 2 cos x tanm x m 2k  tan x tan tan x .  dx  . dx    tan x  dx k n n1 cos x cos cos x cos x ' 1 2 k    1 m   x    xk 1 2 tan . 1 tan .d tan x  1 2  cos x  sin x  . dx   n1 2 m  cos cos x u
   u k 1 2 . 1 du k   2 u    n1 1 u .du
The best or nothing | 13 Quà tặng Valentine Ngọc Huyền LB
Ví dụ 2: Tìm nguyên hàm 6 tan x 5 tan x a. dx  b. dx  . 4 cos x 7 cos x Lời giải
a.Do lũy thừa của cos x là số nguyên dương chẵn nên đặt u  tan x . Từ công
thức tổng quát đã chứng minh ở trên ta có 6 tan x 9 7 9 7 u u tan tan dx  u .   1 u 1 6 2 du    C    C . 4 cos x 9 7 9 7 1
b. Do lũy thừa của tan x là một số lẻ nên ta đặt u  , do vậy, từ công thức cos x
tổng quát chứng minh ở trên ta có 5 tan x      11 9 7 2 2 6 u 2u u dx u 1 .u du     C 7 cos x 11 9 7 1 2 1     C . 11 9 7 11cos x 9 cos x cos x
2. Đổi biến lượng giác
Khi nguyên hàm, tích phân của các hàm số mà biểu thức của nó có chứa các dạng 2 2 2 2 2 2
x  a , x  a , a  x , thì ta có cách biến đổi lượng giác như sau:
Biểu thức có chứa Đổi biến 2 2 x  a    
x  a tan t , t    ;   2 2 
Hoặc x  a cos t,t 0;  2 2 x  a a    x  , t   ; \     0 sin t  2 2  a  Hoặc x  ,t  0;  \     cos t 2  2 2 a  x   
x  a sin t , t   ;    2 2 
Hoặc x  a cos t,t  0;     a  x a  x
x a cos 2t  a  x a  x
x  ab  x  
x  a  b  a 2 sin t,t  0;    2 
3. Nguyên hàm và tích phân của hàm phân thức hữu tỉ P x
Cho hàm số y  f x có dạng f x   
trong đó P và Q là các đa thức, và P STUDY TIP: Kí hiệu Q x
deg P x là bậc của
không chia hết cho Q.
đa thức P x.
Hàm f được gọi là hàm phân thức hữu tỉ thực sự nếu deg P  deg Q . Ngọc Huyền LB | 14
Nguyên hàm – Tích phân và ứng dụng The best or nothing
Trong các bài toán tìm nguyên hàm và tích phân của hàm phân thức hữu tỉ, nếu
f x chưa phải là hàm phân thức hữu tỉ thực sự thì ta thực hiện chia đa thức
tử số cho đa thức mẫu số để được:   Px R x f x      ,
Q x Sx  
Q x Sx h x
Khi đó, h x sẽ là hàm phân thức hữu tỉ thực sự.
Định lý: Một phân thức thực sự luôn phân tích được thành tổng các phân thức đơn giản hơn. 1 1 ax  b ax  b
Đó là các biểu thức có dạng ; là các
x  a    ; ; k 2
x  px  q x a  k 2
x  px  q
hàm số có thế tìm nguyên hàm một cách dễ dàng.Để tách được phân thức ta
dùng phương pháp hệ số bất định.
a. Trường hợp phương trình Q x  0 không có nghiệm phức và các nghiệm
đều là nghiệm đơn.
Qx  a x  b
a x  b ... a x  b 1 1   2 2   k k k 
(Số nhân tử chính bằng bậc của đa thức Q x ).
Trong trường hợp này, g có thể biểu diễn dưới dạng
g x Rx A A A 1 2      Q x ... k a x  b a x  b a x  b 1 1 2 2 k k
Sau khi biểu diễn được gx về dạng này, bài toán trở thành bài toán cơ bản. 4x  3
Ví dụ 3: Họ nguyên hàm của hàm số f x  là 2 x  3x  2 x 
A. F x 1  4ln x  2  ln  C x  2 x 
B. F x 1  4ln x  2  ln  C x  2 x 
C. F x 2  4  ln x  2  ln  C x  1 x 
D. F x 2  4ln x  2  ln  C x  1 Phân tích Đáp án B. 4x  3 4x  3 A B
Ax  2A  Bx  B Ta có     . 2 x  3x  2
x  2x  1 x 1 x  2
x  1x  2
Khi đó  A  B x  2A  B  4x  3 , đồng nhất hệ số thì ta được A  B  4 A  1     2A  B  3 B    5 Lời giải
The best or nothing | 15 Quà tặng Valentine Ngọc Huyền LB 4x  3  1  5  Ta có dx  
dx   ln x  1  5.ln x  2 
Kiểm tra khả năng vận    C 2 x  3x  2
 x  1 x  2 
dụng từ ví dụ 3: x  2  Tìm  x 1 4.ln x  2  ln
 C  4.ln x  2  ln  C . 2   x  1 x  2 x 2x 1 dx  3 2 2x  3x  2x
Đáp số bài tập kiểm tra khả năng vận dụng: 2 x  2x  1 1 1 1 dx  . ln x  . ln 2x  1  . ln x  2  D  3 2 2x  3x  2x 2 10 10 5 3  2 Ví dụ 4: Biết 
 aln 2  bln 3  c ln 5  dln 6  e ln7  x I dx . Khi đó 4 2
x  5x  4 4
6a  3b  6c  3d  2e có giá trị là 19 19 A. 16  B.  C. 16 D. 6 6 Phân tích Đáp án A. 3 3 x  2 x  2 A B C D Ta có      4 2 x  5x  4
x  1x  1x  2x  2 x 1 x  2 x 1 x  2 3 STUDY TIP: đây là
 x  2  A 2
x  4x   1  B  2 x   1 x  2 dạng toán tích phân chống casio đã gặp C   2
x  4x   1  D  2 x  
1 x  2 , x   * trong đề minh họa lần 1 2.
Thay x  1 vào * ta có A   . 2 5
Thay x  2 vào * ta có B  6 1 Thay x  1
 vào * ta có C  6 1 Thay x  2
 vào * ta có D  2 Lời giải 5 3 x  2  I  dx  16 4 2 x  5x  4 4 5 5 5 5 1 dx 5 dx 1 dx 1 dx          2 x  1 6 x  2 6 x  1 2 x  2 4   4 4 4  1 5 1 1  5
  ln x  1  ln x  2  ln x  1  ln x   2   2 6 6 2  4 5 1 1  1 5 1 1   l  2 n  l 3 n  l 6 n  l 7 n   l 3 n  l 2 n  l 5 n   l 6 n  6 6 2  2 6 6 2  11 4 1 1 1   l 2 n  l 3 n  l 5 n  l 6 n  l 7 n 6 3 6 3 2
Khi đó 6a  3b  6c  3d  2e  1
 1  4  1  1  1  1  6 .
b. Trường hợp Q x  0 không có nghiệm phức, nhưng có nghiệm thực là nghiệm bội.
Nếu phương trình Q x  0 có các nghiệm thực a ; a ;...; a trong đó a là 1 2 n 1 R x
nghiệm bội k thì ta phân tích g x    về dạng Q x Ngọc Huyền LB | 16
Nguyên hàm – Tích phân và ứng dụng The best or nothing g x A A A B B B 1 2 k 1 2 n1     ...     ...  k x  a   x  a x  a x  a 1  x a x a n 1 2  1  2 3
Trên đây là phần lý thuyết khá phức tạp, ta đến với bài tập ví dụ đơn giản sau: 2x
Ví dụ 5: Họ nguyên hàm của hàm số f x   là 1  x3 2 1 2 1
A. F x    C
B. F x    C
x  1 x  2 1
x  1 x  2 1 1 1 1 1
C. F x    C
D. F x    C 1  x 41 x4 1  x 41 x4 Phân tích
Nhận thấy x  1 là nghiệm bội ba của phương trình x  3 1  0 , do đó ta biến đổi A 2 x  2x   1  B1 2  x  C x A B C       3 1 1   x x
1 x2 1 x3 1 x3 2 Ax   2
 A  Bx  A  B  C   1  x3 A  0 A  0   Từ đây ta có  2
 A  B  2  B  2   
A  B  C  0 C  2   Lời giải   2x 2  2 2 1
Kiểm tra khả năng vận Ta có        
dụng từ ví dụ 4:  dx dx   C 1  x3 x  2 1 x    3 1  x 1 x  2 1 Tìm
Đáp số bài tập kiểm tra khả năng vận dụng ví dụ 4: 4 2 x  2x  4x  1 dx 4 2 2  3 2 x  2x  4x  1 x 2 x  x  x  1 dx 
 x  ln x  1  ln x  1   C  . 3 2 x  x  x  1 2 x  1
TỔNG QUÁT: Việc tính nguyên hàm của hàm phân thức hữu tỉ thực sự được
đưa về các dạng nguyên hàm sau: A 1. dx  .
A ln x  a  C  x  a A A 1 2.      .  x a dx . C k k  
1 x  ak 1
The best or nothing | 17 Quà tặng Valentine Ngọc Huyền LB
5. Bảng một số nguyên hàm thường gặp n1 1) . k dx  . k x  C  2) n x x dx   C  n  1 1 1 1 3) dx    C  4)
dx  ln x  C  2 x x x 1 1 1 1 5) dx    C  6)
dx  .ln ax  b  C  n n 1 (ax  ) b (
a n  1)(ax  ) b  ax  b a
7) sin xdx  cos x  C 
8) cosxdx  sin x  C 1 1 9) sin
 ax  bdx   cosax  b C 10) cos
 ax  bdx  sinax  b C a a 1 1 11) 2 dx  (1 tan )
x dx  tan x  C   12) 2
dx  (1 cot x)dx  cot x  C   2 cos x 2 sin x 1 1 1 1 13)
dx  tan(ax  ) b  C  14)
dx   cot(ax  ) b  C  2 cos (ax  ) b a 2 sin (ax  ) b a 15) x x
e dx  e  C  16) x x e dx  e  C  n1 ax  b axb 1 n 1 17) axb e dx  e  C 
18) ax  b   dx  .
 C n   1 a a n  1 x 1 19) x a a dx   C  20)
dx  arctan x  C  ln a 2 x  1 1 1 x  1 1 x 21) dx  ln  C  22)
dx  arctan  C  2 x  1 2 x  1 2 2 x  a a 1 1 x  a 1 23) dx  ln  C  24)
dx  arcsin x  C  2 2 x  a 2 x  a 2 1  x 1 x 1 25) dx  arcsin  C  26) 2
dx  ln x  x  1  C  2 2  a a x 2 x  1 1 2 x a x 27) 2 2
dx  ln x  x  a  C  28) 2 2 2 2 a  x dx  a  x  arcsin  C  2 2 x  a 2 2 a 2 x a 29) 2 2 2 2 2 2 x  a dx  x  a 
.ln x  x  a  C  2 2 Ngọc Huyền LB | 18
Nguyên hàm – Tích phân và ứng dụng The best or nothing
III. Ứng dụng của nguyên hàm, tích phân trong thực tế.
1. Dạng bài toán về chuyển động.
Ví dụ 1: Một ô tô đang chạy với vận tốc 10 m/s thì tài xế đạp phanh; từ thời
điểm đó, ô tô chuyển động chậm dần đều với vận tốc v t  5
 t  10m / s ,
trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi
từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 0,2 m B. 2 m C. 10 m D. 20 m
(Trích đề minh họa lần I- BGD&ĐT) Lời giải Đáp án C.
Nguyên hàm của hàm vận tốc chính là quãng đường s t mà ô tô đi được sau
quãng đường t giây kể từ lúc tài xế đạp phanh xe.
Vào thời điểm người lái xe bắt đầu đạp phanh ứng với t  0 .
Thời điểm ô tô dừng lại ứng với t , khi đó vt  0  t  2 . 1  1 1
Vậy từ lúc đạp phanh đến khi dừng lại quãng đường ô tô đi được là 2    s   5  t  10 5 2 2 dt  t  10t    10 m .  2  0 0
Ví dụ 2: Một chiếc ô tô đang đi trên đường với vận tốc vt  2 t 0  t  30 STUDY TIP:
(m/s). Giả sử tại thời điểm t  0 thì s  0 . Phương trình thể hiện quãng đường Hàm số thể hiện quãng
theo thời gian ô tô đi được là
đường vật đi được tính theo thời gian là biểu 4 4 A. 3 s 
t m
B. s  2 t m C. 3 s 
t m
D. s  2t m thức nguyên hàm của 3 3 hàm số vận tốc. Lời giải Đáp án A 1 4
Tương tự như ở ví dụ 1 thì ta có st 1 3 3 2 2
 2 tdt  2 t dt  2. .t  . t   (m) 1 3  1 2
Ví dụ 3: Một vật chuyển động với vận tốc đầu bằng 0, vận tốc biến đổi theo quy luật, và có gia tốc 2
a  0,3(m / s ) .Xác định quãng đường vật đó đi được trong 40 phút đầu tiên. A. 12000m B. 240m C. 864000m D. 3200m
(Trích đề thi thử THPT Hoàng Diệu)
Phân tích: Nhận thấy bài toán này khác với hai ví dụ trên ở chỗ bài toán cho STUDY TIP:
biểu thức gia tốc mà không cho biểu thức vận tốc, ở đây ta có thêm một kiến
Biểu thức gia tốc là đạo thức như sau: hàm cấp một của biểu
Biểu thức gia tốc là đạo hàm của biểu thức vận tốc, đến đây, kết hợp với 2 ví dụ
thức vận tốc, và là đạo hàm cấp hai của biểu
đầu ta kết luận: “Biểu thức gia tốc là đạo hàm cấp một của biểu thức vận tốc, và thức quãng đường
là đạo hàm cấp hai của biểu thức quãng đường”. Từ đây ta có lời giải như sau: Lời giải
Ta có vt  0,3dt  0,3t 
(do ban đầu vận tốc của vật bằng 0).
Vậy quãng đường vật đi được trong 40 phút đầu tiên là 40.60 0, 3 2400 2 0, 3tdt  .t   864000m 2 0 0
The best or nothing | 19 Quà tặng Valentine Ngọc Huyền LB
Bài tập rèn luyện kỹ năng
Câu 1: Một vật chuyển động với vận tốc thay đổi theo
Câu 5: Một ôtô đang chạy với vận tốc 10 m/s thì người
thời gian được tính bởi công thức vt  3t  2, thời gian
lái đạp phanh; từ thời điểm đó, ôtô chuyển động chậm
dần đều với vận tốc v  5  t  15
tính theo đơn vị giây, quãng đường vật đi được tính
(m/s), trong đó t là khoảng thời gian tính bằng giây, kể theo đơn vị .
m Biết tại thời điểm t  2s thì vật đi được quãng đường là
từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến 10 .
m Hỏi tại thời điểm t  30s thì vật
khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét?
đi được quãng đường là bao nhiêu? A. 20m B. 10 m
C. 22,5 m D. 5 m
A. 1410m B. 1140m
C. 300m D. 240m
(Trích đề thi thử THPT chuyên Hạ Long)
Câu 6: Cho chuyển động thẳng xác định bởi phương
Câu 2: Một tàu lửa đang chạy với vận tốc 200 m/s thì trình 3
S  2t  t  1 , trong đó t được tính bằng giây và S
người lái tàu đạp phanh; từ thời điểm đó, tàu chuyển
được tính bằng mét. Gia tốc của chuyển động khi t = 2s
động chậm dần đều với vận tốc vt  200  20t (m/s). là: A. 63m/s2
B. 64m/s2 C. 23m/s2 D. 24m/s2
Trong đó t là khoảng thời gian tính bằng giây, kể từ
(Trích đề thi thử THPT Ngọc Tộ)
lúc bắt đầu đạp phanh. Hỏi thời gian khi tàu đi được
quãng đường 750 m (kể từ lúc bắt đầu đạp phanh) ít
Câu 7: Cho một vật chuyển động có phương trình là:
hơn bao nhiêu giây so với lúc tàu dừng hẳn? 3 2
s  2t   3 (t được tính bằng giây, S tính bằng mét). A. 5 s B. 8 s C. 15 s D. 10 s t 
(Trích đề thi thử THPT Hoàng Văn Thụ)
Vận tốc của chuyển động thẳng t 2s là: 49 47
Câu 3. Giả sử một vật từ trạng thái nghỉ khi t  0s A. 3 B. C. 12 D. 2 2
chuyển động thẳng với vận tốc vt  t5  tm / s.
(Trích đề thi thử THPT Ngọc Tộ)
Tìm quãng đường vật đi được cho đến khi nó dừng lại.
Câu 8. Cho chuyển động thẳng xác định bởi phương 125 125 125 125 A. m B. m C. m D. m trình 4
S  2t  t  1 , trong đó t được tính bằng giây và S 12 9 3 6
được tính bằng mét. Vận tốc của chuyển động khi t = 1s
(Trích đề thi thử THPT Lương Thế Vinh lần 2) là:
Câu 4: Một người đi xe đạp dự định trong buổi sáng đi A. 24m/s
B. 23m/s C. 7m/s D. 8m/s
hết quãng đường 60km. Khi đi được 12 quãng đường,
(Trích đề thi thử THPT Ngọc Tộ)
anh ta thấy vận tốc của mình chỉ bằng 23 vận tốc dự
Câu 9: Một chiếc xe ô tô sẽ chạy trên đường với vận
định, anh ta bèn đạp nhanh hơn vận tốc dự định
tốc tăng dần đều với vận tốc v = 10t (m/s) t là khoảng
3km/h, đến nơi anh ta vẫn chậm mất 45 phút. Hỏi vận
thời gian tính bằng giây, kể từ lúc bắt đầu chạy. Hỏi
tốc dự định của người đi xe đạp là bao nhiêu?
quảng đường xe phải đi là bao nhiêu từ lúc xe bắt đầu
A. 5km / h B. 12km / h C. 7km / h D. 18km / h
chạy đến khi đạt vận tốc 20 (m/s)?
(Trích đề thi thử THPT TVB) A. 10m B. 20m C. 30m D. 40m
(Trích đề thi thử THPT Hoàng Diệu)
Lưu ý: Lời giải chi tiết sẽ được gửi vào 23h ngày 25/02/2017. Đề nghị các bạn đăng ký
tại http://ngochuyenlb.gr8.com/ để được gửi vào đúng thời gian trên. Ngọc Huyền LB | 20

Một số vấn đề chọn lọc nguyên hàm, tích phân và ứng dụng – Vũ Ngọc Huyền Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề nguyên hàm – tích phân Toán 12

Gắn hệ tọa độ Oxyz để giải các bài toán hình học không gian – Phương Nguyễn Toán 12

20 kĩ thuật chinh phục vận dụng cao số phức – Hoàng Xuân Nhàn Toán 12

Phân dạng bài tập và lời giải chi tiết chuyên đề Tích phân – Lưu Huy Thưởng Toán 12

Phương pháp giải các bài toán Tích phân – Trung tâm LTĐH Vĩnh Viễn Toán 12