Thông tin
Quiz

Ngân hàng câu hỏi ứng dụng tích phân để tính diện tích hình phẳng Toán 12

Tài liệu gồm 48 trang, được biên soạn bởi thầy giáo Lê Bá Bảo (Giáo viên Toán trường THPT Đặng Huy Trứ & Admin CLB Giáo Viên Trẻ TP Huế), tuyển chọn 50 bài toán trắc nghiệm liên quan đến ứng dụng tích phân để tính diện tích hình phẳng, có đáp án và lời giải chi tiết, giúp học sinh lớp 12 tham khảo khi học chương trình Giải tích 12 chương 3 và luyện thi THPT Quốc gia môn Toán.

Chủ đề:

Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn:

Toán 12 3.8 K tài liệu

Thông tin:

105 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Ngân hàng câu hỏi ứng dụng tích phân để tính diện tích hình phẳng Toán 12

107 54 lượt tải Tải xuống

TÍCH PHÂN

LÊ BÁ BẢO

TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ

ỨNG DỤNG TÍNH

DIỆN TÍCH HÌNH PHẲNG

 LUYỆN THI THPT QUỐC GIA

 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Ngân hàng câu hỏi:

ỨNG DỤNG TÍCH PHÂN TRONG HÌNH HỌC (1)

NỘI DUNG ĐỀ BÀI

Câu 1: Cho hàm số

 

có đồ thị trên đoạn

 

1;4

như hình vẽ dưới:

Tính tích phân

( )dI f x x







5I 

. B.

I 

. C.

I 

. D.

3I 

Câu 2: Hình phẳng giới hạn bởi đồ thị hàm số

 

y f x

và trục hoành gồm hai phần, phần nằm phía

trên trục hoành có diện tích

S 

và phần nằm phía dưới trục hoành có diện tích

S 

(tham khảo hình vẽ bên).

Tính

 

31I f x x







I 

. B.

I 

. C.

I 

. D.

I 

Câu 3: Cho hàm số

 

liên tục trên . Biết diện tích

2S 

11S 

3S 

4S 

12S 

(tham

khỏa hình vẽ)

Tích phân

 

1 1 df x x x





  





bằng

. B.

. C.

. D.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 4: Cho hàm số

 

y f x

liên tục trên có đồ thị như hình vẽ bên dưới:

Giả sử diện tích phần kẻ dọc trên hình vẽ có diện tích bằng

. Tính theo

giá trị của

   

2 1 d .









I x f x x

50 2Ia

. B.

50Ia

. C.

30 2Ia  

. D.

30 2Ia  

Câu 5: Cho hàm số

 

y f x

liên tục và nhận giá trị không âm trên

1;2





và thỏa mãn

   

1 , 1;2 .f x f x x



    



Đặt

 

S xf x x







là diện tích hình phẳng được giới hạn bởi đồ

thị hàm số

 

y f x

, trục Ox và hai đường thẳng

1, 2xx  

. Khẳng định nào dưới đây đúng?

2SS

. B.

3SS

. C.

2SS

. D.

3SS

Câu 6: Diện tích hình phẳng giới hạn bởi đồ thị hàm số

34y x x  

, trục hoành, các đường thẳng

 

1, 0x x k k   

bằng

. Mệnh đề nào sau đây đúng?

 

1;4k 

. B.

 

3;6k 

. C.

 

0;2k 

. D.









Vậy

 

1;4k 

Câu 7: Cho parabol

 

: 2 1P y x x  

và đường thẳng

:2y x m  

. Để diện tích hình phẳng giới

hạn bởi

 

và



bằng

thì giá trị của tham số

nằm trong khoảng nào dưới đây?

 

5; 3

. B.

 

3;0

. C.

 

0;2

. D.

 

2;3

Câu 8: Cho hình thang cong

 

giới hạn bởi các đường

y 

0y 

0x 

4x 

. Đường thẳng

xa

 

04a

chia hình

 

thành hai phần có diện tích

và

như hình vẽ bên dưới:

Tìm

để

4SS

3a 

. B.

log 13a 

. C.

2a 

. D.

log

a 

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 9: Gọi

 

là phần hình phẳng gạch chéo trong hình vẽ dưới đây được giới hạn bởi đồ thị của

các hàm số

3yx

4yx

và trục hoành (tham khảo hình vẽ)

Diện tích của

 

là bằng

. B.

. C.

. D.

Câu 10: Diện tích hình phẳng giới hạn bởi đồ thị

 

của hàm số

 

y x x  

và hai tiếp tuyến

của

 

xuất phát từ

 

3; 2M 

là

Câu 11: Cho parabol

 

:2P y x

và hai tiếp tuyến của

 

tại các điểm

 

1;3M 

và

 

2;6N

. Diện

tích hình phẳng giới hạn bởi

 

và hai tiếp tuyến đó bằng

. B.

. C.

. D.

Câu 12: Cho hàm số

 

y f x

là một hàm số bậc ba. Gọi

là diện tích giới hạn bởi các đường

 

, 0, 1y f x y x   

và

4x 

(tham khảohình vẽ).

Khi đó diện tích

có giá trị bằng

253

. B.

253

. C.

235

. D.

235

Câu 13: Cho đồ thị hàm số

 

y f x

và

 

y g x

như hình vẽ bên dưới:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Biết đồ thị của hàm số

 

y f x

là một Parabol đỉnh

có tung độ bằng



và

 

y g x

là

một hàm số bậc ba. Hoành độ giao điểm của hai đồ thị là

1 2 3

,,x x x

thỏa mãn

1 2 3

. . 6x x x 

Diện tích hình phẳng giới hạn bởi 2 đồ thị hàm số

 

y f x

và

 

y g x

gần nhất với giá trị

nào dưới đây?

. B.

. C.

. D.

Câu 14: Cho hai hàm số

 

4f x ax bx cx   

và

   

2, , , , ,g x dx ex a b c d e   

. Biết rằng đồ

thị hàm số

 

y f x

và

 

y g x

cắt nhau tại

điểm có hoành độ lần lượt là

3; 1; 2

. Hình

phẳng giới hạn bởi đồ thị hai hàm số đã cho có diện tích bằng

316

. B.

191

. C.

253

. D.

Câu 15: Cho

   

,f x g x

lần lượt là các hàm đa thức bậc ba và bậc nhất có đồ thị như hình vẽ bên

dưới:

Biết diện tích hình

(được tô đậm) bằng

250

. Tính

 



f x x

. B.

. C.

. D.

Câu 16: Cho hàm số

   

36 0;a, ,f x ax bx x c a b c     

có hai điểm cực trị là

6

và

. Gọi

 

y g x

là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

 

y f x

. Diện tích hình

phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

bằng

160

128.

64

672

Câu 17: Cho hai hàm số

 

4 3 2

3f x ax bx cx x   

và

 

g x mx nx x  

; với

, , , ,a b c m n

. Biết

hàm số

   

y f x g x

có ba điểm cực trị là

1

;

và

. Diện tích hình phẳng giới hạn bởi

hai đồ thị hàm số

 



và

 

y g x





bằng

. B.

. C.

125

. D.

131

Câu 18: Cho hàm số

 

y f x

là hàm đa thức bậc bốn và có đồ thị như hình vẽ bên. Hình phẳng giới

hạn bởi đồ thị hai hàm số

 

y f x

 

y f x





có diện tích bằng

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

127

. B.

107

. C.

. D.

127

Câu 19: Cho hàm số

( ) 2 2f x ax x x   

và hàm số

( ) 2g x bx cx  

, có đồ thị như hình vẽ bên

dưới:

Gọi

;SS

là diện tích các hình phẳng gạch chéo trong hình vẽ, biết

221

640

S 

. Khi đó

bằng

1361

640

. B.

271

320

. C.

571

640

. D.

791

640

Câu 20: Tính diện tích

của miền hình phẳng giới hạn bởi đồ thị của hàm số

 

f x ax bx c  

, các

đường thẳng

1x 

2x 

và trục hoành (miền gạch chéo) cho trong hình dưới đây:

S 

. B.

S 

. C.

S 

. D.

S 

Câu 21: Cho đường thẳng

yx

và parabol

y x a

, (

là tham số thực dương). Gọi

,SS

lần

lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên dưới:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Khi

SS

thì

thuộc khoảng nào sau đây?







. B.

;

16 32







. C.

;

4 32







. D.

;

32 4







Câu 22: Cho hai hàm đa thức

 

f x ax bx cx d   

và

 

g x mx nx p  

. Biết rằng đồ thị hai

hàm số

 

y f x

và

 

y g x

cắt nhau tại ba điểm có hoành độ lần lượt là

1;2;4

đồng thời

cắt trục tung lần lượt tại

,MN

sao cho

6MN 

( tham khảo hình vẽ).

Hình phẳng giới hạn bởi đồ thị hai hàm số đã cho ( phần gạch sọc) có diện tích bằng

125

. B.

253

. C.

253

. D.

253

Câu 23: Cho

   

0f x ax bx cx d a    

là hàm số nhận giá trị không âm trên đoạn

 

2;3

có đồ

thị

 



như hình vẽ bên dưới:

Biết diện tích hình phẳng giới hạn bởi các đồ thị của các hàm số

   

g x xf x

;

     

h x x f x f x





và các đường thẳng

2; 3xx

bằng

. Tính

 

12f 

. B.

 

11f 

. C.

 

11f 

. D.

 





Câu 24: Cho hàm số

 

y f x ax bx c   

có đồ thị

 

và cắt trục hoành tại điểm có hoành độ

bằng

1

. Tiếp tuyến

tại điểm có hoành độ

1x 

của

 

cắt

 

tại

điểm khác có

hoành độ lần lượt là

và

. Gọi

,SS

là diện tích các phần hình phẳng giới hạn bởi

và

 

(với

là diện tích phần hình phẳng nằm bên phải trục

). Tỷ số

bằng

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 25: Cho hàm số

lnyx

có đồ thị

 

như hình vẽ bên dưới:

(

)

Đường tròn tâm

có duy nhất một điểm chung

với

 

. Biết

 

0;1C

, diện tích của hình

thang

AB CO

gần nhất với số nào sau đây.

3,01

. B.

2,91

. C.

3,09

. D.

2,98

Câu 26: Cho hàm số

 

4 3 2

f x x bx cx dx e    

(

, , ,b c d e

) có các giá trị cực trị là

1,4

và

. Diện

tích hình phẳng giới hạn bởi đồ thị hàm số

 





và trục hoành bằng

Câu 27: Biết đồ thị

 

của hàm số

   

,f x x bx c b c   

có cực trị là

 

1;0A

. Gọi

 

là

parabol có đỉnh

 

0; 1I 

và đi qua điểm

 

2;3B

. Diện tích hình phẳng giới hạn bởi

 

và

 

thuộc khoảng nào dưới đây?

 

0;1

. B.

 

2;3

. C.

 

3;4

. D.

 

1;2

Câu 28: Đường thẳng

cắt đường cong

 

   f x a x bx cx d

tại ba điểm phân biệt có hoành độ

2x

1x

2x

như hình vẽ bên dưới:

Diện tích hình phẳng gạch sọc thuộc khoảng nào dưới đây?







. B.







. C.







. D.







Câu 29: Cho hai hàm số

 

1f x ax bx cx   

và

 

2g x dx ex  

 

, , , ,a b c d e

. Biết rằng đồ

thị của hàm số

 

y f x

và

 

y g x

cắt nhau tại ba điểm có hoành độ lần lượt là

3; 1;1

(tham khảo hình vẽ) .

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

. B.

. C.

. D.

Câu 30: Cho hai hàm số

 

2f x ax bx cx   

và

 

2g x dx ex  

 

, , , ,a b c d e

. Biết rằng đồ

thị của hàm số

 

y f x

và

 

y g x

cắt nhau tại ba điểm có hoành độ lần lượt là

2; 1;1

(tham khảo hình vẽ).

Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

. B.

145

. C.

. D.

145

Câu 31: Đường thẳng

4y kx

cắt parabol

 

2yx

tại hai điểm phân biệt và diện tích các hình

phẳng

bằng nhau như hình vẽ bên.

Khẳng định nào sau đây đúng?

 

6; 4k   

. B.



  





. C.

 

2; 1k   

. D.









Câu 32: Cho

 

là hình phẳng giới hạn bởi parabol

yx

(với

0 2 2x

), nửa đường tròn

8yx

và trục hoành, trục tung (phần tô đậm trong hình vẽ).

Diện tích của

 

bằng

3 14





. B.





. C.





. D.





Câu 33: Cho hàm số

 

( ) , , , , 0y f x ax bx cx d a b c d a      

có đồ thị là

 

. Biết rằng đồ thị

 

đi qua gốc tọa độ và đồ thị hàm số

'( )y f x

cho bởi hình vẽ bên.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Tính giá trị

(4) (2).H f f

45H 

. B.

64H 

. C.

51H 

. D.

58H 

Câu 34: Cho hàm số

4y x x m  

có đồ thị

 

. Giả sử

 

cắt trục hoành tại bốn điểm phân

biệt sao cho diện tích hình phẳng giới hạn bởi

 

với trục hoành có diện tích phần phía trên

trục hoành bằng diện tích phần phía dưới trục hoành. Khi đó

thuộc khoảng nào dưới đây?

 

1;1m

. B.

 

3;5m

. C.

 

2;3m

. D.

 

5;m  

Câu 35: Cho Parabol

 

:P y x

và đường tròn

 

có tâm

 

0;3A

bán kính bằng

như hình vẽ bên

dưới:

Diện tích phần được tô đậm giữa

 

và

 

gần nhất với số nào dưới đây?

3.44

. B.

1.51

. C.

1.77

. D.

3.54

Câu 36: Cho hàm số bậc bốn

 

y f x

có đồ thị

 

như hình vẽ bên dưới:

Đường thẳng

d y kx

có đúng ba điểm chung với

 

là

,,A B C

và

BC AB

Biết

diện tích hình phẳng

(phần gạch sọc) là

Giá trị của

 





f x x

bằng

2

. B.

321

160



. C.

161



. D.

159

160



Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 37: Cho hàm số

 

f x x bx cx d   

với

.d

Biết hàm số

       

23g x f x f x f x

 

  

có hai giá trị cực trị là

6

và

. Tính diện tích hình phẳng

giới hạn bởi các đường

     

 

f x f x f x

 







và

1.y

ln5.

ln7.

2ln6.

2ln5.

Câu 38: Cho hàm số

y x ax bx c   

có đồ thị

 

. Biết rằng tiếp tuyến

của

 

tại điểm

có

hoành độ bằng

1

cắt

 

tại điểm

có hoành độ bằng

(xem hình vẽ). Diện tích hình

phẳng giới hạn bởi

và

 

(phần gạch chéo trong hình) bằng

. B.

. C.

. D.

Câu 39: Cho hàm số

 

y f x x ax b    

 

a,b

có đồ thị (C) và

 

y g x mx nx p   

 

m,n, p

có đồ thị

 

như hình vẽ. Diện tích hình phẳng giới

hạn bởi

 

và

 

có giá trị nằm trong khoảng nào sau đây?

 

4;4,1

. B.

 

4,2;4,3

. C.

 

4,3;4,4

. D.

 

4,1;4,2

Câu 40: Người ta trồng hoa vào phần đất được tô màu được giới hạn bởi cạnh

,AB CD

, đường trung

bình

của mảnh đất hình chữ nhật

ABCD

và một đường cong hình sin. Biết

2AB





(m),

2AD 

(m). Tính diện tích phần còn lại.





. B.

 





. C.





. D.





Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 41: Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng

cm bằng

cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên dưới:

Biết

5AB 

cm,

4OH 

cm. Tính diện tích bề mặt hoa văn đó.

160

. B.

140

. C.

. D.

50 cm

Câu 42: Một hoa văn trang trí được tạo ra từ một miếng bìa hình vuông cạnh

20 cm

bằng cách khoét

đi bốn phần bằng nhau đều có hình dạng một nửa elip như hình vẽ. Biết một nửa trục lớn là

6AB 

, trục bé

8CD 

. Diện tích bề mặt của hoa văn đó bằng

 

400 48 cm





. B.

 

400 96 cm





. C.

 

400 24 cm





. D.

 

400 36 cm





Câu 43: Một viên gạch hoa hình vuông cạnh

cm được thiết kế như hình bên dưới. Diện tích mỗi

cánh hoa (phần tô đậm) bằng

y =

800

. B.

400

. C.

250

. D.

800

Câu 44: Ông An muốn làm một cánh cửa bằng sắt có hình dạng và kích thước như hình vẽ. Biết rằng

đường cong phía trên là một parabol, tứ giác

ABCD

là một hình chữ nhật.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Giá cánh cửa sau khi hoàn thành là

900000

đồng/

. Số tiền ông An phải trả để làm cánh

cửa đó bằng

A.9 600 000 đồng. B. 15 600 000 đồng. C. 8 160 000 đồng. D. 8 400 000 đồng.

Câu 45: Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là

2,25

mét,

chiều rộng tiếp giáp với mặt đất là

mét. Giá thuê mỗi mét vuông là

1500000

đồng. Vậy số

tiền bác Năm phải trả là

33750000

đồng. B.

3750000

đồng. C.

12750000

đồng. D.

6750000

đồng.

Câu 46: Một khu vườn dạng hình tròn có hai đường kính

, AB CD

vuông góc với nhau,

12AB m

Người ta làm một hồ cá có dạng elip với bốn đỉnh

, , ', 'M N M N

như hình vẽ. Biết

10 , ' ' 8 , 8MN m M N m PQ m  

. Diện tích phần trồng cỏ (phần gạch sọc) bằng:

32,03 m

. B.

20,33 m

. C.

33.02 m

. D.

23,03 m

Câu 47: Một khu vườn có dạng hợp của hai hình tròn giao nhau. Bán kính của hai đường tròn là

20m

và

15m

, khoảng cách giữa hai tâm của hai hình tròn là

30m

. Phần giao của hai hình tròn

được trồng hoa với chi phí

300000

đồng/

. Phần còn lại được trồng cỏ với chi phí

100000

đồng/

. Hỏi chi phí để trồng hoa và cỏ của khu vườn gần nhất với số tiền nào dưới

đây?

202

triệu đồng. B.

208

triệu đồng. C.

192

triệu đồng. D.

218

triệu đồng.

Câu 48: Một khuôn viên dạng nửa hình tròn, trên đó người ta thiết kế phần trồng hoa hồng có dạng

một hình Parabol có đỉnh trùng với tâm hình tròn và trục đối xứng vuông góc với đường

kính của nửa đường tròn, hai đầu mút của Parabol nằm trên đường tròn và cách nhau một

khoảng 4 mét (phần tô đậm). Phần còn lại của khuôn viên (phần không tô đậm) dùng để

trồng hoa cúc. Biết các kích thước cho như hình vẽ. Chi phí trồng hoa hồng và hoa cúc lần

lượt là

120.000

đồng

và

80.000

đồng/

. Hỏi chi phí trồng hoa khuôn viên đó gần nhất

với số nào sau đây (làm tròn đến ngàn đồng).

6.847.000

đồng. B.

6.865.000

đồng. C.

5.710.000

đồng. D.

5.701.000

đồng.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 49: Trong đợt hội trại “Khi tôi

” được tổ chức tại trường THPT X, Đoàn trường có thực hiện

một dự án ảnh trưng bày trên một pano có dạng parabol như hình vẽ. Biết rằng Đoàn trường

sẽ yêu cầu các lớp gửi hình dự thi và dán lên khu vực hình chữ nhật

ABCD

, phần còn lại sẽ

được trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là

200.000

đồng cho một

bảng.

Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng

nghìn)?

900.000

đồng. B.

1.232.000

đồng. C.

902.000

đồng. D.

1.230.000

đồng.

Câu 50: Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh

và hai đường parabol có các đỉnh lần lượt là

(phần tô đậm của hình vẽ).

Hai đường parabol có cùng trục đối xứng

, đối xứng nhau qua trục

, hai parabol cắt

elip tại các điểm

. Biết

8AB m

6CD m

33MN PQ m

2EF m

. Chi

phí để trồng hoa trên vườn là

300.000

đ/

. Hỏi số tiền trồng hoa cho cả vườn gần nhất với

số tiền nào dưới đây?

A. 4477800 đồng. B. 4477000 đồng. C. 4477815 đồng. D. 4809142 đồng.

____________________HẾT____________________

Huế, 15h15’ Ngày 19 tháng 3 năm 2023

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

LỜI GIẢI CHI TIẾT

Câu 1: Cho hàm số

 

có đồ thị trên đoạn

 

1;4

như hình vẽ dưới:

Tính tích phân

( )dI f x x







5I 

. B.

I 

. C.

I 

. D.

3I 

Lời giải:

Gọi

là diện tích của hình thang giới hạn bởi phần trên đồ thị hàm số

 

với trục hoành.

Gọi

là diện tích của hình thang giới hạn bởi phần dưới đồ thị hàm số

 

với trục hoành.

Với

 

1 3 .2

S f x dx





  



 

1 2 .1

S f x dx



   



Ta có:

4 2 4 2 4

1 1 2 1 2

( )d ( )d ( )d ( )d ( )dI f x x f x x f x x f x x f x x

  



     





    

SS



Câu 2: Hình phẳng giới hạn bởi đồ thị hàm số

 

y f x

và trục hoành gồm hai phần, phần nằm phía

trên trục hoành có diện tích

S 

và phần nằm phía dưới trục hoành có diện tích

S 

(tham khảo hình vẽ bên).

Tính

 

31I f x x







I 

. B.

I 

. C.

I 

. D.

I 

Lời giải:

Với

 

31I f x dx







Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Đặt

3 1 3t x dt dx   

. Khi

  





    



Ta được

       

1 1 0 1

2 2 2 0

1 1 1

3 3 3

I f t dt f x dx f x dx f x dx

  



   





   

Trên đoạn

 

 

2;0 : 0fx

nên

 

f x dx







Trên đoạn

 

 

0;1 : 0fx

nên

 

f x dx 



Vậy

   

1 1 8 5 3

3 3 3 12 4

I f x dx f x dx





    







Câu 3: Cho hàm số

 

liên tục trên . Biết diện tích

2S 

11S 

3S 

4S 

12S 

(tham

khỏa hình vẽ)

Tích phân

 

1 1 df x x x





  





bằng

. B.

. C.

. D.

Lời giải:

   

 

d d d

1 1 1

6 6 6

1 1 1 1f x x x f x x x x

  



      



  

Ta có:

 

   

d d d

1 1 1

6 6 1

1 1 1f x x f x x f x x



  

     

  

Xét

 

1 d .







f x x

Đặt

1 d d .     x t x t

Ta có:

     

1 0 5

6 5 0

1 d d 2 11 3 4 12 2f x dx f t t f t t



          

  

Xét

 

1df x x







Đặt

1 d dx t x t   

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Ta có:

   

1 d d 2 11 9f x x f t t



     



Xét

 







Vậy

   

 

1 1 1

6 6 6

21 35

1 1 d 1 d 1 d 2 9 .

  





          



  

f x x x f x x x x

Câu 4: Cho hàm số

 

y f x

liên tục trên có đồ thị như hình vẽ bên dưới:

Giả sử diện tích phần kẻ dọc trên hình vẽ có diện tích bằng

. Tính theo

giá trị của

   

2 1 d .









I x f x x

50 2Ia

. B.

50Ia

. C.

30 2Ia  

. D.

30 2Ia  

Lời giải:

Từ đồ thị suy ra

 

dS f x x a







và

   

3 8; 2 2ff  

Ta có

   

2 1 dI x f x x









   

 

2 1 dx f x







     

2 1 2 dx f x f x x



  



   

5 2 5 3 2f f S   

5.2 5.8 2a  

50 2a

Vậy

50 2Ia

Câu 5: Cho hàm số

 

y f x

liên tục và nhận giá trị không âm trên

1;2





và thỏa mãn

   

1 , 1;2 .f x f x x



    



Đặt

 

S xf x x







là diện tích hình phẳng được giới hạn bởi đồ

thị hàm số

 

y f x

, trục Ox và hai đường thẳng

1, 2xx  

. Khẳng định nào dưới đây đúng?

2SS

. B.

3SS

. C.

2SS

. D.

3SS

Lời giải:

Ta có

 

dS xf x x







Đặt

1 d dt x t x    

. Đổi cận

1 2; 2 1x t x t       

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Suy ra

    

1 1 dS t f t t



   



   

1dt f t t







   

ddf t t tf t t







   

ddf x x xf x x







SS

Vậy

2SS

Câu 6: Diện tích hình phẳng giới hạn bởi đồ thị hàm số

34y x x  

, trục hoành, các đường thẳng

 

1, 0x x k k   

bằng

. Mệnh đề nào sau đây đúng?

 

1;4k 

. B.

 

3;6k 

. C.

 

0;2k 

. D.









Lời giải:

Diện tích hình phẳng cằn tìm

 

3 2 3 3

3 4 d 4 4

4 4 4

S x x x x x k k





         







Mà

 

3 3 2

21 1 1 3 7

8 4 0 3 0

4 4 4 4 4 4

S k k k k k k



           





 

2,07

k TM















Vậy

 

1;4k 

Câu 7: Cho parabol

 

: 2 1P y x x  

và đường thẳng

:2y x m  

. Để diện tích hình phẳng giới

hạn bởi

 

và



bằng

thì giá trị của tham số

nằm trong khoảng nào dưới đây?

 

5; 3

. B.

 

3;0

. C.

 

0;2

. D.

 

2;3

Lời giải:

Ta xét:

     

2 1 2 4 1f x g x x x x m x x m        

Đã biết công thức tính nhanh diện tích giới hạn bởi hai đường cong có

   

f x g x ax bx c  

là

 

20 4 20 4

6 6.1 3





    

Câu 8: Cho hình thang cong

 

giới hạn bởi các đường

y 

0y 

0x 

4x 

. Đường thẳng

xa

 

04a

chia hình

 

thành hai phần có diện tích

và

như hình vẽ bên dưới:

Tìm

để

4SS

3a 

. B.

log 13a 

. C.

2a 

. D.

log

a 

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Lời giải:

Ta có

Sx



;

Sx



Mặt khác,

4SS



2 d 4 2 d

xx





ln 2 ln 2





2 2 2 2

ln2 ln2 ln 2 ln2



  







4.2 2 2 4

  



5.2 20





2a 

Vậy

2a 

Câu 9: Gọi

 

là phần hình phẳng gạch chéo trong hình vẽ dưới đây được giới hạn bởi đồ thị của

các hàm số

3yx

4yx

và trục hoành (tham khảo hình vẽ)

Diện tích của

 

là bằng

. B.

. C.

. D.

Lời giải:

 

H y x

















Xét các phương trình hoành độ giao điểm:

4 0 4xx   

;

3 0 0xx  

;

 

1 ( / )

x t m

x Loai







  









Diện tích hình phẳng

 

3 d 4 d 4

S x x x x x x



      







Câu 10: Diện tích hình phẳng giới hạn bởi đồ thị

 

của hàm số

 

y x x  

và hai tiếp tuyến

của

 

xuất phát từ

 

3; 2M 

là

Lời giải:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Đặt

 

f x x x  

, có

 

2f x x





Tiếp tuyến của

 

tại điểm

 

; ( )A x f x

có phương trình dạng

  

0 0 0

()y f x x x f x



  

Hay

  

 

0 0 0 0

: 2 4 3

y x x x x x      

Tiếp tuyến này xuất phát từ

 

3; 2M 

nên

  

 

0 0 0 0

2 2 3 4 3

x x x x      

3 0

5 : 3 11

x y x



   



     



   



Dựa vào đồ thị đã vẽ, diện tích hình phẳng cần tính là:

   

1 3 1 3

2 1 d 2 3 11 d

2 2 2 2

   

   

          

   

   

   

   



S x x x x x x x x

2 2 3 2 3 2

1 1 1 25 1 1 1 1 5 25 8

d 5 d

2 2 2 2 6 2 2 6 2 2 3

       

            

       

       



x x x x x x x x x x x x

Câu 11: Cho parabol

 

:2P y x

và hai tiếp tuyến của

 

tại các điểm

 

1;3M 

và

 

2;6N

. Diện

tích hình phẳng giới hạn bởi

 

và hai tiếp tuyến đó bằng

. B.

. C.

. D.

Lời giải:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Ta có:

'2yx

Phương trình tiếp tuyến tại

 

1;3M 

là

: 2 1d y x  

Phương trình tiếp tuyến tại

 

2;6N

là

: 4 2d y x

Phương trình hoành độ giao điểm của d1 và d2:

2 1 4 2

x x x     

Vậy diện tích phần giới hạn cần tìm là:

 

2 2 1 d 2 4 2 d

S x x x x x x



         



Câu 12: Cho hàm số

 

y f x

là một hàm số bậc ba. Gọi

là diện tích giới hạn bởi các đường

 

, 0, 1y f x y x   

và

4x 

(tham khảohình vẽ).

Khi đó diện tích

có giá trị bằng

253

. B.

253

. C.

235

. D.

235

Lời giải:

Dựa vào hình vẽ ta có

 

0fx

có 3 nghiệm phân biệt

1; 1; 4x x x   

Mà

 

là hàm bậc ba nên

     

1 1 4f x a x x x   

Cho

0x 

suy ra

aa  

Do đó

     

1 1 4

f x x x x   

Nên diện tích

giới hạn bởi các đường

 

, 0, 1y f x y x   

và

4x 

là

   

1 253

1 1 4

2 24

S x x x dx



    



Câu 13: Cho đồ thị hàm số

 

y f x

và

 

y g x

như hình vẽ bên dưới:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Biết đồ thị của hàm số

 

y f x

là một Parabol đỉnh

có tung độ bằng



và

 

y g x

là

một hàm số bậc ba. Hoành độ giao điểm của hai đồ thị là

1 2 3

,,x x x

thỏa mãn

1 2 3

. . 6x x x 

Diện tích hình phẳng giới hạn bởi 2 đồ thị hàm số

 

y f x

và

 

y g x

gần nhất với giá trị

nào dưới đây?

. B.

. C.

. D.

Lời giải:

Gọi phương trình của Parabol là

y ax bx c  

, từ dữ kiện đề bài ta có hệ phương trình

 

4 2 0 1 .

a b c b f x x x

ac b











        

















Giả sử

 

g x ax bx cx d   

thì đồ thị của nó đi qua









và có 2 cực trị có hoành

độ bằng

và

, tức là phương trình

 

3 2 0g x ax bx c



   

có 2 nghiệm là

và

Kết hợp với giả thiết ta có hệ phương trình

 

1 2 3

133

12 4 0

8 8 4

. . 6

a b c d

g x x x

a b c

x x x







    







     



  







   











Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình

2 3 2

1 1 3 3

2 8 8 4

x x x x x



  



      



  



Vậy diện tích hình phẳng giới hạn bởi 2 đồ thị hàm số

 

y f x

và

 

y g x

bằng

       

1 1 7

3 2 3 2

6,22.

8 8 4 8 8 4

S f x g x x g x f x x

x x x x









   

   

   

   

         

   

   



Câu 14: Cho hai hàm số

 

4f x ax bx cx   

và

   

2, , , , ,g x dx ex a b c d e   

. Biết rằng đồ

thị hàm số

 

y f x

và

 

y g x

cắt nhau tại

điểm có hoành độ lần lượt là

3; 1; 2

. Hình

phẳng giới hạn bởi đồ thị hai hàm số đã cho có diện tích bằng

316

. B.

191

. C.

253

. D.

Lời giải:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Xét phương trình hoành độ giao điểm của hàm số

 

y f x

và

 

y g x

     

60h x ax b d x c e x      

Hàm số

 

y f x

và

 

y g x

cắt nhau tại

điểm có hoành độ lần lượt là

3; 1; 2

nên

     

3 1 2 0h x a x x x    

Xét

   

0 6 .3.1. 2 6 1h a a       

Vậy hàm số:

     

3 1 2h x x x x   

Hình phẳng giới hạn bởi đồ thị hai hàm số đã cho có diện tích bằng:

     

253

d 3 1 2

S h x x x x x



     



Câu 15: Cho

   

,f x g x

lần lượt là các hàm đa thức bậc ba và bậc nhất có đồ thị như hình vẽ bên

dưới:

Biết diện tích hình

(được tô đậm) bằng

250

. Tính

 



f x x

. B.

. C.

. D.

Lời giải:

Ta có

 

là hàm số bậc nhất đi qua







và

 

3;2B

nên

 

g x x

Với

 

1 1 2 2; 1

           y x x C

là giao điểm của

 

và

 

Do đó

       



    





f x g x a x x x

Lại có:

       

250 4 3

d 2 3 d

81 3 20







          













S f x g x x a x x x x a

Suy ra

       

20 3



    





f x g x x x x

     

3 4 3 1

20 3 5 5



      





f x x x x x

Vậy

     

3 4 3 1 34

d 2 3 d

20 3 5 5 15





      











f x x x x x x x

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 16: Cho hàm số

   

36 0;a, ,f x ax bx x c a b c     

có hai điểm cực trị là

6

và

. Gọi

 

y g x

là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

 

y f x

. Diện tích hình

phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

bằng

160

128.

64

672

Lời giải:

   

3 2 2

36 3 2 36f x ax bx x c f x ax bx



       

Theo bài ta được

 

   

6 0 3 6 2 . 6 36 0

3 2 2 . 2 36 0

f a b





      















  





9 3 1

3 9 6

  







  



a b a

a b b

   

3 2 2

6 36 ; 3 12 36f x x x x c f x x x



       

;

Đường thẳng đi qua hai điểm cực trị của hàm số:

 

3 12 36 . 32x 24

y f x x x x c



       





là

 

32 24y g x x c    

Xét phương trình hoành độ giao điểm hai đồ thị

6 36 32 24 2

x x x c x c x







         







Vậy diện tích hình phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

bằng

 

     

2 2 2

3 2 3 2 3 2

6 6 2

6 36 32 24 6 4 24 6 4 24S x x x c x c dx x x x dx x x x dx



  

               

  

128

Câu 17: Cho hai hàm số

 

4 3 2

3f x ax bx cx x   

và

 

g x mx nx x  

; với

, , , ,a b c m n

. Biết

hàm số

   

y f x g x

có ba điểm cực trị là

1

;

và

. Diện tích hình phẳng giới hạn bởi

hai đồ thị hàm số

 



và

 

y g x





bằng

. B.

. C.

125

. D.

131

Lời giải:

Ta có

   

f x g x

là hàm bậc 4 nên

   

432

4f x g x Ax Bx Cx x    

   

4 3 2 4f x g x Ax Bx Cx



    

Hàm số

   

y f x g x

có ba điểm cực trị là

1

;

và

nên ta có hệ phương trình:

4 3 2 4 0

108 27 6 4 0

256 48 8 4 0

A B C

A B C B

A B C







    









     





   











   

f x g x x x x



     

Diện tích của hình phẳng giới hạn bởi hai đồ thị hàm số

 

y f x





và

 

y g x





bằng

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

1 5 131

2 4 d

3 3 12

S x x x x



    



Câu 18: Cho hàm số

 

y f x

là hàm đa thức bậc bốn và có đồ thị như hình vẽ bên. Hình phẳng giới

hạn bởi đồ thị hai hàm số

 

y f x

 

y f x





có diện tích bằng

127

. B.

107

. C.

. D.

127

Lời giải:

Ta thấy đồ thị hàm số

 

y f x

tiếp xúc với trục hoành tại hai điểm có hoành độ bằng

2

và

nên hàm số có dạng

     

21f x a x x  

Mà đồ thị hàm số

 

y f x

đi qua điểm

       

0;1 4 1 2 1

A a a f x x x       

     

2 1 2 1

f x x x x



    

Xét phương trình hoành độ giao điểm của

 

y f x

và

 

y f x





       

2 1 2 1 2 1

x x x x x











      













Hình phẳng giới hạn bởi đồ thị hai hàm số

 

y f x

 

y f x





có diện tích là

       

2 1 2 1 2 1

S x x x x x



       



107

Câu 19: Cho hàm số

( ) 2 2f x ax x x   

và hàm số

( ) 2g x bx cx  

, có đồ thị như hình vẽ bên

dưới:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Gọi

;SS

là diện tích các hình phẳng gạch chéo trong hình vẽ, biết

221

640

S 

. Khi đó

bằng

1361

640

. B.

271

320

. C.

571

640

. D.

791

640

Lời giải:

Từ đồ thị ta thấy hoành độ giao điểm của đồ thị hàm số

()gx

với trục hoành chính là điểm

cực trị của hàm số

()fx

. Do đó:

( ) . ( )f x k g x





. Hay:

 

3 2 3 2

4 3 2 2ax x k bx cx    

Suy ra:

















. Hay:

( ) 4 3 2.  g x ax x

Suy ra:

 

4 3 3 2 4 3 2

( ) ( ) 2 2 4 3 2 1 4 3 2f x g x ax x x ax x ax a x x x            

Khi đó:

 

( ) ( )S f x g x dx



 

4 3 2

221 1

1 4 3 2

640 4

ax a x x x dx a       



Vậy

1 791

2 2 .

4 640

S x x x dx



    







Câu 20: Tính diện tích

của miền hình phẳng giới hạn bởi đồ thị của hàm số

 

f x ax bx c  

, các

đường thẳng

1x 

2x 

và trục hoành (miền gạch chéo) cho trong hình dưới đây:

S 

. B.

S 

. C.

S 

. D.

S 

Lời giải:

Hình phẳng giới hạn bởi đồ thị của hàm số

 

f x ax bx c  

, các đường thẳng

1x 

2x 

và trục hoành được chia thành hai phần:

ền

là hình chữ nhật có hai kích thước lần lượt là

và

3S

ền

gồm:

 

1; 2

f x ax bx c



  









  



Dễ thấy

 

đi qua

điểm

 

1;1A 

 

0;3B

 

2;1C

nên đồ thị

 

có phương trình

 

f x x x  

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

1 3 27

3 1 d

2 2 8

S x x x





     







Vậy diện tích hình phẳng cần tìm là

S S S  

Câu 21: Cho đường thẳng

yx

và parabol

y x a

, (

là tham số thực dương). Gọi

,SS

lần

lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên dưới:

Khi

SS

thì

thuộc khoảng nào sau đây?







. B.

;

16 32







. C.

;

4 32







. D.

;

32 4







Lời giải:

Xét phương trình:

x x a

0 2 3 4 0

x x a x x a       

Ta có:

9 32a  

, theo giả thuyết

a    

Khi đó hoành độ giao điểm là

3 9 32 3 9 32

   



Ta có:

1 3 3 1

2 4 4 2

S S x a x dx x x a dx

   

      

   

   



3 2 2 3

6 8 8 6

x x x x

ax ax

   

     

   

   

3 2 2 3 2 3

1 1 2 2 1 1

1 2 1

3 3 3

6 8 8 6 8 6

x x x x x x

ax ax ax        

ax   



a  

 

3 9 32

9 3 9 32

32 96



   

27 9 9 32 9 6 9 32 9 32 96 0a a a a         

3 9 32 64 9aa   

81 288 4096 1152 81aa    

4096 864 0

128







   









là số thực dương nên

27 3 7

;

128 16 32









Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 22: Cho hai hàm đa thức

 

f x ax bx cx d   

và

 

g x mx nx p  

. Biết rằng đồ thị hai

hàm số

 

y f x

và

 

y g x

cắt nhau tại ba điểm có hoành độ lần lượt là

1;2;4

đồng thời

cắt trục tung lần lượt tại

,MN

sao cho

6MN 

( tham khảo hình vẽ).

Hình phẳng giới hạn bởi đồ thị hai hàm số đã cho ( phần gạch sọc) có diện tích bằng

125

. B.

253

. C.

253

. D.

253

Lời giải:

Phương trình hoành độ giao điểm của đồ thị

 

y f x

và

 

y g x

là:

   

3 2 2 3 2

0ax bx cx d mx nx p ax b m x c n x d p             

Do đồ thị hai hàm số

 

y f x

và

 

y g x

cắt nhau tại ba điểm có hoành độ lần lượt là

1;2;4

nên ta được

       

1 2 4a x x x ax b m x c n x d p         

Mà

   

0 0 6

f g y y MN    

. Suy ra

a 

Do đó:

       

1 2 4

f x g x x x x    

Khi đó:

       

3 253

1 2 4

4 16

S f x g x dx x x x dx



      



Câu 23: Cho

   

0f x ax bx cx d a    

là hàm số nhận giá trị không âm trên đoạn

 

2;3

có đồ

thị

 



như hình vẽ bên dưới:

Biết diện tích hình phẳng giới hạn bởi các đồ thị của các hàm số

   

g x xf x

;

     

h x x f x f x





và các đường thẳng

2; 3xx

bằng

. Tính

 

12f 

. B.

 

11f 

. C.

 

11f 

. D.

 





Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Lời giải:

Từ hình vẽ ta có được

     

2 3 2

3 2 3 6 3f x x x x x f x x x C



       

Diện tích hình phẳng là

         

ddS g x h x x xf x x f x f x x



   



     

 

0, 2;3xf x x f x f x x



   

nên

     

dS xf x x f x f x x











Ta có:

         

2 2 2 2 2 2 2

1 1 9 9

d 3 2 2 2 4

2 2 2 2

S x f x x x f x f f C C





      







Mà

 

72 2 4 72

S C C







     









 

 

   

0, 2;3 3 4 1 2f x x f x x x f        

Câu 24: Cho hàm số

 

y f x ax bx c   

có đồ thị

 

và cắt trục hoành tại điểm có hoành độ

bằng

1

. Tiếp tuyến

tại điểm có hoành độ

1x 

của

 

cắt

 

tại

điểm khác có

hoành độ lần lượt là

và

. Gọi

,SS

là diện tích các phần hình phẳng giới hạn bởi

và

 

(với

là diện tích phần hình phẳng nằm bên phải trục

). Tỷ số

bằng

Lời giải:

Giả sử phương trình tiếp tuyến là

 

y g x

Do tiếp tuyến

tại điểm có hoành độ

1x 

của

 

cắt

 

tại

điểm khác có hoành độ

lần lượt là

và

nên ta có phương trình hoành độ giao điểm của

và

 

là:

       

1 2 0 0

f x g x ax x x x







      







Do đó

   

1 2 d

S ax x x x



   



;

   

1 2 d

S ax x x x   



Suy ra



Câu 25: Cho hàm số

lnyx

có đồ thị

 

như hình vẽ bên dưới:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

(

)

Đường tròn tâm

có duy nhất một điểm chung

với

 

. Biết

 

0;1C

, diện tích của hình

thang

AB CO

gần nhất với số nào sau đây.

3,01

. B.

2,91

. C.

3,09

. D.

2,98

Lời giải:

(

)

e +

Đường thẳng đi qua

 

0;1C

và song song với trục hoành cắt đồ thị

()C

tại

( ;1)Be

Gọi

()d

là tiếp tuyến của

()C

tại

( ;1)Be

thì phương trình

()d

là



()C

tiếp xúc với đường tròn tâm

tại

( ;1)Be

thì

()d

là tiếp tuyến chung của

()C

và đường

tròn tâm

( ) ( ;0)AB d A e

  

Hình thang

AB CO

có:

; ; 1OA e CB e OC

   

Vậy

2,91.

()

OA CB OC

ABCO

S 



  

Câu 26: Cho hàm số

 

4 3 2

f x x bx cx dx e    

(

, , ,b c d e

) có các giá trị cực trị là

1,4

và

. Diện

tích hình phẳng giới hạn bởi đồ thị hàm số

 





và trục hoành bằng

Lời giải:

+) Gọi

1 2 3

x x x

là ba điểm cực trị của hàm số

 

. Ta có bảng biến thiên:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

+) Phương trình hoành độ giao điểm của đồ thị hàm số

 

và trục hoành là:

 

0 ( 1,2,3)

0 (TM)

f x x x i



  









   









+) Diện tích cần tìm là

 

         

2 1 3

2 2 4 2 2 6.

f x f x

S x x f x f x f x f x f x

f x f x



       



Câu 27: Biết đồ thị

 

của hàm số

   

,f x x bx c b c   

có cực trị là

 

1;0A

. Gọi

 

là

parabol có đỉnh

 

0; 1I 

và đi qua điểm

 

2;3B

. Diện tích hình phẳng giới hạn bởi

 

và

 

thuộc khoảng nào dưới đây?

 

0;1

. B.

 

2;3

. C.

 

3;4

. D.

 

1;2

Lời giải:

Đồ thị

 

của hàm số

   

,f x x bx c b c   

có cực trị là

   

1;0 1A A C b c     

 

42f x x bx





vì

 

1;0A

là cực trị nên

 

1 0 4 2 0 2 1.f b b c



        

   

: 2 1   C f x x x

Gọi

   

1 1 1 1

:0P y a x b x c a   

 

là parabol có đỉnh

   

0; 1 1I I P c     

Hoành độ đỉnh

 

    

 

đi qua điểm

 

1 1 1 1

2;3 3 4 2 1B a b c a     

 

:1  P y x

Phương trình hoành độ giao điểm của

 

và

 

4 2 2 4 2

2 1 1 3 2 0

x x x x x





        







Diện tích hình phẳng:

3 2 d 2,537S x x x



   



Câu 28: Đường thẳng

cắt đường cong

 

   f x a x bx cx d

tại ba điểm phân biệt có hoành độ

2x

1x

2x

như hình vẽ bên dưới:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Diện tích hình phẳng gạch sọc thuộc khoảng nào dưới đây?







. B.







. C.







. D.







Lời giải:

Ta có

: d y mx n

Phương trình hoành độ giao điểm:

   

3 2 3 2

           a x bx cx d mx n g x a x bx cx d mx n

có

nghiệm

2x

;

1x

;

2x

Do đó

     

2 1 2   g x a x x x

       

0 3 1 4 2 1 2

           g d n a a g x x x x

Vì vậy

   

1 71

2 1 2 d

2 12



    



S x x x x

Câu 29: Cho hai hàm số

 

1f x ax bx cx   

và

 

2g x dx ex  

 

, , , ,a b c d e

. Biết rằng đồ

thị của hàm số

 

y f x

và

 

y g x

cắt nhau tại ba điểm có hoành độ lần lượt là

3; 1;1

(tham khảo hình vẽ) .

Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

. B.

. C.

. D.

Lời giải:

Hoành độ giao điểm là nghiệm của phương trình

     

3 0 *ax b d x c e x     

Do phương trình

 

có 3 nghiệm nên ta có hệ pt

3 0 1

3 0 3

9a 3 3d 1 0 1

a b d c e a

a b d c e b d

b c e c e

       





        





         



Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Do vậy

   

3 2 3 2

3x 3 d 3x 3 d 8S x x x x x x





        



Câu 30: Cho hai hàm số

 

2f x ax bx cx   

và

 

2g x dx ex  

 

, , , ,a b c d e

. Biết rằng đồ

thị của hàm số

 

y f x

và

 

y g x

cắt nhau tại ba điểm có hoành độ lần lượt là

2; 1;1

(tham khảo hình vẽ).

Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

. B.

145

. C.

. D.

145

Lời giải:

Hoành độ giao điểm là nghiệm của phương trình

   

30ax b d x c e x     

 

Do phương trình

 

có 3 nghiệm là

2

;

1

;

nên ta có hệ pt :

4 0 2

4 0 4

4a 2 2d 2 0 2

a b d c e a

a b d c e b d

b c e c e

       





        





         



Do vậy

   

3 2 3 2

2 4x 2 4 d 2 4x 2 4 d

S x x x x x x





        



Câu 31: Đường thẳng

4y kx

cắt parabol

 

2yx

tại hai điểm phân biệt và diện tích các hình

phẳng

bằng nhau như hình vẽ bên.

Khẳng định nào sau đây đúng?

 

6; 4k   

. B.



  





. C.

 

2; 1k   

. D.









Lời giải:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Phương trình hoành độ giao điểm

 

24x kx  

 

x k x





    







Đường thẳng

4y kx

cắt các trục tọa độ tại các điểm

;0A









 

0;4B

42k

   

20k   

Diện tích hình phẳng

 

4 2 d 4 d 4

S kx x x x k x x k



         



Diện tích hình phẳng

     

 

2 d 4 d 2

S x x kx x k





      



SS

   

 

0,457

6 3 2

5,54

k TM







    









Câu 32: Cho

 

là hình phẳng giới hạn bởi parabol

yx

(với

0 2 2x

), nửa đường tròn

8yx

và trục hoành, trục tung (phần tô đậm trong hình vẽ).

Diện tích của

 

bằng

3 14





. B.





. C.





. D.





Lời giải:

Phương trình hoành độ giao điểm của parabol

yx

và đường

8yx

là:

2 2 4 2

1 1 3

8 1 7 0 2

4 16 2

x x x x x





         







(Vì

0 2 2x

)

Diện tích của (H) là:

2 2 2

2 2 3

1 1 8

4 12 3

S x dx x dx x x I I

   

        

   

   



với

8I x dx



Đặt

2 2 sin , ; 2 2 cos .

x t t dx t dt





    





Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Đổi cận

2 , 2 2 .



     x t x t

2 2 2

4 4 4

8 8sin .2 2 cos . 8cos . 4(1 cos2 ). 4 sin 2 2

I t t dt t dt t dt t t

  



  





        





  

Vậy

8 3 2





  

Câu 33: Cho hàm số

 

( ) , , , , 0y f x ax bx cx d a b c d a      

có đồ thị là

 

. Biết rằng đồ thị

 

đi qua gốc tọa độ và đồ thị hàm số

'( )y f x

cho bởi hình vẽ bên.

Tính giá trị

(4) (2).H f f

45H 

. B.

64H 

. C.

51H 

. D.

58H 

Lời giải:

Theo bài ra

 

( ) , , , , 0y f x ax bx cx d a b c d a      

do đó

 

y f x





là hàm bậc hai có

dạng

 

y f x a x b x c

   

   

Dựa vào đồ thị ta có:

a b c

abc









  

  





  

  

























 

31y f x x



   

Gọi

là diện tích phần hình phẳng giới hạn bởi các đường

 

y f x





, trục

4,x 

2x 

Ta có

 

3 1 dx 58Sx  



Lại có:

       

dx 4 2S f x f x f f



   



Do đó:

   

4 2 58H f f

Câu 34: Cho hàm số

4y x x m  

có đồ thị

 

. Giả sử

 

cắt trục hoành tại bốn điểm phân

biệt sao cho diện tích hình phẳng giới hạn bởi

 

với trục hoành có diện tích phần phía trên

trục hoành bằng diện tích phần phía dưới trục hoành. Khi đó

thuộc khoảng nào dưới đây?

 

1;1m

. B.

 

3;5m

. C.

 

2;3m

. D.

 

5;m  

Lời giải:

Phương trình hoành độ giao điểm của

 

với trục hoành là

40x x m  

 

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Đặt

tx

 

0t 

, phương trình

 

trở thành

40t t m  

 

Để

 

có bốn nghiệm phân biệt thì

 

phải có hai nghiệm dương phân biệt. Điều này xảy ra

khi và chỉ khi





























04m  

 

Gọi

và

 

tt

là hai nghiệm của

 

, khi đó bốn nghiệm (theo thứ tự từ nhỏ đến lớn)

của phương trình

 

là

xt

xt

Do tính đối xứng của

 

nên từ giả thiết ta có

   

4 2 4 2

4 d 4 d

x x m x x x m x     



 

2 8 2 d 0

x x m x   





   





mx   

4 4 4

0 3 20 15 0

mx x x m       

Vậy

là nghiệm của hệ:

3 20 15 0

x x m



  





  





15 60 15 0

3 20 15 0

x x m



  







  





12 40 0

3 20 15 0

x x m











  





12 40 0

3 20 15 0

x x m





































  























Kết hợp điều kiện

 

suy ra

m 

Câu 35: Cho Parabol

 

:P y x

và đường tròn

 

có tâm

 

0;3A

bán kính bằng

như hình vẽ bên

dưới:

Diện tích phần được tô đậm giữa

 

và

 

gần nhất với số nào dưới đây?

3.44

. B.

1.51

. C.

1.77

. D.

3.54

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Lời giải:

+) Phương trình đường tròn

 

tâm

 

0;3A

bán kính bằng

là

   

: 3 5C x y  

+) Do tính chất đối xứng, ta chỉ cần xét phần được tô đậm của

 

và

 

với

0x 

+) Gọi

là diện tích hình phẳng giới hạn bới các đường

 

5 3 , , 1, 4x y x y y y     

Ta có

 

5 3 dS y y y   



1.26032

+) Gọi

là diện tích hình phẳng giới hạn bới các đường

3 5 , , 0, 1y x y x x x     

Ta có





3 5 d 0.5075S x x x



    







Vậy diện tích cần tính

 

2 3,539S S S  

Câu 36: Cho hàm số bậc bốn

 

y f x

có đồ thị

 

như hình vẽ bên dưới:

Đường thẳng

d y kx

có đúng ba điểm chung với

 

là

,,A B C

và

BC AB

Biết

diện tích hình phẳng

(phần gạch sọc) là

Giá trị của

 





f x x

bằng

2

. B.

321

160



. C.

161



. D.

159

160



Lời giải:

Phương trình giao điểm của

 

và

là:

        

2 1 5f x g x a x x x    

(hệ số

0a 

)

Theo giả thiết, ta có:

    

24 24 1

2 1 5

5 5 24

S a x x x dx a        



             

1 1 1

2 1 5 2 1 5

24 4 24

f x g x x x x kx x x x           

* Gọi

1 1 1

2; 2 , 1; , 5; 5

4 4 4

A k B k C k

     

   

     

     

   

4 4 3 3

BC AB k k







       









Đường thẳng nằm ở góc phần tư thứ nhất và thứ ba nên hệ số góc là dương nên ta chọn

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

k

Vậy

      

3 1 1

2 1 5 .

4 4 24

     f x x x x x

Và

      

3 1 1 321

2 1 5

4 4 24 160





       







f x dx x x x x dx

Câu 37: Cho hàm số

 

f x x bx cx d   

với

.d

Biết hàm số

       

23g x f x f x f x

 

  

có hai giá trị cực trị là

6

và

. Tính diện tích hình phẳng

giới hạn bởi các đường

     

 

f x f x f x

 







và

1.y

ln5.

ln7.

2ln6.

2ln5.

Lời giải:

Hàm số

 

là hàm số bậc

nên

 

là hàm số bậc

suy ra

 



là hàm số bậc hai.

Ta có

 

3 3.3! 18fx

;

     

2 18g x f x f x

  

  

có hai nghiệm

(giả sử

xx

) và

 

42gx 

 

6gx 

Xét phương trình tìm cận của tích phân để tính diện tích:

     

 

   

 

2 18

18 18

f x f x f x f x f x

g x g x

   

   

  



Suy ra

     

2 18 0 0

f x f x g x





  

     







Diện tích hình phẳng

     

 

2 2 2

1 1 1

18 18 18

x x x

f x f x f x g x g x

S dx dx dx

g x g x g x

   



   

  

  

Đặt

   

18t g x dt g x dx



   

. Đổi cận

 

1 1 1

2 2 2

x x t g x

   







   





Do đó

ln ln12 ln60 ln ln5 ln5

       



Câu 38: Cho hàm số

y x ax bx c   

có đồ thị

 

. Biết rằng tiếp tuyến

của

 

tại điểm

có

hoành độ bằng

1

cắt

 

tại điểm

có hoành độ bằng

(xem hình vẽ). Diện tích hình

phẳng giới hạn bởi

và

 

(phần gạch chéo trong hình) bằng

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

. B.

. C.

. D.

Lời giải:

Đồ thị

 

đi qua gốc tọa độ

 

0;0O

suy ra

0c 

. Tiếp tuyến

với

 

tại điểm có hoành độ

1x 

có phương trình

 

3 2 2y a b x a    

. Xét phương trình hoành độ giao điểm của hai

đồ thị

và

 

     

3 2 2

3 2 2 1 1 2 0x ax bc a b x a x x a x a



             



   

1 2 0

g x x a x a









     



Vì

cắt

 

tại điểm

có hoành độ bằng

suy ra

 

2 0 0ga  

Vậy diện tích hình phẳng cần tính là

 

3 2 3 2

S x bx b x dx x x dx



        



Câu 39: Cho hàm số

 

y f x x ax b    

 

a,b

có đồ thị (C) và

 

y g x mx nx p   

 

m,n, p

có đồ thị

 

như hình vẽ. Diện tích hình phẳng giới

hạn bởi

 

và

 

có giá trị nằm trong khoảng nào sau đây?

 

4;4,1

. B.

 

4,2;4,3

. C.

 

4,3;4,4

. D.

 

4,1;4,2

Lời giải:

Diện tích hình phẳng giới hạn bởi

 

và

 

   

S f x g x dx











     

h x f x g x

là hàm bậc bốn có hệ số bậc bốn bằng



, có hai nghiệm đơn

2x 

2x 

và một nghiệm kép x=0 (dựa vào sự tương giao của

 

và

 

trong hình vẽ )

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115



        

h x f x g x x x x     



  

1 64

2 2 4 266

2 15



     



S x x x dx , .

Câu 40: Người ta trồng hoa vào phần đất được tô màu được giới hạn bởi cạnh

,AB CD

, đường trung

bình

của mảnh đất hình chữ nhật

ABCD

và một đường cong hình sin. Biết

2AB





(m),

2AD 

(m). Tính diện tích phần còn lại.





. B.

 





. C.





. D.





Lời giải:

Chọn hệ trục toạ độ

Oxy

như hình vẽ

Đồ thị hàm số có dạng

siny a bx

Dựa vào hình vẽ ta thấy đường sin có chu kì

2AB





và biên độ bằng

AM AB

Suy ra đường hình sin có phương trình

sinyx

Đường thẳng

có phương trình





Do đó diện tích phần đất được tô màu là

2 sin d 2cos 4S x x x



   



Diện tích hình chữ nhật là





Diện tích phần còn lại:

4 4 4( 1)S S S



     

Câu 41: Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng

cm bằng

cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên dưới:

Biết

5AB 

cm,

4OH 

cm. Tính diện tích bề mặt hoa văn đó.

160

. B.

140

. C.

. D.

50 cm

Lời giải:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Đưa parabol vào hệ trục

Oxy

ta tìm được phương trình là

 

16 16

25 5

P y x x  

Diện tích hình phẳng giới hạn bởi

 

16 16

25 5

P y x x  

, trục hoành và các đường thẳng

0x 

5x 

là

16 16 40

25 5 3

S x x x



   







Tổng diện tích phần bị khoét đi:

160

SS

Diện tích của hình vuông là

100 cm

S 

Vậy diện tích bề mặt hoa văn là

160 140

100 cm

S S S    

Câu 42: Một hoa văn trang trí được tạo ra từ một miếng bìa hình vuông cạnh

20 cm

bằng cách khoét

đi bốn phần bằng nhau đều có hình dạng một nửa elip như hình vẽ. Biết một nửa trục lớn là

6AB 

, trục bé

8CD 

. Diện tích bề mặt của hoa văn đó bằng

 

400 48 cm





. B.

 

400 96 cm





. C.

 

400 24 cm





. D.

 

400 36 cm





Lời giải:

Gọi

là diện tích hình vuông,

là diện tích khoét đi.

Ta có

 

20 400 cmS 

và

 

2 2 .6.4 48 cmS ab

  

  

(vì mỗi phần bị khoét đi là nửa

elip có

6a 

4b 

Vậy diện tích bề mặt hoa văn là

 

400 48 cmS S S



   

Câu 43: Một viên gạch hoa hình vuông cạnh

cm được thiết kế như hình bên dưới. Diện tích mỗi

cánh hoa (phần tô đậm) bằng

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

y =

800

. B.

400

. C.

250

. D.

800

Lời giải:

Diện tích một cánh hoa là diện tích hình phẳng được tính theo công thức sau:

20 d

S x x x











. 20.

3 60









400



 

Câu 44: Ông An muốn làm một cánh cửa bằng sắt có hình dạng và kích thước như hình vẽ. Biết rằng

đường cong phía trên là một parabol, tứ giác

ABCD

là một hình chữ nhật.

Giá cánh cửa sau khi hoàn thành là

900000

đồng/

. Số tiền ông An phải trả để làm cánh

cửa đó

bằng

A.9 600 000 đồng. B. 15 600 000 đồng. C. 8 160 000 đồng. D. 8 400 000 đồng.

Lời giải:

Chọn hệ trục tọa độ

Oxy

sao cho cạnh

nằm trên

và

là trung điểm

. Khi đó, ta có

phương trình parabol là:

1yx

Diện tích cánh cửa là:

 

2.4 1 d

S x x



   



 

Câu 45: Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là

2,25

mét,

chiều rộng tiếp giáp với mặt đất là

mét. Giá thuê mỗi mét vuông là

1500000

đồng. Vậy số

tiền bác Năm phải trả là

33750000

đồng. B.

3750000

đồng. C.

12750000

đồng. D.

6750000

đồng.

Lời giải:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Gọi phương trình parabol

 

:P y ax bx c  

. Do tính đối xứng của parabol nên ta có thể

chọn hệ trục tọa độ

Oxy

sao cho

 

có đỉnh

I Oy

(như hình vẽ).

Ta có hệ phương trình:

 

c I P

a b c A P

a b c B P







   





   











  











Vậy

 

P y x  

Dựa vào đồ thị, diện tích cửa parabol là:

S x x





  









  



















Số tiền phải trả là:

1500000 675 0

000

đồng.

Câu 46: Một khu vườn dạng hình tròn có hai đường kính

, AB CD

vuông góc với nhau,

12AB m

Người ta làm một hồ cá có dạng elip với bốn đỉnh

, , ', 'M N M N

như hình vẽ. Biết

10 , ' ' 8 , 8MN m M N m PQ m  

. Diện tích phần trồng cỏ (phần gạch sọc) bằng:

32,03 m

. B.

20,33 m

. C.

33.02 m

. D.

23,03 m

Lời giải:

Ta chọn hệ trục tọa độ như hình vẽ:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Khi đó phương trình đường tròn là:

2 2 2

36 36x y y x     

Phương trình elip là:

2 2 2

1 4 1

25 16 25

x y x

y     

Do tính đối xứng nên diện tích phần trồng cỏ sẽ là:

4 36 4 1 d 30,03 .



   







S x x m

Câu 47: Một khu vườn có dạng hợp của hai hình tròn giao nhau. Bán kính của hai đường tròn là

20m

và

15m

, khoảng cách giữa hai tâm của hai hình tròn là

30m

. Phần giao của hai hình tròn

được trồng hoa với chi phí

300000

đồng/

. Phần còn lại được trồng cỏ với chi phí

100000

đồng/

. Hỏi chi phí để trồng hoa và cỏ của khu vườn gần nhất với số tiền nào dưới

đây?

202

triệu đồng. B.

208

triệu đồng. C.

192

triệu đồng. D.

218

triệu đồng.

Lời giải:

215





x-30

( )

=225





=400

+ Gắn hệ trục như hình vẽ.

+ Đường tròn

 

có tâm

 

0;0O

, bán kính

20R 

có phương trình:

400xy

400yx   

+ Đường tròn

 

có tâm

 

30;0I

, bán kính

15R 

có phương trình:

 

30 225xy  

 

225 30yx    

+ Phương trình hoành độ giao điểm của

 

và

 

là:

 

215

400 225 30

xxx     

+ Diện tích trồng hoa:

 

215

2. 225 30 d 2. 400 d 60,255S x x x x m     



Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

+ Diện tích trồng cỏ:

2 2 2 2 2

2 1 2 1

2 .20 .15 2.60,255 1842,985S R R S m

   

      

Tổng chi phí trồng hoa và cỏ là:

300000. 100000. 300000.60,255 100000.1842,985 202375000P S S    

đồng

Vậy chi phí để trồng hoa và cỏ của khu vườn gần nhất với số tiền 202 triệu đồng

Câu 48: Một khuôn viên dạng nửa hình tròn, trên đó người ta thiết kế phần trồng hoa hồng có dạng

một hình Parabol có đỉnh trùng với tâm hình tròn và trục đối xứng vuông góc với đường

kính của nửa đường tròn, hai đầu mút của Parabol nằm trên đường tròn và cách nhau một

khoảng 4 mét (phần tô đậm). Phần còn lại của khuôn viên (phần không tô đậm) dùng để

trồng hoa cúc. Biết các kích thước cho như hình vẽ. Chi phí trồng hoa hồng và hoa cúc lần

lượt là

120.000

đồng

và

80.000

đồng/

. Hỏi chi phí trồng hoa khuôn viên đó gần nhất

với số nào sau đây (làm tròn đến ngàn đồng).

6.847.000

đồng. B.

6.865.000

đồng. C.

5.710.000

đồng. D.

5.701.000

đồng.

Lời giải:

Parabol có phương trình là

yx

Đường tròn tâm

bán kính

2 6 40  R

Phương trình nửa đường tròn đã cho là

2 2 2

40, 0 40     x y y y x

Nửa đường tròn cắt Parabol tại

(2;6), ( 2;6)MN

Ta có diện tích trồng hoa hồng

40 d 16,87



  



S x x x

Diện tích trồng hoa cúc

2 1 1

.40 20 45,9619

   S S S



Từ đó chi phí trồng các loài hoa theo yêu cầu

.120000 .80000 5.701.000T S S

Câu 49: Trong đợt hội trại “Khi tôi

” được tổ chức tại trường THPT X, Đoàn trường có thực hiện

một dự án ảnh trưng bày trên một pano có dạng parabol như hình vẽ. Biết rằng Đoàn trường

sẽ yêu cầu các lớp gửi hình dự thi và dán lên khu vực hình chữ nhật

ABCD

, phần còn lại sẽ

được trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là

200.000

đồng cho một

bảng.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng

nghìn)?

900.000

đồng. B.

1.232.000

đồng. C.

902.000

đồng. D.

1.230.000

đồng.

Lời giải:

Đặt hệ trục tọa độ như hình vẽ, khi đó phương trình đường parabol có dạng:

y ax b

Parabol cắt trục tung tại điểm

 

0;4

và cắt trục hoành tại

 

2;0

nên:

.2 0























Do đó, phương trình parabol là

4yx  

Diện tích hình phẳng giới hạn bởi đường parabol và trục hoành là

 

4dS x x



  







  







Gọi

 

;0Ct

 

;4B t t

với

02t

Ta có

2CD t

và

4BC t

. Diện tích hình chữ nhật

ABCD

là

.S CD BC

 

2 . 4tt

28tt  

Diện tích phần trang trí hoa văn là

S S S

 

tt   

tt  

Xét hàm số

 

f t t t  

với

02t

Ta có

 

6 8 0f t t



  

 

0;2











  





Bảng biến thiên:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Như vậy, diện tích phần trang trí nhỏ nhất là bằng

96 32 3



, khi đó chi phí thấp nhất

cho việc hoàn tất hoa văn trên pano sẽ là

96 32 3

.200000 902000





đồng.

Câu 50: Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh

và hai đường parabol có các đỉnh lần lượt là

(phần tô đậm của hình vẽ).

Hai đường parabol có cùng trục đối xứng

, đối xứng nhau qua trục

, hai parabol cắt

elip tại các điểm

. Biết

8AB m

6CD m

33MN PQ m

2EF m

. Chi

phí để trồng hoa trên vườn là

300.000

đ/

. Hỏi số tiền trồng hoa cho cả vườn gần nhất với

số tiền nào dưới đây?

A. 4477800 đồng. B. 4477000 đồng. C. 4477815 đồng. D. 4809142 đồng.

Lời giải:

+) Gắn hệ trục tọa độ

Oxy

như hình vẽ với

 

0;0O

 

4;0B

và

 

0;3C

+) Khi đó elip

 

có độ dài trục lớn

8AB 

, độ dài trục bé

6CD 



Phương trình của

 

là:

16 9



+) Do

33PQ 

và

 

QE

, suy ra







. Lại có

 

2 1;0EF F

+) Phương trình parabol

 

đỉnh

có dạng:

1x ky

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

+) Vì parabol

 

đi qua điểm







nên phương trình

 

là:

xy

+) Gọi

là diện tích hình phẳng giới hạn bới các đường

16 , 0, 0, 2

y x y x x    

Ta có

16 d

S x x



 

5.73967 m

+) Gọi

là diện tích hình phẳng giới hạn bới các đường

1, 0, 1, 2

y x y x x    

Ta có

 

1d 1,73205

S x x m  



+) Diện tích trồng hoa là:

 

4 16,0305S S S m  

Vậy số tiền trồng hoa cho cả vườn khoảng

16,0305.300000 4809150

đồng.

____________________HẾT____________________

Huế, 15h15’ Ngày 19 tháng 3 năm 2023

TÍCH PHÂN

LÊ BÁ BẢO

TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ

ỨNG DỤNG TÍNH

DIỆN TÍCH HÌNH PHẲNG (Phần 2)

 LUYỆN THI THPT QUỐC GIA

 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Ngân hàng câu hỏi:

ỨNG DỤNG TÍCH PHÂN TRONG HÌNH HỌC (2)

NỘI DUNG ĐỀ BÀI

Câu 1: Cho hàm số

()y f x

có đồ thị như hình vẽ bên dưới:

Biết diện tích hai phần gạch chéo lần lượt là

5, 12SS

Tính

 

(2 1)d 4 d .



   



I f x x f x x



. B.

. C.

. D.

7

Câu 2: Tính diện tích hình phẳng giới hạn bởi parabol

 

:4P y x

và hai tiếp tuyến của

 

tại

các điểm

,AB

có hoành độ lần lượt là

1

và

. B.

. C.

. D.

Câu 3: Gọi

là diện tích của mặt phẳng giới hạn bởi đường thẳng

y mx

với m < 2 và parabol

 

có phương trình

 

2y x x

. Gọi

là diện tích giới hạn bởi

 

và

. Với giá trị nào của

thì

SS

24

. B.

22

. C.

. D.

Câu 4: Cho hàm số

( ) 4f x ax bx cx   

và

()g x mx nx

có đồ thị cắt nhau tại các điểm có

hoành độ là

1; 1; 2

. Diện tích của hình phẳng giới hạn bởi đồ thị của hai hàm số trên bằng

. B.

. C.

. D.

Câu 5: Cho hàm số bậc ba

 

y f x

có đồ thị là đường cong ở hình bên dưới. Gọi

,xx

lần lượt là

hai điểm cực trị thỏa mãn

2xx

và

   

3 0.f x f x

và đồ thị luôn đi qua

( ; ( ))M x f x

trong đó

1xx

()gx

là hàm số bậc hai có đồ thị qua 2 điểm cực trị và M.

1xx

. Tính tỉ số

(

và

lần lượt là diện tích hai hình phẳng được tạo bởi đồ thị hai

hàm

( ), ( )f x g x

như hình vẽ ).

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

. B.

. C.

. D.

Câu 6: Cho hai hàm số

 

f x ax bx cx   

và

 

1g x dx ex  

 

, , , ,a b c d e

. Biết rằng đồ

thị của hàm số

 

y f x

và

 

y g x

cắt nhau tại ba điểm có hoành độ lần lượt là

3

;

1

;

(tham khảo hình vẽ).

Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

. B.

. C.

. D.

Câu 7: Hình phằng

 

được giới hạn bởi đồ thị

 

của hàm đa thức bậc ba và parabol

 

có

trục đối xứng vuông góc với trục hoành. Phần tô đậm như hình vẽ có diện tích bằng

. B.

. C.

. D.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 8: Cho hàm số

 

0y ax bx c a   

và hàm số

 

0y mx nx p m   

có đồ thị là các

đường cong như hình vẽ bên.

Gọi

là diện tích của hình phẳng được tô đậm. Khẳng định nào sau đây đúng?

62 64

;

15 15









. B.

21 13

;









. C.









. D.

13 67

;

3 15









Câu 9: Trong mặt phẳng

Oxy

, cho parabol

   

:0P y ax bx c a   

và đường thẳng

 

:0d y mx n m  

. Tính diện tích hình phẳng

 

giới hạn bởi

 

và đường thẳng

:4y

như hình vẽ bên.

. B.

. C.

. D.

Câu 10: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số

ye

lnyx

1y x e   

với các

trục tọa độ.

ee

. B.

. C.

ee

. D.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 11: Cho hàm số

 

y f x

có đồ thị là

 

. Biết rằng đồ thị

 

cắt trục tung tại điểm có tung độ

bằng

và đồ thị hàm số

 

y f x





cho bởi hình vẽ bên dưới:

Tính diện tích hình phẳng giới hạn bởi đồ thị

 

và đồ thị hàm số

2 2.

  y x x

17 3

. B.

32 3

. C.

16 3

. D.

14 3

Câu 12: Cho hàm số

 

4 3 2

2f x ax bx cx x   

và

 

2g x mx nx x  

với

, , , ,a c b m n

. Biết hàm

số

   

y f x g x

có ba điểm cực trị là

2; 1;3

. Diện tích hình phẳng giới hạn bởi hai

đường

 

y f x





và

 

y g x





bằng

131

. B.

131

. C.

125

. D.

125

Câu 13: Cho hàm số

     

y f x x x u f u du   



có đồ thị

 

. Khi đó diện tích hình phẳng giới

hạn bởi

 

, trục tung, tiếp tuyến của

 

tại điểm có hoành độ

1x 

là

S 

. C.

S 

. D.

S 

Câu 14: Cho hai hàm số

 

f x ax bx cx d   

   

, , , , ; 0g x ax bx e a b c d e a    

có đồ thị

lần lượt là hai đường cong

   

,CC

ở hình vẽ bên dưới:

Biết diện tích hình phẳng giới hạn bởi hai đồ thị

   

,CC

bằng

tính

   

21fg

26

. B.

24

. C.

28

. D.

30

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 15: Cho đồ thị hàm số bậc ba

 

y f x ax bx x c    

và đường thẳng

 

y g x

có đồ thị

như hình vẽ sau:

Biết

5AB 

, diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

y f x

, trục hoành và hai

đường thẳng

1x 

2x 

bằng

. B.

. C.

. D.

Câu 16: Cho hàm số

 

4 3 2

2f x x ax bx cx d    

 

, , ,a b c d 

có ba điểm cực trị là

1, 1

và 3. Gọi

 

y g x

là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số

 

y f x

. Diện

tích hình phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

bằng

256

. B.

265

. C.

128

. D.

182

Câu 17: Cho hàm số

 

4 3 2

6     y f x x ax bx cx d

 

, , ,a b c d 

. Biết đồ thị hàm số

 

y f x

có

ba điểm cực trị có hoành độ lần lượt là

2;1;2

và hàm số

 

y g x

là hàm bậc hai có đồ thị đi

ba điểm cực trị đó. Diện tích hình phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

thuộc

khoảng nào sau đây?

 

71;72

. B.

 

72;73

. C.

 

73;74

. D.

 

74;75

Câu 18: Cho hai hàm số

 

y f x

và

 

y g x

liên tục trên . Biết hàm số

 



   f x ax bx cx d

 



  g x px qx r

với

,0ap

có đồ thị như hình vẽ. Đồng thời

diện tích giới hạn bởi hai đồ thị hàm số

 



y f x

và

 



y g x

bằng

và

   

1 1 1   fg

. Biết rằng diện tích hình phẳng giới hạn bởi hai đồ thị hàm số

 

y f x

và

 

y g x

bằng

. Giá trị

mn

bằng:

. B.

. C.

. D.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 19: Cho số

 

y f x

có đạo hàm là

 

12 4,f x x x



   

và

 

là một nguyên hàm của

 

   

0 1 0fF

. Tính diện tích hình phẳng

giới hạn bởi đồ thị hàm số

 

y F x

và

trục

S 

. B.

116

S 

. C.

576

S 

. D.

S 

Câu 20: Cho hàm số

   

4 3 2

3 , , ,f x x ax bx cx d a b c d     

có ba điểm cực trị

2,1

và

. Gọi

 

y g x

là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số

 

y f x

. Diện

tích hình phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

có giá trị thuộc khoảng nào

dưới đây?

 

34;35

. B.

 

36;37

. C.

 

37;38

. D.

 

35;36

Câu 21: Cho hàm số bậc ba

 

y f x

có đồ thị là đường cong như hình bên dưới. Biết hàm số

 

đạt cực trị tại hai điểm

,xx

thỏa mãn

2xx

và

   

0.f x f x

Gọi

,SS

là diện

tích của hình phẳng như hình bên và

là diện tích phần tô đậm. Tính tỉ số

. B.

. C.

. D.

Câu 22: Cho hàm số bậc ba

 

có đồ thị như hình vẽ bên. Biết hàm số

 

đạt cực trị tại hai điểm

;xx

thỏa mãn

2xx

và

   

2f x f x

. Gọi

;SS

là diện tích của hai hình phẳng

được cho trong hình vẽ bên. Tính tỉ số

. B.

. C.

. D.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 23: Cho hàm số

 

4y f x x ax bx c     

có đồ thị cắt trục hoành tại ba điểm có hoành độ là

 

3, 1, 1; Fx

là một nguyên hàm của

 

và

 

y g x

là hàm số bậc hai đi qua ba điểm

cực trị của đồ thị hàm số

 

y F x

. Diện tích hình phẳng giới hạn bởi hai đường

 

y F x

và

 

y g x

bằng

128

. B.

. C.

. D.

Câu 24: Cho đường cong

( ): 2C y x kx  

và parabol

:2P y x  

tạo thành hai miền phẳng có

diện tích

như hình vẽ.

Biết rằng

S 

, giá trị của

bằng

. B.

. C.

. D.

Câu 25: Cho hàm số

 

f x ax bx c  

có đồ thị

 

, biết

 

10f 

. Tiếp tuyến

tại điểm có hoành

độ

1x 

của

 

cắt

 

tại hai điểm có hoành độ lần lượt là

và

. Gọi

;SS

là diện tích

hình phẳng ( phần gạch chéo trong hình vẽ). Tính

, biết

401

2022

S 

12431

2022

. B.

5614

1011

. C.

2005

2022

. D.

2807

1011

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 26: Cho hàm số

 

là hàm đa thức bậc bốn, có đồ thị nhận đường thẳng

x 

làm trục đối

xứng. Biết diện tích hình phẳng của phần giới hạn bởi đồ thị hàm số

   

,y f x y f x





và

hai đường thẳng

5, 2xx   

có giá trị là

127

(hình vẽ bên)

Diện tích hình phẳng giới hạn bởi

 

y f x

và trục hoành bằng

. B.

. C.

. D.

Câu 27: Cho hàm số bậc ba

 

y f x

có đồ thị như hình vẽ, biết

 

y f x

đạt cực tiểu tại điểm

1x 

và thỏa mãn

 

1fx

và

 

1fx

lần lượt chia hết cho

 

1x 

và

 

1x 

. Gọi

,SS

lần

lượt là diện tích hình phẳng như trong hình dưới. Tính

2SS

. B.

. C.

. D.

Câu 28: Cho hàm số

 

2f x x ax bx c   

với

,,abc

là các số thực. Biết hàm sồ

( ) ( ) ( ) ( )g x f x f x f x

 

  

có hai giá trị cực trị là

4

và 4. Diện tích hình phẳng giới hạn bởi

các đường

()

( ) 12





và

1y 

bằng

2ln3

. B.

ln3

. C.

ln18

. D.

ln 2

Câu 29: Cho hai hàm số

()fx

và

()gx

liên tục trên và hàm số

()f x ax bx cx d



   

'( )g x qx nx p  

với

,0aq

có đồ thị như hình vẽ. Biết diện tích hình phẳng giới hạn bởi

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

hai đồ thị hàm số

()y f x





và

()y g x





bằng

và

(2) (2)fg

. Biết diện tích hình phẳng

giới hạn bởi hai đồ thị hàm số

()y f x

và

()y g x

bằng

. Tính

T a b

. B.

. C.

5

. D.

Câu 30: Cho hàm số

 

y f x

là hàm bậc bốn có đồ thị như hình bên. Biết diện tích hình phẳng giới

hạn bởi đồ thị hai hàm số

 

y f x

và

 

'y f x

bằng

214

. Tính diện tích hình phẳng giới

hạn bởi đồ thị hàm số

 

y f x

và trục hoành.

. B.

. C.

17334

635

. D.

17334

1270

Câu 31: Cho hàm số bậc ba

 

y f x ax bx x d    

và đường thẳng

 

y g x

có đồ thị như hình

vẽ bên dưới:

Biết

2 65

AB 

diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

y f x

và

 

y g x

bằng

. B.

. C.

. D.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 32: Cho hàm số bậc ba

 

y f x ax x cx d    

và parabol

 

y g x

có đồ thị như hình vẽ.

Biết đồ thị

 

y f x

và

 

y g x

cắt nhau tại ba điểm phân biệt

,,A B C

có hoành độ lần lượt

là

2;1;2

và thỏa mãn

AB 

(tham khảo hình vẽ). Tính diện tích hình phẳng giới hạn bởi

hai đồ thị

 

y f x

và

 

y g x

. B.

238

. C.

. D.

Câu 33: Cho hàm số

 

y f x ax bx c   

. Tiếp tuyến

đi qua điểm

có hoành độ

2x 

cắt đồ

thị hàm số

 

y f x

tại hai điểm khác

có hoành độ lần lượt là

4x 

và

0x 

. Gọi

,SS

lần lượt là diện tích phần gạch sọc (như hình vẽ). Tính tỉ số

. B.

. C.

. D.

Câu 34: Cho hàm số

y x x x   

có đồ thị

 

và đường thẳng

đi qua gốc tọa độ tạo

thành hai miền phẳng có diện tích

và

như hình vẽ

Biết

S 

. Khi đó



, giá trị của

2mn

bằng

143

. B.

50

. C.

. D.

142

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 35: Cho hai hàm số

 

4 3 2

f x ax bx cx dx e    

với

0a 

và

 

3g x px qx  

có đồ thị như

hình vẽ bên dưới. Đồ thị hàm số

 

y f x

đi qua gốc tọa độ và cắt đồ thị hàm số

 

y g x

tại

bốn điểm có hoành độ lần lượt là

2

;

1

;

và

. Tiếp tuyến của đồ thị hàm số

   

y f x g x

tại điểm có hoành độ

2x 

có hệ số góc bằng



. Gọi

 

là hình phẳng

giới hạn bởi đồ thị hai hàm số

 

y f x

và

 

y g x

Diện tích của hình

 

bằng

1553

120

. B.

1553

240

. C.

1553

. D.

1553

Câu 36: Cho hàm số

 

liên tục trên và đường thẳng

   

:d g x ax b

có đồ thị như hình vẽ.

Biết diện tích miền tô đậm bằng

và

 

f x x 



. Tích phân

 

. 2 dx f x x







bằng

607

348



. B.



. C.



. D.



Câu 37: Cho parabol

 

:P y x

và hai điểm

thuộc

 

sao cho

2AB 

. Tìm giá trị lớn nhất

của diện tích hình phẳng giới hạn bởi parabol

 

và đường thẳng

. B.

. C.

. D.

Câu 38: Cho hai hàm số

 

    y f x ax bx cx d

và

 

   y g x mx nx k

cắt nhau tại ba điểm

có hoành độ là

1; ;2



và có đồ thị như hình vẽ.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Biết phần diện tích kẻ sọc (hình

) bằng

. Diện tích phần hình phẳng giới hạn bởi đồ thị

   

,y f x y g x

và hai đường thẳng

xx

(phần bôi đen trong hình vẽ) bằng

. B.

243

. C.

. D.

Câu 39: Gọi

là tập hợp tất cả các giá trị của tham số

để đường thẳng

: 45 2d y m  

cùng với

đồ thị

 

của hàm số

y x mx x   

tạo thành hai miền kín có diện tích lần lượt là

,SS

thỏa mãn

SS

(xem hình vẽ). Số phần tử của tập

là

2

1

9

Câu 40: Cho hàm số

 

f x x ax bx c   

với

,,abc

là các số thực. Biết hàm số

       

g x f x f x f x

 

  

có hai giá trị cực trị là

5

và

. Diện tích hình phẳng giới hạn

bởi các đường

 





và

1y 

bằng

ln3

. B.

ln7

. C.

3ln 2

. D.

ln10

Câu 41: Cho đồ thị hàm số bậc ba

 

y f x ax bx cx d    

và đường thẳng

:d y mx n

như

hình vẽ và

, SS

là diện tích hình phẳng được tô đậm trong hình bên. Biết



với

,pq

là một phân số tối giản. Tính

2022pq

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

2043

. B.

2045

. C.

2049

. D.

2051

Câu 42: Cho hàm số

 

với đồ thị là Parabol đỉnh

có tung độ bằng



và hàm số bậc ba

 

Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ

1 2 3

,,x x x

thoả mãn

1 2 3

18 55x x x 

(hình vẽ).

Diện tích miền tô đậm gần số nào nhất trong các số sau đây?

5,7

. B.

5,9

. C.

6,1

. D.

6,3

Câu 43: Cho hàm số

43y x x

có đồ thị

 

và đường thẳng

đi qua gốc tọa độ tạo thành hai

miền hình phẳng có diện tích

,SS

như hình vẽ bên dưới:

Khi

12S 

thì

bằng

. B.

. C.

875

256

. D.

865

256

Câu 44: Cho hàm số bậc ba

 

y f x

có đồ thị

 

như hình vẽ.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Biết rằng đồ thị hàm số đã cho cắt trục

tại ba điểm có hoành độ

1 2 3

,,x x x

theo thứ tự lập

thành cấp số cộng và

23xx

. Diện tích hình phẳng giới hạn bởi

 

và trục

là

diện tích

của hình phẳng giới hạn bởi các đường

 

1y f x

 

1y f x  

xx

và

xx

bằng

. B.

. C.

2 4 3S 

. D.

23S 

Câu 45: Một miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất

bằng 2 đoạn thẳng song song

,AB CD

thành ba phần có diện tích bằng nhau (xem hình vẽ

bên dưới). Tỉ số

bằng:

. B.

1 2 2

. C.

. D.

12

Câu 46: Ông X muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên, biết đường cong

phía trên là một Parabol, chất liệu làm là inox. Giá

vật tư và công làm là

1.300.000

đồng.

Hỏi ông X phải trả bao nhiêu tiền để làm cái cửa sắt như vậy (làm tròn đến hàng nghìn).

13.050.000

đồng. B.

36.630.000

đồng. C.

19.520.000

đồng. D.

21.077.330

đồng.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 47: Một mảnh đất hình chữ nhật có chiều dài

60m

, chiều rộng

20m

. Người ta muốn trồng cỏ ở

hai đầu của mảnh đất hai hình bằng nhau giới hạn bởi hai đường Parabol có hai đỉnh cách

nhau

40m

(như hình vẽ).

Phần còn lại của mảnh đất người ta lát gạch với chi phí là

200.000dm

. Tính tổng số tiền để

lát gạch ( làm tròn đến hàng nghìn)

133.334.000

đồng. B.

213.334.000

đồng. C.

53.334.000

đồng. D.

186.667.000

đồng.

Câu 48: Trên bức tường cần trang trí một hình phẳng dạng paranol đỉnh

như hình vẽ, biết

4 mOS AB

là trung điểm của

. Parabol trên được chia thành ba phần để sơn ba

màu khác nhau với mức chi phí: phần trên là phần kẻ sọc 140000 đồng/

, phần giữa là hình

quạt tâm

, bán kính

2 m

được tô đậm 150000 đồng/

, phần còn lại 160000 đồng/

Tổng chi phí để sơn cả 3 phần gần nhất với số nào sau đây?

A. 1.597.000 đồng. B. 1.625.000 đồng. C. 1.575.000 đồng. D. 1.600.000 đồng.

Câu 49: Hướng tới kỉ niệm ngày thành lập trường Đoàn TNCS Hồ Chí Minh. Khối

thiết kế bồn

hoa gồm hai Elip bằng nhau có độ dài trục lớn bằng

và độ dài trục nhỏ bằng

đặt

chồng lên nhau sao cho trục lớn của Elip này trùng với trục nhỏ của Elip kia và ngược lại

(như hình vẽ).

Phần diện tích nằm trong đường tròn đi qua

giao điểm của hai Elip dùng để trồng cỏ,

phần diện tích bốn cánh hoa nằm giữa hình tròn và Elip dùng để trồng hoa. Biết kinh phí để

trồng hoa là

150.000

đồng

/1m

, kinh phí để trồng cỏ là

100.000

đồng

/1m

. Tổng số tiền dùng

để trồng hoa và trồng cỏ cho bồn hoa gần với số nào nhất trong các số sau?

4.100.000

đồng. B.

4.550.000

đồng. C.

3.100.000

đồng. D.

4.300.000

đồng.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 50: Một công ty có ý định thiết kế một logo hình vuông có độ dài nửa đường chéo bằng 4. Biều

tượng 4 chiếc lá (được tô màu) được tạo thành bởi các đường cong đối xứng với nhau qua

tâm của hình vuông và qua các đường chéo.

Một trong số các đường cong ở nửa bên phải của logo là một phần của đồ thị hàm số bậc ba

dạng

y ax bx x  

với hệ số

0a 

. Để kỷ niệm ngày thành lập

2/3

, công ty thiết kế để tỉ

số diện tích được tô màu so với phần không được tô màu bằng

. Tính

ab

. B.

. C.

. D.

____________________HẾT____________________

Huế, 15h15’ Ngày 19 tháng 3 năm 2023

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

LỜI GIẢI CHI TIẾT

Câu 1: Cho hàm số

()y f x

có đồ thị như hình vẽ bên dưới:

Biết diện tích hai phần gạch chéo lần lượt là

5, 12SS

Tính

 

(2 1)d 4 d .



   



I f x x f x x



. B.

. C.

. D.

7

Lời giải:

Ta có

( ) 5, ( ) 12f x dx S f x dx S



     



Vậy

 

1 0 1 4

0 3 1 1

1 1 19

(2 1) 4 ( ) ( ) .5 12

2 2 2

I f x dx f x dx f x dx f x dx



         

   

Câu 2: Tính diện tích hình phẳng giới hạn bởi parabol

 

:4P y x

và hai tiếp tuyến của

 

tại

các điểm

,AB

có hoành độ lần lượt là

1

và

. B.

. C.

. D.

Lời giải:

+ 3

+ 4

= 2

+ 3

Xét hàm số

42y x y x



   

Ta có

   

1;5 , 1;5AB

là hai điểm thuộc

 

+) Tiếp tuyến của

 

tại

 

1;5A 

là:

 

2 1 5 2 3y x y x       

+) Tiếp tuyến của

 

tại

 

1;5B

là:

 

2 1 5 2 3y x y x     

Hoành độ giao điểm của hai đồ thị hàm số

2 3, 2 3y x y x    

là nghiệm của phương

trình:

2 3 2 3 0x x x     

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Khi đó diện tích hình phẳng giới hạn bởi

 

và hai tiếp tuyến của

 

tại

,AB

là:

   

2 2 3 2 3 2

1 1 2

4 2 3 d 4 2 3 d

3 3 3

S x x x x x x x x x x x x



   

              

   

   



Câu 3: Gọi

là diện tích của mặt phẳng giới hạn bởi đường thẳng

y mx

với m < 2 và parabol

 

có phương trình

 

2y x x

. Gọi

là diện tích giới hạn bởi

 

và

. Với giá trị nào của

thì

SS

24

. B.

22

. C.

. D.

Lời giải:

* Tính

Phương trình hoành độ giao điểm

 





  







Do đó

S x x x  



* Tính

Phương trình hoành độ giao điểm

 

2 2 0

mx x x x m x





      







Do đó

 

   

2 d 2 d

3 2 6

m x m

S x x mx x x m x x









          







 

1 1 4

. 2 4

2 6 2 3

S S m



     

Câu 4: Cho hàm số

( ) 4f x ax bx cx   

và

()g x mx nx

có đồ thị cắt nhau tại các điểm có

hoành độ là

1; 1; 2

. Diện tích của hình phẳng giới hạn bởi đồ thị của hai hàm số trên bằng

. B.

. C.

. D.

Lời giải:

Do hàm số

()fx

và

()gx

có đồ thị cắt nhau các điểm có hoành độ là

1; 1; 2

, nên

( ) ( )f x g x

là hàm số bậc ba.

Suy ra ta có:

( ) ( ) .( 1)( 1)( 2)f x g x k x x x    

Mặt khác ta có:

(0) (0) 4 2f g k   

( ) ( ) 2( 1)( 1)( 2) 2 4 2 4f x g x x x x x x x         

Vậy ta có diện tích là

( ) ( ) 2 4 2 4 dS f x g x dx x x x x



     



3 2 3 2

16 5 37

(2 4 2 4)d (2 4 2 4)d

3 6 6

x x x x x x x x



          



Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 5: Cho hàm số bậc ba

 

y f x

có đồ thị là đường cong ở hình bên dưới. Gọi

,xx

lần lượt là

hai điểm cực trị thỏa mãn

2xx

và

   

3 0.f x f x

và đồ thị luôn đi qua

( ; ( ))M x f x

trong đó

1xx

()gx

là hàm số bậc hai có đồ thị qua 2 điểm cực trị và M.

1xx

. Tính tỉ số

(

và

lần lượt là diện tích hai hình phẳng được tạo bởi đồ thị hai

hàm

( ), ( )f x g x

như hình vẽ ).

. B.

. C.

. D.

Lời giải:

Nhận thấy hình phẳng trên có diện tích không đổi khi ta tịnh tiến đồ thị sang trái sao cho

0x 

Khi đó ta có

1, 3,xx

Xét hàm

()f x ax bx cx d   

và

g( )x mx nx p  

Vì

1, 3,xx

là các điểm cực trị nên ta có:

(1) 0 3 2 0

(1)

(3) 0 27 6 0

f a b c



   









   



Hơn nữa, ta có

(1) 3 (3) 27 9 3 .(2)f f a b c d a b c d        

Từ (1) và(2) suy ra

















Mặt khác dựa vào đồ thị ta thấy:

(0) (0) 2

(1) 3 (3) 2

(0) (3) 3

g f p a

g g m a

g g n a







   





  



Suy ra

( ) ( 6 9 2)f x a x x x   

g( ) ( 2 6 2)x a x x   

Khi đó ta có:

S a x x xdx a   



S a x x xdx a   



Do đó,



Câu 6: Cho hai hàm số

 

f x ax bx cx   

và

 

1g x dx ex  

 

, , , ,a b c d e

. Biết rằng đồ

thị của hàm số

 

y f x

và

 

y g x

cắt nhau tại ba điểm có hoành độ lần lượt là

3

;

1

;

(tham khảo hình vẽ).

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

. B.

. C.

. D.

Lời giải:

Diện tích hình phẳng cần tìm là

       

ddS f x g x x g x f x x





   

   

   



       

3 2 3 2

ax b d x c e x x ax b d x c e x x





   

           

   

   



Trong đó phương trình

   

ax b d x c e x     

 

là phương trình hoành độ giao

điểm của hai đồ thị hàm số

 

y f x

và

 

y g x

Phương trình

 

có nghiệm

3

;

1

;

nên

   

27 9 3 0

a b d c e



      



      





     





   

27 9 3

a b d c e



     



      





    





 







  





  





Vậy

3 2 3 2

1 3 1 3 1 3 1 3

2 2 2 2 2 2 2 2

S x x x x x x x x





   

       

   

   



 

2 2 4   

Câu 7: Hình phằng

 

được giới hạn bởi đồ thị

 

của hàm đa thức bậc ba và parabol

 

có

trục đối xứng vuông góc với trục hoành. Phần tô đậm như hình vẽ có diện tích bằng

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

. B.

. C.

. D.

Lời giải:

Giả sử

   

:0C y ax bx cx d a    

Vì

 

đi qua các điểm

   

1; 2 , 0;2AB

   

1;0 , 2; 2CD

,ta có hệ phương trình:

 

: 3 2

8 4 2 2 2

a b c d a

C y x x

a b c d c

a b c d d

      





  



    



    



     



Giả sử

   

:0P y mx nx q m   

Vì

 

đi qua các điểm

   

1; 2 , 1;0AE

 

2; 2D 

,ta có hệ phương trình:

 

0 1 :

4 2 2 0

m n q m

m n q n P y x x

m n q q

     





        





    



Dựa vào đồ thị của

 

và

 

,ta có diện tích hình phẳng cần tìm là:

   

3 2 2 2 3 2

3 2 3 2

2 2 2 2 .

S x x x x dx x x x x dx

x x x dx x x x dx



   

            

   

   

         

   



Câu 8: Cho hàm số

 

0y ax bx c a   

và hàm số

 

0y mx nx p m   

có đồ thị là các

đường cong như hình vẽ bên.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Gọi

là diện tích của hình phẳng được tô đậm. Khẳng định nào sau đây đúng?

62 64

;

15 15









. B.

21 13

;









. C.









. D.

13 67

;

3 15









Lời giải:

Từ đồ thị ta thấy đồ thị hàm hàm số

 

y f x ax bx c   

đi qua các điểm

 

1;3A

 

0;2B

và đạt cực trị tại

1x 

 

0 2 2

4 2 0

abc





  





   





























 

22f x x x    

Từ đồ thị ta lại thấy đồ thị hàm số

 

y g x mx nx p   

đi qua các điểm

 

0; 1C 

 

1;3A

và

 

1;3D 

 

1 3 3 4 4 1

f m n p m g x x

m n p n





   







          

  

  

   







Diện tích hình phẳng được tô đậm là

   

4 2 2

2 2 4 1 dS x x x x





     





 

2 3 dx x x



   



2 64

5 3 15





    





Câu 9: Trong mặt phẳng

Oxy

, cho parabol

   

:0P y ax bx c a   

và đường thẳng

 

:0d y mx n m  

. Tính diện tích hình phẳng

 

giới hạn bởi

 

và đường thẳng

:4y

như hình vẽ bên.

. B.

. C.

. D.

Lời giải:

Từ đồ thị ta thấy parabol

   

:0P y ax bx c a   

đi qua các điểm

 

2;4A

và có đỉnh là

 

0;0O

4 2 4 0

a b c b







     









yx

Từ đồ thị ta lại thấy đường thẳng

 

:0d y mx n m  

đi qua các điểm

 

2;0B

và

 

0;2C

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

2 0 1

m n m

   











2yx   

Diện tích hình phẳng

 

là:

 

4 2 d 4 dS x x x x     



 

2 d 4 dx x x x   



2 3 6

   

    

   

   

Câu 10: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số

ye

lnyx

1y x e   

với các

trục tọa độ.

ee

. B.

. C.

ee

. D.

Lời giải:

Vì hàm

ye

đồng biến và hàm

1y x e   

nghịch biến, nên phương trình

e x e   

có nghiệm duy nhất

1x 

Tương tự hàm

lnyx

đồng biến và hàm

1y x e   

nghịch biến, nên phương trình

ln 1x x e   

có nghiệm duy nhất

xe

Diện tích hình phẳng cần tính là

   

0 1 0 1

d ln 1 d d 1 ln d

S e x x x e x e x x e x x           

   

 

1 ln d

e e x x x



     







   

1 ln

e x x x



     





ee



Câu 11: Cho hàm số

 

y f x

có đồ thị là

 

. Biết rằng đồ thị

 

cắt trục tung tại điểm có tung độ

bằng

và đồ thị hàm số

 

y f x





cho bởi hình vẽ bên dưới:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Tính diện tích hình phẳng giới hạn bởi đồ thị

 

và đồ thị hàm số

2 2.

  y x x

17 3

. B.

32 3

. C.

16 3

. D.

14 3

Lời giải:

Từ đồ thị của hàm số

 

y f x





ta có

     

11f x a x x



  

       

0 2 2 2 1 1 2 2 2 2f a f x x x x x x



           

Ta có

   

 

3 2 2

2 2 2 2 2

f x f x dx x x x dx x x C



         



Mà

   

1 1 2 1

2 2 2 3 2

f C f x x x        

Phương trình hoành độ giao điểm của đồ thị

 

và đồ thị hàm số

y x x  

là:

4 3 4

2 3 2 4 2

2 1 2 3

2 2 2 0 2 3 0 3

2 3 2 3 2 2

x x x

x x x x x x x x                 

Diện tích hình phẳng giới hạn bởi đồ thị

 

và đồ thị hàm số

y x x  

là:

3 16 3

2 2 5

S x dx



   



Câu 12: Cho hàm số

 

4 3 2

2f x ax bx cx x   

và

 

2g x mx nx x  

với

, , , ,a c b m n

. Biết hàm

số

   

y f x g x

có ba điểm cực trị là

2; 1;3

. Diện tích hình phẳng giới hạn bởi hai

đường

 

y f x





và

 

y g x





bằng

131

. B.

131

. C.

125

. D.

125

Lời giải:

+ Ta có:

         

4 3 2 4. 1f x g x ax b m x c n x



      

+ Mặt khác, vì hàm số

   

y f x g x

có ba điểm cực trị là

2; 1;3

nên

         

2 1 3 2f x g x a x x x



    

+ Từ

   

1 , 2

suy ra:

aa    

. Do đó:

       

2 1 3

f x g x x x x





    

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Vậy diện tích hình phẳng là

       

2 131

2 1 3

S f x g x dx x x x dx







      



Câu 13: Cho hàm số

     

y f x x x u f u du   



có đồ thị

 

. Khi đó diện tích hình phẳng giới

hạn bởi

 

, trục tung, tiếp tuyến của

 

tại điểm có hoành độ

1x 

là

S 

. C.

S 

. D.

S 

Lời giải:

Hàm số

 

có dạng

 

f x x ax b  

, với

()a f u du



và

( ) .b uf u du



432





  

















  







Suy ra

 

5 ; ( ) 2 5.

f x x x f x x



    

 

1; ; (1) 3.

M C f





   





Phương trình tiếp tuyến của

 

tại

 

41 23

3 1 3 .

y x x      

Diện tích hình phẳng cần tìm là:

 

17 23 1

5 3 2 1 .

6 6 3

S x x x dx x x dx



         







Câu 14: Cho hai hàm số

 

f x ax bx cx d   

   

, , , , ; 0g x ax bx e a b c d e a    

có đồ thị

lần lượt là hai đường cong

   

,CC

ở hình vẽ bên dưới:

Biết diện tích hình phẳng giới hạn bởi hai đồ thị

   

,CC

bằng

tính

   

21fg

26

. B.

24

. C.

28

. D.

30

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Lời giải:

Ta có:

 

32f x ax bx c



  

Dựa vào đồ thị, ta có:

    

3 1 3f x a x x



  

6 ; 9b a c a   

Ta có:

   

11f g d e c   

và

   

34 14 12 6 6 18

        



S f x g x dx a b c d e

17 7 3 4 9 12

17 7 3 4 18

  





        





   



b a a

a b c c a b

a b c c

   

3 2 2

2 12 18 18; 2 12        f x x x x e g x x x e

 

   

2 14

2 1 28

1 14







     



  





Câu 15: Cho đồ thị hàm số bậc ba

 

y f x ax bx x c    

và đường thẳng

 

y g x

có đồ thị

như hình vẽ sau:

Biết

5AB 

, diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

y f x

, trục hoành và hai

đường thẳng

1x 

2x 

bằng

. B.

. C.

. D.

Lời giải:

Gọi

   

0g x mx m

. Ta có

 

1;Am

;

 

2;2Bm

Khi đó

 

9 9 5

m tm

AB m







   









Ta có

   

0f x g x ax bx x c     

Mặt khác

 

3 2 2

12ax bx x c a x x     

3 2 3 2

22ax bx x c ax ax ax a       

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Đồng nhất hệ số ta đươc

1a 

2b 

2c 

. Vậy

 

y f x x x x    

Diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

y f x

, trục hoành và hai đường thẳng

1x 

2x 

bằng

1 19

2 2 d .

3 12

S x x x x



    







Câu 16: Cho hàm số

 

4 3 2

2f x x ax bx cx d    

 

, , ,a b c d 

có ba điểm cực trị là

1, 1

và 3. Gọi

 

y g x

là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số

 

y f x

. Diện

tích hình phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

bằng

256

. B.

265

. C.

128

. D.

182

Lời giải:

Ta có

     

 

' 8 1 1 3 8 3 3f x x x x x x x       

 

4 3 2

2 8 4 24f x x x x x d     

Ta có

     

' . 1 8 16 6

f x f x x x x d     

Giả sử

 

i i i

A x y

là điểm cực trị của đồ thị hàm số

 

y f x

thì

 

8 16 6

i i i i

y f x x x d     

Do đó đồ thị hàm số bậc hai qua ba điểm cực trị của đồ thị hàm số

 

y f x

là

 

8 16 6y g x x x d     

Khi đó

   

4 3 2

2 8 4 8 6 0 1

f x g x x x x x x







        







Diện tích hình phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

bằng

   

256

S f x g x x



  



Câu 17: Cho hàm số

 

4 3 2

6     y f x x ax bx cx d

 

, , ,a b c d 

. Biết đồ thị hàm số

 

y f x

có

ba điểm cực trị có hoành độ lần lượt là

2;1;2

và hàm số

 

y g x

là hàm bậc hai có đồ thị đi

ba điểm cực trị đó. Diện tích hình phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

thuộc

khoảng nào sau đây?

 

71;72

. B.

 

72;73

. C.

 

73;74

. D.

 

74;75

Lời giải:

Ta có

 

' ' 24 3 2    y f x x ax bx c

Do đồ thị hàm số

 

y f x

có ba điểm cực trị có hoành độ

2;1;2

nên phương trình

 

'0fx

có ba nghiệm phân biệt

2;1;2

Suy ra

       

' 24 2 1 2 ' 24 24 96 96f x x x x f x x x x        

 

4 3 2

6 8 48 96f x x x x x d     

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Ta có

     

' 26 64 8 26 64 8

4 12

f x x f x x x d g x x x d



           





Vậy diện tích hình phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

là

   

S f x g x dx







   

4 3 2 2

6 8 48 96 26 64 8 74,63.



          



x x x x d x x d dx

Câu 18: Cho hai hàm số

 

y f x

và

 

y g x

liên tục trên . Biết hàm số

 



   f x ax bx cx d

 



  g x px qx r

với

,0ap

có đồ thị như hình vẽ. Đồng thời

diện tích giới hạn bởi hai đồ thị hàm số

 



y f x

và

 



y g x

bằng

và

   

1 1 1   fg

. Biết rằng diện tích hình phẳng giới hạn bởi hai đồ thị hàm số

 

y f x

và

 

y g x

bằng

. Giá trị

mn

bằng:

. B.

. C.

. D.

Lời giải:

Dựa vào đồ thị

      



    f x g x a x x x

và

0a

Theo đề

     

2 1 d 2 1 dS a x x x x a x x x x



     



2 . 4

aa   

Ta có:

      

d 4 2 1 df x g x x x x x x





   





   

4 3 2

44f x g x x x x C     

Theo đề:

       

1 1 1 1 1 1f g f g        

1 1 4 4 0CC      

   

 

4 3 2 2 2 2

4 4 4 4 2f x g x x x x x x x x x         

Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số

 

y f x

và

 

y g x

 

S x x x



   



Vậy giá trị

31mn

Câu 19: Cho số

 

y f x

có đạo hàm là

 

12 4,f x x x



   

và

 

là một nguyên hàm của

 

   

0 1 0fF

. Tính diện tích hình phẳng

giới hạn bởi đồ thị hàm số

 

y F x

và

trục

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

S 

. B.

116

S 

. C.

576

S 

. D.

S 

Lời giải:

+) Ta có:

   

 

d 12 4 d 4 4f x f x x x x x x C



     



 

00f 

nên

0C 

, suy ra

 

44f x x x

   

 

3 4 2

d 4 4 d 2F x f x x x x x x x C     



 

10F 

nên

3C 

, suy ra

 

23F x x x  

+) Xét phương trình

2 3 0





   







Diện tích hình phẳng cần tìm là

2 3d

S x x x



   



Câu 20: Cho hàm số

   

4 3 2

3 , , ,f x x ax bx cx d a b c d     

có ba điểm cực trị

2,1

và

. Gọi

 

y g x

là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số

 

y f x

. Diện

tích hình phẳng giới hạn bởi hai đường

 

y f x

và

 

y g x

có giá trị thuộc khoảng nào

dưới đây?

 

34;35

. B.

 

36;37

. C.

 

37;38

. D.

 

35;36

Lời giải:

Theo bài ra, ta có:

     

 

12 2 1 2 12 4 4f x x x x x x x



       

 

4 3 2

3 4 24 48 .f x x x x x d     

Khi đó

     

2 112, 1 23, 2 16f d f d f d      

Giả sử

 

g x mx nx p  

Theo bài ra, ta có:

 

2 4 2 112 4 2 112

1 23 23 32

2 4 2 16 4 2 16

g m n p d m n p d

g m n p d m n p d n

g m n p d m n p d

          











           

  

  



        





Do vậy,

   

4 3 2 2 4 3 2

3 4 24 48 13 32 3 4 11 16 4f x g x x x x x d x x p x x x x             

Suy ra

   

f x g x









  













Vậy

 

4 3 2

3 4 11 16 4 d 37,31358 37;38 .S x x x x x



      



Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Câu 21: Cho hàm số bậc ba

 

y f x

có đồ thị là đường cong như hình bên dưới. Biết hàm số

 

đạt cực trị tại hai điểm

,xx

thỏa mãn

2xx

và

   

0.f x f x

Gọi

,SS

là diện

tích của hình phẳng như hình bên và

là diện tích phần tô đậm. Tính tỉ số

. B.

. C.

. D.

Lời giải:

+ Tịnh tiến đồ thị hàm số

 

y f x

sang phải một đoạn

xx



đơn vị ta thu được đồ thị

hàm số bậc 3

 

y g x

nhận gốc toa độ làm tâm đối xứng nên

 

là hàm lẻ có

dạng

 

g x ax bx

và hàm số

 

có hai điểm cực trị là

1x 

và

1.x 

Có:

   

3 1 3 0 3 .g x ax b g a b b a



         

Suy ra:

 

3.g x a x x

+ Tịnh tiến đồ thị hàm số

 

y h x

sang phải một đoạn

xx



đơn vị ta thu được đồ thị

hàm bậc nhất

 

y k x

có đồ thị là đường thẳng đi qua gốc tọa độ, điểm

 

;











hay

 

1; .Aa

Phương trình đường thẳng

 

y k x

là

y ax

Ta có:

     

1 2 1

1 . 1 .

S g x dx a S g S a



       



Phương trình hoành độ giao điểm của

 

và

 

là:

 

ax a x x x







   







   

3 4 4 .S a x x x dx a x x dx a     



Vậy:

4 16



Câu 22: Cho hàm số bậc ba

 

có đồ thị như hình vẽ bên. Biết hàm số

 

đạt cực trị tại hai điểm

;xx

thỏa mãn

2xx

và

   

2f x f x

. Gọi

;SS

là diện tích của hai hình phẳng

được cho trong hình vẽ bên. Tính tỉ số

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

. B.

. C.

. D.

Lời giải:

Gọi

là hoành độ điểm uốn

của đồ thị hàm số

 

y f x

. Do

 

đạt cực trị tại hai điểm

;xx

thỏa mãn

2xx

1 0 2 0

1x x x x    

Cố định đồ thị hàm số

 

, tịnh tiến hệ toạ độ

Oxy

theo véc tơ

. Khi đó, trong hệ toạ độ

mới

;SS

không thay đổi so với hệ toạ độ cũ.

Trong hệ toạ độ

Oxy

mới, đường cong là đồ thị của hàm số bậc ba

 

y g x

. Từ hình vẽ suy

 



là tam thức bậc hai có nghiệm

1; 1xx  

    

 

1 1 1 0g x a x x a x a



      

 

g x a x b



   





Đồ thị hàm số

 

y g x

đi qua điểm

 

0;0O

nên

0b 

 

g x a x



  





Ta có:

3 4 2

3 12 2 12

x x x a

S a x x a



   

    

   



   



 

3 3 4 2

1 d d

3 3 3 12 2 3 4

x x a x x x a

S a x g x a x x a

   

     

         

   

     

     

   



Vậy



Câu 23: Cho hàm số

 

4y f x x ax bx c     

có đồ thị cắt trục hoành tại ba điểm có hoành độ là

 

3, 1, 1; Fx

là một nguyên hàm của

 

và

 

y g x

là hàm số bậc hai đi qua ba điểm

cực trị của đồ thị hàm số

 

y F x

. Diện tích hình phẳng giới hạn bởi hai đường

 

y F x

và

 

y g x

bằng

128

. B.

. C.

. D.

Lời giải:

Vì hàm số

 

4y f x x ax bx c     

có đồ thị cắt trục hoành tại ba điểm có hoành độ là

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

3, 1, 1

nên ta có hệ phương trình

9 3 108 12

4 12

a b c a

a b c b

a b c c

     





     





   



hay

 

4 12 4 12y f x x x x     

Ta có

 

3 2 4 3 2

4 12 4 12 d 4 2 12F x x x x x x x x x C          



Mặt khác ta có

   

4 8 3

F x x f x x x C



     





do vậy

 

4 8 3y g x x x C    

là

hàm số bậc hai đi qua 3 điểm cực trị của đồ thị hàm số

 

y F x

Xét phương trình hoành độ giao điểm của hai đồ thị hàm số

 

y F x

và

 

y g x

ta có:

    

4 3 2 2 4 3 2

4 2 12 4 8 3 4 2 4 3 0

1 0 1

1 1 3 0 1 0 1

3 0 3

x x x x C x x C x x x x

x x x x x

               

  





           



   



Khi đó

   

432

d 4 2 4 3dS F x g x x x x x x x



       



   

4 3 2 4 3 2

4 2 4 3 d 4 2 4 3 d

2 3 2 3

5 3 5 3

x x x x x x x x x x

x x x x x x x x









           

   



         

   

   



17 27 47 17 128

15 5 15 15 15

     

Vậy diện tích hình phẳng giới hạn bởi hai đường

 

y F x

và

 

y g x

bằng

128

Câu 24: Cho đường cong

( ): 2C y x kx  

và parabol

:2P y x  

tạo thành hai miền phẳng có

diện tích

như hình vẽ.

Biết rằng

S 

, giá trị của

bằng

. B.

. C.

. D.

Lời giải:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Phương trình hoành độ giao điểm của

()C

và

 

3 2 2

2 2 0

x kx x x x x k

x x k





         



  



Hai đồ thị cắt nhau tại ba điểm phân biệt nên phương trình

0x x k  

có hai nghiệm phân

biệt

khác

và thỏa mãn

0xx

. Do đó ta có

k x x







  





  



Trên đoạn

[ ;0]x

3 2 3 2

2 2 0x kx x x x kx        

. Theo bài ra, diện tích

S 

nên

 

4 3 2

3 2 3 2

8 8 8

3 3 4 3 2 3

x x kx

xxx kx x kxxx



      





   



   

4 3 2 4 3 2 2

1 1 1 1 1 1 1 1

3 4 6 32 3 4 6 32 x x kx x x x x x           

 

4 3 3 2

1 1 1 1 1 1 1

3 2 32 0 ( 2) 3 4 8 16 0 2x x x x x x x            

Với

2 2, 1x k x     

và

2 0, [0;1]x x x x    

, ta có

 

3 2 2 1

2 d .

4 3 12

S x x x x x



        







Câu 25: Cho hàm số

 

f x ax bx c  

có đồ thị

 

, biết

 

10f 

. Tiếp tuyến

tại điểm có hoành

độ

1x 

của

 

cắt

 

tại hai điểm có hoành độ lần lượt là

và

. Gọi

;SS

là diện tích

hình phẳng ( phần gạch chéo trong hình vẽ). Tính

, biết

401

2022

S 

12431

2022

. B.

5614

1011

. C.

2005

2022

. D.

2807

1011

Lời giải:

Giả sử tiếp tuyến

có phương trình

 

y g x mx n  

Tiếp tuyến

tại điểm có hoành độ

1x 

của

 

cắt

 

tại hai điểm có hoành độ lần lượt

là

và

, nên ta có:

       

1 2 , 0.f x g x a x x x a    

Theo giả thiết:

   

401 401

2022 2022



   



S f x g x dx

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

   

401 401 2005

2022 5 2022 2022



       



a x x x dx a

Do đó:

       

2005 5614

1 2 .

2022 1011

S f x g x dx x x x dx



       







Câu 26: Cho hàm số

 

là hàm đa thức bậc bốn, có đồ thị nhận đường thẳng

x 

làm trục đối

xứng. Biết diện tích hình phẳng của phần giới hạn bởi đồ thị hàm số

   

,y f x y f x





và

hai đường thẳng

5, 2xx   

có giá trị là

127

(hình vẽ bên)

Diện tích hình phẳng giới hạn bởi

 

y f x

và trục hoành bằng

. B.

. C.

. D.

Lời giải:

Đặt

     

5 2 , 0f x k x x k   

Khi đó

            

2 5 2 2 5 2 5 2 4 14f x k x x k x x k x x x



         

Xét hàm

        

 

5 2 3 4g x f x f x k x x x x



      

Suy ra

 























Từ đó ta suy ra:

     

2 4 2

5 5 4

  

  

  

g x dx g x dx g x dx

  

 

  

 

5 2 3 4 5 2 3 4



          



k x x x x dx k x x x x dx

23 52 127 127 1

10 5 10 50 5

k k k k     

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Vậy

     

1 81

5 50

S f x dx x x dx



    



Câu 27: Cho hàm số bậc ba

 

y f x

có đồ thị như hình vẽ, biết

 

y f x

đạt cực tiểu tại điểm

1x 

và thỏa mãn

 

1fx

và

 

1fx

lần lượt chia hết cho

 

1x 

và

 

1x 

. Gọi

,SS

lần

lượt là diện tích hình phẳng như trong hình dưới. Tính

2SS

. B.

. C.

. D.

Lời giải:

Theo bài ra, ta có:

      

1 1, 0f x ax b x a    

           

0 0 1 1 1 1 1 1 1 2f b f x ax x f x ax x             

           

1 1 1 5 1 8 4 1 2 2 1f x a x a x a x a          

        

1 1 3

1 1 2 1 0 2 1 1

2 2 2

f x x a a f x x x



            

Vậy

3 3 3 1 1

2 2 1 d d

2 2 4 2 4

x x x x

S S x x





      







Câu 28: Cho hàm số

 

2f x x ax bx c   

với

,,abc

là các số thực. Biết hàm sồ

( ) ( ) ( ) ( )g x f x f x f x

 

  

có hai giá trị cực trị là

4

và 4. Diện tích hình phẳng giới hạn bởi

các đường

()

( ) 12





và

1y 

bằng

2ln3

. B.

ln3

. C.

ln18

. D.

ln 2

Lời giải:

Ta có:

       

3 2 2

2 6 2 12 2 12f x x ax bx c f x x ax b f x x a f x

  

            

Ta lại có

     

( ) 12 12

()

( ) 12 ( ) 12 12

f x g x f x f x

g x g x f x f x f x

 

    

  

 

    

   

     

   

()

1 0 0 12 0

( ) 12 12

f x f x

g x f x f x f x

 

  

 

       

 

   

Ta có

( ) ( ) ( ) ( ) ( ) ( ) 12g x f x f x f x f x f x

     

     

Suy ra:

 

   

     

 

()

12 12 12

f x f x g x

g x f x f x f x g x

  

   

  

 

    

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Gọi

,xx

là 2 nghiệm của

( ) 0gx





Khi và chỉ khi

,xx

là 2 nghiệm của

   

12 0f x f x

 

  

Theo giả thiết ta có

 

( ) 4















 

2 2 2

1 1 1

ln 12 |

12 12 12

x x x

d g x

g x g x

S dx dx g x

g x g x g x





    

  

  

 

ln ln ln ln 2

16 2







   







Câu 29: Cho hai hàm số

()fx

và

()gx

liên tục trên và hàm số

()f x ax bx cx d



   

'( )g x qx nx p  

với

,0aq

có đồ thị như hình vẽ. Biết diện tích hình phẳng giới hạn bởi

hai đồ thị hàm số

()y f x





và

()y g x





bằng

và

(2) (2)fg

. Biết diện tích hình phẳng

giới hạn bởi hai đồ thị hàm số

()y f x

và

()y g x

bằng

. Tính

T a b

. B.

. C.

5

. D.

Lời giải:

Dựa vào đồ thị ta có:

   

 

( ) '( ) 1 2 3 2f x g x a x x x a x x x



      

, với

0a 

Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số

()y f x





và

()y g x





bằng:

 

( ) ( ) 3 2 5

f x g x a x x x a



      



. Suy ra

( ) '( ) 5 15 10f x g x x x x



   

Mặt khác,

     

( ) '( )f x g x ax b q x c n x d p



       

Do đó:







  













Ta có

4 3 2

()

4 3 2

f x x x x dx r    

()

g x x x px s   

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

●

       

(2) (2) 20 2 2 0

f g b q c n d p r s          

Thế vào ta được

0rs

●

   

4 3 2

b q c n

f x g x x x x d p x r s



        

4 3 2

5 5 0

x x x





    







Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số

()y f x

và

()y g x

bằng:

   

4 3 2

d 5 5 d .

f x g x x x x x x    



Suy ra

4, 3ab

. Vậy

7T a b  

Câu 30: Cho hàm số

 

y f x

là hàm bậc bốn có đồ thị như hình bên. Biết diện tích hình phẳng giới

hạn bởi đồ thị hai hàm số

 

y f x

và

 

'y f x

bằng

214

. Tính diện tích hình phẳng giới

hạn bởi đồ thị hàm số

 

y f x

và trục hoành.

. B.

. C.

17334

635

. D.

17334

1270

Lời giải:

Từ đồ thị của hàm số

 

y f x

suy ra

       

2 1 , 0f x a x x a   

Ta có

            

2 2 1 2 2 1 2 2 1 2 1f x a x x a x x a x x x



         

Xét phương trình

           

2 1 2 1 2 2 1 0f x f x a x x x x x



        





  

 

2 1 3 4 0

a x x x x











      











Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số

 

y f x

và

 

'y f x

là

  

 

  

 

428

2 1 3 4 2 1 3 4

S a x x x x dx a x x x x dx a



          



Theo đề bài ta có

 

428 214 1

5 5 2

a a TM  

     

f x x x   

Vậy diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

y f x

và trục hoành là

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

   

1 81

2 20

S x x dx



   



Câu 31: Cho hàm số bậc ba

 

y f x ax bx x d    

và đường thẳng

 

y g x

có đồ thị như hình

vẽ bên dưới:

Biết

2 65

AB 

diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

y f x

và

 

y g x

bằng

. B.

. C.

. D.

Lời giải:

Giả sử

:d y mx n

với

0m 

 

y g x

là hàm nghịch biến.

,A B d

nên tọa độ hai điểm

   

1; , 3;3A m n B m n

Mặt khác

   

2 65 2 65

3 1 3 .

AB m n m n       

()

2 65

( / )

m t m







   









Suy ra

 

y g x x n   

Xét phương trình:

   

f x g x ax bx x d x n

   

       

   

   

ax bx x d n    

Mà

   

f x g x

   

1 1 3 3 3 .a x x x ax ax ax a       

Đồng nhất hệ số ta được

a 

Vậy diện tích hình phẳng giới hạn bởi hai đồ thị là

   

2 16

1 1 3 .

S x x x dx



     



Câu 32: Cho hàm số bậc ba

 

y f x ax x cx d    

và parabol

 

y g x

có đồ thị như hình vẽ.

Biết đồ thị

 

y f x

và

 

y g x

cắt nhau tại ba điểm phân biệt

,,A B C

có hoành độ lần lượt

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

là

2;1;2

và thỏa mãn

AB 

(tham khảo hình vẽ). Tính diện tích hình phẳng giới hạn bởi

hai đồ thị

 

y f x

và

 

y g x

. B.

238

. C.

. D.

Lời giải:

Ta có:

 

     

 

2; , 1; 1 2 2 1

A f x B f x AB f f      

Theo giả thiết

   

3 5 3

AB f f    

 

8 2 2

a c d a c d



         





31ac   

(1).

Mặt khác,

       

 

2 1 2 4 4f x g x a x x x a x x x        

(*)

Nhận xét do đồ thị

 

y g x

là parabol nhận

làm trục đối xứng

 

g x kx m  

Đồng nhất hệ số của phương trình

 

ta có:

4ca

(2)

Từ (1), (2) suy ra

3 1 1

a c a

c a c

   







   



. Vậy

   

44f x g x x x x    

Vậy

   

S f x g x dx



  



Câu 33: Cho hàm số

 

y f x ax bx c   

. Tiếp tuyến

đi qua điểm

có hoành độ

2x 

cắt đồ

thị hàm số

 

y f x

tại hai điểm khác

có hoành độ lần lượt là

4x 

và

0x 

. Gọi

,SS

lần lượt là diện tích phần gạch sọc (như hình vẽ). Tính tỉ số

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

. B.

. C.

. D.

Lời giải:

Gọi phương trình của tiếp tuyến

là

 

y g x

Phương trình hoành độ giao điểm của đồ thị hàm số

 

y f x

và tiếp tuyến

là:

       

f x g x f x g x x







     







       

42f x g x m x x x    

với

0m 

Theo giả thiết ta có:

           

0 0 0

4 4 4

896

d d 4 2 d

S f x g x x f x g x x m x x x x

  

        





  

           

2 2 2

0 0 0

d d 4 2 d

S f x g x x f x g x x m x x x x          





  



Câu 34: Cho hàm số

y x x x   

có đồ thị

 

và đường thẳng

đi qua gốc tọa độ tạo

thành hai miền phẳng có diện tích

và

như hình vẽ

Biết

S 

. Khi đó



, giá trị của

2mn

bằng

143

. B.

50

. C.

. D.

142

Lời giải:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

 Gọi

0a 

là hoành độ giao điểm của

 

và

Khi đó, đường thẳng

có hệ số góc là:

a a a

k a a

  

    

Đường thẳng

đi qua gốc tọa độ nên có phương trình là

d y a a x



   





 Ta có:

3 2 2

1 3 1 3

3 3 d

2 4 2 4

S x x x a a x x



   

       

   



   





4 3 2 2 2

27 1 1 3 1 3 3

4 8 4 2 4 8 2

x x x a a x



   

        

   



   



4 3 2 2 2

27 1 1 3 1 3 3

4 8 4 2 4 8 2

a a a a a a

   

        

   

   

27 1 1

4 8 8

a a a    

Do đó,

d y x

 Phương trình hoành độ giao điểm của

 

và

là:

3 2 3 2

3 1 3 1 3 9

3 0 0

4 2 4 2 4 4

x x x x x x x



        





Phương trình trên có 3 nghiệm:

3x 

0x 

và

x 



1 3 9 135

2 4 4 128

S x x x x





   







Do đó:

135m 

128n 

. Vậy:

2 142mn

Câu 35: Cho hai hàm số

 

4 3 2

f x ax bx cx dx e    

với

0a 

và

 

3g x px qx  

có đồ thị như

hình vẽ bên dưới. Đồ thị hàm số

 

y f x

đi qua gốc tọa độ và cắt đồ thị hàm số

 

y g x

tại

bốn điểm có hoành độ lần lượt là

2

;

1

;

và

. Tiếp tuyến của đồ thị hàm số

   

y f x g x

tại điểm có hoành độ

2x 

có hệ số góc bằng



. Gọi

 

là hình phẳng

giới hạn bởi đồ thị hai hàm số

 

y f x

và

 

y g x

Diện tích của hình

 

bằng

1553

120

. B.

1553

240

. C.

1553

. D.

1553

Lời giải:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Đặt

           

4 3 2

3h x f x g x ax bx c p x d q x e         

     

4 3 2h x ax bx c p x d q



     

Phương trình hoành độ giao điểm của 2 đồ thị

 

y f x

và

 

y g x

là:

         

4 3 2

0 3 0f x g x h x ax bx c p x d q x e           

Đồ thị hàm số

 

y f x

đi qua gốc tọa độ và cắt đồ thị hàm số

 

y g x

tại bốn điểm có

hoành độ lần lượt là

2

;

1

;

và

nên

         

0 2 1 1 0f h h h h m      

     

4 3 2

16 8 4 2 3 1

3 2

3 3

3 0 4

a b c p d q

am bm c p m d q m







      



       





      



      



Mặt khác, tiếp tuyến của đồ thị hàm số

 

y h x

tại điểm có hoành độ

2x 

có hệ số góc

bằng



nên

       

15 15

2 32 12 4 5

h a b c p d q



           

Từ

 

, ta tìm được:















  







Thay vào

 

    

432

1 1 7 1

3 0 3 1 1 2 0

2 2 2 2

m m m m m m m m          

3m

Ngoài ra, ta cũng có:

 

432

1 1 7 1

2 2 2 2

h x x x x x    

Vậy diện tích hình phẳng cần tính là

       

3 1 1 3

2 2 1 1

d d d dS h x x h x x h x x h x x



  

   

   

     

1 1 3

2 1 1

113 58 122 1553

d d d

120 15 15 120

h x x h x x h x x





        

  

Câu 36: Cho hàm số

 

liên tục trên và đường thẳng

   

:d g x ax b

có đồ thị như hình vẽ.

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Biết diện tích miền tô đậm bằng

và

 

f x x 



. Tích phân

 

. 2 dx f x x







bằng

607

348



. B.



. C.



. D.



Lời giải:

Ta có:

   

 

1;3

2 1.

2 3 1

2; 3

A g x ax b

a b a

g x x

a b b

B g x ax b

  



  





    

  

    

    







Mà

       

37 37

2 1 d 2 1 d

12 12

S f x x x x f x x



       

   

   



         

0 1 1 0 0

2 0 0 2 2

37 2

d d 2 1 d 2 1 d d

12 3

f x x f x x x x x x f x x

  

         

    

Khi đó

 



     

0 0 0

2 d 2d d d

d ( )d ( )

1 2 2

. 2 d . d . d

t x t x u t u t

v f t t v f t

x f x x t f t t t f t f t t

     



  

  



  

  





  





  

     

1 1 2 5

2 2 d 2. 3

4 4 3 3

f f x x





       







Câu 37: Cho parabol

 

:P y x

và hai điểm

thuộc

 

sao cho

2AB 

. Tìm giá trị lớn nhất

của diện tích hình phẳng giới hạn bởi parabol

 

và đường thẳng

. B.

. C.

. D.

Lời giải:

y=x

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Gọi

 

;A a a

và

 

;B b b

là hai điểm thuộc

 

sao cho

2AB 

Không mất tính tổng quát giả sử

ab

Theo giả thiết ta có

2AB 

nên

 

4b a b a   

   

14b a b a



    



Phương trình đường thẳng đi qua hai điểm

và

là

 

y b a x ab  

Gọi

là diện tích hình phẳng giới hạn bởi parabol

 

và đường thẳng

ta có

   

 

2 3 6

S a b x ab x x a b abx





        







Mặt khác

   

14b a b a



   



nên

 

42b a b a b a      

Vậy

 

6 6 3



  

Dấu



xảy ra

   

 

1;1

b a a

b a b a

b a b









   





   

   



   

  











Vậy giá trị lớn nhất của diện tích hình phẳng giới hạn bởi parabol

 

và đường thẳng

bằng

Câu 38: Cho hai hàm số

 

    y f x ax bx cx d

và

 

   y g x mx nx k

cắt nhau tại ba điểm

có hoành độ là

1; ;2



và có đồ thị như hình vẽ.

Biết phần diện tích kẻ sọc (hình

) bằng

. Diện tích phần hình phẳng giới hạn bởi đồ thị

   

,y f x y g x

và hai đường thẳng

xx

(phần bôi đen trong hình vẽ) bằng

. B.

243

. C.

. D.

Lời giải:

Ta có:

         

1 2 0



     





f x g x a x x x a

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

           

1 1 1

2 2 2

1 1 1

1 1 81

1 2 1 2 .

2 64

xxS f x g x a x x x a x x x ax

  

   

          



   



   

  

Mà

S

2a

Khi đó:

       

1 81

2 1 2

S g x f x x x xxx



       











Câu 39: Gọi

là tập hợp tất cả các giá trị của tham số

để đường thẳng

: 45 2d y m  

cùng với

đồ thị

 

của hàm số

y x mx x   

tạo thành hai miền kín có diện tích lần lượt là

,SS

thỏa mãn

SS

(xem hình vẽ). Số phần tử của tập

là

2

1

9

Lời giải:

Điều kiện để đồ thị

 

có hai điểm cực trị là

4 1 0y x mx



   

có hai nghiệm phân biệt.

Khi đó

 

2 1 0









     









Đường thẳng

: 45 2d y m  

song song với trục hoành và cắt đồ thị

 

của hàm số

y x mx x   

tạo thành hai miền kín có diện tích lần lượt là

,SS

thỏa mãn

SS

nên

đi qua điểm uốn của đồ thị

 

Ta có:

4 1 2 4 0 2 2 1

y x mx y x m x m y m m



 

            

Khi đó ta có phương trình:

 

16 16

2 1 45 2 47 3 0 *

m m m m m



        

Phương trình

 

có 3 nghiệm

phân biệt và có 2 nghiệm thỏa mãn điều kiện nên tập

có

2 phần tử.

Câu 40: Cho hàm số

 

f x x ax bx c   

với

,,abc

là các số thực. Biết hàm số

       

g x f x f x f x

 

  

có hai giá trị cực trị là

5

và

. Diện tích hình phẳng giới hạn

bởi các đường

 





và

1y 

bằng

ln3

. B.

ln7

. C.

3ln 2

. D.

ln10

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Lời giải:

Xét hàm số

       

g x f x f x f x

 

  

Ta có

       

g x f x f x f x

   

  

   

6f x f x

 

  

Theo giả thiết ta có phương trình

 

0gx





có hai nghiệm

,mn

và

 















Xét phương trình

 





   

 

g x f x

  















   

 

f x f x

 

  



























Diện tích hình phẳng cần tính là:

 













   

 

g x f x









   

 

f x f x

 









 









 

ln 6

gx

   

ln 6 ln 6g n g m   

ln8

3ln 2

Câu 41: Cho đồ thị hàm số bậc ba

 

y f x ax bx cx d    

và đường thẳng

:d y mx n

như

hình vẽ và

, SS

là diện tích hình phẳng được tô đậm trong hình bên. Biết



với

,pq

là một phân số tối giản. Tính

2022pq

2043

. B.

2045

. C.

2049

. D.

2051

Lời giải:

Ta có

 

32y f x ax bx c



   

Do đồ thị hàm số

 

y f x ax bx cx d    

có hai điểm cực trị là

 

1 ; 4

và

 

1 ; 0

nên

3 2 0 1

3 2 0 0

a b c a

a b c b

a b c d c

a b c d d

   





   







      



    



32y x x   

Vì đường thẳng

:d y mx n

đi qua 2 điểm

   

2 ; 0 , 0 ; 2

nên

:2d y x

Ta có

 

2 3 3

.2 3 2 d 2 3 2 d

S x x x x x x        



3 11

4 2 4



    





Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

 

     

2 2 2

3 3 3

0 0 0

2 3 2 d 2 3 2 d 4 d 4S x x x x x x x x x x x             

  

  

Vậy

2022 2049pq  

Câu 42: Cho hàm số

 

với đồ thị là Parabol đỉnh

có tung độ bằng



và hàm số bậc ba

 

Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ

1 2 3

,,x x x

thoả mãn

1 2 3

18 55x x x 

(hình vẽ).

Diện tích miền tô đậm gần số nào nhất trong các số sau đây?

5,7

. B.

5,9

. C.

6,1

. D.

6,3

Lời giải:

Ta có:

1 2 1





Lúc này ta có

2 12









và

      

: 1 2P f x a x x  

Ta có

 

1 7 7

2 12 27

I P a



    





    

f x x x  

Hàm số

 

đạt cực trị tại

1, 2xx  

nên

      

' 1 2 2

g x a x x a x bgx



       





Đồ thị hàm số

 

đi qua

nên

1 7 7 13

2 12 12 12

g a b



      





 

Phương trình hoành độ giao điểm:

      

2 1 2

3 2 27

f x g x a x b x x



       





Theo định lý viet ta có:

1 2 3

28 55

18 55 18. 55 18

x x x b



      

 

Từ

 

ta được

 

1, 2

2 3 2 2

a b g x x      

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Phương trình hoành độ giao điểm là

  

1 2 2

27 3 2 2

x x x     

8 559

























Từ đó suy ra diện tích miền tô đậm là

  

8 559

1 2 2 5,7

27 3 2 2

S x x x dx





       







Câu 43: Cho hàm số

43y x x

có đồ thị

 

và đường thẳng

đi qua gốc tọa độ tạo thành hai

miền hình phẳng có diện tích

,SS

như hình vẽ bên dưới:

Khi

12S 

thì

bằng

. B.

. C.

875

256

. D.

865

256

Lời giải:

Phương trình đường thẳng

có dạng

y mx

Phương trình hoành độ giao điểm giữa đồ thị

 

và đường thẳng

là

4 3 0

x x mx

x x m





  



  



Gọi

là nghiệm dương của phương trình hoành độ giao điểm trên

43b b m  

 

3 2 2 4 3 2 4 3

S mx x x dx mx x x mb b b



        







Theo giả thiết

12S 

2 4 3

mb b b   

 

2 2 4 3

4 3 12

b b b b b    

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

2 24 0 2b b b     

vì

0b 

10m

Khi đó phương trình

4 3 0x x m  

trở thành

4 3 10 0







   







Vậy

 

875

4 3 10 d .

256

S x x x x



   



Câu 44: Cho hàm số bậc ba

 

y f x

có đồ thị

 

như hình vẽ.

Biết rằng đồ thị hàm số đã cho cắt trục

tại ba điểm có hoành độ

1 2 3

,,x x x

theo thứ tự lập

thành cấp số cộng và

23xx

. Diện tích hình phẳng giới hạn bởi

 

và trục

là

diện tích

của hình phẳng giới hạn bởi các đường

 

1y f x

 

1y f x  

xx

và

xx

bằng

. B.

. C.

2 4 3S 

. D.

23S 

Lời giải:

Do đồ thị hàm bậc ba cắt trục hoành tại ba điểm có hoành độ

1 2 3

,,x x x

theo thứ tự lập thành

cấp số cộng nên đồ thị nhận điểm

 

;0Ax

làm tâm đối xứng của đồ thị.

Do đó:

       

1 2 1 2

x x x x

f x dx f x dx f x dx f x dx     

   

Suy ra:

 

;

f x dx 



 

f x dx 



Vì đồ thị hai hàm số

 

1y f x

và

 

1y f x  

đối xứng với nhau qua trục hoành nên ta

có:

     

3 3 3 3

1 1 1 1

1 2 1

2 1 2 1 2 2

2 2 2 2 4 3.

     









       











   

  

x x x x

x x x

S f x dx f x dx f x dx dx

f x dx f x dx dx x x

Câu 45: Một miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất

bằng 2 đoạn thẳng song song

,AB CD

thành ba phần có diện tích bằng nhau (xem hình vẽ

bên dưới). Tỉ số

bằng:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

. B.

1 2 2

. C.

. D.

12

Lời giải:

Chọn hệ trục tọa độ như hình vẽ:

Parabol có dạng

y ax

, do

 

đi qua điểm

 

6;18

a

Diện tích miếng đất là:

18 144

S dx





  







Để diện tích 3 phần bằng nhau thì diện tích mỗi phần là



. Với b, d > 0

Gọi

; ; ;

   

   

   

B b D d

khi đó



AB b

CD d

Ta có:

2 2 2 3

24 24 72

2 2 2 6

   

      

   

   



b x b x x

dx b

Tương tự ta có

48 144



     







d x AB

dx d

Câu 46: Ông X muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên, biết đường cong

phía trên là một Parabol, chất liệu làm là inox. Giá

vật tư và công làm là

1.300.000

đồng.

Hỏi ông X phải trả bao nhiêu tiền để làm cái cửa sắt như vậy (làm tròn đến hàng nghìn).

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

13.050.000

đồng. B.

36.630.000

đồng. C.

19.520.000

đồng. D.

21.077.330

đồng.

Lời giải:

Ta chọn hệ trục tọa độ như hình vẽ.

3,8

1,9

-1,9

Trong đó

19 19

;

10 5









19 19

;

10 5







Đường cong phía trên là một Parabol có phương trình dạng

y ax b

, với

;ab

Do Parabol đi qua các điểm

,IJ

và chiều cao cổng là

nên có

70 9

361 2

yx  

Diện tích

của cửa rào sắt là diện tích phần hình phẳng giới hạn bởi đồ thị hàm số

70 9

361 2

yx  

, trục hoành và hai đường thẳng

x 

;

x 

Ta có

70 9 1216

361 2 75

S x x





   







Vậy ông X phải trả số tiền để làm cái cửa sắt là:

1216

00.000 21.077.3303

1. 

(đồng).

Câu 47: Một mảnh đất hình chữ nhật có chiều dài

60m

, chiều rộng

20m

. Người ta muốn trồng cỏ ở

hai đầu của mảnh đất hai hình bằng nhau giới hạn bởi hai đường Parabol có hai đỉnh cách

nhau

40m

(như hình vẽ).

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Phần còn lại của mảnh đất người ta lát gạch với chi phí là

200.000dm

. Tính tổng số tiền để

lát gạch ( làm tròn đến hàng nghìn)

133.334.000

đồng. B.

213.334.000

đồng. C.

53.334.000

đồng. D.

186.667.000

đồng.

Lời giải:

Ta có diện tích mảnh đất hình chữ nhật trên là.

 

60.20 1200 Sm

Chọn hệ trục tọa độ

,Oxy

như hình vẽ thoả mãn.

     

10;0 ; 10;0 ; 0;10A B C

Phương trình

có dạng.

 

. . 1y a x b x c  

. Do

đi qua các điểm

,,D C I

nên tọa độ

các điểm

     

10;0 ; 10;0 ; 0;10A B C

thỏa mãn phương trình

nên ta có hệ phương trình.

100 10 0

100 10 0 0

10 10

a b c

a b c b









  





    













. Vậy phương trình

 

10 1





Diện tích trồng cỏ ở hai đầu là

 

10 10

2 2 2

10 10

1 1 400 400 800

2. 10 2. 10 2. 10

10 10 30 3 3 3

S x dx x dx x m





   

   

        



   

   







Vậy tổng số tiền để lát gạch là.

800

1200 .200.000 186.666.667



  





( đồng).

Câu 48: Trên bức tường cần trang trí một hình phẳng dạng paranol đỉnh

như hình vẽ, biết

4 mOS AB

là trung điểm của

. Parabol trên được chia thành ba phần để sơn ba

màu khác nhau với mức chi phí: phần trên là phần kẻ sọc 140000 đồng/

, phần giữa là hình

quạt tâm

, bán kính

2 m

được tô đậm 150000 đồng/

, phần còn lại 160000 đồng/

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Tổng chi phí để sơn cả 3 phần gần nhất với số nào sau đây?

A. 1.597.000 đồng. B. 1.625.000 đồng. C. 1.575.000 đồng. D. 1.600.000 đồng.

Lời giải:

Dựng hệ trục

Oxy

như hình vẽ.

Gọi parabol

 

có phương trình:

 

0y ax bx c a   

. Khi đó

 

đi qua các điểm

 

0,4S

 

2;0A 

và

 

2;0B

Suy ra ta có

4 2 0 0

4 2 0 4

a b c b

a b c c

  





    





   



. Vậy parabol

 

4yx  

Đường tròn

 

có tâm

 

0;0O

và bán kính

2OA 

Khi đó phương trình

 

là:

4xy

. Suy ra phương trình nửa đường tròn là

4yx

Gọi

là giao điểm của

 

và

 

Xét phương trình hoành độ giao điểm của

 

và

 

ta có:





4 0 4



  



  



  













       



  

  





  





  



















Suy ra điểm

 

3;1M 

và điểm

 

3;1N

Phương trình đường thẳng

là:

yx

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Chi phí sơn phần kẻ sọc là:





2 4 4 d .140000T x x x



    







Chi phí sơn phần hình quạt là:

2 4 d .150000

T x x x





  













Chi phí sơn phần còn lại là:

 

2 d 2 4 d .160000

T x x x x



   







Vậy tổng chi phí sơn là:

1 2 3

1575349,5T T T T   

đồng.

Câu 49: Hướng tới kỉ niệm ngày thành lập trường Đoàn TNCS Hồ Chí Minh. Khối

thiết kế bồn

hoa gồm hai Elip bằng nhau có độ dài trục lớn bằng

và độ dài trục nhỏ bằng

đặt

chồng lên nhau sao cho trục lớn của Elip này trùng với trục nhỏ của Elip kia và ngược lại

(như hình vẽ).

Phần diện tích nằm trong đường tròn đi qua

giao điểm của hai Elip dùng để trồng cỏ,

phần diện tích bốn cánh hoa nằm giữa hình tròn và Elip dùng để trồng hoa. Biết kinh phí để

trồng hoa là

150.000

đồng

/1m

, kinh phí để trồng cỏ là

100.000

đồng

/1m

. Tổng số tiền dùng

để trồng hoa và trồng cỏ cho bồn hoa gần với số nào nhất trong các số sau?

4.100.000

đồng. B.

4.550.000

đồng. C.

3.100.000

đồng. D.

4.300.000

đồng.

Lời giải:

Chọn hệ trục

Oxy

như hình

Ta có:

2 8 4

2 4 2













Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Gọi

 

là elip nhận

làm trục lớn

 

16 4

E  

Và

 

là elip nhận

làm trục lớn

 

4 16

E  

Tọa độ giao điểm của

 

và

 

là nghiệm của hệ phương trình:

16 4 5

16 4

4 16





  



  

  

  

  

  









Phương trình đường tròn đi qua 4 giao điểm của

 

và

 

là

( ):

C x y

có bán kính

R 

Diện tích hình tròn dùng để trồng

cỏ:

()

S R m



  

Tiền trồng cỏ:

100000. 2 010 619TS

(đồng)

Một cánh hoa được giới hạn bởi đường

 

có phần đồ thị từ phía trên trục

: 2 4Ox y x

và nửa đường tròn

()C

từ phía trên trục

Ox y x

có diện tích

2 2 2

2 4 3.83064( )

S x x dx m





    







Do tính đối xứng của hình nên diện tích của 4 cánh hoa đều bằng nhau



diện tích của 4 cánh

hoa:

4. 15.32256( )S S m  

Số tiền trồng hoa

150 000. 2 298384TS

(đồng).

Tổng số tiền:

4 309 000T T T  

(đồng)

Câu 50: Một công ty có ý định thiết kế một logo hình vuông có độ dài nửa đường chéo bằng 4. Biều

tượng 4 chiếc lá (được tô màu) được tạo thành bởi các đường cong đối xứng với nhau qua

tâm của hình vuông và qua các đường chéo.

Một trong số các đường cong ở nửa bên phải của logo là một phần của đồ thị hàm số bậc ba

dạng

y ax bx x  

với hệ số

0a 

. Để kỷ niệm ngày thành lập

2/3

, công ty thiết kế để tỉ

số diện tích được tô màu so với phần không được tô màu bằng

. Tính

ab

. B.

. C.

. D.

Lời giải:

Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115

Xét hệ trục toạ độ như hình vẽ, diện tích tam giác

OAB

vuông cân tại

Theo giat thiết ta có

 

4, 4;0OA A

. Hình vuông có nửa đường chéo bằng

nên diện tích

hình vuông là

. Diện tích tô màu là

Xét riêng trong tam giác

OAB

có diện tích phần tô màu bằng

Theo giả thiết, diện tích phần tô màu trong tám giác

OAB

được tính bởi công thức

ax bx x dx  



Từ đó ta có hệ:

64 16 4 0

ax bx x dx

















  













   











































Trường hợp

 



















có nghiệm là

0, , 4

(đồ thị cắt

trong

 

0;4

- loại)

Trường hợp

















 

0fx

có nghiệm

0, 4, 5

thoả mãn. Vậy,

ab

____________________HẾT____________________

Huế, 15h15’ Ngày 19 tháng 3 năm 2023

Bấm Tải xuống để xem toàn bộ.

| 1/105

| | Tải xuống

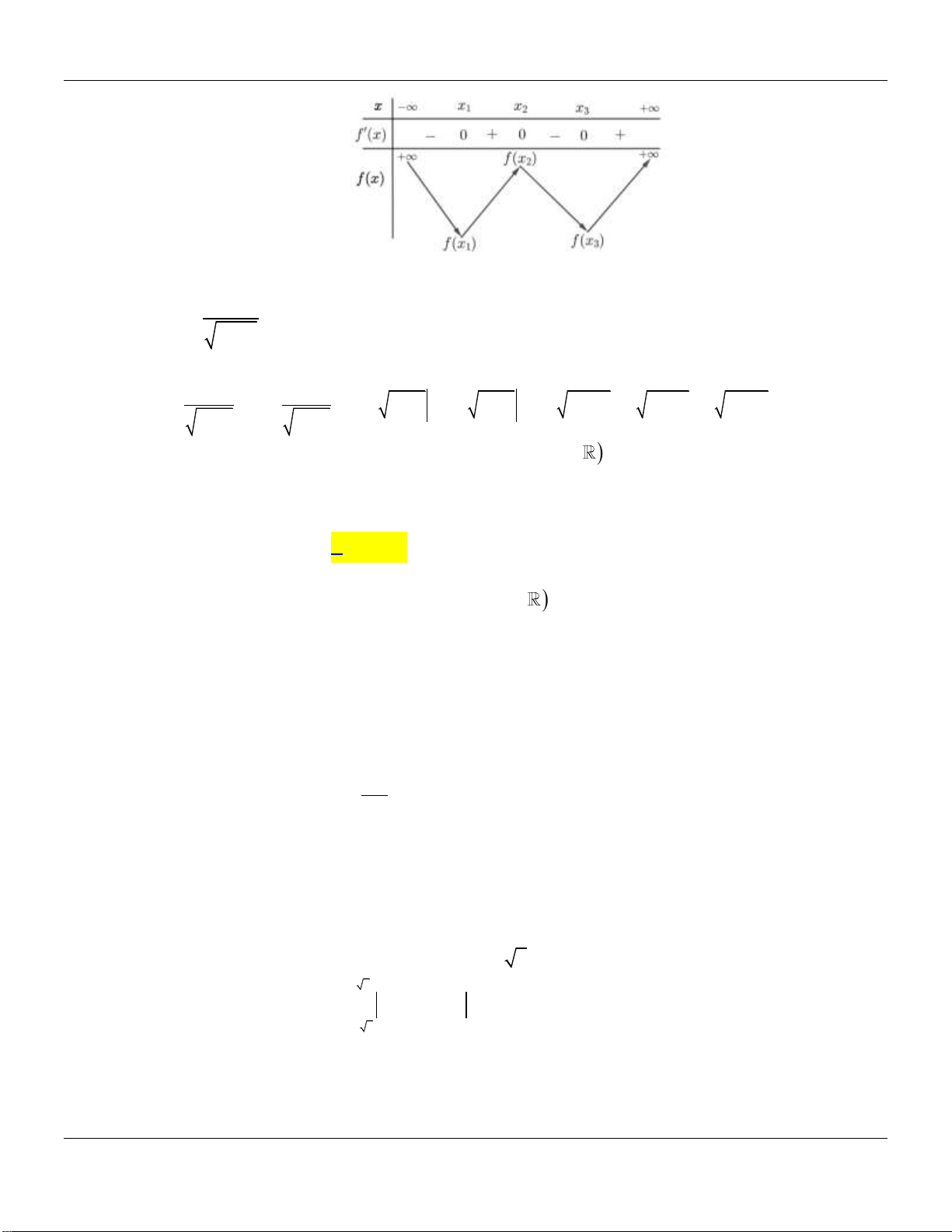
Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TÍCH PHÂN ỨNG DỤNG TÍNH DIỆN TÍCH HÌNH PHẲNG
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Ngân hàng câu hỏi:
ỨNG DỤNG TÍCH PHÂN TRONG HÌNH HỌC (1) NỘI DUNG ĐỀ BÀI Câu 1:
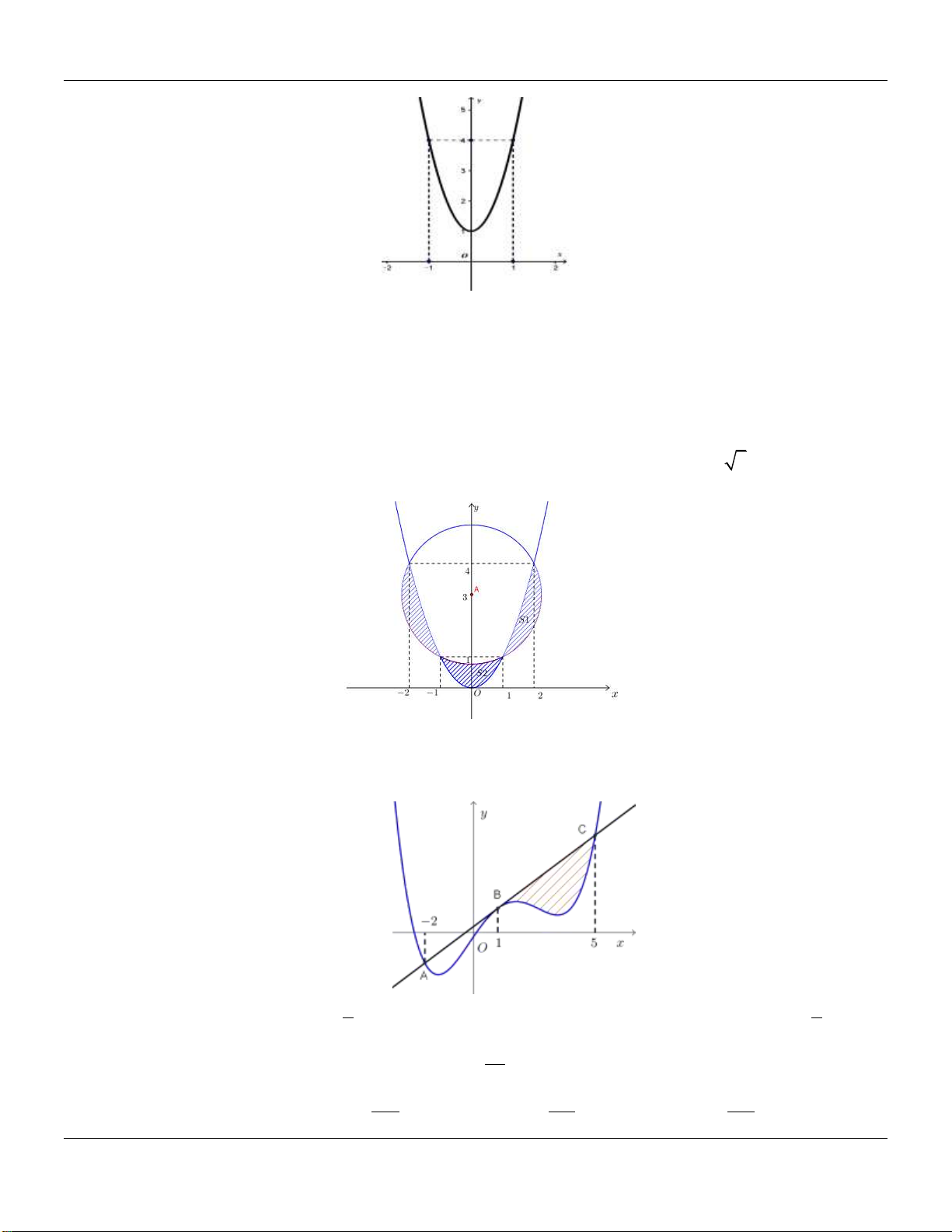
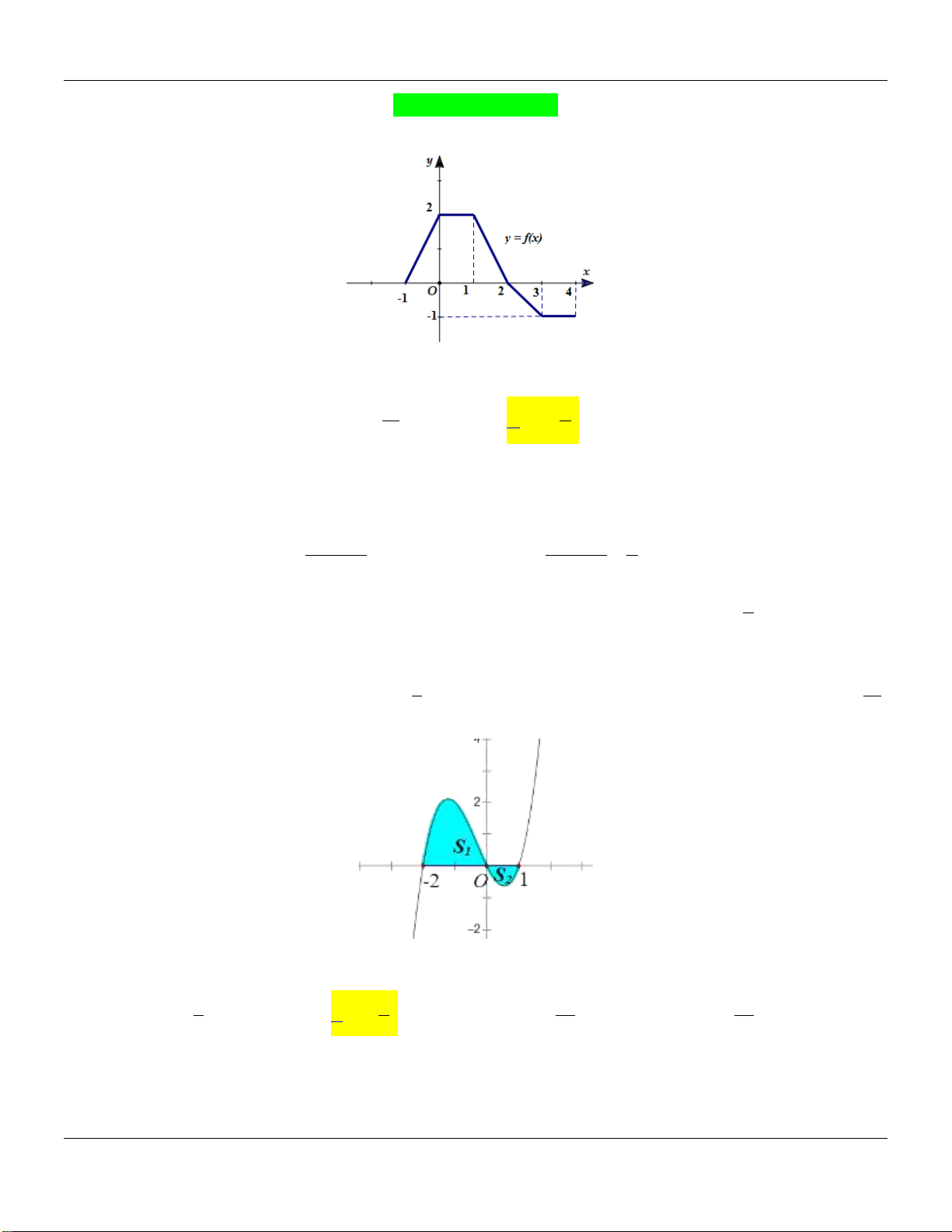
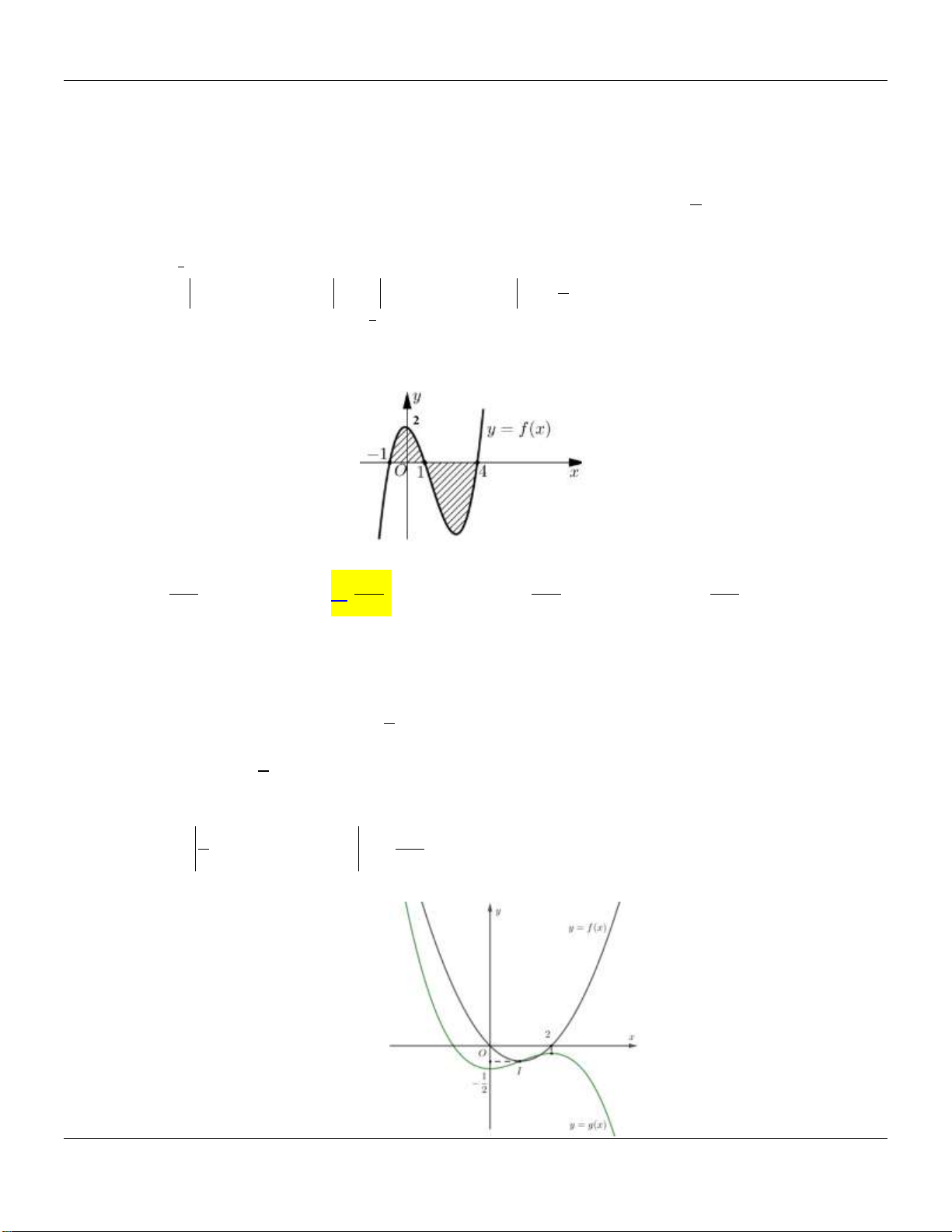
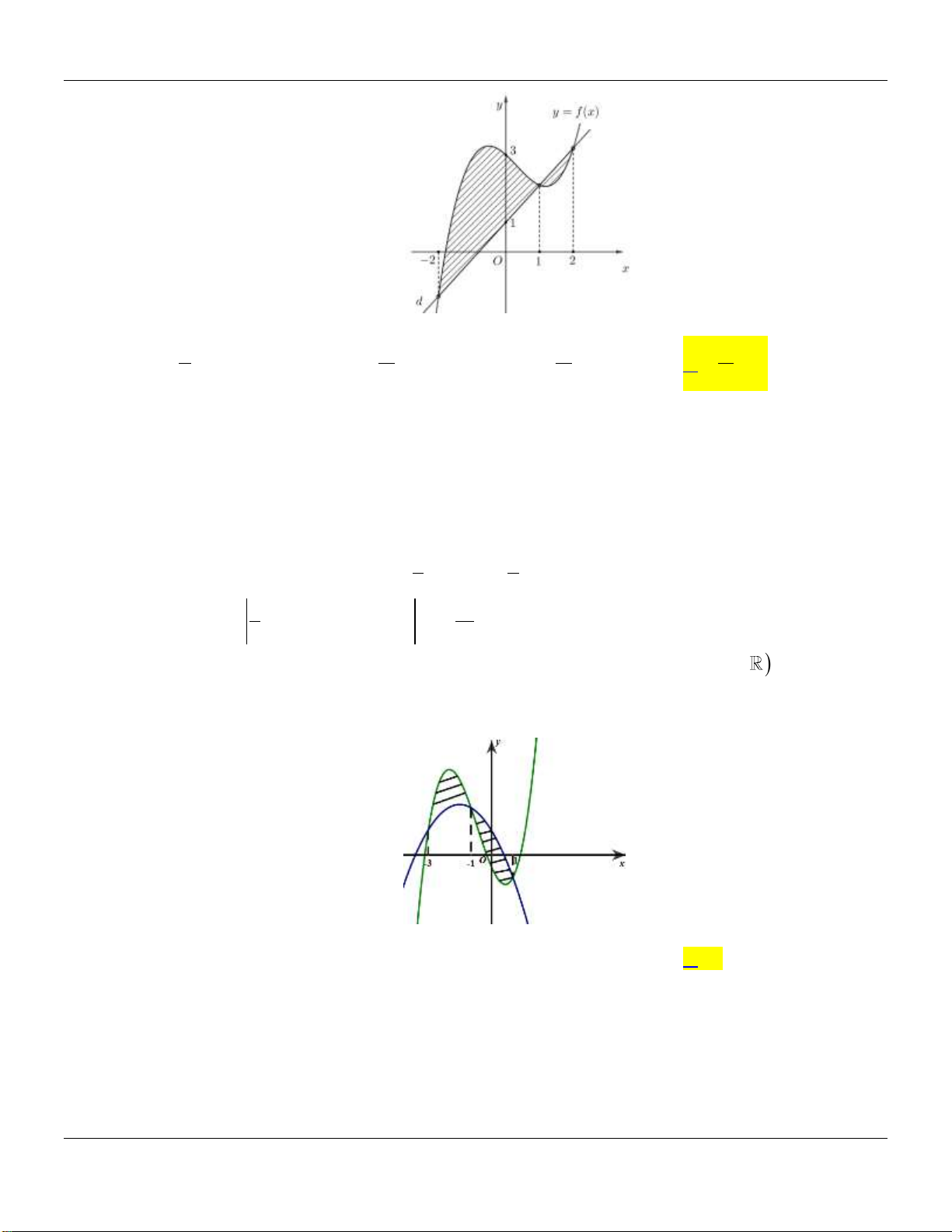
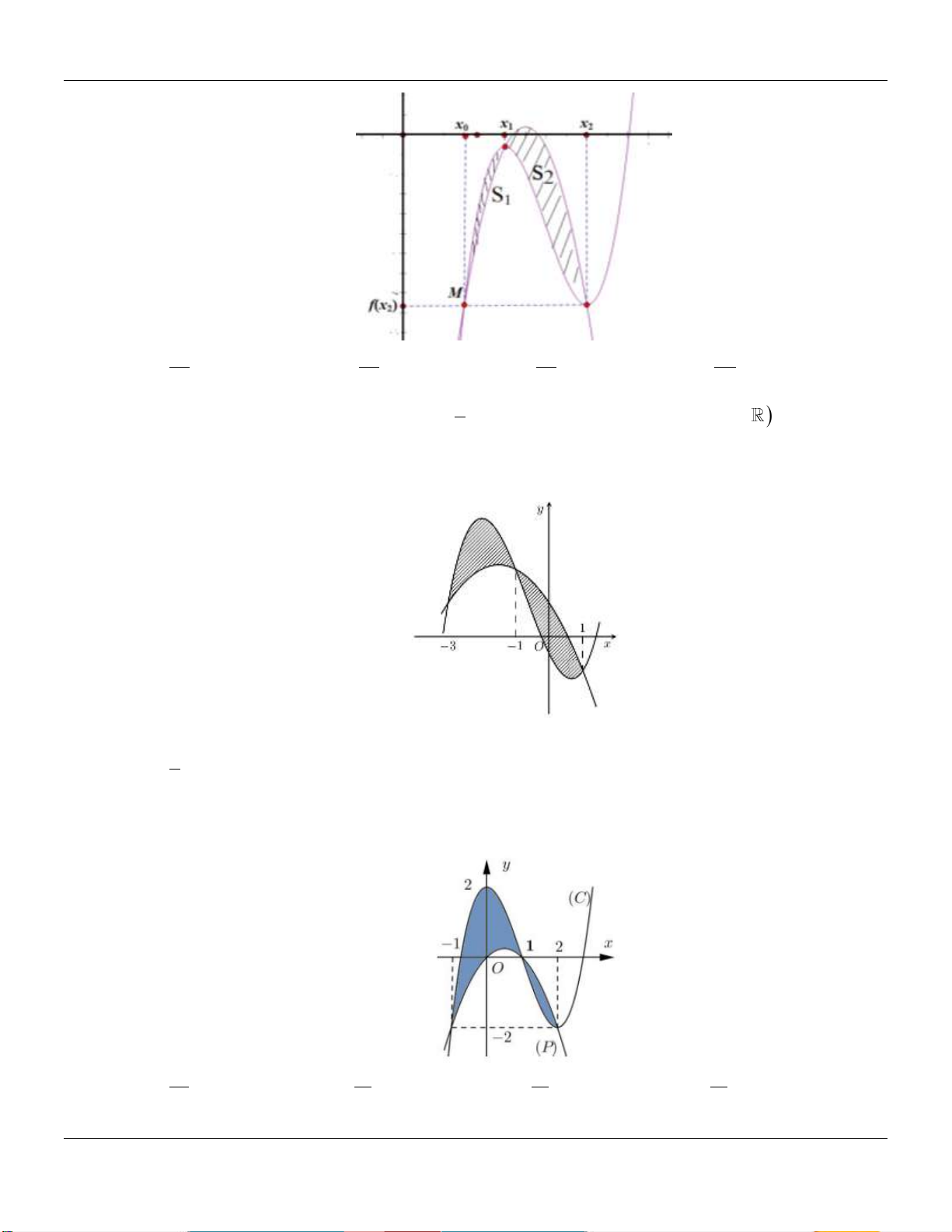
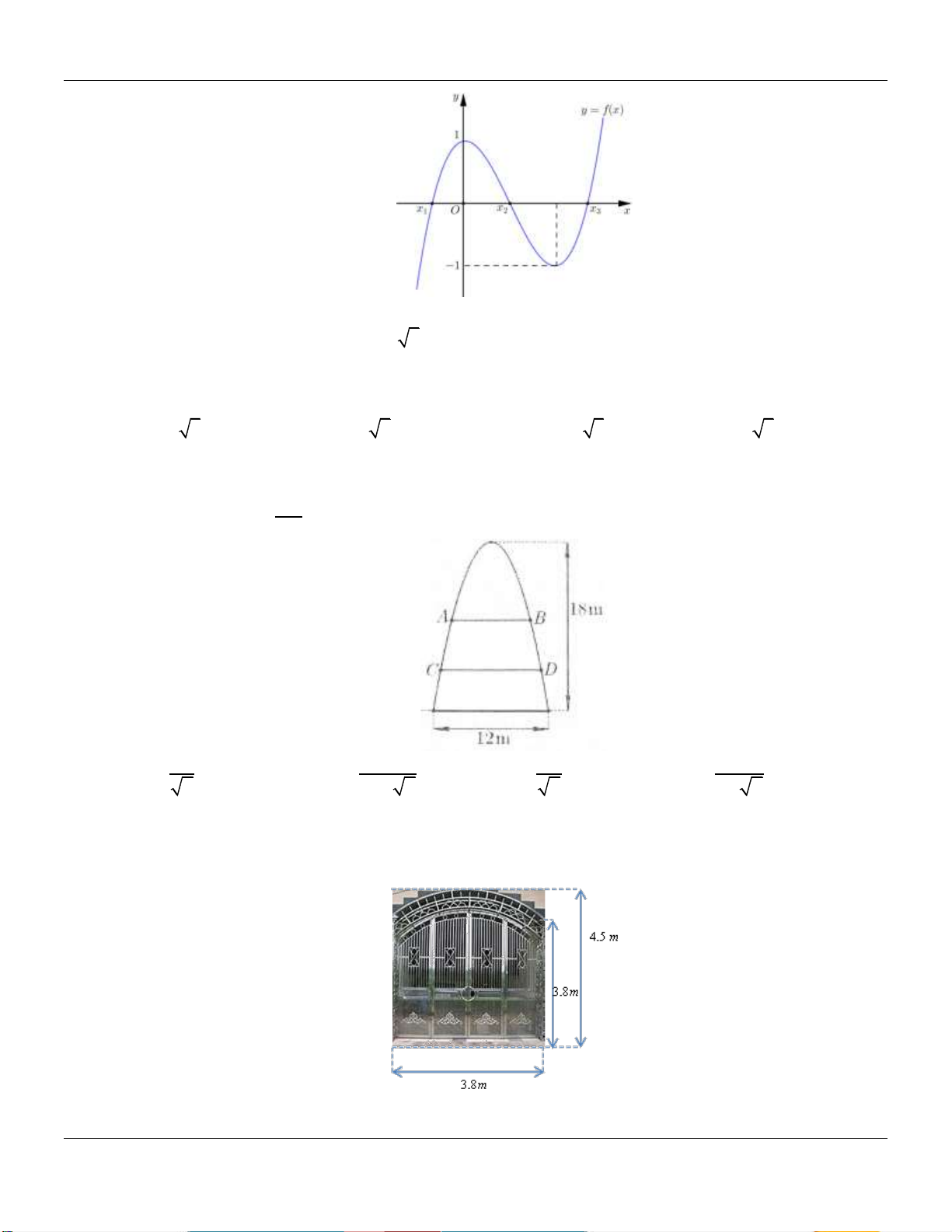
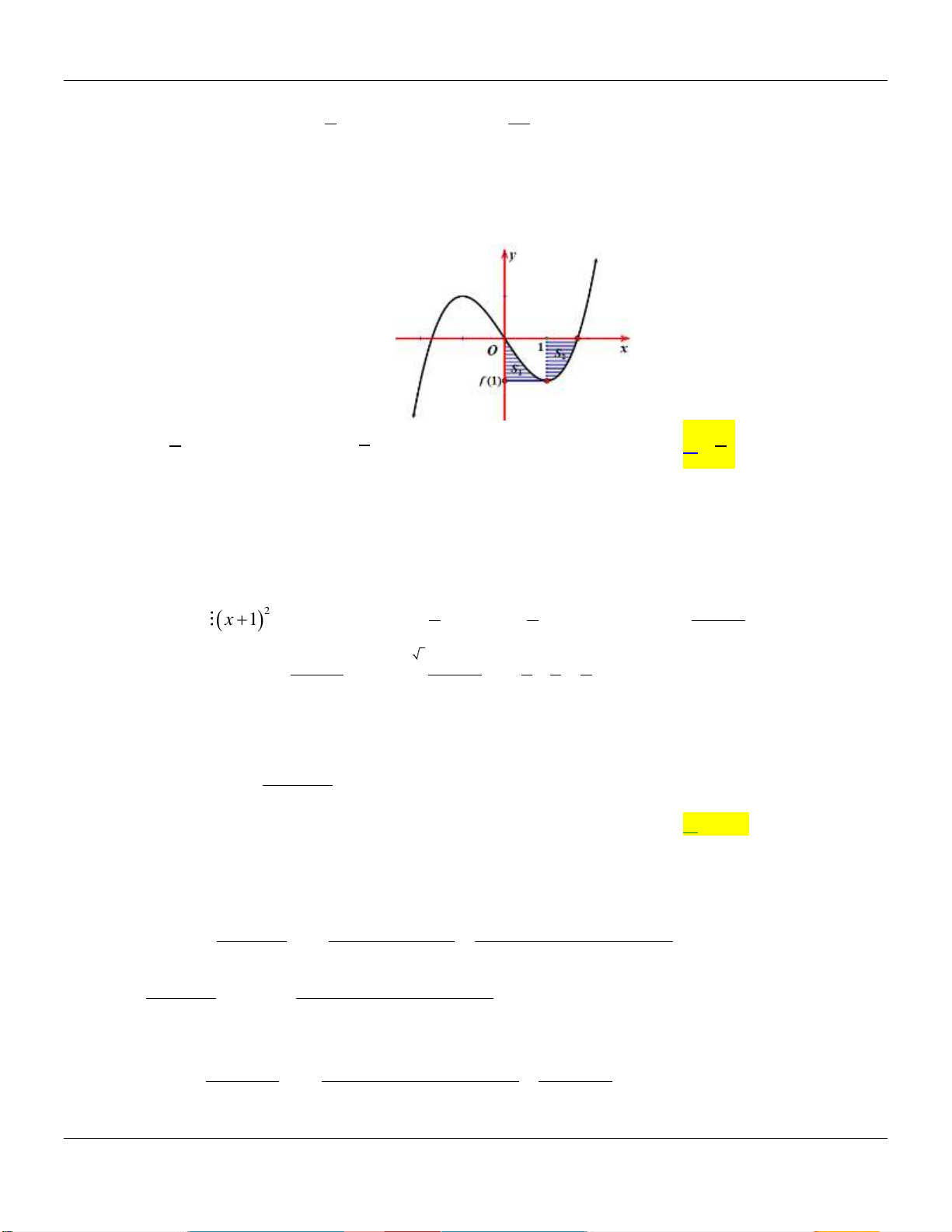
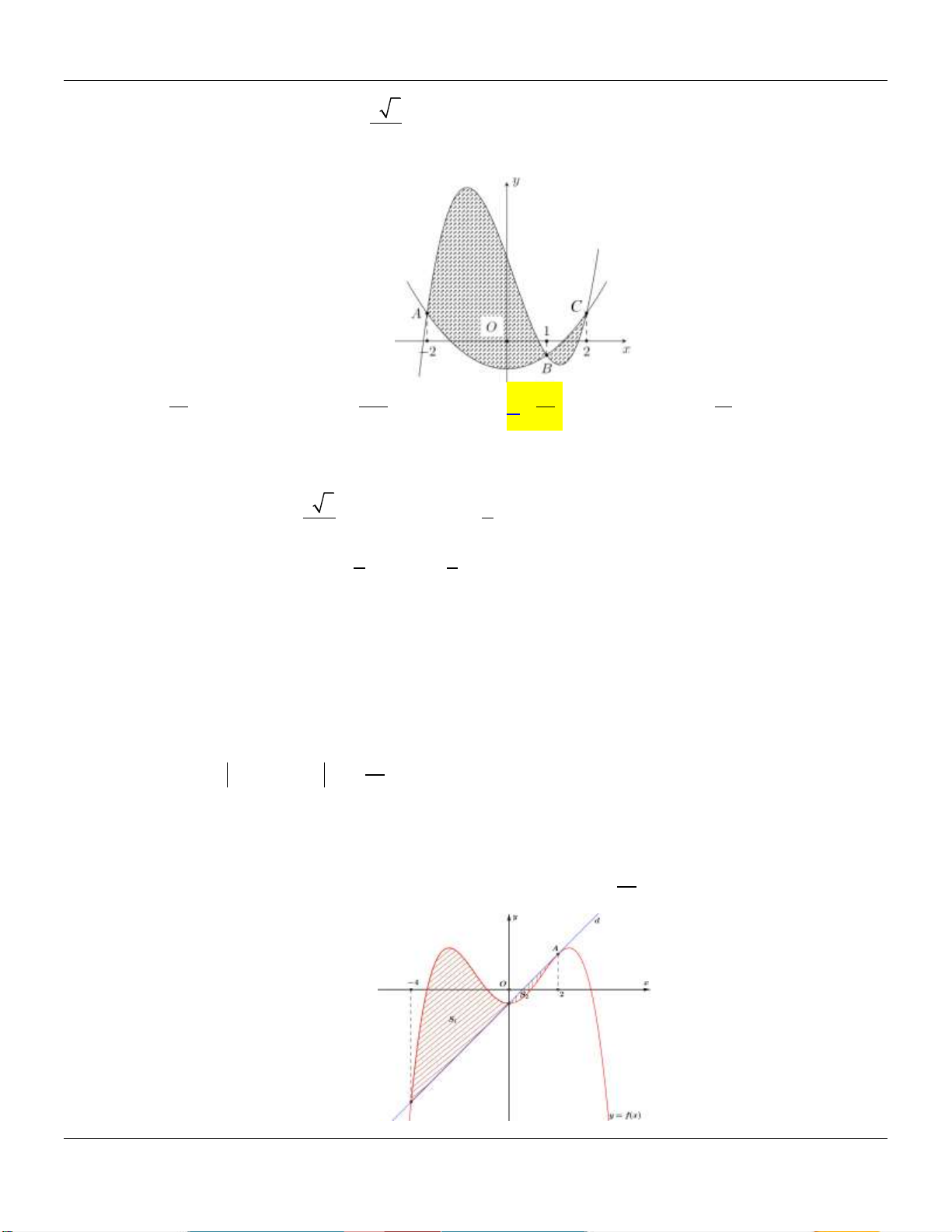
Cho hàm số f  x có đồ thị trên đoạn 1; 4 như hình vẽ dưới: 4 Tính tích phân I  f (x)dx  . 1  11 5
A. I  5 . B. I  . C. I  . D. I  3 . 2 2 Câu 2:
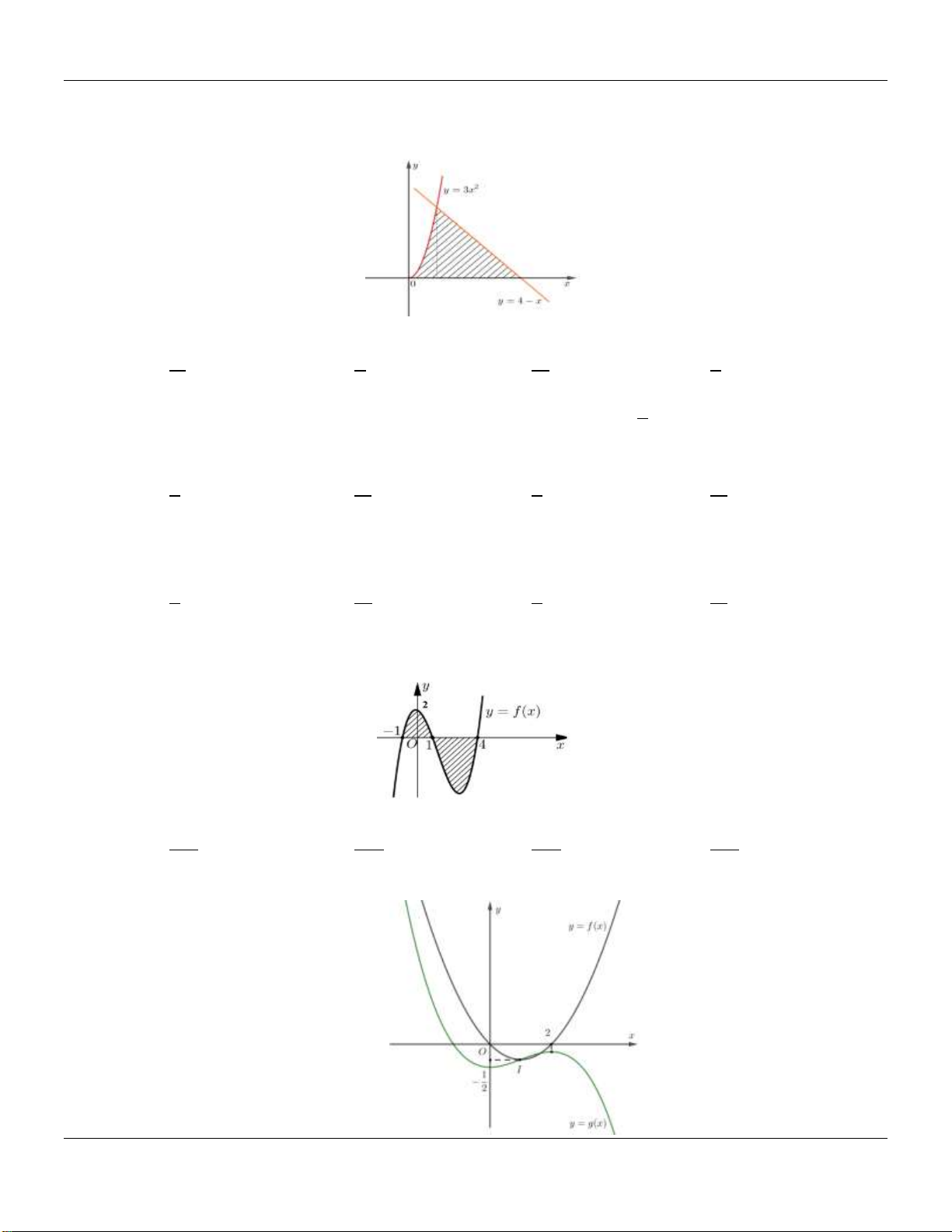
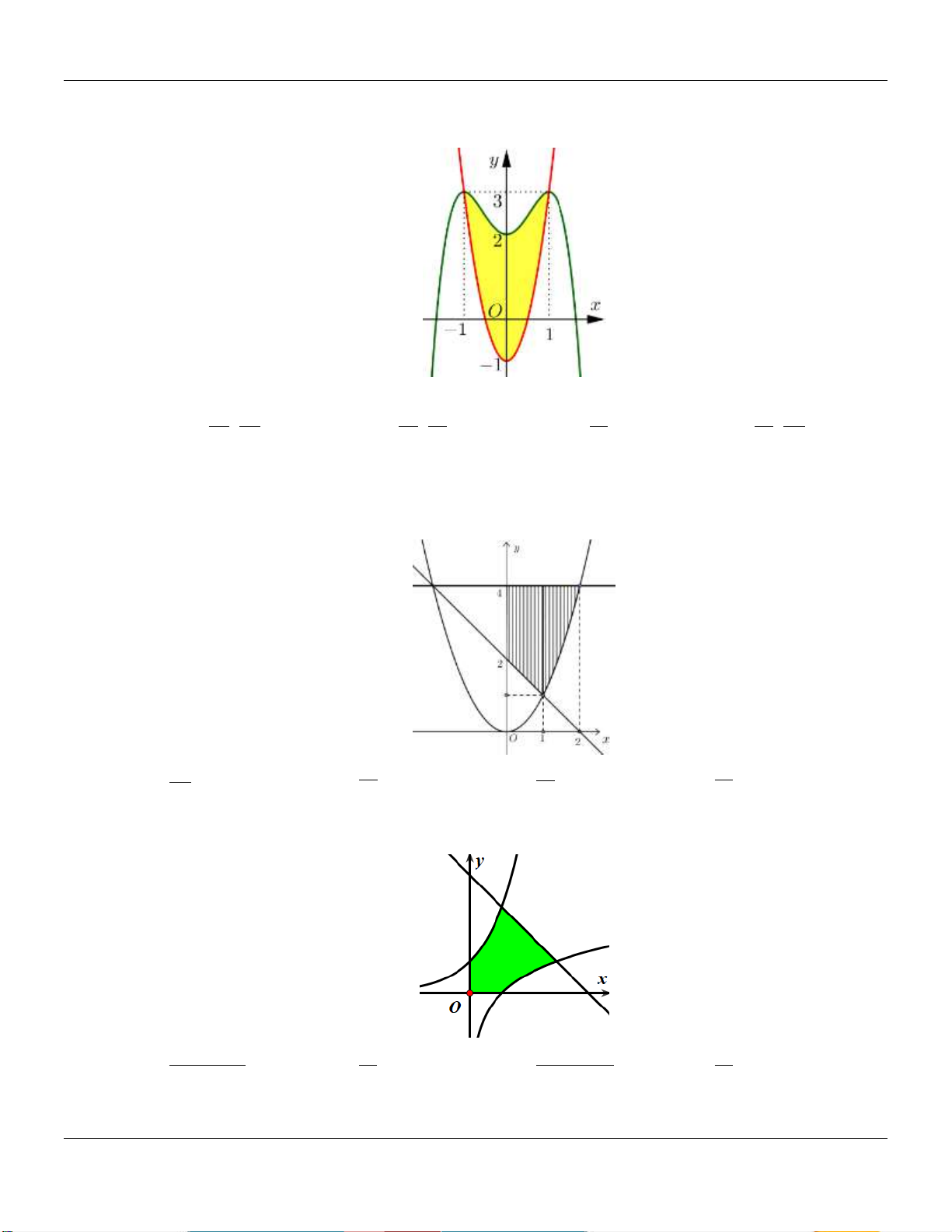
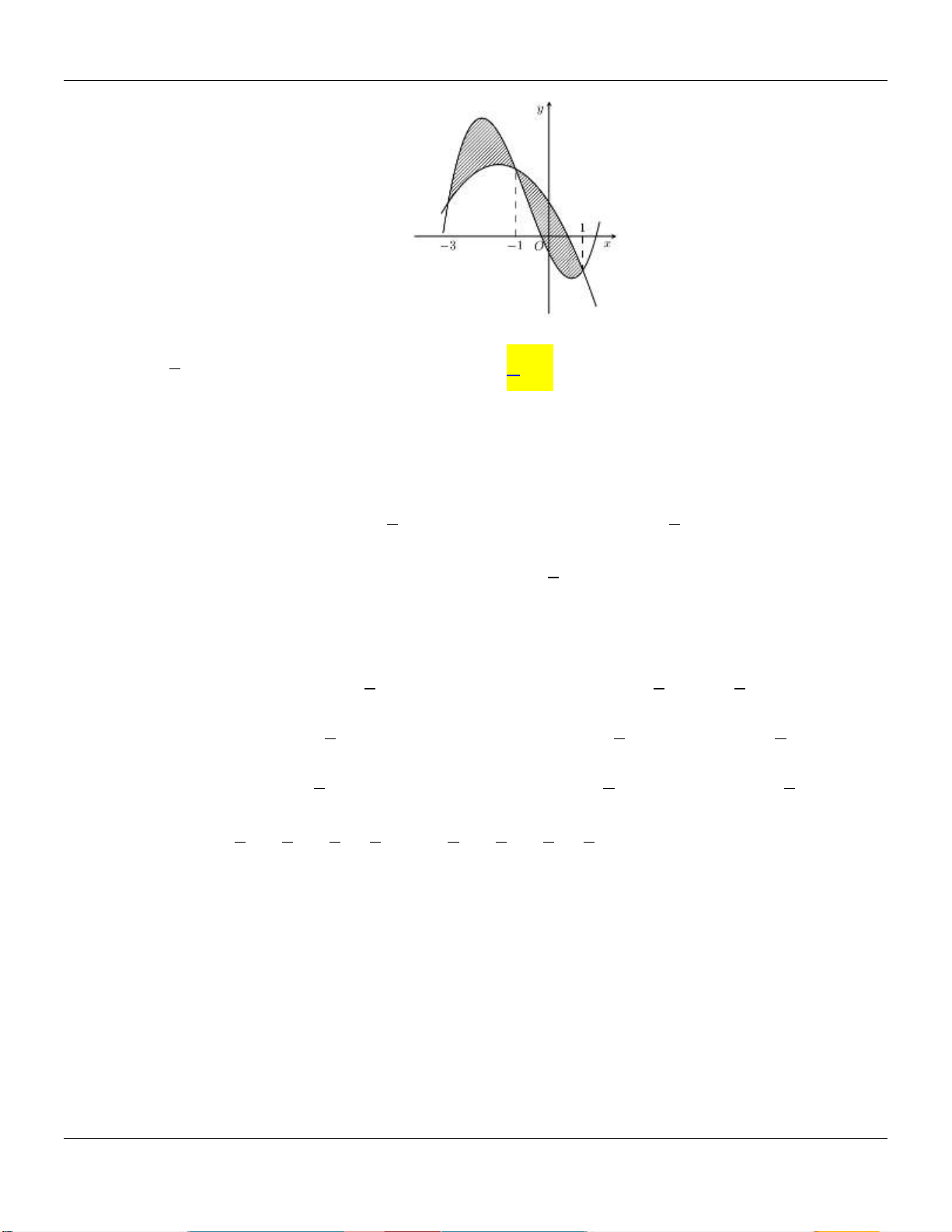
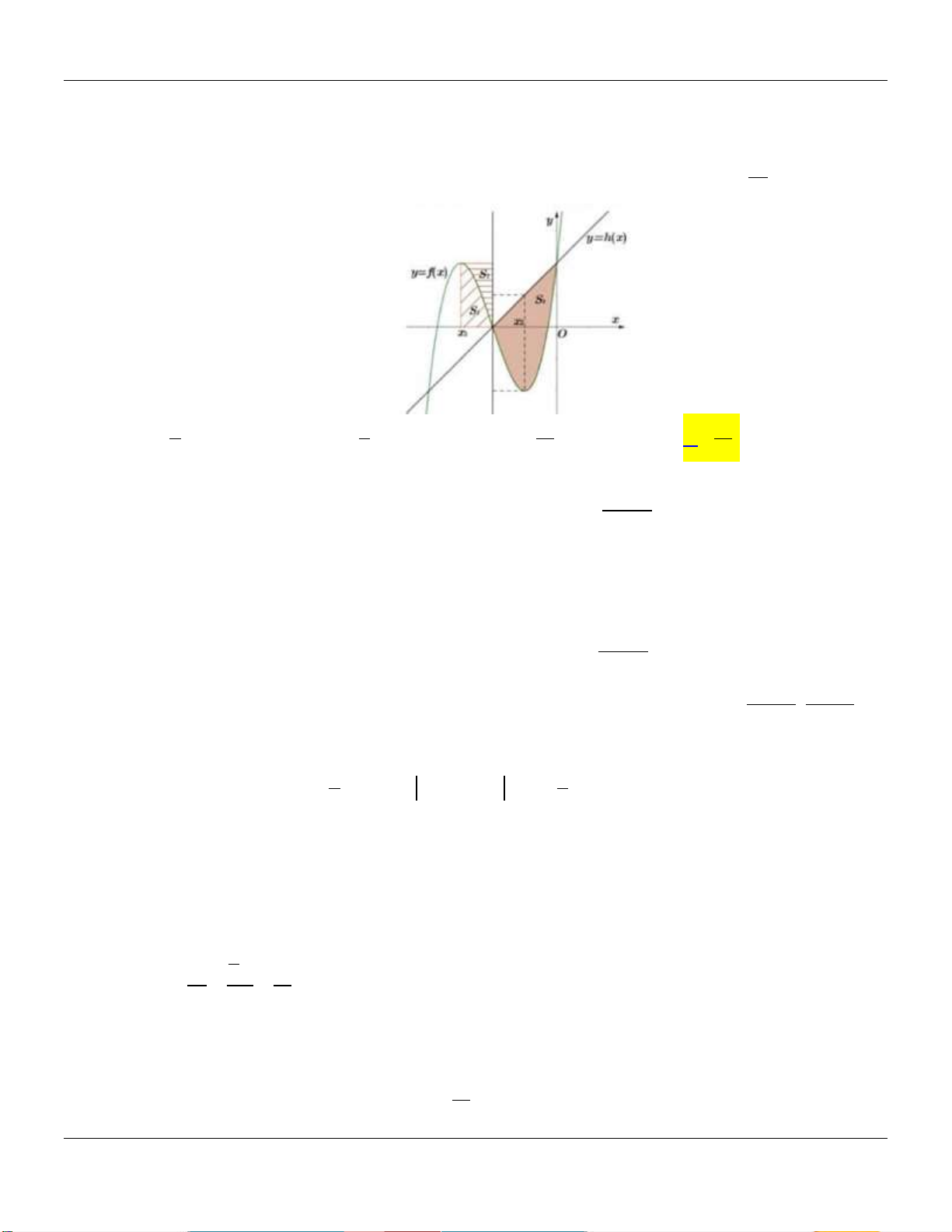
Hình phẳng giới hạn bởi đồ thị hàm số y  f x và trục hoành gồm hai phần, phần nằm phía 8 5
trên trục hoành có diện tích S  và phần nằm phía dưới trục hoành có diện tích S  1 3 2 12
(tham khảo hình vẽ bên). 0 Tính I  f 3x   1dx . 1  5 3 37 27
A. I  . B. I  . C. I  . D. I  . 3 4 36 4 Câu 3:
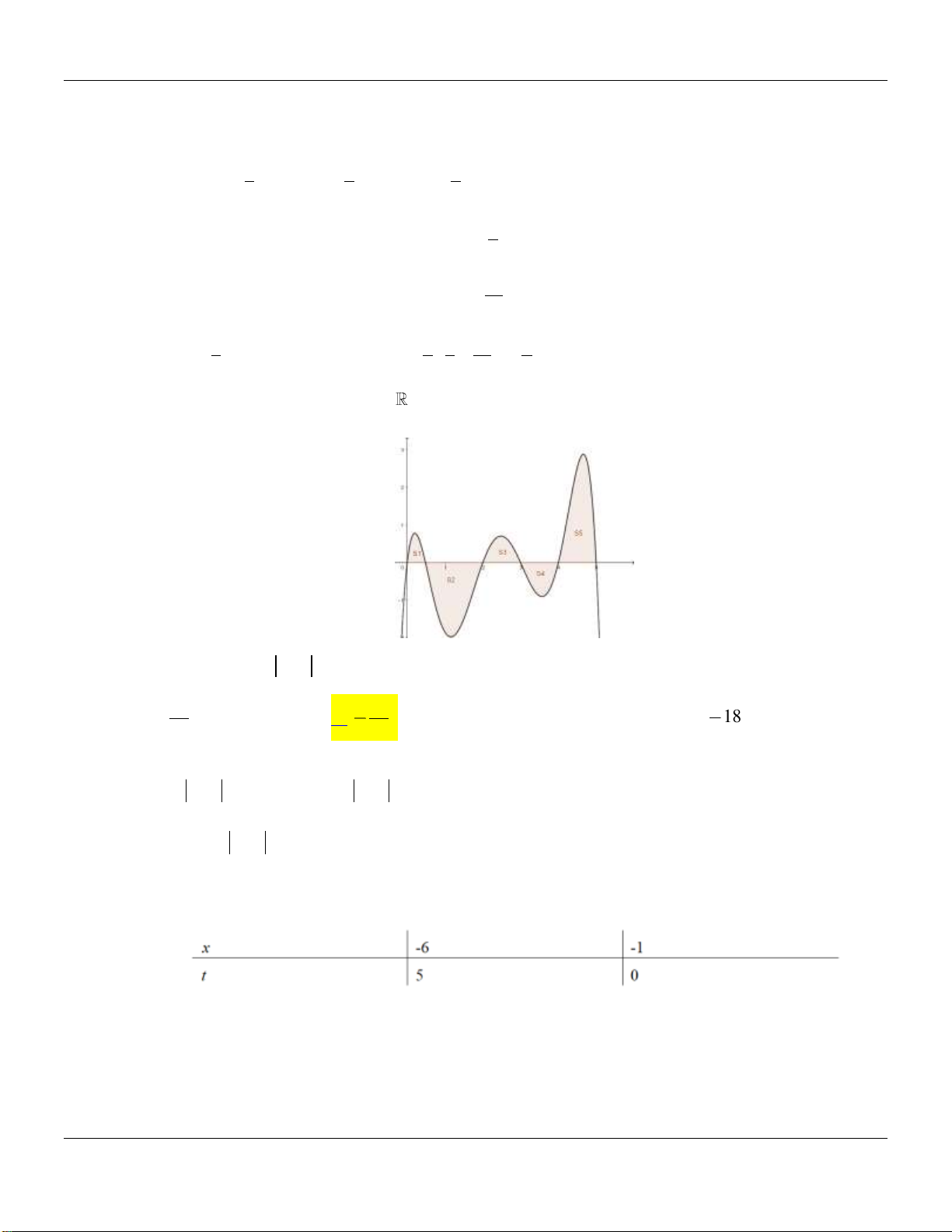
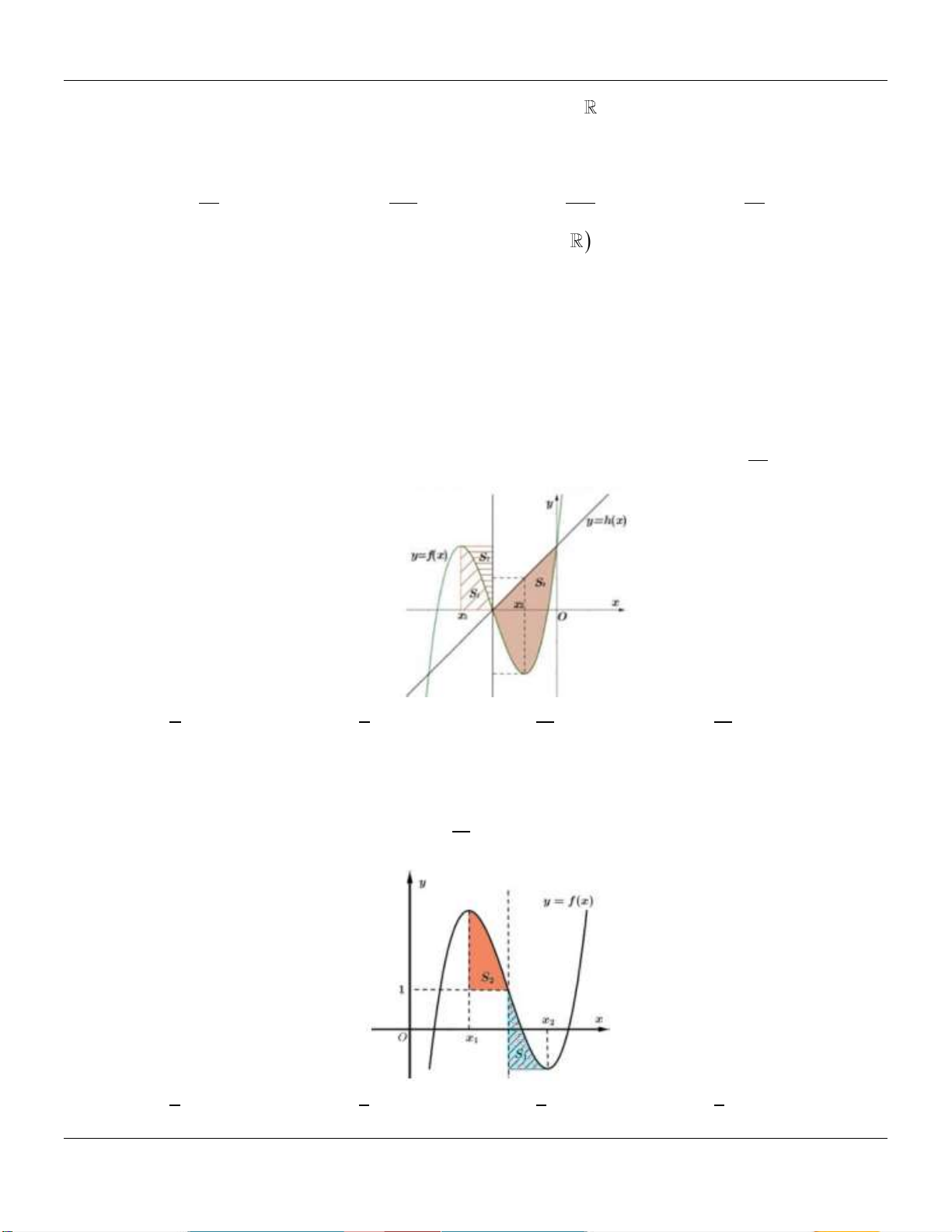
Cho hàm số f  x liên tục trên
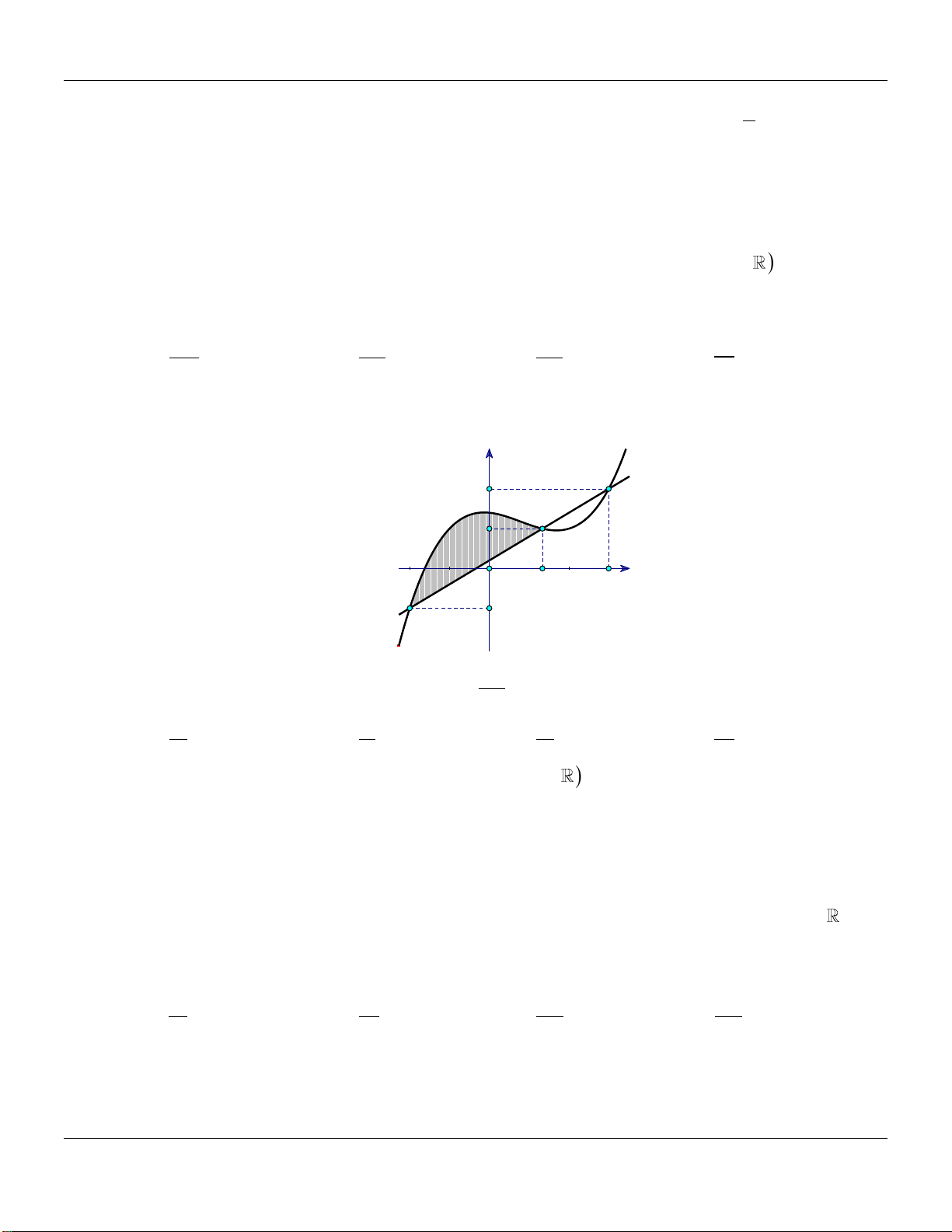
. Biết diện tích S  2 , S  11, S  3 , S  4 , S  12 (tham 1 2 3 4 5 khỏa hình vẽ) S S S 5 1 3 S S4 2 1 Tích phân  f
   x1 x1dx  bằng 6  35 35 A. . B. . C. 18 . D. 18 . 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Câu 4:
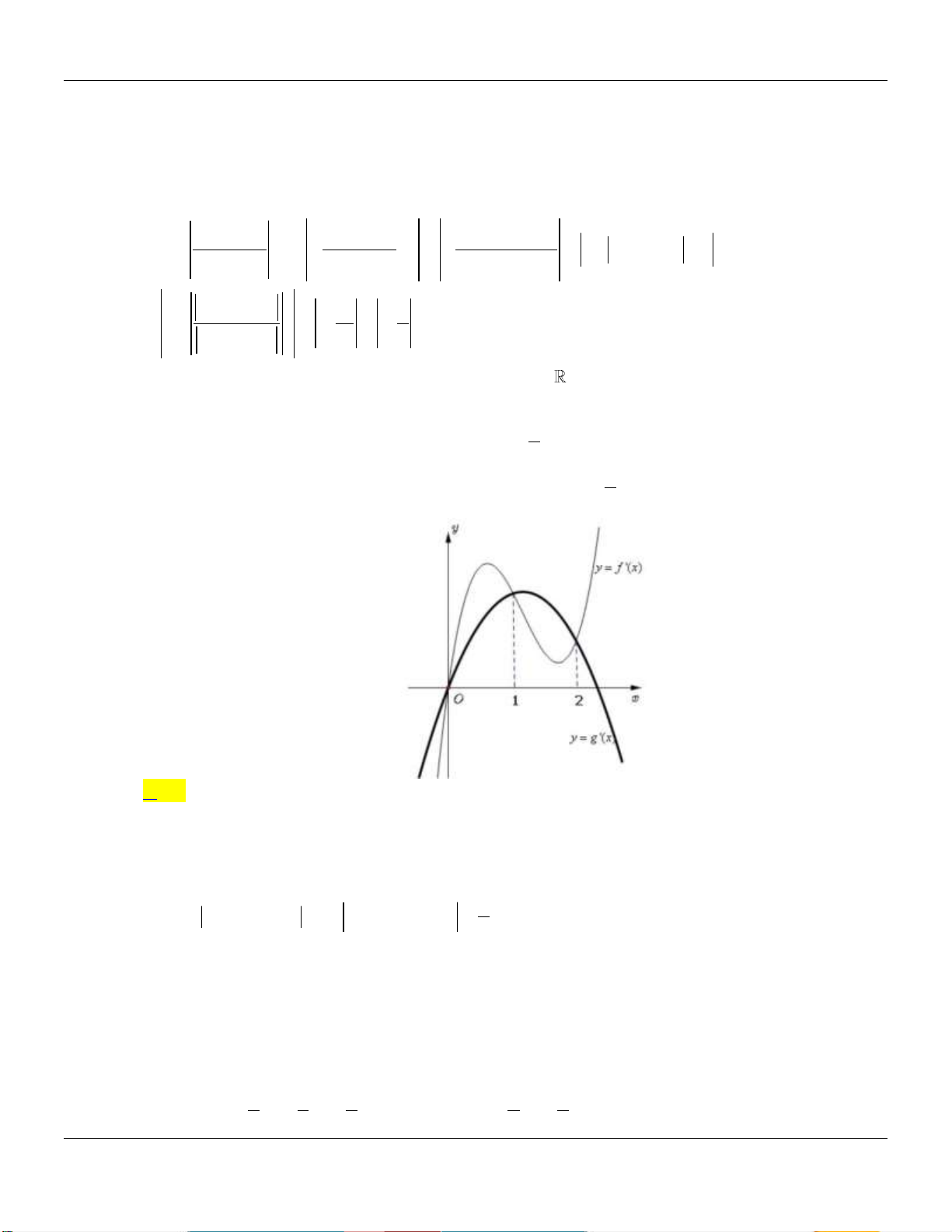
Cho hàm số y  f  x liên tục trên
có đồ thị như hình vẽ bên dưới:
Giả sử diện tích phần kẻ dọc trên hình vẽ có diện tích bằng a . Tính theo a giá trị của 2 I  2x   
1 f  x d . x 3 
A. I  50  2a .
B. I  50  a .
C. I  30  2a .
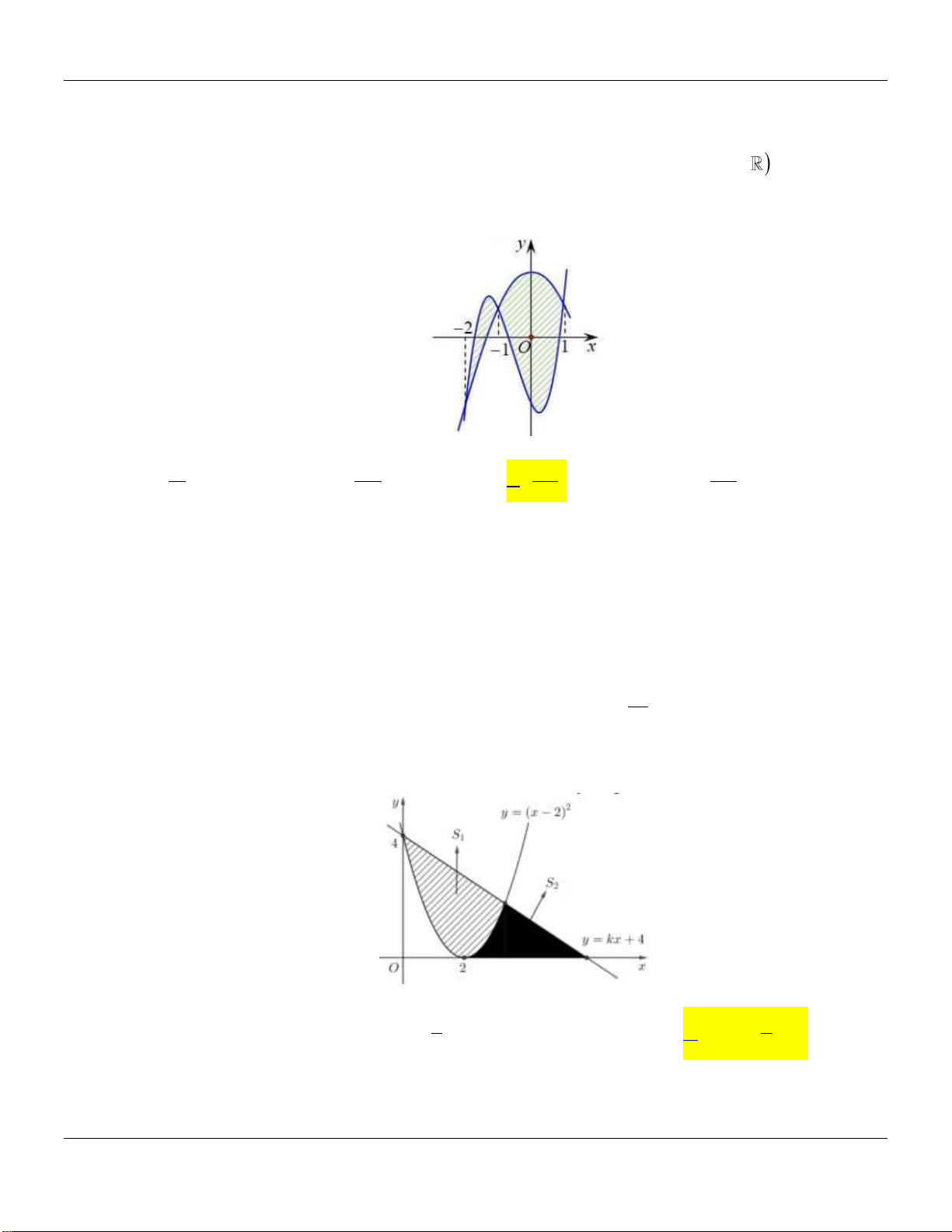
D. I  30  2a . Câu 5:
Cho hàm số y  f x liên tục và nhận giá trị không âm trên 1  ;2   và thỏa mãn 2
f x  f 1  x , x    1  ;2. 
 Đặt S  xf x x 
, S là diện tích hình phẳng được giới hạn bởi đồ 1  d 2 1 
thị hàm số y  f x , trục Ox và hai đường thẳng x  1,x  2 . Khẳng định nào dưới đây đúng?
A. S  2S .
B. S  3S .
C. 2S  S .
D. 3S  S . 1 2 1 2 1 2 1 2 Câu 6:
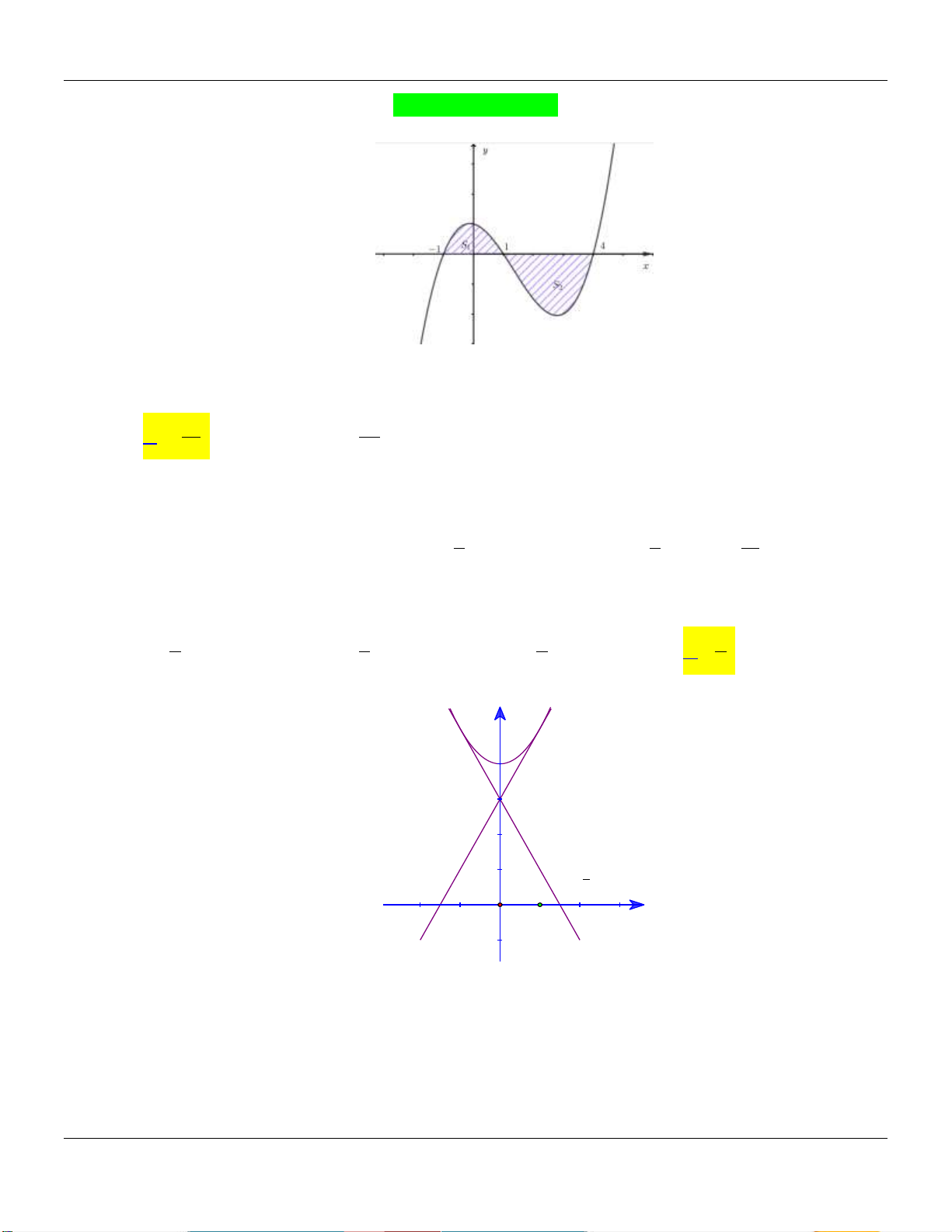
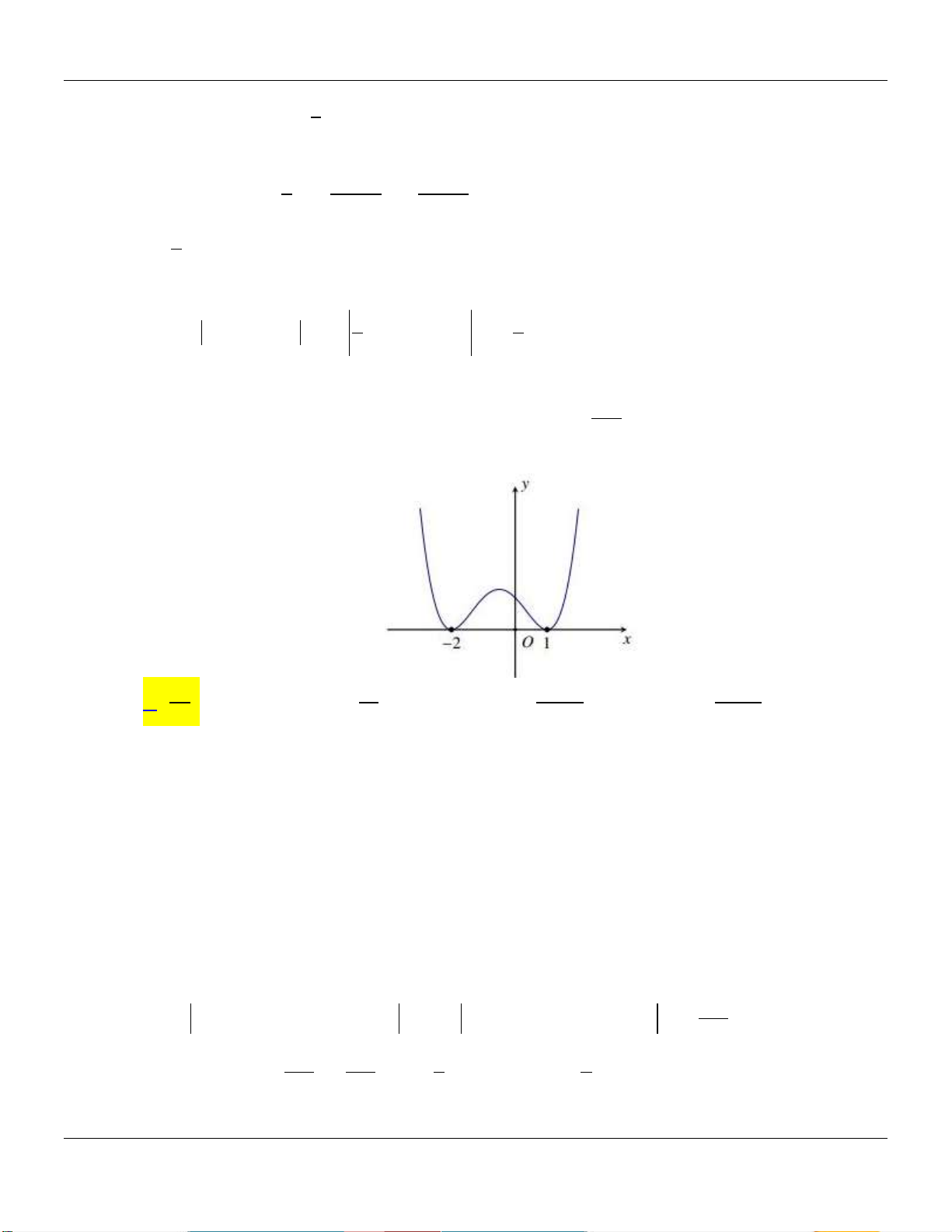
Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y  x  3x  4 , trục hoành, các đường thẳng x  1
 , x  k k  0 bằng 8 . Mệnh đề nào sau đây đúng?  3  A. k   1  ;4 .
B. k  3;6 .
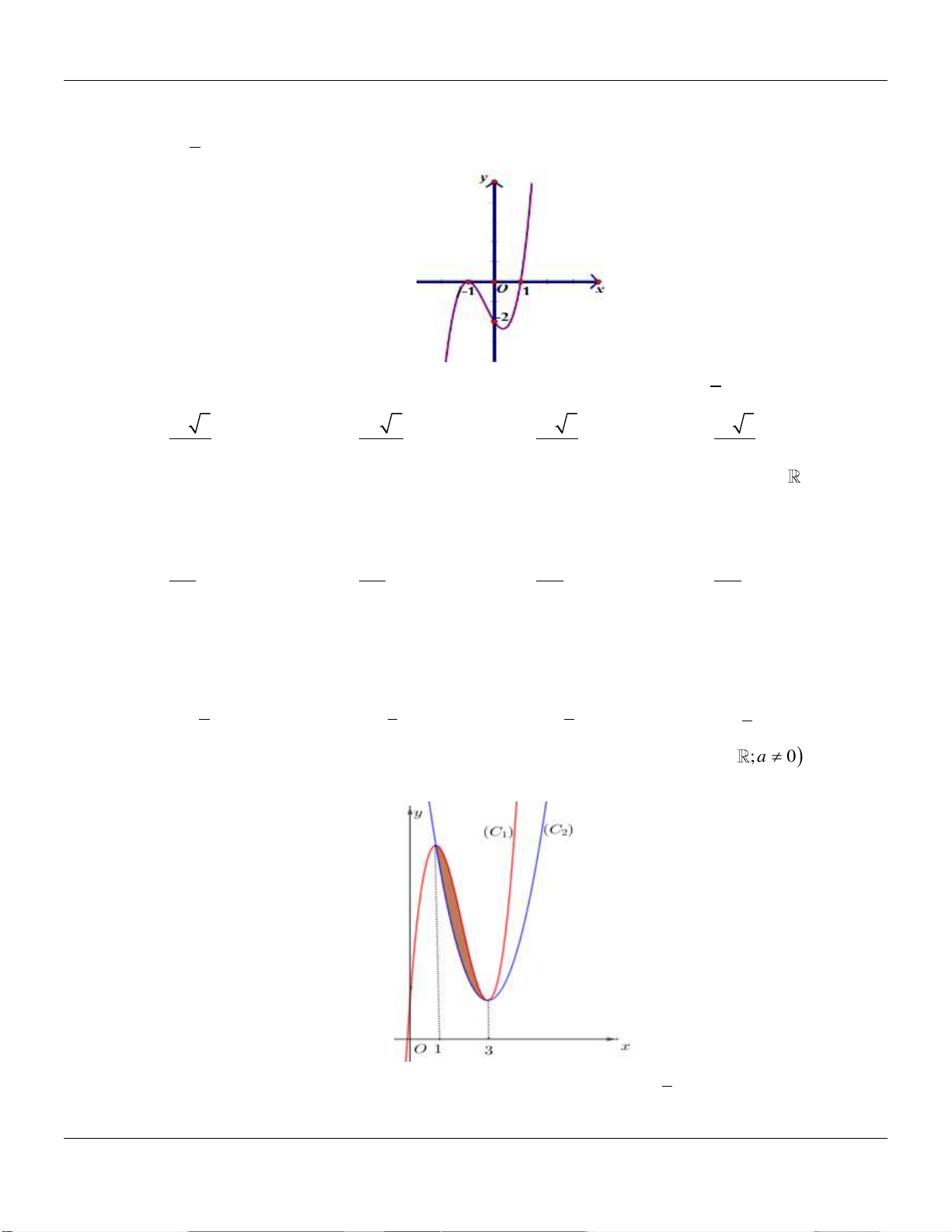
C. k 0; 2 . D. k  3;    .  2  Vậy k   1  ;4 . Câu 7: Cho parabol P 2
: y  x  2x  1 và đường thẳng  : y  2x  m . Để diện tích hình phẳng giới 4
hạn bởi P và  bằng thì giá trị của tham số m nằm trong khoảng nào dưới đây? 3 A. 5;  3 . B.  3  ;0 . C. 0; 2 . D. 2; 3 . Câu 8:
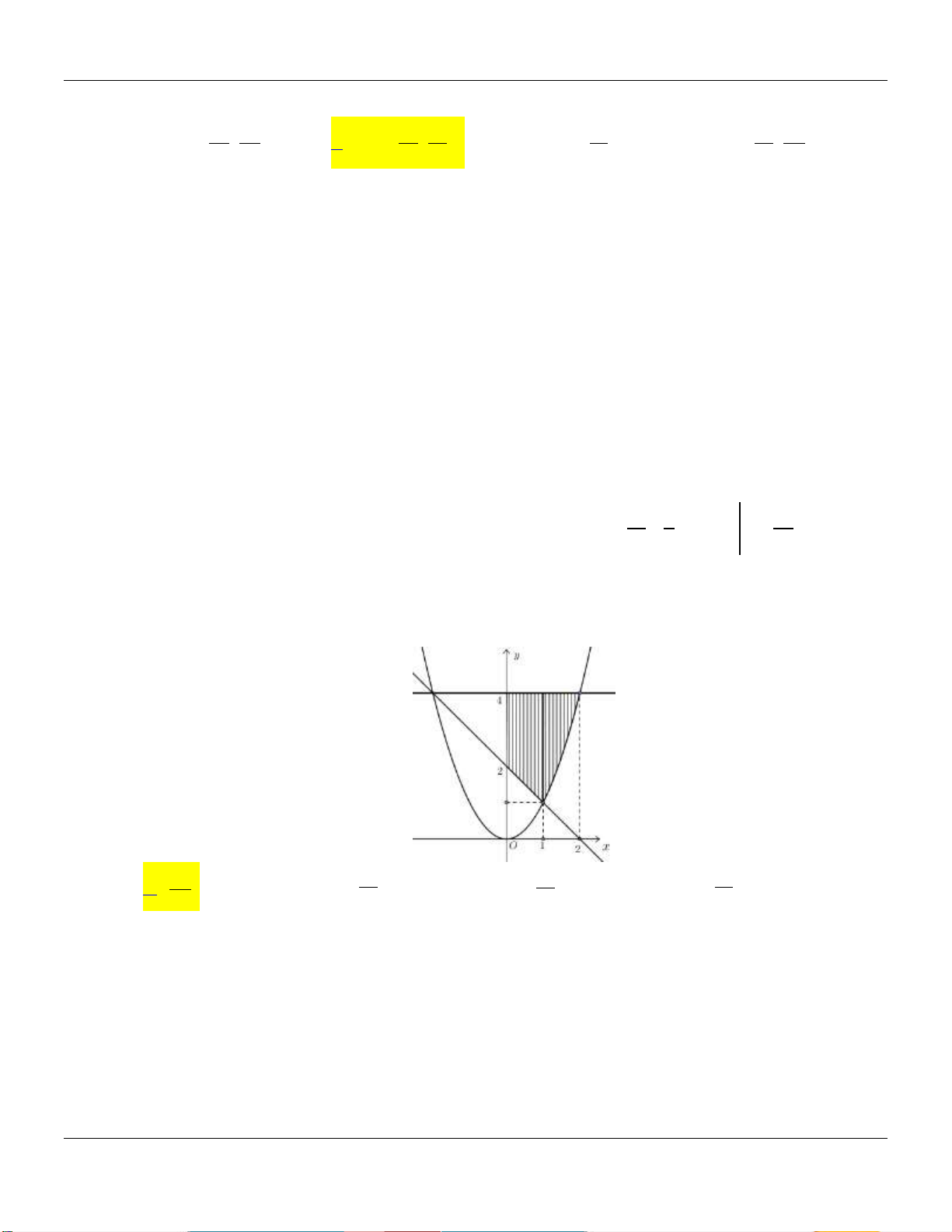
Cho hình thang cong  H  giới hạn bởi các đường 2x y 
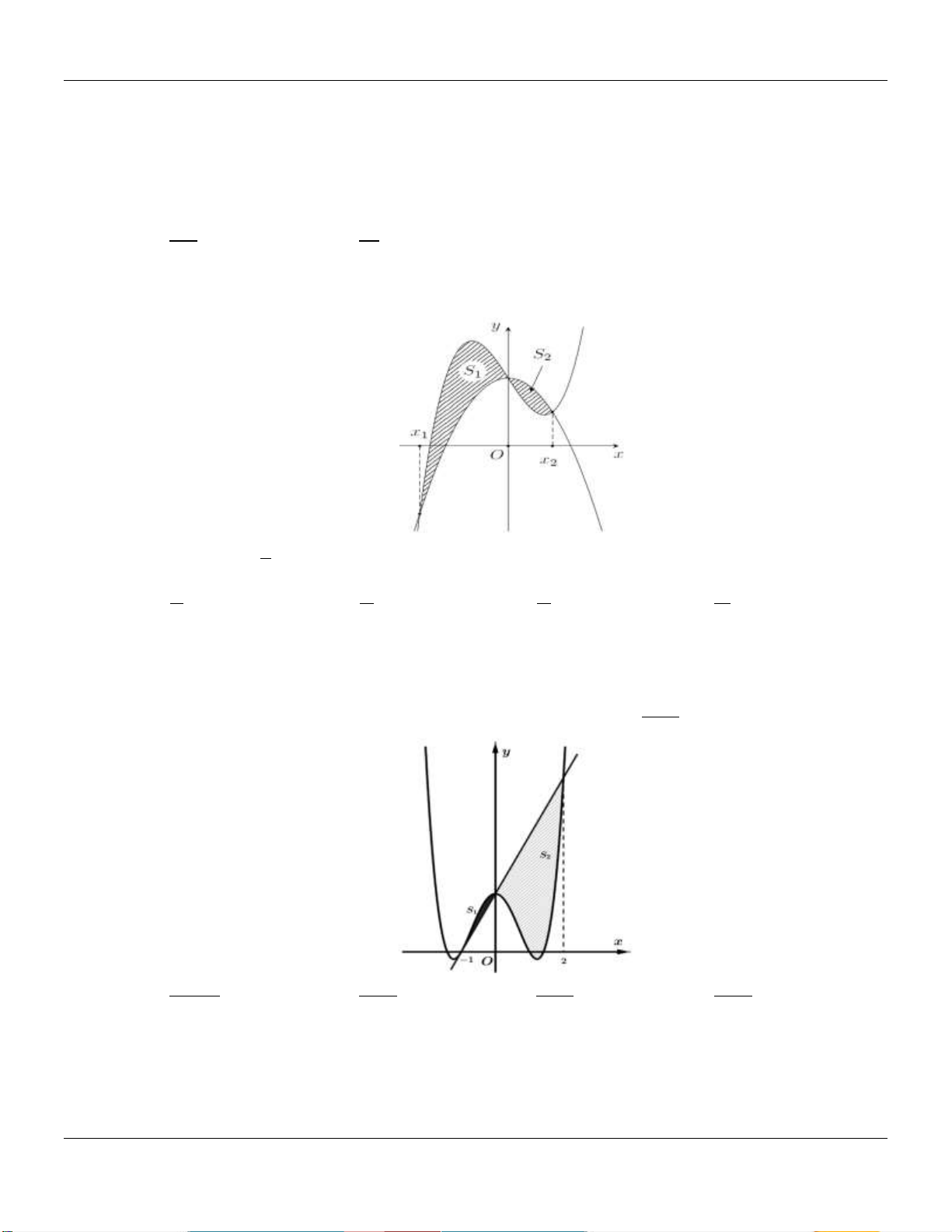
, y  0 , x  0 , x  4 . Đường thẳng
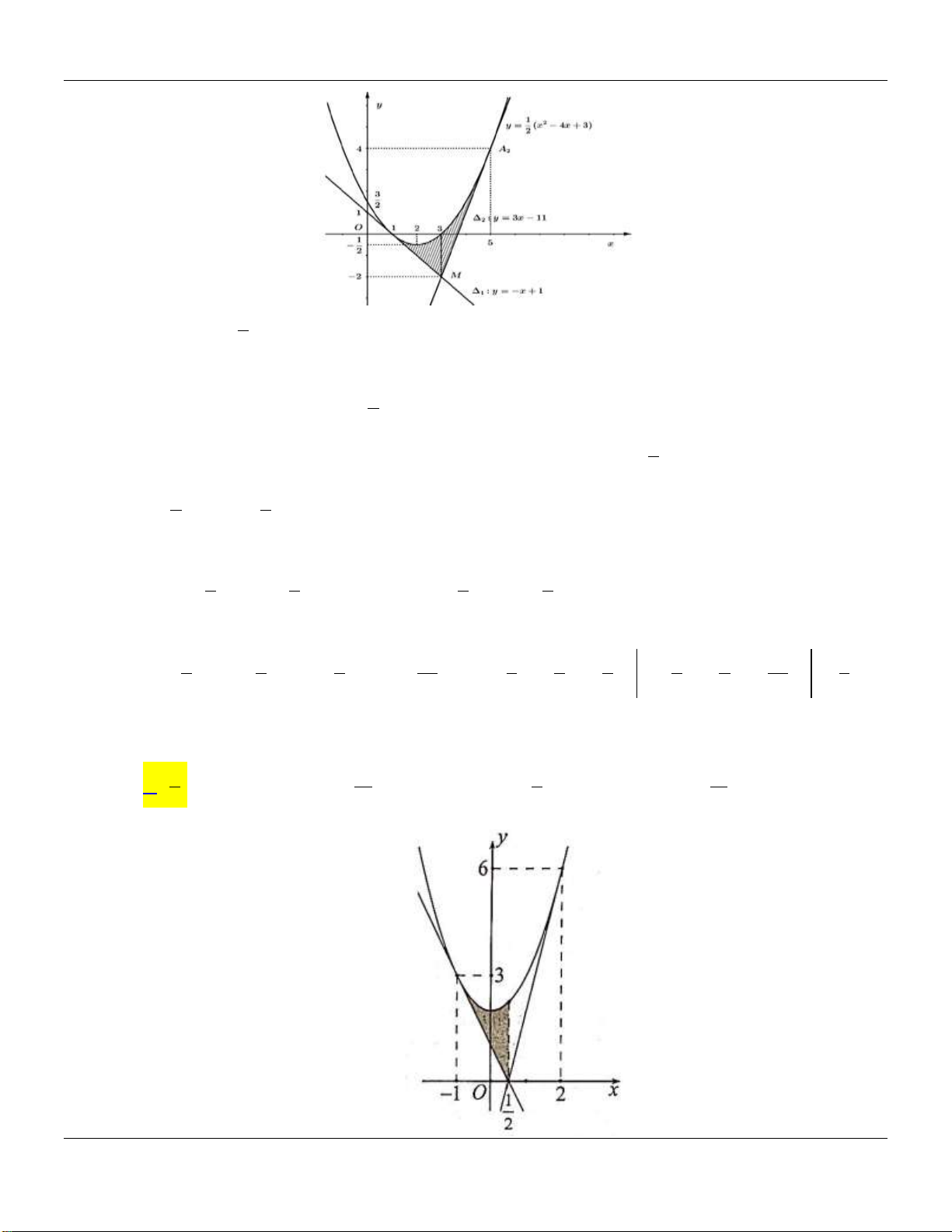
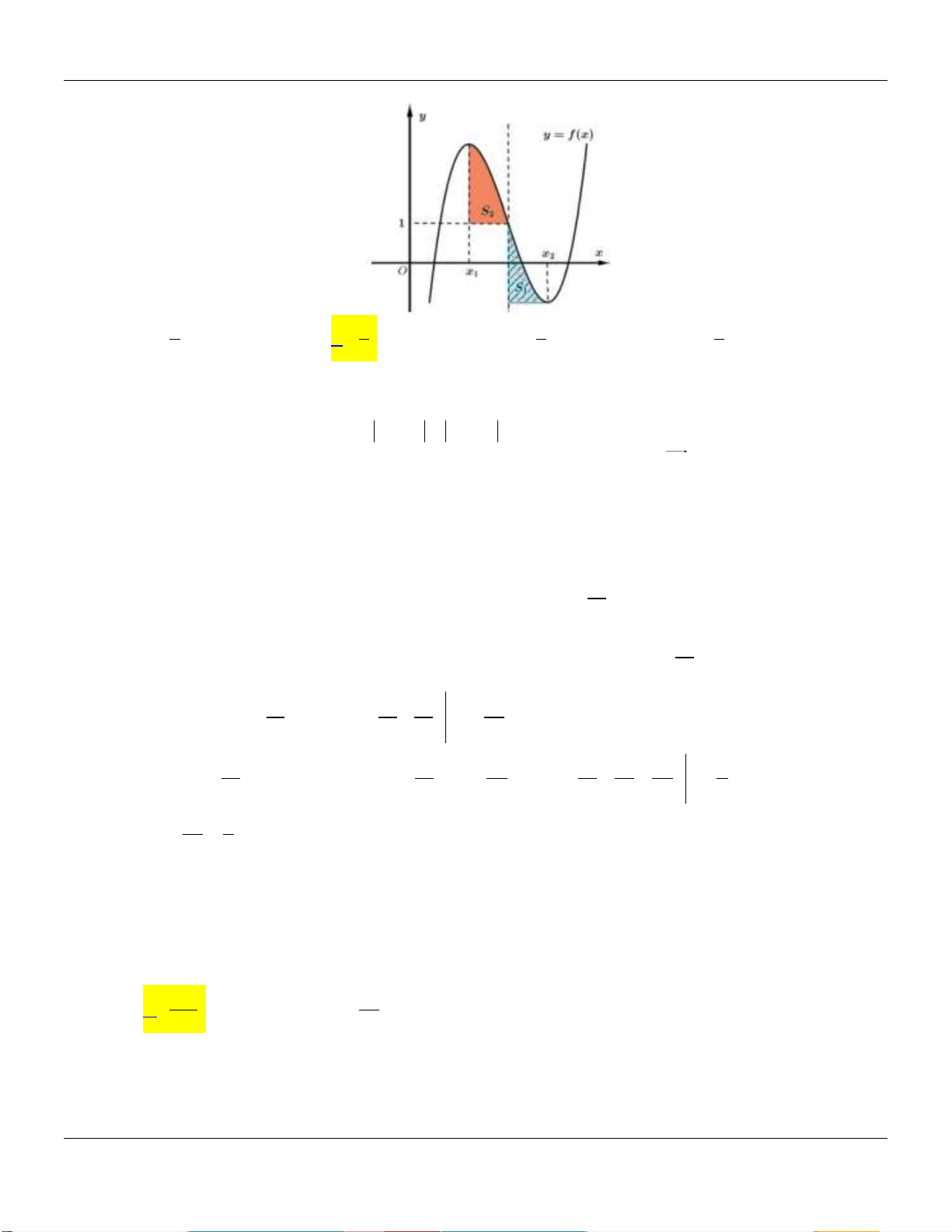
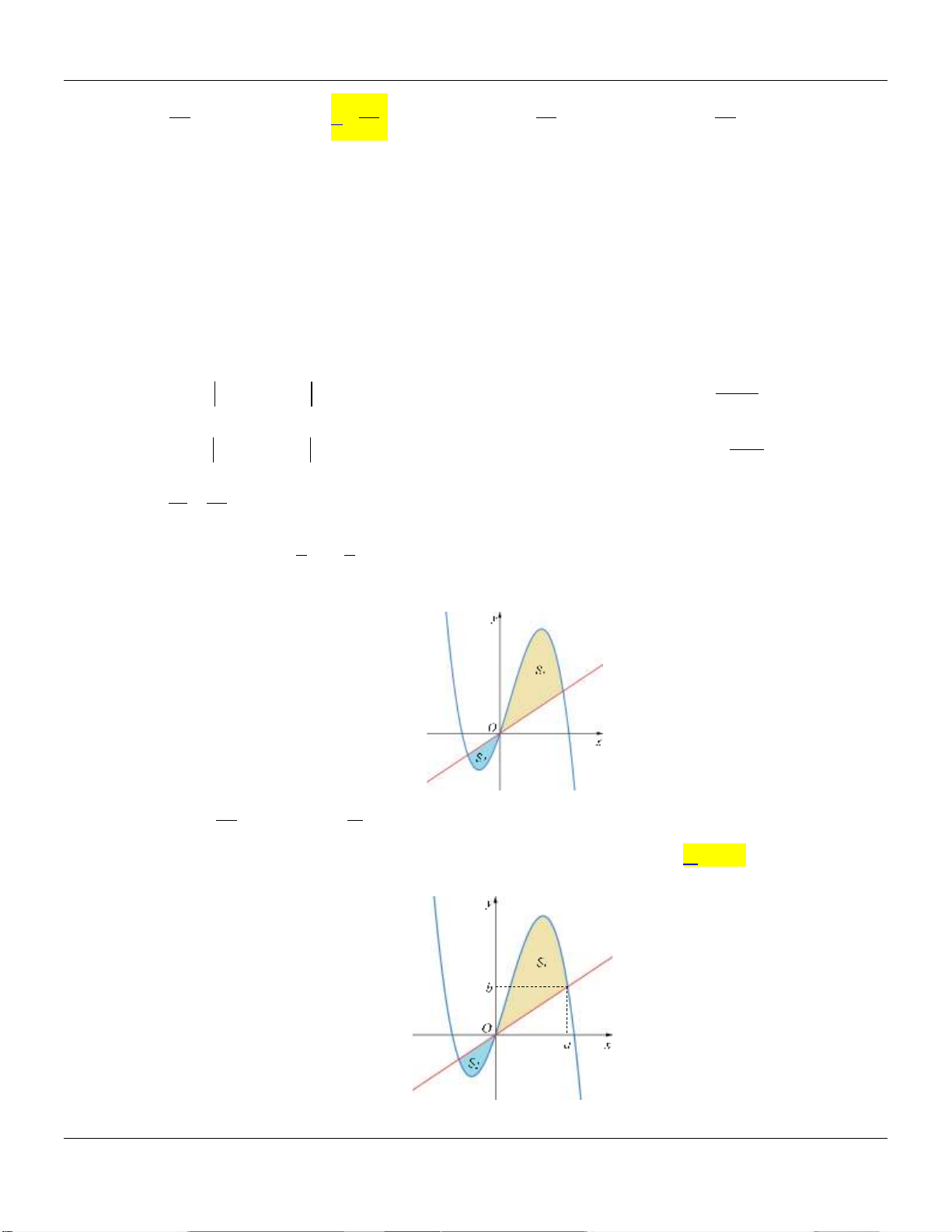
x  a 0  a  4 chia hình  H  thành hai phần có diện tích S và S như hình vẽ bên dưới: 1 2
Tìm a để S  4S . 2 1 16
A. a  3 .
B. a  log 13 .
C. a  2 . D. a  log . 2 2 5
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Câu 9:
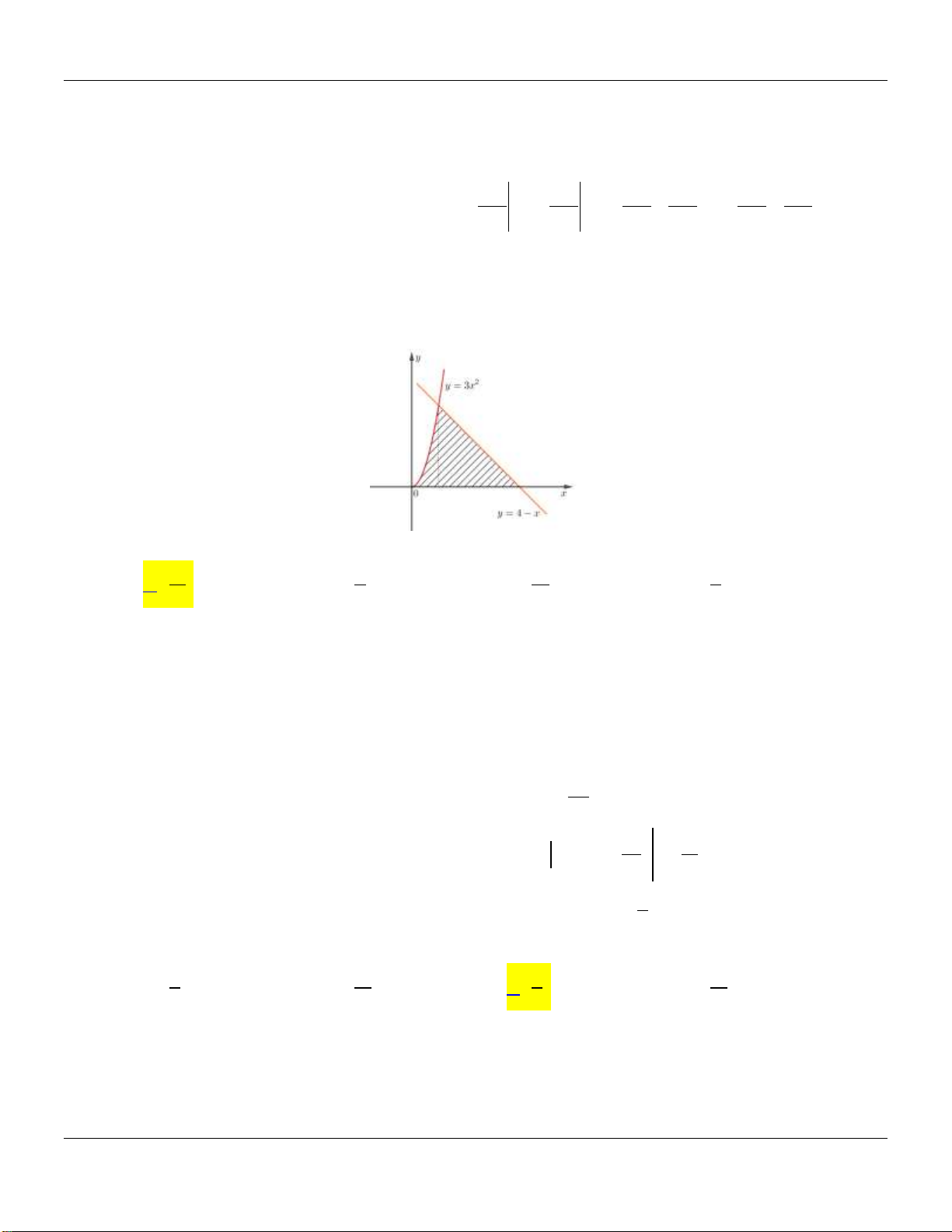
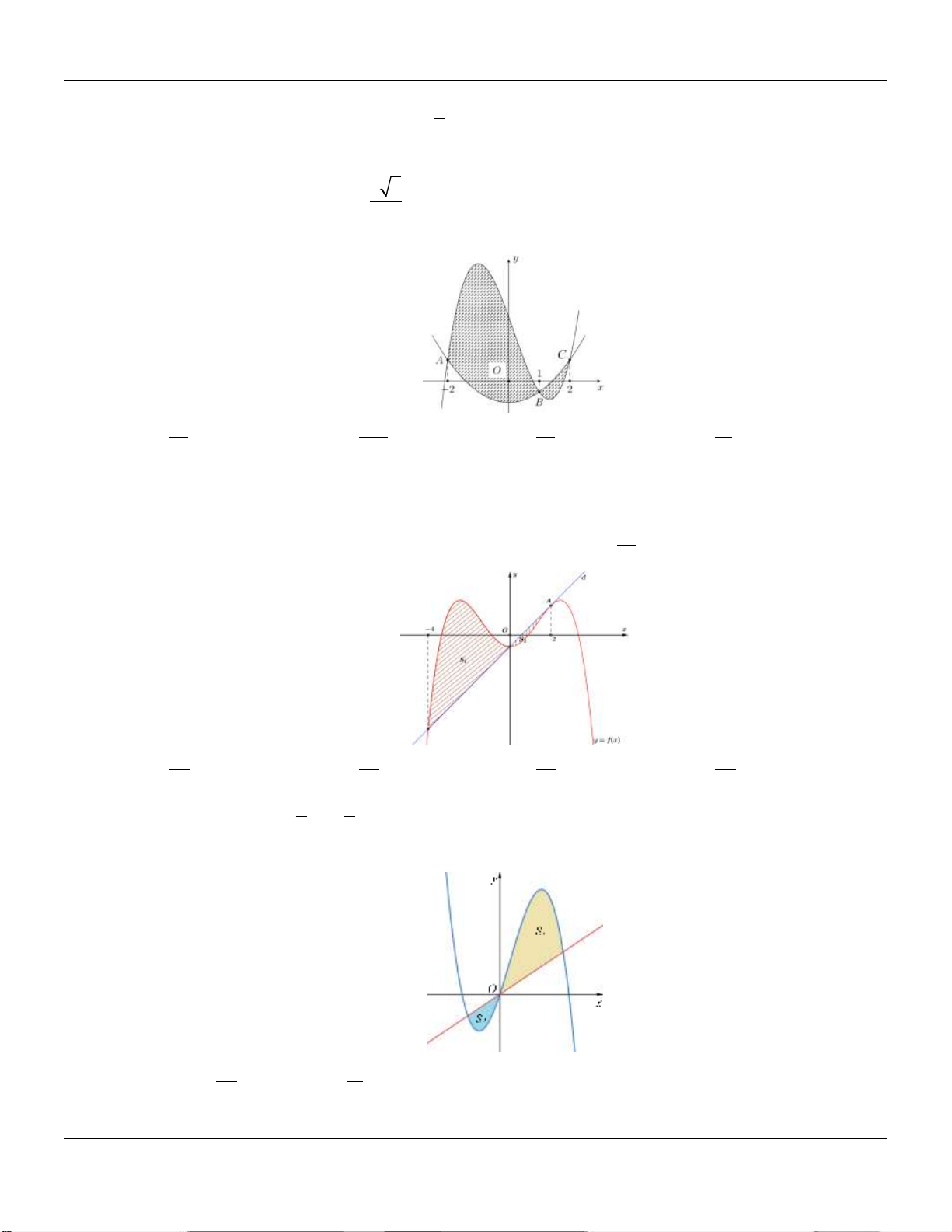
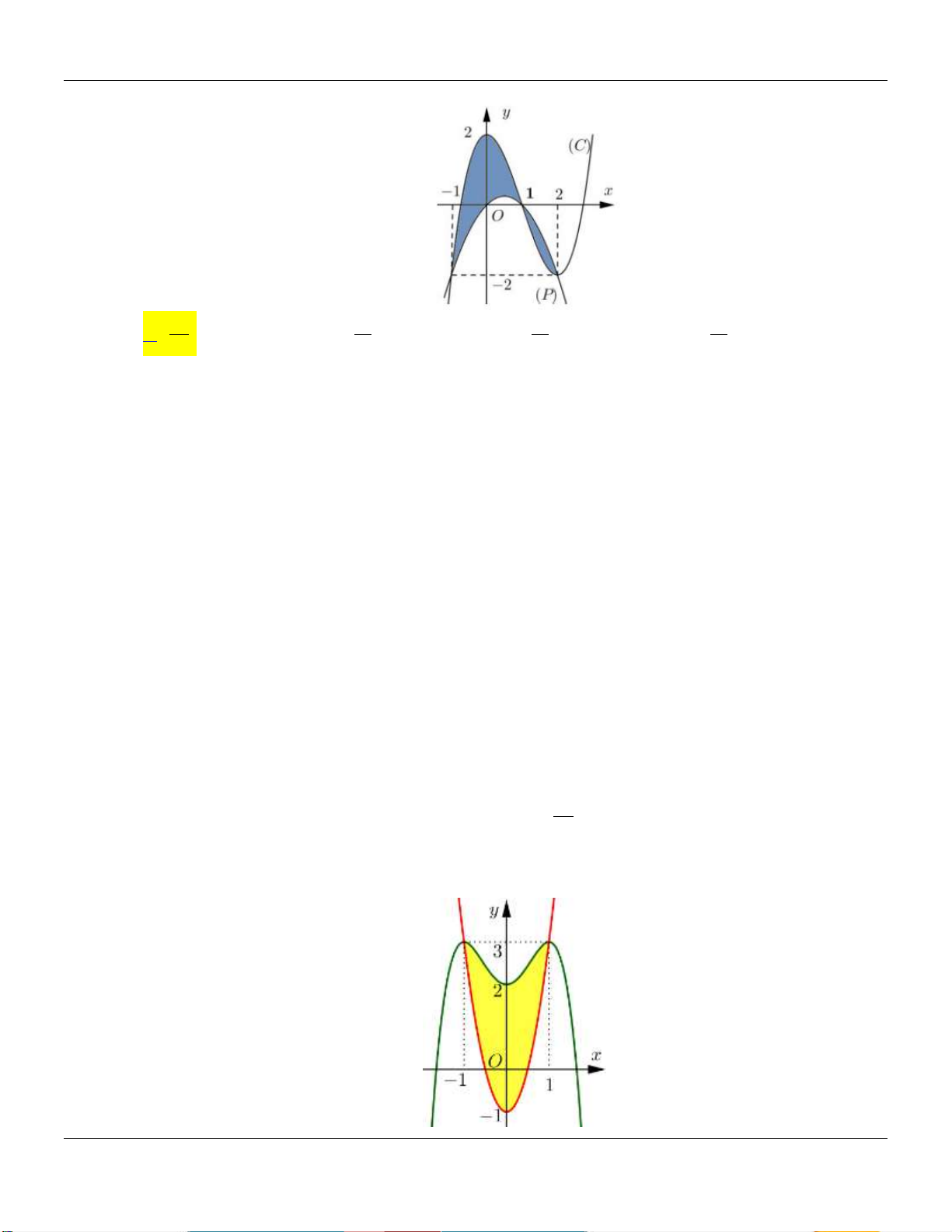
Gọi  H  là phần hình phẳng gạch chéo trong hình vẽ dưới đây được giới hạn bởi đồ thị của các hàm số 2
y  3x , y  4  x và trục hoành (tham khảo hình vẽ)
Diện tích của  H  là bằng 11 9 13 7 A. . B. . C. . D. . 2 2 2 2 1
Câu 10: Diện tích hình phẳng giới hạn bởi đồ thị C  của hàm số y   2
x  4x  3 và hai tiếp tuyến 2
của C  xuất phát từ M 3; 2   là 5 11 8 13 A. . B. . C. . D. . 3 3 3 3
Câu 11: Cho parabol P 2
: y  x  2 và hai tiếp tuyến của P tại các điểm M 1; 3 và N 2;6 . Diện
tích hình phẳng giới hạn bởi P và hai tiếp tuyến đó bằng 9 13 7 21 A. . B. . C. . D. . 4 4 4 4
Câu 12: Cho hàm số y  f  x là một hàm số bậc ba. Gọi S
là diện tích giới hạn bởi các đường
y  f  x, y  0, x  1
 và x  4 (tham khảohình vẽ).
Khi đó diện tích S có giá trị bằng 253 253 235 235 A. . B. . C. . D. . 12 24 24 12
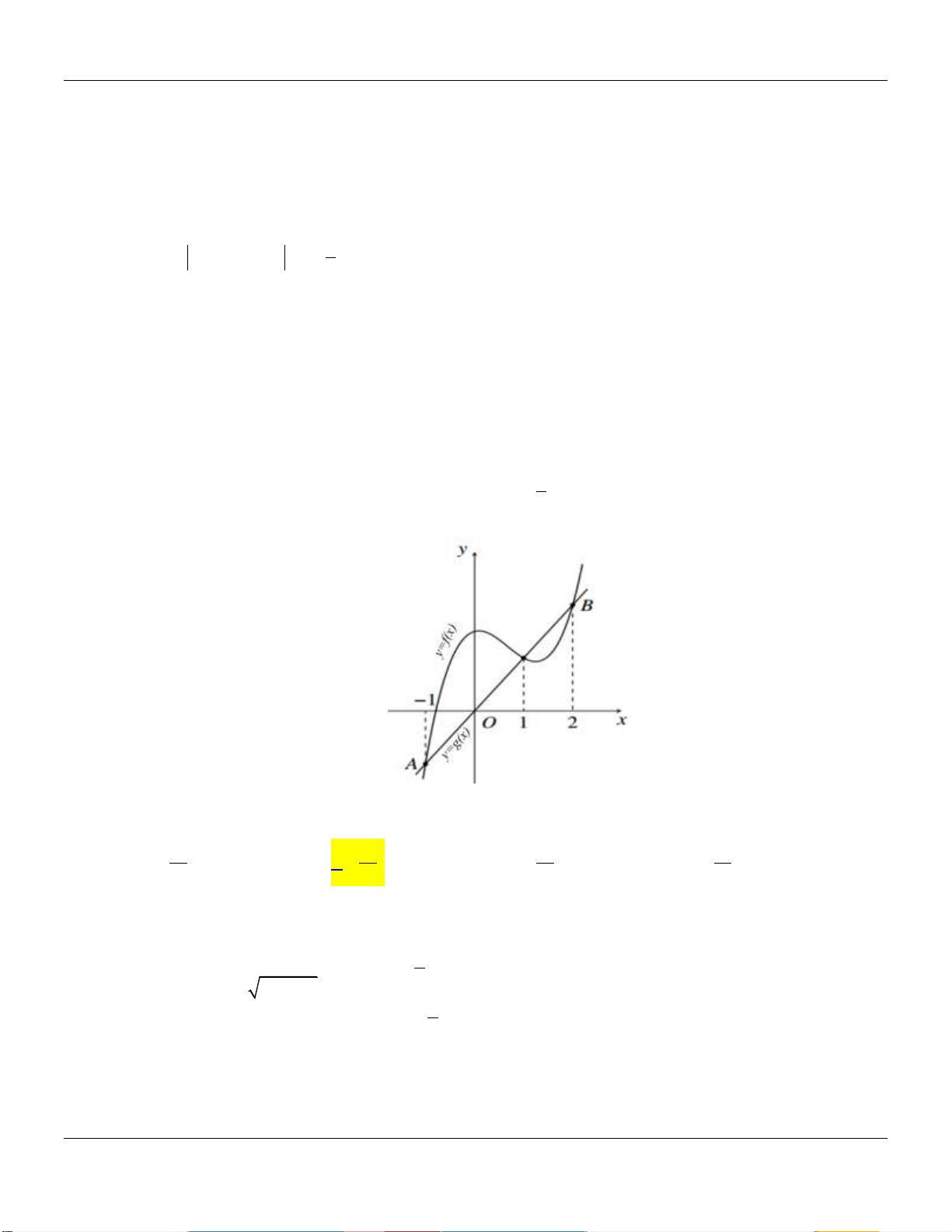
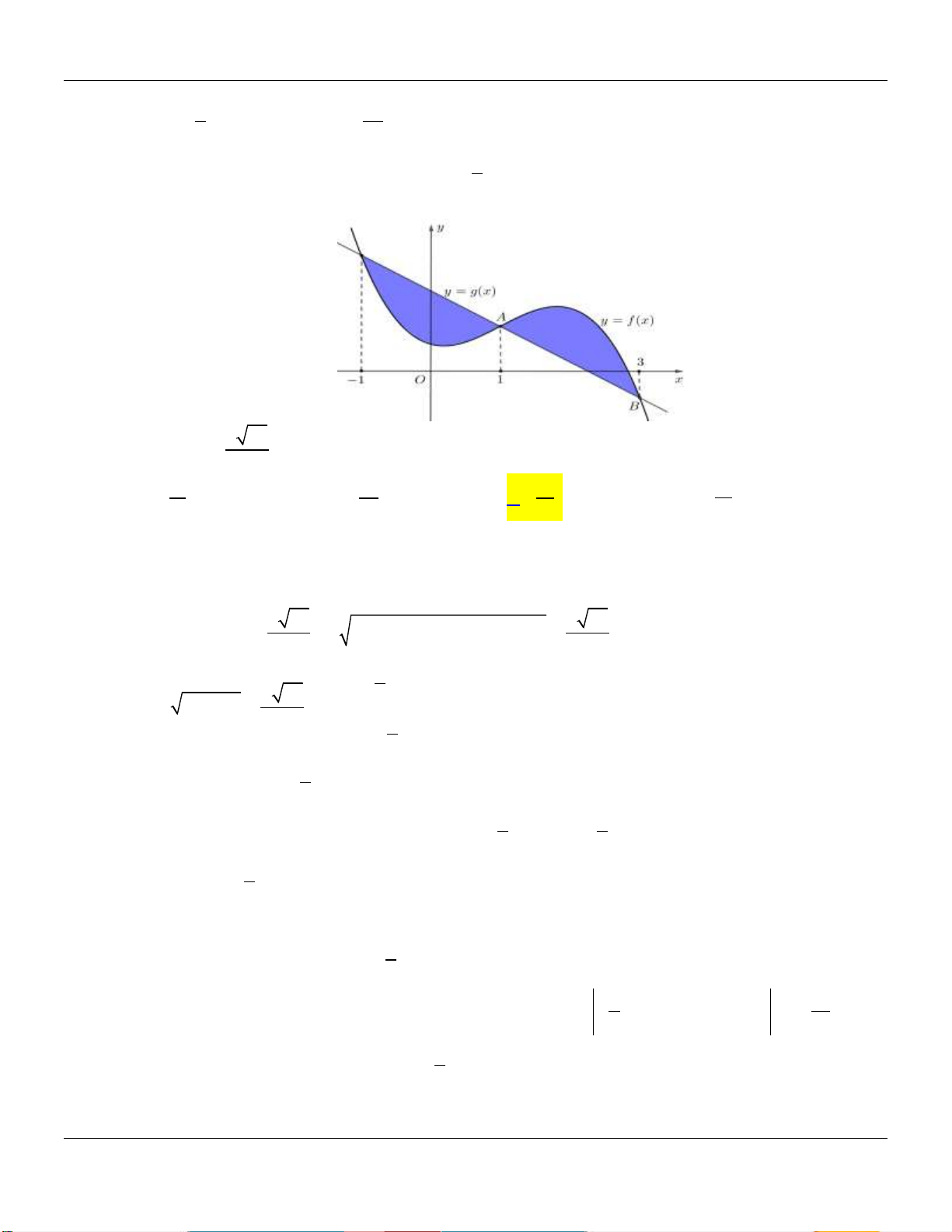
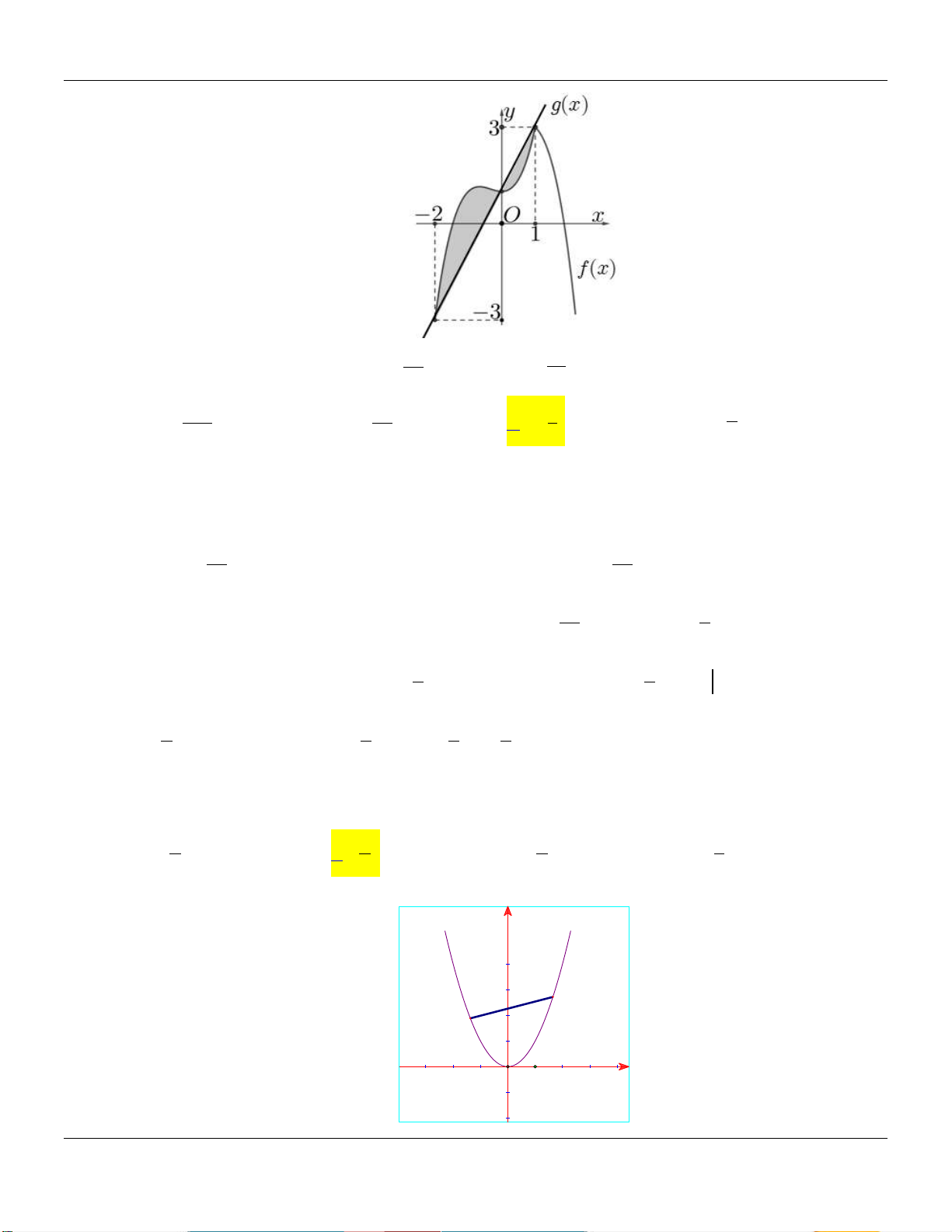
Câu 13: Cho đồ thị hàm số y  f  x và y  g  x như hình vẽ bên dưới:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1
Biết đồ thị của hàm số y  f  x là một Parabol đỉnh I có tung độ bằng  và y  g  x là 2
một hàm số bậc ba. Hoành độ giao điểm của hai đồ thị là x , x , x thỏa mãn x .x .x  6  . 1 2 3 1 2 3
Diện tích hình phẳng giới hạn bởi 2 đồ thị hàm số y  f  x và y  g  x gần nhất với giá trị nào dưới đây? A. 6 . B. 8 . C. 5 . D. 7 .
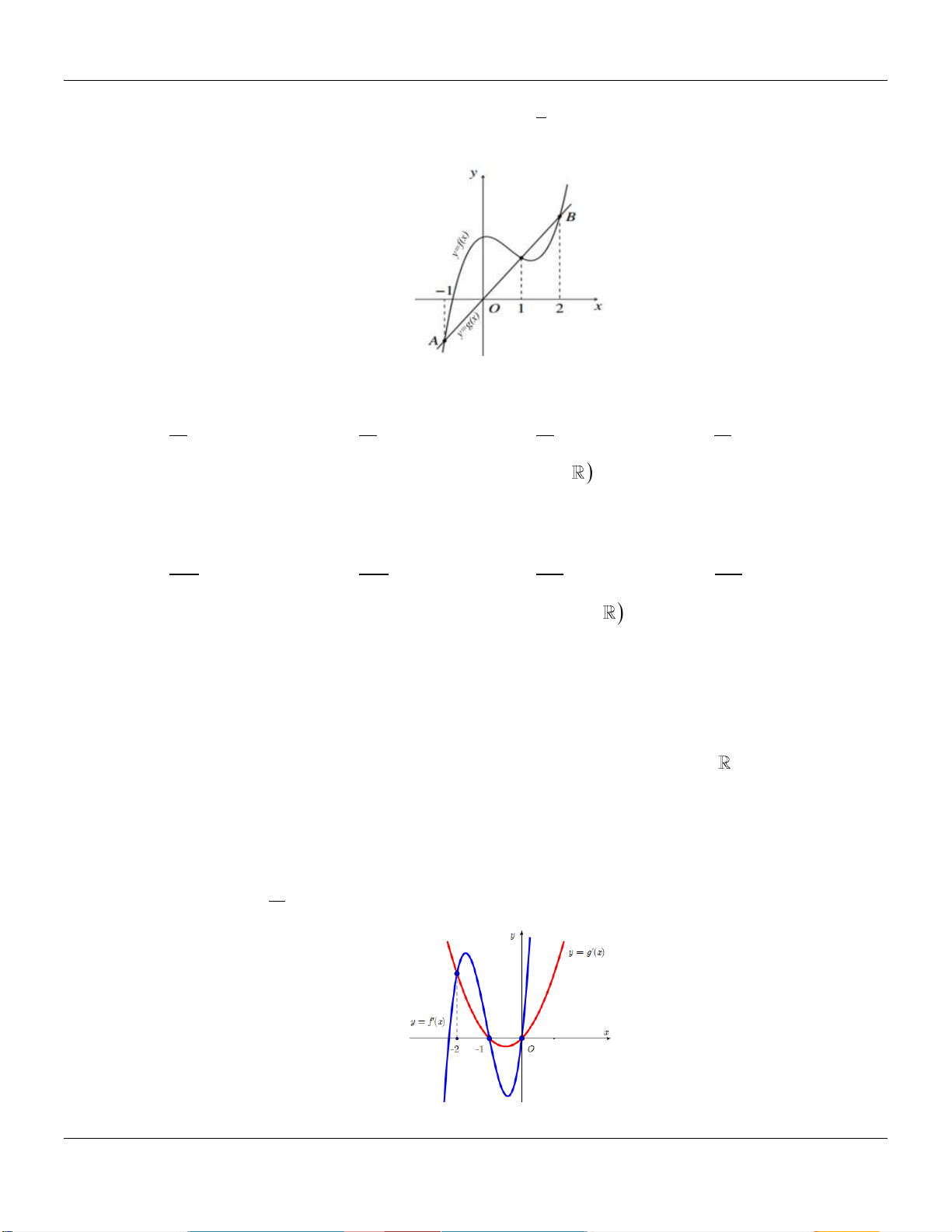
Câu 14: Cho hai hàm số f  x 3 2
 ax  bx  cx  4 và g x 2
 dx  ex  2, a, b, c, d, e  . Biết rằng đồ
thị hàm số y  f  x và y  g  x cắt nhau tại 3 điểm có hoành độ lần lượt là 3; 1; 2 . Hình
phẳng giới hạn bởi đồ thị hai hàm số đã cho có diện tích bằng 316 191 253 97 A. . B. . C. . D. . 15 9 12 6
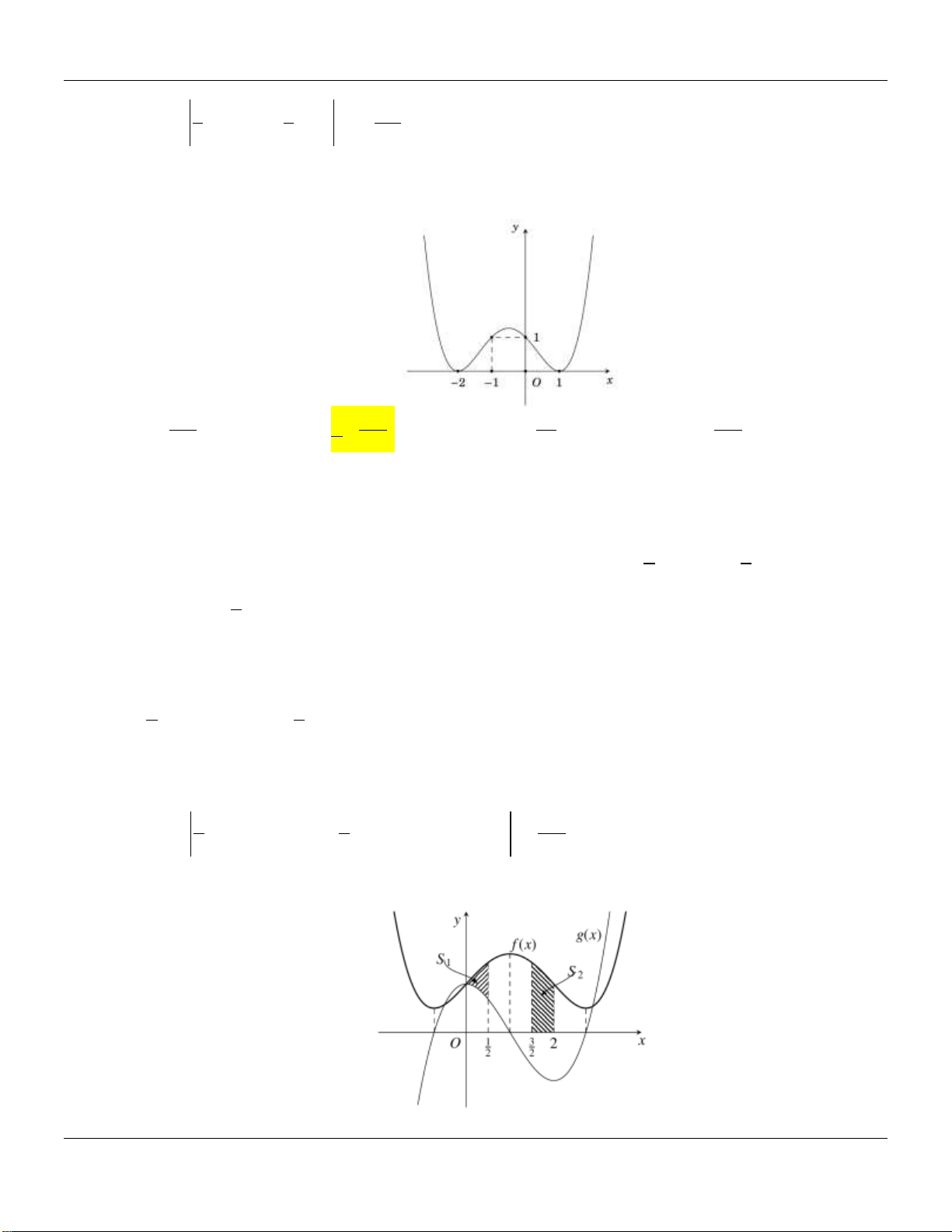
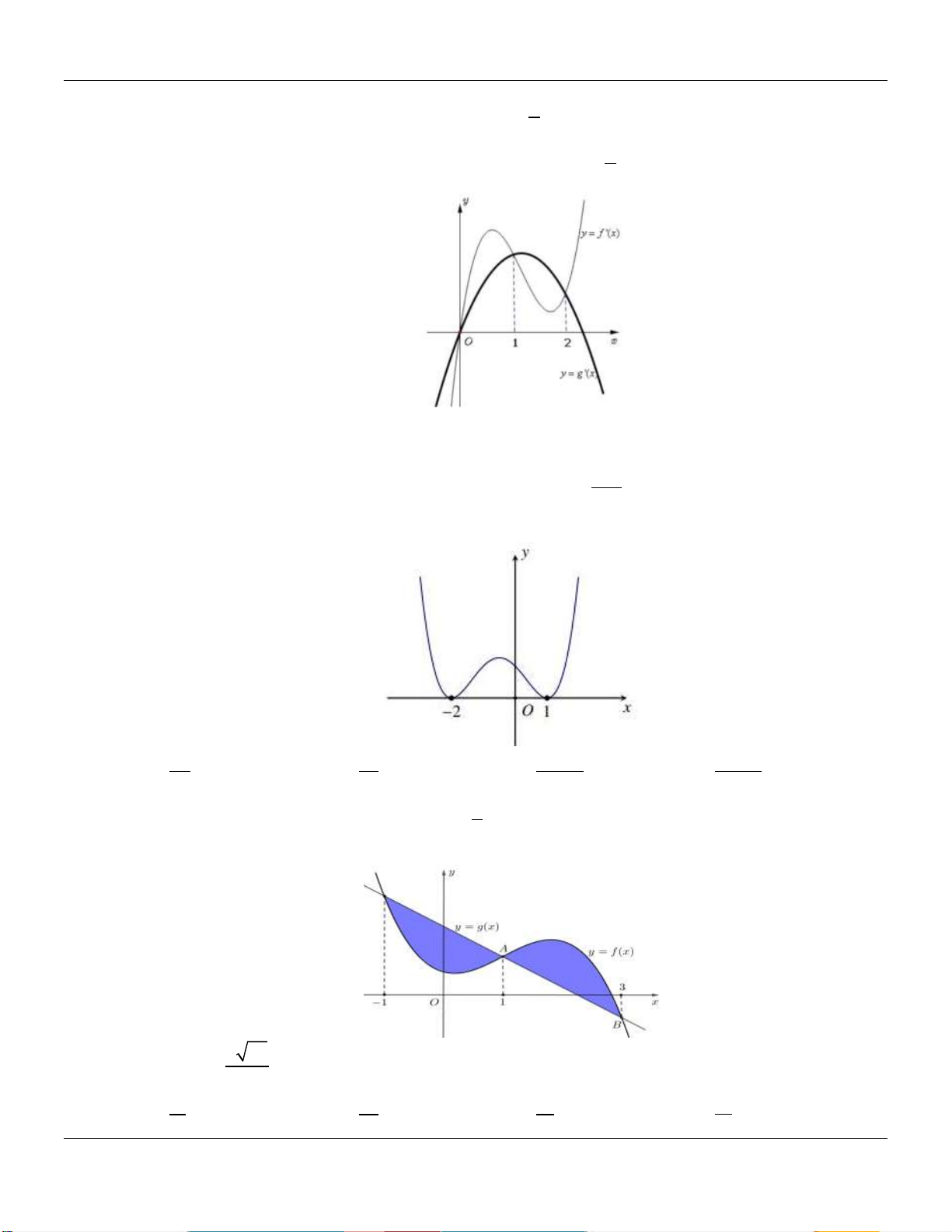
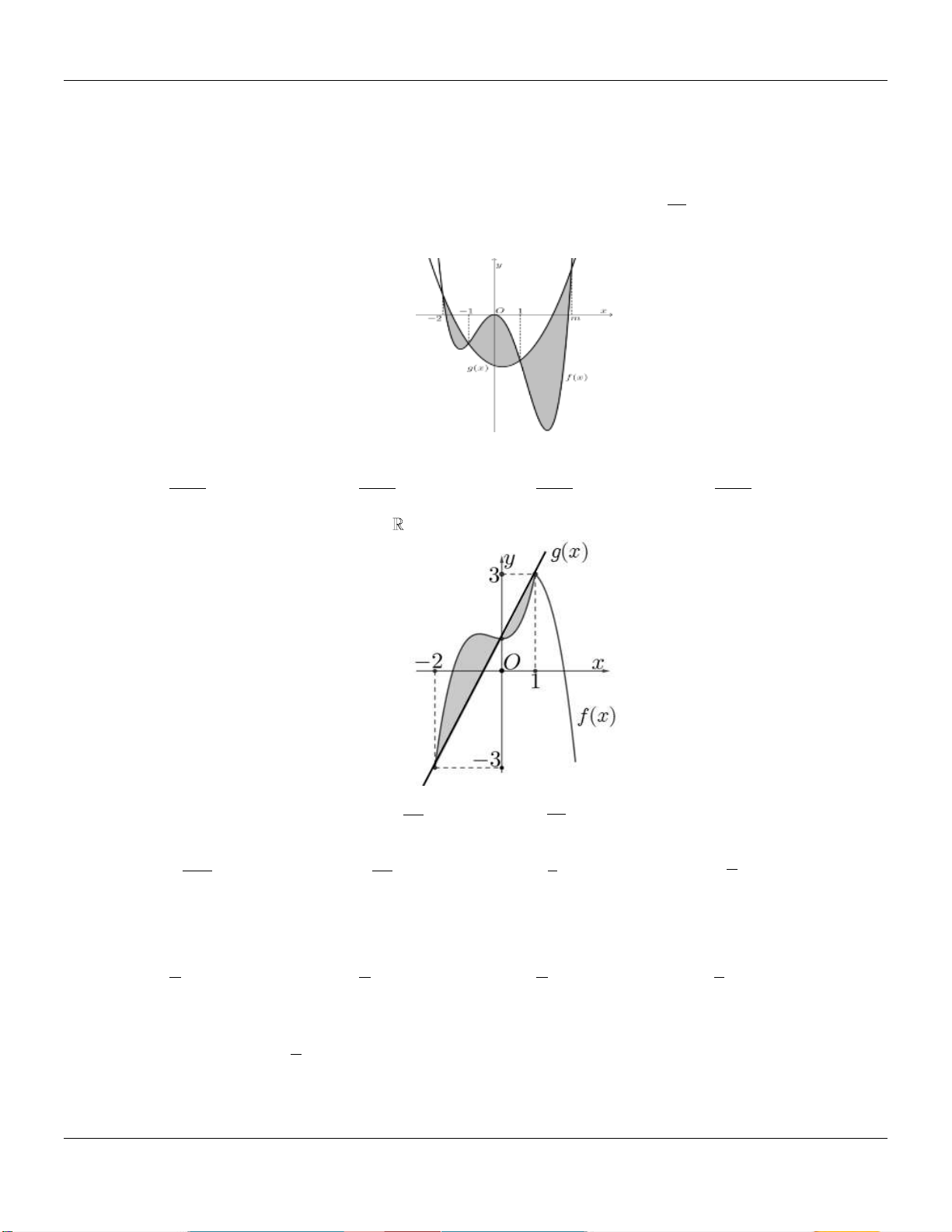
Câu 15: Cho f  x, g  x lần lượt là các hàm đa thức bậc ba và bậc nhất có đồ thị như hình vẽ bên dưới: y 2 1 x O _4 3 3 _ 1 2
Biết diện tích hình S (được tô đậm) bằng 250 . Tính  d  f x x . 81 0 19 11 34 23 A. . B. . C. . D. . 15 9 15 6
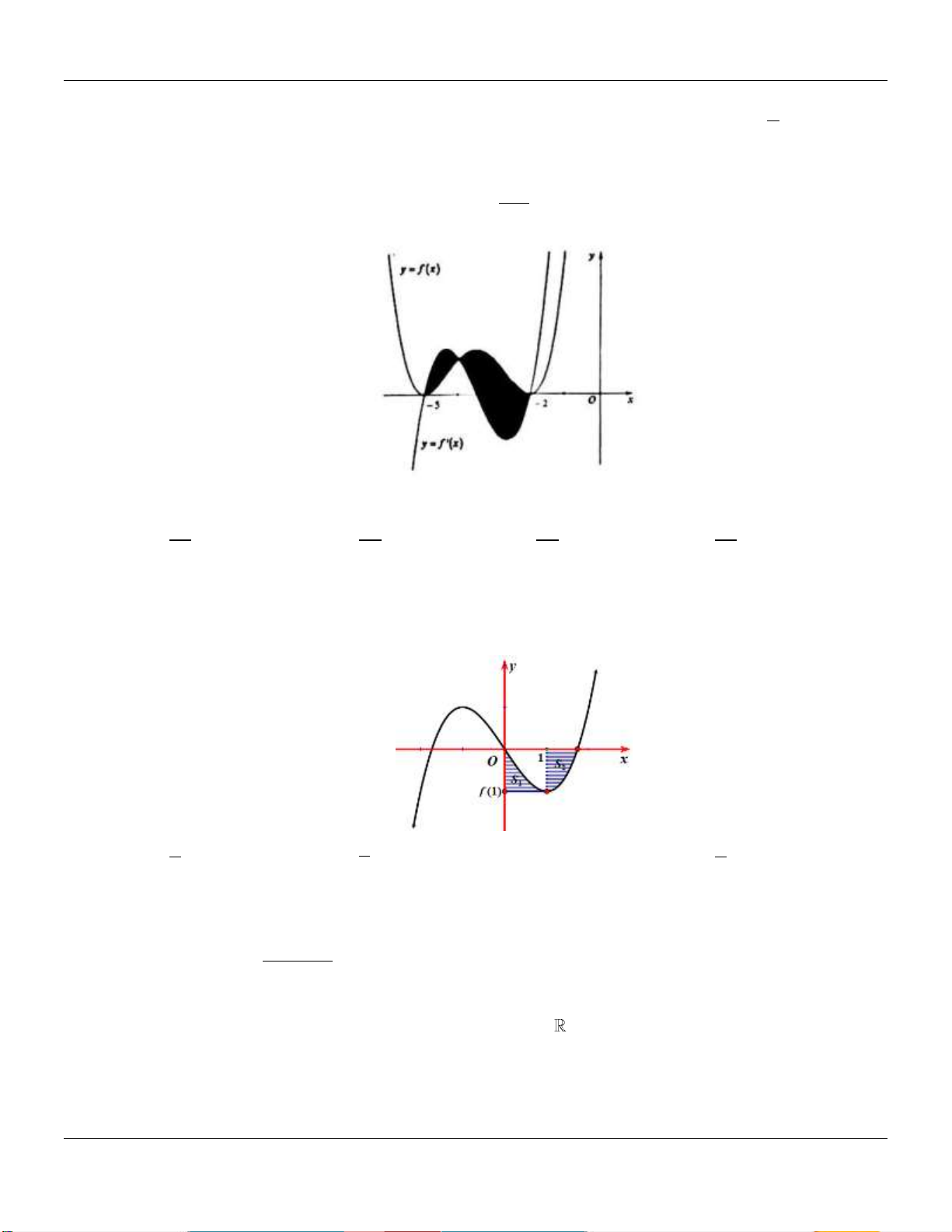
Câu 16: Cho hàm số f  x 3 2
 ax  bx  36x  c a  0;a, , b c 
 có hai điểm cực trị là 6  và 2 . Gọi
y  g  x là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y  f  x . Diện tích hình
phẳng giới hạn bởi hai đường y  f  x và y  g  x bằng A. 160  B. 128. C. 64  D. 672 
Câu 17: Cho hai hàm số f  x 4 3 2
 ax  bx  cx  3x và   3 2
g x  mx  nx  x ; với a,b, c, m, n  . Biết
hàm số y  f  x  g  x có ba điểm cực trị là 1
 ; 3 và 4 . Diện tích hình phẳng giới hạn bởi
hai đồ thị hàm số f  x và y  g x bằng 32 64 125 131 A. . B. . C. . D. . 3 9 12 12
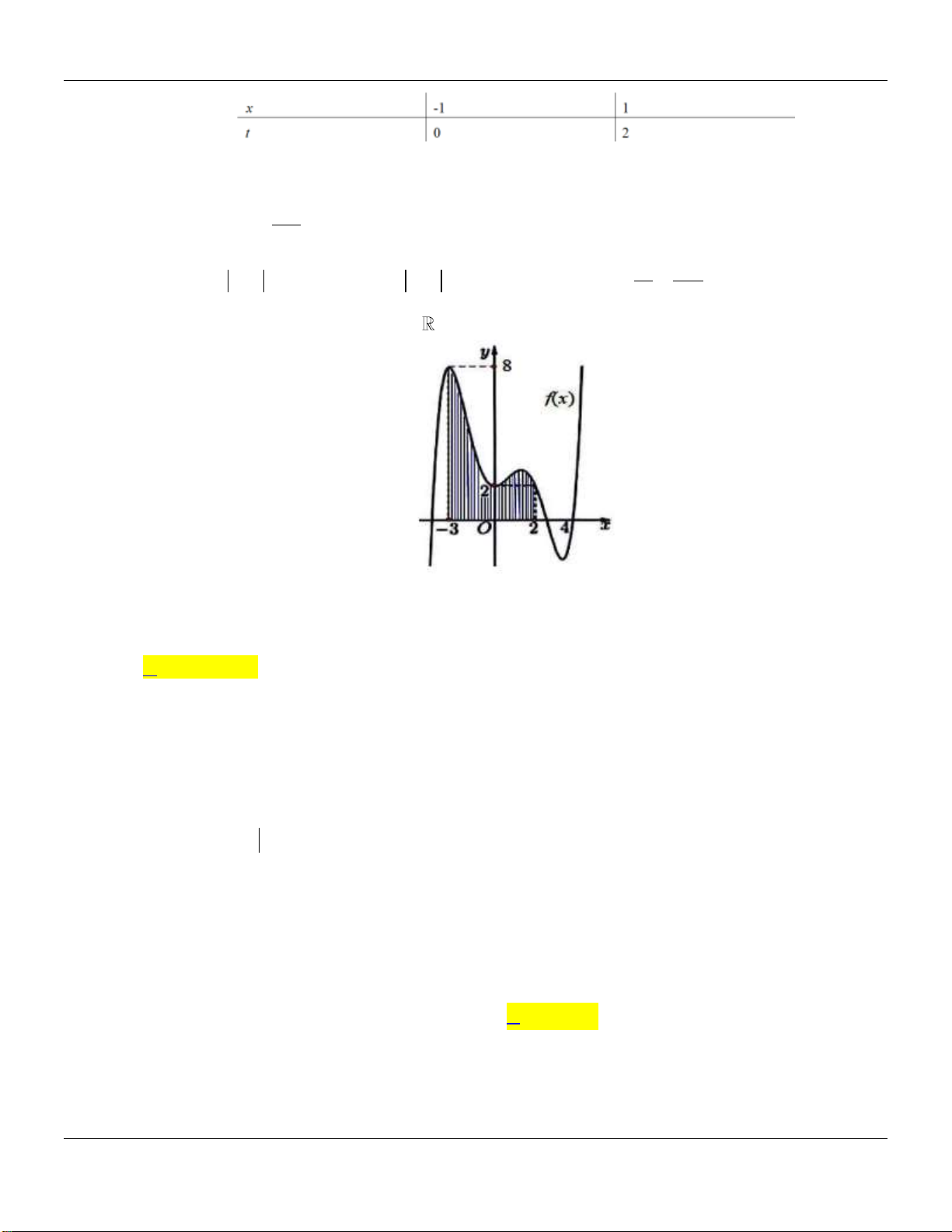
Câu 18: Cho hàm số y  f  x là hàm đa thức bậc bốn và có đồ thị như hình vẽ bên. Hình phẳng giới
hạn bởi đồ thị hai hàm số y  f  x , y  f  x có diện tích bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 127 107 87 127 A. . B. . C. . D. . 40 5 40 10 Câu 19: Cho hàm số 4 3
f (x)  ax  x  2x  2 và hàm số 3 2
g(x)  bx  cx  2 , có đồ thị như hình vẽ bên dưới: 221
Gọi S ; S là diện tích các hình phẳng gạch chéo trong hình vẽ, biết S 
. Khi đó S bằng 1 2 1 640 2 1361 271 571 791 A. . B. . C. . D. . 640 320 640 640
Câu 20: Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số   3 2
f x  ax  bx  c , các
đường thẳng x  1 , x  2 và trục hoành (miền gạch chéo) cho trong hình dưới đây: 51 52 50 53 A. S  . B. S  . C. S  . D. S  . 8 8 8 8 3 1
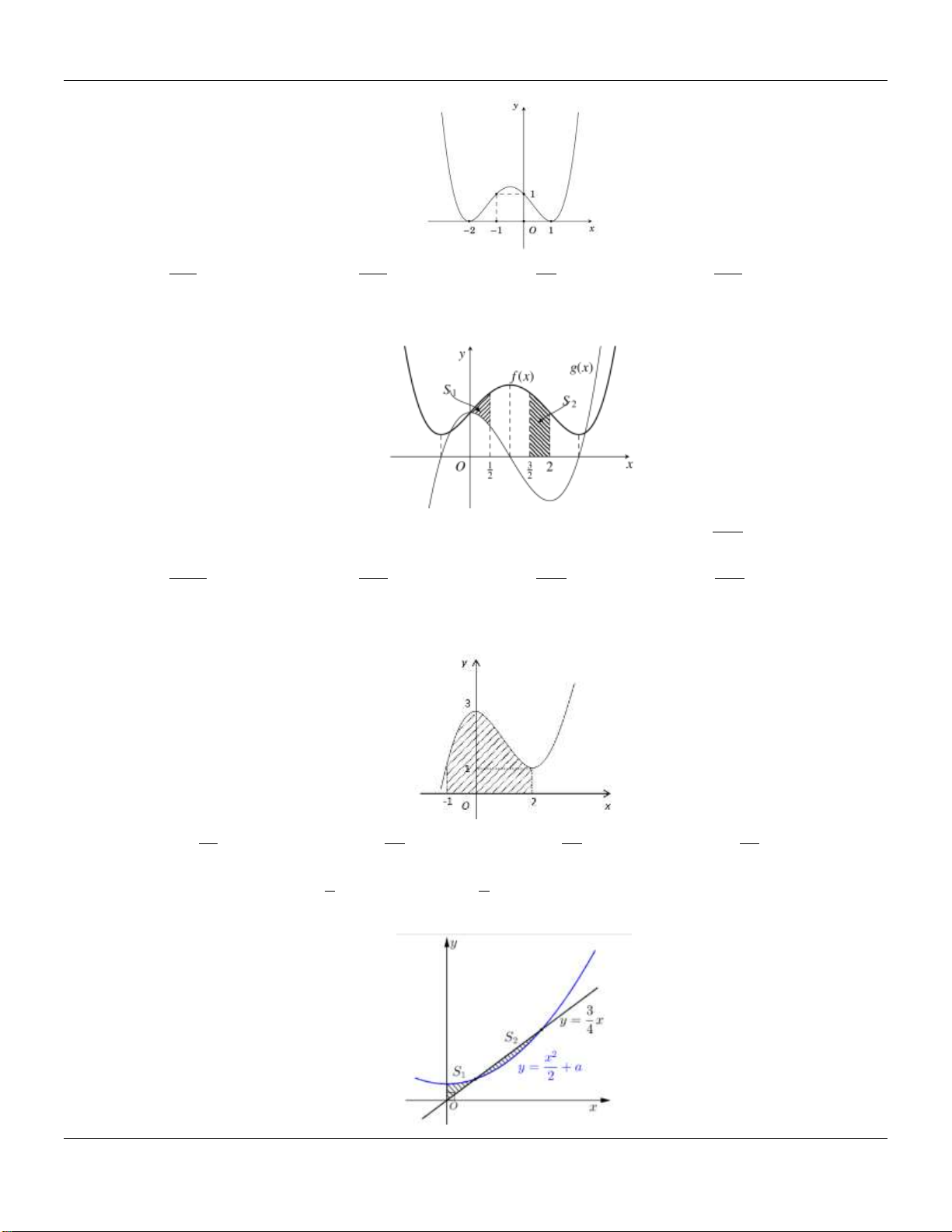
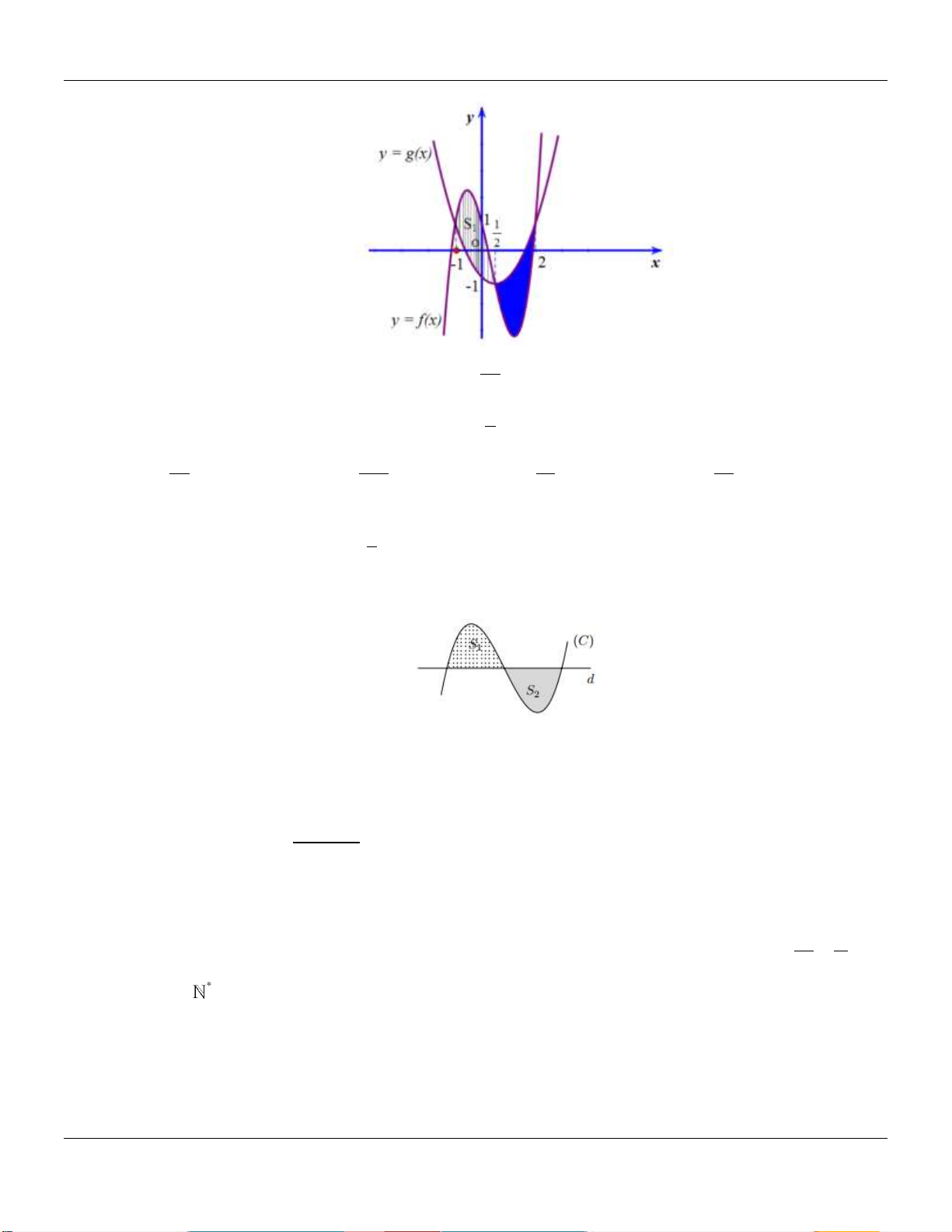
Câu 21: Cho đường thẳng y  x và parabol 2
y  x  a , ( a là tham số thực dương). Gọi S ,S lần 4 2 1 2
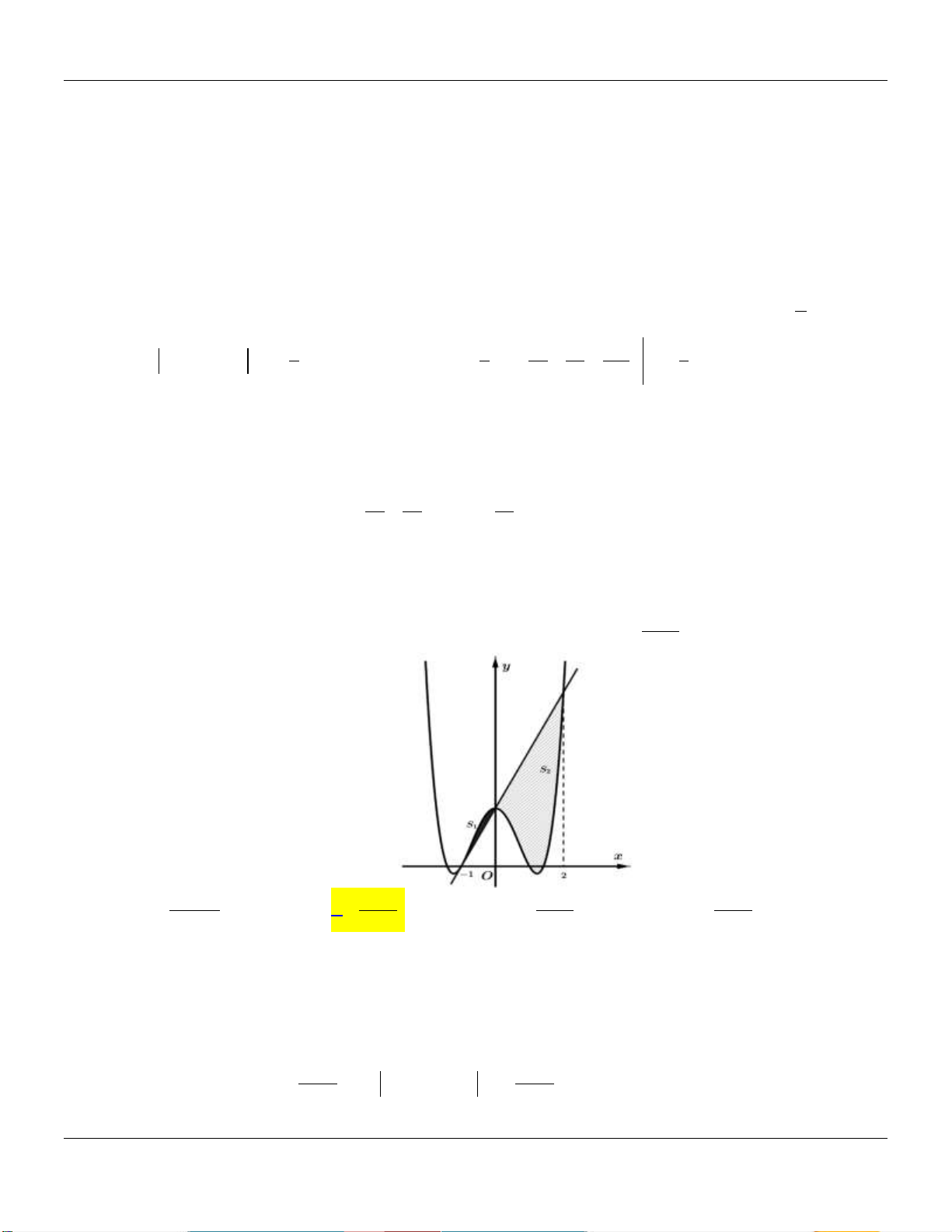
lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên dưới:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Khi S  S thì a thuộc khoảng nào sau đây? 1 2  3   3 7   1 9   7 1  A. 0;  . B.  ;  . C.  ;  . D.  ;  .  16   16 32   4 32   32 4 
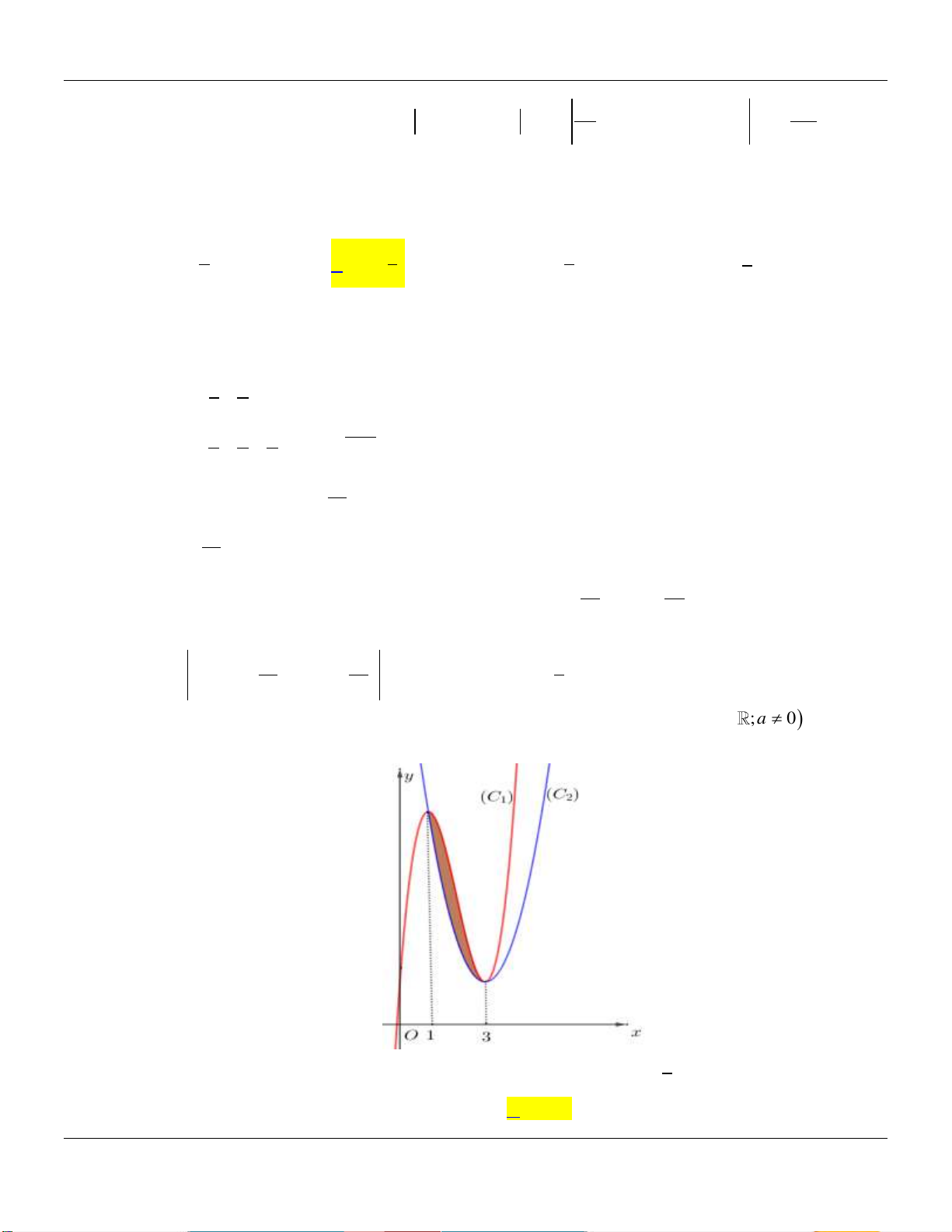
Câu 22: Cho hai hàm đa thức   3 2
f x  ax  bx  cx  d và   2
g x  mx  nx  p . Biết rằng đồ thị hai
hàm số y  f  x và y  g  x cắt nhau tại ba điểm có hoành độ lần lượt là 1; 2; 4 đồng thời
cắt trục tung lần lượt tại M , N sao cho MN  6 ( tham khảo hình vẽ).
Hình phẳng giới hạn bởi đồ thị hai hàm số đã cho ( phần gạch sọc) có diện tích bằng 125 253 253 253 A. . B. . C. . D. . 8 24 16 12
Câu 23: Cho f  x 3 2
 ax  bx  cx  d a  0 là hàm số nhận giá trị không âm trên đoạn 2;  3 có đồ
thị f  x như hình vẽ bên dưới:
Biết diện tích hình phẳng giới hạn bởi các đồ thị của các hàm số   2
g x  xf  x ;   2
h x  x f  x f  x và các đường thẳng x  2; x  3 bằng 72 . Tính f   1 .  A. f   1  2 . B. f   1  1  . C. f   1  1. D. f   62 1  . 5 Câu 24: Cho hàm số    4 2 y
f x  ax  bx  c có đồ thị C  và cắt trục hoành tại điểm có hoành độ bằng 1
 . Tiếp tuyến d tại điểm có hoành độ x  1 của C cắt C tại 2 điểm khác có
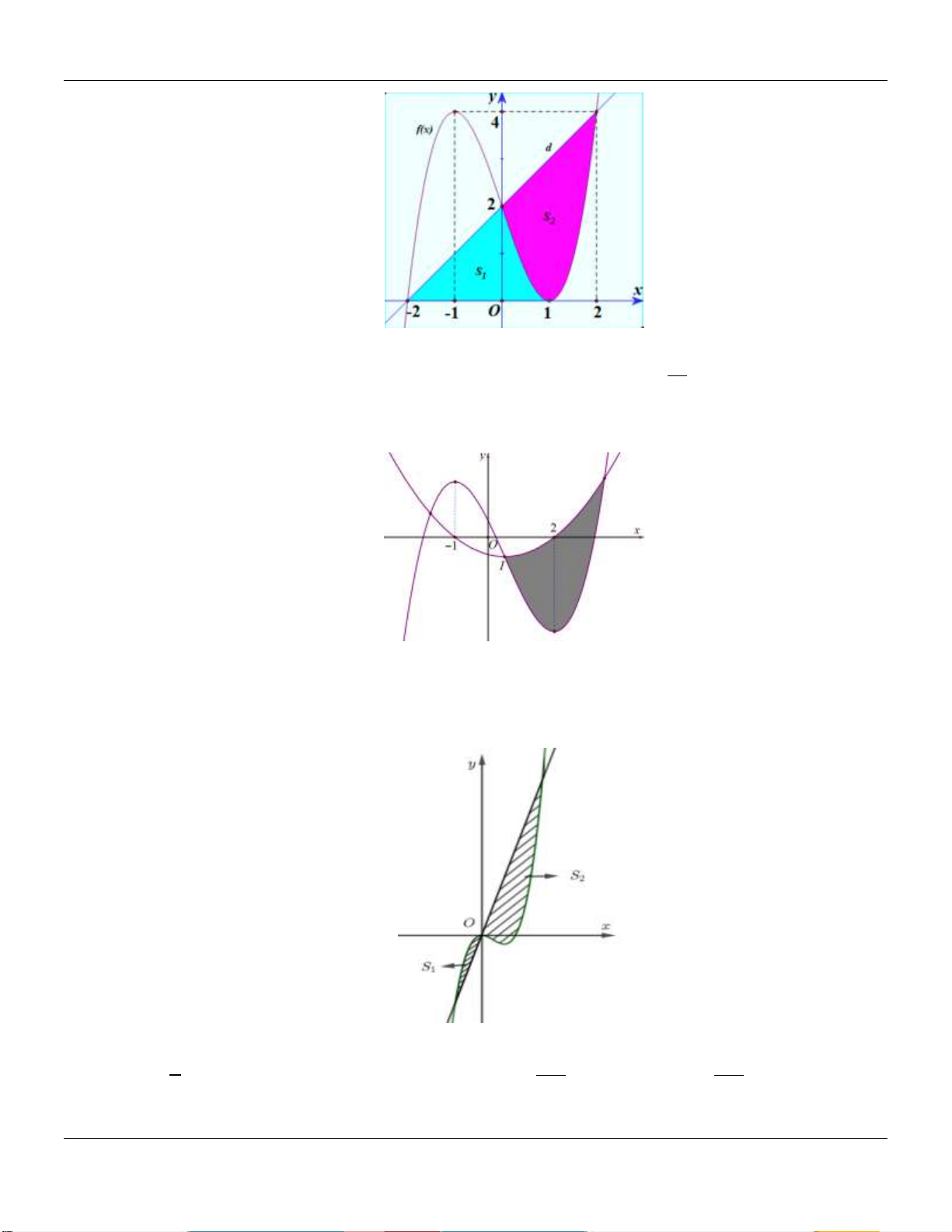
hoành độ lần lượt là 0 và 2 . Gọi S , S là diện tích các phần hình phẳng giới hạn bởi d và 1 2  S
C  (với S là diện tích phần hình phẳng nằm bên phải trục Oy ). Tỷ số 1 bằng 2 S2 1 1 2 1 A. B. C. D. 14 28 25 5
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
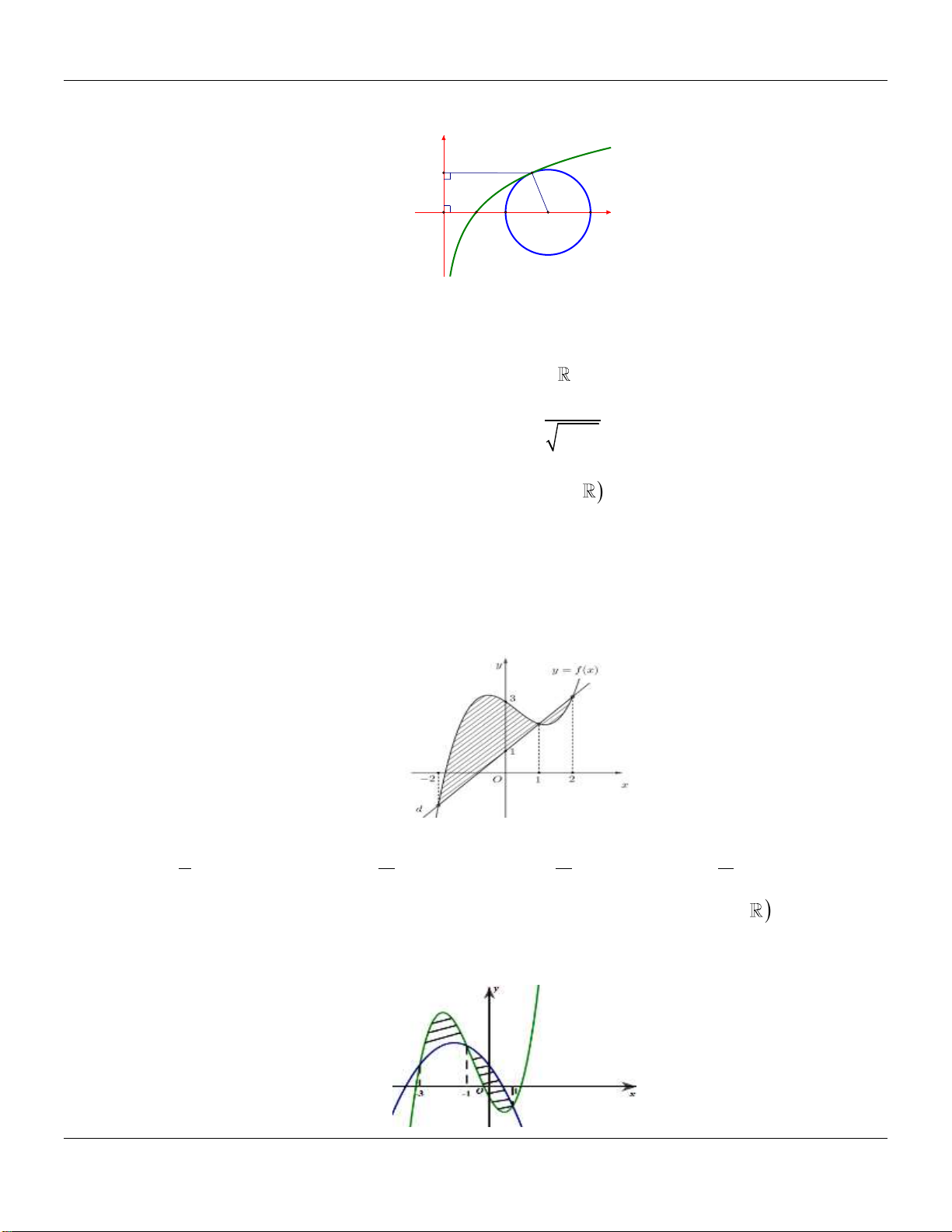
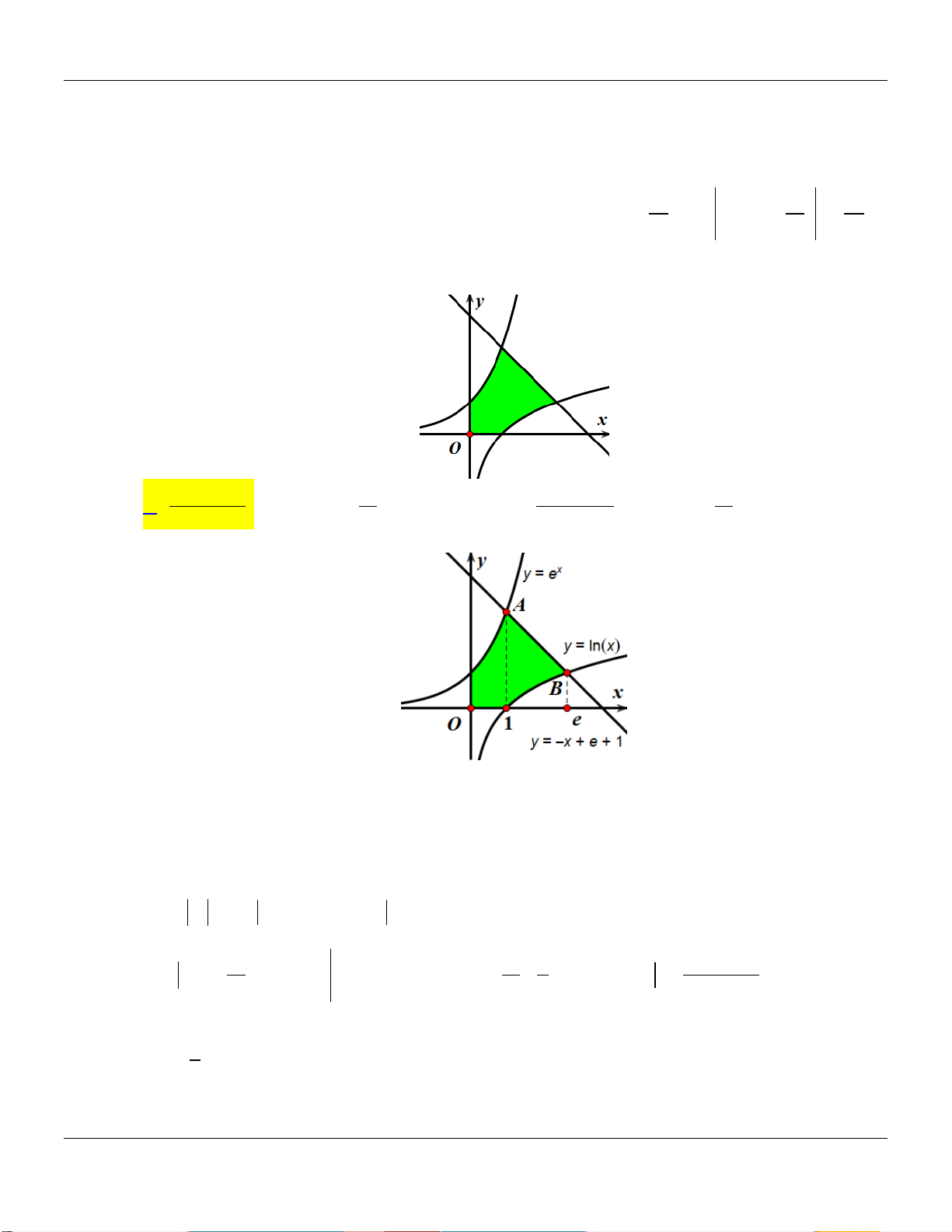
Câu 25: Cho hàm số y  ln x có đồ thị C như hình vẽ bên dưới: y (C) B C A O x
Đường tròn tâm A có duy nhất một điểm chung B với C . Biết C 0;  1 , diện tích của hình
thang ABCO gần nhất với số nào sau đây. A. 3,01. B. 2,91. C. 3,09 . D. 2,98 . Câu 26: Cho hàm số   4 3 2
f x  x  bx  cx  dx  e ( b, c, d, e 
) có các giá trị cực trị là 1, 4 và 9 . Diện f  x
tích hình phẳng giới hạn bởi đồ thị hàm số g  x   
và trục hoành bằng f  x A. 4. B. 6. C. 2. D. 8.
Câu 27: Biết đồ thị C  của hàm số f  x 4 2
 x  bx  c b,c  có cực trị là A1;0 . Gọi P là
parabol có đỉnh I 0;  
1 và đi qua điểm B 2;3 . Diện tích hình phẳng giới hạn bởi C  và
P thuộc khoảng nào dưới đây? A. 0;  1 . B. 2;3 . C. 3; 4 . D. 1; 2 .
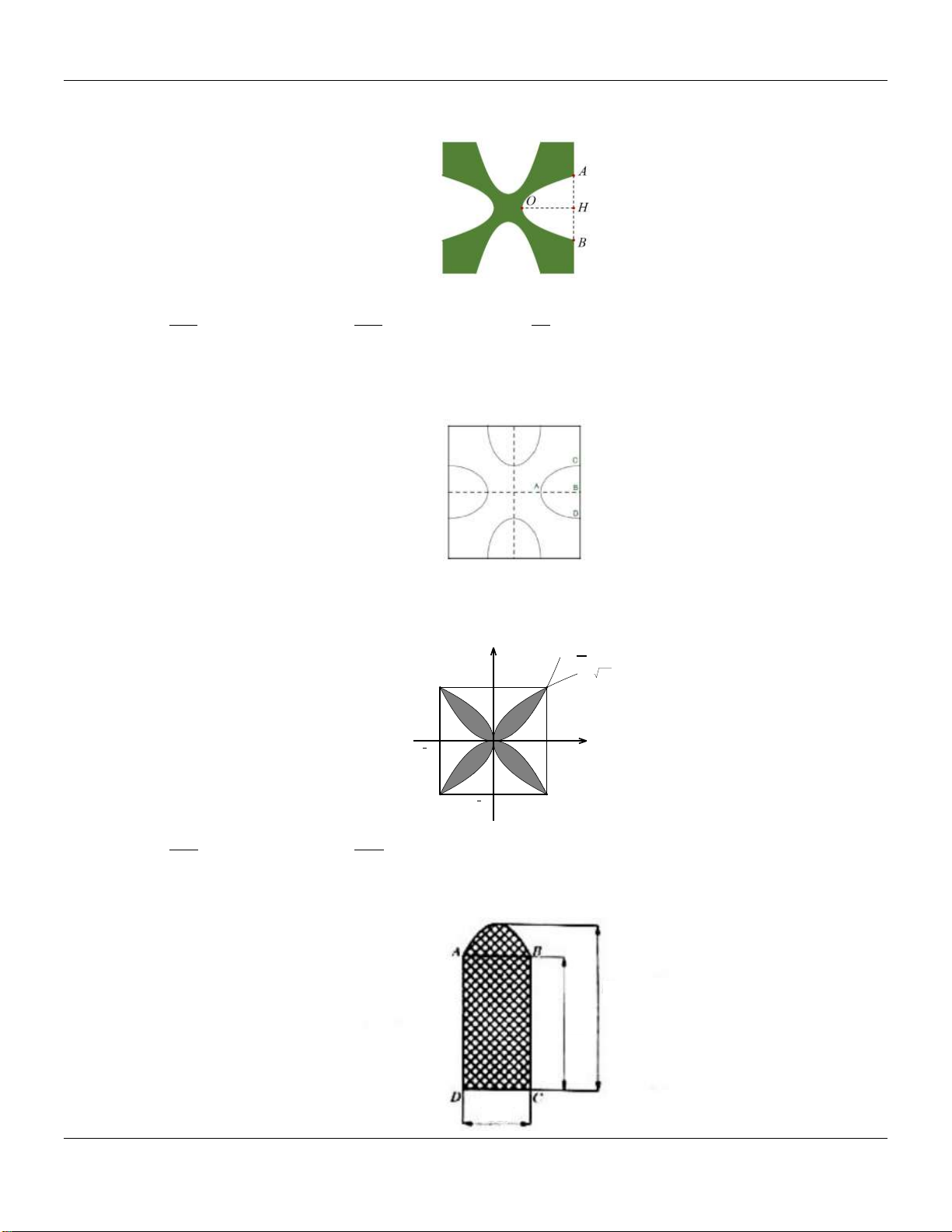
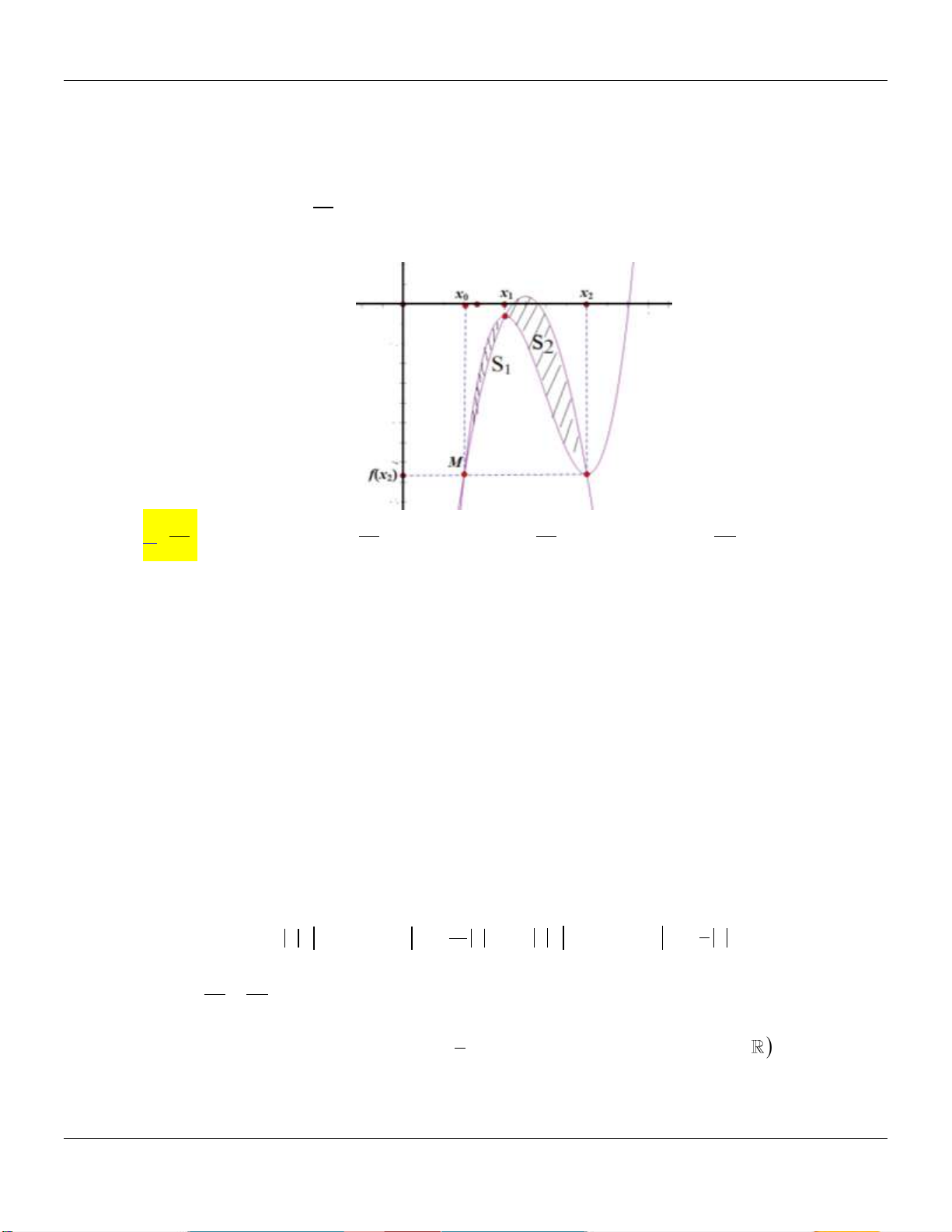
Câu 28: Đường thẳng d cắt đường cong f  x 3 2
 a x  bx  cx  d tại ba điểm phân biệt có hoành độ
x  2 , x  1 , x  2 như hình vẽ bên dưới:
Diện tích hình phẳng gạch sọc thuộc khoảng nào dưới đây?  9   13   11 11  A. ;5   . B. 6;   . C. 5;   . D. ;6   .  2   2   2   2 
Câu 29: Cho hai hàm số f  x 3 2
 ax  bx  cx 1và g x 2
 dx  ex  2 a, ,
b c, d, e   . Biết rằng đồ
thị của hàm số y  f  x và y  g  x cắt nhau tại ba điểm có hoành độ lần lượt là
3; 1;1(tham khảo hình vẽ) .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng A. 6 . B. 9 . C. 7 . D. 8 .
Câu 30: Cho hai hàm số f  x 3 2
 ax  bx  cx  2 và g x 2
 dx  ex  2 a, ,
b c, d, e   . Biết rằng đồ
thị của hàm số y  f  x và y  g  x cắt nhau tại ba điểm có hoành độ lần lượt là
2;1;1(tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng A. 37 . B. 145 . C. 37 . D. 145 . 5 7 6 8
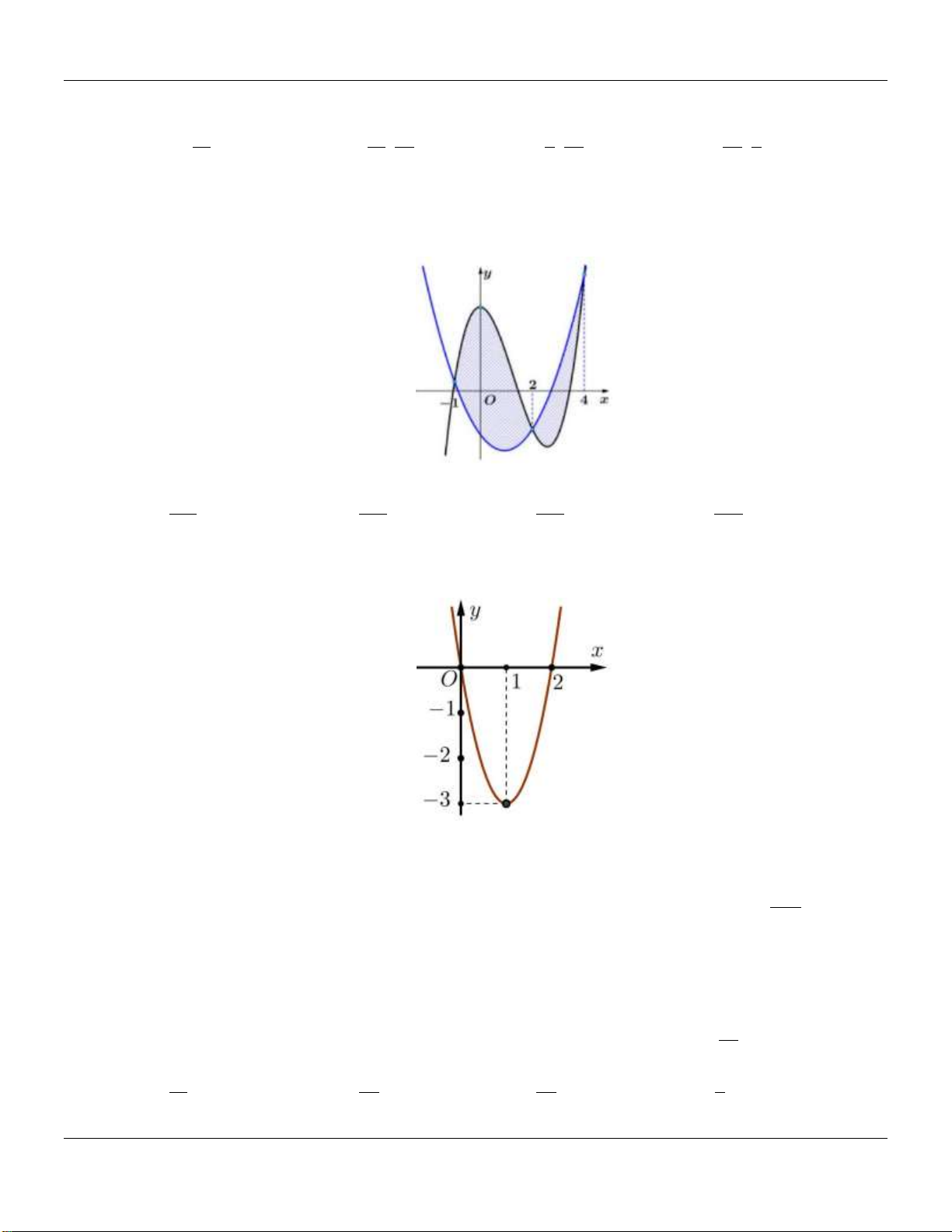
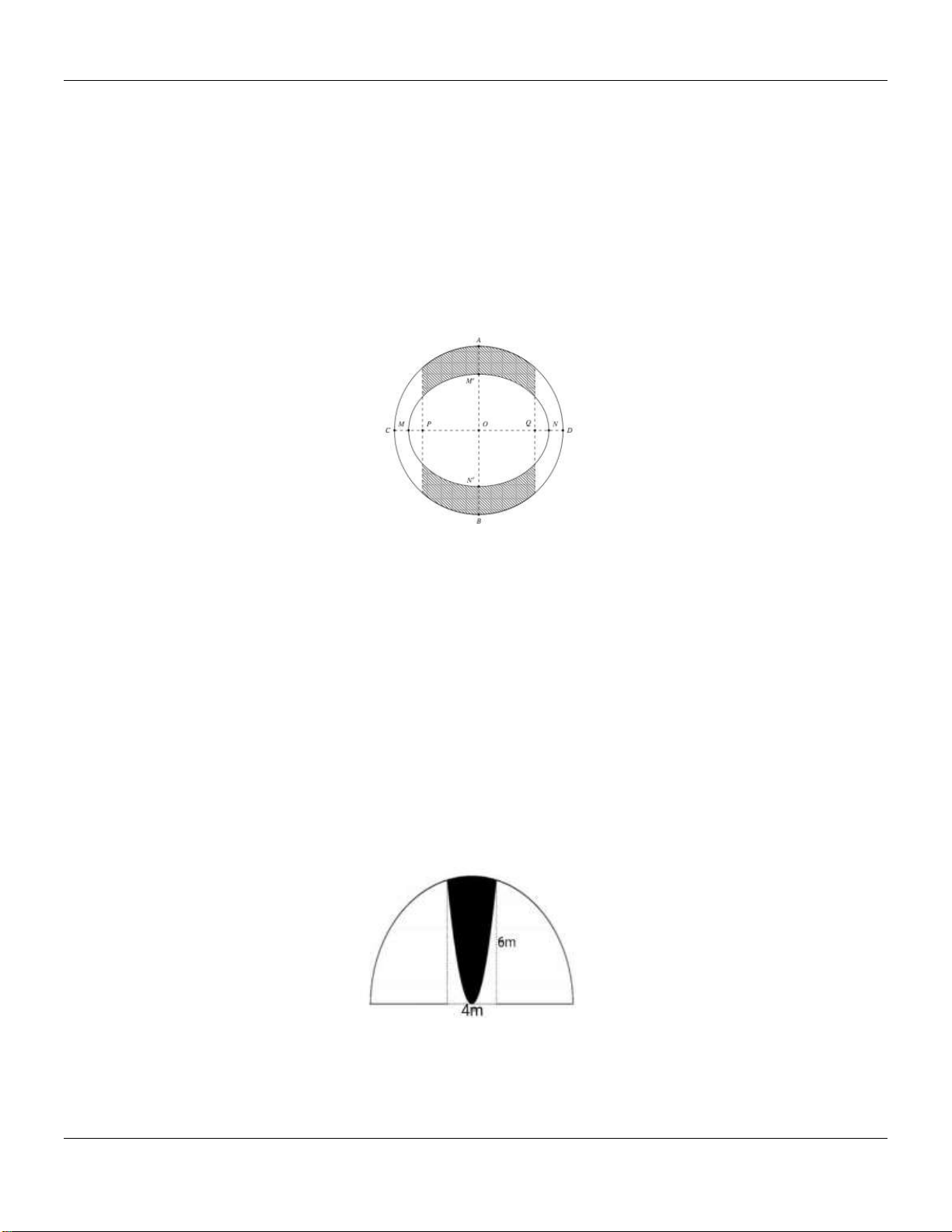
Câu 31: Đường thẳng y  kx  4 cắt parabol y   x  2 2
tại hai điểm phân biệt và diện tích các hình
phẳng S , S bằng nhau như hình vẽ bên. 1 2
Khẳng định nào sau đây đúng?  1   1  A. k   6  ; 4   . B. k  1  ;   . C. k   2  ;  1 . D. k   ;0   .  2   2  1
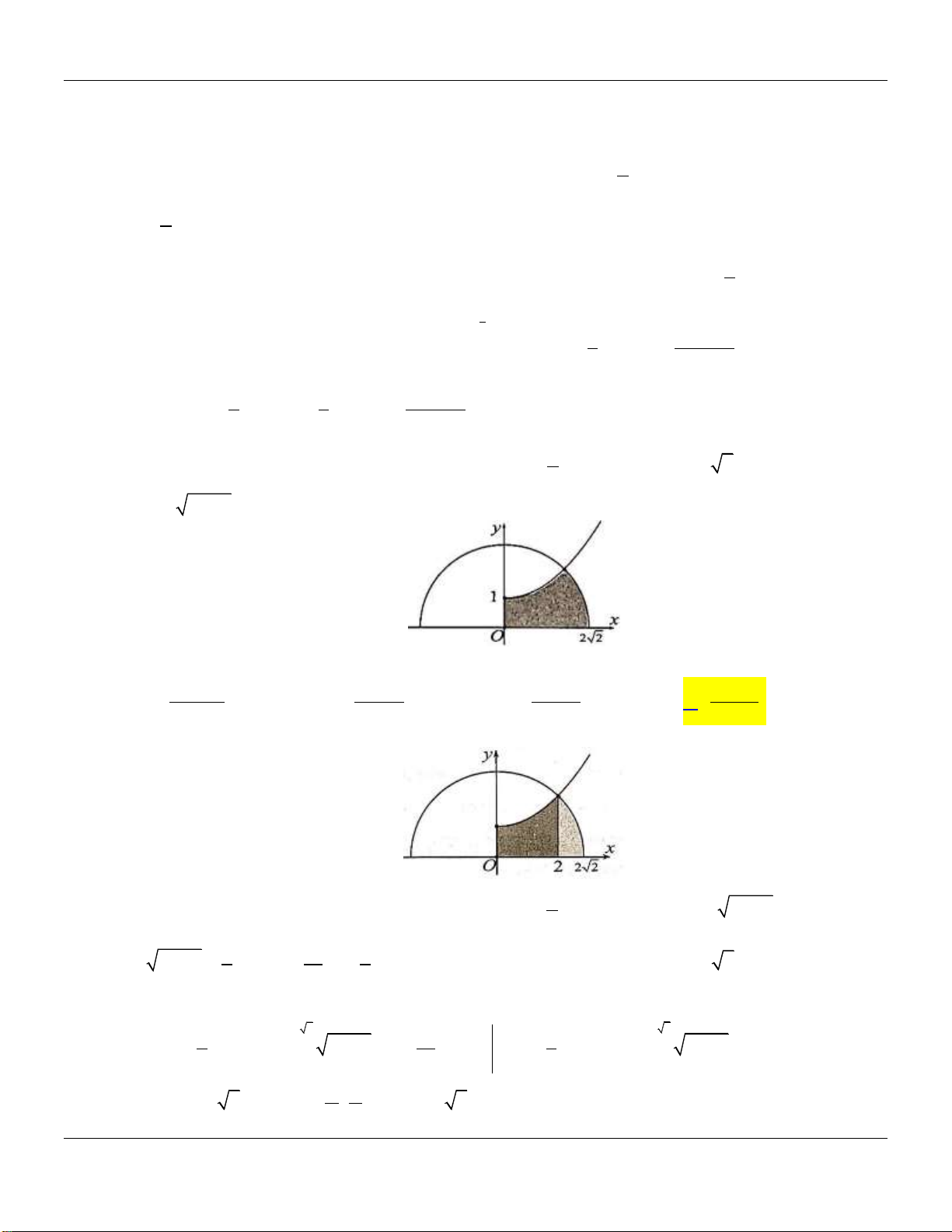
Câu 32: Cho  H  là hình phẳng giới hạn bởi parabol 2 y 
x 1 (với 0  x  2 2 ), nửa đường tròn 4 2
y  8  x và trục hoành, trục tung (phần tô đậm trong hình vẽ).
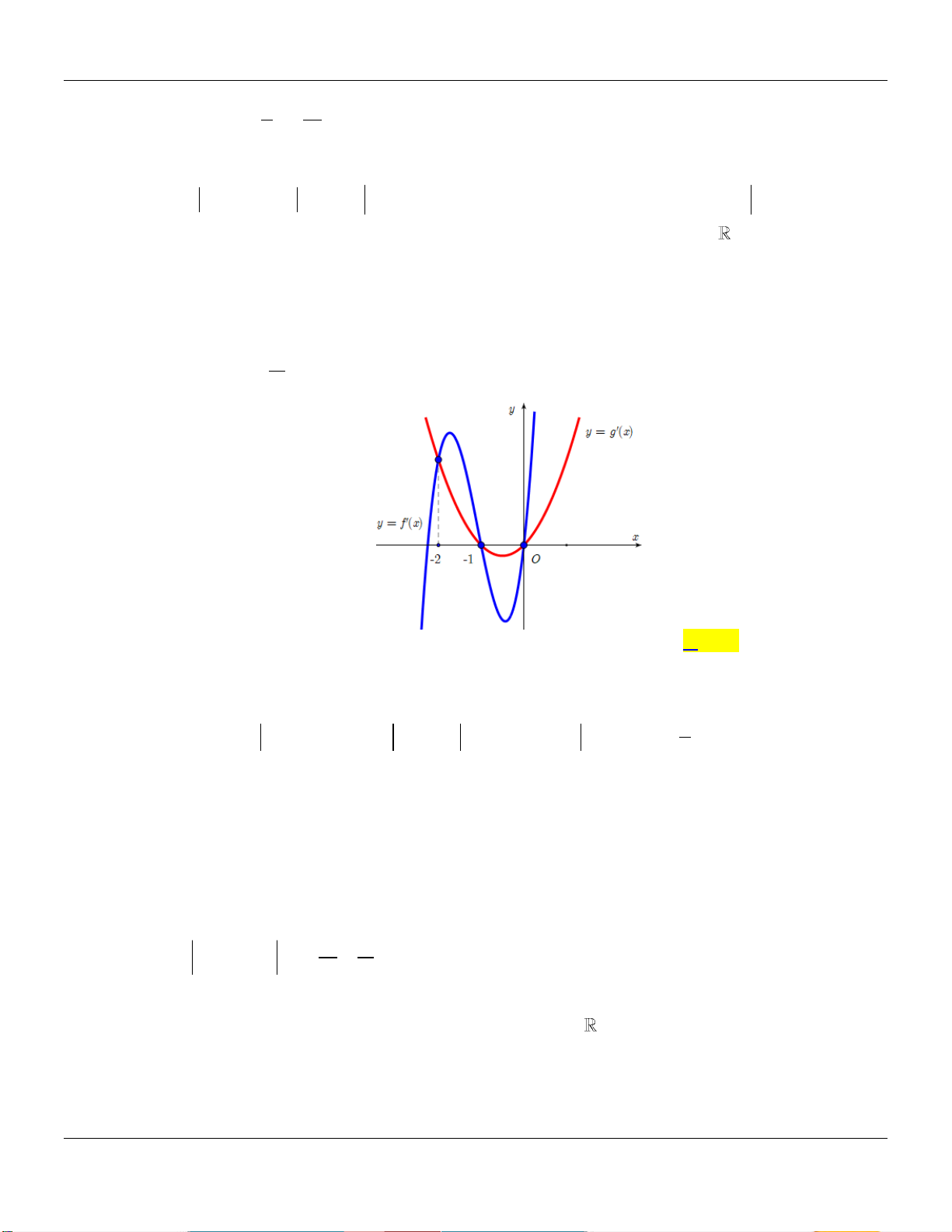
Diện tích của  H  bằng 3 14 2  2 3  4 3  2 A. . B. . C. . D. . 6 3 6 3 Câu 33: Cho hàm số 3 2
y  f (x)  ax  bx  cx  d a, ,
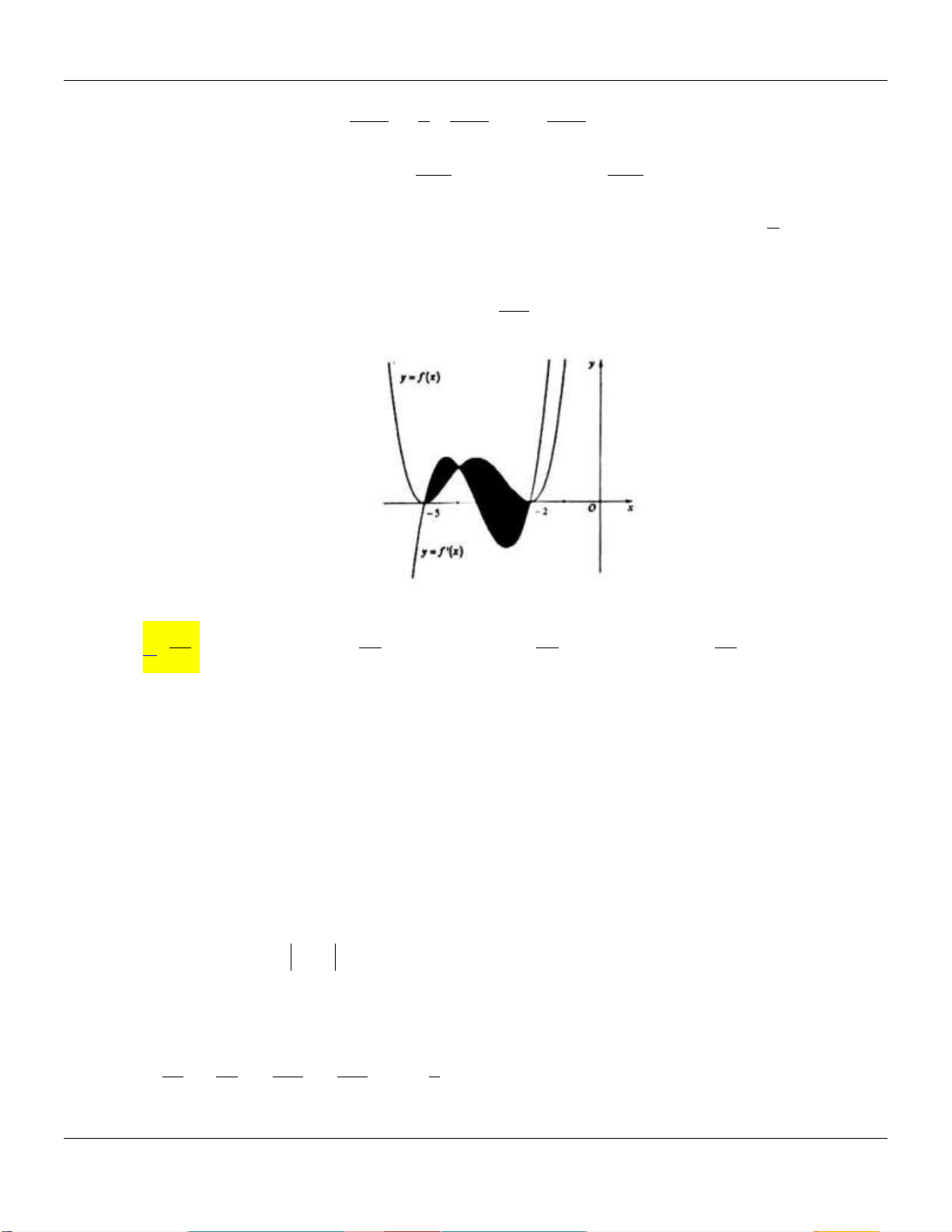
b c, d  , a  0 có đồ thị là C  . Biết rằng đồ thị
Cđi qua gốc tọa độ và đồ thị hàm số y  f '(x) cho bởi hình vẽ bên.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Tính giá trị H  f (4)  f (2).
A. H  45 .
B. H  64 .
C. H  51.
D. H  58 . Câu 34: Cho hàm số 4 2
y  x  4x  m có đồ thị C . Giả sử C
cắt trục hoành tại bốn điểm phân m  m 
biệt sao cho diện tích hình phẳng giới hạn bởi C
với trục hoành có diện tích phần phía trên m 
trục hoành bằng diện tích phần phía dưới trục hoành. Khi đó m thuộc khoảng nào dưới đây? A. m  1   ;1 .
B. m 3;5 .
C. m 2;3 .
D. m  5;   .
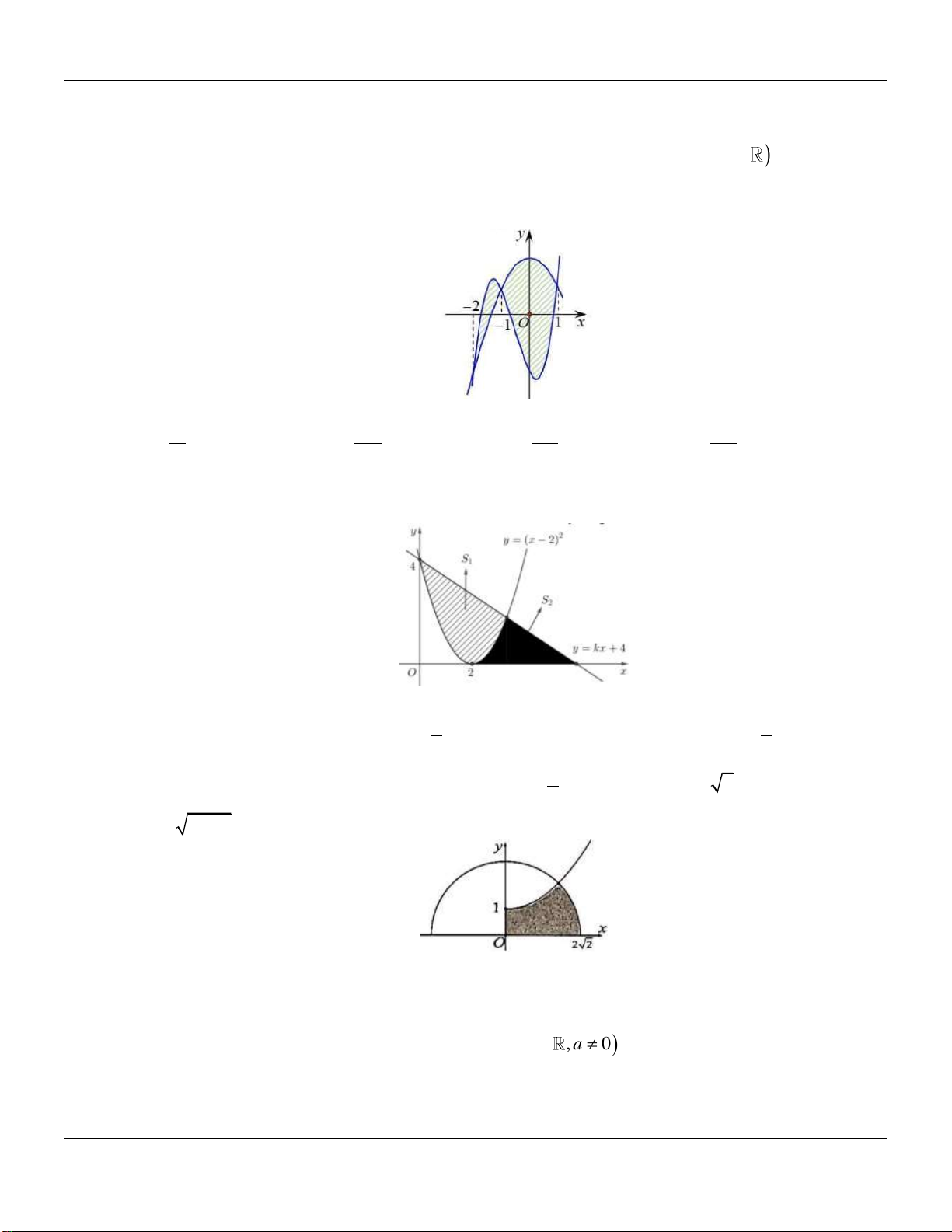
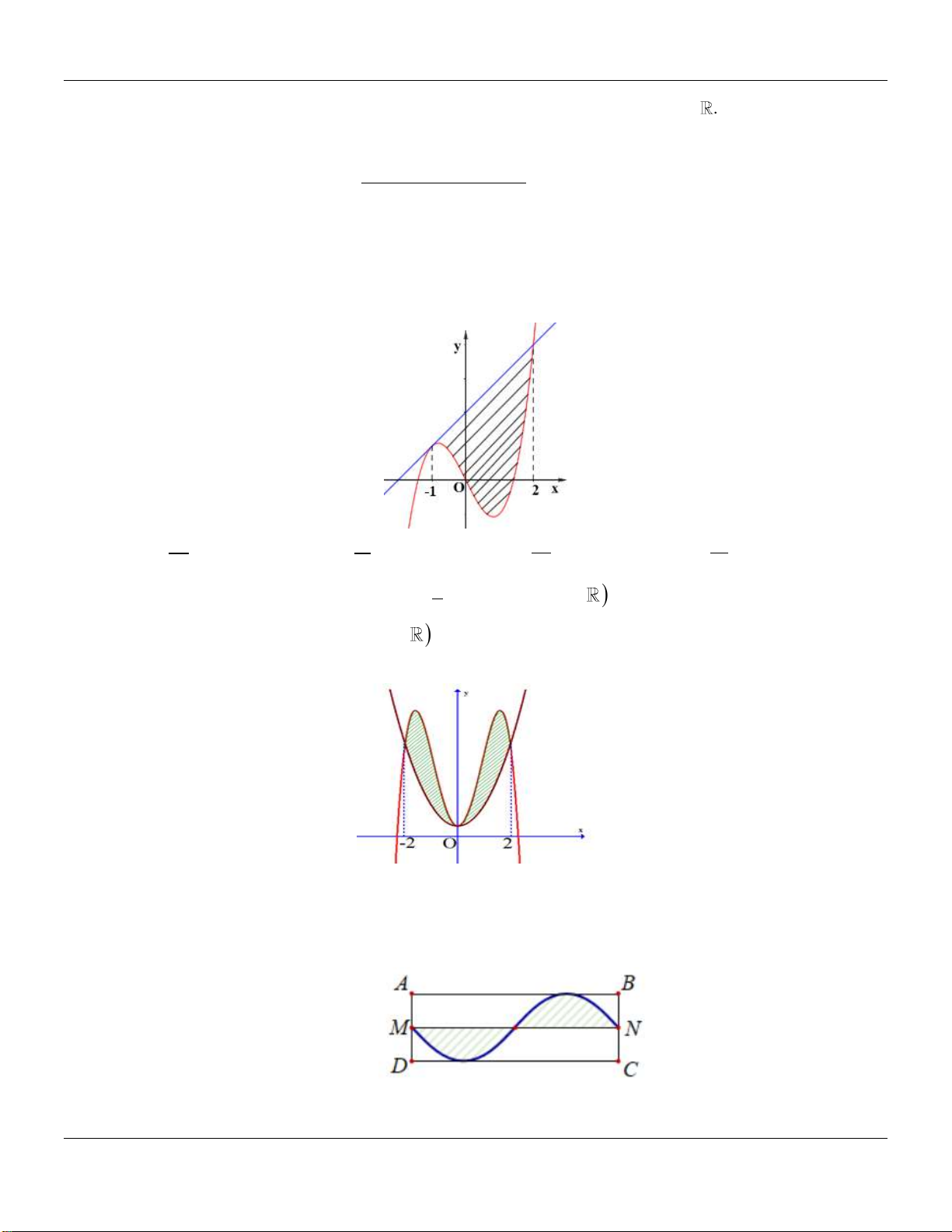
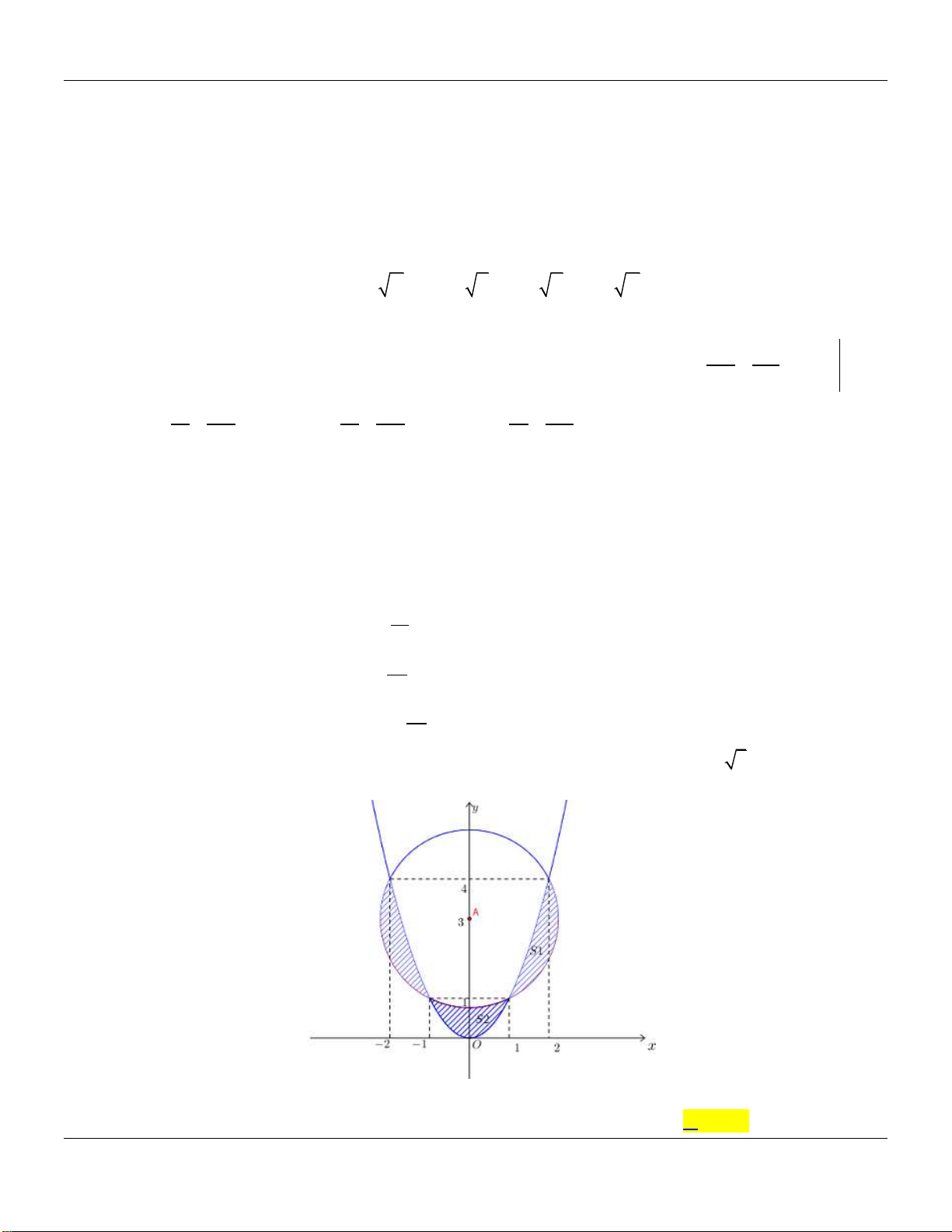
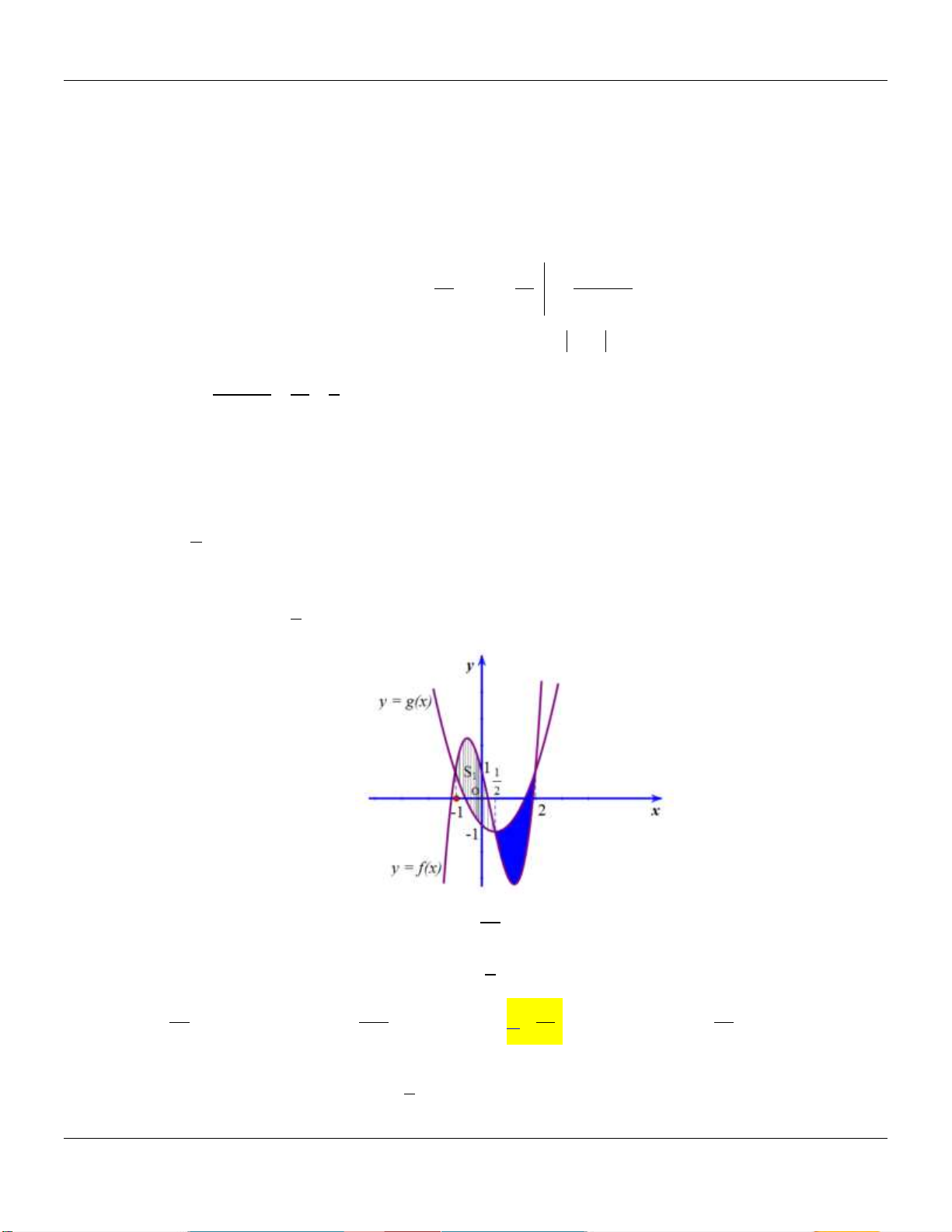
Câu 35: Cho Parabol  P 2
: y  x và đường tròn C  có tâm A0;3 bán kính bằng 5 như hình vẽ bên dưới:
Diện tích phần được tô đậm giữa C  và  P gần nhất với số nào dưới đây? A. 3.44 . B. 1.51. C. 1.77 . D. 3.54 .
Câu 36: Cho hàm số bậc bốn y  f  x có đồ thị C  như hình vẽ bên dưới: 1 5
Đường thẳng d : y  kx  có đúng ba điểm chung với C  là ,
A B, C và BC  AB  . Biết 4 4 24 1
diện tích hình phẳng S (phần gạch sọc) là
. Giá trị của  f xdx bằng 5 2  321 161 159 A. 2  . B.  . C.  . D.  . 160 80 160
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Câu 37: Cho hàm số   3 2
f x  x  bx  cx  d với b , c , d  . Biết hàm số
g  x  f  x  2 f  x  3 f   x có hai giá trị cực trị là 6
 và 42 . Tính diện tích hình phẳng
f  x  f  x  f   x
giới hạn bởi các đường y  và y  1. g  x 18 A. ln 5. B. ln 7. C. 2 ln 6. D. 2 ln 5. Câu 38: Cho hàm số 3 2
y  x  ax  bx  c có đồ thị C  . Biết rằng tiếp tuyến d của C  tại điểm A có hoành độ bằng 1
 cắt C tại điểm B có hoành độ bằng 2 (xem hình vẽ). Diện tích hình
phẳng giới hạn bởi d và C  (phần gạch chéo trong hình) bằng 27 11 25 13 A. . B. . C. . D. . 4 2 4 2 1 Câu 39: Cho hàm số
y  f  x 4 2
  x  ax  b a,b   có đồ thị (C) và 2    2 y
g x  mx  nx  p m,n, p   có đồ thị  P như hình vẽ. Diện tích hình phẳng giới
hạn bởi C  và  P có giá trị nằm trong khoảng nào sau đây? A. 4;4  ,1 . B. 4,2;4,3 . C. 4,3;4,4 . D. 4,1;4, 2 .
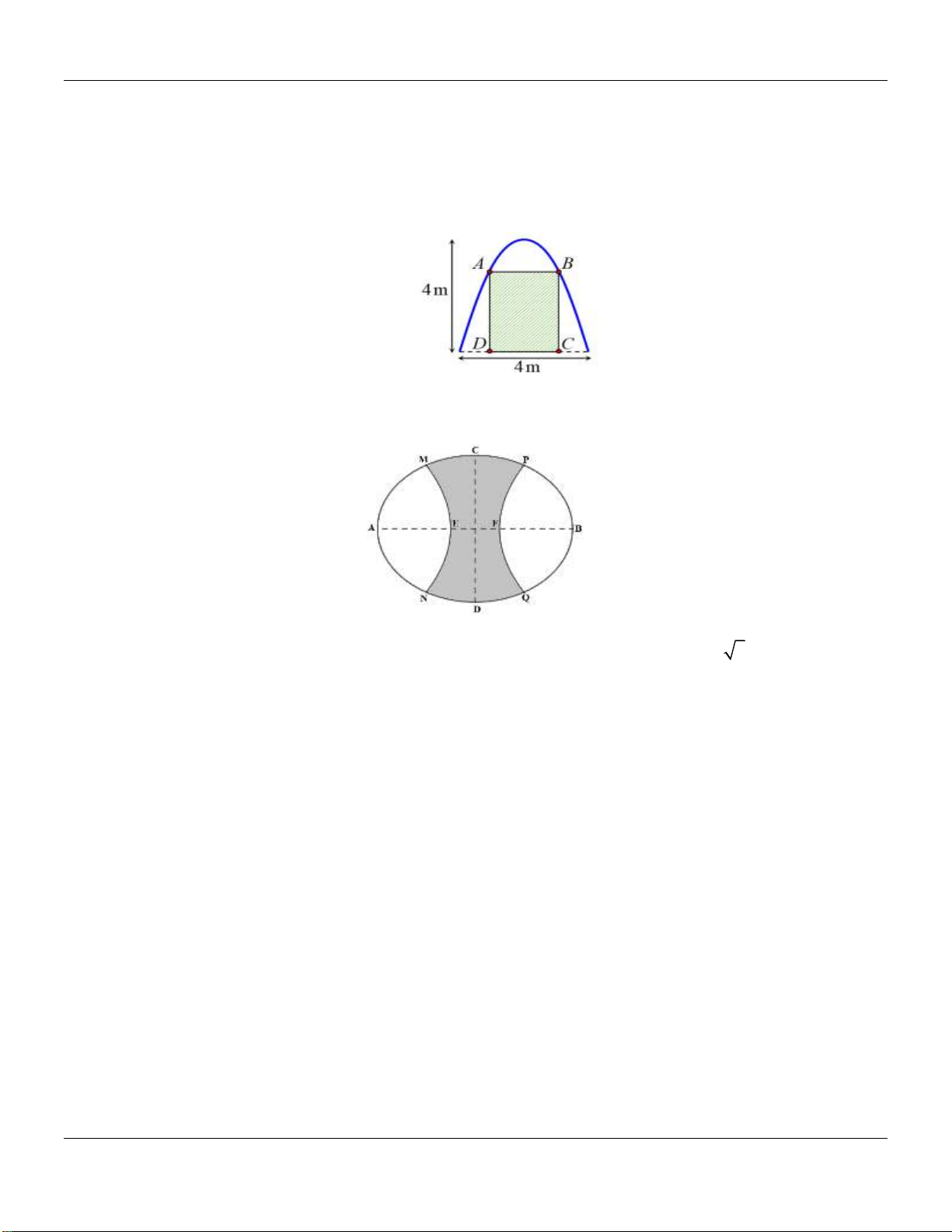
Câu 40: Người ta trồng hoa vào phần đất được tô màu được giới hạn bởi cạnh AB, CD , đường trung
bình MN của mảnh đất hình chữ nhật ABCD và một đường cong hình sin. Biết AB  2 (m),
AD  2 (m). Tính diện tích phần còn lại. A. 4  1 . B. 4  1 . C. 4  2 . D. 4  3 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
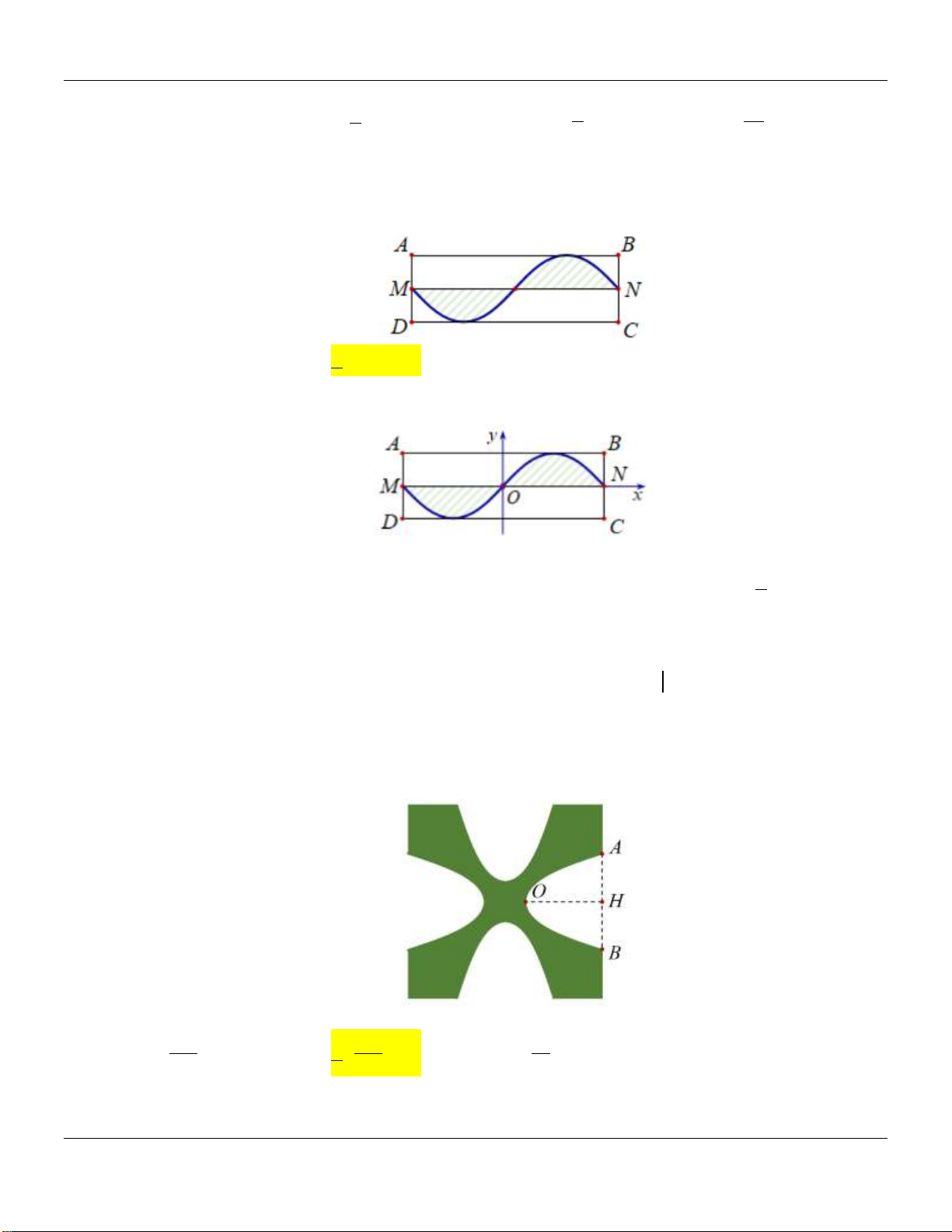
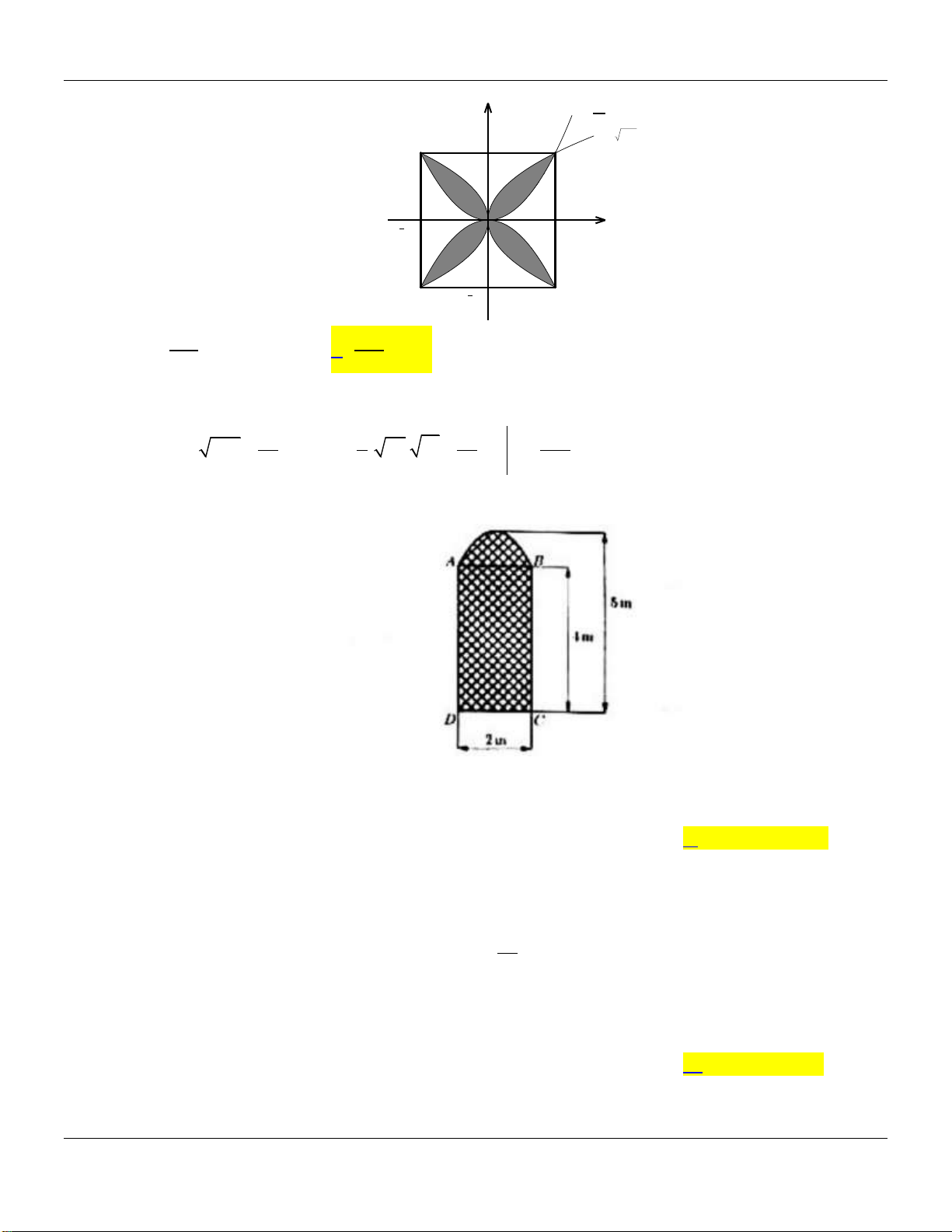
Câu 41: Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng 10 cm bằng
cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên dưới:
Biết AB  5 cm, OH  4 cm. Tính diện tích bề mặt hoa văn đó. 160 140 14 A. 2 cm . B. 2 cm . C. 2 cm . D. 2 50 cm . 3 3 3
Câu 42: Một hoa văn trang trí được tạo ra từ một miếng bìa hình vuông cạnh 20 cm bằng cách khoét
đi bốn phần bằng nhau đều có hình dạng một nửa elip như hình vẽ. Biết một nửa trục lớn là
AB  6 cm , trục bé CD  8 cm . Diện tích bề mặt của hoa văn đó bằng A.    2 400 48 cm  . B.    2 400 96 cm  . C.    2 400 24 cm  . D.    2 400 36 cm  .
Câu 43: Một viên gạch hoa hình vuông cạnh 40 cm được thiết kế như hình bên dưới. Diện tích mỗi
cánh hoa (phần tô đậm) bằng y 1 y = x2 20 y = 20x 20 x 20 20 20 800 400 A. 2 cm . B. 2 cm . C. 250 2 cm . D. 800 2 cm . 3 3
Câu 44: Ông An muốn làm một cánh cửa bằng sắt có hình dạng và kích thước như hình vẽ. Biết rằng
đường cong phía trên là một parabol, tứ giác ABCD là một hình chữ nhật. 5 m 4 m 2 m
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Giá cánh cửa sau khi hoàn thành là 900000 đồng/ 2
m . Số tiền ông An phải trả để làm cánh cửa đó bằng
A.9 600 000 đồng.
B. 15 600 000 đồng.
C. 8 160 000 đồng. D. 8 400 000 đồng.
Câu 45: Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là 2, 25 mét,
chiều rộng tiếp giáp với mặt đất là 3 mét. Giá thuê mỗi mét vuông là 1500000 đồng. Vậy số
tiền bác Năm phải trả là A. 33750000 đồng. B. 3750000 đồng. C. 12750000 đồng. D. 6750000 đồng.
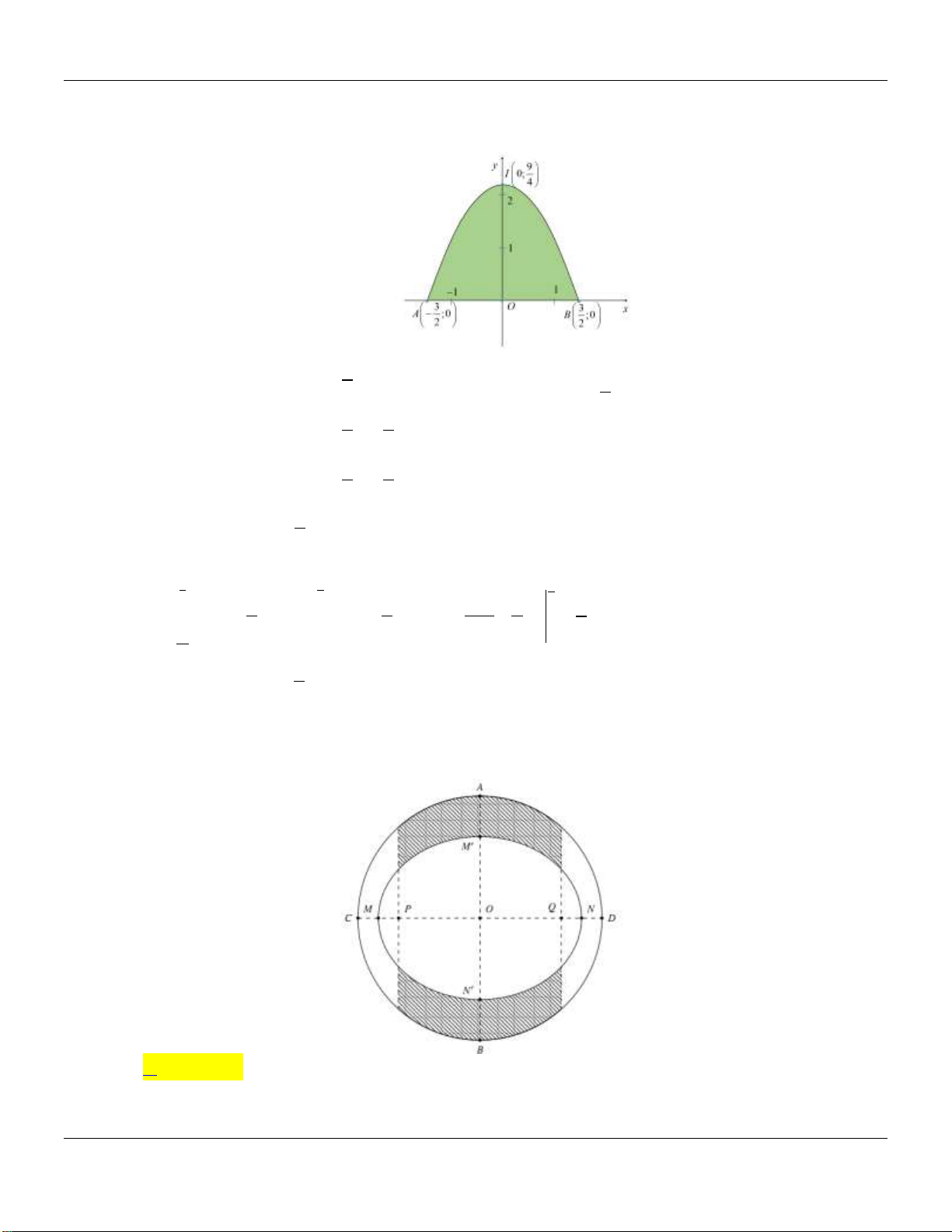
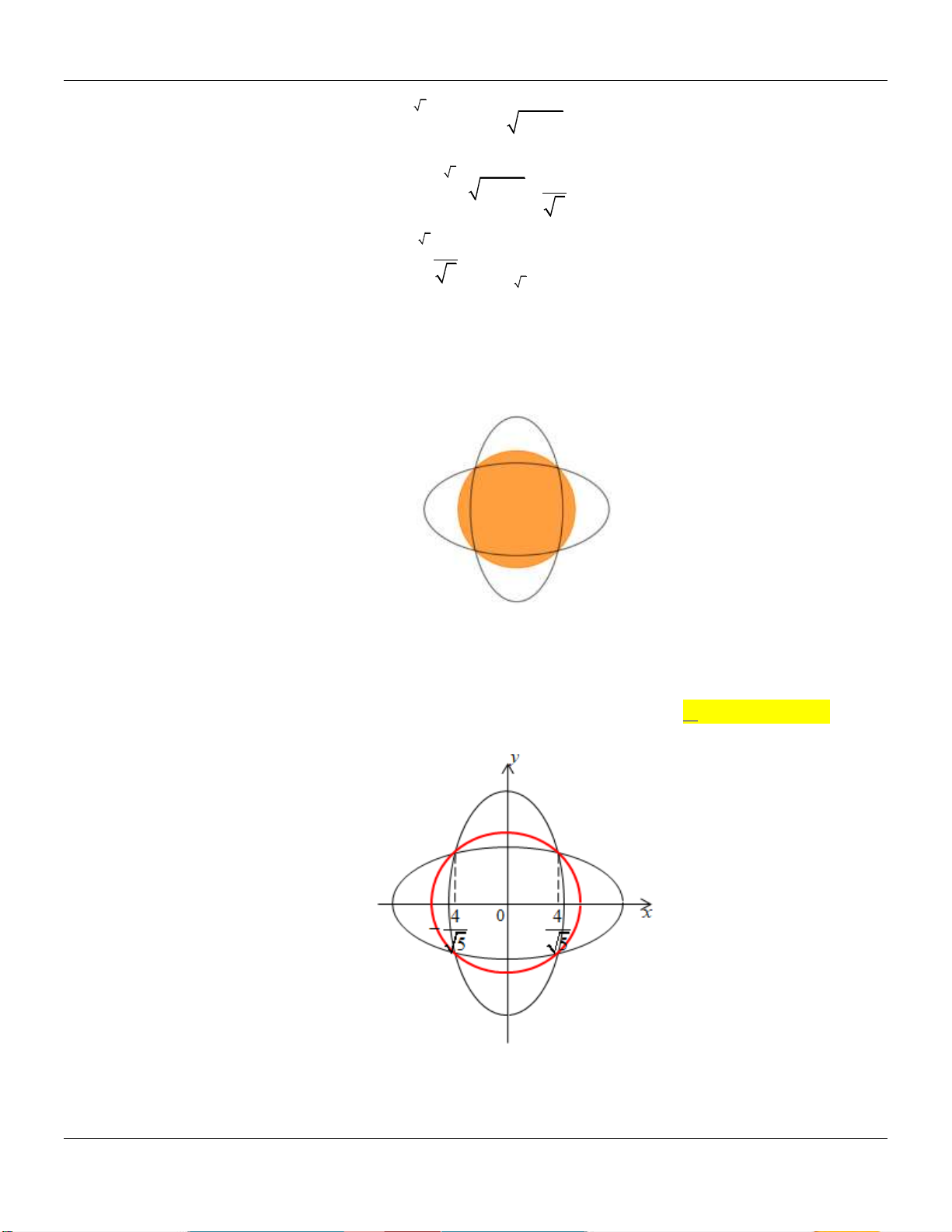
Câu 46: Một khu vườn dạng hình tròn có hai đường kính AB, CD vuông góc với nhau, AB  12m .
Người ta làm một hồ cá có dạng elip với bốn đỉnh M , N , M ', N ' như hình vẽ. Biết MN  10 ,
m M ' N '  8 ,
m PQ  8m . Diện tích phần trồng cỏ (phần gạch sọc) bằng: A. 2 32, 03 m . B. 2 20, 33 m . C. 2 33.02 m . D. 2 23, 03 m .
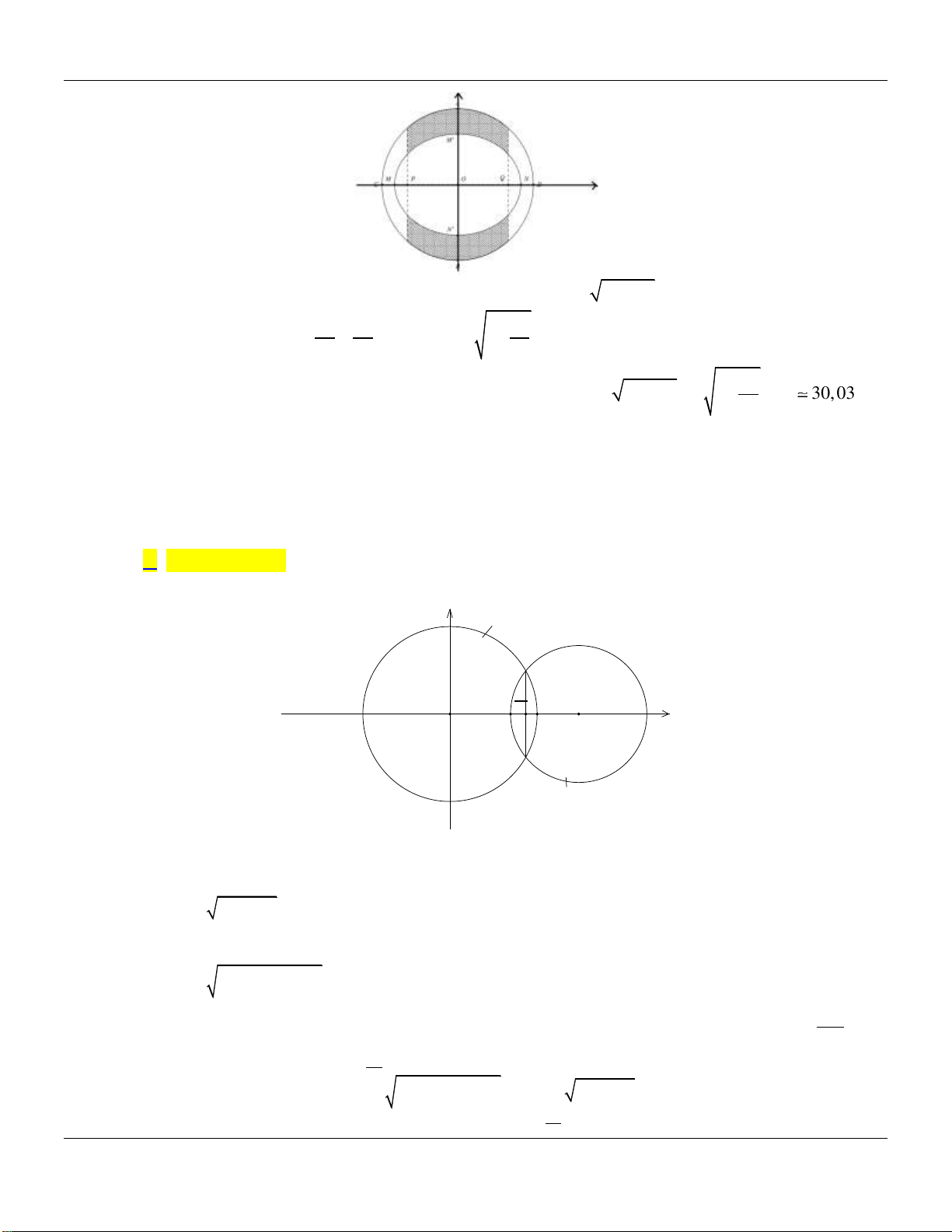
Câu 47: Một khu vườn có dạng hợp của hai hình tròn giao nhau. Bán kính của hai đường tròn là
20m và 15m , khoảng cách giữa hai tâm của hai hình tròn là 30m . Phần giao của hai hình tròn
được trồng hoa với chi phí 300000 đồng/ 2
m . Phần còn lại được trồng cỏ với chi phí 100000 đồng/ 2
m . Hỏi chi phí để trồng hoa và cỏ của khu vườn gần nhất với số tiền nào dưới đây?
A. 202 triệu đồng.
B. 208 triệu đồng.
C. 192 triệu đồng.
D. 218 triệu đồng.
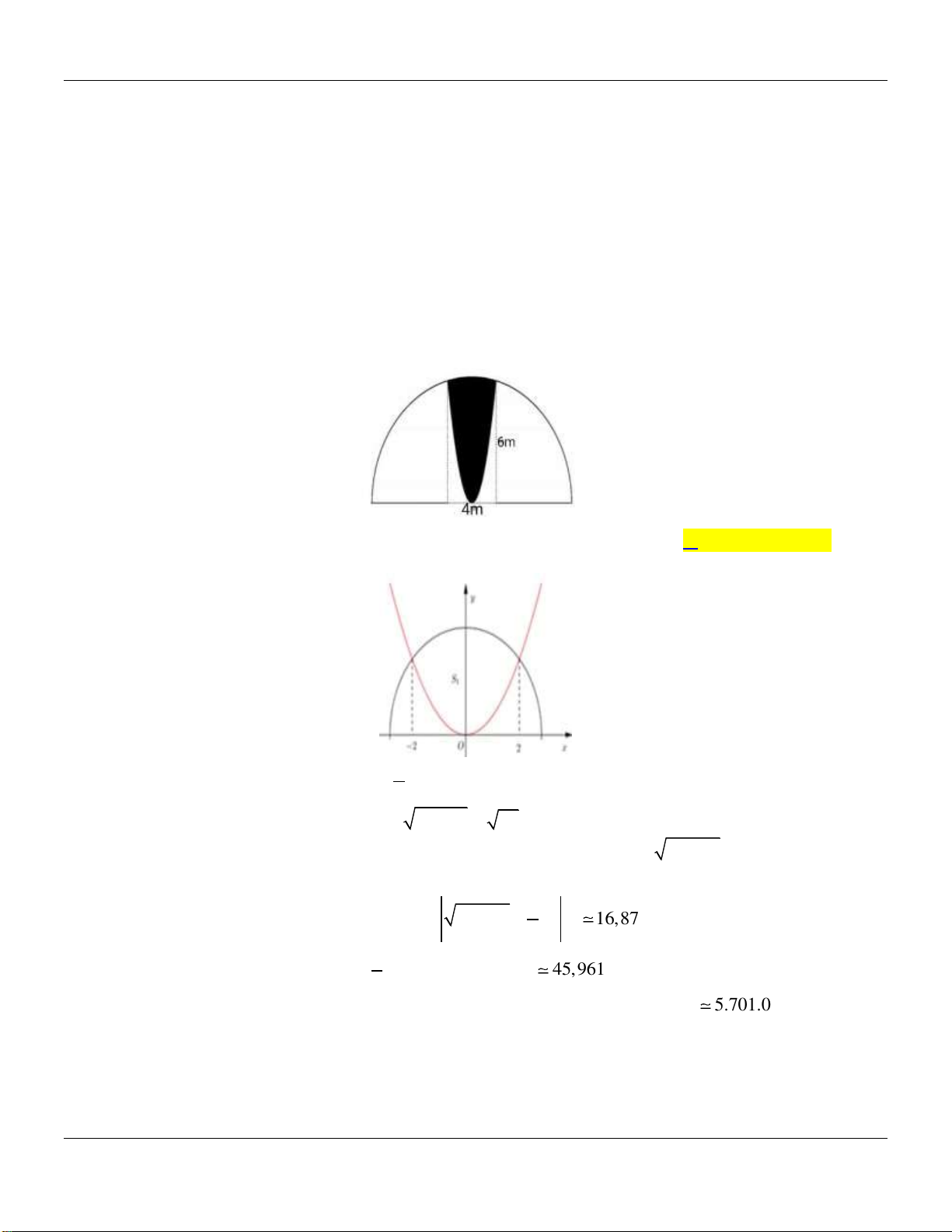
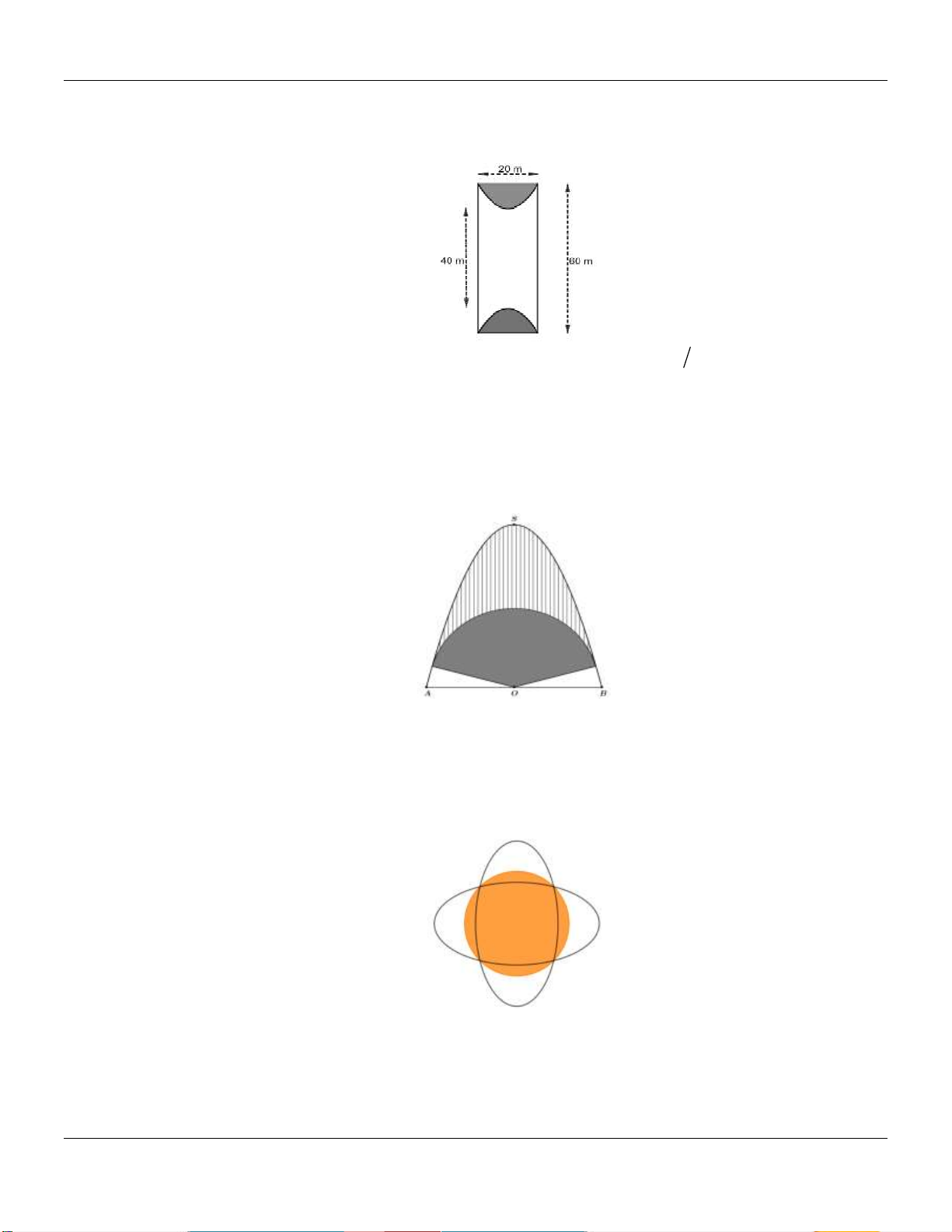
Câu 48: Một khuôn viên dạng nửa hình tròn, trên đó người ta thiết kế phần trồng hoa hồng có dạng
một hình Parabol có đỉnh trùng với tâm hình tròn và trục đối xứng vuông góc với đường
kính của nửa đường tròn, hai đầu mút của Parabol nằm trên đường tròn và cách nhau một
khoảng 4 mét (phần tô đậm). Phần còn lại của khuôn viên (phần không tô đậm) dùng để
trồng hoa cúc. Biết các kích thước cho như hình vẽ. Chi phí trồng hoa hồng và hoa cúc lần lượt là 120.000 đồng 2 m và 80.000 đồng/ 2
m . Hỏi chi phí trồng hoa khuôn viên đó gần nhất
với số nào sau đây (làm tròn đến ngàn đồng). A. 6.847.000 đồng. B. 6.865.000 đồng. C. 5.710.000 đồng. D. 5.701.000 đồng.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 49: Trong đợt hội trại “Khi tôi 18 ” được tổ chức tại trường THPT X, Đoàn trường có thực hiện
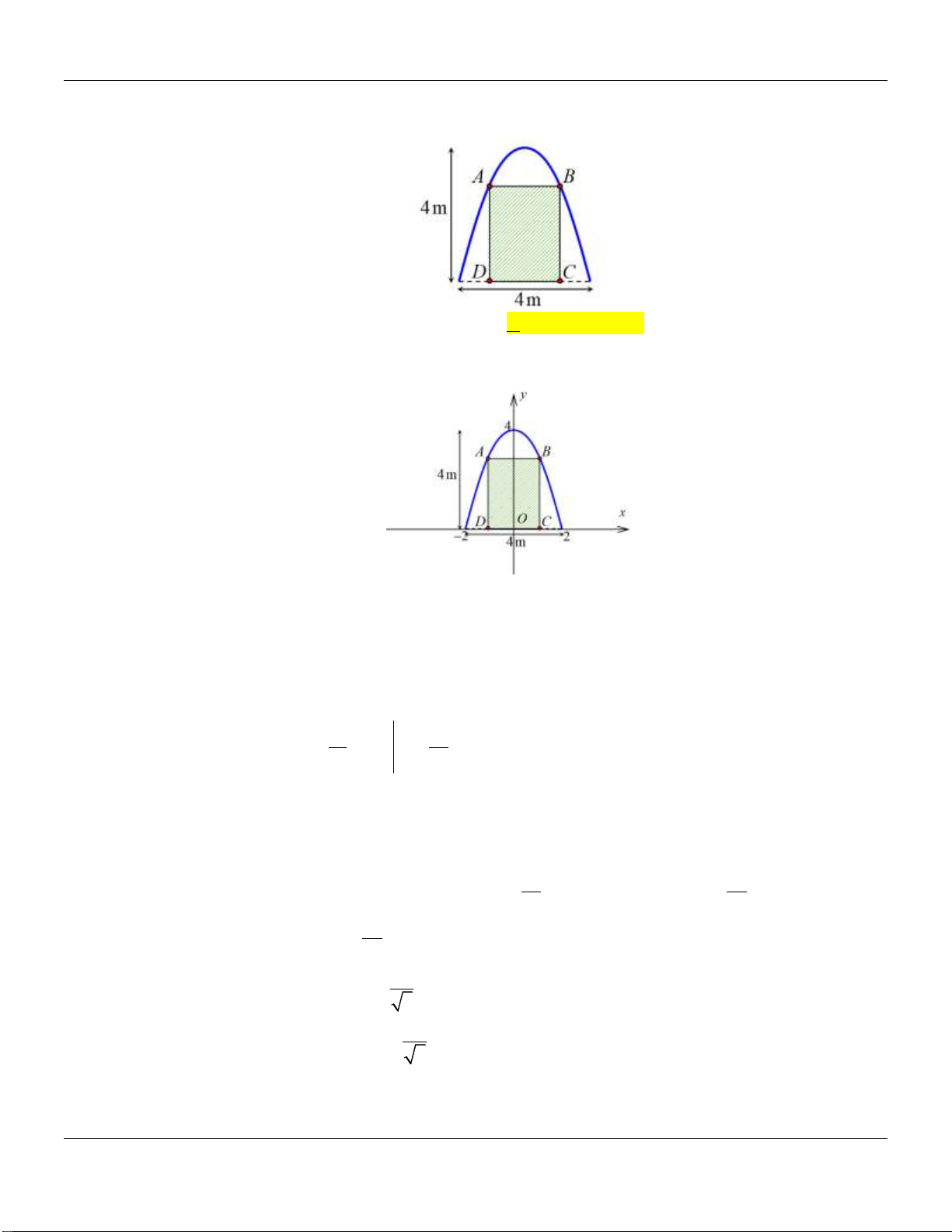
một dự án ảnh trưng bày trên một pano có dạng parabol như hình vẽ. Biết rằng Đoàn trường
sẽ yêu cầu các lớp gửi hình dự thi và dán lên khu vực hình chữ nhật ABCD , phần còn lại sẽ
được trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000 đồng cho một 2 m bảng.
Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng nghìn)? A. 900.000 đồng. B. 1.232.000 đồng. C. 902.000 đồng. D. 1.230.000 đồng.
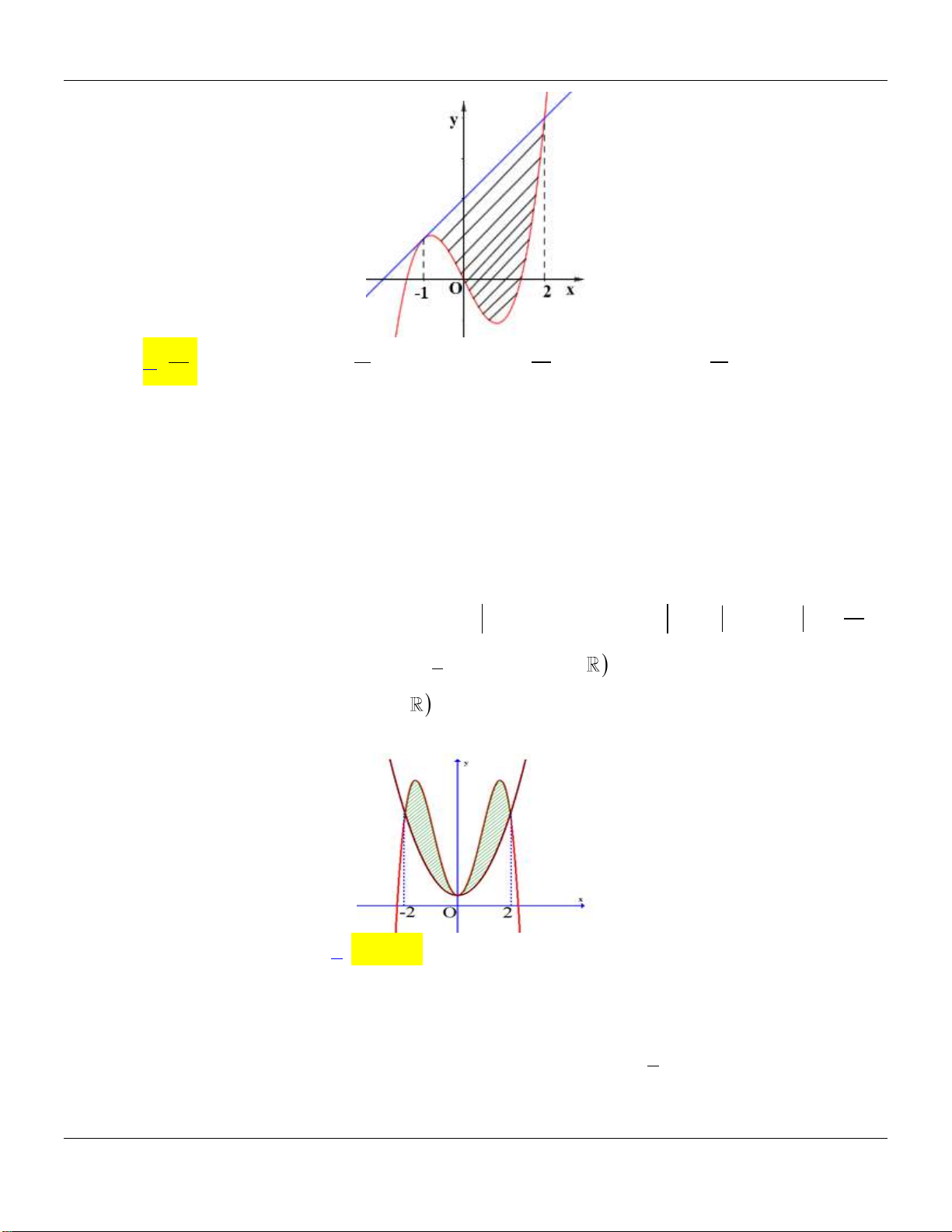
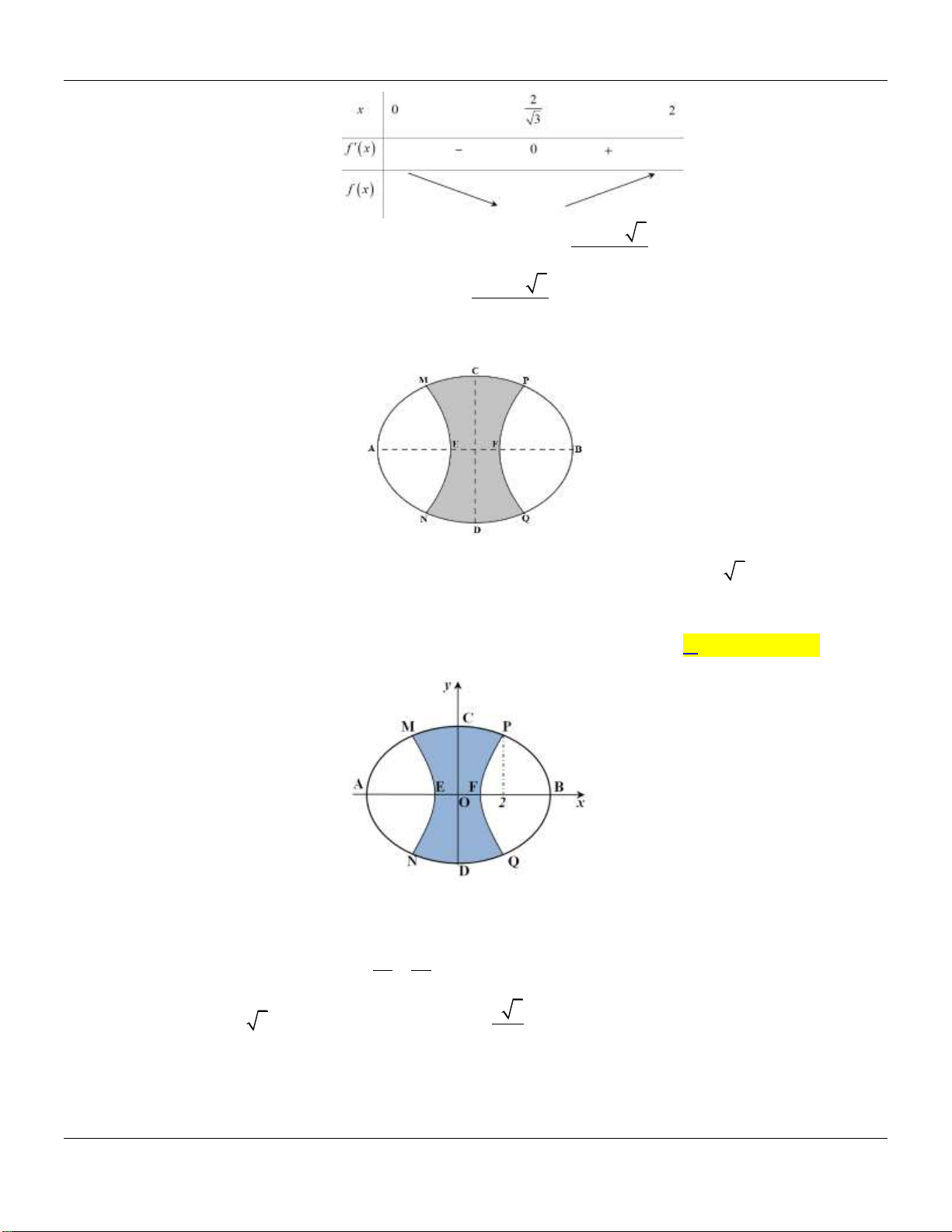
Câu 50: Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh
A , B , C , D và hai đường parabol có các đỉnh lần lượt là E , F (phần tô đậm của hình vẽ).
Hai đường parabol có cùng trục đối xứng AB , đối xứng nhau qua trục CD , hai parabol cắt
elip tại các điểm M , N , P , Q . Biết AB  8m , CD  6m , MN  PQ  3 3m , EF  2m . Chi
phí để trồng hoa trên vườn là 300.000 đ/ 2
m . Hỏi số tiền trồng hoa cho cả vườn gần nhất với
số tiền nào dưới đây? A. 4477800 đồng. B. 4477000 đồng. C. 4477815 đồng. D. 4809142 đồng.
____________________HẾT____________________
Huế, 15h15’ Ngày 19 tháng 3 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
LỜI GIẢI CHI TIẾT Câu 1:
Cho hàm số f  x có đồ thị trên đoạn 1; 4 như hình vẽ dưới: 4 Tính tích phân I  f (x)dx  . 1  11 5
A. I  5 . B. I  . C. I  . D. I  3 . 2 2 Lời giải:
Gọi S là diện tích của hình thang giới hạn bởi phần trên đồ thị hàm số f  x với trục hoành. 1
Gọi S là diện tích của hình thang giới hạn bởi phần dưới đồ thị hàm số f  x với trục hoành. 2 2 1 3 .2 4 1 2 .1 3 Với S  f x dx   4 
, S   f x dx    . 2     1     2 2 2 1  2 4 2 4 2 4   Ta có: I 
f (x)dx 
f (x)dx 
f (x)dx 
f (x)dx     
  f (x)dx   = S  5 S  . 1 2 2 1  1  2 1   2  Câu 2:
Hình phẳng giới hạn bởi đồ thị hàm số y  f x và trục hoành gồm hai phần, phần nằm phía 8 5
trên trục hoành có diện tích S  và phần nằm phía dưới trục hoành có diện tích S  1 3 2 12
(tham khảo hình vẽ bên). 0 Tính I  f 3x   1dx . 1  5 3 37 27
A. I  . B. I  . C. I  . D. I  . 3 4 36 4 Lời giải: 0 Với I  f 3x   1dx . 1 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
x  0  t  1
Đặt t  3x  1  dt  3dx . Khi  . x  1   t  2  1 1 0 1 1 1 1   Ta được I  f
 tdt  f
 xdx   f
 xdx f
 xdx. 3 3 3 2  2   2 0  0 8 Trên đoạn  2
 ;0: f x  0 nên f xdx   . 3 2  1 5 Trên đoạn 0 
;1 : f  x  0 nên f  xdx    . 12 0 0 1 1   1  8 5  3
Vậy I   f
 xdx  f
 xdx      . 3 3    3 12  4 2  0 Câu 3:
Cho hàm số f  x liên tục trên
. Biết diện tích S  2 , S  11, S  3 , S  4 , S  12 (tham 1 2 3 4 5 khỏa hình vẽ) 1 Tích phân  f
   x1 x1dx  bằng 6  35 35 A. . B. . C. 18 . D. 18 . 2 2 Lời giải: 1  f    x1 1 1
 x  1dx  f 
  x 1dx  x 1dx 6  6  6  1 1  1 Ta có: f
  x 1dx  f
 x  1dx  f
 x 1dx 6  6  1  1  Xét  
 f x 1d .x Đặt x 1 t  dx  dt. 6  1  0 5 Ta có: f
 x 1dx   f
 tdt  f
 tdt  2113412  2 6  5 0 1 Xét f  x    1 dx 1 
Đặt x 1  t  dx  dt
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1 2 Ta có: f  x   1 dx 
f t dt  2 11  9    1  0 1 21  Xét  x   1 dx   2 6  1 1 1 21 3  5 Vậy 
  f  x1 x1dx  
 f  x1dx x 1dx  29  . 2 2 6  6  6  Câu 4:
Cho hàm số y  f  x liên tục trên
có đồ thị như hình vẽ bên dưới:
Giả sử diện tích phần kẻ dọc trên hình vẽ có diện tích bằng a . Tính theo a giá trị của 2 I  2x   
1 f  x d . x 3 
A. I  50  2a .
B. I  50  a .
C. I  30  2a .
D. I  30  2a . Lời giải: 2
Từ đồ thị suy ra S  f
 xdx  a và f  3
   8; f 2  2 . 3  2 2
Ta có I  2x   
1 f  x dx  2x   
1 d  f  x 3  3  2  2x  
1 f  x 2  2 f
 xdx  5 f 25 f  3
   2S  5.2  5.8  2a  50  2a . 3  3 
Vậy I  50  2a . Câu 5:
Cho hàm số y  f x liên tục và nhận giá trị không âm trên 1  ;2   và thỏa mãn 2
f x  f 1  x , x    1  ;2. 
 Đặt S  xf x x 
, S là diện tích hình phẳng được giới hạn bởi đồ 1  d 2 1 
thị hàm số y  f x , trục Ox và hai đường thẳng x  1,x  2 . Khẳng định nào dưới đây đúng?
A. S  2S .
B. S  3S .
C. 2S  S .
D. 3S  S . 1 2 1 2 1 2 1 2 Lời giải: 2 Ta có S  xf x dx  . 1   1 
Đặt t  1 x  dt  dx . Đổi cận x  1
  t  2; x  2  t  1  .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1  2 Suy ra S  1 t f 1 t dt 
  1t f tdt 1      2 1  2 2 2 2  f
 tdt  tf
 tdt  f
 xdx xf
 xdx  S  S . 2 1 1  1  1  1 
Vậy 2S  S . 1 2 Câu 6:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y  x  3x  4 , trục hoành, các đường thẳng x  1
 , x  k k  0 bằng 8 . Mệnh đề nào sau đây đúng?  3  A. k   1  ;4 .
B. k  3;6 .
C. k 0; 2 . D. k  3;    .  2  Lời giải: k k  x  k 11
Diện tích hình phẳng cằn tìm S   x  3x  4 4 4 3 2 3 3 dx  
 x  4x    k  4k  .  4  4 4 1  1  4 k 21  1 1 3 7  Mà 3 S  8   k  4k   0  k 3 3 2 k  k  k   0   4 4  4 4 4 4 
k  3 TM    . k  2,07  L Vậy k   1  ;4 . Câu 7: Cho parabol P 2
: y  x  2x  1 và đường thẳng  : y  2x  m . Để diện tích hình phẳng giới 4
hạn bởi P và  bằng thì giá trị của tham số m nằm trong khoảng nào dưới đây? 3 A. 5;  3 . B.  3  ;0 . C. 0; 2 . D. 2; 3 . Lời giải:
Ta xét: f  x  g  x 2
 x  x    x  m 2 2 1 2
x  4x 1 m .
Đã biết công thức tính nhanh diện tích giới hạn bởi hai đường cong có     20  4m     20 4m 2 4 f x g x
ax  bx  c là S    m  4  . 2 2 6a 6.1 3 Câu 8:
Cho hình thang cong  H  giới hạn bởi các đường 2x y 
, y  0 , x  0 , x  4 . Đường thẳng
x  a 0  a  4 chia hình  H  thành hai phần có diện tích S và S như hình vẽ bên dưới: 1 2
Tìm a để S  4S . 2 1 16
A. a  3 .
B. a  log 13 .
C. a  2 . D. a  log . 2 2 5
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Lời giải: a 4 Ta có  2x S dx 
; S  2x dx  . 1 2 0 a 4 a 4 a 2x 2x 4 a a 0 2 2  2 2 
Mặt khác, S  4S 
2x dx  4 2x dx     4    4   2 1 ln 2 ln 2 ln 2 ln 2 ln 2 ln 2   a 0 a 0  a a 4
4.2  2  2  4  5.2a  20  a  2 . Vậy a  2 . Câu 9:
Gọi  H  là phần hình phẳng gạch chéo trong hình vẽ dưới đây được giới hạn bởi đồ thị của các hàm số 2
y  3x , y  4  x và trục hoành (tham khảo hình vẽ)
Diện tích của  H  là bằng 11 9 13 7 A. . B. . C. . D. . 2 2 2 2 Lời giải: 2  y  3x  
H  :  y  4  x  y  0 
Xét các phương trình hoành độ giao điểm:
x 1 (t / m)
4  x  0  x  4 ; 2
3x  0  x  0 ; 2 
3x  4  x  4   x  Loai  3 4 1 4 2 1  x  11 Diện tích hình phẳng 2 S  3x dx 
 x x  x     x    . H 4  3   d 4 0  2  2 0 1 1 1
Câu 10: Diện tích hình phẳng giới hạn bởi đồ thị C  của hàm số y   2
x  4x  3 và hai tiếp tuyến 2
của C  xuất phát từ M 3; 2   là 5 11 8 13 A. . B. . C. . D. . 3 3 3 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1
Đặt f  x   2
x  4x  3 , có f  x  x  2 . 2
Tiếp tuyến của C  tại điểm A x ; f (x ) có phương trình dạng y  f  x x  x  f (x ) . 0   0  0 0  0 1
Hay  : y   x  2 x  x    2 x  4x  3 0 0 0 0  2 1
Tiếp tuyến này xuất phát từ M 3; 2   nên 2
  x  23 x    2 x  4x  3 0 0 0 0  2 1 5 x 1
 : y  x 1 2 0 1
 x  3x   0   0 0   2 2 x  5
 : y  3x 11  0  2
Dựa vào đồ thị đã vẽ, diện tích hình phẳng cần tính là: 3 5  1 3    1 3   2 S  x  2x     x   2 1 dx  x  2x      3x 1  1 d  x  2 2    2 2   1 3 3 5 3 5  1 1   1 25   1 1 1   1 5 25  8 2 2 3 2 3 2  x  x  dx  x  5x  dx  x  x  x  x  x  x          .  2 2   2 2   6 2 2   6 2 2  3 1 3 1 3
Câu 11: Cho parabol P 2
: y  x  2 và hai tiếp tuyến của P tại các điểm M 1; 3 và N 2;6 . Diện
tích hình phẳng giới hạn bởi P và hai tiếp tuyến đó bằng 9 13 7 21 A. . B. . C. . D. . 4 4 4 4 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Ta có: y '  2x .
Phương trình tiếp tuyến tại M  1
 ;3 là d : y  2  x 1. 1
Phương trình tiếp tuyến tại N 2;6 là d : y  4x  2 . 2 1
Phương trình hoành độ giao điểm của d1 và d2: 2
 x 1  4x  2  x  . 2
Vậy diện tích phần giới hạn cần tìm là: 1 2 S   9 2 x  2 2   2  x   1 dx 
 2x 24x2 dx    . 4 1  1 2
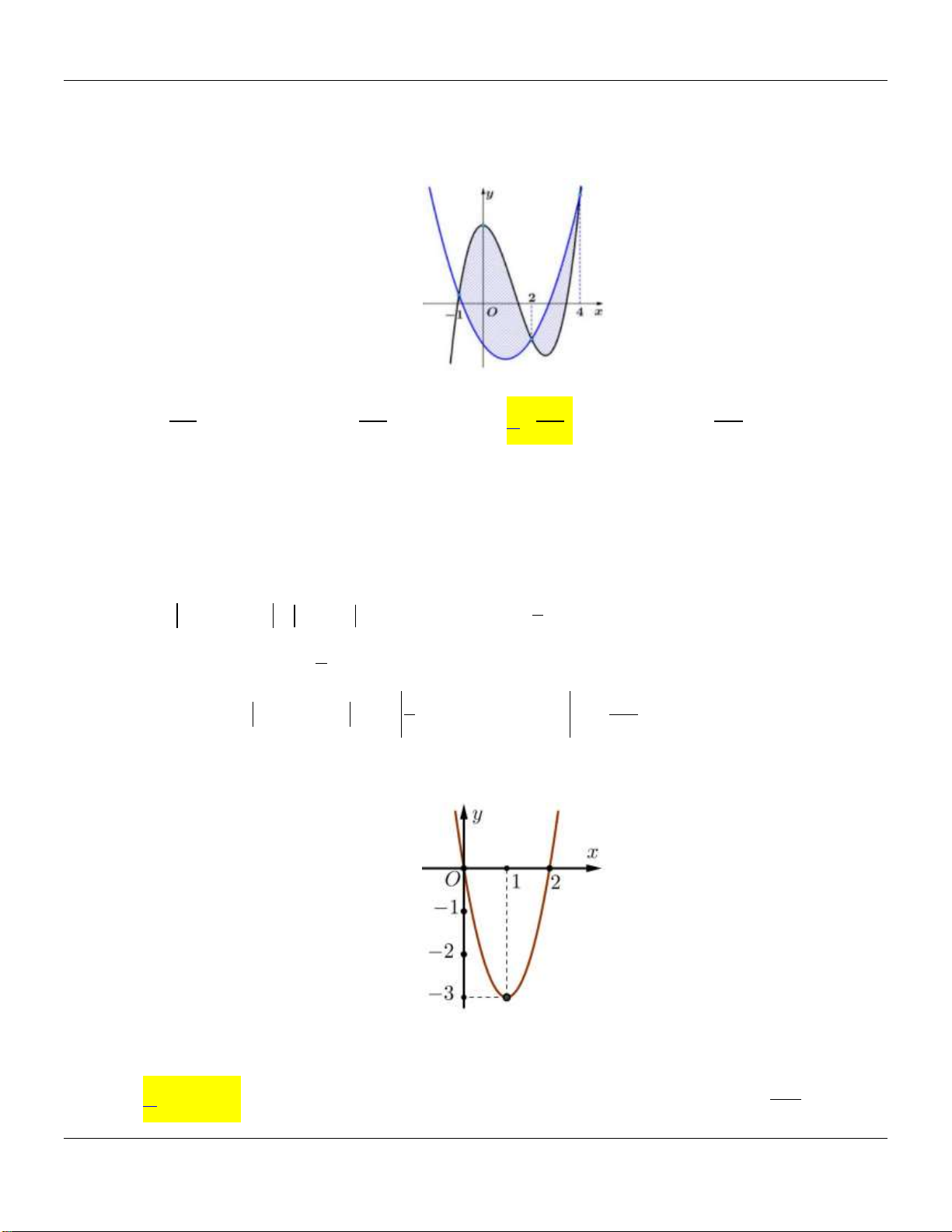
Câu 12: Cho hàm số y  f  x là một hàm số bậc ba. Gọi S
là diện tích giới hạn bởi các đường
y  f  x, y  0, x  1
 và x  4 (tham khảohình vẽ).
Khi đó diện tích S có giá trị bằng 253 253 235 235 A. . B. . C. . D. . 12 24 24 12 Lời giải:
Dựa vào hình vẽ ta có f  x  0 có 3 nghiệm phân biệt x  1; x  1; x  4 .
Mà f  x là hàm bậc ba nên f  x  a x   1  x   1  x  4 1
Cho x  0 suy ra 4a  2  a  2 1
Do đó f  x   x   1  x   1  x  4 2
Nên diện tích S giới hạn bởi các đường y  f  x, y  0, x  1  và x  4 là 4 1 S 
x  x  x   253 1 1 4 dx   . 1  2 24
Câu 13: Cho đồ thị hàm số y  f  x và y  g  x như hình vẽ bên dưới:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1
Biết đồ thị của hàm số y  f  x là một Parabol đỉnh I có tung độ bằng  và y  g  x là 2
một hàm số bậc ba. Hoành độ giao điểm của hai đồ thị là x , x , x thỏa mãn x .x .x  6  . 1 2 3 1 2 3
Diện tích hình phẳng giới hạn bởi 2 đồ thị hàm số y  f  x và y  g  x gần nhất với giá trị nào dưới đây? A. 6 . B. 8 . C. 5 . D. 7 . Lời giải:
Gọi phương trình của Parabol là 2
y  ax  bx  c , từ dữ kiện đề bài ta có hệ phương trình   1 a  c  0  2  
4a  2b  c  0  b   1
  f x 1 2  x  . x 2   2 4ac  b 1 c  0      4a 2   1  Giả sử   3 2
g x  ax  bx  cx  d thì đồ thị của nó đi qua I 1; 
 và có 2 cực trị có hoành  2 
độ bằng 0 và 2 , tức là phương trình g x 2
 3ax  2bx  c  0 có 2 nghiệm là 0 và 2 .
Kết hợp với giả thiết ta có hệ phương trình  1  1 a   a b c d        8 2    3 c  0 b     8  gx 1 3 3 2 3
  x  x  .
12a  4b  c  0 8 8 4  c  0  d 
x .x .x    6   3 1 2 3  a d    4
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình x  1   7 1 1  2 1 3 3 2 3
x  x   x  x   x  1 2 2 8 8 4 x  1   7  3
Vậy diện tích hình phẳng giới hạn bởi 2 đồ thị hàm số y  f  x và y  g  x bằng 1   S   f
  x gx 1 7  dx  g 
  x f xdx  1   7 1 1 3 2 1   7 3 2  x x 3   x x 3 
     x  dx      x  dx  6,22.  8 8 4   8 8 4  1   7 1
Câu 14: Cho hai hàm số f  x 3 2
 ax  bx  cx  4 và g x 2
 dx  ex  2, a, b, c, d, e  . Biết rằng đồ
thị hàm số y  f  x và y  g  x cắt nhau tại 3 điểm có hoành độ lần lượt là 3; 1; 2 . Hình
phẳng giới hạn bởi đồ thị hai hàm số đã cho có diện tích bằng 316 191 253 97 A. . B. . C. . D. . 15 9 12 6 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Xét phương trình hoành độ giao điểm của hàm số y  f  x và y  g  x : h  x 3
 ax  b  d  2
x  c  e x  6  0 .
Hàm số y  f  x và y  g  x cắt nhau tại 3 điểm có hoành độ lần lượt là 3; 1; 2 nên
h  x  a  x  3 x  
1  x  2  0 . Xét h 0  6   .3 a .1. 2    6   a 1 .
Vậy hàm số: h  x   x  3 x   1  x  2
Hình phẳng giới hạn bởi đồ thị hai hàm số đã cho có diện tích bằng: 2 2 S 
h  x x 
x  x  x   253 d 3 1 2    . 12 3  3 
Câu 15: Cho f  x, g  x lần lượt là các hàm đa thức bậc ba và bậc nhất có đồ thị như hình vẽ bên dưới: y 2 1 x O _4 3 3 _ 1 2
Biết diện tích hình S (được tô đậm) bằng 250 . Tính  d  f x x . 81 0 19 11 34 23 A. . B. . C. . D. . 15 9 15 6 Lời giải:  4 
Ta có g  x là hàm số bậc nhất đi qua A ;1 
 và B3;2 nên g  x 3 1  x  .  3  5 5 3 1 Với y  1   x   1   x  2   C  2  ; 
1 là giao điểm của f  x và g  x . 5 5  4 
Do đó f  x  g  x  a x  2 x    x  3 .  3  4 4 3 3 250   4   3 Lại có: S  
  f x gxdx   
 ax  2 x  x 3 dx  a     . 81   3   20 2  2  3  4 
Suy ra f  x  g  x 
x  2 x   x  3 20  3  f  x 3 x  4     x  x   3 1 2 3  x    . 20  3  5 5 2 2  3  4  3 1  34
Vậy  f xdx    x  2 x  x  3  x  dx     . 20  3  5 5  15 0 0
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 16: Cho hàm số f  x 3 2
 ax  bx  36x  c a  0;a, , b c 
 có hai điểm cực trị là 6  và 2 . Gọi
y  g  x là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y  f  x . Diện tích hình
phẳng giới hạn bởi hai đường y  f  x và y  g  x bằng A. 160  B. 128. C. 64  D. 672  Lời giải: f  x 3 2
 ax  bx  x  c f x 2 36
 3ax  2bx  36 .  f    6    0 3a  62  2 .
b 6  36  0 9
 a  b  3 a 1 Theo bài ta được         f   2  0 3  a  a  b  b   22  2 . b 2  36  0 3 9 6  f x 3 2
 x  x  x  c f x 2 6 36 ;
 3x 12x  36 ;
Đường thẳng đi qua hai điểm cực trị của hàm số:  1 2 
y  f  x   2
3x 12x  36. x   32x  c  24    3 3 
là y  g  x  32
 x  c  24 . x  6  
Xét phương trình hoành độ giao điểm hai đồ thị 3 2
x  6x  36x  c  3
 2x  c  24  x  2   x  2 
Vậy diện tích hình phẳng giới hạn bởi hai đường y  f  x và y  g  x bằng 2 
S   x  6x  36x  c   3
 2x  c  24 2
dx   x  6x  4x  24 2 3 2 3 2 dx    3 2
x  6x  4x  24dx 6  6  2   128 .
Câu 17: Cho hai hàm số f  x 4 3 2
 ax  bx  cx  3x và   3 2
g x  mx  nx  x ; với a,b, c, m, n  . Biết
hàm số y  f  x  g  x có ba điểm cực trị là 1
 ; 3 và 4 . Diện tích hình phẳng giới hạn bởi
hai đồ thị hàm số f  x và y  g x bằng 32 64 125 131 A. . B. . C. . D. . 3 9 12 12 Lời giải:
Ta có f  x  g  x là hàm bậc 4 nên f  x  g  x 4 3 2
 Ax  Bx  Cx  4x .
f  x  g x 3 2
 4Ax  3Bx  2Cx  4 .
Hàm số y  f  x  g  x có ba điểm cực trị là 1
 ; 3 và 4 nên ta có hệ phương trình:  1 A   12
4A  3B  2C  4  0    2 1 5 108 
A  27B  6C  4  0  B 
 f x  gx 3 2
 x  2x  x  4 3   3 3
256 A  48B  8C  4  0   5 C   6
Diện tích của hình phẳng giới hạn bởi hai đồ thị hàm số y  f  x và y  g x bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 4 1 5 131 3 2 S  x  2x  x  4 dx   . 3 3 12 1 
Câu 18: Cho hàm số y  f  x là hàm đa thức bậc bốn và có đồ thị như hình vẽ bên. Hình phẳng giới
hạn bởi đồ thị hai hàm số y  f  x , y  f  x có diện tích bằng 127 107 87 127 A. . B. . C. . D. . 40 5 40 10 Lời giải:
Ta thấy đồ thị hàm số y  f  x tiếp xúc với trục hoành tại hai điểm có hoành độ bằng 2  và 2 2
1 nên hàm số có dạng f  x  a  x  2  x   1 . 1 1
Mà đồ thị hàm số y  f  x đi qua điểm A0 
;1  4a  1  a 
 f x  x  22 x  2 1 4 4
 f x 1
 x  2x   1 2x   1 2
Xét phương trình hoành độ giao điểm của y  f  x và y  f  x : x  2   1     2  x  2 1 x x 2 1
 x  2x   1 2x   1 1   4 2 x  1   x  4
 Hình phẳng giới hạn bởi đồ thị hai hàm số y  f x , y  f x có diện tích là 4 1 107 S 
x  2 x  2 1 2 1 
x  2x   1 2x   1   . 4 2 5 2  Câu 19: Cho hàm số 4 3
f (x)  ax  x  2x  2 và hàm số 3 2
g(x)  bx  cx  2 , có đồ thị như hình vẽ bên dưới:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 221
Gọi S ; S là diện tích các hình phẳng gạch chéo trong hình vẽ, biết S 
. Khi đó S bằng 1 2 1 640 2 1361 271 571 791 A. . B. . C. . D. . 640 320 640 640 Lời giải:
Từ đồ thị ta thấy hoành độ giao điểm của đồ thị hàm số g(x) với trục hoành chính là điểm
cực trị của hàm số f (x) . Do đó: f (
 x)  k.g(x) . Hay: 3 2
ax  x   k  3 2 4 3 2
bx  cx  2 k  1 
Suy ra: b  3a . Hay: 3 2
g(x)  4ax  3x  2. c  3  Suy ra: 4 3 3 2 4
f x  g x  ax  x  x   ax  x 
 ax    a 3 2 ( ) ( ) 2 2 4 3 2 1 4
x  3x  2x 1 1 2 2 221 1 Khi đó: S 
f (x)  g(x) dx    4
ax  1 4a 3 2
x  3x  2xdx   a   1   640 4 0 0 2  1  791 Vậy 4 3 S 
x  x  2x  2 dx    . 2  4  640 3 2
Câu 20: Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số   3 2
f x  ax  bx  c , các
đường thẳng x  1 , x  2 và trục hoành (miền gạch chéo) cho trong hình dưới đây: 51 52 50 53 A. S  . B. S  . C. S  . D. S  . 8 8 8 8 Lời giải:
Hình phẳng giới hạn bởi đồ thị của hàm số   3 2
f x  ax  bx  c , các đường thẳng x  1 ,
x  2 và trục hoành được chia thành hai phần:
ền D là hình chữ nhật có hai kích thước lần lượt là 1và 3  S  3. 1 1  f x 3 2
 ax  bx  c 
ền D gồm:  y  1 . 2 x  1  ; x  2 
Dễ thấy C  đi qua 3 điểm A1; 
1 , B 0;3 , C 2; 
1 nên đồ thị C  có phương trình f  x 1 3 3 2
 x  x  3. 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 2  1 3  27 3 2  S  x 
x  3 1 dx   . 2    2 2  8 1  51
Vậy diện tích hình phẳng cần tìm là S  S  S  . 1 2 8 3 1
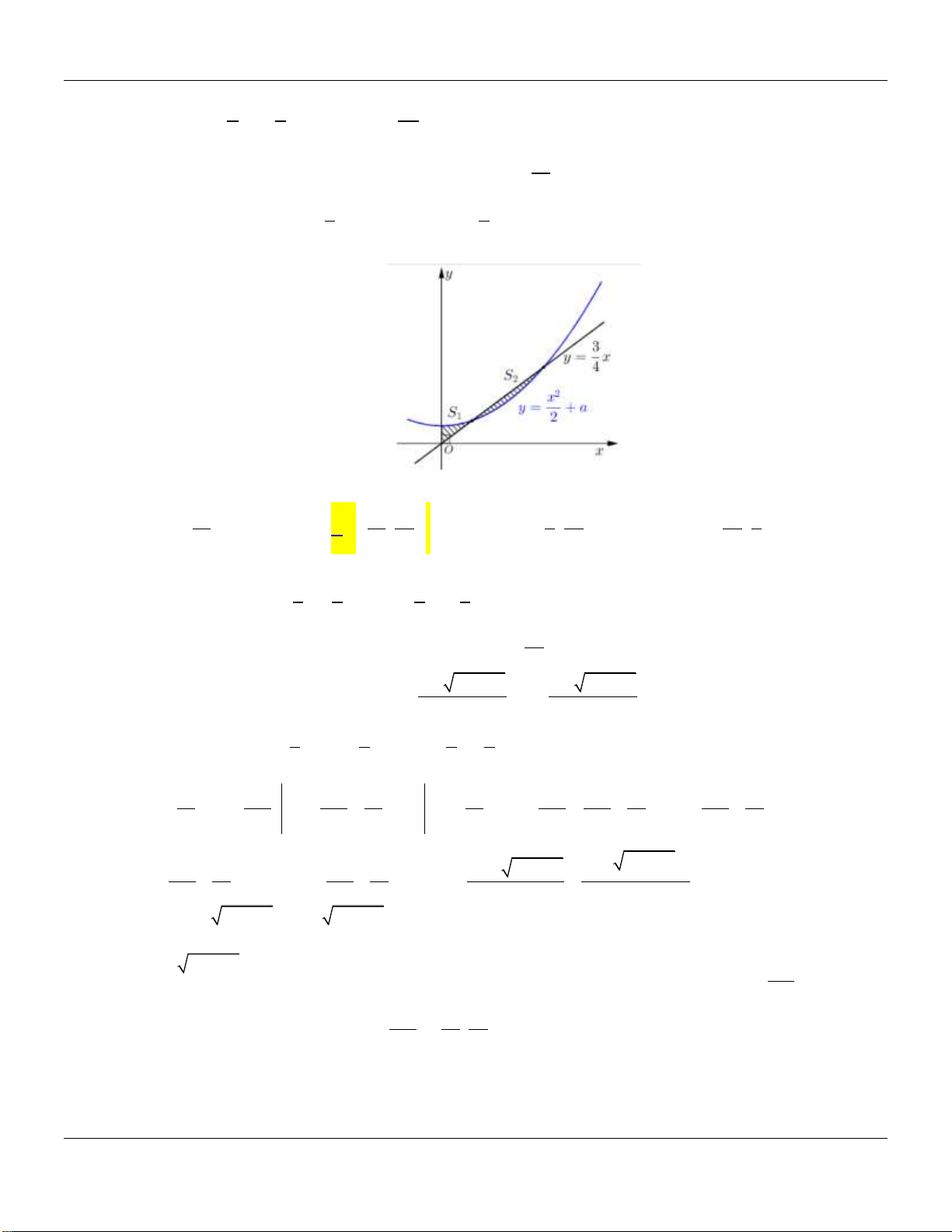
Câu 21: Cho đường thẳng y  x và parabol 2
y  x  a , ( a là tham số thực dương). Gọi S ,S lần 4 2 1 2
lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên dưới:
Khi S  S thì a thuộc khoảng nào sau đây? 1 2  3   3 7   1 9   7 1  A. 0;  . B.  ;  . C.  ;  . D.  ;  .  16   16 32   4 32   32 4  Lời giải: 3 1 1 3 Xét phương trình: 2
x  x  a 2 2
 x  x  a  0  2x  3x  4a  0 4 2 2 4 9
Ta có:   9  32a , theo giả thuyết   0  0  a  32 3  9  32a 3  9  32a
Khi đó hoành độ giao điểm là x  ; x  . 1 2 4 4 x x 1 2  1 3   3 1  Ta có: 2 2 S  S 
x  a  x dx  x  x     a dx 1 2  2 4   4 2  0 x1 x x 1 2 3 2 2 3  x 3x   3x x  3 2 2 3 2 3  x 3x 3x x 3x x   ax       ax 1 1 2 2 1 1   ax     ax    ax  6 8   8 6  1 2 1 6 8 8 6 8 6 0 x1 2     a 3 9 32 9 3 9 32 a  2 3 3x x 2 3x x 2 2    ax  0  2 2   a  0    a  0 2 8 6 8 6 32 96
 27  9 9  32a  9  6 9  32a  9  32a  96a  0 a  0  
3 9  32a  64a  9 2
 81  288a  4096a  1152a  81 2
 4096a  864a  0  27  a   128 27  3 7 
Do a là số thực dương nên a   ;  . 128  16 32 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 22: Cho hai hàm đa thức   3 2
f x  ax  bx  cx  d và   2
g x  mx  nx  p . Biết rằng đồ thị hai
hàm số y  f  x và y  g  x cắt nhau tại ba điểm có hoành độ lần lượt là 1; 2; 4 đồng thời
cắt trục tung lần lượt tại M , N sao cho MN  6 ( tham khảo hình vẽ).
Hình phẳng giới hạn bởi đồ thị hai hàm số đã cho ( phần gạch sọc) có diện tích bằng 125 253 253 253 A. . B. . C. . D. . 8 24 16 12 Lời giải:
Phương trình hoành độ giao điểm của đồ thị y  f  x và y  g  x là: 3 2 2 3
ax  bx  cx  d  mx  nx  p  ax  b  m 2
x  c  n x  d  p  0
Do đồ thị hai hàm số y  f  x và y  g  x cắt nhau tại ba điểm có hoành độ lần lượt là
1;2;4 nên ta được ax  x  x   3
 ax  b  m 2 1 2 4
x  c  n x  d  p . 3
Mà f 0  g 0  y  y  MN  6 . Suy ra a  . M n 4 3
Do đó: f  x  g  x   x  
1  x  2 x  4 . 4 4 4 3 253 Khi đó: S 
f  x  g  x dx  x  
1  x  2 x  4 dx    . 4 16 1  1 
Câu 23: Cho f  x 3 2
 ax  bx  cx  d a  0 là hàm số nhận giá trị không âm trên đoạn 2;  3 có đồ
thị f  x như hình vẽ bên dưới:
Biết diện tích hình phẳng giới hạn bởi các đồ thị của các hàm số   2
g x  xf  x ;   2
h x  x f  x f  x và các đường thẳng x  2; x  3 bằng 72 . Tính f   1 .  A. f   1  2 . B. f   1  1  . C. f   1  1. D. f   62 1  . 5
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Lời giải:
Từ hình vẽ ta có được f  x  x  x   2
 x  x  f  x 3 2 3 2 3 6
 x  3x  C . 3 3
Diện tích hình phẳng là S  g
 xhx 2 dx  xf  x 2
 x f x f x dx 2 2 3 Do 2 xf  x 2
 x f x f x  0, x  2;  3 nên 2 S  xf  x 2
 x f x f x dx   2 3 3  1  1 9 9 2 Ta có: 2 2 S  x f  x 2 2 dx  x f  x 2  f 3 2  2 f 2 2
 C  2C  4   2  2 2 2 2 2  C  4 9 Mà  S  72 
C  2 C  42 2  72  52  . 2 C   5
Do f  x  x
    f x 3 2 0, 2;3
 x  3x  4  f   1  2 . Câu 24: Cho hàm số    4 2 y
f x  ax  bx  c có đồ thị C  và cắt trục hoành tại điểm có hoành độ bằng 1
 . Tiếp tuyến d tại điểm có hoành độ x  1 của C cắt C tại 2 điểm khác có
hoành độ lần lượt là 0 và 2 . Gọi S , S là diện tích các phần hình phẳng giới hạn bởi d và 1 2  S
C  (với S là diện tích phần hình phẳng nằm bên phải trục Oy ). Tỷ số 1 bằng 2 S2 1 1 2 1 A. B. C. D. 14 28 25 5 Lời giải:
Giả sử phương trình tiếp tuyến là y  g  x .
Do tiếp tuyến d tại điểm có hoành độ x  1 của C  cắt C  tại 2 điểm khác có hoành độ
lần lượt là 0 và 2 nên ta có phương trình hoành độ giao điểm của d và C  là: x  1  
f  x  g  x  ax  x  2
1  x  2  0  x  0  . x  2  0 2 2 a 2 28 a Do đó S  ax x 1 x  2 dx  
; S  ax x 1 x  2 dx   . 2     1     5 5 1  0 S 1 Suy ra 1  . S 28 2
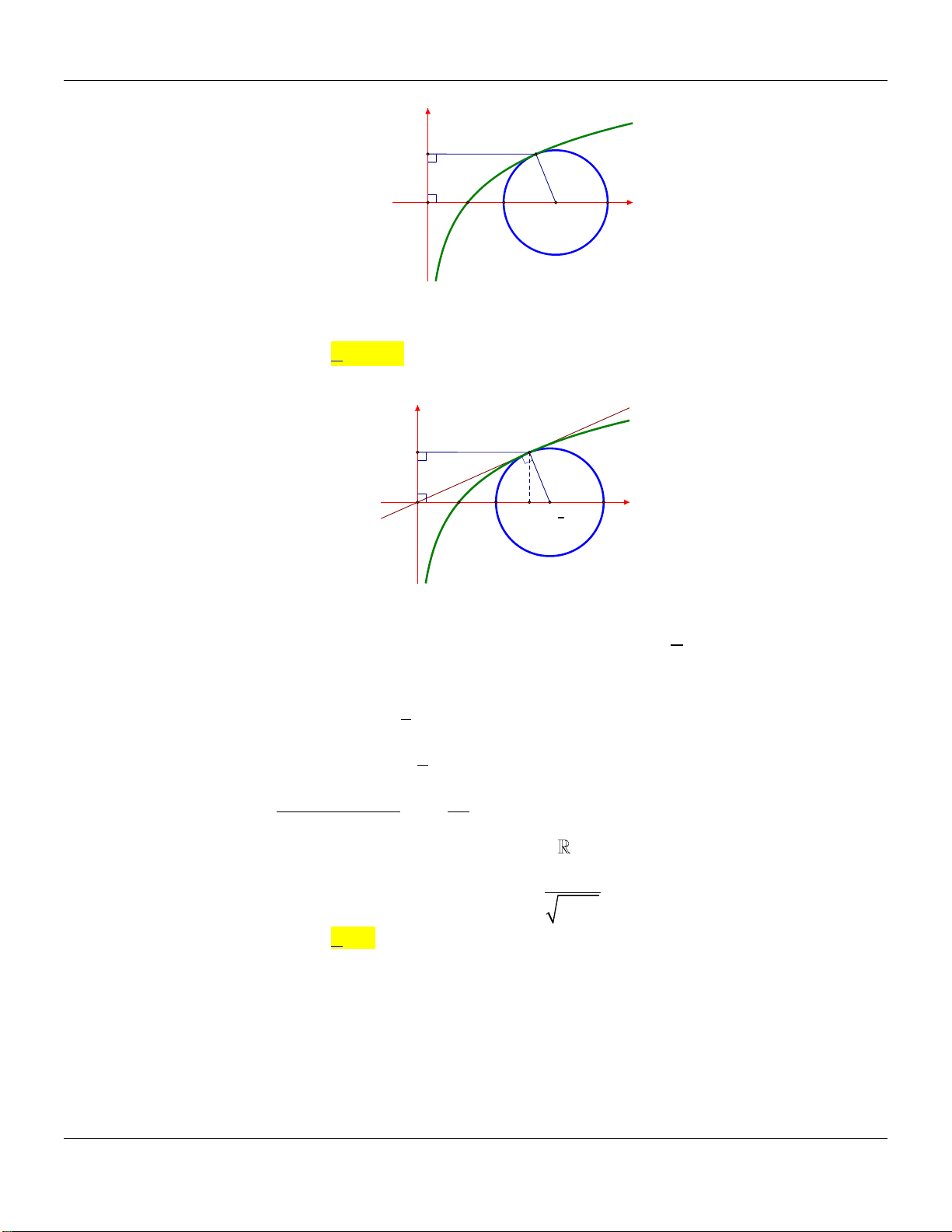
Câu 25: Cho hàm số y  ln x có đồ thị C như hình vẽ bên dưới:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia y (C) B C A O x
Đường tròn tâm A có duy nhất một điểm chung B với C . Biết C 0;  1 , diện tích của hình
thang ABCO gần nhất với số nào sau đây. A. 3,01. B. 2,91. C. 3,09 . D. 2,98 . Lời giải: y d (C) C B 1 A O 1 e x e + e
Đường thẳng đi qua C 0;1 và song song với trục hoành cắt đồ thị (C) tại ( B e;1) . x
Gọi (d) là tiếp tuyến của (C) tại (
B e;1) thì phương trình (d) là y  . e
(C) tiếp xúc với đường tròn tâm A tại (
B e;1) thì (d) là tiếp tuyến chung của (C) và đường 1
tròn tâm A . AB  ( ) d  ( A e  ;0). e 1
Hình thang ABCO có: OA  e  ;CB  e;OC  1 . e (OA C ) B OC 1 Vậy S   e   2,91. ABCO 2 2e Câu 26: Cho hàm số   4 3 2
f x  x  bx  cx  dx  e ( b, c, d, e 
) có các giá trị cực trị là 1, 4 và 9 . Diện f  x
tích hình phẳng giới hạn bởi đồ thị hàm số g  x   
và trục hoành bằng f  x A. 4. B. 6. C. 2. D. 8. Lời giải:
+) Gọi x  x  x là ba điểm cực trị của hàm số f  x . Ta có bảng biến thiên: 1 2 3
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
+) Phương trình hoành độ giao điểm của đồ thị hàm số g  x và trục hoành là: f  x  f    x      g  x   0 x x (i 1, 2, 3) i       f  x 0  f   x  0  f   x  i  0 (TM)
+) Diện tích cần tìm là x x 2 f x 3 f x x x 2 3 S  dx  dx  2 f  
x  2 f x  4 f x  2 f x  2 f x  6. 2   1  3 x f x x f x x x 1 2 1 2
Câu 27: Biết đồ thị C  của hàm số f  x 4 2
 x  bx  c b,c  có cực trị là A1;0 . Gọi P là
parabol có đỉnh I 0;  
1 và đi qua điểm B 2;3 . Diện tích hình phẳng giới hạn bởi C  và
P thuộc khoảng nào dưới đây? A. 0;  1 . B. 2;3 . C. 3; 4 . D. 1; 2 . Lời giải:
Đồ thị C  của hàm số f  x 4 2
 x  bx  c b,c  có cực trị là
A1;0  AC   b  c  1  f  x 3
 4x  2bx vì A1;0 là cực trị nên f  
1  0  4  2b  0  b  2   c 1.
 C f x 4 2 :
 x  2x 1 Gọi  P 2
: y  a x  b x  c a  0 . 1 1 1  1 
P là parabol có đỉnh I 0; 1  I P  c  1. 1 b
Hoành độ đỉnh  P : 1 x    0  b  0 . I 1 2a1
P đi qua điểm B2;3  3  4a  2b  c  a 1. 1 1 1 1  P 2
: y  x 1 .
Phương trình hoành độ giao điểm của C  và  P :  x  1  4 2 2 4 2
x  2x 1  x 1  x  3x  2  0   x   2 2 Diện tích hình phẳng: 4 2 S 
x  3x  2 dx  2,537  .  2
Câu 28: Đường thẳng d cắt đường cong f  x 3 2
 a x  bx  cx  d tại ba điểm phân biệt có hoành độ
x  2 , x  1 , x  2 như hình vẽ bên dưới:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Diện tích hình phẳng gạch sọc thuộc khoảng nào dưới đây?  9   13   11 11  A. ;5   . B. 6;   . C. 5;   . D. ;6   .  2   2   2   2  Lời giải:
Ta có d : y  mx  n
Phương trình hoành độ giao điểm: 3 2 a x bx cx d mx n g  x 3 2      
 a x  bx  cx  d  mx  n có 3nghiệm x  2; x 1; x  2 .
Do đó g  x  a  x  2 x   1  x  2 . Do g   1
 d  n    a  a   g x 1 0 3 1 4
 x  2x   1  x  2 . 2 2 2 1 71 Vì vậy S 
x  2x  
1  x  2 dx   . 2 12 2 
Câu 29: Cho hai hàm số f  x 3 2
 ax  bx  cx 1và g x 2
 dx  ex  2 a, ,
b c, d, e   . Biết rằng đồ
thị của hàm số y  f  x và y  g  x cắt nhau tại ba điểm có hoành độ lần lượt là
3; 1;1(tham khảo hình vẽ) .
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng A. 6 . B. 9 . C. 7 . D. 8 . Lời giải:
Hoành độ giao điểm là nghiệm của phương trình 3
ax  b  d  2
x  c  e x  3  0 * .
a  b  d  c  e  3  0 a   1  
Do phương trình * có 3 nghiệm nên ta có hệ pt a  b  d  c  e  3  0  b
  d  3 .   9a
  3b 3d  c  e 1  0 c  e  1   
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1  1
Do vậy S    3 2
x  3x  x  3dx    3 2
x  3x  x  3dx  8 . 3  1 
Câu 30: Cho hai hàm số f  x 3 2
 ax  bx  cx  2 và g x 2
 dx  ex  2 a, ,
b c, d, e   . Biết rằng đồ
thị của hàm số y  f  x và y  g  x cắt nhau tại ba điểm có hoành độ lần lượt là
2;1;1(tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng A. 37 . B. 145 . C. 37 . D. 145 . 5 7 6 8 Lời giải:
Hoành độ giao điểm là nghiệm của phương trình 3
ax  b  d  2
x  c  e x  3  0 *
Do phương trình * có 3 nghiệm là 2 ; 1  ; 1nên ta có hệ pt :
a  b  d  c  e  4  0 a  2  
a  b  d  c  e  4  0  b
  d  4   4a
  2b  2d  c  e  2  0 c  e  2    1  1 37
Do vậy S   3 2
2x  4x  2x  4dx   3 2
2x  4x  2x  4dx    . 6 2  1 
Câu 31: Đường thẳng y  kx  4 cắt parabol y   x  2 2
tại hai điểm phân biệt và diện tích các hình
phẳng S , S bằng nhau như hình vẽ bên. 1 2
Khẳng định nào sau đây đúng?  1   1  A. k   6  ; 4   . B. k  1  ;   . C. k   2  ;  1 . D. k   ;0   .  2   2  Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia x  0
Phương trình hoành độ giao điểm  x  2 2  kx  4 2
 x  k  4 x  0   . x  k  4  4 
Đường thẳng y  kx  4 cắt các trục tọa độ tại các điểm A  ;0   , B 0;4 .  k  4
  k  4  2  2  k  0 . k k 4 k 4 2 1 3
Diện tích hình phẳng S   kx  4 x  2 dx    2
x  k  4 x dx  k  4 . 1      6 0 0 4  4 k 4 k  2 1 3 k 2
Diện tích hình phẳng S  x  2 dx  kx  4 dx  k  2    . 2         3 2k 2 k 4 4 1 1 k  2 k  0, 457 TM 3 3 S  S 
k  4  k  2        . 1 2 6 3 2k k  5,54  L 1
Câu 32: Cho  H  là hình phẳng giới hạn bởi parabol 2 y 
x 1 (với 0  x  2 2 ), nửa đường tròn 4 2
y  8  x và trục hoành, trục tung (phần tô đậm trong hình vẽ).
Diện tích của  H  bằng 3 14 2  2 3  4 3  2 A. . B. . C. . D. . 6 3 6 3 Lời giải: 1
Phương trình hoành độ giao điểm của parabol 2 y  x 1 và đường 2
y  8  x là: 4 2 1 1 3 x  4 2 2 4 2 8  x  x 1  x  x  7  0  
 x  2 (Vì 0  x  2 2 ) 2 4 16 2 x  28  Diện tích của (H) là: 2 2 2 2  1   1  8 2 2 2 2 3 S  x 1 dx  8  x dx  x  x  I   I      với 2 I  8  x dx   4  12  3 0 2 0 2    
Đặt x  2 2 sin t,t   ;
 dx  2 2 cost.dt    2 2 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia  
Đổi cận x  2  t 
, x  2 2  t  . 4 2     2 2 2 2  1  2 2 I 
8  8sin t .2 2 cos t.dt  8 cos t.dt  4(1 cos 2t).dt  4 t  sin 2t    2      .  2      4 4 4 4 8 3  2
Vậy S   I  . 3 3 Câu 33: Cho hàm số 3 2
y  f (x)  ax  bx  cx  d a, ,
b c, d  , a  0 có đồ thị là C  . Biết rằng đồ thị
Cđi qua gốc tọa độ và đồ thị hàm số y  f '(x) cho bởi hình vẽ bên.
Tính giá trị H  f (4)  f (2).
A. H  45 .
B. H  64 .
C. H  51.
D. H  58 . Lời giải: Theo bài ra 3 2
y  f (x)  ax  bx  cx  d a, ,
b c, d  , a  0 do đó y  f  x là hàm bậc hai có dạng    2 y f x  a x   b x   c . c  1 a  3  
Dựa vào đồ thị ta có: a  b  c  4  b
   0  y  f  x 2  3x 1.  
a  b  c  4  c  1 
Gọi S là diện tích phần hình phẳng giới hạn bởi các đường y  f  x , trục Ox , x  4, x  2 . 4 Ta có S   2 3x   1 dx  58 . 2 4 4 Lại có: S  f 
 xdx  f x  f 4 f 2. 2 2
Do đó: H  f 4  f 2  58 . Câu 34: Cho hàm số 4 2
y  x  4x  m có đồ thị C . Giả sử C
cắt trục hoành tại bốn điểm phân m  m 
biệt sao cho diện tích hình phẳng giới hạn bởi C
với trục hoành có diện tích phần phía trên m 
trục hoành bằng diện tích phần phía dưới trục hoành. Khi đó m thuộc khoảng nào dưới đây? A. m  1   ;1 .
B. m 3;5 .
C. m 2;3 .
D. m  5;   . Lời giải:
Phương trình hoành độ giao điểm của C với trục hoành là 4 2
x  4x  m  0   1 . m 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Đặt 2
t  x t  0 , phương trình   1 trở thành 2
t  4t  m  0 2 . Để  
1 có bốn nghiệm phân biệt thì 2 phải có hai nghiệm dương phân biệt. Điều này xảy ra   0  4  m  0
khi và chỉ khi S  4  0  
 0  m  4 3 .  m  0 P  m  0 
Gọi t và t t  t là hai nghiệm của 2 , khi đó bốn nghiệm (theo thứ tự từ nhỏ đến lớn) 1 2  1 2 của phương trình  
1 là x   t , x   t , x  t , x  t . 1 2 2 1 3 1 4 2
Do tính đối xứng của C
nên từ giả thiết ta có m  x 4 x 3 x 4 5 3  x  2x 8x  4 2
x  4x  m 4 dx    4 2
x  4x  mdx    4 2
2x  8x  2mdx  0     2mx   0  5 3  0 0 3 x 0 5 3 x 4x 5 3 x 4x 5 3 x 4x 4 4    mx  0 4 4    mx  0 4 4 4 2  
 mx  0  3x  20x 15m  0 . 4 5 3 4 5 3 4 4 4 5 3
Vậy x là nghiệm của hệ: 4 4 2
x  4x  m  0 4 2 1
 5x 60x 15m  0 4 2 1
 2x  40x  0 4 4  4 4   4 4   4 2 3
 x  20x 15m  0  4 2 3
 x  20x 15m  0 4 2 3
 x  20x 15m  0 4 4  4 4  4 4 x  0 4  m  0 4 2 12
 x  40x  0  4 4  10  2    . 4 2 x      4 3x 20x 15m 0   4 4  3   20   m   9 20
Kết hợp điều kiện 3 suy ra m  . 9
Câu 35: Cho Parabol  P 2
: y  x và đường tròn C  có tâm A0;3 bán kính bằng 5 như hình vẽ bên dưới:
Diện tích phần được tô đậm giữa C  và  P gần nhất với số nào dưới đây? A. 3.44 . B. 1.51. C. 1.77 . D. 3.54 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Lời giải:
+) Phương trình đường tròn C  tâm A0;3 bán kính bằng 5 là C  x   y  2 2 : 3  5
+) Do tính chất đối xứng, ta chỉ cần xét phần được tô đậm của C  và  P với x  0 .
+) Gọi S là diện tích hình phẳng giới hạn bới các đường x    y  2 5 3 , x 
y , y  1, y  4 1 4 2 Ta có S  5  y  3  y dy   1.26032 . 1     1
+) Gọi S là diện tích hình phẳng giới hạn bới các đường 2 2
y  3  5  x , y  x , x  0, x  1 . 2 1  
Ta có S    2 3  5  x  2
 x dx  0.5075 . 2  0
Vậy diện tích cần tính S  2S  S  3,539 . 1 2 
Câu 36: Cho hàm số bậc bốn y  f  x có đồ thị C  như hình vẽ bên dưới: 1 5
Đường thẳng d : y  kx  có đúng ba điểm chung với C  là ,
A B, C và BC  AB  . Biết 4 4 24 1
diện tích hình phẳng S (phần gạch sọc) là
. Giá trị của  f xdx bằng 5 2  321 161 159 A. 2  . B.  . C.  . D.  . 160 80 160 Lời giải:
Phương trình giao điểm của C  và d là:
f  x  g  x  a  x   x  2 2
1  x  5 (hệ số a  0 ) 5 24 2 24 1
Theo giả thiết, ta có: S 
 a x  2x  
1  x  5 dx   a   1 5 5 24
 f x  g x 1 
x  x  2 x   1 1 2 1 5  kx  
x  2x  2 1  x  5 24 4 24  1   1   1  * Gọi A 2
 ;  2k , B 1;  k ,C 5;  5k        4   4   4   3 k  5  BC  AB     k2    k2 5 2 2 4 4 4 3 3    4 4 3 k    4
Đường thẳng nằm ở góc phần tư thứ nhất và thứ ba nên hệ số góc là dương nên ta chọn
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 3 k  . 4 3 1 1 2
Vậy f  x  x  
x  2x   1 x  5. 4 4 24 1 1  3 1 1 2  321
Và  f xdx  x   
x  2x  
1  x  5 dx     . 2  2  4 4 24  160 Câu 37: Cho hàm số   3 2
f x  x  bx  cx  d với b , c , d  . Biết hàm số
g  x  f  x  2 f  x  3 f   x có hai giá trị cực trị là 6
 và 42 . Tính diện tích hình phẳng
f  x  f  x  f   x
giới hạn bởi các đường y  và y  1. g  x 18 A. ln 5. B. ln 7. C. 2 ln 6. D. 2 ln 5. Lời giải:
Hàm số f  x là hàm số bậc 3 nên g  x là hàm số bậc 3 suy ra g x là hàm số bậc hai. 3 Ta có 3 f x  3.3!18;
g x  f  x  2 f   x 18 có hai nghiệm x , x (giả sử x  x ) và g  x  42 , g  x  6  . 2  1  1 2 1 2
Xét phương trình tìm cận của tích phân để tính diện tích:
f  x  f  x  f   x
f  x  2 f   x 18    . g  x 1  g  x 0 18 18 x  x
Suy ra f  x  2 f   x 18  0  g x 1  0   . x  x  2 2 x
f  x  f  x  f   x 2 x g x 2 x g x
Diện tích hình phẳng S   dx  dx  dx    . g x  g x  g x  x   1 18 x   18 x   18 1 1 1
x  x  t  g x 18  1 1  1
Đặt t  g  x 18  dt  g x dx . Đổi cận  .
x  x  t  g x 18  2 2  2  12 dt 12 12 Do đó S   ln t  ln12  ln 60  ln  ln 5  ln 5  . 60 t 60 60 Câu 38: Cho hàm số 3 2
y  x  ax  bx  c có đồ thị C  . Biết rằng tiếp tuyến d của C  tại điểm A có hoành độ bằng 1
 cắt C tại điểm B có hoành độ bằng 2 (xem hình vẽ). Diện tích hình
phẳng giới hạn bởi d và C  (phần gạch chéo trong hình) bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 27 11 25 13 A. . B. . C. . D. . 4 2 4 2 Lời giải:
Đồ thị C  đi qua gốc tọa độ O 0;0 suy ra c  0 . Tiếp tuyến d với C  tại điểm có hoành độ
x  1 có phương trình y  3  2a  b x  2  a . Xét phương trình hoành độ giao điểm của hai
đồ thị d và C  : 3 2
x  ax  bc    a  b x   a   x   2 3 2 2
1 x  a  
1 x  a  2  0   x  1    . g   x 2
 x  a  
1 x  a  2  0
Vì d cắt C  tại điểm B có hoành độ bằng 2 suy ra g 2  0  a  0 . 2 2 27
Vậy diện tích hình phẳng cần tính là S 
 3x bx3bx2 3 dx 
x  3x  2 dx    . 4 1  1  1 Câu 39: Cho hàm số
y  f  x 4 2
  x  ax  b a,b   có đồ thị (C) và 2    2 y
g x  mx  nx  p m,n, p   có đồ thị  P như hình vẽ. Diện tích hình phẳng giới
hạn bởi C  và  P có giá trị nằm trong khoảng nào sau đây? A. 4;4  ,1 . B. 4,2;4,3 . C. 4,3;4,4 . D. 4,1;4, 2 . Lời giải: 2
Diện tích hình phẳng giới hạn bởi C  và  P : S   f
  x gx dx  . 2 
h  x  f  x  g  x 1
là hàm bậc bốn có hệ số bậc bốn bằng 
, có hai nghiệm đơn x  2 , 2
x  2 và một nghiệm kép x=0 (dựa vào sự tương giao của C  và  P trong hình vẽ )
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 2  1 1 64 2
h  x  f  x  g  x 2
  x x  2x  2  S  
 x x2x2dx   4,266. 2 2 15 2 
Câu 40: Người ta trồng hoa vào phần đất được tô màu được giới hạn bởi cạnh AB, CD , đường trung
bình MN của mảnh đất hình chữ nhật ABCD và một đường cong hình sin. Biết AB  2 (m),
AD  2 (m). Tính diện tích phần còn lại. A. 4 1. B. 4    1 . C. 4  2 . D. 4  3 . Lời giải:
Chọn hệ trục toạ độ Oxy như hình vẽ
Đồ thị hàm số có dạng y  a sin bx . 1
Dựa vào hình vẽ ta thấy đường sin có chu kì AB  2 và biên độ bằng AM  AB  1. 2
Suy ra đường hình sin có phương trình y  sin x .
Đường thẳng BC có phương trình x   .  
Do đó diện tích phần đất được tô màu là S  2 sin x dx  2  cos x  4  . 0 0
Diện tích hình chữ nhật là S  4 . 2
Diện tích phần còn lại: S  S  S  4  4  4( 1) . 2 1
Câu 41: Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng 10 cm bằng
cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên dưới:
Biết AB  5 cm, OH  4 cm. Tính diện tích bề mặt hoa văn đó. 160 140 14 A. 2 cm . B. 2 cm . C. 2 cm . D. 2 50 cm . 3 3 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 16 16
Đưa parabol vào hệ trục Oxy ta tìm được phương trình là  P 2 : y   x  x . 25 5 16 16
Diện tích hình phẳng giới hạn bởi  P 2 : y   x 
x , trục hoành và các đường thẳng 25 5 5  16 16  40
x  0 , x  5 là 2 S   x  x dx    .  25 5  3 0 160
Tổng diện tích phần bị khoét đi: S  4S  2 cm . 1 3
Diện tích của hình vuông là 2 S  100 cm . hv 160 140
Vậy diện tích bề mặt hoa văn là 2
S  S  S  100   cm . 2 hv 1 3 3
Câu 42: Một hoa văn trang trí được tạo ra từ một miếng bìa hình vuông cạnh 20 cm bằng cách khoét
đi bốn phần bằng nhau đều có hình dạng một nửa elip như hình vẽ. Biết một nửa trục lớn là
AB  6 cm , trục bé CD  8 cm . Diện tích bề mặt của hoa văn đó bằng A.    2 400 48 cm  . B.    2 400 96 cm  . C.    2 400 24 cm  . D.    2 400 36 cm  . Lời giải:
Gọi S là diện tích hình vuông, S là diện tích khoét đi. 1 2 Ta có 2 S  20  400  2 cm
và S  2 ab  2 .6.4  48  2 cm
(vì mỗi phần bị khoét đi là nửa 2  1 
elip có a  6 , b  4 ).
Vậy diện tích bề mặt hoa văn là S  S  S  400  48  2 cm . 1 2 
Câu 43: Một viên gạch hoa hình vuông cạnh 40 cm được thiết kế như hình bên dưới. Diện tích mỗi
cánh hoa (phần tô đậm) bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia y 1 y = x2 20 y = 20x 20 x 20 20 20 800 400 A. 2 cm . B. 2 cm . C. 250 2 cm . D. 800 2 cm . 3 3 Lời giải:
Diện tích một cánh hoa là diện tích hình phẳng được tính theo công thức sau: 20  20 1   2 1  400 2 S  20x  x dx   3 3  . 20. x  x     2 cm  .  20   3 60  3 0 0
Câu 44: Ông An muốn làm một cánh cửa bằng sắt có hình dạng và kích thước như hình vẽ. Biết rằng
đường cong phía trên là một parabol, tứ giác ABCD là một hình chữ nhật.
Giá cánh cửa sau khi hoàn thành là 900000 đồng/ 2
m . Số tiền ông An phải trả để làm cánh cửa đó bằng
A.9 600 000 đồng.
B. 15 600 000 đồng.
C. 8 160 000 đồng. D. 8 400 000 đồng. Lời giải:
Chọn hệ trục tọa độ Oxy sao cho cạnh AB nằm trên Ox và O là trung điểm AB . Khi đó, ta có phương trình parabol là: 2 y  1 x . 1 28
Diện tích cánh cửa là: S  2.4   2 1 x dx    2 m  . 3 1 
Câu 45: Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là 2, 25 mét,
chiều rộng tiếp giáp với mặt đất là 3 mét. Giá thuê mỗi mét vuông là 1500000 đồng. Vậy số
tiền bác Năm phải trả là A. 33750000 đồng. B. 3750000 đồng. C. 12750000 đồng. D. 6750000 đồng. Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Gọi phương trình parabol  P 2
: y  ax  bx  c . Do tính đối xứng của parabol nên ta có thể
chọn hệ trục tọa độ Oxy sao cho  P có đỉnh I  Oy (như hình vẽ). 9  c, 
I P  9 4   c   4 9 3 
Ta có hệ phương trình:  a  b  c  0 A P  a  1 . 4 2    b  0 9 3  a 
b  c  0  B   P  4 2 9 Vậy  P 2 : y  x  . 4
Dựa vào đồ thị, diện tích cửa parabol là: 3 3 9 2  9  2  9  3 4  x 9  9 2 S  x  dx    2  2 x  dx    2  x  2  m .   4   4   3 4 2 3  0 0 2 9 Số tiền phải trả là: 1 . 500000  675 0 000 đồng. 2
Câu 46: Một khu vườn dạng hình tròn có hai đường kính AB, CD vuông góc với nhau, AB  12m .
Người ta làm một hồ cá có dạng elip với bốn đỉnh M , N , M ', N ' như hình vẽ. Biết MN  10 ,
m M ' N '  8 ,
m PQ  8m . Diện tích phần trồng cỏ (phần gạch sọc) bằng: A. 2 32, 03 m . B. 2 20, 33 m . C. 2 33.02 m . D. 2 23, 03 m . Lời giải:
Ta chọn hệ trục tọa độ như hình vẽ:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Khi đó phương trình đường tròn là: 2 2 2
x  y  36  y   36  x 2 2 2 x y x Phương trình elip là:  1 y  4  1 25 16 25 4 2  
Do tính đối xứng nên diện tích phần trồng cỏ sẽ là: 2 2
 4  36  x  4 1  dx 30,03m .  x S  25  0  
Câu 47: Một khu vườn có dạng hợp của hai hình tròn giao nhau. Bán kính của hai đường tròn là
20m và 15m , khoảng cách giữa hai tâm của hai hình tròn là 30m . Phần giao của hai hình tròn
được trồng hoa với chi phí 300000 đồng/ 2
m . Phần còn lại được trồng cỏ với chi phí 100000 đồng/ 2
m . Hỏi chi phí để trồng hoa và cỏ của khu vườn gần nhất với số tiền nào dưới đây?
A. 202 triệu đồng.
B. 208 triệu đồng.
C. 192 triệu đồng.
D. 218 triệu đồng. Lời giải: y C  1 :x2+y2=400 215 x 15 12 20 O I C
 2 :(x-30)2+y2=225
+ Gắn hệ trục như hình vẽ.
+ Đường tròn C có tâm O 0;0 , bán kính R  20 có phương trình: 2 2 x  y  400 1  1 2
 y   400  x .
+ Đường tròn C có tâm I 30;0 , bán kính R  15có phương trình:  x  2 2 30  y  225 2  2  y    x  2 225 30 . 215
+ Phương trình hoành độ giao điểm của C và C là: 400  x  225   x  302 2  x  . 2  1  12 215 12 20 2
+ Diện tích trồng hoa: S  2. 225   x30 2 2 dx  2.
400  x dx  60, 255 m  1 . 15 215 12
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia + Diện tích trồng cỏ: 2 2 2 2 2
S   R   R  2S   .20  .15  2.60, 255  1842,985 m 2 1 2 1
Tổng chi phí trồng hoa và cỏ là:
P  300000.S 100000.S  300000.60, 255 100000.1842,985  202375000 đồng 1 2
Vậy chi phí để trồng hoa và cỏ của khu vườn gần nhất với số tiền 202 triệu đồng
Câu 48: Một khuôn viên dạng nửa hình tròn, trên đó người ta thiết kế phần trồng hoa hồng có dạng
một hình Parabol có đỉnh trùng với tâm hình tròn và trục đối xứng vuông góc với đường
kính của nửa đường tròn, hai đầu mút của Parabol nằm trên đường tròn và cách nhau một
khoảng 4 mét (phần tô đậm). Phần còn lại của khuôn viên (phần không tô đậm) dùng để
trồng hoa cúc. Biết các kích thước cho như hình vẽ. Chi phí trồng hoa hồng và hoa cúc lần lượt là 120.000 đồng 2 m và 80.000 đồng/ 2
m . Hỏi chi phí trồng hoa khuôn viên đó gần nhất
với số nào sau đây (làm tròn đến ngàn đồng). A. 6.847.000 đồng. B. 6.865.000 đồng. C. 5.710.000 đồng. D. 5.701.000 đồng. Lời giải: 3
Parabol có phương trình là 2 y  x . 2
Đường tròn tâm O bán kính 2 2 R  2  6  40
Phương trình nửa đường tròn đã cho là 2 2 2
x  y  40, y  0  y  40  x .
Nửa đường tròn cắt Parabol tại M (2;6), N ( 2  ;6) 2 3
Ta có diện tích trồng hoa hồng 2 2 S  40  x  x dx 16,87  . 1 2 2  1
Diện tích trồng hoa cúc S   .40  S  20  S 45, 9619 . 2 1 1 2
Từ đó chi phí trồng các loài hoa theo yêu cầu T  S .120000  S .80000 5.701.000 . 1 2
Câu 49: Trong đợt hội trại “Khi tôi 18 ” được tổ chức tại trường THPT X, Đoàn trường có thực hiện
một dự án ảnh trưng bày trên một pano có dạng parabol như hình vẽ. Biết rằng Đoàn trường
sẽ yêu cầu các lớp gửi hình dự thi và dán lên khu vực hình chữ nhật ABCD , phần còn lại sẽ
được trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000 đồng cho một 2 m bảng.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng nghìn)? A. 900.000 đồng. B. 1.232.000 đồng. C. 902.000 đồng. D. 1.230.000 đồng. Lời giải:
Đặt hệ trục tọa độ như hình vẽ, khi đó phương trình đường parabol có dạng: 2
y  ax  b .
Parabol cắt trục tung tại điểm 0; 4 và cắt trục hoành tại 2;0 nên: b   4 a  1     . 2  . a 2  b  0 b   4
Do đó, phương trình parabol là 2
y  x  4 .
Diện tích hình phẳng giới hạn bởi đường parabol và trục hoành là 2 2 3  x  32 S    2
x  4 d x    4x  . 1   3  3 2  2 
Gọi C t;0  B  2
t; 4  t  với 0  t  2 .
Ta có CD  2t và 2
BC  4  t . Diện tích hình chữ nhật ABCD là S  C . D BC  t  2 2 . 4  t  3  2  t  8t . 2 32 32
Diện tích phần trang trí hoa văn là S  S  S    3 2  t  8t 3  2t 8t  . 1 2 3 3 32
Xét hàm số f t  3  2t 8t  với 0  t  2 . 3  2 t  0;2  3
Ta có f t  2
 6t 8  0   .  2 t   0;2  3 Bảng biến thiên:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 96  32 3
Như vậy, diện tích phần trang trí nhỏ nhất là bằng 2
m , khi đó chi phí thấp nhất 9 96  32 3
cho việc hoàn tất hoa văn trên pano sẽ là .200000  902000 đồng. 9
Câu 50: Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh
A , B , C , D và hai đường parabol có các đỉnh lần lượt là E , F (phần tô đậm của hình vẽ).
Hai đường parabol có cùng trục đối xứng AB , đối xứng nhau qua trục CD , hai parabol cắt
elip tại các điểm M , N , P , Q . Biết AB  8m , CD  6m , MN  PQ  3 3m , EF  2m . Chi
phí để trồng hoa trên vườn là 300.000 đ/ 2
m . Hỏi số tiền trồng hoa cho cả vườn gần nhất với
số tiền nào dưới đây? A. 4477800 đồng. B. 4477000 đồng. C. 4477815 đồng. D. 4809142 đồng. Lời giải:
+) Gắn hệ trục tọa độ Oxy như hình vẽ với O 0;0 , B 4;0 và C 0;3 .
+) Khi đó elip  E  có độ dài trục lớn AB  8 , độ dài trục bé CD  6 . 2 2  x y
Phương trình của  E  là:   1. 16 9  3 3 
+) Do PQ  3 3 và P , Q   E  , suy ra P  2;  
 . Lại có EF  2  F 1;0 . 2  
+) Phương trình parabol  P đỉnh F có dạng: 2 x  ky 1 . 1 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia  3 3  4
+) Vì parabol  P đi qua điểm P  2;
 nên phương trình P là: 2 x  y  1 . 1  1    2   27 3
+) Gọi S là diện tích hình phẳng giới hạn bới các đường 2 y 
16  x , y  0, x  0, x  2 . 1 4 2 3 Ta có 2 S  16  x dx    2 5.73967 m . 1 4 0 3 3
+) Gọi S là diện tích hình phẳng giới hạn bới các đường y 
x 1, y  0, x  1, x  2 . 2 2 2 3 3 Ta có S 
x 1 dx  1, 73205   2 m . 2  2 1
+) Diện tích trồng hoa là: S  4S  S   16,0305 2 m . 1 2 
Vậy số tiền trồng hoa cho cả vườn khoảng 16,0305.300000  4809150 đồng.
____________________HẾT____________________
Huế, 15h15’ Ngày 19 tháng 3 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TÍCH PHÂN ỨNG DỤNG TÍNH
DIỆN TÍCH HÌNH PHẲNG (Phần 2)
 LUYỆN THI THPT QUỐC GIA
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Ngân hàng câu hỏi:
ỨNG DỤNG TÍCH PHÂN TRONG HÌNH HỌC (2) NỘI DUNG ĐỀ BÀI Câu 1:
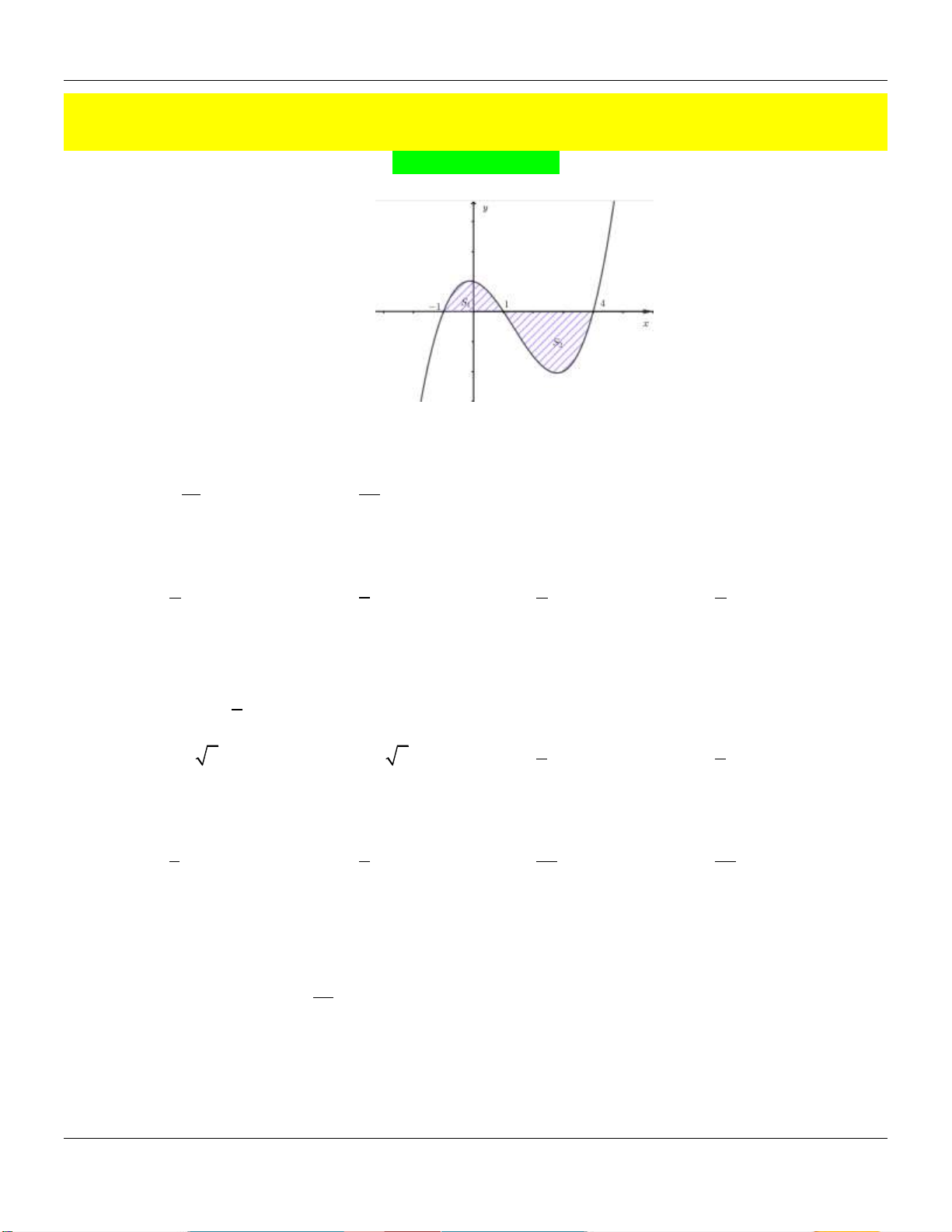
Cho hàm số y  f (x) có đồ thị như hình vẽ bên dưới:
Biết diện tích hai phần gạch chéo lần lượt là S  5, S  12 . 1 2 1 0 Tính I 
f (2x 1)dx  
 f x4d .x 0 3  19 29 A.  . B. . C. 17 . D. 7  . 2 2 Câu 2:
Tính diện tích hình phẳng giới hạn bởi parabol  P 2
: y  x  4 và hai tiếp tuyến của  P tại các điểm ,
A B có hoành độ lần lượt là 1  và 1. 4 1 1 2 A. . B. . C. . D. . 3 3 2 3 Câu 3:
Gọi S là diện tích của mặt phẳng giới hạn bởi đường thẳng y  mx với m < 2 và parabol  P 1
có phương trình y  x 2  x . Gọi S là diện tích giới hạn bởi  P và Ox . Với giá trị nào của 2 1 m thì S  S ? 1 2 2 2 1 A. 3 2  4 . B. 3 2  2 . C. . D. . 5 4 Câu 4: Cho hàm số 3 2
f (x)  ax  bx  cx  4 và 2
g(x)  mx  nx có đồ thị cắt nhau tại các điểm có
hoành độ là 1; 1; 2 . Diện tích của hình phẳng giới hạn bởi đồ thị của hai hàm số trên bằng 9 9 37 37 A. . B. . C. . D. . 4 2 12 6 Câu 5:
Cho hàm số bậc ba y  f  x có đồ thị là đường cong ở hình bên dưới. Gọi x , x lần lượt là 1 2
hai điểm cực trị thỏa mãn x  x  2 và f  x  3 f x  0. và đồ thị luôn đi qua 1   2  2 1
M (x ; f (x )) trong đó x  x 1 g(x) là hàm số bậc hai có đồ thị qua 2 điểm cực trị và M. 0 0 0 1 S
x  x 1 . Tính tỉ số 1 ( S và S lần lượt là diện tích hai hình phẳng được tạo bởi đồ thị hai 1 0 S 1 2 2
hàm f (x), g(x) như hình vẽ ).
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 5 6 7 4 A. . B. . C. . D. . 32 35 33 29 1 Câu 6:
Cho hai hàm số f  x 3 2
 ax  bx  cx  và g x 2
 dx  ex 1 a,b,c,d,e  . Biết rằng đồ 2
thị của hàm số y  f  x và y  g  x cắt nhau tại ba điểm có hoành độ lần lượt là 3  ; 1; 1 (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 9 A. . B. 8 . C. 4 . D. 5 . 2 Câu 7:
Hình phằng  H  được giới hạn bởi đồ thị C  của hàm đa thức bậc ba và parabol  P có
trục đối xứng vuông góc với trục hoành. Phần tô đậm như hình vẽ có diện tích bằng 37 7 11 5 A. . B. . C. . D. . 12 12 12 12
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Câu 8: Cho hàm số 4 2
y  ax  bx  c a  0 và hàm số 2
y  mx  nx  p m  0 có đồ thị là các
đường cong như hình vẽ bên.
Gọi S là diện tích của hình phẳng được tô đậm. Khẳng định nào sau đây đúng?  62 64   21 13   21 13 67  A. S  ;   . B. S  ;   . C. S  4;   . D. S  ;   .  15 15   5 3   5   3 15  Câu 9:
Trong mặt phẳng Oxy , cho parabol  P 2
: y  ax  bx  c a  0 và đường thẳng
d : y  mx  n m  0 . Tính diện tích hình phẳng  D giới hạn bởi  P , d và đường thẳng
 : y  4 như hình vẽ bên. 25 16 19 10 A. . B. . C. . D. . 6 3 6 3
Câu 10: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x
y  e , y  ln x , y  x  e 1 với các trục tọa độ. 2 e  2e  5 2 e 2 2e  e  4 2 e A. . B. . C. . D. . 2 2 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 11: Cho hàm số y  f  x có đồ thị là C  . Biết rằng đồ thị C  cắt trục tung tại điểm có tung độ 1
bằng và đồ thị hàm số y  f  x cho bởi hình vẽ bên dưới: 2 2
Tính diện tích hình phẳng giới hạn bởi đồ thị C  và đồ thị hàm số 3 y 
x  2x  2. 3 17 3 32 3 16 3 14 3 A. . B. . C. . D. . 5 5 5 5
Câu 12: Cho hàm số f  x 4 3 2
 ax  bx  cx  2x và g x 3 2
 mx  nx  2x với a,c,b,m,n . Biết hàm
số y  f  x  g  x có ba điểm cực trị là 2; 1;3 . Diện tích hình phẳng giới hạn bởi hai
đường y  f  x và y  g x bằng 131 131 125 125 A. . B. . C. . D. . 4 6 12 6 1
Câu 13: Cho hàm số y  f  x 2
 x  xu f udu có đồ thị C. Khi đó diện tích hình phẳng giới 0
hạn bởi C  , trục tung, tiếp tuyến của C  tại điểm có hoành độ x  1 là 1 1 2 1 A. S 
B. S  . C. S  . D. S  . 4 3 3 6
Câu 14: Cho hai hàm số   3 2
f x  ax  bx  cx  d , g  x 2
 ax  bx  e a,b,c,d,e  ;a  0 có đồ thị
lần lượt là hai đường cong C , C ở hình vẽ bên dưới: 1   2  8
Biết diện tích hình phẳng giới hạn bởi hai đồ thị C , C bằng , tính f 2  g   1 . 1   2  3 A. 26 . B. 24 .
C. 28 . D. 30 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1
Câu 15: Cho đồ thị hàm số bậc ba y  f  x 3 2
 ax  bx  x  c và đường thẳng y  g x có đồ thị 3 như hình vẽ sau:
Biết AB  5 , diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f  x , trục hoành và hai
đường thẳng x  1 , x  2 bằng 17 19 5 7 A. . B. . C. . D. . 11 12 12 11
Câu 16: Cho hàm số f  x 4 3 2
 2x  ax  bx  cx  d a, , b c, d 
 có ba điểm cực trị là 1, 1 và 3. Gọi
y  g  x là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số y  f  x . Diện
tích hình phẳng giới hạn bởi hai đường y  f  x và y  g  x bằng 256 265 128 182 A. . B. . C. . D. . 15 15 15 15
Câu 17: Cho hàm số y  f  x 4 3 2
 6x  ax  bx  cx  d a, , b c, d 
. Biết đồ thị hàm số y  f x có
ba điểm cực trị có hoành độ lần lượt là 2; 1; 2 và hàm số y  g  x là hàm bậc hai có đồ thị đi
ba điểm cực trị đó. Diện tích hình phẳng giới hạn bởi hai đường y  f  x và y  g  x thuộc khoảng nào sau đây?
A. 71;72 .
B. 72;73 .
C. 73;74 . D. 74;75 .
Câu 18: Cho hai hàm số
y  f  x và
y  g  x liên tục trên . Biết hàm số f  x 3 2 
 ax  bx  cx  d , g x 2 
 px  qx  r với a, p  0 có đồ thị như hình vẽ. Đồng thời
diện tích giới hạn bởi hai đồ thị hàm số y  f  x và y  g x bằng 2 và f   1  g  
1  1. Biết rằng diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y  f  x và m
y  g  x bằng
. Giá trị m  n bằng: n A. 28 . B. 29 . C. 30 . D. 31 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 19: Cho số y  f  x có đạo hàm là f  x 2 12x  4, x
  và F x là một nguyên hàm của
f  x , f 0  F  
1  0 . Tính diện tích hình phẳng S giới hạn bởi đồ thị hàm số y  F  x và trục Ox . 64 116 576 32 A. S  . B. S  . C. S  . D. S  . 15 15 5 15
Câu 20: Cho hàm số f  x 4 3 2
 3x  ax  bx  cx  d a,b,c,d   có ba điểm cực trị 2,1 và 2 . Gọi
y  g  x là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số y  f  x . Diện
tích hình phẳng giới hạn bởi hai đường y  f  x và y  g  x có giá trị thuộc khoảng nào dưới đây?
A. 34;35 .
B. 36;37 .
C. 37;38 . D. 35;36 .
Câu 21: Cho hàm số bậc ba y  f  x có đồ thị là đường cong như hình bên dưới. Biết hàm số f  x
đạt cực trị tại hai điểm x , x thỏa mãn x  x  2 và f  x  f x  0. Gọi S , S là diện 1   2  1 2 2 1 1 2 S
tích của hình phẳng như hình bên và S là diện tích phần tô đậm. Tính tỉ số 2 . 3 S3 1 3 2 3 A. . B. . C. . D. . 4 8 16 16
Câu 22: Cho hàm số bậc ba f  x có đồ thị như hình vẽ bên. Biết hàm số f  x đạt cực trị tại hai điểm
x ; x thỏa mãn x  x  2 và f  x  f x  2 . Gọi S ; S là diện tích của hai hình phẳng 1   2 1 2 2 1 1 2 S
được cho trong hình vẽ bên. Tính tỉ số 1 . S2 5 3 3 5 A. . B. . C. . D. . 4 5 8 8
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 23: Cho hàm số y  f  x 3 2  4
 x  ax  bx  c có đồ thị cắt trục hoành tại ba điểm có hoành độ là 3
 , 1, 1; F x là một nguyên hàm của f  x và y  g x là hàm số bậc hai đi qua ba điểm
cực trị của đồ thị hàm số y  F  x . Diện tích hình phẳng giới hạn bởi hai đường y  F  x và
y  g  x bằng 128 64 A. . B. . C. 16 . D. 64 . 15 15
Câu 24: Cho đường cong 3
(C) : y  x  kx  2 và parabol 2
P : y   x  2 tạo thành hai miền phẳng có
diện tích S , S như hình vẽ. 1 2 8 Biết rằng S 
, giá trị của S bằng 1 2 3 1 1 3 5 A. . B. . C. . D. . 2 4 4 12
Câu 25: Cho hàm số   4 2
f x  ax  bx  c có đồ thị C  , biết f  
1  0 . Tiếp tuyến d tại điểm có hoành
độ x  1 của C  cắt C  tại hai điểm có hoành độ lần lượt là 0 và 2 . Gọi S ; S 1 2 là diện tích 401
hình phẳng ( phần gạch chéo trong hình vẽ). Tính S2 , biết S  . 1 2022 12431 5614 2005 2807 A. . B. . C. . D. . 2022 1011 2022 1011
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 7
Câu 26: Cho hàm số f  x là hàm đa thức bậc bốn, có đồ thị nhận đường thẳng x   làm trục đối 2
xứng. Biết diện tích hình phẳng của phần giới hạn bởi đồ thị hàm số y  f  x, y  f  x và 127
hai đường thẳng x  5, x  2 có giá trị là (hình vẽ bên) 50
Diện tích hình phẳng giới hạn bởi y  f  x và trục hoành bằng 81 91 71 61 A. . B. . C. . D. . 50 50 50 50
Câu 27: Cho hàm số bậc ba y  f  x có đồ thị như hình vẽ, biết y  f  x đạt cực tiểu tại điểm x  1
và thỏa mãn  f  x  
1 và  f  x  
1 lần lượt chia hết cho  x  2 1 và  x  2
1 . Gọi S , S lần 1 2
lượt là diện tích hình phẳng như trong hình dưới. Tính 2S  S . 1 2 3 1 1 A. . B. . C. 4 . D. . 4 2 4 Câu 28: Cho hàm số f  x 3 2
 2x  ax  bx  c với a,b,c là các số thực. Biết hàm sồ
g(x)  f (x)  f (
 x)  f (x) có hai giá trị cực trị là 4
 và 4. Diện tích hình phẳng giới hạn bởi f (x) các đường y  y  bằng g(x)  và 1 12 A. 2 ln 3 . B. ln 3 . C. ln18 . D. ln 2 .
Câu 29: Cho hai hàm số f ( x) và g( x) liên tục trên và hàm số 3 2 f (
 x)  ax  bx  cx  d , 2
g '( x)  qx  nx  p với a, q  0 có đồ thị như hình vẽ. Biết diện tích hình phẳng giới hạn bởi
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 5
hai đồ thị hàm số y  f (
 x) và y  g (x) bằng và f (2)  g(2) . Biết diện tích hình phẳng 2 a
giới hạn bởi hai đồ thị hàm số y  f ( x) và y  g( x) bằng . Tính 2 2
T  a  b . b A. 7 . B. 55 . C. 5  . D. 16 .
Câu 30: Cho hàm số y  f  x là hàm bậc bốn có đồ thị như hình bên. Biết diện tích hình phẳng giới 214
hạn bởi đồ thị hai hàm số y  f  x và y  f ' x bằng
. Tính diện tích hình phẳng giới 5
hạn bởi đồ thị hàm số y  f  x và trục hoành. 81 81 17334 17334 A. . B. . C. . D. . 20 10 635 1270 2
Câu 31: Cho hàm số bậc ba y  f  x 3 2
 ax  bx  x  d và đường thẳng y  g x có đồ thị như hình 7 vẽ bên dưới: 2 65 Biết AB 
diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f  x và y  g  x bằng 7 11 23 16 13 A. . B. . C. . D. . 3 3 7 4
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1
Câu 32: Cho hàm số bậc ba y  f  x 3 2
 ax  x  cx  d và parabol y  g x có đồ thị như hình vẽ. 2
Biết đồ thị y  f  x và y  g  x cắt nhau tại ba điểm phân biệt ,
A B, C có hoành độ lần lượt 3 5
là 2;1; 2 và thỏa mãn AB 
(tham khảo hình vẽ). Tính diện tích hình phẳng giới hạn bởi 2
hai đồ thị y  f  x và y  g  x . 71 238 71 13 A. . B. . C. . D. . 3 3 6 4 Câu 33: Cho hàm số    4 2 y
f x  ax  bx  c . Tiếp tuyến d đi qua điểm A có hoành độ x  2 cắt đồ
thị hàm số y  f  x tại hai điểm khác A có hoành độ lần lượt là x  4 và x  0 . Gọi S , S 1 2 S
lần lượt là diện tích phần gạch sọc (như hình vẽ). Tính tỉ số 2 . S1 3 1 3 1 A. . B. . C. . D. . 20 28 28 20 1 3 Câu 34: Cho hàm số 3 2 y   x 
x  3x có đồ thị C  và đường thẳng d đi qua gốc tọa độ tạo 2 4
thành hai miền phẳng có diện tích S và S như hình vẽ 1 2 27 m Biết S  . Khi đó S 
, giá trị của 2m  n bằng 1 4 2 n A. 143 . B. 50 . C. 50 . D. 142 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 35: Cho hai hàm số   4 3 2
f x  ax  bx  cx  dx  e với a  0 và g  x 2
 px  qx  3 có đồ thị như
hình vẽ bên dưới. Đồ thị hàm số y  f  x đi qua gốc tọa độ và cắt đồ thị hàm số y  g  x tại
bốn điểm có hoành độ lần lượt là 2  ; 1
 ; 1 và m . Tiếp tuyến của đồ thị hàm số 15
y  f  x  g  x tại điểm có hoành độ x  2 có hệ số góc bằng 
. Gọi  H  là hình phẳng 2
giới hạn bởi đồ thị hai hàm số y  f  x và y  g  x .
Diện tích của hình  H  bằng 1553 1553 1553 1553 A. . B. . C. . D. . 120 240 60 30
Câu 36: Cho hàm số f  x liên tục trên và đường thẳng d  : g  x  ax  b có đồ thị như hình vẽ. 1 0 37 19
Biết diện tích miền tô đậm bằng
và f  x dx   . Tích phân . x f  
2xdx bằng 12 12 0 1  607 20 5 5 A.  . B.  . C.  . D.  . 348 3 3 6
Câu 37: Cho parabol  P 2
: y  x và hai điểm A , B thuộc  P sao cho AB  2 . Tìm giá trị lớn nhất
của diện tích hình phẳng giới hạn bởi parabol  P và đường thẳng AB . 3 4 3 5 A. . B. . C. . D. . 2 3 4 6
Câu 38: Cho hai hàm số y f  x 3 2 
 ax  bx  cx  d và y g x 2 
 mx  nx  k cắt nhau tại ba điểm 1 có hoành độ là 1
 ; ;2 và có đồ thị như hình vẽ. 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 81
Biết phần diện tích kẻ sọc (hình S1 ) bằng 32 . Diện tích phần hình phẳng giới hạn bởi đồ thị 1
y  f x,y  gx và hai đường thẳng x  ;x  2 2
(phần bôi đen trong hình vẽ) bằng 79 243 81 45 A. . B. . C. . D. . 24 96 32 16
Câu 39: Gọi X là tập hợp tất cả các giá trị của tham số m để đường thẳng d : y  45
 m  2 cùng với 1
đồ thị C  của hàm số 3 2 y 
x  2mx  x 1 tạo thành hai miền kín có diện tích lần lượt là 3
S , S thỏa mãn S  S (xem hình vẽ). Số phần tử của tập X là 1 2 1 2 A. 0. B. 2  C. 1 D. 9  Câu 40: Cho hàm số   3 2
f x  x  ax  bx  c với a,b, c là các số thực. Biết hàm số
g  x  f  x  f  x  f   x có hai giá trị cực trị là 5
 và 2 . Diện tích hình phẳng giới hạn f  x
bởi các đường y  và y  1 bằng g  x  6 A. ln 3 . B. ln 7 . C. 3ln 2 . D. ln10 .
Câu 41: Cho đồ thị hàm số bậc ba    3 2 y
f x  ax  bx  cx  d và đường thẳng d : y  mx  n như S p
hình vẽ và S , S là diện tích hình phẳng được tô đậm trong hình bên. Biết 1  với 1 2 S q 2 * p, q 
là một phân số tối giản. Tính p  q  2022 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia A. 2043 . B. 2045 . C. 2049 . D. 2051 . 7
Câu 42: Cho hàm số f  x với đồ thị là Parabol đỉnh I có tung độ bằng 
và hàm số bậc ba g  x . 12
Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ x , x , x thoả mãn 1 2 3 18x x x  5  5 (hình vẽ). 1 2 3
Diện tích miền tô đậm gần số nào nhất trong các số sau đây? A. 5, 7 . B. 5,9 . C. 6,1 . D. 6,3 . Câu 43: Cho hàm số 3 2
y  4x  3x có đồ thị C  và đường thẳng d đi qua gốc tọa độ tạo thành hai
miền hình phẳng có diện tích S , S như hình vẽ bên dưới: 1 2
Khi S  12 thì S bằng 2 1 7 875 865 A. . B. 3 . C. . D. . 2 256 256
Câu 44: Cho hàm số bậc ba y  f  x có đồ thị C  như hình vẽ.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Biết rằng đồ thị hàm số đã cho cắt trục Ox tại ba điểm có hoành độ x , x , x theo thứ tự lập 1 2 3
thành cấp số cộng và x  x  2 3 . Diện tích hình phẳng giới hạn bởi C  và trục Ox là S , 3 1
diện tích S của hình phẳng giới hạn bởi các đường y  f  x 1, y   f  x 1, x  x và 1 1
x  x bằng 3 A. 4 3 . B. 2 3 .
C. 2S  4 3 . D. S  2 3 .
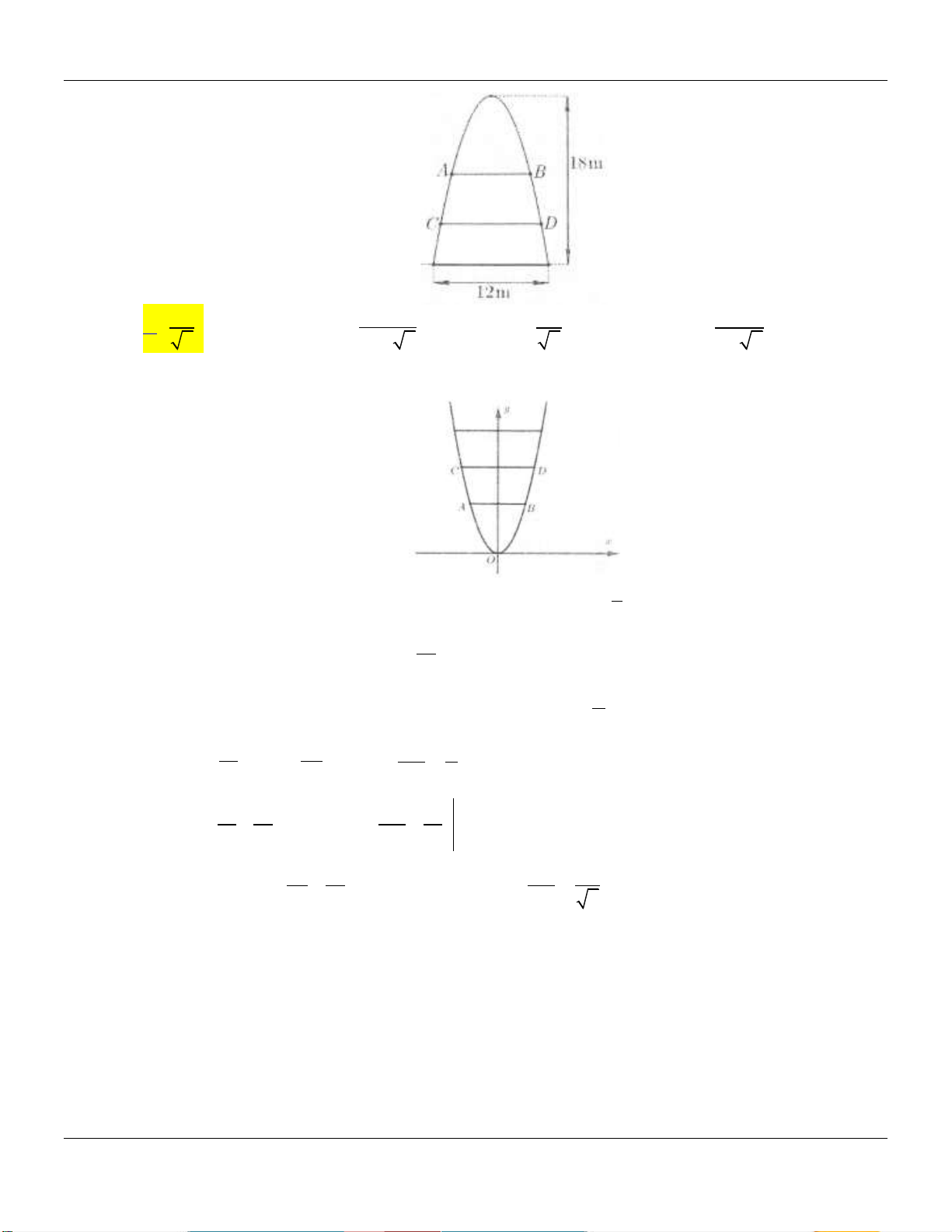
Câu 45: Một miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất
bằng 2 đoạn thẳng song song AB,CD thành ba phần có diện tích bằng nhau (xem hình vẽ AB bên dưới). Tỉ số bằng: CD 1 3 1 1 A. . B. . C. . D. . 3 2 1 2 2 2 1 2
Câu 46: Ông X muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên, biết đường cong
phía trên là một Parabol, chất liệu làm là inox. Giá 2
1m vật tư và công làm là 1.300.000 đồng.
Hỏi ông X phải trả bao nhiêu tiền để làm cái cửa sắt như vậy (làm tròn đến hàng nghìn).
A. 13.050.000 đồng.
B. 36.630.000 đồng. C. 19.520.000 đồng. D. 21.077.330 đồng.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
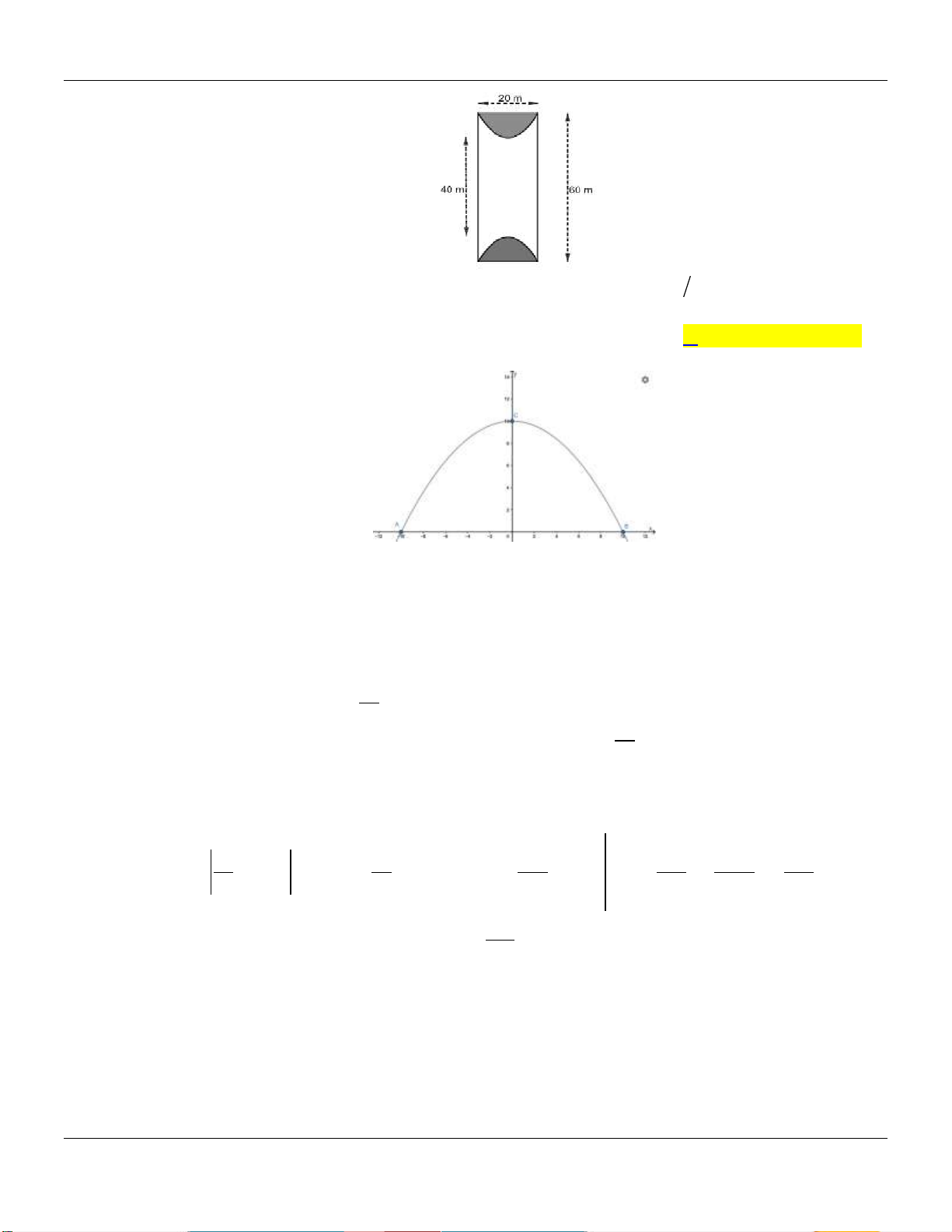
Câu 47: Một mảnh đất hình chữ nhật có chiều dài 60m , chiều rộng 20m . Người ta muốn trồng cỏ ở
hai đầu của mảnh đất hai hình bằng nhau giới hạn bởi hai đường Parabol có hai đỉnh cách
nhau 40m (như hình vẽ).
Phần còn lại của mảnh đất người ta lát gạch với chi phí là 2
200.000 d m . Tính tổng số tiền để
lát gạch ( làm tròn đến hàng nghìn)
A. 133.334.000 đồng. B. 213.334.000 đồng. C. 53.334.000 đồng. D. 186.667.000 đồng.
Câu 48: Trên bức tường cần trang trí một hình phẳng dạng paranol đỉnh S như hình vẽ, biết
OS  AB  4 m , O là trung điểm của AB . Parabol trên được chia thành ba phần để sơn ba
màu khác nhau với mức chi phí: phần trên là phần kẻ sọc 140000 đồng/ 2 m , phần giữa là hình
quạt tâm O , bán kính 2 m được tô đậm 150000 đồng/ 2
m , phần còn lại 160000 đồng/ 2 m .
Tổng chi phí để sơn cả 3 phần gần nhất với số nào sau đây?
A. 1.597.000 đồng.
B. 1.625.000 đồng.
C. 1.575.000 đồng. D. 1.600.000 đồng.
Câu 49: Hướng tới kỉ niệm ngày thành lập trường Đoàn TNCS Hồ Chí Minh. Khối 12 thiết kế bồn
hoa gồm hai Elip bằng nhau có độ dài trục lớn bằng 8m và độ dài trục nhỏ bằng 4m đặt
chồng lên nhau sao cho trục lớn của Elip này trùng với trục nhỏ của Elip kia và ngược lại (như hình vẽ).
Phần diện tích nằm trong đường tròn đi qua 4 giao điểm của hai Elip dùng để trồng cỏ,
phần diện tích bốn cánh hoa nằm giữa hình tròn và Elip dùng để trồng hoa. Biết kinh phí để
trồng hoa là 150.000 đồng 2
/1m , kinh phí để trồng cỏ là 100.000 đồng 2
/1m . Tổng số tiền dùng
để trồng hoa và trồng cỏ cho bồn hoa gần với số nào nhất trong các số sau?
A. 4.100.000 đồng.
B. 4.550.000 đồng.
C. 3.100.000 đồng. D. 4.300.000 đồng.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 50: Một công ty có ý định thiết kế một logo hình vuông có độ dài nửa đường chéo bằng 4. Biều
tượng 4 chiếc lá (được tô màu) được tạo thành bởi các đường cong đối xứng với nhau qua
tâm của hình vuông và qua các đường chéo.
Một trong số các đường cong ở nửa bên phải của logo là một phần của đồ thị hàm số bậc ba dạng 3 2
y  ax  bx  x với hệ số a  0 . Để kỷ niệm ngày thành lập 2 / 3 , công ty thiết kế để tỉ 2
số diện tích được tô màu so với phần không được tô màu bằng
. Tính a  b . 3 41 1 2 9 A. . B. . C. . D. . 80 2 5 10
____________________HẾT____________________
Huế, 15h15’ Ngày 19 tháng 3 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
LỜI GIẢI CHI TIẾT Câu 1:
Cho hàm số y  f (x) có đồ thị như hình vẽ bên dưới:
Biết diện tích hai phần gạch chéo lần lượt là S  5, S  12 . 1 2 1 0 Tính I 
f (2x 1)dx  
 f x4d .x 0 3  19 29 A.  . B. . C. 17 . D. 7  . 2 2 Lời giải: 1 4 Ta có
f (x)dx  S  5,
f (x)dx  S  1  2   1 2 1  1 1 0 1 4 1 1 19 Vậy I 
f (2x 1)dx 
f x  4dx 
f (x)dx 
f (x)dx  .5 12       . 0 3  1  1 2 2 2 Câu 2:
Tính diện tích hình phẳng giới hạn bởi parabol  P 2
: y  x  4 và hai tiếp tuyến của  P tại các điểm ,
A B có hoành độ lần lượt là 1  và 1. 4 1 1 2 A. . B. . C. . D. . 3 3 2 3 Lời giải: y y = x2 + 4 4 3 y = 2x + 3 y = 2x + 3 O x 1 Xét hàm số 2
y  x  4  y  2x . Ta có A 1;
 5, B1;5 là hai điểm thuộc P .
+) Tiếp tuyến của  P tại A1;5 là: y  2  x   1  5  y  2  x  3 .
+) Tiếp tuyến của  P tại B 1;5 là: y  2 x  
1  5  y  2x  3.
Hoành độ giao điểm của hai đồ thị hàm số y  2x  3, y  2
 x  3 là nghiệm của phương trình: 2x  3  2
 x  3  x  0 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Khi đó diện tích hình phẳng giới hạn bởi  P và hai tiếp tuyến của  P tại , A B là:    
S   x  4  2x 3dx  x  4  2x 3 0 1 0 1 1 1 2 2 2 3 2 3 2 dx 
x  x  x 
x  x  x      .  3   3  3 1  0 1  0 Câu 3:
Gọi S là diện tích của mặt phẳng giới hạn bởi đường thẳng y  mx với m < 2 và parabol  P 1
có phương trình y  x 2  x . Gọi S là diện tích giới hạn bởi  P và Ox . Với giá trị nào của 2 1 m thì S  S ? 1 2 2 2 1 A. 3 2  4 . B. 3 2  2 . C. . D. . 5 4 Lời giải: * Tính S 2 x 
Phương trình hoành độ giao điểm x   x 0 2  0   . x  2 2 4 Do đó 2 S 
2x  x dx   . 2 3 0 * Tính S 1 x  0
Phương trình hoành độ giao điểm 2 2
mx  2x  x  x  m  2 x  0   . x  2  m 2m 3 2m 2m 3 2  x 2  m x  2  m Do đó 2 S 
2x  x  mx dx     2
x  2  m x dx      . 1        3 2 6 0 0   0 1 2 m3 1 4 * 3 S  S 
 .  m  2  4 . 1 2 2 6 2 3 Câu 4: Cho hàm số 3 2
f (x)  ax  bx  cx  4 và 2
g(x)  mx  nx có đồ thị cắt nhau tại các điểm có
hoành độ là 1; 1; 2 . Diện tích của hình phẳng giới hạn bởi đồ thị của hai hàm số trên bằng 9 9 37 37 A. . B. . C. . D. . 4 2 12 6 Lời giải:
Do hàm số f (x) và g(x) có đồ thị cắt nhau các điểm có hoành độ là 1; 1; 2 , nên f (x)  g(x) là hàm số bậc ba.
Suy ra ta có: f (x)  g(x)  k.(x 1)(x 1)(x  2)
Mặt khác ta có: f (0)  g(0)  4  k  2 . 3 2
 f (x)  g(x)  2(x 1)(x 1)(x  2)  2x  4x  2x  4 2 2 Vậy ta có diện tích là 3 2 S 
f (x)  g(x) dx 
2x  4x  2x  4 dx   1  1  1 2 16 5 37 3 2 3 2
 (2x  4x  2x  4)dx  (2x  4x  2x  4)dx      . 3 6 6 1  1
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Câu 5:
Cho hàm số bậc ba y  f  x có đồ thị là đường cong ở hình bên dưới. Gọi x , x lần lượt là 1 2
hai điểm cực trị thỏa mãn x  x  2 và f  x  3 f x  0. và đồ thị luôn đi qua 1   2  2 1
M (x ; f (x )) trong đó x  x 1 g(x) là hàm số bậc hai có đồ thị qua 2 điểm cực trị và M. 0 0 0 1 S
x  x 1 . Tính tỉ số 1 ( S và S lần lượt là diện tích hai hình phẳng được tạo bởi đồ thị hai 1 0 S 1 2 2
hàm f (x), g(x) như hình vẽ ). 5 6 7 4 A. . B. . C. . D. . 32 35 33 29 Lời giải:
Nhận thấy hình phẳng trên có diện tích không đổi khi ta tịnh tiến đồ thị sang trái sao cho
x  0 Khi đó ta có x  1, x  3, Xét hàm 3 2
f (x)  ax  bx  cx  d và 2
g(x)  mx  nx  p . 0 1 2  f (1)  0 3
 a  2b  c  0
Vì x  1, x  3, là các điểm cực trị nên ta có:    (1) 1 2  f (3)  0
27a  6b  c  0
Hơn nữa, ta có f (1)  3 f (3)  a  b  c  d  27a  9b  3c  d.(2) b  6a 
Từ (1) và(2) suy ra c  9a d  2a
g(0)  f (0)  p  2a  
Mặt khác dựa vào đồ thị ta thấy: g(1)  3g(3)  m  2  a   g(0)  g(3) n  3  a Suy ra 3 2
f (x)  a(x  6x  9x  2) , 2 g(x)  a( 2
 x  6x  2) 1 5 3 8 Khi đó ta có: 3 2 S  a
x  4x  3x dx  a  3 2 S  a
x  4x  3x dx  a  1 12 2 3 0 1 S 5 Do đó, 1  . S 32 2 1 Câu 6:
Cho hai hàm số f  x 3 2
 ax  bx  cx  và g x 2
 dx  ex 1 a,b,c,d,e  . Biết rằng đồ 2
thị của hàm số y  f  x và y  g  x cắt nhau tại ba điểm có hoành độ lần lượt là 3  ; 1; 1 (tham khảo hình vẽ).
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 9 A. . B. 8 . C. 4 . D. 5 . 2 Lời giải:
Diện tích hình phẳng cần tìm là 1  1 S   f
  x gxdx g 
  x f xdx  3  1  1  1  3   3  3  ax  
b d 2x c e 3 x  dx  ax  
b  d  2x c ex  dx     .  2   2  3  1  3 Trong đó phương trình 3
ax  b  d  2
x  c  e x 
 0 * là phương trình hoành độ giao 2
điểm của hai đồ thị hàm số y  f  x và y  g  x .
Phương trình * có nghiệm 3  ; 1; 1 nên   3  1
a  b  d   c  e 3 27 9 3   0 
27a  9b  d   3c  e   a   2  2  2    3  3
a  b  d   c  e 3   0
 a  b  d   c  e   
 b  d   . 2  2  2    3  1 a  
b  d  c e 3   0 a  
b  d   c e  c e      2  2  2 1  1 1 3 1 3  1 3 1 3  Vậy 3 2 3 2 S  x  x  x  dx  x  x  x  dx        2  2  4 . 2 2 2 2  2 2 2 2  3  1  Câu 7:
Hình phằng  H  được giới hạn bởi đồ thị C  của hàm đa thức bậc ba và parabol  P có
trục đối xứng vuông góc với trục hoành. Phần tô đậm như hình vẽ có diện tích bằng
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 37 7 11 5 A. . B. . C. . D. . 12 12 12 12 Lời giải:
Giả sử C  3 2
: y  ax  bx  cx  d a  0 .
Vì C  đi qua các điểm A 1  ; 2
 , B0;2 ,C 1;0, D2; 2
  ,ta có hệ phương trình:
a  b  c  d  2 a  1    d  2 b   3     C 3 2
: y  x  3x  2 .
a  b  c  d  0 c  0   8
 a  4b  2c  d  2  d  2 Giả sử  P 2
: y  mx  nx  q m  0 .
Vì  P đi qua các điểm A 1  ; 2
 , E 1;0 , D2; 2
  ,ta có hệ phương trình:
 m  n  q  2  m  1   
 m  n  q  0  n  1  P 2
: y  x  x .  
4m  2n  q  2  q  0  
Dựa vào đồ thị của C  và  P ,ta có diện tích hình phẳng cần tìm là: 1 S
 x  3x  2  x  x dx
  x  x  x  x   dx    hp    2 3 2 2 2    3 2 3 2 1  1 1 2 37 3 2 3 2
 x  2x  x  2 dx
  x  2x  x  2 dx  .      12 1  1 Câu 8: Cho hàm số 4 2
y  ax  bx  c a  0 và hàm số 2
y  mx  nx  p m  0 có đồ thị là các
đường cong như hình vẽ bên.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Gọi S là diện tích của hình phẳng được tô đậm. Khẳng định nào sau đây đúng?  62 64   21 13   21 13 67  A. S  ;   . B. S  ;   . C. S  4;   . D. S  ;   .  15 15   5 3   5   3 15  Lời giải:
Từ đồ thị ta thấy đồ thị hàm hàm số    4 2 y
f x  ax  bx  c đi qua các điểm A1;3 , B 0; 2
và đạt cực trị tại x  1  f   1  3
a  b  c  3     a 1   
 f 0  2  c  2  b
  2  f  x 4 2
 x  2x  2 .    f    4a  2b  0 1 0   c  2 
Từ đồ thị ta lại thấy đồ thị hàm số    2 y
g x  mx  nx  p đi qua các điểm C 0;  1 , A1;3  f 0  1   p  1   p  1    
và D 1;3   f  
1  3  m  n  p  3  m  4  g  x 2  4x 1.    f   
m  n  p  3 n  0 1 3   
Diện tích hình phẳng được tô đậm là 1 1 1 5  x 2  64 S     4 2
x  2x  2 2 4x  4 2 3  1dx 
  x 2x 3dx    x 3x  .  5 3  15 1  1  1 Câu 9:
Trong mặt phẳng Oxy , cho parabol  P 2
: y  ax  bx  c a  0 và đường thẳng
d : y  mx  n m  0 . Tính diện tích hình phẳng  D giới hạn bởi  P , d và đường thẳng
 : y  4 như hình vẽ bên. 25 16 19 10 A. . B. . C. . D. . 6 3 6 3 Lời giải:
Từ đồ thị ta thấy parabol  P 2
: y  ax  bx  c a  0 đi qua các điểm A2; 4 và có đỉnh là c  0 a  1  
O 0;0  4a  2b  c  4  b   0 2  y  x .   b  0 c  0  
Từ đồ thị ta lại thấy đường thẳng d : y  mx  n m  0 đi qua các điểm B 2;0 và C 0; 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
2m  n  0 m  1     
 y  x  2 . n  2 n  2
Diện tích hình phẳng  D là: 1 2 1 1 2 2 3  x   x  25 S   2
4  x  2dx   2
4  x dx  x  2dx   2
4  x dx  
 2x   4x    .  2   3  6 0 1 0 1 0 1
Câu 10: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x
y  e , y  ln x , y  x  e 1 với các trục tọa độ. 2 e  2e  5 2 e 2 2e  e  4 2 e A. . B. . C. . D. . 2 2 3 3 Lời giải: Vì hàm x
y  e đồng biến và hàm y  x  e 1 nghịch biến, nên phương trình x
e  x  e 1
có nghiệm duy nhất x  1 .
Tương tự hàm y  ln x đồng biến và hàm y  x  e 1 nghịch biến, nên phương trình
ln x  x  e 1 có nghiệm duy nhất x  e .
Diện tích hình phẳng cần tính là 1 e 1 e x  d  ln        1 d x S e x x x e
x  e dx  
xe1ln xdx 0 1 0 1 e 2 e 2 2 1  x   e 1  e  2e  5 x  e e
   e   1 x   ln d x x   e   1  
  xln x  x  . 0  2  1  2 2  2 1 1
Câu 11: Cho hàm số y  f  x có đồ thị là C  . Biết rằng đồ thị C  cắt trục tung tại điểm có tung độ 1
bằng và đồ thị hàm số y  f  x cho bởi hình vẽ bên dưới: 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 2
Tính diện tích hình phẳng giới hạn bởi đồ thị C  và đồ thị hàm số 3 y 
x  2x  2. 3 17 3 32 3 16 3 14 3 A. . B. . C. . D. . 5 5 5 5 Lời giải: 2
Từ đồ thị của hàm số y  f  x ta có f  x  a  x   1  x   1 . 2
Do f      a   f  x   x    x   3 2 0 2 2 2 1
1  2x  2x  2x  2 . x 2x
Ta có f  x  f 
 xdx  2x 2x 2x2 4 3 3 2 2 dx  
 x  2x  C . 2 3 1 1 x 2x 1
Mà f 0   C   f  x 4 3 2  
 x  2x  . 2 2 2 3 2 2
Phương trình hoành độ giao điểm của đồ thị C  và đồ thị hàm số 3 y 
x  2x  2 là: 3 4 3 4 x 2x 1 2 x 3 2 3 2 4 2 
 x  2x   x  2x  2 
 x   0  x  2x  3  0  x   3 . 2 3 2 3 2 2 2
Diện tích hình phẳng giới hạn bởi đồ thị C  và đồ thị hàm số 3 y 
x  2x  2 là: 3 3 4 x 3 16 3 2 S   x  dx   . 2 2 5  3
Câu 12: Cho hàm số f  x 4 3 2
 ax  bx  cx  2x và g x 3 2
 mx  nx  2x với a,c,b,m,n . Biết hàm
số y  f  x  g  x có ba điểm cực trị là 2; 1;3 . Diện tích hình phẳng giới hạn bởi hai
đường y  f  x và y  g x bằng 131 131 125 125 A. . B. . C. . D. . 4 6 12 6 Lời giải:
+ Ta có: f  x  g x 3
 ax  b  m 2 4 3
x  2 c  n x  4.   1
+ Mặt khác, vì hàm số y  f  x  g  x có ba điểm cực trị là 2; 1;3 nên
f  x  g x  a  x  2 x  
1  x  3 2 2 2  + Từ   1 , 2 suy ra: 4  6
 a  a   . Do đó: f x  gx 
x  2x  1x 3 3 3
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 3 3 2  131
Vậy diện tích hình phẳng là S 
f  x  g x dx 
x  2x  1x 3 dx    3 6 2  2  1
Câu 13: Cho hàm số y  f  x 2
 x  xu f udu có đồ thị C. Khi đó diện tích hình phẳng giới 0
hạn bởi C  , trục tung, tiếp tuyến của C  tại điểm có hoành độ x  1 là 1 1 2 1 A. S 
B. S  . C. S  . D. S  . 4 3 3 6 Lời giải: 1 1
Hàm số f  x có dạng   2
f x  x  ax  b , với a  f (u)du 
và b  uf (u)d . u  0 0  1 a a    b a  5   3 2      17  . 1 a b b  b       6  4 3 2 17
Suy ra f  x 2  x  5x  ; f (
 x)  2x  5. 6  41 M 1;   
 C; f (1)  3  .  6 
Phương trình tiếp tuyến của C  tại M : y    x   41 23 3 1   3  x  . 6 6
Diện tích hình phẳng cần tìm là: 1 1 17  23  1 2 S  x  5x   3  x  dx    
 2x 2x 1dx  . 6  6  3 0 0
Câu 14: Cho hai hàm số   3 2
f x  ax  bx  cx  d , g  x 2
 ax  bx  e a,b,c,d,e  ;a  0 có đồ thị
lần lượt là hai đường cong C , C ở hình vẽ bên dưới: 1   2  8
Biết diện tích hình phẳng giới hạn bởi hai đồ thị C , C bằng , tính f 2  g   1 . 1   2  3 A. 26 . B. 24 .
C. 28 . D. 30 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Lời giải:
Ta có: f  x 2
 3ax  2bx  c
Dựa vào đồ thị, ta có:
+) f  x  3a  x  
1  x  3  b  6  ; a c  9a Ta có: f   1  g  
1  d  e  c và 3
S   f x  g x 8 dx 
 34a 14b 12c  6d  6e 18 3 1 b  6  a a  2  
17a  7b  3c  4  c  9a  b  12  
17a  7b  3c  4 c  18    f x 3 2
 x  x  x  e  g  x 2 2 12 18 18;
 2x 12x  e
 f 2  e 14  
 f 2  g   g   1  28 1  e 14 1
Câu 15: Cho đồ thị hàm số bậc ba y  f  x 3 2
 ax  bx  x  c và đường thẳng y  g x có đồ thị 3 như hình vẽ sau:
Biết AB  5 , diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f  x , trục hoành và hai
đường thẳng x  1 , x  2 bằng 17 19 5 7 A. . B. . C. . D. . 11 12 12 11 Lời giải:
Gọi g  x  mx m  0 . Ta có A 1;
  m ; B2;2m .  4 m  tm  3 Khi đó 2
AB  9  9m  5   . 4
m   l  3
Ta có f  x  g  x 3 2
 ax  bx  x  c  0 . Mặt khác 3 2
ax  bx  x  c  a  2 x   1  x  2 3 2 3 2
 ax  bx  x  c  ax  2ax  ax  2a ,
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1
Đồng nhất hệ số ta đươc a  1 , b  2 , c  2 . Vậy y  f  x 3 2
 x  2x  x  2 . 3
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f  x , trục hoành và hai đường thẳng 2  1  19
x  1 , x  2 bằng 3 2 S  x  2x  x  2 dx  .    3  12 1
Câu 16: Cho hàm số f  x 4 3 2
 2x  ax  bx  cx  d a, , b c, d 
 có ba điểm cực trị là 1, 1 và 3. Gọi
y  g  x là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số y  f  x . Diện
tích hình phẳng giới hạn bởi hai đường y  f  x và y  g  x bằng 256 265 128 182 A. . B. . C. . D. . 15 15 15 15 Lời giải:
Ta có f  x   x   x   x     3 2 ' 8 1 1 3
8 x  3x  x  3  f x 4 3 2
 2x 8x  4x  24x  d 1
Ta có f  x  f ' x.  x   2
1  8x 16x  6  d 4
Giả sử A  x , y là điểm cực trị của đồ thị hàm số y  f  x thì i i i 
y  f  x  2  8
 x 16x  6  d i i i i
Do đó đồ thị hàm số bậc hai qua ba điểm cực trị của đồ thị hàm số y  f  x là
y  g  x 2  8
 x 16x  6  d . x  3 
Khi đó f  x  g  x 4 3 2
 2x 8x  4x  8x  6  0  x 1  x  1  
Diện tích hình phẳng giới hạn bởi hai đường y  f  x và y  g  x bằng 3 S 
f  x  g  x 256 dx   . 15 1 
Câu 17: Cho hàm số y  f  x 4 3 2
 6x  ax  bx  cx  d a, , b c, d 
. Biết đồ thị hàm số y  f x có
ba điểm cực trị có hoành độ lần lượt là 2; 1; 2 và hàm số y  g  x là hàm bậc hai có đồ thị đi
ba điểm cực trị đó. Diện tích hình phẳng giới hạn bởi hai đường y  f  x và y  g  x thuộc khoảng nào sau đây?
A. 71;72 .
B. 72;73 .
C. 73;74 . D. 74;75 . Lời giải:
Ta có y  f  x 3 2 ' '
 24x  3ax  2bx  c .
Do đồ thị hàm số y  f  x có ba điểm cực trị có hoành độ 2;1; 2 nên phương trình
f ' x  0 có ba nghiệm phân biệt 2;1; 2 .
Suy ra f  x 
x  x  x    f x 3 2 ' 24 2 1 2 '
 24x  24x  96x  96  f x 4 3 2
 6x  8x  48x  96x  d .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia  1 1 
Ta có f  x  x  f '   x 2
 26x  64x  d  8  g x 2  2
 6x  64x  d  8 .  4 12 
Vậy diện tích hình phẳng giới hạn bởi hai đường y  f  x và y  g  x là 2 2 S  f
 x  gx dx    4 3 2
6x  8x  48x  96x  d    2 2
 6x  64x  d  8 dx  74,63. 2  2 
Câu 18: Cho hai hàm số
y  f  x và
y  g  x liên tục trên . Biết hàm số f  x 3 2 
 ax  bx  cx  d , g x 2 
 px  qx  r với a, p  0 có đồ thị như hình vẽ. Đồng thời
diện tích giới hạn bởi hai đồ thị hàm số y  f  x và y  g x bằng 2 và f   1  g  
1  1. Biết rằng diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y  f  x và m
y  g  x bằng
. Giá trị m  n bằng: n A. 28 . B. 29 . C. 30 . D. 31 . Lời giải:
Dựa vào đồ thị  f  x  g x  a  x  2 x  
1 x và a  0 . 0 0 1 Theo đề S 
a  x  2 x  
1 x dx  a
x  2x    
1 x dx  2  . a  a  4. 2 2  2  Ta có:  f 
 x gxdx  4
 x  2x     1 d
x x  f  x  g  x 4 3 2
 x  4x  4x  C .
Theo đề: f   1  g  
1  1  f   1  g   1  1
1 1 4  4  C  C  0
 f x  g x  x  x  x  x x  x    x x  2 4 3 2 2 2 2 4 4 4 4 2 .
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y  f  x và y  g  x 0   m S x x  22 16 2 dx    . 15 n 2 
Vậy giá trị m  n  31.
Câu 19: Cho số y  f  x có đạo hàm là f  x 2 12x  4, x
  và F x là một nguyên hàm của
f  x , f 0  F  
1  0 . Tính diện tích hình phẳng S giới hạn bởi đồ thị hàm số y  F  x và trục Ox .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 64 116 576 32 A. S  . B. S  . C. S  . D. S  . 15 15 5 15 Lời giải:
+) Ta có: f  x  f 
 xdx   2 12x  4 3
dx  4x  4x  C . 1
Do f 0  0 nên C  0 , suy ra f  x 3  4x  4x . 1
F  x  f
 xdx   3 4x  4x 4 2
dx  x  2x  C . 2 Do F  
1  0 nên C  3, suy ra F  x 4 2
 x  2x  3 . 2 x  1  +) Xét phương trình 4 2
x  2x  3  0   . x 1 1 64
Diện tích hình phẳng cần tìm là 4 2 S 
x  2x  3dx   . 15 1 
Câu 20: Cho hàm số f  x 4 3 2
 3x  ax  bx  cx  d a,b,c,d   có ba điểm cực trị 2,1 và 2 . Gọi
y  g  x là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số y  f  x . Diện
tích hình phẳng giới hạn bởi hai đường y  f  x và y  g  x có giá trị thuộc khoảng nào dưới đây?
A. 34;35 .
B. 36;37 .
C. 37;38 . D. 35;36 . Lời giải:
Theo bài ra, ta có: f  x 
x  x  x     3 2 12 2 1 2
12 x  x  4x  4  f x 4 3 2
 3x  4x  24x  48x  d. Khi đó f  2
   d 112, f  
1  d  23, f 2  d 16 . Giả sử   2
g x  mx  nx  p . Theo bài ra, ta có: g  2
   4m  2n  p  d 112
4m  2n   p  d   11  2 m  13     g  
1  m  n  p  d  23
 m  n   p  d   23  n  32 .   
g    m  n  p  d 
m  n   p  d   p  d  4 2 4 2 16 4 2 16   
Do vậy, f  x  g  x 4 3 2 2 4 3 2
 3x  4x  24x  48x  d 13x  32x  p  3x  4x 11x 16x  4 . x  2   1 x 
Suy ra f  x  g  x  0   3 . x 1  x  2 2 Vậy 4 3 2 S 
3x  4x 11x 16x  4 dx  37,31358   37;38. 2 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Câu 21: Cho hàm số bậc ba y  f  x có đồ thị là đường cong như hình bên dưới. Biết hàm số f  x
đạt cực trị tại hai điểm x , x thỏa mãn x  x  2 và f  x  f x  0. Gọi S , S là diện 1   2  1 2 2 1 1 2 S
tích của hình phẳng như hình bên và S là diện tích phần tô đậm. Tính tỉ số 2 . 3 S3 1 3 2 3 A. . B. . C. . D. . 4 8 16 16 Lời giải: x  x
+ Tịnh tiến đồ thị hàm số y  f  x sang phải một đoạn 1 2 
đơn vị ta thu được đồ thị 2
hàm số bậc 3 y  g  x nhận gốc toa độ làm tâm đối xứng nên g  x là hàm lẻ có dạng   3
g x  ax  bx và hàm số g  x có hai điểm cực trị là x  1 và x  1.
Có: g x 2
 3ax  b  g 
1  3a  b  0  b  3  .
a Suy ra: g  x  a  3 x  3x. x  x
+ Tịnh tiến đồ thị hàm số y  h  x sang phải một đoạn 1 2 
đơn vị ta thu được đồ thị 2
 x  x g   1 
hàm bậc nhất y  k  x có đồ thị là đường thẳng đi qua gốc tọa độ, điểm 2 1 A ;  2 2  
hay A1; a. Phương trình đường thẳng y  k  x là y  ax . 0 5 3 Ta có: S  g x dx  a  S  1  .g 1   S  . a  1   2     1 1  4 4 x  0 
Phương trình hoành độ giao điểm của g  x và k  x là: ax  a  3
x  3x  x  2  x  2   2
S  a x  x  3x 2 3 dx  a  3 4x  x dx  4 . a 3  0 0 3 a S 3 Vậy: 2 4   . S 4a 16 3
Câu 22: Cho hàm số bậc ba f  x có đồ thị như hình vẽ bên. Biết hàm số f  x đạt cực trị tại hai điểm
x ; x thỏa mãn x  x  2 và f  x  f x  2 . Gọi S ; S là diện tích của hai hình phẳng 1   2 1 2 2 1 1 2 S
được cho trong hình vẽ bên. Tính tỉ số 1 . S2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 5 3 3 5 A. . B. . C. . D. . 4 5 8 8 Lời giải:
Gọi x là hoành độ điểm uốn I của đồ thị hàm số y  f  x . Do f  x đạt cực trị tại hai điểm 0
x ; x thỏa mãn x  x  2  x  x  x  x  1. 1 2 2 1 1 0 2 0
Cố định đồ thị hàm số f  x , tịnh tiến hệ toạ độ Oxy theo véc tơ OI . Khi đó, trong hệ toạ độ
mới S ; S không thay đổi so với hệ toạ độ cũ. 1 2
Trong hệ toạ độ Oxy mới, đường cong là đồ thị của hàm số bậc ba y  g  x . Từ hình vẽ suy
ra g x là tam thức bậc hai có nghiệm x  1; x  1 . 1 2    x
g x  a  x   x    a  2 1 1 x  
1 a  0  g  x 3
 a  x b .  3   x 
Đồ thị hàm số y  g  x đi qua điểm O 0;0 nên b  0  g  x 3
 a  x.  3  0 3 4 2  x   x x  0 5a Ta có: S  a
   xdx  a    2 3 12 2 1      12 1  1 3 1   x 
       3 4 2    x  2a   x x 2x  1 a S a x
g 1  dx   a  x   dx  a     1   3     3  3   12 2 3 0  4 0 0 S 3 Vậy 1  . S 5 2
Câu 23: Cho hàm số y  f  x 3 2  4
 x  ax  bx  c có đồ thị cắt trục hoành tại ba điểm có hoành độ là 3
 , 1, 1; F x là một nguyên hàm của f  x và y  g x là hàm số bậc hai đi qua ba điểm
cực trị của đồ thị hàm số y  F  x . Diện tích hình phẳng giới hạn bởi hai đường y  F  x và
y  g  x bằng 128 64 A. . B. . C. 16 . D. 64 . 15 15 Lời giải:
Vì hàm số y  f  x 3 2  4
 x  ax  bx  c có đồ thị cắt trục hoành tại ba điểm có hoành độ là
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 9
 a  3b  c  10  8 a  12   
3, 1, 1 nên ta có hệ phương trình a b  c  4   b   4  
a  b  c  4 c  12  
hay y  f  x 3 2  4
 x 12x  4x 12
Ta có F  x   3 2
 x  x  x   4 3 2 4 12 4
12 dx  x  4x  2x 12x  C  1 1 
Mặt khác ta có F  x  x  f    x 2
 4x  8x  C  3 do vậy y  g x 2
 4x  8x  C  3 là  4 4 
hàm số bậc hai đi qua 3 điểm cực trị của đồ thị hàm số y  F  x .
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số y  F  x và y  g  x ta có: 4 3 2 2 4 3 2
x  4x  2x 12x  C  4x  8x  C  3  x  4x  2x  4x  3  0 x 1  0 x  1      x   1  x  2
1  x  3  0  x 1  0  x  1   x  3  0 x  3    1 1 Khi đó S  F
 x gx 4 3 2 dx 
x  4x  2x  4x  3dx  3  3  1 
  x  4x  2x  4x 3 1 4 3 2 dx    4 3 2
x  4x  2x  4x  3dx 3  1  1  1 5 5  x 2   x 2  4 3 2 4 3 2  
 x  x  2x  3x   
 x  x  2x  3x   5 3   5 3  3  1  17 27 47 17 128       . 15 5 15 15 15 128
Vậy diện tích hình phẳng giới hạn bởi hai đường y  F  x và y  g  x bằng . 15
Câu 24: Cho đường cong 3
(C) : y  x  kx  2 và parabol 2
P : y   x  2 tạo thành hai miền phẳng có
diện tích S , S như hình vẽ. 1 2 8 Biết rằng S 
, giá trị của S bằng 1 2 3 1 1 3 5 A. . B. . C. . D. . 2 4 4 12 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Phương trình hoành độ giao điểm của (C) và d x  0 3 2
x  kx  2  x  2  x  2
x  x  k   0   2
x  x  k  0.
Hai đồ thị cắt nhau tại ba điểm phân biệt nên phương trình 2
x  x  k  0 có hai nghiệm phân k  0 
biệt x , x khác 0 và thỏa mãn x  0  x . Do đó ta có x  1 x 1 2 1 2 2 1  2
k  x  x .  1 1 8
Trên đoạn [x ; 0] , 3 2 3 2
x  kx  2  x  2  x  x  kx  0 . Theo bài ra, diện tích S  nên 1 1 3 0 0 8  x x kx 
x  x  kx dx   
x  x  kx 4 3 2 8 0 8 3 2 3 2 dx        3 3  4 3 2 x  3 x x 1 1 1   4 3 2
3x  4x  6kx  4 3
 32  3x  4x  6 2 x  x  2 x  3  2 1 1 1 1 1 1 1 1 4 3
 3x  2x  32  0  (x  2) 3 2
3x  4x  8x 16  0  x  2  1 1 1 1 1 1  1 Với x  2   k  2  , x  1 và 3 2
x  x  2x  0, x  [0;1] , ta có 1 2 1    x x  S
x  x  2x 4 3 5 3 2 2 1 dx      x |  . 2 0 4 3 12   0
Câu 25: Cho hàm số   4 2
f x  ax  bx  c có đồ thị C  , biết f  
1  0 . Tiếp tuyến d tại điểm có hoành
độ x  1 của C  cắt C  tại hai điểm có hoành độ lần lượt là 0 và 2 . Gọi S ; S 1 2 là diện tích 401
hình phẳng ( phần gạch chéo trong hình vẽ). Tính S2 , biết S  . 1 2022 12431 5614 2005 2807 A. . B. . C. . D. . 2022 1011 2022 1011 Lời giải:
Giả sử tiếp tuyến d có phương trình y  g  x  mx  n .
Tiếp tuyến d tại điểm có hoành độ x  1 của C  cắt C  tại hai điểm có hoành độ lần lượt 2
là 0 và 2 , nên ta có: f  x  g  x  a  x   1
x  x  2, a  0. 0 401 401
Theo giả thiết: S  
f x  g x dx   1     2022 2022 1 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 0    2    401 401 2005 1 2       a a x x x dx a 2022 5 2022 2022 1  2 2  2005 2  5614
Do đó: S   f x  g x d  x  
x  1 x x  2 dx  .   2           2022  1011 0 0 7
Câu 26: Cho hàm số f  x là hàm đa thức bậc bốn, có đồ thị nhận đường thẳng x   làm trục đối 2
xứng. Biết diện tích hình phẳng của phần giới hạn bởi đồ thị hàm số y  f  x, y  f  x và 127
hai đường thẳng x  5, x  2 có giá trị là (hình vẽ bên) 50
Diện tích hình phẳng giới hạn bởi y  f  x và trục hoành bằng 81 91 71 61 A. . B. . C. . D. . 50 50 50 50 Lời giải: 2 2
Đặt f  x  k  x  5  x  2 , k  0 . 2 2
Khi đó f  x  2k  x  5 x  2  2k  x  5  x  2  k  x  5 x  24x 14
Xét hàm g  x  f  x  f  x  k  x   x   2 5 2
x  3x  4 x  5 x  2
Suy ra g  x  0   x  4  x  1 2  4  2  Từ đó ta suy ra:
g  x dx   g  x dx   
 gxdx 5  5  4  4  2 
 k  x 5x  2 2x 3x  4dx  k  x 5x  2 2x 3x  4dx 5  4  23 52 127 127 1  k  k  k   k  10 5 10 50 5
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 2  2  1 2 2 81 Vậy S 
f  x dx 
x  2 x  5 dx    . 5 50 5  5 
Câu 27: Cho hàm số bậc ba y  f  x có đồ thị như hình vẽ, biết y  f  x đạt cực tiểu tại điểm x  1
và thỏa mãn  f  x  
1 và  f  x  
1 lần lượt chia hết cho  x  2 1 và  x  2
1 . Gọi S , S lần 1 2
lượt là diện tích hình phẳng như trong hình dưới. Tính 2S  S . 1 2 3 1 1 A. . B. . C. 4 . D. . 4 2 4 Lời giải: 2
Theo bài ra, ta có: f  x  ax  b x   1 1,a  0 .
f     b   f  x  ax   x  2   f  x   ax   x  2 0 0 1 1 1 1 1 1 1  2 .
f  x   a  x  3    a x  2 1 1 1 5 1
 8a  4x   1  2 2a   1 .      x   1
 a    a   f x 1
 x  x   3 2 2 x 3x f x 1 1 2 1 0 2 1 1  . 2 2 2 1 3 3 3  x 3x  x  3x 3 1 1
Vậy 2S  S  2 1dx  dx     . 1 2  2  2 4 2 4 0 1 Câu 28: Cho hàm số f  x 3 2
 2x  ax  bx  c với a,b,c là các số thực. Biết hàm sồ
g(x)  f (x)  f (
 x)  f (x) có hai giá trị cực trị là 4
 và 4. Diện tích hình phẳng giới hạn bởi f (x) các đường y  y  bằng g(x)  và 1 12 A. 2 ln 3 . B. ln 3 . C. ln18 . D. ln 2 . Lời giải: Ta có: f x 3 2
 x  ax  bx  c  f x 2 2
 6x  2ax  b  f  x  12x  2a  f x  12 f (x)
f (x)  g  x 12
 f x  f  x 12 Ta lại có 1   g(x) 12 g(x) 12
f  x  f  x  f   x  12 f (x)
 f x  f  x 12 1  0         g x 
f  x  f  x  f   x 0 f  x f  x 12 0 ( ) 12  12 Ta có g (
 x)  f (x)  f (x)  f  (x)  f (x)  f (x) 12. f (x)
 f x  f  x 12 gx Suy ra:    g  x 1 12
f  x  f  x  f   x 12 g  x  12
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Gọi x , x là 2 nghiệm của g (  x)  0 1 2
Khi và chỉ khi x , x là 2 nghiệm của f  x  f   x 12  0 1 2 g(x )  4  1 Theo giả thiết ta có  . g   x  4  2  2 x g x 2 x g x 2
x d g x 12 S  dx  dx     
ln g x 12  x g x  g x  g x  x   12 x   12 x     2 | 1 12 x 1 1 1 
g  x 12  2  8 1  ln      . g  ln ln ln 2 x 12  16 2 1   
Câu 29: Cho hai hàm số f ( x) và g( x) liên tục trên và hàm số 3 2 f (
 x)  ax  bx  cx  d , 2
g '( x)  qx  nx  p với a, q  0 có đồ thị như hình vẽ. Biết diện tích hình phẳng giới hạn bởi 5
hai đồ thị hàm số y  f (
 x) và y  g (x) bằng và f (2)  g(2) . Biết diện tích hình phẳng 2 a
giới hạn bởi hai đồ thị hàm số y  f ( x) và y  g( x) bằng . Tính 2 2
T  a  b . b A. 7 . B. 55 . C. 5  . D. 16 . Lời giải:
Dựa vào đồ thị ta có: f  x  g x  a  x x   x    a  3 2 ( ) '( ) 1 2
x  3x  2x , với a  0 .
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y  f (
 x) và y  g (x) 2 2 5 bằng: f (
 x)  g (x)  a    3 2
x  3x  2x   a  5. Suy ra 3 2 f (
 x)  g '(x)  5x 15x 10x . 2 0 0 Mặt khác, 3
f  x  g x  ax  b  q 2 ( ) '( )
x  c  n x  d  p . a  5 b   q  15 Do đó:  . c  n  10 
d  p  0 5 b c q n Ta có 4 3 2 f (x)  x  x 
x  dx  r , 3 2 g(x)  x 
x  px  s . 4 3 2 3 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 8
● f (2)  g(2)  20  b  q  2c  n  2d  p  r  s  0 . 3
Thế vào ta được r  s  0 . 5 b  q c  n 4 3 2
● f  x  g  x      x  x 
x  d  p x  r  s  0 . 4 3 2 5 x  0 4 3 2
 x  5x  5x  0   . 4 x  2
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y  f (x) và y  g(x) 2 2 5 4 bằng: f
 x gx 4 3 2 dx 
x  5x  5x dx  . 
Suy ra a  4,b  3 . Vậy 2 2
T  a  b  7 . 4 3 0 0
Câu 30: Cho hàm số y  f  x là hàm bậc bốn có đồ thị như hình bên. Biết diện tích hình phẳng giới 214
hạn bởi đồ thị hai hàm số y  f  x và y  f ' x bằng
. Tính diện tích hình phẳng giới 5
hạn bởi đồ thị hàm số y  f  x và trục hoành. 81 81 17334 17334 A. . B. . C. . D. . 20 10 635 1270 Lời giải:
Từ đồ thị của hàm số y  f  x suy ra f  x  a  x  2  x  2 2 1 , a  0 .
Ta có f  x  a  x   x  2  a  x  2 2 2 1 2 2 x  
1  2a  x  2 x   1 2x   1 .
Xét phương trình f  x  f  x  a  x  2 x  
1  x  2 x   1  2 2x   1   0  x  2     x 
a x  2 x   1  1 2
x  3x  4  0   . x  1   x  4
Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y  f  x và y  f ' x là 4 4 S  a
 x2x 1 428 2
x  3x  4dx  a  x  2x   1  2
x  3x  4 dx  a . 5 2  2  428 214 1 1 2 2 Theo đề bài ta có a 
 a  TM   f x  x  2 x   1 . 5 5 2 2
Vậy diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f  x và trục hoành là
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1 1 S 
x  2 x  2 81 2 1 dx   . 1 2 20 2  2
Câu 31: Cho hàm số bậc ba y  f  x 3 2
 ax  bx  x  d và đường thẳng y  g x có đồ thị như hình 7 vẽ bên dưới: 2 65 Biết AB 
diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f  x và y  g  x bằng 7 11 23 16 13 A. . B. . C. . D. . 3 3 7 4 Lời giải:
Giả sử d : y  mx  n với m  0 do y  g  x là hàm nghịch biến. Do ,
A B  d nên tọa độ hai điểm A1; m  n, B 3;3m  n . 2 65 2 2 2 65 Mặt khác AB   3 
1  3m  n  m  n  . 7 7  4 m  (l) 2 65  2 7  4  4m    7 4
m   (t / m)  7
Suy ra y  g  x 4
  x  n . 7  2   4 
Xét phương trình: f  x  g  x 3 2
 ax  bx  x  d   x  n      7   7  2 3 2
 ax  bx  x  d  . n 7
Mà f  x  g  x  a  x   x   x   3 2 1 1
3  ax  3ax  ax  3 . a 2
Đồng nhất hệ số ta được a   . 7 3 2 16
Vậy diện tích hình phẳng giới hạn bởi hai đồ thị là S  
 x 1x 1x3 dx  . 7 7 1  1
Câu 32: Cho hàm số bậc ba y  f  x 3 2
 ax  x  cx  d và parabol y  g x có đồ thị như hình vẽ. 2
Biết đồ thị y  f  x và y  g  x cắt nhau tại ba điểm phân biệt ,
A B, C có hoành độ lần lượt
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 3 5
là 2;1; 2 và thỏa mãn AB 
(tham khảo hình vẽ). Tính diện tích hình phẳng giới hạn bởi 2
hai đồ thị y  f  x và y  g  x . 71 238 71 13 A. . B. . C. . D. . 3 3 6 4 Lời giải: 2
Ta có: A f  x  B  f  x  2 2; , 1;
 AB  1 2   f  2    f   1 A B 2 3 5 3
Theo giả thiết AB   f  2    f   1  . 2 2   
  a   c  d  1 3 8 2 2
 a   c  d   
 3a  c  1 (1).  2  2
Mặt khác, f  x  g  x  a  x   x   x    a  3 2 2 1 2
x  x  4x  4 (*)
Nhận xét do đồ thị y  g  x là parabol nhận Oy làm trục đối xứng    2
g x  kx  m
Đồng nhất hệ số của phương trình * ta có: c  4a (2) 3
 a  c  1  a 1 Từ (1), (2) suy ra   
. Vậy f  x  g  x 3 2
 x  x  4x  4 . c  4  a c   4  2 71 Vậy S 
f  x  g  x dx   . 6 2  Câu 33: Cho hàm số    4 2 y
f x  ax  bx  c . Tiếp tuyến d đi qua điểm A có hoành độ x  2 cắt đồ
thị hàm số y  f  x tại hai điểm khác A có hoành độ lần lượt là x  4 và x  0 . Gọi S , S 1 2 S
lần lượt là diện tích phần gạch sọc (như hình vẽ). Tính tỉ số 2 . S1
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 3 1 3 1 A. . B. . C. . D. . 20 28 28 20 Lời giải:
Gọi phương trình của tiếp tuyến d là y  g  x .
Phương trình hoành độ giao điểm của đồ thị hàm số y  f  x và tiếp tuyến d là: x  4  
f  x  g  x  f  x  g  x  0  x  0  . x  2 
 f x  g x  mx   xx  2 4 2 với m  0 . Theo giả thiết ta có: 0 0 0 2 896m +) S 
f x  g x dx 
 f x  g x  dx  m x  4 x x  2 dx      . 1              5 4  4  4  2 2 2 2 32m +) S 
f x  g x dx    f x  g x  dx  m
x  4 x x  2 dx      . 2              5 0 0 0 S 1 2   . S 28 1 1 3 Câu 34: Cho hàm số 3 2 y   x 
x  3x có đồ thị C  và đường thẳng d đi qua gốc tọa độ tạo 2 4
thành hai miền phẳng có diện tích S và S như hình vẽ 1 2 27 m Biết S  . Khi đó S 
, giá trị của 2m  n bằng 1 4 2 n A. 143 . B. 50 . C. 50 . D. 142 . Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
 Gọi a  0 là hoành độ giao điểm của C và d . 1 3 3 2
 a  a  3a 1 3
Khi đó, đường thẳng d có hệ số góc là: 2 4 2 k 
  a  a  3. a 2 4  1 3 
Đường thẳng d đi qua gốc tọa độ nên có phương trình là 2 d : y   a  a  3 x   .  2 4  a  1 3   1 3    Ta có: 3 2 2 S 
 x  x  3x   a  a  3 x dx  1       2 4   2 4   0 a 27  1 1 3   1 3 3   4 3 2 2 2 
  x  x  x   a  a  x      4  8 4 2   4 8 2   0 27  1 1 3   1 3 3  27 1 1 4 3 2 2 2 
  a  a  a   a  a  a     4 3 
 a  a  a  3. 4  8 4 2   4 8 2  4 8 8 3
Do đó, d : y  x . 4
 Phương trình hoành độ giao điểm của C và d là: 3  1 3  1 3 9 3 2 3 2 x   x 
x  3x  0  x  x  x  0   4  2 4  2 4 4 3
Phương trình trên có 3 nghiệm: x  3 , x  0 và x   . 1 2 3 2 0    1 3 9 135 3 2 S  x  x  x dx   . 2    2 4 4  128 3  2
Do đó: m  135 , n  128 . Vậy: 2m  n  142 .
Câu 35: Cho hai hàm số   4 3 2
f x  ax  bx  cx  dx  e với a  0 và g  x 2
 px  qx  3 có đồ thị như
hình vẽ bên dưới. Đồ thị hàm số y  f  x đi qua gốc tọa độ và cắt đồ thị hàm số y  g  x tại
bốn điểm có hoành độ lần lượt là 2  ; 1
 ; 1 và m . Tiếp tuyến của đồ thị hàm số 15
y  f  x  g  x tại điểm có hoành độ x  2 có hệ số góc bằng 
. Gọi  H  là hình phẳng 2
giới hạn bởi đồ thị hai hàm số y  f  x và y  g  x .
Diện tích của hình  H  bằng 1553 1553 1553 1553 A. . B. . C. . D. . 120 240 60 30 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Đặt h  x  f  x  g  x 4 3
 ax  bx  c  p 2
x   d  
q x   e 3 . h x 3 2
 4ax  3bx  2c  p x  d  q.
Phương trình hoành độ giao điểm của 2 đồ thị y  f  x và y  g  x là:
f  x  g  x  h  x 4 3
  ax  bx  c  p 2 0
x  d  q x  e  3  0 .
Đồ thị hàm số y  f  x đi qua gốc tọa độ và cắt đồ thị hàm số y  g  x tại bốn điểm có
hoành độ lần lượt là 2  ; 1
 ; 1 và m nên f 0  h 2    h  1  h  
1  h m  0 e  0 16
 a  8b  4c  p  2d  q  3    1 
 a b  c  p  d  q  3 2
a bc pd q  3 3   4 3 am  bm   c  p 2
m  d  q m  3  0 4
Mặt khác, tiếp tuyến của đồ thị hàm số y  h  x tại điểm có hoành độ x  2 có hệ số góc 15 15 15 bằng  nên h 2      3
 2a 12b  4c  p  d  q   5 . 2 2 2  1 a   2  1 b    2 Từ  
1 , 2 , 3 , 5 , ta tìm được:  . 7
c  p    2  1 d  q   2 1 1 7 1 Thay vào 4 : 4 3 2 m  m  m 
m  3  0  m  3m   1 m   1 m  2  0 2 2 2 2  m  3. 1 1 7 1
Ngoài ra, ta cũng có: h  x 4 3 2
 x  x  x  x  3 . 2 2 2 2 3 1  1 3
Vậy diện tích hình phẳng cần tính là S  h
 x dx  h
 x dx h
 x dx h  x dx 2  2  1  1 1  1 3
 hx x  hx x  hx 113 58 122 1553 d d dx          . 120 15 15 120 2  1  1
Câu 36: Cho hàm số f  x liên tục trên và đường thẳng d  : g  x  ax  b có đồ thị như hình vẽ.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1 0 37 19
Biết diện tích miền tô đậm bằng
và f  x dx   . Tích phân . x f  
2xdx bằng 12 12 0 1  607 20 5 5 A.  . B.  . C.  . D.  . 348 3 3 6 Lời giải: A
 1;3 g  x  ax  b a  b  3 a  2 Ta có:     
 g x   B   x 2
 ;3 g x 2 1.  ax  b  2
 a  b  3 b   1 0 1 37 37 Mà S    f
  x2x 1dx  
2x 1 f xdx   12 12 2  0 0 1 1 0 0
 f x x  f x x   x   x   x   37 x   f x 2 d d 2 1 d 2 1 d dx        12 3 2  0 0 2  2  0 0 0  
t  x t  x 1
ut  u t 1 0 Khi đó . x f  
2xdx          2 d 2d t. f t t t f t f t t x t     d d d . d 1 2
dv f (t )dt v f (t )     2  x0 t  0 4 4 1 2   2   0 1    
  f    f  x 1 x    2 5 2 2 d 2. 3      . 4 4    3  3 2 
Câu 37: Cho parabol  P 2
: y  x và hai điểm A , B thuộc  P sao cho AB  2 . Tìm giá trị lớn nhất
của diện tích hình phẳng giới hạn bởi parabol  P và đường thẳng AB . 3 4 3 5 A. . B. . C. . D. . 2 3 4 6 Lời giải: y y=x2 B A x 1 O
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Gọi A 2
a; a  và B  2 ;
b b  là hai điểm thuộc P sao cho AB  2 .
Không mất tính tổng quát giả sử a  b . 2 2 Theo giả thiết ta có      
AB  2 nên b  a  b  a 2 2 2 2  4
b a b a 1  4   .
Phương trình đường thẳng đi qua hai điểm A và B là y  b  a x  ab .
Gọi S là diện tích hình phẳng giới hạn bởi parabol  P và đường thẳng AB ta có b b    S  
 a bx ab x  x  a b x x b a3 2 3 2 d  abx       . 2 3 6   a a 2 2
Mặt khác b  a b  a 1  4  
nên b  a2  4  b  a  b  a  2 . b a3 3 2 4 Vậy S    . 6 6 3 b   a  2  b   a  2 a  1 A   1  ;  1 Dấu  xảy ra         . b  a 
2 b  a2 1  4 b   a  0 b   1 B     1;  1
Vậy giá trị lớn nhất của diện tích hình phẳng giới hạn bởi parabol  P và đường thẳng AB 4 bằng . 3
Câu 38: Cho hai hàm số y f  x 3 2 
 ax  bx  cx  d và y g x 2 
 mx  nx  k cắt nhau tại ba điểm 1 có hoành độ là 1
 ; ;2 và có đồ thị như hình vẽ. 2 81
Biết phần diện tích kẻ sọc (hình S1 ) bằng 32 . Diện tích phần hình phẳng giới hạn bởi đồ thị 1
y  f x,y  gx và hai đường thẳng x  ;x  2 2
(phần bôi đen trong hình vẽ) bằng 79 243 81 45 A. . B. . C. . D. . 24 96 32 16 Lời giải:  1 
Ta có: f  x  g  x  a x   1 x  
x  2 a  0  2 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1 1 1 2     S   f
  x gx 2 1 1 81  dx  a 
 x  1 x    x  2 2 dx  a x 1 x  x  2 dx  . a  . 1      2   2  64 1  1  1  81 Mà S   a  2 . 1 32 2 2  1  81
Khi đó: S  g x  f x  dx  2 x 1 x  x  2 dx    . 2           2  32 1 1 2 2
Câu 39: Gọi X là tập hợp tất cả các giá trị của tham số m để đường thẳng d : y  45
 m  2 cùng với 1
đồ thị C  của hàm số 3 2 y 
x  2mx  x 1 tạo thành hai miền kín có diện tích lần lượt là 3
S , S thỏa mãn S  S (xem hình vẽ). Số phần tử của tập X là 1 2 1 2 A. 0. B. 2  C. 1 D. 9  Lời giải:
Điều kiện để đồ thị C  có hai điểm cực trị là 2
y  x  4mx 1  0 có hai nghiệm phân biệt.  1 m    2 Khi đó    2
 m2 1 0   . 1 m   2
Đường thẳng d : y  45
 m  2 song song với trục hoành và cắt đồ thị C của hàm số 1 3 2 y 
x  2mx  x 1 tạo thành hai miền kín có diện tích lần lượt là S , S thỏa mãn S  S 1 2 1 2 3
nên d đi qua điểm uốn của đồ thị C  . 16  Ta có: 2 3
y  x  4mx 1  y  2x  4m  0  x  2m  y  m  2m 1 . I I 3
Khi đó ta có phương trình: 1  6 1  6 3 3
m  2m 1  4  5m  2 
m  47m  3  0 * 3 3
Phương trình * có 3 nghiệm m phân biệt và có 2 nghiệm thỏa mãn điều kiện nên tập X có 2 phần tử. Câu 40: Cho hàm số   3 2
f x  x  ax  bx  c với a,b, c là các số thực. Biết hàm số
g  x  f  x  f  x  f   x có hai giá trị cực trị là 5
 và 2 . Diện tích hình phẳng giới hạn f  x
bởi các đường y  và y  1 bằng g  x  6 A. ln 3 . B. ln 7 . C. 3ln 2 . D. ln10 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia Lời giải:
Xét hàm số g  x  f  x  f  x  f   x
Ta có g x  f  x  f   x  f   x  f  x  f   x  6 . g  m  5
Theo giả thiết ta có phương trình g x  0 có hai nghiệm m, n và  . g  n  2 f  x g
  x  6  f  x  0  f 
  x  f   x  6  0 x  m Xét phương trình        g  x 1  6 g
  x  6  0 g
  x  6  0 x  n
Diện tích hình phẳng cần tính là: n  f  x 
n g  x  6  f  x
n f  x  f   x  6 n g x S  1  x   dx   dx   x  g x   g x  g x  g x  m   d 6 m   6 m   6 m    d 6 
 ln g x  6 n  ln g n  6  ln g m  6  ln8  3ln 2 . m
Câu 41: Cho đồ thị hàm số bậc ba    3 2 y
f x  ax  bx  cx  d và đường thẳng d : y  mx  n như S p
hình vẽ và S , S là diện tích hình phẳng được tô đậm trong hình bên. Biết 1  với 1 2 S q 2 * p, q 
là một phân số tối giản. Tính p  q  2022 . A. 2043 . B. 2045 . C. 2049 . D. 2051 . Lời giải:
Ta có y  f  x 2
 3ax  2bx  c . Do đồ thị hàm số    3 2 y
f x  ax  bx  cx  d có hai điểm cực trị là 1 ; 4 và 1 ; 0 nên 3
 a  2b  c  0 a  1   3
 a  2b  c  0 b   0    2      y x 3x 2 .
a  b  c  d  4 c  3  
a b  c  d  0 d  2
Vì đường thẳng d : y  mx  n đi qua 2 điểm  2
 ; 0,0 ; 2 nên d : y  x  2 . 1 1 1 1 4 2  x 3x  11 Ta có 2 3 S  .2 
x  3x  2 dx 2   3
x  3x  2 dx     2     2x   . 1  2  4 2  4 0 0 0
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 2 2 2
S   x  2  3
x  3x  2 dx  3
x  2  x  3x  2dx  3
x  4x dx 4 . 2  0 0 0 S p 11 1    . S q 16 2
Vậy p  q  2022  2049 . 7
Câu 42: Cho hàm số f  x với đồ thị là Parabol đỉnh I có tung độ bằng 
và hàm số bậc ba g  x . 12
Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ x , x , x thoả mãn 1 2 3 18x x x  5  5 (hình vẽ). 1 2 3
Diện tích miền tô đậm gần số nào nhất trong các số sau đây? A. 5, 7 . B. 5,9 . C. 6,1 . D. 6,3 . Lời giải: 1   2 1 Ta có: x   . I 2 2  1 7  Lúc này ta có I ,  
 và P : f  x  a  x   1  x  2 .  2 12   1 7  7 7 Ta có I , 
P  a     f  x  x   1  x  2 .  2 12  27 27
Hàm số g  x đạt cực trị tại x  1, x  2 nên   
x  a  x   x    g  x 3 2 x x g ' 1 2
 a   2x b  3 2   1  7 7 13
Đồ thị hàm số g  x đi qua I nên g       a  , b     1 .  2  12 12 12 3 2  x x  7
Phương trình hoành độ giao điểm: f  x  g  x  a  
 2xb  x   1  x  2  3 2  27 14 b  28 55a Theo định lý viet ta có: 27 18x x x  5  5  18.  55 18b   2 1 2 3 a 3 3 3 x x Từ  
1 , 2 ta được a  b   g x 3 2 1 1 1,    2x  . 2 3 2 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia x x
Phương trình hoành độ giao điểm là
x  x   3 2 7 1 1 2    2x  27 3 2 2  1 x   2   8  559  x   9   8  559 x   9 8 559 9 3 2  7 x x 1 
Từ đó suy ra diện tích miền tô đậm là S 
  x 1x2   2x dx  5,7.  27 3 2 2 1  2 Câu 43: Cho hàm số 3 2
y  4x  3x có đồ thị C  và đường thẳng d đi qua gốc tọa độ tạo thành hai
miền hình phẳng có diện tích S , S như hình vẽ bên dưới: 1 2
Khi S  12 thì S bằng 2 1 7 875 865 A. . B. 3 . C. . D. . 2 256 256 Lời giải:
Phương trình đường thẳng d có dạng y  mx .
Phương trình hoành độ giao điểm giữa đồ thị C  và đường thẳng d là x  0 3 2
4x  3x  mx   . 2
4x  3x  m  0
Gọi b là nghiệm dương của phương trình hoành độ giao điểm trên 2
 4b  3b  m b b   S   1 1 3 2
mx  4x  3x  2 4 3 2 4 3 dx 
mx  x  x
 mb b  b 2    2  2 0 0 1
Theo giả thiết S  12 2 4 3
 mb  b  b  12 2 2 1   2 4b  3b 2 4 3
b  b  b  12 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 4 3
 2b  b  24  0  b  2 vì b  0  m 10 x  2 Khi đó phương trình 2 
4x  3x  m  0 trở thành 2
4x  3x 10  0  5  . x    4 0 875 Vậy S    3 2
4x  3x 10x dx  . 1  256 5  4
Câu 44: Cho hàm số bậc ba y  f  x có đồ thị C  như hình vẽ.
Biết rằng đồ thị hàm số đã cho cắt trục Ox tại ba điểm có hoành độ x , x , x theo thứ tự lập 1 2 3
thành cấp số cộng và x  x  2 3 . Diện tích hình phẳng giới hạn bởi C  và trục Ox là S , 3 1
diện tích S của hình phẳng giới hạn bởi các đường y  f  x 1, y   f  x 1, x  x và 1 1
x  x bằng 3 A. 4 3 . B. 2 3 .
C. 2S  4 3 . D. S  2 3 . Lời giải:
Do đồ thị hàm bậc ba cắt trục hoành tại ba điểm có hoành độ x , x , x theo thứ tự lập thành 1 2 3
cấp số cộng nên đồ thị nhận điểm A x ;0 làm tâm đối xứng của đồ thị. 2  x x x x 2 3 2 3 S S Do đó:
f  x dx 
f  x dx 
 f xdx   f xdx      . 2 2 1 x 2 x 1 x 2 x x 2 x S 3 S Suy ra: f
 xdx  ; f
 xdx   . 2 2 1 x 2x
Vì đồ thị hai hàm số y  f  x 1 và y   f  x 1đối xứng với nhau qua trục hoành nên ta có: 3 x x x x S  2
f x 1dx  2  f x 1dx  2 f x dx  2     dx 1   3    3    3 1 x 1 x 1 x 1 x x x x 2    S S 
 2  f x 3
dx   f x 3
dx  2 dx  2   2   
x  x  4 3. 3 1  x x  x  2 2   1 2 1
Câu 45: Một miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất
bằng 2 đoạn thẳng song song AB,CD thành ba phần có diện tích bằng nhau (xem hình vẽ AB bên dưới). Tỉ số bằng: CD
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 1 3 1 1 A. . B. . C. . D. . 3 2 1 2 2 2 1 2 Lời giải:
Chọn hệ trục tọa độ như hình vẽ: Parabol có dạng 2
y  ax , do  P đi qua điểm   1 6;18  a  . 2 6 2  x 
Diện tích miếng đất là: S   18 dx 144 .  2  6  S
Để diện tích 3 phần bằng nhau thì diện tích mỗi phần là
 48 . Với b, d > 0 3 2 2  b   d  AB b Gọi B  ; b ; D d;  khi đó   2   2  CD d , b b 2 2 2 3  b x   b x x  Ta có: 3
  dx  24      24  b  72  2 2   2 6  0 0 d 2 2  d x  AB 1 Tương tự ta có 3
  dx  48 d 144  . 3  2 2  CD 2 0
Câu 46: Ông X muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên, biết đường cong
phía trên là một Parabol, chất liệu làm là inox. Giá 2
1m vật tư và công làm là 1.300.000 đồng.
Hỏi ông X phải trả bao nhiêu tiền để làm cái cửa sắt như vậy (làm tròn đến hàng nghìn).
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
A. 13.050.000 đồng.
B. 36.630.000 đồng. C. 19.520.000 đồng. D. 21.077.330 đồng. Lời giải:
Ta chọn hệ trục tọa độ như hình vẽ. y P I 3,8 J x -1,9 0 1,9 1  19 19  19 19  Trong đó I  ;   , J ;   .  10 5  10 5 
Đường cong phía trên là một Parabol có phương trình dạng 2
y  ax  b , với a;b  . 9 70 9
Do Parabol đi qua các điểm I , J và chiều cao cổng là m nên có 2 y   x  . 2 361 2
Diện tích S của cửa rào sắt là diện tích phần hình phẳng giới hạn bởi đồ thị hàm số 70 9 2 19 19 y   x 
, trục hoành và hai đường thẳng x   ; x  . 361 2 10 10 19 10  70 9  1216 Ta có 2 S   x  dx     .  361 2  75 19 10 1216
Vậy ông X phải trả số tiền để làm cái cửa sắt là: 1. 0
3 0.000  21.077.330 (đồng). 75
Câu 47: Một mảnh đất hình chữ nhật có chiều dài 60m , chiều rộng 20m . Người ta muốn trồng cỏ ở
hai đầu của mảnh đất hai hình bằng nhau giới hạn bởi hai đường Parabol có hai đỉnh cách
nhau 40m (như hình vẽ).
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Phần còn lại của mảnh đất người ta lát gạch với chi phí là 2
200.000 d m . Tính tổng số tiền để
lát gạch ( làm tròn đến hàng nghìn)
A. 133.334.000 đồng. B. 213.334.000 đồng. C. 53.334.000 đồng. D. 186.667.000 đồng. Lời giải:
Ta có diện tích mảnh đất hình chữ nhật trên là. S    2 60.20 1200 m 
Chọn hệ trục tọa độ Oxy, như hình vẽ thoả mãn. A 10
 ;0;B10;0;C 0;10 .
Phương trình P có dạng. 2 y  . a x  .
b x  c  
1 . Do P đi qua các điểm D,C, I nên tọa độ các điểm A 10
 ;0;B10;0;C 0;10 thỏa mãn phương trình 1 nên ta có hệ phương trình.  1  a  100 
a 10b  c  0  10   1  100 
a 10b  c  0   b  0 . Vậy phương trình P . 2 y  x  10   1   10 c  10 c  10   
Diện tích trồng cỏ ở hai đầu là 10 10 10 3 1   1    x  400  40  0  800 2 2 S  2.
x  10 dx  2.
x  10 dx  2.      10x        2 m  10  10   30  3  3  3 10  10  10   800 
Vậy tổng số tiền để lát gạch là. T  1200  .200.000  186.666.667   ( đồng).  3 
Câu 48: Trên bức tường cần trang trí một hình phẳng dạng paranol đỉnh S như hình vẽ, biết
OS  AB  4 m , O là trung điểm của AB . Parabol trên được chia thành ba phần để sơn ba
màu khác nhau với mức chi phí: phần trên là phần kẻ sọc 140000 đồng/ 2 m , phần giữa là hình
quạt tâm O , bán kính 2 m được tô đậm 150000 đồng/ 2
m , phần còn lại 160000 đồng/ 2 m .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Tổng chi phí để sơn cả 3 phần gần nhất với số nào sau đây?
A. 1.597.000 đồng.
B. 1.625.000 đồng.
C. 1.575.000 đồng. D. 1.600.000 đồng. Lời giải:
Dựng hệ trục Oxy như hình vẽ.
Gọi parabol  P có phương trình: 2
y  ax  bx  c a  0 . Khi đó  P đi qua các điểm
S 0, 4 , A2;0 và B 2;0 . c  4 a  1   
Suy ra ta có 4a  2b  c  0  b
  0 . Vậy parabol P : 2
y  x  4 .  
4a  2b  c  0 c  4  
Đường tròn C  có tâm O 0;0 và bán kính OA  2 .
Khi đó phương trình C  là: 2 2
x  y  4 . Suy ra phương trình nửa đường tròn là 2 y  4  x .
Gọi M , N là giao điểm của C  và  P .
Xét phương trình hoành độ giao điểm của C  và  P ta có: 2 2 x  4  0  2 x  4  0 x  4  0     x  2  2 2
4  x  x  4     
 x   x    .  4  x    4x  2 2 2 4 0 4 2 2    x   3 2 2     x  3 4 x 1
Suy ra điểm M  3 
;1 và điểm N  3  ;1 . 1
Phương trình đường thẳng ON là: y  x . 3
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia 3  
Chi phí sơn phần kẻ sọc là: T  2   2 2
x  4  4  x dx.140000 . 1    0  3  1   
Chi phí sơn phần hình quạt là: 2 T  2 4  x  x dx    .150000 . 2   3    0  3 2  1 
Chi phí sơn phần còn lại là: T  2 d x x  2    2
x  4 dx.160000 . 3   3   0 3 
Vậy tổng chi phí sơn là: T  T  T  T  1575349,5 đồng. 1 2 3
Câu 49: Hướng tới kỉ niệm ngày thành lập trường Đoàn TNCS Hồ Chí Minh. Khối 12 thiết kế bồn
hoa gồm hai Elip bằng nhau có độ dài trục lớn bằng 8m và độ dài trục nhỏ bằng 4m đặt
chồng lên nhau sao cho trục lớn của Elip này trùng với trục nhỏ của Elip kia và ngược lại (như hình vẽ).
Phần diện tích nằm trong đường tròn đi qua 4 giao điểm của hai Elip dùng để trồng cỏ,
phần diện tích bốn cánh hoa nằm giữa hình tròn và Elip dùng để trồng hoa. Biết kinh phí để
trồng hoa là 150.000 đồng 2
/1m , kinh phí để trồng cỏ là 100.000 đồng 2
/1m . Tổng số tiền dùng
để trồng hoa và trồng cỏ cho bồn hoa gần với số nào nhất trong các số sau?
A. 4.100.000 đồng.
B. 4.550.000 đồng.
C. 3.100.000 đồng. D. 4.300.000 đồng. Lời giải:
Chọn hệ trục Oxy như hình 2a  8 a  4 Ta có:    2b  4 b   2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia x y
Gọi  E là elip nhận Ox làm trục lớn   E :  1 1  2 2 1  16 4 x y
Và  E là elip nhận Oy làm trục lớn   E :  1 2  2 2 2  4 16
Tọa độ giao điểm của  E và  E là nghiệm của hệ phương trình: 2  1  2 2  x y  16  4 2   1 x  x      16 4  5  5     
 Phương trình đường tròn đi qua 4 giao điểm của 2 2  x y 16 4 2     1 y  y    4 16  5  5  32 2
E và  E là 2 2
(C) : x  y  có bán kính R  4
 Diện tích hình tròn dùng để trồng 2  1  5 5 32 cỏ: 2 2 S   R 
 (m )  Tiền trồng cỏ: T 100000.S  2 010 619 (đồng) 1 5 1 1
Một cánh hoa được giới hạn bởi đường  E có phần đồ thị từ phía trên trục 2  32 2
Ox : y  2 4  x và nửa đường tròn (C) từ phía trên trục 2 Ox : y 
 x có diện tích 5 4 5  32  2 2 2
S   2 4  x 
 x dx  3.83064(m )    5 4   5
Do tính đối xứng của hình nên diện tích của 4 cánh hoa đều bằng nhau diện tích của 4 cánh hoa: 2
S  4.S  15.32256(m )  Số tiền trồng hoa T  150 000.S  2 298 384 (đồng). 2 2 2
Tổng số tiền: T  T  T  4 309 000 (đồng) 1 2
Câu 50: Một công ty có ý định thiết kế một logo hình vuông có độ dài nửa đường chéo bằng 4. Biều
tượng 4 chiếc lá (được tô màu) được tạo thành bởi các đường cong đối xứng với nhau qua
tâm của hình vuông và qua các đường chéo.
Một trong số các đường cong ở nửa bên phải của logo là một phần của đồ thị hàm số bậc ba dạng 3 2
y  ax  bx  x với hệ số a  0 . Để kỷ niệm ngày thành lập 2 / 3 , công ty thiết kế để tỉ 2
số diện tích được tô màu so với phần không được tô màu bằng
. Tính a  b . 3 41 1 2 9 A. . B. . C. . D. . 80 2 5 10 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chuyên đề SỐ PHỨC Luyện thi THPT Quốc gia
Xét hệ trục toạ độ như hình vẽ, diện tích tam giác OAB vuông cân tại B .
Theo giat thiết ta có OA  4, A4;0 . Hình vuông có nửa đường chéo bằng 4 nên diện tích 64
hình vuông là 32 . Diện tích tô màu là . 5 8
Xét riêng trong tam giác OAB có diện tích phần tô màu bằng . 5
Theo giả thiết, diện tích phần tô màu trong tám giác OAB được tính bởi công thức 4 8 3 2
ax  bx  x dx   . 0 5  1 a    5 4  8  3 2
ax  bx  x dx    21  0 5 b    20
Từ đó ta có hệ: 64a 16b  4  0     1 a  0 a     20   9  b    20  1 a    5 5 Trường hợp 
 f x  0 có nghiệm là 0, , 4 (đồ thị cắt Ox trong 0;4 - loại) 21 4 b    20  1 a    20 2 Trường hợp 
 f x  0 có nghiệm 0, 4, 5 thoả mãn. Vậy, a  b  . 9 5 b    20
____________________HẾT____________________
Huế, 15h15’ Ngày 19 tháng 3 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Document Outline

ngan-hang-cau-hoi-ung-dung-tich-phan-de-tinh-dien-tich-hinh-phang
NGAN HANG 2023 Ung dung Tich phan (Phan 2)