Nguyên hàm của hàm số lượng giác Toán 12

Nguyên hàm của hàm số lượng giác Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

15 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
Quảng Thuận – Ba Đồn – QB Nguyên hàm của hàm số lượng giác 2020
0
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
MỤC LỤC
Chuû ñeà ④
NGUYEÂN HAØM cuûa haøm soá Löôïng giaùc
........................................................... 1
........ 1
........ 1
1. Dạng 1.
sin sin
dx
I
x a x b

................................................................................................ 1
a. Phương pháp tính ............................................................................................................................................. 1
b. Chú ý ................................................................................................................................................................. 2
c. Ví dụ áp dụng .................................................................................................................................................... 2
2. Dạng 2.
tan tanI x a x b dx
........................................................................................... 3
a. Phương pháp tính ............................................................................................................................................. 3
b. Chú ý ................................................................................................................................................................. 4
c. Ví dụ áp dụng .................................................................................................................................................... 4
3. Dạng 3.
sin cos
dx
I
a x b x
........................................................................................................... 6
a. Phương pháp tính ............................................................................................................................................. 6
b. Ví dụ áp dụng .................................................................................................................................................... 6
4. Dạng 4.
sin cos
dx
I
a x b x c

.................................................................................................... 7
a. Phương pháp tính ............................................................................................................................................. 7
b. Ví dụ áp dụng .................................................................................................................................................... 7
5. Dạng 5.
22
.sin .sin cos .cos
dx
I
a x b x x c x

............................................................................ 8
a. Phương pháp tính ............................................................................................................................................. 8
b. Ví dụ áp dụng .................................................................................................................................................... 8
6. Dạng 6.
11
22
sin cos
sin cos
a x b x
I dx
a x b x
.................................................................................................. 9
a. Phương pháp tính ............................................................................................................................................. 9
b. Ví dụ áp dụng .................................................................................................................................................... 9
c. Chú ý ............................................................................................................................................................... 10
7. Dạng 7. Biến đổi đưa về nguyên hàm cơ bản hoặc 6 dạng ở trên.................................................. 12
Ví dụ áp dụng ...................................................................................................................................................... 12
I.
=I
CÁC DẠNG TOÁN
II.
=I
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
1
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
Chuû ñeà ④
NGUYEÂN HAØM cuûa haøm soá
Löôïng giaùc
Nguyên hàm của hàm số
sơ cấp
Nguyên hàm của hàm số
hợp
u u x
Nguyên hàm của hàm số hợp
;0u ax b a
sin cosxdx x C
sin cosudu u C
1
sin cosax b dx ax b C
a
cos sinxdx x C
cos sinudu u C
1
cos sinax b dx ax b C
a
tan . ln cosx dx x C
tan . ln cosu du u C
1
tan ln cosax b dx ax b C
a
cot . ln sinx dx x C
cot . ln sinu du u C
1
cot ln sinax b dx ax b C
a
2
1
cot
sin
dx x C
x
2
1
cot
sin
du u C
u
2
11
cot
sin
dx ax b C
a
ax b
2
1
tan
cos
dx x C
x

2
1
tan
cos
du u C
u

2
11
tan
cos
dx ax b C
a
ax b
1
ln tan
sin 2
x
dx C
x

1
ln tan
sin 2
u
du C
u

1
ln
2
sin
dx ax b
tg C
a
ax b

1
ln tan
cos 2 4
x
dx C
x



1
ln tan
cos 2 4
u
du C
u



1
ln tan
24
cos
dx ax b
C
a
ax b
1. Dạng 1.
sin sin
dx
I
x a x b

a. Phương pháp tính
Dùng đồng nhất thức:
sin
sin sin cos cos sin
1
sin sin sin
x a x b
a b x a x b x a x b
a b a b a b


Từ đó suy ra:
sin cos cos sin
1
sin sin sin
x a x b x a x b
I dx
a b x a x b
I.
=I
II.
=I
Quảng Thuận – Ba Đồn – QB Nguyên hàm của hàm số lượng giác 2020
2
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
cos cos
1
sin sin sin
x b x a
dx
a b x b x a





1
ln sin ln sin
sin
x b x a C
ab


b. Chú ý
Với cách này, ta có thể tìm được các nguyên hàm:
•
cos cos
dx
J
x a x b

bằng cách dùng đồng nhất thức
sin
1
sin
ab
ab
•
sin cos
dx
K
x a x b

bằng cách dùng đồng nhất thức
cos
1
cos
ab
ab
c. Ví dụ áp dụng
Ví dụ 1
Tìm nguyên hàm sau đây:
sin sin
6
dx
I
xx



Giải
Ta có:
sin
sin
6
6
1 2 sin cos cos sin
1
66
sin
62
xx
x x x x








Từ đó:
sin cos cos sin
cos
66
cos
6
22
sin
sin sin sin
66
x x x x
x
x
I dx dx
x
x x x











sin
sin
6
sin
2 2 2ln
sin
sin sin
66
dx
dx
x
C
x
xx








Ví dụ 2
Tìm nguyên hàm sau đây:
cos3 cos 3
6
dx
I
xx



Giải
Ta có:
sin 3 3
sin
6
6
1 2 sin 3 cos3 cos 3 sin3
1
66
sin
62
xx
x x x x








Từ đó:
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
3
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
sin 3 cos3 cos 3 sin3
sin 3
66
sin3
6
2 2 2
cos3
cos3 cos 3 cos 3
66
x x x x
x
x
I dx dx dx
x
x x x







cos 3
cos3
6
2 2 2 cos3
ln
3 3 cos3 3
cos 3 cos 3
66
dx
dx
x
C
x
xx








Ví dụ 3
Tìm nguyên hàm sau đây:
sin cos
3 12
dx
I
xx


Giải
Ta có:
cos
cos
3 12
4
1
2
cos
4
2
xx



2 cos cos sin sin
3 12 3 12
x x x x


Từ đó:
cos cos sin sin
3 12 3 12
2
sin cos
3 12
x x x x
I dx
xx


cos sin
3 12
22
sin cos
3 12
xx
dx dx
xx






sin cos
sin
3 12
3
2 2 2ln
sin cos cos
3 12 12
d x d x
x
C
x x x




2. Dạng 2.
tan tanI x a x b dx
a. Phương pháp tính
Ta có:
sin sin
tan tan
cos cos
x a x b
x a x b
x a x b


sin sin cos cos cos
11
cos cos cos cos
x a x b x a x b a b
x a x b x a x b
Từ đó:
cos 1
cos cos
dx
I a b
x a x b

Đến đây ta gặp bài toán tìm nguyên hàm ở Dạng 1.
Quảng Thuận – Ba Đồn – QB Nguyên hàm của hàm số lượng giác 2020
4
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
b. Chú ý
Với cách này, ta có thể tính được các nguyên hàm:
•
cot cotJ x a x b dx
•
tan tanK x a x b dx
c. Ví dụ áp dụng
Ví dụ 4
Tìm nguyên hàm sau đây:
cot cot
36
I x x dx

Giải
Ta có:
Ta có:
cos cos
36
cot cot
36
sin sin
36
xx
xx
xx





cos cos sin sin
3 6 3 6
1
sin sin
36
x x x x
xx



cos
36
31
1 . 1
2
sin sin sin sin
3 6 3 6
xx
x x x x


Từ đó:
1
3 1 3
22
sin sin
36
I dx dx I x C
xx



Tính
1
sin sin
36
dx
I
xx


Ta có:
sin
sin
36
6
1
1
sin
62
xx



2 sin cos cos sin
3 6 3 6
x x x x


Từ đó:
1
sin cos cos sin
3 6 3 6
2
sin sin
36
x x x x
I dx
xx


Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
5
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
cos cos sin
6 3 6
2 2 2ln
sin sin sin
6 3 3
x x x
dx dx C
x x x

Suy ra:
sin sin
3
66
.2ln 3ln
2
sin sin
33
xx
I x C x C
xx




Ví dụ 5
Tìm nguyên hàm sau đây:
tan cot
36
K x x dx

Giải
Ta có:
sin cos
36
tan cot
36
cos sin
36
xx
xx
xx





sin cos cos sin
3 6 3 6
1
cos sin
36
x x x x
xx



sin
36
11
1 . 1
2
cos sin cos sin
3 6 3 6
xx
x x x x


Từ đó:
1
1 1 1
22
cos sin
36
K dx dx K x C
xx



Đến đây, bằng cách tính ở Dạng 1, ta tính được:
1
sin
2
6
ln
3
cos sin cos
3 6 3
x
dx
KC
x x x



Suy ra:
sin
3
6
ln
3
cos
3
x
K x C
x






Quảng Thuận – Ba Đồn – QB Nguyên hàm của hàm số lượng giác 2020
6
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
3. Dạng 3.
sin cos
dx
I
a x b x
a. Phương pháp tính
Có:
22
2 2 2 2
sin cos sin cos
ab
a x b x a b x x
a b a b




22
sin cos sina x b x a b x
2 2 2 2
11
ln tan
sin 2
dx x
IC
x
a b a b



b. Ví dụ áp dụng
Ví dụ 6
Tìm nguyên hàm sau đây:
2
3sin cos
dx
I
xx
Giải
2
3sin cos 3 1
sin cos cos sin
sin cos
66
22
dx dx dx
I
xx
xx
xx

6
6
ln tan ln tan
2 2 12
sin sin
66
dx
x
dx x
CC
xx









Ví dụ 7
Tìm nguyên hàm sau đây:
cos2 3sin2
dx
J
xx
Giải
1
2
cos2 3sin2 1 3
cos2 sin2
22
dx dx
J
xx
xx


2
1 1 1
6
2 2 4
sin cos2 cos sin2
sin 2 sin 2
66
66
dx
dx dx
xx
xx






2
11
6
ln tan ln tan
4 2 4 12
x
C x C



Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
7
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
4. Dạng 4.
sin cos
dx
I
a x b x c

a. Phương pháp tính
Đặt
2
2
2
2
2
2
1
2
sin
1
tan
2
1
cos
1
2
tan
1
dt
dx
t
t
x
x
t
t
t
x
t
t
x
t

b. Ví dụ áp dụng
Ví dụ 8
Tìm nguyên hàm sau đây:
3cos 5sin 3
dx
I
xx

Giải
Đặt
2
2
2
2
2
1
2
tan sin
21
1
cos
1
dt
dx
t
xt
tx
t
t
x
t
Từ đó:
2
2
22
22
2
22
1
12
3 3 10 3 3 10 6
3. 5 3
11
dt
dt dt
t
I
tt
t t t t
tt


53
1 1 1
ln 5 3 ln 5tan 3
5 5 3 5 5 2
dt
x
t C C
t
Ví dụ 9
Tìm nguyên hàm sau đây:
2
2sin cos 1
dx
J
xx

Giải
Đặt
2
2
2
2
2
1
2
tan sin
21
1
cos
1
dt
dx
t
xt
tx
t
t
x
t
Quảng Thuận – Ba Đồn – QB Nguyên hàm của hàm số lượng giác 2020
8
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
Từ đó:
2
2
2 2 2
22
2
2.
44
1
2
21
4 1 1 2 4 2
2. 1
11
dt
dt dt dt
t
J
tt
t t t t t t t
tt


11
ln ln 2 ln tan ln tan 2
2 2 2
xx
dt t t C C
tt



Ví dụ 10
Tìm nguyên hàm sau đây:
sin tan
dx
K
xx
Giải
Đặt
2
2
2
2
1
2
tan sin
21
2
tan
1
dt
dx
t
xt
tx
t
t
x
t
Từ đó:
2
2
22
2
1 1 1 1
1
22
2 2 2
11
dt
t dt
t
K dt tdt
tt
tt
tt

22
1 1 1 1
ln ln tan tan
2 4 2 2 4 2
xx
t t C C
5. Dạng 5.
22
.sin .sin cos .cos
dx
I
a x b x x c x

a. Phương pháp tính
22
tan tan .cos
dx
I
a x b x c x

Đặt
2
tan
cos
dx
x t dt
x
. Suy ra
2
dt
I
at bt c

b. Ví dụ áp dụng
Ví dụ 11
Tìm nguyên hàm sau đây:
22
3sin 2sin cos cos

dx
I
x x x x
Giải
•
22
22
3sin 2sin cos cos
3tan 2tan 1 cos
dx dx
I
x x x x
x x x




Đặt
2
tan
cos
dx
x t dt
x
2
3 2 1 1 3 1
dt dt
I
t t t t

Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
9
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
31
1 1 3 1 1
4 1 3 1 4 1 4 3 1
dt
dt
dt
t t t t



1 1 1 tan 1
ln ln
4 3 1 4 3tan 1
tx
CC
tx


Ví dụ 12
Tìm nguyên hàm sau đây:
22
sin 2sin cos 2cos

dx
J
x x x x
Giải
Đặt
2
tan
cos
dx
x t dt
x
2
2
2
1
1 1 3
ln
22
2 3 1 3
13
dt
dt t
JC
tt
t
t





1 tan 1 3
ln
2 3 tan 1 3
x
C
x



6. Dạng 6.
11
22
sin cos
sin cos
a x b x
I dx
a x b x
a. Phương pháp tính
Ta tìm
,AB
sao cho:
1 1 2 2 2 2
sin cos sin cos cos sina x b x A a x b x B a x b x
b. Ví dụ áp dụng
Ví dụ 13
Tìm nguyên hàm sau đây:
4sin 3cos
sin 2cos
xx
I dx
xx
Giải
Ta tìm
,AB
sao cho:
4sin 3cos sin 2cos cos 2sinx x A x x B x x
2 4 2
4sin 3cos 2 sin 2 cos
2 3 1
A B A
x x A B x A B x
A B B



Từ đó:
2 sin 2cos cos 2sin
sin 2cos
x x x x
I dx
xx
sin 2cos
2 2 ln sin 2cos
sin 2cos
d x x
dx x x x C
xx

Ví dụ 14
Tìm nguyên hàm sau đây:
3cos 2sin
cos 4sin
xx
J dx
xx
Giải
Ta tìm
,AB
sao cho:
3cos 2sin cos 4sin sin 4cosx x A x x B x x
Quảng Thuận – Ba Đồn – QB Nguyên hàm của hàm số lượng giác 2020
10
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
3cos 2sin 4 cos 4 sinx x A B x A B x
11
43
17
4 2 10
17
A
AB
AB
B





Từ đó:
11 10
cos 4sin sin 4cos
17 17
cos 4sin
x x x x
J dx
xx
cos 4sin
11 10 11 10
ln cos 4sin
17 17 cos 4sin 17 17
d x x
dx x x x C
xx

c. Chú ý
1. Nếu gặp
11
2
22
sin cos
sin cos
a x b x
I dx
a x b x
ta vẫn tìm
,AB
sao cho:
1 1 2 2 2 2
sin cos sin cos cos sina x b x A a x b x B a x b x
2. Nếu gặp
1 1 1
2 2 2
sin cos
sin cos
a x b x c
I dx
a x b x c


ta tìm
,AB
sao cho:
1 1 1 2 2 2 2 2
sin cos sin cos cos sina x b x c A a x b x c B a x b x C
Ví dụ 15
Tìm nguyên hàm sau đây:
2
8cos
3sin cos
x
I dx
xx
Giải
Ta tìm
,AB
sao cho:
8cos 3sin cos 3cos sinx A x x B x x
8cos 3 sin 3 cosx A B x A B x
2
30
23
38
A
AB
B
AB





Từ đó:
2
2 3sin cos 2 3 3cos sin
3sin cos
x x x x
I dx
xx
1
2
3sin cos
23
2 2 3 2
3sin cos 3sin cos
3sin cos
d x x
dx
IC
x x x x
xx


Tìm
1
11
22
3sin cos 3 1
sin cos cos sin
sin cos
66
22
dx dx dx
I
xx
xx
xx

Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
11
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
1 1 1 1
6
6
ln tan ln tan
2 2 2 2 2 2 12
sin sin
66
dx
x
dx x
CC
xx









Vậy
23
ln tan
2 12
3sin cos
x
IC
xx



Ví dụ 16
Tìm nguyên hàm sau đây:
8sin cos 5
2sin cos 1
xx
J dx
xx


Giải
Ta tìm
,,A B C
sao cho:
8sin cos 5 2sin cos 1 2cos sinx x A x x B x x C
8sin cos 5 2 sin 2 cosx x A B x A B x A C
2 8 3
2 1 2
52
A B A
A B B
A C C





Từ đó:
3 2sin cos 1 2 2cos sin 2
2sin cos 1
x x x x
J dx
xx

2cos sin
3 2 2
2sin cos 1 2sin cos 1
x x dx
dx dx
x x x x

1
3 2ln 2sin cos 1 2x x x J
Tìm
1
2sin cos 1
dx
J
xx

Đặt
2
2
2
2
2
1
2
tan sin
21
1
cos
1
dt
dx
t
xt
tx
t
t
x
t
2
1
2
2
22
2
1 1 1
1
21
2 2 2 2
2. 1
11
dt
dt dt
t
J dt
tt
t t t t t t
tt





tan
11
2
ln ln
2 2 2
tan 2
2
x
t
CC
x
t
Vậy:
tan
2
3 2ln 2sin cos 1 ln
tan 2
2
x
J x x x C
x
Quảng Thuận – Ba Đồn – QB Nguyên hàm của hàm số lượng giác 2020
12
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
7. Dạng 7. Biến đổi đưa về nguyên hàm cơ bản hoặc 6 dạng ở trên
Ví dụ áp dụng
Ví dụ 17
Tìm nguyên hàm sau đây:
cos3 cos4
I x xdx
Giải
1
cos3 cos4 cos cos7
2
I x xdx x x dx

1 1 1 1
cos cos7 sin sin7
2 2 2 14
xdx xdx x x C

Ví dụ 18
Tìm nguyên hàm sau đây:
cos sin2 cos3
I x x xdx
Giải
1
cos sin2 cos3 sin2 cos2 cos4
2
I x x xdx x x x dx

11
sin2 cos2 sin2 cos4
22
x xdx x xdx

11
sin2 sin2 sin2 sin6
44
xd x x x dx

2
1 1 1
sin 2 cos2 cos6
8 8 24
x x x C
Ví dụ 19
Tìm nguyên hàm sau đây:
tan tan tan
33
I x x x dx

Giải
Ta có:
sin sin sin
33
tan tan tan
33
cos cos cos
33
x x x
x x x
x x x





2
2
21
sin cos2 cos sin 1 2sin
32
21
cos cos2 cos cos 2cos 1
32
x x x x
x x x x

2
3
3
2
sin 3 4sin
3sin 4sin sin3
4cos 3cos cos3
cos 4cos 3
xx
x x x
x x x
xx
Từ đó:
cos3
sin3 1 1
ln cos3
cos3 3 cos3 3
dx
x
I dx x C
xx

Ví dụ 20
Tìm nguyên hàm sau đây:
3
sin sin3I x xdx
Giải
Ta có:
33
3sin sin3
sin3 3sin 4sin sin
4
xx
x x x x
Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”
13
https://luyenthitracnghiem.vn
https://www.facebook.com/vietgold
3
3sin 4sin3
sin sin3 .sin3
4
xx
x x x

2
3 1 3 1
sin sin3 sin 3 cos2 cos4 1 cos6
4 4 8 8
x x x x x x
3 3 1 1
cos2 cos4 cos6
8 8 8 8
xxx
Từ đó:
3 3 1 1
cos2 cos4 cos6
8 8 8 8
I x x x dx



3 3 1 1
sin2 sin4 sin6
16 32 48 8
x x x x C
Ví dụ 21
Tìm nguyên hàm sau đây:
33
sin cos3 cos sin3I x x x x dx
Giải
Ta có:
3
3sin sin3
sin
4
xx
x
3
3cos cos3
cos
4
xx
x
Suy ra:
33
3sin sin3 3cos cos3
sin cos3 cos sin3 .cos3 .sin3
44
x x x x
x x x x x x

3 1 3 1
sin cos3 sin3 cos3 cos sin3 cos3 sin3
4 4 4 4
x x x x x x x x
3 3 3
sin 2 sin4 sin 2 sin4 sin2
8 8 4
x x x x x
Vậy
33
sin2 cos2
48
I xdx x C
Ví dụ 22
Tìm nguyên hàm sau đây:
3
sin cos
dx
I
xx
Giải
2
3 4 2 2 2
1 1 1
. . 1 tan
sin cos tan cos tan cos cos tan cos
dx dx dx dx
Ix
x x x x x x x x x
Đặt
2
tan
cos
dx
x t dt
x
2
t t dt
I dt tdt
tt
22
11
ln tan ln tan
22
t t C x x C
Ví dụ 23
Tìm nguyên hàm sau đây:
4
sin cos
dx
I
xx
Giải
Đặt
sin cosx t xdx dt
4 4 2
42
4 2 4 2
11
1
11
dt t t t dt
I dt dt
tt
t t t t

3
42
1 1 1 1
ln
1 1 3 2 1
dt dt dt t
tC
t t t t t t
Quảng Thuận – Ba Đồn – QB Nguyên hàm của hàm số lượng giác 2020
14
https://www.facebook.com/vietgold
https://luyenthitracnghiem.vn
3
1 1 1 sin 1
ln
3sin sin 2 sin 1
x
C
x x x
Ví dụ 24
Tìm nguyên hàm sau đây:
sin3 sin4
tan tan2
xx
I dx
xx
Giải
sin3 sin4 sin3 sin4
sin4 cos2 cos
sin3
tan tan 2
cos cos2
x x x x
I dx dx x x xdx
x
xx
xx
1 1 1
sin6 sin2 cos sin6 cos sin2 cos
2 2 2
x x xdx x xdx x xdx
11
sin7 sin5 sin3 sin
44
x x dx x x dx

1 1 1 1
cos7 cos5 cos3 cos
28 20 12 4
x x x x C
Ví dụ 25
Tìm nguyên hàm sau đây:
3
sin
dx
I
x
Giải
Đặt
2
2
1
cos
sin
sin
cot
sin
x
u
du dx
x
x
dx
vx
dv
x





1
2
cot cot .cos cot
sin sin sin
x x x x
I dx I
x x x
Tính
22
1
3 3 3
cos 1 sin
ln tan
sin sin sin sin 2
x x dx dx x
I dx dx I C
x x x x
1
cot cot
ln tan
sin sin 2
x x x
I I I C
xx
cot 1 cot
2 ln tan ln tan
2 sin 2 2 2sin
x x x x
I C I C
xx
| 1/15
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

 Quảng Thuận – Ba Đồn – QB
Nguyên hàm của hàm số lượng giác 2020 MỤC LỤC
Chuû ñeà ④ NGUYEÂN HAØM cuûa haøm soá Löôïng giaùc ........................................................... 1
I. BẢNG NGUYÊN HÀM CỦA MỘT SỐ THƯỜNG GẶP ........ 1 =I h ttp II. CÁC DẠNG TOÁN s:// ........ 1 =I lu dx ye
1. Dạng 1. I  
................................................................................................ 1
sin  x asin x bn th
a. Phương pháp tính ............................................................................................................................................. 1 it
b. Chú ý ................................................................................................................................................................. 2 rac
c. Ví dụ áp dụng .................................................................................................................................................... 2 n gh
2. Dạng 2. I  tan
 x atanx bdx ........................................................................................... 3 ie
a. Phương pháp tính ............................................................................................................................................. 3 m.vn
b. Chú ý ................................................................................................................................................................. 4
c. Ví dụ áp dụng .................................................................................................................................................... 4 dx
3. Dạng 3. I  
........................................................................................................... 6
asin x b cos x
a. Phương pháp tính ............................................................................................................................................. 6
b. Ví dụ áp dụng .................................................................................................................................................... 6 dx
4. Dạng 4. I  
.................................................................................................... 7
asin x bcos x c
a. Phương pháp tính ............................................................................................................................................. 7 ht b. Ví dụ áp dụng tp
.................................................................................................................................................... 7 s://www dx
5. Dạng 5. I  
............................................................................ 8 2 2 . a sin x  .
b sin x cos x  . c cos x
a. Phương pháp tính ............................................................................................................................................. 8 .fa
b. Ví dụ áp dụng .................................................................................................................................................... 8 ceboo
a sin x b cos x 6. Dạng 6. 1 1 I dx
.................................................................................................. 9 k.com
a sin x b cos x 2 2
a. Phương pháp tính ............................................................................................................................................. 9 /v
b. Ví dụ áp dụng .................................................................................................................................................... 9 iet
c. Chú ý ............................................................................................................................................................... 10 gold
7. Dạng 7. Biến đổi đưa về nguyên hàm cơ bản hoặc 6 dạng ở trên.................................................. 12
Ví dụ áp dụng ...................................................................................................................................................... 12 0
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” Chuû ñeà ④
NGUYEÂN HAØM cuûa haøm soá
Löôïng giaùc
I. BẢNG NGUYÊN HÀM CỦA MỘT SỐ THƯỜNG GẶP m.vn =I ie
Nguyên hàm của hàm số
Nguyên hàm của hàm số
Nguyên hàm của hàm số hợp gh sơ cấp
hợp u ux
u ax ;b a  0 ncar       1 it sin xdx cos x C  sin udu cosu C  sin
 axbdx   cosaxbC a th n 1
cos xdx  sin x C
cosudu  sin u C  cos
 axbdx  sinaxb ye C a lu 1 s:// tan .
x dx   ln cos x C  tan .
u du  ln cosu C
tan ax bdx   ln cosax b  Ca ttp hax b 1 cot
dx  ln sin ax b  C  cot .
x dx  ln sin x C  cot .
u du ln sin u Ca 1 1 1 1
dx   cot x C
du   cot u C
dx   cot ax b C  2 2 sin x 2 sin u
sin ax b   a 1 1 1   1  
dx  tan ax b Cdx tan x Cdu tan u C  2 2 cos x 2 cos u
cos ax b   a gold 1 x 1 u dx 1 ax b iet dx  ln tan  Cdu  ln tan  C   tgC
sin ax b ln /v sin x 2 sin u 2 a 2 1  u        dx 1 ax b    k.com 1  x   du ln tan    C ln tan C dx  ln tan    
C cosu  2 4 
cosax ba 2 4 cos x  2 4  ceboo .fa II. CÁC DẠNG TOÁN =I s://www dx
tp 1. Dạng 1. I   ht
sin  x asin x b
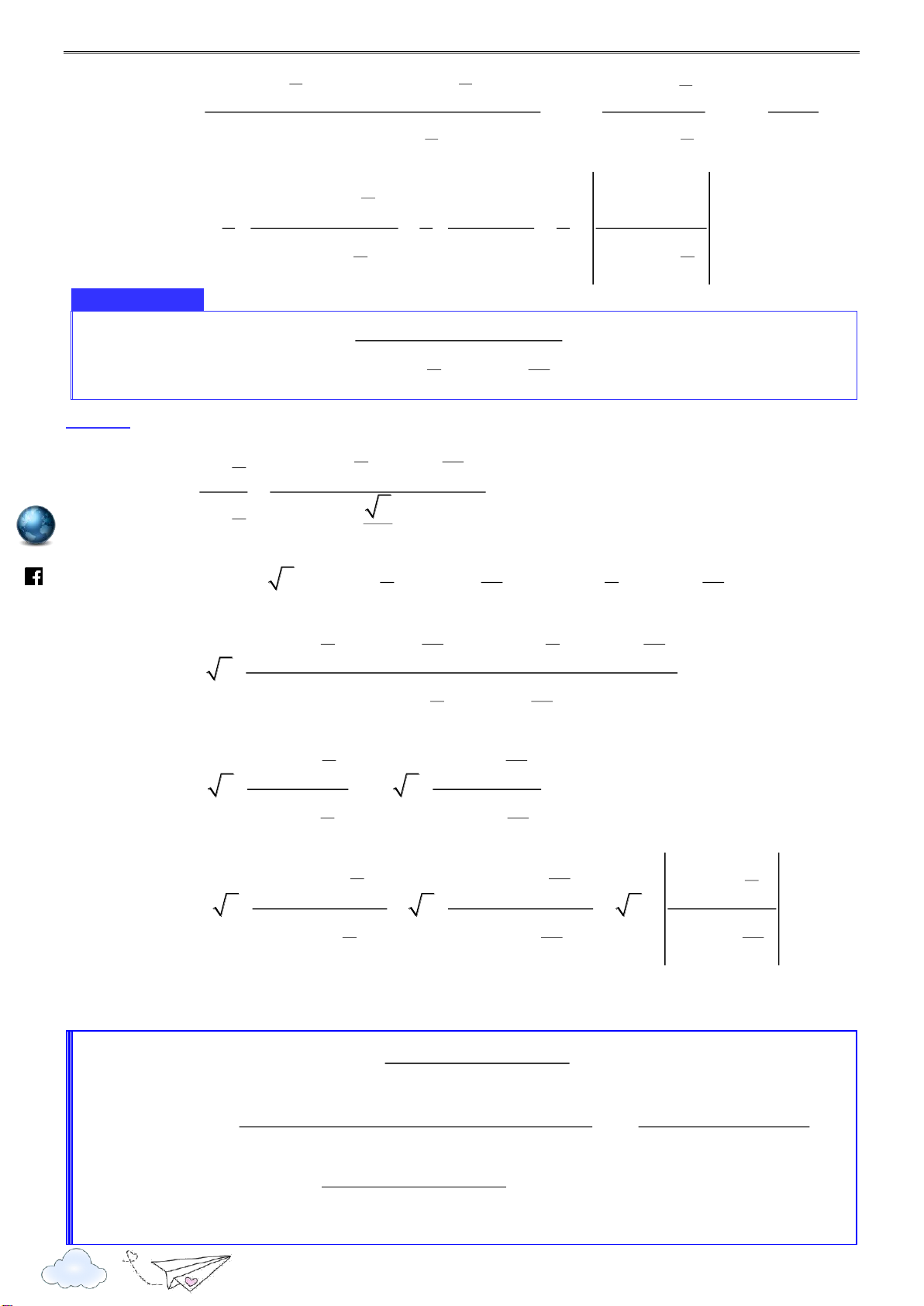
a. Phương pháp tính Dùng đồng nhất thức:
sin a b
sin x a  x b sin 
x acosx bcosx asinx b 1   
sin a b
sin a b sin a b Từ đó suy ra: 1
sin  x acos x b  cos x asin x bI dx
sin a b
sin  x asin x b 1
 Quảng Thuận – Ba Đồn – QB
Nguyên hàm của hàm số lượng giác 2020 1
cosx b cosx a    dx
sin a b sin 
x b sinx a  1   x b
x a   C   sin a b ln sin  ln sin  b. Chú ý
Với cách này, ta có thể tìm được các nguyên hàm:
sin a bh dx •   ttp J
bằng cách dùng đồng nhất thức 1
cos x acos x b sin a bs:// dx cosa blu • K  
bằng cách dùng đồng nhất thức 1  ye
sin  x acos x b cosa bn th
c. Ví dụ áp dụng it Ví dụ 1 ra dx cn
Tìm nguyên hàm sau đây: Igh    sin xsin x    ie  6  m.vn Giải       sin sin x   x     6           Ta có: 6 1    2 sin x
cos x  cos x  sin x      1     6   6  sin  6 2             sin x
cos x  cos x  sin x      cos x        6   6   cos x  6  Từ đó: I  2 dx  2   dx       sin x     ht sin xsin x  sin x      tp 6  6       s://www          xd sin x d sin   6  sin x  2  2  2ln  C   .fa sin x       sin x  sin x  ceboo      6   6  Ví dụ 2 k.com dx
Tìm nguyên hàm sau đây: I   /v    iet cos3x cos 3x     6 gold   Giải Ta có:       sin 3x   3 sin x     6 6           1    2 sin 3x
cos3x  cos 3x  sin 3x      1     6   6  sin  6 2 Từ đó: 2
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”            sin 3x
cos 3x  cos 3x  sin 3x      sin 3x       6   6    6  sin 3x I  2 dx  2 dx  2 dx          cos 3x
cos 3x cos 3x  cos 3x       6   6      d cos 3x     2   6  2 d cos3x 2 cos3x     ln  C   m.vn 3    3 cos3x 3    ie cos 3x  cos 3x       6   6  gh nc Ví dụ 3 ar dx it
Tìm nguyên hàm sau đây: I         th   n sin x cos x      3   12  ye lu Giải s://         cos x   x      ttp cos  3   12  h Ta có: 4 1    2 cos 4 2               2 cos x  cos x   sin x  sin x             3   12   3   12              cos x  cos x   sin x  sin x           3   12   3   12  Từ đó: I  2 dx  gold       sin x  cos x  iet      3   12  /v       cos x  sin x      k.com  3   12   2 dx  2 dx         ceboo sin x  cos x      .fa  3   12             d sin x d cos x        sin x      3     12    3      s://www 2 2 2 ln C            tp sin x  cos x  cos x  ht        3   12   12 
2. Dạng 2. I  tan
 x atanx bdx
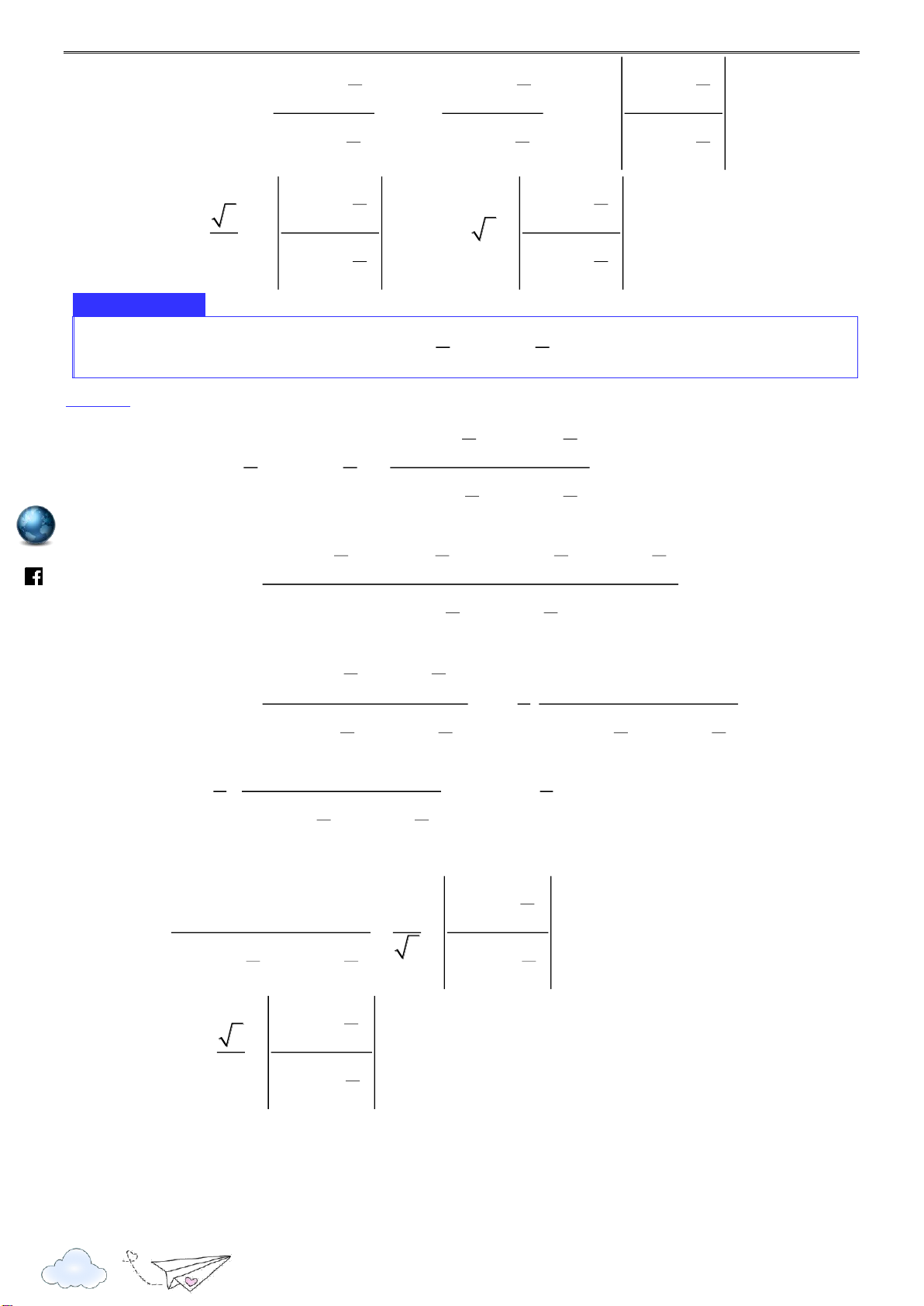
a. Phương pháp tính
sin x a sin x b
Ta có: tan  x a tan  x b    
 cosxacosxb
sin  x asin  x b  cos x acos x b
cos a b      x a x b 1
x a x b 1 cos cos cos cos dx
Từ đó: I  cosa b   x a x b 1 cos cos
Đến đây ta gặp bài toán tìm nguyên hàm ở Dạng 1. 3
 Quảng Thuận – Ba Đồn – QB
Nguyên hàm của hàm số lượng giác 2020 b. Chú ý
Với cách này, ta có thể tính được các nguyên hàm: • J  cot
 x acotx bdx • K  tan
 x atanx bdx
c. Ví dụ áp dụng Ví dụ 4          h
Tìm nguyên hàm sau đây: I cot x cot x dx      ttp  3   6  s:// Giải lu Ta có: ye       n cos x  cos x      th        3   6  Ta có: cot x  cot x   it               r 3 6 a sin x  sin x      c  3   6 ngh ie             m.vn cos x  cos x   sin x  sin x           3   6   3   6   1       sin x  sin x       3   6        cos x   x       3   6  3 1  1 . 1       2       sin x  sin x  sin x  sin x           3   6   3   6  ht 3 1 3 Từ đó: I dx dx
I x C tp   1       s://www 2 2 sin x  sin x       3   6  dx Tính I  .fa  1       ceboo sin x  sin x       3   6  k.com         sin sin x   x       3   6 6  /v Ta có: 1    1 iet sin gold 6 2               2 sin x  cos x   cos x  sin x             3   6   3   6              sin x  cos x   cos x  sin x           3   6   3   6  Từ đó: I  2 dx  1       sin x  sin x       3   6  4
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”          cos x  cos x  sin x         6   3   6   2 dx  2 dx  2ln  C            sin x  sin x  sin x         6   3   3        sin x  sin x      3  6   6  Suy ra: I  .2ln
x C  3 ln  x C m.vn 2       ie sin x  sin x          gh 3 3 nc Ví dụ 5 ar       it
Tìm nguyên hàm sau đây: K  tan x  cot x dx      th  3   6  n ye Giải lu       sin x  cos x s://            3   6     ttp Ta có: tan x cot x              h 3 6  cos x  sin x       3   6              sin x  cos x   cos x  sin x           3   6   3   6   1       cos x  sin x       3   6        sin x   x      gold  3   6  1 1     iet 1 . 1             /v 2 cos x  sin x  cos x  sin x           3   6   3   6  k.com 1 1 1 Từ đó: K dx dx
K x C   1 2       2 ceboo cos x  sin x      .fa  3   6 
Đến đây, bằng cách tính ở Dạng 1, ta tính được:    sin x    s://www dx 2  6  tp K   ln  C  ht 1          3 cos x  sin x  cos x         3   6   3     sin x    3  6  Suy ra: K  ln  x C 3    cos x     3  5
 Quảng Thuận – Ba Đồn – QB
Nguyên hàm của hàm số lượng giác 2020 dx
3. Dạng 3. I  
asin x b cos x
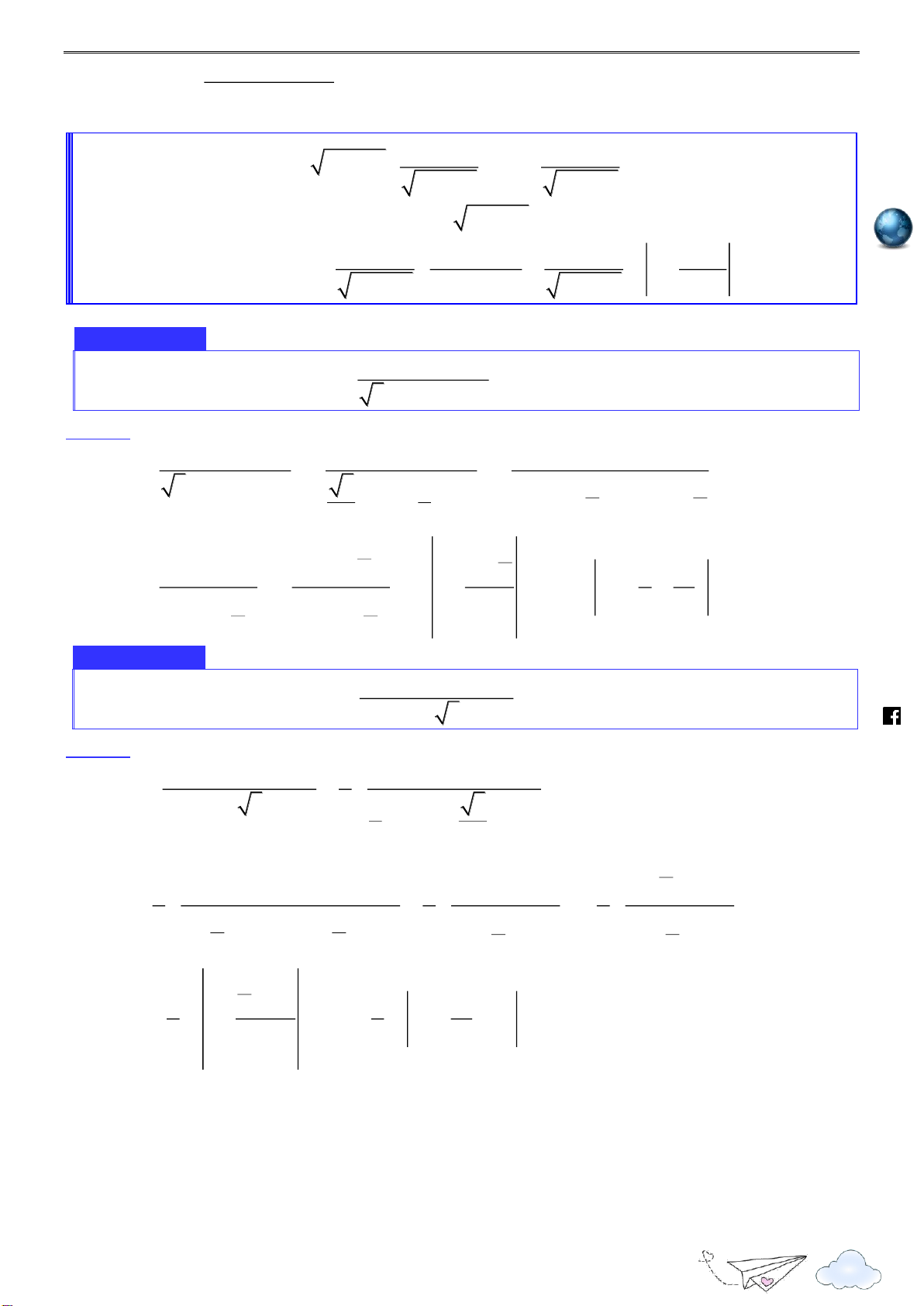
a. Phương pháp tính a b  Có: 2 2
asin x bcos x a b  sin x  cos x  2 2 2 2  a b a b  2 2
asin x bcos x a b sinx   1 dx 1 x   hI   ln tan  C ttp  2 2  sin  x a b   2 2  2 a b s://
b. Ví dụ áp dụng lu Ví dụ 6 ye 2 n
Tìm nguyên hàm sau đây:  thdx I
3 sin x  cos x it ra Giải cn 2dx dx dx gh I          ie 3 sin x cos x 3 1  sin x cos  cos xsin m.vn sin x cos x 6 6 2 2     d x    x dx  6   x   6    ln tan  C  ln tan   C           2  2 12  sin x  sin x       6   6  Ví dụ 7 Tìm nguyên hàm sau đây:   dx J
cos 2x  3 sin 2x ht  Giải tps://www dx 1 dx J    
cos 2x  3 sin 2x 2 1 3 cos 2x  sin 2x 2 2 .fa   ceboo  d  2x   1 dx 1 dx 1  6      k.com    2   2    4    sin
cos 2x  cos sin 2x sin  2x sin  2x     6 6  6   6  /viet  gold  2x 1 1    6   ln tan  C   ln tan  x C   4 2 4 12  6
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” dx
4. Dạng 4. I  
asin x bcos x c
a. Phương pháp tính  2dt dx   2 1  t  2t sin x  2  m.vn x  Đặt 1 t   ie tan t  2 2 1  tgh cos x n 2   c 1 t ar 2t it tan x  2 th  1  t n
b. Ví dụ áp dụng ye Ví dụ 8 lu dx s://
Tìm nguyên hàm sau đây: I  
3cos x  5sin x  3 ttp h Giải  2dt dx   2 1  tx  2t Đặt tan  t  si  n x  2 2 1  t  2  1  t cos x   2  1  t gold 2dt iet/v 2 2dt 2dt  Từ đó: 1 t I       2 2 2 1  t 2t
3  3t  10t  3  3t 10t  6   k.com 3. 5 3 2 2 1  t 1  t
1 d 5t  3 ceboo 1 1 x
 ln 5t  3  C  ln 5tan  3  C  .fa 5 5t  3 5 5 2 Ví dụ 9 s://www 2dx tp
Tìm nguyên hàm sau đây: J   ht
2sin x  cos x 1  Giải  2dt dx   2 1  tx  2t Đặt tan  t  si  n x  2 2 1  t  2  1  t cos x   2  1  t 7
 Quảng Thuận – Ba Đồn – QB
Nguyên hàm của hàm số lượng giác 2020 2dt 2. 2 4dt 4dt dt  Từ đó: 1 t J     2     2 2 2 2 2t 1  t
4t 1  t  1  t 2t  4t t t  2 2.  1 2 2 1  t 1  t 1 1  x x  
dt  ln t  ln t  2  C  ln tan  ln tan  2  C    t t  2  2 2 Ví dụ 10 h dx ttp
Tìm nguyên hàm sau đây: K   sin x  tan x s:// Giải lu ye  2dt dx n  2 1  t thit x  2t r Đặt tan  t  si  n x a 2 c 2 1  t ngh  2t tan x ie  2  1  t m.vn 2dt 2 2  1 1 t 1 dt 1  Từ đó: 1 t K   dt   tdt     2t 2t 2 t 2 t 2  2 2 1  t 1  t 1 1 1 x 1 x 2 2
 ln t t C  ln tan  tan  C 2 4 2 2 4 2 dx
5. Dạng 5. I   2 2 . a sin x  .
b sin x cos x  . c cos x ht
a. Phương pháp tính tps://www dx I    2 a x b x c 2 tan tan .cos x .fa dx dt
Đặt tan x t
dt . Suy ra I   2 2 ceboo cos x
at bt c
b. Ví dụ áp dụng k.com Ví dụ 11 /v
Tìm nguyên hàm sau đây:   dx I 2 2 iet
3sin x  2sin x cos x  cos x gold  Giải dx dx • I     2 2 x x x x  2 xx   2 3sin 2sin cos cos 3tan 2 tan 1 cos x dx
Đặt tan x t   dt 2 cos x dt dtI     2 3t  2t 1 t   1 3t   1 8
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” 1  1 3  1 dt
1 d 3t   1   dt      
4  t 1 3t 1 4 t 1 4 3t 1 1 t 1 1 tan x 1  ln  C  ln  C 4 3t 1 4 3tan x  1 Ví dụ 12 Tìm nguyên hàm sau đây:   dx J m.vn 2 2
sin x  2sin x cos x  2cos x ie Giải gh nc dx a
Đặt tan x t   dt r 2 cos x it th dt d t   1 1 t 1  3 nJ    ln  C   2 ye t  2t  2    t  2   2 2 3 t 1 3 1 3 lu s:// 1 tan x 1  3  ln  C ttp 2 3 tan x 1  3 h
a sin x b cos x 6. Dạng 6. 1 1 I dx
a sin x b cos x 2 2
a. Phương pháp tính Ta tìm , A B sao cho:
a sin x b cos x A a sin x b cos x B a cos x b sin x 1 1  2 2   2 2  gold
b. Ví dụ áp dụng iet Ví dụ 13 /v
4sin x  3cos x
Tìm nguyên hàm sau đây: I dx  k.com sin x  2cos x Giải ceboo Ta tìm , A B sao cho: .fa
4sin x  3cos x Asin x  2cos x  Bcos x  2sin x A B  A
 4sin x  3cos x   A  2Bsin x  2A B 2 4 2    s://www cos x        tp 2A B 3 B 1 ht
2sin x  2cos x  cos x  2sin x Từ đó: I dx  sin x  2cos x
d sin x  2cos x  2 dx
 2x  ln sin x  2cos x C   sin x  2cos x Ví dụ 14
3cos x  2sin x
Tìm nguyên hàm sau đây: J dx  cos x  4sin x Giải Ta tìm , A B sao cho:
3cos x  2sin x Acos x  4sin x  Bsin x  4cos x 9
 Quảng Thuận – Ba Đồn – QB
Nguyên hàm của hàm số lượng giác 2020
 3cos x  2sin x   A 4Bcos x   4
A Bsin x  11 A
A  4B  3  17    
4A B  2 10 B    17 11  x x 10 cos 4sin 
sin x  4cosx Từ đó: 17 17 J dx http cos x  4sin x s:// 11
10 d cos x  4sin x 11 10  dx   x
ln cos x  4sin x C   lu 17 17 cos x  4sin x 17 17 ye c. Chú ý n
a sin x b cos x th 1. Nếu gặp 1 1 I dx  ta vẫn tìm , A B sao cho: 2 it
a sin x b cosx 2 2  rac      n a sin x b cos x A a sin x b cos x
B a cos x b sin x 1 1  2 2   2 2  gh
a sin x b cos x c ie 2. Nếu gặp 1 1 1 I dx  ta tìm , A B sao cho: m.vn
a sin x b cos x c 2 2 2
a sin x b cos x c A a sin x b cos x c
B a cos x b sin x C 1 1 1  2 2 2   2 2  Ví dụ 15 8cos x
Tìm nguyên hàm sau đây: I    dx
3 sin x  cos x2  Giải Ta tìm , A B sao cho: ht tp
8cos x A 3sin x  cos x  B 3cos x  sin x s://www
 8cos x  A 3  Bsin x  AB 3cosx .fa
A 3  B  0 A  2  ceboo    
A B 3  8 B  2 3 k.com
2 3sin x  cos x  2 3 3cos x  sin x Từ đó: I dx  /v
3 sin x  cos x iet  2 gold
d  3sin x  cos x dx  2 3  2  2 3  I   C  
3 sin x  cos x    2 2 1 3 sin x  cos 3 sin cos x x x dx 1 dx 1 dx Tìm I       1
3 sin x  cos x 2 3 1 2    sin x cos  cos xsin sin x cos x 6 6 2 2 10
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”     d x    x  1 dx 1  6  1 1  x   6    ln tan  C  ln tan   C     2    2    2 2 2  2 12  sin x  sin x       6   6   x   2 3 Vậy I  ln tan    C    2 12 
3 sin x  cos x m.vn Ví dụ 16 ie
8sin x  cos x  5 gh
Tìm nguyên hàm sau đây: J dxnc
2sin x  cos x 1 ar it Giải th Ta tìm , A , B C sao cho: n
8sin x  cos x  5  A2sin x  cos x  
1  B2cos x  sin x  ye C lu
 8sin x  cos x  5  2ABsin x  A 2Bcos x AC s://
2A B  8 A  3 ttp   h
 A  2B 1 B  2   A C  5 C  2  
32sin x  cos x  
1  22cos x  sin x  2 Từ đó: J dx
2sin x  cos x 1 2cos x  sin x dx  3 dx  2 dx  2  
2sin x  cos x 1
2sin x  cos x 1
 3x  2ln 2sin x  cos x 1  2J 1 gold dx iet Tìm J   /v 1
2sin x  cos x 1  2dt k.com dx   2 1  t  ceboo x  2t Đặt tan  t  si  n x  .fa 2 2 1  t  2  1  t cos x   2   s://www 1 t tp 2dt ht 2 dt dt 1  1 1 1 t   J      dt     1   2 2 2t 1  t t  2t t t  2 2  t t  2  2.  1 2 2 1  t 1  t x tan 1 t 1 2  ln  C  ln  C 2 t  2 2 x tan  2 2 x tan Vậy: 2
J  3x  2ln 2sin x  cos x 1  ln  C x tan  2 2 11
 Quảng Thuận – Ba Đồn – QB
Nguyên hàm của hàm số lượng giác 2020
7. Dạng 7. Biến đổi đưa về nguyên hàm cơ bản hoặc 6 dạng ở trên
Ví dụ áp dụng Ví dụ 17
Tìm nguyên hàm sau đây: I  cos3x cos 4  xdx Giải 1
I  cos3x cos 4xdx  
cosx cos7xdx 2 h 1 1 1 1 ttp  cos xdx  cos7xdx  sin x  sin 7x C   2 2 2 14 s:// Ví dụ 18 lu ye
Tìm nguyên hàm sau đây: I  cos xsin 2x cos3  xdx n th Giải it 1 ra
I  cos xsin 2x cos3xdx  sin 2x  
cos2x  cos4xdx c 2 n gh 1 1 
sin 2x cos 2xdx  sin 2xcos 4xdx ie   2 2 m.vn 1 1  sin 2xd
sin2x  sin2x sin6xdx 4 4 1 1 1 2
 sin 2x  cos2x  cos6x C 8 8 24 Ví dụ 19      
Tìm nguyên hàm sau đây: I  tan x tan  x tan  x dx       3   3   Giải ht       tp sin xsin  x sin  x     s://www        3   3  Ta có: tan x tan  x tan  x       3   3        cos x cos  x cos  x      3   3  .fa ceboo  2   1  2
sin x cos 2x  cos
sin x 1  2sin x       3   2    k.com  2   1  2
cos x cos 2x  cos
cos x 2cos x 1       3   2  /viet sin x 2 3  4sin x 3
3sin x  4sin x sin 3x gold    cos x 2 4cos x  3 3
4cos x  3cos x cos3x sin 3x 1 d cos3x 1 Từ đó: I dx  
  ln cos3x C   cos3x 3 cos3x 3 Ví dụ 20 Tìm nguyên hàm sau đây: 3
I  sin xsin 3xdx   Giải
3sin x  sin 3x Ta có: 3 3
sin 3x  3sin x  4sin x  sin x  4 12
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
3sin x  4sin 3x 3
 sin xsin3x  .sin 3x 4 3 1 3 1 2
 sin xsin3x  sin 3x  cos2x  cos4x  1 cos6x 4 4 8 8 3 3 1 1 
cos 2x  cos 4x  cos6x  8 8 8 8   m.vn 3 3 1 1 Từ đó: I
cos 2x  cos 4x  cos 6x dx   ie  8 8 8 8  gh n 3 3 1 1 c  sin 2x  sin 4x  sin 6x x C ar 16 32 48 8 it Ví dụ 21 th n
Tìm nguyên hàm sau đây: I   3 3
sin x cos 3x  cos x sin 3xdx yelu Giải
3sin x  sin 3x s:// Ta có: 3 sin x  4 ttp h
3cos x  cos 3x 3 cos x  4
3sin x  sin 3x
3cos x  cos 3x Suy ra: 3 3
sin x cos 3x  cos x sin 3x  .cos 3x  .sin 3x 4 4 3 1 3 1
 sin x cos 3x  sin 3x cos 3x  cos x sin 3x  cos 3x sin 3x 4 4 4 4 3 3 3  sin   2
x  sin 4x  sin    2
x sin 4x   sin 2x  8 8 4 3 3 gold Vậy I   sin 2xdx  cos 2x C  iet 4 8 /v Ví dụ 22
Tìm nguyên hàm sau đây:   dx I k.com 3 sin x cos x Giải ceboo dx dx 1 1 dx 1 dx .fa I    . .       2 1 tan x 3 4 2 2  2 sin x cos x tan x cos x
tan x cos x cos x tan x cos x Đặ dx
t tan x t   dt 2 cos x s://www 2 tp t t dt  1 1 I dt tdt     2 2
t  ln t C  tan x  ln tan x C ht t t 2 2 Ví dụ 23
Tìm nguyên hàm sau đây:   dx I 4 sin x cos x Giải
Đặt sin x t  cos xdx dt 4 4 2 dt 1 t t 1 t dtI   dt dt      4 t  2 1 t  4 t  2 1 t  4 2 t 1 t dt dt dt 1  1 1 t 1 3      t   ln  C    4 2 t tt   1 t   1 3 t 2 t 1 13
 Quảng Thuận – Ba Đồn – QB
Nguyên hàm của hàm số lượng giác 2020 1 1 1 sin x 1     ln  C 3 3sin x sin x 2 sin x 1 Ví dụ 24 sin 3 sin 4
Tìm nguyên hàm sau đây:   x x I dx tan x  tan 2x Giải sin 3x sin 4x sin 3x sin 4x I dx
dx  sin 4x cos 2x cos xdx    tan x  tan 2x sin 3x h ttp cos x cos 2x 1 1 1 s://
 sin6x sin2xcos xdx  sin6xcos xdx  sin2xcos xdx   2 2 2 lu 1 1 ye
 sin7x sin5xdx  sin3x sin xdx 4 4 n th 1 1 1 1   cos 7x  cos 5x  cos 3x  cos x C it 28 20 12 4 rac Ví dụ 25 n gh dx
Tìm nguyên hàm sau đây: I   3 ie sin x m.vn Giải  1 u   cos x     Đặ sin du dx x t 2    sin x dxdv  
v  cot x 2  sin x cot x cot . x cos x cot xI    dx    I  2 1 sin x sin x sin x 2 2 cos x 1 sin x dx dx x Tính I dx dx  
I  ln tan  C     1 3 3 3 sin x sin x sin x sin x 2 ht cot x cot x x tp  I    I  
I  ln tan  C 1 s://www sin x sin x 2 x cot x 1 x cot x  2I  ln tan 
C I  ln tan   C 2 sin x 2 2 2sin x .fa ceboo k.com /vietgold 14
Document Outline

  • 1. Dạng 1.
    • a. Phương pháp tính
    • b. Chú ý
    • c. Ví dụ áp dụng
  • 2. Dạng 2.
    • a. Phương pháp tính
    • b. Chú ý
    • c. Ví dụ áp dụng
  • 3. Dạng 3.
    • a. Phương pháp tính
    • b. Ví dụ áp dụng
  • 4. Dạng 4.
    • a. Phương pháp tính
    • b. Ví dụ áp dụng
  • 5. Dạng 5.
    • a. Phương pháp tính
    • b. Ví dụ áp dụng
  • 6. Dạng 6.
    • a. Phương pháp tính
    • b. Ví dụ áp dụng
    • c. Chú ý
  • 7. Dạng 7. Biến đổi đưa về nguyên hàm cơ bản hoặc 6 dạng ở trên
    • Ví dụ áp dụng