Nguyên hàm, tích phân chống casio – phân thức và đổi biến – Mẫn Ngọc Quang Toán 12

Nguyên hàm, tích phân chống casio – phân thức và đổi biến – Mẫn Ngọc Quang Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

80 40 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

24 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page 1
0989 850 625
Daïng 1: ÑOÀNG NHAÁT HEÄ SOÁ - MAÃU COÙ DAÏNG TÍCH
Phương pháp hệ số bất định: Khi mẫu có thể phân tích thành nhân tử.
Câu 1: Cho
1
( 2)( 5)( 4) ( 2) ( 5) ( 4)
A B C
x x x x x x
Khi đó tổng
S A B C
bằng:
A.
1
18
B.
0
C.
1
14
D.
1
63
Giải:
ĐÁP ÁN B.
Bình luận: Bài toán này chúng ta sẽ tách phân số ở mẫu số có tích thành các phân số đơn giản hơn. Để
làm đươc điều này ta dùng phương pháp đồng nhất hệ số .
Câu 2: Cho
1
( 3)( 3) 3 3
A B C
x x x x x x
. Khi đó
2S A B C
bằng:
A.
1
18
B. 0 C.
1
18
D.
2
9
Giải:
1
( 3)( 3) 3 3
A B C
x x x x x x
1 ( 3)( 3) ( 3) ( 3)A x x Bx x Cx x
1
) 0 9 1
9
x A A
1
) 3 18 1
18
x B B
1
) 3 18 1
18
2
2
9
x C C
A B C
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page 2
0989 850 625
ĐÁP ÁN D
Câu 3: Cho các hằng số
,,A B C R
thỏa mãn:
32
2
.
3 2 1 2
A B C
x x x x x x
Khi đó
..P ABC
bằng:
A.
2
B.
1
2
C.
1
D.
2
Giải:
( 1)( 2) ( 2) ( 1) 2
) 0 1
) 1 2
) 2 1
A x x Bx x Cx x
xA
xB
xC
2ABC
ĐÁP ÁN D
Câu 4. Cho
2
2 3 1 1
.
21
21
x
AB
x x C
xx



. Khi đó tổng
S A B C
bằng:
A.
1
3
B.
1
3
C.
2
3
D.
2
3
Giải:
2
23
21
x
xx

=
23
(2 1)( 1)
x
xx

=
4 1 5 1
..
3 2 1 3 1xx





4 5 2
, , 1
3 3 3
A B C S A B C

ĐÁP ÁN D
Daïng 2: NHAÛY LAÀU
Câu 6: Nguyên hàm của hàm
5
5
1
1
x
I dx
xx
có dạng
55
ln ln 1a x b x C


Khi đó
10S a b
bằng
A. 1 B. 2 C. 0 D.3
Giải:





5 4 5 5
5
55
5 5 5 5
11
1 1 1 2
55
1
11
x x dx x d x
I d x
xx
x x x x
55
1
ln 2ln 1
5
x x C


Suy ra :
1
,2
5
ab
10 0ab
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page 3
0989 850 625
ĐÁP ÁN C
Câu 7: Cho
22
53
ln
12
5 6 2 1


x a x b
I dx C
xx
x x x x
Khi đó
2P a b
bằng:
A. 0 B. 1 C. 2 D. 3
Giải:
Ta co:
22
0
2 2 2
22
1
5 6 2 1
23
2 1 5 6
5 6 2 1
1
x x x x
dx dx dx dx
I dx
xx
x x x x
x x x x
x

2
1 1 1 3
1 ln
3 2 1 2
x
I x dx dx C
x x x x





Suy ra:
1, 3 2 1a b P a b
ĐÁP ÁN B
Câu 8. Cho
2
2
32
1
ln ln 1
1
a
I dx b x c x
x
xx
Khi đó
S a b c
bằng:
A. -2 B. -1 C. 0 D.
1
2
Giải:
2 2 2 2
33
3 2 2 2
11
1 1 1
1 1 1
x x x x
I dx dx
xx
x x x x x x

32
11
1
x
dx
x
xx



2
2
3 2 2
1
1 1 1 1 1
ln ln 1
22
12
dx
dx x x
x
x x x




11
, 1, 1
22
a b c S
ĐÁP ÁN B
Câu 9. Cho
2
2
11
ln 1 ln
1
x
I dx a x b x c
x
xx
. Khi đó
2P a b c
bằng:
A. 2 B. -2 C. 1 D. 0
Giải:
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page 4
0989 850 625
2
2
2 2 2
1
1 1 1 1
1
1
11
x x x
x
I dx dx dx
x
xx
x x x x x





22
1 1 1 1 2 1 1
1 1 1
dx
x x x x x
xx






1
2ln 1 lnxx
x
2, 1, 0 0a b c P
ĐÁP ÁN D.
Câu 10: Tnh tch phân
2
2
1
1
ln
1
I dt a b
xx
. Khi đó
2S a b
bằng:
A.
2
3
B.
2
3
C. 1 D.
1
Giải:
2 2 2 2
2 2 2
1 1 1 1
1 1 1 1
1
1 1 1
xx
I dx dx dx dx
xx
x x x x x

Suy ra
22
21
11
22
1 1 4 1
1 1 ln 1 ln
11
1 1 3 6
x
I dx x dx x x
x x x






41
,1
36
a b S
ĐÁP ÁN C
Câu 11: Nguyên hàm của có dạng
22
2
1
ln 1 ln
2
a
F x x bx x c C
x
.
Khi đó
4
2P a b c b
bằng
A. 1 B.
1
2
C.
1
2
D. 0
Giải:
Ta có:
Vậy
2
3 2 2
11
( ) ln ln( 1)
2
12
dx dx xdx
f x dx x x C
x
x x x
1
, 0, 1 0
2
a b c P
ĐÁP ÁN D
Câu 12: Cho
1
0
ln
1
xdx
I a b c
x
. Biết b + c = 1
35
1
fx
xx
22
3 5 3
3 2 2
1
1 1 1
11
xx
fx
x x x
x x x x


22
3 3 2
2
1
1 1 1
1
1
xx
x
x x x x
xx

Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page 5
0989 850 625
Với
,3bc
. Khi đó
2
2016
42
ac
Sb
bằng:
A. 0 B. -1 C.
1
4
D.
1
2
Giải:
11
1
0
00
( 1) 1 1
1 ln( 1) 1 ln2
11
x
I dx dx x x
xx








2
2016
1
1; 1; 2
4 2 4
ac
a b c S b
ĐÁP ÁN C
Câu 13: Cho
1
4
2
2
0
1
ln
2
1
x dx
I a b
x
. Khi đó
24 12
3
b
Sa
bằng:
A. 0 B. -1 C. 1 D.
1
2
Giải:
13
, 3 24 12 0
24 3
b
a b S a
ĐÁP ÁN A
Daïng 3: MAÃU SOÁ COÙ CHÖÙA BIEÅU THÖÙC BÌNH PHÖÔNG
Câu 14: Cho
2
32
3 3 5
12
32
1



x x A B C
y
xx
xx
x
. Khi đó
S A B C
bằng:
A. 1 B.
2
3
C.
5
8
D.
5
8
Giải:
1 1 1
44
2 2 2
2
2 2 2
0 0 0
1 1 1
1
1 1 1
xx
I dx dx x dx
x x x




1
3
2
2
0
13 1
ln 1 ln3
3 24 2
x
xx



Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page 6
0989 850 625
2
32
22
3 3 5
12
32
1
( 2) ( 1)( 2) ( 1) 3 3 5
11
)1
3
11
)2
9



x x A B C
xx
xx
x
A x B x x C x x x
xA
xC
Tính tổng các hệ số không có x , rồi đồng nhất 2 vế ta có
22
16
) 2 5
9
11 16 11
1 2 9( 1) 9( 2)
1 3 1

A B C B
A B C
x x x x
xx
2
3
A B C
ĐÁP ÁN B
Câu 14. Nguyên hàm của
2
3
3 3 5
32


xx
y
xx
có dạng
ln 1 ln
1
a
f x b x c x d C
x
Biết
,0ac
. Chọn nhận định đúng
A.
0
3
a
b
B.
3a b c d
C.
ab cd
D.
3bc
Giải:
2
2
3
3 3 5 11 16 11
3 2 9( 1) 9( 2)
31






xx
dx dx
x x x x
x
11 16 11
ln 1 ln 2
3( 1) 9 9
x x C
x
11 16 11
, , , 2
3 9 9
a b c d
ĐÁP ÁN D
Câu 15. Cho
3 2 2
31
2 2 5
4 28 65 50
25
x A B C
xx
x x x
x

Khi đó
2S A B C
bằng
A. 10 B. 13 C. -13 D. -10
Giải:
Ta phân tích:
22
31
2 2 5
2 2 5 2 5
x A B C
xx
x x x

2
3 1 2 5 2 2 5 2x A x B x x C x
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page 7
0989 850 625
Cho x =
5
2; ;0
2

ta được:
5
10
13
A
B
C

13S
ĐÁP ÁN C
Câu 16: Cho A, B, C thỏa mãn
22
1
12
1 2 2
A B C
xx
x x x

Tính S = A + B +2C
A. 2 B. 1 C. 0 D. -1
Gợi ý:
Đồng nhất ta được
1, 1A B C
Daïng 4: BAÄC TÖÛ SOÁ LÔÙN HÔN MAÃU
Chúng ta thường thực hiện phép chia cho đa thức rồi tiếp tục tiến hành với phần dư.
Câu 17: Cho


2
2
1
1
ln
1
xx
ab
x
.
Chọn mệnh đề đúng
A.
2ab
B.
2
2
20
3
a b b
C.
ab
D.
ab
Giải:
33
,
22
a b a b
ĐÁP ÁN C
Câu 18. Tìm hàm số
2
( ) ln 1f x x ax bx c
biết

2
4 4 3
'
21
xx
fx
x
và
01f
. Khi đó
3
2S a b c
bằng
A. 0 B. 1 C.
2
3
D. 4
Giải:
Ta có
2
4 4 3
()
21
xx
f x dx
x

=
2
2
2 1 ln 2 1
21
x dx x x x c
x



2
2 2 2 2
22
1 1 1 1
1
1 1 1
ln 1
1 1 1 2
x x x
dx x dx xdx dx x
x x x







1 3 3
2 ln3 ln2 ln
2 2 2
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page 8
0989 850 625
Mà f(0) = 1
2
1 ( ) ln 2 1 1c f x x x x
3
1, 2, 1 2 0a b c S a b c
ĐÁP ÁN A
Câu 19. Cho
32
1
2
0
2
33
ln 1 .
23

x x x
I dx a b
xx
Khi đó
2 ab
bằng:
A. 2 B. 3 C.
1
3
D.
2
3
Giải:.
Ta co
3 2 2
3 3 1 2 3 .x x x x x x
Đt
2
1
2 3 1 .
2
t x x dt x dx
Đổi cận
0 3, 1 6x t x t
Khi đo
6
2
3
16
2
t
I dt
t
=
6
6
2
3
3
1 1 6 1 6
ln
22
dt t
tt
t
1
ln2 1
2

1
, 2 2 3
2
a b a b
ĐÁP ÁN B
Câu 20:
2
1
2
0
1
= a + lnb
1
x
I dx
x
. Khi đó
a
S
b
bằng
A.
1
3
B.
2
3
C.
1
3
D.
1
2
Giải:
1 1 1 1
2
4
2 2 2
0 0 0 0
1 2 2 2
1
1 1 1
x x x x
I dx dx dx dx
x x x




2
11
2
2
00
1
1
ln 1 1 ln 2
0
1
dx
dx x x
x

1
1, 2
2
a
ab
b
ĐÁP ÁN D
Câu 21: Cho
1
3
2
0
3
5 ln ln
2
23
xc
I dx a b b c
xx

. Khi đó
..P a b c
bằng
A.
32
B.
30
B.
26
D.
26
Giải:
1 1 1 1
3
22
0 0 0 0
6 1 3
3 7 3 6 1
2 2 2
31
13
2 3 2 3
xx
xx
I dx x dt x dt x dx
xx
xx
x x x x







Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page 9
0989 850 625
1
2
0
5
2 6ln 3 ln 1 7ln 2 6ln3
22
x
x x x



5
, 2, 6 30
2
a b c P
ĐÁP ÁN B
Câu 22: Cho
2
1
2
1
AB
xx




. Khi đó
2.S A B I
bằng:
A.
2
B.
2
ln 2
3
C.
2
3
D.
ln2
Giải:
Ta có:
Nên
Suy ra
Vậy
2 . ln2S A B I I
ĐÁP ÁN D
Câu 23: Cho
2
1
21
21






dx A B
I
x
x
xx
Khi đó
2P A B
bằng:
A.
1
B.
3
2
C.
3
D.
0
Giải:
2
2 1 2 1
1 2 1 1 2 1
21
xx
dx dx
I dx
x x x x
xx

1 1 2 1 2
ln 1 ln 1
3 1 2 1 3 3
dx x x C
xx




Khi đó
12
, 2 0 0
33
A B A B P
ĐÁP ÁN D
2
1
2
1
dx
I
xx
1
1 1 1
A B x A
AB
x x x x x x

01
11
A B A
AB




1 1 1
11x x x x


2 2 2
2
2
1
1
2
1 1 1
2
2 2 2
ln ln 1 | ln2
11
dx dx dx
I x x
x x x x

Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
10
0989 850 625
Câu 24:
2
43
ln ln 1
2 3 2
x
I dx x a b cx C
xx

. Khi đó
a
Sc
b

bằng:
A.
2
B.
2
C.
4
D.
3
Giải:
2
2 1 2 2
4 3 1 2
()
2 2 1
2 1 2
2 3 2



xx
x
I dx dx dx
xx
xx
xx
12
ln 2 2ln 2 1
2 2 1
dx x x C
xx




2, 2, 2 3
a
a b c S c
b
ĐÁP ÁN D
Câu 25: Cho
32
4 2 2 2
21
x x x
I dx
x
3
ln 2 1ax x b x C
Và các mệnh đều sau:
1
a < b
2
16
3
S a b
3
,ab
là các số nguyên dương.
4
1P ab
Số mệnh đề đúng là:
A.
0
B.
1
C.
2
D.
3
Giải:
32
2
4 2 2 2 3
21
2 1 2 1
x x x
I dx x dx
xx





3
23
ln 2 1
32
x
x x C



23
,
32
ab
1
. Đúng
2
.
13
6
S a b
. Đúng
3.
,ab
không phải là số nguyên. Sai
4
1.P ab
Đúng
ĐÁP ÁN D.
Câu 26: Cho
32
2
36
43
x x x
I dx
xx

2
3
ln
1
x
ax x b C
x



Và các mệnh đều sau:
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
11
0989 850 625
1

3
a 1,b
2
2
2S a b
3
ab
4
3
2
P ab
Số mệnh đề sai là:
A.
0
B.
1
C.
2
D.
3
Giải:
32
22
2
3 6 3
1
4 3 4 3
3 3 3 3
1 ln
2( 3) 2( 1) 2 2 1
x x x
I dx x dx
x x x x
xx
x dx x C
x x x










13
,
22
ab
1
.
3
a 1,
2
. Sai
2
.
2S a b
. Đúng
3.
,ab
không phải là số nguyên. Sai
4
3
4
P ab
. Sai
ĐÁP ÁN D
Câu 27: Cho
32
2
8 4 2
4 4 1
xx
I dx
xx


2
1
ln 2 1
21




ax x b x C
x
Và các mệnh đều sau:
1
Modun của số phức
22z a bi
bằng
5
2
2S a b
3
ab
4
3
2
P ab
Số mệnh đề đúng là:
A.
0
B.
1
C.
2
D.
3
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
12
0989 850 625
Giải:
32
2 2 2
8 4 2 2 3 1 2
2 1 2 1
21
4 4 1 4 4 1
21







x x x
I dx x dx x dx
x
x x x x
x
2
1
ln 2 1
21




x x x C
x
1, 1 ab
1
. Sai
22
2 2 4 4 8 z a b
.
2
.
2S a b
. Đúng
3.
,ab
không phải là số nguyên. Sai
4
3
4
P ab
. Sai
ĐÁP ÁN B
Câu 28: Cho
2
1
2
0
1
1
x
I dx
x
lnab
. Cho các mệnh đề sau:
1.
ab
2
32
26S a b
3
lnI ab
4
1
log 2
a
không tồn tại
Số mệnh đề đúng là:
A.
0
B.
1
C.
2
D.
3
Giải:
1 1 1 1
2
4
2 2 2
0 0 0 0
1 2 2 2
1
1 1 1
x x x x
I dx dx dx dx
x x x




2
11
2
2
00
1
1
ln 1 1 ln 2
0
1
dx
dx x x
x

1, 2ab
1.
ab
. Sai
2
32
29S a b
. Sai
3
ln ln1 ln2 0 ln2I ab
. Đúng.
4
Đúng vì cơ số 1 không tồn tại.
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
13
0989 850 625
ĐÁP ÁN C
LUYEÄN TAÄP
Câu 1: Cho
1
3
1
42
0
=ln ln
32
x
I dx a b c
xx


. Chọn đáp án đúng
A.
5
2
a b c
B.
13
2
c
a
b

C.
2 2 2 1b c c a a b
D.
a c b
Câu 2: Cho
2
32
1
1
1
dx
xx
5
ln
8
ab
. Chọn đáp án đúng
A.
7
2
ab
B.
43ab
C.
8
53
27
ab
D.
3
18
ab
Câu 3. Cho
1
3
42
0
32
x
I dx
xx

ln3 ln2bc
. Chọn đáp án đúng
A.

3
4
bc
B.
2bc
C.
0bc
D.
,bc
là các số nguyên
Câu 4: Cho
I
2
0
13
AB
xx





. Khi đó
.I A B
bằng:
A.
125
2 ln
3
B.
125
2ln
3
C.
125
ln
9
D.
1 125
ln
29
Câu 5: Cho
0
2
1
1
ln
5
23
dx
I a b
xx

Và các mệnh đều sau:
1
Modun của số phức
25z a bi
bằng 30
2
7S a b
3
ab
4
6P ab
Số mệnh đề đúng là:
A.
0
B.
1
C.
2
D.
3
Câu 6: Cho
2
45
ln ln
2
x
I dx x a b x c C
xx


1
Modun của số phức
z a b ci
bằng
22
2
2S a b c
2
2
0
23
43
x
dx
xx

Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
14
0989 850 625
3
c b a
4
,,a b c
là các số thực dương.
Số mệnh đề sai là:
A.
0
B.
1
C.
2
D.
3
Câu 7: Cho
22
22
11
32
21
4 4 1
21
x A B
I dx dx
x
xx
x


Khi đó
.P A B
bằng:
A.
ln3
B.
3
ln 2
2
C.
ln2
D.
21
4
Câu 8. Cho
2
1 2 1 2 3
1 4 8 3
dx A B C
I dx
xxx
x x x





Khi đó
.P A B C I
bằng
A.
2
2ln 1 ln 4 8 3x x x C
B.
2
1
ln 1 ln 4 8 3
2
x x x C



C.
2
1
ln 4 8 3
2
x x C



D.
2
ln 4 8 3x x C
Câu 9: Tìm nguyên hàm của
2
3
12
32
x A B
dx dx
xx
xx







Khi đó
S A B
bằng
A.
0
B.
1
C.
2
D.
1
2
Câu 10: Tính
11
2
00
2 1 6ln ln
2 3 2 3 12
49
x A B a b
I dx dx
xx
x





Khi đó
2P A B a b
A.
2
3
B.
3
C.
5
2
D.
6
Câu 11: Cho
a) Xác định các hằng số A, B, C để
A.
3, 1, 2A B C
B.
1, 2, 3A B C
C.
2, 1, 3A B C
D.
3, 2, 1A B C
b) Tìm nguyên hàm của f(x).
2
3
3 3 3
32
xx
fx
xx


2
12
1
A B C
fx
xx
x

Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
15
0989 850 625
A.
3
2ln 1 ln 2
1
x x C
x
B.
3
2ln 1 ln 2
1
x x C
x
C.
3
2ln 1 ln 2
1
x x C
x
D.
3
2ln 1 ln 2
1
xx
x
Câu 12: Nguyên hàm của
2
82
ln 1 ln 5
45
x
a x b x C
xx

Tính S = a+b
A. 1 B. 2 C. 4 D. -2
Câu 13: Để
1
2
0
.
32
ax dx
xx
9
ln
8
Khi đó
a
bằng:
A.
4
B.
1
C.
2
D.
3
Câu 14. Tìm
a
để
2
2
1
33
ln
1 2 2
x x a
dx
x


A.
0
B.
1
C.
2
D.
3
Câu 15. Tính
I
2
0
13
AB
xx





Khi đó
..P A B I
bằng:
A.
3 125
ln
49
B.
3 125
ln
29
C.
3 125
ln
89
D.
125
ln
9
Câu 16.Tìm hàm số
fx
biết
'fx
2
4 4 3
21
xx
x

và
0 1.f
A.
2
ln 2 1x x x
B.
2
ln 2 1 1x x x C
C.
2
ln 2 1 1x x x
D.
2
ln 2 1 1x x x
Câu 17. Tnh tch phân
1
1
3 2 2
0
0
42
ln
2 2 2 1





x A Bx C
dx dx a b
x x x x x
Khi đó
.S A B C ab
bằng:
A.
0
B.
4
ln
9
C.
1
D.
4
2 ln
9
Câu 18. Tìm A, B, C:
2
2 1 2
12
dx A B C
dx
x x x
xx





A.
1, 1A B C
B.
1 A B C
C.
2, 1 A B C
D.
1 A B C
2
2
0
23
43
x
dx
xx

Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
16
0989 850 625
Giải:
Câu 1:
Đáp án D.
Câu 2:
ĐÁP ÁN D
Câu 3.
ĐÁP ÁN C
Câu 4:
ĐÁP ÁN C
Câu 5:
ĐÁP SỐ B
Câu 6:
ĐÁP ÁN D
Câu 7:
ĐÁP ÁN D
Câu 8.
ĐÁP ÁN B.
Câu 9:
ĐÁP ÁN B
Câu 10
ĐÁP ÁN D
Câu 11:
ĐÁP ÁN D
ĐÁP ÁN C
Câu 12:
ĐÁP ÁN C
Câu 13:
ĐÁP ÁN B
Câu 14.
ĐÁP ÁN B
Câu 15
ĐÁP ÁN C
Câu 16.
ĐÁP ÁN C
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
17
0989 850 625
Câu 17.
ĐÁP ÁN A
Câu 18.
ĐÁP ÁN A
ÑOÅI BIEÁN
Câu 6 : Cho
2
2
3
3
b
x
I x x dx C
a
. Tính
2
ba
S log a log b 2016
?
A. 2018 B. 2020 C. 2025 D. 2030
Giải:
Đt
2 2 2
t x 3 t x 3 2tdt 2xdx xdx tdt
.
Suy ra
3 2 3
2
( 3)
.
33
tx
I t tdt t dt C C

Vậy
2
33
S log 3 log 3 2016 2018
Bình luận: khi có căn
2
3x
ta sẽ tìm cách đt
2
3tx
.Tiếp đó ta biến đổi các phần còn lại
theo t , kể cả dx cũng biểu diễn theo dt .
xdx tdt
Câu 7. Cho
x
2x 1 ln 2x 1 4
2x 1 4
n
d
IC

. Tính
.
()
8
n
S Sin
A.
1
2
B.
0
C.
1
D.
1
Giải:
Chọn C
Đt
2
2x 1 2x 1 d xt t t t d
d4
1 4ln 4
44
tt
I dt t t C
tt





4
2x 1 ln 2x 1 4 C
Vậy n = 4 vậy
.
( ) 1
8
n
S Sin

Bình luận: Việc suất hiện căn
2x 1
ta đt
2x 1t 
, sau đó vẫn như thói quen, ta biểu diễn dx
theo dt:
dxt t d
Câu 8. Cho
22
1
3 1 3 1
b
I x x dx x C
a
. Giá trị a và b lần lượt là:
A. 4 và 3 B. 9 và 3 C. 3 và 9 D. 4 và 9
Giải:
Chọn B
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
18
0989 850 625
Đt
2
1
3 1 2 6
3
t x tdt xdx tdt xdx
2
2
23
1
1
3
2 3 2
1 1 7
3 9 9
1 1 1
31
3 9 9
I t dt t
I t dt t C x C
Vậy a = 9; b = 3
Bình luận: Việc xuất hiện căn
2
31x
ta đt
2
31tx
, sau đó vẫn như thói quen, ta biểu diễn
dx theo dt .
Câu 9: Cho
5 2 7 5 3
1
A x x dx at bt ct C
, với
2
1tx
. Tính
A a b c
A.
12
79
B.
95
103
C.
22
105
D.
48
109
Giải:
Chọn C
Đt
2 2 2
11t x x t xdx tdt
73
2
2 2 6 4 2 5
2 1 2 1
1 2 ; ;
7 5 3 7 5 3
22
105

tt
A t t dt t t t dt t C a b c
abc
Câu 10. Cho
2
2
3
sin 1 2
ln 4 3 ln 2 2 1
3
sin 1 cos 2 2
x
dx a b
xx
.
Tính

15
A a b
2
A. 30 B. 24 C. 36 D.75
Giải:
Chọn D
Đt
2
1 cos 1 cos 2 sin t x t x tdt xdx
3
;1
3 2 2

x t x t
1 1 1
3 3 3
22
2
22
2
2 2 2
2 2 1 1
2
2
2
11










tdt
C dt dt
tt
tt
t
1
2 3 2 1
1 2 1 1 2
2 ln ln 1
3
3
2 2 2 2 2
2 3 2 1
2










t
t
t
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
19
0989 850 625
12
ln 7 4 3 ln 3 2 2 1 7; 3
3
22
ab
Câu 11. Cho
3
2
1
1
ln ln 3
x
I dx a b
x
. Tính

11
a b 3
2
.
A. 0 B. 1 C. 2 D. 3
Giải:
Chọn A
Đt
2 2 2
11 t x t x tdt xdx
và
:1 3x
thì
: 2 2t
Khi đó
3 2 2 2
22
2 2 2 2
1
2 2 2
1 1 1 1
.1
1 1 1



x t t
I xdx tdt dt dt
x t t t
2
2
2
2
1 1 1 1 1 1
1 ln 2 2 ln 2 1 ln3
2 1 1 2 1 2
11
2 2; 2 1 3 0
2





t
dt t
t t t
a b a b
Bình luận: Việc xuất hiện căn
2
1 x
ta đt
2
1tx
, ta tiếp tục công việc biểu diễn
22
2
11xx
x
xx

và dồn về ẩn t , có xdx = tdt. Kinh nghiệm cho thấy khi có căn bậc 2 ta cứ
đt căn đó bằng một biến t rồi kiên trì biến đổi là giải được bài toán.
Câu 12. Cho
1
2
0
2
2ln
1
43






dx a
I
b
xx
. Tính
A a b
A.
3
B.
2
C.
5
D.
7
Giải:
Chọn C
Đt
13t x x
1 1 1 3 2
.
2 1 2 3
2 1 3 2 1 3 1 3




x x dx dx dt
dt dx dx t
t
xx
x x x x x x
Và
:0 1x
thì
:1 3 2 2t
.
Khi đó:
22
22
4
13
13
22
2 2ln 2ln 2; 3
13




dt
I t a b
t
Câu 13. Cho tích phân
2
2
3
28
(4 )
3
1
a
x
I dx
x
. Giá trị a là: (biết a có giá trị nguyên)
A. 0 B. 1 C. - 1 D. 3
Giải:
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
20
0989 850 625
Chọn A
Ta có
22
2
3
4
1


aa
x
I dx dx
x
Tính
2
2
3
1
a
x
B dx
x
. Đt
3 3 2 2
2
11
3
x t x t x dx tdt
Khi đó
2
2
2
33
3
22
1 2 1
33
1
a
a
x
B dx x b
x
Ta có:
2
33
22
4 1 10 4 1
33



a
I x x a a
3 3 3
28 2 2 2
10 4 1 4 1 6 1 1
3 3 3 3
0



a a a a a a
SHIFT SOLVE a
LUYEÄN TOÁC ÑOÄ
ÑEÀ 1:
Câu 1. Cho tích phân:
6
1
31
2ln
2
x
I dx a a
x

. Tính
3
S 4 4a
A. 10 B. 5 C. 15 D. 8
Câu 2. Cho tich phân
3
1
0 2 4
1
3
1


x dx a
I
xx
. Giá trị của a là:
A. 1 B. 2 C. 3 D. 4
Câu 3. Tnh tich phân
3
0
22

b
a
xdx
Ib
x
. Biết
z a bi
là căn bậc hai của số phức
35
3i
4

A.
12
5
B.
7
5
C.
6
5
D.
11
5
Câu 4. Tnh tch phân
2
1
19
1 ln ln
I x x x dx b
a
. Tính

52
3b a
S 76
3
A.100 B.-100 C.-200 D.200
Câu 5. Tính tích phân
2
1
2
.0
1
1
3

x
ab
I x x e dx
. Giá trị của a và b là:
A. 3 và 1 B. 2 và 3 C. 3 và 2 D. 2 và 1
Câu 6. Cho tích phân:
1
2
0
3 1 3
I x ax b x dx
, biết
a b 1
. Tính
33
S a b
A.-15 B. 20 C. -19 D. 15
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
21
0989 850 625
Câu 7. Tnh tch phân
5
2
03
1

xa
I dx
b
x
. Tính
32
a a 370
S
10b 10b 729
.
A.
2
9
B.
2
9
C.
4
9
D.
4
9
Câu 8. Cho

3
1
dx f x C
1 x 1 x
. Tính
f ' 8 ?
A.
1
5
B.
4
5
C.
1
6
D.
7
6
Câu 9. Cho tích phân
lna lnb
. Tính
8 ln2a ln2b
e
A.
4
9
B.
25
9
C.
9
4
D.
9
25
Câu 10. Cho tích phân =
a
ln16
b
. Giá trị của a và b là bao nhiêu (a, b tối giản)
A. 4 và 15 B. 5 và 3 C. 6 và 3 D. 5 và 6
ÑEÀ 2:
Câu 1. Cho =
e
53
1
a 3 1 3ln x 5 1 3ln x



. Giá trị của a là
A.
7
125
B.
2
135
C.
9
145
D.
4
115
Câu 2. Cho
sin2x sin x
I dx f x C
1 3cosx
. Biết rằng f(x) không có hằng số tự do. Tính f(0)
A.
5
27
B.
13
27
C.
44
27
D.
19
27
Câu 3. Cho





6
35
tt
1 cos x.sin x.cos xdx 2 C
với
6
3
t 1 cos x
. Tỉ số
bằng bao nhiêu?
A.
5
13
B.
7
5
C.
7
13
D.
5
6
Câu 4. Tìm nguyên hàm của
7
3
0
( 2)
1

x dx a
I
b
x
biết rằng a,b tối giản . Tính a + b
A.
214
B.
124
C.
421
D.
241
Câu 5. Cho
2
53
ln x
I dx a bt ct d.t C
x ln x 1
, biết
t lnx 1
. Tính
A abcd
23
2
5
4
dx
I
xx
2
1
11
x
I dx
x

1
1 3ln ln
e
xx
I dx
x
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
22
0989 850 625
A. -30 B. -60 C. -45 D. -27
Câu 6. Cho
22
sin2 2
3
cos 4sin

x
I dx
xx
, biết



2
, 0;
2
. Tính
A cos
A.
1
2
B. 1 C.
1
2
D. 0
Câu 7. Tính
2
0
42
1 cos sin
3
b
B x xdx a
. Tính
44
A sin a b
A.
43
4
B.
29
C.
37
4
D.
16
Câu 8.
1
3 2ln 5
3
1 2ln
a
x
I dx
xx

. Giá trị của a là:
A.
3
e
B.
2
e
C.e D.
3
e
Câu 9.
2
3
1
x
x
e dx
I at bt C
e
.Với
1
x
te
; Tính
22
A a b
A.
52
9
B.
40
9
C.
47
9
D.
46
9
Câu 10. Cho
ln3
0
11
x
xx
e dx
I a b
ee

. Tính
44
A 2 a b
A. 23 B. 34 C. 21 D. 45
ÑEÀ 3:
Câu 1. Cho tích phân sau
1
0
2 1 28
ln
27
1 3 1

x b a
I dx
ab
x
.
Tính




2
a 3997 cosa
S cos
bb
. Biết a, b tối giản.
A.
2
cos 5 cos 5 1999
B. 1999
C. 2016 D.
2
cos 3 cos 3 2016
Câu 2. Tính tích phân:
6
1
31
ln
2

x
I dx a b
x
.Tính
S z z
. Biết
z a bi
.
A. 2 B. 4 C. 3 D. 1
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
23
0989 850 625
Câu 3. Tính tích phân
10
32
5
34
ln
2

xx
I dx a b
x
. Chọn phát biểu đúng
A. a < b B. a = b C. b < 21 D. a, b đều nguyên
Câu 4. Cho tích phân:
2
1
ln

e
eb
I x xdx
a
. Tính
S ab
.
A. 12 B. 4 C. 6 D. 8
Câu 5. Cho tích phân:
7
3
0
.1
a
x x dx
b

. Giá trị của a là: (biết a, b tối giải)
A. 64 B. 356 C. 346 D. 1029
Câu 6. Cho tích phân
1
2
1
11
dx
a
xx
. Tính
2016 2000
S ai ai
A. 3 B. 2 C. 0 D. 1
Câu 7. Tnh tch phân:
2
0
4
1 cos (sin )
3
ab
I x x dx
. Tính
44
S sin a b
A. 1 B. 9 C. 25 D.
16
Câu 8. Cho tch phân
8
3
ln ln
ln ln

e
e
dx
ab
x x ex
. Tính



2
10ab
cos 11
6
S cos a b
2
A.-10 B.-5 C.-20 D.-40
Câu 9. Cho tich phân:
2
32
2
0
23
1
1


x x x b
I dx
a
xx
. Tính
729
22
1999
S log a log b
? biết a, b tối giản.
A.
1
9
B.
1
27
C.
1
81
D.
1
36
Câu 10. Cho
22
33
3
3 1 3 1 3 1
1
31
x x b x
x
D dx C
a
x
. Tìm a + b
A. 20 B. 75 C. 55 D. 45
LÔØI GIAÛI
ÑEÀ 1:
Câu 1. Chọn D
Câu 2. Chọn B
Câu 3. Chọn A
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Thầy Mẫn Ngọc Quang
Page
24
0989 850 625
Câu 4. Chọn B
Câu 5. Chọn D
Câu 6. Chọn C
Câu 7. Chọn A
Câu 8. Chọn C
Câu 9. Chọn D
Câu 10. Chọn B
ÑEÀ 2:
Câu 1. Chọn B
Câu 2. Chọn C
Câu 3. Chọn C
Câu 4. Chọn D
Câu 5. Chọn A
Câu 6. Chọn B
Câu 7. Chọn D
Câu 8. Chọn D
Câu 9. Chọn B
Câu 10. Chọn B
ÑEÀ 3:
Câu 1. Chọn B
Câu 2. Chọn B
Câu 3. Chọn C
Câu 4. Chọn B
Câu 5. Chọn D
Câu 6. Chọn B
Câu 7. Chọn D
Câu 8. Chọn B
Câu 9. Chọn D
Câu 10. Chọn A.
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

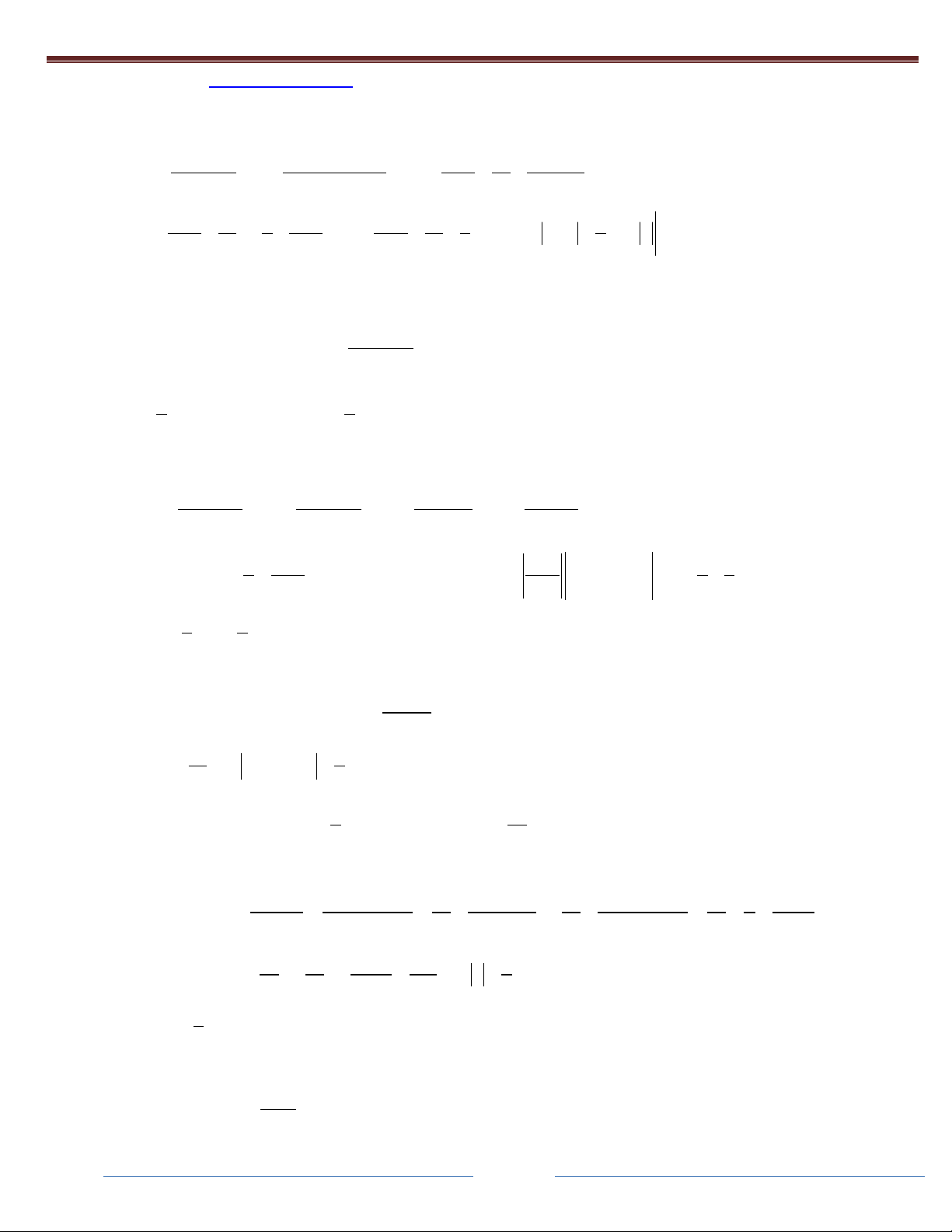
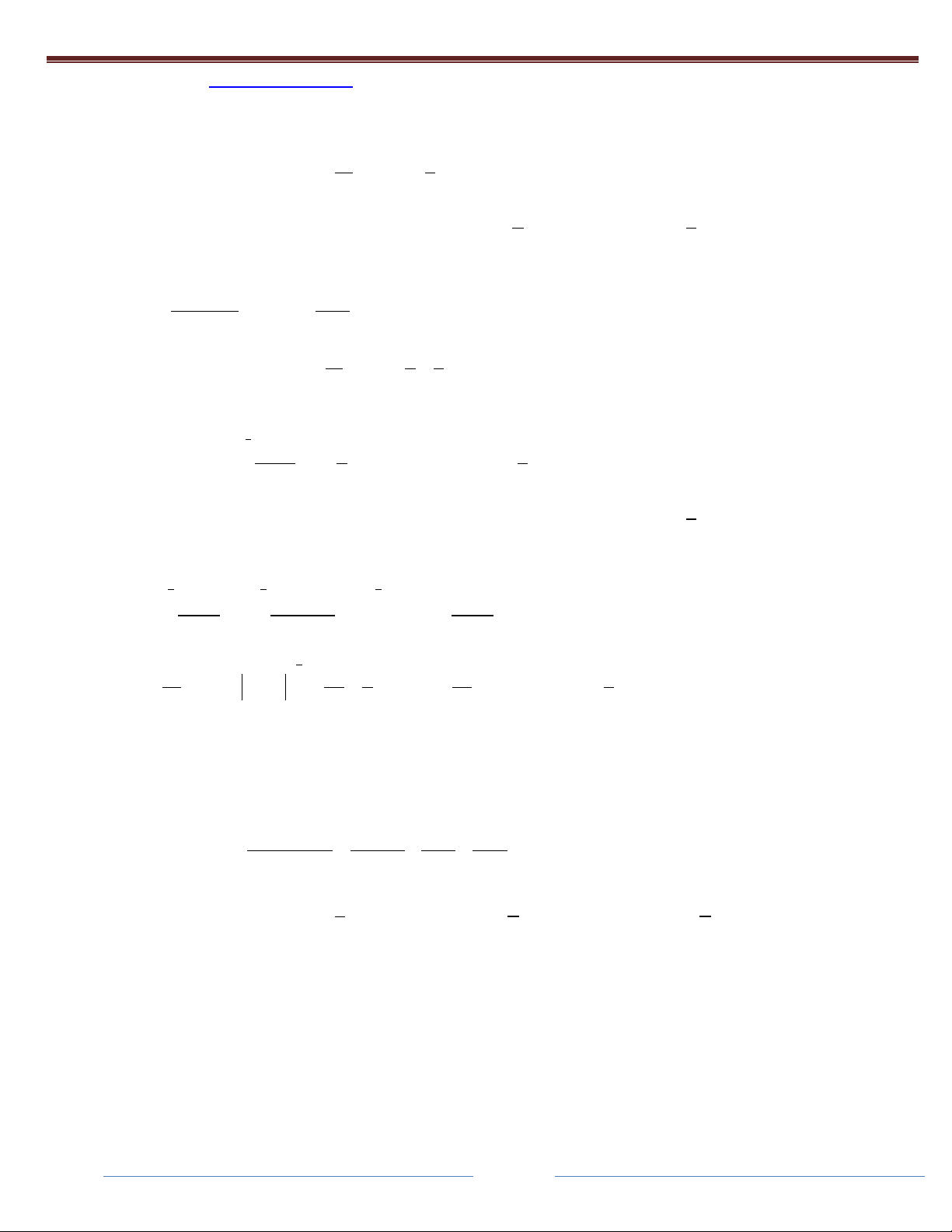
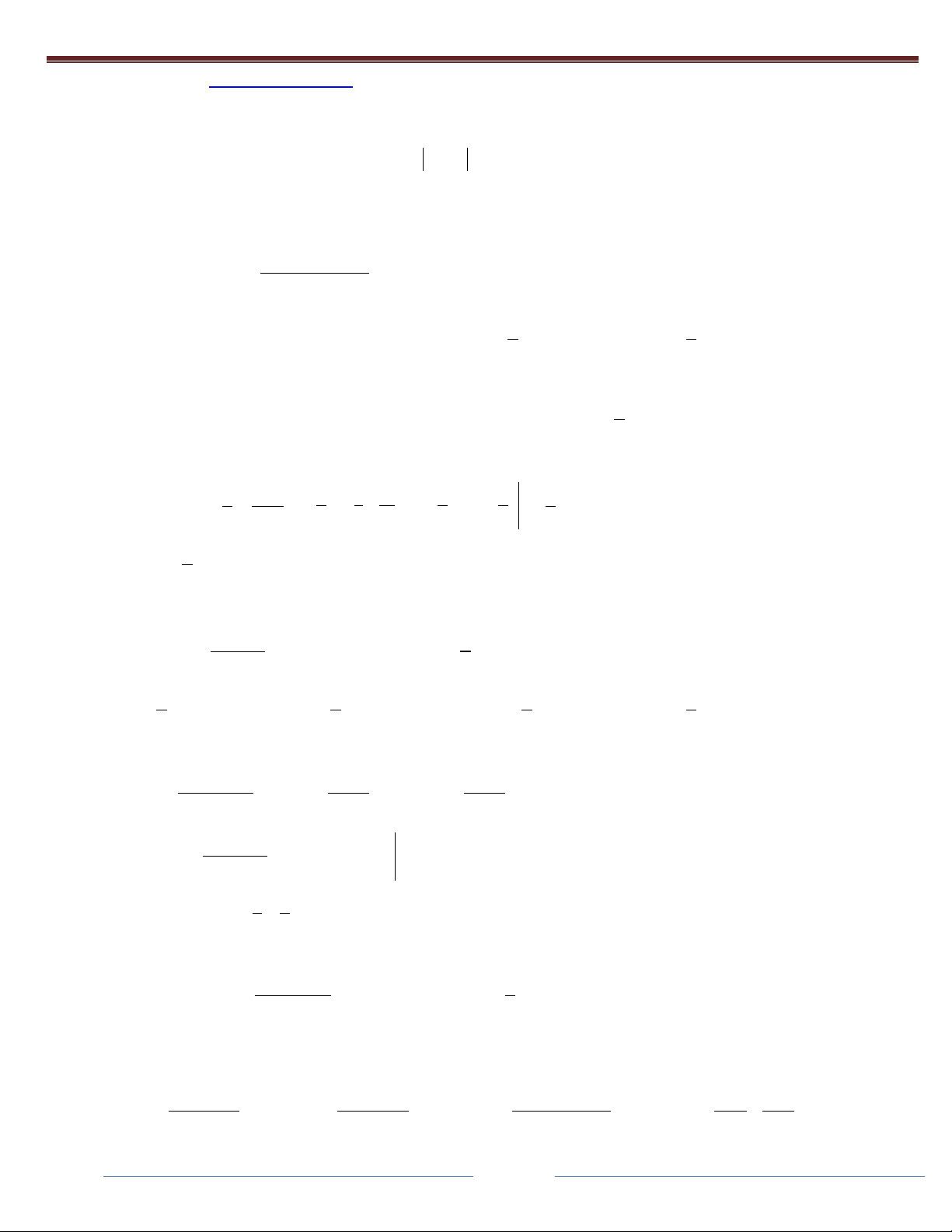
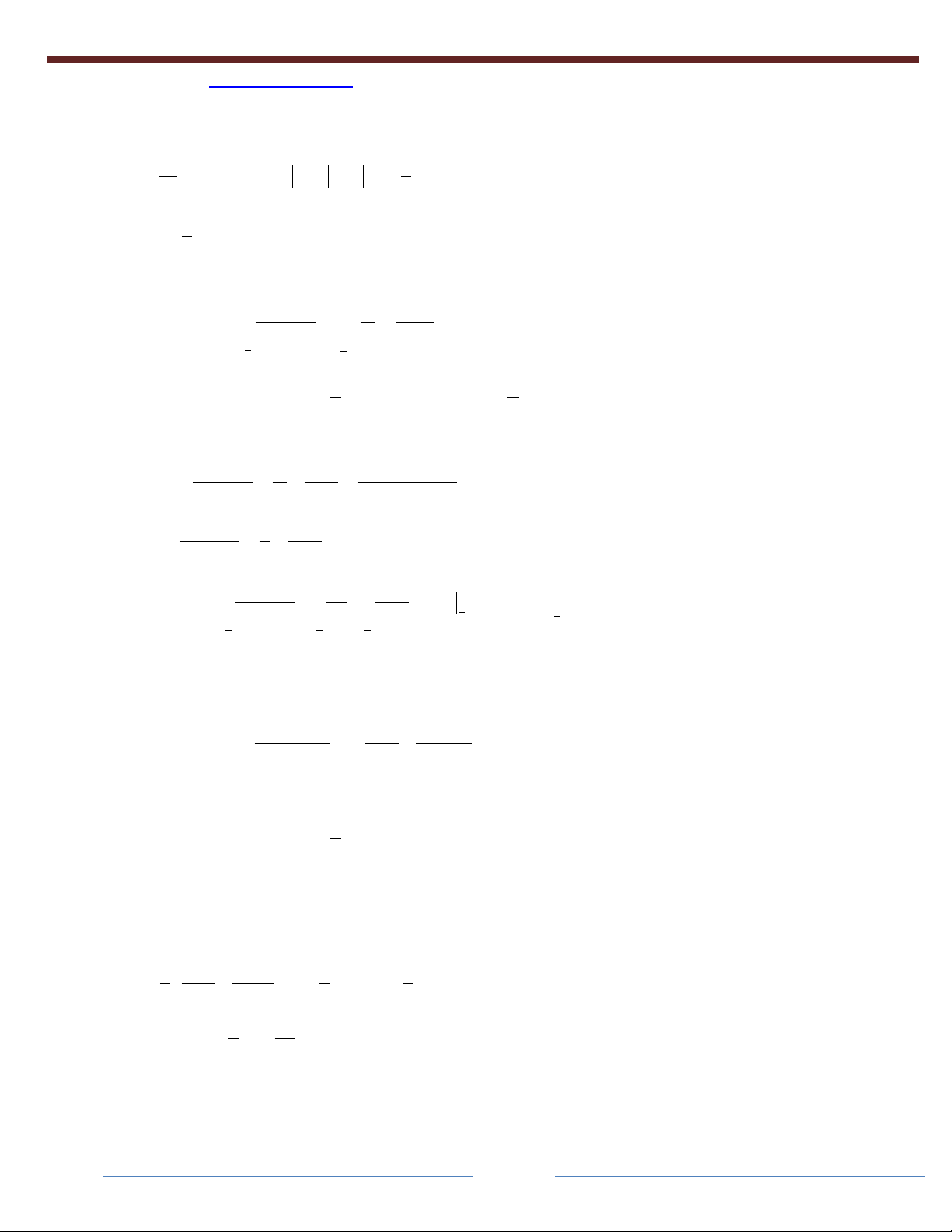
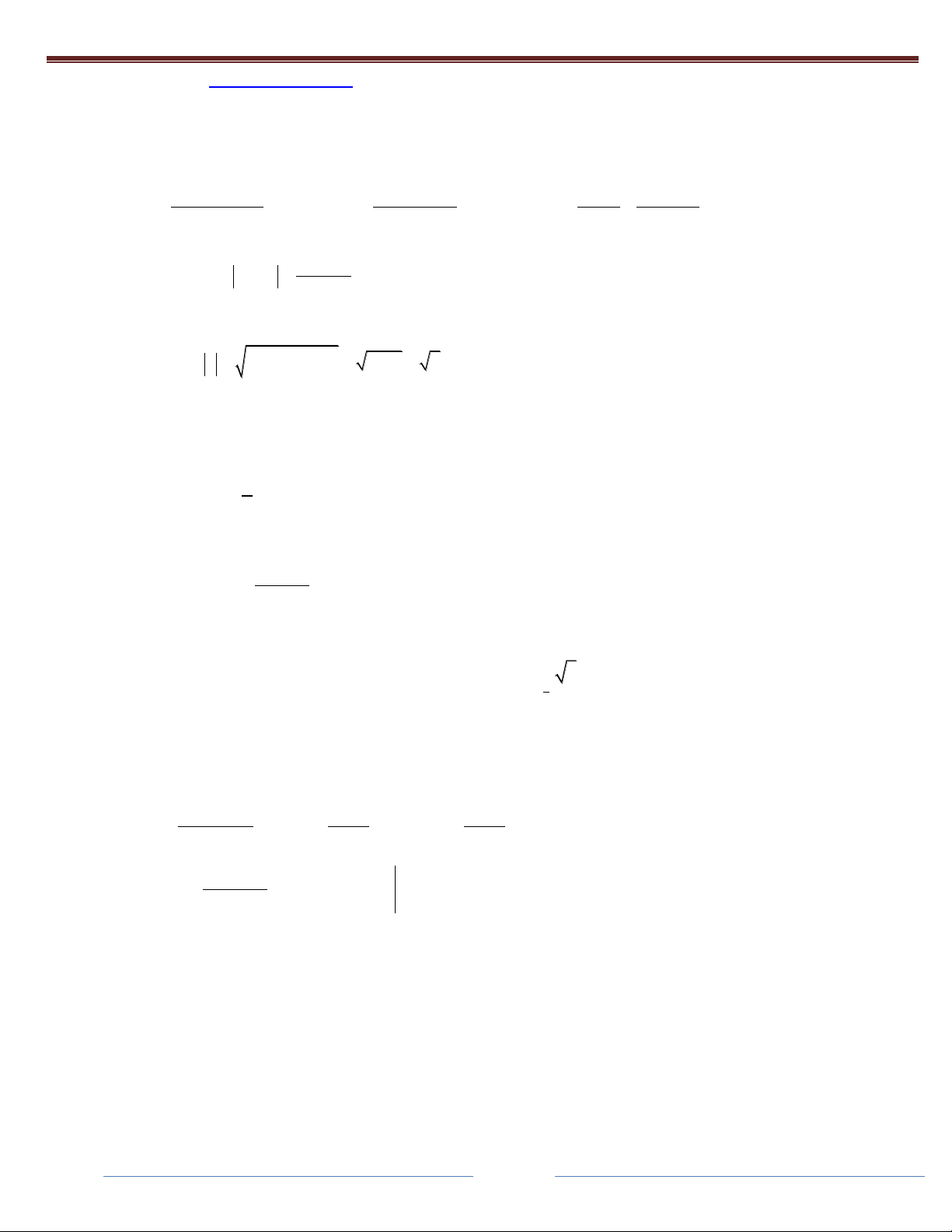
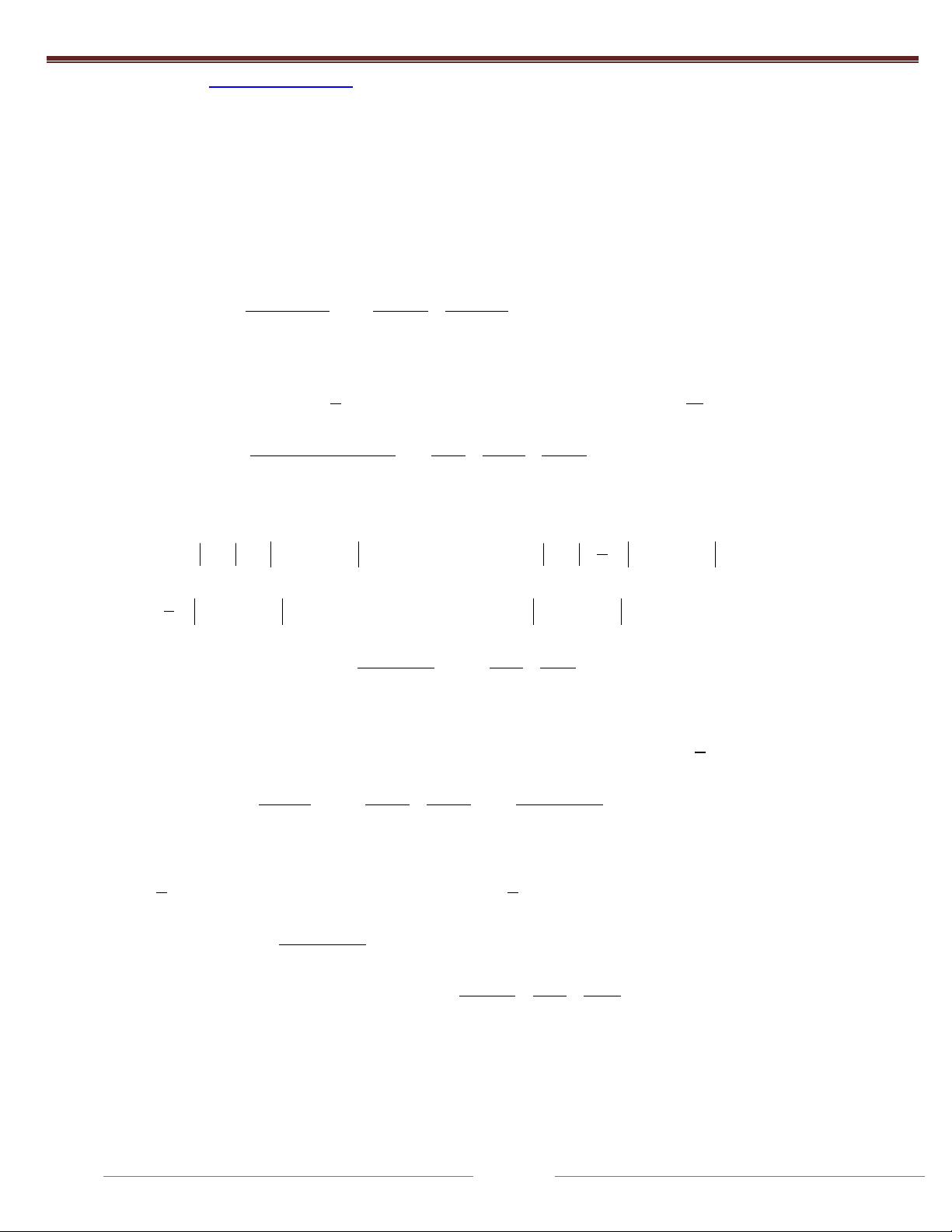
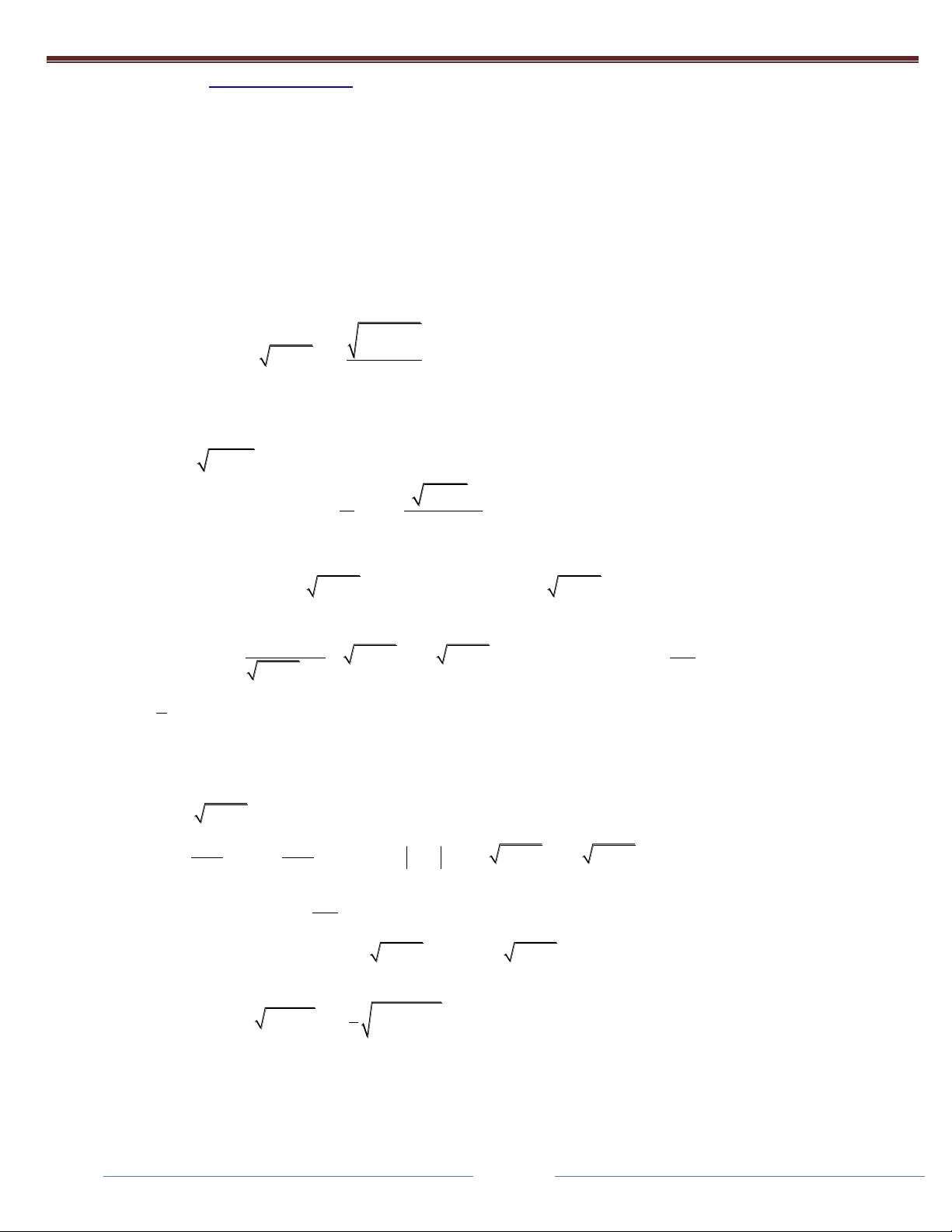
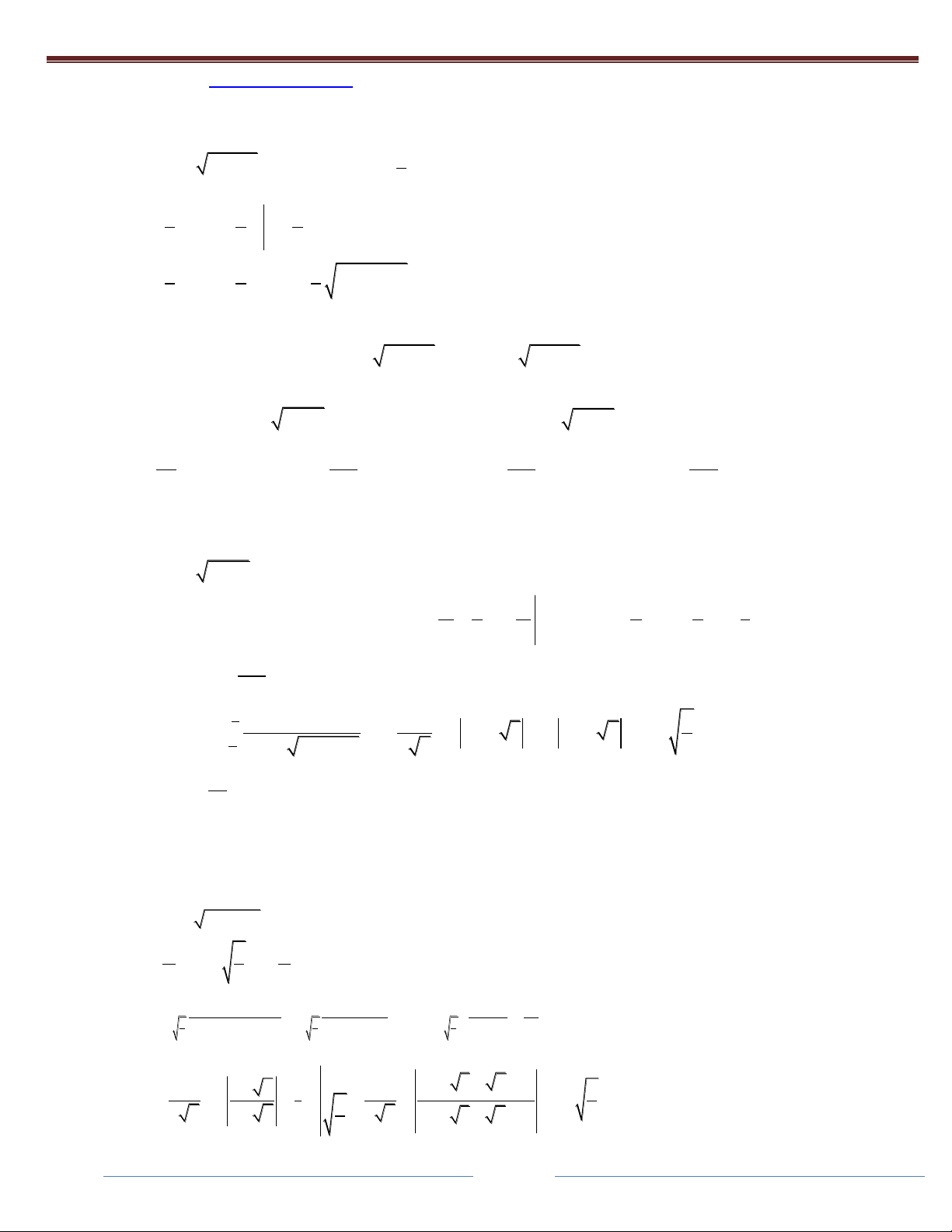
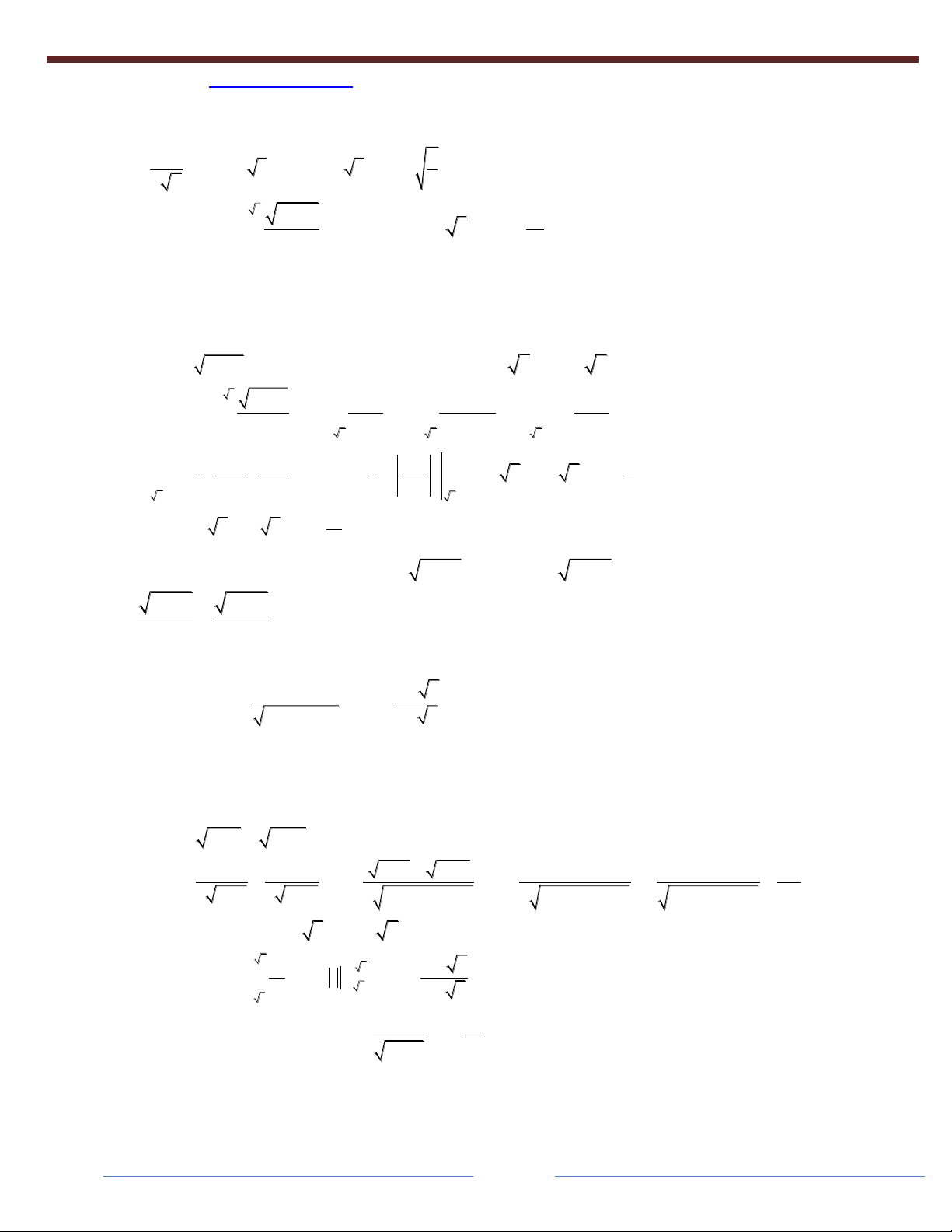
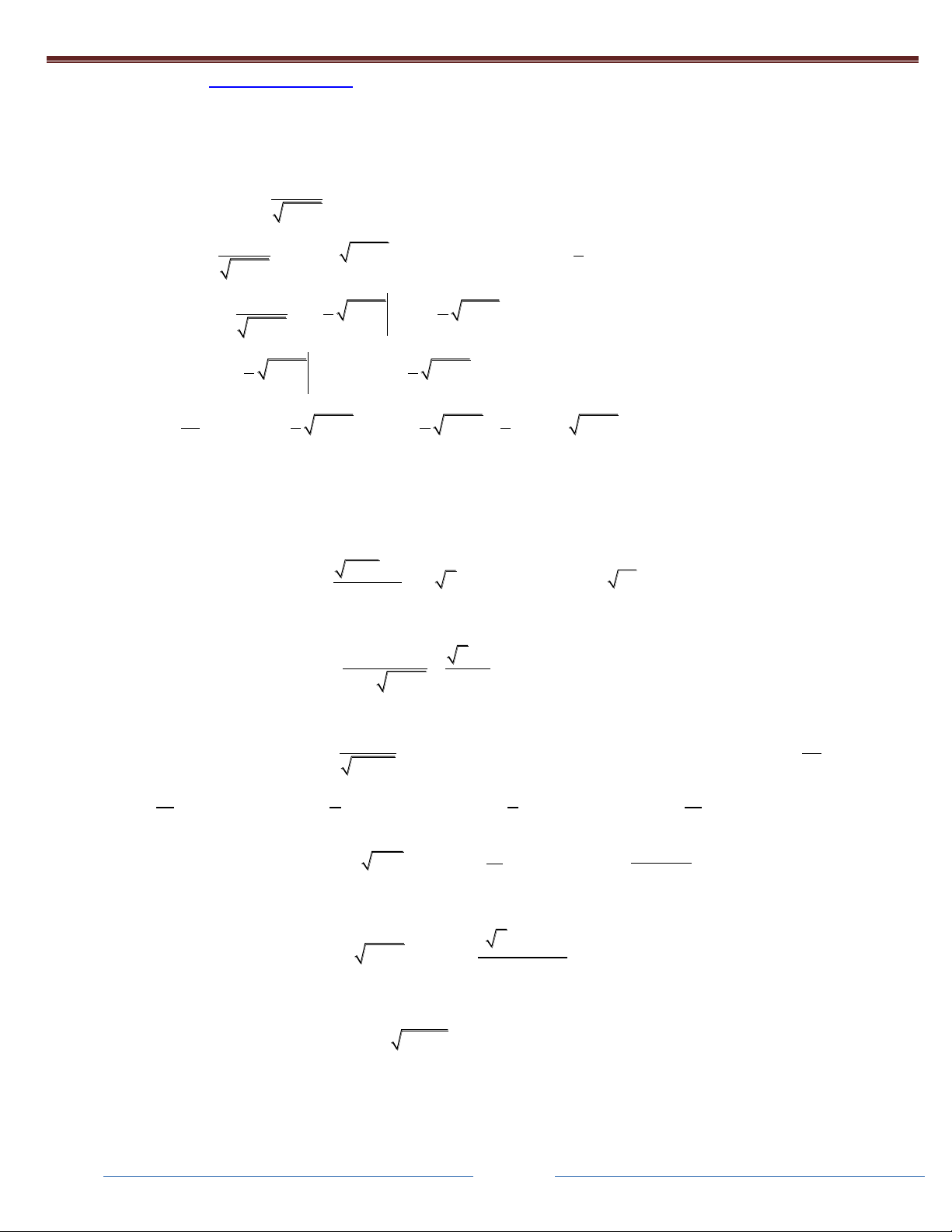
Preview text:

Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Daïng 1: ÑOÀNG NHAÁT HEÄ SOÁ - MAÃU COÙ DAÏNG TÍCH
Phương pháp hệ số bất định: Khi mẫu có thể phân tích thành nhân tử. 1 A B C Câu 1: Cho   
(x  2)(x  5)(x  4) (x  2) (x  5) (x  4)
Khi đó tổng S A B C bằng: 1 1 1 A. B. 0 C. D.  18 14 63 Giải: 1  ABC
(x  2)(x  5)(x  4) (x  2) (x  5) (x  4)  (
A x  5)(x  4)  B(x  2)(x  4)  C(x  2)(x  5)  1 1 ) x  2   14
A 1 A  14 1
) x  5  63B 1 B  63 1 ) x  4
 18C 1 C  18
A B C  0 ĐÁP ÁN B.
Bình luận: Bài toán này chúng ta sẽ tách phân số ở mẫu số có tích thành các phân số đơn giản hơn. Để
làm đươc điều này ta dùng phương pháp đồng nhất hệ số . 1 A B C Câu 2: Cho   
. Khi đó S  2A B C bằng:
x(x  3)(x  3) x x  3 x  3 1 1 2 A. B. 0 C. D.  18 18 9 Giải: 1 A B C    (
x x  3)(x  3) x x  3 x  3 1  (
A x  3)(x  3)  B (
x x  3)  C ( x x  3)
x    A   A   1 ) 0 9 1 9
x   B   B  1 ) 3 18 1 18 1 )x  3
  18C  1 C  18 2 
 2A B C  9
Thầy Mẫn Ngọc Quang 0989 850 625 Page 1
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. ĐÁP ÁN D 2 A B C
Câu 3: Cho các hằng số , A ,
B C R thỏa mãn:    . 3 2
x  3x  2x x x 1 x  2 Khi đó P  . A . BC bằng: 1 A. 2 B. C.1 D. 2  2 Giải: (
A x  1)(x  2)  B (
x x  2)  C ( x x  1)  2
) x  0  A  1
) x  1 B  2
) x  2  C  1  ABC  2  ĐÁP ÁN D 2x  3 1 1 Câu 4. Cho  A  . B
. Khi đó tổng S A B C bằng: 2 2x x  1 2x  1 x C 1 1 2 2 A. B. C. D.  3 3 3 3 Giải: 2x  3 2x  3  4 1 5 1  = =  .  .   2
2x x  1 (2x  1)(x  1)  3 2x  1 3 x  1 4  5 2   A  ,B  ,C  1
  S A B C  3 3 3 ĐÁP ÁN D Daïng 2: NHAÛY LAÀU 5 1  x
Câu 6: Nguyên hàm của hàm I   có dạng 5 5
aln x bln 1 x   C   xdx 5 1  x
Khi đó S  10a b bằng A. 1 B. 2 C. 0 D.3 Giải:
1 5x 4xdx 1 1 5xd 5x 1  1 2  I   d x 5 x  5  5 5  5 1  x   5
x 1 x     5 5    5  x 1  x  1 5 5
 ln x  2ln 1 x   C 5   1
Suy ra : a  ,b  2
  10a b  0 5
Thầy Mẫn Ngọc Quang 0989 850 625 Page 2
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. ĐÁP ÁN C 5  3  Câu 7: Cho   x a x b Idx   ln  C 2
x  5x  6 2 x  2x   1 x 1 x  2
Khi đó P  2a b bằng: A. 0 B. 1 C. 2 D. 3 Giải:
Ta có:  2x5x6 2x2x 1 0 dx dx dx dx I    dx         2
x  5x  6 2 x  2x   2 2 1 1 x  2x  1 x  5x  6 x  2 1
x 2x 3     
I   x   2 1 1 1 x 3 1 dx   dx   ln     C
x  3 x  2  x  1 x  2 Suy ra: a  1
 ,b  3  P  2a b  1 ĐÁP ÁN B 1 Câu 8. Cho    ln  ln 1  a I dx b x c x 3 x  2 1 x   2 2  x
Khi đó S a b c bằng: 1 A. -2 B. -1 C. 0 D. 2 Giải:  2 1  x  2  x     2 1    1 1 1 x  2 x  1 1 xI dx    dx           dx 3 x  2 1  x  3  x x 3 2   2 1  x  3   x x    2 1  x    x x 1  x d 2 1 1 1 1    x  1 1   dx     ln x  ln    2 1    x 3 2 2   x x  2 1  x 2x 2 1  1  a  ,b  1
 ,c   S  1  2 2 ĐÁP ÁN B 2 x  1 1
Câu 9. Cho I
dx aln x  1 
bln x c
. Khi đó P  2a bc bằng: 2 x x   1 x A. 2 B. -2 C. 1 D. 0 Giải:
Thầy Mẫn Ngọc Quang 0989 850 625 Page 3
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. 2 2 x  1
x  x   1  x  1 1 1  I dx dx     dx    2 x x   2 1 x x   2 1  x 1 x x  x 1  1 1  1 1   2 1 1            dx  1  
 2ln x  1   ln x 2 2  x  1 xx x  1  x  1 x x x
a  2,b  1
 ,c  0  P  0 ĐÁP ÁN D. 2 1
Câu 10: Tính tích phân I    
. Khi đó S a  2b bằng:
xx   dt ln a b 2 1 1 2 2 A. B. C. 1 D. 1  3 3 Giải: 2 2   2 2 1 x 1 x 1 1 I            dx dx dx dx 2   2 xx x x x x   1 1 1 x 2 1 1 1 1 1 2   2 1 1 2  x 2 1  2 4 1 Suy ra I   dx  
 x 1 dxx 1  ln  x   1  ln    1 1  x x  1 x  1 1 1 3 6 4 1
a  ,b    S  1 3 6 ĐÁP ÁN C 1
Câu 11: Nguyên hàm của f x  có dạng 3 5 x x F xa 2 1 
 ln x bx  1  ln 2
x c C Khi đó P  a b c 4 2 b bằng 2  x 2 . 1 1 A. 1 B. C. D. 0 2 2 Giải:  2 1  2 1 1  x  2 1  x  2  x 1 1  x 1 1 x
Ta có: f x          3 5 3 x x x  2 1 x  3 x x  2 1 x  3 x x  2 1 x  3 2 x x 1 x dx dx xdx 1  1 Vậy 2
f (x)dx    
 ln x  ln(x  1)  C     3 2 2 x x 1  x 2x 2 1
a   ,b  0,c  1 P  0 2 ĐÁP ÁN D 1 xdx
Câu 12: Cho I   a  
b lnc . Biết b + c = 1 x  1 0
Thầy Mẫn Ngọc Quang 0989 850 625 Page 4
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. 2 a c Với , b c  3 . Khi đó 2016 S   b  bằng: 4 2 1 1 A. 0 B. -1 C. D. 4 2 Giải: 1 1 (x  1)  1  1  1 I dx  1 
dx  x  ln(x  1)  1     ln 2  0 x  1  x  1  0 0 2 a 2016 c 1
a  1;b  1
 ;c  2  S   b   4 2 4 ĐÁP ÁN C 1 2 4 1 b Câu 13: Cho    ln  x dx I a
b . Khi đó S  24a   12 bằng: 2 x  1 2 3 0 1 A. 0 B. -1 C. 1 D. 2 Giải: 1 1 1 2 4 2 4 2 x x 11  1  2 I dx dx x 1 dx     2 2 2 x 1 x 1  x 1  0 0 0 1 3 2  x  13 1 2 13 
x  ln x 1   ln 3   b   a
,b  3  S  24a   12  0  3  24 2 24 3 0 ĐÁP ÁN A
Daïng 3: MAÃU SOÁ COÙ CHÖÙA BIEÅU THÖÙC BÌNH PHÖÔNG 2 3x  3x  5 A B C
Câu 14: Cho y    
. Khi đó S A B C bằng: 3 x  3x  2
x  2 x 1 x 2 1 2 5 5 A. 1 B.  3 C. D. 8 8 Giải:
Thầy Mẫn Ngọc Quang 0989 850 625 Page 5
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. 2
3x  3x  5  A B C 3 x  3x  2
x 12 x 1 x  2 2 2  ( A x  2)  (
B x  1)(x  2)  C(x  1)  3x  3x  5 11
)x  1  A  3 11 )x  2   C  9
Tính tổng các hệ số không có x , rồi đồng nhất 2 vế ta có 16
) A B  2C  5  B  9 A B C 11 16 11      
x 2 x 1 x  2 x 2 9(x 1) 9(x    2) 1 3 1 2
A B C  3 ĐÁP ÁN B 2 3x  3x  5 a
Câu 14. Nguyên hàm của y
có dạng f x  
b ln x  1  c ln x d C 3 x  3x  2 x  1 Biết ,
a c  0 . Chọn nhận định đúng a A.b  0
B.a b c d  3
C.ab cd
D.b c  3 3 Giải: 2 3x 3x 5  11 16 11     11 16 11 dx        dx    ln x 1  ln x  2  C 3 x  3x  2  3x   2 1 9(x 1) 9(x  2)  3(x 1) 9 9
a   11 b  16 c  11 , , ,d  2 3 9 9 ĐÁP ÁN D 3x  1 A B C Câu 15. Cho    3 2
4x  28x  65x  50 x  2 2x  5 2x  52
Khi đó S  2A B C bằng A. 10 B. 13 C. -13 D. -10 Giải: Ta phân tích: 3x  1 A B C   
x   Ax  2 3 1 2
5  Bx  22x  5  Cx  2
x  x 2 x  2 2x    5 2 2 5 2x  52
Thầy Mẫn Ngọc Quang 0989 850 625 Page 6
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. A  5  5  Cho x = 2
 ; ;0 ta được: B  10 S  13  2 C  13  ĐÁP ÁN C 1 A B C
Câu 16: Cho A, B, C thỏa mãn   
x x 2 x 2 x 1 x     2 1 2 2 Tính S = A + B +2C A. 2 B. 1 C. 0 D. -1 Gợi ý:
Đồng nhất ta được A B  1,C  1 
Daïng 4: BAÄC TÖÛ SOÁ LÔÙN HÔN MAÃU
Chúng ta thường thực hiện phép chia cho đa thức rồi tiếp tục tiến hành với phần dư. 2 2 x x  1 Câu 17: Cho  a   lnb . x  1 1
Chọn mệnh đề đúng 2
A.a  2b B. 2
2a b b  0 C.a b D.a b 3 Giải: 2 2 2 2 2 2 2 x x 1  1  1  xdx x dx xdx dx       1 3 3 
 ln x 1   2 ln3 ln 2   ln x 1  x 1 x 1  2  2 2 2 1 1 1 1 1 3 3  a  ,b   a b 2 2 ĐÁP ÁN C 2 4x 4x 3
Câu 18. Tìm hàm số f x  2
( ) x ax  ln bx  1  c biết f ' x    
và f 0  1 . Khi đó 2x  1
S   a b3 2 c bằng 2 A. 0 B. 1 C. D. 4 3 Giải: 2 4x  4x  3  2  Ta có f (x)  dx  = 2 2x  1 
dx x x  ln 2x  1    c 2x  1  2x  1 
Thầy Mẫn Ngọc Quang 0989 850 625 Page 7
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. Mà f(0) = 1 2
c  1 f ( )
x x x  ln 2x  1  1
a b c   S   a b3 1, 2, 1 2 c  0 ĐÁP ÁN A 3 2 1  3   3 Câu 19. Cho   ln  1 .  x x x I dx a b
Khi đó 2a b bằng: 2   0
 2x 2x3 1 2 A. 2 B. 3 C. D. 3 3 Giải:. Ta có 3 2
x x x   x   2 3 3
1 x  2x  3. Đặt 2 1
t x  2x  3  dt  x   1 d . x 2
Đổi cận x  0  t  3,x  1 t  6 6 6 1 t  6 6 1  1 6  1  6  1 Khi đó I dt  =  dt  lnt        ln 2   1 2 3 2 t 2 3 2  t t  2  t  2 3 1
a  ,b  2  2a b  3 2 ĐÁP ÁN B   2 1 1 a Câu 20:  = a + lnb  x I dx . Khi đó S  bằng 2 x  1 b 0 1 2 1 1 A. B. C. D. 3 3 3 2 Giải: 1 2 1 1 1 x  1  2x  2x  2x I dx  1  dx dx     dx   4 2 2 2 x  1  x  1  x  1 0 0 0 0 d 2 1 1 x   1  dx     xln 1 2 x  1  1 ln2 2  x  1 0 0 0 a 1
a  1,b  2   b 2 ĐÁP ÁN D 1 3 x  3 c
Câu 21: Cho I
dx a b  5 lnb c ln  . Khi đó P  . a . b c bằng 2   x  2x  3 2 0 A. 32 B. 30 B. 26 D. 26 Giải: 1 3 1 1 x  3  7x  3   6 x   1 1  x  3   6 1  I dx x  2 
dt   x  2      dt   x 2  dx 2 2 x  2x  3  x  2x  3  
x  1 x  3   x  3 x  1  0 0 0      0
Thầy Mẫn Ngọc Quang 0989 850 625 Page 8
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. 1 2  x  5  
 2x  6ln x  3  ln x  1    7ln2  6ln3  2  2 0
a  5 ,b  2,c  6  P  30 2 ĐÁP ÁN B 2 2 dxA B
Câu 22: Cho I     
 . Khi đó S  2A B.I bằng: x x 1 1   x x  1 1   2 2 2 2 A. 2 B. ln 2 C. D. ln 2 3 3 Giải: 1 A B
ABx A AB  0 A 1 Ta có:        x x   1 x x 1 x x   1 A 1 B  1  1 1 1 Nên   x x   1 x x 1 2 2 2 dx dx dx 2 Suy ra 2 I           x x   ln x 1 ln  x  1 | ln 2 1 1 x x 1 2 1 1 1 2 2 2 2
Vậy S  2A B.I I  ln2 ĐÁP ÁN D   dx A B
Câu 23: Cho I        2 2x x  1  x 1  2x  1
Khi đó P  2A B bằng: 3 A. 1 B. C. 3 D. 0 2 Giải: dx dx
2x 12x 1 I    dx    2 2x x  1
x  12x  1
x  12x 1 1  1 2  1 2  
dx  ln x  1  ln x  1     C
3  x  1 2x  1  3 3 1 2 
Khi đó A  ,B
 2A B  0  P  0 3 3 ĐÁP ÁN D
Thầy Mẫn Ngọc Quang 0989 850 625 Page 9
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. 4x  3 a Câu 24: I
dx  ln x a bln cx  1  C
. Khi đó S   c bằng: 2   2x  3x  2 b A. 2 B. 2  C. 4 D. 3 Giải: 4x  3
2x  1 2x2 1 2 I dx dx  (  )    dx 2 2x  3x  2
2x  1x 2 x  2 2x  1  1 2    a dx  
ln x2 2ln 2x1  
C a  2,b  2,c  2  S   c  3
x  2 2x  1 b ĐÁP ÁN D 3 2
4x  2x  2x  2
Câu 25: Cho I dx  3
ax x bln 2x 1  C 2x  1 Và các mệnh đều sau: 1 a < b  16
2 S a b  3
3 a,b là các số nguyên dương.
4 P ab 1 Số mệnh đề đúng là: A. 0 B.1 C. 2 D. 3 Giải: 3 2
4x  2x  2x  2   3   2 3 2x 3 I dx  2x  1    dx  
x  ln 2x  1   C 2x  1  2x  1   3 2  2 3  a  ,b  3 2 1 . Đúng  13
2 . S a b  . Đúng 6
3. a,b không phải là số nguyên. Sai
4 P ab 1.Đúng ĐÁP ÁN D. 3 2
x  3x x  6  x  
Câu 26: Cho I dx  2 3
 ax x bln   C 2 x  4x  3 x   1  Và các mệnh đều sau:
Thầy Mẫn Ngọc Quang 0989 850 625 Page 10
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.  3 1 a  1,b  2
2 S ab  2 3 a b  3
4 P ab  2
Số mệnh đề sai là: A. 0 B.1 C. 2 D. 3 Giải: 3 2
x  3x x  6  3  I dx x  1    dx 2 2 x  4x  3 
x  4x  3  2  3 3   x 3 x  3   x 1  dx    x  ln   C  2(x  3) 2(x  1)   2 2 x  1  1 3  a  ,b  2 2  3 1. a 1,2 . Sai
2. S a b  2. Đúng
3. ,ab không phải là số nguyên. Sai  3
4 P ab . Sai 4 ĐÁP ÁN D 3 2 8x  4x  2  
Câu 27: Cho I dx   2 1
ax x bln 2x  1    C 2 4x  4x  1  2x   1 Và các mệnh đều sau:
1 Modun của số phức z  2a 2bi bằng 5
2 S a b  2 3 a b  3
4 P ab  2
Số mệnh đề đúng là: A. 0 B.1 C. 2 D. 3
Thầy Mẫn Ngọc Quang 0989 850 625 Page 11
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. Giải:   3 2 8x  4x  2  2x  3  1 2 I dx   2x1 dx    2x  1     dx 2 2 4x  4x  1  4x  4x  1  
2x  1 2x   2 1    2 1
  x x  ln 2x  1      C 2x   1
a  1,b  1  2 2
1 . Sai z  2a  2b  4  4  8 .
2. S a b  2. Đúng
3. ,ab không phải là số nguyên. Sai  3
4 P ab . Sai 4 ĐÁP ÁN B x  2 1 1
Câu 28: Cho I dx
a  lnb . Cho các mệnh đề sau: 2 x  1 0 1.a b 2 3 2
S a  2b  6
3 I  lnab
4 log 2 không tồn tại 1 a
Số mệnh đề đúng là: A. 0 B.1 C. 2 D. 3 Giải: 1 2 1 1 1 x  1  2x  2x  2x I dx  1  dx dx     dx   4 2 2 2 x  1  x  1  x  1 0 0 0 0 d 2 1 1 x   1  dx     xln 1 2 x  1  1 ln2 2  x  1 0 0 0
a  1,b  2
1.a b . Sai 2 3 2
S a  2b  9 . Sai
3 I  lnab  ln1 ln2  0  ln2. Đúng.
4Đúng vì cơ số 1 không tồn tại.
Thầy Mẫn Ngọc Quang 0989 850 625 Page 12
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. ĐÁP ÁN C LUYEÄN TAÄP 1 3 x
Câu 1: Cho I
dx = ln a bln c
. Chọn đáp án đúng 1 4 2 x  3x  2 0 5 1 3c
A. a b c B. a   2 b 2
C. b  2cc  2aa  2b  1
D. a c b 2 1 Câu 2: Cho dx  5
a bln . Chọn đáp án đúng 3 x  2  8 1 1 x  7
A. a b
B. 4a  3b 2 3
C. a b 8 5 3  D. ab  27 18 1 3 x
Câu 3. Cho I dx
 ln3  bln2  c . Chọn đáp án đúng 4 2 x  3x  2 0
A. b c  3
B. 2b c 4 C. bc  0
D. b,c là các số nguyên 2 2 2x  3  A B
Câu 4: Cho I dx    2 
 . Khi đó I.A B bằng: x  4x  3 0
x  1 x  3  0 125 125 125 1 125 A. 2  ln B. 2ln C. ln D. ln 3 3 9 2 9 0 dx 1
Câu 5: Cho I   a  lnb  2    2x x 3 5 1 Và các mệnh đều sau:
1 Modun của số phức z  2a5bi bằng 30
2 S ab 7 3 a b
4 P ab 6
Số mệnh đề đúng là: A. 0 B.1 C. 2 D. 3 4x  5
Câu 6: Cho I
dx  ln x a bln x c C  2   x x  2
1 Modun của số phức z  a b ci bằng 2 2
2 S a b c  2
Thầy Mẫn Ngọc Quang 0989 850 625 Page 13
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
3 c b a
4 ,a ,bc là các số thực dương.
Số mệnh đề sai là: A. 0 B.1 C. 2 D. 3 2 2 3x  2 A B
Câu 7: Cho I dx   dx   2 4x  4x  1
2x  1 2x 2 1 1 1 Khi đó P  . A B bằng: 3 21 A. ln 3 B. ln 2 C. ln 2 D. 2 4 dxA B C
Câu 8. Cho I         x   dx 1  2
4x  8x  3
x  1 2x  1 2x  3 
Khi đó P  A B C.I bằng  1  A.  2 2
 ln x  1  ln 4x  8x  3  C B. 2
ln x  1  ln 4x  8x  3    C  2   1  C. 2
ln 4x  8x  3    C D.  2
ln 4x  8x  3   C  2  x  3  A B
Câu 9: Tìm nguyên hàm của dx     dx 2 x  3x  2
x  1 x  2 
Khi đó S A B bằng 1 A. 0 B.1 C. 2 D. 2 1 1 2x  1  A B  6  lna  lnb
Câu 10: Tính I dx   dx     2 4  9x
 2  3x 2  3x  12 0 0
Khi đó P  A Ba  2b 2 5 A. B. 3 C. D. 6 3 2 3x  3x  3
Câu 11: Cho f x 2  3 x  3x  2 A B C
a) Xác định các hằng số A, B, C để f x    x  2 1 x 1 x  2
A. A  3,B  1,C  2
B. A  1,B  2,C  3
C. A  2,B  1,C  3
D. A  3,B  2,C  1
b) Tìm nguyên hàm của f(x).
Thầy Mẫn Ngọc Quang 0989 850 625 Page 14
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. 3 3 A.
 2ln x 1  ln x  2  C B.
 2ln x 1  ln x  2  C x  1 x  1 3  3 C.
 2ln x 1  ln x  2  C D.
 2ln x 1  ln x  2 x  1 x  1 8  2x
Câu 12: Nguyên hàm của
aln x 1  bln x  5  C 2 x  4x  5 Tính S = a+b A. 1 B. 2 C. 4 D. -2 1 a . x dx Câu 13: Để  9  ln 2 x  3x  2 8 0 Khi đó a bằng: A. 4 B. 1 C. 2 D. 3 2 2
x x a 3 3
Câu 14. Tìm a để dx   ln  x1 2 2 1 A. 0 B. 1 C. 2 D. 3 2 2 2x  3  A B
Câu 15. Tính I dx    2   x  4x  3 0
x  1 x  3  0 Khi đó P  . A . B I bằng: 3 125 3 125 3 125 125 A. ln B. ln C. ln D. ln 4 9 2 9 8 9 9 2 4x  4x  3
Câu 16.Tìm hàm số f x biết f 'x  và f 0  1. 2x  1 A. 2
x x  ln 2x  1 B. 2
x x  ln 2x  1  1  C C. 2
x x  ln 2x  1  1 D. 2
x x  ln 2x  1  1 1 1 4x  2  A Bx C
Câu 17. Tính tích phân dx   dx a  ln    b 3 2 2
0 x  2x x  2  x  2 x 1  0
Khi đó S  A B C .ab bằng: 4 4 A. 0 B. ln C.1 D. 2  ln 9 9 Câu 18. Tìm A, B, C: dx AB C       
x  x   dx 2 x  2
x  1 x  2 1 2 
A. A B 1,C  1 
B. A B C 1
C. A B  2,C  1 
D. A B C  1 
Thầy Mẫn Ngọc Quang 0989 850 625 Page 15
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. Giải: Câu 1: Đáp án D. Câu 2: ĐÁP ÁN D Câu 3. ĐÁP ÁN C Câu 4: ĐÁP ÁN C Câu 5: ĐÁP SỐ B Câu 6: ĐÁP ÁN D Câu 7: ĐÁP ÁN D Câu 8. ĐÁP ÁN B. Câu 9: ĐÁP ÁN B Câu 10 ĐÁP ÁN D Câu 11: ĐÁP ÁN D ĐÁP ÁN C Câu 12: ĐÁP ÁN C Câu 13: ĐÁP ÁN B Câu 14. ĐÁP ÁN B Câu 15 ĐÁP ÁN C Câu 16. ĐÁP ÁN C
Thầy Mẫn Ngọc Quang 0989 850 625 Page 16
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. Câu 17. ĐÁP ÁN A Câu 18. ĐÁP ÁN A ÑOÅI BIEÁN b 2 x  3 Câu 6 : Cho 2
I x x  3dx   C  . Tính 2
S  log a  log b  2016 ? a b a A. 2018 B. 2020 C. 2025 D. 2030 Giải: Đặt 2 2 2
t  x  3  t  x  3  2tdt  2xdx  xdx  tdt . 3 2 3 t ( x  3) Suy ra 2
I t.tdt t dt   C   C   3 3 Vậy 2
S  log 3  log 3  2016  2018 3 3
Bình luận: khi có căn 2
x  3 ta sẽ tìm cách đặt 2
t x  3 .Tiếp đó ta biến đổi các phần còn lại
theo t , kể cả dx cũng biểu diễn theo dt . xdx tdt x n d . n
Câu 7. Cho I   2x 1  ln 
 2x14 C. Tính SS (in ) 2x  1  4 8 1 A. B. 0 C.1 D. 1 2 Giải: Chọn C Đặt 2
t  2x  1  t  2x  1  d t t  x d d t t  4   I   1 
dt t  4ln t  4     C       4 2x 1 ln 2x 1 4  C t  4  t  4  . n
Vậy n = 4 vậy S S ( in )  1 8
Bình luận: Việc suất hiện căn
2x  1 ta đặt t  2x  1 , sau đó vẫn như thói quen, ta biểu diễn dx theo dt: d t t  x d 1 b Câu 8. Cho 2
I x 3x  1dx    2 3x  
1  C . Giá trị a và b lần lượt là: a A. 4 và 3 B. 9 và 3 C. 3 và 9 D. 4 và 9 Giải: Chọn B
Thầy Mẫn Ngọc Quang 0989 850 625 Page 17
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. 1 Đặt 2
t  3x 1  2tdt  6xdx tdt xdx 3 2 2 1 1 7 2 3 I t dt t   3 9 9 1 1 1 1 1 I t dt t C   3x  3 2 3 2 1  C 3 9 9 Vậy a = 9; b = 3
Bình luận: Việc xuất hiện căn 2 3x 1 ta đặt 2
t  3x 1 , sau đó vẫn như thói quen, ta biểu diễn dx theo dt . Câu 9: Cho 5 2 7 5 3 A x
1 x dx at bt ct   C , với 2
t  1 x . Tính A  a  b  c 12 95 22 48 A. B. C. D. 79 103 105 109 Giải: Chọn C Đặt 2 2 2 t
x 1  x t 1 xdx tdt      t t A t
1 t dt   t  2t t  7 3 2 2 1 2 1 2 2 6 4 2 5 dt   t
C a  ;b   ;c  7 5 3 7 5 3 22
a b c  105  sin x 1 2 Câu 10. Cho 2 dx
ln a  4 3  ln b  2 2 1   . 2   sin x 1 cos x 2 2 3 3 15 Tính A  a  b 2 A. 30 B. 24 C. 36 D.75 Giải: Chọn D Đặt 2
t  1 cos x t 1 cos x  2tdt  sin xdx  3  x   t  ; x   t 1 3 2 2 1  1 tdt  1 2 2  1 1   C   dt  2     dt 3       t t   t    t  1   3 2 2 1  2 2 2 2 t  2 2  3 2 2 2    1   t   2 3 2  1 1 2 1 1 2  2 ln    ln     2 2 t  2   t  2 2  2 3 2   1 3 1 3 2
Thầy Mẫn Ngọc Quang 0989 850 625 Page 18
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. 1         2 ln 7 4 3 ln 3 2 2 1
a  7;b  3 2 2 3 3 2 1 x     11 a  b  Câu 11. Cho I dx a ln b ln 3  . Tính  3 . x 2 1 A. 0 B. 1 C. 2 D. 3 Giải: Chọn A Đặt 2 2 2
t  1 x t 1 x tdt xdx và x :1  3 thì t : 2  2 3 2 2 2 2 2 1 x t t 11  1  Khi đó I xdx  .tdt dt  1      dt 2 2 2 2 x t 1 t 1  t 1 1 2 2 2 2 2  1  1 1   1 1     dt t      t         1 1 ln 2 2 ln 2 1  ln 3 
2  t 1 t 1  2 t 1  2 2 2 11
a  2  2;b  2 1
a b 3  0 2
Bình luận: Việc xuất hiện căn 2 1 x ta đặt 2
t  1 x , ta tiếp tục công việc biểu diễn 2 2 1 x 1 x
x và dồn về ẩn t , có xdx = tdt. Kinh nghiệm cho thấy khi có căn bậc 2 ta cứ 2 x x
đặt căn đó bằng một biến t rồi kiên trì biến đổi là giải được bài toán. 1  2  a
Câu 12. Cho I   2ln  dx     . Tính A  a  b 2 x  4x  3 1 b 0   A. 3 B. 2 C. 5 D. 7 Giải: Chọn C
Đặt t x 1  x  3  1 1  x 1  x  3 dx dx 2    dx dx t   dt dt    x x  
x  x   . 2 1 2 3 2 1 3 2  x   1  x  3 x   1  x  3 t
Và x : 0 1 thì t :1 3  2  2 . 2 2    2 2 2 2 Khi đó:  2  2ln  2ln  dt I t
  a  2;b  3 4 1 3   t 1 3   1 3 2 2 x 28
Câu 13. Cho tích phân I  (4  )dx  
. Giá trị a là: (biết a có giá trị nguyên) 3 a  3 1 x A. 0 B. 1 C. - 1 D. 3 Giải:
Thầy Mẫn Ngọc Quang 0989 850 625 Page 19
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. Chọn A 2 2 2 x
Ta có I  4dx    dx 3 a a 1 x 2 2 x 2 Tính B   dx . Đặt 3 3 2 2
1 x t 1 x t x dx tdt 3 3 a 1  x 2 2 2 x 2 2 Khi đó 3 3 B dx  1 x  2  1  b 3 a  3 3 1 x a 2 2  2  Ta có: 3 3 I  4x  1 x 10  4a  1  a  3 a  3  28  2  2 2 3 3 3  10  4a  1  a  4a  1 a
 6a  1 a 1   3  3  3 3
SHIFT SOLVE a  0 LUYEÄN TOÁC ÑOÄ ÑEÀ 1: 6 x  3 1
Câu 1. Cho tích phân: I
dx a  2ln a  . Tính  3 S 4 4a x  2 1 A. 10 B. 5 C. 15 D. 8 3 1 1
Câu 2. Cho tích phân    x dx a I . Giá trị của a là: 0 2 4 x x  3 1 A. 1 B. 2 C. 3 D. 4 xdx 35
Câu 3. Tính tích phân I  b
b  0 . Biết z  a  bi là căn bậc hai của số phức  3i a 3 2x  2 4 12 7 6 11 A. B. C. D. 5 5 5 5 5 2 2 19 3b  a
Câu 4. Tính tích phân I   xx 1  ln xdx   lnb . Tính S   76 1 a 3 A.100 B.-100 C.-200 D.200 a b 1
Câu 5. Tính tích phân I xx 1  e   2 1 2 dx   x
. Giá trị của a và b là: 3 .0 A. 3 và 1 B. 2 và 3 C. 3 và 2 D. 2 và 1 1
Câu 6. Cho tích phân: I   x 2
ax b 3x 1dx  3 , biết a  b  1  . Tính 3 3 S  a  b 0 A.-15 B. 20 C. -19 D. 15
Thầy Mẫn Ngọc Quang 0989 850 625 Page 20
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. 5 3 2 2  a   a  370
Câu 7. Tính tích phân    x a I dx . Tính S        . 0 3 1 b x  10b   10b  729 2 2 4 4 A. B.  C. D.  9 9 9 9 1 Câu 8. Cho dx  
f x  C . Tính f '8  ? 1  x   1 x 3 1 4 1 7 A. B. C. D. 5 5 6 6 2 3 dx  8 ln 2aln 2b
Câu 9. Cho tích phân I   lna  ln b . Tính e  2  5 x x 4 4 25 9 9 A. B. C. D. 9 9 4 25 2 x a
Câu 10. Cho tích phân I dx =
 ln16 . Giá trị của a và b là bao nhiêu (a, b tối giản) 1 x1 b 1 A. 4 và 15 B. 5 và 3 C. 6 và 3 D. 5 và 6 ÑEÀ 2: e e 1 3ln x ln x 5 3  
Câu 1. Cho I dx =  a 
3 1 3ln x  5 1 3ln x  . Giá trị của a là x   1 1 7 2 9 4 A. B. C. D. 125 135 145 115  Câu 2. Cho   sin2x sinx I dx
f x  C . Biết rằng f(x) không có hằng số tự do. Tính f(0) 1  3cos x 5 13 44 19 A. B. C. D. 27 27 27 27    t t   Câu 3. Cho 1  cos x.sin x.cos xdx   6 3 5 2    C với 6 3 t  1 cos x . Tỉ số      bằng bao nhiêu? 5 7 7 5 A. B. C. D. 13 5 13 6 7 (  2)
Câu 4. Tìm nguyên hàm của    x dx a I
biết rằng a,b tối giản . Tính a + b 3 x 1 b 0 A. 214 B. 124 C. 421 D. 241 2 ln x Câu 5. Cho I  dx   a  5 bt  3
ct  d.t   C , biết t  ln x 1 . Tính A  abcd x ln x  1
Thầy Mẫn Ngọc Quang 0989 850 625 Page 21
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. A. -30 B. -60 C. -45 D. -27         sin 2x 2  2
Câu 6. Cho I dx   , biết 
. Tính A  cos 2 2    x  3 cos 4sin x ,0;    2  1 A. B. 1 C.  1 D. 0 2 2  2 4  2 Câu 7. Tính  1 cos sin    b B x xdx a . Tính 4 4 A  sin a  b 3 0 43 37 A. B. 29 C. D.16 4 4 a 3  2 ln x 5 Câu 8. I dx   . Giá trị của a là: x 1 2 ln x 3 1 A. 3 e B. 2 e C.e D. 3e 2 x e dx Câu 9. 3 I
at bt C  .Với x
t e 1 ; Tính 2 2 A  a  b x e 1 52 40 47 46 A. B. C. D. 9 9 9 9 ln 3 x e dx
Câu 10. Cho I   a b  . Tính   4 4 A 2 a  b  x x   0 e 1 e 1 A. 23 B. 34 C. 21 D. 45 ÑEÀ 3: 1 2 1 28
Câu 1. Cho tích phân sau    ln  x b a I dx . 1 3x 1 27 a b 0 a 3997 cosa 2    Tính S  cos   
. Biết a, b tối giản.  b  b A. 2 cos   5  cos  5 1999 B. 1999 C. 2016 D. 2
cos 3  cos3  2016 6  3 1
Câu 2. Tính tích phân:    ln  x I dx a
b .Tính S  z  z . Biết z  a  bi . x  2 1 A. 2 B. 4 C. 3 D. 1
Thầy Mẫn Ngọc Quang 0989 850 625 Page 22
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực. 10 3 2  3  4
Câu 3. Tính tích phân    ln  x x I dx a
b . Chọn phát biểu đúng x  2 5 A. a < b B. a = b C. b < 21 D. a, b đều nguyên e 2 e b
Câu 4. Cho tích phân: I x ln xdx   . Tính S  ab . a 1 A. 12 B. 4 C. 6 D. 8 7 a
Câu 5. Cho tích phân: 3 . x x 1dx  
. Giá trị của a là: (biết a, b tối giải) b 0 A. 64 B. 356 C. 346 D. 1029 1 2016 2000
Câu 6. Cho tích phân   dx
a . Tính S  ai  ai 1  2
1 x  1 x A. 3 B. 2 C. 0 D. 1  2 4 
Câu 7. Tính tích phân:  1 cos (sin )   a b I x x dx . Tính  4   4 S sin a b 3 0 A. 1 B. 9 C. 25 D.16  10ab  8 cos  e   11 dx 2  6 
Câu 8. Cho tích phân  ln a  ln 
b . Tính S  cos a  b  2 3 x ln x ln ex e A.-10 B.-5 C.-20 D.-40 2 3 2 2  3 
Câu 9. Cho tích phân:   1  x x x b I dx . Tính 2 S  log a 2  log b ? biết a, b tối giản. 1999   2 x x a 729 0 1 1 1 1 1 A. B. C. D. 9 27 81 36 x 1 3   1 3  2 1  3  2 3 3 1
Câu 10. Cho D dx    x x b x C . Tìm a + b 3 3x 1 a A. 20 B. 75 C. 55 D. 45 LÔØI GIAÛI ÑEÀ 1: Câu 1. Chọn D
Câu 2. Chọn B Câu 3. Chọn A
Thầy Mẫn Ngọc Quang 0989 850 625 Page 23
Truy cập website http://qstudy.vn/ để tham gia Khóa HọcToán và các bài thi Test năng lực.
Câu 4. Chọn B Câu 5. Chọn D
Câu 6. Chọn C Câu 7. Chọn A Câu 8. Chọn C Câu 9. Chọn D Câu 10. Chọn B ÑEÀ 2: Câu 1. Chọn B Câu 2. Chọn C Câu 3. Chọn C Câu 4. Chọn D Câu 5. Chọn A Câu 6. Chọn B Câu 7. Chọn D Câu 8. Chọn D Câu 9. Chọn B Câu 10. Chọn B ÑEÀ 3: Câu 1. Chọn B Câu 2. Chọn B Câu 3. Chọn C Câu 4. Chọn B Câu 5. Chọn D Câu 6. Chọn B
Câu 7. Chọn D Câu 8. Chọn B
Câu 9. Chọn D Câu 10. Chọn A.
Thầy Mẫn Ngọc Quang 0989 850 625 Page 24