Phá đường dây hàm số Toán 12

Phá đường dây Hàm số

- Nắm chắc lý thuyết toán lớp 12

- Tư duy nhanh các bài toán trắc nghiệm

- Phân tích sâu các lỗi sai HS thường mắc phải

- Hệ thống câu hỏi đa dạng có chọn lọc

- Đánh giá năng lực theo thang 4 mức độ

- Extra Techniques bổ sung kinh nghiệm thực

chiến đề

DÚI

TOÁN

NHÓM

ANH

Nhóm toán anh Dúi

Nguyễn Thành Nhân

Phan Thành Tường

Nhóm toán anh Dúi

Nguyễn Thành Nhân

Phan Thành Tường

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

1

[ I can't, I can! ]

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

2

[ I can't, I can! ]

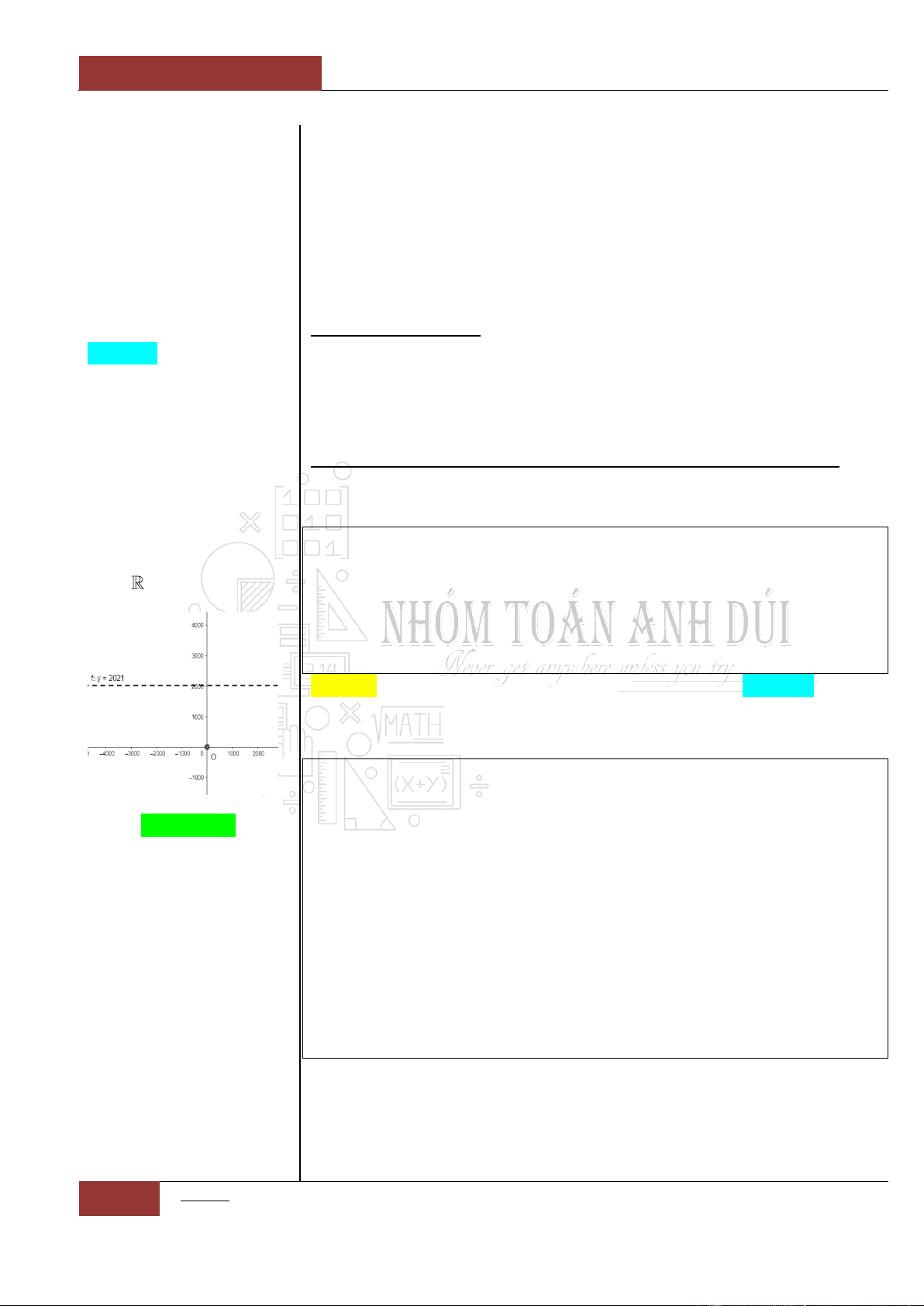
Ví dụ 1: Xét hàm số

2021y 

.

Dễ thấy,

'00y 

(hoặc

0

).

Tuy nhiên,

2021y 

là

một hàm hằng (hàm

không đổi trên trường số

thực ).

Đồ thị I.I.1

CHỦ ĐỀ 1:

HÀM SỐ & ỨNG DỤNG ĐẠO HÀM

I.I. Tính đơn điệu của hàm số

A. Lý thuyết cần nắm

1. Đơn điệu là gì?

Một hàm số được gọi là đơn điệu nếu nó hoặc đồng biến hoặc

nghịch biến trên

K

, trong đó

K

có thể là một khoảng (đoạn),

nửa khoảng (nửa đoạn).

2. Mối quan hệ giữa tính đơn điệu và dấu của đạo hàm

Điều kiện cần để một hàm số đơn điệu:

Giả sử hàm số

 

y f x

có đạo hàm trên khoảng

I

. Khi đó:

 

i

Nếu hàm số

 

y f x

đồng biến thì

 

' 0,f x x I  

 

ii

Nếu hàm số

 

y f x

nghịch biến thì

 

' 0,f x x I  

Lưu ý: Điều ngược lại chưa chắc đúng. (Xem Ví dụ 1)

Điều kiện đủ để một hàm số đơn điệu trên khoảng:

Giả sử hàm số

 

y f x

có đạo hàm trên khoảng

I

. Khi đó:

 

i

Nếu

 

' 0,f x x I  

và dấu

""

chỉ xảy ra ở hữu hạn điểm

của khoảng

I

thì hàm số

 

y f x

đồng biến trên

I

.

 

ii

Nếu

 

' 0,f x x I  

và dấu

""

chỉ xảy ra ở hữu hạn

điểm của khoảng

I

thì hàm số

 

y f x

nghịch biến trên

I

.

 

iii

Nếu

 

' 0,f x x I  

thì hàm số

 

y f x

không đơn điệu

(không đổi) trên

I

.

*Mở rộng khoảng đơn điệu trên nữa khoảng, đoạn:

Điều kiện đủ để một hàm số đơn điệu trên nữa khoảng:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

3

[ I can't, I can! ]

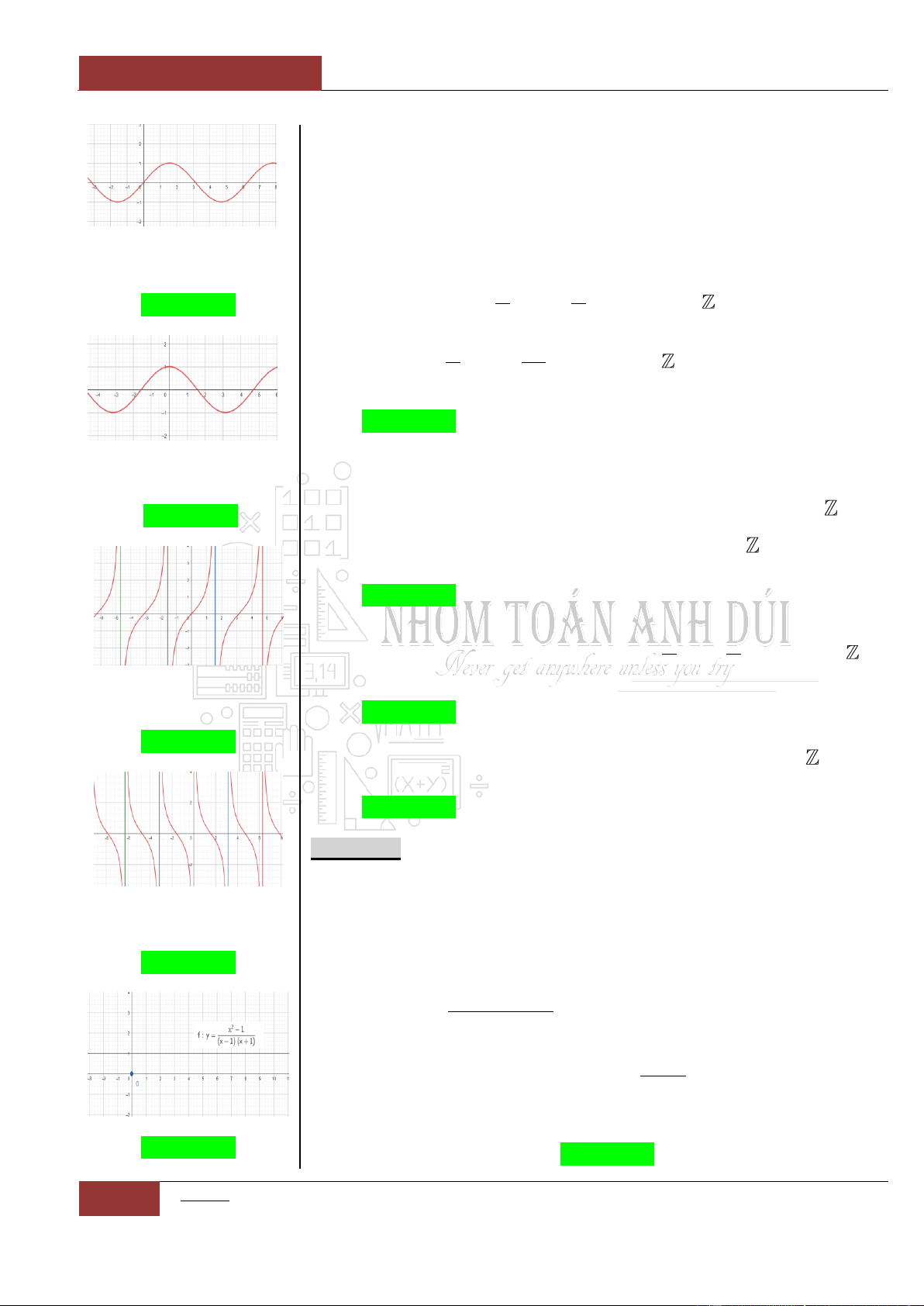
Ví dụ 2: Cho đồ thị hàm

số

 

y f x

liên tục

trên như hình 2 bên

dưới

Đồ thị I.I.2

Ta có nhận xét như sau:

Hàm số

 

y f x

nghịch biến trên khoảng

 

;2

.

Hàm số

 

y f x

không đổi trên khoảng

 

2;6

.

Hàm số

 

y f x

đồng

biến trên khoảng

 

6;

.

Lưu ý: Trên khoảng

 

6;

có một điểm

(hữu hạn) làm đồ thị

hàm số đi ngang (đạo

hàm tại điểm đó bằng

không).

Vì hàm số liên tục trên

đoạn , nên hoàn toàn

ta có thể thay các

khoảng

I

thành các nửa

khoảng, đoạn

'I

tương

ứng.

Giả sử hàm số liên tục trên nửa khoảng





;ab

(hoặc





;ab

)

và có đạo hàm trên khoảng

 

;ab

. Khi đó:

 

i

Nếu

   

' 0, ;f x x a b  

và dấu

""

chỉ xảy ra ở hữu hạn

điểm của khoảng

 

;ab

thì hàm số

 

y f x

đồng biến trên nửa

khoảng





;ab

(hoặc





;ab

).

 

ii

Nếu

   

' 0, ;f x x a b  

và dấu

""

chỉ xảy ra ở hữu hạn

điểm của khoảng

 

;ab

thì hàm số

 

y f x

nghịch biến trên nửa

khoảng





;ab

(hoặc





;ab

).

 

iii

Nếu

   

' 0, ;f x x a b  

thì hàm số

 

y f x

không đơn

điệu (không đổi) trên nửa khoảng





;ab

(hoặc





;ab

).

Điều kiện đủ để một hàm số đơn điệu trên đoạn:

Giả sử hàm số

 

y f x

liên tục trên đoạn

 

;ab

và có đạo hàm trên

khoảng

 

;ab

. Khi đó:

 

i

Nếu

   

' 0, ;f x x a b

và dấu

""

chỉ xảy ra ở hữu hạn

điểm của khoảng

 

;ab

thì hàm số

 

y f x

đồng biến trên đoạn

 

;ab

.

Nếu

   

' 0, ;f x x a b

và dấu

""

chỉ xảy ra ở hữu hạn

điểm của khoảng

 

;ab

thì hàm số

 

y f x

nghịch biến trên đoạn

 

;ab

.

Nếu

   

' 0, ;f x x a b

thì hàm số

 

y f x

không đơn

điệu (không đổi) trên đoạn

 

;ab

.

Nhận xét chiều biến thiên: Nếu hàm số đồng biến trên

K

thì đồ thị

hàm số có chiều hướng đi lên từ trái sang phải. Nếu hàm số nghịch

biến thì đồ thị hàm số có chiều hướng đi xuống từ trái sang phải. Tất

nhiên, hàm hằng thì chỉ là một đường thẳng song song hoặc trùng với

trục hoành. (Xem Ví dụ 2).

 

y f x

 

ii

 

iii

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

4

[ I can't, I can! ]

Hàm số

sinyx

Đồ thị I.I.3

Hàm số

cosyx

Đồ thị I.I.4

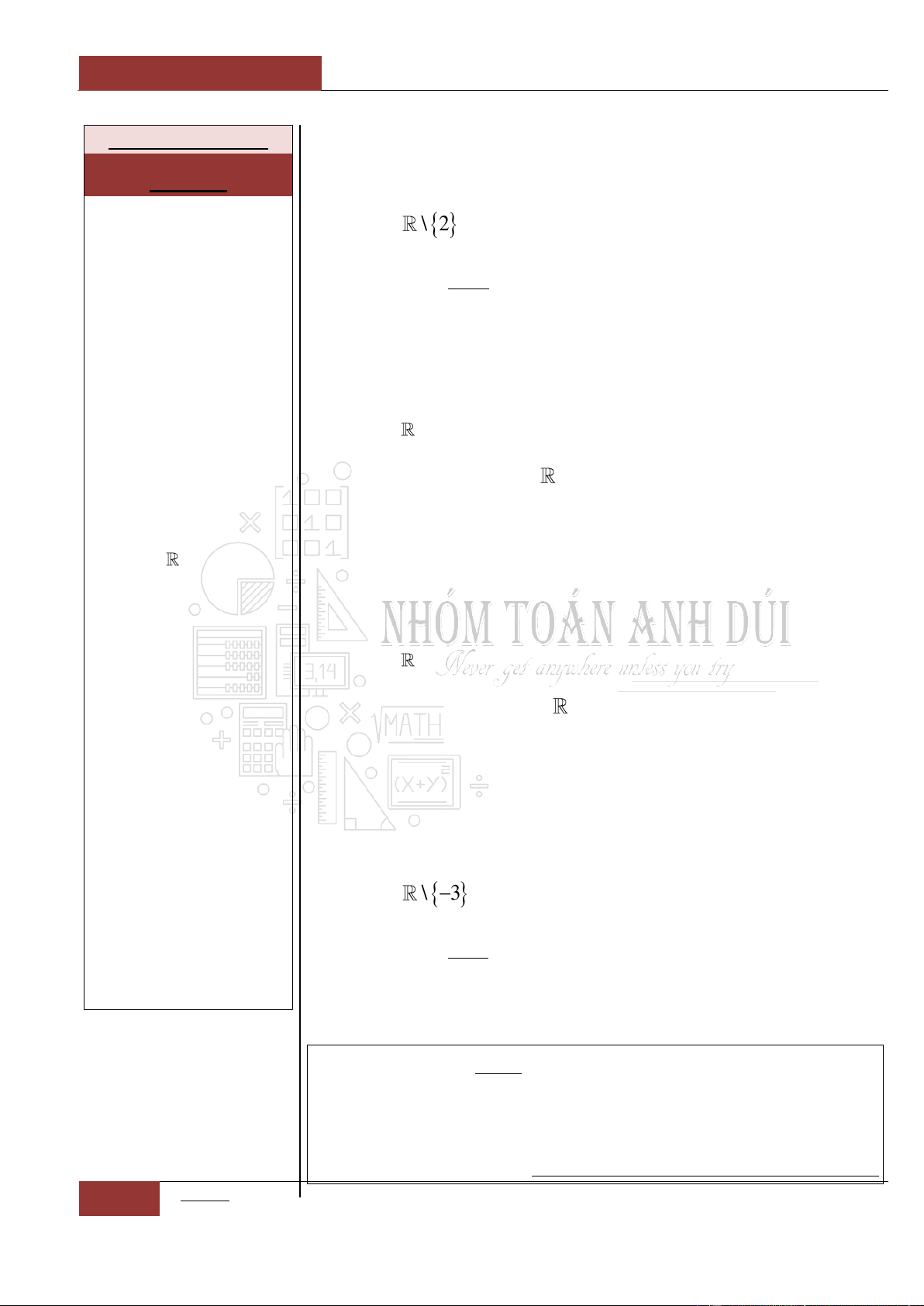
Hàm số

tanyx

Đồ thị I.I.5

Hàm số

cotyx

Đồ thị I.I.6

Đồ thị I.I.7

Những trường hợp đặc biệt:

Ta xét những hàm số tuần hoàn, hàm số lượng giác:

sinyx

hay

cosyx

sẽ có một số vô hạn điểm mà tại đó hàm số đạo hàm bằng

không. Nhưng ta vẫn có thể kết luận rằng hàm số

sinyx

đồng biến

trên họ các khoảng

2 ; 2 ,

22

k k k





    





và nghịch biến trên

họ các khoảng

3

2 ; 2 ,

22

k k k





   





.

(Xem Đồ thị I.I.3).

Một cách tương tự, ta có kết luận rằng hàm số:

cosyx

đồng biến trên họ các khoảng

 

2 ; 2 ,k k k

  

   

và

nghịch biến trên họ các khoảng

 

2 ; 2 ,k k k

  

  

.

(Xem Đồ thị I.I.4).

tanyx

đồng biến trên họ các khoảng

;,

22

k k k





    





.

(Xem Đồ thị I.I.5).

cotyx

nghịch biến trên họ các khoảng

 

;,k k k

  

  

.

(Xem Đồ thị I.I.6).

Nhận xét : Khi xác định tính đơn điệu của đồ thị hàm số bằng đạo

hàm ta phải đặc biệt lưu ý về câu chuyện phải có dấu bằng xảy ra tại

hữu hạn điểm là bởi: Nếu dấu bằng xảy ra tại một số vô hạn điểm

trên

K

hay xảy ra trên toàn tập

K

thì mảy may một trường hợp nào

đó giống như hàm số

 

y f x

trên đoạn

 

2;6

thì hàm số không đổi.

Hay hàm số

  

2

1

11

x

y

xx







chẳng hạn, trên khoảng

 

1; 

, hàm

số liên tục và có đạo hàm bằng 0 do

 

2

1

1, 1;

1

x

yx

x



    



nên

khi đó:

 

' 0, 1;yx   

. Vậy hàm số có hay không tính đơn

điệu? Đáp án là không. (Xem Đồ thị I.I.7).

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

5

[ I can't, I can! ]

Extra Techniques:

Remark:

Để đánh giá dấu trong

khoảng

 

1

,

ii

xx



ta có

thể dùng công cụ Casio

để hỗ trợ bằng cách

"CALC" một giá trị

trung gian trong khoảng

 

1

,

ii

xx



, dấu của

   

0 0 1

' , ,

ii

f x x x x





cũng chính là dấu của

dấu của

 

'fx

trong

khoảng

 

1

,

ii

xx



.

Ngoài ra, công cụ đạo

hàm cũng khá hữu hiệu

trong việc xác định dấu

của

 

'fx

trên từng

khoảng con trên

K

.

Extra Techniques:

Tips:

Để đạo hàm hàm số

ax b

y

cx d







ta có thể áp

dụng công thức đạo hàm

nhanh như sau:

 

2

'

ad bc

y

cx d







3. Quy tắc xét tính đơn điệu của hàm số

Bước 1: Tìm tập xác định

D

.

Bước 2: Tính đạo hàm

 

''y f x

. Tìm tất cả các điểm

, 1,

i

x i n

mà

tại đó

 

'0

i

fx

hoặc

 

'

i

fx

không xác định.

Bước 3: Lập bảng biến thiên và sắp xếp các điểm vừa tìm được theo

thứ tự tăng dần cùng các kí hiệu tương ứng.

Bước 4: Kết luận khoảng đơn điệu của hàm số.

B. Bài tập trong các đề thi thử

Dạng 1: Bài toán không chứa tham số

Câu 1. Cho hàm số

2

1

x

y

x







. Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng

 

; 

.

B. Hàm số nghịch biến trên khoảng

 

1; 

.

C. Hàm số nghịch biến trên khoảng

 

;1 

.

D. Hàm số đồng biến trên khoảng

 

;1 

.

(Trích đề tham khảo BGD&ĐT năm 2017)

Đáp án: D

Lời giải

TXĐ:

 

\1D 

Xét hàm số:

2

1

x

y

x







Ta có:

 

2

3

' 0,

1

y x D

x

   



Vì vậy, hàm số

2

1

x

y

x







đồng biến trên

 

;1 

và

 

1; 

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

6

[ I can't, I can! ]

Extra Techniques:

Casio:

Cơ sở: Dựa vào đáp án

ta có thể dễ dàng loại trừ

các phương án sai:

Đạo hàm tại

5x 

Vì:

 

' 5 0y 

Loại B.

Đạo hàm tại

0.5x 

Vì:

 

' 0.5 0y 

Loại C, D.

Chọn A.

Câu 2. Cho hàm số

2

21yx

. Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng

 

0;

.

B. Hàm số đồng biến trên khoảng

 

;0

.

C. Hàm số nghịch biến trên khoảng

 

0;

.

D. Hàm số nghịch biến trên khoảng

 

1;1

.

(Trích đề thi THPTQG năm 2017 MĐ 104)

Đáp án: A

Lời giải

TXĐ:

D 

Xét hàm số:

2

21yx

Ta có:

22

42

' 0 0

2 2 1 2 1

xx

yx

xx

    



Vậy hàm số

2

21yx

nghịch biến trên khoảng

 

;0

và đồng

biến trên khoảng

 

0;

.

Câu 3. Hàm số nào dưới đây đồng biến trên khoảng

 

; 

?

A.

1

2

x

y

x







. B.

3

y x x

. C.

3

3y x x  

. D.

1

3

x

y

x







.

(Trích đề thi THPTQG năm 2017 MĐ 110)

Đáp án: B

Lời giải

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

7

[ I can't, I can! ]

Extra Techniques:

Remark:

Cơ sở: Dựa vào đáp án

ta có thể dễ dàng loại trừ

các phương án sai:

Đáp án A và D đều là

các hàm nhất biến vì thế

đồ thị hoặc đồng biến

hoặc nghịch biến hoặc

không đổi trên từng

khoảng xác định. Hay

nói cách khác đồ thị

hàm nhất biến không

liên tục và không đơn

điệu trên .

Loại A, D.

Đáp án C là một hàm

bậc ba có hệ số

0a 

nên:

 

3

lim 3

x

xx



   

Hay hàm số có xu

hướng đi theo chiều từ

trên xuống dưới khi

x

dần đến một khoảng đủ

lớn.

Loại C.

Chọn B.

Ta xét từng đáp án:

+) Đáp án A:

TXĐ:

 

\2D 

Vậy hàm số

1

2

x

y

x







không thể nào liên tục trên khoảng

 

; 

Loại A.

+) Đáp án B:

TXĐ:

D 

Ta có:

2

' 3 1 0,y x x    

Vậy hàm số

3

y x x

đồng biến trên khoảng

 

; 

.

Chọn B.

+) Đáp án C:

TXĐ:

D 

Ta có:

2

' 3 3 0,y x x     

Vậy hàm số

3

3y x x  

nghịch biến trên khoảng

 

; 

.

Loại C.

+) Đáp án D:

TXĐ:

 

\3D 

Vậy hàm số

1

3

x

y

x







không thể nào liên tục trên khoảng

 

; 

Loại D.

Câu 4. Hàm số

2

1

y

x





nghịch biến trên khoảng nào dưới đây?

A.

 

; 

. B.

 

0;

. C.

 

;0

. D.

 

1;1

.

(Trích đề thi THPTQG năm 2017 MĐ 123)

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

8

[ I can't, I can! ]

Extra Techniques:

Casio:

Cơ sở: Dựa vào đáp án

ta có thể dễ dàng loại trừ

các phương án sai:

Đạo hàm tại

0.5x 

Vì:

 

' 0.5 0y 

Loại A, C, D.

Chọn B.

Đáp án: B

Lời giải

TXĐ:

D 

Xét hàm số:

2

1

y

x





Ta có:

 

2

4

' 0 0

1

x

yx

x



   



Từ bảng biến thiên của đồ thị hàm số ta nhận thấy rằng đồ thị hàm số

đã cho nghịch biến trên khoảng

 

0;

.

Câu 5. Cho hàm số

 

fx

có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào sau đây?

A.

 

;1 

. B.

 

0;1

. C.

 

1;0

. D.

 

1; 

.

(Trích đề thi THPTQG năm 2019 MĐ 103)

Đáp án: C

Lời giải

Dựa vào bảng biến thiên của đồ thị hàm số ta thấy rằng: Hàm số đồng

biến trên hai khoảng rời nhau:

 

1;0

và

 

1; 

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

9

[ I can't, I can! ]

Extra Techniques:

Remark:

Cơ sở: Dựa vào đáp án

ta có thể dễ dàng loại trừ

các phương án sai:

Đáp án B là hàm nhất

biến vì thế đồ thị hoặc

đồng biến hoặc nghịch

biến hoặc không đổi trên

từng khoảng xác định.

Hay nói cách khác đồ thị

hàm nhất biến không

liên tục và không đơn

điệu trên .

Loại B.

Đáp án C là một hàm

bậc bốn trùng phương

có tích hệ số

0ab 

nên

có

3

điểm cực trị, vì

0a 

nên đồ thị hàm số

có dạng hình chữ

"W"

Loại C.

Đáp án D có tập xác

định:

 

\ 2;2D 

vì

vậy hàm không xác định

trên toàn tập . Vì thế

nó không thể nào đồng

biến trên .

Loại D.

Chọn A.

Câu 6. Trong các hàm số sau hàm nào đồng biến trên ?

A.

3

5y x x

. B.

2

7

x





.

C.

42

46xx

. D.

2

1

4

x





.

(Trích đề thi Nhóm toán anh Dúi 2020 - 2021)

Đáp án: A

Lời giải

Xét từng đáp án:

+) Đáp án A:

TXĐ:

D 

. Ta có:

2

' 3 5 0yx  

Vì vậy hàm số:

3

5y x x

đồng biến trên .

+) Đáp án B:

TXĐ:

 

\7D 

Vì vậy hàm số

2

7

x

y

x







không liên tục trên

Loại B.

+) Đáp án C:

TXĐ:

D 

. Ta có:

3

2

' 4 8 0 0

2

x

y x x x

x







    







Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

10

[ I can't, I can! ]

Extra Techniques:

Tips:

Đối với các bài toán

phân thức bậc hai trên

bậc hai có dạng:

2

1 1 1

2

2 2 2

a x b x c

y

a x b x c







Ta có thể áp dụng công

thức đạo hàm nhanh như

sau:

 

   

 

1 1 1 1 1 1

2

2 2 2 2 2 2

2

2 2 2

2

1 2 2 1 1 2 2 1 1 2 2 1

2

2 2 2

2

'

2

a b a c b c

xx

a b a c b c

y

a x b x c

a b a b x a c a c x b c b c

a x b x c







    





Extra Techniques:

Casio:

Ví dụ cần đạo hàm phân

thức:

2

23

4 5 6

xx

y

xx







bằng Casio ta làm theo

các bước sau:

B1: Vào mode Vector.

B2: Khai báo vector A

với

3

kích thước lần

lượt là hệ số của

2

x

,

x

và hệ số tự do của tử số.

Từ bảng biến thiên của đồ thị hàm số đã cho ta thấy rằng đồ thị hàm

số nghịch biến trên hai khoảng rời nhau:

 

;2 

và

 

0; 2

.

Vì vậy hàm số:

42

46y x x  

không thể nào đồng biến trên .

Loại C.

+) Đáp án D:

TXĐ:

 

\ 2;2D 

Vì vậy hàm số

2

1

4

x

y

x







không liên tục trên .

Loại D.

Câu 7. Hàm số

2

3

2

y

x





đồng biến trên khoảng nào?

A.

 

0;

. B.

 

;0

.

C.

 

; 

. D.

 

;2 

.

(Trích đề thi Nhóm toán anh Dúi 2020 - 2021)

Đáp án: B

Lời giải

TXĐ:

D 

.

Ta có:

 

   

22

32

6

' 0 0

22

x

yx

xx

      



Dựa vào bảng biến thiên, ta thấy hàm số

2

3

2

y

x





đồng biến trên

khoảng

 

;0

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

11

[ I can't, I can! ]

B3: Thoát ra chế độ chờ

bằng phím .

Nhấn liên tiếp hai phím

và phím .

để khai báo tương tự

cho vector B với ba kích

thước

2

x

,

x

và hệ số tự

do của mẫu số.

B4: Thoát ra chế độ chờ

bằng phím .

Nhấn liên tiếp ba phím

, phím và

phím để xuất ra

màn hình vector A.

B5: Nhấn phím .

B6: Nhấn liên tiếp ba

phím , phím và

phím để xuất ra

màn hình vector B.

B7: Nhấn phím .

B8: Đọc kết quả từ sau

ra trước, nhân thêm

""2

vào số thứ hai.

 

2

33

'

4 5 6

12xx

y

xx











Câu 8. Trên đoạn

 

0;2



, hàm số

   

2

9

cos 2 3 2 6

2

f x x x x    

nghịch biến trên khoảng nào sau đây?

A.

0;

2









. B.

;2

2









.

C.

 

0;2



. D.

 

;2



.

(Trích đề thi Nhóm toán anh Dúi 2020 - 2021)

Đáp án: C

Lời giải

TXĐ:

D 

Ta có:

   

2

9

cos 2 3 2 6

2

f x x x x    

   

 

2

4 12 9

cos 2 3

2

23

cos 2 3

2

xx

f x x

x

f x x



   



   

Khi đó:

     

' 2sin 2 3 2 2 3 0f x x x     

 

sin 2 3 2 3 0

3

2 3 0

2

xx

x x L

    

     

Vậy hàm số:

   

2

9

cos 2 3 2 6

2

f x x x x    

nghịch biến trên

khoảng

 

0;2



.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

12

[ I can't, I can! ]

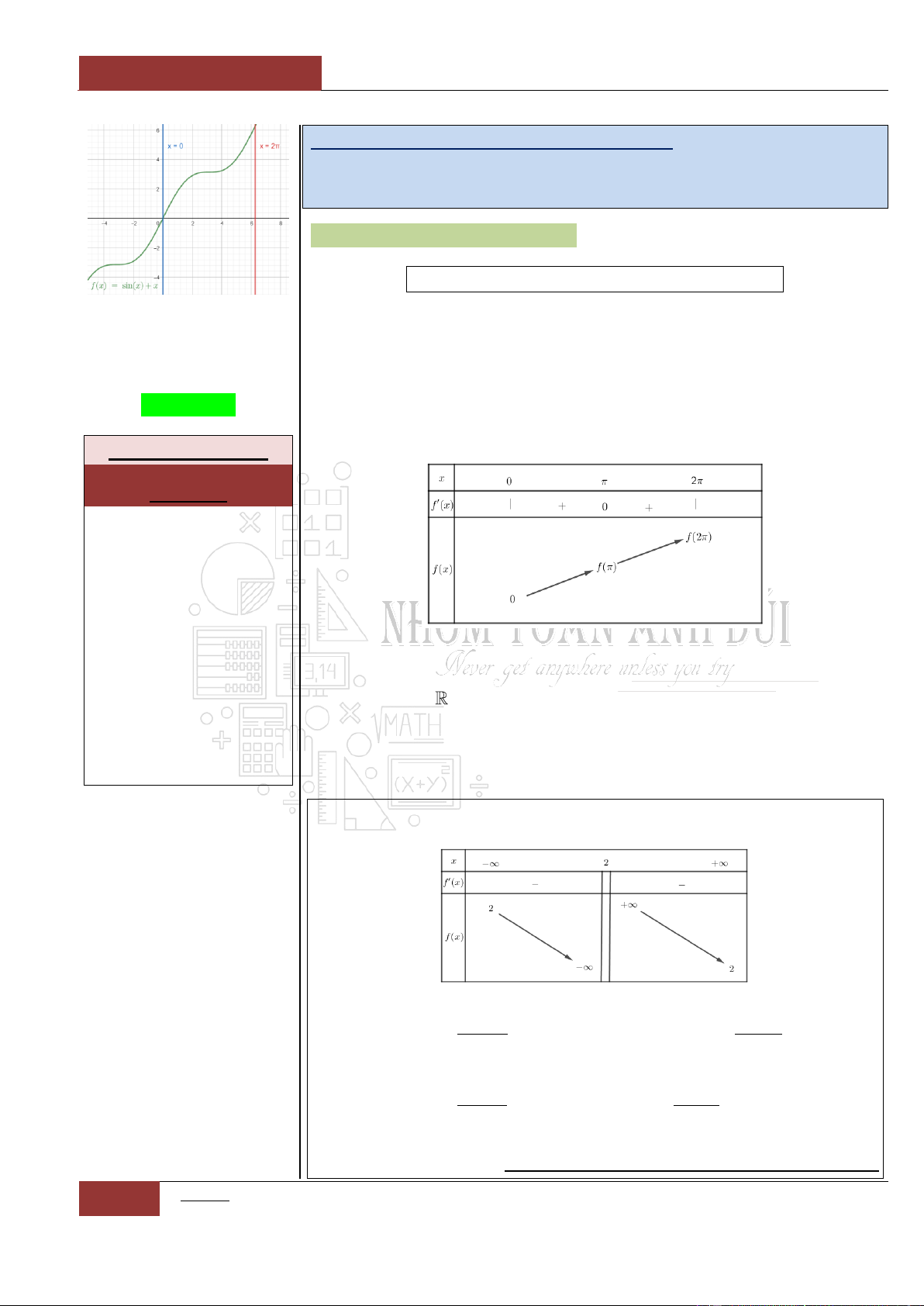
Đồ thị hàm số

 

siny f x x x  

Đồ thị I.I.8

Extra Techniques:

Remark:

Giả sử đồ thị hàm số

 

y f x

tăng ngặt

(luôn đồng biến) hay

giảm ngặt (luôn nghịch

biến) trên khoảng

K

,

khi đó trên khoảng

K

,

phương trình

 

0fx

,

nếu có nghiệm, thì tối đa

chỉ có

1

nghiệm.

Một câu hỏi được đặt ra, rằng tại sao ta có:

 

sin 2 3 2 3 0 2 3 0x x x      

???

Ta xét một bài toán phụ như sau:

Tìm giá trị của

x

thỏa mãn:

sin 0xx

???

Ta xét hàm số:

 

sinf x x x

Ta có:

 

' cos 1 0 2f x x x k



     

Bảng biến thiên:

Từ đồ thị hàm số

 

siny f x x x  

ta nhận thấy đồ thị là một hàm

đồng biến trên . Nên phương trình

 

0fx

có nhiều nhất một

nghiệm. Mà mặt khác ta lại có:

 

00f 

. Vậy

0x 

là nghiệm duy

nhất của phương trình:

sin 0xx

.

Câu 9. Hàm số nào có bảng biến thiên như hình vẽ dưới đây?

A.

 

24

2

x

fx

x







. B.

 

21

2

x

fx

x







.

C.

 

25

2

x

fx

x







. D.

41

2

x 

.

(Trích đề thi Nhóm toán anh Dúi 2020 - 2021)

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

13

[ I can't, I can! ]

Đáp án: B

Lời giải

Từ bảng biến thiên, ta nhận thấy rằng:

 Hàm số

 

y f x

nghịch biến trên từng khoảng xác định,

khoảng

 

;2

và

 

2;

.

 Đồ thị hàm số nhận đường thẳng

2x 

làm tiệm cận đứng.

 Đồ thị hàm số nhận đường thẳng

2y 

làm tiệm cận ngang.

Xét từng đáp án:

+) Đáp án A:

Ta lưu ý rằng tuy mới nhìn vào hàm số

 

24

2

x

fx

x







ta nhận thấy

đồ thị hàm số có hai đường tiệm cận ngang và đứng lần lượt là

2, 2xy

thật. Tuy nhiên, sau một phép biến đổi thì:

 

24

2

x

fx

x







Vì vậy đồ thị hàm số đơn giản chỉ là đường thẳng

2y 

trên hai

khoảng rời nhau

 

;2

và

 

2;

(bị gián đoạn tại

2x 

).

Loại A.

+) Đáp án B:

 Đồ thị hàm số nhận đường thẳng

2x 

làm tiệm cận đứng.

 Đồ thị hàm số nhận đường thẳng

2y 

làm tiệm cận ngang.

Ta có:

   

 

2

2 1 3

'0

2

x

f x f x

x



   



 Hàm số

 

y f x

nghịch biến trên từng khoảng xác định,

khoảng

 

;2

và

 

2;

.

Chọn B.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

14

[ I can't, I can! ]

Đồ thị I.I.9

Đồ thị I.I.10

+) Đáp án C:

Ta có:

 

2

1

'0

2

y

x





.

Vì thế hàm số đã cho đồng biến trên từng khoảng xác định, khoảng

 

;2

và

 

2;

.

Loại C.

Đáp án D:

Dễ thấy rằng, đồ thị hàm số

 

4 1 1

2

22

x

y f x x



   

là phương

trình đường thẳng có

20a 

, nên hàm số luôn đồng biến trên .

Loại D.

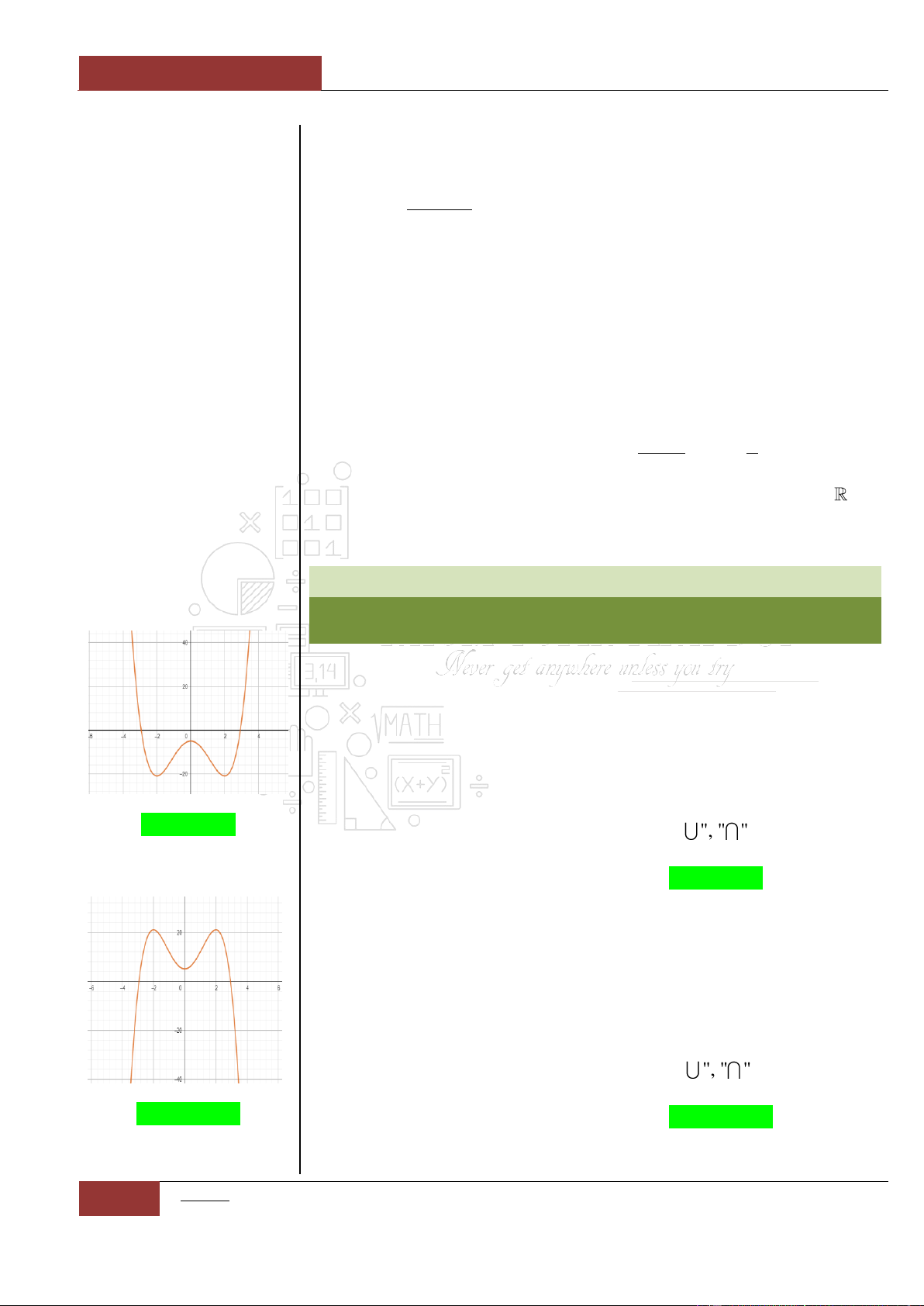
Một số Tips để làm tốt các bài toán không chứa tham số

 

1

Xét hàm số:

 

42

0y ax bx c a   

, ta có các nhận xét:

 Trường hợp 1:

0

ab

a











hay

0

a

b











Khi đó đồ thị hàm số có dạng hình chữ

"W"

, ta có thể loại trừ các

phương án với đồ thị có dạng hình chữ

" ", " ", " "

.

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.I.9).

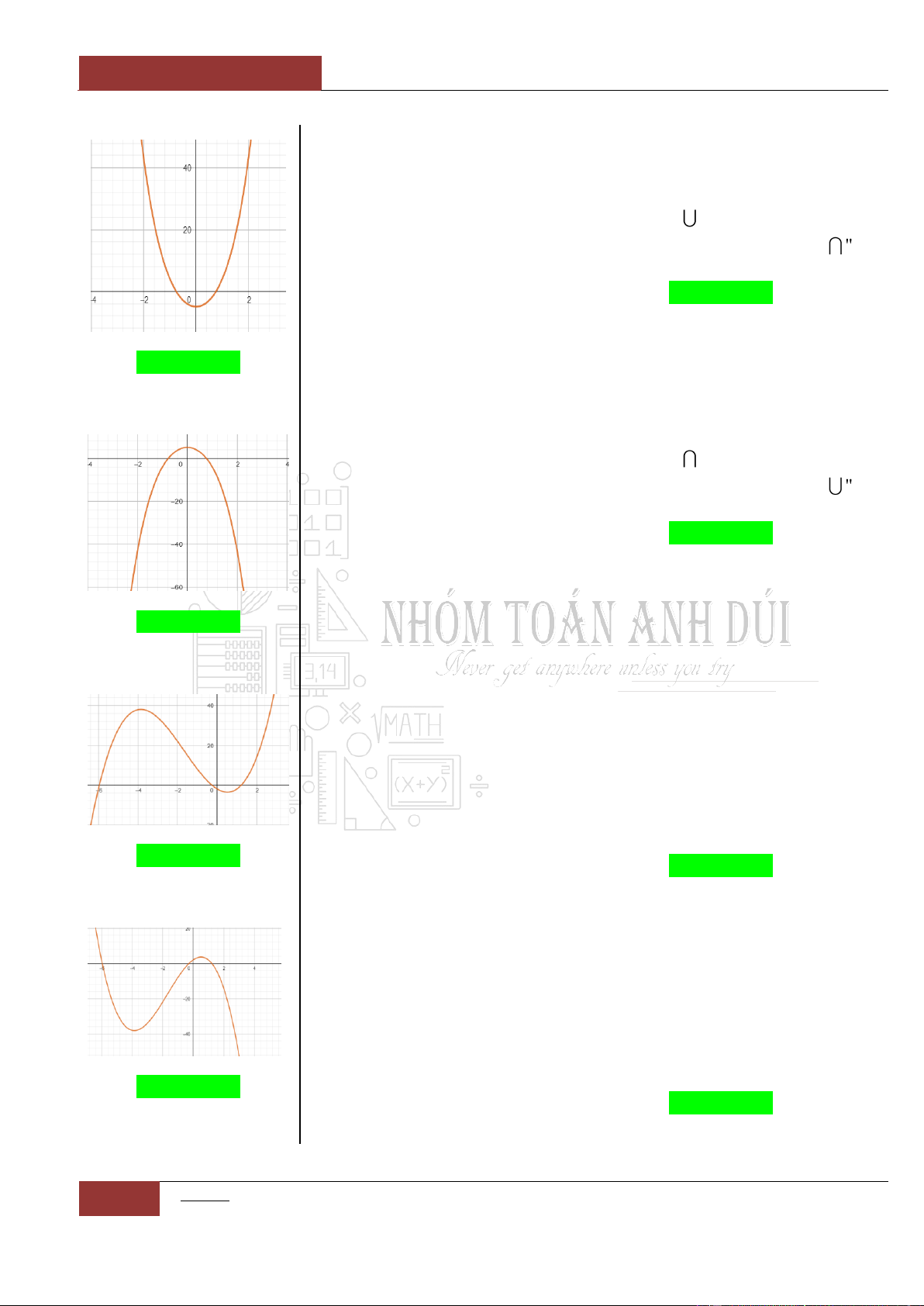
 Trường hợp 2:

0

ab

a











hay

0

a

b











Khi đó đồ thị hàm số có dạng hình chữ

""

, ta có thể loại trừ các

phương án với đồ thị có dạng hình chữ

"W", " ", " "

.

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.I.10).

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

15

[ I can't, I can! ]

Đồ thị I.I.11

Đồ thị I.I.12

Đồ thị I.I.13

Đồ thị I.I.14

Trường hợp 3:

0

ab

a











hay

0

a

b











Khi đó đồ thị hàm số có dạng giống hình chữ của Parabol ta có thể

loại trừ các phương án với đồ thị có dạng hình chữ

"W", " ", " "

.

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.I.11).

 Trường hợp 4:

0

ab

a











hay

0

a

b











Khi đó đồ thị hàm số có dạng giống hình chữ của Parabol ta có thể

loại trừ các phương án với đồ thị có dạng hình chữ

"W", " ", " "

.

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.I.12).

 

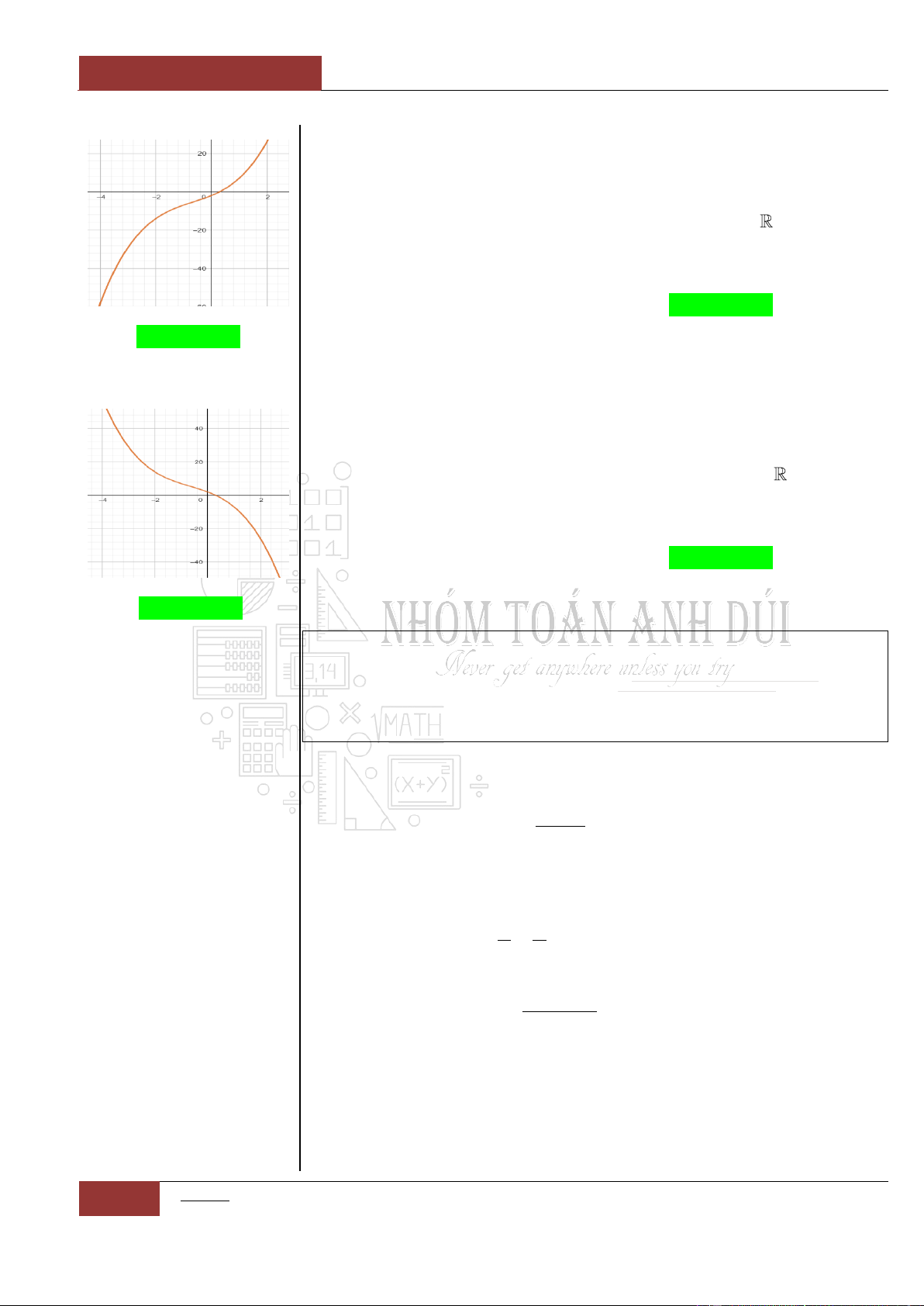
2

Xét hàm số:

 

32

0y ax bx cx d a    

 Trường hợp 1:

2

30

0

b ac

a











hay

2

3

0

b ac

a











Khi đó đồ thị hàm số có dạng giống chữ

""

ta có thể loại trừ các

phương án khác.

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.I.13).

 Trường hợp 2:

2

30

0

b ac

a











hay

2

3

0

b ac

a











Khi đó đồ thị hàm số có dạng giống chữ

"

И

"

ta có thể loại trừ các

phương án khác.

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.I.14).

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

16

[ I can't, I can! ]

Đồ thị I.I.15

Đồ thị I.I.16

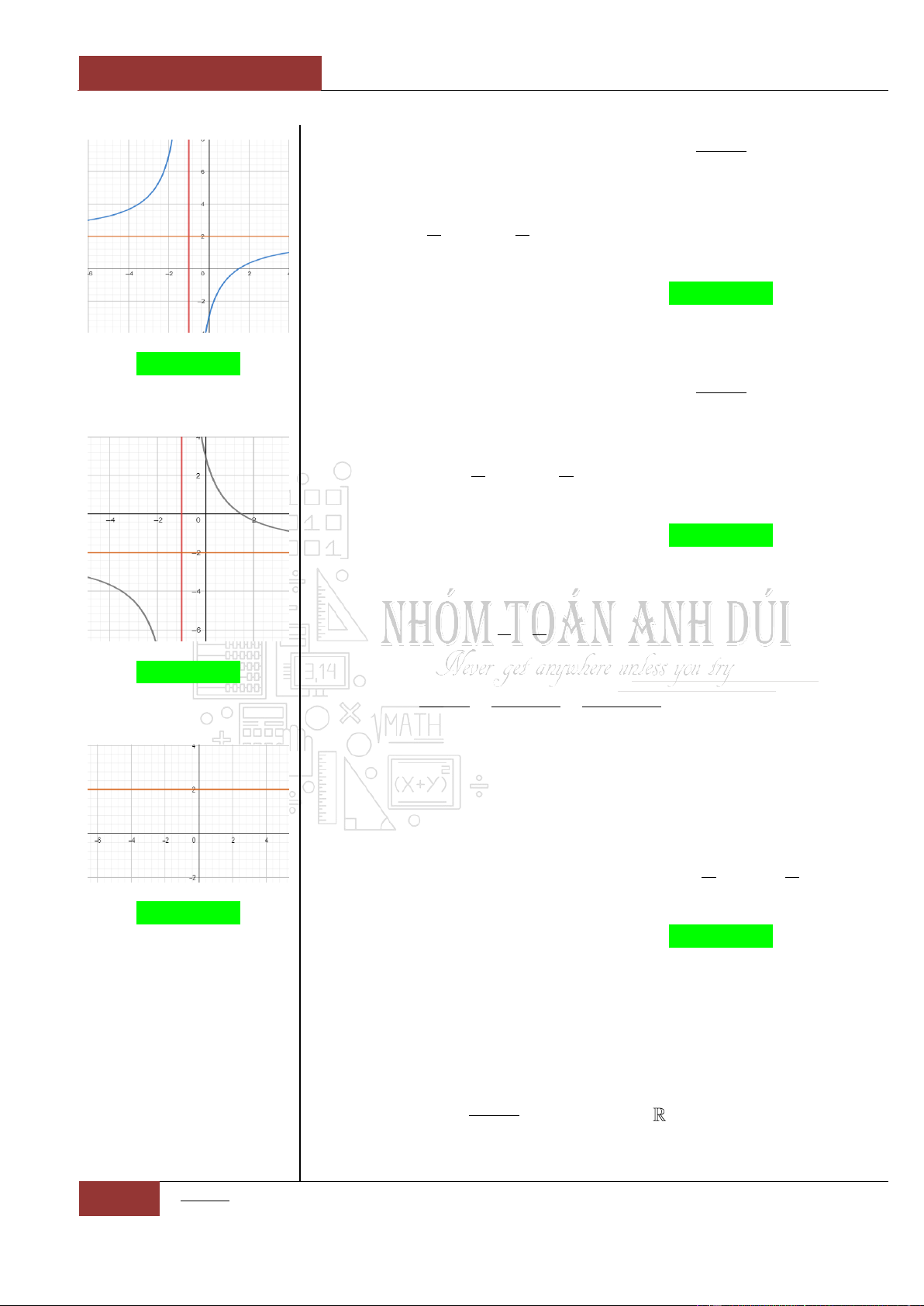
 Trường hợp 3:

2

30

0

b ac

a











hay

2

3

0

b ac

a











Đặc biệt rằng khi đó đồ thị hàm số luôn đồng biến trên

(Hàm số không có điểm cực trị).

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.I.15).

 Trường hợp 2:

2

30

0

b ac

a











hay

2

3

0

b ac

a











Đặc biệt rằng khi đó đồ thị hàm số luôn nghịch biến trên

(Hàm số không có điểm cực trị).

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.I.16).

"Hai Tips trên đã chỉ rõ cho ta

8

trường hợp thường gặp của

2

dạng đồ thị, tiếp theo, chúng tôi xin trình bài các yếu tố có liên

quan đến sự đồng biến, nghịch biến của các loại hàm cơ bản để áp

loại trừ các hàm sai trong các bài toán thường gặp."

 

3

Xét hàm số

ax b

y

cx d







 Trường hợp 1:

ab

cd



Hàm số có đạo hàm:

 

2

'

ad bc

y

cx d







Khi đó sự đồng biến, nghịch biến (trên từng khoảng xác định) của đồ

thị hàm số phụ thuộc duy nhất vào tính âm, dương của tử số. Hay nói

cách khác, nếu:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

17

[ I can't, I can! ]

Đồ thị I.I.17

Đồ thị I.I.18

Đồ thị I.I.19



0ad bc

hay

ad bc

thì hàm số

ax b

y

cx d







đồng biến trên

từng khoảng xác định (đồng biến trên hai khoảng rời nhau

;

d

c



 





và

;

d

c



 





).

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.I.17).



0ad bc

hay

ad bc

thì hàm số

ax b

y

cx d







nghịch biến

trên từng khoảng xác định (nghịch biến trên hai khoảng rời

nhau

;

d

c



 





và

;

d

c



 





).

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.I.18).

 Trường hợp 2:

ab

k

cd



Hàm số:

 

k cx d

ax b kcx kd

yk

cx d cx d cx d





   

  

Hàm số có đạo hàm:

'0y 

Khi đó sự đồng biến, nghịch biến (trên từng khoảng xác định) của đồ

thị không tồn tại. Hay nói cách khác hàm số đã cho là một hàm không

đổi (hàm hằng) trên hai khoảng rời nhau

;

d

c



 





và

;

d

c



 





.

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.I.19).

Hàm nhất biến chỉ hoặc đồng biến hoặc nghịch biến hoặc không đổi

trên từng khoảng xác định. Trong thực tế nhiều câu hỏi lại dựa vào

yếu tố không để ý vào vấn đề này mà có thể bẫy học sinh. Chẳng hạn,

các nhận định được cho dưới đây là hoàn toàn sai.

 Hàm số

ax b

y

cx d







đồng biến trên .

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

18

[ I can't, I can! ]

Extra Techniques:

Remark:

Sở dĩ ta không kết luận

hàm số đồng biến,

nghịch biến trên một tập

(

\

d

c









hay

;;

dd

cc

   

    

   

   

)

vì theo chương trình

biên soạn của Sách giáo

khoa hiện hành không

đề cập đến vấn đề biến

thiên trên một tập, nên

ta không có cơ sở để kết

luận rằng hàm số đồng

biến hoặc nghịch trên

tập. Nói cách khác ta

không thừa nhận việc

kết luận sự biến thiên

của hàm số cùng các

phép toán trên tập hợp

( , ,\,...)

.

Minh họa sự đan dấu

qua điểm mà tại đó hàm

số không xác định.

 Hàm số

ax b

y

cx d







nghịch biến trên

 Hàm số

ax b

y

cx d







đồng biến trên

\

d

c









 Hàm số

ax b

y

cx d







đồng biến trên

\

d

c









 Hàm số

ax b

y

cx d







nghịch biến trên

\

d

c









 Hàm số

ax b

y

cx d







đồng biến trên

;;

dd

cc

   

    

   

   

 Hàm số

ax b

y

cx d







nghịch biến trên

;;

dd

cc

   

    

   

   

 

4

Hàm số

 

42

0y ax bx c a   

 Hàm số bậc bốn trùng phương có ít nhất một điểm cực trị là

điểm

0x 

do đó hàm số luôn có khoảng đồng biến và khoảng

nghịch biến. Đặc biệt hơn khi hàm số chỉ có một điểm cực trị

thì hàm số trên chỉ có một khoảng nghịch biến và một khoảng

đồng biến lần lượt là

 

;0

và

 

0;

hoặc ngược lại.

 Hàm số bậc bốn trùng phương là một hàm chẵn vì thế đồ thị

của chúng có điểm cực trị đối xứng nhau qua trục tung do đó

có các khoảng đồng biến, nghịch biến cũng đối xứng nhau qua

trục tung (các khoảng đối dấu nhau).

 

5

Xét dấu đạo hàm giai đoạn bảng biến thiên

 Khi xét dấu ở giai đoạn bảng biến thiên ta chỉ cần chọn một

điểm giữa mỗi khoảng để xét dấu đạo hàm trên khoảng đó.

 Điểm

0

xx

mà tại đó

 

0

fx

không xác định cũng có thể làm

thay đổi dấu của đạo hàm khi qua nó. (Một lỗi sai thường thấy

của học sinh).

Xem bảng biến thiên như hình minh họa.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

19

[ I can't, I can! ]

Hình 10.1

Hình 10.2

Hình 10.3

Hình 10.4

Hình 10.5

Hình 10.6

Hình 10.7

"Tiếp theo, chúng tôi xin trình bày một số Tips có thể hữu dụng với

các bạn trong quá trình tính toán, lựa chọn những đáp án đúng

bằng công cụ Casio."

 

6

Đối với bài toán đồng biến, nghịch biến trên một khoảng

cho trước.

Câu 10. Hàm số

4 3 2

12 46 60 20y x x x x    

đồng biến trên

khoảng nào?

A.

 

;1

. B.

 

3;5

.

C.

 

2;4

. D.

 

7;9

.

(Trích đề thi Nhóm toán anh Dúi 2020 - 2021)

Đáp án: D

Lời giải

Đối với dạng toán như thế này, ta nảy ra ý tưởng sử dụng công cụ

Casio với mode Table để tìm khoảng đồng biến nghịch biến.

Ta vào mode Table và nhập biểu thức

 

fx

đề bài đã cho

(Xem Hình 10.1 và Hình 10.2.)

Chọn:

 

:9

99

:

29

Start

End

Step



















(Xem Hình 10.3, Hình 10.4, Hình 10.5.)

Màn hình Casio hiện thời sau khi nhấn phím (Xem Hình 10.6.)

Ta nhấn liên tục phím để di chuyển con trỏ chuột xuống các giá

trị bên dưới và note lại khoảng đồng biến, nghịch biến của hàm số.

Chẳng hạn, ta thấy rằng trên khoảng

 

9;0.931...x

hàm số giảm từ

một số rất lớn (



) về

4.921...

rồi có dấu hiệu tăng dần khi vượt

qua

1x 

.

(Xem Hình 10.7)

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

20

[ I can't, I can! ]

Hình 10.8

Hình 10.9

Hình 10.10

Hình 10.11

Extra Techniques:

Tips:

Sở dĩ, ta chọn khoảng

 

9;9

vì đáp án có

điểm nhỏ nhất là



nên ta một số đủ nhỏ để

xét, ta chọn

 

9

và

điểm lớn nhất là

9

thì

hiển nhiên.

Một cách tương tự, trên khoảng

 

1.55...;2.79...x

hàm số tăng từ

1.38...

đến

10.659...

và có dấu hiệu giảm khi vượt qua điểm

3x 

.

(Xem Hình 10.8)

Một lần nữa, ta thấy trên khoảng

 

3.413...;4.655...x

hàm số giảm

từ

9.659...

đến

3.411...

và có dấu hiệu tăng khi vượt qua điểm

5x 

.

(Xem Hình 10.9)

Cuối cùng, trên khoảng

 

5.27...;9x

hàm số tăng từ

3.608...

đến

một số rất lớn (



).

(Xem Hình 10.10)

Thống kê lại ta phát thảo được chiều đồng biến, nghịch biến của hàm

số lên bảng biến thiên như sau:

Lưu ý: Ở đây nếu nhìn vào Hình 10.9 chắc hẵn ai cũng có thắc mắc

tại sao hàm số đi qua

5x 

thì giá trị

y

vẫn còn giảm mà chúng tôi

lại bảo có dấu hiệu tăng. Thực chất, chúng tôi đưa bài toán này để các

bạn lưu ý hơn vì sự bất tiện của các dòng máy Casio đời cũ, vì Step

khá lớn nên nó có thể gây một xíu sai lầm nếu chúng ta dùng phương

pháp Casio. Lỗi sai được minh họa như Hình 10.11.

Một phương pháp Casio khác có thể giải quyết nhanh dạng toán này

là công cụ đạo hàm. Xem Câu 11.

Câu 11. Hàm số

32

6 9 3y x x x   

nghịch biến trên khoảng nào?

A.

 

1;3

. B.

 

;1

. C.

 

2;4

. D.

 

3;

.

(Trích đề thi Nhóm toán anh Dúi 2020 - 2021)

Đáp án: A.

Lời giải

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

21

[ I can't, I can! ]

Hình 11.1

Hình 11.2

Hình 11.3

Hình 11.4

Bước 1: Gọi công cụ đạo hàm ra màn hình chính của Casio và nhập

biểu thức

32

6 9 3y x x x   

như hình minh họa.

(Xem Hình 11.1)

Bước 2: Sau biểu thức đạo hàm có vị trí để CALC giá trị của

x

.

 Ta nhập

10x 

(vì

 

10 ;1  

) thu được kết quả như

hình minh họa.

(Xem Hình 11.2.)

Vì

 

' 10 0y 

nên khoảng

 

;1

không thể nghịch biến.

Loại B.

 Ta nhập

3.5x 

(vì

 

3.5 2;4

) thu được kết quả như hình

minh họa.

(Xem Hình 11.3.)

Vì

 

15

' 3.5 0

4

y 

nên khoảng

 

2;4

không thể nghịch biến.

Loại C.

 Ta nhập

9x 

(vì

 

9 3; 

) thu được kết quả như hình

minh họa.

(Xem Hình 11.4.)

Vì

 

' 9 144 0y 

nên khoảng

 

3;

không thể nghịch biến.

Loại D.

Dễ dàng ta chọn được phương án A.

"Trên đây là một số Tips chúng tôi cảm thấy rất hữu dụng trong

các bài toán hiện hành. Do mục đích phục vụ cho phần đông các

bạn học sinh nên phần trình bày khá chi tiết và khá dài. Nhưng nếu

bạn đọc hiểu bản chất vấn đề, thao tác sẽ ngắn gọn hơn, chuẩn xác

hơn và quan trọng nhất vẫn là lợi thế về thời gian nếu biết các Tips

này.”

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

22

[ I can't, I can! ]

TỰ LUYỆN 4 MỨC ĐỘ

Câu 1. [Nhận biết].

Cho hàm số

 

fx

có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới

đây?

A.

 

;1 

. B.

 

0;1

.

C.

 

1;1

. D.

 

1;0

.

Câu 2. [Nhận biết].

Cho hàm số

 

y f x

có bảng xét dấu đạo hàm

như sau

Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng

 

;2 

.

B. Hàm số đồng biến trên khoảng

 

2;0

.

C. Hàm số đồng biến trên khoảng

 

;0

.

D. Hàm số nghịch biến trên khoảng

 

0;2

.

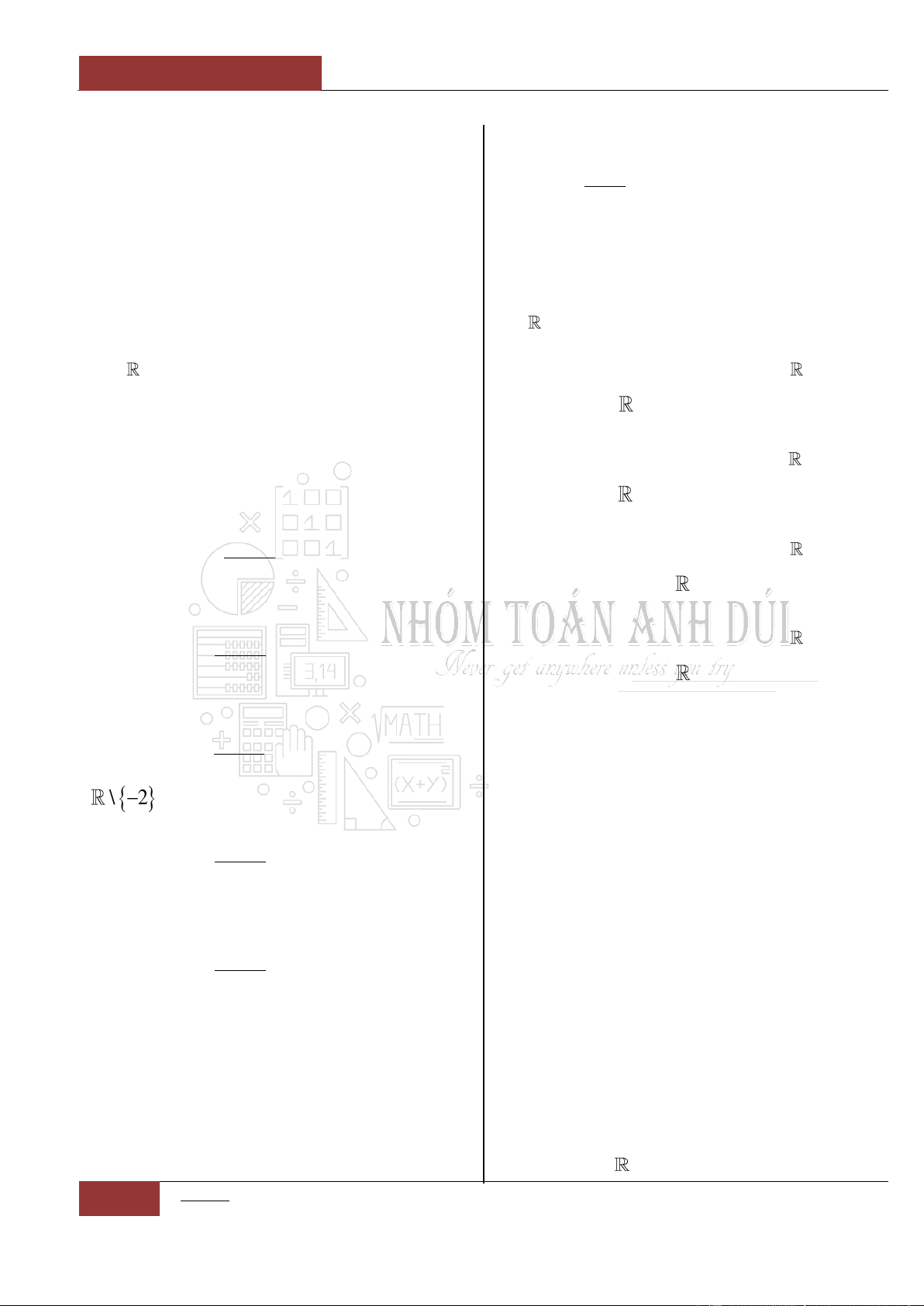
Câu 3. [Nhận biết].

Đồ thị của hàm số dưới đây nghịch biến trên

khoảng nào?

A.

 

;1

. B.

 

2;0

.

C.

 

2;

. D.

 

2;1

.

Câu 4. [Thông hiểu].

Hàm số

 

2

f x x

x



nghịch biến trên khoảng

nào dưới đây?

A.

 

;1

. B.

 

;0

.

C.

 

1; 

. D.

 

2;1

.

Câu 5. [Thông hiểu]

Cho hàm số

 

y f x

có đồ thị hàm số

 

'y f x

như hình vẽ dưới đây. Mệnh đề nào

sao đây là sai?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

23

[ I can't, I can! ]

A. Hàm số

 

y f x

nghịch biến trên khoảng

 

0;1

.

B. Hàm số

 

y f x

đồng biến trên khoảng

 

1;1

.

C. Hàm số

 

y f x

là một hàm số đồng biến

trên .

D. Hàm số

 

y f x

đồng biến trên khoảng

 

;1 

.

Câu 6. [Thông hiểu].

Cho hàm số

3

2

x

y

x







. Khẳng định nào sau

đây đúng?

A. Hàm số

3

2

x

y

x







đồng biến trên từng

khoảng xác định.

B. Hàm số

3

2

x

y

x







nghịch biến trên

 

\2

.

C. Hàm số

3

2

x

y

x







nghịch biến trên khoảng

   

; 2 2;    

.

D. Hàm số

3

2

x

y

x







nghịch biến trên khoảng

 

;2 

và

 

2; 

.

Câu 7. [Nhận biết].

Hàm số nào sau đây đồng biến trên tập xác định

của nó?

A.

4

yx

. B.

3

24y x x  

.

C.

1

2

x

y

x







. D.

siny x x

.

Câu 8. [Vận dụng].

Cho hàm số

 

y f x

liên tục và có đạo hàm

trên . Nhận định nào sau đây đúng?

A. Hàm số

 

y f x

đồng biến trên khi

 

' 0,f x x  

.

B. Hàm số

 

y f x

đồng biến trên khi

 

' 0,f x x  

.

C. Hàm số

 

y f x

đồng biến trên khi và

chỉ khi

 

' 0,f x x  

.

D. Hàm số

 

y f x

đồng biến trên khi và

chỉ khi

 

' 0,f x x  

.

Câu 9. [Vận dụng].

Biết hàm số

32

6 9 2y x x x   

nghịch biến

trên khoảng lớn nhất

 

;ab

. Khi đó tổng lập

phương của

a

và

b

có giá trị là?

A.

64

. B.

27

.

C.

28

. D.

27

.

Câu 10. [Vận dụng].

Biết rằng hàm số

 

42

,0y ax bx c a   

đồng biến trên khoảng

 

;0

. Mệnh đề nào

dưới đây chắc chắn sai?

A.

0

a

b

c

















. B.

0

a

ab

ac

















.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

24

[ I can't, I can! ]

C.

0

a

b

c

















. D.

0

a

ab

c

















.

Câu 11. [Nhận biết].

Hàm số

32

1

3 5 3

3

y x x x   

đồng biến trên

khoảng nào dưới đây?

A.

 

5;

. B.

 

1;5

.

C.

 

;5

. D. .

Câu 12. [Nhận biết].

Hàm số nào sau đây đồng biến trên khoảng

 

0;



?

A.

1x

y

x





. B.

2

yx

.

C.

cosyx

. D.

tanyx

.

Câu 13. [Vận dụng].

Giả sử hàm số

 

y f x

nghịch biến và có đạo

hàm trên khoảng

 

9;9

. Mệnh đề sau đây chắc

chắn sai?

A.

   

' 1 . ' 2 0ff

. B.

 

' 3 0f 

.

C.

   

38ff

. D.

   

' 3 ' 8ff

.

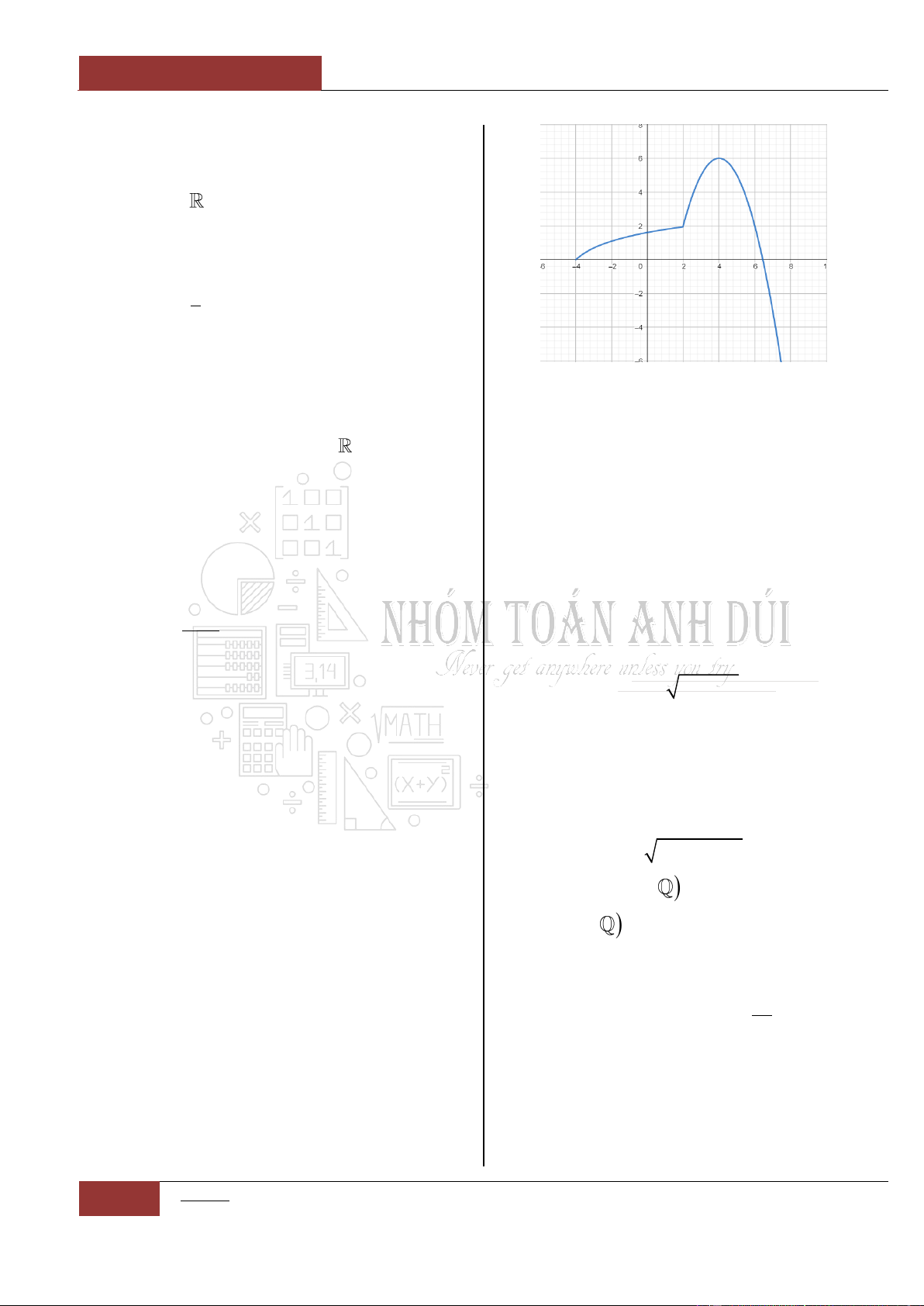
Câu 14. [Nhận biết].

Đồ thị hàm số

 

y f x

liên tục và có đạo hàm

trên khoảng

 

4; 

. Biết đồ thị hàm số

 

y f x

có đồ thị như hình vẽ dưới đây.

Mệnh đề nào sau đây đúng nhất?

A. Hàm số đồng biến trên khoảng

 

4;2

.

B. Hàm số đồng biến trên khoảng

 

2;6

.

C. Hàm số đồng biến trên khoảng

 

4;4

.

D. Hàm số đồng biến trên khoảng

 

4;2

và

 

2;4

.

Câu 15. [Nhận biết].

Biết rằng hàm số

2

2y x x

nghịch biến trên

đoạn có độ lớn bằng

a

. Giá trị

a

là?

A.

1a 

. B.

2a 

. C.

3a 

. D.

4a 

.

Câu 16. [Nhận biết].

Giả sử hàm số

2

65y x x  

có đoạn đồng

biến là

 

 

; , ,a b a b

và đoạn nghịch biến là

 

 

; , ,c d c d 

. Khi đó tổng

S a b c d   

bằng?

A.

10S 

. B.

5S 

. C.

15

2

S 

. D.

0S 

.

Câu 17. [Nhận biết].

Hàm số

 

y f x

được cho như hình vẽ dưới

đây nghịch biến trên những khoảng nào?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

25

[ I can't, I can! ]

A. Hàm số nghịch biến trên khoảng

 

;2 

.

B. Hàm số nghịch biến trên khoảng

 

0;2

.

C. Hàm số nghịch biến trên khoảng

 

2;0

và

 

2;

.

D. Hàm số nghịch biến trên khoảng

 

;2 

và

 

0;2

.

Câu 18. [Nhận biết].

Biết hàm số

 

'y f x

có đồ thị như hình vẽ

dưới đây. Nhận định nào sau đây là sai về hàm

số

 

y f x

?

A. Hàm số nghịch biến trên khoảng

 

0;2

.

B. Hàm số đồng biến trên khoảng

 

2;0

.

C. Hàm số nghịch biến trên khoảng

 

3; 2

.

D. Hàm số nghịch biến trên khoảng

 

2;3

.

Câu 19. [Thông hiểu].

Biết hàm số

ln x

y

x



đồng biến trên khoảng

 

;ab

. Tính giá trị biểu thức

lnS a b

?

A.

0S 

. B.

1 ln2S 

.

C.

1S 

. D.

ln2S 

.

Câu 20. [Thông hiểu].

Hàm số

lny x x x

đồng biến trên khoảng

nào dưới đây?

A.

 

0;1

. B.

 

1; 

.

C.

 

1;0

. D.

 

1; 

.

Câu 21. [Vận dụng cao].

Hàm số

2

3sin cos

3

2sin cos2

xx

yx

xx







đồng biến

trên khoảng nào dưới đây?

A.

0;

2









. B.

;

62









.

C.

0;

3









. D.

;

3









.

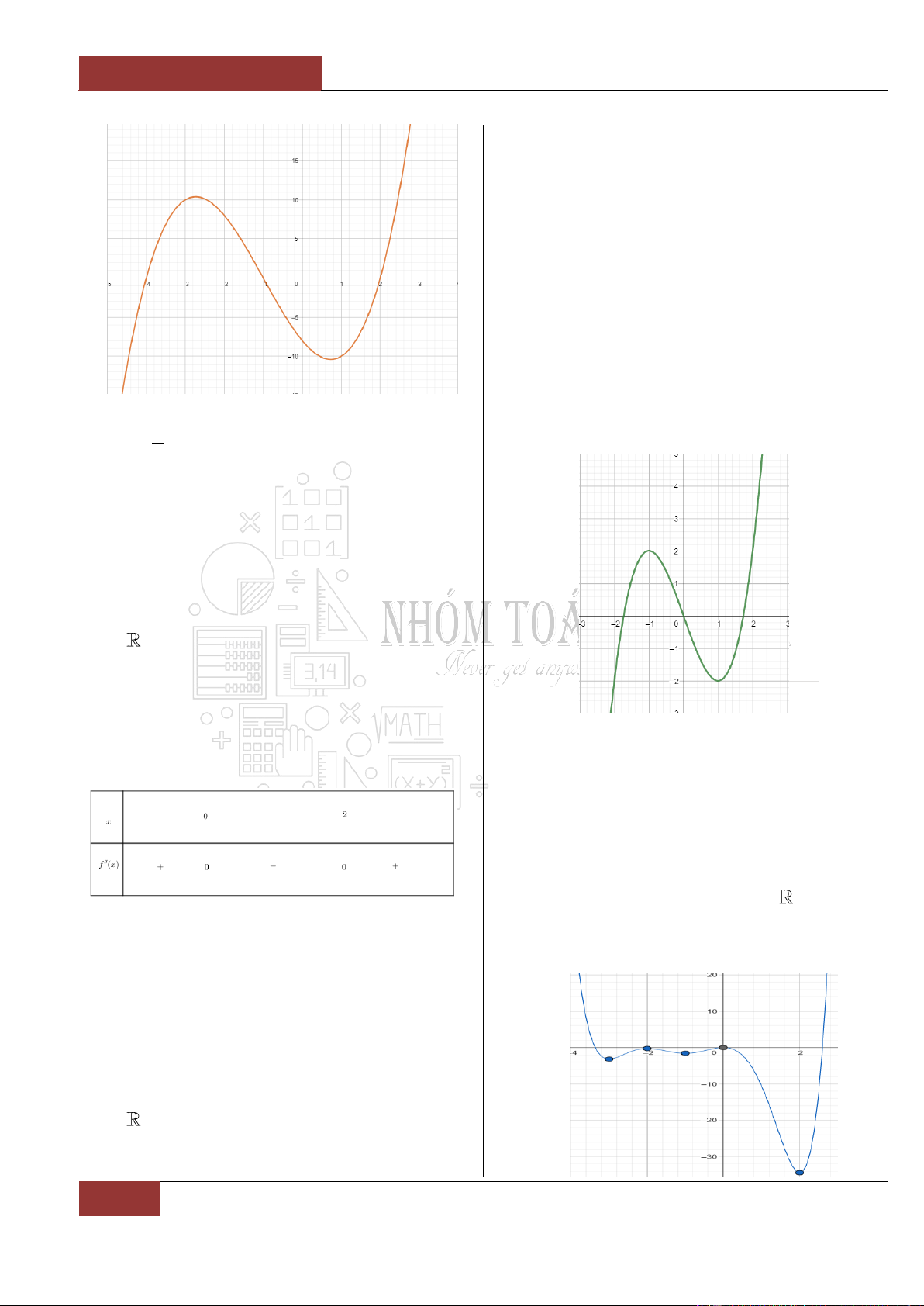
Câu 22. [Vận dụng cao].

Cho hàm số

 

y f x

, biết đồ thị hàm số

 

'y f x

như hình vẽ dưới đây. Hàm số

 

2

y f x x

nghịch biến trong khoảng nào

sau đây?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

26

[ I can't, I can! ]

A.

1

1;

2









. B.

 

2;

.

C.

 

;1 

. D.

 

1;2

.

Câu 23. [Vận dụng cao].

Cho hàm số

 

y f x

có đạo hàm đến cấp hai

trên . Biết rằng

 

' 0 1f 

,

 

' 2 2021f 

và

 

' 1 2021f   

. Biết hàm số

 

''y f x

có

bảng xét dấu như hình vẽ dưới đây. Hàm số

   

2022 2021y g x f x x   

đồng biến trên

khoảng nào dưới đây?

A.

 

;2

. B.

 

2;

.

C.

 

; 2023 

. D.

 

2023; 

.

Câu 24. [Thông hiểu].

Cho hàm số

 

y f x

liên tục và có đạo hàm

trên . Biết rằng:

     

2

' 2 3y f x x x x   

.

Hàm số đã cho nghịch biến trên đoạn

 

;ab

.

Khi đó, giá trị biểu thức

S b a

bằng?

A.

3S 

. B.

2S 

.

C.

2S 

. D.

3S 

.

Câu 25. [Thông hiểu].

Cho hàm số

 

y f x

có đồ thị hàm số đạo

hàm như hình vẽ dưới đây.

Hàm số

 

2 2021y f x x  

đồng biến trên

khoảng nào dưới đây?

A.

 

;1 

và

 

1; 

. B.

 

1; 

.

C.

 

;1 

. D.

 

2;

.

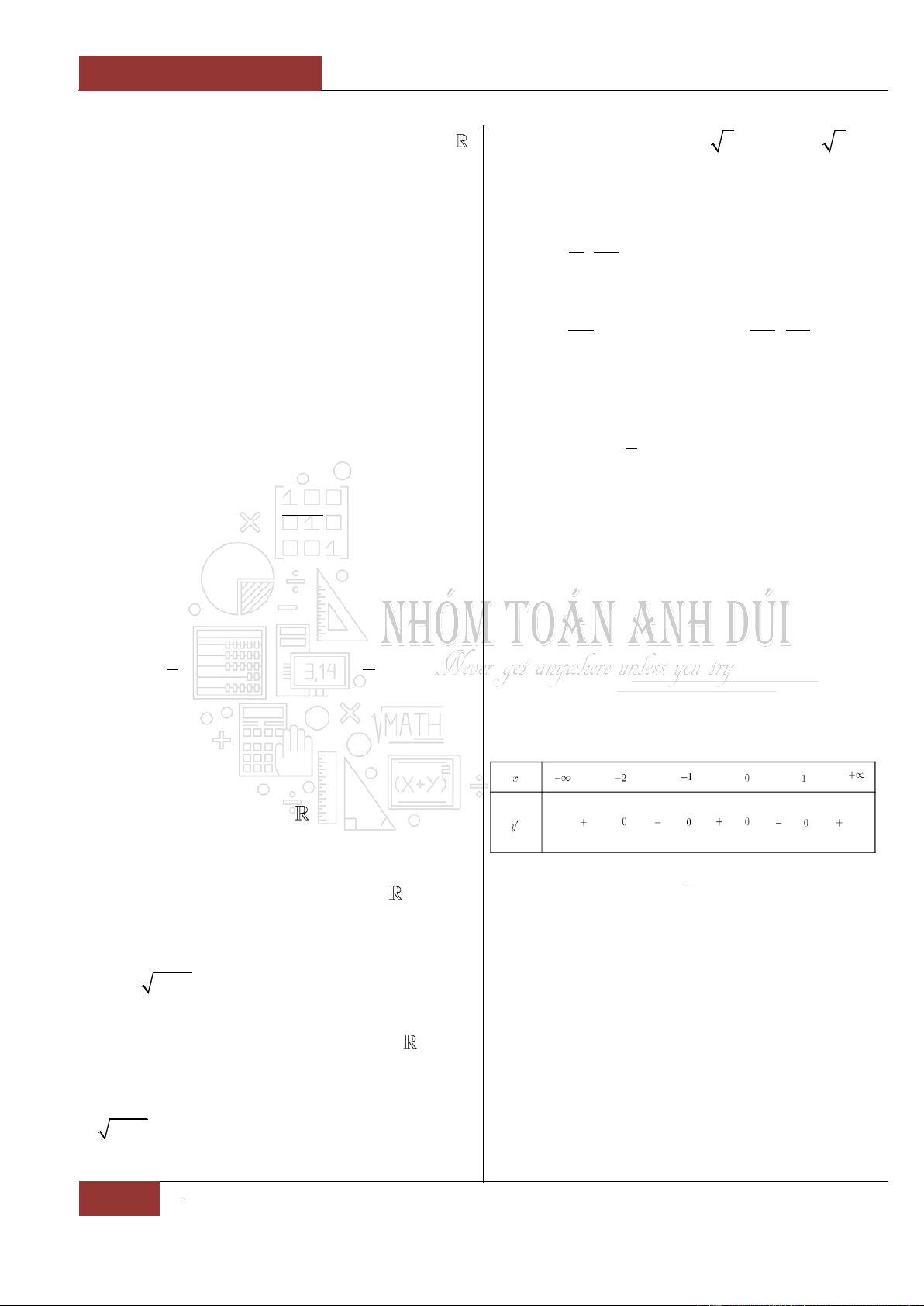
Câu 26. [Thông hiểu].

Cho hàm số

 

y f x

liên tục trên có đồ thị

hàm số như hình vẽ. Hàm số

 

2021y f x

nghịch biến trên những khoảng nào?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

27

[ I can't, I can! ]

A. Hàm số

 

2021y f x

nghịch biến trên .

B. Hàm số

 

2021y f x

nghịch biến trên

khoảng

 

2; 1

.

C. Hàm số

 

2021y f x

nghịch biến trên

khoảng

 

2019;2020

.

D. Hàm số

 

2021y f x

nghịch biến trên

khoảng

 

3; 2

.

Câu 27. [Thông hiểu].

Hàm số

 

3

ln 2

2

yx

x

  



đồng biến trên

khoảng nào?

A.

 

;1

. B.

 

1; 

.

C.

1

;1

2







. D.

1

;

2



 





.

Câu 28. [Thông hiểu].

Hàm số

 

y f x

liên tục và có đạo hàm

 

2

' 2021,f x x x    

. Mệnh đề nào sau

đây đúng?

A. Hàm số

 

y f x

đồng biến trên .

B. Hàm số

 

y f x

đồng biến trên khoảng

 

; 2021 

.

C. Hàm số

 

y f x

nghịch biến trên .

D. Hàm số

 

y f x

nghịch biến trên khoảng

 

2021;

.

Câu 29. [Thông hiểu].

Hàm số

  

cos 2cos 3 2cos 3y x x x  

đồng biến trên khoảng nào trên đoạn

 

0;2



?

A.

2

;

33









. B.

 

0;



.

C.

2

;

3









. D.

45

;

33









.

Câu 30. [Thông hiểu].

Biết hàm số

 

2

1

2ln 1

4

y x x

nghịch biến

trên khoảng lớn nhất là

 

0;a

và đồng biến trên

khoảng lớn nhất là

 

;b 

. Khi đó giá trị của

biểu thức

S b a

?

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 31. [Vận dụng cao].

Cho hàm số

 

y f x

có bảng xét dấu đạo hàm

như sau:

Đặt

   

4 3 2

1

2 1 5

4

g x f x x x x     

.

Khẳng định nào sau đây là đúng?

A. Hàm số

 

gx

đồng biến trên khoảng

 

;2 

.

B. Hàm số

 

gx

đồng biến trên khoảng

 

1;0

.

C. Hàm số

 

gx

đồng biến trên khoảng

 

0;1

.

D. Hàm số

 

gx

nghịch biến trên khoảng

 

1; 

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

28

[ I can't, I can! ]

Câu 32. [Vận dụng cao].

Hàm số

 

y f x

liên tục và có đạo hàm luôn

không âm trên khoảng

 

2022;2022

. Biết rằng

trên khoảng

 

2022;2022

có duy nhất một

đoạn con nào đó có độ lớn bằng

2021

mà trên

đoạn đó đồ thị hàm số là một đường thẳng song

song với trục hoành. Mệnh đề nào dưới đây có

thể xảy ra?

A. Hàm số

 

y f x

là một hàm đồng biến trên

khoảng

 

2022;2022

.

B.

   

2021 2021ff

.

C.

   

' 2020 ' 2021 0ff

.

D. Có ít nhất

2021

điểm mà tại đó

 

0fx

.

Câu 33. [Vận dụng cao].

Hàm số

5 4 3 2

4 3 2

6 3 12 6 2

22

x x x x x

yx

x x x x

    



  

nghịch biến trên khoảng nào dưới đây?

A.

 

;2 

. B.

 

2; 1

.

C.

 

1; 

. D. Cả ba phương án đều sai.

Câu 34. [Vận dụng].

Cho hàm số

 

y f x

có đồ thị như hình vẽ

Hàm số

 

y f x

đồng biến trên khoảng nào

dưới đây?

A.

 

1;0

. B.

 

0;1

.

C.

 

1; 

. D.

 

;1 

.

Câu 35. [Vận dụng].

Cho hàm số

 

y f x

có đồ thị như hình vẽ

Hàm số

 

y f x

đồng biến trên khoảng nào

dưới đây?

A.

 

1;0

. B.

 

0;1

.

C.

 

0;

. D.

 

;1 

.

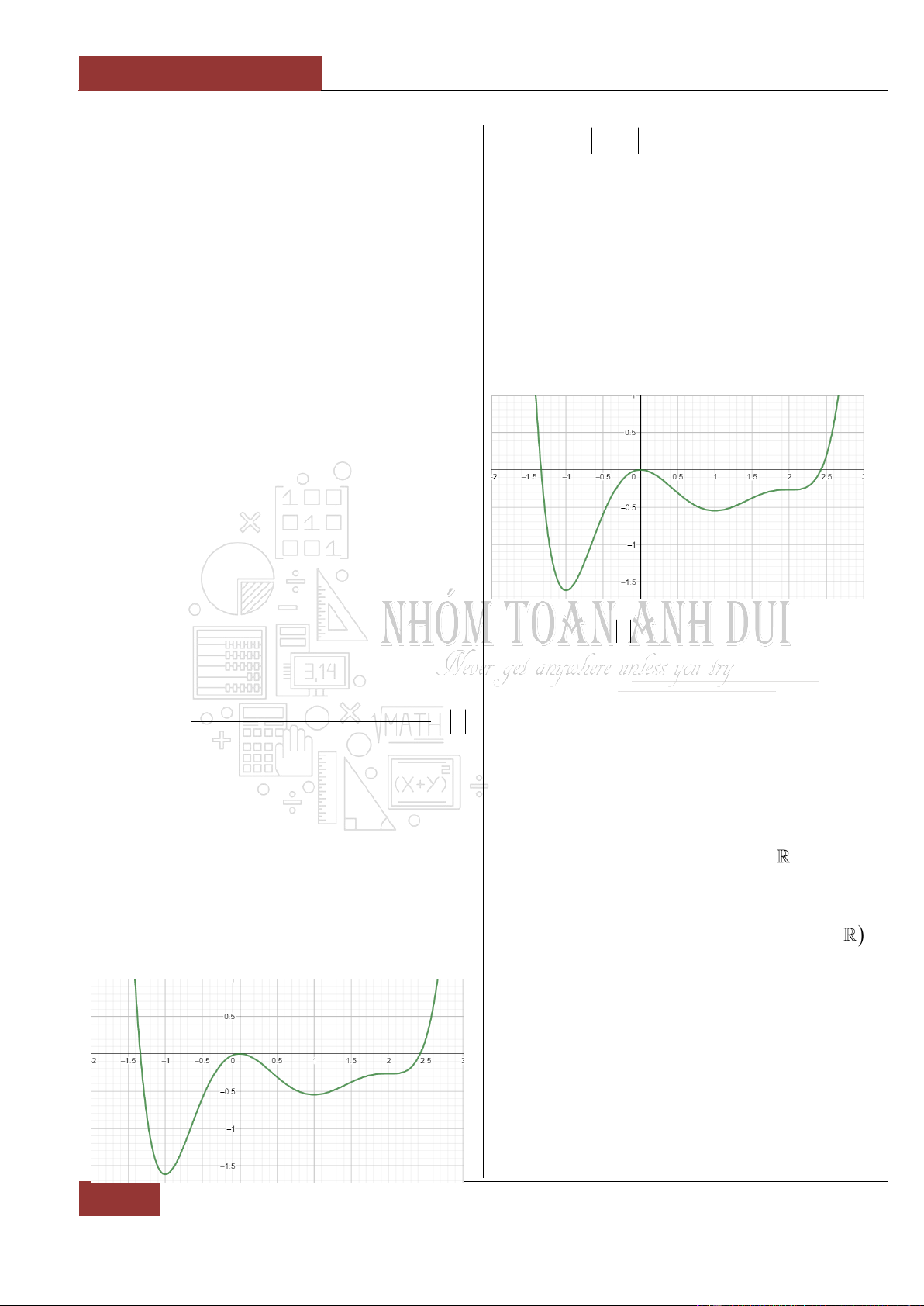
Câu 36. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục trên và có đạo

hàm đến cấp hai. Biết rằng:

 

4 3 2

'f x mx nx px qx r    

,

 

, , , ,m n p q r 

.

Hàm số

 

''y f x

có đồ thị như hình vẽ dưới

đây. Biết đồ thị hàm số

   

y g x f x rx  

đồng biến trên một khoảng duy nhất

 

;ab

.

Tích

S ab

bằng?

A.

5

. B.

5

.

C.

3

. D.

0

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

29

[ I can't, I can! ]

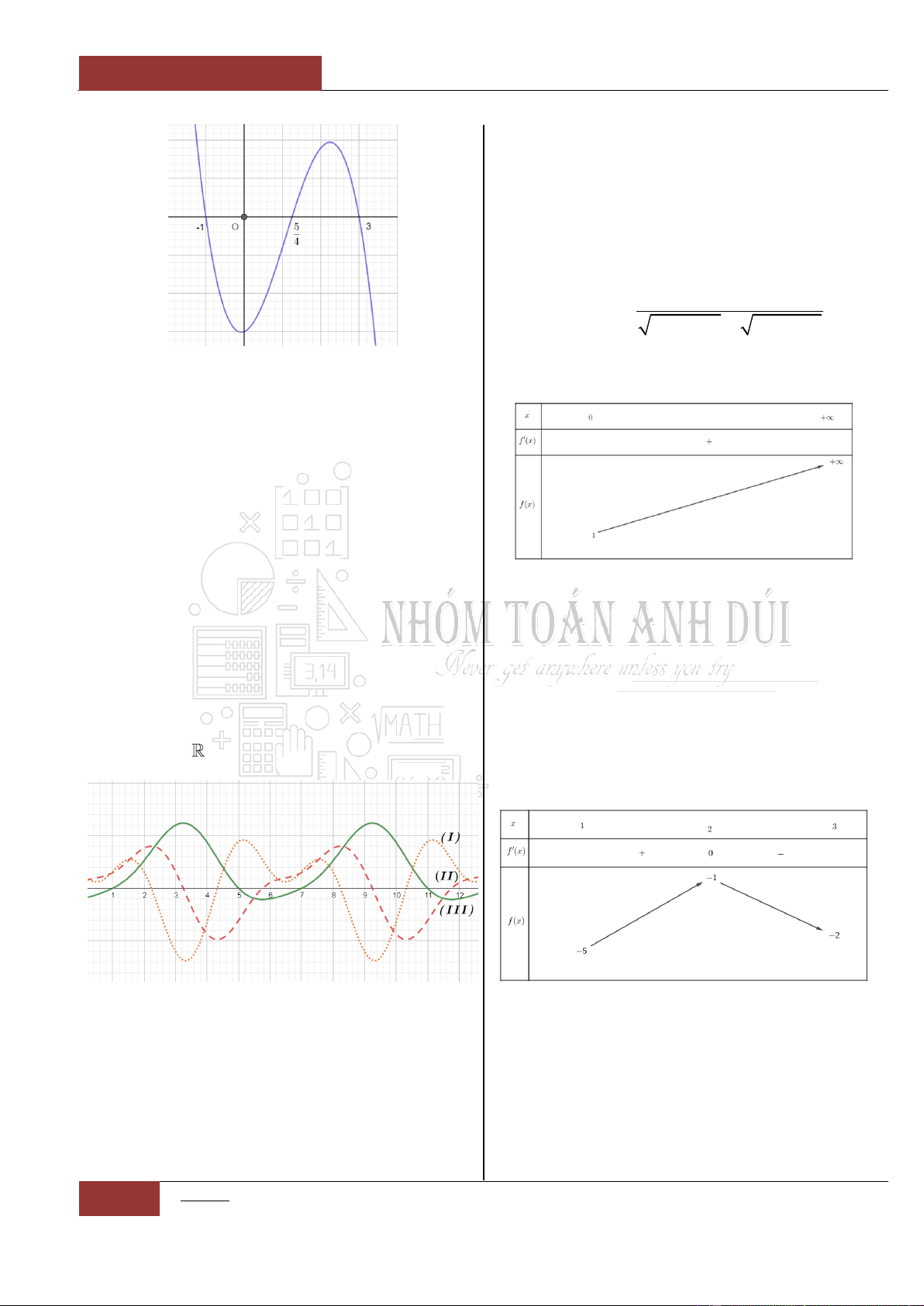
Câu 37. [Vận dụng].

Để phục vụ công tác cho đề thi thử TN năm học

2021 2022

của "Nhóm toán anh Dúi". Bạn

Lành đã dùng phần mềm toán học vẽ ba đồ thị

hàm số

 

y f x

,

 

'y f x

và

 

''y f x

trên cùng một hình biểu diễn (Minh họa bằng

hình vẽ bên dưới). Vì bất cẩn, bạn Lành đã sơ

ý quên ghi lại dấu hiệu để phân biệt ba đồ thị

hàm số trên. Hãy giúp bạn Lành xác định chính

xác các đồ thị hàm số

     

,,I II III

bằng cách

sắp xếp chúng theo thứ tự

 

y f x

,

 

'y f x

và

 

''y f x

. Biết rằng đồ thị hàm số

 

y f x

liên tục trên và có đạo hàm đến cấp hai.

A.

     

,,I II III

.

B.

     

,,II I III

.

C.

     

,,II III I

.

D.

     

,,III II I

.

Câu 38. [Vận dụng].

Cho hàm số

 

y f x

liên tục và xác định trên

nữa khoảng





0;

và có bảng biến thiên như

hình vẽ bên dưới. Hàm số

 

2022 2021

fx

y g x

xx



  

có khoảng đồng biến là khoảng nào dưới đây?

A.

 

0;2022

. B.

 

0;2021

.

C.

 

2021;2022

. D.

 

0;

.

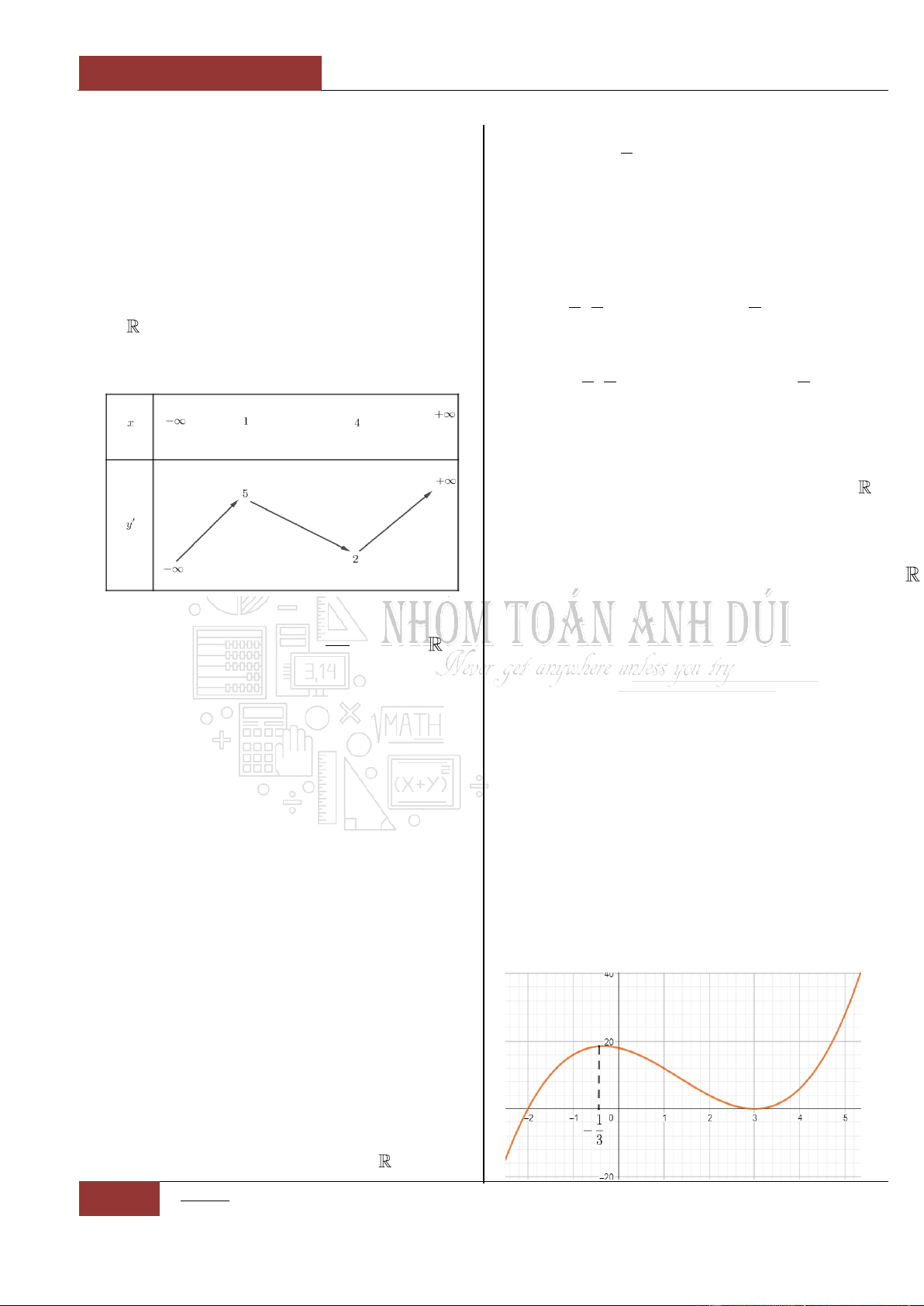
Câu 39. [Vận dụng].

Cho hàm số

 

y f x

liên tục trên đoạn

 

1;3

và có bảng biến thiên như hình vẽ bên dưới.

Xét hàm số:

   

 

2

1 . 6 12y g x f x x x    

trên đoạn

 

2;4

. Mệnh đề nào sau đây đúng?

A. Hàm số

 

y g x

không liên tục trên

 

2;4

.

B. Hàm số

 

y g x

đồng biến trên

 

2;4

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

30

[ I can't, I can! ]

C. Hàm số

 

y g x

nghịch biến trên

 

2;4

.

D. Hàm số

 

y g x

nghịch biến trên

 

3;4

.

Câu 40. [Vận dụng].

Cho hàm số

 

y f x

liên tục và có đạo hàm

trên . Hàm số

 

'y f x

có bảng biến thiên

như hình vẽ bên dưới.

Hàm số:

 

2

cos ,

4

y f x x m m



    

đồng biến trên khoảng

 

2;3

. Mệnh đề trên

đúng hay sai?

A. Mệnh đề trên là sai, bởi vì

 

y f x

là một

hàm số nghịch biến trên

 

2;3

.

B. Mệnh đề trên là sai, bởi vì trên khoảng

 

2;3

 

y f x

có cả khoảng đồng biến và nghịch

biến.

C. Mệnh đề trên là đúng, vì:

 

' 0, 2;3yx  

.

D. Mệnh đề trên là đúng, vì:

 

' 0, 2;3yx  

và

 

0, 2;3yx  

.

Câu 41. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục trên . Biết

rằng:

2

7

' 2 3 12 9

2

f x x x



    





.

Hàm số

 

y f x

nghịch biến trên khoảng nào

sau đây.

A.

19

;

44







. B.

9

;

4









.

C.

53

;

22









. D.

5

;

2



 





.

Câu 42. [Vận dụng].

Cho hàm số

 

y f x

xác định, liên tục trên

và có đạo hàm

 

'fx

thỏa mãn:

       

' 2 1 2021 2 2 3 . , 0,f x x x g x g x x      

Khi đó hàm số:

 

1 2021 2022y f x x   

đồng biến trên khoảng nào?

A.

 

1; 

. B.

 

0;3

.

C.

 

;3

. D.

 

4;

.

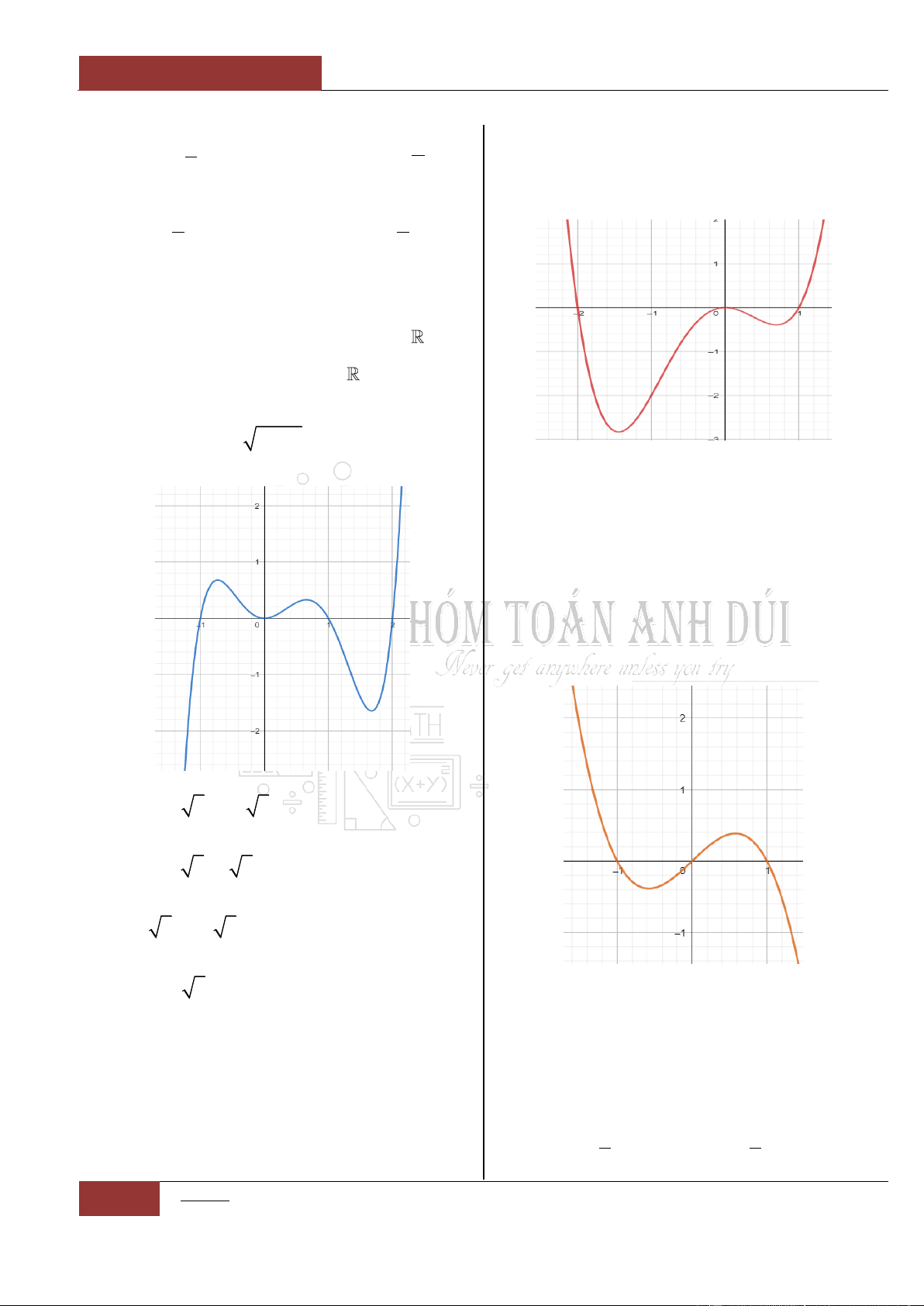
Câu 43. [Vận dụng].

Cho hàm số

 

y f x

có đồ thị như hình vẽ.

Giả sử hàm số

 

25fx

nghịch biến trên

khoảng

 

;mn

. Giá trị nhỏ nhất của biểu thức

S m n

là bao nhiêu?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

31

[ I can't, I can! ]

A.

min

5

3

S 

. B.

min

5

2

S 

.

C.

min

5

3

S 

. D.

min

5

2

S 

.

Câu 44. [Vận dụng].

Cho hàm số

 

y f x

có đạo hàm trên . Biết

hàm số

 

'y f x

liên tục trên và có đồ thị

như hình vẽ. Tìm tất cả các khoảng đồng biến

của hàm số





2

1y f x

.

A.

   

; 3 , 0; 3 

.

B.

   

; 3 , 3;  

.

C.

   

3;0 , 3; 

.

D.

 

; 3 , 0;  

.

Câu 45. [Vận dụng].

Cho hàm số

 

y f x

có đồ thị

 

'fx

như

hình vẽ dưới đây.

Hàm số:

     

2

1 2 6 3y g x f x f x x x       

đồng biến trên khoảng nào dưới đây?

A.

 

;0

. B.

 

0;3

.

C.

 

1;2

. D.

 

3;

.

Câu 46. [Vận dụng].

Cho hàm số

 

y f x

. Đồ thị

 

'y f x

như

hình bên dưới.

Hàm số

   

3

21g x f x





nghịch biến trên

các khoảng nào trong các khoảng sau.

A.

 

1;0

. B.

 

0;1

.

C.

1

0;

2







. D.

1

;1

2







.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

32

[ I can't, I can! ]

Câu 47. [Vận dụng].

Cho hàm số

 

y f x

. Đồ thị

 

'y f x

như

hình bên dưới.

Hàm số

   

2021

1g x f x





nghịch biến trên

các khoảng nào trong các khoảng sau?

A.

 

1;5

. B.

 

2;1

.

C.

 

1;3

. D.

 

3;5

.

Câu 48. [Vận dụng].

Cho hàm số

 

y f x

. Đồ thị

 

'y f x

như

hình vẽ bên dưới và

   

1 2 0ff  

.

Hàm số

 

2

3g x f x







đồng biến trên

khoảng nào sau đây?

A.

 

1;2

. B.

 

0;1

.

C.

 

1;0

. D.

 

2; 1

.

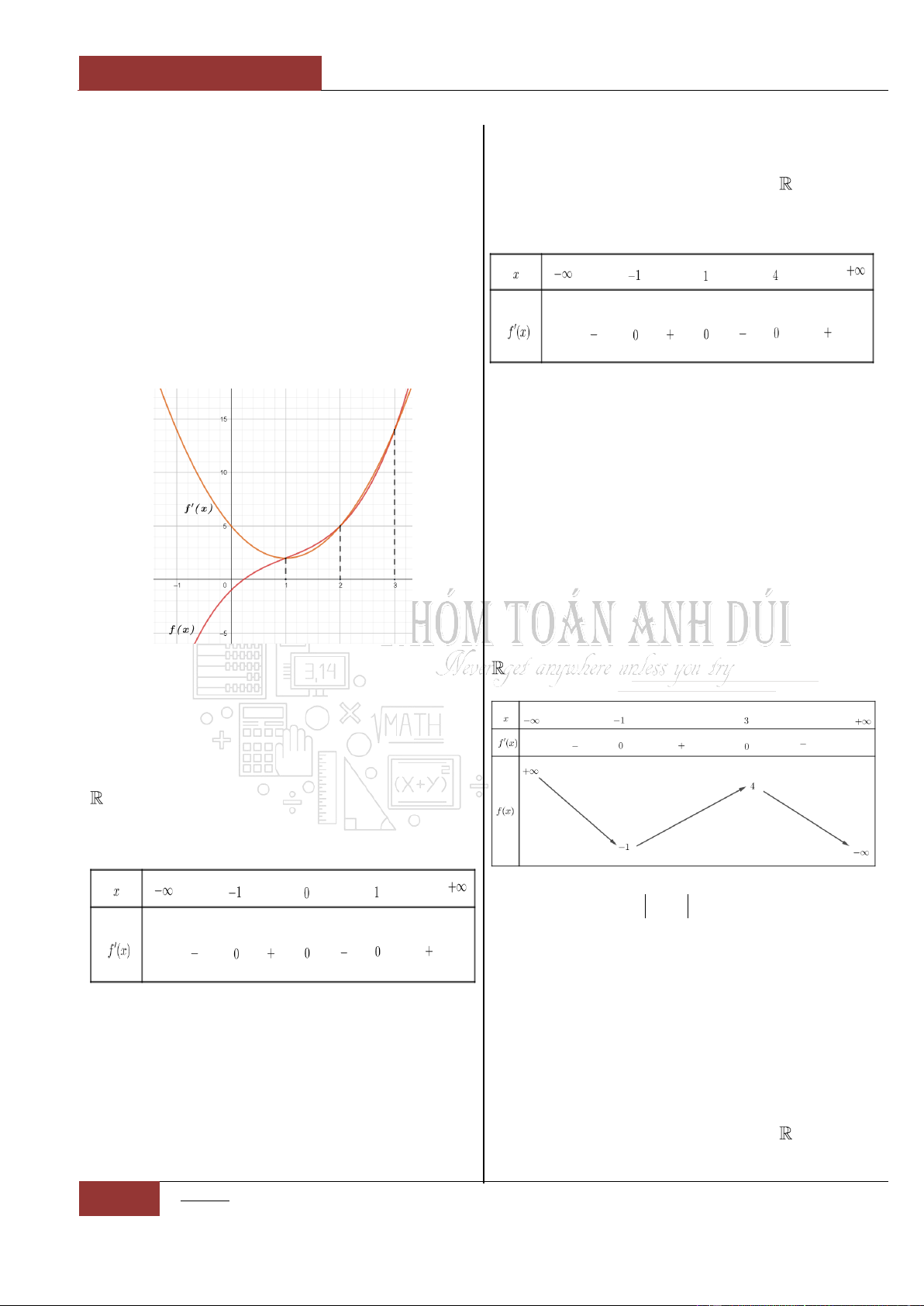
Câu 49. [Vận dụng].

Cho hàm số

 

y f x

có đồ thị hàm số

3

'2

2

y f x









như hình vẽ bên dưới.

Biết hàm số

 

y f x

đồng biến trên hai

khoảng rời nhau

 

;ab

và

 

;c 

 

,,abc

.

Khi đó biểu thức

2S a b c  

có giá trị bằng?

A.

18S 

. B.

12S 

.

C.

10S 

. D.

14S 

.

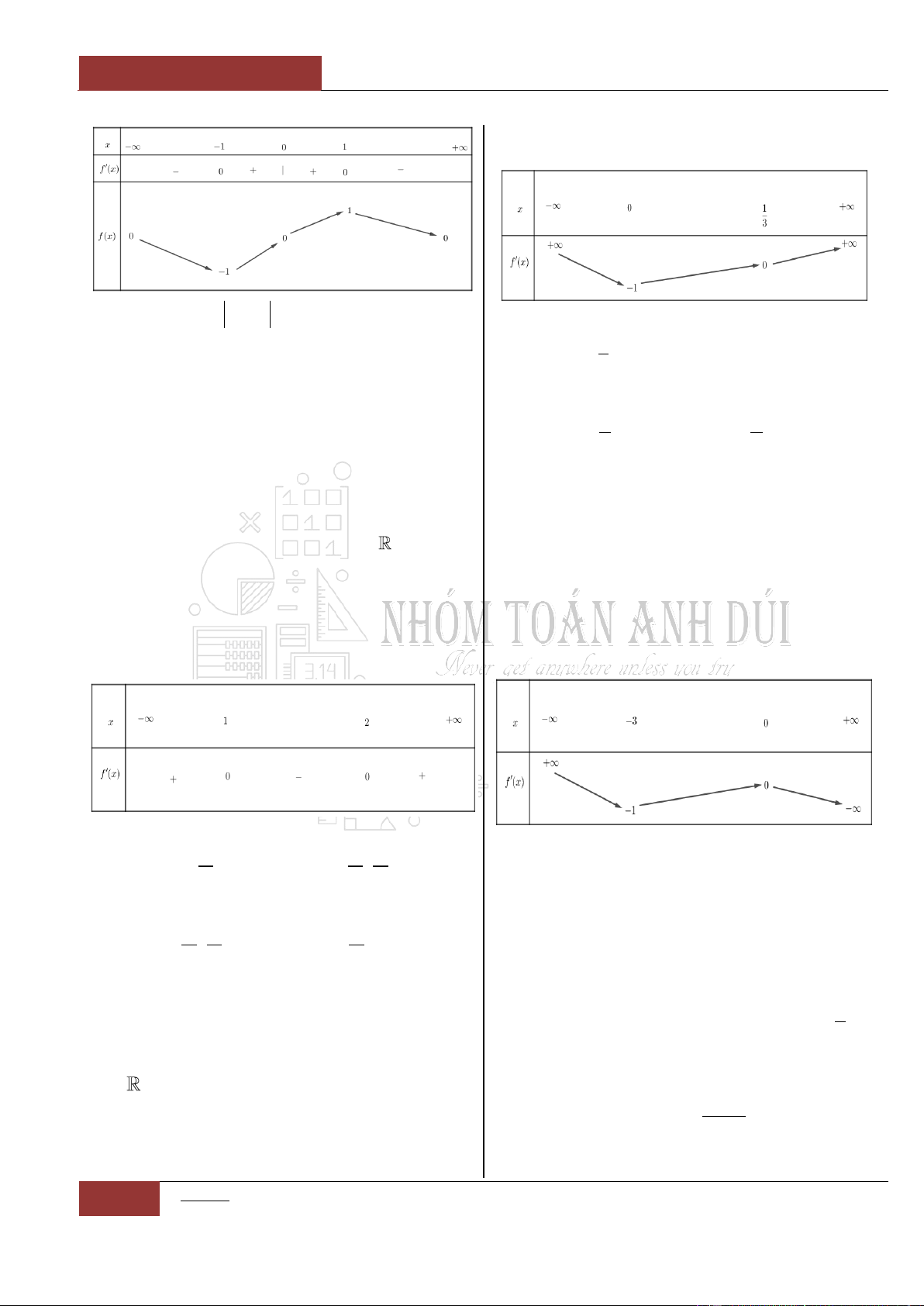
Câu 50. [Vận dụng].

Cho đồ thị hàm số

 

3

'1y f x

như hình vẽ.

Hàm số

 

fx

nghịch biến trong khoảng nào

trong các khoảng sau?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

33

[ I can't, I can! ]

A.

 

2;2

. B.

 

2;5

.

C.

 

5;10

. D.

 

10;

.

Câu 51. [Vận dụng].

Cho hàm số

   

,'y f x y f x

có đồ thị như

hình vẽ. Hàm số

 

.

x

y e f x





có bao nhiêu

khoảng đồng biến?

A.

1

. B.

3

. C.

2

. D.

4

.

Câu 52. [Vận dụng].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

và bảng xét dấu của hàm số đạo hàm của

hàm số

 

y f x

như sau:

Hàm số

   

 

2

ln 1g x f x x x   

nghịch

biến trên khoảng nào dưới đây?

A.

 

;0

. B.

 

0;1

.

C.

 

1; 

. D.

 

1;0

.

Câu 53. [Vận dụng].

Cho hàm số

 

y f x

liên tục trên và có

bảng xét dấu đạo hàm như sau:

Hàm số

 

2

x

y f e

nghịch biến trên khoảng

nào trong các khoảng dưới đây?

A.

 

;1

. B.

 

1;4

.

C.

 

0;ln3

. D.

 

2;

.

Câu 54. [Vận dụng].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

và có bảng biến thiên như hình vẽ dưới đây.

Hàm số

 

2g x f x

nghịch biến trên

khoảng nào dưới đây.

A.

 

3;

. B.

 

2;3

.

C.

 

1;2

. D.

 

;1 

.

Câu 55. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục trên , có bảng

biến thiên như hình vẽ:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

34

[ I can't, I can! ]

Hàm số

 

y f f x

đồng biến trên khoảng

nào sau đây?

A.

 

;2 

. B.

 

1;1

.

C.

 

2;

. D.

 

0;2

.

Câu 56. [Vận dụng].

Cho hàm số

 

y f x

liên tục trên . Biết hàm

số

 

'y f x

có bảng xét dấu như hình vẽ bên

dưới. Hàm số

   

2cos 1g x f x

đồng biến

trên khoảng nào dưới đây?

A.

0;

6









. B.

;

43









.

C.

;

32









. D.

;

2









.

Câu 57. [Vận dụng].

Cho hàm số

 

y f x

liên tục và có đạo hàm

trên . Bảng biến thiên của đồ thị hàm số

 

'y f x

như hình vẽ bên dưới. Hàm số

 

2 3 3 2

15y g x f x x x x      

nghịch

biến trên khoảng nào dưới đây?

A.

1

0;

3







. B.

 

;0

.

C.

2

0;

3







. D.

2

;

3









.

Câu 58. [Vận dụng].

Cho hàm số

 

y f x

. Biết rằng

 

00f 

và

hàm số

 

'y f x

có bảng biến thiên như hình

vẽ dưới đây. Hàm số

 

y xf x

đồng biến trên

khoảng nào?

A.

 

;0

. B.

 

2;0

.

C.

 

0;2

. D.

 

2;2

.

Câu 59. [Vận dụng].

Cho hàm số bậc ba

 

y f x

có

 

1

0

3

f 

.

Bảng biến thiên của hàm số

 

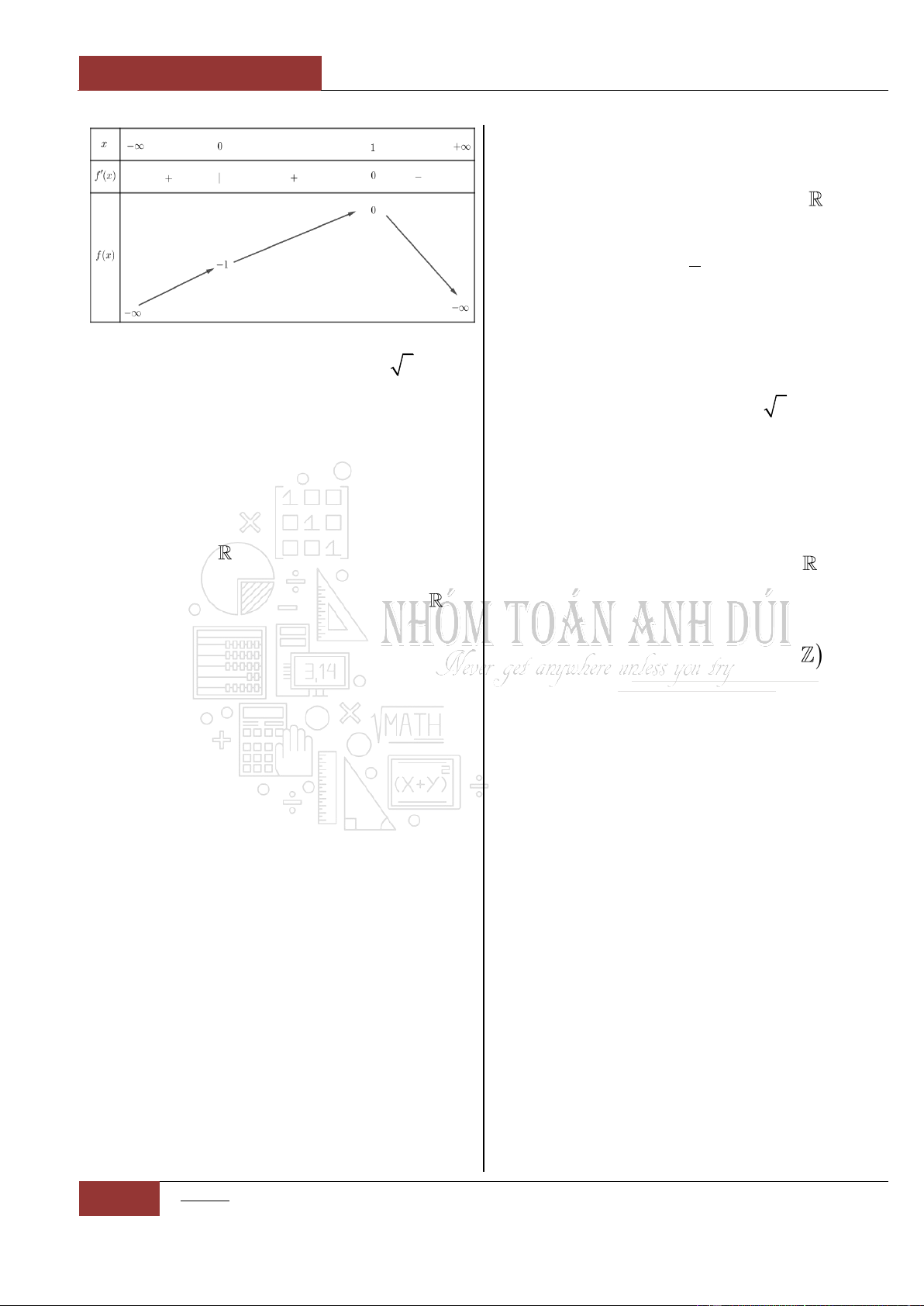
'fx

như hình vẽ

dưới đây. Hàm số

 

x

fx

gx

e



đồng biến trên

khoảng nào dưới đây?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

35

[ I can't, I can! ]

A.

 

;1

. B.

 

2;2 3

.

C.

 

4;

. D.

 

3;

.

Câu 60. [Vận dụng].

Cho hàm số

 

y f x

liên tục và có đạo hàm

đến cấp ba trên thỏa mãn hệ thức sau:

       

23

. ''' 1 4 ,f x f x x x x x    

.

Biết hàm số

   

 

   

2

' 2 . ''g x f x f x f x

đồng biến trên khoảng

 

;ab

. Tích

S ab

có

giá trị bằng?

A.

3S 

. B.

1S 

.

C.

0S 

. D.

4S 

.

Câu 61. [Vận dụng].

Cho hàm số

 

y f x

liên tục và có đạo hàm

   

3

'2f x x x

. Khoảng nghịch biến của đồ

thị hàm số

     

3

2g x f x x  

là khoảng

nào dưới đây? Chọn đáp án đúng nhất.

A.

 

1;2

. B.

 

1;3

.

C.

 

2;3

. D.

 

;1 

.

Câu 62. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục và có đạo hàm

   

 

2021

2

' 2 8 ,f x x x x    

.

Hàm số

 

2 4 2

1

2 4 2021

2

y f x x x    

nghịch biến trên khoảng nào sau đây?

A.

 

;2 

. B.

 

2;0

.

C.

 

0;2

. D.

 

0; 5

.

Câu 63. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục và có đạo hàm

 

  

' 2 ,

xx

f x e e x x    

Biết hàm số

   

ln 2lny g x f x x x   

nghịch biến trên khoảng

   

; , ,a b a b

.

Mệnh đề sau đây là đúng về tổng

S a b

?

A.

S

là một số chính phương.

B.

S

là một số lẻ.

C.

S

là số nguyên tố chẵn duy nhất.

D.

S

là một số chẵn.

Câu 64. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục và có đạo hàm

 

3

' 4 2f x x x

và

 

01f 

.

Hàm số

 

32

23y g x f x x   

đồng biến

trên khoảng nào sao đây?

A.

 

;1 

. B.

 

1;3

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

36

[ I can't, I can! ]

C.

 

1;1

. D.

 

1;3

.

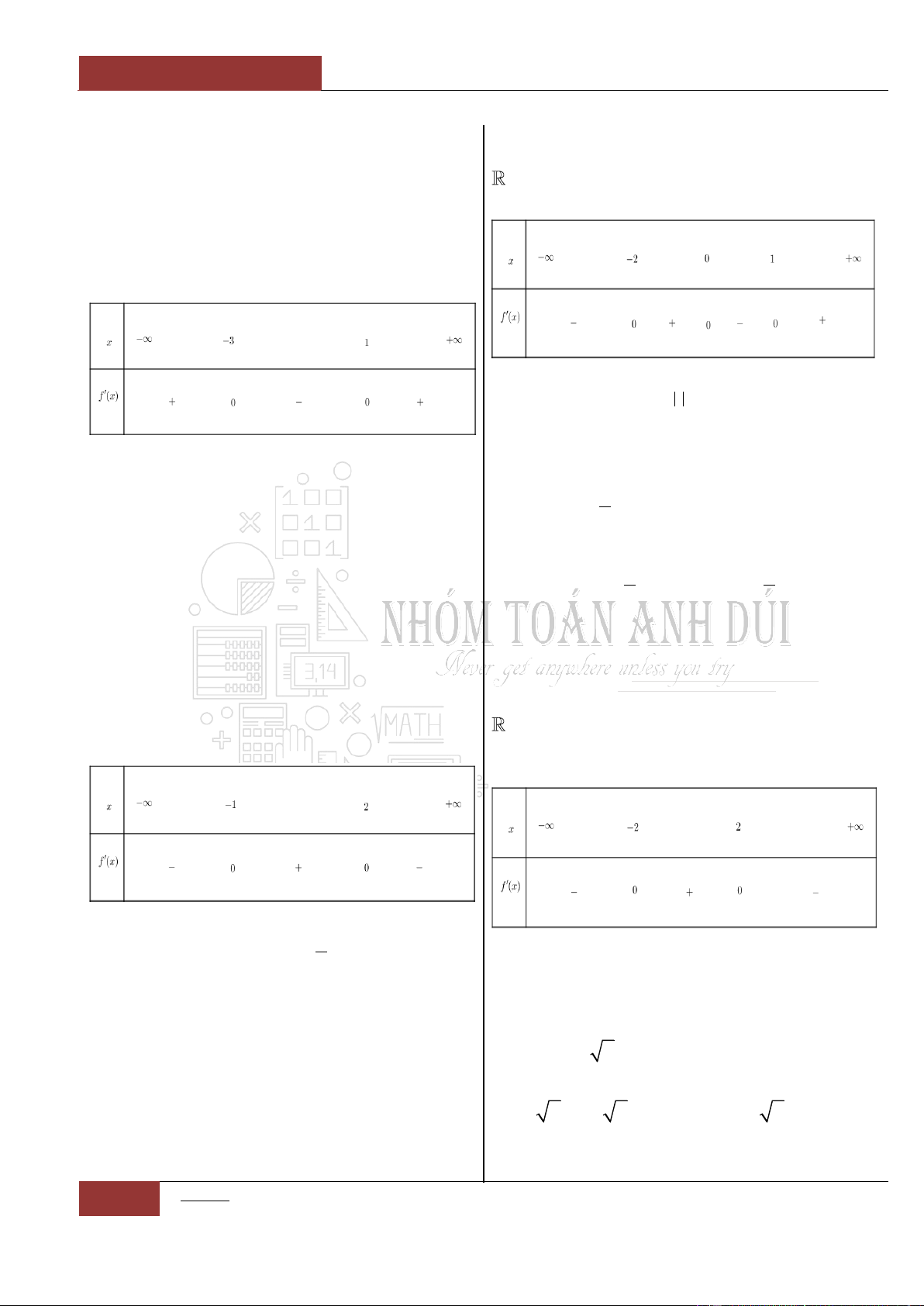
Câu 65. [Vận dụng cao].

Cho hàm số

 

y f x

có bảng xét dấu đạo hàm

như hình vẽ dưới đây.

Hàm số

   

32

3 9 5g x f x x x x    

đồng

biến trên các khoảng nào dưới đây?

A.

   

; 3 , 1;  

. B.

 

3;1

.

C.

 

; 

. D.

 

3; 

.

Câu 66. [Vận dụng cao].

Cho hàm số

 

y f x

có bảng xét dấu đạo hàm

như hình vẽ dưới đây.

Hàm số

   

32

3

6 2020

2

g x f x x x x    

đồng biến trên các khoảng nào dưới đây?

A.

   

; 1 , 2;  

. B.

 

1;2

.

C.

 

; 

. D.

 

1; 

.

Câu 67. [Vận dụng].

Cho hàm số

 

y f x

xác định và liên tục trên

và

 

'fx

có bảng xét dấu như sau:

Hàm số

 





2

2xx

g x f e





nghịch biến trên

khoảng nào dưới đây?

A.

1

0;

2







. B.

 

2;

.

C.

1

2;

2









. D.

1

;0

2









.

Câu 68. [Vận dụng cao].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

và có bảng xét dấu đạo hàm như hình vẽ bên

dưới.

Hàm số

 

4 2 6 4 2

3 4 6 2 3 12y f x x x x x      

đồng biến trên các khoảng nào dưới đây?

A.

 

;0 , 2; 

. B.

 

;0

.

C.

   

2;0 , 2; 

. D.

 

2; 

.

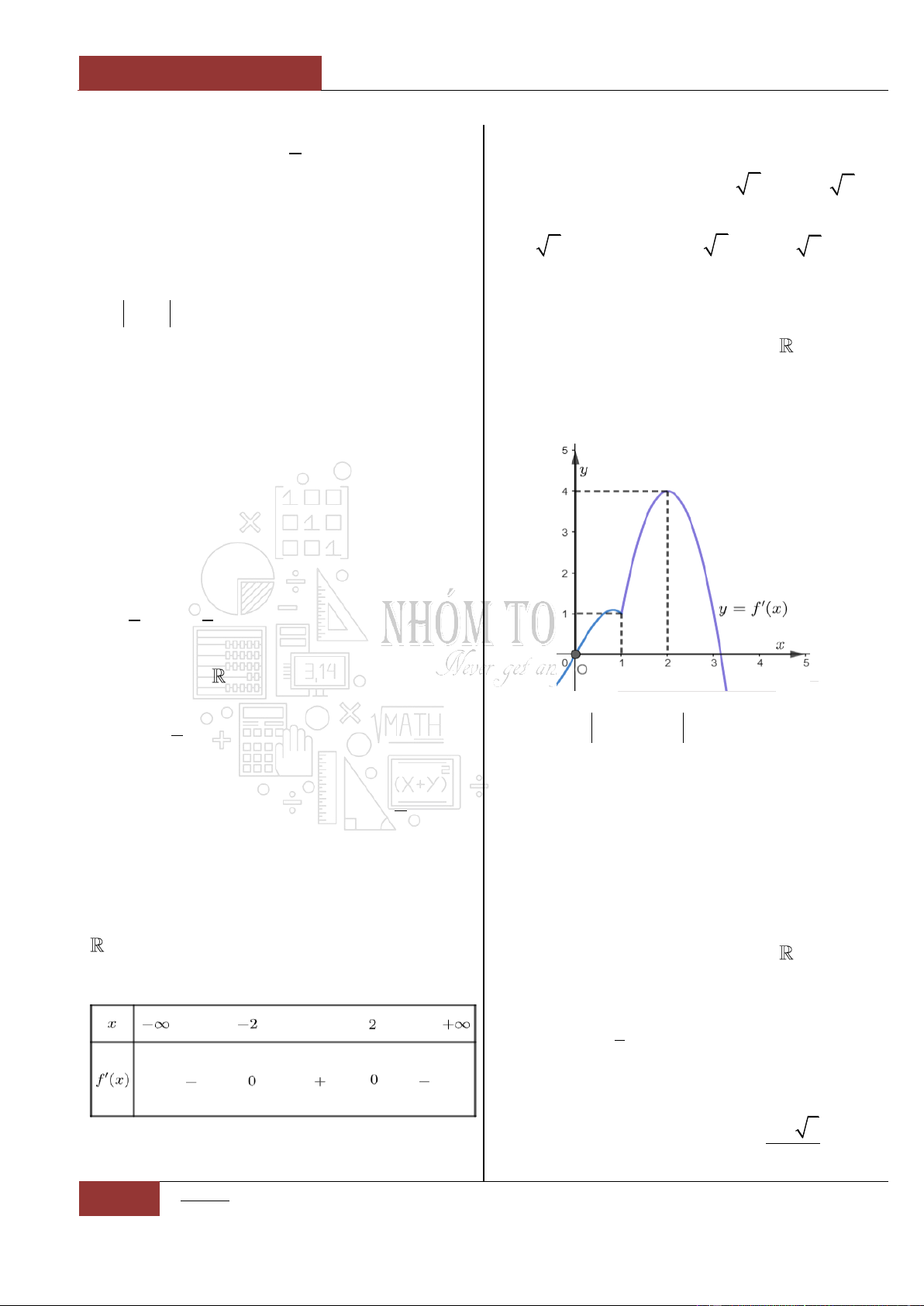
Câu 69. [Vận dụng].

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

37

[ I can't, I can! ]

Cho hàm số

2021

1

logy

x









có đồ thị hàm số

 

1

C

và đồ thị hàm số

 

y f x

có đồ thị

 

2

C

.

Biết rằng hai đồ thị hàm số

 

1

C

và

 

2

C

đối

xứng với nhau qua gốc tọa độ. Khi đó hàm số

 

y f x

nghịch biến trên khoảng nào sau

đây?

A.

 

;1 

. B.

 

1;0

.

C.

 

0;1

. D.

 

1; 

.

Câu 70. [Vận dụng].

Tích tất cả các giá trị thực của tham số

m

để

hàm số:

 

2 5 3 2 2

11

10 20 1

53

y m x mx x m m x      

đồng biến trên là?

A.

5

2

. B.

2

.

C.

5

. D.

1

2

.

Câu 71. [Vận dụng].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

và bảng xét dấu đạo hàm như hình vẽ bên

dưới:

Hàm số

 

4 2 6 4 2

3 4 6 2 3 12y f x x x x x      

đồng biến trên những khoảng nào dưới đây?

A.

 

;0

. B.

 

;2 

và

 

0; 2

.

C.

 

2;0

. D.

 

2;0

và

 

2;

.

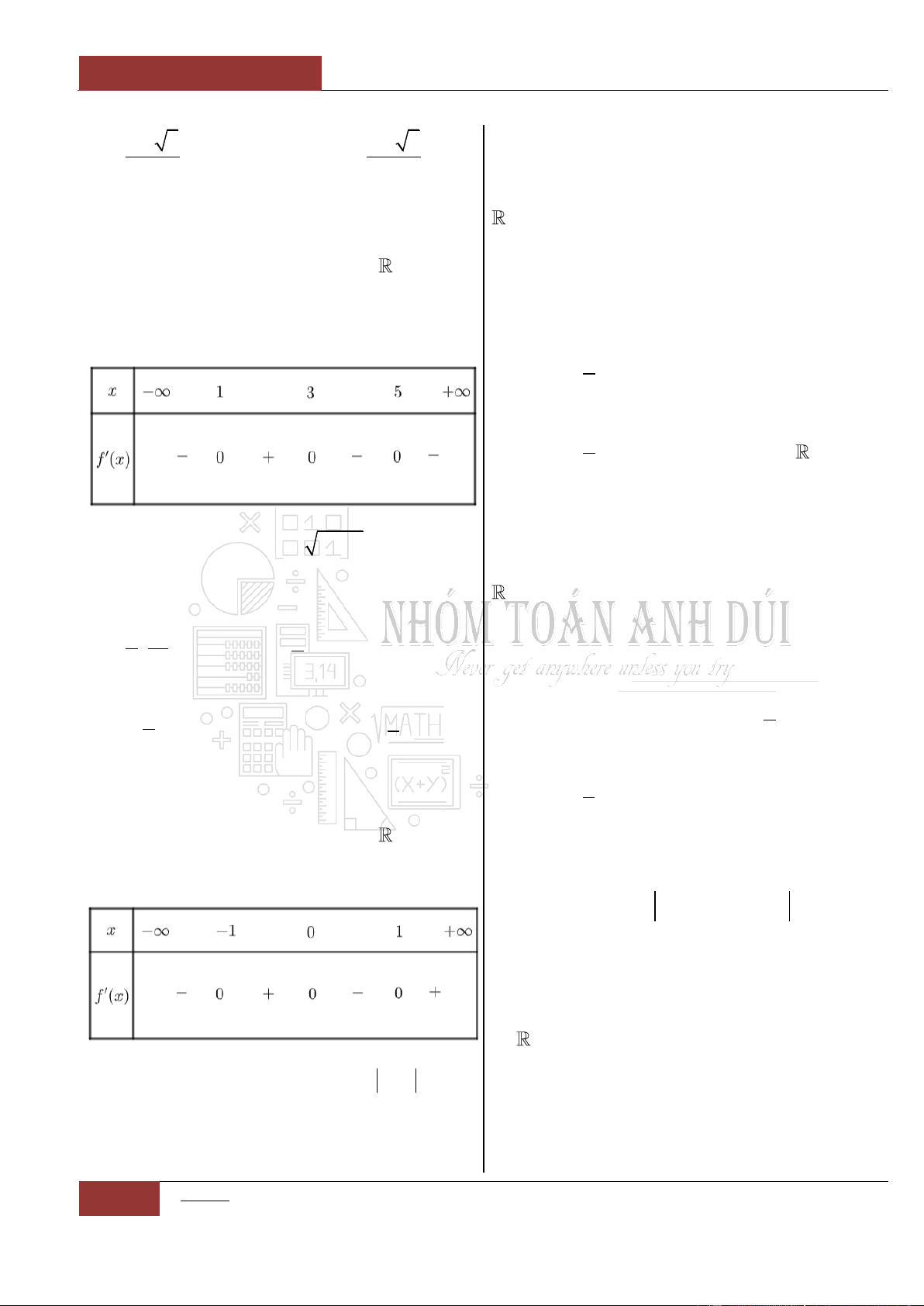
Câu 72. [Vận dụng].

Cho hàm số

 

y f x

liên tục trên có

 

00f 

và đồ thị hàm số

 

'y f x

như hình

vẽ bên dưới:

Hàm số

 

3

3y f x x

đồng biến trên khoảng

nào dưới đây?

A.

 

2;

. B.

 

;2

.

C.

 

0;2

. D.

 

1;3

.

Câu 73. [Vận dụng].

Cho hàm số

 

y f x

liên tục trên , có đạo

hàm

     

2

' 1 3f x x x x  

. Khi đó hàm số

   

3

1

2021

3

g x f x x  

đồng biến trên

khoảng nào trong các khoảng dưới đây?

A.

 

0;2

. B.

35

2;

2









.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

38

[ I can't, I can! ]

C.

35

;2

2









. D.

35

0;

2









.

Câu 74. [Vận dụng].

Cho hàm số

 

y f x

liên tục trên . Biết

hàm số

 

'y f x

có bảng xét dấu như hình vẽ

dưới đây:

Hàm số

 





2

1y g x f x x   

nghịch biến

trên khoảng nào dưới đây?

A.

4 12

;

35







. B.

4

;

3









.

C.

4

0;

3







. D.

 

;0

và

4

;

3









.

Câu 75. [Vận dụng].

Cho hàm số

 

y f x

liên tục trên và có

bảng xét dấu đạo hàm

 

'y f x

như sau:

Hàm số

 

2

2 1 1y g x f x x x     

đồng

biến trên bao nhiêu khoảng hữu hạn?

A.

1

. B.

3

. C.

2

. D.

4

.

Câu 76. [Vận dụng].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

, thỏa mãn

   

2

2 2 1 2 12f x f x x  

.

Phương trình tiếp tuyến của đồ thị hàm số

 

y f x

tại điểm có hoành độ bằng

1

đồng

biến trên khoảng nào sau đây?

A.

1

;

2









. B.

 

;2

.

C.

1

;2

2







. D. .

Câu 77. [Vận dụng].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

. Đồ thị hàm số

 

' 3 5y f x

như hình vẽ

bên. Hàm số

 

y f x

nghịch biến trên khoảng

nào dưới đây?

A.

 

;8

. B.

7

;

3



 





.

C.

4

;

3









. D.

 

;10

.

Câu 78. [Vận dụng].

Hàm số

 

32

3 9 5y f x x x x    

đồng

biến trên những khoảng nào dưới đây?

A.

 

32;0

. B.

 

1;3

và

 

5;

.

C. . D.

 

;1 

và

 

3;5

.

Câu 79. [Vận dụng].

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

39

[ I can't, I can! ]

Cho hàm số

 

y f x

có đạo hàm liên tục trên

đoạn

 

0;1

, thỏa mãn đồng thời

 

01f 

và

 

2

2 6 4 2

' 4 6 1 . 40 44 32 4f x x f x x x x       



 

 

, 0;1 *x

.

Hàm số

 

y f x

nghịch biến trên khoảng có

độ dài bằng bao nhiêu?

A.

22

2



. B.

1

. C.

2

. D.

2

.

Câu 80. [Vận dụng].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

đoạn

 

0;1

thỏa mãn đồng thời ba điều kiện:

 

 

1

2

0

1

3

0

11

' 9, 0;1

1

.

2

f

f x dx x

x f x dx









    















.

Mệnh đề nào sau đây là đúng về

 

y f x

?

A. Hàm số đồng biến trên .

B. Hàm số nghịch biến trên .

C. Hàm số nghịch biến trên khoảng

 

0;1

.

D. Hàm số đồng biến trên khoảng

 

0;1

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

45

[ I can't, I can! ]

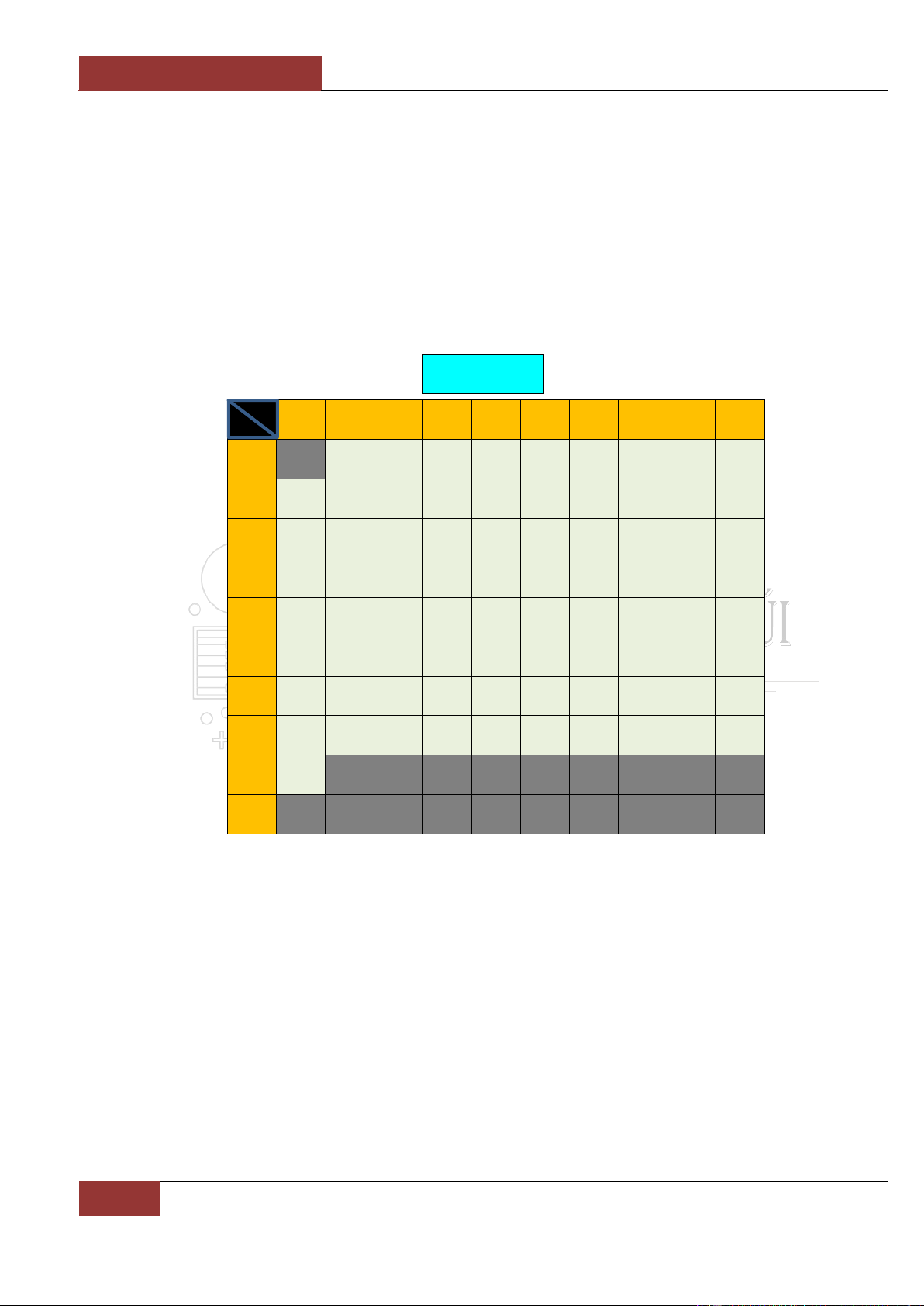
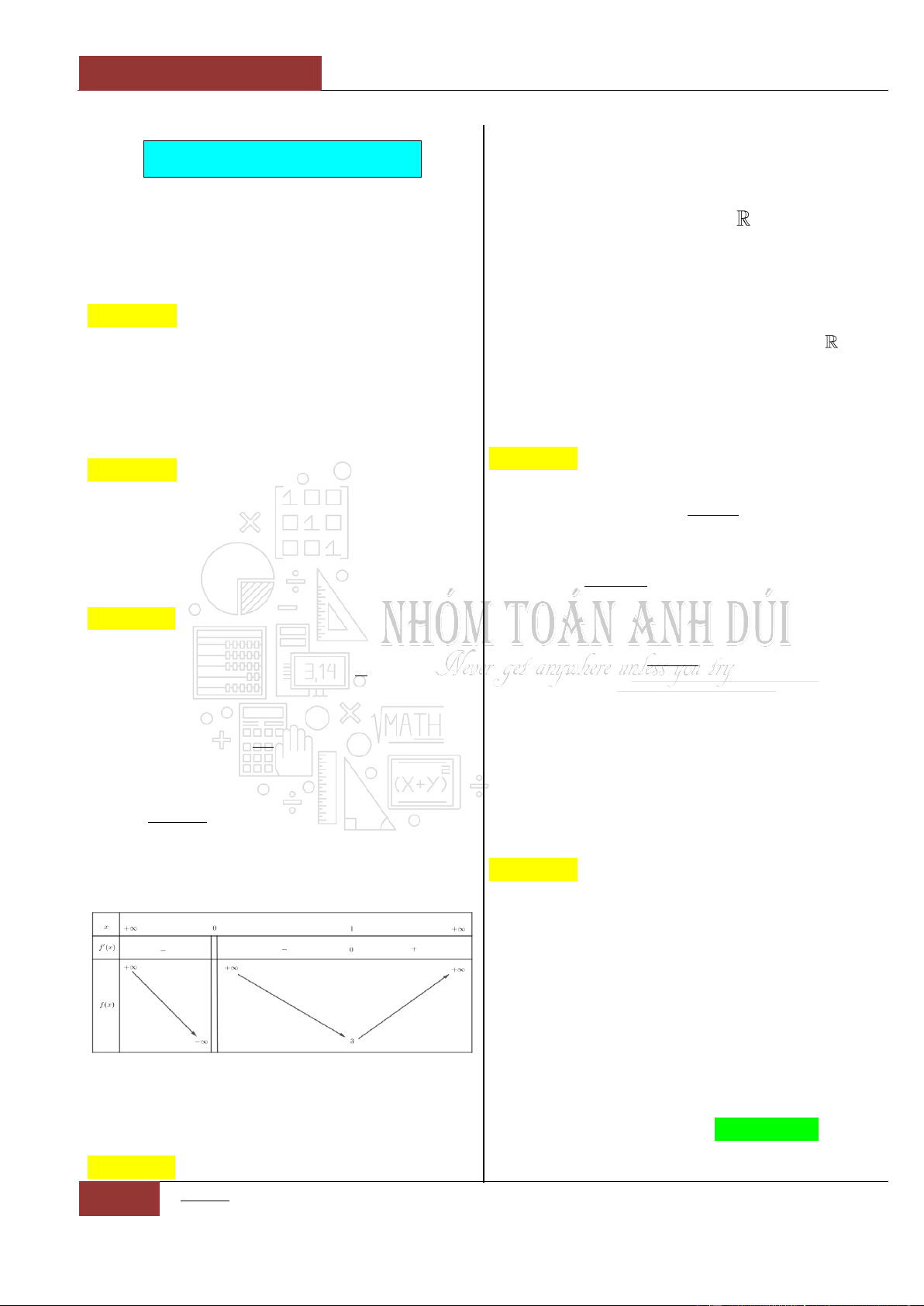
ĐÁP ÁN

0

1

2

3

4

5

6

7

8

9

0

D

B

A

D

B

A

C

1

C

A

B

C

A

D

A

C

2

B

C

D

B

C

A

3

A

C

D

B

A

D

B

D

4

C

B

A

C

D

C

A

5

B

C

B

C

A

C

B

C

6

C

B

C

B

C

A

B

D

C

A

7

C

D

C

D

B

D

A

B

C

8

C

9

Ghi chú: Đáp án là sự kết hợp giữa dòng

i

và cột

j

. Ví dụ: Câu 24D (giao của dòng 2 và cột 4).

i

j

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

46

[ I can't, I can! ]

LỜI GIẢI CHI TIẾT

Câu 1. Dựa vào bảng biến thiên của đồ thị hàm

số ta nhận thấy rằng: Hàm số đã cho đồng biến

trên khoảng

 

1;0

và

 

1; 

.

Đáp án: D

Câu 2. Theo bảng xét dấu thì

'0y 

khi

 

2;0x

hoặc

 

0;2x

nên hàm số nghịch biến

trên khoảng

(0;2)

.

Đáp án: D

Câu 3. Dựa vào đồ thị hàm số, ta nhận thấy

rằng hàm số có duy nhất một khoảng nghịch

biến là khoảng

 

2;0

.

Đáp án: B

Câu 4. Xét hàm số:

 

2

f x x

x



Ta có:

 

2

' 2 0f x x

x

  

3

2

22

01

x



   

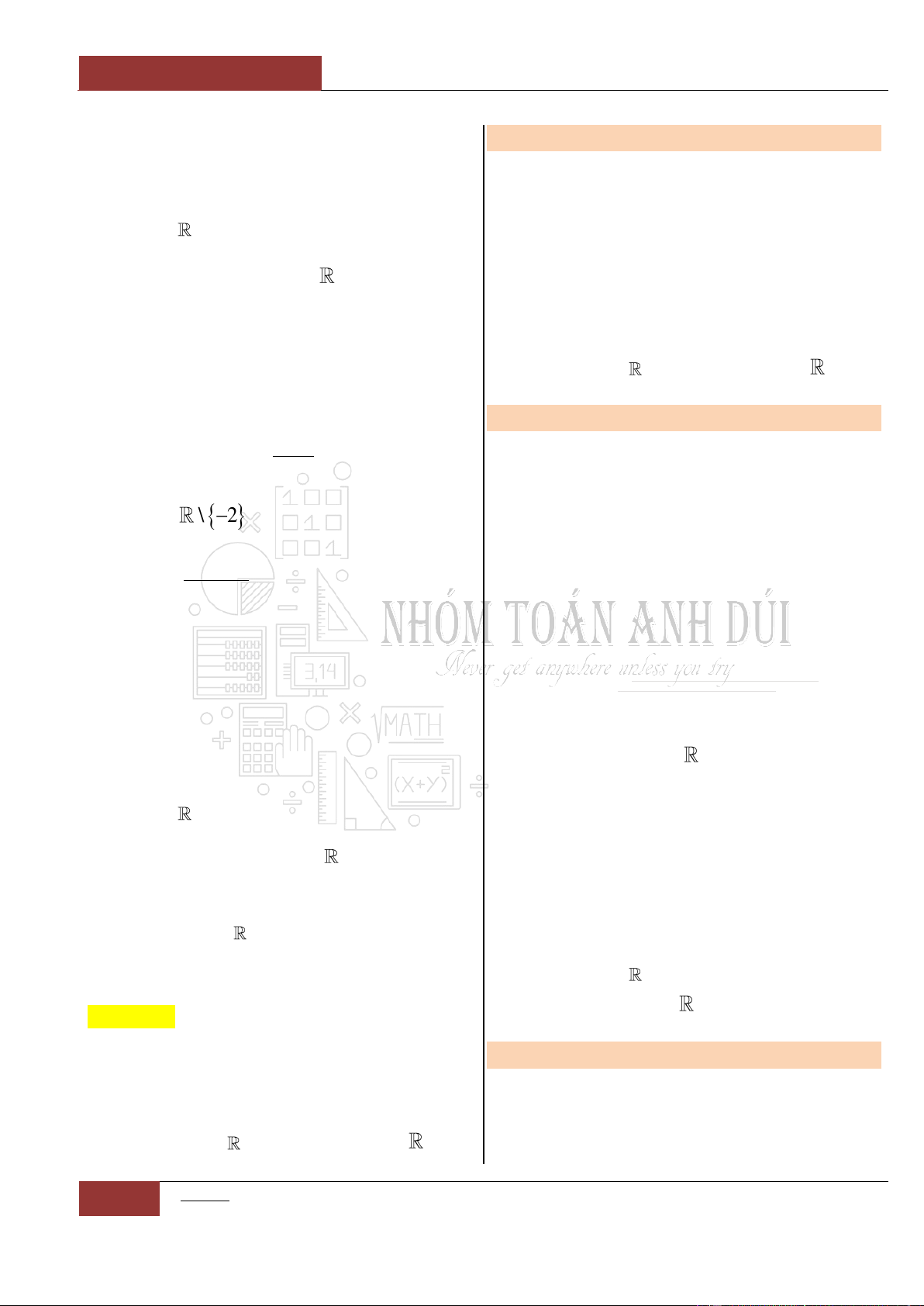
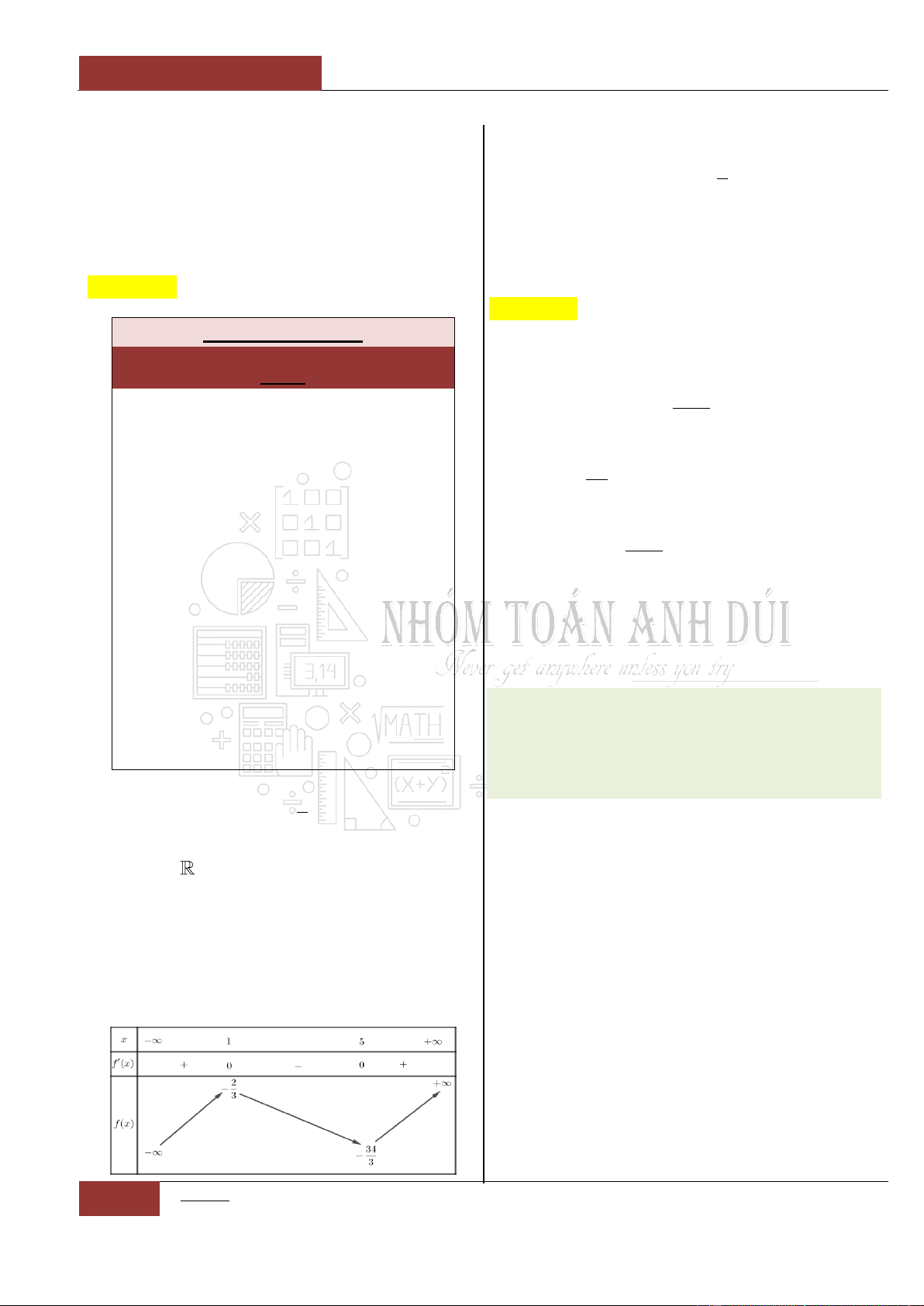
Bảng biến thiên:

Từ bảng biến thiên, ta thấy hàm số nghịch biến

trên khoảng

 

;0

và

 

0;1

.

Đáp án: B

Câu 5. Dựa vào bảng biến thiên của đồ thị hàm

số

 

'y f x

, ta lưu ý một điều:

 

' 0,f x x  

Và dấu

""

chỉ xảy ra tại hữu hạn điểm (tại

điểm

1x 

và điểm

1x 

).

Vì vậy, hàm số

 

y f x

đồng biến trên .

Thế nên, các kết luận về đồng biến ở nhận định

B, C, D hoàn toàn đúng.

Đáp án: A

Câu 6. Xét hàm số:

3

2

x

y

x







Ta có:

 

2

5

'0

2

y

x







.

Khi đó hàm số

3

2

x

y

x







nghịch biến trên

từng khoảng xác định.

Loại A.

Nhận định B, C cũng bị loại vì ở phần lưu ý

 

3

đã chỉ ra lỗi sai.

Đáp án: D

Câu 7. Ta xét từng đáp án:

 Đáp án A:

4

yx

.

Đây là hàm số bậc bốn trùng phương có

0ab 

và

0a 

. Khi đó: hàm số

4

yx

có dạng tương

tự một Parabol với hệ số

0a 

. Vì thế hàm số

4

yx

vừa có khoảng nghịch biến vừa có

khoảng đồng biến (Xem lại Đồ thị I.I.11).

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

47

[ I can't, I can! ]

Loại A.

 Đáp án B:

3

24y x x  

TXĐ:

D 

.

Ta có:

2

' 3 2 0,y x x    

.

Vì vậy hàm số

3

24y x x  

đồng biến trên

toàn tập xác định.

Chọn B.

 Đáp án C:

1

2

x

y

x







TXĐ:

 

\2D 

.

Ta có:

 

2

3

' 0,

2

y x D

x



   



.

Vì thế, hàm số nghịch biến trên từng khoảng

xác định

 

;2 

và

 

2; 

.

Loại C.

 Đáp án D:

siny x x

TXĐ:

D 

.

Ta có:

' cos 1 0,y x x    

Vì thế hàm số:

siny x x

nghịch biến trên

toàn tập xác định .

Loại D.

Đáp án: B

Câu 8. A. Ta xét từng nhận định:

 Nhận định A: Hàm số

 

y f x

đồng

biến trên khi

 

' 0,f x x  

.

Đây là một nhận định đúng.

Vì theo lý thuyết: Trên một khoảng

K

bất kì,

nếu ta có

 

' 0,f x x K  

thì hàm số là một

hàm đồng biến (tăng ngặt) trên

K

.

Chọn A.

 Nhận định B: Hàm số

 

y f x

đồng

biến trên khi

 

' 0,f x x  

.

Nhận định B chưa hẵn là đúng.

Lí do:

Giả sử ta xét hàm số cho bởi hai biểu thức:

 

2 9 , 0

9 , 0 100

9 891, 100

xx

y f x x

xx







   









Khi đó:

 

2 , 0

' 0 , 0 100

9 , 100

x

y f x x

x







   









Mặc dù

 

' 0,f x x  

nhưng hàm số trên

đoạn

 

0;100

là không đổi (dấu

""

xảy ra ở

vô hạn điểm nên vi phạm nội dung điều kiện

đủ để hàm số đơn điệu trên một khoảng).

Loại B.

 Nhận định C: Hàm số

 

y f x

đồng

biến trên khi và chỉ khi

 

' 0,f x x  

.

Nhận định C chưa hẵn là đúng.

Ta phải nhận ra rằng mối quan hệ trong nhận

định C là một mối quan hệ hai chiều, có nghĩa

là hai nhận định dưới đây đều phải đúng.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

48

[ I can't, I can! ]

 



Nếu hàm số

 

y f x

đồng biến

trên thì

 

' 0,f x x  

.

 



Nếu

 

' 0,f x x  

thì hàm số

 

y f x

đồng biến trên .

Tuy nhiên, do ta đã xác định được nhận định B

là sai nên nhận định C cũng sai do nhận định B

và nhận định

 



là tương đương.

Loại C.

 Nhận định D: Hàm số

 

y f x

đồng

biến trên khi và chỉ khi

 

' 0,f x x  

.

Nhận định D chưa hẵn là đúng.

Ta phải nhận ra rằng mối quan hệ trong nhận

định C là một mối quan hệ hai chiều, có nghĩa

là hai nhận định dưới đây đều phải đúng.

M

 



Nếu hàm số

 

y f x

đồng biến

trên thì

 

' 0,f x x  

.

 



Nếu

 

' 0,f x x  

thì hàm số

 

y f x

đồng biến trên .

Nhận định

 



đúng do tương đương với nhận

định A.

Tuy nhiên, nhận định

 



chưa hẵn là hoàn

toàn đúng. Chẳng hạn, ta xét một hàm số đồng

biến trên quen thuộc, hàm số

 

3

y f x x

.

Tuy nhiên,

 

2

' 3 0,f x x x   

.

Loại D.

Đáp án: A

Câu 9. Xét hàm số:

32

6 9 2y x x x   

.

TXĐ:

D 

.

Ta có:

2

1

' 3 12 9 0

3

x

y x x

x





    







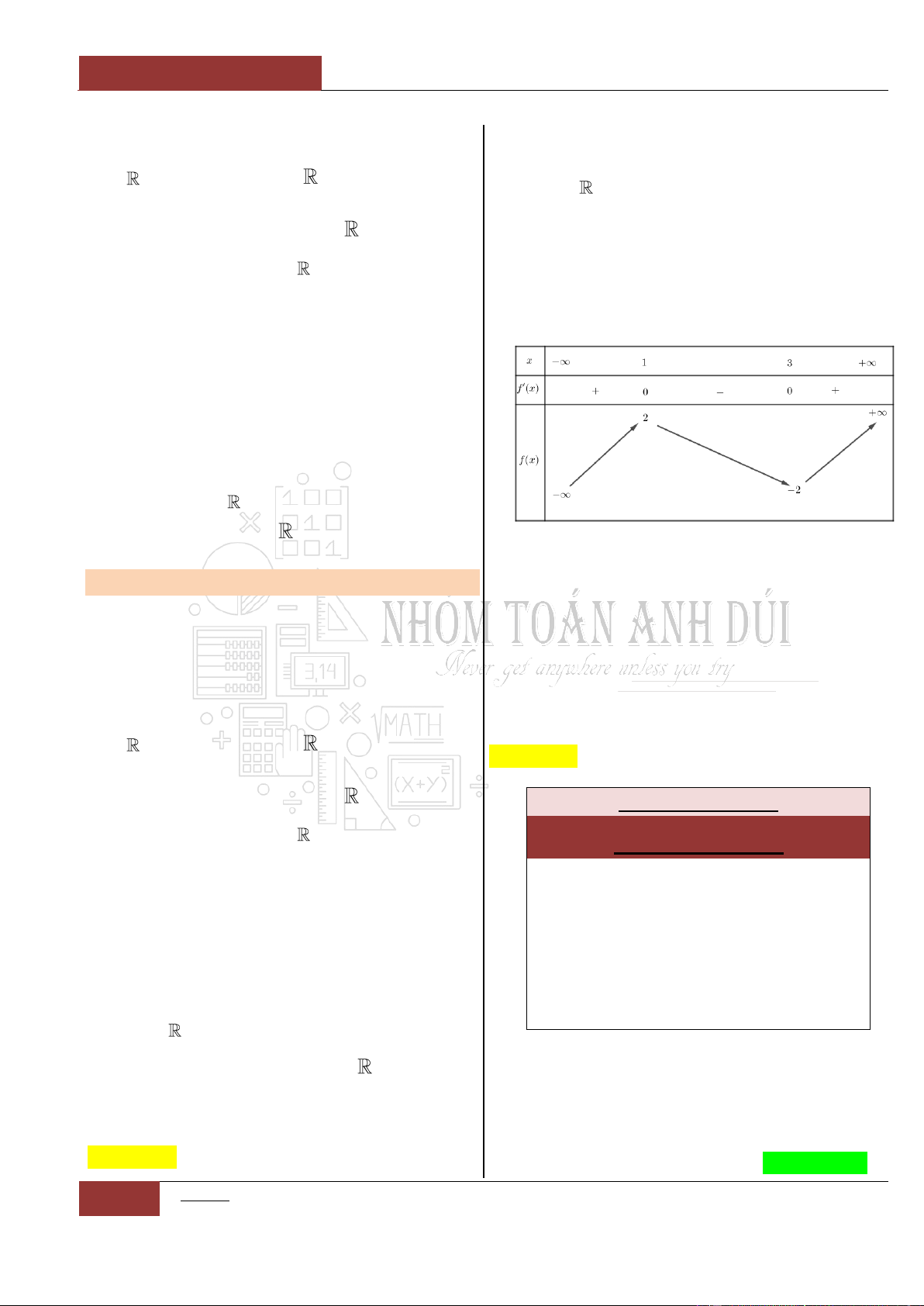
Bảng biến thiên:

Dựa vào bảng biến thiên ta thấy rằng, đồ thị

hàm số

32

6 9 2y x x x   

nghịch biến trên

khoảng lớn nhất là khoảng

 

1;3

.

Khi đó:

3 3 3 3

1

1 3 28

3

a

ab

b





    







Đáp án: C

Extra Techniques:

Confusing answers:

Nhiều bạn sẽ chọn đáp án A. Vì các bạn

không phân biệt được hai khái niệm:

+) Tổng lập phương của a và b:

33

ab

+) Lập phương của một tổng:

 

3

ab

Câu 10. Để hàm số đồng biến trên khoảng

 

;0

thì hàm số

 

42

,0y ax bx c a   

chỉ có duy nhất một cực trị và

0a 

.

(Xem Đồ thị I.I.12).

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

49

[ I can't, I can! ]

Khi đó ta có:

0

ab

a











hay

0

a

b











(*).

Như vậy trong bốn đáp án, duy chỉ có đáp án C

không thể nào thỏa mãn (*) (do

0b 

).

Đáp án: C

Extra Techniques:

Tips:

Ở đây, tham số

c

không ảnh hưởng đến

tính đơn điệu hay chiều biến thiên của

hàm số (do đạo hàm của hằng số bằng

0

)

nhưng thay vào đó, tham số

c

lại đóng

vai trò là "điểm trượt" dọc theo trục Oy.

Chẳng hạn, ta xét hàm số:

 

y f x

liên

tục trên khoảng

K

. Khi đó ta thu được

hàm số

 

y f x c

bằng cách tịnh tiến

đồ thị

 

y f x

lên

c

đơn vị đồ thị theo

trục Oy nếu

0c 

và tịnh tiến đồ thị

 

y f x

xuống

c

đơn vị đồ thị theo

trục Oy nếu

0c 

.

Câu 11. Xét hàm số:

32

1

3 5 3

3

y x x x   

TXĐ:

D 

Ta có:

2

1

' 6 5 0

5

x

y x x

x





    







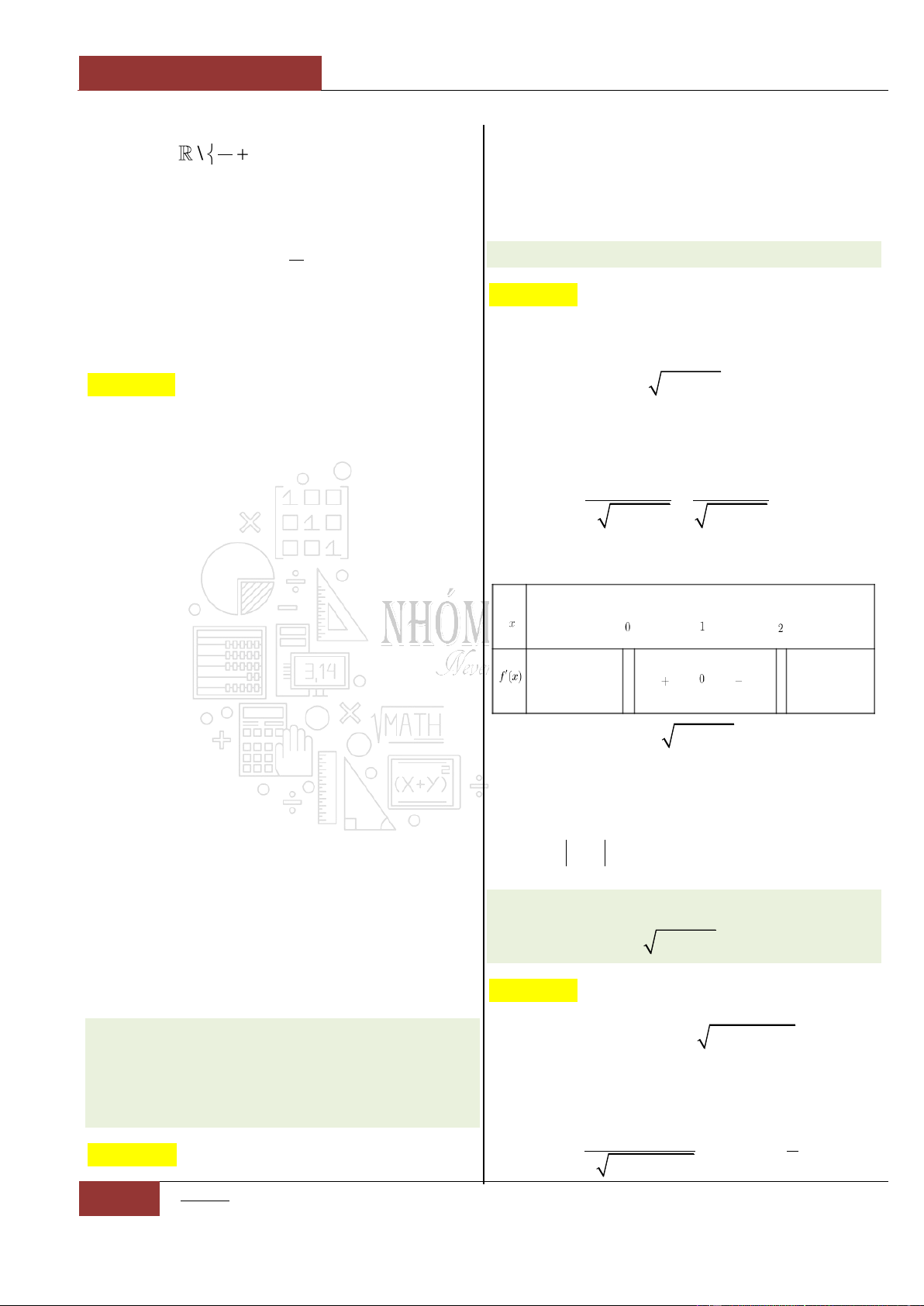
Bảng biến thiên:

Dựa vào bảng biến thiên của đồ thị hàm số ta

nhận thấy rằng, hàm số

32

1

3 5 3

3

y x x x   

đồng biến trên hai khoảng rời nhau là

 

;1

và

 

5;

.

Đáp án: A

Câu 12. Ta xét từng đáp án:

 Đáp án A:

1x

y

x





Ta có:

 

2

1

' 0, 0;yx

x





   

.

Nên hàm số

1x

y

x





nghịch biến trên

 

0;



.

Loại A.

 Đáp án B:

2

yx

Note: Hàm số

 

2

,0y kx k

là một Parabol

nghịch biến trên khoảng

 

;0

và đồng biến

trên khoảng

 

0;

.

Mà

   

0; 0;



 

;

Nên hàm số

2

yx

đồng biến trên

 

0;



.

Chọn B.

 Đáp án C:

cosyx

Ta có:

 

' sin 0, 0;y x x



    

;

Nên hàm số

cosyx

nghịch biến trên

 

0;



.

Loại C.

 Đáp án D:

tanyx

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

50

[ I can't, I can! ]

TĐX:

\

2

Dk











.

Vì thế hàm số

tanyx

không liên tục trên

khoảng

 

0;



vì tại

2

x





, hàm số

tanyx

không xác định.

Loại D.

Đáp án: B

Câu 13. Vì hàm số

 

y f x

nghịch biến trên

khoảng

 

9;9

nên

 

9;9x  

ta luôn có:

 

'0fx

. Mặt khác, cũng vì hàm số

 

y f x

nghịch biến trên khoảng

 

9;9

nên với mọi

     

1 2 1 2 1 2

, 9;9 ,x x x x f x f x    

.

Một số điểm đặc biệt:

 

   

' 3 0

' 1 0

' 2 0

' 3 0

' 8 0

38

f

ff





























(*).

Từ (*) trên ta có thể suy ra được những kết quả

có thể xảy ra như sau:

     

   

     

' 1 . ' 2 0 1

' 3 0 2

3 8 3

' 3 ' 8 4

ff

f

ff





















Note: Kết quả

 

4

, tuy không hẳn luôn đúng

nhưng vẫn có thể xảy ra do

 

' 3 0

' 8 0

f















.

Đáp án: C

Câu 14. Dựa vào đồ thị hàm số ta thấy rằng đồ

thị hàm số đồng biến trên khoảng

 

4;4

và

nghịch biến trên khoảng

 

4;

.

Note: Nhận định A, D tuy đúng nhưng chưa đủ.

Đáp án: C

Câu 15.

Ta xét hàm số:

2

2y x x

TXĐ:

 

0;2D 

.

Ta có:

22

2 2 1

' 0 1

2 2 2

xx

yx

x x x x



    



.

Bảng biến thiên:

Như vậy hàm số

2

2y x x

nghịch biến trên

đoạn

 

1;2

.

Khi đó độ lớn của khoảng nghịch biến của hàm

số là

2 1 1a   

.

Note: Tuy

 

'2f

không xác định nhưng tại

2x 

, hàm số

2

2y x x

xác định.

Đáp án: A

Câu 16. Xét hàm số:

2

65y x x  

TXĐ:

 

1;6D 

Ta có:

2

5 2 5

'0

2

2 6 5

x

yx

xx



   



.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

51

[ I can't, I can! ]

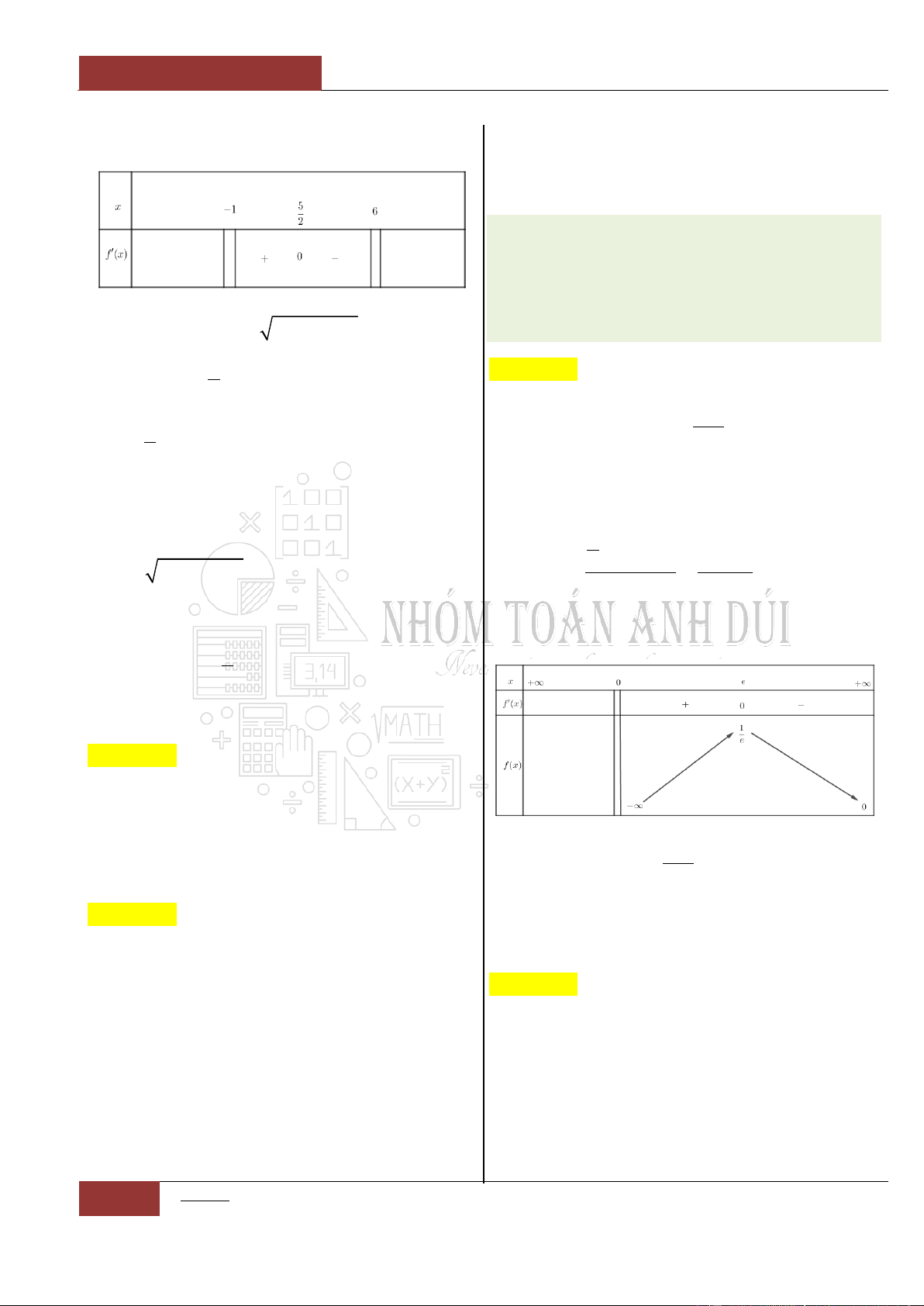
Bảng biến thiên:

Như vậy hàm số

2

65y x x  

đồng biến

trên đoạn

5

1;

2









và hàm số nghịch biến trên

đoạn

5

;6

2







.

Note: Tuy tại

1x 

và

6x 

, hàm số

 

'fx

không xác định nhưng tại

1x 

và

6x 

, hàm

số

2

65y x x  

xác định.

Do đó:

1

5

10

2

6

a

b c S a b c d

d







       











.

Đáp án: A

Câu 17. Dựa vào đồ thị hàm số ta dễ dàng nhận

thấy rằng, hàm số

 

y f x

nghịch biến trên

khoảng

 

;2 

và

 

0;2

.

Đáp án: D

Câu 18. Dựa vào đồ thị hàm số hàm

 

'y f x

ta nhận thấy:

     

' 0, 3; 2 2;3f x x     

.

Suy ra: Hàm số

 

y f x

nghịch biến trên

khoảng

 

3; 2

và

 

2;3

. Hơn thế nữa hàm số

đồng biến trên ba khoảng rời nhau,

 

;3 

và

 

2;2

và

 

3;

.

Vì

   

0;2 2;2

nên hàm số đồng biến trên

khoảng

 

0;2

. Vì thế A sai.

Note: Tuy đồ thị là hàm số đạo hàm

 

'y f x

nhưng yêu cầu đề bài lại hỏi khoảng đơn điệu

của hàm số

 

y f x

nên dễ gây nhầm lẫn cho

một số bạn đọc.

Đáp án: A

Câu 19. Xét hàm số

ln x

y

x



.

TXĐ:

 

0;D  

.

Ta có:

22

1

. ln .1

1 ln

'0

xx

x

y x e

xx



    

.

Bảng biến thiên:

Như vậy hàm số

ln x

y

x



đồng biến trên

khoảng

 

0;e

. Suy ra:

0

ln 1

a

S a b

be





   







.

Đáp án: C

Câu 20. Xét hàm số:

lny x x x

.

TXĐ:

 

0;D  

Loại C, D.

Bảng biến thiên:

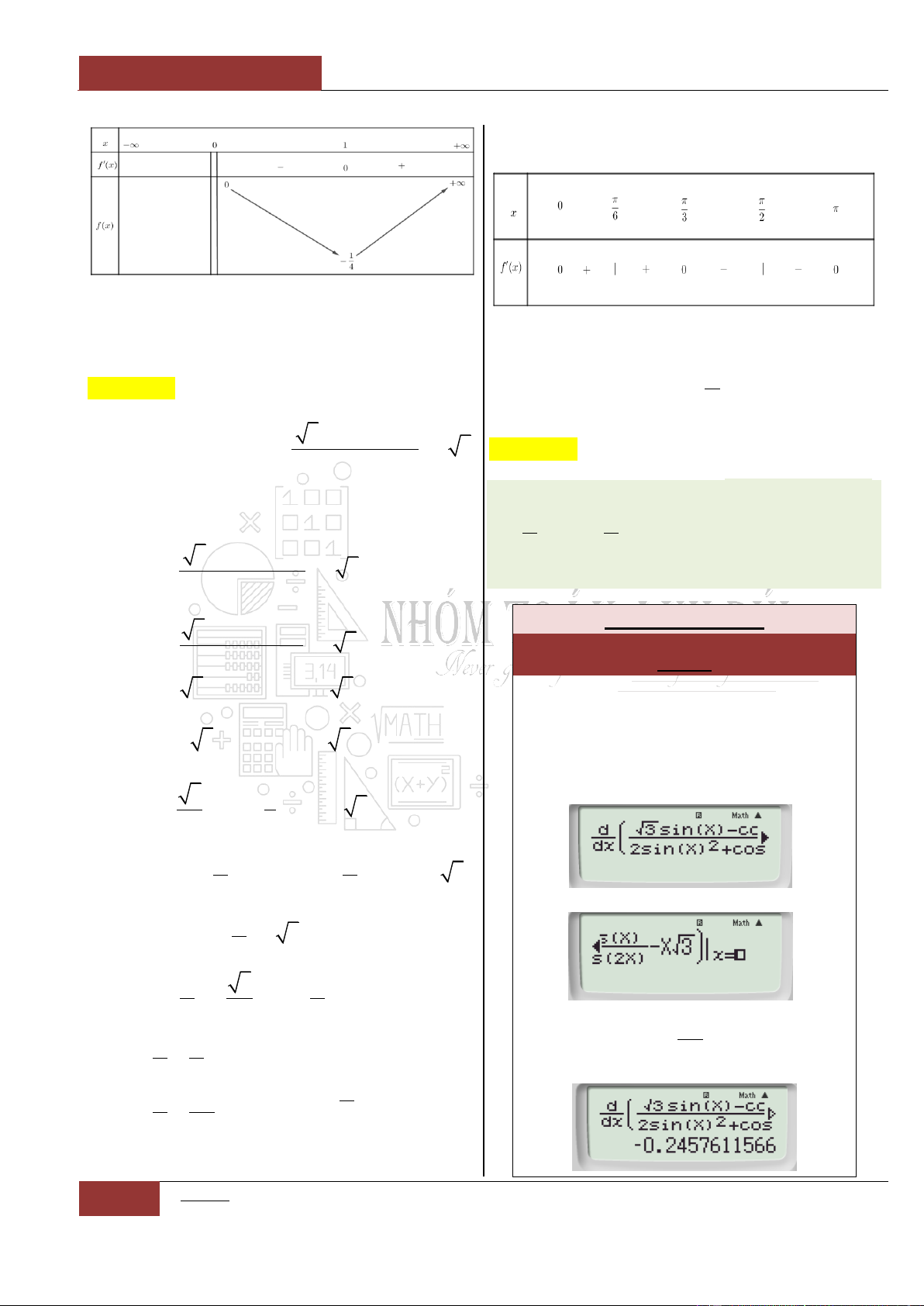
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

52

[ I can't, I can! ]

Dựa vào bảng biến thiên ta thấy rằng, hàm số

lny x x x

đồng biến trên khoảng

 

1; 

.

Đáp án: B

Câu 21. Xét hàm số:

2

3sin cos

3

2sin cos2

xx

yx

xx







Vì:

22

cos2 1 2sin 2sin cos2 1x x x x    

.

Ta có:

2

3sin cos

3

2sin cos2

xx

yx

xx







3sin cos

3

1

3sin cos 3

xx

yx

y x x x



  

   

Suy ra:

' 3cos sin 3y x x  

31

' 2 cos sin 3

22

' 2 sin .cos cos .sin 3

33

' 2sin 3 0

3

sin sin

3 2 3

2

33

2

3

33

y x x

yx

x

xk















   







   

   

   



   





    





   

   

   

   





  













  







Bảng biến thiên:

Dựa vào bảng biến thiên, ta thấy rằng hàm số

đồng biến trên khoảng

0;

3









.

Đáp án: C

Note: Dựa trên bốn đáp án ta xen các điểm phụ

6

x





và

2

x





và

x





vào bảng biến thiên

để có một bảng biến thiên hoàn chỉnh.

Extra Techniques:

Casio:

Cơ sở: Dựa vào đáp án ta có thể dễ dàng

loại trừ các phương án sai.

Nhập vào màn hình như sau:

+) Đạo hàm tại

2

5

x





Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

53

[ I can't, I can! ]

Ta có:

2

'0

5

y











Suy ra hàm số không thể đồng biến trên

cả ba khoảng

0;

2









và

;

62









và

;

3









vì điểm

2

5

x





thuộc trong cả

ba khoảng ấy mà đạo hàm tại điểm đó là

một số âm (Nghịch biến).

Câu 22. Xét hàm số:

 

2

y f x x

.

Ta có:

 

2

' 2 1 . ' 0y x f x x   

2

1

2 1 0

2

4

1

2

x

xx

x

xx

x

xx











  



   



  











Bảng biến thiên:

Dựa vào bảng biến thiên, ta nhận thấy rằng hàm

số

 

2

y f x x

nghịch biến trên hai khoảng

rời nhau

 

;1 

và

1

;2

2







.

Đáp án: C

Extra Techniques:

Tips:

Để xét dấu bảng biến thiên, ta chỉ cần

chọn một số đủ lớn

 

2;x 

,

10x 

chẳng hạn để xét dấu biểu thức:

   

 

2

' 2 1 'g x x f x x  

.

Ta có:

   

' 10 19. ' 90 0gf

do

 

' 90 0f 

.

Vậy ta điền dấu

""

ở khoảng

 

2;

.

Note: Khi ta giải phương trình

 

'0gx

ta nhận được

3

nghiệm bội lẻ. Khi đó ta

thừa nhận tính chất đổi dấu đạo hàm qua

nghiệm bội lẻ của nó. Hay nói cách

khác, ta chỉ cần đan dấu giữa các điểm

cực trị (điểm mà tại đó đạo hàm bằng

0

hoặc không xác định (nếu điểm đó cũng

là bội lẻ)).

Câu 23. Ta xét hàm số:

   

2021h x f x x

.

Ta có:

   

' ' 2021h x f x

và

   

'' ''h x f x

.

Bảng biến thiên:

Kẻ thường thẳng

0y 

như hình bên dưới.

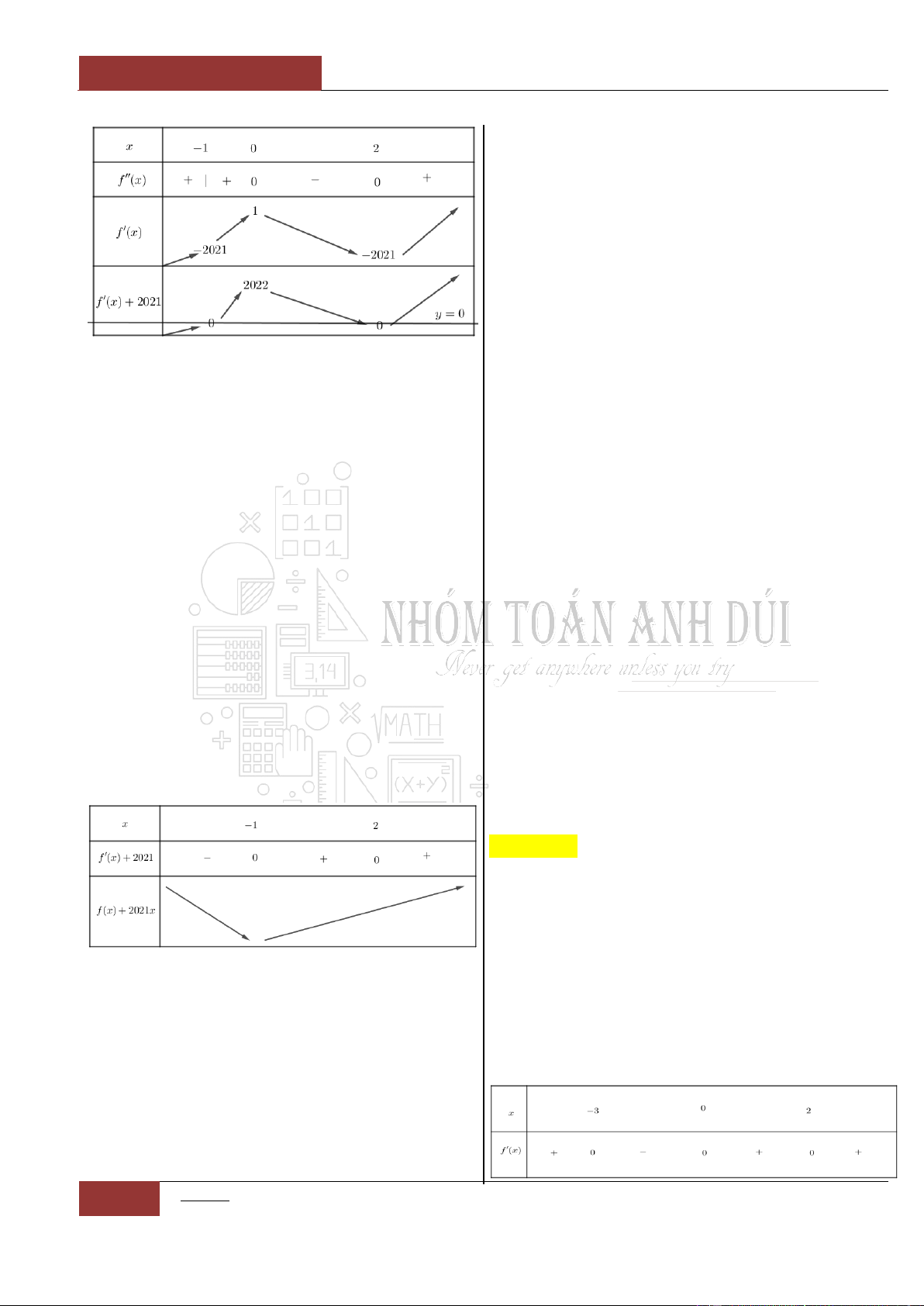
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

54

[ I can't, I can! ]

Dựa vào bảng biến thiên, ta thấy rằng đồ thị

hàm số

 

' 2021fx

cắt đường thẳng

0y 

tại hai điểm phân biệt là

1x 

và

2x 

.

Suy ra:

 Hàm số

 

2021y f x x

nghịch biến

trên khoảng

 

;1 

(do

 

;1x   

hàm số

 

' 2021 0fx

).

 Hàm số

 

2021y f x x

đồng biến

trên khoảng

 

1; 

(do

 

1;x   

hàm số

 

' 2021 0fx

).

Bảng biến thiên:

Vì:

     

2022 2022 2021 2022h x f x x    

Đặt:

2022tx

.

Khi đó ta có một biểu thức tương đương:

   

2021h t f t t

Vì:

 

2021y f x x

đồng biến trên

 

1; 

Nên hàm số

   

2021h t f t t

cũng đồng

biến trên khoảng

 

1; 

.

Khi đó:

1 2022 1 2023t x x        

.

Như vậy, hàm số

 

2022y h x

đồng biến

trên khoảng

 

2023; 

.

Mặt khác, ta xét hàm:

     

2022 2022 2021 2022h x f x x    

 

2022 2021 4086462f x x   

Suy ra:

   

2022 4086462h x g x  

.

Vì: hàm số

 

2022y h x

đồng biến trên

khoảng

 

2023; 

.

Nên hàm số

 

2022 4086462y h x  

cũng

đồng biến trên khoảng

 

2023; 

.

Vậy hàm số

   

2022 2021y g x f x x   

đồng biến trên khoảng

 

2023; 

.

Đáp án: D

Câu 24. Xét:

     

2

' 2 3y f x x x x   

.

Khi đó:

 

0

' 0 2

3

x

f x x

x







  







.

Bảng biến thiên:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

55

[ I can't, I can! ]

Như vậy hàm số

 

y f x

nghịch biến trên

đoạn

 

3;0

.

Suy ra:

 

3

0 3 3

0

a

S b a

b





      







.

Đáp án: D

Extra Techniques:

Remark:

Đạo hàm

 

'fx

của hàm số

 

y f x

đổi dấu qua nghiệm bội lẻ của phương

trình

 

'0fx

.

Đạo hàm

 

'fx

của hàm số

 

y f x

không đổi dấu qua nghiệm bội chẵn

của phương trình

 

'0fx

.

Câu 25. Xét hàm số:

   

2 2021g x f x x  

.

Ta có:

     

' ' 2 0 ' 2g x f x f x    

.

Kẻ đường thẳng:

2y 

.

(Minh họa như hình vẽ)

Bảng biến thiên:

Khi đó hàm số

   

2 2021y g x f x x   

đồng biến trên khoảng

 

2;

.

Đáp án: D

Note: Đề bài cho đồ thị minh họa là đồ thị đạo

hàm của hàm số

 

fx

có nghĩa là đồ thị hàm

số

 

'y f x

.

Câu 26. Hàm số:

 

y f x

có đồ thị như hình

minh họa dưới đây.

Đồ thị hàm số

 

y f x

.

Đồ thị hàm số

 

2021y f x

.

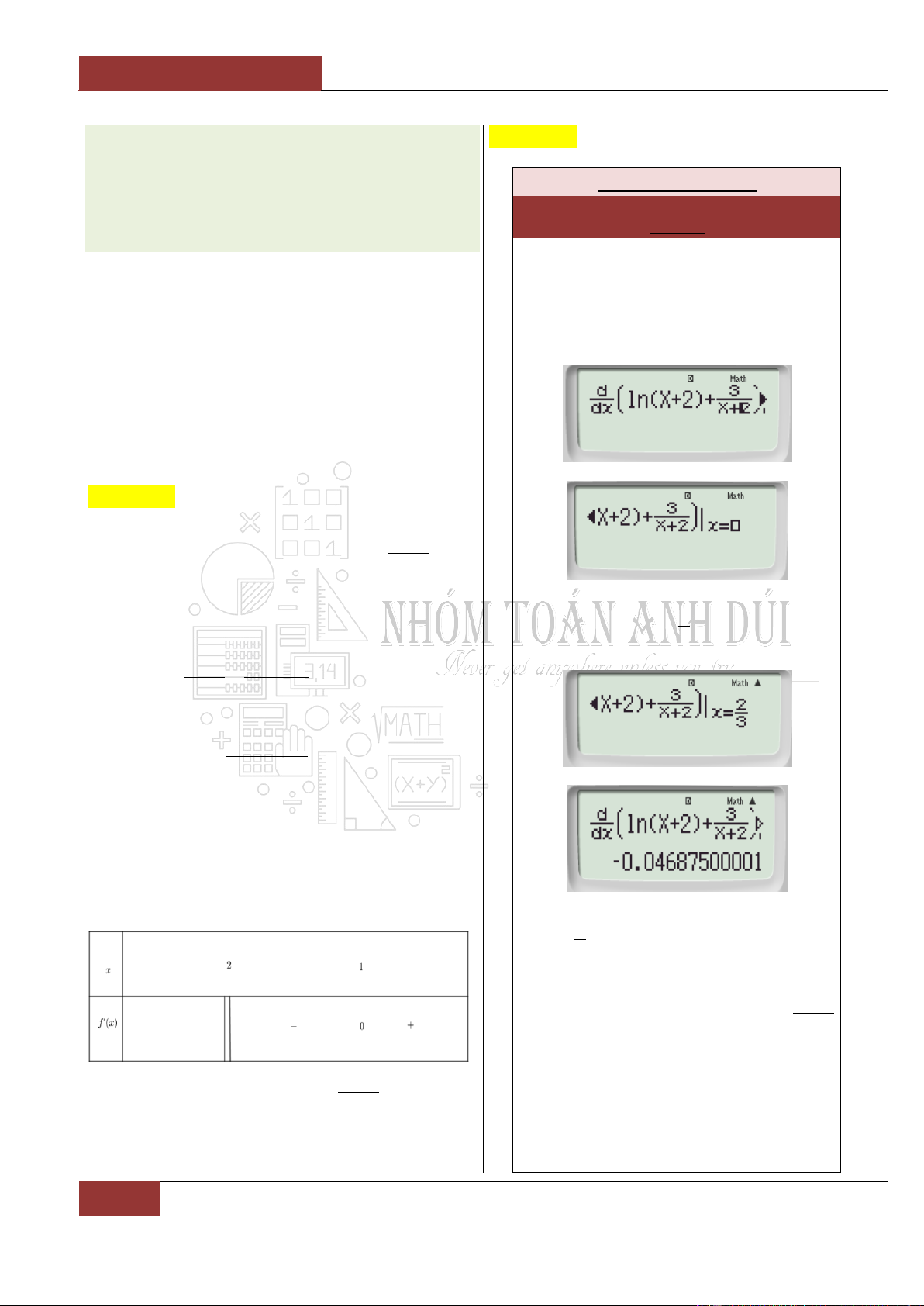
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

56

[ I can't, I can! ]

Note: Đồ thị hàm số

 

2021y f x

là một đồ

thị có hình dáng giống hệt với đồ thị hàm số

 

y f x

nhưng được tịnh tiến lên phía trên

2021 đơn vị.

Vì vậy khoảng đơn điệu của hàm số

 

y f x

và hàm số

 

2021y f x

là như nhau.

Khi đó đồ thị hàm số

 

2021y f x

nghịch

biến trên các khoảng

 

;3 

và

 

2; 1

và

 

0;2

.

Đáp án: B

Câu 27. Xét hàm số:

 

3

ln 2

2

yx

x

  



.

TXĐ:

 

2;D   

.

Ta có:

 

2

13

'0

2

y

x

  



 

2

23

0

2

1

0

2

1

x















Bảng biến thiên:

Khi đó hàm số

 

3

ln 2

2

yx

x

  



đồng biến

trên khoảng

 

1; 

.

Đáp án: B

Extra Techniques:

Casio:

Cơ sở: Dựa vào đáp án ta có thể dễ

dàng loại trừ các phương án sai.

Nhập vào màn hình như sau:

+) Đạo hàm tại

2

3

x 

Vì

2

'0

3

y









Nên hàm số:

 

3

ln 2

2

yx

x

  



không thể đồng biến trên các khoảng

 

;1

hoặc

1

;1

2







hoặc

1

;

2



 





.

Loại A, C, D.

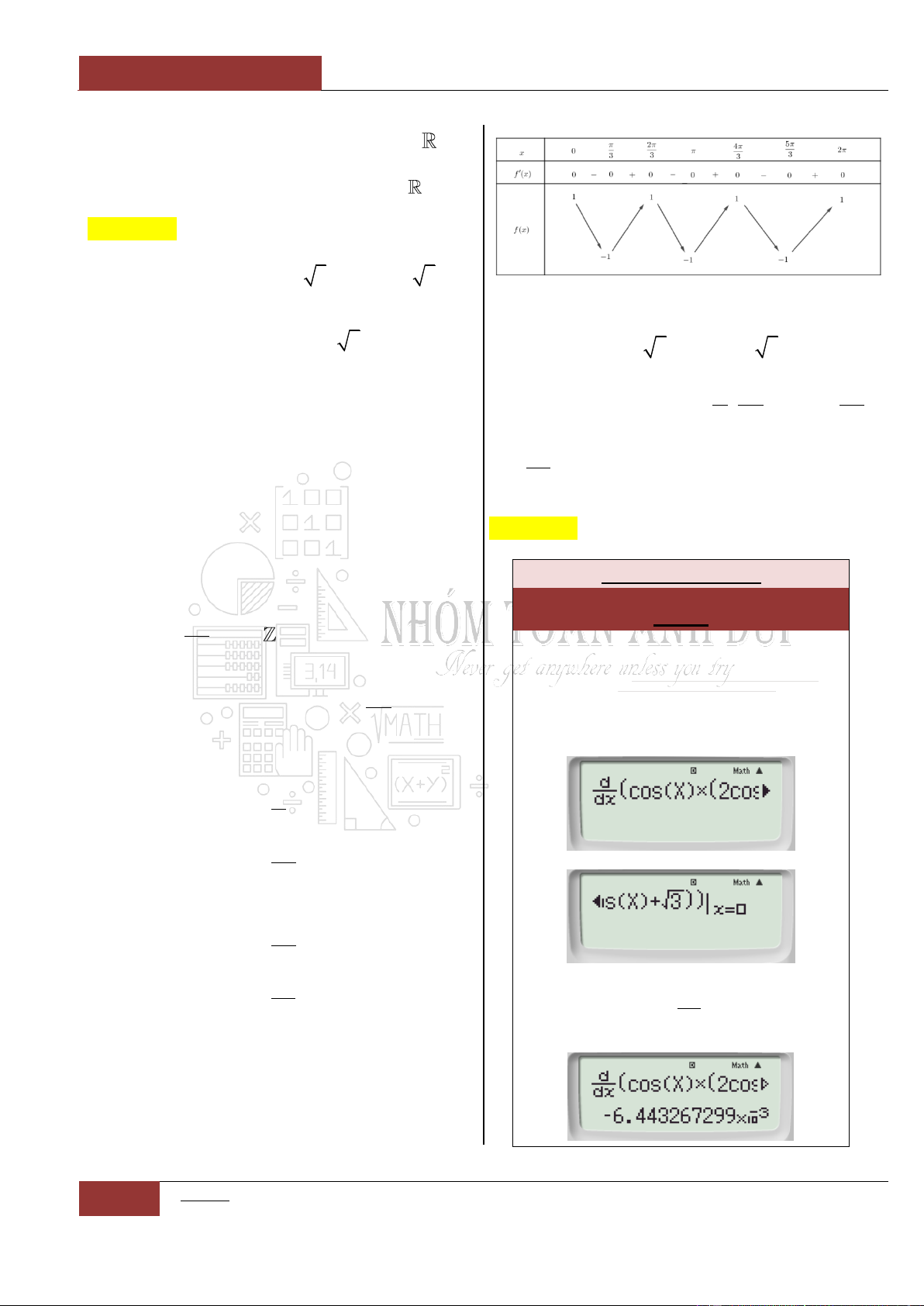
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

57

[ I can't, I can! ]

Câu 28. Ta có:

2

' 2021 0,y x x     

.

Khi đó hàm số đã cho nghịch biến trên .

Đáp án: C

Câu 29. Vì:

  

cos 2cos 3 2cos 3x x x

 

2

3

cos 2cos 3

cos 4cos 3

4cos 3cos

cos3

xx

x

yx















Suy ra:

' 3sin3 0yx  

sin3 0 3x x k



   

,

3

k

xk



   

.

Xét trong đoạn

 

0;2



, ta có:

02

3

k





.

Hay:

0

3

2

3

06

4

3

5

3

2

x

kx

x

















   















.

Bảng biến thiên:

Vậy trên đoạn

 

0;2



, đồ thị hàm số

  

cos 2cos 3 2cos 3y x x x  

đồng biến

trên các khoảng rời nhau:

2

;

33









và

4

;

3









và

5

;2

3









.

Đáp án: A

Extra Techniques:

Casio:

Cơ sở: Dựa vào đáp án ta có thể dễ

dàng loại trừ các phương án sai.

Nhập vào màn hình như sau:

+) Đạo hàm tại

3

4

x





.

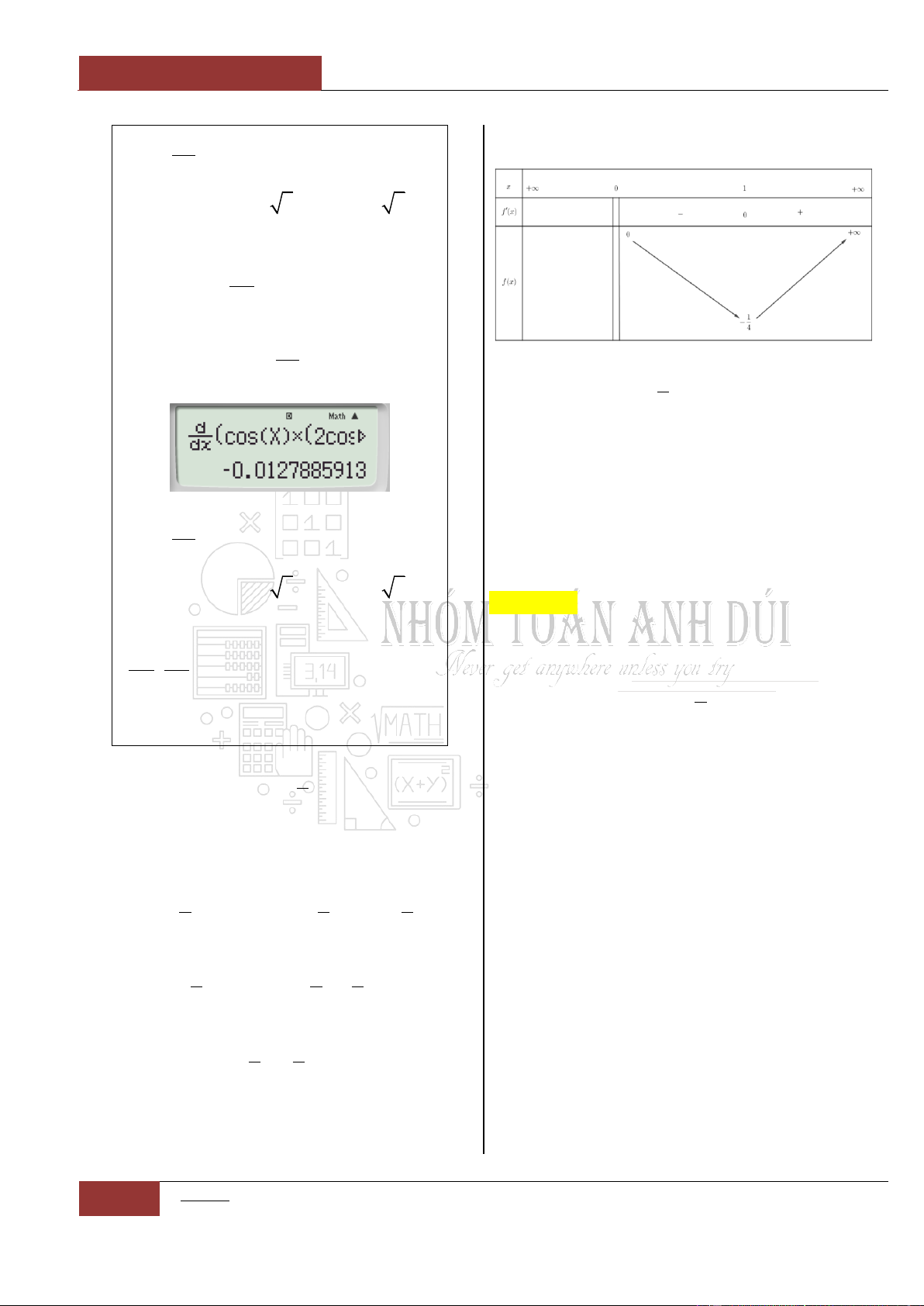
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

58

[ I can't, I can! ]

Vì

3

'0

4

y











. Nên hàm số:

  

cos 2cos 3 2cos 3y x x x  

không thể đồng biến trên các khoảng

 

0;



hoặc

2

;

3









.

+) Đạo hàm tại

3

2

x





.

Vì

3

'0

2

y











. Nên hàm số:

  

cos 2cos 3 2cos 3y x x x  

không thể đồng biến trên khoảng

45

;

33









.

Loại A, B, C.

Câu 30. Xét hàm số:

 

2

1

2ln 1

4

y x x

.

TXĐ:

 

0;D  

.

Ta có:

 

2 2 2

1 1 1

2ln 1 ln

4 2 4

y x x x x x   

.

Suy ra:

2

1 1 1

' 2 ln .

22

y x x x x

x



  





11

' ln ln 0

22

00

ln 0 1

y x x x x x x

xx

    













Bảng biến thiên:

Như thế hàm số

 

2

1

2ln 1

4

y x x

nghịch biến

trên khoảng

 

0;1

và đồng biến trên khoảng

 

1; 

.

Suy ra:

1

1 1 0

1

a

S b a

b





     







Đáp án: A

Câu 31. Ta xét hàm số:

   

4 3 2

1

2 1 5

4

g x f x x x x     

Ta có:

   

32

' 2 ' 1 3 2g x f x x x x     

   

 

       

32

3

' 2 ' 1 3 3 1 1

' 2 ' 1 1 1

g x f x x x x x

g x f x x x

          

       

       

Đặt:

1tx

. Khi đó

 

'gx

tương đương với:

   

3

2'h t f t t t   

Ta xét điều kiện lỏng để

 

'0gx

.

(Điều kiện lỏng:

 

3

2 ' 0

0

ft

ht

tt











  





)

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

59

[ I can't, I can! ]

 

3

21

'0

01

21

01

1

0

01

2 1 1 2 3

0 1 1 0 1

t

ft

t

tt

t

xx



   













   



 

  





























      







    



Vậy

 

'gx

nhận giá trị dương (hàm số

 

gx

đồng biến) trên khoảng

 

0;1

và

 

2;3

.

Một cách tương tự, ta xét điều kiện lỏng để

 

'0gx

.

(Điều kiện lỏng:

 

3

2 ' 0

0

ft

ht

tt











  





).

 

3

2

10

'0

10

1

0

10

1

t

ft

t

tt

t

  







  









  









  

















  















1 1 0 1 2

1 1 0

xx

     







  



Vậy

 

'gx

nhận giá trị âm (hàm số

 

gx

nghịch biến) trên khoảng

 

;0

và

 

1;2

.

Đáp án: C

Câu 32. Một số nhận xét rút ra từ giả thuyết để

bài:

Vì hàm số

 

y f x

liên tục và có đạo

hàm luôn không âm trên khoảng

 

2022;2022

nên

   

2022;2022 , ' 0x f x   

. (

1

)

Vì trên khoảng

 

2022;2022

, hàm số

 

y f x

, có duy nhất một đoạn con

K

nào đó

có độ lớn bằng

2021

mà trên đoạn đó đồ thị

hàm số là một đường thẳng song song với trục

hoành nên trên đoạn con

K

,

 

0f x m

. (

2

)

Vì (

2

), nên trên khoảng con

K

có độ lớn

là

2021

, ta luôn có:

 

'0fx

. (

3

)

Note: Hàm số

 

0y f x

là một đường

thẳng "trùng" với trục hoành (Trục

Ox

).

Xét từng đáp án:

 Đáp án A: Do (

3

) nên ta không thể kết

luận được rằng hàm số

 

y f x

đồng

biến trên khoảng

 

2022;2022

.

Loại A.

Note: Theo lý thuyết đồng biến, nghịch biến,

dấu

""

chỉ xảy ra tại hữu hạn điểm.

 Đáp án B: Do (

1

) nên:

   

12

f x f x

với mọi

12

2022 2022xx   

. Dấu

""

chỉ xảy ra ở một đoạn con

K

nào

đó có độ lớn là

2021

. Vì thế:

   

2021 2021ff

Loại B.

Note: Khoảng

K

chứa

2021x 

thì không

thể chứa

2021x 

và ngược lại.

 Đáp án C: Do

 

3

, nên biểu thức:

   

' 2020 ' 2021 0ff

hoàn toàn có thể xảy

ra. Chẳng hạn, ta xét trên khoảng

 

1;2021K 

.

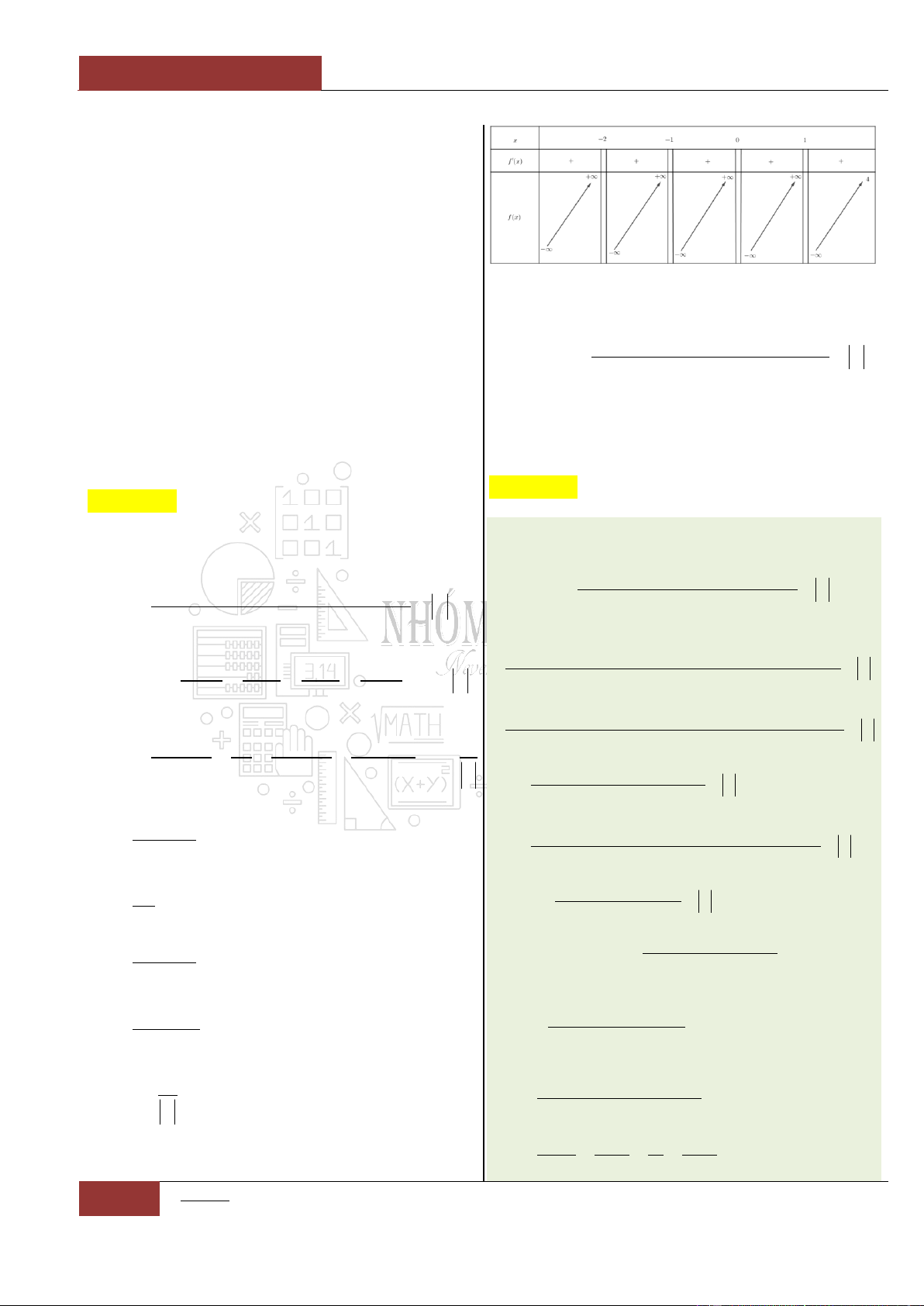
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

60

[ I can't, I can! ]

Theo

 

3

, ta có:

   

' 2020 ' 2021 0ff

.

Chọn C.

 Đáp án D: Do

 

2

nên trên

K

, ta luôn

có

 

0fx

. Và ở "các khoảng bù với

khoảng

K

trong

 

2022;2022

", hàm

số

 

y f x

đồng biến nên nếu có giao

điểm với trục hoành (

 

0fx

) thì số

giao điểm, nếu có, tối đa là

1

.

Loại D.

Đáp án: C

Câu 33. Xét hàm số:

5 4 3 2

4 3 2

6 3 12 6 2

22

x x x x x

yx

x x x x

    



  

Ta có:

2 1 1

1 1 2

x x x x

y x x

x x x x

  

     

  

     

2 2 2 2

1 1 1 1

'1

1 1 2

x

y

x

x x x

      

  

Vì:

 

2

1

0

1

0

1

0 ' 0

1

0

2

10

x

y

x

















  





















.

Bảng biến thiên:

Dựa vào đồ thị bảng biến thiên, ta thấy rằng:

Hàm số

5 4 3 2

4 3 2

6 3 12 6 2

22

x x x x x

yx

x x x x

    



  

đồng biến trên các khoảng rời nhau

 

;2 

và

 

2; 1

và

 

1;0

và

 

0;1

và

 

1; 

.

Đáp án: D

Note: Kĩ thuật tách phân thức hữu tỉ (thực sự)

Ta có:

5 4 3 2

4 3 2

6 3 12 6 2

22

x x x x x

yx

x x x x

    



  

 

5 4 3 2 4 3 2

4 3 2

4 3 2 4 3 2

4 3 2

4 3 2 3 2

4 3 2

32

4 3 2

2 2 4 4 10 6 2

22

2 2 4 4 10 6 2

22

4 4 10 6 2

22

4 2 2 4 6 2 2

22

4 6 2 2

4

22

x x x x x x x x

x

x x x x

x x x x x x x x x

x

x x x x

xx

x x x x

x x x x x x x

xx

x x x x

x x x

xx

x x x x

       



  

       



  

   

  

  

      

  

  

   

  

Ta tách biểu thức:

32

4 3 2

4 6 2 2

22

x x x

x x x x

  

Ta có:

32

4 3 2

4 6 2 2

22

x x x

x x x x

  

    

32

4 6 2 2

2 1 1

x x x

x x x x

A B C D

x x x x

  



  

   

  

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

61

[ I can't, I can! ]

       

    

      

    

   

    

 

    

32

1 1 2 1 ...

2 1 1

... 2 1 1 2 1

2 1 1

2 3 ...

2 1 1

... 2 2 2

2 1 1

A x x x B x x x

x x x x

C x x x D x x x

x x x x

A B C D x B C D x

x x x x

A B C D x C

x x x x

     



  

      

  

      



  

     

  

Đồng nhất hệ số của

32

,,x x x

và hệ số tự do,

được hệ bốn phương trình:

41

2 3 6 1

2 2 2 1

2 2 1

A B C D A

B C D B

A B C D C

CD

    





   







      



   



32

4 3 2

4 6 2 2 1 1 1 1

2 1 1

22

x x x

x x x x

  

    

  

  

.

Suy ra:

1 1 1 1

4

1 1 2

y x x

x x x x

      

  

1 1 1 1

1 1 2

2 1 1

1 1 2

xx

x x x x

xx

x x x x

       

         

       

  

       

  

     

  

Vậy:

2 1 1

1 1 2

x x x x

y x x

x x x x

  

     

  

.

Extra Techniques:

Tips:

Cho hàm số

 

y f x

có dạng phân thức

hữu tỉ

 

Px

fx

Gx



trong đó

 

Px

,

 

Qx

là hai đa thức với hệ số thực theo biến

x

và

 

Px

không chia hết cho

 

Qx

.

Hàm số

 

y f x

được gọi là hàm phân

thức hữu tỉ thực sự khi và chỉ khi:

   

deg degPQ

Nếu hàm số

 

y f x

chưa là hàm phân

thức hữu tỉ thực sự.

Phương pháp: Thực hiện lấy phép chia tử

thức cho mẫu thức để được:

 

   

P x R x

f x S x S x g x

Q x Q x

    

Khi đó: ta thu được một hàm

 

Sx

là một

đa thức và một phân thức hữu tỉ thực sự

 

gx

.

Phương pháp phân tách một phân thức

hữu tỉ thực sự thành tổng các phân thức

hữu tỉ thực sự khác đơn giản hơn.

Trường hợp 1: Phương trình

 

0Qx

có các nghiệm thực đơn.

Giả sử đa thức

 

Qx

có bậc

n

và có

n

nghiệm đơn. Khi đó:

    

 

1 1 2 2

...

nn

Q x a x b a x b a x b   

Nên hàm phân thức hữu tỉ

 

gx

bằng:

 

12

1 1 2 2

...

n

nn

Rx

A

AA

Q x a x b a x b a x b

   

  

Việc còn lại ta chỉ cần quy đồng và đồng

nhất hệ số ở tử như ở kĩ thuật tách phân

thức hữu tỉ (thực sự) như ở phần Note đã

trình bày ở trên.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

62

[ I can't, I can! ]

Trường hợp 2: Phương trình

 

0Qx

có

các nghiệm thực bội.

Giả sử đa thức

 

Qx

có bậc

n

và có các

nghiệm thực là

1 2 3

, , ,...,

k

a a a a

trong đó

1

xa

là một nghiệm bội

m

. Khi đó:

     

 

12

...

m

k

Q x x a x a x a   

Nên hàm phân thức hữu tỉ

 

gx

bằng:

 

   

12

2

1

11

1

12

23

...

m

k

Rx

A

AA

Q x x a

x a x a

B

BB

x a x a x a



   





   

  

Việc còn lại ta chỉ cần quy đồng và đồng

nhất hệ số ở tử như ở kĩ thuật tách phân

thức hữu tỉ (thực sự) như ở phần Note đã

trình bày ở trên.

Extra Techniques:

Casio:

Cơ sở: Dựa vào sự tăng giảm của hàm số,

ta có thể xác định trên một khoảng nào đó

hàm số tăng hay giảm bằng mode Table.

Ta vào mode Table và nhập biểu thức

 

fx

đề bài cho (như hình minh họa).

Chọn

 

:5

55

:

29

Start

End

Step



















Dựa vào kết quả hàm

 

fx

(Lưu ý những

điểm không xác định như điểm

2x 

,

1x 

,

0x 

,

1x 

). Ta thấy:

Trên đoạn

 

5; 2.241...

hàm số tăng từ

5.05

đến

5.2203...

.

Trên đoạn

 

1.896...; 1.206...

hàm số

tăng từ

7.471...

đến

6.4403...

.

Trên đoạn

 

0.862...; 0,172...

hàm số

tăng từ

4.155...

đến

8.5526...

.

Trên đoạn

 

0.1724...;0.862...

hàm số tăng

từ

1.904...

đến

9.2035...

.

Trên đoạn

 

1.2068...;5

hàm số tăng từ

2.426...

đến

3.2404...

.

Ta để ý rằng hàm số đồng biến trên các

khoảng rời nhau, và điểm phân cách các

khoảng con đó chính là những điểm mà tại

đó không xác định:

2x 

,

1x 

,

0x 

,

1x 

.

Vậy hàm số:

5 4 3 2

4 3 2

6 3 12 6 2

22

x x x x x

x

y

x x x

    



 



đồng biến trên các khoảng rời nhau

 

;2 

và

 

2; 1

và

 

1;0

và

 

0;1

và

 

1; 

.

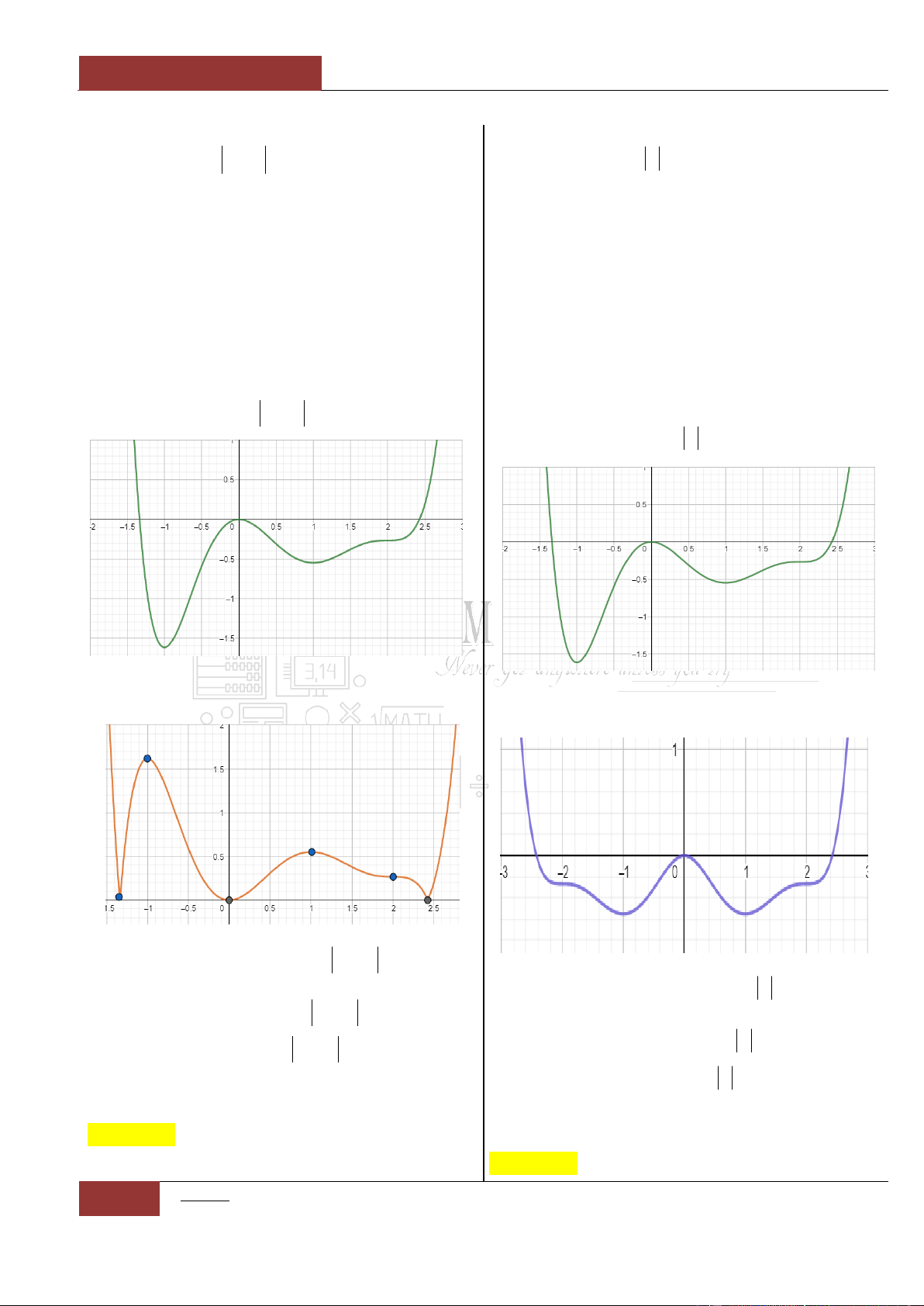
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

63

[ I can't, I can! ]

Câu 34. Vì

 

   

,0

f x f x

y f x

f x f x

















.

Nên phần hàm số nằm từ trục hoành (Trục

Ox

)

(kể cả trục hoành) đi lên theo chiều của tia

Oy

,

được giữ không đổi. Còn phần hàm số nằm từ

trục hoành đi xuống theo chiều của tia đối tia

Oy

được lấy đối xứng qua trục

Ox

.

Theo lý thuyết được trình bày ở trên, ta có thể

phác họa đồ thị hàm

 

fx

như hình bên dưới:

Đồ thị hàm số

 

y f x

.

Đồ thị hàm số

 

y f x

.

Dựa vào đồ thị hàm số

 

y f x

, dễ dàng

nhận ra rằng hàm số

 

y f x

đồng biến trên

khoảng

 

0;1

.

Đáp án: B

Câu 35. Vì

 

,0

f x x

y f x

f x x

















.

Nên phần hàm số nằm từ trục tung (Trục

Oy

)

(kể cả trục tung) đi qua theo chiều của tia

Ox

,

được giữ không đổi. Còn phần hàm số nằm từ

trục tung đi qua theo chiều của tia đối tia

Ox

được thay bằng phần đối xứng của đồ thị nằm

bên phải trục tung (Trục

Oy

).

Theo lý thuyết được trình bày ở trên, ta có thể

phác họa đồ thị hàm

 

fx

như hình bên dưới:

Đồ thị hàm số

 

y f x

.

Đồ thị hàm số

 

y f x

.

Dựa vào đồ thị hàm số

 

y f x

, dễ dàng

nhận ra rằng hàm số

 

y f x

đồng biến trên

khoảng

 

1;0

.

Đáp án: A

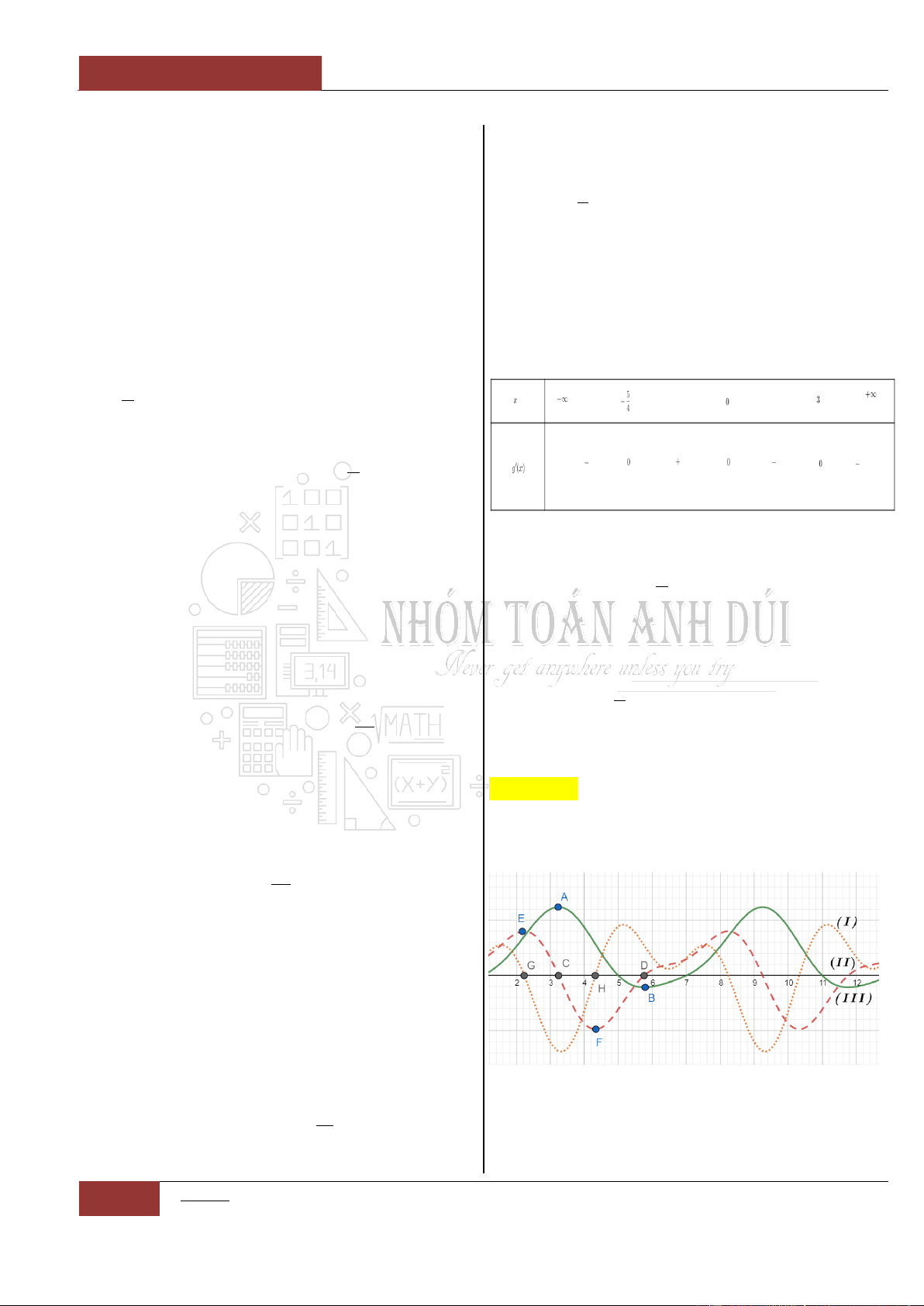
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

64

[ I can't, I can! ]

Câu 36. Xét hàm số:

 

4 3 2

'y f x mx nx px qx r     

Ta có:

   

32

'' 4 3 2 1y f x mx nx px q    

Vì đồ thị hàm

 

''fx

cắt trục hoành tại ba điểm

phân biệt (Phương trình

 

'' 0fx

có ba

nghiệm thực phân biệt) lần lượt là:

1x 

,

5

4

x 

,

3x 

.

Khi đó:

     

5

'' 4 1 3

4

f x m x x x



   





     

 

   

32

'' 1 4 5 3

'' 4 13 2 15

'' 4 13 2 15 2

f x m x x x

f x mx mx mx m

    

    

Đồng nhất hệ số giữa

 

1

và

 

2

, ta có:

13

44

3

3 13

22

15

mm

nm

pm

qm















  















Suy ra:

 

4 3 2

13

' 15

3

f x mx mx mx mx r    

.

Dễ thấy:

0m 

. Do hàm số

 

''fx

có hệ số

40am

(Đồ thị hàm số

 

''y f x

có xu

hướng đi xuống khi

x

đủ lớn).

Xét hàm số:

   

y g x f x rx  

Ta có:

 

4 3 2

13

' ' 15

3

y f x r mx mx mx mx     

Khi đó:

4 3 2

' 0 3 13 3 45 0y x x x x     

1

2

3,4

5

3

0

3

x

















(Nghiệm

3x 

là nghiệm kép).

Bảng biến thiên:

Dựa vào bảng biến thiên được vẽ ở trên, ta nhận

thấy trên khoảng

5

;0

4









, đồ thị hàm số

   

y g x f x rx  

đồng biến.

Khi đó:

5

0

4

0

a

S ab

b







  









.

Đáp án: D

Câu 37. Ta kí hiệu một số điểm đặc biệt lên đồ

thị hàm số như hình vẽ.

Dễ thấy trên cung

AB

của đồ thị

 

III

, hàm số

giảm và đồng thời hàm số

 

II

nhận giá trị âm

trên cung

CD

.

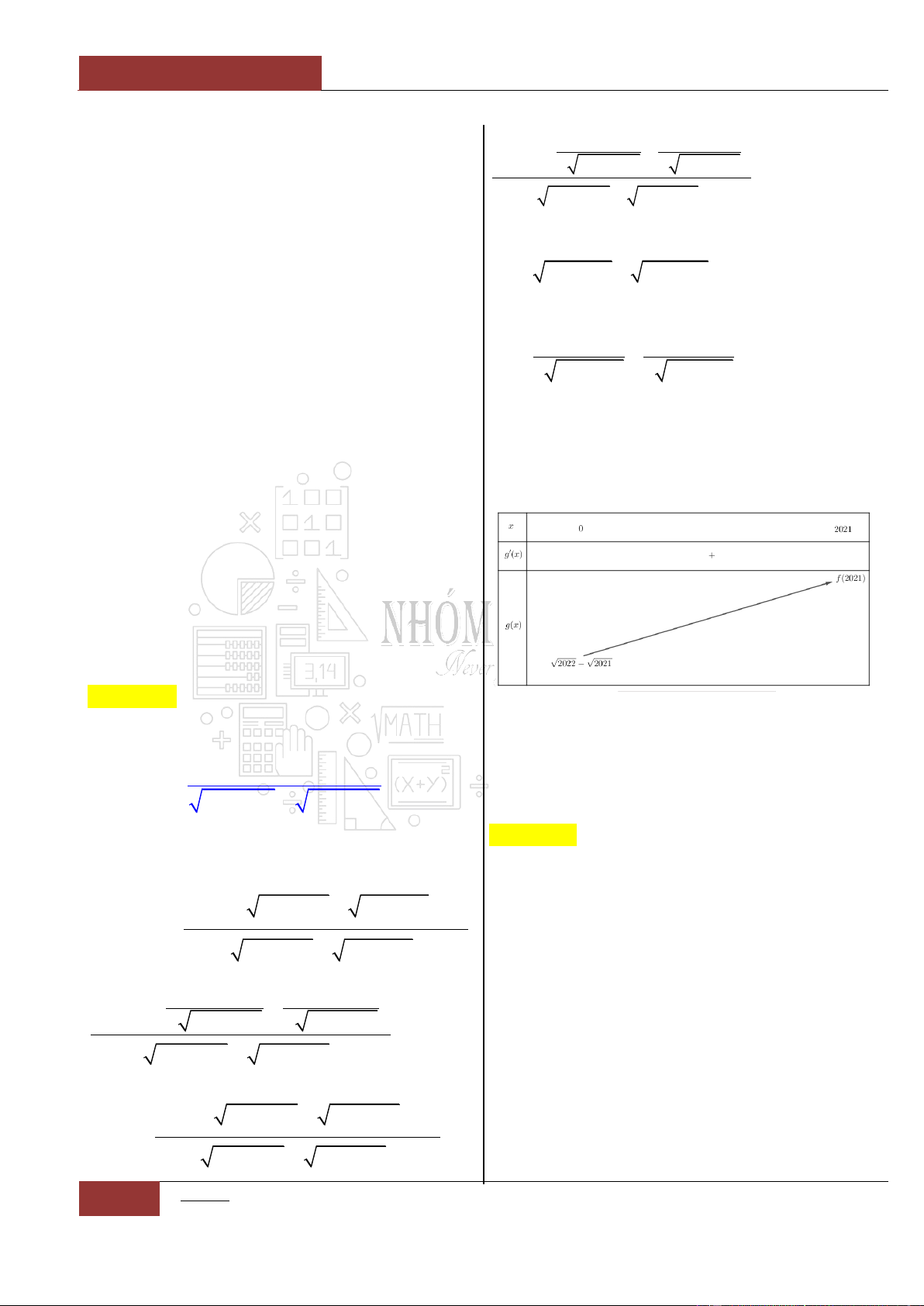
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

65

[ I can't, I can! ]

Như vậy hàm số

 

II

là đồ thị đạo hàm của

hàm số

 

III

.

Mặt khác: Trên cung

EF

của đồ thị

 

II

, hàm

số giảm và đồng thời hàm số

 

I

nhận giá trị

âm trên cung

GH

.

Như vậy hàm số

 

I

là đồ thị đạo hàm của hàm

số

 

II

.

Khi đó: Hàm số

 

II

là đồ thị đạo hàm của hàm

số

 

III

và hàm số

 

I

lại là đồ thị đạo hàm

của hàm số

 

II

.

Vậy hàm số

 

fx

là đồ thị hàm số

 

III

, hàm

số

 

'fx

là đồ thị hàm số

 

II

và hàm số

 

''fx

là đồ thị hàm số

 

I

.

Đáp án: D

Câu 38. Xét hàm số:

 

2022 2021

fx

y g x

xx



  

.

TXĐ:

 

0;2021D 

.

Ta có:

 

2

' . 2022 2021 ...

'

2022 2021

f x x x

y

xx

   



  

 

2

11

... .

2 2022 2 2021

2022 2021

fx

xx













  

 

2

' 2022 2021 ...

'

2022 2021

f x x x

y

xx

   



  

 

 

2

11

... .

2 2022 2 2021

0, 0;2021

2022 2021

fx

xx

x

xx











  

  

Vì:

 

 

 

 

' 0, 0;2021

2022 2021 0, 0;2021

0, 0;2021

11

0, 0;2021

2 2022 2 2021

f x x

x x x

f x x

x

xx



  



     





  



   







Khi đó:

 

 

' ' 0, 0;2021y g x x   

.

Bảng biến thiên hàm

 

y g x

.

Dựa vào bảng biến thiên của đồ thị hàm số

 

y g x

ta thấy hàm số đồng biến trên một

khoảng duy nhất là

 

0;2021

.

Đáp án: B

Câu 39. Xét hàm số:

   

 

 

2

1 . 6 12 , 2;4y g x f x x x x      

.

Ta có:

   

 

   

2

' ' 1 . 6 12 1 . 2 6g x f x x x f x x      

Xét trên đoạn

 

2;4

, ta có:

+) Trường hợp 1:

 

2;3x

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

66

[ I can't, I can! ]

Khi đó:

 

2

10

1 1 2

2 6 0

' 1 0

6 12 0

fx

x

fx

xx





  







  







  





  



Suy ra:

 

 

' 0, 2;3g x x  

.

Vì thế hàm số

 

y g x

đồng biến trên khoảng

 

2;3

.

+) Trường hợp 2:





3;4x

.

Khi đó:

 

2

10

2 1 3

2 6 0

' 1 0

6 12 0

fx

x

fx

xx





  







  







  





  



Suy ra:

  



' 0, 3;4g x x  

.

Vì thế hàm số

 

y g x

nghịch biến trên

khoảng

 

3;4

.

Đáp án: D

Note: Hàm số

 

y f x

liên tục trên

 

1;3

, nên

hàm số

 

1y f x

liên tục trên

 

2;4

. Vì vậy

hàm số

   

 

2

1 6 12g x f x x x   

liên tục

trên đoạn

 

2;4

.

Câu 40. Xét hàm:

 

2

cos

4

y f x x m



   

.

Ta có:

 

' ' siny f x x





.

Dễ thấy: trên đoạn

   

2;3 1;4

, ta có:

   

 

' 0 ' 0

' 0, 2;3

2 3 sin 0

f x f x

yx

xx

  





    



  



.

Như vậy, mệnh đề trên hoàn toàn đúng do

   

' 0, 2;3y f x x   

.

Đáp án: C

Note: Ta loại đáp án D bởi vì đồ thị hàm số

 

2

cos

4

y f x x m



   

mang giá trị dương

hay âm trên khoảng

 

2;3

vẫn bị phụ thuộc bởi

tham số

m

.

Câu 41. Xét hàm:

2

7

' 2 3 12 9

2

f x x x



    





.

Ta có:

2

7

' 2 0 3 12 9 0

2

f x x x



      





Suy ra:

7

' 2 0 1 3

2

f x x



     





.

Đặt:

7 7 2

2

24

t

t x x



    

.

Khi đó ta có:

 

72

' 0 1 3

4

t

ft



   

Suy ra:

 

53

'0

22

f t t    

.

Vậy hàm số:

 

y f x

nghịch biến trên khoảng

53

;

22









.

Đáp án: C

Câu 42.

Ta có:

     

' 2 1 2021 2 2 3 .f x x x g x   

Đặt:

1

21

2

t

t x x



   

.

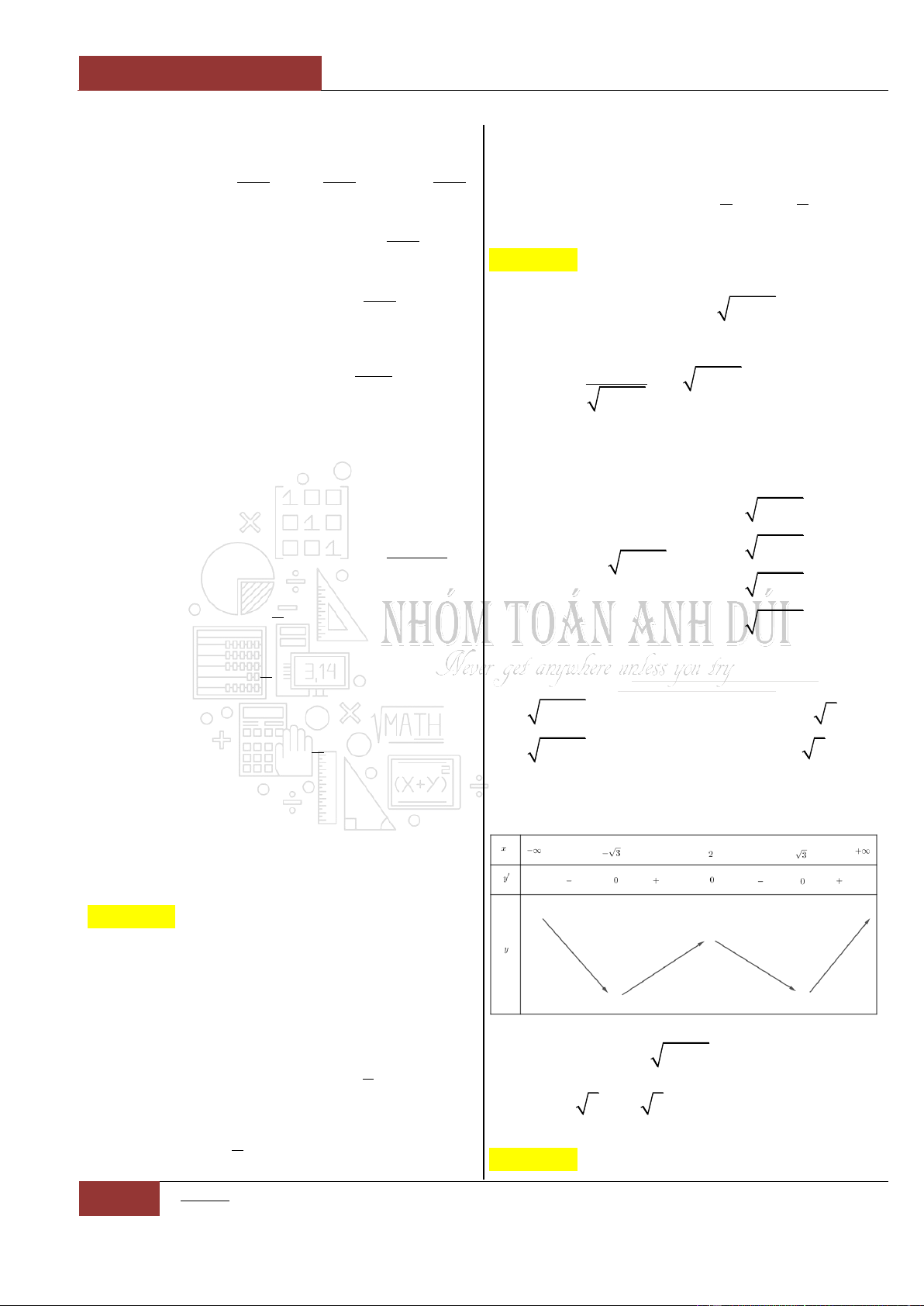
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

67

[ I can't, I can! ]

Hàm số đã cho trở thành:

 

1 1 1

' 2021 2. . 2. 3 .

2 2 2

t t t

f t g

  



     

  

     



     



    

1

' 2021 1 1 3

2

1

' 2021 1 2

2

t

f t t t g

t

f t t t g





     









    





Suy ra:

    

1

' 1 2 2021

2

x

f x x x g





   





.

Ta xét hàm số:

 

1 2021 2022y f x x   

.

Ta có:

 

' ' 1 2021y f x   

   

 

11

' 1 1 1 2

2

'3

2

'3

2

x

y x x g

x

y x x g

x

y x x g





      

   



   





    







   





Cho

 

' 0 3 0

2

x

y x x g



    





Suy ra:

 

3 0 0 3x x x    

.

Vậy hàm số đồng biến trên khoảng

 

0;3

.

Đáp án: B

Câu 43. Xét hàm số:

 

25y f x

.

Ta có:

 

' 2 ' 2 5y f x

Cho

 

1

' 0 ' 2 5 0 2 5 3

3

y f x x        

Suy ra:

7

' 0 4

3

yx   

.

Hàm số

 

25y f x

đồng biến trên

 

;mn

.

Suy ra:

min min max

75

4

33

S m n     

.

Đáp án: A

Câu 44. Xét hàm số





2

1y f x

Ta có:





2

' . ' 1 0

1

x

y f x

x

  



Khi đó:





2

0

11

0

' 0 1 0

' 1 0

11

12

x

yx

fx

x







  









    

















22

2

0

1 1 1 1 3

14

3

12

x

x x x

x











        















.

Bảng biến thiên:

Vậy hàm số





2

1y f x

đồng biến trên các

khoảng

   

3;0 , 3; 

.

Đáp án: C

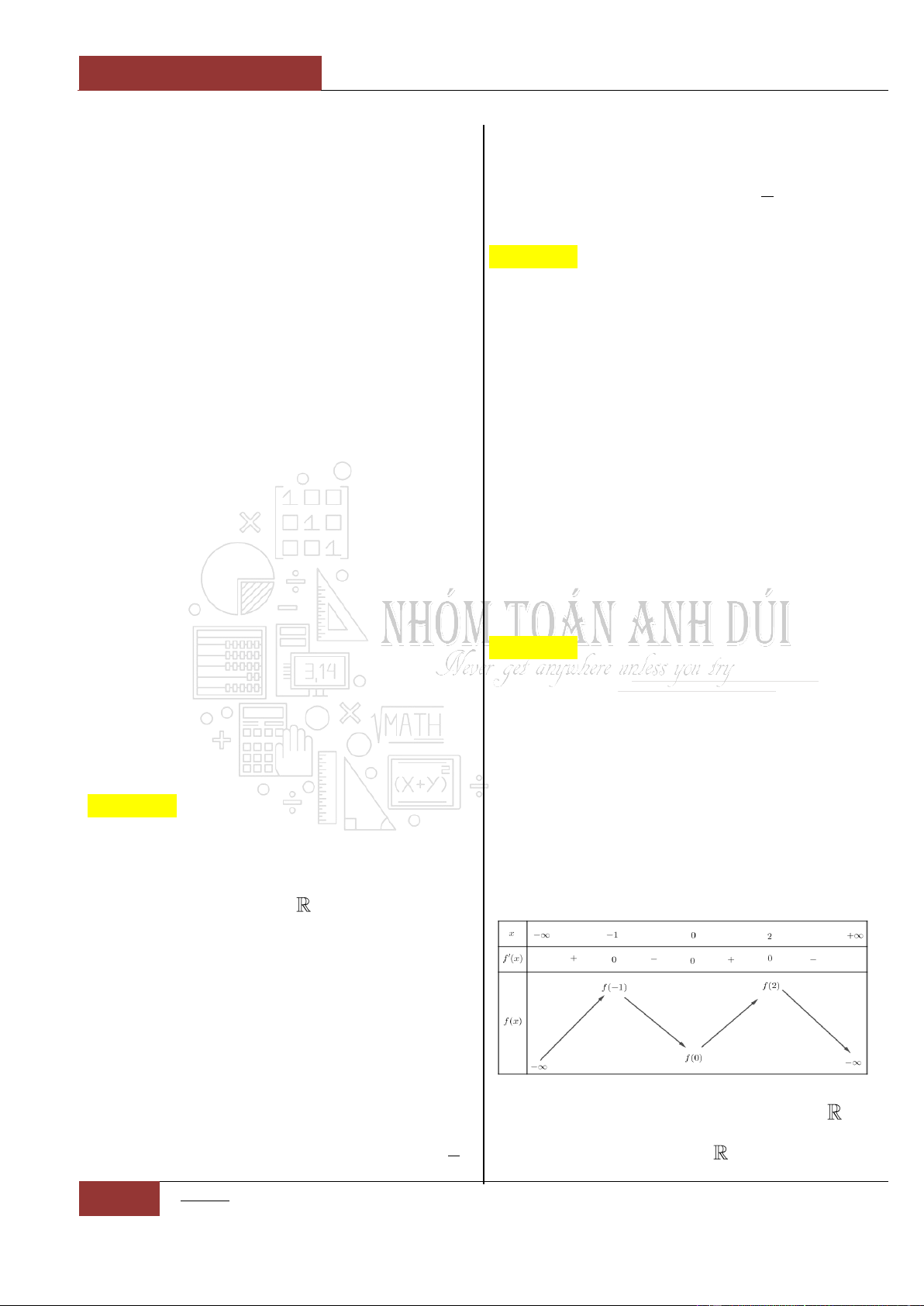
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

68

[ I can't, I can! ]

Câu 45. Xét hàm số

 

y g x

.

Ta có:

     

' ' 1 ' 2 6 2g x f x f x x     

.

Điều kiện lỏng:

 

     

' 1 0

' 2 0 * ' 0

6 2 0

fx

f x g x

x







    









.

Khi đó:

 

*

tương đương với:

 

' 1 0

' 2 0

3

fx

x

















1 1 0

1 2 3

2 2 1 1 4 1 3

33

xx

x x x

xx

    







    





          











.

Mà

 

 

1;2 1;3

.

Vậy hàm số

 

y g x

đồng biến trên khoảng

 

1;2

.

Đáp án: C

Câu 46. Ta có:

     

2

' 6 2 1 . ' 2 1g x f x f x  

Vì:

 

2

6 2 1 0,f x x   

.

Nên:

     

2

' 0 6 2 1 ' 2 1 0g x f x f x    

Suy ra:

   

' 0 ' 2 1 0g x f x   

.

Dựa vào đồ thị hàm số

 

'y f x

, ta thấy rằng:

 

1

2 1 1

' 2 1 0

1

1 2 1 0

0

2

x

fx

x











   



   





Vậy hàm số

   

3

21y g x f x  





nghịch

biến trên hai khoảng rời nhau

 

1

0; , 1;

2









.

Đáp án: C

Câu 47. Xét hàm số

   

2021

1g x f x





.

Ta có:

     

2020

' 2021 1 . ' 1g x f x f x   





.

Khi đó:

 

'0gx

     

2020

2021 1 . ' 1 0 ' 1 0f x f x f x       





Dựa vào đồ thị hàm số

 

'y f x

ta có:

 

' 1 0 1 2 3f x x x       

.

Vậy hàm số đồng biến trên khoảng

 

3;

.

Đáp án: D

Câu 48. Xét hàm số

 

2

3g x f x







.

Ta có:

 

   

22

' 4 3 . ' 3g x xf x f x  

.

Dựa vào đồ thị hàm số

 

'y f x

, ta mô phỏng

hình dạng đồ thị hàm số

 

y f x

dưới dạng

bảng biến thiên như hình vẽ:

Vì

   

1 2 0ff  

nên

 

0,f x x  

.

Suy ra:

 

2

3 0,f x x   

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

69

[ I can't, I can! ]

Hàm số

 

y g x

đồng biến khi và chỉ khi:

 

   

22

' 4 3 . ' 3 0g x xf x f x   

Hay:

 

2

' 3 0xf x 

.

 Trường hợp 1:

 

2

0

1

' 3 0

x

fx















.

 

2

32

1 3 0 2 3

1

32

5

x

xx

x



   





     





















Kết hợp với điều kiện

 

1

, được:

23

5

x













.

 Trường hợp 2:

 

2

0

2

' 3 0

x

fx















.

 

2

53

0 3 2

2 3 5

31

22

x



   





  

   



  





  





Kết hợp điều kiện

 

2

, được:

53

20

x



   



  





.

Vậy hàm số đã cho đồng biến trên các khoảng

       

5; 3 , 2;0 , 2; 3 , 5;   

.

Đáp án: C

Câu 49. Dựa vào đồ thị hàm số

3

'2

2

y f x









.

Ta có:

 

11

3

' 2 0 *

3

2

x

fx

x

  





  











Đặt:

3 2 3

2

24

t

t x x



   

.

Khi đó:

   

23

11

4

* ' 0

23

3

4

t

ft

t





  



  













17

22

15

2

t



  













Do đó hàm số

 

y f x

đồng biến trên các

khoảng

1 7 15

; , ;

2 2 2

   

 

   

   

.

Khi đó:

1

2

7

2 18

2

15

2

a

b S a b c

c







     











Đáp án: A

Câu 50. Dựa vào đồ thị hàm số

 

3

'1fx

.

Ta suy ra:

 

3

20

' 1 0

12

x

fx

x

  



  







.

Đặt:

3

11t x x t    

.

Suy ra:

 

3

2 1 0

'0

1 1 2

t

ft

t



   





  





8 1 0 7 1

1 1 8 2 9

tt

      







    



.

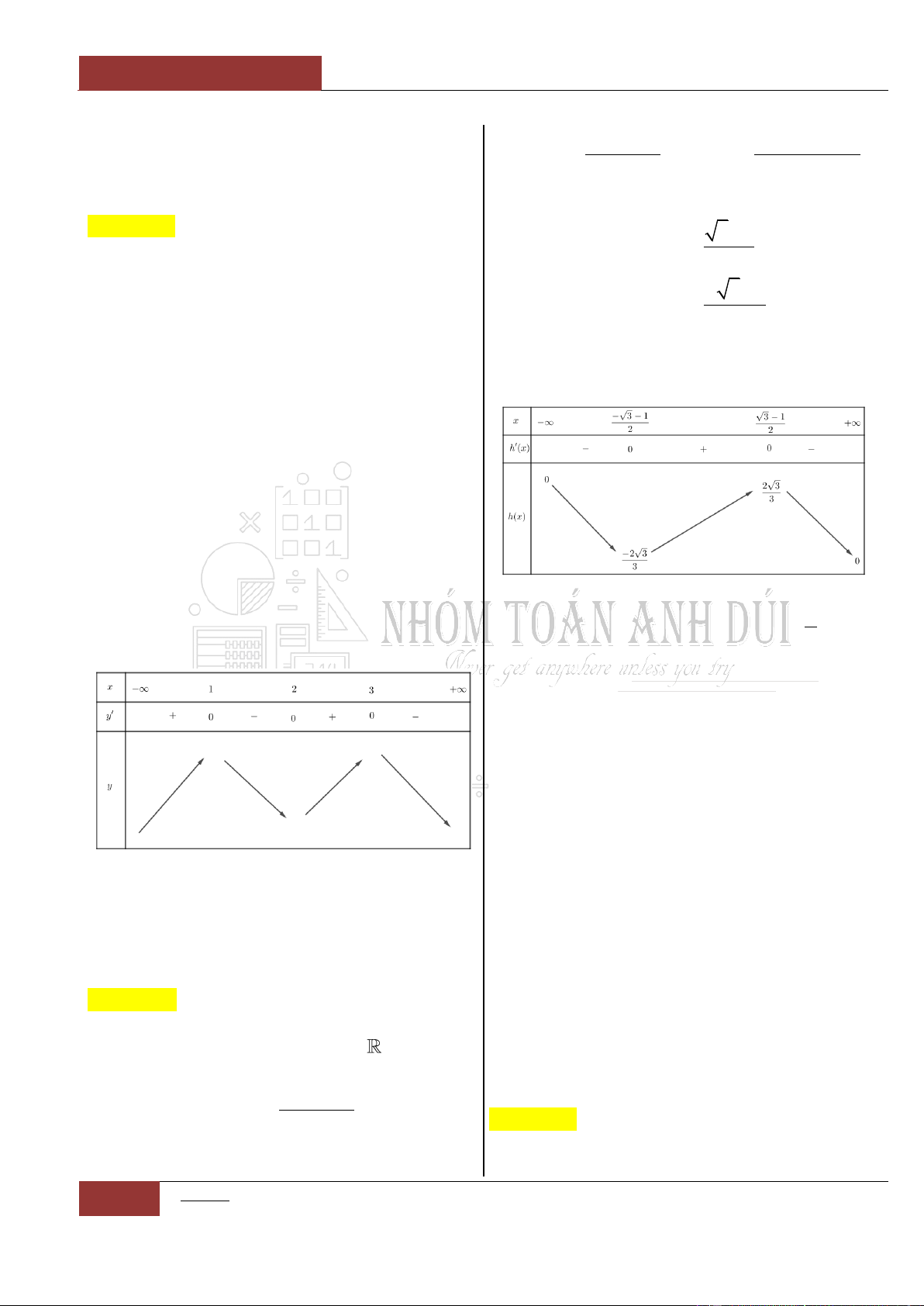
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

70

[ I can't, I can! ]

Vậy hàm số

 

y f x

nghịch biến trên các

khoảng

   

7;1 , 2;9

.

Đáp án: B

Câu 51. Xét hàm số

 

.

x

y e f x





.

Ta có:

   

' . . '

xx

y e f x e f x



  

   

 

   

' . ' 0

'0

'

x

y e f x f x

f x f x



   

  



Dựa vào đồ thị hàm số

 

y f x

và

 

'y f x

,

ta thấy

   

1

'2

3

x

f x f x x

x







  







.

Bảng biến thiên:

Dựa vào bảng biến thiên của đồ thị hàm số dễ

dàng thấy hàm số

 

x

y e f x





có hai khoảng

đồng biến là

 

;1

và

 

2;3

.

Đáp án: C

Câu 52. Tập xác định

 

gx

:

D 

.

Ta có:

   

2

21

''

1

x

g x f x

xx







.

Đặt

   

 

2

22

2

2 1 2 2 1

'

1

x x x

h x h x

xx

   

  



Khi đó:

 

31

2

'0

31

2

x

hx

x





















Bảng biến thiên của hàm số

 

y h x

như sau:

Ta có:

     

1

1 1; 0 1 1; 0

2

h h h h



      





.

Bảng biến thiên hàm số

 

y h x

.

Ta có:

   

1, 0;1h x x  

.

Khi đó:

   

1 0, 0;1h x x     

.

Mặt khác dựa vào bảng xét dấu của đồ thị đạo

hàm

 

'y f x

.

Ta có:

     

' 0, ; 1 0;1f x x     

.

Vì vậy trên khoảng

 

0;1

, ta có:

     

' ' 0g x f x h x  

.

Suy ra hàm số

 

y g x

nghịch biến trên

 

0;1

.

Đáp án: B

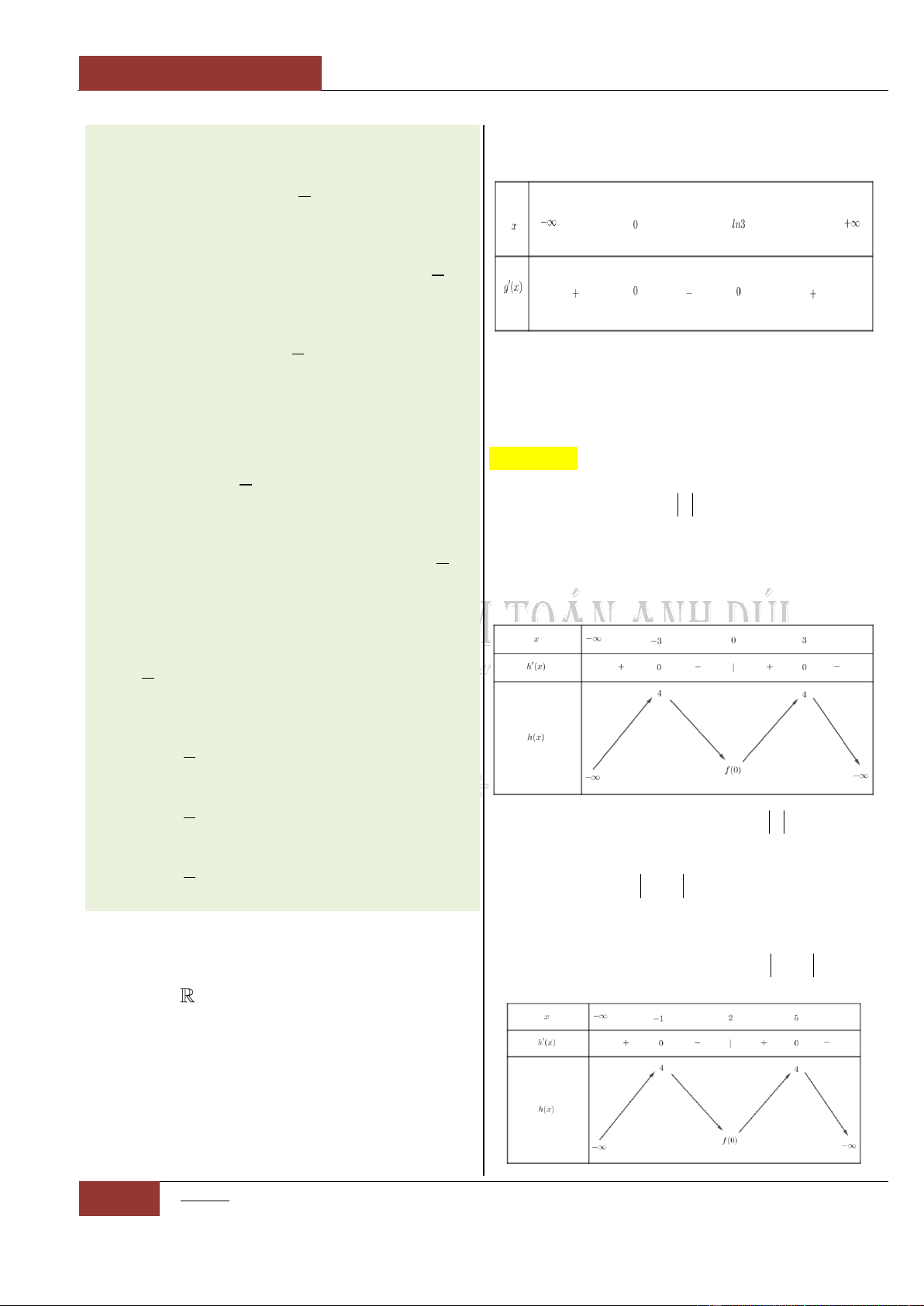
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

71

[ I can't, I can! ]

Note: Lý do loại các phương án A, C, D.

Ta xét trên khoảng

1

1;

2









.

Vì hàm số

 

y h x

đồng biến trên

1

1;

2









.

Nên

     

1

1 1 0

2

h h x h h x



       





Suy ra:

 

0hx

hay

 

0hx

.

Ta có:

   

1

1; 1;0 , ' 0

2

x f x



      





Vậy:

     

1

' ' 0, 1;

2

g x f x h x x



      





.

Do đó hàm số

 

y g x

đồng biến trên

1

1;

2









.

Mà

 

1

1; ;0

2

1

1; 1;

2

1

1; 1;0

2





   











    











   









nên ta loại A, C, D.

Câu 53. Đặt

 

2

x

g x f e

.

TXĐ:

D 

.

Ta có:

 

' ' 2

xx

g x e f e  

.

 

21

ln3

' 0 2 1

0

24

x

e

x

g x e

x

e



  







    













Bảng xét dấu đạo hàm của hàm số

 

y g x

:

Suy ra hàm số

 

y g x

nghịch biến trên các

khoảng

 

0;ln3

.

Đáp án: C

Câu 54. Do

 

h x f x

là hàm chẵn, đồ thị

hàm số

 

y h x

nhận trục tung làm trục đối

xứng nên từ bảng biến thiên của hàm số

 

y f x

suy ra bảng biến thiên của hàm số

 

h x f x

như sau:

Tịnh tiến đồ thị hàm số

 

h x f x

sang phải

(theo trục hoành)

2

đơn vị ta thu được đồ thị

hàm số

 

2g x f x

.

Khi đó ta dễ dàng phác họa được bảng biến

thiên của đồ thị hàm số

 

2g x f x

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

72

[ I can't, I can! ]

Dựa vào bảng biến thiên của đồ thị hàm số

 

2g x f x

ta thấy hàm số nghịch biến

trên

 

1;2

và

 

5;

.

Đáp án: C

Câu 55. Đặt

   

 

g x f f x

Suy ra:

   

 

   

 

.'

' ' .

f x f x

g x f f x

fx



.

Dễ thấy:

 

'gx

không xác định khi và chỉ khi

 

0fx

hay

0x 

.

Mặt khác:

 

'0

fx

gx

f f x















 

1

1 1 1

1

x

f x f x x

fx







      









.

Từ bảng biến thiên của

 

fx

ta có:

   

 

1 1 0;1 ,f x f x x      

.

Vì thế

 

' 0,f f x x  

.

Bảng xét dấu của hàm số đạo hàm

 

'gx

:

Suy ra hàm số đồng biến trên mỗi khoảng

   

; 1 , 0;1 

.

Đáp án: A

Câu 56. Xét hàm số:

   

2cos 1y g x f x  

.

Ta có:

   

' 2sin . ' 2cos 1g x x f x  

Cho

 

'0gx

.

Khi đó:

 

2sin . ' 2cos 1 0x f x  

Ta xét trên khoảng

 

0;



.

Vì

0 x





. Suy ra:

sin 0 sin 0xx   

.

Vì thế:

   

' 2cos 1 0 *fx

.

Từ bảng biến thiên của hàm số

 

'y f x

, ta

suy ra:

 

1

* 1 2cos 1 2 0 cos

2

xx      

.

Hay

32

x





.

Vậy hàm số đồng biến trên khoảng

;

32









.

Đáp án: C

Note: Sở dĩ ta xét trên đoạn

 

0;



vì ta dựa

vào khoảng nghiệm của bốn đáp án. Hay nói

cách khác là do:

 

0; 0;

6

; 0;

43

; 0;

32

; 0;

2



































 































.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

73

[ I can't, I can! ]

Câu 57. Xét hàm số

 

y g x

.

Ta có:

 

   

 

   

2 2 3 2

2 2 3

' 3 2 . ' 1 3 2

' 3 2 . ' 1 1

g x x x f x x x x

g x x x f x x

     



     



Dựa vào bảng biến thiên của hàm số

 

'fx

.

Suy ra:

 

' 1,f x x   

.

Nên

 

23

' 1 1 0,f x x x     

.

Khi đó:

 

2

' 0 3 2 0 0

3

g x x x x      

.

Đáp án: C

Câu 58. Xét hàm số

 

y xf x

.

Ta có:

   

''y f x xf x

.

Từ bảng biến thiên của hàm số

 

'y f x

.

Ta có:

 

0

'0

,3

x

fx

x a a









  



.

Bảng biến thiên của đồ thị hàm số

 

y f x

.

Dựa vào bảng biến thiên của hàm số

 

y f x

ta luôn có

 

0fx

và

 

'0fx

 

, 2;0x  

.

Vì thế:

 

0

, 2;0

'0

fx

x

xf x







  









.

Vậy hàm số

 

y xf x

đồng biến trên khoảng

 

2;0

.

Đáp án: B

Note: Sở dĩ ta không chọn các phương án A, C,

D là vì:

+) Trên khoảng

 

;0

ta không thể nào

kết luận dấu của

   

'0f x xf x

được vì

 

fx

và

 

'xf x

có thể âm hoặc dương trên

khoảng

 

;0

. Vì thế đáp án A sai.

+) Trên khoảng

 

0;2

, hàm số

 

y xf x

nghịch biến. Thật vậy!

 

0;2x

ta

luôn có:

 

   

0

'0

fx

f x xf x

xf x







  









.

Vì thế đáp án C sai.

+) Vì

   

0;2 2;2

nên đáp án D sai.

Câu 59.

Dựa vào bảng biến thiên của đồ thị hàm số.

Ta dễ dàng suy ra phương trình của cả ba hàm

số:

     

, ' , ''f x f x f x

.

 

32

2

11

33

' 2 1

'' 2 2

f x x x x

f x x x

f x x



    



   





  





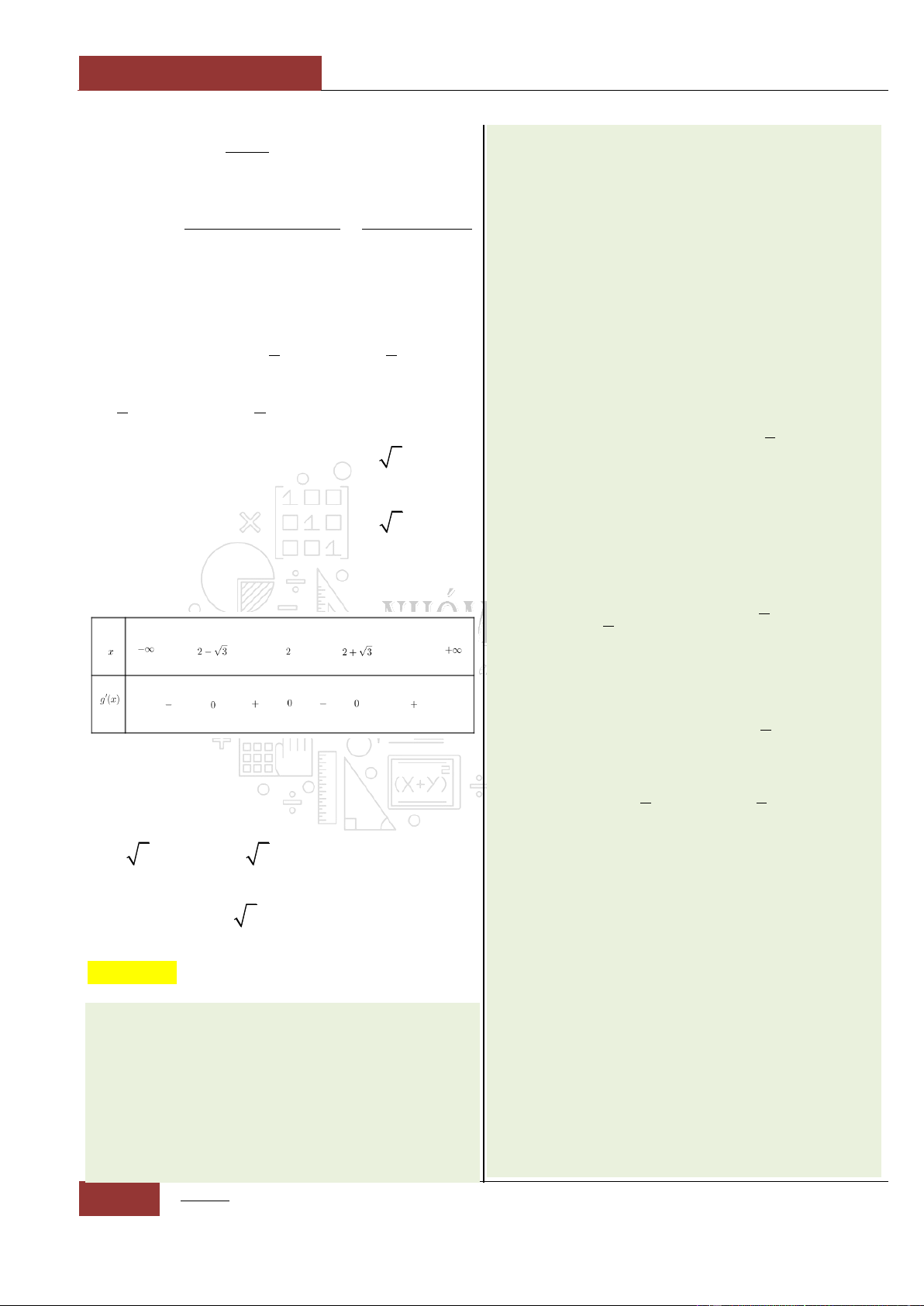
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

74

[ I can't, I can! ]

Xét hàm số:

 

x

fx

y

e



.

Ta có:

       

2

' . . '

'

xx

f x e f x e f x f x

y

ee





Khi đó:

     

' 0 ' 0g x f x f x   

 

2 3 2

32

11

2 1 0

33

12

2 3 0

33

23

6 9 2 0 2

23

x x x x x

x x x

x

x x x x

x



         





    







      







Bảng xét dấu hàm

 

'y g x

.

Dựa vào bảng xét dấu của hàm số

 

'y g x

.

Khi đó hàm số đồng biến trên khoảng

 

2 3;2

và

 

2 3; 

.

Vì

 

4; 2 3;   

.

Đáp án: C

Note: Vì hàm số

 

y f x

là hàm số bậc ba

nên hàm số

 

'y f x

là một hàm số bậc hai

(Parabol) và

 

''y f x

là một hàm số bậc nhất

(đường thẳng).

Cách 1:

Ta hoàn toàn có thể giả sử:

   

32

,0y f x ax bx cx d a     

.

Khi đó:

 

2

' 3 2y f x ax bx c   

.

Và

 

'' 6 2y x ax b

.

Từ giả thuyết ta có hệ:

 

1

0

3

' 0 1

*

' 1 0

'' 1 0

f























.

 

1

3

1

*

1

3 2 0

1

6 2 0

3

a

d

b

c

a b c

ab

d



























  











Suy ra:

 

32

2

11

33

' 2 1

'' 2 2

f x x x x

f x x x

f x x



    



   





  





.

Cách 2:

Gọi

   

2

' , 0f x ax bx c a   

.

Suy ra:

 

'' 2f x ax b

Từ giả thuyết ta có hệ

sau:

 

'' 1 0

' 1 0 **

' 0 1

f

















.

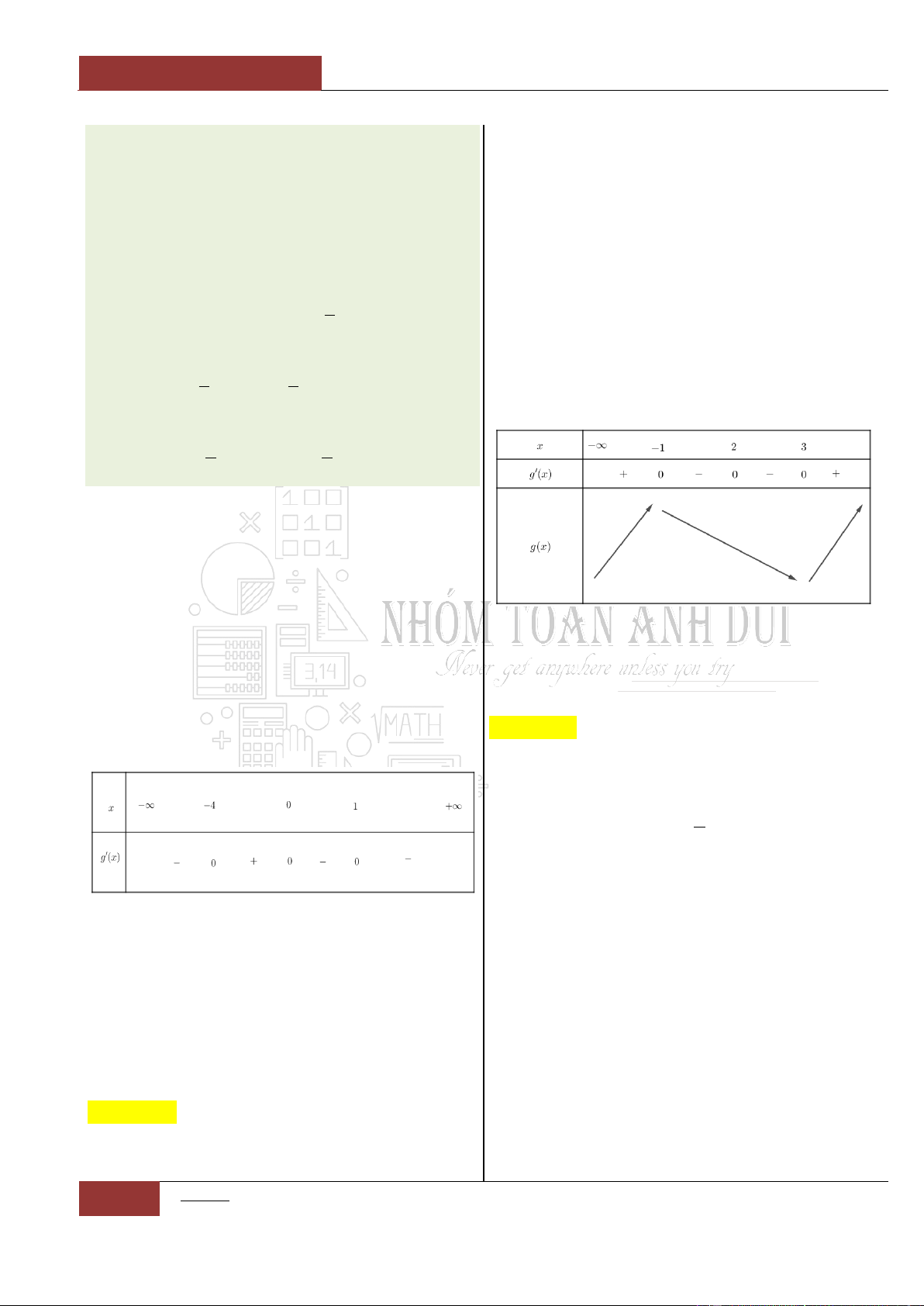
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

75

[ I can't, I can! ]

 

2 0 1

** 0 2

11

a b a

a b c b

cc

   





     





   



.

Vậy:

 

2

' 2 1f x x x   

.

Ta có:

   

32

1

'

3

f x f x dx x x x C     



.

Mà

 

11

0

33

fC    

.

Hay

 

32

11

33

f x x x x    

.

Câu 60. Xét hàm số

 

y g x

.

Ta có:

         

' 2 ' '' 2[ ' ''g x f x f x f x f x  

   

... . ''' ]f x f x

.

         

23

' 2 ''' 2 1 4g x f x f x x x x      

.

Bảng biến thiên của đồ thị hàm số

 

y g x

.

Dựa vào bảng biến thiên của đồ thị hàm số đạo

hàm

 

'y g x

ta có thể suy ra: Hàm số

 

y g x

đồng biến trên khoảng

 

4;0

. Thế

nên ta có:

4

0

a

S ab

b





  







.

Đáp án: C

Câu 61. Xét hàm số

 

y g x

.

Ta có:

     

2

' ' ' 3 2y g x f x x   

     

 

3 2 2

2

' 2 3 2 2 2 3y x x x x x x        

Ta có:

 

2

' 0 1

3

x

g x x

x







   







(

2x 

là nghiệm kép).

Bảng biến thiên hàm số

 

gx

.

Từ bảng biến thiên ta suy ra hàm số

 

y g x

nghịch biến trên khoảng

 

1;3

.

Đáp án: B

Câu 62. Xét hàm số

 

2 4 2

1

2 4 2021

2

g x f x x x    

Ta có:

 

23

' 2 . ' 2 2 8g x x f x x x   

.

Ta có:

 

'0gx

 

23

22

2 . ' 2 2 8 0

2 . ' 2 4 0

0

' 2 4 0 *

x f x x x

x f x x

x

f x x

    



    











   





Giải phương trình

 

*

.

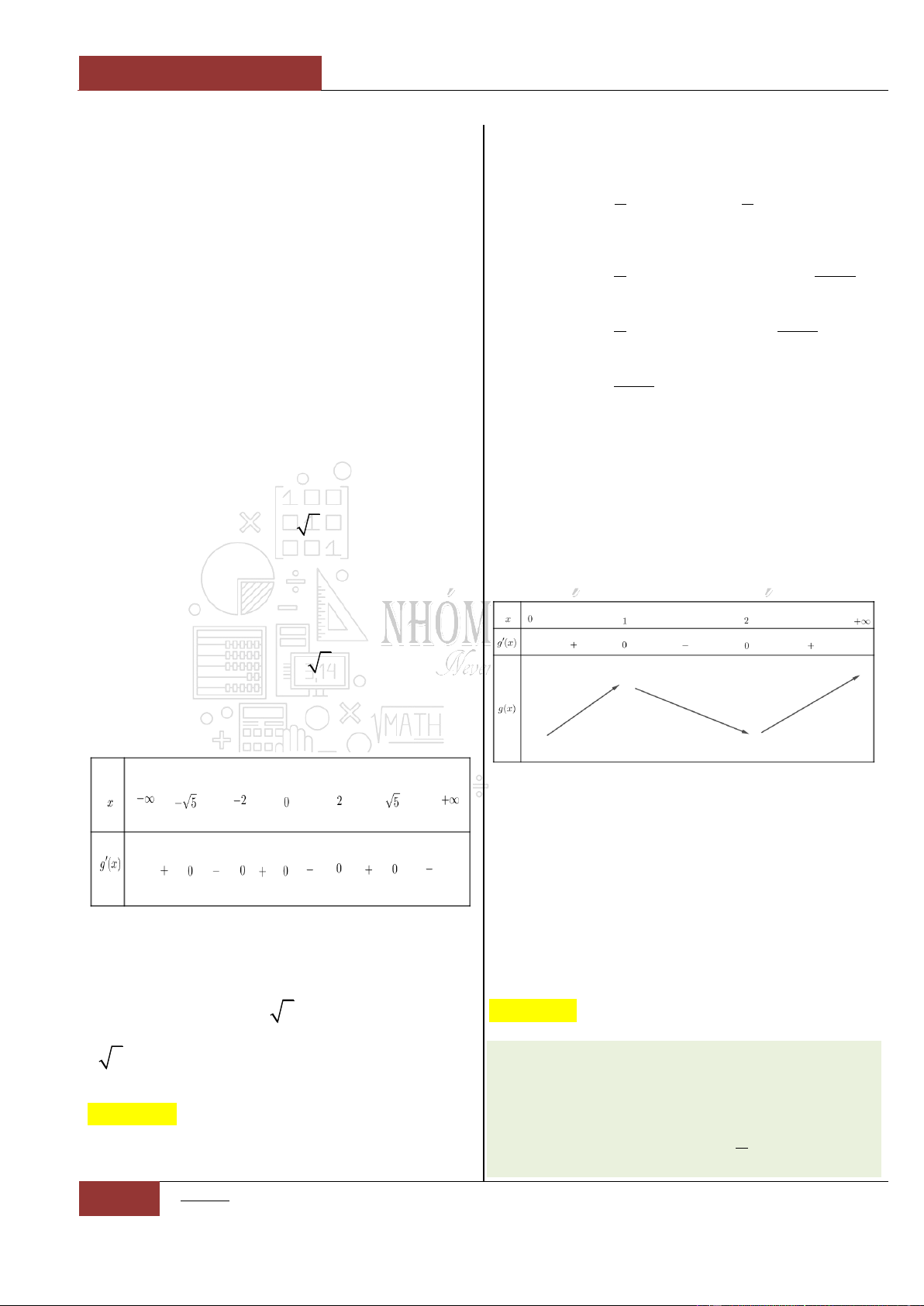
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

76

[ I can't, I can! ]

Đặt

2

2tx

.

Khi đó:

   

* ' 2 0f t t   

 

2021

2

2021

2

2021

2

2 8 2 0

2 8 1 0

2

3

81

3

22

2

23

5

23

t t t

tt

t

x

     

     



    















   























    













Suy ra

 

0

' 0 2

5

x

g x x

x







   







Bảng biến thiên của đồ thị hàm số

 

y g x

.

Dựa vào bảng biến thiên của hàm số

 

y g x

ta thấy rằng hàm số nghịch biến trên ba khoảng

rời nhau lần lượt là

 

5; 2

và

 

0;2

và

 

5;

.

Đáp án: C

Câu 63. Xét hàm số

   

ln 2lng x f x x x  

.

TXĐ:

 

0;D  

.

Ta có:

   

12

' . ' ln 1g x f x

xx

  

  

 

ln ln

12

2 ln

12

2 ln

2

ln 1

xx

x

e e x

xx

x

x x x

xx

x

xx

x



   



   



  

Ta có:

 

0

2

'0

20

1

ln 1 0

x

gx

x

xx











  

















  





.

Bảng biến thiên của đồ thị hàm số

 

y g x

.

Từ bảng biến thiên của đồ thị hàm số

 

y g x

ta suy ra hàm số nghịch biến trên khoảng

 

1;2

.

Hay:

1

3

2

a

S a b

b





   







.

Khi đó tổng

S

là một số nguyên lẻ.

Đáp án: B

Note: Sở dĩ ta có:

ln 1 0 1x x x    

là vì:

Hàm số

 

ln 1y h x x x   

là một hàm đồng

biến trên

 

0;

. Do

 

1

' 1 0, 0h x x

x

    

.

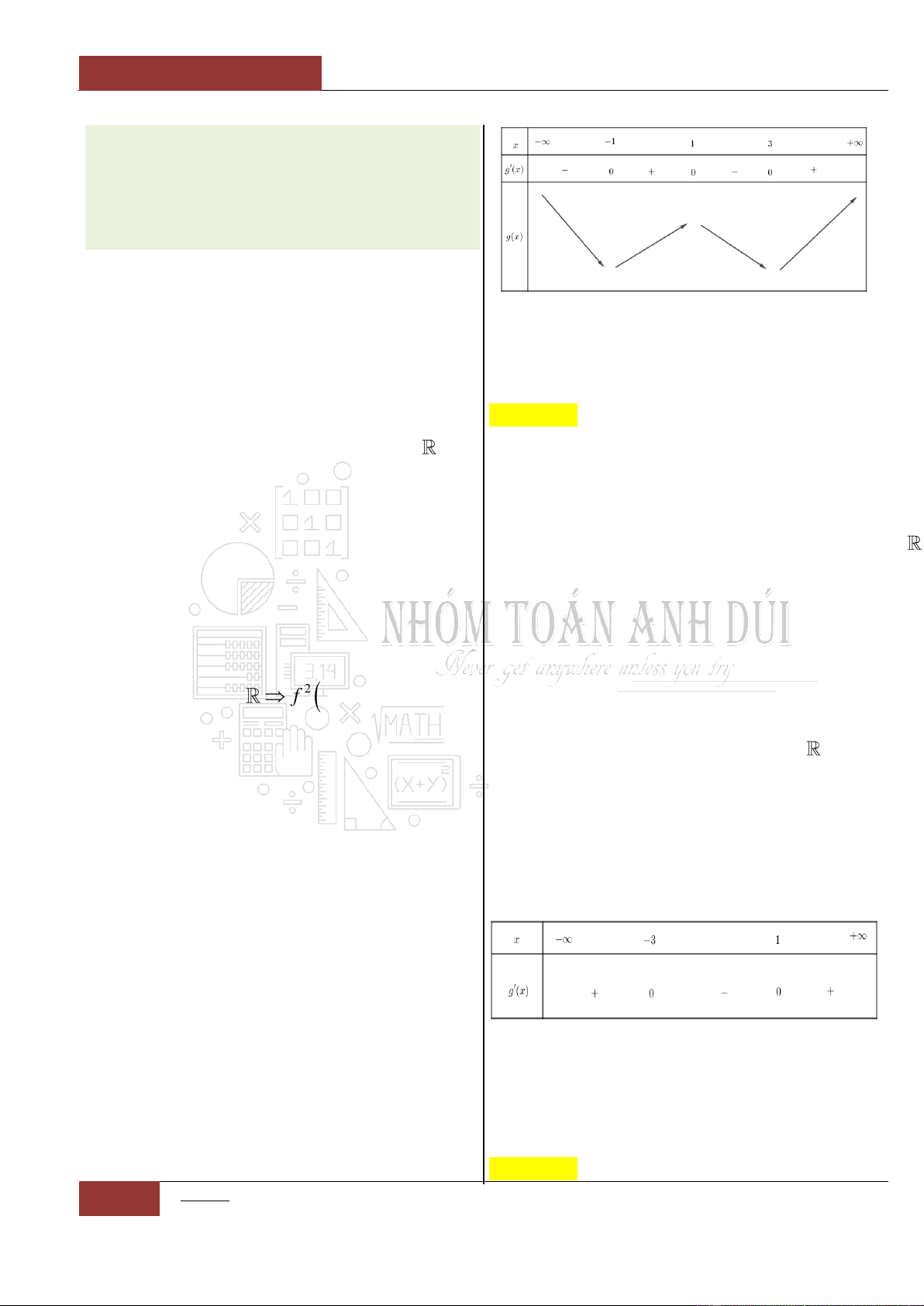
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

77

[ I can't, I can! ]

Vì vậy nếu phương trình

ln 1 0xx  

có

nghiệm thì nghiệm đó là duy nhất.

Ta nhẩm thấy

1x 

là một nghiệm của phương

trình

ln 1 0xx  

, nên nó là duy nhất.

Câu 64. Ta có:

   

'f x f x dx



Khi đó:

 

3 4 2

42f x x x dx x x C    



Vì

 

0 1 1fC  

.

Do đó ta có:

 

42

1 0,f x x x x     

.

Xét hàm số

 

32

23y g x f x x   

.

   

2 2 2

' 3 2 2 2 3 ' 2 3g x x f x x f x x     

Ta có:

 

2

2 2 0

'0

' 2 3 0 *

x

gx

f x x









  





Do

 

22

0, 2 3 0f x x f x x      

.

 

   

 

3

22

2

22

2

* 4 2 3 2 2 3 0

2 3 4 2 3 2 0

2 3 0

1

3

4 2 3 2 0

x x x x

xx

x

xx

      



      







  















   



Do vậy:

 

1

' 0 1

3

x

g x x

x







   







.

Bảng biến thiên của đồ thị hàm số

 

y g x

.

Từ bảng biến thiên của đồ thị hàm số

 

y g x

đồng biến trên khoảng

 

1;1

và

 

3;

.

Đáp án: C

Câu 65. Từ bảng biến thiên của đồ thị hàm số

 

'fx

ta dễ dàng suy ra dạng tổng quát nó:

        

2 1 2 1

' 3 1 , 0,

nm

f x A x x x A x x



     

Ta có:

   

2

' ' 3 6 9g x f x x x   

.

         

         

2 1 2 1

22

' 3 1 3 3 1

' 3 1 3 1 3

nm

g x A x x x x x

g x x x A x x x



     



     



Do

 

0Ax

    

22

3 1 3 0,

nm

A x x x x      

.

Khi đó:

    

3

' 0 3 1 0

1

x

g x x x

x





     







Bảng biến thiên hàm số

 

y g x

.

Dựa vào bảng biến thiên của đồ thị hàm số

 

y g x

ta nhận thấy hàm số đồng biến trên

hai khoảng lần lượt là

 

;3 

và

 

1; 

.

Đáp án: A

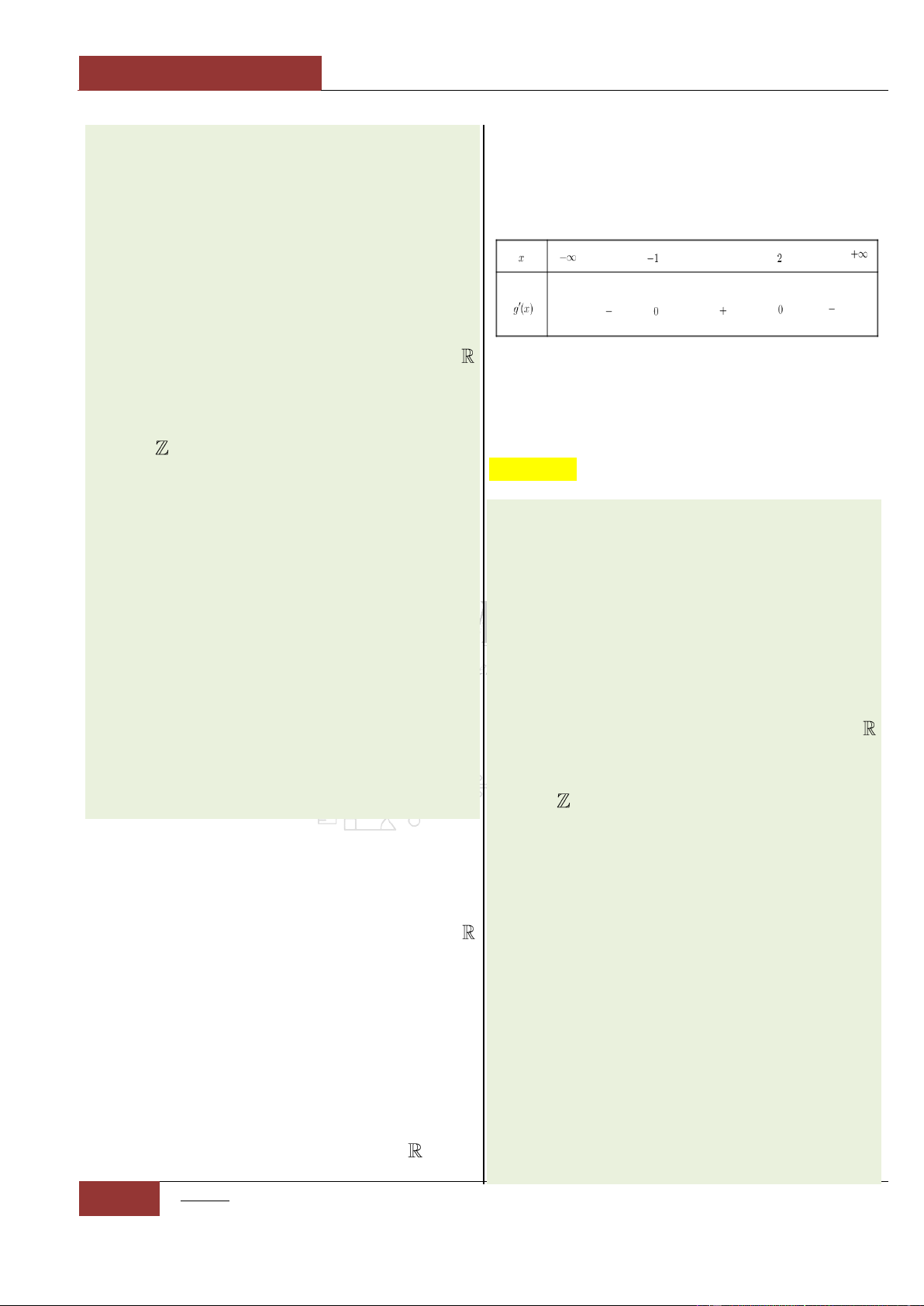
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

78

[ I can't, I can! ]

Note: Sở dĩ ta chọn được hàm

 

'fx

như trên

là bởi phương trình

 

3

'0

1

x

fx

x













.

Mà hai nghiệm

3x 

và

1x 

đều là những

nghiệm mà qua nó đạo hàm đổi dấu (Nghiệm

bội lẻ). Vì thế ý tưởng đặt hàm số có dạng:

        

2 1 2 1

' 3 1 , 0,

nm

f x A x x x A x x



     

hoàn toàn thỏa mãn do:

,mn

,

2 1, 2 1nm

đều là những số lẻ.

Mặt khác:

 

lim ' 0

x

f x t





.

Do đó hàm số sẽ có hệ số

0a 

.

Nếu mở rộng thêm thì nếu

 

'0

i

f x x x  

và

i

xx

là một nghiệm bội chẵn thì qua nó

đạo hàm không đổi dấu. Vì thế bảng biến thiên

không thay đổi gì nhiều về khoảng đan dấu.

Nên tổng quát nhất ta nhân thêm lượng

 

Ax

vào biểu thức

   

2 1 2 1

31

nm

xx





với

     

 

2

22

12

... 0

k

pq

n

A x a x x x x x x    

.

Câu 66. Từ bảng biến thiên của đồ thị hàm số

 

'fx

ta dễ dàng suy ra dạng tổng quát nó:

        

2 1 2 1

' 1 2 , 0,

nm

f x A x x x A x x



     

Ta có:

   

2

' ' 3 3 6g x f x x x   

.

         

         

2 1 2 1

22

' 1 2 3 2 1

' 1 2 1 2 3

nm

g x A x x x x x

g x x x A x x x



     



     



Do

 

0Ax

    

22

1 2 3 0,

nm

A x x x x      

.

Khi đó:

    

1

' 0 1 2 0

2

x

g x x x

x





     







Bảng biến thiên hàm số

 

y g x

.

Dựa vào bảng biến thiên của đồ thị hàm số

 

y g x

ta nhận thấy hàm số đồng biến trên

khoảng

 

1;2

.

Đáp án: B

Note: Sở dĩ ta chọn được hàm

 

'fx

như trên

là bởi phương trình

 

1

'0

2

x

fx

x













.

Mà hai nghiệm

1x 

và

2x 

đều là những

nghiệm mà qua nó đạo hàm đổi dấu (Nghiệm

bội lẻ). Vì thế ý tưởng đặt hàm số có dạng:

        

2 1 2 1

' 1 2 , 0,

nm

f x A x x x A x x



     

hoàn toàn thỏa mãn do:

,mn

,

2 1, 2 1nm

đều là những số lẻ.

Mặt khác:

 

lim ' 0

x

f x t





.

Do đó hàm số sẽ có hệ số

0a 

.

Nếu mở rộng thêm thì nếu

 

'0

i

f x x x  

và

i

xx

là một nghiệm bội chẵn thì qua nó

đạo hàm không đổi dấu. Vì thế bảng biến thiên

không thay đổi gì nhiều về khoảng đan dấu.

Nên tổng quát nhất ta nhân thêm lượng

 

Ax

vào biểu thức

   

2 1 2 1

12

nm

xx





với

     

 

2

22

12

... 0

k

pq

n

A x a x x x x x x    

.

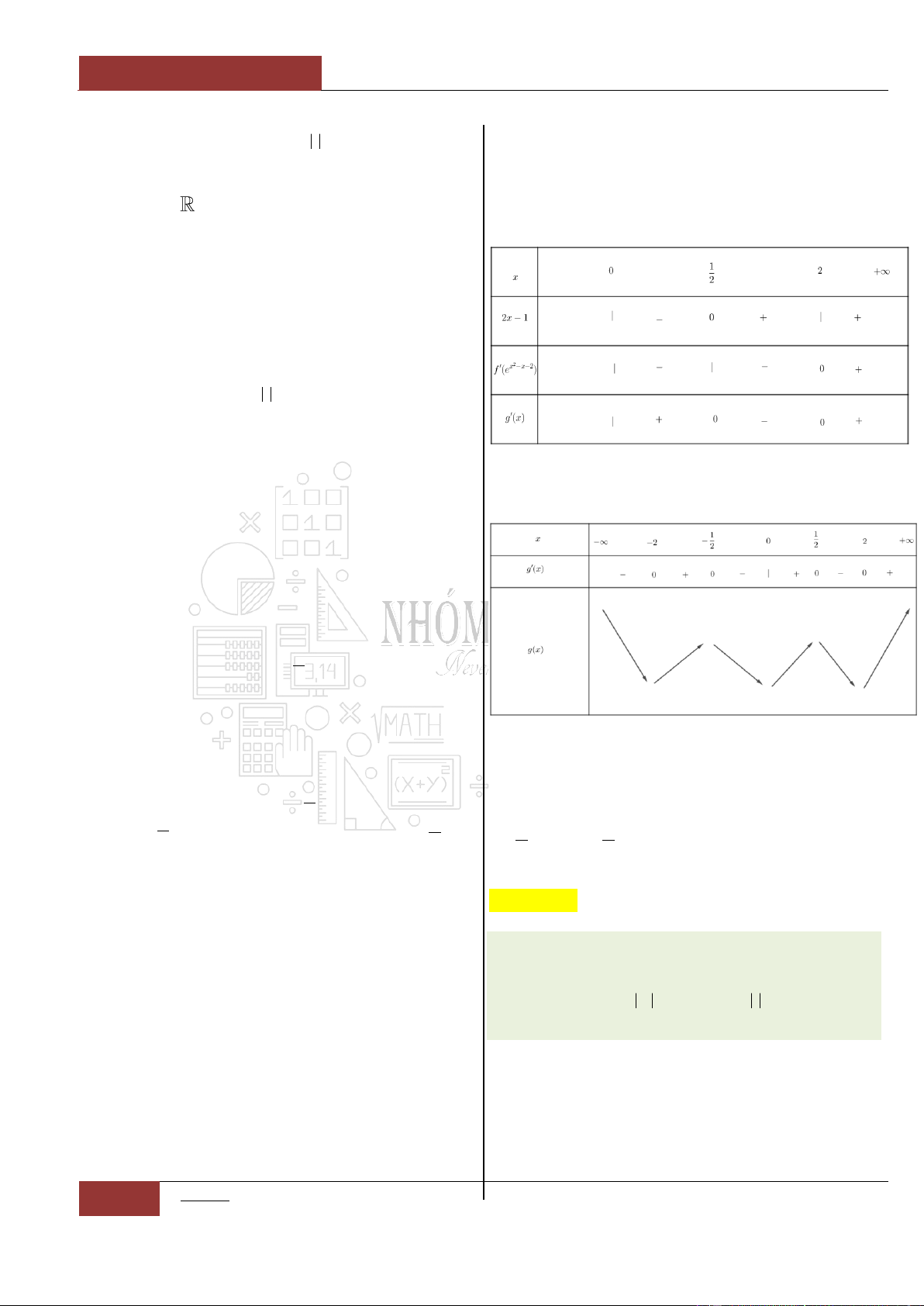
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

79

[ I can't, I can! ]

Câu 67. Đặt

 





2

2xx

g x f e





.

TXĐ:

D 

.

Dễ thấy hàm số

 

gx

là một hàm chẵn thì thế

 

gx

đối xứng nhau qua trục

Oy

.

Vì thế ta chỉ cần xét trên khoảng

 

0;

Ta có:

 









2

,0

xx

g x f e f e x



   

.

Suy ra:

   





22

' 2 1 . . '

x x x x

g x x e f e

   



Ta có:

 





2

2 1 0

'0

xx

x

gx

fe

















2

2 1 0

1

2

0

1

xx

x

e

x

e





































(Do

2

0

xx

e





)

 

2

1

2

1

2

20

2

x

xL

x

xx

x

















    





  













 Trường hợp 1:

2x 

Khi đó:

2

20xx  

.

Suy ra:





22

1 ' 0

x x x x

e f e

   

  

.

 Trường hợp 2:

02x

Khi đó:

2

20xx  

.

Suy ra:





22

0 1 ' 0

x x x x

e f e

   

   

.

Bảng xét dấu

 

'gx

trên nữa khoảng





0;

.

Do đó bảng biến thiên đồ thị

 

y g x

Dựa vào đồ thị hàm số

 

y g x

ta nhận thấy

hàm số nghịch biến trên khoảng

 

;2 

và

1

;0

2









và

1

;2

2







.

Đáp án: D

Note: Hàm số

 

y g x

là hàm số chẵn là vì:

 





 

2

22x x x x

g x f e f e g x

     

   

.

Câu 68. Xét hàm số:

 

4 2 6 4 2

3 4 6 2 3 12y f x x x x x      

Ta có:

   

2 4 2

' 12 2 . ' 4 6y x x f x x      

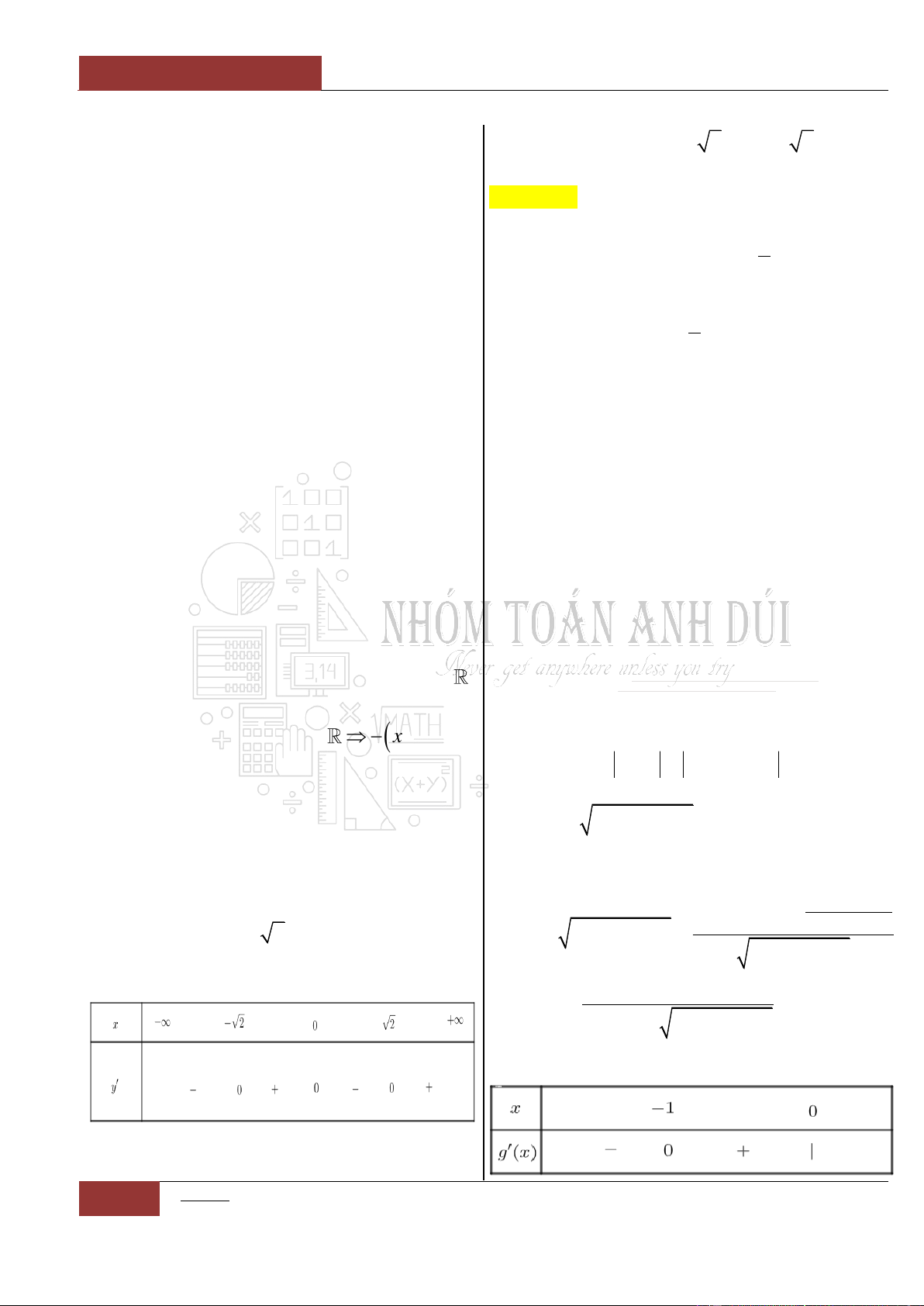
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

80

[ I can't, I can! ]

.

Ta có:

Xét phương trình

Ta có:

Suy ra: .

Mặt khác:

Vì vậy

Nên phương trình vô nghiệm.

Vậy .

Bảng xét dấu đạo hàm

Dựa vào bảng biến thiên ta nhận thấy hàm số

đồng biến trên khoảng và .

Đáp án: C

Câu 69. Xét hàm số

2021

1

logy

x









.

Ta có:

 

1 2021 2021

1

: log logC y x

x



  





.

Gọi đồ thị hàm số

 

C

là đồ thị đối xứng của

đồ thị

 

1

C

qua trục hoành

Ox

.

 

C

là đồ thị của hàm số

2021

logyx

.

Nhận thấy

 

2

C

đối xứng với đồ thị hàm số

 

C

qua trục tung

Oy

.

 

2

C

là đồ thị của hàm số

 

2021

logyx

,0x

.

Hay ta đặt:

   

2021

log , 0f x x x   

.

Do đó:

     

2021

logg x f x x  

   

2

2021

logg x x  

.

Suy ra:

   

 

2021

2

2021

2

2021

2

2021

1

2log .

.ln2021

' log

log

2log

' 0 1

ln2021. log

x

g x x

x

g x x

xx



  



     



Bảng xét dấu đạo hàm:

 

42

... 12 2x x x  

   

2 4 2

' 12 2 . ' 4 6y x x f x x       

  

22

... 12 2 1x x x  

     

2 4 2 2

' 12 2 ' 4 6 1y x x f x x x



        



   

 

2

4 2 2

0

' 0 2 0

' 4 6 1 0 *

x

yx

f x x x







   



     





 

*

 

4 2 4 2

4 6 4 4 2x x x x       

 

2

2 2 2x     

 

42

4 6 2 0,f x x f x       

 

22

1 1 0, 1 0x x x        

   

4 2 2

' 4 6 1 0f x x x     

 

*

0

'0

2

x

y

x













 

2;0

 

2;

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

81

[ I can't, I can! ]

Vì thế hàm số

 

y f x

nghịch biến trên

khoảng

 

;1 

.

Đáp án A

Extra Techniques:

Remark:

Giả sử, ta xét đồ thị hàm số

   

y f x C

liên tục trên khoảng

K

. Khi đó:

Đồ thị hàm số

 

y f x

là đồ thị

đối xứng với đồ thị

 

C

qua trục hoành

(trục

Ox

) trên khoảng

K

.

Đồ thị hàm số

 

y f x

là đồ thị

đối xứng với đồ thị

 

C

qua trục tung

(trục

Oy

) trên khoảng đối của khoảng

K

.

Đồ thị hàm số

 

y f x  

là đồ thị

đối xứng với đồ thị

 

C

qua gốc tọa độ

O

trên khoảng đối của khoảng

K

.

Câu 70. TXĐ:

D 

.

Xét hàm số:

 

2 5 3 2 2

11

10 20 1

53

y m x mx x m m x      

.

Ta có:

2 4 2 2

' 20 20y m x mx x m m     

.

Để hàm số đồng biến trên thì khi đó:

2 4 2 2

' 20 20 0,y m x mx x m m x        

Lưu ý: Dấu

""

chỉ đạt tại hữu hạn điểm.

Điều kiện cần:

Phương trình

'0y 

có hiệu hệ số bậc chẵn và

lẻ bằng

0

vì thế

'0y 

có một nghiệm

1x 

.

Nên để

' 0,yx  

thì dấu của đạo hàm

phải không đổi khi đi qua điểm

1x 

.

Dùng lược đồ Hoocner chia đa thức, ta được:

 

2 3 2 2 2 2

' 1 20y x m x m x m m x m m       

Như vậy:

 

10g 

, với:

 

2 3 2 2 2 2

20g x m x m x m m x m m      

.

Khi đó:

 

2

1 4 2 20 0

5

2

m

g m m

m







      







.

Điều kiện đủ:

+) Với

2m 

, ta có:

42

' 4 2 20 14y x x x   

   

22

5

' 4 1 1 0,

2

y x x x



       





.

Vì vậy hàm số đã cho đồng biến trên .

Nhận

2m 

.

+) Với

5

2

m 

, ta có:

42

25 5 65

' 20

4 2 4

y x x x   

   

22

25 8

' 1 1 0,

45

y x x x



       





.

Vì vậy hàm số đã cho đồng biến trên .

Nhận

5

2

m 

.

Tích các giá trị thỏa mãn:

 

5

2 . 5

2

S    

.

Đáp án C

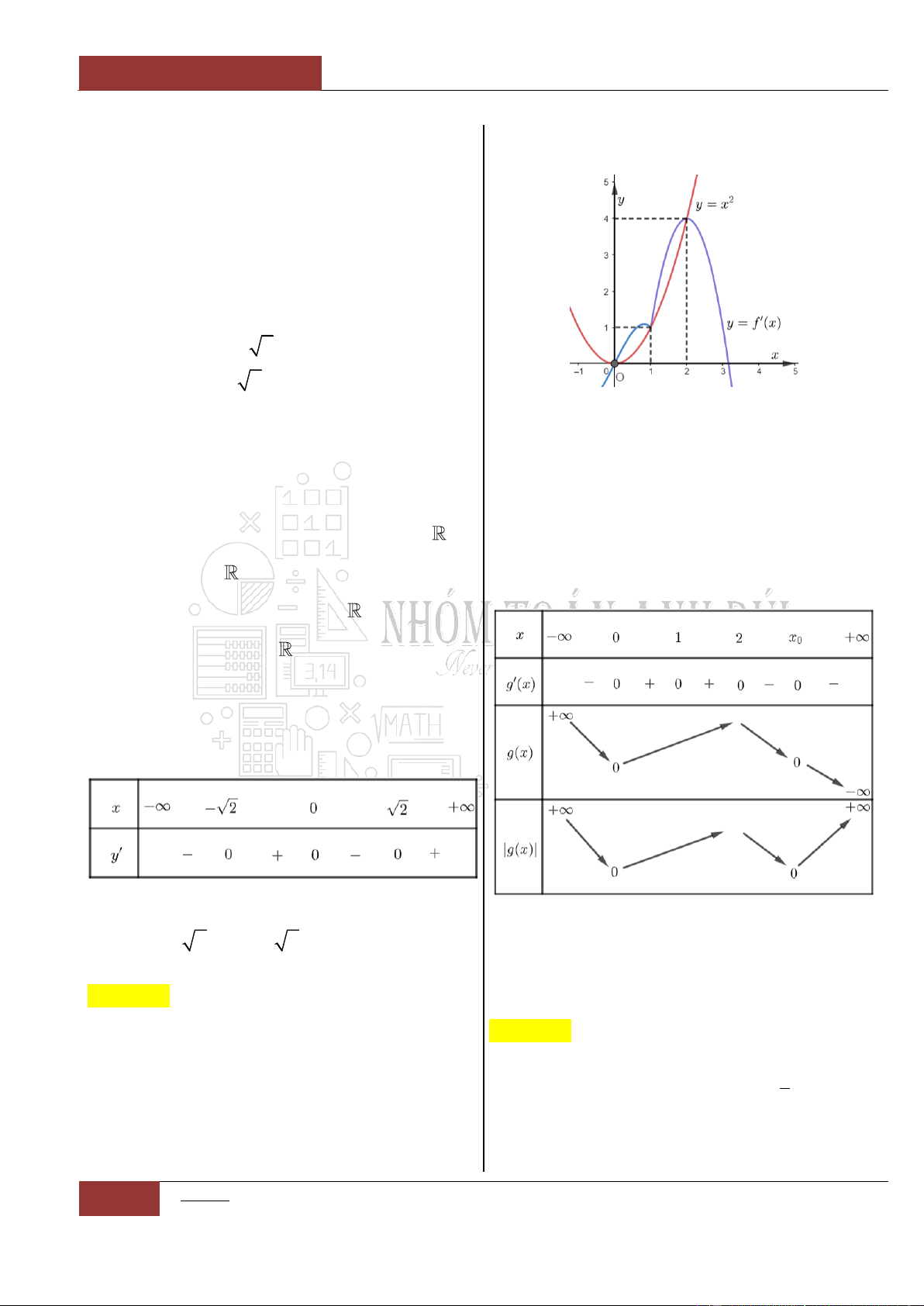
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

82

[ I can't, I can! ]

Câu 71. Ta có:

   

     

      

     

3 4 2 5 3

2 4 2 4 2

2 4 2 2 2

2 4 2 2

' 12 24 . ' 4 6 12 12 24

12 2 . ' 4 6 12 2

12 2 . ' 4 6 12 2 1

12 2 . ' 4 6 1

y x x f x x x x x

x x f x x x x x

x x f x x x

        

        



       



 

4 2 2

0

2

'0

2

' 4 6 1 *

x

y

x

f x x x











  







    



.

Để giải quyết

 

*

, trước hết ta đánh giá:

 

2

4 2 2

2

42

2

4 6 2 2 2,

1 1,

' 4 6 0,

1 1 0,

x x x x

xx

f x x x

xx



          







   





     







    





Vậy phương trình

 

*

vô nghiệm.

Bảng xét dấu:

Vậy hàm số đã cho đồng biến trên hai khoảng

rời nhau

 

2;0

và

 

2;

.

Đáp án D

Câu 72. Đặt:

   

3

3g x f x x

, ta có:

     

22

' 3 ' 0 'g x f x x f x x



    



.

Vẽ đồ thị hàm số

2

yx

tương giao với đồ thị

hàm số

 

'y f x

trên cùng một trục tọa độ.

Suy ra:

 

0

' 0 1

2

x

g x x

x







  







.

Theo giả thuyết, ta có:

   

0 3 0 0 0gf  

.

Bảng biến thiên mở rộng:

Từ bảng biến thiên mở rộng ta dễ dàng suy ra

hàm số đã cho đồng biến trên hai khoảng rời

nhau là

 

0;2

và

 

00

; , 2xx 

.

Đáp án C

Câu 73. Xét hàm số

   

3

1

2021

3

g x f x x  

.

       

2

2 2 2

' ' 1 3g x f x x x x x x      

.

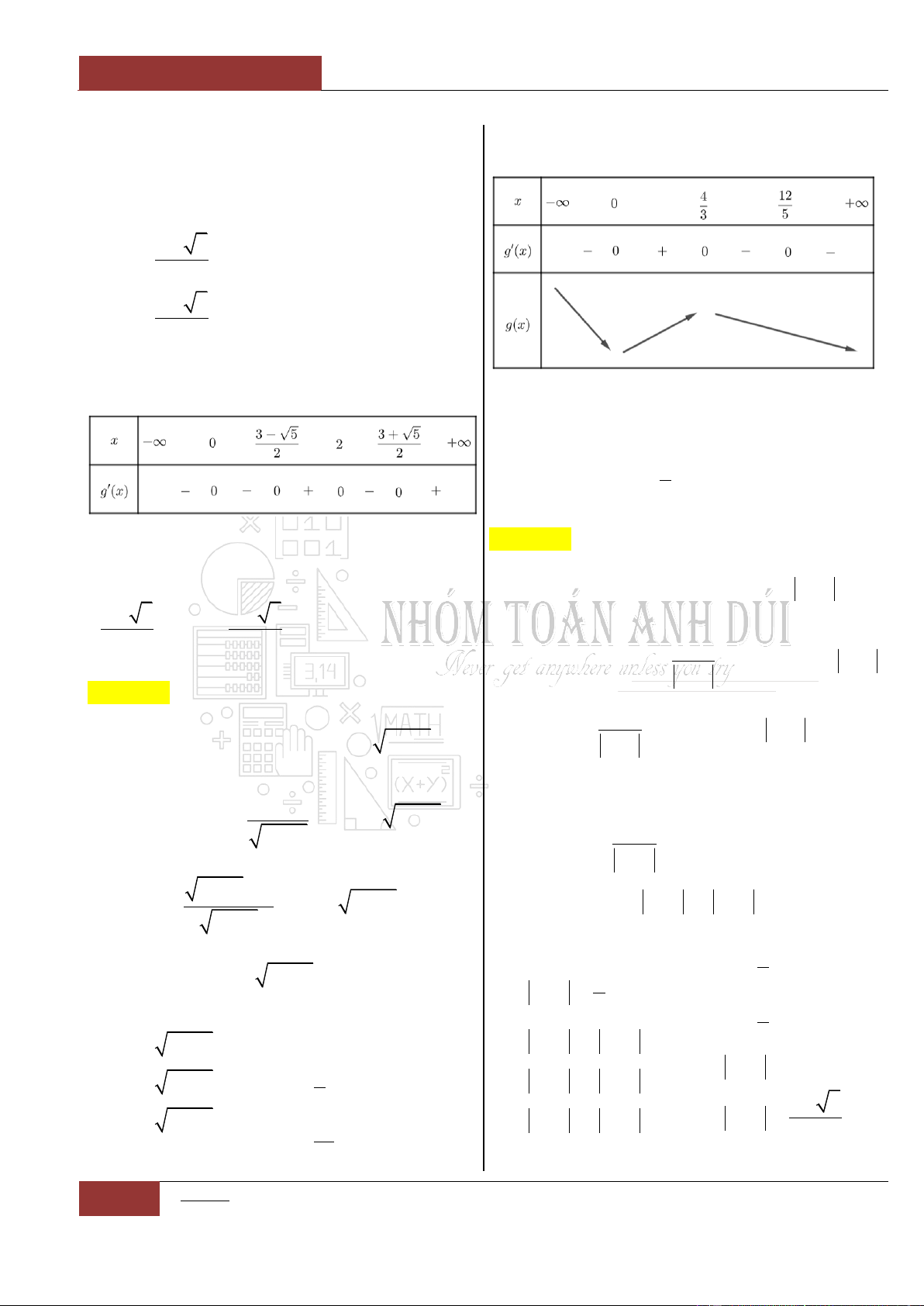
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

83

[ I can't, I can! ]

 

2 3 2

' 0 5 7 2 0

0

2

35

2

35

2

g x x x x x

x

     



























Bảng xét dấu đạo hàm

 

'gx

.

Từ bảng xét dấu đạo hàm

 

'gx

, ta thấy hàm số

đã cho đồng biến trên hai khoảng rời nhau:

35

;2

2









và

35

;

2











.

Đáp án C

Câu 74. Xét hàm số

 





2

1g x f x x  

.

Ta có:

 





2

' 1 . ' 1

1

x

g x f x x

x



   







.

 





2

1

' . ' 1

1

xx

g x f x x

x



   



.

 





2

' 0 ' 1 0

0

11

4

13

3

15

12

5

g x f x x

x

xx

x x x

xx

x

    









  



     



  









.

Bảng biến thiên hàm số

 

y g x

:

Dựa vào bảng biến thiên của đồ thị hàm số

 

y g x

, ta thấy hàm số nghịch biến trên

khoảng

 

;0

và

4

;

3









.

Đáp án D

Câu 75. Xét:

 

2

2 1 1g x f x x x    

.

     

   

2

1

' 2 1 . ' 1 1

1

1 2 . ' 1 1 , 1

1

x

g x x f x x

x

x f x x x

x







      













      









 

2

1

' 0 2

1

' 1 1 0

1

3

1

2

1

2

1

2

1 1 1

11

1 1 0

15

1

1 1 1

2

x

gx

x

f x x

xL

x

xx

x

xx

x

xx







  





   





















      







   









   





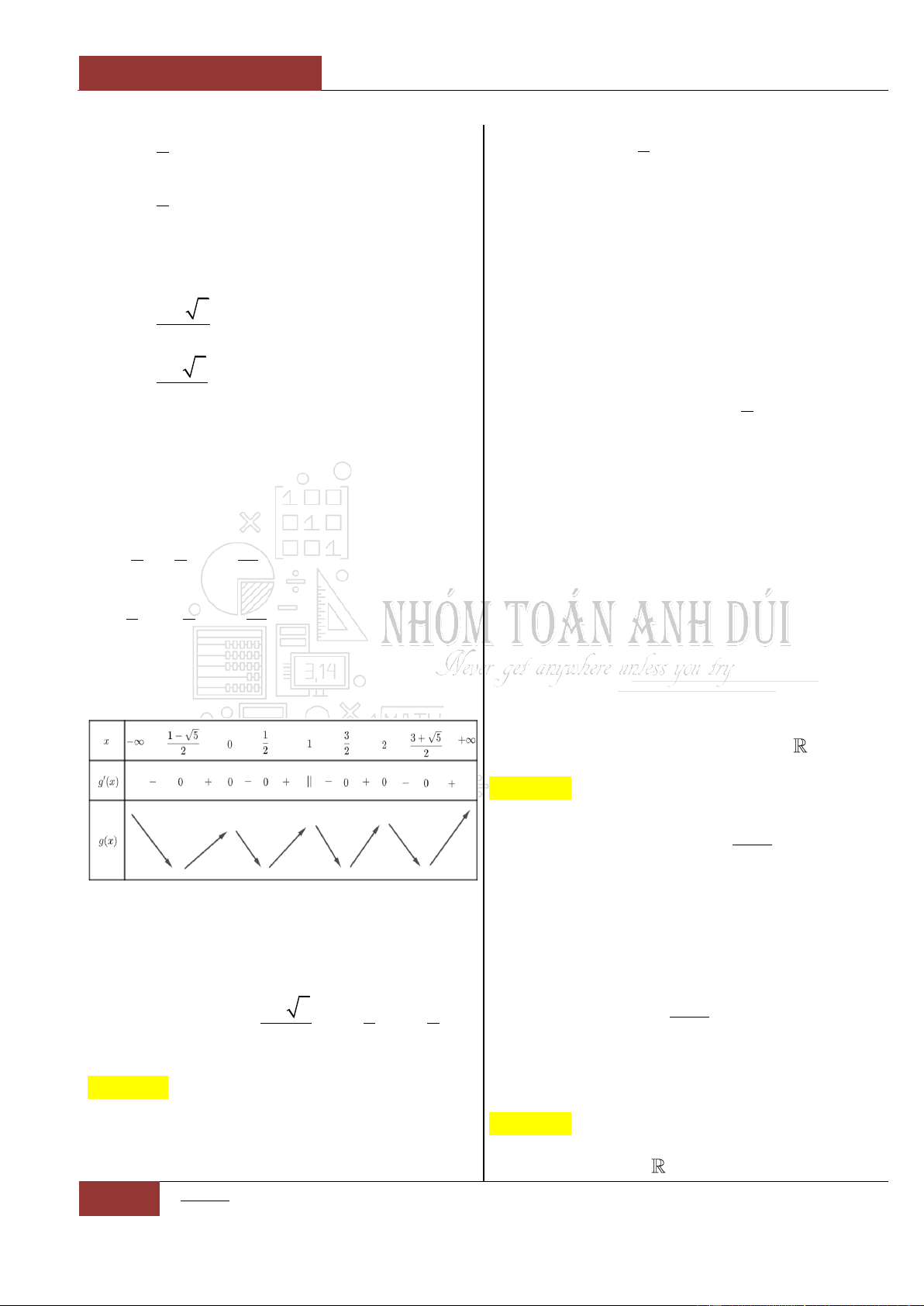
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

84

[ I can't, I can! ]

3

2

1

2

0

35

2

15

2

x









































.

Tính toán tại một số điểm đặc biệt để xét dấu:

   

' 1 3 ' 2 0

3 1 3

' . ' 0

4 2 16

5 1 3

. ' 0

4 2 16

gf





   



   

  



   

   



   

   



   

   



.

Bảng biến thiên đồ thị hàm số

 

y g x

.

Dựa vào bảng biến thiên của đồ thị hàm số

 

y g x

, ta thấy, hàm số đồng biến trên

4

khoảng rời nhau nhưng chỉ đồng biến trên

3

khoảng hữu hạn là:

1 5 1 3

;0 , ;1 , ;2

2 2 2





   



   

   



.

Đáp án B

Câu 76. Xét:

     

2

2 2 1 2 12 *f x f x x  

.

Cho

0x 

và

1

2

x 

, ta có hệ phương trình:

   

 

2 0 1 0

12

0 2 1 3

ff

f

ff

















.

Đạo hàm hai vế

 

*

theo ẩn

x

, ta được:

   

4 ' 2 2 ' 1 2 24f x f x x  

.

Một lần nữa, cho

0x 

và

1

2

x 

, ta có:

   

 

4 ' 0 2 ' 1 0

' 1 4

4 ' 1 2 ' 0 12

ff

f

ff

















.

Như vậy dễ dàng viết được phương trình tiếp

tuyến của đồ thị hàm số

 

y f x

tại điểm

1x 

là:

    

' 1 1 1y f x f  

.

Hay:

 

4 1 2 4 2y x y x     

.

Tiếp tuyến là một đường thẳng có hệ số góc

40k 

nên hàm số đồng biến trên .

Đáp án D

Câu 77. Đặt:

5

35

3

x

x t t



   

.

Khi đó:

       

3 5 ' 3 ' 3 5g t f t g t f t    

.

Ta có:

   

' 0 ' 3 5 0 1g t f t t     

.

Do vậy:

 

5

' 0 1 8

3

x

f x x



    

.

Vậy hàm số nghịch biến trên khoảng

 

;8

.

Đáp án A

Câu 78. TXĐ:

D 

.

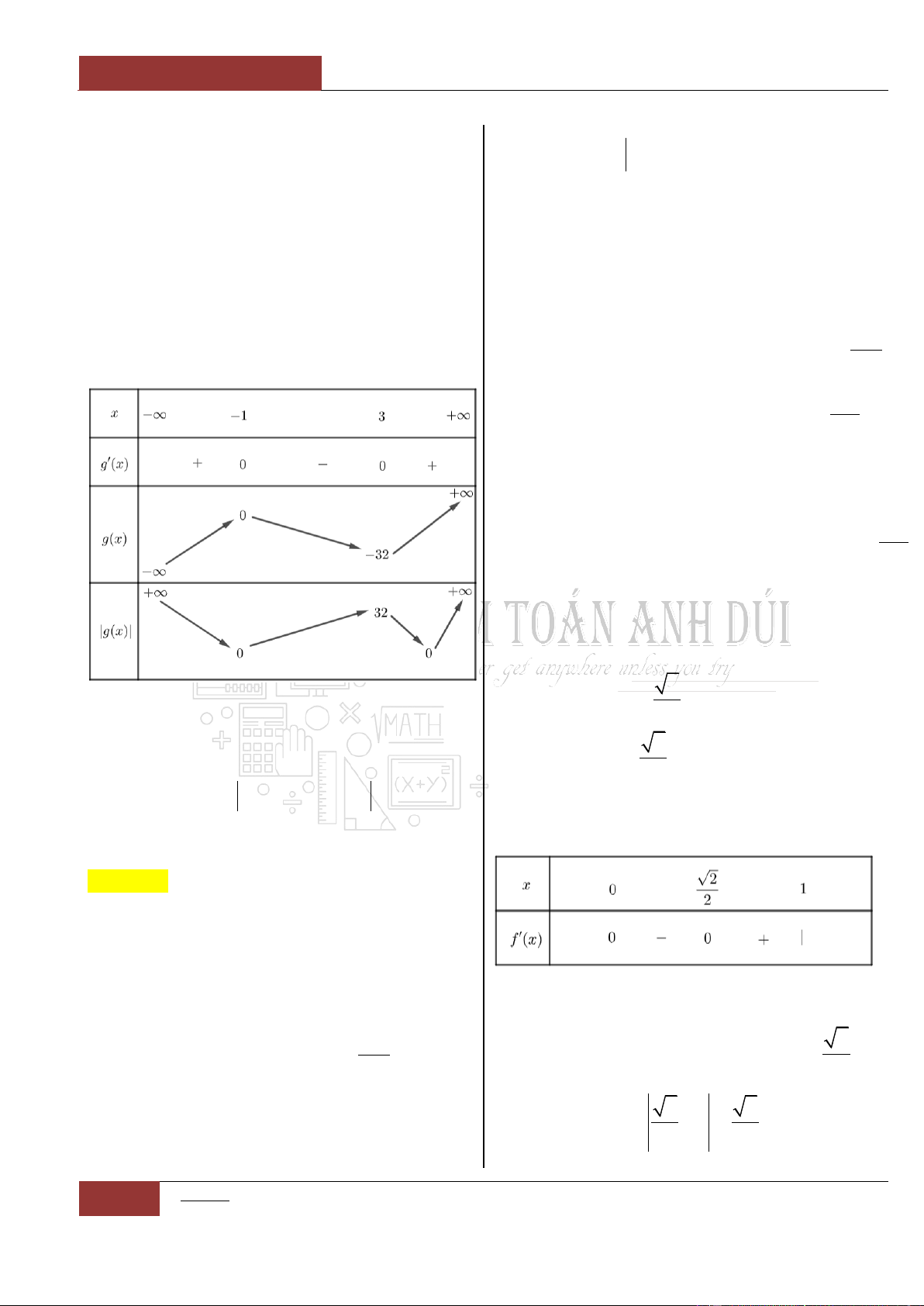
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

85

[ I can't, I can! ]

Xét hàm số

 

32

3 9 5g x x x x   

.

Ta có:

 

2

1

' 3 6 9 0

3

x

g x x x

x





    







.

Ta có:

 

10

3 32

g















.

Bảng biến thiên mở rộng:

Ta có:

 

50g 

.

Dựa vào bảng biến thiên mở rộng ta thấy rằng,

đồ thị hàm số

32

3 9 5y x x x   

đồng biến

trên

2

khoảng rời nhau

 

1;3

và

 

5;

.

Đáp án B

Câu 79. Từ

 

*

, ta có:

 

11

2

00

1

6 4 2

0

' 4 6 1 .

376

40 44 32 4 **

105

f x dx x f x dx

x x x dx

  





    





Mặt khác:

 

   

 

11

23

00

6 1 2x f x dx f x d x x  



 

1

33

0

11

23

00

2 2 . '

6 1 . 1 2 . '

x x f x x x f x dx

x f x dx x x f x dx

   

    





Thay vào

 

*

, ta được:

 

 

11

2

3

00

11

2

3

00

1

2

3

0

1

2

3

0

33

376

' 4 1 2 . '

105

44

' 4 2 . ' 0

105

' 2 2 0

44

: 4 2

105

' 2 2 4 2 , 0;1

f x dx x x f x dx

f x x x dx

Do x x dx

f x x x x x x



   







    







   











      





   

0

2

'0

2

x

f x x L

x









   









.

Bảng xét dấu hàm số

 

'y f x

:

Dựa vào bảng xét dấu của hàm số

 

'y f x

, ta

thấy hàm số nghịch biến trên khoảng

2

0;

2







có độ dài bằng

22

0

22

L   

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

86

[ I can't, I can! ]

Đáp án C

Câu 80. Tính:

 

1

3

0

.I x f x dx



.

Đặt:

 

4

3

'

4

du f x dx

u f x

x

dv x dx

v





















.

Ta có:

   

1

44

0

11

. . '

44

I x f x x f x dx



.

   

 

1

4

0

11

. ' : 1 1

44

I x f x dx Do f  



.

Vì:

   

11

34

00

1 1 1 1

. . '

2 2 4 4

x f x dx x f x dx   



     

11

44

00

. ' 1 18 . ' 18 1x f x dx x f x dx     



Ta có:

   

1

2

0

' 9 2f x dx 







.

Lại có:

 

1

11

9

88

00

0

1

81 9 3

99

x

x dx x dx   



.

Cộng vế theo vế ba đẳng thức

     

1 , 2 , 3

, ta

được:

   





1

2

48

0

' 18 . ' 81 0f x x f x x dx  







.

   

1

2

44

0

' 9 0 ' 9f x x dx f x x



     





.

Mà:

 

 

4

' 9 0, 0;1f x x x    

.

Vậy hàm số

 

y f x

nghịch biến trên khoảng

 

0;1

.

Đáp án C

Extra Techniques:

Remark:

Lý do nói hàm số

 

y f x

nghịch

biến trên khoảng

 

0;1

mà không

phải nghịch biến trên toàn tập .

Cơ sở: Đề bài chỉ cho hàm số có đạo

hàm và liên tục trên đoạn

 

0;1

. Vì thế

ta chỉ có thể xét lận cận trong của đoạn

 

0;1

. Có thể đồ thị hàm số không có

đạo hàm, hoặc hàm số không liên tục

tại các khoáng

 

;0

và khoảng

 

1; 

. Vì thế ta không thể nào gộp

chung kết luận hàm số nghịch biến trên

mặc dù

 

4

' 9 0,f x x x    

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

91

[ I can't, I can! ]

Dạng 2: Bài toán chứa tham số

Lý thuyết cần nắm:

Tương tự với bài toán không chứa tham số. Ta xét hàm số theo biến

x

phụ thuộc tham số

m

xác định trên khoảng

K

, kí hiệu:

 

,y f x m

.

 

i

Hàm số đồng biến trên

K



' 0,y x K  

và dấu

""

chỉ xảy ra tại hữu hạn điểm.

 

ii

Hàm số nghịch biến trên

K



' 0,y x K  

và dấu

""

chỉ xảy ra tại hữu hạn điểm.

Một số Tips để làm tốt các bài toán chứa tham số

m

Đối với dạng bài tập cho hàm số

 

y f x

là phương trình bậc ba

theo

x

có ẩn

m

. Khi đó:

 

''y f x

là một hàm số bậc hai có dạng

tổng quát như sau:

 

2

,0y ax bx c a   

.

Để xét dấu

'y

ta thường sử dụng định lý về dấu của tam thức bậc hai

, định lý Viéte,…

 

1

Định lý về dấu của tam thức bậc hai:

Cho tam thức bậc hai

   

2

,0g x ax bx c a   

.

.a

Nếu

0

(hoặc

'0

) thì

 

. 0,a g x x K  

hay

nói cách khác,

 

gx

cùng dấu với hệ số

a

.

.b

Nếu

0

(hoặc

'0

) thì

 

. 0, \

2

b

a g x x K

a



   





hay nói cách khác,

 

gx

cùng dấu với hệ số

a

(trừ

2

b

x

a



) vì

0

2

b

g

a









.

.c

Nếu

0

(hoặc

'0

) thì hiễn nhiên hàm số có

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

92

[ I can't, I can! ]

Hình I.2.1.

Hình I.2.2.

Extra Techniques:

Tips:

Cơ sở hình thành các

điều kiện:

 

1

:Phương trình có hai

nghiệm phân biệt nên

0

hoặc

'0

. Do

tổng của hai số âm là

một số âm và tích của

hai số âm là một số

dương.

 

2

:Phương trình có hai

nghiệm phân biệt nên

0

hoặc

'0

. Do

tổng của hai số dương là

một số dương và tích

của hai số dương là một

số dương.

hai nghiệm (bội lẻ) thực phân biệt:

 

1

2

0

xx

gx

xx













nên qua

1

xx

và

2

xx

đạo hàm đổi dấu.

 Trường hợp 1:

0a 

.

(Xem Hình I.2.1.).

 Trường hợp 2:

0a 

.

(Xem Hình I.2.2.).

Nói cách khác, dấu của

 

gx

trong khoảng hai nghiệm thì trái dấu

với hệ số

a

và ở ngoài hai khoảng nghiệm thì cùng dấu với hệ số

a

.

(Trong trái - ngoài cùng).

 

2

Định lý về dấu kết hợp định lý Viéte cho tam thức bậc hai:

Đặt:

12

.

S x x

P x x











.

.a

So sánh nghiệm với hằng số

0

.

 

i

Điều kiện để:

12

0xx

là:

 

1

0 ' 0

0

S

P

   















.

 

ii

Điều kiện để:

12

0 xx

là:

 

2

0 ' 0

0

S

P

   















.

 

iii

Điều kiện để:

12

0xx

là:

 

0 3P 

.

.b

So sánh nghiệm với hằng số

,



(Với

,



là các tham số thực

cho trước).

 

i

Điều kiện để:

12

xx





là:

   

.04af





.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

93

[ I can't, I can! ]

Extra Techniques:

Tips:

Cơ sở hình thành các

điều kiện:

 

3

:Sỡ dĩ chỉ cần một

điều kiện

0P 

là vì khi

00

c

PP

a

   

hay

00ac ac   

. Khi

đó:

2

40b ac    

.

Đã thỏa mãn điều kiện

cần và đủ để phương

trình có hai nghiệm thực

phân biệt.

       

4 , 7 , 8 , 9

:

 

gx

trong khoảng hai nghiệm

thì trái dấu với hệ số

a

và ở ngoài hai khoảng

nghiệm thì cùng dấu với

hệ số

a

. Và tích của

một số dương với một số

âm là một số âm.

 

5

: Vì

21

xx





nên

1 2 1

22

2

S

x x x



    

 

6

: Vì

12

xx





nên

1 2 2

22

2

S

x x x



    

 

6

: Vì

12

xx



  

nên

1 1 2 2

22x x x x  

.

Khi đó:

22S





2

S



  

.

 

ii

Điều kiện để:

12

xx





là:

 

   

5

0 ' 0

.0

2

af

S







   













.

 

iii

Điều kiện để:

12

xx





là:

 

   

6

0 ' 0

.0

2

af

S







   













.

 

iv

Điều kiện để:

12

xx



  

là:

 

7

.0

af



















.

 

v

Điều kiện để:

12

xx



  

là:

 

8

.0

af



















.

 

vi

Điều kiện để:

12

xx



  





  



là:

     

0 9.ff





.

 

vii

Điều kiện để:

12

xx



  

là:

 

0

0 ' 0

.0

2

1

af

S







   





















.

Để tiết kiệm thời gian cho một số bài toán ta có thể tính trực tiếp dựa

trên hàm số bậc ba:

 

32

0y ax bx cx d a    

.

Khi đó:

 Hàm số đồng biến trên khi và chi khi .

 Hàm số nghịch biến trên khi và chi khi

'2

'

0

30

f

a

b ac









   





.

'2

'

0

30

f

a

b ac









   





Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

94

[ I can't, I can! ]

Extra Techniques:

Tips:

Cơ sở hình thành các

điều kiện:

Lưu ý: Ở các điều kiện

   

5 , 6 ,

 

10

thì dấu

của các tích

 

.,af



 

.af



đều được xét

dấu tương tự với

 

4,

     

7 , 8 , 9

. Và vì

phương trình có hai

nghiệm phân biệt nên

0

hoặc

'0

.

Extra Techniques:

Remark:

Ngoài ra ta còn có thể cô

lập tham số

m

để việc

tính toán trở nên dễ dàng

hơn.

Câu 1. Tìm tất cả các giá trị thực của tham số

m

để hàm số

   

32

1

1 2 1 2

3

y x m x m x m      

đồng biến trên khoảng

 

; 

?

A.

15m

. B.

5

1

m











.

C.

0m 

. D.

0m 

.

(Trích đề thi Nhóm toán anh Dúi 2020 - 2021)

Đáp án: C

Lời giải

TXĐ: .

Xét hàm số:

   

32

1

1 2 1 2

3

y x m x m x m      

.

Ta có:

 

2

' 2 1 2 1y x m x m    

.

Cách 1: Định lý về dấu.

Để hàm số đồng biến trên khoảng

 

; 

thì

 

'

0

*

'0

y

a 













.

 

   

2

10

*0

0

1 2 1 0

m

mm











   





   





(Do

2

0m 

).

Vậy với

0m 

hàm số

   

32

1

1 2 1 2

3

y x m x m x m      

đồng

biến trên khoảng

 

; 

.

Cách 2: Cô lập

m

.

Ta có:

 

     

2

' 2 1 2 1 1 2 1y x x m x x m x        

.

Để hàm số đồng biến trên khoảng

 

; 

thì:

'0y 

.

D 

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

95

[ I can't, I can! ]

Extra Techniques:

Remark:

Không phải lúc nào cô

lập tham số

m

cũng là

phương án tối ưu cho bài

toán đồng biến nghịch

biến trên khoảng

K

cho

trước. Vì thế ngoài việc

biết giải một cách máy

móc ta còn phải biết sử

dụng các phương pháp

một cách phù hợp.

Khi đó:

         

22

1 2 1 2 1 1 **x m x m x x      

.

Ta xét các khả năng:

 Trường hợp 1:

1x 

.

 

** 0 0

luôn đúng

 

1m

.

 Trường hợp 2:

1 1 0xx   

.

Khi đó:

 

1;

11

** , 1 min 0 0 2

22

xx

m x m m





        

.

 Trường hợp 3:

1 1 0xx   

.

Khi đó:

 

;1

11

** , 1 max 0 0 3

22

xx

m x m m





        

.

Từ

     

1 , 2 , 3 0m

.

Câu 2. Tìm tất cả các giá trị thực của tham số để hàm số

   

32

1

1 1 1

3

y x m x m x      

nghịch biến trên khoảng ?

A.

21m   

. B.

1

2

m











.

C.

21m   

. D.

2

1

m











.

(Trích đề thi Nhóm toán anh Dúi 2020 - 2021)

Đáp án: A

Lời giải

TXĐ: .

Xét hàm số: .

Ta có: .

Cách 1: Định lý về dấu

m

 

; 

D 

   

32

1

1 1 1

3

y x m x m x      

   

2

' 2 1 1y x m x m     

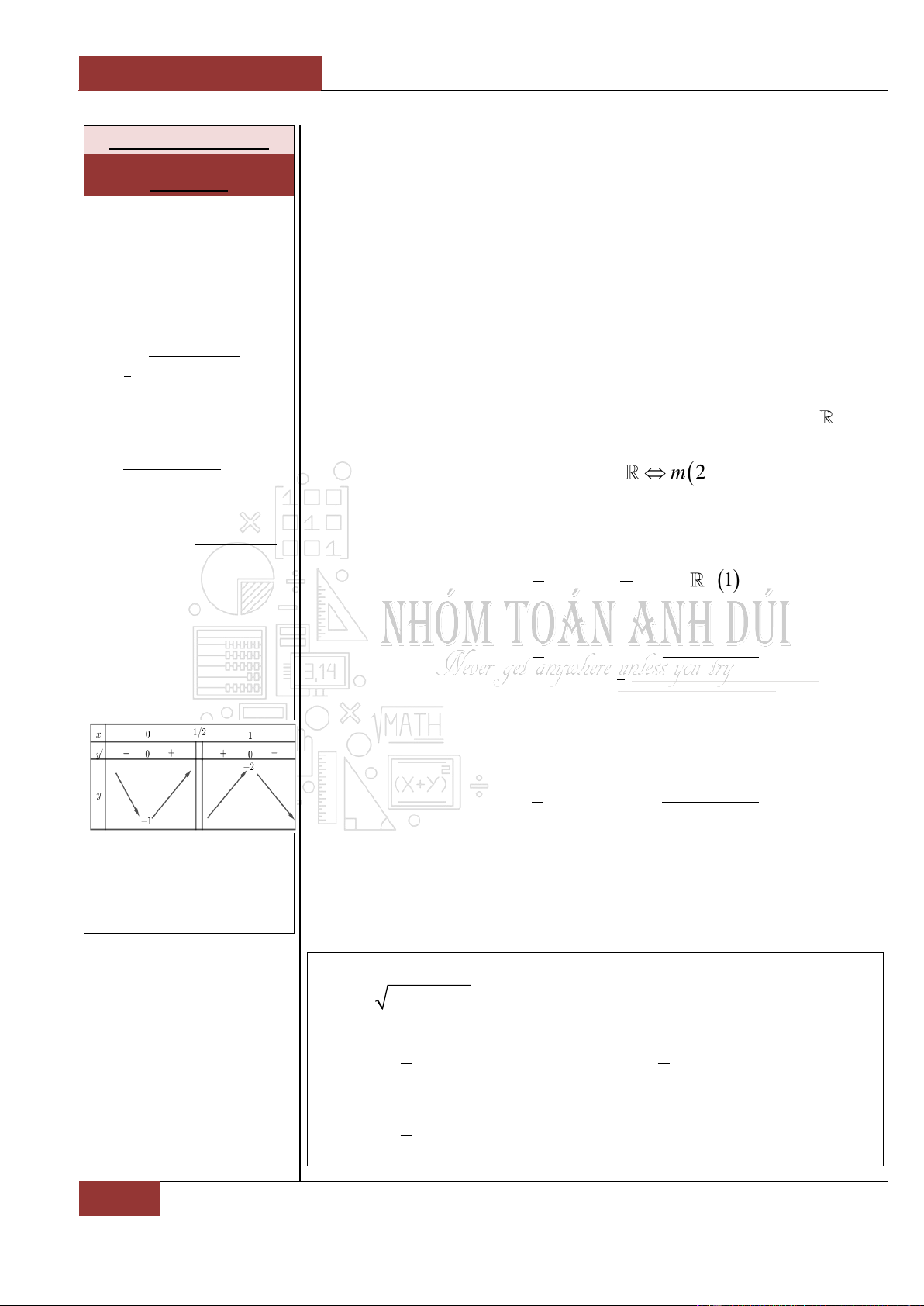
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

96

[ I can't, I can! ]

Extra Techniques:

Remark:

Cơ sở kết luận:

2

1

;

2

1

;

2

21

max 2

21

min 1

21

xx

x

xx

x





















  















   















Ta xét hàm số:

2

21

xx

y

x

  





Khi đó:

 

2

22

'

21

xx

y

x







Cho

0

'0

1

x

y

x













.

Bảng biến thiên:

Dựa vào bảng biến thiên

ta có ngay kết luận bên

trên.

Để hàm số nghịch biến trên khoảng thì

 

'

0

*

'0

y

a 









.

 

2

10

* 2 1

3 2 0

1 1 0

m

mm











      



  

   





.

Cách 2: Cô lập tham số

m

.

Ta có:

 

2

' 2 1 2 1y x x m x     

.

Để hàm số nghịch biến trên khoảng

 

; 

thì:

' 0,yx  

.

 

   

22

2 1 2 1 0, 2 1 2 1x x m x x m x x x              

.

Ta xét các trường hợp:

 Trường hợp 1:

 

11

0 , 1

24

xm     

.

 Trường hợp 2:

2

1

;

2

1 2 1

max 2

2 2 1

xx

xm

x











  

    







.

Suy ra:

 

22m 

.

 Trường hợp 3:

2

1

;

2

1 2 1

min 1

2 2 1

xx

xm

x











  

    







.

Suy ra:

 

13m 

.

Từ

     

1 , 2 , 3 2 1m    

.

Câu 3. Tìm tất cả các giá trị thực của tham số để hàm số

2

y x x x m   

nghịch biến trên khoảng ?

A.

1

4

m 

. B.

1

4

m 

.

C.

1

4

m 

. D. Không có giá trị

m

thỏa mãn.

 

; 

m

 

; 

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

97

[ I can't, I can! ]

Đáp án: D

Lời giải

ĐKXĐ:

22

11

00

44

x x m x x m

   

         

   

   

.

Suy ra:

 

2

;

1 1 1

min 0 1

4 2 4

m x m

 

   

     

   

   

.

1

,

4

m

ta có:

2

21

'1

2

x

y

x x m







.

Để hàm số nghịch biến trên khoảng

 

; 

thì:

'0y 

và dấu

""

đạt tại hữu hạn điểm. Vì thế ta cho

2

21

' 0 1

2

x

y

x x m



  



.

Vì

2

20x x m  

. Nên:

 

2

22

1

2 1 2 *

2

4 4 1 4 4 4

x

x x x m

x x x x m







     





    



.

   

1

2

*2

1

4

x

m



















.

Từ

  

1

2

12

1

4

x

m



















.

Thử lại, với

1

4

m 

, ta có:

2

1 1 1 1 1

4 2 2 2 2

y x x x x x x x x x

   

             

   

   

.

Khi đó:

 

' 0, ;yx    

(Loại).

Vậy không tồn tại giá thực

m

để hàm số nghịch biến trên .

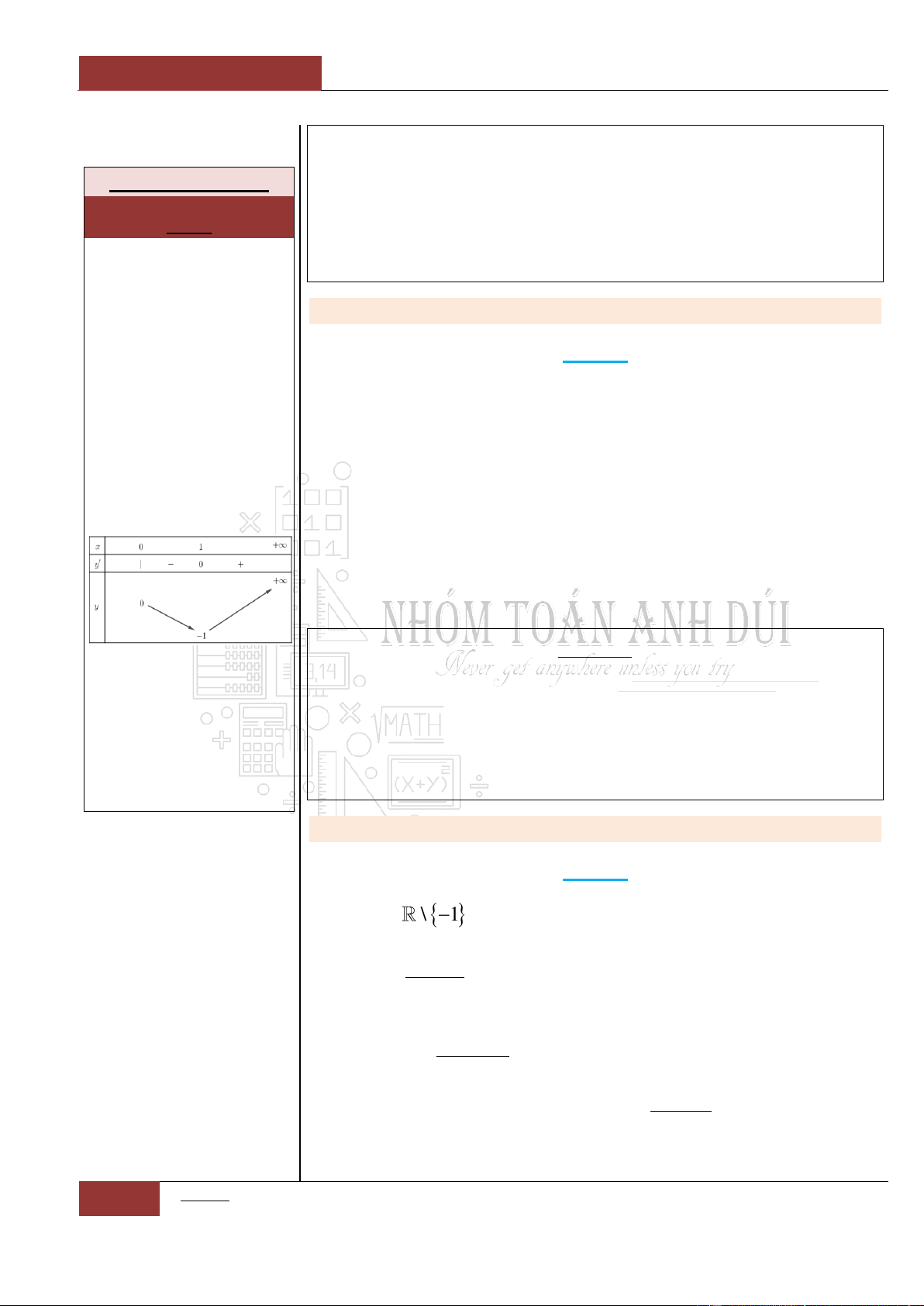
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

98

[ I can't, I can! ]

Extra Techniques:

Tips:

Cơ sở khẳng định:

 

2

0;

min 2 1xx





  



.

Ta xét hàm số:

 

2

2 , 0;y x x x    

Ta có:

' 2 2 0 1y x x    

.

Bảng biến thiên:

Dựa vào bảng biến thiên

của đồ thị hàm số, ta dễ

dàng kết luận được:

 

2

0;

min 2 1xx





  



Câu 4. Tìm

m

để hàm số

32

3 3 1y x x mx    

nghịch biến trên

khoảng

 

0;

?

A.

1m 

. B.

1m 

.

C.

1m 

. D.

1m 

.

Đáp án: A

Lời giải

Xét hàm số:

32

3 3 1y x x mx    

.

Ta có:

2

' 3 6 3y x x m   

.

Để hàm số nghịch biến trên khoảng

 

0;

thì

 

' 0, 0;yx   

.

Khi đó:

   

22

3 6 3 0, 0; 2 , 0;x x m x m x x x            

.

Suy ra:

 

2

0;

min 2 1 1m x x m





      



.

Câu 5. Tìm

m

để hàm số

2

1

xm

y

x







giảm trên từng khoảng mà nó

xác định?

A.

1m 

. B.

1m 

.

C.

3m 

. D.

3m 

.

Đáp án: B

Lời giải

TXĐ:

 

\1D 

.

Ta có:

 

2

1

'

1

m

y

x







.

Để hàm số

2

1

xm

y

x







nghịch biến (giảm) trên từng khoảng xác

định thì

   

 

2

1

' 0, ; 1 , 1; 0

1

m

yx

x



        



.

Hay:

1 0 1mm   

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

99

[ I can't, I can! ]

Extra Techniques:

Tips:

Cơ sở khẳng định:

 

2

;

max 3 0x

 







là vì:

22

0, 3 0x x x     

Câu 6. Với giá trị nào của

a

thì hàm số

3

y ax x

đồng biến trên .

A.

0a 

. B.

0a 

.

C.

0a 

. D. Với mọi giá trị thực của tham số

a

.

Đáp án: A

Lời giải

Xét hàm số

3

y ax x

.

Ta có:

2

'3y a x

.

Để hàm số

3

y ax x

đồng biến trên thì

' 0,yx  

.

Hay

 

2 2 2

;

3 0, 3 , max 3 0a x x a x x a x

 



            



.

Suy ra:

0a 

.

Câu 7. Hàm số nào sau đây nghịch biến trên với mọi

m

?

A.

23

y m x m  

. B.

2 3 2

31y m x mx x    

.

C.

1mx

y

xm







. D.

3

21y x mx  

.

Đáp án: B

Lời giải

Xét từng đáp án:

 Đáp án A sai vì với

00my  

. Khi đó hàm số là hàm

không đổi trên .

Loại A.

 Đáp án B đúng vì ta có:

2

2 2 2 2

1 8 3 8

' 3 2 3 3 2 3

3 3 3 3

y m x mx m x mx mx



            





Khi đó:

8

' 0, ,

3

y x m    

. Nên hàm số nghịch biến trên với

mọi giá trị thực

m

.

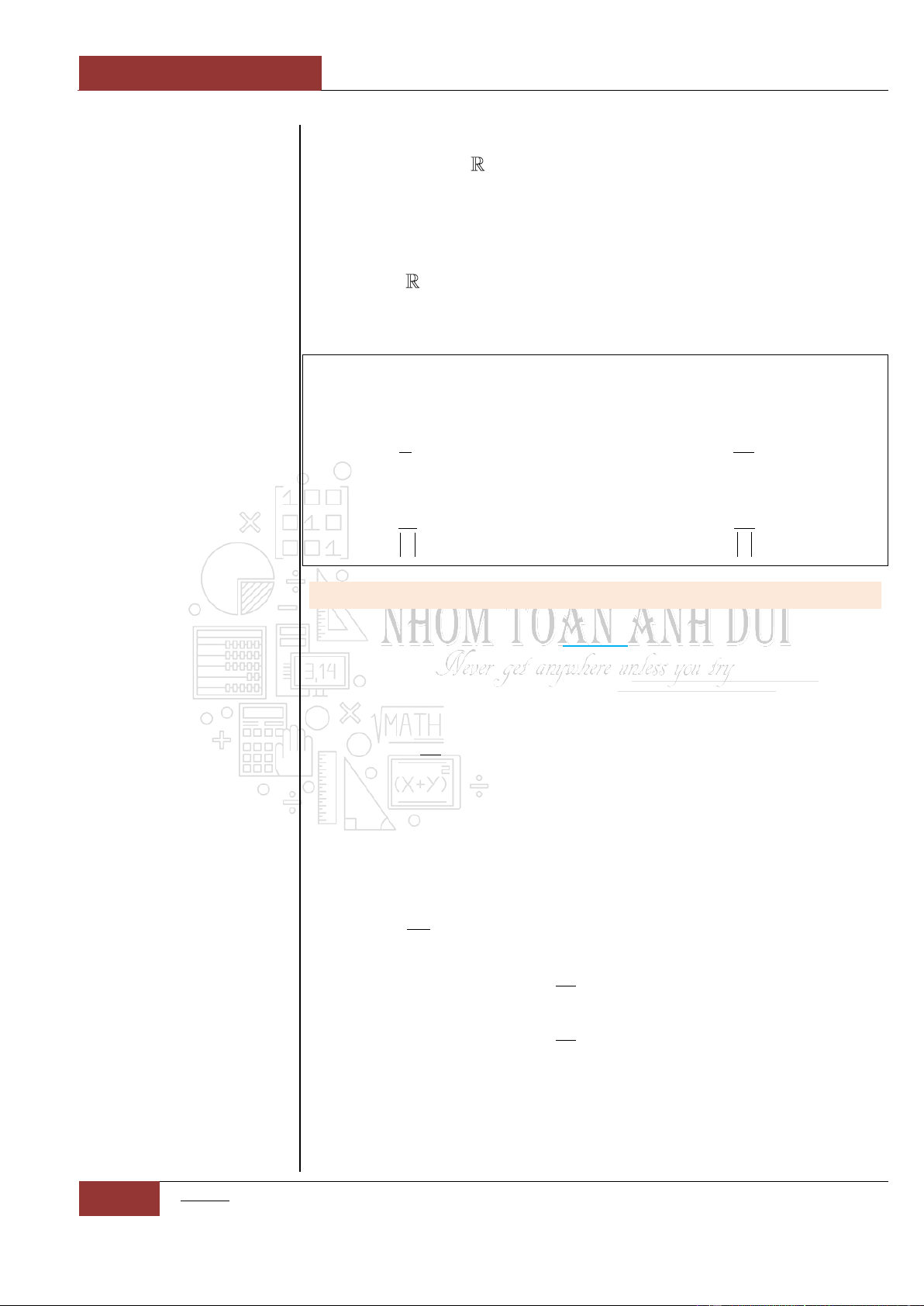
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

100

[ I can't, I can! ]

 Đáp án C sai vì hàm số là hàm nhất biến nên hàm số không

liên tục trên .

Loại C.

 Đáp án D sai vì với

3

01m y x   

là một hàm đồng biến

trên .

Loại D.

Câu 8. Hàm số nào trong các hàm số sau chỉ có một chiều biến thiên

trên tập xác định của nó?

A.

1

y

x



. B.

2

1

y

x



.

C.

1

y

x



. D.

2

x

y

x



.

Đáp án: A

Lời giải

Xét từng đáp án:

 Đáp án A đúng vì trên khoảng

 

;0

và

 

0;

, ta có:

2

1

'0y

x

  

. Nên hàm số đã cho luôn nghịch biến trên từng

khoảng xác định.

Chọn A.

 Đáp án B sai vì trên khoảng

 

;0

và

 

0;

, ta có:

3

2

'y

x





. Và dấu của đạo hàm bị đổi khi

x

đi qua

0

. Hay ta có

thể kết luận do

3

2

0, 0

'

2

0, 0

x

y

x



   









   





.

Loại B.

 Đáp án C sai vì

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

101

[ I can't, I can! ]

2

1

0, 0

,0

'

11

, 0 0, 0

x

xx

yy

xx

x



  







  





   





.

Loại C.

 Đáp án D sai vì:

2

,0

1, 0

'

1, 0

,0

x

xx

x

yy

x

xx

x













  









  







.

Loại D.

Câu 9. Tập hợp tất cả các giá trị của tham số

m

để hàm số

3 1 2xm

y

xm







nghịch biến trên khoảng

 

5;

là?

A.





1; 

. B.





1;5

.

C.

 

1;5

. D.

 

1; 

.

Đáp án: B

Lời giải

Xét hàm số:

3 1 2xm

y

xm







.

TXĐ:

 

\Dm

.

Ta có:

 

2

1

'

m

y

xm







.

Để hàm số nghịch biến trên khoảng

 

5;

thì trước hết, trên khoảng

 

5;

, hàm số

3 1 2xm

y

xm







phải liên tục và có

'0y 

 

*

.

 

10

* 1 5

5

m





   







.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

102

[ I can't, I can! ]

Câu 10. Tìm tất cả các giá trị thực của tham số

m

sao cho hàm số

32

2sin 3sin siny x x m x  

tăng trên khoảng

0;

2









.

A.

0m 

. B.

3

2

m 

.

C.

3

2

m 

. D.

3

2

m 

.

Đáp án: C

Lời giải

Đặt:

sintx

. Vì

 

0; 0;1

2

xt





  





.

Ta biết rằng

cos 0, 0; sin

2

x x y x





    





là một hàm đồng biến

trên

0;

2









. Vì thế tính đơn điệu của hàm số được giữ không đổi.

Xét hàm số:

 

32

2 3 , 0;1y t t mt t   

.

Ta có:

2

' 6 6y t t m  

Cách 1: Định lý về dấu.

Để hàm số

32

23y t t mt  

đồng biến trên khoảng

 

0;1

thì

phương trình

'0y 

hoặc là vô nghiệm hay có nghiệm kép (

0

)

hoặc là có hai nghiệm thực phân biệt

 

0

nằm ngoài đoạn

 

0;1

(có thể nằm về trái, hoặc nằm về phải).

Xét các khả năng:

 Trường hợp 1: Phương trình

'0y 

vô nghiệm hoặc có nghiệm

kép. Khi đó:

3

' 9 6 0

2

mm     

.

 Trường hợp 2: Phương trình

'0y 

có hai nghiệm thỏa mãn:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

103

[ I can't, I can! ]

Extra Techniques:

Tips:

Cơ sở khẳng định:

 

2

0;1

3

max 6 6

2

tt







là do:

Hàm số

2

66y t t

trên

khoảng

 

0;1

, có:

1

' 6 12 0

2

y t t    

và:

 

0;1

00

13

max

22

10

y

yy

y























.

Extra Techniques:

Remark:

Cơ sở xét

3

2

m 

là vì ở

cả ba đáp án B, C, D giá

trị

3

2

đều thuộc vào các

khoảng. Nếu C đúng thì

B, D đều sai.

Cơ sở xét

1m 

là vì

 

1 0; , 

3

1;

2



 







.

12

01

tt

  





  



Khi đó ta có:

  

12

3

2

'0

10

0

6

' 0 3

2

1

2

1

2

1 1 0

6

m

S

m

P

m

S

tt

m















  







































   











































  













  









.

Vậy

3

2

m 

.

Cách 2: Cô lập

m

.

Ta có:

 

22

0;1

3

6 6 0, 0;1 max 6 6

2

t t m t m t t



        



.

Vậy

3

2

m 

.

Cách 3: Casio

Với

 

2

3 3 6

' 6 6 6 0, 0;1

2 2 2

m y t t t t



         





và dấu

""

chỉ xảy ra tại

 

1

0;1

2

t 

. Vì thế hàm số đồng biến trên

 

0;1

.

Loại B, D.

Với

2

1 ' 6 6 1 0m y t t     

có hai nghiệm thực phân biệt.

Theo định lý Viéte ta có:

12

10

01

1

.0

6

tt

  





   









(Mâu thuẫn).

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

104

[ I can't, I can! ]

Loại A.

Chọn B.

Câu 11. Xác định giá trị của tham số m để hàm số

     

32

1 3 1 2 4y f x m x m x mx      

đồng biến trên khoảng có độ dài bằng

1

.

A.

9m 

. B.

1m 

.

C.

9

1

m











. D. Không có giá trị

m

thỏa mãn.

Đáp án: A

Lời giải

Ta xét các khả năng:

 Trường hợp 1:

1m 

, khi đó:

 

24y f x x   

là một

đường thẳng có hệ số góc

20k   

. Nên hàm số nghịch biến

trên .

 Trường hợp 2:

1m 

, khi đó:

Nếu

 

'0fx

vô nghiệm hoặc có nghiệm kép thì hàm số luôn đồng

biến trên . (Loại)

Nếu

 

'0fx

có hai nghiệm thực

12

,xx

thì hàm số đồng biến trên

hai khoảng

 

1

;x

và

 

2

;x 

. (Loại)

Như vậy ở Trường hợp 2 không tồn tại giá trị thực

m

nào để cho

hàm số đồng biến trên khoảng có độ dài bằng

1

.

 Trường hợp 3:

1m 

, khi đó:

Nếu

 

'0fx

vô nghiệm hoặc có nghiệm kép thì hàm số luôn

nghịch biến trên . (Loại)

Nếu

 

'0fx

có hai nghiệm thực

12

,xx

thì hàm số đồng biến trên

khoảng

 

12

;xx

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

105

[ I can't, I can! ]

Đồ thị I.2.1

Như vậy để hàm số đồng biến trên khoảng có độ lớn bằng

1

thì:

 

'

12

1

' 0 *

1

fx

m

xx



















.

Ta có:

     

2

' 3 1 6 1 2f x m x m x m    

.

 

      

2

'

1

' 9 1 6 1 1 3 9 0

3

fx

m

m m m m m

m





          







.

Theo định lý Viéte, ta có:

 

12

2

31

xx

m

xx

m

















.

Mà

   

22

1 2 1 2 1 2 1 2

1 1 4 1x x x x x x x x        

 

2

1

3

1

*9

2

2 4. 1

3

31

2

2 4. 1

31

m





















    





























.

Đáp án A.

Một số Tips để làm tốt các bài toán chứa tham số

m

 

1

Xét hàm số

 

32

,0y ax bx cx d a    

, ta có các nhận

xét:

Hàm số có đạo hàm

2

' 3 2y ax bx c  

liên tục trên .

 Trường hợp 1:

0

'0

a 









hay

2

0

3

a

b ac











Khi đó phương trình

'0y 

hoặc vô nghiệm, hoặc có nghiệm kép và

hàm số

32

y ax bx cx d   

đồng biến trên .

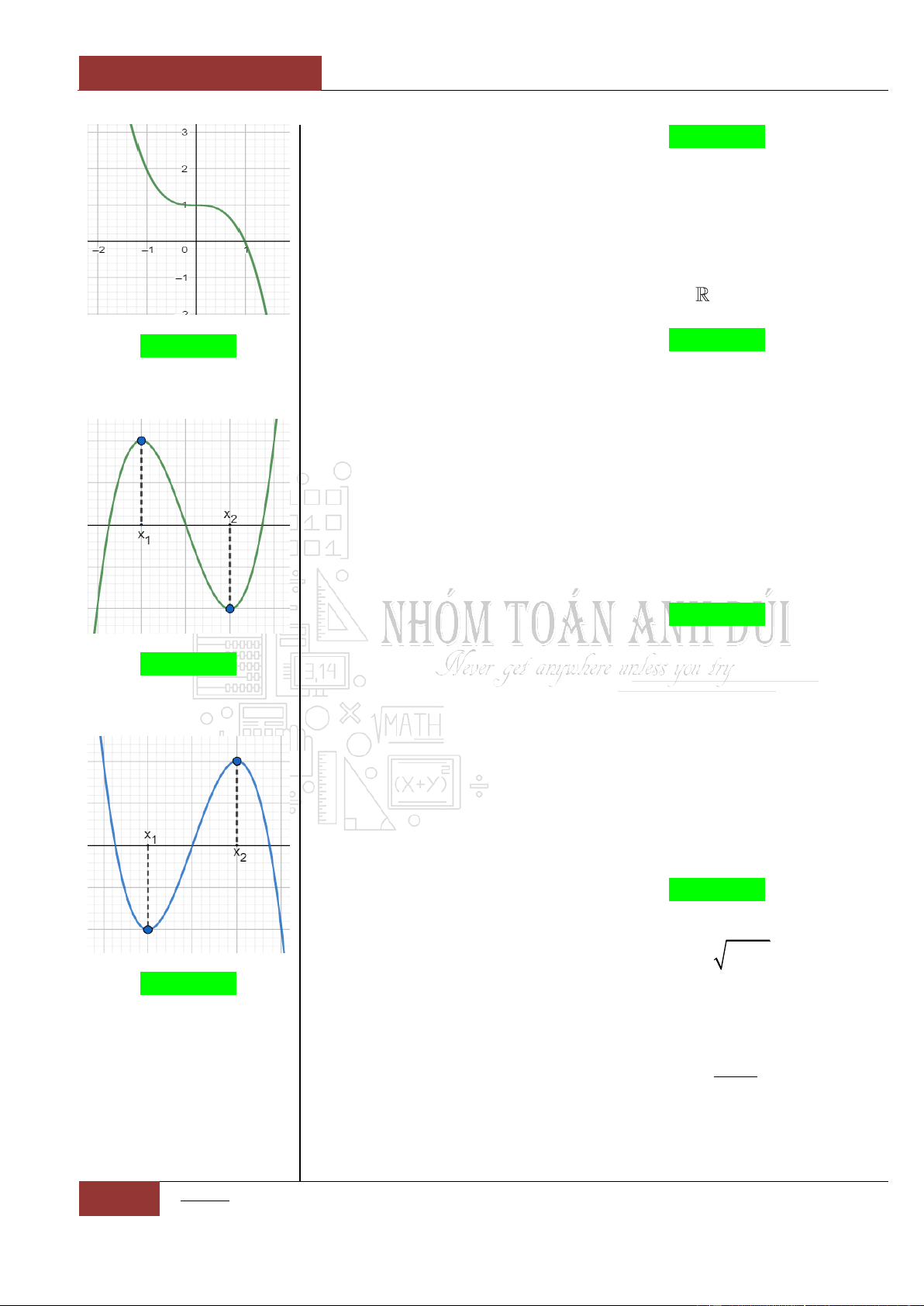
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

106

[ I can't, I can! ]

Đồ thị I.2.2

Đồ thị I.2.3

Đồ thị I.2.4

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.2.1).

 Trường hợp 2:

0

'0

a 









hay

2

0

3

a

b ac











Khi đó phương trình

'0y 

hoặc vô nghiệm, hoặc có nghiệm kép và

hàm số

32

y ax bx cx d   

nghịch biến trên .

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.2.2).

 Trường hợp 3:

0

'0

a 









hay

2

0

3

a

b ac











Khi đó phương trình

'0y 

có hai nghiệm thực phân biệt

12

xx

và

hàm số

32

y ax bx cx d   

nghịch biến trong khoảng giữa hai

nghiệm

 

12

;xx

và đồng biến trên hai khoảng không chứa

12

,xx

là

 

1

;x

và

 

2

;x 

.

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.2.3).

 Trường hợp 4:

0

'0

a 









hay

2

0

3

a

b ac











Khi đó phương trình

'0y 

có hai nghiệm thực phân biệt

12

xx

và

hàm số

32

y ax bx cx d   

đồng biến trong khoảng giữa hai

nghiệm

 

12

;xx

và nghịch biến trên hai khoảng không chứa

12

,xx

là

 

1

;x

và

 

2

;x 

.

Minh họa hình dạng chung của đồ thị (Xem Đồ thị I.2.4).

 

2

Đối với một số hàm số đặc biệt như

 

tan

cot

1

....

y f x

y

fx























.

Trước tiên ta cần phải xác định ĐKXĐ và đối chiếu lại với kết quả

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

107

[ I can't, I can! ]

vừa tính được để thu được kết quả chính xác.

 

3

Đối với dạng câu hỏi về đồng biến, nghịch biến trên toàn tập

thì một số hàm phân thức, căn thức, hàm lượng giác có thể loại

ngay, điển hình như một số hàm dưới đây:

 

42

2

,0

......

ax b

ya

cx d

y ax bx c a













   





   





.

 

4

Đối với dạng toán tìm

m

để hàm số

32

y ax bx cx d   

đồng biến, nghịch biến trên một khoảng, đoạn

 

;



cho trước.

Nếu dấu của đạo hàm phụ thuộc vào dấu của tam thức bậc hai

2

' 3 2y ax bx c  

thì ta phải chia thành hai trường hợp để xét.

 Trường hợp 1:

 

0*

.

Nếu

0a 

, hàm số luôn đồng biến trên nên sẽ đồng biến

trên khoảng

 

;



. Nếu yêu cầu đề bài buộc hàm số đồng biến trên

khoảng

 

;



thì ta nhận toàn bộ giá trị

m

giải được từ

 

*

, ngược

lại ta sẽ loại trường hợp 1.

Nếu

0a 

, hàm số luôn nghịch biến trên nên sẽ nghịch

biến trên khoảng

 

;



. Nếu yêu cầu đề bài buộc hàm số nghịch biến

trên khoảng

 

;



thì ta nhận toàn bộ giá trị

m

giải được từ

 

*

,

ngược lại ta sẽ loại trường hợp 1.

 Trường hợp 2:

 

0 **

.

Ta sẽ lập bảng biến thiên để tham chiếu và xác định khoảng biến thiên

theo yêu cầu đề bài. Bên cạnh kết hợp sử dụng định lý về dấu và

định lý Viéte như đã trình bài ở phần mở đầu để giải quyết bài toán.

 

5

Đối với dạng toán có hệ số của bậc cao nhất thay đổi theo

tham số

m

:

       

1

....

nn

y g m x h m x p m x q m



    

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

108

[ I can't, I can! ]

Khi đó:

       

12

' . . 1 . . ...

nn

y n g m x n h m x p m



    

.

Ta xét hai trường hợp:

 Trường hợp 1:

 

0gm

.

 Trường hợp 2:

 

0gm

.

 

6

Xét hàm số:

     

1

...

nn

y a f x b f x cf x d



    

   

   

.

Đối với một số bài toán tìm

m

để hàm số đồng biến, nghịch biến trên

khoảng

K

phức tạp, hàm lồng hàm, để giải quyết bài toán một cách

gọn gàng hơn, người ta thường dùng phương pháp đặt ẩn phụ.

Đặt:

 

t f x

.

Khi đó hàm số đã cho trở thành:

1

...

nn

y at bt ct d



    

.

Tuy nhiên một số lỗi sai HS thường hay mắc phải là:

 Quên tìm tập giá trị của

t

.

 Quên xét tính đơn điệu của hàm số

 

fx

trên khoảng

K

.

 Kết luận theo tập giá trị của

x

.

Tuy nhiên lỗi sai thứ hai là thường thấy nhất. Ta rút ra lưu ý như sau:

Xét hàm số

     

1

...

nn

y a f x b f x cf x d



    

   

   

trên

1

K

. Đặt

 

2

,t f x t K

, trong đó

2

K

là khoảng, nữa khoảng, hoặc đoạn được

tính chặt chẽ theo

 

fx

trên

1

K

.

Nếu

 

1

' 0,f x x K  

và dấu

""

xảy ra tại hữu hạn điểm

(Hàm số đồng biến trên

1

K

) thì tính đơn điệu của hàm không đổi

(Đồng



Đồng, Nghịch



Nghịch) sau khi đặt ẩn phụ.

Nếu

 

1

' 0,f x x K  

và dấu

""

xảy ra tại hữu hạn điểm

(Hàm số nghịch biến trên

1

K

) thì tính đơn điệu của hàm bị thay đổi

(Đồng



Nghịch, Nghịch



Đồng) sau khi đặt ẩn phụ.

Nếu

 

'fx

đan dấu trên

1

K

thì ta xét từng trường hợp rồi áp dụng

phương pháp ở trên. Thông thường dạng này ta sẽ dùng cô lập

m

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

109

[ I can't, I can! ]

Extra Techniques:

Tips:

Định lý Viéte đối với

phương trình bậc hai:

Nếu

12

,xx

là hai nghiệm

của phương trình:

 

2

0, 0ax bx c a   

thì:

12

b

x x S

a

c

x x P

a



   













.

 

7

Đối với dạng toán hàm phân thức có mẫu số chứa

m

. Ta cần

lưu ý một số điều sau:

Muốn hàm số đơn điệu trên khoảng

K

thì trước hết hàm số phải

liên tục trên khoảng

K

.

Đối với hàm nhất biến

ax b

y

cx d







, có:

 

2

'

ad bc

y

cx d







.

Nếu hàm số đồng biến thì

0ad bc

, nghịch biến thì

0ad bc

.

Tuy nhiên đối với hàm phân thức bậc hai trên bậc hai:

2

ax bx c

y

dx ex f







, có:

   

 

2

'

ae bd x af cd x bf ce

y

dx ex f

    





Nếu hàm số đồng biến thì

   

2

20ae bd x af cd x bf ce     

nghịch biến thì

   

2

20ae bd x af cd x bf ce     

.

 

8

Đối với dạng toán tìm

m

để hàm số đồng biến, nghịch biến

trên khoảng có độ lớn bằng

k

.

Ta thường sử dụng định lý Viéte kết hợp hằng đẳng thức để giải

quyết một cách nhanh chóng.

Định lý Viéte mở rộng:

Cho phương trình:

 

1

1 1 0

... 0, 0 *

nn

n n n

a x a x a x a a



     

có

12

, ,...,

n

x x x

là

n

nghiệm của phương trình

 

*

. Khi đó:

 

1

12

2

1 2 2 3 1

0

1 2 3

...

.........

... 1 .

n

a

x x x

a

x x x x x x

a

x x x x

a





    



   













.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

110

[ I can't, I can! ]

Extra Techniques:

Remarks:

Hàm số bậc ba đơn điệu

(Hoặc đồng biến, hoặc

nghịch biến) trên khoảng

có độ dài

k

khi phương

trình

'0y 

có hai

nghiệm thực phân biệt

thỏa mãn:

22

4S P k

.

"Trên đây là một số

Tips chúng tôi cảm thấy

rất hữu dụng trong các

bài toán hiện hành. Do

mục đích phục vụ cho

phần đông các bạn học

sinh nên phần trình bày

khá chi tiết và khá dài.

Nhưng nếu bạn đọc

hiểu bản chất vấn đề,

thao tác sẽ ngắn gọn

hơn, chuẩn xác hơn và

quan trọng nhất vẫn là

lợi thế về thời gian nếu

biết các Tips này.

Một số đẳng thức cần lưu ý:

 

   

     

   

 

2

2 2 2 2 2

1

2 1 1 2 2 1 2 1 2 1 2

2 2 2

4 4 2 2 2 2 2 2

1 2 1 2 1 2 1 2

2

22

2

3 3 2 2

1 1 1 2 1

2

1 2 2 1 1 2 1 2

3

1 2 1 2

1

22

1 2 1 2 1

2

3

33

2 2 2

2

22

1

2

1

x x x x x x x x x x x x x x

x x x x x x x x x x x x S P

x x x x

xx

x x x x

x x x x x

x x x x S SP

x S P

x

P

x



        



     



         

     



      



   

2

2 1 1 2 1 2 1

12

2

4 4 ,

x

x x x x x x S P x

xS

xP

x





     

 

9

Bài toán tịnh tiến đồ thị:

Giả sử hàm số:

 

y f x

đồng biến (nghịch biến) trên khoảng

K

.

Khi đó hàm số

   

y f x g m

với

 

gm

là một hàm theo tham số

m

, cũng đồng biến (nghịch biến) trên khoảng

K

.

Giả sử hàm số:

 

y f x

đồng biến (nghịch biến) trên

 

;ab

.

 

i

Hàm số

 

,0y f x m m  

đồng biến (nghịch biến) trên

khoảng

 

;a m b m

.

 

ii

Hàm số

 

,0y f x m m  

đồng biến (nghịch biến) trên

khoảng

 

,a m b m

.

Giả sử hàm số:

 

y f x

đồng biến (nghịch biến) trên

 

;ab

.

 

i

Hàm số

 

,0y f mx n m  

đồng biến (nghịch biến) trên

khoảng

;

a n b n

mm









.

 

ii

Hàm số

 

,0y f mx n m  

nghịch biến (đồng biến) trên

khoảng

;

b n a n

mm









.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

111

[ I can't, I can! ]

TỰ LUYỆN 4 MỨC ĐỘ

Câu 1. [Nhận biết].

Tìm tất cả các giá trị của tham số thực

m

để hàm số

   

32

12

2 5 4

33

y x m x m x     

đồng biến

trên khoảng

 

; 

.

A.

1

8

m











. B.

18m

.

C.

1

8

m











. D.

18m

.

Câu 2. [Nhận biết].

Hàm số

   

32

1

1 1 2

3

y x m x m x     

đồng biến trên tập xác định của nó khi

A.

4m 

. B.

21m   

.

C.

2m 

. D.

4m 

.

Câu 3. [Thông hiểu].

Trong tất cả các giá trị thực của tham số

m

làm

cho hàm số

   

32

32f x x mx m x m    

đồng biến trên , giá trị lớn nhất là?

A.

0

. B.

1

.

C.

2

. D.

2

3



.

Câu 4. [Thông hiểu].

Trong tất cả các giá trị của tham số

m

để hàm

số

32

1

3

y x mx mx m   

đồng biến trên ,

giá trị nhỏ nhất của

m

là?

A.

4

. B.

1

.

C.

0

. D.

1

.

Câu 5. [Nhận biết].

Cho hàm số

 

32

4 9 5y x mx m x     

với

m

là tham số. Có bao nhiêu giá trị nguyên của

m

để hàm số nghịch biến trên

 

; 

?

A.

7

. B.

4

.

C.

6

. D.

5

.

Câu 6. [Thông hiểu].

Tất cả các giá trị của tham số

m

để hàm số

   

32

2 3 2 1 6 1 1y x m x m m x     

đồng

biến trên khoảng

 

2;

là?

A.





;1m 

. B.

 

1;m 

.

C.

 

\1m

. D.

1m 

.

Câu 7. [Vận dụng].

Điều kiện của tham số

m

để hàm số

 

32

2 3 6 1f x x x mx   

nghịch biến trên

khoảng

 

0;2

là?

A.

6m 

. B.

6m 

.

C.

1

4

m 

. D.

1

6

4

m  

.

Câu 8. [Vận dụng].

Tất cả các giá trị của

m

để hàm số

   

32

3 3 2 1f x x mx m x   

đồng biến trên

khoảng

 

2;3

là?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

112

[ I can't, I can! ]

A.

3

2

m 

. B.

3

2

m 

.

C.

3

2

m 

. D.

3

;1

2

mm

.

Câu 9. [Vận dụng].

Tìm tất cả các giá trị của tham số

m

để hàm số

 

42

2 4 2y x m x m    

nghịch biến trên

đoạn

 

1;0

.

A.

4m 

. B.

4m 

.

C.

2m 

. D.

2m 

.

Câu 10. [Nhận biết].

Điều kiện cần và đủ để hàm số

5

1

mx

y

x







đồng biến trên từng khoảng xác định là?

A.

5m 

. B.

5m 

.

C.

5m 

. D.

5m 

.

Câu 11. [Nhận biết].

Cho hàm số

22mx m

y

xm







. Tìm

m

để hàm

số đồng biến trên từng khoảng xác định?

A.

31m  

. B.

31m  

.

C.

1

3

m











. D.

13

m



  



  





.

Câu 12. [Thông hiểu].

Tìm

m

để hàm số

22xm

y

xm







đồng biến

trên khoảng

 

1;2

?

A.

2

3

m 

. B.

1m 

.

C.

2

3

m  

. D.

2

1

3

m

.

Câu 13. [Thông hiểu].

Cho hàm số

23mx m

y

xm







. Tìm tất cả các

giá trị thực của

m

để hàm số nghịch biến trên

khoảng

 

2;

.

A.

2

3

m 

. B.

1m 

.

C.

2

3

m  

. D.

2

1

3

m

.

Câu 14. [Vận dụng].

Giá trị của

m

để hàm số

32

3y x x mx m   

nghịch biến trên đoạn có độ dài bằng

2

là?

A.

2m 

. B.

4m 

.

C.

1m 

. D.

0m 

.

Câu 15. [Vận dụng].

Tìm tất cả các giá trị thực của tham số

m

để

hàm số

32

1

2 10

3

y x x mx   

nghịch biến

trên đoạn có độ dài bằng

1

?

A.

2m 

. B.

4m 

.

C.

15

4

m 

. D.

15

4

m 

.

Câu 16. [Vận dụng].

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

113

[ I can't, I can! ]

Tìm

m

để hàm số

 

32

2

1 2 5

3

y x m x mx     

đồng biến trên

khoảng

 

0;2

.

A.

2

3

m 

. B.

0m 

.

C.

2

3

m 

. D.

0m 

.

Câu 17. [Vận dụng].

Tìm

m

để hàm số

 

32

11

2

33

y x mx m x     

đồng biến trên

đoạn có độ dài bằng

4

.

A.

2m 

. B.

2m 

.

C.

3m 

. D. Cả A và C đều đúng.

Câu 18. [Thông hiểu].

Tìm

m

để hàm số

32

61y x x mx   

đồng

biến trên khoảng

 

0;

?

A.

0m 

. B.

12m 

.

C.

0m 

. D.

12m 

.

Câu 19. [Nhận biết].

Tìm

m

để hàm số

2

1

xm

y

x







giảm trên các

khoảng mà nó xác định?

A.

1m 

. B.

1m 

.

C.

3m 

. D.

3m 

.

Câu 20. [Nhận biết].

Tìm

m

để hàm số

32

1

4

3

y x mx  

đồng biến

trên ?

A.

20m  

. B.

20m  

.

C.

2m 

. D.

0m 

.

Câu 21. [Thông hiểu].

Tìm

m

để hàm số

4mx

y

xm







giảm trên khoảng

 

;1

?

A.

21m   

. B.

21m   

.

C.

21m   

. D.

21m   

.

Câu 22. [Nhận biết].

Tìm giá trị nhỏ nhất của

m

để hàm số

3

2

3

x

y mx mx m   

đồng biến trên ?

A.

0m 

. B.

4m 

.

C.

4m 

. D.

1m 

.

Câu 23. [Nhận biết].

Hàm số

 

3

2

23

3

x

y m x mx m     

nghịch

biến trên khoảng xác định khi:

A.

0m 

. B.

4m 

.

C.

4m 

. D.

1m 

.

Câu 24. [Nhận biết].

Hàm số

3

2

4

3

x

y mx x  

đồng biến trên

khi và chỉ khi?

A.

22m  

. B.

2

m











.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

114

[ I can't, I can! ]

C.

2m 

. D.

2m 

.

Câu 25. [Nhận biết].

Hàm số

3

2

4

3

x

y mx x   

nghịch biến trên

khi và chỉ khi?

A.

22m  

. B.

2

m











.

C.

2m 

. D.

2m 

.

Câu 26. [Nhận biết].

Tìm

m

để hàm số

   

2 1 sin 3y m x m x   

đồng biến trên ?

A.

2

4

3

m  

. B.

2

4

3

m  

.

C.

4m 

. D.

2

3

m 

.

Câu 27. [Vận dụng].

Với giá trị nào của tham số thực

m

thì hàm số

2 1 cosy m x m x   

đồng biến trên ?

A.

1m 

. B.

1m 

.

C.

11m  

. D.

m

.

Câu 28. [Thông hiểu].

Tìm

m

để hàm số

32

3 4 2y x x mx    

nghịch biến trên nữa khoảng





;0

.

A.

3

4

m 

. B.

3

4

m 

.

C.

3

4

m 

. D.

3

4

m 

.

Câu 29. [Thông hiểu].

Cho hàm số

 

3 2 2

12y x m x m x m      

. Mệnh đề

nào sau đây là đúng?

A. Hàm số đồng biến trên

 

2;4

.

B. Hàm số có cả khoảng đồng biến và khoảng

nghịch biến.

C. Hàm số luôn nghịch biến trên .

D. Hàm số nghịch biến trên

 

2

;1mm

.

Câu 30. [Nhận biết].

Với giá trị nào của tham số

m

để hàm số

3

2

22

3

x

y x mx    

nghịch biến trên tập

xác định?

A.

4m 

. B.

4m 

.

C.

4m 

. D.

4m 

.

Câu 31. [Nhận biết].

Với điều kiện nào của

m

thì hàm số

 

3 2 2

2 4 9y x m x m x     

đồng biến

trên ?

A.

1

2

m











. B.

2

4

m











.

C.

0

1

m











. D.

3

m











.

Câu 32. [Nhận biết].

Với giá trị nào của tham số thực

m

để hàm số

 

2m x m

y

xm







đồng biến trên mỗi khoảng

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

115

[ I can't, I can! ]

xác định của nó?

A.

2

0

m











. B.

3

0

m











.

C.

2

0

m











. D.

3

0

m











.

Câu 33. [Thông hiểu].

Với giá trị nào của tham số thực

m

thì hàm số

32

32y x x mx   

đồng biến trên

 

0;

?

A.

2m 

. B.

3m 

.

C.

0m 

. D.

4m 

.

Câu 34. [Nhận biết].

Tất cả các giá trị của số thực

m

để hàm số

 

1

xm

fx

x







nghịch biến trên từng khoảng

xác định của nó là?

A.

1m 

. B.

1m 

.

C.

1m 

. D.

1m 

.

Câu 35. [Nhận biết].

Tất cả các giá trị của

m

để hàm số

 

3

2

4

3

x

f x mx x  

đồng biến trên là?

A.

22m  

. B.

22m  

.

C.

2m 

. D.

2m 

.

Câu 36. [Nhận biết].

Hàm số

 

1 2 2m x m

y

xm

  





nghịch biến trên

khoảng

 

1; 

khi

A.

1m 

. B.

2m 

.

C.

12m

. D.

12m  

.

Câu 37. [Thông hiểu].

Tìm tất cả các giá trị

m

để hàm số

3

2

21

32

xm

y x x   

đồng biến trên khoảng

 

1; 

?

A.

11m  

. B.

1m 

.

C.

1m 

. D.

2m 

.

Câu 38. [Nhận biết].

Tìm tất cả các giá trị thực của

m

để hàm số

 

3

2

2 1 1

3

x

y m x mx



    

nghịch biến trên

?

A.

1

4

m

. B.

1

4

m   

.

C.

m 

. D.

1m 

.

Câu 39. [Vận dụng].

Tìm tất cả các giá trị thực của tham số

m

sao

cho hàm số

2

x

em

y

em







đồng biến trên

khoảng

1

ln ;0

4







.

A.

 

1;2m

. B.

11

;

22

m









.

C.

 

1;2m

. D.





11

; 1;2

22

m



  





.

Câu 40. [Nhận biết].

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

116

[ I can't, I can! ]

Tìm tất cả các giá trị thực của tham số

m

để

hàm số

3x

y

xm







đồng biến trên từng khoảng

xác định của nó.

A.

3m 

. B.

3m 

.

C.

3m 

. D.

3m 

.

Câu 41. [Vận dụng].

Cho hàm số

 

1 1 2

1

mx

y

xm

  





. Tìm tất cả

các giá trị của tham số

m

để hàm số đồng biến

trên khoảng

 

17;37

.

A.

41m   

. B.

2

6

41

m











   



.

C.

2

4

m











. D.

12m  

.

Câu 42. [Thông hiểu].

Xác định các giá trị của tham số

m

để hàm số

32

3y x mx m  

nghịch biến trên khoảng

 

0;1

?

A.

1

2

m 

. B.

1

2

m 

.

C.

0m 

. D.

0m 

.

Câu 43. [Nhận biết].

Để hàm số

32

3y x m x

đồng biến trên thì:

A.

0m 

. B.

0m 

.

C.

0m 

. D.

0m 

.

Câu 44. [Nhận biết].

Cho hàm số

 

32

1

3 2 1

3

y x mx m x     

.

Tìm tất cả các giá trị thực của tham số

m

để

hàm số nghịch biến trên khoảng

 

; 

.

A.

2

1

m











. B.

2m 

.

C.

21m   

. D.

10m  

.

Câu 45. [Nhận biết].

Cho hàm số

 

12mx

y

xm







. Tìm tất cả các

giá trị của tham số

m

để hàm số đồng biến trên

từng khoảng xác định.

A.

21m  

. B.

1

2

m











.

C.

21m  

. D.

1

2

m











.

Câu 46. [Thông hiểu].

Cho hàm số

32

34y x x mx   

. Tìm tất cả

các giá trị của tham số

m

để hàm số đồng biến

trên khoảng

 

;0

.

A.

1m 

. B.

3m 

.

C.

3m 

. D.

3m 

.

Câu 47. [Vận dụng].

Với giá trị nào của tham số

m

thì hàm số

sin cos 2021 2y x x mx  

đồng biến trên .

A.

2021m 

. B.

0m 

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

117

[ I can't, I can! ]

C.

1

2021

m 

. D.

1

2017

m 

.

Câu 48. [Thông hiểu].

Tìm tất cả các giá trị của

m

để hàm số

2sin 1

sin

x

y

xm







đồng biến trên khoảng

0;

2









.

A.

1m 

. B.

1m 

.

C.

0m 

. D.

1m 

.

Câu 49. [Thông hiểu].

Tìm tất cả các giá trị thực của tham số

m

để

hàm số

sin

xm

y

xm







nghịch biến trên

;

2









.

A.

0

1

m











. B.

0m 

.

C.

01m

. D.

1m 

.

Câu 50. [Thông hiểu].

Tìm tất cả các giá trị thực của tham số

m

để

hàm số:

   

32

1

1 3 10

3

y x m x m x      

đồng biến trong khoảng

 

0;3

?

A.

12

7

m 

. B.

12

7

m 

.

C.

m

. D.

7

12

m 

.

Câu 51. [Thông hiểu].

Tìm tất cả các giá trị của

m

để hàm số

 

32

12y mx mx m m x    

đồng biến trên

?

A.

4

3

m 

. B.

4

3

0

m











.

C.

0

4

3

m











. D.

4

3

m 

.

Câu 52. [Thông hiểu].

Tìm tất cả các giá trị thực của

m

để hàm số

     

32

1 3 1 3 2 3y m x m x m x m      

nghịch biến trên là?

A.

1m 

. B.

1m 

.

C.

1m 

. D.

1m 

.

Câu 53. [Nhận biết].

Tìm tất cả các giá trị thực của tham số

m

để

hàm số

   

32

12

1 2 3

33

y x m x m x     

đồng biến trên

 

1; 

.

A.

2m 

. B.

2m 

.

C.

1m 

. D.

1m 

.

Câu 54. [Nhận biết].

Tìm tất cả các giá trị thực của tham số

m

để

hàm số

2

3

1

2 2021

32

mx

y x x   

đồng biến

trên ?

A.

2 2 2 2m  

. B.

22m 

.

C.

22m 

. D.

2 2 2 2m  

.

Câu 55. [Nhận biết].

Tìm tập hợp tất cả các giá trị thực của tham số

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

118

[ I can't, I can! ]

m

để hàm số:

 

32

1 3 1y x m x x    

đồng

biến trên khoảng

 

; 

.

A.

 

4;2

. B.

   

; 4 2;   

.

C.

 

4;2

. D.



 



; 4 2;   

.

Câu 56. [Vận dụng].

Tìm

m

để hàm số

 

32

21y x x m x     

tăng trên đoạn có độ dài bằng

2

.

A.

11

3

m 

. B.

7

3

m 

.

C.

5

3

m 

. D.

14

3

m 

.

Câu 57. [Vận dụng].

Tất cả các giá trị thực của tham số

m

để hàm số

 

32

3 3 1 2y x mx m x    

nghịch biến trên

đoạn có độ dài lớn hơn

4

là?

A.

 

1;2m 

.

B.

1 21 1 5

;

22

m











.

C.

1 5 1 21

;

22

m











.

D.

1 21 1 21

;;

22

m

   



   

   

   

.

Câu 58. [Thông hiểu].

Tập hợp tất cả các giá trị thực của tham số

m

để hàm số

4mx

y

xm







luôn nghịch biến trên

khoảng

 

;1

là?

A.

 

2; 1m  

. B.

 

2;2m

.

C.





2; 1m  

. D.

 

2; 1m  

.

Câu 59. [Thông hiểu].

Cho hàm số

32

31

3

m

y x mx x   

(

m

là tham

số thực). Tìm giá trị nhỏ nhất của

m

để hàm số

trên luôn đồng biến trên .

A.

1m 

. B.

0m 

.

C.

2m 

. D.

3m 

.

Câu 60. [Vận dụng].

Tìm tập hợp các giá trị của tham số thực

m

để

hàm số

sin 7 5 3y m x x m   

đồng biến trên

.

A.

77m  

. B.

1m 

.

C.

7m 

. D.

7m 

.

Câu 61. [Nhận biết].

Hàm số

   

32

12

1 2 5

33

y x m x m x      

nghịch biến trên thì điều kiện của

m

là?

A.

2m 

. B.

22m  

.

C.

2m 

. D.

22m  

.

Câu 62. [Thông hiểu].

Tìm tất cả các giá trị thực của tham số

m

để

hàm số

1x

y

xm







nghịch biến trên khoảng

 

2;

?

A.

21m  

. B.

2m 

.

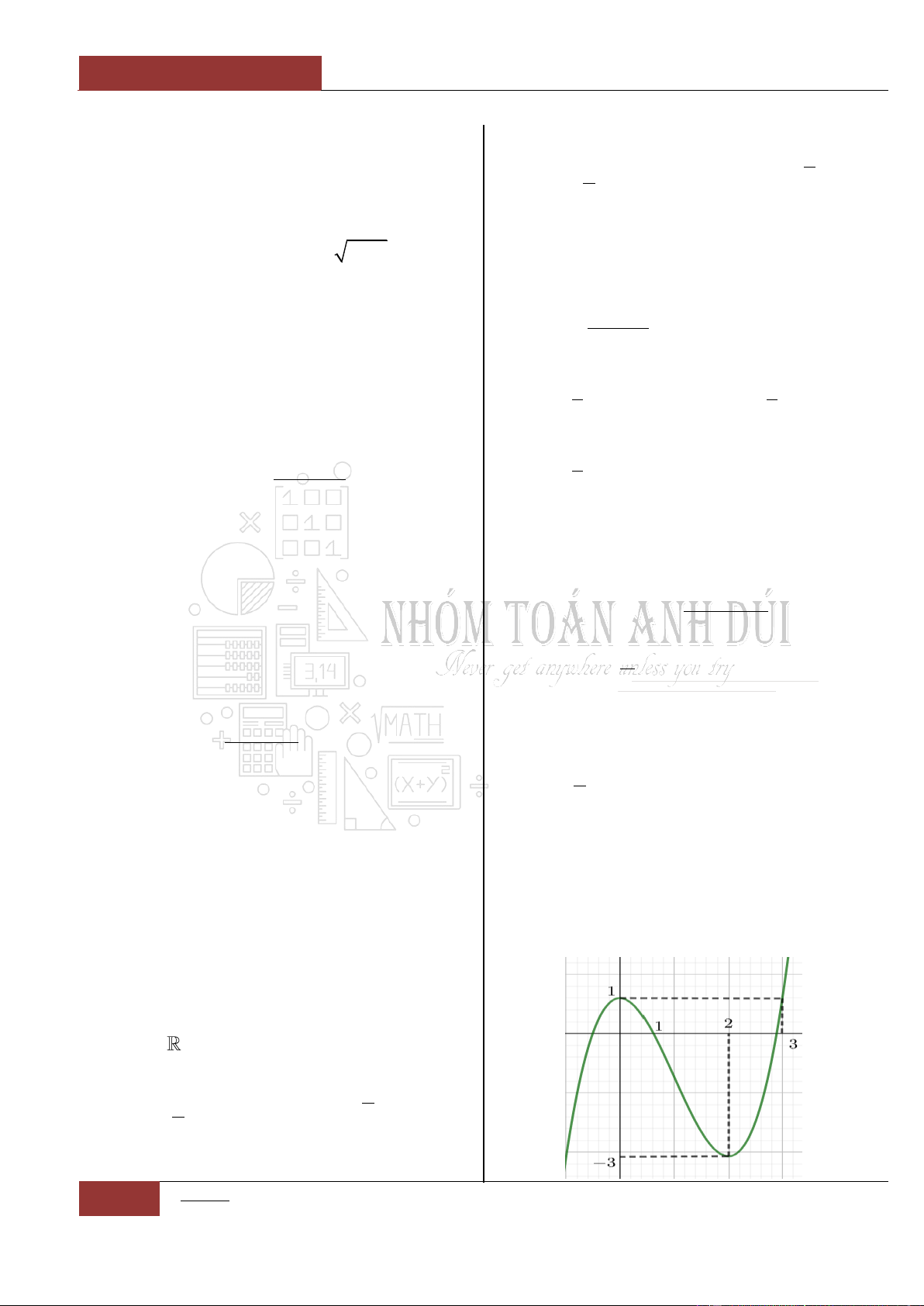
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

119

[ I can't, I can! ]

C.

2m 

. D.

2m 

.

Câu 63. [Vận dụng].

Tìm tập hợp tất cả các giá trị thực của tham số

m

để hàm số

 

1 2 1y mx m x    

nghịch

biến trên nữa khoảng





2;

.

A.

0m 

. B.

1m 

.

C.

1m 

. D.

21m  

.

Câu 64. [Nhận biết].

Tìm

m

để hàm số

2

3

mx

y

xm







nghịch biến

trên các khoảng xác định của nó.

A.

12m

. B.

12m

.

C.

2

1

m











. D.

2

1

m











.

Câu 65. [Thông hiểu].

Cho hàm số

3

4

mx

y

xm







. Tất cả các giá trị

của tham số thực

m

để hàm số nghịch biến trên

các khoảng xác định của nó là?

A.

3m 

. B.

1m 

.

C.

13m

. D.

13m

.

Câu 66. [Nhận biết].

Tìm tất cả các giá trị thực của tham số

m

để

hàm số

 

32

12y mx mx m m x    

đồng

biến trên .

A.

4

3

m 

. B.

4

3

0

m











.

C.

0

4

3

m











. D.

4

3

m 

.

Câu 67. [Vận dụng].

Tìm tất cả các giá trị của tham số thực

m

để

hàm số

33

3

x

y

m







nghịch biến trên

 

1;1

.

A.

1

3

m 

. B.

1

3

m

.

C.

1

3

m 

. D.

3m 

.

Câu 68. [Vận dụng].

Tìm tất cả các giá trị thực của tham số

m

sao

cho hàm số

 

2

2sin

1 cos

mx

y f x

x







nghịch biến

trên khoảng

0;

6









.

A.

1m 

. B.

0m 

.

C.

9

2

m 

. D.

35m

.

Câu 69. [Vận dụng].

Cho hàm số

 

y f x

có đồ thị hàm số

 

'y f x

như hình vẽ bên dưới.

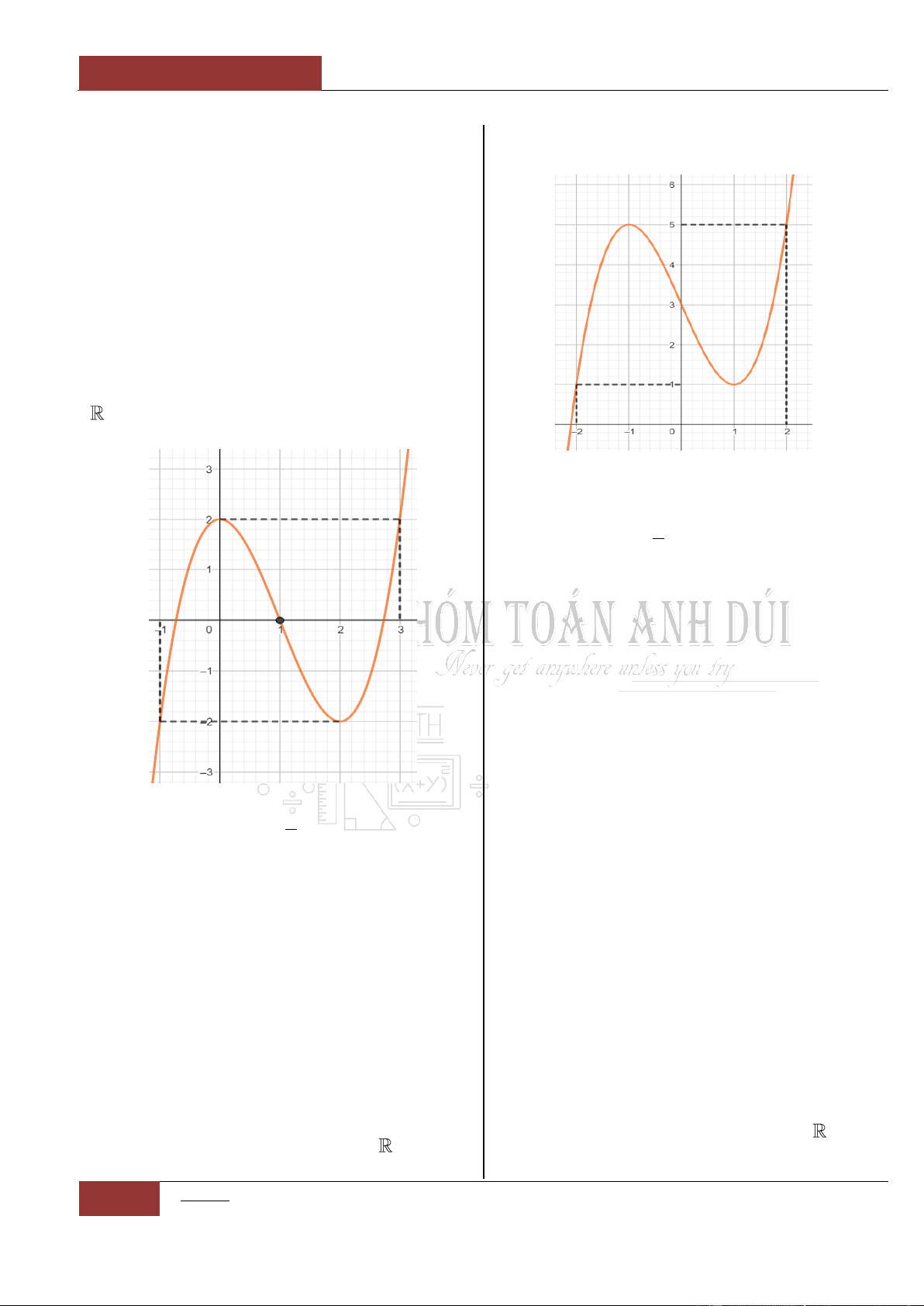
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

120

[ I can't, I can! ]

Tập hợp các giá trị thực của tham số

m

để hàm

số

   

1y f x m x  

đồng biến trên khoảng

 

0;3

là?

A.

4m 

. B.

4m 

.

C.

4m 

. D.

04m

.

Câu 70. [Vận dụng].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

và đồ thị của hàm số

 

'y f x

như hình vẽ.

Đặt:

     

2

1

1 2021

2

g x f x m x m     

với

m

là tham số thực. Gọi

S

là tập các giá trị

nguyên dương của tham số

m

để hàm số

 

y g x

đồng biến trên khoảng

 

5;6

.

Tổng các phần tử của

S

bằng?

A.

4

. B.

11

.

C.

14

. D.

20

.

Câu 71. [Vận dụng].

Cho hàm số

 

y f x

liên tục trên có đồ thị

hàm số

 

'y f x

như hình vẽ

Xét hàm số

   

 

22

1

3

2

g x f x x m x m    

.

Khẳng định nào sau đây là đúng?

A. Với mọi giá trị thực của

m

, hàm số nghịch

biến trên các khoảng

 

2;0

và

 

2;

, đồng

biến trên các khoảng

 

;2 

và

 

0;2

.

B. Có duy nhất một giá trị của

m

để hàm số

nghịch biến trên các khoảng

 

2;0

và

 

2;

,

đồng biến trên các khoảng

 

;2 

và

 

0;2

.

C. Với mọi giá trị thực của

m

, hàm số đồng

biến trên các khoảng

 

2;0

và

 

2;

, nghịch

biến trên các khoảng

 

;2 

và

 

0;2

.

D. Có duy nhất một giá trị của

m

để hàm số

đồng biến trên các khoảng

 

2;0

và

 

2;

,

nghịch biến trên các khoảng

 

;2 

và

 

0;2

.

Câu 72. [Vận dụng].

Cho hàm số

 

y f x

có đạo hàm trên và có

bảng xét dấu như sau:

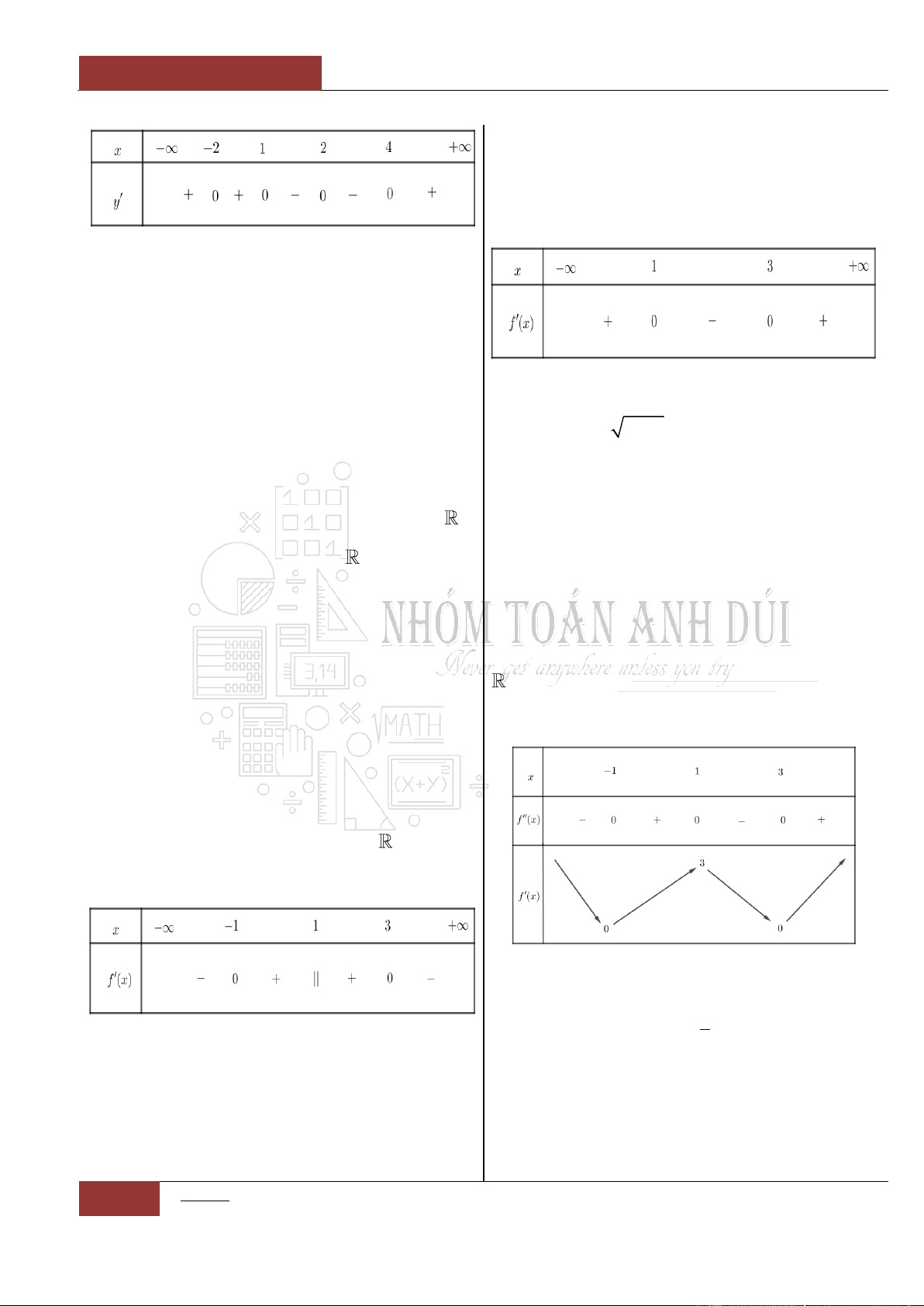
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

121

[ I can't, I can! ]

Có bao nhiêu giá trị nguyên của

 

0;2021m

để hàm số

 

2

g x f x x m  

nghịch biến

trên khoảng

 

1;0

?

A.

2016

. B.

2021

.

C.

2017

. D.

2020

.

Câu 73. [Vận dụng].

Cho hàm số

 

fx

có đạo hàm liên tục trên ,

   

 

2

' 1 2 ,f x x x x x    

. Có bao

nhiêu giá trị thực của tham số

m

thỏa mãn

2021m 

và

 

2

8g x f x x m  

đồng biến

trên khoảng

 

4;

?

A.

2003

. B.

2002

.

C.

2004

. D.

2021

.

Câu 74. [Vận dụng].

Cho hàm số

 

y f x

liên tục trên và có

bảng xét dấu đạo hàm như sau:

Có bao nhiêu giá trị nguyên của tham số

m

để

hàm số

   

g x f x m

đồng biến trên

 

0;2

?

A.

3

. B.

4

.

C.

2

. D.

1

.

Câu 75. [Vận dụng].

Cho hàm số

 

y f x

là một hàm đa thức và có

bảng xét dấu đạo hàm như hình vẽ:

Có bao nhiêu giá trị nguyên của tham số

m

để

hàm số

 

2y f x m  

nghịch biến trên

khoảng

 

11;27

?

A.

1

. B.

0

.

C.

2

. D.

3

.

Câu 76. [Vận dụng cao].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

và

 

12f 

. Biết

 

'y f x

có bảng biến

thiên như hình vẽ.

Có bao nhiêu giá trị nguyên

 

2021;2021m

để hàm số

 

32

1

ln 3 9

3

y f x x x x m



    





đồng biến trên

 

1;3

?

A.

2011

. B.

2022

.

C.

4042

. D.

4043

.

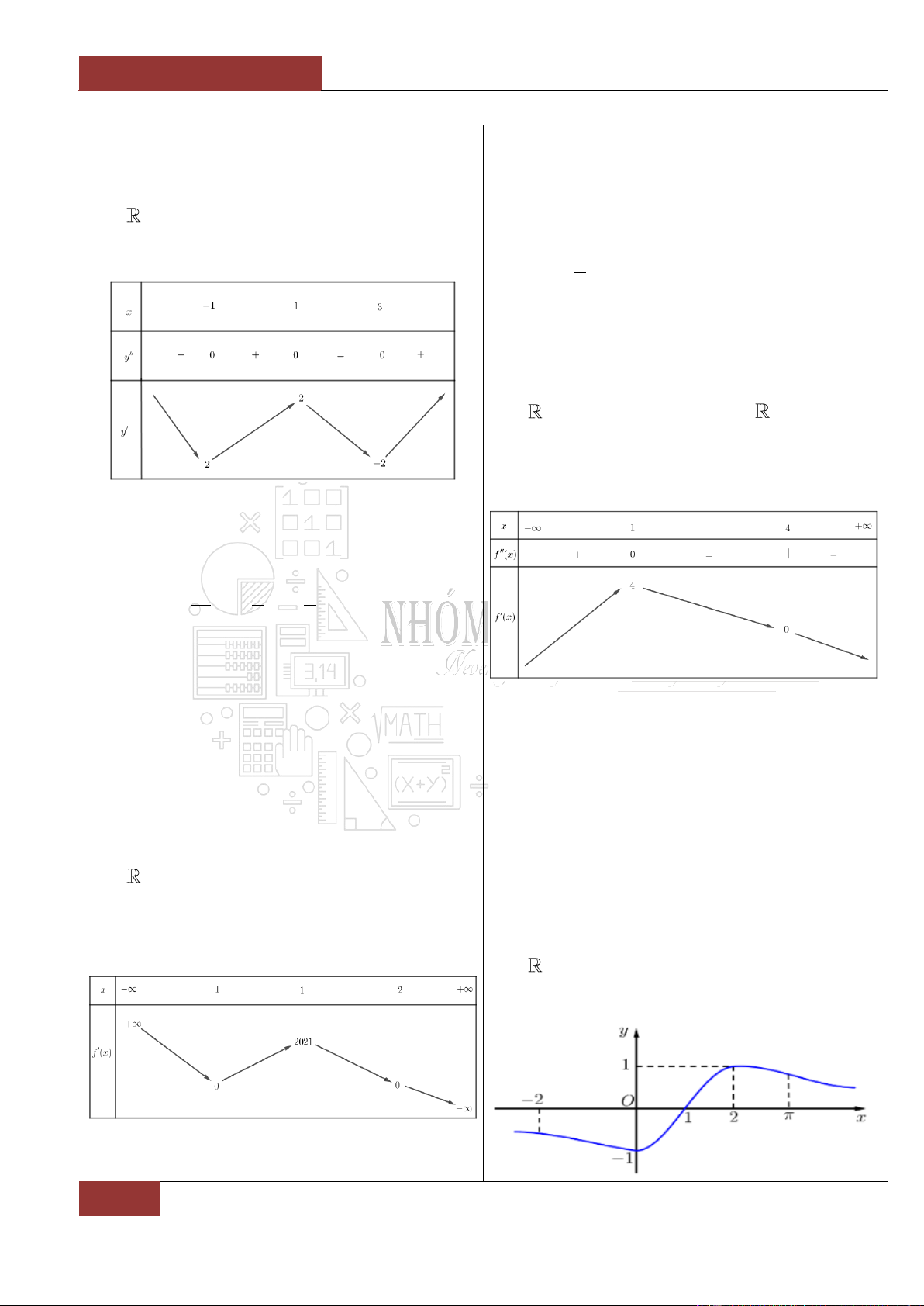
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

122

[ I can't, I can! ]

Câu 77. [Vận dụng cao].

Cho hàm số

 

2y f x

có đạo hàm liên tục

trên . Biết

 

'2y f x

có bảng biến thiên

như hình vẽ dưới đây.

Có bao nhiêu giá trị nguyên

 

2021;2021m

để hàm số

   

4 3 2

1 2 3

21

12 3 2

y f x x x x m x m      

đồng biến trên khoảng

 

1;3

.

A.

2023

. B.

2022

.

C.

4043

. D.

4042

.

Câu 78. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục và có đạo hàm

trên , thỏa mãn

 

10f 

. Biết bảng biến

thiên của hàm số

 

'y f x

có đồ thị như hình

vẽ dưới đây?

Hàm số

 

2

2g x x x f x  

nghịch biến

trên khoảng nào dưới đây?

A.

 

2;

. B.

 

;1 

.

C.

1

1;

2









. D.

 

1;1

.

Câu 79. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục và có đạo hàm

trên thỏa mãn

 

0,f x x  

. Biết rằng

hàm số

 

'y f x

có bảng biến thiên như hình

vẽ.

Có bao nhiêu số nguyên

 

2021;2021m

để

hàm số

 

2

1x mx

y e f x

  



đồng biến trên

 

1;4

.

A.

2021

. B.

4043

.

C.

2013

. D.

2014

.

Câu 80. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục và có đạo hàm

trên . Đồ thị hàm số đạo hàm được cho hình

hình vẽ bên dưới.

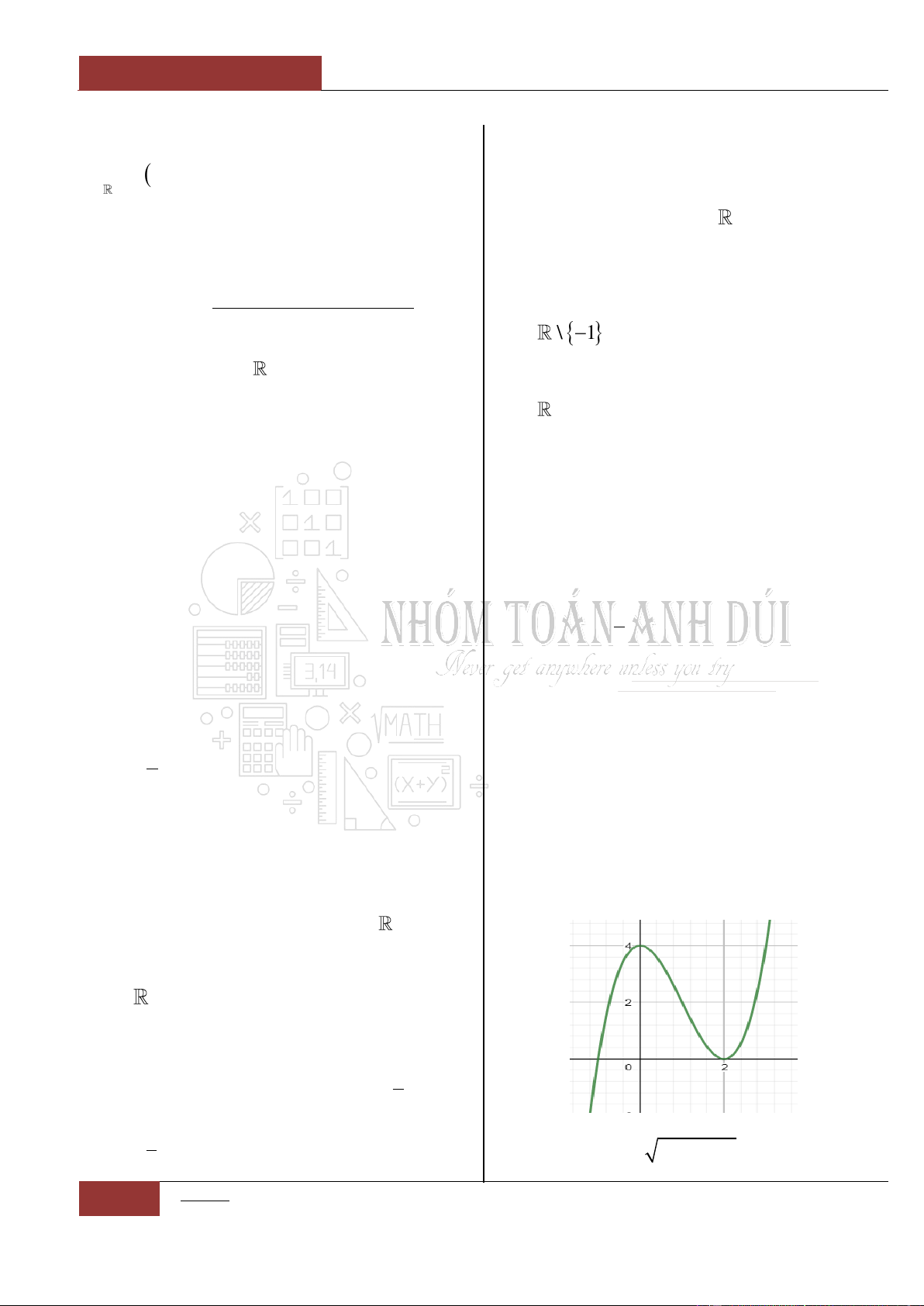
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

123

[ I can't, I can! ]

Biết rằng phương trình

 

0fx

vô nghiệm và

 

max 1fx

. Phương trình

 

'0fx

có

một nghiệm duy nhất. Có bao nhiêu giá trị của

tham số

m

để hàm số

 

2

1 1 2x m x m

gx

fx



  





luôn đồng biến trên .

A.

1

. B.

2

.

C.

0

. D.

5

.

Câu 81. [Vận dụng cao].

Cho Parabol

   

2

: , 0P y f x ax bx c a    

Biết rằng

 

P

đi qua điểm

 

4;3M

, cắt trục

Ox

tại

 

3;0N

và

Q

sao cho diện tích tam giác

INQ

bằng

1

và đồng thời hoành độ điểm

Q

nhỏ hơn

3

. Khi đó hàm số

 

21y f x

đồng

biến trên khoảng nào dưới đây?

A.

1

;

2









. B.

 

0;2

.

C.

 

5;7

. D.

 

;2

.

Câu 82. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục trên thỏa mãn

 

10f 

và

   

6 4 2

. 3 2f x x f x x x x   





,

x

. Hàm số

   

2

2g x f x x

đồng biến

trên khoảng nào dưới đây?

A.

 

1;3

. B.

1

0;

3







.

C.

1

;1

3







. D.

 

1; 

.

Câu 83. [Vận dụng cao].

Cho đa thức

 

fx

hệ số thực và thỏa điều kiện

   

2

2 1 ,f x f x x x    

. Hàm số

 

2

3 . 4 1y x f x x x   

đồng biến trên

khoảng nào dưới đây?

A.

 

\1

. B.

 

0;

.

C. . D.

 

;0

.

Câu 84. [Vận dụng cao].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

đoạn

 

1;1

và thỏa mãn đồng thời:

 

10f 

và

   

2

' 4 8 16 8f x f x x x   





. Hàm số

   

3

1

23

3

g x f x x x   

đồng biến trên

khoảng nào dưới đây?

A.

 

1;2

. B.

 

0;3

.

C.

 

0;2

. D.

 

2;2

.

Câu 85. [Vận dụng cao].

Cho hàm số

 

32

y f x ax bx cx d    

có

đồ thị hàm số như hình bên dưới.

Hàm số

 





2

2g x f x x  

. Khẳng định

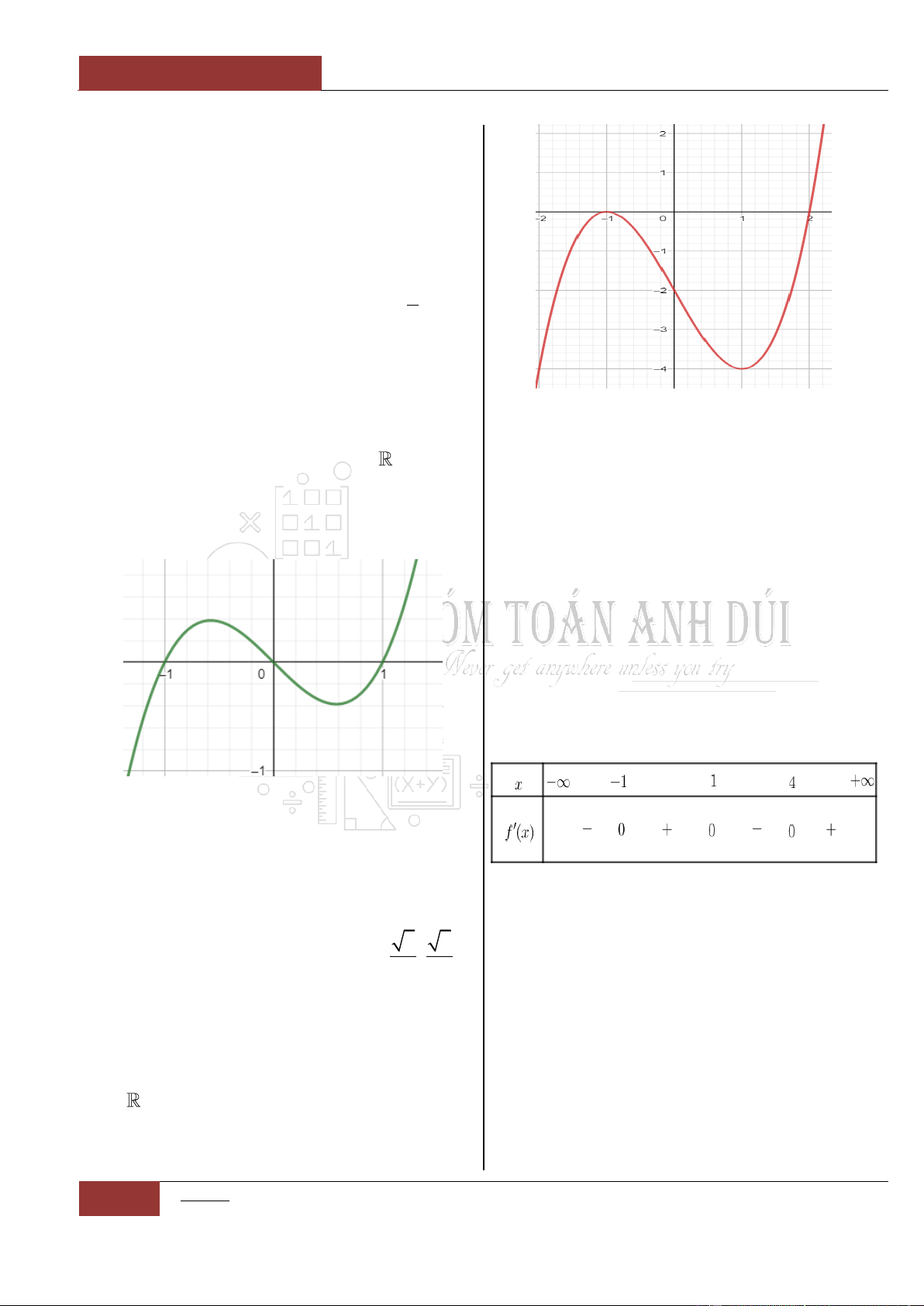
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

124

[ I can't, I can! ]

nào sau đây là khẳng định đúng về

 

gx

?

A. Hàm số nghịch biến trên khoảng

 

0;2

.

B. Hàm số đồng biến trên khoảng

 

1;0

.

C. Hàm số nghịch biến trên khoảng

1

;0

2









.

D. Hàm số đồng biến trên khoảng

 

;1 

.

Câu 86. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục trên và có đồ

thị đạo hàm

 

32

'y f x x ax bx c    

có đồ

thị như hình vẽ bên dưới.

Hàm số

   

 

'g x f f x

nghịch biến trên

khoảng nào dưới đây?

A.

 

1; 

. B.

 

;2 

.

C.

 

1;0

. D.

33

;

33









.

Câu 87. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục và có đạo hàm

trên . Biết đồ thị hàm số

 

'y f x

như hình

vẽ bên dưới:

Biết

S

là tập tất cả các giá trị nguyên của tham

số

m

thỏa mãn

 

2021;2021m

sao cho hàm

số

   

g x f x m

đồng biến trên khoảng

 

2;0

. Số phần tử của tập

S

là?

A.

2017

. B.

2019

.

C.

2018

. D.

2021

.

Câu 88. [Vận dụng cao].

Cho hàm số

 

fx

có bảng xét dấu đạo hàm

như sau:

Hàm số

   

3 2 1 2

3

f x f x

ye

  



đồng biến trên

khoảng nào dưới đây?

A.

 

1; 

. B.

 

1;3

.

C.

 

;2 

. D.

 

2;1

.

Câu 89. [Vận dụng cao].

Cho hàm số

 

y f x

có bảng biến thiên như

hình vẽ bên dưới:

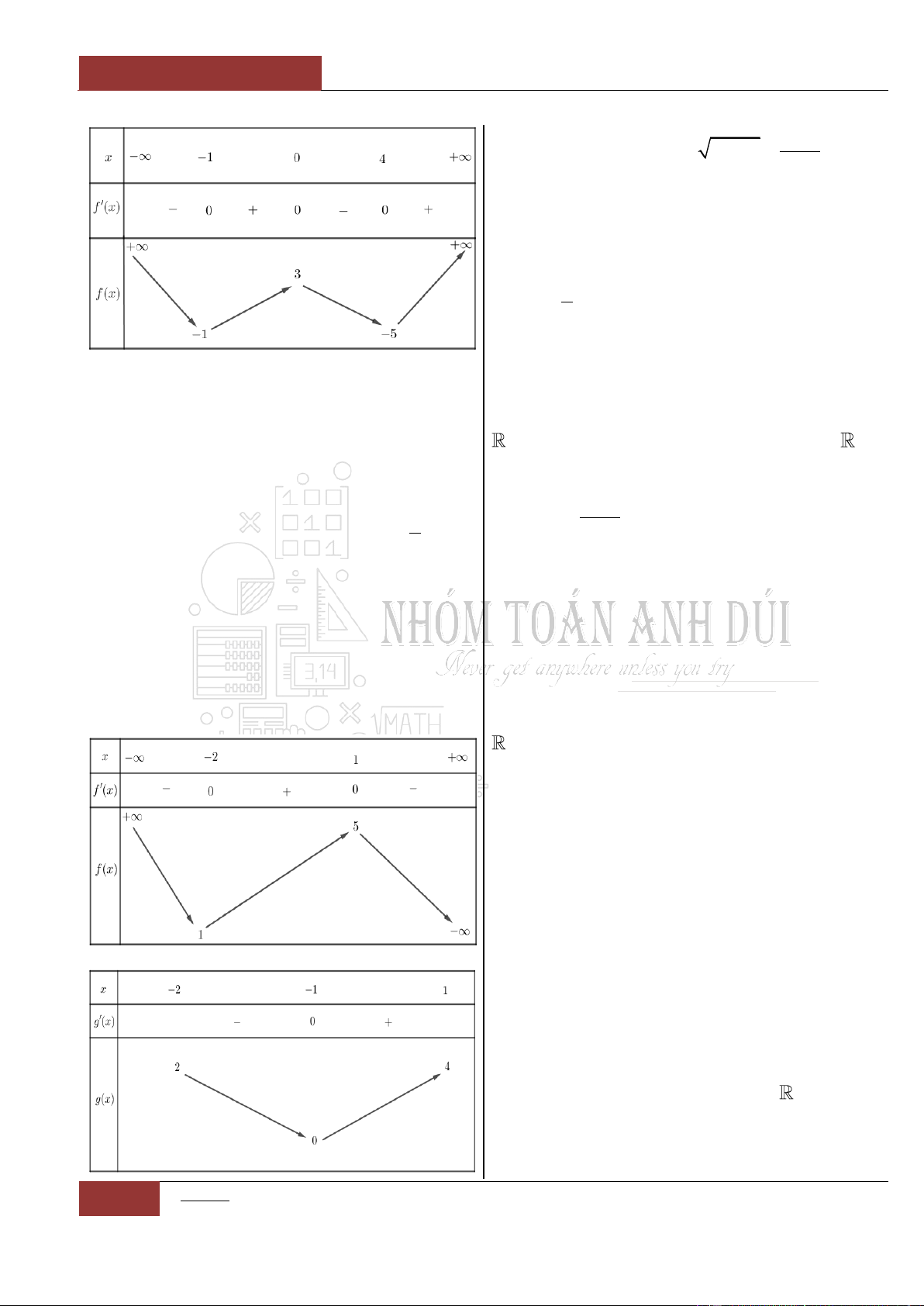
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

125

[ I can't, I can! ]

Hàm số

 

2

2f x m

ye





nghịch biến trên khoảng

nào dưới đây?

A.

 

4;

. B.

 

1;4

.

C.

 

1;2

. D.

1

;

2









.

Câu 90. [Vận dụng cao].

Cho bảng biến thiên của hàm số

 

y f x

và

 

y g x

lần lượt là hai bảng biến thiên như

hình vẽ dưới đây.

Hàm số

   

1

. 2 3

2

y f x g x x

x

   



chắc

chắn đồng biến trên khoảng nào dưới đây?

A.

 

2;1

. B.

 

1;1

.

C.

3

;1

2









. D.

 

1;4

.

Câu 91. [Vận dụng cao].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

, biết:

     

' 1 1 4 ,f x x x x x     

.

Có bao nhiêu số nguyên

2021m 

để hàm số

 

2

1

x

g x f m

x













đồng biến trên

 

2;

?

A.

2018

. B.

2019

.

C.

2020

. D.

2021

.

Câu 92. [Vận dụng cao].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

thỏa mãn:

   

'1

x

f x x e

. Có tất cả bao

nhiêu giá trị nguyên của tham số

m

trong đoạn

 

2021;2021

để hàm số

   

2

ln 2y g x f x mx mx    

nghịch biến trên

 

2

1; e

?

A.

2018

. B.

2019

.

C.

2020

. D.

2021

.

Câu 93. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục trên và có

       

3 4 5

' 1 . 1 . 4f x x x x x   

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

126

[ I can't, I can! ]

Giá trị của tham số

m

để hàm số

   

22

1

y g x f x

x mx m

   

  

chắc chắn luôn đồng biến trên khoảng

 

3;0

.

A.

 

2; 1m  

. B.

 

;2m  

.

C.

 

1;0m

. D.





;0m 

.

Câu 94. [Vận dụng cao].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

, biết

 

2

',

1

x

f x x

x



  



. Có bao nhiêu

số nguyên

m

thuộc khoảng

 

20;20

để hàm

số

   

11g x f x mx   

đồng biến trên .

A.

20

. B.

19

.

C.

17

. D.

18

.

Câu 95. [Vận dụng cao].

Cho hàm số

 

y f x

có đạo hàm tục trên ,

biết

    

' 1 2f x x x  

. Tìm

m

để hàm số

   

2y g x f x mx   

đồng biến trên

khoảng

 

2;1

.

A.

9

4

m 

. B.

9

10

4

m  

.

C.

9

4

m 

. D.

10m 

.

Câu 96. [Vận dụng cao].

Có tất cả bao nhiêu giá trị nguyên của tham số

 

20;20m

để hàm số:

cot cot

8 ( 3).2 3 2

xx

y m m    

đồng biến trên khoảng

;

4









?

A.

10

. B.

12

.

C.

11

. D.

9

.

Câu 97. [Vận dụng cao].

Cho họ đường cong

 

2

2 2 4

:

m

m x m m

Cy

xm

   





.

Gọi

 

,f x ax b

 

,g x cx d b d  

lần

lượt là đồ thị hàm số của hai đường thẳng luôn

tiếp xúc với

 

m

C

.

Hàm số

   

3

f g x g x







đồng biến trên khoảng

nào sau đây, chọn phương án đúng nhất?

A.

18 3 18 3

;

33









.

B.

18 3

;

3











và

18 3

;

3











.

C.

6 3 6 3

;

33



   





.

D.

63

;

3











và

63

;

3











.

Câu 98. [Vận dụng cao].

Cho hàm số

 

y f x

có đồ thị hàm số

 

'y f x

như hình vẽ dưới đây.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

127

[ I can't, I can! ]

Xét hàm số

 

y g x

liên tục và có đạo hàm

trên

 

0;1

,

 

8 3 2

'

48 1

x

fx

g x m

x



  



,

với

m

là tham số thực. Giá trị thực

m

nào dưới

đây làm cho hàm số

 

y g x

luôn tăng trên

khoảng

 

0;1

.

A.

 

0

8

48

32

f

m 



.

B.

 

0

8

48

32

f

m 



.

C.

 

1

2

48

f

m 

.

D.

 

1

2

48

f

m 

.

Câu 99. [Vận dụng cao].

Cho hàm số

 

fx

có đạo hàm liên tục trên

và có đồ thị của hàm số

 

y f x





như hình vẽ

dưới đây.

Để hàm số

 

3

2 6 3y f x x  

đồng biến với

mọi

 

x m m R

thì

sin ,

b

ma

c





trong đó

*

, , , 2 .a b c N c b

Tổng

23S a b c  

bằng?

A.

9

. B.

7

.

C.

5

. D.

2

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

131

[ I can't, I can! ]

ĐÁP ÁN

0

1

2

3

4

5

6

7

8

9

0

D

B

A

C

1

D

B

A

D

C

B

D

B

2

D

C

A

C

A

C

3

B

D

B

C

B

C

B

C

D

4

A

B

A

B

C

A

C

B

5

A

D

A

D

A

D

C

B

6

A

B

A

B

A

C

D

C

7

C

A

C

D

8

A

C

B

C

D

C

9

B

D

B

A

B

C

B

Ghi chú: Đáp án là sự kết hợp giữa dòng

i

và cột

j

. Ví dụ: Câu 24A (giao của dòng 2 và cột 4).

i

j

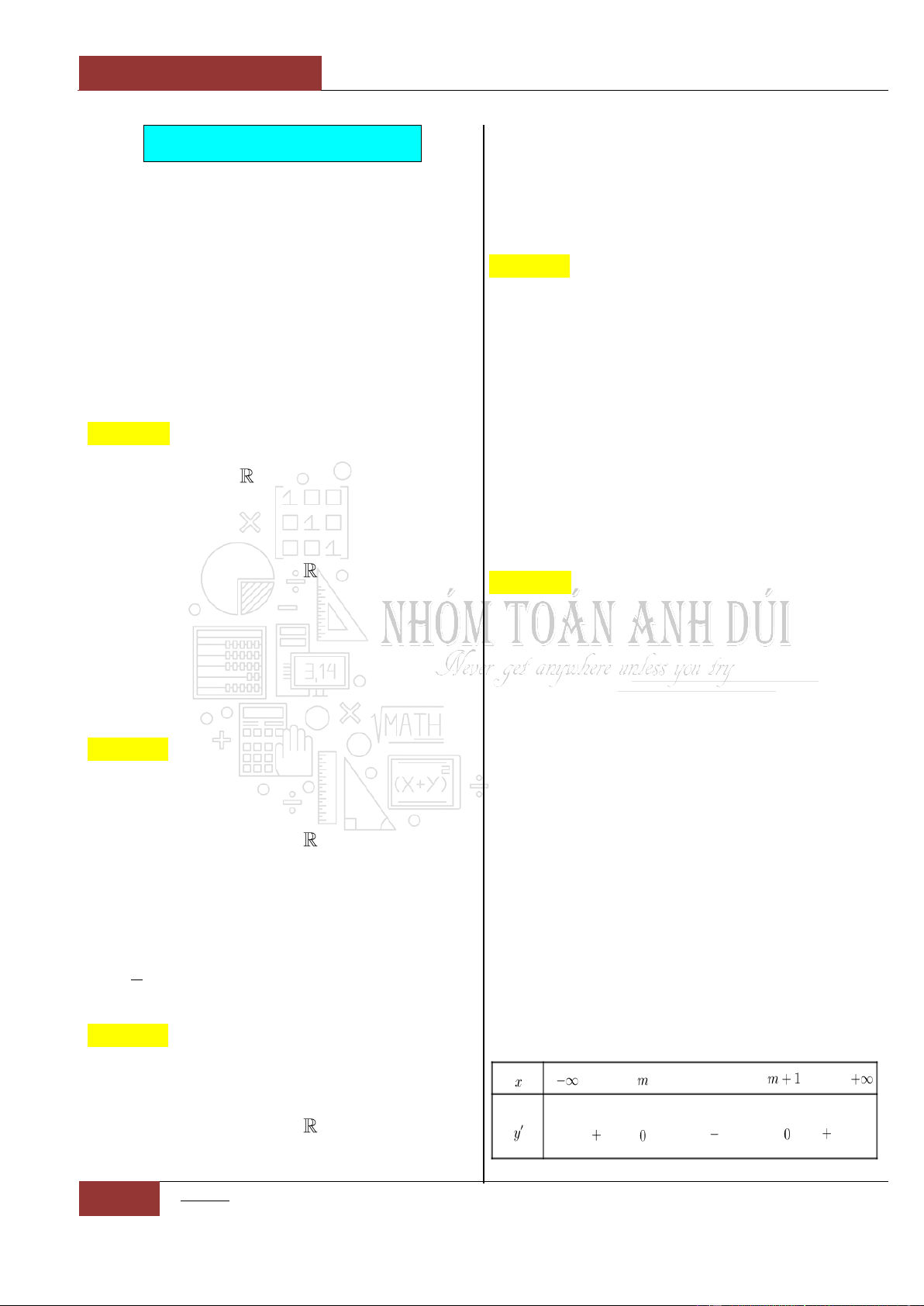
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

134

[ I can't, I can! ]

LỜI GIẢI CHI TIẾT

Câu 1. Ta có:

 

2

' 2 2 5 4y x m x m    

.

Để hàm số đồng biến trên khoảng

 

; 

thì:

 

2

10

2 5 4 0

a

mm









   





2

9 8 0 1 8m m m      

.

Đáp án D

Câu 2. TXĐ:

D 

.

Ta có:

 

3

' 2 1 1y x m x m    

.

Để hàm số đồng biến trên thì:

 

2

10

' 1 1 0

a

mm









     





2

3 2 0 2 1m m m        

.

Đáp án B

Câu 3. Ta có:

2

' 3 6 2y x mx m   

.

Để hàm số đồng biến trên thì:

2

30

' 9 3 6 0

a

mm







    



max

2

11

3

mm     

.

Đáp án B

Câu 4. Ta có:

2

2y x mx m  

.

Để hàm số đồng biến trên thì:

10

'0

a

mm









   



.

min

1 0 1mm      

.

Đáp án B

Câu 5. Ta có:

2

' 3 2 4 9y x mx m    

.

Để hàm số nghịch biến trên

 

; 

thì:

2

30

' 12 27 0

a

mm

  





    



 

9 3 9; 8;...; 3mm         

.

Như vậy có tất cả

7

giá trị

m

thỏa mãn.

Đáp án A

Câu 6. Ta có:

   

2

' 6 6 2 1 6 1y x m x m m    

.

Để hàm số đồng biến trên khoảng

 

2;

thì:

 

' 0, 2;yx   

     

2

6 6 2 1 6 1 0, 2;

1 1 0, 2;

x m x m m x

x m m x m m x

        

         





Ta có:

   

2

1 1 0x m m x m m     





  

10

1

xm

x m x m

xm





     







Bảng xét dấu:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

135

[ I can't, I can! ]

Dựa vào bảng xét dấu, ta suy ra: Hàm số đồng

biến trên khoảng

 

2;

khi và chỉ khi:

1 2 1mm   

.

Đáp án A

Câu 7. Ta có:

2

' 6 6 6y x x m  

.

Cách 1: Cô lập

m

.

Để hàm số nghịch biến trên khoảng

 

0;2

thì:

 

2

6 6 6 0, 0;2x x m x    

.

 

22

0;2

, 0;2 minm x x x m x x         

Ta xét hàm số:

 

2

, 0;2y x x x   

.

Ta có:

 

1

' 2 1 0

2

y x x L      

.

Và:

 

 

0;2

00

2 6 min

y

yy









  





.

Khi đó:

6m 

.

Đáp án A

Cách 2:

Ta có:

'

' 9 36

y

m  

.

Trường hợp 1:

'

1

'0

4

y

m   

.

Hàm số luôn đồng biến trên (loại).

Trường hợp 2:

'

1

'0

4

y

m   

.

Hàm số có hai nghiệm phân biệt

12

xx

.

Vì hàm số có hệ số

60a 

. Hàm số có một

khoảng nghịch biến duy nhất là

 

12

;xx

.

Để hàm số nghịch biến trên khoảng

 

0;2

thì:

12

02xx  

 

6. ' 0 0

36 0

6

36 216 0

6. ' 2 0

f

m

f











    













.

Câu 8. Ta có:

 

2

' 3 6 3 2 1y x mx m   

.

Để hàm số đồng biến trên khoảng

 

2;3

thì:

 

2

3 6 6 3 0, 2;3x mx m x     

Khi đó:

     

2

6 1 3 3 , 2;3 *m x x x    

.

Vì với mọi

2 3 2 1 1 0xx        

.

 

 

2

2;3

3 3 1 1

* , 2;3 min

6 1 2 2

x x x

m x m

x

  

     



Vì hàm số

1

2

x

y





đồng biến trên .

Suy ra:

 

2;3

1 2 1 3 3

min

2 2 2 2

x

m



   

.

Đáp án C

Câu 9. Cách 1: Đặt ẩn phụ.

Đặt:

2

tx

. Do

   

1;0 0;1xt   

.

Tuy nhiên ta hàm số:

2

yx

là một Parabol có

đỉnh

 

0;0I

và hệ số

10a 

nên hàm số

nghịch biến trên khoảng

 

;0

. Do đó trên

đoạn

 

1;0

hàm số nghịch biến. Vì thế sau khi

đặt ẩn phụ, tính đơn điệu của hàm số bị thay

đổi. Như vậy, yêu cầu đề bài tương đương với:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

136

[ I can't, I can! ]

Hàm số:

 

2

2 4 2y t m t m    

đồng biến

trên đoạn

 

0;1

.

Ta có:

 

' 2 2 0, 0;1y t m x     

.

 

 

0;1

min 2 2 2.0 2 2 2m t m       

do

hàm số

22yt

đồng biến trên .

Đáp án C

Cách 2: Cô lập

m

.

Ta có:

3

' 4 4 2y x x mx  

.

Để hàm số nghịch biến trên đoạn

 

1;0

thì:

 

 

3

4 4 2 0, 1;0 *x x mx x     

 

3

2 4 4 , 1;0mx x x x     

.

Xét các khả năng:

Trường hợp 1:

0 0 0x   

(Hiển nhiên).

Do đó

m

.

Trường hợp 2:

10x  





 

 

3

2

22

1;0

44

2 2, 1;0

2

min 2 2 2.0 2 2 2

xx

m x x

x

m x m





      

       

Do hàm số

2

22yx

nghịch biến trên khoảng

 

1;0

.

Vậy

2m 

.

Cách 3: Vì

0x 

. Suy ra

 

*

tương đương với:

 

 

22

2 2 2 0 2 2 0, 1;0x x m x m x         

 

 

22

1;0

min 2 2 2.0 2 2 2m x m



       

Do hàm số

2

22yx

nghịch biến trên khoảng

 

1;0

.

Vậy

2m 

.

Câu 10. TXĐ:

 

\1D 

.

Ta có:

 

2

5

' 0 5 0 5

1

m

y m m

x



      



.

Đáp án D

Câu 11. TXĐ:

 

\Dm

.

Ta có:

 

2

22

'0

mm

y

xm







2

13

2 2 0

13

m

mm

m



  

    



  





.

Đáp án D

Câu 12. TXĐ:

 

\Dm

.

Ta có:

   

22

2 2 3 2

'

m m m

y

x m x m

  





.

Để hàm số đồng biến trên khoảng

 

1;2

thì

trước hết hàm số phải liên tục trên

 

1;2

và

'0y 

. Điều đó tương đương với:

2

3 2 0

3

1

2

m













  

  





























.

Đáp án B

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

137

[ I can't, I can! ]

Câu 13. TXĐ:

 

\Dm

.

Ta có:

 

2

23

'

mm

y

xm

  





.

Để hàm số nghịch biến trên khoảng

 

2;

thì

trước hết hàm số phải liên tục trên khoảng

 

2;

và

'0y 

. Điều đó tương đương với:

2

3

2 3 0

1

12

2

m

mm

m

  



  

    





























.

Đáp án A.

Câu 14. Ta có:

2

' 3 6y x x m  

.

Để hàm số nghịch biến trên đoạn có độ dài bằng

2

thì phương trình:

'0y 

có hai nghiệm thực

phân biệt

12

xx

sao cho:

22

4S P k

. Điều

đó tương đương với hệ sau:

 

2

' 9 3 0

3

0

2 4. 2

3

m

   









  





  







.

Đáp án D

Câu 15. Ta có:

2

'4y x x m  

.

Để hàm số nghịch biến trên đoạn có độ dài bằng

1

thì phương trình:

'0y 

có hai nghiệm thực

phân biệt

12

xx

sao cho:

22

4S P k

. Điều

đó tương đương với hệ sau:

   

2

4

' 4 0

15

4

4 4. 1

4

m





   





   





   





.

Đáp án C.

Câu 16. Ta có:

 

2

' 2 2 1 2y x m x m    

.

Để hàm số đồng biến trên khoảng

 

0;2

thì

phương trình

'0y 

có hai nghiệm thực phân

biệt

12

xx

thỏa mãn:

12

02xx  

. Điều đó

tương đương với hệ:

 

. 0 0

2.2 0 0

0

2 12 0 6

. 2 0

af

mm

m

mm

af





  





   





    









Đáp án B

Câu 17. Ta có:

22

' 2 2y x mx m    

.

Để hàm số đồng biến trên đoạn có độ dài bằng

4

thì phương trình:

'0y 

có hai nghiệm thực

phân biệt

12

xx

sao cho:

22

4S P k

. Điều

đó tương đương với hệ sau:

   

2

' 2 0

1

2 4. 2 4

4 4 24 0

2

1

3

2

3

2

m

mm

m

mm

m

  





    













   





  















































Đáp án D

Câu 18. Ta có:

 

2

' 3 12 , 0;y x x m x     

Để hàm số đồng biến trên khoảng

 

0;

thì:

 





 

2

0;

3 12 0, 0;

max 3 12

x x m x

m x x



     

   

Xét hàm số

 

2

3 12 , 0;y x x x     

.

Ta có:

' 6 12 0 2y x x     

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

138

[ I can't, I can! ]

Và:

 

00

2 12

lim

x

y















 





.

Vì thế





 

2

0;

max 3 12 12xx



  

.

Vậy:

12m 

.

Đáp án B

Câu 19. TXĐ:

 

\1D 

.

Ta có:

 

2

1

' 0 1 0 1

1

m

y m m

x



      



.

Đáp án B

Câu 20. Ta có:

2

'2y x mx

.

Để hàm số đồng biến trên thì:

2

10

'0

a

m







  



.

Suy ra:

0m 

vì

2

0m 

.

Đáp án D

Câu 21. TXĐ:

 

\Dm

.

Ta có:

 

2

4

'

m

y

xm







.

Để hàm số nghịch biến trên khoảng

 

;1

thì

trước hết hàm số phải liên tục trên khoảng

 

;1

và

'0y 

. Điều đó tương đương với:

2

22

40

21

1

m

   

  

     









.

Đáp án D

Câu 22. Ta có:

2

'2y x mx m  

.

Để hàm số đồng biến trên thì:

min

2

10

1 0 1

'0

a

mm





      



   



.

Đáp án D

Câu 23. Ta có:

 

2

' 2 2y x m x m    

.

Để hàm số nghịch biến trên thì:

 

2

10

5 4 0

' 2 0

a

mm

  





   



    





14m  

.

Đáp án C

Câu 24. Ta có:

2

' 2 4y x mx  

.

Để hàm số đồng biến trên thì:

2

10

22

' 4 0

a

m





   



   



.

Đáp án A

Câu 25. Ta có:

2

' 2 4y x mx   

.

Để hàm số đã cho nghịch biến trên thì:

2

10

22

' 4 0

a

m

  



   



   



.

Đáp án A

Câu 26. Ta có:

 

' 2 1 cos 3y m x m   

.

Để hàm số đồng biến trên thì:

' 0,yx  

Đặt:

 

cos 1;1t x t   

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

139

[ I can't, I can! ]

Khi đó:

 

' 0 2 1 3 0y m t m     

.

Cách 1:

Vì

   

 

2 1 3 , 1;1y f t m t m t       

là

phương trình đoạn thẳng. Khi đó:

 

0ft

tương đương với:

 

10

f















3 2 0

2

4

40

3

m

  



    







.

Cách 2:

Xét các khả năng:

Trường hợp 1:

1

2

m 

.

Ta có:

 

7

' 0, 1;1

2

yt    

(Thỏa mãn).

Trường hợp 2:

1

2

m 

.

Khi đó hàm số

   

2 1 3f t m t m   

là một

hàm đồng biến suy ra:

 

 

   

1;1

0, 1;1 min 1 0f t t f t f



       

.

Suy ra:

2

3 2 0

3

mm    

.

Suy ra:

12

23

m  

.

Trường hợp 3:

1

2

m 

.

Khi đó hàm số

   

2 1 3f t m t m   

là một

hàm nghịch biến suy ra:

 

 

   

1;1

0, 1;1 min 1 0f t t f t f



      

.

Suy ra:

4 0 4mm    

.

Suy ra:

1

4

2

m   

.

Kết hợp ba trường hợp, ta có:

2

4

3

m  

.

Đáp án A

Câu 27. Ta có:

' 1 siny m x

.

Để hàm số đồng biến trên thì:

' 0,yx  

Đặt:

 

sin , 1;1t x t  

.

Khi đó:

 

' 0, 1 0, 1;1y x mt t        

.

Cách 1:

Vì

 

 

1 , 1;1y f t mt t     

là phương

trình đoạn thẳng. Khi đó:

 

0ft

tương

đương với:

 

10

f















10

11

10

m





    







.

Cách 2:

Xét các khả năng:

Trường hợp 1:

0m 

.

Ta có:

 

' 1 0, 1;1yt    

(Thỏa mãn).

Trường hợp 2:

0m 

.

Khi đó hàm số

 

1f t mt

là một hàm đồng

biến suy ra:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

140

[ I can't, I can! ]

 

 

   

1;1

0, 1;1 min 1 0f t t f t f



       

.

Suy ra:

1 0 1mm    

.

Suy ra:

10m  

.

Trường hợp 3:

0m 

.

Khi đó hàm số

 

1f t mt

là một hàm nghịch

biến suy ra:

 

 

   

1;1

0, 1;1 min 1 0f t t f t f



      

.

Suy ra:

1 0 1mm   

.

Suy ra:

01m

.

Kết hợp ba trường hợp, ta có:

11m  

.

Cách 3:

Để hàm số đồng biến trên thì:

 

' 1 sin 0, sin 1, *y m x x m x x        

Ta thấy

0m 

, thỏa mãn

 

*

, ta xét hai trường

hợp sau:

Trường hợp 1:

0m 

.

Khi đó:

 

11

* sin , maxsin 1x x x

mm

      

.

Suy ra:

1m 

. Kết hợp với điều kiện, được:

01m

.

Trường hợp 2:

0m 

.

Khi đó:

 

11

* sin , minsin 1x x x

mm

       

.

Suy ra:

1m 

. Kết hợp với điều kiện, được:

10m  

.

Từ ba điều kiện trên ta có:

11m  

.

Đáp án C

Câu 28. Ta có:

2

' 3 6 4y x x m   

.

Cách 1: Cô lập

m

.

Để hàm số nghịch biến trên nữa khoảng





;0

thì:





 

' 0, ;0 *yx   

.

  







2

;0

* 3 6 4 0, ;0

36

min

4

x x m x

xx

m



       











Ta có:

 

2

3 6 3 3 3 3 3 3 3

1

4 4 2 4 4 4 4 4

xx

x x x





        





Dấu

""

xảy ra khi

1x 

.

Suy ra:





2

;0

3 6 3

min

44

xx













.

Hay:

3

4

m 

.

Cách 2:

Ta có:

'

' 9 12

y

m  

.

Ta xét các khả năng:

Trường hợp 1:

'

'0

y



.

Vì:

30a   

nên hàm số nghịch biến trên .

Khi đó:

3

9 12 0

4

mm    

.

Vậy hàm số nghịch biến trên khoảng





;0

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

141

[ I can't, I can! ]

Trường hợp 2:

'

12

'0

0

y

xx











.

Khi đó:

9 12 0

20

4

0

3

m

S

m

P









  





  



(Vô lý).

Vậy:

3

4

m 

.

Đáp án A.

Câu 29. Ta có:

 

22

' 3 2 1 2y x m x m     

.

 

2

22

' 1 3 2 2 2 5m m m m        

.

Vì:

22

19

2 2 5 2

42

m m m m



       





2

1 9 9

20

2 2 2

m



      





.

Suy ra:

'0

. Vì thế hàm số luôn nghịch biến

trên (do

30a   

).

Đáp án C

Câu 30. Ta có:

2

'4y x x m   

.

Để hàm số nghịch biến trên thì:

10

4

' 4 0

a

m

  







   



.

Đáp án B

Câu 31. Ta có:

 

22

' 3 2 2 4y x m x m    

.

Để hàm số đồng biến trên thì:

 

2

30

2 4 16 0

' 2 3 4 0

a

mm







    



     





4

2

m













.

Đáp án B

Câu 32. TXĐ:

 

\Dm

.

Ta có:

 

2

3

'0

mm

y

xm







.

2

3

30

0

m

mm

m





   







.

Đáp án D

Câu 33. Ta có:

2

' 3 6y x x m  

.

Để hàm số đồng biến trên

 

0;

thì:

 

' 0, 0;yx   

 

22

0;

3 6 0, 0; min 3 6x x m x m x x



        

Mà:

 

2

22

3 6 3 6 3 3 3 1 3 3x x x x x         

Và dấu

""

xảy ra tại

 

1 0;x   

.

Vì thế

 

2

0;

min 3 6 3xx



  

.

Suy ra:

3m 

.

Đáp án B

Câu 34. TXĐ:

 

\1D 

.

Ta có:

 

2

1

' 0 1 0 1

1

m

y m m

x



      



.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

142

[ I can't, I can! ]

Đáp án C

Câu 35. Ta có:

2

' 2 4y x mx  

.

Để hàm số đồng biến trên thì:

2

10

22

' 4 0

a

m





   



   



Đáp án B

Câu 36. TXĐ:

 

\Dm

.

Ta có:

 

2

'

mm

y

xm







.

Để hàm số nghịch biến trên khoảng

 

1; 

thì trước hết hàm số phải liên tục trên khoảng

 

1; 

và

'0y 

. Khi đó:

 

2

0

20

12

1

mm

m

xm

m









  



   











  



Đáp án C

Câu 37. Ta có:

2

'2y x mx  

.

Để hàm số đồng biến trên khoảng

 

1; 

thì:

 

' 0, 1;yx   

. Khi đó:

 





2

22

1;

2 0, 1;

2, 1;

22

, 1; min

x mx x

mx x x

xx

m x m

xx



     

     





      





Ta xét hàm số

2

22x

yx

xx



  

, có:

 

2

' 1 0, 1;yx

x

     

.

Suy ra:





 

1;

min 1 1yy



  

.

Nên:

1m 

.

Đáp án B

Câu 38. Ta có:

 

2

' 2 2 1y x m x m    

.

Để hàm số nghịch biến trên thì:

 

2

10

4 3 1 0

' 2 1 0

a

m m m

mm

  





      



    





Vậy không có giá trị thực nào của

m

thỏa mãn.

Đáp án C

Câu 39. TXĐ:

 

 

2

\ lnDm

Đặt:

1

, ;1

4

x

t e t









.

Vì:

1

ln

0

4

11

ln 0 1

44

xx

x e e e e       

.

Hàm số đã cho trở thành:

2

21

, ;1

4

tm

yt

tm













.

Ta có:

 

2

'

mm

y

tm

  





.

Để hàm số đồng biến trên khoảng

1

;1

4







thì

trước hết hàm số phải liên tục trên khoảng

1

;1

4







và

1

' 0, ;1

4

yx



  





.

Khi đó, ta được:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

143

[ I can't, I can! ]

2

11

1

22

11

4

1

22

1

12

20

12

m

mm

m





  























  































   





  



Đáp án D

Extra Techniques:

Tips:

Sở dĩ hàm số sau khi đặt ẩn

phụ không bị thay đổi tính

đơn điệu là vì hàm số

x

ye

là một hàm đồng biến trên

(do

'0

x

ye

).

Câu 40. TXĐ:

 

\Dm

.

Ta có:

 

2

3

'

m

y

xm







.

Để hàm số đồng biến trên từng khoảng xác định

thì:

' 0,y x D  

.

Khi đó:

 

2

3

0 3 0 3

m

mm

xm



       



.

Đáp án A.

Câu 41. Đặt:

 

1, 4;6t x t  

.

Vì:

17 37 16 1 36 4 6x x t        

.

Khi đó hàm số đã cho trở thành:

 

12

, 4;6

mt

yt

tm







.

Ta có:

 

2

'

mm

y

tm







.

Để hàm số đồng biến trên khoảng

 

4;6

thì

trước hết hàm số phải liên tục trên khoảng

 

4;6

và thỏa mãn

 

' 0, 4;6yt  

. Khi đó:

2

4

41

4

6

2

6

1

20

2

m

mm

m





    



  



































  















Đáp án B

Extra Techniques:

Tips:

Sở dĩ hàm số sau khi đặt ẩn phụ

không bị thay đổi tính đơn điệu

là vì hàm số

1yx

là một

hàm đồng biến trên nữa khoảng





1; 

(do trên khoảng

 

1; 

,

1

'0

21

y

x





).

Để có:

41

2

6

m

   

















ta thực hiện

như sau:

4

1

44

41

62

2

6

16

21

6

2

m

mm

m

mm

m

mm

m

mm

m



















   

     











  





 











   

















  

























.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

144

[ I can't, I can! ]

Câu 42. Ta có:

 

2

' 3 6 0 *y x mx  

 

0

*

2

x

xm













.

Ta xét các khả năng:

Trường hợp 1:

0m 

, khi đó:

 

2

' 3 0, 0;1y x x   

.

Suy ra hàm số luôn đồng biến trên

 

0;1

(Loại).

Trường hợp 2:

0m 

.

Để hàm số nghịch biến trên khoảng

 

0;1

thì:

   

1

0;1 0;2 1 2

2

m m m    

(Nhận).

Trường hợp 3:

0m 

.

Để hàm số nghịch biến trên khoảng

 

0;1

thì:

   

20

0;1 2 ;0

10

m













(Vô lý).

Vậy

1

2

m 

.

Đáp án A

Extra Techniques:

Tips:

Vì hàm số là hàm số bậc ba

có hệ số

30a 

. Vì thế,

nếu có khoảng nghịch biến thì

bắt buộc hàm số phải có dạng

hình chữ

""

. Hay khoảng

nghịch biến là khoảng giữa

hai cực trị của hàm số.

Câu 43. Ta có:

22

' 3 3y x m

.

Để hàm số đồng biến trên thì:

' 0,yx  

Hay

22

3 3 0,x m x   

.

2 2 2 2 2

, min 0 0m x x m x m        

Vì:

2

00mm  

.

Đáp án B

Extra Techniques:

Remark:

Vì

2

0,xx  

nên:

 

2

min 0x 

.

Câu 44. Ta có:

2

' 2 3 2y x mx m    

.

Để hàm số nghịch biến trên thì:

10

'0

a   









.

Khi đó:

2

' 3 2 0 2 1m m m         

.

Đáp án C

Câu 45. TXĐ:

 

\Dm

.

Ta có:

 

2

2mm

y

xm

  





.

Để hàm số đồng biến trên từng khoảng xác định

thì

' 0,y x D  

.

Hay:

2

2 0 2 1m m m       

.

Đáp án A

Câu 46. Ta có:

2

' 3 6y x x m  

.

Để hàm số đồng biến trên khoảng

 

;0

thì:

   

' 0, ;0 *yx   

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

145

[ I can't, I can! ]

   

 

2

;0

* 3 6 0, ;0

3 6 , ;0

min 3 6

x x m x

m x x x

m x x



      

     

  

Xét hàm số:

 

2

3 6 , ;0y x x x   

.

Ta có:

' 6 6 0 1y x x     

Vì:

 

;0

lim

1 3 min

00

x

y

yy

y







 



   









.

Nên:

3m 

.

Đáp án C

Câu 47. Xét hàm số:

sin cos 2021 2y x x mx  

Ta có:

2sin 2021 2

4

y x mx





  





.

Khi đó:

' 2cos 2021 2

4

y x m





  





Để hàm số đồng biến trên thì:

' 0,yx  

2 cos 2021 2 0,

4

2021 2 2 cos ,

4

1

cos ,

2021 4

11

max cos

2021 4 2021

1

2021

x m x

m x x

mx

m





     







     







     









    











Đáp án C

Extra Techniques:

Remark:

Vì:

1 cos 1

4

x





   





.

Nên:

1 1 1

cos

2021 2021 4 2021

x





    





Suy ra:

11

max cos

2021 4 2021

x







  









Câu 48. Đặt:

 

sin , 0;1t x t

.

Khi đó:

 

21

, 0;1

t

yt

tm







.

TXĐ:

 

\Dm

Ta có:

 

2

21

'

m

y

tm







.

Để hàm số

21t

y

tm







đồng biến trên khoảng

 

0;1

thì trước hết hàm số phải liên tục trên

khoảng

 

0;1

và

 

' 0, 0;1yx

. Khi đó, ta có:

0

1

0

1

2 1 0

2

m





















  









  









.

Đáp án C

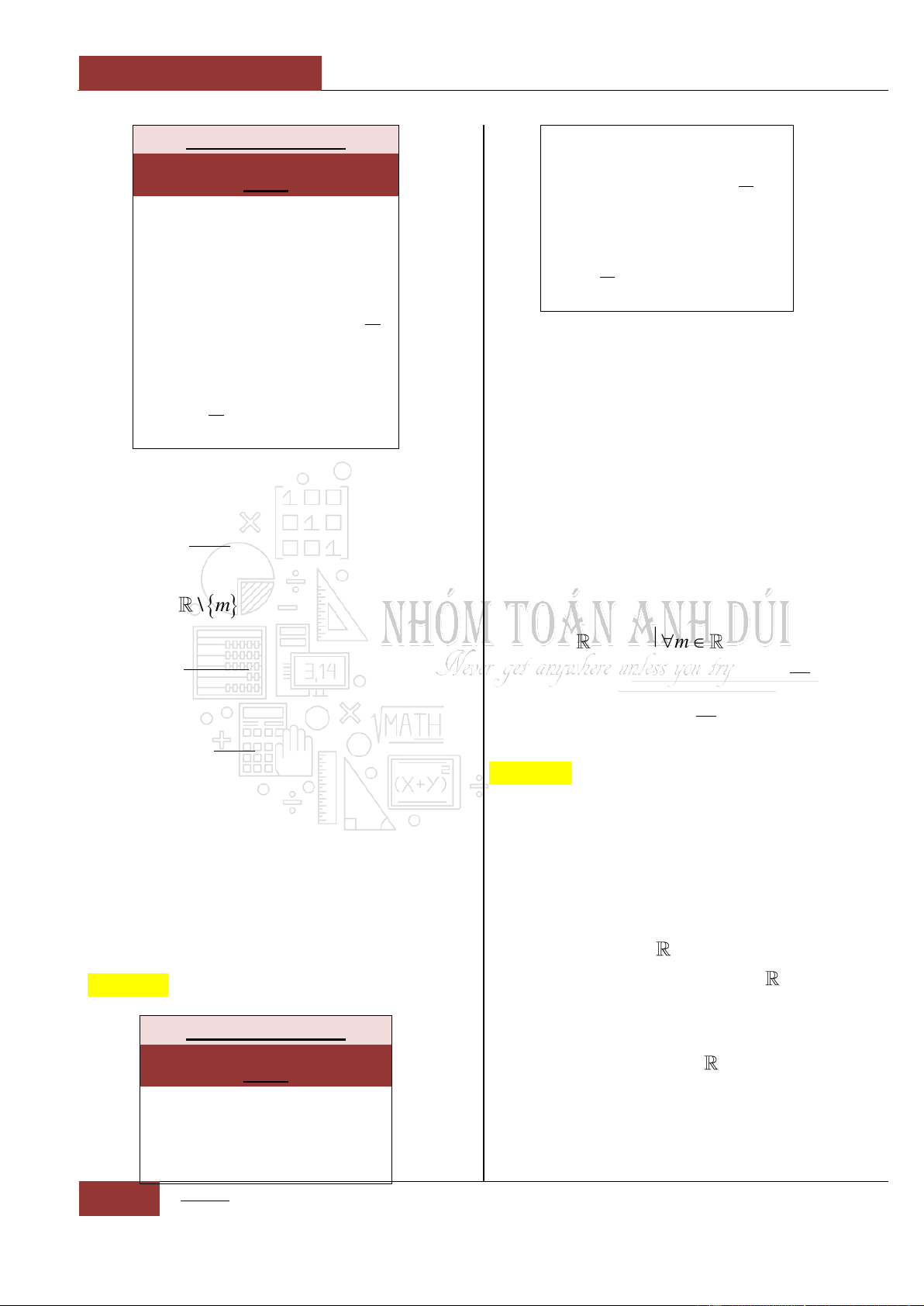
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

146

[ I can't, I can! ]

Extra Techniques:

Tips:

Sở dĩ hàm số sau khi đặt ẩn phụ

không bị thay đổi tính đơn điệu

là vì hàm số

sinyx

là một

hàm đồng biến trên

0;

2









(do

' cosyx

mà

cos 0,x 

0;

2

x











).

Câu 49. Đặt:

 

sin , 0;1t x t

.

Khi đó:

 

, 0;1

tm

yt

tm







.

TXĐ:

 

\Dm

Ta có:

 

2

'

m

y

tm







.

Để hàm số

tm

y

tm







đồng biến trên khoảng

 

0;1

thì trước hết hàm số phải liên tục trên

khoảng

 

0;1

và

 

' 0, 0;1yx

. Khi đó, ta có:

00

0

11

2 0 0

mm

m

mm

   







  









  



.

Đáp án B

Extra Techniques:

Tips:

Sở dĩ hàm số sau khi đặt ẩn

phụ bị thay đổi tính đơn

điệu là vì:

hàm số

sinyx

là một hàm

nghịch biến trên

;

2









(do

' cosyx

mà

cos 0,x 

;

2

x











).

Câu 50. Ta có:

 

2

' 2 1 3y x m x m     

.

Để hàm số đồng biến trên

 

0;3

thì phương

trình:

'0y 

có hai nghiệm phân biệt

12

,xx

thỏa

mãn:

12

03xx  

. Khi đó:

 

   

 

2

' 1 3 0

' 4 0

1 . 0 0 0 0

1 . 3 0 3 0

12

3 0 3

7

7 12 0 12

7

mm

ff

mm

m m m

m



     



    



   





  











   





       















Đáp án A

Câu 51. Ta có:

22

' 3 2y mx mx m m   

.

Xét các khả năng:

Trường hợp 1: Với

0m 

.

Khi đó:

' 0,yx  

. Nên hàm số không đổi

hay hàm số không đồng biến trên (Loại).

Trường hợp 2: Với

0m 

.

Để hàm số đồng biến trên thì:

 

22

30

*

' 3 0

am

m m m m









    





Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

147

[ I can't, I can! ]

 

32

0

4

0

*

3

3 4 0

4

3

m

mm

m















   





  















Đáp án D

Câu 52. Ta có:

     

2

' 3 1 6 1 3 2 3y m x m x m     

.

Xét các khả năng:

Trường hợp 1: Với

1m 

.

Khi đó:

' 3,yx   

. Nên hàm số nghịch

biến trên (Nhận).

Trường hợp 2: Với

1m 

.

Để hàm số nghịch biến trên thì:

 

    

 

2

3 1 0

*

' 9 1 9 1 2 3 0

am

m m m

  







      





 

  

1

*1

1

9 1 2 0

2

m

mm

m











   







  













Từ hai trường hợp trên ta suy ra:

1m 

.

Đáp án A

Câu 53. Ta có:

 

2

' 2 1 2 3y x m x m    

.

Để hàm số đồng biến trên

 

1; 

thì:

 

' 0, 1;yx   

Hay:

    

2

2 3 2 1 0, 1; *x x m x x       

 

2

1;

23

* max 1 1

22

xx

mm

x





  

    







.

Đáp án D

Note: Chứng minh:





2

1;

23

max 1

22

xx

x





  









.

Xét hàm số:

 

2

23

, 1;

22

xx

yx

x

  

  



Ta có:

 

2

2 4 2

' 0 1

22

xx

yx

x

  

    



(Loại).

Và:

 





1;

1 1 max

lim

x

y













 





.

Suy ra:





2

1;

23

max 1

22

xx

x





  









.

Câu 54. Ta có:

2

'2y x mx  

.

Để hàm số đồng biến trên thì:

2

10

2 2 2 2

80

a

m





   



   



.

Đáp án A

Câu 55. Ta có:

 

2

' 3 2 1 3y x m x   

.

Để hàm số đồng biến trên khoảng

 

; 

thì:

 

2

30

3 1 3 4 2

' 1 9 0

a

mm

m







        



    





Đáp án A

Câu 56. Ta có:

2

' 3 2 2y x x m    

.

Để hàm số đồng biến trên một khoảng có độ lớn

bằng

2

thì:

 

22

' 1 3 6 0

*

4 2 4

m

SP

    





  



.

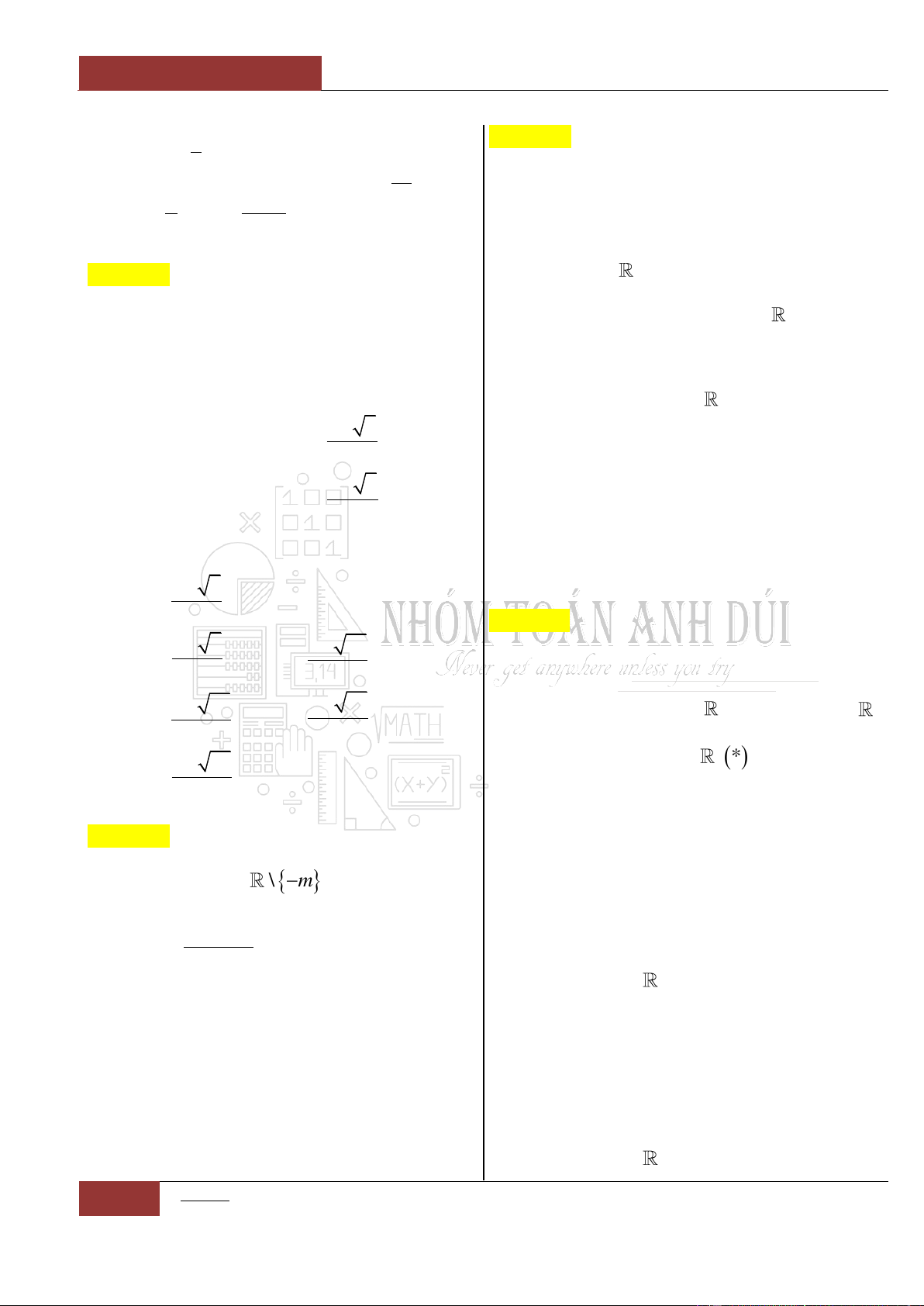
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

148

[ I can't, I can! ]

 

2

5

3

14

*

3

22

4. 4

33

m







  





   





   





   



.

Đáp án D

Câu 57. Ta có:

2

' 3 6 3 3y x mx m   

.

Để hàm số nghịch biến trên một khoảng có độ

dài lớn hơn

4

thì:

   

2

22

2

15

2

9 9 9 0

15

4 4 16

2

2 4 1 16

15

2

15

1 21

2

1 21

2

1 21

2

m

mm

m

SP

mm

m



















  















  









   





















































































Đáp án D

Câu 58. TXĐ:

 

\Dm

.

Ta có:

 

2

4

'

m

y

xm







.

Để hàm số nghịch biến trên khoảng

 

;1

thì

trước hết hàm số phải liên tục trên khoảng

 

;1

và

 

' 0, ;1yx   

. Khi đó ta có:

2

1

21

22

40

m



  



     



  





.

Đáp án C

Câu 59. Ta có:

2

' 2 3y mx mx  

.

Trường hợp 1: Với

0m 

, ta có:

' 3 0,yx   

.

Vì thế hàm số luôn đồng biến trên (Nhận).

Trường hợp 2: Với

0m 

.

Để hàm số đồng biến trên thì:

2

0

03

' 3 0

am

m

mm







   





   



.

Kết hợp hai trường hợp, ta được:

03m

.

Vậy giá trị nhỏ nhất của

m

thỏa mãn yêu cầu đề

bài là

0m 

.

Đáp án B

Câu 60. Ta có:

' cos 7y m x

.

Để hàm số đồng biến trên thì:

' 0,yx  

Hay:

 

cos 7 0, *m x x   

.

Xét hàm số

cos 7y m x

.

Ta xét các khả năng:

Trường hợp 1:

0m 

.

Khi đó:

7 cos 7 7m m x m     

.

Để

 

*

đúng

x

thì:

7 0 7mm    

.

Khi đó:

07m

.

Trường hợp 2:

0m 

.

Khi đó:

7 cos 7 7m m x m     

.

Để

 

*

đúng

x

thì:

7 0 7mm    

.

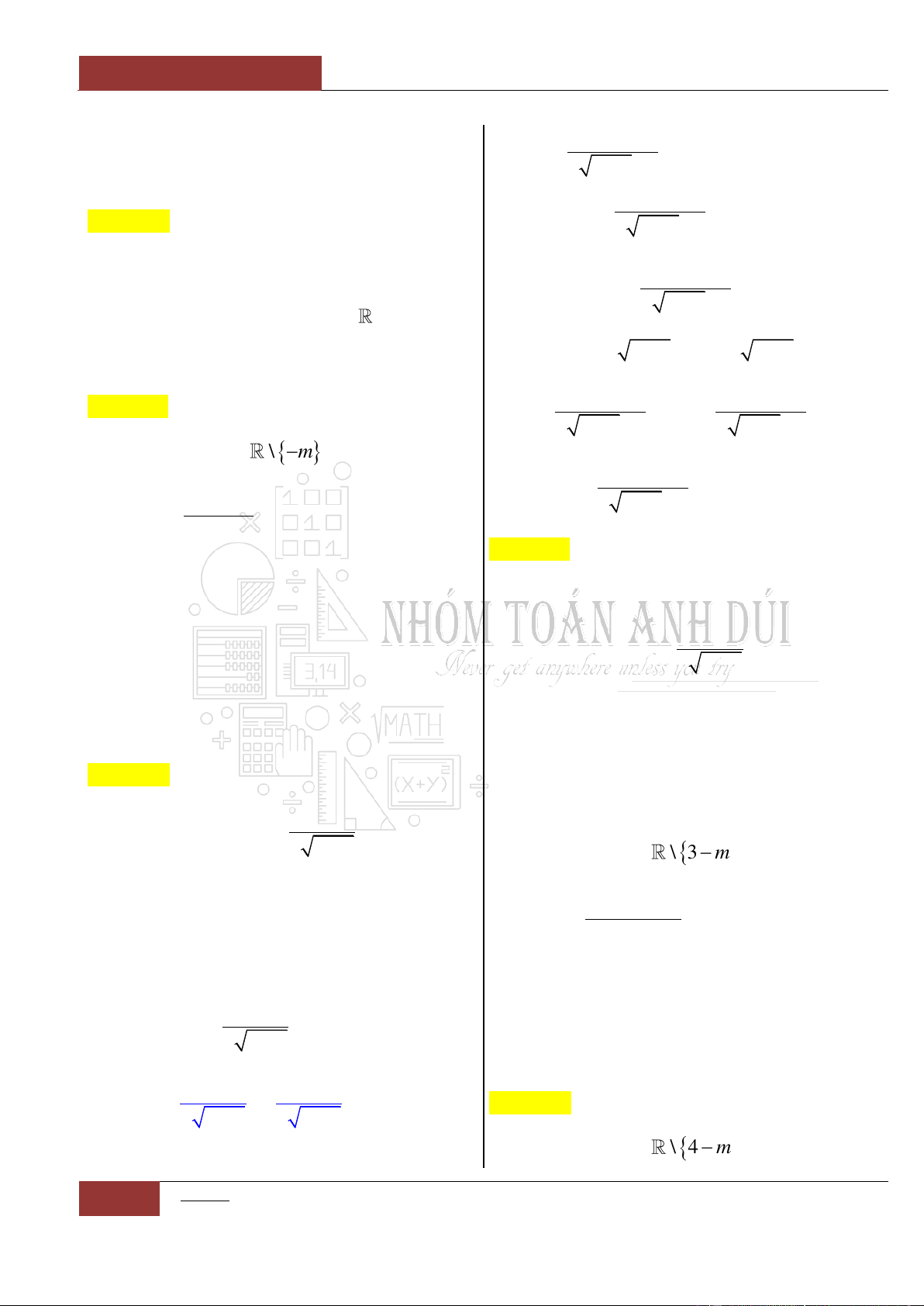
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

149

[ I can't, I can! ]

Khi đó:

70m  

.

Kết hợp hai trường hợp, ta được:

77m  

.

Đáp án A

Câu 61. Ta có:

 

2

' 2 1 2 5y x m x m     

.

Để hàm số luôn nghịch biến trên thì:

 

2

10

4 0 2 2

' 1 2 5 0

a

mm

  





      



     





Đáp án B

Câu 62. TXĐ:

 

\Dm

.

Ta có:

 

2

1

'

m

y

xm







.

Để hàm số nghịch biến trên khoảng

 

2;

thì

trước hết hàm số phải liên tục trên khoảng

 

2;

và

 

' 0, 2;yx   

. Khi đó, ta có:

22

21

1 0 1

mm

m

mm

   



    



  



.

Đáp án A

Câu 63. Ta có:

1

'

22

m

ym

x







.

Để hàm số nghịch biến trên nữa khoảng





2;

thì:





' 0, 2;yx   

.

Cách 1: Cô lập

m

.

Khi đó:

 

1

' 0, 2;

22

m

y m x

x



     



.

 

11

' 1 0, 2;

2 2 2 2

y m x

xx



      















2;

1

, 2;

2 2 1

1

min

2 2 1

mx

x

m

x



     





  







.

Xét hàm số:





1

, 2;

2 2 1

yx

x

    



.

Ta có:

2 2 0 2 2 1 1x x x       

.

Suy ra:

11

2 2 1 2 2 1xx

    

   

.

Vậy:





2;

1

min 1 1

2 2 1

m

x





     







.

Đáp án B

Cách 2:

Ta có:

 

1

'1

22

y m m

x

  



.

Điều kiện cần để:

2

' 0, 2 lim ' 0

x

y x y





    

.

Khi đó:

1 0 1mm    

.

Thử lại:

1m 

thỏa mãn yêu cầu đề bài.

Câu 64. TXĐ:

 

\3Dm

.

Ta có:

 

2

32

'

3

mm

y

xm







.

Để hàm số đã cho nghịch biến trên từng khoảng

xác định thì:

' 0,y x D  

. Khi đó, ta có:

2

3 2 0 1 2m m m     

.

Đáp án A

Câu 65. TXĐ:

 

\4Dm

.

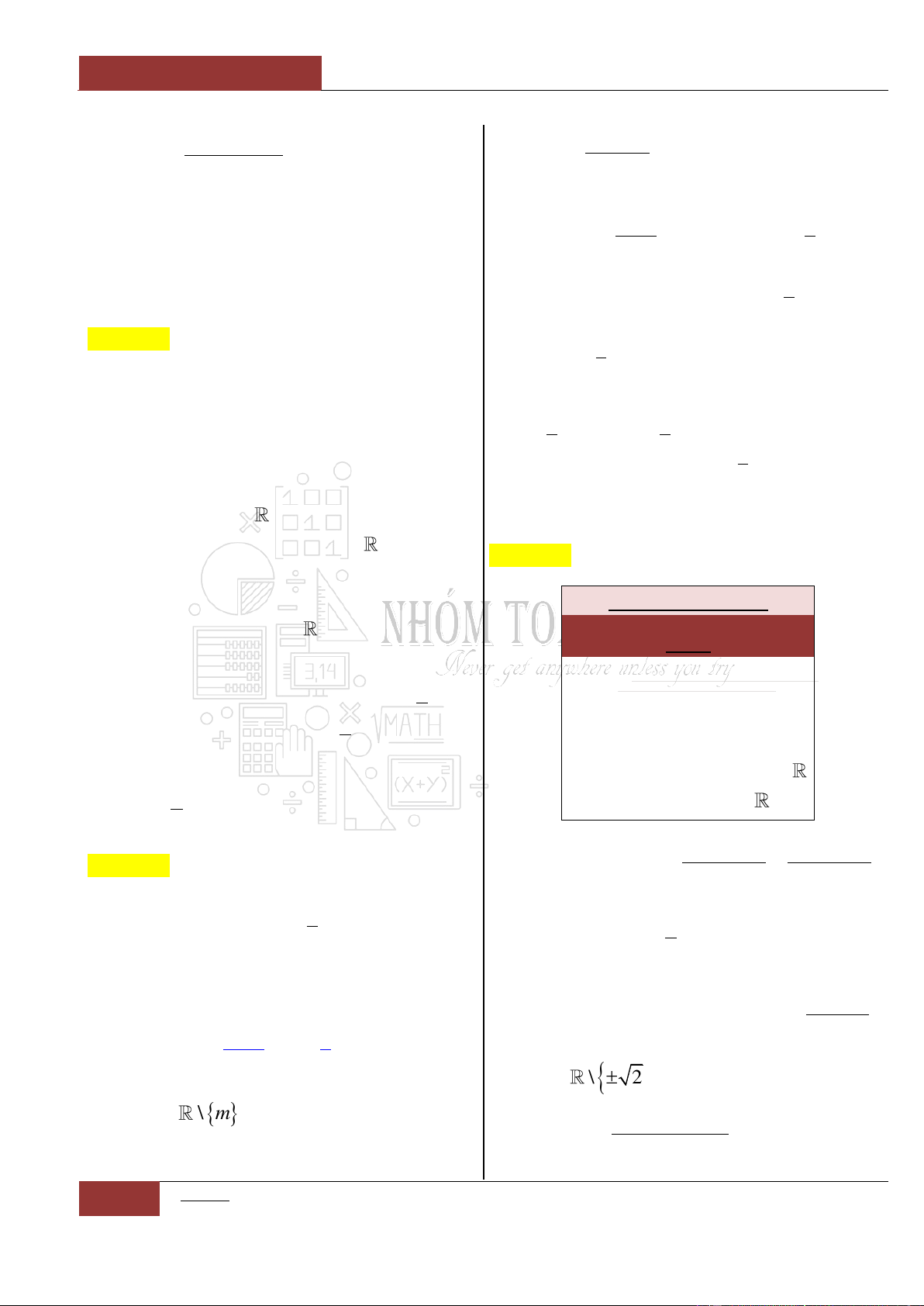
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

150

[ I can't, I can! ]

Ta có:

 

2

43

'

4

mm

y

xm







.

Để hàm số đã cho nghịch biến trên từng khoảng

xác định thì:

' 0,y x D  

. Khi đó, ta có:

2

4 3 0 1 3m m m     

.

Đáp án C

Câu 66. Ta có:

22

' 3 2y mx mx m m   

.

Xét các trường hợp:

Trường hợp 1:

0m 

.

Khi đó:

' 0,yx  

. Nên hàm số không đổi

hay hàm số không đồng biến trên (Loại).

Trường hợp 2:

0m 

.

Để hàm số đồng biến trên thì:

23

0

30

4

0

3

' 4 3 0

4

3

m

am

m

mm

m















  





   















.

Vậy:

3

4

m 

.

Đáp án D

Câu 67. Đặt:

1

3 , ;3

3

x

tt











.

Khi đó hàm số đã cho trở thành:

31

, ;3

3

t

yt

tm













.

TXĐ:

 

\Dm

.

Ta có:

 

2

3

'

m

y

tm







.

Để hàm số

3t

y

tm







đồng biến trên

1

;3

3







thì

hàm số trước hết phải liên tục trên

1

;3

3







và

1

' 0, ;3

3

yt



  





. Khi đó, ta có:

11

33

1

33

3

3 0 3

mm

m

mm















  









  



.

Đáp án C

Extra Techniques:

Tips:

Sở dĩ hàm số sau khi đặt ẩn

phụ bị thay đổi tính đơn

điệu là vì: hàm số

x

ye





là

một hàm nghịch biến trên

(do

' 0,

x

y e x



    

).

Câu 68. Ta có:

 

22

2sin 2sin

1 cos 2 sin

m x m x

fx

xx







Đặt:

1

sin , 0;

2

t x t









.

Khi đó hàm số đã cho có dạng:

 

2

tm

ft

t







.

TXĐ:

 

\2t 

.

Ta có:

 

2

2 2 4

'

2

t mt

ft

t

  





.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

151

[ I can't, I can! ]

Để hàm số

 

2

tm

ft

t







nghịch biến trên

1

0;

2







thì

 

1

' 0, 0;

2

f t t



  





.

Hay:

2

1

2 2 4 0, 0;

2

t mt t



     





Suy ra:

2

11

0; 0;

22

2 4 2

min min

2

t

mt

tt

   





   







  





.

Xét hàm số:

21

, 0;

2

y t t

t



  





.

Ta có:

2

21

' 1 0, 0;

2

yt

t



    





.

Nên:

1

0;

2

2 1 2 9

min

1

22

2

t











   





.

Vậy:

9

2

m 

.

Đáp án C

Câu 69. Ta có:

 

' ' 1y f x m  

.

Để hàm số đồng biến trên

 

0;3

thì:

   

 

0;3

' 1 0, 0;3 1 min 'f x m x m f x       

Suy ra:

1 3 4mm    

.

Đáp án C

Câu 70. Ta có:

     

' ' 1g x f x m x m    

.

Đặt:

       

' 1 0 ' 1h x f x x f x x      

.

Kẻ đường thẳng:

1yx

tương giao với đồ thị

 

'y f x

.

Dựa vào sự tương giao hàm số ta thấy:

   

3

0 ' 1

11

x

h x f x x

x





    



  



.

Do đó:

   

'0g x h x m  

.

33

1 1 1 1

x m x m

x m m x m

   







       



.

Vì hàm số

 

y g x

đồng biến trên khoảng

 

5;6

nên ta có:

35

2

15

56

16

m

































.

Kết hợp với điều kiện ta có:

 

1;2;5;6m 

.

Suy ra:

1 2 5 6 14S     

.

Đáp án C

Câu 71. Ta có:

   

' ' 3g x f x x  

.

Cho

   

' 0 ' 3g x f x x   

.

Vẽ đường thẳng

3yx

tương giao với đồ thị

hàm số

 

'y f x

trên cùng một hệ trục tọa độ.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

152

[ I can't, I can! ]

Dựa vào đồ thị tương giao ta có kết luận:

 

2

' 0 0

2

x

g x x

x







  







.

Bảng biến thiên:

Vậy: với mọi giá trị thực của

m

, hàm số đồng

biến trên các khoảng

 

2;0

và

 

2;

, nghịch

biến trên các khoảng

 

;2 

và

 

0;2

.

Đáp án C

Câu 72. Ta có:

   

 

2

' 2 1 . 'g x x f x x m   

.

Để hàm số nghịch biến trên khoảng

 

1;0

thì:

     

' 0, 1;0 *g x x   

.

Ta có:

1 0 3 2 1 1 0xx         

.

Như vậy:

 

   

2

' * ' 0, 1;0 **g f x x m x      

.

Dựa vào bảng xét dấu của đồ thị đạo hàm ta có:

 

 

 

 

 

2

1;0

2

1;0

1, 1;0

**

4, 1;0

min 1 1

1

4

max 4 4

x x m x

m x x

m

m x x





     





     







     















    





Kết hợp với điều kiện ta có:

4 2021m

.

 

4;5;6;...;2020m

.

Vậy có

2017

giá trị của

m

thỏa mãn yêu cầu

đề bài.

Đáp án C

Extra Techniques:

Tips:

Hai hàm số

2

y x x k   

với

k

là tham số thực là hai

hàm số đồng biến trên khoảng

 

1;0

do

2 1 0x  

. Vì thế

trên đoạn

 

1;0

giá trị nhỏ

nhất đạt tại

1x 

và giá trị

lớn nhất đạt tại

0x 

.

Câu 73. Ta có:

   

 

2

' 1 2 0f x x x x   

.

Khi đó:

 

0

1

2

x











.

Xét hàm số:

 

2

8g x f x x m  

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

153

[ I can't, I can! ]

Ta có:

   

 

2

' 2 8 . ' 8g x x f x x m   

.

Để hàm số đồng biến trên khoảng

 

4;

thì:

   

' 0, 4 *g x x  

.

   

 

2

* 2 8 . ' 8 0, 4

' 8 0, 4 2

x f x x m x

f x x m x

      

     

(Do

4 2 8 0xx   

).

Từ

  

2

8 0, 4

12

8 2, 4

x x m x



    





    





.





 









 

2

4;

2

4;

2

4;

min 8 ###

max 8 2

max 8 2 18

18 2021 18;19;...;2020

m x x

mm







  











   









     



    

Như vậy có tất cả

2003

giá trị

m

thỏa mãn.

Đáp án A

Extra Techniques:

Tips:

Bất

 

###

vô nghiệm là vì:

Hàm số

2

8y x x  

không

có GTNN trên





4;

.

Câu 74. Dựa vào bảng xét dấu đạo hàm ta nhận

thấy: Hàm số

 

y f x

đồng biến trên hai

khoảng rời nhau

 

1;1

và

 

1;3

nhưng liên tục

trên toàn khoảng

 

1;3

.

Ta có:

   

''g x f x m

.

Xét trên khoảng

 

0;2

, ta có:

0 2 2x m x m m      

.

Để hàm số

 

y g x

đồng biến trên

 

0;2

thì:

   

1

; 2 1;3 1 1

23

m

m m m

m





       







Do vậy:

 

1;0;1m 

.

Đáp án A

Câu 75. Ta có:

11 27 3 2 5x m x m m        

.

Đặt:

 

2 , 3; 5t x m t m m     

.

Khi đó yêu cầu bài toán chuyển về việc tìm m

để hàm số

 

y f t

nghịch biến trên khoảng

   

3; 5 *mm

.

Dựa vào bảng xét dấu đạo hàm, ta thấy rằng:

Hàm số

 

y f t

nghịch biến trên khoảng

 

1;3

. Do đó để

 

*

xảy ra thì:

3 1 2

2

5 3 2

mm

m

mm

   



   



   



.

Vậy chỉ có duy nhất một giá trị thực của tham

số

m

thỏa mãn yêu cầu bài toán.

Đáp án A

Câu 76. Tìm ĐKXĐ:

Để hàm số

 

32

1

ln 3 9

3

y f x x x x m



    





tồn tại thì:

   

32

1

39

3

g x f x x x x m    

phải thỏa mãn:

    

0, 1;3 *g x x   

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

154

[ I can't, I can! ]

Ta có:

   

 

   

2

' ' 6 9 ' 3g x f x x x f x x      

.

Dựa vào bảng xét dấu đồ thị đạo hàm ta thấy:

   

' 0, 1;3f x x   

.

Dễ thấy:

   

2

3 0, 1;3xx    

.

Khi đó:

   

' 0, 1;3g x x   

. Hay nói cách

khác trên khoảng

 

1;3

hàm số

 

y g x

đồng biến.

Suy ra:

 

   

1;3

31

min 1

3

g x g m



   

.

Để

 

*

xảy ra thì:

31 31

0

33

mm   

.

Mặt khác:

31

3

m

, ta có:

   

 

2

32

'3

' 0, 1;3

1

39

3

f x x

yx

f x x x x m



    

   

Vậy:

 

31

;2021 11;12;...;2021

3

mm



  





.

Hay có

2011

giá trị thực của tham số

m

thỏa

mãn yêu cầu đề bài.

Đáp án A

Câu 77. Ta có:

 

32

1

' ' 2 3 2 1

3

y f x x x x m     

.

Để hàm số đồng biến trên khoảng

 

1;3

thì:

   

' 0, 1;3 *yx  

.

Đặt:

 

2, 1;1x t t   

.

Khi đó:

 

1;1t  

,

 

*

tương đương với:

       

32

1

' 2 2 2 2 3 2 2 1 0

3

f t t t t m         

    

3

11

' 2 2 , 1;1 **

33

f t t t m t        

.

Xét hàm số:

   

3

11

'2

33

g t f t t t    

.

Ta có:

   

2

' '' 2 1g t f t t   

.

Dựa vào bảng xét dấu của đồ thị đạo hàm, ta

thấy:

   

'' 2 0, 1;1f t t    

.

Dễ thấy:

22

1 1 1 1 0t t t        

.

Vậy:

     

2

' '' 2 1 0, 1;1g t f t t t       

.

Suy ra: Hàm số

 

y g t

đồng biến trên

 

1;1

Để

 

**

xảy ra thì:

   

2 , 1;1g t m t   

.

 

     

1;1

1 1 1 3

min 1 ' 1 1

2 2 2 2

m g t g f



      





Kết hợp điều kiện ta có:

3

2021

2

m  

.

Suy ra:

 

2021; 2020;...;1m   

.

Vậy có tất cả

2023

giá trị nguyên của

m

thỏa

mãn yêu cầu đề bài.

Đáp án A

Câu 78. Ta dễ dàng phát họa được bảng biến

thiên của hàm số

 

y f x

dựa trên bảng biến

thiên của đồ thị hàm số

 

'y f x

như sau:

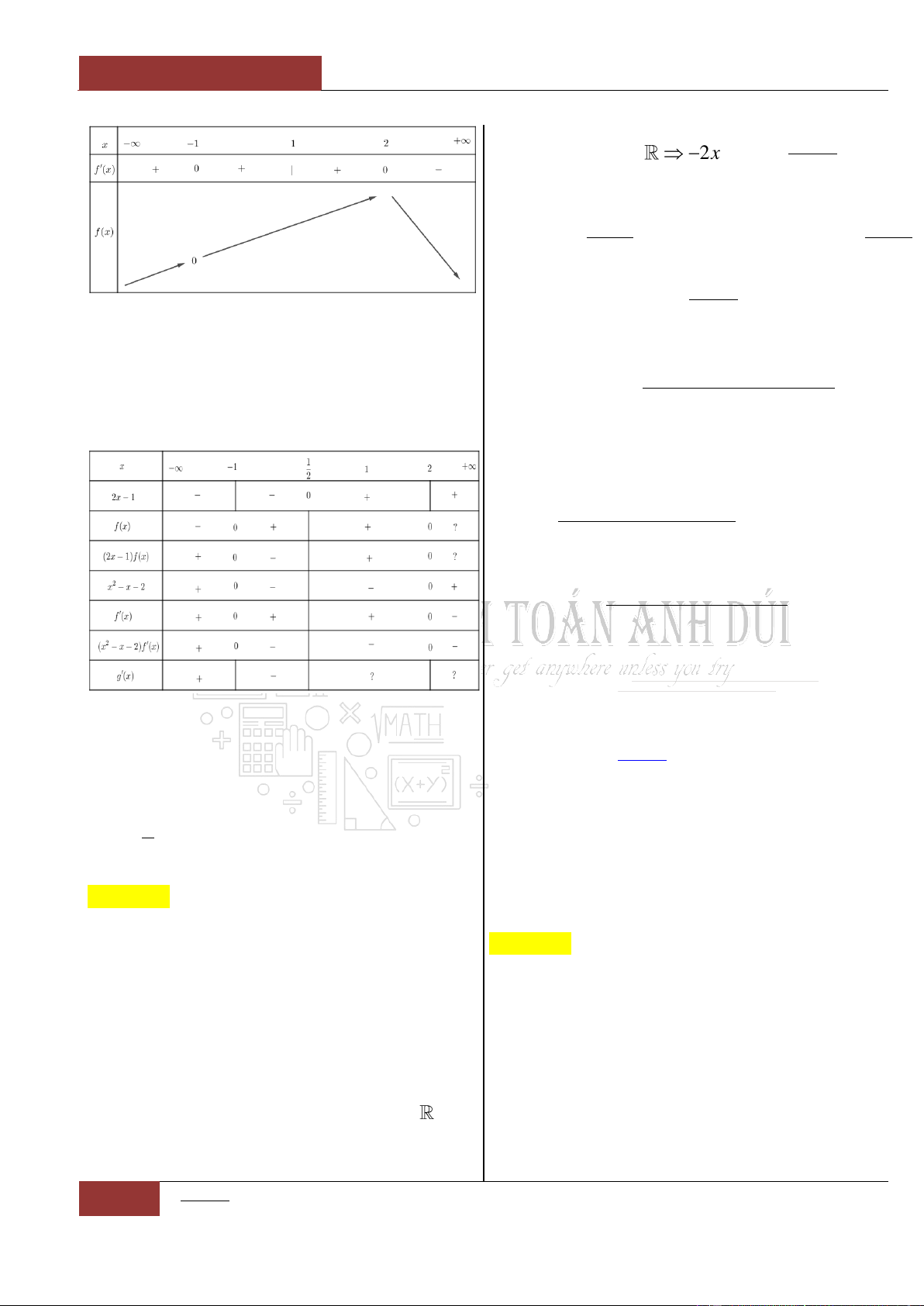
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

155

[ I can't, I can! ]

Mặt khác:

     

 

2

' 2 1 2 'g x x f x x x f x    

.

Bảng xét dấu của hàm số đạo hàm

 

'gx

.

Dựa vào bảng xét dấu của

 

'y g x

ta chỉ có

thể chắc chắc được rằng: Hàm số đồng biến trên

khoảng

 

;1 

và nghịch biến trên khoảng

1

1;

2









.

Đáp án C

Câu 79. Ta có:

     

2

1

' 2 '

x mx

y e x m f x f x

  

   





.

Hàm số đồng biến trên

 

1;4

khi và chỉ khi:

       

' 0, 1;4 2 ' 0,y x x m f x f x       

   

1;4 *x

(Do

2

1

0, ,

x mx

e x m

  

  

).

Vì:

 

'

0, 2

fx

f x x x m

fx

       

.

 

1;4

''

2 , 1;4 max 2

f x f x

m x x m x

f x f x



       





Xét hàm số

 

'

2 , 0;4

fx

g x x x

fx

  

.

Ta có:

 

     

 

2

'' . '

'2

f x f x f x

gx

fx









.

Vì:

         

'' 0, 1;4 '' . 0, 1;4f x x f x f x x      

Khi đó:

     

 

2

'' . '

0, 1;4

f x f x f x

x

fx







  

 

     

 

2

'' . '

' 2 0, 1;4

f x f x f x

g x x

fx







     

Vậy hàm số

 

y g x

đồng biến trên

 

1;4

.

Suy ra:

 

   

1;4 1;4

'

max 2 max 4 8

fx

m x g x g

fx



    





.

Kết hợp điều kiện ta có:

 

8;9;10;...;2021m 

.

Vậy có tất cả

2014

giá trị thực

m

thỏa mãn yêu

cầu đề bài.

Đáp án D

Câu 80. Dựa vào dữ kiện đã được cho ở đề bài

ta có thể suy ra các "manh mối" sau:

 Đồ thị hàm số

 

y f x

không có giao

điểm với trục hoành.

 Đồ thị hàm số

 

'y f x

cắt trục hoành

tại một điểm duy nhất.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

156

[ I can't, I can! ]



 

0,f x x  

(Vì:

 

max 1fx

).

Ta có:

 



 

2

2 1 2 1 ...

'

x m x m

gx

fx



    





 



 

2

... 1 2 1 . ...x m f x

fx

    

 

2

... 1 2 1 . 'x m x m f x

fx



   



.

 

   

 

2

1 2 1 3 1 2 ...

'

x m x m f x

gx

fx



     





 

2

... 1 2 1 . 'x m x m f x

fx



   



.

 

   



 

2

1 2 1 3 1 2 ...

'

x m x m f x

gx

fx



     





 



 

2

... 1 2 1 . 'x m x m f x

fx



   



.

Đặt:

 

   

2

2 1 3 1 2 ...h x m x m f x



     



 

2

... 1 2 1 . 'x m x m f x



   



.

Vì:

 

'0gx

có một nghiệm bội lẻ

1x 

nên

điều kiện cần để

 

'0gx

là:

 

10h 

.

Ta có:

 

2

1 2 2 1 . 1 0h m m f    

.

2

1

2 1 0

2

1

m

mm

m







     







.

Thử lại:

 Với

 

1

2

mL

. Do:

 

       

 

23

2

3 1 . 1 . '

1

' . 0,

2

x f x x f x

g x x

fx

  

   

 Với

1m 

.

 

       

 

23

2

3 1 . 1 . '

' 0,

x f x x f x

g x x

fx

   

   

.

Vậy có duy nhất một giá trị

m

thỏa mãn yêu

cầu bài toán.

Đáp án A

Extra Techniques:

Tips:

Sỡ dĩ ta có thể kết luận dấu

của

 

'gx

tại

1

2

m 

và

1m 

là do:

 





 





   

2

3

1 0,

0,

1 0, 1;

' 0, 1;

1 0, ;1

' 0, ;1

xx

f x x

xx

f x x

xx

f x x



   



  



  



    





   



    



   



Câu 81. Ta có:

   

16 4 3 1M P a b c    

.

Mặt khác: Giao điểm của đồ thị hàm số

 

P

với

trục hoành là điểm

 

3;0N

và

   

;0 , 3Q t t 

.

Hay nói cách khác: Phương trình

 

0fx

có

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

157

[ I can't, I can! ]

hai nghiệm thực phân biệt:

 

,3

3

x t t

x











.

Theo định lý Viéte, ta có:

3

b

t

a

c

t

a



  













.

Gọi

H

là chân đường vuông góc kẻ từ

;

24

b

I

aa











lên trục hoành.

Khi đó:

   

,

4

IH d I Ox y I

a



   

.

Ta có:

 

11

. . . 3

2 2 4

INQ

S IH NQ t

a



   

.

Vì:

1

INQ

S





.

Suy ra:

 

1

. . 3 1

24

t

a



  

   

 

   

22

2

3

1 4 4

. 3 1 . 3 2

2 4 4

8

. 3 2 . 3

4

2

.3

2

3

22

3 . 3 3 2

4

b ac b ac

tt

aa

b b c

c t t

a a a

a

bc

t

a a a

t

t t t

aa



     

       



   







      

Vì:

   

3 0 9 3 0 3f a b c    

.

Từ

  

16 4 3

1 3 7 3

9 3 0

a b c

ab

a b c

  



   



  



.

37ba  

.

Ta có:

7 3 3 1 4

37

3

b a t

t

a a a a



       

.

Thay vào

 

2

, ta được:

 

3

84

3*

3

t





.

 

32

* 3 27 73 49 0 1t t t t      

.

Suy ra:

 

2

1

4 4 3

3

a

b y f x x x

c







      









.

Khi đó:

     

2

2 1 2 1 4 2 1 3 4 12 8f x x x x x        

Hàm số trở thành một Parabol có hệ số

0a 

và

đỉnh

3

;1

2

I









nên hàm số có dạng hình chữ .

Nên hàm số đồng biến trên khoảng

3

;

2









.

Mà:

 

3

5;7 ;

2



 





.

Vậy hàm số đổng biến trên khoảng

 

5;7

.

Đáp án C

Câu 82. Ta có:

     

6 4 2

. 3 2 *f x x f x x x x   





.

     

2 6 4 2

* . 3 2 0f x x f x x x x     

.

Đặt:

 

t f x

, phương trình đã cho trở thành:

 

2 6 4 2

3 2 0 **t xt x x x    

.

Xem phương trình

 

**

như một phương trình

theo ẩn

t

, tham số

x

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

158

[ I can't, I can! ]

Ta có:

 

2

6 4 2 3

4 12 9 2 3x x x x x     

.

Suy ra:

3

23

2

23

2

x x x

xx

x

t

x x x

xx



















  





.

Vậy:

 

3

2f x x x

f x x x







  





.

Do

   

3

10f f x x x    

.

Ta có:

   

2

' ' 4 3 1 4 0g x f x x x x      

1

3

x  

.

Đáp án C

Câu 83. Xét biểu thức:

   

2

21f x f x x  

.

Thay đỏi vai trò của

x

và

1 x

bằng cách đặt:

1xt

, ta được:

     

2

2 1 1f t f t t   

.

Hay:

     

2

2 1 1f x f x t   

.

Ta có hệ:

   

     

2

21

2 1 1

f x f x x



  





   





.

     

2

4 2 1 2 1

2 1 2 1 2

f x f x x

f x f x x x



  







    





Lấy

   

12

theo từng vế, ta được:

 

2

3 2 1f x x x  

.

Do vậy:

 

2 2 2

3 . 4 1 2 1 4 1y x f x x x x x x x x         

 

3

32

3 3 1 1y x x x y x       

.

Ta có:

 

2

' 3 1 0,y x x    

.

Nên hàm số đồng biến trên toàn tập .

Đáp án C

Câu 84. Chọn hàm:

Chọn:

   

2

,0f x ax bx c a   

.

Khi đó:

 

'2f x ax b

.

Ta có:

   

2

' 4 8 16 8f x f x x x   





 

2

22

2 2 2 2

2 4 8 16 8

4 4 4 4 4 8 16 8

ax b ax bx c x x

a a x ab b x b c x x

       

        

Đồng nhất hai vế, ta có:

 

22

2

4 1 8

4 4 8 4 4 8

4 4 16 4 1 16 2

4 8 8

48

4

2

4

1

6

2 4 6

2

1

23

8

2

4

3

aa

a a a a

ab b b a b a

b c b

bc

c

a

b

a

c

f x x x

ba

a

f x x x

b

c

b

c









   



      

  

  

    

  











  



  



























   





   







  





































Vì:

   

2

1 0 2 3f f x x x    

.

Suy ra:

   

3 2 2

1

'2

3

g x x x g x x x      

.

 

0

'0

2

x

gx

x













.

Bảng biến thiên:

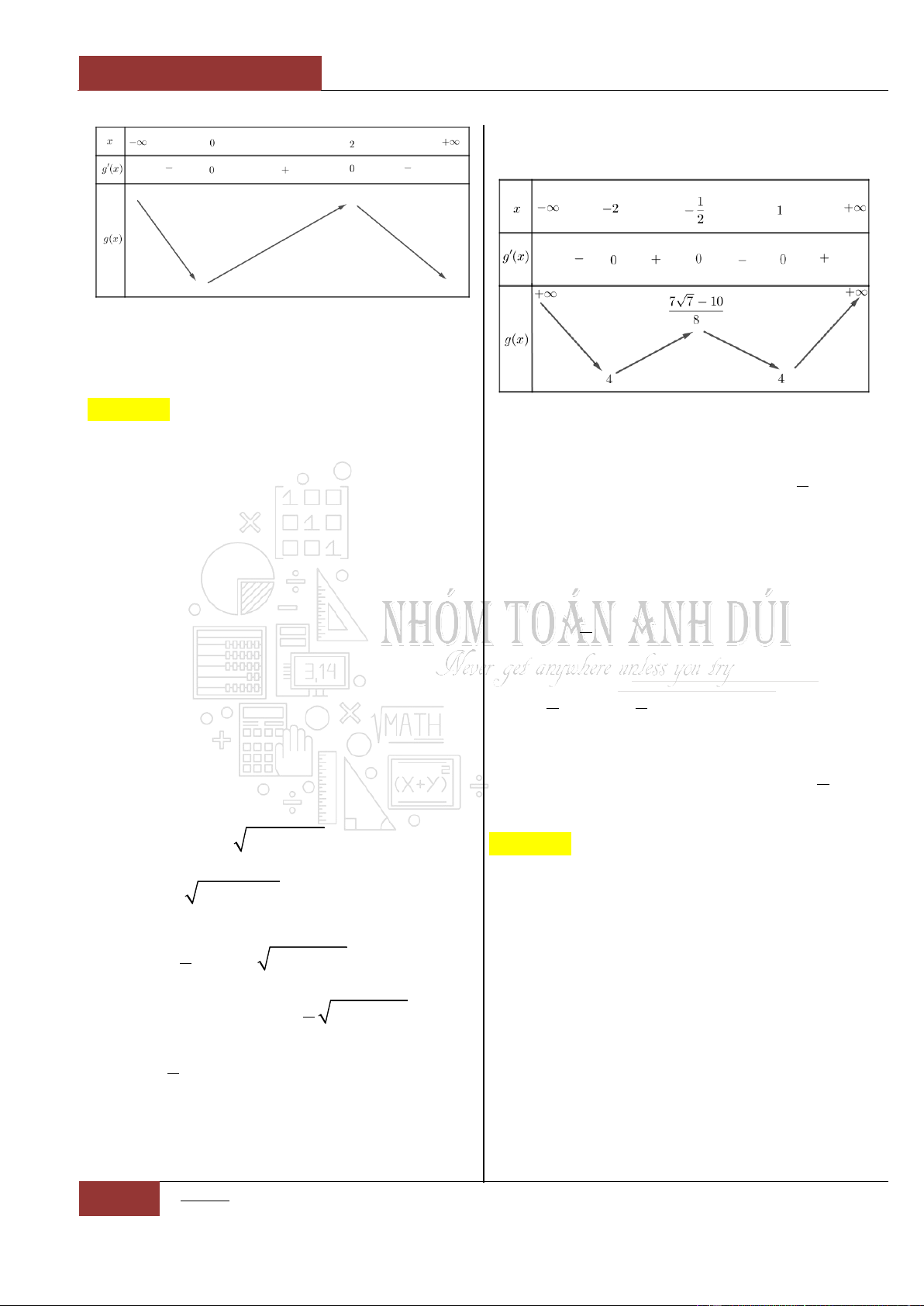
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

159

[ I can't, I can! ]

Dựa vào bảng biến thiên, ta thấy hàm số đồng

biến trên khoảng

 

0;2

.

Đáp án C

Câu 85. Dựa vào đồ thị hàm số được cho ở trên

ta có một số điểm đáng lưu ý để tìm hàm:

Đặt:

 

32

f x ax bx cx d   

.

Suy ra:

 

2

' 3 2f x ax bx c  

.

 

04

41

20

8 4 0 3

00

' 0 0

12 4 0 4

' 2 0

f

da

f

a b c d b

cc

f

a b c d

f















     







  





  

   







.

Khi đó:

 

32

34f x x x  

.

Suy ra:

 





2

2 ...g x f x x   





 

3

22

... 2 3 2 4x x x x     

.

     

   

2

3

' 2 1 2 3 2 1

2

1

' 0 3 2 1 2 1 0

2

1

2

1

2

g x x x x x

g x x x x

x

      



       





















Bảng xét dấu của hàm số

 

y g x

:

Dựa vào bảng biến thiên ta thấy:

Hàm số đồng biến trên khoảng

1

2;

2









và

khoảng

 

1; 

.

Hàm số nghịch biến trên khoảng

 

;2 

và

khoảng

1

;1

2









.

Vì:

11

;0 ;1

22

   

  

   

   

.

Vậy hàm số nghịch biến trên khoảng

1

;0

2









.

Đáp án C

Câu 86. Dựa vào đồ thị hàm số ta có:

 

' 1 0

1 0 0

' 0 0 0 1

1 0 0

' 1 0

f

a b c a

f c b

a b c c

f





     







     

  

  

    







.

Như thế:

   

32

' '' 3 1f x x x f x x    

.

Xét hàm số:

   

 

'y g x f f x

.

Ta có:

   

 

' ' ' . '' 0g x f f x f x

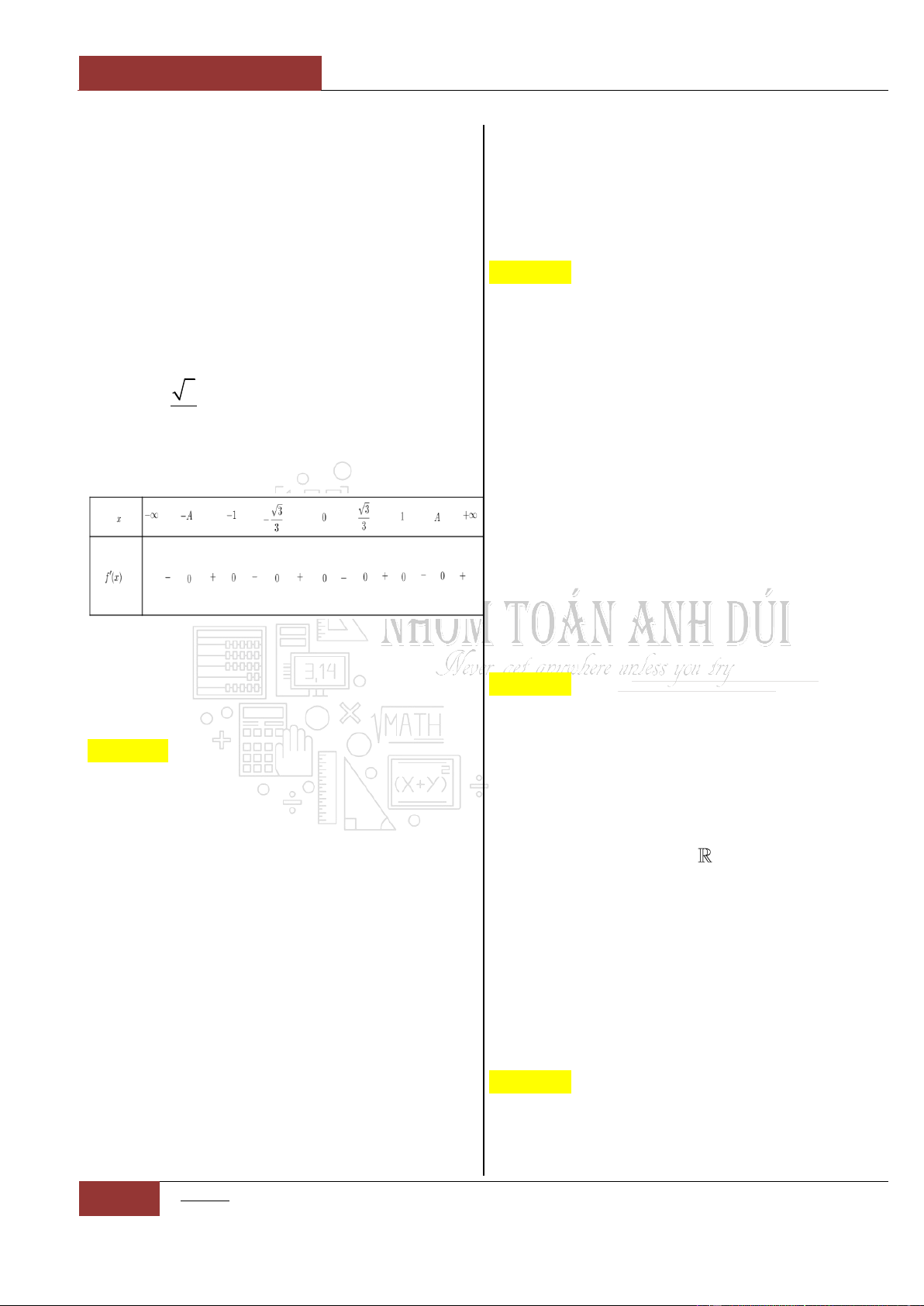
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

160

[ I can't, I can! ]

   

3

32

3

2

0

1

' . 3 1 0

1

3 1 0

xx

f x x x

xx

x











    



  







 

1

0

, 1,325

3

x

x A A

x













  









.

Bảng biến thiên:

Vì:

   

; 2 ; A    

.

Nên hàm số nghịch biến trên khoảng

 

;2 

.

Đáp án B

Câu 87. Ta có:

   

''g x f x m

.

Cho

 

'0gx

, ta được:

11

22

x m x m

    







   



.

Ta có:

   

' 0 ' 0 2 2g x f x m x m x m         

Để hàm số đồng biến trên khoảng

 

2;0

thì:

   

 

 

 

2;0

' 0, 2;0 min 0

2 min 2 4

g x x f x m

m x m



      





       

Kết hợp với điều kiện, ta có:

2021 4m   

.

Hay:

 

2021; 2020;...; 4m    

.

Như vậy tập

S

có tất cả

2018

phần tử.

Đáp án C

Câu 88. Ta có:

 

3 2 1 2

' 3 ' 2 . ' 2 .3 .ln3

f x f x

y f x e f x

  

    

 

   

3 2 1 2

' ' 2 . 3 3 .ln3

f x f x

y f x e

  



    



.

Vì:

   

3 2 1 2

3 3 .ln3 0

f x f x

e

  



.

Nên:

   

' 0 ' 2 0 ' 2 0y f x f x       

.

Dựa vào bảng xét dấu đạo hàm

 

'fx

, ta có:

 

2 1 3

' 2 0

1 2 4 2 1

xx

fx

xx

   



   



     



.

Đáp án D

Câu 89. Ta có:

 

2

' ' .

f x m

y f x e









.

Để

'0y 

thì:

 

2

' . 0 *

f x m

f x e









.

Vì:

 

2

0, ,

f x m

e x m



  

.

Do đó:

   

1

* ' 0

04

x

fx

x





  







.

Mà:

 

 

1;2 0;4

.

Nên hàm số nghịch biến trên khoảng

 

1;2

.

Đáp án C

Câu 90. Xét hàm số:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

161

[ I can't, I can! ]

     

1

. 2 3 *

2

y f x g x x

x

   



.

TXĐ:

3

;

2

D



  







.

Đoạn xét hàm số

 

*

:

3

' ;1

2

D









.

Vì:

 

3

2;1 ;1

2

3

1;4 ;1

2





  





  

















Nên ta có thể loại ngay phương án A, D.

Ta có:

       

 

2

11

' ' '

23

2

y f x g x f x g x

x

   



Vì:

 

2

11

0, '

23

2

xD

x

   



. Nên ta chỉ

có thể kết luận rằng:

'0y 

trên khoảng con

'KD

nếu và chỉ nếu ta có được:

       

' ' 0,f x g x f x g x x K   

.

Dựa vào bảng biến thiên của hai đồ thị

   

,y f x y g x

ta nhận thấy rằng:

Trên đoạn

 

1;1

, ta có:

 

0

'0

0

'0

fx

gx





















.

Do đó:

       

 

' ' 0, 1;1f x g x f x g x x    

Vậy hàm số chắc chắn đồng biến trên khoảng

 

1;1

.

Đáp án B

Extra Techniques:

Tips:

Sở dĩ ta có loại đáp án C là

vì:

 

3

0, ; 1

2

3

' 0, ; 1

2

3

' 0, ; 1

2

3

0, ; 1

2

f x x

g x x

f x x

g x x





    











    





  







    













    









Suy ra:

   

3

' 0, ; 1

2

3

' 0, ; 1

2

f x g x x





    





  







    









Vì vậy ta không thể kết luận

dấu của

'y

.

Câu 91. Xét hàm số:

 

2

1

x

y g x f m

x





  







.

Ta có:

 

2

32

' . '

1

x

g x f m

x





  









.

Để hàm số đồng biến trên khoảng

 

2;

, thì:

     

' 0, 2; *g x x   

.

     

2

* ' 0, 2; **

1

x

f m x

x





     







.

Mặt khác, xét hàm số:

 

y f x

, có:

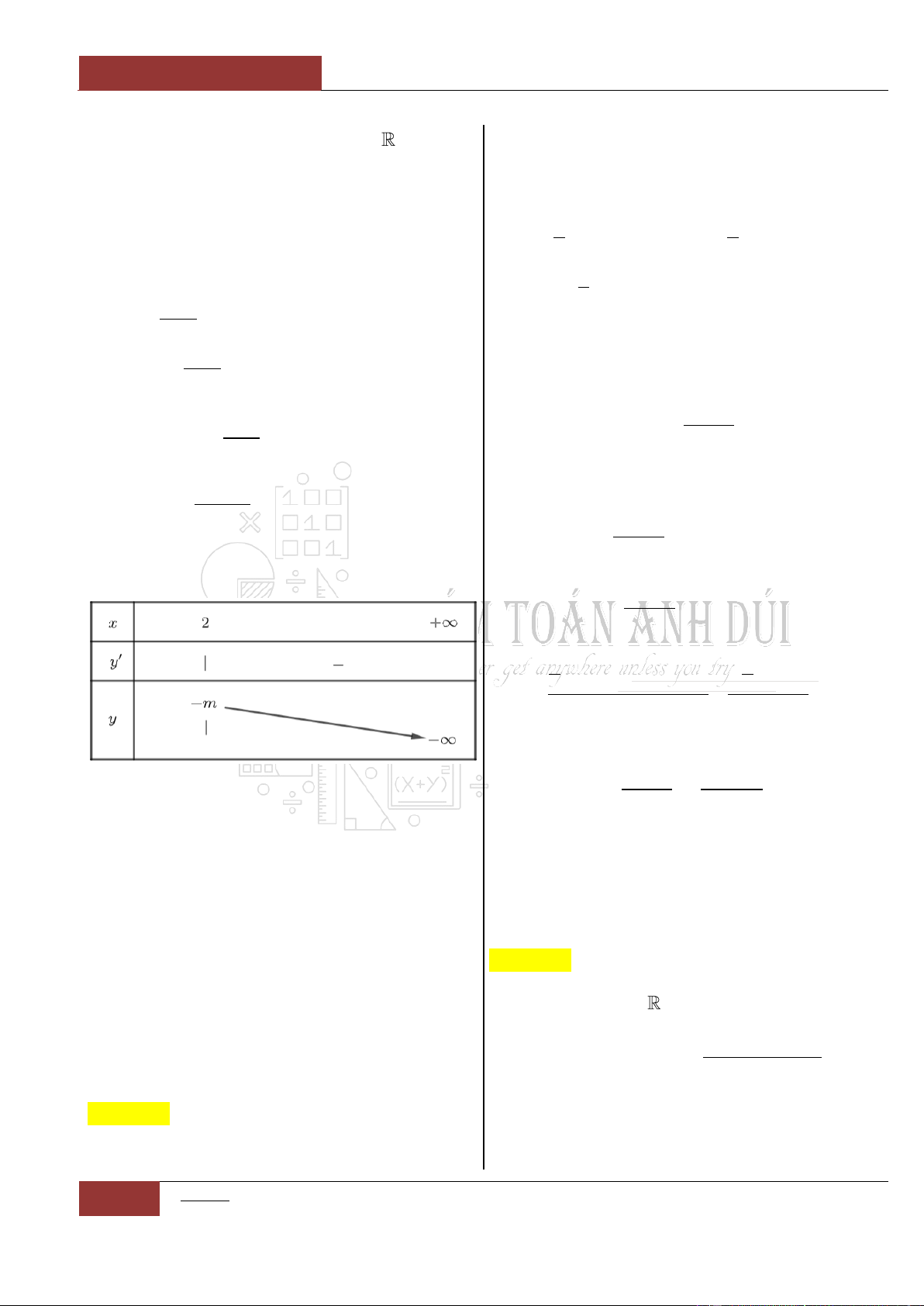
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

162

[ I can't, I can! ]

     

' ' 1 1 4 ,y f x x x x x      

.

     

1

' 0 1 1 4 0

14

x

f x x x x

x





      







.

Từ hai điều trên ta suy ra:

 

2

11

1

** , 2;

2

1 4 2

1

x

m

x

m

x





  





   







  







.

Xét hàm số:

 

2

, 2;

1

x

y m x

x



    



.

Ta có:

 

2

3

' 0, 2;

1

yx

x

     



.

Bảng biến thiên:

Dựa vào bảng biến thiên, ta thấy hàm số không

tồn tại giá trị nhỏ nhất, vì thế

 

2

không thế xảy

ra (Do

min 1

x

y





).

 

1 1 1mm     

.

Kết hợp với điều kiện đề bài:

2021m 

.

Khi đó:

1 2021m

.

Vậy có tất cả

2021

giá trị thực của tham số

m

thỏa mãn yêu cầu đề bài.

Đáp án D

Câu 92. Xét hàm số:

 

y g x

trên khoảng

 

2

1; e

, ta có:

     

       

ln

11

' ' ln 2 . ln 1 . 2

1

' ln 1 . 2 1 ln 1 2 1

x

g x f x mx m x e mx m

xx

g x x x m x x x m

x

      

        

Hàm số

 

y g x

nghịch biến trên khoảng

 

2

1; e

khi và chỉ khi:

 

2

ln 1 2 1 0, 1;x x m x e     

 

2

ln 1

ln 1 2 1 , 1;

21

x

x x m m x e

x



       



.

(Do

1 2 1 1 0xx    

).

Vậy:

2

1;

ln 1

max

21

e

x

m

x

















.

Xét hàm số:

 

2

ln 1

, 1;

21

x

y x e

x



  



.

   

 

2

22

11

2 1 2 ln 1 2ln

' 0, 1;

2 1 2 1

x x x

xx

y x e

xx

    

     



Hàm số nghịch biến trên khoảng

 

2

1; e

hay nói

cách khác

 

2

1;

ln 1 1

ln 1

max 1 1

2 1 2.1 1

e

x

m

x









   







.

Kết hợp với điều kiện đề bài, ta có:

1 2021m

Vậy có tất cả

2021

giá trị thực của tham số

m

thỏa mãn yêu cầu đề bài.

Đáp án D

Câu 93. TXĐ:

D 

.

Ta có:

   

22

2

' ' 1

1

xm

g x f x

x mx m



   

  

.

Điều kiện “lỏng” để hàm số

 

y g x

đồng biến

trên khoảng

 

3;0

là:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

163

[ I can't, I can! ]

   

 

22

' 1 0, 3;0

2

0, 3;0

1

f x x

xm

x

x mx m

     









    



  



 



Hàm số

 

'1y f x  

trên

 

3;0

.

Ta đặt:

11t x x t    

.

Vì:

3 0 3 1 0 1 4x t t          

.

Suy ra:

       

' 1 0, 3;0 ' 0, 1;4f x x f t x          

Hay

         

3 4 5

1 1 . 4 0, 1;4 *t t t t t      

.

 

*

hiển nhiên, do:

 

5

3

4

4 1 0

243 4 0

1

8 1 12

1

4

5

0 81

t





  





  



     











Như vậy, yêu cầu bài toán quay về việc định giá

trị của tham số

m

để hàm số:

   

22

2

0, 3;0 **

1

xm

x

x mx m



    

  

Vì:

2 2 2 2 2

13

11

44

x mx m x mx m m



       





2

3

1 0,

24

mm

xm



      





.

   

 

 

3;0

** 2 0, 3;0 min 2x m x m x



        

Mà

 

   

3;0

min 2 2.0 0 0xm



     

.

Đáp án D

Câu 94. Xét hàm

   

11y g x f x mx    

,

ta có:

   

' ' 1g x f x m  

.

Để hàm số

 

y g x

đồng biến trên thì:

   

' 0, *g x x  

     

* ' 1 0, ' 1f x m x m f x        

Nói cách khác:

   

min ' min ' 1m f x f x  

.

Mà

 

22

12

3

'1

22

11

x

fx

xx

x





  



.

Xét hàm số

2

3

22

x

y

xx







.

Ta có:

 

2

1

2 2 3 .

22

'

22

x

x x x

xx

y

xx



   







  

 





2

3

22

2

2 2 3 1

21

2 2 2 2

22

x x x x

x

x x x x

xx

    





   



.

1

' 0 2 1 0

2

y x x       

.

Và:

2

3

lim 1 min

22

13

5 max

2

22

lim 1

x

y

xx

x

y

xx

y

































  





















.

Suy ra:

1m 

.

Kết hợp với điều kiện

 

20;20m

.

Suy ra:

 

19; 18;...; 1m    

.

Vậy có tất cả

19

giá trị thực của tham số

m

để

hàm số đồng biến trên .

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

164

[ I can't, I can! ]

Đáp án B

Câu 95. Ta có:

   

2y g x f x mx   

.

Suy ra:

   

' ' 2g x f x m  

.

Để hàm số

 

y g x

đồng biến trên khoảng

 

2;1

thì

   

' 0, 2;1g x x   

.

Hay:

     

' 2 0, 2;1 *f x m x     

.

     

   

 

 

2

2;1

* ' 2 , 2;1

3 3 , 2;1

min 3

m f x x

m x x x x x

m x x



     

       

  

Xét hàm số

 

2

3 , 2;1y x x x    

.

Ta có:

3

' 2 3 0

2

y x x     

.

Và

 

 

 

2;1

22

39

min

24

14

y

yy

y



   





   













.

Vậy

9

4

m 

.

Đáp án B

Câu 96. Đặt

 

cot

2 0;2

x

t 

.

Để hàm số

cot cot

8 ( 3).2 3 2

xx

y m m    

đồng biến trên khoảng

;

4









thì hàm số

 

3

3 3 2y t m t m    

phải nghịch biến trên

khoảng

 

0;2

.

Hay:

 

2

3 3 0, 0;2t m x    

.

 

 

22

0;2

min 3 3 3 3.2 9mt      

.

Do

 

20;20m

nên

 

20; 19;...; 9m   

.

Vậy có tất cả

12

giá trị nguyên của tham số

m

để hàm số đồng biến trên khoảng

;

4









.

Đáp án B

Extra Techniques:

Remark:

Sở dĩ hàm số

 

y g x

đồng

biến trên khoảng

 

2;1

thì

   

' 0, 2;1g x x   

là vì

hàm số

cot

2

x

y 

là một hàm

nghịch biến trên khoảng

;

4









. Thật vậy! Ta có:

cot

2

1

' 2 .ln2. 0

sin

x

y

x



  





,;

4

x











.

Câu 97. Giả sử

 

m

C

luôn tiếp xúc với đường

thẳng

y ax b

, khi đó phương trình sau có

nghiệm với mọi

m

:

 

2

2 2 4

4

m x m m

ax b

xm

a

xm



   





















  

 

2

24

4

m x m

a x m am b

xm

a

xm

  



   





















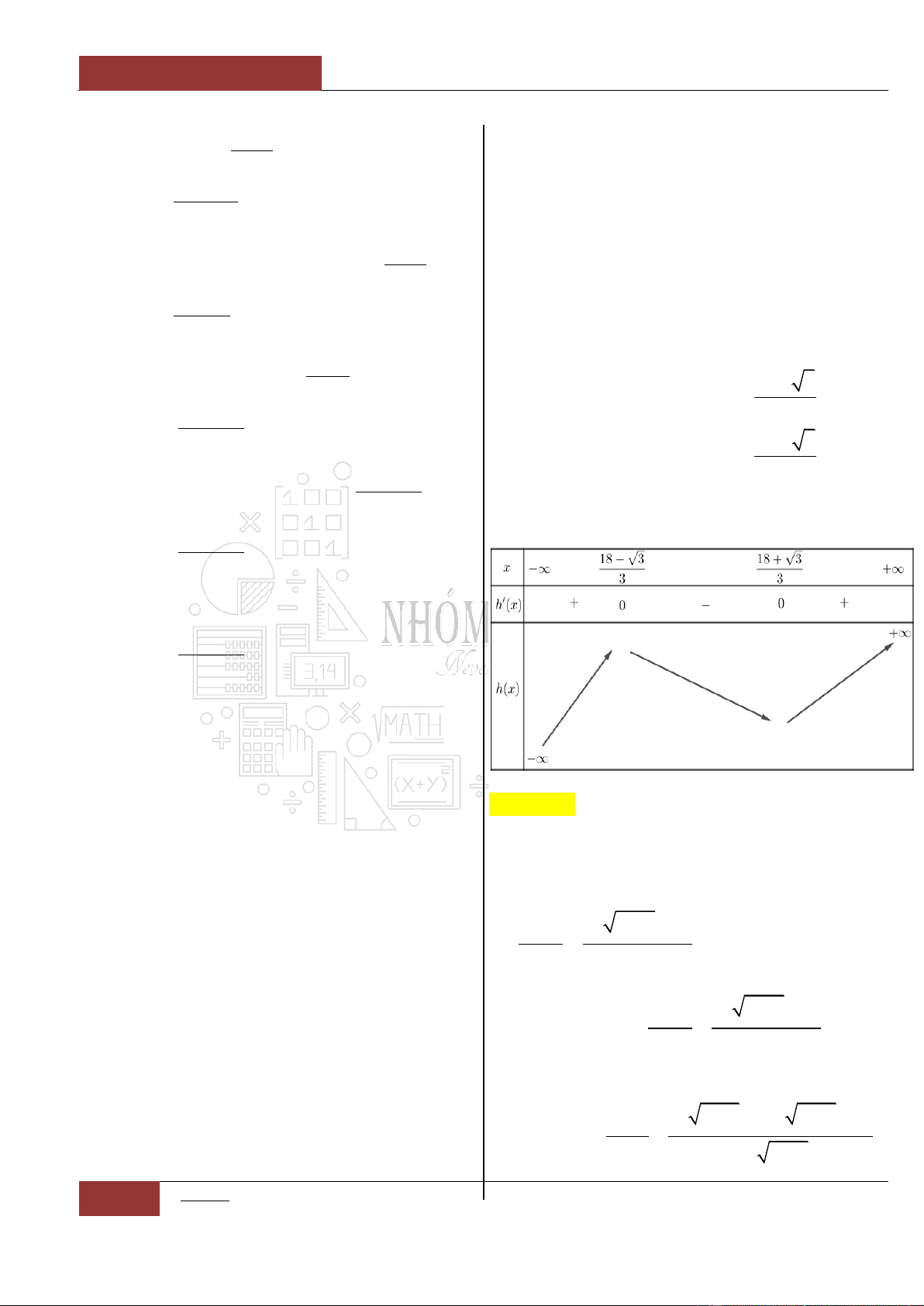
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

165

[ I can't, I can! ]

 

2

4

2

4

2

4

m a x m am b

xm

a

xm

m am b a x m

xm

a x m

xm



     























     





















 

   

 

     

 

2

8

2

4

64

12

4

1 2 16 *

4

m am b

xm

a

xm

m a b

xm

a

xm

m a b a

a

xm



   























   



























   





















      

2

* 1 2 1 2a m a b m     

 

2

2 16 0ba



   



Để tìm được hệ số

,ab

không phụ thuộc

vào tham số

m

thì:

 

  

 

2

1

10

1

2 1 2 0

2

2 16

a

ab

b

ba



















    





















.

 

2

1

2 16

1

2

2 16

a

ba

a

b VN

ba





















































 

1

2

6

1

6

a

f x x

b

yx

g x x

a

b

























  





























Như vậy:

     

 

   

3

6 6 2h x f g x g x x x      

Suy ra:

   

2

18 3

3

' 3 6 1 0

18 3

3

x

h x x

x









    











.

Bảng biến thiên:

Đáp án B.

Câu 98. Để hàm số

 

y g x

luôn tăng trên

khoảng

 

0;1

thì

   

' 0, 0;1g x x  

.

 

8 3 2

, 0;1

48 1

x

fx

mx

x



    



.

Xét hàm số

 

8 3 2

48 1

x

fx

hx

x







trên

khoảng

 

0;1

.

Ta có:

 

  

 

8 3 2 3 2

48

1 3 2

xx

fx

hx

xx

   



  

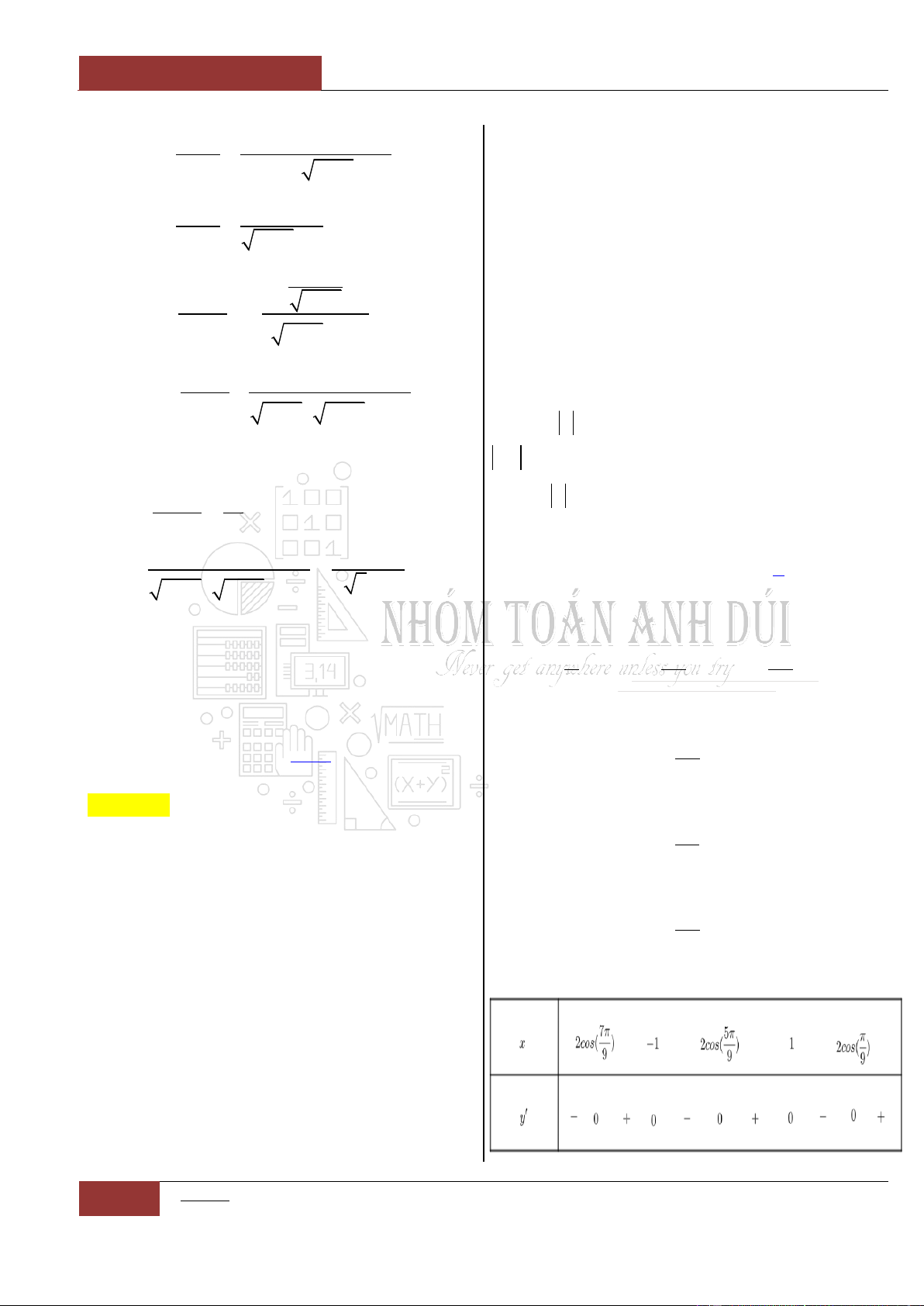
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

166

[ I can't, I can! ]

 

   

 

8 3 4

48

1 3 2

8

48

32

f x x

hx

xx

fx

hx

x



  

  

  



 

2

1

'

3

' 8.

48

32

'

8

'0

48

3 3 2

, 0;1

fx

x

hx

x

fx

hx

xx

x



  



   

  



(do

 

'

1

0 0,0625

48 16

fx

  

và

 

2

88

0,25 0,3

7 3 12

3 3 2xx

  



  

với mọi

 

0;1x

).

     

1 , 0;1h x h x   

Vậy để

   

' 0, 0;1g x x  

, thì:

 

1

12

48

f

mh  

.

Đáp án C

Câu 99. Xét hàm số:

 

3

2 6 3y f x x  

.

Ta có:

   

23

6 6 . ' 2 6 3y x f x x



   

.

Dựa vào bảng biến thiên hàm số

 

'y f x

, ta

có:

 

2

3

10

0 2 6 3 1 0

2 6 3 5

k

x

y x x

xx











      





  



 

2

3*

3

1

2 6 3 1 0 *

3 1 **

k

x

x x k N

xx











      









Xét phương trình

 

*

, nếu phương trình có

nghiệm thì tất cả các nghiệm đều là nghiệm bội

chẵn nên dấu đạo hàm khi đi qua các điểm đó

không đổi dấu. Vì thế, ta không xét nghiệm

 

*

.

Xét phương trình:

3

31xx

.

+) Với

2x 

Phương trình vô nghiệm do

21VT VP  

.

+) Với

2x 

.

Đặt

2cosxt

. Khi đó phương trình trở thành :

 

3

*

1

8cos 6cos 1 cos **3

2

t t t   

Phương trình

 

***

có

3

nghiệm phân biệt:

57

2cos , 2cos , 2cos

9 9 9

x x x

  

  

.

Suy ra phương trình

0y





có

5

nghiệm bội lẻ,

lần lượt là:

2

3

4

5

6

7

2cos

9

1

5

2cos

9

1

7

2cos

9

x





























.

Bảng xét dấu đạo hàm:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

167

[ I can't, I can! ]

Dựa vào bảng xét dấu, ta thấy:

Hàm số đồng biến trên các khoảng rời nhau:

75

2cos ; 1 , 2cos ;1 , 2cos ;

9 9 9

  

     

 

     

     

.

Do đó để hàm số đồng biến với mọi

xm

,

 

7

; 2cos ; 2cos 2sin

9 9 18

mm

  



      





Vậy

2, 7, 18 2 3 7a b c a b c      

.

Đáp án B

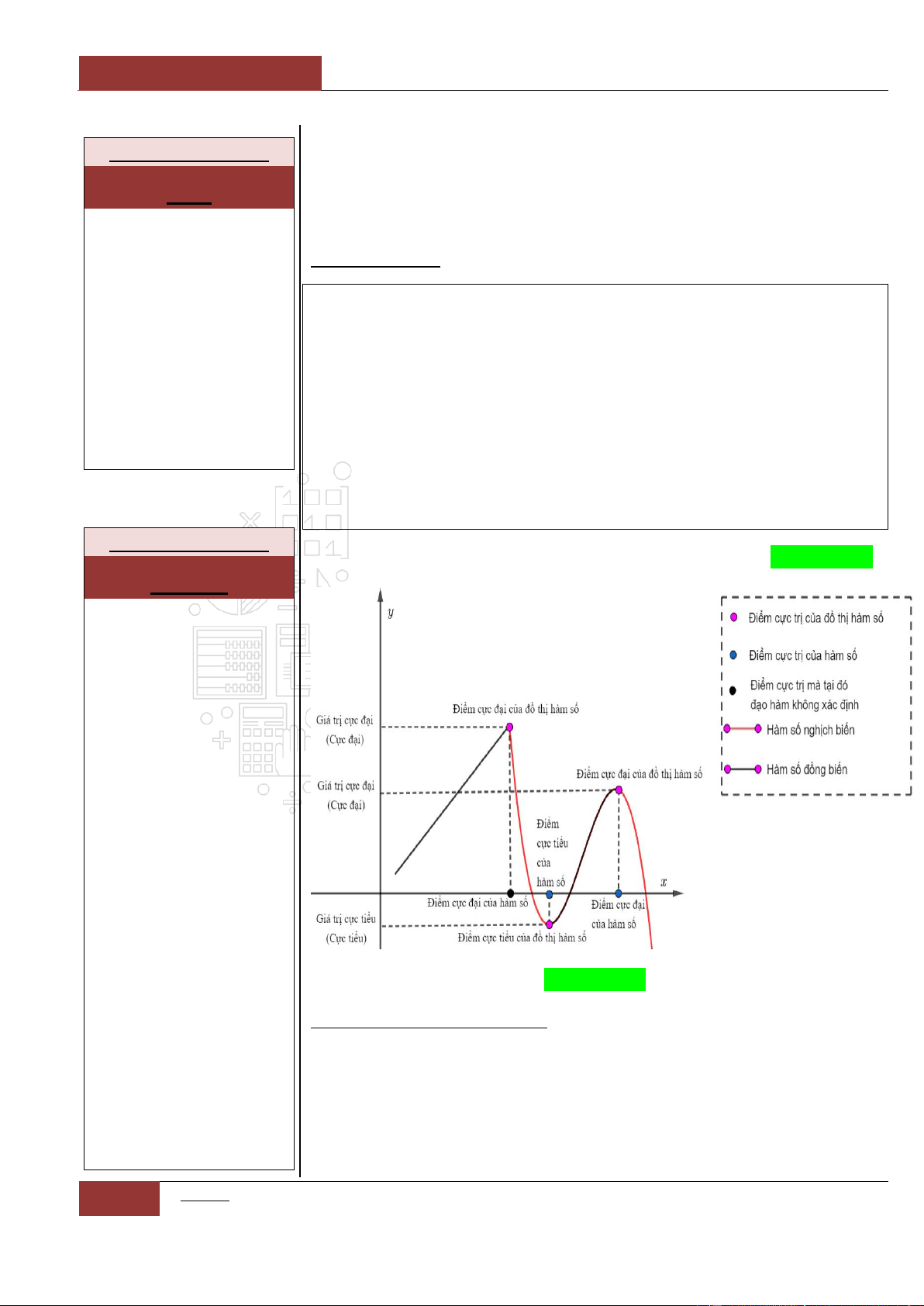
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

170

[ I can't, I can! ]

Extra Techniques:

Tips:

Giả sử hàm số

 

y f x

liên tục trên khoảng

K

và đạt cực trị tại điểm

0

x x K

thì hoặc đạo

hàm của

 

y f x

bằng

0

hoặc đạo hàm của

 

y f x

không xác

định.

Extra Techniques:

Remark:

Giả sử hàm số

 

y f x

liên tục trên khoảng

K

và đạt cực đại tại điểm

x a K

và đạt cực

tiểu tại điểm

x b K

thì ta gọi:

xa

là điểm cực đại

của hàm số

 

y f x

.

xb

là điểm cực tiểu

của hàm số

 

y f x

.

 

;A a f a

là điểm cực

đại của đồ thị hàm số

 

y f x

.

 

;B b f b

là điểm cực

tiểu của đồ thị hàm số

 

y f x

.

I.II. Cực trị - Điểm cực trị - Giá trị lớn nhất -

Giá trị nhỏ nhất của hàm số

A. Lý thuyết cần nắm

1. Định nghĩa

Cho hàm số

 

y f x

xác định và liên tục trên khoảng

 

;ab

,

 

;ab

có thể là khoảng hữu hạn hoặc vô hạn

 



và điểm

 

0

;x a b

.

 

i

Nếu tồn tại số

0h 

sao cho

 

   

0 0 0

,;f x f x x x h x h    

và

0

xx

thì ta nói hàm số

 

y f x

đạt cực đại tại điểm

0

xx

.

 

ii

Nếu tồn tại số

0h 

sao cho

 

   

0 0 0

,;f x f x x x h x h    

và

0

xx

thì ta nói hàm số

 

y f x

đạt cực tiểu tại điểm

0

xx

.

(Minh họa Đồ thị I.II.1)

Đồ thị I.II.1

2. Giá trị cực trị (Cực trị)

Một cách đơn giản hóa khái niệm thế nào là cực trị hay giá trị cực trị

đó là việc tính toán giá trị

 

0

fx

với

0

x

là điểm cực trị của hàm số

 

y f x

. Từ đây khi ta muốn xác định giá trị cực trị thì ta chỉ cần

tính giá trị

 

0

fx

. Lưu ý: Giá trị cực trị là tên gọi khác của cực trị.

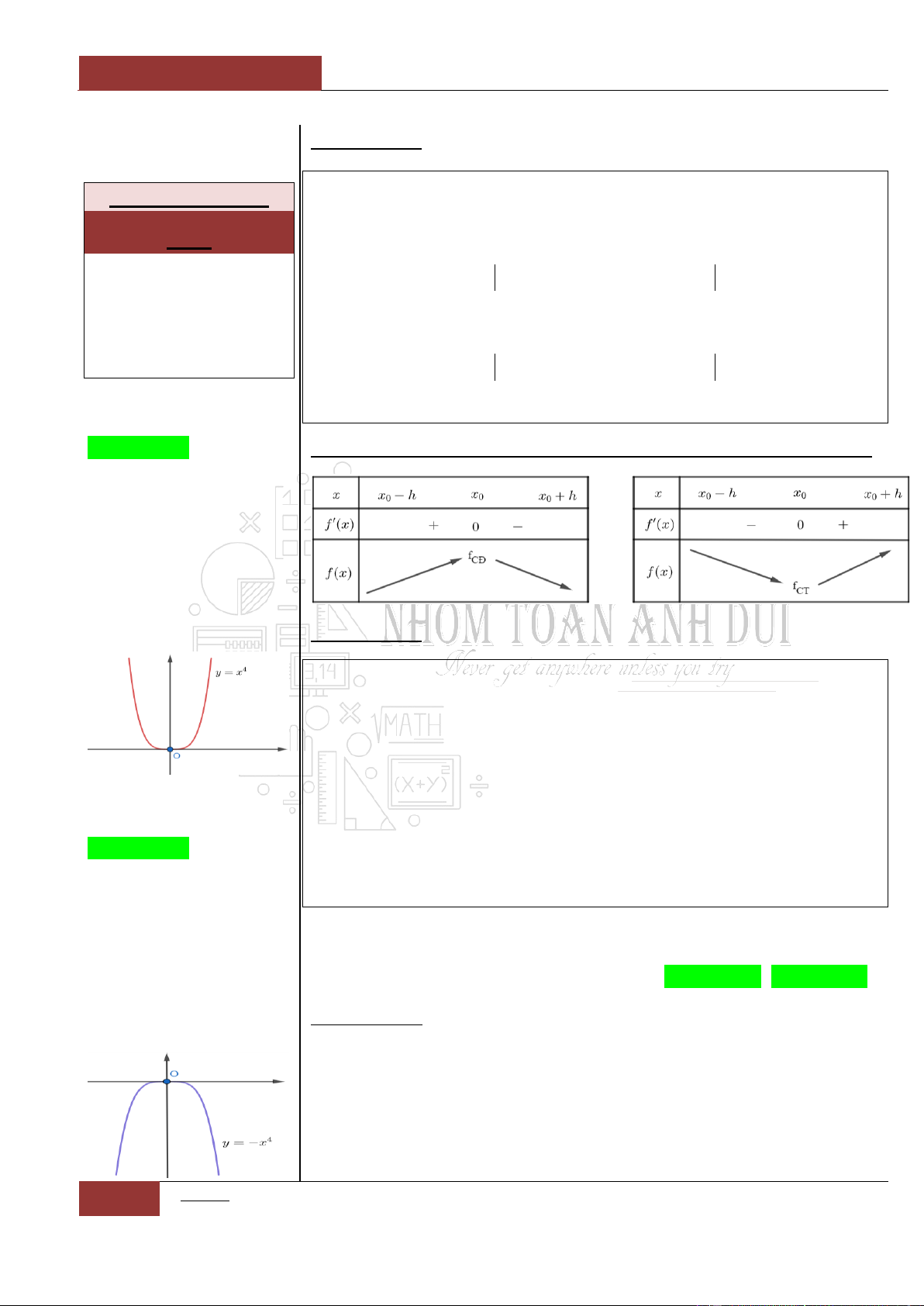
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

171

[ I can't, I can! ]

Extra Techniques:

Tips:

Mối quan hệ giữa cực trị

và bảng biến thiên thực

chất là Định lý 1 dạng

hình ảnh.

Ví dụ I.II.1.

Hàm số

4

yx

có:

 

' 0 0

'' 0 0

y















nhưng vẫn

đạt cực tiểu tại điểm

0x 

.

Ví dụ I.II.2.

Hàm số

4

yx

có:

 

' 0 0

'' 0 0

y















nhưng vẫn

đạt cực đại tại điểm

0x 

.

3. Định lý 1

Cho hàm số

 

y f x

liên tục trên khoảng

 

00

; , 0x h x h h  

và

có đạo hàm trên

 

00

; , 0x h x h h  

hoặc

   

0 0 0

;\x h x h x

.

Nếu

 

 

0 0 0 0

' 0 ; , ' 0 ;f x x x h x f x x x x h       

thì ta nói hàm số đạt cực đại tại điểm

0

xx

.

Nếu

 

 

0 0 0 0

' 0 ; , ' 0 ;f x x x h x f x x x x h       

thì ta nói hàm số đạt cực tiểu tại điểm

0

xx

.

4. Mối quan hệ giữa cực trị và bảng biến thiên của hàm số

5. Định lý 2

Cho hàm số

 

y f x

có đạo hàm cấp hai trên khoảng

K

, cụ thể:

 

00

; , 0K x h x h h   

.

Nếu

 

0

'0

'' 0

fx













thì

0

xx

là điểm cực tiểu của hàm số

 

fx

Nếu

 

0

'0

'' 0

fx













thì

0

xx

là điểm cực đại của hàm số

 

fx

Tuy nhiên điều ngược lại không đúng.

(Xem thêm Ví dụ I.II.1, Ví dụ I.II.2).

6. Nhận xét

Khi

 

'fx

đổi dấu từ dương sang âm khi qua điểm

0

xx

thì

0

xx

được gọi là điểm cực đại của hàm số.

Khi

 

'fx

đổi dấu từ dương sang âm khi qua điểm

0

xx

thì

0

xx

được gọi là điểm cực đại của hàm số.

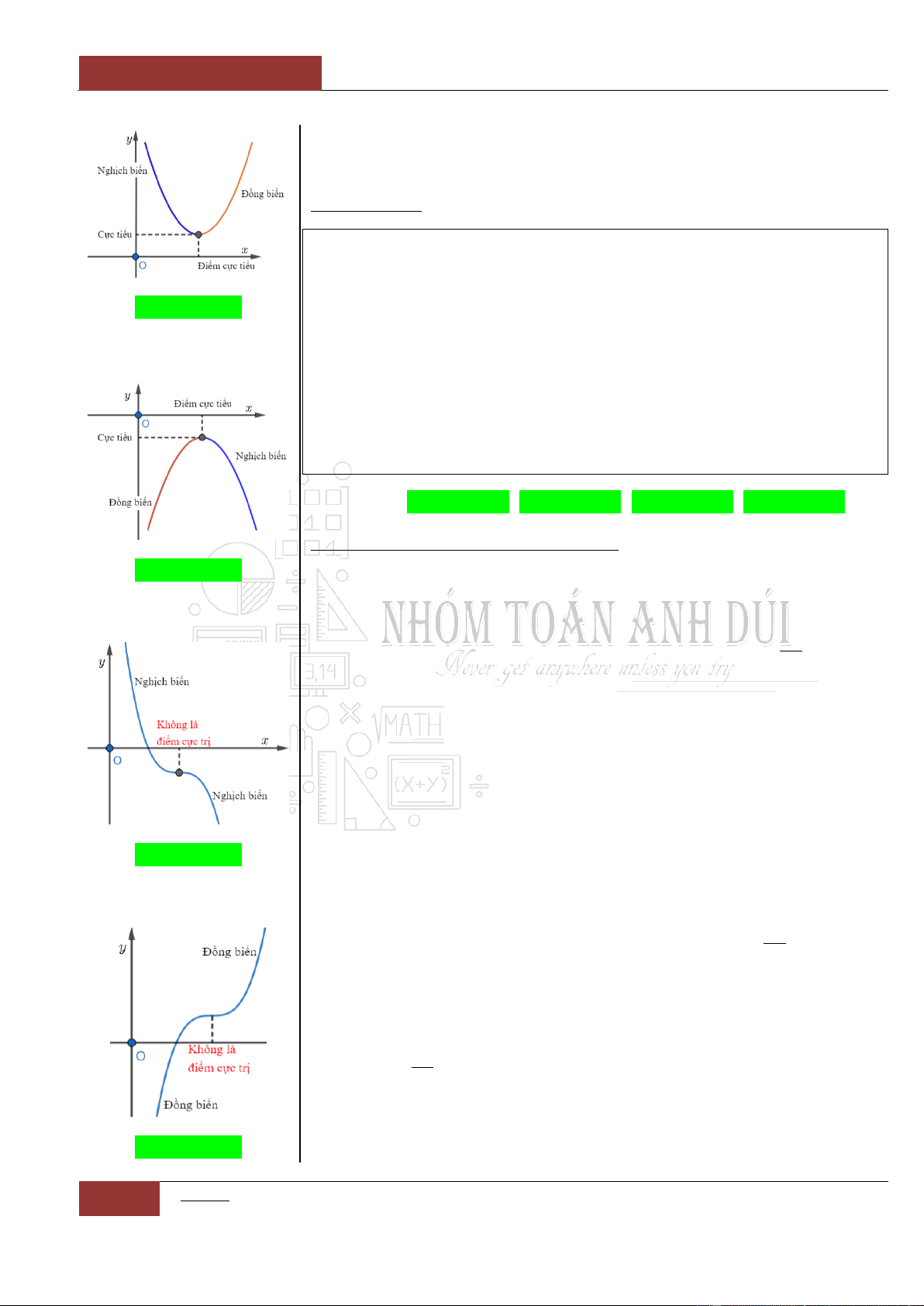
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

172

[ I can't, I can! ]

Đồ thị I.II.2.

Đồ thị I.II.3.

Đồ thị I.II.4.

Đồ thị I.II.5.

Tổng quát, từ các định lý và ví dụ trên ta thừa nhận định lý về điều

kiện cần và đủ để hàm số có cực trị.

7. Định lý 3

Giả sử hàm số

 

y f x

liên tục trên khoảng

 

00

;K x h x h

và có

đạo hàm trên

K

hoặc

 

0

\Kx

, với

0h 

.

Nếu

 

'0fx

trên khoảng

 

00

;x h x

và

 

'0fx

trên

khoảng

 

00

;x x h

thì

0

xx

là một điểm cực đại của hàm số

 

fx

.

Nếu

 

'0fx

trên khoảng

 

00

;x h x

và

 

'0fx

trên

khoảng

 

00

;x x h

thì

0

xx

là một điểm cực tiểu của hàm số

 

fx

.

(Xem thêm Đồ thị I.II.2, Đồ thị I.II.3, Đồ thị I.II.4, Đồ thị I.II.5.)

8. Phương pháp xác định cực trị

1.Phương pháp 1. (Áp dụng cho dạng toán cổ điển).

Bước 1: Tìm tập xác định.

Bước 2: Tính đạo hàm

 

'fx

và tìm tập các giá trị

, 1,

i

x i n

thỏa

mãn

 

'0

i

fx

hoặc

 

'

i

fx

không xác định.

Bước 3: Lập bảng biến thiên, xét dấu đạo hàm.

Bước 4: Xác định cực trị của hàm số.

2. Phương pháp 2. (Áp dụng cho dạng toán tìm điểm cực trị với tham

số

m

hoặc điều kiện đủ để

0

xx

là điểm cực trị của

 

y f x

).

Bước 1: Tìm tập xác định.

Bước 2: Tính đạo hàm

 

'fx

và tìm tập nghiệm

, 1,

i

x i n

của

phương trình

 

'0fx

.

Bước 3: Tính đạo hàm cấp hai

 

''fx

và đạo hàm cấp hai tại các

điểm

, 1,

i

x i n

vừa tìm được.

Bước 4: Xét dấu theo Định lý 2.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

173

[ I can't, I can! ]

B. Bài tập trong các đề thi thử

Dạng 1. Xác định các vấn đề liên quan đến cực trị

Câu 1. Điểm cực tiểu của đồ thị hàm số

32

1 3 1

2

3 2 3

y x x x   

là?

A.

1x 

. B.

2x 

.

C.

7

1;

6

A







. D.

 

2;1B

.

Đáp án: D

Lời giải

Xét hàm số:

32

1 3 1

2

3 2 3

y x x x   

.

Ta có:

2

32y x x  

.

Khi đó:

2

1

' 0 3 2 0

2

x

y x x

x





     







.

Bảng biến thiên:

Dựa vào bảng biến thiên ta nhận thấy điểm cực tiểu của đồ thị hàm

số là điểm

 

2;1B

.

Câu 2. Số cực tiểu của đồ thị hàm số

42

22y x x  

là?

A.

1

. B.

2

.

C.

3

. D.

4

.

Đáp án: A

Lời giải

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

174

[ I can't, I can! ]

Extra Techniques:

Tips:

Cực tiểu của hàm số

chính là giá trị cực tiểu

của hàm số. Các giá trị

cực tiểu của hàm số thực

ra là những hằng số, nếu

các giá trị đó bằng nhau

thì ta chỉ tính là

1

.

Đồ thị I.II.6.

Xét hàm số

42

22y x x  

.

Ta có:

3

1

' 4 4 0 0

1

x

y x x x

x







    







.

Bảng biến thiên:

Đồ thị hàm số có duy nhất một cực tiểu (Giá trị cực tiểu) là

1y 

.

Câu 3. Cho hàm số

42

2020 2021y x x   

.

Mệnh đề nào sau đây đúng?

A. Hàm số số có hai điểm cực đại và một điểm cực tiểu.

B. Hàm số có một điểm cực đại và hai điểm cực tiểu.

C. Hàm số chỉ có một điểm cực đại.

D. Hàm số chỉ có một điểm cực tiểu.

Đáp án: A

Lời giải

Đồ thị hàm số là hàm bậc bốn trùng phương có hệ số

10a   

nên

hàm số có xu hướng đi xuống khi

x

dần đến một số đủ lớn.

Và tích hệ số

2020 0ab   

nên hàm số có ba điểm cực trị.

Khi đó đồ thị hàm số có dạng hình chữ

""

.

Nên hàm số có hai điểm cực đại và một điểm cực tiểu.

(Xem thêm Đồ thị I.II.6).

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

175

[ I can't, I can! ]

Extra Techniques:

Tips:

Ta cần đọc kĩ đề để

tránh những sai phạm

không đáng có đã được

lưu ý ở phần Remark về

cách gọi tên của điểm

cực trị của hàm số và đồ

thị hàm số.

Đồ thị hàm số

yx

.

Đồ thị I.II.7.

Câu 4. Điểm cực tiểu của hàm số

2

2x 3  yx

là?

A.

0x 

. B.

1x 

.

C.

 

0;3A

. D.

 

1;2B

.

Đáp án: B

Lời giải

Ta có:

' 2 2 0 1y x x    

.

Vì

 

'' 1 2 0y 

.

Nên

1x 

là điểm cực tiểu của hàm số.

Câu 5. Phát biểu nào sau đây đúng?

A. Hàm số

 

y f x

đạt cực trị tại

0

x

khi và chỉ khi

 

0

fx



.

B. Nếu

 

0

0fx





và

 

0

0fx





thì hàm số đạt cực đại tại

0

x

.

C. Nếu

 

fx



đổi dấu khi qua điểm

0

x

và

 

fx

liên tục tại

0

x

thì hàm số

 

y f x

đạt cực trị tại điểm

0

x

.

D. Nếu

 

0

0fx





thì

0

x

không phải là điểm cực trị của hàm số.

Đáp án: C

Lời giải

Ta xét từng đáp án:

Đáp án A sai, vì tại những điểm mà đạo hàm không xác định,

hàm số

 

y f x

vẫn có thể có cực trị.

Chẳng hạn hàm số

yx

không có đạo hàm tại

0x 

nhưng

0x 

vẫn là điểm cực tiểu của hàm số.

Thật vậy:

,0

xx

yx

xx













. Nên

1, 0

'

1, 0

x

y

x













.

Vì vậy hàm số không có đạo hàm tại

0x 

.

(Xem thêm Đồ thị I.II.7).

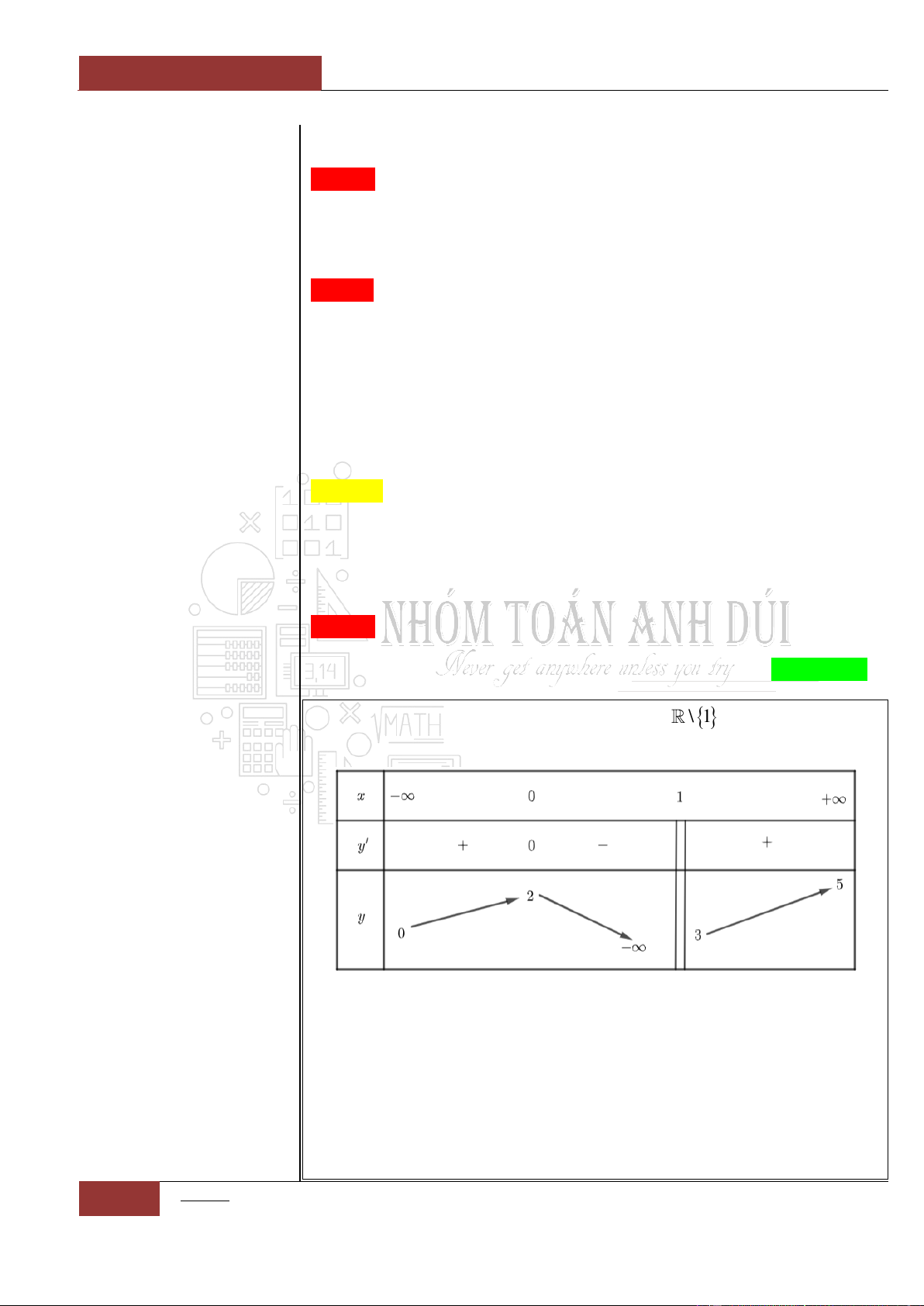
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

176

[ I can't, I can! ]

Dựa vào đồ thị hàm số ta thấy: Hàm số đạt cực tiểu tại điểm

0x 

.

Loại A.

Đáp án B sai, vì nếu

 

0

0fx





và

 

0

0fx





thì hàm số đạt cực

tiểu tại

0

x

.

Loại B.

(Xem thêm Định lý 2).

Đáp án C đúng vì:

"Nếu

 

fx



đổi dấu khi qua điểm

0

x

và

 

fx

liên tục tại

0

x

thì

hàm số

 

y f x

đạt cực trị tại điểm

0

x

."

Chọn C.

Đáp án D sai, vì:

Hàm số

4

yx

có một điểm cực đại là

0x 

. Mặc dù:

 

'' 0 0f 

.

Loại D.

(Xem thêm Ví dụ I.II.2).

Câu 6. Cho hàm số

 

y f x

xác định trên

 

\1

liên tục trên mỗi

khoảng xác định và có bảng biến thiên như sau:

Mệnh đề nào dưới đây đúng?

A. Đồ thị hàm số có hai tiệm cận ngang là

0, 5yy

và tiệm cận

đứng là

1x 

.

B. Giá trị cực tiểu của hàm số là

3

CT

y 

.

C. Giá trị cực đại của hàm số là

5

CĐ

y 

.

D. Hàm số đồng biến trên khoảng

 

0;

.

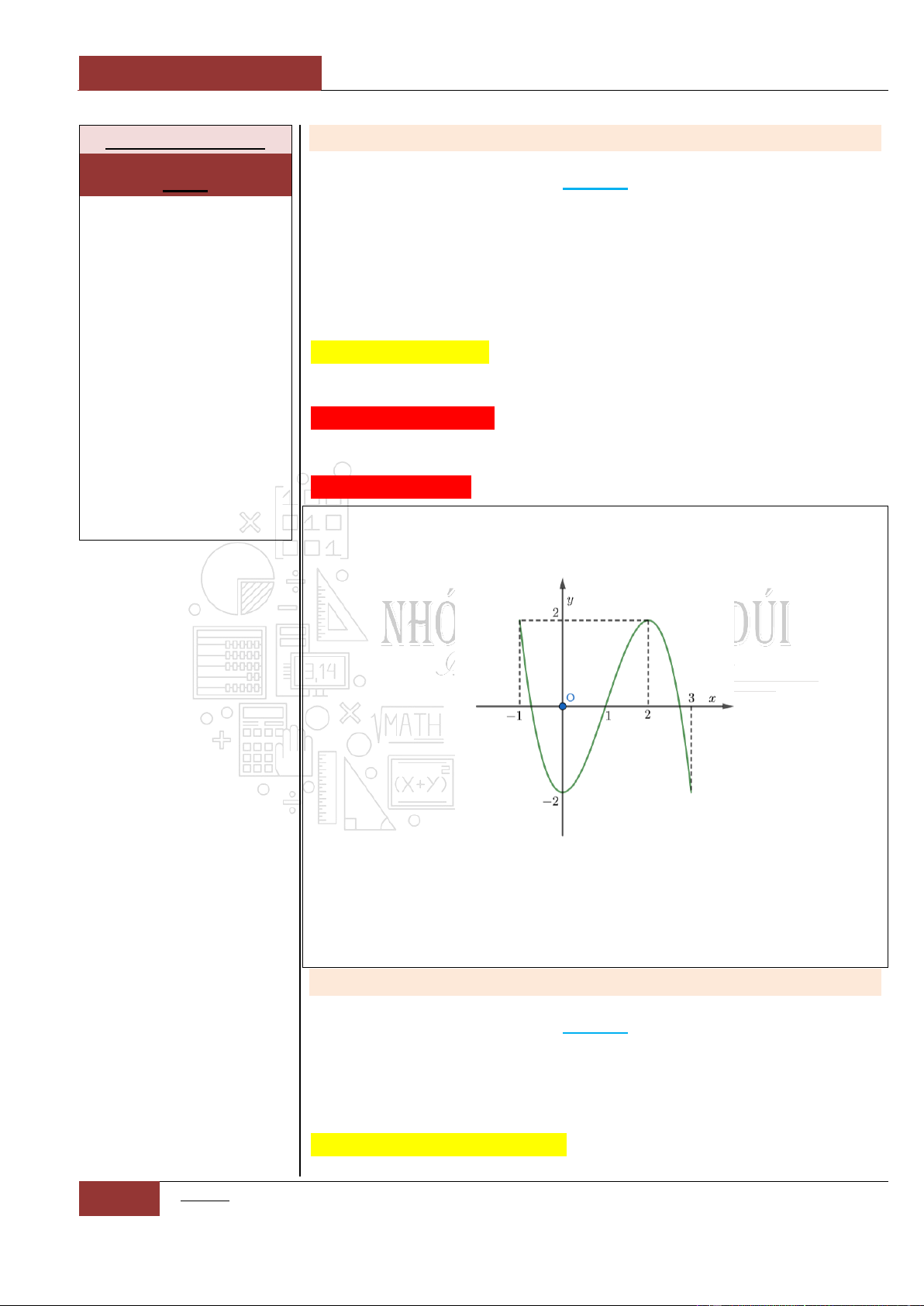
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

177

[ I can't, I can! ]

Extra Techniques:

Tips:

Theo định nghĩa:

Nếu

lim ( )

o

x

f x y





hoặc

lim ( )

o

x

f x y





thì đồ thị

hàm số có tiệm cận

ngang là

o

yy

.

Nếu

lim ( )

o

xx

fx





 

hoặc

lim ( )

o

xx

fx





 

thì

đồ thị hàm số có tiệm

cận đứng là

o

xx

.

Đáp án: A

Lời giải

Dựa vào bảng biến thiên:

Vì

lim 5

x

y





và

lim 0

x

y





nên đồ thị hàm số có hai tiệm cận ngang

0, 5yy

.

Vì

1

lim

x

y





 

nên đồ thị hàm số có tiệm cận đứng là

1x 

.

Do đó đáp án A đúng.

Hàm số đạt cực đại tại

0x 

và giá trị cực đại

2

CĐ

y 

.

Do đó đáp án B, C sai.

Hàm số đồng biến trên khoảng

 

;0

và

 

1; 

.

Do đó đáp án D sai.

Câu 7. Cho hàm số

 

y f x

xác định, liên tục trên đoạn

 

1;3

và

có đồ thị như hình vẽ bên dưới. Khẳng định nào sau đây đúng?

A. Hàm số đạt cực đại tại

1x 

và

2x 

.

B. Hàm số đạt cực tiểu tại

0, 3xx

.

C. Hàm số đạt cực tiểu tại

0x 

, cực đại tại

2x 

.

D. Hàm số đạt cực tiểu tại

0x 

, cực đại tại

1x 

.

Đáp án: C

Lời giải

Dựa vào đồ thị hàm số như hình vẽ, ta nhận thấy:

Hàm số đạt cực tiểu tại điểm

0x 

.

Hàm số đạt cực đại tại điểm

2x 

.

Do đó đáp án C là đáp án đúng.

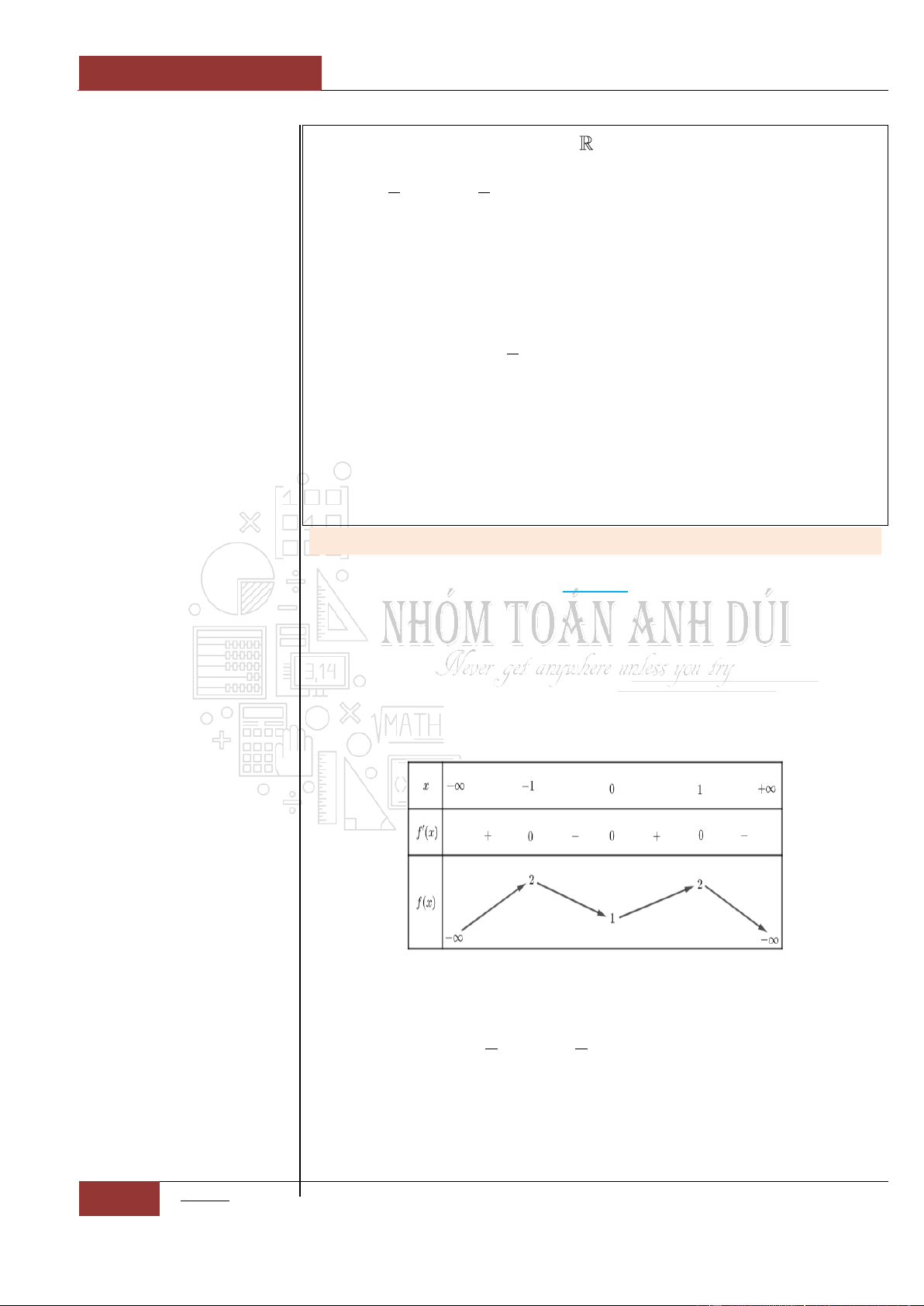
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

178

[ I can't, I can! ]

Câu 8. Xét hai hàm đa thức trên ,

 

42

21f x x x   

và hàm số

 

42

15

44

g x x x   

.

Mệnh đề nào sau đây là mệnh đề đúng trong các mệnh đề sau?

A. Hàm số

 

fx

có hai điểm cực đại là

 

1;2A

và

 

1;2B 

.

B. Hàm số

 

y f x

có điểm cực tiểu là

0x 

và hàm số

 

y g x

có giá trị cực đại là

5

4

y 

.

C. Hàm số

 

y f x

có hai điểm cực tiểu và một điểm cực đại, hàm

số

 

y g x

có duy nhất một điểm cực đại.

D. Hàm số

 

y f x

và hàm số

 

y g x

có cùng điểm cực tiểu là

điểm

0x 

.

Đáp án: B

Lời giải

Xét hàm số

 

42

21f x x x   

.

Ta có:

 

3

1

' 4 4 0 0

1

x

f x x x x

x







     







.

Bảng biến thiên hàm số

 

y f x

.

Xét hàm số

 

42

15

44

g x x x   

.

Ta có:

 

3

' 2 0 0g x x x x     

.

Bảng biến thiên hàm số

 

y g x

.

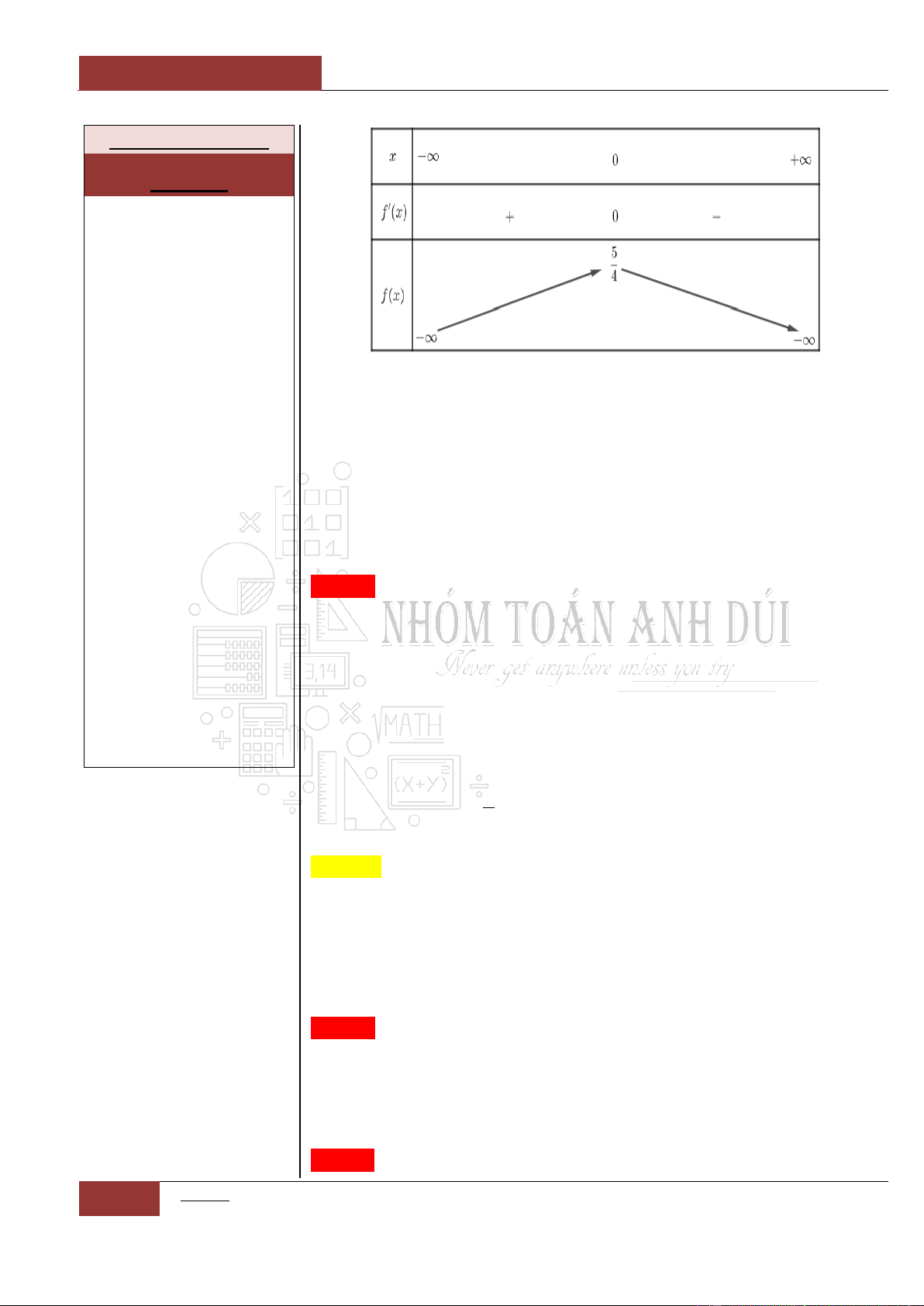
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

179

[ I can't, I can! ]

Extra Techniques:

Remark:

Giả sử hàm số

 

y f x

liên tục trên khoảng

K

và đạt cực đại tại điểm

x a K

và đạt cực

tiểu tại điểm

x b K

thì ta gọi:

xa

là điểm cực đại

của hàm số

 

y f x

.

xb

là điểm cực tiểu

của hàm số

 

y f x

.

 

;A a f a

là điểm cực

đại của đồ thị hàm số

 

y f x

.

 

;B b f b

là điểm cực

tiểu của đồ thị hàm số

 

y f x

.

Xét từng đáp án:

Đáp án A:

Đồ thị hàm số

 

fx

có hai điểm cực đại là

 

1;2A

và

 

1;2B 

.

Nhưng hàm số

 

fx

lại có hai điểm cực đại là

1x 

và

1x 

.

Loại A.

Đáp án B:

Dựa vào bảng biến thiên của đồ thị hàm số

 

y f x

và

 

y g x

, ta

thấy rằng:

Hàm số

 

y f x

có điểm cực tiểu là

0x 

và hàm số

 

y g x

có

giá trị cực đại là

5

4

y 

.

Chọn B.

Đáp án C:

Hàm số

 

y f x

có hai điểm cực đại và một điểm cực tiểu, hàm

số

 

y g x

có duy nhất một điểm cực đại.

Loại C.

Đáp án D:

Hàm số

 

y f x

nhận điểm

0x 

làm điểm cực tiểu trong khi đó

hàm số

 

y g x

lại nhận

0x 

làm điểm cực đại.

Loại D.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

180

[ I can't, I can! ]

Extra Techniques:

Remark:

Hàm số bậc bốn trùng

phương có dạng tổng

quát:

42

y ax bx c  

có ba điểm cực trị khi và

chỉ khi tích hệ số

0ab 

Extra Techniques:

Remark:

Hàm số bậc bốn trùng

phương có dạng tổng

quát:

42

y ax bx c  

 

0a 

có một điểm cực

trị khi và chỉ khi tích hệ

số

0ab 

.

Nếu

0a 

thì hàm số có

một điểm cực trị khi và

chỉ khi

0b 

.

Câu 9. Tìm tất cả các giá trị thực của tham số

m

để hàm số bậc bốn

trùng phương

 

42

13y m x mx   

có ba điểm cực trị.

A.

 





; 1 0;m    

. B.

 

1;0m

.

C.



 



1 0;m    

. D.

   

; 1 0;m    

.

Đáp án: D

Lời giải

Để đồ thị hàm số

42

y ax bx c  

có ba điểm cực trị

  

0

0 1 0

1

m

ab m m

m





      







.

   

; 1 0;m     

.

Câu 10. Đồ thị hàm số nào dưới đây luôn có một điểm cực trị với mọi

giá trị

m

?

A.

 

2 4 2 2

1 2 1y m x x m    

. B.

 

4 2 2

3y x m m x m    

.

C.

2 4 2 2

1y m x x m m     

. D.

 

4 2 2

1 1 3y x m m x m     

.

Đáp án: D

Lời giải

Xét từng đáp án:

Đáp án A:

Xét hàm số:

 

2 4 2 2

1 2 1y m x x m    

.

Ta có:

 

22

1 . 1 1 1 0,ab m m m          

.

Vì thế hàm số có ba điểm cực trị.

Loại A.

Đáp án B:

Xét hàm số:

 

4 2 2

3y x m m x m    

.

Ta có:

 

22

1.ab m m m m   

.

Ta không thể xác định được dấu của tích

ab

nên số cực trị của hàm

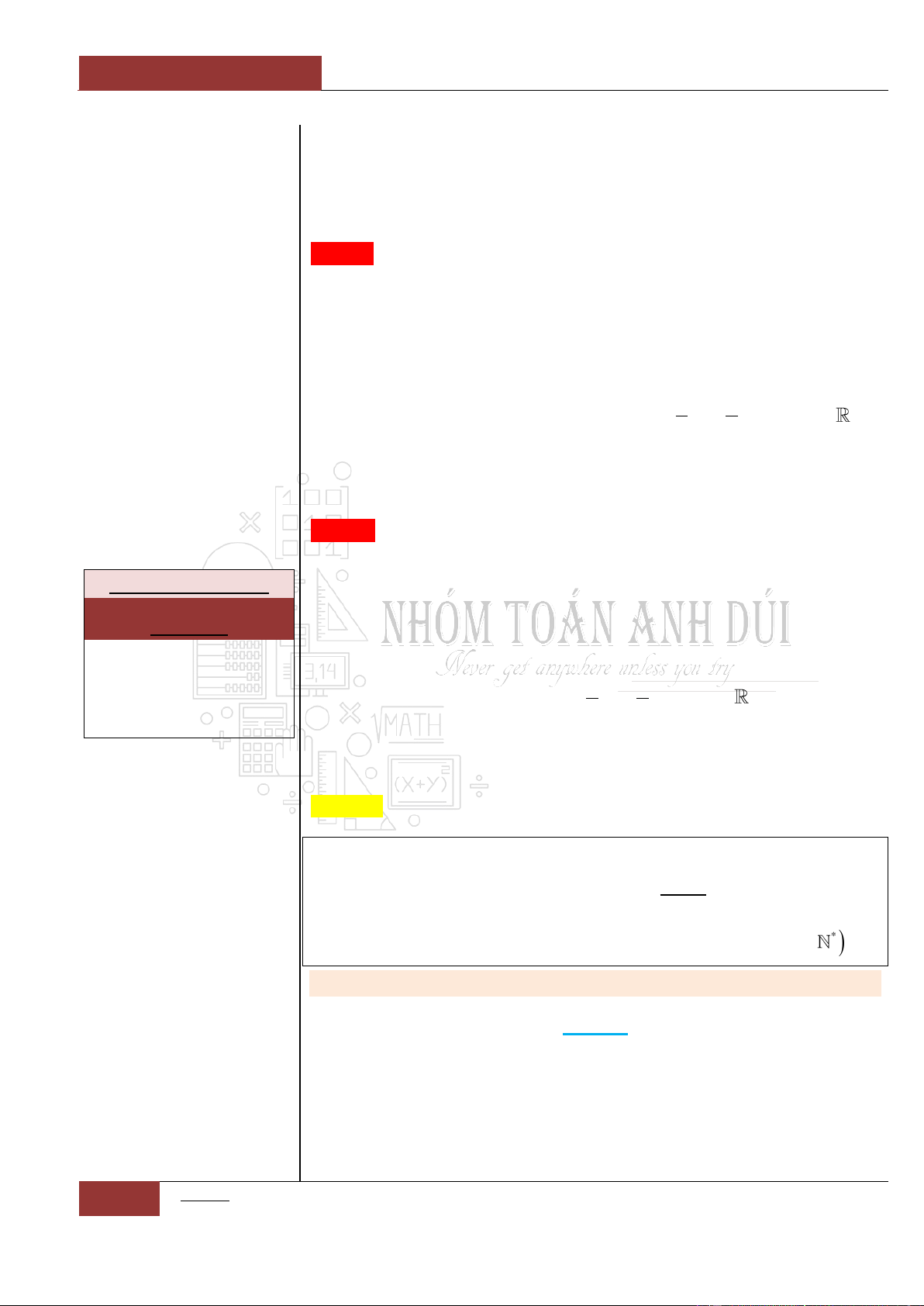
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

181

[ I can't, I can! ]

Extra Techniques:

Remark:

Hàm số bậc bốn trùng

phương có ít nhất một

điểm cực trị:

0x 

.

số không cố định.

Vì thế ta không thể xác định một cách chính xác số cực trị của hàm

số.

Loại B.

Đáp án C:

Xét hàm số:

2 4 2 2

1y m x x m m     

.

Ta có:

   

2

2 2 2

13

. 1 0,

24

ab m m m m m m





          











.

Vì thế hàm số có ba điểm cực trị.

Loại C.

Đáp án D:

Xét hàm số:

 

4 2 2

1 1 3y x m m x m     

.

Ta có:

 

2

13

1. 1 0,

24

ab m m m m



        





.

Vì thế hàm số chỉ có một cực trị.

Chọn D.

Câu 11. Hàm số nào sau đây không có cực trị?

A.

3

31y x x  

. B.

28

7

x

y

x







.

C.

43

4 3 1y x x x   

. D.

 

4*

2021 ,

m

y x x m   

.

Đáp án: B

Lời giải

Xét từng đáp án:

Đáp án A:

Xét hàm số:

3

31y x x  

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

182

[ I can't, I can! ]

Extra Techniques:

Remark:

Hàm số nhất biến (Hàm

bậc nhất trên bậc nhất).

ax b

y

cx d







không có

cực trị.

Ta có:

2

1

' 3 3 0

1

x

yx

x





   







.

Vậy hàm số có hai cực trị.

Loại A.

Đáp án B:

Xét hàm số:

28

7

x

y

x







.

TXĐ:

 

\7D 

.

Ta có:

 

2

28 28 35

'0

77

7

xx

yy

xx

x

   

    





.

Vậy hàm số không có điểm cực trị.

Chọn B.

Đáp án C:

Xét hàm số:

43

4 3 1y x x x   

.

Ta có:

32

0,46

' 4 12 3 0 0,55

2,91

xa

y x x x b

xc

  





      







.

Như vậy: Hàm số đã cho có

3

điểm cực trị.

Loại C.

Đáp án D:

Xét hàm số:

 

4*

2021 ,

m

y x x m   

.

Ta có:

41

2021

' 4 2021 0

4

m

y mx x

m



     

.

Như vậy hàm số có một điểm cực trị.

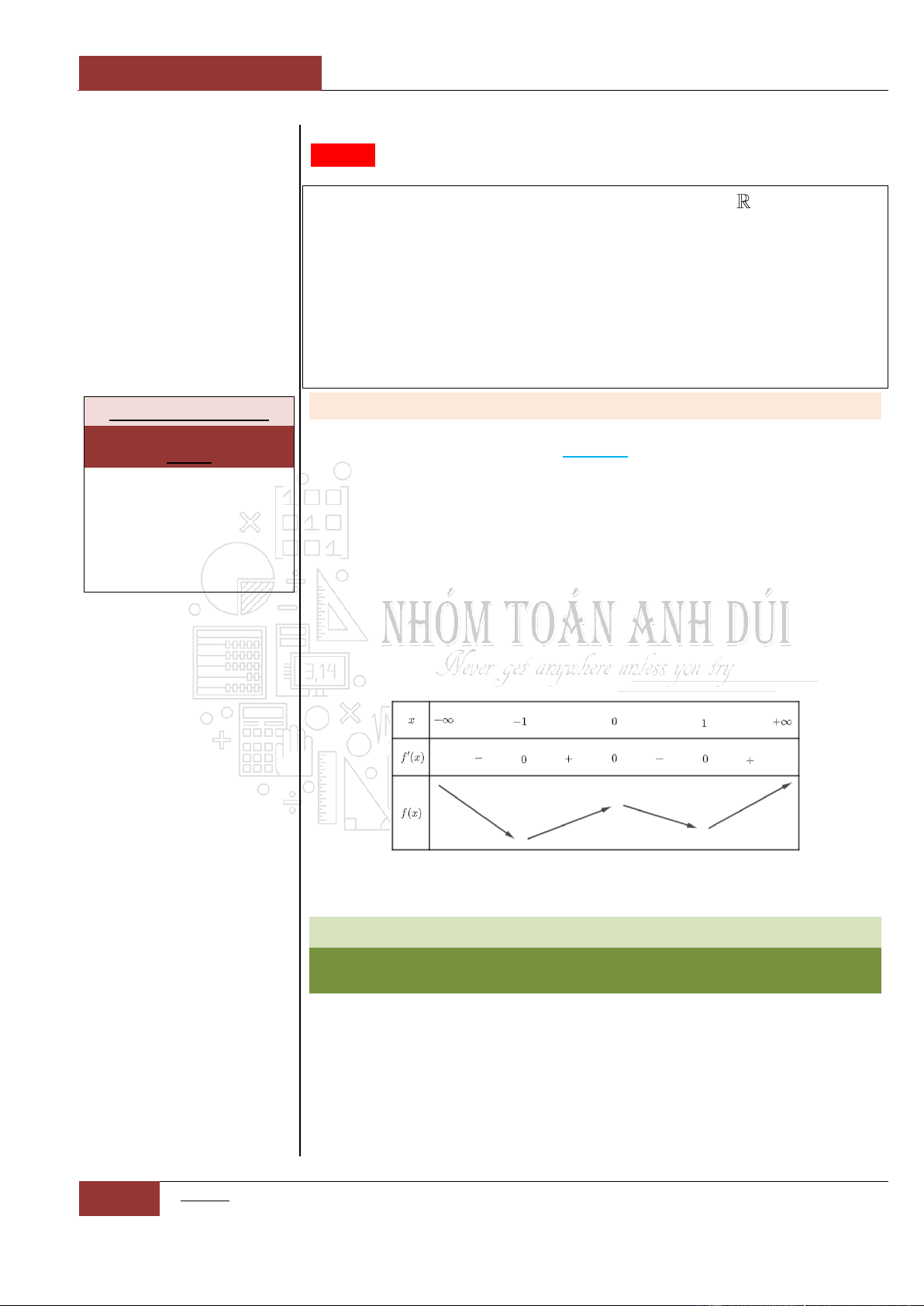
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

183

[ I can't, I can! ]

Extra Techniques:

Tips:

Số điểm cực trị của hàm

đa thức chính bằng tổng

số nghiệm bội lẻ của

phương trình đạo hàm.

Loại D.

Câu 12. Hàm số

 

y f x

có đạo hàm liên tục trên và

   

  

2

22

' 1 1 2f x x x x x   

. Phát biểu nào sau đây là đúng?

A. Hàm số có một điểm cực tiểu.

B. Hàm số có hai điểm cực đại.

C. Hàm số có ba điểm cực trị.

D. Hàm số có một điểm cực trị.

Đáp án: C

Lời giải

Ta có:

   

  

2

22

' 1 1 2 0f x x x x x    

   

 

3

2

0

1 1 2 0 1

1

x

x x x x x

x







      







.

Bảng biến thiên:

Như vậy hàm số đã cho có

3

điểm cực trị.

Một số Tips để làm tốt các bài toán cực trị

 

1

Xét hàm số bậc ba:

 

32

,0y ax bx cx d a    

.

Ta có:

22

' 3 2 ' 3y ax bx c b ac      

.

 Trường hợp 1:

2

'

' 3 0

y

b ac   

:

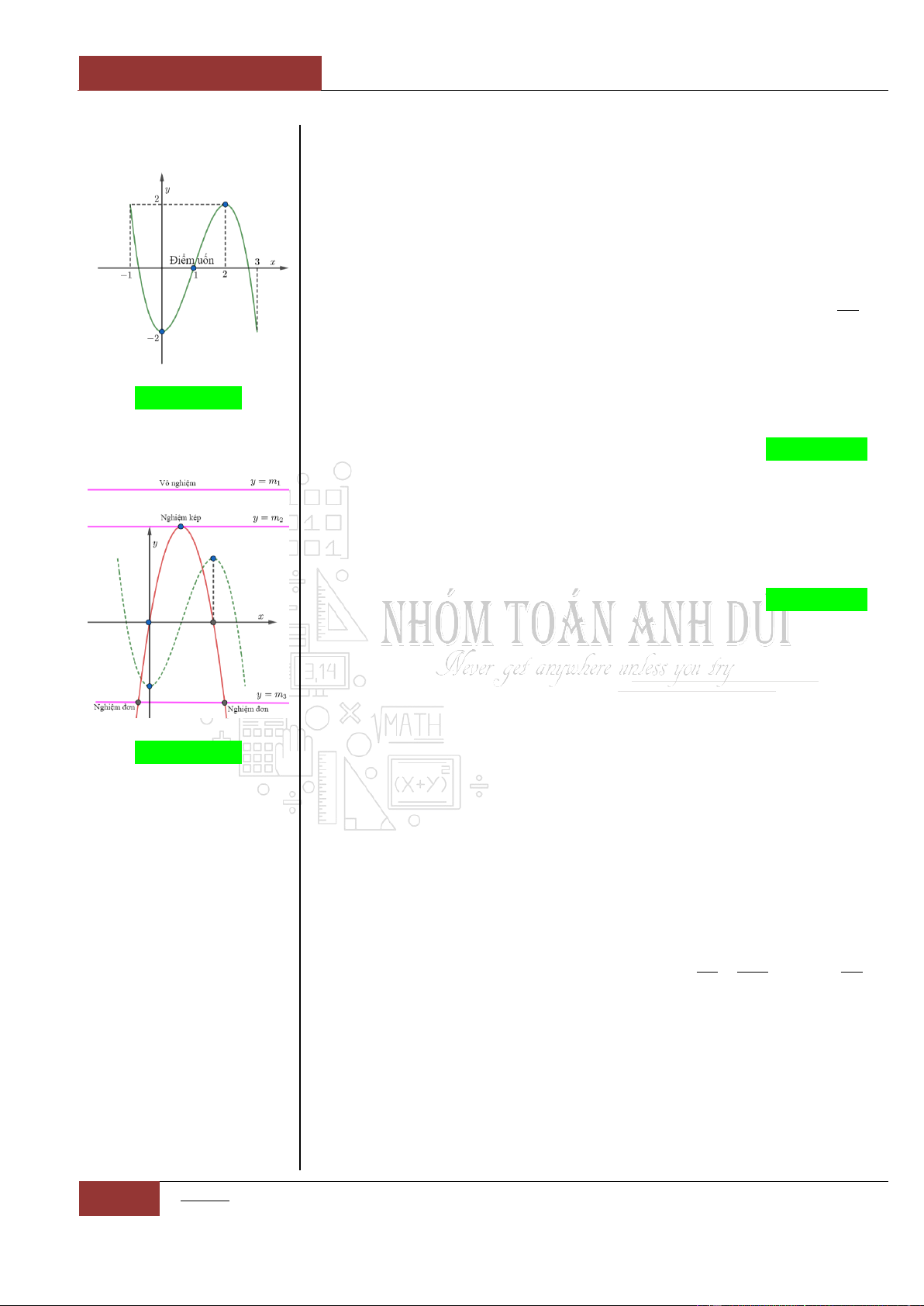
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

184

[ I can't, I can! ]

Đồ thị I.II.8.

Đồ thị I.II.9.

Khi đó đồ thị hàm số

32

y ax bx cx d   

có hai điểm cực trị.

 Trường hợp 2:

2

'

' 3 0

y

b ac   

:

Khi đó đồ thị hàm số

32

y ax bx cx d   

không có cực trị.

Mở rộng, hàm số bậc ba

32

y ax bx cx d   

nhận điểm

3

b

x

a



làm điểm uốn và hai điểm cực trị (nếu có) của hàm số trên cũng đối

xứng qua điểm uốn. Và hoành độ điểm uốn chính là nghiệm của

phương trình của đạo hàm cấp hai.

(Xem thêm Đồ thị I.II.8).

 Hàm số bậc ba

32

y ax bx cx d   

hoặc có

2

cực trị, hoặc

không có cực trị. Vì hàm bậc ba đạo hàm cho hàm đa thức bậc hai

có dạng Parabol.

(Xem thêm Đồ thị I.II.9).

Thật vậy, nếu ta kẻ các đường thẳng

1 2 3

,,y m y m y m  

như hình

vẽ minh họa, thì hoặc không có giao điểm (vô nghiệm), hoặc có một

giao điểm (nghiệm kép), hoặc có hai giao điểm (hai nghiệm đơn).

 Qua nghiệm kép, dấu của đạo hàm không thay đổi.

 Qua nghiệm đơn (hoặc gọi chung nghiệm bội lẻ nếu xét các hàm

khác), dấu của đạo hàm đổi dấu từ dương

   

  

sẽ tạo thành

cực đại và từ

   

  

sẽ tạo thành cực tiểu.

 Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số bậc ba

32

y ax bx cx d   

có phương trình

2

22

3 9 9

c b bc

y x d

aa



   





.

Thật vậy!

Giả sử ta xét hàm số

   

32

,0y f x ax bx cx d a     

.

Nếu

 

y f x

được phân tích thành

       

.'f x g x f x h x

, thì

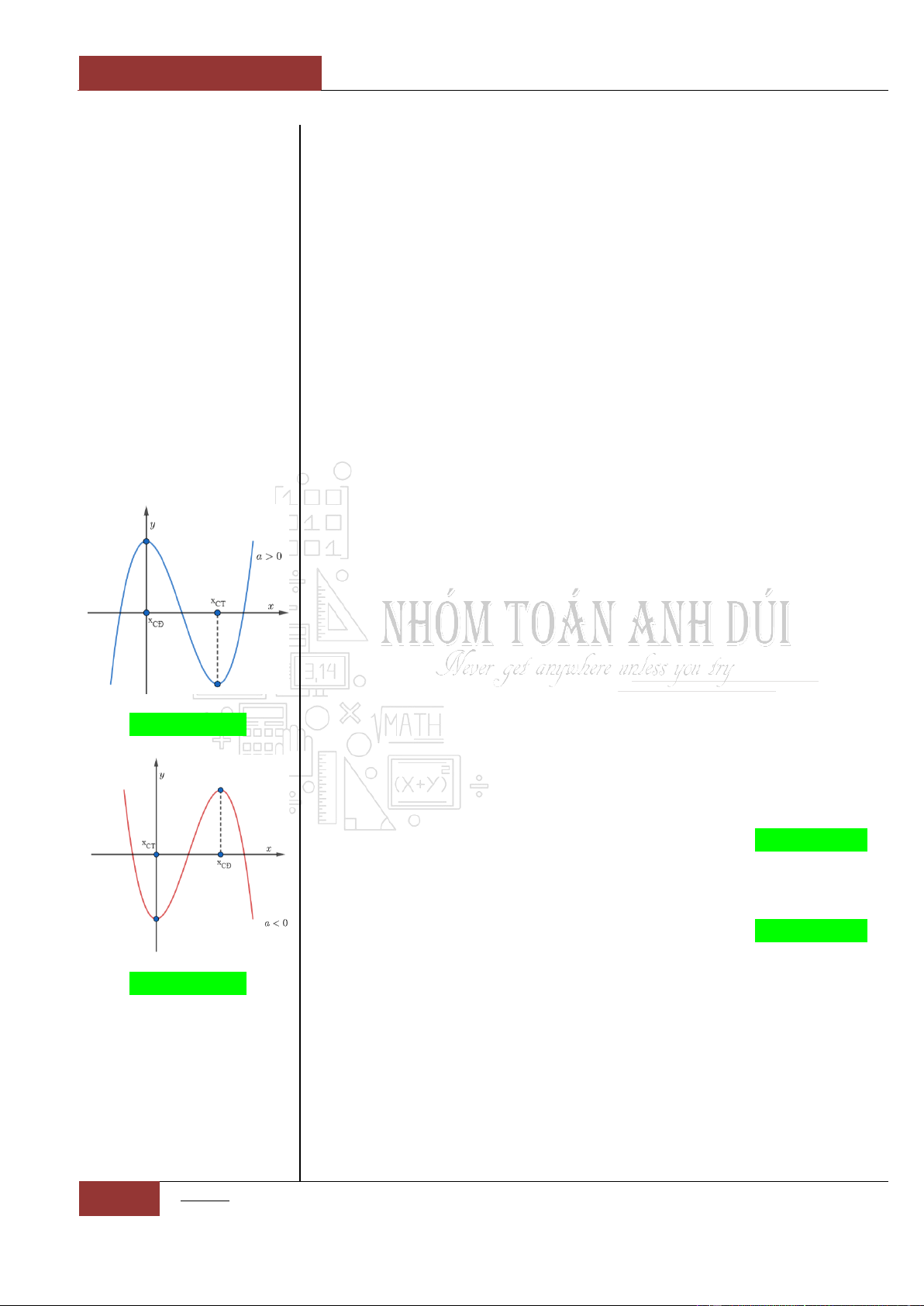
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

185

[ I can't, I can! ]

Đồ thị I.II.10.

Đồ thị I.II.11.

 

y h x

là phương trình đi qua điểm cực trị của hàm số

 

fx

.

Do nếu hàm số

 

y f x

nhận

12

,xx

lần lượt là các điểm cực đại và

cực tiểu của hàm số

 

y f x

thì:

     

12

*' ' 0f x f x

.

Ta có:

         

1 1 1 1

222 22

1

. '

'.

f

x

x g x h x h x

f x g x h

fx

f x h x

  







  





(Do

 

*

).

Đến đây ta thấy rằng hàm số

 

y h x

đi qua hai điểm cực trị của

hàm số

 

y f x

là

 

1 1 2 2

; , ;A x f x B x f x

.

Nên

 

y h x

là đường thẳng đi qua hai điểm cực trị của hàm số

 

y f x

.

Mà

 

hx

có được trong phép chia lấy dư của

 

fx

với

 

'fx

.

Từ đây, khi tìm đường thẳng đi qua hai điểm cực trị của hàm số bậc

ba, chúng tôi sẽ trình bày theo cách này, trong một số bài toán khác

có thể mở rộng thêm ở cách viết phương trình đường thẳng qua hai

điểm cực trị theo lý thuyết đường thẳng.

 Đối với hàm số bậc ba

32

y ax bx cx d   

ta luôn có:

CCĐ T

y y

.

 Nếu

0a 

thì:

CĐ CT

xx

.

(Xem thêm Đồ thị I.II.10).

 Nếu

0a 

thì:

CĐ CT

xx

.

(Xem thêm Đồ thị I.II.11).

 Hàm số có

2

cực trị nằm về hai phía đối với trục hoành khi và

chỉ khi:

.0

CT CĐ

yy

.

 Hàm số có

2

cực trị nằm về hai phía đối với trục tung khi và

chỉ khi:

.0

CT CĐ

xx

.

 Hàm số có hai cực trị nằm về phía trên đối với trục hoành khi

và chỉ khi:

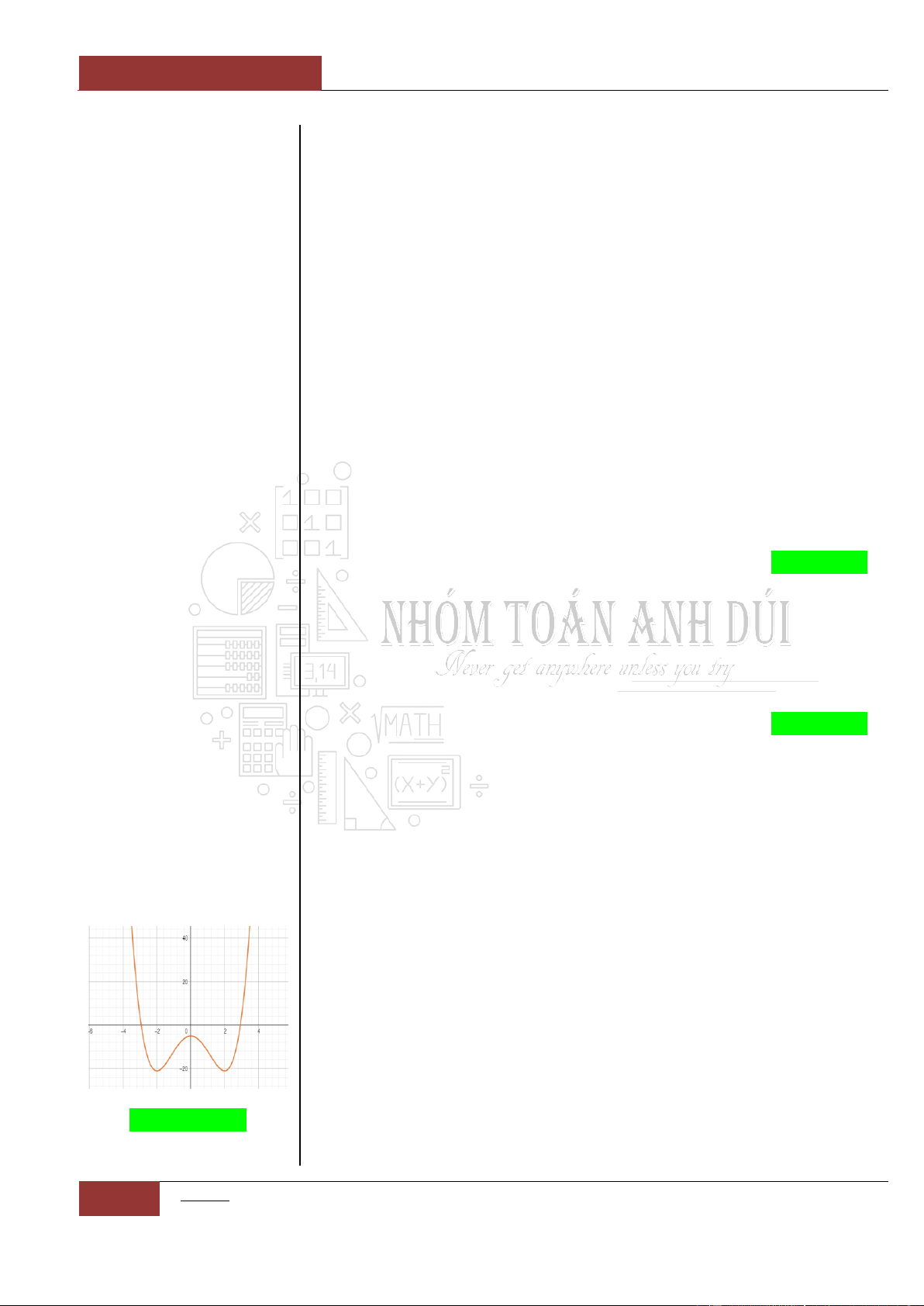
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

186

[ I can't, I can! ]

Đồ thị I.II.12.

0

.0

CT CĐ

yy











.

 Hàm số có hai cực trị nằm phía dưới đối với trục hoành khi và

chỉ khi:

0

.0

CT CĐ

yy











.

 Hàm số có cực trị tiếp xúc với trục hoành khi và chỉ khi:

.0

CT CĐ

yy

.

 Nếu tồn tại điểm

0

xx

thỏa mãn

 

0

'0

'' 0

fx













thì hàm số đạt

cực tiểu tại điểm

0

xx

. Điều ngược lại chưa chắc đúng.

(Xem lại Ví dụ I.II.1).

 Nếu tồn tại điểm

0

xx

thỏa mãn

 

0

'0

'' 0

fx













thì hàm số đạt

cực đại tại điểm

0

xx

. Điều ngược lại chưa chắc đúng.

(Xem lại Ví dụ I.II.2).

 

2

Xét hàm bậc bốn trùng phương

 

42

,0y ax bx c a   

.

Ta có:

 

32

' 4 2 0 2 2 0 *y ax bx x ax b     

.

Số điểm cực trị của hàm số

 

42

,0y ax bx c a   

phụ thuộc rất

lớn vào phương trình

 

*

, nếu phương trình

 

*

có bao nhiêu nghiệm

bội lẻ thì phương trình bậc bốn trùng phương đang xét sẽ có bấy

nhiêu nghiệm.

 Trường hợp 1:

0

ab

a











hay

0

a

b











.

Khi đó đồ thị hàm số có dạng hình chữ

"W"

nên hàm số sẽ có

3

điểm

cực trị,

2

cực trị (giá trị cực trị, nếu trùng nhau, chỉ tính

1

),

1

điểm

cực đại,

2

điểm cực tiểu,

1

cực đại (giá trị cực đại),

1

cực tiểu (giá trị

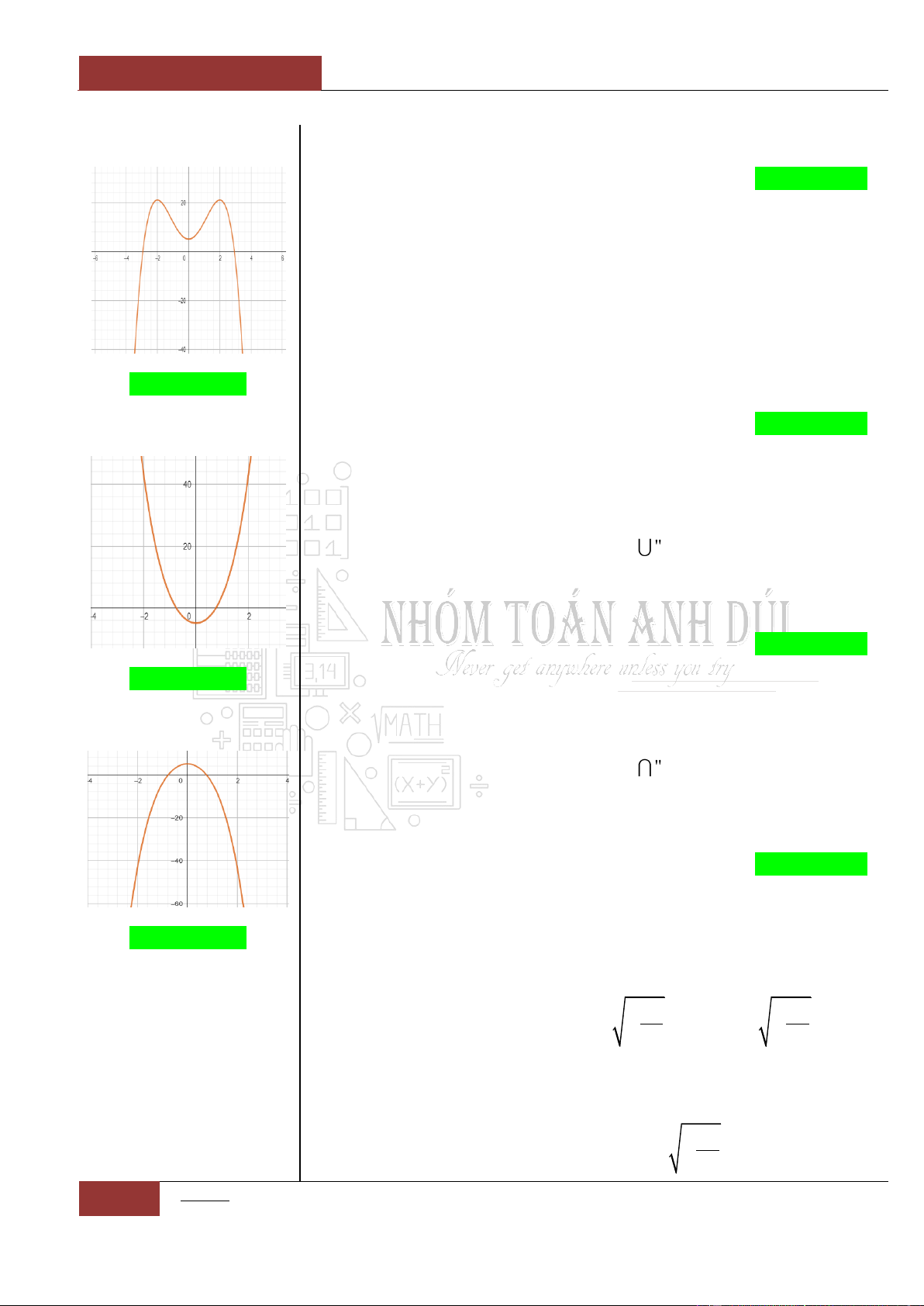
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

187

[ I can't, I can! ]

Đồ thị I.II.13.

Đồ thị I.II.14.

Đồ thị I.II.15.

cực tiểu, nếu trùng nhau, chỉ tính

1

).

(Xem thêm Đồ thị I.II.12).

 Trường hợp 2:

0

ab

a











hay

0

a

b











.

Khi đó đồ thị hàm số có dạng hình chữ

""

nên hàm số sẽ có

3

điểm

cực trị,

2

cực trị (giá trị cực trị, nếu trùng nhau, chỉ tính

1

),

1

điểm

cực tiểu,

2

điểm cực đại,

1

cực tiểu (giá trị cực tiểu) và

1

cực đại (giá

trị cực đại, nếu trùng nhau, chỉ tính

1

).

(Xem thêm Đồ thị I.II.13).

 Trường hợp 3:

0

ab

a











hay

0

a

b











.

Khi đó đồ thị hàm số có dạng hình chữ

""

của Parabol nên hàm số

sẽ có

1

điểm cực trị,

1

cực trị (giá trị cực trị), chính xác hơn:

1

điểm

cực tiểu và

1

cực tiểu (giá trị cực tiểu).

(Xem thêm Đồ thị I.II.14).

 Trường hợp 4:

0

ab

a











hay

0

a

b











.

Khi đó đồ thị hàm số có dạng hình chữ

""

của Parabol nên hàm số

sẽ có

1

điểm cực trị,

1

cực trị (giá trị cực trị), chính xác hơn:

1

điểm

cực đại và

1

cực đại (giá trị cực đại).

(Xem thêm Đồ thị I.II.15).

 Hàm số bậc bốn trùng phương có ít nhất một điểm cực trị là

điểm

0x 

.

 Nếu tích hệ số

0ab 

, hàm số bậc bốn trùng phương có

3

điểm cực trị, lần lượt là:

, 0,

22

bb

x x x

aa

     

.

 Xét riêng trường hợp hàm số có

3

điểm cực trị

 

0ab 

.

Nếu

0a 

, thì

0x 

là điểm cực tiểu,

2

b

x

a

  

là hai điểm cực

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

188

[ I can't, I can! ]

Đồ thị I.II.16.

đại của hàm số.

Ngược lại, nếu

0a 

, thì

0x 

là điểm cực đại,

2

b

x

a

  

là hai

điểm cực tiểu của hàm số.

 Mở rộng lên hàm đa thức bậc

4

có dạng tổng quát:

Hàm số

 

4 3 2

,0y ax bx cx dx e a     

hoặc có một cực trị hoặc

có ba cực trị.

Do ta có:

 

32

' 4 3 2 0 *y ax bx cx d    

là một phương trình bậc

ba theo ẩn

x

.

Xét các khả năng có nghiệm của phương trình

 

*

.

(Xem thêm Đồ thị I.II.16).

Dựa vào Đồ thị I.II.16 ta thấy rằng với sự tương giao của đồ thị hàm

số

32

4 3 2y ax bx cx d   

với đường thẳng

1

ym

chỉ cắt duy

nhất tại

1

điểm duy nhất (phương trình

 

*

có

1

nghiệm đơn); sự

tương giao của đồ thị hàm số

32

4 3 2y ax bx cx d   

với đường

thẳng

2

ym

cắt đồ thị tại

3

điểm phân biệt (phương trình

 

*

có

3

nghiệm đơn); tương giao của đồ thị hàm số

32

4 3 2y ax bx cx d   

với đường thẳng

3

ym

tại

2

điểm, tuy nhiên trong đó có một

nghiệm đơn và một nghiệm kép. Nói tóm lại trong cả

3

sự tương giao

được bàn ở trên, số nghiệm đơn của phương trình

 

*

hoặc là

1

hoặc

là

3

thì ta đã đủ điều kiện để suy ra điều cần chứng minh.

 

3

Xét một số hàm phân thức hữu tỉ.

 Hàm nhất biến (Bậc nhất trên bậc nhất):

,

ax b d

yx

cx d c



  



.

Ta có:

 

2

'

ad bc

y

cx d







.

Vì:

ad bc const

nên hàm số hoặc đồng biến hoặc nghịch biến trên

từng khoảng xác định. Do đó hàm số không có cực trị.

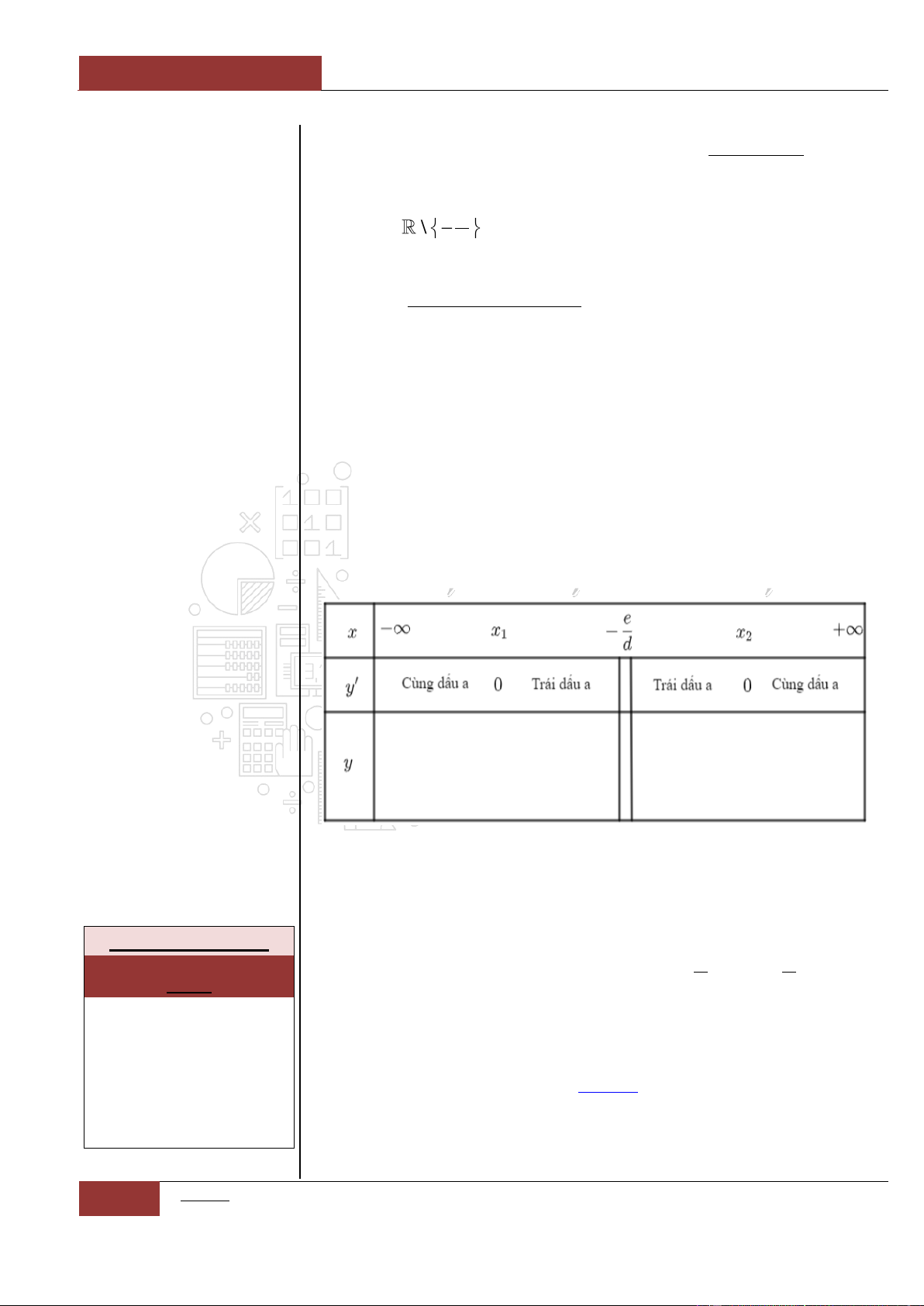
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

189

[ I can't, I can! ]

Extra Techniques:

Tips:

Đường thẳng đi qua hai

điểm cực trị có phương

trình là hàm phân thức

hữu tỉ của đạo hàm tử

trên đạo hàm mẫu.

Hàm phân thức bậc hai trên bậc nhất:

2

,0

ax bx c

ya

dx e







.

TXĐ:

\

e

D

d









.

Ta có:

 

2

'

adx aex be cd

y

dx e

  





.

Đặt

 

2

2P x adx aex be cd   

.

Ta có:

   

2

2 2 2

'

P

ae ad be cd a e acd abde      

.

 Với

2 2 2

'0

P

a e acd abde    

thì hàm số không có cực trị

 Với

2 2 2

'0

P

a e acd abde    

thì hàm số có hai điểm cực

trị

12

,xx

.

Tóm lại hàm số có cực trị khi và chỉ khi:

2 2 2

2

0

a e acd abde

a

ee

a b c

dd













   



    

   



   



.

 Đường thẳng đi qua hai điểm cực trị (nếu có) có phương trình:

2ax b

y

d





.

Thật vậy!

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

190

[ I can't, I can! ]

Ta giả sử hàm số

2

ax bx c

y

dx e







có hai điểm cực trị là

12

,xx

.

Ta có:

 

,

ux

y

vx



với

 

2

u x ax bx c

v x dx e



  











.

Khi đó:

       

 

       

2

' . . '

' 0 ' . . '

u x v x u x v x

y u x v x u x v x

vx



   

.

Dấu

""

đạt tại

1

2

xx











.

Suy ra:

 

1 1 1 1

1

1 1 1 1

''

2

''

u x u x u x u x

ax b

yx

v x v x v x v x d



    

.

Một cách tương tự, ta có:

 

2

2ax b

yx

d





.

Suy ra: đường thẳng

2ax b

y

d





đi qua hai điểm cực trị của đồ thị

hàm số

 

1 1 2 2

; , ;A x y x B x y x

.

Như vậy từ các dữ kiện trên ta đã có thể suy ra điều cần chứng minh.

“Trên đây là một số Tips chúng tôi cảm thấy rất hữu dụng trong

các bài toán hiện hành. Do mục đích phục vụ cho phần đông các

bạn học sinh nên phần trình bày khá chi tiết và khá dài. Nhưng nếu

bạn đọc hiểu được bản chất vấn đề, thao tác sẽ ngắn gọn hơn,

chuẩn xác hơn và quan trọng nhất vẫn là lợi thế về thời gian nếu

các bạn biết thêm một số Tips làm bài.”

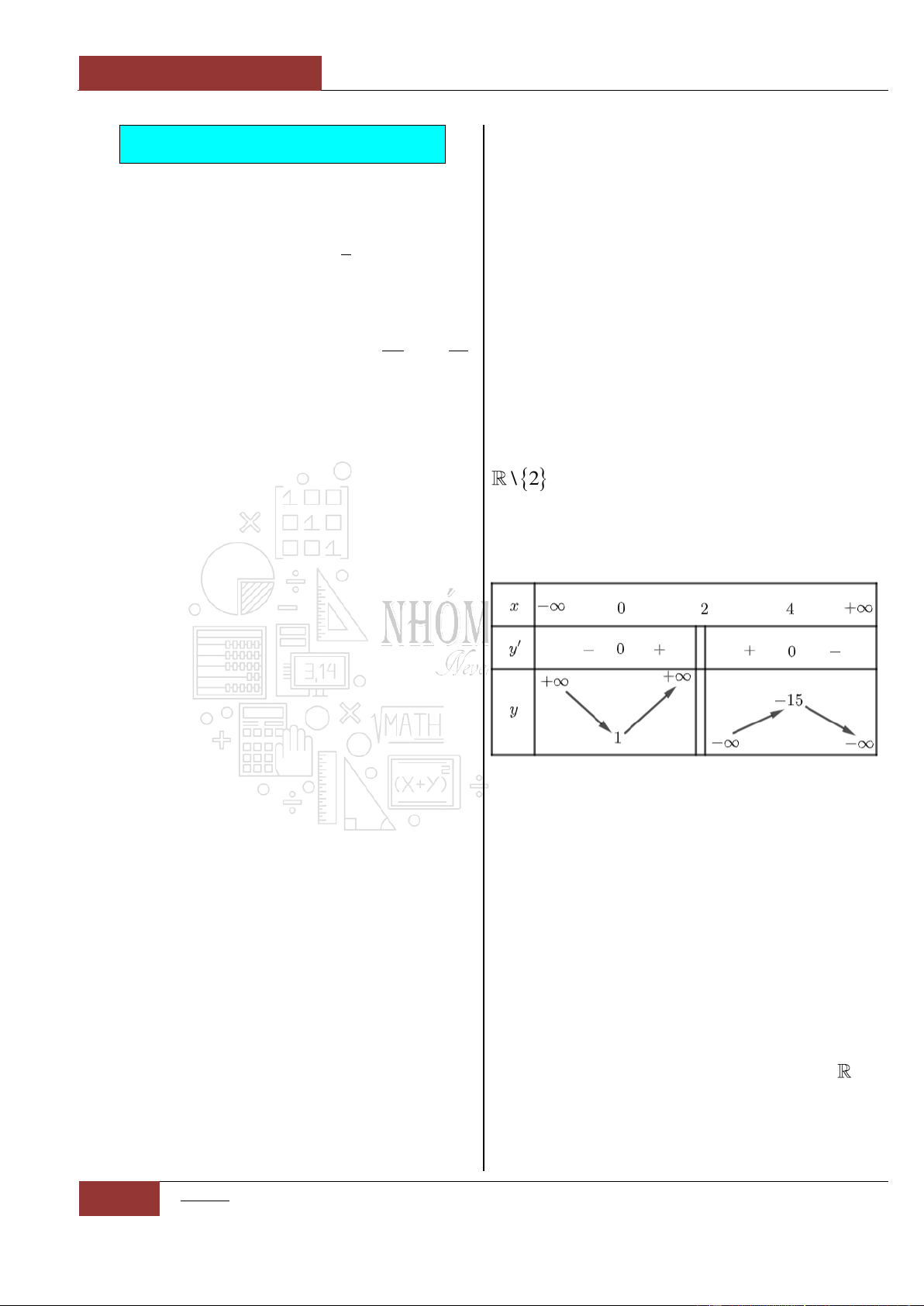
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

191

[ I can't, I can! ]

TỰ LUYỆN 4 MỨC ĐỘ

Câu 1. [Nhận biết].

Điểm cực trị của hàm số

 

32

1

31

3

f x x x x   

là các điểm nào dưới đây?

A.

1, 3xx  

. B.

22 10

,

33

xx  

.

C.

1, 5xx  

. D.

4, 3xx

.

Câu 2. [Nhận biết].

Điểm cực trị của hàm số

 

32

3 3 5f x x x x   

là?

A.

1, 3xx   

.

B.

1, 3xx  

.

C.

0, 1xx

.

D. Hàm số không có điểm cực trị.

Câu 3. [Nhận biết].

Cho hàm số

42

21y x x   

. Mệnh đề nào sau

đây là đúng?

A. Hàm số có một cực đại và hai cực tiểu

B. Hàm số có hai cực đại và một cực tiểu.

C. Hàm số có một cực đại và không có cực tiểu.

D. Hàm số có một cực đại và một cực tiểu.

Câu 4. [Nhận biết].

Cho hàm số

42

6 8 1y x x x    

. Nhận định

nào sau đây là đúng?

A. Hàm số đạt cực đại tại

2x 

và đạt cực

tiểu tại

1x 

.

B. Hàm số có giá trị cực đại là

25y 

và giá trị

cực tiểu là

2y 

.

C. Hàm số có duy nhất một điểm cực trị

2x 

là điểm cực đại.

D. Đồ thị hàm số đã cho có một điểm cực tiểu

là

 

2;25A 

.

Câu 5. [Nhận biết].

Cho hàm số

 

y f x

xác định, liên tục trên

 

\2

và có bảng biến thiên như hình vẽ bên

dưới.

Nhận định nào sau đây là đúng?

A. Hàm số đạt cực đại tại điểm

0x 

và đạt cực

tiểu tại điểm

4x 

.

B. Hàm số có đúng một điểm cực trị.

C. Hàm số có giá trị cực tiểu bằng

1

.

D. Hàm số có giá trị lớn nhất bằng

1

và có giá

trị nhỏ nhất bằng

15

.

Câu 6. [Nhận biết].

Cho hàm số

 

y f x

xác định, liên tục trên và

có bảng biến thiên như hình vẽ bên dưới.

Nhận định nào sau đây là đúng?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

192

[ I can't, I can! ]

A. Hàm số đã cho có hai điểm cực trị.

B. Hàm số đã cho không có giá trị cực đại.

C. Hàm số đã cho có đúng một điểm cực trị.

D. Hàm số đã cho không có giá trị cực tiểu.

Câu 7. [Nhận biết].

Hàm số

 

y f x

có đạo hàm liên tục trên thỏa

mãn

     

2

' 1 3f x x x  

.

Nhận định nào dưới đây là đúng?

A. Hàm số đã cho có một điểm cực đại.

B. Hàm số đã cho có hai điểm cực trị.

C. Hàm số đã cho có đúng một điểm cực trị.

D. Hàm số đã cho không có điểm cực trị.

Câu 8. [Nhận biết].

Hàm số nào dưới đây có ba điểm cực trị?

A.

42

2 10y x x  

.

B.

42

23y x x   

.

C.

32

1

3 5 2

3

y x x x   

.

D.

4

24yx

.

Câu 9. [Nhận biết].

Số điểm cực đại của đồ thị hàm số

4

100yx

là?

A.

0

. B.

1

.

C.

3

. D.

2

.

Câu 10. [Nhận biết].

Hàm số

42

2 2021y x x  

có bao nhiêu điểm

cực trị?

A.

1

. B.

2

.

C.

0

. D.

3

.

Câu 11. [Nhận biết].

Cho hàm số

32

1

4 8 5

3

y x x x   

có hai điểm

cực trị là

12

,xx

. Hỏi tổng

12

xx

là bao nhiêu?

A.

12

8xx

. B.

12

8xx  

.

C.

12

5xx

. D.

12

5xx  

.

Câu 12. [Nhận biết].

Hàm số

 

y f x

có đạo hàm liên tục trên ,

thỏa mãn:

     

2

' 1 3f x x x  

.

Nhận định nào sau đây là nhận định đúng?

A. Hàm số có một điểm cực đại.

B. Hàm số có hai điểm cực trị.

C. Hàm số có đúng một điểm cực trị.

D. Hàm số không có điểm cực trị.

Câu 13. [Nhận biết].

Đồ thị hàm số

32

31y x x  

có điểm cực đại

là điểm nào dưới đây?

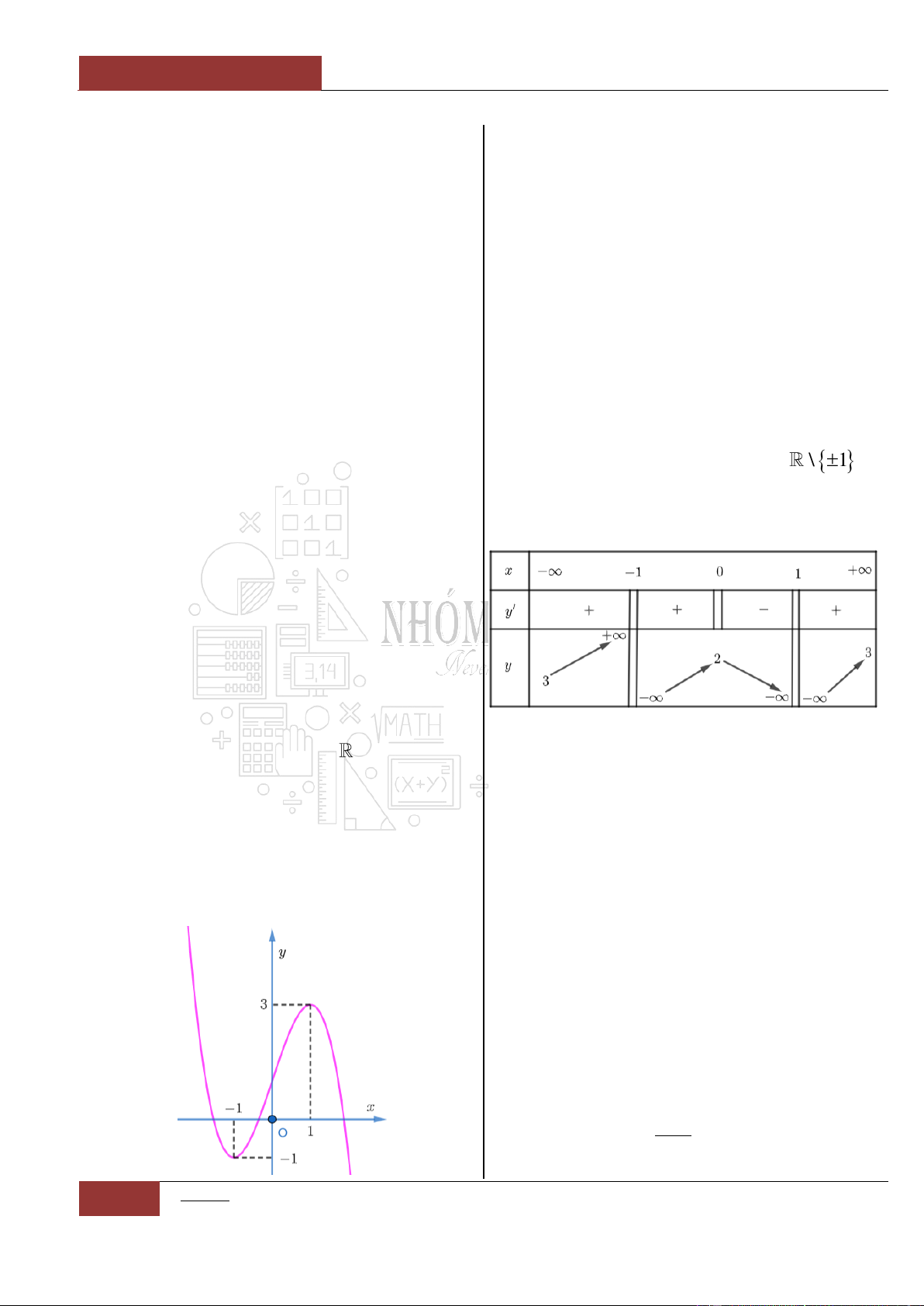
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

193

[ I can't, I can! ]

A.

 

2; 3I 

. B.

 

0;1I

.

C.

 

0;2I

. D. Đáp án khác.

Câu 14. [Nhận biết].

Hàm số

42

2 2021y x x  

có bao nhiêu điểm

cực trị?

A.

1

. B.

2

.

C.

0

. D.

3

.

Câu 15. [Nhận biết].

Cho hàm số

32

3 3 1y x x x   

. Khẳng định

nào sau đây là đúng?

A. Hàm số đạt cực tiểu tại điểm

1x 

.

B. Hàm số đồng biến trên khoảng

 

1; 

và nghịch biến trên khoảng

 

;1

.

C. Hàm số đạt cực đại tại điểm

1x 

.

D. Hàm số đồng biến trên .

Câu 16. [Nhận biết].

Cho hàm số

 

y f x

có đồ thị như hình vẽ

bên dưới. Khẳng định nào sau đây là khẳng

định đúng?

A. Hàm số đạt giá trị nhỏ nhất bằng

1

và đạt

giá trị lớn nhất bằng

3

.

B. Đồ thị hàm số có điểm cực tiểu

 

1; 1A 

và

điểm cực đại

 

1;3B

.

C. Hàm số có giá trị cực đại bằng

1

.

D. Hàm số đạt cực tiểu tại

 

1; 1A 

và cực đại

tại

 

1;3B

.

Câu 17. [Nhận biết].

Cho hàm số

 

y f x

xác định trên

 

\1

,

liên tục trên mỗi khoảng xác định và có bảng

biến thiên như hình vẽ bên dưới:

Khẳng định nào dưới đây là khẳng định sai?

A. Hàm số không có đạo hàm tại điểm

0x 

nhưng vẫn đạt cực trị tại điểm

0x 

.

B. Hàm số đạt cực tiểu tại điểm

1x 

.

C. Đồ thị hàm số có hai đường tiệm cận đứng là

các đường thẳng

1x 

và

1x 

.

D. Đồ thị hàm số có hai đường tiệm cận ngang

là các đường thẳng

3y 

và

3y 

.

Câu 18. [Nhận biết].

Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số

1

2

1

yx

x





có hai điểm cực trị.

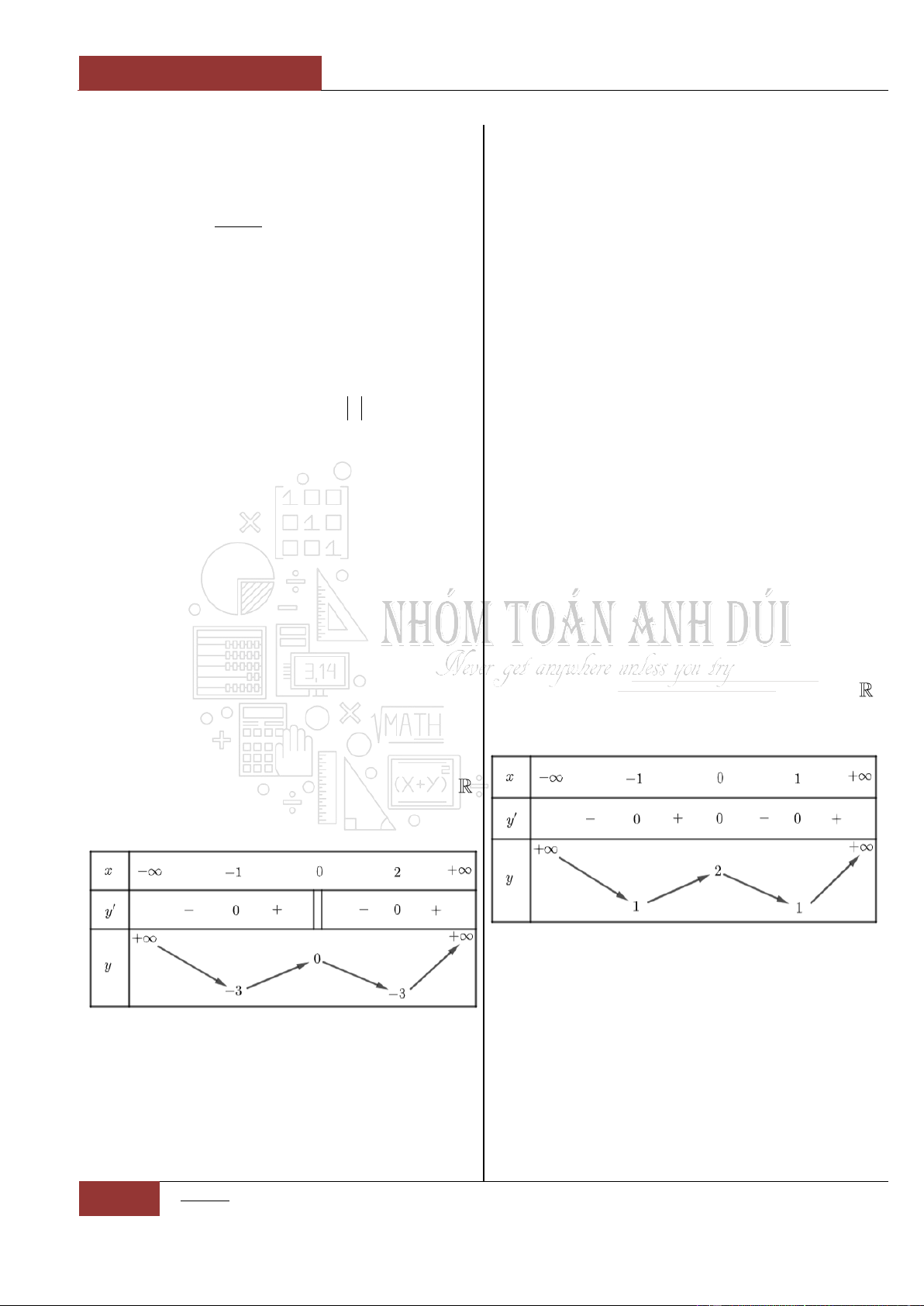
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

194

[ I can't, I can! ]

B. Hàm số

3

3 2021 2022y x x  

có hai điểm

cực trị.

C. Hàm số

21

1

x

y

x







có một điểm cực trị.

D. Hàm số

42

32y x x   

có một điểm cực

trị.

Câu 19. [Thông hiểu].

Số điểm cực trị của hàm số

3

2

43y x x  

bằng?

A.

2

. B.

0

.

C.

3

. D.

4

.

Câu 20. [Nhận biết].

Hàm số

42

1y x x  

đạt cực tiểu tại:

A.

1x 

. B.

0x 

.

C.

2x 

. D.

1x 

.

Câu 21. [Nhận biết].

Cho hàm số

 

y f x

xác định, liên tục trên

và có bảng biến thiên như hình vẽ dưới đây:

Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có đúng hai cực trị.

B. Hàm số có giá trị cực tiểu bằng

1

hoặc

1

.

C. Hàm số có giá trị lớn nhất bằng

0

và giá trị

nhỏ nhất bằng

3

.

D. Hàm số đạt cực đại tại

0x 

.

Câu 22. [Nhận biết].

Hàm số

32

31y x x  

đạt cực trị tại các điểm

nào sau đây?

A.

2x 

. B.

1x 

.

C.

0; 2xx

. D.

0; 1xx

.

Câu 23. [Thông hiểu].

Hệ thức liên hệ giữa giá trị cực đại

CĐ

y

và giá

trị cực tiểu

CT

y

của hàm số

3

2y x x

là?

A.

0

CT CĐ

yy

. B.

2 3

CT CĐ

yy

.

C.

2

CT CĐ

yy

. D.

CT CĐ

yy

.

Câu 24. [Nhận biết].

Cho hàm số

 

y f x

xác định, liên tục trên

và có bảng biến thiên như hình vẽ bên dưới:

Khẳng định nào sau đây là sai?

A.

 

0;2M

được gọi là điểm cực đại của hàm

số.

B.

 

1f 

được gọi là giá trị cực tiểu của hàm

số.

C. Hàm số đồng biến trên các khoảng

 

1;0

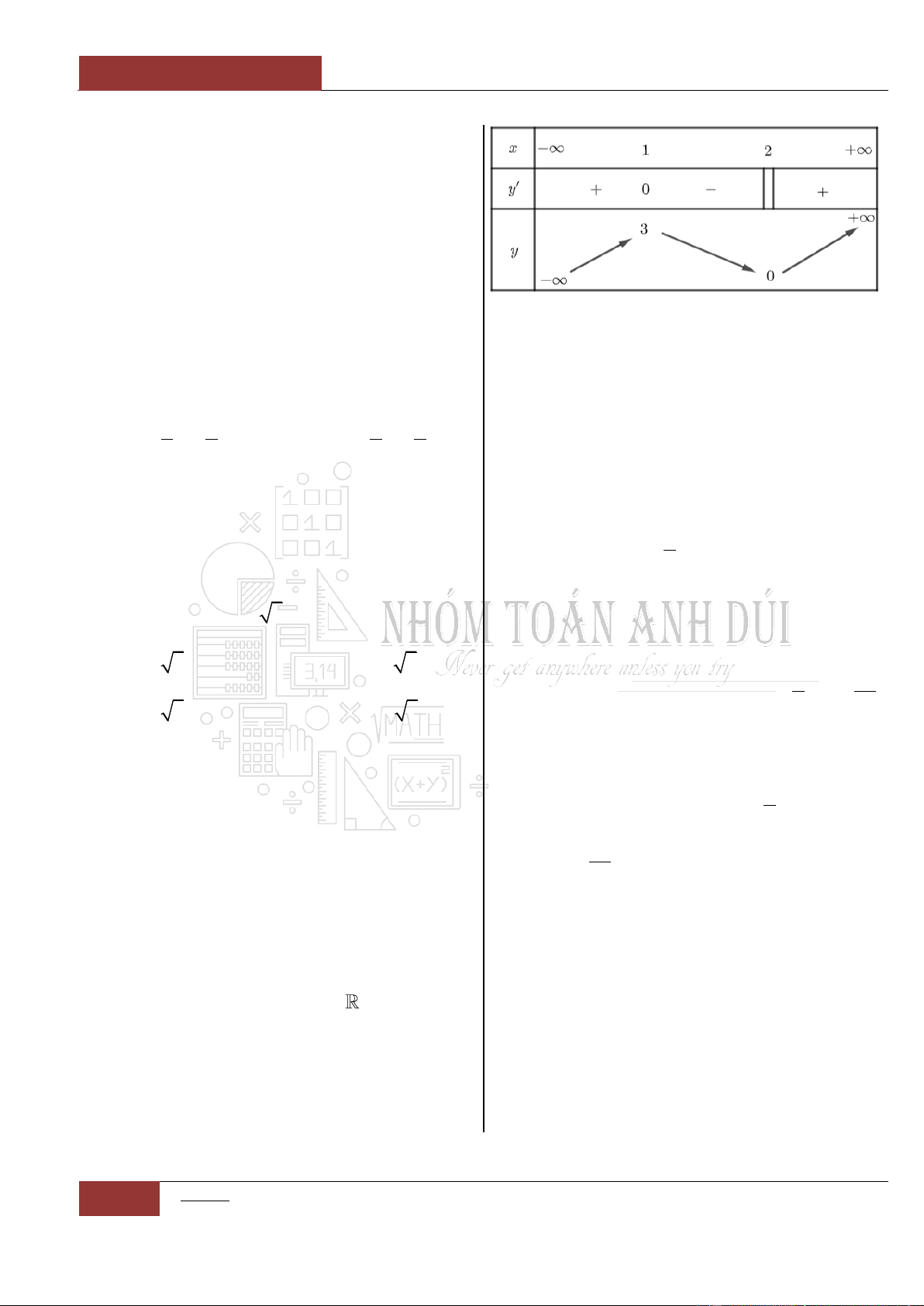
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

195

[ I can't, I can! ]

và

 

1; 

.

D.

0

1x 

được gọi là điểm cực tiểu của hàm số.

Câu 25. [Thông hiểu].

Cho hàm số

 

32

6 9 2y x x x C   

. Đường

thẳng đi qua điểm

 

1;1A 

và vuông góc với

đường thẳng đi qua hai điểm cực trị của

 

C

là?

A.

13

22

yx  

. B.

13

22

yx

.

C.

3yx

. D.

2 3 0xy  

.

Câu 26. [Thông hiểu].

Tính khoảng cách giữa hai điểm cực tiểu của đồ

thị hàm số

42

2 3 1y x x  

.

A.

4

23

. B.

3

.

C.

23

. D.

4

3

.

Câu 27. [Nhận biết].

Tìm tất cả các điểm cực đại của hàm số

42

21y x x   

.

A.

1x 

. B.

1x 

.

C.

1x 

. D.

0x 

.

Câu 28. [Nhận biết].

Hàm số

 

y f x

liên tục trên và có bảng

biến thiên như hình vẽ bên dưới.

Trong các mệnh đề được cho dưới đây, mệnh

đề nào đúng?

A. Hàm số đã cho có hai điểm cực trị.

B. Hàm số đã cho không có giá trị cực đại.

C. Hàm số đã cho có đúng một điểm cực trị.

D. Hàm số đã cho không có giá trị cực tiểu.

Câu 29. [Nhận biết].

Cho hàm số

4 3 2

2

3

y x x x  

. Mệnh đề nào

sau đây là đúng?

A. Hàm số có giá trị cực tiểu là

0

.

B. Hàm số có hai giá trị cực tiểu là

2

3



và

5

48



C. Hàm số chỉ có một giá trị cực tiểu.

D. Hàm số có giá trị cực tiểu là

2

3



và giá trị

cực đại là

5

48



.

Câu 30. [Thông hiểu].

Cho hàm số

  

2

12y x x  

. Trung điểm

của đoạn thẳng nối hai điểm cực trị của đồ thị

hàm số nằm trên đường thẳng nào sau đây?

A.

2 4 0xy  

. B.

2 4 0xy  

.

C.

2 4 0xy  

. D.

2 4 0xy  

.

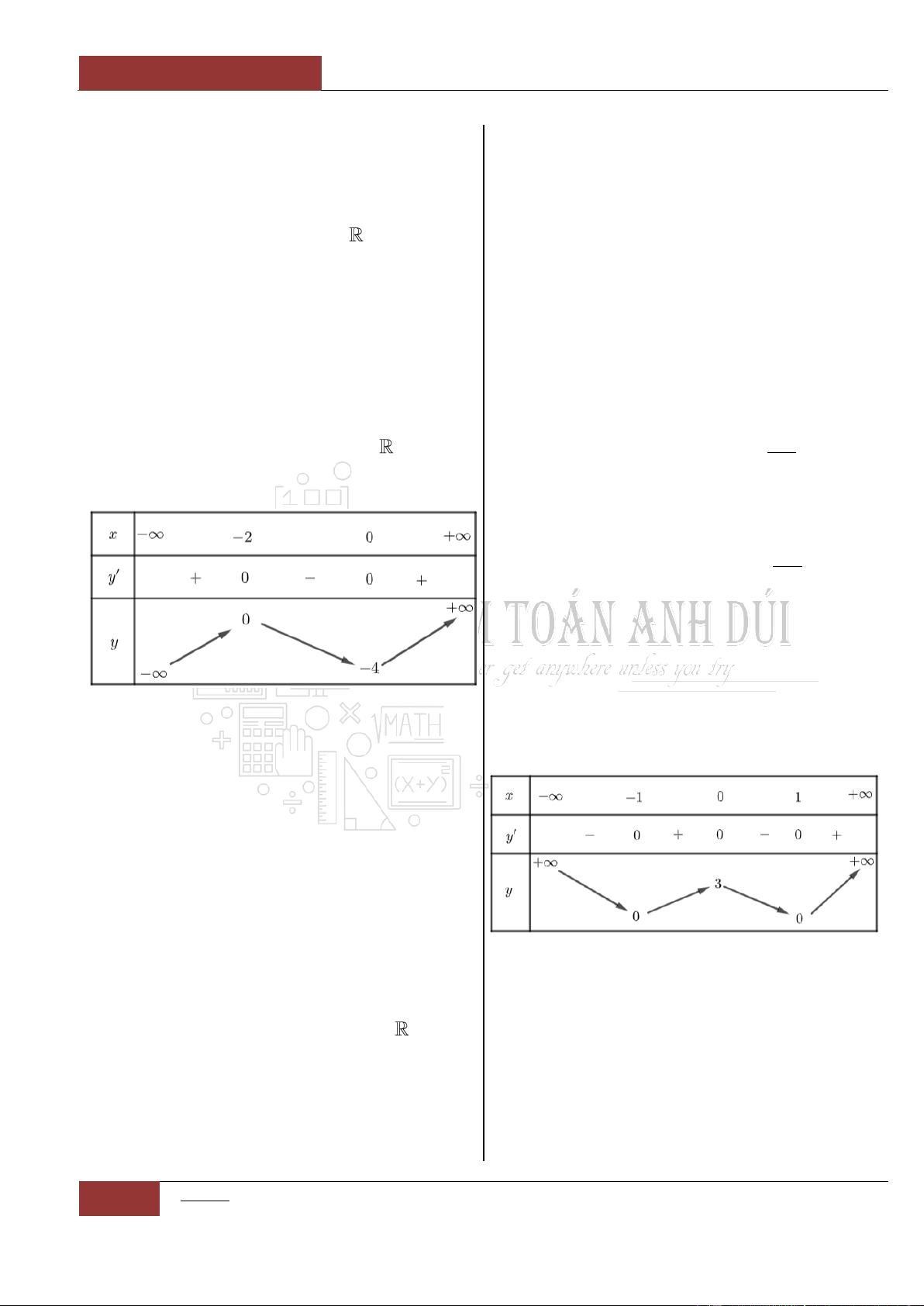
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

196

[ I can't, I can! ]

Câu 31. [Thông hiểu].

Cho hàm số

 

y f x

có đạo hàm thỏa mãn

     

23

' 1 2 ,f x x x x x    

. Số điểm cực

trị của hàm số

 

y f x

là?

A.

0

. B.

1

.

C.

2

. D.

3

.

Câu 32. [Nhận biết].

Cho hàm số

 

y f x

liên tục trên và có

bảng biến thiên như hình vẽ bên dưới:

Khẳng định nào sau đây là sai?

A. Hàm số đồng biến trên khoảng

 

0;

.

B. Hàm số đạt cực tiểu tại

0x 

.

C. Hàm số đạt cực tiểu tại

2x 

.

D. Hàm số nghịch biến trên khoảng

 

2;0

.

Câu 33. [Thông hiểu].

Cho hàm số

 

y f x

có đạo hàm thỏa mãn

     

2

' 1 2f x x x  

xác định trên . Mệnh

đề nào sau đây là mệnh đề đúng?

A. Hàm số

 

y f x

đồng biến trên khoảng

 

2; 

.

B. Hàm số

 

y f x

đạt cực đại tại

2x 

.

C. Hàm số

 

y f x

đạt cực tiểu tại

1x 

.

D. Hàm số

 

y f x

nghịch biến trên khoảng

 

2;1

.

Câu 34. [Thông hiểu].

Kết luận nào sau đây về cực trị của hàm số

.5

x

yx





là đúng?

A. Hàm số có điểm cực đại là

1

ln5

x 

.

B. Hàm số không có cực trị.

C. Hàm số có điểm cực tiểu là

1

ln5

x 

.

D. Hàm số có điểm cực đại là

ln5x 

.

Câu 35. [Thông hiểu].

Cho hàm số

 

y f x

có bảng biến thiên như

hình vẽ bên dưới:

Mệnh đề nào dưới đây là sai?

A. Hàm số có ba điểm cực trị.

B. Hàm số có giá trị cực đại bằng

3

.

C. Hàm số có giá trị cực đại bằng

0

.

D. Hàm số có

2

điểm cực tiểu.

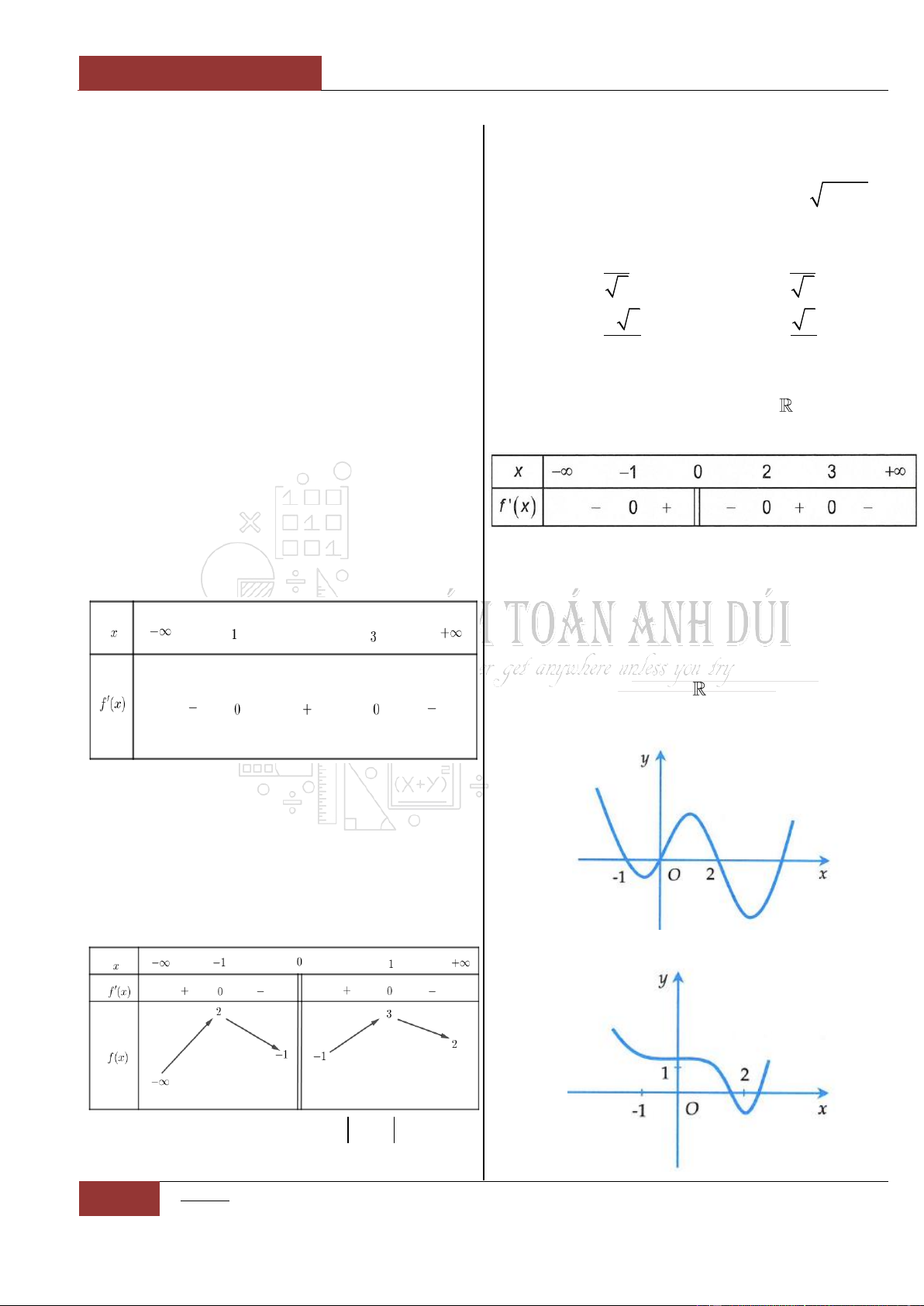
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

197

[ I can't, I can! ]

Câu 36. [Thông hiểu].

Đồ thị của hàm số

32

3 9 1y x x x   

có hai

điểm cực trị

A

và

B

. Điểm nào dưới đây thuộc

đường thẳng

AB

?

A.

 

1;0P

. B.

 

0; 1M 

.

C.

 

1; 10N 

. D.

 

1;10Q 

.

Câu 37. [Thông hiểu].

Số cực trị của hàm số

42

( ) 3 2f x x x  

là:

A.

1

. B.

2

.

C.

3

. D.

4

.

Câu 38. [Thông hiểu].

Cho hàm số

()y f x

là hàm đa thức có bậc

không vượt quá

3

có bảng xét dấu của hàm số

đạo hàm như hình vẽ sau:

Hàm số

2

()y f x mx

có tối đa bao nhiêu

điểm cực trị?

A. 2. B. 3.

C. 4 D. 5.

Câu 39. [Thông hiểu].

Cho hàm số

 

y f x

có bảng biến thiên sau:

Số điểm cực trị của hàm số

 

y f x

là?

A.

5

. B.

6

.

C.

7

. D.

8

.

Câu 40. [Thông hiểu].

Giá trị cực đại của hàm số

 

2

21f x x x  

là số nào dưới đây?

A.

3

y 

. B.

3

y





.

C.

3

y





. D.

3

y 

.

Câu 41. [Thông hiểu].

Cho hàm số

 

y f x

liên tục trên và có

bảng xét dấu đạo hàm như hình vẽ dưới đây:

Số điểm cực trị của hàm số

 

y f x

là?

A.

1

. B.

2

.

C.

3

. D.

4

.

Câu 42. [Thông hiểu].

Một trong các đồ thị dưới đây là đồ thị của hàm

số

()y f x

liên tục trên thỏa mãn

(0) 0f





và

( ) 0, ( 1;2)f x x



   

. Hỏi đó là đồ thị nào?

A. .

B. .

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

198

[ I can't, I can! ]

C. .

D. .

Câu 43. [Thông hiểu].

Cho hàm số

 

y f x

có đồ thị như hình vẽ. Số

cực trị của hàm số

 

y f x

là?

A.

7

. B.

6

.

C.

3

. D.

4

.

Câu 44. [Thông hiểu].

Cho đa thức

 

fx

hệ số thực và thỏa mãn điền

kiện

   

2

2 1 1,f x f x x x     

. Biết hàm

số

 

2

6 . 11 78 78y x f x x x   

đạt cực trị tại

hai điểm

 

1 2 1 2

,,x x x x

. Tích

12

.xx

bằng?

A.

12

. B.

1

2



.

C.

24

. D.

8

3

.

Câu 45. [Thông hiểu].

Cho hàm số

32

()f x ax bx cx d   

có đồ thị

như hình vẽ bên dưới. Số điểm cực trị của

hàm số

2

( 2 4 )y f x x  

là?

A.

3

. B.

4

.

C.

2

. D.

5

.

Câu 46. [Thông hiểu].

Cho hàm số

3

4 2 3

( 27) 1

3

x

y m x m x    

. Tìm

các giá trị của tham số

m

để hàm số có hai cực

trị nằm về hai phía của trục tung.

A.

3m 

. B.

3m 

.

C.

3m 

. D.

3m 

.

Câu 47. [Thông hiểu].

Cho hàm số

32

y ax bx cx d   

với

0a 

có

hai hoành độ cực trị là

1x 

và

3x 

. Tập hợp

tất cả các giá trị của tham số

m

để phương trình

   

f x f m

có đúng ba nghiệm phân biệt là:

A.

   

 

1 ; 3ff

. B.

 

0;4

.

C.

 

1;3

. D.

   

0;4 \ 1;3

.

Câu 48. [Thông hiểu].

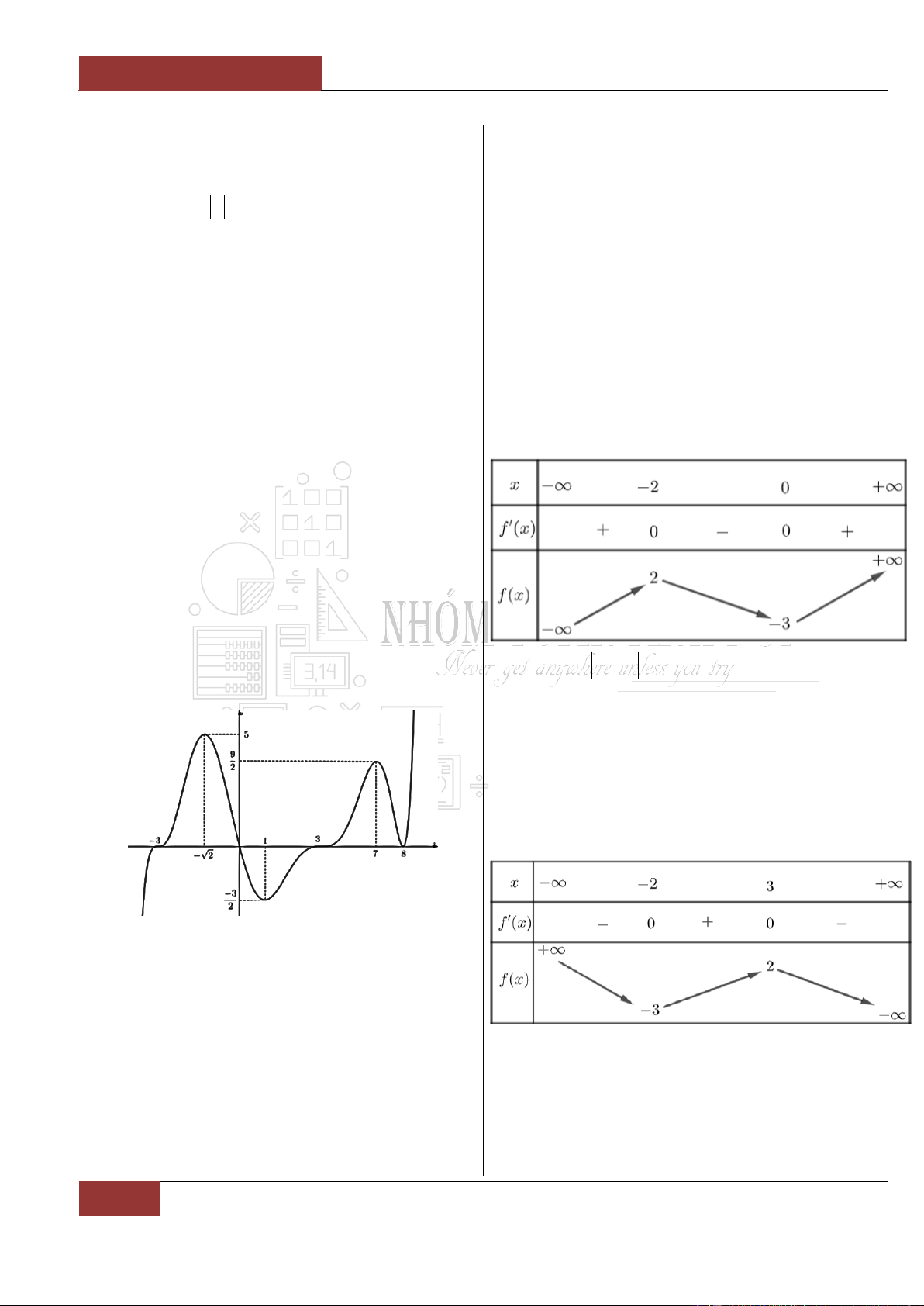
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

199

[ I can't, I can! ]

Cho hàm số

   

32

1 5 3 3y m x x m x     

.

Có tất cả bao nhiêu giá trị nguyên của

m

để

hàm số

 

y f x

có đúng

3

điểm cực trị?

A.

5

. B.

3

.

C.

4

. D.

0

.

Câu 49. [Thông hiểu].

Nếu hàm số đa thức

 

y f x

có

2

điểm cực

trị thì hàm số

 

12y f x

có bao nhiêu điểm

cực trị?

A.

1

. B.

2

.

C.

3

. D.

4

.

Câu 50. [Nhận biết].

Cho hàm số

42

4 6 4 2021y x x x   

. Số điểm

cực đại của hàm số là:

A.

0.

B.

1.

C.

2.

D.

3.

Câu 51. [Thông hiểu].

Cho đồ thị

 

y f x

xác định và có đồ thị của

hàm số

 

fx



như hình vẽ:

Số điểm cực trị của hàm số

 

y f x

là:

A.

3

. B.

4

.

C.

1

. D.

2

.

Câu 52. [Thông hiểu].

Cho đồ thị hàm số

 

32

: 3 5 2C y x x x    

.

Trong các mệnh đề sau, mệnh đề nào không sai

khi nói về

 

C

?

A.

 

C

không có điểm cực trị.

B.

 

C

có hai điểm cực trị.

C.

 

C

có ba điểm cực trị.

D.

 

C

có một điểm cực trị.

Câu 53. [Thông hiểu].

Tìm tất cả các giá trị thực của tham số

m

để

hàm số

42

y x mx

đạt cực tiểu tại

0x 

?

A.

0m 

. B.

0m 

.

C.

0m 

. D.

0m 

.

Câu 54. [Thông hiểu].

Cho hàm số

 

y f x

có bảng biến thiên như

hình vẽ dưới đây:

Hàm số

 

y f x

có bao nhiêu cực tiểu?

A.

1

. B.

2

.

C.

3

. D.

4

.

Câu 55. [Nhận biết].

Cho hàm số

 

y f x

có bảng biến thiên như

hình vẽ sau:

Cực tiểu của hàm số đã cho là?

A.

3x 

. B.

3y 

.

C.

3x 

. D.

2y 

Câu 56. [Nhận biết].

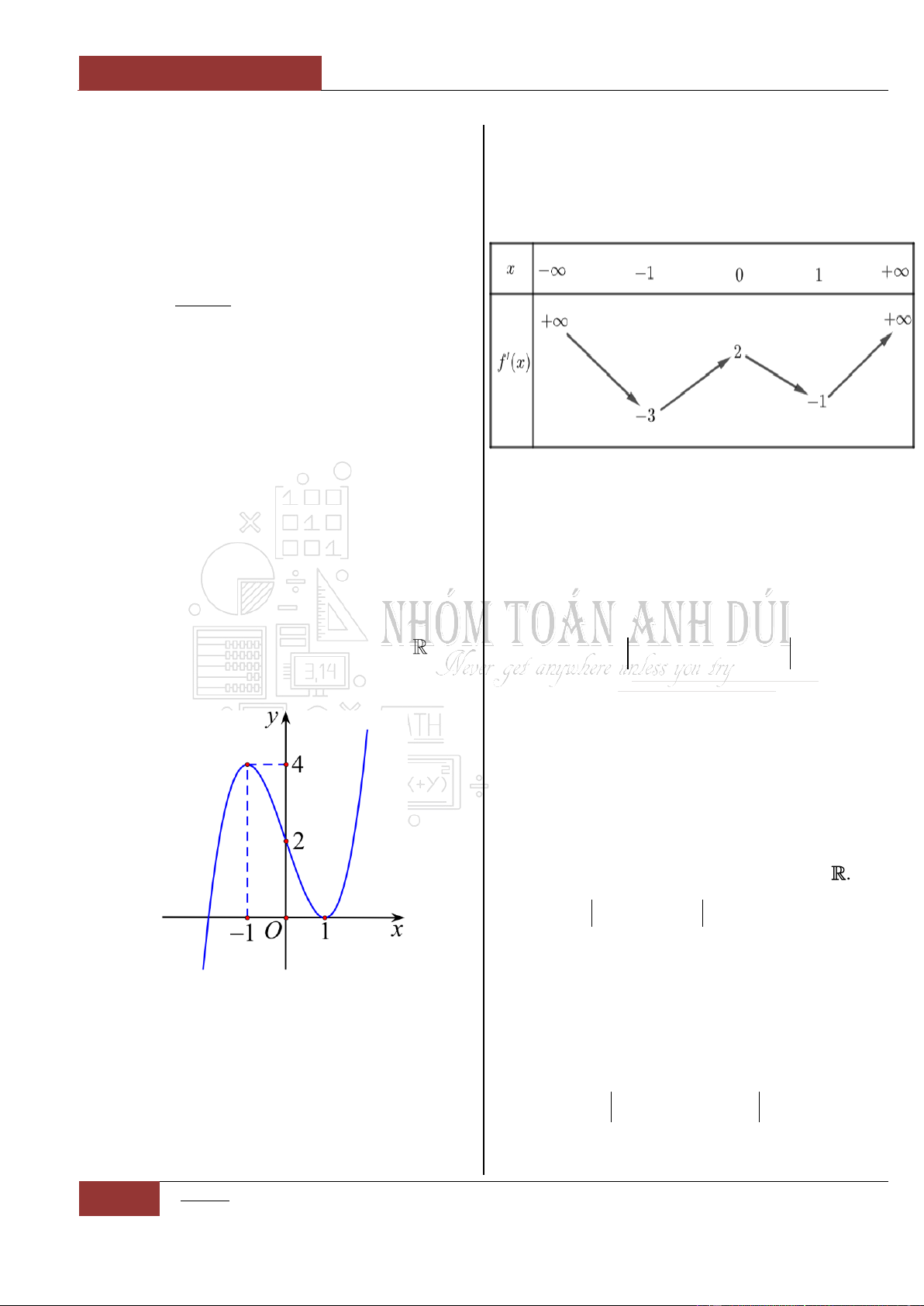
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

200

[ I can't, I can! ]

Trong các hàm số dưới đây, hàm số nào có

đúng

2

cực trị?

A.

42

32y x x  

.

B.

32

57y x x  

.

C.

2

21

3

x

y

x





.

D.

64

2017 2016y x x

.

Câu 57. [Nhận biết].

Cho hàm số

42

53y x x  

đạt cực trị tại

1 2 3

,,x x x

. Khi đó, giá trị của tích

1 2 3

..x x x

là?

A.

1

. B.

3

.

C.

5

. D.

0

.

Câu 58. [Thông hiểu].

Cho hàm số

 

y f x

có đạo hàm trên và

có đồ thị đường cong trong hình vẽ bên dưới.

Đặt

   

 

g x f f x

. Số điểm cực trị của hàm

số

 

y g x

là?

A.

5

. B.

6

.

C.

7

. D.

8

.

Câu 59. [Vận dụng].

Cho hàm số

 

fx

, biết bảng biến thiên của hàm

số

 

fx



như hình vẽ dưới đây.

Số điểm cực trị của hàm số

 

2

2y f x x

là?

A.

3

. B.

9

.

C.

5

. D.

7

.

Câu 60. [Vận dụng].

Cho hàm số

42

2 2 1y x mx m   

. Có bao

nhiêu giá trị nguyên của tham số

 

2;2m

để

hàm số có đúng

3

điểm cực trị là:

A.

1

. B.

2

.

C.

3

. D.

4

.

Câu 61. [Vận dụng cao].

Cho hàm số

 

y f x

có đạo hàm thỏa mãn:

 

  

3 2 3

2 2 ,f x x x x x



  

với mọi

.x

Hàm số

 

1 2018y f x

có nhiều nhất bao

nhiêu điểm cực trị?

A.

9

. B.

2018

.

C.

2021

. D.

2022

.

Câu 62. [Vận dụng cao].

Cho hàm số

()y f x

có đồ thị như hình vẽ bên

dưới. Có bao nhiêu giá trị thực của tham số

m

để hàm số

   

2

y f x f x m  

có đúng

3

điểm cực trị?

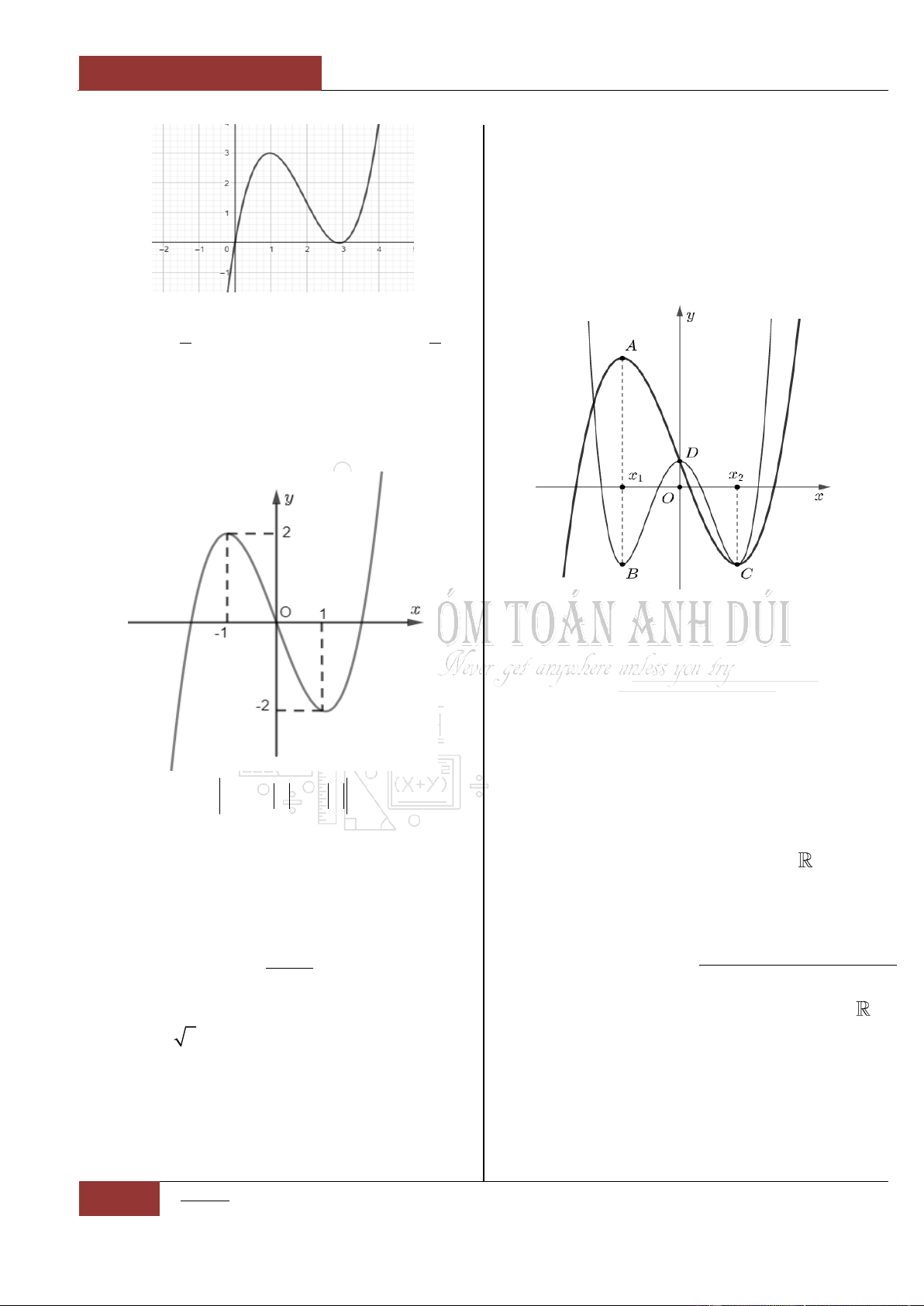
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

201

[ I can't, I can! ]

A.

1

4

m 

. B.

1

4

m 

.

C.

1m 

. D.

1m 

.

Câu 63. [Vận dụng].

Cho hàm số đa thức bậc ba có đồ thị như hình

vẽ bên dưới:

Hàm số

 

()g x f f x x

có bao nhiêu

điểm cực trị?

A.

15

. B.

17

.

C.

18

. D.

19

.

Câu 64. [Vận dụng].

Cho hàm số

32

21

2 2022

2

m

y x x x





   





. Biết

rằng tồn tại hai giá trị tham số

12

mm

;

12

m m a b c  

thỏa mãn hàm số đạt cực trị

tại hai điểm

12

,xx

sao cho

12

2 3 3x x m  

. Giá

trị của

 

12A a b c  

bằng bao nhiêu biết

,,abc

là các phân số tối giản.

A.

896

. B.

825

.

C.

887

. D.

927

.

Câu 65. [Vận dụng cao].

Cho hàm số

   

42

1

32

2

:2

:

C y f x x ax b

C y g x x cx dx e



   





    





có

đồ thị như hình vẽ bên dưới.

Gọi

, BC

là hai điểm cực tiểu của

 

1

C

;

, AC

lần lượt là điểm cực đại và điểm cực tiểu của

 

2

C

(

, AC

đối xứng nhau qua

D Oy

). Biết

hoành độ của

, AB

bằng nhau. Có bao nhiêu

giá trị nguyên của

a

để

2022AB 

.

A.

113

. B.

116

.

C.

118

. D.

114

.

Câu 66. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục trên có đạo

hàm cấp

3

với

 

0fx





và thỏa mãn:

   

 

2 2023

2022

2 1 2022

'1

x x x

f x f x

fx







   

   



, x

.

Hàm số

     

2023

1g x f x f x

 



   

   

có bao

nhiêu điểm cực trị?

A.

1

. B.

2

.

C.

3

. D.

4

.

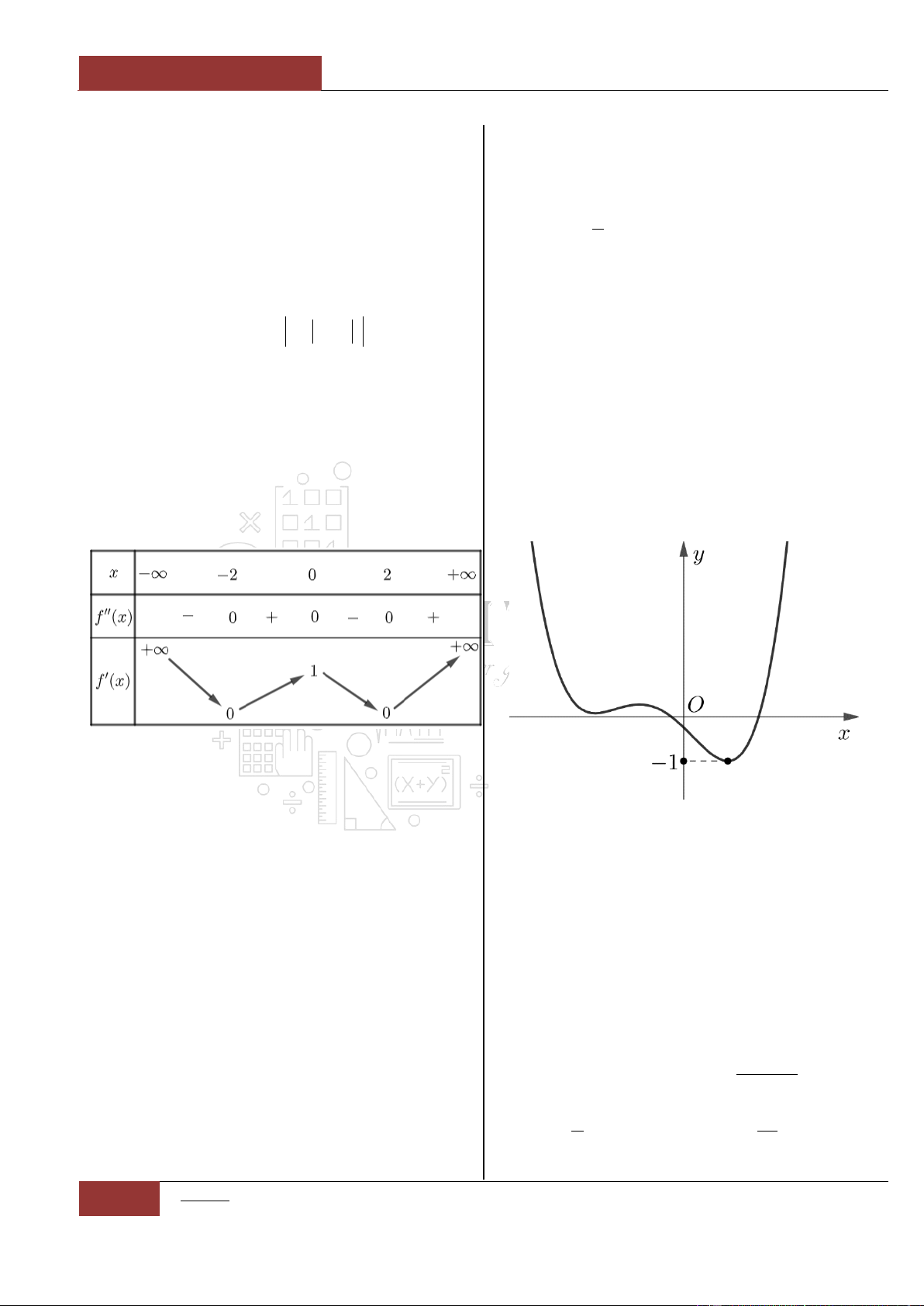
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

202

[ I can't, I can! ]

Câu 67. [Vận dụng].

Cho Parabol

   

2

,0y f x ax bx c a    

cắt trục hoành tại hai điểm có hoành độ bằng

1

và bằng

2

, biết rằng hàm số

 

y f x

nghịch

biến trên khoảng

 

0

;x 

và khoảng cách từ

giao điểm của Parabol với trục tung đến điểm

O

bằng

4

. Hàm số

 

1y f x

có tất cả bao

nhiêu điểm cực trị?

A.

2

. B.

3

.

C.

5

. D.

7

.

Câu 68. [Thông hiểu].

Cho hàm số

 

y f x

có bảng biến thiên hàm

số đạo hàm như hình vẽ sau:

Số điểm cực trị của hàm số đã cho là?

A.

3

. B.

2

.

C.

0

. D.

1

.

Câu 69. [Thông hiểu].

Hàm số

 

32

y f x ax bx cx d    

đạt cực

đại tại

1x 

,

 

12f 

; đạt cực tiểu tại

2x 

,

 

21f   

. Khi đó, giá trị của biểu thức

22A a b c d   

là?

A.

1

. B.

2

.

C.

3

. D.

4

.

Câu 70. [Vận dụng].

Có bao nhiêu giá trị nguyên của tham số

 

10;10m

để hàm số:

 

2

32

3

4 1 1

2

y x mx m x    

có hai điểm cực trị

12

,xx

thỏa mãn bất phương

trình:

1 2 1 2

x x x x

là?

A.

12

. B.

18

.

C.

16

. D.

15

.

Câu 71. [Vận dụng cao].

Cho hàm số

 

y f x

có đồ thị như hình vẽ

sau:

Số điểm cực trị của hàm số

   

34

f x f x

y 

là?

A.

3

. B.

4

.

C.

5

. D.

6

.

Câu 72. [Vận dụng cao].

Biết đồ thị hàm số

42

2 4 1y x mx  

có 3

điểm cực trị

A

(thuộc trục tung) và

,.BC

Giá

trị nhỏ nhất của biểu thức

4

.AB AC

T

BC



là:

A.

1

4

. B.

1

16

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

203

[ I can't, I can! ]

C.

3

4

. D.

3

16

.

Câu 73. [Vận dụng].

Cho hàm số

 

fx

có đạo hàm liên tục trên .

Đồ thị hàm số

 

y f x





như hình vẽ bên. Hàm

số

 

22

44y f x x x x   

có bao nhiêu điểm

cực trị thuộc khoảng

 

5;1

?

A.

5

. B.

4

.

C.

6

. D.

3

.

Câu 74. [Vận dụng].

Biết rằng hàm số

 

fx

có đồ thị được cho như

hình vẽ bên. Tìm số điểm cực trị của hàm số

 

y f f x





.

A.

5

. B.

3

.

C.

4

. D.

6

.

Câu 75. [Vận dụng cao].

Cho hàm số

 

y f x

có đồ thị như hình vẽ.

Biết tất cả các điểm cực trị của hàm số

 

y f x

là

2

;

0

;

2

;

a

;

6

với

46a

. Số điểm cực trị

của hàm số

 

62

3y f x x

là?

A.

8

. B.

11

.

C.

9

. D.

7

.

Câu 76. [Vận dụng cao].

Cho hàm số

( 1)y f x





có đồ thị như hình vẽ.

Hàm số

 

24f x x

y







đạt cực tiểu tại điểm nào?

A.

1x 

. B.

0x 

.

C.

2x 

. D.

1x 

.

Câu 77. [Vận dụng cao].

Cho hàm số đa thức

 

y f x

có đạo hàm trên ,

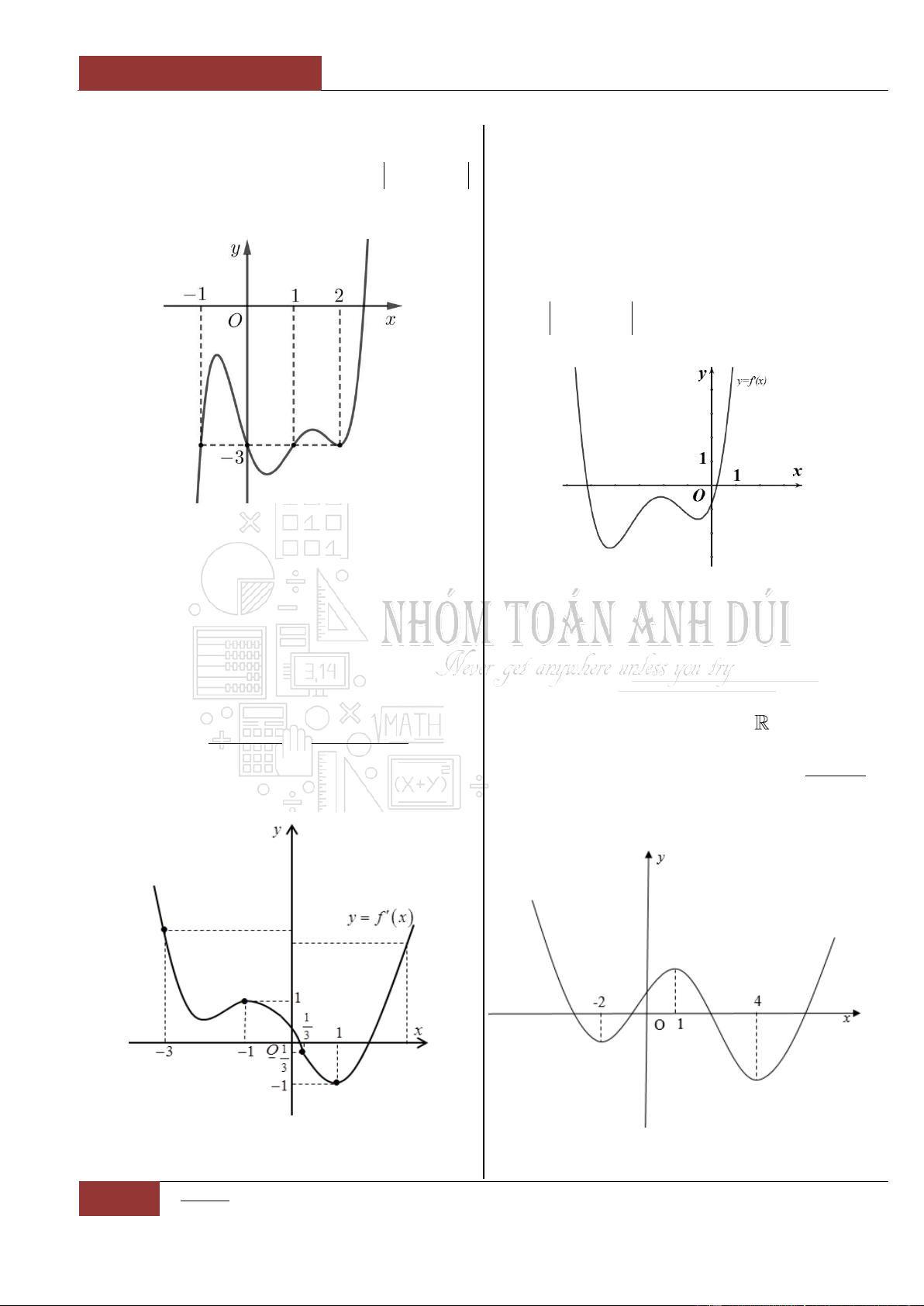
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

204

[ I can't, I can! ]

 

00f 

và đồ thị hình bên dưới là đồ thị đạo

hàm

 

y f x





. Hỏi hàm số

   

3g x f x x

có bao nhiêu cực trị?

A.

4

. B.

5

.

C.

3

. D.

6

.

Câu 78. [Vận dụng cao].

Cho hàm số

 

y f x

, biết hàm số đạo hàm

 

y f x





có đồ thị như hình vẽ bên dưới. Hàm

số

2

5sin 1 (5sin 1)

( ) 2 3

24

xx

g x f





  





có

bao nhiêu điểm cực trị trên khoảng

 

0;2



?

A.

9

. B.

7

.

C.

6

. D.

8

.

Câu 79. [Vận dụng cao].

Cho hàm số

 

fx

có

 

00f 

. Biết

 

y f x





là hàm số bậc bốn và có đồ thị là đường cong

như hình bên dưới. Số điểm cực trị của hàm số

 

3

()g x f x x

là?

A.

5

. B.

4

.

C.

6

. D.

3

.

Câu 80. [Vận dụng cao].

Cho hàm số

 

fx

liên tục trên và có đồ thị

như hình vẽ. Hàm số

 

2

x

xx

g x f e











có bao nhiêu điểm cực trị?

A.

3

. B.

7

.

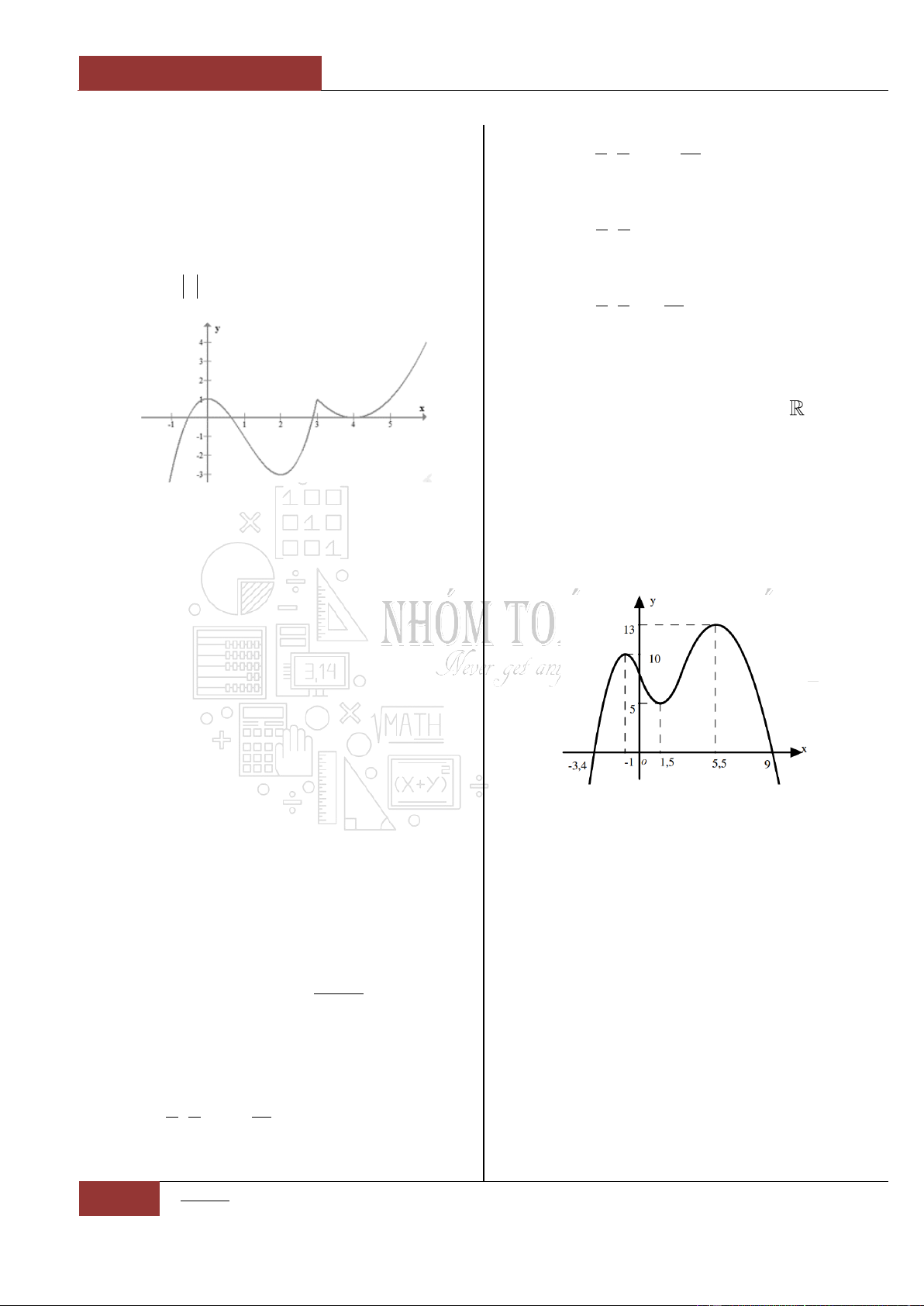
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

205

[ I can't, I can! ]

C.

6

. D.

4

.

Câu 81. [Vận dụng cao].

Cho hàm số

 

y f x

đồng biến trên

 

4;

có đồ thị như hình vẽ. Số điểm cực trị của hàm

số

 

22y f x

bằng?

A.

7

. B.

5

.

C.

4

. D.

9

.

Câu 82. [Vận dụng cao].

Cho hàm số

 

fx

có đạo hàm thỏa mãn:

       

43

22

2 4 2 3 6 18f x x x x x m x m





      



Có tất cả bao nhiêu giá trị nguyên của

m

để

hàm số

 

fx

có đúng một điểm cực trị?

A.

7

. B.

5

.

C.

8

. D.

6

.

Câu 83. [Vận dụng cao].

Cho hàm số

 

fx

có đạo hàm thỏa mãn

    

3

2

13 15f x x x a x



  

. Tập hợp các giá

trị của

a

để hàm số

2

5

4

x

yf

x











có

6

điểm

cực trị là?

A.

5 5 15

; \ 0;

4 4 13

   







   

.

B.

5 5 15

; \ 0;

4 4 13

   







   

.

C.

 

55

; \ 0

44









.

D.

5 5 15

;\

4 4 13

   







   

.

Câu 84. [Vận dụng cao].

Cho hàm số

 

y f x

xác định trên và hàm

số

 

'y f x

có đồ thị như hình bên dưới. Biết

rằng

 

'0fx

   

, ; 3,4 9;x     

. Có

bao nhiêu giá trị nguyên dương của tham số

m

để hàm số

   

5g x f x mx  

có đúng hai

điểm cực trị?

A.

7.

B.

8.

C.

6.

D.

5.

Câu 85. [Vận dụng cao].

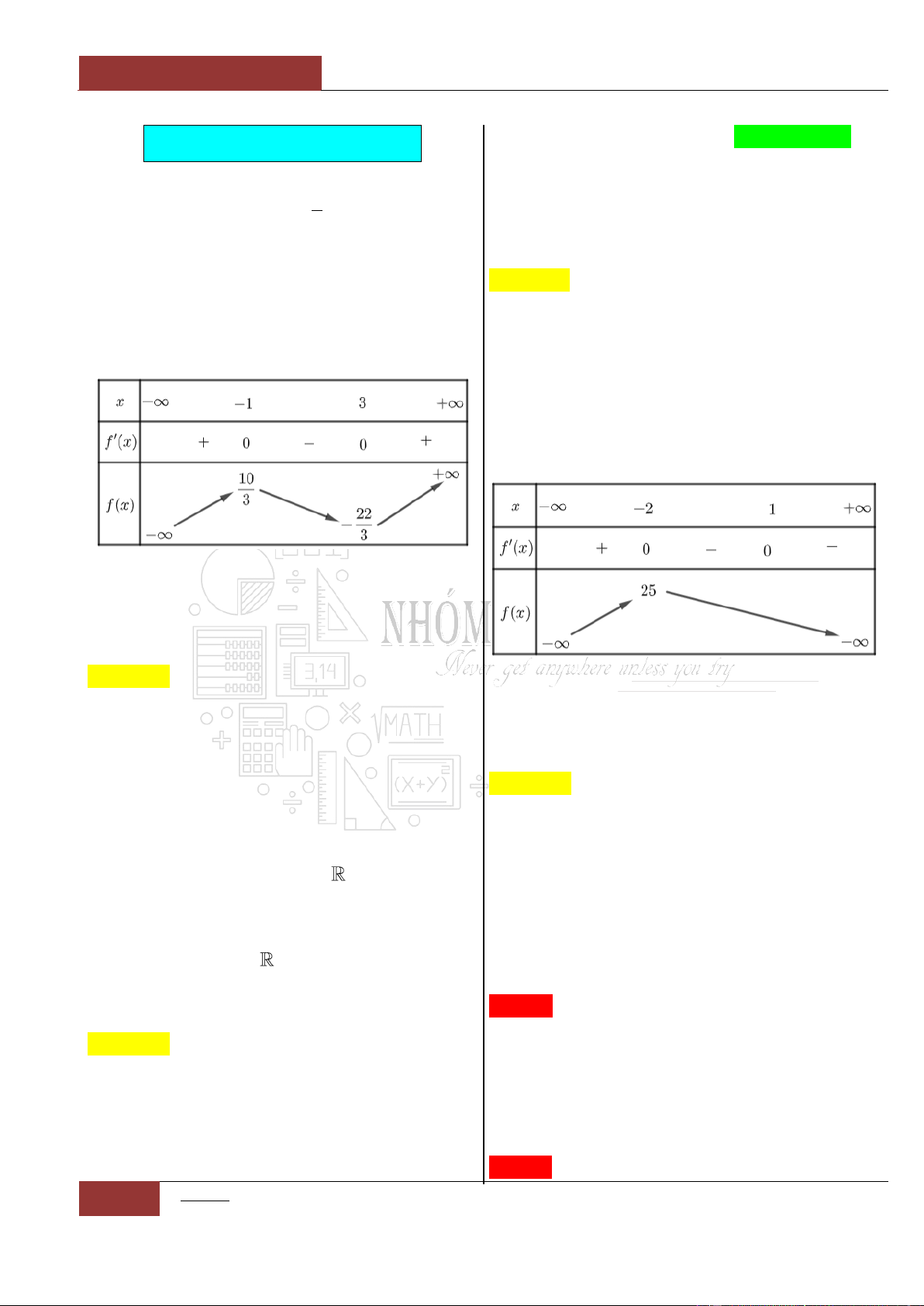
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

213

[ I can't, I can! ]

LỜI GIẢI CHI TIẾT

Câu 1. Xét hàm số

 

32

1

31

3

f x x x x   

.

Ta có:

 

2

1

' 2 3 0

3

x

f x x x

x





    







.

Bảng biến thiên:

Dựa vào bảng biến thiên của đồ thị hàm số, ta

nhận thấy hàm số đạt cực trị tại điểm

1x 

và

3x 

.

Đáp án A

Câu 2. Xét hàm số:

 

32

3 3 5f x x x x   

.

Ta có:

 

32

3 3 1 4f x x x x    

.

   

3

2

14

' 3 1 0,

f x x

f x x x

   

     

Nên hàm số

 

32

3 3 5f x x x x   

đồng biến

trên toàn tập số thực .

Vậy hàm số không có điểm cực trị.

Đáp án D

Câu 3. Xét hàm số:

42

21y x x   

.

Dễ thấy hàm số có hệ số

10a   

và tích hệ

số

 

1 .2 2 0ab     

. Nên theo phần Tips

đã trình bày ở trên (xem thêm Đồ thị I.II.13.).

Đồ thị hàm số

42

21y x x   

có dạng hình

chữ

""

và có hai điểm cực đại và một điểm

cực tiểu.

Đáp án B

Câu 4. Xét hàm số

42

6 8 1y x x x    

.

Ta có:

3

2

' 4 12 8 0

1

x

y x x

x





     







.

Bảng biến thiên:

Dựa vào bảng biến thiên, ta nhận thấy điểm

2x 

là điểm cực đại của hàm số và hàm số

chỉ có duy nhất một điểm cực trị.

Đáp án C

Câu 5. Xét từng nhận định:

+) Đáp án A:

Dựa vào bảng biến thiên của đồ thị hàm số, ta

thấy rằng hàm số đạt cực tiểu tại điểm

0x 

và

đạt cực đại tại điểm

4x 

.

Loại A.

+) Đáp án B:

Hàm số

 

y f x

có hai điểm cực trị là điểm

0x 

và điểm

4x 

.

Loại B.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

214

[ I can't, I can! ]

+) Đáp án C:

Hàm số

 

y f x

có giá trị cực tiểu là

1y 

và

giá trị cực đại là

15y 

.

Chọn C.

+) Đáp án D:

Hàm số

 

y f x

không tồn tại giá trị lớn nhất

và giá trị nhỏ nhất trân tập xác định.

Loại D.

Đáp án C

Extra Techniques:

Remark:

Giá trị cực đại không nhất thiết

phải lớn hơn giá trị cực tiểu, bài

tập trên là một ví dụ minh họa cụ

thể.

Extra Techniques:

Tips:

Bài toán cho bảng biến thiên có

các giá trị ở dạng các đại lượng



ta cần phải lưu ý về giá trị lớn

nhất, giá trị nhỏ nhất.

Nếu bài toán có giá trị là



,

thông thường, hàm số sẽ không có

giá trị lớn nhất.

Tương tự, nếu bài toán có giá trị

là



, thông thường, hàm số sẽ

không có giá trị nhỏ nhất.

Giá trị cực trị khác GTLN, GTNN

Câu 6. Ta xét các nhận định:

+) Đáp án A:

Mặc dù hàm số

 

y f x

có đạo hàm

 

'fx

không liên tục tại điểm

2x 

, tuy nhiên, tại

điểm

2x 

, hàm số

 

y f x

vẫn liên tục nên

hàm số vẫn có cực trị tại điểm

2x 

, nếu qua

đó, đạo hàm hàm số đổi dấu.

Thật vậy! Hàm số

 

y f x

đạt cực đại tại

điểm

1x 

và đạt cực tiểu tại điểm

2x 

.

Vậy hàm số đã cho có hai điểm cực trị.

Chọn A.

+) Đáp án B:

Giá trị cực đại của đồ thị hàm số là:

3y 

.

Loại B.

+) Đáp án C:

Kết hợp với cách giải thích ở đáp án A, ta hoàn

toàn kết luận được hàm số

 

y f x

có đúng

hai điểm cực trị là

1x 

và

2x 

.

Loại C.

+) Đáp án D:

Hàm số

 

y f x

có giá trị cực tiểu là

0y 

.

Loại D.

Đáp án A

Extra Techniques:

Remark:

Hàm số

yx

không có đạo hàm tại

0x 

, nhưng đạt cực tiểu tại

0x 

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

215

[ I can't, I can! ]

Câu 7. Xét hàm:

     

2

' 1 3f x x x  

.

Ta có:

 

1

'0

3

x

fx

x













.

Nhưng trong đó nghiệm

1x 

là nghiệm kép

(nghiệm bội chẵn) nên qua

1x 

, đạo hàm

không đổi dấu, còn

3x 

là nghiệm đơn nên

3x 

là điểm cực trị của hàm số

 

y f x

.

Vậy hàm số

 

y f x

có một cực trị duy nhất

là điểm

3x 

và nó là điểm cực tiểu do đạo

hàm đổi dấu từ âm sang dương khi đi qua điểm

3x 

.

Đáp án C

Câu 8. Xét từng hàm số:

+) Đáp án A:

Xét hàm số:

42

2 10y x x  

.

Ta có:

10

1.2 2 0

a

ab







  



.

Nên theo phần Tips đã trình bày ở trên (xem

thêm Đồ thị I.II.14.).

Hàm số đã cho có duy nhất một điểm cực tiểu.

Loại A.

+) Đáp án B:

Xét hàm số:

42

23y x x   

.

Ta có:

 

10

1 .2 2 0

a

ab

  





    



.

Nên theo phần Tips đã trình bày ở trên (xem

thêm Đồ thị I.II.13.).

Hàm số đã cho có ba điểm cực trị.

Chọn B.

+) Đáp án C:

Hàm số

32

1

3 5 2

3

y x x x   

là một hàm số

bậc ba nên tối đa chỉ có hai cực trị.

Loại C.

+) Đáp án D:

Xét hàm số:

4

24yx

.

Ta có:

20

2.0 0 0

a

ab







  



.

Nên theo phần Tips đã trình bày ở trên (xem

thêm Đồ thị I.II.14.).

Hàm số đã cho có duy nhất một điểm cực tiểu.

Loại D.

Đáp án B

Câu 9. Xét hàm số

4

100yx

.

Ta có:

10

1.0 0 0

a

ab







  



.

Nên theo phần Tips đã trình bày ở trên (xem

thêm Đồ thị I.II.14.).

Hàm số đã cho có duy nhất một điểm cực tiểu

và không có điểm cực đại.

Vậy số cực đại của đồ thị hàm số

4

100yx

là

0

.

Đáp án A

Câu 10. Xét hàm số

42

2 2021y x x  

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

216

[ I can't, I can! ]

Ta có:

10

1.2 2 0

a

ab







  



.

Nên theo phần Tips đã trình bày ở trên (xem

thêm Đồ thị I.II.14.).

Hàm số đã cho có duy nhất một điểm cực tiểu.

Đáp án A

Câu 11. Xét hàm số

32

1

4 8 5

3

y x x x   

.

Ta có:

 

2

' 8 8 *y x x  

.

Hai điểm cực trị

12

,x x x x

là nghiệm của

phương trình

 

*

.

Theo định lý Viéte, ta có:

12

8

1

b

xx

a

      

.

Vậy:

12

8xx  

.

Đáp án B

Câu 12. Ta có:

     

2

' 1 3f x x x  

.

 

1

'0

3

x

fx

x













.

Trong đó,

1x 

là nghiệm kép nên

1x 

không

là điểm cực trị và

3x 

là nghiệm đơn nên

3x 

là một điểm cực trị của hàm số

 

y f x

.

Vậy hàm số có đúng một điểm cực trị.

Đáp án C

Câu 13. Ta có:

32

31y x x  

.

Suy ra:

 

2

' 3 6 0 3 2 0y x x x x     

.

0

2

x













.

Nên theo phần Tips đã trình bày ở trên (xem

thêm Đồ thị I.II.10.).

Vì

1 0 0

CĐCTCĐ

a xxx     

.

Mà

   

0 1 0;1yI

là điểm cực đại của đồ

thị hàm số

32

31y x x  

.

Đáp án B

Câu 14. Xét hàm số:

42

2 2021y x x  

.

Ta có:

 

10

1. 2 2 0

a

ab







    



.

Nên theo phần Tips đã trình bày ở trên (xem

thêm Đồ thị I.II.12.).

Hàm số

42

2 2021y x x  

có ba điểm cực trị.

Đáp án D

Câu 15. Xét hàm số:

32

3 3 1y x x x   

.

Ta có:

 

22

' 3 6 3 3 2 1y x x x x     

 

2

' 3 1 0,y x x     

.

Vậy hàm số

32

3 3 1y x x x   

luôn đồng

biến trên .

Đáp án D

Câu 16. Xét các phương án:

+) Đáp án A:

Hàm số bậc ba có dạng:

32

y ax bx cx d   

nên

lim

x

y





vì thế hàm số không tồn tại giá

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

217

[ I can't, I can! ]

trị nhỏ nhất và giá trị lớn nhất.

Tuy nhiên, nếu ta nói:

1

CT

y 

và

3

CĐ

y 

thì

đây là mệnh đề đúng.

Loại A.

+) Đáp án B:

Dựa vào đồ thị hàm số như hình vẽ, ta thấy đồ

thị hàm số có điểm cực tiểu

 

1; 1A 

và điểm

cực đại

 

1;3B

.

Chọn B.

+) Đáp án C:

Hàm số có giá trị cực đại là:

3

CĐ

y 

.

Tuy nhiên, nếu ta nói: Hàm số đạt cực đại tại

điểm

1x 

thì mệnh đề đúng.

Loại C.

+) Đáp án D:

Dựa vào đồ thị hàm số

 

y f x

, ta thấy đồ thị

hàm số đạt cực tiểu tại điểm

 

1; 1A 

và đạt

cực đại tại điểm

 

1;3B

.

Loại D.

Đáp án B.

Câu 17. Xét từng đáp án:

+) Đáp án A:

Dựa vào bảng biến thiên của đồ thị hàm số ta dễ

dàng thấy hàm số

 

y f x

không có đạo hàm

tại điểm

0x 

do tại

0x 

,

'y

có kí hiệu

"||"

.

Loại A.

+) Đáp án B:

Hàm số

 

y f x

không liên tục tại điểm

1x 

nên không thể đạt cực tiểu tại điểm

1x 

mặc

dù qua điểm

1x 

đạo hàm của hàm số đổi dấu.

Chọn B.

+) Đáp án C:

Dựa vào bảng biến thiên của đồ thị hàm số, ta

thấy rằng:

1

lim

x

y









 







 





.

Vì thế đồ thị hàm số

 

y f x

nhận đường

thẳng

1x 

và

1x 

làm tiệm cận đứng.

Loại C.

+) Đáp án D:

Dựa vào bảng biến thiên của đồ thị hàm số, ta

thấy rằng:

lim 3

x

y



















.

Vì thế đồ thị hàm số

 

y f x

nhận đường

thẳng

3y 

và

3y 

làm tiệm cận ngang.

Loại D.

Đáp án B

Câu 18. Xét các nhận định:

+) Đáp án A:

Xét hàm số:

1

2

1

yx

x





.

Ta có:

 

 

2

1

' 2 0, \ 1

1

yx

x

     



.

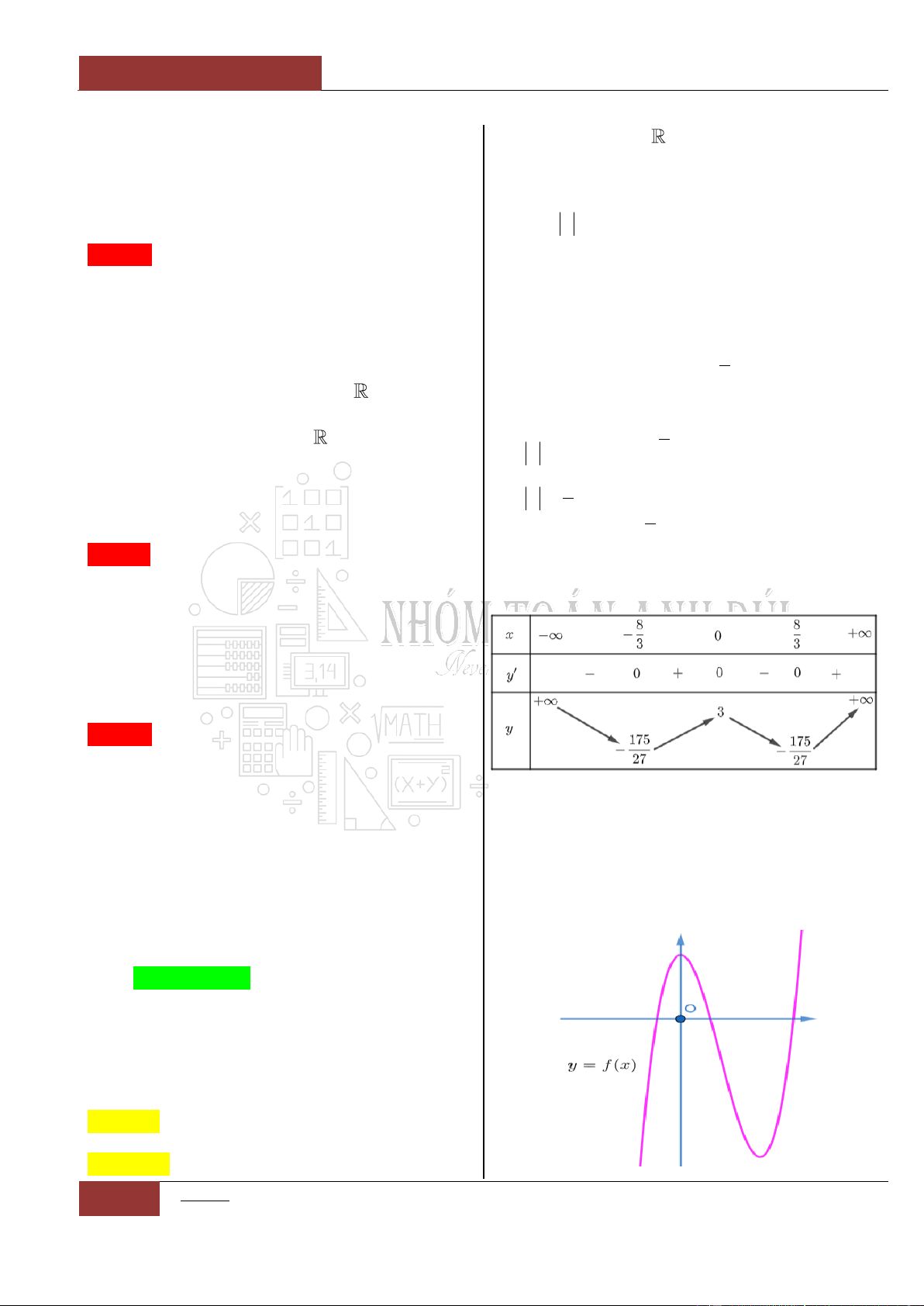
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

218

[ I can't, I can! ]

Vậy hàm số là một hàm đồng biến trên hai

khoảng rời nhau

 

;1 

và

 

1; 

.

Vậy hàm số không có điểm cực trị.

Loại A.

+) Đáp án B:

Xét hàm số:

3

3 2021 2022y x x  

.

Ta có:

2

' 9 2021 0,y x x    

.

Vậy hàm số đồng biến trên .

Khi đó hàm số

3

3 2021 2022y x x  

không

có điểm cực trị.

Loại B.

+) Đáp án C:

Hàm số nhất biến hoặc đồng biến hoặc nghịch

biến hoặc không đổi trên từng khoảng xác định

và không có cực trị.

Loại C.

+) Đáp án D:

Xét hàm số:

42

32y x x   

.

Ta có:

   

10

1 . 3 3 0

a

ab

  





    



.

Nên theo phần Tips đã trình bày ở trên (xem

thêm Đồ thị I.II.15.).

Suy ra hàm số

42

32y x x   

có duy nhất

một điểm cực trị, chính xác hơn là một điểm

cực đại.

Chọn D.

Đáp án D

Câu 19. TXĐ:

D 

.

Cách 1:

Đặt:

0tx

.

Khi đó:

32

43y t t  

.

Và:

2

0

' 3 8 0

8

3

t

y t t

t







   







.

8

0

3

0

8

3

x













  















.

Bảng biến thiên:

Như vậy, hàm số đã cho có

3

điểm cực trị.

Cách 2: Xét hàm số

32

43y x x  

.

Vẽ phác họa đồ thị hàm số

32

43y x x  

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

219

[ I can't, I can! ]

Xét hàm số:

 

y f x

.

Ta có:

 

   

, 0 1

, 0 2

f x x

y f x

f x x

















.

Mặt khác, hàm số

 

y f x

là hàm chẵn vì

   

f x f x

nên hàm số

 

y f x

đối

xứng nhau qua trục tung

 

3

.

Suy ra cách vẽ đồ thị hàm số

 

y f x

từ đồ

thị hàm số

 

y f x

như sau:

Cách vẽ:

+) Giữ nguyên phần đồ thị hàm số

 

y f x

nằm bên phải trục tung (do

 

1

).

+) Lấy đối xứng qua trục tung phần đồ

thị hàm số

 

y f x

nằm bên phải trục tung

(do

 

3

).

Vẽ đồ thị hàm số

 

2

3

43y x x  

.

Bước 1:

Bước 2:

Vậy hàm số có ba điểm cực trị.

Cách 3:

Nhận xét:

Do

 

y f x

là hàm chẵn nên hàm số đối

xứng nhau qua trục

Oy

. Vì thế giả sử hàm số

 

y f x

có

n

điểm cực trị dương thì hàm số

 

y f x

sẽ có

21n 

điểm cực trị (Có thêm

1

điểm cực trị là

0x 

vì nếu trên khoảng

 

1

0; x

hàm số

 

y f x

đồng biến (nghịch biến) thì

trên khoảng

 

1

;0x

hàm số

 

y f x

sẽ

nghịch biến (đồng biến)).

Xét hàm số:

32

43y x x  

.

Ta có:

2

0

' 3 8 0

8

0

3

x

y x x

x







   







.

Do đó:

1n 

.

Nên số điểm cực trị của hàm số

 

y f x

là

2.1 1 3

điểm cực trị.

Vậy hàm số

3

2

43y x x  

có

3

điểm cực

trị.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

220

[ I can't, I can! ]

Đáp án C

Câu 20. Xét hàm số:

42

1y x x  

.

Ta có:

10

1.1 1 0

a

ab







  



.

Nên theo phần Tips đã trình bày ở trên (xem

thêm Đồ thị I.II.14.).

Suy ra hàm số:

42

1y x x  

có duy nhất một

điểm cực tiểu là điểm

0x 

.

Đáp án B

Câu 21. Xét các nhận định:

+) Đáp án A:

Dựa vào bảng biến thiên của đồ thị hàm số, ta

dễ dàng nhận thấy:

Hàm số có ba điểm cực trị là:

1x 

,

0x 

,

2x 

.

Loại A.

+) Đáp án B:

Hàm số có giá trị cực tiểu là

3y 

.

Loại B.

+) Đáp án C:

Hàm số có giá trị nhỏ nhất trùng với giá trị cực

tiểu là

3y 

. Tuy nhiên hàm số không tồn tại

giá trị lớn nhất do

lim

x

y



 

.

Giá trị cực đại và giá trị lớn nhất không

giống nhau.

Loại C.

+) Đáp án D:

Hàm số đạo hàm

 

'y f x

không xác định tại

điểm

0x 

nhưng hàm số

 

y f x

liên tục

trên và đạo hàm đổi dấu từ dương sang âm

khi qua điểm

0x 

. Vì vậy

0x 

là điểm cực

đại của đồ thị hàm số

 

y f x

.

Chọn D.

Đáp án D

Câu 22. Xét hàm số:

32

31y x x  

.

Ta có:

2

0

' 3 6 0

2

x

y x x

x





   







.

Vì

0, 2xx

đều là hai nghiệm bội lẻ nên

đạo hàm đổi dấu khi qua hai điểm này.

Vậy

0, 2xx

là hai điểm cực trị của hàm số

32

31y x x  

.

Đáp án C

Câu 23. Xét hàm số:

3

2y x x

.

Ta có:

2

6

3

' 3 2 0

6

3

x

yx

x







   









.

Nên theo phần Tips đã trình bày ở trên (xem

thêm Đồ thị I.II.10.).

Ta suy ra:

6

3

0

6

3

CT

C

Đ

T

Đ

C

x

xx

x







  











.

Đáp án A

Câu 24. Xét các nhận định:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

221

[ I can't, I can! ]

+) Đáp án A:

Điểm

 

0;2M

được gọi là điểm cực đại của đồ

thị hàm số.

Chọn A.

+) Đáp án B:

   

1 1 1ff  

được gọi là giá trị cực tiểu

của hàm số.

Loại B.

+) Đáp án C:

Dựa vào bảng biến thiên của đồ thị hàm số, ta

thấy rằng:

Hàm số nghịch biến trên hai khoảng rời nhau

 

;1 

và

 

0;1

.

Hàm số đồng biến trên hai khoảng rời nhau

 

1;0

và

 

1; 

.

Loại C.

+) Đáp án D:

1x 

,

1x 

là hai điểm đều được gọi là điểm

cực tiểu của hàm số.

Loại D.

Đáp án A

Câu 25. Xét hàm số:

32

6 9 2y x x x   

.

Ta có:

2

' 3 12 9y x x  

.

Thực hiện phép chia đa thức

y

cho

'y

ta được:

 

2

'. 2 4

33

x

y y x



    





.

Suy ra:

 

: 2 4yx   

là đường thẳng đi qua

hai điểm cực trị của hàm số bậc ba.

Gọi

 

d

là đường thẳng đi qua điểm

 

1;1A 

và vuông góc với đường thẳng

 



.

Khi đó đường thẳng

 

d

có dạng:

1

2

y x c

.

Vì:

     

13

1;1 1 . 1

22

A d c c       

.

Vậy đường thẳng đi qua điểm

 

1;1A 

và

vuông góc với đồ thị hàm số

 

C

có phương

trình:

 

13

:

22

d y x

.

Đáp án B

Extra Techniques:

Tips:

Cho đường thẳng

 

,0y ax b a  

.

Khi đó một đường thẳng có phương

trình

 

,0y cx d c  

được gọi là

vuông góc với đường thẳng cho trước

khi và chỉ khi:

1ac 

.

Câu 26. Xét hàm số:

42

2 3 1y x x  

.

Khi đó:

4

3

4

3

2

' 8 2 3 0 0

3

2

x

y x x x

x







    









.

Do:

 

20

2. 3 2 3 0

a

ab









    





.

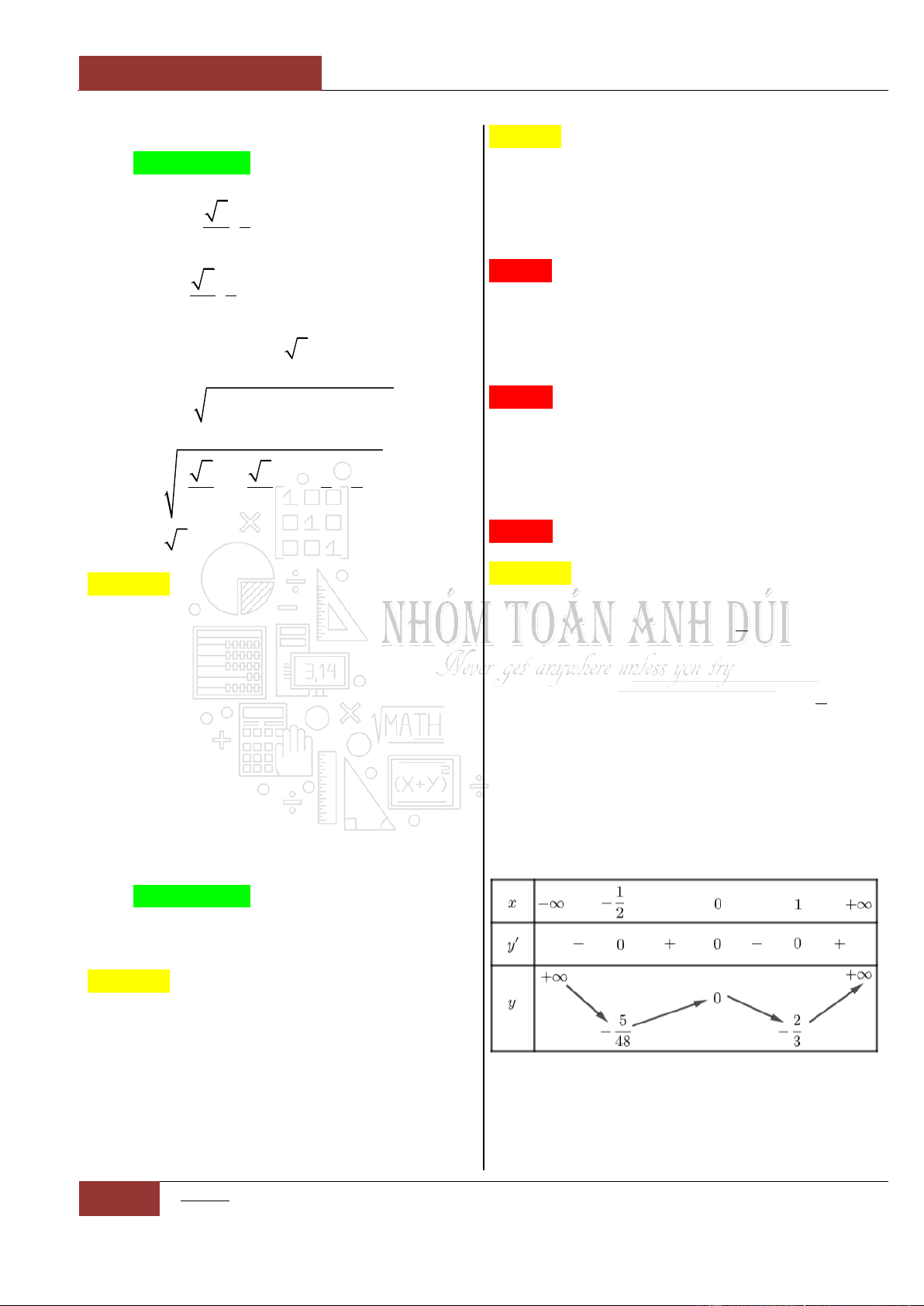
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

222

[ I can't, I can! ]

Nên theo phần Tips đã trình bày ở trên (xem

thêm Đồ thị I.II.12.).

Suy ra:

4

35

;

28

35

;

28

A

B





























là hai điểm cực tiểu của

đồ thị hàm số

42

2 3 1y x x  

.

Ta có:

   

22

B A B A

AB x x y y   

.

2

44

4

3 3 5 5

2 2 8 8

3

AB



     







Đáp án D

Câu 27. Xét hàm số:

42

21y x x   

.

Ta có:

3

1

' 4 4 0 0

1

x

y x x x

x







     







.

Do:

 

10

1 .2 2 0

a

ab

  





    



.

Nên theo phần Tips đã trình bày ở trên (xem

thêm Đồ thị I.II.13.).

Suy ra:

1x 

là điểm cực trị của hàm số.

Đáp án A

Câu 28. Xét từng mệnh đề:

+) Đáp án A:

Hàm số đã cho nhận điểm

1x 

và

2x 

làm

hai điểm cực trị.

Chọn A.

+) Đáp án B:

Hàm số

 

y f x

có giá trị cực đại là

3y 

.

Loại B.

+) Đáp án C:

Nếu A đúng thì chắc chắn C sai.

Loại C.

+) Đáp án D:

Hàm số

 

y f x

có giá trị cực tiểu là

0y 

.

Loại D.

Đáp án A

Câu 29. Xét hàm số:

4 3 2

2

3

y x x x  

.

Ta có:

32

1

2

' 4 2 2 0 0

1

x

y x x x x

x







     









.

Bảng biến thiên:

Dựa vào bảng biến thiên của đồ thị hàm số, ta

xét từng mệnh đề:

+) Đáp án A:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

223

[ I can't, I can! ]

Hàm số có giá trị cực đại là

0y 

.

Loại A.

+) Đáp án B:

Hàm số có hai giá trị cực tiểu, lần lượt là

2

3

y 

và

5

48

y 

.

Chọn B.

+) Đáp án C:

Vì đáp án B đúng nên hàm số có hai giá trị cực

tiểu.

Loại C.

+) Đáp án D:

Hàm số có giá trị cực tiểu là

2

3

y 

,

5

48

y 

và hàm số có giá trị cực đại là

0y 

.

Loại D.

Đáp án B

Câu 30. Xét hàm số:

  

2

12y x x  

.

Cách 1: Chia đa thức.

Thực hiện phép chia đa thức

y

cho

'y

ta được:

 

32

1

3 4 '. 2 4

33

x

y x x y x



       





.

Suy ra đường thẳng đi qua hai điểm cực trị của

hàm số

  

2

12y x x  

có phương trình là:

 

: 2 4d y x  

.

Vì hai điểm cực trị của đồ thị hàm số thuộc

đường thẳng

 

d

nên trung điểm của hai điểm

cực trị của đồ thị hàm số cũng thuộc vào đường

thẳng

 

: 2 4d y x  

hay

2 4 0xy  

.

Đáp án A

Cách 2: Tính toán trực tiếp bằng đạo hàm.

Ta có:

  

2

32

1 2 3 4y x x x x     

.

Khi đó:

2

' 3 6 0

0

x

y x x

x





   







.

Suy ra:

 

2;0A 

và

 

0; 4B 

là hai điểm cực

trị của hàm số

  

2

12y x x  

.

Trung điểm

I

của

AB

có tọa độ:

 

1; 2I 

.

+) Đáp án A:

Ta có:

   

2. 1 2 4 0    

.

Chọn A.

+) Đáp án B:

Ta có:

   

2. 1 2 4 8 0      

.

Loại B.

+) Đáp án C:

Ta có:

   

2. 1 2 4 4 0      

.

Loại C.

+) Đáp án D:

Ta có:

   

2. 1 2 4 4 0     

.

Loại D.

Cách 3: CASIO.

Xét hàm số:

32

34y x x  

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

224

[ I can't, I can! ]

Ta có:

2

' 3 6

'' 6 6

y x x

yx











.

Sử dụng máy tính cầm tay bằng cách nhập biểu

thức

'. ''

18

yy

y

a



như sau:

Chọn MODE 2.

Nhập vào màn hình:

 

2

32

3 6 . 6 6

34

18

X X X

XX



  

.

Ấn CALC, nhập

xi

(

i

là đơn vị ảo, nhấn nút

ENG để gọi

i

ra màn hình).

Màn hình xuất hiện kết quả:

Vậy phương trình đường thẳng đi qua hai điểm

cực trị có phương trình là:

42yx  

, hay

2 4 0xy  

.

Vì hai điểm cực trị của đồ thị hàm số thuộc

đường thẳng

 

d

nên trung điểm của hai điểm

cực trị của đồ thị hàm số cũng thuộc vào đường

thẳng

 

: 2 4d y x  

hay

2 4 0xy  

.

Extra Techniques:

Remark:

Sở dĩ ta có thể ứng dụng phương pháp

CASIO ở trên vì ta có cơ sở toán học.

Chứng minh trình tự các bước CASIO

trình bày ở Cách 3 là hợp lý.

Theo Tips về phương pháp giải nhanh các

bài toán về đường thẳng đi qua ba điểm

cực trị của hàm số bậc ba, ta đã chứng

minh rằng: Nếu sau khi thực hiện phép

chia đa thức

 

fx

cho

 

'fx

ta được:

       

.'f x g x f x h x

thì phương trình

 

y h x

là đường thẳng

đi qua hai điểm cực trị của hàm số

 

y f x

.

Một cách khác, ta có thể ghi dưới dạng:

     

.'

39

xb

f x f x h x

a



  





     

.'

39

xb

h x f x f x

a



   





là

phương trình đường thẳng đi qua hai điểm

cực trị của đồ thị hàm số.

Xét hàm số:

 

3 6 2 ''

3 9 9 18 3. '''

x b ax b ax b y

gx

a a a y



    

Vì:

32

2

' 3 2

'' 6 2

''' 6

y ax bx cx d

y ax bx c

y ax b

ya



   



  













.

Như vậy:

 

'. '' '. ''

3 ''' 18

y y y y

h x y y

ya

   

.

Ta CALC giá trị

xi

hợp lý là vì nếu ta

CALC một giá trị thực thì kết quả ta sẽ

nhận được một số thực. Ngược lại, khi

CALC

xi

, giá trị của

x

sẽ đóng vai trò

là “biến”

i

trong kết quả, không hòa lẫn

giá trị của hệ số tự do.

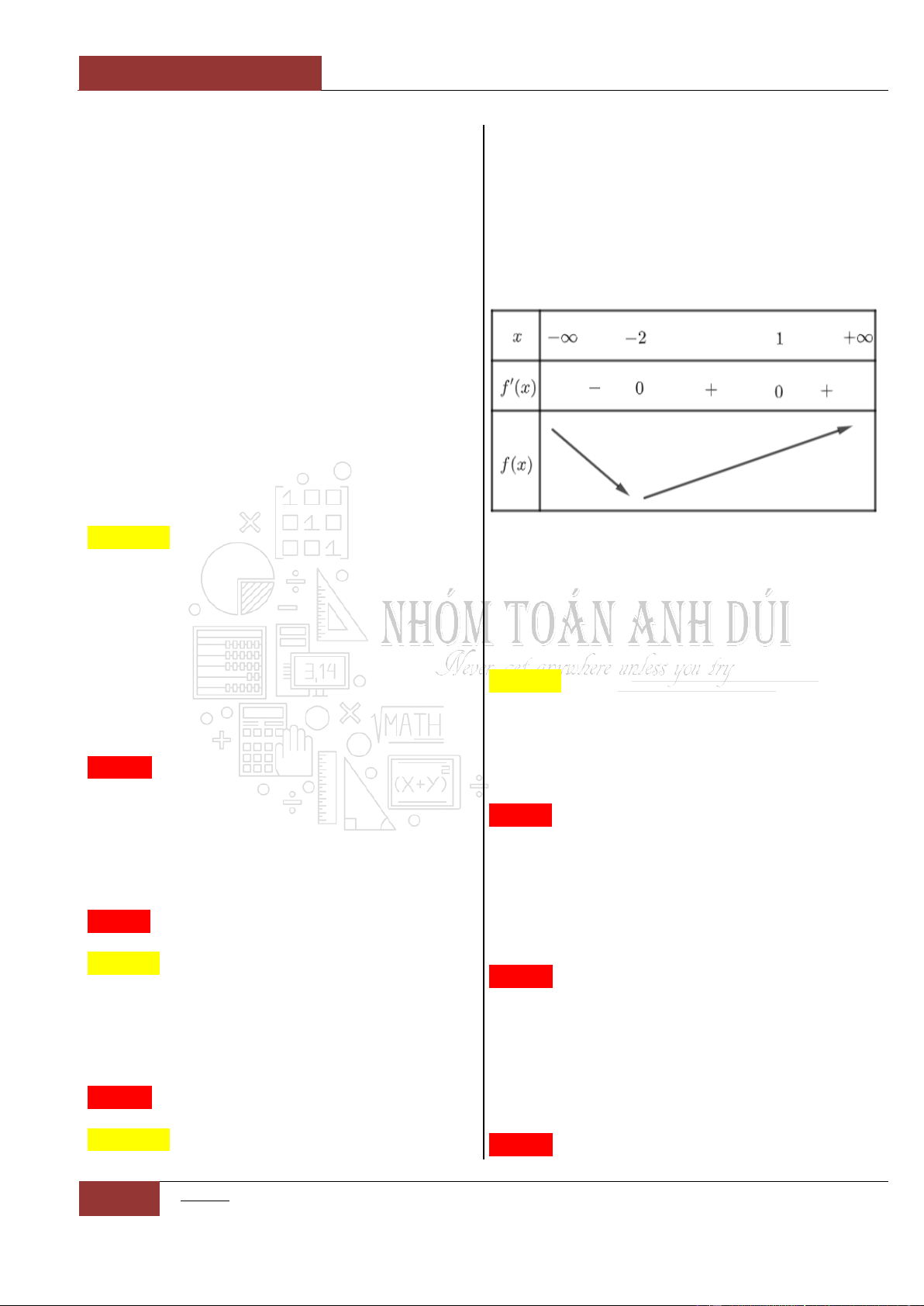
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

225

[ I can't, I can! ]

Câu 31. Ta có:

     

23

' 1 2f x x x x  

.

   

0

' 0 1

2

x

f x x NBC

x







  







.

Nhận thấy trong ba nghiệm

2, 0, 1x x x   

,

chỉ có nghiệm

1x 

là nghiệm kép (nghiệm bội

chẵn). Do đó qua điểm

2, 0xx  

, đạo hàm

đổi dấu còn khi qua điểm

1x 

, đạo hàm không

đổi dấu.

Vậy hàm số có hai điểm cực trị là các điểm

2, 0xx  

.

Đáp án C

Câu 32. Xét các nhận định:

+) Đáp án A:

Dựa vào bảng biến thiên của đồ thị hàm số, ta

thấy hàm số đồng biến trên hai khoảng rời nhau

 

;2 

và

 

0;

.

Loại A.

+) Đáp án B:

Hàm số đạt cực tiểu tại điểm

0x 

và đạt cực

đại tại điểm

2x 

.

Loại B.

Chọn C.

+) Đáp án D:

Hàm số nghịch biến trên khoảng

 

2;0

.

Loại D.

Đáp án C

Câu 33. Ta có:

     

2

' 1 2f x x x  

.

 

1

'0

2

x NBC

fx

x













.

Bảng biến thiên:

Xét các nhận định:

+) Đáp án A:

Hàm số đồng biến trên khoảng

 

2; 

.

Chọn A.

+) Đáp án B:

Hàm số

 

y f x

không có điểm cực đại.

Loại B.

+) Đáp án C:

Điểm

1x 

không là điểm cực trị của hàm số

 

y f x

.

Loại C.

+) Đáp án D:

Hàm số

 

y f x

đồng biến trên khoảng

 

2;1

.

Loại D.

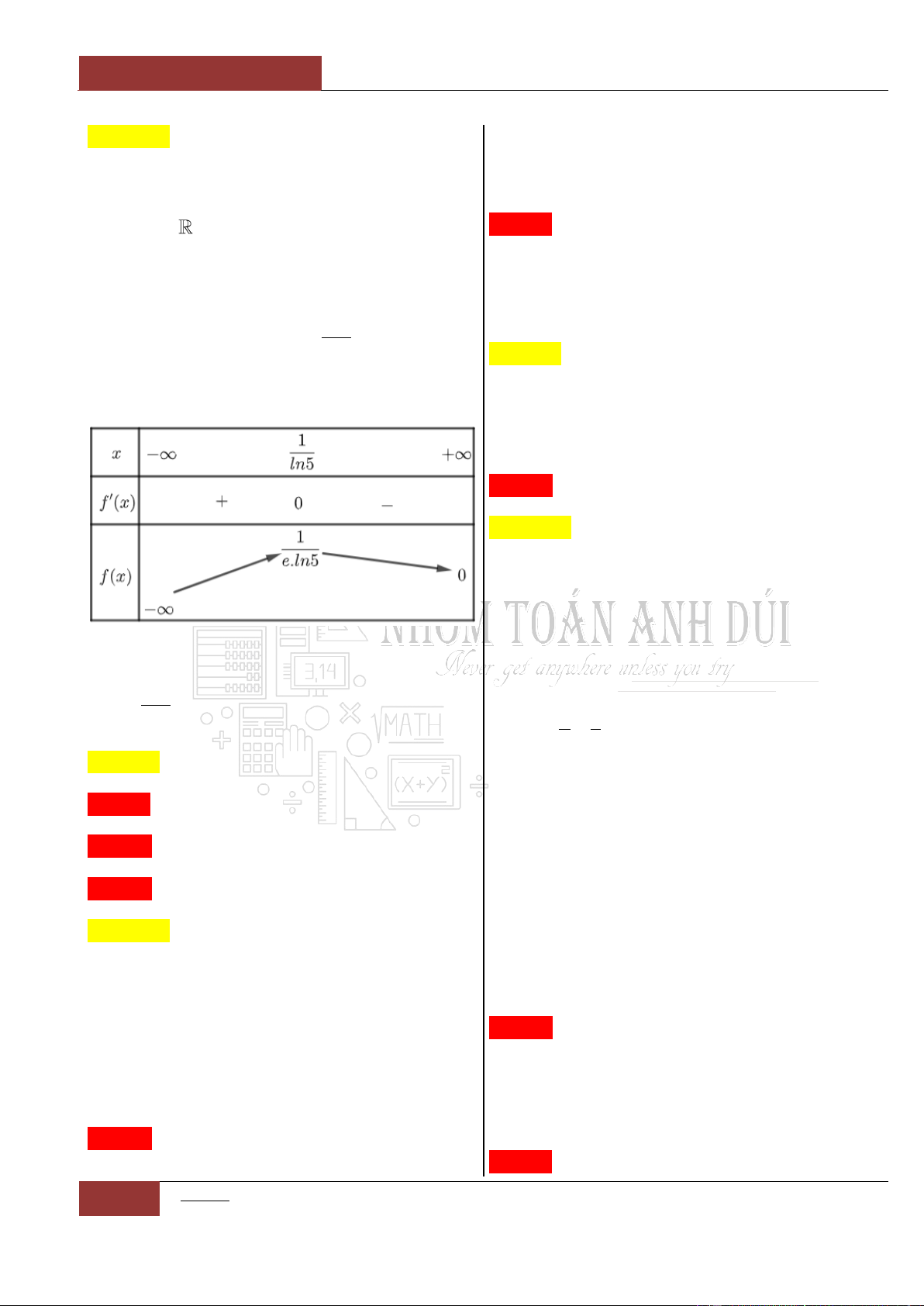
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

226

[ I can't, I can! ]

Đáp án A

Câu 34. Xét hàm số:

.5

x

yx





.

TXĐ:

D 

.

Ta có:

 

' 5 .5 .ln5 5 1 ln5

x x x

y x x

  

   

.

1

' 0 1 ln5 0

ln5

y x x     

.

Bảng biến thiên:

Hàm số

.5

x

yx





có duy nhất một điểm cực đại

là

1

ln5

x 

.

Chọn A.

Loại B.

Loại C.

Loại D.

Đáp án A

Câu 35. Xét các mệnh đề:

+) Đáp án A:

Hàm số

 

y f x

có ba điểm cực trị lần lượt là

1, 0, 1x x x   

.

Loại A.

+) Đáp án B:

Hàm số có giá trị cực đại là

3y 

.

Loại B.

+) Đáp án C:

Hàm số có giá trị cực tiểu là

0y 

.

Chọn C.

+) Đáp án D:

Hàm số có hai điểm cực tiểu là

1, 1xx  

.

Loại D.

Đáp án C

Câu 36. Ta có:

32

3 9 1y x x x   

.

Suy ra:

2

' 3 6 9y x x  

.

Thực hiện phép chia đa thức

y

cho

'y

, ta được:

 

1

'. 8 2

33

x

y y x



    





.

Vậy đường thẳng đi qua hai điểm cực trị của đồ

thị hàm số

32

3 9 1y x x x   

có phương trình

là

82yx  

.

Xét từng đáp án:

+) Đáp án A:

Ta có:

 

0 8. 1 2  

.

Loại A.

+) Đáp án B:

Ta có:

 

1 8. 0 2   

.

Loại B.

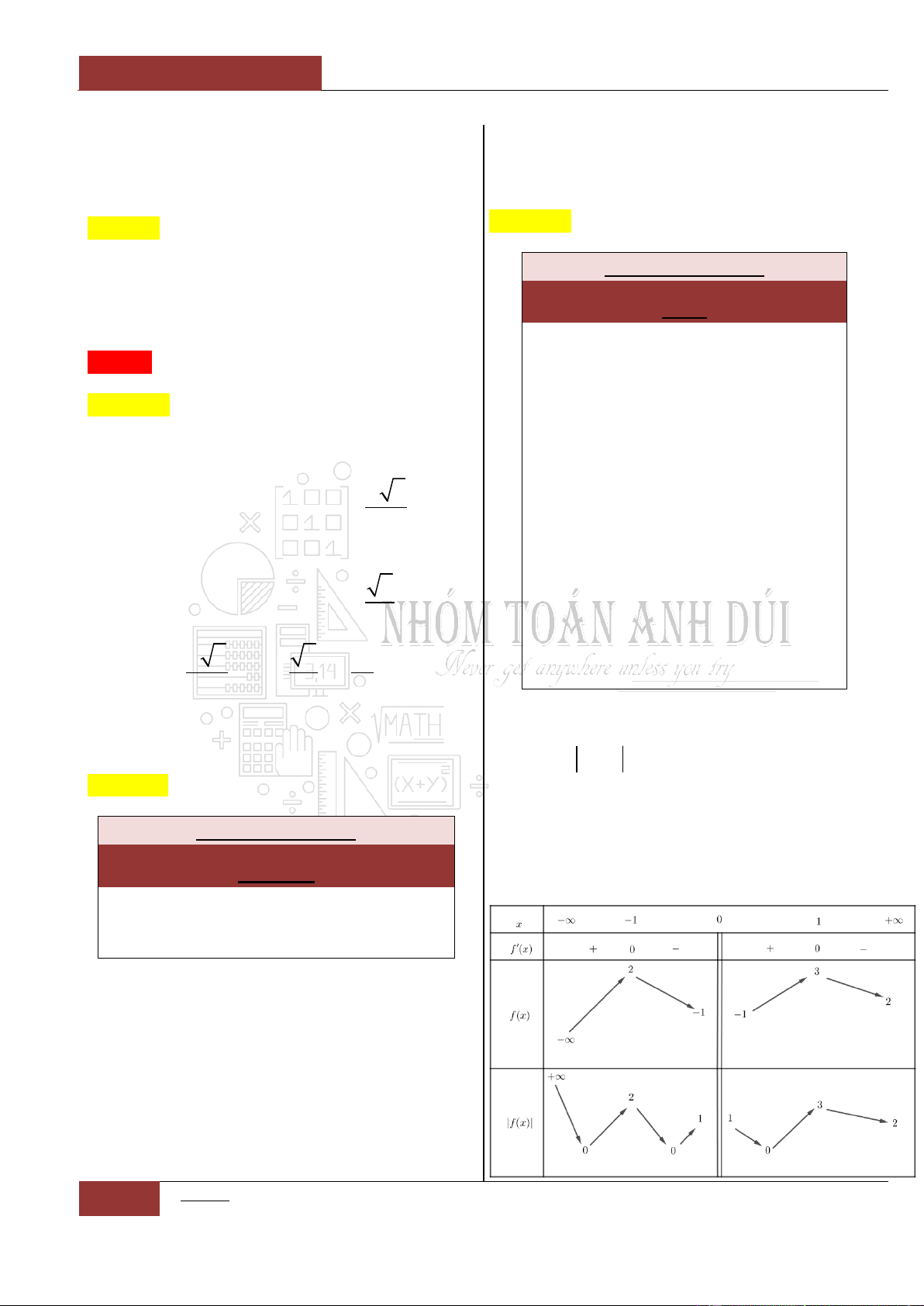
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

227

[ I can't, I can! ]

+) Đáp án C:

Ta có:

 

10 8. 1 2   

Chọn C.

+) Đáp án D:

Ta có:

 

10 8. 1 2   

.

Loại D.

Đáp án C

Câu 37. Xét hàm số:

42

( ) 3 2f x x x  

.

Ta có:

3

6

2

' 4 6 0 0

6

2

x

y x x x

x









    









.

Ta có:

6 6 1

2 2 4

(0) 2

ff

f



   







   



   







Vì thế hàm số có 2 cực trị.

Đáp án B

Extra Techniques:

Remark:

Cực trị của hàm số, tức giá trị cực trị của

hàm số.

Câu 38. Xét hàm số:

 

2

y f x mx

.

Ta có:

' '( ) 2y f x mx

= 0.

Dựa vào sự tương giao ta thấy, đạo hàm là tổng

của hàm đa thức bậc

2

: (

 

1

'y f x

) với hàm

đa thức bậc

1

:

 

2

2y mx

.

Khi đó phương trình

'0y 

có nhiều nhất

2

nghiệm.

Do đó hàm số có nhiều nhất

2

điểm cực trị.

Đáp án A

Extra Techniques:

Tips:

Dựa vào bảng xét dấu của hàm số đạo

hàm ta dễ dàng nhận ra hàm số

 

y f x

là một hàm đa thức bậc ba

(Vì bậc cao nhất không quá

3

và hàm

số có hai cực trị). Vì thế việc tìm số

nghiệm tối đa của phương trình

 

' 2 0f x mx

được quy về bài

toán tìm số nghiệm tối đa của phương

trình bậc hai

 

2

0*ax bx c  

. Vì

phương trình

 

*

có tối đa hai

nghiệm nên hàm số

 

2

y f x mx

có tối đa

2

cực trị.

Câu 39. Từ bảng biến thiên, ta dễ dàng suy ra

đồ thị

 

y f x

bằng hai bước sau:

- Giữ nguyên phần đồ thị

 

y f x

phía trên

Ox

.

- Với phần đồ thị

 

y f x

phía dưới

Ox

, ta

lấy đối xứng qua trục

Ox

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

228

[ I can't, I can! ]

Dựa vào bảng biến thiên mở rộng, ta thấy đồ thị

có

5

điểm cực trị.

Đáp án A

Extra Techniques:

Remark:

Dựa vào đồ thị hàm số ta thấy hàm số có

hai điểm cực trị. Mặt khác nếu ta kẻ đường

thẳng

0y 

, thì đường thẳng sẽ tương

giao với đồ thị hàm số tại

3

điểm phân

biệt khác

1x 

.

Minh họa như hình vẽ.

Vậy hàm số:

 

y f x

có tất cả

5

điểm

cực trị.

Câu 40. TXĐ:

D 

.

Ta có:

 

2

1

x

fx

x







.

 

2

22

2

20

0 1 2

14

0

3

31

x

f x x x

xx

x







    











  







Bảng biến thiên:

Vậy hàm số đạt cực đại tại

3

x 

và đại giá trị

cực đại của hàm số

3

yf



  





.

Đáp án B

Câu 41. Dễ thấy, hàm số có 3 điểm cực trị là:

1, 2, 3.x x x   

Dựa vào bảng biến thiên, ta thấy rằng đạo hàm

không xác định tại điểm

0x 

.

Và

 

0

lim ' 0

x

f x m

f x n





















.

(Đạo hàm đổi dấu khi đi qua điểm

0x 

).

Hơn thế nữa, hàm số liên tục trên nên tại

0x 

, hàm số

 

y f x

xác định và liên tục.

Vậy hàm số có tất cả

4

điểm cực trị.

Đáp án D

Câu 42. Ta có:

( ) 0, ( 1;2)f x x



   

.

Suy ra:

 

'' 0 0f 

.

Như vậy theo giả thuyết ta có:

 

' 0 0

'' 0 0

f















.

Do vậy hàm số đạt cực đại tại điểm

0x 

.

Trong bốn hình vẽ chỉ thấy đồ thị hàm số ở hình

3

thỏa mãn tính chất trên.

Đáp án C

Câu 43. Để vẽ đồ thị hàm số

 

y f x

, ta chỉ

cần giữ nguyên phần phía trên trục hoành của

đồ thị hàm số

 

y f x

và vẽ đối xứng phần

phía dưới trục hoành lên phía trên.

Theo cách trên, ta thu được đồ thị sau:

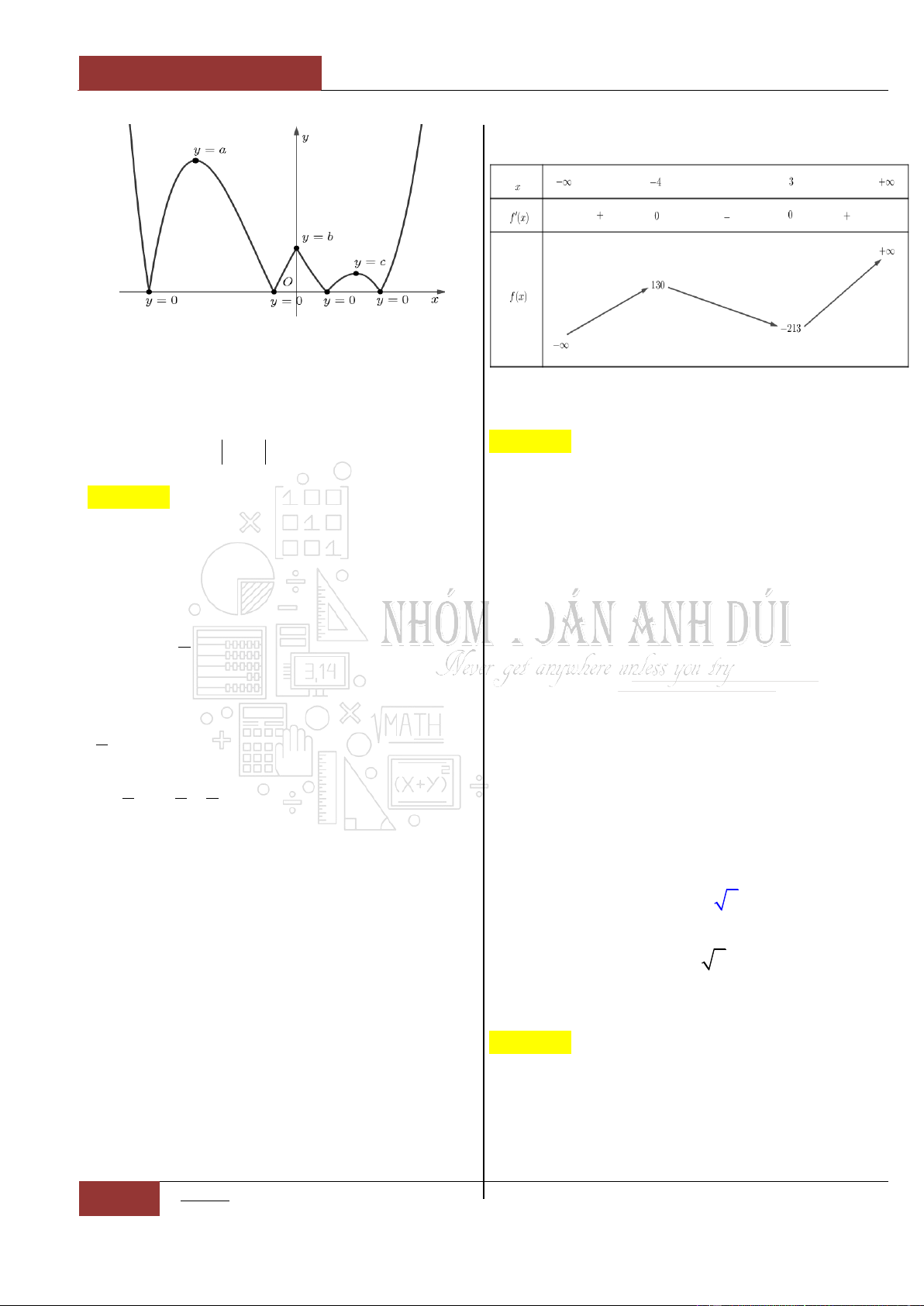
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

229

[ I can't, I can! ]

Nhìn vào đồ thị trên, ta nhận được các giá trị

cực trị là:

; ; ; 0y a y b y c y   

.

Vậy hàm số

 

y f x

có 4 giá trị cực trị.

Đáp án D

Câu 44. Thay

x

thành

1 x

, ta được:

     

2

1 2 2 2 *f x f x x x    

.

Theo giả thiết suy ra:

   

 

2

1

11

2

f x x f x   

thay vào phương

trình

 

*

ta có:

 

   

22

2

1

1 2 2 2 0

2

1 1 1

2 2 2 0

2 2 2

3 4 3 1

x f x f x x x

f x x x

      

       

   

Thay

 

1

vào giả thiết ta có:

 

2

22

3 2 2

32

6. . 11 78 78

2 4 3 11 78 78

2 8 6 11 78 78

2 3 72 78 ( )

y x f x x x

y x x x x x

y x x x g x

   

      

     

Xét hàm số

()y g x

ta có:

 

2

4

' 6 6 72 0

3

x

g x x x

x





    







.

Bảng biến thiên:

Vậy

1 2 1 2

4, 3 . 12x x x x     

.

Đáp án A

Câu 45. Quan sát đồ thị

 

y f x

, ta thấy:

Hàm số có hai điểm cực trị

2; 0xx  

.

Vì vậy:

2

'( ) 3 2f x ax bx c  

có hai nghiệm

2; 0xx  

nên

'( ) 3 ( 2)f x ax x

.

Ta có:

 

2

' 2 4 'y f x x



  



.

 

  

2

22

2

' 4 4 . ' 2x 4

' 3 4 4 2 4 2 4 2

' 48 ( 2)( 1)( 2 1)

y x f x

y a x x x x x

y ax x x x x

     

        

      

  

 

2

' 0 48 2 1 2 1 0y ax x x x x       

.

0

1

2

12

x

























.

Đạo hàm của hàm số đổi dấu khi qua các điểm

0; 2; 1; 1 2x x x x    

, vì cả năm giá trị

đều là nghiệm bội lẻ.

Vậy hàm số đã cho có

5

điểm cực trị.

Đáp án D

Câu 46. Ta có:

2 4 3

' 2 27y x m x m   

.

Và:

2 4 3

' 0 2 27 0y x m x m     

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

230

[ I can't, I can! ]

Để hàm số có hai cực trị nằm về phía của trục

tung thì phương trình

2 4 3

2 27 0x m x m   

có hai nghiệm trái dấu

3

0 27 0 3ac m m      

.

Với

3m 

, hàm số có hai cực trị nằm về hai

phía của trục tung.

Đáp án D

Câu 47. Xét hàm số:

 

32

y f x ax bx cx d    

.

Ta có:

 

2

' 3 2f x ax bx c  

.

Do hàm số có hoành độ hai điểm cực trị là:

12

1, 3xx

nên:

12

2

4

6

3

9

3

b

xx

ba

a

c c a

xx

a



   

























.

Xét phương trình

   

f x f m

, ta được:

   

3 2 3 2

3 3 2 2

( ) 0

ax bx cx d am bm cm d

a x m b x m c x m

      

      

   

 

  

 

   

 

3 3 2 2

22

6 9 0

6 ...

... 9 0

6 6 9 0

0

6 6 9 0

a x m a x m a x m

x m x mx m x m x m

xm

x m x mx m x m

x m x m x m m

xm

x m x m m

      

       

  



       





       











     



Để phương trình

   

f x f m

có ba nghiệm

phân biệt thì phương trình:

22

( 6) 6 9 0x m x m m     

có hai nghiệm

phân biệt khác

 

*xm

.

 

22

2

( 6) 4 6 9 0

*

( 6) 6 9 0

3 12 0

3 12 9 0

04

1, 3

m m m

m m m m m

mm

m

mm



      







     







  





  















Vậy

(0;4) \{1,3}m

.

Đáp án D

Câu 48. Để hàm số

 

y f x

có đúng

3

điểm

cực trị thì hàm số

   

32

1 5 3 3y m x x m x     

có 2 cực trị trái dấu.

Trước hết cần điều kiện:

1 0 1mm   

.

Ta có:

 

2

3 1 10 3'y m x x m    

.

Để hàm số

   

32

1 5 3 3y m x x m x     

có

2

cực trị trái dấu thì phương trình

0'y 

có

2

nghiệm trái dấu.

  

3 1 3 0 3 1m m m       

.

Kết hợp điều kiện

{ 2; 1;0}mm    

.

Với

1m 

thì hàm số trở thành:

2

5 4 3y x x   

có

1

cực trị

2

0

5

x 

.

Khi đó hàm số

 

fx

có đúng

3

điểm cực trị.

Vậy

 

2; 1;0;1m  

.

Đáp án C

Extra Techniques:

Tips:

Xét hàm số:

 

y f x

liên tục trên

K

. Giả sử hàm số có

n

điểm cực trị

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

231

[ I can't, I can! ]

dương khi đó số điểm cực trị của đồ

thị hàm số

 

y f x

là

21n 

.

Câu 49. Xét hàm số:

 

12y f x

.

Ta có:

 

' 2 ' 1 2 0y f x   

.

1

12

2

1 2 1

2

a

x

xa

x b b

x

















  











, với

;x a x b

là

hai điểm cực trị của hàm số

 

y f x

.

Vậy hàm số

 

12y f x

có hai điểm cực trị

là

11

;

22

ab

xx





.

Đáp án B

Extra Techniques:

Remark:

Số điểm cực trị của hàm

 

f ax b

bằng

số điểm cực trị của hàm

 

fx

vì hàm

 

f ax b

được sinh ra bởi các phép tịnh

tiến và co dãn hàm

 

fx

.

Câu 50. Ta có:

3

' 16 12 4 0y x x   

.

 

2

1

(2 1) ( 1) 0

2

1

x NBC

xx

x







    







.

Nhận thấy, hàm số có đúng một nghiệm bội lẻ

và đạo hàm đổi dấu từ âm sang dương khi đi

qua nghiệm

1x 

(do:

 

' 1 0

ya

yb



















).

Nên hàm số có đúng một điểm cực tiểu.

Đáp án A

Câu 51. Số điểm cực trị của hàm số

 

y f x

chính bằng tổng số nghiệm bội lẻ của phương

trình

 

'0fx

.

Ta có:

 

3

0

'0

3

8

x

fx

x

x NBC

























.

Như vậy chỉ có ba nghiệm

3, 0, 3x x x   

là ba nghiệm bội lẻ.

Vậy hàm số

 

y f x

có ba điểm cực trị.

Đáp án A

Extra Techniques:

Tips:

Dấu hiện để nhận biết nghiệm bội lẻ.

Nghiệm bội lẻ của phương trình

 

'0fx

được hiểu đơn giản là

nghiệm của phương trình

 

'0fx

mà tại đó dấu của

 

'fx

thay đổi

(Đổi từ âm sang dương hoặc ngược

lại).

Câu 52. Xét hàm số:

32

3 5 2y x x x    

.

Ta có:

2

' 3 6 5y x x   

.

 

2

' 3 6 3 2

' 3 1 2 2 0,

y x x

     

         

Nên hàm số

32

3 5 2y x x x    

nghịch biến

trên .

Vậy hàm số

32

3 5 2y x x x    

không có

điểm cực trị.

Đáp án A

Câu 53. Cho hàm số

 

y f x

xác định.

+) Nếu

 

0

fx

















nên

0

xx

là điểm cực

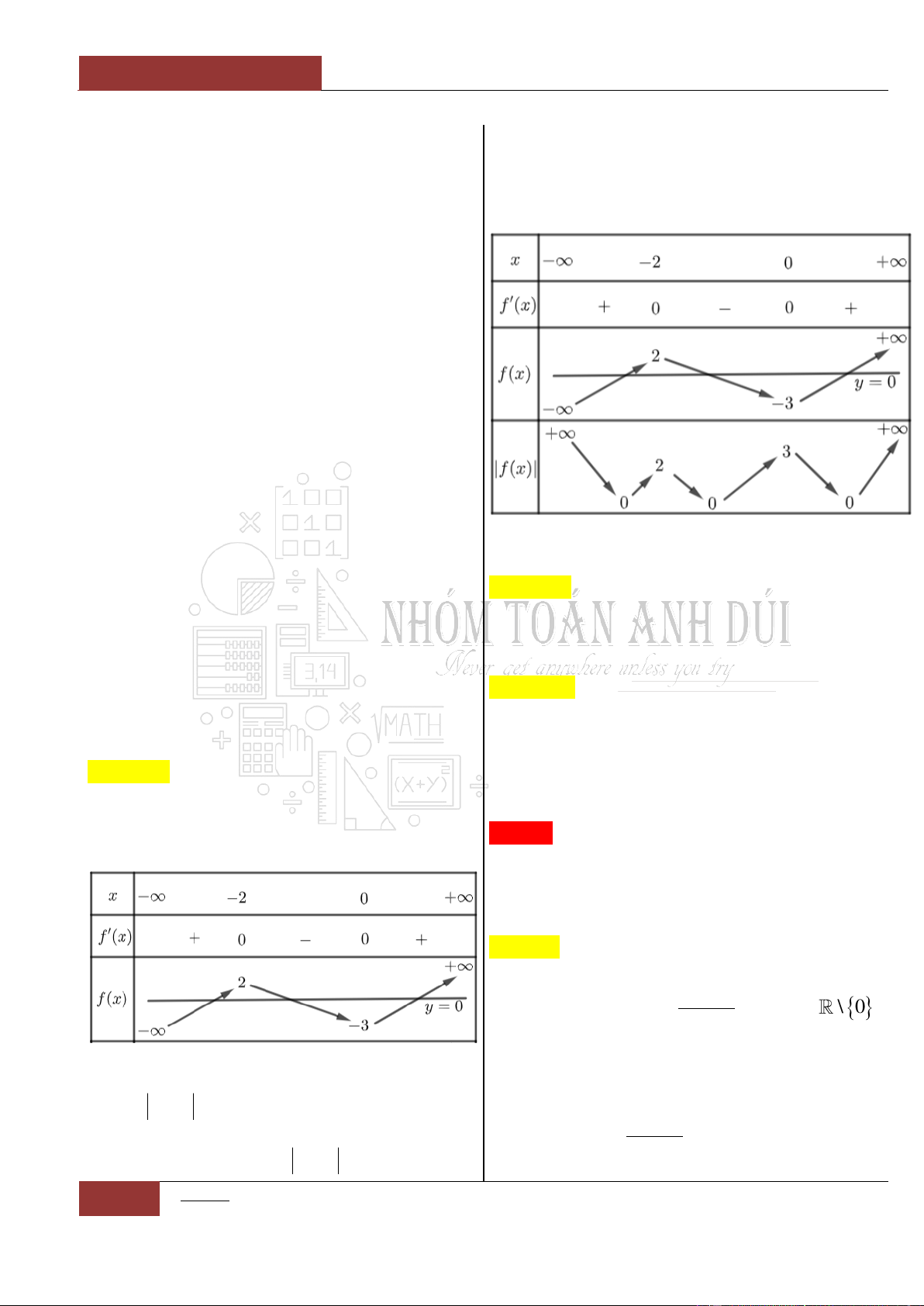
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

232

[ I can't, I can! ]

tiểu của hàm số

 

y f x

.

+) Nếu

 

0

fx

















nên

0

xx

là điểm cực đại

của hàm số

 

y f x

.

+) Trường hợp

 

0

'0

'' 0

fx













thì ta cần phải

kiểm tra lại lần nữa.

Hàm số

42

y x mx

có:

3

2

42

12 2

y x mx

y x m



















. Để

hàm số đạt cực tiểu tại

0x 

thì điều kiện ban

đầu, hàm số phải thỏa

3

2

4.0 2 .0 0

12.0 2 0

m















00

0

m





  







.

Với

3

2

4.0 2 .0 0

0

12.0 2 0

m

















.

Thử lại, với

 

4

0m f x x  

là hàm số nhận

điểm

0x 

là điểm cực tiểu.

Vậy:

0m 

.

Đáp án C

Câu 54.

Ta tiến hành kẻ đường thẳng

0y 

trên bảng

biến thiên khi đó ta có:

Ta có:

 

   

,0

f x f x

fx

f x f x

















.

Do đó đồ thị hàm số

 

y f x

gồm hai phần:

Phần 1: Là phần đồ thị nằm trên trục hoành.

Phần 2: Lấy đối xứng phần của đồ thị dưới trục

Ox

qua

Ox

.

Khi đó bảng biến thiên sẽ là:

Nhìn vào bảng biến thiên ta thấy hàm số có

5

điểm cực trị, trong đó có

3

cực tiểu.

Đáp án C

Câu 55. Dựa vào bảng biến thiên ta có giá trị

cực tiểu là

3

CT

y 

.

Đáp án B.

Câu 56. Xét từng đáp án:

Đáp án A: Hàm số

42

32y x x  

có

1

cực

trị.

Loại A.

Đáp án B: Đây là hàm số bậc

3

có

2

3 25 0b ac  

. Do đó, hàm số có

2

cực trị.

Chọn B.

Đáp án C: Ta có:

 

2

21

0, \ 0

3

x

yx

x





   

Do đó, hàm số này đồng biến trên từng khoảng

xác định của nó.

Vậy hàm số

2

21

3

x

y

x





không có cực trị.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

233

[ I can't, I can! ]

Loại C.

Đáp án D: Ta có:

53

2017.6 2016.4y x x





.

 

32

0 2017.6 2016.4 0y x x x



    

Do đó hàm số này có đúng

1

cực trị.

Loại D.

Đáp án B

Câu 57. Hàm số trùng phương luôn đạt cực trị

tại

0x 

. Do đó:

1 2 3

. . 0x x x 

.

Đáp án D

Câu 58. Ta có:

   

 

0

. 0 1

1

fx

g x f f x f x f x

fx









  

   







.

Phương trình

 

1

0

1

x

fx

x















.

Phương trình

   

1

1 0;1

1

xa

f x x b

xc

  





   







.

Phương trình

 

11f x x d     

.

Như vậy phương trình

 

'0gx

có

6

nghiệm

thực phân biệt.

Vậy hàm số

 

y g x

có

6

cực trị.

Đáp án B

Câu 59. Ta có:

 

2

2 2 2y x f x x



  

.

Suy ra:

 

2

2 2 0

0

20

x

y

f x x



















.

 

2

1

2 ; 1

2 1;0

2 0;1

2 1;

x

x x a

x x b

x x c

x x d







    



    



  



   



.



2

20x x a  

có

 

1 0 ; 1aa



       

nên phương trình

vô nghiệm.



2

20x x b  

có

 

1 0 1;0bb



      

nên phương trình có 2 nghiệm phân biệt.



2

20x x c  

có

 

1 0 0;1cc



     

nên phương trình có 2 nghiệm phân biệt.



2

20x x d  

có

 

1 0 1;dd



      

nên phương trình có 2 nghiệm phân biệt.

Như vậy phương trình đạo hàm

 

2

2 2 2 0y x f x x



   

có tất cả

7

nghiệm đơn.

Vậy hàm số

 

2

2y f x x

có tất cả

7

điểm

cực trị.

Đáp án D

Câu 60. Xét hàm số:

42

( ) 2y f x x mx  

, có:

3

2

0

' 4 4 0

x

y x mx

xm





   







.

Ta xét các trường hợp:

Trường hợp 1: Hàm số

42

( ) 2y f x x mx  

có đúng một cực trị là

0

tức là

0m 

.

(Vì hàm số bậc bốn trùng phương có một cực trị

khi và chỉ khi tích

0ab 

).

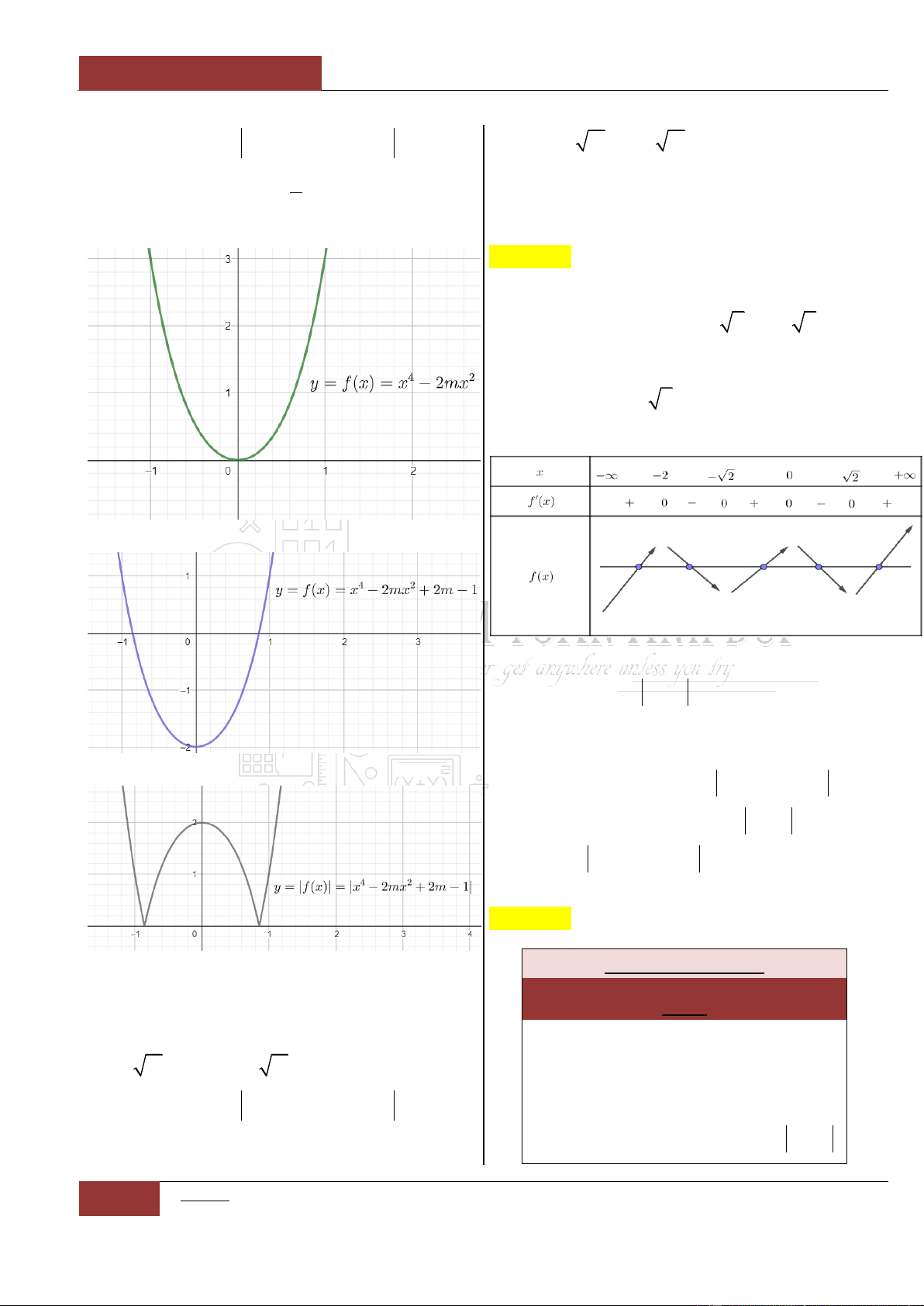
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

234

[ I can't, I can! ]

Do đó hàm số

42

2 2 1y x mx m   

có ba cực

trị khi

1

2 1 0

2

mm   

.

Minh họa bằng hình vẽ bên dưới:



Vậy:

 

2; 1;0m   

.

Trường hợp 2: Hàm số

42

( ) 2y f x x mx  

có đúng

3

điểm cực trị lần lượt là:

, 0,x m x x m   

tức là

0m 

.

Do đó hàm số

42

2 2 1y x mx m   

có ba

cực trị khi:

   

2

2 1 0 1

CT

y y m y m m m m         

(thỏa mãn).

Vậy qua hai trường hợp trên ta thấy có

4

giá trị

của

m

thỏa mãn.

Đáp án D

Câu 61. Xét hàm số

 

y f x

, ta có:

   

  

3

2 2 2f x x x x x



   

.

Do đó hàm số

 

fx

có

4

điểm cực trị là:

0; 2; 2x x x    

.

Bảng biến thiên của hàm số

 

fx

:

Suy ra

 

0fx

có tối đa

5

nghiệm phân biệt.

Do đó hàm số

 

y f x

có tối đa

4 5 9

điểm cực trị.

Mặt khác:

Số điểm cực trị hàm số

 

1 2018y f x

bằng

số điểm cực trị của hàm số

 

.y f x

Do đó

hàm số

 

1 2018y f x

có tối đa

9

điểm cực

trị.

Đáp án A

Extra Techniques:

Tips:

Số điểm cực trị của hàm số

 

y f x

và số điểm cực trị của hàm số

 

y f ax b

là như nhau. Điều đó

cũng đúng đối với hàm số:

 

y f x

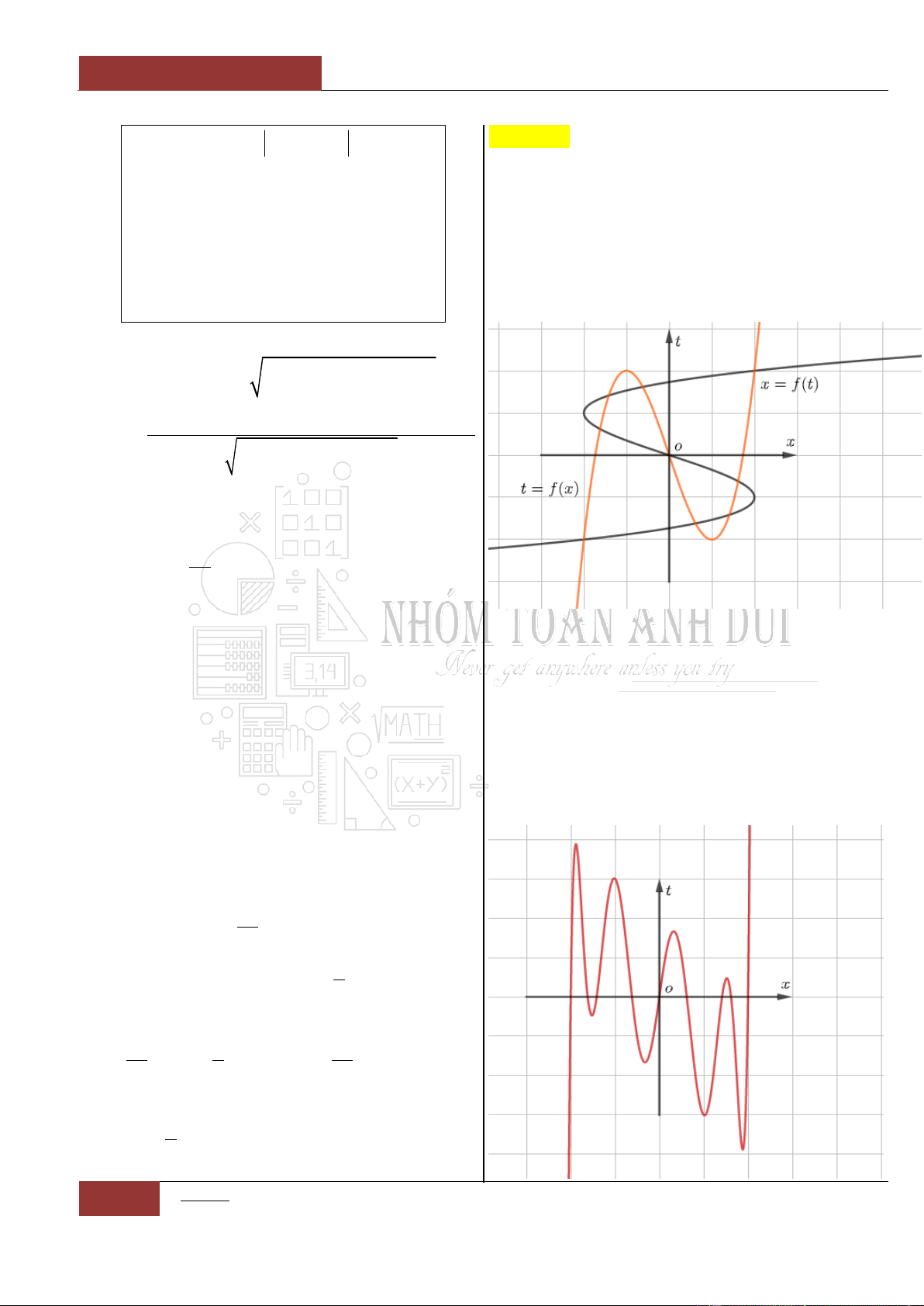
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

235

[ I can't, I can! ]

và hàm số

 

y f ax b

. Do hàm

số

 

y f ax b

thực chất là hàm số

 

y f x

qua các phép co dãn đồ thị

và tịnh tiến đồ thị sang ngang (trái,

phải). Nên sẽ không làm ảnh hưởng

đến số cực trị hàm trị tuyệt đối.

Câu 62. Ta có:

   

2

y f x f x m



  



.

         

   

2

2 ' '

'

f x f x m f x f x f x

y

f x f x m



  













'0y 

.

 

   

     

2

0

2

'0

1

2

0

1

3

0

01

fx

f x f x m

x

xx

f x f x m















  





















  





Đặt

 

t f x

,

 

2

10t t m   

 

*

.

Ta đã tìm được

3

điểm cực trị là

0

1; 3; 0x x x x   

.

Nên để hàm số đã cho có đúng

3

điểm cực trị

thì phương trình

 

*

vô nghiệm hoặc có

nghiệm kép là

1

2

t





.

Suy ra:

1

1 4 0

4

mm     

.

Thử lại, ta thấy:

2

1 1 1

0

4 2 2

m t t





     





(Thỏa mãn

yêu cầu đề bài).

Vậy

1

4

m 

.

Đáp án B

Câu 63. Cách 1:

Đặt

( ) ( ( ))k x f f x x

và

()t f x

. Bây giờ ta

xét số nghiệm của phương trình

( ) 0 ( )k x f t x  

. Để khảo sát ta xét tương

giao hàm

 

fx

và hàm

 

ft

trên hệ trục tọa

độ

Oxt

.

Trong đó đường màu cam là đồ thị

()t f x

.

Từ đồ thị ta thấy được chúng có

9

giao điểm

tức là phương trình

 

0kx

có

9

nghiệm và

 

kx

là đa thức bậc

9

nên buộc có

8

cực trị.

Trong đó có

4

nghiệm dương,

4

nghiệm âm và

một nghiệm bằng

0

. Ta có thể phác họa đồ thị

 

y k x

như sau:

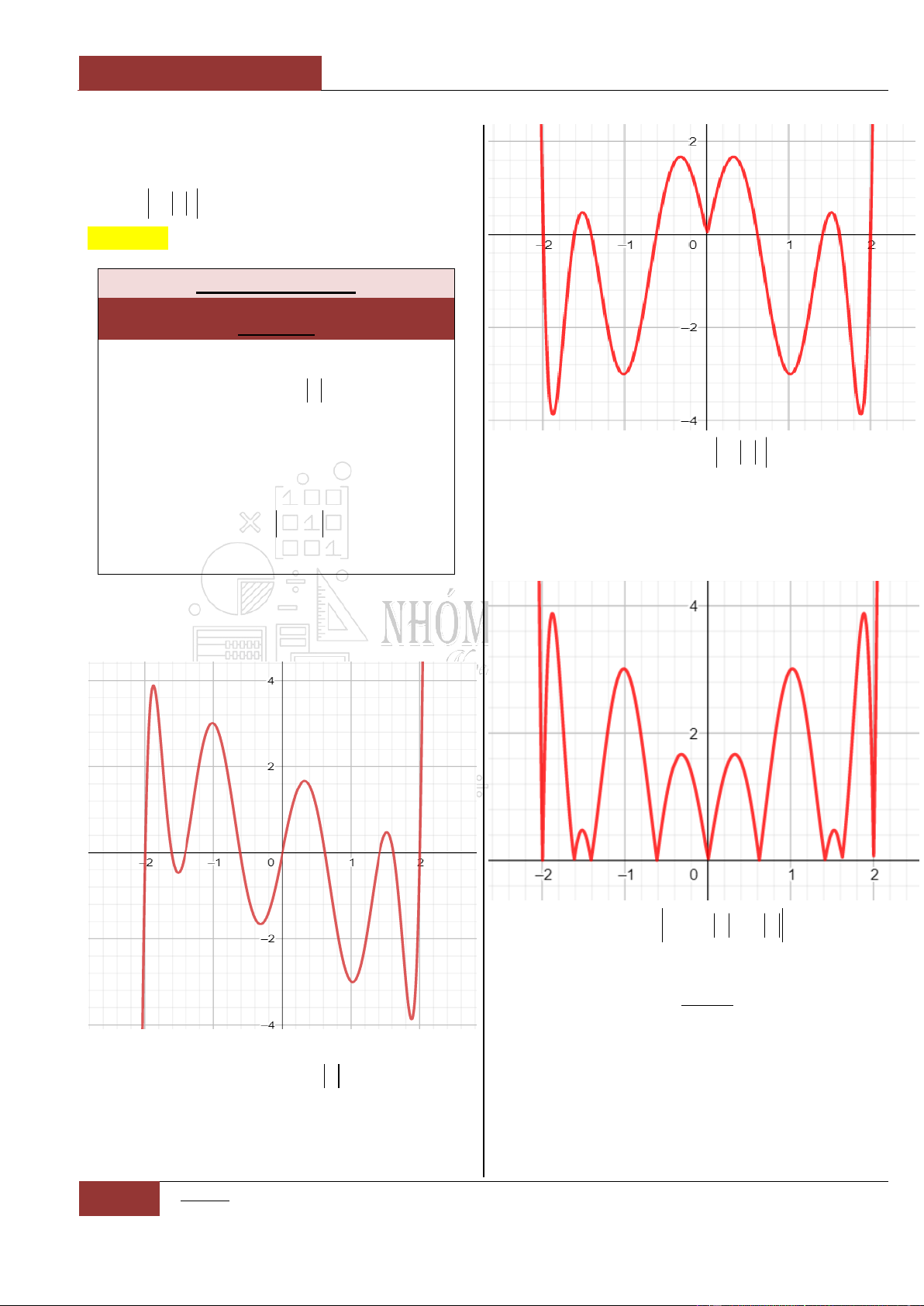
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

236

[ I can't, I can! ]

Rõ ràng

 

y k x

không chỉ có

4

nghiệm

dương mà còn có

4

cực trị dương nên hàm

 

()g x k x

có

2.8 1 17

điểm cực trị.

Đáp án B

Extra Techniques:

Remark:

Giả sử hàm số

 

y f x

có

n

điểm cực trị

dương thì hàm số

 

y f x

có tất cả

21Sn

điểm cực trị.

Giả sử hàm số

 

y f x

có

m

điểm cực

trị và phương trình

 

0fx

có

n

nghiệm

bội lẻ thì hàm số

 

y f x

có tất cả

S m n

điểm cực trị.

Cách 2:

Phác họa đồ thị hàm số:

 

y k x

.

Khi đó đồ thị hàm số:

 

y k x

có được bằng

cách lấy đối xứng phần bên phải trục tung sang

trái (Bỏ phần đồ thị bên trái trục hoành). Minh

họa như hình vẽ.

Tiếp đó, đồ thị hàm số:

 

y k x

có được

bằng cách giữ lấy phần phần đồ thị nằm trên

trục tung và lấy đối xứng phần đồ thị nằm ở

dưới trục tung lên phía trên. Minh họa bằng đồ

thị như hình vẽ bên dưới.

Như vậy hàm số

 

y f f x x

có tất cả

17

cực trị.

Câu 64. Xét:

32

21

2 2022

2

m

y x x x





   





.

Ta có:

 

2

' 3 2 1 2y x m x   

.

Hàm số có hai điểm cực trị khi phương trình

'0y 

có hai nghiệm phân biệt.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

237

[ I can't, I can! ]

   

22

1

2 1 6 0 2 1 24 (*)

4

mm



       

Theo định lý Viete ta có:

12

21

3

2

3

m

xx



















.

Vì:

 

1

12

2

1

21

32

5

3

1

2 3 3

11

15

m

xm

xx

x x m

xm



















  







.

Thế vào

12

2

.

3

xx

, ta được:

   

 

12

2

2 1 1 2

3 2 . 11

3 5 15 3

12

3 31 22

75 3

x x m m

mm

   

    

   

   

   

.

 

2

1

2

3 31 22 50

3 31 72 0

1

5 73 31

6

1

5 73 31

6

mm

m

   













  





12

5 73

3

5

, 73, 0

3

mm

a b c

  

   

12( ) 896A a b c   

.

Đáp án A

Câu 65. Dựa vào đồ thị ta có

be

và

0c 

.

Khi đó

   

3

2

:C y g x x dx b   

. Ta cần tìm

tung độ của hai điểm

,AB

(theo

a

).

 

2

'( ) 2 4

'3

f x x x a

g x x d















.

 

2

0

'0

4

'0

3

x

a

fx

x

gx

d

x

































.

Theo đề bài ta có

0

a

d











và

3

4 3 4

a d a

d



  

Khi đó:

2

48

34

B

A

aa

y f b

d a a

y f b







   

















   









.

2

84

aa

AB a



  

.

Đặt:

0

2

a

t





.





 

43

2

2022

22

0 7.64311

0

116.834;0

7.64

116; 115;...; 1

tt

AB

t

a

t

a

   

  





  







    

Suy ra có

116

giá trị nguyên của

a

thỏa mãn

yêu cầu đề bài.

Đáp án B

Câu 66. Ta có:

       

   

2022

2023

2023 . 1 ...

...

g x f x f x f x

f x f x

   

  

   

   

 





Do:

 

0fx





.

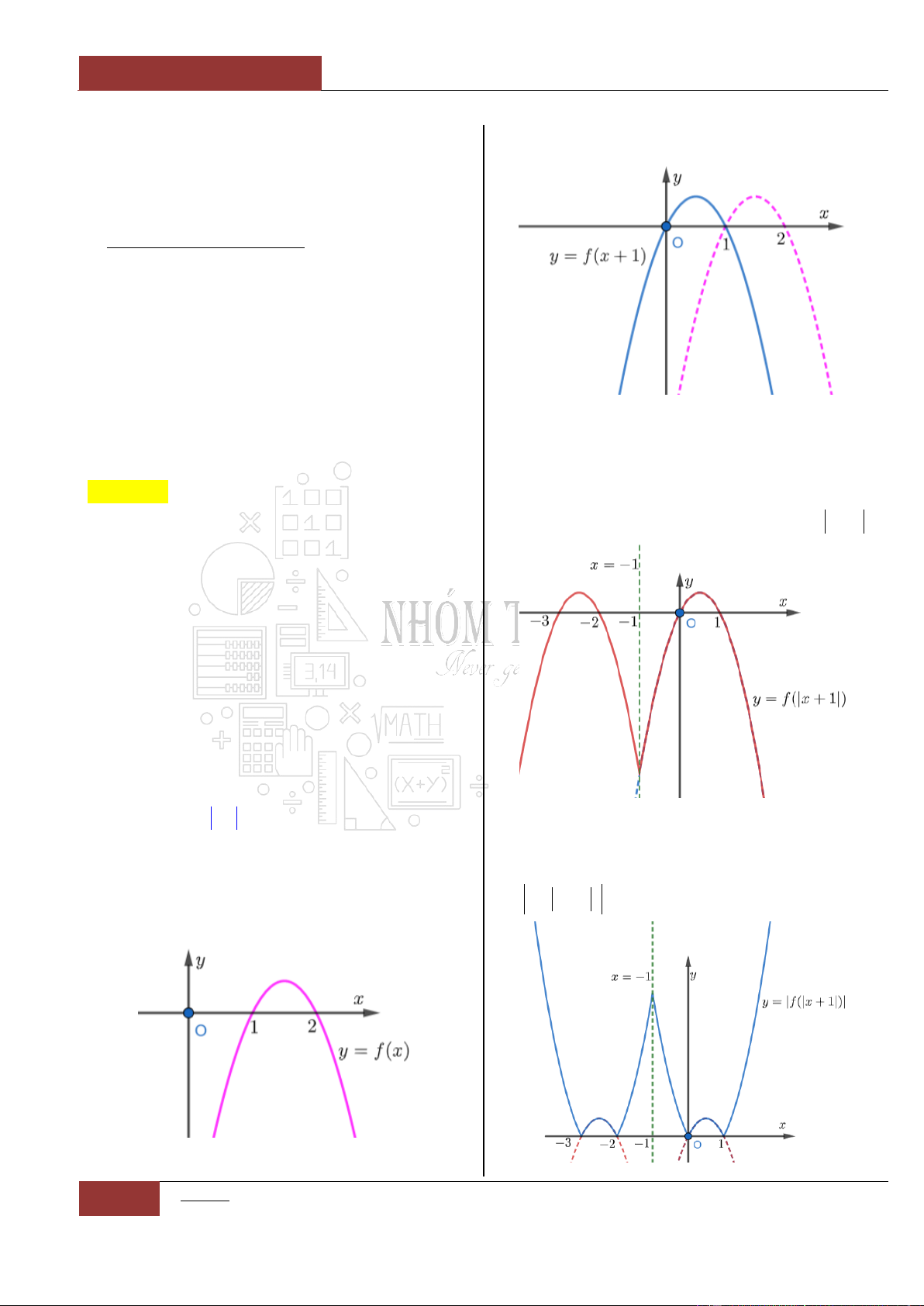
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

238

[ I can't, I can! ]

       

2022

2023 . . 1g x f x f x f x

   

  

   

   

.

Từ giả thuyết ta có:

   

2022

'1f x f x





   

   

   

 

2 2023

2 1 2022

''

x x x

fx





.

     

   

2022

2 2023

. 1 .

2 1 2022

f x f x f x

x x x

  

  

   

   

  

.

     

2 2023

2023.2 1 2022g x x x x



   

.

Ta thấy:

0, 2022xx

là các nghiệm đơn nên

hàm số

 

y g x

có

2

điểm cực trị.

Đáp án B

Câu 67. Do hàm số

 

y f x

nghịch biến trên

khoảng

 

0

;x 

nên

0a 

.

Mặt khác, đồ thị hàm số

 

y f x

cắt trục

hoành tại hai điểm có hoành độ là

1, 2xx

nên

 

10

20

f















, hay:

    

12f x a x x  

.

Suy ra:

 

2

32f x ax ax a  

.

Khoảng cách từ giao điểm của Parabol với trục

tung đến điểm

O

bằng

4

nên ta có:

2 4 2aa   

.

Vì:

02aa   

.

Vậy:

 

2

2 6 4f x x x   

.

Vẽ đồ thị hàm số:

 

2

2 6 4y f x x x    

.

Tịnh tiến đồ thị hàm số

 

y f x

sang trái

1

đơn vị, ta thu được đồ thị hàm số

 

1y f x

.

Giữ nguyên phần đồ thị phía bên phải đường

thẳng

1x 

, bỏ phần đồ thị phía bên trái

đường thẳng

1x 

, sau đó lấy đối xứng sang

trái phần đồ thị nằm bên phải đường thẳng

1x 

, ta thu được đồ thị hàm số

 

1y f x

Giữ nguyên phần đồ thị phía trên trục hoành và

lấy đối xứng phần đồ thị nằm bên dưới trục

hoành lên trên, ta thu được đồ thị hàm số

 

1y f x

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

239

[ I can't, I can! ]

Vậy hàm số

 

1y f x

có tất cả

7

điểm

cực trị.

Đáp án D

Câu 68. Theo bảng biến thiên ta thấy đồ thị

hàm số

 

y f x





chỉ chạm (tiếp xúc) trục

hoành chứ không cắt qua trục hoành nên

phương trình

 

0fx





có hai nghiệm bội chẵn

là

2x 

và

2x 

, suy ra đồ thị hàm số

 

y f x

không có điểm cực trị.

Đáp án C

Extra Techniques:

Remark:

Hàm số

 

y f x

đạt cực trị tại các điểm

mà tại đó đạo hàm

 

'fx

đổi dấu và hàm

số

 

y f x

liên tục.

Vì:

 

' 0,f x x  

.



Hàm số

 

y f x

đồng biến trên .

Vậy hàm số

 

y f x

không có điểm cực

trị.

Câu 69. Ta có:

 

2

32f x ax bx c



  

.

Theo giả thuyết, ta có:

 

12

10

21

20

f















  









.

2

3 2 0

8 4 2 1

12 4 0

a b c d

a b c

a b c d

a b c

   





  







     



  



.

2

9

1

3

4

3

11

9

a

b

A

c

d











  













.

Đáp án C

Câu 70. Ta có:

 

2

9

81

2

y x mx m



   

.

Hàm số

y

có hai điểm cực trị khi phương trình

0y





có hai nghiệm phân biệt.

 

23 18 9mm



    

.

Theo định lý Viéte ta có:

 

12

2

12

16

9

21

9

m

xx

m

xx



  















.

Khi đó:

1 2 1 2

x x x x

 

2

2 16

1

99

mm   

.

2

2 2 3

6 1 0

2 2 3

m

mm

m





    



  





   

10; 6 0;10m    

.

Vậy có

16

giá trị nguyên của

m

thỏa mãn.

Đáp án C

Câu 71. Đặt

 

   

34

f x f x

y g x  

.

Quan sát đồ thị ta thấy hàm số

 

y f x

có ba

điểm cực trị hay phương trình

 

'0fx

có ba

nghiệm thực phân biệt.

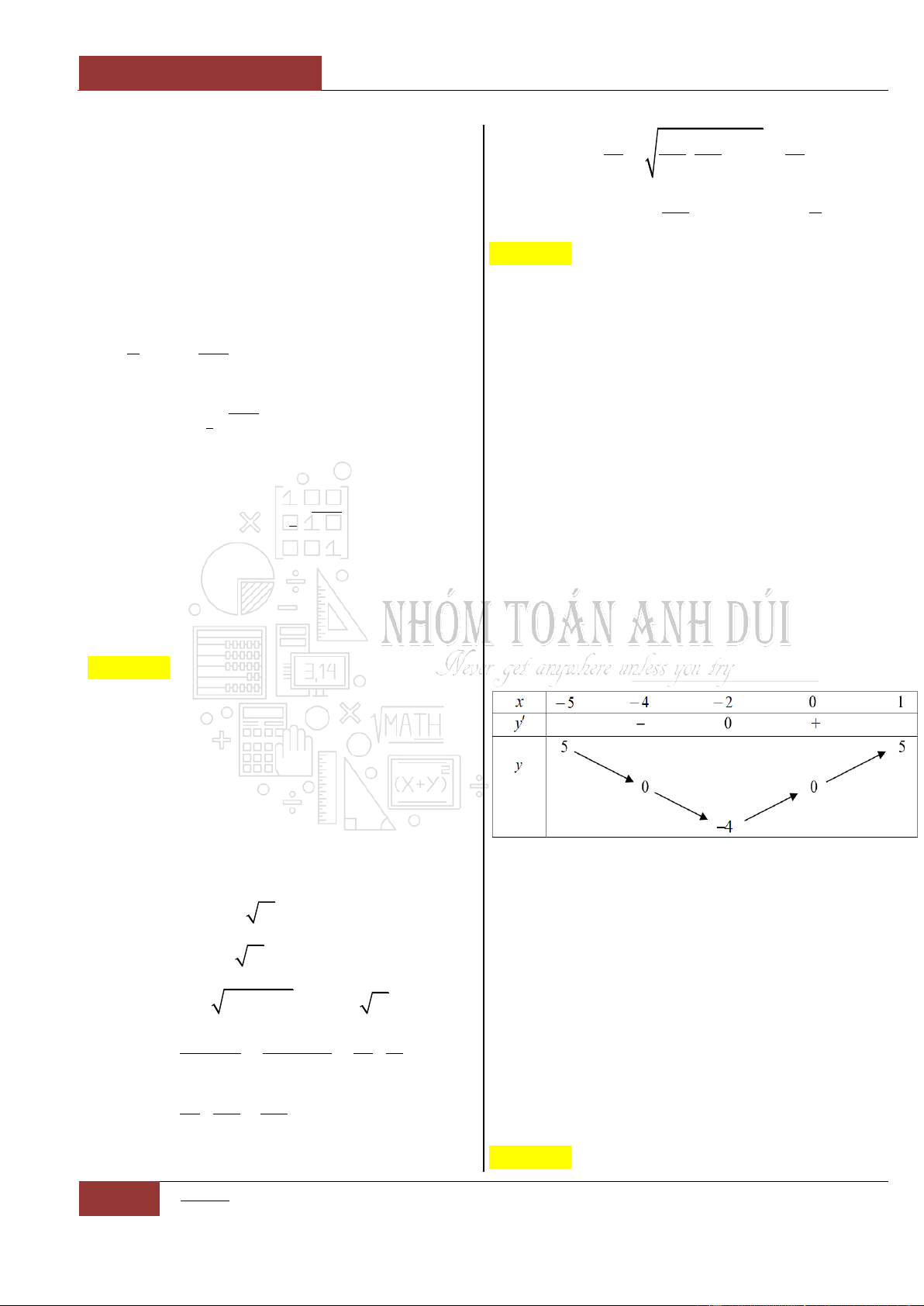
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

240

[ I can't, I can! ]

Ta có:

 

   

. 3 .ln3 4 .ln4

f x f x

y f x









.

 

   

0

3 .ln3 4 .ln4 0

f x f x

fx

y









  









.

Ta có:

   

3 .ln3 4 .ln4 0

f x f x



.

 

3

4

3 ln4

4 ln3

ln4

log 0.8

ln3

fx











   





.

Dựa vào đồ thị hàm số

 

y f x

, ta thấy

phương trình

 

3

4

ln4

log

ln3

fx









có

2

nghiệm

phân biệt khác các nghiệm của phương trình

 

0fx





nên hàm số

   

34

f x f x

y 

có tất cả

5

điểm cực trị.

Đáp án C

Câu 72. Ta có

3

88y x mx





.

2

0

x

y

xm















.

Hàm số có ba cực trị khi và chỉ khi

0m 

.

Khi đó tọa độ ba điểm cực trị là:

 

2

(0;1)

; 2 1

A

B m m

C m m





  









.

4

4 , 2AB AC m m BC m    

.

Ta có:

4

2

42

. 4 1 1

4

16

AB AC m m

Tm

m

BC m





   





.

2

1 1 1

4

16 2 2

Tm

mm



  





.

Ta có:

2

3

1 1 1 3

.3. . .4

16 2 2 16

Cauchy

Tm

mm



.

Dấu

""

xảy ra khi

2

11

4 0.

22

mm

m

   

Đáp án D

Câu 73. Đặt:

 

22

44g x f x x x x   

.

   

 

2

2 4 4 2 4g x x f x x x



     

   

 

2

' 2 4 4 1g x x f x x





    



.

Ta có:

 

   

2

2 4 0

4 4 1

0

4 0 2

4 1;5 3

x

xx

gx

xx

x x a







  













  



.

Xét phương trình

 

2

4 1;5x x a  

, ta có bảng

biến thiên của hàm số

2

4y x x

trên

 

5;1

như sau:

Suy ra

 

1

có nghiệm kép

2x 

,

 

2

có

2

nghiệm phân biệt

4; 0xx  

,

 

3

có

2

nghiệm phân biệt

12

;x x x x

khác

2; 0; 4

.

Do đó phương trình

 

0gx





có

5

nghiệm

trong đó có

2x 

là nghiệm bội ba, các

nghiệm

4; 0xx  

;

12

;x x x x

là các

nghiệm đơn.

Vậy

 

gx

có

5

điểm cực trị.

Đáp án A

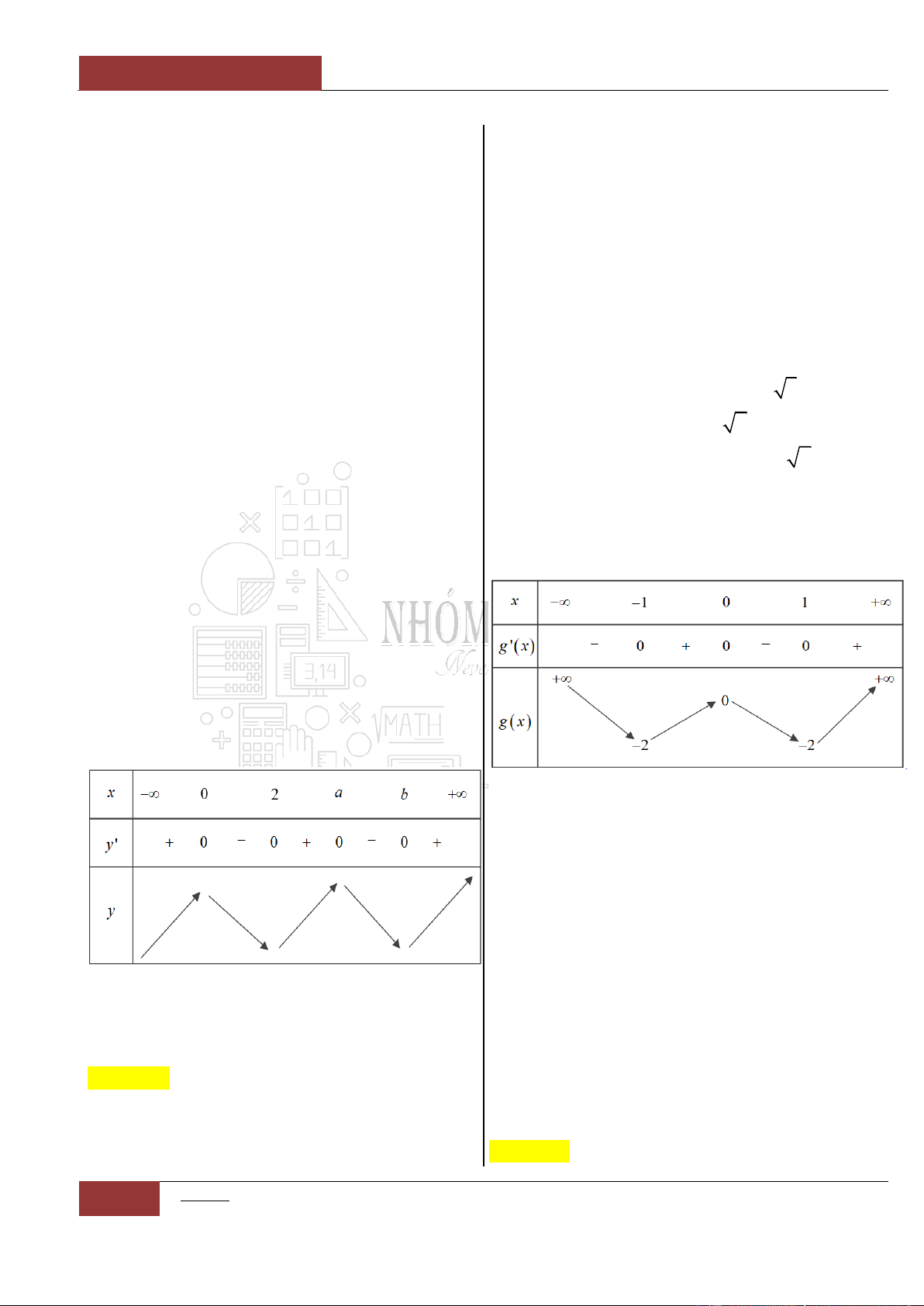
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

241

[ I can't, I can! ]

Câu 74.

Xét hàm số

 

y f f x





.

Ta có:

   

.y f x f f x

  







.

 

0

fx

y

f f x

























 

00

22

0 2;

2;

xx

f x x a

f x x b a















   



   





.

Với

xb

, ta có:

 

2fx

 

0f f x









.

Với

a x b

, ta có:

 

02fx

 

0f f x









.

Với

0 xa

hoặc

0x 

, ta có:

 

0fx

 

0f f x









.

Bảng biến thiên:

Dựa vào bảng biến thiên suy ra hàm số

 

y f f x





có

4

điểm cực trị.

Đáp án C

Câu 75.

Từ đồ thị ta thấy:

2

;

0

;

2

;

a

;

6

là tất cả các

nghiệm của phương trình:

 

0fx





.

Ta có:

     

6 2 5 6 2

' 3 6 6 . 3y f x x x x f x x



    

.

 

5

62

6 6 0

'0

30

xx

y

f x x

















62

0, 1

32

30

32

3

36

xx

x x a

xx

  





  























4

0, 1

1

0, 3

2

,2

,

xx

x

xx

x

x m m

x n n m

  









  











  



  



.

Bảng biến thiên của hàm số

 

62

3g x x x

.

Dựa vào bảng biến thiên của hàm số

 

62

3g x x x

, ta suy ra

1x 

là nghiệm kép

của phương trình

62

32xx  

và

0x 

là

nghiệm kép của phương trình

62

30xx

. Do

đó

1x 

và

0x 

là nghiệm kép của

 

62

3f x x





. Do vậy

1x 

và

0x 

là

nghiệm bội ba của phương trình

0y





.

Các nghiệm khác

1x 

và

0x 

của

y



đều là

nghiệm đơn.

Vậy hàm số đã cho có

11

cực trị.

Đáp án B

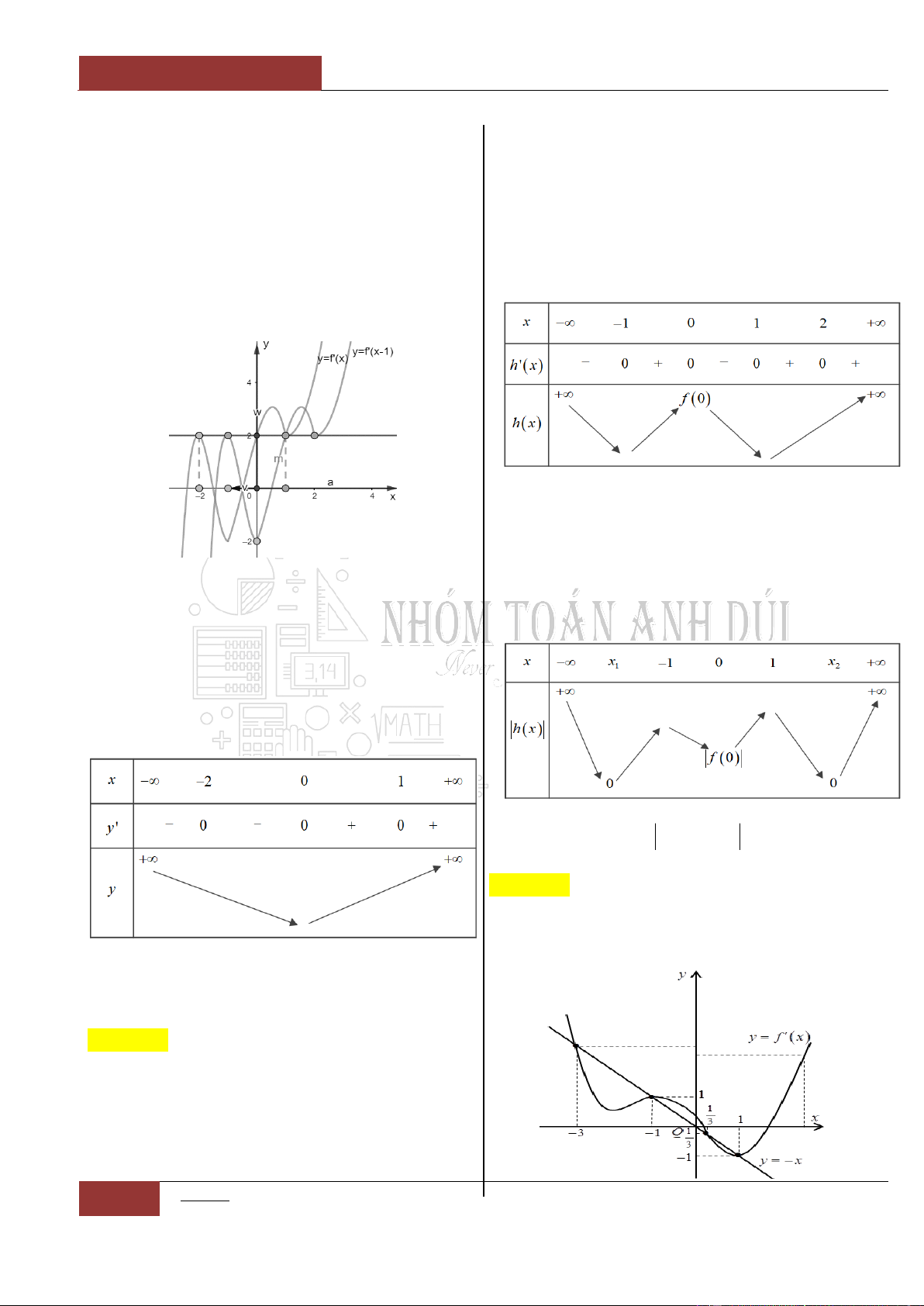
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

242

[ I can't, I can! ]

Câu 76. Ta có:

 

24

2 4 ln

f x x

y f x













.

Suy ra:

   

0 2 4 0 2y f x f x

  

     

.

Đồ thị hàm số

 

y f x





nhận được từ việc tịnh

tiến đồ thị hàm số

 

1y f x





sang trái

1

đơn vị.

Nên:

 

2fx





2

0

1

x















.

Do

2x 

và

1x 

là nghiệm bội chẵn nên ta

có bảng biến thiên sau:

Từ bảng biến thiên ta có hàm số đạt cực tiểu tại

0x 

.

Đáp án B

Câu 77. Đặt

   

3h x f x x

.

Ta có:

   

3h x f x





.

     

0 3 0 3h x f x f x

  

      

.

Theo đồ thị của hàm số

 

fx



, thì phương trình

 

3fx





có

4

nghiệm

 

1;0;1;2

.

Ta có bảng biến thiên

Theo bảng biến thiên ta có phương trình

 

0hx

có hai nghiệm

1

1x 

và

2

1x 

(do

có

 

00f 

).

Khi đó ta có:

Vậy hàm số

   

3g x f x x

có

5

cực trị.

Đáp án B

Câu 78.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

243

[ I can't, I can! ]

   

5sin 1 5

5cos cos 5sin 1

22

x

g x xf x x







  





Ta có:

 

0gx





 

5sin 1 5

5cos . cos . 5sin 1 0

22

x

x f x x







   





cos 0

5sin 1

3

2

cos 0

5sin 1

1

5sin 1 5sin 1

2

22

5sin 1 1

23

5sin 1

1

2

x

xx

f

x



























   







































cos 0

sin 1

5sin 1 6

1

5sin 1 2 sin

5

2

1

5sin 1

sin

3

5sin 1 2

3

sin

5

x

xx

x





















  



      























3

22

3

2

11

sin 2 sin

55

11

sin sin

33

sin sin

55

xx

x

x arc x arc













  







   

       



   

   



   

   



   

   



   

   



   

   



(Vì:

02x





).

Suy phương trình

 

0gx





có

9

nghiệm,

trong đó có nghiệm

3

2

x





là nghiệm kép.

Vậy hàm số

 

y g x

có

7

cực trị.

Đáp án B

Câu 79. Xét hàm số:

 

3

h x f x x

.

Ta có:

 

23

' 3 . ' 1 0h x x f x  

.

   

2 3 3

2

1

3 . 1 0 0 1

3

x f x f x x

x



     

Đặt:

3

3 2 2

x t x t  

phương trình

 

1

trở

thành:

     

3

2

1

0 2

3

f t t

t





.

Vẽ đồ thị hàm

3

2

1

3

y

x



trên cùng hệ trục tọa

độ với hàm

 

y f x





.

Dựa vào đồ thị ta có:

 

3

2

1

3

ft

t





.

3

0 0 0

0

t b x b x b

ta

xa



     



  













.

Bảng biến thiên:

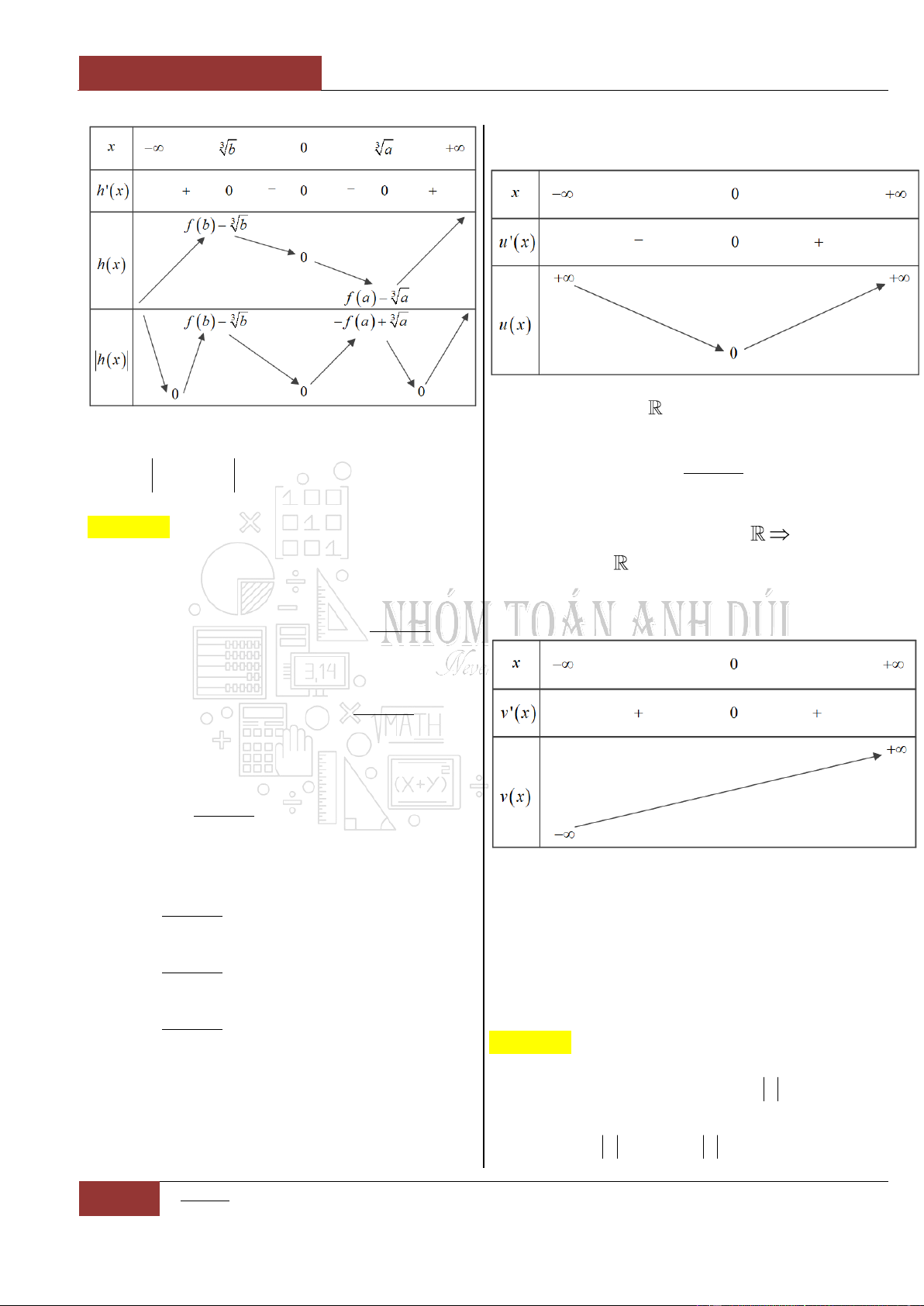
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

244

[ I can't, I can! ]

Dựa vào bảng biến thiên ta thấy: hàm số

 

3

g x f x x

có

5

điểm cực trị.

Đáp án A

Câu 80.

Ta có:

 

2

' 1 '

2

xx

g x e x f e





   





.

 

2

' 0 1 ' 0

2

xx

g x e x f e





     





.

2

10

2

'0

2

x

ex

xx

fe



  





















 

2

1 0 1

2

2 2

2

1 3

2

4 4

2

x

ex

xx

e

xx

e

xx

e



  







  























Xét hàm số:

 

1

x

u x e x  

.

Ta có:

   

' 1 ' 0 0

x

u x e u x x     

.

Bảng biến thiên:

Vậy

( ) 0,u x x  

.

Xét hàm số:

2

()

2

x

xx

v x e





.

Ta có

'( ) 1 0,

x

v x e x x      

hàm số

đồng biến trên .

Bảng biến thiên:

Khi đó các phương trình

     

2 , 3 , 4

có

nghiệm duy nhất và

 

'gx

đổi dấu qua các

nghiệm đó.

Vậy hàm số

 

gx

có

3

điểm cực trị.

Đáp án A

Câu 81. Xét hàm số:

 

22g x f x

.

 

   

'

' 2 2 ' 2 2g x x f x   

.

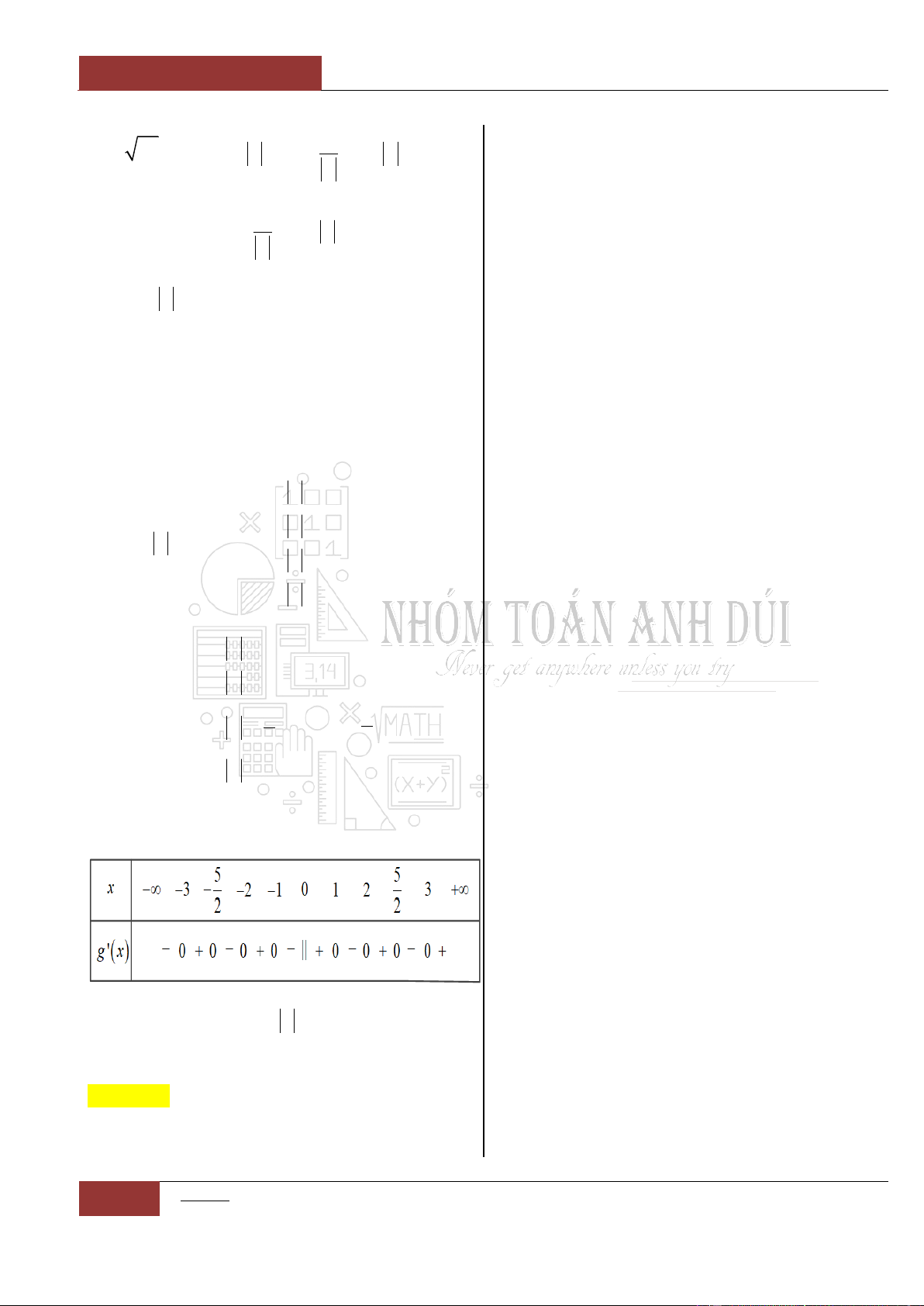
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

245

[ I can't, I can! ]





2

'

2 2 '(2 2) . '(2 2)

x

x f x f x

x

    

.

Ta có:

 

' 0 . ' 2 2 0

x

g x f x

x

   

 

' 2 2 0, 0f x x   

.

Dựa vào đồ thị ta có

0

2

'( ) 0

3

4

x

fx

x























.

2 2 0

2 2 2

'(2 2) 0

2 2 3

2 2 4

x

fx

x

  







   











.

1

2

5

2

3

x





































Ta có bảng xét dấu

 

'gx

:

Suy ra hàm số

 

22y f x

có

9

điểm cực

trị.

Đáp án D

Câu 82.

Ta có:

     

43

2

2 4 ...f x x x x



  

 

2

... 2 3 6 18x m x m



   



.

 

2

4

3

2

0

20

0

40

2 3 6 18 0

x

fx

x

x m x m





















    





   

2

0

2

4

2 3 6 18 0 *

x

x m x m



















    





.

Để hàm số

 

fx

có đúng một điểm cực trị thì

phương trình

 

*

vô nghiệm, có nghiệm kép

hoặc có hai nghiệm phân biệt trong đó có

nghiệm là

4

.

Trường hợp 1: Phương trình

 

*

vô nghiệm.

22

4 24 36 24 72 4 36 0m m m m         

33m   

 

2; 1;0;1;2m   

.

Trường hợp 2: Phương trình

 

*

có nghiệm kép.

2

3

4 36 0

3

m





     







.

Trường hợp 3: Phương trình

 

*

có hai

nghiệm phân biệt

1

x

,

2

x

. Trong đó

1

4x 

.

Phương trình có hai nghiệm phân biệt:

2

12

3

, 4 36 0

3

m

x x m

m





     







.

Theo định lí Viéte ta có:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

246

[ I can't, I can! ]

1 2 2

4 2 6

. 4. 6 18

S x x x m

P x x x m

       





    



.

2

22

39

22

xm

  









  





39

2 2 5

22

m m m       

.

Vậy

 

3; 2; 1;0;1;2;3;5m   

thỏa mãn yêu

cầu đề bài.

Đáp án C

Câu 83. Ta có:

2

5

4

x

yf

x













23

2 2 2 2

5 5 5 5

. 13 15

4 4 4 4

x x x x

a

x x x x



      

  

      

   

      

   

2 2 2

22

20 5 25 5 4

. ...

4

44

x x ax x a

x

xx



   











3

2

15 65 60

...

4

xx

x



  







.

0y







 

2

0

3

4

3

5 4 0 1

Nghieäm keùp

x

ax x a





















   



.

Đặt:

 

2

54g x ax x a   

.

Yêu cầu được thỏa mãn khi phương trình

0y





có

6

nghiệm bội lẻ hay phương trình có

hai nghiệm phân biệt khác

 

2;0;1;4

.

(Nếu

 

00g 

thì

0y





chỉ có

5

nghiệm bội

lẻ).

Điều kiện cần và đủ:

 

2

0

5 4 .4 0

20

00

30

4

0

3

a

aa

g









   



































0

55

44

5

4

0

15

13

a







  





















55

44

0

15

13

a



  













.

Đáp án B

Câu 84. Ta có:

   

''g x f x m

.

Số điểm cực trị của hàm số

 

gx

bằng số

nghiệm đơn (bội lẻ) của phương trình

 

'f x m

.

Dựa và đồ thị ta có điều kiện:

05

10 13

m











.

Vậy có

8

giá trị nguyên dương của

m

thỏa

mãn.

Đáp án B

 

1

Nhóm toán anh Dúi

[NG DÂY HÀM S]

251

[ I can't, I can! ]

Dạng 2. Cực trị hàm số và mối ràng buộc về điều kiện.

Câu 1. ng thm cc tr c th hàm

s

32

2 3 1y x x x   

là?

A.

26 15

99

yx  

. B.

25 15

99

yx

.

C.

26 15

99

yx

. D.

25 15

99

yx

.

 A

Li gii

Cách 1: Xét hàm s:

32

2 3 1y x x x   

.

Ta có:

2

2 13

' 3 4 3 0

3

y x x x



     

.

Gi

,AB

lm cm cc tiu c th hàm s

32

2 3 1y x x x   



2 13 97 26 13

;

3 27

2 13 97 26 13

;

3 27

A

B





  













  











.

Vector ch ng thng

AB

:

2 13 52 13

;

3 27

AB









.

Hay:

26 26

1; ;1

99

AB

AB n

   

  

   

   

là vector pháp tuyn cng thng

AB

.

ng thm cc tr

,AB

c th hàm s có



 

26

:0

9

d x y C  

mà

 

Ad

.



26 2 13 97 26 13 5

.

9 3 27 3

C

  

    

.

Vy:

 

26 5 26 15

:

9 3 9 9

d y x x     

ng thng cn tìm.

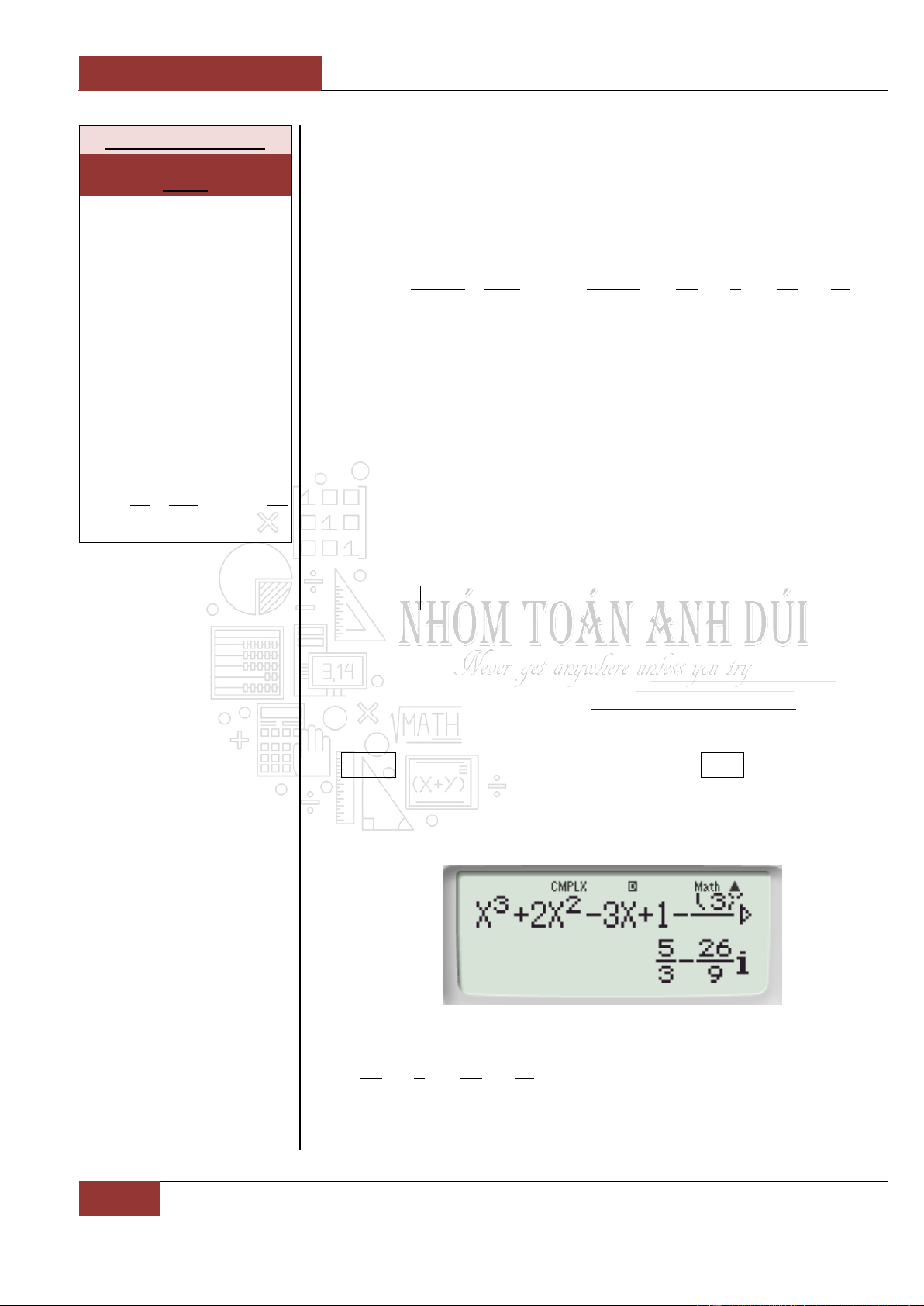
Nhóm toán anh Dúi

[NG DÂY HÀM S]

252

[ I can't, I can! ]

Extra Techniques:

Tips:

  c trình

bài  phn L

chc rng:

ng th

m cc tr (c i,

cc tiu) c th hàm

s

32

dy x xba cx   



2

22

3 9 9a

y

cb

a

d

c b

x



   





Cách 2: Dùng công thc.

ng thm cc tr c th hàm s:

32

2 3 1y x x x   

:

   

2

9

22. .

2. 26 5 26 15

3 9. 911. 9 3

1

3

2

9

3

y x x x



         









.

Cách 3: CASIO.

Xét hàm s:

32

2 3 1y x x x   

.

Ta có:

2

' 3 4 3

'' 6 4

y x x

yx



  







.

S dng máy tính cm tay bng cách nhp biu thc 

Chn MODE 2.

Nhp vào màn hình:

 

2

32

3 4 3 . 6 4

2 3 1

18.1

X X X

  

   

.

n CALC, nhp (  o, nhn nút ENG  gi ra màn

hình).

Màn hình xut hin kt qu:

Vng thm cc tr 

26 5 26 15

9 3 9 9

y x x     

.

(Xem thêm Câu 30).

'. ''

18

yy

y

a



xi

i

Nhóm toán anh Dúi

[NG DÂY HÀM S]

253

[ I can't, I can! ]

Extra Techniques:

Tips:

i vi mt s bài toán

có cha tham s

m

ta

ng gán cho

100m 

khi CALC.

i vi mt s bài toán

có cha tham s

,mn

 ng gán cho

100m 

và

0,01n 

khi CALC.

i vi mt s bài toán

ng th

 m cc tr thì ta

CALC giá tr ca

xi

.

Câu 2. Cho hàm s

 

32

3 3 1 1 3y x x m x m     

, tìm

m



th hàm s m ci, cc ting thng th

m cc tr c th hàm s 

A.

 

0

: 2 2 2 0

m

d mx y m







   



. B.

 

0

: 2 2 2 0

m

d mx y m







   



.

C.

 

0

: 202 200

m

d y x











. D.

 

0

: 202 200

m

d y x











.

 B

Li gii

Xét hàm s:

 

32

3 3 1 1 3y x x m x m     

.

Ta có:

2

' 3 6 3 3

'' 6 6

y x x m

yx



   







.

 hàm s m cc tr thì:

'

'0

y



.



 

'

' 0 9 3 3 3 0 9 0 0

y

m m m         

.

S dng máy tính cm tay và nhp biu thc 

Chn MODE 2.

Nhp vào màn hình:

 

2

32

3 6 3 3 6 6

3 3 1 1 3

18

X X X

X

M

MMXX

   

     

.

n CALC, nhp

, 100X i M

(  o, nhn nút ENG  gi

ra màn hình).

Màn hình xut hin kt qu:

'. ''

18

yy

y

a



i

Nhóm toán anh Dúi

[NG DÂY HÀM S]

254

[ I can't, I can! ]

Vì:

202 200 2 2.100 2 2 2

200 2.100 2

m

     





    



.

Vy:

2 2 2y mx m   

là ng thm cc tr c th

hàm s

 

32

3 3 1 1 3y x x m x m     

.

Câu 3. Tìm  

m



 

: 3 1 3d y m x m   





32

31y x x  

.

A.

1

3

m 

. B.

1

6

m 

.

C.

1

6

m 

. D.

1

3

m 

.

 B

Li gii

Xét hàm s

32

31y x x  

.

Ta có:

2

36y x x





,

11

21

33

y x y x





   





.









21yx  

.



d

vuông góc vi



thì

   

3 1 . 2 1m    

1

6

m  

.

Vy giá tr cn tìm ca

m

là

1

6

m 

.

Câu 4. 

m





4yx

song song 



   

32

2 3 1 6 1 2y x m x m m x    

.

A.

1

3

m 

. B.

2

3

m 

.

C.

2

3

m 

. D.

1m 

.

 A

Nhóm toán anh Dúi

[NG DÂY HÀM S]

255

[ I can't, I can! ]

Extra Techniques:

Tips:

ng thng

 

11

2 2

1

2

:

d

x

b

y a x

y ad















ng thng ct

nhau khi và ch khi:

12

aa

.

ng thng song

song vi nhau khi và

ch khi:

1

2

a

b

a

b











.

ng thng trùng

vi nhau khi và ch khi:

1

2

a

b

a

b











.

ng thng vuông

góc vi nhau khi và ch

khi:

12

. 1aa

.

Li gii

Ta có:

   

2

6 6 1 6 1 2y x m x m m



    

.

Suy ra:

0

12

xm

y

xm















.

 hàm s có hai cc tr thì:

12mm

1

3

m

.

m cc tr c th hàm s là:

 

3

32

2

;

; 7 3

1 2 20 24 9 1

A

B m m m m

m m m



















.



 

3

1 3 ; 3 1AB m m  



AB

n là

 

2

3 1 ;1nm

.

Sng thng

 

2

32

: 3 1 2 3 0AB m x y m m m     

.

Hay:

 

2

32

: 3 1 2 3AB y m x m m m     

.

 ng thng

AB

song song vng thng

4yx

thì:

 

2

1

2

3

1

3

0

34

20

4

1

a

m

b

m

b

m

a

b

a





   







  





  







1

3

0

1

2

1

m













































1

3

m  

.

Vy:

1

3

m 

là giá tr tham s thc duy nht ca

m

tha mãn yêu c

bài.

Nhóm toán anh Dúi

[NG DÂY HÀM S]

256

[ I can't, I can! ]

Extra Techniques:

Tips:

Ngoài vic tìm ng

thm

cc tr bng công thc,

c

y

o hàm

'y

c



ng

thng cn tìm.

Câu 5. Tìm tt c các giá tr ca tham s

m

  th hàm s

 

32

23y x x m x m    

m cc tr m

 

9; 5M 

nm

ng thm cc tr c th.

A.

1m 

. B.

5m 

.

C.

3m 

. D.

2m 

.

 C

Li gii

Ta có:

2

3 4 3y x x m



   

.

 hàm s m cc tr 

0y





có hai nghim phân

bit

 

0 4 3 3 0m



      

 

13

*

3

m

.

Ta có:

1 2 2 26 7 2

.

3 9 3 9 9 3

mm

y y x x

   



     

   

   

ng

thm cc tr là:

2 26 7 2

3 9 9 3

mm

yx



   





. Theo gi

thing th

 

9; 5M 

nên ta có:

2 26 7 2

5 .9 3

3 9 9 3

mm

m



      





(thu kin

 

*

).

Vy:

3m 

là giá tr thc ca tham s

m

cn tìm.

Câu 6. Gi s

A

,

B

  m cc tr c  th hàm s

 

32

f x x ax bx c   

 ng thng

AB

  c t . Giá tr

nh nht ca

P abc ab c  

bng?

A.

16

25

P 

. B.

9P 

.

C.

25

9

P 

. D.

1P 

.

 C

Li gii



D 

.

Ta có:

 

2

32f x x ax b



  

.

Nhóm toán anh Dúi

[NG DÂY HÀM S]

257

[ I can't, I can! ]

u ki hàm s m cc tr là

 

0fx





có hai nghim phân

bit

2

30ab  

.

Ly

 

fx

chia cho

 

fx



.

Ta có:

   

1 1 2 2 1

.

3 9 3 9 9

f x f x x a b x c ab

   



     

   

   

.

ng th

A

,

B

là:

 

2 2 1

:

3 9 9

d y b x c ab



   





.

u bài

 

d

c t

1

0

9

c ab  

9ab c

.

:

P abc ab c  

2

9 10P c c  

2

5 25

3

39

Pc



   





.

Suy ra:

25

min

9

P 

.

Du

""

xy ra khi và ch khi:

5

9

ab

c















.

Vy giá tr nh nht ca biu thc là:

min

25

9

P 

.

Câu 7. Vi giá tr nào ca tham s

m

  th hàm s

32

3y x x m  

m cc tr

A

,

B

tha mãn

OA OB

(

O

là gc t)?

A.

3

2

m 

. B.

3m 

. C.

1

2

m 

. D.

5

2

m 

.

 D

Li gii

Tnh:

D 

.

2

36y x x





,

2

0

0 3 6 0

2

x

y x x

x







    







.

 th hàm s m cc tr lt có t

Nhóm toán anh Dúi

[NG DÂY HÀM S]

258

[ I can't, I can! ]

Extra Techniques:

Tips:

 ng thng

 

d

:

0ax by c  

m

 

;A x y

, t m

B

c g  i xng

vi

A

qua

 

d

khi và

ch khi:

 

.0

d

AB u

Id















vi

;

22

A B A B

x x y y

I











   n

thng

AB

và

d

u

là

vector ch  a

ng thng

 

d

.

là

 

0;Am

và

 

2; 4Bm

.

Ta có:

   

22

2 2 2 2

0 2 4 4 4OA OB m m m m         

5

20 8 0

2

mm    

.

Câu 8. Cho hàm s

3 2 3

34y x mx m  

(vi

m

là tham s   th

 

m

C

. Tp tt c các giá tr ca

m

 m cc tr c th

 

m

C

i

xng vng thng

:d y x

là?

A.

1

2







. B.

11

;

22









.

C.

11

; ;0

22









. D.

1

0;

2









.

B

Li gii

Xét hàm s:

3 2 3

34y x mx m  

.

Ta có:

2

0

' 3 6 0

2

x

y x mx

xm





   







.

 hàm s m cm cc tiu thì:

0m 

.

Gi s hàm s t cc tr ti:

 

3

0;4

2 ;0

Am

Bm











.

Suy ra:

 

3

2 ; 4AB m m

.

Ta có:

 

3

;2I m m

n thng

AB

,



,AB

i xng vng thng

yx

có vector ch 

là

 

1;1

d

u

, thì:

 

3

2

2 4 0

2

0L

m

mm

m































.

Nhóm toán anh Dúi

[NG DÂY HÀM S]

259

[ I can't, I can! ]

Extra Techniques:

Tips:

 ng thng

 

d

:

yekx

 m

,AB

m cc tr

ca hàm s bc ba

 

Q

:

32

y ax bx cx d   

 

A

và

B

i

xng nhau qua

 

Q

khi

và ch khi:

 

2

1

2

33

..

d

b

c

I

k

a

























vi

;

33

bb

Iy

aa



  





là

t m un c

th

 

Q

.



2

9

2

33

bc

y x d

a

b

c

a



















   ng

th    m

cc tr c  th hàm

s

 

Q

.

Vy

11

;

22

m









.

Câu 9. nh tt c các giá tr ca

m

 m cc tr c th

hàm s

32

3y x x mx  

i xng v   ng thng

2 5 0xy  

?

A.

0m 

. B.

2m 

.

C.

m 

. D.

2m 

.

A

Li gii

Xét hàm s:

32

3y x x mx  

.

Ta có:

2

' 3 6 '' 6 6 0 1y x x m y x x        

.

Suy ra:

 

1; 2Im

i xng c th hàm s:

32

3y x x mx  

.

ng thng

2 5 0xy  

có th vit li thành:

15

22

yx

.

Vì th:

1

2

k 

.

 m cc tr c th hàm s

32

3y x x mx  

i xng vi nhau

ng thng

2 5 0xy  

thì:

 

2

0

2

.1

1 2 2

3

.

3 3.

50

1

2

m













   

















.

Câu 10. Tt c các giá tr ca

m

  th

 

3 2 2 3

: 3 3 1

m

C y x mx m x m m     

  m cc tr  

A

m ci và

B

m cc tiu sao cho

2OA OB

là?

A.

3 2 2m 

. B.

2 3 2

m



  



  



.

C.

3 2 3m   

. D.

3 2 2

m



  



  



.

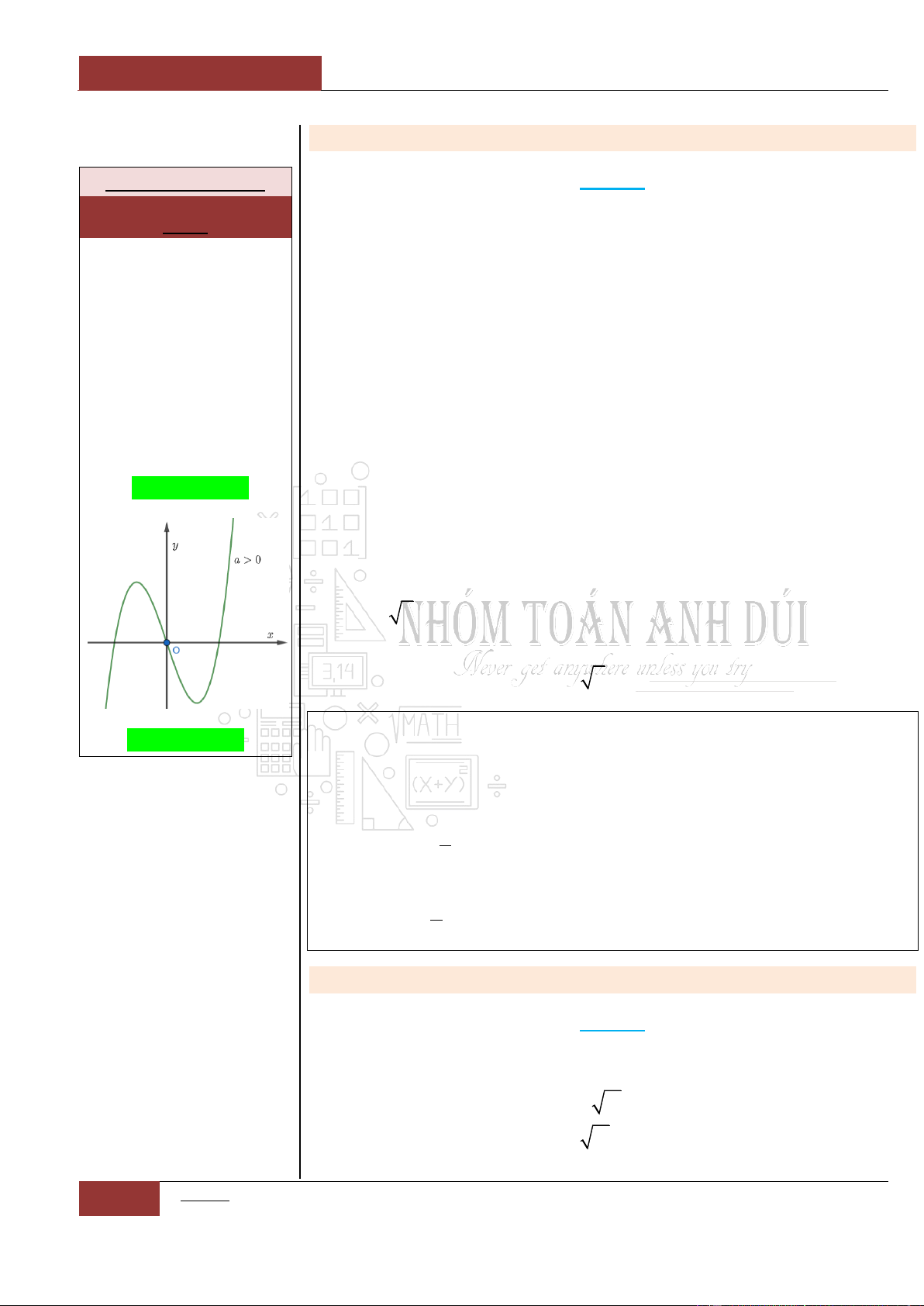
Nhóm toán anh Dúi

[NG DÂY HÀM S]

260

[ I can't, I can! ]

Extra Techniques:

Tips:

S 

AB

xx

khi

0a 

 th hàm

s bm

cc tr và h s

0a 

 th hàm s

có dng hình ch



,

do vy

CÑ CT

xx

.

Xem  th I.II.17.

 th I.II.17.

D

Li gii

Xét hàm s:

 

3 2 2 3

3 3 1y x mx m x m m     

.

Ta có:

 

2 2 2 2

' 3 6 3 1 0 2 1 0y x mx m x mx m         

.

      

2

1

1 1 1 1 0

1

xm

x m m x m m

xm







         









.

Vì hàm s

 

3 2 2 3

3 3 1y x mx m x m m     

có h s

0a 

.

Nên:

1xm

m ci và

1xm

m cc tiu ca hàm s.



 

1;2 2

1; 2 2

A m m

B m m









  





.



2OA OB

thì:

       

2 2 2 2

1 2 2 2. 1 2 2m m m m



       





2

6 1 0 3 2 2m m m       

.

Câu 11. Giá tr ca

m

  th hàm s

 

3

: 3 1

m

C y x mx  

có hai

m cc tr

,BC

sao cho tam giác

ABC

cân ti

A

vi

 

2;3A

là?

A.

0

1

2

m













. B.

1

2

m











.

C.

1

2

m 

. D.

2m 

.

C

Li gii

Xét hàm s:

3

31y x mx  

.

Ta có:

2

' 3 3 0 , 0

xm

y x m m

xm





     







.

Nhóm toán anh Dúi

[NG DÂY HÀM S]

261

[ I can't, I can! ]

Extra Techniques:

Tips:

Tam giác

ABC

cân

ti

A

có

I

là trung

m

BC



.0AI BC AI BC  

Extra Techniques:

Tips:

Tam giác

OAB

vuông

ti

O



.0OA OB OAOB  

 hàm s m cc tr thì:

0m 

.

y:













3

;2 1

2 ; 4

; 2 1

B m m

BC m m

C m m

















.

Ta có:

 

0;1I

n thng

 

2; 2BC AI  

.

ABC

cân ti

A

khi và ch khi:

 

3

0L

. 0 4 8 0

1

2

m

AI BC m m

m







     









.

Câu 12. Tìm tt c các giá tr thc ca tham s

m

  th hàm s

 

3 2 2 3

: 3 3 1 4 1

m

C y x mx m x m m      

 m cc tr

,AB

sao cho tam giác

OAB

vuông ti

O

?

A.

1

2

m











. B.

1

2

m











.

C.

1

m











. D.

1

0

m











.



Li gii

Xét hàm s:

 

3 2 2 3

3 3 1 4 1y x mx m x m m      

.

Ta có:

 

22

1

' 3 6 3 1 0

1

xm

y x mx m

xm





     







.

(Xem thêm Câu 10).

Suy ra:

 

1; 3 1; 3

1; 1

A m m OA m m

B m m

OB m m



    









  





.

Do tam giác

OAB

vuông ti

O

nên

.0OA OB 

.

Nhóm toán anh Dúi

[NG DÂY HÀM S]

262

[ I can't, I can! ]

        

1 1 3 1 0 1 2 4 0m m m m m m          

.

Suy ra:

1

2

m











.

Mt s T làm tt các bài toán cc tr ràng buc

Xét hàm s bc ba: .

Dng th

2

m cc tr.

ng th

2

m cc tr ca hàm s bc ba là

pha phép chia ca

y

cho

'y

.

Phân tích (bc

y

cho



y

):

   

 

11

22









    









y h x

y y q x h x

y h x

ng thng qua

2

m cc tr là

 

y h x

.

ng thm cc tr c th hàm s

32

   y ax bx cx d



2

3 3 9



   





b bc

y c x d

aa

.

Dng 2. Tìm

m

 hàm s có cc tr thu kic.

★:

Cho hàm s

 

32

;    y f x m ax bx cx d

. Tìm tham s

m

  th

hàm s có

2

c tr

12

, xx

thu kin

K

c?

 :

 ::

D

.

2

32



  y ax bx c

.

 :

2

m 

0



y



2



 

2

30

2 4.3 0













   





y

aa

b ac



1

mD

.

 

1

 

32

,0y ax bx cx d a    

Nhóm toán anh Dúi

[NG DÂY HÀM S]

263

[ I can't, I can! ]

 :

12

, xx



2



0



y

.e



12



   













b

S x x

a

c

P x x

a

.

 :

K



S



P





2

mD

.

 :

m



12

m D D

.

 





0



y



2





0



  

y

.



K





2



   

1 1 2 2

; , ;A x y B x y



12

, xx



2





0



y

. 

2







0



y

,

12

, xx





 

;y f x m



12

, yy





A



B

.





0



y

,

2



12

, xx





12

, yy



2





 ving thng nm cc tr ng dùng

o hàm (phc nht trong phép chia

y

cho



y

),



Phân tích (bc

y

cho



y

):

   

 

11

22









   









y h x

y y q x h x

y h x

.

ng thng qua

2

m cc tr là

 

y h x

.

D

m





d

):

Nhóm toán anh Dúi

[NG DÂY HÀM S]

264

[ I can't, I can! ]

Extra Techniques:

Tips:

c gi là

ni vi

ng thng nng

thm

ng th

cho ti phn kéo dài ca

nó.

 th I.II.18.

Extra Techniques:

Tips:

c gi là

ni vi

ng thng nng

thm

ng th

cho ti mm nm

gia (không nht thit

pha



 th I.II.19.



2



Cho

2



   

; , ;

A A B B

A x y B x y



:0  d ax by c

.







   

0     

A A B B

ax by c ax by c



, AB



2





d

.

(Xem thêm  th I.II.18.).





   

0     

A A B B

ax by c ax by c



, AB





d

.

(Xem thêm  th I.II.19.).







 

y f x



2





Oy



0



y



2







 

y f x



2





Ox



 

y f x



Ox



3









 

0fx



3





D

m





★  m

m



2



, AB





d

:



 :

1

mD

.

 :

2



, AB



2





0



y



12

, ,xx



   

1 1 2 2

; , ;A x y B x y

.



0



y

ph



2







   

1 1 2 2

; , ; A x y B x y

Nhóm toán anh Dúi

[NG DÂY HÀM S]

265

[ I can't, I can! ]

Extra Techniques:

Tips:

i vi mt s bài toán

trc nghim cn tính

nhanh giá tr tham s

m

 m ci và

m cc tiu c th

hàm s bc ba tng quát

32

y ax bx cx d   

vi

0a 

i xng

ng thng

y kx e

thì

m

chính

là nghim ca h

 theo tham

s

m

:

2

. . 1

33

II

y kx e

b

ck

a











  













;

33

bb

Iy

aa









là

t m un c

th hàm s b

cho.

 :

1 2 1 2

;

22









x x y y

I



AB

.

Do

, AB



d

:

2

0











  









d

AB u

mD

Id

.

 

12

m D D

.

★ 

m



2



, AB





d

:



 

1

mD

.

 

2



, AB

.

2







0



y



12

, xx

,

   

1 1 2 2

; , ;A x y B x y

.



0



y





2







   

1 1 2 2

; , ; A x y B x y

.

 . Do

, AB



d

nên

2

( ; ) ( ; )  d A d d B d m D

.

 

12

m D D

.

☞

, AB



II



AB

.

★ . Tìm khong cách gim cc tr ca hàm s bc

ba tng quát

 

32

,0y ax bx cx d a    

.



Xét hàm s:

   

32

,0y f x ax bx cx d a     

.

Nhóm toán anh Dúi

[NG DÂY HÀM S]

266

[ I can't, I can! ]

Extra Techniques:

Tips:

Xét hàm s bc ba

32

y ax bx cx d   

vi

0a 

. Nu bit s

2

'

30'

y

b ac   

thì

khong cách gia hai

m cc tr c  th

hàm s   nh

 ln

biu thc:

3

4

2

a

k

d

k





'

9

y

k

a





.

Extra Techniques:

Tips:



 

2

' 3 2 0f x ax bx c   

nh lý Viéte

Ta có:

12

2

3

b

xx

a

c

xx

a



  













.

   

2

' 3 2 0 *f x ax bx c   

.

Ta có:

2

'

'3

y

b ac  

.

Nu

2

'

' 3 0

y

b ac   



 

*

có hai nghim thc

phân bit và t  th hàm s

 

y f x

m cc tr ln

t là

 

11

22

;

A x y

B x y











.



     

22

1 2 1 2

**

AB

d x x y y   

M ng thng

m cc tr c th hàm s

32

y ax bx cx d   

ng

th

2

22

3 9 9

c b bc

y x d

aa



   





.

t:

2

3

9

b ac

k

a







 

2 2 2

2 2 3

2. 2. 2 ***

3 9 9 3 9

c b b c b ac

k

a a a

   



       

   

   

.

T

  

11

22

2

9

** *** 2

9

2

9

bc

y kx d

bc

a

y kx d

a

bc

y kx d

a



   



     





   





.

 

1 2 1 2

2y y k x x    

.

y, d c:

     

 

2 2 2

2 2 2 2

1 2 1 2 1 2

2

2 2 2

1 2 1 2

4 1 4

2

1 4 4 1 4 4.

33

AB

d AB x x k x x x x k

bc

AB k x x x x k

aa

       



   





        

   







   



(Xem thêm nh lý Viéte).

Nhóm toán anh Dúi

[NG DÂY HÀM S]

267

[ I can't, I can! ]

   

 

22

2 2 2

2

3

22

4 12 4 3

1 4 . 1 4 . .

9

44

. 1 4 2

b ac b ac

AB k k

aa

a

kk

AB k k AB

a a a





    







     

 

2

Xét hàm s bc b

 

42

,0y ax bx c a   

.

ng toán, tôi xin trình bài mt s tính cht, ni

dung cn thit và s c áp di.

Xét hàm s:

 

42

,0y ax bx c a   

.

Ta có:

3

' 4 2 0y ax bx  

.

i vi các du ht chúng tôi ch trình bài mt khía

cnh nh v bài toán cc tr ng hp hàm s 

m cc tr (có th hom ci và mm cc tiu hoc là

m cc tiu và mm ci

0ab 

.



 

0;

;

24

;

24

Ac

b

B

aa

b

C

aa











  































vi

 

2

4 ib ac  

.

Tht vt rng khi

0ab 

thì:

Hàm s

42

y ax bx c  

m cc tr là

0

2

x

b

x

a

b

x

a









  











.

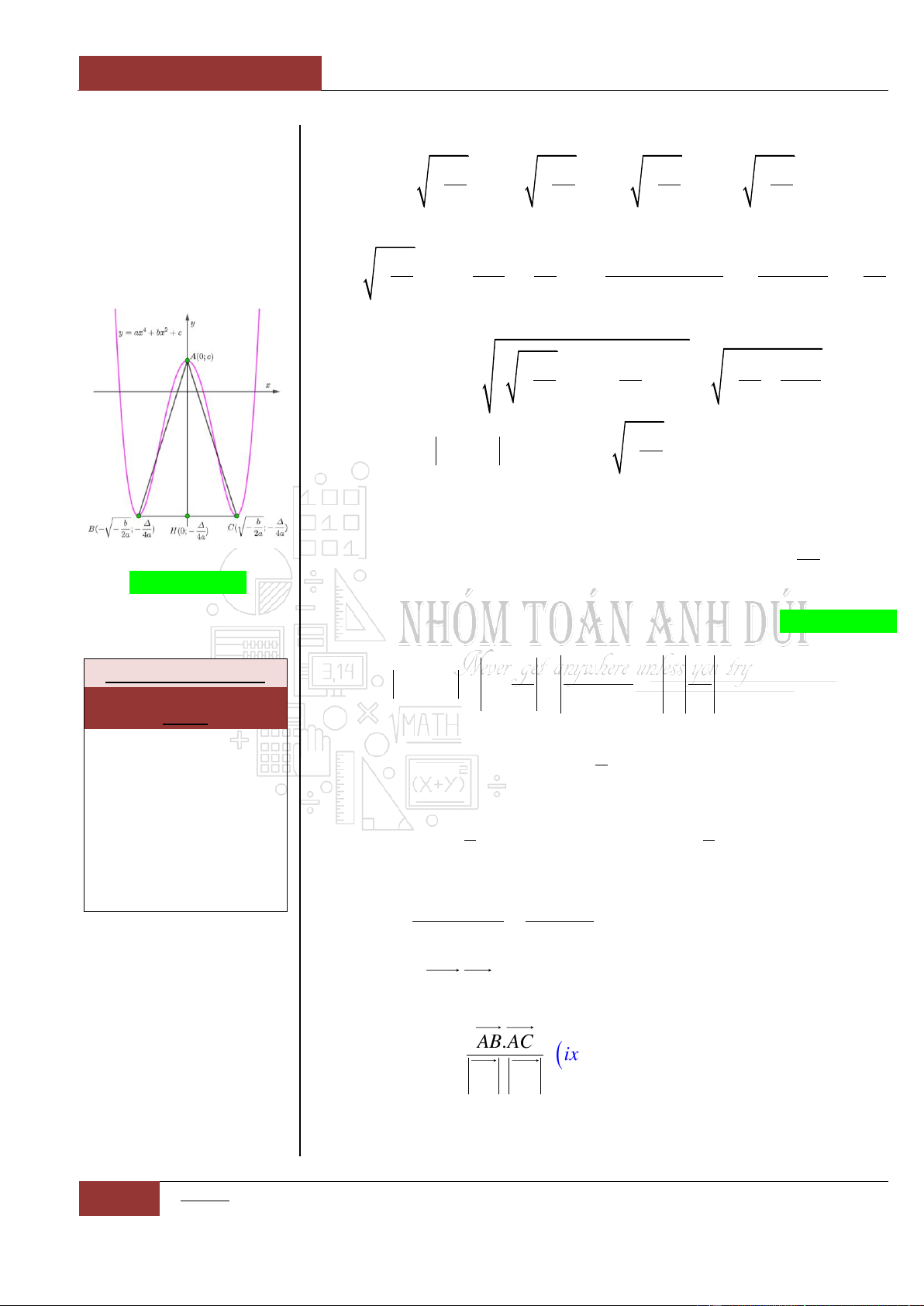
Nhóm toán anh Dúi

[NG DÂY HÀM S]

268

[ I can't, I can! ]

 th I.II.20.

Extra Techniques:

Tips:

Các kí hiu:

R

ng

tròn ngoi tip

ABC

.

r

ng

tròn ni tip

ABC

.



42

2 2 2 2

b b b b

f f a b c

a a a a

       

        

       

       

2 2 2 2 2

2

2 4 4

.

2 2 4 4 4

4

b b b b b ac b ac

f a c

a a a a a

a



   

         





.

Suy ra:

 

2

4

2

2 4 2

16

2

C B C B

i

b b b

AB AC c

a a a

a

b

BC x x x x

a

i









        















     





Gi

H

m

BC

thì

H

ng thi ca nm trên trc tung và có

 b ca

,BC

. Hay nói cách khác:

 

0;

4

iH i

a

i











.

 th  th I.II.20.).

Và

 

22

4

4 4 4

AH

iv

b ac b

AH y y c c

a a a



      

.

Din tích tam giác

 

1

: . . .

2

ABC

vABC S AH BC AH HB AH HC



   

.

Hay:

   

11

..

22

ABC

viS pr AB AC BC r AB BC r





     





.

Và:

 

2

. . .

44

ABC

vii

AB AC BC AB BC

S

RR





.

 

.0viiiMN PQ MN PQ  

.

 

.

cos cos

.

ix

AB AC

BAC

AB AC





.

Nu

 

00

0 90 cos 0 x



   

.

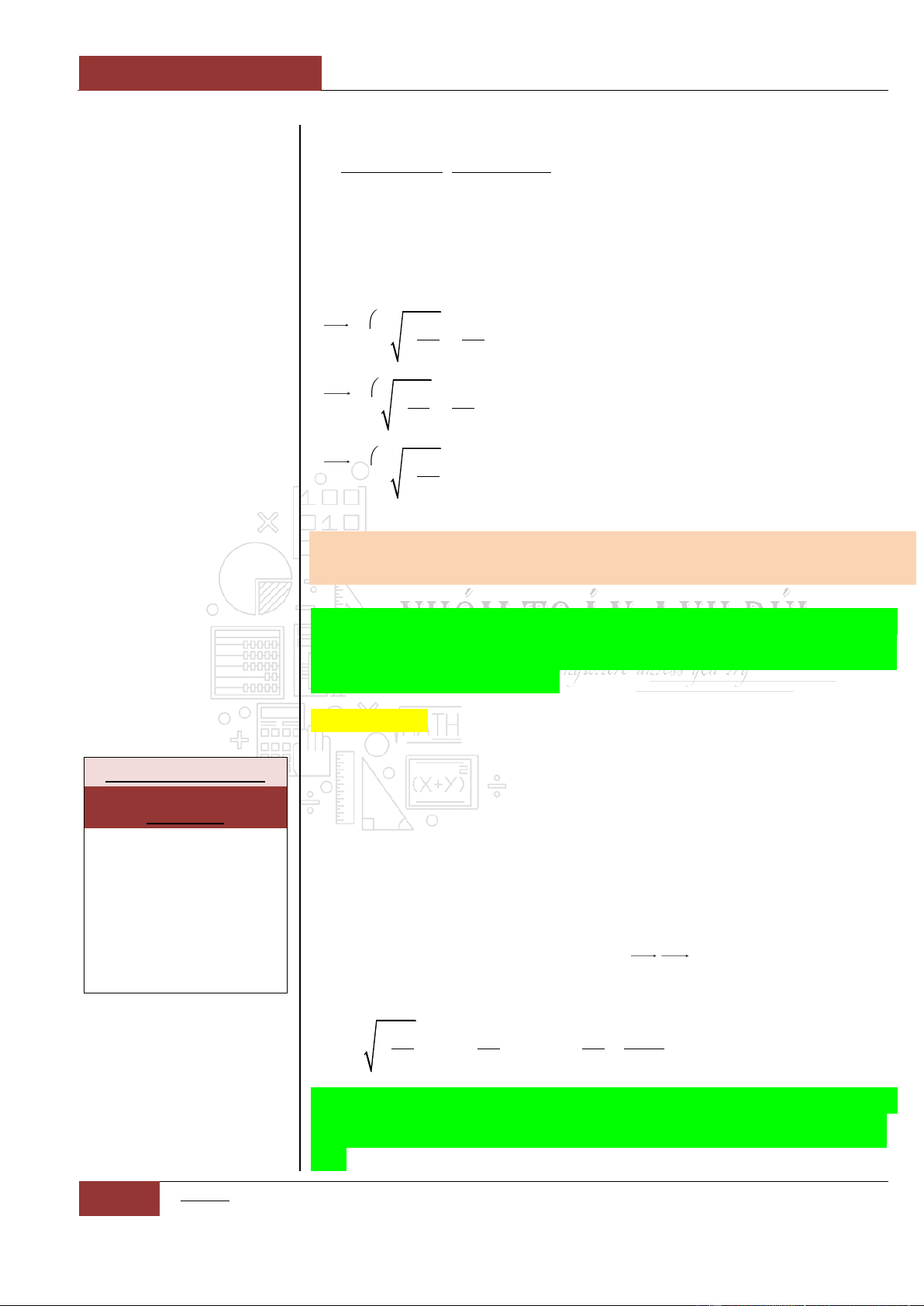
Nhóm toán anh Dúi

[NG DÂY HÀM S]

269

[ I can't, I can! ]

Extra Techniques:

Remark:

  th hàm s

 

42

,0y ax bx c a   

m cc tr lp

thành mt tam giác

vuông thì:

3

80ba

.

;

33

A B C A B C

x x x y y y

G



   





là t trng tâm ca

 

iABC x

.

ng dng vi t l

k

thì t s di

th t t l 

 

2

k xii

.

 

2

;

24

;

24

2 ;0

2

bb

A

i

B

aa

bb

AC

aa

b

BC

xii

a





   















  





























D

m



các yu t tam giác, góc, di):

★ . Tìm tt c các giá tr thc ca tham s

m

  th hàm

s

 

42

,0y ax bx c a   

m cc tr lp thành mt tam giác

vuông (có th nói vuông cân).



Do tam giác

ABC

cân ti

A

nên nu vuông thì chc chn

o

90BAC 

.

Tht vy, gi s c li:

o

90ABC 

.









o o o o

90 90 90 180ACB BAC ABC ACB ABC ACB         

(Vô lý).

Suy ra:

AB AC

, theo

   

.0,v AB Aiii xi Cii 

.

 

2

24

3

2

0 0 8 0

2 4 2

16

b b b b

ba

a a a

a





           





.

★ . Tìm tt c các giá tr thc ca tham s

m

  th hàm

s

 

42

,0y ax bx c a   

m cc tr lp thành mt tam giác

u.

Nhóm toán anh Dúi

[NG DÂY HÀM S]

270

[ I can't, I can! ]

Extra Techniques:

Remark:

  th hàm s

 

42

,0y ax bx c a   

m cc tr lp

thành mt tam giác u

thì:

3

24 0ba

.

Extra Techniques:

Remark:

 th hàm s

 

42

,0y ax bx c a   

m cc tr lp

thành mt tam giác có

 ln din tích bng:

5

0

3

32

b

S

a



.

Extra Techniques:

Remark:

 th hàm s

 

42

,0y ax bx c a   

m cc tr

,,AB

C

sao cho

,B C Ox

(nm trên trc hoành)

thì

2

40

0

b ac

c















.

Theo

 

4

2

22

16

2

b b b

aa

a

   

.

 

4

3

2

4

24 0

22

16

b b b

ba

aa

a



      

.

★ . Tìm tt c các giá tr thc ca tham s

m

  th hàm

s

 

42

,0y ax bx c a   

m cc tr lp thành mt tam giác có

din tích bng

0

S

.



Theo

   

,ii iv

và  th I.II.20 ta suy ra:

2

2 2 2 2

00

1

. 4 . 4 . 2

2 4 2

ABC

bb

S AH BC S AH BC S

aa





     





.

 

4 5 5

2

00

2 3 3

.

2

16 32 32

b b b b

SS

a

a a a





       





.

★ . Tìm tt c các giá tr thc ca tham s

m

  th hàm

s

 

42

,0y ax bx c a   

m cc tr lp thành mt tam giác có

din tích ln nht, nh nht .



ng minh  trên và kt lun  phn Remark gii quyt bài

toán dng này ta cn tìm giá tr ln nht, nh nht ca biu thc

 

5

3

32

b

fm

a



theo bin

m

(tham s

m

m xét tính

ln nht, nh nht ca các giá tr có th xy ra).

★ . Tìm tt c các giá tr thc ca tham s

m

  th hàm

s

 

42

,0y ax bx c a   

m cc tr

,,A B C

sao cho

,B C Ox

(nm trên trc hoành) .





,B C Ox

thì:

 

2

0

40

4

0

44

BC

c

b ac

c

yy

aa





















     









.

Nhóm toán anh Dúi

[NG DÂY HÀM S]

271

[ I can't, I can! ]

Extra Techniques:

Remark:

 th hàm s

 

42

,0y ax bx c a   

m cc tr

,,AB

C

tha mãn:

 

.,BC k AB k







k

tha mãn:

 

3 2 2

84b k a k

Extra Techniques:

Remark:

 th hàm s

 

42

,0y ax bx c a   

m cc tr to

thành mt tam giác cân

có góc  nh bng



khi và ch khi



tha

ng thc theo

3

8

cos:

8

cos

ba









hoc theo

tan :

32

8 .tan

2

ab





.

★ . Tìm tt c các giá tr thc ca tham s

m

  th hàm

s

 

42

,0y ax bx c a   

m cc tr

,,A B C

tha mãn

 

.,BC k AB k





.



Theo

 

4

2

. 2 .

22

16

b b b

BC k AB k

aa

ii

a

     

 

4

2 3 2 2 3 2 2

2

4

32 8 8 4

22

16

b b b

k a b k ak b k a k

aa

a





          





.

★ . Tìm tt c các giá tr thc ca tham s

m

  th hàm

s

 

42

,0y ax bx c a   

m cc tr to thành mt tam giác

cân có góc  nh bng



.



Theo

 

ix

2

.

cos . . .cos .cos

.

AB AC

AB AC AB AC AB

AB AC

  

    

Mt khác theo

   

,ii xiii

,

 

2

24

2

44

22

3

33

3

.cos

2 4 2

16

8

.cos

2

16 16

8

8 8 cos cos

8

b b b b

a a a

a

b b b ab

a

aa

ba

a b b a

ba









   

       



   



   







  







     



.

Mt khác, nu ta dùng theo giá tr ng giác

tan

 thu mu

khá thú v:

Ta có:

tan tan

22

HC BC

HAC

AH AH



  

Suy ra:

2

2 2 2 2

2

tan 4tan .

22

4

BC

BC AH

AH



  

.

Theo

   

2

24

22

2

4

, 2 4 tan . 4 tan .

2 2 4 2 2

16

b b b b

a a a

ii i

a

v





     





 

32

8 tan 0

2

ab





  

.

Nhóm toán anh Dúi

[NG DÂY HÀM S]

272

[ I can't, I can! ]

Extra Techniques:

Remark:

 th hàm s

 

42

,0y ax bx c a   

m cc tr to

thành mt tam giác có

ba góc u nhn thì ta

có th kim tra mt

trong hai cách sau:



3

8

0

8

ba







;



 

3

80b b a

.

Extra Techniques:

Remark:

 th hàm s

 

42

,0y ax bx c a   

m cc tr to

thành mt tam giác có

bán ng tròn ni

tip là

r

khi và ch khi

r

tha mãn biu thc:

2

3

4 . 1 1

8

b

r

b

a













.

★ . Tìm tt c các giá tr thc ca tham s

m

  th hàm

s

 

42

,0y ax bx c a   

m cc tr to thành mt tam giác có

ba góc nhn.



ng minh  trên và  phn Remark nh có

 ln thng thi vi

3

8

cos

8

ba









.

Theo

 

x

, nu

o

0 90





, thì:

 

3

8

0

8

ba









.

 dùng li cách chng minh  Bài toán 7  

ra kt qu 

Ta có:

4

2

.

cos 0 0 . 0 0

2

16

.

AB AC b b

AB AC

a

AB AC



       

 

43

8 0 8 0b ab b b a



    

.

★ . Tìm tt c các giá tr thc ca tham s

m

  th hàm

s

 

42

,0y ax bx c a   

m cc tr to thành mt tam giác có

ng tròn ni tip là

r

.



Theo

     

,,ii vi



ta có:

5

3

4

2

32

1

.2

2

2 2 2

16

ABC

b

S

a

r

b b b

AB BC

aa

a









  

 

54

4 2 2 3 2 2

22

32

3

2 16 16 2 16 16

2 16 4

4 . 1 1

8

bb

r

ab a b a b ab a a

bb

ab a a

b

a





  

     





  









★ . Tìm tt c các giá tr thc ca tham s

m

  th hàm

s

 

42

,0y ax bx c a   

m cc tr to thành mt tam giác có

ng tròn ngoi tip là

R

.



Nhóm toán anh Dúi

[NG DÂY HÀM S]

273

[ I can't, I can! ]

Extra Techniques:

Remark:

 th hàm s

 

42

,0y ax bx c a   

m cc tr to

thành mt tam giác có

bán ng tròn

ngoi tip là

R

khi và

ch khi

R

tha mãn

biu thc:

3

8

8.

ba

R

ab





.

Extra Techniques:

Tips:

 th hàm s

 

42

,0y ax bx c a   

m cc tr to

thành mt tam giác

ABC

cân ti

A

, khi



0

4

0

2

16

b

m

a

bb

n

a

















.

Extra Techniques:

Remark:

 th hàm s

m cc tr to

thành mt tam giác

nhn

O

làm trng tâm

khi:

2

60b ac

.

Theo

   

,v vii

, ta có:

2

1.

..

24

ABC

AB BC

S AH BC

R





.

Suy ra:

2 2 2 4

2 . 4 .AH R AB AH R AB  

 

2

4

2

24

2

22

4 3 3

22

2

8

16

4. .

42

16 2

4

8 8 8

8

8.

8

b ab

b b b

a

RR

aa

ab

a

b ab b a b a

R R R

ab













    









   

  

     

   

   

★ . Tìm tt c các giá tr thc ca tham s

m

  th hàm

s

 

42

,0y ax bx c a   

m cc tr to thành mt tam giác:

 dài c

0

BC m

;

 dài cnh bên

0

AB AC n

.



Theo

 

ii

, ta có:

 

0

4

0

2

16

b

BC m

a

bb

AB AC n

a





  







   





.

★ . Tìm tt c các giá tr thc ca tham s   th hàm

s m cc tr to thành mt tam giác:

a) Có trng tâm là gc t

O

;

b) Có trc tâm là gc t

O

;

ng tròn ngoi tip là gc t

O

.



a) Theo

   

,i xi

ta có:

3

A B C O

x x x x

y y y y



  





  





 

2

22

0 3.0

22

3 6 0

2

3.0

44

bb

aa

b

c b ac

a

bb

ccc

aa







     









     



   



      

   



   

   



.

 

42

,0y ax bx c a   

m

 

42

,0y ax bx c a   

Nhóm toán anh Dúi

[NG DÂY HÀM S]

274

[ I can't, I can! ]

Extra Techniques:

Remark:

 th hàm s

m cc tr to

thành mt tam giác

nhn

O

làm trc tâm

khi:

3

4 8 0b abc a  

.

Extra Techniques:

Remark:

 th hàm s

m cc tr to

thành mt tam giác

nhn

O

làm tng

tròn ngoi tip khi:

3

8 8 0b abc a  

.

b) Do tam giác

ABC

cân ti

A

, hin nhiên

AO BC

.

 tam giác

ABC

nhn gc t

O

làm trng tâm thì

BO AC

hay

.0OB AC 

.

Theo

   

,i xiii

ta suy ra:

22

4

. . 0

2 2 4 4

b b b ac b

a a a a



   



      



   



   



 

42

4 2 3

2

0 8 4 0 4 8 0

24

16

b b b c

ab b ab c b abc a

aa

a



           

c) Do tam giác

OBC

cân ti

O

(do

O

thung trung trc ca

BC

)

nên ta có:

OB OC

.

 tam giác

ABC

nhn gc t

O

ng tròn ngoi tip thì

OA OB

u ki u kin c là:

OA OB OC

).

Theo

 

i

, ta suy ra:

2

4

24

b b ac

OA OB c

aa





      





 

4 2 4 2

22

4 2 3

0

2 2 2 2

16 16

8 8 0 8 8 0

b b b c b b b c

cc

a a a a

aa

ab b ab c b abc a



          

        

★ . Tìm tt c các giá tr thc ca tham s   th hàm

s m cc tr to thành mt tam giác

nhn trc hoành trn tích (trc hoành

chia tam giác thành hai bng có din tích bng nhau).



Gi

,MN

m c th hàm s vi trc hoành.

(Xem thêm  th I.II.21.)

D thy:

AMN ABC

.

Theo yêu c bài ta có:

11

22

AMN

AMN MNCB AMN ABC

MNCB

S

S S S S

S

    

.

Theo

 

xii

ta suy ra:

 

42

,0y ax bx c a   

 

42

,0y ax bx c a   

m

 

42

,0y ax bx c a   

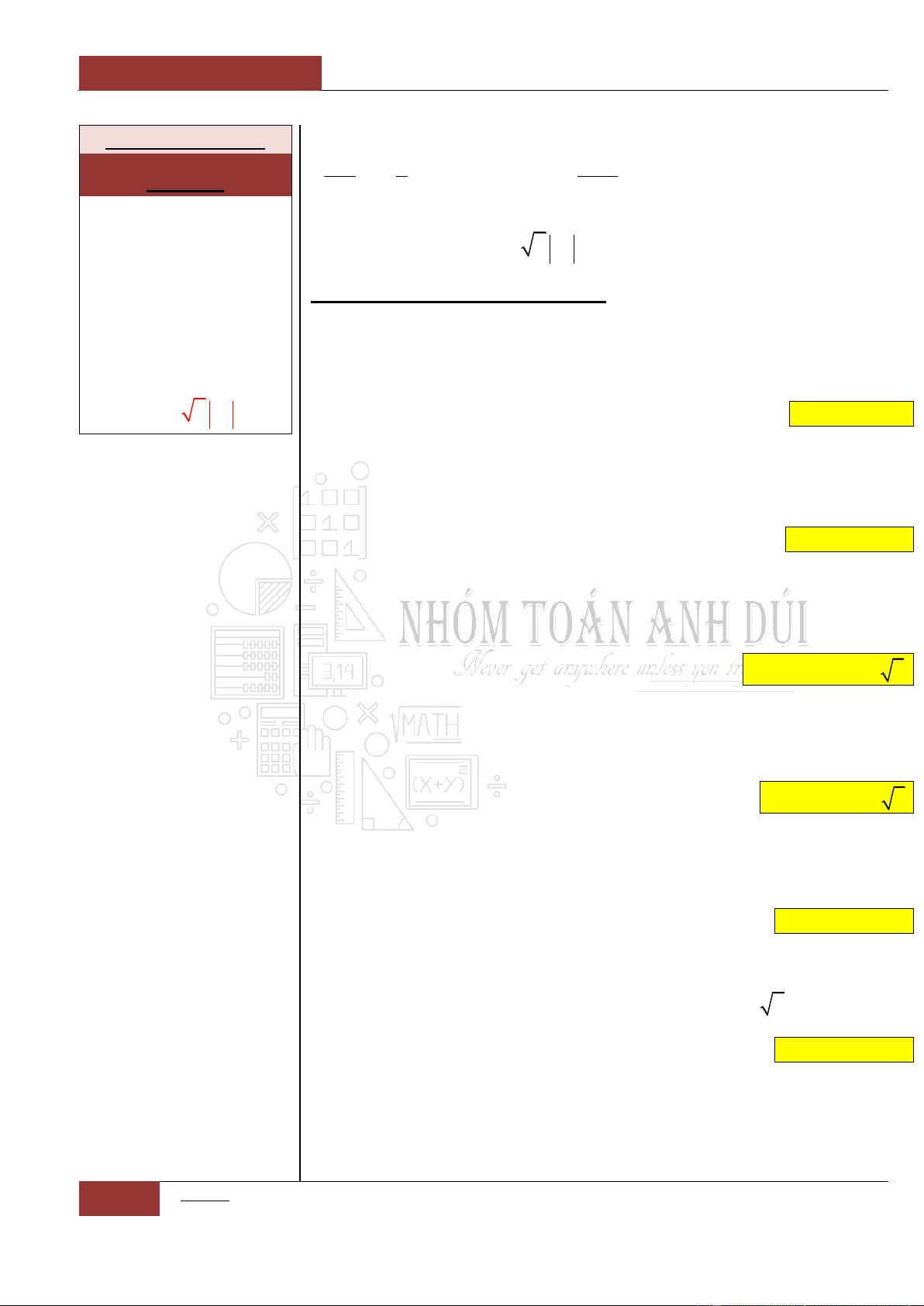
Nhóm toán anh Dúi

[NG DÂY HÀM S]

275

[ I can't, I can! ]

Extra Techniques:

Remark:

 th hàm s

m cc tr to

thành mt tam giác

nhn trc hoành trc

ng phân

 din tích :

2

42b ac

.

2

4

2 2 2

2

1

22

2

16

AO b

AH AO c

AH

a



    





 

4 2 2 2

32 4 2b a c b ac



   

.

Một số bài tập áp dụng:

Câu 1. Cho hàm s

4 2 2

22y x mx m   

. Tìm

m

  th hàm s có

m cc tr to thành mt tam giác vuông cân?

 s:

1m 

.

Câu 2. Cho hàm s

 

4 2 2

21y x m x m   

. Tìm

m

  th hàm s có

m cc tr to thành mt tam giác vuông?

 s:

0m 

.

Câu 3. Cho hàm s

 

4 2 2

2 2 5 5y x m x m m     

. Tìm

m

  th

hàm s m cc tr to thành mu?

 s:

3

23m 

.

Câu 4. Cho hàm s

42

2y mx mx m   

. Tìm

m

  th hàm s có ba

m cc tr to thành mu?

 s:

3m 

.

Câu 5. Cho hàm s

4 2 2

21y x m x  

. Tìm

m

  th hàm s có ba

m cc tr to thành mt tam giác có din tích bng

32

?

 s:

2m 

.

Câu 6. Cho hàm s

42

21y x mx m   

. Tìm

m

  th hàm s có ba

m cc tr to thành mt tam giác có din tích bng

42

?

 s:

2m 

.

 

42

,0y ax bx c a   

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

276

[ I can’t, I can! ]

TỰ LUYỆN 4 MỨC ĐỘ

Câu 1. Đồ thị hàm số

32

3 9 1   y x x x

có

hai cực trị

A

và

B

. Điểm nào dưới đây thuộc

đường thẳng

AB

?

A.

 

0; 1M

. B.

 

1; 10N

.

C.

 

1;0P

. D.

 

1;10Q

.

Câu 2. Tìm giá trị thực của tham số

m

để

đường thẳng

 

: 2 1 3   d y m x m

vuông

góc với đường thẳng đi qua hai điểm cực trị của

đồ thị hàm số

32

31  y x x

.

A.

3

2

m

. B.

3

4

m

.

C.

1

2

m

. D.

1

4

m

.

Câu 3. Tìm giá trị thực của tham số

m

để

đường thẳng

 

2 1 3   y m x m

song song

với đường thẳng đi qua các điểm cực trị của đồ

thị hàm số

32

31  y x x

.

A.

3

4

m

. B.

1

2

m

.

C.

3

4

m

. D.

1

2

m

.

Câu 4. Đồ thị của hàm số

32

3 9 1   y x x x

có hai điểm cực trị

A

và

B

. Điểm nào dưới đây

thuộc đường thẳng

AB

.

A.

 

1;0P

. B.

 

0; 1M

.

C.

 

1; 10N

. D.

 

1;10Q

.

Câu 5. Tìm giá trị thực của tham số

m

để

đường thẳng

 

: 3 1 3   d y m x m

vuông

góc với đường thẳng đi qua hai điểm cực trị của

đồ thị hàm số

32

31  y x x

.

A.

1

3

m

. B.

1

6

m

.

C.

1

6

m

. D.

1

3

m

.

Câu 6. Tìm tổng tất cả các giá trị thực của

tham số

m

sao cho đường thẳng đi qua hai

điểm cực trị của đồ thị hàm số

   

32

2 3 1 6 1 2    y x m x m m x

song song

đường thẳng

4yx

.

A.

1

3

m

. B.

2

3

m

.

C.

2

3

m

. D.

1m

.

Câu 7. Biết đồ thị hàm số

3

31y x x

có hai

điểm cực trị

A

,

B

. Khi đó phương trình đường

thẳng

AB

là?

A.

21yx

. B.

2 1.  yx

C.

2.  yx

D.

2yx

.

Câu 8. Tìm tất cả các giá trị của tham số

m

để

đồ thị hàm số

 

32

23    y x x m x m

có

hai điểm cực trị và điểm

 

9; 5M

nằm trên

đường thẳng đi qua hai điểm cực trị của đồ thị.

A.

1.m

B.

5.m

C.

3.m

D.

2.m

Câu 9. Đường thẳng nối hai điểm cực đại và

cực tiểu của đồ thị hàm số

3

2  y x x m

đi

qua điểm

 

3;7M

khi

m

bằng bao nhiêu?

A.

1

. B.

1

.

C.

3

. D.

0

.

Câu 10. Tìm giá trị thực của tham số

m

để

đường thẳng

 

: 3 1 3   d y m x m

vuông

góc với đường thẳng đi qua hai điểm cực trị của

đồ thị hàm số

32

31  y x x

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

277

[ I can’t, I can! ]

A.

1

6

m

. B.

1

3

m

.

C.

1

3

m

. D.

1

6

m

.

Câu 11. Giả sử

A

,

B

là hai điểm cực trị của đồ

thị hàm số

 

32

   f x x ax bx c

và đường

thẳng

AB

đi qua gốc tọa độ. Tìm giá trị nhỏ

nhất của

  P abc ab c

.

A.

16

25



. B.

9

.

C.

25

9



. D.

1

.

Câu 12. Tìm tất cả giá trị thực của tham số

m

để đồ thị hàm số

32

32  y x mx

có hai điểm

cực trị

A

và

B

sao cho các điểm

A

,

B

và

 

1; 2M

thẳng hàng.

A.

2m

. B.

2m

.

C.

2m

. D.

2













m

.

Câu 13. Với giá trị nào của tham số

m

để đồ

thị hàm số

32

3  y x x m

có hai điểm cực trị

A

,

B

thỏa mãn

OA OB

(

O

là gốc tọa độ)?

A.

3

2

m

. B.

3m

.

C.

1

2

m

. D.

5

2

m

.

Câu 14. Gọi

S

là tập hợp tất cả các giá trị thực

của tham số

m

để đồ thị của hàm số

 

3 2 2

1

3

   y x mx m x

có hai điểm cực trị

A

và

B

sao cho

,AB

nằm khác phía và cách

đều đường thẳng

: 5 9d y x

. Tính tổng tất cả

các phần tử của

S

.

A.

3

. B.

6

. C.

6

. D.

0

.

Câu 15. Có tất cả bao nhiêu giá trị thực của

tham số

m

để đồ thị hàm số

 

3 2 2

22

2 3 1

33

    y x mx m x

có hai điểm

cực trị có hoành độ

1

x

,

2

x

sao cho

 

1 2 1 2

21  x x x x

.

A.

1

. B.

0

. C.

3

. D.

2

.

Câu 16. Có bao nhiêu giá trị nguyên của tham

số m để đồ thị hàm số

32

(2 1) 2 1     y mx m x mx m

có hai điểm

cực trị nằm về hai phía của trục hoành?

A.

4

. B.

2

. C.

1

. D.

3

.

Câu 17. Cho đồ thị hàm số bậc ba có phương

trình

   

32

6 2 9 2.     y x m x m x

Tìm

m

để đồ thị hàm số có hai điểm cực trị nằm về

hai phía của trục hoành.

A.

2

.

6











m

B.

2.m

C.

6.m

D.

2

6

.

3

2

  

























m

Câu 18. Cho hàm số bậc ba có phương trình

   

32

1

1 3 2 2018

3

     y mx m x m x

với

m

là tham số. Tổng bình phương tất cả các giá

trị của

m

để hàm số có hai điểm cực trị

12

;xx

thỏa mãn

12

21xx

bằng?

A.

40

9

. B.

22

9

.

C.

25

4

. D.

8

3

.

Câu 19. Cho hàm số

32

3 3 1    y x mx m

với

m

là một tham số thực. Giá trị của

m

thuộc

tập hợp nào sau đây để đồ thị hàm số đã cho có

hai điểm cực trị đối xứng nhau qua đường thẳng

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

278

[ I can’t, I can! ]

: 8 74 0  d x y

.

A.





1;1m

. B.





3; 1  m

.

C.





3;5m

. D.





1;3m

.

Câu 20. Có bao nhiêu giá trị nguyên của tham

số

m

để đồ thị hàm số

 

3 2 2 2

8 11 2 2     y x x m x m

có hai điểm

cực trị nằm về hai phía của trục

Ox

.

A.

4.

B.

5.

C.

6.

D.

7.

Câu 21. Cho hàm số bậc ba có phương trình

   

32

2 1 1 1      y x m x m x m

. Có bao

nhiêu giá trị của số tự nhiên

20m

để đồ thị

hàm số có hai điểm cực trị nằm về hai phía trục

hoành?

A.

18

. B.

19

.

C.

21

. D.

20

.

Câu 22. Có bao nhiêu giá trị nguyên của tham

số

m

để đồ thị của hàm số

 

3 2 2 2

1 2 3      y x m x m x m

có hai

điểm cực trị và hai điểm cực trị đó nằm về hai

phía khác nhau đối với trục hoành?

A.

2

. B.

1

.

C.

3

. D.

4

.

Câu 23. Tìm tất cả cả các giá trị của tham số

m

để

32

31   y x x mx

đạt cực trị tại

12

,xx

thỏa mãn

22

12

6xx

.

A.

3m

. B.

3m

.

C.

1m

. D.

1m

.

Câu 24. Có bao nhiêu giá trị nguyên của

m

để

hàm số

 

32

2 6 1   f x x x m

có các giá trị

cực trị trái dấu?

A.

7

. B.

9

. C.

2

. D.

3

.

Câu 25. Cho hàm số bậc ba có phương trình

   

32

2 3 1 6 2 1     y x m x m x

với

m

là

tham số thực. Tìm tất cả các giá trị của

m

để

hàm số có điểm cực đại và điểm cực tiểu nằm

trong khoảng

 

2;3

.

A.

   

1;4 \ 3m

. B.

 

3;4m

.

C.

 

1;3m

. D.

 

1;4m

.

Câu 26. Cho hàm số

3 2 2

3 4 2   y x mx m

có đồ thị

 

C

và điểm

 

1;4C

. Tính tổng các

giá trị nguyên dương của

m

để

 

C

có hai

điểm cực trị

,AB

sao cho tam giác

ABC

có

diện tích bằng 4.

A.

6

. B.

5

. C.

3

. D.

4

.

Câu 27. Cho hàm số bậc ba có phương trình

   

32

2 3 1 6 2 1     y x m x m x

với

m

là

tham số thực. Tìm tất cả các giá trị của

m

để

hàm số có điểm cực đại và điểm cực tiểu nằm

trong khoảng

 

2;3

.

A.

   

1;3 3;4  m

. B.

 

1;3m

.

C.

 

3;4m

. D.

 

1;4m

.

Câu 28. Tổng tất cả các giá trị thực của tham số

m

để hàm số bậc ba có phương trình:

 

32

3 2 1 3 5     y x m x mx m

có hai điểm

cực trị

12

;xx

đồng thời

   

12

.0y x y x

là?

A.

21

. B.

39

.

C.

8

. D.

3 11 13

.

Câu 29. Gọi

S

là tập các giá trị dương của

tham số

m

sao cho hàm số bậc ba

32

3 27 3 2    y x mx x m

đạt cực trị tại

12

,xx

thỏa mãn

12

5xx

. Biết





;S a b

.

Tính

2T b a

.

A.

51 6T

. B.

61 3T

.

C.

61 3T

. D.

51 6T

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

279

[ I can’t, I can! ]

Câu 30. Gọi

S

là tập hợp các giá trị nguyên

của tham số

m

để hàm số

3

2

23

3

   

x

y x mx

có hai điểm cực trị

12

,4xx

. Số phần tử của

S

bằng?

A.

5

. B.

3

. C.

2

. D.

4

.

Câu 31. Tìm giá trị thực của tham số

m

để hàm

số

 

32

4 2 7 1    y x m x x

có hai điểm cực

trị

12

;xx

 

12

xx

thỏa mãn

12

4  xx

.

A.

5m

. B.

1

2

m

.

C.

3m

. D.

7

2

m

.

Câu 32. Có bao nhiêu giá trị nguyên của tham

số

m

để điểm

 

3

2;M m m

tạo với hai điểm cực

đại, cực tiểu của đồ thị hàm số

     

32

: 2 3 2 1 6 1 1     C y x m x m m x

một tam giác có diện tích nhỏ nhất?

A.

0

. B.

1

.

C.

2

. D. Không tồn tại.

Câu 33. Tìm tất cả các giá trị thực của tham số

thực

m

để đường thẳng đi qua hai điểm cực đại,

cực tiểu của đồ thị hàm số

3

32  y x mx

cắt

đường tròn

 

C

có tâm

 

1;1I

, bán kính bằng

1

tại hai điểm phân biệt

,AB

sao cho diện tích

tam giác

IAB

đạt giá trị lớn nhất.

A.

23

3



m

. B.

23

2



m

.

C.

13

2



m

. D.

25

2



m

.

Câu 34. Biết đồ thị hàm số bậc ba

32

   y x ax bx c

có hai điểm cưc trị

   

1 1 2 2

; , ;M x y N x y

thỏa mãn biểu thức

   

1 1 2 1 1 2

  x y y y x x

. Giá trị nhỏ nhất của

biểu thức

23  P abc ab c

bằng?

A.

49

4



. B.

25

4



.

C.

841

36



. D.

7

6



.

Câu 35. Cho hàm số bậc ba có phương trình

 

3 2 2 3

3 3 1     y x mx m x m m

( với

m

là

tham số). Gọi

A

,

B

là hai điểm cực trị của đồ

thị hàm số và

 

2; 2I

. Tổng tất cả các giá trị

của

m

để ba điểm

I

,

A

,

B

tạo thành tam giác

nội tiếp đường tròn có bán kính bằng

5

là?

A.

4

17

. B.

14

17

.

C.

2

17



. D.

20

17

.

Câu 36. Cho hàm số

3

64  y x mx

có đồ thị

 

m

C

. Gọi

0

m

là giá trị của

m

để đường thẳng

đi qua điểm cực đại, điểm cực tiểu của

 

m

C

cắt

đường tròn tâm

 

1;0I

, bán kính

2

tại hai

điểm phân biệt

,AB

sao cho tam giác

IAB

có

diện tích lớn nhất. Chọn khẳng định đúng.

A.

 

0

3;4m

. B.

 

0

1;2m

.

C.

 

0

0;1m

. D.

 

0

2;3m

.

Câu 37. Cho hàm số

 

3 2 2 3

3 3 1    y x mx m x m

,

với

m

là tham số; gọi

 

C

là đồ thị của hàm số đã

cho. Biết rằng khi

m

thay đổi, điểm cực đại của đồ

thị

 

C

luôn nằm trên một đường thẳng

d

cố định.

Xác định hệ số góc

k

của đường thẳng

d

.

A.

1

3

k

. B.

1

3

k

.

C.

3k

. D.

3k

.

Câu 38. Biết

o

m

là giá trị của tham số

m

để

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

280

[ I can’t, I can! ]

hàm số

32

31   y x x mx

có hai điểm cực trị

12

,xx

sao cho

22

1 2 1 2

13  x x x x

. Mệnh đề nào

dưới đây đúng?

A.

 

0

1;7m

. B.

 

0

7;10m

.

C.

 

0

15; 7  m

. D.

 

0

7; 1  m

.

Câu 39. Biết rằng đồ thị hàm số bậc ba

 

32

11

2

32

   f x x mx x

có giá trị tuyệt đối

của hoành độ hai điểm cực trị là độ dài hai cạnh

của tam giác vuông có cạnh huyền là

7

. Hỏi

có mấy giá trị của

m

?

A.

3

. B.

1

.

C. Không có

m

. D.

2

.

Câu 40. Gọi

A

,

B

là hai điểm cực trị của đồ thị

hàm số

 

3

34   f x x x

và

 

0

;0Mx

là điểm

trên trục hoành sao cho tam giác

MAB

có chu

vi nhỏ nhất, đặt

0

4 2015Tx

. Trong các

khẳng định dưới đây, khẳng định nào đúng?

A.

2017T

. B.

2019T

.

C.

2016T

. D.

2018T

.

Câu 41. Tổng tất cả các giá trị của tham số thực

m

sao cho đồ thị hàm số

3 2 3

34  y x mx m

có

điểm cực đại và cực tiểu đối xứng với nhau qua

đường phân giác của góc phần tư thứ nhất là?

A.

2

. B.

1

2

.

C.

0

. D.

1

4

.

Câu 42. Tìm tất cả các giá trị của tham số thực

m

sao cho đồ thị hàm số bậc ba có phương

trình

 

32

54    y x x m x m

có hai điểm cực

trị nằm về hai phía đối với trục hoành.

A.



. B.

  



;3 3;4 

.

C.

   

;3 3;4 

. D.

 

;4

.

Câu 43. Biết

a

b

(trong đó

a

b

là phân số tối giản

và

a

,

*b

) là giá trị của tham số

m

để hàm

số

 

3 2 2

22

2 3 1

33

    y x mx m x

có

2

điểm

cực trị

1

x

,

2

x

sao cho

 

1 2 1 2

21  x x x x

. Tính

giá trị biểu thức

22

S a b

.

A.

13S

. B.

25S

.

C.

10S

. D.

34S

.

Câu 44. Gọi

S

là tập hợp tất cả các giá trị

nguyên của tham số

m

để điểm cực tiểu của đồ

thị hàm số

32

1   y x x mx

nằm bên phải trục

tung. Tìm số phần tử của tập hợp

 

5;6S

.

A.

2

. B.

5

.

C.

3

. D.

4

.

Câu 45. Cho hàm số bậc ba có phương trình

 

3 2 2 2

3 3 1 3 1      y x x m x m

. Có bao nhiêu

giá trị nguyên của

m

để đồ thị hàm số có điểm

cực đại, cực tiểu nằm bên trái đường thẳng

2x

?

A.

3

. B.

1

. C.

2

. D.

0

.

Câu 46. Tìm tất cả giá trị thực của tham số

m

để đồ thị hàm số

32

32  y x mx

có hai điểm

cực trị

A

và

B

sao cho các điểm

A

,

B

và

 

1; 2M

thẳng hàng.

A.

2m

. B.

2m

.

C.

2m

. D.

2m

;

2m

.

Câu 47. Cho hàm số bậc ba có phương trình

   

32

1 3 2 2

3

     

m

y x m x m x

. Hàm số đạt

cực trị tại

12

,xx

thỏa mãn

12

21xx

khi

ma

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

281

[ I can’t, I can! ]

và

mb

. Hãy tính tổng

ab

.

A.

8

3



. B.

8

3

. C.

5

2



. D.

5

2

.

Câu 48. Cho hàm số bậc ba có phương trình

 

3 2 3

2 3 1 6    y x m x mx m

. Tìm

m

để đồ thị

hàm số có hai điểm cực trị

,AB

sao cho độ dài

2AB

.

A.

0m

. B.

0m

hoặc

2m

.

C.

1m

. D.

2m

.

Câu 49. Tìm tất cả các giá trị của tham số

m

để

đồ thị hàm số

32

3 3 3   y mx mx m

có hai

điểm cực trị

,AB

thỏa

 

2 2 2

2 20  AB OA OB

(trong đó

O

là gốc tọa độ)

A.

1m

. B.

1m

.

C.

1

17

11











m

. D.

1

17

11











m

.

Câu 50. Cho hàm số

42

22  y x x

. Diện

tích

S

của tam giác có ba đỉnh là ba điểm cực

trị của đồ thị hàm số đã cho có giá trị là

A.

3S

. B.

1

2

S

.

C.

1S

. D.

2S

.

Câu 51. Tìm

m

đề đồ thị hàm số

42

21  y x mx

có ba điểm cực trị

 

0; 1 , , A B C

thỏa mãn

4?BC

A.

2m

. B.

4m

.

C.

4m

. D.

2m

.

Câu 52. Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị của hàm số

42

21  y x mx

có ba điểm cực trị tạo thành một tam giác

vuông cân

A.

3

1

9

m

. B.

1m

.

C.

3

1

9

m

. D.

1m

.

Câu 53. Tìm tất cả các giá trị thực của tham số

m

để đồ thị của hàm số

42

2y x mx

có ba

điểm cực trị tạo thành một tam giác có diện tích

nhỏ hơn

1

.

A.

01m

. B.

0m

.

C.

3

04m

. D.

1m

.

Câu 54. Cho hàm số

4 2 2 4

22   y x mx m m

có đồ thị (C). Biết đồ thị (C) có ba điểm cực trị

A, B, C thỏa mãn ABCD là hình thoi với

 

0; 3D

. Số

m

thuộc khoảng nào sau đây?

A.

19

;

25









m

. B.

9

;2

5









m

.

C.

1

1;

2









m

. D.

 

2;3m

.

Câu 55. Gọi S là tập hợp tất cả các giá trị của

tham số m để đồ thị hàm số

 

4 2 2

21   y x m x m

có ba điểm cực trị tạo

thành ba đỉnh của một tam giác vuông. Số phần

tử của tập hợp S là?

A.

2

. B.

0

.

C.

4

. D.

1

.

Câu 56. Cho hàm số

 

42

2 1 1  y x mx

.

Tổng lập phương các giá trị của tham số

m

để

đồ thị hàm số

 

1

có ba điểm cực trị và đường

tròn đi qua

3

điểm này có bán kính

1R

bằng?

A.

55

2



. B.

15

2



.

C.

25

. D.

15

.

Câu 57. Tìm tất cả các giá trị thực của tham số

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

282

[ I can’t, I can! ]

m

để đồ thị hàm số

4 2 2

24   y x m x m

có

ba điểm cực trị tạo thành ba đỉnh của một tam

giác đều?

A.

 

0; 3; 3m

. B.

 

66

0; 3; 3m

.

C.

 

66

3; 3m

. D.

 

3; 3m

.

Câu 58. Tìm

m

để đồ thị hàm số

4 2 2

21  y x m x

có 3 điểm cực trị lập thành

một tam giác vuông cân.

A.

1m

. B.

 

1;1m

.

C.

 

1;0;1m

. D.

m

.

Câu 59. Tìm tất cả các giá trị

m

sao cho đồ thị

hàm số

 

42

1 2 1    y x m x m

có ba điểm

cực trị là ba đỉnh của một tam giác có một góc

bằng

120

.

A.

3

2

1

3

  m

.

B.

3

2

1

3

  m

,

1m

.

C.

3

1

3

m

.

D.

1m

.

Câu 60. Gọi

S

là tập hợp tất cả các giá trị thực

của tham số

m

để đồ thị

 

C

của hàm số

4 2 2 4

25   y x m x m

có ba điểm cực trị,

đồng thời ba điểm cực trị đó cùng với gốc tọa

độ

O

tạo thành một tứ giác nội tiếp. Tìm số

phần tử của

S

.

A.

1

. B.

0

. C.

2

. D.

3

.

Câu 61. Cho hàm số

4 2 2 4

22   y x mx m m

có đồ thị

 

C

. Biết đồ thị

 

C

có ba điểm cực

trị

A

,

B

,

C

và

ABDC

là hình thoi trong đó

 

0; 3D

,

A

thuộc trục tung. Khi đó

m

thuộc

khoảng nào?

A.

9

;2

5









m

. B.

1

1;

2









m

.

C.

 

2;3m

. D.

19

;

25









m

.

Câu 62. Cho hàm số

42

22   y x mx

có đồ

thị

 

m

C

. Tìm

m

để đồ thị hàm số có ba điểm

cực trị tạo thành một tam giác vuông.

A.

3

3m

. B.

3

3m

.

C.

5

0

4

x

. D.

1m

.

Câu 63. Gọi

A

,

B

,

C

là các điểm cực trị của

đồ thị hàm số

42

24  y x x

. Bán kính đường

tròn nội tiếp tam giác

ABC

bằng?

A.

1

. B.

21

. C.

21

. D.

2

.

Câu 64. Cho hàm số bậc bốn trùng phương

 

42

2 4 5    y x m x m

có đồ thị

 

m

C

.

Tìm

m

để

 

m

C

có ba điểm cực trị tạo thành

một tam giác nhận gốc tọa độ

O

làm trọng tâm.

A.

1m

hoặc

17

2

m

. B.

1m

.

C.

4m

. D.

17

2

m

.

Câu 65. Tìm tất cả các giá trị thực của tham số

m

để đồ thị của hàm số

42

2y x mx

có ba

điểm cực trị tạo thành một tam giác có diện tích

nhỏ hơn

1

.

A.

1m

. B.

01m

.

C.

3

04m

. D.

0m

.

Câu 66. Gọi

0

m

là giá trị của tham số

m

để đồ

thị hàm số

42

21  y x mx

có ba điểm cực trị

tạo thành một tam giác có diện tích bằng

42

.

Mệnh đề nào sau đây đúng

A.





0

1;0m

. B.





0

2; 1  m

.

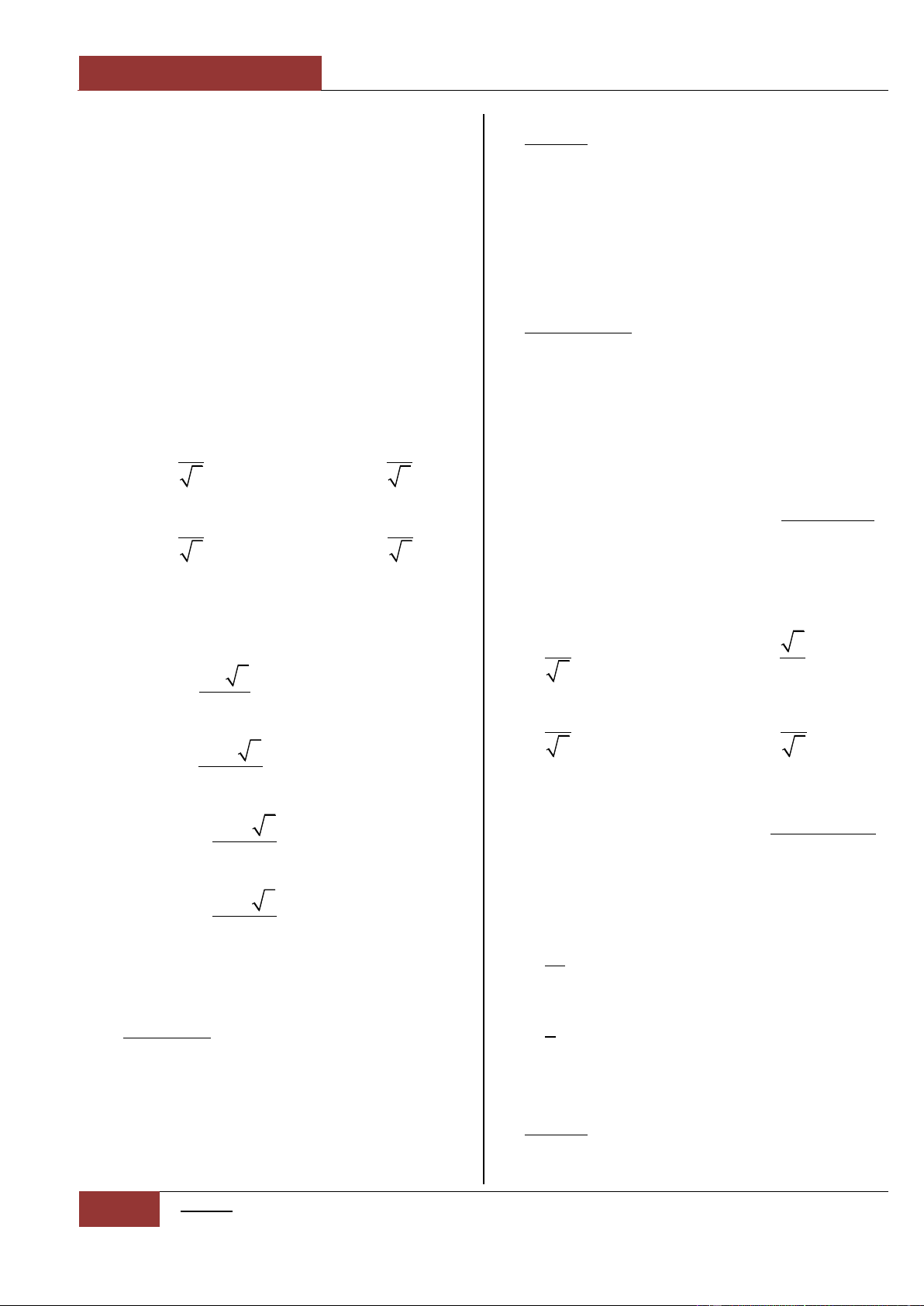
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

283

[ I can’t, I can! ]

C.





0

;2  m

. D.

 

0

1;0m

.

Câu 67. Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị của hàm số

 

4 2 2

21   y x m x m

có ba điểm cực trị tạo

thành một tam giác vuông cân.

A.

0m

.

B.

1; 0  mm

.

C.

1m

. D.

1; 0mm

.

Câu 68. Cho hàm số:

4 2 2

2   y x mx m m

.

Tìm

m

để đồ thị hàm số có 3 điểm cực trị lập

thành tam giác có một góc bằng

120

.

A.

1

3



m

. B.

3

1

3

m

.

C.

3

1

3



m

. D.

1

3

m

.

Câu 69. Đồ thị hàm số

42

2  y x mx m

có ba

điểm cực trị và đường tròn đi qua ba điểm cực

trị này có bán kính bằng

1

thì giá trị của

m

là:

A.

15

1;

2



mm

.

B.

15

1;

2



mm

.

C.

15

1;

2



  mm

.

D.

15

1;

2



  mm

.

Câu 70. Viết phương trình đường thẳng đi qua

hai điểm cực trị của đồ thị hàm số

2

23

21







xx

y

x

.

A.

22yx

. B.

1yx

.

C.

21yx

. D.

1yx

.

Câu 71. Điều kiện của tham số

m

để hàm số

2

1







x mx

y

x

có cực đại và cực tiểu là?

A.

1m

. B.

1m

.

C.

2m

. D.

2m

.

Câu 72. Gọi

S

là tập hợp tất cả các giá trị thực

của tham số

m

để đồ thị hàm số

2

1







x mx m

y

x

có hai điểm cực trị

A

,

B

và

tam giác

OAB

vuông tại

O

. Tổng tất cả các

phần tử của

S

bằng

A.

9

. B.

1

.

C.

4

. D.

5

.

Câu 73. Biết rằng đồ thị

 

2

:

2







x x m

Hy

x

(với

m

là tham số thực) có hai điểm cực trị là

,AB

. Hãy tính khoảng cách từ gốc tọa độ

 

0;0O

đến đường thẳng

AB

.

A.

2

5

. B.

5

.

C.

3

5

. D.

1

5

.

Câu 74. Gọi

S

là tập hợp các giá trị thực của

tham số

m

để đồ thị hàm số

22

1







x mx m

y

x

có hai điểm cực trị

,AB

. Khi

90AOB

thì

tổng bình phương tất cả các phần tử của

S

bằng:

A.

1

16

. B.

8

.

C.

1

8

. D.

16

.

Câu 75. Với tham số

m

, đồ thị của hàm số

2

1







x mx

y

x

có hai điểm cực trị

A

,

B

và

5AB

. Mệnh đề nào dưới đây đúng?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

284

[ I can’t, I can! ]

A.

2m

. B.

01m

.

C.

12m

. D.

0m

.

Câu 76. Cho hàm số

2

4





x m x

y

xm

. Biết

rằng đồ thị hàm số có hai điểm cực trị phân biệt

là

A

,

B

. Tìm số giá trị

m

sao cho ba điểm

A

,

B

,

 

4;2C

phân biệt và thẳng hàng.

A.

0

. B.

2

.

C.

1

. D.

3

.

Câu 77. Giá trị của tham số

m

để hàm số

2

1





x mx

y

xm

đạt cực đại tại điểm

0

2x

là:

A.

1m

. B.

3m

.

C.

1m

. D.

3m

.

Câu 78. Cho hàm số

2

22

  





x mx m

y

xm

. Để

hàm số có cực đại và cực tiểu, điều kiện của

tham số

m

là:

A.

1

2











m

B.

12  m

.

C.

21  m

. D.

2

1











m

.

Câu 79. Để hàm số

2

1





x mx

y

xm

đạt cực đại

tại

2x

thì

m

thuộc khoảng nảo?

A.

 

0;2

. B.

 

4; 2

.

C.

 

2;0

. D.

 

2;4

.

Câu 80. Cho hàm số

1

  



q

y x p

x

đạt cực

đại tại điểm

 

2; 2A

. Tính

pq

.

A.

2pq

. B.

1

2

pq

.

C.

3pq

. D.

1pq

.

Câu 81. Cho hàm số

2

1





x mx

y

xm

( với

m

là

tham số). Tìm tất cả các giá trị của tham số

m

để hàm số có giá trị cực đại là 7.

A.

7m

. B.

5m

.

C.

9m

. D.

5m

.

Câu 82. Tìm tất cả các giá trị của tham số thực

m

để đồ thị hàm số bậc ba

     

32

2 1 3y f x mx m x m x      

có hai điểm cực trị có hoành độ dương là?

A.

1

;0

2

m









. B.

1

0;

2

m









.

C.

1

0;

2

m











. D.

1

;0

2

m











.

Câu 83. Có bao nhiêu giá trị nguyên của tham

số

 

10;10m

để hàm số:

 

2

32

3

4 1 1

2

y x mx m x    

có hai điểm cực trị

12

,xx

thỏa mãn

1 2 1 2

x x x x

là?

A.

12

. B.

18

. C.

16

. D.

15

.

Câu 84. Cho phương trình bậc hai

   

2

1 2 2 1 0m x m x m     

có hai nghiệm

12

,xx

. Định

m

để phương trình

có nghiệm thỏa mãn:

12

2xx

.

A.

16 3 33m 

. B.

3 13

2

m





.

C.

29

12

m 

. D.

1

3

m 

.

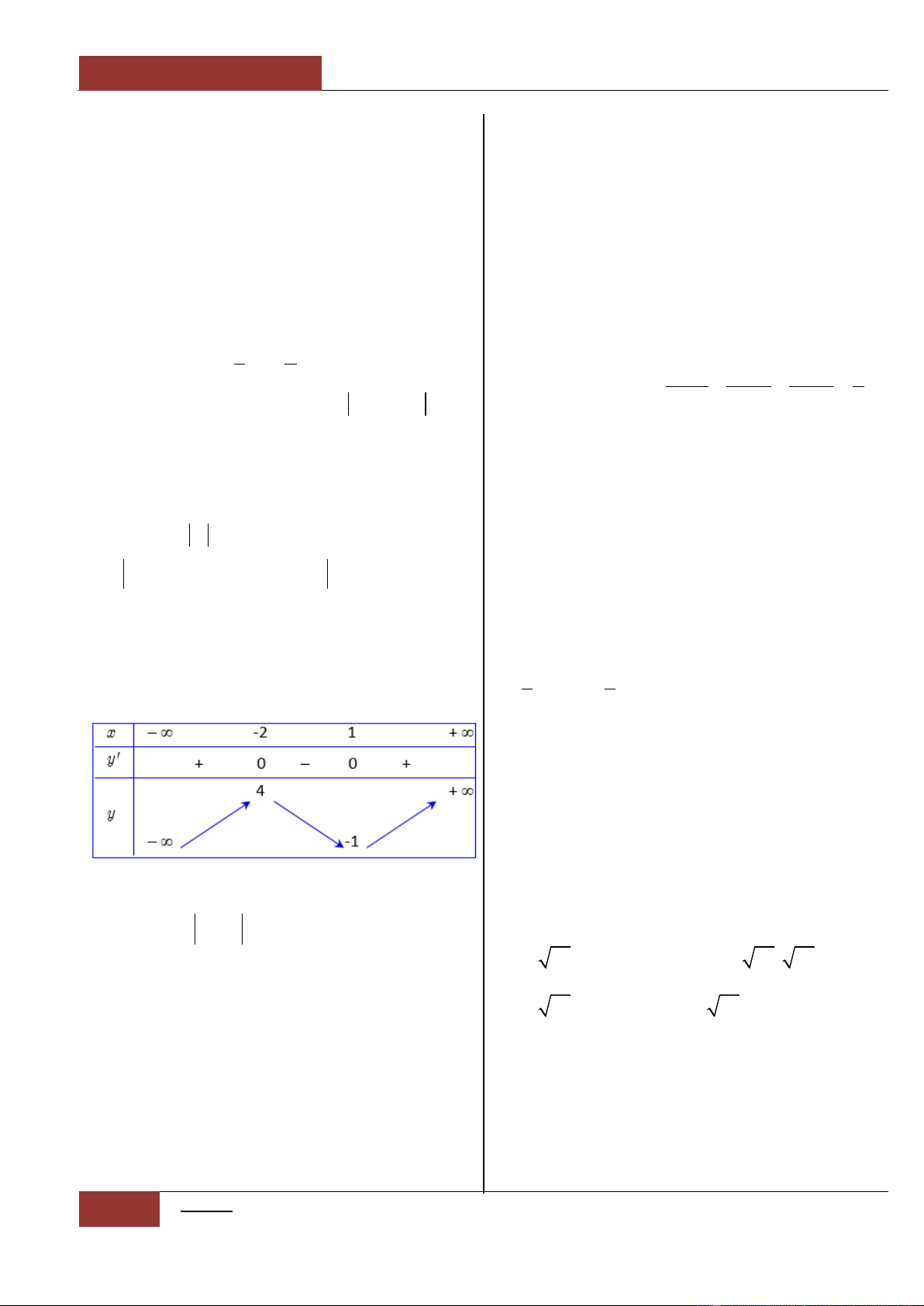
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

285

[ I can’t, I can! ]

Câu 85. Tìm tất cả các giá trị của tham số

m

để

hàm số

4 2 3

2 2017 2016y mx x m   

có 3

cực trị tạo thành tam giác có bán kính ngoại tiếp

bằng

1

.

A.

2m 

. B.

1

2

m











.

C.

1m 

. D.

1m 

.

Câu 86. Tìm tất cả các giá trị thực của tham số

m

để hàm số

 

32

11

5

32

y x m x mx   

có

cực đại, cực tiểu thỏa điều kiện

5

CD CT

xx

.

A.

0m 

. B.

6m 

.

C.

 

0;6m 

. D.

 

0; 6m 

.

Câu 87. Có bao nhiêu giá trị nguyên của tham

số

 

5mm

để hàm số

 

3 2 2

2    y x m x mx m

có ba điểm cực

tiểu?

A.

6

. B.

3

. C.

5

. D.

4

.

Câu 88. Cho hàm số bậc ba có bảng biến thiên

như hình vẽ dưới đây:

Số giá trị nguyên của tham số

m

để hàm số

 

32

31   y f x x m

có

10

điểm cực trị?

A.

2

. B.

3

. C.

0

. D.

1

.

Câu 89. Cho hai đường cong hàm bậc bốn

trùng phương

   

42

1

: 1 2   C y x m x

và

   

4

2

: 2 1 4 8 3    C y x x x m

. Biết rằng

mỗi đường cong

   

12

,CC

đều có ba điểm cực

trị tạo thành tam giác, đồng thời hai tam giác đó

đồng dạng với nhau. Hỏi

m

thuộc khoảng nào

dưới đây?

A.

 

1;2

. B.

 

0;1

.

C.

 

2;3

. D.

 

3;4

.

Câu 90. Có bao nhiêu số thực

m

để đường

thẳng

 

64y m x  

cắt đồ thị hàm số

32

31y x x x   

tại ba điểm phân biệt có tung

độ

1 2 3

,,y y y

thỏa mãn

1 2 3

1 1 1 2

4 4 4 3

  

  y y y

?

A.

2

. B.

0

. C. 3. D. 1.

Câu 91. Cho hàm số

42

2y x x

có đồ thị

 

C

.

Có bao nhiêu đường thẳng

d

có đúng ba điểm

chung với đồ thị

 

C

và các điểm chung có

hoành độ

1 2 3

,,x x x

thỏa mãn

333

1 2 3

1?   xxx

A. 0. B. 1. C. 2. D. 3.

Câu 92. Biết rằng đồ thị hàm số

2

11

3

2

y x x

x

  

có ba điểm cực trị thuộc một

đường tròn

 

.C

Bán kính của

 

C

gần với giá

trị nào dưới đây ?

A.

12,4

. B.

6,4

. C.

4,4

. D.

11,4

.

Câu 93. Tập hợp tất cả các giá trị thực của tham

số m để hàm số bậc ba

   

32

3 1 3 4 9 1      y x m x m x

đạt cực trị tại các điểm lớn hơn -1 là

A.

 

10 1;4 .

B.

 

1 10; 10 1 .  

C.

 

10 1; . 

D.



10 1; .



 



Câu 94. Cho hàm số bậc ba

   

3 2 2 2

2 3 1 6 6     y x m m x m m x

,

với m là tham số. Gọi

S

là tập hợp các giá trị

của m để đồ thị hàm số đã cho có hai điểm cực

trị, đồng thời đường thẳng đi qua hai điểm cực

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

286

[ I can’t, I can! ]

trị đó vuông góc với đường thẳng

2yx

. Số

phần tử của tập hợp

S

là ?

A. 2. B. 3. C. 1. D. 4.

Câu 95. Gọi S là tập hợp các giá trị của tham số

a để đồ thị hàm số bậc bốn trùng phương

 

2

4 2 2

2 2 3 1    y x a a x

có ba điểm cực

trị và ba điểm cực trị đó tạo thành một tam giác

có chu vi bằng

2 2 2

. Số tập hợp con của tập

hợp

S

là?

A. 2. B. 8. C. 16. D. 4.

Câu 96. Cho hàm số

42

22  y x mx

có đồ

thị

 

C

. Để đồ thị

 

C

có

3

điểm cực trị cùng

với

 

2; 4M

nằm trên một parabol thì m nằm

trong khoảng nào?

A.

 

2;0

. B.

 

0;2

.

C.

 

2;4

. D.

 

4;

.

Bài tập tương tự

Câu 97. Cho hàm số

32

6 9 4   y x x x

có

đồ thị

 

C

. Biết rằng trên

 

C

tồn tại hai điểm

phân biệt

, MN

mà tiếp tuyến tại đó có cùng

hệ số góc

m

, đồng thời đường thẳng

MN

đi

qua điểm

 

1; 2018A

. Hỏi

m

nằm trong

khoảng nào?

A.

 

2017; 4000

. B.

 

2019;0

.

C.

 

0;2017

. D.

(4000; )

.

Câu 98. Biết đồ thị hàm số

2

33   

m

y x x

x

(

m

là tham số) có ba điểm cực trị. Parabol

2

  y ax bx c

đi qua ba điểm cực trị đó. Tính

24abc

.

A.

2 4 3  abc

. B.

2 4 0  abc

.

C.

2 4 4   abc

. D.

2 4 1  abc

.

Câu 99. Cho hàm số bậc ba

 

32

0    y ax bx cx d a

đạt cực trị tại các điểm

12

,xx

thỏa mãn

 

1

1;0 ;x

 

2

1;2 .x

Biết hàm số đồng biến trên khoảng

 

12

;xx

, đồ thị hàm số cắt trục tung tại điểm có

tung độ dương. Khẳng định nào dưới đây đúng?

A.

0, 0, 0, 0.   a b c d

B.

0, 0, 0, 0.   a b c d

C.

0, 0, 0, 0.   a b c d

D.

0, 0, 0, 0.   a b c d

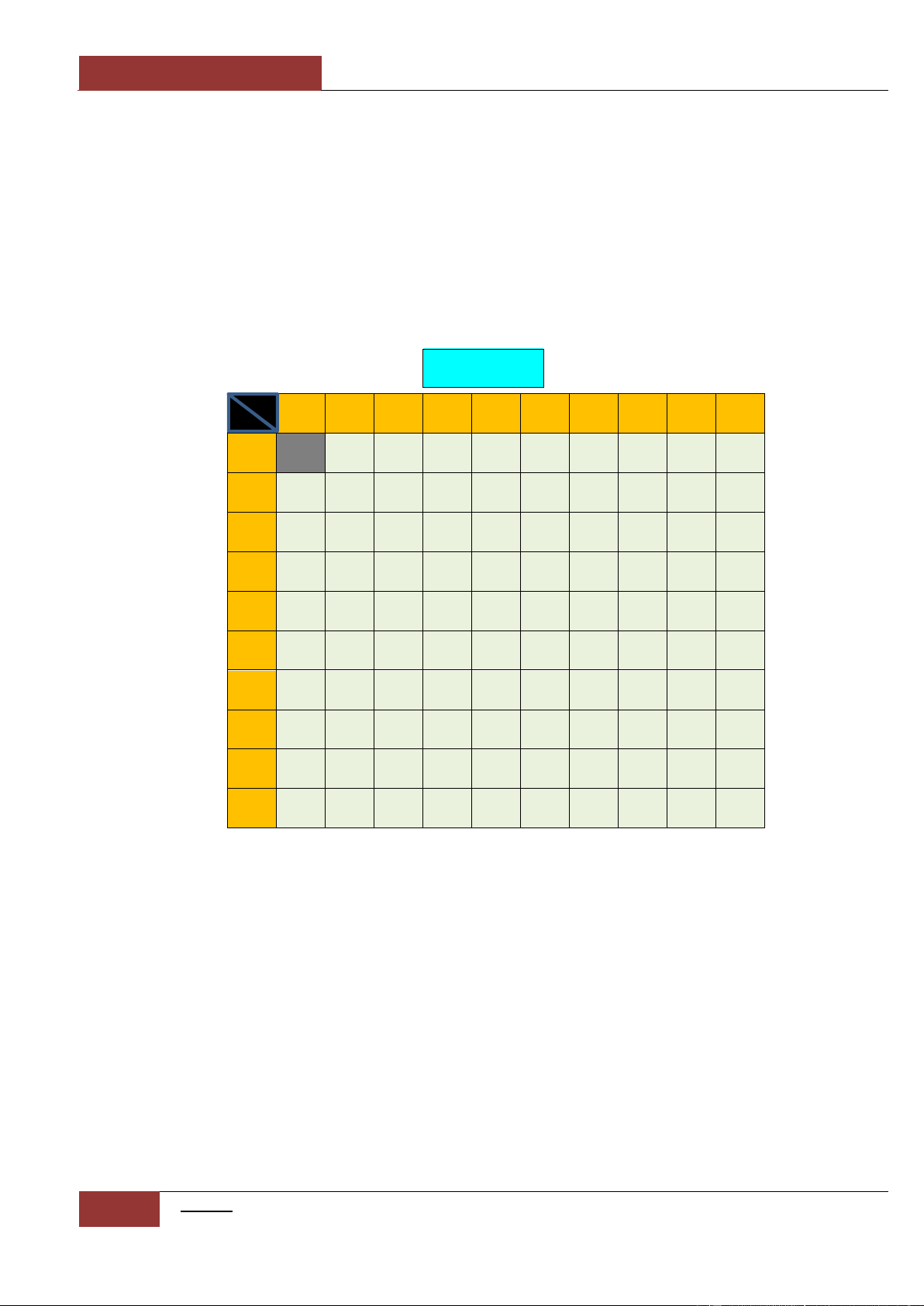
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

287

[ I can’t, I can! ]

ĐÁP ÁN

0

1

2

3

4

5

6

7

8

9

0

B

D

C

B

A

B

C

1

D

C

D

A

C

D

A

D

2

D

B

A

C

A

C

3

D

B

A

D

C

D

4

A

C

A

D

B

D

5

C

B

D

A

D

C

B

A

6

C

D

C

B

C

A

C

B

7

B

A

B

A

B

8

D

C

A

D

C

9

D

B

A

D

C

B

D

A

Ghi chú: Đáp án là sự kết hợp giữa dòng và cột . Ví dụ: Câu 24A (giao của dòng 2 và cột 4).

i

j

i

j

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

288

[ I can't, I can! ]

LỜI GIẢI CHI TIẾT

Câu 1. Ta có:

2

3 6 9



  y x x

thực hiện phép

chia

y

cho



y

ta được số dư là

82  yx

.

Như thế điểm

 

1; 10N

thuộc đường thẳng

AB

.

Đáp án B

Câu 2. Ta có:

2

36



y x x

. Từ đó ta có tọa độ

hai điểm cực trị

 

0;1A

,

 

2; 3B

. Đường

thẳng qua hai điểm cực trị có phương trình

21  yx

. Đường thẳng này vuông góc với

đường thẳng

 

2 1 3   y m x m

khi và chỉ

khi:

  

3

2 1 2 1

4

     mm

.

Đáp án B

Câu 3. Hàm số

32

31  y x x

có TXĐ: ;

2

36



y x x

;

0

'0

2













x

y

x

.

Suy ra đồ thị hàm số có hai điểm cực trị là:

 

0;1A

,

   

2; 3 2; 4   B AB

.

Đường thẳng

d

đi qua hai điểm

A

,

B

có

phương trình:

1

21

24



    



xy

yx

.

Đường thẳng

 

2 1 3   y m x m

song song

với đường thẳng

2 1 2

1

31

2

  



   







m

dm

m

.

Đáp án D

Câu 4. TXĐ:

D

.

2

' 3 6 9  y x x

.

2

16

' 0 3 6 9 0

3 26

   



     



   



xy

y x x

xy

Ta có:

   

1;6 , 3; 26AB

 

4; 32  AB

nên chọn

1x

.

Phương trình đường thẳng

AB

là:

   

8 1 1 6 0 8 2 0       x y x y

.

Thay tọa độ các điểm

, , ,P M N Q

vào phương

trình đường thẳng

AB

ta có điểm

 

1; 10N

thuộc đường thẳng.

Đáp án C

Câu 5. Xét hàm số

32

31  y x x

.

Ta có:

2

36



y x x

,

11

21

33





   





y x y x

.

Do đó, đường thẳng



qua hai điểm cực trị của

đồ thị hàm số này có phương trình là

21  yx

.

Để

d

vuông góc với



thì

   

3 1 . 2 1   m

1

6

  m

.

Vậy giá trị cần tìm của

m

là

1

6

m

.

Đáp án B

Câu 6. TXĐ:

D 

.

Ta có:

   

2

6 6 1 6 1 2



    y x m x m m

,

0

12















xm

y

xm

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

289

[ I can't, I can! ]

Để hàm số có hai cực trị thì

12mm

1

3

m

.

Hai điểm cực trị của đồ thị hàm số là:

 

32

; 7 3A m m m

,

 

32

1 2 ;20 24 9 1   B m m m m

.

Do đó:

 

3

1 3 ; 3 1  AB m m

. Do đó

AB

có

vectơ pháp tuyến là

 

2

3 1 ;1nm

.

Do đó:

 

2

32

: 3 1 2 3 0     AB m x y m m m

 

2

32

3 1 2 3      y m x m m m

.

Để đường thẳng

AB

song song với đường

thẳng

4yx

thì:

 

2

32

3 1 4

2 3 0



   





  





m

m m m

1

3

0

1

2

1













































m

1

3

  m

.

Câu 7. Thực hiện phép chia

y

cho



y

ta được:

 

1

. 2 1

3





   





y y x x

.

Giả sử hai điểm cực trị của đồ thị hàm số lần

lượt là:

 

11

;A x y

và

 

22

;B x y

. Ta có:

     

1 1 1 1 1 1

1

. 2 1 2 1

3





       





y y x y x x x x

     

2 2 2 2 2 2

1

. 2 1 2 1

3





       





y y x y x x x x

.

Ta thấy, toạ độ hai điểm cực trị

A

và

B

thoả

mãn phương trình

21  yx

.

Vậy phương trình đường thẳng qua hai điểm

cực trị là:

21  yx

.

Đáp án B

Câu 8. Ta có:

2

3 4 3



   y x x m

, để hàm số

có hai điểm cực trị thì phương trình

0



y

có

hai nghiệm phân biệt

0



  

 

13

*

3

m

Ta có:

1 2 2 26 7 2

.

3 9 3 9 9 3

   



     

   

   

mm

y y x x

nên phương trình đường thẳng đi qua hai điểm

cực trị là

2 26 7 2

3 9 9 3



   





mm

yx

. Theo giả

thiết, đường thẳng này đi qua

 

9; 5M

nên

3m

(thỏa mãn điều kiện

 

*

).

Đáp án C

Câu 9. Tập xác định:

D

.

2

32



yx

.

3

14

2.

33





      





y x x m x y x m

Suy ra đường thẳng đi qua các điểm cực trị của

đồ thị hàm số có phương trình là

4

3

  y x m

đường thẳng này đi qua điểm

 

3;7M

khi và

chỉ khi

 

4

7 . 3 3

3

     mm

.

Đáp án C

Câu 10. Xét hàm số

32

31  y x x

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

290

[ I can't, I can! ]

Ta có:

2

36



y x x

,

11

21

33





   





y x y x

.

Do đó, đường thẳng



qua hai điểm cực trị của

đồ thị hàm số này có phương trình là

21  yx

.

Để

d

vuông góc với



thì

   

3 1 . 2 1   m

1

6

  m

.

Vậy giá trị cần tìm của

m

là

1

6

m

.

Câu 11. TXĐ:

D

.

 

2

32



  f x x ax b

. Điều kiện để hàm số có

hai điểm cực trị là

 

0



fx

có hai nghiệm

phân biệt

2

30  ab

.

Lấy

 

fx

chia cho

 



fx

.

Ta có:

   

11

. ...

39





  





f x f x x a

2 2 1

...

3 9 9



   





b x c ab

.

Suy ra đường thẳng đi qua

A

,

B

là:

 

2 2 1

3 9 9



   





y b x c ab d

.

Theo đầu bài

 

d

đi qua gốc tọa độ

1

0

9

  c ab

9ab c

.

Khi đó:

  P abc ab c

2

9 10  P c c

2

5 25

3

39



   





Pc

.

Suy ra:

25

min

9

P

.

Đáp án C

Câu 12. Ta có:

2

36



y x mx

;

0



y



2

3 6 0x mx



0x

,

2xm

.

Đồ thị hàm số có hai điểm cực trị khi và chỉ khi

phương trình

0



y

có hai nghiệm phân biệt



20m



0m

.

Khi đó hai điểm cực trị là:

 

0;2A

,

 

3

2 ;2 4B m m

.

Ta có:

 

1;4MA

,

 

3

2 1;4 4  MB m m

.

Ba điểm

A

,

B

và

 

1; 2M

thẳng hàng



MA

,

MB

cùng phương



3

2 1 4 4

14







mm



3

2 1 1

11







mm



3

2 1 1  mm



3

2mm



2

2m



2m

(do

0m

).

Đáp án D

Câu 13. Tập xác định:

D

.

2

36



y x x

,

2

0

0 3 6 0

2







    







x

y x x

x

.

Do đó đồ thị hàm số đã cho luôn có hai điểm

cực trị lần lượt có tọa độ là

 

0;Am

và

 

2; 4Bm

.

Ta có:

 

2

2 2 2

0 2 4     OA OB m m

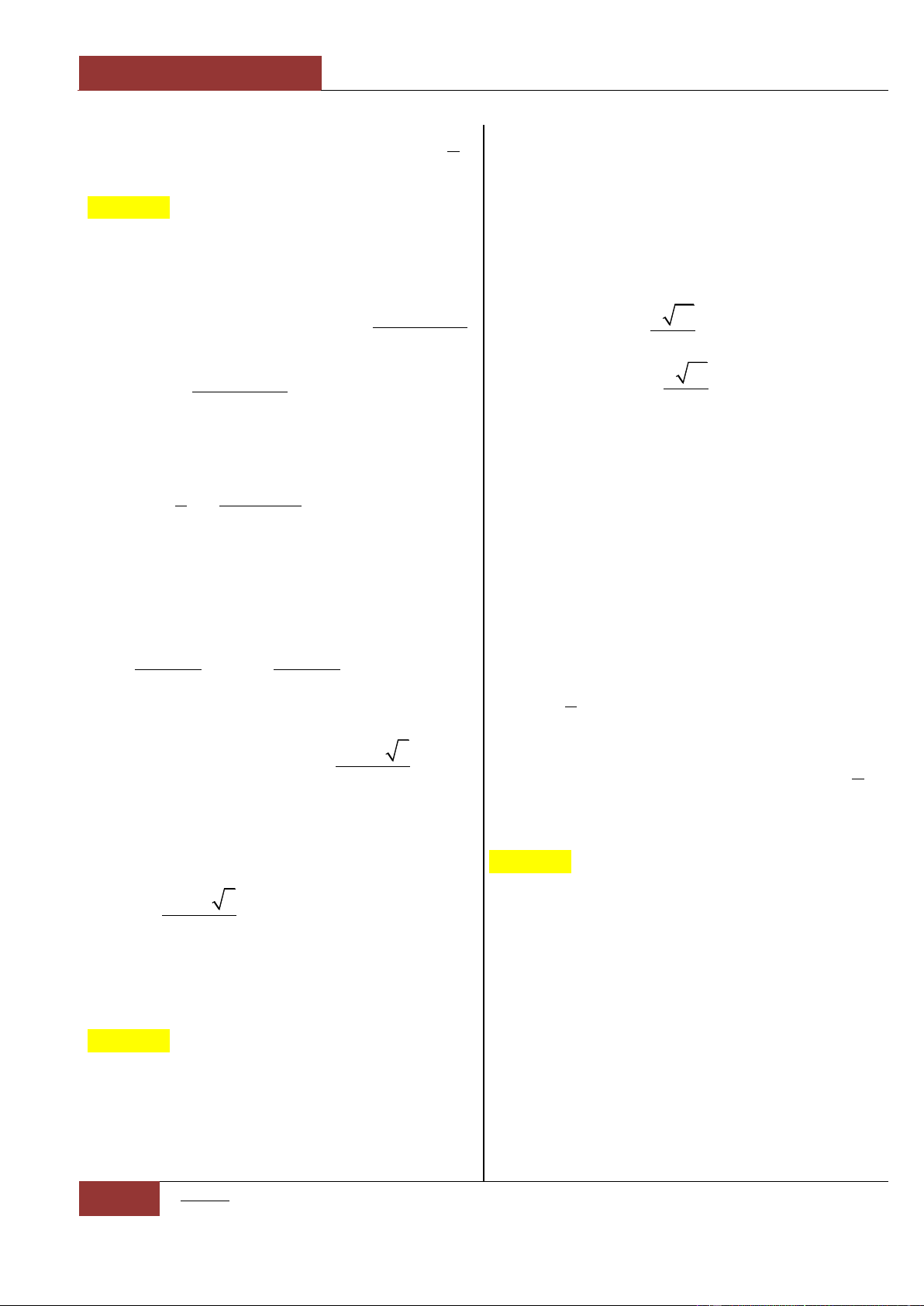
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

291

[ I can't, I can! ]

 

2

44   mm

5

20 8 0

2

    mm

.

Đáp án D

Câu 14. Ta có:

 

22

' 2 1   y x mx m

3

1

32

' 0 1;

1

3









    











xm

mm

y A m

xm

và

3

32

1;

3











mm

Bm

Dễ thấy phương trình đường thẳng

 

2

1

2

:

33



  

mm

AB y x

nên

AB

không thể

song song hoặc trùng với

d

, AB

cách đều

đường thẳng

: 5 9d y x

nếu trung điểm

I

của

AB

nằm trên

d

.

33

3

33

; 5 9

33

3

18 27 0

3 3 5

2





   











    











m m m m

I m d m

m

mm

m

Với

3,m A B

thỏa điều kiện nằm khác

phía so với

d

.

Với

3 3 5

,

2



m A B

thỏa điều kiện nằm

khác phía so với

d

.

Tổng các phần tử của

S

bằng 0.

Đáp án D

Câu 15. Ta có:

 

22

' 2 2 2 3 1   y x mx m

;

 

22

' 2 3 1   y x mx m

.

 

22

31   g x x mx m

;

2

13 4  m

.

Đồ thị hàm số có hai điểm cực trị khi và chỉ khi

'y

có hai nghiệm phân biệt



 

gx

có hai nghiệm phân biệt



0



2 13

13

2 13

13













m

. (*)

1

x

,

2

x

là các nghiệm của

 

gx

nên theo định lý

Vietè, ta có:

12

2

12

31









  





x x m

.

Do đó:

 

1 2 1 2

21  x x x x



2

3 2 1 1   mm



2

3 2 0  mm



0

2

3











m

.

Đối chiếu với điều kiện

 

*

, ta thấy chỉ

2

3

m

thỏa mãn yêu cầu bài toán.

Đáp án A

Câu 16. Đồ thị hàm số bậc ba đã cho có hai

điểm cực trị nằm về hai phía đối với trục hoành

khi và chỉ khi phương trình:

   

32

2 1 2 1 10     mx m x mx m

có

3

nghiệm phân biệt.

Ta có

     

2

1 1 1 01



      



x mx m x m

Phương trình

 

1

có

3

nghiệm phân biệt khi và

chỉ khi phân biệt

 

2

1 1 0    mx m x m

có

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

292

[ I can't, I can! ]

2

nghiệm phân biệt khác

1

.

 

   

2

0

1 1 0

1 4 1 0







     





   





m

m m m

2

0

20

3 6 1 0







  





   



m

mm

0

2

3 2 3 3 2 3

33









  





   









m

Do

1   mm

.

Đáp án C

Câu 17.

 

2

' 3 2 6 2 9.    y x m x m

 

2

' 3 2 6 2 9 0

1

.

29

3

     

















y x m x m

x

m

x

Hàm số có

2

cực trị khi và chỉ khi:

29

13

3



   

m

 

*

 

12ym

.

 

2

29

2

3 27





  





m

ym

.

Yêu cầu đề bài

 

29

1 . 0

3











m

yy

 

2

32

29

2 . 2 0

27

2 . 4 36 81 54 0

6

2

.

3

2





    





     

  



























m

mm

m m m m

m

Kết hợp điều kiện

 

*

, ta có:

2

6

.

3

2

  

























m

Đáp án D

Câu 18. TXĐ:

D 

.

Ta có:

   

2

' x 2 1 3 2    y m m x m

.

Để hàm số có hai điểm cực trị thì phương trình

   

2

x 2 1 3 2 0    m m x m

phải có hai

nghiệm phân biệt.

   

2

0

1 3 2 0

0

2 4 1 0













     













   



m

m m m

m

mm

.

Theo định lý Vietè, ta có:

 

12

21

.

32

.





















m

xx

m

xx

m

.

Theo bài ta có hệ phương trình:

 

12

1

21

2

.

















xx

m

xx

m

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

293

[ I can't, I can! ]

 

1

2

34

21

1

2

























m

x

m

x

m

mm

.

 

    

 

32

3 4 2

.

3 2 3 4 2 0

2 thoûa maõn

2

thoûa maõn

3

m

mm

m m m

m m m m

m







     

















Vậy

22

12

40

9

mm

.

Đáp án A

Câu 19.

2

36



  y x mx

;

0

2















x

y

xm

Đồ thị có hai cực trị khi:

0m

.

Khi đó hai điểm cực trị là:

 

3

0; 3 1 , 2 ;4 3 1   A m B m m m

.

Tọa độ trung điểm

AB

là:

 

3

;2 3 1I m m m

.

A

và

B

đối xứng qua

d

khi và chỉ khi:

.0















d

Id

AB u

.

 

3

2 ;4 , 8; 1  

d

AB m m u

.

+

3

0

. 0 16 4 0 2

2







     







d

m

AB u m m m

m

.

Với

0m

, loại.

Với

2m

, ta có:

 

2;9 I I d

.

Với

2m

, ta có:

 

2; 11   I I d

.

Do đó

2m

thỏa mãn yêu cầu.

Đáp án D

Câu 20. Yêu cầu bài toán



đồ thị hàm số cắt

trục hoành tại ba điểm phân biệt.

 

3 2 2 2

8 11 2 2 0      x x m x m

có ba

nghiệm phân biệt.

 

3 2 2 2

8 11 2 2 0     x x m x m

 

22

2 6 1 0     x x x m

;

 

22

2

6 1 0 *









   



x

x x m

Suy ra phương trình

 

*

có hai nghiệm phân

biệt khác

2

.

2

' 10 0

80



   













m

22

10 10











  





m

Vậy có

7

giá trị nguyên của tham số thỏa mãn

đề bài.

Đáp án D

Câu 21. Ta có:

 

2

1 2 1    y x x mx m

.

+ Hàm số có hai điểm cực trị nằm về hai phía

trục hoành khi và chỉ khi đồ thị

y

cắt trục hoành

tại ba điểm phân biệt.

 

2

1 2 1 0      y x x mx m

có ba

nghiệm phân biệt.

2

2 1 0    x mx m

có hai nghiệm phân

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

294

[ I can't, I can! ]

biệt khác 1.

2

15

2

10

15

2 3 0

2

3



















  



























m

mm

m

.

+ Do

, 20m N m

nên

1 20m

.

Vậy có

19

số tự nhiên thỏa mãn bài toán.

Đáp án B

Câu 22. TXĐ:

D 

.

 

22

0 3 2 1 2 0



      y x m x m

.

Để hàm số có hai điểm cực trị:

 

2

0 2 2 7 0

1 15 1 15

*

22



       



  

mm

m

.

Ta lần lượt thử bốn giá trị nguyên của

m

thỏa

mãn

 

*

là

1; 0;1; 2

.

Ta được bốn hàm số:

3

32

2

23

22

31



  



   





   



   



y x x

y x x x

.

Khi đó ta nhận thấy chỉ có

1m

thỏa mãn yêu

cầu bài toán.

Đáp án B

Câu 23. Ta có:

2

' 3 6  y x x m

.

Hàm số đạt cực trị tại

12

,xx

.

Vậy

12

,xx

là nghiệm của phương trình

'0y

.

Theo Vietè, ta có:

12

2

.

3















xx

m

xx

.

2 2 2

1 2 1 2 1 2

( ) 2   x x x x x x

2

4

3



m

2

46

3

  

m

3  m

.

Đáp án A

Câu 24. Ta có:

 

2

' 6 12f x x x

.

 

0

'0

2













x

fx

x

 

0 0 1    x f m

 

2 2 7    x f m

Hàm số có các giá trị cực trị trái dấu

  

1 7 0     mm

  

1 7 0 7 1       m m m

.

Vậy có

7

giá trị nguyên của

m

thỏa mãn.

Đáp án A

Câu 25. Ta có:

   

2

6 6 1 6 2



    y x m x m

.

   

2

1

0 1 2 0

2







       



  



x

y x m x m

xm

Để hàm số có điểm cực đại cực tiểu nằm trong

khoảng

 

2;3

thì

0



y

có hai nghiệm phân

biệt nằm trong khoảng

 

2;3

.

2 1 3

2 2 3 1 4

    







       



mm

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

295

[ I can't, I can! ]

Đáp án A

Câu 26. Ta có:

2

0

' 3 6 0

2





   







x

y x mx

xm

.

Đồ thị

 

C

có hai điểm cực trị

2 0 0   mm

.

Khi đó:

   

2 3 2

0;4 2 , 2 ; 4 4 2   A m B m m m

.

2 6 4

4 16 2 4 1    AB m m m m

.

Phương trình đường thẳng

AB

là:

 

2

22

3

42

0

2 4 2 0

20

4





     



ym

x

m x y m

m

 

2 2 2

44

2 4 4 2 2 3

,

4 1 4 1

   





m m m

d C AB

mm

.

Diện tích tam giác

ABC

là:

 

2

4

1

. . , 4

2

23

1

.2 . 4 1. 4

2

41





  



S AB d C AB

m

mm

m

 

   

2 6 4 2

2

22

3 2 6 9 4 0

1

1 4 0

2

       





    







m m m m m

m

mm

m

Do

m

nguyên dương nên ta được

1, 2mm

,

tổng thu được là

3

.

Đáp án C

Câu 27. Ta có:

   

2

' 6 6 1 6 2    y x m x m

Để hàm số có điểm cực đại và điểm cực tiểu

nằm trong khoảng

 

2;3

.



Phương trình:

'0y

có

2

nghiệm thuộc

khoảng

 

2;3

.

   

2

1 2 0     x m x m

có 2 nghiệm

thuộc khoảng

 

2;3

.

  

1 2 0    x x m

.

 

1 2;3

2

   











x

xm

.

2 1 3

2 2 3 1 4

   







      



mm

YCBT

mm

.

Đáp án A

Câu 28. +) Để hàm số có hai cực trị thì phương

trình

0



y

phải có hai nghiệm phân biệt:

 

2

9 4 1 3



   y x m x m

có hai nghiệm phân

biệt

 

2

4 1 27 0



     mm

+) Xét

   

12

.0y x y x

nên ta có

 

32

3 2 1 3 5     y x m x mx m

phải tiếp

xúc với trục hoành

 

32

3 2 1 3 5 0      x m x mx m

phải có

nghiệm kép

     

2

1 3 2 5 5 0 1



      



x x m x m

phải

có nghiệm kép

+) TH1: Phương trình

 

2

3 2 5 5 0    x m x m

có một nghiệm

1

1 13   xm

.

+) TH2: Phương trình

 

2

3 2 5 5 0    x m x m

có nghiệm kép khác

1

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

296

[ I can't, I can! ]

   

2

23

2 5 12 5 0

4 32 35 0

8

      

   

   

mm

1 2 3

21    m m m

.

Đáp án A

Câu 29. +) Ta có:

2

3 6 27



  y x mx

,

2

0 2 9 0



    y x mx

 

1

.

+) Theo giả thiết hàm số đạt cực trị tại

12

,xx



phương trình

(1)

có

2

nghiệm phân biệt

0



  

2

3

90

3





   







m

 

*

.

+) Với điều kiện

 

*

thì phương trình

(1)

có

2

nghiệm

12

,xx

, theo Vietè, ta có:

12

2

9











x x m

xx

.

+) Ta lại có:

12

5xx

   

22

1 2 1 2 1 2

25 4 25 0       x x x x x x

2

61 61

4 61 0

22

      mm

 

**

+) Kết hợp

   

* , **

và điều kiện

0m

, ta

được:

61

3

2

m

3

2 61 3

61

2







     









a

T b a

b

.

Đáp án C

Câu 30. TXĐ:

D 

3

22

2 3 ' 4

3

       

x

y x mx y x x m

.

Hàm số có hai điểm cực trị

12

,xx

thì phương

trình

'0y

có hai nghiệm phân biệt

' 0 4 0 4       mm

.

Khi đó giả sử

12

xx

,

1

2

24

'0

24



  





  





xm

y

xm

.

Yêu cầu bài toán trở thành:

2

4 2 4 4 0 4       x m m

.

Kết hợp với

4m

ta được

04m

. Do

m

nguyên nên

 

0;1;2;3m

. Vậy có

4

giá trị của

m

thỏa mãn yêu cầu bài toán.

Đáp án D

Câu 31. Ta có

   

32

14 2 7 1    y x m x x

.

 

2

' 3 8 2 7    y x m x

.

Xét phương trình

   

2

23 8 2 7 0   x m x

.

 

2

' 4 2 21 0    





m

, với mọi m



Hàm

số

 

1

luôn có hai điểm cực trị

12

;xx

với mọi

m

.

*Ta thấy:

21 0  ac



phương trình

 

2

có

2

nghiệm trái dấu.

12

0; 0  xx

1 1 2 2

;   x x x x

.

*Ta có:

12

4  xx



12

4   xx

 

12

82

44

3



       

m

xx

1

2

m

.

Đáp án B

Câu 32. Ta có:

   

2

' 6 6 2 1 6 1    y x m x m m

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

297

[ I can't, I can! ]

'0

1





    







xm

ym

xm

, hàm số luôn có

cực đại, cực tiểu.

Tọa độ các điểm cực đại, cực tiểu của đồ thị là

   

3 2 3 2

;2 3 1 , 1;2 3   A m m m B m m m

.

Suy ra

2AB

và phương trình đường thẳng

32

: 2 3 1 0     AB x y m m m

.

Do đó, tam giác

MAB

có diện tích nhỏ nhất khi

và chỉ khi khoảng cách từ

M

tới

AB

nhỏ nhất

Ta có:

 

2

3 1 1

,

22





m

d M AB

, dấu

""

khi

0m

.

Đáp án B

Câu 33. Ta có:

2

33



y x m

suy ra đồ thị hàm

số có điểm cực đại và cực tiểu khi

0m

. Các

điểm cực đại, cực tiểu của đồ thị hàm số là

   

;2 2 ; ;2 2 .  C m m m D m m m

Đường thẳng



đi qua các điểm cực đại, cực

tiểu của đồ thị hàm số có phương trình là:

22  y mx

.

Do:

 

2

21

,1

41



   



m

d I R

m

(vì

0m

)





luôn cắt đường tròn tâm

 

1;1I

, bán kính

1R

tại

2

điểm

,AB

phân biệt. Dễ thấy

1

2

m

không thỏa mãn do

,,A I B

thẳng hàng.

Với

1

2

m

:



không đi qua

I

, ta có:

2

1 1 1

. .sin

2 2 2



  

ABI

S IA IB AIB R

.

Do đó

IAB

S

lớn nhất bằng

1

2

khi

sin 1AIB

hay

AIB

vuông cân tại

I

1

22

  

R

IH

2

21

1 2 3

2

41





   



m

(

H

là trung

điểm của

AB

)

Đáp án B

Câu 34. Ta có:

2

32



  y x ax b

.

Chia

y

cho



y

ta được:

2

1 1 2

3 9 9 3 9





      





a b ab

y y x a x c

.

Do

   

1 1 2 2

; , ;M x y N x y

là hai điểm cực trị

nên:

   

12

0, 0



y x y x

.

Do đó:

2

11

2

22

2

;

9 3 9

2

9 3 9





    





  







    









a b ab

y x c

a b ab

y x c

.

Theo giả thiết:

   

1 1 2 1 1 2 1 2 2 1

    x y y y x x x y x y

2

12

2

21

2

9 3 9

2

9 3 9





     













    









a b ab

x x c

a b ab

x x c

 

12

99

09

9

   

   

   

   

     

ab ab

x c x c

ab

c x x ab c

.

Ta có:

2

2 3 9 21    P abc ab c c c

.

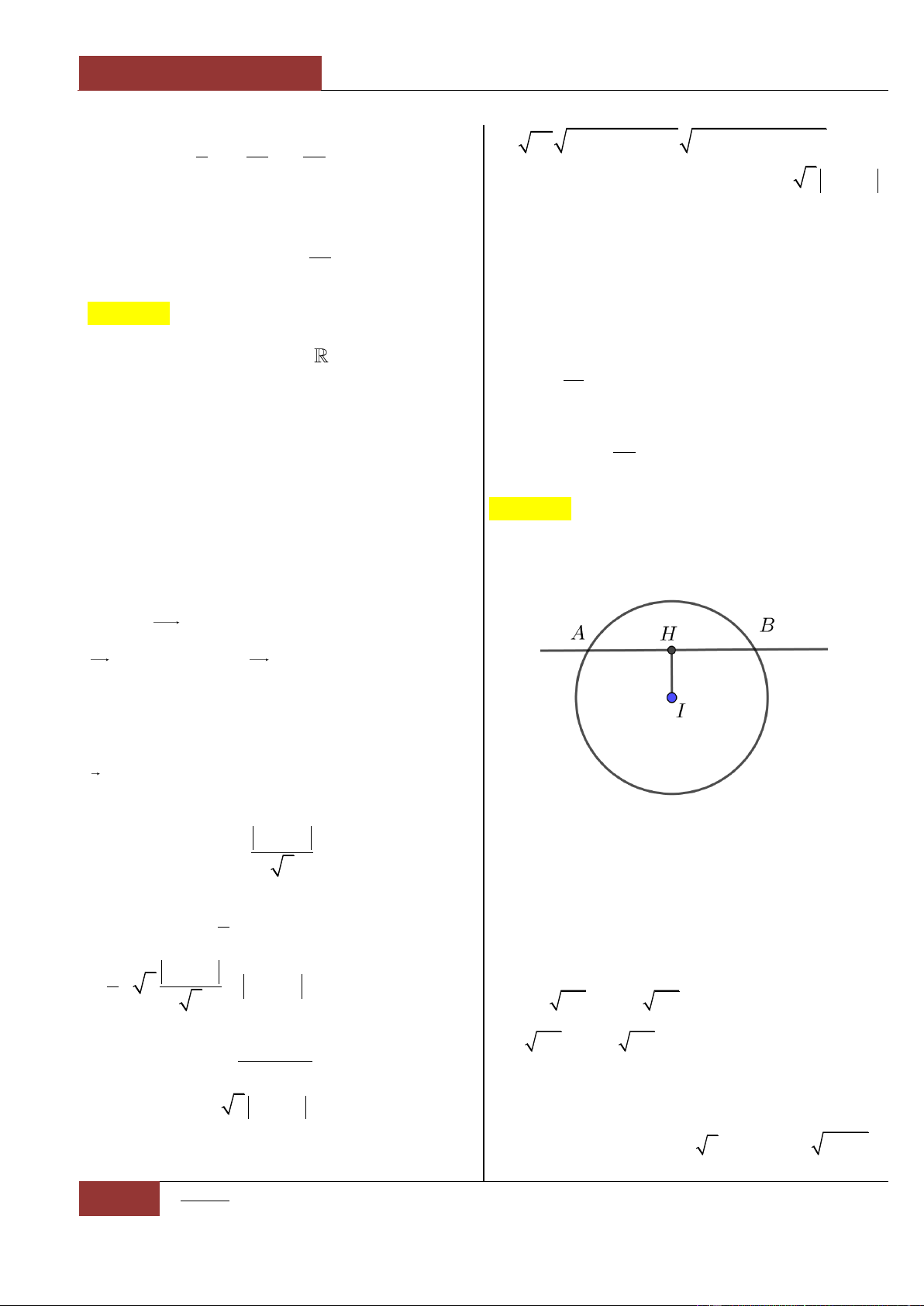
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

298

[ I can't, I can! ]

2

7 49 49

3

2 4 4



     





Pc

Vậy giá trị nhỏ nhất của biểu thức

23  P abc ab c

bằng

49

4



.

Đáp án A

Câu 35. Tập xác định:

D

.

 

22

3 6 3 1



   y x mx m

.

Cho

0



y

22

2 1 0    x mx m

.

Vì

10



   m

nên phương trình

0



y

luôn

có hai nghiệm phân biệt

1xm

.

Gọi

 

1; 4 2  A m m

,

 

1; 4 2  B m m

.

Suy ra:

   

2;4 2 1; 2    AB

,

 

1; 4  IA m m

,

 

3; 4 4   IB m m

.

Phương trình đường thẳng

AB

qua

 

1; 4 2  A m m

và có vectơ pháp tuyến

 

2;1n

là:

:2 2 0  AB x y m

.

Suy ra:

 

22

,

5





m

d I AB

.

Khi đó:

 

1

.,

2





IAB

S AB d I AB

22

1

25

2

5





m

22m

.

Mặt khác:

..

4





IAB

AB IA IB

S

R

. . 4 5 2 2  AB IA IB m

.

22

20 17 2 1 17 38 25

4 5 2 2

    



m m m m

m

  

 

22

2

17 2 1 17 38 25

4 4 8 4

    

  

m m m m

mm

4 3 2

289 680 502 120 9 0     m m m m

.

1

3

17















m

.

Vậy

12

20

17

mm

.

Đáp án D

Câu 36.

Ta có:

2

36



y x m

.

2

02



  y x m

.

Hàm số có cực đại, cực tiểu

0



y

có hai

nghiệm phân biệt

0m

Gọi

 

2 ;4 4 2A m m m

và

 

2 ;4 4 2B m m m

Phương trình đường thẳng

:4 4 0  AB mx y

.

Đặt

 

,a d I AB

 

02a



2

2HB a

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

299

[ I can't, I can! ]

Suy ra:

 

2 2 2

1

2 2 1

2



     

IAB

S a a a a

.

Dấu

“”

xảy ra

2

21    a a a

.

Khi đó:

 

2

4 0 4

;1

16 1







m

d I AB

m

.

2

16 1 4 1   mm

22

15

16 1 16 32 16

32

      m m m m

.

Đáp án C

Câu 37. Tập xác định:

D

.

Ta có:

 

22

3 6 3 1



   y x mx m

và

66



y x m

.

Khi đó:

 

22

0 3 6 3 1 0



     y x mx m

.

 

22

9 9 1 9



    mm

nên hàm số luôn có hai

điểm cực trị

1xm

và

1xm

.

   

1 6 1 6



   y m m m

60  

1  xm

là

điểm cực đại của hàm số.

 

1; 3 2   A m m

là điểm cực đại của đồ thị

 

C

.

Ta có:

1

32







  



A

xm

ym

31   

AA

yx

.

 A

luôn thuộc đường thẳng

d

có phương

trình

31  yx

.

Do đó hệ số góc

k

của đường thẳng

d

là

3

.

Đáp án C

Câu 38. TXĐ:

D

.

2

36



  y x x m

.

Xét:

2

0 3 6 0



    y x x m

;

93



   m

.

Hàm số có hai điểm cực trị

03



    m

.

Hai điểm cực trị

12

;xx

là nghiệm của

0



y

nên:

1 2 1 2

2; .

3

  

m

x x x x

.

Để

 

2

22

1 2 1 2 1 2 1 1

13 3 . 13      x x x x x x x x

.

4 13 9     mm

.

Vậy

 

0

9 15; 7    m

.

Đáp án C

Câu 39. Ta có:

 

2

1



  y x x mx

;

2

0 1 0



    y x mx

 

1

.

Để hàm số có cực trị thì

 

1

phải có hai nghiệm

phân biệt. Điều này tương đương với

0

2

40  m

2













m

.

Gọi hai nghiệm của

 

1

là

1

x

,

2

x

. Khi đó, ta có:

12

.1











x x m

xx

.

Độ dài hai cạnh của tam giác vuông đó là

1

x

,

2

x

.

Theo bài ra ta có phương trình:

22

12

7xx

 

2

1 2 1 2

27   x x x x

2

27  m

2

9m

3  m

(Thỏa mãn).

Vậy có hai giá trị của

m

thỏa mãn yêu cầu bài

toán.

Đáp án D

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

300

[ I can't, I can! ]

Câu 40. Tập xác định:

D

.

Đạo hàm:

 

2

33



  f x x

.

Xét

 

2

0 3 3 0



    f x x

12

16

   







    



xy

.

Đặt

 

1; 2A

và

 

1; 6B

.

Ta thấy hai điểm

A

và

B

nằm cùng phía với

trục hoành.

Gọi

 

1;2



A

là điểm đối xứng với điểm

A

qua

trục hoành. Chu vi tam giác

MAB

đạt giá trị

nhỏ nhất khi và chỉ khi ba điểm

B

,

M

và



A

thẳng hàng.

Ta có:

 

0

1; 2



  A M x

và

 

2; 8



  AB

0

1

2

28







x

0

1

2

x

1

;0

2









M

.

Vậy

1

4. 2015 2017

2

  T

.

Đáp án A

Câu 41. Ta có:

2

36



y x mx

,

0

2















x

y

xm

Để hàm số có cực đại cực tiểu thì

0m

.

Khi đó các điểm cực trị của đồ thị hàm số là:

 

3

0;4Am

,

 

2 ;0Bm

.

Ta có:

 

3

;2I m m

là trung điểm của đoạn thẳng

AB

.

Đường phân giác của góc phần tư thứ nhất là

:0d x y

.

Do đó để điểm cực đại và cực tiểu đối xứng với

nhau qua

d

thì:

3

2

3

2 4 0

2

1 2 0

2

20







     









mm

.

Vậy tổng tất cả các giá trị của tham số thực

m

là

0

.

Đáp án C

Câu 42. TXĐ:

D 

.

   

 

3 2 2

5 4 1 4        y x x m x m x x x m

.

Đồ thị hàm số đã cho có hai điểm cực trị nằm về

hai phía trục hoành khi và chỉ khi phương trình

0y

có ba nghiệm phân biệt

2

40   x x m

có

hai nghiệm phân biệt khác

1

.

4 0 4

1 4 0 3

  







   



mm

.

Đáp án C.

Câu 43. Tập xác định:

D

.

Đạo hàm:

22

2 2 6 2



   y x mx m

.

Hàm số có hai điểm cực trị:

0



  

 

22

2 6 2 0    mm

2

13 4 0  m

2 13

13

2 13

13

















m

Theo định lý Vietè, thì:

12

2

12

31







  



x x m

.

Ta có:

 

1 2 1 2

21  x x x x

2

3 1 2 1    mm

2

3 2 0  mm

0

2

3















m

.

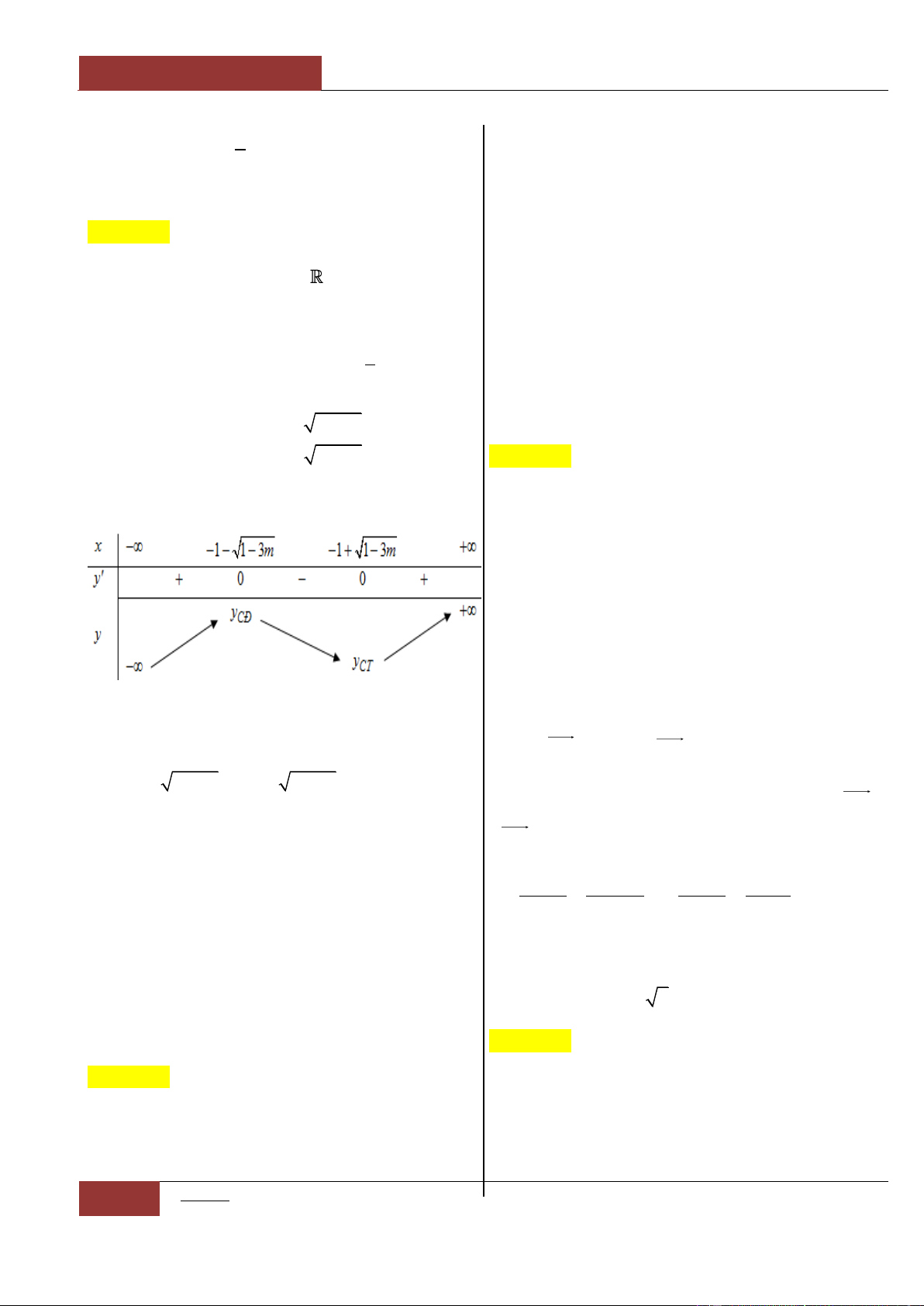
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

301

[ I can't, I can! ]

Chỉ có giá trị

2

3

m

thỏa điều kiện, khi đó

2 2 2 2

2 3 13    S a b

.

Đáp án A

Câu 44. Tập xác định:

D

;

2

32



  y x x m

.

Hàm bậc ba có cực trị khi

0



y

có

2

nghiệm

phân biệt



1 3 0



   m



 

1

3

m

.

Khi đó:

0



y



1 1 3



   



   





xm

.

Bảng biến thiên:

Điểm cực tiểu của đồ thị hàm số nằm về phía

bên phải trục tung khi

1 1 3 0   m



1 3 1m



0m

.

Kết hợp với

 

1

, ta có:

0m

thì điểm cực tiểu

của đồ thị hàm số đã cho nằm bên phải trục

tung.

Khi đó

S

là tập hợp tất cả các giá trị nguyên

âm.

Vậy

   

5;6 4; 3; 2; 1      S

 

5;6   S

có

4

phần tử.

Đáp án D

Câu 45.

 

3 2 2 2

3 3 1 3 1      y x x m x m

 

22

3 6 3 1



     y x x m

.

1

0

1















xm

y

xm

.

Để đồ thị hàm số có điểm cực đại, cực tiểu nằm

bên trái đường thẳng

2x

thì:

00

1 2 1







   





   



mm

.

Vậy không có giá trị nguyên nào của

m

thỏa

yêu cầu bài toán.

Đáp án D

Câu 46. Ta có:

2

36



y x mx

;

0



y



2

3 6 0x mx



0x

,

2xm

.

Đồ thị hàm số có hai điểm cực trị khi và chỉ khi

phương trình

0



y

có hai nghiệm phân biệt



20m



0m

.

Khi đó hai điểm cực trị là

 

0;2A

,

 

3

2 ;2 4B m m

.

Ta có:

 

1;4MA

,

 

3

2 1;4 4  MB m m

.

Ba điểm

A

,

B

và

 

1; 2M

thẳng hàng



MA

,

MB

cùng phương



3

2 1 4 4

14







mm



3

2 1 1

11







mm



3

2 1 1  mm



3

2mm

.



2

2m



2m

(do

0m

).

Đáp án D

Câu 47. Ta có:

   

2

2 1 3 2



    y mx m x m

.

Hàm số đạt cực trị tại

12

,xx

thỏa mãn

12

21xx

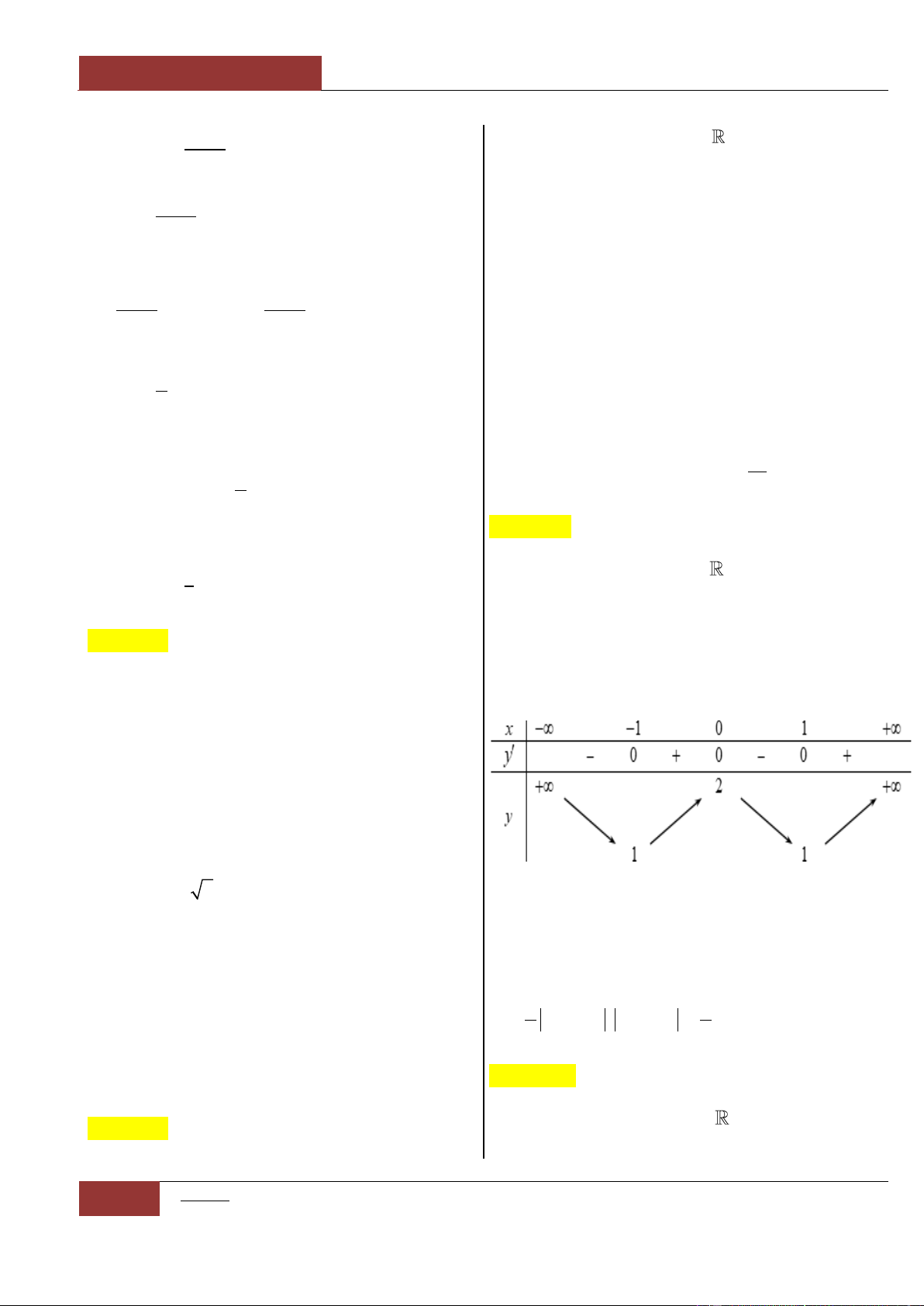
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

302

[ I can't, I can! ]

suy ra

2

2



m

x

m

.

Do

2

2



m

x

m

là nghiệm của phương trình

   

2

2 1 3 2 0    mx m x m

nên

   

2

22

2 1 3 2 0



   

    

   

   

mm

m m m

mm

2

3















m

.

Thử lại thấy

2

3











m

đều thỏa mãn yêu cầu bài

toán.

Vậy

8

3

ab

.

Đáp án B

Câu 48. Ta có:

 

2

' 6 6 1 6   y x m x m

;

 

2

1

' 0 1 0





      







x

y x m x m

xm

.

Để đồ thị hàm số có hai điểm cực trị thì

1m

.

Khi đó ta có:

   

32

1; 3 1 , ;3A m m B m m

.

Ta có:

2AB

.

 

   

2

32

26

1 3 3 1 2

1 1 2

      

    

m m m m

mm

 

2

0

11

2





   







m

(thỏa mãn yêu cầu bài

toán).

Đáp án B

Câu 49. Tập xác định:

D

.

Ta có:

2

' 3 6y mx mx

.

Hàm số có hai điểm cực trị

0m

Khi đó

0

'0

2





  







x

y

x

Tọa độ điểm cực trị:

   

0;3 3 , 2; 3  A m B m

Theo giả thiết:

 

2 2 2

2 20  AB OA OB

2

1

22 12 34 0

17

11







    







m

mm

m

.

Đáp án D

Câu 50. Tập xác định

D

.

Ta có

3

02

4 4 0

11

  





   



   



xy

y x x

xy

Bảng biến thiên

Đồ thị hàm số có ba điểm cực trị

 

0;2A

,

 

1;1B

,

 

1;1C

.

Nhận xét

ABC

cân tại

A

. Vì vậy

11

. .1.2 1

22

    

A B C B

S y y x x

.

Đáp án C.

Câu 51. Tập xác định:

D

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

303

[ I can't, I can! ]

3

2

0

' 4 4 0





   







x

y x mx

xm

.

Hàm số đã cho có ba điểm cực trị

0m

.

Tọa độ điểm cực trị của đồ thị hàm số:

 

   

22

0;1 , ; 1 , ; 1 .    A B m m C m m

4 4 16 4.    BC m m

Đáp án B.

Câu 52. Hàm số

42

21  y x mx

có tập xác

định:

D

.

Ta có:

33

' 4 4 ; ' 0 4 4 0     y x mx y x mx

 

2

0

40





   



  



x

x x m

xm

Hàm số có

3

cực trị khi và chỉ khi phương trình

 



có

2

nghiệm phân biệt khác

0

.

00    mm

.

Vậy tọa độ

3

điểm lần lượt là:

 

   

22

0;1 ; ;1 ; ;1    A B m m C m m

Ta có:

   

22

; ; ;      AB m m AC m m

.

Vì

ABC

vuông cân tại

2 2 2

. 0 . 0     A AB AC m m m

44

00      m m m m

1  m

( vì

0m

)

Vậy với

1m

thì hàm số có 3 cực trị tạo

thành một tam giác vuông cân.

Đáp án D

Câu 53. Tập xác định

D

Ta có:

3

44



y x mx

.

3

2

0

0 4 4 0







    







x

y x mx

xm

.

Hàm số có ba điểm cực trị khi và chỉ khi

0m

.

Khi đó đồ thị hàm số có ba điểm cực trị là:

 

0;0O

,

 

2

;A m m

,

 

2

;B m m

.

Do đó:

2

11

. .2

22





OAB

S OH AB m m

2

1 0 1



     

OAB

S m m m

Đáp án A

Câu 54. Tập xác định:

D

.

Ta có

3

2

0

' 4 4 ' 0





    







x

y x mx y

xm

.

Hàm số đã cho có ba điểm cực trị

0m

.

Khi đó ba điểm cực trị của đồ thị hàm số là:

 

24

0; 2A m m

;

 

42

; 3 ;B m m m

 

42

;3C m m m

.

Gọi I trung điểm của BC

 

42

0; 3I m m

x

y

A

O

H

B

m

m

2

m

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

304

[ I can't, I can! ]

Vì

, A D Oy

, B và C đối xứng nhau qua Oy

nên tứ giác ABCD là hình thoi



I là trung

điểm của AD

 

4 2 2 4

2

42

2

0

2 3 2 3

1

4 3 0

3

11

33



     





    









  



 



  



m

m m m m

m

mm

m

mm

.

Đáp án A

Câu 55.

 

4 2 2

21   y x m x m

.

 

32

' 4 4 1 4 1      y x m x x x m

Hàm số có 3 điểm cực trị

'0y

có 3

nghiệm phân biệt.

2

10   xm

có 2 nghiệm phân biệt khác 0.

10   m

1  m

.

Khi đó:

1

' 0 0

1



  



  







xm

yx

xm

.

Giả sử

,,A B C

là ba điểm cực trị của đồ thị

hàm số

 

2

1; 2 1

0;

1; 2 1



   









  





A m m

Bm

C m m

.

 

2

1; 1



  









   



AB m m

CB m m

ABC

vuông tại

B

.0AB CB

   

4

1

1 1 0 0

0





        







m

m m m

m

.

Đáp án D

Câu 56. TXĐ:

.D

 

32

' 4 4 4 .   y x mx x x m

Để đồ thị hàm số

 

1

có 3 điểm cực trị

0.m

Gọi

 

   

22

0;1 , ; 1 , ; 1    A B m m C m m

là các điểm cực trị của đồ thị hàm số

 

1

,

 

2

0; 1Im

là trung điểm

.BC

Ta có:

24

,.   AI m AB AC m m

Suy ra:

1 . . 2

.

2 4 .

  

AB AC BC AI

AI BC R

R AB AC

2

42

4

2

1 2 0

0 ( )

1 ( )

15

()

2

15

()

2

     





























m

m m m

mm

ml

mn

ml

mn

Ta có:

 

3

15

1 5 1

2





   





S

.

Đáp án D

Câu 57. Đồ thị hàm số có

3

điểm cực trị



0m

.

Khi đó,

3

điểm cực trị của đồ thị hàm số là:

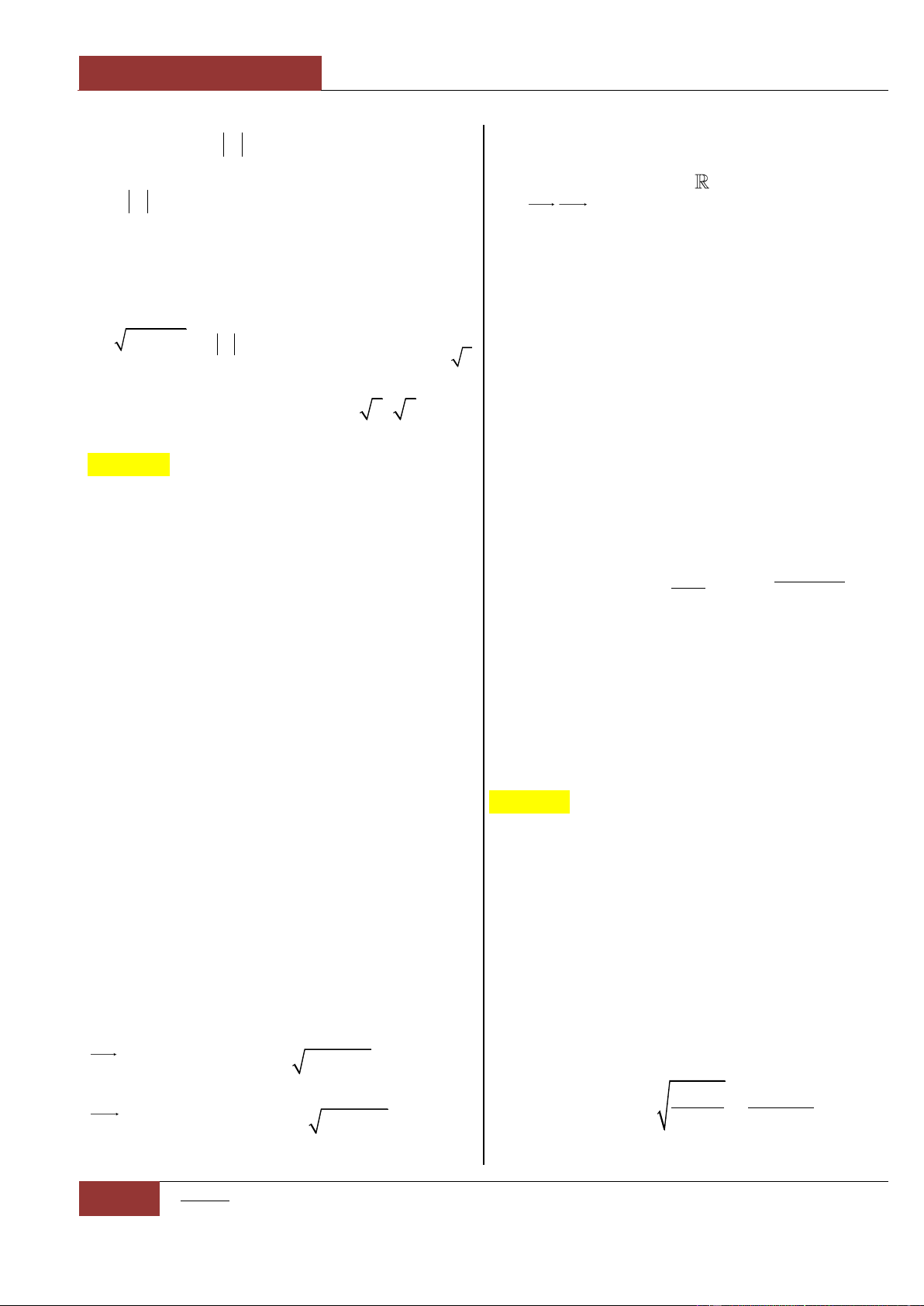
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

305

[ I can't, I can! ]

 

0; 4Am

,

 

4

;4  B m m m

,

 

4

;4   C m m m

.

Tam giác

ABC

có

AB AC

nên tam giác

ABC

cân tại

A

, suy ra tam giác

ABC

đều

AB BC

2 8 8 2 2

6

0

24

3





      







m

m m m m m m

m

Kết hợp điều kiện ta được

 

66

3; 3m

.

Đáp án C

Câu 58.

4 2 2

21  y x m x

.

+ Cách 1:

Hàm số có 3 cực trị

2

0 2 0 0      ab m m

.

32

44



y x m x

 

32

22

1

4

22

4

3

0 4 4 0

40

1

0

1



   

  











     





  



y x m x

x x m

y

x

x m y m

xm

ym

Giả sử

 

0;1A

,

 

4

;1B m m

,

 

4

;1  C m m

là 3 điểm cực trị của đồ thị

hàm số.

 

4

;AB m m

28

  AB m m

.

 

4

;  AC m m

28

  AC m m

.

Yêu cầu bài toán



ABC

vuông cân tại

A

.0

















AB AC

28

0









  



m

mm

 

26

10   mm

0 ( )

1 ( )

1( )















ml

mn

.

Vậy

 

1;1m

.

+ Cách 2: (Áp dụng công thức tính nhanh cực

trị hàm trùng phương)

Yêu cầu bài toán



 

2

3

2

3

20

0

8

1

2















 









m

ab

a

m

b

6

0

1 ( )

1

1( )

































m

mn

m

mn

.

Vậy

 

1;1m

.

Đáp án B

Câu 59. Ta có:

 

32

4 2 1 2 2 1



     y x m x x x m

.

2

0

21











  



x

y

xm

Hàm số có ba điểm cực trị khi và chỉ khi

0



y

có ba nghiệm phân biệt



1 0 1    mm

.

 

0; 2 1Am

,

 

2

1

; 2 1

24







   





m

Bm

,

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

306

[ I can't, I can! ]

 

2

1

; 2 1

24







  





m

Cm

,

là các điểm cực trị của đồ thị.

Ta thấy:

 

4

1

2 16



   

m

AB AC

nên

tam giác

ABC

cân tại

A

.

Từ giả thiết suy ra

120A

.

Gọi

H

là trung điểm

BC

, ta có:

 

2

1

0; 2 1

4





  





m

Hm

 

2

1

tan60 . 3

42



    

m

BH AH

 

4

3

31

1

16 2

3 1 8

2

1

3



  

   

   

m

.

Đáp án A

Câu 60. Ta có:

32

44



y x m x

.

Hàm số có cực đại cực tiểu



phương trình

0



y

có ba nghiệm phân biệt

0m

.

Gọi

 

4

0; 5Am

,

 

;5Bm

,

 

;5Cm

lần lượt

là ba điểm cực trị của đồ thị hàm số.

Gọi

I

là tâm đường tròn ngoại tiếp tứ giác

ABOC

khi đó ta có ba điểm

A

,

I

,

O

thẳng

hàng.

Mặt khác do hai điểm

B

và

C

đối xứng nhau

qua

AO

nên

AO

là đường kính của đường tròn

ngoại tiếp tứ giác

ABOC

AB OB

.0AB OB

.

Trong đó:

 

4

;AB m m

,

 

;5OB m

. Ta có

phương trình:

24

50mm

5

  m

.

Đáp án C

Câu 61. Ta có

 

2

4



y x x m

2

0







  







x

y

xm

;

Với điều kiện

0m

đồ thị hàm số có ba điểm

cực trị là

 

42

0; 2A m m

;

 

42

;3B m m m

;

 

42

;3C m m m

. Để

ABDC

là hình thoi điều

kiện là

BC AD

và trung điểm

I

của

BC

trùng với trung điểm

J

của

AD

. Do tính đối

xứng ta luôn có

BC AD

nên chỉ cần

IJ

với

 

42

0; 3 ,I m m

42

23

0;

2









mm

J

.

ĐK:

4 2 4 2

2 3 2 6   m m m m

42

4 3 0   mm

1

3













m

19

;

25









m

Đáp án D

Câu 62. Cách 1:

Ta có

 

32

4 4 4



     y x mx x x m

.

Để hàm số có ba cực trị thì phương trình

0



y

có ba nghiệm phân biệt

 

2

40   x x m

có

ba nghiệm phân biệt

0m

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

307

[ I can't, I can! ]

Gọi

 

0;2A

,

 

2

,2B m m

,

 

2

,2C m m

là ba điểm cực trị của đồ thị hàm số.

Vì

ABC

cân tại

A

nên

ABC

chỉ có thể

vuông tại

A

0ABAC

.

Với

 

2

;AB m m

,

 

2

;AC m m

 

43

0 1 0 1        m m m m m

.

Cách 2: Áp dụng công thức tính nhanh: Ba

điểm cực trị của đồ thị hàm số

42

  y ax bx c

tạo thành một tam giác vuông khi

33

8 0 8 8 0 1      a b m m

.

Đáp án D

Câu 63. Ta có:

3

4 4 0



  y x x

.

 

0 0;4

1 1;3







    







xA

xB

xC

.

 

1; 1 2    AB AB

;

 

1; 1 2   AC AC

;

 

2;0 2  BC BC

.

Ta có

ABC

vuông cân tại

A

có:

 

2

1

21

2

S

,

21

2



  

AB AC BC

p

.

Vậy

1

21

   



S

r

p

.

Đáp án C

Câu 64. Ta có

 

3

4 4 4



  y x m x

;

2

0

4















x

y

xm

.

Để hàm số có ba điểm cực trị

4m

. Khi đó

các điểm cực trị của

 

m

C

là

 

0; 5Am

,

 

2

4 ; 5 4   B m m m

,

 

2

4 ; 5 4    C m m m

.

Do

O

là trọng tâm tam giác

ABC

nên

   

2

3 5 2 4  mm

1

17

2















m

.

Do

4m

nên

1m

.

Đáp án B

Câu 65. Hàm số

42

2y x mx

có

TXĐ : D 

. Ta có

3

44



y x mx

;

2

0















x

y

xm

.

Để đồ thị hàm số có ba điểm cực trị thì

0m

.

Khi đó ba điểm cực trị là

 

0;0O

,

 

2

;B m m

,

 

2

;C m m

. Ta giác

OBC

cân tại

O

, với

 

2

0;Im

trung điểm của

BC

Theo yêu cầu bài toán, ta có:

2

11

. .2 1 0 1

22

      

ABC

S OI BC m m m

.

Đáp án B

Câu 66. Ta có:

42

21  y x mx

3

44



  y x mx

.

0



y

 

2

1

0











x

xm

.

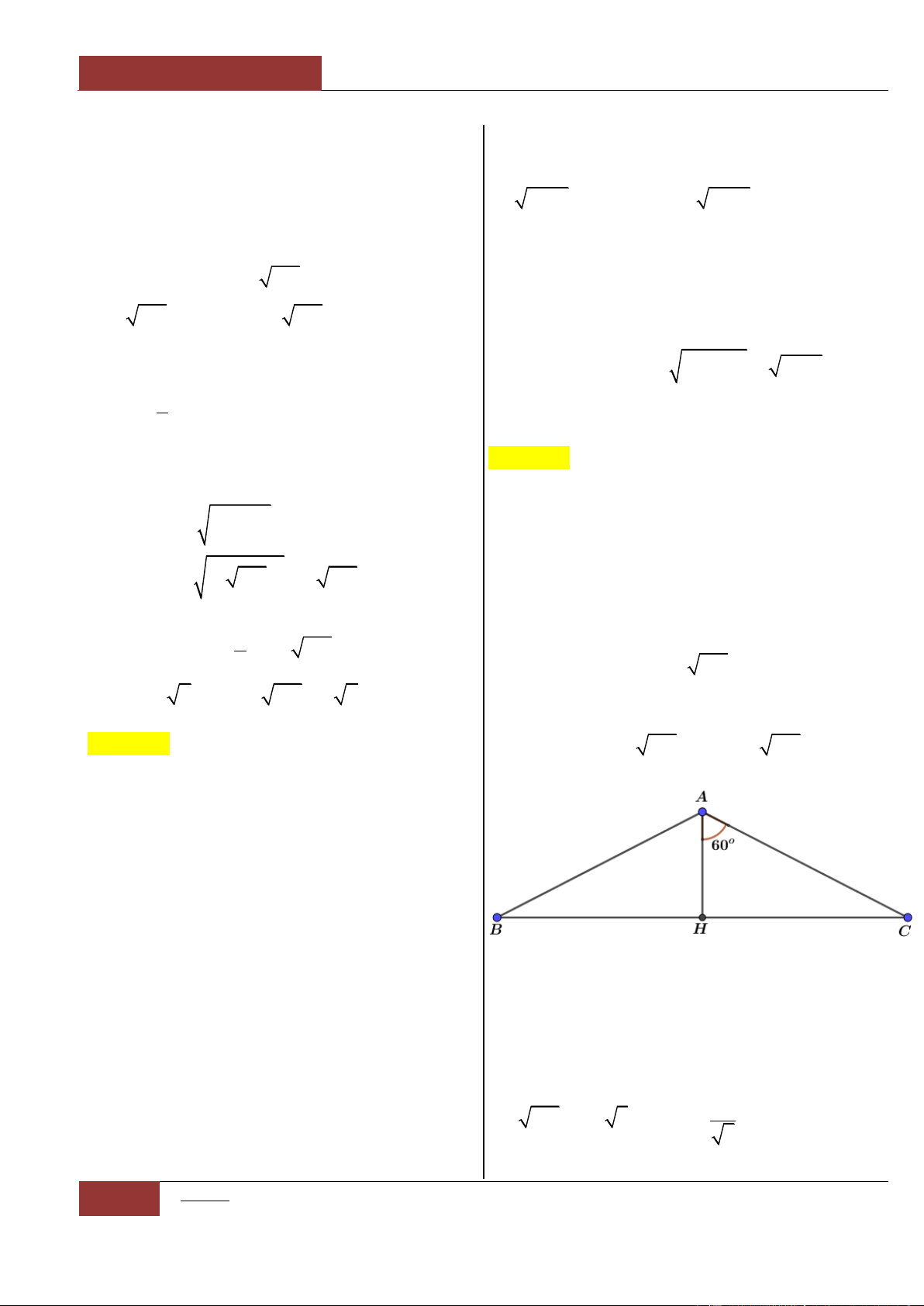
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

308

[ I can't, I can! ]

Để đồ thị hàm số

42

21  y x mx

có ba điểm

cực trị thì

0



y

phải có ba nghiệm phân biệt

tức là

0m

.

Khi đó

 

0

1









  



x

xm

nên ta gọi

 

0; 1A

,

 

2

;1   B m m

,

 

2

;1  C m m

Tam giác

ABC

cân tại

A

nên

1

.

2





ABC

S AH BC

với

H

là trung điểm của

BC

nên

 

2

0; 1Hm

.

Nên:

 

2

22

2

22



  







   



AH m m

BC m m

.

Ta có:

2

1

. .2

2





ABC

S m m

theo giả thiết

42





ABC

S

nên

2

4 2 2    m m m

.

Đáp án C

Câu 67. Cách 1: Điều kiện để đồ thị hàm trùng

phương

42

  y ax bx c

có ba điểm cực trị là

01    ab m

loại B

Khi đó ba điểm cực trị lập thành tam giác vuông

cân khi

3

80ba

 

3

8 1 8 0 0      mm

Cách 2: Ta có

 

2

41



  y x x m

Xét

2

0

1















x

y

xm

. Để đồ thị số có ba

điểm cực trị thì

1m

 

*

Tọa độ ba điểm cực trị là

 

2

0; ,Am

 

1; 2 1 ,  B m m

 

1; 2 1   C m m

Gọi

H

là trung điểm của đoạn thẳng

BC

thì

 

0; 2 1Hm

Khi đó ba điểm cực trị lập thành tam giác vuông

cân khi

AH BH

 

4

11   mm

 

0 : Thoûa maõn *m

.

Đáp án A

Câu 68.

 

32

4 4 4



   y x mx x x m

.

Hàm số có ba điểm cực trị

0



y

có ba

nghiệm phân biệt

0m

.

Khi đó

0



y

0







  



x

xm

.

Ba điểm cực trị của đồ thị hàm số là

 

2

0; A m m

,

 

;B m m

,

 

;C m m

.

Do

ABC

cân tại

A

nên gọi

 

0;Hm

là trung

điểm của

BC

thì

AHC

vuông tại

H

.

ABC

có một góc bằng

120

khi và chỉ khi

60  HAB HAC



.tanHB AH HAB

2

3  mm

3

1

3

  m

.

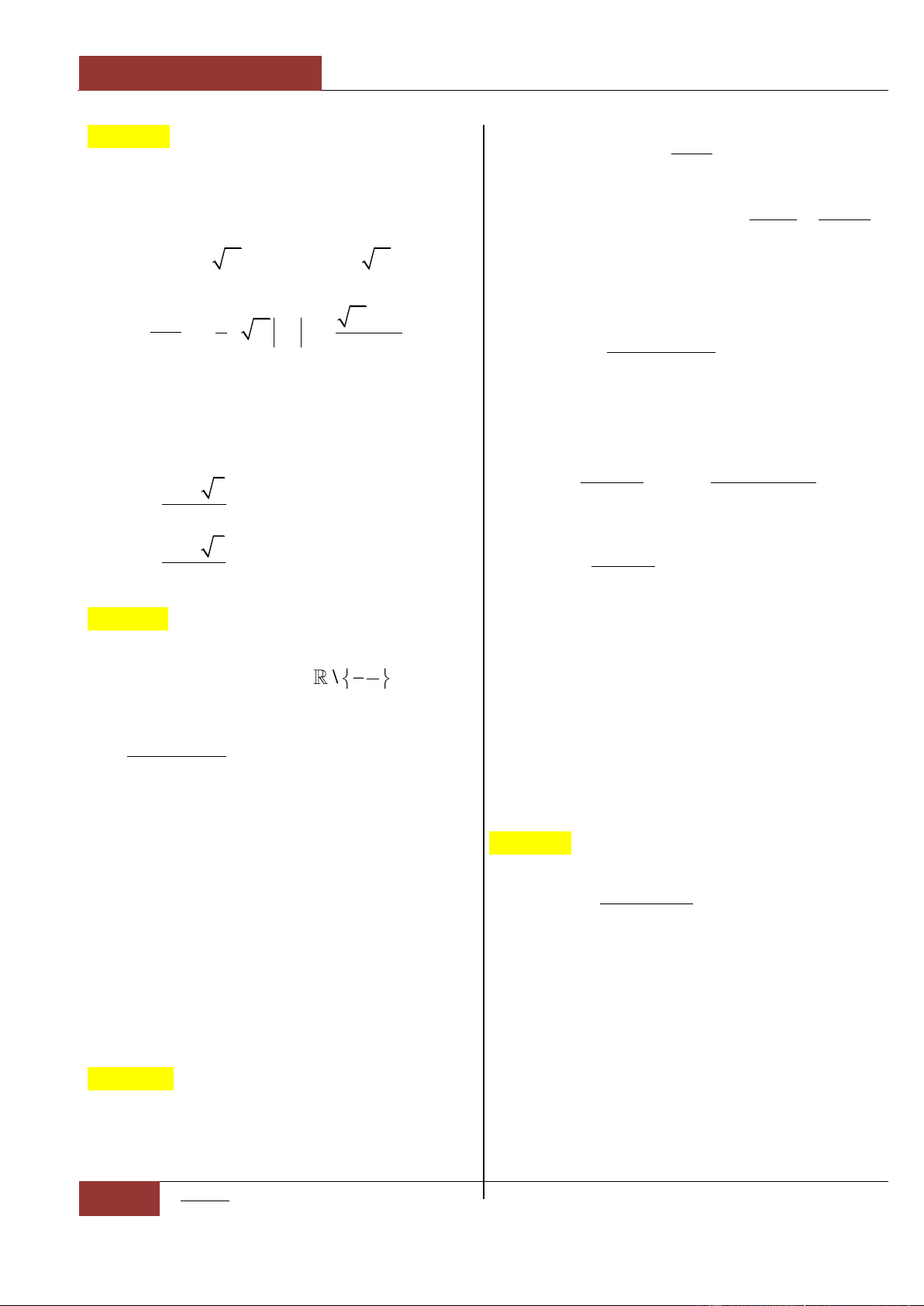
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

309

[ I can't, I can! ]

Đáp án C

Câu 69.

4 2 3

2 4 4



     y x mx m y x mx

.

Với

0m

ta có ba cực trị

 

   

22

0; ; ; ; ;     A m B m m m C m m m

4R



ABC

abc

S

2

1

22

24



mAB

mm

2 4 4 2

2 2 0      m m m m m m

.

 

0

1

15

2

15

2































ml

mn

ml

Đáp án B

Câu 70. Tập xác định:

1

\

2









D

.

 

2

2 2 4

21









xx

y

x

,

2

0 2 2 4 0



    y x x

 

12

21



  





    





xy

.

Đồ thị hàm số có hai điểm cực trị là

 

1;2M

và

 

2; 1N

.

Vậy phương trình đường thẳng qua hai điểm

cực trị

,MN

của đồ thị hàm số đã cho là:

1yx

.

Đáp án B.

Cách khác:

Áp dụng tính chất: Nếu

0

x

là điểm cực trị của

hàm số hữu tỷ

 



ux

y

vx

thì giá trị cực trị

tương ứng của hàm số là

 

00

0

00







u x u x

y

v x v x

.

Suy ra với bài toán trên ta có phương trình

đường thẳng qua hai điểm cực trị của đồ thị

hàm số là

 

2

23

1

21





  





xx

yx

x

.

Câu 71. Điều kiện

1x

.

Ta có:

2

1







x mx

y

x

 

2

1

  







x x m

y

x

.

Hàm số

2

1







x mx

y

x

có cực đại và cực tiểu

0



y

có hai nghiệm phân biệt và đổi dấu

khi đi qua hai điểm đó

2

20    x x m

có

hai nghiệm phân biệt khác

1

0 1 0

1

1 2 0 1



   



   



    



m

mm

.

Vậy

1m

thì hàm số đã cho có cực đại và cực

tiểu.

Đáp án A

Câu 72.

 

2

,1

1





  





xx

xy

m

x

. Đặt

 

2

2 x x mfx

,

 

2

2 x mx mhx

,

 

1gx x

.

Đồ thị hàm số đã cho có hai điểm cực trị

A

,

B

khi

 

fx

có hai nghiệm phân biệt

1

x

,

2

x

khác

1

 

10

1 1 0



   







    



m

fm

 

11  m

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

310

[ I can't, I can! ]

Khi đó

 

1

11

1

2

22

2

()

(

2

2)











  



  





hx

y x x m

gx

hx

y x x m

gx

.

Suy ra:

 

11

;2 A x x m

,

 

22

;2 B x x m

.

Suy ra:

 

11

;2OA x x m

,

 

22

;2 OB x x m

.

OAB

vuông tại

O

khi

 

    

1 2 1 2

, 0 2

2.32.0













   



OA OB

OA OB x x x m x m

.

   

2 1 2

2

1

5 . 2 03  m x x m x x

. Kết hợp

với định lí Vietè cho phương trình

 

0fx

ta

được

2

5 4 0 mmm

 

   

 

0 khoâng thoûa maõn 2

9 thoûa maõn 1 , 2

m















 

9S

.

Vậy tổng tất cả các phần tử của

S

bằng 9.

Đáp án A

Câu 73. + Phương trình của đường thẳng

AB

là:

 

/

2

/

2







x x m

y

x

2 2 2 2 0      y x x y

.

+ Khoảng cách

 

2

2.0 0 2

2

;

5

21







d O AB

.

Đáp án A

Câu 74.

  

 

22

2

21

1

    







x m x x mx m

y

x

 

22

2

1

  





x x m m

x

Để đồ thị hàm số có hai điểm cực trị

,AB

thì

0



y

phải có hai nghiệm phân biệt khác 1

2

10





    







   





mm

  m

.

Phương trình đường thẳng đi qua 2 điểm cực

đại, cực tiểu là

2

A

y x m

.

Gọi

;

A

x

B

x

là hoành độ của

A

,

B

khi đó

;

A

x

B

x

là nghiệm của

 

22

2  x x m m

.

Theo định lí Vietè, ta có:

2

AB

xx

;

2

.   

AB

x x m m

.

2

AA

y x m

;

2

BB

y x m

.

90AOB

. . 0  

A B A B

x x y y

 

2

4 2 0     

A B A B A B

x x x x m x x m

 

22

5 4 0     m m m m

2

40   mm

1

0;

4

   mm

.

Tổng bình phương tất cả các phần tử của

S

bằng:

2

11

0

4 16



  





.

Đáp án A

Câu 75. Ta có:

 

\1D

Và có đạo hàm là

 

2

1









x x m

y

x

.

Để hàm số có hai điểm cực trị ta phải có:

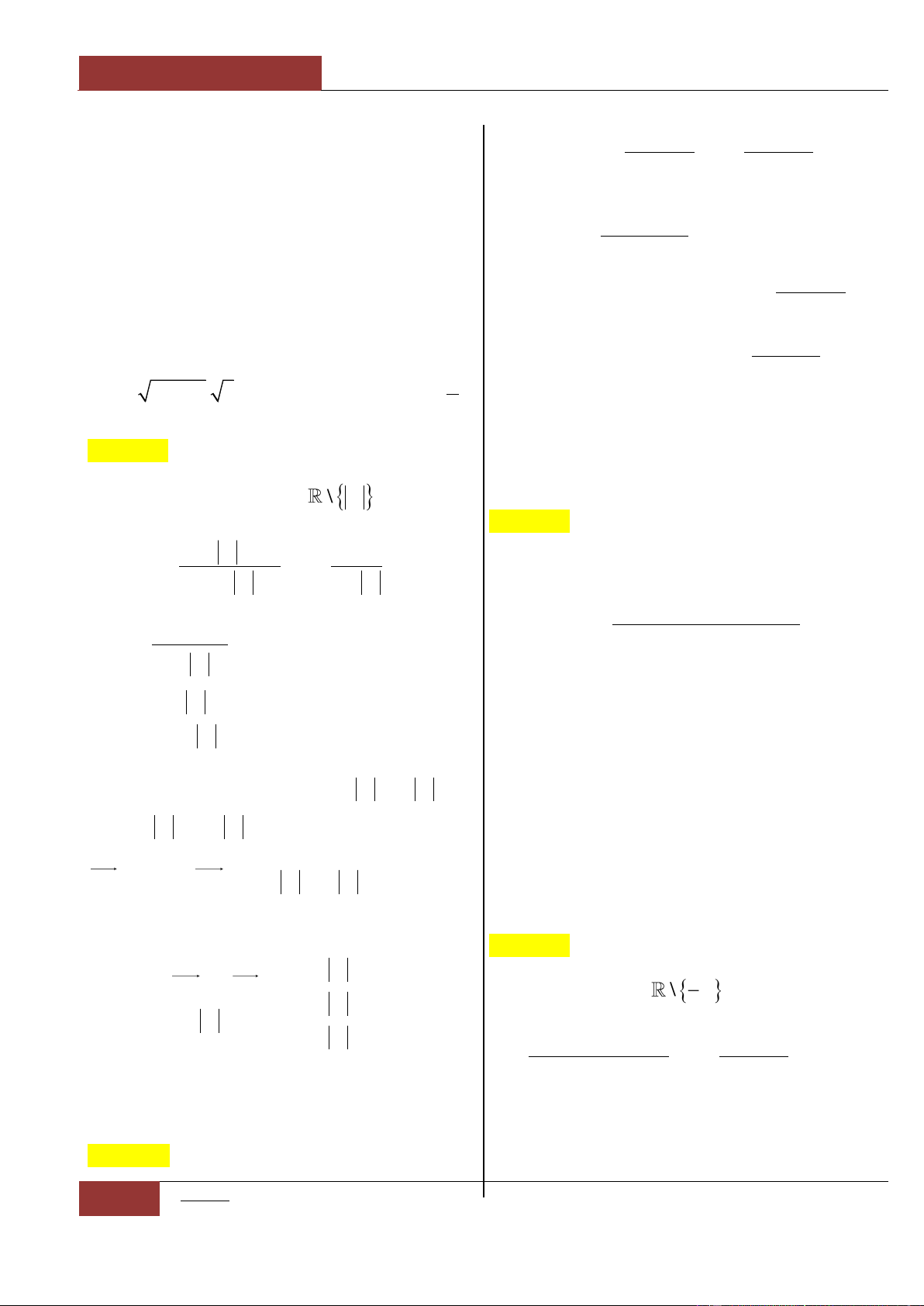
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

311

[ I can't, I can! ]

10

1 2 0







  



m

1  m

.

Gọi hai hoành độ cực trị là

1

x

và

2

x

ta có:

12

2  









xx

x x m

.

Khi đó điểm

 

11

,2 A x x m

và

 

22

,2 B x x m

.

4 4 . 5 5  AB m

1

4 4 5

4

    mm

.

Đáp án B

Câu 76. Tập xác định

 

\Dm

.

Ta có:

2

4



  



x m x

yx

x m x m

.

 

2

4

1







y

xm

,

xD

,

0



y

2

  





  





xm

.

Tọa độ hai điểm cực trị là

 

2 ;4B m m

,

 

2 ; 4   A m m

.

 

4;8AB

,

 

6 ;6  AC m m

.

Ba điểm

A

,

B

,

 

4;2C

phân biệt và thẳng

hàng

60

















AC k AB

m

64

68

60







  









mk

m

(vô

nghiệm).

Vậy không có giá trị

m

nào thỏa mãn.

Đáp án A

Câu 77.

   

23

12

' 1 ; ''  



yy

x m x m

.

Hàm số

2

1





x mx

y

xm

đạt cực đại tại điểm

0

2x

khi

 

' 2 0

'' 2 0















y

 

2

3

1

10

2

0

2

























m

1

3

2

  







   













m

. Thử lại thấy thỏa mãn.

Đáp án B

Câu 78. Điều kiện:

xm

.

Đạo hàm:

 

22

2

2 2 2

2

   







x mx m m

y

xm

.

Để hàm số có cực đại và cực tiểu, thì

0



y

22

2 2 2 0     x mx m m

có hai nghiệm

phân biệt khác

m

.

Ta có:

2

22

20

2 . 2 2 0





     





    





mm

m m m m m

2

12

20

  







  



m

mm

12   m

.

Đáp án B

Câu 79. TXĐ:

 

\Dm

   

22

23

2 1 2

,

  

 





x mx m

yy

x m x m

Hàm số đạt cực đại tại

2x

nên

 

20



















y

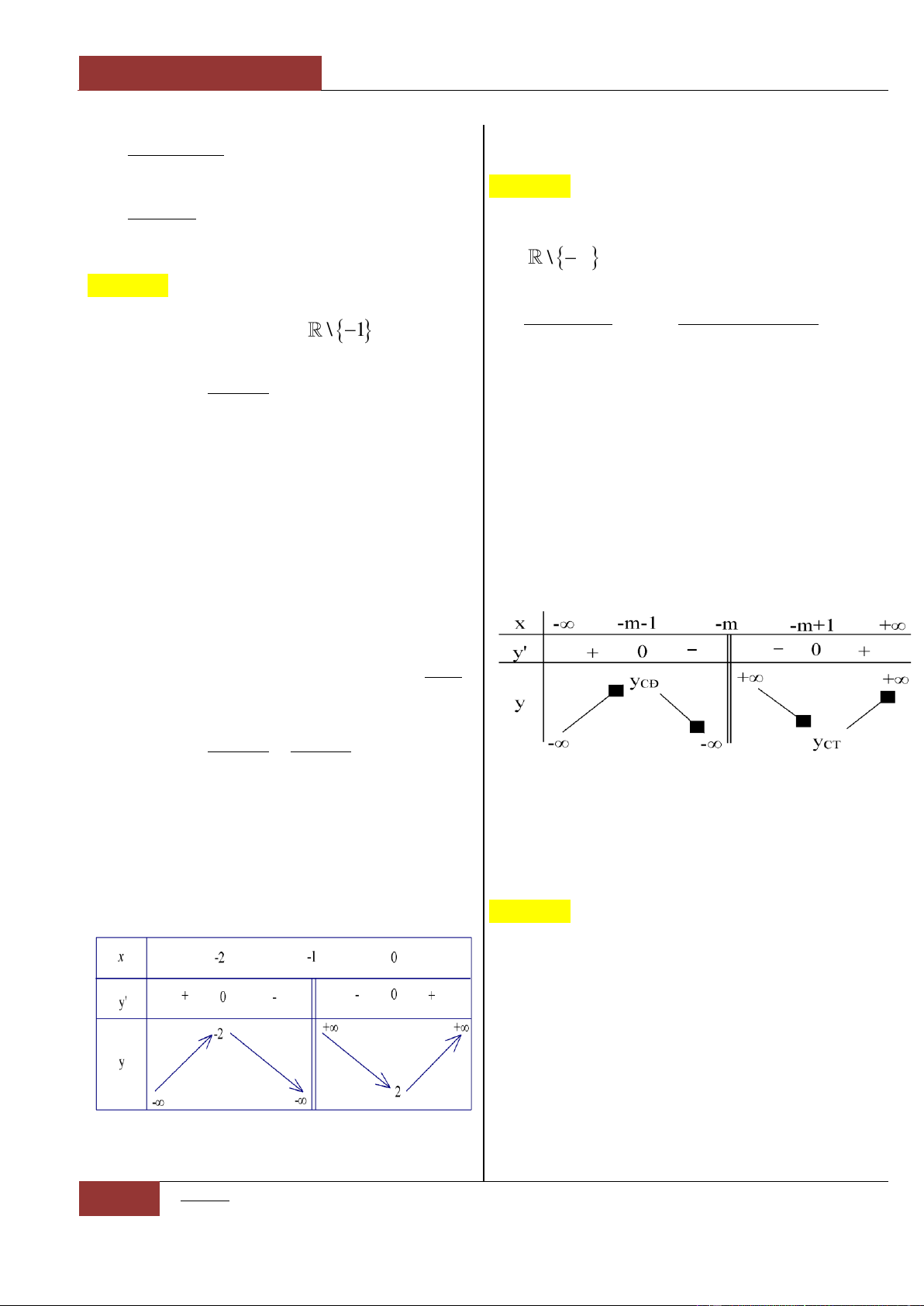
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

312

[ I can't, I can! ]

 

2

3

43

0

2

3

2

0

2













   













mm

m

thuộc

 

4; 2

.

Đáp án B

Câu 80. Tập xác định

 

\1D

.

Ta có:

 

2

1







q

y

x

.

Hàm số đạt cực đại tại

2x

, suy ra:

 

2 0 0 1 1



      y q q

.

Lại có đồ thị hàm số đi qua điểm

 

2; 2A

nên

2 2 0       p q p q

.

Do đó:

1pq

.

Thử lại: với

1pq

ta được

1

  



yx

x

.

Ta có:

   

2

22

12

10

11





   



xx

y

xx

2

0

20

2





   







x

xx

x

.

Từ đó có bảng biến thiên của hàm số:

Rõ ràng đồ thị hàm số đạt cực đại tại điểm

 

2; 2A

. Vậy

11   p q pq

.

Đáp án D

Câu 81. Tập xác định của hàm số là:

 

\Dm

 

2 2 2

2

1 2 1    



  



x mx x mx m

yy

xm

22

0

2 1 0

1











   







  







  







  







  





xm

y

x mx m

xm

Bảng biến thiên

Từ bảng biến thiên ta thấy hàm số đạt cực đại

tại

1  xm

.

Vậy

 

1 7 2 7 9         y m m m

.

Đáp án C

Câu 82.

     

2

3 2 2 1f x mx m x m



    

.

Để đồ thị hàm số có hai điểm cực trị có hoành

độ dương thì:

0



















S

P

.

Khi đó, ta có thể suy ra:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

313

[ I can't, I can! ]

   

 

2

2 3 1 0

22

0

3

1

0



   







  















m m m

m

1

4

2

1

2 0 0

2

0

1





  



       





















m

mm

m

Đáp án A

Câu 83. Ta có:

 

2

9

81

2

y x mx m



   

.

Hàm số

y

có hai điểm cực trị khi phương trình

0y





có hai nhgiệm phân biệt

 

23 18 9mm



    

.

Theo định lý Vietè, ta có:

12

16

9

m

xx

;

 

2

12

21

9

m

xx





,

1 2 1 2

x x x x

 

2

2 16

1

99

10 1 0

5 2 6

  

   















mm

m

.

 

 

10;0 10m   

.

Vậy có

12

giá trị nguyên thỏa mãn.

Đáp án A

Câu 84. Điều kiện để phương trình có nghiệm

là:

1

5

,1

' 4 5 0

4

m

mm

m





   



   



.

Theo giả thuyết, ta có:

2

1 2 2

2

1 2 2

2

3

2































S

x

x x x

P

x x x

x

.

 

2

24

1

9 2 2 1

91



   



m

S P m

m

.

    

2

2 2 4 9 1 1

32 41 0 16 3 33

    

      

m m m

(thỏa mãn).

Vậy:

16 3 33m 

là các giá trị cần tìm.

Đáp án A

Câu 85. Áp dụng công thức giải nhanh:

3

8

ba

R

ab





.

Với:

,2a m b  

.

Hàm số có

3

cực trị là:

0ab 

, tức là phải có:

 

. 2 0 0mm   

.

 

3

28

8

1

8 8 2

1

12

1

3





  









   









m

ba

R

ab m

m

mm

ml

Vậy:

1m 

.

Đáp án D

Câu 86. Xét hàm số:

 

32

11

5

32

y x m x mx   

, ta có:

 

2

5,y x m x m x



     

.

Phương trình:

   

2

5 0 * y x m x m



    

,

có:

 

2

5 4 6 10m m m m      

.

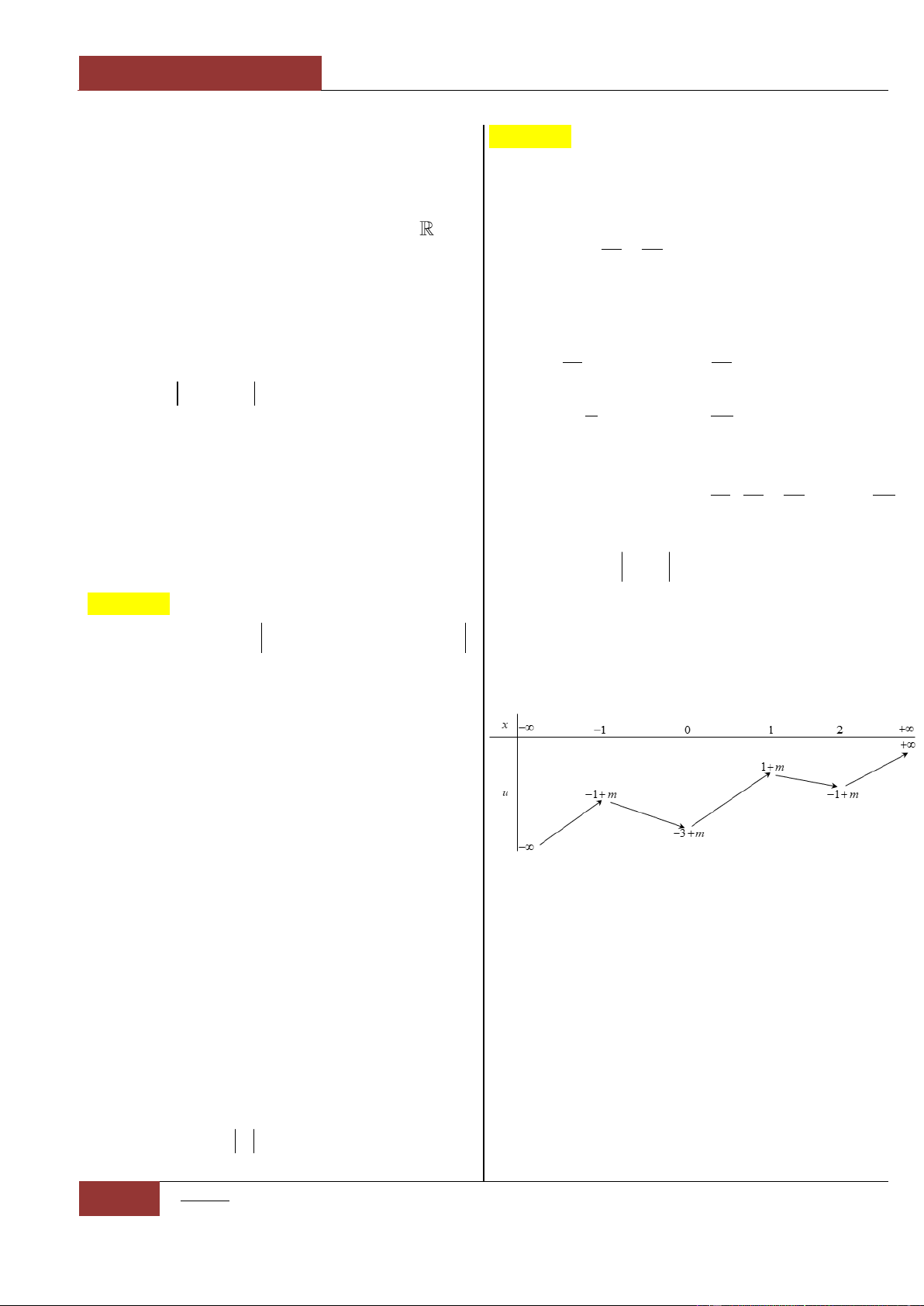
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

314

[ I can't, I can! ]

Để hàm số đã cho có hai điểm cực trị

0y





có hai nghiệm phân biệt.

 

*

có hai nghiệm phân biệt

 

2

6 10 3 1,m m m m         

.

Khi đó, gọi:

,

CD CT

xx

lần lượt là hoành độ điểm

cực đại và cực tiểu của hàm số.

Theo Vietè, ta có:

5

.

CD CT

x x m

  









.

Mặt khác:

 

2

5 25

CD CT CD CT

x x x x    

.

 

2

4 . 25

5 4 25

0

60

6

   

   





   







CD CT CD CT

x x x x

mm

m

mm

m

Vậy giá trị cần tìm của

m

là:

 

0; 6m 

.

Đáp án D

Câu 87. Hàm số

 

3 2 2

2    y x m x mx m

có ba điểm cực tiểu khi và chỉ khi:

 

3 2 2

2    y x m x mx m

có hai điểm cực

trị nằm về hai phía của trục hoành



   

3 2 2

2 0 1    x m x mx m

có ba

nghiệm phân biệt.

Ta có:

 

3 2 2

20    x m x mx m

 

2

20    x m x x m

 

2

2 0 2









  



xm

x x m

.

Để

 

1

có ba nghiệm phân biệt thì

 

2

có hai

nghiệm phân biệt khác

m

.

2

10

0













m

mm

1

0













m

   

1;0 0;     m

.

Do

m

nguyên và

5m

nên suy ra

 

1;2;3;4m

.

Đáp án D

Câu 88. Ta có:

    

21



  f x a x x

 

32

2

32



    





xx

f x a x b

.

Đồ thị hàm số đi qua

   

2;4 , 1; 1AB

nên ta

có:

10 10

4

39

78

1

6 27



  









    





a b a

a b b

.

Hàm số ban đầu là:

 

32

10 8

2

9 3 2 27



   





xx

f x x

.

Đặt:

   

32

31

2

0

1



   











  











u x x m

x

f x f x

x

.

Bảng biến thiên:

Yêu cầu bài toán xảy ra khi và chỉ khi:

 

2 3 1

1 1 2

3 2 1 1 1

1 1 1 0 2

2 1 1

1 1 0

      







   





         









      







     









  





mm

loai

mm

m m m

mm

loai

mm

.

Vậy

 

0;1m

không có giá trị nào của

m

thoả mãn.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

315

[ I can't, I can! ]

Đáp án C

Câu 89. Xét

   

42

1

: 1 2   C y x m x

.

Ta có:

 

3

4 2 1 ;



  y x m x

2

0

0.

1

2



















x

y

m

x

Đồ thị

 

1

C

có 3 điểm cực trị thì:

1

0

2





m

1  m

.

Ba điểm cực trị của

 

1

C

là:

 

2

1

0;2 , ; 2 ,

24

1

;2

24















  





m

AB

m

C

.

Ta có:

 

4

1

2 16

21







  







   





m

AB AC

BC m ABC

cân tại

A

Xét

   

4

2

: 2 1 4 8 3    C y x x x m

.

Ta có:

   

3

8 1 8 1 ;



   y x x

 

2

1 4 3

10

0 0 2 3

11

2 2 3

    











      











    



x y m

x

y x y m

x

x y m

Ba điểm cực trị của

 

2

C

là:

     

1;4 3 , 0;2 3 , 2;2 3    M m N m P m

.

Ta có:

5, 5, 2    MN MP NP MNP

cân tại

M

.

    

AB AC BC

ABC MNP

MN MP NP

 

4

1

21

2 16

2

5





m

 

3

1

15

8



  

m

 

3

1 32 2 4 1     mm

và

 

3

2 4 1 2,17 2;3   m

.

Đáp án C

Câu 90. Phương trình hoành độ giao điểm:

   

3 2 3 2

3 1 6 4 3 3 0           x x x m x x x m x

Gọi

1 2 3

,,x x x

là ba nghiệm phân biệt của phương

trình này ta có

1 2 3

1 2 2 3 1 3

1

3

   





   



x x x

x x x x x x m

và tung

độ các giao điểm là:

     

1 1 2 2 3 3

6 4; 6 4; 6 4        y m x y m x y m x

Vậy điều kiện bài toán:

     

1 2 3

1 1 1 2

4 4 4 3

1 1 1 2

6 6 6 3

  

  

   

  

y y y

m x m x m x

1 2 2 3 3 1

1 2 3

12

63

1 3 2

9

6 3 3

















   







x x x x x x

m x x x

m

.

Thử lại:

32

9 6 3 0     m x x x

có

3

nghiệm

phân biệt nên

9m

thỏa mãn.

* Note: Phương trình

32

0   ax bx cx d

có ba

nghiệm

1 2 3

,,x x x

thì

1 2 3

1 2 2 3 3 1

1 2 3



   



  











b

x x x

a

c

x x x x x x

a

d

x x x

a

Đáp án D

Câu 91. Giả sử đường thẳng cần tìm có dạng

.y kx m

Phương trình hoành độ giao

điểm:

4 2 2 2

2 2 0.x x kx m x x kx m       

Theo giả thiết đường thẳng

d

có đúng ba điểm

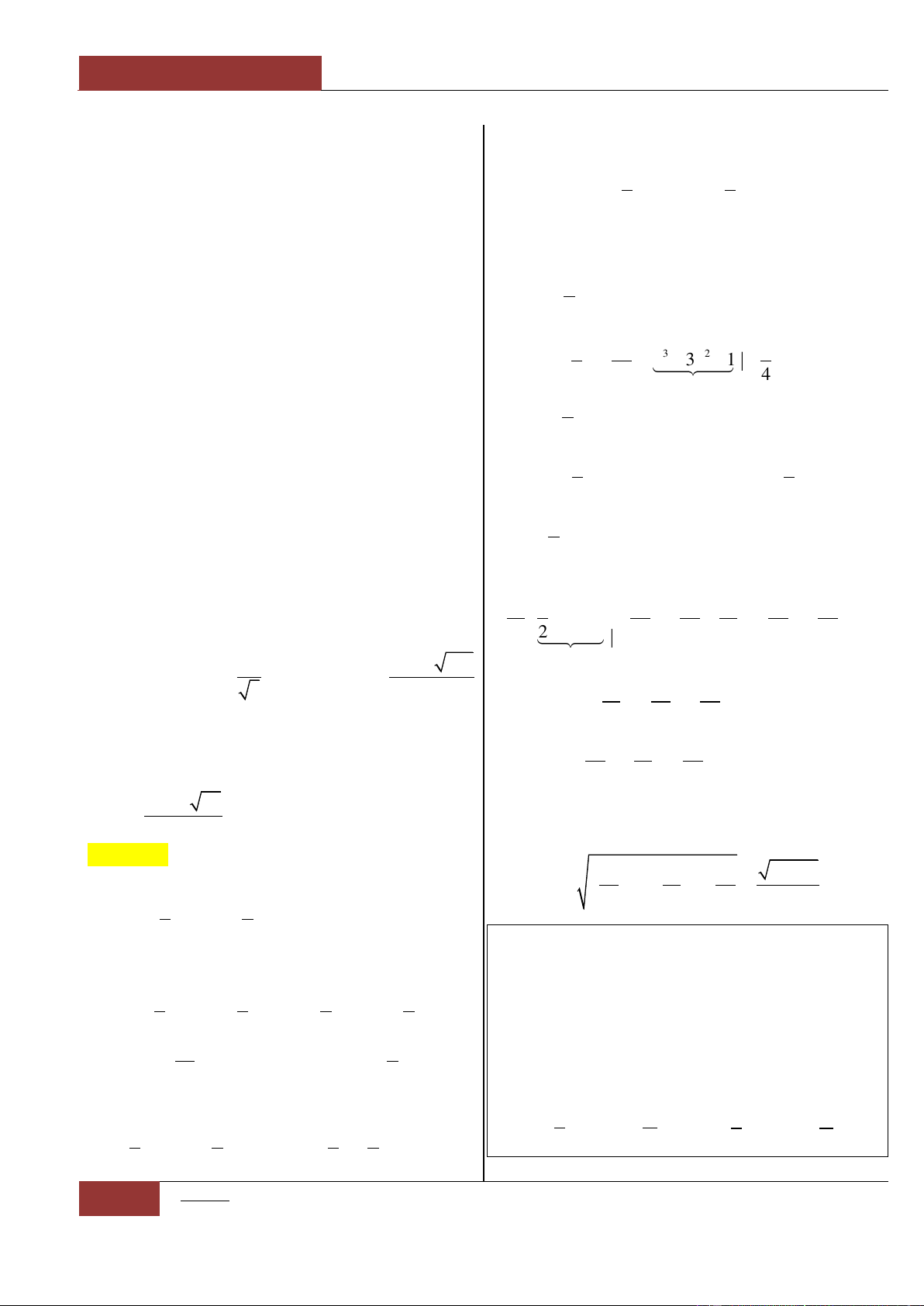
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

316

[ I can't, I can! ]

chung với đồ thị

 

C

và các điểm chung có

hoành độ

1 2 3

,,x x x

nên:

4 2 2

1 2 3

2 ( ) ( )( )x x kx m x x x x x x      

.

Do đó

d

là tiếp tuyến của (C) có hoành độ

 

3 4 2

1 1 1 1 1 1

: 4 4 2 .      x x d y x x x x x x

Phương trình hoành độ giao điểm lúc này là:

 

4 2 3 4 2

1 1 1 1 1

2 4 4 2     x x x x x x x x

 

2

22

1 1 1

1

22

11

2 3 2 0

2 3 2 0 1

     









   



x x x x x x

xx

x x x x

Yêu cầu bài toán tương đương với

 

1

có hai

nghiệm phân biệt

2 3 1

,x x x

và

333

1 2 3

1.xxx   

Vì vậy:

 

22

11

2 2 2

1 1 1

3

1 2 3 2 3 2 3

' 3 2 0

2 3 2 0

3 ( ) 1



    



   





     





xx

x x x

x x x x x x x

.

 

1

11

3 3 2

1 1 1 1

11

1 11 165

22

3

8 6 3 2 1



  



  

    





    



x

xx

x x x x

Vì vậy có duy nhất một đường thẳng thoả mãn

là tiếp tuyến tại điểm có hoành

độ

11 65

.

22

x





Đáp án B

Câu 92. Toạ độ ba điểm cực trị là nghiệm của

hệ:

2

11

3

2

'0



  











y x x

x

y

 

22

2

1 1 1 1

33

22

11

3 0 1 0 3



     









     





y x x y x x

xx

x x x

xx

.

Cộng lại theo vế có:

2 2 2

1 1 1 3

3 3 6

22

   

       

   

   

y x x x x x x

xx

.

Khi đó:

2

2 2 2 2 4 3 2

39

6 18 37

24



      





x y x x x x x x

.

Mặt khác từ

 

1

, có:

32

3 1 0,  xx

ta có:

2 2 4 3 2

9

18 37

4

   x y x x x

 

3 2 2

0

2

9 45 1

3 1 13 9 45

4 4 4

1

13 9 45 .

4



      





  

x x x x x

xx

Biến đổi:

 

2

1

13 9 45

4

xx

theo

2

3

6

2

y x x

.

Ta có:

 

2

1

13 9 45

4

xx

2

13 3 43 45 13 43 45

6

6 2 4 4 6 4 4





      





y

x x x y x

.

Vậy

22

13 43 45

6 4 4

   x y y x

 

22

43 13 45

0*

4 6 4

     x y x y

.

Vậy ba điểm cực trị cùng thuộc đường tròn có

phương trình

 

*

và bán kính của đường tròn

này là

22

43 13 45 23797

6,4

8 12 4 24

   

    

   

   

R

.

Note: Mẹo trắc nghiệm giải phương trình

 

1

sau khi quy đồng là phương trình bậc ba bấm

máy phương trình bậc ba có ba nghiệm lẻ lưu

vào các biến nhớ A – B – C.

Khi đó toạ độ các điểm cực trị của đồ thị hàm

số đã cho là

2

11

; 3 ,

2









M A A A

A

2

11

; 3 ,

2









N B B B

B

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

317

[ I can't, I can! ]

2

11

;3

2









P C C C

C

.

Sau đó tính bán kính đường tròn ngoại tiếp tam

giác có toạ độ các đỉnh như trên.

Đáp án B

Câu 93. Tập xác định:

.D

Ta có

   

2

3 6 1 3 4 9 .



     y x m x m

Hàm số đã cho đạt cực trị tại các điểm lớn hơn -

1 khi và chỉ khi phương trình

   

2

3 6 1 3 4 9 0     x m x m

có hai

nghiệm phân biệt lớn hơn -1

   

2

2 1 4 9 0     x m x m

có hai nghiệm

phân biệt

12

,xx

lớn hơn -1.

 

  

2

12

1 4 9 0

2 2 0 10 1 4.

1 1 8 2 0





     



       





    





mm

x x m m

x x m

Đáp án A

Câu 94. Đặt:

2

k m m

thì:

 

2

6 6 1 6 ; 0 1



      y x k x k y x

hoặc

.xk

Đồ thị hàm số có hai điểm cực trị khi và chỉ

khi:

1.k

Ta có:

 

32

1;3 1 ; ; 3  A k B k k k

là hai điểm

cực trị của đồ thị hàm số đã cho.

Hệ số góc của đường thẳng AB là:

 

2

1.k

Đường thẳng

AB

vuông góc với đường thẳng

2yx

khi và chỉ khi

 

2

1 1 0     kk

hoặc

2k

(cả hai giá trị này đều thỏa mãn).

+) Với

0k

thì

2

00   m m m

hoặc

1;m

+) Với

2k

thì

2

21    m m m

hoặc

2.m

Vậy

 

1;0;1;2S

.

Đáp án D

Câu 95. Đặt:

2

23  m a a

.

Ta có:

 

3 2 2 2

' 4 4 4   y x m x x x m

.

 

2

0 *'0   y x x m

22

0















x

xm

.

Hàm số có ba cực trị khi và chỉ khi

 

*

có ba

nghiệm phân biệt

0m

.

Tọa độ các điểm cực trị của đồ thị hàm số là:

 

   

44

0;1 , ;1 ; ;1  A B m m C m m

.

Chu vi tam giác

ABC

là:

28

22    AB BC CA m m m

.

Theo giả thiết, ta có:

28

2 2 2 2 2   m m m

28

1 2 1 1         m m m m m

.

- Với

1m

, ta có:

22

2 3 1 2 4 0 1 5         a a a a a

.

- Với

1m

, ta có:

22

2 3 1 2 2 0 1 3          a a a a a

.

Do đó,

S

có

4

phần tử. Vậy S có

4

2 16

tập

hợp con.

Đáp án C

Câu 96.

3

2

0

' 4 4 , ' 0





   







x

y x mx y

xm

Hàm số có cực đại, cực tiểu khi và chỉ khi:

0m

.

Gọi

 

,

oo

xy

là tọa độ điểm cực trị. Ta có:

 

'0

o

yx

Ta lại có:

2

'. 2

4

  

x

y y mx

.

Vậy các điểm cực luôn nằm trên parabol có

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

318

[ I can't, I can! ]

phương trình

2

( ): 2  P y mx

.

3

M ( ) 4 4 2

2

       P m m

.

Đáp án B

Note: Phương pháp giải bài toán trên là cách

làm gián tiếp, nó phù hợp cho nhiều bài toán

mà việc tính toán phức tạp, thay vào đó ta sử

dụng kết quả tổng quát dùng các giả thiết để

biến đổi đi đến công thức hoặc phương trình

mong muốn. Ta xét một số bài toán tương tự ở

bên dưới.

Câu 97. Đáp án D

Câu 98. Đáp án A

Câu 99. Đồ thị hàm số cắt trục tung tại điểm có

tung độ dương nên:

0.d

Hàm số đồng biến trên khoảng

 

12

;xx

nên:

0.a

Vì

   

12

1;0 ; 1;2  xx

nên

21

.xx

Do đó,

ta có:

12

0xx

.

Đạo hàm

2

32



  y ax bx c

có hai nghiệm

phân biệt

12

;xx

thỏa mãn

12

0xx

và

12

0.xx

Suy ra:

2

0

3

  

b

S

a

và

0.

3



c

P

a

Do đó:

0b

và

0c

(do

0a

).

Vậy:

0, 0, 0, 0.   a b c d

Đáp án A

Note: Cho hàm số

32

   y ax bx cx d

có

hai điểm cực trị

12

;.xx

+ Nếu

0,a

đồ thị hàm số có dạng “dấu

ngã”, hàm số nghịch biến trên khoảng

 

12

;xx

;

+ Nếu

0,a

đồ thị hàm số có dạng “dấu đồng

dạng”, hàm số đồng biến trên khoảng

 

12

;xx

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

319

[ I can't, I can! ]

Đồ thị I.II.1.1.

Minh họa giá trị lớn

nhất & giá trị nhỏ nhất

của hàm số

Weierstrass

1815 –1897

I.II. Cực trị - Điểm cực trị - Giá trị lớn nhất –

Giá trị nhỏ nhất của hàm số (Tiếp theo)

A. Lý thuyết cần nắm

1. Định nghĩa

Giá trị

M

(Max) được gọi là giá trị lớn nhất của hàm số

 

y f x

trên

K

nếu

 

,f x M x K  

và tồn tại một giá trị

0

xx

nào đó

thuộc

K

thỏa mãn

 

0

f x M

.

Kí hiệu:

 

max

xK

M f x





.

Giá trị

m

(min) được gọi là giá trị nhỏ nhất của hàm số

 

y f x

trên

K

nếu

 

,f x m x K  

và tồn tại một giá trị

0

xx

nào đó thuộc

K

thỏa mãn

 

0

f x m

.

Kí hiệu:

 

min

xK

m f x





.

2. Định lý Weierstrass thứ nhất

Nếu hàm số

 

y f x

liên tục trên đoạn

;ab





thì nó bị chặn trên

đoạn đó.

Chứng minh

Giả sử hàm số không bị chặn trên đoạn

;ab





. Khi đó với mỗi số tự

nhiên

n

luôn tồn tại

;

n

x a b







sao cho

 

n

f x n

.

Cho

n

thay đổi ta được dãy

 

n

x

bị chặn (do

;,

n

x a b n



  



).

Theo bổ đề Bolzano – Weierstrass thì từ dãy

 

n

x

bị chặn rút ra được

một dãy con

 

n

x

hội tụ. Giả sử

0

lim ;

k

n

k

x x a b









.

Do hàm

 

fx

liên tục trên

;ab





và

0

;x a b







nên

 

fx

liên tục

tại

0

x

. Suy ra:

 

0

lim

k

n

k

f x f x





.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

320

[ I can't, I can! ]

Điều này mâu thuẫn do

 

**

,,

k

n n k

f x n n f x n n      

 

lim

k

n

k

fx



  

.

Vậy hàm

 

y f x

“bị chặn trên” trên

;ab





.

Một cách tương tự, ta chứng minh được rằng hàm số

 

y f x

“bị

chặn dưới” trên

;ab





.

Vậy hàm số

 

y f x

“bị chặn” trên

;ab





.

3. Định lý Weierstrass thứ 2

Nếu hàm số

 

y f x

liên tục trên đoạn

;ab





thì nó đạt giá trị lớn

nhất và giá trị nhỏ nhất trên đoạn đó.

Tức là:

   

11

;

22

;

; : sup

; : inf

x a b

x a b f x f x

















  









  







.

Chứng minh

Ta chứng minh hàm số đạt giá trị lớn nhất trên

;ab





.

Do hàm số

 

y f x

liên tục trên

;ab





nên theo định lý Weierstrass

thứ 1 thì hàm số bị chặn trên

;ab





.

Suy ra hàm số có cận trên đúng trên

;ab





.

Đặt

 

;

sup

x a b

M f x









, khi đó:

 

,;f x M x a b



  



.

Để chứng minh

 

fx

đạt giá trị lớn nhất trên

;ab





ta cần chứng

minh tồn tại

1

;x a b







sao cho

 

1

f x M

.

Thật vậy! Bằng phản chứng ta giả sử

 

,;f x M x a b



  



.

Khi đó, ta có:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

321

[ I can't, I can! ]

Extra Techniques:

Tips:

Bên đây, chúng tôi nhắc

lại cho bạn đọc những

kiến thức liên quan đến

cực trị để so sánh với

một khái niệm mới –

Giá trị lớn nhất, giá trị

nhỏ nhất.

 

1

0, ; 0, ;M f x x a b x a b

M f x

   

       

   



.

Do hàm số

 

y f x

liên tục trên

;ab





nên hàm số

 

1

M f x

cũng

liên tục trên

;ab





. Theo định lý Weierstrass thứ 1 thì hàm số

 

1

M f x

bị chặn trên

;ab





, tức là tồn tại

0c 

sao cho

 

11

,;c f x M x a b

c

M f x



     





(Điều này mâu thuẫn với

M

là cận trên đúng).

Vậy tồn tại

1

;x a b







sao cho

 

1

f x M

hay hàm số đạt giá trị lớn

nhất trên

;ab





.

Một cách tương tự, ta chứng minh hàm số đạt giá trị nhỏ nhất trên

;ab





.

4. Cực trị và giá trị lớn nhất, nhỏ nhất liệu có giống?

Cho hàm số

 

y f x

xác định và liên tục trên khoảng

 

;ab

,

 

;ab

có thể là khoảng hữu hạn hoặc vô hạn

 



và điểm

 

0

;x a b

.

 

i

Nếu tồn tại số

0h 

sao cho

và

0

xx

thì ta nói hàm số đạt cực đại tại điểm .

Nếu tồn tại số

0h 

sao cho

và

0

xx

thì ta nói hàm số

 

y f x

đạt cực tiểu tại điểm

0

xx

.

Giả sử hàm số

 

y f x

liên tục trên khoảng

K

và đạt cực đại tại

điểm

x a K

và đạt cực tiểu tại điểm

x b K

thì ta gọi:

xa

là điểm cực đại của hàm số

 

y f x

.

xb

là điểm cực tiểu của hàm số

 

y f x

.

 

   

0 0 0

,;f x f x x x h x h    

 

y f x

0

xx

 

ii

 

   

0 0 0

,;f x f x x x h x h    

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

322

[ I can't, I can! ]

Extra Techniques:

Tips:

Giá trị cực trị hay cực trị

chỉ đơn giản là giá trị tại

điểm mà qua đó, đạo

hàm đổi dấu hay hàm số

đổi chiều biến thiên.

Trong trường hợp trên

thì cực tiểu đồng thời là

giá trị nhỏ nhất, tuy

nhiên ví dụ dưới đây sẽ

giúp chúng ta nhận ra

rằng hai lý thuyết trên

hoàn toàn khác nhau.

Hàm số không có cực trị

vẫn có giá trị lớn nhất và

nhỏ nhất trên một đoạn

liên tục nào đó.

 

;A a f a

là điểm cực đại của đồ thị hàm số

 

y f x

.

 

;B b f b

là điểm cực tiểu của đồ thị hàm số

 

y f x

.

Cho hàm số

 

y f x

liên tục trên khoảng và

có đạo hàm trên hoặc .

Nếu

thì ta nói hàm số đạt cực đại tại điểm .

Nếu

thì ta nói hàm số đạt cực tiểu tại điểm .

Như vậy, ta có thể khẳng định rằng: Cực trị (Giá trị cực trị) và giá trị

lớn nhất, nhỏ nhất là những khái niệm hoàn toàn tách biệt, chỉ do sự

nhầm lẫn trong cách hiểu hoặc trong những hình vẽ đặc biệt (hai khái

niệm trên trùng nhau) mà ra. Các bạn đọc lưu ý, chúng ta nên tìm hiểu

một cách tổng quát chứ không nên chỉ tham khảo một vài trường hợp

có sẵn, để hiểu rõ về vấn đề này.

5. Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

liên tục trên một đoạn

Một số quy tắc cũng như mẹo bên dưới đây có thể giúp đọc giả đốt

cháy được một số giai đoạn trong việc thực hiện hàn lâm.

 

00

; , 0x h x h h  

 

00

; , 0x h x h h  

   

0 0 0

;\x h x h x

 

 

0 0 0 0

' 0 ; , ' 0 ;f x x x h x f x x x x h       

0

xx

 

 

0 0 0 0

' 0 ; , ' 0 ;f x x x h x f x x x x h       

0

xx

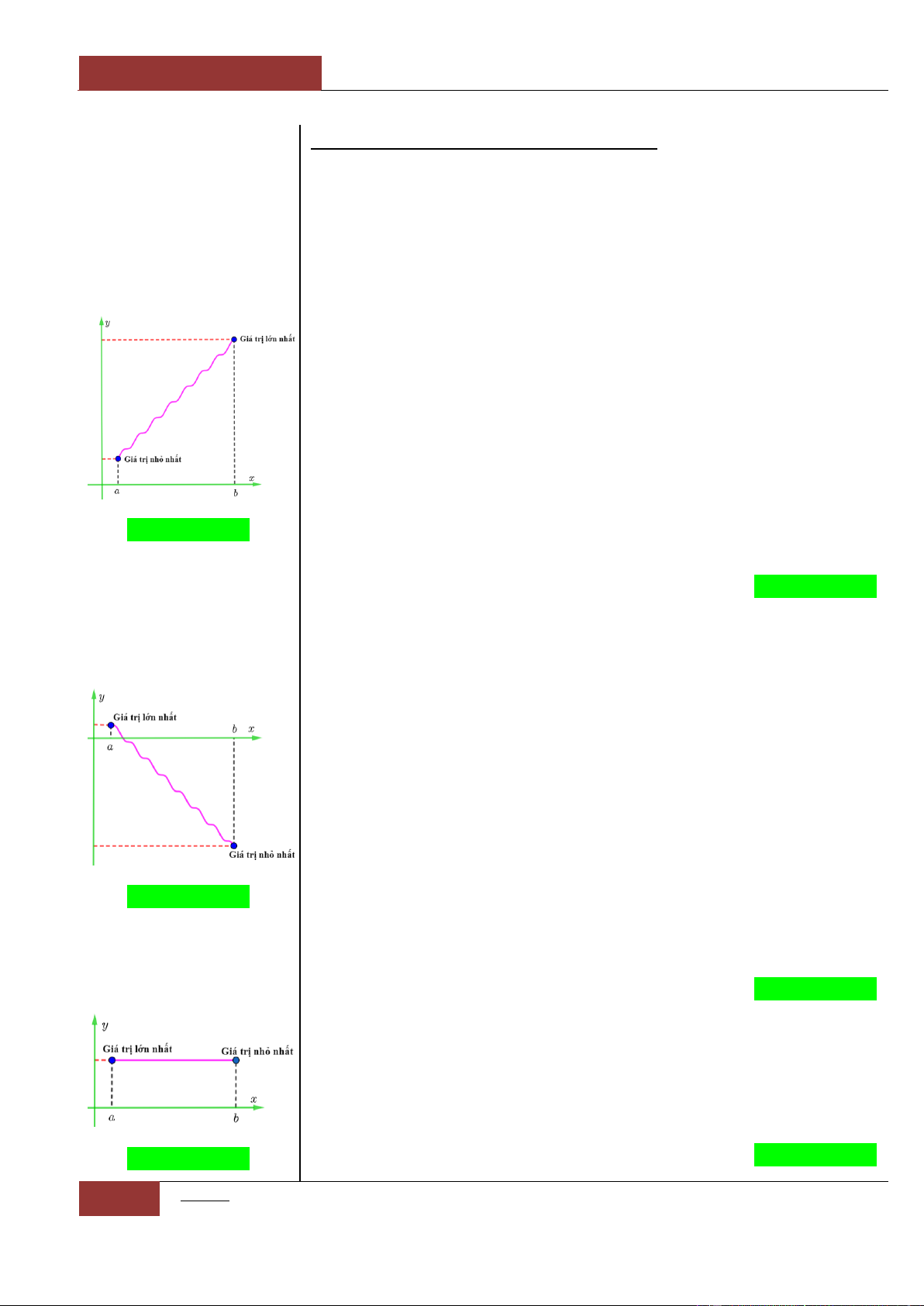
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

323

[ I can't, I can! ]

Đồ thị I.II.1.2.

Đồ thị I.II.1.3.

Đồ thị I.II.1.4.

5.1. Nhận xét 3 trường hợp đặc biệt

Xét hàm số

 

y f x

liên tục và có đạo hàm trên

;K a b







.

Trường hợp 1: Nếu

 

' 0, ;f x x a b



  



thì hàm số đạt giá trị lớn

nhất tại

xb

và có giá trị là

 

fb

. Tương tự, hàm số đạt giá trị nhỏ

nhất tại

xa

và có giá trị là

 

fa

Lưu ý: Nếu

b

là một đại lượng vô cùng

 



thì ta phải xét biểu thức

 

lim

x

fx



, nhưng phần lớn đều không tồn tại giá trị lớn nhất ở phần này

(mặc dù sau khi tính

 

lim

x

fx



cho ta một số hữu hạn nhưng nếu không

tồn tại một giá trị

0

xx

nào đó thuộc

K

sao cho

   

0

lim

x

f x f x





thì

vẫn vô nghĩa). Tương tự với

a

khi là một đại lượng âm vô cùng

 



.

Xem thêm Đồ thị I.II.1.2.

Trường hợp 2: Nếu

 

' 0, ;f x x a b



  



thì hàm số đạt giá trị nhỏ

nhất tại

xb

và có giá trị là

 

fb

. Tương tự, hàm số đạt giá trị lớn

nhất tại

xa

và có giá trị là

 

fa

Lưu ý: Nếu

b

là một đại lượng vô cùng

 



thì ta phải xét biểu thức

 

lim

x

fx



, nhưng phần lớn đều không tồn tại giá trị lớn nhất ở phần này

(mặc dù sau khi tính

 

lim

x

fx



cho ta một số hữu hạn nhưng nếu không

tồn tại một giá trị

0

xx

nào đó thuộc

K

sao cho

   

0

lim

x

f x f x





thì

vẫn vô nghĩa). Tương tự với

a

khi là một đại lượng âm vô cùng

 



.

Xem thêm Đồ thị I.II.1.3.

Trường hợp 3: Nếu

 

'0fx

thì hàm số là một hàm hằng, không đổi,

tuy nhiên ta vẫn có thể định nghĩa

   

min max

KK

f x f x const

vì vẫn

thỏa mãn định nghĩa của giá trị lớn nhất, giá trị nhỏ nhất của hàm số.

Xem thêm Đồ thị I.II.1.4.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

324

[ I can't, I can! ]

Extra Techniques:

Tips:

Giá trị lớn nhất và nhỏ

nhất không nhất thiết đạt

tại các điểm cực trị,

cũng không nhất thiết

đạt tại hai biên của một

đoạn liên tục, cũng

không nhất thiết phải tồn

tại (trường hợp có sự có

mặt của các đại lượng

vô cùng).

Extra Techniques:

Tips:

Điều kiện cần và đủ để

tồn tại

max

K

M 

là:

 

00

,

x K f x M



  





  





Hoàn toàn tương tự:

Điều kiện cần và đủ để

tồn tại

min

K

m 

là:

 

00

,

x K f x m



  





  





5.2. Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm

số.

Bước 1: Tìm tập tất cả các điểm

, 1, ;

ii

x i n x K a b



  



mà tại đó

 

'fx

bị triệt tiêu (bằng

0

) hoặc không xác định.

Bước 2: Tính các giá trị

 

1

2

...

n

fa

fx

fb











.

Bước 3: Tìm số lớn nhất

M

và nhỏ nhất

m

trong

2n 

giá trị vừa

tính được.

Bước 4: Kết luận: Vậy

   

;;

max , min

a b a b

M f x m f x

   

   



.

B. Bài tập trong các đề thi thử

Dạng 1: Bài toán không chứa tham số

Câu 1. Cho hàm số

2

1

mx n

y

x







. Giá trị của

,mn

sao cho giá trị lớn

nhất và giá trị nhỏ nhất của hàm số trên lần lượt là

4, 1

là?

A.

   

; 3;4mn 

. B.

     

 

; 4; 3 ; 4; 3mn    

.

C.

   

; 3; 4mn   

. D.

     

 

; 4;3 ; 4;3mn 

.

Đáp án: D

Lời giải

+)

 

2

0

00

0

2

0

4,

1

max 4

,4

1

mx n

x

yx

x

y

mx n

x y x

x





  





  





  





  





  







.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

325

[ I can't, I can! ]

 

   

2

0 0 0

4 4 0,

, 4 4 0 1

x mx n x

x x mx n



     







     





 

   

1

2

1

0

0 16 4 0 *

0

mn







       









Tương tự, ta có:

+)

 

2

0

00

0

2

0

1,

1

min 1

,1

1

mx n

x

yx

x

y

mx n

x y x

x





   





   





   





   





   







 

   

2

0 0 0

1 0,

, 1 0 2

x mx n x

x x mx n



     







     





 

   

2

0

0 4 1 0 **

0

mn







       









.

Từ

   

 

2

4

16 4 0

3

1 , 2

4

4 1 0

3

m

mn

n

m

mn

m













  



















  

















.

Câu 2. Giá trị lớn nhất và giá trị nhỏ nhất của

2

2 10 3

3 2 1

xx

A

xx







trên

tập xác định lần lượt là?

A.

52

max , min

23

AA

. B.

5

max 7, min

2

AA

.

C.

max 5, min 1AA

. D.

1 3 17 1 3 17

max , min

33

AA





.

Đáp án: D

Lời giải

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

326

[ I can't, I can! ]

Extra Techniques:

Tips:

Đối với dạng toán

phương trình tổng quát

1

10

...

nn

a x a x a



  

,

trong đó hệ số

n

a

có

chứa tham số thì ta phải

xét hai trường hợp như

đã trình bày trong Câu 2

Để hàm số có giá trị lớn

nhất và nhỏ nhất thì

A

phải tồn tại, nhưng vì để

A

tồn tại thì phương

trình bậc hai bên phải

tồn tại nghiệm.

TXĐ:

D 

.

Ta có:

     

2

2 10 3

3 2 2 5 3 0 *

3 2 1

xx

A A x A x A

xx



       



.

Trường hợp 1:

27

3 2 0

3 26

A A x      

.

Trường hợp 2:

2

3 2 0

3

AA   

thì ta xem

 

*

như là một

phương trình bậc hai theo

x

. Do đó, để phương trình

 

*

có nghiệm

thì:

 

    

2

*

' 0 5 3 2 3 0 2 19 0A A A A A            

Suy ra:

1 3 17 1 3 17

44

A





.

Do đó:

1 3 17 1 3 17

max , min

44

AA





.

Câu 3. Hàm số

 

2

sin 1

sin sin 1

x

y g x

xx







có giá trị lớn nhất và giá

trị nhỏ nhất lần lượt là?

A.

   

max 1, min 2g x g x  

. B.

   

max 0, min 1g x g x  

.

C.

   

max 1, min 0g x g x

. D.

   

max 1, min 1g x g x  

.

Đáp án: C

Lời giải

Ta có:

2

13

sin sin 1 sin 0,

24

x x x x



       





.

Đặt:

sin , 1;1t x t



  



. Lúc đó:

 

2

1

; 1;1

1

t

y f t t

tt





   





.

 

2

0

2

' ; ' 0

2 1;1

1

t

tt

f t f t

t

tt







  





  









Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

327

[ I can't, I can! ]

Extra Techniques:

Remark:

Đối với dạng toán có

hàm số quá phức tạp và

không thấy miền cụ thể,

ta có thể dựa vào TXĐ

để tìm ra miền hay dùng

phương pháp đổi biến số

để đưa bài toán về dạng

đã biết với cách thực

hiện nhẹ nhàng hơn.

Lưu ý: Đổi biến – Tìm

điều kiện miền theo biến

mới

Tính toán tại một số điểm cần thiết:

 

10

01

2

1

3

f





















.

Khi đó, ta suy ra:

   

1;1

max max 1 sin 0 ,

min min 0 sin 1 2 ,

2

g x f x x x k k

















      







         





.

Câu 4. Tìm giá trị lớn nhất của hàm số

4

5

x

y

x





trên

4;







?

A.

4;

1

max

40

y









. B.

4;

1

max

30

y









.

C.

4;

1

max

10

y









. D.

4;

1

max

20

y









.

Đáp án: D

Lời giải

TXĐ:

4;D



 



.

Ta có:

14

4

44

2

.2

22

41

2

5 5 5 10 20

x

y

x x x x















    

.

Dấu

""

xảy ra khi và chỉ khi:

4

28

2

x



  

.

Vậy:

4;

1

max

20

y









khi

8x 

.

Câu 5. Tìm giá trị lớn nhất và nhỏ nhất của hàm số

53

1y x x  

trên đoạn

1;3





?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

328

[ I can't, I can! ]

Extra Techniques:

Remark:

Thông thường, những

hàm số là dãy tổng của

những hàm cùng tính

đơn điệu thì min và max

đạt tại các đầu mút.

Thật vậy! Tổng những

hàm đồng biến sẽ là một

hàm đồng biến và tổng

của những hàm nghịch

biến sẽ là một hàm

nghịch biến.

Extra Techniques:

Tips:

Xét phương trình bậc

nhất đối với

sin x

và

cos x

có dạng:

 

sin cos *b cxxa 

Phương trình

 

*

có

nghiệm khi và chỉ khi:

2 2 2

a cb

A.

   

max 271, min 3g x g x

.

B.

   

max 1, min 1g x g x  

.

C.

   

max 271, min 3g x g x  

.

D.

   

max 273, min 3g x g x  

.

Đáp án: A

Lời giải

ĐKXĐ:

 

53

10D x x x    

.

Ta có:

42

53

' 0,

21

xx

y x D

xx



   



.

Vậy hàm số đã cho luôn đồng biến trên đoạn

1;3





, từ đây suy ra:

   

1;3

min 1 3

max 3 271

f x f























Câu 6. Cho hàm số

sin 1

cos 2

kx

y

x







. Điều kiện của

k

để

min 1y 

là?

A.

1

k











. B.

 

2 2;2 2k 

.

C.

 

2 2; 1;1;2 2k   

. D.

22

k











.

Đáp án: D

Lời giải

Xét phương trình

 

sin 1

*

cos 2

kx

y

x







 

* sin cos 2 1k x y x y   

.

Phương trình

 

*

có nghiệm khi và chỉ khi:

 

2

2 2 2 2

2 1 3 4 1 0k y y y y k       

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

329

[ I can't, I can! ]

Extra Techniques:

Tips:

44

2

22

sin cos ...

1

... 1 sin 2

2

sin cos 1

2sin cos sin 2

xx

x

xx

x x x









22

2 3 1 2 3 1

33

kk

y

   

  

Vậy:

2

2 3 1

min

3

k

y





.

Theo đề bài ta có:

2

22

2 3 1

1 3 1 5 3 1 25

3

k

kk



       

2

22

8

22

k





  







.

Câu 7. Cho hàm số

44

sin cos sin cosy x x m x x  

. Điều kiện của

m

để

min 1y 

là?

A.

 

1;1m 

. B.

1m 

.

C.

1m 

. D. Không tồn tại.

Đáp án: D

Lời giải

TXĐ:

D 

.

Ta có:

 

   

2

4 2 2 4

1

sin 2sin cos cos 2sin cos 2sin cos

22

m

y x x x x x x x x    

.

 

2

2 2 2

2

1

sin cos sin 2 sin 2

22

1

1 sin 2 sin 2

22

m

y x x x x

m

y x x

    

   

Đặt

sin 2 , 1;1t x t



  



.

Ta có:

2

1

1 ' 0

2 2 2 2

m m m

y t t y t t          

.

Trường hợp 1:

12

2

m

m    

.

Khi đó:

   

1

1 max

2

1

1 min

2

m

f f x

m

f f x





  















Trường hợp 2:

1 1 2 2

2

m

m      

.

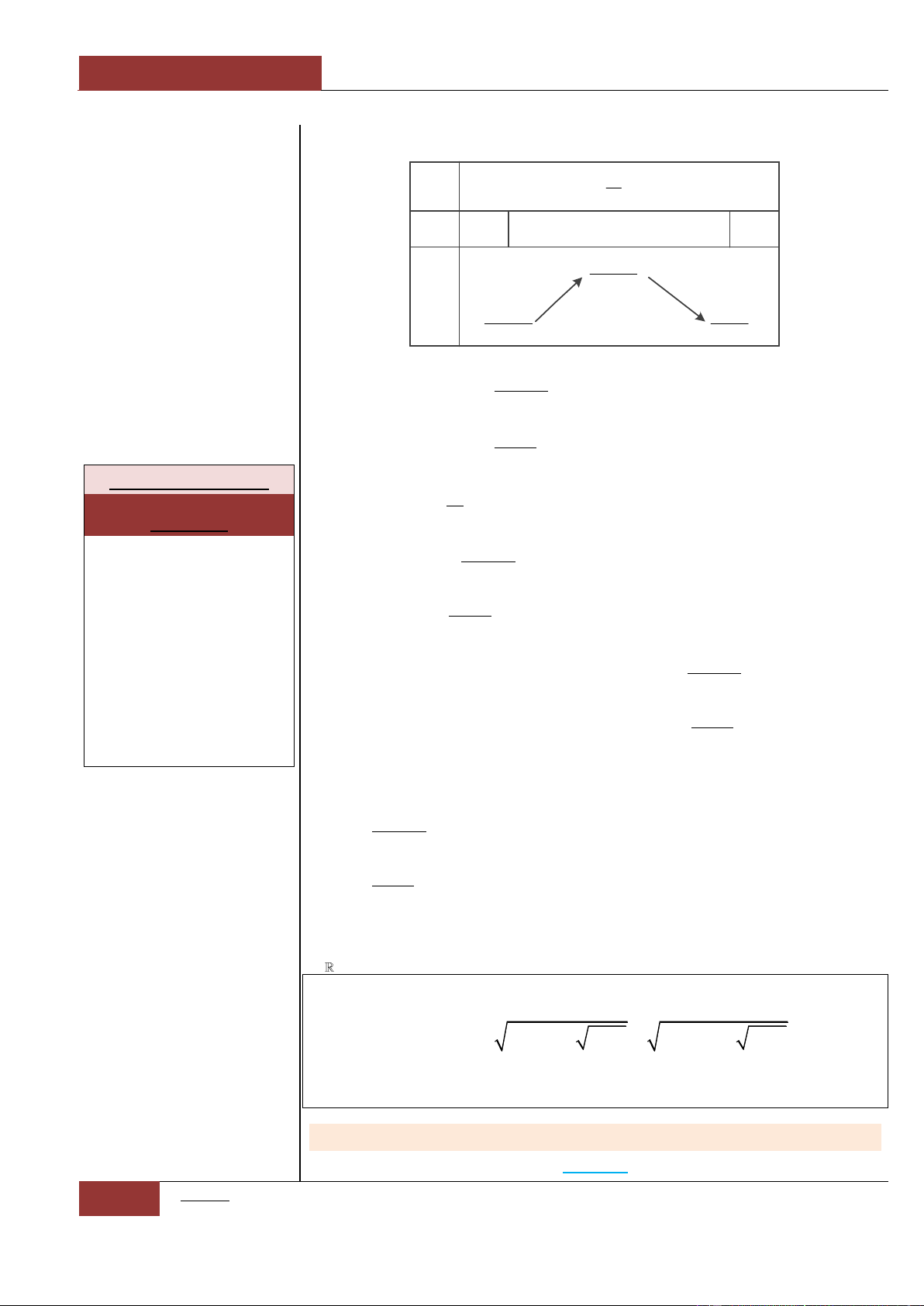
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

330

[ I can't, I can! ]

Extra Techniques:

Remark:

Đối với những bài toán

ta không tổng quát được

hoặc với từng khoảng,

từng miền thì bài toán sẽ

nhận những giá trị khác

nhau thì ta phải chia nhỏ

các trường hợp có thể

một cách khoa học nhất.

Bảng biến thiên:

t

 

'ft

 

ft

1

2

m

0

1





2

8

m 

1

2

m 

1

2

m

Dễ thấy,

  

   

1;1

1

min , 0;2

2

1

min , 2;0

2

m

f x x

m

f x x



















  













   





.

Trường hợp 3:

12

2

m

m  

.

Khi đó:

   

1

1 min

2

1

1 max

2

m

f f x

m

f f x





  















.

Kết hợp cả ba trường hợp, ta có:

  

   

1

min , 0;

2

1

max , ;0

2

m

f x x

m

f x x







  













  





.

Khi đó việc tìm

m

thỏa mãn được chuyển sang việc giải hai phương

trình:

1

1, 0

2

1 1, 0

1, 0

2

m

mm

m m m

m











  





  











.

Vậy phương trình vô nghiệm hay không tại giá trị thực của

m

nào để

min 1y 

.

Câu 8. Tìm giá trị nhỏ nhất của hàm số

 

3 4 1 15 8 1y f x x x x x        

A.

1

. B.

2

. C.

3

. D.

4

.

Đáp án: B

Lời giải

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

331

[ I can't, I can! ]

Extra Techniques:

Remark:

Đối với những bài toán

có chứa căn thức lồng

căn thức, thì việc phá

căn bằng lũy thừa là một

điều tất yếu và thường

thấy nhất.

Lưu ý: Đối với các căn

bậc chẵn, ta phải lưu ý

dấu của biểu thức sau

khi phá trị tuyệt đối.

Extra Techniques:

Tips:

Bất đẳng thức vector:

 

1a b a b  

Dấu

""

xảy ra khi

,ab

cùng hướng.

 

2a b a b  

Dấu

""

xảy ra khi

,ab

cùng hướng.

 

3..a b a b

Dấu

""

xảy ra khi

,ab

cùng phương.

Ta có:

 

1 4 1 4 1 8 1 16f x x x x x         

.

 

   

22

1 2 1 4 1 2 1 4f x x x x x            

.

 

1 2 4 1 1 2 4 1 2f x x x x x             

.

Dấu

""

xảy ra khi và chỉ khi:

  

1 2 4 1 0

2 1 4

5 17

1

xx

x



    



  

   













.

Vậy



 

1;

min 2fx









.

Câu 9. Tìm giá trị nhỏ nhất của hàm số

 

22

2 2 2 2y f x x x x x      

A.

0

. B.

23

. C.

22

. D.

4

.

Đáp án: C

Lời giải

Ta có:

 

2

22

2

22

2 2 2 1 1 1 1 0,

x x x x x x



           







           



.

Như vậy:

     

22

1 1 1 1y f x x x      

.

Trong mặt phẳng tọa độ

Oxy

, xét hai vector

   

1;1 , 1 ;1u x v x   

.

Khi đó:

     

 

2

1;1 1 ;1 2;2

11

22

u v x x

ux

vx

uv



     



  







  









.

Áp dụng bất đẳng thức

u v u v  

, ta có:

 

22

2 2 2 2 2 2y f x x x x x       

.

Dấu đẳng thức xảy ra khi và chỉ khi hai vector

,uv

cùng hướng.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

332

[ I can't, I can! ]

Extra Techniques:

Remark:

Đối với những hàm số

có dạng:

  

...

y x a x b

x c c d

  



Với

a d b c  

, thì ta

biến đổi phương trình về

dạng:

  

 

2

...

y x a x d

x b x c

y x kx ad

x kx bc



  









   



Với

k a d b c   

.

Vì hai vector

,uv

có tung độ bằng nhau nên hoành độ cũng phải bằng

nhau. Như vậy, ta có:

1 1 0x x x    

.

Vậy:

 

min 2 2fx

đạt tại

0x 

.

Câu 10. Tìm giá trị nhỏ nhất của hàm số

      

1 2 3 4y f x x x x x     

A.

1

. B.

1

. C.

2

. D.

2

.

Đáp án: A

Lời giải

Cách 1: Dùng hằng đẳng thức.

Ta có:

          

1 2 3 4 1 4 2 3y x x x x x x x x         

   

   

.

  

   

 

22

2

22

2

5 4 5 6

5 5 1 5 5 1

25 5

5 5 1 5 1

44

55

11

24

     

   

       

   





         













      











y x x x x

yx

Dấu

""

xảy ra khi và chỉ khi:

2

5 5 5 5

2 4 2

xx





    





.

Vậy giá trị nhỏ nhất của hàm số

    

1 2 3 4y x x x x    

là

1

.

Dấu

""

xảy ra khi và chỉ khi:

55

2

x





.

Cách 2: Khảo sát hàm số.

Ta có:

    

 

2

1 2 3 4 5 5 1y x x x x x x        

(Do Cách 1).

Suy ra:

 

2

' 2 5 5 . 2 5 0    y x x x

.

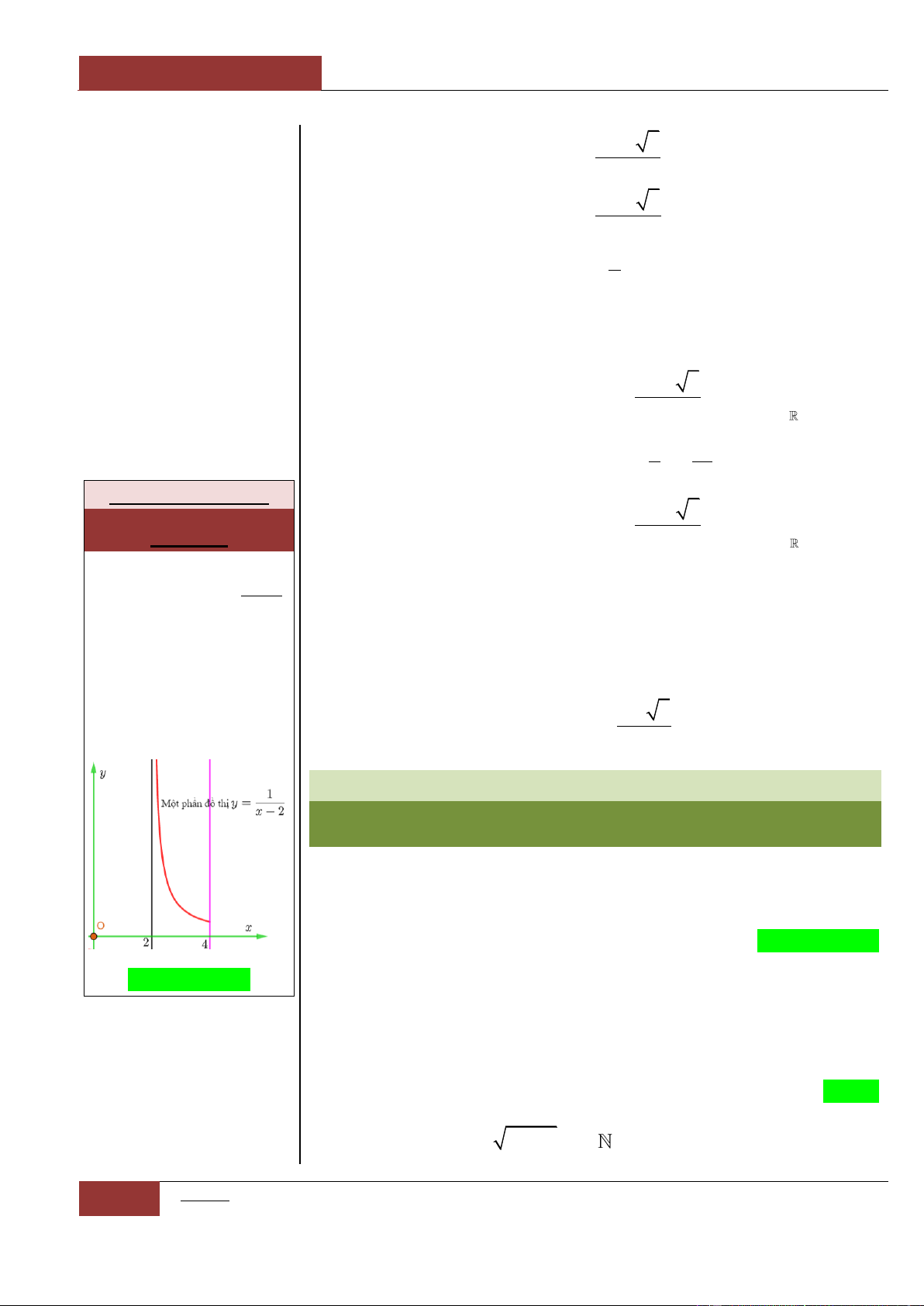
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

333

[ I can't, I can! ]

Extra Techniques:

Remark:

Đồ thị hàm số

1

2

y

x





không có giá trị lớn nhất

và nhỏ nhất trên khoảng

 

2;4

, mặc dù, đồ thị

hàm số trên vẫn liên tục.

Đồ thị I.II.1.5.

55

2

55

2

5

2





















x

Tính toán tại một số điểm đặc biệt:

lim

55

1 min

2

59

2 16

55

1 min

2

lim

x

y

yy

y

yy

y





 









  





























  









 





.

Vậy giá trị nhỏ nhất của hàm số

    

1 2 3 4y x x x x    

là

1

.

Dấu

""

xảy ra khi và chỉ khi:

55

2

x





.

Một số Tips để làm tốt các bài toán Min – Max

 

1

Hàm số liên tục trên một khoảng chưa chắc đã có giá trị lớn nhất,

nhỏ nhất tuy nhiên vẫn có trường hợp có cả giá trị lớn nhất, nhỏ nhất.

Xem thêm Đồ thị I.II.1.5.

 

2

Các hàm đa thức chỉ bao gồm các hạng tử có bậc lẻ và hệ số tự

do có hệ số là các số cùng tính âm, dương thì luôn đơn điệu trên tập

xác định nên sẽ đạt Min – Max tại những đầu mút.

Xem thêm Câu 5.

 

3

Các hàm có dạng

,

n

ax b n

thì thường đồng biến trên TXĐ

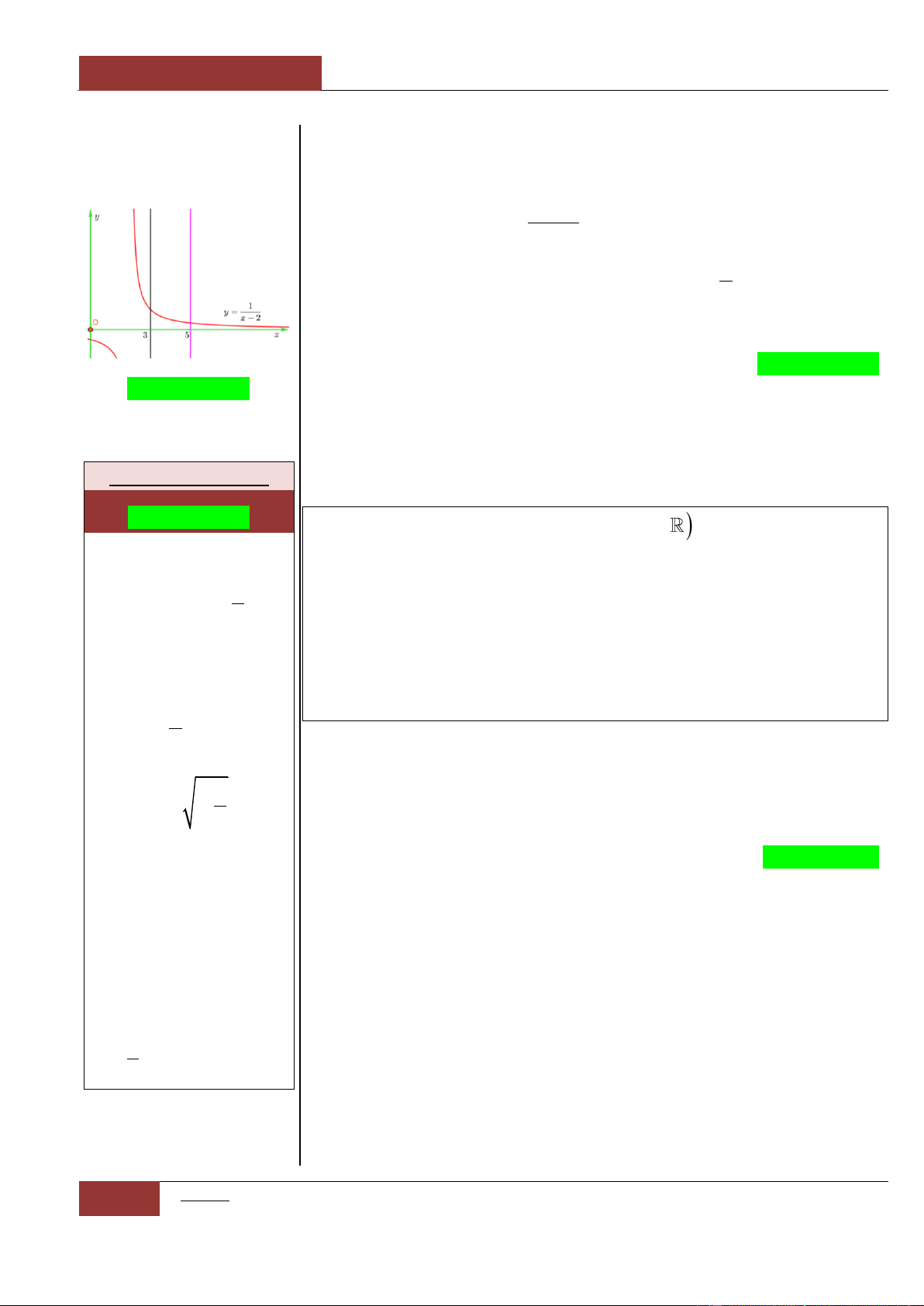
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

334

[ I can't, I can! ]

Đồ thị I.II.1.6.

Extra Techniques:

Ví dụ I.II.1.1.

Tìm giá trị nhỏ nhất của

biểu thức

1

yx

x



trên

đoạn

2;3





. Nếu ta

dùng Cauchy cho hai số

dương

1

,x

x

thì ta được:

1

2 . 2

Cauchy

yx

x



Dấu

""

xảy ra khi:

1 2;3x







.

Như vậy, bài toán không

được chấp nhận.

Giá trị nhỏ nhất phải là:

5

2

m 

, tại

2x 

.

khi

0a 

và nghịch biến trên TXĐ khi

0a 

. Việc tìm Min – Max ta

có thể lưu ý nhanh các giá trị tại đầu mút.

 

4

Hàm số nhất biến

ax b

y

cx d







luôn đồng biến hoặc nghịch biến

trên một đoạn liên tục nào đó (đoạn không chứa

d

c



). Vì thế việc tìm

Min – Max ta thường chỉ tính toán các giá trị ở đầu mút.

Xem thêm Đồ thị I.II.1.6.

 

5

Các bài toán cho ta trước giá trị Min – Max cụ thể và yêu cầu ta

định giá trị các tham số để

min , maxab

thì ta nên dùng định

nghĩa để giải quyết bài toán.

Giả sử

f

là một hàm xác định trên

 

KK

.

 

00

,

max

:

,

min

:

K

f x M x K

M f x

x K f x M

f x m x K

m f x

x K f x m



  







  







  







  





 

6

Với các bài toán có liên quan đến đánh giá hoặc dùng bất đẳng

thức thì điều kiện đủ để kết luận bài toán đúng hay chưa là việc xem

xét dấu đẳng thức có xảy ra hay không.

Xem thêm Ví dụ I.II.1.1.

 

7

Một số phương pháp để giải quyết bài toán tìm Max – Min.

 

i

Phương pháp miền giá trị:

Đối với hàm

 

y f x

một biến, xác định trên

K

:

 

o

y f K

phương trình

 

0

y f x

có nghiệm

 

*

.

Giải phương trình

 

*

, suy ra:

   

0

min max

KK

f x y f x

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

335

[ I can't, I can! ]

Extra Techniques:

Tips:

Trong trường hợp tìm

giá trị lớn nhất, giá trị

nhỏ nhất của hàm số

 

y f x

trên đoạn

;ab





, ta có thể trình

bày đơn giản như sau:

Bước 1: Tìm

 

'fx

và

tìm các điểm tới hạn

12

, ,...,

n

x x x

của

 

fx

trên đoạn

;ab





;

Bước 2: Tính

2n 

giá

trị:

     

1 2 3

, , ,f x f x f x

     

..., , ,

n

f x f a f b

.

Bước 3: Tìm số lớn nhất

 

maxM f x

trong

2n 

số đó, và số nhỏ

nhất

 

minm f x

trong

2n 

số đó.

Nếu hàm số

 

y f x

liên tục trên đoạn

;ab





,

thì giá trị lớn nhất, giá

trị nhỏ nhất luôn tồn tại.

Đối với hàm số

 

,y f x y

hai biến, xác định trên

K

.

Xem

 

,y f x y

là phương trình đối với ẩn

x

và

y

là tham số.

Tìm điều kiện của

y

để phương trình

 

y f x

có nghiệm.

Từ điều kiện trêm, biến đổi đưa đến dạng

m y M

. Xét dấu

""

xảy ra và kết luận

   

max , min

KK

f x M f x m

.

Tổng quát lên bài toán như sau:

Cho các số thực

,xy

thỏa mãn điều kiện

 

,0F x y 

. Tìm giá trị nhỏ

nhất và giá trị lớn nhất của biểu thức

 

,P G x y

.

Bước 1: Gọi

T

là tập giá trị của

P

. Khi đó

mT

khi và chỉ khi hệ

phương trình

 

;0

1

,

F x y

G x y m















có nghiệm.

Bước 2: Tìm các giá trị

m

để hệ

 

1

có nghiệm (thường đưa về điều

kiện có nghiệm của phương trình bậc hai), rồi suy ra tập giá trị

T

của

P

. Từ đó suy ra giá trị nhỏ nhất và giá trị lớn nhất của biểu thức

 

;P G x y

.

 

ii

Phương pháp đạo hàm

Khảo sát sự biến thiên của hàm số

 

y f x

;

Dựa vào bảng biến thiên để kết luận

   

max , minf x f x

.

Dựa vào bảng biến thiên để kết luận min, max.

 

iii

Phương pháp dùng bất đẳng thức

Dùng các bất đẳng thức quen thuộc để chứng mình

 

f x M

f x m

m f x M

















Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

336

[ I can't, I can! ]

Augustin Louis Cauchy

1789 – 1857

Victor Yakovlevich

Bunyakovsky

1804 - 1889

Phải chỉ ra sự tồn tại của

01

,x x K

sao cho

   

01

,f x M f x m

.

Khi đó:

   

max , min

KK

f x M f x m

.

Các bất đẳng thức quen thuộc phải kể đến như:

Bất đẳng thức Cauchy:

Cho

n

số thực

12

, ,...,

n

a a a

không âm. Thế thì:

12

...

Cauchy

n

a a a

n

  



Dấu

""

xảy ra khi và chỉ khi:

12

...

n

a a a  

.

Bất đẳng thức Bunyakovsky

Cho

n

cặp số thực

 

, , 1,...,

ii

a b i n

.

Thế thì:

2

22

1 1 1

.

n n n

i i i i

i i i

a b a b

  

     



     

     

  

.

Dấu

""

xảy ra khi và chỉ khi tồn tại

k 

sao cho

. , 1,...,

ii

b k a i n

.

Hệ quả:

  

2 2 2 2

4a b c d abcd  

.

Bất đẳng thức về dấu giá trị tuyệt đối

 

1 2 1 2

1a a a a  

 

1 2 1 2

2a a a a  

 

1 2 1 2

... ... 3

nn

a a a a a a      

Dấu

""

trong

   

1 , 2

xảy ra khi và chỉ khi

12

.0aa

.

Dấu

""

trong

 

3

xảy ra khi và chỉ khi

0, 1,

i

a i n

hoặc

0, 1,

i

a i n

.

 

iv

Phương pháp tọa độ vector

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

337

[ I can't, I can! ]

Bất đẳng thức vector:

 

1a b a b  

Dấu

""

xảy ra khi

,ab

cùng hướng.

 

2a b a b  

Dấu

""

xảy ra khi

,ab

cùng hướng.

 

3..a b a b

Dấu

""

xảy ra khi

,ab

cùng phương.

 

v

Phương pháp đổi biến (đặt ẩn phụ) để tìm Min – Max.

+) Nếu đặt

2

tx

thì

0t 

và giả sử

2

; 0;x a a t a



   



.

+) Nếu đặt

2

tx

thì

0t 

và giả sử

22

; ; , , 0x a b t a b a b



   



.

+) Nếu đặt

2

tx

thì

0t 

và giả sử

2

; 0; ,x a b t a



  



0,ab b a

.

+) Nếu đặt

2

tx

thì

0t 

và giả sử

2

; 0; ,x a b t b



  



0,ab a b

.

+) Nếu đặt

sintx

hoặc

costx

thì ta suy ra

1;1t







.

+) Nếu đặt

22

sin , cost x t x

thì suy ra

0;1t







.

+) Nếu đặt

sin cos 2; 2t x x t



    



.

+) Nếu đặt

1

, 0 2t x x t

x

    

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

338

[ I can't, I can! ]

 

vi

Phương pháp dùng CASIO.

Cách 1: Sử dụng Table.

Sử dụng Table xét hàm số

 

fx

trên đoạn

 

;

min

;

max

x a b

fx

ab

fx





























.

Chọn các giá trị nhập vào: Start, End, Step.

Start? Nhập giá trị

a

.

End? Nhập giá trị

b

.

Step? Nhập bước nhảy phù hợp với từng bài.

Dựa vào Table ta sẽ hình dung được hình dáng tổng quát của đồ thị

hàm số trên đoạn

;ab





để đưa ra những kết luận phù hợp.

Cách 2: Chức năng Solve, Calc.

Giải phương trình

 

'0fx

bằng cách sử dụng chức năng Solve, lưu

ý ta chỉ lấy những giá trị trong đoạn

;ab





để dò nghiệm, ta sẽ thu

được tập các nghiệm của phương trình

 

'0fx

.

Dùng Calc để tìm các giá trị của

 

fx

tại

2n 

điểm (

2

điểm đầu

mút và

n

nghiệm của phương trình đạo hàm) rồi so sánh, đưa ra kết

luận về Max – Min.

 

vii

Một số lưu ý khi giải các bài toán Max – Min.

Bước 1: Tính đạo hàm

 



fx

.

Bước 2: Tìm tất cả các nghiệm

 

;

i

x a b

của phương trình

 

0



fx

và tất cả các điểm

 

;





i

ab

làm cho

 



fx

không xác định.

Bước 3. Tính

 

lim







xa

A f x

,

 

lim







xb

B f x

,

 

i

fx

,

 



i

f

.

Bước 4. So sánh các giá trị tính được và kết luận Max – Min.

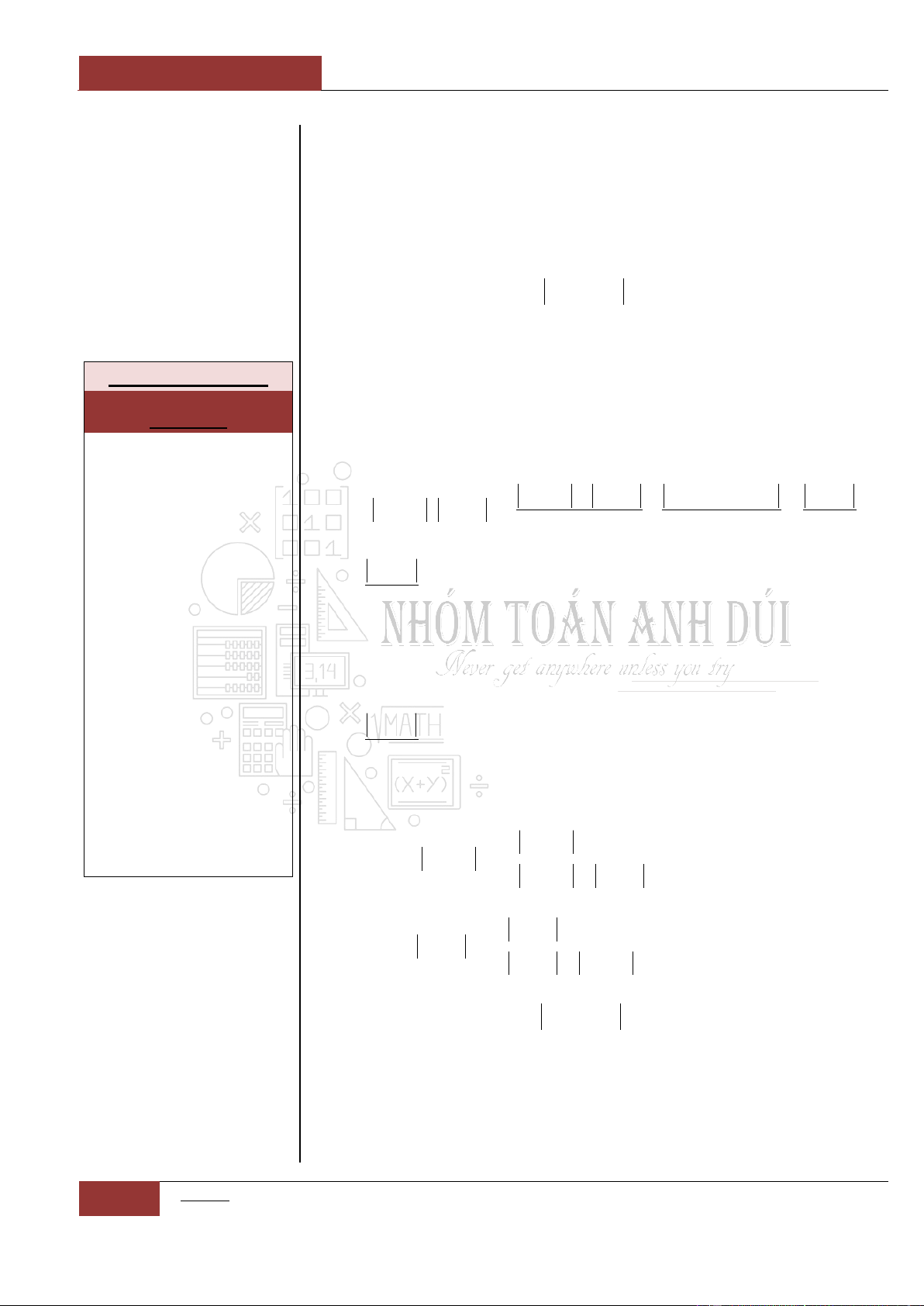
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

339

[ I can't, I can! ]

Extra Techniques:

Remark:

Các dng v tr tuyi

ng rng,

chúng ta nên tìm cho

mình mt s 

pháp phù h có th

hc tt dng này.  

chúng tôi trình bày cho

bn các dng ng

thy và các công thc

giúp các bn có th làm

 phn

bày tp, chúng tôi s 

ng t lu

khai thác nhiu khía

ca dng toán

này.

Nu giá tr ln nht (nh nht) là A hoc B thì ta kt lun không có

giá tr ln nht (nh nht).

 

viii

nh

m

 Max  Min ca hàm s cha du giá tr tuyt

i thu kic

Dạng 1: Tìm

m



 

   

;

max 0 .



   y f x m a a

Phương pháp:

Cách 1: c tiên tìm

 

 

 

   

;

max ; min .



  f x K f x k K k

Kim tra:

 

max , .

2 2 2

      

    

m K m k m K m k K k

m K m k

TH1:

.

2





Kk

a



 

 

;

max ;



     



       



   



m k a m a k

y a m a k a K

m K a m a K

.

TH2:

2





Kk

a

 m

.

Cách 2: ng hp

TH1:

  



  



  





m K a

Max m K

m K m k

TH2:

  



  



  





m k a

Max m k

m k m K

Dạng 2: Tìm

m



 

   

;

min 0 .



   y f x m a a

Phương pháp:

c tiên tìm

 

 

 

   

;

max ; min .



  f x K f x k K k

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

340

[ I can't, I can! ]

 

;

min .

00



         

   

    

   

       

   

m k a m K a m a k m a K

ya

m k m K m k m K

Vy

12

.m S S

Dạng 3: Tìm

m



 

 

;

max



y f x m

t quá giá tr

M

cho

c.

Phương pháp: c tiên tìm:

 

 

 

   

;

max ; min .



  f x K f x k K k



 

;

max .



  



       







m k M

y M M k m M K

m K M

Dạng 4: Tìm

m



 

 

;

min



y f x m

t quá giá tr

a

cho

c.

Phương pháp: c tiên tìm:

 

 

 

   

;

max ; min .



  f x K f x k K k

 

  

;

min 0

00

.



    



      



   



    



      



   



m k a m K a

y a m K m k

m k m K

m a k m a K

K m k

m k m K

Dang 5: Tìm

m



 

 

;

max 

ab

y f x m

t min.

Phương pháp:

c tiên tìm

 

 

 

   

;

max ; min .  

ab

f x K f x k K k

 hi tìm

.

2



  

Kk

mm

 hi tìm min ca

 

;

max 

ab

y

giá tr

này là

.

2

Kk

Dạng 6: Tìm

m



 

 

;

min 

ab

y f x m

t min.

Phương pháp: c tiên tìm:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

341

[ I can't, I can! ]

 

 

 

   

;

max ; min .  

ab

f x K f x k K k

 hi tìm

  

0        m m K m k K m k

 hi tìm min

ca

 

;

min 

ab

y

giá tr này là

0.

Dạng 7: Cho hàm s

 

y f x m

.

Tìm

m



 

 

;

max .min 0

ab

y h y h

hoc

min max ....

Phương pháp: c tiên tìm:

 

 

 

   

;

max ; min .  

ab

f x K f x k K k

TH1:

1

cuøng daáu

.

K m k m

K m h k m m S

  



    

TH2:

2

cuøng daáu

.

k m K m

K m k m

k m h K m m S

  



    

Vy

12

.m S S

Dạng 8: Cho hàm s

 

y f x m

.

Phương pháp: c tiên tìm:

 

 

 

   

;

max ; min .  

ab

f x K f x k K k

TH1: Tìm

m



 

;

min max



      

ab

y y m K m k

.

TH2: Tìm

m



 

;

min .max .



    

ab

y y m K m k

.

"Trên đây là một số Tips chúng tôi cảm thấy rất hữu dụng trong

các bài toán hiện hành. Do mục đích phục vụ cho phần đông các

bạn học sinh nên phần trình bày khá chi tiết và khá dài. Nhưng nếu

bạn đọc hiểu bản chất vấn đề, thao tác sẽ ngắn gọn hơn, chuẩn xác

hơn và quan trọng nhất vẫn là lợi thế về thời gian nếu biết các Tips

này.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

342

[ I can't, I can! ]

TỰ LUYỆN 4 MỨC ĐỘ

Câu 1. Cho hàm s

 

y f x

liên tn

 

1;3

 th  bên. Gi

M

và

m

lt là giá tr ln nht và nh nht ca

hàm s    n

 

1;3

. Giá tr ca

Mm

bng?

A.

1

. B.

4

. C.

5

. D.

0

.

Câu 2. (Đề Minh Họa 2017) Cho hàm s

 

y f x

 nh, liên tc trên và có bng

bin thiên:

Kh

A. Hàm s có giá tr cc tiu bng

1

.

B. Hàm s có giá tr ln nht bng 0 và giá tr

nh nht bng

1

.

C. Hàm s t ci ti

0x

t cc tiu

ti

1x

.

D. Hàm s t cc tr.

Câu 3. Cho hàm s

 

y f x

liên tn

 

1;1

 th .

Gi

M

và

m

lt là giá tr ln nht và nh

nht ca hàm s n

 

1;1

. Giá tr

ca

Mm

bng?

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 4. Cho hàm s

 

y f x

liên tc trên

 

3;2

và có bng bi    i

,Mm

lt là giá tr ln nht và giá tr nh

nht ca hàm s

 

y f x

 n

 

1;2

.

Tính

Mm

.

A.

3

. B.

2

. C.

1

. D.

4

.

Câu 5. Cho hàm s

 

y f x

nh và liên

tc trên  th  bên. Tìm giá

tr nh nht

m

và giá tr ln nht

M

ca hàm

s

 

y f x

trên

 

2;2

.

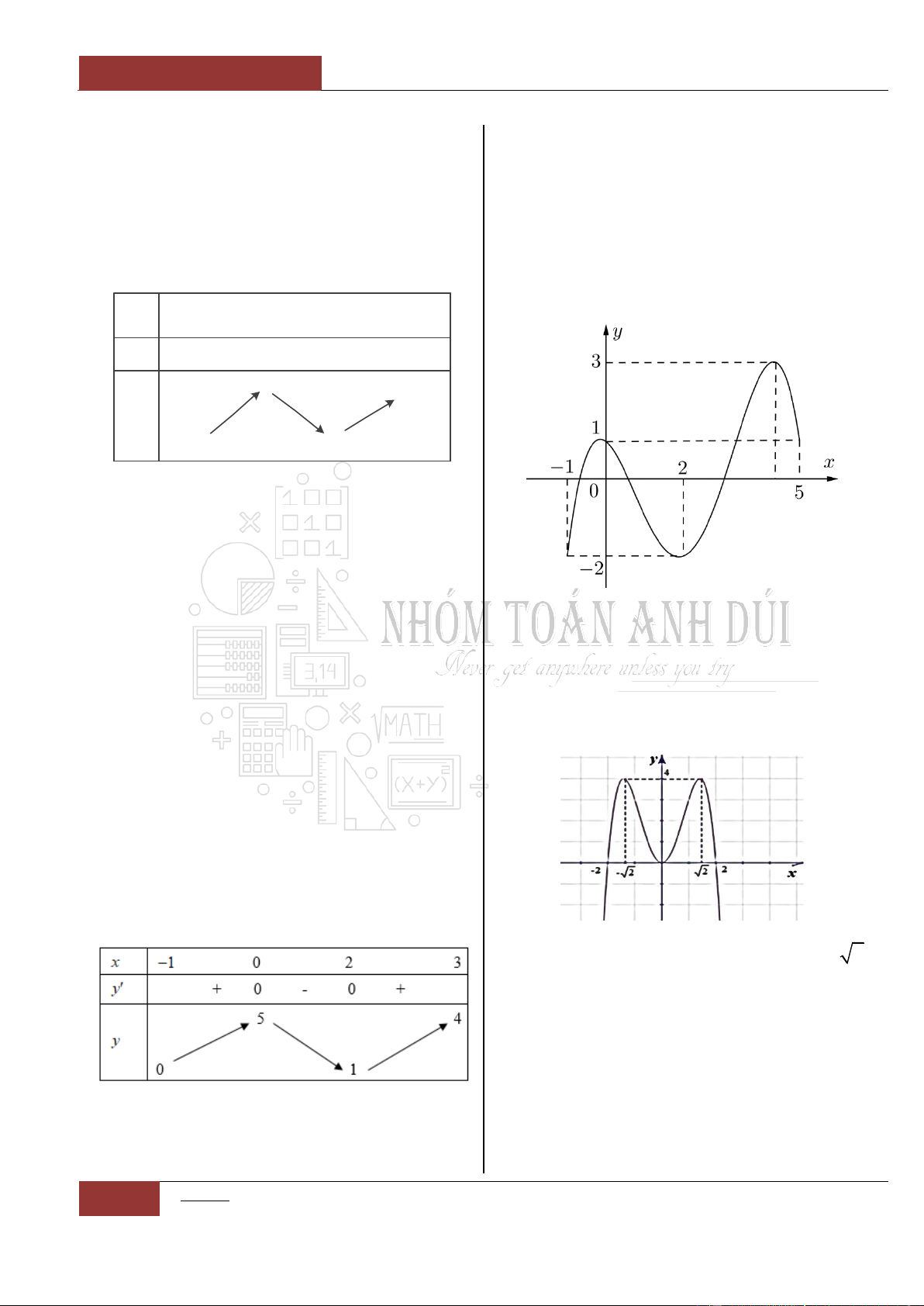
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

343

[ I can't, I can! ]

A.

5; 1   mM

. B.

2; 2  mM

.

C.

1; 0  mM

. D.

5; 0  mM

.

Câu 6. Xét hàm s

 

y f x

vi có

bng bi

x

 

'fx

 

fx

1

0

5





4



3

2

0



0

Kh?

A. Hàm s    n ta GTLN trên

n .

B. Hàm s   t GTNN ti và

n .

C. Hàm s t GTNN ti t

GTLN ti n .

D. Hàm s   t GTNN ti trên

n .

Câu 7. Cho hàm s

 

y f x

liên tc và có

bng bi   n

 

1;3

  

bên. Kh?

A.

 

   

1;3

max 0



f x f

. B.

 

   

1;3

max 3



f x f

.

C.

 

   

1;3

max 2



f x f

. D.

 

   

1;3

max 1



f x f

.

Câu 8. Cho hàm s

 

fx

liên tc trên

 

1;5

 th n

 

1;5

 bên

i. Tng giá tr ln nht và giá tr nh nht

ca hàm s

 

fx

n

 

1;5

bng?

A.

1

. B.

4

. C.

1

. D.

2

.

Câu 9. Cho hàm s

 

y f x

  th 

hình v. Giá tr ln nht ca hàm s

 

fx

trên

n

 

0;2

là:

A.

 

 

0;2

2Max f x

. B.

 

 

0;2

2Max f x

.

C.

 

 

0;2

4Max f x

. D.

 

 

0;2

0Max f x

.

Câu 10. (Sở Bắc Giang 2019) Cho hàm s

 

y f x

liên tn

 

1;3

 th

 bên. Gi

,Mm

lt là giá tr ln

 

1;5x

 

1;5

1x 

2x 

 

1;5

1x 

5x 

 

1;5

0x 

 

1;5

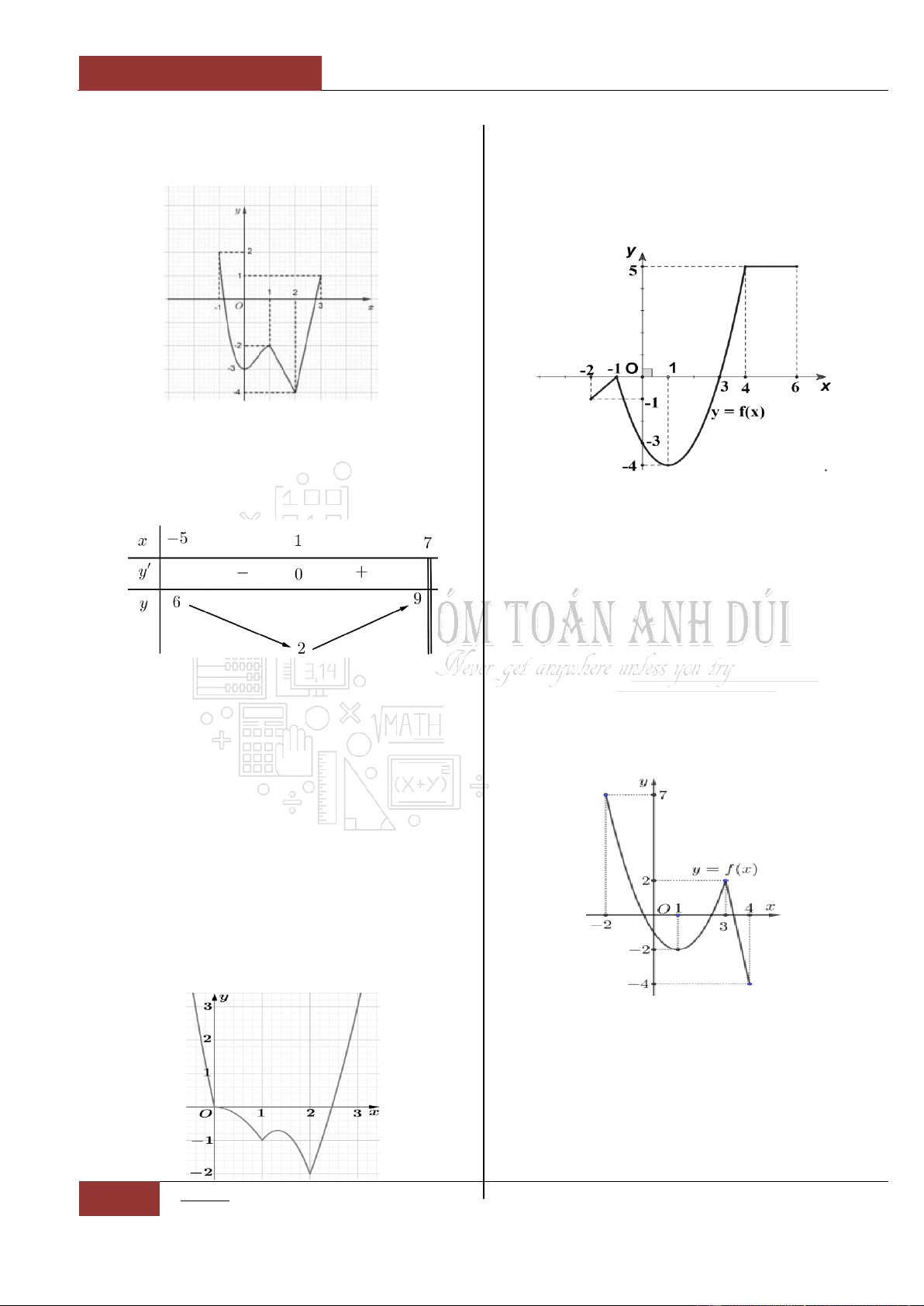
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

344

[ I can't, I can! ]

nht và giá tr nh nht ca hàm s 

n

 

1;3

. Giá tr ca

Mm

là?

A.

2

. B.

6

. C.

5

. D.

2

.

Câu 11. (S Hà Ni 2019) Cho hàm s

 

y f x

có bng bin thiên trên





5;7



sau

M 

A.





 

5;7

Min 6



fx

. B.





 

5;7

Min 2



fx

.

C.





 

-5;7

Max 9fx

. D.





 

5;7

Max 6



fx

.

Câu 12.  

 

fx

 

 

0;3



M



m

 

    

 

0;3

   

Mm

b

A.

4

. B.

3

. C.

2

. D.

1

.

Câu 13. Cho hàm s

 

y f x

liên tc trên

n

 

2;6

 th  bên i.

Gi

M

và

m

lt là giá tr ln nht và nh

nht ca hàm s n

 

2;6

. Giá

tr ca

Mm

bng?

A.

9

. B.

8

. C.

9

. D.

8

.

Câu 14. Cho hàm s

 

y f x

liên tc và có

 th n

 

2;4

 bên. Tng

giá tr ln nht và nh nht ca hàm s

 

y f x

n

 

2;4

bng?

A.

5

. B.

3

. C.

0

. D.

2

.

Câu 15. Giá tr ln nht ca hàm s

 

42

12 1   f x x x

trên n

 

1;2

bng?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

345

[ I can't, I can! ]

A.

1

. B.

37

. C.

33

. D.

12

.

Câu 16. Giá tr nh nht ca hàm s

 

42

10 2  f x x x

n

 

1;2

bng?

A.

2

. B.

23

. C.

22

. D.

7

.

Câu 17. Giá tr nh nht ca hàm s

 

3

24f x x x

n

 

2;19

bng?

A.

32 2

. B.

40

.

C.

32 2

. D.

45

.

Câu 18. Giá tr nh nht ca hàm s

 

42

12 4  f x x x

n

 

0;9

bng?

A.

39

. B.

40

. C.

36

. D.

4

.

Câu 19. Giá tr nh nht ca hàm s

 

42

12 1  f x x x

n

 

0;9

bng?

A.

28

. B.

1

. C.

36

. D.

37

.

Câu 20. Tìm giá tr nh nht ca hàm s

2

3

1







x

y

x

n

 

2;4

.

A.

 

2;4

min 3y

. B.

 

2;4

19

min

3

y

.

C.

 

2;4

min 6y

. D.

 

2;4

min 2y

.

Câu 21. Tìm giá tr nh nht

m

ca hàm s

2

yx

x

n

1

;2

2







.

A.

5m

. B.

3m

.

C.

17

4

m

. D.

10m

.

Câu 22. (Chuyên Bắc Ninh 2018) Tìm tp giá

tr ca hàm s

19   y x x

A.

 

1; 9T

. B.

2 2; 4







T

.

C.

 

1; 9T

. D.

0; 2 2







T

.

Câu 23. Tìm giá tr nh nht

m

ca hàm s

32

7 11 2   y x x x

n

 

0;2

.

A.

3m

. B.

0m

.

C.

2m

. D.

11m

.

Câu 24. (Sở Quảng Trị 2019) Tìm giá tr ln

nht

M

ca hàm s

31

3







x

y

x

n

 

0;2

.

A.

1

3

M

. B.

1

3

M

.

C.

5M

. D.

5M

.

Câu 25. Giá tr ln nht ca hàm s

2

4yx

là?

A.

2

. B.

0

. C.

4

. D.

1

.

Câu 26. Tìm giá tr nh nht ca hàm s

2

sin 4sin 5  y x x

.

A.

20

. B.

8

. C.

9

. D.

0

.

Câu 27. Gi

m

,

M

lt là giá tr nh nht

và giá tr ln nht ca hàm s

 

1

2

  f x x x

n

 

0;3

. Tính tng

23S m M

.

A.

7

2

S

. B.

3

2

S

.

C.

3

. D.

4S

.

Câu 28. Tìm giá tr ln nht ca hàm s

 

sin cos2f x x x

trên

 

0;



.

A.

9

8

. B.

5

4

. C.

2

. D.

1

.

Câu 29. Giá tr ln nht ca hàm s

3

4

2cos os

3

y x c x

trên

 

0;



.

A.

 

0;

2

ax

3



my

. B.

 

0;

10

ax

3



my

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

346

[ I can't, I can! ]

C.

 

0;

22

ax

3



my

. D.

 

0;

ax 0



my

.

Câu 30. Gi

,Mm

lt là giá tr ln nht

và giá tr nh nht ca hàm s

3sin 2

sin 1







x

y

x

n

0;

2









 ca

22

Mm

là?

A.

31

2

. B.

11

2

. C.

41

4

. D.

61

4

.

Câu 31. 

2

sin 1

sin sin 1







x

y

xx



M



m





A.

3

2

Mm

. B.

3

2

Mm

.

C.

1Mm

. D.

2

3

Mm

.

Câu 32. Tính giá tr nh nht ca hàm s

2

4

3yx

x

trên khong

 

0;

.

A.

 

0;

33

min

5



y

. B.

 

3

0;

min 2 9



y

.

C.

 

3

0;

min 3 9



y

. D.

 

0;

min 7



y

.

Câu 33. Gi

m

là giá tr nh nht ca hàm s

4

1

  



yx

x

trên khong

 

1; 

. Tìm

m

?

A.

5m

. B.

4m

.

C.

2m

. D.

3m

.

Câu 34. Giá tr nh nht ca hàm s

1

5  yx

x

trên khong

 

0;

bng bao

nhiêu?

A.

0

. B.

1

. C.

3

. D.

2

.

Câu 35. Giá tr nh nht ca hàm s

43  yx

trên tnh ca nó là

A.

2 3.

B.

2 3.

C.

0.

D.

3.

Câu 36. Vi giá tr nào ca

x

thì hàm s

2

1

yx

x

t giá tr nh nht trên khong

 

0;

?

A.

3

4

. B.

1

2

. C.

1

. D.

3

1

2

.

Câu 37. Giá tr nh nht ca hàm s

 

2

12   yx

x

trên khong

 

0;

A. Không tn ti. B.

3

.

C.

12

. D.

0

.

Câu 38. Cho hàm s

 

2

1

2







x

fx

x

vi

x

thuc





3

; 1 1;

2



   





D

. M i



A.

   

max 0;min 5  

D

f x f x

.

B.

 

max 0

D

fx

; không tn ti

 

min

D

fx

.

C.

   

max 0;min 1  

D

f x f x

.

D.

 

min 0

D

fx

; không tn ti

 

max

D

fx

.

Câu 39. M  hàm

s

2

1

5







x

y

x

trên tnh ca nó.

A. Hàm s không có giá tr ln nht và không

có giá tr nh nht.

B. Hàm s không có giá tr ln nht và có giá tr

nh nht.

C. Hàm s có giá tr ln nht và giá tr nh nht.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

347

[ I can't, I can! ]

D. Hàm s có giá tr ln nht và không có giá

tr nh nht.

Câu 40. Cho hàm s

1







xm

y

x

(

m

là tham s

thc) tha mãn

[2;4]

min 3.y

M   i

?

A.

4m

. B.

34m

.

C.

1m

. D.

13m

.

Câu 41. Cho hàm s

2

1





x

y

xm

(m là tham s

thc) tha mãn

 

3; 2

1

min

2



y

. M i



A.

34m

. B.

23  m

.

C.

4m

. D.

2m

.

Câu 42. Tìm giá tr  a tham s

m



giá tr nh nht ca hàm s

2

1

2







mx

y

x

trên

n

 

1;3

bng

1

.

A.

2m

. B.

3m

.

C.

4m

. D.

2m

.

Câu 43. Cho hàm s

2

8







xm

y

x

vi

m

là tham

s thc. Gi s

0

m

là giá tr a tham s

m

 hàm s có giá tr nh nhn

 

0;3

bng 3. Giá tr

0

m

thuc khong nào trong các

kho

A.

 

2;5

. B.

 

1;4

.

C.

 

6;9

. D.

 

20;25

.

Câu 44. Tìm giá tr ca tham s thc

m

 giá

tr nh nht ca hàm s

2

1







xm

y

x

n

 

0;4

bng

3

.

A.

3m

. B.

1m

.

C.

7m

. D.

5m

.

Câu 45. Tìm các giá tr ca tham s

m

 giá

tr nh nht ca hàm s

2

1







x m m

y

x

trên

n

 

0;1

bng

2

.

A.

1

2











m

. B.

1

2











m

.

C.

1

2











m

. D.

1

2











m

.

Câu 46. Tìm tt c các giá tr ca tham s

m



giá tr nh nht ca hàm s

32

3   y x x m

n

 

1;1

bng

0

.

A.

2.m

B.

6.m

C.

0.m

D.

4.m

Câu 47. Có mt giá tr

0

m

ca tham s

m



hàm s

 

32

11    y x m x m

t giá tr nh

nht bng

5

n

 

0;1

. M nào sau



A.

2

00

2018 0mm

. B.

0

2 1 0m

.

C.

2

00

60mm

. D.

0

2 1 0m

.

Câu 48. Nu hàm s có giá

tr ln nht bng thì giá tr ca là.

A. . B. . C. . D. .

Câu 49. Bit là tp giá tr ca  tng giá

tr ln nht và giá tr nh nht ca hàm s

 n bng

. Tính tích các phn t ca .

A. . B. . C. . D. .

2

1   y x m x

22

m

2

2

2



S

m

4 2 3 2

2   y x m x x m

 

0;1

16

S

2

2

15

17

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

348

[ I can't, I can! ]

Câu 50. Tìm tt c giá tr thc ca tham s

 hàm s liên tt giá tr

nh nh  n ti m m

.

A. . B. .

C. . D. .

Câu 51. Cho hàm s . Có bao

nhiêu giá tr nguyên ca tham s thun

 giá tr nh nht ca hàm s nh 

?

A. . B. . C. . D. .

Câu 52. Cho hàm s có

 

   

;0

min 2

 



x

f x f

. Giá tr ln nht ca hàm

s n bng?

A. . B. .

C. . D. .

Câu 53. Tìm tt c các giá tr ca tham s m 

hàm s có giá tr ln nht trên

nh c bng 1.

A. . B. .

C. . D. .

Câu 54. Giá tr ln nht ca hàm s

trên bng . Tham s

nhn giá tr là?

A. . B. . C. . D. .

Câu 55. Cho hàm s . Tng

tt c các giá tr ca tham s sao cho giá tr

nh nht ca hàm s  n bng

là?

A. . B. . C. . D. .

Câu 56. Tìm tt c các giá tr ca  giá

tr nh nht ca hàm s trên

n  .

A. . B. .

C. . D. .

Câu 57. Bit rng giá tr nh nht ca hàm s

trên bng . M 

nào sau 

A. . B. .

C. . D. .

Câu 58. Cho hàm s b

. Có tt c

bao nhiêu giá tr nguyên ca sao cho hàm s

có giá tr nh nht trên khong ?

A. . B. . C. Vô s. D. .

Câu 59. Cho hàm s ( là

tham s thc khác ). Gi là hai giá tr

ca tho mãn:

.

Giá tr ca bng?

A.

3

. B.

5

. C.

10

. D.

2

.

Câu 60. Cho hàm s có bao

nhiêu giá tr nguyên ca tham s thun

 giá tr nh nht ca nh  .

A. . B. . C. . D. .

m

2

1





x mx

y

xm

 

0;2

 

0

0;2x

01m

1m

2m

11  m

1 sin

cos 2







mx

y

x

m

 

0;10

2

1

9

3

6

3

,0   y ax cx d a

 

y f x

 

1;3

11da

16da

2da

8da

2

1







xm

y

xx

1m

1m

1m

1m

32

1







x x m

y

x

 

0;2

5

m

5

1

3

8

 

2

3

3  y x x m

m

 

1;1

1

4

0

4

0m

3

31y x x

 

1; 2mm

3

 

0;2m

 

0;1m

 

1;  m

 

0;  m

36

1





y mx

x

 

0;3

20

02m

48m

24m

8m

 

3 2 2

3 3 1 2020    y x mx m x

m

 

0;

2

1

3

 

1f x m x

m

0

12

,mm

m

 

 

 

 

2

2;5

min ax 10  f x m f x m

12

mm

sin 1

cos 2

mx

y

x







m

 

5;5

y

1

4

2

6

8

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

349

[ I can't, I can! ]

Câu 61. Gi là tp hp tt c các giá tr thc

ca tham s sao cho giá tr nh nht ca hàm

s  n

bng 2. Tng tt c các phn t ca bng?

A. . B. . C. . D.

1

.

Câu 62. Cho hàm s .

Tng tt c các giá tr ca tham s sao cho

giá tr nh nht ca hàm s  n

bng là?

A. . B. . C. . D. .

Câu 63. Cho hàm s

Tính tng tt c các giá tr ca  hàm s

có giá tr nh nht bng .

A. . B. . C. . D. .

Câu 64. Cho hàm s vi

. M i ?

A. .

B. khi .

C. .

D. khi .

Câu 65. (Chuyên Sư Phạm Hà Nội - 2020) Có

bao nhiêu s nguyên thun

 giá tr ln nht ca hàm s

n là s ?

A.

9

. B.

8

. C.

11

. D.

10

.

Câu 66. Gi S là tp hp tt c các giá tr ca

tham s thc m sao cho giá tr ln nht ca hàm

s

3

3  y x x m

n

 

0;2

bng

3

. S

phn t ca

S

là?

A.

0

. B.

6

. C.

1

. D.

2

.

Câu 67. Cho hàm s

 

1







xm

fx

x

(

m

là tham

s thc). Gi

S

là tp hp tt c các giá tr ca

m

sao cho

 

 

 

 

0;1

max min 2f x f x

. S phn

t ca

S

là?

A.

6

. B.

2

. C.

1

. D.

4

.

Câu 68. Tìm

m

 giá tr ln nht ca hàm s

3

3 2 1   y x x m

 n

 

0;2

là nh

nht. Giá tr ca

m

thuc khong nào?

A.

3

;1

2









. B.

2

;2

3







.

C.

 

1;0

. D.

 

0;1

.

Câu 69. Tính tng tt c các giá tr ca tham s

m

sao cho giá tr ln nht ca hàm s

2

2  y x x m

n

 

1;2

bng

5

.

A.

1

. B.

2

. C.

2

. D.

1

.

Câu 70. Cho hàm s

2

24   y x x a

(

a

là

tham s). Tìm

a

 giá tr ln nht ca hàm s

n

 

2;1

t giá tr nh nht

A.

1a

. B.

3a

.

C.

2a

. D.

5a

.

S

m

 

2

3

34

3 2 1

fx

x x m



  

 

0;3

S

8

8

6

 

2

3

31   y x x m

m

 

1;1

1

2

4

4

0

 

22

2 2 4 4 1        y f x m x x x m

m

 

y f x

4

7

2



5

2

1

2



1

2

 

2

1







xm

fx

x

2m

 

 

1;3

26

max max ;

24











mm

fx

 

 

1;3

6

max

4





m

fx

2m

 

 

1;3

26

min min ;

24











mm

fx

 

 

1;3

2

min

2





m

fx

2m

m

 

20 ; 20

6





xm

y

xm

 

1; 3

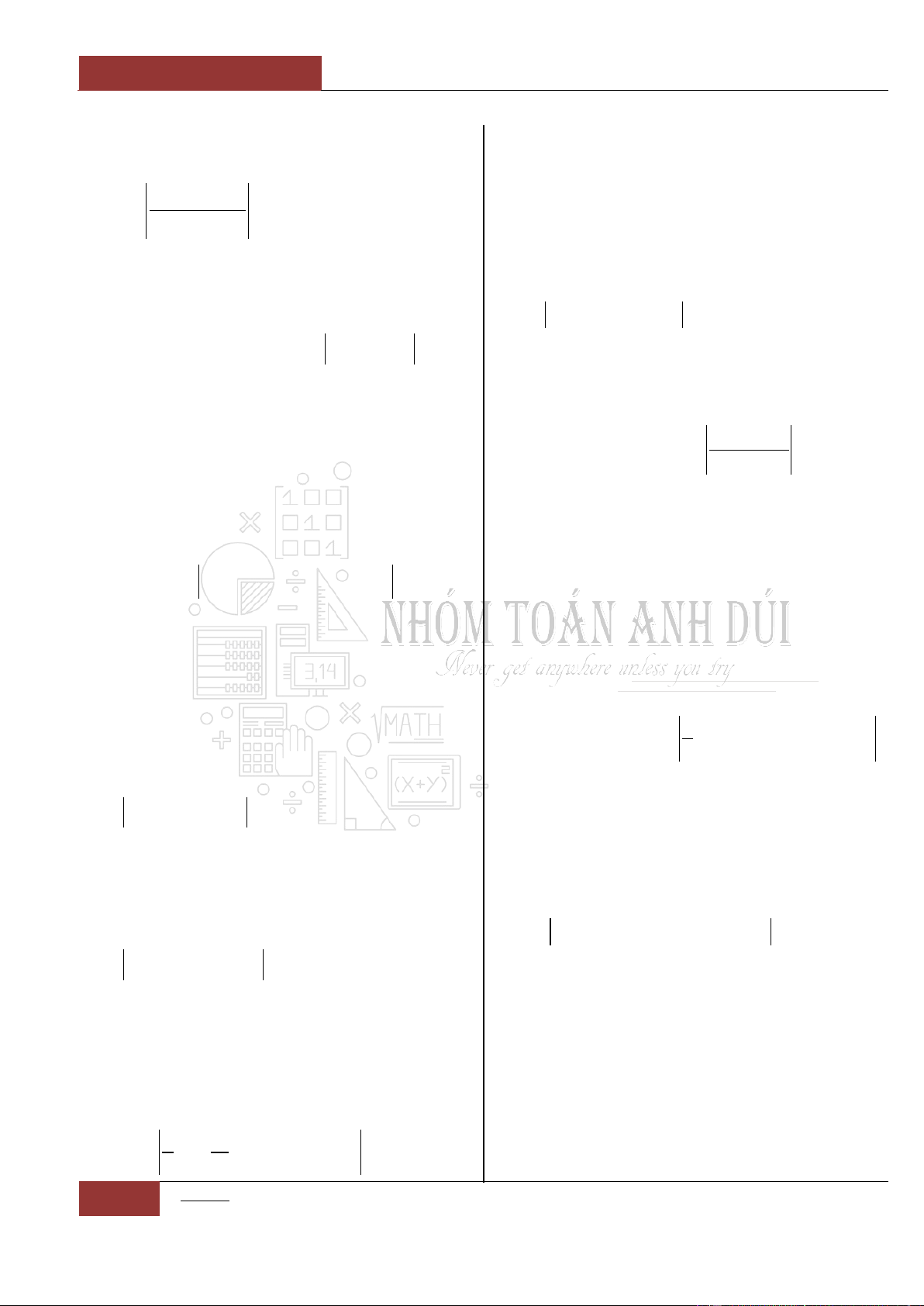
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

350

[ I can't, I can! ]

Câu 71. Gi

S

là tp hp tt c các giá tr thc

ca tham s

m

sao cho giá tr ln nht ca hàm

s

2

1







x mx m

y

x

trên

 

1;2

bng

2

. S phn

t ca tp

S

?

A.

3

. B.

1

. C.

4

. D.

2

.

Câu 72. Xét hàm s

 

2

  f x x ax b

, vi

a

b

là tham s. Gi

M

là giá tr ln nht ca

hàm s trên

 

1;3

. Khi

M

nhn giá tr nh

nht có th c, tính

2ab

.

A.

2

. B.

4

. C.

4

. D.

3

.

Câu 73. Cho hàm s

 

3 2 2

1 27    y x x m x

.

Giá tr ln nht ca hàm s tn

 

3; 1

có giá tr nh nht bng?

A.

26

. B.

18

. C.

28

. D.

16

.

Câu 74. Có bao nhiêu giá tr thc ca tham s

m

 giá tr ln nht ca hàm s

2

24   y x x m

n

 

2;1

bng

4

?

A.

1

. B.

2

. C.

3

. D.

4

.

Câu 75. Gi

S

là tp hp tt c các giá tr ca

tham s

m

sao cho giá tr ln nht ca hàm s

32

39   y x x x m

 n

 

2;4

bng

16

. S phn t ca

S

là?

A.

0

. B.

2

. C.

4

. D.

1

.

Câu 76. Gi

S

là tp tt c các giá tr nguyên

ca tham s

m

sao cho giá tr ln nht ca hàm

s

42

1 19

30 20

42

    y x x x m

 n

 

0;2

t quá

20

. Tng các phn t ca

S

bng?

A.

210

. B.

195

. C.

105

. D.

300

.

Câu 77. Gi

S

là tp hp tt c các giá tr thc

ca tham s

m

sao cho giá tr ln nht ca hàm

s

2

sin 2sin  y x x m

bng

1

. S phn t ca

S

là?

A.

0

. B.

1

. C.

4

. D.

3

.

Câu 78. Cho hàm s

4

1







x ax a

y

x

, vi

a

là

tham s thc. Gi

,Mm

lt là giá tr ln

nht và giá tr nh nht ca hàm s 

n

 

1;2

. Có bao nhiêu giá tr nguyên ca

tham s

a



2Mm

?

A.

10

. B.

14

. C.

5

. D.

20

.

Câu 79. Gi

S

là tp hp tt c các giá tr

nguyên ca tham s thc

m

sao cho giá tr ln

nht ca hàm s

42

1

14 48 30

4

    y x x x m

 n

 

0;2

 t quá

30

. Tng giá

tr các phn t ca tp hp

S

bng bao nhiêu?

A.

120

. B.

210

. C.

108

. D.

136

.

Câu 80. Cho hàm s

 

4 3 2

3 4 24 48    

x x x x

f x e e e e m

. Gi

A

,

B

l t là giá tr ln nht và giá tr nh nht

ca hàm s   

 

0;ln2

.Gi

S

là tp

hp tt c các giá tr nguyên ca tham s

m

thuc





23;10

tha mãn

3AB

. Tng các

phn t ca tp

S

bng?

A.

33

. B.

0

. C.

111

. D.

74

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

351

[ I can't, I can! ]

Câu 81. 

4 3 2

2   y x x x a





a



   

1;2 1;2

min max 10yy

?

A.

3

. B.

5

. C.

2

. D.

1

.

Câu 82. Cho hàm s

 

32

3  f x x x m

. Có

bao nhiêu s nguyên

m

 giá tr nh nht ca

hàm s

 

fx

 n

 

1;3

không l 

2020

?

A.

4045

. B.

4046

. C.

4044

. D.

4042

.

Câu 83. Xét hàm s

 

24







mx x

fx

x

, vi

m

là tham s thc. Có bao nhiêu s nguyên

m

thu kin

 

 

1;1

0 min 1



fx

?

A.

4

. B.

8

. C.

2

. D.

1

.

Câu 84. Gi

S

là tp hp nhng giá tr ca

tham s

m

 giá tr ln nht ca hàm s

  f x x x m

3

( ) 12

 n

[1;3]

bng

12

.Tng tt c các phn t ca tp

S

bng

A.

25.

B.

4.

C.

15.

D.

21.

Câu 85. Gi

0

S

là tp tt c các giá tr nguyên

ca tham s thc

m

sao cho giá tr ln nht ca

hàm s

42

1

14 48

4

   y x x x m

 n

 

2;4

t quá

30

. S phn t ca

S

là

A.

50

. B.

49

. C.

66

. D.

73

.

Câu 86. Có bao nhiêu giá tr ca tham s

m



giá tr nh nht ca ham s

 

2

e 4e  

xx

f x m

n

 

0;ln4

bng

6

?

A.

3

. B.

4

. C.

2

. D.

1

.

Câu 87. Gi

S

là tp tt c các giá tr nguyên

ca tham s

m

sao cho giá tr ln nht ca hàm

s

3

1

9 10

3

   y x x m

 n

 

0;3

không

t quá

12

. Tng giá tr các phn t ca

S

bng bao nhiêu?

A.

7

. B.

0

. C.

3

. D.

12

.

Câu 88. Gi

S

là tp tt c các giá tr nguyên

ca tham s thc

m

sao cho giá tr ln nht ca

hàm s

42

1

14 48 30

4

    y x x x m

 n

 

0;2

t quá

30

. Tng tt c các giá tr

ca

S

là?

A.

180

. B.

136

. C.

120

. D.

210

.

Câu 89. Bit giá tr ln nht ca hàm s

 

3

2 15 5 9     y f x x x m x

trên

 

0;3

bng

60

.

Tính tng tt c các giá tr ca tham s thc

m

.

A.

48

. B.

5

. C.

6

. D.

62

.

Câu 90. Gi

S

là tp hp tt c các giá tr ca

tham s thc

m

sao cho giá tr ln nht ca

hàm s

3

3  y x x m

n

 

0;2

bng

3

.

S phn t ca

S

là?

A.

2.

B.

6.

C.

1.

D.

0.

Câu 91. Cho hàm s

 

4 3 2

2   f x x x x m

(

m

là tham s thc). Gi

S

là tp hp tt c các

giá tr ca

m

sao cho

 

 

 

 

1;2

min max 10



f x f x

.

S phn t ca

S

là?

A.

2

. B.

3

. C.

5

. D.

1

.

Câu 92. Có tt c bao nhiêu giá tr nguyên

 a tham s

m

 hàm s

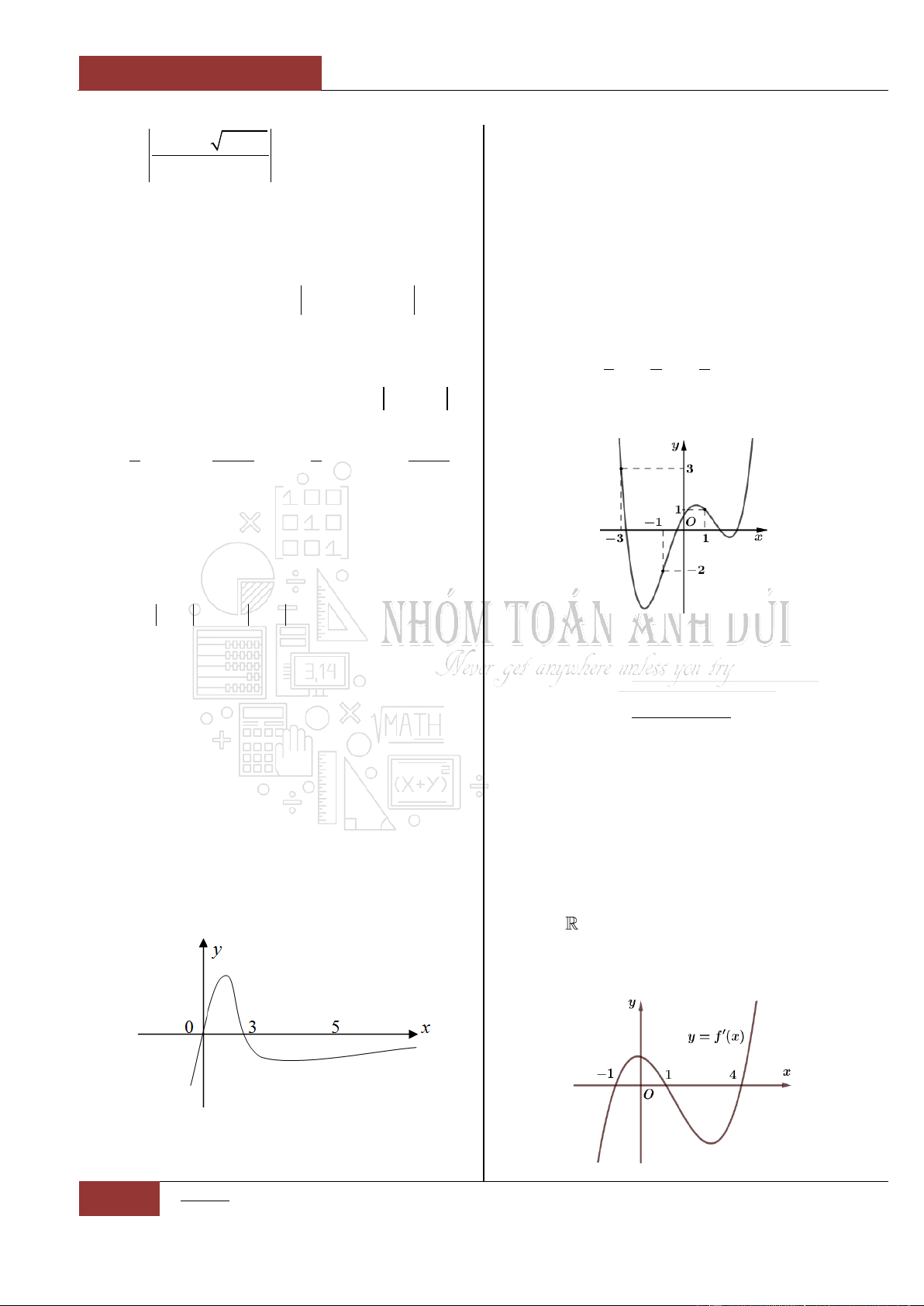
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

352

[ I can't, I can! ]

 

2 2 4 8

2







mx x

fx

x

có giá tr nh nht trên

n

 

1;1

là

a

tha mãn

0 1.a

A.

3.

B.

4.

C.

5.

D.

2.

Câu 93. Cho hàm s

42

23  y x x m

vi

m

là tham s. Bit r

12

,mm

ca

m

 giá tr nh nht ca hàm s  

trên

 

1;2

bng

2021

. Tính giá tr

12

mm

.

A.

1

3

. B.

4052

3

. C.

8

3

. D.

4051

3

.

Câu 94. Cho hàm s

 

32

31   f x x x m

(

m

là tham s thc). Gi

S

là tp hp tt c các giá

tr nguyên ca

m

thun

 

2020;2020

sao

cho

 

 

 

 

1;4

max 3minf x f x

. S phn t ca

S

là

A.

4003

. B.

4002

. C.

4004

. D.

4001

.

Câu 95. Cho hàm s

 

fx

o hàm là

 



fx

 th ca hàm s

 



y f x



v bên. Bit rng:

         

0 1 2 3 5 4   f f f f f

.

Tìm giá tr nh nht

m

và giá tr ln nht

M

ca

 

fx

n

 

0;5

.

A.

   

5 , 3m f M f

.

B.

   

5 , 1m f M f

.

C.

   

0 , 3m f M f

.

D.

   

1 , 3m f M f

.

Câu 96. Cho hàm s

 

y f x

  th

 



y f x

 hình v bên. Xét hàm s

   

32

1 3 3

2018,

3 4 2

    g x f x x x x

m 



A.

 

   

3;1

min 1



g x g

.

B.

 

 

   

3;1

31

min

2







gg

gx

.

C.

 

   

3;1

min 3



g x g

.

D.

 

   

3;1

min 1



g x g

.

Câu 97. Cho hàm s

 

y f x

o hàm liên

tc trên . Hàm s

 

'y f x

  th 

hình sau:

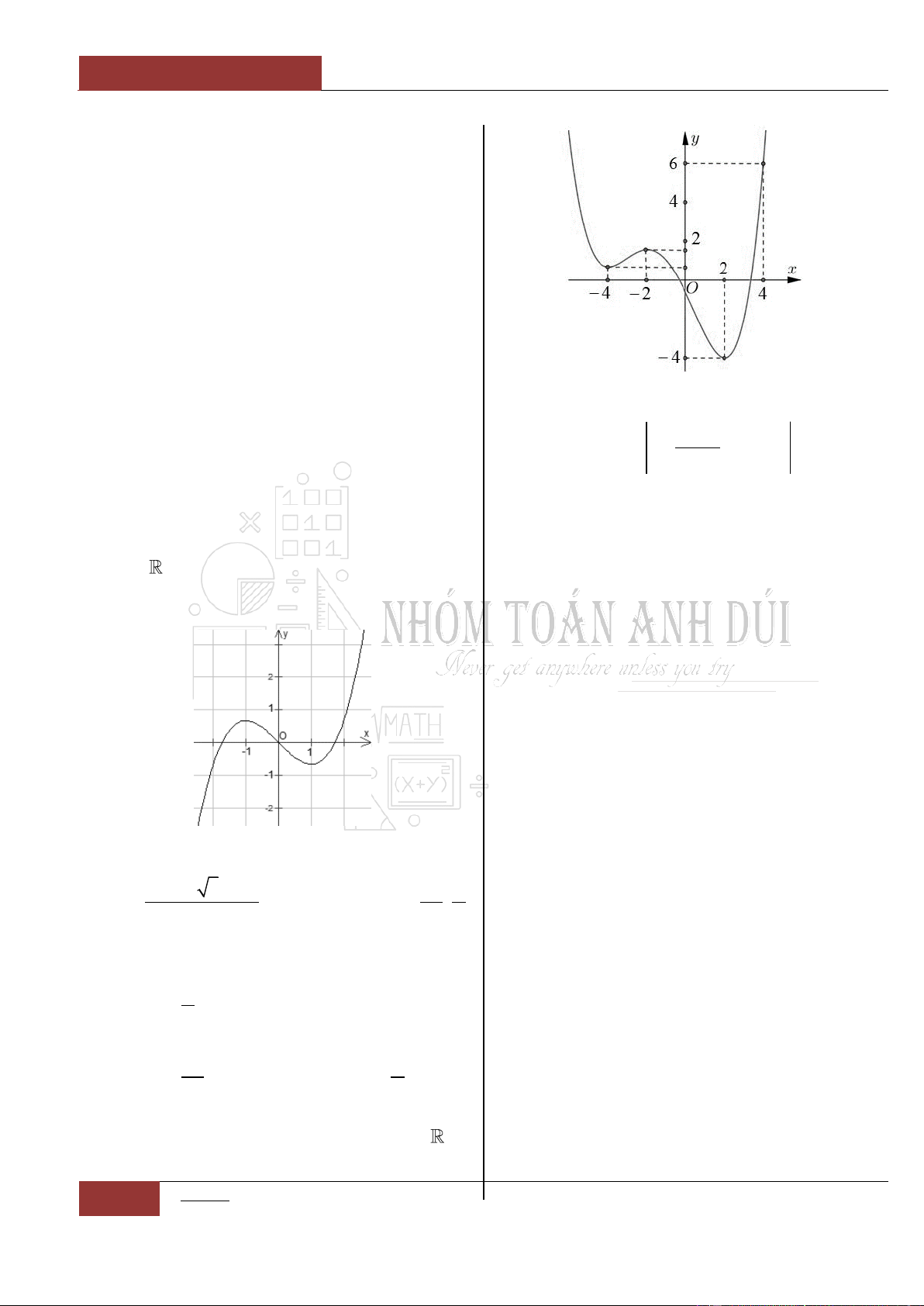
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

353

[ I can't, I can! ]

Cho bn m sau:

1) Hàm s

 

y f x

có hai cc tr.

2) Hàm s

 

y f x

ng bin trên khong

 

1; 

.

3)

     

1 2 4 .f f f

n

 

1;4

, giá tr ln nht ca hàm s

 

y f x

là

 

1.f

S m n m trên là:

A.

3.

B.

1.

C.

4.

D.

2.

Câu 98. Cho hàm s

 

y f x

o hàm cp

2

trên , hàm s

 



y f x

 th 

v bên.

Giá tr ln nht ca hàm s

sin 3cos

2











xx

yf

 n

5

;

66











bng?

A.

3











f

. B.

 

0f

.

C.

5

6











f

. D.

6









f

.

Câu 99. Cho hàm s

 

fx

liên tc trên , có

 th 

Có tt c bao nhiêu giá tr nguyên ca tham s

m

 hàm s

2

8

1



  







x

y f m

x

có giá tr

ln nht quá

2020

?

A.

4029

. B.

4035

. C.

4031

. D.

4041

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

354

[ I can't, I can! ]

ĐÁP ÁN

0

1

2

3

4

5

6

7

8

9

0

C

B

A

C

1

D

B

D

A

B

C

B

D

2

C

B

C

A

B

A

C

3

C

B

C

D

B

A

D

4

A

B

A

C

D

A

C

5

A

D

B

A

C

B

C

D

A

6

C

B

A

C

B

A

D

B

D

C

7

B

D

C

B

D

C

A

B

D

8

A

C

A

B

A

B

C

A

B

C

9

A

D

B

A

D

A

C

Ghi chú:  kt hp gia dòng và ct . Ví d: Câu 25A (giao ca dòng 2 và ct 5).

i

j

i

j

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

355

[ I can't, I can! ]

LỜI GIẢI CHI TIẾT

Câu 1. Da và  th suy ra:

   

3 3; 2 2    M f m f

.

Vy

5Mm

.

Đáp án C

Câu 2. Ta xét t

Đáp án A sai vì hàm s có

2

m cc tr.

Đáp án B sai vì hàm s có giá tr cc tiu

1y

khi

0x

.

Đáp án C sai vì hàm s không có GTLN và

GTNN trên .

Đáp án D  vì hàm s t ci ti

0x

t cc tiu ti

1x

.

Đáp án C

Câu 3. T  th ta thy

1, 0Mm

nên

1Mm

.

Đáp án B

Câu 4. Trên n

 

1;2

ta có giá tr ln nht

3M

khi

1x

và giá tr nh nht

0m

khi

0x

.

:

3 0 3   Mm

.

Đáp án A

Câu 5.  th ta thy:

 

 

2;2

max 1



  M f x

khi

1x

hoc

2x

.

 

 

2;2

min 5



  m f x

khi

2x

hoc

1x

.

Đáp án A

Câu 6. Ta xét t

A. 

5

lim





 

x

y

nên hàm s không có

n .

B. Sai. Hàm s  t GTNN ti

n .

C. Sai. Hàm s  t GTNN ti

n và .

D. Sai. Hàm s  t GTNN ti

n .

Đáp án A

Câu 7. Nhìn vào bng bin thiên ta thy:

 

   

1;3

max 0 .



f x f

Đáp án A

Câu 8. T  th ta thy:

 

 

 

 

1;5

max 3

1.

min 2









  



  





M f x

Mn

n f x

Đáp án C

Câu 9. D th ta thn

 

0;2

hàm

s

 

fx

có giá tr ln nht bng

4

khi

2x

Suy ra:

 

 

0;2

4Max f x

.

Đáp án C

Câu 10. D th ta thy GTLN ca hàm

s  n

 

1;3

là

2M

 c ti

1x

và GTNN ca hàm s s  n

 

1;3

là

4m

c ti

2x

.

 

2 4 2      Mm

.

 

1;5

2x 

 

1;5

2x 

 

1;5

5

lim

x

y



 

2x 

 

1;5

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

356

[ I can't, I can! ]

Đáp án D

Câu 11. Da vào bng bin thiên trên





5;7

,

ta có:





   

5;7

Min 1 2



f x f

.

Đáp án B

Câu 12. 

3M

,

2m

nên

1Mm

.

Đáp án D

Câu 13. T  th suy ra:

 

45  fx

 

2;6 ;  x

   

1 4; 4 5  ff

5

4













M

m

9  Mm

.

Đáp án A

Câu 14. D th hàm s ta có:

 

 

2;4

4



  

x

m Min f x

,

 

 

2;4

7





x

M Max f x

:

3Mm

.

Đáp án B

Câu 15.

 

42

12 1   f x x x

liên tc trên

 

1;2

và

 

32

0

' 4 24 0 6 ( )

6 ( )







     







x

f x x x x L

xL

Ta có:

     

1 12; 2 33; 0 1   f f f

Vy GTLN ca hàm s

 

42

12 1   f x x x

n

 

1;2

bng 33 ti

2x

.

Đáp án C

Câu 16. Hàm s n

 

1;2

.

Ta có:

   

3

0

4 20 , 0

5







   







x

f x x x f x

x

.

Xét hàm s n

 

1;2

có:

     

1 7; 0 2; 2 22     f f f

.

Vy

 

 

1;2

min 22





x

fx

.

Đáp án C

Câu 17. Ta có:

 

 

2

2 2 2;19

3 24 0 .

2 2 2;19









   



  



x

f x x

x

 

3

2 2 24.2 40   f

;

   

3

2 2 2 2 24.2 2 32 2   f

;

 

3

19 19 24.19 6403  f

.

Vy giá tr nh nht ca hàm s

 

3

24f x x x

n

 

2;19

bng

32 2

.

Đáp án C

Câu 18. Ta có:

 

3

4 24



f x x x

;

 

0

6















x

fx

x

c:

 

04f

;

 

9 5585f

và

 

6 40f

.

Suy ra:

 

 

0;9

min 40fx

.

Đáp án B

Câu 19. Ta có

 

3

4 24



f x x x

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

357

[ I can't, I can! ]

 

 

3

0 0;9

0 4 24 0 6 0;9

6 0;9









      



  





x

f x x x x

x

 

01f

,

 

6 37f

,

 

9 5588f

.

Đáp án D

Câu 20. Tnh:

 

\1D

.

Hàm s

2

3

1







x

y

x

nh và liên tc trên

n

 

2;4

.

Ta có:

 

2

23

;

1









xx

y

x

 

2

3

0 2 3 0

1







     







x

y x x

xl

Suy ra:

     

19

2 7; 3 6; 4

3

  y y y

.

Vy

 

2;4

min 6y

ti

3x

.

Đáp án C

Câu 21. t:

 

2

  y f x x

x

.

Ta có:

3

22

2 2 2

2





  

x

yx

xx

,

1

0 1 ;2

2





   





yx

.

:

   

1 17

1 3, , 2 5

24



  





f f f

.

Vy

   

1

;2

2

min 1 3







  m f x f

.

Đáp án B

Câu 22. Tnh:

 

1;9D

11

0 9 1

2 1 2 9



      



y x x

xx

1

5

91





  







x

xx

.

   

1 9 2 2ff

;

 

54f

Vy tp giá tr là

2 2; 4







T

.

Đáp án B

Câu 23. Xét hàm s n

[0 ;2]

. Ta có

2

3 14 11



  y x x

suy ra:

01



  yx

Tính

     

0 2; 1 3, 2 0   f f f

. Suy ra

 

   

0;2

min 0 2   f x f m

.

Đáp án C

Câu 24. Trên n

 

0;2

, ta luôn có

 

2

8

0 0;2

3



    



yx

x

(o hàm vô

nghim trên

 

0;2

).

Vì

   

1

0 , 2 5

3

 yy

nên

 

0;2

1

max

3

My

.

Đáp án A

Câu 25. Tnh:

 

2;2D



2

'

4







x

y

x

 

0 0 2;2



     yx



   

 

 

2;2

2 2 0

max 2

02



  















yy

y

.

Đáp án A

Câu 26. t

 

sin , 1;1  t x t

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

358

[ I can't, I can! ]

Xét

2

( ) 4 5  f t t t

,

 

1;1t

.

 

( ) 2 4 0 2 1;1



      f t t t

.

   

1 8, 1 0   ff

.

Ta thy

 

   

1;1

min 1 8



  f t f

. Vy giá tr nh

nht ca hàm s là

8

.

Đáp án B

Câu 27. Kho sát hàm s n

0;3





.

 

1 1 1 1

2

2 1 2 1





  



x

fx

xx

Cho:

 

 

0 1 1 0 0;3



      f x x x

.

Khi 

 

01f

,

 

1

3

2

f

nên

1m

và

1

2

M

.

Vy

7

23

2

   S m M

.

Đáp án A

Câu 28.

 

sin cos2 ...  f x x x

2

... sin 1 2sin  xx

t:

sin xt

 

01t

 

2

21   f t t t

,

 

41



  f t t

 

0



ft

1

4

t

 

01f

,

 

10f

,

19

48









f

.

Vy

 

 

0;1

9

max

8

fx

.

Đáp án A

Câu 29. t:

costx

 

1;1  t

3

4

2

3

  y t t

.

2

' 2 4yt

;

'0y

 

1

1;1

2

1

1;1

2





  







  





x

.

Tính các giá tr cn thit:

 

2

1

3

1 2 2

3

2

1 2 2

3

2

1

3



  















  























y

.

Vy:

 

0;

22

ax

3



my

.

Đáp án C

Câu 30. t:

sintx

,

 

0;1t

.

Xét hàm

 

32

1







t

ft

t

liên tn

 

0;1

có

 

 

2

1

0, 0;1

1



  



f t t

t

.

Suy ra hàm s ng bin trên

 

0;1

.

 

0;1

5

Max ( ) (1)

2

   M f t f

và

 

0;1

Min ( ) (0) 2  m f t f

.

:

2

2 2 2

5 41

2

24



   





Mm

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

359

[ I can't, I can! ]

Đáp án C

Câu 31. :

sin xt

,

 

11  t



2

1







t

y

tt

.

:

2

1







t

y

tt

trên 

 

1;1

ta có

 

2

1









tt

y

tt

.

:

0



y

2

20   tt

 

0 thoûa maõn

2 (loaïi)

t















.

Vì

 

10y

;

 

01y

;

 

2

1

3

y

nên

 

 

1;1

max 0 1



yy

1M

;

 

 

1;1

min 1 0



  yy

0m

.



1Mm

.

Đáp án C

Câu 32. Cách 1:

3

2 2 2

4 3 3 4 3 3 4

3 3 . . 3 9

2 2 2 2

      

x x x x

yx

x x x

Du

""

xy ra khi

3

2

3 4 8

23

  

x

.

Vy

 

3

0;

min 3 9



y

.

Cách 2:

Xét hàm s:

2

4

3yx

x

trên khong

 

0;

.

Ta có:

23

48

3 ' 3    y x y

xx

.

Cho

3

8 8 8

' 0 3

33

      y x x

x

.

 

3

0;

8

min 3 9

3





  





yy

.

Đáp án C

Câu 33. Tnh

 

\1DR

.

 

2

1

23

,0

3

1









  









x

xx

yy

x

.

Bng bin thiên:

 

1;

min 4



  my

khi

3x

.

Đáp án B

Câu 34. Áp dng bng thc Cauchy, ta có:

11

5 2 . 5 3      y x x

xx

Du bng xy ra khi

2

1

11    x x x

x

(vì

0x

).

Vy

 

0;

min 3



y

.

x

0



3

8

3

'y

y

3

39

0





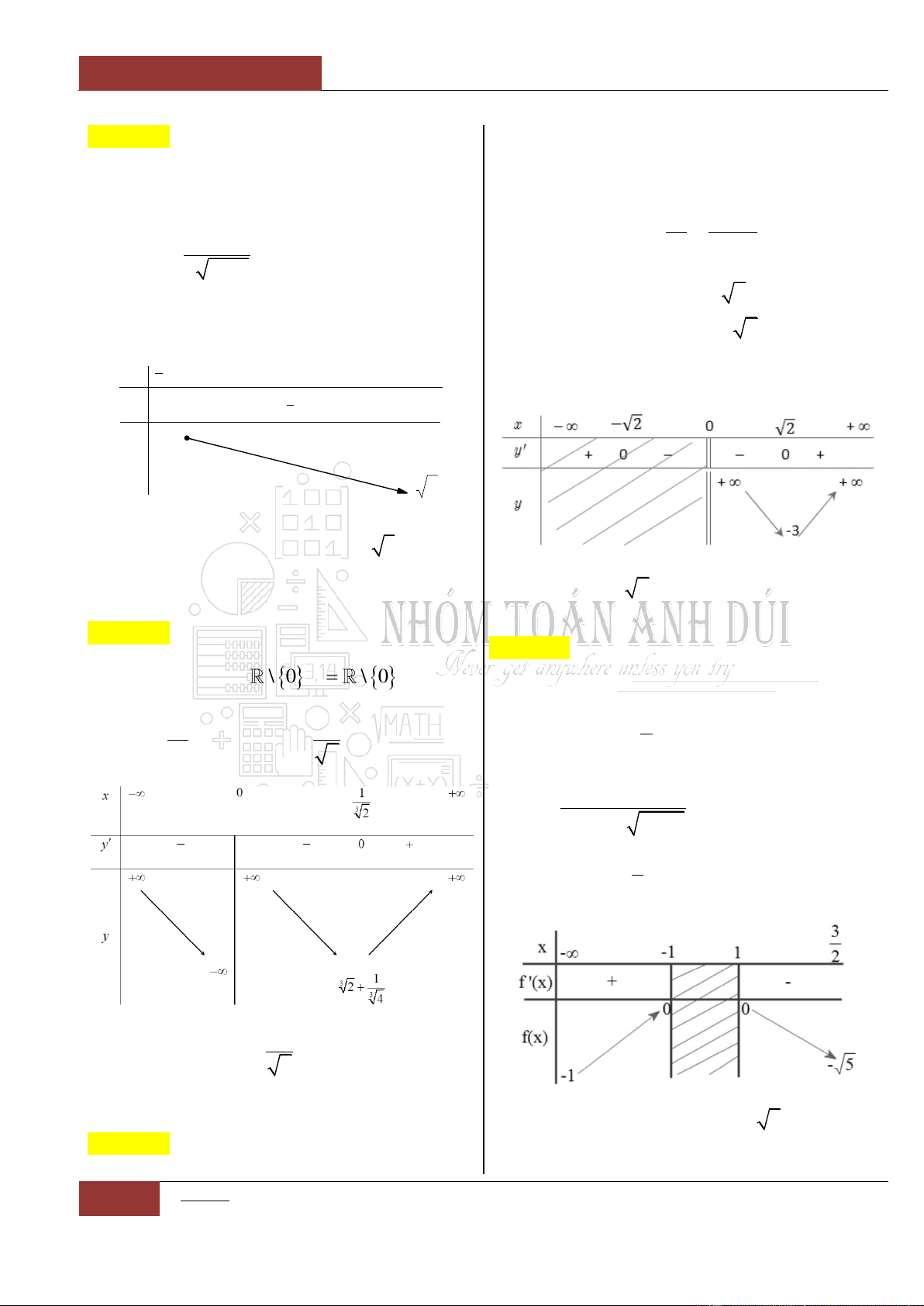
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

360

[ I can't, I can! ]

Đáp án C

Câu 35. Tnh ca hàm s là:





;4 . D

Ta có:

1

' 0,

24



   



y x D

x

Bng bin thiên

T bng bin thiên suy ra





;4

min 3



y

khi

4x

. Vy chn

D

.

Đáp án D

Câu 36. :

   

\ 0 \ 0DD

.

2

1

'2yx

x

,

3

1

' 0 .

2

  yx

Da vào BBT thì

3

1

2

x





 

0;

.

Đáp án D

Câu 37. Hàm s nh và liên tc trên

khong

 

0; .

2

22

1.





  

x

y

xx

2

0.

2

















x

y

x

Bng bin thiên:

Vy

 

0;

min 2 3.



  yf

Đáp án B

Câu 38. Hàm s nh và liên tc trên





3

; 1 1;

2



   





D

.

 

2

21

'

21







x

fx

xx

;

 

1

'0

2

   f x x D

Vy

   

max 0;min 5  

D

f x f x

.

3

+



x

y'

y



4

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

361

[ I can't, I can! ]

Đáp án A

Câu 39. Tnh:

D

.

 

   

2

22

2 2 2 2

2

51

25

'

5

55

'

5 5 5 5

  







   

  

   

x

xx

x

y

x

x x x x

y

x x x x

.

 

22

5

' 0 0

55

5 0 5



  



    

x

y

xx

Bng bin thiên:

T bng bin thiên có

 

30

max 5

5

yy

khi

5x

.

Hàm s

2

1

5







x

y

x

không có giá tr nh nht.

Vy hàm s có giá tr ln nht và không có giá

tr nh nht.

Đáp án D

Câu 40. Ta có:

 

2

1

'

1







m

y

x

.

* TH1.

1 0 1     mm

suy ra

y

ng

bin trên

 

2;4

suy ra:

 

   

2;4

2

min 2 3 1

1



    

m

f x f m

(loi)

* TH2.

1 0 1     mm

suy ra

y

nghch

bin trên

 

2;4

suy ra:

 

   

2;4

4

min 4 3 5

3



    

m

f x f m

suy ra

4m

.

Đáp án A

Câu 41. 

 

 

2

\ , 3; 2   D m D

.

+ Ta có:

 

2

1

' 0,



   



m

y x D

xm

. Nên hàm

s nghch bin trên tng khonh.

Nên:

 

 

2

3; 2

1 2 1

min 2

2





   



yy

m

2

2 2 0 2 3          m m m

.

Đáp án B

Câu 42. Tnh:

 

\2D

.

Ta có:

 

2

21

0, 2

2





    



m

yx

x

.

Hàm s ng bin

 

1;3

nên

 

 

1;3

max 3yy

2

31

1

5





m

2m

(vì

0m

).

Đáp án A

Câu 43. 

 

\8D

.

+

 

2

'

2

8

0,

8



   



m

y x D

x

Vy hàm s

2

8







xm

y

x

ng bin trên

 

0;3

.

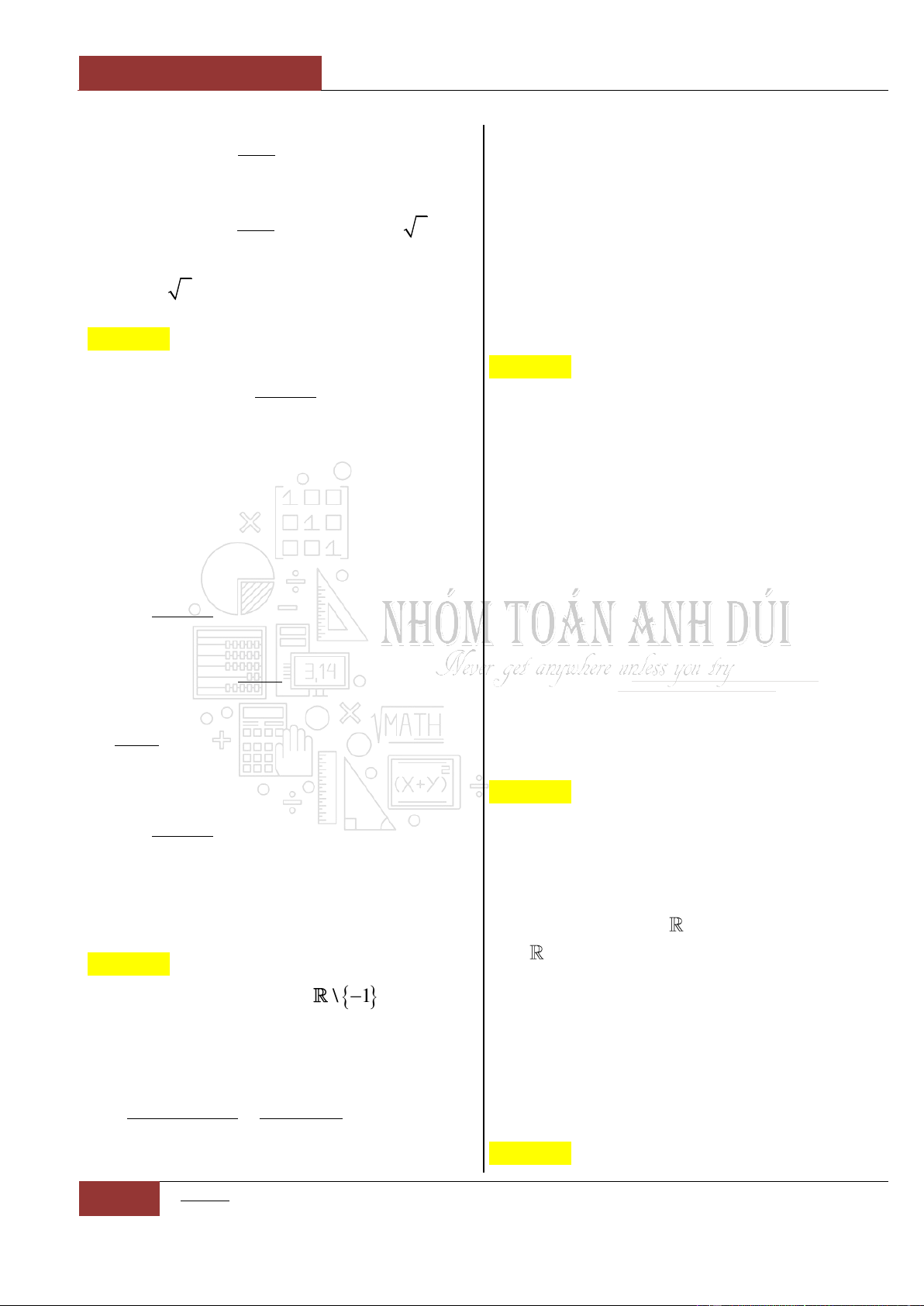
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

362

[ I can't, I can! ]

 

2

0;3

min (0)

8



  

m

yy



 

2

0;3

min 3 3 2 6.

8



       

m

ym

 

0

2 6 2;5  m

. Vy chn A.

Đáp án A

Câu 44. Ta có:

 

2

'

1







m

y

x

.

+ Xét

2m

.



Hàm s tr thành:

2y

là hàm s hng nên

t giá tr nh nht bng

3

2m

(loi)

+ Xét

2m

.

 

2

' 0 ( 1)

1



     



m

yx

x

 

0;4

8

min (4)

5



  

m

yy

.

8

37

5



   

m

(tho mãn).

+ Xét

2m

.

 

2

' 0 ( 1)

1



     



m

yx

x

 

 

0;4

min 0  y y m

3m

(loi).

Vy

7m

.

Đáp án C

Câu 45. Tnh:

 

\1D

.

Hàm s c trên

 

0;1

.

 

   

2

22

1

0

11

  





  



mm

y

xx

;

xD

.



Hàm s ng bin

 

0;1

.

Trên

 

0;1

hàm s t giá tr nh nht ti

0x

.

Ta có:

 

2

0 2 2      y m m

2

1

20

2





    







m

mm

m

.

Đáp án D

Câu 46. Xét hàm s

32

3   y x x m

trên

n

 

1;1

, ta có:

 

2

0 1;1

3 6 ; 0

2 1;1



  



    



   





x

y x x y

x

Mà

( 1) m 2

(0) m

(1) m 4



  



















y



 

1;1

min 4 0 4.



     y m m

Vy

4m

tha yêu cu bài toán.

Đáp án D

Câu 47. t

 

32

11    f x x m x m

.

+ Ta có:

22

31



  y x m

. D thy rng

0



y

vi mi

x

,

m

thuc nên hàm s ng bin

trên , suy ra hàm s ng bin trên . Vì

th .

+ Theo bài ra ta có: , suy ra .

  y và m   

.

Đáp án A

 

0;1

 

0;1

min y

 

 

0;1

min fx

 

0 f

1m

15m

4m

0

4m

2

00

2018 0mm

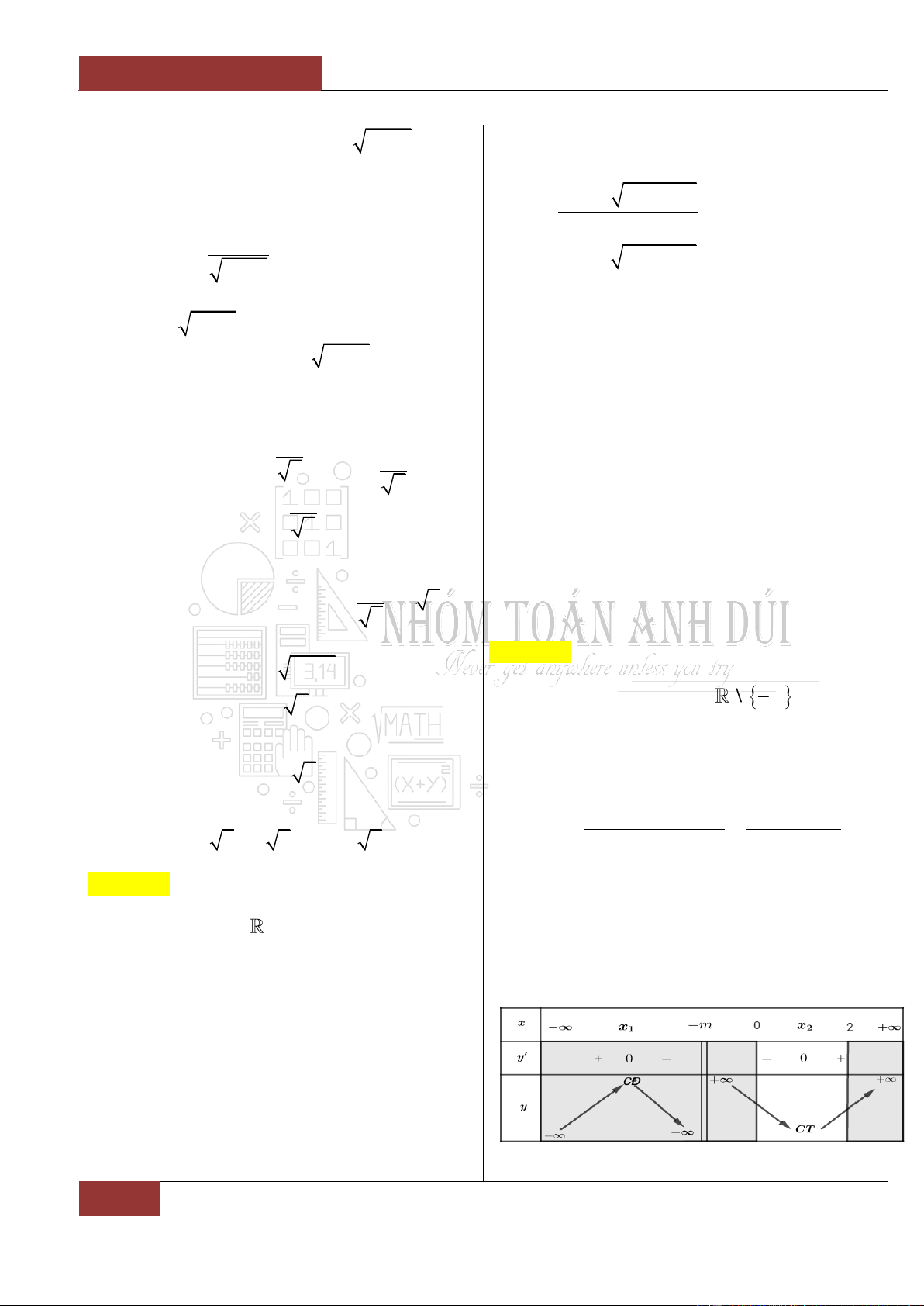
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

363

[ I can't, I can! ]

Câu 48. Xét hàm s .

Tnh: .

Ta có: .

.

Do hàm s liên tc trên

nên .

Theo bài ra thì , suy ra

.

Đáp án C

Câu 49.  .

Ta có: .

3 2 2

' 0 4 3 4 0y x m x x    

;

22

0

4 3 4 0

x

x m x









  



Nên hàm s u trên .

Tng giá tr ln nht và giá tr nh nht ca

hàm s n bng nên:

   

 

2

0 1 16 1 16y y m m m          

1

12

2

3

15

55

m

x

mm

xm











    





   







Vy .

Đáp án C

Câu 50. Tnh: . Hàm s

liên tc trên . .

Ta có: .

Cho .

Ta có bng bin thiên:

2

1   y x m x

 

1;1D

2

1







x

y

x

2

1

0

10



















xx

y

x

2

10

1

















x

xx

2

10

1

10

1

2

21

2

1

2





















   

























x

   

1

1 1 , 1 1 , 2

2



       





y m y m y m

2

1   y x m x

 

1;1

 

1;1

Max 2



ym

 

1;1

Max 2 2



y

2 2 2 2   mm

D

3 2 2

4 3 4



  y x m x x

24

0

3 9 64

1

8

3 9 64

0

8











  











x

mm

x

mm

x

 

0;1

 

0;1

16

12

. 15mm

 

\ Dm

 

0;2

00

22

  







   



mm

 

2

22

1

21



  







xm

x mx m

y

x m x m

1

2

1

0

1

  









  



xm

y

xm

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

364

[ I can't, I can! ]

Hàm s t giá tr nh nht ti nên

So vu kin hàm s liên tn

. Ta có .

 gi

u kinh: .

Hàm s liên tn nên

.

có hai nghim là ,

nên ch có nhiu nht mt nghim

thuc

Ta thy 

hàm s liên tt giá tr nh nht trên

ti mm

 

0

0;2x

thì

T

   

* , **

ta có: .

Đáp án A

Câu 51. Tnh: .

Ta có:

.

m khi và ch khi:

.

 bài, ta có:

.

Vy có

6

giá tr nguyên ca tham s tha

yêu cu bài toán.

Đáp án D

Câu 52. Vì là hàm s

bc ba và có nên và

có hai nghim phân bit.

Ta có có hai nghim phân bit

.

Vy vi thì có hai nghim

i nhau

T 

 

0

0;2x

0 1 2 1 1       mm

 

0;2

01m

xm

 

0;2

 

 

00

0;2 *

22

  



   



   



mm

m

mm

 

2

22

1

21

'



  





xm

x mx m

y

x m x m

'0y

1

2

1

  





  



xm

12

2xx

 

0;2

1 1,      m m m

 

0;2

 

0 1 2 1 1 **       mm

01m

D

1 sin

cos 2







mx

y

x

cos sin 1 2   y x m x y

2 2 2

1 4 4   y m y y

22

3 4 1 0    y y m

22

2 1 3 2 1 3

33

   

  

mm

y

 

2

2 1 3

min 2

3

0;10







  















x

m

y

m

 

2

1 3 8

0;10



















m

 

2

3 63

0;10

















m

 

2

21

0;10

















m

 

5,6,7,8,9,10m

m

3

,0   y ax cx d a

 

   

;0

min 2

 



x

f x f

0a

'0y

2

' 3 0  y ax c

0ac

0, 0ac

'0y

3

  

c

x

a

 

;0

min

3

 



  





x

c

f x f

a

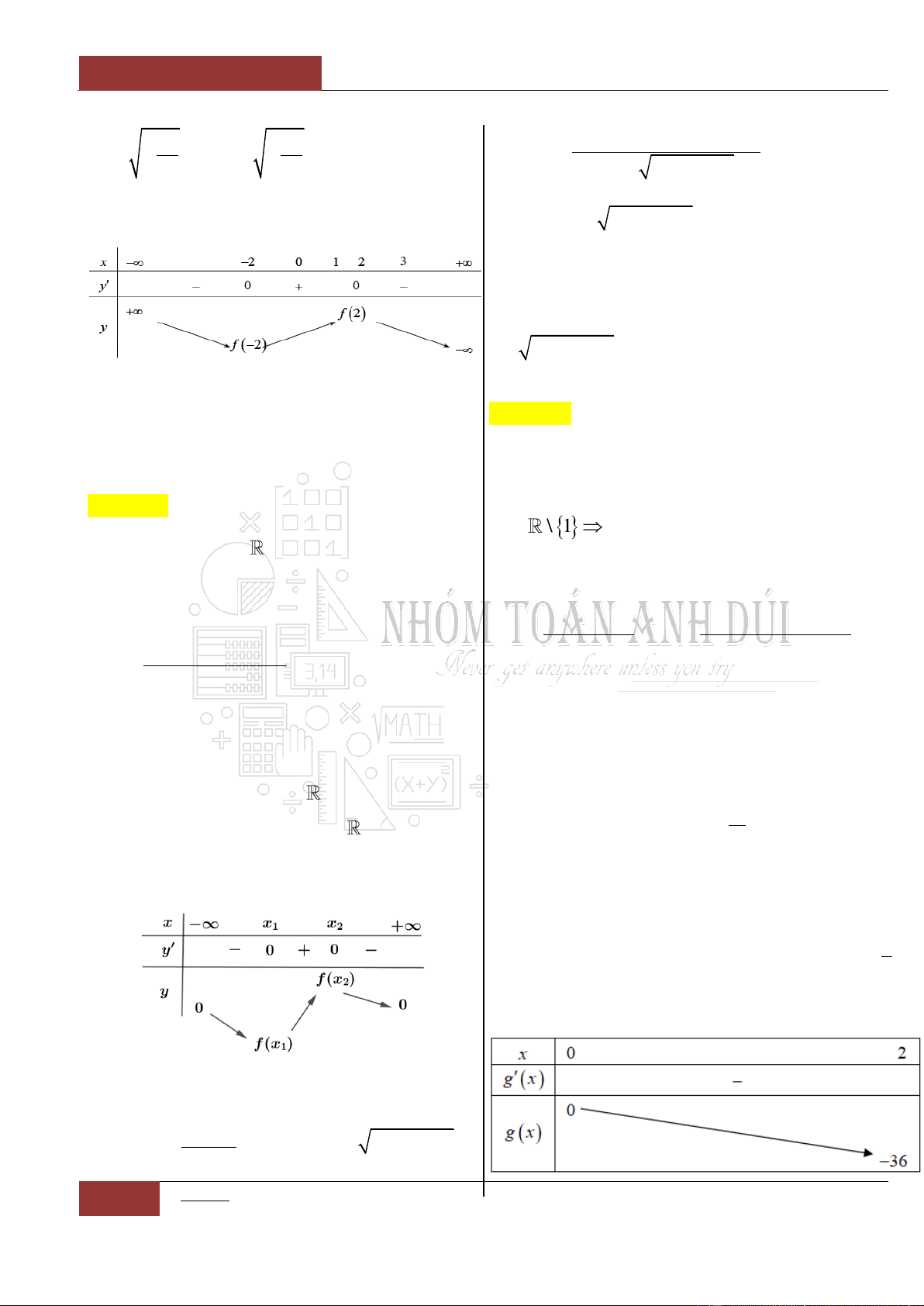
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

365

[ I can't, I can! ]

Ta có bng bin thiên

Ta suy ra:

.

Đáp án B

Câu 53.  .

+ .

nên có 2

nghim phân bit

+ Bng bin thiên:

Vy hàm s t giá tr ln nht là:

vi

2

1

2 2 1 1



    

YCBT

m m m

2

1 2 2 1 1     m m m

.

(vì

 

22

0 2 1 0   f x x

).

2

22

0

11

1









      









  





m

m m m m

m m m

Đáp án A

Câu 54. Cách 1:

Tnh ca hàm s:

.

Ta có:

.

32

' 0 2 4 2 0y x x x m     

 

32

2 4 2 1m x x x    

Ta có: .

t :

 

2

1

6 8 2 0 1

3



           g x x x x x

Trên ta có bng bin thiên:

2 2 12

33

          

cc

ca

aa

 

   

1;3

max 2 8 2 16



      

x

f x f a c d a d

D

lim 0





x

y

 

2

21

1

   







x mx m

y

xx

 

2

0 2 1 0 *



      y x mx m

2

(*)

1 0,



      m m m

 

*

12

,  x x m

 

2

1

21





fx

x

2

1    x m m m

 

 

\ 1 0;2  DD

 

3 2 3 2

2

2 4 2

1

    



  



x x m x x x m

yy

x

   

0 ; 2 4

3

   

m

y m y

 

32

2 4 2   g x x x x

 

0;2

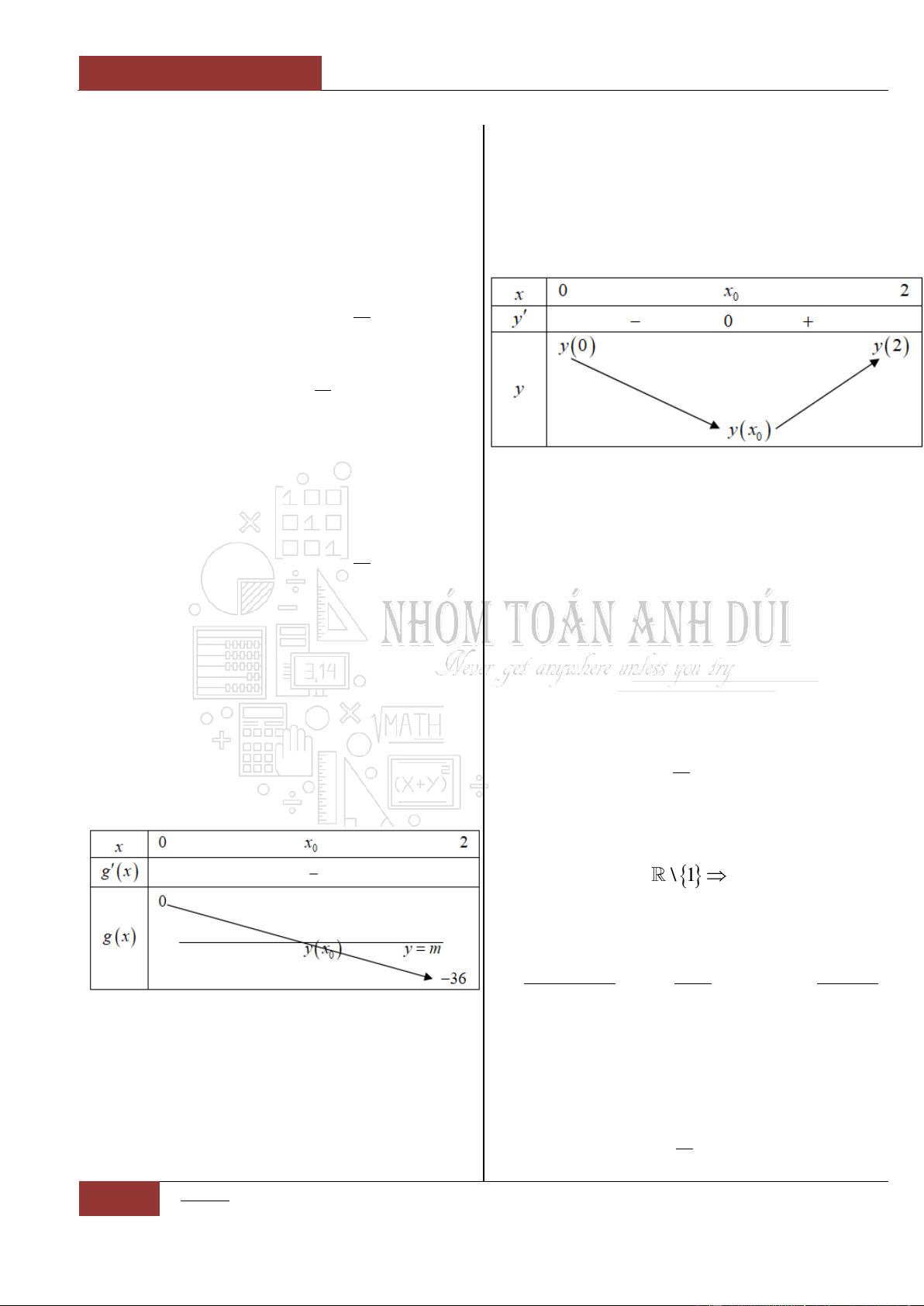
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

366

[ I can't, I can! ]

T bng bin thiên ta có:

.

Trường hợp 1: 

nghim  vô nghim.

D thy .

:

loi do .

Trường hợp 2: 

vô nghim  vô nghim.

D thy

 loi

do .

Trường hợp 3: 

có nghim duy nht (gi s ).

Trên ta có bng bin thiên:

Nhìn vào bng bin thiên ta có:

 

32

0

32

: 2 4 2

2 4 2 0 0

      



      

x x g x m x x x m

x x x m y

   

 

32

0

) 0; : 2 4 2x x g x m x x x m       

32

2 4 2 0 ' 0x x x m y      

   

 

32

0

32

) ;2 : 2 4 2

2 4 2 0 ' 0

x x g x m x x x m

x x x m y

       

      

Ta có bng bin thiên sau:

T bng bin thiên ta thy:

.

Nu

   

36; 6 0 2m y y



    



   

0;2

max 0 5 5y y m m l





       

.

Nu

   

6;0 0 2m y y



   



   

0;2

max 2 4 5 3

3

m

y y m n





       

.

Vy th.

Cách 2: : .

Ta có:

Trường hợp 1:

Hàm s ng bin trên .

 

   

36;0 , 0;2   g x x

0m



0



y

   

0 2 4 0

3

     

m

y m y khi m

 

 

0;2

max 2 4 5 3

3

      

m

y y m

0m

36  m



0



y

   

0 2 4 36

3

      

m

y m y khi m

 

 

0;2

max 0 5 5      y y m m

36m

 

36;0  m

0



y

0

xx

 

0;2

 

   

 

0;2

Max 2 ; 0y y y

3m

 

 

\ 1 0;2  DD

 

32

2

11

1





     





x x m m m

y x y x

xx

x

 

0 0, 0;2



    m y x



 

0;2

 

 

0;2

Max 2 4 5 3

3

       

m

y y m

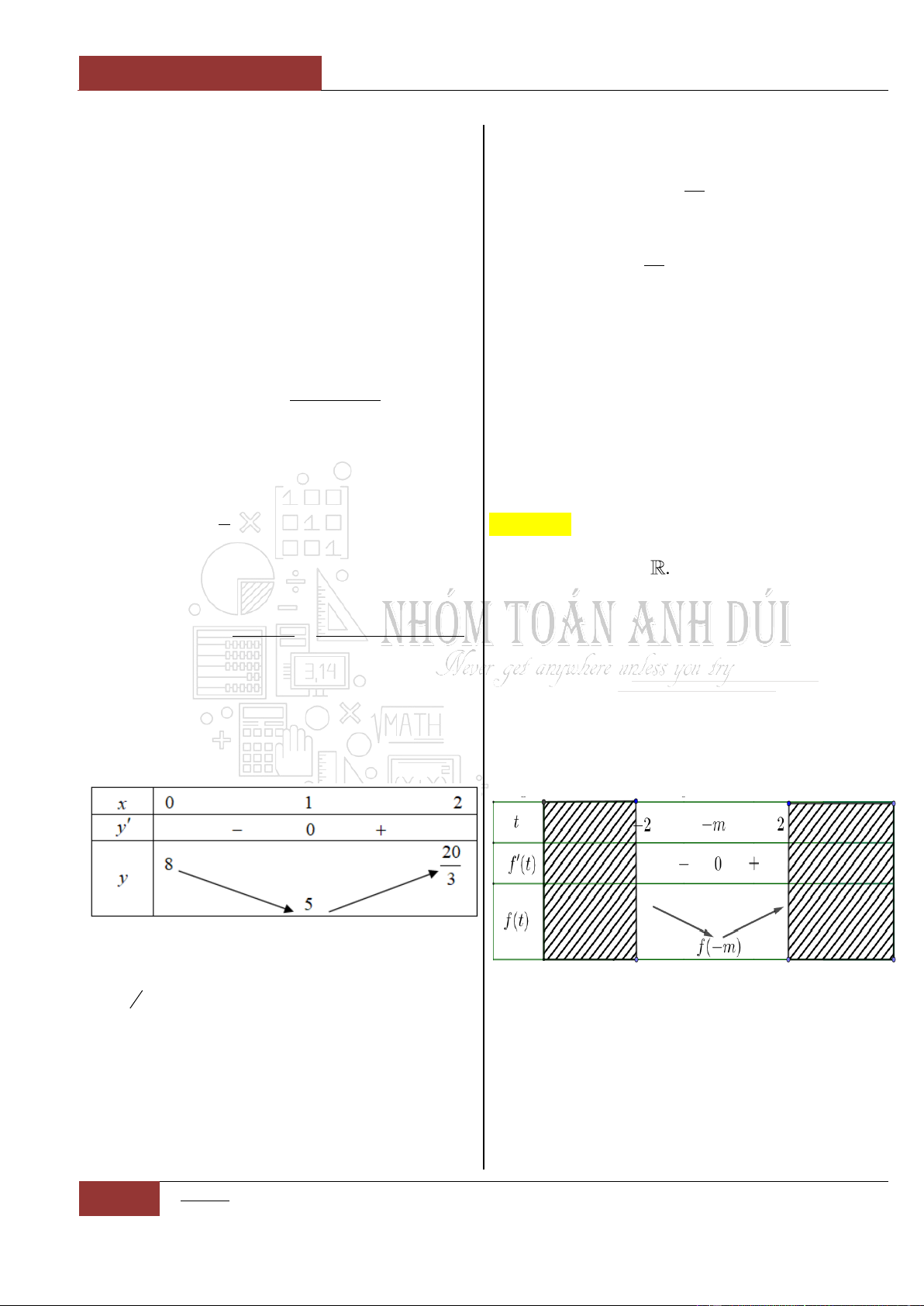
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

367

[ I can't, I can! ]

loi do .

Trường hợp 2: , gi s

 

0

M y x

.

vi .

Do hàm s liên tc trên

   

 

2

32

0 0 0 0 0

0

2 1 5 1

5

3

8

1

x x x x x

xl

m

xn

     







   











   

32

22

8 2 4 2 8

'2

11

x x x

yx

xx

  

  



' 0 1yx  

.

Ta có bng biên thiên:

không tha yêu c.

Nên

 

0

0;2x

 .

.

Nu

 

05

5

17

2

3

y

m

y







  









   

0;2

17

max 2 5 5

3

y y m l





      

Nu

 

03

3

25

y

m

y







  









   

0;2

max 2 5 3y y m n





     

Vy th.

Đáp án C

Câu 55. 

t



Trường hợp 1:

T bng bin thiên ta thy:

không tha mãn yêu cu.

Trường hợp 2:

0m

0m

 

 

0

0;2

Maxy y x

 

0

0;2x

 

0;2

 

2

00

0

32

00

0

21

0

5

1



  























m x x

yx

x x m

yx

x

8  m

 

 

0

0;2

Max y y x

 

 

 

 

0;2

Max 2 5

Max 0 3

   









   





y y m

3m

.D

   

3

3 , 1;1 2;2 .      t x x x t

   

2

.f t t m

     

2 ; 0 .



     f t t m f t t m

2 2 2 2.       mm

 

   

2;2

min 0



  f t f m

22    mm

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

368

[ I can't, I can! ]

T bng bin thiên ta thy:

.

Theo yêu cu bài toán:

Trường hợp 3:

T bng bin thiên ta thy:

Theo yêu cu bài toán:

Vy tng các giá tr ca tham s tha mãn

yêu cu là:

Đáp án C

Câu 56. Ta có: , .

D: và .

Thy ngay, vi   n

hàm s ng bin.

Vy giá tr nh nht ca hàm s   

n là:

.

Giá tr nh nht  :

.

Kt hu kin c

.

Đáp án B

Câu 57.

Trường hợp 1:

0m

, ta có:

.

: (loi).

Trường hợp 2:

Nu , ta có , .

:

(loi).

Nu 

.

,

 

     

2

2;2

min 2 2



   f t f m

 

2

3

2 1 3.

1







    







m

mm

m

22    mm

 

     

2

2;2

min 2 2 .



  f t f m

 

2

3

2 1 3.

1







     







m

mm

m

 

3 3 0.  

2

33



yx

01



   yx

 

11  

CT

yy

 

C

13  

Đ

yy

0m

 

1; 2mm

 

1; 2mm

     

3

1 1 3 1 1     y m m m

3

   

3

1 3 1 2 0     mm

12

11









  



m

1

2













m

0m

 

0;1m

36

1





y mx

x

 

2

36

1



  



ym

x

 

2

36

0, 1

1



     



yx

x

 

 

0;3

min 3 9





x

yy

0m

0m

0



y

1  x

 

 

0;3

min 3





x

yy

11

20 3 9

3

    mm

0m

 

2

36

00

1



   



ym

x

 

2

36

1  x

m

 

6

1

6

1











  





x

m

xl

m

64

0 1 3 36

9

     m

m

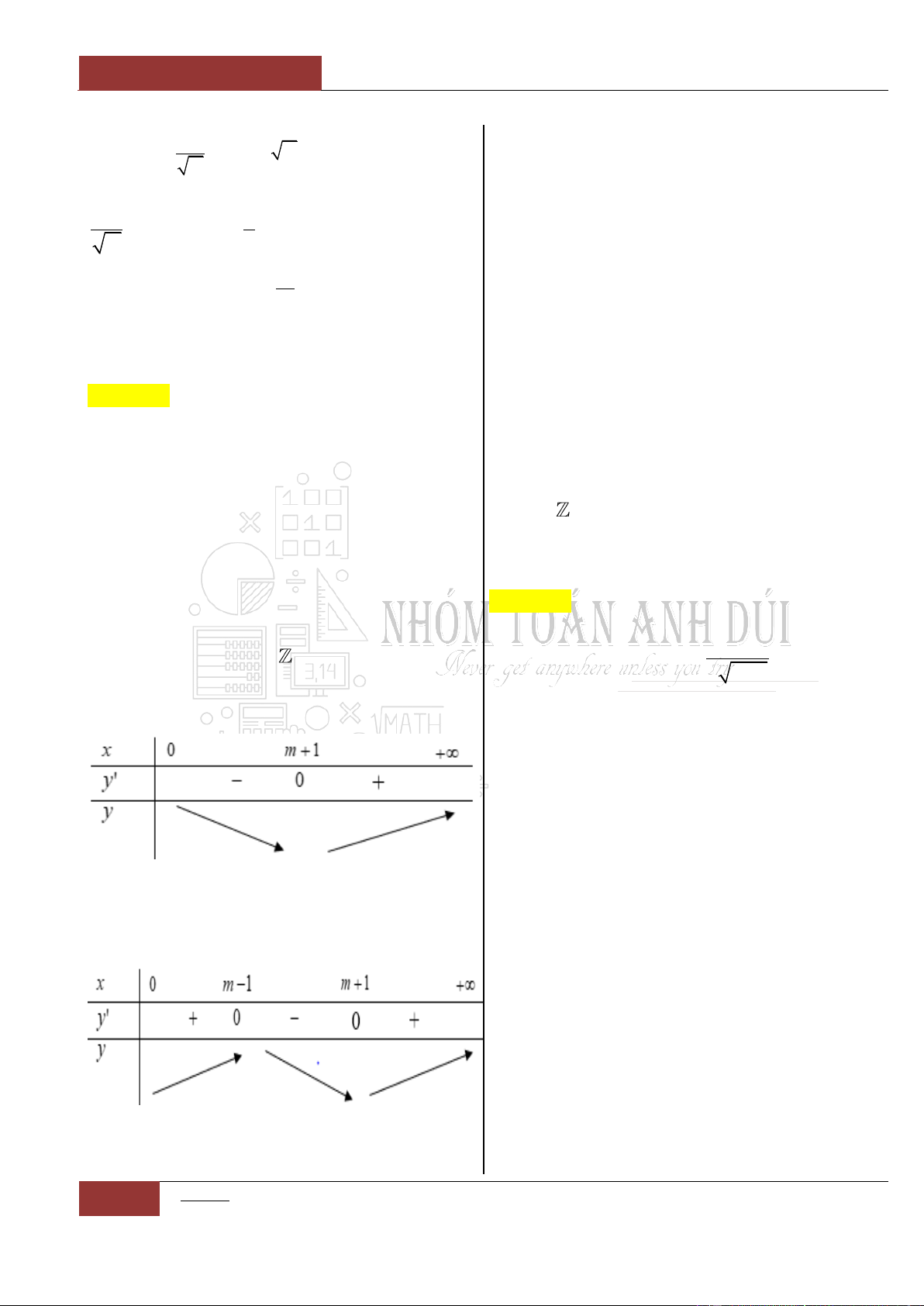
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

369

[ I can't, I can! ]

,

.

Vy .

Đáp án C

Câu 58. Ta có:

.

 hàm s có giá tr nh nht trên khong

thì hoc .

TH1:

. Do .

Bng bin thiên ca hàm s:

TH2: .

Bng bin thiên ca hàm s

Hàm s có giá tr nh nht trên khong

khi và ch khi .

.

Do .

Vy .

Đáp án D

Câu 59. Ta có: ;

Do nên khác 0 và có du không

i vi

Nu thì . 

Do nên nhn

Nu thì .

 

 

0;3

4

6

min 1 12 20

100









     











x

m

y y m m

ml

m

69

13

4

   m

m

 

 

0;3

min 3





x

yy

 

11

20 3 9

3

    m m l





4 2;4m

 

1

22

2

1

' 3 6 3 1 0

1





     







xm

y x mx m

xm

 

0;

12

0xx

12

0 xx

12

0xx

1 0 1    mm

11   m

m

 

0;1m

12

0 xx

 

0;

   

10











m

y m y

   

 

32

2

1

1 3 1 3 1 1 2020 2020











       





m

m m m m m

   

2

1

1 2 0











  





m

mm

1

2

1

























m

12  m

m

2m

 

0;1;2m

 

'

1

.

21





f x m

x

0m

 

'

fx

 

1; .  x

0m

 

 

'

0, 2;5  f x x

 

   

 

   

2;5

min 2 ; ax 5 2 .   f x f m m f x f m

 

 

 

 

2

2;5

2

1

2

min ax 10

2 10

2

3 10 0

5

  

   





    







f x m f x m

m m m

m

mm

m

0m

2

5.m

0m

 

 

'

0, 2;5  f x x

 

   

 

   

2;5

min 5 2 ; ax 2 .   f x f m m f x f m

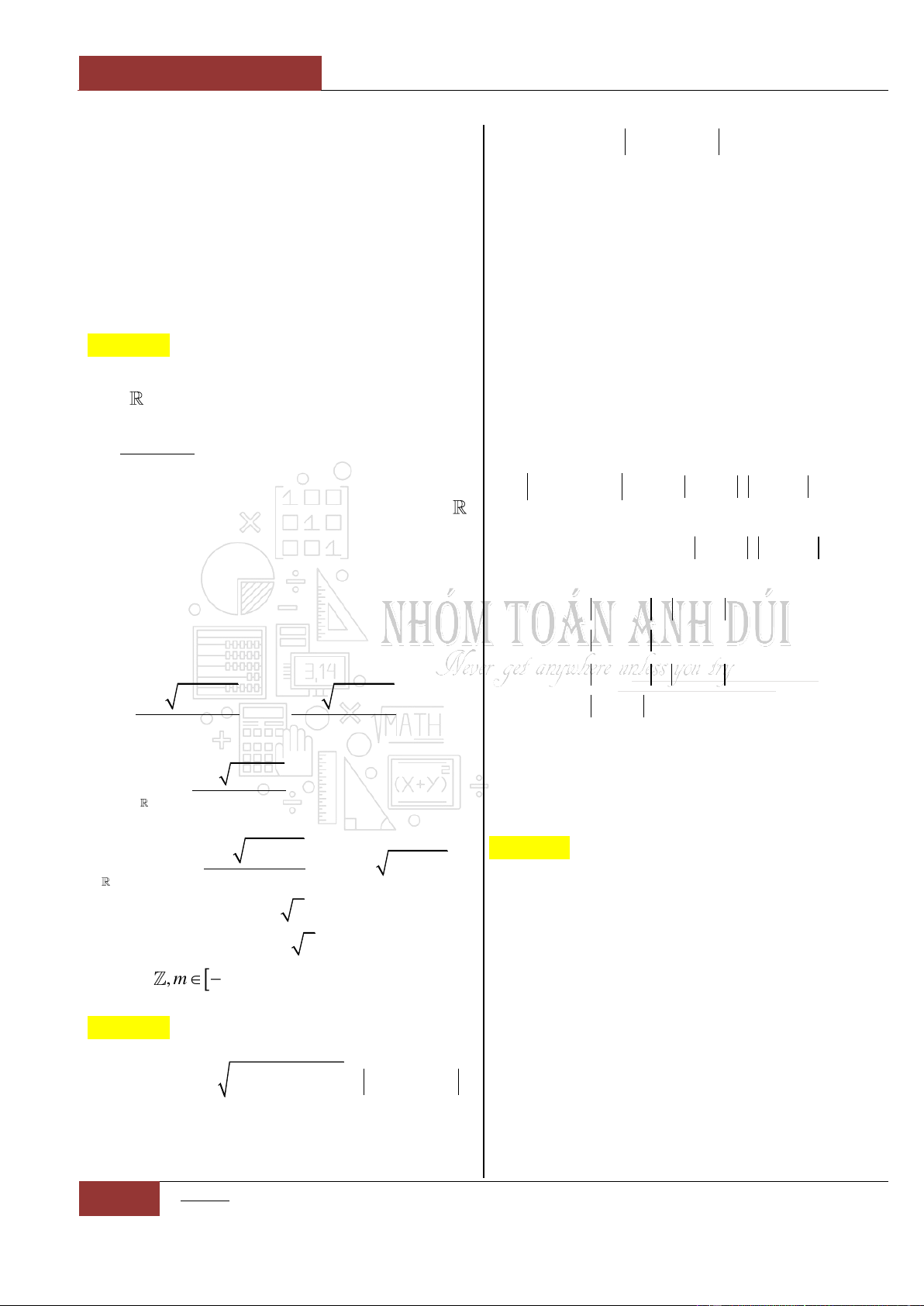
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

370

[ I can't, I can! ]

Do nên nhn

Vy

Đáp án A

Câu 60. u kin:  

.

(do  )

.

 có nghim

 

2

2 2 2 2

22

2 1 3 4 1 0

2 1 3 2 1 3

33

m y y y y m

mm

y

       

   

  

Vy .

2

2 1 3

min 1 1 1 3 5

3

2 2 2,82

80

2 2 2,82

m

ym

m



       





   



   



Mà nên .

Đáp án C

Câu 61. Ta có:

Nhn thy:

.

Xét hàm s: trên , ta có:

+ ,

+

: , tc:

.

T :

.

Suy ra .

Vy, tng các phn t ca là .

Đáp án B

Câu 62. t là

hàm s nh và liên tn .

Ta có: .

.

Ta kho sát hàm s n .

 

 

 

 

2

2;5

2

1

2

min ax 10

2 10

2

3 10 0

5

  

   





    







f x m f x m

m m m

m

mm

m

0m

1

2.m

12

3.mm

cos 2 0x

x

 

sin 1

cos 2 sin 1

cos 2

mx

y y x m x

x



    



cos 2 0x

x

sin cos 2 1m x y x y   

 

*

 

*

2

2 1 3

3

m

Min y





 

, 5;5mm  





5; 4; 3;3;4;5m   

 

2

33

3 2 3 2x x m x x m    

 

 

0;3

min 2fx

 

 

3

0;3

max 3 2 16 1x x m   

 

3

32g x x x m  

 

0;3

 

2

' 3 3g x x

 

2

' 3 3 0g x x  



 

1 0;3

x







  





     

0 2 , 1 2 2, 3 2 18g m g m g m    

 

 

2 2 2 18, 0;3m g x m x     

   

 

3

0;3 0;3

max 3 2 max 2 2 ; 2 18x x m m m    

 

 

 

0;3

1 max 2 2 ; 2 18 16mm   

2 18 2 2

2 18 16

1

7

2 18 2 2

2 2 16

mm

m

mm

m



   

























   



















 

7; 1S   

S

8

 

2

3

31    y f x x x m

 

1;1

  

32

( ) 2 3 1 3 3



     y f x x x m x

 

3

1

0

31











    



x

fx

m x x g x

 

gx

 

1;1

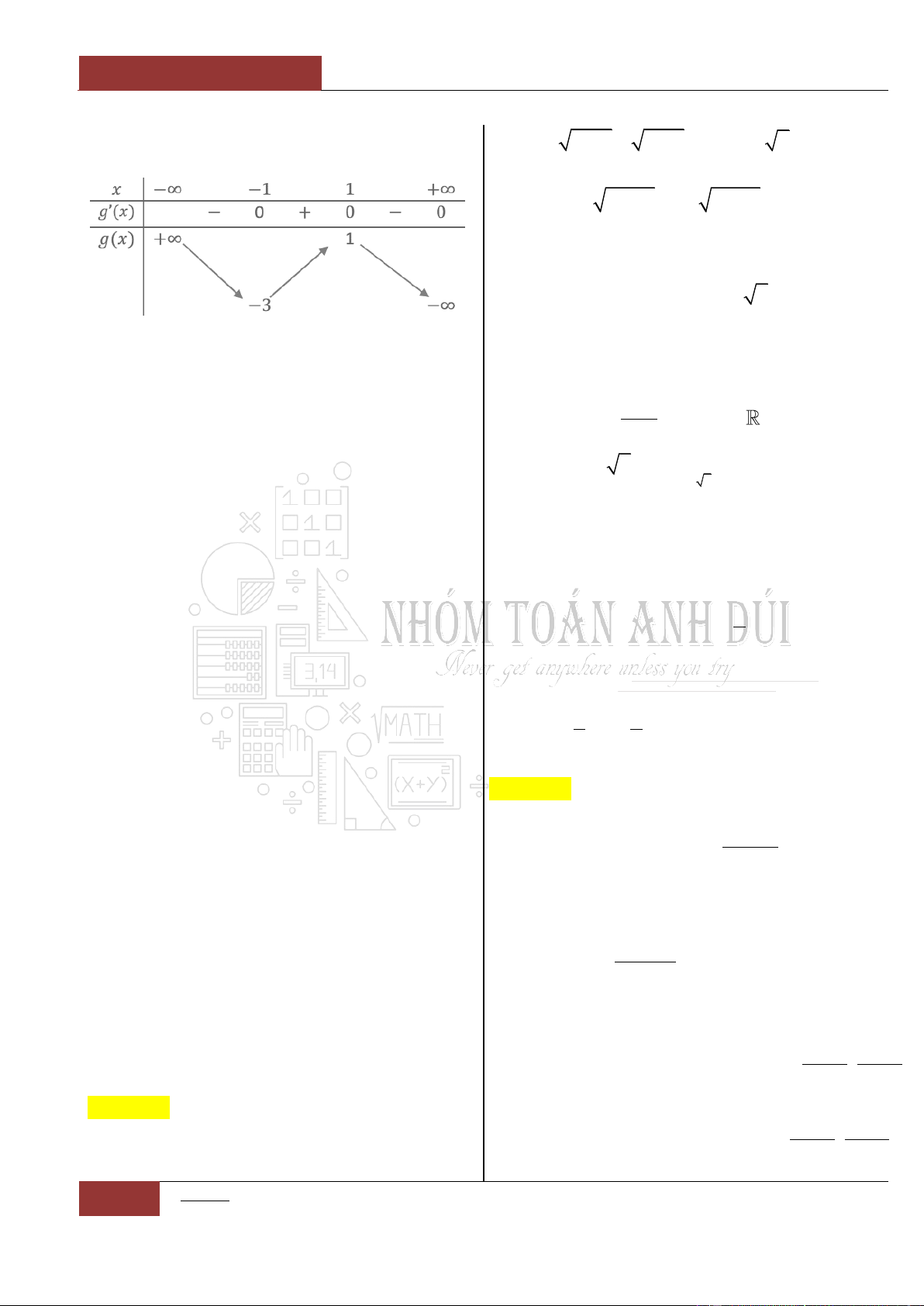
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

371

[ I can't, I can! ]

Bng bin thiên ca

Nu thì luôn tn ti sao

cho hay . Suy ra

, tc là không tn ti tha mãn yêu

cu bài toán.

Nu thì .

Ta có:

     

 

1;1

min min 1 ; 1f x f f









;

     

 

22

1;1

min min 1 ; 3f x m m







   

Trường hợp 1: tc là

suy ra:

Trường hợp 2: tc là

suy ra:

Vy có hai giá tr ca tha mãn yêu cu bài

toán: , t ng tt c các giá tr

ca là .

Đáp án A

Câu 63.  .

t: ; .

.

vi .

Ta có: .

ng

bin trên .

Mà



.

Tng các giá tr ca tha mãn ycbt là

.

Đáp án C

Câu 64. Xét hàm s vi .

Tnh: .

Ta có: i

du suy ra:

.

 

gx

 

3;1m

 

0

1;1x

 

0

m g x

 

0

0fx

 

1;1

min 0



y

m

 

3;1m

 

( ) 0 1 1;1



     f x x

1m

3 1 0   mm

 

 

2

1;1

2 ( )

min ( ) 1 1

0 ( )







   







m TM

f x m

m KTM

3m

1 3 0   mm

 

 

2

1;1

4 ( )

min ( ) 3 1

2 ( )







   







m TM

f x m

m KTM

m

2; 4  mm

m

2

 

2;2D

22   t x x

2;2 2







t

22

4 2 4   tx

22

2 4 4   xt



 

22

2 4 1     y g t m t t m

22

27   t m t m

2;2 2







t

 

2

4



g t t m

 

2

0

4





  

m

g t t

0;  m

 

 gt

2;2 2





   

2;2 2

min 2





g t g

4

 

2

2 2 1  g m m

2

2 1 4   mm

1

3

2











m

31

1

22



    





S

 

2

1







xm

fx

x

2m

1x

 

2

1









m

fx

x

 

1;3x

 

     

 

1;3

26

max max 1 ; 3 max ;

24











mm

f x f f

 

     

 

1;3

26

min min 1 ; 3 min ;

24











mm

f x f f

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

372

[ I can't, I can! ]

Xét vi .

Vy: .

.

Xét vi . Vy

.

Đáp án B

Câu 65. Tnh:

 hàm s có giá tr ln nht trên thì:

Trường hợp 1:

:

 giá tr ln nhn là s 

thì:

Vy các s tha là:

Trường hợp 2:



 giá tr ln nhn là s 

thì:

Vy các s nguyên tha mãn là 0.

Trường hợp 3:

: Nên

Vy tha.

Kt lun: có

9

s nguyên tha mãn yêu cu

bài toán.

Đáp án A

Câu 66. Xét hàm s

 

3

3  f x x x m

, ta có

 

2

33



f x x

. Ta có bng bin thiên ca

 

fx

:

TH1:

2 0 2   mm

.

:

 

   

0;2

22    max f x m m

2 3 1   mm

(loi).

TH2:

20

0





   







m

.



2 2 2 2     m m m

.

 

   

0;2

22     max f x m m

2 3 1   mm

(tha mãn).

2m

 

0



fx

 

1;3x

 

   

2

1;3 1

2



    

m

x f x f

 

 

1;3

2

max

2





m

fx

2m

 

0



fx

 

1;3x

 

   

2

1;3 1

2



    

m

x f x f

 

 

1;3

2

min

2





m

fx

 

\.Dm

 

1; 3

 

1; 3 .m

 

2

26

.









m

y

xm

2 6 0 3.     mm

 

 

1 ; 3

9

max 3 .

3









x

m

yy

m

 

1;3

9

0 9 0 9.

3



      



m

mm

m

8,

7,

6,

5,

4.

2 6 0 3.     mm

 

 

1;3

7

max 1 .

1









x

m

yy

m

 

1; 3

7

0 1 0 1.

1



     



m

mm

m

2,

1,

2 6 0 3.     mm

1.y

 

1 ; 3

max 1.





x

y

3m

m

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

373

[ I can't, I can! ]

TH3:

0

02

20





  



  



m

.



2 2 2 2     m m m

.

 

 

0;2

2  max f x m

2 3 1   mm

(tha mãn).

TH4:

2 0 2    mm

.

:

 

 

0;2

2max f x m

.

2 3 1   mm

(loi).

Vy:

1m

.

Đáp án D

Câu 67. Do hàm s

 

1







xm

fx

x

liên tc trên

n

 

0;1

.

Khi

1m

, hàm s là hàm hng nên:

 

 

 

 

0;1

max min 1f x f x

.

Khi

1m

, hàm s u trên

 

0;1

, nên:

+ Khi

   

0 ; 1ff

cùng du thì:

 

 

 

     

0;1

max min 0 1

1

2

  





f x f x f f

m

+ Khi

   

0 ; 1ff

trái du thì:

 

 

0;1

min 0fx

,

 

     

 

0;1

1

max max 0 ; 1 max ;

2











m

f x f f m

TH1:

   

0 . 1 0ff

;

 

1

10

0





   







m

mm

m

.

 

 

 

 

0;1

max min 2f x f x

1

2

5

2

3









   







m

(tho mãn).

TH2:

   

0 . 1 0ff

;

 

1 0 1 0      m m m

 

 

 

 

0;1

max min 2f x f x

2

5

1

2

3

2









   













m

(không tho mãn).

S phn t ca

S

là

2

.

Đáp án B

Câu 68. Xét hàm s:

 

3

3 2 1    y f x x x m

n

 

0;2

.

Ta có:

 

 

2

1 0;2

' 3 3 0

1



  

   







x

f x x

x

.

Ta có:

 

0 2 1

1 2 3

2 2 1

















fm

.

Suy ra:

 

 

 

0;2

2 1; 2 3 ; 2 1   max f x max m m m

.

 

2 3 ; 2 1   max m m P

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

374

[ I can't, I can! ]

Trường hợp 1: Xét

2 3 2 1  mm

;

 

1

4 4 2 0

2

     mm

.

:

2 3 2  Pm

,

1

2

m

.

Suy ra:

min

1

2

  Pm

.

Trường hợp 2: Xét

2 3 2 1  mm

;

 

1

4 4 2 0

2

     mm

.

:

2 1 2  Pm

,

1

2

m

.

Suy ra:

min

P

không tn ti.

Vy

1

2

m

.

Đáp án D

Câu 69. Ta có:

2

22

2









x

y

x x m

;

01



  yx

.

:

     

 

max 1 , 2 , 1 5y y y

.

 

max 3 , , 1 5   mmm

.

ng hp

1m

, ta có:

 

max 3 , , 1 5

3 5 2

  

    

mmm

mm

ng hp

1m

, ta có:

 

max 3 , , 1 5 1 5 4        m m m m m

Vy tng các giá tr

m

bng

2

.

Đáp án C.

Câu 70.         



 

2;1

.



   

2

2 4 1 5         y x x a x a

:

 

   

2

1 , 2;1 0;4     t x x a

.

 

 

5  f t t a

vi

 

0;4t

.

Nên:

     

 

0;4

2;1

0;4

max max max 0 ; 4

















t

x

t

y f t f f

 

0;4

max 5 ; 1







  

t

aa

1 5 1 5

2

22

     

  

a a a a

ng thc xy ra khi:

1 5 2 3     a a a

.

 nh nh

 

0;4

max





t

ft

là

2

khi

3a

.

Đáp án B

Câu 71. Xét:

2

1







x mx m

y

x

.

Ta có:

 

2

1









xx

fx

x

,

 

 

0 1;2

0

2 1;2











  





x

fx

x

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

375

[ I can't, I can! ]

Mà

   

2 1 3 4

1 ,f 2

23





mm

f

;

 

1;2

2 1 3 4

max ;

23













x

mm

y

.

Trường hợp 1:

 

1;2

3

21

2

max 2

5

2











  









x

m

y

m

.

i

3 3 4 17

2

2 3 6



   

m

(loi).

i

5 3 4 7

2

2 3 6



    

m

(tha mãn).

Trường hợp 2:

 

1;2

34

max 2

3

2

3 4 6

3

3 4 6 10

3





















  











x

m

y

m

i

2 2 1 7

2

3 2 6



   

m

(tha mãn)

i

10 2 1 17

2

3 2 6



    

m

(loi)

Vy có

2

giá tr ca

m

tha mãn.

Đáp án D

Câu 72. Xét hàm s

 

2

  f x x ax b

.

 bài,

M

là giá tr ln nht ca hàm s

trên

 

1;3

.

Suy ra:

 

1

3

1

















Mf

1

93

1

  





   





  



M a b

.

4 1 9 3 2 1          M a b a b a b

1 9 3 2( 1 )         a b a b a b

48M

2M

.

Nu

2M

u kin cn là:

1 9 3 1 2         a b a b a b

và

1ab

,

93ab

,

1  ab

cùng du

1 9 3 1 2

         







          



a b a b a b

2

1













a

b

.

c li, khi

2

1











a

b

ta có, hàm s

 

2

21  f x x x

trên

 

1;3

.

Xét hàm s

 

2

21  g x x x

nh và liên

tc trên

 

1;3

.

 

22



g x x

;

 

 

0 1 1;3



    g x x

M

là giá tr ln nht ca hàm s

 

fx

trên

 

1;3

     

 

max 1 ; 3 ; 1  M g g g

2

.

Vy

2

1











a

b

. Ta có:

24  ab

.

Đáp án C

Câu 73. Xét

 

3 2 2

1 27    u x x m x

trên

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

376

[ I can't, I can! ]

n

 

3; 1

, ta có:

22

3 2 1 0,



      u x x m x

.

:

 

 

 

 

2

3; 1

2

3; 1

max 1 26

min 3 6 3





    





    





A u u m

a u u m

;

Do

 

 

22

3; 1

22

M max max 26 , 6 3

4 3 26 6 3 72





   







    



y m m

M m m

.

Vy

18M

.

Du bng xy ra khi và ch khi:

22

26 6 3 18 2 2      m m m

.

Đáp án B

Câu 74. Xét hàm s

 

2

24   f x x x m

.

Ta có:

 

22



f x x

,

 

01



   f x x

.

:

 

2

2;1

max 2 4



  x x m

;

 

max 1; 4 ; 5   m m m

Ta thy:

5 4 1    m m m

vi mi

m

,

suy ra:

 

2;1

max



y

ch có th là

5m

hoc

1m

.

Nu

 

2;1

max 5



ym

thì:

54

51

  





  





m

mm

1m

.

Nu

 

2;1

max 1



ym

thì:

14

15

  





  





m

mm

5m

.

Vy

 

1; 5m

.

Đáp án B

Câu 75. Xét hàm s:

 

32

39   f x x x x m

n

 

2;4

.

2

3 6 9



  f x x

;

 

1

0

3















x

fx

x

(tha mãn).

c:

 

22

15

3 27

4 20

   





  





  



  



fm

 

 

 

 

2;4

min 27;max 5



    f x m f x m

;

 

 

 

2;4

max max 27 ; 5



   f x m m

.

+) Trường hợp 1: Nu

 

27 5 *  mm

 

 

2;4

11

max 5 5 16

21







      







m

f x m m

m

i chiu kin

 

* 11m

.

+) Trường hợp 2: Nu

 

27 5 **  mm

 

 

2;4

43

max 27 27 16

11







      







m

f x m m

m

(Không thu kin

 

**

).

Vy

 

11S

 S

có

1

phn t.

Đáp án D

Câu 76. Xét hàm s:

 

42

1 19

30 20

42

    g x x x x m

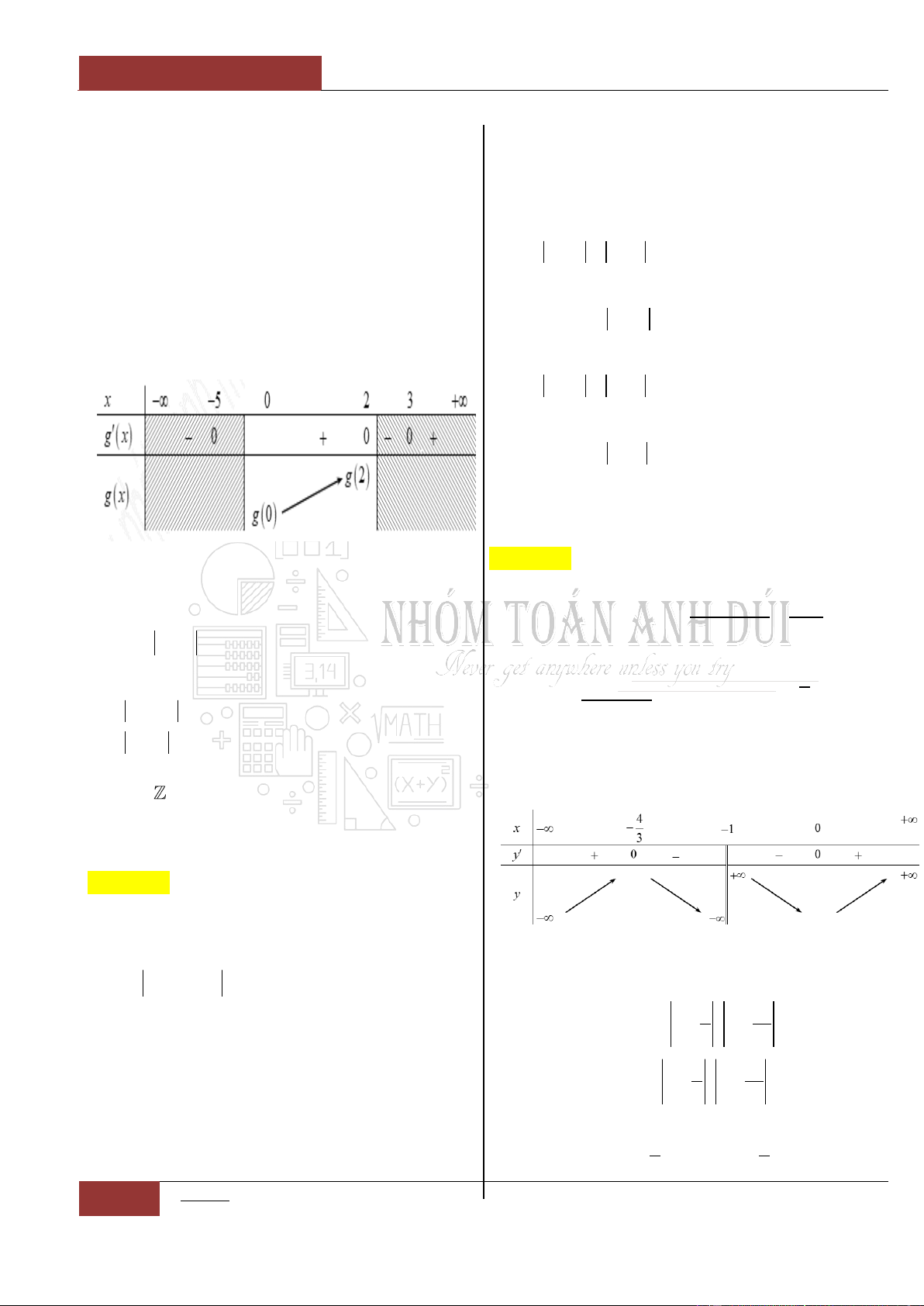
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

377

[ I can't, I can! ]

n

 

0;2

.

Ta có:

 

3

19 30



  g x x x

;

 

 

5 0;2

02

3 0;2



  





  







x

g x x

x

Bng bin thiên

 

0 20gm

;

 

26gm

.



 

 

0;2

max 20gx

thì

 

0 20

2 20















g

;

20 20

6 20

  













m

0 14  m

.

Mà

m

nên

 

0;1;2;...;14m

.

Vy tng các phn t ca

S

là

105

.

Đáp án C

Câu 77. t:

 

 

sin 1;1  x t t

;

2

2   y t t m

.

Xét hàm s:

 

2

2  f t t t m

, ta có:

 

 

' 2 2 0 1 1;1      f t t t

.

Ta có:

   

1 3, 1 1    f m f m

.



 

 

 

 

 

 

1;1

max max 3; 1 3

min min 3; 1 1



    







    





f x m m m

TH1:

3 1 1     m m m

 

2

max 3 1

4





    









ml

f x m

ml

TH2:

3 1 1     m m m

 

2

max 1 1

0





    









ml

f x m

ml



Không tn ti

m

tha mãn.

Đáp án A

Câu 78. Xét hàm s

44

11



  



x ax a x

ya

xx

.

Ta có:

 

43

2

4

34

0

3

1

0











   









x

xx

yy

x

.

Bng bin thiên

Da vào bng bin thiên suy ra:

1 16

max ;

23

1 16

min ;

23





  





  







  









M a a

m a a

.

Trường hợp 1.

11

0

22

    aa

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

378

[ I can't, I can! ]

16 16

33

11

22



   









   





M a a

m a a

.

:

16 1 13

22

3 2 3



      





M m a a a

.

Kt h u kin, ta có:

1 13

23

  a



có

5

giá tr nguyên thu kin.

Trường hợp 2.

16 16

0

33

    aa

;

11

22

16 16

33



    









    





M a a

m a a

1 16 61

22

2 3 6



         





M m a a a

.

Kt hu kin ta có

61 16

63

   a

.

Suy ra có

5

giá tr nguyên ca

a

tha mãn.

Trường hợp 3.

1

0

16 1

2

16

32

0

3







    











a

.

Nu

1 16 1 16

2 3 2 3

       a a a a

35

12

  a

thì:

1

2

16

3



  















Ma

Mm

ma

1 16 67

2

2 3 18



       





a a a

.

Kt hu kin, ta có

16 67

3 18

   a

.

Suy ra có

2

giá tr nguyên ca

a

thu

ki bài.

Nu

1 16 1 16

2 3 2 3

       a a a a

35

12

  a

thì:

16

3

2

1

2













  





Ma

Mm

ma

;

16 1 19

2

3 2 9



       





a a a

.

Kt hu kin, ta có

19 1

92

   a

.

Suy ra có

2

giá tr nguyên ca

a

thu

kin.

Vy có

14

giá tr nguyên ca

a

thu

kin.

Đáp án B

Câu 79. t

 

42

1

14 48 30

4

    f x x x x m

là

hàm s nh và liên tc trên

 

0;2

.

Vi mi

 

0;2x

, ta có:

 

3

' 0 28 48 0 2      f x x x x

.

Suy ra:

 

 

 

0;2

max max (0) ; (2)f x f f

.



 

 

0;2

max 3fx

30 30

14 30

30 14



  







  











  









  







m

mm

m

mm

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

379

[ I can't, I can! ]

30 30

14 30

  













m

30 30 30

30 14 30

   







   



m

0 60

0 16

44 16





   



  



m

.

Do

 

0;1;2;...;16 .   m m S

Vy tng tt c

17

giá tr trong tp

S

là

136

.

Đáp án D

Câu 80. t

   

, 0;ln2 1;2   

x

t e x t

Xét hàm s:

 

4 3 2

|3 4 24 48 |    h t t t t t m

trên

n

 

1;2

.

t:

 

4 3 2

3 4 24 48    g t t t t t m

 

32

12 12 48 48



   g t t t t

;

 

0



gt

2 [1;2]

2

1

  













t

;

 

1 23gm

,

 

2 16gm

.

TH1:

16 10  m

23 16 0    mm

 

 

1;2

maxA h t

23m

;

 

 

1;2

minB h t

16m

.

Suy ra:

16 10

25

23 3 48

2

  



  











  









m

mm

m

25

10

2



  m

.



22

giá tr ca

m

tha mãn.

TH2:

23 16   m

23 23, | 16| 16       m m m m

.

D thy

0B

.

Suy ra:

23 16

16 0

23 16

23 0

    







  





   















mm

m

mm

m

 

16 19.5

Voâ lyù

19.5 23

m



   





   



Vy





12; 11;...;0;1;...9  S

và tng các phn

t ca tp

S

bng

   

12 11 10 33      

.

Đáp án A

Câu 81. 

4 3 2

2 ( )    y x x x a f x

.

Xét hàm s

 

4 3 2

2   f x x x x a



 

32

4 6 2 0



   f x x x x

;

 

2

1

2 2 3 1 0 0; ;1

2



     





x x x x

.

 

 

0, 1;2



   f x x

và

 

1

24















fa

.

:

 

1;2x

thì

 

max , 4

min ,0, 4















y a a

.

:

+

max 4

0

min













ya

a

ya

2 4 10 3    aa

.

+

max

4

min 4





  



  



ya

a

ya

,

4 10 2 4 10 7           a a a a



Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

380

[ I can't, I can! ]

+

0

40





   







a

4 10 6

10 10

  







   



aa





a



Đáp án C

Câu 82. Vi

32

3  u x x m

, ta có:

2

3 6 ; 0 0; 2



     u x x u x x

:

 

     

 

 

     

 

1;3

min min 1 ; 3 ; 2

max max 1 ; 3 ; 2















u u u u

 

 

 

 

1;3

min min 2; ; 4 4

max max 2; ; 4

    







   





u m m m m

* Nu

4 0 4   mm

;

 

 

 

1;3

min 4 2020

2024 4,...,2024 .

   

   

f x m

mm

* Nu

 

 

1;3

0 min 2020    m f x m

;

 

2020 2020;...;0 .     mm

* Nu

0 m 4



 

 

1;3 1;3

1;3

min 0; max 0 min 0   u u f x

(tha mãn).

Vy

 

2020,...,2024m

có tt c

4045

s

nguyên tha mãn.

Đáp án A

Câu 83. Cách 1:

Xét hàm s

 

24







mx x

gx

x

liên tc trên

n

 

1;1

và

   

f x g x

.

Ta có:

 

01

25

1

6

23

1

2

























g

m

g

m

g

.

- Nu

 

10

25

10

23





















g

m

g

m

thì

 

 

1;1

min 0



fx

,

không tha mãn bài toán.

- Nu

 

10

2 3 2 5

10







   









g

m

g

Mà

m

nguyên nên

 

3; 2; 1;0;1;2;3;4   m

.

Ta có:

 

2

2 12

4

24









x

m

x

gx

x

.

TH1:

0m

.

 

 

 

0 1;1



   g x x

    

 

gx

ng bin trên

 

1;1

.

Mà

   

0 1 1 1    gg



 

1 1 0  g

.

Vy

 

 

1;1

0 min 1



fx

hay

 

0;1;2;3;4m

tha

mãn bài toán.

TH2:

0m

.

Xét hàm s

 

2 12

4







x

hx

x

trên

 

1;1

. Ta có:

 

 

2

0 1;1

44





    



x

h x x

xx

.

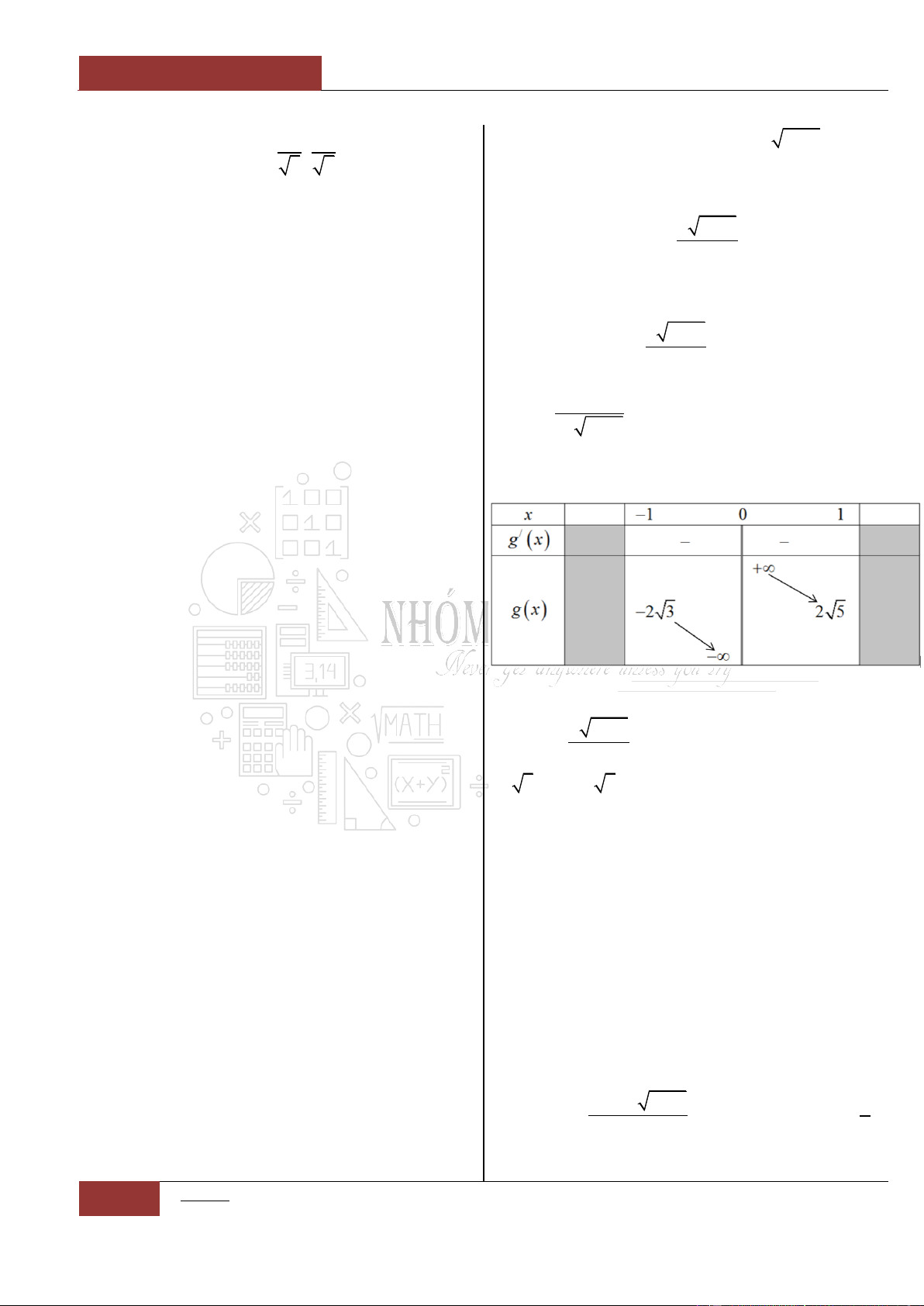
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

381

[ I can't, I can! ]

 thy

 

10 14

;

35









hx

.

* Khi

 

 

1 4 0, 1;1       m m h x x

 

 

0 1;1



    g x x

hay hàm s

 

gx

ng

bin trên

 

1;1

.



 

1 1 0  g

nên

 

 

1;1

0 min 1



fx

. Vy

1m

tha mãn.

* Khi

 

3; 2  m

 

 

 

 

4 0 1;1 0 1;1



          m h x x g x x

hay hàm s

 

gx

nghch bin trên

 

1;1

.

:

     

1 0 1 1 0      g g g

nên

 

 

1;1

0 min 1



fx

.

Vy

 

3; 2  m

tha mãn.



 

3; 2; 1;0;1;2;3;4   m

hay có

8

giá tr

nguyên ca

m

.

Cách 2:

Nhn thy

 

fx

liên tc trên

 

1;1

nên tn ti

giá tr nh nht ca

 

fx

n

 

1;1

.

Ta có:

 

 

 

0, 1;1

01



   











f x x

f

, nên suy ra:

 

 

1;1

0 min 1





x

fx

.

Vu kin:

 

 

 

 

 

 

1;1

min 0 (1)

0 min 1

min 1 (2)









  









x

fx

.

Ta có

 

1 

 

2 4 0  mx x

vô

nghim trên

 

1;1



 

24



x

m

x

vô nghim trên

 

 

1;1 \ 0

Xét hàm s

 

 

 

24

, 1;1 \ 0



   

x

g x x

x

 

 

 

/

2

8

0, 1;1 \ 0

4



    



x

g x x

xx

Bng bin thiên

T bng bi    u ki 

trình

24



x

m

x

vô nghim trên

 

 

1;1 \ 0



2 3 2 5  m

.

Do

m

nguyên nên

 

3; 2; 1;0;1;2;3;4   m

.

 gii

 

2

c h    u ki 

 

 

1;1

min 1





x

fx

.

Do

 

01f

nên

 

   

1;1

min 0





x

f x f

, mà

 

0 1;1

, suy ra

0x

m cc tr ca hàm

s

 

fx

.

t

   

/

24

00

24



  



mx x

h x h

x

3

2

  m

.

i

m

nguyên thì

 

2

chc chn xy ra.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

382

[ I can't, I can! ]

Vy

 

3; 2; 1;0;1;2;3;4   m

th  u

kin

 

2

Kt lun: Có

8

giá tr nguyên ca

m

tha mãn

yêu cu.

Đáp án B

Câu 84. Xét hàm s:

    

      

3

2

( ) 12 (1 3)

'( ) 3 12 0 2, 2

g x x x m x

g x x x x

.

(1) 11, (2) 16, (3) 9g m g m g m     

Suy ra:

 

  f x m m

[1;3]

max ( ) 16 ; 9

.

Gi s

    m m m16 12 28, 4

th li ta

thy

m 4

nhn.

Gi s

     m m m9 12 21, 3

th li ta

thy

m 21

nhn.

Vy

m 4

và

m 21

.

Đáp án A

Câu 85. Xét hàm s

 

42

1

14 48

4

   f x x x x m

 

3

28 48



  f x x x

 

6

04

2









  







x ktm

f x x tm

x tm

.

   

2 44; 4 32   f m f m

.

 

 

 

 

2;4

min 32; max 4    f x m f x m

.

 

 

2;4

max max 44 ; 32   y m m

.

 giá tr ln nht ca hàm s

42

1

14 48

4

   y x x x m

n

 

2;4

t quá

30

thì:

44 30

74 14

62 14

62 2

32 30

  

   





     



   









m

Đáp án B

Câu 86. t

e

x

t

, vì

 

0;ln4x

 

1;4t

.

u bài toán tr thành tìm

m

 giá

tr nh nht ca hàm s

 

2

4  f t t t m

trên

n

 

1;4

bng

6

.

t

2

4s t t

, vì

 

1;4t

 

4;0  s

.

Xét hàm s

 

g s s m

vi

 

4;0s

suy ra

hàm s

 

gs

ng bin

 

4;0

.

    nh nht ca

 

f s s m

,

 

4;0s

ch t tu mút.

TH1:

 

 

4;0

min 4 6

4



   











f s m

mm

10

2

10

4











  











m

mm

tha mãn.

TH2:

 

 

4;0

min 6

4



  











f s m

mm

6

4











   











m

mm

tha mãn.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

383

[ I can't, I can! ]

Vy có

2

giá tr ca tham s

m

tha mãn yêu

cu bài toán.

Đáp án C

Câu 87. Xét hàm s

 

3

1

9 10

3

   g x x x m

.

D thy hàm s

 

gx

liên tc trên n

 

0;3

.

Ta có:

 

2

9



g x x

;

 

 

3

0

3 0;3











  



x

gx

x

Ta có:

 

0 10gm

;

 

38gm

.

Theo yêu cu bài toán,

   

 

0;3 0;3

max max 12y g x

 

0 12

3 12

















g

10 12

8 12

  













m

42   m

Mà

m

nên

 

4; 3; 2; 1;0;1;2    m

.

Vy tng các phn t ca

S

là

7

.

Đáp án A

Câu 88. Xét

42

1

14 48 30

4

    u x x x m

trên

n

 

0;2

 

3

6 0;2

0 28 48 0 2 0;2

4 0;2



  





       







x

u x x x

x

.



 

 

 

0;2

max u max (0), 2 uu

 

max 30, 14 14    m m m

;

Suy ra:

 

 

0;2

max -30 , 14Max y m m

.

Trường hợp 1:

 

0;2

14Max y m

22

14 30

30 14 30



   

  









   





mm

m

88 704

44 16









  



m

8

44 16









  



m

8 16  m

, mà

m

.

 

8;9;10;...;16m

.

Trường hợp 2:

 

0;2

-30Max y m

.

22

30 14

14 30

30 30

30 30 30



   

  









   





mm

m

88 704

0 60













m

8

0 60













m

08  m

, mà

m

.

 

0;1;2;...;8m

.

Vy tng các giá tr

m

tha mãn là:

0 1 2 ... 16 136    

.

Đáp án B

Câu 89. Ta có:

 

   

 

0;3

max 60 60, 0;3    f x f x x

và

 

0

0;3x

sao cho

 

0

60.fx

Ta có:

 

3

60 2 15 5 9 60      f x x x m x

3

2 15 5 60 9     x x m x

.

3

9 60 2 15 5 60 9       x x x m x

 

33

2 24 55 2 6 65, 0;3 .          x x m x x x

Ta có:

 

3

2 6 65 29, 0;3     x x x

nên

 

3

2 6 65, 0;3 29.       m x x x m

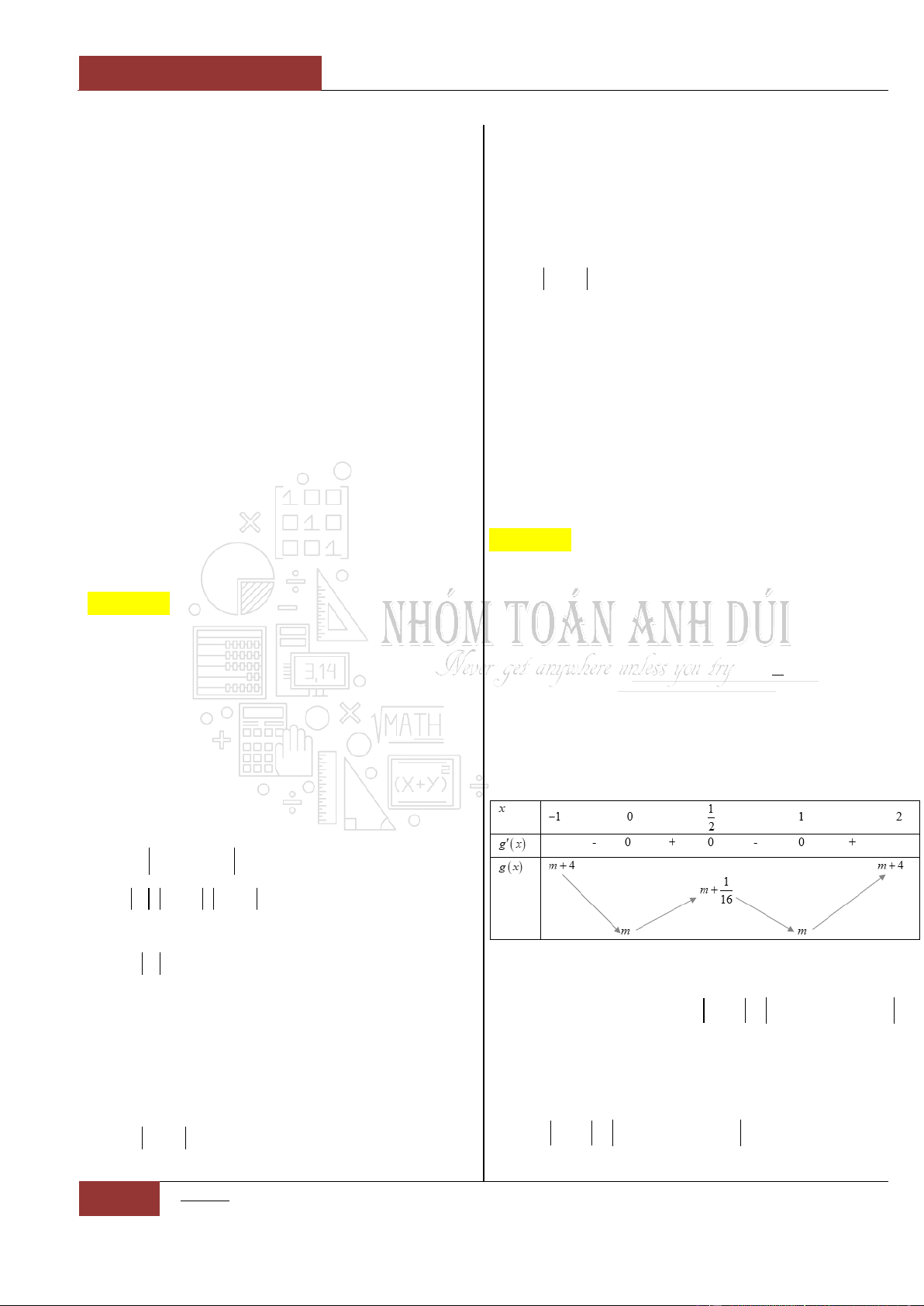
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

384

[ I can't, I can! ]

:

3

2 24 55 23    xx

nên:

 

3

2 24 55 , 0;3 23.        x x m x m

Vy

23 29m

thì

 

 

60, 0;3 .  f x x



 

0

0;3x

sao cho

 

0

60fx

thì:

3

2 24 55

2 6 65



   



   



x x m

có nghim trên

 

0;3 .

Hay

29

.

23











m

Vy

29

23











m

thì

 

 

0;3

max 60.fx

ng các giá tr ca

m

là

29 23 6.

Đáp án C

Câu 90. Xét hàm s

 

3

3  g x x x m

, ta có:

 

 

2

1 0;2

' 3 3 0

1 0;2



  

   









x

g x x

x

.

 

0 gm

,

 

12gm

,

 

22gm

.

Vy giá tr ln nht ca hàm s

 

3

3  f x x x m

bng max ca

 

; 2 ; 2  F m m m

TH1:

3

3.

3













m

Vi

 

3 3;1;5  mF

loi vì max bng

5

.

Vi

 

3 3;5;1   mF

loi vì max bng

5

.

TH2:

5

2 3 .

1





  







m

Vi

 

5 5;3;7  mF

loi vì max bng

7

.

Vi

 

1 1;3;1   mF

có max bng

3

. Chn

1.m

TH3:

1

2 3 .

5





  







m

Vi

 

1 1;1;3  mF

có max bng

3

. Chn

1.m

Vi

 

5 5;7;3   mF

loi vì max bng

7

.

Vy

 

1;1  S

có

2

giá tr

m

tho mãn yêu

c bài.

Đáp án A

Câu 91. t

 

4 3 2

2   g x x x x m

 

32

0

1

4 6 2 0

2

1









      







x

g x x x x x

x

.

Bng bin thiên ca hàm

 

gx

Da vào bng bin thiên ca

 

gx

ta suy ra bng

bin thiên hàm s:

   

4 3 2

2    f x g x x x x m

.

ng hp sau:

Trường hợp 1:

0m

. Bng bin thiên ca

   

4 3 2

2    f x g x x x x m

.

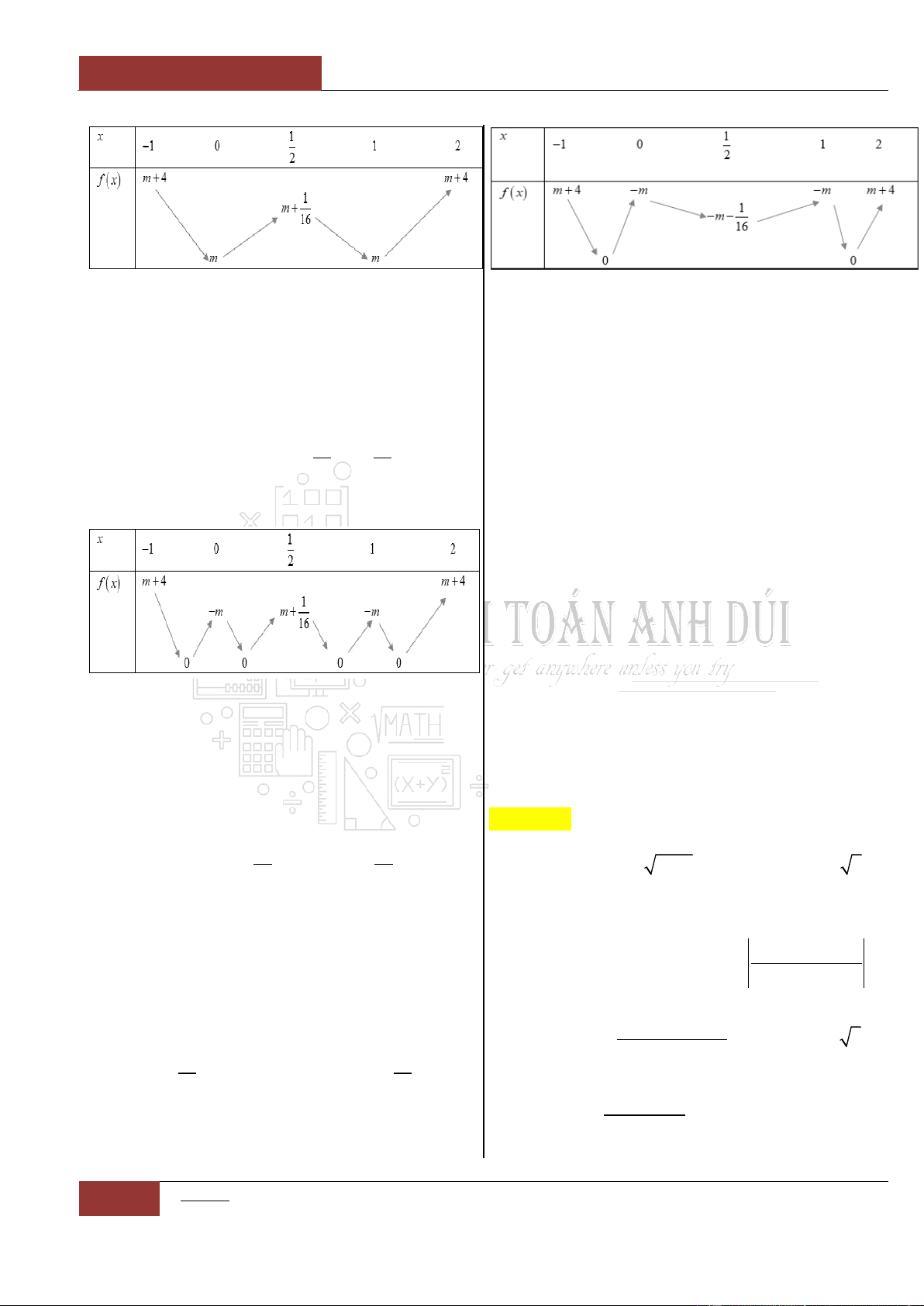
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

385

[ I can't, I can! ]

Da vào bng bin thiên, ta có:

 

 

 

 

1;2

min max 10



f x f x

4 10 3     m m m

(tha mãn)

Trường hợp 2:

11

00

16 16

      m m m

.

Bng bin thiên:

Da vào bng bin thiên ta có:

 

 

 

 

1;2

min max 10



f x f x

0 4 10 6     mm

(loi)

Trường hợp 3:

11

0

16 16

    mm

.

 ta có:

 

 

 

 

1;2

min max 10



f x f x

0 4 10 6     mm

(loi)

Trường hợp 4:

11

0 4 4

16 16

        m m m

.

Bng bin thiên:

Da vào BBT, ta có:

 

 

 

 

 

 

 

 

1;2

min max 10















f x f x

 

0 4 10

6

0 10

10

  











  





m

(loi).

Trường hợp 5:

4 0 4    mm

.

Ta có:

 

 

 

 

1;2

min max 10



f x f x

0 10 10     mm

(loi)

Trường hợp 6:

4 0 4    mm

.

Ta có:

 

 

 

 

1;2

min max 10



f x f x

4 10 7       m m m

(tha mãn)

Vy

 

7;3m

.

Đáp án A

Câu 92. t

 

2, 1;1 1; 3



     



t x x t

;

2

2.xt

Hàm s  thành

 

2

2 4t 4



mt m

gt

t

.

Xét hàm

 

2

2 4t 4



mt m

ht

t

n

1; 3





.

Ta có:

 

2

22

'





mt

ht

t

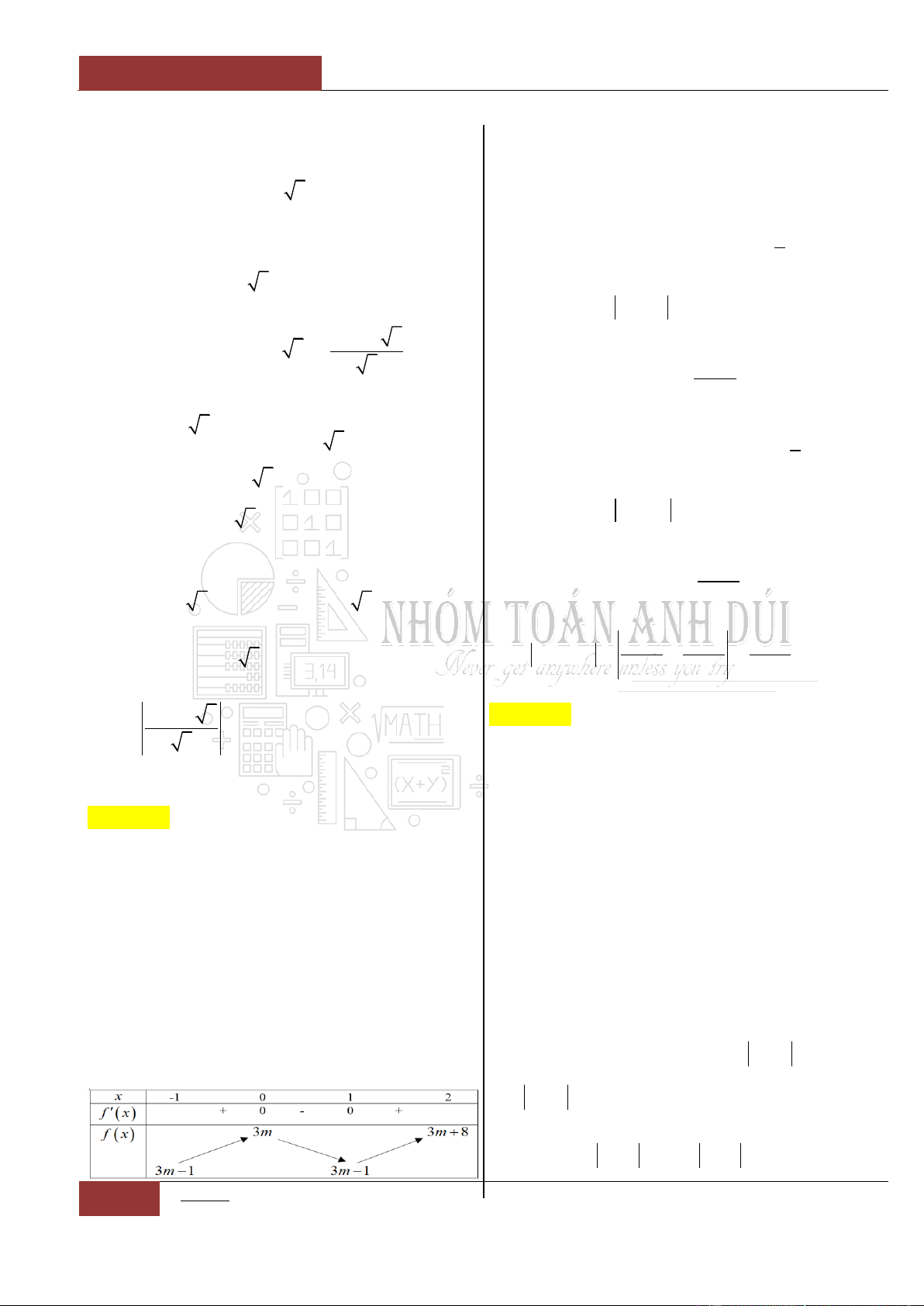
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

386

[ I can't, I can! ]

TH1:

0m

thì:

 

4ht

 

4, 1; 3 4



     



g t t a

(loi).

TH2:

0m

thì hàm s

 

ht

ng bin hoc

nghch bin trên

1; 3





Ta có:

 

2 4 3

1 2 4; 3

3



   

m

h m h

.

Nu

 

2

1 .h 3 0

23













m

h

m

và hàm s

 

ht

liên tn

1; 3





 th hàm s

 

ht

n

1; 3





ct trc hoành

0a

(loi).

Nu

 

1 . 3 0 2 2 3    h h m

.



 

(1) 0; 3 0hh

2 4 3

3





m

a

. Suy ra

3

4











m

là các giá tr



01a

.

Đáp án D

Câu 93. Xét hàm s

 

42

23  f x x x m

.

Ta có:

 

32

4 4 4 1



   f x x x x x

 

0

1















x

fx

x

.

Bng bin thiên ca hàm s trên

 

1;2

:

Vì

 

1;2

min 2021



y





 

0fx

không có nghim thuc

 

1;2

.

Trường hợp 1 :

1

3 1 0

3

   mm

.

Ta có:

 

1;2

min 3 1 3 1 2021



    y m m

2022

3

m

Trường hợp 2 :

8

3 8 0

3

    mm

.

Ta có:

 

1;2

min 3 8 3 8 2021



     y m m

2029

3

  m

.

Vy

12

2022 2029 4051

3 3 3

   mm

.

Đáp án D

Câu 94. Xét hàm s:

 

32

31    y f x x x m

 

2

36



   y f x x x

.

 

2

0

0 3 6 0

2







    







xl

f x x x

x

.

     

1 1; 2 3; 4 17     f m f m f m

.

 

 

 

 

1;4

max 17; min 3   f x m f x m

.

+Nu

3 0 3   mm

thì

 

 

1;4

max 17f x m

,

 

 

1;4

min 3f x m

.



 

 

 

 

1;4

max 3minf x f x

.

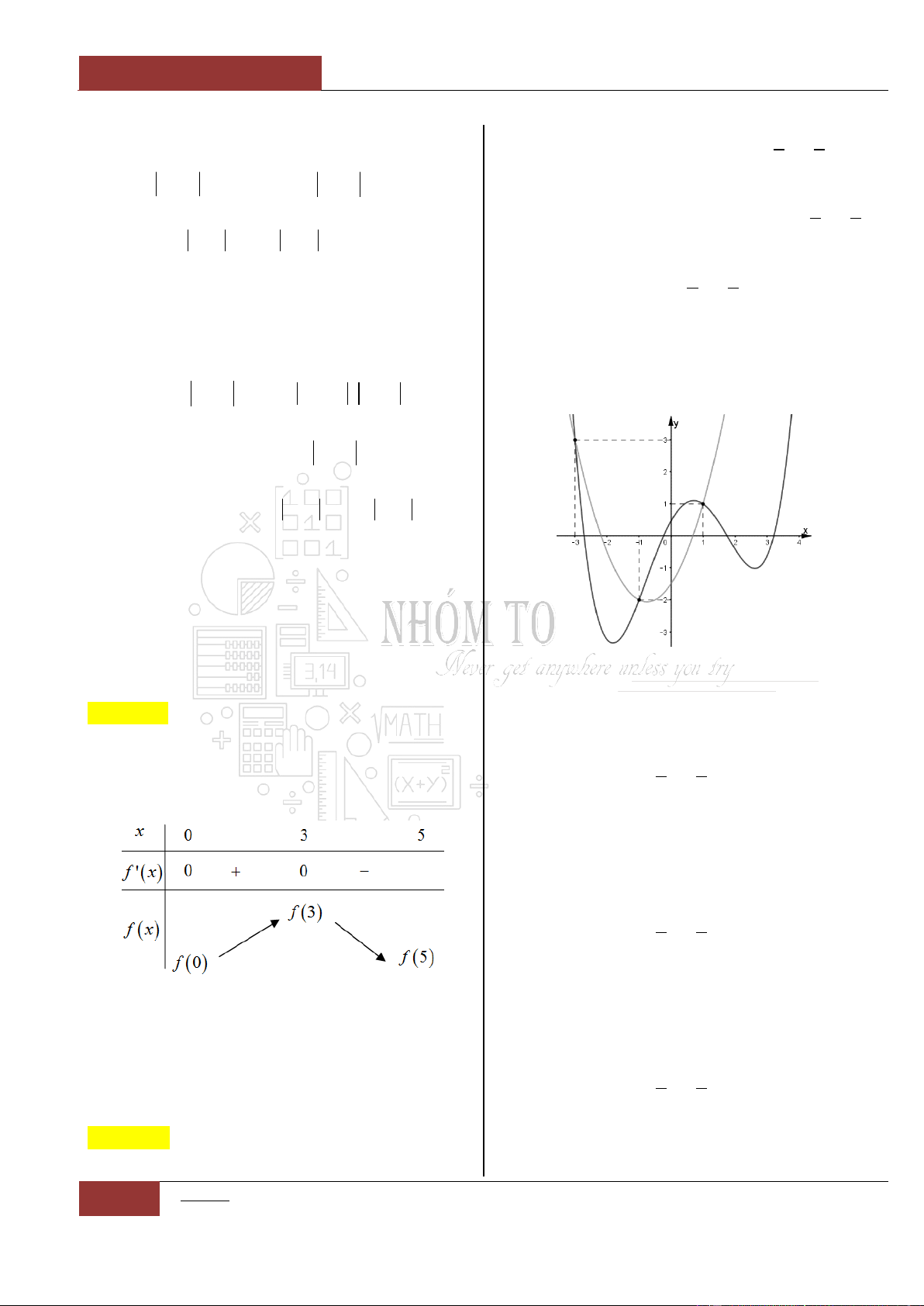
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

387

[ I can't, I can! ]

+ Nu

17 0 17    mm

thì:

 

 

1;4

max 3  f x m

,

 

 

1;4

min 17  f x m

.



 

 

 

 

1;4

max 3minf x f x

 

3 3 17 27        m m m

+ Nu

  

3 17 0 17 3      m m m

thì:

 

 

 

1;4

max max 17 , 3  f x m m

 

 

 

1;4

max 17,3 0;min 0    m m f x

.

a

 

 

 

 

1;4

max 3minf x f x

.



27

13











m

kt hp vi

 

2020;2020m

,

ta có:

   

2020; 27 13;2020   m

Vy

4002

giá tr nguyên ca

m

cn tìm.

Đáp án B

Câu 95. T  th ta có bng bin thiên ca

 

fx

n

 

0;5

 

3Mf

và

       

1 3 , 4 3f f f f

           

     

5 0 1 3 4 3 0

5 0 5

     

   

f f f f f f

f f m f

Đáp án A

Câu 96. Ta có:

   

2

33

...

22



    g x f x x x

 

2

33

...

22





   





f x x x

.

V parabol

 

2

33

:

22

  P y x x

.

Ta thy

 

P

m có to 

 

3;3

,

 

1;2

,

 

1;1

.

Trên khong

 

3; 1

 th hàm s

 



fx

nm

i

 

P

nên:

   

2

33

0

22





    





f x x x g x

.

Trên khong

 

1;1

 th hàm s

 



fx

nm

phía trên

 

P

nên:

   

2

33

0

22





    





f x x x g x

.

Trên khong

 

1;

 th hàm s

 



fx

nm

i

 

P

nên:

   

2

33

0

22





    





f x x x g x

.

Bng bin thiên

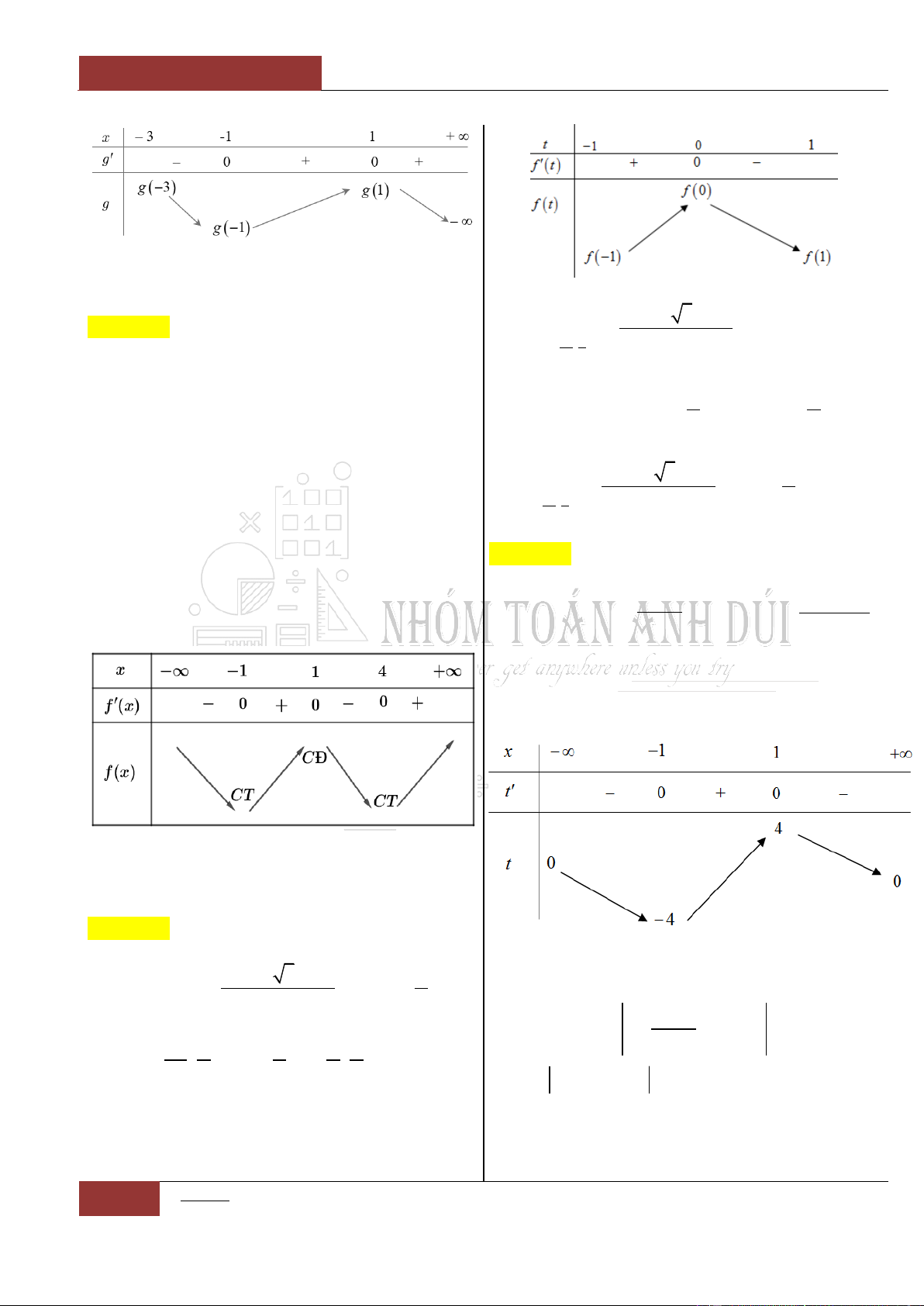
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

388

[ I can't, I can! ]

T bng bin thiên, ta có:

 

   

3;1

min 1



g x g

.

Đáp án A

Câu 97. D th ca hàm s

 

'y f x

,

ta thy:

 

1

' 0 1

4







  







x

f x x

x

     

' 0 ; 1 1;4     f x x

     

' 0 1;1 4;     f x x

Ta có bng bin thiên ca hàm s

 

y f x

Da vào bng binh

 s

3

và

4

.

Đáp án D

Câu 98. t

sin 3cos

sin

23







  





xx

tx

.

Vì

 

5

; ; 1;1

6 6 3 2 2

    

   

        

   

   

x x t

.

D  th ca hàm s

 



fx

, ta có bng

bin thiên

Ta có:

 

 

5

1;1

;

66

sin 3cos

max max

2























xx

f f t

0 sin 0

33





       





t x x

.

Vy

5

;

66

sin 3cos

max

23

























xx

ff

.

Đáp án A

Câu 99. t

2

8

1





x

t

x

. Ta có:

 

2

88

1









x

t

x

;

01



   tx

.

Bng bin thiên:

 

4;4  t

.

Hàm s

2

8

1



  







x

y f m

x

tr thành

   

 

1, 4;4    g t f t m t

.

t

   

 

1, 4;4    h t f t m t

, ta có:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

389

[ I can't, I can! ]

   



h t f t

.

   

00



  h t f t

 

4 4;4

2 4;4



   



    



  



t

.

Ta có:

 

4 0,8 1 0,2     h m m

;

 

4 6 1 5    h m m

;

 

2 1,6 1 0,6     h m m

;

 

2 4 1 5     h m m

.

 

 

4;4

Max Max



y h t

 

Max 5 ; 5  mm

.

Yêu cu bài toán

5 2020

















m

2020 5 2020

   







   



m

2025 2015

2015 2025

  







  



m

2015 2015   m

.

Vy có tt c

4031

giá tr nguyên ca tham s

m

tha mãn yêu cu bài toán.

Đáp án C

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

390

[ I can't, I can! ]

Extra Techniques:

Tips:

Sở dĩ có được đẳng thức

 

120 2.2. 2hr

là do

ta nhận thấy, dải Ribbon

tạo thành hai hình chữ

nhật bao quanh chiếc

hộp, do đó tổng chiều

dài cần thiết để bao

quanh hộp (không kể

phần dư để thắt nơ) là

tổng chu vi của hai hình

chữ nhật đó.

I.III. Ứng dụng Min – Max trong toán tối ưu

Câu 1. Một người có một dải Ribbon dài

130cm

, người đó cần bọc

dải Ribbon đỏ đó quanh một hộp quà hình trụ. Khi bọc quà, người này

dùng

10cm

của dải Ribbon để thắt nơ ở trên nắp hộp (như hình vẽ bên

dưới). Hỏi dải Ribbon có thể bọc được hộp quà có thể tích lớn nhất là

bao nhiêu?

A.

3

4000 cm



. B.

3

32000 cm



.

C.

3

1000 cm



. D.

3

16000 cm



.

Đáp án: C

Lời giải

Gọi

,hr

lần lượt là chiều cao và bán kính đáy của hình trụ.

Tổng chiều dài dây sử dụng để gói phần quà hình trụ (không kể chiều

dài dải Ribbon dùng để thắt nơ) là

130 10 120 cm

.

Ta có đẳng thức liên hệ giữa

,hr

:

 

2.2. 2. 120 2 30 30 2       h r h r h r

.

Do đó, thể tính của hình hộp được tính bởi công thức:

 

2 2 2 3

. 30 2 30 2

   

     V Bh r h r r r r

Xem

 

Vr

là một hàm số bậc ba theo biến

r

, ta xét trên khoảng

 

0;15

.

Ta có:

 

2

' 60 6 0 10



    V x r r r

.

Tính toán tại một số điểm cần thiết:

 

 

 

0;15

00

10 1000 max

15 0



















V

V V r

V

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

391

[ I can't, I can! ]

Extra Techniques:

Tips:

Vận tốc tức thời

Một chuyển động thẳng

có phương trình dạng

 

s s t

là một hàm số

có đạo hàm, khi đó vận

tốc tức thời xác định

bằng công thức

   

 

0

00

0

' lim

tt

s t s t

v t s t

tt









trong đó nếu:

00

t t t t



   

sẽ có độ chính xác càng

cao.

Extra Techniques:

Remark:

Gia tốc tức thời

Với đạo hàm cấp hai

 

ft



ta có là gia tốc tức

thời của chuyển động

 

s f t

tại thời điểm

t

.

Tất cả các kiến thức kể

trên đều có trong SGK

Đại số và Giải tích 11,

Sách nâng cao Đại số và

Giải tích 11 nâng cao và

Sách Giáo viên Đại số

Giải tích 11 nâng cao.

Vậy thể tích lớn nhất mà hộp quà có thể có là

 

3

1000



cm

.

Câu 2. Một vật chuyển động theo quy luật

32

1

9

2

  S t t

, với

t

(giây)

là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và

s

(mét) là

quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời

gian

10s

, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt

được bằng

A.

 

400 /ms

. B.

 

216 /ms

.

C.

 

30 /ms

. D.

 

54 /ms

.

Đáp án: C

Lời giải

Vận tốc của vật là

2

3

18

2



   v s t t

Xét trên đoạn

 

0,10

, ta có:

3 18 ; 0 6



     v t v t

Mà

     

 

0;10

0 0; 6 54 ; 10 30 54    v v v maxv

.

Vậy trong khoảng thời gian

10s

, kể từ lúc bắt đầu chuyển động, vận

tốc lớn nhất của vật đạt được bằng

 

54 /ms

.

Câu 3. Một sợi dây không giãn dài

1

mét được cắt thành hai đoạn.

Đoạn thứ nhất được uốn thành tam giác đều có diện tích

1

S

, đoạn thứ

hai được uốn thành đường tròn có diện tích

2

S

. Khi

12

SS

đạt giá trị

nhỏ nhất, tính

1

2

S

.

A.

23



. B.

93



. C.

3



. D.

33



.

Đáp án: D

Lời giải

Giả sử sợi dây được cắt thành hai đoạn lần lượt là

 

mx

và

 

1mx

với điều kiện

01x

.

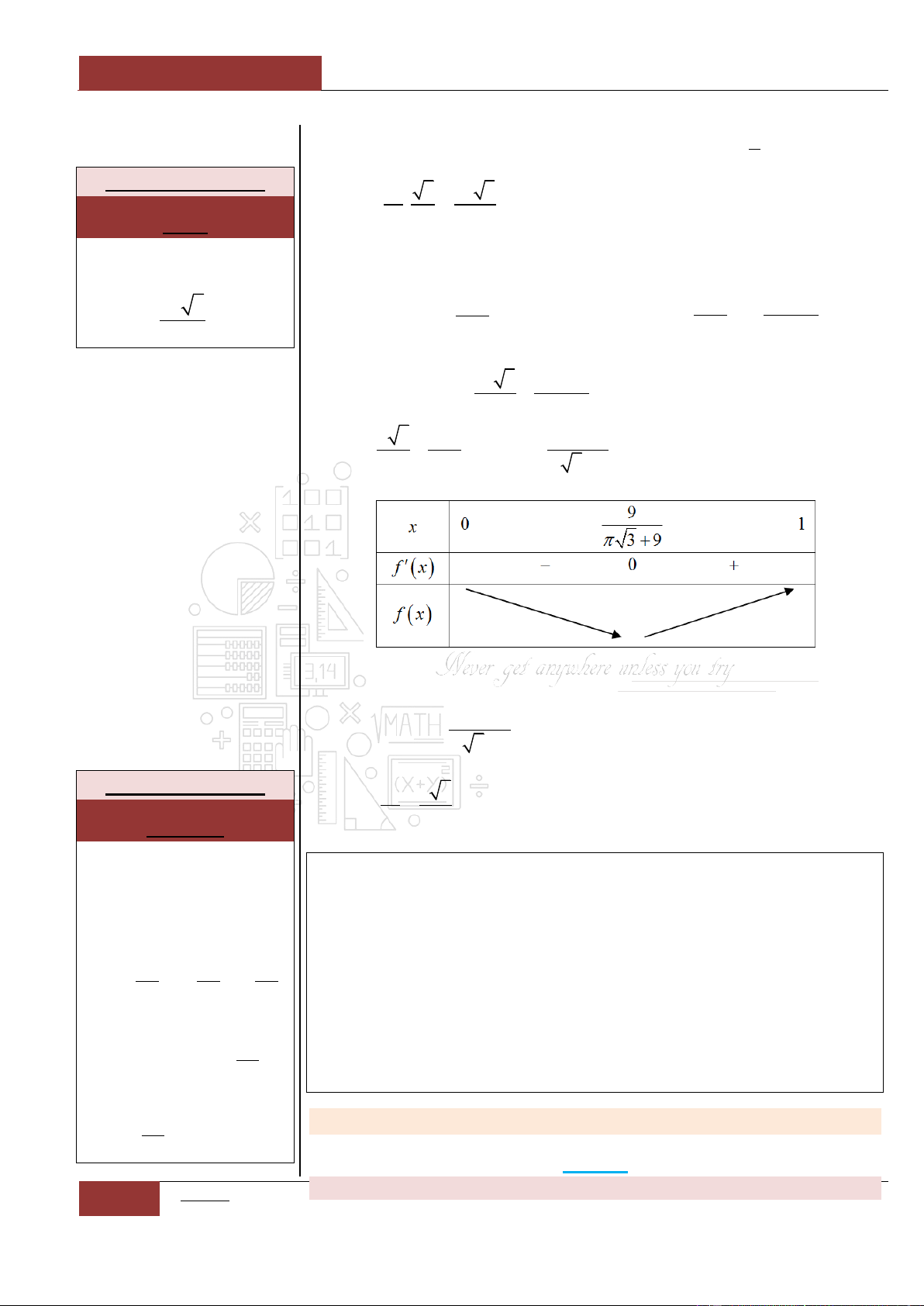
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

392

[ I can't, I can! ]

Extra Techniques:

Tips:

Diện tích tam giác đều có

độ dài một cạnh là

a

có

độ lớn là

2

3

4

a

.

Extra Techniques:

Remark:

Đối với hàm số bậc hai

 

2

,0y ax bx c a   

có hệ số

0a 

thì ta luôn

đưa được về dạng

2

2 4 4

b

ax

a a a





   





khi đó hàm số đạt giá trị

nhỏ nhất tại

2

b

x

a



và

giá trị nhỏ nhất khi đó

bằng

4a





.

Đoạn

 

mx

được quấn thành tam giác đều có cạnh là

3

x

nên có diện

tích

22

1

33

.

9 4 36

xx

S 

.

Đoạn

 

1mx

được quấn thành đường tròn bán

R

nên ta có

1

12

2

x

x R R





   

nên có diện tích

 

2

1

24

x

S















.

Đặt

 

2

12

1

3

36 4

x

f x S S





   

, có

 

3 1 9

0

18 2

39

xx

f x x







    



Dựa vào bảng biến thiên của hàm số

   

, 0;1f x x

ta thấy

12

SS

nhỏ nhất khi

9

39

x







.

Khi đó:

1

2

33

S





.

Câu 4. Một công ty kinh doanh thực phẩm ước tính rằng số tiền thu

được ở việc kinh doanh rau được tính xấp xỉ bằng công thức

 

2

29000 1000100000h x x x  

và tiền lãi được tính bằng công

thức

 

1000 100000g x x

với

x

là số tiền cho mỗi kg rau. Tìm

x

để số tiền vốn bỏ ra là ít nhất.

A.

15000

đồng. B.

30000

đồng.

C.

10000

đồng. D.

20000

đồng.

Đáp án: A

Lời giải

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

393

[ I can't, I can! ]

Extra Techniques:

Remark:

Đối với hàm số bậc hai

 

2

,0y ax bx c a   

có hệ số

0a 

thì ta

luôn đưa được về dạng

2

2 4 4

b

ax

a a a





   





khi đó hàm số đạt giá trị

lớn nhất tại

2

b

x

a



và

giá trị lớn nhất khi đó

bằng

4a





.

Extra Techniques:

Remark:

Đối với hàm số bậc ba

32

y ax bx cx d   

 

0a 

.

Với

2

30b ac

, ta gọi

12

,xx

là hai điểm cực trị

của hàm số, khi đó với

12

xx

, ta có nhận xét:

Trường hợp 1:

0a 

.

 

1

fx

là giá trị cực đại

của hàm số và

 

2

fx

là

giá trị cực tiểu của hàm

số.

Trường hợp 2:

0a 

.

 

1

fx

là giá trị cực tiểu

của hàm số và

 

2

fx

là

giá trị cực đại của hàm

số.

Số tiền vốn đầu tư vào việc mua rau được biểu thị bằng công

thức

     

2

30000 1000000000T x h x g x x x    

.

Ta có:

 

2

30000 225000000 775000000T x x x   

   

2

15000 775000000 775000000T x x    

.

Dấu

""

xảy ra khi và chỉ khi

15000x 

đồng.

Câu 5. Một công ty sản xuất khoai tây chiên giới hạn về kích thước

hộp sao cho tổng chiều dài

l

của hộp khoai tây chiên và

chu vi đường tròn đáy không vượt quá

84cm

(để phù hợp

với phương thức vận chuyển và chiều dài truyền thống của

dòng sản phẩm này, minh họa như hình bên). Công ty đang

tìm kích thước phù hợp để thiết kế hộp sao cho thể tích

đựng khoai tây chiên là lớn nhất, thể tích đó là?

A.

3

21952

cm



. B.

3

29152 cm

.

C.

3

14576 cm

. D.

3

14576

cm



.

Đáp án: A

Lời giải

Do đề bài yêu cầu tìm thể tích lớn nhất của hộp khoai tây chiên và

tổng chiều dài

l

và chu vi đường tròn đáy không vượt quá

84cm

nên:

Nếu muốn thể tích lớn nhất ta sẽ lấy giới hạn

max

của tổng độ dài tức

là

84 2 84l P l r



    

với

r

là bán kính đường tròn đáy.

Khi đó:

84 2lr





.

Thể tích của hộp khoai tây chiên được tính bằng công thức:

   

2 2 2 2 3

84 2 84 2V r l r r r r f r

    

     

.

Ta có:

   

22

0

' 168 6 6 28 0

28

r

f r r r r r

r

   









     







Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

394

[ I can't, I can! ]

Extra Techniques:

Tips:

Đây là bài toán tổng

quát, nên ta xét chi tiết

bài toán này và ghi nhận

công thức tổng quát để

về sau có thể tối ưu hóa

thời gian khi giải bài

toán về hình trụ như thế

này.

Extra Techniques:

Remark:

Bài giải bên không đi

theo hướng dùng đạo

hàm để khảo sát hàm số

mà dùng bất đẳng thức

Cauchy cho ba số không

âm.

Review: Bất đẳng thức

Cauchy

Với

n

số thực không âm

12

, ,...,

n

x x x

, bất đẳng

thức Cauchy được định

nghĩa theo công thức

sau:

1 2 1 2

... ...

n

nn

x x x n x x x   

Ta xét hàm số trên đoạn

42

0;









, nên ta chỉ cần tính toán tại một số

điểm đặc biệt:

 

42

0;

00

28 21952

max

42

0

f

f f r

f















































.

Câu 5. Cần thiết kế các thùng dạng hình trụ có nắp đậy để đựng sản

phẩm đã chế biến có dung tích

 

3

V cm

. Hãy xác định bán kính

đường tròn đáy của hình trụ theo

V

để tiết kiệm vật liệu nhất.

A.

3

3V

cm



. B.

3

V

cm



.

C.

3

2V

cm



. D.

3

2

V

cm



.

Đáp án: D

Lời giải

Gọi hai kích thước của hình trụ lần lượt là

,rh

, trong đó

r

là bán

kính đường tròn đáy và

h

là chiều cao của hình trụ.

Ta có mối quan hệ:

2

V

V r h h

r



  

.

Để tiết kiệm chi phí nhất thì diện tích toàn phần của hình trụ phải nhỏ

nhất .

Tức là:

 

2 2 2

2

2 2 2 . 2 2

VV

f r rh r r r r

rr

    



     

2 2 2

3

2 3. . .2 3 2

Cauchy

V V V V

r r V

r r r r

  

    

.

Dấu

""

xảy ra khi và chỉ khi:

2

3

2

VV

rr

r



  

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

395

[ I can't, I can! ]

Extra Techniques:

Remark:

Bài bên thay vì dùng

cách đánh giá theo bất

đẳng thức ta cũng có thể

thông qua đạo hàm để

giải quyết bài toán.

Chẳng hạn ta có:

' 100000 500000Sx  

và

' 0 5Sx  

.

Tính toán tại một số

điểm cần thiết, ta có:

 

 

 

0;50

0 100000000

5 101250000 max

50 0

S

S S x

S

















Như vậy ta cũng thu

được

5x 

là giá trị

thỏa mãn yêu cầu đề bài,

việc còn lại chỉ cần đi

tính giá tiền cho thuê

của mỗi một phòng là

bao nhiêu.

Câu 6. Một công ty bất động sản có

50

căn hộ cho thuê. Biết rằng

nếu cho thuê mỗi căn hộ với giá

2000000

đồng một tháng thì mọi căn

hộ đều có người thuê và cứ tăng thêm giá cho thuê mỗi căn hộ

100000

đồng một tháng thì sẽ có

2

căn hộ bị bỏ trống. Hỏi muốn có

thu nhập cao nhất thì công ty đó phải cho thuê mỗi căn hộ với giá là

bao nhiêu một tháng?

A.

2225000

. B.

2100000

.

C.

2200000

. D.

2250000

.

Đáp án: D

Lời giải

Gọi số căn hộ bị bỏ trống là

 

 

, 0; 50xx

.

Số tiền

1

tháng thu được khi cho thuê nhà là:

  

2

2000000 50000 50 50000 500000 100000000S x x x x      

Ta có:

 

2

50000 10 25 101250000S x x    

 

2

50000 5 101250000 101250000x    

Dấu

""

xảy ra khi và chỉ khi

5x 

.

Như vậy, mỗi căn hộ được cho thuê với giá

2000000 5.50000 2250000

thì công ty sẽ nhận được thu nhập cao nhất.

Câu 7. Khi nuôi cá thí nghiệm trong một hồ, nếu trên mỗi đơn vị diện

tích mặt hồ nuôi

n

con cá

 

*

n

thì trung bình sau mỗi vụ mỗi con

cá nặng

 

480 20P n n

(gram). Hỏi phải thả bao nhiêu con cá trên

mỗi đơn vị diện tích mặt hồ để sau mỗi vụ khối lượng cá thu được là

nhiều nhất.

A.

10

con. B.

12

con.

C.

9

con. D.

15

con.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

396

[ I can't, I can! ]

Extra Techniques:

Remark:

Do đề bài cho mối

tương quan giữa chiều

rộng và chiều sâu của

bể, nên ta có thể quy hết

về một ẩn, biểu diễn

diện tích toàn phần của

bể theo ẩn đó, từ đó xét

hàm số để tìm giá trị

nhỏ nhất của hàm số

này.

Đáp án: D

Lời giải

Số lượng cá thu được trên mỗi đơn vị diện tích mặt hồ là:

     

2

. . 480 20 20 480f n n P n n n n n     

 

2

20 480 2880 2880 2880 20 12f n n n n        

Mà

 

2

*

2880 20 12 2880,nn    

.

Dấu

""

xảy ra khi và chỉ khi

12n 

.

Hay nói cách khác, ta cần phải thả

12

con cá trên mỗi đơn vị diện tích

mặt hồ để sau mỗi vụ khối lượng cá thu được là nhiều nhất.

Câu 8. Một trang tại chăn nuôi dự định xây dựng một hầm biogas với

thể tích

3

12 m

để chứa chất thải chăn nuôi và tạo khí sinh học. Dự

kiến hầm chứa có dạng hình hộp chữ nhật có chiều sâu gấp rưỡi chiều

rộng. Hãy xác định các kích thước đáy (dài, rộng) của hầm biogas để

thi công tiết kiệm nguyên vật liệu nhất có thể (không tính đến ề dày

của thành bể). Ta có kích thước (dài; rộng – tính theo đơn vị

m

, làm

tròn đến một chữ số thập phân sau dấu phẩy) phù hợp yêu cầu là:

A. Dài

2,42m

và rộng

1,82m

. B.

Dài

2,74m

và rộng

1,71m

.

C.

Dài

2,26m

và rộng

1,88m

. D. Dài

2,19m

và rộng

1,91m

.

Đáp án: C

Lời giải

Nếu đặt chiều rộng của bể là

 

xm

thì chiều sâu của bể sẽ có độ lớn là

 

1,5xm

. Lúc này chiều dài đáy của bể sẽ bằng:

 

22

12 8

. 1,5

d

rs

V

lm

l l x x

  

Diện tích toàn phần của bể là:



    





22

88

2 2. .1,5 2. .

tp xq ñaùy

S S S x x x

xx

       

2 2 2

3

40 20 20 20 20

3 3 3 3 . . 3 1200

Cauchy

tp

S x x x

x x x x x

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

397

[ I can't, I can! ]

Extra Techniques:

Remark:

Do đề bài cho mối

tương quan giữa chiều

rộng và chiều dài của

đáy hình hộp chữ nhật

và thể tích của hộp nên

ta chỉ cần một biến để

biểu thị sự biến thiên

của chiều rộng (hoặc

chiều dài) rồi dùng mối

liên quan thứ nhất (tỉ lệ)

để biểu diện chiều dài

(chiều rộng) thông qua

biến đã cho. Vận dụng

mối liên quan trong

công thức tính thể tích

hình hộp

V abc

với

,,a b c

là độ dài ba kích

thước là có thể biểu diễn

cạnh còn lại theo ẩn ban

đầu.

Dấu

""

xảy ra khi và chỉ khi:

 

   

2

3

20 20

3 1,88

3

x x m

x

Và chiều dài của bể có độ lớn bằng

 



2

8

2,26 m

x

.

Câu 9. Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật

không có nắp và có các kích thước

 

,,x y z dm

. Biết tỉ số hai cạnh

đáy là

: 1: 3xy

, thể tích của hộp bằng

18

lít. Để tốn ít vật liệu nhất

thì kích thước của thùng là

A.

3

2; 6;

2

x y z  

. B.

1; 3; 6x y z  

.

C.

3 9 8

;;

2 2 3

x y z  

. D.

13

; ; 24

22

x y z  

.

Đáp án: A

Lời giải

Ta có:

 3yx

, lúc này theo đề bài ta có:

    

2

6

18 3 18xyz x z z

x

.

Khi đó:

 

    

2

6

2 3 . .3

tp xq ñaùy

S S S x x x x

x

       

2 2 2

3

48 24 24 24 24

3 3 3 . .3 36

Cauchy

tp

S x x x

x x x x x

.

Dấu

""

xảy ra khi









    









2

24

3 2 6

3

2

x

x x y

x

z

.

Một cách khác, ta có thể xét hàm

 

2

48

3

tp

S x x

x



trên khoảng

 

0;

.

Ta có:

2

48

6 0 2

tp

S x x

x



     

(nhận).

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

398

[ I can't, I can! ]

Extra Techniques:

Remark:

Do chi phí thuê nhân

công tính theo mét

vuông, nên để chi phí

thấp nhất thì ta đi tìm

kích thước của hồ sao

cho có tổng diện tích

xung quanh và diện tích

đáy nhỏ nhất.

Tính toán tại một số giá trị cần thiết:

 

0

0;

lim

2 36 min

lim

tp

x

tp tp

tp

x

Sx

S S x

Sx











 









 



.

Câu 10. Người ta cần xây một hồ bơi với dạng khối hộp chữ nhật

không nắp có thể tích là

3

500

3

m

. Đáy hồ là hình chữ nhật có chiều

dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ được tính theo

mét vuông (gồm đáy hồ và bồn xung quanh thành hồ). Để chi phí thuê

công nhân thấp nhất thì cần xây bờ hồ có chiều rộng là:

A.

5 m

. B.

4 m

. C.

10 m

. D.

12 m

.

Đáp án: A

Lời giải

Gọi độ dài chiều rộng của bể bơi là

 

x cm

khi đó chiều dài bể bơi là

 

2xm

. Chiều cao của bể bơi bằng:

 

2

500 250

3. .2

3

hm

xx

x



Ta có biểu thức tính tổng diện tích xung quanh và diện tích đáy theo

x

như sau:

   

22

2

250 500 250 250

2. 2 . .2 2 2

3

S f x x x x x x x

x x x

x

        

Khi đó:

2

3

250 250

3. . .2 150

Cauchy

Sx

xx



 

2

m

.

Dấu

""

xảy ra khi và chỉ khi

 

2

250

25x x m

x

  

.

"Trên đây là một số Tips chúng tôi cảm thấy rất hữu dụng trong

các bài toán hiện hành. Do mục đích phục vụ cho phần đông các

bạn học sinh nên phần trình bày khá chi tiết và khá dài. Nhưng nếu

bạn đọc hiểu bản chất vấn đề, thao tác sẽ ngắn gọn hơn, chuẩn xác

hơn và quan trọng nhất vẫn là lợi thế về thời gian nếu biết các Tips

này.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

399

[ I can't, I can! ]

TỰ LUYỆN 4 MỨC ĐỘ

Câu 1. Cho số

0a

. Trong số các tam giác

vuông có tổng một cạnh góc vuông và cạnh

huyền bằng

a

, tam giác có diện tích lớn nhất

bằng?

A.

2

3

a

. B.

2

3

6

a

.

C.

2

3

9

a

. D.

2

3

18

a

.

Câu 2. Ông

A

dự định dùng hết

2

6,5m

kính để

làm một bể cá có dạng hình hộp chữ nhật không

nắp, chiều dài gấp đôi chiều rộng (các mối ghép

có không đáng kể). Bể cá có dung tích lớn nhất

bằng bao nhiêu (kết quả làm tròn đến hàng phần

trăm).

A.

3

2,26 m

. B.

3

1,61m

.

C.

3

1,33 m

. D.

3

1,50 m

.

Câu 3. Một vật chuyển động theo quy luật

32

1

6

3

  s t t

với

t

(giây) là khoảng thời gian

tính từ khi vật bắt đầu chuyển động và

s

(mét)

là quãng đường vật di chuyển được trong

khoảng thời gian đó. Hỏi trong khoảng thời

gian

9

giây kể từ khi bắt đầu chuyển động, vận

tốc lớn nhất của vật đạt được bằng bao nhiêu?

A.

243

(m/s). B.

27

(m/s).

C.

144

(m/s). D.

36

(m/s).

Câu 4. Ông Nhân dự định sử dụng hết

2

5 m

kính để làm một bể cá bằng kính có dạng hình

hộp chữ nhật không nắp, chiều dài gấp đôi

chiều rộng (các mối ghép có kích thước không

đáng kể). Bể cá có dung tích lớn nhất bằng bao

nhiêu (kết quả làm tròn đến hàng phần trăm)?

A.

3

1,01m

. B.

3

0,96 m

.

C.

3

1,33 m

. D.

3

1,51m

.

Câu 5. Một loại thuốc được dùng cho một bệnh

nhân và nồng độ thuốc trong máu của bệnh

nhân được giám sát bởi bác sĩ. Biết rằng nồng

độ thuốc trong máu của bệnh nhân sau khi tiêm

vào cơ thể trong

t

giờ được cho bởi công thức

 

2

1





t

ct

t

 

/mg L

. Sau khi tiêm thuốc bao

lâu thì nồng độ thuốc trong máu của bệnh nhân

cao nhất?

A. 4 giờ. B. 1 giờ.

C. 3 giờ. D. 2 giờ.

Câu 6. Cho một tấm nhôm hình vuông cạnh

12

cm. Người ta cắt ở bốn góc của tấm nhôm đó

bốn hình vuông bằng nhau, mỗi hình vuông có

cạnh bằng

x

(cm), rồi gập tấm nhôm lại như

hình vẽ dưới đây để được một cái hộp không

nắp. Tìm

x

để hộp nhận được có thể tích lớn

nhất.

A.

3x

. B.

2x

.

C.

4x

. D.

6x

.

Câu 7. Một sợi dây có chiều dài

28m

được cắt

thành hai đoạn để làm thành một hình vuông và

một hình tròn. Tính chiều dài (theo đơn vị mét)

của đoạn dây làm thành hình vuông được cắt ra

sao cho tổng diện tích của hình vuông và hình

tròn là nhỏ nhất?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

400

[ I can't, I can! ]

A.

56

4





. B.

112

4





.

C.

84

4





. D.

92

4





.

Câu 8. Cho một tấm nhôm hình chữ nhật có

chiều dài bằng

10cm

và chiều rộng bằng

8cm

.

Người ta cắt bỏ ở bốn góc của tấm nhôm đó bốn

hình vuông bằng nhau, mỗi hình vuông có cạnh

bằng

 

x cm

, rồi gập tấm nhôm lại (như hình

vẽ) để được một cái hộp không nắp. Tìm

x

để

hộp nhận được có thể tích lớn nhất.

A.

8 2 21

3



x

. B.

10 2 7

3



x

.

C.

9 21

9



x

. D.

9 21

3



x

.

Câu 9. Một người nông dân có 15.000.000

đồng muốn làm một cái hàng rào hình chữ E

dọc theo một con sông (như hình vẽ) để làm

một khu đất có hai phần chữ nhật để trồng rau.

Đối với mặt hàng rào song song với bờ sông thì

chi phí nguyên vật liệu là 60.000 đồng một mét,

còn đối với ba mặt hàng rào song song nhau thì

chi phí nguyên vật liệu là 50.000 đồng một mét.

Tìm diện tích lớn nhất của đất rào thu được

A.

2

3125m

. B.

2

50m

.

C.

2

1250m

. D.

2

6250m

.

Câu 10. Ông Khoa muốn xây một cái bể chứa

nước lớn dạng một khối hộp chữ nhật không

nắp có thể tích bằng

3

288m

. Đáy bể là hình

chữ nhật có chiều dài gấp đôi chiều rộng, giá

thuê nhân công để xây bể là

500000

đồng/

2

m

.

Nếu ông Khoa biết xác định các kích thước của

bể hợp lí thì chi phí thuê nhân công sẽ thấp

nhất. Hỏi ông Khoa trả chi phí thấp nhất để xây

dựng bể đó là bao nhiêu (Biết độ dày thành bể

và đáy bể không đáng kể)?

A.

90

triệu đồng. B.

168

triệu đồng.

C.

54

triệu đồng. D.

108

triệu đồng.

Câu 11. Một người nông dân có 3 tấm lưới thép

B40, mỗi tấm dài

 

12 m

và muốn rào một

mảnh vườn dọc bờ sông có dạng hình thang cân

ABCD

như hình vẽ (bờ sông là đường thẳng

DC

không phải rào, mỗi tấm là một cạnh của

hình thang). Hỏi ông ta có thể rào được mảnh

vườn có diện tích lớn nhất là bao nhiêu

2

m

?

A.

100 3

. B.

106 3

.

C.

108 3

. D.

120 3

.

Câu 12. Cho nửa đường tròn đường kính

2AB

và hai điểm

C

,

D

thay đổi trên nửa

đường tròn đó sao cho

ABCD

là hình thang.

Diện tích lớn nhất của hình thang

ABCD

bằng?

A.

1

2

. B.

33

4

.

C

D

B

A

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

401

[ I can't, I can! ]

C.

1

. D.

33

2

.

Câu 13. Một người đàn ông muốn chèo thuyền

ở vị trí

A

tới điểm

B

về phía hạ lưu bờ đối

diện, càng nhanh càng tốt, trên một bờ sông

thẳng rộng

3 km

(như hình vẽ). Anh có thể

chèo thuyền của mình trực tiếp qua sông để đến

C

và sau đó chạy đến

B

, hay có thể chèo trực

tiếp đến

B

, hoặc anh ta có thể chèo thuyền đến

một điểm

D

giữa

C

và

B

và sau đó chạy đến

B

. Biết anh ấy có thể chèo thuyền

6 km/h

,

chạy

8 km/h

và quãng đường

8 kmBC

. Biết

tốc độ của dòng nước là không đáng kể so với

tốc độ chèo thuyền của người đàn ông. Tính

khoảng thời gian ngắn nhất (đơn vị: giờ) để

người đàn ông đến

B

.

A.

3

2

. B.

9

7

.

C.

73

6

. D.

7

1

8



.

Câu 14. Một cái hồ rộng có dạng hình chữ nhật.

Tại một góc nhỏ của hồ, người ta đóng một cái

cọc ở vị trí

K

cách bờ

AB

một khoảng có độ

dài

1m

và cách bờ

AC

8m

, rồi dùng một cây

sào ngăn một góc nhỏ của hồ để thả bèo (như

hình vẽ bên dưới). Tính chiều dài ngắn nhất của

cây sào để cây sào có thể chạm vào

2

bờ

,AB AC

và cây cọc

K

(giả thuyết đường kính

cây sào không đáng kể).

A.

5 65

4

. B.

55

.

C.

92

. D.

5 71

4

.

Câu 15. Một màn ảnh hình chữ nhật cao

1,5m

được đặt trên cao

2m

so với tầm mắt (tính từ

mép dưới của màn hình). Để nhìn rõ nhất phải

xác định vị trí đứng sao cho góc nhìn lớn nhất.

Hãy xác định vị trí đó (Biết góc

BAC

được coi

là góc nhìn)?

A.

5 m

. B.

2 m

.

C.

7 m

. D.

3 m

.

Câu 16. Bên trong một khối gỗ đồ chơi dạng

hình chóp đều có thể tích

V

, người ta đục một

khối hộp hình chữ nhật sao cho một mặt của

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

402

[ I can't, I can! ]

khối hộp đó nằm trên mặt đáy của khối chóp,

các đỉnh còn lại của khối hộp lần lượt nằm trên

các cạnh bên của khối chóp. Thể tích lớn nhất

của khối hộp là?

A.

2

V

. B.

4

V

.

C.

4

9

V

. D.

8

27

V

.

Câu 17. Một cái ao hình

ABCDE

(như hình

vẽ), ở giữa ao có một mảnh vườn hình tròn có

bán kính

10m

. Người ta muốn bắc một cầu từ

bờ

AB

của ao đến vườn.

Tính gần đúng độ dài tối thiểu

l

của cây cầu

biết:

- Hai bờ

AE

và

BC

nằm trên hai đường thẳng

vuông góc với nhau, hai đường thẳng này cắt

nhau tại điểm

O

;

- Bờ

AB

là một phần của một Parabol có đỉnh

là điểm

A

và có trục đối xứng là đường thẳng

OA

.

- Độ dài đoạn

OA

và

OB

lần lượt là

40m

và

20m

;

- Tâm

I

của mảnh vườn lần lượt cách đường

thẳng

AE

và

BC

lần lượt

40m

và

30m

.

A.

17,7lm

. B.

25,7lm

.

C.

27,7lm

. D.

15,7lm

.

Câu 18. Cho đường kính và chiều cao của hình

trụ bằng

4

. Một đường thẳng



thay đổi luôn

cắt trục hình trụ và tạo với trục góc

o

30

, đồng

thời cắt hai hình tròn đáy. Quay



quanh trục

hình trụ thu được một vật thể tròn xoay. Thể

tích lớn nhất và nhỏ nhất của vật thể đó là?

A.

16



và

16

9



. B.

 

208 96 3

9





và

16

9



.

C.

64

9



và

16

9



. D.

 

209 96 3

9





và

16

93



.

Câu 19. Một ô tô đang chạy với vận tốc 20

(m/s) thì người lái xe phát hiện có hàng rào

chắn ngang đường ở phía trước cách xe 45 m

(tính từ đầu xe tới hàng rào) nên người lái đạp

phanh. Từ thời điểm đó, xe chuyển động chậm

dần đều với vận tốc

 

5 20  v t t

(m/s), trong

đó t là thời gian được tính từ lúc người lái đạp

phanh. Khi xe dừng hẳn, khoảng cách từ xe đến

hàng rào là bao nhiêu?

A. 4 m. B. 5 m. C. 3 m. D. 6 m.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

403

[ I can't, I can! ]

Câu 20. Nhà thầy Hiếu trồng rất nhiều hoa ly

để bán phục vụ tết. Trog ngày 29 tết âm lịch

Thầy Hiếu bán hàng tại vườn từ lúc 6 giờ sáng

đến 4 giờ chiều, cứ sau 1 tiếng thầy Hiếu lại

đếm số cây hoa ly đã bán thì thấy số cây hoa ly

bán được theo thời gian là

 

23

15f t t t

(t: thời gian, đơn vị giờ). Giả sử

 

'ft

là số cây

bán được trong 1 giờ tại thời điểm t. Hỏi số cây

hoa ly bán được nhiều nhất vào lúc mấy giờ?

A.

9

giờ sáng. B. 11 giờ trưa.

C. 2 giờ chiều. D. 4 giờ chiều.

Câu 21. Một xưởng sản xuất hai loại sản phẩm.

Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và

30 giờ. Mỗi kg sản phẩm loại II cần 4 kg

nguyên liệu và 15 giờ. Xưởng có 200 kg

nguyên liệu và 1200 giờ làm việc, Biết rằng giá

bán 1 kg sản phầm loại I là 40 nghìn và 1 kg

sản phẩm loại II là 30 nghìn. Xưởng sản xuất

mỗi loại sản phẩm là bao nhiêu để thu được

nhiều lợi nhuận nhất

A. 30 kg loại I và 40 kg loại II.

B. 20 kg loại I và 40 kg loại II.

C. 30 kg loại I và 20 kg loại II.

D. 25 kg loại I và 45 kg loại II.

Câu 22. Cho hình nón

 

N

có đường cao

SO h

và bán kính đáy bằng

R

, gọi

M

là

điểm trên đoạn

SO

, đặt

 

0  OM x x h

.

 

C

là thiết diện của mặt phẳng

 

P

vuông góc

với trục

SO

tại

M

, với hình nón

 

N

. Giá trị

x

theo

h

để thể tích khối nón đỉnh

O

đáy là

 

C

lớn nhất là:

A.

2



h

x

. B.

2



h

x

.

C.

3

2



h

x

. D.

3



h

x

.

Câu 23. Khi sản xuất vỏ lon sữa bò có hình trụ

với thể tích bằng

V

, nhà thiết kế luôn đặt mục

tiêu sao cho chi phí nguyên liệu làm vỏ lon sữa

bò là ít nhất, tức là diện tích toàn phần của hình

trụ là nhỏ nhất. Muốn thể tích khối trụ đó bằng

V

và diện tích toàn phần hình trụ là nhỏ nhất

thì chiều cao

h

của lon sữa bò bằng bao nhiêu?

A.

3

4





V

h

. B.

3





V

h

.

C.

3

4





V

h

. D.

3

5

4





V

h

.

Câu 24. Một gia đình cần ít nhất

900

đơn vị

protein và

400

đơn vị lipit trong thức ăn mỗi

ngày. Mỗi kilogram thịt bò chứa

800

đơn vị

protein và

200

đơn vị lipit. Mỗi kilogram thịt

lợn chứa

600

đơn vị protein và

400

đơn vị

lipit. Biết rằng gia đình này chỉ mua nhiều nhất

1,6 kg

thịt bò và

1,1 kg

thịt lợn. Giá tiền của

một kg thịt bò là

160

nghìn đồng, một kg thịt

lợn là

110

nghìn đồng. Gọi

, xy

lần lượt là số

kg thịt bò và thịt lợn mà gia đình đó cần mua để

tổng số tiền họ phải trả là ít nhất mà vẫn đảm

bảo lượng protein và lipit trong thức ăn. Tính

22

xy

?

A.

22

1,3xy

. B.

22

2,6xy

.

C.

22

1,09xy

. D.

22

0,58xy

.

Câu 25. Một cửa hàng bán cam với giá bán mỗi

kg là

50.000

đồng. Với giá bán này thì cửa hàng

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

404

[ I can't, I can! ]

chỉ bán được khoảng

40kg

. Cửa hàng này dự

định giảm giá bán, ước tính nếu cửa hàng cứ

giảm mỗi kg

5000

đồng thì số kg bán đươc

tăng thêm là

50kg

. Xác định giá bán để cửa

hàng đó thu được lợi nhuận lớn nhất, biết rằng

giá nhập về ban đầu mỗi kg là

30.000

đồng:

A.

44.000

đ. B.

43.000

đ.

C.

42.000

đ. D.

41.000

đ.

Câu 26. Một sợi dây có chiều dài

 

Lm

được

chia thành ba phần. Phần thứ nhất được uốn

thành hình vuông, phần thứ hai được uốn thành

tam giác đều có cạnh gấp hai lần cạnh của hình

vuông, phần thứ ba được uốn thành hình tròn

(như hình vẽ).

Hỏi độ dài cạnh hình tam giác đều bằng bao

nhiêu để tổng diện tích 3 hình thu được là nhỏ

nhất?

A.

 

7

.

49 3 1





L

m

B.

 

5

.

49 3 1





L

m

C.

 

5

.

25 3 1





L

m

D.

 

7

.

25 3 1





L

m

Câu 27. Thầy Nhân dạy toán ở trường Đại học

An Giang, tỉnh An Giang muốn xây dựng một

hố ga dạng hình hộp chữ nhật có nắp bằng bê

tông với thể tích

3

3m

, biết tỉ số chiều cao và

chiều rộng của hố ga bằng

1,5

. Xác định chiều

cao của hố ga để khi xây hố tiết kiêm được

nguyên liệu nhất?

A.

 

1,2 m

. B.

 

3

45

m

8

.

C.

 

2m

. D.

 

3

34

m

29

.

Câu 28. Cho tam giác

SOA

vuông tại

O

có

//MN SO

với

, MN

lần lượt nằm trên cạnh

, SA OA

như hình vẽ bên dưới. Đặt

SO h

không đổi. Khi quay hình vẽ quanh

SO

thì tạo

thành một hình trụ nội tiếp hình nón đỉnh

S

có

đáy là hình tròn tâm

O

bán kính

R OA

. Tìm

độ dài của

MN

theo

h

để thể tích khối trụ là

lớn nhất.

A.

2



h

MN

. B.

3



h

MN

.

C.

4



h

MN

. D.

6



h

MN

.

Câu 29. Một thư viện nọ có

4

phương án cho

thuê sách như sau

 

1

Không cần mua thẻ mượn. Thuê mỗi cuốn

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

405

[ I can't, I can! ]

sách trả

5000

đ.

 

2

Mua thẻ mượn loại

20000

đ

/1

năm. Thuê

mỗi cuốn sách trả

3000

đ.

 

3

Mua thẻ mượn loại

10000

đ

/1

năm. Thuê

mỗi cuốn sách trả

4000

đ.

 

4

Mua thẻ mượn loại

60000

đ

/1

năm. Thuê

mỗi cuốn sách trả

1000

đ.

Nếu bạn mượn trên

20

cuốn sách trong

1

năm,

nên chọn phương án nào để tốn ít tiền nhất?

A. Chọn

 

1

. B. Chọn

 

2

.

C. Chọn

 

3

. D. Chọn

 

4

.

Câu 30. Một xí nghiệp chế biến sữa muốn sản

xuất những lon đựng sữa dạng hình trụ bằng vật

liệu thiếc. Để giảm giá thành khi chế tạo một

lon sữa người ta phải chọn kích thước phù hợp

để ít tốn kém vật liệu nhưng đựng được nhiều

sữa nhất. Hỏi phải chọn chiều cao

h

và bán

kính đáy

r

của hình trụ theo tỉ lệ nào dưới đây

để thỏa mãn yêu cầu đặt ra? (Thể tích khối trụ

lớn nhất).

A.

2 3 .hr

B.

.hr

C.

3.hr

D.

2.hr

Câu 31. Một vật chuyển động theo quy luật

32

1

95

2

   S t t

với

t

(giây) là khoảng thời

gian tính từ khi vật bắt đầu chuyển động và

S

(mét) là quãng đường vật di chuyển được trong

khoảng thời gian đó. Hỏi trong khoảng thời

gian

8

giây, kể từ khi vật bắt đầu chuyển động,

vận tốc lớn nhất của vật đạt được bằng bao

nhiêu ?

A.

84

(m/s). B.

48

(m/s).

C.

54

(m/s). D.

104

(m/s).

Câu 32. Một tấm nhôm hình vuông cạnh

10cm

.

Người ta cắt ở bốn góc của tấm nhôm đó bốn

tam giác cân bằng nhau (xem hình vẽ), mỗi tam

giác cân có chiều cao bằng

x

, rồi gấp tấm nhôm

đó dọc theo đường nét đứt để được một hình

chóp tứ giác đều. Tìm

x

để khối chóp nhận

được có thể tích lớn nhất.

A.

4x

. B.

2x

.

C.

1x

. D.

3

4

x

.

Câu 33. Trên một đoạn đường giao thông có

2

con đường vuông góc với nhau tại

O

như hình

vẽ. Một địa danh lịch sử có vị trí đặt tại

M

, vị

trí

M

cách vị trí đường

125 OE m

và cách

đường

1OH km

. Vì lý do thực tiễn, người ta

muốn làm một đoạn đường thẳng

AB

đi qua vị

trí

M

, biết rằng giá để làm

100m

đường là

150

triệu đồng.

O

H

M

E

A

B

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

406

[ I can't, I can! ]

Chọn vị trí

A

và

B

để hoàn thành con đường

với chi phí thấp nhất. Hỏi chi phí thấp nhất để

hoàn thành con đường là bao nhiêu?

A.

1,9603

(tỷ đồng). B.

2,3965

(tỷ đồng). .

C.

2,0963

(tỷ đồng). D.

3

(tỷ đồng).

Câu 34. Hãng pha lê nổi tiếng Swarovski của

Áo dự định thiết kế một viên pha lê hình cầu và

đặt vào bên trong nó

7

viên ruby hình cầu nhỏ

hơn, trong đó viên ruby ở chính giữa có tâm

trùng với tâm của viên pha lê và tiếp xúc với

6

viên ruby còn lại,

6

viên ruby còn lại có kích

thước bằng nhau và nằm ở các vị trí đối xứng

nhau (qua tâm của viên pha lê) và tiếp xúc với

viên pha lê (như hình vẽ). Biết viên pha lê có

đường kính

10

cm và hãng này muốn thiết kế

sao cho tổng thể tích các viên ruby bên trong là

nhỏ nhất để tiết kiệm được lượng ruby. Khi đó

bán kính của viên ruby ở giữa mà hãng pha lê

cần thiết kế gần giá trị nào nhất sau đây?

A.

2,2

cm. B.

2,3

cm.

C.

2,4

cm. D.

2,5

cm.

Câu 35. Một tấm bìa hình chữ nhật có chiều dài

40cm và chiều rộng 10cm được cắt thành hai

phần. Một phần được uốn thành hình hộp chữ

nhật có hai đáy là hình vuông cạnh

a

, phần còn

lại được uốn thành hình trụ có hai đáy là hình

tròn bán kính r (không tính hai đáy của hình

hộp chữ nhật và hình trụ) như hình vẽ sao cho

tổng thể tích của khối hộp chữ nhật và khối trụ

là nhỏ nhất. Khi đó tổng

 

ar

gần giá trị nào

nhất trong các giá trị sau?

A. 8,3cm. B. 8,4cm.

C. 8,5cm. D. 8,6cm.

Câu 36. Nam muốn xây một bình chứa hình trụ

có thể tích

3

72m .

Đáy làm bằng bêtông giá 100

nghìn đồng

2

/m ,

thành làm bằng tôn giá 90 nghìn

đồng

2

/m ,

nắp bằng nhôm giá 140 nghìn đồng

2

/m .

Vậy đáy của hình trụ có bán kính bằng bao

nhiêu để chi phí xây dựng là thấp nhất ?

A.

 

3

2

m.



B.

 

3

m.



C.

 

3

m.



D.

 

3

m.

2



Câu 37. Người ta thiết kế một thùng chứa hình

trụ (như hình vẽ) có thể tích

V

không đổi. Biết

rằng giá của vật liệu làm mặt đáy và nắp của

thùng bằng nhau và đắt gấp

3

lần so với giá vật

liệu để làm mặt xung quanh của thùng (chi phí

cho mỗi đơn vị diện tích). Gọi chiều cao của

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

407

[ I can't, I can! ]

thùng là

h

và bán kính đáy là

.r

Tính tỷ số

h

r

sao cho chi phí vật liệu sản xuất thùng nhỏ nhất.

A.

1.

h

r

B.

2.

h

r

C.

6.

h

r

D.

9.

h

r

Câu 38. Công ty của ông Bình dự định đóng

một thùng phi hình trụ (có đáy dưới và nắp đậy

phía trên) bằng thép không rỉ để đựng nước. Chi

phí trung bình cho

2

1m

thép không rỉ là

350000

đồng. Với chi phí không quá

6594000

đồng, hỏi công ty ông Bình có thể có được một

thùng phi đựng được tối đa bao nhiêu tấn nước?

(Lấy

3,14





)

A.

3,14.

B.

6,28.

C.

12,56.

D.

9,52.

Câu 39. Một nhà máy sản xuất bột trẻ em cần

thiết kê bao bì cho một loại sản phẩm mới dạng

khối trụ có thể tích

3

1.dm

Hỏi phải thiết kế hộp

đựng này với diện tích toàn phần bằng bao

nhiêu để tiết kiệm nguyên vật liệu nhất.

A.

2

3

3 2 .



dm

B.

2

3 2 .



dm

C.

2

3

3.



dm

D.

2

3

4.



dm

Câu 40. Trong một cuộc thi pha chế, mỗi đội

chơi được sử dụng tối đa

24g

hương liệu,

9

lít

nước và

210g

đường để pha chế nước cam và

nước táo. Để pha chế

1

lít nước cam cần

30g

đường,

1

lít nước và

1

g hương liệu; pha chế

1

lít nước táo cần

10g

đường,

1

lít nước và

4g

hương liệu. Mỗi lít nước cam nhận được

60

điểm thưởng và mỗi lít nước táo nhận được

80

điểm thưởng. Số điểm thưởng cao nhất mỗi đội

chơi có thể nhận được bằng?

A. 620. B.

640

.

C.

660

. D.

600

.

Câu 41. Từ một miếng tôn hình tam giác đều

cạnh

3m

, người ta dùng để chế tạo một thùng

hình trụ không đáy có thể tích

V

bằng cách cắt

ra một hình chữ nhật như hình vẽ. Giá trị lớn

nhất của

V

bằng bao nhiêu lít? (kết quả làm

tròn đến hàng phần trăm).

A.

45,92

. B.

40,72

.

C.

65,03

. D.

53,05

.

Câu 42. Một khối thủy tinh có dạng khối nón

có chiều cao bằng

20

cm, bán kính đáy bằng

5

cm. Anh A cần cắt gọt khối thủy tinh trên để tạo

thành một viên thủy tinh mới có dạng khối lăng

trụ tứ giác đều. Thể tích lớn nhất của viên thủy

tinh mới gần giá trị nào dưới đây?

A.

3

158,20 cm

. B.

3

148,15 cm

.

C.

3

125 cm

. D.

3

150 cm

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

408

[ I can't, I can! ]

Câu 43. Một vật chuyển động theo quy luật

32

1

9

2

  s t t

với

t

(giây) là khoảng thời gian

tính từ lúc bắt đầu chuyển động và

s

(mét) là

quãng đường vật đi được trong khoảng thời

gian đó. Hỏi trong khoảng thời gian

10

giây, kể

từ lúc bắt đầu chuyển động, vận tốc lớn nhất

của vật đạt được bằng bao nhiêu?

A.

 

216 m/s .

B.

 

30 m/s .

C.

 

400 m/s .

D.

 

54 m/s .

Câu 44. Một ngôi biệt thự có

10

cây cột nhà

hình trụ tròn, tất cả đều có chiều cao

4,2

m.

Trong đó,

4

cây cột trước đại sảnh có đường

kính

40

cm và

6

cây cột còn lại bên thân nhà

có đường kính

26

cm. Chủ nhà dùng loại sơn

giả đá để sơn

10

cây cột đó. Nếu giá của một

loại sơn giả đá là

380.000

đồng/

2

m

(gồm cả

tiền thi công) thì người chủ phải chi ít nhất bao

nhiêu tiền để sơn

10

cây cột đó ? (Số tiền làm

tròn đến hàng nghìn).

A.

14.647.000

(đồng). B.

13.627.000

(đồng).

C.

16.459.000

(đồng). D.

15.844.000

(đồng).

Câu 45. Người ta thiết kế một thùng chứa hình

trụ có thể tích

V

cho trước. Biết rằng đơn giá

của vật liệu làm mặt đáy và nắp của thùng bằng

nhau và gấp

3

lần so với đơn giá vật liệu để

làm mặt xung quanh của thùng (chi phí cho mỗi

đơn vị diện tích). Gọi chiều cao của thùng là

h

và bán kính đáy là

r

. Tính tỉ số

h

r

sao cho chi

phí vật liệu sản xuất thùng là nhỏ nhất?

A.

2

h

r

. B.

2

h

r

.

C.

6

h

r

. D.

32

h

r

.

Câu 46. Một nhà máy sản xuất bột trẻ em cần

thiết kê bao bì cho một loại sản phẩm mới dạng

khối trụ có thể tích

3

1.dm

Hỏi phải thiết kế hộp

đựng này với diện tích toàn phần bằng bao

nhiêu để tiết kiệm nguyên vật liệu nhất.

A.

2

3

3 2 .



dm

B.

2

3 2 .



dm

C.

2

3

3.



dm

D.

2

3

4.



dm

Câu 47. Để cắt được

40

thanh sắt có chiều dài

2,5

m và

60

thanh sắt có chiều dài

1,6

m từ các

thanh sắt có chiều dài

6

m thì cần ít nhất bao

nhiêu thanh sắt có chiều dài

6

m?

A.

33

. B.

35

. C.

34

. D.

36

.

Câu 48. Trong một cuộc thi pha chế, mỗi đội

chơi được sử dụng tối đa

24

g hương liệu,

9

lít

nước và

210

g đường để pha chế nước cam và

nước táo. Để pha chế

1

lít nước cam cần

30

g

đường,

1

lít nước và

1

g hương liệu; pha chế

1

lít nước táo cần

10

g đường,

1

lít nước và

4

g

hương liệu. Mỗi lít nước cam nhận được

60

điểm thưởng và mỗi lít nước táo nhận được

80

điểm thưởng. Số điểm thưởng cao nhất mỗi đội

chơi có thể nhận được bằng?

A.

620

. B.

640

. C.

660

. D.

600

.

Câu 49. Trong tất cả các hình nón tròn xoay mà

đường sinh có độ dài bằng

1

, hình nón có thể

tích lớn nhất

max

V

bằng bao nhiêu?

A.

62





max

V

. B.

24





max

V

.

C.

6





max

V

. D.

2

93





max

V

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

409

[ I can't, I can! ]

Câu 50. Trong tất cả các hình trụ mà tổng độ

dài đường sinh và bán kính đường tròn đáy

bằng

1

thì hình trụ có thể tích lớn nhất

 

max

V

bằng bao nhiêu?

A.

max

8



V

. B.

max

4

27



V

.

C.

max

6



V

. D.

max

63



V

.

Câu 51. Người ta cưa một cây gỗ hình trụ tròn

dài

1

m, với đường kính cây gỗ là

60

cm thành

một hộp gỗ hình chữ nhật dài 1m. Người ta phải

tìm cách để hộp đó có thể tích lớn nhất. Thể

tích lớn nhất đó bằng bao nhiêu?

A.

3

max

0,18Vm

. B.

3

max

12

Vm





.

C.

3

max

6

Vm





. D.

3

max

0,2Vm

.

Câu 52. Xét các hình trụ có diện tích xung

quanh bằng nhau và bằng

2



thì hình trụ có thể

tích

V

lớn nhất bằng bao nhiêu?

A.

max

V

3





. B.

max

V 

.

C.

3

max

V

9





. D.

max

V

không tồn tại.

Câu 53. Trong các hình chóp lục giác đều nội

tiếp trong mặt cầu bán kính bằng

1

thì hình

chóp có thể tích

max

V

bằng bao nhiêu?

A.

max

16 3

V

27



. B.

max

3

V

2



.

C.

max

V3

. D.

max

4

V

3



.

Câu 54. Xét các hình trụ tròn mà thiết diện với

hình trụ với một mặt phẳng đi qua trục hình trụ

là một hình chữ nhật có chu vi bằng

4

. Tìm thể

tích lớn nhất

 

max

V

của hình trụ đó.

A.

max

8

27



V

. B.

max

8



V

.

C.

max

4



V

. D.

max

2

27



V

.

Câu 55. Xét các hình nón có đường sinh

1l

. Xác

định thể tích lớn nhất của hình nón (

max

V?

).

A.

max

V

24





. B.

max

V

62





.

C.

max

V

6





. D.

max

2

V

93





.

Câu 56. Xét các trụ tròn có tổng bình phương

của đường sinh và bán kính đường tròn bằng

3

,

hình trụ có thể tích lớn nhất

 

max

V

bằng bao

nhiêu?

A.

 

3

max

3

2









V

. B.

 

max

2V

.

C.

 

max

23V

. D.

 

max

2V

.

Câu 57. Trong các hình chóp tứ giác đều nội

tiếp trong mặt cầu bán kính bằng

2

thì hình

chóp có thể tích lớn nhất

 

max

V

bằng bao

nhiêu?

A.

3

max

8

9









V

. B.

9

max

2

9

V

.

C.

3

max

4

3









V

. D.

max

256

27

V

.

Câu 58. Xét các tam giác cân

ABC

(đỉnh

A

)

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

410

[ I can't, I can! ]

ngoại tiếp đường tròn có bán kính

1r

. Tìm

min

ABC

S

?

A.

 

2

min 1 2 .S

B.

min 4S

.

C.

min 3 2.S

D.

min 3 3.S

Câu 59. Cho tứ diện

ABCD

có

2CD x

 

0x

các cạnh còn lại đều bằng

2

. Xác định

x

để thể tích

ABCD

đạt giá trị lớn nhất.

A.

2x

. B.

1x

.

C.

2 2.x

D.

3

.

2

x

Câu 60. Một nóc tòa nhà cao tầng có dạng hình

nón. Người ta muốn xây một bể nước có dạng

một hình trụ nội tiếp trong hình nón để chứa

nước (như hình vẽ minh họa). Cho biết

 

; ; , 0 .    SO h OB R OH x x h

Tìm thể tích

lớn nhất của hình trụ.

A.

2

4 R h

27



. B.

2

2 R h

9



.

C.

2

2 R h

27



. D.

2

4 R h

9



.

Câu 61. Một nhà sản xuất cần thiết kế một

thùng sơn dạng hình trụ có nắp đậy với dug tích

là

20

lít. Cần phải thiết kế thùng sơn đó với

bán kính nắp đậy là bao nhiêu (cm) để nhà sản

xuất tiết kiệm được vật liệu nhất?

A.

200



. B.

3

100



.

C.

3

10000



. D.

200



.

Câu 62. Đến mùa sinh sản, một con cá hồi bơi

ngược dòng để vượt một quãng đường

240

km.

Vận tốc dòng nước là

3

km/h. Nếu vận tốc bơi

của cá khi nước yên lặng là

v

(km/h) thì năng

lượng tiêu hao của con cá trong

t

giờ được cho

bởi công thức

 

3

E v cv t

, trong đó

c

là hằng

số,

E

được tính bằng jun. Tìm vận tốc của con

cá khi nước đứng yên để năng lượng tiêu hao là

ít nhất.

A.

5

km/h. B.

6

km/h.

C.

9

km/h. D.

4,5

km/h.

Câu 63. Một người cần đi từ địa điểm

A

bên

bờ biển đến hòn đảo

B

. Biết rằng khoảng cách

từ đảo

B

đến bờ biển là

15BC km

(như hình

vẽ), khoảng cách

50AC km

. Người đó có thể

đi đường thủy hoặc đi đường bộ rồi đi đường

thủy. Biết rằng kinh phí đi đường thủy là

7

(nghìn đồng/km), đi đường bộ là

5

(nghìn

đồng/km). Hỏi người đó phải đi đường bộ một

khoảng bằng bao nhiêu để kinh phí đi là nhỏ

nhất? (làm tròn đến chữ số thập phân thứ nhất)

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

411

[ I can't, I can! ]

A.

35,5

. B.

34,7

.

C.

36,5

. D.

33,7

.

Câu 64. Có một cái hồ rộng

50

m, dài

200

m.

Một vận động viên chạy phối hợp với bơi (bắt

buộc cả hai) cần đi từ góc này qua góc đối diện

bằng cách cả chạy và bơi (như hình vẽ). Hỏi

rằng sau khi chạy được bao xa (quãng đường x)

thì nên nhảy xuống bơi để đến đích nhanh nhất?

Biết rằng vận tốc bơi là

1,5

m/s và vận tốc chạy

là

4,5

m/s.

A.

197,5xm

. B.

183,3xm

.

C.

182,3xm

. D.

152,3xm

.

Câu 65. Trong hội trại kỉ niệm ngày thành lập

Đoàn thanh niên Cộng sản Hồ Chí Minh 26/3,

ban tổ chức phát cho mỗi lớp một đoạn dây dài

16

m không co dãn để khoanh trên một khoảng

đất trống một hình chữ nhật có các cạnh là các

đoạn của sợi dây đó. Phần đất để dựng trại

chính là hình chữ nhật được tạo thành. Hỏi diện

tích lớn nhất có thể của phần dựng trại là bao

nhiêu mét vuông?

A.

2

16m

. B.

2

8m

.

C.

2

10m

. D.

2

12m

.

Câu 66. Trên một đoạn đường giao thông có

hai con đường vuông góc với nhau tại

O

như

hình vẽ. Một địa danh có vị trí đặt tại

M

, vị trí

M

cách đường

216Oy m

và cách đường

1000Ox m

. Vì lý do thực tiễn, người ta muốn

làm một đoạn đường thẳng

AB

đi qua vị trí

M

, biết rằng giá để làm

100

m đường là

200

triệu

đồng. Chọn vị trí

A

và

B

để hoàn thành con

đường với chi phí thấp nhất. Hỏi chi phí thấp

nhất để hoàn thành con đường là bao nhiêu?

A.

2,093

tỷ đồng. B.

2,153

tỷ đồng.

C.

1,967

tỷ đồng. D.

3,172

tỷ đồng.

Câu 67. Một hình cầu nội tiếp trong một hình nón

tròn xoay. Một hình trụ ngoại tiếp hình cầu đó và

có đáy dưới nằm trong mặt phẳng đáy của hình

nón. Gọi

12

,VV

lần lượt là thể tích của khối nón và

khối trụ. Giá trị nhỏ nhất của của

1

2

V

là?

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

412

[ I can't, I can! ]

A.

1

3

. B.

3

7

.

C.

4

3

. D.

7

3

.

Câu 68. Một xưởng làm cơ khí nhận làm những

chiếc thùng phi với thể tích theo yêu cầu là

2000



lít mỗi chiếc. Hỏi bán kính đáy và chiều

cao của thùng lần lượt bằng bao nhiêu để tiết

kiệm vật liệu nhất?

A.

1

m và

2

m. B.

2

dm và

1

dm.

C.

2

m và

1

m. D.

1

dm và

2

dm.

Câu 69. Chi phí nhiên liệu của một chiếc tàu

chạy trên sông được chia làm hai phần.

Phần thứ nhất không phụ thuộc vào vận tốc

bằng

480

nghìn đồng trên

1

giờ.

Phần thứ hai tỷ lệ thuận với lập phương của vận

tốc, khi

 

10 /v km h

thì phần thứ hai bằng

30

nghìn đồng/giờ.

Hãy xác định vận tốc của tàu để tổng chi phí

nguyên liệu trên 1km đường sông là nhỏ nhất

(kết quả làm tròn đến số nguyên)

A.

10

(km/giờ). B.

25

(km/giờ).

C.

15

(km/giờ). D.

20

(km/giờ).

Câu 70. Bên trong một khối cầu có bán kính

1

m, người ta đặt

1

khối cầu

A

có tâm trùng với

tâm của khối cầu ban đầu, khối cầu

A

có bán

kính thay đổi. Tiếp đó người ta đặt

4

khối cầu

, , B C D

và

E

giống nhau và nằm ở các vị trí

đối xứng nhau, tiếp xúc với khối cầu

A

và tiếp

xúc với khối cầu ban đầu. Hỏi tổng thể tích của

5

khối cầu

, , , , A B C D E

nhỏ nhất là bao

nhiêu?

A.

3

0,72m

. B.

3

0,70m

.

C.

3

0,68m

. D.

3

0,66m

.

Câu 71. Cho hình nón có chiều cao

h

. Tính

chiều cao

x

của khối trụ có thể tích lớn nhất nội

tiếp trong hình nón theo

h

.

A.

2



h

x

. B.

3



h

x

.

C.

2

3



h

x

. D.

3



h

x

.

Câu 72. Một kĩ sư được một công ty xăng dầu

thuê thiết kế một mẫu bồn cầu chứa xăng với

thể tích

V

cho trước, hình dạng như hình bên,

các kích thước

, rh

thay đổi sao cho nguyên

vật liệu làm bồn xăng là ít nhất.

Người kĩ sư này phải thiết kế kích thước

h

như

thế nào để đảm bảo được đúng yêu cầu mà công

ty xăng dầu đã đưa ra

A.

0h

. B.

3





V

h

.

C.

3

2hV

. D.

3

2



V

h

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

413

[ I can't, I can! ]

ĐÁP ÁN

0

1

2

3

4

5

6

7

8

9

0

D

A

B

D

1

D

C

B

D

B

C

A

B

2

B

D

A

C

B

D

3

D

C

B

C

B

A

4

B

D

B

D

C

A

B

D

5

B

A

D

A

D

B

D

6

A

C

D

B

C

A

D

C

A

D

7

A

B

A

8

9

Ghi chú: Đáp án là sự kết hợp giữa dòng và cột . Ví dụ: Câu 24A (giao của dòng 2 và cột 4).

i

j

i

j

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

414

[ I can't, I can! ]

LỜI GIẢI CHI TIẾT

Câu 1. Giả sử tam giác

ABC

vuông ở

A

thỏa

mãn yêu cầu đề bài.

Giả sử

AB BC a

  AB a BC

Đặt

;0  BC x x a

.

  AB a x

và

 

2

22

2    AC x a x ax a

.

Diện tích tam giác

ABC

là:

 

2

11

.2

22

   S AB AC a x ax a

.

Xét hàm số:

   

2

1

2

  f x a x ax a

.

   

2

1

2.

2





    







a

f x ax a a x

ax a

2 2 2

2 2 2 2

1 2 1 2 3

.

22



    









ax a a ax a ax

x a x a

 

2

0

3



  

a

f x x

.

Vậy diện tích lớn nhất của tam giác

ABC

là:

2

2a 3

3 18









S f a

.

Đáp án D

Câu 2.

Giả sử hình hộp chữ nhật có kích thước như

hình vẽ. Ta có dung tích của bể cá:

V abc

Mặt khác theo giả thiết ta có:

2 2 6,5

2

  









ab bc ac

ab

2

2 6 6,5

2













b bc

ab

2

6,5 2

6

2



















b

c

b

ab

Khi đó:

2

6,5 2

2.

6





b

Vb

b

3

6,5 2

3





bb

V

.

Xét hàm số:

 

3

6,5 2

3





bb

fb

.

Bảng biến thiên:

Vậy bể cá có dung tích lớn nhất là:

3

39

1,50

6









fm

.

Đáp án D

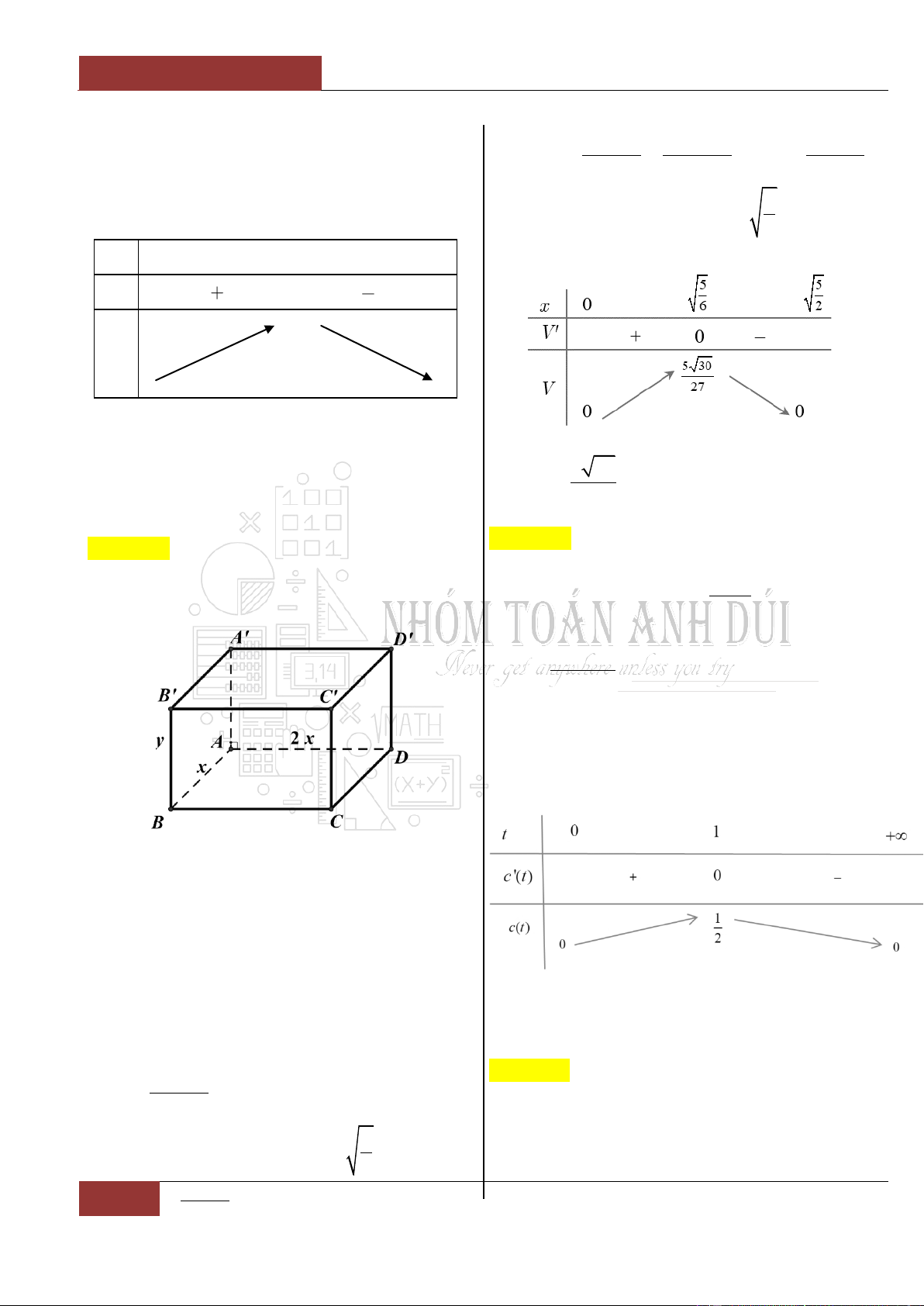
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

415

[ I can't, I can! ]

Câu 3. Ta có:

2

12



   v s t t

;

2 12



  vt

;

06



  vt

.

Bảng biến thiên:

Nhìn bảng biến thiên ta thấy vận tốc đạt giá trị

lớn nhất khi

6t

.

Giá trị lớn nhất là

 

6 36m/sv

.

Đáp án D

Câu 4.

Gọi

,xy

lần lượt là chiều rộng và chiều cao của

bể cá (điều kiện

,0xy

).

Ta có thể tích bể cá:

2

2V x y

.

Theo đề bài ta có:

2

2 2.2 2 5  xy xy x

2

6 2 5  xy x

2

52

6





x

y

x

(Điều kiện kiện

2

0 5 2 0   yx

5

0

2

  x

)

23

2

5 2 5 2

2

63



  

x x x

Vx

x

2

56

3







x

V

2

0 5 6 0



    Vx

5

6

x

3

max

5 30

1,01

27

  V m

.

Đáp án A

Câu 5. Xét hàm số:

 

2

1





t

ct

t

,

( 0)t

.

 

2

1









t

ct

t

.

 

1

0

1















t

ct

t

.

Với

1t

giờ thì nồng độ thuốc trong máu của

bênh nhân cao nhất.

Đáp án B

Câu 6. Ta có:

 

h x cm

là đường cao hình hộp

Vì tấm nhôm được gấp lại tạo thành hình hộp

t

v



v

0

9

6

0

36

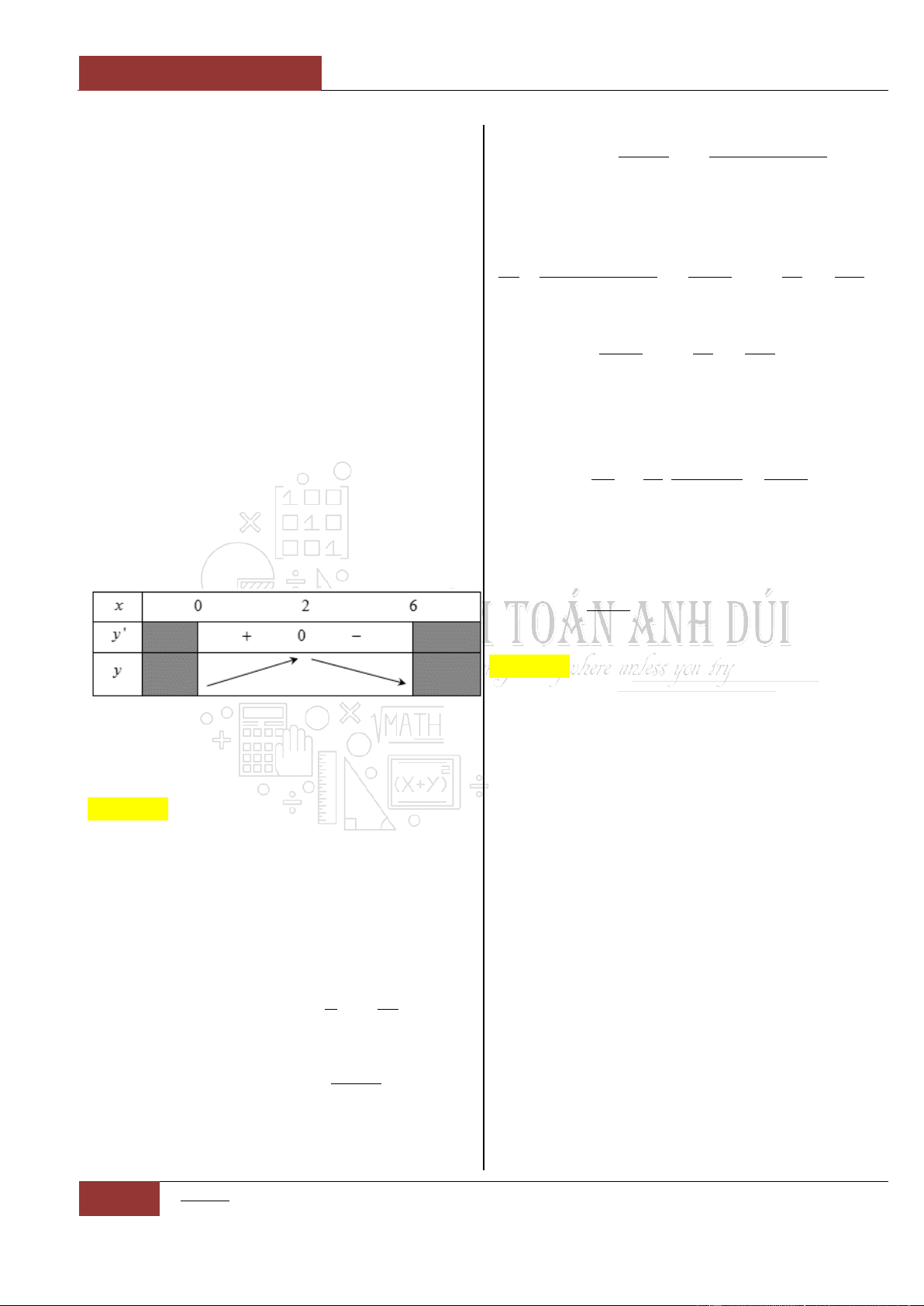
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

416

[ I can't, I can! ]

nên cạnh đáy của hình hộp là:

 

12 2 x cm

Vậy diện tích đáy hình hộp có độ lớn bằng:

 

2

12 2S x cm

.

Ta có:

 

00

0;6

12 2 0 6





  



  



xx

x

xx

Thể tích của hình hộp là:

 

2

.1. 22 V xh xS

Xét hàm số:

   

2

. 12 2 , 0;6   y x x x

.

Ta có:

      

2

' 12 2 4 12 2 12 2 12 6      y x x x x x

   

' 0 12 2 . 12 6 0 2      y x x x

hoặc

6x

(loại).

Suy ra với

2x

thì thể tích hộp là lớn nhất và

giá trị lớn nhất đó là

 

2 128y

.

Đáp án B

Câu 7. Gọi chiều dài của đoạn dây làm thành

hình vuông là

x

(

m

) (

0 28x

)

 chiều dài của đoạn dây làm thành hình tròn

là

28 x

(

m

)

+) Diện tích hình vuông là:

2

4 16









xx

.

+) Bán kính hình tròn là: R =

28

2



 x

.

 Diện tích hình tròn:

2

28 784 56

.

24



  









x x x

R

.

+) Tổng diện tích hai hình:

22

2

784 56 4 14 196

16 4 16



   

  



   





x x x

xx

.

Xét

 

2

4 14 196

16



  





  





f x x x

.

Nhận thấy

 

fx

đạt giá trị nhỏ nhất tại

2





b

x

a

 

14 16 112

.

2 4 4



  





Vậy chiều dài của đoạn dây làm thành hình

vuông để tổng diện tích của hai hình đạt giá trị

nhỏ nhất là

112

4





m

.

Đáp án B

Câu 8. Ta có:

 

h x cm

là đường cao hình hộp.

Vì tấm nhôm được gấp lại tạo thành hình hộp

nên cạnh đáy của hình hộp là:

 

10 2 x cm

và

 

82 x cm

.

Vậy diện tích đáy hình hộp có độ lớn bằng:

  

 

2

10 2 8 2  S x x cm

.

Ta có:

 

0

10 2 0 0;4

4

8 2 0











    













x

xx

x

.

Thể tích của hình hộp là:

   

. 10 8. 2 . 2 x x xV S h

.

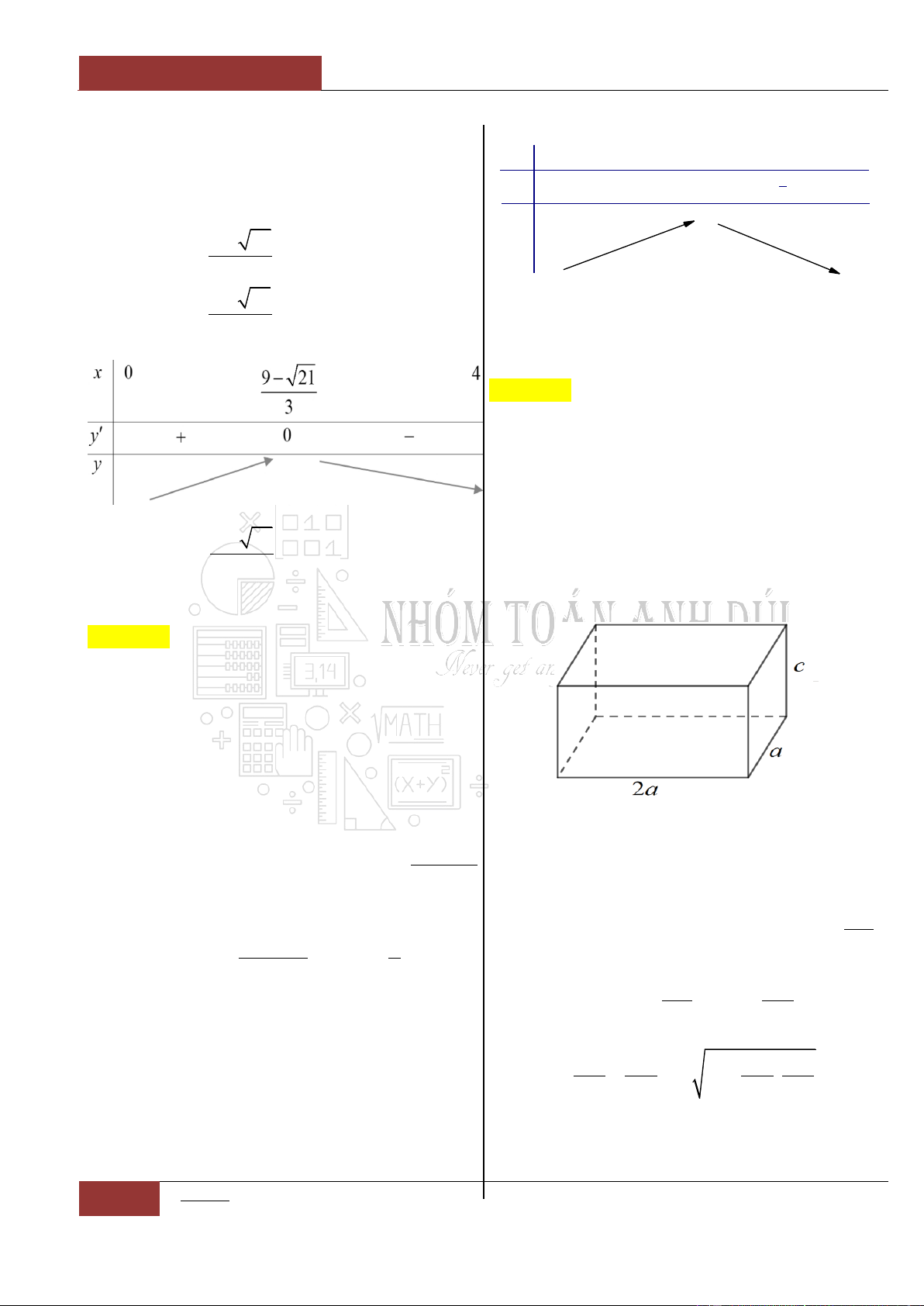
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

417

[ I can't, I can! ]

Xét hàm số:

     

. 10 2 . 8 2 0;4    y x x x x

Ta có:

2

' 12 72 80  y x x

;

 

9 21

4

3

'0

9 21

3





















xl

y

xn

.

Suy ra với

9 21

3



x

thì thể tích hộp là lớn

nhất và giá trị lớn nhất.

Đáp án D

Câu 9. Gọi

x

là chiều dài 1 mặt hàng rào hình

chữ E ( trong ba mặt song song,

0x

).

Gọi

y

là chiều dài mặt hàng rào hình chữ E

song song với bờ sông (

0y

).

Số tiền phải làm là:

500 5

.3.50000 .60000 15.000.000

2



   

x

x y y

Diện tích đất:

2

500 5 5

. . 250

22



   

x

S x y x x x

Ta có:

' 250 5Sx

.

' 0 250 5 50.    S x x

Bảng biến thiên:

Vậy:

 

2

0;

max 6250 ( )



Sm

khi

50.x

Đáp án D

Câu 10. Theo bài ra ta có để chi phí thuê nhân

công là thấp nhất thì ta phải xây dựng bể sao

cho tổng diện tích xung quanh và diện tích đáy

là nhỏ nhất.

Gọi ba kích thước của bể là

a

,

2a

,

c

   

 

0, 0a m c m

.

Ta có diện tích cách mặt cần xây là:

22

2 4 2 2 6    S a ac ac a ac

.

Thể tích bể:

2

.2 . 2 288  V a a c a c



2

144

c

a

Suy ra:

22

2

144 864

2 6 . 2   S a a a

a

22

3

432 432 432 432

2 3. 2 . . 216    S a a

a a a a

.

Vậy

2

min

216mS

, khi đó chi phí thấp nhất là:

216.500000 108

triệu đồng.

-

∞

50

0

S'

S

0

x

+

∞

0

6250

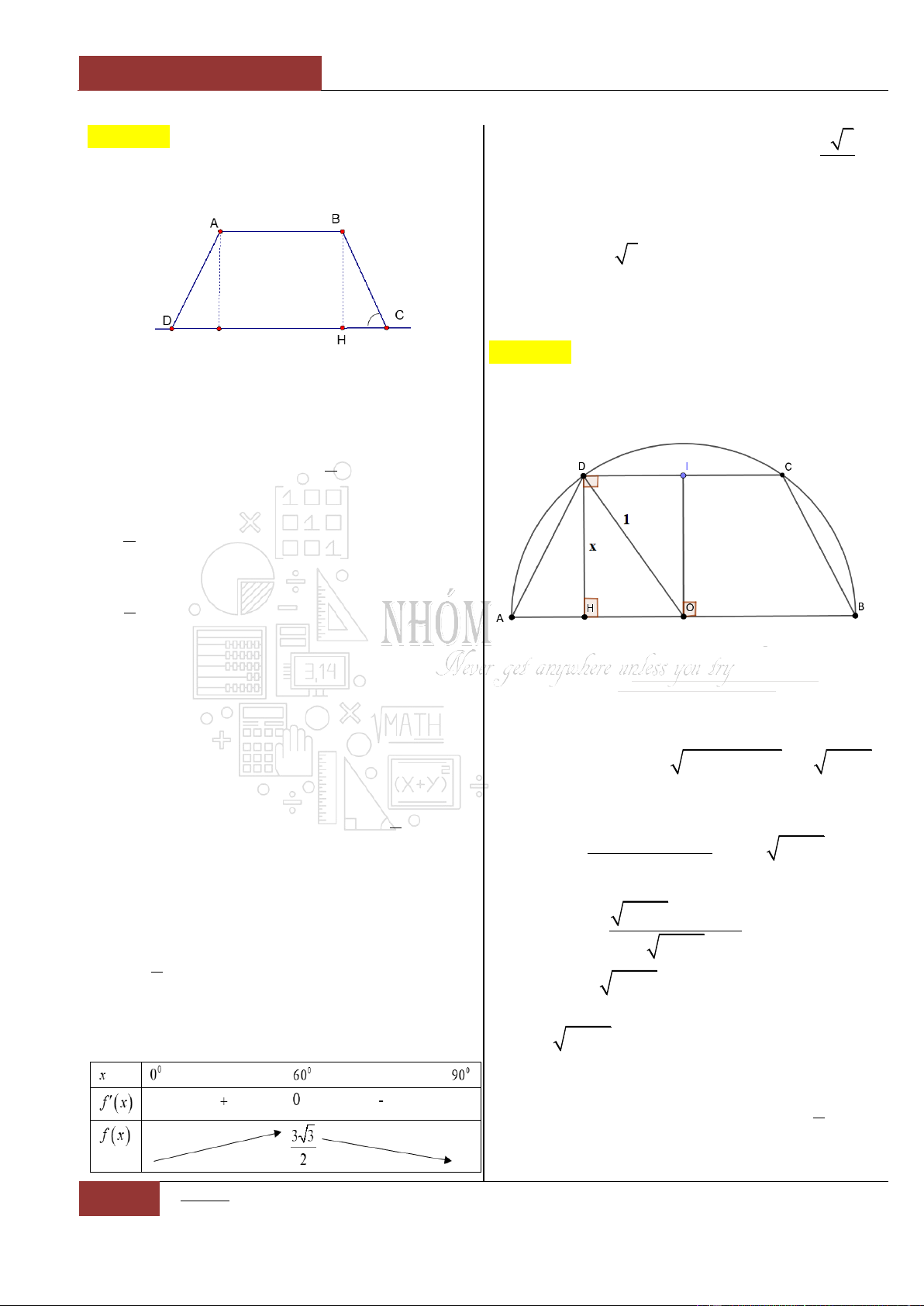
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

418

[ I can't, I can! ]

Đáp án D

Câu 11.

Kẻ đường cao

BH

, gọi số đo 2 góc ở đáy

CD

của hình thang là

 

, 0 ;90  xx

.

Diện tích mảnh vườn là:

 

1

2

S BH AB C D

 

1

.sin 2. 2 .cos

2

S BC x AB BC x

 

2

1

2sin sin2

2

S AB x x

Xét hàm số

 

2sin sin2f x x x

với

 

00

0 ;90x

có

 

2cos 2cos2



f x x x

.

Ta có:

 

0 2cos 2cos2 0



   f x x x

2

1

cos

2cos cos 1 0

2

cos 1







    







x

xx

x

Do

 

00

0 ;90x

nên ta nhận

0

1

cos 60

2

  xx

.

Ta có bảng biến thiên:

Từ bảng biến thiên ta thấy:





 

00

0 ;90

33

max

2

fx

đạt được tại

0

60x

.

 

2

max 108 3Sm

khi góc ở đáy

CD

của

hình thang bằng

0

60

 

0

60CD

.

Đáp án C

Câu 12.

Gọi

H

là hình chiếu vuông góc của

D

lên

AB

,

I

là trung điểm của đoạn

CD

và

O

là trung

điểm của

AB

. Đặt

DH x

,

01x

. Ta có

2 2 2

2 2 2 2 1     DC DI OH OD DH x

.

Diện tích của hình thang

ABCD

là

 





2

11

2



    

AB CD DH

S f x x x

.

Ta có

 

22

2

1 1 2

1

  







xx

fx

x

.

 

22

0 1 1 2 0



     f x x x

(*)

Đặt

2

1tx

, (điều kiện

0t

) khi đó phương

trình (*) trở thành

2

1

2 1 0

1

2







   







t

tt

t

.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

419

[ I can't, I can! ]

Với

1t

 loại.

Với

1

2

t

ta có:

22

1 3 3

1

2 4 2

      x x x

.

Bảng biến thiên

Vậy diện tích lớn nhất của hình thang

ABCD

bằng

33

4

.

Đáp án B

Câu 13. Cách 1: Anh chèo thuyền của mình

trực tiếp qua sông để đến

C

và sau đó chạy đến

B

Thời gian chèo thuyền trên quãng đường

AC

:

3

0,5

6



(giờ)

Thời gian chạy trên quãng đường

CB

:

8

1

8



(giờ)

Tổng thời gian di chuyển từ

A

đến

B

là

1,5

(giờ).

Cách 2: Chèo trực tiếp trên quãng đường

22

3 8 73  AB

mất

h

73

1 26

6





.

Cách 3:

Gọi

 

kmx

là độ dài quãng đường

BD

;

 

8 km x

là độ dài quãng đường

CD

.

Thời gian chèo thuyền trên quãng đường

2

9AD x

là:

2

9

6

x

(giờ)

Thời gian chạy trên quãng đường

DB

là:

8

 x

(giờ)

Tổng thời gian di chuyển từ

A

đến

B

là

 

2

98

68





xx

fx

Xét hàm số

 

2

98

68





xx

fx

trên khoảng

 

0; 8

.

Ta có:

 

2

1

8

69







x

fx

x

;

 

2

9

0 3 9 4

7



     f x x x x

Bảng biến thiên

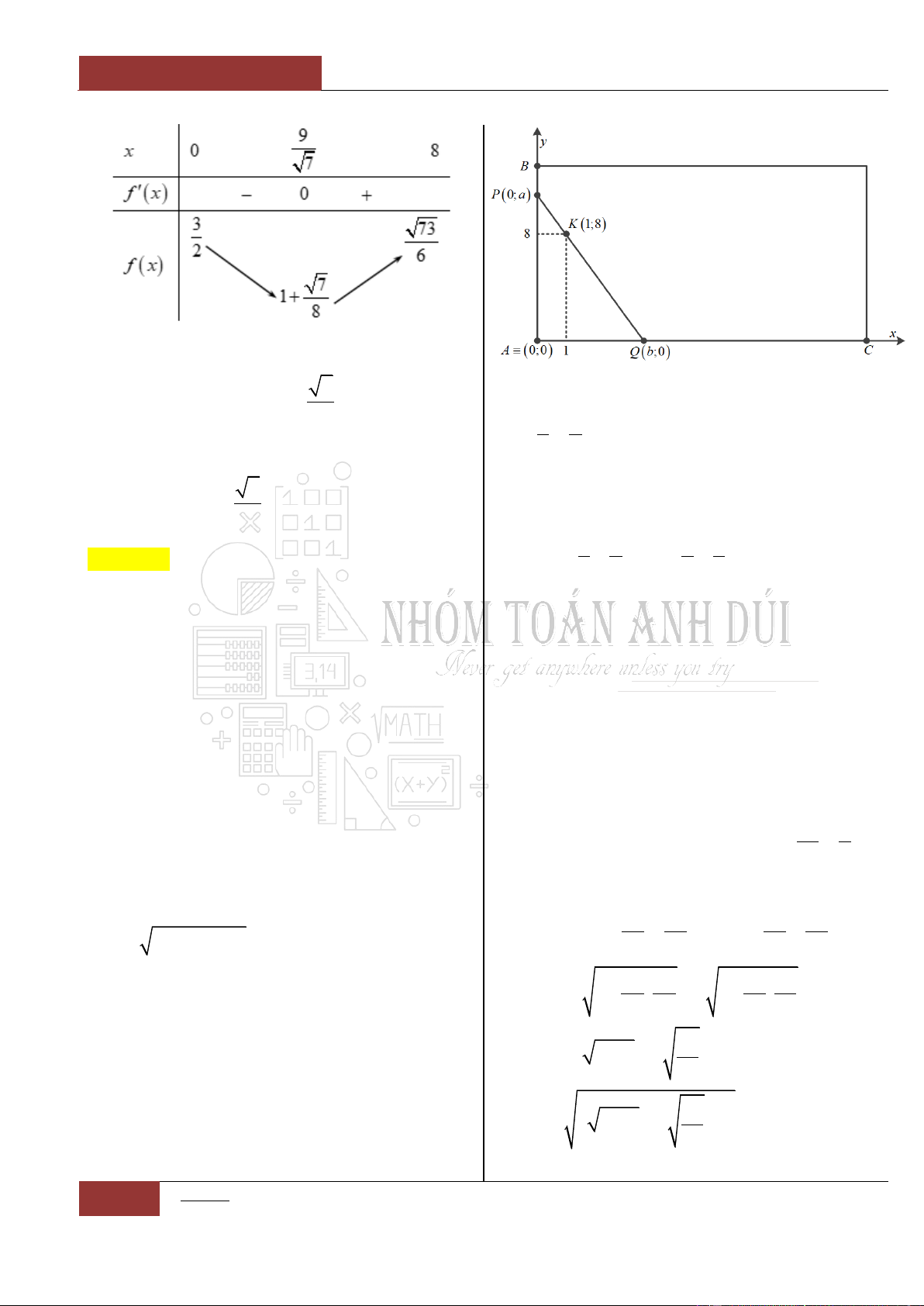
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

420

[ I can't, I can! ]

Dựa vào BBT ta thấy thời gian ngắn nhất để di

chuyển từ

A

đến

B

là:

h

7

1 1 20

8





.

Vậy khoảng thời gian ngắn nhất để người đàn

ông đến

B

là:

h

7

1 1 20

8





.

Đáp án D

Câu 14. Phân tích hướng giải

- Hình chữ nhật không rõ kích thước dài và

rộng nên ta không thể nào tính toán một cách

hàn lâm theo độ dài cạnh được



Chuyển sang

tọa độ hóa.

- Gắn trục tọa độ

Oxy

.

- Xác định tọa độ điểm

,AK

.

- Xác định phương trình đường thẳng:

PQ

.

- Tìm giá trị nhỏ nhất của đoạn thẳng

PQ

biết

22

PQ AP AQ

.

- Các phương pháp: Dùng bất đẳng thức, dùng

đạo hàm khảo sát hàm số.

Lời giải

Lắp trục

Oxy

, có

Ox

theo phương cạnh

AC

và

Oy

theo phương

AB

như hình vẽ dưới đây.

Phương trình đường thẳng

AB

theo đoạn chắn:

 

:1

xy

d

ba



.

Mặt khác, vì:

 

Kd

, nên ta có:

 

1 8 8 1

1 1 *

b a a b

    

.

Cách 1: Bất đẳng thức Cauchy.

Ta có:

2 2 2 2 2

PQ AP AQ a b   

.

Vì:

2

max maxPQ PQ  

.

Ta có:

 

2 2 2 2 2

2 2 2 2

2 2 2

33

2

3

22

3

2

3

2

3

8

.1 ,

0

44

22

44

3 . . 3 . .

22

3 16 3

4

3 16 3

4

     

        



   

       

   

   

   

PQ AP AQ a b k k

kk

a b k k a b k

ab

k

k k k k

PQ a b k

a a b b

k k k k

PQ a b k

a a b b

k

PQ k k

k

PQ k k

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

421

[ I can't, I can! ]

Dấu

""

xảy ra khi và chỉ khi:

2

3

2

3

4

22

81

1









  











k

a

ak

a

kk

bb

b

ab

33

3

3 3 3

3

33

44

22

8 2 128 2

11

4

10

5

2

250

128 2









   





   

















   















a k a k

kk

bb

k

k k k

ak

a

k

bb

k

.

Vậy

2 2 2 2

min

10 5 5 5PQ a b    

là

chiều dài ngắn nhất có thể của cây sào để cây

sào có thể chạm vào

2

bờ

,AB AC

và cây cọc

K

.

Đáp án B

Cách 2: Dùng đạo hàm để khảo sát hàm số.

Từ

   

8 1 1 8 8

* 1 1 0 8

8

aa

ba

a b b a a a



           



.

Ta có:

2

2 2 2 2

8



   







a

PQ a b a

a

.

Xét hàm:

   

2

, 8;

8

a

f a a a

a



    







.

Suy ra:

 

   

23

2 8 16

' 2 . 2 0

8

88



    





aa

f a a a

a

aa

.

 

3

8 8 8 2 10       a a a

Bảng biến thiên:

Dựa vào bảng biến thiên của đồ thị hàm số

 

y f a

, ta thấy:

 

   

2

min min

8;

min 10 125 5 5



    PQ f a f PQ

Dấu

""

xảy ra tại

10

5

AP a

AQ b











.

Câu 15. Phân tích hướng giải

- Thấy rằng góc nhìn

BAC

không thể tính trực

tiếp vì tam giác thiếu yếu tố vuông góc, tuy

nhiên ta hoàn toàn có thể gián tiếp biểu diễn

BAC

từ góc

OAC

và

OAB

.

- Dùng hàm lượng giác

tan

có thể giải quyết

bài toán.

-

 

0

max tan max, 0;90BAC BAC BAC    

.

-

 

tan tan

tan

1 tan .tan

ab







.

- Các phương pháp: Đạo hàm, khảo sát hàm số

và bất đẳng thức.

Lời giải

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

422

[ I can't, I can! ]

Ta có:

 

tan tanBAC OAC OAB

tan tan

1 tan .tan







OAC OAB

.

Mặt khác, vì:

3,5

tan

2

tan

OC

OAC

OA x

OB

OAB

OA x

















.

Suy ra:

tan tan

tan

1 tan .tan







OAC OAB

BAC

OAC OAB

 

2

3,5 2

1,5

tan *

3,5 2

7

1.







x

xx

BAC

x

xx

Cách 1: Xét hàm số:

2

1,5

7

x

y

x





.

Ta có:

 

2

1,5 10,5

' 0 7 7

7

0Do



      





x

y x x

x

.

Bảng biến thiên:

Dựa vào bảng biến thiên của đồ thị hàm số, ta

thấy rằng:

 

37

max tan

28

BAC

 

37

max arctan

28

BAC

Dấu

""

xảy ra khi và chỉ khi:

7x 

.

Đáp án C

Cách 2: Dùng bất đẳng thức Cauchy.

 

2

1,5 1,5 1,5

* tan

7

27

77

2 . 2 7Do

   





  





x

BAC

x

xx

Suy ra:

   

1,5 1,5

max tan max arctan

2 7 2 7

BAC BAC  

Dấu

""

xảy ra khi và chỉ khi:

 

7

70Dox x x

x

   

.

Câu 16. Phân tích hướng giải

- Bài toán không cho dữ kiện liên quan đến độ

dài cạnh mà chỉ cho yếu tố thể tích. Và bài toán

yêu cầu tính thể tích khối hộp nhỏ bên trong

nên ta sẽ vận dụng hình học vào bài toán để tính

thể tích theo phương pháp phân chia tỉ lệ.

- Dùng định lý Thales có thể giải quyết nhanh

được bài toán.

Lời giải

Ta kí hiệu như hình vẽ bên dưới:

S

N

P

Q

A

B

C

M

D

O

T

'O

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

423

[ I can't, I can! ]

Đặt:

 

, 0 1

SP

kk

SC

  

.

Ta có:

1

NP SP

k

BC SC

CP SC SP

k

SC SC

PT CP

k

SO SC











  





  





.

Suy ra:

 

.

1.

NP k BC

PT k SO















2

khoái hoäp chöõ nhaät

. . .V NP PQ PT NP PT  

   

22

khoái hoäp chöõ nhaät

1 . . 1V k k BC SO  

Mặt khác:

 

2

khoái choùp

11

. . . 2

33

V V BC CD SO BC SO  

.

Từ

   

1 , 2

ta suy ra:

   

2 2 2

khoái hoäp chöõ nhaät

1

3. 1 . . . 3 1 .

3

V k k BC SO k k V   

Xét hàm số:

   

 

2 2 3

3 1 . 3 3 . , 0 1f k k k V k k V k     

Ta có:

 

2

' 6 9 . 0

3

f k k k V k    

.

Bảng biến thiên:

k

 

fk

0

2

3

1

0



 

'fk



0

4

9

V

0

Dựa vào bảng biến thiên của đồ thị hàm số, ta

thấy rằng thể tích khối hộp lớn nhất khi và chỉ

khi

2

3

NP

k

BC



và khi đó, thể tích khối hộp

chữ nhật là

khoái hoäp chöõ nhaät

4

9

V

V 

.

Đáp án C

Câu 17. Phân tích hướng giải

- Đề bài không cho các dữ kiện về số quá nhiều,

chỉ cho khoảng cách của một số điểm nào đó và

những hình vẽ là những phần của các đồ thị

hàm số nào đó (Parabol, đường tròn,…)



tọa

độ hóa bài toán.

- Viết phương trình:

+ Parabol.

+ Đường tròn.

- Phương pháp áp dụng:

+ Bất đẳng thức trong tam giác.

+ Độ dài đoạn thẳng trong

Oxy

.

+ Khảo sát hàm số.

Giả sử: Ta lấy

1

đvđd

10m

.

Khi đó ta có thể chuyển bài toán như hình vẽ sau:

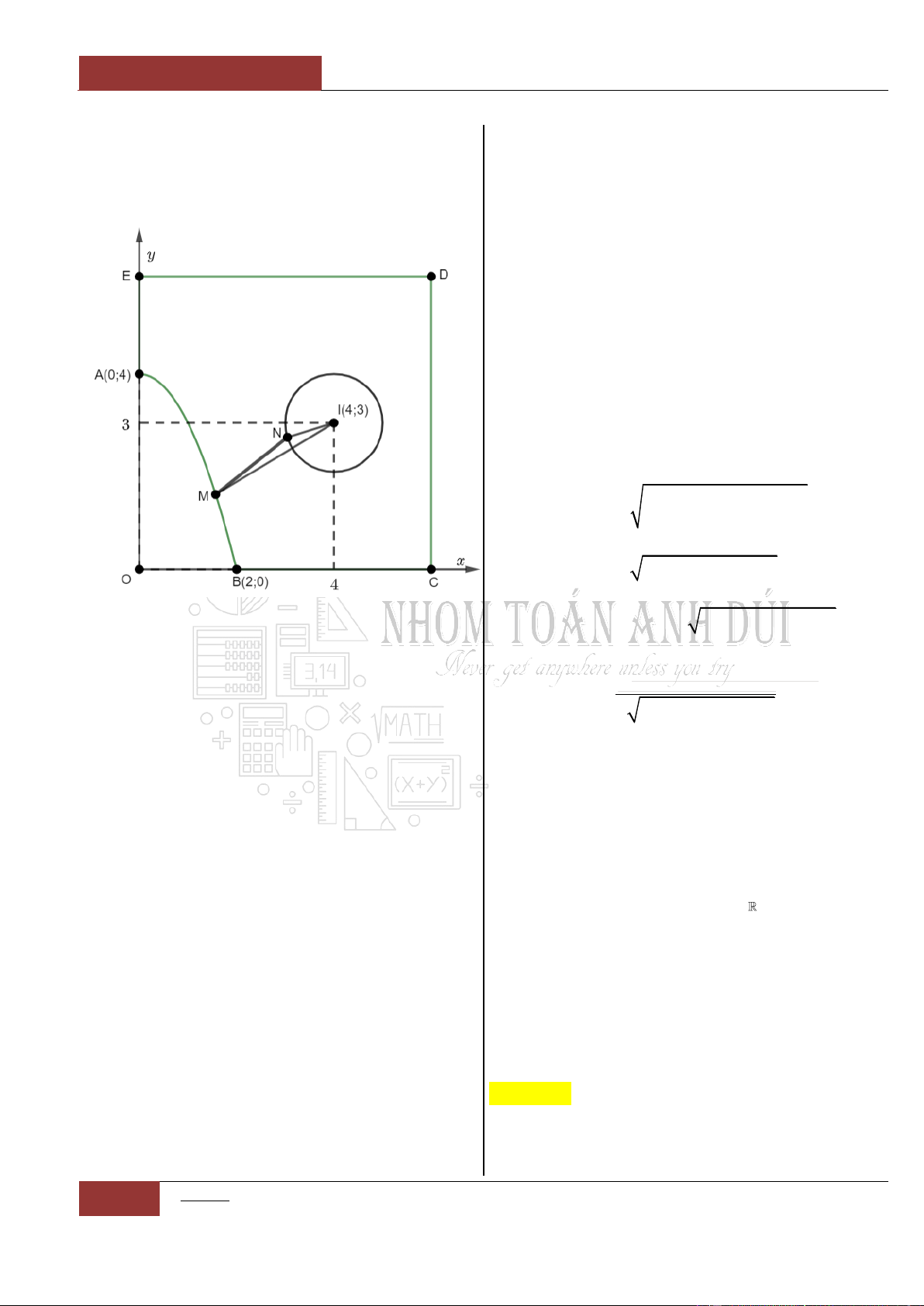
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

424

[ I can't, I can! ]

Gắn hệ trục tọa độ

Oxy

với

Ox

theo phương

của cạnh

OC

và trục

Oy

theo phương

OE

như

hình vẽ, ta thu được:

- Phương trình Parabol:

Giả sử Parabol có dạng:

 

2

:P y ax bx c  

.

Vì:

   

0;4

2;0

' 2;0

AP

BP



















 

Do Parabol nhaän truïc Oy laøm truïc ñoái xöùng haøm chaün

Nên ta có:

4

4 2 0

0

c

a b c

b







  









 

2

1

0 : 4

4

a

b P y x

c







     









Phương trình đường tròn tâm

 

4;3I

bán kính

1R 

có phương trình:

 

   

22

, ,1 : 4 3 1C I x y   

.

Ta có:

1MN MI NI MI   

(đvđd) (Bất

đẳng thức trong tam giác).

Dấu

""

xảy ra khi và chỉ khi:

,,M N I

thẳng

hàng.

Suy ra:

min

1MN MI

.

Gọi

 

2

;4M x x P  

.

Khi đó:

 

2

1 4 1 1MI x x      

42

8 17 1x x x    

.

Xét hàm số:

 

42

8 17 1y f x x x x     

.

Ta có:

 

3

42

4 2 8

'0

2 8 17

xx

fx

x x x





  

1,39176...xA  

.

Tính toán tại một số điểm cần thiết:

 

     

 

lim

1,77 ñvñd min

lim

x

fx

f A f x

fx







 









 





.

Như vậy:

   

min

1 1,77 ñvñdMN MI  

min

17,7MN m

.

Đáp án A

Câu 18. Phân tích hướng giải

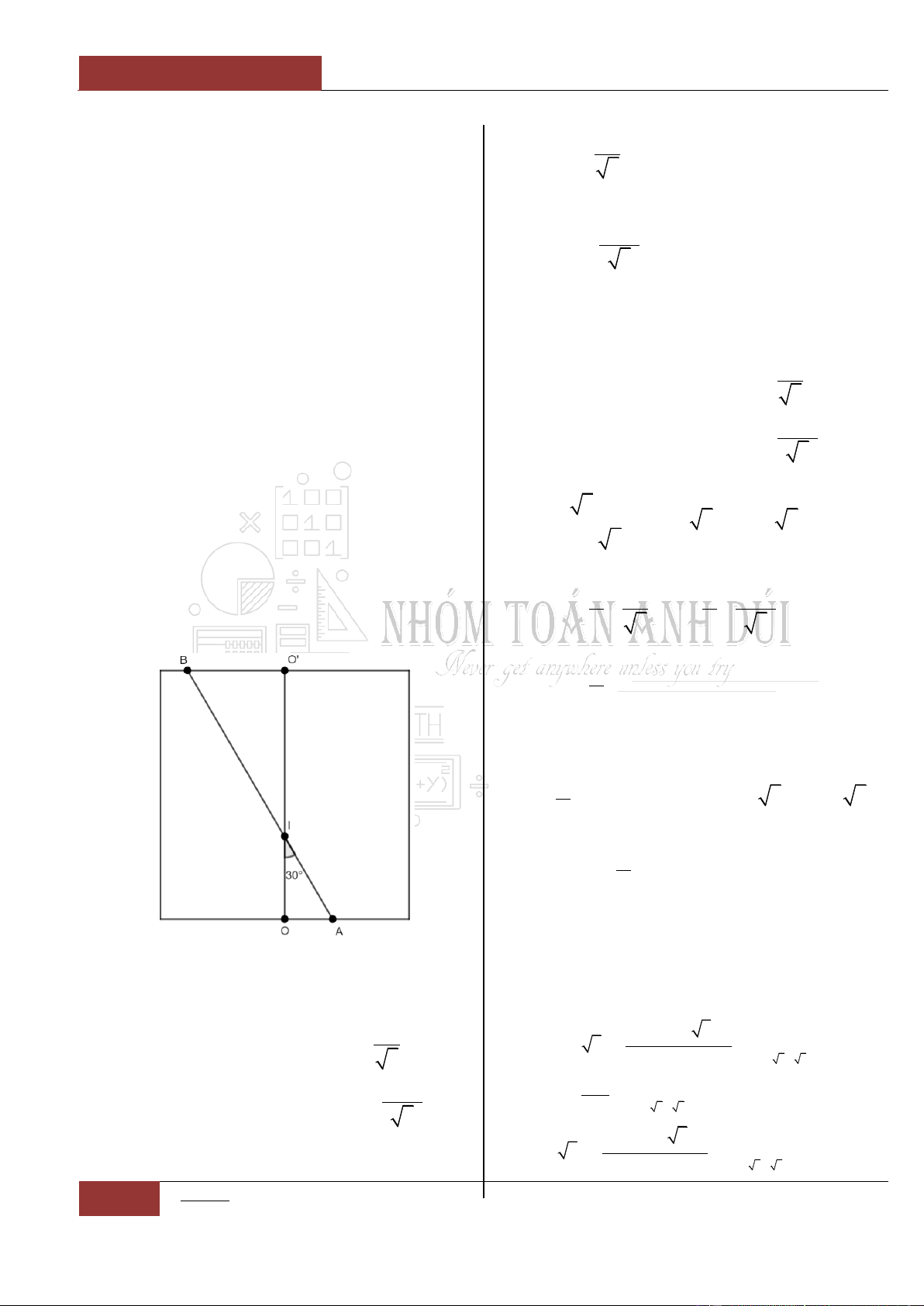
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

425

[ I can't, I can! ]

- Đề bài chỉ cho yếu tố độ dài cạnh nên ta nhất

thiết phải “dồn” độ dài các cạnh cần thiết qua

cùng một biến qua yếu tố góc đã được cho như

giả thuyết đề bài.

- Dùng các giá trị lượng giác để tính toán các

cạnh còn lại theo ẩn (ưu tiên sử dụng hàm

tan

).

- Thể tích khối vật thể cần tính là hợp của hai

khối nón.

- Khảo sát hàm số trên miền giá trị thỏa mãn:

Tìm điều kiện của ẩn để điều kiện đề bài

(đường thẳng

 



cắt hai hình tròn đáy tại các

điểm phân biệt).

Lời giải

Giả sử:

 



cắt trục

 



tại

I

và cắt hai hình

tròn đáy tại

,AB

.

Đặt:

o

'4

.tan30

3

4

'.tan30

3









   













IO x

x

IO x OA IO

x

OB IO

.

Như vậy: Vật thể thu được là

2

khối nón có:

 

1

2

:

3

4

:

3

4







































x

r

N

hx

x

r

N

hx

.

Điều kiện cần và đủ để đường thẳng cắt cả hai

đường tròn đáy:

2

3

' 2 4

2

3

















  











x

OA R

O B R x

23

4 2 3 2 3

4 2 3







    









x

.

Suy ra:

 

22

4

. . . . 4

33





   

  

   

   

xx

V x x

 

3

4

9





   



V x x

Xét hàm số:

   

 

3

. 4 , 4 2 3 2 3

9





     



f x x x x

Ta có:

   

2

' . 3 3 4 0

9





   



f x x x

 

2

42    x x x

.

Tính toán tại một số điểm cần thiết:

 

   

 

4 2 3;2 3

208 96 3

4 2 3 max

9

16

2 min

9

208 96 3

2 3 max

9



























  



















f f x

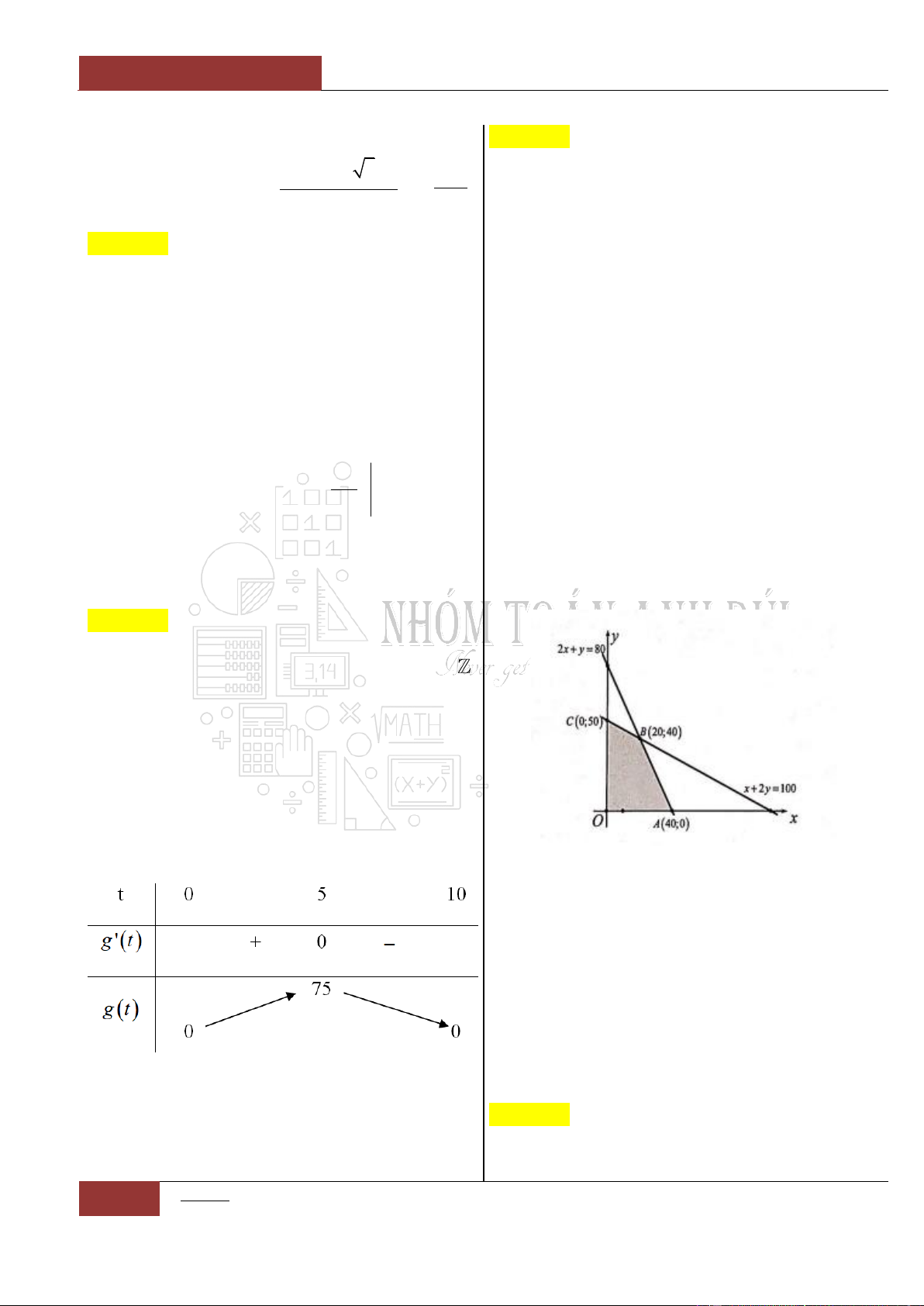
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

426

[ I can't, I can! ]

Vậy thể tích lớn nhất và nhỏ nhất của vật thể

được tạo ra lần lượt là:

 

208 96 3

9





và

16

9



.

Đáp án B

Câu 19. Xe dừng lại khi:

   

0 5 20 0 4      v t t t s

.

Quãng đường xe đi được kể từ lúc đạp phanh

đến khi dừng lại là:

   

4

0





s t v t dt

.

   

4

2

0

4

5

5 20 20 40

0

2



     







t

s t t dt t m

.

Khi xe dừng hẳn, khoảng cách từ xe đến hàng

rào là:

45 40 5m

.

Đáp án B

Câu 20. Ta có:

  



23

15 , 0;10 ,   f t t t t t

 

2

' 30 3  f t t t

.

Xét hàm

   

2

' 30 3  g t f t t t

   

' 30 6 , ' 0 5     g t t g t t

.

Bảng biến thiên:

Dựa vào bảng biến thiên ta thấy: Hàm số

 

'ft

đạt giá trị lớn nhất tại

5t

nên số cây hoa ly

bán được nhiều nhất vào lúc 11 giờ trưa.

Đáp án B

Câu 21. Giả sử

 

, 0; 0x y x y

lần lượt là số

sản phẩm I và loại II được sản xuất.

Lợi nhuận thu được là:

40x 30Ty

(nghìn).

Khi đó:

2x 4 y

là số kg nhiên liệu

30x 15 y

là số giờ làm việc

Theo đề bài:

00

2x 4 200 2 100

30x 15 1200 2x 80















   



   



xx

yy

y x y

yy

Vẽ trục tọa độ ta điểm được tọa độ các điểm:

     

40;0 ; 20;40 ; 0;50A B C

Nhận xét:

     

1600, 2000, 1500  T A T B T C

Vậy lợi nhuận lớn nhất là 2 triệu tại điểm

 

20;40B

hay

20; 40xy

.

Vậy để thu được lợi nhuận cao nhất thì cần sản

xuất 20 sản phẩm loại I và 40 sản phẩm loại II.

Đáp án B

Câu 22. Ta có:

BM

là bán kính đường tròn

 

C

.

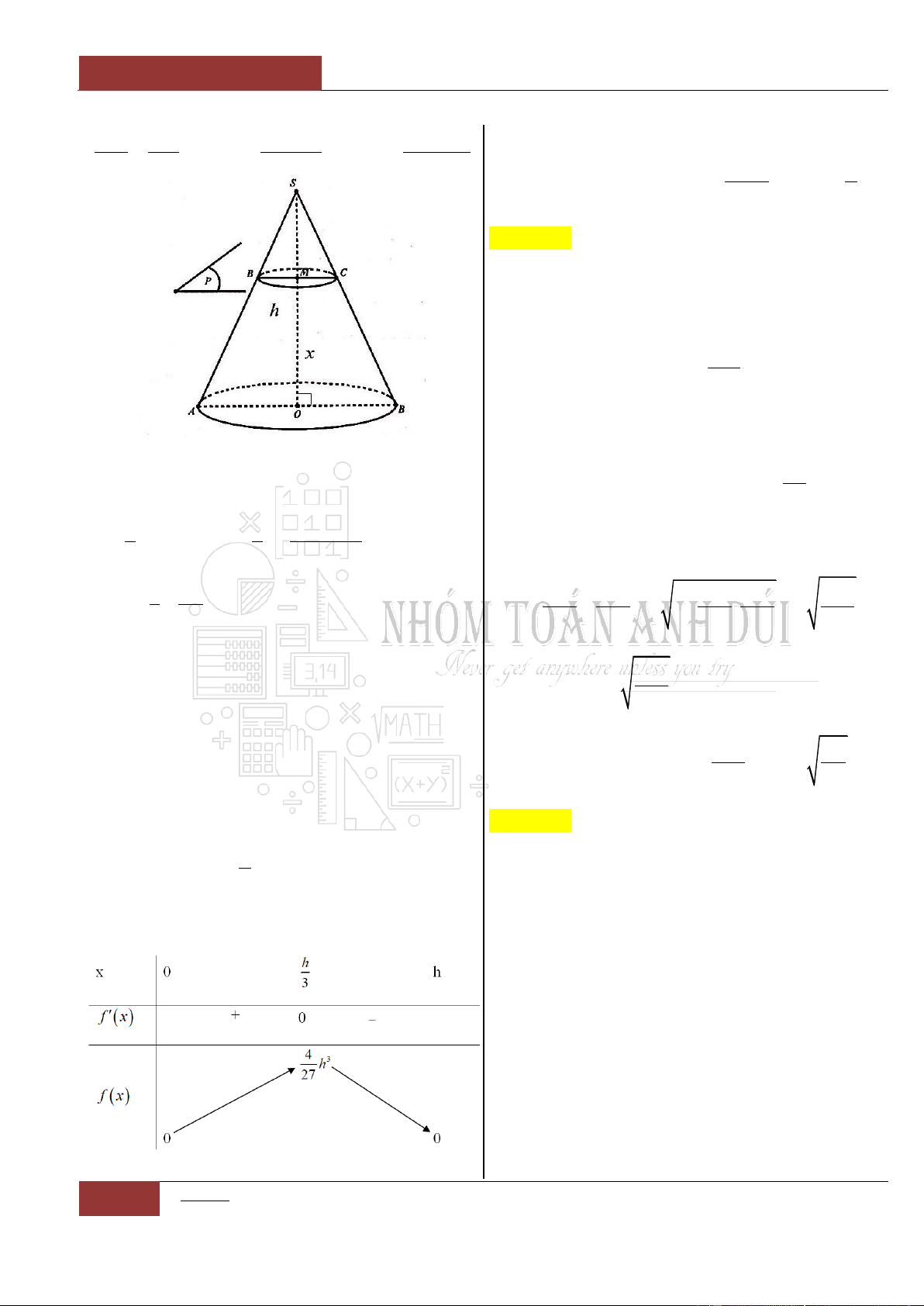
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

427

[ I can't, I can! ]

 

.



    

R h x

BM SM AO SM

BM BM

AO SO SO h

Thể tích của khối nón đỉnh

O

đáy là

 

C

là:

 

2

11

.

33

1

.

3















  

R h x

V BM OM x

h

R

V h x x

h

Xét hàm số:

     

2

,0   f x h x x x h

Ta có:

     

2

' 2 .    f x h x x h x

    

'3   f x h x h x

.

 

'0

3















xh

fx

h

x

Bảng biến thiên:

Từ bảng biến thiên ta có thể tích khối nón đỉnh

O

đáy là

 

C

lớn nhất bằng

2

4

khi .

81 3



hR h

x

Đáp án D

Câu 23. Gọi

, rh

lần lượt là bán kính đáy và

chiều cao của lon sữa bò cần thiết kế.

Khi đó:

2



V r h

hay

2





V

h

r

.

Diện tích toàn phần của hình trụ là:

22

2 2 2

  





   





tp

V

S r rh r

r

.

Áp dụng bất đẳng thức Cauchy, ta có:

2

22

3

2

3 . . 3

2 2 2 2

4

   



   

V V V V V

rr

r r r r

.

Suy ra:

2

3

2

6

4





tp

V

S

.

Đẳng thức xảy ra khi:

2

3

22



  

VV

rr

r

.

Đáp án A

Câu 24. Gọi

, ab

lần lượt là số kg thịt bò và

thịt lợn mà gia đình đó cần mua đảm bảo lượng

protein và lipit trong thức ăn. Theo bài ra ta có

số tiền gia đình cần trả là

160 110ab

với

, ab

thỏa mãn:

0 1,6

0 1,1











a

b

.

Số đơn vị protein gia đình có là:

 

1

0,8 0,6 0,9 8 6 9    a b a b d

Số đơn vị lipit gia đình có là:

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

428

[ I can't, I can! ]

 

2

0,2 0,4 0,4 2 2    a b a b d

Bài toán đã cho trở thành bài toán:

Tìm

, ab

thỏa mãn hệ bất phương trình

0 1,6

0 1,1

8 6 9

22





















a

b

ab

sao cho

 

; 160 110T a b a b

nhỏ nhất.

Vẽ hệ trục tọa độ ta tìm được tọa độ các điểm

       

1;6;1;1 ; 1;6;0;2 ; 0;6;0;7 ; 0;3;1;1A B C D

Nhận xét

 

1;6;1;1 377T

nghìn;

 

1;6;0;2 278T

nghìn;

 

0;6;0;7 173T

nghìn;

 

0;3;1;1 169T

nghìn

Do đó, tổng số tiền họ phải trả là ít nhất mà vẫn

đảm bảo lượng protein và lipit trong thức ăn thì

0,3; 1,1   x a y b

Vậy

22

1,3xy

.

Đáp án A

Câu 25. Gọi

5000t

 

0 4;  tt

là tổng số

tiền giảm.

Lúc đó giá bán sẽ là

50000 – 5000t

, số kg bán

ra là

40 50 t

suy ra tổng số tiền bán được cả

vốn lẫn lãi là

   

50000 5000 . 40 50tt

;

Số tiền vốn nhập ban đầu là

 

30000. 40 50 t

.

Ta có lợi nhuận thu được là:

      

50000 5000 40 50 30000 40 50    f t t t t

Ta tìm

t

để

 

fx

lớn nhất:

    

4 5 20 5 .10000  f t t t

 

2

25 80 80

10000

     

ft

g t t t

   

2

144 5 8 144,      g t t t

Để

 

ft

lớn nhất khi

 

gt

lớn nhất;

 

gt

lớn

nhất bằng

144

khi:

8

5 8 0

5

   tt

.

8

5000 8000

5

  tt

.

Do đó giảm số tiền 1 kg là 8000đ, tức giá bán ra

1

kg là

50000 8000 42000

đ thì lợi nhuận

thu được cao nhất.

Đáp án C

Câu 26. Gọi độ dài cạnh của hình vuông là

 

xm

thì độ dài cạnh tam giác đều là

 

2 xm

.

Chiều dài phần dây được uống thành hình

vuông (chính là chu vi hình vuông) là

 

4 xm

;

chiều dài phần dây được uốn thành tam giác

đều (chính là chu vi hình tam giác đều) là

 

3.2 6x x m

.

Suy ra chiều dài phần dây được uốn thành hình

tròn là

 

4 6 10   L x x L x m

.

Từ đó ta có:

0;

10









L

x

.

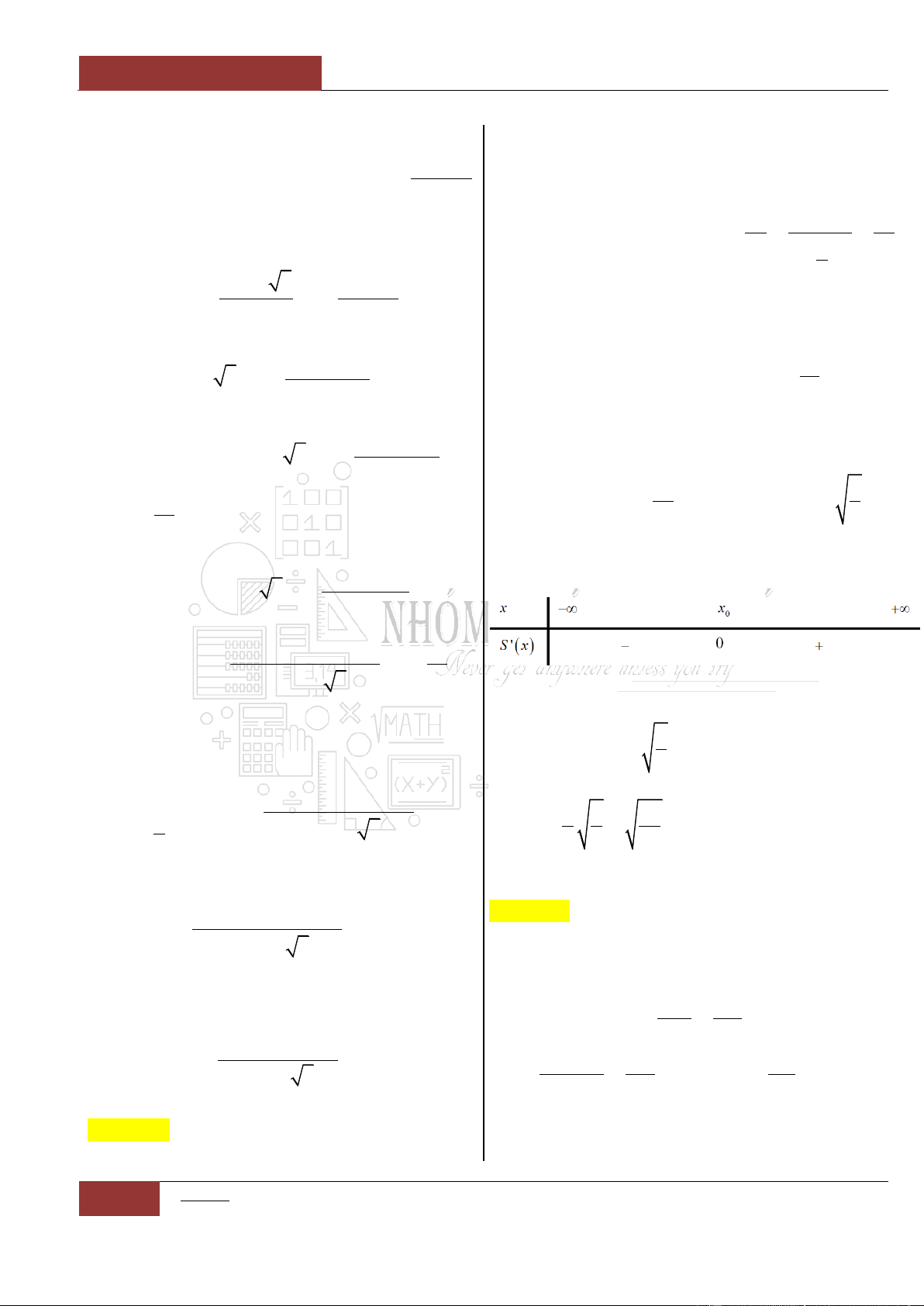
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

429

[ I can't, I can! ]

Gọi

r

là bán kính của đường tròn thì chu vi

đường tròn là

10

2 10

2





    

Lx

P r L x r

Tổng diện tích của ba hình là:

 

2

23

10

42







  





x

Lx

Sx

 

2

10

13

4





   

Lx

Sx

Xét hàm số

 

2

10

13

4





  

Lx

f x x

trên

0;

10







L

.

Ta có:

 

5 10

' 2 1 3 ;





  

Lx

f x x

 

5

' 0 0;

10

2 25 1 3





   











LL

f x x

.

Lập bảng biến thiên ta thấy:

 

0;

10

5

min .

2 25 1 3



























L

f x f

Vậy tổng diện tích của ba hình thu được nhỏ

nhất khi

 

5

2 25 1 3











L

x

.

Suy ra độ dài cạnh của tam giác đều là:

 

5

2

25 1 3







L

xm

.

Đáp án C

Câu 27. Gọi

,,x y h

lần lượt là chiều rộng, chiều

dài, chiều cao của hố ga

 

0, 0, 0,  x y h m

Thể tích hố ga:

2

32

3

.

2

    







V

V xyh y

xh

x

xx

.

Diện tích cần xây dựng hố ga là:

 

2

10

2 2 2 3    S x xy xh yh x

x

.

Bài toán trở thành tìm

x

để

 

Sx

nhỏ nhất

Ta có:

   

3

0

2

10 5

' 6 , ' 0

3

    S x x S x x

x

.

Lập bảng xét dấu

 

'Sx

Dựa vào bảng xét dấu

 

'Sx

, thấy

 

Sx

đạt giá

trị nhỏ nhất

3

5

3

x

.

Vậy

 

33

3 5 45

2 3 8

hm

là chiều cao xây hố

ga tiết kiệm được nguyên liệu nhất.

Đáp án B

Câu 28. Đặt

MN x

,

 

0 xh

.

Ta có

// MN SO

nên



MN NA

SO OA



..



MN OA x R

NA

SO h



R



x

ON R

h

.

Khối trụ thu được có bán kính đáy và chiều cao

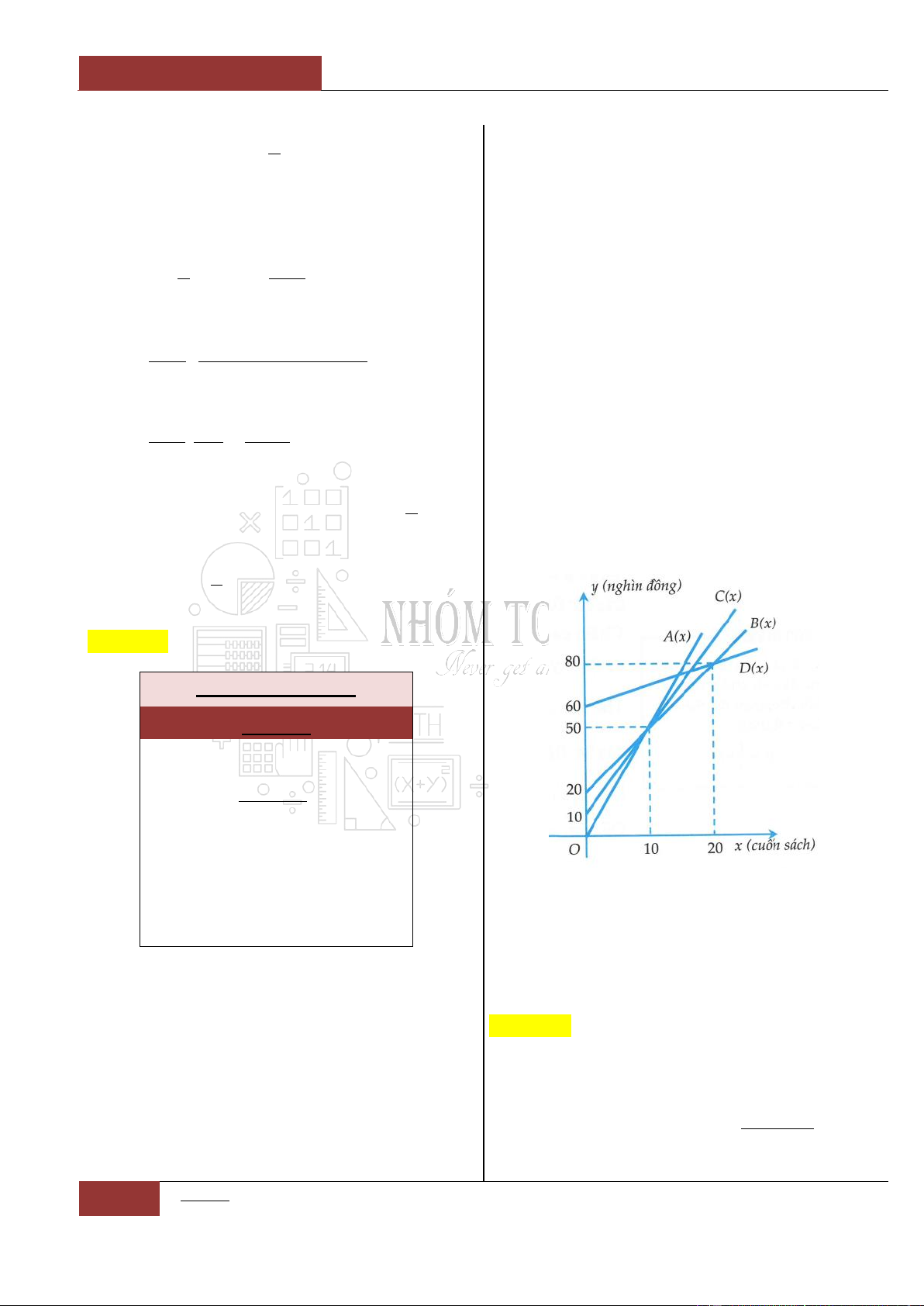
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

430

[ I can't, I can! ]

lần lượt là:

1.









x

ON R

h

và

MN x

.

Thể tích khối trụ là:

2

..



V ON MN

  

2

. 1 . .2

2





    





xR

V R x h x h x x

h



   

3

2

2x

3

2



   









h x h x

R

V

h

2 3 2

2

8 4R

.

27 27

2



  

R h h

V

h

Dấu bằng xảy ra khi

2x hx



3



h

x

.

Khi đó:

3



h

MN

.

Đáp án B

Extra Techniques:

Review:

Note: Với ba số dương

, , a b c

thì:

3











abc

(Bất đẳng thức Cauchy).

Dấu

“”

xảy ra khi và chỉ khi

abc

.

Câu 29. Gọi

 

Ax

là tổng số tiền phải trả để

thuê

x

cuốn sách theo phương án

 

1

:

 

5A x x

(nghìn đồng).

Gọi

 

Bx

là tổng số tiền phải trả để thuê

x

cuốn sách theo phương án

 

2

:

 

3 20B x x

(nghìn đồng).

Gọi

 

Cx

là tổng số tiền phải trả để thuê

x

cuốn sách theo phương án

 

3

:

 

4 10C x x

(nghìn đồng)

Tương tự, theo phương án

 

4

phải trả

 

60D x x

(nghìn đồng)

Vẽ đồ thị các hàm số

 

1

: 5 ;d y x

 

2

: 3 20d y x

;

 

3

: 4 10d y x

;

 

4

: 60d y x

trên cùng hệ trục tọa độ như

hình vẽ.

Dễ dàng nhận thấy khi

20x

, đồ thị

 

4

d

nằm

dưới các đồ thị kia.

Vậy chọn phương án

 

4

sẽ tốn ít tiền nhất.

Đáp án D

Câu 30. Diện tích toàn phần hình trụ là:

2

2 2 .

2









   

Sr

S rh r h

r

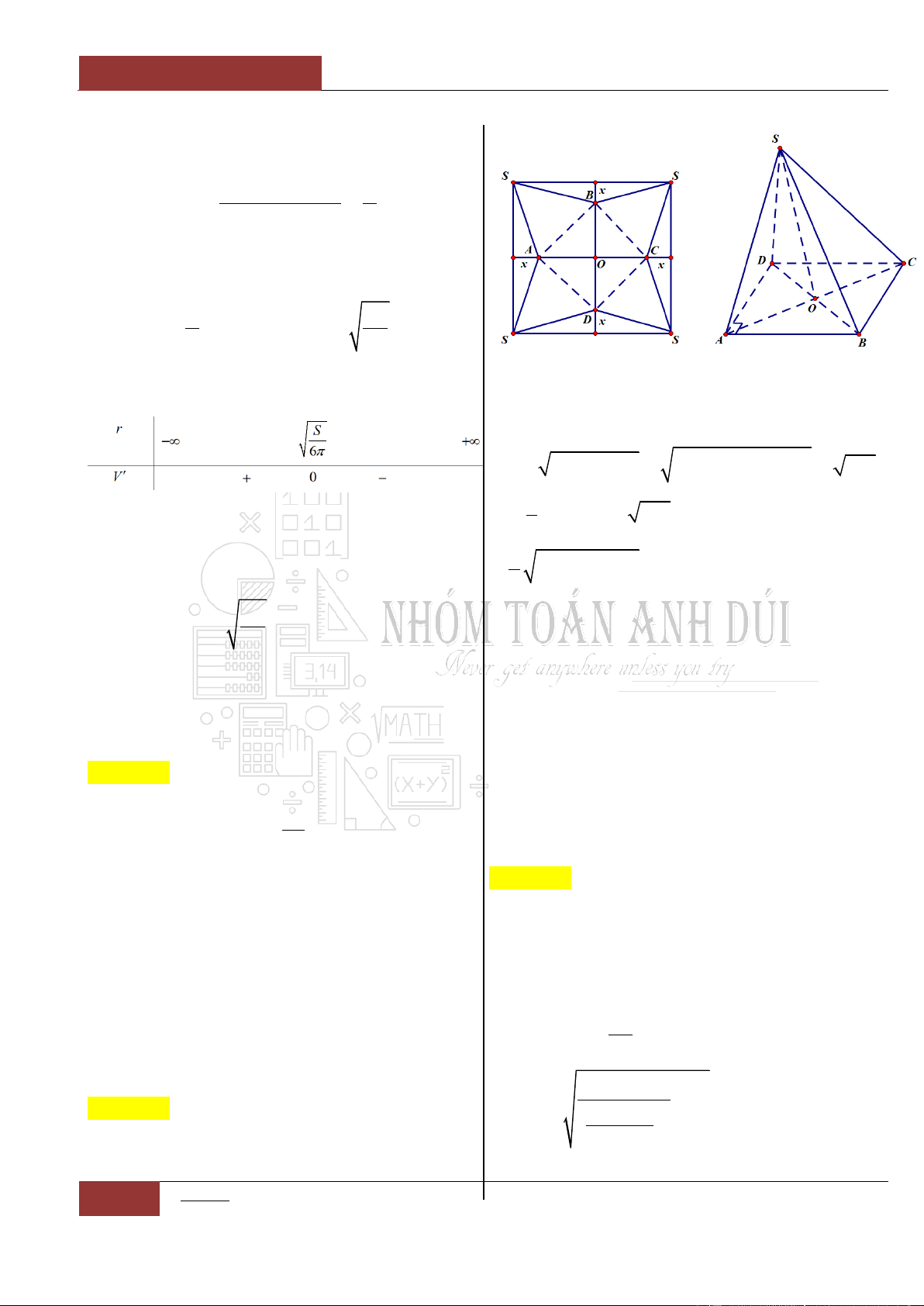
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

431

[ I can't, I can! ]

Do đó thể tích khối trụ là:

 

22

23

2

.

22







   

r S r

S

V r h r r

r

Xem

r

là biến với

 

0; r

.

Ta có:

2

3 0 0

26





     

SS

V r r

.

Lập bảng xét dấu



V

Dựa vào bảng xét dấu



V

.

Ta thấy

V

đạt giá trị lớn nhất khi:

2

6



  

S

r S r

Khi đó:

22

6 2 2 2 .

  

   r rh r h r

Đáp án D

Câu 31. Ta có:

2

3

' 18 0

2



   v s t t

' 3 18 0 6      v t t

xét trên đoạn

 

0;8

.

Ta có:

 

   

00

6 54 /

8 48 /

















v

v m s

.



 

max 6 54( / )v v m s



C

Đáp án C

Câu 32. Đặt tên các điểm như hình vẽ dưới đây

     

 

2

2 2 2

2

2 2 2

2

4

5 5 2 5

5 5 10

1

.2. 5 . 10

3

2

10. 5 .

3



     

      



AB OA OB

x x x

SO SA AO x x x

V x x

xx

Đặt

   

4

5 . , 0 5   y x x x

   

34

3

' 4 5 . 5

5 5 5

' 0 1

    

  

  

y x x x

xx

yx

Lập bảng biến thiên, ta thấy:

 

max

1yy

.

Vậy

1x

.

Đáp án C

Câu 33. Gọi phương trình

: y ax bAB

y

qua

 

125;1000M

125 1000  ab

 

2

0;b ,B ;0

min 139

3

7,5

0

2,09

10 0

()

6

125











   





b

A

a

b

AB b

b

S

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

432

[ I can't, I can! ]

Đáp án C

Câu 34. Bán kính viên ở giữa:

a

.

Bán kính 6 viên còn lại:

b

.

4 2 10  ba

10 2

4





a

b

.

 

3

3 3 3

4 4 10 2

6 . 6.

3 3 4









   











bi

a

V b a a

.

 

(min)

2,3  

bi

TABLE V V

.

Đáp án B

Câu 35.

2 2 2 2

40 2

4 2 40

4

40 2

10 10 10.( ) 10

4

min 2,75 5,68 8,4







   



   

       

r

a r a

r

V a r r

V r a a r

Đáp án B

Câu 36. Ta có:

2

22

72

.





   

V

V r h h

rr

Tổng chi phí xây dựng là:

22

2

100 90.2 140

72

240 90.2 .

  





  

  

P r rh r

P r r

r

2

3

12960

240

6480 6480

240 6480 .





  

    

Pr

r

Pr

rr

Dấu

""

xảy ra khi và chỉ khi:

 

2

3

6480 3

240 m .



   rr

r

Đáp án C

Câu 37. Ta có:

2

.



  

V

V r h h

r

Gọi

t

là giá tiền của một đơn vị diện tích vật liệu

để làm mặt xung quanh, suy ra giá tiền của một

đơn vị diện tích vật liệu để làm mặt đáy là

3.t

Diện tích mặt xung quanh

1

2.



S r h



giá

tiền mặt xung quanh là

1

2.



T rh t

Diện tích hai mặt đáy

2



Sr



giá tiền

hai mặt đáy là

2

2 3 .



T r t

Tổng tiền hoàn thành sản phẩm:

 

22

12

2 3 2 3

  



     





V

T T T t rh r t r

r

n

22

3

2 3 2 3 .

2 2 4





    





VV

t r t V

rr

Dấu

""

xảy ra khi và chỉ khi:

2

do

2

3 6 .

2





   

V r h

V

r h r

r

Đáp án C

Câu 38. Giả sử thùng phi có chiều cao

,h

bán

kính đáy

.r

Diện tích thép tối đa cần dùng là:

6594000

18,84

350000



suy ra

2

2 2 18,84



r rh

22

3 3 .     r rh rh r

Ta có:

 

22

3



  V r h r r

.

  

2 2 2

2 3 3

2



   V r r r

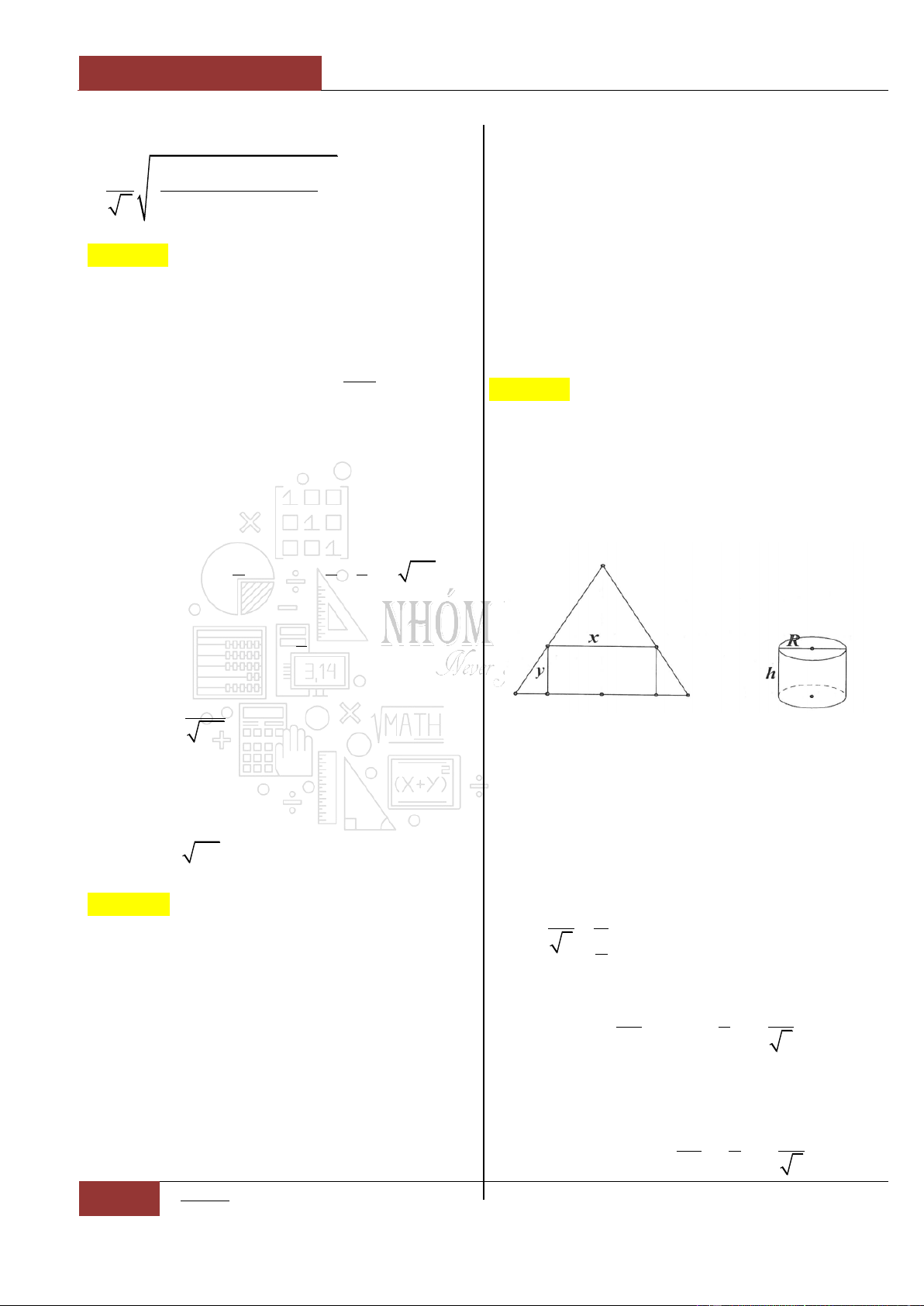
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

433

[ I can't, I can! ]

3

222

2 3 3

2 6,28.

3

2





   

  





rrr

Đáp án B

Câu 39. Giả sử hộp trụ có bán kính đáy

r

, ,

chiều cao là

h

. Theo giả thiết ta có:

2

1

1.



   V r h h

r

Để tiết kiệm nguyên vật liệu nhất thì diện tích

toàn phần phải nhỏ nhất:

2

22



   

tp xq day

S S S r rh

22

3

2 1 1

2 2 3 2

  

     

tp

S r r

r r r

Dấu bằng đạt tại:

2

1

2



r

r

3

1

0,54 1,084

2



    r dm h dm

Vậy phải thiết kế một khối trụ có bán kính đáy

0,54dm

và chiều cao

1,084dm

.

Vậy

3

3 2 .





tp

S dm

Đáp án A

Câu 40. Đặt

, ab

lần lượt là số lít nước cam và

táo mỗi đội pha chế được:

30 10 ab

là số g đường cần dùng

ab

là số lít nước cần dùng

4 ab

là số

g

hương liệu cần dùng

Theo giả thiết bài toán có:

 

30 10 210 3 21

9 9 * .

3 24 3 24

   





    





   



a b a b

Số điểm thưởng mà mỗi đội nhận được là

 

; 60 80F a b a b

sẽ đạt giá trị lớn nhất tại

một trong các đỉnh

, , A B C

. Kiểm tra trực tiếp

có:

( , )max

(4,5) 640.

ab

FF

Đáp án B

Câu 41. Phân tích: Để tìm được giá trị lớn nhất

của

V

, ta phải thiết lập được hàm tính

V

theo

một ẩn đã chọn, để đưa bài toán về tìm giá trị

lớn nhất, nhỏ nhất của hàm số một biến.

Hướng dẫn giải:

Cắt từ miếng tôn lấy một hình chữ nhật có kích

thước

,xy

như hình vẽ. Sau đó, từ miếng tôn

hình chữ nhật, chế tạo thành hình trụ không đáy

có bán kính

R

, chiều cao bằng

h

.

Ta có:

1, 2 ,

3

2



   

xy

x R y h

3

, 1 .

22

3





    





xx

R h y

Thể tích khối trụ đã cho có độ lớn là:

2

3

.1

22

3







  





xx

V R h

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

434

[ I can't, I can! ]

   

23

3

3 , 0; 3 .

83



  V x x x

Khảo sát hàm số

V

, ta được

 

3

max

1

6



Vm

tại

23

.

3

x

Vậy

max

1

.1000 53,05

6



V

lít.

Đáp án D

Câu 42. Phân tích: Đây là dạng toán khối nón,

khối trụ lồng khối đa diện nên chúng ta cần hiểu

được bản chất của bài toán là xử lí các bài toán

về đáy của các khối lồng nhau. Vì vậy chúng ta

cần lưu ý các công thức bán kính đường tròn

nội ngoại tiếp các đa giác thường gặp.

Lăng trụ nội tiếp nón, nên chúng ta cần đưa bài

toán về khối trụ nội tiếp nón và ngoại tiếp lăng

trụ.

Với bài toán khối xoay lồng nhau, thì chúng ta

cần đưa về hình phẳng thể hiện các hình biểu

diễn của các khối tròn xoay lồng nhau. Cụ thể,

nón ngoại tiếp trụ có nghĩa là tam giác cân

ngoại tiếp hình chữ nhật.

Một vấn đề đề cập trong bài toán này là tìm giá

trị lớn nhất – nhỏ nhất của một đại lượng. Chúng

ta phải thiết lập được công thức tính đại lượng

đó theo một ẩn do chúng ta chọn để đưa về bài

toán tìm giá trị lớn nhất – nhỏ nhất của hàm số.

Hướng dẫn giải.

Xét hình trụ

 

T

nội tiếp hình nón đã cho và

ngoại tiếp khối lăng trụ tứ giác đều đã cho, có

chiều cao là

h

, bán kính đáy bằng

x

với

 

0;5x

.

Theo định lý Thales:

20

1 20 1

5 20 20 5





     





x h h x

h

Đáy khối lăng trụ tứ giác đều là hình vuông nội

tiếp đáy hình trụ

 

T

nên có cạnh bằng

2x

.

Thể tích khối lăng trụ tứ giác đều bằng:

 

2 2 3 2

2 .20 1 8 5 8 40

5



      





x

V x x x x x

Khảo sát hàm

V

trên

 

0;5

, ta được:

4000

27



max

V

tại

10

3

x

.

Đáp án B

Câu 43. Vận tốc tại thời điểm

t

là:

   

2

3

18

2



   v t s t t t

với

 

0;10 .t

Ta tìm được

 

     

0;10

max 6 .54 m/sv t v

Đáp án D

Câu 44. Diện tích cần sơn chính là tổng diện

tích xung quanh của các hình trụ.

Tổng diện tích xung quanh của

4

cây cột đường

kính

40

cm là

11

4.



S rh

Tổng diện tích xung quanh của

6

cây cột đường

kính

26

cm là

22

6 2 .



S r h

Số tiền cần dùng là

 

12

.380000F S S

2

40 26

2 4. 6. .10 .4,2.380000 15844000

22







  





F

(đồng).

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

435

[ I can't, I can! ]

Đáp án D

Câu 45. Thể tích khối trụ là:

2



  

V

V r h h

r

.

Giả sử đơn giá làm mặt xung quanh là

1

thì đơn

giá làm mặt đáy và nắp là

3

.

Số tiền để làm thùng là:

22

2

2 1 2 3 2 3

3

2 3 6 .

22

4

  









     







   





V

T rh r r

r

V V V

Tr

rr

Dấu

“”

xảy ra khi:

22

3 2 6.

22



    

V rh h

rr

Đáp án C

Câu 46. Giả sử hộp trụ có bán kính đáy

r

,

chiều cao là

h

. Theo giả thiết có:

2

1

1.



   V r h h

r

Để tiết kiệm nguyên vật liệu nhất thì diện tích

toàn phần phải nhỏ nhất:

22

2

3

2

2 2 2

11

2 3 2 .

  



     

   

tp xq day

tp

S S S r rh r

r

Sr

rr

Dấu bằng đạt tại:

2

3

11

2 0,54 1,084 .

2



     r r dm h dm

r

Vậy phải thiết kế một khối trụ có bán kính đáy

0,54

dm và chiều cao

1,084

dm.

Vậy

3

3 2 .





tp

S dm

Đáp án A

Câu 47. Với thanh sắt

6

m có các cách cắt ra

các thanh sắt có chiều dài

2,5

m và

1,6

m là

Cách 1: Cắt thành

2

thanh sắt chiều dài

2,5

m;

Cách 2: Cắt thành

1

thanh sắt chiều dài

2,5

m

và

2

thanh sắt chiều dài

1,6

m;

Cách 3: Cắt thành

3

thanh sắt có chiều dài

1,6

m.

Gọi

 

, , , ,



x y z x y z

lần lượt là số thanh sắt

chiều dài

6

m được cắt theo cách 1, cách 2 và

cách 3.

Ta có hệ phương trình

2 40

.

2 3 60











xy

yz

Do đó:

 

2 3 3 100 3 100.       x y z x y z z

Số thanh sắt chiều dài

6

m cần sử dụng là:

100

.

3



   

x

M x y z

Do

100

33,3.

3



   x Z M

+) Nếu

34 2  Mx

 

4 40 36

;

2 3 60 4

  







   



yy

l

y x z

+) Nếu

35 5  Mx

 

10 40 30

;

2 3 60 0

  







  



yy

TM

y z z

Vậy số thanh sắt chiều dài

6

m tối thiểu cần

dùng là

35

.

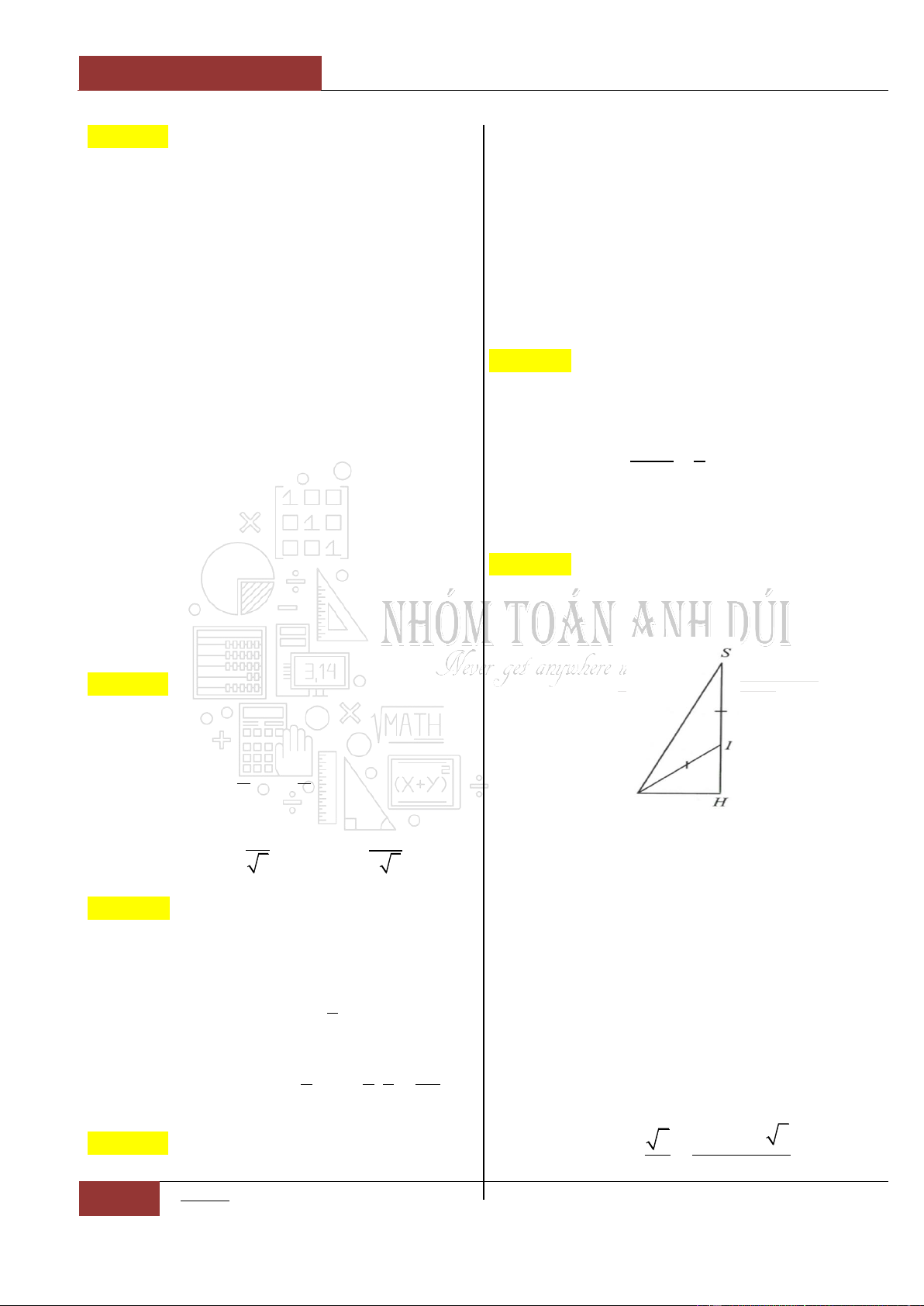
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

436

[ I can't, I can! ]

Đáp án B

Câu 48. Đặt

,ab

lần lượt là số lít nước cam và

táo mỗi đội pha chế được:

30 10 ab

là số g đường cần dùng

ab

là số lít nước cần dùng

4 ab

là số g hương liệu cần dùng

Theo giả thiết bài toán có:

 

30 10 210 3 21

9 9 * .

3 24 3 24

   





    





   



a b a b

Số điểm thưởng mà mỗi đội nhận được là

 

; 60 80F a b a b

sẽ đạt giá trị lớn nhất tại một

trong các đỉnh

, , A B C

. Kiểm tra trực tiếp có

 

( , )max

4,5 640.

ab

FF

Đáp án B

Câu 49. Ta có:

22

11   l r h

;

 

22

1.

33



   V r h h h

Ta có:

1

0

3



  yh

khi đó

2

93



V

.

Đáp án D

Câu 50. Ta có:

 

22

1;    V r h r r

2

0

3



  Vr

Khi đó:

2

max

2 4 1 4

1 . .

3 9 3 27





    





V h V

.

Đáp án B

Câu 51. Hộp gỗ đó có thể tích lớn nhất khi và

chỉ khi hình chữ nhật nội tiếp đường tròn có

đường kính

0,6

(mét) phải có diện tích lớn

nhất. Gọi kích thước hai cạnh chữ nhật đó là

,ab

nên

 

2

22

0,6 2a b ab

 

3

0,18 0,18.1 0,18ab V abc m     

Đáp án A

Câu 52. Ta có:

2 rh 2 rh 1    

.

22

2

rh

V r h khi h 0

hh





       

 Không tồn tại

max

V

.

Đáp án D

Câu 53.

Gọi

SH

là đường cao hình chóp,

a

là độ dài

cạnh đáy và cũng là bán kính đường tròn ngoại

tiếp đáy.

Lúc đó tâm mặt cầu là

1   I SH SH IH

hoặc

1–SH IH

.

Đặt

 

22

0 1 1–   IH x x a x

, đáy hình

chóp là ghép của

6

tam giác.

Như vậy: Diện tích lục giác đều đã cho bằng:

 

2

3 1 3

3

6. .

42





x

Va

.

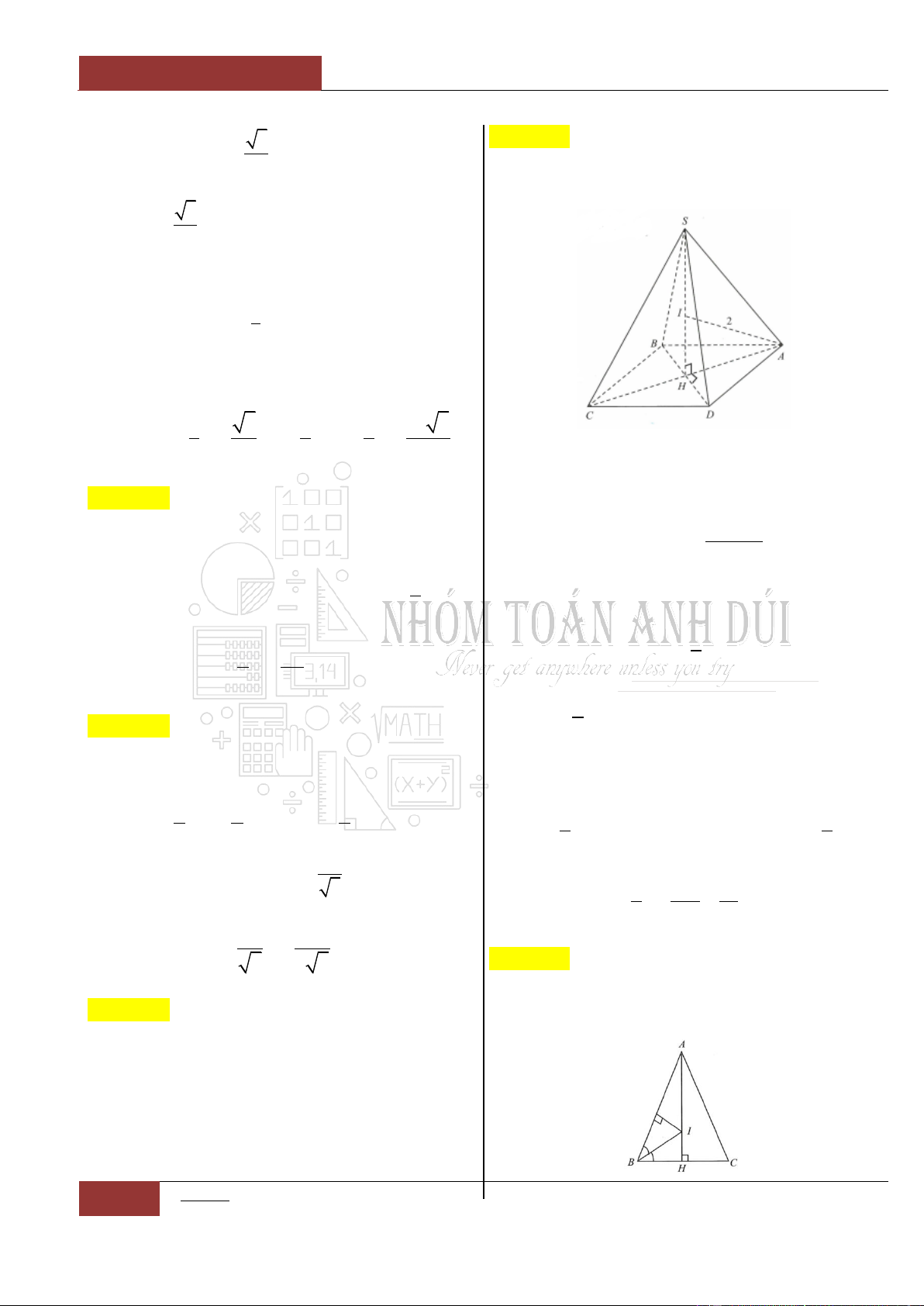
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

437

[ I can't, I can! ]

 

2

3

V 1 x 1 x

2

   

(hoặc

 

2

3

V 1 x 1 x

2

  

 loại khi phải tìm

max

V

).

Ta có:

1

V' 0 x

3

  

.

Khi đó:

max

1 3 1 1 16 3

. 1 . 1

3 2 3 9 27

     

    

     

     

VV

.

Đáp án A

Câu 54. Ta có:

2 4 4hr

.

 

2

2 2 0

3





      V r r V r

Khi đó:

max

28

3 27











VV

.

Đáp án A

Câu 55. Ta có:

   

2 2 2 2

V r h l h h l h h

3 3 3

  

    

,

1

V 0 h

3



  

.

Khi đó:

max

12

3 9 3











VV

.

Đáp án D

Câu 56. Ta có:

 

22

3 , 0 1



       V r h h h V h

.

Khi đó:

 

max

12  VV

.

Đáp án B

Câu 57.

Lưu ý:

I

thuộc đường thẳng

SH

, đặt

IH x

,

lúc đó:

2 2 2

.

4 , 2

2

ABCD

AC BD

AH x S AH   

Do

2SH x

hoặc

 

2

2 2 4

3

     SH x V x x

hoặc:

 

2

24

3

  V x x

mà ta tìm

max

V

suy ra

2SH x

bị loại.

Với

 

2

24

3

  V x x

thì

2

0

3



  Vx

.

Khi đó:

9

max

2

2 512 2

3 81 9



  





VV

.

Đáp án B

Câu 58.

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

438

[ I can't, I can! ]

Hạ

AH BC

 AH

đi qua tâm

I

của đường tròn.

Đặt

 

, 0 45



  

oo

IBH

 

1

, tan .

tan



   

IH

BH x

x

22

2tan 2

.tan2 .

1 tan 1

AH BH BH

x



  



 

2

.2

..

2

1



    



ABC

AH BC

S HA HB S

xx

Xét

 

2

1g x x x

có

 

'0gx

khi

1

3

x

.

Khi đó:

min

1

33

3









SS

.

Đáp án D

Câu 59. Gọi

, MN

lần lượt là trung điểm

, CD AB

, ta có:

 

CD ABM

.

2 . 2

. . .

3 3 2 3



   

ABM

CD x MN AB x

V S MN



Do



2

4  AM BM x

.

Ta có:

 

2 2 2 2 2

4 1 3      MN AM AN x x

2

. 3 .

3

V x x  

 

2

22

3

23

3 2 2













xx

V

max

3

2

V

khi

2

3

2

   x x x

.

Đáp án D

Câu 60. Ta có:

SO' SB'

SO SB



.

 

   

22

2 2 2

2

h x R h

SO'.SB

SB'

SO h

Rh

O'B' SB' SO' h x h x

h



  



      

Ta có:

2

tru

V .O'B' .OO'

 

22

2

tru

2

hR

V 1 h x .x

h





   





 

22

2

h R h

V' x 1 3x 4hx h 0 x

h3





       





Khi đó, dễ dàng tính được thể tích lớn nhất của

hình trụ là:

 

2

22

tru max

2

h R h h

V 1 h .

h 3 3







   





 

2 2 2

tru max

2

R 4h h 4 R h

V . . .

h 9 3 27



  

Đáp án A

Câu 61. Đổi

20

lít

3

20000  cm

.

Gọi bán kính nắp đậy của thùng sơn là

x

(cm),

0x

, chiều cao của thùng sơn là

h

(cm)

Khi đó thể tích của thùng sơn là:

2

20 000

V x h 20 000 h

x

    



Diện tích toàn phần của thùng sơn là:

22

tp

40 000

S 2 xh 2 x 2 x

x

      

Để nhà sản xuất tiết kiệm được vật liệu nhất tức

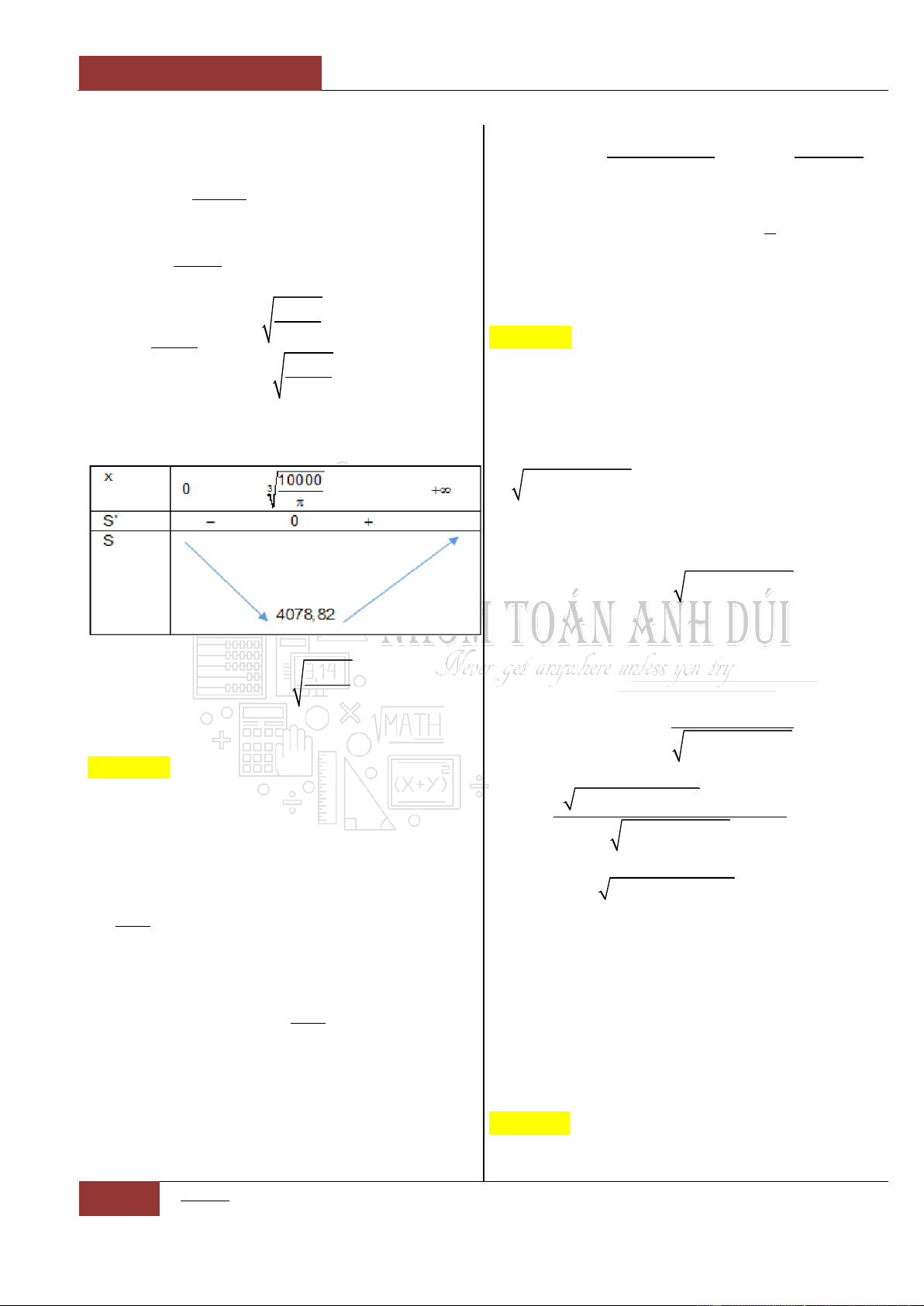
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

439

[ I can't, I can! ]

là

tp

S

nhỏ nhất.

Ta có:

2

40 000

S' 4 x

x

   

.

2

3

40000

S' 0 4 x 0 4 x 40000

x

10000

x

10000

x

10000

x

        











  













Bảng biến thiên

Vậy bán kính nắp đậy là

3

10000



thì sẽ tiết

kiệm vật liệu nhất.

Đáp án C

Câu 62. Vận tốc của con cá khi bơi ngược dòng

được là

 

3/v km h

.

Thời gian cá bơi được quãng đường

240

km là

 

240

3





th

v

.

Năng lượng tiêu hao của cá để vượt quãng

đường đó là

 

3

240 .

3





v

E v c

v

.

Bài toán trở thành tìm

3v

để

 

Ev

là nhỏ

nhất.

 

   

23

32

22

33

29

240 . 240 .

33

   









   



   

v v v

vv

E v c c

vv

     

2

9

0 2 9 0 3 .

2



      E v v v v do v

Vậy

 

4,5 /v km h

thỏa mãn đề bài.

Đáp án D

Câu 63. Gọi

x

(km) là quãng đường bộ mà

người đó đi,

0 50x

.

Suy ra, người đó phải đi với quãng đường thủy

là

 

2

50 15x

(km)

Kinh phí cho cả quãng đường đi là:

   

2

5 7 50 15   S x x x

Yêu cầu bài toán



ta cần tìm

x

để

 

Sx

đạt

giá trị nhỏ nhất.

Đạo hàm

 

2

50

5 7.

50 15









x

Sx

x

 

2

5 100 2725 7 50

'

50 15

   





x x x

Sx

x

   

2

0 5 100 2725 7 50



     S x x x x

   

2 2 2

25 100 2725 49 50 100     x x x x

34,7x

(km) thỏa mãn điều kiện

0 50x

.

Lập bảng biến thiên ta được

34,7x

thì

 

Sx

đạt giá trị nhỏ nhất trên

 

0;50

.

Đáp án B

Câu 64. Gọi quãng đường vận động viên chạy

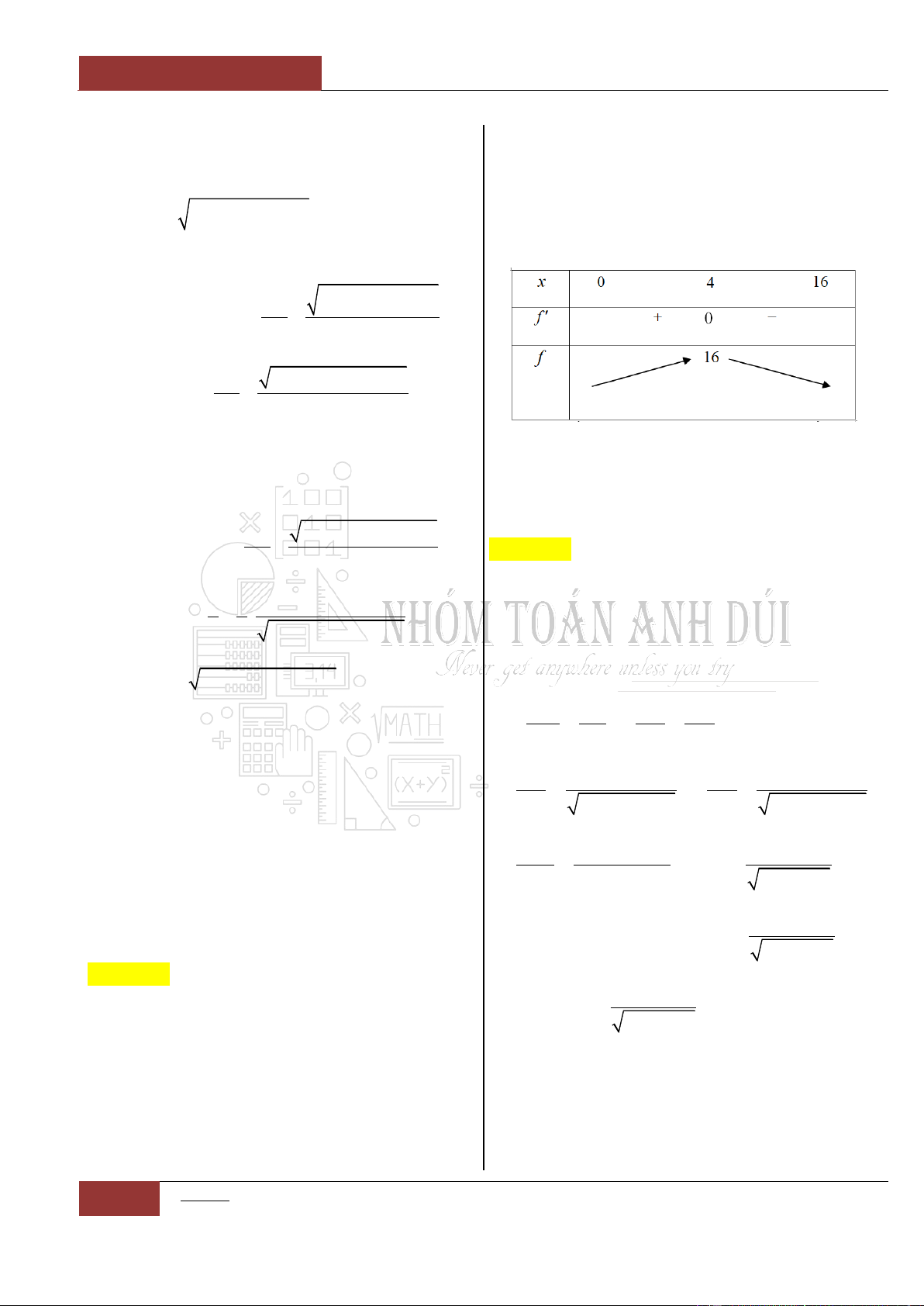
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

440

[ I can't, I can! ]

trên bờ là

x

(m).

Khi đó quãng đường vận động viên bơi dưới

nước sẽ là

   

2

50 200xm

Thời gian cho cả quãng đường đi (cả trên bờ và

dưới nước) là

 

2

50 200

4,5 1,5





x

Tx

 

2

42500 400

4,5 1,5





x x x

Tx

Yêu cầu bài toán tương đương với: Tìm

x

để

 

Tx

đạt giá trị nhỏ nhất.

Xét hàm số

 

2

42500 400

4,5 1,5





x x x

Tx

.

Ta có:

 

2

2 2 200

.

93

42500 400









x

Tx

xx

   

 

2

0 42500 400 3 200 0,

0 200



      



T x x x x

x

 

22

42500 400 9 400 40000     x x x x

 

217,7

182,3















xL

xN

Lập bảng biến thiên ta được

182,3x

thì

 

Tx

đạt giá trị nhỏ nhất.

Đáp án C

Câu 65. Gọi

, ab

lần lượt là chiều dài và chiều

rộng của hình chữ nhật

 

0 b a 16  

. Theo

bài ra ta có:

 

2 a b 16 a b 8 b 8 a.       

Diện tích của hình chữ nhật là

 

2

a 8 a 8a a  

.

Ta tìm giá trị lớn nhất của hàm số

 

2

f a 8a a .

 

f a 8 2a 0 a 4.



    

Ta có bảng biến thiên

Vậy diện tích hình chữ nhật lớn nhất khi

a b 4m

. Diện tích lớn nhất của hình chữ nhật

bằng

2

16m .

Đáp án A

Câu 66. Theo bài ra ta có

216IM m

,

1000MN m

.

Đặt

 

,0AM x x

.

Tam giác

AIM

đồng dạng với tam giác

MNB

nên

216

  

AM IM x

BM NB MB NB

22

216

1000





x

MB

22

216

1000





x MB

MB

 

22

2 2 2

22

1000

216

216 1000

216

    



x MB x

MB x

MB

x

Vậy độ dài đoạn thẳng

AB

:

2

1000

216





x

.

Đặt

 

22

1000

216





x

f x x

x

.

Để chi phí làm con đường nhỏ nhất thì độ dài

AB

là nhỏ nhất. Ta tìm giá trị nhỏ nhất của

hàm số

 

fx

.

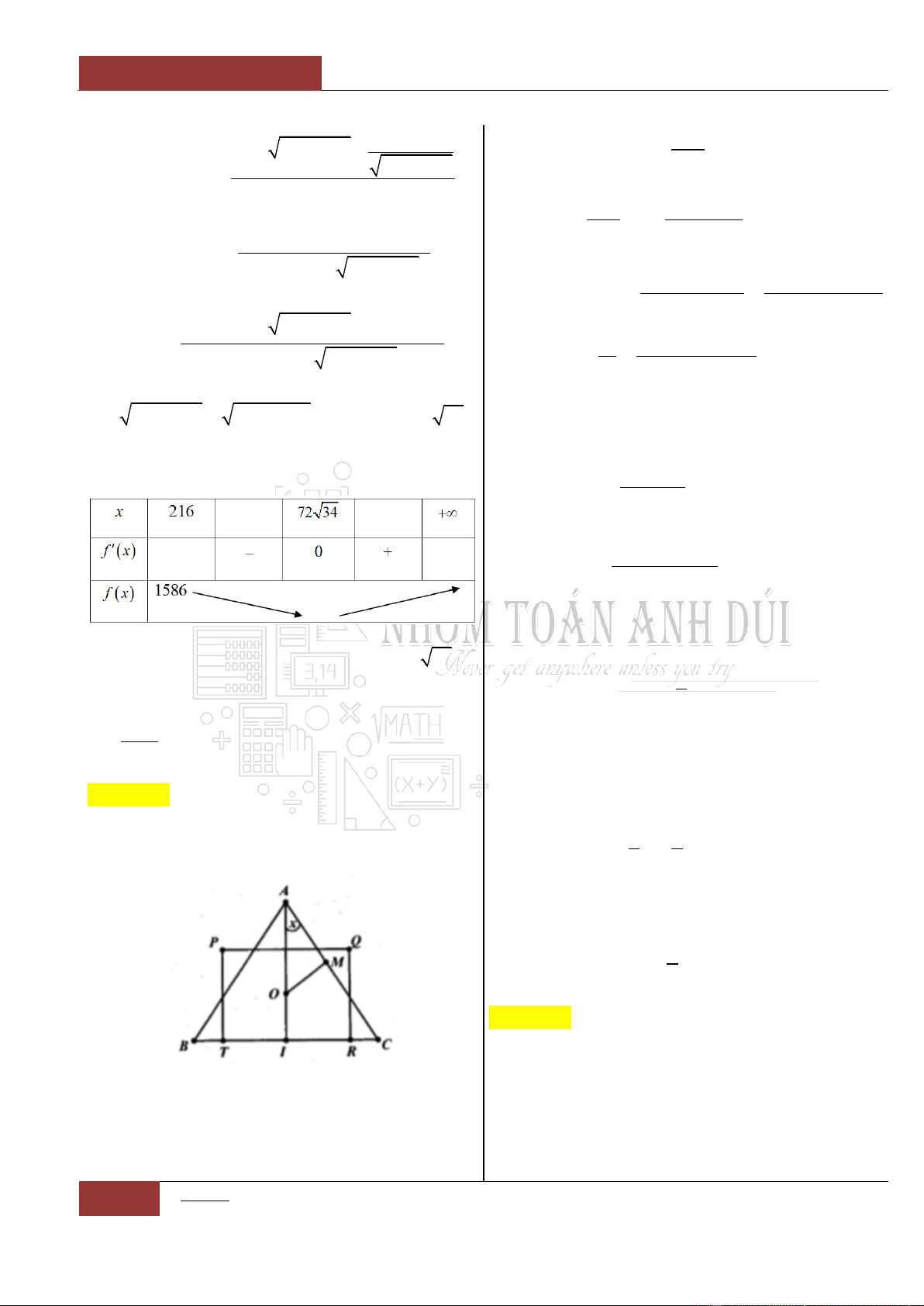
Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

441

[ I can't, I can! ]

Ta có:

 

2

22

1000

1000 216

216

1

216











x

fx

x

 

2 2 2

2 2 2 2

1000 216 1000

'1

216 216



  



xx

fx

xx

.

 

2 2 2 2 2

2 2 2 2

216 216 1000.216

'0

216 216

  

  



xx

fx

xx

3

2 2 2

216 1000.216 360 72 34xx     

.

Ta có bảng biến thiên

Vậy độ dài

AB

đạt cực tiểu khi

72 34AM m

.

Chi phí phải sử dụng nhỏ nhất là

1586

.200 3172

100

S

(triệu).

Đáp án D

Câu 67.

Hình nón có chiều cao

h AI

, bán kính đáy

R IC

, góc giữa đường sinh và trục là

,x

bán

kính khối cầu nội tiếp khối nón là

OM r

.

Ta có:

sinx

   

OM

AI AO OI OI

 

sinx 1

sinx sinx



   

r

AI r

   

 

32

33

2

1

2

sinx 1 sinx 1

.tanx ,

3sin .cos 3sin . 1 sinx

sinx 1

2. .

6sin . 1 sinx







   





  



rr

R IC AI

x x x

V

Vr

Vx

Đặt

 

sinx t 0;1 .

Xét hàm

 

2

1

, 0;1 .

6 . 1







t

f t t

tt

Ta có:

 

2

18 12 6

'0

66







tt

ft

tt

 

1 0;1

1

3

  















t

Tính toán tại một số giá trị cần thiết:

 

0

0;1

1

lim

14

min

33

lim







 

















 





x

ft

f f t

ft

Tìm được

 

4

.

3

Min f x

Đáp án C

Câu 68. Gọi

, Rh

lần lượt là bán kính đáy và

chiều cao của thùng.

+ Gọi

,

tp

VS

lần lượt là thể tích và diện tích toàn

phần của thùng

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

442

[ I can't, I can! ]

2000



V

lít

2000





33

2.



dm m

2 2 2

2

22

2 2 2 2 2 .



    



     





V R Rh R R R

RR

22

3

2 2 . . 2

   

  



    





V R R

R R R R

.

Dấu

""

xảy ra khi và chỉ khi:

2

12



     R R m h m

R

Đáp án A

Câu 69. Gọi

 

/x km h

là vận tốc của tàu,

0x

Thời gian tàu chạy quãng đường

1

km là

 

1

h

x

Chi phí tiền nhiên liệu cho phần thứ nhất là:

1 480

.480 

xx

(ngàn đồng)

Hàm chi phí cho phần thứ hai là

3

p kx

(ngàn

đồng/giờ)

Mà khi

10 30 0,03    x p k

nên

2

0,03px

(ngàn đồng)

Vậy tổng chi phí

 

2

480

0,03f x x

x

 

2

3

240 240

0,03 3 1728 36     f x x

xx

Dấu

“”

xảy ra khi

20x

.

Đáp án D

Câu 70. Gọi bán kính của quả cầu

A

là

1

R

của

4

quả cầu

, , B C D

và

E

là

2

R

.

Khi đó ta có:

 

2

1 2 1

24

1 2 0 1

2



    

R

R R R

.

Từ đó ta có:

 

2

1

0 1 2 1 0

2

     RR

.

Tổng thể tích của

5

khối cầu là

4

A BCDE

S S S

 





3

3 3 3

1 2 2 2

4 4 4

4. 1 2 4

3 3 3







     



S R R R R

 

32

2 2 2 2

41

4 12 6 1 , 0

32





      





S R R R R

Khảo sát hàm

 

32

1

4 12 6 1 0

2



      





f t t t t t

 

2

12 24 6



   f t t t

 

22

2

0

22

2











  











t

ft

t

Lập bảng biến thiên và từ bảng biến thiên ta

thấy

 

ft

đạt nhỏ nhất tại

22

2



t

Từ đó ta có

3

min

4 2 2

0,72

32













S f m

.

Đáp án A

Câu 71.

Theo định lí Thales, ta có:

 

''

0.

''



   



SO h x r

xh

SO x h r

Nhóm toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

443

[ I can't, I can! ]

Thể tích hình trụ là:

 

2

22

' . .











   

h x r

r

V r x x x h x

hh

Xét hàm số:

   

2

M x x h x

, ta có:

 

4. .

22





h x h x

M x x

Theo bất đẳng thức Cauchy, ta có thể suy ra:

3

2

4

22

4.

3 27















Cauchy

h x h x

x

h

M

Dấu

“”

xảy ra khi

.

23



  

h x h

xx

Đáp án B

Câu 72. Điều kiện:

0h

.

Ta có:

3

32

2

4

3









   

Vr

V r r h h

r

.

Diện tích toàn phần của bồn xăng là:

 

33

2

8

42

3

42





   

r V r

S r r rh h

r

.

Ta có:

 

3

2

8

2

3

0









rV

Sr

r

3

83

2

34



   

V

r V r

Lập bảng biến thiên ta sẽ thấy:

3

min

3

4





V

Sr

3 8 3

4 . 2 .

4 3 4

0





  

VV

V

h

r

Để nguyên vật liệu làm bồn xăng là ít nhất

min

0  Sh

.

Đáp án A

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

444

[ I can't, I can! ]

Minh họa đường

tiệm cận ngang!

Extra Techniques:

Study tips:

Việc ôn tập nội dung

“Giới hạn” của chương

trình lớp 11 là một yêu

cầu gần như là bắt buộc

nếu độc giả muốn làm

tốt dạng toán này!

Extra Techniques:

Remark:

Thực chất việc tìm tiệm

cận của đồ thị hàm số là

công đoạn đi tìm giới

hạn hữu hạn tại vô cực.

Extra Techniques:

Study Tips:

Một số công thức giới

hạn thường xuyên gặp

bên đây có thể giúp các

bạn tối ưu hóa thời gian

của các bạn trong quá

trình thực chiến đề!

I.IV. Đường tiệm cận

I. Đường tiệm cận ngang

1. Định nghĩa

Trên một khoảng

 

;

a

Kb







 



  





vô hạn nào đó, xét một hàm

số xác định

 

y f x

. Đường thẳng

0

yy

được gọi là đường

tiệm cận ngang của đồ thị hàm số

 

y f x

nếu ít nhất một

trong hai điều kiện đưới đây được thỏa mãn:

   

00

lim ; lim

xx

f x y f x y

 



.

2. Một số giới hạn đặc biệt – dạng cơ bản

a. Giới hạn của hằng số tại vô cực

 

lim , 2.1

x

c c c



  

.

b. Giới hạn của tỉ số giữa hằng và biến

 

lim 0, , 2.2

k

x

c

ck

x





  

.

c. Ba trường hợp thường thấy của giới hạn hàm

k

yx

 

lim , 2.3

k

x

xk





  

.

 

, , 2 1 2.4

lim

, , 2 2.5

k

x

k k m

x

k k m





   





  





.

d. Giới hạn

 

2.2

dạng đặc biệt.

 

1

lim 0, 2.6

k

x

k

x







.

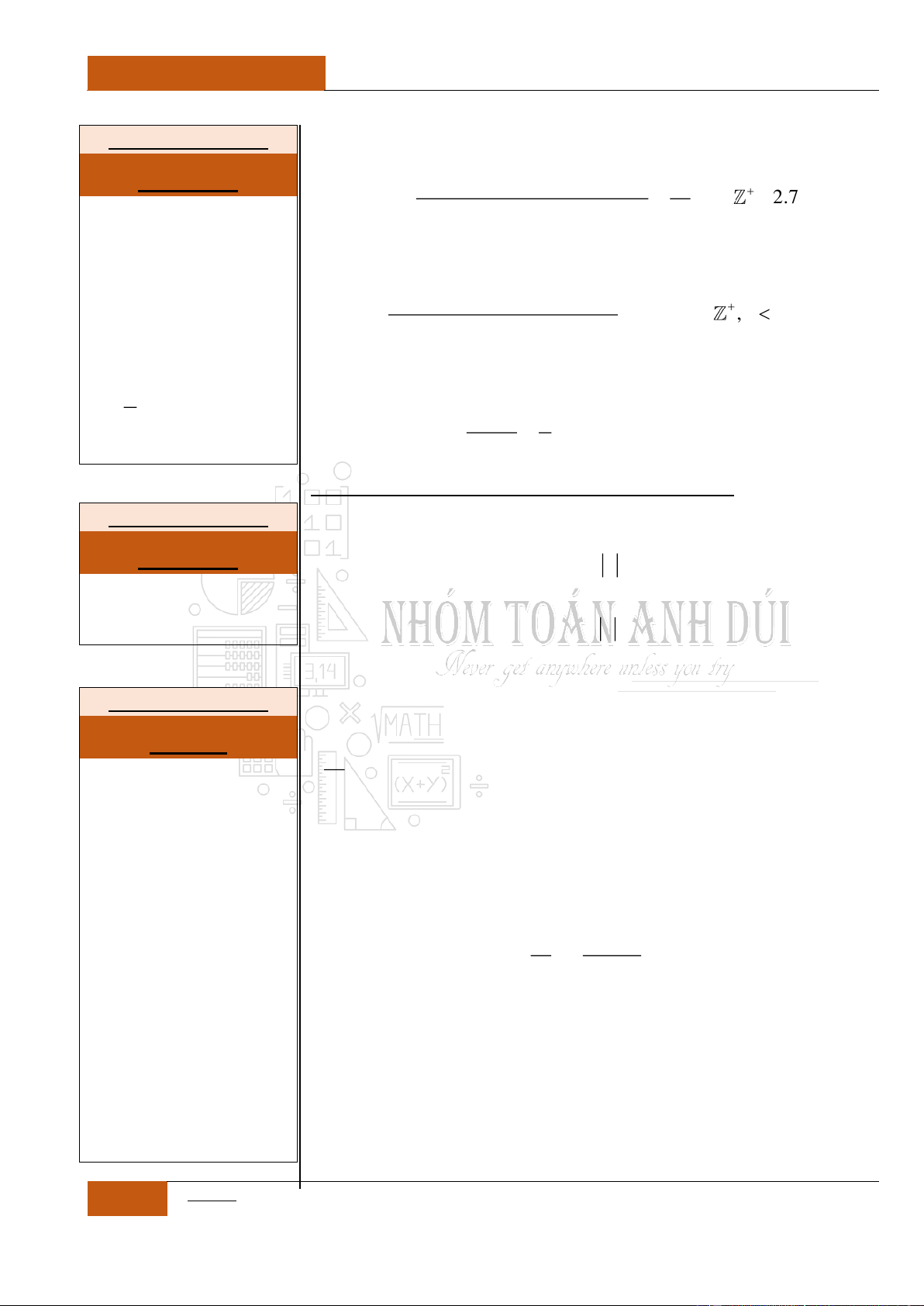
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

445

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Giới hạn thường thấy

trong các bài toán vận

dụng tính chất đồ thị

hàm số của Bộ giáo dục

và Đào tạo hiện nay là

giới hạn

 

2.9

. Khi đó,



a

y

c

là tiệm cận ngang

của đồ thị hàm số.

Extra Techniques:

Study Tips:

Giới hạn của dãy số

(nếu có) là duy nhất.

Extra Techniques:

Remark:

Những giới hạn chỉ

đúng khi cả hai dãy

n

a

và

n

b

hội tụ.

Cho dù

 



nn

ab

hội tụ

các công thức bên vẫn

có trường hợp sai.

Chẳng hạn:

 

1















n

a

b

,

khi đó:

 

n

a

hội tụ,

 

n

b

phân kỳ nhưng

 



nn

ab

hội tụ!!!

e. Giới hạn hàm phân thức (đồng bậc tử mẫu)

 

1

1 1 0

1

1 1 0

...

lim , 2.7

...

nn

n n n

nn

x

n

nn

a x a x a x a a

n

b

b x b x b x b











   



   

.

f. Giới hạn hàm phân thức (bậc tử nhỏ hơn mẫu)

 

1

1 1 0

1

1 1 0

...

lim 0, , , 2.8

...











   

  

   

kk

nn

x

nn

a x a x a x a

k n k n

b x b x b x b

.

g. Giới hạn

 

2.7

dạng đặc biệt

 

lim , 0, 0 2.9





   



x

ax b a

c ad bc

cx d c

.

3. Một số giới hạn đặc biệt – dạng nâng cao

a. Giới hạn của hàm số mũ

 

,1

lim 1, 1 2.10

0, 1





 











x

a

aa

a

.

b. Giới hạn của các dãy (hội tụ) với các phép toán

Nếu các dãy số

 

n

a

và

 

n

b

hội tụ thì các dãy

   

,,

n n n n

a b a b







n

a

b

với

0,

n

bn

và

lim 0





n

b

cũng hội tụ và khi đó:

 

lim lim lim 2.11

  

  

n n n n

n n n

a b a b

.

     

 

lim lim . lim 2.12

  



n n n n

n n n

a b a b

.

 

lim

lim 2.13

lim











n

nn

n

nn

n

a

bb

.

c. Giới hạn của hằng số và dãy (hội tụ) trên các phép toán

 

lim lim 2.14

 

  

nn

a c a c

.

   

 

lim . lim 2.15

 



nn

ka k a

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

446

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Những công thức bên

trên vẫn còn đúng nếu

thay

0

lim lim

 



x x x

.

Extra Techniques:

Study Tips:

Cách xét dấu trên tương

tự như xét dấu các hàm

số với các phép toán

cộng và nhân thông

thường (âm cộng âm

được âm, dương cộng

dương thành dương, tích

cùng dấu được dương,

tích trái dấu được âm,

lấy âm một số dương

thu được số âm và

ngược lại.

Minh họa đường

tiệm cận đứng!

d. Giới hạn hữu hạn của các hàm (xác định) với các phép toán

Cho các hàm số

   

,y f x g x

xác định trong một tập

X

nào

đó. Nếu

 

lim





x

f x A

và

 

lim , ,





x

g x B A B

, thì ta có:

     

lim 2.16



    



x

f x g x A B

.

     

lim . . 2.17



  



x

f x g x A B

.

 

lim 2.18











x

fx

A

g x B

.

 

   

lim , 0 2.19





gx

B

x

f x A A

.

d. Giới hạn vô tận của các hàm (xác định) với các phép toán

Cho các hàm số

   

,y f x g x

xác định trong một tập

X

nào

đó. Nếu

 

lim



 

x

fx

và

 

lim



 

x

gx

, thì ta có:

     

lim 2.20



    



x

f x g x

.

     

lim . 2.21



   



x

f x g x

.

Cho các hàm số

   

,y f x g x

xác định trong một tập

X

nào

đó. Nếu

 

lim



 

x

fx

và

 

lim





x

gx

, thì ta có:

     

lim 2.22



    



x

f x g x

.

     

lim . 2.23



   



x

f x g x

.

II. Đường tiệm cận đứng

1. Định nghĩa

Đường thẳng

0

xx

được gọi là đường tiệm cận đứng (hay

tiệm cận đứng) của đồ thị hàm số

 

y f x

nếu ít nhất một

trong các điều kiện sau thỏa mãn:

   

00

lim , lim





   

x x x x

f x f x

.

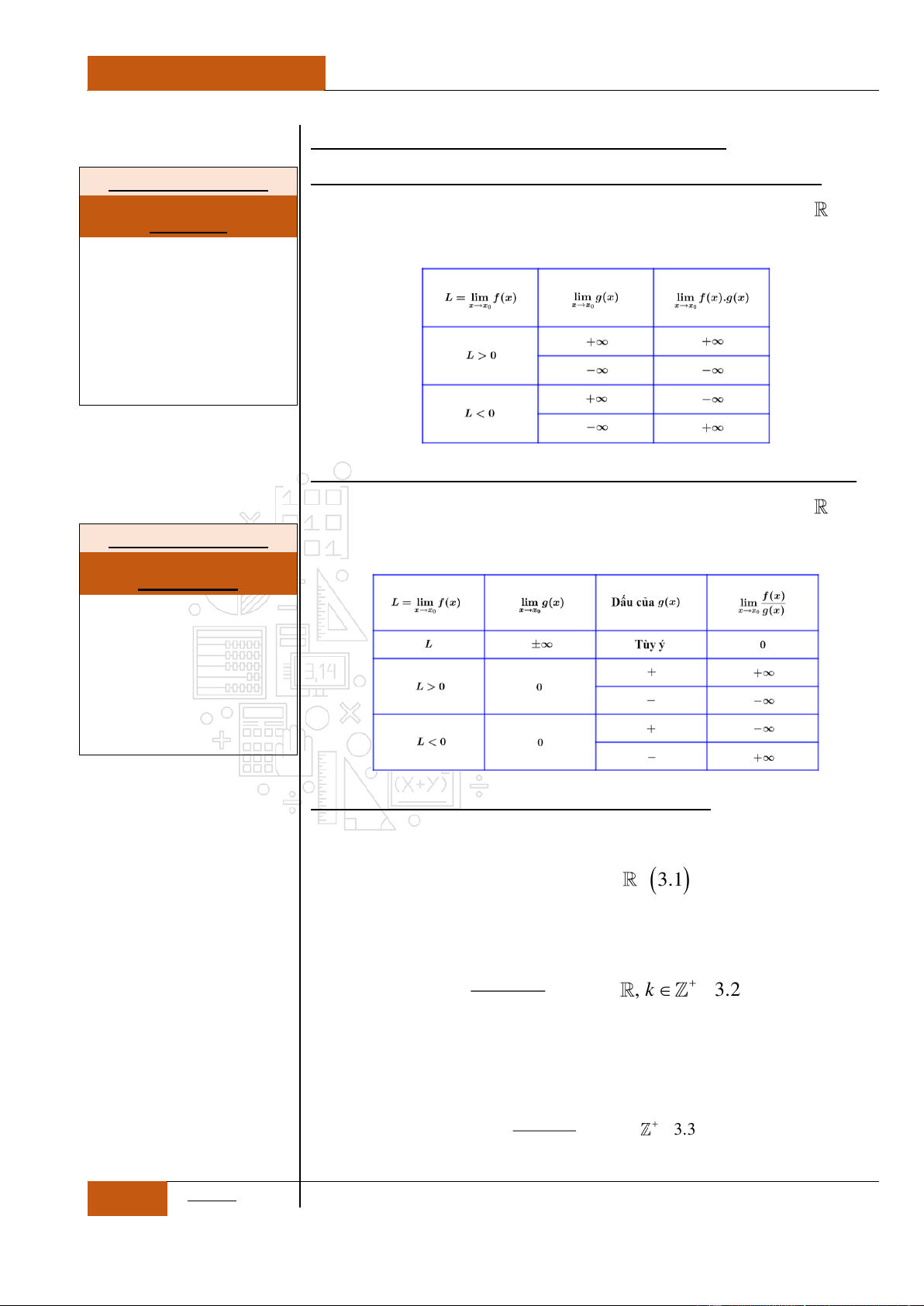
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

447

[ I can't, I can! ]

Extra Techniques:

Remark:

Các quy tắc bên đây

được áp dụng cho mọi

trường hợp

0

xx

,

00

,,

,





   

x x x x

xx

Extra Techniques:

Study Tips:

Ở quy tắc 2, chúng tôi

dùng thuật ngữ “dấu” thể

hiện tính “âm, dương”

của hàm số trên khoảng

 

0

\Xx

đang xét.

2. Một số quy tắc tìm giới hạn tại một điểm

a. Quy tắc 1 – Quy tắc xác định dấu giới hạn của tích

Cho các hàm số

   

,y f x g x

xác định trong một tập

X

nào

đó. Khi đó:

b. Quy tắc 2 – Quy tắc xác định dấu giới hạn của thương

Cho các hàm số

   

,y f x g x

xác định trong một tập

X

nào

đó với

 

0gx

. Khi đó:

3. Một số giới hạn đặc biệt – dạng cơ bản

a. Giới hạn của hằng số tại một điểm

 

0

lim , 3.1

xx

c c c



  

.

b. Giới hạn của tỉ số giữa hằng và biến

 

0

lim , , 3.2

k

xx

c

ck

xx





   



.

d. Giới hạn

 

2.2

dạng đặc biệt.

 

0

1

lim 0, 3.3

k

xx

k

xx









.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

448

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Những công thức bên

trên vẫn còn đúng nếu

thay

0

lim lim

 



x x x

.

Extra Techniques:

Study Tips:

Cách xét dấu trên tương

tự như xét dấu các hàm

số với các phép toán

cộng và nhân thông

thường (âm cộng âm

được âm, dương cộng

dương thành dương, tích

cùng dấu được dương,

tích trái dấu được âm,

lấy âm một số dương

thu được số âm và

ngược lại.

e. Đối với những hàm phân thức có dạng

 



fx

y

gx

thỏa mãn

 

0















fx

gx

thì:

 

0

lim , 3.4





xx

fx

gx

f. Giới hạn phân thức bậc nhất trên bậc nhất (hàm nhất biến)

 

lim , 0, 0 3.5





    



d

x

c

ax b

c ad bc

cx d

.

4. Một số giới hạn đặc biệt – dạng nâng cao

a. Giới hạn hữu hạn của các hàm (xác định) với các phép toán

Cho các hàm số

   

,y f x g x

xác định trong một tập

X

nào

đó. Nếu

 

0

lim





xx

f x A

và

 

0

lim , ,





xx

g x B A B

, thì ta có:

     

0

lim 3.6



    



xx

f x g x A B

.

     

0

lim . . 3.7



  



xx

f x g x A B

.

 

0

lim 3.8











xx

fx

A

g x B

.

 

   

0

lim , 0 3.9





gx

B

xx

f x A A

.

b. Giới hạn vô tận của các hàm (xác định) với các phép toán

Cho các hàm số

   

,y f x g x

xác định trong một tập

X

nào

đó.

Nếu

 

0

lim



 

xx

fx

và

 

0

lim



 

xx

gx

, thì ta có:

     

0

lim 3.10



    



xx

f x g x

.

     

0

lim . 3.11



   



xx

f x g x

.

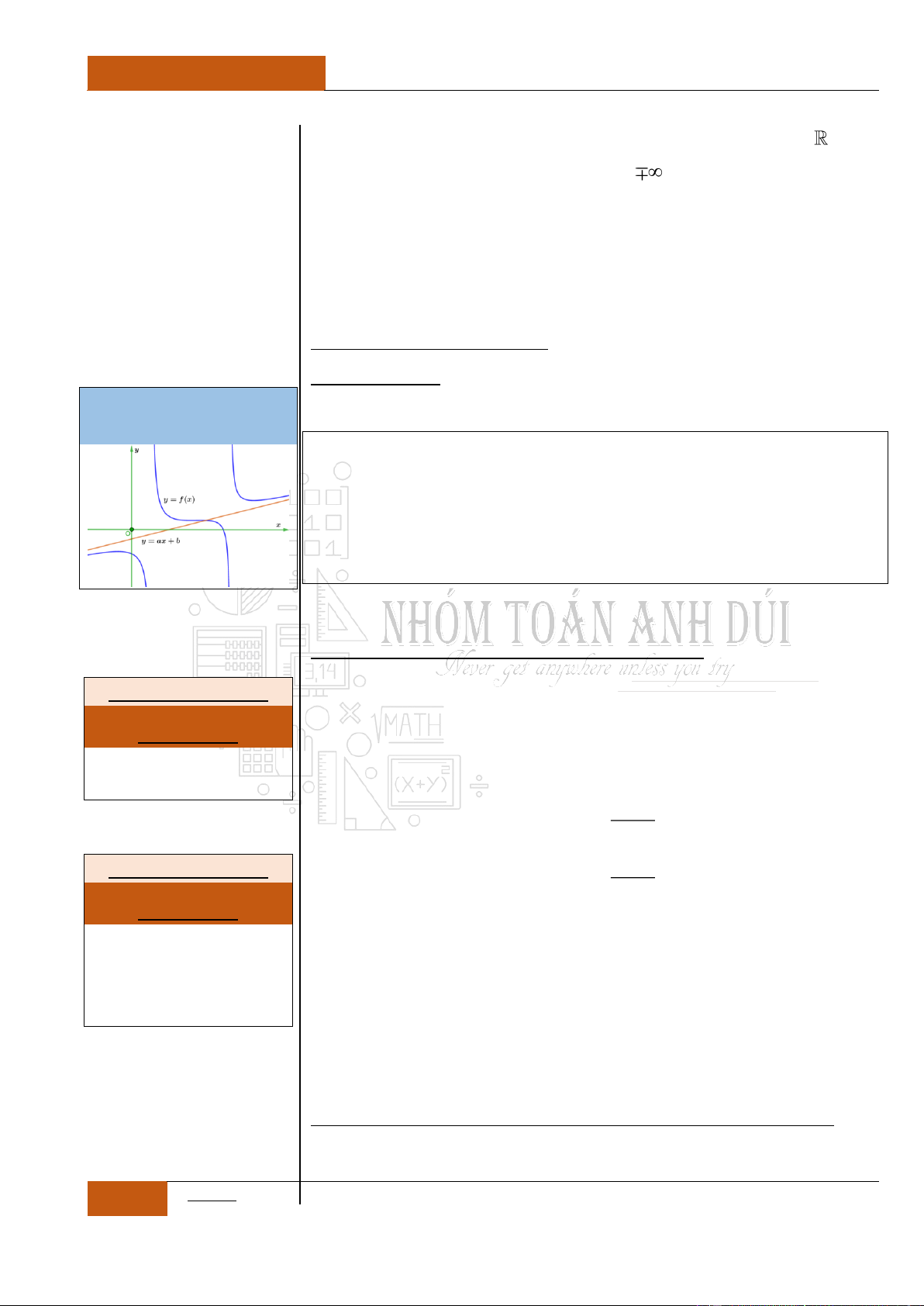
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

449

[ I can't, I can! ]

Minh họa đường

tiệm cận xiên!

Extra Techniques:

Study Tips:

Nếu

0a

Ta chỉ có

đường tiệm cận ngang.

Extra Techniques:

Study Tips:

Hàm phân thức chỉ có

đường tiệm cận xiên khi

bậc của tử lớn hơn bậc

của mẫu một bậc!

Cho các hàm số

   

,y f x g x

xác định trong một tập

X

nào

đó. Nếu

 

0

lim



 

xx

fx

và

 

0

lim





xx

gx

, thì ta có:

     

0

lim 3.12



    



xx

f x g x

.

     

0

lim . 3.13



   



xx

f x g x

.

III. Đường tiệm cận xiên

1. Định nghĩa

Đường thẳng

,0  y ax b a

được gọi là đường tiệm cận xiên

của đồ thị hàm số

 

y f x

nếu ít nhất một trong các điều

kiện sau thỏa mãn:

   

lim 0, lim 0

 

         

   

xx

f x ax b f x ax b

.

2. Cách xác định hệ số của tiệm cận xiên

Để xác định hệ số

,ab

trong phương trình đường tiệm cận

xiên

y ax b

, ta có thể áp dụng các công thức sau đây:

a. Hệ số

a

Hệ số

a

được tính bởi:

 

lim















x

fx

x

a

fx

x

.

b. Hệ số

b

Hệ số

b

được xác định bằng cách:

 

lim







  









  





x

f x ax

b

f x ax

.

3. Cách xác định đường tiệm cận xiên của hàm cơ bản

a. Hàm số bậc hai trên bậc nhất

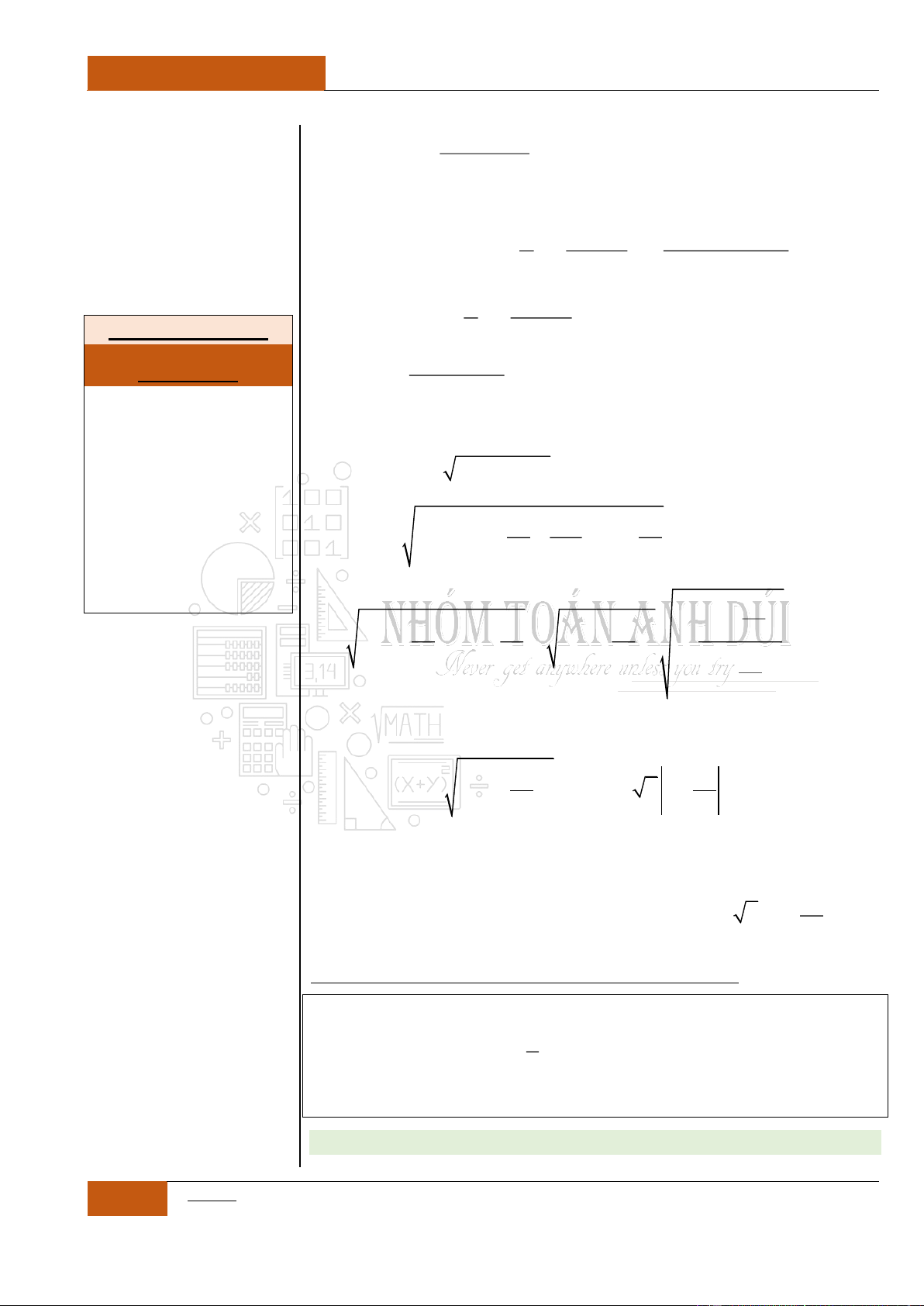
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

450

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Những dạng toán về

đường tiệm cận xiên, tôi

chỉ cung cấp thêm kiến

thức cho độc giả. Bởi lẽ,

rất hiếm khi thấy xuất

hiện trong các đề thi thử

đặc biệt đề thi tốt nghiệp

THPTQG những năm

gần đây!

Xét hàm số

2

, , 0







ax bx c

y a d

dx e

.

Thực hiện phép chia đa thức

2

ax bx c

cho

dx e

, ta thu được

thương và dư lần lượt là:

2





a bd ae

x

d

và

22

2

cd bde ae

d

.

Khi đó đường

2





a bd ae

yx

d

là đường tiệm cận xiên của đồ thị

hàm số

2

, , 0







ax bx c

y a d

dx e

.

b. Căn thức bậc hai của hàm bậc hai

Xét hàm số

2

,0   y ax bx c a

.

Ta có:

22

2

2. .

24

4



    





b b b

y a x x c

aa

a

2

22

2

4

.1

2 4 2

2



   

      

   

   









b

c

b b b

a

y a x c a x

a a a

b

x

a

Khi đó, ta hoàn toàn có thể phân tích thành

   

2

22





     





bb

y a x x a x x

aa

Với

 

lim 0







x

.

Do thế ta thu được hai đường tiệm cận xiên là

2



  





b

y a x

a

.

IV. Một số bài tập ứng dụng đường tiệm cận

Câu 1. Đồ thị hàm số

1

y

x

có bao nhiêu đường tiệm cận ngang?

A.

0

. B.

1

. C.

2

. D.

3

.

Đáp án: B

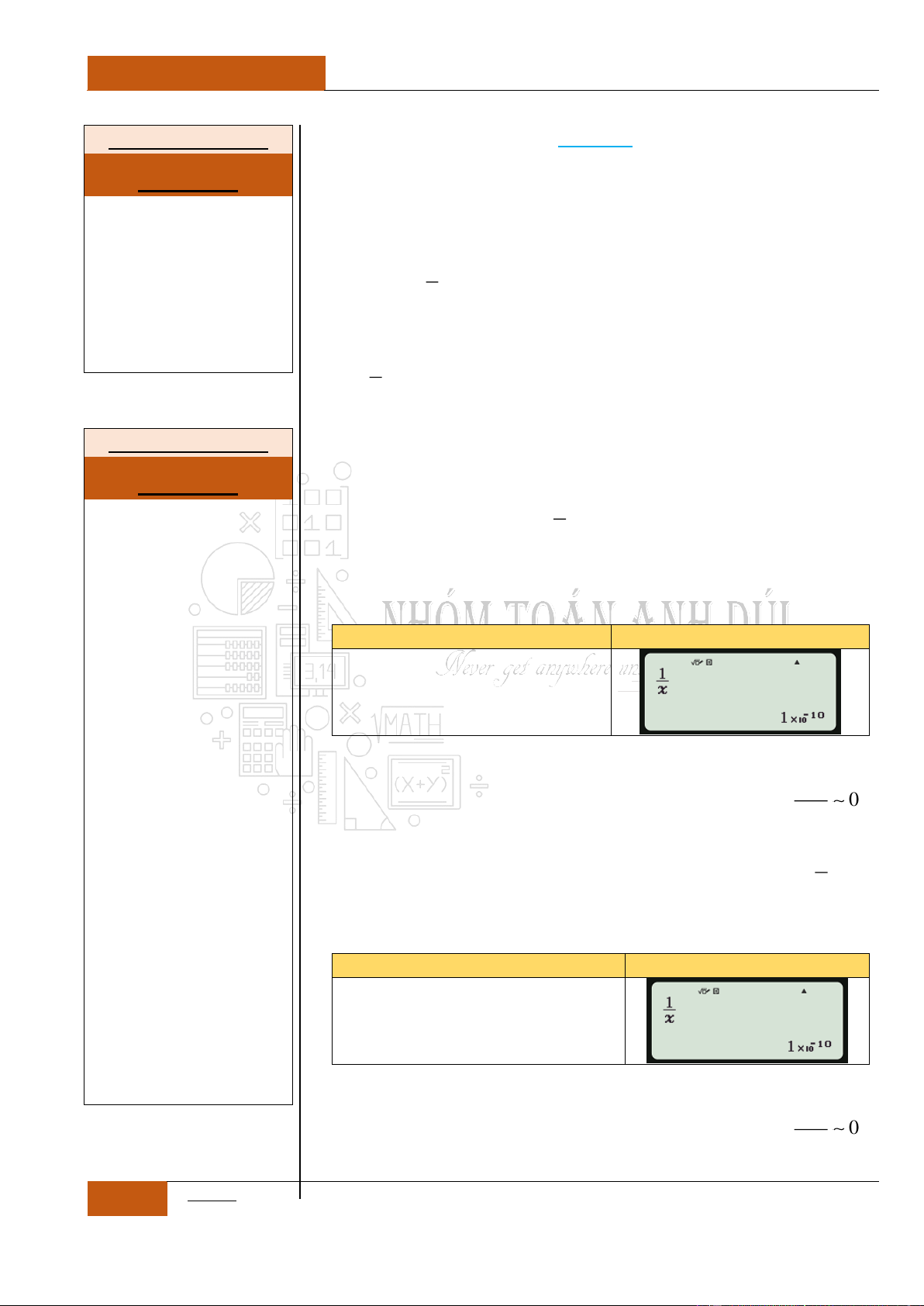
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

451

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Trong chương trình sách

giáo khoa hiện thời, ta

không định nghĩa đường

tiệm cận (tiệm cận) của

hàm số mà chỉ có đường

tiệm cận của đồ thị hàm

số!

Extra Techniques:

Study Tips:

Các bước sử dụng

CASIO để tính giới hạn

tại vô cực.

Bước 1: Nhập hàm số

vào CASIO.

Bước 2: CALC một giá

trị phù hợp, chẳng hạn:

Nếu dần về



, ta

CALC

10

a

x

(Tùy bài

có dạng phân thức, đa

thức, hàm số mũ mà ta

chọn

 

5;15a

cho phù

hợp, những trường hợp

hiếm thấy có thể chọn

số

a

ngoài khoảng trên.

Nếu dần về



, ta

CALC

10 ,

a

x

với

 

5;15a

.

Lời giải

Cách 1: Tự luận thông thường.

Đồ thị hàm số xác định trên

   

;0 0;   

.

Dễ thấy:

1

lim 0





x

.

Do vậy đường thẳng

0y

là đường tiệm cận ngang của đồ thị hàm

số

1

y

x

.

Vậy đồ thị hàm số có duy nhất một đường tiệm cận ngang.

Cách 2: CASIO.

Nhập vào máy tính biểu thức

1

x

, sử dụng lệnh CALC để tính toán tại

một giá trị có độ lớn giá trị tuyệt đối đủ lớn,

10

.

Quy trình bấm máy

Màn hình hiển thị

1a[r10

^10==

Kết quả máy tính thu được là một số khá nhỏ

10

1

10 0

10





.

Do vậy

0y

là đường tiệm cận ngang của đồ thị hàm số

1

y

x

.

Tiếp tục CALC một giá trị vô cùng nhỏ,

10

10

.

Quy trình bấm máy

Màn hình hiển thị

rp10^10==

Kết quả máy tính thu được là một số khá nhỏ

10

1

10 0

10





.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

452

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Bài toán vẫn nhận

trường hợp 1, mẫu số có

nghiệm của tử là vì với

4

3

m

thì:

2

44

33







x

y

xx

Hay:

 

2

3













x

y

xx

Khi đó:

1

lim lim 0

2

3

 





xx

y

x

Do vậy

0y

là đường tiệm cận ngang của đồ thị hàm số

1

y

x

.

Hai đường thẳng trên giống nhau nên ta chỉ lấy một.

Câu 2. Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị hàm

số

2

2





x

y

x mx m

có đúng một đường tiệm cận đứng?

A.

 

m

. B.

04

4

3











m

.

C.

4

;0;4

3









m

. D.

0

4











m

.

Đáp án: C

Lời giải

Để đồ thị hàm số

2

2





x

y

x mx m

có một đường tiệm cận đứng thì:

Trường hợp 1: Mẫu số

2

0  x mx m

có một nghiệm bội chẵn có

thể trùng hoặc không trùng nghiệm của tử,

2x

.

Hay

2

0

40

4





    







m

mm

m

.

Trường hợp 2: Mẫu số có một nghiệm

2x

và một nghiệm khác,

khác

2x

. Hay:

2

4

40

3

0

4

2 2 0

3

4













   







   



  











m

mm

m

mm

m

.

Vậy tập các giá trị

m

thỏa mãn yêu cầu đề bài là

4

;0;4

3









m

.

Mở rộng đề bài: Hàm số

2

2





x

y

x mx m

luôn có một đường tiệm

cận ngang là đường

0y

. Do bậc tử nhỏ hơn bậc mẫu! Ta có thể

dùng những nhận xét ở phần lý thuyết để giải quyết bài toán!

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

453

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Những bài toán không

cho một hàm số cụ thể

mà chỉ cho “kết quả”

của các giới hạn thì

công cụ hiểu quả nhất là

định nghĩa và các quy

tắc tìm đường tiệm cận

đã được trình bày ở trên!

Câu 3. Cho hàm số

 

y f x

có

   

lim 2, lim

 

  

xx

f x f x

.

Khẳng định nào dưới đây là chắc chắn đúng?

A. Đồ thị hàm số có hai đường tiệm cận ngang.

B. Đồ thị hàm số không có đường tiệm cận đứng.

C. Đồ thị hàm số có duy nhất một đường tiệm cận.

D. Đồ thị hàm số có đúng một đường tiệm cận ngang.

Đáp án: D

Lời giải

Dựa vào lý thuyết đường tiệm cận, ta dễ dàng nhận thấy:

Đường

2y

là đường tiệm cận ngang của đồ thị hàm số.

Tuy nhiên, ta không thể kết luận hàm số chỉ có một đường tiệm cận

(Do còn có đường tiệm cận đứng chưa được kể vào).

 Loại A, B, C.

Đáp án đúng phải là Đáp án D vì: đồ thị hàm số có thể có nhiều hơn

một đường tiệm cận (nếu tồn tại tiệm cận đứng).

Câu 4. Số đường tiệm cận của đồ thị hàm số

2

43

2 15







xx

y

xx

là?

A.

0

. B.

1

. C.

2

. D.

3

.

Đáp án: C

Lời giải

Cách giải sai:

Tìm tiệm cận ngang:

Ta có:

2

43

1

43

lim lim lim 1

2 15

1

  



  



x x x

xx

x

y

xx

.

Vậy

1y

là đường tiệm cận ngang của đồ thị hàm số.

Tìm tiệm cận đứng:

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

454

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Những bài toán phân

thức hữu tỉ thường “bẫy”

Học sinh những điểm

như bài toán được nêu ra

ở bên! Để tối ưu cách

giải, hay tìm ra dạng bên,

ta có thể dùng CASIO để

giải phương trình tìm

nghiệm mẫu và tử. Nếu

có nghiệm chung, chắc

chắn sẽ được đưa về

dạng bên.

Tìm nghiệm của mẫu:

Ta có:

2

3

2 15 0

5





   







x

xx

x

.

Vậy

5, 3  xx

là hai đường tiệm cận của đồ thị hàm số trên.

Vậy có tất cả

3

đường tiệm cận của đồ thị hàm số!

Đáp án D.

Cách giải đúng:

Nhận xét: Tử số và mẫu số đều có lượng nhân tử

 

3x

.

Do,

  

2

4 3 1 3    x x x x

và

  

2

2 15 3 5    x x x x

.

Khi đó:

  

2

13

4 3 1

3 5 5

2 15



  



  



xx

x x x

xx

.

Như vậy đồ thị hàm số trở thành hàm số nhất biến

1

5







x

y

x

.

Hay đồ thị hàm số hai đường tiệm cận (một đường tiệm cận đứng

5x

và một đường tiệm cận ngang

1y

).

Câu 5. Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị hàm

số

2

2 2021

2022







x mx

y

x

có đúng hai đường tiệm cận ngang.

A.

0m

. B.

03

3











m

. C.

0m

. D.

0m

.

Đáp án: C

Lời giải

Điều kiện xác định:

2

2022

2021 0











x

mx

.

Ta có:

2

2021

2

2 2021

lim lim 2

2022

1

 



  



xx

m

x mx

x

m

x

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

455

[ I can't, I can! ]

Extra Techniques:

Remark:

Một trong những lỗi sai

dễ thấy nhất của Học

sinh chính là “quên” điều

kiện cần để hàm số có

tiệm cận.

Đối với đồ thị hàm số

nhất biến

ax b

y

cx d







thì

điều kiện cần và đủ để có

đường tiệm cận đứng

(ngang) là:

0

a

c

ad bc

















Mặt khác:

2

2021

2

2 2021

lim lim 2

2022

1

 





  



xx

m

x mx

x

m

x

.

Để hai đồ thị hàm số có hai đường tiệm cận thì điều kiện cần và đủ là:

0

22

m

mm











  





  





.

Câu 6. Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

45x

y

xm







có tiệm cận đứng nằm bên phải trục

Oy

.

A.

0m

. B.

0m

. C.

0m

. D. Đáp án khác.

Đáp án: D

Lời giải

Điều kiện cần để có đường tiệm cận đứng là:

   

5

4. 5 .1 0 4 5

4

m m m         

.

Thật vậy! Vì với

5

4

m 

thì:

45

4

5

4

x

y

x







không có đường tiệm cận.

Tiệm cận đứng của đồ thị hàm số là đường

xm

. Để đường thẳng

xm

nằm bên phải trục

Oy

thì

0m 

.

Vậy

 

5

0; \

4

m



  





.

Câu 7. Tiệm cận đứng của đồ thị hàm số

2

2 1 3

56

x x x

y

xx

   





là?

A.

2x

. B.

3x

. C.

2

3











x

. D. Đáp án khác.

Đáp án: B

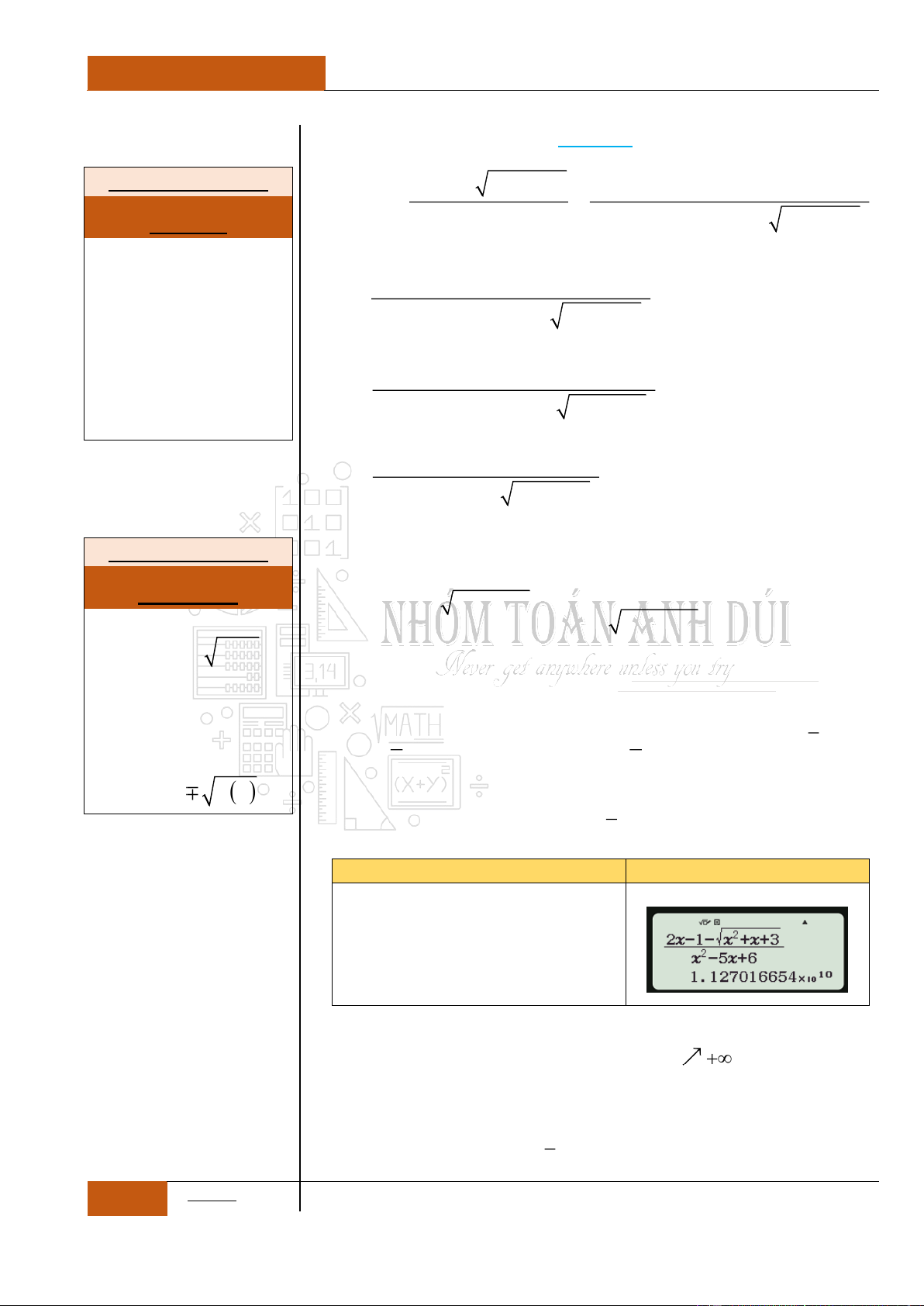
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

456

[ I can't, I can! ]

Extra Techniques:

Remark:

Học sinh thường gặp rắc

rối trong những dạng

toán này, bởi lẻ, các bạn

không quan tâm đến việc

khử đi lượng nhân tử

“chung” ở tử và mẫu.

Dẫn đến có sự nhận sai

đáp án!

Extra Techniques:

Study Tips:

Những bài toán có chứa

lượng

   

f x g x

, ta

thường “trục” căn thức

bằng cách nhân thêm

lượng liên hợp cho cả tử

và mẫu, lượng liên hợp

đó là:

   

f x g x

.

Lời giải

Ta có:

 





2 2 2

2

22

2 1 3 4 4 1 3

56

5 6 2 1 3

x x x x x x x

y

xx

x x x x x

        





     

 





2

22

3 5 2

5 6 2 1 3

xx

y

x x x x x





     

  





2

2 3 1

2 3 2 1 3





     

xx

y

x x x x x

 





2

31

3 2 1 3





    

x

y

x x x x

Tìm nghiệm mẫu số:

 





2

3

3 2 1 3 0

3 1 2





      



   





x

x x x x

x x x

2 2 2

33

3

3 1 4 4 3 5 2 0

1

11

3

22













       





  























xx

x

x x x x x x

x

xx

.

Tính giới hạn tại

10 10

1

3 10 , 10

3



    xx

bằng máy tính CASIO.

Quy trình bấm máy

Màn hình hiển thị

a2[p1ps[d

+[+3$$[dp

5[+6r3+10

^p10==

Màn hình hiển thị kết quả

10

1.127016654 10 

.

Vì thế

3x

là đường tiệm cận đứng của đồ thị hàm số.

Một cách tương tự với

10

1

10

3



  x

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

457

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Tìm điều kiện để đồ thị

hàm số có đường tiệm

cận

00

,x x y y

xác

định thì việc định các giá

trị của tham số thực

,ab

được chuyển thành bài

toán tìm nghiệm ẩn

“tham số” và ẩn

x

được

thay thế thành những

hằng số cụ thể,

0

x

.

Tương tự với

0

y

.

Quy trình bấm máy

Màn hình hiển thị

a2[p1ps[d

+[+3$$[dp

5[+6rp1a3

+10^p10==

Vì màn hình cho ra kết quả là một giá trị hữu hạn, vì thế

1

3

x

Vậy chỉ có một đường tiệm cận đứng duy nhất là đường

3x

.

Câu 8. Biết đồ thị hàm số

 

2

21  





a b x bx

y

x x b

có đường tiệm cận

đứng và đường tiệm cận ngang lần lượt là

1, 0xy

. Tính

2ab

.

A.

6

. B.

7

. C.

8

. D. Đáp án khác.

Đáp án: C

Lời giải

Để

1x

là đường tiệm cận đứng thì:

2

1 1 0 2    bb

.

Để đường tiệm cận ngang là

0y

thì:

 

2

21

lim lim 2 0 2 4

 

  

      



xx

a b x bx

y a b a b

x x b

.

Như vậy tổng

2 4 2.2 8   ab

.

Thử lại với

4, 2ab

, ta có:

2

21

2







x

y

xx

quả thật thỏa mãn yêu

cầu đề bài!

Câu 9. Số giá trị

m

để đồ thị hàm số

1





mx

y

xm

có tiệm cận đứng.

A.

0

. B.

1

. C.

2

. D.

3

.

Đáp án: C

Lời giải

Để hàm số có tiệm cận đứng thì:

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

458

[ I can't, I can! ]

   

2

1

. 1 .1 0 1 0

1





        







m

m m m

m

.

Câu 10. Cho hàm số

 

y f x

có đồ thị đạo hàm như hình vẽ dưới

đây.

Tổng số tiệm cận của đồ thị hàm số:

 

2 2021

2021

2 2021

1

...

1 2 2021





    

  

f x f x

fx

y g x

f x f x f x

A.

2022

. B.

2

. C.

2021

. D.

0

.

Đáp án: A

Lời giải

Dựa vào đồ thị hàm số đạo hàm ta thấy:

   

'1f x f x x C   

.

Khi đó hàm số là một hàm đồng biến và

 

   

lim lim lim

lim

lim lim

  



 



    









 







x x x

x

xx

f x f x x C

fx

f x x C

Xét hàm số:

 

2 3 2021

3 2021

2 3 2021

1

...

1 2 3 2021

f x f x f x

fx

y g x

f x f x f x f x

  



     

   

TXĐ:

 

\ 2021 ; 2020 ;...; 1D C C C      

.

Với mọi số

   

0

2021 ; 2020 ;...; 2x f a C C C       

.

Ta có:

   

00

lim , lim

x x x x

g x g x





   

.

Suy ra:

0

xx

là tiệm cận đứng của đồ thị hàm số.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

459

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Điều kiện 1 thực chất là

dựa vào tính “đơn điệu”

của đồ thị hàm số. Bởi lẽ,

đồ thị hàm số không đơn

điệu – hàm không đổi thì

hàm số đạo hàm phải

bằng

0

. Như vậy, để

hàm số không trở thành

“đường thẳng song song

hoặc trùng” với trục

hoành – hàm hằng thì

'0y

.

Extra Techniques:

Study Tips:

Mẹo bên cạnh đây sẽ là

một công cụ hữu hiệu để

các độc giả có thể hoàn

thành bài tập một cách

nhanh chóng và đầy hiệu

quả.

Như vậy hàm số

 

y g x

có tất cả

2020

tiệm cận đứng. (Lưu ý:

 

0

1x x f a   

không là tiệm cận đứng).

Ta có:

 

2021 1

lim 1 1 ... 1 2021

x

elementsof

gx



    

Bên cạnh đó:

 

2021

2 2021

2021

2 2021

11

lim lim 1 ...

2 2021

11

lim lim 1 ...

2 2021

lim 1 1 1 ... 1 1 1 1

 









   











  



   









       

xx

x

f x f x

gx

f x f x

gx

f x f x

gx

Vì thế đồ thị hàm số

 

y g x

có hai tiệm cận ngang là đường

2021y 

và

1y 

. Như vậy hàm số có tất cả

2022

đường tiệm cận.

Một số Tips để làm tốt các bài toán về đường tiệm cận

1. Điều kiện có tiệm cận của đồ thị hàm số nhất biến

Đồ thị hàm số

, 0, 0



  



ax b

y a c

cx d

có đường tiệm cận đứng và

đường tiệm cận ngang khi và chỉ khi:

' 0 0   y ad bc

.

Khi đó, đồ thị hàm số có một đường tiệm cận đứng là



d

x

c

và

đường tiệm cận ngang là



a

y

c

.

2. Mẹo “nhìn” đường tiệm cận

a. Hàm phân thức hữu tỉ

Xét hàm số

 



fx

y

gx

với

   

,f x g x

là các đa thức. Khi đó:

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

460

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Mẹo bên cạnh đây sẽ là

một công cụ hữu hiệu để

các độc giả có thể hoàn

thành bài tập một cách

nhanh chóng và đầy hiệu

quả.

Extra Techniques:

Study Tips:

Khi làm những bài tập

dạng tìm tiệm cận xiên

của đồ thị hàm bậc hai

trên bậc nhất, ta không

nên “học thuộc” công

thức bên, thay vào đó,

công cụ “Lược đồ

Hoocner” để tìm ra phần

thương và phần dư, nhất

là những hàm bậc cao.

a.1. Hàm số có tiệm cận đứng là

xc

nếu

 

0















fc

gc

(Xét sau khi đã thu gọn phân thức – nếu có lượng nhân tử chung).

a.2. Nếu bậc tử bằng bậc mẫu thì tiệm cận ngang chính là “tỉ lệ” của

hệ số cao nhất của hạng tử ở tử và ở mẫu.

Chẳng hạn:

 

1

1 1 0

1

1 1 0

...

lim lim

...



 



   



   

nn

n n n

nn

xx

n

nn

fx

a x a x a x a a

g x b

b x b x b x b

.

a.3. Nếu bậc tử lớn hơn bậc mẫu thì tiệm cận ngang không tồn tại

thay vào đó nếu bậc tử lớn hơn bậc mẫu đúng một bậc thì luôn tồn tại

đường tiệm cận xiên theo định nghĩa “đường tiệm cận xiên” đã được

trình bày ở trên.

Một ví dụ về đường tiệm cận xiên của đồ thị hàm bậc hai trên bậc

nhất tổng quát:

Xét hàm số

2

, , 0







ax bx c

y a d

dx e

.

Thực hiện phép chia đa thức

2

ax bx c

cho

dx e

, ta thu được

thương và dư lần lượt là:

2





a bd ae

x

d

và

22

2

cd bde ae

d

.

Khi đó đường

2





a bd ae

yx

d

là đường tiệm cận xiên của đồ thị

hàm số

2

, , 0







ax bx c

y a d

dx e

.

a.4. Nếu bậc tử nhỏ hơn bậc mẫu thì đồ thị hàm số có duy nhất một

đường tiệm cận ngang, đó là đường thẳng

0y

.

b. Các dạng hàm khác

b.1. Hàm số mũ

Hàm số

, 0, 1  

x

y a a a

có một đường tiệm cận duy nhất. Cụ thể

hàm số



x

ya

có một tiệm cận ngang là đường

0y

- Trục hoành.

b.2. Hàm số logarit

Hàm số

log , 0, 1, 0   

a

y x a a x

có một đường tiệm cận duy

nhất.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

461

[ I can't, I can! ]

Minh họa khoảng cách

từ một điểm điến các

đường tiệm cận

Extra Techniques:

Study Tips:

Một cách nhớ nhanh

công thức tính tích

khoảng cách từ một điểm

đến hai đường tiệm cận

(đứng và ngang) của đồ

thị hàm số nhất biến.

Ta đưa ra một tương

quan so sánh giữa công

thức tính đạo hàm của

hàm số







ax b

y

cx d

, tức

là

 

2

'







ad bc

y

cx d

với

công thức vừa được

chứng minh:

2

ad bc

c

thì cách nhớ sẽ trở nên dễ

dàng hơn rất nhiều.

Cụ thể hàm số

log , 0, 1, 0   

a

y x a a x

có một tiệm cận đứng là

đường

0x

- Trục tung.

3. Một số dạng toán thường gặp liên quan đến đường tiệm cận

của đồ thị hàm số

a. Khoảng cách từ một điểm

 

00

;M x y

thuộc đồ thị hàm nhất

biến







ax b

y

cx d

đến các tiệm cận của nó

Công thức:

 

0

1

12

2

0

.





























cx d

d

c

ad bc

dd

c

ad bc

d

c cx d

.

Chứng minh:

Xét hàm số

 

, 0, 0, 0



    



ax b

y a c ad bc

cx d

.

Gọi

 

00

;M x y

là điểm thuộc đồ thị hàm số







ax b

y

cx d

.

Suy ra:

0

;











ax b

Mx

cx d

.

Đồ thị hàm số có đường tiệm cận đứng:



d

x

c

và đường tiệm cận

ngang



a

y

c

.

Khi đó, khoảng cách từ

M

đến hai đường tiệm cận lần lượt là:

 

0

10

20

0





  









  







cx d

d

dx

cc

a ad bc

dy

c c cx d

.

Nếu ta tính tích hai khoảng cách đến các đường tiệm cận trên, ta dễ

dàng thu được:

 

0

12

2

0

..









cx d

ad bc ad bc

dd

c c cx d

c

.

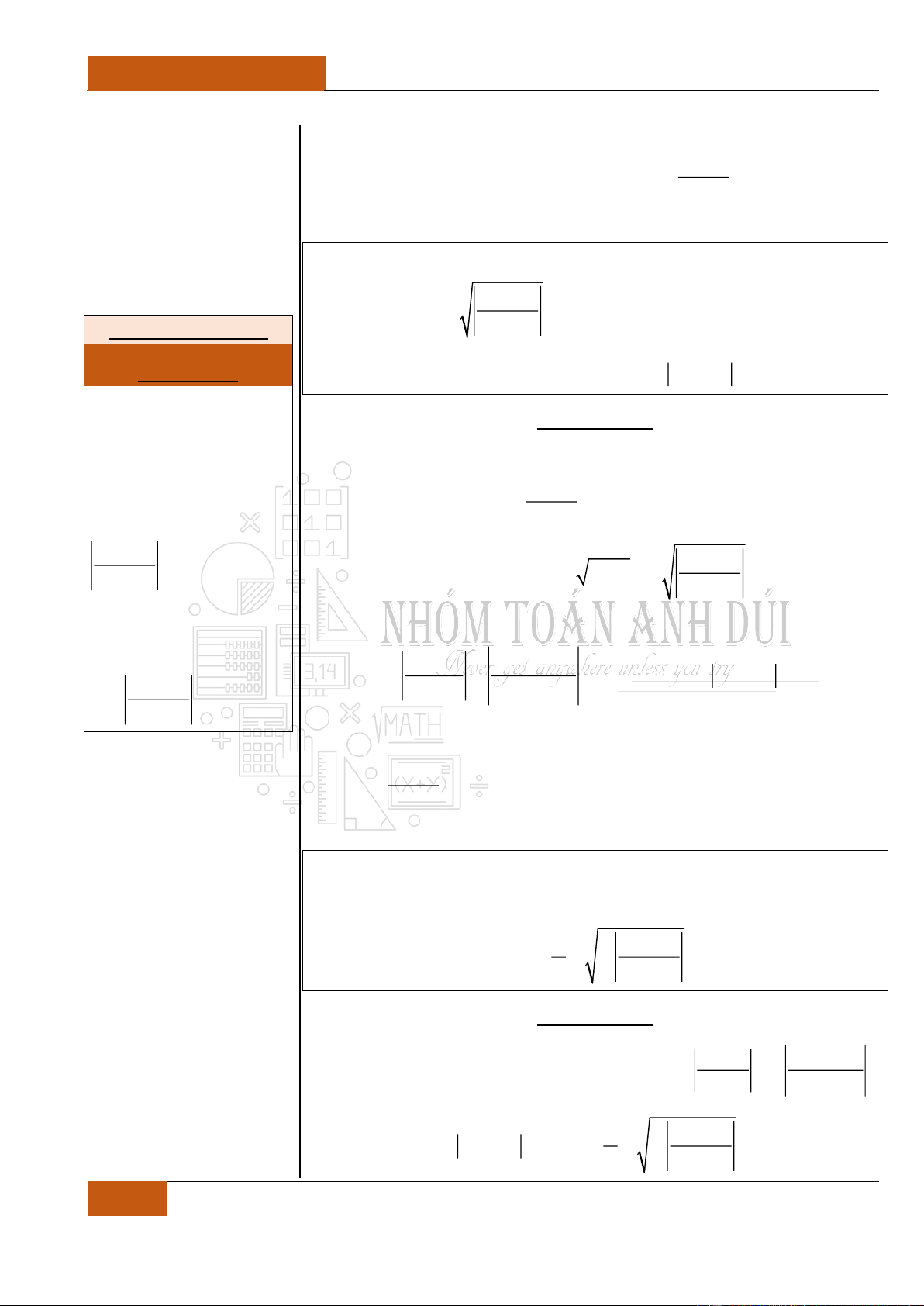
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

462

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Để ý một điều, khi chúng

ta chứng minh để đưa ra

công thức áp dụng cho

các bài toán tổng quát,

chúng ta luôn chỉ ra

lượng không đổi

2

ad bc

c

. Để công thức

được gọn hơn, ta có thể

gán biểu thức trên cho

một ẩn nào đó, có thể là

2





ad bc

p

c

chẳng hạn.

b. Giá trị nhỏ nhất của tổng các khoảng cách từ một điểm

 

00

;M x y

thuộc đồ thị hàm nhất biến







ax b

y

cx d

đến các tiệm

cận của nó

Giá trị nhỏ nhất của tổng các khoảng cách từ

 

00

;M x y

đến các tiệm

cận của nó bằng

2

ad bc

c

.

Dấu

""

xảy ra khi và chỉ khi

 

2

0

  cx d ad bc

.

Chứng minh:

Gọi

12

,dd

lần lượt là khoảng cách từ điểm

M

đến hai đường tiệm

cận của đồ thị hàm số







ax b

y

cx d

.

Khi đó:

1 2 1 2

2

2 . 2



    



Cauchy

ad bc

S d d d d d

c

.

Dấu

""

xảy ra khi và chỉ khi:

 

2

0

1 2 0

0





      



cx d

ad bc

d d cx d ad bc

c c cx d

.

c. Khoảng cách từ một điểm

 

00

;M x y

thuộc đồ thị hàm nhất

biến







ax b

y

cx d

đến đường tiệm cận đứng bằng

k

lần khoảng

cách từ đó đến đường tiệm cận ngang.

Điều kiện của

 

00

;M x y

để khoảng cách đến đường tiệm cận đứng

bằng

k

lần khoảng cách đến đường tiệm cận ngang là:

0

2

.



  

d ad bc

xk

c

.

Chứng minh:

Theo kết quả đã chứng minh, ta có:

 

0

12

0

..





  



cx d

ad bc

d k d k

c c cx d

 

2

00

2

..



       

d ad bc

cx d k ad bc x k

c

.

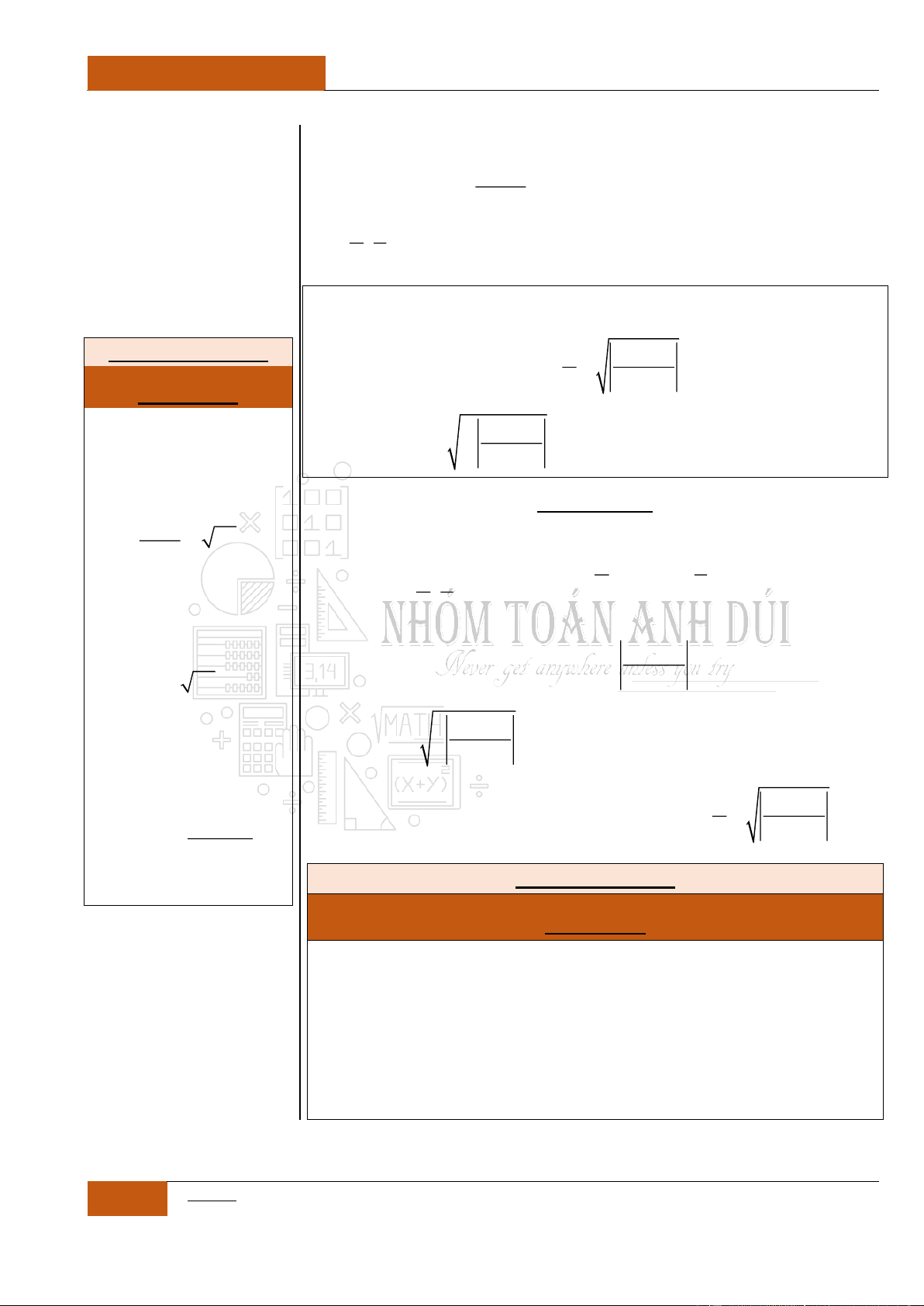
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

463

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Bất đẳng thức Cauchy:

Cho hai số thực dương

,ab

khi đó:

2





ab

Hoặc các “biến thể”

khác có thể sử dụng

như:

1.

2a b ab

.

2.

22

2a b ab

.

3.

 

2

22

2   a b a b

.

4.

 

2

22

2





ab

.

…

d. Khoảng cách ngắn nhất từ một điểm

 

00

;M x y

thuộc đồ thị

hàm nhất biến







ax b

y

cx d

đến giao điểm hai đường tiệm cận

;









da

I

cc

.

Điều kiện của

 

00

;M x y

để khoảng cách

MI

ngắn nhất là

0

2



  

d ad bc

x

c

Khi đó:

min

2

2.





ad bc

MI

c

.

Chứng minh:

Ta có:

 

22

00

2 2 2

0 0 1 2

;





   

      



   





   









M x y

da

MI x y d d

da

cc

I

cc

Do đó:

2 2 2

1 2 1 2

2

22



   

Cauchy

ad bc

MI d d d d

c

.

Hay

min

2





ad bc

MI

c

.

Dấu

""

xảy ra khi và chỉ khi:

1 2 0

2



    

d ad bc

d d x

c

.

Extra Techniques:

Study Tips:

"Trên đây là một số Tips chúng tôi cảm thấy rất hữu dụng trong

các bài toán hiện hành. Do mục đích phục vụ cho phần đông các

bạn học sinh nên phần trình bày khá chi tiết và khá dài. Nhưng nếu

bạn đọc hiểu bản chất vấn đề, thao tác sẽ ngắn gọn hơn, chuẩn xác

hơn và quan trọng nhất vẫn là lợi thế về thời gian nếu biết các Tips

này.

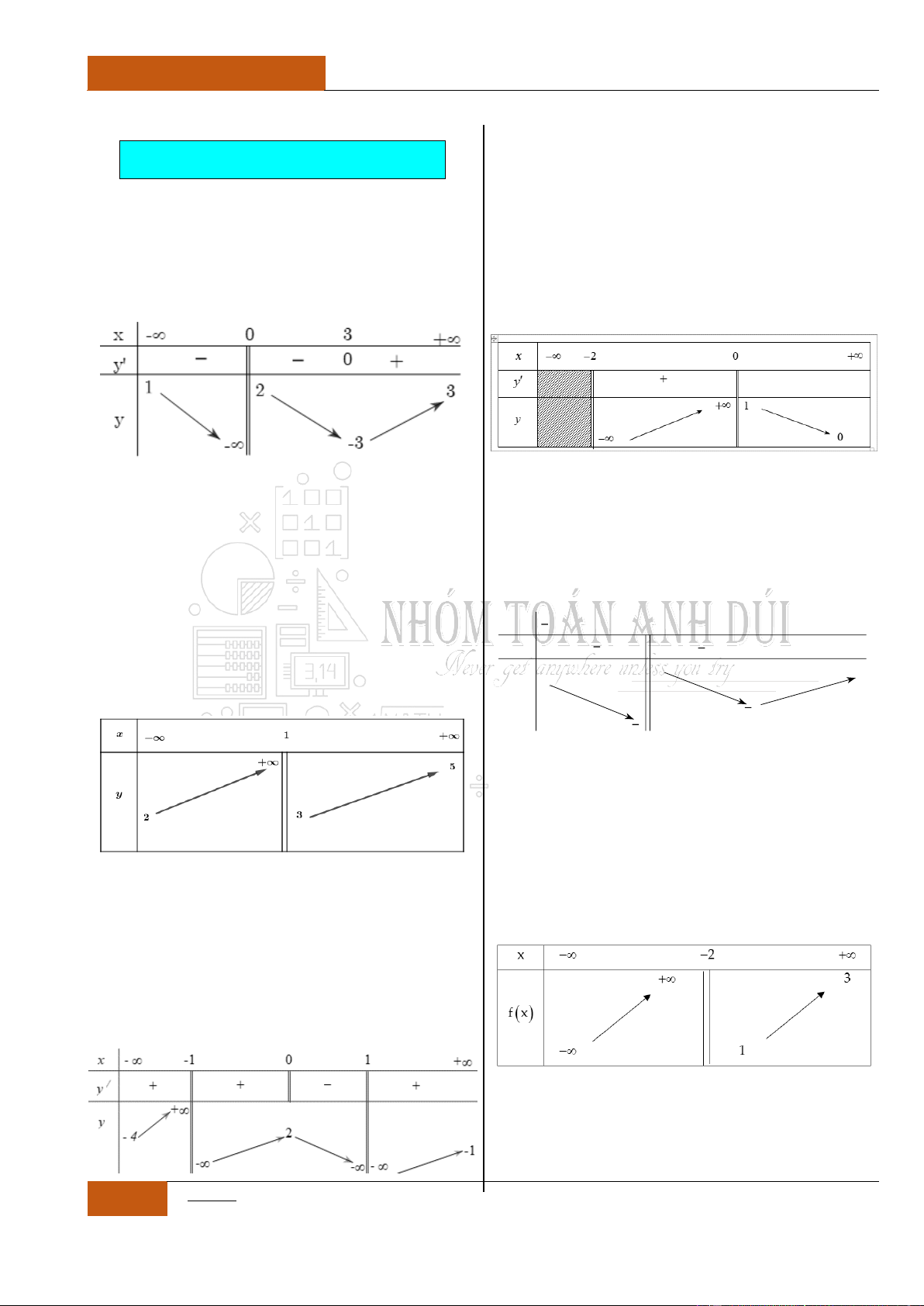
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

464

[ I can't, I can! ]

TỰ LUYỆN 4 MỨC ĐỘ

Câu 1. [Nhận biết].

Cho hàm số

 

y f x

có bảng biến thiên như

sau:

Tổng số tiệm cận đứng và tiệm cận ngang của đồ

thị hàm số đã cho là:

A.

2

. B.

3

.

C.

4

. D.

1

.

Câu 2. [Nhận biết].

Cho hàm số

 

y f x

có bảng biến thiên như

sau

Tổng số đường tiệm cận ngang và đường tiệm

cận đứng của đồ thị hàm số đã cho là

A.

3

. B.

2

. C.

4

. D.

1

.

Câu 3. [Nhận biết].

Cho hàm số có bảng biến thiên như hình sau

Tổng số đường tiệm cận ngang và tiệm cận

đứng của đồ thị hàm số là

A.

3

. B.

2

. C.

4

. D.

1

.

Câu 4. [Nhận biết].

Cho hàm số

 

y f x

có bảng biến thiên như

hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho

có bao nhiêu đường tiệm cận?

A.

3

. B.

2

. C.

4

. D.

1

.

Câu 5. [Nhận biết].

Cho hàm số

 

y f x

có bảng biến thiên như

sau:

Tổng số tiệm cận đứng và tiệm cận ngang của đồ

thị hàm số đã cho là

A.

1

. B.

3

. C.

4

. D.

2

.

Câu 6. [Nhận biết].

Cho hàm số

 

fx

có bảng biến thiên như sau:

Tổng số tiệm cận ngang và tiệm cận đứng của

đồ thị hàm số đã cho là:

A.

4

. B.

3

. C.

1

. D.

2

.

y'

+

∞

0

3

4

3

0

+

3

0

+

∞

y

x

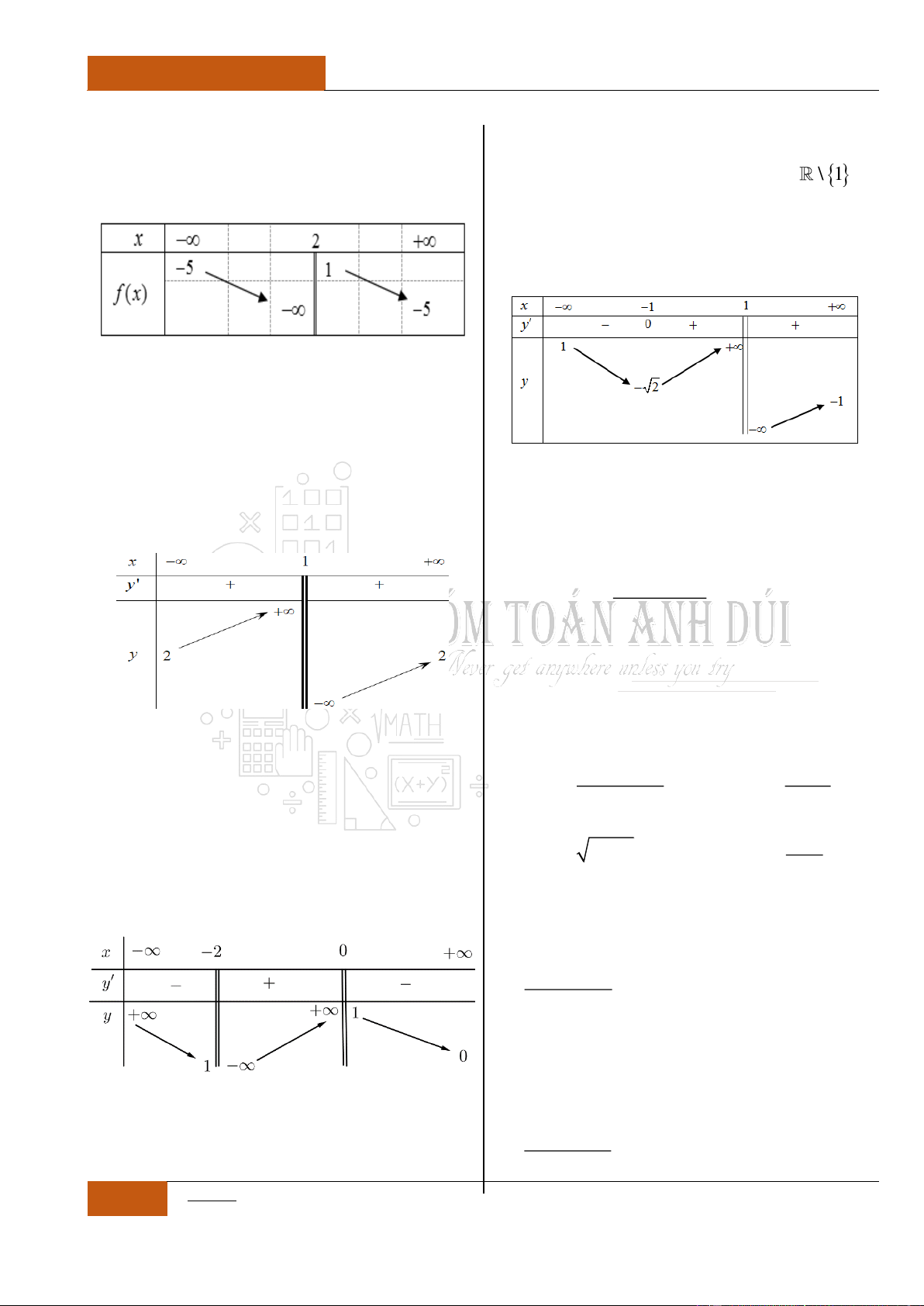
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

465

[ I can't, I can! ]

Câu 7. [Nhận biết].

Cho hàm số

 

y f x

có bảng biến thiên như

sau

Tổng số tiệm cận ngang và tiệm cận đứng của đồ

thị hàm số đã cho là?

A.

4

. B.

2

. C.

3

. D.

1

.

Câu 8. [Nhận biết].

Cho hàm số

 

y f x

có bảng biến thiên như

sau

Tổng số tiệm cận ngang và tiệm cận đứng của

đồ thị hàm số đã cho là

A.

4

. B.

1

. C.

3

. D.

2

.

Câu 9. [Nhận biết].

Cho hàm số

 

y f x

có bảng biến thiên như

sau

Tổng số đường tiệm cận đứng và tiệm cận

ngang của đồ thị hàm số đã cho bằng

A.

2

. B.

1

. C.

0

. D.

3

.

Câu 10. [Nhận biết].

Cho hàm số

 

y f x

liên tục trên

 

\1

có

bảng biến thiên như hình vẽ. Tổng số đường tiệm

cận đứng và đường tiệm cận ngang của đồ thị

hàm số

 

y f x

A.

1

. B.

4

. C.

2

. D.

3.

Câu 11. [Nhận biết].

Tổng số tiệm cận đứng và tiệm cận ngang của đồ

thị hàm số

2

5 4 1

1







xx

y

x

là

A.

0.

B.

1.

C.

2.

D.

3.

Câu 12. [Thông hiểu].

Đồ thị của hàm số nào dưới đây có tiệm cận

đứng?

A.

2

32

1







xx

y

x

. B.

2

1





x

y

x

.

C.

2

1yx

. D.

1





x

y

x

.

Câu 13. [Nhận biết].

Tìm số tiệm cận của đồ thị hàm số

2

54

1







xx

y

x

.

A.

2

. B.

3

. C.

0

. D.

1

.

Câu 14. [Nhận biết].

Tìm số tiệm cận đứng của đồ thị hàm số:

2

34

16







xx

y

x

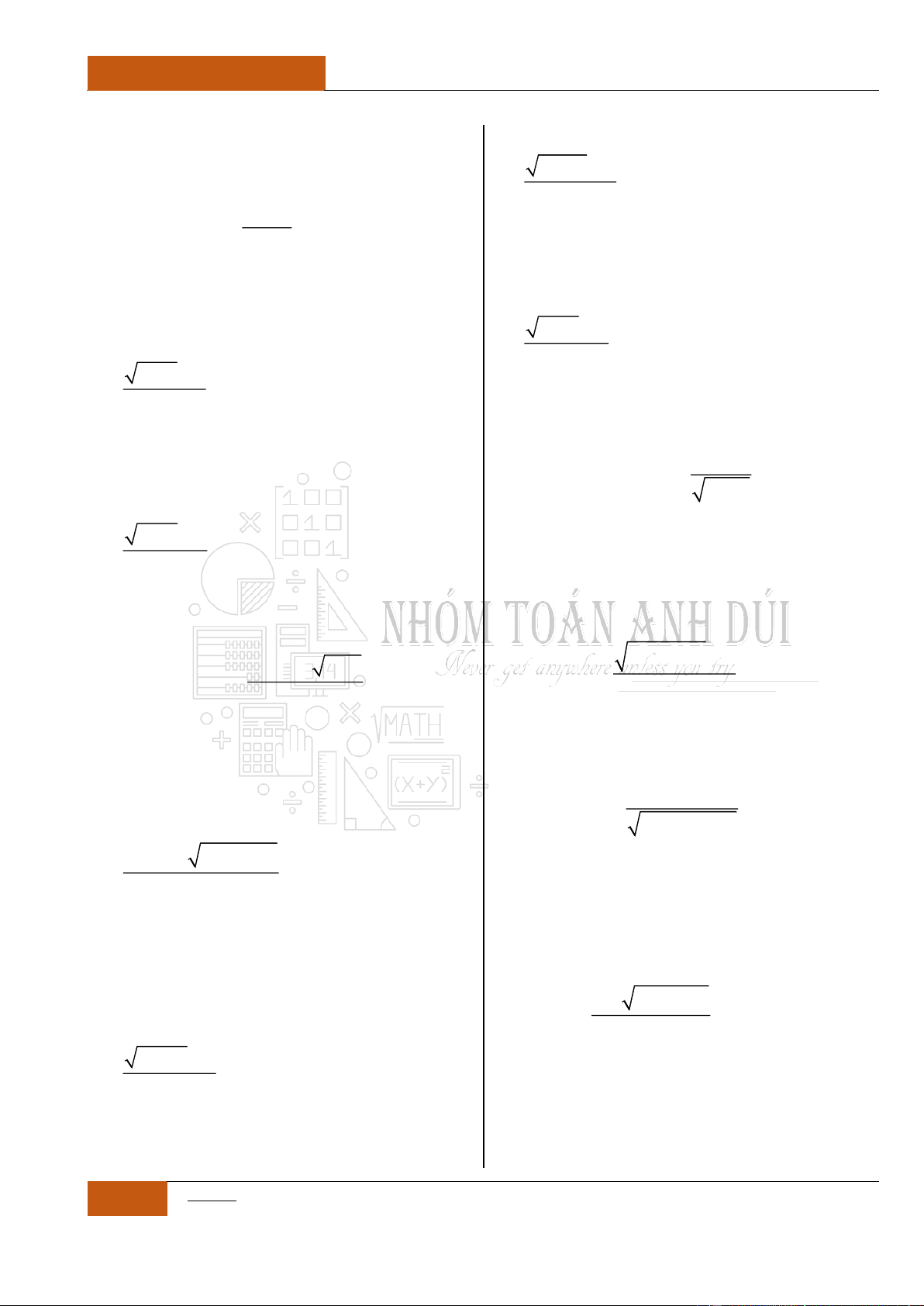
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

466

[ I can't, I can! ]

A.

2

. B.

3

. C.

1

. D.

0

.

Câu 15. [Nhận biết].

Đồ thị hàm số

2

4







x

y

x

có mấy tiệm cận.

A.

3

. B.

1

. C.

2

. D.

0

.

Câu 16. [Thông hiểu].

Số tiệm cận đứng của đồ thị hàm số

2

93





x

y

xx

là?

A.

1

. B.

2

. C.

0

. D.

3

.

Câu 17. [Thông hiểu].

Số tiệm cận đứng của đồ thị hàm số

2

42





x

y

xx

là?

A.

2

. B.

1

. C.

3

. D.

0

.

Câu 18. [Thông hiểu].

Đồ thị hàm số

2

5 1 1

2

  





xx

y

xx

có tất cả bao

nhiêu đường tiệm cận?

A.

3

. B.

0

. C.

2

. D.

1

.

Câu 19. [Thông hiểu].

Tìm tất cả các tiệm cận đứng của đồ thị hàm số

2

2 1 3

56

   





x x x

y

xx

.

A.

3x

và

2x

. B.

3x

.

C.

3x

và

2x

. D.

3x

.

Câu 20. [Thông hiểu].

Số tiệm cận đứng của đồ thị hàm số

2

25 5





x

y

xx

là?

A.

3

. B.

2

. C.

0

. D.

1

.

Câu 21. [Thông hiểu].

Số tiệm cận đứng của đồ thị hàm số

2

16 4





x

y

xx

là?

A.

3

. B.

2

. C.

1

. D.

0

.

Câu 22. [Thông hiểu].

Số tiệm cận đứng của đồ thị hàm số

2

42





x

y

xx

là?

A.

3

. B.

0

. C.

1

. D.

2

.

Câu 23. [Thông hiểu].

Đồ thị hàm số

 

2

1







x

fx

x

có tất cả bao

nhiêu tiệm cận đứng và tiệm cận ngang?

A.

4

. B.

3

. C.

1

. D.

2

.

Câu 24. [Thông hiểu].

Tổng số tiệm cận đứng và tiệm cận ngang của đồ

thị hàm số

 

4 6 2

2







xx

y

x

là?

A.

1

. B.

3

. C.

2

. D.

4

.

Câu 25. [Thông hiểu].

Cho hàm số

2

42

23

32







xx

y

xx

.

Đồ thị hàm số đã cho có bao nhiêu đường tiệm

cận?

A.

4

. B.

5

. C.

3

. D.

6

.

Câu 26. [Thông hiểu].

Hàm số

2

3

1  





x x x

y

xx

có bao nhiêu đường

tiệm cận?

A.

1

. B.

3

. C.

2

. D.

4

.

Câu 27. [Thông hiểu].

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

467

[ I can't, I can! ]

Số đường tiệm cận đứng và tiệm cận ngang của

đồ thị hàm số

2

21

32







x

y

xx

là?

A.

4

. B.

1

. C.

3

. D.

2

.

Câu 28. [Vận dụng].

Cho hàm số

2

3

5 6 12

4 3 1

  





xx

y

xx

có đồ thị

 

C

Mệnh đề nào sau đây là đúng?

A. Đồ thị

 

C

không có tiệm cận.

B. Đồ thị

 

C

chỉ có một tiệm cận ngang

0y

.

C. Đồ thị

 

C

có một tiệm cận ngang

0y

và

hai tiệm cận đứng

1

1;

2

  xx

.

D. Đồ thị

 

C

chỉ có một tiệm cận ngang

0y

và một tiện cận đứng

1x

.

Câu 29. [Thông hiểu].

Đồ thị hàm số

2

31







x x x

y

x

có tất cả bao

nhiêu đường tiệm cận?

A.

2

. B.

3

. C.

0

. D.

1

.

Câu 30. [Thông hiểu].

Đồ thị hàm số

2

14

23







x

y

xx

có số đường tiệm

cận đứng là

m

và số đường tiệm cận ngang là

n

Giá trị của

mn

là?

A.

1

. B.

2

. C.

3

. D.

0

.

Câu 31. [Thông hiểu].

Gọi

,nd

lần lượt là số đường tiệm cận ngang và

số tiệm cận đứng của đồ thị hàm số

 

1







x

y

xx

. Khẳng định nào sau đây là đúng?

A.

0, 2nd

. B.

1nd

.

C.

1, 2nd

. D.

0, 1nd

.

Câu 32. [Thông hiểu].

Đồ thị hàm số

2

5 1 1

2

  





xx

y

xx

có tất cả bao

nhiêu đường tiệm cận?

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 33. [Thông hiểu].

Tìm số đường tiệm cận của đồ thị hàm số

1

4 3 1 3 5





  

x

y

xx

.

A.

2

. B.

3

. C.

1

. D.

0

.

Câu 34. [Thông hiểu].

Cho hàm số

2

42

23

32







xx

y

xx

. Đồ thị hàm số

đã cho có bao nhiêu đường tiệm cận?

A.

4

. B.

5

. C.

3

. D.

6

.

Câu 35. [Thông hiểu].

Đồ thị hàm số

2

58

3







x

y

xx

có bao nhiêu đường

tiệm cận?

A. 2. B. 4. C. 1. D. 3.

Câu 36. [Thông hiểu].

Đồ thị hàm số

2

4 2 1

1

  





x x x

y

x

có bao

nhiêu đường tiệm cận?

A.

1

. B.

0

. C.

2

. D.

3

.

Câu 37. [Thông hiểu].

Tìm tất cả các giá trị thực của tham số

m

sao cho

đồ thị của hàm số

2

1







x

y

mx

có hai tiệm cận

ngang.

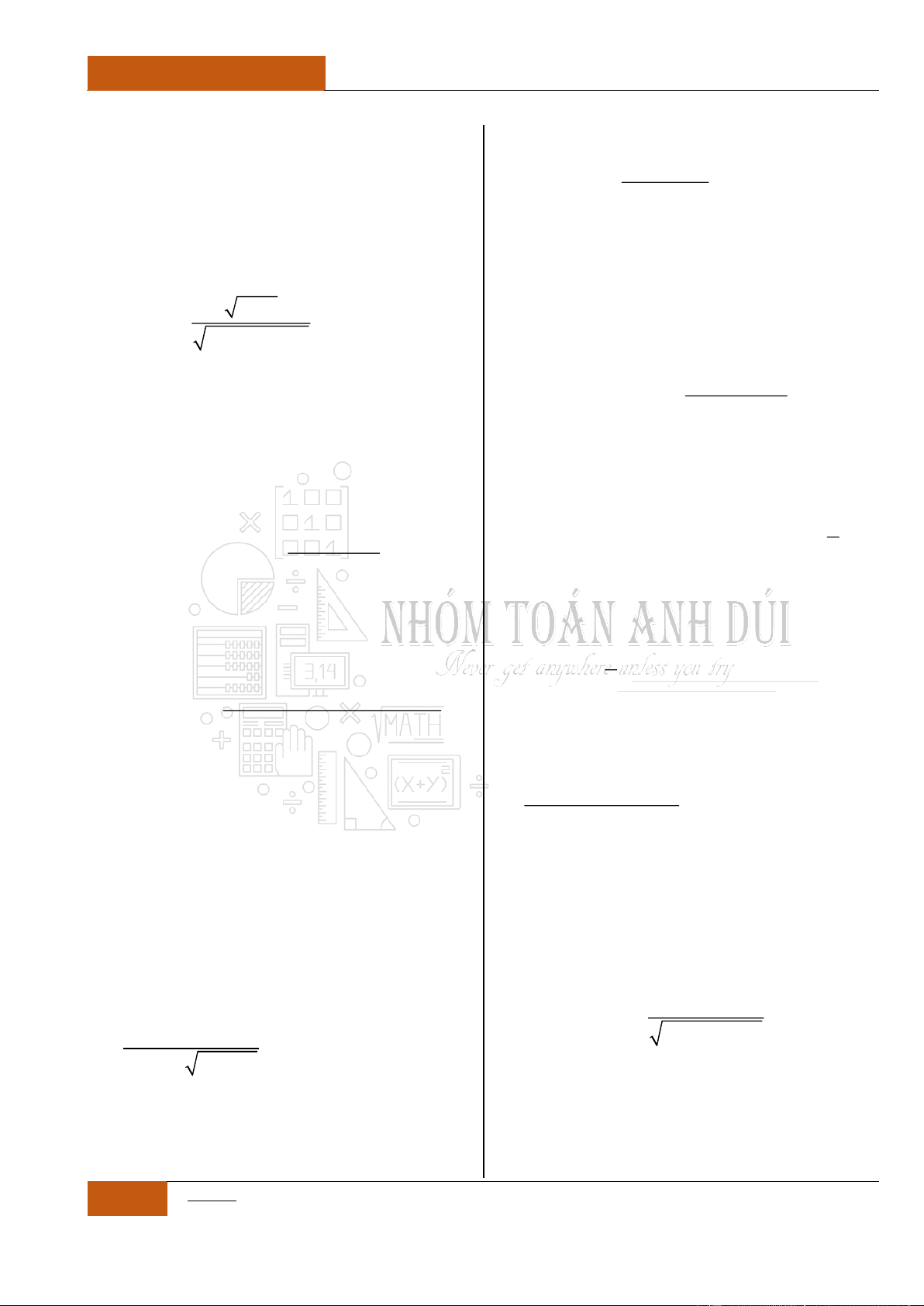
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

468

[ I can't, I can! ]

A.

0m

. B.

0m

.

C.

0m

. D.

m

.

Câu 38. [Vận dụng].

Gọi

S

là tập hợp các giá trị nguyên

m

để đồ thị

hàm số

2

62







x

y

x x m

có hai đường tiệm

cận đứng. Số phần tử của

S

là?

A. vô số. B.

12

.

C.

14

. D.

13

.

Câu 39. [Thông hiểu].

Có bao nhiêu giá trị nguyên dương của tham số

m

để đồ thị hàm số

2

1

8







x

y

x x m

có 3 đường

tiệm cận?

A.

14

. B.

8

. C.

15

. D.

16

.

Câu 40. [Vận dụng].

Cho hàm số

 

3 2 2

3

3 2 1





   

x

y

x mx m x m

. Có

bao nhiêu giá trị nguyên của tham số

m

thuộc

đoạn

 

2020;2020

để đồ thị hàm số có

4

đường tiệm cận?

A.

4039

. B.

4040

.

C.

4038

. D.

4037

.

Câu 41. [Vận dụng].

Có bao nhiêu số nguyên của

m

thuộc đoạn

 

100;100

để đồ thị hàm số

 

2

1

2





y

x m x x

có đúng hai đường tiệm

cận?

A.

200.

B.

2.

C.

199.

D.

0.

Câu 42. [Thông hiểu].

Tìm tất cả các giá trị của tham số thực

m

để đồ

thị hàm số

2

32







xm

y

xx

có đúng hai đường

tiệm cận.

A.

1m

. B.

 

1;4m

.

C.

4m

. D.

 

1; 4  m

.

Câu 43. [Thông hiểu].

Cho hàm số

 

2

1

24









x

mx

yf

. Tìm tất cả

các giá trị của tham số

m

để đồ thị có ba đường

tiệm cận

A.

2m

. B.

2

5

2















m

.

C.

2

5

2



























m

. D.

2











m

.

Câu 44. [Vận dụng].

Biết rằng đồ thị của hàm số

 

3 2017

3

  





n x n

y

xm

(

,mn

là các số thực)

nhận trục hoành làm tiệm cận ngang và trục tung

là tiệm cận đứng. Tính tổng

mn

.

A.

0

. B.

3

. C.

3

. D.

6

.

Câu 45. [Vận dụng].

Có bao nhiêu giá trị nguyên của tham số

m

để

đồ thị hàm số

2

1

82







x

y

mx x

có đúng bốn

đường tiệm cận?

A.

8

. B.

6

. C.

7

. D. Vô số.

Câu 46. [Vận dụng].

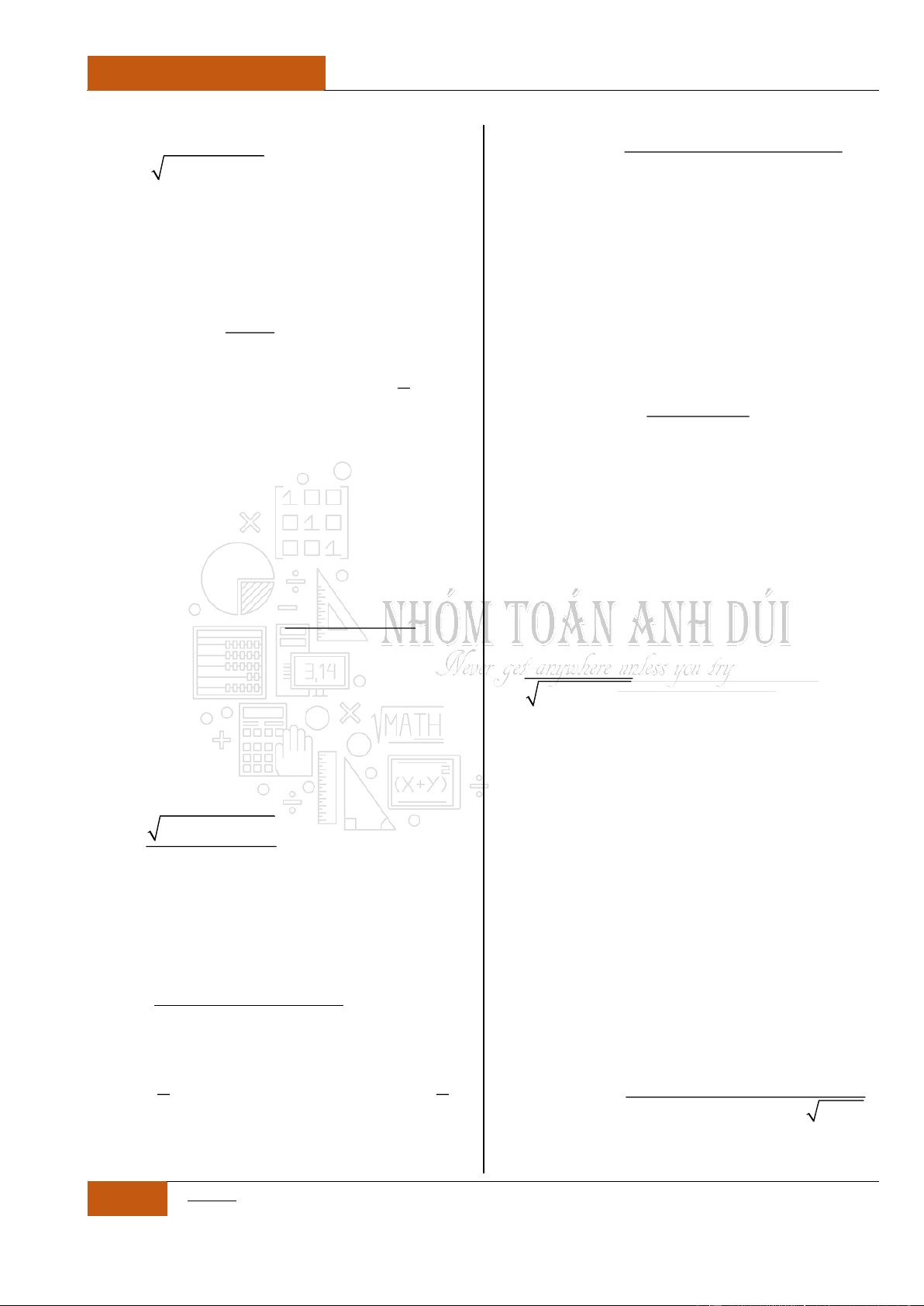
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

469

[ I can't, I can! ]

Với giá trị nào của hàm số

m

để đồ thị hàm số

2

37   y x mx x

có tiệm cận ngang.

A.

1m

. B.

1m

.

C.

1m

. D. Không có

m

.

Câu 47. [Thông hiểu].

Cho hàm số

1

.

2







ax

y

bx

Tìm

,ab

để đồ thị hàm

số có

1x

là tiệm cận đứng và

1

2

y

là tiệm

cận ngang.

A.

1; 2  ab

. B.

4; 4ab

.

C.

1; 2ab

. D.

1; 2   ab

.

Câu 48. [Thông hiểu].

Có bao nhiêu giá trị nguyên

 

10;10m

sao

cho đồ thị hàm số

2

1

2 6 3





  

x

y

x x m

có hai

đường tiệm cận đứng?

A.

19

. B.

15

. C.

17

. D.

18

.

Câu 49. [Vận dụng].

Có bao nhiêu giá trị nguyên của

m

để tổng số

tiệm cận ngang và tiệm cận đứng của đồ thị hàm

số

2

34

2







mx mx

y

x

bằng

3

?

A.

4

. B.

2

. C. Vô số. D.

3

.

Câu 50. [Thông hiểu].

Tổng các giá trị của tham số

m

để đồ thị của hàm

số

 

22

1

2 1 2





   

x

y

x m x m

có đúng một

tiệm cận đứng.

A.

1

2



. B.

2

. C.

3

. D.

3

2

.

Câu 51. [Vận dụng].

Cho hàm số

 

3 2 2

3

3 2 1





   

x

y

x mx m x m

. Có

bao nhiêu giá trị nguyên thuộc đoạn

 

6;6

của

tham số

m

để đồ thị hàm số có bốn đường tiệm

cận?

A.

12

. B.

9

. C.

8

. D.

11

.

Câu 52. [Thông hiểu].

Tìm tất cả các giá trị thực của tham số m sao cho

đồ thị hàm số

2

23





x x m

y

xm

không có tiệm

cận đứng.

A.

1m

. B.

1m

.

C.

1m

và

0m

. D.

0m

.

Câu 53. [Thông hiểu].

Có bao nhiêu giá trị nguyên của tham số thực

m

thuộc đoạn

 

2017;2017

để đồ thị hàm số

2

4







x

y

x x m

có hai tiệm cận đứng.

A.

2019

. B.

2021

.

C.

2018

. D.

2020

.

Câu 54. [Vận dụng].

Cho hàm số

 

y f x

thỏa mãn

 

lim 2019





x

f x m

,

 

4

lim 2020





x

f x m

(với

m

là tham số thực). Hỏi có tất cả bao nhiêu giá

trị của

m

để đồ thị của hàm số

 

y f x

có duy

nhất một tiệm cận ngang?

A.

4

. B.

2

. C.

3

. D.

1

.

Câu 55. [Vận dụng].

Cho hàm số

 

2

1

2 1 2





   



y

x m x m x m

.

Tìm tất cả các giá trị thực của tham số

m

để đồ

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

470

[ I can't, I can! ]

thị hàm số có

4

đường tiệm cận.

A.

01

1

2















m

. B.

1

2















m

.

C.

1m

. D.

01

1

2















m

.

Câu 56. [Vận dụng].

Có bao nhiêu giá trị nguyên của

m

để đồ thị hàm

số

  

22

63

6 3 9 6 1





   

x

y

mx x x mx

có đúng

1

đường tiệm cận?

A.

0.

B. 2. C.

1.

D. Vô số.

Câu 57. [Thông hiểu].

Tìm tất cả các giá trị thực của tham số m để đồ

thị hàm số:

2

1  y x mx

có tiệm cận ngang.

A.

0 1.m

B.

1.m

C.

1.m

D.

1.m

Câu 58. [Thông hiểu].

Cho hàm số

2

24







x

y

mx x

. Có tất cả bao

nhiêu giá trị của tham số

m

để đồ thị hàm số có

đúng hai đường tiệm cận (tiệm cận đứng và tiệm

cận ngang)?

A.

0

. B.

2

. C.

3

. D.

1

.

Câu 59. [Vận dụng].

Gọi

S

là tập các giá trị nguyên của

m

sao cho

đồ thị hàm số

2

2019

17 1





x

y

x m x

có bốn

đường tiệm cận (bao gồm tiệm cận đứng và tiệm

cận ngang). Tính số phần tử của tập

S

.

A. Vô số. B.

3

.

C.

5

. D.

4

.

Câu 60. [Vận dụng].

Gọi

S

là tập hợp tất cả các giá trị của tham số

thực

m

sao cho đồ thị hàm số

 

3

3 4 2

11



     

x

fx

x mx x x m x

nhận

trục tung làm tiệm cận đứng. Khi đó tổng các

phần tử của

S

bằng?

A.

1

2

. B.

1

2



. C.

1

3

. D.

1

3



.

Câu 61. [Vận dụng].

Có bao nhiêu giá trị

m

nguyên thuộc khoảng

 

10;10

để đồ thị hàm số

 

1

2







x x m

y

x

có đúng ba đường tiệm cận?

A.

12

. B.

11

. C.

0

. D.

10

.

Câu 62. [Vận dụng].

Tìm số giá trị nguyên thuộc đoạn

 

2019;2019

của tham số

m

để đồ thị hàm số

2

3





x

y

x x m

có đúng hai đường tiệm cận.

A.

2007

. B.

2010

.

C.

2009

. D.

2008

.

Câu 63. [Thông hiểu].

Cho hàm số

2

1

23







x

y

mx x

. Có tất cả bao

nhiêu giá trị

m

để đồ thị hàm số có đúng hai

đường tiệm cận.

A.

2

. B.

3

. C.

0

. D.

1

.

Câu 64. [Vận dụng].

Cho hàm số

32

1

31



  

y

x x m

với

m

là

tham số. Tìm tất cả các giá trị của

m

để đồ thị

hàm số đã cho có

4

đường thẳng tiệm cận.

A.

15m

. B.

12  m

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

471

[ I can't, I can! ]

C.

1m

hoặc

5m

. D.

2m

hoặc

1m

.

Câu 65. [Vận dụng].

Hàm số

 

2

31

1

  





x ax b

y

x

không có tiệm cận

đứng.

Khi đó hiệu

ab

bằng:

A.

1

2

.

B.

3

4



. C.

5

4



.

D.

1

2



.

Câu 66. [Vận dụng].

Có bao nhiêu giá trị nguyên của tham để

m

đồ

thị hàm số

2

2016 2017 24 7   





xx

y

xm

có

tiệm cận đứng?

A. vô số.

B.

2

.

C.

2017

D.

2019

.

Câu 67. [Thông hiểu].

Tìm tất cả các giá trị thực của

m

sao cho đồ thị

hàm số

2

1







mx

y

x

có đúng một đường tiệm

cận.

A.

10  m

. B.

10  m

.

C.

1m

. D.

0m

.

Câu 68. [Vận dụng].

Cho đồ thị hàm số

 

31

1







x

y f x

x

. Khi đó

đường thẳng nào sau đây là đường tiệm cận đứng

của đồ thị hàm số

 

1

2





y

fx

?

A.

1x

. B.

2x

.

C.

1x

. D.

2x

.

Câu 69. [Vận dụng].

Cho hàm số

 

y f x

có đồ thị như hình vẽ

Số tiệm cận đứng của đồ thị hàm số

 

2019

1





y

fx

là?

A.

1

. B.

2

. C.

3

. D.

4

.

Câu 70. [Vận dụng].

Cho hàm số

 

fx

xác định và liên tục trên

 

\1

có bảng biến thiên như sau:

Hỏi đồ thị hàm số

 

1

y

fx

có tất cả bao nhiêu

đường tiệm cận đứng và tiệm cận ngang?

A.

4

. B.

3

. C.

2

. D.

1

.

Câu 71. [Vận dụng].

Cho hàm số

 

y f x

thỏa mãn

 

lim 1





x

fx

và

 

lim

 



x

f x m

. Có bao nhiêu giá trị thực của

tham số

m

để hàm số

 

1

2





y

fx

có duy nhất

một tiệm cận ngang.

A.

1

. B.

0

. C.

2

. D. Vô số.

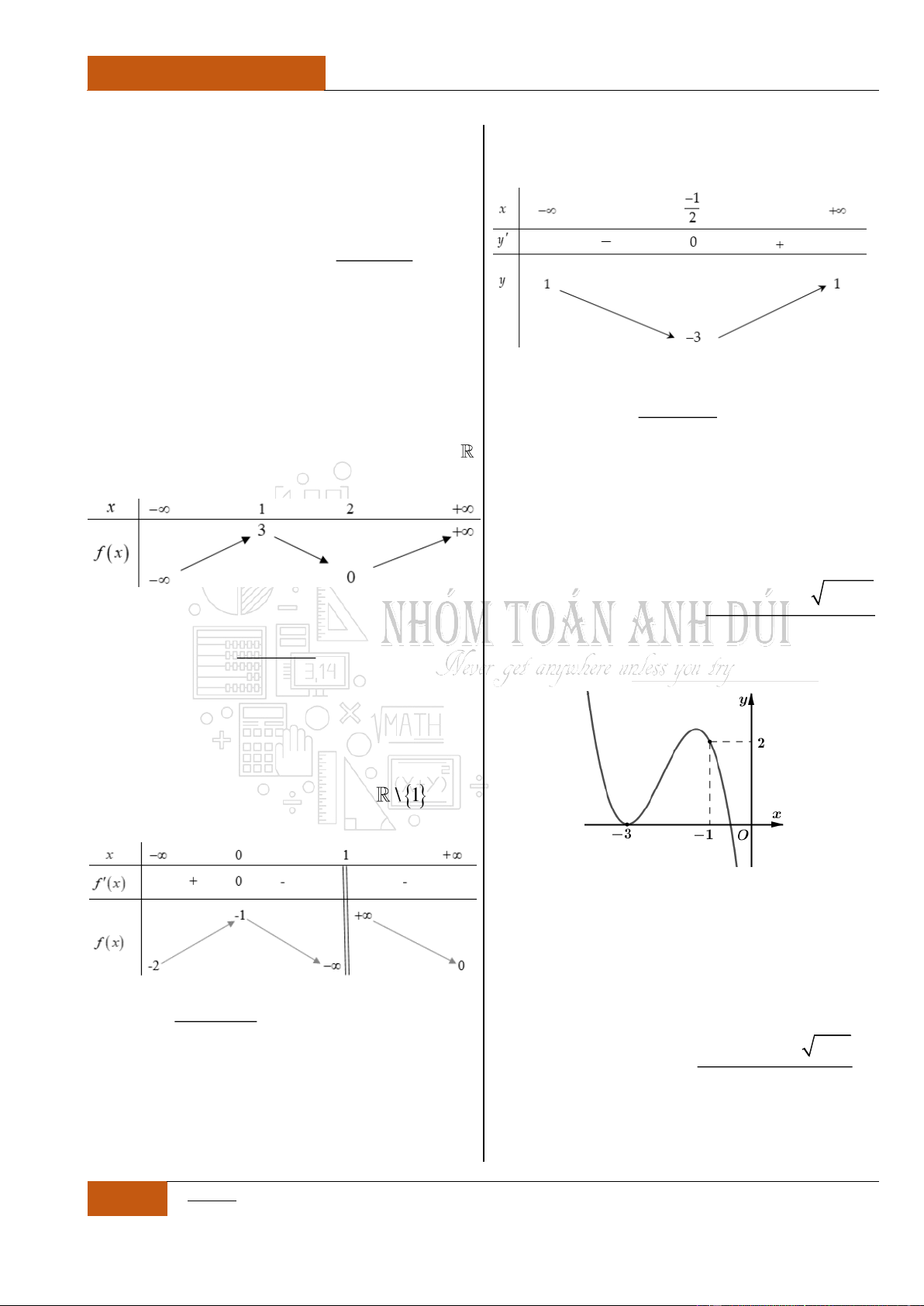
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

472

[ I can't, I can! ]

Câu 72. [Vận dụng].

Cho hàm số

 

y f x

thỏa mãn

 

4

tan cosf x x

. Tìm tất cả các giá trị thực của

m

để đồ thị hàm số

 

2019





gx

f x m

có hai

tiệm cận đứng.

A.

0m

. B.

01m

.

C.

0m

. D.

1m

.

Câu 73. [Vận dụng].

Cho hàm số

 

y f x

xác định, liên tục trên

và có bảng biến thiên như hình bên dưới:

Tổng số tiệm cận ngang và tiệm cận đứng của

đồ thị hàm số

 

1

21





y

fx

là:

A.

4

. B.

3

. C.

1

. D.

2

.

Câu 74. [Vận dụng].

Cho hàm số

 

y f x

liên tục trên

 

\1

và có

bảng biến thiên như sau:

Đồ thị

 

1

23





y

fx

có bao nhiêu đường tiệm

cận đứng?

A.

2

. B.

0

. C.

1

. D.

3

.

Câu 75. [Vận dụng].

Cho hàm số

 

y f x

có bảng biến thiên như

hình dưới đây.

Tổng số tiệm cận ngang và tiệm cận đứng của

đồ thị hàm số

 

1

21





y

fx

là?

A.

0.

B.

1.

C.

2.

D.

3.

Câu 76. [Vận dụng].

Cho hàm bậc ba

 

y f x

có đồ thị như hình vẽ

bên. Hỏi đồ thị hàm số

 

   

22

2

43

2

  









x x x x

y

x f x f x

có bao nhiêu đường tiệm cận đứng?

A.

2

. B.

3

. C.

4

. D.

6

.

Câu 77. [Vận dụng cao].

Cho hàm số

 

32

   f x ax bx cx d

có đồ thị

như hình vẽ bên dưới.

Hỏi đồ thị hàm số

 

   

2

3 2 1  









x x x

gx

x f x f x

có

bao nhiêu tiệm cận đứng?

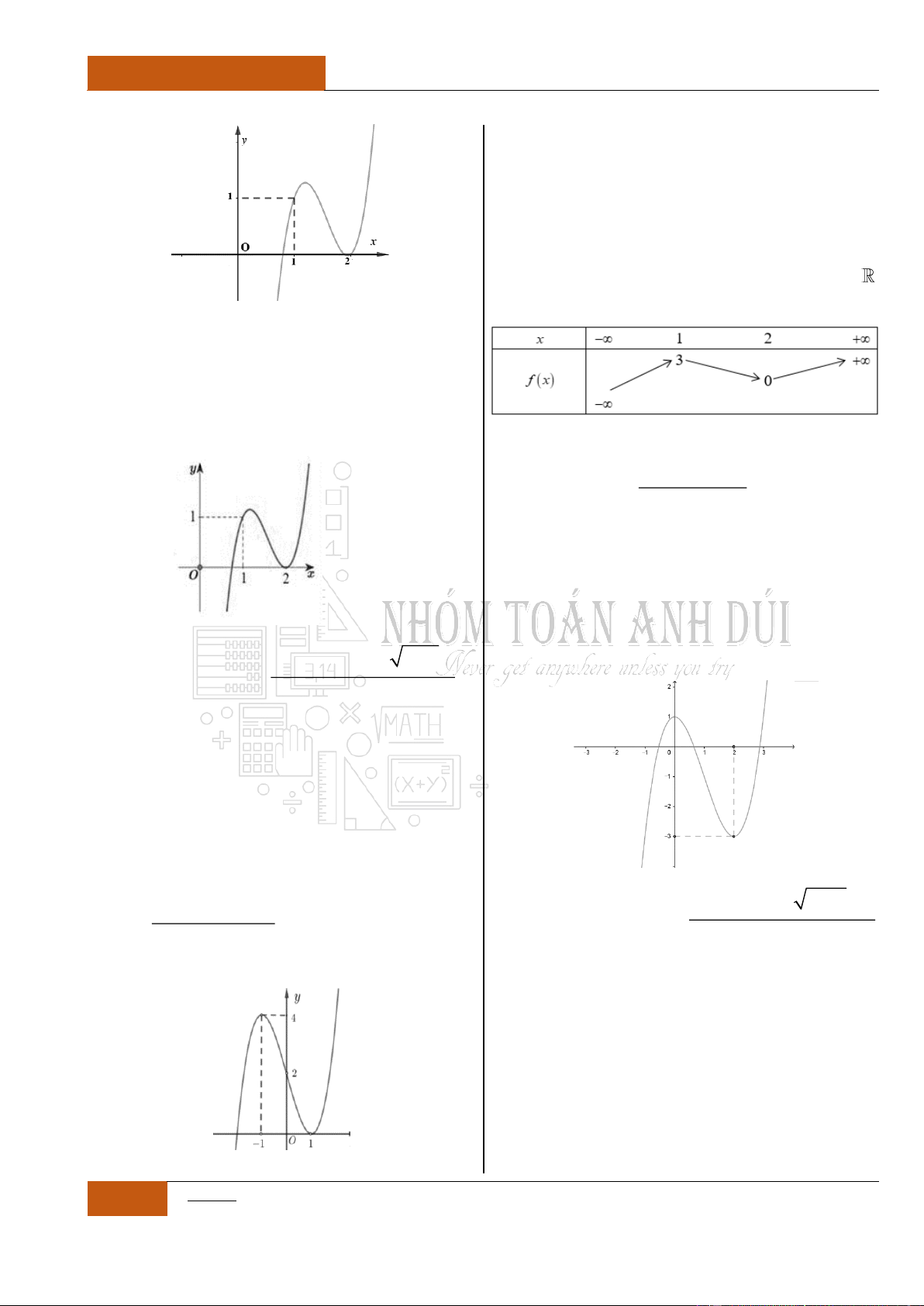
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

473

[ I can't, I can! ]

A.

2

. B.

4

. C.

3

. D.

5

.

Câu 78. [Vận dụng].

Cho hàm số bậc ba

 

32

   f x ax bx cx d

có

đồ thị như hình vẽ sau.

Đồ thị hàm số

 

     

2

3 2 1

1

  









x x x

gx

x f x f x

có bao nhiêu tiệm cận đứng?

A.

5

. B.

4

. C.

6

. D.

3

.

Câu 79. [Vận dụng].

Cho hàm số

 

y f x

là hàm số đa thức có đồ

thì như hình vẽ dưới đây, đặt

 

   

2







xx

gx

f x f x

.

Hỏi đồ thị hàm số

 

y g x

có bao nhiêu tiệm

cận đứng?

A.

5

. B.

3

. C.

4

. D.

2

.

Câu 80. [Vận dụng cao].

Cho hàm số

 

y f x

xác định, liên tục trên

và có bảng biến thiên như hình bên dưới.

Tổng số tiệm cận ngang và tiệm cận đứng của

đồ thị hàm số

 

3

1

3





y

f x x

là?

A.

2

. B.

4

. C.

3

. D.

1

.

Câu 81. [Vận dụng cao].

Cho hàm số

 

32

    y f x ax bx cx d

có đồ

thị như bên dưới.

Hỏi đồ thị hàm số

 

     

2

22

3











x x x

y

x f x f x

có bao nhiêu đường tiệm cận đứng?

A.

4

. B.

6

. C.

3

. D.

5

.

Câu 82. [Vận dụng cao].

Cho hàm số

32

   y ax bx cx d

,

 

0a

có

đồ thị như hình dưới đây.

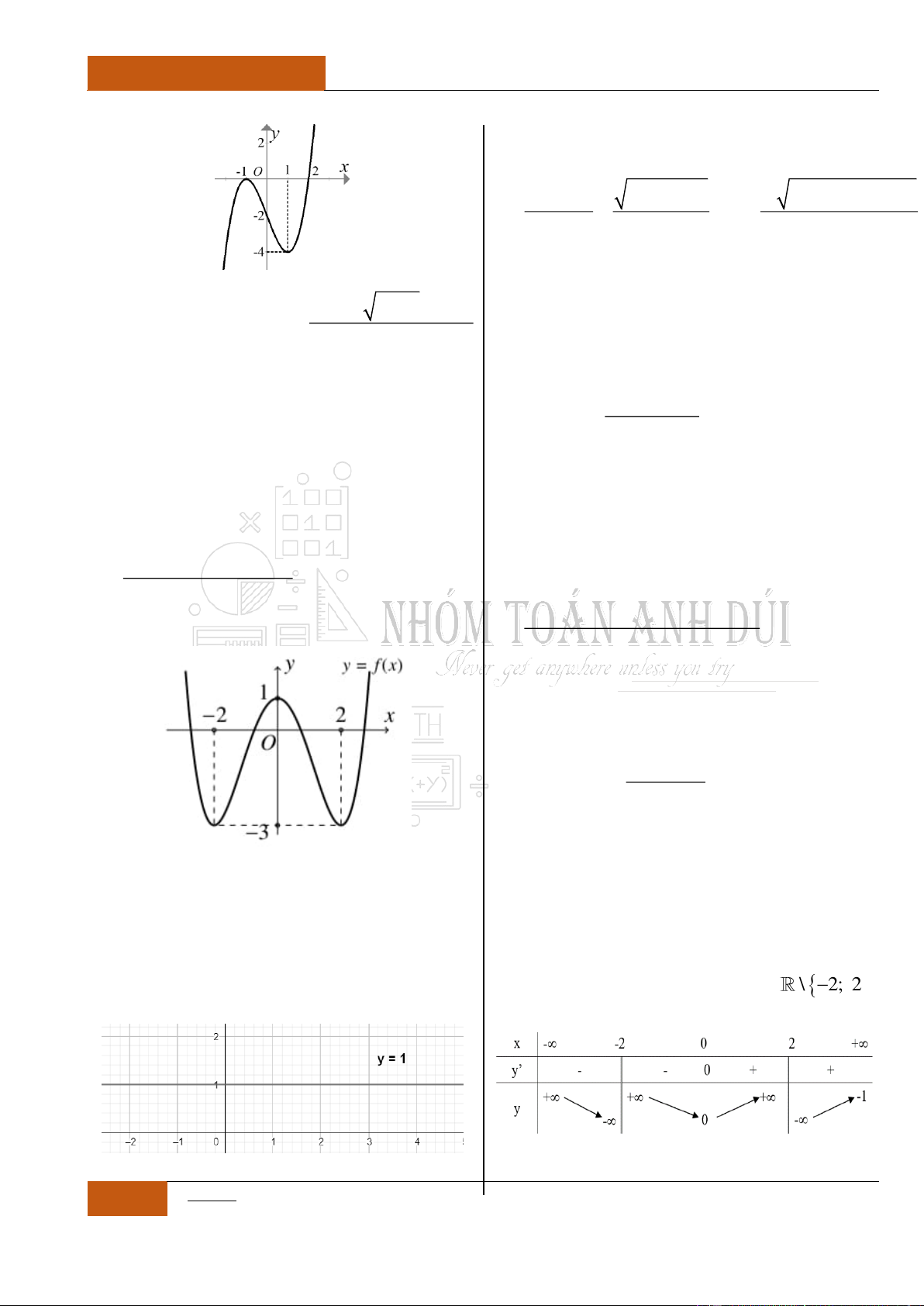
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

474

[ I can't, I can! ]

Hỏi đồ thị hàm số

 

2

1 4 3



  

fx

gx

x x x

có bao nhiêu đường tiệm cận đứng?

A.

2

. B.

1

. C.

3

. D.

4

.

Câu 83. [Vận dụng cao].

Cho hàm số trùng phương

42

  y ax bx c

có

đồ thị như hình vẽ. Hỏi đồ thị hàm số

  

   

22

2

42

23





   



x x x

y

f x f x

có tổng cộng bao

nhiêu tiệm cận đứng?

A.

5

. B.

2

. C.

3

. D.

4

.

Câu 84. [Vận dụng cao].

Cho hàm số

 

y f x

có đồ thị đạo hàm như

hình vẽ dưới đây.

Số tiệm cận của đồ thị hàm số:

 

y g x

với

 

2 2021

2021

2 2021

1

...

1 2 2021





   

  

f x f x

fx

y

f x f x f x

là bao nhiêu?

A.

2022

. B.

2

. C.

2021

. D.

0

.

Câu 85. [Vận dụng].

Cho hai số thực

a

và

b

thỏa mãn

2

4 3 1

lim 0

21







  







x

xx

ax b

x

.

Khi đó

2ab

bằng?

A. –4. B. –5. C. 4. D. –3.

Câu 86. [Vận dụng cao].

Có tất cả bao nhiêu giá trị nguyên thuộc đoạn

 

9;9

của tham số

m

để đồ thị hàm số

 

3 2 2 2

2

32





   

x

y

x mx m m x m

có đúng bốn

đường tiệm cận?

A. 15. B. 14. C. 16. D. 17.

Câu 87. [Vận dụng].

Cho hàm số

2

3

1







x

y

xm

(m là tham số;

2m

). Có bao nhiêu giá trị của tham số m để

hình phẳng giới hạn bởi hai trục tọa độ và hai

đường tiệm cận của đồ thị hàm số đã cho là một

hình vuông.

A.

1

. B.

3

. C.

2

. D.

4

.

Câu 88. [Vận dụng].

Hàm số

 

y f x

có đạo hàm trên

 

\ 2; 2

,

có bảng biến thiên như sau:

Gọi

, kl

lần lượt là số tiệm cận đứng và tiệm

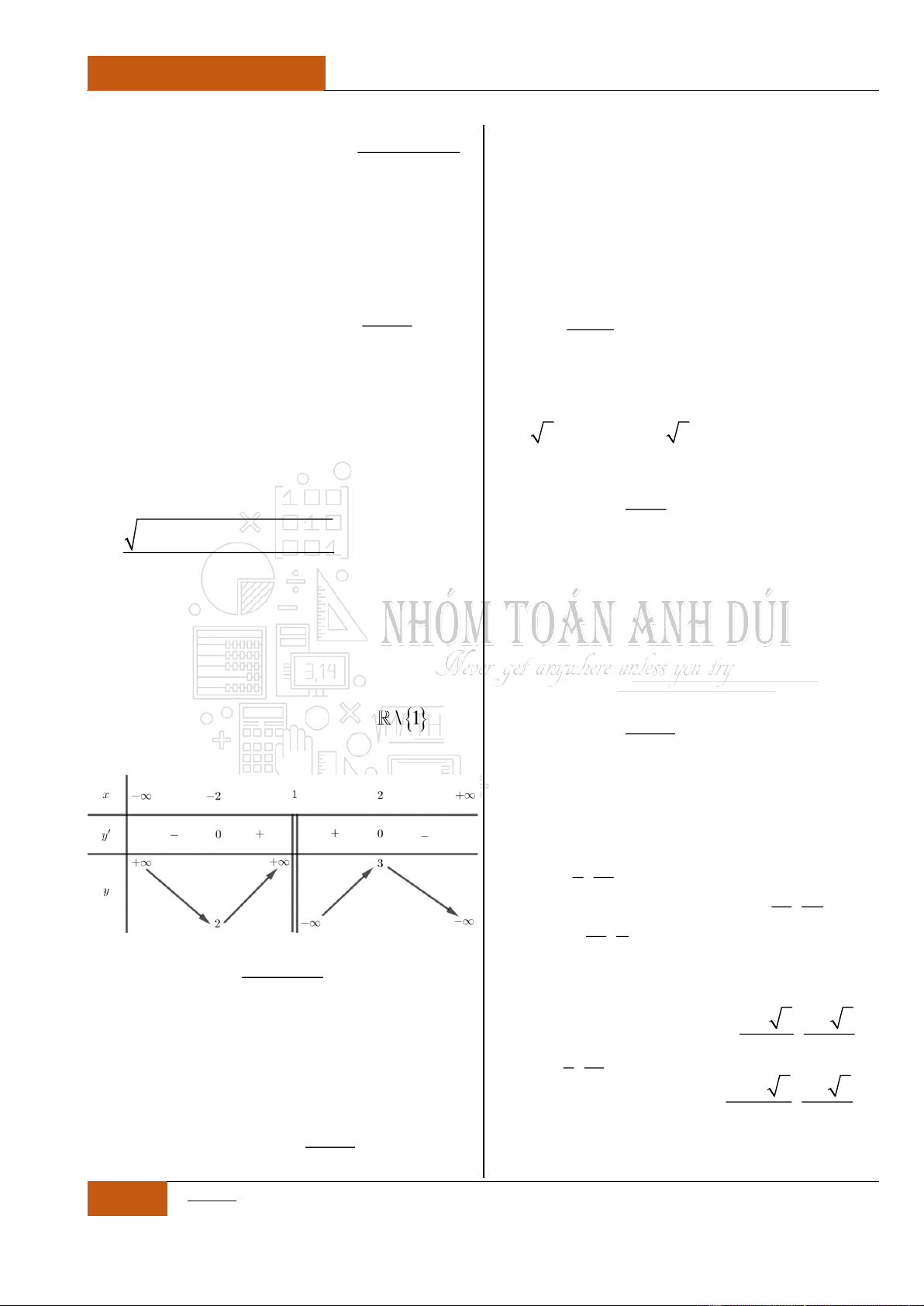
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

475

[ I can't, I can! ]

cận ngang của đồ thị hàm số

 

1

2018





y

fx

.

Tính

kl

?

A.

2.kl

B.

3.kl

C.

4.kl

D.

5.kl

Câu 89. [Vận dụng].

Tiếp tuyến của đồ thị hàm số

23

21







x

y

x

cùng

với hai đường tiệm cận tạo thành tam giác có

diện tích bằng?

A.

5

. B.

7

. C.

3

. D.

4

.

Câu 90. [Vận dụng cao].

Tính tổng

S

gồm tất cả các giá trị nguyên

dương của tham số

m

sao cho đồ thị hàm số

 

2

4 2 x 3

2

   





m x m m

y

x

có

2

tiệm cận

ngang.

A.

5S

. B.

3S

.

C.

10S

. D.

6S

.

Câu 91. [Vận dụng].

Cho hàm số

 

y f x

liên tục trên

 

\1

và có

bảng biến thiên như sau:

Đồ thị hàm số

 

1

25





y

fx

có bao nhiêu

đường tiệm cận đứng?

A.

0

. B.

4

. C.

2

. D.

1

.

Câu 92. [Vận dụng cao].

Cho đường cong

 

23

:

1







x

Cy

x

và

M

là một

điểm nằm trên

 

C

. Giả sử

12

,dd

tương ứng là

các khoảng cách từ

M

đến hai đường tiệm cận

của đồ thị hàm số

 

C

. Tính tích

12

.dd

.

A.

4

. B.

3

. C.

6

. D.

5

.

Câu 93. [Vận dụng cao].

Tìm hoành độ điểm

M

thuộc đồ thị hàm số

 

21

:

1







x

Cy

x

biết rằng

0

M

x

và tổng

khoảng cách từ

M

đến hai tiệm cận của đồ thị

hàm số

 

C

là nhỏ nhất.

A.

31

. B.

13

. C.

3

. D.

1

.

Câu 94. [Vận dụng cao].

Cho hàm số

2

3







x

y

x

có đồ thị là

 

C

. Có tất

cả bao nhiêu điểm

M

thuộc

 

C

sao cho

khoảng cách từ

M

đến đường tiệm cận ngang

bằng

5

lần khoảng cách từ

M

đến đường tiệm

cận đứng?

A.

4

. B.

3

. C.

2

. D.

1

.

Câu 95. [Vận dụng cao].

Cho hàm số

2

39







x

y

x

có đồ thị

 

C

. Điểm

M

trên đồ thị

 

C

thỏa mãn khoảng cách từ

M

đến giao điểm

I

của hai đường tiệm cận

ngắn nhất có tọa độ là?

A.

8 14

;

3 51

10 4

;

33

























M

. B.

10 16

;

3 57







M

.

C.

8 14

;

3 51







M

. D.

9 3 1 3

;

33

9 3 1 3

;

33





















  











M

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

444

[ I can't, I can! ]

ĐÁP ÁN

0

1

2

3

4

5

6

7

8

9

0

B

A

C

A

B

D

B

D

1

D

C

D

A

C

A

B

D

B

2

D

C

B

C

A

C

D

A

3

A

C

A

B

C

B

A

4

D

A

D

C

A

B

A

C

B

5

A

B

C

D

B

A

C

B

D

C

6

B

A

D

B

A

C

A

C

7

A

C

B

A

D

C

D

C

8

A

C

B

D

A

D

C

B

D

9

D

B

D

A

C

D

Ghi chú: Đáp án là sự kết hợp giữa dòng

i

và cột

j

. Ví dụ: Câu 24C (giao của dòng 2 và cột 4)

i

j

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

444

[ I can't, I can! ]

LỜI GIẢI CHI TIẾT

Câu 1. Nhìn bảng biến thiên ta thấy

0x

hàm

số không xác định nên

0x

là tiệm cận đứng

của đồ thị hàm số.

 

lim 3 3



  

x

f x y

là tiệm cận ngang của

đồ thị hàm số

 

lim 1 1



  

x

f x y

là tiệm cận ngang của

đồ thị hàm số

Vậy hàm số có 3 tiệm cận

Đáp án B.

Câu 2. Từ bảng biến thiên ta có:

1

lim





 

x

y

nên đường thẳng

1x

là đường

tiệm cận đứng của đồ thị hàm số

lim 2, lim 5

 



xx

yy

nên đường thẳng

2y

và

5y

là các đường tiệm cận ngang của đồ

thị hàm số

Tổng số đường tiệm cận ngang và đường tiệm

cận đứng của đồ thị hàm số đã cho là

3

.

Đáp án A.

Câu 3. Vì

lim 4, lim 1

 

   

xx

yy

Đồ thị

hàm số có hai tiệm cận ngang là

1y

và

4y

.

11

lim , lim



 

    

xx

yy

Đồ thị hàm số có

tiệm cận đứng

1x

.

11

lim , lim





    

xx

yy

Đồ thị hàm số có

tiệm cận đứng

1x

.

Nên đồ thị hàm số có 4 đường tiệm cận.

Đáp án C.

Câu 4. Dựa vào bảng biến thiên ta có :

 

2

lim





 

x

fx

, suy ra đường thẳng

2x

là tiệm cận đứng của đồ thị hàm số.

 

0

lim





 

x

fx

, suy ra đường thẳng

0x

là

tiệm cận đứng của đồ thị hàm số.

 

lim 0





x

fx

, suy ra đường thẳng

0y

là

tiệm cận ngang của đồ thị hàm số.

Vậy đồ thị hàm số có 3 đường tiệm cận.

Đáp án A.

Câu 5. Ta có:

 

lim 3

 



x

fx

và

 

lim 0

 



x

fx

nên đồ thị hàm số có 2 tiệm cận ngang là các

đường thẳng có phương trình

3y

và

0.y

Và

 

0

lim





 

x

fx

nên hàm số có 1 tiệm cận

đứng là đường thẳng có phương trình

0.x

Vậy tổng số đường tiệm cận đứng và ngang là

3

.

Đáp án B.

Câu 6. Vì

 

lim 3





x

fx

ta được tiệm cận

ngang

3y

.

Do

 

2

lim





 

x

fx

ta được tiệm cận đứng

2x

.

Vậy có tất cả

2

đường tiệm cận.

Đáp án D.

Câu 7. Từ bảng biến thiên ta có:

+ Tiệm cận ngang

5y

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

445

[ I can't, I can! ]

+ Tiệm cận đứng

2.x

Vậy có tất cả

2

đường tiệm cận.

Đáp án B.

Câu 8. Dựa vào bảng biến thiên của hàm số ta

có:

lim ( ) 2 2



  

x

f x y

là một tiệm cận ngang

1

lim ( ) 1





   

x

f x x

là một tiệm cận đứng

Vậy đồ thị hàm số có tổng số đường tiệm cận

là

2

.

Đáp án D.

Câu 9. Ta có:

2

lim 2





    

x

yx

là tiệm

cận đứng của đồ thị hàm số đã cho.

Ta có:

0

lim 0





   

x

yx

là tiệm cận đứng

của đồ thị hàm số đã cho.

lim 0 0



  

x

yy

là tiệm cận ngang của đồ

thị hàm số đã cho.

Vậy đồ thị hàm số đã cho có tổng đường tiệm

cận đứng và tiệm cận ngang là

3

.

Đáp án D.

Câu 10. Do

11

lim ; lim





    

xx

y

Tiệm

cận đứng:

1.x

lim 1; lim 1

 

   

xx

yy

đồ thị có 2 tiệm cận

ngang là

1y

Vậy, đồ thị hàm số đã cho có tổng số tiệm cận

đứng và tiệm cận ngang là 3.

Đáp án D.

Câu 11. Tiệm cận ngang:

Ta có:

2

5 4 1

lim lim

1

 







xx

y

x

2

41

5

lim lim

1

 



















xx

x

y

x

2

41

5

lim lim 5

1

 



  



xx

x

y

x

nên đồ thị hàm

số có một tiệm cận ngang

5y

.

Tiệm cận đứng:

Cho

2

1













x

Ta có:

2

11

5 4 1

lim lim

1









xx

y

x

  

1 1 1

5 1 1

5 1 6

lim lim lim 3

1 1 1 2

  





   

  

x x x

xx

x

y

x x x

nên

1x

không là tiệm cận đứng.

Vì:

   

2

11

5 4 1

lim lim

1



   







xx

y

x

   

  

2

11

5 4 1

lim lim

11



   







xx

y

xx

   

2

11

1 5 4 1

lim lim .

11



   





   







xx

y

xx

.

vì

 

1

2

1

lim

1

5 4 1

lim 4 0

1







 













  







x

xx

x

.

Khi đó, đồ thị hàm số có một tiệm cận đứng

1x

.

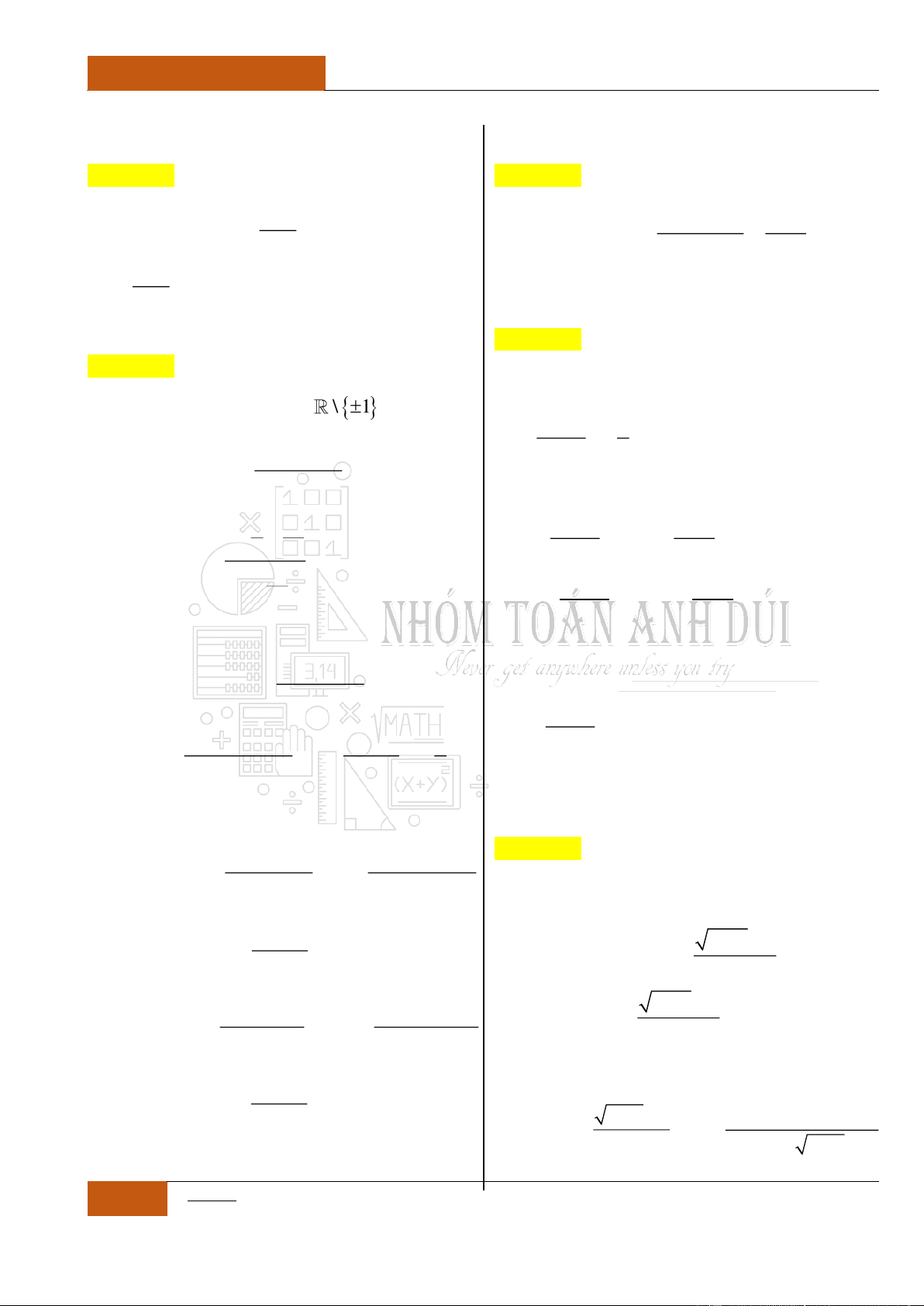
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

446

[ I can't, I can! ]

Tổng cộng đồ thị hàm số có

2

tiệm cận.

Đáp án C.

Câu 12. Ta có:

1

lim

1





 



x

và ta cũng có

1

lim

1





 



x

nên đường thẳng

1x

là

tiệm cận đứng của đồ thị hàm số.

Đáp án D.

Câu 13. Tập xác định:

 

\1D

Ta có:

2

54

lim lim

1

 







xx

y

x

2

54

1

lim lim 1

1

 



  



xx

x

y

x

1y

là một

đường tiệm cận ngang của đồ thị hàm số.

Mặc khác:

2

11

54

lim lim

1









xx

y

x

  

 

11

1

1 4 4

3

lim lim lim

1 1 1 2





  

   

  

xx

x

x x x

y

x x x

1x

không là đường tiệm cận đứng.

   

  

2

1

11

14

54

lim lim lim

11

1

  



   











x

xx

y

xx

x

   

 

11

4

lim lim

1



   



   



xx

x

y

x

.

     

  

2

1 1 1

14

54

lim lim lim

11

1

  

     











x x x

xx

y

xx

x

   

 

11

4

lim lim

1



   



   



xx

x

y

x

.

1  x

là đường tiệm cận đứng.

Vậy đồ thị hàm số có 2 đường tiệm cận.

Đáp án A.

Câu 14. Ta có:

2

3 4 1

4

16

  







x x x

y

x

(với

điều kiện xác định), do đó đồ thị hàm có 1 tiệm

cận đứng.

Đáp án C.

Câu 15. Ta có:

2

4 0 2    xx

2

21

lim

4















x

nên đường thẳng

2x

không phải là tiệm cân đứng của đồ thị hàm số.

2

22

21

lim lim ,

2

4



 





  









xx

x

   

2

22

21

lim lim ,

2

4



   





  









xx

x

nên

đường thẳng

2x

là tiệm cân đứng của đồ

thị hàm số.

2

lim 0

4















x

nên đường thẳng

0y

là

tiệm cận ngang của đồ thị hàm số.

Vậy có đồ thị có hai đường tiệm cận.

Đáp án C.

Câu 16. TXĐ:



  

9; \ 0; 1   D

.

Ta có:

 

1

lim







x

y

 

2

1

93

lim









x

xx

 

và

 

1

lim



x

y

 

2

1

93

lim











x

xx

 

.



Tiệm cận đứng:

1x

.

0

lim







x

y

2

0

93

lim









x

xx

 

2

0

lim

93







  

x

x x x

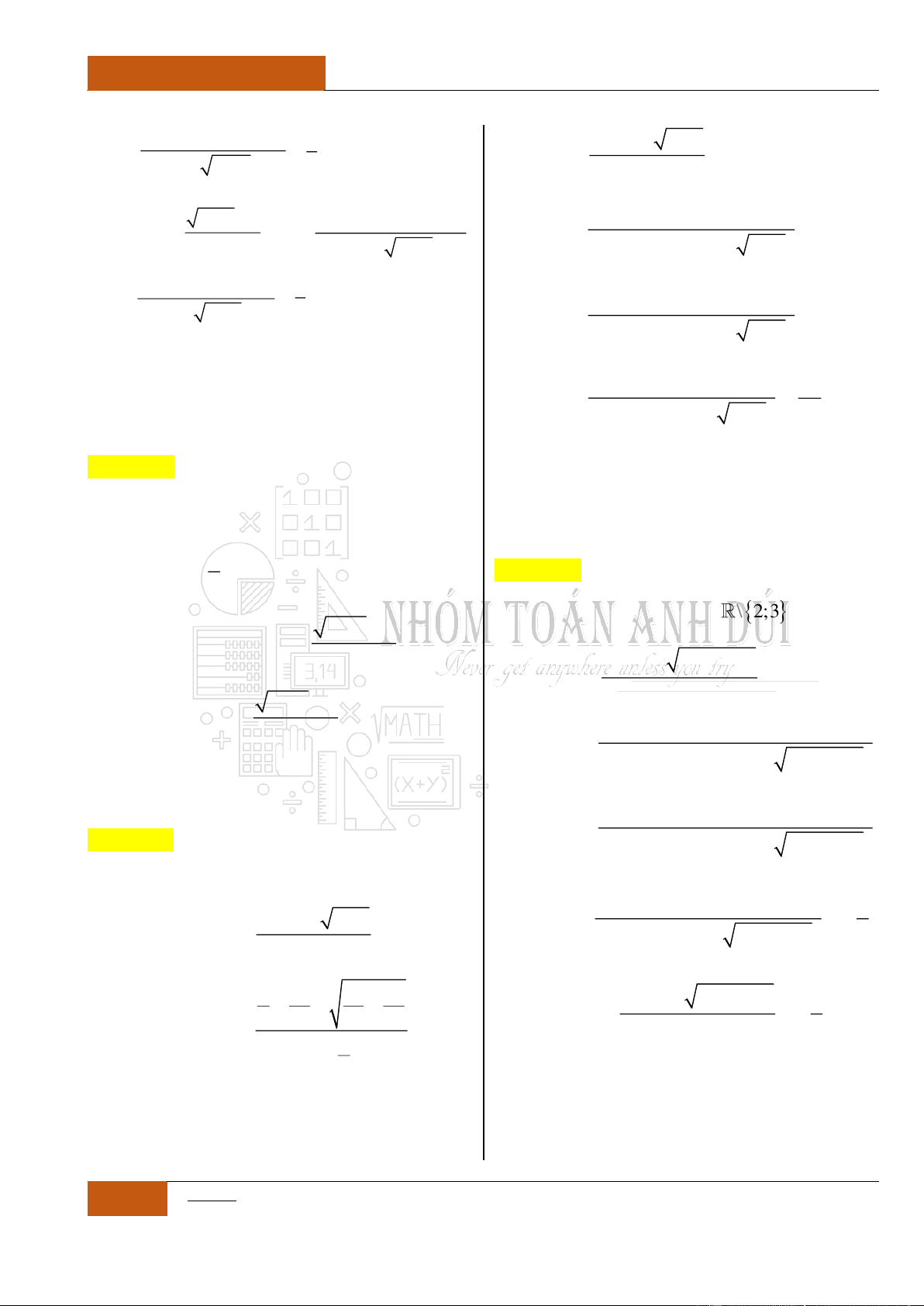
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

447

[ I can't, I can! ]

 

0

1

lim

1 9 3







  

x

xx

1

6



.

0

lim







x

y

2

0

93

lim









x

xx

 

2

0

lim

93







  

x

x x x

 

0

1

lim

1 9 3







  

x

xx

1

6



.



0x

không là đường tiệm cận đứng của đồ

thị hàm số.

Vậy đồ thị hàm số có

1

tiệm cận đứng.

Đáp án A.

Câu 17. TXĐ:



  

4; \ 0; 1   D

Ta có:

0

1

lim

4





x

y

.

Mặt khác:

   

2

11

42

lim lim



   



  



xx

x

y

xx

Và

   

2

11

42

lim lim



   



  



xx

x

y

xx



Tiệm cận đứng:

1x

.

Vậy đồ thị hàm số có

1

tiệm cận đứng.

Đáp án B.

Câu 18. Tập xác định:



  

1; \ 0   D

.

Ta có:

lim

x

y

2

5 1 1

lim

2



  





x

xx

2 3 4

5 1 1 1

lim

2

1



  





x

x x x

x

0

0y

là đường tiệm cận ngang của đồ thị

hàm số.

0

lim

x

y

2

0

5 1 1

lim

2



  





x

xx

 

2

0

5 1 1

lim

2 5 1 1



  



   

x

xx

x x x x

 

2

0

25 9

lim

2 5 1 1







   

x

xx

x x x x

 

0

25 9

lim

2 5 1 1







   

x

x x x

9

4





0x

không là đường tiệm cận đứng của đồ

thị hàm số.

Vậy đồ thị hàm số có tất cả

1

đường tiệm cận.

Đáp án D.

Câu 19. Tập xác định:

 

2;3\D

.

 





 





2

22

2

22

2

22

2

2 1 3

lim lim

56

2 1 3

lim

5 6 2 1 3

2 1 3

lim

5 6 2 1 3









   





   



     

   



     

xx

x

x x x

y

xx

x x x

x x x x x

x x x

x x x x x

 





2

31

7

lim

6

3 2 1 3







  

    

x

x x x x

Tương tự:

2

2 1 3 7

lim

6

56





   





x

x x x

xx

.

(Học sinh tự chứng minh).

Suy ra đường thẳng

2x

không là tiệm cận

đứng của đồ thị hàm số đã cho.

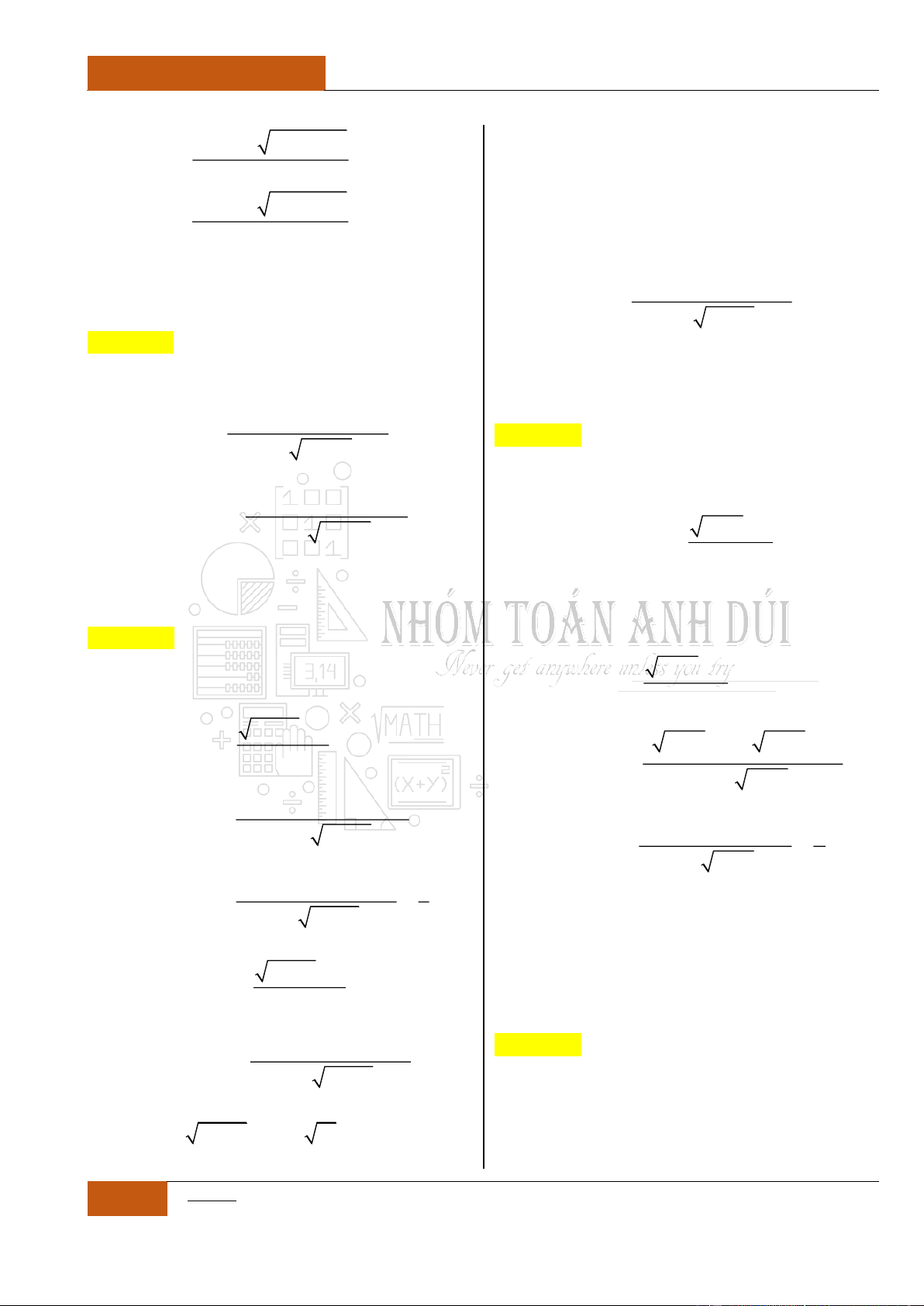
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

448

[ I can't, I can! ]

Ta có:

2

3

2

3

2 1 3

lim

56

2 1 3

lim

56









   

 









   

 







x

x x x

xx

x x x

xx

.

Suy ra đường thẳng

3x

là tiệm cận đứng của

đồ thị hàm số đã cho.

Đáp án B.

Câu 20. Tập xác định:



  

25; \ 1;0   D

.

Biến đổi

 

1

.

1 25 5



  

fx

xx

Vì

   

 

11

1

lim lim

1 25 5



   

  

  

xx

y

xx

nên đồ thị hàm số đã cho có 1 tiệm cận đứng

1x

.

Đáp án D.

Câu 21. TXĐ:



  

16; \ 1;0   D

.

Ta có:

 

00

16 4

lim lim

1









xx

x

y

xx

 

0

lim

1 16 4





  

x

x x x

 

0

11

lim

8

1 16 4





  

x

xx

.

Và

   

 

11

16 4

lim lim

1



   







xx

x

y

xx

 

1

lim

1 16 4





  

  

x

xx

.

Vì :

 

1

lim 16 4 15 4 0





    

x

,

 

1

lim 1 0







x

.

Và

 

1



x

thì

1 1 0    xx

.

Tương tự : (Độc giả tự chứng minh).

   

 

11

1

lim lim

1 16 4



   

  

  

xx

y

xx

.

Vậy đồ thị hàm số đã cho có tiệm cận đứng là

1x

.

Đáp án C.

Câu 22. TXĐ:



  

4; \ 1;0   D

.

Ta có:

   

2

11

42

lim lim



   



  



xx

x

y

xx

Nên đường thẳng

1x

là một đường tiệm cận

đứng của đồ thị hàm số đã cho.

Ta có:

2

00

42

lim lim









xx

x

y

xx

  

 

0

4 2 4 2

lim

1 4 2



   



  

x

xx

x x x

 

0

11

lim

4

1 4 2





  

x

xx

.

Nên đường thẳng

0x

không là tiệm cận đứng

của đồ thị hàm số đã cho.

Vậy đồ thị hàm số đã cho có một tiệm cận đứng

1x

.

Đáp án C.

Câu 23. TXĐ:

   

; 1 1;    D

.

Trường hợp 1:

1 1 0    xx

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

449

[ I can't, I can! ]

Khi đó:

 

  

2

1

11

1











x

fx

xx

x

Hay

 

1







x

fx

x

.

Suy ra hàm số tiệm cận ngang

1y

, không

có tiệm cận đứng.

Trường hợp 2:

1 1 0   xx

. Khi đó

 

  

2

1

11

1

11

1





  







x

xx

fx

x

xx

x

.

Suy ra hàm số tiệm cận ngang

1y

, tiệm cận

đứng

1x

.

Vậy hàm số có 2 tiệm cận ngang và 1 tiệm cận

đứng.

Đáp án B.

Câu 24. Ta có:

 

62

4

4 6 2

lim lim 2

2

1

 







xx

x

 

62

4

4 6 2

lim lim 2

2

1

 

  



  



xx

x

 

  

   

 

22

4 6 2

2 4 2

lim lim

2

2 4 6 2



 







  

xx

x

x x x

 

2

4 2 5

lim

2

4 6 2











x

xx

.

Vậy hàm số có hai tiệm cận ngang

2y

.

Đáp án C.

Câu 25. TXĐ:

 

; 2 1;1 2;     

.

Do

lim lim

 



xx

yy

2

42

23

lim

32









x

xx

2

24

23

1

lim 1

32

1









x

xx

1y

là đường tiệm cận ngang của đồ thị

hàm số.

Ta có:

1

lim





 

x

y

nên đường thẳng

1x

là

đường tiệm cận đứng.

Ta có:

 

1

lim







x

y

 

  

 

1

12

lim

1 2 1 2









   

x

xx

x x x x

 

   

 

1

12

lim 0

2 1 2









  

x

xx

x x x

Nên đường thẳng

1x

không là đường tiệm

cận đứng.

Ta có:

 

2

lim





 

x

y

nên đường thẳng

2x

là đường tiệm cận đứng.

Ta có:

 

2

lim





 

x

y

nên đường thẳng

2x

là đường tiệm cận đứng.

Vậy đồ thị hàm số có

4

đường tiệm cận (

1

tiệm

cận ngang,

3

tiệm cận đứng).

Đáp án A.

Câu 26. TXĐ:

 

\0D

.

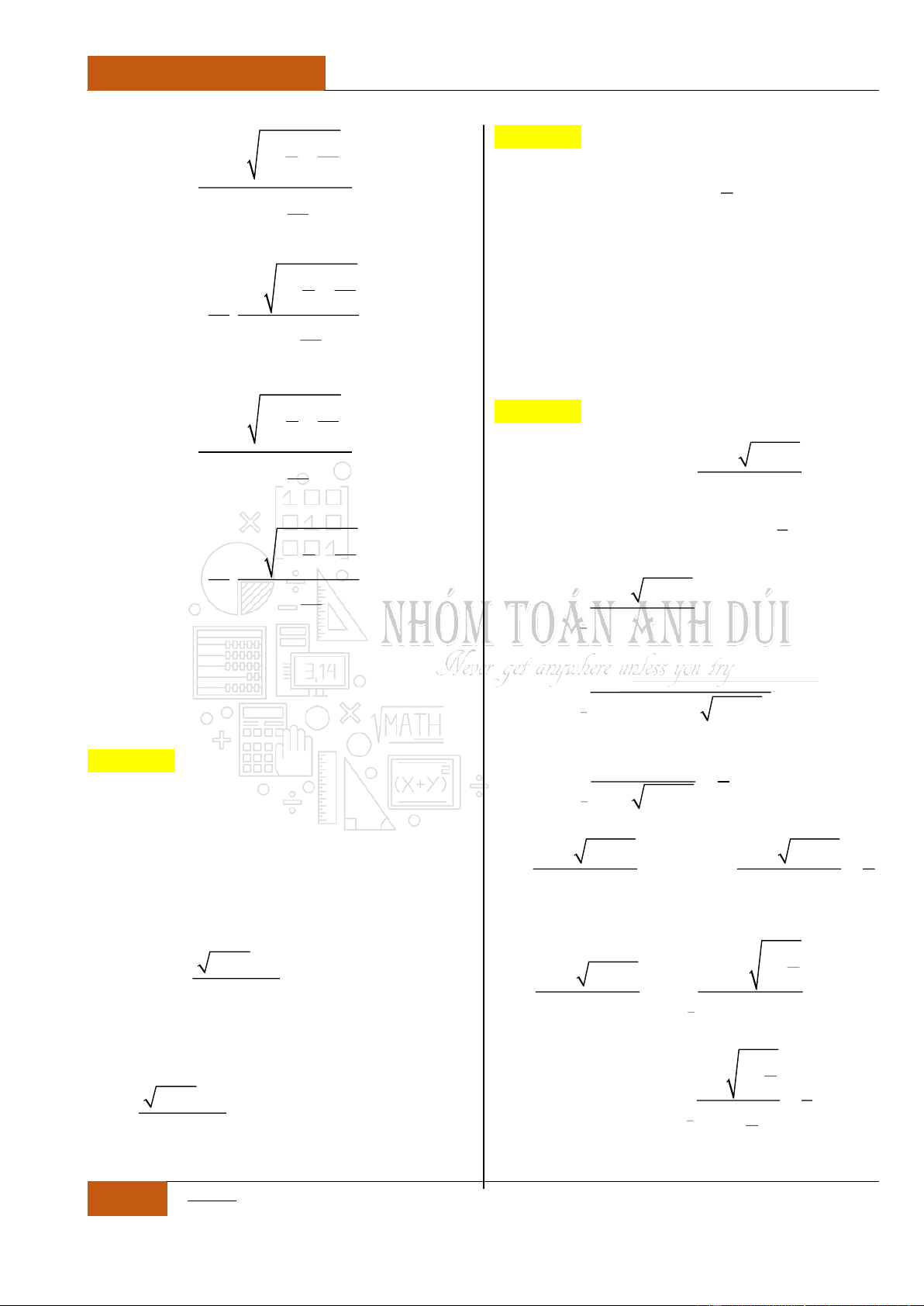
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

450

[ I can't, I can! ]

2

3

2

11

lim lim

1

 



  















xx

x

y

x

2

11

1

lim . 0

1





  













x

;

2

3

2

11

lim lim

1

 



  















xx

x

y

x

2

11

1

lim . 0

1





  













x

.



Tiệm cận ngang:

0y

.

0

lim





 

x

y



Tiệm cận đứng:

0x

.

Đáp án C.

Câu 27. ĐKXĐ:

2

20

3 2 0







  



x

xx

2

2, 1





  







x

xx

.

Ta có:

2

21

lim

32









 







x

xx

nên đường

thẳng

2x

là tiệm cận đứng của đồ thị hàm

số.

2

21

lim 0

32















x

xx

nên đường thẳng

0y

là tiệm cận ngang của đồ thị hàm số.

Đáp án D.

Câu 28. TXĐ:

1

\ 1;

2









DR

Ta có:

11

lim ; lim





   

xx

yy



Đồ thị hàm

số có một tiệm cận đứng là

1x

lim 0





x

y



Đồ thị hàm số có một tiệm cận

ngang là

0y

.

Đáp án D.

Câu 29. Xét hàm số

2

31







x x x

y

x

có tập

xác định



 



1

;0 1; \

3



    





D

.

Ta có:

2

1

3

2

lim

31







x

x x x

x

 





2

1

2

3

lim

3 1 2







  

x

xx

x x x x

1

2

3

lim

2







x

x x x

1

4



;

2

0

2

lim 0

31











x

x x x

x

và

2

1

21

lim

3 1 2











x

x x x

x

nên đồ thị không có tiệm cận đứng.

2

1

3

1

21

2

lim lim

3 1 3 1













x

xx

x x x

x

xx

1

3

1

21

1

lim

1

3









x

,

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

451

[ I can't, I can! ]

và

2

1

3

1

21

2

lim lim

3 1 3 1











x

xx

x x x

x

xx

1

3

1

21

lim 1

1

3









x

.

Nên đồ thị có hai tiệm cận ngang là

1

3

y

và

1y

.

Vậy đồ thị hàm số có tất cả hai đường tiệm

cận.

Đáp án A.

Câu 30.

 

 

2;2 \ 1  D

.

   

2

11

14

lim lim ;

23



   



  



xx

x

y

xx

   

2

11

14

lim lim

23



   



  



xx

x

y

xx

1  x

là tiệm cận đứng.

Đồ thị hàm số không có đường tiệm cận ngang.

Vậy

1mn

.

Đáp án A.

Câu 31. Tập xác định:

 

0;1D

.

Từ tập xác định suy ra đồ thị hàm số không có

tiệm cận ngang.

0n

.

+

 

0 0 0

11

lim lim lim

11

  

  



   



x x x

x

y

x x x x

+

 

1 1 1

11

lim lim lim

11

  

  



   



x x x

x

y

x x x x

Suy ra đồ thị hàm số có hai tiệm cận đứng,

2d

.

Đáp án A.

Câu 32. TXĐ:



  

1;0 2;   D

.

Ta có:

 

2

00

25 9

lim lim

2 5 1 1

   





   

xx

y

x x x x

 

0

25 9 9

lim

4

2 5 1 1





  

   

x

x x x

.

Mặt khác:

2

lim



 

x

y

.

Và

2 3 4

5 1 1 1

lim lim 0

2

1

 

  





xx

x

x x x

y

x

.

Vậy đồ thị của hàm số có hai đường tiệm cận

có phương trình

2x

và

0y

.

Đáp án C.

Câu 33. Tập xác định:

 

1

; \ 1

3



  







D

+ Ta có:

1

lim

4 3 1 3 5







  

x

xx

 

2

1

1 4 3 1 3 5

lim

91





   





x

x x x

x

 

1

4 3 1 3 5

lim

91





  

  



x

xx

x

.

Do đó đường thẳng

1x

là đường tiệm cận

đứng của đồ thị hàm số.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

452

[ I can't, I can! ]

Mặt khác:

1

lim

4 3 1 3 5





  

x

xx

2

1

lim

3

3 1 5

43





  

  

x

xx

x

.

Do đó đường thẳng

1

3

y

là đường tiệm cận

ngang của đồ thị hàm số.

Vậy đồ thị hàm số có 2 đường tiệm cận.

Đáp án A.

Câu 34. Tập xác định của hàm số:

 

; 2 1;1 2;      D

.

   

11

22

lim lim lim lim

   

  

    

xx

y y y y

.



Các đường tiệm cận đứng của đồ thị là

2x

,

1x

.

lim lim 1

 



xx

yy



đồ thị có một tiệm cận

ngang

1y

.

Đáp án B.

Câu 35. Tập xác định:

   

;0 3;   D

.

2

58

lim lim

3

 







xx

x

y

xx

8

5

58

lim lim 5

33

11

 



  



xx

x

xx



Đường thẳng

5y

là tiệm cận ngang của

đồ thị hàm số.

2

5 8 5 8

lim lim lim

3

1

  









x x x

xx

y

xx

x

8

5

lim 5

3

1





  



x

.



Đường thẳng

5y

là tiệm cận ngang của

đồ thị hàm số.

2

00

58

lim lim

3







  



xx

x

y

xx

Vì:

 

0

22

0

lim 5 8 8 0

lim 3 0; 3 0 0











   





     





x

x x x x x

.

Suy ra đường thẳng

0x

là tiệm cận đứng của

đồ thị hàm số.

2

33

58

lim lim

3







  



xx

x

y

xx

Vì

 

2

33

2

lim 5 8 7 0; lim 3 0

3 0 3









    







   



xx

x x x

.

Suy ra đường thẳng

3x

là tiệm cận đứng của

đồ thị hàm số.

Đáp án B.

Câu 36. Điều kiện xác định của hàm số:

2

4 2 1 0

10



  







xx

x

15

4

15

4

1











































x

.

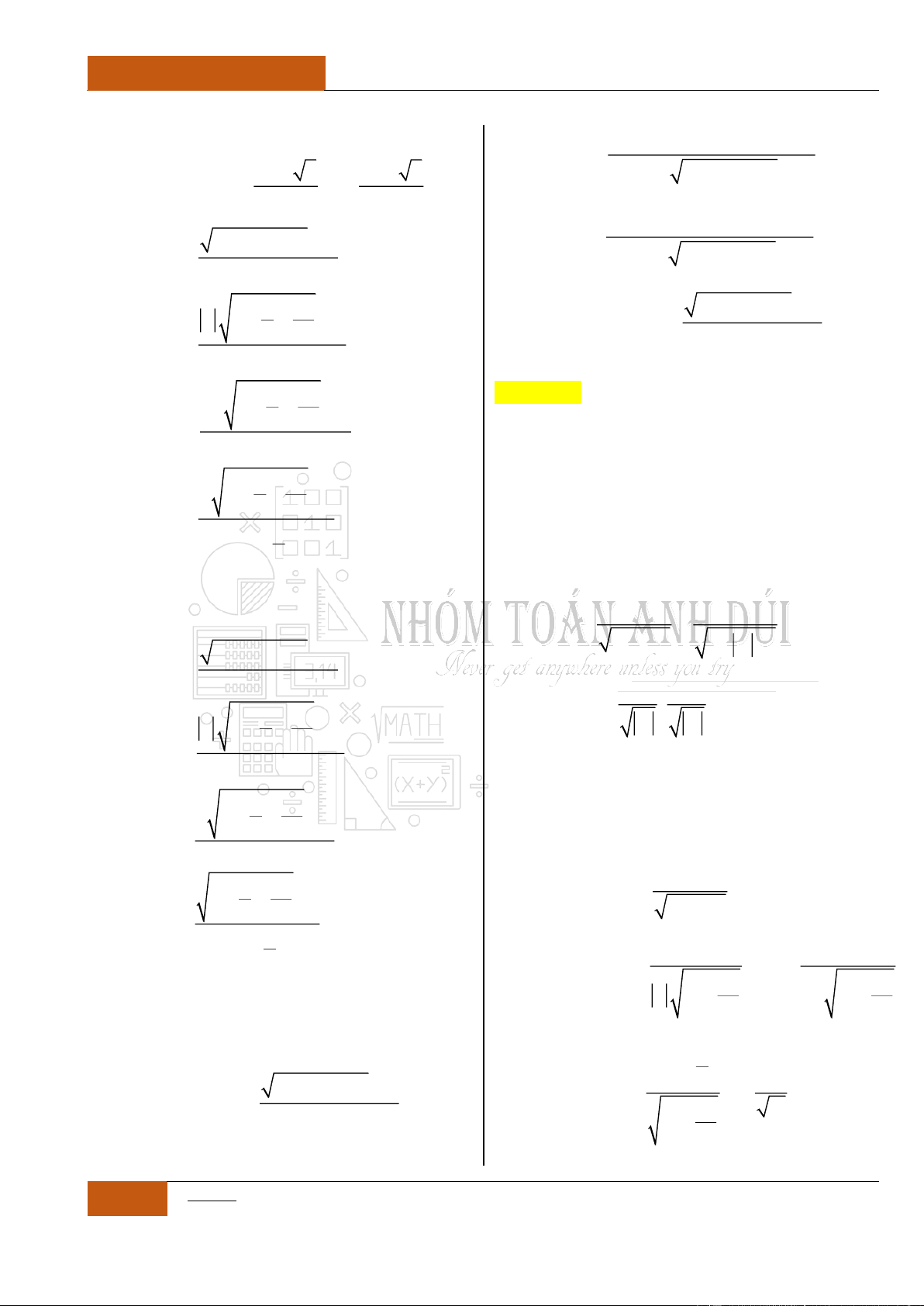
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

453

[ I can't, I can! ]

Tập xác định của hàm số đã cho là:

 

1 5 1 5

; 1 1; ;

44

   

   

      





   

D

2

4 2 1

lim lim

1

 

  





xx

x x x

y

x

2

21

4

lim

1



  





x

xx

x

2

21

4

lim

1



   





x

xx

x

2

21

41

lim 1

1



   

  



x

.

1  y

là đường tiệm cận ngang của đồ thị

hàm số khi

 x

.

2

4 2 1

lim lim

1

21

4

lim

1

 



  





  





xx

x

x x x

y

x

xx

x

2

21

4

lim

1

21

41

lim 3

1





  





  





x

xx

x

3y

là đường tiệm cận ngang của đồ thị

hàm số khi

 x

.

Mặt khác, ta lại có:

2

11

4 2 1

lim lim

1

 

  





xx

x x x

y

x

 





22

1

2

4 2 1

lim

1 4 2 1



  



   

x

x x x

x x x x

  

 





1

2

1 3 1

lim 2

1 4 2 1





  

   

x

xx

x x x x

Vậy đồ thị hàm số

2

4 2 1

1

  





x x x

y

x

có

2

đường tiệm cận.

Đáp án C.

Câu 37. Xét các trường hợp sau:

Với

0m

:

Hàm số trở thành

1yx

nên không có tiệm

cận ngang.

Với

0m

:

Hàm số

22

11







xx

y

mx m x

có tập xác

định là

11

;











D

mm

suy ra không tồn

tại giới hạn

lim

x

y

hay hàm số không có tiệm

cận ngang.

Với

0m

:

Ta có:

2

1

lim lim

1

 







xx

x

y

mx

2

1

lim

1









x

xm

x

2

1

lim

1









x

xm

x

2

1

lim .

1











  



x

m

x

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

454

[ I can't, I can! ]

Và ta có:

2

1

lim lim

1

 







xx

x

y

mx

2

1

lim

1









x

xm

x

2

1

lim

1









x

xm

x

2

1

lim .

1















x

m

x

Vậy hàm số có hai tiệm cận ngang là :

11

;  yy

mm

khi

0m

.

Đáp án C.

Câu 38. Điều kiện xác định

2

20

6 2 0







  



x

x x m

.

Để đồ thị hàm số có hai đường tiệm cận đứng

thì phương trình

2

6 2 0  x x m

có hai

nghiệm phân biệt

12

,xx

lớn hơn

2

   

12

2

9 2 0

2

2 6 2 2 0





   



   





     





m

xx

m

9

2

32

2

8

4 12 2 0













   







  







m

.

Do đó tập

 

7; 6; 5;...;4   S

có

12

giá trị.

Đáp án B.

Câu 39. Ta có:

2

1

lim

8







x

x x m

2

1

lim 0

8









x

x x m

nên hàm

số có một tiệm cận ngang

0y

.

Hàm số có

3

đường tiệm cận khi và chỉ khi

hàm số có hai đường tiệm cận đứng



phương

trình

2

80  x x m

có hai nghiệm phân biệt

khác

1

16 0 16

7 0 7



    







  



mm

.

Kết hợp với điều kiện

m

nguyên dương ta có:

 

1;2;3;...;6;8;...;15m

.

Vậy có

14

giá trị của

m

thỏa mãn đề bài.

Đáp án A.

Câu 40. Ta có:

lim 0, lim 0

 



xx

yy



đồ thị hàm số đã cho có 1 tiệm cận ngang.

Do đó đồ thị hàm số đã cho có 4 đường tiệm

cận khi và chỉ khi nó có 3 tiệm cận đứng

 

*

.

Ta có:

 

3 2 2

3 2 1   x mx m x m

 

2

21   x m x mx

 

3 2 2

2

3 2 1 0

2 1 0 2

    









  





x mx m x m

xm

x mx

 

*



 

3 2 2

3 2 1 0    x mx m x m

có

3

nghiệm phân biệt khác

3

.



3m

và

 

2

có

2

nghiệm phân biệt khác

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

455

[ I can't, I can! ]

m

và khác

3

.

2

3

5

3,

2 . 1 0

3

1

3 2 .3 1 0

1

10









  











  













   



m

mm

m m m

m

.

Do đó tập tất cả giá trị nguyên của

m

thỏa yêu

cầu đề bài là:

 

2020; 2019;...; 2;2;4;5;...;2020  

.

Vậy có

4037

giá trị

m

thỏa yêu cầu đề bài.

Đáp án D.

Câu 41. Điều kiện xác định:

 

0;2















xm

x

, khi đó

đồ thị hàm số sẽ không có tiệm cận ngang.

Ta có:

02

lim , lim





   

xx

yy

.

Suy ra

0, 2xx

là hai đường tiệm cận đứng.

Vậy để đồ thị hàm số có đúng hai đường tiệm

cận thì

0

2











m

, theo bài

m

thuộc đoạn

 

100;100

. Vậy có

200

số nguyên của

m

thỏa

mãn đầu bài.

Đáp án A.

Câu 42.

  

22

2

12

32









x m x m

y

xx

.

lim 1





x

y

1y

là đường tiệm cận ngang.

Đồ thị hàm số

2

32







xm

y

xx

có đúng hai

đường tiệm cận.



Đồ thị hàm số có đúng một tiệm cận đứng.



Phương trình

2

0xm

nhận nghiệm

1x

hoặc

2x

.

Khi đó:

1

4











m

.

Với

1m

có một tiệm cận đứng

2x

.

Với

4m

có một tiệm cận đứng

1x

.

Vậy

 

1; 4  m

.

Đáp án D.

Câu 43. Để đồ thị có ba đường tiệm cận thì

2

2 4 0  x mx

có hai nghiệm phân biệt

1

   

2

0

2

1 2 1 4 0

5

2

























    





  





m

Đáp án C.

Câu 44. Theo công thức tìm nhanh tiệm cận của

đồ thị hàm số





d

ax b

y

cx

ta có:

Đồ thị hàm số nhận

30     

d

xm

c

làm

tiệm cận đứng

3  m

.

Đồ thị hàm số nhận

30   

a

yn

c

làm tiệm

cận ngang

3n

.

Vậy

0mn

.

Đáp án A.

Câu 45. Trường hợp 1:

0m

suy ra tập xác

định của hàm số là

 

12

;D x x

, (

12

;xx

là

nghiệm của phương trình

2

8 2 0  mx x

).

Do đó

0m

không thỏa yêu cầu của bài toán.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

456

[ I can't, I can! ]

Trường hợp 2:

1

0

82



  



x

my

x

suy ra

tập xác định của hàm số là

 

;4 D

.

4

lim ; lim







   

x

yy

. Khi đó ta có

4x

là đường tiệm cận đứng của đồ thị hàm số.

Do đó

0m

không thỏa yêu cầu của bài toán

Trường hợp 3:

0m

suy ra tập xác định của

hàm số là

   

12

;;   D x x

(

12

;xx

là

nghiệm của phương trình

2

8 2 0  mx x

).

Do đó đồ thị hàm số có bốn đường tiệm cận

khi phương trình

2

8 2 0  mx x

có hai

nghiệm phân biệt khác

1

khi và chỉ khi:

16 2 0 8

0; 0;

8 2 0 6

  





    





   



mm

m m m m

mm

 

1;2;3;4;5;7m

.

Suy ra có tất cả

6

giá trị nguyên của tham số

m

thỏa mãn yêu cầu của bài toán.

Đáp án B.

Câu 46. Đồ thị hàm số có tiệm cận ngang



Hàm số xác định trên một trong các miền

  



 

; , ; , ,  a a a

hoặc





;a

khi

0m

.

Trường hợp 1:

0 3 7, lim



       

x

m y x x y

đồ thị

không có tiệm cận ngang

Trường hợp 2:

2

0, 3 7    m y x mx x

Khi

2

3 7 3

lim lim

2





    





x

y x x m

x

đồ

thị hàm số có tiệm cận ngang khi và chỉ khi

1m

.

Vậy

1m

.

Đáp án A.

Cách trắc nghiệm:

Thay

1m

.

2

37    y x x x





2

3

lim 3 7

2



    

x

x x x

đồ thị hàm số

có tiệm cận ngang.





2

lim 3 7



     

x

x x x

không có tiệm

cận ngang.

Thay

1m

.

2

37     y x x x





2

lim 3 7



    

x

x x x

không xác định.





2

lim 3 7



   

x

x x x

không xác định.

Vậy

1m

.

Đáp án A.

Câu 47. +)

0b

đồ thị hàm số

1

2







ax

y

không có tiệm cận.

+)

0b

, tập xác định của hàm số

1

2







ax

y

bx

là

2

\









DR

b

.

1

lim lim lim

2

  



  



x x x

a

ax a

x

y

bx b

b

x

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

457

[ I can't, I can! ]



Đồ thị hàm số

1

2







ax

y

bx

có tiệm cận

ngang là đường thẳng

1

2

    

aa

y b a

bb

.

22

1

lim lim

2





















xx

bb

ax

y

bx

.



Đồ thị hàm số

1

2







ax

y

bx

có tiệm cận đứng

là đường thẳng

2

x

b

2

1 2 1     ba

b

.

Vậy

1; 2ab

.

Đáp án C.

Câu 48. Đồ thị hàm số

2

1

2 6 3





  

x

y

x x m

có

hai đường tiệm cận đứng khi phương trình

2

2 6 3 0   x x m

có hai nghiệm phân biệt

khác

1

.

 

2

3 2 3 0

2.1 6.1 3 0



   







   





m

15

2

5

















m

.

Từ đó ta suy ra tập các giá trị nguyên của

m

thỏa mãn là:

 

7,...,3, 4, 6,...,10

.

Vậy có

17

giá trị nguyên của

m

thỏa mãn.

Đáp án C.

Câu 49. Đồ thị hàm số

2

34

2







mx mx

y

x

có

nhiều nhất một tiệm cận đứng và hai tiệm cận

ngang.

Điều kiện để

2

34

2







mx mx

y

x

có 3 tiệm

cận là nó có đúng

1

tiệm cận đứng và

2

tiệm

cận ngang.

* Xét điều kiện tồn tại

lim

x

y

và

lim

x

y

.

Trường hợp 1:

 

2

3 4 0   g x mx mx

với

x

2

0

16

0

9

9 16 0









   









   





m

mm

Trường hợp 2:

 

2

3 4 0   g x mx mx

với

   

12

;;    x x x

với

1

x

;

2

x

là nghiệm

của

 

gx

2

0

16

9

9 16 0





  



   



m

mm

.

Vậy

0m

thì tồn tại

lim

x

y

và

lim

x

y

.

Khi đó:

2

34

lim lim

2

 







xx

mx mx

y

x

2

34

lim

2

1









x

m

x

m

x

.

Và

2

34

lim lim

2

 







xx

mx mx

y

x

2

34

lim

2

1



  

  



x

m

x

m

x

.

Vậy điều kiện để đồ thị hàm số có hai đường

tiệm cận ngang là

0m

.

* Xét trường hợp

2x

là nghiệm của tử số.

2  x

là nghiệm của

 

0gx

với

 

2

34  g x mx mx

.



 

2 0 2   gm

.

Khi đó:

2

2 6 4

2







xx

y

x

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

458

[ I can't, I can! ]

  

2

2 1 2

lim

2











x

xx

y

x

 

2

21

lim

2









   









x

.



Đồ thị hàm số có

1

tiệm cận đứng

2x

.



2m

thỏa mãn.

* Xét trường hợp

2x

không là nghiệm của

tử số.

Để

2x

là tiệm cận đứng của đồ thị hàm số

thì

 

20















g

 

2 0 4 2 0 2       g m m

.



Đồ thị hàm số có một đường tiệm cận đứng

2x

với





0;2m

.

Vậy điều kiện để đồ thị hàm số

2

34

2







mx mx

y

x

có 3 tiệm cận là





0;2m

.

Vậy có hai giá trị nguyên của

m

thỏa mãn đề

bài là

1m

;

2m

.

Đáp án B.

Câu 50. Đặt

   

22

2 1 2   f xmx xm

.

Đồ thị hàm số có đúng một tiệm cận đứng khi

và chỉ khi

 

0fx

có

2

nghiệm phân biệt

trong đó có

1

nghiệm

1x

hoặc

 

0fx

có

nghiệm kép.

 

2

1 2 0

0

1 2 1 2 0

10

3

0

2





   























    





























mm

f

m

3

1

2

3

1; 3

3

2





















   

  

















m

mm

m

Vậy tổng các giá trị

m

thỏa mãn là:

1

2



.

Đáp án A.

Câu 51. Do

lim lim 0

 



xx

yy

nên đồ thị hàm

số có tiệm cận ngang là đường thẳng

0y

.

Do đó, đồ thị hàm số có tất cả bốn đường tiệm

cận khi phương trình:

 

3 2 2

3 2 1 0    x mx m x m

có

3

nghiệm phân biệt

3x

.

Xét phương trình:

 

3 2 2

3 2 1 0    x mx m x m

 

*

, ta có:

 

3 2 2

3 2 1 0    x mx m x m

 

2

2 1 0    x m x mx

2

2 1 0









  



xm

x mx

.

Phương trình

 

*

có ba nghiệm phân biệt

3x

khi và chỉ khi

3m

và phương trình

2

2 1 0  x mx

có hai nghiệm phân biệt

3x

.

Hay:

2

5

3

3,

3

10

1

3 2.3. 1 0

1











  











  











m

mm

m

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

459

[ I can't, I can! ]

Do

m

nguyên và

 

6;6m

nên:

 

6; 5; 4; 3; 2;2;4;5;6     m

.

Vậy có

9

giá trị nguyên của

m

thỏa mãn đề bài.

Đáp án B.

Câu 52. TXĐ:

 

\ m

.

Ta có:

2

23

lim







xm

x x m

xm

2

22

lim 2 2 3







   







xm

mm

xm

.

Để đồ thị hàm số không có tiệm cận đứng thì

phải tồn tại

2

23

lim







xm

x x m

xm

.

2

0

2 2 0

1





   







m

mm

m

.

Vậy đáp án C là đáp án đúng.

Đáp án C.

Câu 53. Để đồ thị hàm số

2

4







x

y

x x m

có hai tiệm cận đứng thì phương trình

2

40  x x m

có hai nghiệm thực phân biệt

khác

2

40

12 0













m

2017 4

12

  





  









m

   

2017; 2016;..;3 \ 12    m

.

Do đó số giá trị nguyên của tham số

m

thỏa đề

bài là:

 

3 2017 1 1 2020    

giá trị.

Đáp án D.

Câu 54. Đồ thị hàm số

 

y f x

có duy nhất

một tiệm cận ngang

4

2019 2020mm

3

0

2019

2020

















m

.

Vậy có

2

giá trị của

m

thỏa bài toán.

Đáp án B.

Câu 55. Điều kiện:

.xm

Ta có:

lim 0





x

y

0y

là tiệm cận ngang của đồ thị hàm số.

Xét phương trình:

 

2

2 1 2 0



    



x m x m x m

   

2

2 1 2 0 *









   





xm

x m x m

.

Để hàm số có

4

đường tiệm cận thì phương

trình

 

*

có

2

nghiệm phân biệt

12

m x x

.

Khi đó, ta có điều kiện:

 

  

2

12

2 1 0

0

2







  











m

x m x m

x x m

 

2

1 2 1 2

1

2

0

2 1 2







    











m

x x m x x m

mm

2

1

2

1

0

2

01

10















   















m

mm

m

.

Đáp án A.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

460

[ I can't, I can! ]

Câu 56. Đặt

 

2

63  f x mx x

và

 

2

9 6 1  g x x mx

.

Ta xét các trường hợp:

+ Trường hợp 1:

0m

.

Khi đó ta có:

 

2

63

6 3 9 1





  

x

y

xx

đồ thị

hàm số có một đường tiệm cận ngang là đường

thẳng

0y

do đó

0m

thỏa mãn yêu cầu bài

toán.

+ Trường hợp 2:

0m

và cả hai tam thức

 

fx

và

 

gx

đều vô nghiệm.

Khi đó:

2

'0

9 3 0

'0

9 9 0























f

g

m

3

11





  



  



m

.

+ Trường hợp 3: Tam thức

 

gx

nhận

1

2

x

làm nghiệm

1 13

0

2 12



   





gm

khi đó

 

fx

luôn có 2 nghiệm phân biệt nên đồ thị

hàm số đã cho có nhiều hơn

1

đường tiệm cận.

Vậy có

1

giá trị nguyên của

m

để đồ thị hàm

số

  

22

63

6 3 9 6 1





   

x

y

mx x x mx

có đúng

1 đường tiệm cận.

Đáp án C.

Câu 57. Điều kiện cần và đủ để đồ thị hàm số:

2

1  y x mx

có tiệm cận ngang là tồn tại số

thực

k

sao cho:









2

lim 1 k







  



  





x

x mx

.

Hiển nhiên nếu

0m

thì giới hạn





2

lim 1





x

x mx

không hữu hạn.

Nếu

0m

ta có:

+





2

lim 1 .



   

x

x mx

+





2

lim y lim 1

 

  

xx

x mx

 

2

1

11

lim lim

1

 









xx

xm

x

x mx

m

x

Để giới hạn trên hữu hạn khi và chỉ khi

1m

.

Đáp án B.

Câu 58. Với

0m

, ta có:

2

24



  



x

y

x



Không thỏa mãn yêu cầu bài toán.

Với

0m

, ta có:

2

lim 0

24









x

mx x



0y

là tiệm cận ngang của đồ thị hàm số.

Đồ thị hàm số có đúng hai đường tiệm cận



Đồ thị hàm số có đúng 1 tiệm cận đứng



2

2 4 0  mx x

có nghiệm duy nhất hoặc

2

2 4 0  mx x

có hai nghiệm phân biệt trong

đó có một nghiệm

2x

.

Trường hợp 1:

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

461

[ I can't, I can! ]

2

2 4 0  mx x

có nghiệm duy nhất.

1

0 1 4 0

4



       mm

.

Trường hợp 2:

2

2 4 0  mx x

có hai nghiệm phân biệt trong

đó có một nghiệm

2x

.

1

0

4

40

0



























m



0m

không thỏa

mãn điều kiện.

Vậy chỉ có một giá trị của

m

thỏa mãn yêu cầu

bài toán.

Đáp án D.

Câu 59.

2019 2019

lim , lim

17 17

 





xx

yy

mm

.

Với

17m

thì đồ thị hàm số có hai đường

tiệm cận ngang là

2019 2019

,

17 17





yy

mm

.

Khi đó đồ thị hàm số đã cho có

4

đường tiệm

cận khi và chỉ khi phương trình

 

2

17 1 0 1  x m x

có hai nghiệm phân biệt khác

0

.

Ta có:

 

2

1 17 1  x m x

 

22

2 2 2

0

17 1 2

17 1























m

mx

x m x

.

Phương trình

 

1

có

2

nghiệm phân biệt khác

0

khi và chỉ khi phương trình

 

2

có hai

nghiệm phân biệt khác

0

.

2

0

0 17

17 0





   







m

.

Suy ra

 

0,1,2,3,4S

.

Đáp án C.

Câu 60. Ta có:

 

3

3 4 2

00

1

lim lim

11





     

xx

fx

x mx x x m x

x

Mà

3

3 4 2

0

11

lim



     

x

x mx x x m x

x





 

3

3 4 2

0

3

0

3

4

2

3

44

3

1 1 1 1

lim

11

1 1 1





     

  















  



















     









x

x mx x x m x

x x x

x mx

x x mx

xx

m

x x x x x

Đồ thị hàm số

 

fx

nhận trục tung làm tiệm

cận đứng

 





 

2

0

3

2

3

4 2 4

3

22

lim

11

1

0

( 1) 1 1

1

0 6 3 2 0

23













  











  



     



       

x

xm

x mx

x

m

x x x x

m

m m m

Vậy

12

1

.

2

  mm

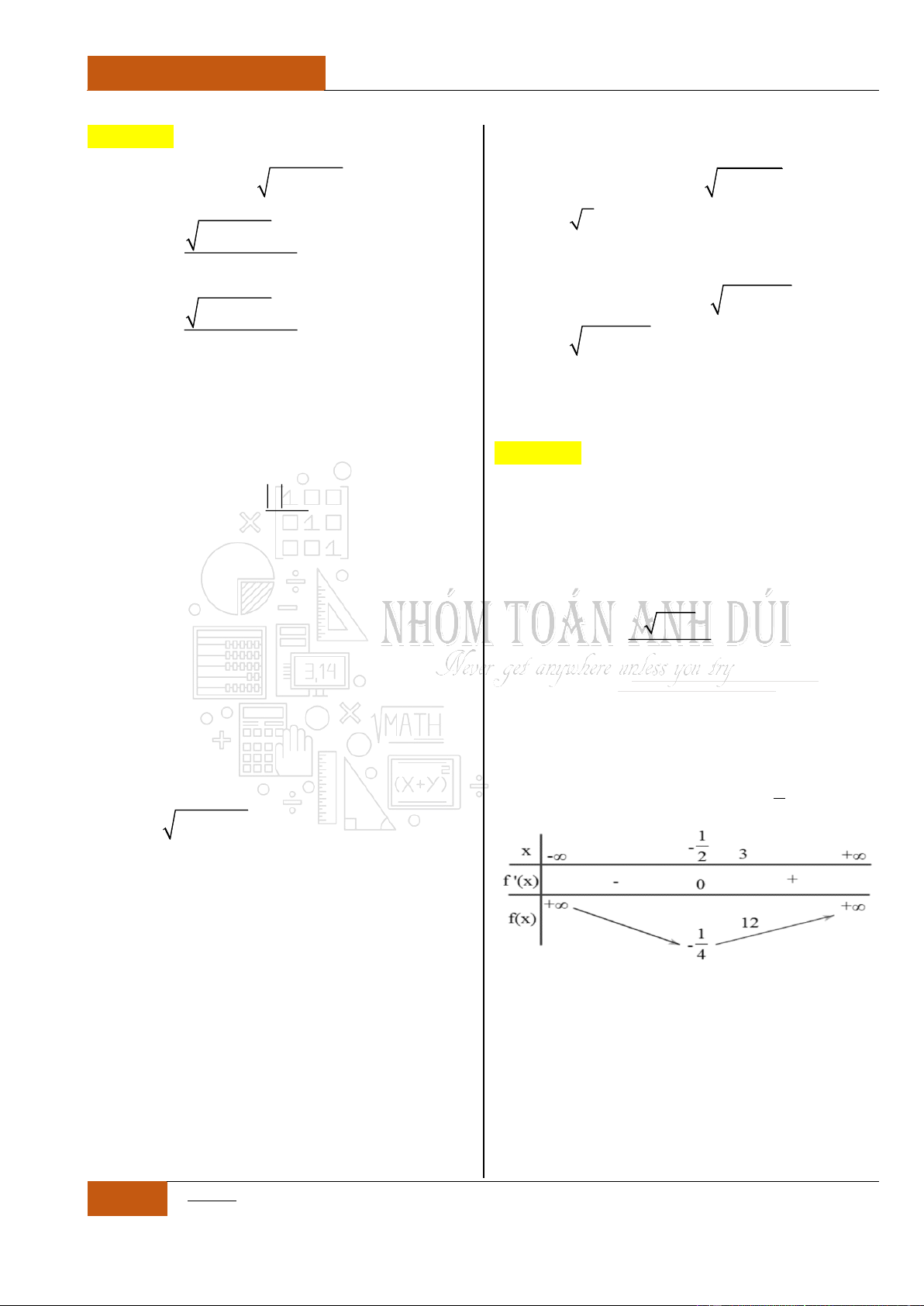
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

462

[ I can't, I can! ]

Đáp án B.

Câu 61. Xét

   

1  g x x x m

.

Ta có:

 

1

lim 1

2









x

x x m

x

và

 

1

lim 1

2









x

x x m

x

.

Nên đồ thị hàm số luôn có hai đường tiệm cận

ngang

1y

và

1y

.

Trường hợp 1:

0m

.

Khi đó hàm số là

1

2







x

y

x

.

Đồ thị hàm số có tiệm cận đứng là

2x

.

Vậy

0m

thỏa mãn yêu cầu đề bài.

Trường hợp 2:

0m

.

Hàm số

 

gx

có tập xác định là:



 



;0 ;    Dm

.

Vì:

2  xD

.

   

2 2 2 1 0    gm

nên

2x

là tiệm

cận đứng của đồ thị hàm số.

Vậy

1m

,

2m

,

9m

thỏa mãn.

Nên có

9

giá trị

m

.

Trường hợp 3:

0m

.

Hàm số

 

gx

có tập xác định là



 



; 0;    Dm

.

Để

2x

là tiệm cận đứng của đồ thị hàm số

thì trước hết

2  xD

hay

2m

.

Nên chỉ có

2m

,

1m

thỏa mãn.

Với

1m

ta có

   

11  g x x x

,

 

2 2 1 0   g

nên

2x

là tiệm cận

đứng của đồ thị hàm số.

Với

2m

ta có:

   

21  g x x x

,

   

2 2 1 1 0      g x x

nên

2x

là

tiệm cận đứng của đồ thị hàm số.

Vậy

12

giá trị

m

nguyên thỏa mãn yêu cầu.

Đáp án A.

Câu 62. Điều kiện xác định:

2

30









x

x x m

.

Dựa vào điều kiện xác định ta suy ra hàm số đã

cho không có giới hạn khi

 x

.

2

3

lim 0,









x

m

x x m

.

0y

là phương trình đường tiệm cận

ngang.

Xét hàm số

 

2

f x x x

.

   

1

' 2 1; ' 0

2

     f x x f x x

.

Dựa vào bảng biến thiên ta thấy:

Khi

12m

thì đồ thị hàm số không có tiệm

cận đứng.

Khi

12m

thì đồ thị hàm số có 1 tiệm cận

đứng.

Do đó để hàm số có đúng 2 đường tiệm cận thì

 

12;2019m

.

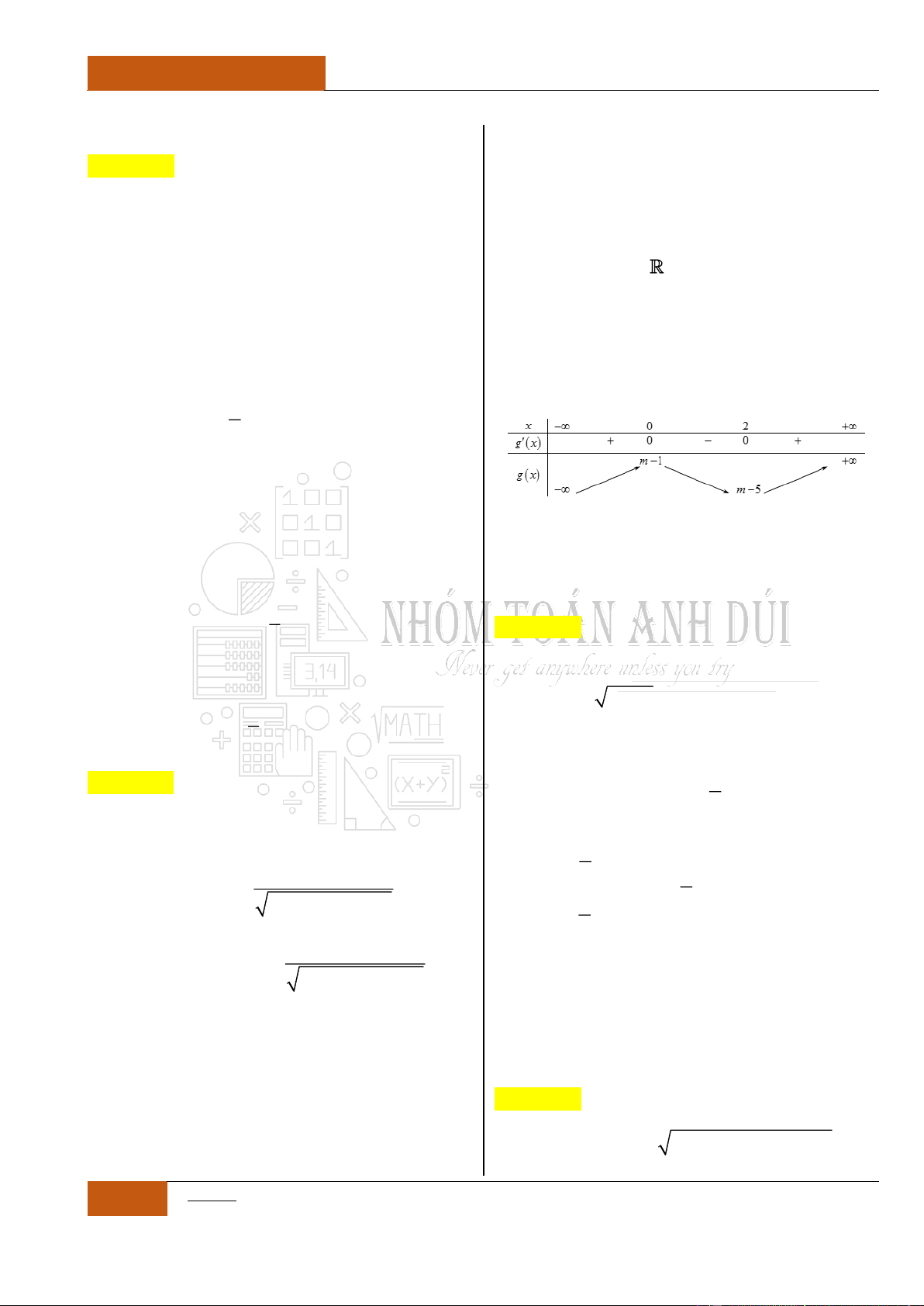
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

463

[ I can't, I can! ]

Vậy có

2008

giá trị nguyên của

m

.

Đáp án D.

Câu 63. Nhận xét:

+

 

2

23  f x mx x

có bậc

1

nên đồ thị

hàm số luôn có

1

tiệm cận ngang.

+ Do đó: Yêu cầu bài toán

9

đồ thị hàm số có

đúng

1

tiệm cận đứng.

+

0m

, đồ thị hàm số có

1

tiệm cận đứng là

đường thẳng

3

0

2

  xm

thỏa bài toán.

+

0m

, đồ thị hàm số có đúng

1

tiệm cận

đứng khi và chỉ khi phương trình

2

2 3 0  mx x

có nghiệm kép hoặc nhận

1x

làm nghiệm

 

1

0

3

10

1

























f

m

f

m

.

+ Kết luận:

1

0; ; 1

3









m

.

Đáp án B.

Câu 64. Ta có:

lim

x

y

32

1

lim 0

31





  

x

x x m

.

Mặt khác:

32

1

lim lim

31

 



  

xx

y

x x m

không tồn tại.

Suy ra

0y

là đường tiệm cận ngang của đồ

thị hàm số.

Do đó, để đồ thị hàm số đã cho có

4

đường

thẳng tiệm cận thì phương trình

32

3 1 0   x x m

có

3

nghiệm phân biệt.

Xét hàm số

 

32

31   g x x x m

.

Tập xác định:

D

.

 

2

36



g x x x

;

 

0

2















x

gx

x

.

Bảng biến thiên:

Từ bảng biến thiên, ta thấy phương trình

32

3 1 0   x x m

có

3

nghiệm phân biệt

khi và chỉ khi

5 0 1 1 5      m m m

.

Đáp án A.

Câu 65. Do hàm số không có tiệm cận đứng

nên

     

2

3 1 1     f x x ax b x g x

.

Suy ra

 

20

10

3

0

' 1 0

4

  



















ab

f

a

f

3

1

4

5

2

4







   











a

ab

b



Đáp án A.

Note: Với

 

0



n

f x x x g x

thì ta luôn có

     

 

1

0 0 0 0

' '' ... 0



    

n

f x f x f x f x

.

Đáp án A.

Câu 66. Biểu thức:

2

2016 2017  xx

có

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

464

[ I can't, I can! ]

nghĩa khi:

2

2016 2017 0 1 2017       x x x

.

Đặt

 

2

2016 2017   f x x x

.

Xét

0   x m x m

.

Vậy đồ thị nếu có tiệm cận đứng chỉ có thể là

xm

, khi đó điều kiện là:

 

1 2017

0

  













x

fm

 

 

2

7

1;2017 1

2016 201 2

7*

4











   





m

mm

.

Ta có:

 

2

* 2016 2015 0   mm

 

1

2

2015













m

.

Từ

   

 

 

1 , 2 1;2017 \ 1;2015



   

m

có

2019 2 2017

số nguyên

m

thỏa mãn bài

toán



Đáp án C.

Câu 67. Nếu

0m

thì

1





y

x

.

Hàm số này có tập xác định

 

\1D

.

Ta có

1

lim 0

1







x

nên đồ thị hàm số có tiệm

cận ngang là

0y

.

 

1

lim

1





 



x

nên đồ thị hàm số có tiệm cận

đứng

1x

.

Vậy với

0m

thì đồ thị hàm số có hai đường

tiệm cận (loại).

Nếu

0m

thì

2

10mx

với mọi

x

và tập xác

định của hàm số là

 

\1D

.

2

1

lim

1





x

mx

x

2

1

lim

1









x

m

x

m

x

,

2

1

lim

1





x

mx

x

2

1

lim

1





  



x

m

x

m

x

.

Suy ra đồ thị hàm số có hai tiệm cận ngang là :

ym

và

ym

.

 

2

1

lim

1







 



x

mx

x

nên

1x

là đường

tiệm cận đứng của đồ thị hàm số.

Vậy

0m

không thỏa mãn.

Nếu

0m

thì tập xác định của hàm số là

 

11

; \ 1



    





D

mm

.

Trường hợp này đồ thị hàm số không có tiệm

cận ngang.

Để đồ thị hàm số có đúng một đường tiệm cận

thì đồ thị hàm số phải có một tiệm cận đứng.

Điều này xảy ra khi:

1

1   

m

1

1  

m

1

1  

m

1  m

.

Vậy với

10  m

thì đồ thị hàm số có đúng

một đường tiệm cận.

Đáp án A.

Câu 68.

 

31

22

1



  



x

fx

x

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

465

[ I can't, I can! ]

3 1 2 2 1      x x x

.

Với

 

1

2





y

fx

ta có:

   

11

lim ; lim



   

   

xx

yy

Vậy đồ thị hàm số

 

1

2





y

fx

có đường tiệm

cận đứng

1x

.

Đáp án C.

Câu 69. Từ đồ thị của hàm số

 

y f x

suy ra

tập xác định của hàm số

 

y f x

là

D

Do đó số đường tiệm cận đứng của đồ thị hàm

số

 

2019

1





y

fx

đồng thời chính là số nghiệm

của phương trình

 

1fx

.

Qua đồ thị ta có: Đường thẳng

1y

cắt đồ thị

hàm số

 

y f x

tại

3

điểm phân biệt nên

phương trình

 

1fx

có

3

nghiệm phân biệt.

Vậy đồ thị hàm số

 

2019

1





y

fx

có 3 đường

tiệm cận đứng.

Đáp án C.

Câu 70. Ta có:

 

11

lim 2 lim

2

 

  

xx

fx

;

 

11

lim 2 lim

2

 

    

xx

fx

.

Suy ra đồ thị hàm số

 

1

y

fx

có hai đường

tiệm cận ngang là

1

2

y

và

1

2

y

.

Dựa vào bảng biến thiên của hàm số

 

y f x

ta thấy phương trình

 

0fx

có hai nghiệm

phân biệt

12

1  xx

.

Khi đó:

   

12

0f x f x

.

Ta có:

 

1

lim 0

0





















xx

fx

f x khi x x

 

1

lim





  

xx

fx

.

Và

 

2

lim 0

0 khi





















xx

fx

f x x x

 

2

1

lim





  

xx

fx

.

Vậy đồ thị hàm số

 

1

y

fx

có hai tiệm cận

đứng là đường thẳng

1

xx

và

2

xx

.

Đáp án A.

Câu 71. Ta có:

 

1

lim lim 1

2

 





xx

y

fx



Đồ thị hàm số có tiệm cận ngang

1y

.

Trường hợp 1: Nếu

1m

thì:

 

1

lim 1

2







x

fx

và

 

1

lim 1

2

 





x

fx

thì đồ

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

466

[ I can't, I can! ]

thị hàm số có một tiệm cận.

Trường hợp 2: Nếu

1m

Để đồ thị hàm số có một tiệm cận ngang

 

1

lim

2







x

fx

không có giá trị hữu hạn

2 0 2     mm

.

Vậy khi

 

2; 1  m

thì đồ thị hàm số có duy

nhất một tiệm cận ngang.

Đáp án C.

Câu 72. Theo giả thuyết, ta có:

   

 

4

2

1

tan cos tan

1 tan

  



f x x f x

x

 

2

1





ft

t

.

Hàm số

 

2019





gx

f x m

 

2

2019

1







gx

m

x

.

Hàm số

 

gx

có hai tiệm cận đứng khi và chỉ

khi phương trình

 

2

1

0

1





m

x

có hai

nghiệm phân biệt.

 

2

1

1 1 0 1      xm

m

.

Vậy

01m

.

Đáp án B.

Câu 73. Đặt

 

1

21





hx

fx

.

* Tiệm cận ngang:

Ta có:

 

1

lim lim 0

21

 





xx

hx

fx

.

 

1

lim lim 0

21

 





xx

hx

fx

.

Suy ra đồ thị hàm số có một đường tiệm cận

ngang

0y

.

* Tiệm cận đứng:

Xét phương trình:

 

2 1 0fx

 

1

2

fx

.

Dựa vào bảng biến thiên ta thấy phương trình

 

1

2

fx

có ba nghiệm phân biệt

,,abc

thỏa

mãn

12   a b c

.

Đồng thời, ta cũng có:

     

lim lim lim

  

  

   

x a x b x c

h x h x h x

Nên đồ thị hàm số

 

y h x

có ba đường tiệm

cận đứng là

xa

,

xb

và

xc

.

Vậy tổng số tiệm cận ngang và tiệm cận đứng

của đồ thị hàm số

 

y h x

là

4

.

Đáp án A.

Câu 74. Đặt

 

1

23





y g x

fx

có tử số là

1 0,  x

.

Ta có:

     

1

3

2 3 0

2

   f x f x

.

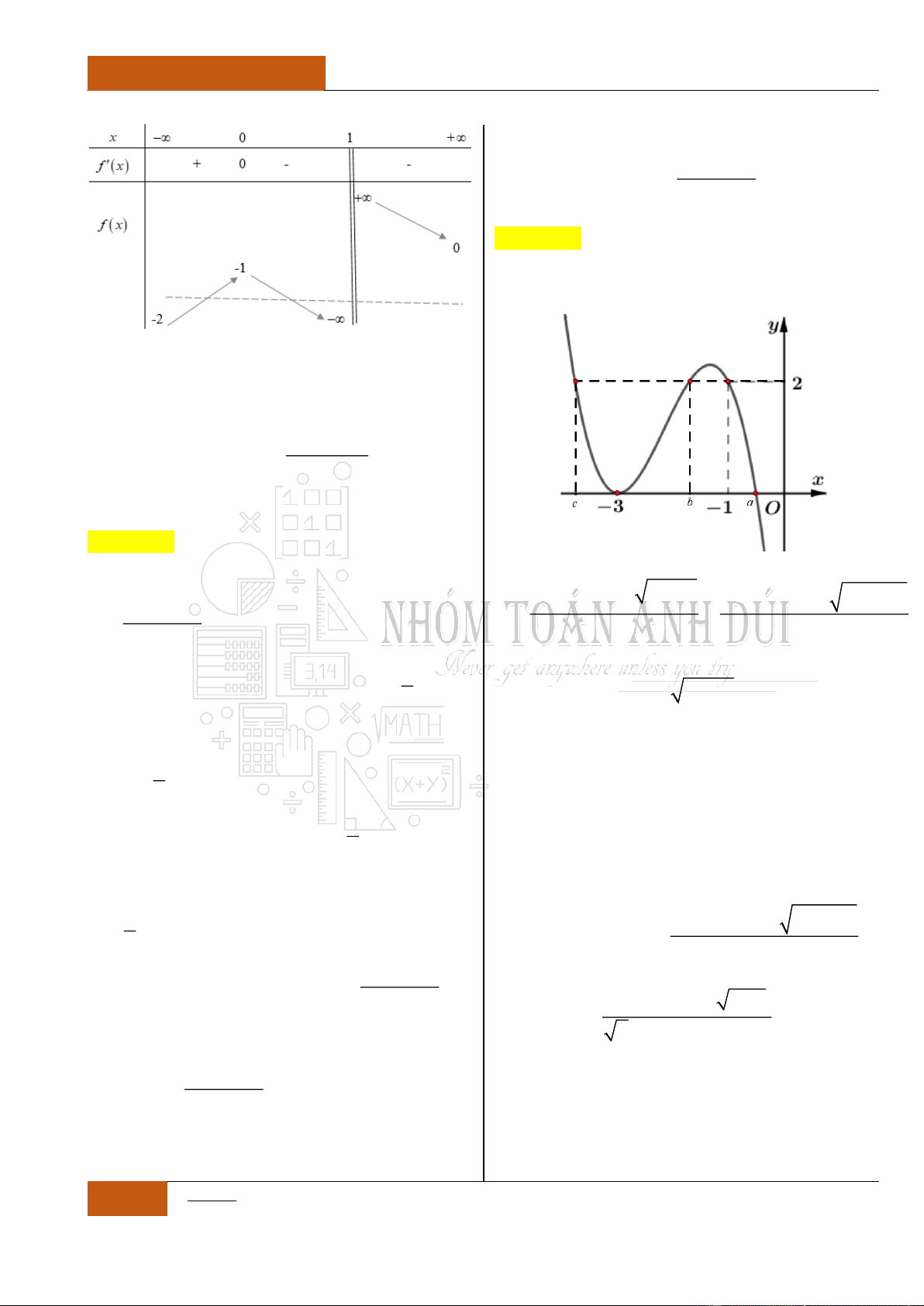
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

467

[ I can't, I can! ]

Từ bảng biến thiên có phương trình

 

1

có

2

nghiệm phân biệt:

   

12

;0 , 0;1  xx

.

Do đó đồ thị hàm số

 

1

23





y

fx

có

2

đường

tiệm cận đứng.

Đáp án A.

Câu 75. Số tiệm cận đứng của đồ thị hàm số

 

1

21





y

fx

đúng bằng số nghiệm thực của

phương trình

   

1

2 1 0

2

   f x f x

.

Mà số nghiệm thực của phương trình

 

1

2

fx

bằng số giao điểm của đồ thị hàm số

 

y f x

với đường thẳng

1

2

y

.

Dựa vào bảng biến thiên ta thấy đường thẳng

1

2

y

cắt đồ thị hàm số

()y f x

tại

2

điểm

phân biệt. Vậy đồ thị hàm số

 

1

21





y

fx

có

2

tiệm cận đứng.

Lại có

 

1

lim 1

21







x

fx

đồ thị hàm số có

một tiệm cận ngang là

1y

.

Vậy tổng số tiệm cận ngang và tiệm cận đứng

của đồ thị hàm số

 

1

21





y

fx

là

3

.

Đáp án D.

Câu 76.

 

   

    

   

22

2

43

1 3 1

. . 2

2

  



    





x x x x

y

x f x f x

Điều kiện tồn tại căn

2

xx

:

0

1











x

.

Xét phương trình:

     

 

2

0

2 0 0

2









   











x

x f x f x f x

fx

.

Với

0x

ta có:

    

   

0

1 3 1

lim

. . 2





  

  



x

x x x x

x f x f x

  

   

0

1 3 1

lim

. . 2





  

  

  



x

x x x

x f x f x

.

Suy ra

0x

là tiệm cận đứng.

Với

 

0fx

3  x

(nghiệm bội

2

) hoặc

xa

(loại vì

10  a

).

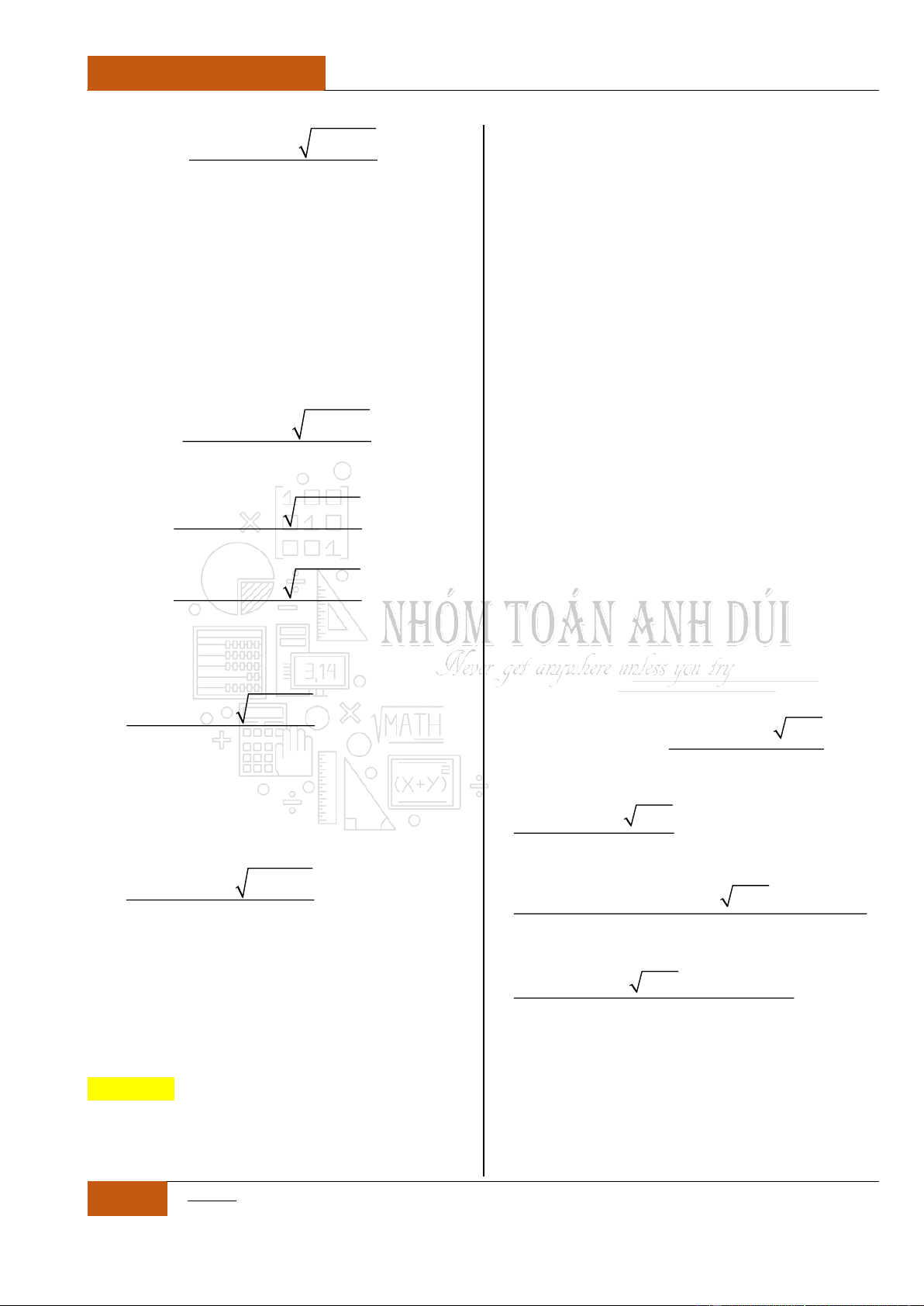
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

468

[ I can't, I can! ]

Ta có:

    

   

3

1 3 1

lim

. . 2





  

 

  



x

x x x x

x f x f x

nên

3x

là tiệm cận đứng.

Với

 

2fx

 

1

31

3







    



  



x

x b b

x c c

(nghiệm bội

1

).

Ta có:

    

   

1 3 1

lim 0

. . 2





  



  



xb

x x x x

x f x f x

Vì:

    

   

    

   

1

1 3 1

lim 0

. . 2

1 3 1

lim 0

. . 2









  





  



  



  







  







x

x x x x

x f x f x

x x x x

x f x f x

.

Nên

1x

không là tiệm cận đứng.

    

   

1 3 1

lim

. . 2





  

 

  



xb

x x x x

x f x f x

(Do



xb

thì

 

2



fx

)

Nên

xb

là tiệm cận đứng.

    

   

1 3 1

lim

. . 2





  

 

  



xc

x x x x

x f x f x

(Do



xc

thì

 

2



fx

)

Nên

xc

là tiệm cận đứng.

Vậy đồ thị hàm số có

4

tiệm cận đứng.

Đáp án C.

Câu 77. Nhận xét 1: Với

0

1x

và

 

0

lim



xx

gx

hoặc

 

0

lim



xx

gx

có kết quả là



hoặc



thì

0

xx

là tiệm cận đứng của của đồ thị hàm số

 

gx

.

Nhận xét 2: Dựa vào đồ thị hàm số

 

fx

ta có:

 

2

1

2  f x a x x x

.

Ta có:

     

 

2

0

00

1









   











x

x f x f x f x

fx

.

 

11

,0 1

0

2



  









x x x

fx

x

.

Vì:

 

22

33

1

1 ,1 2

,2







    







x

f x x x x

x x x

suy ra:

   

  

23

11    f x a x x x x x

.

Khi đó ta có:

 

   

2

3 2 1  









x x x

gx

x f x f x

  

   

1 2 1

.1

  



  



x x x

x f x f x

  

 

   

  

2

1 2 3

1 2 1

. 2 . 1

  



    

x x x

x a x x x a x x x x x

 

  

2

1 2 3

1

2





   

x

a x x x x x x x x

.

Do vậy,

1

0,x x x

không phải tiệm cận đứng

của đồ thị hàm số

 

y g x

do không thỏa mãn

điều kiện

0

1x

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

469

[ I can't, I can! ]

Đồ thị hàm số

 

gx

có

3

đường tiệm cận đứng

là:

23

2, ,  x x x x x

.

Đáp án C.

Câu 78. Ta có:

 

  

     

1 2 1

11

  



   



x x x

gx

x f x f x

ĐKXĐ:

 

1

0

1

















x

fx

.

Dựa vào đồ thị hàm số

 

y f x

, ta có:

 

1

2

0













x

fx

xx

với

2x

là nghiệm kép,

 

1

0;1x

.

 

2

3

1







  







x

f x x x

xx

với

 

23

1;2 ; 2xx

.

Suy ra, ta có:

 

gx

  

      

 

2

1 2 3

1 2 1

  



     

x x x

a x x x x x x x x x

    

 

2

1 2 3

1

12





    

x

a x x x x x x x x

.

Vậy đồ thị hàm số có

3

tiệm cận đứng là:

23

2; ;  x x x x x

(do

1x

nên ta loại

1

1;  x x x

).

Đáp án D.

Câu 79. Ta xét phương trình

   

2

20f x f x

 

1

2

3 3 1

1

0

2

1

1,









  































   



x

xx

fx

x

fx

xx

x x x x

.

Nên

 

    

 

2

1 2 3

1





   

xx

gx

ax x x x x x x x

   

 

1 2 3

1

; 0

1



   

a

a x x x x x x x

.

Vậy đồ thị hàm số

 

y g x

có

4

đường tiệm

cận đứng.

Đáp án C.

Câu 80. Tính tiệm cận ngang.

Ta có:

3



 

x

xx

 

3

1

lim 0

3







x

f x x

.

Và

3



 

x

xx

 

3

1

lim 0

3







x

f x x

.

Vậy đồ thị hàm số có 1 tiệm cận ngang

0y

.

Tính tiệm cận đứng.

Số đường tiệm cận đứng của đồ thị hàm số là

số nghiệm của phương trình

 

3

30  f x x

.

Dựa vào bảng biến thiên ta có:

 

3

30  f x x

 

33

00

3 ; ;1        f x x x x x x

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

470

[ I can't, I can! ]

Vì hàm số

3

y x x

đồng biến trên do đó

 

3

00

; ;1   x x x x

có một nghiệm duy

nhất.

Vậy đồ thị hàm số

 

3

1

3





y

f x x

có

1

tiệm

cận đứng.

Đáp án A.

Câu 81. Ta có:

 

2

32



  y x ax bx c

.

Dựa vào đồ thị hàm số, ta thấy hàm số đạt cực

trị tại

0x

,

2x

.

Do đó, ta có hệ:

 

01

23

00

20

























y

1

0

12 4 0

8 4 4



















  



d

c

ab

1

3

0

1























a

b

c

d

.

Vậy

 

32

31   y f x x x

.

Khi đó:

 

     

2

22

3











x x x

y

x f x f x

 

  

2

3 2 3 2

22

3 3 1 3





   

x x x

x x x x x

 

2

2 3 2

22

3 3 1





  

x x x

x x x x

.

Ta có:

 

2

2 3 2

3 3 1 0   x x x x

 

1

2

3

0

3

1;0

0;1

2;3











   











x

xx

.

Hàm số

 

2

2 3 2

22

3 3 1





  

x x x

y

x x x x

có tập xác

định





 

12

;2 \ 0; ; D x x

.

Và:

 

2

2 3 2

0

22

lim

3 3 1







  

x

x x x

x x x x

 

2

2 3 2

0

22

lim

3 3 1









  

x

x x x

x x x x

 

2

32

0

22

lim

3 3 1







  

  

x

xx

x x x x

.

Suy ra

0x

là đường tiệm cận đứng.

 

1

2

2 3 2

22

lim

3 3 1







 

  

xx

x x x

x x x x

,

 

2

2 3 2

22

lim

3 3 1







 

  

xx

x x x

x x x x

.

Suy ra

1

xx

và

2

xx

cũng là các đường tiệm

cận đứng của đồ thị hàm số.

Đáp án C.

Câu 82. Điều kiện xác định:

 

2

0

1

4 3 0











  



fx

x

xx

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

471

[ I can't, I can! ]

2

1

3























x

2

3













x

.

Ta có:

 

3

lim



x

gx

 

2

3

lim

1 4 3







  

x

fx

x x x

 

và

 

3

lim



x

gx

 

2

3

lim

1 4 3







  

x

fx

x x x

 

.

Vậy đồ thị

 

2

1 4 3



  

fx

gx

x x x

có một

đường tiệm cận đứng là:

3x

.

Đáp án B.

Câu 83. Ta có:

  

   

22

2

42

23





   



x x x

y

f x f x

   

2

22

23





   



x x x

f x f x

.

Ta có:

   

2

2 3 0    



f x f x

 

1

3















fx

 

2

0

2

   







  











x m m

x

x n n

x

.

Dựa vào đồ thị hàm số, ta thấy các nghiệm

0;x

2x

là các nghiệm kép (nghiệm bội

2) và đa thức

   

2

23   



f x f x

có bậc là 8

nên

   

      

2

22





   

x x x

y

a x x x x m x n

.

Vậy hàm số có các tiệm cận đứng là:

0; 2; ;   x x x m x n

.

Đáp án D.

Câu 84. Dựa vào đồ thị hàm số đạo hàm ta

thấy:

   

'1f x f x x C   

.

Khi đó hàm số là một hàm đồng biến và

 

   

lim lim lim

lim

lim lim

  



 



    









 







x x x

x

xx

f x f x x C

fx

f x x C

Xét hàm số:

 

y g x

 

2 2021

2021

2 2021

1

...

1 2 2021





   

  

f x f x

fx

f x f x f x

TXĐ:

 

\ 2021 ;...; 1    D C C

.

Với mọi

   

0

2021 ;...; 2     x f a C C

.

Ta có:

   

00

lim , lim

x x x x

g x g x





   

.

Suy ra:

0

xx

là tiệm cận đứng của đồ thị hàm

số.

Như vậy hàm số

 

y g x

có tất cả

2020

tiệm

cận đứng.

(Lưu ý: đường thẳng

 

0

1x x f a   

không là tiệm cận đứng).

Ta có:

 

2021 1

lim 1 1 ... 1 2021

x

elementsof

gx



    

Bên cạnh đó:

 

lim





x

gx

 

2021

2 2021

11

lim 1 ...

2 2021









   









x

f x f x

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

472

[ I can't, I can! ]

 

3

23

2020 2021

23

11

lim 1 ...

23

2020 2021

11

...

2020 2021

lim 1 1 1 ... 1 1 1 1





  



   











  













       

x

f x f x

gx

Vì thế đồ thị hàm số

 

y g x

có hai tiệm cận

ngang là đường

2021y 

và

1y 

.

Như vậy hàm số có tất cả

2022

đường tiệm

cận.

Đáp án A.

Câu 85. Cách 1:

2

4 3 1

lim

21















x

xx

ax b

x

   

2

4 2 2 3 1

lim 0

21



     





x

a x a b x b

x

2

4 2 0

23

5

2 3 0

2











     



  









a

ab

b

.

Cách 2: Ta có:

2

4 3 1

lim

21















x

xx

ax b

x

 

57

lim 2

2 2 2 1





    







x

x ax b

x

.

Mà

2

4 3 1

lim 0

21







  







x

xx

ax b

x

 

57

lim 2 0

2 2 2 1





     







x

x ax b

x

2 0 2

55

0

22

  









    





aa

bb

.

Khi đó

23  ab

.

Đáp án D.

Lưu ý: Với

   

,f x g x

là các đa thức thì

 

lim 0





x

fx

gx

Bậc

 

fx

Bậc

 

gx

.

Câu 86. Xét hàm số

 

3 2 2 2

2

32





   

x

yC

x mx m m x m

Ta có:

lim 0





x

y

nên đồ thị

 

C

luôn có một

đường tiệm cận ngang

0y

.

Do đó đồ thị

 

C

có đúng

4

đường tiệm cận



Đồ thị

 

C

có

3

đường tiệm cận đứng



Phương trình

 

3 2 2 2

3 2 0 1    x mx m m x m

có

3

nghiệm phân biệt khác

2

.

Mặt khác, phương trình:

   

 

2

01 2    x m x mx m

 

2

2 0 2











  





xm

x mx m

Phương trình

 

1

có

3

nghiệm phân biệt khác

2

22

2

01

2

0

20

4

4 3 0

3





  









    





  







  















m

m m m

m

m m m

m

.

Do

 

, 9;9  mm

nên có

16

giá trị của

m

thỏa mãn yêu cầu bài toán.

Đáp án C.

Câu 87. Phân tích hướng giải.

Trước hết ta tìm các đường tiệm cận đứng và

ngang của đồ thị hàm số theo tham số

m

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

473

[ I can't, I can! ]

Đường tiệm cận ngang của đồ thị hàm số là

1y

và trục hoành

0y

nên hình vuông có

cạnh bằng

1

.

Hướng dẫn giải.

Tập xác định của hàm số

 

2

\1Dm

.

Đồ thị hàm số

2

3

1







x

y

xm

có đường tiệm

cận ngang là

1y

và đường tiệm cận đứng là

2

x1m

(do

2m

).

Yêu cầu bài toán

2

11  m

2

11

2

0

11













  





m

.

Đáp án B.

Câu 88. Vì phương trình

 

2018fx

có ba

nghiệm phân biệt nên đồ thị hàm số

 

1

2018





y

fx

có ba đường tiệm cận đứng.

Mặt khác, ta có:

 

11

lim lim

2018 2019

 

  



xx

y

fx

Nên đường thẳng

1

2019

y

là đường tiệm

cận ngang của đồ thị hàm số

 

1

2018





y

fx

.

Và

 

1

lim lim 0

2018

 





xx

y

fx

nên đường

thẳng

0y

là đường tiệm cận ngang của đồ

thị hàm số

1

2019

y

.

Vậy

5kl

.

Đáp án D.

Câu 89.

Phương trình tiếp tuyến tại điểm

 

00

;M x y

thuộc đồ thị hàm số là:

 

0

2

0

84

: y 1

21

    



xx

x

.

Giao của đường tiếp tuyến với tiệm cận ngang

là

0

41

;1

2









x

A

.

Giao của đường tiếp tuyến với tiệm cận đứng

là

0

27

1

;

2 2 1











x

B

x

.

Giao của hai tiệm cận là:

1

;1

2









I

.

 

0

8

2 1;0 ; 0;

21



    







IA x IB

x

.

Diện tích tam giác

IAB

là

0

1 1 8

. . 2 1. 4

2 2 2 1



   



IAB

S IA IB x

x

.

Đáp án D.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

474

[ I can't, I can! ]

Câu 90. Đặt

   

2

4 2 x 3    f x m x m m

.

Để đồ thị hàm số đã cho có

2

tiệm cận ngang

thì

4 0 4   mm

.

Suy ra các giá trị nguyên dương của

m

là

 

1;2;3m

.

Vậy tổng các giá trị nguyên dương cần tìm của

m

là

6

.

Đáp án D.

Câu 91. Ta có:

     

5

2 5 0 1

2

   f x f x

Khi đó, phương trình

 

1

có

4

nghiệm phân

biệt

1 2 3 4

, , , 1x x x x

và giới hạn của hàm số

 

1

25





y

fx

tại các điểm

1 2 3 4

, , ,x x x x

đều

bằng



.

Mặt khác

 

1

lim 0

25









x

fx

nên

1x

không

phải tiệm cận đứng.

Vậy đồ thị hàm số

 

1

25





y

fx

có

4

đường

tiệm cận đứng.

Đáp án B.

Câu 92. Áp dụng công thức tính nhanh, ta có:

 

12

22

2. 1 3.1

.5

1





  

ad bc

dd

c

.

Đáp án D.

Câu 93. Áp dụng công thức tính nhanh, ta có

ngay điều kiện để tổng khoảng cách từ

M

đến

hai tiệm cận là nhỏ nhất:

 

2

0

  cx d ad bc

 

2

0

1 3 1 3      xx

.

Vì:

0 1 3    

MM

xx

.

Đáp án A.

Câu 94. Ta chú ý, đề bài yêu cầu ngược lại với

công thức ta chứng minh ở phần lý thuyết (Lý

thuyết: Khoảng cách từ điểm

M

thuộc đồ thị

đến đường tiệm cận đứng bằng

k

lần khoảng

cách từ điểm

M

thuộc đồ thị đến đường tiệm

cận ngang. Câu hỏi: Khoảng cách từ điểm

M

thuộc đồ thị đến đường tiệm cận ngang bằng

k

lần khoảng cách từ điểm

M

thuộc đồ thị đến

đường tiệm cận đứng).

Do vậy:

1

5

k

.

Lúc này, lượng:

2

5





ad bc

p

c

.

Và theo công thức đã được chứng minh, ta dễ

dàng định được điều kiện thỏa mãn yêu cầu đề

bài:

0



  



  





d

x kp

c

d

x kp

c

00

1

3 .5 4 6

5

1

3 .5 2 4

5



    







     





xy

.

Vậy, có tất cả

2

điểm thỏa mãn yêu cầu đề bài.

Đáp án C.

Câu 95. Áp dụng công thức tính nhanh, ta có:

00

2

0

2

9 6 9 3 1 3

3

33

3

13

93

96

3



   

     







  





    





xy

y

x

.

Do vậy, ta có tất cả hai điểm

M

thỏa mãn là

9 3 1 3

;

33









M

.

Đáp án D.

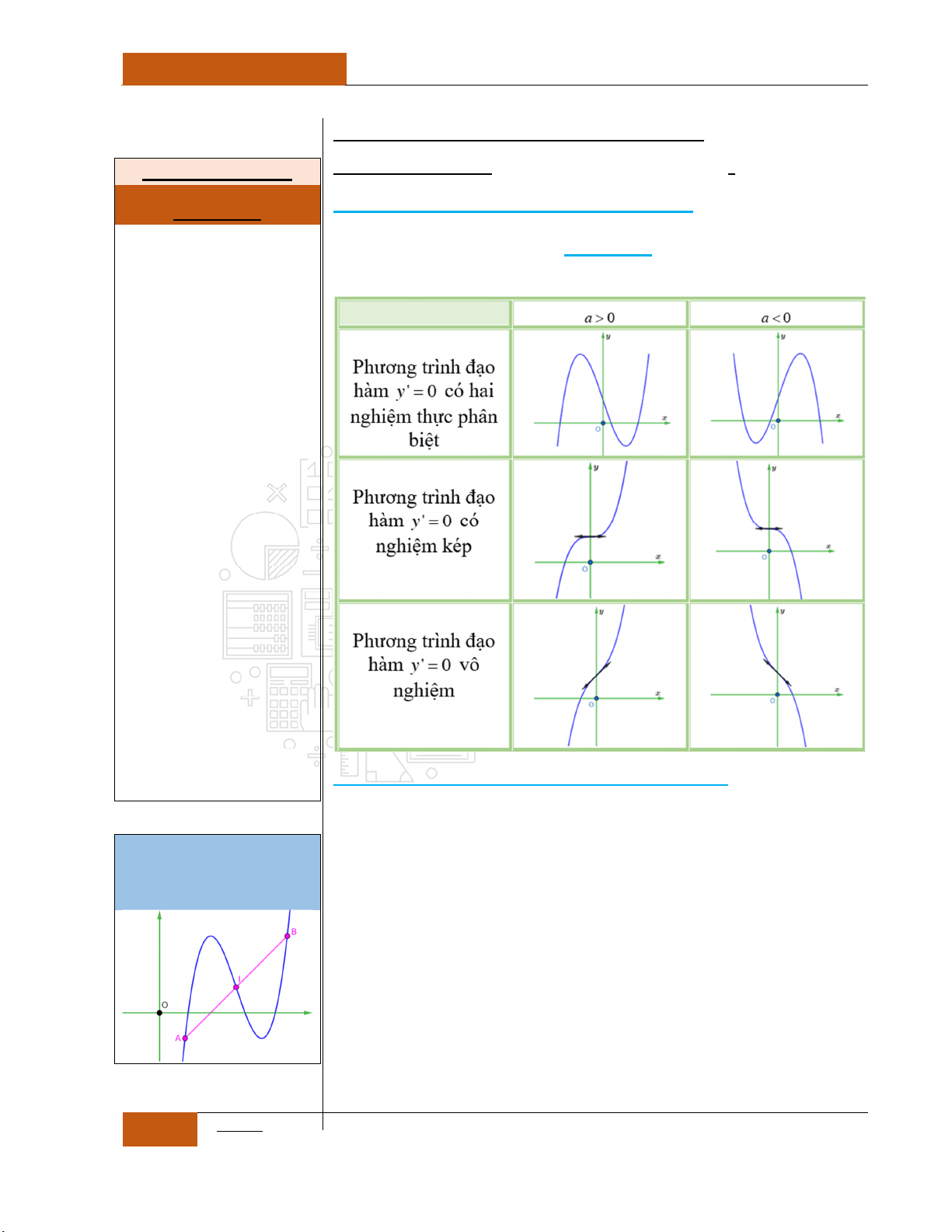
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

475

[ I can't, I can! ]

Extra Techniques:

Study tips:

Sở dĩ số giao điểm của

đồ thị hàm số bậc ba với

trục hoành ít nhất là 1 vì

giả sử ta xét tổng quát đồ

thị hàm số bậc ba

3 2

   y ax bx cx d

với

0a

. Khi đó, dễ

thấy:

lim





 







 





x

y

do

đó, tồn tại ít nhất hai

khoảng “gần bù nhau”,

   

0 0

; , ;  x x

sao

cho

 

0

;



  x

và

 

0

;



  x thỏa mãn

   

. 0

 

y y . Theo

định lý Bolzano –

Cauchy thì tồn tại một

điểm

 

;

 

x sao cho

 

0y x .

Minh họa tâm đối

xứng (điểm uốn) của

đồ thị hàm số bậc ba

I. V. Các dạng đồ thị hàm số thường gặp

1. Hàm số bậc ba

 

3 2

0    y ax bx cx d a

.

Sáu minh họa hình dáng các đồ thị hàm số bậc ba

 

3 2

0    y ax bx cx d a

thường gặp

Một số nhận xét về đồ thị hàm số bậc ba tổng quát

- Đồ thị hàm số bậc ba hoặc có hai cực trị (hoặc điểm cực trị)

hoặc không có cực trị (hoặc điểm cực trị).

+ Đồ thị hàm số có hai điểm cực trị khi

2

'

3 0   

y

b ac .

+ Đồ thị hàm số không có điểm cực trị khi

2

'

3 0   

y

b ac .

- Đồ thị hàm số bậc ba có ít nhất một giao điểm với trục hoành.

- Đồ thị hàm số bậc ba nhận điểm uốn làm tâm đối xứng.

- Tung độ giao điểm của đồ thị hàm số bậc ba với trục tung nằm trên

trục hoành khi 0d và nằm dưới trục hoành khi 0d .

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

476

[ I can't, I can! ]

Extra Techniques:

Study tips:

Những bước thực hiện

bên đây vô cùng quan

trọng, tuy cảm thấy khá

dài và rắc rối, nhưng nếu

các bạn hiểu được bản

chất của sơ đồ tư duy bên

thì việc tăng tốc là hoàn

toàn có căn cứ.

Extra Techniques:

Study tips:

Ngoài ra, để làm trắc

nghiệm, ta cần lưu ý các

điều dưới đây để định

dấu của các hệ số!

1. Xác định dấu của

d

:

dựa vào vị trí (tung độ)

của giao điểm giữa đồ thị

hàm số với trục tung.

2. Xác định dấu của a :

dựa vào “hướng lên,

xuống” của đồ thị khi x

dần đến một giá trị đủ

lớn.

3. Định dấu của ,b c :

dựa vào hai điểm cực trị

của “hàm số” kết hợp

định lý Vietè để định dấu

thông qua tổng và tích

các điểm cực trị.

Các bước nhận dạng đồ thị hàm số bậc ba:

Cho hàm số bậc ba

 

3 2

0    y ax bx cx d a .

Để nhận biết được hình dáng đồ thị hàm số bậc ba, ta có thể tham

khảo các bước được minh họa như hình vẽ dưới đây:

2. Hàm số bậc bốn trùng phương

 

4 2

0   y ax bx c a

.

Bốn minh họa hình dáng các đồ thị hàm số bậc bốn trùng phương

 

4 2

0   y ax bx c a thường gặp

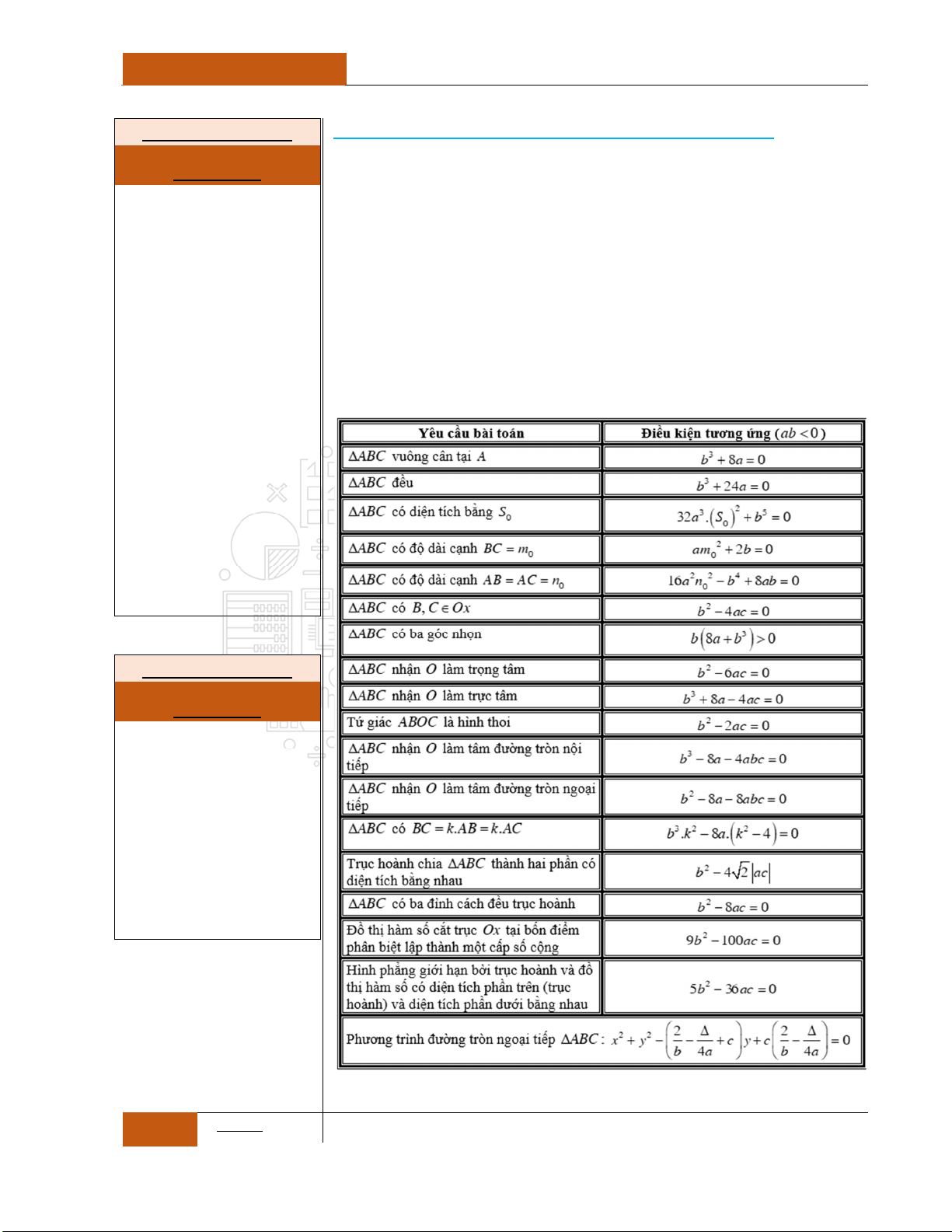
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

477

[ I can't, I can! ]

Extra Techniques:

Study tips:

Đồ thị hàm số bậc bốn

trùng phương

 

4 2

, 0   y ax bx c a

có hàm số là một hàm

chẵn vì nếu ta đặt:

 

4 2

  f x ax bx c

thì dễ thấy rằng:

   

,   f x f x x

Do đó, đồ thị hàm số bậc

bốn trùng phương đối

xứng với nhau qua trục

tung!

Extra Techniques:

Study tips:

Những công thức ở bên

chỉ mang tính chất gợi

mở, không khuyến khích

bạn đọc học thuộc lòng

một cách sáo rỗng, rất dễ

nhầm lẫn giữa các công

thức mang tính tương tự

nhau.

Một số nhận xét về đồ thị hàm số bậc bốn trùng phương

- Đồ thị hàm số bậc bốn hoặc có một cực trị khi 0ab , hoặc

có ba cực trị khi

0ab

.

- Đồ thị hàm số bậc bốn trùng phương nhận trục tung (trục Oy ) làm

trục đối xứng.

- Đồ thị hàm số

 

4 2

0   y ax bx c a với

0ab

thì ta luôn luôn

thu được một tam giác cân có đỉnh là

 

0;I c , hai đỉnh còn lại là hai

điểm cực trị còn lại của đồ thị hàm số.

- Một số công thức nhanh đáng lưu ý!

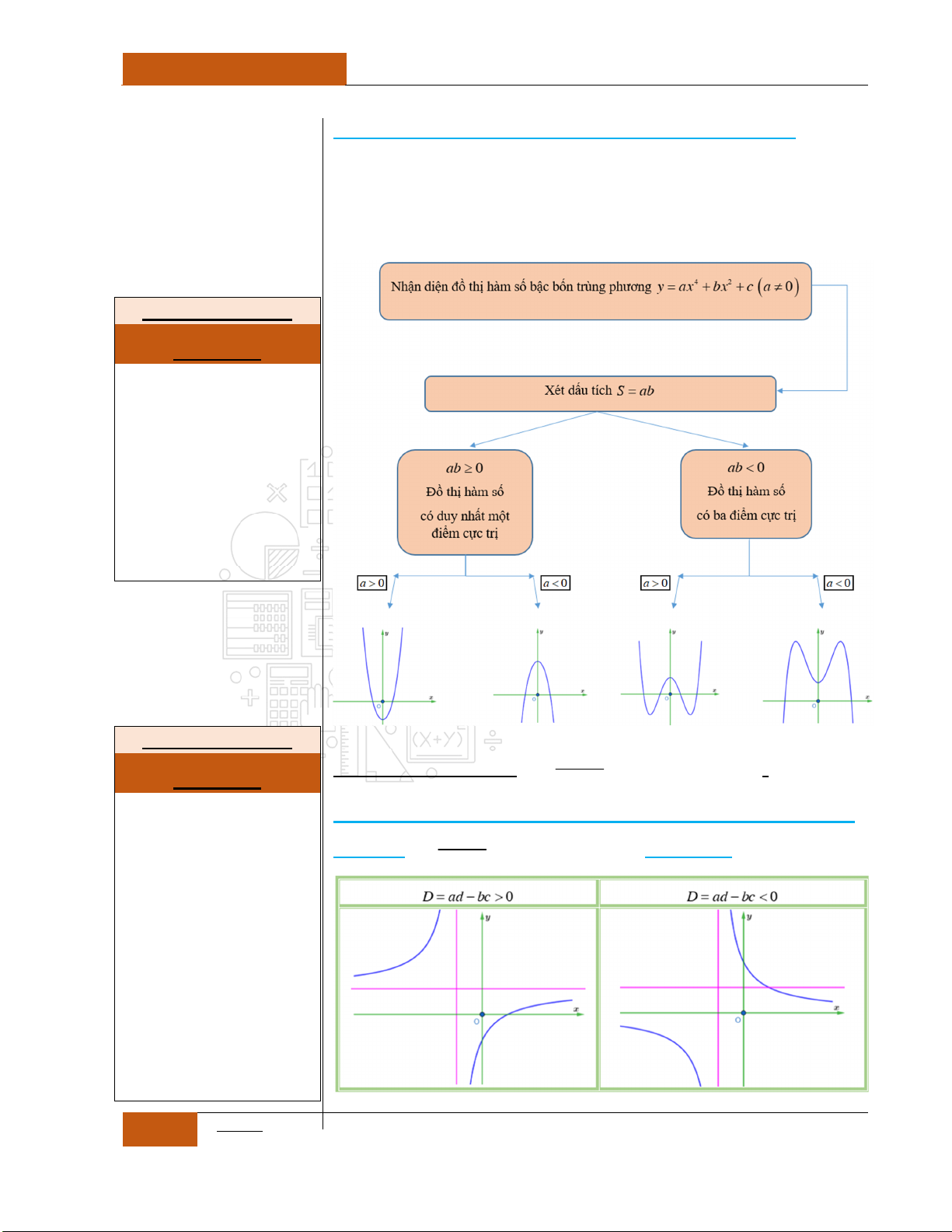
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

478

[ I can't, I can! ]

Extra Techniques:

Study tips:

Những bước thực hiện

bên đây vô cùng quan

trọng, tuy cảm thấy khá

dài và rắc rối, nhưng nếu

các bạn hiểu được bản

chất của sơ đồ tư duy bên

thì việc tăng tốc là hoàn

toàn có căn cứ.

Extra Techniques:

Study tips:

Đối với trường hợp

0c

thì đồ thị hàm số

nhất biến bên sẽ được

đưa về phương trình

đường thẳng.

Hoặc đối với trường hợp

0 ad bc

, thì đồ thị

hàm số hàm nhất biến chỉ

là một đường thẳng song

song hoặc trùng với trục

hoành.

Các bước nhận dạng đồ thị hàm số bậc bốn trùng phương:

Cho hàm số bậc bốn trùng phương

 

4 2

0   y ax bx c a .

Để nhận biết được hình dáng đồ thị hàm số bậc bốn trùng phương, ta

có thể tham khảo các bước được minh họa như hình vẽ dưới đây:

3. Hàm số nhất biến

 

0, 0



   



ax b

y c ad bc

cx d

.

Hai minh họa hình dáng các đồ thị hàm số nhất biến (hàm bậc nhất trên

bậc nhất)

 

0, 0



   



ax b

y c ad bc

cx d

thường gặp

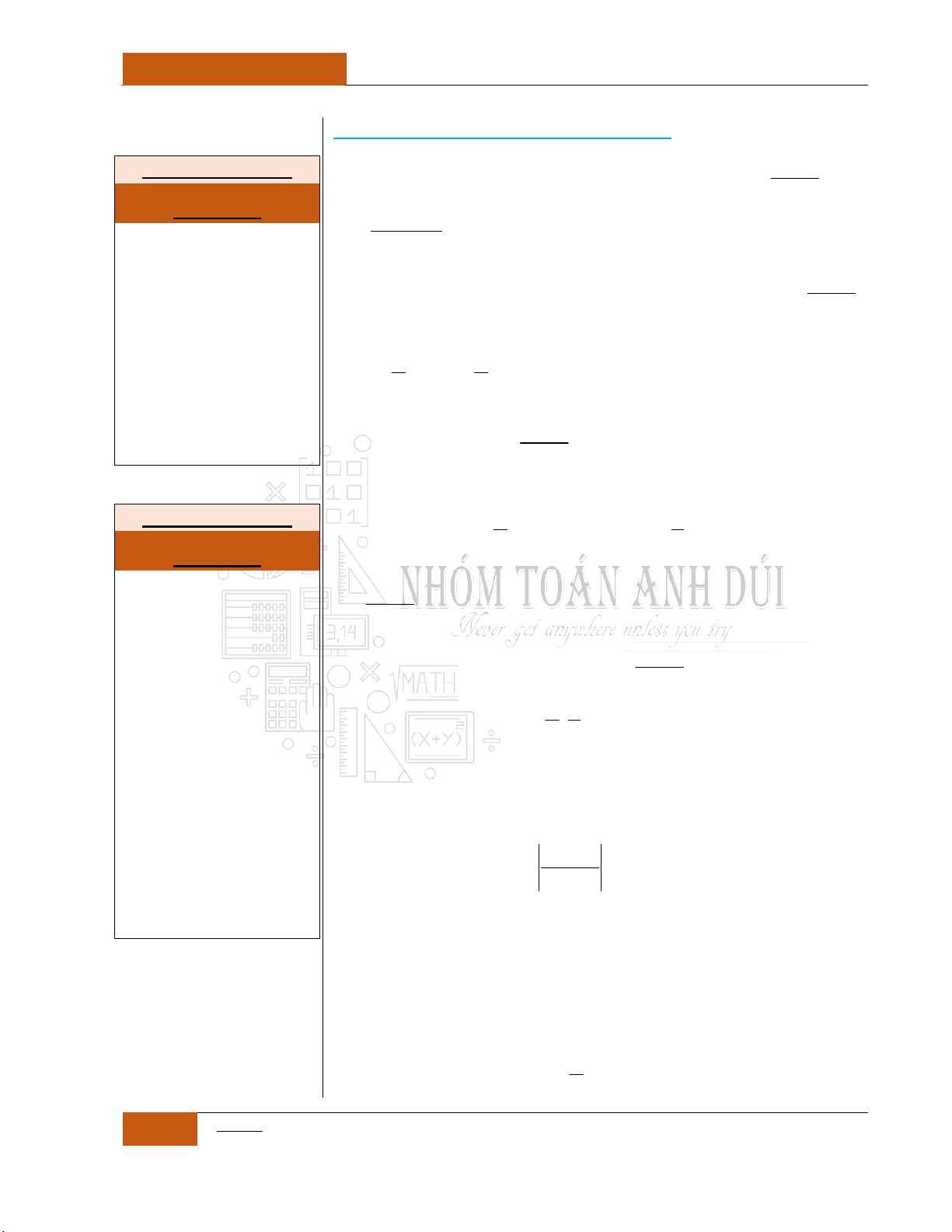
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

479

[ I can't, I can! ]

Extra Techniques:

Study tips:

Hàm số nhất biến là một

trong những nguồn cảm

hứng sáng tác rất lớn

trong kỳ thi TN – THPT

QG nhiều năm gần đây

bởi những tính chất rất

đẹp của nó, đơn giản hóa

như những kiến thức

nhận xét trong phần bên.

Extra Techniques:

Study tips:

Ngoài ra, các công thức

có liên quan đến các tính

chất đặc biệt và thường

xuyên xuất hiện trong

các kỳ thi cũng được đưa

vào bảng thống kê các

công thức nhanh ở trên.

Nếu các bạn cảm thấy

mất thời gian để giải đi

giải lại những dạng Toán

này, các bạn có quyền

học thuộc, nhưng đó

không phải là cách tối ưu

nhất, các bạn nhé!

Một số nhận xét về đồ thị hàm số nhất biến

- Trong điều kiện

0, 0

  

c ad bc , thì hàm số







ax b

y

cx d

có

 

2

'







ad bc

y

cx d

hoặc luôn đồng biến, hoặc luôn nghịch biến

trên từng khoảng xác định (Nói cách khác, hàm số







ax b

y

cx d

hoặc luôn đồng biến, hoặc luôn nghịch biến trên các khoảng

;

 

 

 

 

d

c

và ;

 

  

 

 

d

c

).

- Hàm số nhất biến,

, 0, 0



    



ax b

y c ad bc

cx d

, không có điểm

cực trị.

- Đường thẳng

 

d

x

c

và đường thẳng



a

y

c

lần lượt được gọi là

đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số

, 0, 0



   



ax b

y c ad bc

cx d

.

- Điểm đối xứng của đồ thị hàm số

, 0, 0



   



ax b

y c ad bc

cx d

,

đồng thời là giao điểm

;

 



 

 

d a

I

c c

của hai đường tiệm cận của đồ thị

hàm số.

- Cho





0 0

;

M x y

là một điểm di động trên đồ thị hàm số hàm nhất

biến, khi đó, tích hai khoảng cách từ điểm

M

đến hai đường tiệm cận

là một hằng số không đổi,

2





ad bc

const

c

.

- Một đường thẳng bất kỳ có dạng

 

y mx n

tương giao với đồ thị

hàm số hàm nhất biến tại hai điểm phân biệt,

,

M N

. Đồng thời cắt

hai đường tiệm cận của đồ thị hàm số tại hai điểm

,

A B

thì đẳng thức



MA NB

.

- Dựa vào giao điểm của đồ thị hàm số với trục tung ta xác định được

dấu của tích

bd

(hoặc thương

b

d

) là âm hay dương.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

480

[ I can't, I can! ]

Extra Techniques:

Remark:

Đối với dạng toán này ta

thường bỏ sót điều kiện

0m , do ta chưa thật sự

hiểu được điều kiện cần

và điều kiện đủ, hoặc

chúng ta chưa thật sự

nắm vững kiến thức về

cực trị, điểm cực trị.

Nhiều hàm số đạt cực trị

tại điểm

0

x x thỏa mãn

     

0 0 0

' '' 0  f x f x f x

là đằng khác, chẳng hạn

hàm số

4

y x hay hàm

4

 y x là một ví dụ

điển hình.

IV. Một số bài tập ứng dụng nhận diện đồ thị hàm số

Câu 1. Tìm tất cả các giá trị thực của tham số

m

để hàm số

4 2

y x mx  đạt cực tiểu tại 0x  ?

A.

0m 

. B.

0m 

. C.

0m 

. D.

0m 

.

Đáp án: C

Lời giải

Cho hàm số

 

y f x

xác định.

+) Nếu

 

0

f x



 













nên

0

x x là điểm cực tiểu của hàm số

 

y f x .

+) Nếu

 

0

f x



 













nên

0

x x là điểm cực đại của hàm số

 

y f x

.

+) Trường hợp

 

0

' 0

'' 0

f x

 











thì ta cần phải kiểm tra lại lần nữa.

Hàm số

4 2

y x mx 

có:

3

2

4 2

12 2

y x mx

y x m





 







 





. Để hàm số đạt cực tiểu tại

0x 

thì điều kiện ban đầu, hàm số phải thỏa

3

2

4.0 2 .0 0

12.0 2 0

m



 





 





0 0

0

m





  







. Với

3

2

4.0 2 .0 0

0

12.0 2 0

m



 



 



 





.

Thử lại, với

 

4

0m f x x   là hàm số nhận điểm 0x  là điểm

cực tiểu. Vậy: 0m  .

Câu 2. Cho hàm số

 

3 2

, , ,y ax bx cx d a b c d     có đồ thị là

đường cong như hình vẽ.

Chọn khẳng định đúng trong các khẳng định sau:

A.

0

a

b











. B.

0

c

b











. C.

0

b

d











. D.

0

ac

bd











.

Đáp án: C

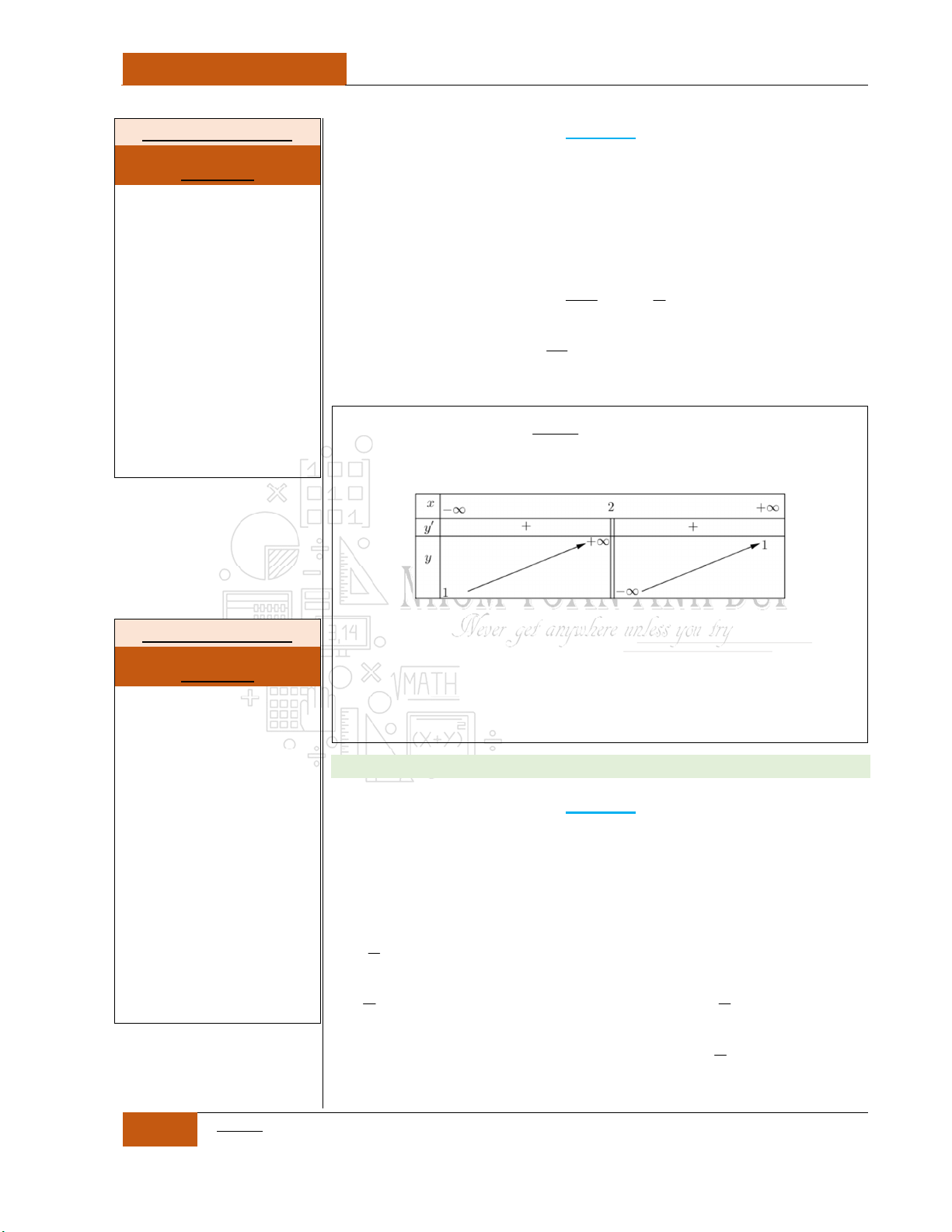
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

481

[ I can't, I can! ]

Extra Techniques:

Remark:

Bài toán trên thuộc dạng

toán nhận diện mới tư

duy khá cao vì không có

thêm một gợi ý số nào cả,

tuy nhiên, bằng vị trí của

đồ thị, ta có thể đoán

được tổng và tích các

điểm cực trị của hàm số

là âm hay dương mà đưa

ra những kết luận có lý

dựa trên Định lý Vietè.

Extra Techniques:

Remark:

Bài toán cho bảng biến

thiên của đồ thị hàm số

hàm nhất biến thì trước

hết ta cần phải xác định

được những điều dưới

đây để định dấu các hệ

số:

1. Tiệm cận đứng.

2. Tiệm cận ngang.

3. Đồng biến/ Nghịch

biến?

Lời giải

Ta có:

lim 0

x

y a



   

.

Gọi

1 2

,x x là hoành độ hai điểm cực trị của hàm số suy ra

1 2

,x x

nghiệm phương trình

2

3 2 0y ax bx c



   

nên theo định lí Viéte, ta

có:

+) Tổng hai nghiệm:

1 2

2

0 0 0

3

b b

x x b

a a



       .

+) Tích hai nghiệm:

1 2

. 0 0

3

c

x x c

a

   

.

Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên 0d  .

Câu 3. Cho hàm số

1ax

y

bx c







(Với , ,a b c là các tham số) có bảng

biến thiên như hình vẽ bên dưới

Xét các phát biểu sau:

       

1 : 1; 2 : 0; 3 : 0; 4 : 0c a b a b c a      

.

Số phát biểu đúng là?

A. 1. B. 2 . C.

3

. D. 4 .

Đáp án: B

Lời giải

Dựa vào bảng biến thiên ta có hàm số luôn đồng biến trên từng

khoảng xác định, đồ thị hàm số có tiệm cận đứng là đường thẳng

2x 

và tiệm cận ngang là đường thẳng 1y  nên ta có hệ:

2

0 1

2 2

1

1 0

2

0 2 0

1

0

2

0









 



 



   

 



  

        

   

   

    

 

 

 

  

 





  



c

b

c b c b

a

a b a b a

b

ac b b b

ac b

b

a b c

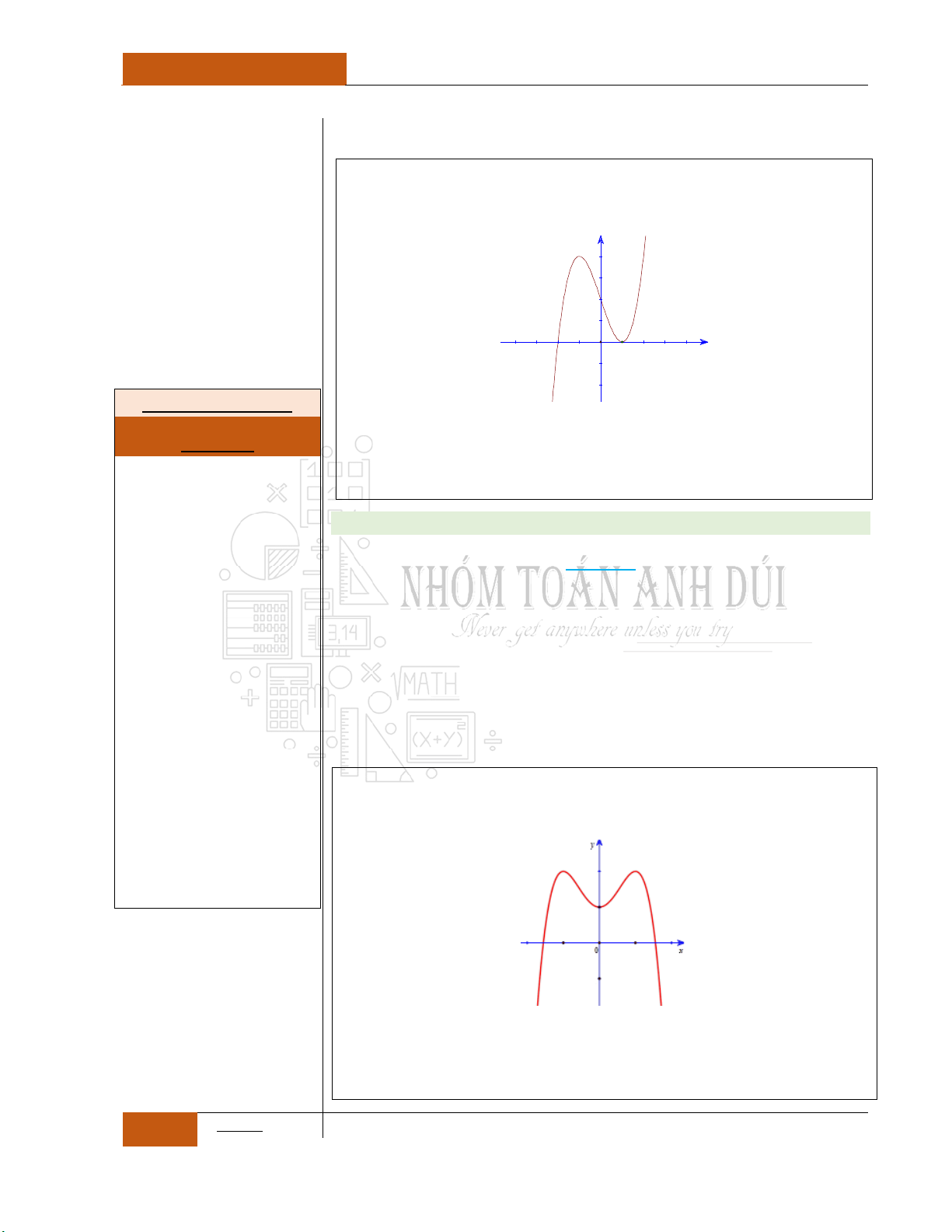
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

482

[ I can't, I can! ]

Extra Techniques:

Remark:

Bài toán cho đồ thị hàm

số bậc ba, bậc bốn trùng

phương để xác định dấu

của các hệ số của đồ thị,

ta cần phải dựa vào các

dấu hiệu dưới đây.

1. Dạng của đồ thị hàm

số (có xu hướng đi lên

hay xuống khi

x

dần đến

một giá trị đủ lớn).

2. Tung độ giao điểm của

đồ thị hàm số với trung

tung.

3. Điểm cực trị.

4. Các điểm thuộc.

Dựa vào hệ trên ta có các phát biểu

   

1 , 4 là sai,

   

2 , 3 đúng.

Câu 4. Đồ thị của hàm số nào dưới đây có dạng như đường cong

trong hình bên dưới?

A.

3 2

3 2   y x x . B.

4 2

2 2  y x x .

C.

3

3 2  y x x

. D.

3

3 2  y x x

.

Đáp án: C

Lời giải

Đây là dạng của đồ thị hàm số bậc ba

3 2

   y ax bx cx d

có hệ số

0a nên loại phương án ,A B .

Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên loại

phương án D .

Vậy đồ thị trên là của hàm số

3

3 2  y x x .

Câu 5. Đồ thị của hàm số nào dưới đây có dạng như đường cong

trong hình bên?

A.

4 2

2 1   y x x . B.

3 2

3 1   y x x .

C.

3 2

3 1  y x x . D.

4 2

2 1  y x x .

x

y

O

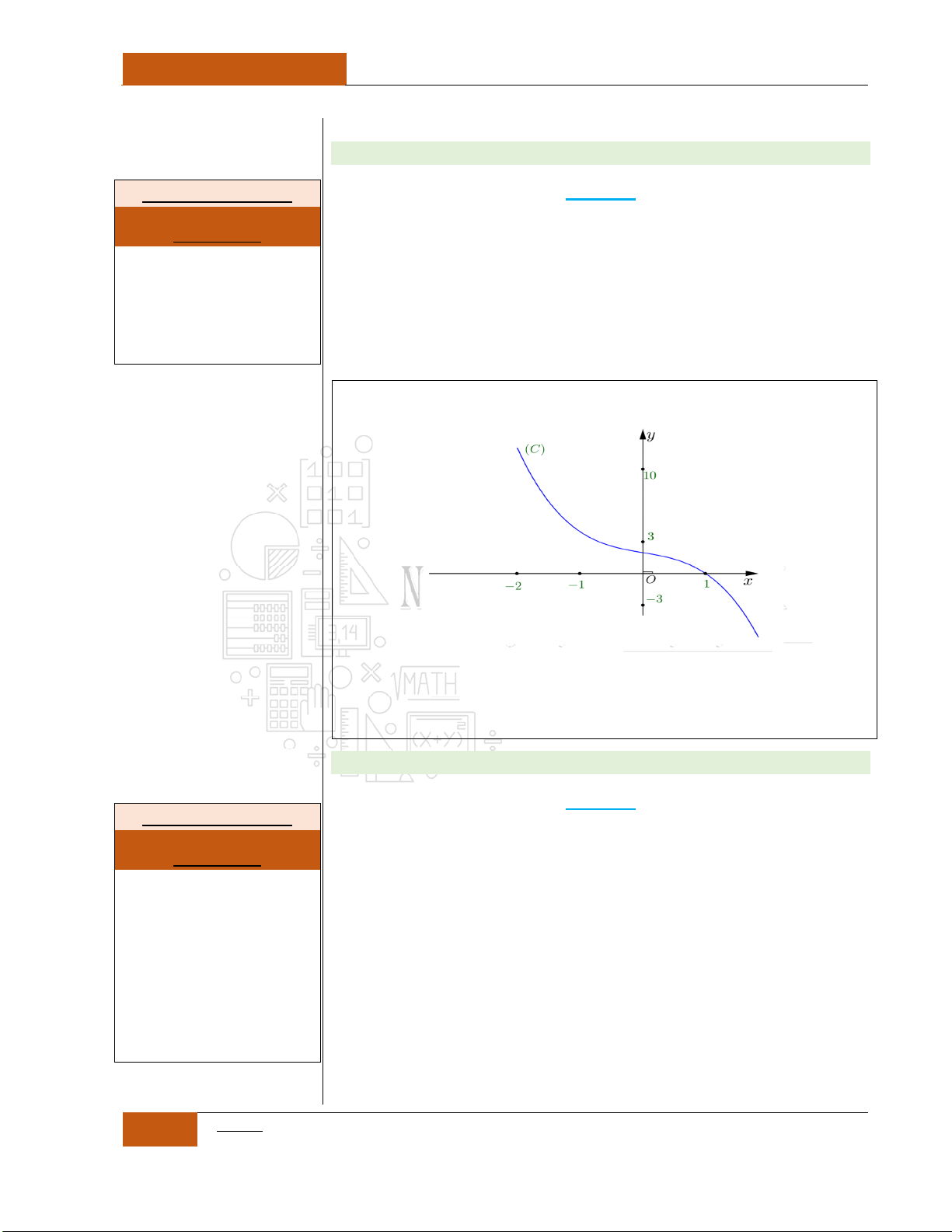
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

483

[ I can't, I can! ]

Extra Techniques:

Study tips:

Đồ thị có dạng chữ " "

đặc trưng cho đồ thị hàm

số bậc bốn trùng phương

có hệ số

0a

.

Extra Techniques:

Study tips:

Đối với dạng toán trắc

nghiệm, ta không nhất

thiết phải giải tường tận

từng giá trị. Phương

pháp loại trừ sẽ phát huy

được tác dụng khi ta ứng

dụng vào dạng toán này.

Đáp án: A

Lời giải

 Gọi

 

C

là đồ thị đã cho.

 Thấy

 

C là đồ thị của hàm trùng phương có

0a

và có

3

cực trị.

 Suy ra

0

. 0











a

a b

. Nên A (đúng).

Câu 6. Đường cong

 

C

hình bên là đồ thị của hàm số nào?

A.

3 2

3 2  y x x . B.

3

2   y x x .

C.

3

3 2   y x x

. D.

3

3 2  y x x

.

Đáp án: B

Lời giải

Cách 1:

Đồ thị đi xuống trên toàn trục số nên hàm số luôn nghịch biến trên



.

Với

3 2

3 2  y x x

2

0

3 6 0

2







    







x

y x x

x



 y

đổi dấu nên

hàm số không nghịch biến trên  . Nên loại phương án A.

Ta có,

3

2   y x x

2

3 1 0,



       y x x

. Chọn phương án B.

Với

3

3 2   y x x

2

0

3 6 0

2







     







x

y x x

x

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

484

[ I can't, I can! ]

Extra Techniques:

Study tips:

Bài toán cho đồ thị hàm

số nhất biến để xác định

phương trình, ta cần phải

dựa vào các dấu hiệu

dưới đây.

1. Dạng của đồ thị hàm

số (có xu hướng đi lên

hay xuống khi

x

dần đến

một giá trị đủ lớn).

2. Tung độ giao điểm của

đồ thị hàm số với trung

tung.

3. Tiệm cận đứng,

ngang.

4. Tâm đối xứng.

5. Các điểm thuộc.



 y

đổi dấu nên hàm số không nghịch biến trên



. Nên loại

phương án C.

Với

3

3 2  y x x

2

1

3 3 0

1







    



 



x

y x

x



 y

đổi dấu nên

hàm số không nghịch biến trên  . Nên loại phương án D.

Cách 2:

Nhận thấy, đồ thị đã cho là đồ thị hàm số bậc 3:

3 2

   y ax bx cx d

 

0a .

Từ đồ thị ta có,

 

lim



 

x

f x



hàm số có hệ số

0a 

Loại

phương án A và D.

Đồ thị cắt trục Oy tại điểm

 

0; d

nằm phía trên trục hoành nên

0d



Loại phương án C.

Câu 7. Đồ thị của hàm số nào dưới đây có dạng như đường cong

trong hình bên?

A.

2

1







x

y

x

. B.

2

1







x

y

x

.

C.

2 1

1







x

y

x

. D.

3

3 2   y x x .

Đáp án: A

Lời giải

Đường cong có dạng của đồ thị hàm số hữu tỉ bậc

1

trên bậc

1

, đồ thị

có các đường tiệm cận đứng

1x

và tiệm cận ngang 1y .

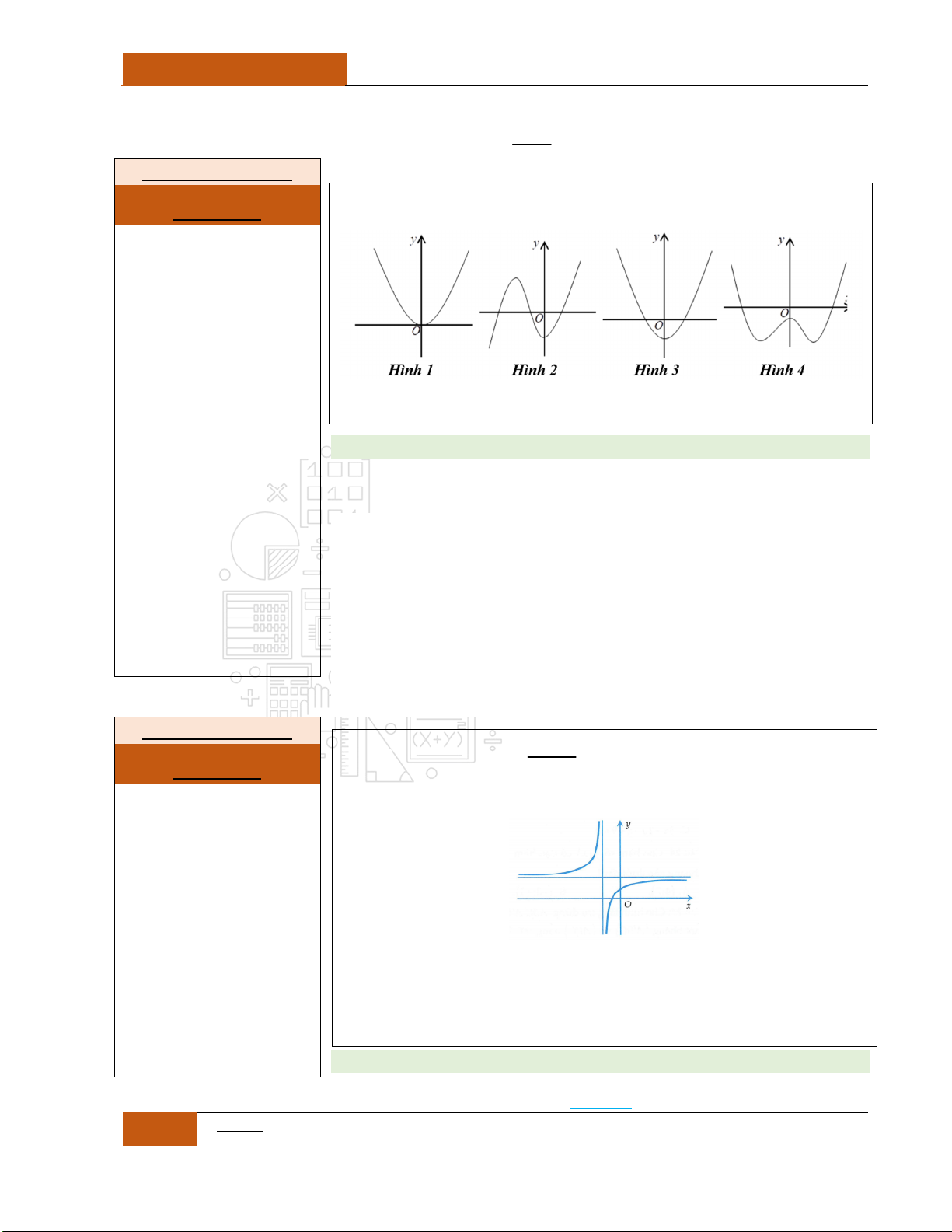
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

485

[ I can't, I can! ]

Extra Techniques:

Study tips:

Bài toán dự đoán đồ thị

hàm số trong các hình thì

chúng ta chỉ cần để ý một

cách logic về những tính

chất của đồ thị, chẳng

hạn:

1. Loại đồ thị (Bậc hai,

ba, nhất biến, bậc bốn

trùng phương,..).

2. Giao điểm với trục

tung.

3. Cực trị, điểm cực trị.

4. Dấu của hệ số

a

hoặc

xu hướng đồ thị (đối với

hàm nhất biến).

Extra Techniques:

Study tips:

Dạng toán cho thêm một

điều kiện về dấu của một

trong các hệ số sẽ là

manh mối đưa về đáp án.

Tư duy như sau: Ta sẽ

tìm những mối liên hệ

kép, có chứa điều kiện

ràng buộc lẫn nhau giữa

các hệ số  tiệm cận,

tung độ giao điểm với

trục tung,…

Nên chỉ có hàm số

2

1







x

y

x

thỏa yêu cầu bài toán.

Câu 8. Hàm số

4

1 y x

có đồ thi là hình nào dưới đây?

A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.

Đáp án: C

Lời giải

Ta có:

3

4



y x

,

3

0 4 0 0



    y x x

.

Hàm số đã cho là hàm trùng phương, có một cực trị nên chỉ còn “phân

vân” giữa đồ thị hình 1 với hình 3.

Dễ thấy

 

0; 1I  là giao điểm của đồ thị hàm số

4

1y x 

với trục

hoành

Ox

.

Như vậy, đồ thị hàm số chính xác phải là đồ thị hàm số ở hình 3.

Câu 9. Cho hàm số







ax b

y

cx d

có đồ thị như hình vẽ bên dưới,

trong đó 0.d

Mệnh đề nào dưới đây đúng?

A.

0, 0, 0.  a b c

B.

0, 0, 0.  a b c

C. 0, 0, 0.  a b c D. 0, 0, 0.  a b c

Đáp án: B

Lời giải

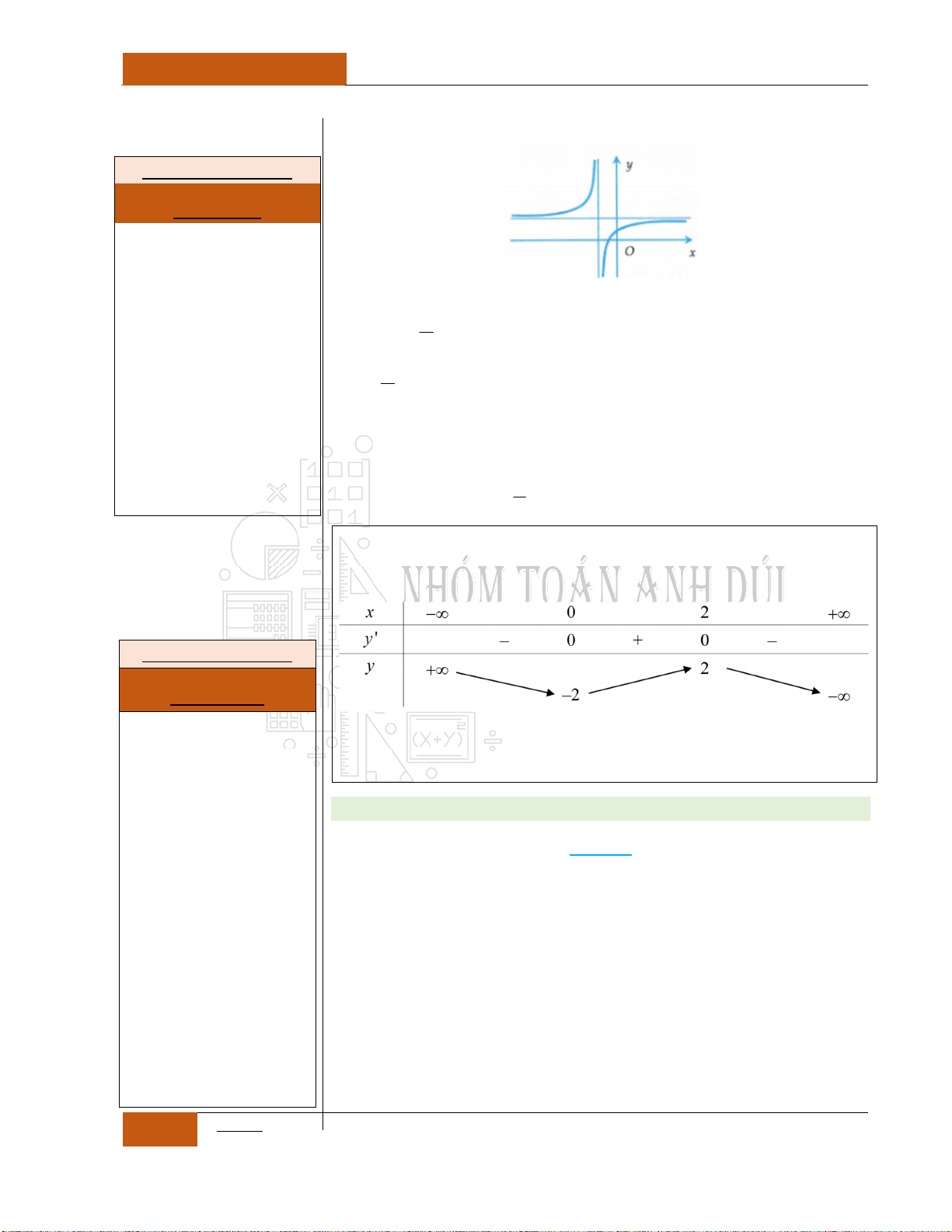
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

486

[ I can't, I can! ]

Extra Techniques:

Study tips:

Dạng toán cho thêm một

điều kiện về dấu của một

trong các hệ số sẽ là

manh mối đưa về đáp án.

Tư duy như sau: Ta sẽ

tìm những mối liên hệ

kép, có chứa điều kiện

ràng buộc lẫn nhau giữa

các hệ số  tiệm cận,

tung độ giao điểm với

trục tung,…

Extra Techniques:

Study Tips:

"Trên đây là một số

Tips chúng tôi cảm thấy

rất hữu dụng trong các

bài toán hiện hành. Do

mục đích phục vụ cho

phần đông các bạn học

sinh nên phần trình bày

khá chi tiết và khá dài.

Nhưng nếu bạn đọc

hiểu bản chất vấn đề,

thao tác sẽ ngắn gọn

hơn, chuẩn xác hơn và

quan trọng nhất vẫn là

lợi thế về thời gian nếu

biết các Tips này.

Từ đồ thị hàm số

Ta có: giao điểm của đồ thị hàm số với trục tung nằm phía trên trục

hoành nên 0.

b

d

Tiệm cận đứng của đồ thị nằm bên phải trục tung

nên 0. 

d

c

Do

0d

nên

0, 0. b c

Có thể tìm được dấu của

a

thông qua tiệm cận ngang

 

0 0 Do: 0    

a

y a c

c

.

Câu 10. Bảng biến thiên sau là bảng biến thiên của một hàm số trong

bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi

đó là hàm số nào?

A.

3 2

3 1  y x x

. B.

3 2

3 2   y x x

.

C.

3 2

3 1   y x x . D.

3

3 2   y x x .

Đáp án: B

Lời giải

Từ bảng biến thiên suy ra hệ số của

3

x

âm nên ta loại phương án A.

Tại

0x

thì 2 y suy ra loại C.

0



y

có hai nghiệm phân biệt nên loại D.

Do vậy phương án B thỏa mãn.

Như vậy những kiến thức về nhận dạng đồ thị hàm số đã được chúng

tôi nhắc khá kỹ trước khi chúng ta chuyển sang phần tự luyện bốn

mức độ, do dạng toán khá dễ nên những câu Vận dụng cao chỉ mang

tính phân loại so với các câu “dễ” hơn trong dạng toán này.

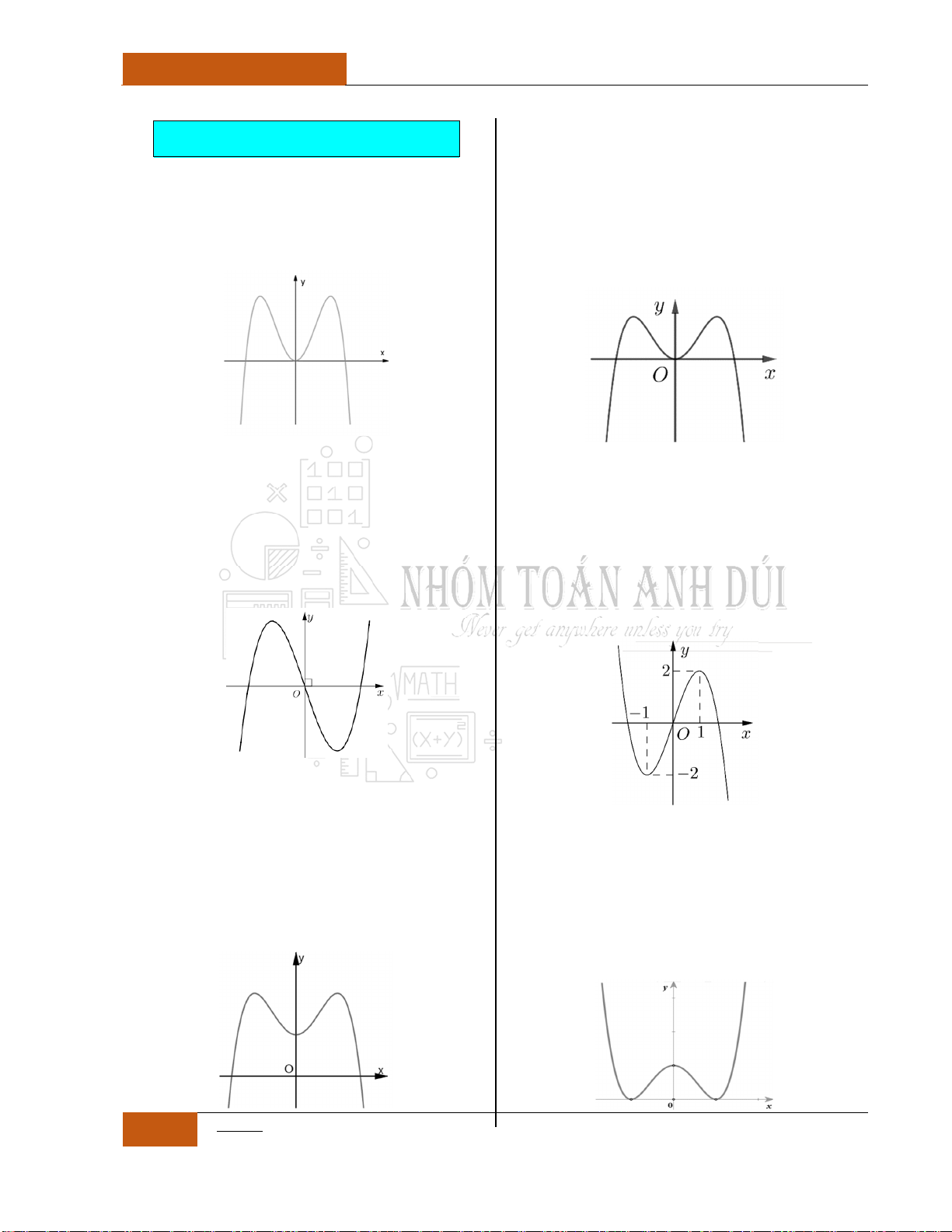
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

475

[ I can't, I can! ]

TỰ LUYỆN 4 MỨC ĐỘ

Câu 1. [Nhận biết].

Đồ thị của hàm số nào dưới đây có dạng như

đường cong trong dưới đây?

A.

4 2

2  y x x . B.

4 2

2 y x x .

C.

3 2

3 y x x . D.

3 2

3  y x x .

Câu 2. [Nhận biết].

Đồ thị của hàm số nào dưới đây có dạng như

đường cong trong hình bên?

A.

3

3 y x x . B.

3

3  y x x .

C.

4 2

2 y x x . D.

4 2

2  y x x .

Câu 3. [Nhận biết].

Đồ thị hàm số nào dưới đây có dạng như đường

cong trong hình bên?

A.

3 2

3 1  y x x . B.

3 2

3 1   y x x .

C.

4 2

2 1   y x x . D.

4 2

2 1  y x x .

Câu 4. [Nhận biết].

Đồ thị hàm số nào dưới đây có dạng như đường

cong trong hình bên?

A. . B. .

C. . D. .

Câu 5. [Nhận biết].

Cho hàm số bậc ba

 

y f x có đồ thị là đường

cong trong hình bên.

Số nghiệm thực của phương trình

 

1f x là

A. 1. B.

0

. C. 2 . D.

3

.

Câu 6. [Nhận biết].

Đồ thị hàm số nào dưới đây có dạng như đường

cong trong hình bên?

4 2

2

y x x

  

3

y x x

  

4 2

2

y x x

 

3

y x x

 

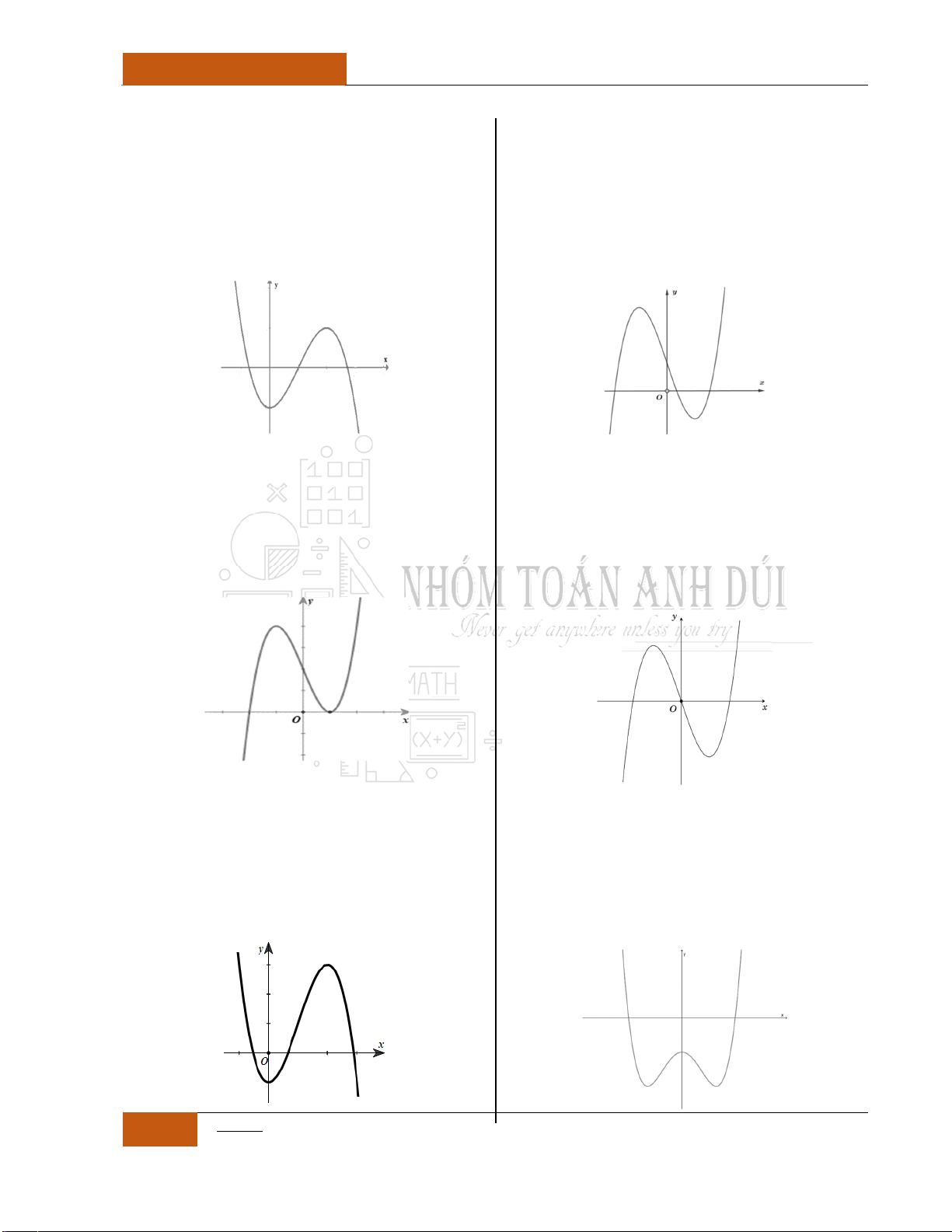
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

476

[ I can't, I can! ]

A.

4 2

2 1  y x x . B.

3 2

3 1   y x x .

C.

3 2

3 1  y x x . D.

4 2

2 1   y x x .

Câu 7. [Nhận biết].

Đồ thị hàm số nào dưới đây có dạng như đường

cong hình bên

A.

4 2

2x 2  y x . B.

3 2

2x 2   y x .

C.

3 2

3x 2  y x . D.

4 2

2x 2   y x .

Câu 8. [Nhận biết].

Đường cong hình bên là đồ thị của một trong bốn

hàm số dưới đây. Hàm số đó là hàm số nào?

A.

3

3 2   y x x . B.

4 2

1  y x x .

C.

4 2

1  y x x . D.

3

3 2  y x x .

Câu 9. [Nhận biết].

Đồ thị của hàm số nào dưới đây có dạng như

đường cong trong hình bên?

A.

4 2

2 1   y x x . B.

4 2

2 1  y x x .

C.

3 2

3 1  y x x . D.

3 2

3 1   y x x .

Câu 10. [Nhận biết].

Đồ thị của hàm số dưới đây có dạng như đường

cong bên?

A.

3

3 1  y x x . B.

4 2

2 1  y x x .

C.

4 2

2 1   y x x . D.

3

3 1   y x x .

Câu 11. [Nhận biết].

Đồ thị của hàm số nào dưới đây có dạng như

đường cong trong hình bên?

A.

4 2

2 y x x . B.

3

3  y x x .

C.

3

3 y x x . D.

4 2

2  y x x .

Câu 12. [Nhận biết].

Đường cong trong hình vẽ bên là đồ thị của hàm

số nào dưới đây?

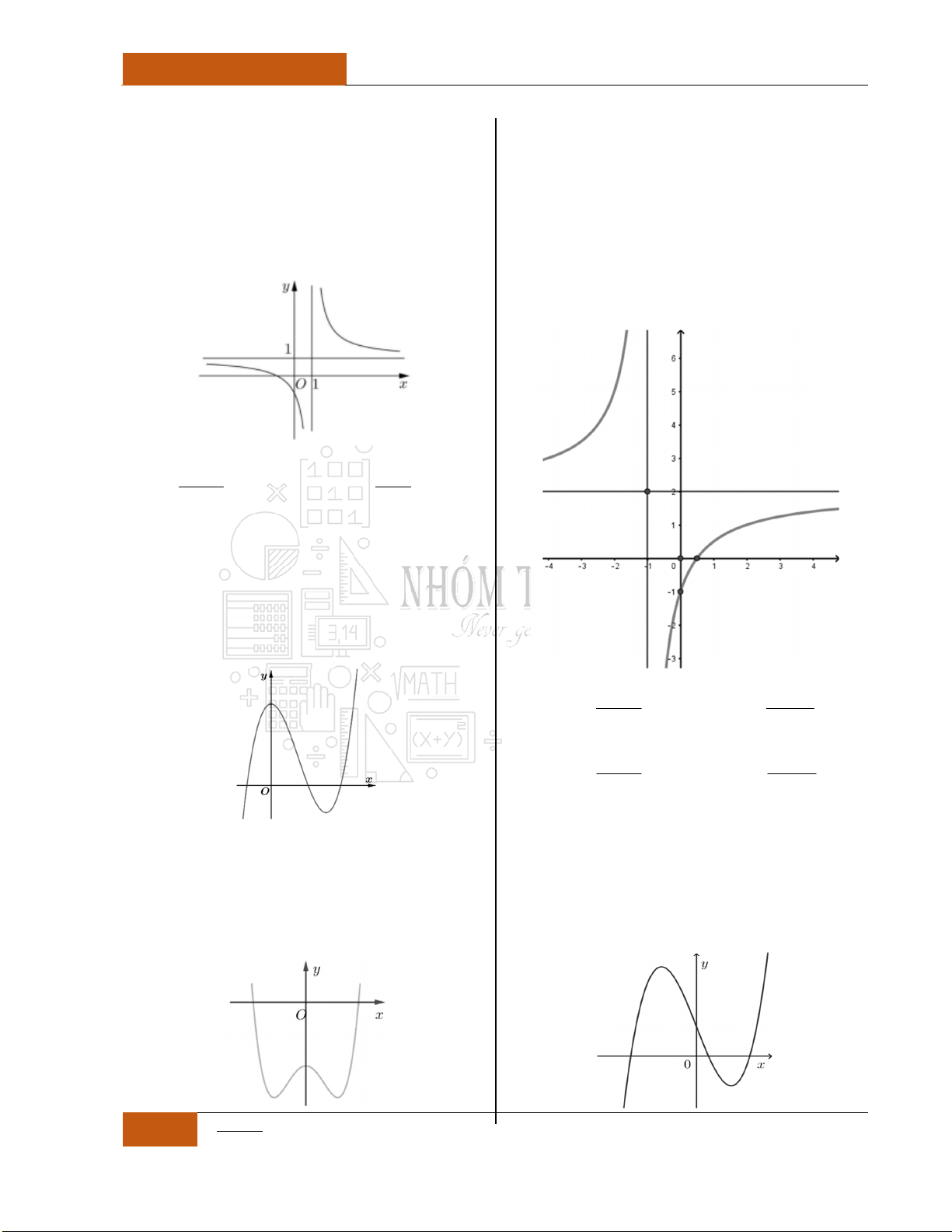
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

477

[ I can't, I can! ]

A.

3 2

1   y x x . B.

4 2

2 1   y x x .

C.

3 2

1  y x x . D.

4 2

2 1  y x x .

Câu 13. [Nhận biết].

Đường con trong hình vẽ bên là đồ thị của hàm

số nào dưới đây?

A.

2 1

1







x

y

x

. B.

1







x

y

x

.

C.

4 2

1  y x x . D.

3

3 1  y x x .

Câu 14. [Nhận biết].

Đường cong ở hình bên dưới là đồ thị của một

trong bốn hàm số dưới đây. Hàm số đó là hàm số

nào?

A.

3 2

3 1   y x x . B.

3 2

3 3  y x x .

C.

4 2

2 1   y x x . D.

4 2

2 1  y x x .

Câu 15. [Nhận biết].

Đồ thị hàm số nào dưới đây có dạng như đường

cong trong hình vẽ bên?

A.

3 2

3 2  y x x . B.

4 2

2 2  y x x .

C.

3 2

3 2   y x x . D.

4 2

2 2   y x x .

Câu 16. [Nhận biết].

Cho đường cong hình vẽ bên là đồ thị của một

hàm số trong bốn hàm số được liệt kê ở bốn

phương án A, B, C, D dưới đây. Hỏi đó là hàm

số nào?

A.

2 1

y

1







x

. B.

2 3

1







x

y

x

.

C.

2 1

1







x

y

x

. D.

2 2

1







x

y

x

.

Câu 17. [Nhận biết].

Đường cong trong hình bên là đồ thị của một

hàm số trong bốn hàm số

được liệt kê ở bốn phương án , , ,A B C D dưới

đây. Hỏi hàm số đó là hàm số nào?

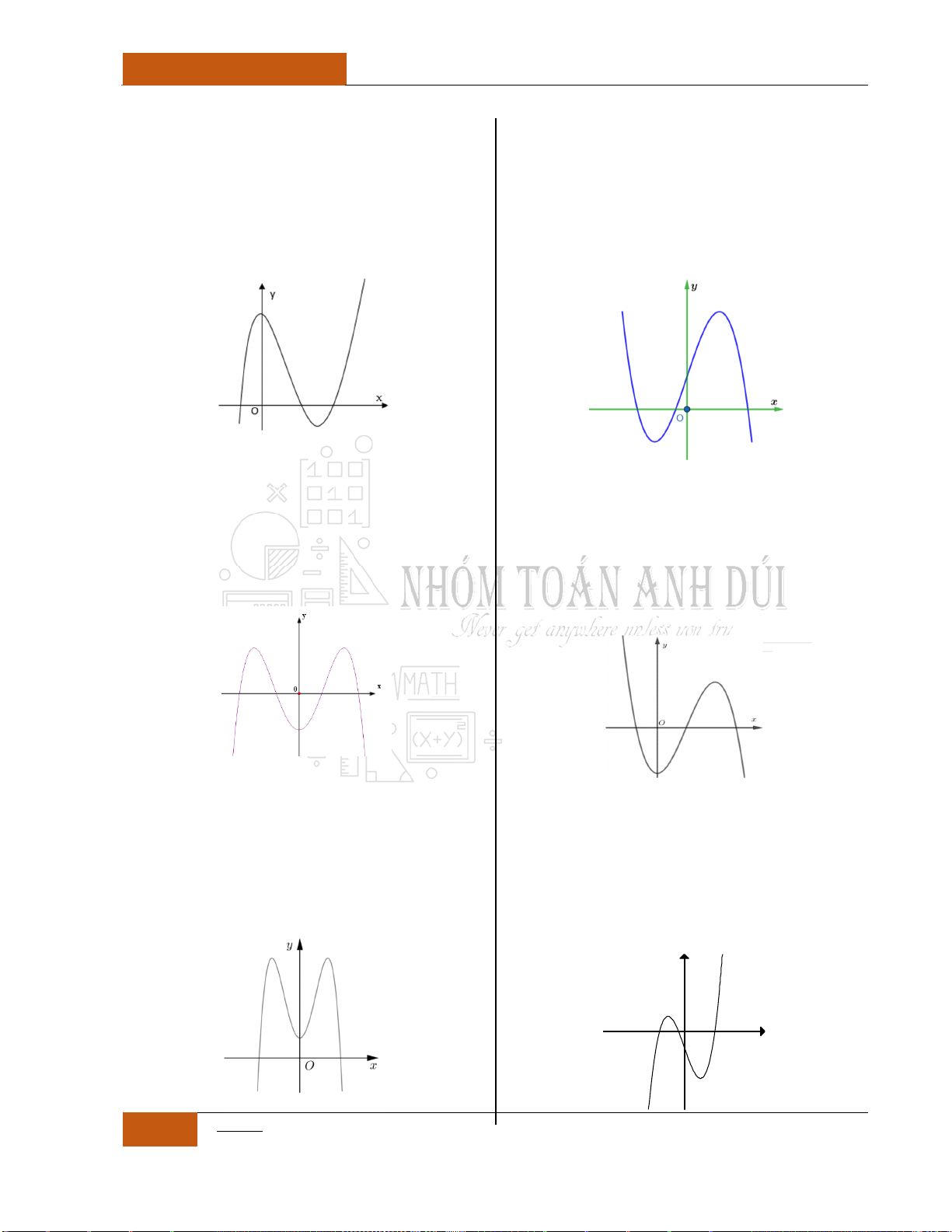
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

478

[ I can't, I can! ]

A.

3

3 1  y x x . B.

3

3 1   y x x .

C.

4 2

1  y x x . D.

2

1   y x x .

Câu 18. [Nhận biết].

Đồ thị của hàm số nào dưới đây có dạng như

đường cong trong hình vẽ bên?

A.

3 2

3 3  y x x . B.

3 2

3 3   y x x .

C.

4 2

2 3  y x x . D.

4 2

2 3   y x x .

Câu 19. [Nhận biết].

Đường cong trong hình vẽ bên là đồ thị của hàm

số nào dưới đây?

A.

3 2

3 1  y x x . B.

3 2

3 1   y x x .

C.

4 2

3 1   y x x . D.

4 2

3 1  y x x .

Câu 20. [Nhận biết].

Đồ thị hàm số nào dưới đây có dạng như đường

cong trong hình vẽ bên?

A.

4 2

2 4 1  y x x . B.

3

2 3 1   y x x .

C.

3

2 3 1  y x x . D.

4 2

2 4 1   y x x .

Câu 21. [Nhận biết].

Đồ thị của hàm số nào dưới đây có dạng như

đường cong trong hình vẽ bên

A.

3

3 1   y x x . B.

3

3 1  y x x .

C.

4 2

2 1  y x x . D.

4 2

2 1   y x x .

Câu 22. [Nhận biết].

Đường cong trong hình vẽ bên là đồ thị của hàm

số nào dưới đây?

A.

4 2

2  y x x . B.

4 2

2   y x x .

C.

3 2

3 2   y x x . D.

3 2

3 2  y x x .

Câu 23. [Nhận biết].

Đường cong trong hình vẽ bên là đồ thị của hàm

số nào dưới đây?

x

y

O

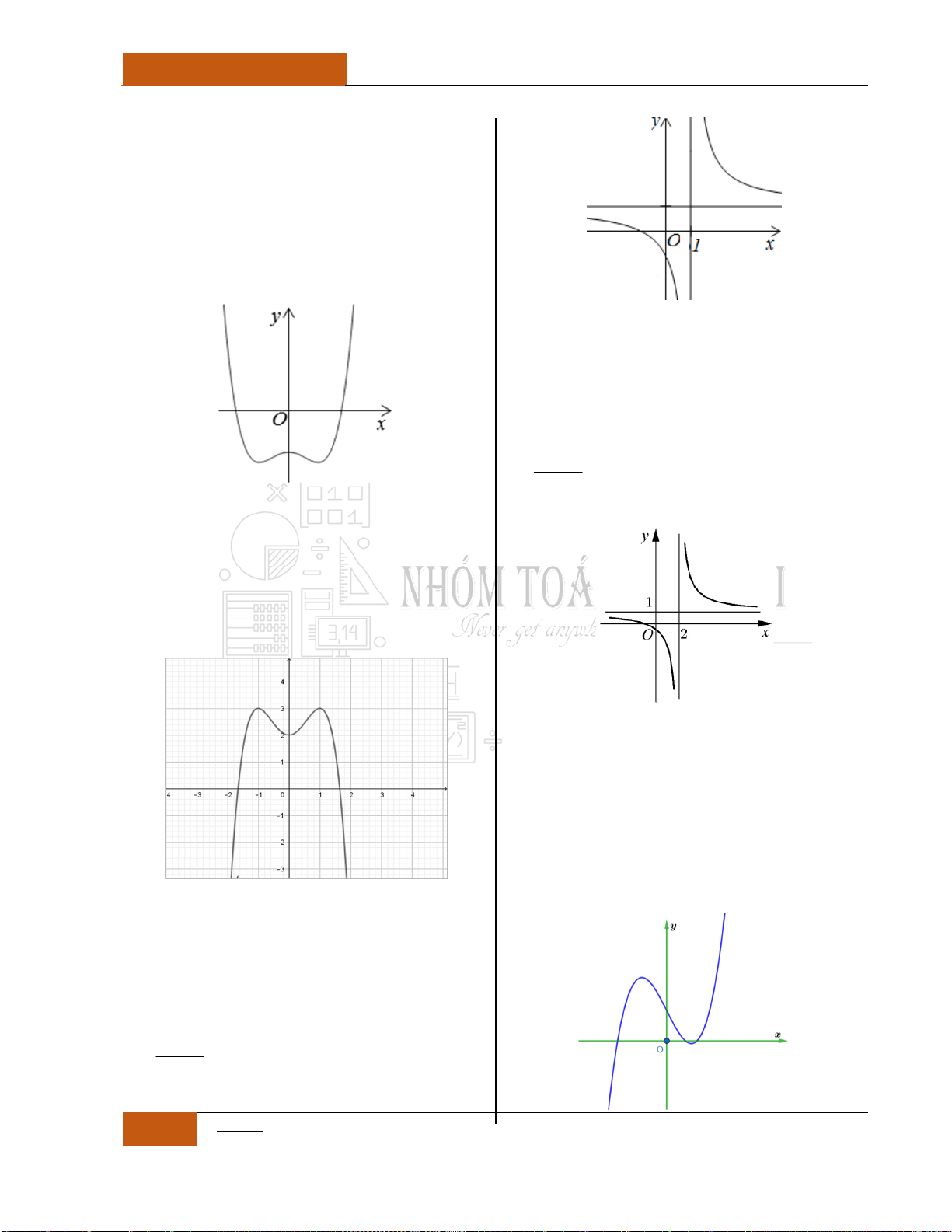
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

479

[ I can't, I can! ]

A.

3

3 1  y x x . B.

4 2

3 1  y x x .

C.

3

3 1   y x x . D.

4 2

1   y x x .

Câu 24. [Nhận biết].

Đường cong ở hình bên là đồ thị của một trong

bốn hàm số dưới đây.

Hàm số đó là hàm số nào?

A.

4 2

1  y x x . B.

4 2

1   y x x .

C.

3 2

1  y x x . D.

3 2

1   y x x .

Câu 25. [Nhận biết].

Đường cong trong hình bên là của đồ thị hàm số

nào dưới đây?

A.

3 2

3 2  y x x . B.

3 2

3 2   y x x .

C.

4 2

2 2   y x x . D.

4 2

2 2  y x x .

Câu 26. [Thông hiểu].

Đường cong ở hình bên là đồ thị của hàm số







ax b

y

cx d

với , , ,a b c d là các số thực. Mệnh đề

nào dưới đây đúng?

A.

0,



  y x

. B.

0, 1



  y x

.

C. 0, 1



  y x . D. 0,



  y x .

Câu 27. [Thông hiểu].

Đường cong ở hình bên là đồ thị của hàm số







ax b

y

cx d

với , , ,a b c d là các số thực. Mệnh đề

nào dưới đây đúng?

A.

y 0, 1



  x

. B.

y 0, 1



  x

.

C. y 0, 2



  x . D. y 0, 2



  x .

Câu 28. [Thông hiểu].

Hình vẽ sau đây là đồ thị của một trong bốn hàm

số cho ở các đáp án

, , ,A B C D

.

Hỏi đó là hàm số nào?

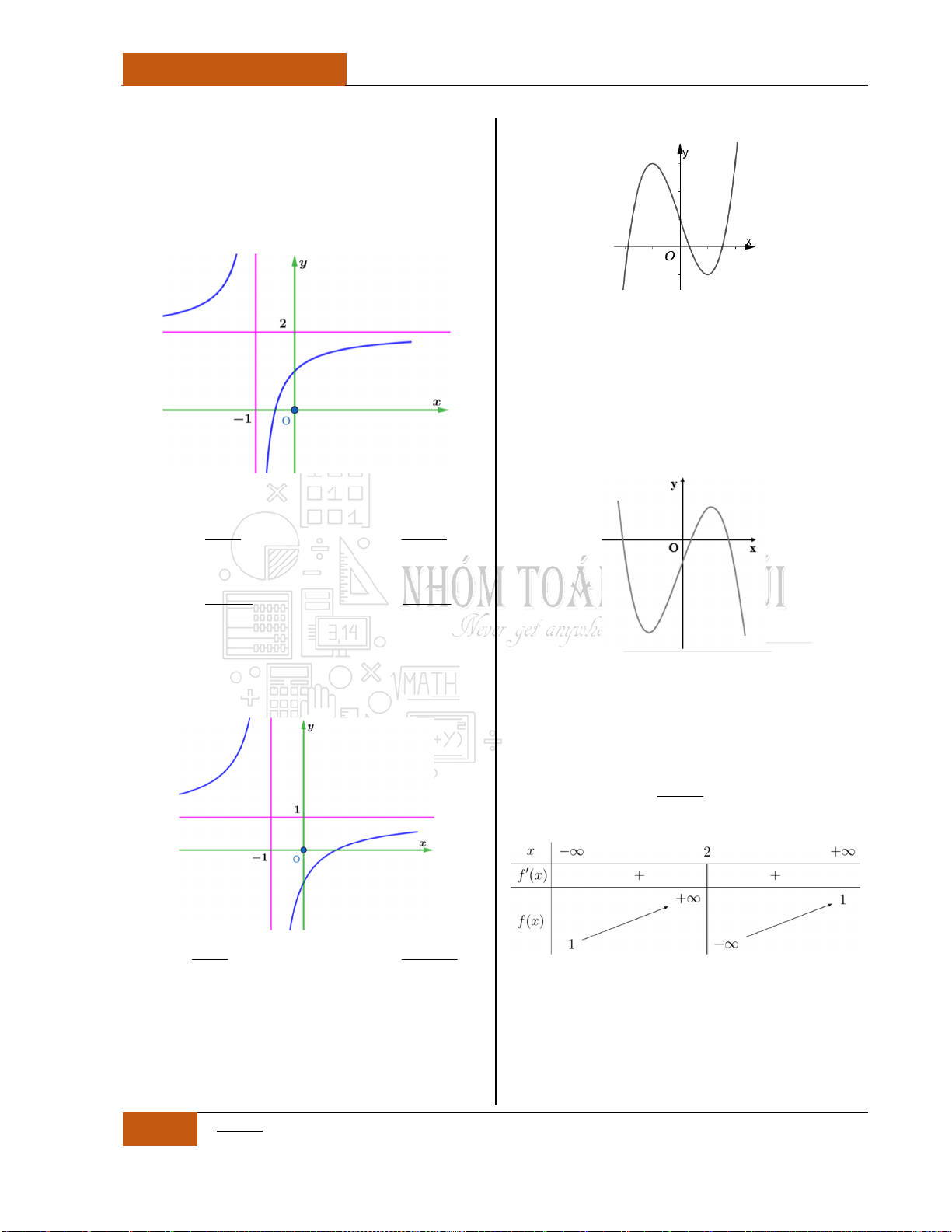
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

480

[ I can't, I can! ]

A.

3

2 1  y x x . B.

3 2

3 1  y x x .

C.

3

2 1  y x x . D.

3

2 1   y x x .

Câu 29. [Nhận biết].

Hình vẽ bên dưới là đồ thị của hàm số nào

A.

1







x

y

x

. B.

2 1

1







x

y

x

.

C.

2 3

1







x

y

x

. D.

2 5

1







x

y

x

.

Câu 30. [Nhận biết].

Đường cong trong hình là đồ thị của hàm số nào

dưới đây?

A.

1







x

y

x

. B.

2 1

2

 





x

y

x

.

C.

4 2

3 y x x . D.

3 2

3 y x x .

Câu 31. [Nhận biết].

Đường cong trong hình vẽ bên là đồ thị của hàm

số nào sau đây?

A.

3

3 1   y x x . B.

4 2

1  y x x .

C.

2

1   y x x . D.

3

3 1  y x x .

Câu 32. [Thông hiểu].

Cho hàm số

 

3

3 ;    y ax x d a d có đồ thị

như hình bên. Mệnh đề nào dưới đây đúng?

A. 0, 0 a d . B. 0, 0 a d .

C.

0, 0 a d

. D.

0, 0 a d

.

Câu 33. [Vận dụng].

Cho hàm số

 

1





ax

f x

bx c

 

, ,  a b c có bảng

biến thiên như sau:

Trong các số ,a b và c có bao nhiêu số dương?

A. 2 . B.

3

. C. 1. D.

0

.

Câu 34. [Vận dụng].

Cho hàm số

3 2

   y ax bx cx d

 

, , ,  a b c d

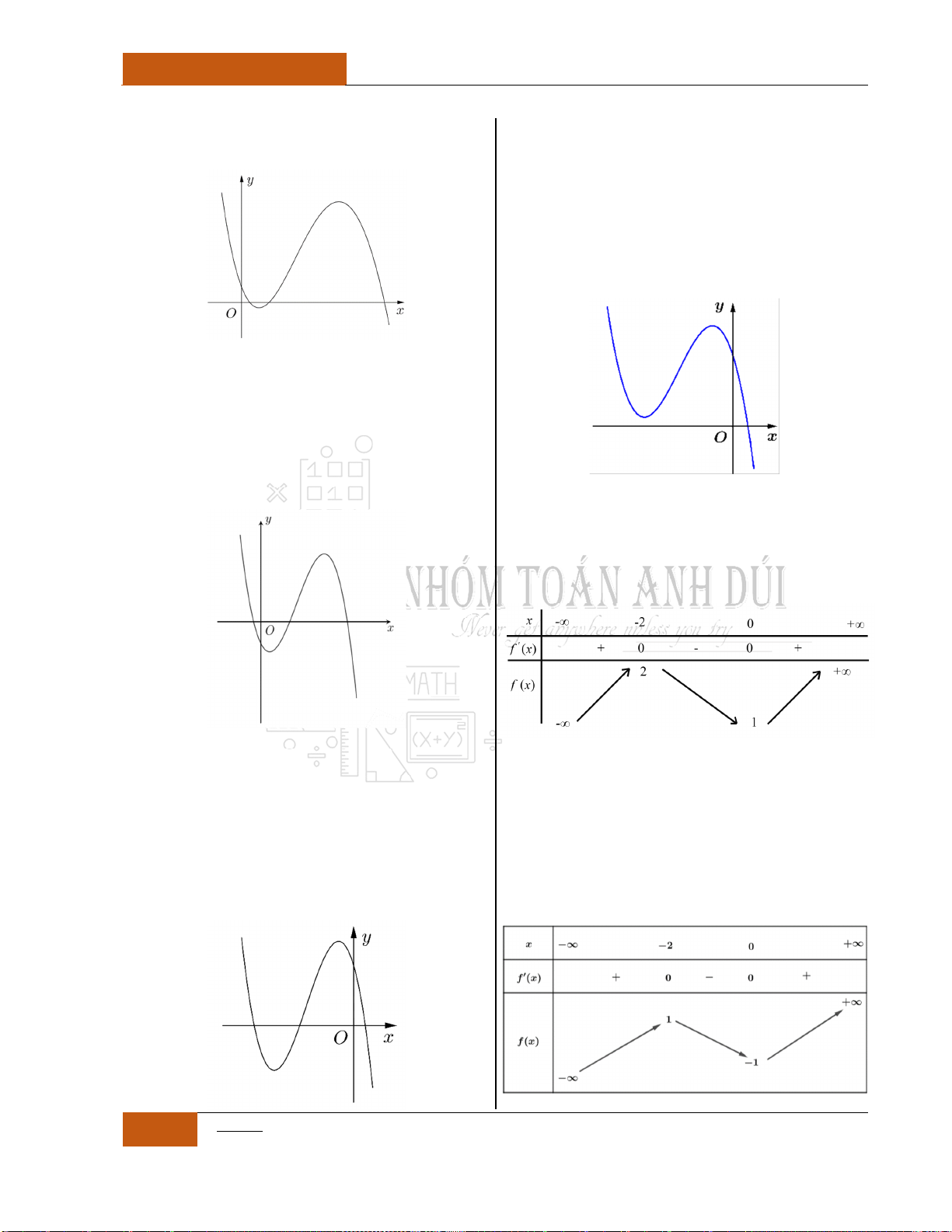
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

481

[ I can't, I can! ]

có đồ thị là đường cong trong hình bên. Có bao

nhiêu số dương trong các số a , b , c , d ?

A.

4

. B.

1

. C.

2

. D. 3.

Câu 35. [Vận dụng].

Cho hàm số

3 2

   y ax bx cx d





, , , 



a b c d có đồ thị là đường cong trong

hình bên. Có bao nhiêu số dương trong các hệ số

, , ,

a b c d

?

A. 4 . B.

3

. C. 1. D. 2 .

Câu 36. [Vận dụng].

Cho hàm số

3 2

y ax bx cx d    trong đó,

 

, , ,a b c d  có đồ thị là đường cong trong

hình bên. Có bao nhiêu số dương trong các số

, , ,a b c d ?

A.

4

. B.

2

. C.

1

. D. 3.

Câu 37. [Vận dụng].

Cho hàm số bậc ba

3 2

,y ax bx cx d    trong

đó,

 

, , ,a b c d  , có đồ thị là đường cong trong

hình bên. Có bao nhiêu số dương trong các số

, , ,a b c d ?

A.

4

. B.

2

. C.

1

. D. 3.

Câu 38. [Vận dụng].

Cho hàm số bậc ba





3 2

f x ax bx cx d

   

với

 

, , ,a b c d   có bảng biến thiên như sau

Có bao nhiêu số dương trong các số , , , a b c d ?

A.

2

. B.

4

. C.

1

. D. 3.

Câu 39. [Vận dụng].

Cho hàm số bậc ba

 

3 2

f x ax bx cx d   

với

 

, , ,a b c d  có bảng biến thiên như sau:

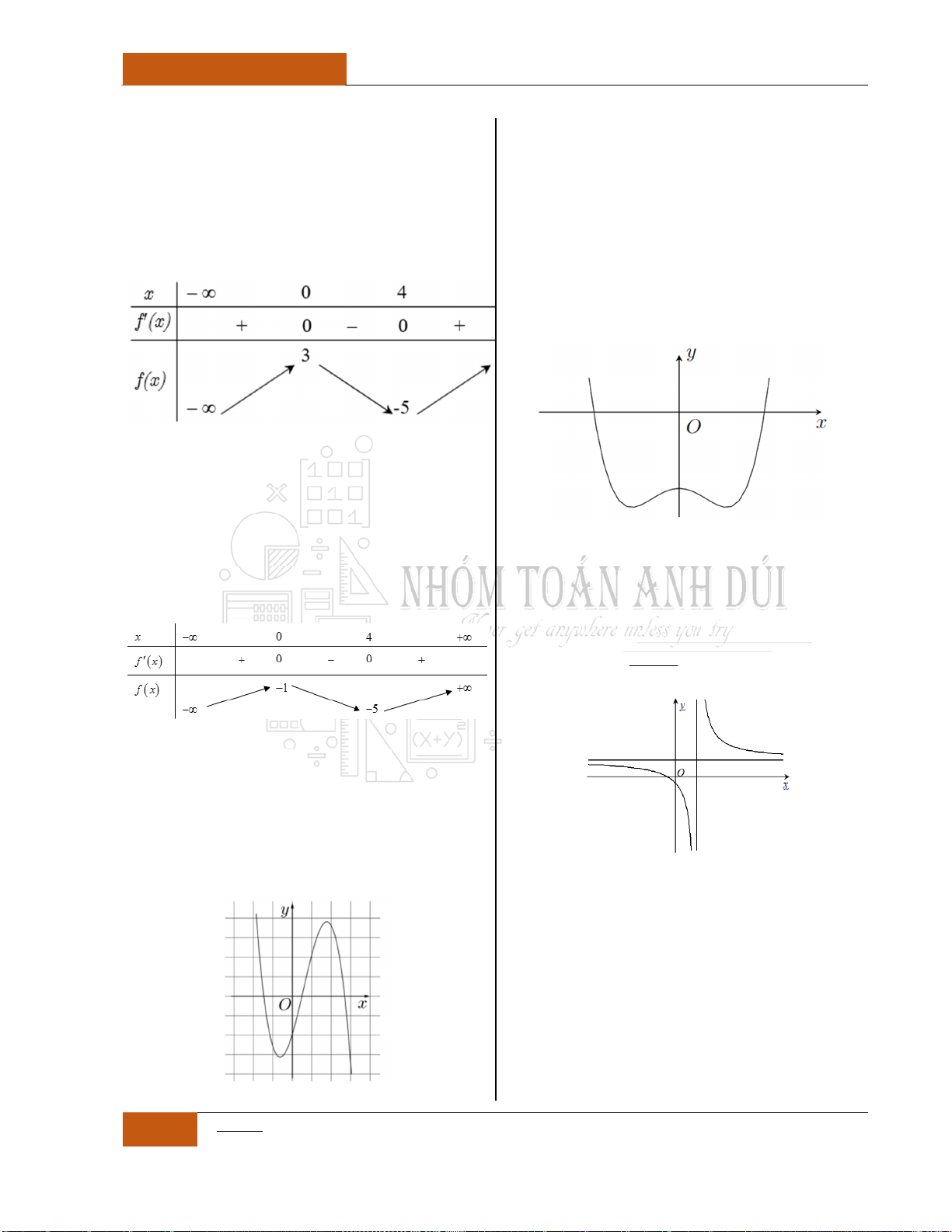
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

482

[ I can't, I can! ]

Có bao nhiêu số dương trong các số , , , ?a b c d

A.

3.

B.

4.

C.

2.

D.

1.

Câu 40. [Vận dụng].

Cho hàm số bậc ba

 

3 2

f x ax bx cx d   

với

 

, , ,a b c d  có bảng biến thiên như sau:

Có bao nhiêu số dương trong các số , , ,a b c d ?

A. 2 . B. 4 . C. 1. D.

3

.

Câu 41. [Vận dụng].

Cho hàm số bậc ba

 

3 2

f x ax bx cx d   

với

 

, , ,a b c d  có bảng biến thiên như sau:

Có bao nhiêu số dương trong các số , , ,a b c d ?

A.

4

. B.

2

. C. 3. D.

1

.

Câu 42. [Vận dụng cao].

Cho hàm số

3 2

   y ax bx cx d có đồ thị như

hình vẽ bên. Mệnh đề nào dưới đây đúng?

A.

0, 0, 0, 0   a b c d

.

B. 0, 0, 0, 0   a b c d .

C. 0, 0, 0, 0   a b c d .

D.

0, 0, 0, 0   a b c d

.

Câu 43. [Vận dụng].

Cho hàm số

4 2

  y ax bx c có đồ thị như hình

bên. Mệnh đề nào dưới đây là đúng?

A. 0, 0, 0  a b c . B. 0, 0, 0  a b c .

C. 0, 0, 0  a b c . D. 0, 0, 0  a b c .

Câu 44. [Vận dụng cao].

Cho hàm số







ax b

y

cx d

có đồ thị như sau.

Mệnh đề nào sau đây đúng?

A. 0; 0 ac bd . B. 0; 0 ab cd .

C. 0; 0 bc ad . D. 0; 0 ad bd .

Câu 45. [Vận dụng].

Cho hàm số

 

3 2

0    y ax bx cx d a

có đồ

thị như hình vẽ dưới đây.

Chọn khẳng định đúng về dấu của a , b , c , d ?

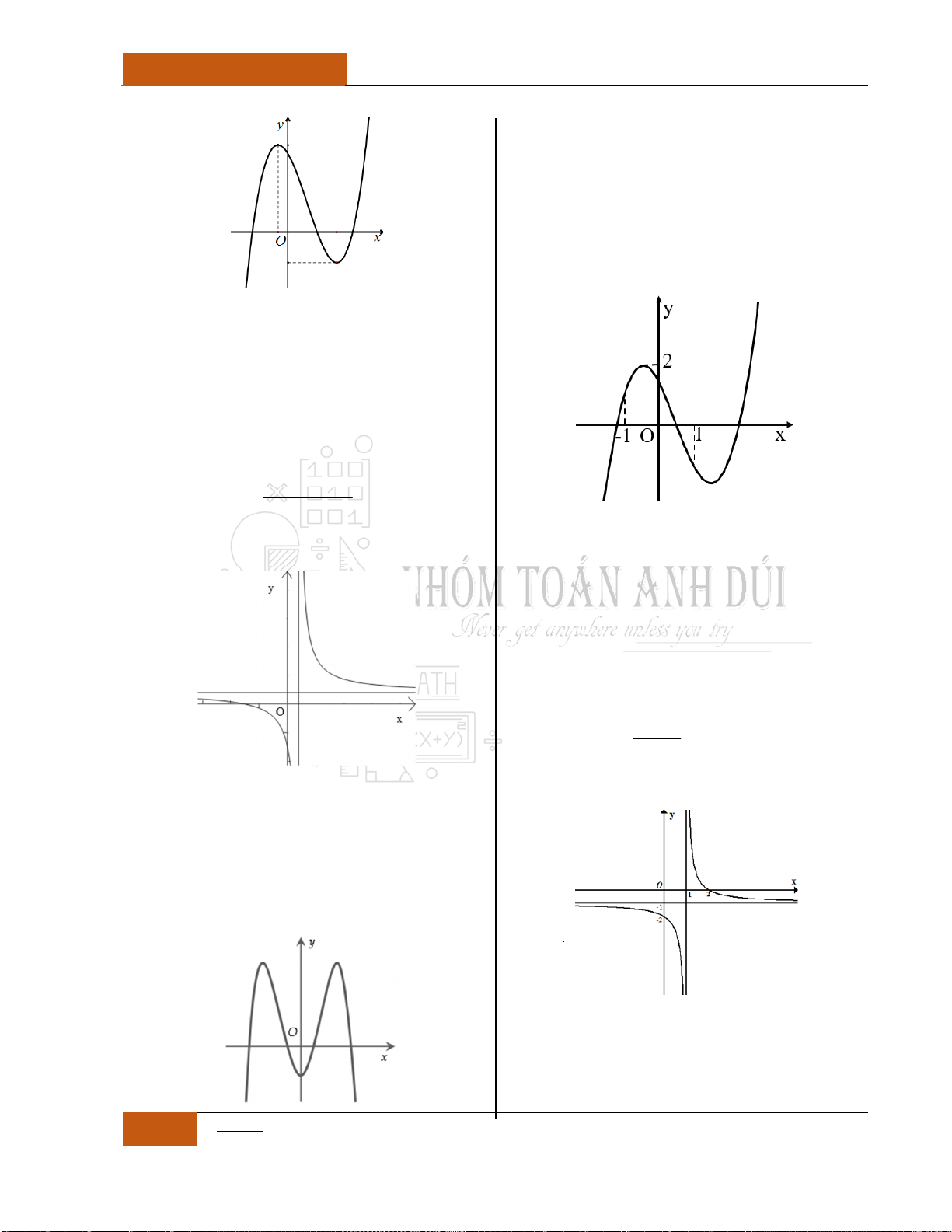
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

483

[ I can't, I can! ]

A. 0a , 0b , 0d , 0c .

B.

0a

,

0 c b

,

0d

.

C. 0, 0, 0, 0.   a b c d

D.

0a

,

0b

,

0c

,

0d

.

Câu 46. [Vận dụng].

Cho hàm số





 

1

, 0

1

 

 

 

a x b

y d

c x d

có đồ thị

như hình trên.

Khẳng định nào dưới đây là đúng?

A. 1, 0, 1.  a b c B. 1, 0, 1.  a b c

C. 1, 0, 1.  a b c D. 1, 0, 1.  a b c

Câu 47. [Vận dụng].

Cho hàm số

4 2

  y ax bx c

 

0a có đồ thị

như hình vẽ dưới đây.

Mệnh đề nào dưới đây đúng?

A. 0a , 0b , 0c . B. 0a , 0b , 0c .

C. 0a , 0b , 0c . D. 0a , 0b , 0c .

Câu 48. [Vận dụng].

Hàm số

3 2

   y ax bx cx d có đồ thị như hình

vẽ bên dưới:

Khẳng định nào là đúng?

A. 0a , 0b , 0c , 0d .

B. 0a , 0b , 0c , 0d .

C. 0a , 0b , 0c , 0d .

D. 0a , 0b , 0c , 0d .

Câu 49. [Vận dụng].

Cho hàm số







ax b

y

x c

có đồ thị như hình bên

dưới, với a ,

b

,

c

.

Tính giá trị của biểu thức

2 3  T a b c

?

A.

8 T

. B. 2T .

C.

6T

. D.

0T

.

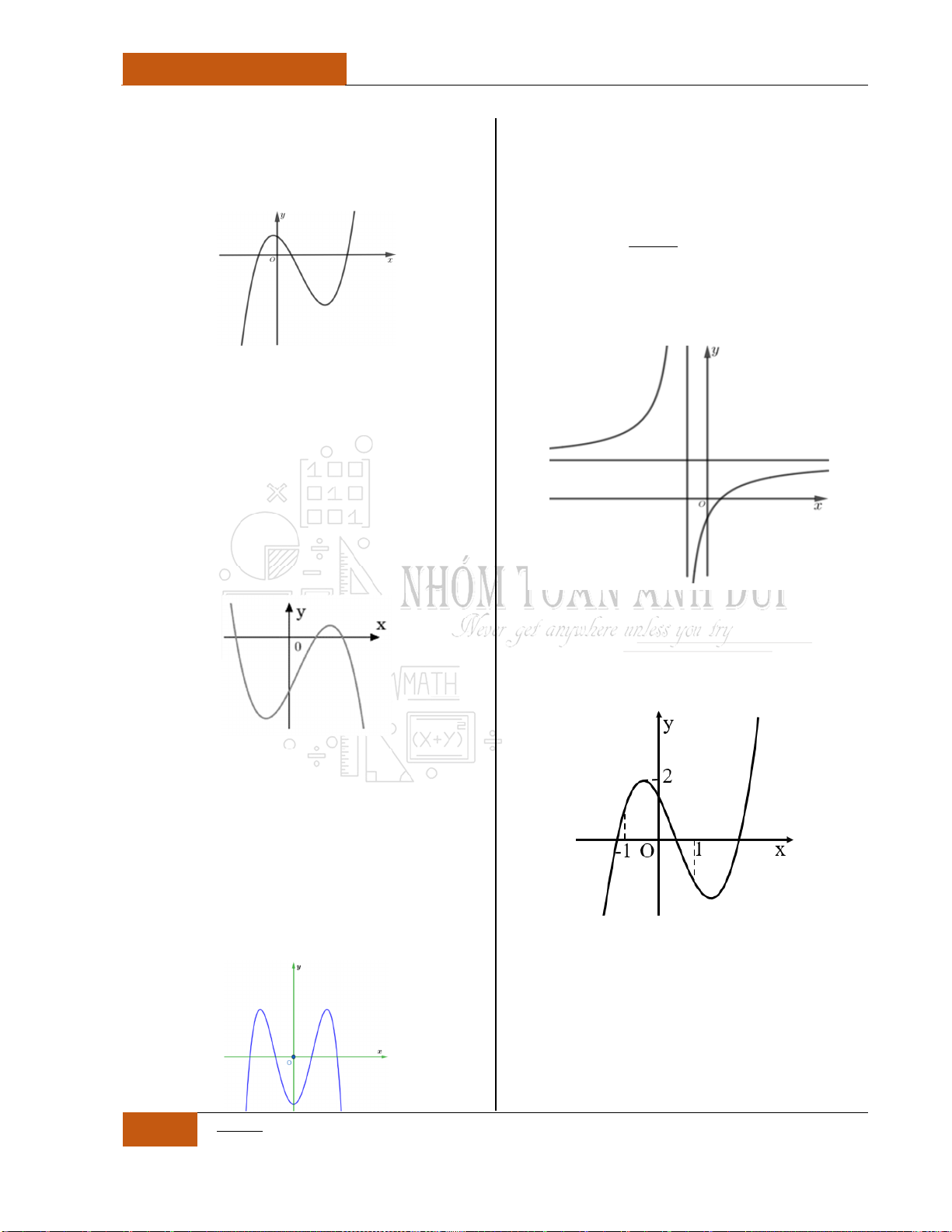
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

484

[ I can't, I can! ]

Câu 50. [Vận dụng cao].

Cho hàm số

3 2

   y ax bx cx d có đồ thị như

hình bên. Trong các mệnh đề sau mệnh đề nào

đúng?

A. 0, 0, 0  ab bc cd .

B.

0, 0, 0  ab bc cd

.

C. 0, 0, 0  ab bc cd .

D. 0, 0, 0  ab bc cd .

Câu 51. [Vận dụng].

Cho hàm số

3 2

   y ax bx cx d có đồ thị như

hình dưới. Khẳng định nào sau đây đúng ?

A. 0, 0, 0, 0   a b c d .

B. 0, 0, 0, 0   a b c d .

C.

0, 0, 0, 0   a b c d

.

D. 0, 0, 0, 0   a b c d .

Câu 52. [Vận dụng].

Cho hàm số có đồ thị như hình

vẽ. Mệnh đề nào dưới đây đúng ?

A. 0, 0, 0  a b c . B. 0, 0, 0  a b c .

C.

0, 0, 0

  

a b c

. D.

0, 0, 0

  

a b c

.

Câu 53. [Vận dụng].

Cho hàm số







ax b

y

cx d

có đồ thị như trong hình

bên dưới. Biết rằng

a

là số thực dương, hỏi trong

các số

, ,b c d

có tất cả bao nhiêu số dương?

A.

1

. B.

2

. C. 0 . D. 3.

Câu 54. [Vận dụng].

Hàm số

3 2

   y ax bx cx d có đồ thị như hình

vẽ bên dưới:

Khẳng định nào là đúng?

A. 0a , 0b , 0c , 0d .

B. 0a , 0b , 0c , 0d .

C. 0a , 0b , 0c , 0d .

D. 0a , 0b , 0c , 0d .

4 2

y ax bx c

  

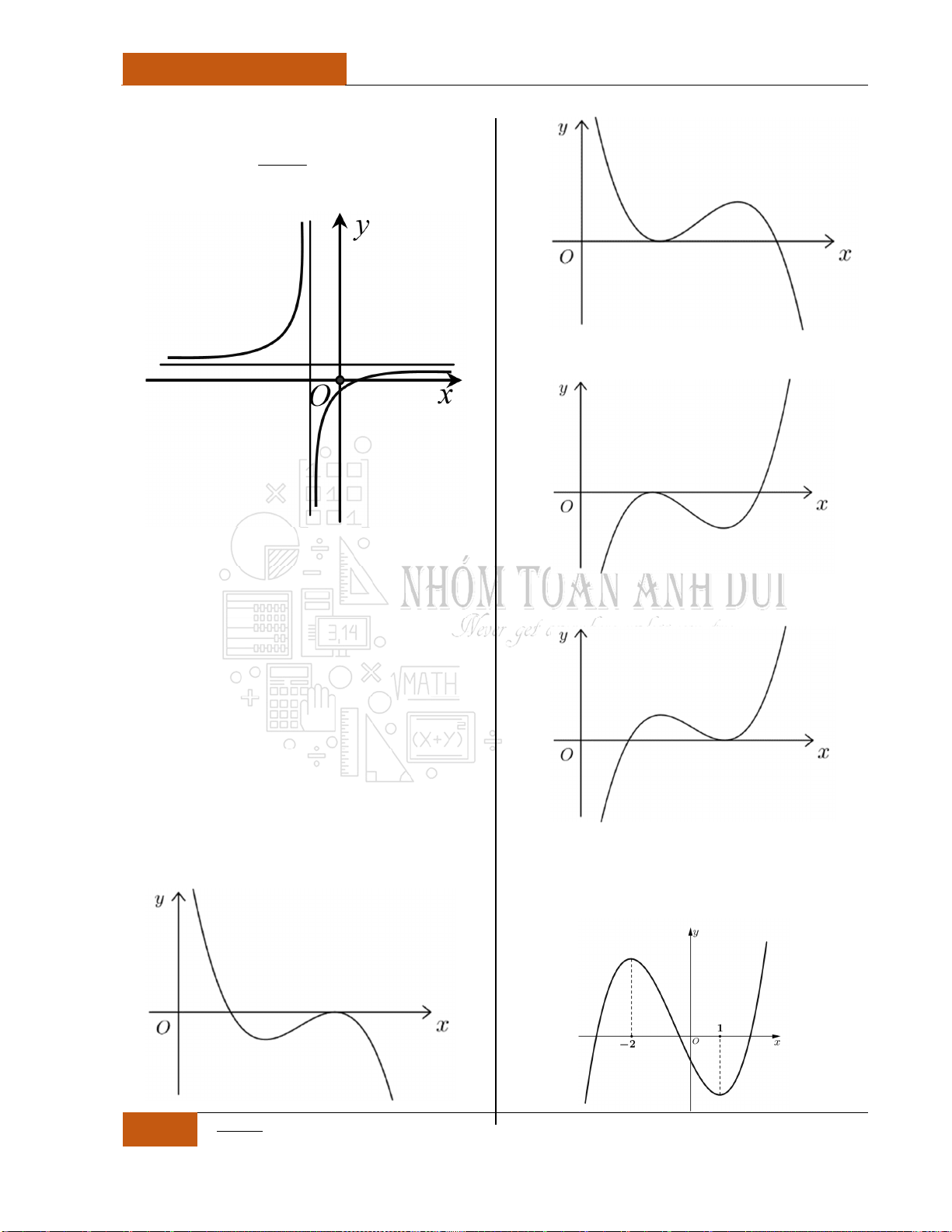
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

485

[ I can't, I can! ]

Câu 55. [Vận dụng].

Cho hàm số







ax b

y

cx d

có đồ thị như hình vẽ

bên.

Khẳng định nào sau đây là khẳng định đúng?

A.

0











ad

bc

. B.

0











ad

bc

.

C.

0











ad

bc

. D.

0











ad

bc

.

Câu 56. [Vận dụng].

Tìm đồ thị hàm số







y f x

được cho bởi một

trong các phương án dưới đây, biết

    

2

  

f x a x b x

với a b .

A. .

B. .

C. .

D. .

Câu 57. [Vận dụng].

Cho đường cong





3 2

:

   

C y ax bx cx d

có

đồ thị như hình bên.

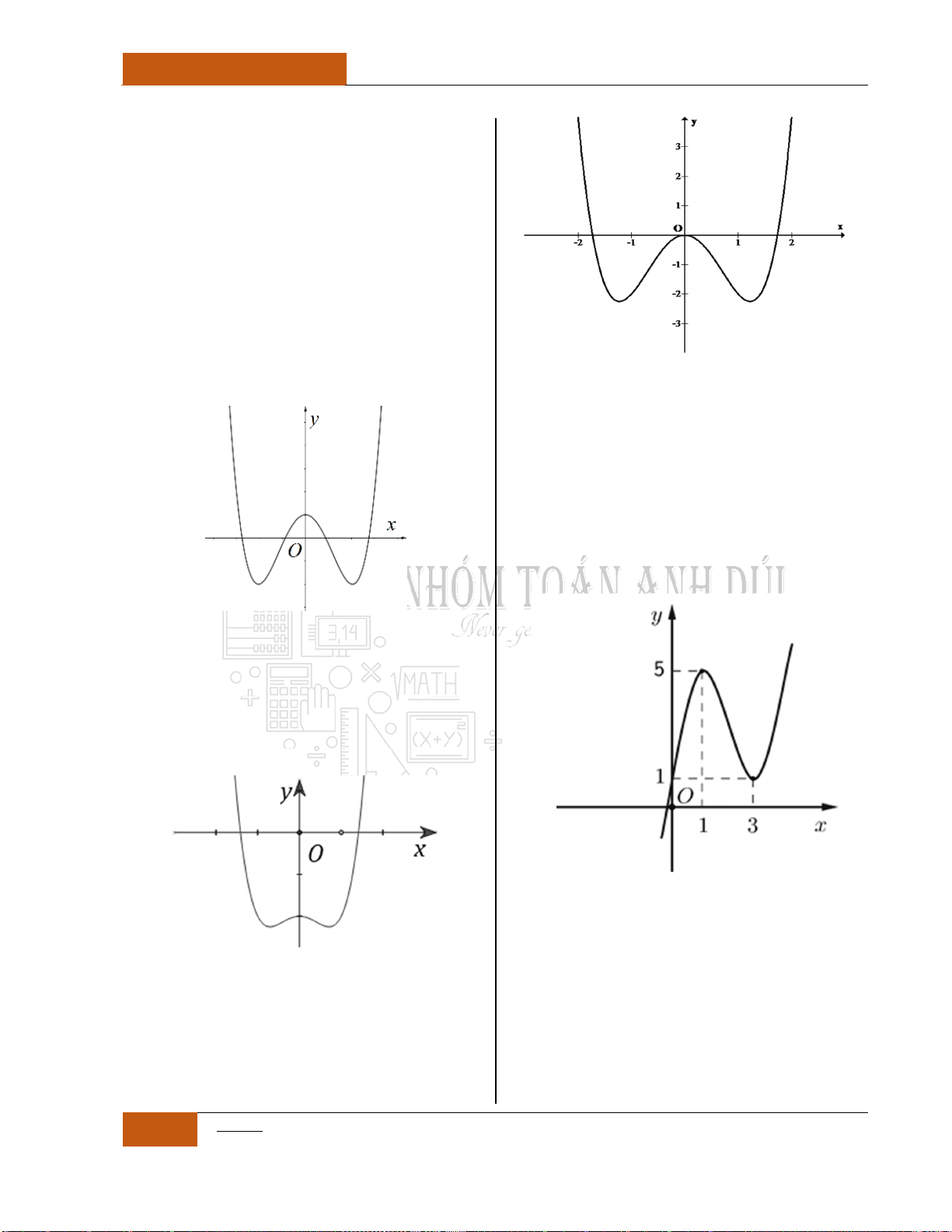
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

486

[ I can't, I can! ]

Khẳng định nào sau đây là đúng?

A. 0, 0, 0, 0   a b c d .

B. 0, 0, 0, 0   a b c d .

C. 0, 0, 0, 0   a b c d .

D. 0, 0, 0, 0   a b c d .

Câu 58. [Vận dụng].

Hàm số

4 2

  y ax bx c có đồ thị như hình vẽ

bên. Mệnh đề nào sau đây đúng?

A. 0a , 0b , 0c . B. 0a , 0b , 0c .

C. 0a , 0b , 0c . D. 0a , 0b , 0c .

Câu 59. [Vận dụng].

Cho hàm số

4 2

  y ax bx c có đồ thị như hình

vẽ. Tìm kết luận đúng

A. 0 a b . B. 0bc .

C. 0ab . D. 0ac .

Câu 60. [Vận dụng].

Cho hàm số

4 2

( 0)   y ax bx c a có đồ thị

như hình bên.

Hãy chọn mệnh đề đúng.

A. 0, 0, 0  a b c . B. 0, 0, 0  a b c .

C. 0, 0, 0  a b c . D. 0, 0, 0  a b c .

Câu 61. [Vận dụng].

Cho hàm số

 

3 2

    y f x ax bx cx d

có đồ

thị như hình vẽ ở bên.

Mệnh đề nào sau đây đúng?

A.

0a

,

0b

,

0c

,

0d

.

B.

0a

,

0b

,

0c

,

0d

.

C.

0a

,

0b

,

0c

,

0d

.

D.

0a

, 0b ,

0c

, 0d .

Câu 62. [Vận dụng].

Cho hàm số bậc bốn trùng phương

4 2

  y ax bx c có đồ thị như hình vẽ bên.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

487

[ I can't, I can! ]

Mệnh đề nào dưới đây là đúng?

A. 0, 0, 0  a b c . B. 0, 0, 0  a b c .

C. 0, 0, 0  a b c . D. 0, 0, 0  a b c .

Câu 63. [Vận dụng].

Cho hàm số

4 2

  y ax bx c có đồ thị như hình

vẽ bên. Hỏi khẳng định nào sau đây đúng?

A. 0, 0, 0  a b c . B. 0, 0, 0  a b c .

C. 0, 0, 0  a b c . D. 0, 0, 0  a b c .

Câu 64. [Vận dụng].

Cho hàm số

3







ax

y

x c

có đồ thị như hình vẽ

bên. Tính giá trị của

2 .a c

A. 2 3. a c B. 2 3.  a c

C.

2 1.  a c

D.

2 2.  a c

Câu 65. [Vận dụng].

Hình vẽ bên là đồ thị hàm số







ax b

y

cx d

.

Mệnh đề nào dưới đây đúng?

A. 0ad và 0bd . B. 0ad và 0ab .

C. 0bd và 0ab . D. 0ad và 0ab .

Câu 66. [Vận dụng].

Cho hàm số

1







ax b

y

x

có đồ thị như hình vẽ

dưới đây:

Khẳng định nào sau đây đúng?

A.

0 b a

. B.

0 a b

.

C.

b a

và

0a

. D.

0 a b

.

Câu 67. [Vận dụng].

Đồ thị trong hình bên dưới là của hàm số







ax b

y

x c

(với

, , a b c

).

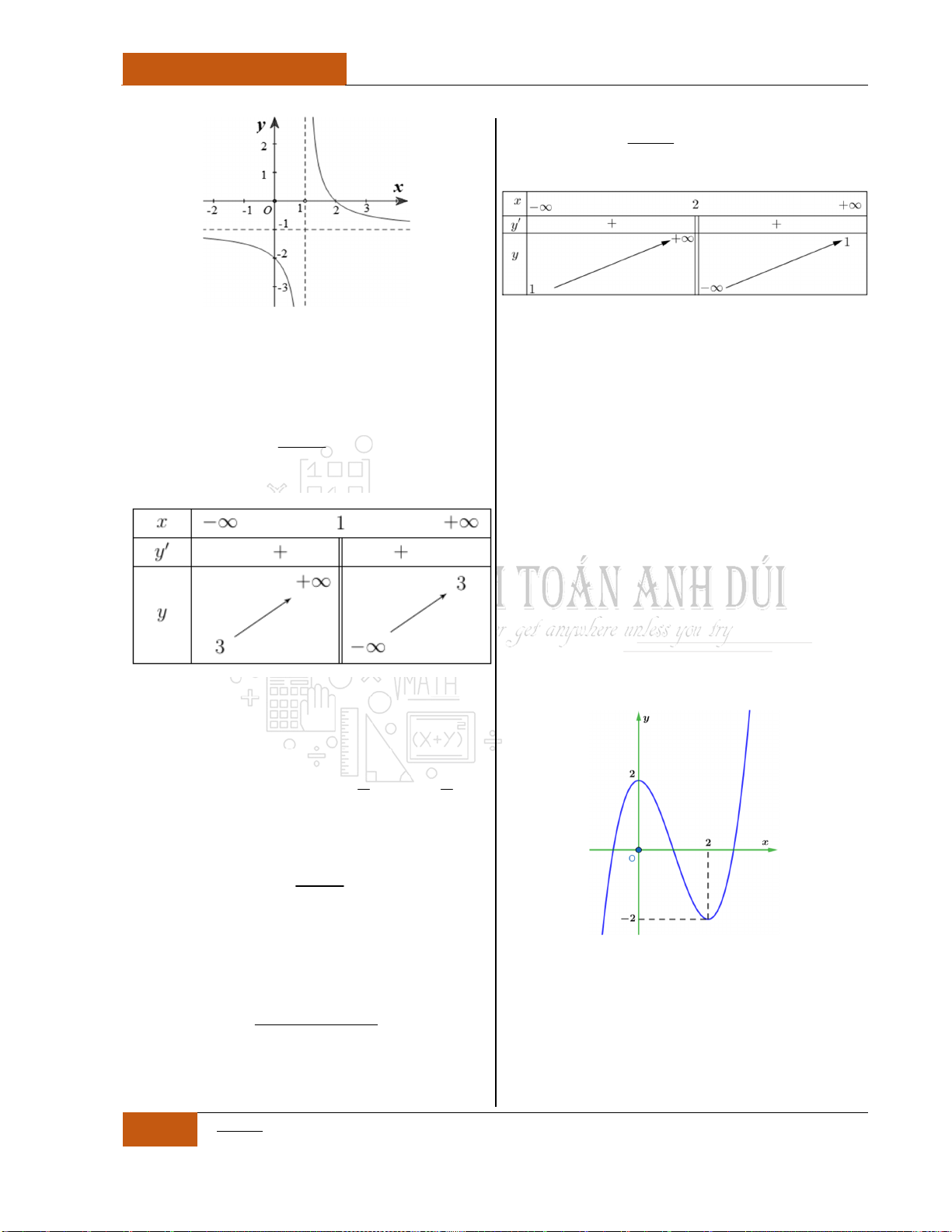
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

488

[ I can't, I can! ]

Khi đó tổng

 a b c

bằng?

A. 1 . B. 1. C. 2 . D.

0

.

Câu 68. [Vận dụng].

Cho hàm số

 

2 





ax

f x

bx c

 

, , , 0 a b c b

có

bảng biến thiên như sau:

Tổng các số

 

2

 a b c

thuộc khoảng nào sau

đây

A.

 

1;2 . B.

 

2;3 . C.

4

0;

9

 

 

 

. D.

4

;1

9

 

 

 

.

Câu 69. [Vận dụng].

Cho hàm số

 







ax b

f x

cx d

( , , , a b c d  và

0c

). Biết rằng đồ thị hàm số đã cho đi qua

điểm





1;7

 và giao điểm hai tiệm cận là

 

2;3 .

Giá trị biểu thức

2 3 4

7

  a b c d

c

bằng?

A.

7

. B. 4 . C.

6

. D.

5

.

Câu 70. [Vận dụng].

Cho hàm số

1





ax

y

bx c

(

, ,a b c

là các tham số) có

bảng biến thiên như hình vẽ

Xét các phát biểu sau:

   

1 : 1; 2 : 0;c a b  

   

3 : 0; 4 : 0a b c a    .

Số phát biểu đúng là?

A.

1

. B.

2

. C. 3 . D.

4

.

Câu 71. [Vận dụng].

Ta xác định được các số , ,a b c để đồ thị hàm số

3 2

   y x ax bx c đi qua điểm

 

1;0 và có

điểm cực trị





2;0

 .

Tính giá trị biểu thức

2 2 2

  T a b c .

A. 25. B. 1. C. 7. D. 14.

Câu 72. [Vận dụng].

Cho hàm số có đồ thị như

hình vẽ. Tính ?

A. . B. .

C. . D. .

Câu 73. [Vận dụng].

Cho hàm số

3 2

   y ax bx cx d có đồ thị như

hình vẽ bên. Mệnh đề nào dưới đây đúng?

3 2

y ax bx cx d

   

S a b

 

2

S

 

0

S



1

S



1

S

 

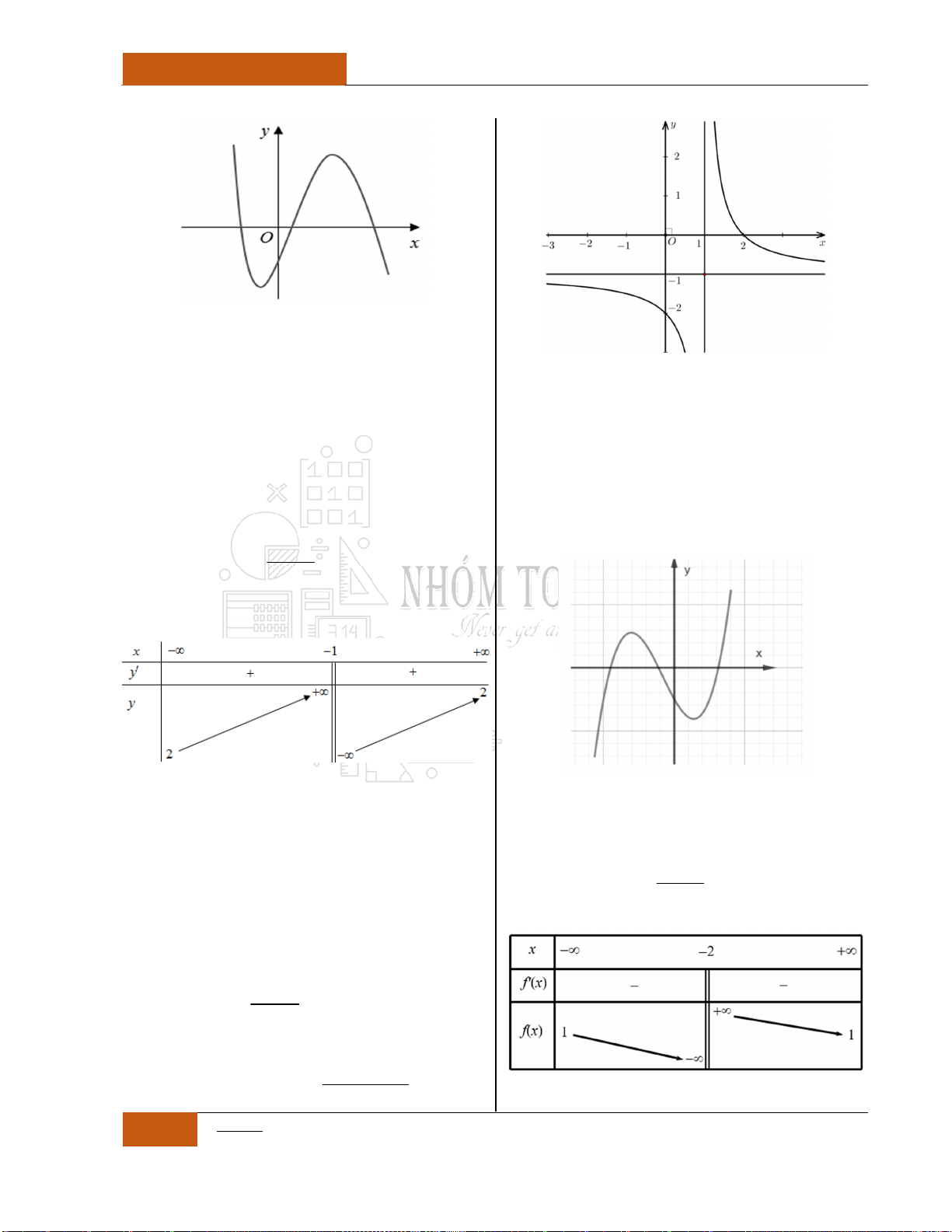
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

489

[ I can't, I can! ]

A.

0, 0, 0, 0   a b c d

.

B. 0, 0, 0, 0   a b c d .

C.

0, 0, 0, 0   a b c d

.

D. 0, 0, 0, 0   a b c d .

Câu 74. [Vận dụng].

Cho hàm số

 

, ,

1



 





ax b

y a b c

cx

có bảng

biến thiên như sau:

Tập các giá trị b là tập nghiệm của bất phương

trình nào dưới đây?

A.

3

8 0. b

B.

2

4 0.  b

C.

2

3 2 0.  b b D.

3

8 0. b

Câu 75. [Vận dụng].

Cho hàm số







ax b

y

cx d

(với , , ,a b c d là số thực)

có đồ thị như hình dưới đây.

Tính giá trị biểu thức

2 3 



a b d

T

c

.

A.

6T

. B.

0T

.

C.

8 T

. D. 2T .

Câu 76. [Vận dụng].

Cho hàm số

3 2

   y ax bx cx d có đồ thị như

hình vẽ. Trong các số

, ,

a b c

và d có bao nhiêu

số dương?

A. 1. B. 4 . C.

3

. D. 2 .

Câu 77. [Vận dụng].

Cho hàm số

 

6





ax

f x

bx c

 

, ,  a b c có bảng

biến thiên như sau:

Trong các số

, ,

a b c

có bao nhiêu số âm?

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

490

[ I can't, I can! ]

A. 0 . B. 3. C.

1

. D.

2

.

Câu 78. [Vận dụng].

Cho hàm số

3 2

3 2  y x x

có đồ thị như hình

1. Đồ thị hình 2 là của hàm số nào dưới đây?

A.

3 2

3 2 .  y x x

B.

3

2

3 2  y x x .

C.

 

2

1 2 2 .   y x x x

D.

 

2

1 2 2 .   y x x x

Câu 79. [Vận dụng].

Hàm số

 

2

2 1  y x x

có đồ thị như hình vẽ

bên dưới.

Hình nào dưới đây là đồ thị của hàm số

 

2

2 1  y x x

?

A. Hình 1. B. Hình 2.

C. Hình 3. D. Hình 4.

Câu 80. [Vận dụng cao].

Cho hàm số

 

y f x có đồ thị hàm số







y f x

như hình vẽ.

Chọn kết luận đúng trong các kết luận sau:

A.

 

3 2

4 4    f x x x x .

B.

 

3 2

4 4   f x x x x

.

C.

 

3 2

4 4    f x x x x .

D.

 

3 2

4 4.   f x x x x

Câu 81. [Vận dụng cao].

Biết phương trình

3 2

0   ax bx cx d

 

0a

có đúng hai nghiệm thực.

Hỏi đồ thị hàm số

3 2

   y ax bx cx d có bao

nhiêu điểm cực trị?

A.

4

. B. 5 . C.

2

. D. 3.

Câu 82. [Vận dụng].

Cho hàm số

 

2

2 1  y x x

có đồ thị như

hình vẽ

Một trong bốn hình dưới đây là đồ thị của hàm

số

 

2

2 1  y x x . Hỏi đó là hình nào?

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

491

[ I can't, I can! ]

A. Hình 2. B. Hình 4.

C. Hình 3. D. Hình 1.

Câu 83. [Vận dụng].

Cho hàm số

3 2

3 2  y x x

có đồ thị như hình

1. Đồ thị hình 2 là của hàm số nào dưới đây?

A.

3 2

3 2 .  y x x

B.

3

2

3 2  y x x

C.

 

2

1 2 2 .   y x x x

D.

 

2

1 2 2 .   y x x x

Câu 84. [Vận dụng].

Cho hàm số

1

2 1

 





x

y

x

có đồ thị như hình 1. Đồ

thị hình 2 là của hàm số nào dưới đây?

A.

1

2 1

 





x

y

x

. B.

1

2 1







x

y

x

.

C.

1

2 1

 





x

y

x

. D.

1

2 1

 





x

y

x

.

Câu 85. [Vận dụng].

Cho hàm số

3 2

6 9  y x x x có đồ thị như

Hình 1. Khi đó đồ thị Hình 2 là của hàm số nào

dưới đây?

A.

3 2

6 9   y x x x .

B.

3 2

6 9  y x x x

.

C.

3

2

6 9  y x x x

.

D.

3 2

6 9  y x x x

.

Câu 86. [Vận dụng].

Cho hàm số

2 1





x

y

x

có đồ thị như Hình 1. Đồ

thị Hình 2 là của hàm số nào trong các đáp án A,

B, C, D dưới đây?

A.

2 1





x

y

x

. B.

2 1





x

y

x

.

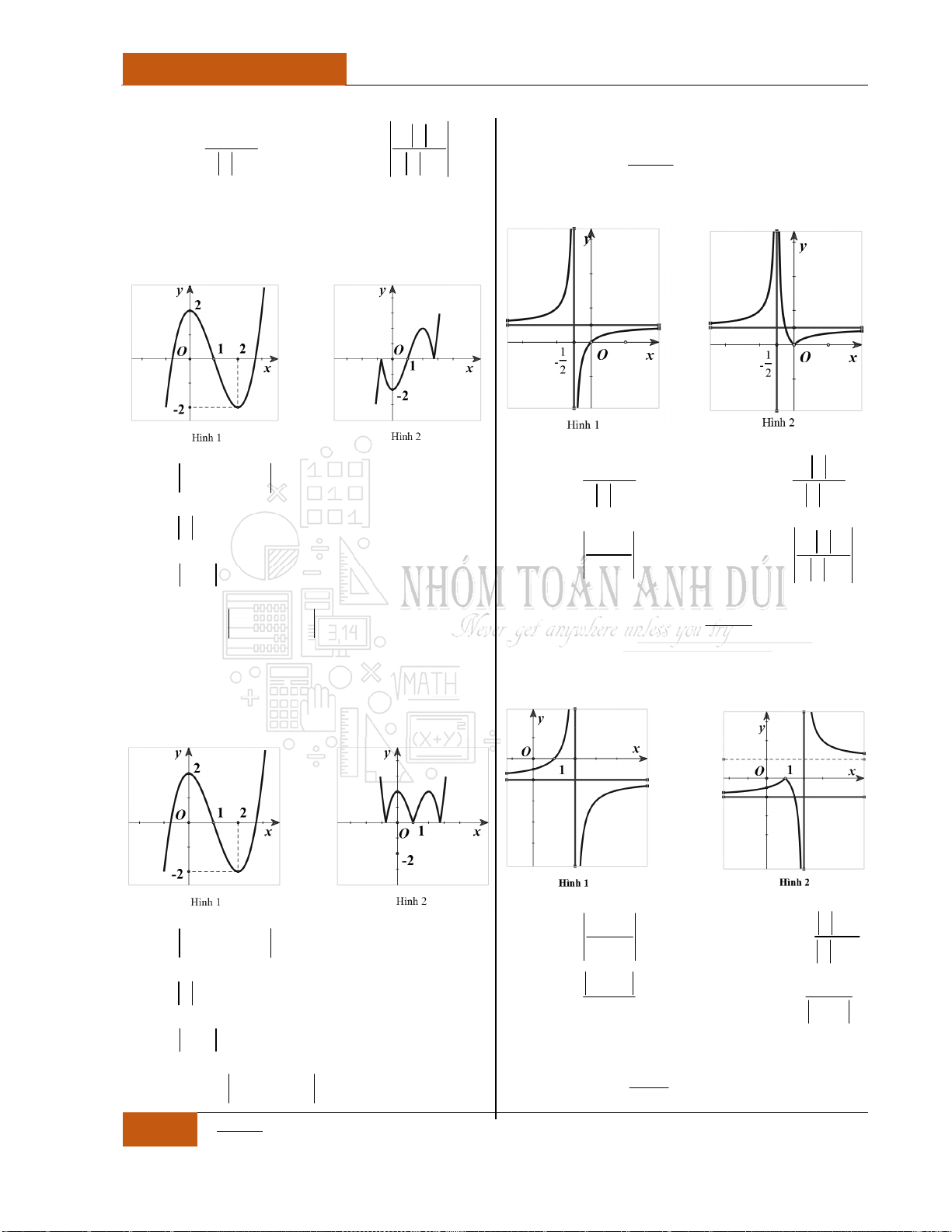
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

492

[ I can't, I can! ]

C.

2 1





x

y

x

. D.

2 1





x

y

x

.

Câu 87. [Vận dụng].

Cho hàm số

3 2

3 2  y x x

có đồ thị như hình

1. Đồ thị hình 2 là của hàm số nào dưới đây?

A.

3 2

3 2 .  y x x

B.

3

2

3 2  y x x

.

C.

 

2

1 2 2 .   y x x x

D.

 

2

1 2 2 .   y x x x

Câu 88. [Vận dụng].

Cho hàm số

3 2

3 2  y x x

có đồ thị như hình

1. Đồ thị hình 2 là của hàm số nào dưới đây?

A.

3 2

3 2 .  y x x

B.

3

2

3 2  y x x

.

C.

 

2

1 2 2 .   y x x x

D.

 

2

1 2 2 .   y x x x

Câu 89. [Vận dụng].

Cho hàm số

2 1





x

y

x

có đồ thị như hình 1. Đồ

thị hình 2 là của hàm số nào dưới đây?

A.

2 1





x

y

x

. B.

2 1





x

y

x

.

C.

2 1





x

y

x

. D.

2 1





x

y

x

.

Câu 90. Cho hàm số

1

2

 





x

y

x

có đồ thị như

hình 1. Đồ thị hình 2 là của hàm số nào dưới

đây?

A.

1

.

2

 





x

y

x

B.

1

.

2







x

y

x

C.

1

2

 





x

y

x

. D.

1

2

 





x

y

x

.

Câu 91. [Vận dụng].

Cho hàm số

1

2







x

y

x

có đồ thị như hình 1.

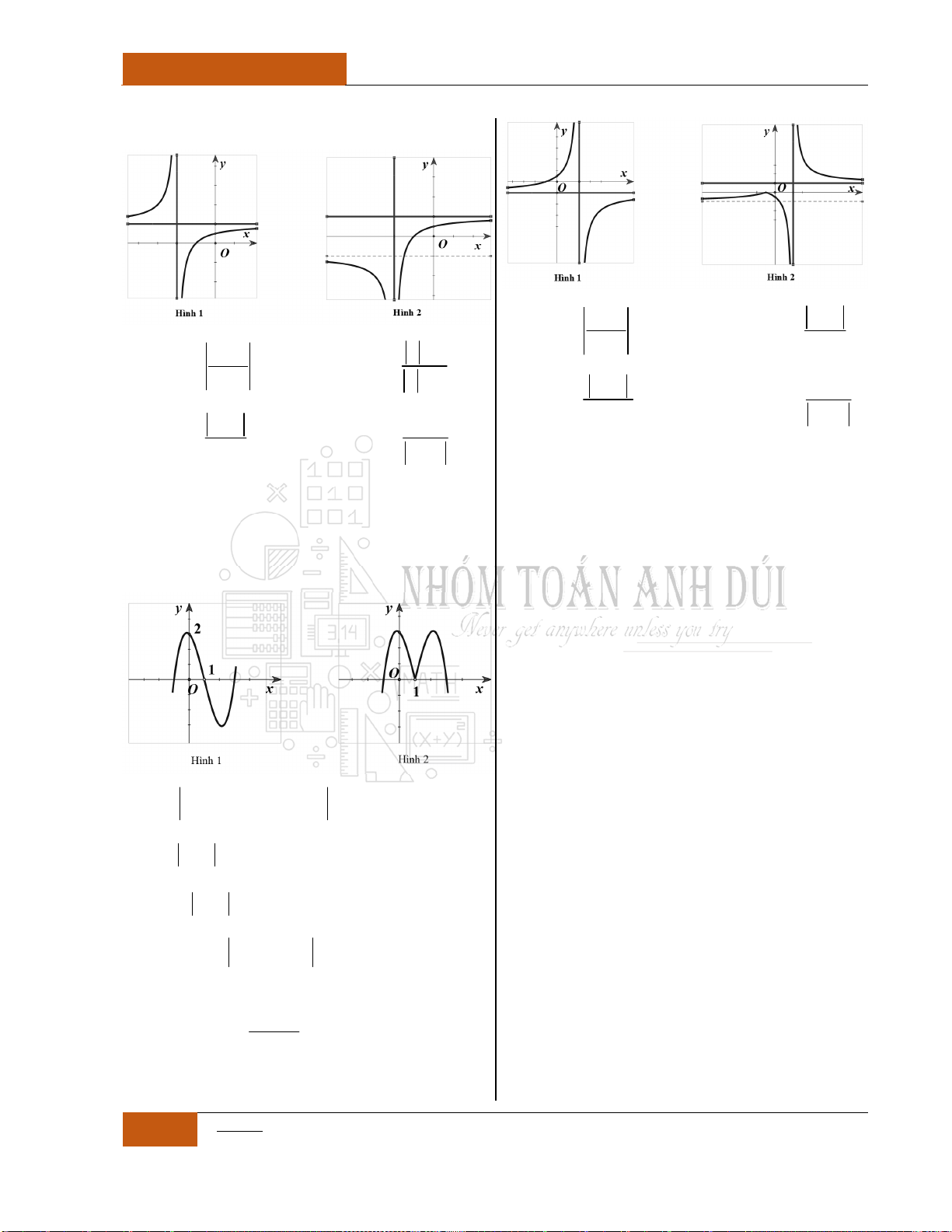
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

493

[ I can't, I can! ]

Đồ thị hình 2 là của hàm số nào dưới đây?

A.

1

.

2







x

y

x

B.

1

.

2







x

y

x

C.

1

.

2







x

y

x

D.

1

.

2







x

y

x

Câu 92. [Vận dụng].

Cho hàm số

 

2

1 2 3   y x x x

có đồ thị

như hình 1. Đồ thị hình 2 là của hàm số nào dưới

đây?

A.

 

2

1 2 3 .   y x x x

B.

 

2

1 2 3 .   y x x x

C.

 

2

1 2 3    y x x x

.

D.

 

2

1 2 3   y x x x

.

Câu 93. [Vận dụng].

Cho hàm số

1

2





 

x

y

x

có đồ thị như hình 1. Đồ

thị hình 2 là của hàm số nào dưới đây?

A.

1

.

2







x

y

x

B.

1

.

2







x

y

x

C.

1

.

2





 

x

y

x

D.

1

.

2







x

y

x

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

494

[ I can't, I can! ]

ĐÁP ÁN

0 1 2 3 4 5 6 7 8 9

0

A A C A D A B D D

1

A C D B B B C A A C

2

D A C A A C C C C B

3

A D D C C C C C D C

4

A D A B C D D A D D

5

A D C B D C A D C B

6

C C C A A B A D C C

7

B A A D D C D D C A

8

A D C B B C A D A C

9

C D C B

Ghi chú: Đáp án là sự kết hợp giữa dòng

i

và cột

j

. Ví dụ: Câu 23A (giao của dòng 2 và cột 3).

i

j

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

495

[ I can't, I can! ]

LỜI GIẢI CHI TIẾT

Câu 1. Từ hình dạng của đồ thị (đồ thị hàm bậc

bốn trùng phương) ta loại phương án C và D.

Nhận thấy lim ( )



 

x

f x suy ra hệ số của

4

x

âm nên chọn phương án A.

Đáp án A.

Câu 2. Đường cong có dạng của đồ thị hàm số

bậc 3 với hệ số 0a nên chỉ có hàm số

3

3 y x x thỏa yêu cầu bài toán.

Đáp án A.

Câu 3. Từ hình có đây là hình dạng của đồ thị

hàm bậc 4.

   

lim lim 0

 

    

x x

f x f x a .

Đáp án C.

Câu 4. Đường cong trong hình là đồ thị hàm

trùng phương có hệ số

.

Đáp án A.

Câu 5. Từ đồ thị hàm số ta có số nghiệm thực

của phương trình

 

1f x là

3

.

Đáp án D.

Câu 6. Dựa vào hình vẽ, ta thấy đồ thị hàm số có

ba điểm cực trị nên loại các đáp án B và C.

Mặt khác, ta thấy

 

4 2

lim 2 1



   

x

x x nên

chọn đáp án A.

Đáp án A.

Câu 7. Qua đồ thị là hàm bậc 3 nên loại A, D.

Bên phải ngoài cùng của đồ thị đi xuống nên hệ

số a < 0



Loại đáp án C.

Đáp án B.

Câu 8. Đồ thị hình vẽ là đồ thị hàm số bậc ba

có hệ số 0a nên chỉ có hàm số

3

3 2  y x x thỏa mãn điều kiện trên.

Đáp án D.

Câu 9. Dựa vào đồ thị có dạng đồ thị của hàm

số bậc

3

có hệ số

0a

nên đáp án D đúng.

Đáp án D.

Câu 10. Dựa vào đồ thị hàm số, ta thấy ngay

đây là dạng của đồ thị hàm số hàm bậc

3



Loại đáp án B, C.

Hàm số có xu hướng đi lên khi x dần đến một

giá trị đủ lớn 

0a

.

Đáp án A.

Câu 11. Đây là đồ thị của hàm số bậc ba với hệ

số

0a

nên chọn C.

Đáp án C.

Câu 12. Dựa vào hình vẽ suy ra hàm số đã cho

có

3

cực trị



loại A, C.

Mặt khác nhánh bên tay phải của đồ thị hàm số

đi lên suy ra hệ số 0a  Chọn D.

Đáp án D.

Câu 13. Vì từ đồ thị ta suy ra đồ thị của hàm

phân thức có tiệm cận đứng và ngang

1; 1 x y .

Đáp án B.

Câu 14. Dựa vào đồ thị ta thấy đây là hình ảnh

đồ thị của hàm số bậc ba nên loại đáp án C và

4 2

y ax bx c

  





0

a



0

a



Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

496

[ I can't, I can! ]

D; Mặt khác dựa vào đồ thị ta có lim



 

x

y

nên hệ số của

3

x

dương nên ta chọn đáp án

3 2

3 3

  

y x x .

Đáp án B.

Câu 15. Quan sát đồ thị ta thấy đây là đồ thị của

hàm số





4 2

0

   

y ax bx c a .

Vậy chọn B.

Đáp án B.

Câu 16. Dựa vào đồ thị suy ra tiệm cận đứng

1

 

x

loại A, D.

Đồ thị hàm số giao với trục hoành có hoành độ

dương suy ra chọn C.

Đáp án C.

Câu 17. Từ đồ thị:

lim



 

x

y

và đây là đồ thị

hàm bậc ba nên ta chọn phương án

3

3 1.

  

y x x

Đáp án A.

Câu 18. Dạng hàm bậc ba nên loại C, D.

Từ đồ thị ta có

0



a

. Do đó loại B.

Đáp án A.

Câu 19. Ta có một số nhận xét sau:

+ Nhìn đồ thị khẳng định đồ thị hàm trùng

phương loại A, B.

+ lim



 

x

y nên chọn C.

Đáp án C.

Câu 20. Dạng đồ thị hình bên là đồ thị hàm số

trùng phương

4 2

  

y ax bx c

có hệ số

0



a

.

Do đó, chỉ có đồ thị ở đáp án D là thỏa mãn.

Đáp án D.

Câu 21. Trong bốn hàm số đã cho thì chỉ có

hàm số

3

3 1

   

y x x

(hàm số đa thức bậc ba

với hệ số

0



a

) có dạng đồ thị như đường cong

trong hình.

Đáp án A.

Câu 22. Dựa trên hình dáng đồ thị, ta loại

4 2

2

   

y x x và

4 2

2

  

y x x .

Mặt khác từ đồ thị, ta thấy lim



 

x

y nên loại

3 2

  

y x x .

Đáp án C.

Câu 23. Đồ thị hàm số là đồ thị của hàm số bậc

ba nên loại B và D.

Đồ thi hàm số bậc ba có hệ số

0



a

nên A

đúng.

Đáp án A.

Câu 24. Đây là hình dáng của đồ thị hàm bậc

bốn trùng phương có hệ số

0



a

.

Đáp án A.

Câu 25. Đồ thị hàm số trên là đồ thị hàm trùng

phương có 3 cực trị và có

0



a

.

Đáp án C.

Câu 26. Dựa vào hình dáng của đồ thị ta được:

+ Điều kiện:

1



x

.

+ Đây là đồ thị của hàm nghịch biến.

Từ đó ta được

0, 1.



  

y x

Đáp án C.

Câu 27. Dựa vào đồ thị ta nhận thấy tiệm cận

đứng bằng

2

và hàm số nghịch biến vậy chọn

C.

Đáp án C.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

497

[ I can't, I can! ]

Câu 28. Dựa vào đồ thị, ta có: lim



 

x

y ,

loại phương án D.

Xét phương án A, có:

2

3 2 0,



    



y x x

,

hàm số không có cực tri, loại phương án A.

Xét phương án B, có:

2

3 6



 

y x x

và



y

đổi

dấu khi đi qua các điểm

0, 2

 

x x

nên hàm

số đạt cực tri tại

0



x

và

2



x

, loại phương án

B.

Vậy phương án đúng là C.

Đáp án C.

Câu 29. Đồ thị hàm số cắt trục Oy tai điểm có

tọa độ









0 0

0; , 0; 2

y y

nên chọn phương án

B.

Đáp án B.

Câu 30. Hình vẽ trên là đồ thị của hàm số dạng

 

0; 0



    



ax b

y c ad bc

cx d

Loại phương

án C, D.

Ta thấy: Đồ thị có đường tiệm cận đứng là

1

 

x

và đường tiệm cận ngang là

1



y

.

Phương án B: Đồ thị có đường tiệm cận đứng

là

2

  

x

loại B.



A đúng.

Đáp án A.

Câu 31. Đồ thị đã cho có hình dạng của đồ thị

hàm số bậc ba

3 2

   

y ax bx cx d

nên loại

phương án B và C.

Dựa vào đồ thị, ta có:

lim 0



   

x

y a nên

loại phương án D.

Đáp án D.

Câu 32. Ta có: lim



  

x

đồ thị nhánh ngoài

cùng của hàm số hướng đi xuống nên hệ số

0



a

.

Giao điểm của đồ thị hàm số với trục tung

: 0



Oy x

là điểm nằm bên dưới trục hoành nên

khi

0 0

   

x y d .

Đáp án D.

Câu 33. Hàm số

 

1







ax

f x

bx c

có đường tiệm

cận đứng là đường thẳng

 

c

x

b

và đường

tiệm cận ngang là đường thẳng



a

y

b

.

Từ bảng biến thiên ta có:

2

1



 



   











c

b

a b

a

b





1

Mặt khác:

 

2

'







ac b

f x

bx c

.

Vì hàm số đã cho đồng biến trên các khoảng





;2



và





2;



nên

 

2

' 0 0



    



ac b

f x ac b

bx c





2

Thay





1

vào





2

, ta được:

2

0 0 0 1

2 2

         

c c

c c c

.

Suy ra

c

là số dương và

,

a b

là số âm.

Đáp án C.

Câu 34. Ta có:

lim



 

x

y



0



a

.

Gọi

1

x

,

2

x

là hoành độ hai điểm cực trị của

hàm số suy ra

1

x

,

2

x

nghiệm phương trình

2

3 2 0



   

y ax bx c

nên theo Định lý Vietè:

+) Tổng hai nghiệm

1 2

2

0

3

   

b

x x

a

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

498

[ I can't, I can! ]



0



b

a



0



b .

+) Tích hai nghiệm

1 2

0

3

 

c

x x

a



0



c

.

Lại có đồ thị hàm số cắt trục tung tại điểm có

tung độ dương nên

0



d

.

Vậy có

2

số dương trong các số

a

,

b

,

c

,

d

.

Đáp án C.

Câu 35. Ta có:





lim 0



   

x

f x a

.

Đồ thị hàm số có hai điểm cực trị nằm cùng

phía của trục tung nên

0 0

  

ac c

.

Đồ thị hàm số có điểm uốn nằm bên phải trục

tung nên

0 0

  

ab b .

Đồ thị hàm số cắt trục tung ở dưới trục hoành

0

 

d

.

Đáp án C.

Câu 36. Ta có:

2

3 2



  

y ax bx c

. Dựa vào đồ

thị ta thấy

0



a

.

Hàm số có 2 cực trị âm nên:

2

9 0

0

2

0 0

0

3

0

3







 



 







 

     

  





 



 



 



y

b ac

b

S

c

a

P

c

a

.

Đồ thị cắt trục

Oy

tại điểm





0;

d

nên

0



d

.

Vậy có đúng một số dương trong các số

, , ,

a b c d

.

Đáp án C.

Câu 37. Ta có:

2

3 2



  

y ax bx c

.

Dựa vào đồ thị ta thấy

0



a

.

Hàm số có 2 cực trị âm nên

2

9 0

0

2

0 0

0

3

0

3







 



 











    

  





 













y

b ac

b

S

c

a

P

c

a

.

Đồ thị cắt trục

Oy

tại điểm





0;

d

nên

0



d

.

Vậy có đúng

1

số dương trong các số

, , ,

a b c d

.

Đáp án C.

Câu 38. Từ dáng điệu sự biến thiên hàm số ta

có

0.



a

Khi

0



x

thì

1 0

  

y d

.

Mặt khác:





2

3 2



  

f x ax bx c

. Từ bảng biến

thiên ta có

 

2

0

 





 







x

f x

x

.

Từ đó suy ra

2

0; 2 3 0

3



     

b

c b a

a

.

Vậy có 3 số dương là

, ,

a b d

.

Đáp án D.

Câu 39. Một số nhận xét:







lim 0.



   

x

f x a







0 1 1 0.

     

f d







2

3 2 .



  

f x ax bx c

Ta có:

1 2

2

3 0

3

.

0 0

0

3



  



  

 





 

  

 











b

x x

b a

a

x x c c

a

Có

2

số dương là

,

a b

.

Đáp án C.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

499

[ I can't, I can! ]

Câu 40. Từ bảng biến thiên, ta có:

 

1

0 3

3

4

4 5

64 16 4 5 3

2

0

0 0

0

48 8 0

4 0

3





 









 

    



 

 

 

  







  



  

  















a

f

d

f

a b c d

b

c

f

c

a b c

f

d

.

Vậy trong các số

, , ,

a b c d

có

2

số dương.

Đáp án A.

Câu 41. Ta có:





3 2

f x ax bx cx d

   





, , ,a b c d 







2

3 2



   

f x ax bx c

.

Đồ thị hàm số





f x

có

2

điểm cực trị





0; 1 ,

A







4; 5

B



nên ta có hệ:





 

0 1

4 5

0 0

4 0

f



 



 

















1

8

64 16 4 5

3

4

0

48 8 0

1

a

d

a b c d

b

c

a b c

d







 





    

 

 

 

 



 



 

  





 



.

Trong các số

, , ,

a b c d

có

1

số dương.

Đáp án D.

Câu 42. Dựa vào đồ thị suy ra hệ số

0



a



loại phương án C.

2

3 2 0



   

y ax bx c có

2

nghiệm

1 2

,

x x

trái

dấu (do hai điểm cực trị của đồ thị hàm số nằm

hai phía với

Oy

)

3 . 0 0

   

a c c



loại

phương án D.

Do









0; 0.

   

C Oy D d d

Dễ thấy:

1 2

2

0 0 0

3

b

x x ab

a

      





0 Do : 0

b a

  

.

Đáp án A.

Câu 43. Đồ thị trên có hình dạng hàm bậc bốn

trùng phương có hai điểm cực tiểu và một điểm

cực đại nên

0, 0

 

a b .

Giá trị cực đại nhỏ hơn

0

(giao điểm với trục

tung nằm bên dưới trục hoành) nên

0



c

.

Đáp án B.

Câu 44. Theo đồ thị, ta có:

Tiệm cận ngang:

0

 

a

y

c





1

Tiệm cận đứng:

0 0

    

d d

x

c c





2

0 0 0

      

b b

y x

a a





3

.

Mặt khác, giao điểm của đồ thị hàm số nằm bên

dưới trục hoành, hay

 

0 4



b

d

.

Lấy





 

1

2

theo từng vế, ta được:

: 0 0 0

    

a d a

ad

c c d

.

Lấy









1 . 3

theo từng vế, ta được:

. 0 0 0

    

a b b

bc

c a c

.

Đáp án C.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

500

[ I can't, I can! ]

Câu 45. Dựa vào đồ thị ta có

0



a

, đồ thị cắt

Oy

tại

1

điểm có tung độ dương nên

0



d

, đồ

thị có

2

cực trị trái dấu nên

1 2

. 0

x x



.

0 0

c

a

   

.

Dễ thấy:

1 2

2

0 0 0

3

b

x x ab

a

      





0 Do : 0

b a

  

.

Vậy đáp án D.

Đáp án D.

Câu 46. Theo bài ra, đường tiệm cận đứng của

đồ thị hàm số là

.

1

 



d

x

c

Đường tiệm cận ngang của đồ thị hàm số là:

1

.

1







a

y

c

Nhìn đồ thị ta thấy:

0

1

  



d

x

c

mà

0 1 0 1

     

d c c

.

1

0 1 0 1

1



      



a

y a a

c

.

Đồ thị cắt trục tung tại điểm có tung độ bằng

0 0

  

b

d

.

Đáp án D.

Câu 47. Đồ thị cắt trục tung tại điểm





0;

c

, từ

đồ thị suy ra

0



c

.

Mặt khác đồ thị hàm số có ba điểm cực trị nên

0





y có ba nghiệm phân biệt, hay





3 2

4 2 2 2 0



    

y ax bx x ax b

có ba

nghiệm phân biệt. Suy ra

,

a b

trái dấu.

Mà

0 0

  

a b

.

Đáp án A.

Câu 48. Một số nhận xét quan trọng:

+ Dựa vào hình dạng đồ thị ta khẳng định được

0



a

.

+ Đồ thị cắt trục

Oy

tại điểm có tọa độ





0;

d

.

Dựa vào đồ thị suy ra

0



d

.

+ Ta có:

2

3 2



  

y ax bx c

. Hàm số có hai điểm

cực trị

1

x

,

2

x





1 2



x x

trái dấu nên phương trình

0





y có hai nghiệm phân biệt

1

x

,

2

x

trái dấu.

Vì thế

3 . 0



a c

, nên suy ra

0



c

.

+ Mặt khác từ đồ thị ta thấy

1

2

1

 









x

nên

1 2

0

 

x x

.

Mà

1 2

2

3



 

b

x x

a

nên suy ra

2

0

3





b

a

0

 

b .

Vậy

0



a

,

0



b

,

0



c

,

0



d

.

Đáp án D.

Câu 49. Từ đồ thị hàm số, ta suy ra:

+) Đồ thị hàm số có tiệm cận đứng là đường

thẳng

1



x

, tiệm cận ngang là đường thẳng

1

 

y

.

+) Đồ thị hàm số đi qua các điểm





2;0

A

,





0; 2



B

.

Từ biểu thức hàm số







ax b

y

x c

(vì đồ thị hàm

số là đồ thị hàm nhất biến nên

0

 

ac b ), ta

suy ra:

+) Đồ thị hàm số có tiệm cận đứng là đường

thẳng

 

x c

, tiệm cận ngang là đường thẳng



y a

.

+) Đồ thị hàm số đi qua

;0

 



 

 

b

A

a

,

0;

 

 

 

b

B

c

.

Đối chiếu lại, ta suy ra

1

 

c

,

1

 

a

,

2



b

.

Vậy









2 3 1 2.2 3 1 0

        

T a b c

.

Đáp án D.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

501

[ I can't, I can! ]

Câu 50. Từ dáng điệu của đồ thị ta có ngay

được:

+)

lim ; lim 0

 

     

x x

y y a .

+) Đồ thị hàm số cắt trục tung tại một điểm có

tung độ dương nên

0



d .

Ta có:

2

' 3 2

  

y ax bx c

.

Mặt khác dựa vào đồ thị ta thấy phương trình

' 0



y

có hai nghiệm trái dấu và tổng hai

nghiệm này luôn dương nên

0

2

0

3













 



 







ac

c

b

a

(do

0



a

).

Do đó:

0, 0, 0

  

ab bc cd .

Đáp án A.

Câu 51. Một số nhận xét quan trọng:

- Dựa vào hình dáng của đồ thị suy ra hệ số

0



a

.

- Đồ thị cắt trục

Oy

tại điểm có tung độ âm nên

0



d

.

- Ta thấy đồ thị như hình vẽ có hai điểm cực trị,

hoành độ các điểm cực trị trái dấu suy ra phương

trình

2

3 2 0



   

y ax bx c

có

2

nghiệm

1 2

,

x x

trái dấu kéo theo

3 . 0 0

  

a c c

.

- Mặt khác

1 2

0 0

2 3



    

x x b

b

a

.

Đáp án D.

Câu 52. Một số nhận xét quan trọng:

- Dựa vào hình dạng đồ thị suy ra

0



a

.

- Hàm số có

3

điểm cực trị nên

0 0

  

ab b .

- Giao điểm với trục tung nằm dưới trục hoành

nên

0



c

.

Đáp án C.

Câu 53. Nhìn vào đồ thị ta thấy

 Tiệm cận ngang



a

y

c

nằm trên trục hoành

nên

0



c

(vì

0



a

).

 Tiệm cận đứng





d

x

c

nằm bên trái trục tung

nên

0.





d

c

Suy ra

0



d (vì

0



c

).

 Giao điểm của đồ thị và trục tung nằm bên

dưới trục hoành nên

0.



b

d

Suy ra

0



b

(vì

0



d

)

Vậy

0, 0

 

c d

.

Đáp án B.

Câu 54. Một số nhận xét quan trọng:

+) Dựa vào hình dạng đồ thị ta khẳng định được

0



a

.

+) Đồ thị cắt trục

Oy

tại điểm có tọa độ





0;

d

.

Dựa vào đồ thị suy ra

0



d

.

+) Ta có:

2

3 2



  

y ax bx c

.

Hàm số có hai điểm cực trị

1

x

,

2

x





1 2



x x

trái

dấu nên phương trình

0





y

có hai nghiệm phân

biệt

1

x

,

2

x

trái dấu.

Vì thế

3 . 0



a c

, nên suy ra

0



c

.

+ Mặt khác từ đồ thị ta thấy

1

2

1

 









x

nên

1 2

0

 

x x

.

Mà

1 2

2

3



 

b

x x

a

nên suy ra

2

0

3





b

a

0

 

b

.

Vậy

0



a

,

0



b

,

0



c

,

0



d

.

Đáp án D.

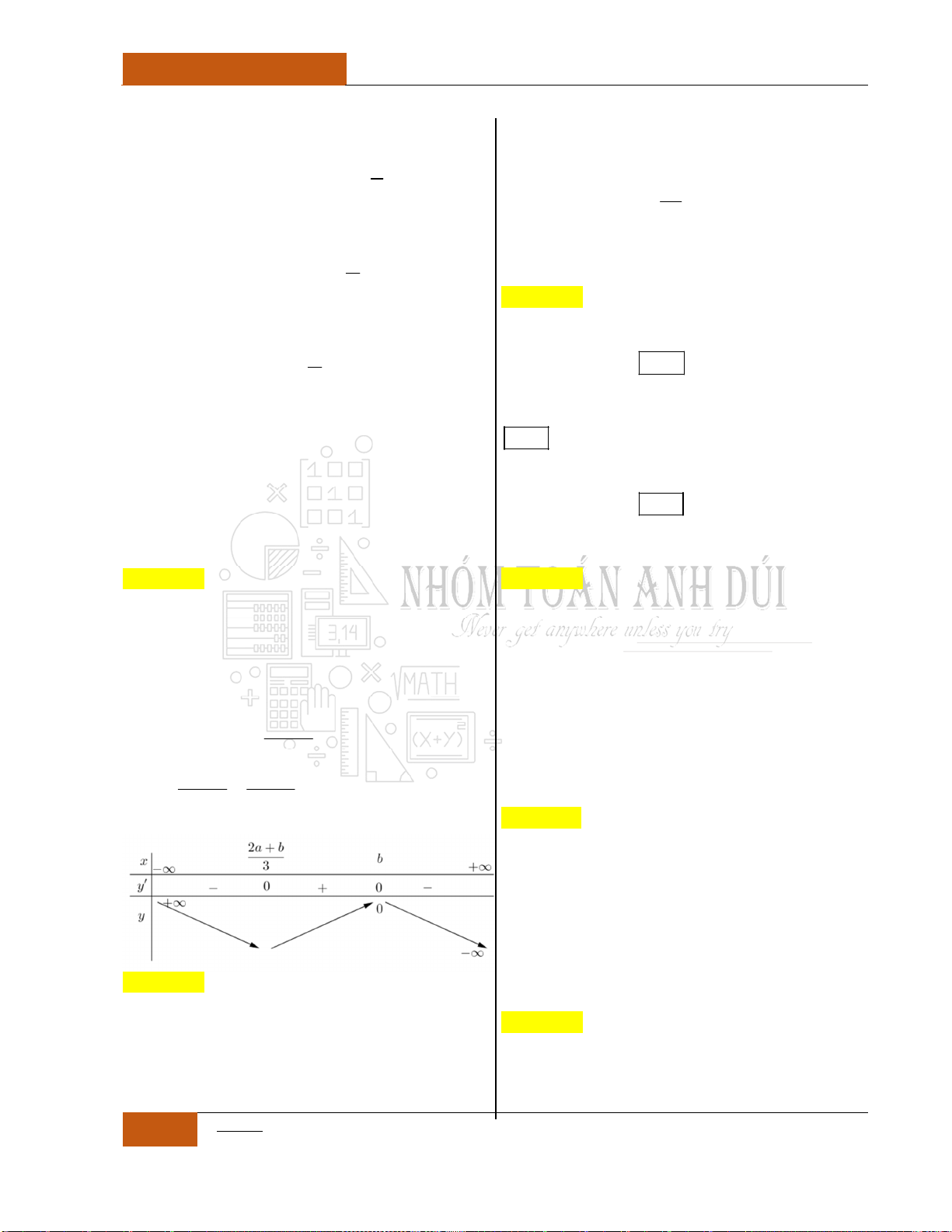
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

502

[ I can't, I can! ]

Câu 55. Nhận xét từ đồ thị:

+ Giao với trục hoành tại

0   

o

b

x

a

và

b trái dấu

 

1 .

+ Giao với trục tung tại 0  

o

b

y b

d

và

d

trái dấu

 

2 .

+ Tiệm cận đứng: 0   

d

x d

c

và c cùng

dấu

 

3

.

Từ

 

1 và

 

2 suy ra: a và

d

cùng dấu hay

0ad

.

Từ

 

2 và

 

3 suy ra: b và c trái dấu hay

0bc .

Đáp án C.

Câu 56. Lấy đạo hàm hàm số

 

y f x .

        

2

. 2

f x b x a x b x



      

     

2 2 2 3b x b x a x b x b a x          

 

0

2

3

x b

f x

a b

x









 









.

Ta có:

2 2

3 3

 

 

a b b b

b

.

Ta có bảng biến thiên:

Đáp án A.

Câu 57. Từ đồ thị ta có: 0 0   x y d , từ

dạng đồ thị suy ra 0a .

Mặt khác

2

' 3 2  y ax bx c từ đồ thị ta có

phương trình ' 0y có hai nghiệm trái dấu suy

ra 0ac mà 0a suy ra 0c .

Hơn nữa phương trình ' 0y có hai nghiệm

phân biệt

1 2

2

1

3

    

b

x x

a

suy ra

3 2 0  a b b

.

Vậy chọn đáp án D.

Đáp án D.

Câu 58. Dựa vào đồ thị:

+

lim



 

x

y

 0a .

+ Đồ thị hàm số có ba điểm cực trị 0ab 

0b .

+ Giao điểm của đồ thị hàm số và trục tung có

tung độ dương

 0c

.

Vậy 0a , 0b , 0c .

Đáp án C.

Câu 59. Từ hình vẽ ta thấy:

Đồ thị hàm số có bề lõm hướng lên

0 a

.

Đồ thị hàm số cắt trục tung tại điểm có tung độ

âm 0 c .

Đồ thị hàm số có 3 điểm cực trị

0 0   ab b

.

Vậy chỉ có 0bc .

Đáp án B.

Câu 60. Dựa vào hình dạng đồ thị hàm số ta

nhận thấy:

Hệ số

0a

.

Đồ thị hàm số đi qua gốc tọa tọa

0 c

.

Hàm số có 3 điểm cực trị . 0 0   a b b .

Đáp án C.

Câu 61. Đồ thị hàm số đi qua các điểm

 

0;1A ,

 

1;5B và

 

3;1C và đạt cực trị tại các điểm B

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

503

[ I can't, I can! ]

và

C

.

Đạo hàm:





2

3 2



  

f x ax bx c

.

Ta có:





 

0 1

1 1

1 5

5 6

1 0

3 2 0 9

3 0

27 6 0 1

 

 

 



 



     

  

 

  





   

  





   

 



f

d a

f a b c d b

f

a b c c

f

a b c d

.

Đáp án C.

Câu 62. Dựa vào hình dạng đồ thị hàm số ta

nhận thấy:

Hệ số

0



a

.

Hàm số có

3

điểm cực trị

. 0 0

   

a b b .

Đồ thị hàm số đi qua gốc tọa tọa

0

 

c

.

Vậy

0, 0, 0

  

a b c

.

Đáp án C.

Câu 63. Nhìn vào đồ thị ta có:

Khi



x





2;

 

hàm số đồng biến

0

 

a

.

Hàm số có

3

điểm cực trị nên

. 0



a b

mà

0 0

  

a b

.





0 1 0

    

y c c .

Đáp án A.

Câu 64. Đồ thị hàm số có tiệm cận ngang:

1 1 1.

1

       

a

y a

Mặt khác Đồ thị hàm số có TCĐ

2



x

nên

2 0 2.

    

c c





2 1 2. 2 3.

      

a c

Dựa vào đồ thị ta thấy các điểm





3;0

và

3

0;

2

 



 

 

thuộc vào đồ thị hàm số đã cho nên ta

được hệ phương trình

.3 3

0

3

3 .0 3

2 0

















 







a

c

a

c

3 3 0

3 6

 







 



a

c

1

2

 







 



a

c





2 1 2. 2 3.

      

a c

Đáp án A.

Câu 65. Đồ thị hàm số giao với trục

Ox

tại điểm

có hoành độ

 

b

x

a

, giao với

Oy

tại điểm có

tung độ



b

y

d

.

Dựa vào hình vẽ ta có:

0 0

0

0 0

 

  

 





 

   

  





 

 

 

 

b b

ab

a a

ad

b b bd

d d

.

Trong các phương án chỉ có phương án B thỏa

mãn.

Đáp án B.

Câu 66. Ta thấy đồ thị hàm số có tiệm cận

ngang

1

 

y

suy ra

1

 

a

.

Do đồ thị hàm số đi qua điểm





2;0

nên

2 0 2 0 2

        

a b b b

.

Vậy

0

 

b a

.

Đáp án A.

Câu 67. Đồ thị hàm số







ax b

y

x c

có đường tiệm

cận ngang



y a

, đường tiệm cận đứng

 

x c

và cắt

Oy

tại điểm

0;

 

 

 

b

c

.

Từ đồ thị hàm số ta có đường tiệm cận ngang

1

 

y

, đường tiệm cận đứng

1



x

và cắt

Oy

tại điểm





0; 2



.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

504

[ I can't, I can! ]

Từ đó suy ra:

1 1 1

2 2

2





     

 



 

       

  

  

  

 



 



a a a

c c c

b b c b

c

.

Vậy

1 1 2 0

      

a b c

.

Đáp án D.

Câu 68. Ta có:

2

lim



 





x

ax a

bx c b

, theo giả thiết

suy ra:

3 3



   

a

a b

b

.

Hàm số không xác định tại

1 0

     

x b c b c

.

Hàm số đồng biến trên từng khoảng xác định

nên

 

2

0





 



ac b

f x

bx c

với mọi

x

khác

1

.

Suy ra:

2

2 2

2 0 3 2 0 0 0

3 3

             

ac b b b b b

Lại có: 3

       

a b c b b b b

.

Suy ra

 

2

4

0;

9

 

   

 

 

a b c b

Vậy tổng

 

a b c

thuộc khoảng

4

0;

9

 

 

 

.

Đáp án C.

Câu 69. Một số nhận xét quan trọng:

+ Ta có đồ thị hàm số ( )







ax b

f x

cx d

có đường

tiệm cận ngang là



a

y

c

, đường tiệm cận đứng

là





d

x

c

.

Theo bài ra, ta có:

3

2















 

 





 





a

a c

c

d d c

c

.

+ Điểm





1;7



thuộc đồ thị hàm số





f x

nên

3

7 7 10

2

   

    

   

a b c b

b c

c d c c

.

Vậy

2 3 4

7

a b c d

c

  

2.(3 ) 3.(10 ) 4 2

6

7

c c c c

c

  

 

.

Đáp án C.

Câu 70. Dựa vào bảng biến thiên ta có hàm số

luôn đồng biến trên từng khoảng xác định, đồ

thị hàm số có tiệm cận đứng là đường thẳng

2



x

và tiệm cận ngang là đường thẳng

1



y

nên ta có hệ

2

1

0

c

b

c b

a

a b

b

ac b



 



 





 

  

 

 

 



 





2

0 1

2

1

0

2

2 0

1

0

2

0

c

c b

a b a

b b

b

a b c





 



 





     

 

 

  





  



  



.

Dựa vào hệ trên ta có các phát biểu









1 , 4

là

sai,









2 , 3

đúng.

Đáp án B.

Câu 71. Ta có:

3 2

y x ax bx c

   

2

3 2

y x ax b



   

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

505

[ I can't, I can! ]

Theo đề, ta có hệ phương trình:

 

     

   

3 2

2

0 1 .1 .1

1 0

2 0 0 2 . 2 . 2

2 0

0 3. 2 2 . 2



   

 



         

 

 



 

    







a b c

y

y a b c

y

a b

.

1 3

4 2 8 0

4 12 4

    

 

 

     

 

 

     

 

a b c a

a b c b

a b c

.

Vậy





2

2 2 2 2 2

3 0 4 25.

       T a b c

Đáp án A.

Câu 72. Vì đồ thị hàm số cắt trục tung tại điểm

2



y

nên

2



d

.

2

3 2



  

y ax bx c

.

Hàm số đạt cực trị tại

0



x

và

2



x

nên:





 

0 0

0

3 1

12 4 0

2 0

y

c

b a

a b c

y



 









 

 

  

 

  













Từ đồ thị ta nhận thấy









2 2 8 4 2 8 4 4 2 1 2

              y a b d a b a b

Thay





1

vào





2

ta tìm được

1, 3

  

a b .

Vậy

2

 

S

.

Đáp án A.

Câu 73. Ta có:

2

3 2



  

y ax bx c

,

6 2



 

y ax b

Từ đồ thị ta thấy:

+) lim



 

x

y . Ta suy ra

0



a

.

+)





0 0 0

  

y d

loại C.

Đồ thị hàm số có hai điểm cực trị với

1

x

,

2

x

trái

dấu và

1 2

0

 

x x . Ta suy ra phương trình

' 0



y

có hai nghiệm trái dấu và

1 2

0

 

x x .

Ta suy ra

1 2

0

3

 

c

x x

a

,

0

 

c

loại B.

Hơn nữa,

1 2

0

3

0



   



 









b

x x

b

a

. Loại A.

Đáp án D.

Câu 74. Đồ thị hàm số

1







ax b

y

cx

có đường tiệm

cận đứng là đường thẳng

1

 

x

c

và đường tiệm

cận ngang là đường thẳng



a

y

c

.

Nhìn vào bảng biến thiên, ta thấy

1

1 1

    

c

và

2 2

  

a

c

(vì

1



c

).

Ta có:

 

2

1









a bc

y

cx

.

Vì hàm số đã cho đồng biến trên các khoảng





; 1

 

và





1;

 

nên

 

2

0

a bc

y

bx c





 



0 2 0 2

a bc b b

       

.

Suy ra:

3 3

8 8 0

b b

   

.

Vậy tập các giá trị

b

là tập nghiệm của bất

phương trình

3

8 0.

 

b

Đáp án D.

Câu 75. Từ đồ thị ta có:

Tiệm cận đứng:

1 1 1



     

d d

x

c c

  

d c

.

Tiệm cận ngang: 1 1

       

a

y a c

c

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

506

[ I can't, I can! ]

Đồ thị cắt trục hoành tại điểm:

2 2 2 2

 

      



b b b

x

a c c

2

 

b c

.

Vậy

2 3 4 3

8

    

   

a b d c c c

T

c c

.

Đáp án C.

Câu 76. Từ hình dạng đồ thị hàm số ta có

0



a

Đồ thị hàm số cắt trục tung tại điểm có tung độ

âm

0

 

d

Ta có:

2

' 3 2

  

y ax bx c

.

Hàm số có hai điểm cực trị trái dấu

' 0

 

y

có

hai nghiệm trái dấu

0

 

ca

Mà

0



a

nên

0



c

.

Ta lại có:

'' 6 2

 

y ax b

.

'' 0 6 2 0

3

      

b

y ax b x

a

.

Từ đồ thị hàm số ta thấy tâm đối xứng có hoành

độ âm.

Do đó

0

3

 

b

a

.

Mà

0



a

nên

0



b

.

Vậy trong các số

, ,

a b c

và

d

có

2

số dương là

a

và

b

.

Đáp án D.

Câu 77. Từ bảng biến thiên của hàm số, ta thấy

đồ thị có hai đường tiệm cận, trong đó tiệm cận

đứng là đường thẳng

2

 

x

và tiệm cận ngang

là đường thẳng

1



y

.

Suy ra

2

1



 













c

b

a

b

0













bc

ab





 

1

0, 0, 0

2

0, 0, 0

  







  



b c a

.

Lại có hàm số nghịch biến trên mỗi khoảng xác

định

 

2

6

0

 



 



ac b

f x

bx c

6

 

ac b

.

Ta thấy





1

không thể xảy ra do nếu

0



b

thì

6 0

 

ac b ; và





2

có thể xảy ra do nếu

0, 0

 

c a

thì

6 0

 

b ac .

Vậy trong các số

, ,

a b c

có hai số âm.

Đáp án D.

Câu 78. Ta có:

3 2

y x x

  









2

1 2 2

x x x

   

Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2

(hình 2) ta thấy

Toàn bộ đồ thị ứng với

1



x

được giữ nguyên.

Phần đồ thị ứng với

1



x

lấy đối xứng qua trục

hoành.



Chọn đáp án C.

Đáp án C.

Câu 79. Ta có nhận xét sau:

 





 

2

2 1 , 2

2 1

2 1 , 2



  



   



   





x x x

y x x

x x x

.

Đồ thị gồm 2 phần:

+) Giữ nguyên phần đồ thị đã cho ứng với

2



x

.

+) Lấy đối xứng phần đồ thị đã cho ứng với

2



x

qua trục

Ox

.

Hình 1 nhận vì đồ thị là hàm





2

2 1

  

y x x

.

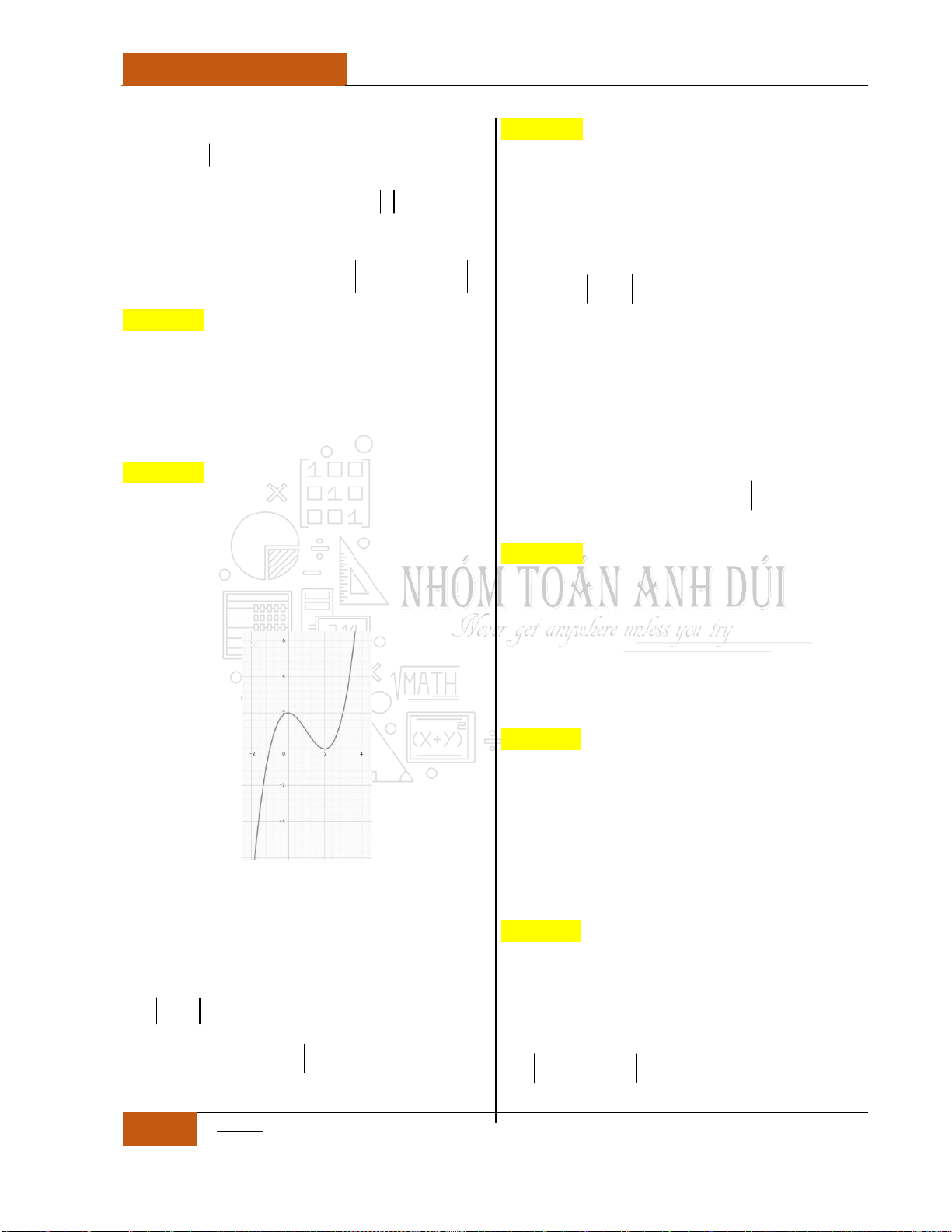
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

507

[ I can't, I can! ]

Hình 2 loại vì đồ thị là hàm

   

2 1 1   y x x x .

Hình 3 loại vì đồ thị hàm số

 

2

2 1  y x x

.

Hình 4 loại vì đồ thị hàm

 

2

2 1  y x x .

Đáp án A.

Câu 80. Do đồ thị giao với trục Oy tại điểm có

tung độ bằng 4 và

lim



 

x

y

 Loại B, D.

Mặt khác:

   

1;0 A f x  Loại C.

Đáp án A.

Câu 81. Phương trình

3 2

0   ax bx cx d

 

0a có đúng hai nghiệm thực.

Nên đồ thị hàm số

3 2

   y ax bx cx d được

minh họa như hình vẽ.

Gọi m là số điểm cực trị của hàm số

 

y f x

và k là nghiệm bội lẻ của phương trình

 

0f x .

 Số điểm cực trị của đồ thị hàm số

 

y f x

là m k .

Vậy đồ thị hàm số

3 2

   y ax bx cx d có số

điểm cực trị là

2 1 3 

.

Đáp án D.

Câu 82. Gọi

 

C là đồ thị hàm số biểu diễn của

hàm

 





2

2 1

  

y x x

.

Ta có nhận xét khá quan trọng như sau:

 

2

1

2 1 khi

1

2 1

2 1 khi 1 1

x

x x

x

y x x

x x x

  



 











   





     





Cách vẽ đồ thi như sau:

+ Giữ nguyên phần đồ

 

C ứng với









; 1 1;

    

x

ta được

 

1

C .

+ Lấy đối xứng phần

 

C ứng với

 

1;1 x

qua trục hoành ta được





2

C

.

Khi đó đồ thị hàm số

 

2

2 1  y x x

gồm

 

1

C và

 

2

C .

Đáp án C.

Câu 83. Từ đồ thị ban đầu (hình 1) sang đồ thị

thứ 2 (hình 2) ta thấy

Toàn bộ đồ thị phía “phải” Oy sau đó lấy đối

xứng sang trái.



Chọn đáp án B.

Đáp án B.

Câu 84. Từ đồ thị ban đầu (hình 1) sang đồ thị

thứ 2 (hình 2) ta thấy:

Toàn bộ đồ thị phía bên phải Oy được giữ

nguyên.

Sau đó, được lấy đối xứng sang trái.

Đáp án B.

Câu 85. +) Loại đáp án A vì:

 

3 2 3 2

6 9 6 9       y x x x x x x .

+) Loại đáp án B, vì đồ thị của hàm số

3 2

6 9  y x x x

giữ lại phần đồ thị phía trên

trục hoành và chỉ lấy đối xứng phần dưới trục

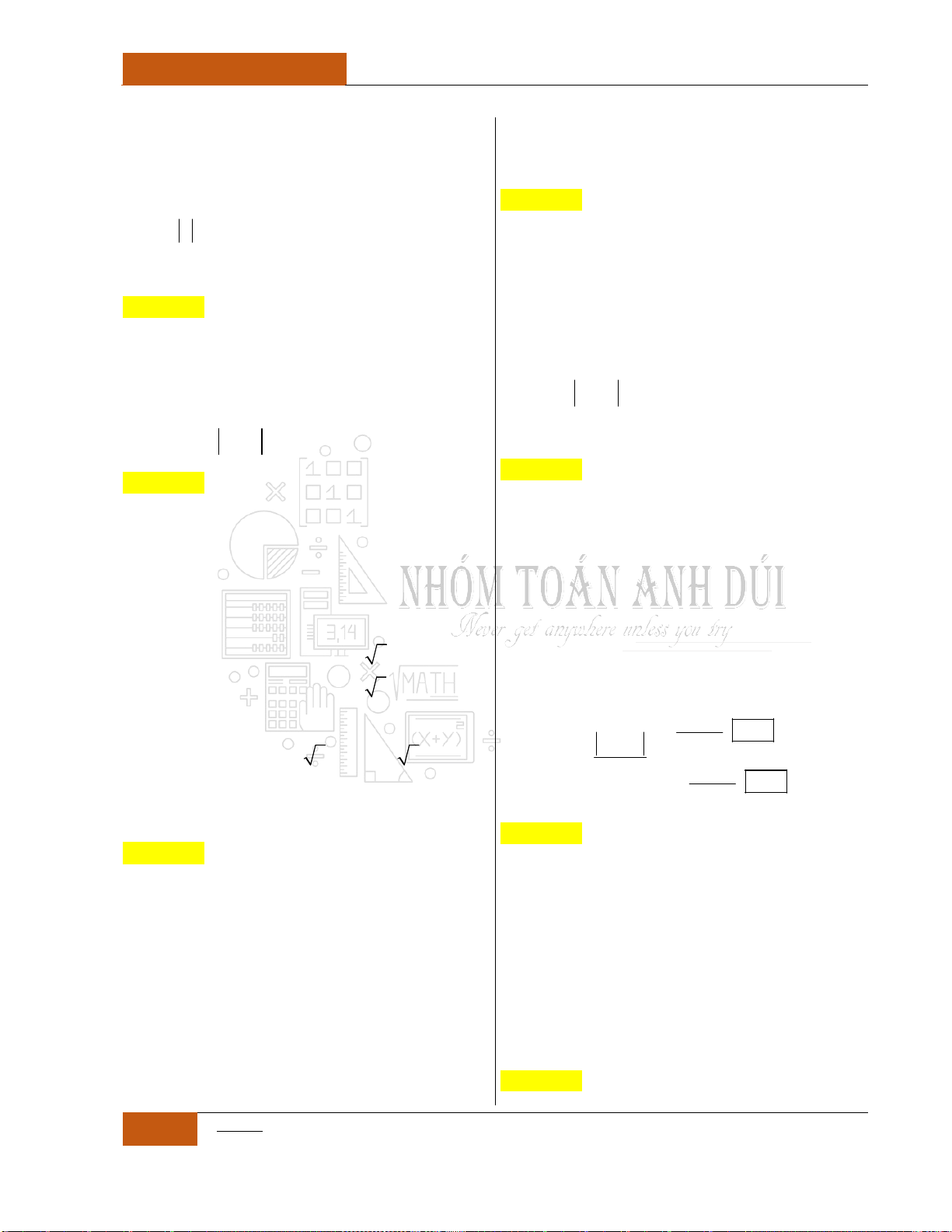
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

508

[ I can't, I can! ]

hoành của đồ thị Hình 1.

+) Loại đáp án D vì hệ số của

2

x

khác

6



.

+) Đồ thị ở đáp án C là đồ thị của hàm số dạng







y f x

.

Chọn đáp án C.

Đáp án C.

Câu 86. Dễ thấy, phần đồ thị nằm trên trục

hoành được giữ không đổi và phần đồ thị nằm

bên dưới trục hoành được lấy đối xứng lên trên

và bỏ đi phần bên dưới. Đây là cách vẽ của đồ

thị hàm







y f x

từ đồ thị hàm số







y f x

.

Đáp án A.

Câu 87. Ta có sự phân tích đa thức như sau:

 





3 2 2

3 2 1 2 2

      

y x x x x x

.

Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2

(hình 2) ta thấy:

Toàn bộ đồ thị ứng với

1 3



 



 





x

được giữ

nguyên.

Phần đồ thị ứng với

1 3 1 3

   x

lấy đối

xứng qua trục hoành.



Chọn đáp án D.

Đáp án D.

Câu 88. Ta có:

 





3 2 2

3 2 1 2 2

      

y x x x x x

.

Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2

(hình 2) ta thấy:

Toàn bộ đồ thị nằm phía trên

Ox

được giữ

nguyên.

Phần đồ thị phía dưới

Ox

được lấy đối xứng

qua

Ox

.



Chọn đáp án A.

Đáp án A.

Câu 89. Từ đồ thị ban đầu (hình 1) sang đồ thị

thứ 2 (hình 2) ta thấy:

Toàn bộ đồ thị phía trên

Ox

giữ nguyên.

Toàn bộ phần phía dưới

Ox

được lấy đối xứng

lên trên.



dạng





f x

.

Chọn đáp án C.

Đáp án C.

Câu 90. Từ đồ thị ban đầu (hình 1) sang đồ thị

thứ 2 (hình 2) ta thấy

Toàn bộ đồ thị phía bên trái đường thẳng

1



x

được giữ nguyên

Toàn bộ đồ thị phía bên phải đường thẳng

1



x

lấy đối xứng qua

Ox

Chọn đáp án C.

Chú ý:

1

, 1

1

2

1

2

, 1

2

 







 





 



 





 







x

y

x

.

Đáp án C.

Câu 91. Từ đồ thị ban đầu (hình 1) sang đồ thị

thứ 2 (hình 2) ta thấy:

Toàn bộ đồ thị phía bên phải đường thẳng

2

 

x

được giữ nguyên.

Toàn bộ đồ thị phía bên trái đường thẳng

2

 

x

lấy đối xứng qua

Ox

.

Chọn đáp án D.

Đáp án D.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

509

[ I can't, I can! ]

Câu 92. Từ đồ thị ban đầu (hình 1) sang đồ thị

thứ 2 (hình 2) ta thấy:

Toàn bộ đồ thị nằm bên trái (ứng với

1)



x

đường thẳng

1



x

được giữ nguyên.

Toàn bộ đồ thị nằm bên phải (ứng với

1)



x

đường thẳng

1



x

được lấy đối xứng qua

.

Ox



Chọn đáp án C.

Đáp án C.

Câu 93. Từ đồ thị ban đầu (hình 1) sang đồ thị

thứ 2 (hình 2) ta thấy:

Toàn bộ đồ thị phía bên trái đường thẳng

1

 

x

(ứng với

1)

 

x được giữ nguyên

Toàn bộ đồ thị phía bên phải đường thẳng

1

 

x

(ứng với

1)

 

x

được lấy đối xứng qua

trục

.

Ox

Chọn đáp án B.

Đáp án B.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

510

[ I can't, I can! ]

Extra Techniques:

Study tips:

Trong một số trường hợp

để giải phương trình ta

có thể làm một cách

ngược lại để minh họa

lời giải Logic hơn.

Chẳng hạn:

Phương trình

 

0hx

,

ta khó để có thể giải

được vì là phương trình

bậc cao (phương trình có

bậc từ

5

trở lên không có

công thức nghiệm để giải

một cách tổng quát) hoặc

có thêm các tham số

m

,

hàm nhiều ẩn,… ta cần

tách hàm

     

h x f x g x

.

Khi đó, việc giải phương

trình

 

0hx

được quy

về việc giải phương trình

   

f x g x

.

Extra Techniques:

Study tips:

Trong quyển tài liệu

Nghiên cứu định lý

Vietè của tác giả Nguyễn

Thành Nhân đã trình bày

rất chi tiết về cơ sở cũng

như ứng dụng. Nếu có cơ

hội, các bạn tìm đọc nhé!

VI. Sự tương giao của hai đồ thị hàm số

Xét vấn đề tổng quát:

Xét sự tương giao giữa hai đồ thị hàm số tổng quát

 

y f x

và

 

y g x

.

Phương pháp giải

Bước 1: Lập phương trình hoành độ giao điểm:

   

f x g x

.

Bước 2: Xét nghiệm phương trình

   

f x g x

.

Ta có ba khả năng có thể xảy ra sau:

Thứ 1: Phương trình

   

f x g x

vô nghiệm. Điều đó có nghĩa hai

đồ thị hàm số là rời nhau, tức không có điểm chung,

Thứ 2: Phương trình

   

f x g x

có nghiệm kép. Điều đó có nghĩa

là tại điểm

 

00

;A x f x

(trong đó

   

00

f x g x

) hai đồ thị hàm số

tiếp xúc với nhau.

Thứ 3: Phương trình

   

f x g x

có

n

nghiệm (không nhất thiết

nghiệm bội lẻ hay chẵn). Điều đó có nghĩa là hai đồ thị hàm số

 

fx

và

 

gx

khi biểu diễn trên cùng một hệ trục tọa độ thì chúng cắt nhau

tại

n

điểm. Lưu ý:

*

n

.

VI. 1. Sự tương giao giữa đồ thị hàm số bậc ba tổng quát

   

32

,0y f x ax bx cx d a     

với trục hoành.

Cách 1: Sử dụng phương pháp đại số (Phương pháp giải

phương trình bằng các phương pháp thường gặp).

Ta biết rằng số giao điểm của đồ thị hàm số bậc ba với trục hoành

bằng đúng với số nghiệm của phương trình

 

0fx

.

Giả sử ta xét phương trình

32

0ax bx cx d   

. Ta có một số mẹo

giải như sau:

Thứ 1: Hàm số có dấu hiệu nhận biết bằng Hệ quả của Định lý

Vietè. Tổng các hệ số của phương trình bằng

0

thì phương trình chắc

chắn có nghiệm

1x 

hoặc hiệu của các tổng hệ số bậc chẵn và lẻ

bằng

0

thì phương trình có một nghiệm

1x 

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

511

[ I can't, I can! ]

Extra Techniques:

Study tips:

Khi biết một nghiệm cụ

thể nào đó của phương

trình đa thức thì ta luôn

có thể dùng Lược đồ

Horner để phân tích và

giải phương trình như

bình thường.

Hình VI.1.1.

Hình VI.1.2.

Thứ 2: Nếu phương trình

32

0ax bx cx d   

có một nghiệm

x 

thì ta hoàn toàn có thể đưa về một phương trình tương đương

như sau:

   

 

22

. . . 0

gx

x ax a b x a b c





          





Khi đó:

   

0*

x

gx











.

Việc giải phương trình

 

*

ta hoàn toàn dùng được công thức

nghiệm.

Một số trường hợp có thể xảy ra như sau:

Thứ 1: Đồ thị hàm số bậc ba cắt trục hoành tại một điểm duy nhất khi

và chỉ khi phương trình

 

0gx

vô nghiệm thực. Hoặc nếu có

nghiệm thì bắt buộc

x 

chính là nghiệm kép. Trường hợp này ta

gọi

x 

là nghiệm bội ba.

Thứ 2: Đồ thị hàm số bậc ba cắt trục hoành tại hai điểm khi và chỉ

khi phương trình

 

0gx

có một nghiệm kép khác

x 

. Hoặc có

một nghiệm

x 

và một nghiệm

x    

.

Thứ 3: Đồ thị hàm số bậc ba cắt trục hoành tại ba điểm phân biệt khi

và chỉ khi phương trình

 

0gx

có hai nghiệm thực phân biệt thỏa

mãn

 

0g 

.

Cách 2: Sử dụng phương pháp hàm số.

Đối với những trường hợp đã trình bày ở Study tips trên, ta

luôn có những phương trình nghiệm “xấu”, không thể nhẩm

được nghiệm là bao nhiêu (Điều kiện không dùng CASIO để

giải phương trình bậc ba) thì ta sẽ có một số tips như sau:

Thứ nhất: Đồ thị hàm số bậc ba có một giao điểm duy nhất với trục

hoành. Khi đó, hai khả năng có thể xảy ra: Hoặc đồ thị hàm số không

có cực trị (Hình VI.1.1), hoặc đồ thị hàm số có hai điểm cực trị cùng

nằm về một phía (Hình VI.1.2).

Xem thêm Hình VI.1.1.

Xem thêm Hình VI.1.2.

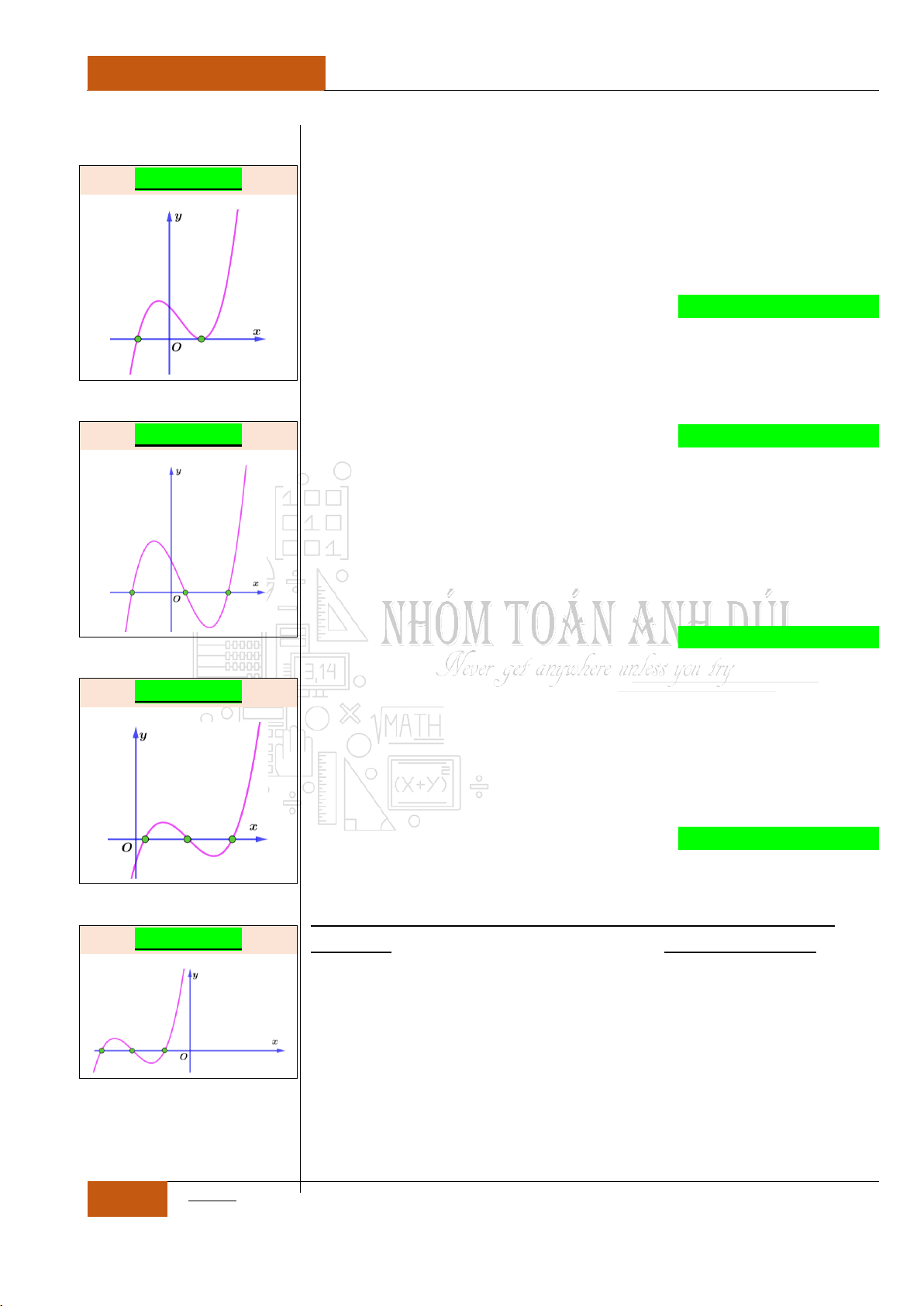
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

512

[ I can't, I can! ]

Hình VI.1.3.

Hình VI.1.4.

Hình VI.1.5.

Hình VI.1.6.

Thứ hai: Đồ thị hàm số bậc ba có hai giao điểm với trục hoành. Khi

đó đồ thị hàm số tiếp xúc với trục hoành tại một điểm

0

xx

nào đó

thỏa mãn

 

0

0fx 

.

Hay nói cách khác, một điểm cực trị của đồ thị hàm số thuộc trục

hoành. Khi đó, ta có thể “Hàm số hóa” thành dạng:

.0

CD CT

yy

.

Xem thêm Hình VI.1.3.

Thứ ba: Đồ thị hàm số bậc ba có ba giao điểm với trục hoành khi hai

điểm cực trị của đồ thị hàm số nằm ở hai phía đối với trục hoành. Khi

đó, ta có thể “Hàm số hóa” thành dạng:

.0

CD CT

yy

.

Xem thêm Hình VI.1.4.

Thứ tư: Đồ thị hàm số bậc ba cắt trục hoành tại ba điểm có hoành độ

dương khi và chỉ khi: Đồ thị hàm số bậc ba có hai điểm cực trị thỏa

mãn

 

.0

0, 0

. 0 0

CD CT

yy

xx

a f ad

















.

Xem thêm Hình VI.1.5.

Thứ năm: Đồ thị hàm số bậc ba cắt trục hoành tại ba điểm có hoành

độ âm khi và chỉ khi: Đồ thị hàm số bậc ba có hai điểm cực trị thỏa

mãn

 

.0

0, 0

. 0 0

CD CT

yy

xx

a f ad

















.

Xem thêm Hình VI.1.6.

VI. 2. Sự tương giao giữa đồ thị hàm số bậc bốn trùng

phương

   

42

,0y f x ax bx c a    

với trục hoành.

Ta biết rằng số giao điểm của đồ thị hàm số bậc bốn trùng phương với

trục hoành bằng đúng với số nghiệm của phương trình

 

0fx

.

Giả sử ta xét phương trình

42

0ax bx c  

. Ta có một số mẹo giải

như sau:

Thứ 1: Hàm số có dấu hiệu nhận biết bằng Hệ quả của Định lý

Vietè. Tổng các hệ số của phương trình bằng

0

thì phương trình chắc

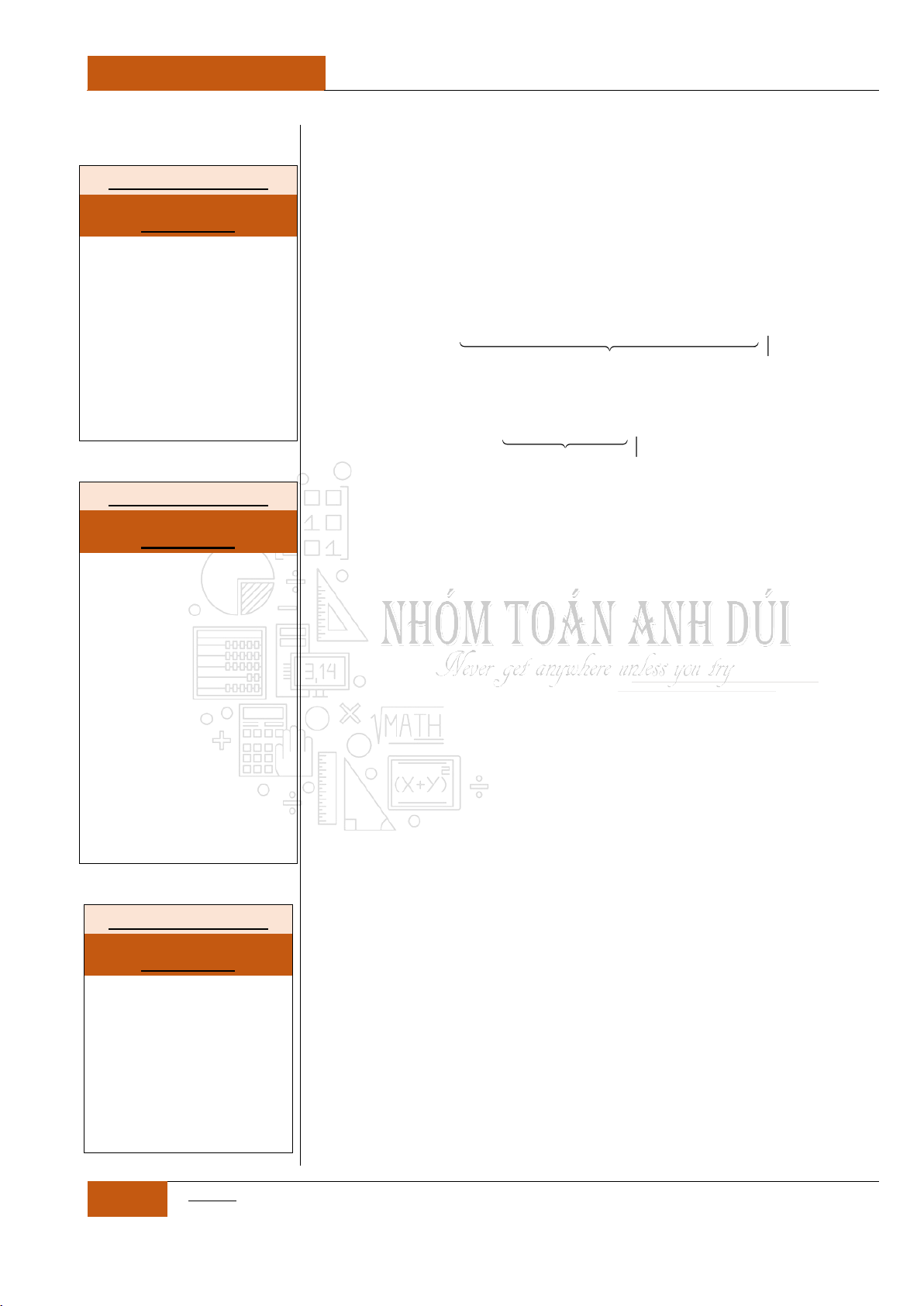
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

513

[ I can't, I can! ]

Extra Techniques:

Study tips:

Khi biết một nghiệm cụ

thể nào đó của phương

trình đa thức thì ta luôn

có thể dùng Lược đồ

Horner để phân tích và

giải phương trình như

bình thường.

Extra Techniques:

Study tips:

Một số trường hợp

thường thấy ở đây đưa ta

về bài toán biện luận

phương trình bậc bốn

trùng phương. Để làm tốt

dạng này ta nên mô

phỏng những trường hợp

trên với những hình ảnh

minh họa để khắc sâu

hơn trong đầu những

dạng đồ thị hàm số đó.

Extra Techniques:

Study tips:

Trong một vài trường

hợp khác, ta có thể đưa

dạng trùng phương về

dạng bậc hai theo một ẩn

khác để tiện lợi hơn

trong quá trình giải bài

tập.

chắn có nghiệm

1x 

hoặc hiệu của các tổng hệ số bậc chẵn và lẻ

bằng

0

thì phương trình có một nghiệm

1x 

.

Thứ 2: Nếu phương trình

42

0ax bx c  

có một nghiệm

x 

thì

chắc chắn

x  

cũng là một nghiệm. Khi đó ta hoàn toàn có thể

tách thành

 

   

 

3 2 2 3

2 2 2 2

. . . . 0

.0

gx

hx

x ax ax a b x a b

x ax a b





           









      





Khi đó:

   

0*

x

hx











.

Việc giải phương trình

 

*

ta hoàn toàn dùng được công thức

nghiệm.

Một số trường hợp có thể xảy ra như sau:

Trường hợp 1: Đồ thị hàm số bậc bốn trùng phương không có bất cứ

giao điểm nào với trục hoành khi và chỉ khi phương trình

42

0ax bx c  

vô nghiệm.

Trường hợp 2: Đồ thị hàm số bậc bốn trùng phương có một giao

điểm duy nhất đối với trục hoành khi và chỉ khi

0

và phương

trình

 

0hx

vô nghiệm hoặc có nghiệm kép (trường hợp này ta thu

được phương trình:

4

0ax 

, khi đó, nghiệm

0x 

được gọi là

nghiệm bội bậc bốn).

Trường hợp 3: Đồ thị hàm số bậc bốn trùng phương có hai giao điểm

với trục hoành khi và chỉ khi

0

và phương trình

 

*

vô nghiệm.

Trường hợp 4: Đồ thị hàm số bậc bốn trùng phương có ba giao điểm

với trục hoành khi và chỉ khi

0

và

 

0hx

có hai nghiệm thực

phân biệt. Hoặc

0

và

2

.ba 

.

Trường hợp 5: Đồ thị hàm số bậc bốn trùng phương có bốn giao

điểm với trục hoành khi và chỉ khi

0

và phương trình

 

0hx

có hai nghiệm thực phân biệt khác

x  

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

514

[ I can't, I can! ]

Extra Techniques:

Study tips:

Quá trình lựa chọn các

trường hợp được nêu ở

bên được ghi nhận qua

quá trình giải toán và

nhận xét, có thể còn một

số trường hợp ngoại lệ,

chúng ta có thể kết hợp

các điều kiện với nhau

trong những bài toán

phức hợp. Chúng tôi

không yêu cầu các bạn

thuộc lòng, tuy nhiên,

quá trình ngẫm và hiểu là

một yêu cầu cấp thiết đối

với bài toán loại này.

Thứ 3: Xét phương trình hoành độ giao điểm

 

42

0*ax bx c  

.

Đặt:

2

0,t x x   

.

Khi đó:

   

2

* 0 **at bt c   

Trường hợp 1: Đồ thị hàm số không cắt trục hoành khi và chỉ khi

phương trình

 

*

vô nghiệm hay phương trình

 

**

vô nghiệm hoặc

có hai nghiệm âm.

Trường hợp 2: Đồ thị hàm số cắt trục hoành tại duy nhất một điểm,

khi đó, phương trình

 

*

có duy nhất một nghiệm thực, hay nói cách

khác, phương trình

 

**

có một nghiệm kép

0t 

hoặc có hai

nghiệm phân biệt trong đó có một nghiệm

0t 

và nghiệm còn âm,

0t 

.

Trường hợp 3: Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt,

khi đó phương trình

 

*

có hai nghiệm phân biệt, hay nói cách khác

phương trình

 

**

có một nghiệm kép dương hoặc có hai nghiệm

phân biệt trái dấu.

Trường hợp 4: Đồ thị hàm số cắt trục hoành tại ba điểm phân biệt,

khi đó phương trình

 

*

có ba nghiệm phân biệt, hay nói cách khác

phương trình

 

**

có một nghiệm

0t 

và một nghiệm

0t 

.

Trường hợp 5: Đồ thị hàm số cắt trục hoành tại bốn điểm phân biệt,

khi đó phương trình

 

*

có bốn nghiệm thực phân biệt, hay nói cách

khác phương trình

 

**

có hai nghiệm thực dương phân biệt.

VI. 3. Sự tương giao giữa đồ thị hàm số hàm nhất biến

   

, 0, 0

ax b

y f x ad bc c

cx d



    



với đường thẳng

:d y kx m

.

Bài toán tổng quát:

Cho hàm số

 

, 0, 0

ax b

y ad bc c

cx d



   



có đồ thị

 

C

. Tìm điều

kiện của tham số

m

để đường thẳng

:d y kx m

cắt đồ thị

 

C

tại

hai điểm phân biệt thỏa mãn một điều kiện nào đó…

Phương pháp chung

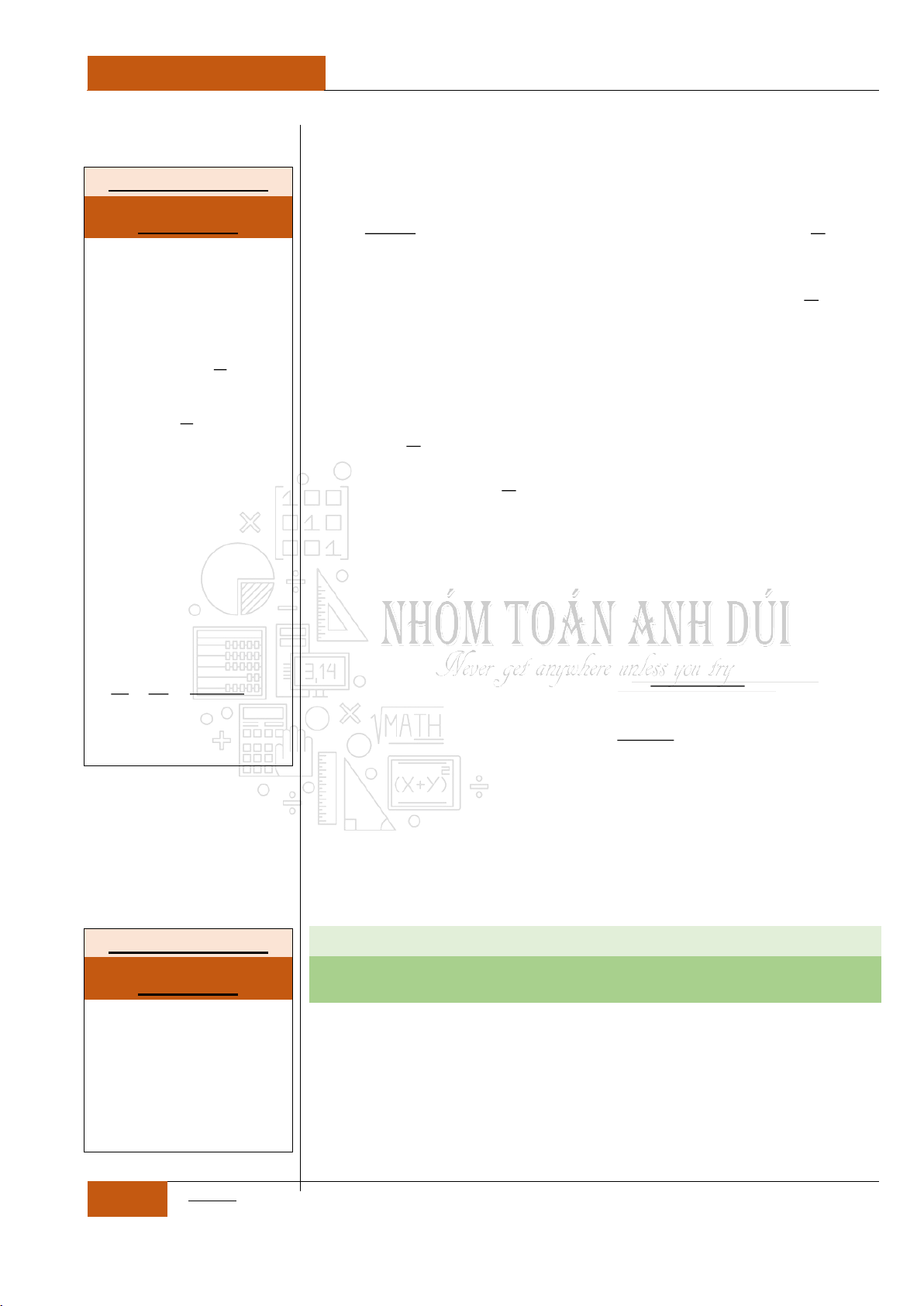
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

515

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Nhắc lại định lý Vietè

đối với hai nghiệm phân

biệt của phương trình

bậc hai:

2

0ax bx c  

là:

12

b

xx

a

c

xx

a



  













.

Một số biểu thức cần lưu

ý:

1.

 

2

22

1 2 1 2 1 2

2x x x x x x   

2.

 

3

33

1 2 1 2

x x x x  

 

1 2 1 2

3x x x x

3.

12

1 2 1 2

11xx

x x x x





.

…

Extra Techniques:

Study Tips:

Mẹo bên cạnh đây sẽ là

một công cụ hữu hiệu để

các độc giả có thể hoàn

thành bài tập một cách

nhanh chóng và đầy hiệu

quả.

Bước 1: Xét phương trình hoành độ giao điểm của đồ thị

hàm số

y kx m

và đồ thị hàm số

 

C

, ta có:

    

*,

ax b d

kx m ax b cx d kx m x

cx d c



        



   

2

0,

d

g x kcx mc kd a x md b x

c

          

.

Để

d

cắt

 

C

tại hai điểm phân biệt

 

0gx

có hai nghiệm phân

biệt khác

.0

0

ck

d

c

d

g

c









   



















.

Giải hệ này ta tìm được

 

1

1mD

.

Gọi

   

1 1 2 2

; , ;A x kx m B x kx m

với

12

,xx

là hai nghiệm phân biệt

của phương trình

 

0gx

.

Áp dụng định lý Vietè, ta có:

 

12

2

mc kd a

xx

ck

md b

xx

kc





  















.

Bước 2: Biến đổi điều kiện đề bài về dạng có chứa tổng và tích của

hai điểm

 

12

,3xx

.

Kết hợp ba điều kiện

     

1 , 2 , 3

, ta thu được điều kiện của tham

số thực

m

.

Một Tip để làm tốt các bài toán về tương giao hàm

Đối với dạng toán tương giao giữa đồ thị hàm số bậc bốn trùng

phương, ta có thể kết hợp với bảng công thức tính nhanh để luận điều

kiện của tham số

m

!

Bảng công thức tính nhanh (Nhắc lại).

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

516

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Đây là một trong số ít

những bài toán được

khai thác mạnh ở khía

cạnh CASIO, nên nếu

các bạn nhớ được một

vài công thức cơ bản thì

việc vượt tốc độ đối thủ

chỉ còn thuộc về kỹ năng

của các bạn với nhau

thôi.

Extra Techniques:

Study Tips:

Để giải tương giao hàm

 

0af x b

, ta vẽ

đường thẳng

b

y

a



và

cho cắt đồ thị hàm số,

bảng biến thiên đồ thị

hàm số… rồi đưa ra kết

luận theo yêu cầu đề bài.

IV. Một số bài tập ứng dụng nhận diện đồ thị hàm số

Câu 1. Cho hàm số bậc ba

 

y f x

có đồ thị là đường cong trong

hình bên. Số nghiệm thực của phương trình

 

1fx

là:

A.

3

. B.

1

. C.

0

. D.

2

.

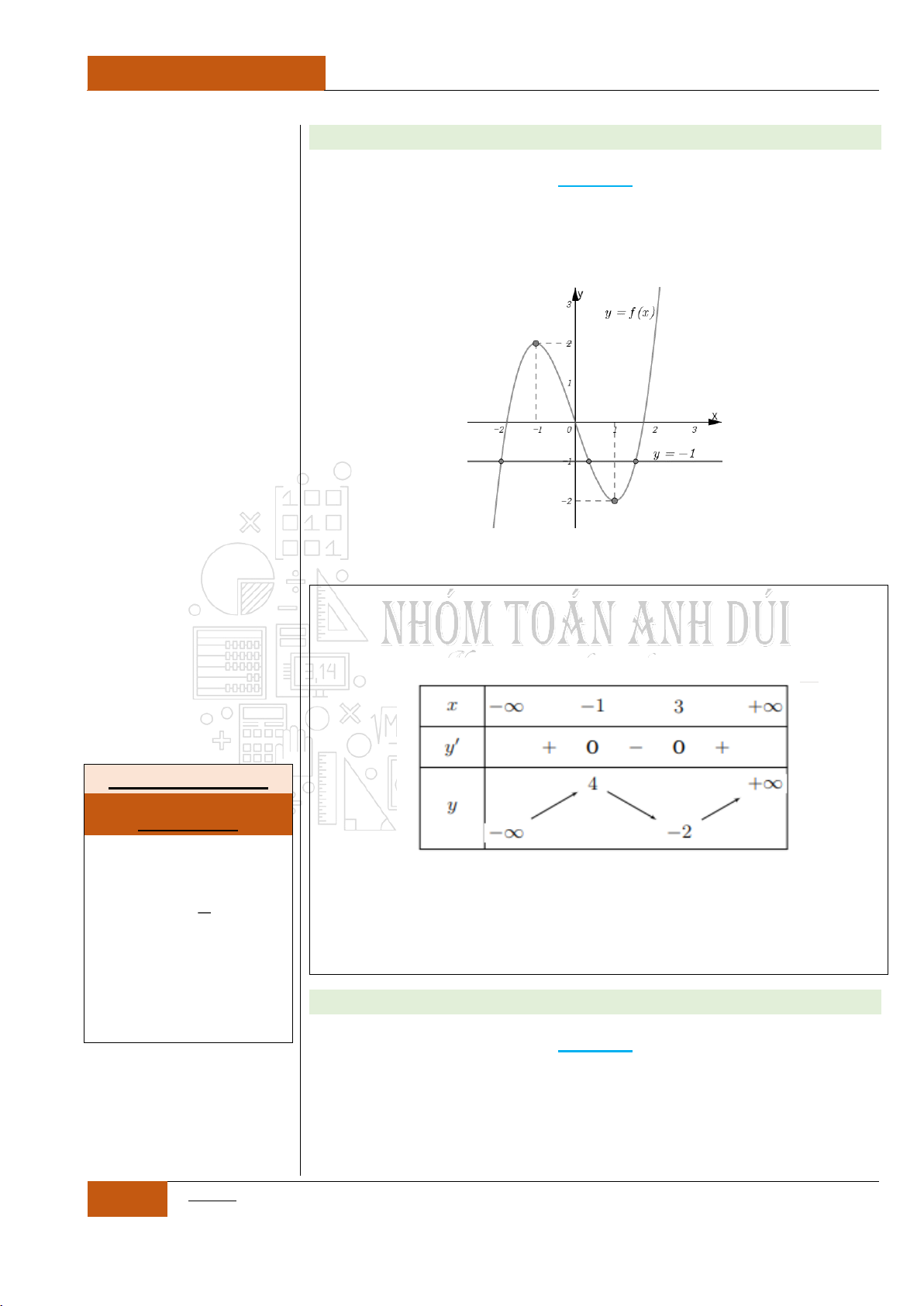
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

517

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Một cách tương tự cho

bảng biến thiên, ta vẫn vẽ

đường

b

y

a



lên trên

bảng biến thiên và kết

luận giá trị của tham số

m

thỏa mãn yêu cầu của

đề bài.

Đáp án: A

Lời giải

Số nghiệm thực của phương trình

 

1fx

chính là số giao điểm

của đồ thị hàm số

 

y f x

và đường thẳng

1y 

.

Từ hình vẽ suy ra

3

nghiệm.

Câu 2. [Nhận biết].

Cho hàm số có bảng biến thiên như hình bên.

Số nghiệm của phương trình là

A. B. C. D.

Đáp án: A

Lời giải

Ta có: , theo bảng biến thiên ta có phương

trình có 3 nghiệm.

Lưu ý: Ta kẻ đường thẳng

3y 

lên bảng biến thiên để xét!

 

y f x

 

30fx

3

2

1

0

   

3 0 3f x f x   

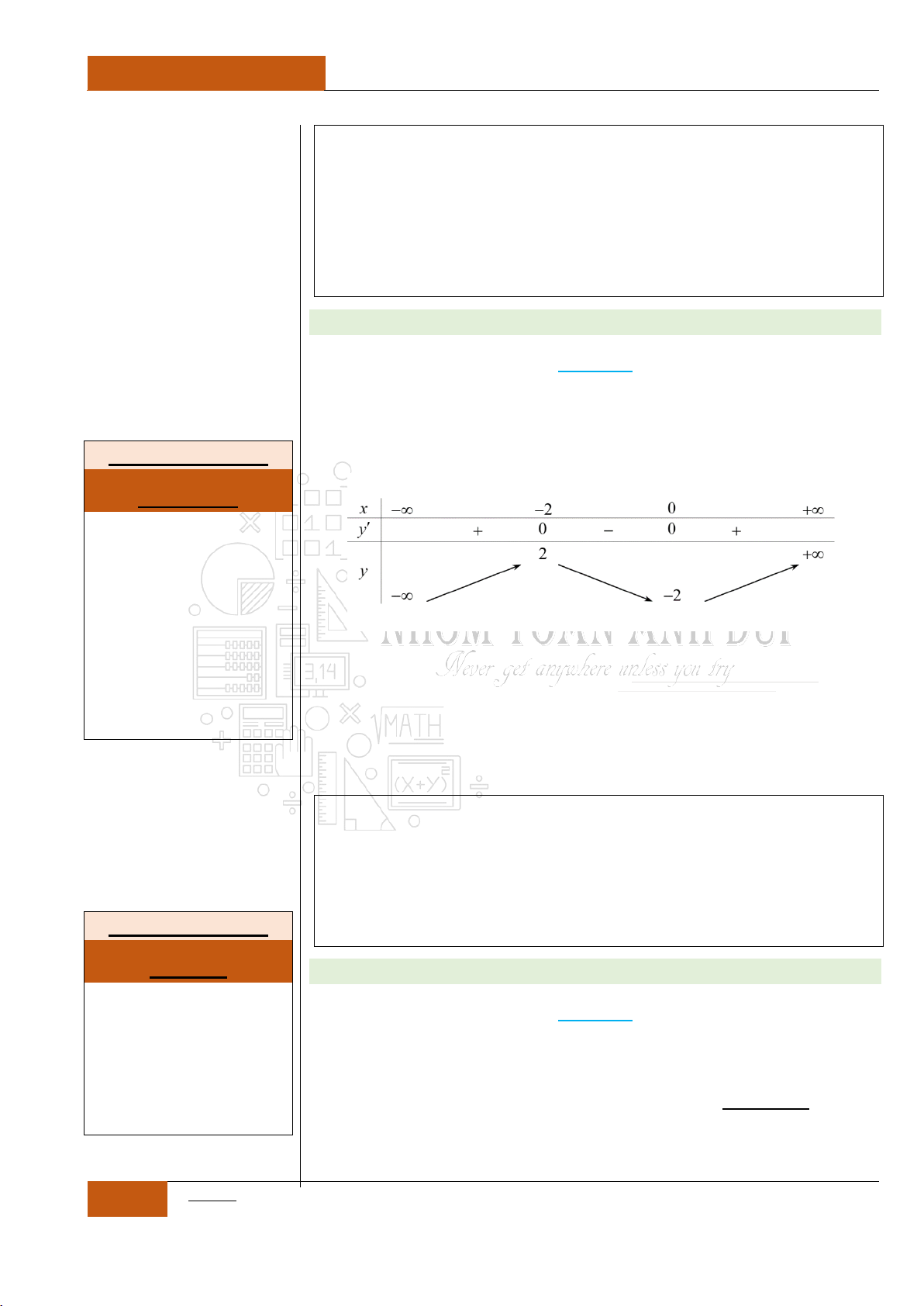
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

518

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Thay vì ta giải phương

trình bậc ba theo công

thức nghiệm thì bài toán

vô cùng phức tạp và

dường như không có

điểm ra, ta nảy ra ý tưởng

tương giao với đồ thị

hàm số theo ẩn

x

với

đường thẳng tham số.

Extra Techniques:

Remark:

Sở dĩ ta chỉ thu được điều

kiện là

0m 

là do

nghiệm bội kép vẫn được

xem là một nghiệm nên

ta không nhận giá trị

0m 

.

Câu 3. [Nhận biết].

Tìm tất cả các giá trị của tham số

m

để phương trình

32

32x x m  

có ba nghiệm phân biệt.

A.





2;m 

. B.





;2m  

.

C.

 

2;2m

. D.

 

2;2m

.

Đáp án: C

Lời giải

Xét hàm số

32

32y x x  

,

2

36y x x





.

Lập bảng biến thiên

Số nghiệm của phương trình

 

32

3 2 *x x m  

bằng số giao điểm

của đồ thị hàm số

32

32y x x  

và đường thẳng

ym

.

Dựa vào bảng biến thiên suy ra phương trình

 

*

có

3

nghiệm phân

biệt khi

22m  

.

Câu 4. [Nhận biết].

Có bao nhiêu giá trị nguyên của tham số

 

2018;2019m

để đồ thị

hàm số

3

33y x mx  

và đường thẳng

31yx

có duy nhất một

điểm chung?

A.

1

. B.

2019

. C.

4038

. D.

2018

.

Đáp án: D

Lời giải

Phương trình hoành độ giao điểm:

3

3 3 3 1x mx x   

3

3 2 3x x mx   

 

3

32

13

xx

m

x





.

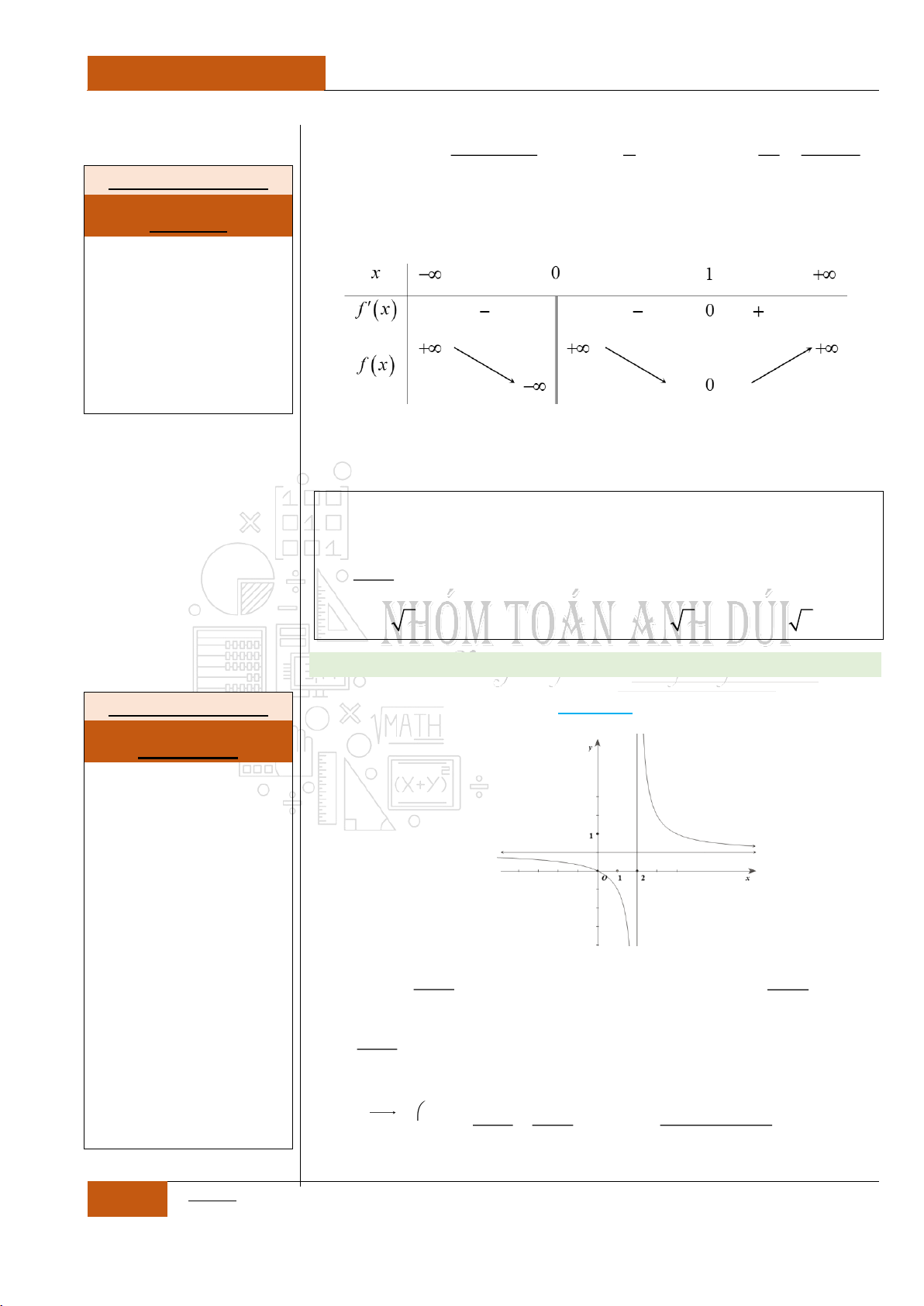
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

519

[ I can't, I can! ]

Extra Techniques:

Remark:

Đối với những điểm

không xác định, ta rất dễ

quên không điền vào

bảng xét dấu, đó là lý do

hơn 40% học sinh giải

các bạn toán dạng này bị

sai!

Extra Techniques:

Study Tips:

Đối với dạng toán tìm

khoảng cách

min

AB

như

vầy, ta có một mẹo như

sau (tối ưu khoảng 80%

dạng toán hiện tại, tuy

nhiên vẫn còn một số

trường hợp chưa chuẩn

xác do gài điều kiện).

Chúng ta kẻ một đường

thẳng

y x k

đi qua

tâm đối xứng của đồ thị

hàm số nhất biết, xác

định đoạn thẳng nối hai

giao điểm. Đó là đoạn

thẳng ngắn nhất.

Xét hàm

 

3

2

3 2 2

3

xx

f x x

xx



   

;

 

3

22

2 2 2

2

x

f x x

xx





  

;

 

01f x x



  

.

Bảng biến thiên.

Khi đó yêu cầu bài toán

0m

. Mà

m

nguyên và

 

2018;2019m

nên có

2018

giá trị thỏa mãn.

Câu 5. [Vận dụng].

Gọi

A

và

B

là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số

2

x

y

x





. Khi đó độ dài đoạn

AB

ngắn nhất bằng

A.

42

. B.

4

. C.

22

. D.

22

.

Đáp án: B

Lời giải

Hàm số

2

x

y

x





có đồ thị

 

C

như hình vẽ. Gọi

;

2

a

Aa

a









và

;

2

b

Bb

b









là hai điểm thuộc hai nhánh của

 

C

 

2ab

.

Ta có:

  

;;

2 2 2 2

b a b a

AB b a b a

b a b a







    



   



.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

520

[ I can't, I can! ]

Extra Techniques:

Study Tips:

Ví dụ: Đường thẳng

được giới thiệu ở trên có

dạng

 

:d y x k

. Vì

   

2;1 1I d k   

.

Phương trình hoành độ

giao điểm:

1

2

x





22

x















.

Khi đó hai giao điểm

được hoàn toàn xác định:

 

' 2 2;1 2

A

B















.

Hay

min

' ' 4AB A B

.

Extra Techniques:

Remark:

Giả sử ta có tam giác

ABC

, khi đó trọng tâm

O

của tam giác

ABC

có tọa độ là:

 

,

GG

G x y

,

trong đó

,

GG

xy

được

xác định bởi công thức:

3

A B C

G

A B C

G

xxx

x

yyy

y





















.

Áp dụng bất đẳng thức Cauchy, ta có:

  

 

2

22

4

ba



  

.

Suy ra:

 

  

2

22

ba

AB b a

ba



  

   



 

2

64

16ba

ba

   



4AB

. Dấu bằng xảy ra khi và chỉ khi

22a 

và

22b 

.

Vậy

min

4AB 

.

Câu 6. [Vận dụng].

Giả sử

b

m

a



,

,ab





,

 

,1ab 

là giá trị thực của tham số

m

để

đường thẳng

:3d y x m  

cắt đồ thị hàm số

21

1

x

y

x







 

C

tại hai

điểm phân biệt

A

,

B

sao cho trọng tâm tam giác

OAB

thuộc đường

thẳng

2 2 0xy    

, với

O

là gốc toạ độ. Tính

2ab

.

A.

2

. B.

5

. C.

11

. D.

21

.

Đáp án: D

Lời giải

Phương trình hoành độ giao điểm:

21

3

1

x

xm

x



  



,

1x 

.

 

2

3 1 1 0x m x m     

 

*

.

Để

 

C

cắt

d

tại hai điểm phân biệt thì

 

*

phải có hai nghiệm

phân biệt khác 1.

Suy ra:

   

2

1 12 1 0

10

1 12

3.1 1 .1 1 0

mm

m

mm



   















    







1

11

m













.

Khi đó

 

11

;3A x x m

,

 

22

;3B x x m

, với

1

x

và

2

x

là nghiệm

của phương trình

 

*

đồng thời thoả mãn

12

1

3

m

xx





.

Gọi

G

là trọng tâm của

OAB

, ta có

11

;

93

mm

G









.

Mà

G 

nên

1 1 11

2 2 0

9 3 5

mm

m



     

. Suy ra

11

5

a

b











.

Vậy

2 21ab

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

521

[ I can't, I can! ]

Extra Techniques:

Remark:

Nếu

A

và

B

là hai điểm

đối xứng với nhau qua

M

thì

M

là trung điểm

của đoạn thẳng

AB

hay

nói cách khác, ta có:

2

AB

M

xx

x





.

Extra Techniques:

Remark:

Đối với một số bài toán

điều kiện của mẫu số đã

bị loại khỏi nhờ yêu cầu

đề bài, tuy nhiên, không

nên dựa vào số đông bài

tập không “bẫy” về điều

kiện này mà quên mất

những điều kiện đủ để

logic các vấn đề toán học

trong việc trình bày nhé!

Câu 7. [Vận dụng].

Cho hàm số

2

1

x

y

x





có đồ thị là

 

C

. Tìm tập hợp tất cả các giá trị

a 

để qua điểm

 

0;Ma

có thể kẻ được đường thẳng cắt

 

C

tại

hai điểm phân biệt đối xứng nhau qua điểm

M

.

A.

   

;0 2;  

. B.

 

3;

.

C.

 

;0

. D.



 



; 1 3;   

.

Đáp án: A

Lời giải

Đường thẳng có hệ số góc

k

đi qua điểm

 

0;Ma

có dạng

y kx a

.

Phương trình hoành độ giao điểm của đồ thị

 

C

và đường thẳng

y kx a

là:

2

1

2

1

2

x

kx a

x

x kx kx ax a





  





   



   

2

1

2 0 *

x

kx a k x a











    





.

Ta cần tìm điều kiện của

a

để phương trình

 

*

có hai nghiệm phân

biệt

1

x

;

2

x

khác 1 và thỏa mãn

12

00

2

xx



   

.

Điều kiện này tương đương với

 

2

12

0

2 4 0

.1 2 .1 0

0

k

a k ka

k a k a

xx







   





    







 

2

0

2 4 0

20

2

0

k

a k ka

ka

k







   





















 

0

2

4 2 0

k

ka

aa







  









   

20

2

;0 2;

a

ka

a







  





   



   

;0 2;a    

.

Vậy đáp án A là đáp án chính xác.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

522

[ I can't, I can! ]

Extra Techniques:

Remark:

Đối với dạng toán này,

không đơn thuần là định

giá trị của tham số

m

để

độ dài đoạn thẳng đạt

một độ lớn nhất định,

đây là một khoảng,

đoạn,… Tuy nhiên,

phương pháp chung vẫn

thế, ta lưu ý những kỹ

năng tách, thêm, bớt để

đưa về việc ứng dụng

Định lý Vietè trong giải

bài toán dạng này.

Câu 8. [Vận dụng].

Gọi

S

là tập hợp tất cả các giá trị nguyên của tham số

m

để

đườngthẳng

:d y x m  

cắt đồ thị hàm số

21

1

x

y

x







tại hai điểm

phân biệt

,AB

sao cho

22AB 

. Tổng giá trị các phần tử của

S

bằng

A.

6

. B.

27

. C.

9

. D.

0

.

Đáp án: A

Lời giải

Phương trình hoành độ giao điểm:

 

1

21

1

x

xm

x



  



Điều kiện:

1x 

.

Phương trình

 

1

21

1

x

xm

x



   



  

2 1 1x x m x      

   

2

2.1 1 0x m x m      

Để đường thẳng

:d y x m  

cắt đồ thị hàm số

21

1

x

y

x







tại hai

điểm phân biệt

,AB

thì phương trình

 

2

có hai nghiệm phân biệt

khác

1

2

0

6 3 0.

30

mm





    







   

 

3; 3 2 3 3 2 3;m        

.

Gọi

   

; , ;

A A B B

A x x m B x x m   

là tọa độ giao điểm:

Theo đề ta có:

   

22

2 2 2 2

B A B A

AB x x x x     

 

2

28

BA

xx  

22

2 . 4 0

B A B A

x x x x    

 

2

4 . 4 0

A B A B

x x x x    

.

   

2

1 4 1 4 0mm     

   

2

6 7 0 7;1 4m m m      

Từ

 

3

và

 

4

, ta có:

   

7; 3 2 2 3 2 2;1m      

.

Vì

 

6;0mm   

Đáp án A.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

523

[ I can't, I can! ]

Extra Techniques:

Remark:

Những dạng toán yêu

cầu định giá trị tham số

m

để các “nghiệm” hay

những hoành độ tương

giao thỏa mãn một tính

chất số học nào đó, công

cụ tương giao giữa hàm

số biến thiên với hàm

hằng là không thể thiếu,

bên đây là một ý tưởng

ứng dụng kỹ năng ấy!

Extra Techniques:

Remark:

Đối với một số bài toán

dạng hàm số bậc bốn

trùng phương có chưa

tham số, không bắt buộc

lúc nào cũng đặt ẩn phụ,

cô lập

m

vẫn là một

hướng đi rất khả thi, tuy

nhiên, khi cô lập và chia

hai vế cho một biểu thức

nào đó, ta cần xem xét

khi chia có đưa phương

trình trước đó thành

phương trình hệ quả

hay không? Đó là một sai

lầm trong giải phương

trình. Tác giả Nguyễn

Thành Nhân có một bài

viết về sai lầm phương

trình được đăng trên tạp

chí giáo dục, các bạn có

thời gian có thể xem

thêm những lưu ý quan

trọng khi giải toán.

Câu 9. [Vận dụng].

Có bao nhiêu giá trị nguyên của

m

để đồ thị hàm số

 

4 3 2

4 2 8 4y x x m x x     

cắt trục hoành tại đúng hai điểm có

hoành độ lớn hơn

1

.

A.

8

. B.

7

. C.

5

. D.

3

.

Đáp án: A

Lời giải

Phương trình hoành độ giao điểm

 

4 3 2

4 2 8 4 0x x m x x     

Đồ thị hàm số

 

4 3 2

4 2 8 4y x x m x x     

cắt trục hoành tại đúng

hai điểm có hoành độ lớn hơn

1



có đúng hai nghiệm lớn hơn

1

.

   

4 3 2

* 4 8 4 2x x x m x     

2

84

24m x x

x

     

Đây là phương trình hoành độ giao điểm của

   

2

84

: 4 1C y x x x

x

    

với đường thẳng

2ym

song

song với trục hoành.

Xét hàm số

 

2

84

41y x x x

x

    

.

23

88

24yx

xx



   

43

2

2 4 8 8x x x

x

  



.

Cho

0y





 

1 3 l

1 3 n

x















.

Bảng biến thiên

Dựa vào bảng biến thiên ta thấy, yêu cầu đề bài

0 2 9m   

72m   

.

Vì

m

nguyên nên

 

6, 5,...,1m  

.

Vậy có

8

giá trị nguyên của

m

thỏa bài toán.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

524

[ I can't, I can! ]

Extra Techniques:

Remark:

Phương trình bậc hai

 

2

00ax bx c a   

có hai nghiệm dương

phân biệt khi và chỉ khi:

12

0

b

xx

a

c

xx

a









   











.

Câu 10. [Vận dụng].

Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

   

42

1 2 2 3 6 5y m x m x m     

cắt trục hoành tại 4 điểm phân

biệt có các hoành độ

1 2 3 4

, , ,x x x x

thỏa mãn

1 2 3 4

1.x x x x   

A.

5

1;

6

m











. B.

 

3; 1m  

.

C.

 

3;1m

. D.

 

4; 1m  

.

Đáp án: D

Lời giải

Cách 1: Phương trình hoành độ giao điểm của đồ thị hàm số và trục

hoành là

     

42

1 2 2 3 6 5 0 1m x m x m     

Đặt

2

0tx

, phương trình đã cho trở thành

     

2

1 2 2 3 6 5 0 2m t m t m     

     

2

1 2 2 3 6 5g t m t m t m     

Để phương trình

 

1

có 4 nghiệm phân biệt thì phương trình

 

2

phải

có 2 nghiệm dương phân biệt

Hay

    

2

12

1

10

2 3 1 6 5 0

0

65

0

.0

1

0

23

0

1

m

m m m

m

tt

m

tt

m











    





































 

1

23 561 23 561

44

*

5

1

6

3

1

2

m

mm







   











    



   





Để phương trình

 

1

có 4 nghiệm thỏa mãn

1 2 3 4

1x x x x   

thì phương trình

 

2

phải có 2 nghiệm thỏa

12

01tt  

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

525

[ I can't, I can! ]

Extra Techniques:

Remark:

Cách làm bên đây rất

thích hợp cho các bạn có

kiến thức nền khá rộng,

chúng ta có thể xử lý

điều kiện một cách trực

tiếp bằng việc khảo sát

hàm số ngay vấn đề. Tuy

nhiên, để làm được bài

toán này, ta phải biết

được cách cô lập tham số

m

cũng như xem xét

điều kiện của mẫu và

mức độ khả thi để cô lập

m

. Một bất lợi của dạng

này là chỉ sử dụng cho

một vài trường hợp đặc

biệt, không thể tổng quát

hóa thành phương pháp

chung.

    

1

1 2 1 2 1 2

2

10

1 1 0 1 0

10

t

t t t t t t

t





         







 

2 2 3

6 5 3 12

1 0 0 4 1

1 1 1

m

mm

m

m m m





          

  

Kết hợp với

 

*

ta có

 

4; 1m  

thỏa yêu cầu bài toán.

Cách 2:

Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là

     

42

1 2 2 3 6 5 0 1m x m x m     

Đặt

2

0tx

, phương trình đã cho trở thành

     

2

1 2 2 3 6 5 0 2m t m t m     

Để phương trình

 

1

có 4 nghiệm thỏa mãn

1 2 3 4

1x x x x   

thì phương trình

 

2

phải có 2 nghiệm thỏa

12

01tt  

Phương trình

 

2

65

2

46

tt

m

tt

  





(biểu thức

2

4 6 0,t t t    

)

Xét hàm số

 

2

65

46

tt

ft

tt

  





, với

 

0;t  

Ta có

 

ft

liên tục trên

 

0;

và có

 

2

10 2 56

'

46

tt

ft

tt







 

1 561

0

10

'0

1 561

1

10

t

ft

t





















Bảng biến thiên

Dựa vào bảng biến thiên ta thấy đường thẳng

ym

cắt đồ thị hàm số

 

2

65

46

tt

ft

tt

  





tại hai giao điểm có hoành độ thỏa

12

01tt  

khi

41m   

.

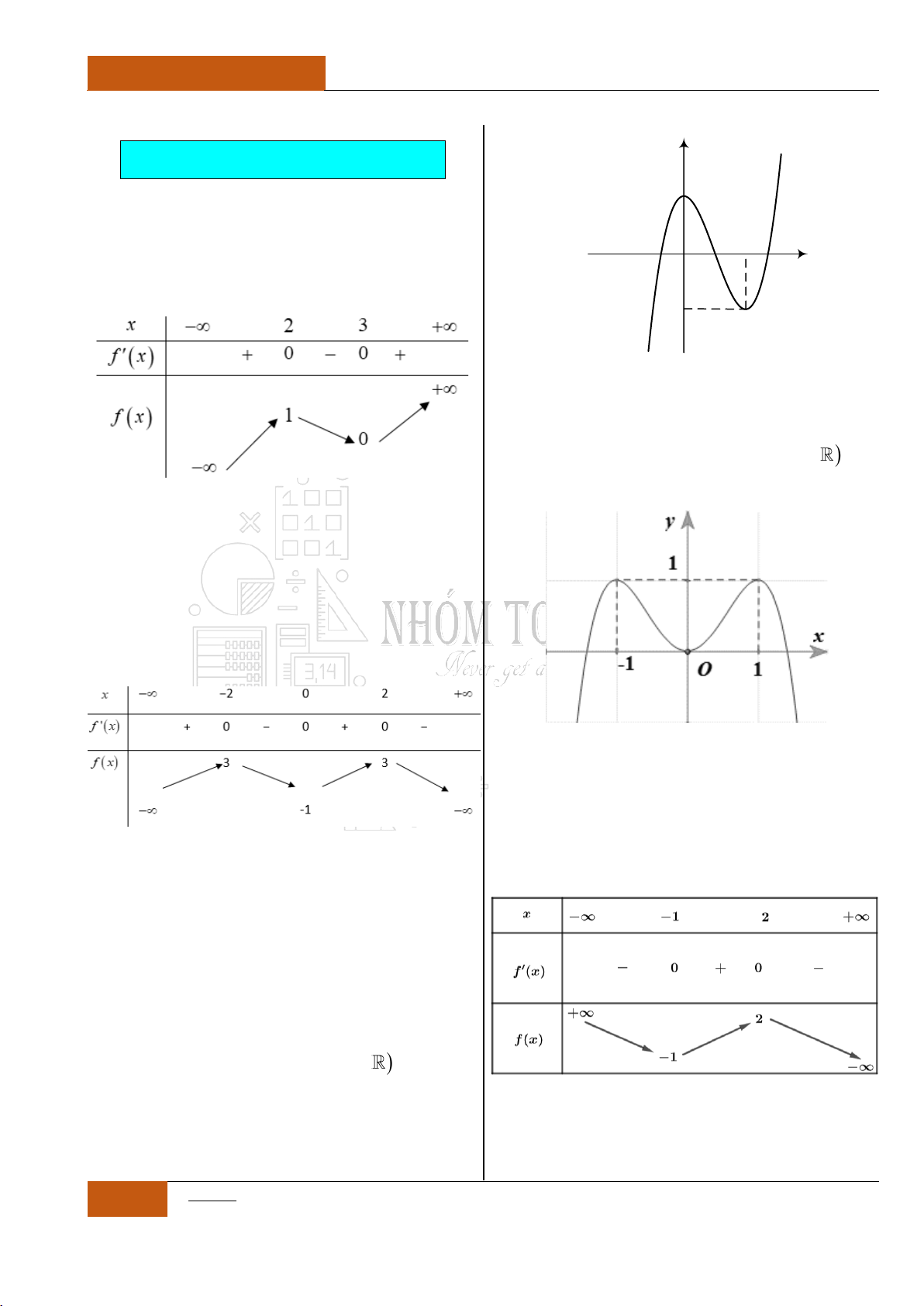
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

526

[ I can't, I can! ]

TỰ LUYỆN 4 MỨC ĐỘ

Câu 1. [Nhận biết].

Cho hàm số

 

fx

có bảng biến thiên như sau

Số nghiệm của phương trình

 

3 2 0fx

là

A.

2.

B.

0.

C.

3.

D.

1.

Câu 2. [Nhận biết].

Cho hàm số có bảng biến thiên như sau:

Số nghiệm thực của phương trình

là

A. . B. . C. . D. .

Câu 3. [Nhận biết].

Cho hàm số bậc ba có dạng tổng quát

. Đồ thị

của hàm số như hình vẽ bên. Số

nghiệm thực của phương trình là?

A. . B. . C. . D. .

Câu 4. [Nhận biết].

Cho hàm số . Đồ

thị của hàm số như hình vẽ bên.

Số nghiệm của phương trình là

A. . B. . C. . D. .

Câu 5. [Nhận biết].

Cho hàm số

 

fx

bảng biến thiên như sau:

Số nghiệm thực của phương trình

 

2 3 0fx

là

 

fx

 

2 3 0fx

2

1

4

3

   

32

, , ,f x ax bx cx d a b c d    

 

y f x

 

3 4 0fx

x

y

O

2

2

0

1

3

   

42

,,f x ax bx c a b c   

 

y f x

 

4 3 0fx

2

0

4

3

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

527

[ I can't, I can! ]

A. . B. . C. . D. .

Câu 6. [Nhận biết].

Cho hàm số có bảng biến thiên như sau

Số nghiệm thực của phương trình

là

A.

3

. B. . C. . D. .

Câu 7. [Thông hiểu].

Cho hàm số liên tục trên và có đồ

thị như hình vẽ.

Số nghiệm của phương trình là

A. . B. . C. . D. .

Câu 8. [Thông hiểu].

Đường cong ở hình bên là đồ thị của hàm số

, với là các số thực. Mệnh

đề nào dưới đây đúng?

A. Phương trình vô nghiệm trên tập số

thực.

B. Phương trình có đúng một nghiệm thực.

C. Phương trình có đúng hai nghiệm thực

phân biệt.

D. Phương trình có đúng ba nghiệm thực

phân biệt.

Câu 9. [Nhận biết].

Cho hàm số

 

y f x

liên tục trên đoạn

 

2;4

và có đồ thị như hình vẽ bên. Số nghiệm thực của

phương trình

 

3 5 0fx

trên đoạn

 

2;4

là

A. . B. . C. . D. .

Câu 10. [Nhận biết].

Cho hàm số

 

y f x

liên tục trên đoạn

và có đồ thị là đường cong như hình vẽ bên.

3

0

1

2

 

fx

 

3 5 0fx

4

0

2

 

y f x

 

2fx

3

2

4

6

42

y ax bx c  

,,abc

0y





0y





0y





0y





2

1

0

3

 

2;2

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

528

[ I can't, I can! ]

Tìm số nghiệm của phương trình

 

1fx

trên

đoạn .

A. 3. B. 5. C. 6. D. 4.

Câu 11. [Nhận biết].

Cho hàm số

 

y f x

có đồ thị là đường cong

trong hình bên. Số nghiệm thực của phương trình

 

1

2

fx

là

A.

4

. B.

2

. C.

1

. D.

3

.

Câu 12. [Thông hiểu].

Số giao điểm của đồ thị hàm số

3

31y x x

và trục hoành là

A.

3

. B.

0

. C.

2

. D.

1

.

Câu 13. [Thông hiểu].

Số giao điểm của đồ thị hàm số

32

3y x x

và

đồ thị hàm số

2

33y x x

là

A.

3

. B.

1

. C.

2

. D.

0

.

Câu 14. [Thông hiểu].

Số giao điểm của đồ thị hàm số

3

3y x x  

với

trục hoành là

A.

2

. B.

0

. C.

3

. D.

1

.

Câu 15. [Thông hiểu].

Cho hàm số

 

2

21y x x  

có đồ thị

 

C

.

Mệnh đề nào dưới đây đúng?

A.

 

C

cắt trục hoành tại một điểm.

B.

 

C

cắt trục hoành tại ba điểm.

C.

 

C

cắt trục hoành tại hai điểm.

D.

 

C

không cắt trục hoành.

Câu 16. [Thông hiểu].

Biết rằng đường thẳng

22yx  

cắt đồ thị

hàm số

3

2y x x  

tại điểm duy nhất; kí hiệu

 

00

;xy

là tọa độ của điểm đó. Tìm

0

y

A.

0

4y 

. B.

0

0y 

.

C.

0

2y 

. D.

0

1y 

.

Câu 17. [Thông hiểu].

Gọi

P

là số giao điểm của hai đồ thị

32

1y x x  

và

2

1yx

. Tìm

P

.

A.

0P 

. B.

2P 

.

C.

1P 

. D.

3P 

.

Câu 18. [Thông hiểu].

Cho hàm số

42

3y x x

có đồ thị

 

C

. Số giao

điểm của đồ thị

 

C

và đường thẳng

2y 

là

A.

2

. B.

1

. C.

0

. D.

4

.

Câu 19. [Thông hiểu].

Đồ thị của hàm số

42

31y x x   

cắt trục

tung tại điểm có tung độ bao nhiêu

A.

3

. B.

0

. C.

1

. D.

1

.

Câu 20. [Thông hiểu].

Số giao điểm của đường cong

32

2 2 1y x x x   

và đường thẳng

1yx

là

A.

1

. B.

2

. C.

3

. D.

0

.

Câu 21. [Thông hiểu].

Cho hàm số

3

25y x x  

có đồ thị

 

C

Tìm

số giao điểm của

 

C

và trục hoành.

 

2;2

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

529

[ I can't, I can! ]

A.

2

. B.

3

. C.

1

. D.

0

.

Câu 22. [Thông hiểu].

Biết rằng đường thẳng

2yx

cắt đồ thị hàm

số

32

4y x x x   

tại điểm duy nhất, kí hiệu

 

00

;xy

là tọa độ của điểm đó. Tìm

0

y

.

A.

0

1y 

. B.

0

3y 

.

C.

0

2y 

. D.

0

4y 

.

Câu 23. [Thông hiểu].

Đồ thị hàm số nào sau đây cắt trục tung tại điểm

có tung độ âm?

A.

1

3

x

y

x







. B.

1

4

x

y

x







.

C.

1

2

x

y

x







. D.

21

5

x

y

x







.

Câu 24. [Thông hiểu].

Gọi

,MN

là giao điểm của đường thẳng

1yx

và đường cong

24

1

x

y

x







. Khi đó

hoành độ

I

x

của trung điểm

I

của đoạn

MN

bằng bao nhiêu?

A.

2

I

x 

. B.

1

I

x 

.

C.

5

I

x 

. D.

5

2

I

x 

.

Câu 25. [Thông hiểu].

Cho hàm số

1

3

x

y

x







có đồ thị

 

C

và các

đường thẳng

1

:2d y x

,

2

: 2 2d y x

,

3

: 3 3d y x

,

4

:3d y x  

. Hỏi có bao nhiêu

đường thẳng trong bốn đường thẳng

1 2 3 4

, , ,d d d d

đi qua giao điểm của

 

C

và trục hoành.

A.

1

. B.

2

. C.

3

. D.

4

.

Câu 26. [Thông hiểu].

Tìm số giao điểm của đồ thị hàm số

4

45yx  

và đường thẳng

yx

A.

3

. B.

0

. C.

2

. D.

1

.

Câu 27. [Thông hiểu].

Cho hàm số

32

32y x mx m  

. Có bao nhiêu

giá trị của tham số thực

m

để đồ thị hàm số cắt

trục hoành tại ba điểm phân biệt có hoành độ lập

thành cấp số cộng?

A.

1

. B.

2

. C.

3

. D.

0

.

Câu 28. [Thông hiểu].

Tìm tất cả các giá trị thực của tham số

m

để đồ

thị hàm số

 

32

32y x x C  

cắt đường

thẳng

 

:1d y m x

tại ba điểm phân biệt

1 2 3

,,x x x

.

A.

2m 

. B.

2m 

.

C.

3m 

. D.

3m 

.

Câu 29. [Thông hiểu].

Đường thẳng



có phương trình

21yx

cắt

đồ thị của hàm số

3

3y x x  

tại hai điểm

A

và

B

với tọa độ được kí hiệu lần lượt là

 

;

AA

A x y

và

 

;

BB

B x y

trong đó

BA

xx

. Tìm

BB

xy

?

A.

5

BB

xy  

. B.

2

BB

xy  

.

C.

4

BB

xy

. D.

7

BB

xy

.

Câu 30. [Vận dụng].

Cho hàm số

3 2 3

3y x mx m  

có đồ thị

 

m

C

và

đường thẳng

23

:2d y m x m

. Biết rằng

 

1 2 1 2

,m m m m

là hai giá trị thực của

m

để

đường thẳng

d

cắt đồ thị

 

m

C

tại

3

điểm phân

biệt có hoành độ

1 2 3

,,x x x

thỏa mãn

4 4 4

1 2 3

83x x x  

. Phát biểu nào sau đây là đúng

về quan hệ giữa hai giá trị

12

,mm

?

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

530

[ I can't, I can! ]

A.

12

0mm

. B.

2

12

24mm

.

C.

2

21

24mm

. D.

12

0mm

.

Câu 31. [Vận dụng].

Tìm tất cả các giá trị thực của tham số

m

để đồ

thị hàm số

32

3y x x

cắt đường thẳng

ym

tại ba điểm phân biệt.

A.

 

;4m  

. B.

 

4;0m

.

C.

 

0;m 

. D.

   

; 4 0;m    

.

Câu 32. [Thông hiểu].

Tìm tất cả các giá trị thực của tham số

m

để

đường thẳng

1y mx m  

cắt đồ thị hàm số

32

32y x x x   

tại ba điểm

,,A B C

phân

biệt sao

AB BC

.

A.

5

;

4

m



  





. B.

 

2;m  

.

C.

m

. D.

 





;0 4;m   

.

Câu 33. [Vận dụng].

Tất cả giá trị của tham số

m

để đồ thị hàm số

 

3 2 2

2 2 4y x m x m    

cắt các trục tọa độ

,Ox

Oy

lần lượt tại

,A

B

sao cho diện tích tam

giác

OAB

bằng 8 là

A.

2m 

. B.

1m 

.

C.

3m 

. D.

2m 

.

Câu 34. [Vận dụng].

Tìm tất cả các giá trị thực của tham số

m

để

đường thẳng

y mx

cắt đồ thị của hàm số

32

32y x x m   

tại ba điểm phân biệt

,,A B C

sao cho

AB BC

.

A.

 

;1m  

. B.

 

:m  

.

C.

 

1:m 

. D.

 

;3m 

.

Câu 35. [Vận dụng].

Tìm tất cả các giá trị thực của tham số

m

để

đường thẳng

5yx  

cắt đồ thị hàm số

32

2 x 3( 1) 5y x m m x    

tại

3

điểm phân

biệt.

A.

1

2

m











. B.

2

3

1

2

m





























.

C.

2

3

1

2

m





























. D.

1

2

m











.

Câu 36. [Vận dụng].

Cho hàm số bậc ba

 

y f x

có đồ thị

 

C

như

hình vẽ, đường thẳng

d

có phương trình

1yx

. Biết phương trình

 

0fx

có ba

nghiệm

1 2 3

x x x

. Giá trị của

13

xx

bằng

A.

3

. B.

7

3



. C.

2

. D.

5

2



.

Câu 37. [Vận dụng].

Tính tổng tất cả các giá trị của

m

biết đồ thị hàm

số

 

32

2 3 4y x mx m x    

và đường thẳng

4yx

cắt nhau tại ba điểm phân biệt

 

0;4A

,

B

,

C

sao cho diện tích tam giác

IBC

bằng

82

với

 

1;3I

.

A.

3

. B.

8

. C.

1

. D.

5

.

Câu 38. [Vận dụng].

Đường thẳng d có phương trình

4yx

cắt đồ

thị hàm số

 

32

2 3 4y x mx m x    

tại 3

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

531

[ I can't, I can! ]

điểm phân biệt

 

0;4A

, B và C sao cho diện

tích của tam giác MBC bằng

4

, với

 

1;3M

.

Tìm tất cả các giá trị của

m

thỏa mãn yêu cầu

bài toán.

A.

3m 

. B.

2

3

m











.

C.

2

3

m











. D.

2

3

m











.

Câu 39. [Vận dụng].

Tìm tất cả các giá trị thực của tham số

m

để

đường thẳng

5yx  

cắt đồ thị hàm số

 

32

2 3 1 5y x mx m x    

tại ba điểm phân

biệt.

A.

1

2

m











. B.

2

3

1

2

m





























.

C.

2

3

1

2

m





























. D.

1

2

m











.

Câu 40. [Vận dụng].

Giá trị lớn nhất của

m

để đường thẳng

 

:1d y x m  

cắt đồ thị hàm số

   

32

2 2 8 5 5y x m x m x m      

tại 3

điểm phân biệt có hoành độ

1 2 3

,,x x x

thỏa mãn

điều kiện

222

1 2 3

20xxx  

là?

A.

3

. B.

1

. C.

0

. D.

3

2



.

Câu 41. [Vận dụng].

Có bao nhiêu giá trị của

m

để đồ thị hàm số

 

3 2 2 3

2 3 2 2y x m x m m x     

cắt trục

hoành tại ba điểm phân biệt có hoành độ là ba số

hạng liên tiếp của một cấp số nhân?

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 42. [Vận dụng].

Tìm

m

để đồ thị

 

C

của

32

34y x x  

và

đường thẳng

y mx m

cắt nhau tại 3 điểm

phân biệt

 

1;0A 

,

B

,

C

sao cho

OBC

có

diện tích bằng

64

.

A.

14m 

. B.

15m 

.

C.

16m 

. D.

17m 

.

Câu 43. [Vận dụng].

Cho hàm số

32

88y x x x  

có đồ thị

 

C

và

hàm số

 

2

8y x a x b   

( với

,ab

) có

đồ thị

 

P

. Biết đồ thị hàm số

 

C

cắt

 

P

tại

ba điểm có hoành độ nằm trong

 

1;5

. Khi

a

đạt giá trị nhỏ nhất thì tích

ab

bằng

A.

729

. B.

375

.

C.

225

. D.

384

.

Câu 44. [Vận dụng].

Có bao nhiêu giá trị nguyên của tham số

m

để

đường thẳng

y mx m  

cắt đồ thị hàm số

32

y x mx m  

tại

3

điểm phân biêt có hoành

độ

1 2 3

,,x x x

thỏa mãn

1 2 3

13x x x    

?.

A.

6

. B.

5

. C.

2

. D.

3

.

Câu 45. [Vận dụng].

Cho hàm số

 

32

2 3 4y x mx m x    

 

m

C

.

Tất cả các giá trị của tham số

m

để đường thẳng

 

:4d y x

cắt

 

m

C

tại ba điểm phân biệt

 

0;4A

,

B

,

C

sao cho tam giác

KBC

có diện

tích bằng

82

với điểm

 

1;3K

là:

A.

1 137

2

m





. B.

1 137

2

m





.

C.

1 137

2

m





. D.

1 137

2

m





.

Câu 46. [Vận dụng].

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

532

[ I can't, I can! ]

Cho đồ thị hàm số

 

32

f x x bx cx d   

cắt

trục hoành tại 3 điểm phân biệt có hoành độ

1 2 3

,,x x x

. Tính giá trị của biểu thức

   

 

1 2 3

1 1 1

.P

f x f x f x

  

  

A.

32P b c  

. B.

0P 

.

C.

P b c d  

. D.

11

2

P

bc



.

Câu 47. [Vận dụng].

Cho hàm số bậc ba

 

y f x

có đồ thị đi qua

điểm

     

1;1 , 2;4 , 3;9A B C

. Các đường thẳng

,,AB AC BC

lại cắt đồ thị lần lượt tại các điểm

,,M N P

(

M

khác

A

và

B

,

N

khác

A

và

C

,

P

khác

B

và

C

. Biết rằng tổng các hoành độ

của

,,M N P

bằng 5, giá trị của

 

0f

là

A.

6

. B.

18

. C. 18. D. 6.

Câu 48. [Vận dụng].

Tìm giá trị thực của tham số

m

để đồ thị hàm số

32

32y x x  

cắt đường thẳng

 

:1d y m x

tại ba điểm phân biệt có hoành

độ

1

x

,

2

x

,

3

x

thỏa mãn

222

1 2 2

5xxx  

.

A.

3m 

. B.

2m 

.

C.

3m 

. D.

2m 

.

Câu 49. [Vận dụng].

S

là tập tất cả các giá trị của tham số

m

để đồ

thị hàm số

32

3 9 2 1y x x x m    

và trục

Ox

có đúng hai điểm chung phân biệt. Tính tổng

T

của các phần tử thuộc tập

S

A.

10T 

. B.

10T 

.

C.

12T 

. D.

12T 

.

Câu 50. [Vận dụng].

Có tất cả bao nhiêu giá trị nguyên thuộc đoạn

 

2020;2020

của tham số

m

để đường thẳng

y x m

cắt đồ thị hàm số

23

1

x

y

x







tại hai

điểm phân biệt?

A.

4036.

B.

4040.

C.

4038.

D.

4034.

Câu 51. [Vận dụng].

Có bao nhiêu giá trị của

m

để đồ thị của hàm số

1

x

y

x





cắt đường thẳng

y x m

tại hai

điểm phân biệt

,AB

sao cho góc giữa hai đường

thẳng

OA

và

OB

bằng

0

60

( với

O

là gốc tọa

độ)?

A.

2

. B.

1

. C.

3

. D.

0

.

Câu 52. [Vận dụng].

Cho hàm số

2

1

xm

y

x







có đồ thị

 

,

m

C

trong

đó

m

là tham số thực. Đường thẳng

:d y m x

cắt

 

m

C

tại hai điểm

   

; , ;

A A B B

A x y B x y

với

;

AB

xx

đường

thẳng

': 2d y m x  

cắt

 

m

C

tại hai điểm

 

; , ;

C C D D

C x y D x y

với

.

CD

xx

Gọi

S

là

tập hợp tất cả các giá trị của tham số

m

để

. 3.

AD

xx

Số phần tử của tập

S

là

A.

1.

B.

2.

C.

0.

D.

3.

Câu 53. [Vận dụng].

Cho hàm số

42

32y x x  

. Tìm số thực

dương

m

để đường thẳng

ym

cắt đồ thị hàm

số tại

2

điểm phân biệt

A

,

B

sao cho tam giác

OAB

vuông tại

O

, trong đó

O

là gốc tọa độ.

A.

2m 

. B.

3

2

m 

.

C.

3m 

. D.

1m 

.

Câu 54. [Vận dụng].

Cho hàm số

42

2y x mx m  

(với

m

là tham

số thực). Tập tất cả các giá trị của tham số

m

để

đồ thị hàm số đã cho cắt đường thẳng

3y 

tại

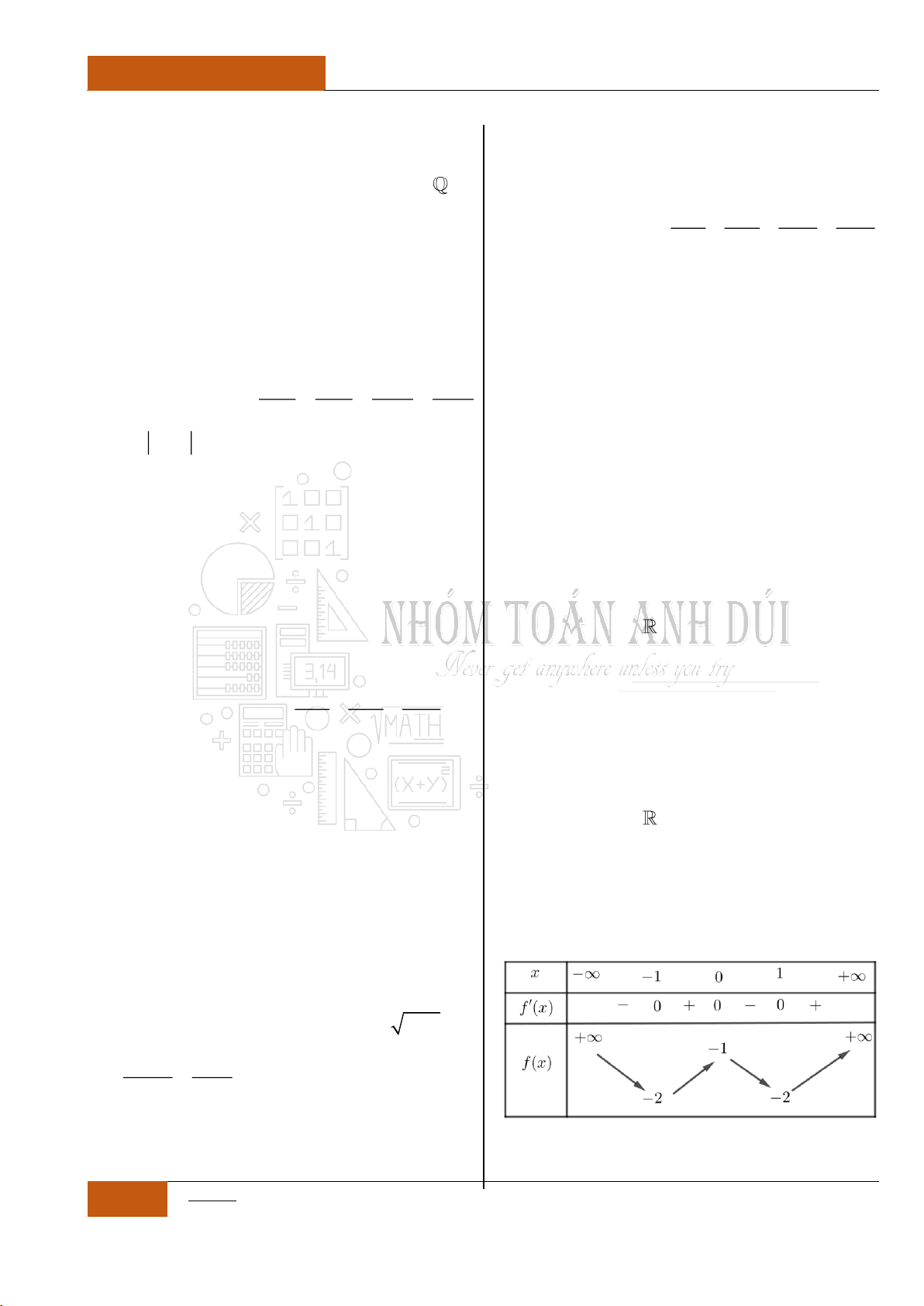
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

533

[ I can't, I can! ]

bốn điểm phân biệt, trong đó có một điểm có

hoành độ lớn hơn

2

còn ba điểm kia có hoành

độ nhỏ hơn

1

, là khoảng

 

;ab

(với

,ab

,

a

,

b

là phân số tối giản).

Khi đó,

15ab

nhận giá trị nào sau đây?

A.

63

. B.

63

.

C.

95

. D.

95

.

Câu 55. [Vận dụng cao].

Cho hai hàm số

1 1 2

1 2 3

x x x x

y

x x x x

  

   

  

và

2y x x m   

(

m

là tham số thực) có đồ

thị lần lượt là

   

12

,CC

. Tập hợp tất cả các giá

trị của

m

để

 

1

C

và

 

2

C

cắt nhau tại đúng bốn

điểm phân biệt là

A.

 

2;  

. B.





;2 

.

C.





2;  

. D.

 

;2 

.

Câu 56. [Vận dụng].

Cho hai hàm số

12

11

x x x

y

x x x



  



và

2020 3

x

y e m  

(

m

là tham số thực) có đồ

thị lần lượt là

 

1

C

và

 

2

C

. Có bao nhiêu số

nguyên

m

thuộc

 

2019;2020

để

 

1

C

và

 

2

C

cắt nhau tại 3 điểm phân biệt?

A.

2692

. B.

2691

.

C.

2690

. D.

2693

.

Câu 57. [Vận dụng cao].

Tìm tập hợp tất cả các giá trị của tham số

m

để

đồ thị hai hàm số

 

2

2 1 1y x x  

và

11 1

11

3 4 2

ym

xx

   



cắt nhau tại

2

điểm

phân biệt?

A.

 

;0

. B.

 

;1

.

C.





;1

. D.





;2

.

Câu 58. [Vận dụng cao].

Cho hai hàm số

1 1 2

1 2 3

x x x x

y

x x x x

  

   

  

và

1

22

x

ym





( là tham số thực) có đồ thị

lần lượt là

 

1

C

và

 

2

C

. Tập hợp tất cả các giá

trị của để

 

1

C

và

 

2

C

cắt nhau tại đúng

năm điểm phân biệt là

A.

 

2;

. B.





;2

.

C.

 

;2

. D.

 

;4

.

Câu 59. [Vận dụng cao].

Gọi

S

là tập hợp tất cả các giá trị của tham số

m

để bất phương trình

 

2 4 3 2 2

2 1 0m x m x x m x     

nghiệm

đúng với mọi

x

. Số phần tử của tập

S

là

A.

3

. B.

2

. C.

0

. D.

1

.

Câu 60. [Vận dụng cao].

Có bao nhiêu cặp số thực

 

;ab

để bất phương

trình

  

 

2

1 2 2 0x x ax bx    

nghiệm

đúng với mọi

x

A.

3

. B.

2

. C.

0

. D.

1

.

Câu 61. [Vận dụng cao].

Cho hàm số

 

fx

có bảng biến thiên như sau:

Số nghiệm thuộc đoạn

 

;2



của phương

m

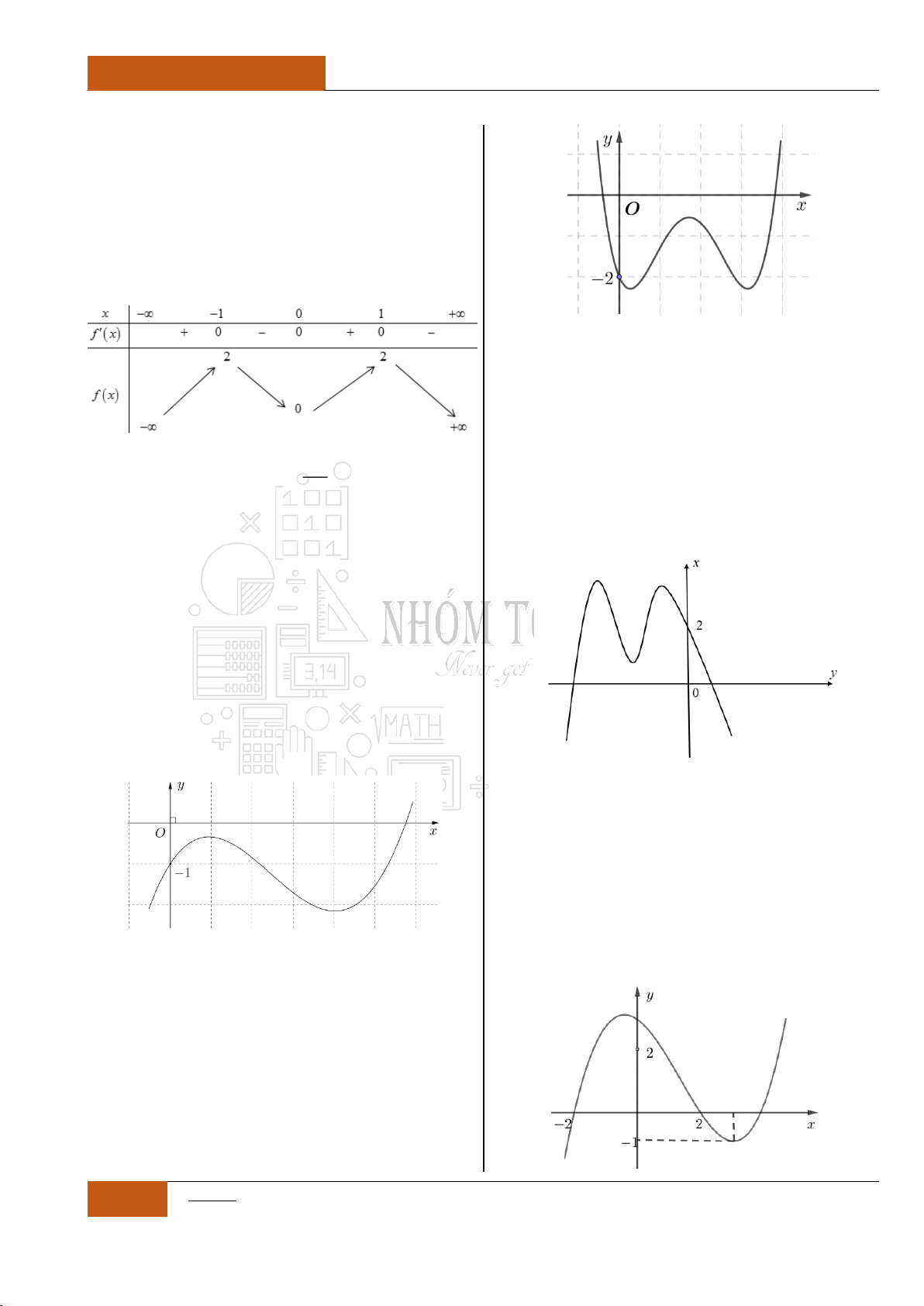
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

534

[ I can't, I can! ]

trình

 

2 sin 3 0fx

là

A.

4

. B.

6

. C.

3

. D.

8

.

Câu 62. [Vận dụng cao].

Cho hàm số

 

fx

có bảng biến thiên như sau

Số nghiệm thuộc đoạn

5

0;

2









của phương

trình

 

sin 1fx

là

A.

7

. B.

4

. C.

5

. D.

6

.

Câu 63. [Vận dụng cao].

Cho hàm số bậc ba

()y f x

có đồ thị là đường

cong trong hình bên. Số nghiệm thực phân biệt

của phương trình

 

3

( ) 1 0f x f x 

là

A.

8

. B.

5

. C.

6

. D.

4

.

Câu 64. [Vận dụng cao].

Cho hàm số bậc bốn

 

y f x

có đồ thị là

đường cong trong hình vẽ bên.

Số nghiệm thực phân biệt của phương trình

 

2

( ) 2 0f x f x 

là

A.

8

. B.

12

. C.

6

. D.

9

.

Câu 65. [Vận dụng cao].

Cho hàm số

 

y f x

có đồ thị là đường cong

trong hình vẽ bên.

Số nghiệm thực của phương trình

 

2

2f x f x 

là:

A. 6. B. 12. C. 8. D. 9.

Câu 66. [Vận dụng cao].

Cho hàm số bậc ba

 

y f x

có đồ thị như hình

vẽ dưới đây.

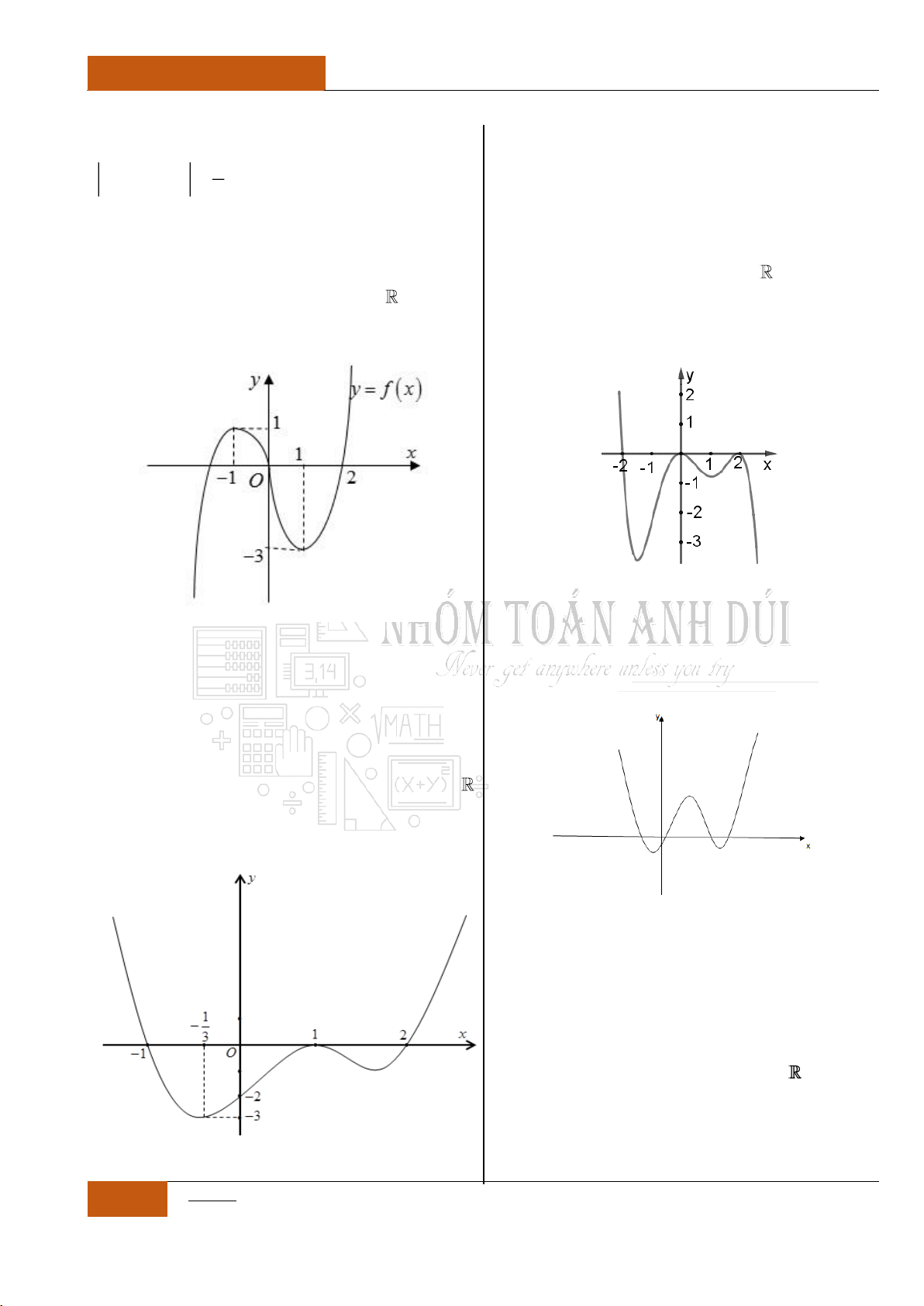
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

535

[ I can't, I can! ]

Số nghiệm thực của phương trình

 

3

2

f x x

là

A.

7

. B.

3

. C.

8

. D.

4

.

Câu 67. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục trên và có đồ

thị như hình vẽ sau

Số nghiệm của phương trình

 

2 e 1

x

ff

là

A.

4

. B.

2

. C.

1

. D.

3

.

Câu 68. [Vận dụng cao].

Cho hàm số

 

y f x

có đạo hàm cấp 2 trên

và có đồ thị

 

fx



là đường cong trong hình vẽ

bên.

Đặt

   

 

1.g x f f x





Gọi

S

là tập nghiệm

của phương trình

 

0.gx





Số phần tử của tập

S

là

A.

8

. B.

10

. C.

9

. D.

6

.

Câu 69. [Vận dụng cao].

Cho hàm số

 

fx

liên tục trên và có đồ thị

như hình vẽ. Đặt

   

 

g x f f x

. Hỏi phương

trình

 

0gx





có mấy nghiệm thực phân biệt?

A.

14

. B.

10

. C.

8

. D.

12

.

Câu 70. [Vận dụng cao].

Biết rằng đồ thị hàm số

()y f x

được cho như

hình vẽ sau

Số giao điểm của đồ thị hàm số

     

2

.y f x f x f x

 

   



và trục

Ox

là:

A.

4

. B.

6

. C.

2

. D.

0

.

Câu 71. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục trên và có đồ

thị như hình vẽ bên. Phương trình

 

10f f x 

có tất cả bao nhiêu nghiệm

thực phân biệt?

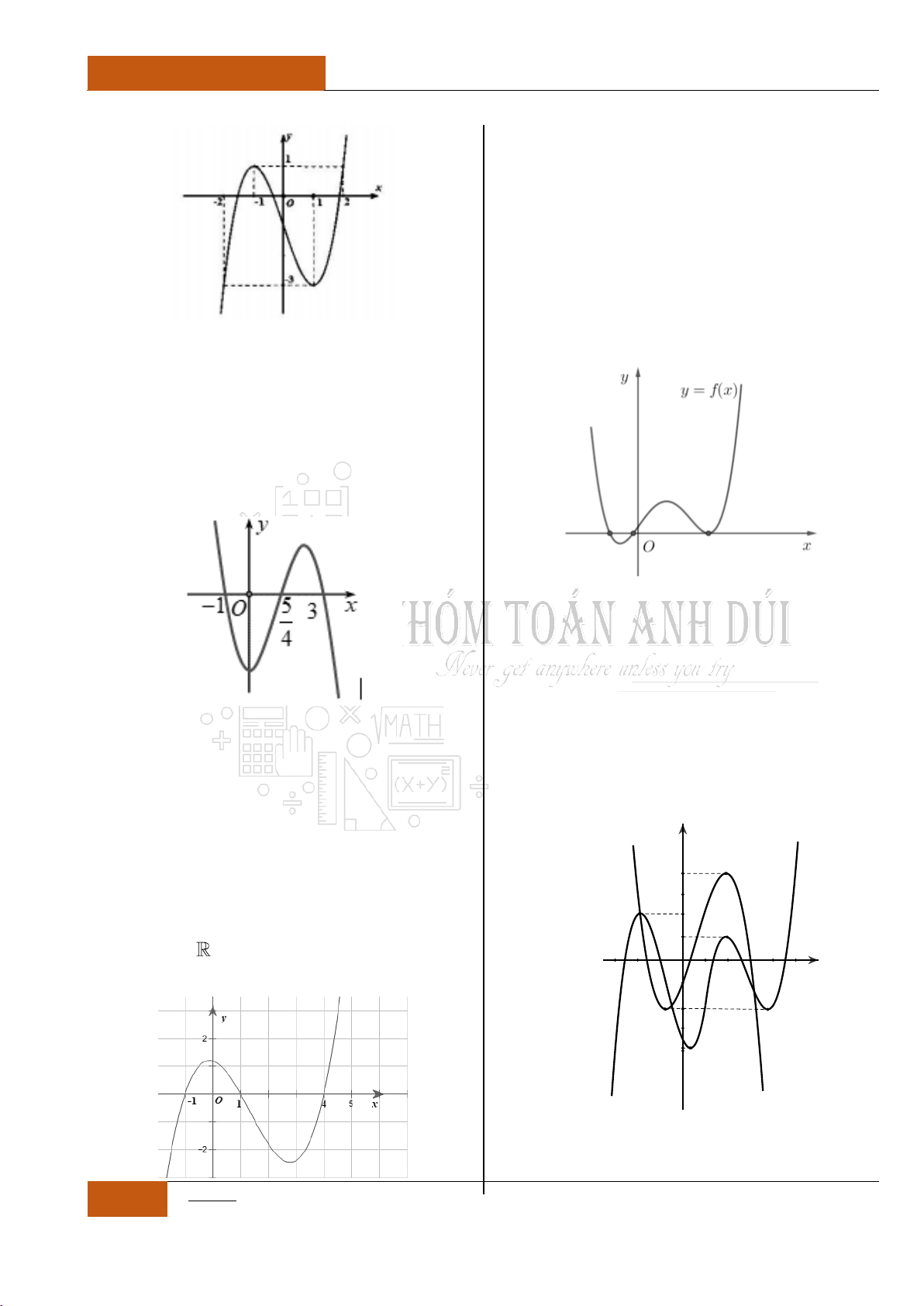
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

536

[ I can't, I can! ]

A.

6

. B.

5

. C.

7

. D.

4

.

Câu 72. [Vận dụng cao].

Cho hàm số

 

4 3 2

f x mx nx px qx r    

,.

Hàm số

 

y f x





có đồ thị như hình vẽ bên

dưới:

Tập nghiệm của phương trình

 

f x r

có số

phần tử là

A.

4

. B.

3

. C.

1

. D.

2

.

Câu 73. [Vận dụng cao].

Cho hàm số bậc bốn tổng quát như sau

 

4 3 2

y f x mx nx px qx r     

, trong đó

, , , ,m n p q r 

. Biết rằng hàm số

 

'y f x

có

đồ như hình vẽ dưới.

Tập nghiệm của phương trình

 

16 8 4 2f x m n p q r    

có tất cả bao

nhiêu phần tử.

A.

4

. B.

3

. C.

5

. D.

6

.

Câu 74. [Vận dụng cao].

Cho

 

fx

là một hàm đa thức bậc bốn có đồ thị

như hình dưới đây.

Tập nghiệm của phương trình

     

2

.f x f x f x

 

  



có số phần tử là

A.

1.

B.

2.

C.

4.

D.

0.

Câu 75. [Vận dụng cao].

Cho hai hàm số

   

,y f x y g x

có đồ thị

như hình sau:

Khi đó tổng số nghiệm của hai phương trình

 

0f g x 

và

 

0g f x 

là

5

y=g

(

x

)

y=f

(

x

)

y

x

-4

-3

-2

-1

4

3

2

1

4

3

2

1

O

-1

-2

-3

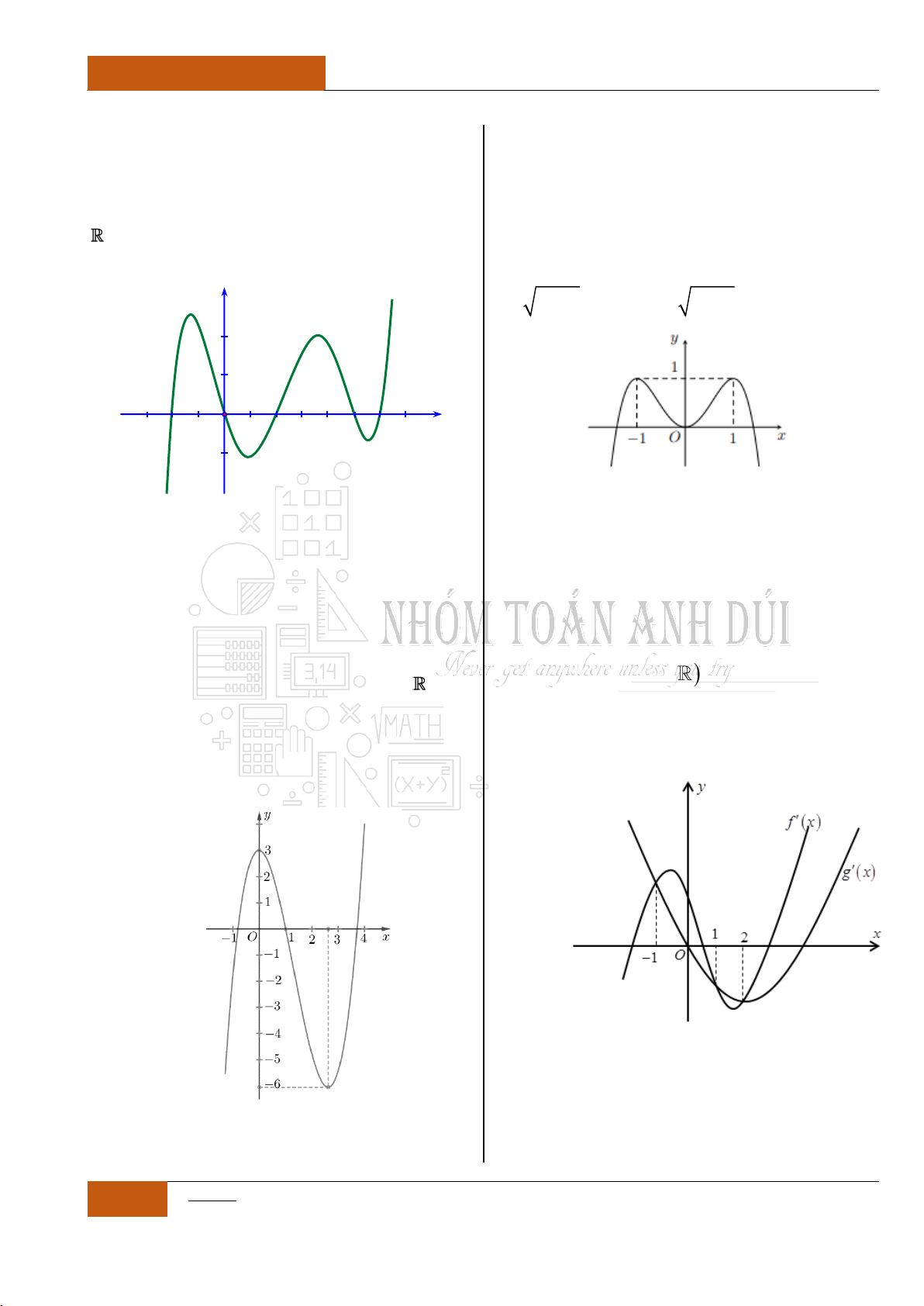
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

537

[ I can't, I can! ]

A.

25

. B.

22

. C.

21

. D.

26

.

Câu 76. [Vận dụng cao].

Cho hàm số

 

y f x

có đạo hàm liên tục trên

. Hàm số

 

y f x





có đồ thị như hình vẽ bên

dưới:

Số nghiệm thuộc đoạn

 

2;6

của phương trình

   

0f x f

là

A. 5. B. 2. C. 3. D. 4.

Câu 77. [Vận dụng cao].

Cho hàm số

 

y f x

có đạo hàm trên và có

đồ thị là đường cong trong hình vẽ dưới. Đặt

   

g x f f x  



. Tìm số nghiệm của phương

trình

 

0gx





.

A.

2

. B.

8

. C.

4

. D.

6

.

Câu 78. [Vận dụng cao].

Cho hàm số

 

4 3 2

y f x ax bx cx dx e     

có đồ thị như hình vẽ bên đây, trong đó

, , , ,a b c d e

là các hệ số thực. Số nghiệm của

phương trình

 

   

2 1 0f f x f x f x   

là

A. 3. B. 4. C. 2. D. 0.

Câu 79. [Vận dụng cao].

Cho các hàm số bậc bốn có phương trình

 

4 3 2

f x mx nx px qx r    

và hàm số bậc

ba có phương trình

 

32

g x ax bx cx d   

,

 

, , , , , , , ,n n p q r a b c d 

thỏa mãn

   

00fg

. Các hàm số

   

,f x g x



có đồ

thị như hình vẽ dưới đây

Tập nghiệm của phương trình

   

f x g x

có

số phần tử là

A.

4

. B.

2

. C.

1

. D.

3

.

O

1

2

3

1

2

3

4

5

6

7

x

y

4

2

2

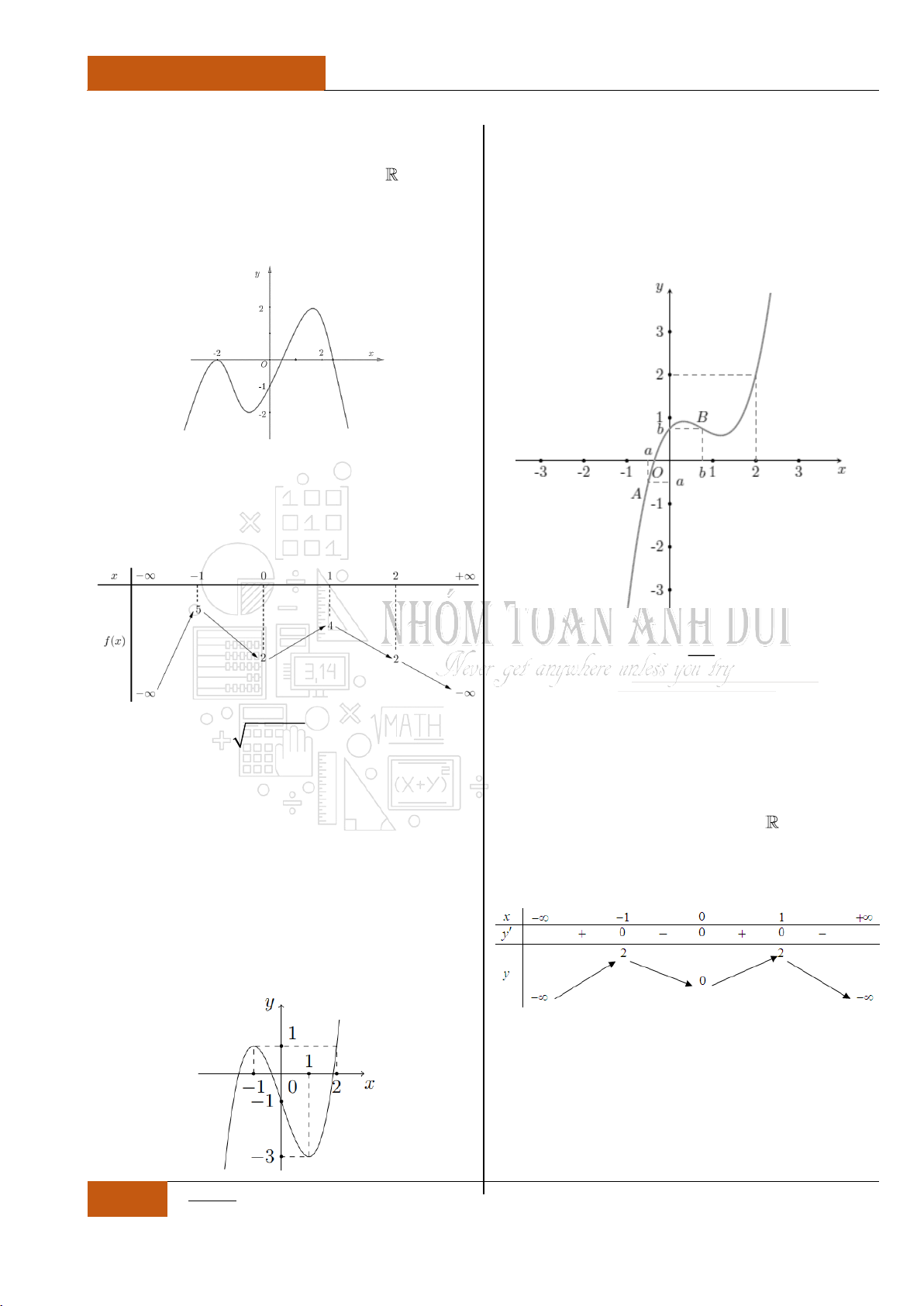
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

538

[ I can't, I can! ]

Câu 80. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục trên

và có đồ

thị như hình vẽ. Tập hợp nghiệm của phương

trình

 

10f f x 

có bao nhiêu phần tử?

A.

4

. B.

7

. C.

6

. D.

9

.

Câu 81. [Vận dụng cao].

Cho hàm số

 

fx

có bảng biến thiên

Phương trình





2

23f x x

có bao nhiêu

nghiệm?

A. 1. B. 2. C. 3. D. 4.

Câu 82. [Vận dụng cao].

Cho hàm số

 

fx

có đồ thị như hình bên.

Phương trình

 

cos 1 0f f x   



có bao nhiêu

nghiệm thuộc đoạn

 

0;2



?

A.

2

. B.

5

. C.

4

. D.

6

.

Câu 83. [Vận dụng cao].

Cho hàm số

 

32

f x ax bx bx c   

có đồ thị

như hình vẽ:

Số nghiệm nằm trong

;3

2











của phương

trình

 

cos 1 cos 1f x x  

là

A.

2

. B.

3

. C. 5. D. 4.

Câu 84. [Vận dụng cao].

Cho hàm số

 

fx

liên tục trên và có bảng

biến thiên như sau:

Số nghiệm thuộc khoảng

 

;ln2

của phương

trình

 

2019 1 2021 0

x

fe  

là

A.

1

. B.

2

. C.

3

. D.

4

.

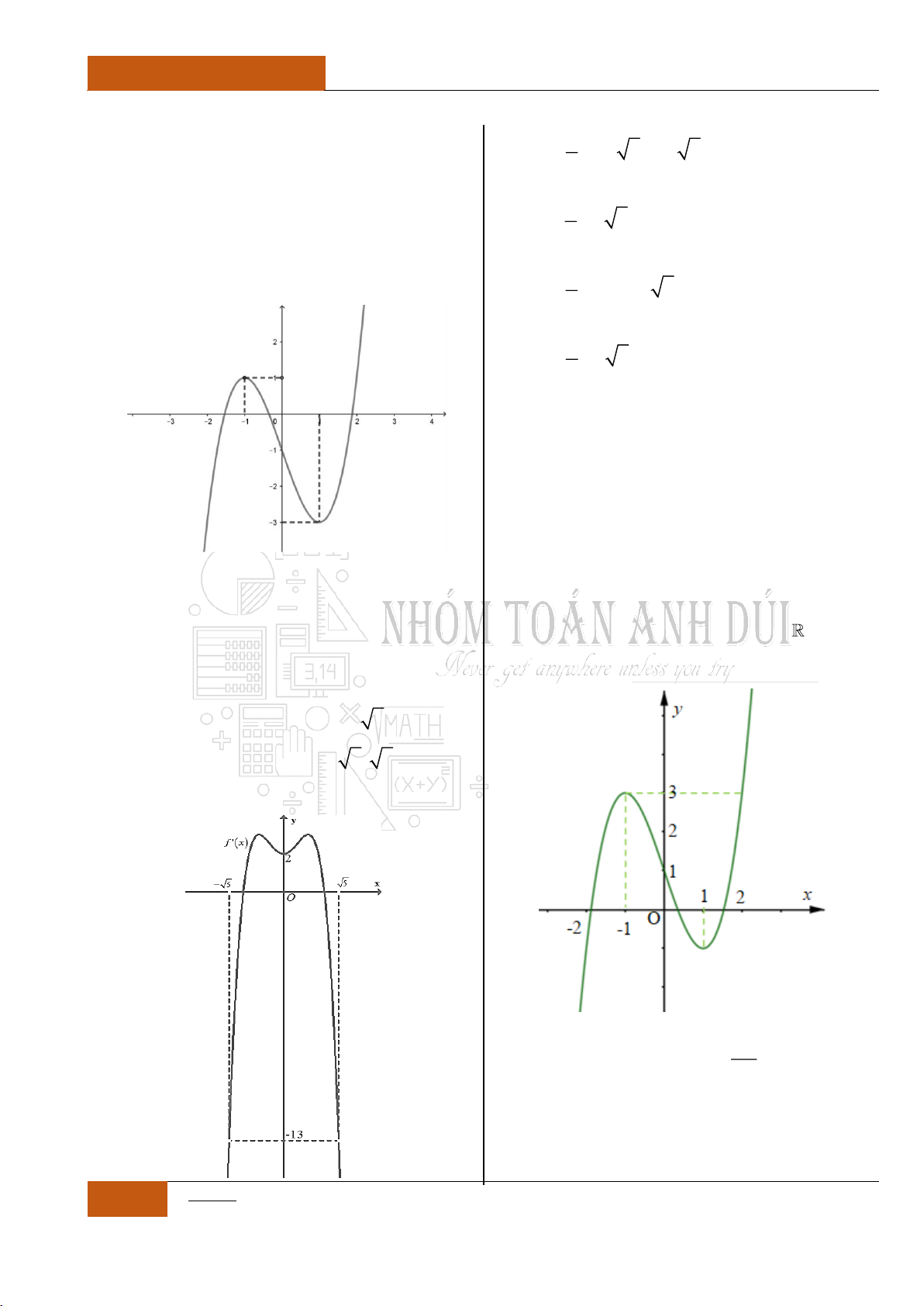
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

539

[ I can't, I can! ]

Câu 85. [Vận dụng cao].

Cho

 

y f x

là hàm số đa thức bậc 3 và có đồ

thị như hình vẽ bên. Hỏi phương trình

 

cos 1 0f f x 

có bao nhiêu nghiệm thuộc

đoạn

 

0;3



?

A.

2

. B.

4

. C.

5

. D.

6

.

Câu 86. [Vận dụng cao].

Cho hàm số

 

y f x

có đồ thị

 

'y f x

như

hình vẽ. Xét hàm số

   

3

2 2 4 3 6 5g x f x x x m    

với

m

là

số thực. Để

 

0, 5; 5g x x



   



thì điều

kiện của

m

là

A.

 

2

5 4 5

3

mf  

.

B.

 

2

5

3

mf

.

C.

 

2

0 2 5

3

mf

.

D.

 

2

5

3

mf

.

Câu 87. [Vận dụng cao].

Cho hàm số

 

fx

có đồ thị như hình vẽ. Đặt

   

 

1g x f f x

. Số nghiệm của phương

trình

 

0gx





là

A.

6

. B.

10

. C.

9

. D.

8

.

Câu 88. [Vận dụng cao].

Cho hàm số

()y f x

liên tục trên và có đồ

thị như hình vẽ bên

Số nghiệm thuộc đoạn

7

0;

2









của phương

trình

 

cos 0f f x 

là

A.

7

. B.

5

. C.

8

. D.

6

.

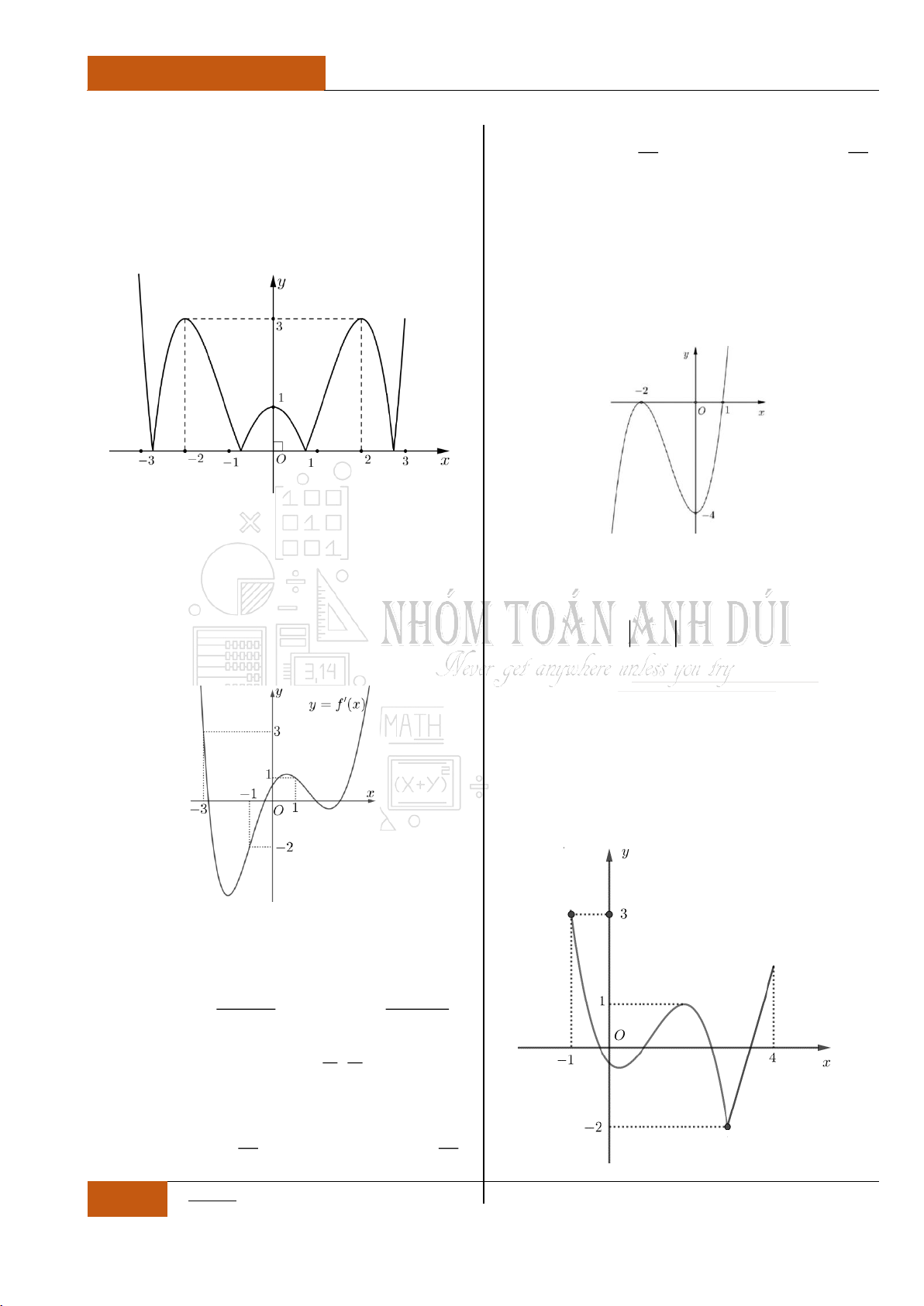
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

540

[ I can't, I can! ]

Câu 89. [Vận dụng cao].

Cho hàm số

 

y f x

có đồ thị như hình vẽ bên.

Tìm số nghiệm thuộc đoạn

 

2017 ;2020



của

phương trình

 

3 2cos 8fx

.

A.

8

. B.

3

. C.

4

. D.

6

.

Câu 90. [Vận dụng cao].

Cho hàm số

 

fx

. Hàm số

 

y f x





có đồ thị

như hình sau.

Tìm tất cả các giá trị thực của tham số

m

để bất

phương trình

 

3

2sin 5cos2

2 sin 2 sin

34

xx

f x x m    

nghiệm đúng với mọi

;

22

x











.

A.

 

11

2 3 .

12

mf  

B.

 

19

2 1 .

12

mf  

C.

 

19

2 1 .

12

mf  

D.

 

11

2 3 .

12

mf  

Câu 91. [Vận dụng cao].

Cho hàm số

 

32

y f x ax bx cx d    

có

đồ thị như hình dưới đây

Có tất cả bao nhiêu giá trị nguyên của tham số

 

5;5m

để phương trình

     

2

4 2 4 0f x m f x m    

có

6

nghiệm phân biệt

A.

2

. B.

4

. C.

3

. D.

5

.

Câu 92. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục trên đoạn

 

1;4

và có đồ thị như hình vẽ.

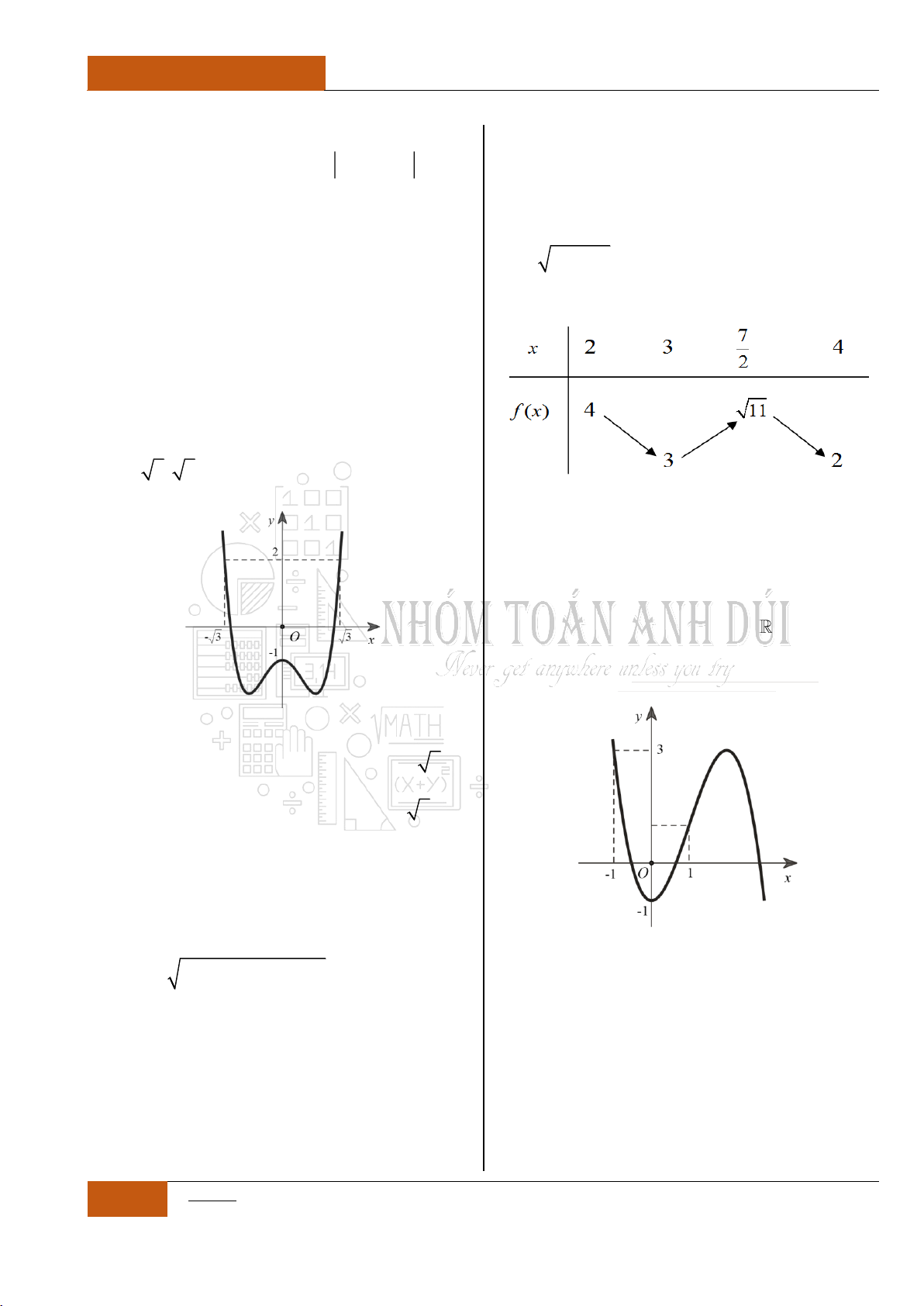
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

541

[ I can't, I can! ]

Có bao nhiêu giá trị

nguyên của

m

thuộc đoạn

 

10;10

để bất phương trình

 

2f x m m

đúng với mọi

x

thuộc đoạn

 

1;4

.

A.

6

. B.

5

. C.

7

. D.

8

.

Câu 93. [Vận dụng cao].

Cho hàm số

 

y f x

. Đồ thị hàm số

 

'y f x

như hình vẽ. Cho bất phương trình

 

3

33f x x x m

(

m

là tham số thực). Điều

kiện cần và đủ để bất phương trình

 

3

33f x x x m

đúng với mọi

3; 3x







là

A.

 

31mf

. B.

 

33mf

.

C.

 

30mf

. D.

 

33mf

.

Câu 94. [Vận dụng cao].

Cho hàm số

 

3

2f x x x  

. Có tất cả bao

nhiêu giá trị nguyên của tham số

m

để phương

trình

   





33

3

2f f x f x m x x     

có

nghiệm

 

1;2x 

?

A.

1750

. B.

1748

.

C.

1747

. D.

1746

.

Câu 95. [Vận dụng cao].

Cho hàm số

 

fx

liên tục trên

 

2;4

và có bảng

biến thiên như hình vẽ bên. Có bao nhiêu giá trị

nguyên của

m

để phương trình

2

2 2 . ( )x x x m f x  

có nghiệm thuộc đoạn

 

2;4

?

A.

6

. B.

5

. C.

4

. D.

3

.

Câu 96. [Vận dụng cao].

Cho hàm số

 

fx

liên tục trên và có đồ thị

như hình vẽ.

Số giá trị nguyên của

m

để phương trình

     

2

cos 2019 cos 2020 0f x m f x m    

có đúng 6 nghiệm phân biệt thuộc đoạn

 

0;2



là

A.

1

. B.

3

. C.

2

. D.

5

.

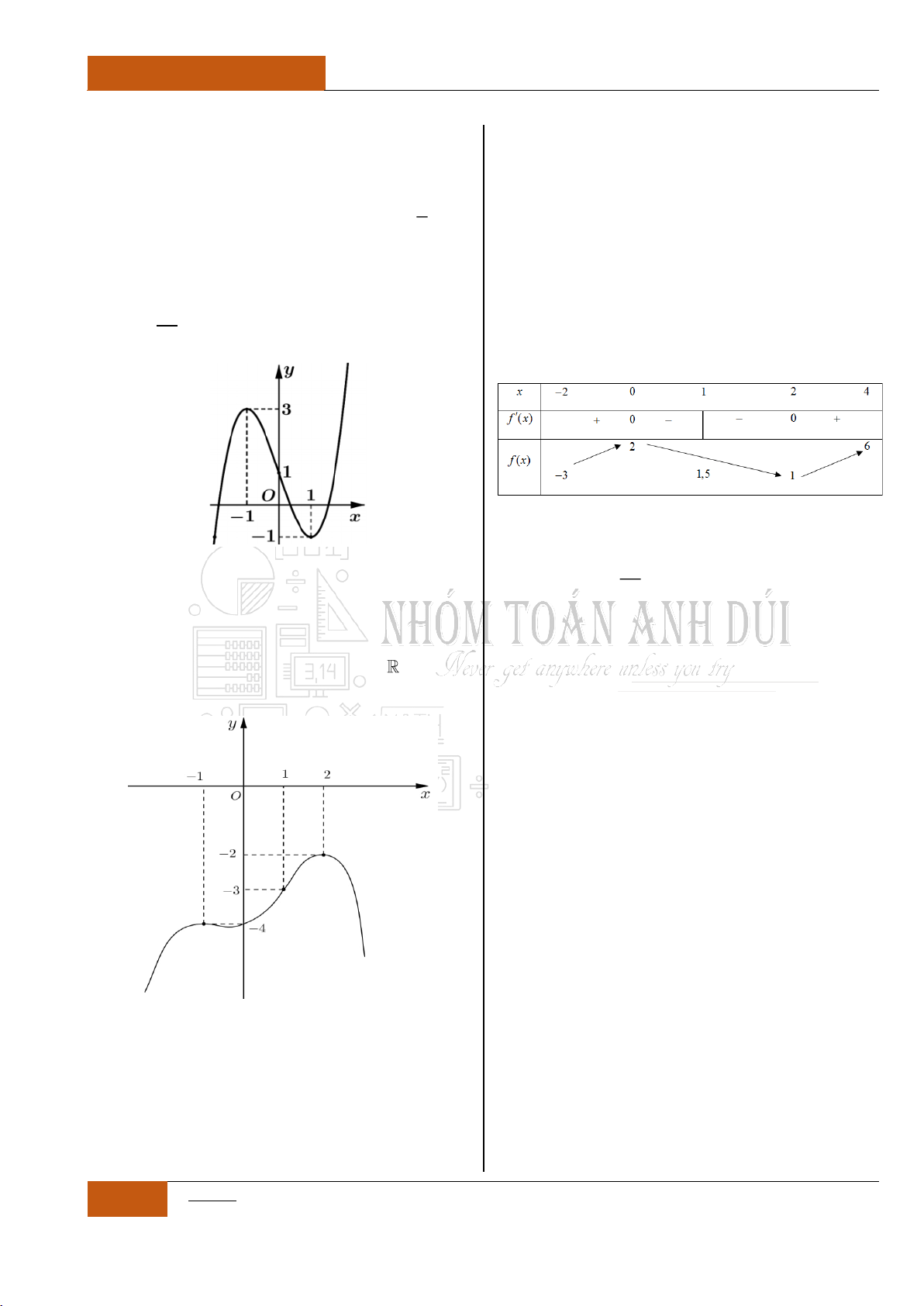
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

542

[ I can't, I can! ]

Câu 97. [Vận dụng cao].

Cho hàm số

 

y f x

. Hàm số

()y f x





có đồ

thị như hình bên. Biết

 

1

1 1; 2ff

e



   





.

Tìm tất cả các giá trị của

m

để bất phương trình

   

lnf x x m  

nghiệm đúng với mọi

1

1;x

e











.

A.

2m 

. B.

3m 

.

C.

2m 

. D.

3m 

.

Câu 98. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục trên và có đồ

thị như hình vẽ bên.

Số các giá trị nguyên của tham số

m

để bất

phương trình

 

( ) 2 2

16.8 5 .4 4 .16

f x f x

fx

m m f x    

nghiệm đúng với mọi số thực

x

là

A.

3.

B.

5.

C.

1.

D.

4.

Câu 99. [Vận dụng cao].

Cho hàm số

 

y f x

liên tục và có đạo hàm

trên đoạn

 

2;4

và có bảng biến thiên như sau

Có bao nhiêu giá trị nguyên của tham số

m

để hệ

phương trình

 

2

3

9

40

6 2 1 8 6 0

x

f x x x m











     



có

ba nghiệm phân biệt?

A.

9

. B.

11

. C.

10

. D.

8

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

543

[ I can't, I can! ]

ĐÁP ÁN

0

1

2

3

4

5

6

7

8

9

0

C

D

C

A

B

C

D

1

C

A

C

A

C

B

A

C

2

A

B

A

C

B

A

B

C

A

3

A

B

D

C

A

C

4

A

C

B

C

B

D

C

5

A

B

A

C

B

A

C

D

6

C

B

C

D

C

B

C

B

7

D

C

B

C

A

B

8

D

B

C

B

D

C

B

D

9

C

D

A

C

B

D

Ghi chú: Đáp án là sự kết hợp giữa dòng

i

và cột

j

. Ví dụ: Câu 23C (giao của dòng 2 và cột 3).

i

j

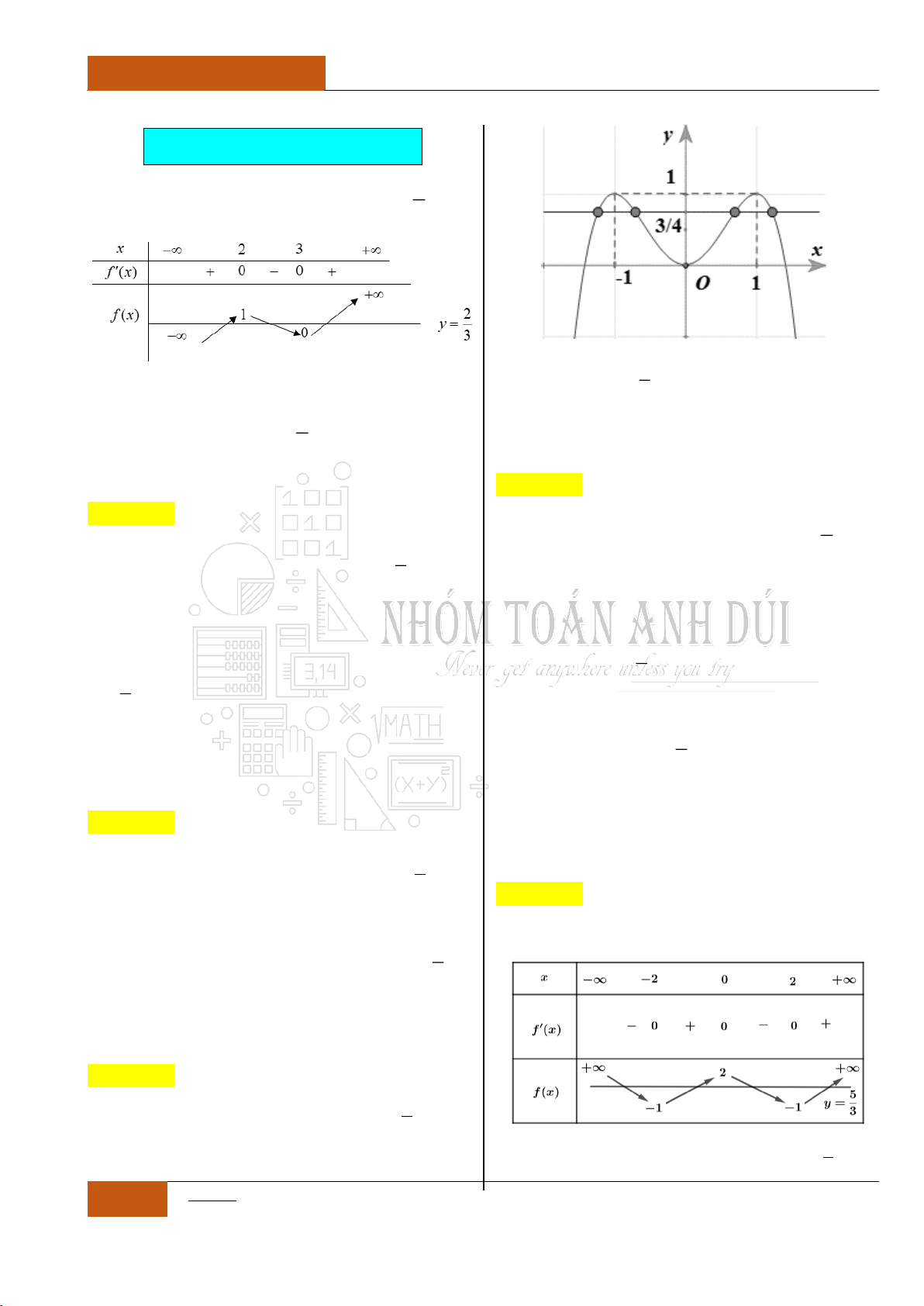
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

544

[ I can't, I can! ]

LỜI GIẢI CHI TIẾT

Câu 1. Ta có:

   

2

3 2 0

3

f x f x   

Căn cứ vào bảng biến thiên thì phương trinh

   

2

3 2 0

3

f x f x   

có 3 nghiệm phân

biệt.

Đáp án C.

Câu 2. Ta có: .

Số nghiệm của phương trình bằng số giao điểm

của đồ thị hàm số và đường thẳng

.

Dựa vào bảng biến thiên của ta có số giao

điểm của đồ thị là

4

.

Đáp án C.

Câu 3. Ta có:

là phương trình hoành độ giao điểm của đồ

thị hàm số và đường thẳng .

Dựa vào đồ thị hàm số, ta thấy có

nghiệm.

Đáp án D.

Câu 4. Ta có:

Đường thẳng cắt đồ thị hàm số

tại điểm phân biệt nên phương trình đã cho

có nghiệm phân biệt.

Đáp án C.

Câu 5. Ta có:

   

3

2 3 0

2

f x f x   

.

Số nghiệm thực của phương trình

 

1

bằng số

giao điểm của đồ thị hàm số

 

y f x

với

đường thẳng .

Từ bảng biến thiên đã cho của hàm số

 

fx

, ta

thấy đường thẳng cắt đồ thị hàm số

 

y f x

tại ba điểm phân biệt.

Do đó phương trình

 

1

có ba nghiệm thực

phân biệt.

Đáp án A.

Câu 6. Bảng biến thiên

Xét phương trình .

   

3

2 3 0

2

f x f x   

 

y f x

3

2

y 

 

fx

 

3 4 0fx

 

4

3

fx  

 

*

 

*

 

y f x

4

3

y 

 

*

3

 

4 3 0fx

 

3

4

fx 

3

4

y 

 

y fx

4

3

2

y 

3

2

y 

   

5

3 5 0

3

f x f x   

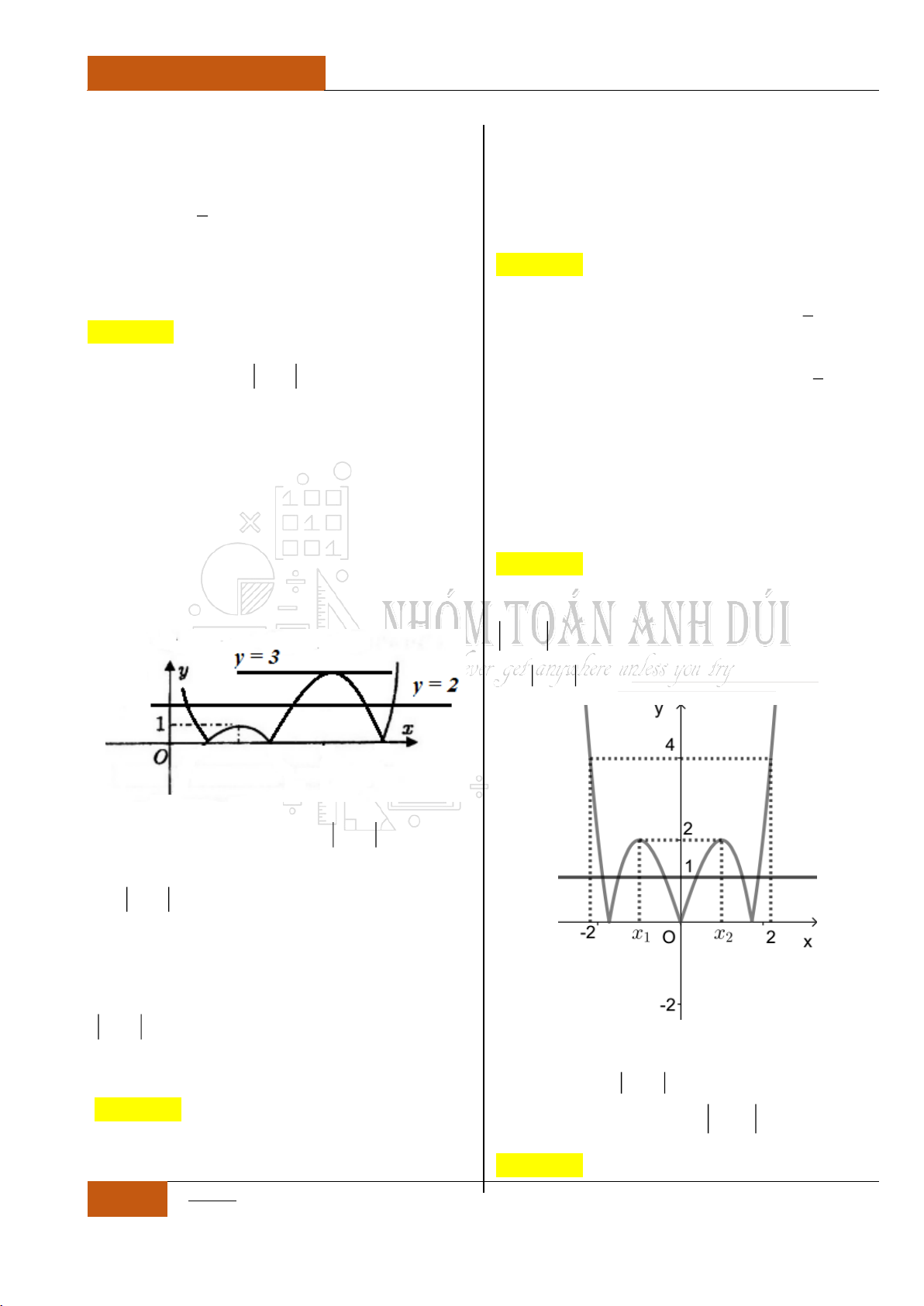
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

545

[ I can't, I can! ]

Số nghiệm của phương trình bằng số giao điểm

của đồ thị hàm số và đường

thẳng

5

:

3

dy

. Dựa vào bảng biến thiên ta

thấy đường thẳng cắt đồ thị tại bốn điểm

phân biệt.

Đáp án B.

Câu 7. *Đồ thị

- Bước 1: Giữ nguyên phần đồ thị của

nằm phía trên Ox

- Bước 2: Lấy đối xứng phần đồ thị của

nằm phía dưới Ox qua trục hoàn.

- Bước 3: Xóa phần đồ thị của nằm

phía dưới trục hoành

Số nghiệm của phương trình cũng

chính là số giao điểm cũng đồ thị hàm số

và đường thẳng . Dựa vào hình

vẽ trên, ta thấy có 4 giao điểm.

*Cách giải khác:

, dựa vào đồ thị suy ra

phương trình đã cho có 4 nghiệm.

Đáp án C.

Câu 8. Dựa vào hình dáng của đồ thị hàm số

ta thấy đây là đồ thị của hàm

số bậc bốn trùng phương có 3 điểm cực trị nên

phương trình có ba nghiệm thực phân

biệt.

Đáp án D.

Câu 9. Ta có: .

Dựa vào đồ thị ta thấy đường thẳng cắt đồ

thị hàm số tại ba điểm phân biệt thuộc

đoạn .

Do đó phương trình có ba nghiệm

thực.

Đáp án D.

Câu 10. Ta có số nghiệm của phương trình

 

1fx

là số giao điểm của đồ thị hàm số

()y f x

với đường thẳng

1y 

.

Từ hình vẽ ta thấy đường thẳng

1y 

cắt đồ

thị hàm số

()y f x

tại 6 điểm. Vậy số

nghiệm của phương trình

 

1fx

là 6.

Đáp án C.

   

:C y f x

d

 

C

 

y f x

 

y f x

 

y f x

 

y f x

 

2fx

 

y f x

2y 

 

( ) 2

2

( ) 2

fx













42

y ax bx c  

0y





   

5

3 5 0

3

f x f x   

5

3

y 

()y f x

 

2;4

3 ( ) 5 0fx

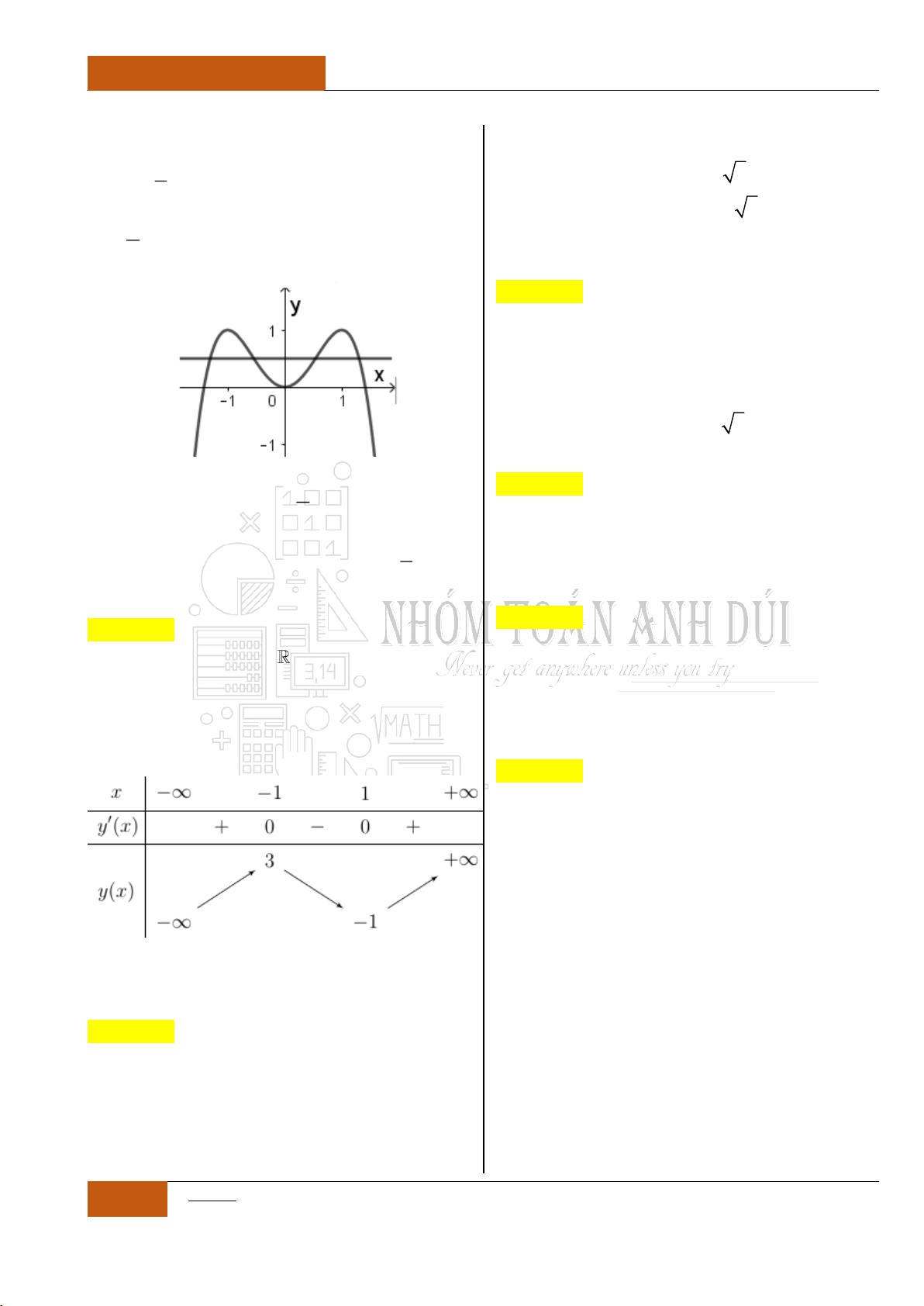
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

546

[ I can't, I can! ]

Câu 11. Số nghiệm thực của phương trình

 

1

2

fx

bằng số giao điểm của đường thẳng

1

2

y 

và có đồ thị hàm số

 

y f x

.

Ta thấy đường thẳng

1

2

y 

cắt đồ thị hàm số tại

4

điểm nên phương trình

 

1

2

fx

có

4

nghiệm.

Đáp án A.

Câu 12. Tập xác định: .

Ta có:

 

22

3 3 3 1 ; 0 1y x x y x



       

.

Bảng biến thiên

Từ bảng biến thiên ta thấy đồ thị hàm số cắt trục

hoành tại

3

điểm phân biệt.

Đáp án A.

Câu 13. Phương trình hoành độ giao điểm của

hai đồ thị đã cho là:

3 2 2 3

3 3 3 3 0x x x x x x     

.

 

2

0

3 0 3

3

x

xx

x







    







.

Hai đồ thị đã cho cắt nhau tại 3 điểm.

Đáp án A.

Câu 14. Xét phương trình hoành dộ giao điểm

3

30xx  

.

 

2

0

30

3

x

xx

x





    







.

Vậy có 3 giao điểm.

Đáp án C.

Câu 15. Dễ thấy phương trình

 

2

2 1 0xx  

có 1 nghiệm

2x 

 

C

cắt trục hoành tại một điểm.

Đáp án A.

Câu 16. Xét phương trình hoành độ giao điểm:

33

2 2 2 3 0 0x x x x x x         

Với

00

02xy  

.

Đáp án C.

Câu 17. Xét phương trình hoành độ giao điểm

của hai đồ thị

32

1y x x  

và

2

1yx

:

3 2 2 3 2

0

1 1 2 0

2

x

x x x x x

x





       







Với

01xy  

.

Với

25xy  

.

Nên hai đồ thị trên có hai giao điểm là

 

0;1

và

 

2;5

.

Vậy

2P 

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

547

[ I can't, I can! ]

Đáp án B.

Câu 18. Số giao điểm của đồ thị

 

C

và đường

thẳng

2y 

là số nghiệm của phương trình sau:

4 2 4 2

2

3 2 3 2 0

3 17

2

3 17

0

2

x x x x

x

     













   











.

Phương trình hoành độ giao điểm có 2 nghiệm

nên số giao điểm của đồ thị

 

C

và đường thẳng

là 2.

Đáp án A.

Câu 19. Trục tung có phương trình:

0x 

. Thay

0x 

vào

42

31y x x   

được:

1y 

.

Đáp án C.

Câu 20. Xét phương trình hoành độ giao điểm

32

2 2 1 1x x x x    

.

 

32

2

2 3 0

2 3 0 0

x x x

x x x x

   

     

.

Đáp án A.

Câu 21. Phương trình hoành độ giao điểm của

 

C

và trục hoành là:

3

0

2 5 0

5

2

x

xx

x







   









có

3

giao điểm.

Chú ý: Ở bài toán này hoàn toàn có thể giải

trực tiếp bằng Casio với phương trình

3

2 5 0xx  

, nhưng chắc chắn thao tác bấm

máy sẽ chậm hơn việc tính tay (thậm chí bài

này không cần nháp khi mà kết quả đã hiện ra

luôn khi ta đọc đề xong). Vì vậy, Casio là điều

không cần thiết với câu hỏi này.

Đáp án B.

Câu 22. Phương trình hoành độ giao điểm:

3 2 3 2

0

2 4 2 0

11

x x x x x x

xy

        

    

Đáp án A.

Câu 23. Trục tung có phương trình

0x 

, ta

thay

0x 

lần lượt vào các phương án thì chỉ

có phương án C cho ta

1

0

2

y   

.

Đáp án C.

Câu 24. Phương trình hoành độ giao điểm:

 

24

11

1

x

xx

x



  



2

2 5 0xx   

(*)

Khi đó

1

2

MN

I

xx

x





.

Chú ý: có thể giải

 

*

, tìm được

1 6, 1 6 1

M N I

x x x     

.

Đáp án B.

Câu 25. Ta có

 

C

cắt trục hoành

 

0y 

tại

điểm

 

1;0M 

.

Trong các đường thẳng

1 2 3 4

, , ,d d d d

chỉ có

3

Md

, có nghĩa là có

1

đường thẳng đi qua

 

1;0M 

.

Đáp án A.

Câu 26. Cách 1: Phương trình hoành độ giao

điểm

44

4 5 4 5x x x x      

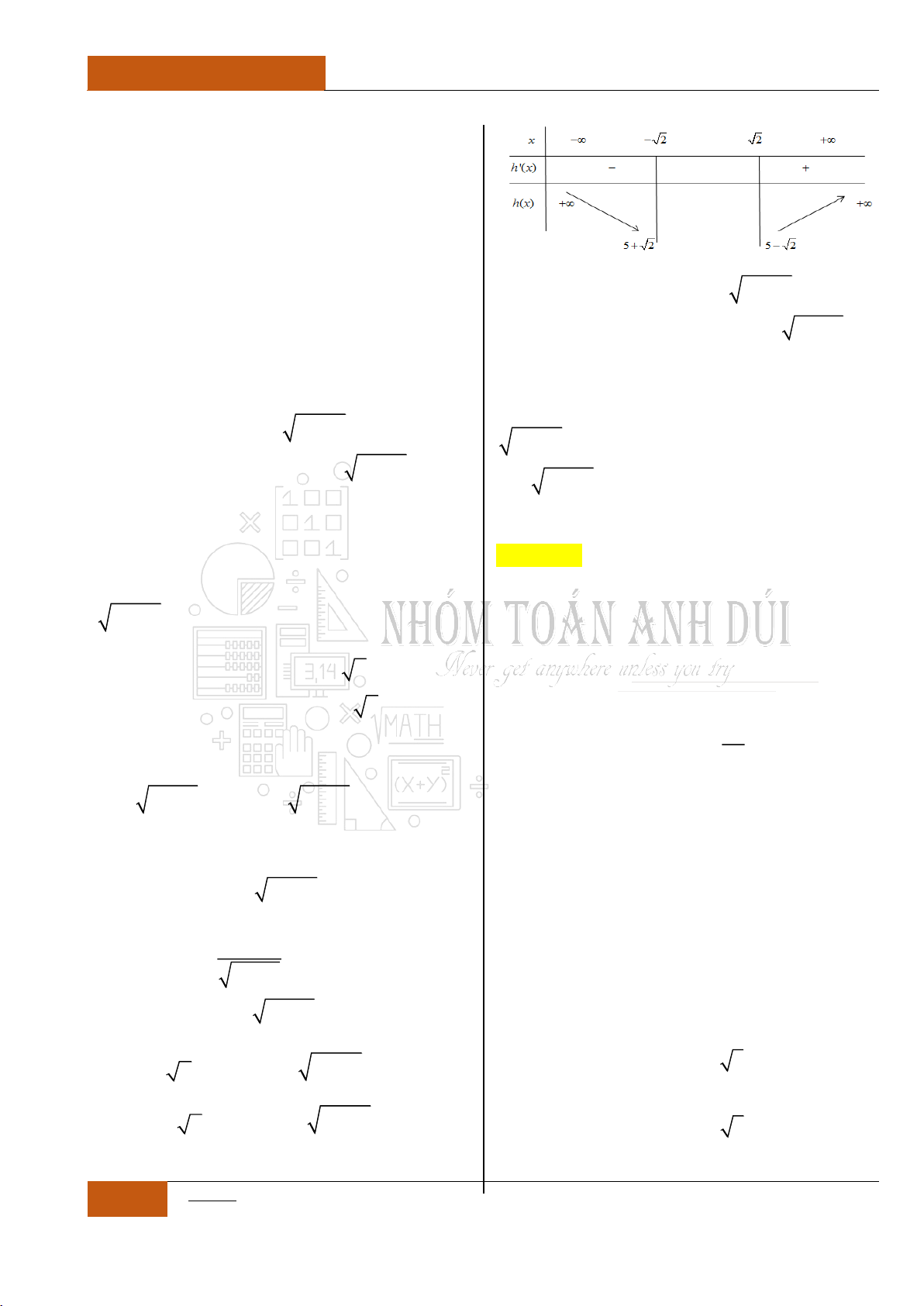
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

548

[ I can't, I can! ]

 

2

4

5

45

x

xx











  





 

42

5

10 29 0 *

x

x x x











   





Do

5x 

nên

 

4 2 2 2

10x x x x   

và

10 29 0x 

.

Vì vậy

 

*

vô nghiệm.

Như vậy phương trình

4

45xx  

vô

nghiệm hay đồ thị hàm số

4

45yx  

và

đường thẳng

yx

không có giao điểm nào.

Cách 2:

Phương trình hoành độ giao điểm

4

45xx  

.

Ta có điều kiện xác định

2

x













Với điều kiện trên ta có:

44

4 5 4 5 0x x x x       

Xét hàm số

 

4

45h x x x   

.

Ta có:

 

3

4

2

'1

4

x

hx

x





;

 

34

' 0 2 4h x x x   

Với

2x 

ta có

34

24xx

.

Với

2x 

ta có

34

24xx

Ta có bảng biến thiên:

Số nghiệm của phương trình

4

45xx  

là

số giao điểm của đồ thị

 

4

45y h x x x    

và trục hoành

0y 

.

Dựa vào bảng biến thiên, ta thấy phương trình

4

45xx  

vô nghiệm hay đồ thị hàm số

4

45yx  

và đường thẳng

yx

không

có giao điểm nào.

Đáp án B.

Câu 27. Phương trình hoành độ giao điểm:

32

3 2 0x mx m  

 

*

Phương trình

32

0ax bx cx d   

có ba

nghiệm lập thành cấp số cộng



phương

trình có một nghiệm

0

3

b

x

a



.

Suy ra phương trình

 

*

có một nghiệm

.xm

Thay

xm

vào phương trình

 

*

, ta được:

32

3

3 . 2 0

1

2 2 0

0

m m m m

m

mm

m

  





    







.

Thử lại:

 Với

1m 

, ta được

32

13

3 2 0 1

13

x

x x x

x







    







.

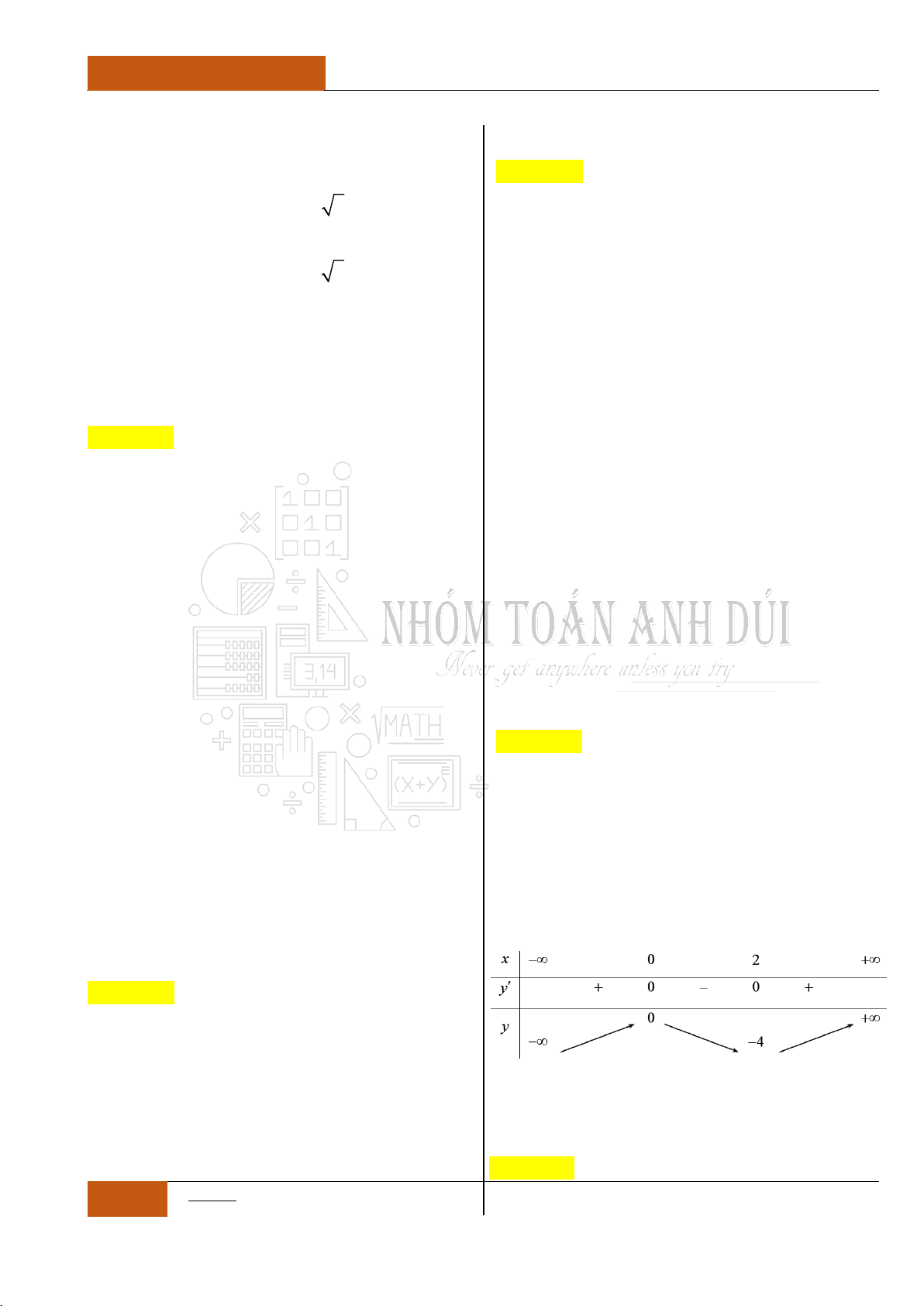
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

549

[ I can't, I can! ]

Do đó

1m 

thỏa mãn.

 Với

1m 

, ta được

32

13

3 2 0 1

13

x

x x x

x



  



     



  



.

Do đó

1m 

thỏa mãn.

 Với

0m 

, ta được

3

00xx  

.

Do đó

0m 

không thỏa mãn.

Vậy

1m 

là hai giá trị cần tìm.

Đáp án B.

Câu 28. Phương trình hoành độ giao điểm của

 

C

và

d

là

   

32

3 2 1 1x x m x   

Phương trình

32

3 2 0x x mx m     

 

2

1 2 2 0x x x m     

 

   

2

10

2 2 0

1

2 2 0 2

x

f x x x m

x

f x x x m









    













    





Phương trình

 

1

luôn có nghiệm

1x 

, vậy để

phương trình

 

1

có ba nghiệm phân biệt thì

phương trình

 

2

phải có hai nghiệm phân biệt

khác 1.

 

' 1 2 0

3

10

3

m

f

m

    









    











.

Vậy

3m 

thỏa mãn yêu cầu bài toán.

Đáp án C.

Câu 29. Phương trình hoành độ giao điểm của



và

3

3y x x  

:

33

3 2 1 3 2 0x x x x x       

23

13

xy

    







  



Vậy

   

1;3 ; 2; 3 5

BB

A B x y     

.

Đáp án A.

Câu 30. Xét phương trình hoành độ giao điểm

của

d

và

 

m

C

3 2 3 2 3

32x mx m m x m   

3 2 2 3

3 3 0x mx m x m    

   

3 2 2 3

3 3 0x m x mx m    

   

 

2 2 2 2

22

30

3

30

x x m m x m

xm

x m x m x m

xm

    







     







Để đường thẳng

d

cắt đồ thị

 

m

C

tại

3

điểm

phân biệt có hoành độ

1 2 3

,,x x x

0m

.

Khi đó,

   

44

4 4 4 4

1 2 3

83 3 83x x x m m m        

4

83 83 1mm    

Vậy

12

1, 1mm  

hay

12

0mm

.

Đáp án A.

Câu 31. Ta có:

32

3y x x

2

3 6 ;

0

2

y x x

x

y

x



  















Bảng biến thiên:

Dựa vào bảng biến thiên ta thấy đồ thị hàm số

32

3y x x

cắt đường thẳng

ym

tại ba điểm

phân biệt khi

40m  

.

Đáp án B.

 

1

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

550

[ I can't, I can! ]

Câu 32. Ta có phương trình hoành độ giao

điểm là:

32

3 2 1x x x mx m     

 

32

3 1 0 1x x x mx m      

 

2

1 2 1 0

1

2 1 0

x x x m

x

x x m

     









   



.

Để đường thẳng cắt đồ thị hàm số tại ba điểm

phân biệt thì phương trình

2

2 1 0x x m   

có

hai nghiệm phân biệt khác

1

.

Hay

1 1 0 2

2

1 2 1 0 2

mm

m

mm

    



   



     



.

Với

2m 

thì phương trình

 

1

có ba nghiệm

phân biệt là

12

1, ,xx

(

12

,xx

là nghiệm của

2

2 1 0x x m   

).

Mà

12

1

2

xx



suy ra điểm có hoành độ

1x 

luôn là trung điểm của hai điểm còn lại. Nên

luôn có 3 điểm A,B,C thoả mãn

AB BC

. Vậy

2m 

.

Đáp án B.

Câu 33. Giao điểm của đồ thị hàm số đã cho với

trục tung là

 

2

0;2 4Bm

Phương trình hoành độ giao điểm của đồ thị đã

cho với trục hoành là:

 

3 2 2

22

2 2 4 0

2 2 2 0

x m x m

x x x m

    

     

   

2

1 1 0

x

x m vn









   





Giao điểm của đồ thị đã cho với trục hoành là

 

2;0A 

.

Diện tích tam giác

ABC

là:

 

2

11

. .2. 2 4 8 2.

22

S OAOB m m      

Đáp án D.

Câu 34. Hoành độ giao điểm là nghiệm của

phương trình

32

32x x m mx    

 

2

1 2 2 0x x x m     

2

1

2 2 0

x

x x m









   



Đặt nghiệm

2

1.x 

Từ giải thiết bài toán trở

thành tìm

m

để phương trình có 3 nghiệm lập

thành cấp số cộng.

Khi đó phương trình

2

2 2 0x x m   

phải

có 2 nghiệm phân biệt (vì theo Vietè rõ ràng:

1 3 2

22x x x  

).

Vậy ta chỉ cần

 

1 2 0 3mm



      

.

Đáp án D.

Câu 35. Phương trình hoành độ giao điểm

chung là:

 

32

2 x 3 1 5 5x m m x x      

 

32

2 3 2 0x mx m x    

 

2

0

2 3 2 0 1

x

x mx m









   





Đường thẳng

5yx  

cắt đồ thị hàm số

 

32

2 x 3 1 5y x m m x    

tại 3 điểm phân

biệt



Phương trình

 

1

có hai nghiệm phân

biệt khác

0



2

3 2 0

mm

m





    







2

1

2

3

m





























2

3

1

2

m





























.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

551

[ I can't, I can! ]

Đáp án C.

Câu 36. +) Ta có:

 

1

11

3

x

f x x x

x







   







.

Vì:

 

fx

là hàm bậc ba nên:

       

1 1 1 3f x x a x x x     

     

1 1 3 1f x a x x x x      

;

Mà:

 

0 2 1fa  

.

     

1 1 3 1f x x x x x      

.

+)

 

    

2

1

0

1 3 1 0 2

xx

fx

xx









   



.

Vì:

13

,xx

là các nghiệm của

 

2

nên ta có

13

2xx 

.

Đáp án C.

Câu 37. +) Gọi đồ thị hàm số

 

32

2 3 4y x mx m x    

là

 

m

C

và đồ thị

hàm số

4yx

là

 

d

.

+) Phương trình hoành độ giao điểm của

 

m

C

và

 

d

là

 

32

2 3 4 4x mx m x x     

   

32

2 2 0x mx m x     

2

0

2 2 0

x

x mx m









   



+) Gọi

 

2

22g x x mx m   

.

+)

 

d

cắt

 

m

C

tại ba điểm phân biệt



phương trình

 



có ba nghiệm phân biệt



phương trình

 

0gx

có hai nghiệm phân

biệt khác

0

.

 

0

00

g



















2

20

mm

m



  









 

1

2

m

a

m

























.

+)

0x 

là hoành độ điểm

A

, hoành độ điểm

B

,

C

là hai nghiệm

1

x

,

2

x

của phương trình

 

0gx

.

+)

     

2

2 1 2 1

44BC x x x x       



 

2

21

2 xx

(do

B

,

C

thuộc đường thẳng

 

d

.

 

2

2 1 1 2

24x x x x



  



 

2

82mm  

+) Viết phương trình đường thẳng

 

d

dưới

dạng

40xy  

, ta có

 

1 3 4

,2

2

d I d





.

+)

82

IBC

S 

 

1

. , 8 2

2

BC d I d

 

2

1

. , 128

4

BC d I d







 

2

1

8 2 .2 128

4

mm   

.

2

1 137

2

34 0

1 137

2

m

mm

m









    











(thỏa

điều kiện

 

a

)

+) Vậy tổng tất cả các giá trị

m

là

1

.

Đáp án C.

Câu 38. Hoành độ giao điểm của hai đồ thị là

nghiệm của phương trình

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

552

[ I can't, I can! ]

 

   

32

2

2 3 4 4

2 2 0

0

2 2 0 *

x mx m x x

x mx m x

x

x mx m

     

    









   





.

Đường thẳng

d

cắt đồ thị hàm số

 

1

tại 3

điểm phân biệt khi phương trình

 

*

có hai

nghiệm phân biệt khác 0 .

2

1

20

2

20

2

m

mm

m









  























.

Giả sử

   

1 1 2 2

; 4 ; ; 4B x x C x x

với

12

;xx

là

nghiệm của phương trình

 

*

khi đó:

22

1 2 1 2 1 2

2

2( ) 2( ) 8 .

8 8 16

BC x x x x x x

mm

    

  

.

 

1 3 4

11

. , . . 4

22

2

42

MBC

S BC d M d BC

BC



  



Ta có:

2

60

3

m

mm

m





   







.

Đối chiếu điều kiện ta có

3m 

.

Đáp án A.

Câu 39. Ta có phương trình hoành độ giao điểm

 

32

2 3 1 5 5x mx m x x      

 

32

2

2 3 2 0

0

2 3 2 0 1

x mx m x

x

x mx m

    









   





.

Yêu cầu bài toán tương đương phương trình

 

1

có hai nghiệm phân biệt, khác

0

.

2

0 2 .0 3 2 0

3 2 0

mm



   









    





2

3

21

1

2

m

mm

m













































.

Đáp án C.

Câu 40. Hoành độ giao điểm của

 

d

và đồ

thị hàm số là nghiệm của phương trình:

   

32

2 2 8 5 5 1x m x m x m x m        

   

2

2 2 2 3 0x x m x m



      



   

3

2

2 2 3 0 1

x

x m x m









    





.

Đường thẳng

 

d

cắt đồ thị hàm số tại 3 điểm

phân biệt



phương trình

 

1

có hai nghiệm

phân biệt

12

;xx

khác 2

   

 

2

1 3 0

4 2 2 .2 3 0

mm





     







    





1

2

1

m

























 

2.

1

2

m













Khi đó,

 

12

22

3

x x m



   





  





.

Theo giả thiết

222

1 2 3

20xxx  

 

2

1 2 1 2 3

2 20x x x x x    

   

2

2 2 2 3 4 20mm     

2

3

2 3 9 0

3

2

m

mm

m







    







(thỏa mãn).

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

553

[ I can't, I can! ]

Vậy giá trị lớn nhất của

m

thỏa mãn yêu cầu

bài toán là

3

.

Đáp án A.

Câu 41. Hoành độ giao điểm của đồ thị với

trục hoành là nghiệm của phương trình

 

3 2 2 3

2 3 2 2 0. *x m x m m x     

Giả sử đồ thị cắt trục hoành tại 3 điểm có

hoành độ

1 2 3

, , x x x

.

Khi đó ta có:

  

 

1 2 3

32

1 2 3

1 2 2 3 3 1 1 2 3

2

2 2 ...

... 2 2 .

y x x x x x x

x x x x x

x x x x x x x x x x

    

     

   

Đồng nhất thức ta được

 

2

1 2 3

3

1 2 2 3 3 1

1 2 3

2

1 2 3

3

1 2 2 3 3 1

1 2 3

23

22

3

1

2

1 3

x x x m

x x x x x x m m

x x x

m

x x x

mm

x x x x x x

x x x



   



    













   





    











Vì

1 2 3

, , x x x

lập thành cấp số nhân nên

 

2

1 3 2

. 4x x x

Từ

 

2

và

 

3

:

2

1.x 

Thay vào phương trình

 

*

rút ra được

0

1.

2

m















Với

0m 

phương trình

 

*

:

3

2 2 0 1xx    

(không thỏa mãn).

Với

1m 

phương trình

 

*

:

1

32

2

3

2

2 3 3 2 0 1

1

2

x

x x x x

x









      









(thỏa mãn).

Với

2m 

phương trình

 

*

:

1

32

2

3

7 45

2

6 6 1 0 1

7 45

2

x

x x x x

x









     













(thỏa mãn).

Vậy có 2 giá trị

m

thỏa mãn.

Đáp án C.

Câu 42. Cách 1:

 

   

 

2

22

2

,

1

14

1

,.

2

64 16.

B C b c

BC

B C B C

OBC

m

d O BC

m

BC x x y y

m x x

m x x x x

mm

S d O BC BC

m m m







   

  



   







   

Cách 2:

Phương trình hoành độ giao điểm:

 

   

32

2

34

1 4 4 0

1

2

x x mx m

x x x m

x

xm

   

     









  





Để

d

cắt

 

C

tại 3 điểm phân biệt phương trình

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

554

[ I can't, I can! ]

 



có 2 nghiệm phân biệt khác

0

1

9

m













 

2 2 ;3

2

2 ;3

x m B m m m m

xm

C m m m m



    







  







 

2 ;3OB m m m m  

 

2 ;3OC m m m m  

1

, 64 16.

2

OBC

S OB OC m m m





     



Đáp án C.

Câu 43. Cách 1:

Phương trình hoành độ giao điểm là

 

3 2 2

32

8 8 8

9 10

x x x x a x b

x x ax b

     

    

.

Gọi

,,m n p

là

3

nghiệm của phương trình

 

1

ta có

9m n p

mn np pm a

mnp b

  





  









Do

 

C

cắt

 

P

tại ba điểm có hoành độ nằm

trong

 

1;5

nên

   

1 1 1 0

5 5 5 0

m n p



   





   





.

Hay:

   

10

5 25 125 0

mnp mn np pm m n p



       





        





Cộng vế theo vế của hệ phương trình trên ta có

   

6 24 124 0

15 15.

mn np pm m n p

mn np pm a

      

     

Dấu bằng xảy ra khi và chỉ khi:

25

25 25

25

mnp

mnp b

mnp





    







Vậy tích

375.ab 

Đáp án B.

Cách 2: Phương trình hoành độ giao điểm là

 

3 2 2

32

8 8 8

9 10

x x x x a x b

x x ax b

     

    

.

Khi đó phương trình

 

1

có 3 nghiệm nằm

trong

 

1;5

.

Đặt

 

32

9f x x x ax b   

suy ra

 

2

' 3 18f x x x a  

. Để phương trình

 

1

có

3

nghiệm nằm trong

 

1;5

thì

 

2

' 3 18 0f x x x a   

có hai nghiệm phân

biệt thuộc

 

1;5



2

3 18a x x  

có hai

nghiệm phân biệt thuộc

 

1;5

.

Xét hàm số

 

2

3 18g x x x  

suy ra

 

' 6 18g x x  

, ta có:

 

' 0 3g x x  

.

Bảng biến thiên của

 

y g x

Từ bảng biến thiên, ta có:

15 27a

suy ra

giá trị nhỏ nhất của

a

bằng 15 khi

5x 

, khi

đó

25b 

.

Vậy tích

375.ab 

Đáp án B.

Câu 44.

 

:d y mx m  

,

 

32

:C y x mx m  

.

Phương trình hoành độ giao điểm của

 

d

và

 

C

:

 

32

01x mx mx  

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

555

[ I can't, I can! ]

 

2

0

02

x

x mx m









  





.

Gọi

12

,xx

là

2

nghiệm của phương trình

 

2

,

3

0x 

.

 

1

có

3

nghiệm phân biệt



 

2

có

2

nghiệm

12

,xx

phân biệt và khác

0

.

2

0, 4

0

mm

m



    









   

;0 4;m    

.

 

1

có

3

nghiệm phân biệt

1 2 3

,,x x x

thỏa

1 2 3

13x x x    

, với

12

x x m  

,

3

0x 

.

13m    

31m   

, mà

   

;0 4;m   

,

m

 

2; 1m   

. Vậy có

2

giá trị

m

.

Đáp án C.

Câu 45. Phương trình hoành độ giao điểm của

 

m

C

và

 

d

là:

   

32

2 3 4 4 1x mx m x x     

 

32

2 2 0x mx m x    

 

2

. 2 2 0x x mx m



    



 

2

04

2 2 0 2

xy

x mx m

  







   





.

 

d

cắt

 

m

C

tại ba điểm phân biệt

 

1

có ba nghiệm phân biệt

 

2

có hai nghiệm phân biệt khác 0

2

0

20

0 2 .0 2 0 2 0

2

11

2

mm

m m m

m

mm

m







  





     

















   





















Khi đó,

 

2

có hai nghiệm phân biệt

1

x

và

2

x

tương ứng cũng là hoành độ của

B

và

C

.

 

11

;4B x x

và

 

22

;4C x x 

.

 

12

1; 1KB x x   

và

 

22

1; 1KC x x  

     

1 2 2 1

12

1 1 1 1

2

KBC

x x x x

S

xx



    





.

Theo đề bài:

12

8 2 8 2

KBC

S x x



   

 

2

12

128 4 128x x S P     

   

2

1 137

2 4 2 128

2

m m m



      

(nhận).

Vậy tất cả các giá trị

m

thỏa đề là

1 137

2

m





Đáp án C.

Câu 46. Vì

1 2 3

,,x x x

là ba nghiệm của phương

trình bậc ba

 

0fx

    

 

1 2 3

f x x x x x x x    

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

556

[ I can't, I can! ]

Ta có:

    

12

...f x x x x x



   

 

2 3 1 3

... x x x x x x x x     

.

Khi đó:

   

 

    

1 1 2 1 3

2 2 3 2 1

3 3 1 3 2

f x x x x x





  





  







  



Suy ra

 

1 2 1 3

1

...P

x x x x





 

  

2 3 2 1 3 1 3 2

11

... .

x x x x x x x x



   

   

 

  

2 3 1 3 1 2

1 2 1 3 2 3

0

x x x x x x

    



  

.

Đáp án B.

Câu 47. Từ giả thuyết bài toán ta giả sử

     

2

1 2 3f x a x x x x    

(

0a 

)

Ta có:

: 3 2AB y x

,

: 4 3AC y x

,

: 5 6BC y x

.

Khi đó:

Hoành độ của

M

là nghiệm của phương trình:

   

2

1 2 3 3 2

M M M M M

a x x x x x     

   

  

1 2 3 ...

... 1 2 0

M M M

MM

a x x x

xx

    

   

 

3 1 0

M

ax   

1

3

M

x

a

  

.

Hoành độ của

N

là nghiệm của phương trình:

   

2

1 2 3 4 3

N N N N N

a x x x x x     

   

  

1 2 3 ...

... 1 3 0

N N N

NN

a x x x

xx

    

   

 

2 1 0

N

ax   

1

2

N

x

a

  

.

Hoành độ của

P

là nghiệm của phương trình:

   

2

1 2 3 5 6

P P P P P

a x x x x x     

      

1 2 3 2 3 0

P P P P P

a x x x x x       

 

1 1 0

P

ax   

1

P

x

a

  

.

Từ giả thuyết ta có:

3

5 6 5 3

M N P

x x x a

a

       

.

Do đó:

     

2

3 1 2 3f x x x x x    

 

0 18f 

.

Đáp án B.

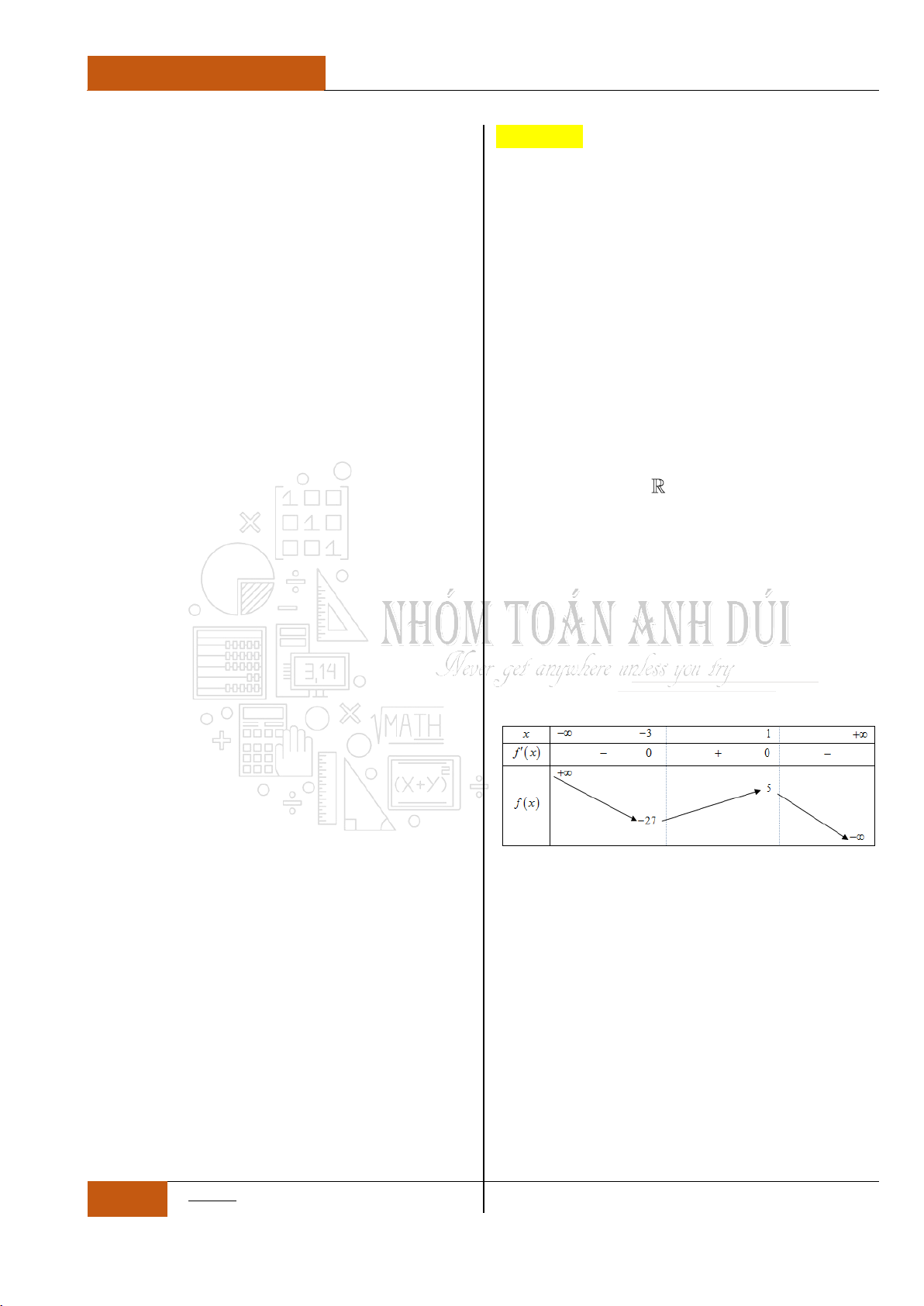
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

557

[ I can't, I can! ]

Câu 48. Phương trình hoành độ giao điểm:

 

32

3 2 1

3 2 0

x x m x

x x mx m

   

     

 

2

1 2 2 0x x x m     

     

1

2

1

2 2 0 *

x

g x x x m









    





.

Để hai đồ thị cắt nhau tại ba điểm phân biệt thì

phương trình

 

*

phải có hai nghiệm phân biệt

khác

1

 

2

0

1 2 0

10

1 2 2 0

m

g

m







  









   





3

m





   







.

Gọi

2

x

,

3

x

là hai nghiệm phương trình

 

*

.

Theo định lý Vietè, ta có:

 

23

2

.2

xx

x x m









  





.

Theo bài ta có:

222

1 2 3

5xxx  

.

2 2 2 2

2 3 2 3

1 5 4x x x x      

 

2

2 3 2 3

24x x x x   

 

4 2 2 4 2mm      

.

So sánh với điều kiện ở trên suy ra

2m 

.

Kết luận:

2m 

thỏa mãn yêu cầu bài toán.

Đáp án D.

Câu 49. Hoành độ giao điểm của đồ thị hàm số

32

3 9 2 1y x x x m    

với trục

Ox

chính là

nghiệm của phương trình:

32

3 9 2 1 0x x x m    

.

32

3 9 2 1x x x m     

Xét hàm số

 

32

39f x x x x   

.

Tập xác định:

D 

.

   

2

3 6 9, 0

1

3 6 9 0

3

f x x x f x

x

xx

x



    





     







.

Bảng biến thiên:

Đồ thị hàm số

32

3 9 2 1y x x x m    

cắt

trục

Ox

tại hai điểm phân biệt khi và chỉ khi

đường thẳng

21ym

cắt đồ thị hàm số

 

32

39f x x x x   

tại hai điểm phân biệt.

Từ bảng biến thiên suy ra :

2 1 5

2 1 27

m







  



 

2

14;2

14

m

S

m





   







.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

558

[ I can't, I can! ]

Tổng của các phần tử thuộc tập

S

là :

14 2 12T     

.

Đáp án C.

Câu 50. Ta có phương trình hoành độ giao điểm

của đường thẳng

y x m

và đường cong

23

1

x

y

x







. Tức là nghiệm của phương trình:

    

23

1 2 3 1

1

x

x m x m x x x

x



       



   

22

2 3 3 3 0 *x mx x m x x m x m           

Ta có:

   

2

3 4 3mm     

22

6 9 4 12 2 3m m m m m       

.

Để đường thẳng

y x m

cắt đồ thị hàm số

23

1

x

y

x







tại hai điểm phân biệt thì phương

trình

 

*

có hai nghiệm phân biệt khác

1

.

 

2

0

1 3 .1 3 0

2 3 0

1

3

10

mm

m

lđ











    







  























.

Theo giả thiết:

2020 2020m  

và

1

3

m











nên

2020 1

3 2020

m

   









.

Vì

m

và

2020 1m   

, suy ra có

 

2 2020

1 2019

1

  



giá trị nguyên

m

.

Vì

m

và

3 2020m

, suy ra có

2020 4

1 2017

1





giá trị nguyên

m

.

Tóm lại có tất cả

2019 2017 4036

giá trị

nguyên của tham số

m

.

Đáp án A.

Câu 51. Xét phương trình hoành độ giao điểm

 

2

1

0*

x

xm

x

x mx m







  





  





Để có hia điểm phân biệt

,AB

thì phương

trình

 

*

phải có hai nghiệm phân biệt khác

1

2

10

4

0

40

mm

m

mm

  





















Khi đó phương trình

 

*

có hai nghiệm phân

biết

1

x

,

2

x

thỏa mãn:

12

x x m











Giả sử

   

1 1 2 2

; , ;A x x m B x x m

, suy ra:

   

1 1 2 2

; , ;OA x x m OB x x m

Theo giả thiết góc giữa hai đường thẳng

OA

và

OB

bằng

0

60

suy ra:

 

0

cos ; cos60OA OB 

  

   

1 2 1 2

22

1 1 2 2

1

2

x x x m x m

x x m x x m

  



   

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

559

[ I can't, I can! ]

 

      

2

1 2 1 2

2

22

2 2 2

1 2 1 2 2 1 1 2 1 2

2

1

2

x x m x x m

x x x x mx x x x m x m x m

  



        



     

22

2

22

2 1 1 2 1 2

2

1

2

m m m

m m mx m mx x x m x x m







       



   

2

22

2 2 2

21

2

1

2

m

m m mx m mx m m m





      



   

22

21

2

2 1 1xx



   

   

22

21

2 1 1 16xx     

   

2

1 2 1 2 1 2

2 2 12x x x x x x     

2

6

4 12 0

2

m

mm

m





    







.

Đáp án A.

Câu 52. Hoành độ điểm

A

và

B

là nghiệm

phương trình:

  

2

21x m x m x   

 

22

30x m x m m     

suy ra:

2

. ; 3

A B A B

x x m m x x m     

Hoành độ điểm

C

và

D

là nghiệm phương

trình:

  

2

2 1 2x m x m x    

 

22

1 2 0x m x m m      

suy ra

2

. 2; 1

C D C D

x x m m x x m       

.

Mặc khác

A

x

và

D

x

là nghiệm của phương

trình:

2

3

2 3 0

1

A

D

x

xx

x





   







. Suy ra:

22

0

6 9 5 2 9

2

m

m m m m

m





     







.

Đáp án B.

Câu 53. Hoành độ giao điểm của hai đồ thị

hàm số là nghiệm của phương trình:

42

32x x m  

 

42

3 2 0 1x x m    

.

Vì

0 2 0mm    

hay phương trình

 

1

luôn có hai nghiệm phân biệt thỏa mãn:

2

3 4 17

2

m

x





1

3 4 17

2

m

x





và

2

3 4 17

2

m

x





.

Khi đó:

 

1

;A x m

,

 

2

;B x m

.

Ta có tam giác

OAB

vuông tại

O

, trong đó

O

là gốc tọa độ

2

12

. 0 . 0OAOB x x m    

.

2

42

0

2 3 0

3 4 17

2

2 3 0

4 12 4 8 0

2

m

m m m

m



















   





 

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

560

[ I can't, I can! ]

Vậy

2m 

là giá trị cần tìm.

Đáp án A.

Câu 54. Xét phương trình hoành độ giao điểm

42

23x mx m   

. Đặt

2

xt

,

0t 

. Khi đó

phương trình trở thành

2

2 3 0t mt m   

 

1

và đặt

 

2

23f t t mt m   

.

Để đồ thị hàm số cắt đường thẳng

3y 

tại

4

điểm phân biệt thì phương trình

 

1

có hai

nghiệm thỏa mãn

12

0 tt

và khi đó hoành độ

bốn giao điểm là

2 1 1 2

t t t t    

.

Do đó, từ điều kiện của bài toán suy ra

2

1

2

1

t















hay

12

0 1 4tt   

.

Điều này xảy ra khi và chỉ khi

 

00

10

40

f















30

3 4 0

9 19 0

m







  









19

3

9

m    

.

Vậy

3a 

,

19

9

b 

nên

15 95ab 

.

Đáp án C.

Câu 55. Xét phương trình hoành độ giao điểm

 

1 1 2

2

1 2 3

1 1 2

21

1 2 3

x x x x

x x m

x x x x

x x m

x x x x

  

      

  

  

        

  

Xét hàm số:

 

1 1 2

2

1 2 3

x x x x

f x x x

x x x x

  

      

  

 

\ 3; 2; 1;0xD    

Ta có:

 

1

2

1 1 2

2,

1 2 3

1 1 2

2 2,

1 2 3

x x x x

xD

x x x x

fx

x x x x

x x D

x x x x

  



    



  





  



     



  



Trong đó:

 

1

2

2;

;2

DD



    





   





.

Ta có:

 

fx





     

1

2 2 2 2

2

2 2 2 2

1 1 1 1

,

1 2 3

1 1 1 1

2,

1 2 3

xD

x

x x x

xD

x

x x x



    



  







     



  



Dễ thấy

 

12

0,f x x D D



   

, ta có bảng

biến thiên

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

561

[ I can't, I can! ]

Hai đồ thị cắt nhau tại đúng 4 điểm phân biện

khi và chỉ khi phương trình

 

1

có đúng 4

nghiệm phân biệt, từ bảng biến thiên ta có:

22mm    

.

Đáp án B.

Câu 56. Xét phương trình hoành độ giao điểm

12

11

2020 3

x

x x x

em





  

 

12

11

2020 3 1

x

x x x

em





   

.

Đặt

 

12

11

2020

x

x x x

g x e





  

.

Ta có

 

   

2 2 2

1

1 1 1

0

1

x

g x e

x

x 



     



với mọi

x

thuộc các khoảng sau

 

;1 

,

 

1;0

,

 

0;1

và

 

1; 

nên hàm số

 

y g x

nghịch biến trên mỗi khoảng đó.

Mặt khác ta có

 

lim 2017

x

gx





và

 

lim

x

gx



 

.

Bảng biến thiên hàm số

 

y g x

Do đó để

 

1

C

và

 

2

C

cắt nhau tại đúng ba

điểm phân biệt thì phương trình

 

1

phải có ba

nghiệm phân biệt. Điều này xảy ra khi và chỉ

khi đường thẳng

3ym

cắt đồ thị hàm số

 

y g x

tại ba điểm phân biệt khi và chỉ khi

2017

3 2017 672,3

3

mm      

.

Do

m

nguyên thuộc

 

2019;2020

nên

 

672; 671;...;2019m  

. Vậy có tất cả 2692

giá trị

m

thỏa mãn.

Đáp án A.

Câu 57. Xét phương trình hoành độ giao điểm:

 

2

11 1

2 1 1 11 *

3 4 2

x x m

xx

     



Điều kiện:

1 0 1

44

33

22

xx

  





  











-



2

-



-



-



+



+



+



+



-



+

f(x)

f'(x)

+



-



x

-3

-2

1

0

+

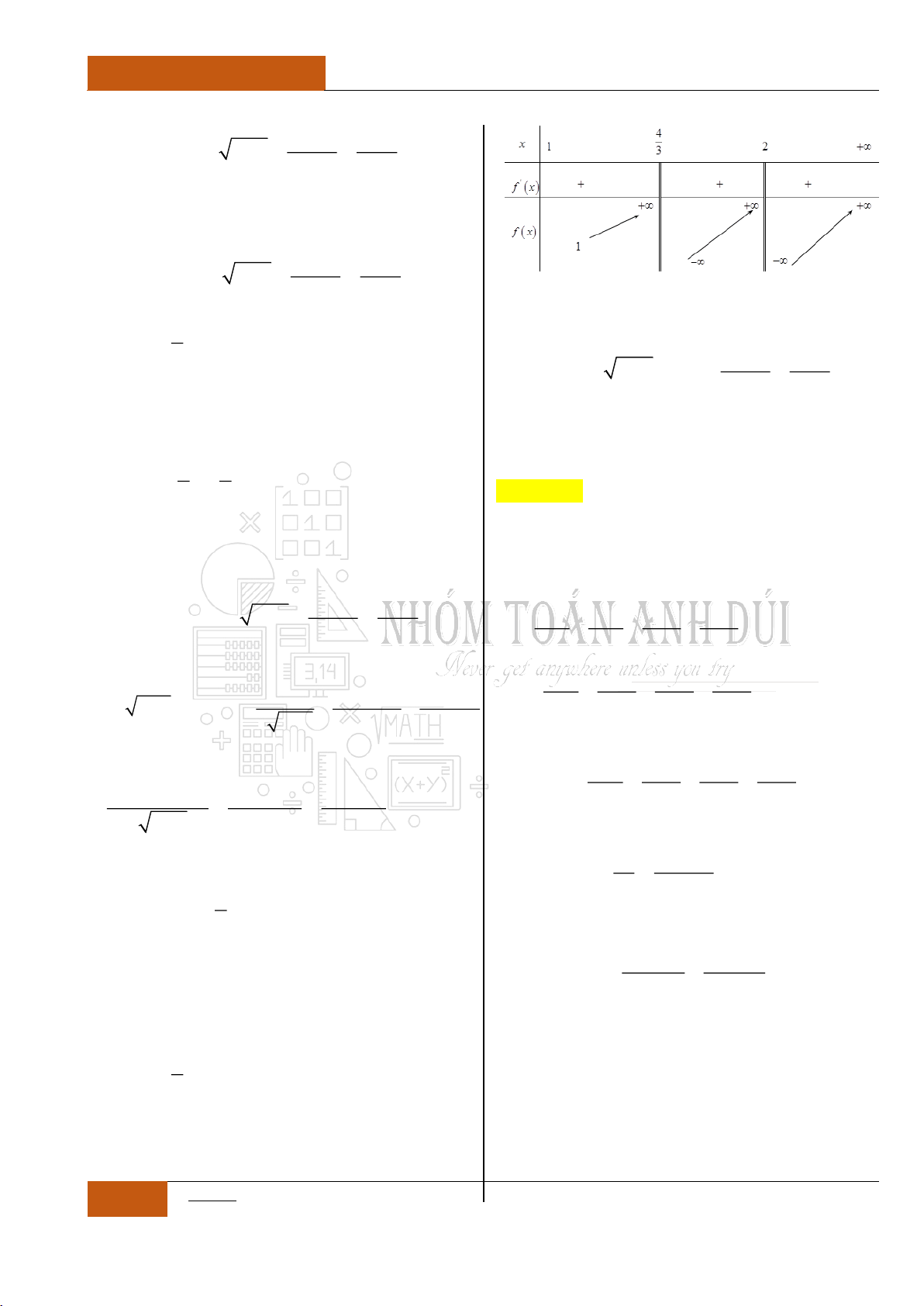
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

562

[ I can't, I can! ]

 

* 

 

2

11 1

2 1 1 11

3 4 2

x x m

xx

     



Xét hàm số

 

2

11 1

( ) 2 1 1 11

3 4 2

f x x x

xx

     



trên





4

1; \ ;2

3









.

Nhận thấy, hàm số

 

fx

liên tục trên các

khoảng

 

44

1; , ;2 , 2;

33

   



  



   

Ta có:

 

2

11 1

2 1 1 11

3 4 2

f x x x

xx







     







 

   

2

22

1 33 1

4 1 2 1

21

3 4 2

x x x

x

xx

     





   

2

22

10 8 1 33 1

0

21

3 4 2

xx

x

xx



   





với





4

1; \ ;2

3

x



   





.

Suy ra, đồ thị hàm số

 

fx

đồng biến trên





4

1; \ ;2

3









.

Bảng biến thiên

Từ bảng biến thiên ta suy ra đồ thị hai hàm số

 

2

2 1 1y x x  

và

11 1

11

3 4 2

ym

xx

   



cắt nhau tại

2

điểm phân biệt khi





;1m 

.

Đáp án C.

Câu 58. Xét phương trình hoành độ giao điểm

1

1 1 2

1 2 3

22

x

x x x x

m



  

  



1

1 2 3

1 2 3 4

22

x

x x x x

m



  



   

  

.

Đặt

 

1

1 2 3

1 2 3 4

2

x

x x x x

gx



  



   



.

Ta có:

 

22

1

11

...

x

gx

x





  

   

1

22

...

23

11

2 ln2 0

x

xx







với mọi

x

thuộc các khoảng sau

 

;3 

,

 

3; 2

 

2; 1

,

 

1;0

và

 

0;

nên hàm số

 

y g x

đồng biến trên mỗi khoảng đó.

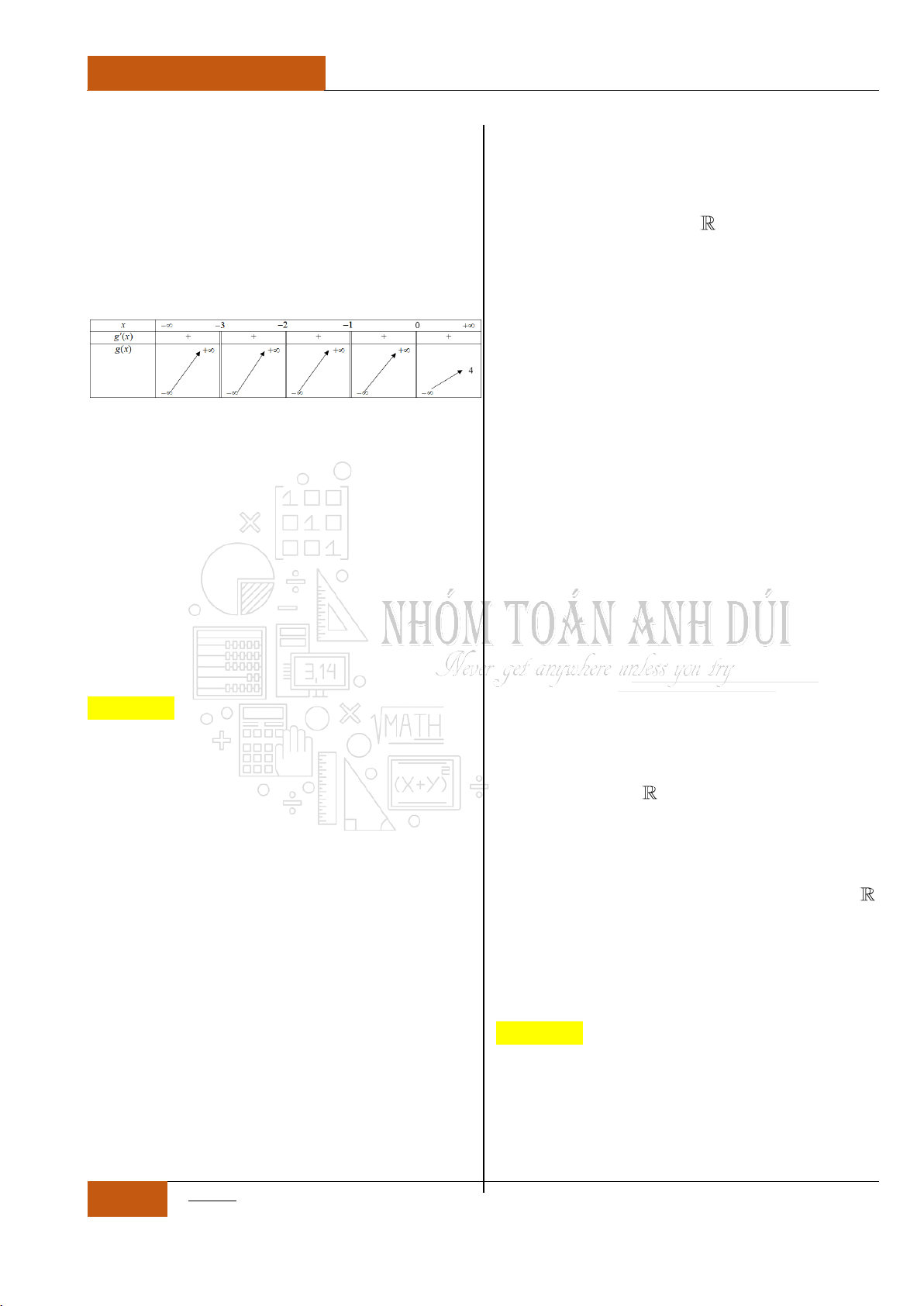
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

563

[ I can't, I can! ]

Mặt khác ta có

 

lim 4

x

gx





và và

 

lim

x

gx



 

.

Bảng biến thiên hàm số

 

y g x

Do đó

 

1

C

và

 

2

C

cắt nhau tại đúng năm

điểm phân biệt thì phương trình

 

1

phải có 5

nghiệm phân biệt. Điều này xảy ra khi và chỉ

khi đường thẳng

2ym

cắt đồ thị hàm số

 

y g x

tại 5 điểm phân biệt khi và chỉ khi

2 4 2mm  

.

Đáp án C.

Câu 59. Đặt hàm số:

   

 

2 4 3 2 2

21f x m x m x x m x     

Ta có:

   

 

2 4 3 2 2

21f x m x m x x m x     

 

2 3 2 2

21x m x m x x m



     



.

Giả sử

0x 

không phải là nghiệm của phương

trình

   

 

2 3 2 2

2 1 0g x m x m x x m      

thì hàm số bậc bốn

 

y f x

với

   

 

2 4 3 2 2

21f x m x m x x m x     

sẽ đổi

dấu khi qua điểm

0x 

, nghĩa là

 

2 4 3 2 2

2 1 0m x m x x m x     

không có

nghiệm đúng với mọi

x

.

Do đó, để yêu cầu bài toán được thỏa mãn thì

một điều kiện cần là:

   

 

2 3 2 2

2 1 0g x m x m x x m      

phải có nghiệm

0x 

, suy ra

2

1 0 1mm    

Điều kiện đủ:

Với

1m 

:

 

4 3 2 2 2

3 3 1f x x x x x x x     

khi đó

 

1 1 0f   

không thỏa mãn điều kiện

 

2 4 3 2 2

2 1 0m x m x x m x     

nghiệm

đúng với mọi

x

. (loại)

Với

1:m 

 

4 3 2 2 2

10f x x x x x x x      

,

x

Vậy

 

1S 

.

Đáp án D.

Câu 60. Đặt

    

 

2

1 2 2f x x x ax bx    

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

564

[ I can't, I can! ]

Giả sử

1x 

không phải là nghiệm của phương

trình

   

 

2

2 2 0g x x ax bx    

thì hàm

số

    

 

2

1 2 2f x x x ax bx    

sẽ đổi

dấu khi qua điểm

1x 

, nghĩa là

  

 

2

1 2 2 0x x ax bx    

không có

nghiệm đúng với mọi

x

.

Do đó, để yêu cầu bài toán được thỏa mãn thì

một điều kiện cần là

   

 

2

2 2 0g x x ax bx    

có nghiệm

1x 

suy ra

20ab  

 

1

Lí luận tương tự có:

   

 

2

1 2 0h x x ax bx    

cũng phải nhận

2x 

là nghiệm, suy ra

4 2 2 0ab  

 

2

Từ

 

1

và

 

2

ta có hệ

2 0 1

4 2 2 0 1

a b a

a b b

    







    



Điều kiện đủ:

Với

1

a

b











, ta có:

    

 

2

1 2 2f x x x x x     

   

22

1 2 0xx    

,

x

.

Vậy không tồn tại cặp số thực

 

;ab

nào thỏa

mãn yêu cầu bài toán.

Đáp án C.

Câu 61. Đặt

sintx

. Do

 

;2x



nên

 

1;1t 

.

Khi đó ta có phương trình

   

3

2 3 0

2

f t f t    

.

Dựa vào bảng biến thiên ta thấy phương trình

 

3

2

ft

có 2 nghiệm

 

1;0ta  

và

 

0;1tb

.

Trường hợp 1:

 

1;0ta  

Ứng với mỗi giá trị

 

1;0t 

thì phương trình

có 4 nghiệm thỏa mãn:

1 2 3 4

0 2 .x x x x       

  

Trường hợp 2:

 

0;1tb

Ứng với mỗi giá trị

 

0;1t 

thì phương trình

có 4 nghiệm

56

0.xx  



Hiển nhiên cả 6 nghiệm trong 2 trường hợp

trên đều khác nhau.

Vậy phương trình đã cho có 6 nghiệm thuộc

đoạn

 

;2



.

Đáp án B.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

565

[ I can't, I can! ]

Câu 62. Đặt

sintx

,

 

5

0; 1;1

2

xt



   







Khi đó phương trình

 

sin 1fx

trở thành

 

 

1, 1;1f t t   

Đây là phương trình hoành độ giao điểm của

hàm số

 

y f t

và đường thẳng

1y 

.

Dựa vào bảng biến thiên, ta có:

 

1;0

1

0;1

ta

ft

tb



  











.

Trường hợp 1:

 

1;0ta  

Ứng với mỗi giá trị

 

1;0t 

thì phương trình

sin xt

có

2

nghiệm

12

,xx

thỏa mãn

12

2xx  



.

Trường hợp 2:

 

0;1tb

Ứng với mỗi giá trị

 

0;1t 

thì phương trình

có

3

nghiệm

1 2 3

,,xxx

thỏa mãn

3 4 5

5

0 ; 2 ;

2

x x x    





Hiển nhiên cả 5 nghiệm trong 2 trường hợp

trên đều khác nhau.

Vậy phương trình đã cho có 5 nghiệm thuộc

đoạn

5

0;

2









.

Đáp án C.

Câu 63.

   

33

( ) 1 0 ( ) 1f x f x f x f x    

3

0

( ) 0

( ) (do 0)

( ) 0

( ) (do 0)

x

fx

x f x

a

x f x a

f x x

x

x f x b

b

f x x

x















   



















 

0fx

có một nghiệm dương

xc

.

Xét phương trình

 

3

k

fx

x



với

0, 0xk

.

Đặt

   

3

k

g x f x

x



,

   

4

3

'

k

g x f x

x





.

Với

xc

, nhìn hình ta ta thấy

 

0fx





   

4

3

0

k

g x f x

x



   

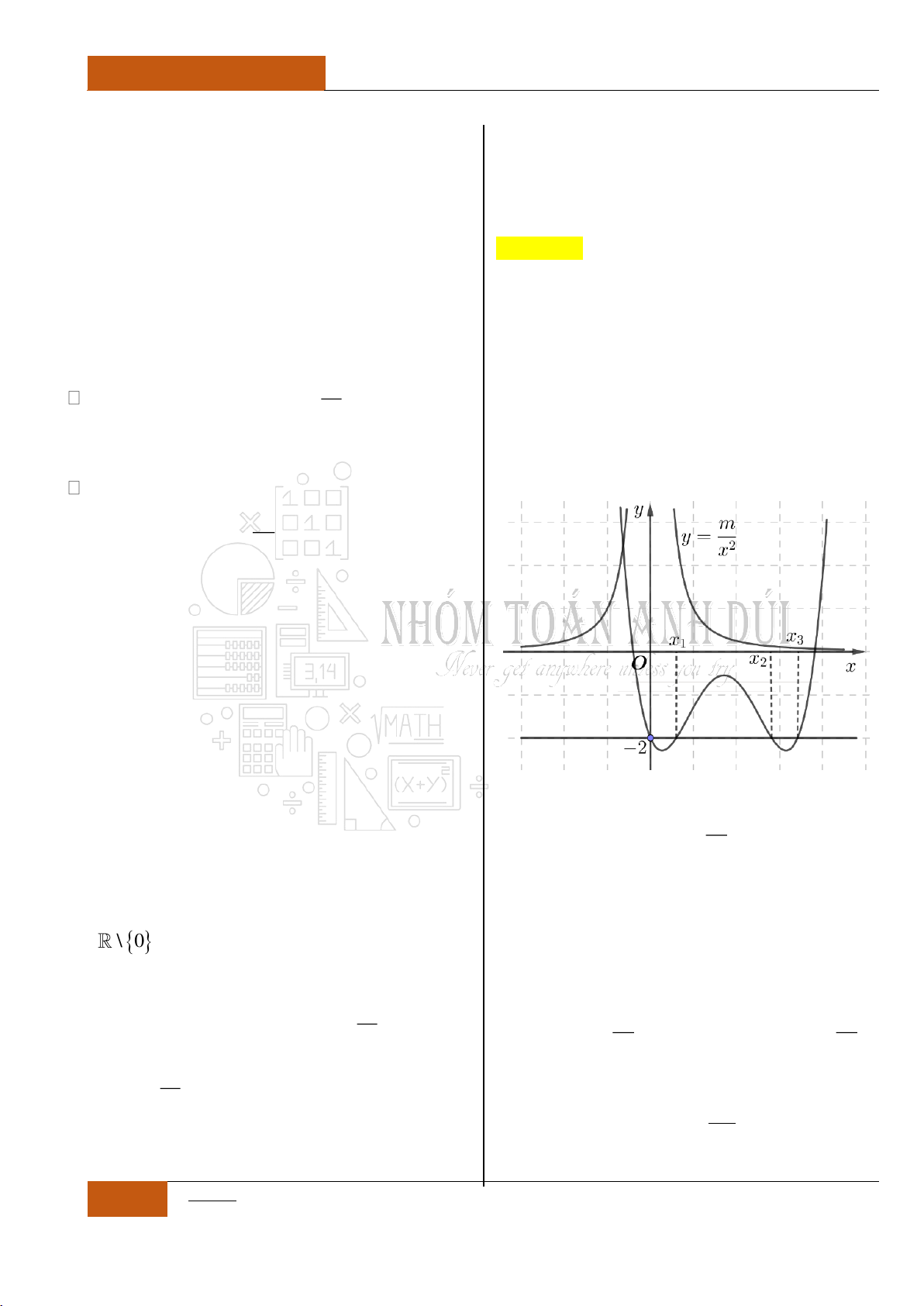
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

566

[ I can't, I can! ]

 

0gx

có tối đa một nghiệm.

Mặt khác

 

0

lim

x

gc

gx









 





và

 

gx

liên tục

trên

 

;c 



 

0gx

có duy nhất nghiệm trên

 

;c 

.

Với

0 xc

thì

3

( ) 0

k

fx

x





 

0gx

vô

nghiệm.

Với

0x 

, nhìn hình ta ta thấy

 

0fx





   

4

3

0

k

g x f x

x



   

 

0gx

có tối đa một nghiệm.

Mặt khác

 

0

lim 0

lim

x

gx















 





và

()gx

liên tục

trên

 

;0

.



 

0gx

có duy nhất nghiệm trên

 

;0

.

Tóm lại

 

0gx

có đúng hai nghiệm trên

 

\0

.

Suy ra hai phương trình

 

3

a

fx

x



,

 

3

b

fx

x



có 4 nghiệm phân biệt khác 0 và

khác

c

.

Vậy phương trình

 

3

( ) 1 0f x f x 

có đúng 6

nghiệm.

Đáp án C.

Câu 64.

 

2

( ) 0

( ) 1

( ) 2 0

( ) 2

( ) 3

x f x

x f x a

f x f x

x f x b

x f x c











  













với

0 abc  

.

Xét phương trình

     

2

10

m

f x m

x



.

Gọi

,



là hoành độ giao điểm của

   

:C y f x

và

Ox

;

0



.

   

2

10x

m

f

x

  

. Đặt

   

2

g x f x

x

m



Đạo hàm

   

3

2m

g x f x

x





.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

567

[ I can't, I can! ]

Trường hợp 1:

   

3

2

; 0; 0 0

m

x f x g x

x



    



Ta có

   

2

0lim ,

x

m

g x g



    



.

Phương trình

 

0gx

có một nghiệm thuộc

 

;



.

Trường hợp 2:

x



 

0fx

,

2

0

m

x



   

0,g x x  



.

Trường hợp 3:

   

3

2

; 0; 0 0

m

x f x g x

x



    



Ta có

   

2

0lim ,

x

m

g x g



    



.

Phương trình

 

0gx

có một nghiệm thuộc

( ; )



.

Vậy phương trình

 

2

m

fx

x



có hai nghiệm

0m

.

Ta có:

2

( ) 0 0 ( ) 0x f x x f x    

: có ba

nghiệm.

Vậy phương trình

 

1

có 9 nghiệm.

Đáp án D.

Câu 65. Ta có:

 

2

2f x f x 

 

2

0

x f x

x f x a

x f x b

x f x c























.

Xét phương trình:

 

2

0x f x 

 

0

x

fx













mà

 

0fx

có hai nghiệm

 

2

.0x f x

có

ba nghiệm.

Xét phương trình:

 

2

0x f x a

Do

2

0x 

;

0x 

không là nghiệm của phương

trình

 

2

0

a

fx

x

  

.

Xét

   

23

2aa

g x g x

xx





  

.

Bảng biến thiên:

Từ bảng biến thiên với

 

0fx

 

2

a

fx

x



có 2 nghiệm.

Tương tự:

 

2

x f x b

và

 

2

x f x c

 

,0bc

mỗi phương trình cũng có hai nghiệm.

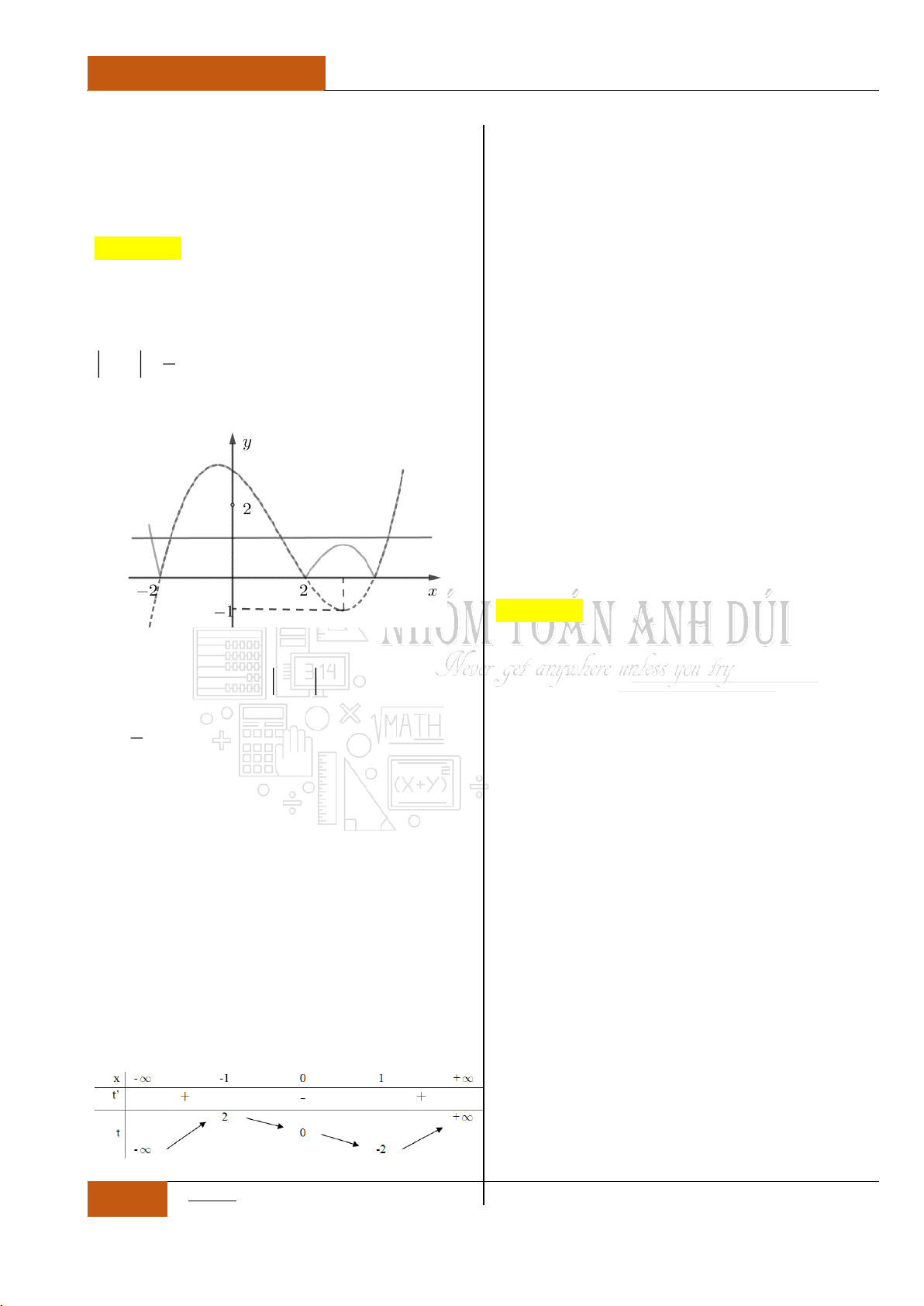
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

568

[ I can't, I can! ]

Vậy số nghiệm của phương trình

 

2

2f x f x 

là 9 nghiệm.

Đáp án D.

Câu 66. Đặt

3

3t x x

ta có phương trình

   

3

*

2

ft

.

Từ đồ thị hàm số

 

y f t

và đường thẳng

3

2

y 

ta suy ra phương trình

 

*

có 4 nghiệm

1 2 3 4

2 0 2t t t t      

Xét hàm

3

3t x x

.

Ta có

2

1

3 3 0

1

x

tx

x







   







.

Ta có bảng biến thiên

Với

1

2t 

phương trình:

3

1

3t x x

cho ta 1

nghiệm.

Với

2

20t  

phương trình:

3

2

3t x x

cho

ta 3 nghiệm.

Với

3

02t

phương trình:

3

3t x x

cho

ta 3 nghiệm.

Với

4

2 t

phương trình:

3

4

3t x x

cho ta 1

nghiệm.

Vậy phương trình đã cho có tất cả 8 nghiệm.

Đáp án C.

Câu 67. Đặt

e0

x

u 

, từ đồ thị suy ra:

 

3, 0f u u   

.

Đặt

 

2t f u

,

1t 

.

Ứng với mỗi nghiệm

1t 

, có một nghiệm

1u 

.

Ứng với mỗi nghiệm

 

1;2t 

, có hai nghiệm

 

0;2u 

.

Ứng với mỗi nghiệm

2t 

, có một nghiệm

2u 

.

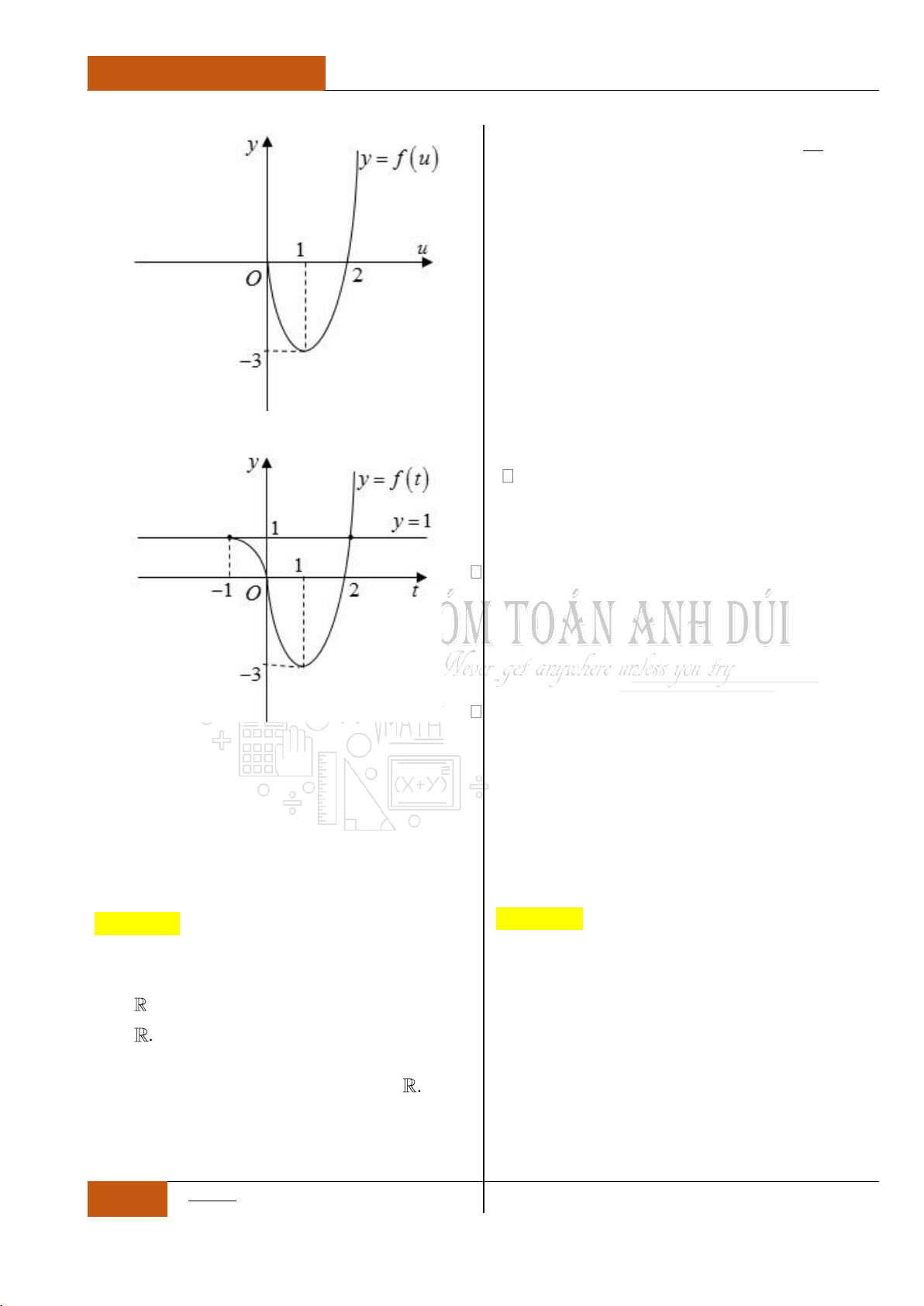
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

569

[ I can't, I can! ]

Phương trình

 

1ft

có một nghiệm

1t 

và

một nghiệm

2t 

.

Vậy phương trình đã cho có hai nghiệm.

Đáp án B.

Câu 68. Hàm số

 

y f x

có đạo hàm cấp 2

trên nên hàm số

 

fx

và

 

fx



xác định

trên

.

Do đó, TXĐ của hàm số

 

gx

là

.D 

Ta có:

     

 

.1g x f x f f x

   



.

 

0

1

3

1

0

1 ; 2

0

10

11

12

x

fx

xx

gx

f f x

fx























  











  

















Từ đồ thị ta cũng có:

   

1

1 1 0 1 .

2

x

f x f x x

x









       







   

 

1

2

; 1

1 1 2 .

2 ; +

xx

f x f x

xx



   



    



  





   

 

31

42

;

1 2 3 .

; +

x x x

f x f x

x x x



  



    



  





Vậy phương trình

 

0gx





có 9 nghiệm.

Đáp án C.

Câu 69. Ta có:

   

 

.g x f f x f x

  



 

0

f f x

gx

fx





















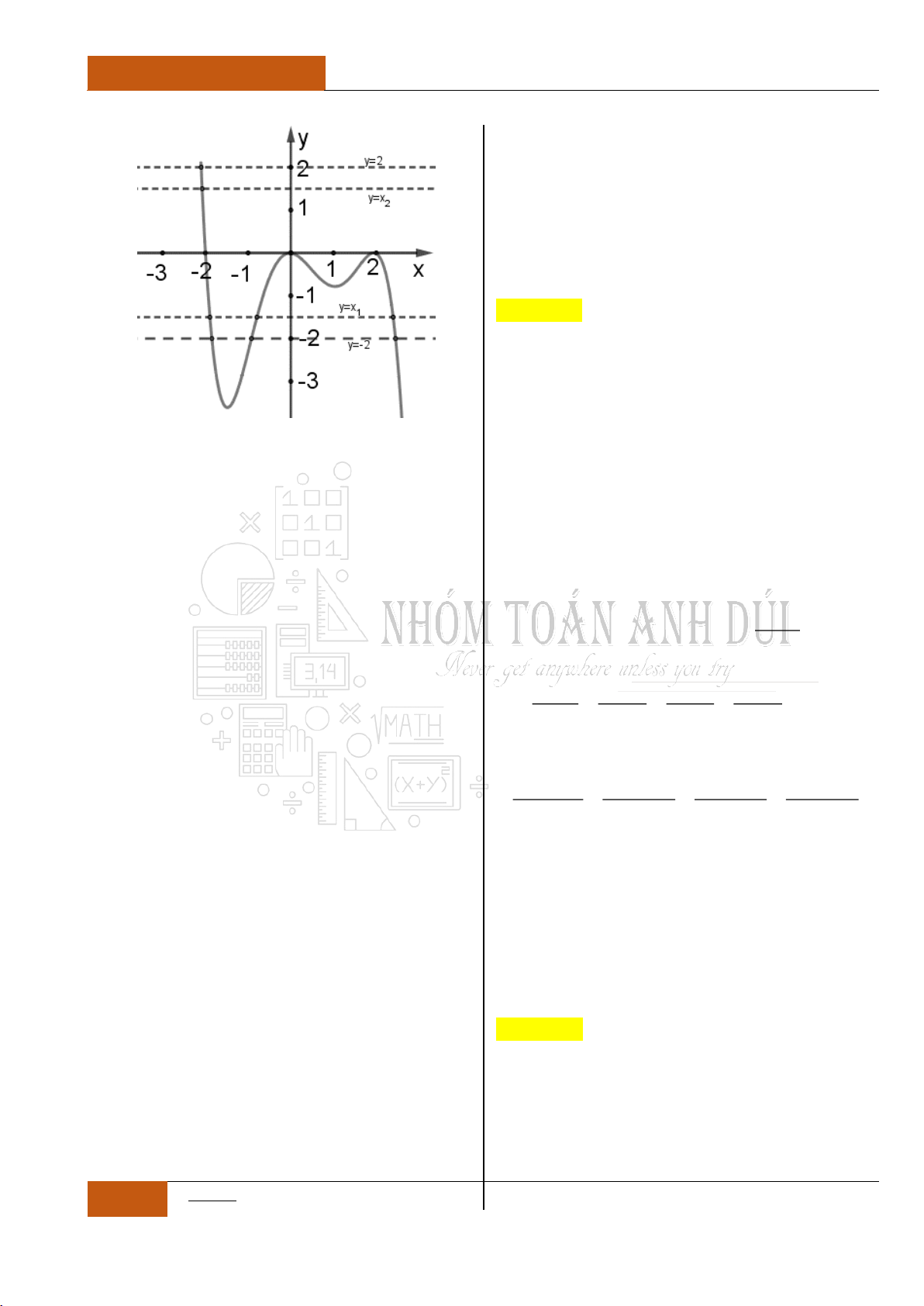
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

570

[ I can't, I can! ]

Ta có:

 

11

22

, 2 1

0

, 1 2

2

x x x

x

fx

x x x

x



    













  









;

 

1

2

0

2

f x x

fx

f f x

f x x

fx

























Dựa vào đồ thị ta thấy:

 

0fx

có

3

nghiệm phân biệt là

2, 0, 2x x x   

, trong đó có

2

nghiệm

trùng với nghiệm của

 

0fx





.

 

1

f x x

có

3

nghiệm phân biệt

     

3 4 5

2; 1 , 1;1 , 2;x x x      

.

 

2

f x x

có

1

nghiệm duy nhất

 

6

;2x   

.

 

2fx

có

1

nghiệm duy nhất

 

7

;2x   

.

Cũng từ đồ thị có thể thấy các nghiệm

12

,,xx

3 4 5 6 7

, , , , , 2,0,2x x x x x 

đôi một khác nhau.

Vậy

 

0gx





có tất cả

10

nghiệm phân biệt.

Đáp án B.

Câu 70. Với mọi

1 2 3 4

0,a x x x x   

, đặt:

    

 

1 2 3 4

,f x a x x x x x x x x    

.

Phương trình hoành độ giao điểm của đồ thị

hàm số

     

2

.y f x f x f x

 

   



và trục

Ox

là:

     

2

1 2 3 4

()

. 0 0

()

1 1 1 1

0

fx

f x f x f x

fx

x x x x x x x x





 

     









    



   



   

 

2 2 2 2

1 2 4

3

1 1 1 1

0

x x x x x x

xx

    

  



vô nghiệm.

Vậy số giao điểm của đồ thị hàm số

     

2

.y f x f x f x

 

   



và trục

Ox

là

0

.

Đáp án D.

Câu 71. Ta có:

 

1

2

3

2; 1

0 1;0

1;2

xx

f x x x

xx

    



    







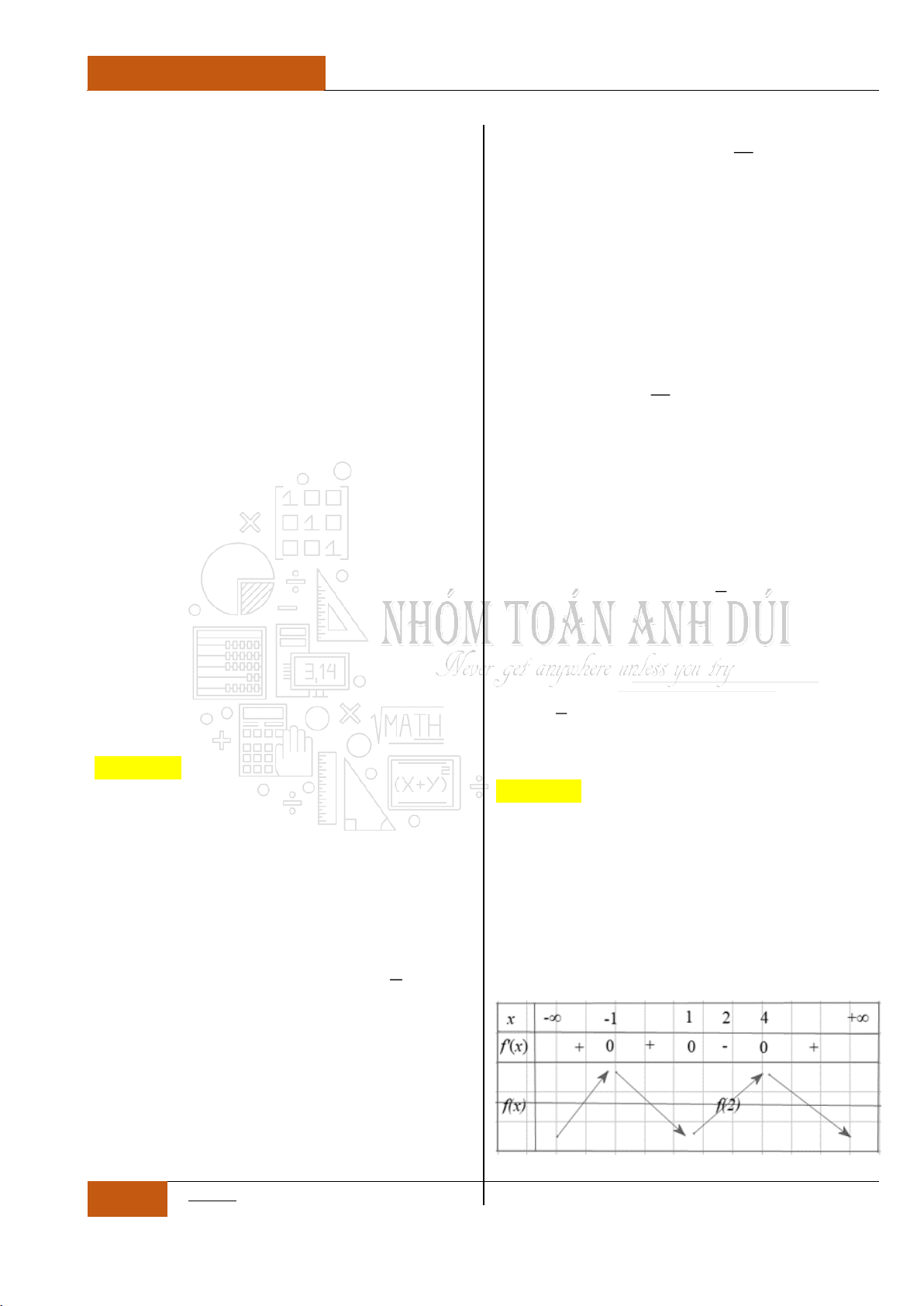
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

571

[ I can't, I can! ]

Khi đó:

 

10f f x 

   

1

2

3

1 2; 1

1 1;0

1 1;2

f x x

     



    



  



   

1

2

3

1 1;0

1 0;1

1 2;3

f x x

    



   



  



+ Ta thấy hai phương trình

   

1

1 1;0f x x   

;

   

2

1 0;1f x x  

đều có ba nghiệm phân biệt.

Phương trình

   

3

1 2;3f x x  

có một

nghiệm.

Vậy phương trình

 

10f f x 

có

7

nghiệm.

Đáp án C.

Câu 72. Ta có:

 

32

4 3 2f x mx nx px q



   

 

1

Dựa vào đồ thị

 

y f x





ta thấy phương trình

 

0fx





có ba nghiệm đơn là

1

,

5

4

,

3

.

Do đó

     

1 4 5 3f x m x x x



   

và

0m 

.

Hay

 

32

4 13 2 15f x mx mx mx m



   

 

2

.

Từ

 

1

và

 

2

suy ra

13

3

nm

,

pm

và

15qm

.

Khi đó phương trình

 

f x r



4 3 2

0mx nx px qx   



4 3 2

13

15 0

3

m x x x x



   







4 3 2

3 13 3 45 0x x x x   



  

2

3 5 3 0x x x  



5

03

3

x x x     

.

Vậy tập nghiệm của phương trình

 

f x r

là

5

;0;3

3

S









.

Đáp án B.

Câu 73. Từ đồ thị ta thấy

 

'0fx

1 1 4x x x      

.

Ta có bảng biến thiên

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

572

[ I can't, I can! ]

Phương trình

 

16 8 4 2f x m n p q r    

   

2f x f

.

Từ bảng biến thiên ta thấy phương trình có 4

nghiệm.

Câu 74. Xét phương trình

       

2

.1f x f x f x

 

  



Do

 

0fx

có ba nghiệm

 

1 2 2 1 2 3

,,x x x x x x

và

 

3

'0fx

suy ra

3

x

là một nghiệm của

 

1

.

Ta có:

    

 

2

1 2 3

f x a x x x x x x   

 

,0a 

Với

 

3

10

fx

xx

fx







   





1 2 3

1 1 2

0

x x x x x x





   



  



.

   

 

2 2 2

12

3

1 1 2

0

x x x x

xx

    





vô

nghiệm.

Vậy, phương trình

 

1

có đúng một nghiệm

3

.xx

Đáp án A.

Câu 75. Quan sát đồ thị ta thấy:

 

11

22

33

44

32

1

0 1 2

23

45

x x x

x

f x x x x

x x x



    







    



  



  



.

Do đó:

 

0f g x 

   

1

2

3

4

1

12

3

4

5

g x x

gx

g x x





















Phương trình

 

1

có đúng

1

nghiệm; Phương

trình

 

2

có đúng

3

nghiệm; Phương trình

 

3

có đúng

3

nghiệm; Phương trình

 

4

có đúng

3

nghiệm; Phương trình

 

5

có đúng

1

nghiệm. Tất cả các nghiệm trên đều phân biệt

nên phương trình

 

0f g x 

có đúng

11

nghiệm.

Quan sát đồ thị ta thấy:

 

0gx

 

55

66

21

01

3

x x x

x



    



   







Do đó:

 

0g f x 

   

5

6

7

38

f x x

fx













Phương trình

 

6

có

5

nghiệm;

Phương trình

 

7

có

5

nghiệm;

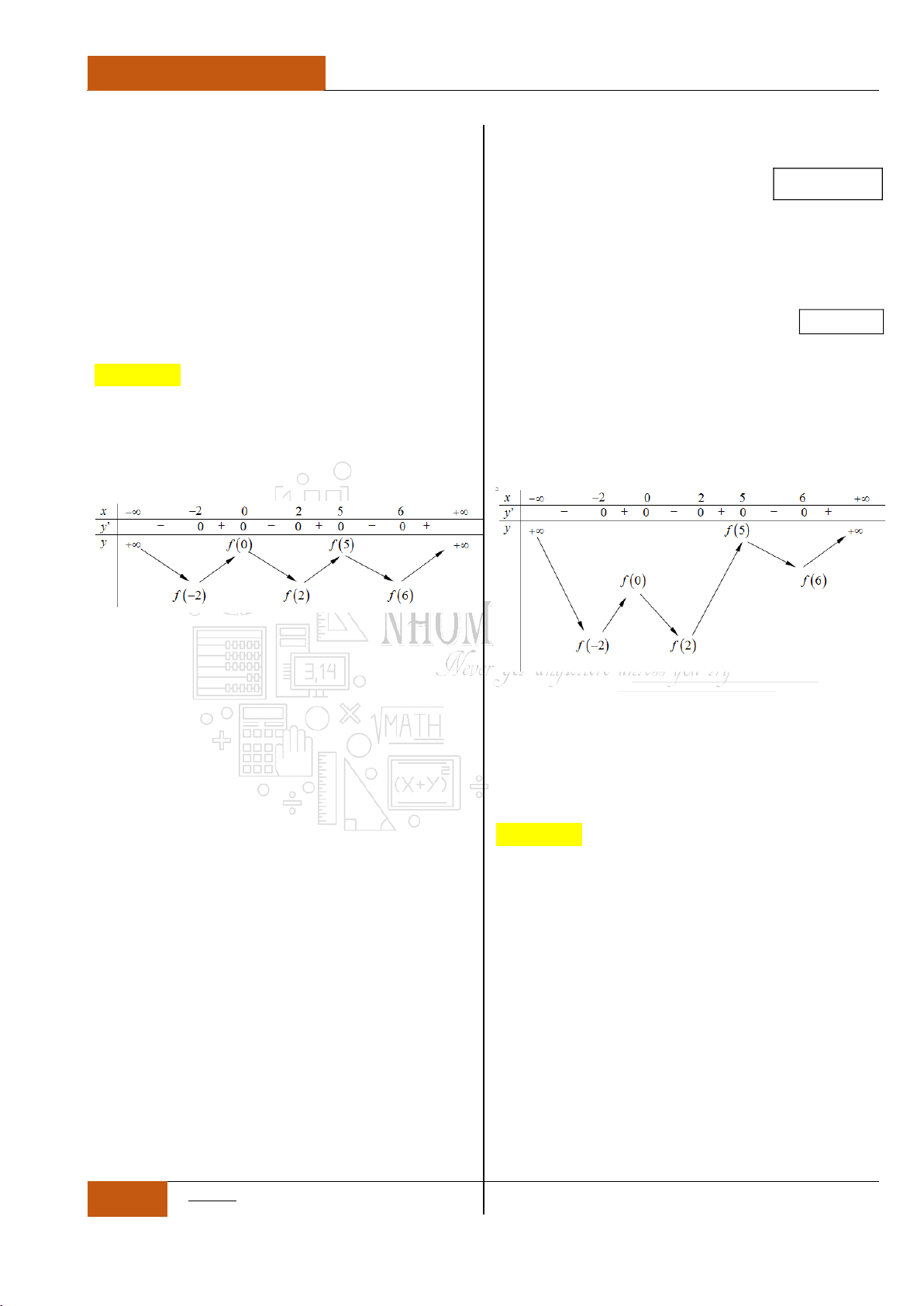
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

573

[ I can't, I can! ]

Phương trình

 

8

có

1

nghiệm.

Tất cả các nghiệm này đều phân biệt nên

phương trình

 

0g f x 

có đúng

11

nghiệm.

Vậy tổng số nghiệm của hai phương trình

 

0f g x 

và

 

0g f x 

là

22

nghiệm.

Đáp án B.

Câu 76. Từ đồ thị của hàm số

 

'fx

ta có

bảng biến thiên của đồ thị hàm số như sau:

Gọi

1

S

là diện tích hình phẳng giới hạn bởi

 

' ; 0; 0; 2y f x y x x   

.

Gọi

2

S

là diện tích hình phẳng giới hạn bởi

 

' ; 0; 2; 5y f x y x x   

.

Gọi

3

S

là diện tích hình phẳng giới hạn bởi

 

' ; 0; 5; 6y f x y x x   

.

     

2

1

0

' 0 2S f x dx f f   



;

     

5

2

' 5 2S f x dx f f  



;

     

6

3

5

' 5 6S f x dx f f   



Từ đồ thị ta thấy

21

SS

           

5 2 0 2 5 0f f f f f f     

và

1 3 2

S S S

               

0 2 5 6 5 2 6 0f f f f f f f f       

Khi đó ta có bảng biến thiên chính xác (dạng

đồ thị chính xác) như sau:

Vậy phương trình

   

0f x f

có 2 nghiệm

thuộc đoạn

 

2;6

.

Đáp án B.

Câu 77. Ta có:

     

0g x f x f f x

  

   



 

0

fx

f f x











  







 

*

.

Theo đồ thị hàm số suy ra.

 

1

0

x

fx

xa















, với

1

23a

.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

574

[ I can't, I can! ]

 

   

1

0 , 1

0

,2

fx

f f x

f x a







   











.

Phương trình

 

1

:

 

0fx

có

3

nghiệm phân

biệt khác nghiệm phương trình

 

*

.

Phương trình

 

2

:

 

1

f x a

có 3 nghiệm

phân biệt khác nghiệm phương trình

 

1

và

phương trình

 

*

.

Vậy phương trình ban đầu có 8 nghiệm phân

biệt.

Đáp án B.

Câu 78. Từ hình vẽ ta có dạng đồ thị của hàm

trùng phương nên

0bd

 

42

xf x ax c e   

Ta có

 

3

4ax 2 x.f x c





Từ đồ thị

 

10

4a 2 0

0 0 0

1

11

f

c

fe

a c e

f











   





  





 

42

1

0 2x .

2

a

e f x x

c







    









 

2

2xf x x  

và

 

   

2

2.f f x f x f x

Như vậy phương trình

 

   

2 1 0.f f x f x f x   

       

2

2 2 1 0f x f x f x f x     

với

 

0.fx

Đặt

  

0t f x t

ta được phương trình

 

0gt

với

 

2

3 2 1.g t t t t   

Nhận thấy: Hàm số

 

gt

liên tục trên đoạn

 

0;1

và

   

0 . 1 0gg

 

0gt

có ít nhất 1 nghiệm thuộc

 

0;1

.

Hàm số

 

gt

liên tục trên đoạn

 

1;4

và

   

1 . 4 0gg

 

0gt

có ít nhất 1 nghiệm thuộc

 

1;4

.

Mà

 

0gt

là phương trình bậc hai chỉ có tối

hai nghiệm nên

 

0gt

có duy nhất một

nghiệm thuộc

 

0;1

.

Suy ra:

 

   

2 1 0f f x f x f x   

có duy nhất một nghiệm

   

0;1 .fx

Suy ra phương trình

 

f x a

với

 

0;1a 

luôn có 4 nghiệm x phân biệt.

Đáp án B.

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

575

[ I can't, I can! ]

Câu 79. +) Từ giả thiết suy ra

rd

do đó phương trình tương

đương với:

     

32

0

x mx n a x p b x q c

x

mx n a x p b x q c



      











      





+) Từ đồ thị của các hàm số suy

ra

0m 

và

   

11

22

fg



   

















   

4 3 2 0

32 12 4 0

8

3

2

8

m n a p b q c

n a m

p b m

q c m

       



       





      





  



   











Từ đó ta có phương trình:

32

8

2 8 0

3

8

2 8 0

3

mx mx mx m

x x x

   

    

.

Sử dụng máy tính Casio ta được phương trình

có 1 nghiệm và nghiệm đó khác

0

.

Vậy tập nghiệm của phương trình

có 2 phần tử.

Đáp án B.

Câu 80. Dựa vào đồ thị ta có

 

10f f x 

 

1f f x 

 

   

 

2

2; 1

0

2

f x a

f x b

fx

f x c



  



   















.

+ Với

 

2f x a  

1

2

xx

  











.

+ Với

   

2; 1f x b   

 

3

4

5

6

2

2; 1

1;0

2

xx

  





   







  







+ Với

 

0fx

 

7

8

9

2

0;1

2;3

xx



  



  







.

+ Với

 

2f x c

vô nghiệm.

Ta thấy hàm số

 

y f x

đơn điệu trên

 

;2 

,

 

13

f x a b f x  

nên

13

xx

.

Hàm số

 

y f x

đơn điệu trên

 

2;

,

   

69

0f x b f x  

nên

69

xx

.

Vậy phương trình đã cho có 9 nghiệm phân biệt.

Đáp án D.

   

00fg

   

f x g x

   

,f x g x



   

f x g x

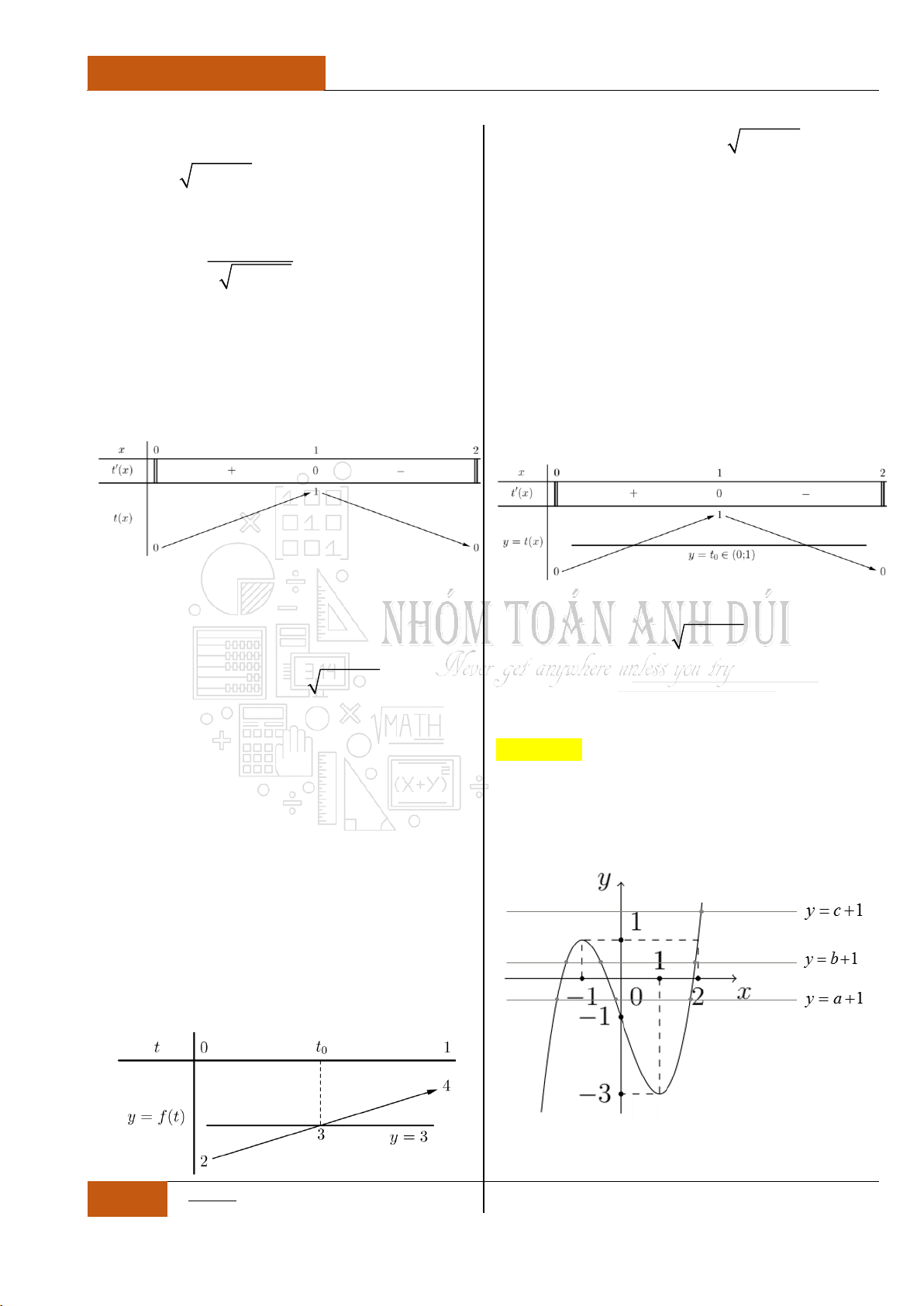
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

576

[ I can't, I can! ]

Câu 81. Trước hết, xét hàm số

 

2

2t t x x x  

,

 

0;2x

.

Ta có

 

2

22

x

tx

xx









,

 

0;2x

.

   

0 1 0;2t x x



   

.

Bảng biến thiên của

 

tx

:

01t  

,

 

0;2x

.

Lúc này, phương trình





2

23f x x

trở

thành

   

3 1ft

với

 

0;1t 

.

Theo bảng biến thiên của hàm số

 

ft

trên

đoạn

 

0;1

thì đường thẳng

3y 

cắt đồ thị

hàm số

 

y f t

tại đúng 1 điểm có hoành độ

thuộc khoảng

 

0;1

nên phương trình

 

2

có

đúng 1 nghiệm

0

tt

với

 

0

0;1t 

.

Khi đó, phương trình

 

2

0

12x x t  

 

2

,

 

0

0;1t 

.

Mặt khác, theo bảng biến thiên của hàm số

 

tx

, với mỗi

 

0

0;1t 

thì đường thẳng

0

yt

cắt đồ thị hàm số

 

y t x

tại đúng 2

điểm phân biệt nên phương trình

 

2

có đúng

2 nghiệm phân biệt.

Vậy phương trình





2

23f x x

có đúng 2

nghiệm.

Đáp án B.

Câu 82. Dựa vào đồ thị hàm số ta thấy:

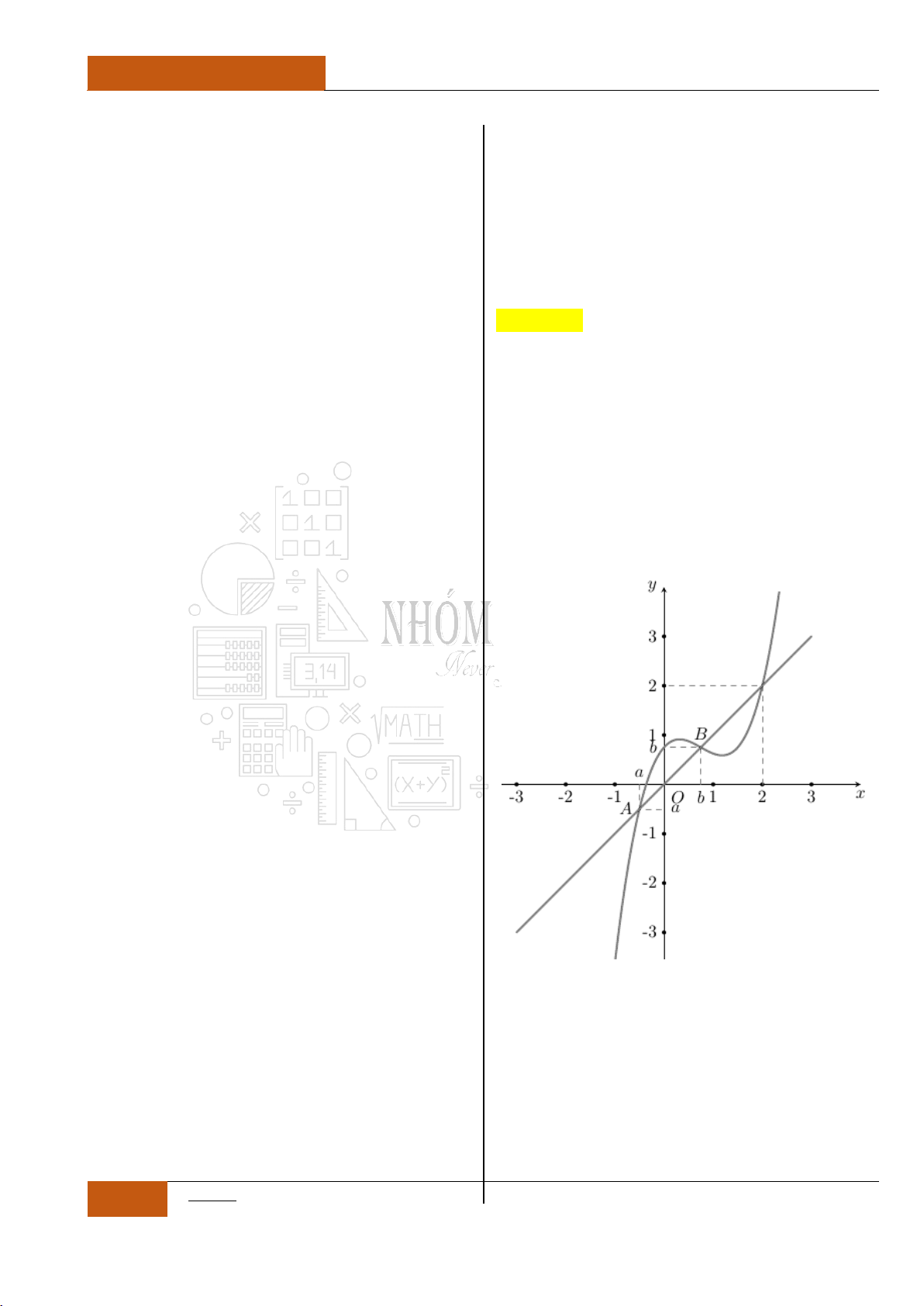
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

577

[ I can't, I can! ]

 

   

cos 1 0

cos 1 2; 1

cos 1 1;0

cos 1 1;2

f f x

f x a

f x b

f x c

   



     



    



  



   

cos 1 1;0

cos 1 0;1

cos 1 2;3

f x a

f x b

f x c

    



   



  



• Xét phương trình

 

cos 1f x a

 

   

 

1

2

3

cos 1 1

cos 1;0 2

cos 1 3

x

   



   









Vì

 

cos 1;1x

nên phương trình

   

1 , 3

vô

nghiệm và phương trình

 

2

có 2 nghiệm thuộc

đoạn

 

0;2



.

• Xét phương trình

 

cos 1f x b

 

   

 

1

2

3

cos 1 4

cos 1;0 5

cos 1 6

x

   



   









Vì

 

cos 1;1x

nên phương trình

   

4 , 6

vô

nghiệm và phương trình

 

5

có 2 nghiệm thuộc

đoạn

 

0;2



.

• Xét phương trình

 

cos 1f x c

cos 2xt  

(vô nghiệm)

Nhận xét hai nghiệm của phương trình

 

5

không trùng với nghiệm nào của phương trình

 

2

nên phương trình

 

cos 1 0f f x   



có 4

nghiệm phận biệt.

Đáp án C.

Câu 83. Từ đồ thị ta có:

 

;0

0;1

2

xa

f x x x b

x

   



   







Do đó

 

cos 1 cos 1f x x  

 

cos 1 ;0

cos 1 0;1

cos 1 2

xa

xb

x

    



   







Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

578

[ I can't, I can! ]

   

 

1

2

cos 1 ; 1

cos 1 1;0 1

cos 1 2

x a t VN

x b t

x

      



     







Dựa vào đường tròn lượng giác, phương trình

 

1

có 3 nghiệm nằm trong

;3

2











.

Phương trình (2) có

2

nghiệm nằm trong

;3

2











.

Vậy phương trình ban đầu có tất cả 5 nghiệm

nằm trong

;3

2











.

Đáp án C.

Câu 84. Đặt

1

x

te

;

 

;ln2x  

 

1;1t  

.

Nhận xét:

 

ln 1xt



với mỗi giá trị của

 

1;1t 

ta được một

giá trị của

 

;ln2x  

.

Phương trình tương đương:

 

2021

2019

ft

.

Sử dụng bảng biến thiên của

 

fx

cho

 

ft

như sau:

Dựa vào bảng biến thiên ta thấy phương trình

 

2021

2019

ft

có 2 nghiệm

 

12

, 1;1tt

.

Vậy phương trình

 

2019 1 2021 0

x

fe  

có

2 nghiệm

 

;ln2x 

.

Đáp án B.

Câu 85. Đặt

costx

, với

 

0;3x



.

Khi đó:

 

1;1t 

.

Với

1t 

, phương trình

costx

có hai

nghiệm

 

0;3x



.

Với

1t 

, phương trình

costx

có hai

nghiệm

 

0;3x



.

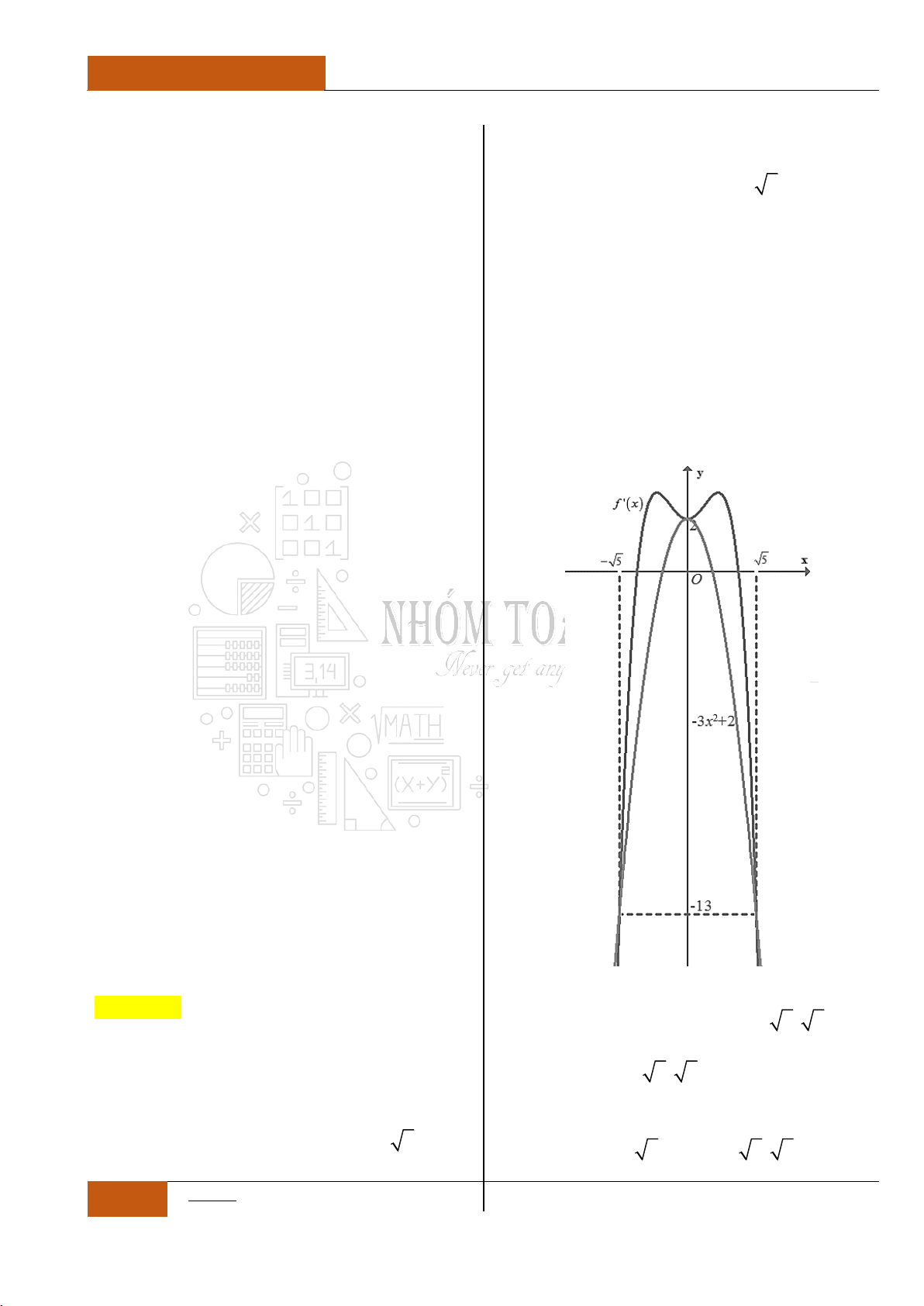
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

579

[ I can't, I can! ]

Với

11t  

, phương trình

costx

có ba

nghiệm

 

0;3x



.

Thay

costx

vào phương trình

 

cos 1 0f f x 

, ta được phương trình:

 

   

1 2; 1

1 0 1 1;0

1 1;2

f t a

f f t f t b

f t c

     



      



  



     

1 1;0 1

1 0;1 2

1 2;3 3

f t a

f t b

f t c

    



   



  



.

Từ đồ thị ta có:

+) Phương trình

 

1

có 1 nghiệm

 

1;0t 

,

suy ra phương trình đã cho có 3 nghiệm.

+) Phương trình

 

2

có 1 nghiệm

 

1;0t 

,

suy ra phương trình đã cho có 3 nghiệm.

+) Phương trình

 

3

có 1 nghiệm

1t 

, suy ra

phương trình đã cho vô nghiệm.

Vậy phương trình đã cho có 6 nghiệm.

Đáp án D.

Câu 86. Ta có:

 

0gx

 

3

2 2 4 3 6 5f x x x m    

.

Đặt

   

3

2 2 4h x f x x x  

thì bất phương

trình

   

0 3 6 5g x h x m   

   

 

2

' 2 ' 2.3 4

2 ' 3 2

h x f x x

f x x

  

   

.

Vẽ đồ thị hàm số

2

32yx  

trên cùng hệ

trục tọa độ với hàm số

 

'y f x

.

Ta thấy

 

2

' 3 2f x x  

5; 5x



  



nên

 

' 0, 5; 5h x x



   



.

Suy ra

 

5 , 5; 5h x h x



   



.

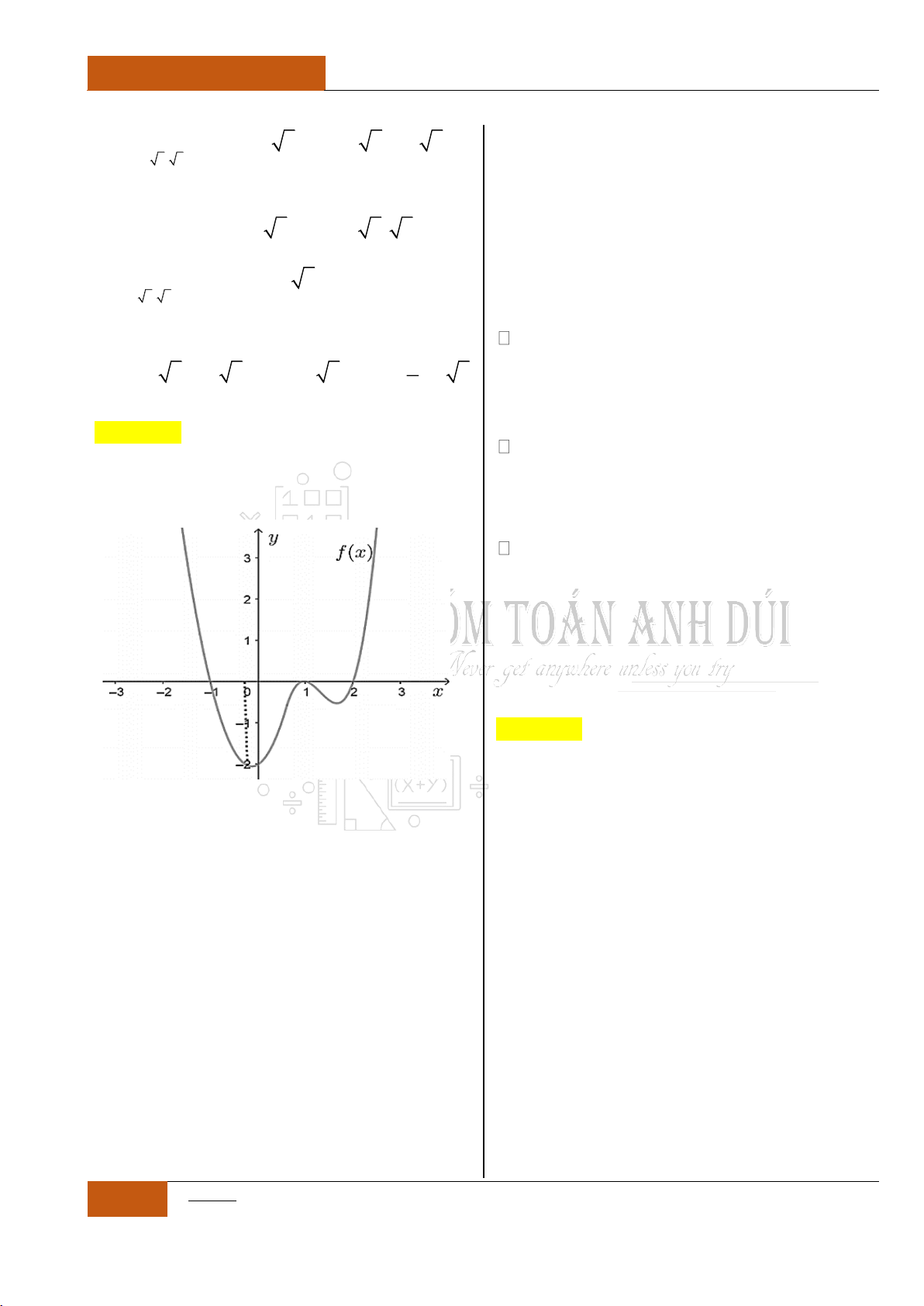
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

580

[ I can't, I can! ]

Hay

 

   

5; 5

max 5 2 5 6 5h x h f







  

Do đó

 

3 6 5, 5; 5h x m x



    



 

5; 5

max 3 6 5h x m







  

.

   

2

2 5 6 5 3 6 5 5

3

f m m f     

Đáp án D.

Câu 87. Ta có:

     

 

.1g x f x f f x

  



     

 

0 . 1 0

0

10

g x f x f f x

fx

f f x

  

   

















.

+)

 

11

22

1;0

01

1;2

x a a

f x x

x a a



  





  









+)

 

10f f x





 

     

   

     

11

22

1 1 0;1 1

1 1 2 2

1 1 2;3 3

f x a f x a

f x f x

f x a f x a

      



    



    



Từ đồ thị suy ra:

Phương trình

 

1

có hai nghiệm phân biệt

   

12

2; 1 ; 2;3bb   

Phương trình (2) có hai nghiệm phân biệt

   

1 1 2 2

2; ; ;3c b c b  

Phương trình (3) có hai nghiệm phân biệt

   

1 1 2 2

2; ; ;3d c d c  

Vậy phương trình đã cho có 9 nghiệm phân

biệt.

Đáp án C.

Câu 88. Đặt

 

cosf x t

ta được phương trình

 

0ft

.

Quan sát đồ thị

 

y f x

ta suy ra

 

1

2

3

2; 1

0 0;1 .

t t 1;2

tt

f t t t

    



   







* Với

1

tt

ta có

 

1

cosf x t

.

Xét tương giao giữa hai đồ thị

 

y f x

và

   

11

1

2; 1 cos

cos 1

y t f x t

xx

     

   

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

581

[ I can't, I can! ]

nên phương trình vô nghiệm.

* Với

2

tt

ta có

 

2

cosf x t

.

Xét tương giao giữa hai đồ thị

 

y f x

và

   

22

0;1 cosy t f x t   

 

2

3

4

cos 1

cos 0;1 .

cos 1;2

xx



  



  







Chỉ có

3

cosxx

thỏa mãn.

Khi đó tồn tại 3 giá trị

7

0;

2

x











tương ứng để

3

cosxx

.

* Với

3

tt

tương tự ta có

5

6

7

cos 1

cos ( 1;0).

cos 1

xx

  





  







Chỉ có

6

cosxx

thỏa mãn. Khi đó tồn tại 2 giá

trị

7

0;

2

x











tương ứng để

6

cosxx

.

Vậy phương trình đã cho có 5 nghiệm thuộc

đoạn

7

0;

2









.

Đáp án B.

Câu 89. Đặt

2costx

, ta có bảng biến thiên

của

t

như sau

Khi đó:

   

8

3 2cos 8

3

f x f t  

.

Vẽ thêm đường thẳng

8

3

y 

trên đồ thị

 

y f x

đã cho.

Xét trên đoạn

 

2;2

, đường thẳng

8

3

y 

cắt đồ

thị hàm số

 

ft

tại hai điểm

 

1

2; 1t   

và

 

2

1;2t 

.

Từ bảng biến thiên của

t

, ứng với giá tị

1

t

, ta

tìm được 3 nghiệm

x

thỏa

1

2cos xt

, tương tự,

ta cũng tìm được 3 nghiệm

x

thỏa

2

2cos xt

.

Vậy phương trình

 

3 2cos 8fx

có 6 nghiệm

x

thuộc đoạn

 

2017 ;2020



.

Đáp án D.

Câu 90. Ta có

 

3

2

3

2sin 5cos2

2 sin 2 sin

34

5 1 2sin

2sin

2 sin 2 sin

34

xx

f x x m

x

m f x x

    



     

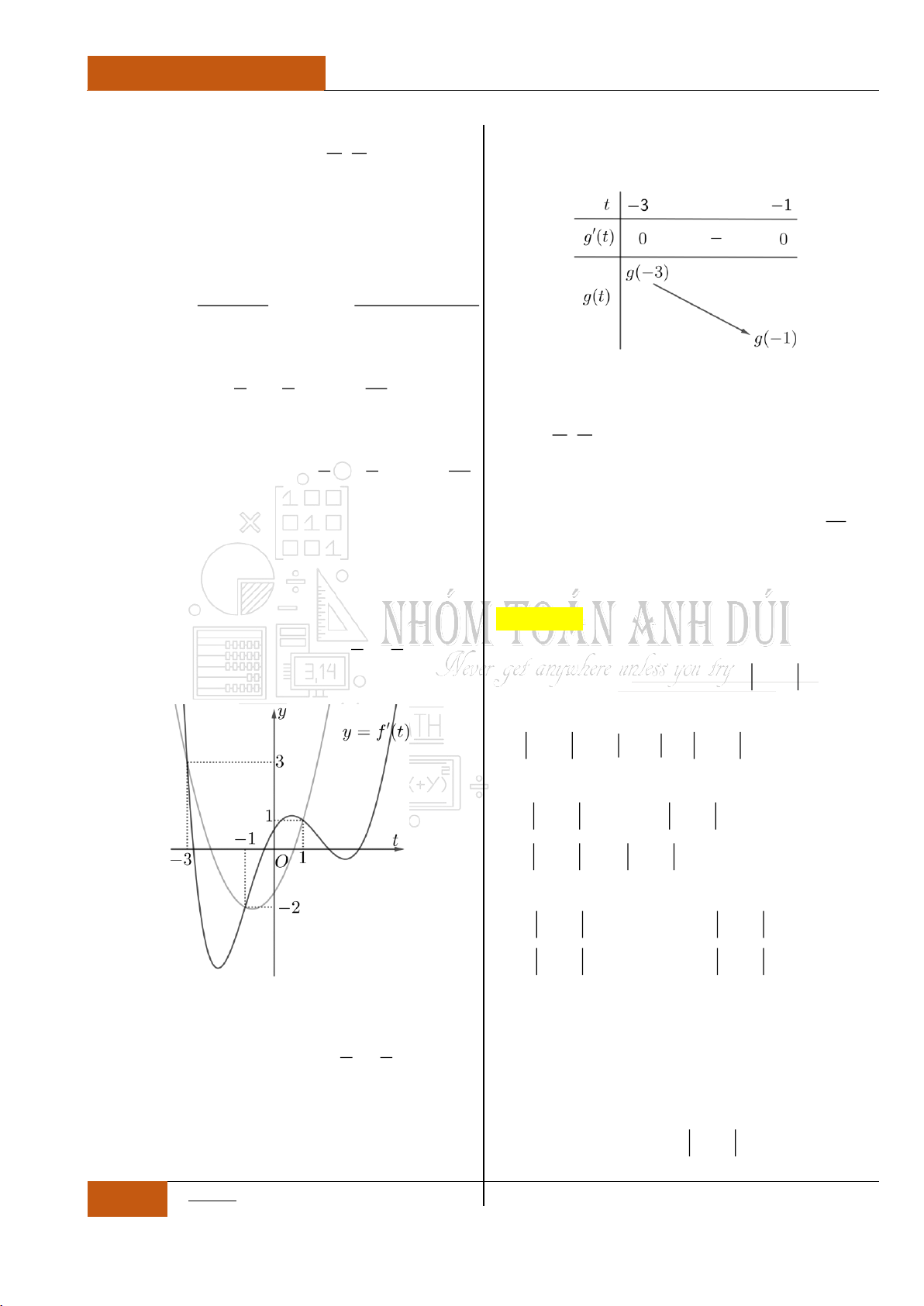
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

582

[ I can't, I can! ]

Đặt

sin 2tx

(với

;

22

x











thì

 

3; 1t   

, khi đó bất phương trình được viết

lại thành:

 

2

3

5 1 2 2

22

34

t

m f t t









    

hay

   

32

2 3 65

2 3 *

3 2 12

m f t t t t    

.

Xét hàm số

   

32

2 3 65

23

3 2 12

g t f t t t t    

trên đoạn

 

3; 1

.

Ta có

   

2

2 2 3 3g t f t t t



   

.

Do đó

   

2

33

0

22

g t f t t t



    

.

Dựa vào sự tương giao của đồ thị hàm số

 

y f t





và Parabol

2

33

22

y t t  

trên đoạn

 

3; 1

thì

   

0 3; 1g t t



    

.

Suy ra bảng biến thiên của hàm số

 

gt

trên

đoạn

 

3; 1

như sau:

Bất phương trình đã cho nghiệm đúng với mọi

;

22

x











khi và chỉ khi bất phương trình

 

*

nghiệm đúng với mọi

 

3; 1t   

. Điều đó

tương đương với

   

19

1 2 1

12

m g f    

dựa vào tính liên tục của hàm số

 

gt

.

Đáp án C.

Câu 91. Ta có:

     

2

4 2 4 0f x m f x m    

   

2

( ) 4 2 4 0f x m f x f x m     

 

2

2 2 0

f x m f x

f x f x m

    

 

   

2 0 2 1

2 0 2 2

f x f x

f x m f x m



  







    





Dựa vào đồ thị hàm số bậc ba

 

32

y f x ax bx cx d    

ta có đồ thị hàm số

 

y f x

như sau:

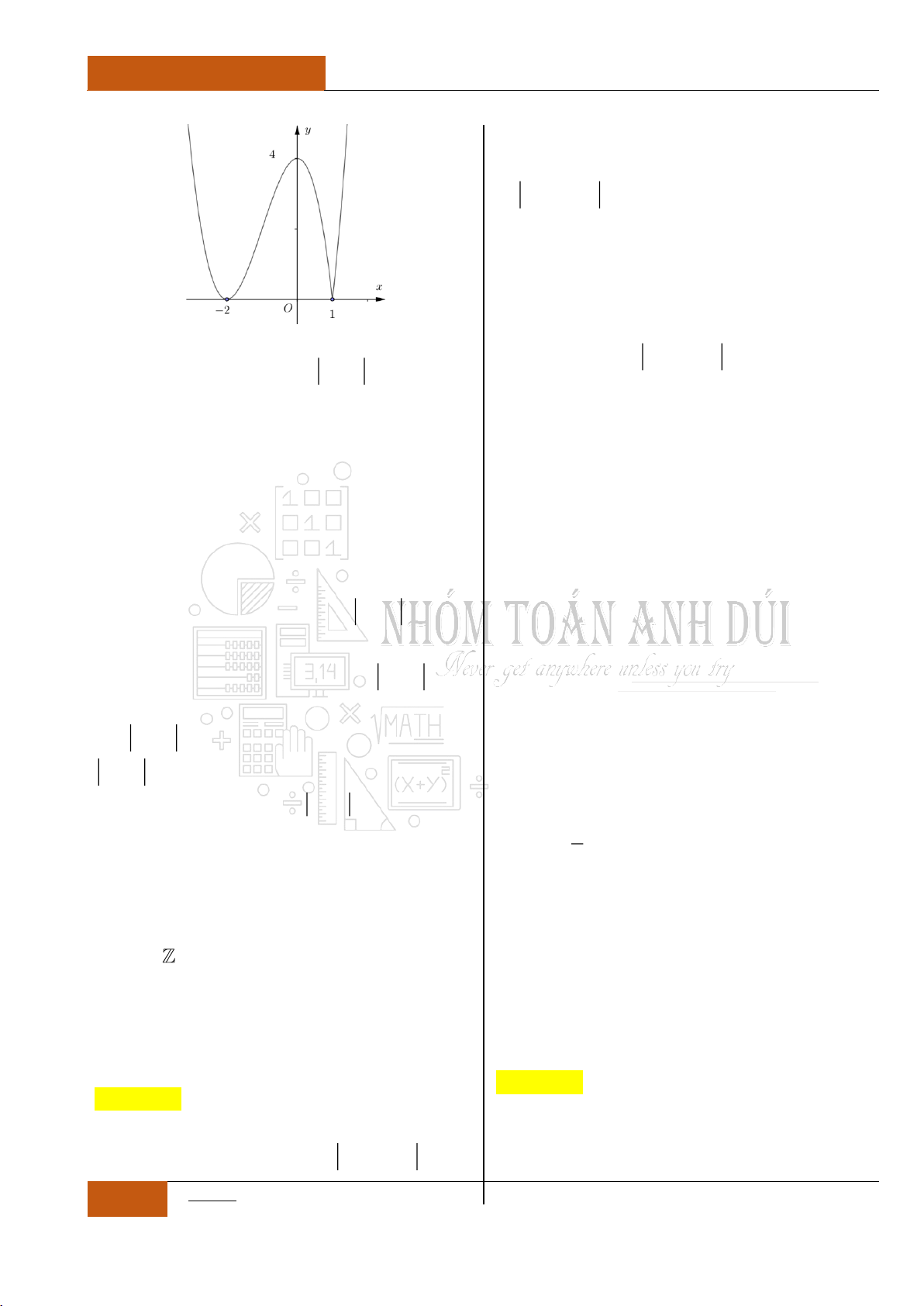
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

583

[ I can't, I can! ]

Dựa vào đồ thị hàm số

 

y f x

suy ra

phương trình

 

1

có 4 nghiệm phân biệt.

Suy ra phương trình đã cho có 6 nghiệm phân

biệt

 

2

có 2 nghiệm phân biệt khác các

nghiệm của phương trình

 

1

.

Ta có phương trình

 

2

là phương trình hoành

độ giao điểm của hai đường

 

y f x

và

2ym

. Số nghiệm phương trình

 

2

là số

giao điểm của 2 đồ thị hàm số

 

y f x

và

2ym

. Dựa vào hình vẽ đồ thị hàm số

 

y f x

ta được phương trình

 

2f x m

có 2 nghiệm phân biệt khác các

nghiệm của phương trình

( ) 2fx

20

2

24

2

22

m











   













Do

m

và

   

5;5 2;3;4mm    

.

Vậy có 3 giá trị nguyên

 

5;5m

thỏa mãn

điều kiện bài toán.

Đáp án C.

Câu 92. Để bất phương trình

 

2f x m m

có nghiệm ta suy ra điều kiện

0m 

.

   

2 2 2f x m m m f x m m      

 

3f x m

f x m

















.

Bất phương trình

 

2f x m m

đúng với

mọi

x

thuộc đoạn

 

1;4

 

3f x m

f x m

















đúng với mọi

x

thuộc đoạn

 

1;4

 

 

 

 

1;4

3 min

max

m f x



















.

Từ đồ thị hàm số

 

y f x

ta suy ra

 

 

 

 

1;4

min 2; max 3f x f x



  

.

 

 

 

 

1;4

3 min

32

3

max

2

3

m f x

m

m f x

m







  























  









(thỏa mãn điều kiện

0m 

)

Vậy trên đoạn

 

10;10

có

7

giá trị nguyên của

m

thỏa mãn điều kiện bài toán.

Đáp án C.

Câu 93. Ta có:

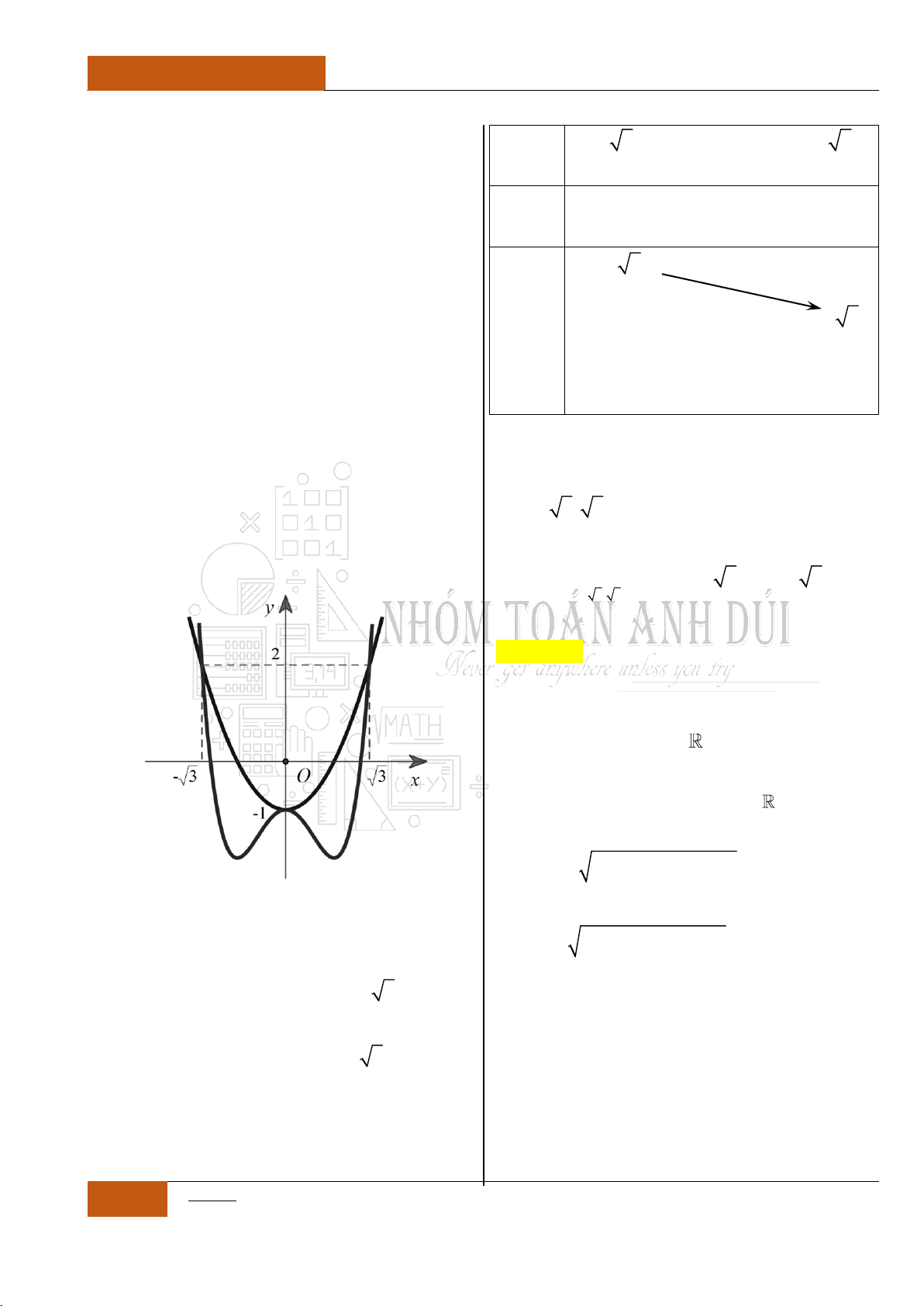
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

584

[ I can't, I can! ]

   

33

3 3 3 3f x x x m f x x x m      

Đặt

   

3

33g x f x x x  

.

Tính

   

2

' 3 ' 3 3g x f x x  

Ta có:

   

2

' 0 ' 1g x f x x   

Nghiệm của phương trình

 

'0gx

là hoành

độ giao điểm của đồ thị hàm số

 

'y f x

và

parabol

2

1yx

.

Minh họa sự tương giao giữa đồ thị hàm số

 

'y f x

và Parabol

2

1yx

.

Dựa vào đồ thị hàm số ta có:

 

2

3

' 1 0

3

x

f x x x

x







   







Bảng biến thiên:

x

3

1

3

 

'gx

0



0



0

 

gx

 

3g 

 

3g

Để bất phương trình nghiệm đúng với mọi

3; 3x







thì:

 

   

3; 3

min 3 3 3m g x g f







  

.

Đáp án D.

Câu 94. Xét hàm số

 

3

2f t t t  

, ta có

 

2

3 1 0,f t t t



    

.

Do đó hàm số

f

đồng biến trên .

Ta có:

   





 

3

f f f x m f xx    

   

     

3

33

01

x f f x m

f x x m

x

x f

    

    

Xét

     

33

h x f f xx xm   

trên đoạn

 

1;2

.

Ta có:

       

22

33xh x f x f f x x

  

   

Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

585

[ I can't, I can! ]

   

22

3 1 3 .f xf x x





  



Ta có:

 

2

3 1 0, [ 1;2]f x x x



     

 

0, [ 1;2]h x x



    

.

Hàm số

 

hx

đồng biến trên

[ 1;2]

nên

   

[ 1;2]

min 1 1

max 2 1748.

h x h m





   





  





Phương trình

 

1

có nghiệm khi và chỉ khi

       

  

[ 1;2]

min max 0 1 2

1 1748 0

1748 1.

h x h x h h

mm

m



    

   

   

Do

m

nguyên nên tập các giá trị

m

thỏa mãn

là

 

1748; 1747; ;0;1S    

.

Vậy có tất cả 1750 giá trị nguyên của

m

thỏa

mãn.

Đáp án A.

Câu 95. Dựa vào bảng biến thiên ta có

 

   

2;4

24f x fMin 

và

 

   

2;4

42f x fMax 

Hàm số

 

2

22g x x x x  

liên tục và đồng

biến trên

 

2;4

.

Suy ra:

 

   

2;4

22xgMin g 

và

 

   

2;4

4442xgMax g   

Ta có

 

2

2 2 .x x x m f x  

 

2

22

()

gx

x x x

mm

f x f x



   

.

Xét hàm số

 

gx

hx

fx



liên tục trên

 

2;4

.

Vì

 

xg

nhỏ nhất và

 

fx

lớn nhất đồng thời

xảy ra tại

2x 

nên:

 

 

 

 

 

 

2;4

2

1

2

22

x

f x f

Min g

g

Minh x h

Max

   

Vì

 

xg

lớn nhất và

 

fx

nhỏ nhất đồng thời

xảy ra tại

4x 

nên

 

 

 

 

2;4

4

( ) 4 2 2 2

4

x

f x f

Max g

g

Maxh x h

Min

    

Từ đó suy ra phương trình

 

h x m

có

nghiệm khi và chỉ khi:

1

2 2 2

2

m  

.

Vậy có 4 giá trị nguyên của

m

để phương trình

có nghiệm.

Đáp án C.

Câu 96. Ta có:

     

 

2

cos 2019 cos 2020 0

1

cos 1

cos 2020

f x m f x m

fx

f x m

    















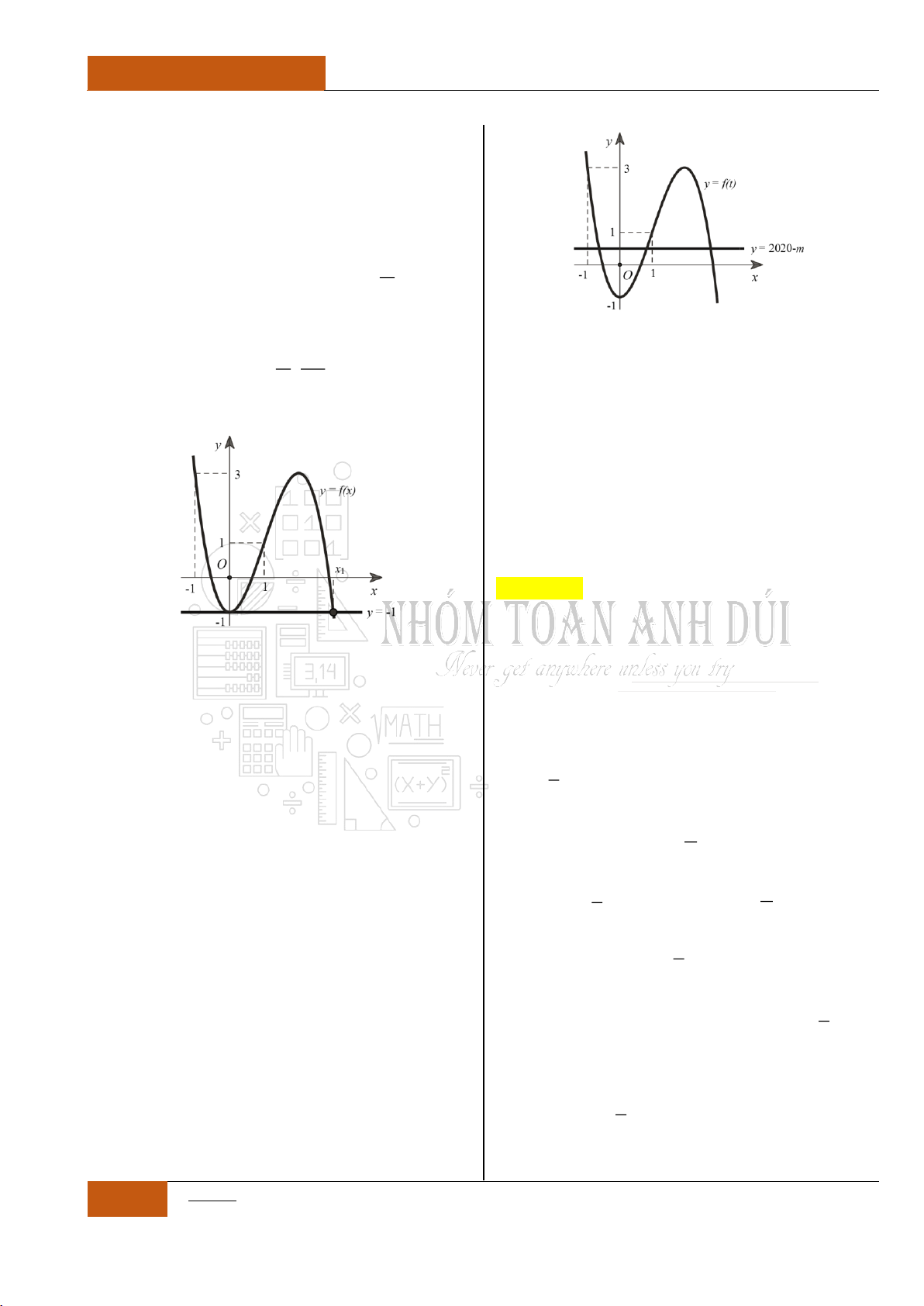
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

586

[ I can't, I can! ]

* Với

 

cos 1fx

Dựa vào đồ thị ta có

 

cos 1fx

 

11

cos 0

cos 1 ( )

2

x

xk

x x x VN





   









.

Vì

 

3

0;2 ;

22

xx



  









* Với

 

cos 2020f x m

Đặt

 

 

cos 1;1t x t  

Với





1;1t 

thì phương trình

costx

có hai

nghiệm phân biệt thuộc

 

0;2



.

Với

1t 

thì phương trình

costx

có một

nghiệm thuộc

 

0;2



Phương trình trở thành

 

2020f t m

Để phương trình (1) có tất cả 6 nghiệm phân biệt

thì phương trình

 

cos 2020f x m

có 4

nghiệm phân biệt, hay phương trình

 

2020f t m

có hai nghiệm





1;1t 

Dựa vào đồ thị ta có để phương trình

 

2020f t m

có hai nghiệm





1;1t 

thì

1 2020 1 2019 2021mm      

Vì

m

nguyên nên

 

2019;2020m

Vậy có 2 giá trị nguyên của

m

thỏa mãn.

Đáp án C.

Câu 97. Ta có:

   

lnf x x m  

   

lnm f x x   

.

Xét hàm số

     

lng x f x x  

trên

1

1;

e









.

Ta có:

   

1

g x f x

x





.

Trên

1

1;

e









có

 

0fx





và

1

0

x



nên

 

1

0, 1;g x x

e





    





.



Hàm số

 

gx

đồng biến trên

1

1;

e









.

Vậy nên

   

lnf x x m  

nghiệm đúng với

mọi

1

1;x

e



  





.

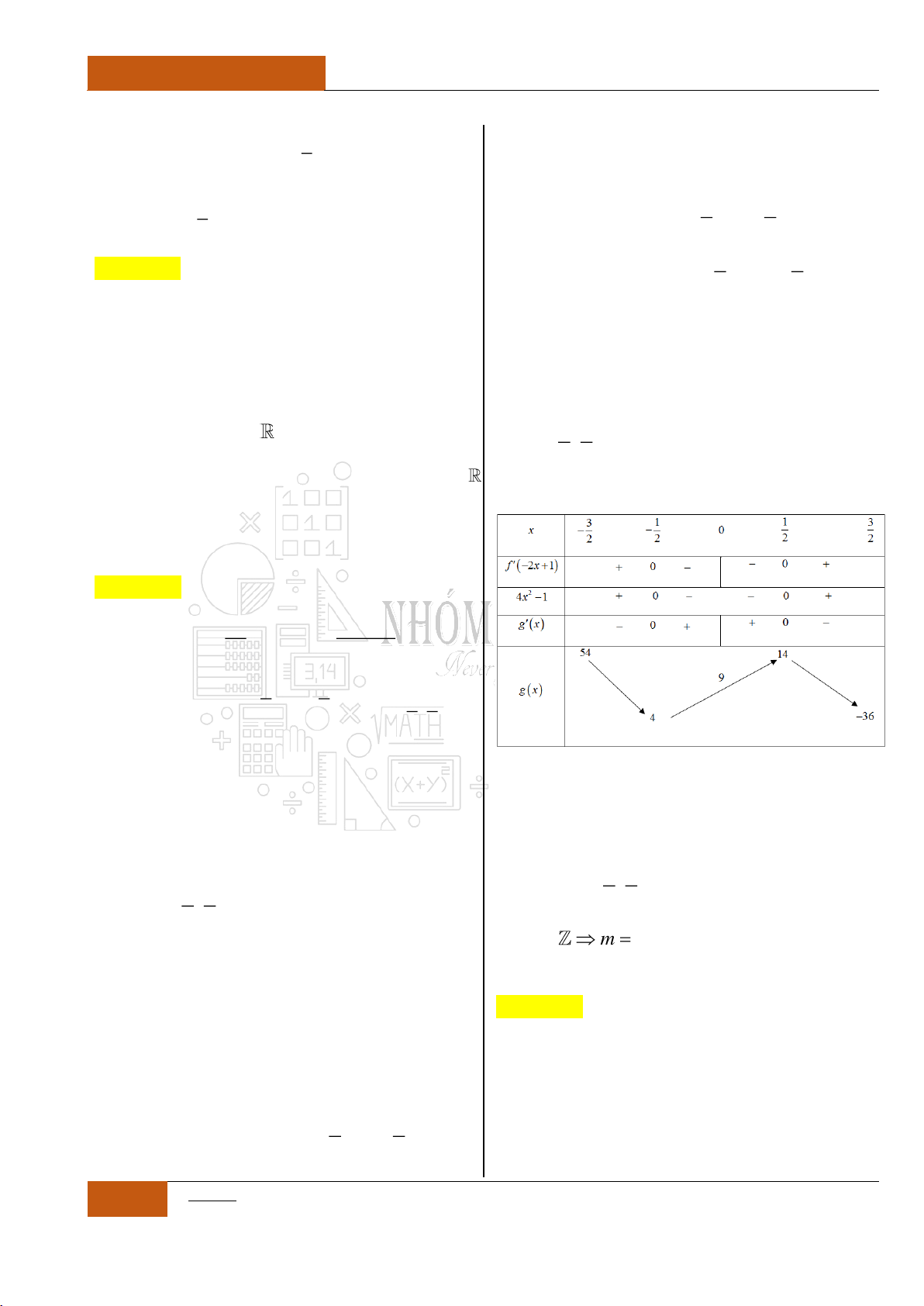
Nhóm Toán anh Dúi

[PHÁ ĐƯỜNG DÂY HÀM SỐ]

587

[ I can't, I can! ]

 

1

, 1;m g x x

e



     





1

mg

e



  





3m

.

Đáp án B.

Câu 98. Ta có :

 

22

16.8 5 .4 4 .16

f x f x f x

m m f x    

 

22

5 16.2 4 .4

f x f x

m m f x     

Vì

 

2,f x x   

nên ta có:

 

22

16.2 4 .4 16.2 0 4,

f x f x

f x x



      

22

5 4 5 4 0

14

m m m m

m

       

  

.

Đáp án D.

Câu 99. Ta có:

2

22

9 9 4

4 0 0

x

xx



   

 

2

33

9 4 0

33

; \ 0

22

0

x



  







    

















Xét phương trình

 

3

6 2 1 8 6 0f x x x m     

   

3

6 2 1 8 6 1m f x x x     

Xét hàm số

   

3

6 2 1 8 6g x f x x x    

,

với

 

33

; \ 0

22

x









.

Ta có:

   

2

12 2 1 24 6g x f x x



     

 

2

6 2 2 1 4 1f x x





     



Từ giả thiết ta suy ra:

 

2 1 0fx



  

2 1 2

11

2 1 0

22

x

  



    



  



;

 

2 2 1 0

2 1 0

2 2 1 4

13

22

31

22

x

fx

x

    





   



   













   





.

Bảng biến thiên của hàm số

   

3

6 2 1 8 6g x f x x x    

trên

 

33

; \ 0

22









.

Từ bảng biến thiên ta suy ra hệ có đúng ba

nghiệm

 

1

có đúng ba nghiệm

 

33

; \ 0

22

x









4 14

9

m













.

Vì

5;6;7;8;10;11;12;13mm  

.

Vậy có

8

số nguyên

m

.

Đáp án D.

TÀI LIỆU THAM KHẢO

1. Sách giáo khoa Toán cơ bản lớp 10, 11, 12, NXB Giáo Dục.

2. Sách giáo khoa Toán nâng cao lớp 10, 11, 12, NXB Giáo Dục.

3. Sách bài tập Toán cơ bản lớp 10, 11, 12, NXB Giáo Dục.

4. Sách bài tập Toán nâng cao lớp 10, 11, 12, NXB Giáo Dục.

5. Công phá Toán 3 – Ngọc Huyền LB.

6. Tài liệu Thầy Nguyễn Bảo Vương.

7. Tài liệu của tác giả Phan Thành Tường – Đồng chủ biên.

8. Tài liệu của tác giả Nguyễn Thành Nhân – Đồng chủ biên.

Lời kết

Thật ra, đây là quyển tài liệu lớn đầu tiên, tôi và người bạn thân Phan Thành

Tường cùng kết hợp để viết. Một tài liệu hết sức tâm huyết của một cậu học

sinh năm nhất trường Đại học An Giang gửi gắm đến các thế hệ học sinh “đàn

em” sau này.

Ngay từ khi vừa kết thúc kỳ thi THPTQG năm 2020, tôi đã lên ý tưởng và sắp

xếp lại bố cục trong đầu của mình về một “quyển sách” nhỏ tầm 1000 trang

gửi đến các bạn đọc làm tài liệu tham khảo. Những câu hỏi liên tiếp được đặt

ra trong đầu tôi ngay lúc đó, chẳng có một phương tiện nào có thể hỗ trợ, bản

thân lại chưa đủ trình độ chuyên môn. Tuy nhiên, sau một năm gắn bó với

các thành viên của đại gia đình “Nhóm Toán anh Dúi”, tôi đã tự tin hơn rất

nhiều, và đem hết tâm huyết mình vào những dự án mang tính nhân văn này

đến tất cả các “em học sinh” của tôi. Hơn thế nữa, tôi muốn đưa đến các bạn,

một nguồn tài liệu mở, mang tinh thần giúp đỡ nhau trong học tập đến rộng

khắp trái tim của những nhân tài đất nước sau này, một nguồn tài liệu về

Hàm số, gồm những nội dung Lý thuyết cơ bản, nâng cao, thử sức với bốn

dạng mức độ của bài tập cũng như tự luyện nâng khả năng tư duy và phản

xạ. Sau 6 tháng, miệt mài nghiên cứu các dạng tài liệu phổ biến, dạng câu hỏi

thường gặp và sáng tạo nội dung. Tôi và người bạn, Phan Thành Tường

(Kaito Tường) đã cho ra mắt cuốn sách “Phá đường dây Hàm số” này.

Không lấy lý do còn non trẻ và là bài đầu tay để biện hộ cho những sai sót

trong quá trình thực hiện. Nhưng thật sự, để đạt được một sự hoàn hảo tuyệt

đối thì cá nhân tôi chưa đảm bảo được. Tôi thực sự rất biết ơn các độc giả phát

hiện và tích cực chỉ ra những lỗi sai còn tồn đọng trong quyển tài liệu này. Tôi

xin đặt tình cảm của các độc giả vào những lần sửa chữa tiếp theo.

Các độc giả có những góp ý, vui lòng mail cho tôi vào tài khoản cá nhân:

nhannguyen.6760@gmail.com

ntnhan_21to@student.agu.edu.vn

tuongkaito@gmail.com

Phá đường dây hàm số Toán 12

Tài liệu liên quan:

Kĩ Thuật Giải Nhanh Cực Trị Hàm Bậc 4 Trùng Phương | Toán 12

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số