Phân dạng bài tập và lời giải chi tiết chuyên đề hàm số – Lưu Huy Thưởng Toán 12

Phân dạng bài tập và lời giải chi tiết chuyên đề hàm số – Lưu Huy Thưởng Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

81 41 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 1

LÝ THUYẾT KHẢO SÁT HÀM SỐ

I. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

1. Định nghĩa:

Hàm số f đồng biến trên K

1 2 1 2 1 2

, , ( ) ( )

x x K x x f x f x

⇔ ∀ ∈ < ⇒ <

Hàm số f nghịch biến trên K

1 2 1 2 1 2

, , ( ) ( )

x x K x x f x f x

⇔ ∀ ∈ < ⇒ >

2. Điều kiện cần:

Giả sử f có đạo hàm trên khoảng I.

a) Nếu f đồng biến trên khoảng I thì

'( ) 0,

f x x I

≥ ∀ ∈

b) Nếu f nghịch biến trên khoảng I thì

'( ) 0,

f x x I

≤ ∀ ∈

3. Điều kiện đủ:

Giả sử f có đạo hàm trên khoảng I.

a) Nếu

'( ) 0,

f x x I

≥ ∀ ∈

(

'( ) 0

f x

tại một số hữu hạn điểm) thì f đồng biến trên I.

b) Nếu

'( ) 0,

f x x I

≤ ∀ ∈

(

'( ) 0

f x

tại một số hữu hạn điểm) thì f nghịch biến trên I.

c) Nếu

'( ) 0

f x

thì f không đổi trên I.

Chú ý: Nếu khoảng I được thay bởi đoạn hoặc nửa khoảng thì f phải liên tục trên đó.

4. Điều kiện hàm số luôn đồng biến trên một miền xác định.

Cho hàm số

( , )

y f x m

, m là tham số, có tập xác định D.

• Hàm số f đồng biến trên D

' 0,

y x D

⇔ ≥ ∀ ∈

• Hàm số f nghịch biến trên D

' 0,

y x D

⇔ ≤ ∀ ∈

Từ đó suy ra điều kiện của m.

Chú ý:

●

' 0

chỉ xảy ra tại một số hữu hạn điểm.

●Nếu

y ax bx c

= + +

thì:

•

••

•

' 0,

a b

y x R







= =











≥







≥ ∀ ∈ ⇔



















∆ ≤







•

' 0,

a b

y x R







= =











≤







≤ ∀ ∈ ⇔



















∆ ≤







●Định lí về dấu của tam thức bậc hai

( )

g x ax bx c

= + +

♣ Nếu

∆ <

thì

( )

g x

luôn cùng dấu với

♣ Nếu

∆ =

thì

( )

g x

luôn cùng dấu với

(trừ

= −

)

♣ Nếu

∆ >

thì

( )

g x

có hai nghiệm

1 2

x x

và trong khoảng hai nghiệm thì

( )

g x

khác dấu

với

, ngoài khoảng hai nghiệm thì

( )

g x

cùng dấu với

●So sánh các nghiệm

1 2

x x

của tam thức bậc hai

( )

g x ax bx c

= + +

với số 0:

♣

1 2

0 0

x x P





∆ >



< < ⇔ >







♣

1 2

0 0

x x P





∆ >



< < ⇔ >







♣

1 2

0 0

x x P

< < ⇔ <

●Để hàm số

3 2

y ax bx cx d

= + + +

có độ dài khoảng đồng biến (nghịch biến)

1 2

( ; )

x x

bằng d thì

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 2

ta thực hiện các bước sau:

Bước 1: Tính

Bước 2: Tìm điều kiện để hàm số có khoảng đồng biến và nghịch biến:





≠







∆ >





(1)

Bước 3: Biến đổi

1 2

x x d

− =

thành

2 2

1 2 1 2

( ) 4

x x x x d

+ − =

(2)

Bước 4: Sử dụng định lí Viet đưa (2) thành phương trình theo m.

Bước 5: Giải phương trình, so với điều kiện (1) để chọn nghiệm.

II. CỰC TRỊ CỦA HÀM SỐ

1. Khái niệm cực trị của hàm số

Giả sử hàm số f xác định trên tập D (D

⊂

R) và

x D

∈

– điểm cực đại của f nếu tồn tại khoảng

( ; )

a b D

∈

và

( ; )

x a b

∈

sao cho

{ }

0 0

( ) ( ), ( ; ) \

f x f x x a b x

< ∀ ∈

Khi đó

( )

f x

được gọi là giá trị cực đại (cực đại) của f.

– điểm cực tiểu của f nếu tồn tại khoảng

( ; )

a b D

∈

và

( ; )

x a b

∈

sao cho

{ }

0 0

( ) ( ), ( ; ) \

f x f x x a b x

> ∀ ∈

Khi đó

( )

f x

được gọi là giá trị cực tiểu (cực tiểu) của f.

c) Nếu

là điểm cực trị của f thì điểm

(

)

0 0

; ( )

x f x

được gọi là điểm cực trị của đồ thị hàm số f.

2. Điều kiện cần để hàm số có cực trị

Nếu hàm số f có đạo hàm tại

và đạt cực trị tại điểm đó thì

'( ) 0

f x

Chú ý: Hàm số f chỉ có thể đạt cực trị tại những điểm mà tại đó đạo hàm bằng 0 hoặc không có đạo

hàm.

3. Điểu kiện đủ để hàm số có cực trị

1. Định lí 1: Giả sử hàm số f liên tục trên khoảng

( ; )

a b

chứa điểm

và có đạo hàm trên

{ }

( ; ) \

a b x

a) Nếu

'( )

f x

đổi dấu từ âm sang dương khi

đi qua

thì f đạt cực tiểu tại

b) Nếu

'( )

f x

đổi dấu từ dương sang âm khi

đi qua

thì f đạt cực đại tại

2. Định lí 2: Giả sử hàm số f có đạo hàm trên khoảng (a; b) chứa điểm

'( ) 0

f x

và có đạo

hàm cấp hai khác 0 tại điểm

a) Nếu

''( ) 0

f x

thì f đạt cực đại tại

b) Nếu

''( ) 0

f x

thì f đạt cực tiểu tại

4. Quy tắc tìm cực trị

Qui tắc 1: Dùng định lí 1.

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 3

• Tìm

'( )

f x

• Tìm các điểm

(i = 1, 2, …) mà tại đó đạo hàm bằng 0 hoặc không có đạo hàm.

• Xét dấu

'( )

f x

. Nếu

'( )

f x

đổi dấu khi

đi qua

thì hàm số đạt cực trị tại

Qui tắc 2: Dùng định lí 2.

• Tính

'( )

f x

• Giải phương trình

'( ) 0

f x

tìm các nghiệm

(i = 1, 2, …).

• Tính

''( )

f x

và

''( )

f x

(i = 1, 2, …).

Nếu

''( ) 0

f x

thì hàm số đạt cực đại tại

Nếu

''( ) 0

f x

thì hàm số đạt cực tiểu tại

III. SỰ TƯƠNG GIAO CỦA CÁC ĐỒ THỊ

1. Cho hai đồ thị

( ) : ( )

C y f x

và

( ) : ( )

C y g x

. Để tìm hoành độ giao điểm của (C

) và (C

) ta

giải phương trình:

( ) ( )

f x g x

(*) (gọi là phương trình hoành độ giao điểm).

Số nghiệm của phương trình (*) bằng số giao điểm của hai đồ thị.

2. Đồ thị hàm số bậc ba

3 2

( 0)

y ax bx cx d a= + + + ≠

cắt trục hoành tại 3 điểm phân biệt

⇔ Phương trình

3 2

ax bx cx d

+ + + =

có 3 nghiệm phân biệt.

⇔ Hàm số

3 2

y ax bx cx d

= + + +

có cực đại, cực tiểu và

. 0

CÑ CT

y y

IV. TOÁN TIẾP TUYẾN

Bài toán 1: Viết phương trình tiếp tuyến ∆ của

( ) : ( )

C y f x

tại điểm

(

)

0 0 0

;

M x y

• Nếu cho

thì tìm

0 0

( )

y f x

Nếu cho

thì tìm

là nghiệm của phương trình

( )

f x y

• Tính

' '( )

y f x

. Suy ra

0 0

'( ) '( )

y x f x

• Phương trình tiếp tuyến ∆ là:

0 0 0

'( ).( )

y y f x x x

− = −

Bài toán 2: Viết phương trình tiếp tuyến ∆ của

( ) : ( )

C y f x

, biết ∆ có hệ số góc k cho trước.

Cách 1: Tìm toạ độ tiếp điểm.

• Gọi

(

)

0 0 0

;

M x y

là tiếp điểm. Tính

'( )

f x

• ∆ có hệ số góc

'( )

k f x k

⇒ =

(1)

• Giải phương trình (1), tìm được

và tính

0 0

( )

y f x

. Từ đó viết phương trình của ∆.

Cách 2: Dùng điều kiện tiếp xúc.

• Phương trình đường thẳng ∆ có dạng:

y kx m

= +

• ∆ tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:

( )

'( )

f x kx m

f x k





= +









(*)

• Giải hệ (*), tìm được

. Từ đó viết phương trình của ∆.

Chú ý: Hệ số góc

của tiếp tuyến ∆ có thể được cho gián tiếp như sau:

+ ∆ tạo với chiều dương trục hoành góc α thì

tan

+ ∆ song song với đường thẳng

d y ax b

= +

thì

k a

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 4

+ ∆ vuông góc với đường thẳng

: ( 0)

d y ax b a

= + ≠

thì

= −

+ ∆ tạo với đường thẳng

d y ax b

= +

một góc α thì

tan

k a

−

Bài toán 3: Viết phương trình tiếp tuyến ∆ của (C):

( )

y f x

, biết ∆ đi qua điểm

( ; )

A A

A x y

Cách 1: Tìm toạ độ tiếp điểm.

• Gọi

(

)

0 0 0

;

M x y

là tiếp điểm. Khi đó:

0 0 0 0

( ); ' '( )

y f x y f x

• Phương trình tiếp tuyến ∆ tại

0 0 0

: '( )( )

M y y f x x x

− = −

• ∆ đi qua

( ; )

A A

A x y

nên:

0 0 0

'( )( ) (2)

A A

y y f x x x

= − = −

• Giải phương trình (2), tìm được

. Từ đó viết phương trình của ∆.

Cách 2: Dùng điều kiện tiếp xúc.

• Phương trình đường thẳng ∆ đi qua

( ; )

A A

A x y

và có hệ số góc

: ( )

A A

k y y k x x

− = −

• ∆ tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:

( ) ( )

'( )

A A

f x k x x y

f x k





= − +









(*)

• Giải hệ (*), tìm được

(suy ra

). Từ đó viết phương trình tiếp tuyến ∆.

V. ĐIỀU KIỆN TIẾP XÚC

1. Điều kiện cần và đủ để hai đường

( ) : ( )

C y f x

và

( ) : ( )

C y g x

tiếp xúc nhau là hệ phương

trình sau có nghiệm:

( ) ( )

'( ) '( )

f x g x











(*)

Nghiệm của hệ (*) là hoành độ của tiếp điểm của hai đường đó.

2. Nếu

( ) :

C y px q

= +

và

( ) :

C y ax bx c

= + +

thì

) và (C

) tiếp xúc nhau ⇔ phương trình

ax bx c px q

+ + = +

có nghiệm kép.

VI. KHOẢNG CÁCH

1. Khoảng cách giữa hai điểm A, B: AB =

2 2

( ) ( )

B A B A

x x y y− + −

2. Khoảng cách từ điểm M(x

; y

) đến đường thẳng

: 0

ax by c

∆ + + =

d(M, ∆) =

0 0

2 2

ax by c

a b

+ +

VII. ĐỒ THỊ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI

Cách 1: Khảo sát sự biến thiên và vẽ đồ thị.

• Xét dấu biểu thức có chứa dấu giá trị tuyệt đối.

• Chia miền xác định thành nhiều khoảng, trong mỗi khoảng ta bỏ dấu giá trị tuyệt đối.

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 5

• Vẽ đồ thị hàm số tương ứng trong các khoảng của miền xác định.

Cách 2: Thực hiện các phép biến đổi đồ thị.

Dạng 1: Vẽ đồ thị hàm số

( )y f x=

Đồ thị (C′) của hàm số

( )y f x=

có thể được suy từ đồ thị (C) của hàm số y = f(x) như sau:

+ Giữ nguyên phần đồ thị (C) ở phía trên trục hoành.

+ Lấy đối xứng phần đồ thị của (C) ở phía dưới trục hoành qua trục hoành.

+ Đồ thị (C′) là hợp của hai phần trên.

Dạng 2: Vẽ đồ thị của hàm số

( )

y f x=

Đồ thị (C′) của hàm số

( )

y f x=

có thể được suy từ đồ thị (C) của hàm số y = f(x) như sau:

+ Giữ nguyên phần đồ thị (C) ở bên phải trục tung, bỏ phần bên trái trục tung.

+ Lấy đối xứng phần bên phải trục tung qua trục tung.

+ Đồ thị (C′) là hợp của hai phần trên.

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 6

PHẦN I: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

HT 1. Cho hàm số

3 2

( 1) (3 2)

y m x mx m x

= − + + −

(1). Tìm tất cả các giá trị của tham số m để

hàm số (1) đồng biến trên tập xác định của nó.

Giải

• Tập xác định: D = R.

( 1) 2 3 2

y m x mx m

′

= − + + −

(1) đồng biến trên R ⇔

y x

′

≥ ∀

( 1) 2 3 2 0,

1 2 0

3 2 0

1 0

2 5 2 0

( 1)(3 2) 0

m x mx m x

m m

m m m

⇔ − + + − ≥ ∀







− = =



















− ≥



> 











⇔ ⇔ ⇔ ⇔ ≥



 

≤





 

− >

 − + − ≤



 











≥







− − − ≤

















HT 2. Cho hàm số

3 2

3 4

y x x mx

= + − −

(1). Tìm tất cả các giá trị của tham số m để hàm số (1)

đồng biến trên khoảng

( ;0)

−∞

Giải

• Tập xác định: D =

ℝ

;

' 3 6

y x x m

= + −

(1) đồng biến trên khoảng (-∞;0) ⇔ y’ ≥ 0, ∀x ∈ (-∞;0)

⇔

3 6 0

x x m

+ − ≥

∀x ∈ (-∞;0)

⇔

3 6

x x m

+ ≥

∀x ∈ (-∞;0)

Xét hàm số f(x) =

3 6

x x m

+ −

trên (-∞;0]

Có f’(x) = 6x + 6; f’(x) = 0 ⇔ x = -1

Từ bảng biến thiên: ⇒

≤ −

HT 3. Cho hàm số

3 2

2 3(2 1) 6 ( 1) 1

y m x m m x

= − + + + +

có đồ thị (C

). Tìm m để hàm số đồng

biến trên khoảng

(2; )

+∞

Giải

-3

f’(x)

f(x)

∞

0 -1

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 7

• Tập xác định: D =

ℝ

' 6 6(2 1) 6 ( 1)

y x m x m m

= − + + +

có

2 2

(2 1) 4( ) 1 0

m m m

∆ = + − + = >

' 0

x m





= ⇔



= +





Ta có: y’ ≥ 0, ∀x (-∞;m) và (m + 1; +∞)

Do đó: hàm số đồng biến trên

(2; )

+∞

⇔

1 2

+ ≤

⇔

≤

HT 4. Cho hàm số

3 2

(1 2 ) (2 ) 2

y x m x m x m

= + − + − + +

. Tìm m để hàm đồng biến trên

(

)

+∞

Giải

• Tập xác định: D =

ℝ

3 ( 2 ) ( )

2 1 2

y x m x m

′

= − + −+

Hàm đồng biến trên

(0; )

+∞

3 (1 2 ) ( 0

2 2 )y x m x m

′

⇔ = − + − ≥

với

0; )

(

∀ ∈

+∞

( )

4 1

2xx

f x m

⇔ =

≥

với

0; )

(

∀ ∈

+∞

Ta có:

2(2

( ) 0 2

(

1 0

4 )

f x x

′

= = ⇔



= −



+ −



+ − = ⇔





Lập bảng biến thiên của hàm

( )

f x

trên

(0; )

+∞

, từ đó ta đi đến kết luận:

1 5

2 4

f m m

 







≥ ⇔ ≥











 

HT 5. Cho hàm số

4 2

2 3 1

y x mx m

= − − +

(1), (m là tham số). Tìm m để hàm số (1) đồng biến

trên khoảng (1; 2).

Giải

• Tập xác định: D =

ℝ

Ta có

3 2

' 4 4 4 ( )

y x mx x x m

= − = −

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 8

≤

0, (1;2)

′

≥ ∀ ∈y x

⇒

≤

thoả mãn.

′

có 3 nghiệm phân biệt:

, 0,

m m

−

Hàm số (1) đồng biến trên (1; 2) khi chỉ khi

1 0 1

m m

≤ ⇔ < ≤

. Vậy

(



∈ −∞





HT 6. Cho hàm số

x m

(1). Tìm tất cả các giá trị của tham số m để hàm số (1) nghịch

biến trên khoảng

( ;1)

−∞

Giải

• Tập xác định: D = R \ {–m}.

( )

x m

−

′

Hàm số nghịch biến trên từng khoảng xác định ⇔

0 2 2

y m

′

< ⇔ − < <

(1)

Để hàm số (1) nghịch biến trên khoảng

( ;1)

−∞

thì ta phải có

1 1

m m

− ≥ ⇔ ≤ −

(2)

Kết hợp (1) và (2) ta được:

2 1

− < ≤ −

HT 7. Chứng minh rằng, hàm số

sin cos

y x x

= +

đồng biến trên đoạn

 

 

và nghịch biến trên

đoạn

;

 

 

 

Giải

Hàm số đã cho xác định trên

 

 

 

Ta có:

' sin (2 cos 1), (0; )

y x x x

= − ∈

Vì

(0; ) sin 0

x x

∈ ⇒ >

nên trên

(0; ) : ' 0 cos

2 3

y x x

= ⇔ = ⇔ =

+ Trên khoảng

0; : ' 0

 

















 

nên hàm số đồng biến trên đoạn

 

 

 

+ Trên khoảng

; : ' 0

 

















 

nên hàm số nghịch biến trên đoạn

;

 

 

 

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 9

HT 8. Cho hàm số

3 2

y x x mx m

= + + +

. Tìm m để hàm số nghịch biến trên đoạn có độ dài bằng

Giải

Hàm số đã cho xác định trên

ℝ

Ta có:

' 3 6

y x x m

= + +

có

' 9 3

∆ = −

+ Nếu m ≥ 3 thì y’ ≥ 0, ∀x ∈

ℝ

, khi đó hàm số đồng biến trên

ℝ

, do đó m ≥ 3 không thỏa mãn.

+ Nếu m < 3, khi đó: y’ = 0 có hai nghiệm phân biệt

1 2

( )

x x

và hàm số nghịch biến

trong đoạn:

1 2

;

x x

 

 

 

với độ dài l =

2 1

x x

−

Theo Vi-ét ta có:

1 2 1 2

x x x x+ = − =

Hàm số nghịch biến trên đoạn có độ dài bằng 1 ⇔ l = 1

⇔

( )

2 1 1 2 1 2

4 9

1 ( ) 4 1 4 1

3 4

x x x x x x m m

− = ⇔ + − = ⇔ − = ⇔ =

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 10

PHẦN 2: CỰC TRỊ CỦA HÀM SỐ

HT 9. Cho hàm số

3 2

(1 – 2 ) (2 – ) 2

y x m x m x m

= + + + +

(m là tham số) (1). Tìm các giá trị của

m để đồ thị hàm số (1) có điểm cực đại, điểm cực tiểu, đồng thời hoành độ của điểm cực tiểu nhỏ

hơn 1.

Giải

• Tập xác định: D =

ℝ

3 2(1 2 ) 2 ( )

y x m x m g x

′

= + − + − =

YCBT ⇔ phương trình

′

có hai nghiệm phân biệt

1 2

x x

thỏa mãn:

1 2

x x

< <

⇔

4 5 0

(1) 5 7 0

2 1

2 3

m m

g m

S m





′

∆ = − − >



 = − + >





−



= <





⇔

5 7

4 5

< <

HT 10. Cho hàm số

3 2

( 2) 3 5

y m x x mx

= + + + −

, m là tham số. Tìm các giá trị của m để các điểm

cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương.

Giải

• Các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương

⇔

' 3( 2) 6 0

y m x x m

= + + +

có 2 nghiệm dương phân biệt

( 2) 0

' 9 3 ( 2) 0

' 2 3 0 3 1

0 0 3 2

3( 2)

2 0 2

a m

m m

m m m

m m





= + ≠





∆ = − + >





∆ = − − + > − < <



⇔ ⇔ < ⇔ < ⇔ − < < −

  

= >

  

+ < < −

  



−



= >





HT 11. Cho hàm số

3 2 3

2 3( 2) 6(5 1) (4 2).

y x m x m x m

= − + + + − +

Tìm

để hàm số đạt cực tiểu tại

(

1;2



∈



Giải

Vì hàm số bậc 3 nên để hàm số có hai điểm cực trị

' 0

⇔ =

có 2 nghiệm phân biệt.

Do hệ số của

là dương nên khi đó:

CT CD

x x

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 11

Ta có

2 2

' 6[ ( 2) 5 1], ' 0 ( 5) 2 1 (1)

y x m x m y m x x x

= − + + + = ⇔ − = − +

không là nghiệm của (1)

2 1

(1) ( )

x x

m g x

− +

⇒ ⇔ = =

−

10 9

'( ) 0

( 5)

x x

g x

− +



= = ⇔





−

Bảng biến thiên:

Từ bảng biến thiên và kết hợp với nhận xét trên

⇒

Hàm số đạt cực tiểu tại

(1;2] 0

x m

∈ ⇔ − ≤ <

HT 12. Cho hàm số

4 2

1 3

2 2

y x mx

= − +

(1). Xác định m để đồ thị của hàm số (1) có cực tiểu mà

không có cực đại.

Giải

• Tập xác định: D =

ℝ

3 2

2 2 2 ( )

y x mx x x m

′

= − = −

x m





′

= ⇔





Đồ thị của hàm số (1) có cực tiểu mà không có cực đại ⇔ PT

′

có 1 nghiệm ⇔

≤

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 12

HT 13. Cho hàm số

4 2

2 4 ( ).

y x mx C= − + −

Tìm các giá trị của m để tất cả các điểm cực trị

của

( )

đều nằm trên các trục tọa độ.

Giải

Ta có:

' 4 4 ; ' 0

y x mx y

x m





= − + = ⇔





Nếu m ≤ 0 ⇒ đồ thị hàm số có 1 điểm cực trị duy nhất và điểm đó nằm trên trục tung.

Nếu m > 0 thì đồ thị hàm số khi đó có 3 điểm cực trị. Một điểm cực trị nằm trên trục tung và

hai điểm cực trị còn lại có tọa độ:

( ; 4)

m m

± −

⇒ Các điểm này chỉ có thể nằm trên trục

hoành.

⇒ Điều kiện các điểm nằm trên trục hoành là

4 0









− =





⇔ m = 2

Kết luận:





≤





HT 14. Cho hàm số

3 2 2

(2 1) ( 3 2) 4

y x m x m m x

= − + + − − + −

(m là tham số) có đồ thị là (C

Xác định m để (C

) có các điểm cực đại và cực tiểu nằm về hai phía của trục tung.

Giải

•Tập xác định: D =

ℝ

2 2

3 2(2 1) ( 3 2)

y x m x m m

′

= − + + − − +

) có các điểm CĐ và CT nằm về hai phía của trục tung ⇔ PT

′

có 2 nghiệm trái dấu

⇔

3( 3 2) 0

m m

− + <

⇔

1 2

< <

HT 15. Cho hàm số

3 2

(2 1) 3

y x mx m x

= − + − −

(m là tham số) có đồ thị là (C

). Xác định m để

) có các điểm cực đại, cực tiểu nằm về cùng một phía đối với trục tung.

Giải

• TXĐ: D =

ℝ

;

– 2 2 – 1

y x mx m

′

= +

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 13

Đồ thị (C

) có 2 điểm CĐ, CT nằm cùng phía đối với trục tung ⇔

′

có 2 nghiệm phân biệt

cùng dấu ⇔

2 1 0

m m





′

∆ = − + >







− >









≠



⇔







HT 16. Cho hàm số

3 2

3 – 2

y x x mx m

= + + +

(m là tham số) có đồ thị là (C

). Xác định m để

) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành.

Giải

• PT hoành độ giao điểm của (C) và trục hoành:

3 2

3 – 2 0 (1)

x x mx m

+ + + =

⇔

( ) 2 2 0 (2)

g x x x m



= −



= + + − =





) có 2 điểm cực trị nằm về 2 phía đối với trục 0x

⇔

PT (1) có 3 nghiệm phân biệt

⇔ (2) có 2 nghiệm phân biệt khác –1 ⇔

3 0

( 1) 3 0

g m





′

∆ = − >







− = − ≠





⇔

HT 17. Cho hàm số

3 2 3

1 4

( 1) ( 1) ( ).

3 3

y x m x m C

= − + + +

Tìm

để các điểm cực trị của hàm số

2 2

4 3 0.

x y x

+ − + =

Giải

Ta có:

' 2( 1)

y x m x

= − +

' 0

2( 1)

(0) ( 1) ; (2 2) 0

x m

y m y m





= ⇔



= +





= + + =

Đề hàm số có cực trị thì

≠ −

Gọi hai điểm cực trị của đồ thị hàm số là:

0; ( 1) ; (2 2;0)

A m B m

 







+ +











 

Gọi I là tâm đường tròn, khi đó

(2;0)

và

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 14

A và B nằm về hai phía của đường tròn khi và chỉ khi:

(

)

(

)

2 2 2 2

IA R IB R

− − <

6 2

4 ( 1) ; 4

IA m IB m

= + + =

(

)

(

)

2 2 2 2 6 2

0 3 ( 1) (4 1) 0 (*)

IA R IB R m m

 







− − < ⇔ + + − <











 

Ta có:

3 ( 1) 0

m x

 







+ + > ∀











 

Suy ra:

(*) 4 1 0

m m

⇔ − < ⇔ <

Kết hợp điều kiện ta có:

HT 18. Cho hàm số

3 2 3

3 4

y x mx m

= − +

(m là tham số) có đồ thị là (C

). Xác định m để (C

) có

các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng y = x.

Giải

• Tập xác định: D =

ℝ

Ta có:

3 6

y x mx

′

= −

;

x m





′

= ⇔





. Để hàm số có cực đại và cực tiểu thì m ≠ 0.

Đồ thị hàm số có hai điểm cực trị là: A(0; 4m

), B(2m; 0) ⇒

(2 ; 4 )

AB m m

= −



Trung điểm của đoạn AB là I(m; 2m

)

A, B đối xứng nhau qua đường thẳng d: y = x ⇔

AB d

I d





⊥







∈





⇔

2 4 0

m m





− =









⇔

m = ±

HT 19. Cho hàm số

3 2

3 3 1

y x mx m

= − + − −

. Với giá trị nào của m thì đồ thị hàm số có điểm cực

đại và điểm cực tiểu đối xứng với nhau qua đường thẳng

: 8 74 0

d x y

+ − =

Giải

• Tập xác định: D =

ℝ

3 6

y x mx

′

= − +

;

0 0 2

y x x m

′

= ⇔ = ∨ =

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 15

Hàm số có CĐ, CT ⇔ PT

′

có 2 nghiệm phân biệt ⇔

≠

Khi đó 2 điểm cực trị là:

(0; 3 1), (2 ; 4 3 1)

A m B m m m

− − − −

⇒

(2 ;4 )

AB m m



Trung điểm I của AB có toạ độ:

( ;2 3 1)

I m m m

− −

Đường thẳng d:

8 74 0

x y

+ − =

có một VTCP

(8; 1)

= −



A và B đối xứng với nhau qua d ⇔

I d

AB d





∈







⊥





⇔

8(2 3 1) 74 0

. 0

m m m

AB u





+ − − − =









 

⇔

HT 20. Cho hàm số

3 2 2 3 2

3 3(1 )

y x mx m x m m

= − + + − + −

(1). Viết phương trình đường thẳng

qua hai điểm cực trị của đồ thị hàm số (1).

Giải

• Tập xác định: D =

ℝ

2 2

3 6 3(1 )

y x mx m

′

= − + + −

′

có

1 0,

∆ = > ∀

⇒ Đồ thị hàm số (1) luôn có 2 điểm cực trị

1 1 2 2

( ; ), ( ; )

x y x y

Chia y cho y′ ta được:

3 3

y x y x m m

 





′



= − + − +







 

Khi đó:

1 1

y x m m

= − +

;

2 2

y x m m

= − +

PT đường thẳng qua hai điểm cực trị của đồ thị hàm số (1) là

y x m m

= − +

HT 21. Cho hàm số

3 2

3 2 ( ).

y x x mx C= − + +

Tìm

để

( )

có cực đại và cực tiểu, đồng thời

các điểm cực trị của hàm số cách đều đường thẳng

: 1 0.

d x y

− − =

Giải

Ta có :

2 2

' 3 6 ; ' 0 3 6 0 (1).

y x x m y x x m= − + = ⇔ − + =

Hàm số

( )

có cực đại, cực tiểu khi và chỉ khi (1) có 2 nghiệm phân biệt

⇔ <

Giả sử

(

)

1 1 2 2

( ; ), ;

A x y B x y

là hai điểm cực trị của hàm số

1 2

( ),( ,

C x x

là 2 nghiệm của (1).

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 16

Ta có :

' 2 1 2

3 3 3 3

x m m

y y x

   

 

 

 

= − + − + +

 

 

 

 

 

   

và

1 2

'( ) '( ) 0

y x y x

= =

Nên phương trình đường thẳng đi qua

A B

là :

' : 2 1 2 .

3 3

m m

d y x

 







= − + +











 

Do đó, các điểm

A B

cách đều đường thẳng (d) trong hai trường hợp sau :

Trường hợp 1 : (d’) cùng phương với (d)

2 1 1

3 2

 







⇔ − = ⇔ =











 

(Không thỏa mãn)

Trường hợp 2 : Trung điểm

của

A B

nằm trên (d). Do (I) là trung điểm của AB nên tọa độ (I)

là :

1 2

x x

y y

y m





= =







= =





Vì I nằm trên (d) nên ta có

1 1 0 0

m m

− − = ⇔ =

(thỏa mãn)

KL :

HT 22. Cho hàm số

3 2

y x x mx

= − − +

(m là tham số) có đồ thị là (C

). Xác định m để (C

) có

các điểm cực đại và cực tiểu cách đều đường thẳng

y x

= −

Giải

• Tập xác định: D =

ℝ

Ta có:

' 3 6

y x x m

= − −

Hàm số có CĐ, CT

' 3 6 0

y x x m

⇔ = − − =

có 2 nghiệm phân biệt

1 2

;

x x

' 9 3 0 3

m m

⇔ ∆ = + > ⇔ > −

(*)

Gọi hai điểm cực trị là

(

)

(

)

1 2

; ; ;

A B x

y y

Thực hiện phép chia y cho y′ ta được:

1 1 2

' 2 2

3 3 3 3

m m

y x y x

     

  

  

  

= − − + + −

  

  

  

  

  

     

⇒

( ) ( )

1 1 1 22 2

2 2

2 2 ; 2 2

3 3 3 3

y y x

m m m

y xx y

       

   

   

   

− + + − − + + −

   

   

   

   

   

       

= = = =

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 17

⇒

Phương trình đường thẳng đi qua 2 điểm cực trị là ∆:

2 2

3 3

m m

y x

   

 

 

 

= − + + −

 

 

 

 

 

   

Các điểm cực trị cách đều đường thẳng

y x

= −

⇔

xảy ra 1 trong 2 trường hợp:

TH1: Đường thẳng đi qua 2 điểm cực trị song song hoặc trùng với đường thẳng

y x

= −

2 3

2 1

3 2

 







− + = ⇔ = −









 

⇔



(thỏa mãn)

TH2: Trung điểm I của AB nằm trên đường thẳng

y x

= −

( ) ( )

1 2 1 2

1 2 1

2 2 2 2

3 3

2 2

3 .2 6

3 3

1 1

2 2

I I

m m

x x x x

y x

+ +

⇔ = − ⇔ = −

   

 

 

 

− + + + − = + −

 

 

 

 

 

   

 







⇔ + = − ⇔ =











 

⇔

Vậy các giá trị cần tìm của m là:

 

 

= −

 

 

 

HT 23. Cho hàm số

3 2

y x x mx

= − +

(1). Với giá trị nào của m thì đồ thị hàm số (1) có các

điểm cực đại và điểm cực tiểu đối xứng với nhau qua đường thẳng

: – 2 – 5 0

d x y

Giải

• Tập xác định: D =

ℝ

Ta có

3 2 2

3 ' 3 6

y x x mx y x x m

= − + ⇒ = − +

Hàm số có cực đại, cực tiểu ⇔

′

có hai nghiệm phân biệt

9 3 0 3

m m

′

⇔ ∆ = − > ⇔ <

Ta có:

1 1 2 1

3 3 3 3

y x y m x m

   

 

 

′

 

= − + − +

 

 

 

 

 

   

Tại các điểm cực trị thì

′

, do đó tọa độ các điểm cực trị thỏa mãn phương trình:

2 1

3 3

y m x m

 







= − +











 

Như vậy đường thẳng

∆ đi qua các điểm cực trị có phương trình

2 1

3 3

y m x m

 







= − +











 

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 18

nên ∆ có hệ số góc

k m

= −

– 2 – 5 0

x y

1 5

2 2

y x

⇔ = −

⇒ d có hệ số góc

Để hai điểm cực trị đối xứng qua d thì ta phải có d ⊥ ∆

⇒

1 2

1 2 1 0

2 3

k k m m

 







= − ⇔ − = − ⇔ =











 

Với m = 0 thì đồ thị có hai điểm cực trị là (0; 0) và (2; –4), nên trung điểm của chúng là I(1; –2).

Ta thấy I ∈ d, do đó hai điểm cực trị đối xứng với nhau qua d.

Vậy: m = 0

HT 24. Cho hàm số

3 2

3( 1) 9 2

y x m x x m

= − + + + −

(1) có đồ thị là (C

). Với giá trị nào của m thì

đồ thị hàm số có điểm cực đại và điểm cực tiểu đối xứng với nhau qua đường thẳng

d y x

Giải

• Tập xác định: D =

ℝ

' 3 6( 1) 9

y x m x

= − + +

Hàm số có CĐ, CT ⇔

' 9( 1) 3.9 0

∆ = + − >

( ; 1 3) ( 1 3; )

⇔ ∈ −∞ − − ∪ − + +∞

Ta có

1 1

2( 2 2) 4 1

3 3

y x y m m x m

 





′



= − − + − + +











 

Giả sử các điểm cực đại và cực tiểu là

1 1 2 2

( ; ), ( ; )

A x y B x y

, I là trung điểm của AB.

1 1

2( 2 2) 4 1

y m m x m

⇒ = − + − + +

;

2 2

2( 2 2) 4 1

y m m x m

= − + − + +

và:

1 2

2( 1)

. 3

x x m

x x





+ = +









Vậy đường thẳng đi qua hai điểm cực đại và cực tiểu là

2( 2 2) 4 1

y m m x m

= − + − + +

A, B đối xứng qua (d):

y x

⇔

AB d

I d





⊥







∈





⇔

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 19

HT 25. Cho hàm số

3 2

1 1

( 1) 3( 2)

3 3

y x m x m x

= − − + − +

, với

là tham số thực. Xác định

để

hàm số đã cho đạt cực trị tại

1 2

x x

sao cho

1 2

2 1

x x

+ =

Giải

• Tập xác định: D =

ℝ

Ta có:

2( 1) 3( 2)

y x m x m

′

= − − + −

Hàm số có cực đại và cực tiểu ⇔

′

có hai nghiệm phân biệt

1 2

x x

⇔

5 7

0 0

m m

′

∆ > ⇔ − + >

(luôn đúng với ∀m)

Khi đó ta có:

1 2

2( 1)

3( 2)

x x m





+ = −







= −





⇔

(

)

2 2

3 2

1 2 3( 2)

x m

x x m





= −







− = −





4 34

8 16 9 0

m m m

− ±

⇔ + − = ⇔ =

HT 26. Cho hàm số

3 2

3( 1) 9

y x m x x m

= − + + −

, với

là tham số thực. Xác định

để hàm số

đã cho đạt cực trị tại

1 2

x x

sao cho

1 2

x x

− ≤

Giải

• Tập xác định: D =

ℝ

Ta có

' 3 6( 1) 9.

y x m x

= − + +

+ Hàm số đạt cực đại, cực tiểu tại

1 2

x x

⇔

' 0

có hai nghiệm phân biệt

1 2

x x

⇔

2( 1) 3 0

x m x

− + + =

có hai nghiệm phân biệt là

1 2

x x

1 3

' ( 1) 3 0

1 3



> − +



⇔ ∆ = + − > ⇔



< − −



(1)

+ Theo định lý Viet ta có

1 2 1 2

2( 1); 3.

x x m x x

+ = + =

Khi đó:

(

)

(

)

2 2

1 2 1 2 1 2

2 4 4 4 1 12 4

x x x x x x m

− ≤ ⇔ + − ≤ ⇔ + − ≤

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 20

( 1) 4 3 1

m m

⇔ + ≤ ⇔ − ≤ ≤

(2)

+ Từ (1) và (2) suy ra giá trị của m cần tìm là

3 1 3

− ≤ < − −

và

1 3 1.

− + < ≤

HT 27. Cho hàm số

3 2

(1 2 ) (2 ) 2

y x m x m x m

= + − + − + +

, với

là tham số thực. Xác định

để hàm số đã cho đạt cực trị tại

1 2

x x

sao cho

1 2

x x

− >

Giải

• Tập xác định: D =

ℝ

Ta có:

' 3 ( 2 ( )

1 ) 2

y x m x m

= − + −

Hàm số có CĐ, CT

' 0

⇔ =

có 2 nghiệm phân biệt

1 2

x x

(giả sử

1 2

x x

)

2 2

' (1 2 ) 3(2 ) 4 5 0

m m m m





⇔ ∆ = − − − = − − > ⇔



< −





(*)

Hàm số đạt cực trị tại các điểm

1 2

x x

. Khi đó ta có:

1 2

(1 2 )

x x





−



+ = −







−





( ) ( )

2 2

1 2 1 21 2 1 2

x x x x x x x x⇔ = + −−

− >

2 2

3 29 3 29

4(1 2 ) 4(2 ) 1 16 12 5 0

8 8

m m m m m m

+ −

⇔ − − − > ⇔ − − > ⇔ > ∨ <

Kết hợp (*), ta suy ra

3 29

m m

> ∨ < −

HT 28. Cho hàm số

3 2

2 4

( 1) ( 1)( 3) (1),

3 3

y x m x m m x m

= + + + + + +

là tham số. Tìm

để hàm

số (1) đạt cực đại, cực tiểu tại

1 2

x x

sao cho

1 2 1 2

x x x x

+ −

đạt giá trị lớn nhất.

Giải

Ta có :

' 2 2( 1) ( 1)( 3)

y x m x m m

= + + + + +

;

Hàm số đạt cực đại, cực tiểu khi và chỉ khi

' 0

có hai nghiệm phân biệt

( 1) 2( 1)( 3) 0

m m m

⇔ + − + + >

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 21

( 1)( 5) 0 5 1

m m m

⇔ − + + > ⇔ − < < −

Khi đó :

1 2 1 2

( 1)( 3)

m m

x x m x x

+ +

+ = − − =

Nên

1 2 1 2

1 1 1

1 ( 1)( 3) ( 8 7)

2 4 4

x x x x m m m m m

+ − = − − − + + = − + +

2 2

1 1 9 9

( 8 7) ( 4) ,

4 4 4 4

m m m m

= − + + = − + + ≤ ∀

Suy ra :

1 2 1 2

x x x x

+ −

đạt giá trị lớn nhất bằng

khi

4( / )

m t m

= −

HT 29. Cho hàm số

3 2

4 – 3

y x mx x

= +

. Tìm m để hàm số có hai điểm cực trị

1 2

x x

thỏa

1 2

x x

= −

Giải

• Tập xác định: D =

ℝ

12 2 – 3

y x mx

′

= +

. Ta có:

36 0,

m m

′

∆ = + > ∀

⇒ hàm số luôn có 2 cực trị

1 2

x x

Khi đó:

1 2

x x





= −



+ = −





= −





⇒ = ±

Câu hỏi tương tự:

3 2

3 1

y x x mx

= + + +

;

1 2

2 3

x x

+ =

ĐS:

1 5

= −

HT 30. Tìm các giá trị của m để hàm số

3 2 2

1 1

( 3)

3 2

y x mx m x

= − + − có cực đại

, cực tiểu

đồng

thời

;

là độ dài các cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng

Giải

Cách 1: Miền xác định: D =

ℝ

có

2 2 2 2

' 3; ' 0 0

y x mx m y x mx m

= − + − = ⇔ − + =

Hàm số đạt cực đại tại

cực tiểu tại

thỏa mãn yêu cầu bài toán khi và chỉ khi pt y’= 0 có hai

nghiệm dương phân biệt, triệt tiêu và đồi dấu qua hai nghiệm đó:

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 22

0 4 0 2 2

0 0 0 3 2 (*)

3 0

3 3

m m

S m m m

m m









∆ > − > − < <



 

> ⇔ > ⇔ > ⇔ < <

  

  

− >

< − ∨ >

  











Theo Vi-ét ta có:

1 2

x x m





+ =







= −





Mà

2 2 2 2 2

1 2 1 2 1 2

5 14

2( ) 4 5 5 2 4( 3) 5

2 2

x x x x x x m m m+ = ⇔ + − = = ⇔ − − = ⇔ = ±

Đối chiếu điều kiện (*) ta được:

m =

HT 31. Cho hàm số

3 2 2

( 1) ( 4 3) 1.

y x m x m m x

= + + + + + +

Tìm

để hàm số có cực trị. Tìm

giá trị lớn nhất của biểu thức

1 2 1 2

2( )

A x x x x

= − +

với

1 2

x x

là các điểm cực trị cửa hàm số.

Giải

Ta có:

2 2

' 2 2( 1) 4 3

y x m x m m

= + + + + +

Hàm số có cực trị

' 0

⇔ =

có hai nghiệm phân biệt.

6 5 0 5 1

m m m

⇔ + + < ⇔ − < < −

Khi đó ta có:

1 2

8 7

( 4 3)

x x m

A m m

x x m m





+ = − −



⇒ = + +





= + +





Xét

( 8 7)

t m m= + + trên

( 5; 1) 0

− − ⇒ − ≤ <

Từ đó ta có

≤

khi

= −

HT 32. Cho hàm số

3 2

3( 1) 9 (1)

y x m x x m= − + + − với

là tham số thực. Xác định

để hàm

số (1) đạt cực đại , cực tiểu sao cho

CD CT

y y

+ =

Giải

Ta có:

' 3 6( 1) 9

y x m x

= − + +

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 23

Hàm số đạt cực đại, cực tiểu tại

1 2

, ' 0

x x y

⇔ =

có 2 nghiệm phân biệt

1 2

x x

2( 1) 3 0

x m x

⇔ − + + =

có hai nghiệm phân biệt

1 2

x x

1 3

' ( 1) 3 0 (*)

1 3



> − +



⇔ ∆ = + − > ⇔



< − −



Theo Viet ta có:

1 2

2( 1)

x x m

x x





+ = +









3 2 3 2

1 1 1 2 2 2

2 3( 1) 9 3( 1) 9 2

CD CT

y y x m x x m x m x x m

+ = ⇔ − + + − + − + + − =

3 3 2 2

1 2 1 2 1 2

3( 1)( ) 9( ) 2 2 0

( 1)( 2 3) 0

x x m x x x x m

m m m

⇔ + − + + + + − − =

⇔ + + − =

1( )

1( / )

3( / )

m l

m t m



= −



⇔ =



= −





HT 33. Cho hàm số

3 2 2

( 1) 1 ).

y x mx m x= − + − +

Tìm m để hàm số có cực đại cực tiểu và:

C CT

y y

+ >

Giải

Ta coù:

2 2

' 2 ( 1)

' 1 1 0

' 0

y x mx m

m m

x m

= − + −

∆ = − + = >



= +



⇒ = ⇔



= −





⇒

( 1) ( 1)

CD CT m m

y y y y

+ −

+ = +

[ [

KL:

3 3

2 2 2 2

3 2

( 1) ( 1)

( 1) ( 1)( 1) 1] ( 1) ( 1)( 1) 1]

3 3

1 0

2 2 2 2 ( 1) 0

1 0

m m

m m m m m m m m

m m m m

+ −

= − + + − + + + − − + − − +



− < <



= − + > ⇔ − > ⇔







− < <





GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 24

HT 34. Cho hàm số

3 2

( 2) 3( 1) 1 (1),

y x m x m x m

= − − − − +

là tham số. Tìm

để đồ thị

hàm số (1) có giá trị cực đại, cực tiểu lần lượt là

CD CT

y y

thỏa mãn:

2 4

CD CT

y y

+ =

Giải

Ta có:

' 3 3( 2) 3( 1),

y x m x m x

= − − − − ∀ ∈

ℝ

' 0 ( 2) 1 0

x x

y x m x m

x x m



= = −



= ⇔ − − − + = ⇔



= = −





Chú ý rằng với

thì

1 2

x x

Khi đó hàm số đạt cực đại tại

= −

và đạt cực tiểu tại

x m

= −

Do đó:

3 1

( 1) , ( 1) ( 2)( 1) 1

2 2

CD CT

y y y y m m m

= − = = − = − + − +

Từ giả thiết ta có:

2 2

3 1

2. ( 2)( 1) 1 4 6 6 ( 2)( 1) 0

2 2

m m m m m

− + − + = ⇔ − − + − =

( 1)( 8) 0

1 33

m m m





⇔ − + − = ⇔

− ±





Đối chiếu điều kiện

ta có giá trị của

là

1 33

m m

− +

= =

HT 35. Cho hàm số

3 2

– 3 2

y x x

= +

(1). Tìm điểm M thuộc đường thẳng

: 3 2

d y x

= −

sao tổng

khoảng cách từ M tới hai điểm cực trị nhỏ nhất.

Giải

• Các điểm cực trị là: A(0; 2), B(2; –2).

Xét biểu thức

( , ) 3 2

g x y x y

= − −

ta có:

( , ) 3 2 4 0; ( , ) 3 2 6 0

A A A A B B B B

g x y x y g x y x y

= − − = − < = − − = >

⇒ 2 điểm cực đại và cực tiểu nằm về hai phía của đường thẳng d:

3 2

y x

= −

Do đó MA + MB nhỏ nhất ⇔ 3 điểm A, M, B thẳng hàng ⇔ M là giao điểm của d và AB.

Phương trình đường thẳng AB:

2 2

y x

= − +

Tọa độ điểm M là nghiệm của hệ:

3 2

2 2 2

y x









= −



⇔

 

 

= − +

 







⇒

4 2

;

5 5

 

















 

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 25

HT 36. Cho hàm số

3 2 2 3

3 3( 1)

y x mx m x m m

= − + − − +

(1). Tìm m để hàm số (1) có cực trị

đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng

lần khoảng

cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.

Giải

• Tập xác định: D =

ℝ

Ta có

2 2

3 6 3( 1)

y x mx m

′

= − + −

Hàm số (1) có cực trị thì PT

′

có 2 nghiệm phân biệt

2 2

2 1 0

x mx m

⇔ − + − =

có 2 nhiệm phân biệt

1 0,

⇔ ∆ = > ∀

Khi đó: điểm cực đại

( 1;2 2 )

A m m

− −

và điểm cực tiểu

( 1; 2 2 )

B m m

+ − −

Ta có

3 2 2

2 6 1 0

3 2 2

OA OB m m



= − +



= ⇔ + + = ⇔



= − −



HT 37. Cho hàm số

3 2

3( 1) 3 ( 2) 2 ( )

y x m x m m x m C

= − + + + − +

.Tìm

để đồ thị hàm số (C)

có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số (C) tới trục

bằng khoảng

cách từ điểm cực tiểu của đồ thị hàm số (C) tới trục

Giải

Ta có:

' 3 6( 1) 3 ( 2); ' 0

x m

y x m x m m y

x m





= + + + + = ⇔



= +





Hàm số có cực trị với mọi

. Hai điểm cực trị của đồ thị hàm số (C) là:

3 2 3 2

( ; 3 2), ( 2; 3 6)

A m m m m B m m m m

+ + − + + + −

Ta có hàm số là hàm bậc ba với hệ số

1 0

= >

⇒

điểm cực đại nhỏ hơn điểm cực tiểu.

Vậy A là điểm cực đại, B là điểm cực tiểu.

Ta có:

( ; ) 3 2 , ( , ) 2

d A Ox m m m d B Oy m

= + + − = +

Theo giả thiết ta có:

3 2 2

m m m m

+ + − = +



= −



= −



⇔





GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 26

HT 38. Cho hàm số

3 2

y x x mx

= − − +

có đồ thị là (C

). Tìm m để (C

) có các điểm cực đại,

cực tiểu và đường thẳng đi qua các điểm cực trị song song với đường thẳng

: 4 3

d y x

= − +

Giải

• Tập xác định: D =

ℝ

Ta có:

' 3 6

y x x m

= − −

Hàm số có CĐ, CT

' 3 6 0

y x x m

⇔ = − − =

có 2 nghiệm phân biệt

1 2

;

x x

' 9 3 0 3

m m

⇔ ∆ = + > ⇔ > −

(*)

Gọi hai điểm cực trị là

(

)

(

)

1 2

; ; ;

A B x

y y

Thực hiện phép chia y cho y′ ta được:

1 1 2

' 2 2

3 3 3 3

m m

y x y x

     

  

  

  

= − − + + −

  

  

  

  

  

     

⇒

( ) ( )

1 1 1 22 2

2 2

2 2 ; 2 2

3 3 3 3

y y x

m m m

y xx y

       

   

   

   

− + + − − + + −

   

   

   

   

   

       

= = = =

⇒

Phương trình đường thẳng đi qua 2 điểm cực trị là d:

2 2

3 3

m m

y x

   

 

 

 

= − + + −

 

 

 

 

 

   

Đường thẳng đi qua các điểm cực trị song song với d:

4 3

y x

= − +

2 4

2 3



 











− + = −

 











 



⇔ ⇔ =



 











− ≠















 





(thỏa mãn)

HT 39. Cho hàm số

3 2

y x x mx

= − − +

có đồ thị là (C

). Tìm m để (C

) có các điểm cực đại,

cực tiểu và đường thẳng đi qua các điểm cực trị tạo với đường thẳng

: 4 – 5 0

d x y

+ =

một góc

Giải

• Tập xác định: D =

ℝ

Ta có:

' 3 6

y x x m

= − −

Hàm số có CĐ, CT

' 3 6 0

y x x m

⇔ = − − =

có 2 nghiệm phân biệt

1 2

;

x x

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 27

' 9 3 0 3

m m

⇔ ∆ = + > ⇔ > −

(*)

Gọi hai điểm cực trị là

(

)

(

)

1 2

; ; ;

A B x

y y

Thực hiện phép chia y cho y′ ta được:

1 1 2

' 2 2

3 3 3 3

m m

y x y x

     

  

  

  

= − − + + −

  

  

  

  

  

     

⇒

( ) ( )

1 1 1 22 2

2 2

2 2 ; 2 2

3 3 3 3

y y x

m m m

y xx y

       

   

   

   

− + + − − + + −

   

   

   

   

   

       

= = = =

⇒

Phương trình đường thẳng đi qua 2 điểm cực trị là ∆:

2 2

3 3

m m

y x

   

 

 

 

= − + + −

 

 

 

 

 

   

Đặt

 







= − +











 

. Đường thẳng d:

4 – 5 0

x y

+ =

có hệ số góc bằng

−

Ta có:

1 1 3 39

4 4 5 10

tan 45

1 1 5 1

4 4 3 2

k k k m

  

  

+ = − = = −

  

= ⇔ ⇔ ⇔

  

+ = − + = − = −

−

  

  



Kết hợp điều kiện (*), suy ra giá trị m cần tìm là:

= −

HT 40. Cho hàm số

3 2

y x x m

= + +

(1). Xác định m để đồ thị của hàm số (1) có hai điểm cực trị

A, B sao cho



120

AOB

Giải

• Tập xác định: D =

ℝ

Ta có:

3 6

y x x

′

= +

;

2 4

x y m



= − ⇒ = +



′

= ⇔



= ⇒ =





Vậy hàm số có hai điểm cực trị A(0 ; m) và B(−2 ; m + 4)

(0; ), ( 2; 4)

OA m OB m

= = − +

 

. Để



120

AOB

thì

cos

AOB

= −

(

)

( )

2 2

4 0

( 4) 1

4 ( 4) 2 ( 4)

3 24 44 0

4 ( 4)

m m

m m m m

m m





− < <



⇔ = − ⇔ + + = − + ⇔





+ + =



+ +





GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 28

4 0

12 2 3





− < <



− +



⇔ ⇔ =



− ±





HT 41. Cho hàm số

3 2 2 3

3 3( 1) 4 1 (1),

y x mx m x m m m

= − + − − + −

là tham số thực. Tìm các giá

trị của

để đồ thị hàm số (1) có hai điểm cực trị

A B

sao cho tam giác

OAB

vuông tại

với

là gốc tọa độ.

Giải

Ta có:

2 3

' 3( 2 1).

y x mx m

= − + −

Hàm số có cực trị khi và chỉ khi phương trình

' 0

có hai

nghiệm phân biệt.

∆ > ⇔ ∀ ∈

ℝ

' 0

x m



= +



= ⇔



= −





⇒

Hai điểm cực trị:

( 1; 1), ( 1; 3)

A m m B m m

− + + −

( 1; 1), ( 1; 3).

OA m m OB m m

= − + = + −

 

OAB

∆

vuông tại O khi O, A, B phân biệt và

. 0

OAOB

 

2( 2) 0

m m



= −



⇔ − − = ⇔





HT 42. Cho hàm số

3 2 2 3

– 3 3( – 1) –

y x mx m x m

= +

). Chứng minh rằng (C

) luôn có điểm

cực đại và điểm cực tiểu lần lượt chạy trên mỗi đường thẳng cố định.

Giải

• Tập xác định: D =

ℝ

2 2

3 6 3( 1)

y x mx m

′

= − + −

;

x m



= +



′

= ⇔



= −





Điểm cực đại

( – 1;2 – 3 )

M m m

chạy trên đường thẳng cố định:

2 3

x t

y t





= − +







= −





Điểm cực tiểu

( 1; 2 – )

N m m

+ −

chạy trên đường thẳng cố định:

2 3

x t

y t





= +







= − −





HT 43. Cho hàm số

3 2 3 2

3( 1) 3 ( 2) 3 .

y x m x m m x m m

= + + + + + +

Chứng minh rằng với mọi m

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 29

hàm số luôn có 2 cực trị và khoảng cách giữa hai điểm này không phụ thuộc vào vị trí của m.

Giải

Ta có:

' 3 6( 1) 6 ( 2); ' 0

x m

y x m x m m y

x m



= − −



= + + + + = ⇔



= −





Hàm số đồng biến trên các khoảng (-∞;-2 - m) và (-m;+∞), nghịch biến trên khoảng (-2 - m;-m)

và

2 ; 4; ; 0

CD CD CT CT

x m y x m y

= − − = = − =

Khi đó, khoảng cách giữa hai điểm cực trị là:

2 2

( 2 ) (4 0) 2 5

m m

− − + + − =

⇒ Điều phải chứng minh.

HT 44. Cho hàm số

3 2

y x x mx

= − − +

(1) với m là tham số thực. Định m để hàm số (1) có

cực trị, đồng thời đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tạo với hai trục tọa độ

một tam giác cân.

Giải

Ta có:

' 3 6

y x x m

= − −

Hàm số có cực trị khi và chỉ khi y’ = 0 có 2 nghiệm phân biệt

' 9 3 0 3

m m

⇔ ∆ = + > ⇔ > −

(1)

Lấy y chia cho y’ ta được:

3 2

1 2

3 2 ( 1). ' ( 2) 2

3 3 3

m m

y x x mx x y x= − − + = − + − − + −

Đường thẳng qua hai điểm cực trị của đồ thị hàm số có phương trình

( 2) 2

3 3

m m

y x= − − + −

Đường thẳng này cắt 2 trục Ox và Oy lần lượt tai

6 6

;0 , 0;

2( 3) 3

m m

A B

   

− −

 

 

 

 

 

 

 

 

   

Tam giác OAB cân khi và chỉ khi

OA OB

6 6

2( 3) 3

m m

− −

⇒ =

9 3

6; ;

2 2

m m m

⇒ = = − = −

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 30

Với m = 6 thì

A B O

≡ ≡

do đó so với điều kiện ta nhận

= −

HT 45. Cho hàm số

3 2

1 1

( 1) ( 2) 1.

3 2

y x m x m x

= − − + − +

Tìm

để đồ thị hàm số có hai điểm

cực trị A, B đồng thời các điểm cực trị tạo với hai điểm

 

















 

và gốc tọa độ O tạo thành hình

bình hành

OADB

Giải

Ta có:

' ( 1) 2, ' 0

y x m x m y

x m





= − + + − = ⇔



= −





Hàm số có cực trị

' 0

⇔ =

có hai nghiệm phân biệt

2 1 3

m m

⇔ − ≠ ⇔ ≠

Ta có OADB là hình bình hành nên trung điểm của AB cũng chính là trung điểm của OD.

Từ đó, ta có hệ:

2 2

A B D

x x x

y y y











Giả sử:

1, 2.

A B

x x m

= = −

Từ phương đầu tiên của hệ ta có:

1 3 4.

m m

− = ⇔ =

Với

ta có: A

11 5

1; ; 2;

6 3

A B

   

 

 

 

 

 

 

 

 

   

Thay vào phương trình thứ hai của hệ ta thấy thỏa mãn.

Kết hợp điều kiện

≠

ta đi đến kết luận:

là giá trị cần tìm.

HT 46. Cho hàm số

4 2 2

( ) 2( 2) 5 5

y f x x m x m m

= = + − + − +

( )

. Tìm các giá trị của m để đồ

thị

( )

của hàm số có các điểm cực đại, cực tiểu tạo thành 1 tam giác vuông cân.

Giải

• Tập xác định: D =

ℝ

Ta có

( )

4 4( 2) 0

f x x m x

x m





′

= + − = ⇔



= −





Hàm số có CĐ, CT ⇔ PT

( ) 0

f x

′

có 3 nghiệm phân biệt ⇔

(*)

Khi đó toạ độ các điểm cực trị là:

(

)

(

)

(

)

0; 5 5 , 2 ;1 , 2 ;1

A m m B m m C m m

− + − − − − −

⇒

(

)

(

)

2 2

2 ; 4 4 , 2 ; 4 4

AB m m m AC m m m

= − − + − = − − − + −

 

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 31

Do ∆ABC luôn cân tại A, nên bài toán thoả mãn khi ∆ABC vuông tại A

⇔

(

)

. 0 2 1 1

AB AC m m

= ⇔ − = − ⇔ =

 

(thoả (*))

HT 47. Cho hàm số

(

)

4 2 2

2( 2) 5 5 .

y x m x m m C= + − + − +

Với những giá trị nào của m

thì đồ thị (C

) có điểm cực đại và điểm cực tiểu, đồng thời các điểm cực đại và điểm cực tiểu lập

thành một tam giác đều.

Giải

• Tập xác định: D =

ℝ

Ta có

( )

4 4( 2) 0

f x x m x

x m





′

= + − = ⇔



= −





Hàm số có CĐ, CT ⇔ PT

( ) 0

f x

′

có 3 nghiệm phân biệt ⇔

(*)

Khi đó toạ độ các điểm cực trị là:

(

)

(

)

(

)

0; 5 5 , 2 ;1 , 2 ;1

A m m B m m C m m

− + − − − − −

⇒

(

)

(

)

2 2

2 ; 4 4 , 2 ; 4 4

AB m m m AC m m m

= − − + − = − − − + −

 

Do ∆ABC luôn cân tại A, nên bài toán thoả mãn khi



⇔

cos

⇔

. 1

AB AC

 

⇔

2 3

= −

Câu hỏi tương tự đối với hàm số:

4 2

4( 1) 2 1

y x m x m

= − − + −

HT 48. Cho hàm số

4 2 2

y x mx m m

= + + +

có đồ thị (C

) . Với những giá trị nào của m thì đồ

thị (C

) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có một góc bằng

120

Giải

• Tập xác định: D =

ℝ

Ta có

4 4

y x mx

′

= +

;

0 4 ( ) 0

y x x m

x m





′

= ⇔ + = ⇔



= ± −





(m < 0)

Khi đó các điểm cực trị là:

(

)

(

)

(0; ), ; , ;

A m m B m m C m m

+ − − −

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 32

( ; )

AB m m

= − −



;

( ; )

AC m m

= − − −



. ∆ABC cân tại A nên góc

120



chính là



120



1 . 1 . 1

cos

2 2 2

AB AC m m m

m m

AB AC

− − − +

⇔ = − ⇔ = − ⇔ = −

−

 

4 4 4

0 ( )

2 2 3 0

m loaïi

m m

m m m m m m

m m





⇔ = − ⇒ + = − ⇔ + = ⇔



= −

−





Vậy

m = −

HT 49. Cho hàm số

4 2

2 1

y x mx m

= − + −

có đồ thị (C

) . Với những giá trị nào của m thì đồ thị

) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có bán kính đường

tròn ngoại tiếp bằng

Giải

• Tập xác định: D =

ℝ

Ta có

3 2

4 4 4 ( ) 0

y x mx x x m

x m





′

= − = − = ⇔





Hàm số đã cho có ba điểm cực trị

⇔

′

có ba nghiệm phân biệt và

′

đổi dấu khi

đi

qua các nghiệm đó

⇔ >

. Khi đó ba điểm cực trị của đồ thị (Cm) là:

(

)

(

)

2 2

(0; 1), ; 1 , ; 1

A m B m m m C m m m

− − − + − − + −

ABC B A C B

S y y x x m m

= − − =

△

;

, 2

AB AC m m BC m

= = + =

. . ( )2

1 1 2 1 0

5 1

ABC

AB AC BC m m m

R m m

m m





= = ⇔ = ⇔ − + = ⇔

−





△

Câu hỏi tương tự:

4 2

2 1

y x mx

= − +

ĐS:

1 5

m m

− +

= =

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 33

HT 50. Cho hàm số

4 2 4

2 2

y x mx m m

= − + +

có đồ thị (C

) . Với những giá trị nào của m thì đồ

thị (C

) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có diện tích

bằng 4.

Giải

• Tập xác định: D =

ℝ

Ta có

' 4 4 0

( ) 0

y x mx

g x x m





= − = ⇔



= − =





Hàm số có 3 cực trị

' 0

⇔ =

có 3 nghiệm phân biệt

0 0

m m

⇔ ∆ = > ⇔ >

(*)

Với điều kiện (*), phương trình

′

có 3 nghiệm

1 2 3

; 0;

x m x x m

= − = =

. Hàm số đạt

cực trị tại

1 2 3

; ;

x x x

. Gọi

(

)

(

)

4 4 2 4 2

(0;2 ); ; 2 ; ; 2

A m m B m m m m C m m m m

+ − + − − +

là 3

điểm cực trị của (C

) .

Ta có:

2 2 4 2

; 4

AB AC m m BC m ABC

= = + = ⇒ ∆

cân đỉnh A

Gọi M là trung điểm của BC

4 2 2 2

(0; 2 )

M m m m AM m m

⇒ − + ⇒ = =

Vì

ABC

∆

cân tại A nên AM cũng là đường cao, do đó:

2 5

1 1

. . . 4 4 4 16 16

2 2

ABC

S AM BC m m m m m

∆

= = = ⇔ = ⇔ = ⇔ =

Vậy

Câu hỏi tương tự:

4 2 2

2 1

y x m x

= − +

, S = 32 ĐS:

= ±

HT 51. Cho hàm số

4 2

2 2

x mx

− +

có đồ thị

( )

. Tìm tất cả các giá trị của tham số m để đồ thị

( )

có ba điểm cực trị tạo thành một tam giác có đường tròn ngoại tiếp đi qua điểm D

3 9

;

5 5

 

















 

Giải

' 4 4 0 ( 0)

y x mx m

x m





= − = ⇔ >



= ±





Vậy các điểm thuộc đường tròn (P) ngoại tiếp các điểm

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 34

cực trị là: A (0;2);

2 2

3 9

( ; 2); ( ; 2); ;

5 5

B m m C m m D

 







− − + − +











 

. Gọi I(x;y) là tâm đường tròn (P)

2 2

2 2 2 2 2

3 1 0

2 2 1

0( )

( ) ( 2) ( 2)

1( / )

x y

IA ID

IB IC x m x m y

m l

IB IA

x m y m x y

m t m













− + =



  

= ⇔ = − ⇔ =

  

  



  

+ + + − = + −

  

























Kết luận: m = 1

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN

PHẦN 3: SỰ TƯƠNG GIAO

HT 52.   

3 2

6 9 6

y x x x

= − + −

          

( ) : 2 4

d y mx m

= − −

 !"!#$"!%

 Giải

•&'!!()*+

3 2

6 9 6 2 4

x x x mx m

− + − = − −



  ⇔

( 2)( 4 1 ) 0

x x x m

− − + − =

⇔

( ) 4 1 0

g x x x m





= − + − =







 * !"!#$"!%⇔&

( ) 0

g x

,!%#$"!%-.,⇔

> −



HT 53. 

3 2

y x m x m

= − −





&/



)012,!3

#$"!%

Giải

&+

' 3 6 ' 0

y x mx y

x m





= − ⇒ = ⇔











)452,!3#$"!%

⇔

CÑ, CT

y hoaëc y

0 0

CÑ CT

y coù









= =







67 !87!3⇔,≠9⇔≠ 0

&+

3 3

. 0 2 (8 6 2 ) 0

CD CT

y y m m m m





= ⇔ − − − = ⇔



= ±







:;<#!3-!%+

= ±



 

HT 54. 

3 2

2 6 1

y x x

= − + +

&/

y mx

= +

 !!#$

"!%=8>8=9?@)>03!(=

Giải

A0/'!!(

y mx

= +

)B!+

3 2 2

2 6 1 1 (2 6 ) 0

2 6 0

x x mx x x x m

x x m





− + + = + ⇔ − + = ⇔



− + =







 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNC

DB!5E9⇒FE@⇒=9?@



y mx

= +

 !"!#$"!%=8>8

⇔

2 6 0

x x m

− + =

!!%#$"!%

8

-.9

⇔

' 0 9 2 0

0 0

m m





 



 

∆ > − >



 



⇔ ⇔

  

  

≠ ≠

  

≠

 







:!+

1 1 2 2

( ; 1); ( ; 1).

B x mx C x mx

+ +

D/03!(=G

2 1

2 (1)

x x



H

8

!%(#A0/+

2 6 0

x x m

− + =

G

1 2

(2)

x x





+ =











&I@),⇒EJ



HT 55. 

3 2 2 2

3 3( 1) ( 1)

y x mx m x m

= − + − − −



@&/.!.0

(@01 !!#$"!%'*A

 •&6K@01 !!#$"!%'*A8#L!+

  

(1) 2

. 0

0, 0

. (0) 0









> >





CÑ CT

coù cöïc trò

y y

x x

a y

 M

 &0+N

3 2 2 2

3 3( 1) ( 1)

y x mx m x m

= − + − − −

⇒

2 2

3 6 3( 1)

y x mx m

′

= − + −



   N

2 2

1 0 0,

m m m

′

∆ = − + = > ∀



   N

CÑ

x m x



= − =



′

= ⇔



= + =







 K3F0+M

2 2 2

1 0

3 1 2

( 1)( 3)( 2 1) 0

( 1) 0

m m m m





− >



+ >



⇔ ⇔ < < +





− − − − <



− − <







 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNO

HT 56. 

3 2

1 2

3 3

y x mx x m

= − − + +

PQ !R

( )

&STU

( )

V 01TR!

!U#W"!WRPU"ST#APTWRAP A@

 Giải

•X>&⇔

3 2

1 2

3 3

x mx x m

− − + + =

MP!WR#W"!WRY

2 2 2

1 2 3

x x x+ + >



 &+M

( 1)( (1 3 ) 2 3 ) 0

x x m x m

⇔ − + − − − =

⇔

( ) (1 3 ) 2 3 0

g x x m x m





= + − − − =







 Z+X>&⇔

( ) 0

g x

P,!WR

1 2

x x

#W "!WR-P@)TY

2 2

1 2

x x+ >



   

⇔ >



 $3[!A7!)B!+

3 2

3 3 3 2

y x mx x m

= − − + +



HT 57. 

3 2

3 9

y x x x m

= − − +

80

7&/\L.!.0(



]01 !!#$"!%'^#

\#'

 Giải

•01 !!#$"!%'^#\#'



⇔

A0/

3 2

3 9 0

x x x m

− − + =

!%#$"!%^#\#'



⇔

A0/

3 2

3 9

x x x m

− − = −

!%#$"!%^#\#'



⇔



y m

= −

!_3!3(



11 11.

m m

⇔ − = − ⇔ =



HT 58. 

3 2

3 9 7

y x mx x

= − + −





80

7&/







01 !!#$"!%'^#\#'

 Giải

•6'.!!!%(#A0/+

3 2

3 9 7 0

x mx x

− + − =

@

 `a!'.!!b<

1 2 3

; ;

x x x

+

1 2 3

x x x m

+ + =



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNc

 

1 2 3

; ;

x x x

^#\#'/

x m

!%(#A0/@

 

⇒



2 9 7 0

m m

− + − =



⇔



1 15





− +



− −







 &d !

1 15

− −

!.0b/



HT 59. 

3 2

y x mx mx

= − −





80

7&/









: 2

d y x

= +

 !!#$"!%'^#\#$

 Giải

•ef#A0/'!!(



)*+



(

)

(

)

3 2 3 2

3 2 3 1 2 0

x mx mx x g x x mx m x

− − = + ⇔ = − − + − =



 -b+`!Ld * ! !#$"!% '

1 2 3

; ;

x x x

b<^#\#

$:!+

(

)

(

)

(

)

(

)

1 2 3

g x x x x x x x

= − − −



 K3F0+

1 2 3

1 2 2 3 1 3

1 2 3

x x x m

x x x x x x m

x x x





+ + =



+ + = − −









 D/

2 3

1 3 2 2 2

2 2

x x x x x= ⇒ = ⇒ =

G+

1 4 2.3

3 2 1

m m m− − = + ⇔ = −



 -(+DB!

3 2 1

m = −

8F)g!%\F[]

 D^F

3 2 1

m = −



HT 60. +

3 2

2 3 1 (1)

y x x= − +

&/0Gh!H!;#3F;(

 !H013 !!3'"ic



Giải

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNj

`!LdH5

?F



∈



⇒

E,5



k5

N@

&+

' 3 6

y x x

= −

    

&!;#3F;

∆

( !H+

FEC5

kC5

5k5

N,5



k5

N@    



∆

!_3!9?c

⇔

cEkJ5



N5

N@

⇔

5

N@J5

kO5

NOE9       

⇔

Ek@?J5

kO5

NOl98

∀

     

D^F8*3F\!Hk@?kJb/ 



HT 61.   

3 2

2 ( 3) 4

y x mx m x

= + + + +

     



      

*+

y x

= +

)!:@?&/.!.0(*



 !"!#$"!%

=9?J8>8!.:>*!%g"i

8 2



 Giải

•A0/'!!(



)*+

 

3 2 2

2 ( 3) 4 4 ( 2 2) 0

x mx m x x x x mx m

+ + + + = + ⇔ + + + =



0 ( 4)

( ) 2 2 0 (1)

x y

g x x mx m



= =



⇔



= + + + =







 *



 !"!#$"!%=9?J8>8

⇔

,,!%#$"!%-.9



/ 2

1 2

2 0

(0) 2 0

m m

g m





≤ − ∨ ≥

∆ = − − >



⇔ ⇔

 

 

≠ −

= + ≠

 







 M

 :!+

2 ; . 2

B C B C

x x m x x m

+ = − = +



 Hm-.+

1 3 4

( , ) 2

d K d

− +

= =

Z+

 

8 2 . ( , ) 8 2 16 256

KBC

S BC d K d BC BC

∆

= ⇔ = ⇔ = ⇔ =



2 2

( ) ( ) 256

B C B C

x x y y⇔ − + − =



2 2

( ) (( 4) ( 4)) 256

B C B C

x x x x⇔ − + + − + =



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNJ9



2 2

2( ) 256 ( ) 4 128

B C B C B C

x x x x x x⇔ − = ⇔ + − =



2 2

1 137

4 4( 2) 128 34 0

m m m m m

⇔ − + = ⇔ − − = ⇔ =

[M

 D^F

1 137





HT 62. 

3 2

3 4

y x x

= − +

`a!

!_3!

( 1;0)

−



)B!%

( )

∈

ℝ

&/



 !"!#$"!%=8>8)

,!!>8n)B! '

 '!.*!%g"i



 Giải

•&+

d y kx k

= +

⇔

kx y k

− + =



 A0/'!!(



)*+

 

3 2 2

3 4 ( 1) ( 2) 0 1

x x kx k x x k x

 

− + = + ⇔ + − − = ⇔ = −

 

 

m

( 2)

x k

− =



 !!#$"!%





⇔





≠







 :!.!!

(

)

(

)

( 1;0), 2 ;3 , 2 ;3

A B k k k k C k k k k

− − − + +



 

2 1 , ( , ) ( , )

BC k k d O BC d O d

= + = =



 

2 3

. .2 . 1 1 1 1 1

OBC

S k k k k k k

∆

= + = ⇔ = ⇔ = ⇔ =



HT 63.  

3 2

y x x

= − +

     `a! o  $ ! 5p(    D!;

#A0/_3o) !"!o8=8>#$"!%*!%g

!.4=>"i



 Giải

•&+o@?9&∆_3o* 

( 1)

y k x

= −



 &'!!()

∆+

( 1)( 2 2 ) 0

x x x k

− − − − =



 ∆ !!#$"!%⇔&

2 2 0

x x k

− − − =

!!%#$"!%-.@

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNJ@

  ⇔

> −



( , ). 3

OAB

S d O AB k k

∆

= ∆ = +

⇒

3 2

k k

+ =

⇔

1 3



= −



= − ±







 D^FLX>&+

(

)

1; 1 3 ( 1)

y x y x

= − + = − ± −



HT 64. 

3 2

4 1

(2 1) ( 2)

3 3

y x m x m x

= − + + + +



( ),

C m

`a!



!!(

( )

)B!013&/

!;#3F;(

( )

 !

 )B!!01a'

'!.*!%g"i



Giải

&+

 

 

 

)

' 4 2(2 1) 2.

y x m x m

= − + + +

K3F0

'(0) 2

y m

= +



&!;#3F;( !



: ( 2) .

d y m x= + +





 !

3 6

 

−

















 



:!*!%g!. "q!

)B!!01a'+

1 1 1 1 1

. . .

2 2 3 3 6

18 2

S OAOB

−

= = =



&!L!;+

1 1 1

3 6

18 2





= −



= ⇔ + = ⇔



= −







HT 65. 

y x mx

= + +





&/



01 !'

!*3F\

Giải

 •A0/'!!(



)B!01+

 

2 0

x mx

+ + =

( 0)

m x x

⇔ = − − ≠



 ef+

2 2

2 2 2 2

( ) '( ) 2

f x x f x x

x x

− +

= − − ⇒ = − + =



 &"L"!;!G+

 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNJ,

f x

( )

′

f x

( )

−∞

+∞

−∞

+∞

−∞



 



01 !'!*3F\

⇔ > −





HT 66. 

3 2

2 3( 1) 6 2

y x m x mx

= − + + −





&/



01

 !'!*3F\

 Giải

•

&^#5.+ZE

ℝ



' 6 6( 1) 6

y x m x m

= − + +



2 2

' 9( 1) 36 9( 1)

m m m∆ = + − = −



&@+E@⇒"!;0G

ℝ

⇒01 !@!*3F\

⇒E@[]

&,+

≠

⇒

⇒⇒

⇒ 67 !)7!3`a!

8

.!70(

⇒

8

.!%(#A0/FrE9

&D!+

1 2

x x m





+ = +











s\FF!Fr<+

( ) ' ( 1) 2 ( 1)

3 6

x m

y y m x m m

= − − − − + +



⇒A0/!_3!7 !)7!3(

( 1) 2 ( 1)

y m x m m

= − − − + +



01 !@!*3F\

⇔



. 0

CD CT

y y



 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNJ

[ ][ ] 0

[ ]

2 2

1 2

4 2 2 2 2

1 2 1 2

4 2 2 2 2

2 2 2 2

3 2 3 2 2

( 1) 2 ( 1) ( 1) 2 ( 1)

( 1) ( 1) ( 2)( ) ( 2) 0

( 1) ( 1) ( 2)( 1) ( 2) 0

2 2 2 4 4 0(

m x m m m x m m

m x x m m m x x m m

m m m m m m m m

m m m m m m m

m m m m m m m m V m

− − − + + − − − + + >

⇔ − − − + − + + + − >

⇔ − − − + − + + + >

⇔ − + − − + + + + + >

2 2 0

1 3 1 3

m m

≠

⇔ − − <

⇔ − < < +



:;3^+

1 3 1 3

− < < +



HT 67. 

3 2

– 3 1

y x x

= +

&/

∆

+

(

2 1) – 4 – 1

y m x m

= −



 !2!!#$"!%

Giải



•

A0/'!()

∆

+

(

3 2

– 3 – 2 – 1) 4 2 0

x x m x m

+ + =



 

⇔



( 2)( – – 2 – 1) 0

x x x m

− =



( ) 2 1 0 (1)

f x x x m





⇔



= − − − =







 

∆

 !2,!#$"!%

⇔

@#L!!%

1 2

x x

[]+

1 2

x x



≠ =



= ≠







 

⇔



(2) 0







∆ =















− ≠

















∆ >



















⇔



8 5 0

2 1 0







+ =















≠

















+ >











− + =











⇔







= −







 D^F+

= −

?





HT 68. 

3 2

6 9 (1).

y x x x= − +

&/*+

y mx

 !"!4

9?98=)>p[0i-!Ft!803!u( =>3vi0G'

)B!4F

Giải

A0/'!!(*)B!+

 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNJJ

3 2

6 9 (1)

6 9 0 (2)

x x x mx

x x m





− + = ⇔



− + − =







* !!#$"!%49?98=8>

⇔

@!%#$"!%

⇔

,,!%#$"!%-.5

≠

9

⇔



' 0

0 9 (*)

9 0





∆ >



⇔ < ≠





− ≠







DB!!w3-!%M8=8>,!'b<

;

A B

x x

,!%(#A0/

,

u03!( =>G'u+

A B

x x

= =



⇒

∈ ∆

#A0/5E8

∆

)B!4F-!Ft!

(0 9)

< ≠



HT 69. 

3 2

3 ( 1) 1

y x mx m x m

= − + − + +



( )

&/\L.!.0(

*+

2 1

y x m

= − −



( )

 !"!#$"!%'BAm"i@

Giải

A0/'!!(

( )

)B!*+

3 2

3 ( 1) 1 2 1

3 ( 3) 2 2 0

( 1) (1 3 ) 2 2 0 (1)

(1 3 ) 2 2 0 (2)

x mx m x m x m

x mx m x m

x x m x m

x m x m

− + − + + = − −

⇔ − + − + + =

 

⇔ − + − − − =

 

 





⇔



+ − − − =







( )

* !!#$"!%'BAm"i@

⇔

@!%#$"!%BAm"i@

⇔

,!!%#$"!%BA@

ef#A0/,?&+

2 2

(1 3 ) 8 8 9 2 9 0,

m m m m m

∆ = − + + = + + > ∀



⇒

∀

,3v,!%#$"!%

1 2

;

x x



@ ,!%BA@

⇔



1 2 1 2

1 0 1 1

x x x x

< < ⇔ < − < −



 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNJ

mE5k@

⇔

5EN@⇒,

⇔



( 1) (1 3 )( 1) 2 2 0

t m t m

+ + − + − − =



⇔



3(1 ) 5 0 (3)

t m t m+ − − = 

, ,!%[]+

1 2

x x

< <

⇔

,!%*A#$"!%+

⇔



3( 1) 0

5 0

S m vn

p m





∆ >



= − > ⇔





= − >







:;3^+-v!.0



HT 70. 

3 2

y x x

= − +

D!;#A0/ !!

#$"!%=8>8

)

2 2



Giải

DB!

2 4

A A

x y

= ⇒ =

A0/*!_3!=,?J+

( ) : ( 2) 4

A A

y k x x y d y k x

= − + ⇒ = − +



A0/'!!()B!*

3 2

3 2 ( 2) 4 ( 2)( 2 1) 0

( ) 2 1

x x k x x x x k

g x x x k

− + = − + ⇔ − + − + =





⇔



= + − +







!w3-!%>+

' 0 0

(2) 0 9

g k

 



∆ > >





⇔







≠ ≠





 



:!&a'(

1 1 2 2

( ; ); ( ; )

B x y C x y

[]%#A0/+

2 1 0 (1)

2 4 (2)

x x k

y kx k





+ − + =







= − +







&+

2 1

2 1 2 1

(1) 2 ' 2

(2) ( 2

x x k

y y k x x k k

⇔ − = ∆ =

⇔ − = − =



&!L!;+>E

2 2

⇔



3 3

4 4 2 2 4 4 8 0 1

k k k k k

+ = ⇔ + − = ⇔ =



D^F+

: 2

d y x

= +



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNJC



HT 71. 

3 2

4 6 1

y x mx

= − +

8&/

: 1

d y x

= − +



 !!=9?@8>8)B!>8!5p3_3#$!.p\

Giải

`!()*'!%(#A0/+

3 2 2

4 6 1 1 (4 6 1) 0

x mx x x x mx

− + = − + ⇔ − + =



#A0/!%#$"!%/

4 6 1 0

x mx

− + =

!!%#$"!%

⇒

2 2

' 9 4 0 ;

3 3

m m m

−

∆ = − > ⇔ > < 

`a!

1 1 2 2

( ; 1), ( ; 1)

B x x C x x

− + − +

>8!5p_3#$!.p\/+

1 2 1 2

1 2

1 2 2 1

3 2

1 1

2 3

x y x x

x x m m

y x x x

 

 

= = − +

 

⇔ ⇔ + = ⇔ = ⇔ =

 

 

= = − +

 

 



K.!w3-!%\F-v!.0[]

HT 72. 

3 2

3 1

y x x mx

= + + +

@&/

: 1

d y



@ !"!#$"!%=9?@8>8.!;#3F;(@

 !>))3v)B!3

 Giải

•

&'!!(@)*+

3 2 2

3 1 1 ( 3 ) 0

x x mx x x x m

+ + + = ⇔ + + =



 *@ !!#$"!%=9?@8>8

⇔



, 0

m m

< ≠



 :!+

B C

x x

.!%(&+

3 0

x x m

+ + =

⇒

3; .

B C B C

x x x x m

+ = − =



 6%(!;#3F; !>

3 6

B B

k x x m

= + +

) !

3 6

C C

k x x m

= + +



 &!;#3F;( !>))3v)B!3

⇔



1 2

. 1

k k

= −



⇔



4 9 1 0

m m

− + =



  

⇔



9 65 9 65

8 8

m m

− +

= ∨ = 



 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNJO

HT 73. 

– 3 1

y x x

= +

)*+

y mx m

= + +

&/

* !Hx@?8y8!;#3F;( !y))3v)B!3

 Giải

•

A0/'!!()*+

(

– 3) – – 2 0

x m x m

+ =



 

⇔



( 1)( – – – 2) 0

x x x m

+ =



⇔



1 ( 3)

( ) 2 0

x y

g x x x m



= − =



= − − − =







 *@ !!#$"!%Hx@?8y8

⇔



, 0

m m

> − ≠



 :!+

N P

x x

.!%(&+

2 0

x x m

− − − =

⇒

1; . 2

N P N P

x x x x m

+ = = − −



 6%(!;#3F; !y

3 3

k x

= −

) !

3 3

k x

= −



 &!;#3F;( !y))3v)B!3

⇔



1 2

. 1

k k

= −



⇔



9 18 1 0

m m

+ + =



        

⇔



3 2 2 3 2 2

3 3

m m

− + − −

= ∨ = 



HT 74. 

3 2

3 4

y x x

= − +

`a!*!_3!=,?9%

-&/-* !"!#$"!%=8H8y!!;#3F;( !H)y

)3v)B!3

 Giải

•

&*+

( 2)

y k x

= −



 N&'!!()*+

3 2

3 4 ( 2)

x x k x

− + = −



 

⇔



( 2)( 2 ) 0

x x x k

− − − − =



⇔



( ) 2 0

x x

g x x x k



= =



= − − − =







 N* !!#$"!%=8H8y

⇔

&

( ) 0

g x

,!%#$"!%8-.,

 

⇔



(2) 0





∆ >



⇔ − < ≠





≠





  M

 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNJc

 N&gD!+

M N

x x

x x k





+ =







= − −







 N.!;#3F; !H)y)3v)B!3

⇔

( ). ( ) 1

M N

y x y x

′ ′

= −



 

⇔



2 2

(3 6 )(3 6 ) 1

M M N N

x x x x

− − = −



⇔



9 18 1 0

k k

+ + =

3 2 2

− ±

⇔ =  LM



HT 75.    

y x x

= −

   p ! 0i -!  F t!8   *+

( 1) 2

y m x

= + +

3v !'!H)5..!.0(*

 !!#$"!%H8y8!;#3F;( !y))3v)B!3

 Giải

•

&'!!

( 1)( 2 ) 0

x x x m

+ − − − =

@

⇔



1 0

2 0 (2)

x x m



+ =



− − − =







 @3v@!%

= −



⇒*3v !!Hx@?,

 * !!#$"!%

⇔

,,!%#$"!%8-.x@

⇔

  M

 &!;#3F; !y8)3v

⇔

 

⇔



3 2 2

− ±

= LM



HT 76. 

1 ( ).

y x mx m C= − + − &/!;#3F;(]

 !!

= −

0z+

2 2

( 2) ( 3) 4

x y

− + − =

'*$F3'*![

\

Giải

Cách 1:&+

' 3

y x m

= −

⇒

( 1)

' 1

y m

−

= −



A/!;#3F; !!'5Ek@+

(3 ) 1 (3 ) 1 ( )

y m x m m x y m d

= − + + ⇔ − − + +





> −







≠



'( ). '( ) 1

N P

y x y x

= −

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNJj

2 2 2

4 1 (3 )

2 (3 ) 1

,( ) 2

(3 ) 1 (3 ) 1 (3 ) 1

m m

d I d

m m m

− + −

− +

 

= = ≤ =

 

 

− + − + − +



&!;#3F;0z !!!=8>=>!

⇔

*u8*5

Z\3E5LF0-!E,:!8#A0/!;#3F;5kFNE9

Cách 2: A0/!;#3F; !!5Ek@+FEk5NN@

⇒&!;#3F;3v!_3!H@?J

&0z$u,?8".-g{E,

⇒uHE

|{⇒Hi00z

`a!6/!;3(uG!;#3F;`!Ld!;#3F;0z*$F3=>

⇒=>E,=6E

2 2

R IH

−



⇒=>!-!u65&p60n)B!H:!8!;# 3F;^



)fA #.#

3F;

&+



k@?@⇒E,:!8#A0/!;#3F;+FE5N



HT 77. 

(

)

3 2 .

y x mx C= − + &/

!_3!7 !87!3

(

(

)

0z$

(

)

1;1 ,

".-g"i@ !!!#$"!%=8>*!%g

!.u=> !.0B\

Giải



&

' 3 3

y x m

= −



7 !87!3/#A0/

' 0

!!%#$"!%

⇔ >



D/

. ' 2 2

y x y mx

= − +

G

∆

!_37 !87!3(#A

0/

2 2

y mx

= − +



&

( )

2 1

, 1

4 1

d I R

−

∆ = < =

)/l98p[

∆

3v0z$

u@?@8".-g{E@ !,!=8>#$"!%

 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN9

DB!

≠

8

∆

-v!_3u8+

1 1 1

. .sin

2 2 2

ABI

S IAIB AIB R

∆

= ≤ =



yG

IAB

∆

   !. 0 B \ "i } -! !=u> E @ F  !. =u> )3v $  ! u

2 2

IH⇔ = =

603!(=>

2 1

1 2 3

4 1

−

⇔ = ⇔ =



HT 78. 

4 2

y x mx m

= − + −



(

)



(

)

0101

 !"!#$"!%

 Giải

•

A0/'!!()B!01+

4 2

1 0 (1)

x mx m− + − =



m+E



≥

9⇒@

⇔



1 0

t mt m

t m





− + − = ⇔



= −







01 !J!#$"!%

⇔

@J!%#$"!%

⇔

9|k@

≠

⇔











≠







HT 79. 

4 2

2( 1) 2 1 ( ).

y x m x m C= − + + +

&/\L.!.0(

∈

ℝ



]01 !J!#$"!%

, , ,

A B C D

b<'

1 2 3 4

, , ,

x x x x

1 2 3 4

( )

x x x x

< < <

!.

ACK

*!%g"iJ"!;

(3; 2).

−



Giải

A0/'!!(

( )

)B!01+

4 2

2( 1) 2 1 0 (1)

x m x m− + + + =

m+

( 0)

t x t

= ≥



:!+

(1) 2( 1) 2 1 0 (2).

t m t m⇔ − + + + =



01 !J!#$"!%/#A0/@J!%#$"!%

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN@

⇔

A0/,!%*A#$"!%

' ( 1) (2 1) 0

2( 1) 0

2 1 0

m m

S m

P m





∆ = + − + > 



≠



⇔ = + > ⇔

 

 

> −

 

= + >

 











DB!

− < ≠

/01 !J!#$"!%'p7

1 2 2 1

; ; ;

t t t t

− −

)B!

1 2

t t



&!L!;+

. ( ; ) (3)

ACK

S AC d K AC=

)B!

( ; )

d K AC y



:!+

1 2 1 2 1 2

(3) 4 2 16

t t t t t t⇔ + = ⇔ + + =



&D!+

2( 1) 2 2 1 16 2 1 7

m m m m

+ + + = ⇔ + = −



7 0

16 48 0

m m





− ≥



⇔ ⇔ =





− + =







HT 80. 

(

)

4 2

2 1 2 1

y x m x m

= − + + +



(

)





(

)



01 !J!#$"!%'^#\#'

 Giải

•

ef#A0/'!!+

(

)

4 2

2 1 2 1 0

x m x m

− + + + =

  @

 m

, 0

t x t

= ≥

/@0q+

(

)

( ) 2 1 2 1 0

f t t m t m

= − + + + =



 



45 !J!#$"!%/

( ) 0

f t

#L!,!%*A#$"!%

 

( )

' 0

2 1 0

S m

P m





∆ = >





> −



 

⇔ = + > ⇔

 

 

≠

= + >

 









M

 DB!M8a!

1 2

t t

,!%(

( ) 0

f t

8-!'!!(



)B!45b<

+

1 2 2 1 3 1 4 2

; ; ;

x t x t x t x t

= − = − = =



1 2 3 4

, , ,

x x x x

^#\#'

2 1 3 2 4 3 2 1

x x x x x x t t

⇔ − = − = − ⇔ =



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN,

 

( )

5 4 4

1 9 1 5 4 1

5 4 4

m m

m m m m m m

m m



= +



⇔ + + = + − ⇔ = + ⇔ ⇔



− = +

= −











 D^F

 

 

= −

 

 

 



 $3[!A7!)B!

4 2

2( 2) 2 3

y x m x m

= − + + − −

K+

m m= = −





HT 81. 

4 2

– (3 2) 3

y x m x m

= + +

 



8&/



= −





 !J!#$"!%w3'[A,

 Giải

•

A0/'!!(



)

= −

+

 

4 2

– (3 2) 3 1

x m x m

+ + = −



⇔



4 2

– (3 2) 3 1 0

x m x m

+ + + =

⇔



3 1 (*)

x m



= ±



= +







 

= −





 !J!#$"!%'[A,-!)~-!#A

0/M!!%#$"!%-.

@)[A,

 

⇔



0 3 1 4

3 1 1





< + <







+ ≠







⇔







− < <







≠







HT 82. 

4 2 2 2

( 2) 1 ( )

y x m x m Cm

= − + + +

&/.!.0(



( )



01 !J!#$"!%/#!B! "q!

( )

)B!01#b#g

0G

*!%g"i



Giải



4 2 2 2 2 2 2

( 2) 1 ( 1)( 1)

y x m x m x x m

= − + + + = − − −



A 0/

2 2 2

0 ( 1)( 1) 0

y x x m

= ⇔ − − − =

  J !% #$ "!% 

1; 1

± ± +

-!

≠



Z!% g #b / # !B!   "q!

( )

 )B! 01  #b #g 0G 01  +

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN

( )

4 2 2 2

20 16 96

2 ( 2) 1 2

15 15

S x m x m dx m

= − + + + = = ⇔ = ±

∫



D^F

= ±

!.0b/



HT 83. FE5



x5

N5NNJ



&/*!%g/#!B!

 "q!



)01#bi#g0G01"i#bi#g*B!

01



6"^^!3$!5p

⇒F"

⇔



Coù hai cöïc trò

Ñieåm uoán thuoäc truïc Ox













M6   7 0 -! #A 0/ F• E 9  , !% #$ "!% |El 5

kC5NE9  ,

!%#$"!%|El

9(1 ) 0 1

m m

∆ = − > ⇔ <



MF••EC5kCE9|El5E@ElFECN,El^!€@?CN,!3

!33'45-!F

€

E9|ElCN,E9|El

−



D^F

−

!.0b/



HT 84. 

(

)

4 2

2 1 2 1

y x m x m

= − + + +





8&/





01 !!#$"!%w3'[A

 Giải

•

ef#A0/'!!+

(

)

4 2

2 1 2 1 0

x m x m

− + + + =

  @

 m

, 0

t x t

= ≥

/@0q+

(

)

( ) 2 1 2 1 0

f t t m t m

= − + + + =



 



45 !!#$"!%'[A

 

(

)

f t

⇔

,!%#$"!%

1 2

t t

+

1 2

0 3

t t



= < <



< < ≤







 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNJ

 

( )

' 0

3 4 4 0

(0) 2 1 0 1

2 1 0

2 1 3

2 1 0

f m

f m m m

S m

P m





∆ = >







∆ = >



= − ≤





⇔ = + = ⇔ = − ∨ ≥

 

 

= + >

 

= + <

 





= + >







 D^F+

m m

= − ∨ ≥



HT 85. 

4 2 2 4

2 2

y x m x m m

= − + +

@8)B!p!

@3v0145 !g\!!#$"!%8)B!a!



 Giải

•

A0/'!!(@)0145+

 

4 2 2 4

2 2 0

x m x m m

− + + =

 @

 m

(

)

t x t= ≥

8@0q+

2 2 4

2 2 0

t m t m m

− + + =

 ,

 &+

' 2 0

∆ = − >

)

2 0

S m

= >

)B!a!

yG,!%*A

 ⇒@g\,!%#$"!%⇒@3v0145 !g\!!

#$"!%

HT 86. +

4 2

5 4

= − +

y x x

&/\L.!H0G(

!;#3F;( !H !!!#$"!%-.H

Giải

`a!

4 2

( ; 5 4) ( )

M m m m C

− + ∈



A0/!;#3F;( !

3 4 2

: (4 10 )( ) 5 4 ( )

M y m m x m m m d

= − − + − +



6'!!(

( )

)

( )

!%(#A0/+

4 2 3 4 2

5 4 (4 10 )( ) 5 4 ( )

x x m m x m m m d

− + = − − + − +



2 2 2

( ) ( 2 3 5) 0 (1)

x m x mx m⇔ − + + − =



XG3b3"!.

2 2

2 3 5 0

x mx m

⇔ + + − =

!!%#$"!%-.

5 2 0

6 5 0





− >



⇔





− ≠







 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN

10 10

2 2





− < <



⇔





≠ ±







HT 87.   

2 1

      p ! 0i  

d y x m

= − +



3v !!!#$"!%=8>&/ =>'*![\

 Giải

•

&'!!()*+

2 1

x m

= − +



     

⇔



( ) (4 ) 1 2 0 (1)

f x x m x m





≠ −







= + − + − =







 Z@

1 0

∆ = + >

)

( 2) ( 2) (4 ).( 2) 1 2 3 0,

f m m m

− = − + − − + − = − ≠ ∀



 G*3v3v !!!#$"!%=8>

 &+

;

A A B B

y m x y m x

= − = −

G

2 2 2 2

( ) ( ) 2( 12)

B A B A

AB x x y y m= − + − = +



 K3F0=>\

⇔



[\

⇔



:!+



 $3[!A7!)B!+

  

−

  K+E,  "

−

K+





HT 88. 

−

D!;#A0/*_3!

( 1;1)

−

)

 !!!H8yu03!( Hy

 Giải

•

A0/

(

)

: 1 1

d y k x

= + +



 * !,!#$"!%H8y

kx k

−

⇔ = + +

,!%#$"!%-.

−





⇔



( ) 2 4 0

f x kx kx k

= + + + =

,!%#$"!%-.

−



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNC



⇔



4 0 0

( 1) 4 0

k k





≠



∆ = − > ⇔ <





− = ≠







 Hm-.+

2 2

M N I

x x x

+ = − = ⇔

u03!Hy)B!

∀ <



 :;3^+A0/b/

y kx k

= + +

)B!





HT 89. 

2 4

−

`a!*_3=@?@)%-&/-

* !!!H8y

3 10





•

A0/

( ) : ( 1) 1.

d y k x

= − +



 >!.0q+&/-%#A0/3!!%

1 1 2 2

( ; ), ( ; )

x y x y

#$"!%



(

)

(

)

2 2

2 1 2 1

x x y y− + − =

 

 

2 4

( 1) 1

k x

y k x





= − +





− +



= − +





u&+

(2 3) 3 0

( )

( 1) 1

kx k x k

y k x





− − + + =



⇔





= − +







 u ! !% #$ "!%

⇔

 &

(2 3) 3 0 ( )

kx k x k b

− − + + =

  ! !% #$ "!%



⇔



0, .

k k≠ <



 &"!;t!0q+

(

)

(

)

2 2

2 1 2 1 2 1

(1 ) 90 (1 ) 4 90

k x x k x x x x

 

+ − = ⇔ + + − =

 

 



 &  g D!  "  +

1 2 1 2

2 3 3

, ,

k k

x x x x

k k

− +

+ = =

; )    #A

0/+

3 2 2

8 27 8 3 0 ( 3)(8 3 1) 0

k k k k k k

+ + − = ⇔ + + − =



  

3 41 3 41

3; ;

16 16

k k k

− + − −

⇔ = − = =



 :;3^+D^F!.0(-L]0G



HT 90.



2 2

−

&/*+

y x m

= +

 !!!

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNO

#$"!%=8>



 Giải

•

&'!!+

2 2

x m

−

= +



⇔



2 2 0 ( 1)

x mx m x

+ + + = ≠ −

 @

 * !,!#$"!%=8>

⇔

@,!%#$"!%

1 2

x x

-.x@

 

⇔



8 16 0

m m

− − >

 ,

 :!+

1 2

x x





+ = −









`a!

(

)

(

)

1 1 2 2

;2 , ;2

A x x m B x x m

+ +



 =>

E

⇔



2 2

1 2 1 2

( ) 4( ) 5

x x x x

− + − =



⇔



1 2 1 2

( ) 4 1

x x x

+ − =



⇔



8 20 0

m m

− − =



  

⇔







= −





 L,

 D^F+

10; 2

m m

= = −





HT 91.    

x m

−

  @ &/ . !. 0 (        *+

y x

= +

@ !!!=)>

2 2



 Giải

•

&'!!+

( 1) 2 1 0 (*)

x m

x m x m

x m





≠ −

−



= + ⇔





+ + + + =







 *@ !!!=8>#$"!%

⇔

M!!%#$"!%-.

−



 

6 3 0

3 2 3 3 2 3

m m

x m





∆ >

− − >

< − ∨ > +



 

⇔ ⇔ ⇔

  

  

≠ −

  











 MM

 :!a!

1 2

x x

.!%(M8

1 2

( 1)

. 2 1

x x m





+ = − +







= +







 .!!(*)@

1 1 2 2

( ; 2), ( ; 2)

A x x B x x

+ +



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNc

 K3F0

2 2 2 2

1 2 1 2 1 2

2( ) 2 ( ) 4 2( 6 3)

AB x x x x x x m m

 

= − = + − = − −

 

 



 &!L!;<

2 2

2( 6 3) 8 6 7 0

m m m m



= −



− − = ⇔ − − = ⇔







 :;<#)B!!w3-!%MM<

!.0b/



HT 92.   

( ).

2 2

y C

−

 &/ \ L . !. 0 (  

∈

ℝ

   

d y x m

= +

 !!!#$"!%

A B



2 2

OA OB+ =



Giải

A0/'!!(*)+

( ) 2 (2 3) 2( 1) 0, 1

2 2

x m g x x m x m x

= + ⇔ = + − − + = ≠

−



D/

4 4 25 0

(1) 3 0

m m





∆ = + + >



∀ ∈





= ≠





ℝ

G* !!!#$"!%)B!a!

∈

ℝ



`a!

1 1 2 2

( ; ), ( ; )

A x x m B x x m

+ +

a'!!(*)

&•D!+

1 2 1 2

2 3

; ( 1)

x x x x m

−

+ = − = − +



&+

2 2 2 2 2 2

1 1 2 2

( ) ( )

OA OB x x m x x m

+ = + + + + +

2 2

1 2 1 2 1 2

2( ) 4 2 ( ) 2

x x x x m x x m

= + − + + +



2 2

2 3 2 3 1

2 4( 1) 2 2 (4 2 17)

2 2 2

m m

m m m m m

   

− −

 

 

 

= − + + + − + = + +

 

 

 

 

 

   



`!L!;+

2 2 2

37 1 37

(4 2 17)

2 2 2

OA OB m m+ = ⇔ + + =



2 10 0

m m m

⇔ + − = ⇔ = −

m



:;3^+

m m

= − ∨ =



 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNj

HT 93. 

( ).

y C

−

&/\L.!.0(

∈

ℝ



: 1

d y mx m

= − −

 !!!#$"!%

A B



2 2

MA MB

 !.0[

\DB!

( 1;1)

−



Giải

A0/'!!(*)+

1 (1)

mx m

= − −

−



DB!!w3-!%

≠

/+

(1) ( 1)(1 )

x mx m x

⇔ = − − −



2 1 0 (2)

mx mx m⇔ − + + = 

* !!!#$"!%-!)~-!@,!%#$"!%

!w3FAA)B!,,!%#$"!%-.@m+

( ) 2 1

f x mx mx m

= − + +



' 0

(1) 0





≠



⇔ ∆ >





≠





2 2

0 0

2 1 0

m m m m

m m m





≠



⇔ − − > ⇔ <





− + + ≠







:!8a'!!

(

)

(

)

1 1 2 2

; 1 ; ; 1

A x mx m B x mx m

− − − −



DB!

1 2

x x

,!%(,

&+

2 2 2

1 1

( 1) ( 2)

MA x mx m= + + − −

?

2 2 2

2 2

( 1) ( 2)

MB x mx m= + + − −



2 2 2 2 2 2

1 1 2 2

( 1) ( 2) ( 1) ( 2)

MA MB x mx m x mx m⇒ + = + + − − + + + − −



2 2 2 2 2 2 2 2

1 1 1 2 2 2

2 1 2( 2) ( 2) 2 1 2( 2) ( 2)

x x m x m m x x m x m m= + + + − + + + + + + + − + + +



2 2 2 2

1 2 1 2 1 2

( 1)( ) 2( ) 2 ( 2)( ) 2( 2) 2

m x x x x m m x x m

= + + + + − + + + + +



2 2 2

1 2 1 2 1 2 1 2

( 1) ( ) 2 2( ) 2 ( 2)( ) 2( 2) 2

m x x x x x x m m x x m

 

= + + − + + − + + + + +

 

 



&D!+

1 2 1 2

x x x x

+ = ∨ = 

2 2

16 2

MA MB m

⇒ + = − − 

ef+

( ) 16 2

f m m

= − − 0G

( ;0)

−∞



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNC9

&<+

min ( ) 20

f m

 !

= −



:;3^+

= −



HT 94. 

( )

y C

−

&/!.0(



d y x m

= − +



 !!!#$"!%=8>+

2 2 2

OA OB AB

+ +

 !.0[\4a'

Giải

6'!!(

)!%#A0/+

; 1

x m x

−

= − + ≠

−



( ) 2 0 (1)

g x x mx m

⇔ = − + − = 

 !!!#$"!%

⇔

#A0/@,!%#$"!%-.@

4 8 0

(1) 1 0

m m





∆ = − + >



⇔ ⇔ ∀





= − ≠







D^F

( )

d C

∩

 !!!#$"!%)B!

∀



`a!.!!b<+

1 1 2 2

( ; ), ( ; )

A x x m B x x m

− + − +

)B!

1 2

x x

.!%(#A

0/@

&+

2 2 2 2 2 2 2 2 2

1 1 2 2 1 2 1 2

( ) ( ) ( ) ( )

OA OB AB x x m x x m x x x x

+ + = + − + + + − + + − + −



2 2

1 2 1 2 1 2

4( ) 12 2 ( ) 2

x x x x m x x m

= + − − + +



2 2

4 12 24 (2 3) 15 15

m m m m

= − + = − + ≥ ∀



D^F8

2 2 2

OA OB AB

+ +

 !.0[\"i@-!



HT 95. 

( ).

y C

−

`a!*_3

(2;0)

)%

&/



* !!!#$"!%

A B

+

MA MB

= −

 



Giải

A0/

: 2

d y kx k

= −



A0/'!!(*)+

2 (1)

kx k

= −

−



DB!

≠

/@

( ) (4 1) 4 1 0 (2)

f x kx k x k⇔ = − + + − =



* !!!#$"!%

A B



(1)

⇔

!!%#$"!%

⇔

,,!%#$"!%-.,

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNC@

12 1 0 (*)

(2) 3 0





≠ 



≠



⇔ ∆ = + > ⇔

 

 

> −

 

= − ≠

 











m

1 1 2 2

( ; ), ( ; )

A x y B x y

)B!

1 2

x x

!!%(,)

1 1 2 2

2 ; 2 2

y kx k y x k

= − = −



:!+

1 2

2 2( 2)

2. 2 6 (3)

2 2( 2)

x x

MA MB x x

y y





− = − −



= − ⇔ ⇔ + =





− = − −





 



&•D!+

1 2

4 1

(4)

4 1

(5)

x x





+ =







−







&I)J3F0+

1 2

2 2 4 1

; (6)

k k

x x

k k

+ −

= =



&I)C<+

2 2 2 1 4 1 2

k k k

+ − −

= ⇔ =

[]M

:s+



HT 96. 

6&/*+FE,5N6 !!

!#$"!%

. 4

OAOB

= −

 

)B!4a'

Giải

A0/'!!(6)B!*+

2 3 2 3(1 ) 6 3 0 (1)( 2)

x m x m x m x

= + ⇒ + + + − = ≠ −



6* !!!#$"!%=)>

⇔

@!!%#$"!%-.k,

⇔



9 30 33 0

8 6(1 ) 6 3 0

m m





∆ = − + >



⇔ ∀





− + + − ≠







`a!,!%(#@

/=

N?>

N

+

. 4

OAOB

= −

 

⇒

N,

N,

NEkJ⇒

12 15 7

2 12

−

= − ⇒ =



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNC,

HT 97. &/0G6+

− +

−

.!=8>'*!  =>"iJ)

=>)3v)B!

y x



Giải

Z=>

⊥

*+FE5⇒#=>+FEk5N

A0/'!!(6)B!=>+

( ) ( 3) 2 1 0 ( 2) (1)

x m g x x m x m x

− +

= − + ⇔ = − + + + = ≠

−



 !,!=8>/#@b!!%#$"!%

;

A B

x x

)-.,

2( )

( 3) 4(2 1) 0

( 1) 4 0;

(2) 0

4 ( 3).2 2 1 0

g x

m m





∆ >

+ − + >



⇔ ⇔ ⇔ − + > ∀

 

 

≠

− + + + ≠

 









&D!+

. 2 1

A B

x x m





+ = +







= +





Hm-.+

;

A A B B

y x m y x m

= − + = − +



2 2 2 2

2 2

: 4 16 ( ) ( ) 16 ( ) 4 . 8

( 3) 4(2 1) 0 2 3 0

B A B A B A A B

Maø AB AB x x y y x x x x

m m m m

= ⇔ = ⇔ − + − = ⇔ + − =



= −



⇔ + − + = ⇔ − − = ⇔







NDB!EF)#@+

6 7 0 3 2 2

x x x y

− + = ⇔ = ± ⇒ = ±



⇒

(3 2; 2); (3 2; 2) (3 2; 2); (3 2; 2)

A B hoaëc A B+ − − + − −



NDB!Ek@F)@+

2 1 0 1 2 2 2

x x x y

− − = ⇔ = ± ⇒ = − ±



⇒

(1 2; 2 2); (1 2; 2 2) (1 2; 2 2); (1 2; 2 2)

A B hoaëc A B+ − − − − + − − + + − −



:;3^+

HT 98. 

2 3

( ).

y C

−

&/



: 2 0

d x y m

− + =

 !

!!#$"!%3'*A

Giải

A0/'!!()

+

2 3

2 2 3 0 (1)

x m x mx m

−

= + ⇔ + + + =





 !!!#$"!%-!)~-!+@!!%#$"!%-.k@

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNC

4 40

8 24 0

2 3 0

4 40

m m







> +

∆ = − − >





⇔ ⇔







− + + ≠



< −









6!!!3'*A-!)~-!+

1 2

1 2 1 2

2 2 0

(2 )(2 ) 0

4 2 ( ) 0

x x m

x m x m

x x m x x m





+ + >



+ + + >



⇔

 

 

+ + >

+ + + >

 









2( 3) 2 ( ) 0

m m m





− + >



⇔





+ + − + >





⇔ >



:;<#!w3-!%+

4 40

> +



HT 99. 

−

6&/

: 1

d y x m

= − + +

 !!!

#$"!%=8>



AOB

a

Giải

A0/'!!(6)B!*+

1 ( 2) 2 5 0 ( 2)

x m x m x m x

= − + + ⇔ − + + + = ≠

−



#A0/0G!!%#$"!%/+

4 16 0

0; 2

2 2( 2) 2 5 0

m m

x m

m m





− + >



∆ > ≠ ⇔ ⇔ ∀





− + + + ≠







`a!

1 1 2 2

( ; 1); ( ; 1)

A x x m B x x m

− + + − + +

,!!(6)*





AOB

a/

2 2 2 2 2 2

2 1 1 2

2( ) ( 1) ( 1)

AB OA AB x x x m x m< + ⇔ − < − + + + − + +



1 2 1 2

2 ( 1)( ) ( 1) 0 3

x x m x x m m

⇔ − + + + − + < ⇔ > −



:;3^+lk



HT 100. 

3 2

( )

y C



y x

 !!!

=8>&/

y x m

= +

 !!!8Z=>Z/"/

Giải

 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNCJ

6'!=8>!%(#A0/+

3 2

( 1; 1); (2;2) 3 2

x A B AB



= −



= ⇔ ⇒ − − ⇒ =







&+8Z3'FE5N)

D AB



G

≠

9)ZE=>E

3 2



A0/'!!(*)+

3 2

( 1) 2 2 0 (*)

x m x m x m

= + ⇔ + − + − =



* !!!#$"!%#L!+

10 9 0

m m





∆ = − + > ⇔







`a!?N?Z"?"N)B!8"!%(#A0/M

ZE

3 2



⇔



2( ) 3 2

a b

− =

⇔



0 ( )

10 9 9

10 ( / )

m loai

m m

m t m





− + =







:s+E@9



HT 101. 

2 1

−

&/*+

y x m

= +



 !!!#$"!%=8>

∆

4=>)3v !4

Giải



•

A0/'!!()*+

( 3) 1 0, 1

x m x m x

+ − + − = ≠

 M

 M

2 5 0,

m m m R

∆ = − + > ∀ ∈

)M-v!%5E@

 ⇒M3v,!%#$"!%

A B

x x

&gD!f+

. 1

A B

x x m





+ = −







= −







 :!+

(

)

(

)

; , ;

A A B B

A x x m B x x m

+ +



OAB

∆

)3v !4/

(

)

(

)

. 0 0

A B A B

OAOB x x x m x m

= ⇔ + + + =

 



      

(

)

2 0 2

A B A B

x x m x x m m

⇔ + + + = ⇔ = −



 D^F+Ex,

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNC



HT 102. +

−

p!0i)B!a!!.0/0G

3vm#!=8>i)w!.()[

A A

B B

x y m





− + =







− + =







 Giải

•

&+

, ( ) :

A A A A

B B B B

x y m y x m

A B d y x m

x y m y x m

 

 

− + = = +

 

⇔ ⇒ ∈ = +

 

 

− + = = +

 

 



 ⇒=8>!!()*A0/'!!()*+

 

( ) ( 3) (2 2) 0 ( 2)

x m f x x m x m x

+ = ⇔ = + − − + = ≠

−

 M

 M

2 17 0,

m m m

∆ = + + > ∀

⇒*3v !!!#$"!%=8>

 D 

1. (2) 4 0 2

A B

f x x

= − < ⇒ < <

m

B A

x x

< <

#



HT 103. 

x m

−

@p!0i)B!a!

≠



@*+

2 2

y x m

= −

 !!!#$"!%=8>3''6

*014584Fb< !.!H8y&/

OAB OMN

S S



Giải

A0/'!!(@)*+

2 2

2 1

2 2 2 2 0 (2)

x m

x m mx m x m x

mx m

 

−







= − ⇔ − − = ≠ −











 



Z

≠

G

(2) ( ) 2 2 1 0 (*)

f x mx mx x

 







⇔ = − − = ≠ −











 



 !!!=8>/#A0/M#L!,!%#$"!%

;

A B

x x

-.

−



' 2 0

1 2

1 0





∆ = + >



 

⇔ ⇔ ∀ ≠











− = + ≠















 







 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNCC

Hm-.8+

A B

x x

G=8>3vi0G'6

:‚46

⊥

=>⇒46

( , )

O d

−

= =

s !=8>

∈

*⇒



HT 104. 

2 1

−

&/0G!.(!H)y

!;#3F; !H)y!!%^ !J!^#'/

Giải

`a!H8y,!3'!.(

&!;#3F; !H!!%^ !!!=8>

&!;#3F; !y!!%^ !!!8Z

A0/!;#3F; !H* +

( ) ( )

( ) ' ( )

m m

f x f x m f

= − +



⇒&a'!

( )

2 4

1; , 2 1;2

A B m

 







−











−

 



&A7+

( )

2 1

1; , 2 1;2

C D n

 







−











−

 



A0/A=Z+

3 6(2 4)(2 1)

( 1)( 1) (2 2)( 1)

m n

y x

m n m n

− + −

= +

− − − −



=Z%+

( 1)( 1)

m n

−

− −



&A7ƒ>%+

( 1)( 1)

m n

−

− −



⇒

BC AD



⇒Ha!!H8y3',.(w3[]FG3b3"!.

HT 105. +

4 3

mx m

x m

− +

−

p[0i)B!a!

≠

83v!_3

!

)

&I!!

)

]F^##A0/(!%

"i@8&g*!%g/!B! "q!

!F)01

Giải

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNCO

`a!

0 0

( ; )

x y

!(

⇒

#A0/+

0 0 0 0

( 4) 3 0

x y m x y

+ − + − =

2)B!

∀ ≠



0 0

4 0

3 0

4 3 0

x y

x x

∆

















+ − =

+ − =







⇔ ⇔ ⇔

 





 

− =



− + =



 

























D^F!!+

(1;3), (3;1).

A B



A0/!_3=%"i



3 3 3

3 ( 1) ( )

2 2 2

y x y x d

− = − ⇔ = + 

A0/_3>%

+

3 3 7

1 ( 3) ( )

2 2 2

y x y x d

− = − ⇔ = −

`!!(

( )

)B!



( 1; 0),

−

(

( )

)B!



 

















 



:L.!h

1 2

( ),( )

d d

ƒg!w3(/

3 7

2 2

13 3

 







− −











 

= = =

 

















 



D^F*!%g/#L!/+

13 5 4 5 20

( ) 13 . . 13.

2 3 3 3

13 13

S AC BD

 









= + = + = =













 



HT 106. 

2 1

( ).

y C

−

`a!u!!(!!%^(DB!!.0(

/

y x m

= − +

 !!!#$"!%=8>)!.u=>w3

Giải



y x m

= − +

 !!!#$"!%-!)~-!#A0/3

 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNCc

,!%#$"!%+

2 1

(1 ) 1 0

x m

x m x m





≠

−



= − + ⇔





+ − + − =

−







(1 ) 4( 1) 0

(*)

1 1 1 0

m m







∆ = − − − >





⇔ ⇔







+ − + − ≠













&+

1 2 1 2

(1;2), 1 & 1

I x x m x x m

+ = − = −



`a!

1 1 2 2

( ; ), ( ; )

A x y B x y

)603!(=>

:!+

1 1 2 2

;

y x m y x m

= − + = − +

)

2 1 1 2

1 1 3 3

; ; ; ; ( ; )

2 2 2 2

m m m m

H IH AB x x x x

   

− + − −

 

 

 

= − −

 

 

 

 

 

   

 



IAB

∆

w3

2 2

(**)

IA IB

IH AB





 

⇔ ⇔

 

 











&+

2 2

1 2 1 2

( ) ( 1) 0

IA IB x x x x m

 

= ⇔ − + − − =

 

 



Z

1 2

x x m

+ = −

GpF2)B!a![]M

&+

2 2

2 1 1 2

( 3) 3

(**) ( ) 4 3 ( 1) 4( 1)

2 2

x x x x m m

−

   

⇔ = − − = − − −

   

   



6 3 0 3 6

m m m

⇔ − + = ⇔ = ±

.!.0F[]M

:s+

3 6

= ±



HT 107. 

( )

y C

−

&/.!.0(



y x m

= − +



 !!!#$"!%

A B



OA OB

"i

60 .

DB!

a'

Giải

A0/'!!+

( ) 0 (1)

x m g x x mx m

= − + ⇔ = − + =

−

)B!

≠





y x m

= − +

 !!!#$"!%+

⇔

A0/@!!%#$"!%

≠



 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾNCj

4 0

(*)

(1) 0

1 0

m m















∆ = − >







⇔ ⇔ ⇔

 





 

≠



 







 ≠







`a!

1 2

x x

!!%(„8+

1 2

. (**)

( ) ( ) 0

x x m

g x g x





+ =







= =







.!!

1 1 2 2

( ; ), ( ; )

A x x m B x x m

− + − +

)

1 1

2 2

( ; )

OA x x m

OB x x m





= − +







= − +









:!+

1 2 1 2

2 2 2 2

1 1 2 2

( )( )

cos60 cos( ;

2 2 2 2

x x x m x m

OA OB

x mx m x mx m

+ − + − +

= =

− + − +

 



2 2

1 2 1 2 1 2 1 2

2 2 2 2

1 2

2 ( ) 2 ( )

2 ( ) 2 2 ( ) 2 2 2

x x m x x m x x m x x m

m m

g x m m g x m m m m m m

− + + − + +

⇔ = = =

−

+ − + − − −



2 4

m m m



= −





− =



⇔ ⇔ =



− = −











:;<#!w3-!%M+

2 6

m m

= − ∨ =



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN 

PHẦN 4: TIẾP TUYẾN

HT 108. 

3 2

3 1 ( ).

y x x C

= − +

 !"

#$ %$&'

Giải

()* !"$+,#$&

0 0 1 1 1

( ; ), ( ; )

M x y M x y



-$./01234

2 3 2

0 0 0 0

(3 6 ) 2 3 1

y x x x x x

= − − + +

!

2 3 2

1 1 1 1

(3 6 ) 2 3 1

y x x x x x

= − − + +



5012673012864

2 2

0 0 1 1

3 2 3 2

0 0 1 1

3 6 3 6

2 3 1 2 3 1

x x x x





− = −







− + + = − + +







()96$0:4

0 1

x x

;$<)'



HT 109. = > 

2 1

−

' ? 01 2    /@ A) B C $&

(1;2)

$@

'

 Giải

•D#$&

0 0

( ; ( )) ( )

M x f x C

∈

.0124

  

0 0 0

'( )( ) ( )

y f x x x f x

= − +

⇔

2 2

0 0 0

( 1) 2 2 1 0

x x y x x

+ − − + − =

E

 -)BC$&F8GH$E@

2 2

1 ( 1)

−

⇔ =

+ −

⇔









 BI24

1 0

x y

+ − =

!

5 0

x y

+ − =



HT 110. 

3 2

(1 2 ) (2 ) 2

y x m x m x m

= + − + − + +

83'D2

 $& $+ ,    8 .   # !" $0J K L4

7 0

x y

+ + =

 .

/ @

cos

α =

'

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN 8

 Giải

•(MA39.

⇒

.?DD

( ; 1)

n k

= −



 N0JKL.?DD

(1;1)



'

 D.

1 2

1 1

cos 12 26 12 0

2 1

n n

k k

n n





−



= ⇔ = ⇔ − + = ⇔





 



 OPD)Q⇔RS%012.94

 



′



′





⇔

3 2(1 2 ) 2

x m x m





+ − + − =



+ − + − =





⇔



∆ ≥



∆ ≥





⇔

8 2 1 0

4 3 0

m m



− − ≥



− − ≥







 ⇔

1 1

;

4 2

; 1

m m





≤ − ≥



≤ − ≥





⇔

≤ −

T

≥



HT 111. 

3 2

2 ( ).

y x x x C

= − + −

D2M$%B$&6UV$&

$.AW$0:!"$+,!.X@

45 .



Giải

Y$&Z6[/3\AW$0:!"3



(.3

45 ,



.9.369.

]3#.

9.@^8T8'

(M

0 0

( ; )

M x y

3$&L!

0 0

' 3 4 1 1

y x x





⇒ = − + − = ± ⇔









-

0 0

0 0 :

x y d y x M O

= ⇒ = ⇒ = − ⇒ ≡



-

0 0

4 4 4 32 32

: ;0

3 27 3 27 27

x y d y x x M

   

 

 

 

= ⇒ = − ⇒ = − − = − + ⇒

 

 

 

 

 

   



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN H

HT 112. 

3 2

3 1

y x x

= − +

.$+,'D2$&_/P%$+,

#_!P!"!$%L$#_P`

4 2

'

 Giải

•()*

3 2 3 2

( ; 3 1), ( ; 3 1)

A a a a B b b b

− + − +

%/!"

a b

≠

'

 ?2#_!P!"64

 

( ) ( )

y a y b

′ ′

⇔

2 2 2 2

3 6 3 6 2( ) 0 ( )( 2) 0

a a b b a b a b a b a b

− = − ⇔ − − − = ⇔ − + − =



 ⇔

2 0 2

a b b a

+ − = ⇔ = −

'?2

a b

≠

6

2 1

a a a

≠ − ⇔ ≠



 D.4

2 3 2 3 2 2 2 3 3 2 2 2

( ) ( 3 1 3 1) ( ) ( 3( ))

b a b b a a b a b a b a= − + − + − + − = − + − − −



  

2 3

( ) ( ) 3 ( ) 3( )( )

b a b a ab b a b a b a

 

= − + − + − − − +

 

 



  

2 2 2

( ) ( ) ( ) 3 3.2

b a b a b a ab

 

= − + − − + −

 

 



  

2 2 2

( ) ( ) ( ) 6

b a b a b a ab

 

= − + − + − −

 

 

2 2 2

( ) ( ) ( 2 )

b a b a ab

= − + − − −



 

2 2 2 2 2

( ) 1 ( 2 ) (2 2 ) 1 ( 2 2)

b a ab a a a

   

= − + − − = − + − −

   

   



  

2 2 2 4 2

4( 1) 1 ( 1) 3 4( 1) ( 1) 6( 1) 10

a a a a a

 

   

 

= − + − − = − − − − +

   

   

 



  

6 4 2

4( 1) 24( 1) 40( 1)

a a a

= − − − + −



 Z

4 2

AB =

6

6 4 2

4( 1) 24( 1) 40( 1) 32

a a a

− − − + − =



 

6 4 2

( 1) 6( 1) 10( 1) 8 0

a a a

⇔ − − − + − − =

 E

 NT

( 1) , 0

t a t

= − >

'-$.Ea4

 

3 2 2

6 10 8 0 ( 4)( 2 2) 0 4

t t t t t t t

− + − = ⇔ − − + = ⇔ =

 ⇒

3 1

( 1) 4

1 3

a b



= ⇒ = −



− = ⇔



= − ⇒ =







 ?bH$&)QOPD34

(3;1), ( 1; 3)

A B

− −

'

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN c

HT 113. 

−

'D26[S)B$&C$.AW$0:LS%

"'

 Giải

•(M

(0; )

M y

3$&I2'D$0JKVZ.L#4

y kx y

= +

L

 L3

( 1) 2( 1) 1 0 (1)

( 1)

o o o

y x y x y

kx y

x k









− − + + + =

= +



−

 

⇔ ⇔

 

−

 

≠ =

 

−

 



−





E

 OPD⇔9E.89

⇔

8.89AB8

 

1 1

; 1 8

' ( 1) ( 1)( 1) 0

0; 1 2

o o o

x y k

y y y

x y k

 







≠



= = ⇒ = −



 



⇔ ∨ ⇔

 



 

∆ = + − − + =

 

= = − ⇒ = −









 



 ?b.H$&I234ZG8!ZGd8'



HT 114. 

y x x

= −

 'D26 $0JK

d y x

= −

B$&  C $.AW

$0:$ He@9!"$+,'

 Giải

•(M

( ; ) ( )

M m m d

− ∈

'

 D$0JK∆$V$&Z!.9.A.L#4

( )

y k x m m

= − −



 ∆3⇔9D.9

3 ( ) (1)

3 3 (2)

x x k x m m

x k





− = − −







− =





 E'

 DH!8$0:4

3 2

3 (3 3 )( ) 0

2 3 4 0

(**)

3 4

x x x x m m

x mx m

− − − − + =

⇔ − + =

⇔ =

−



fg4

( )

3 4

f x

−

'DbB$,4h`

ℝ

ij

2 3 2 3

;

3 3

−

k

.4lm`

4 2

6 24

3 4

x x

−

Glm`⇔





= ±







 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN n

  



DCZAW$0:$ "$+,

⇔EE.9e@9'

ho!@)@6.4EE.H9e@9⇔





= −







⇒B$&I234_HGdH!PdHGH'



HT 115. 4

3 2

y x x

= − +

'D2S)$&6$0JK

/C$.AW

$0:$ H"$+,'

Giải

(MZ

Gn3$&I2'

012$0JKLVZ!"9.A34`A^



pn

L3$+,⇔9.94

( ) 4 3 2 (1)

3 3 (2)

k x x x x

k x





− + = − +







= −







DH!8$0:4



( )

2 3

3 2 3

3 2

0 0

(3 3)( ) 4 3 2

3 3 3 3 3 2

2 3 3 2 0

1 2 (3 2) 3 2 0 (3)

o o

x x x x x

x x x x x x x

x x x x

x x x x x

− − + = − +

⇔ − − + = − +

⇔ − + − =

 

⇔ + − + + + =

 

 



N&AW$0:H"$+,A!Ac.$ H9'

-2

∞

-2 0

∞

0 0 2 - - + - - +

f’(x)

f(x)

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN q

⇔

0 0

2 (3 2) 3 2 0

x x x x

⇔ − + + + =

.4

pH9$.89@^8G

p.9AgAB^8'

()2$ c$&4^8GnG^HrcGnGHGn

  

HT 116. 

3 2

y x x

= − + −

'D26$0JK

: 2

d y

B$&C$.

AW$0:ce@9!"$+,'

 Giải

•(M

( ;2) ( )

M m d

∈

'

 D$0JK∆$V$&Z!.9.A.L#4

( ) 2

y k x m

= − +



 ∆3⇔9D.9

3 2

3 2 ( ) 2 (1)

3 6 (2)

x x k x m

x x k





− + − = − +







− + =





 E'

 DH!8$0:4

3 2 2

2 3( 1) 6 4 0 ( 2) 2 (3 1) 2 0

x m x mx x x m x

 

− + + − = ⇔ − − − + =

 

 



  ⇔

(3)

( ) 2 (3 1) 2 0

f x x m x





= − − + =







 DCZAW$0:c$$+,

⇔

9E.c9e@9

 

⇔

c.9e@9ABH

(2) 0

m hoÆc m









∆ >

< − >



⇔ ⇔

 

 

≠

 

≠







'

 ?bCB$&ZGH∈L4`H!"

m hoÆc m





< − >







≠





.&AW$0:c$$+

,'

HT 117. 

(

)

(

)

2 2

1 . 1

y x x

= + −

'$&

( ;0)

A a

'D2$&C_AW$0:c

e@9!"$+,'

 Giải

•D.

4 2

2 1

y x x

= − +

'

 012$0JKL$V

( ;0)

A a

!.9.A4

( )

y k x a

= −



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN s

 L3⇔9012.94

4 2

2 1 ( )

( )

4 4

x x k x a

x x k





− + = −







− =







 D.4

( ) ( )

1 0

I A





⇔





− =





 tu

4 ( 1)

( )

( ) 3 4 1 0 (1)

x x k

f x x ax





− =







= − + =







 pD0= vu_/%LS3

: 0

d y

'

 p?b$&C_AW$0:ce@9!"2$<A9w!= $x3=vuPxyH

vuv@9

( ; )

x k

!1y 

≠ ±

/0y 3=01z=8).H9e@9AB

⇔

4 3 0

( 1) 0





′

∆ = − >







± ≠





⇔

3 3

1 1

2 2

− ≠ < − ≠ >

hoÆc

a a



HT 118. 

3 2

3 2.

y x x

= − +

D26$0JK

B$&C$..&AW

$0:H"$+,!H$.!\.!"'

Giải

(M$&I23

( ;2).

M m



{bg4$0JK

x m

$VZ|$0J!!"U!.A\

&36MVZ$<.L#4

( ) 2.

= − +

y k x m



?b/9).94

3 2

3 2 2

3 2 ( ) 2

3 2 ( )(3 6 ) 2

3 6





− + = − +



⇒ − + = − − +





− =





x x k x m

x x x m x x

x x k



3 2

0 0

2 (3 3) 6 0

2 3( 1) 6 0 (1)



= ⇒ =



⇔ − − + = ⇔



− + + =





x k

x m x mx

x m x m



D0J:84

D3

$0JK!\.!"..L#4

x c

?b

A\.$0J!\.!"'

?b/$&$0J.!\.20128).H9

1 2

x x



4

1 2

'( ). '( ) 1 (2).

= −

y x y x



0128.H9e@9A

∆ >



2 2

9 18 9 48 0 9 30 9 0 (2)





⇔ + + − > ⇔ − + > ⇔





m m m m m



 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN 

D$,3}?.4

1 2 1 2

3 3

; . 3

+ = =

x x x x m



D.4

2 2

3 3

3 6 2 3( 1) 6 (3 1) 9

2 2

 

− = − + + + − −

 

 

x x x m x m m x m



2 2

1 1 1 1 1 2 2 2

3 3

'( ) 3 6 (3 1) 9 , '( ) 3 6 (3 1) 9

2 2

⇒ = − = − − = − = − −

y x x x m x m y x x x m x m



1 2 1 2

3 3

(2) '( ). '( ) 1 (3 1) 9 (3 1) 9 1

2 2

   

   

⇔ = − ⇔ − − − − = −

   

   

y x y x m x m m x m



2 2

1 2 1 2

9 27

(3 1) (3 1).( ) 81 1

4 2

⇔ − − − + + = −

m x x m m x x m



2 2

9 27 3 3

(3 1) .3 (3 1). 81 1

4 2 2

⇔ − − − + = −

m m m m m



27 1 0

⇔ + = ⇔ = −

m m

~Q$<A9H

-•4

 







−











 



HT 119. 

3 2

( ) ( 1) (4 3 ) 1

y f x mx m x m x

= = + − + − +

.$+,3



'D2BB,

  6 $+, 



+ # % $& L S .  $% e    # $.

!\.!"$0JK

: 2 3 0

d x y

+ − =

'

Giải

 •L.9.

−

⇒.9.

'(M3$%$&24



2 2

'( ) 2 2( 1) (4 3 ) 2 2( 1) 2 3 0

f x mx m x m mx m x m

= ⇔ + − + − = ⇔ + − + − =

8

 OPD⇔8.$ %9e'

 p{

28

2 2 1

x x

⇔ − = − ⇔ =

3#

 p{

≠

2L€S0128.H93

hay x=

2 3

−



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN •

 h$.$&8.%9e2

2 3





−



< ⇔







 ?b

hay

m m

< >

'



HT 120. D2S)BB,6$+,

( )

3 2

( 1) (4 3) 1

y mx m x m x

= + − + − +

 + # $   $& .  $% L01  

#$.!\.!"$0JK•4

2 3 0

x y

+ − =



Giải

Cách 1: .m`

2( 1) 4 3

mx m x m

+ − + −



DC6I@B.4

'. 1

 







− = −











 

.$ 9L01e@9

⇔

2( 1) 2 3 0

mx m x m

+ − + − =

.9e@9'

1 1

4 4 1 0

' 0

2 2

0 0 1 1 2

2 3

0 2

2 3

m m

S m





≠



≠







≠







 − + >







≠ < <

∆ >





  

−

⇔ ⇔ ⇔ ⇔

  



  

> < <



  

< <

  



  

> 

−

  





 

< <

 





?b

1 1 2

0; ;

2 2 3

   

 

 

 

∈ ∪

 

 

 

 

 

   

3BB,I2

Cách 2: .

' 2( 1) 4 3

y mx m x m

= + − + −



DC6I@B.4

'. 1

 







− = −











 

.$ 9L01e@9

⇔

2( 1) 2 3 0

mx m x m

+ − + − =

8.9e@9'

+) D584`C8.4`^83#

pD5H4

C8.`±83#

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN ‚

pDc4

m m

≠ ≠

DC8.H9

2 3

x x

−

= ∨ =



N<A9@B⇒

2 3 2

0 0

−

> ⇔ < <



-:)c0J:6.B,I234

1 1 2

0; ;

2 2 3

   

 

 

 

∈ ∪

 

 

 

 

 

   



 

HT 121. 

4 2

( ) 2

y f x x x

= = −

'D63S$&e@9_!P.$%3I

30:3!@'D2$<A9$!"!@$&#_!P!"

'

 Giải

•D.4

'( ) 4 4

f x x x

= −



 59.#_!P3

3 3

'( ) 4 4 , '( ) 4 4

A B

k f a a a k f b b b

= = − = = −



 D#_/P3I30:.01234

 

( )( ) ( ) ( ) ( ) ( )

y f a x a f a y f a x f a a

′ ′ ′

= − + ⇔ = + −



 

( )( ) ( ) ( ) ( ) ( )

y f b x b f b y f b x f b b b

′ ′ ′

= − + ⇔ = + −



 5#_!PT7A!A4

 

3 3

a a = 4b

2 2

4 4 4 ( )( 1) 0

A B

k k b a b a ab b

= ⇔ − − ⇔ − + + − =

  8

 ?2_!Pe@96

a b

≠

/L$.8⇔

2 2

1 0

a ab b

+ + − =

  H

 ZTAB#_!P7A!A4

 

2 2

4 2 4 2

1 0

( )

3 2 3 2

( ) ( ) ( ) ( )

a ab b

a b

a a b b

f a af a f b bf b





+ + − =



 

⇔ ≠ ⇔

 

 

′ ′

− + = − +

− = −

 











 ()9$0:93

( ; ) ( 1;1)

a b

= −

T

( ; ) (1; 1)

a b

= −

/901!"

7%T$&6$+,3

( 1; 1)

− −

!

(1; 1)

−



 ?b$<A9I!$$&#_!P!"34

 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN •

   

2 2

1 0

a ab b

a a b





+ + − =







≠ ± ≠







HT 122. 

'?012$+,/@A)

BCe$$+,$33"S'

Giải

 •DL$+,#$&Z.$%

≠ −

%.0124

 

2 2

4 2

( ) 4 ( 2) 2 0

( 2)

y x a x a y a

= − + ⇔ − + + =



 De$3

(

)

2;2

−

'D.4

 

4 2

8 2 8 2 8 2

( , ) 2 2

2 2 2

16 ( 2) 2.4.( 2)

a a a

d I d

a a

+ + +

= ≤ = =

+ + +



( , )

d I d

3"SA

( 2) 4





+ = ⇔



= −





'

 DC$..

y x

!

y x

= +

'



HT 123. 

2 3

 8'?012$+,8/@

$.|U/U3I30:#$&e@9_/P!B[_Pe#

M$%['

 Giải

•(M

0 0

( ; )

x y

3#$%$&⇒

( ) 0

(2 3)

y x

−

′

= <



 ∆[_Pe#[6∆!"$0JK

y x

= −

!2.9.

e'{ƒ34

( ) 1

(2 3)

y x

−

′

= = −

⇒

0 0

1 1

2 0

x y



= − ⇒ =



= − ⇒ =







 p?"

0 0

1; 1

x y

= − =

⇒∆4

1 ( 1)

y x y x

− = − + ⇔ = −

3#

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN •8

 p?"

0 0

2; 0

x y

= − =

⇒∆4

0 ( 2) 2

y x y x

− = − + ⇔ = − −

b

 ?b012I234

y x

= − −

'



HT 124. `

2 1

−

'•b012$+,

|BU[/[3I30:#B$&_!P)Q[_`n[P'

 Giải

•()*L#

0 0

( ; ) ( )

M x y C

∈

|[#_/[#P

OA B

'

 h∆[_P!\#[6

tan

= =

⇒59.L@

T

−

'

 59.L3

2 2

0 0

1 1 1

( ) 0

( 1) ( 1)

y x

x x

′

= − < ⇒ − = −

− −

⇔

0 0

1 ( )

3 ( )

x y





= − =



= =







 -$..H)Q34

1 3 1 5

( 1)

4 2 4 4

1 5 1 13

( 3)

4 2 4 4

y x y x

 

 

= − + + = − +

 

⇔

 

= − − + = − +

 

 

'



HT 125. ?012$+,

−

@|[/[3I30:

#_!PB[_P~Q4

AB OA



Giải

B84(M

( ; )

o o

M x y

/

( 2)

≠

%$+,'012#Z.L#4

( )

( 2)

y x x

−

− = −

−



hB|U[/[#B$&_/P!B[_P.

AB OA

6B

[_P!\e#['• $L!\.!"%H$0JeB`

T`^

pD584L!\.!"$0JeB`

 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN •H

.4

2 : ( )

1 ( 2) 4

4 : 8

( 2)

x pt d y x loai

x pt d y x



= ⇒ = −

−



= − ⇔ − = ⇔



= ⇒ = − +

−







pD5H4L!\.!"$0JeB`^

.4

( 1) 1

( 2)

ptvn

−

− = − ⇔

−



-3b4?b.8~Q6I@BL4`^p•

Cách 2:

{bgB_[P!\#[6.4_P[`

sin

= =

6B_[P

!\e#[/012#$&

( ; )

o o

M x y

.L#4

( )

( 2)

y x x

−

= − +

−



h€LR$0:4

2 2

;0 ; 0; ( 4) 0

( 2)

o o

x x

A B x x

   

 

 

 

 

= ⇔ − =

 

 

 

 

 

 

−

   



p?"

= 0.01234`^3#

p?"

= 4.01234`^p•



HT 126. 

2 3

−

.$+,'D26X$&Z#Z

|9b#_/P_P|S'

 ••S$&

; 2

M m

 

















−

 

(

)

∈

'D.4

( )

( 2)

y m

′

= −

−



 DL#Z.0124

1 1

( ) 2

( 2)

y x m

= − − + +

−



 ($&L!"9b$34

2;2

 

















−

 



 ($&L!"9b34

(2 – 2;2)

B m



 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN •c

 D.4

2 2

4 ( 2) 8

( 2)

AB m

 

 

= − + ≥

 

−

 

 

'hS„`…)⇔









 ?b$&ZI2.M$%34

(3;3)

T

(1;1)



HT 127. 

2 3

−

'Z3$&@SA26'D#Z|B

$0J9b#_!P'(MF3$&B$0J9b'D2#$%$&

Z$0J]#BF_P.L9R~S'

 Giải

•()*

0 0

2 3

; , 2

M x x

 

−









≠









−

 

/

(

)

'( )

y x

−



 012∆!"#Z4

(

)

2 3

( )

y x x

−

= − +

−



 D#$%$&_/P∆!"9b34

( )

2 2

2; ; 2 2;2

A B x

 

−









−









−

 



 D S

2 2 2

2 2

A B

x x x

x x

+ + −

= = =

/

2 3

2 2

A B

y y x

+ −

= =

−

    Z 3  $&

_P'

 ZTABFHGH!∆F_P!\#F6$0J]#BF_P.L9R

  ;`

2 2 2

0 0

2 3

( 2) 2 ( 2) 2

( 2)

IM x x

π π π π

 

 

−

 





 





= − + − = − + ≥

 



 





 





−

 

 

 

 

 



 hS„`…)A

( 2)





− = ⇔



−







 h$.$&ZI23Z8G8TZcGc

HT 128. 

3 2 2

2 1 ( ).

y x mx m x m C= − + − +

D2

$&$+, !"U

'

Giải

N+,

3 2 2

2 1

y x mx m x m

= − + − +

 !"U

 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN •n

3 2 2

2 2

2 1 0

3 4 0

x mx m x m

x mx m





− + − + =



⇔





− + =





.9'

3 2 2

2 1 0(1)

x mx m x m

x m





− + − + =





⇔









=













?"

x m

!8$0:4



?"

x m

!8$0:4

3 3 3 3

6 9 3 1 0 4 3 1 0

1 3

2 2

x x x x x x

x m

− + − + = ⇔ − + =



= − ⇒ = −



⇔



= ⇒ =







-3b4

1 3

m m m

= ∨ = − ∨ =



HT 129. 

2 1

−

.$+,'(MF3$&9b'D2$&Z

%#Z|H9b#_!P!"!BF_P$#B

,~S'

 Giải

•($&H9b3

(1;2)

'(MZ

 

















−

 

∈'

 pDDD#Z.L#4

3 3

( ) 2

( 1)

y x x

−

= − + +

−



 pD#$%B$&!"H9b4_

1;2

 

















−

 

/P

(2 1;2)

−



 pD.4

1 1 6

. 2 1 2.3 6

2 2

IAB

S IA IB x

∆

= = ⋅ ⋅ − = =

−

$!L

 p∆F_P!\.L9RA\$†⇒!∆F_P$#B,~SAF_`FP

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN •q

  ⇔

1 3

2 1

1 3



= +



= − ⇒



−

= −





 ?b.$&Z~Q$<A9

(

)

1 3;2 3

M + +

/

(

)

1 3;2 3

M − −



 -$.!∆_FP`

4 3 2 6

'

 Chú ý: ?"HL01/@)@`;A\$†2@&`

2 2

a b a b

+ + +

~S

A!A`@'

 Db!b4`

2 2

a b a b

+ + +

≥

2 2 (2 2) (2 2)

ab ab ab S

+ = + = +

'

  hS‡`‡)⇔`@'



HT 130. 4

−

'$&

(0; )

A a

'D2$&C_AW$0:H"$+

,H$&01!<HRU'

 Giải

•012$0JKL$V

(0; )

A a

!.9.A4

y kx a

= +



 L3⇔59D

( 1)

kx a





= +



−





−



−





.9

    ⇔ D4

(1 ) 2( 2) ( 2) 0

a x a x a

− + + − + =

 8 . 9

≠

'

 N&V_.H28).H9e@9

1 2

x x



  ⇔

3 6 0





≠



≠



⇔

 

′

 

> −

∆ = + >

 







 E

 -$..4

1 2 1 2

2( 2) 2

;

1 1

a a

x x x x

a a

+ +

+ = =

− −

!

1 2

3 3

1 ; 1

1 1

y y

x x

= + = +

− −



 N&H$&!<HR$!"U2

1 2

. 0

y y



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN •s

  ⇔

1 2

3 3

1 . 1 0

1 1x x

   

 

 

 

+ + <

 

 

 

 

 

− −

   

⇔

1 2 1 2

. 2( ) 4

. ( ) 1

x x x x

+ + +

− + +

⇔

3 2 0

+ >

⇔

> −



 -:!"$<A9E$0:4





> −







≠





'



HT 131. 

−

'$&

( ; )

o o o

M x y

%$+,'D#Z



|

B9b#B$&_!P'Z



3$&$#K_P'

 Giải

•

( ; )

o o o

M x y

∈⇒

= +

−

'

 012L#Z



4

0 0

( )

( 1)

y y x x

− = − −

−



 ($&L!"B9b34

0 0

(2 1;1), (1;2 1)

A x B y

− −

'

  ⇒

0 0

;

2 2

A B A B

x x y y

x y

+ +

= =

⇒Z



3$&_P'



HT 132. 4

−

'M$+,$<3b!"

$0J9b%B.L9RA\$†'

 Giải

•()*Z

;

 

















−

 

∈'

 DDDL#Z4

( ).( )

y y a x a

′

= − +

−

⇔

2 2

3 4 2

( 1) ( 1)

a a

y x

a a

− + −

= +

− −



 B$&L!"B9b34

 













 

−

/

(2 1;1)

B a

−

'



→

 

















−

 



⇒

−

G

(2 2;0)

IB a

→

= −



⇒

2 1

IB a

= −



 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN •

 h9R

IAB

∆

4;

IAB

∆

`

IA IB

`s$!L

⇒

NZ'

 e~01o$!"

2 4

−

N;4;`8H'



HT 133. `

'(MF3$&H$0J9b/

∆

3%@SAˆ

$+,'L3A)BCF$

∆

'D2B,3"SL'

 Giải

•

( 1)

−

′

'($&$0J9b3Fd8G8'()*

; ( )

M x C

 









∈









 



 012

∆

!"$+#Z34

 

(

)

( )

y x x

−

= − +



(

)

(

)

(

)

0 0 0 0

1 1 2 0

x x y x x x

⇔ + + − − + + =



 -)BCF$

∆

3L`

(

)

2 1

1 1

+ +

(

)

( )

≤

+ +



 ?b(D•{L@

A

T

= −

'



HT 134. 

2 1

'?012$+,/@

B$<$&_HGn/P−nG−H'

 Giải

•(M



3$%$&

≠ −

'

 DDDL3

2 1

( )

( 1)

y x x

= − +

⇔

2 2

0 0 0

( 1) 2 2 1 0

x x y x x

− + + + + =



 D.4

( , ) ( , )

d A d d B d

⇔

2 2 2 2

0 0 0 0 0 0

2 4( 1) 2 2 1 4 2( 1) 2 2 1

x x x x x x

− + + + + = − + + + + +



     ⇔

0 0 0

1 0 2

x x x

= ∨ = ∨ = −



 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN ••

 ?b.@0124

1 5

; 1; 5

4 4

y x y x y x

= + = + = +



HT 135. 

2 1

−

'(MF3$&$0J9b/_3$&6.

$%3'D#_|$0J9b#!Y'~_3

$&Y!RL9RBFY'

 Giải

•

2 1

(1; 2), ;

I A a

 

−







−







 

−

'DL#_4

1 2 1

( )

(1 )

y x a

−

= − +

−



 ($&9b$!L4

 













 

−



 ($&9b!L4

(2 – 1; 2)

Q a

−



 D.4

2 2

P Q A

x x a x

+ = =

'?b_3$&Y'

  F`

2 2

+ =

−

GFY`

2( 1)

−



 ;

FY

`

F'FY`H$!L



HT 136. 

2 3

−

'?012#$&Z%@

$.|9b$!9b3I30:#_/P\.



ABI

@

/!"F3H9b'

 Giải

•FHGH'(M

2 3

; ( )

M x C

 

−









∈









−

 

/

≠



 012∆#Z4

2 3

( )

( 2)

y x x

−

= − − +

−



 ($&

∆!"B9b4

2 2

 

−

















−

 

/

(2 2;2)

B x

−

'

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN •‚

 h



cos

ABI =

6



tan

ABI

= = ⇔

2 2

16.

IB IA



⇔

( 2) 16

x − =



⇔









 -3b4D#

 













 

0124

1 3

4 2

y x

= − +



   D#

 













 

0124

1 7

4 2

y x

= − +



HT 137. 

2 1

−

'D2B,~S+#RS%$&Z

∈

#Z#!"UM$%%B.Me6

$0JK

2 1

y m

= −



Giải

(M

( ; )

o o

M x y

3M$%$&

⇒012#$&

( ; )

o o

M x y

3

( )

(2 1)

o o

y x x y

= − − +

−



(M_/P3$&!"U/U01

{6.4

2 4 1

(2 1)

o o

x x

+ −

−

!Me(B[_P.

2 4 1

3(2 1)

o o

x x

+ −

−



D)Me6$0JK`Hp86

2 4 1

2 1

3(2 1)

o o

x x

+ −

= −

−



D3#.4

2 2 2 2

2 2

2 4 1 6 (2 1) 6

1 1

(2 1)

3(2 1) (2 1)

o o o o o

o o

x x x x x

x x

+ − − −

= = − ≥ −

−

− −



?b/+#RS%$&Z~Q$<A9@BH^8≥

−

⇒

≥



HT 138. 

3 10 ( ).

y x x C

= + − ?012$+,

!"@3

( ) : 5 6.

P y x x

= − +



Giải

(M

y ax b

= +

3'(M

1 2

x x

3$&.90124

 

GV.Lưu Huy Thưởng 0968.393.899  

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN ‚

1 1 1

2 2 2

5 6 (1)

2 5 (2)

3 10 (3)

3 3 (4)

ax b x x

a x

ax b x x

a x





+ = − +



 = −







+ = + −



= +







DCH!n

1 2 1

3 8

2 5 3 3 (5)

x x x

⇒ − = + ⇔ = 

DC8/H

2 2

1 1 1 1 1

5 6 (2 5) 6 (6)

x x x x b b x⇒ − + = − + ⇒ = − 

Dq/s!H/c

( )

2 3 4 3 2

22 2 2 2 2 2 2

3 8

3 3 . 6 3 10 2 12 0

2 4

x x x x x x x

 









+ + − = + − ⇔ − + − =













 



2 2

2 2 2

2 2

(9 8 48) 0

9 8 48 0 ( )

x x x

x x vn





⇔ − − + = ⇔



− + =







3 10

y x

⇒ = −

3012I2



HT 139. 

2 1

( ).

y C

−

D2BB,

$&$+, !"$0J

K

y mx

= +

Giải

(M

3$%$&_/012#_34

0 0 0 0 0 0

'( )( ) ( ) '( ) ( ).

y y x x x y x y x x y x

= − + = +



D3.4

'( )

( 1)

m y x

= = −

−

!

0 0 0

'( ) ( ) 4

y x x y x

− + =



DC$..4

0 0 0 0

2 1

5 3 8 4 0 2

( 1)

x x x x

−

+ = ⇔ − + = ⇔ =

−

T



-•4

= −

T

= −



HT 140. 

4 2

6 5 ( ).

y x x C

= − + D2

$&$0JK

y mx m

= −

 !"$+

 

GV.Lưu Huy Thưởng 0968.393.899



BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN ‚8

,'

Giải

N0JK

y mx m

= −

 !"$+,

4 2

6 5

4 12

x x mx m

x x m





− + = −



⇔





− =





.9

3 2 3 2

1 8

5 5 5 5

( )

4 12

x m

x x x m x x x m

x x m

 





= ⇒ =

















+ − − = + − − =

⇔ ⇔























− =











 



()9F4

3 2

5 5

4 12

x x x m

x x m





+ − − =







− =







D.4

3 2 3 3 2

5 5 4 12 3 7 5 0

x x x x x x x x

+ − − = − ⇔ − − + =



1 8

5 40

3 27

x m





= ⇒ = −



⇔





= − ⇒ =







-•4



= −







 

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 92

PHẦN 5: BIỆN LUẬN SỐ NGHIỆM CỦA PHƯƠNG TRÌNH

HT 141. Cho hàm số

3 2

3 1

y x x

= − + +

1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

2) Tìm m để phương trình

3 2 3 2

3 3

x x m m

− = −

có ba nghiệm phân biệt.

• PT

3 2 3 2

3 3

x x m m

− = −

⇔

3 2 3 2

3 1 3 1

x x m m

− + + = − + +

. Đặt

3 2

3 1

k m m

= − + +

Số nghiệm của PT bằng số giao điểm của đồ thị (C) với đường thẳng d:

y k

Dựa vào đồ thị (C) ta có PT có 3 nghiệm phân biệt ⇔

1 5

< <

⇔

{

( 1;3) \ 0;2}

∈ −

HT 142. Cho hàm số

4 2

5 4

y x x

= − +

có đồ thị (C).

1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

2) Tìm m để phương trình

4 2

| 5 4 | log

x x m

− + =

có 6 nghiệm.

• Dựa vào đồ thị ta có PT có 6 nghiệm ⇔

log 12 144 12

m m= ⇔ = =

HT 143. Cho hàm số:

4 2

2 1

y x x

= − +

1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

2) Biện luận theo m số nghiệm của phương trình:

4 2

2 1 log 0

x x m

− + + =

(m > 0)

•

4 2

2 1 log 0

x x m

− + + =

⇔

4 2

2 1 log

x x m

− + = −

(*)

+ Số nghiệm của (*) là số giao điểm của 2 đồ thị

4 2

2 1

y x x

= − +

và

log

y m

= −

+ Từ đồ thị suy ra:

< <

2 nghiệm 3 nghiệm 4 nghiệm 2 nghiệm vô nghiệm

HT 144. Cho hàm số

4 2

( ) 8 9 1

y f x x x

= = − +

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 93

1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

2) Dựa vào đồ thị (C) hãy biện luận theo m số nghiệm của phương trình:

4 2

8 cos 9 cos 0

x x m

− + =

với

[0; ]

∈

• Xét phương trình:

4 2

8 cos 9 cos 0

x x m

− + =

với

[0; ]

∈

(1)

Đặt

cos

t x

, phương trình (1) trở thành:

4 2

8 9 0

t t m

− + =

(2)

Vì

[0; ]

∈

nên

[ 1;1]

∈ −

, giữa x và t có sự tương ứng một đối một, do đó số nghiệm của

phương trình (1) và (2) bằng nhau.

Ta có:

4 2

(2) 8 9 1 1

t t m

⇔ − + = −

(3)

Gọi (C

4 2

8 9 1

y t t

= − +

với

[ 1;1]

∈ −

và (d):

y m

= −

. Phương trình (3) là phương trình

hoành độ giao điểm của (C

) và (d).

Chú ý rằng (C

) giống như đồ thị (C) trong miền

1 1

− ≤ ≤

Dựa vào đồ thị ta có kết luận sau:

0 1

< <

m≤ <

m =

m >

vô nghiệm 1 nghiệm 2 nghiệm 4 nghiệm 2 nghiệm vô nghiệm

HT 145. Cho hàm số

3 4

−

(C).

1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

2) Tìm các giá trị của m để phương trình sau có 2 nghiệm trên đoạn

 

 

 

(

6 6 4 4

sin cos sin cos )

x x m x x

+ = +

• Xét phương trình:

(

6 6 4 4

sin cos sin cos )

x x m x x

+ = +

(*)

2 2

3 1

1 sin 2 1 sin 2

4 2

x m x

 







⇔ − = −











 

⇔

2 2

4 3 sin 2 2 (2 sin 2 )

x m x

− = −

(1)

Đặt

sin 2

t x

. Với

 

 

∈

 

 

thì

0;1

 

∈

 

. Khi đó (1) trở thành:

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 94

3 4

−

với

0;1

 

∈

 

 

Nhận xét : với mỗi

0;1

 

∈

 

 

ta có :

sin2

sin 2

sin2

x t



= −



⇔ =





Để (*) có 2 nghiệm thuộc đoạn

 

 

 

thì

3 3

;1 ;1

2 4

t t

 











∈ ⇒ ∈



















Dưa vào đồ thị (C) ta có:

3 7

(1) 2 1 2

4 5

y m y m

 







< ≤ ⇔ < ≤







 

⇔

1 7

2 10

m< ≤

HT 146. Cho hàm số

−

1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

2) Biện luận theo m số nghiệm của phương trình

−

• Số nghiệm của

−

bằng số giao điểm của đồ thị (C′):

−

và

y m

Dựa vào đồ thị ta suy ra được:

1; 1

m m

< − >

= −

1 1

− < ≤

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 95

PHẦN 6: ĐIỂM ĐẶC BIỆT CỦA ĐỒ THỊ

HT 147. Cho hàm số

3 2

y x x

= − + +

(C). Tìm 2 điểm trên đồ thị hàm số sao cho chúng đối xứng

nhau qua tâm M(–1; 3).

Giải

• Gọi

(

)

0 0

;

A x y

là điểm đối xứng với A qua điểm

( 1; 3)

−

(

)

0 0

2 ;6

B x y

⇒ − − −

, ( )

A B C

∈

⇔

0 0 0

3 2

6 ( 2 ) 3( 2 ) 2

y x x





= − + +







− = − − − + − − +





(

)

(

)

3 2

0 0 0 0 0 0

6 3 2 2 3 2 2 6 12 6 0

x x x x x x

⇔ = − + + − − − + − − + ⇔ + + =

⇔

0 0

1 0

x y

= − ⇒ =

Vậy 2 điểm cần tìm là:

(

)

1;0

−

và

(

)

1;6

−

HT 148. Cho hàm số

3 2

y x x

= − + +

(C). Tìm trên (C) hai điểm đối xứng nhau qua đường thẳng

: 2 – 2 0

d x y

+ =

Giải

• Gọi

(

)

(

)

1 1 2 2

; ; ;

M x y N x y

thuộc (C) là hai điểm đối xứng qua đường thẳng d

I là trung điểm của AB nên

1 2 1 2

;

2 2

x x y y

 

+ +

















 

, ta có

I d

∈

Có:

(

)

(

)

3 3

1 1 2 2

1 2 1 2

3 2 3 2

2. 2

2 2 2

x x x x

y y x x

− + + + − + +

+ +

= = +

( ) ( ) ( ) ( )

1 2

2 2

1 2 1 2 1 2 1 2 1 2

1 1 2 2

3 3 2

x x

x x x x x x x x x x

x x x x



+ =



⇒ − + + + + + = + ⇒



− + =





Lại có:

(

)

(

)

2 1 2 1

.1 .2 0

MN d x x y y

⊥ ⇒ − + − =

( ) ( )

(

)

2 2 2 2

2 1 2 1 1 1 2 2 1 1 2 2

7 2 0

x x x x x x x x x x x x

⇒ − − − + + = ⇒ + + =

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 96

- Xét

1 2

x x

+ =

1 2

7 7

;

2 2

x x⇒ = ± = ∓

- Xét

2 2

1 1 2 2

1 2

2 2

1 1 2 2

1 2

x x x x

x x

x x x x

x x









− + =

+ =



 

⇔ ⇒

 

 

+ + =

 









vô nghiệm

Vậy 2 điểm cần tìm là:

7 1 7 7 1 7

;2 ; ;2

2 2 2 2 2 2

   

 

 

 

 

− − +

 

 

 

 

 

 

   

HT 149. Cho hàm số

3 3

y x= − + + −

. Tìm trên đồ thị (C) hai điểm phân biệt M, N đối

xứng nhau qua trục tung.

Giải

• Hai điểm

1 1 2 2

( ; ), ( ; ) ( )

M x y N x y C

∈

đối xứng nhau qua Oy ⇔

2 1

1 2

x x

y y





= − ≠









⇔

2 1

3 3

2 3

1 2

1 1 2

11 11

3 3

3 3 3 3

x x

x x x x





= − ≠







− + + − = − + + −





⇔









= −





hoặc





= −









Vậy hai điểm thuộc đồ thị (C) và đối xứng qua Oy là:

16 16

3; , 3;

3 3

M N

   

 

 

 

−

 

 

 

   

HT 150. Cho hàm số

2 1

−

(C). Tìm điểm M thuộc đồ thị (C) để tiếp tuyến của (C) tại M với

đường thẳng đi qua M và giao điểm hai đường tiệm cận có tích các hệ số góc bằng –9.

Giải

• Giao điểm 2 tiệm cận là

( 1;2)

−

Gọi

3 3

;2 ( )

( 1)

M I

y y

M x C k

x x x

 

−







− ∈ ⇒ = =











+ −

 

+ Hệ số góc của tiếp tuyến tại M:

(

)

( )

k y x

′

= =

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 97

+ YCBT

. 9

M IM

k k

⇔ = −

⇔





= −





. Vậy có 2 điểm M thỏa mãn: M(0; –3) và M(–2; 5)

HT 151. Cho hàm số

2 1

(C). Tìm trên (C) những điểm có tổng khoảng cách đến hai tiệm

cận của (C) nhỏ nhất.

Giải

• Gọi

0 0

( ; )

M x y

∈ (C), (

≠ −

)

thì

0 0

2 1

1 1

x x

= = −

+ +

Gọi A, B lần lượt là hình chiếu của M trên TCĐ và TCN thì:

0 0

1 , 2

MA x MB y

= + = − =

Áp dụng BĐT Cô-si ta có:

2 . 2 1 . 2

MA MB MAMB x

+ ≥ = + =

⇒

MA + MB nhỏ nhất bằng 2 khi





+ = ⇔



= −





Vậy ta có hai điểm cần tìm là (0; 1) và (–2; 3).

Câu hỏi tương tự:

2 1

−

ĐS:

1 3

x = − ±

HT 152. Cho hàm số

3 4

−

(C). Tìm các điểm thuộc (C) cách đều 2 tiệm cận.

Giải

• Gọi

( ; )

M x y

∈ (C) và cách đều 2 tiệm cận x = 2 và y = 3.

Ta có:

3 4

2 3 2 2 2

2 2

x x

x y x x

x x

−

− = − ⇔ − = − ⇔ − =

− −

( 2)





⇔ = ± − ⇔



−





GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 98

Vậy có 2 điểm thoả mãn đề bài là : M

( 1; 1) và M

(4; 6)

HT 153. Cho hàm số

4 2

1 1

1 ( ).

4 2

y x x C

= − +

Tìm điểm M thuộc (C) sao cho tổng khoảng cách từ

điểm M đến hai trục tọa độ là nhỏ nhất.

Giải

Đồ thị (C) cắt Oy tại

(0;1)

, nên tổng khoảng cách từ A đến hai trục tọa độ bằng 1. Đồ thị hàm số

có hai điểm cực tiểu:

3 3

1; ; 1;

4 4

   

 

 

 

−

 

 

 

 

 

   

và nhận trục Oy làm trục đối xứng nên ta chỉ cần xét

0 0

( ; ) ( )

M x y C

∈

và

0 1

≤ ≤

Tổng khoảng cách từ M đến hai trục tọa độ là:

4 2 4

0 0 0 0 0 0 0 0 0 0

1 1 1 1

1 (2 ) 1 1

4 2 4 2

x y x y x x x x x x

+ = + = + − + = + − + ≥

Với mọi

0 0

: 0 1,

x x

≤ ≤

đẳng thức xảy ra khi và chỉ khi

0 0

0 1.

x y

= ⇒ =

Vậy điểm

(0;1)

HT 154. Cho hàm số

4 2

0 0 0 0

2 3 2 1

= − + +

y x x x

có đồ thị là (C) và đường thẳng

( ) 2 1

∆ = −

.Tìm

trên đồ thị (C) điểm A có khoảng cách đến

( )

∆

là nhỏ nhất

Giải

Giả sử

0 0

( , )

A x y

( )

∈

,ta có:

4 2

0 0 0 0

2 3 2 1

y x x x

= − + +

Khoảng cách từ A đến (

∆

) là :

4 2

0 0 0 0

| 2 3 2 1 2 1 |

( , )

x x x x

d A

− + + − +

∆ =

4 2

0 0

| 2 3 2 |

x x− +

4 2

0 0

2 3 2

x x

− +

4 2

0 0

2 3

2 1

x x

 







= − +











 

2 3 7

4 16

 

 

 







= − +



 









 

 

 

 

8 5

≥

⇒

Mind=

8 5

khi

x = ±

Vậy có hai điểm cần tìm:

3 1

; 3

2 8

 









− − −













 

3 1

; ; 3

2 8

 









− +













 

HT 155. Cho hàm số

−

. Tìm trên đồ thị hàm số điểm M sao cho tồng khoảng cách từ M đến

hai trục tọa độ là nhỏ nhất.

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 99

Giải

Giả sử

0 0

( ; ) ( )

M x y C

∈

0 0

; | | | |

d x y

= +

Ta có :

 







−











 

( )

∈

và

Dựa vào đồ thị ta có:

| |

thì

ii)

< <

thì

< −

⇒ >

0 0 0

d x y x

= − − = − −

−

0 0

x x

− + −

−

Tìm GTNN của y

x x

− + −

−

trên

 

 

−

 

 

Ta có:

4 1 1

0, ;0

( 2)

x x

y x

 

− + −

 

= < ∀ ∈ −

 

−

 

⇒

y giảm trên

 

 

−

 

 

Vậy miny=

(0)

và điểm M cần tìm là

 







−











 

HT 156. Cho hàm số

2 4

−

. Tìm trên (C) hai điểm đối xứng nhau qua đường thẳng MN biết

M(–3; 0) và N(–1; –1).

Giải

•

(2; 1)

= −



⇒ Phương trình MN:

2 3 0

x y

+ + =

Phương trình đường thẳng (d)

⊥

MN có dạng:

y x m

= +

Phương trình hoành độ giao điểm của (C) và (d):

2 4

x m

−

= +

⇔

2 4 0 ( 1)

x mx m x

+ + + = ≠ −

(1)

(d) cắt (C) tại hai điểm phân biệt A, B

⇔

– 8 – 32 0

m m

∆ = >

(2)

Khi đó

1 1 2 2

( ;2 ), ( ;2 )

A x x m B x x m

+ +

với

1 2

x x

là các nghiệm của (1)

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 100

Trung điểm của AB là

1 2

;

x x

I x x m

 









+ +









 

≡

;

4 2

m m

 







−







 

(theo định lý Vi-et)

A, B đối xứng nhau qua MN

⇔

∈

⇔

= −

Suy ra (1)

⇔

2 4 0

x x





− = ⇔





⇒ A(0; –4), B(2; 0).

HT 157. Cho hàm số

−

. Tìm trên đồ thị (C) hai điểm B, C thuộc hai nhánh sao cho tam giác

ABC vuông cân tại đỉnh A với A(2; 0).

Giải

•

Ta có

( ) : 2

C y

= +

−

. Gọi

2 2

;2 , ;2

1 1

B b C c

b c

+ +

− −

   

 

 

 

 

 

 

   

với

b c

< <

Gọi H, K lần lượt là hình chiếu của B, C lên trục Ox.

Ta có:



0 0

; 90 90

AB AC BAC CAK BAH CAK ACK BAH ACK

+ = + ⇒

= = ⇒ = =

và:



AH CK

BHA CKA ABH CAK

HB AK

= = ⇒ ∆ = ∆ ⇒











Hay:

2 2

− = +

= −

−

⇔

+ = −

−









 

 







Vậy

( 1;1), (3;3)

B C

−

HT 158. Cho hàm số

2 1

−

. Tìm tọa độ điểm M

∈

( 1;2)

−

tới tiếp tuyến của (C) tại M là lớn nhất.

Giải

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 101

•

Giả sử

;2 ( )

M x C

 









− ∈









 

. PTTT

∆

của (C) tại M là:

3 3

2 ( )

( 1)

y x x

− + = −

⇔

0 0 0

3( ) ( 1) ( 2) 3( 1) 0

x x x y x

− − + − − + =

Khoảng cách từ

( 1;2)

−

tới tiếp tuyến

∆

là:

( )

0 0 0

4 4

3( 1 ) 3( 1) 6 1

9 ( 1)

9 1

( 1)

x x x

− − − + +

= = =

+ +

Theo BĐT Cô–si:

( 1) 2 9 6

( 1)

+ + ≥ =

⇒

≤

Khoảng cách d lớn nhất bằng

khi

( )

0 0 0

( 1) 1 3 1 3

( 1)

x x x

= + ⇔ + = ⇔ = − ±

Vậy có hai điểm cần tìm là:

(

)

1 3;2 3

M − + −

hoặc

(

)

1 3;2 3

M − − +

HT 159. Cho hàm số

2 1

−

. Tìm những điểm trên đồ thị (C) cách đều hai điểm A(2; 0) và

B(0; 2).

Giải

•

PT đường trung trực đọan AB:

y x

Những điểm thuộc đồ thị cách đều A và B có hoành độ là nghiệm của PT:

2 1

−

⇔

1 5

1 0

1 5

x x



−



− − = ⇔





Hai điểm cần tìm là:

1 5 1 5 1 5 1 5

, ; ,

2 2 2 2

   

− −  + + 

 

 

 

 

 

 

 

 

 

   

HT 160. Cho hàm số

−

. Tìm trên hai nhánh của đồ thị (C) hai điểm A và B sao cho AB

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 102

ngắn nhất.

Giải

•

Tập xác định D =

{

\ 1}

−

. Tiệm cận đứng

= −

Giả sử

4 4

1 ;1 , 1 ;1A a B b

a b

   

 

 

 

− − + − + −

 

 

 

   

(với

0, 0

a b

> >

) là 2 điểm thuộc 2 nhánh của (C)

2 2 2

2 2 2 2

1 1 16 16 64

( ) 16 ( ) 1 4 1 4 32

AB a b a b ab ab

a b ab

a b a b

     





   



= + + + = + + ≥ + = + ≥







   

 

   

AB nhỏ nhất

⇔

4 2 4

a b

AB a b









 

= ⇔ ⇔ ⇔ = =

 

 









Khi đó:

(

)

(

)

4 4 4 4

1 4;1 64 , 1 4;1 64

A B− − + − + −

HT 161. Cho hàm số

4 2

2 1

y x x

= − +

Tìm tọa độ hai điểm P. Q thuộc (C) sao cho đường thẳng PQ

song song với trục hoành và khoảng cách từ điểm cực đại của (C) đến đường thẳng PQ bằng 8

Giải

Phương trình đường thẳng PQ có dạng: y = m (m

≥

Vì điểm cực đại A(0;1) cách PQ một khoảng bằng 8 nên m = 9

Khi đó, hoành độ P, Q là nghiệm của phương trình:

4 2

2 8 0 2

x x x

− − = ⇔ = ±

Vậy, P(-2;9), Q(2;9) hoặc P(2;9); Q(-2;9)

HT 162. Cho hàm số

3 2

1 5

3 3

y x x x

= + − +

(C). Gọi A và B là giao điểm của (C) và trục Ox. Chứng

minh rằng, trên đồ thị tồn tại hai điểm cùng nhìn đoạn AB dưới một góc vuông.

Giải

Phương trình hoành độ giao điểm của đồ thị với trục hoành:

3 2

1 5

3 0

3 3

x x x





+ − + = ⇔



= −





⇒ A(-5;0) và B(1;0)

Gọi M thuộc (C) ⇒

3 2

1 5

; 3

3 3

M a a a a

 







+ − +











 

khác A, B

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 103

3 2 3 2

1 5 1 5

5; 3 ; 1; 3

3 3 3 3

AM a a a a BM a a a a

   

 

 

 

+ + − + − + − +

 

 

 

 

 

   

 

Theo giả thiết:

. 0

AM BM AM BM

⊥ ⇔ =

 

⇔

2 2

( 5)( 1) ( 1) ( 5) 0

a a a a

 

 

+ − + − + =

 

 

Do M khác A, B nên a khác -5 và a khác 1 nên phương trình tương đương:

3 4 3 2

1 ( 1) ( 5) 0 2 12 14 4 0 (*)

a a hay a a a a+ − + = + − + + =

Đặt:

4 3 2

2 12 14 4

y a a a a

= + − + +

có tập xác định là

ℝ

3 2

' 4 6 12 14; ' 0

y a a a y

= + − + =

có 1 nghiệm thực

7 2043

2 16

o o

a y

−

≈ − ⇒ ≈

Từ bảng biến thiên ta có: (*) luôn có hai nghiệm khác 1 và -5

Vậy luôn tồn tại 2 điểm cùng nhìn đoạn AB dưới một góc vuông

HT 163. Cho hàm số

x m

Chứng minh rằng mọi điểm không nằm trên đường phân giác

thứ nhất của mặt phẳng luôn có duy nhất một đồ thị của hàm số đi qua.

Giải

Gọi

0 0 0 0

( ; ) ;

M x y d y x x y

∉ = ⇔ ≠

Điều kiện để đồ thị hàm số đi qua

0 0

( ; )

M x y

là phương trình sau có nghiệm :

0 0 0 0 0

3 8

y x y y m x m

x m

= ⇔ + = +

∞

y’

∞

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 104

0 0

0 0 0 0

0 0

3 8

( ) 3 8 (*)

x y

x y m x y m

x y

−

⇔ − = − ⇔ =

−

Nhìn vào biểu thức (*) ta thấy, ứng với mỗi cặp điểm

(

)

0 0

;

x y

ta luôn có 1 giá trị của m duy nhất

tương ứng. Suy ra điều phải chứng minh.

HT 164. Cho hàm số

(3 1)

m x m m

x m

+ − +

Tìm các điểm thuộc đường thẳng

mà không

có đồ thị đi qua.

Giải

Gọi điểm

(1; )

M a

là điểm thỏa mãn yêu cầu bài toán.

Vì không có đồ thị nào đi qua điểm

(1; )

M a

⇒

Phương trình :

3 1

(1)

m m m

+ − +

không có

nghiệm m.

Với điều kiện

≠ −

ta có

(1) ( 4) 1 0 (2)

m a m a⇔ + − + − =

Để (1) vô nghiệm thì phương trình (2) xảy ra 1 trong hai trường hợp :

- (2) vô nghiệm

- (2) có nghiệm kép

1,2

= −

Trường hợp 1 : (2) vô nghiệm

2 2

0 ( 4) 4( 1) 0 12 20 0 2 10

a a a a a

⇔ ∆ < ⇔ − − − < ⇔ − + < ⇔ < <

Trường hợp 2 : (2) có nghiệm kép bằng -1











∆ =







⇔ ⇔ ⇔

 

−





 

= −

 

  =









Kết luận : Như vậy tập hợp các điểm thuộc đường thẳng

có tung độ bằng a với a thỏa mãn :

2 10

< <

HT 165. Cho hàm số

4 2 2

2 1.

y x mx m

= − + +

Chứng minh rằng mỗi điểm thuộc đường thẳng

luôn có duy nhất một đồ thị của hàm số đi qua.

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 105

Giải

Gọi

( ;1) : 1

A a d y

∈ =

Đồ thị hàm số qua A

4 2 2 4 2 2

2 1 1 2 0

a ma m a ma m

⇔ − + + = ⇔ − + =

2 2 2

( ) 0 (*)

m a m a

⇔ − = ⇔ =

Dựa vào (*) ta có, ứng với mỗi giá trị của a ta luôn có 1 giá trị

tương ứng.

Suy ra, mỗi điểm trên

luôn có duy nhất 1 giá trị m để đồ thị hàm số đi qua.

Suy ra điều phải chứng minh.

HT 166. Cho hàm số

3 2 .

y x mx m

= − +

Chứng minh rằng với mọi

thì đồ thị hàm số luôn đi

qua điểm cố định duy nhất.

Giải

Giả sử

( ; )

A a b

là điểm cố định của đồ thị hàm số.

3 2

b a ma m

⇒ = − +

( 3 2) 0 (1)

m a a b⇔ − + + − =

Đề đồ thị hàm số luôn qua A với mọi m thì phương trình (1) có nghiệm với

∀

3 2 0

a b









− + =



 

⇔ ⇔

 

 

− =

 









Vậy đồ thị hàm số luôn đi qua điểm cố định duy nhất :

2 8

;

3 27

 

















 

. Suy ra điều phải chứng minh.

HT 167. Cho hàm số

3 2

( 2) 2( 2) ( 3) 2 1.

y m x m x m x m

= + + + − + − +

Chứng minh rằng đồ thị

hàm số luôn đi qua 3 điểm cố định thẳng hàng.

Giải

Xét họ đường cong:

3 2

( 2) 2( 2) ( 3) 2 1.

y m x m x m x m

= + + + − + − +

Gọi

0 0

( ; )

M x y

là điểm cố định cần tìm. Khi đó ta có:

3 2

0 0 0 0

( 2) 2( 2) ( 3) 2 1

y m x m x m x m m

= + + + − + − + ∀

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 106

3 2 3 2

0 0 0 0 0 0 0

( 2 2) (2 4 3 1 ) 0

x x x m x x x y m

⇔ + − − + + − + − = ∀

3 2

0 0 0

3 2

0 0 0 0

2 2 0 (1)

2 4 3 1 0 (2)

x x x

x x x y





+ − − =



⇔





+ − + − =





0 0

0 0 0 0

0 0

2 7

(1) ( 2)( 1) 0 1 6

1 4

x y

x x x y

x y



= − ⇒ =



⇔ + − = ⇔ = − ⇒ =



= ⇒ =





Vậy ta được 3 điểm cố định là:

( 2;7), ( 1;6), (1;4)

A B C

− −

(1; 1), (3; 3) 3

AB AC AC AB

= − = − ⇒ =

   

Suy ra A, B, C thẳng hàng.

HT 168. Cho hàm số

( 1) (2 1) 1.

y m x m x m

= + − − − +

Chứng minh rằng đồ thị hàm số luôn đi

qua 3 điểm cố định thẳng hàng.

Giải

Xét họ đường cong:

( 1) (2 1) 1

y m x m x m

= + − − − +

Gọi

0 0

( ; )

M x y

là điểm cố định cần tìm. Tương tự bài trước ta có hệ phương trình sau:

0 0

0 0 0

2 1 0 (1)

1 0 (2)

x x

y x x





− − =







− + − =





(

)

0 0 0 0 0

(2) 2 1 2 2

y x x x x

⇔ = − − + + = +

0 0 0

(1) ( 1)( 1) 0 (1)

x x x⇔ + − − = ⇒

có 3 nghiệm phân biệt.

Nên 3 điểm đều thỏa mãn:

0 0

y x

= +

Vậy 3 điểm thuộc đường thẳng

y x

= +

HT 169. Cho hàm số

3 2

( 3) 4( 3) ( 1) .

y m x m x m x m

= − − − − + +

Chứng minh rằng đồ thị hàm số

luôn đi qua 3 điểm cố định thẳng hàng.

Giải

Xét họ đường cong

3 2

( 3) 4( 3) ( 1) .

y m x m x m x m

= − − − − + +

Gọi

0 0

( ; )

M x y

là điểm cố định cần tìm. Tương tự bài trên ta có hệ sau để xác định

0 0

x y

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 107

3 2

0 0 0

3 2

0 0 0 0

4 1 0 (1)

3 12 0 (2)

x x x

y x x x





− − + =







+ − + =





3 2 3 2

0 0 0 0 0 0 0 0 0

(2) 3 12 3( 4 1) 4 3 4 3

y x x x x x x x x

⇔ = − − − = − − − + − + = − +

Ta chứng minh (1) có 3 nghiệm phân biệt:

Xét hàm số:

3 2

( ) 4 1

f x x x x

= − − +

Hàm số liên tục trên

ℝ

Có:

( 1) 3, (0) 1, (1) 3, (5) 21

f f f f

− = − = = − =

1 1

( 1). (0) 3 0 ( 1;0) : ( ) 0

f f x f x

− = − < ⇒ ∃ ∈ − =

2 2

(0). (1) 3 0 (0;1) : ( ) 0

f f x f x

= − < ⇒ ∃ ∈ =

3 3

(1). (5) 63 0 (1;5) : ( ) 0

f f x f x

= − < ⇒ ∃ ∈ =

Vì

1 2 3

x x x

< <

nên phương trình có 3 nghiệm phân biệt.

Vậy 3 điểm cố định thẳng hàng đều nằm trên đường thẳng

4 3

y x

= − +

HT 170. Cho hàm số

(1 ) .

y mx m x

= + −

Tìm các điểm trên mặt phẳng tọa độ sao cho không có

đường cong nào của họ đồ thị đi qua.

Giải

Gọi

0 0

( ; )

M x y

là điểm cần tìm. Khi đó phương trình sau với m là ẩn:

0 0 0

(1 ) (1)

y mx m x= + −

vô nghiệm.

Dễ thấy (1)

0 0 0 0

( ) (2).

y x m x x⇔ − = −

Ta có: (2) vô nghiệm khi và chỉ khi hệ sau thỏa mãn:

0 0

x x

y x













− =





= ±

⇔

 





 

− ≠

 





 ≠





Vậy các điểm cần tìm nằm trên 3 đường thẳng:

0, 1, 1

x x x

= = − =

bỏ đi 3 điểm

(0; 0), (1;1), ( 1; 1)

A B C

− −

HT 171. Cho hàm số

3 3 2 2

2 1.

y x m x mx m

= − + + −

Tìm các điểm trên mặt phẳng tọa độ mà đồ

thị hàm số không qua với mọi

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 108

Giải

Gọi

0 0

( ; )

M x y

là điểm cần tìm. Khi đó phương trình sau với m là ẩn:

3 3 2 2

0 0 0 0

2 1 (1)

y x m x mx m= − + + −

vô nghiệm

Ta viết lại:

3 2 2 3

0 0 0 0

2 1 0 (2)

m x m mx y x− − + + − =

vô nghiệm

Nếu

x m

≠

thì (2) là phương trình bậc 3. Ta biết rằng mọi phương trình bậc 3 đều có ít nhất 1

nghiệm. Vì thế để (2) vô nghiệm thì

Với

thì (2) trở thành:

2 2

0 0

1 0 1 (3)

m y m y− + + = ⇔ = +

Để (3) vô nghiệm

0 0

1 0 1.

y y

+ < ⇔ < −

Vậy tập hợp các điểm là nửa đường thẳng:

với

< −

HT 172. Cho hàm số

3 2 2 2

2( 1) ( 4 1) 2( 1).

y x m x m m x m

= + − + − + − +

Tìm các điểm trên mặt

phẳng tọa độ sao cho đồ thị không qua với mọi

Giải

Gọi

0 0

( ; )

M x y

là điểm cần tìm. Khi đó phương trình sau với m là ẩn:

3 2 2 2

0 0 0 0

2( 1) ( 4 1) 2( 1) (1)

y x m x m m x m= + − + − + − +

vô nghiệm.

Viết lại (1) thành:

2 3 2

0 0 0 0 0 0 0

( 2) 2 ( 2) 2 2 0 (2).

x m x x m x x x y− + − + − + − − =

Xét các khả năng sau:

Trường hợp 1:

≠

Khi đó (2) vô nghiệm khi:

2 2 3 2

0 0 0 0 0 0 0

' ( 2) ( 2 2 )( 2) 0

x x x x x y x

∆ = − − − + − − − <

3 2 3 2

0 0 0 0 0 0 0

( 2)( 2 2 2 ) 0

x x x x x x y

⇔ − − − + − + + <

0 0

0 0 0

0 0

2 0

( 2)( 2) 0

2 0

x y

x x y

x y







− <











− + + >







⇔ − − + + < ⇔







− >













− + + <







GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 109

HT 173. Cho hàm số

2 1

( ).

y C

−

Tìm trên đồ thị (C) hai điểm

A B

phân biệt sao cho ba điểm

, , (0; 1)

A B I

−

thẳng hàng đồng thời thỏa mãn:

. 4.

IA IB

Giải

, , (0; 1)

A B I

−

thẳng hàng nên

A B

nằm trên đường thẳng

∆

qua

(0; 1).

−

A B

thuộc đồ

thị hàm số (C) nên

A B

là giao điểm của đồ thị hàm số (C) với đường thẳng

: 1

y kx

∆ = −

Xét phương trình hoành độ giao điểm của (C) và

∆

ta có:

2 1

1 ( 3) 2 0 (*);( 1)

kx kx k x x

−

= − ⇔ − + + = ≠

−

∆

cắt (C) tại hai điểm phân biệt

A B

⇔

phương trình (*) có hai nghiệm phân biệt khác 1

2 9 0 0

( 3) 2 0

k k k

k k





≠



⇔ ∆ = − + > ⇔ ≠





− + + ≠





Gọi

1 1 2 2

( ; ); ( ; )

A x y B x y

A B

thuộc

∆

nên

1 1 2 2

1; 1

y kx y kx

= − = −

Ta có:

2 2 2 2 2

1 1 2 2 1 2

. 4 . 4 ( 1) 4

IA IB x kx x kx x x k

= ⇔ + + = ⇔ + =

Theo Viet ta có:

1 2

x x

thay vào ta được:

( 1) 4 1

k k

+ = ⇔ = ±

Với

ta được:

(

)

(

)

2 2;1 2 ; 2 2;1 2

A B− − + +

Với

= −

ta được:

(

)

(

)

1 3; 2 3 ; 1 3; 2 3

A B− − + + − −

HT 174.

Cho hàm số

2 4

( )

y C

−

. Tìm trên đồ thị

( )

hai điểm A, B đối xứng nhau qua đường

thẳng MN, biêt

( 3;0), ( 1; 1)

M N

− − −

Giải

Phương trình đường thẳng MN:

2 3 0

x y

+ + =

Xét hai điểm A, B trên đồ thị (C), ta có:

6 6

;2 , ;2 , , 1

1 1

A a B b a b

a b

   

 

 

 

− − ≠ −

 

 

 

 

 

+ +

   

Gọi

3 3

2 1 1

a b

 







− −











+ +

 

là trung điểm của đoạn AB

Theo yêu cầu bài toán ta có:

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 110

3 3

. 0

1 1

6 6

2 1 1

b a

AB MN

a b

I MN b a

I MN

a b







− − + =





⊥



 

+ +

⇔ ⇔

  

  

∈ +

∈

  



− − = −







+ +





 

...





















⇔ ⇔

























Vậy,

(2;0); (0; 4)

A B

−

hoặc

(2;0); (0; 4)

B A

−

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 111

CÁC BÀI TỔNG HỢP

HT 175. Cho hàm số

2 3

( ).

y C

−

Tìm

để đường thẳng

: 2

d y x m

= +

cắt đồ thị tại hai điểm

phân biệt sao cho tiếp tuyến tại hai điểm đó của đồ thị hàm số song song với nhau.

Giải

Phương trình hoành độ giao điểm của d với đồ thị (C) là:

2 3

2 2 ( 6) 2 3 0(1)

x m x m x m

= + ⇔ + − − − =

−

( 2

không là nghiệm của phương trình)

cắt (C) tại hai điểm phân biệt mà tiếp tuyến tại đó song song với nhau

(1)

⇔

có hai nghiệm phân biệt

1 2

;

x x

thỏa mãn:

1 2

'( ) '( )

y x y x

hay

1 2

x x

+ =

( 6) 8(2 3) 0

m m





∆ = − + + >



⇔ ⇔ = −



−





HT 176. Cho hàm số

3 2

4 1

(2 1) ( 2) ( ).

3 3

y x m x m x C= − + + + +

Gọi

là giao điểm của

( )

với

trục tung. Tìm

sao cho tiếp tuyến của

( )

tại

tạo với hai trục tọa độ một tam giác có diện

tích bằng

Giải

Ta có:

 

















 

và

' 4 2(2 1) 2.

y x m x m

= − + + +

Suy ra

'(0) 2.

y m

= +

Tiếp tuyến của đồ thị tại

là

: ( 2) .

d y m x= + +

Đường thẳng

cắt

tại

;0 .

3 6

 

−

















 

Khi đó, diện tích tam giác tạo bởi

với hai trục tọa độ là:

1 1 1 1 1

. .

2 2 3 3 6

18 2

S OAOB

−

= = =

Theo giả thiết ta có:

1 1 1

3 6

18 2





= −



= ⇔ + = ⇔



= −





GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 112

HT 177. Cho hàm số

3 2

2 2 1 ( ).

y x mx mx C

= − + −

Tìm

để đồ thị hàm số (C) cắt trục hoành tại

3 điểm phân biệt

(1;0),

A B

và

sao cho

1 2

. 5

k k BC+ =

trong đó

1 2

k k

lần lượt là hệ số góc tiếp

tuyến tại B, C của đồ thị hàm số (C).

Giải

Phương trình hoành độ giao điểm của đồ thị với

3 2 2

2 2 1 0 ( 1) (1 2 ) 1 0

x mx mx x x m x

 

− + − = ⇔ − + − + =

 

 

(1 2 ) 1 0 (*)

x m x





⇔



+ − + =





Đề đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân

biệt khác 1.

Tức là phương trình:

(1 2 ) 1 0

x m x

+ − + =

có 2 nghiệm phân biệt khác 1

4 4 3 0

1 (1 2 ) 1 0

m m









≤ −















≤ −





∆ = − − >





 



⇔ ⇔ ⇔

 

≥



 

+ − + ≠





 

≥















≠





Giả sử

1 2

( ;0), ( ;0)

B x C x

Vì

1 2

x x

là 2 nghiệm phân biệt của phương trình (*) nên theo định lý Viet ta có:

1 2

2 1

x x m

+ = −

và

1 2

. 1

x x

Ta có:

2 2 2

2 1 1 2 1 2

( ) ( ) 4 . 4 4 3

BC x x x x x x m m

= − = + − = − −

Mặt khác:

2 2

1 2 1 1 2 2

3 4 2 3 4 2

k k x mx m x mx m

+ = − + + − +

2 2

1 2 1 2 1 2

3( ) 6 4 ( ) 4 4 4 3

x x x x m x x m m m

= + − − + + = − −

Theo giả thiết ta có:

1 2

k k BC+ =

2 2

4 4 3 5(4 4 3)

m m m m

⇔ − − = − −

4 4 3 5

m m

⇒ − − =

Vì

4 4 3 0

m m

− − >

1 ( / )

2 0

2 ( / )

m t m

m m

m t m



= −



⇔ − − = ⇔





GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 113

KL:



= −





HT 178. Cho hàm số

3 2

3 2 ( ).

y x x mx m C= − + + −

Tìm

để

( )

cắt trục hoành tại 3 điểm

phân biệt

, ,

A B C

sao cho tổng các hệ số góc của tiếp tuyến của

( )

tại

, ,

A B C

bằng 3.

Giải

Phương trình hoành độ giao điểm của

( )

với trục hoành là:

3 2 2

3 2 0 (1) ( 1)( 2 2) 0

2 2 0 (2)

x x mx m x x x m

x x m





− + + − = ⇔ − − + − = ⇔



− + − =





( )

cắt trục

tại 3 điểm phân biệt

⇔

(1) có 3 nghiệm phân biệt

⇔

(2) có 2 nghiệm phân biệt

khác 1

3 0

3(*)

(1) 0, ( ) 2 2

f f x x x m





∆ > 

− >



⇔ ⇔ ⇔ <

 

 

≠

≠ = − + −

 







Khi đó, gọi

1 2

x x

là hai nghiệm của (2). Theo Viet ta có:

1 2

(**), '( ) 3 6

x x

f x x x m

x x m





+ =



= − +





= −





3 6 2

m m

⇔ − = − ⇔ =

(thỏa mãn (*))

KL:

HT 179. Cho hàm số

( )

y C

−

Lập phương trình tiếp tuyến

với đồ thị (C) biết tiếp

tuyến cắt hai đường tiệm cận của (C) tại hai điểm phân biệt A, B sao cho diện tích đường tròn

ngoại tiếp tam giác IAB bằng

, với I là giao điểm của hai đường tiệm cận.

Giải

Gọi

; ( )

M x C

 









∈









−

 

là tiếp điểm

Phương trình tiếp tuyến của

tại M là

( )

( 1)

y x x

−

= − +

−

Tiếp tuyến

cắt với tiệm cận đứng tại

 

















−

 

Tiếp tuyến

cắt với tiệm cận ngang tại

(

)

2 1;1

B x

−

Vì tam giác IAB vuông tại I nên bán kính đường tròn ngoại tiếp tam giác IAB:

( 1)

R x

= = − +

−

Theo giả thiết ta có:

2 4 2

0 0

17 17 ( 1) 17( 1) 16 0

S R x xπ π π

= ⇔ = ⇔ − − − + =

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 114



= −



⇔ ⇒





4 tiếp tuyến:

4 3

4 13

y x



= − −



= − −



= − +



= − +





HT 180. Cho hàm số

( 1) (1).

x m

y m

= ≠

Gọi

là hệ số góc của tiếp tuyến tại giao điểm

của đồ thị hàm số (1) với trục hoành. Gọi

là hệ số góc của tiếp tuyến với đồ thị hàm số (1) tại

điểm có hoành độ

Tìm tất cả các giá trị của tham số

sao cho

1 2

k k

đạt giá trị nhỏ nhất.

Giải

Ta có:

( 1)

−

Hoành độ giao điểm của đồ thị hàm số (1) với trục hoành là

x m

= −

Hệ số góc của tiếp tuyến:

Tại điểm có hoành độ

x m

= −

là

−

Tại điểm có hoành độ

là

−

Ta có:

1 2

1 1 1 1

1, 1

1 4 1 4

m m

k k m

m m

− −

+ = + = + ≥ ∀ ≠

− −

Đẳng thức xảy ra khi:

1 2 1

1 2 3

m m

 

−

− = = −

 

= ⇔ ⇔

 

− = − =

−

 

 

Vậy:

1 2

k k

đạt giá trị nhỏ nhất bằng 1 khi

{

1; 3}

∈ −

HT 181. Cho hàm số

1 2

( ).

3 3

y x x C

= − + − Gọi M là điểm thuộc đồ thị (C) có hoành độ

. Tìm các giá trị của tham số

để tiếp tuyến với (C) tại M song song với đường thẳng

9 5

: ( 4)

d y m x

= − +

Giải

Ta có

4 4

(2) 2;

3 3

y M

 







= − ⇒ −











 

Tiếp tuyến

∆

với (C) tại M có phương trình:

4 4 14

'(2)( 2) 3( 2) 3

3 3 3

y y x y x y x= − − ⇔ = − − − ⇔ = − +

Ta có:

4 3

/ /

9 5 14

3 3





− = −



∆ ⇔





≠









⇔ ⇔ = −





≠





Kết luận:

= −

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 115

HT 182. Cho hàm số:

( )

y C

−

Viết phương trình đường thẳng

1 2

;

d d

đi qua giao điểm I

của hai tiệm cận và cắt đồ thị (C) tại 4 điểm phân biệt là các đỉnh của một hình chữ nhật biết

đường chéo hình chữ nhật có độ dài bằng

30.

Giải

(1;1)

là tâm đối xứng của đồ thị hàm số. Giả sử

cắt (C) tại A, B;

cắt (C) Tại C và D thì I là

trung điểm của AB và CD. Do đó, ACBD là hình bình hành. Để ACBD là hình chữ nhật thỏa mãn đề

bài thì

AB CD

= =

Gọi

là đường thẳng qua I có hệ số góc là

Phương trình đường thẳng

: ( 1) 1 1

d y k x y kx k

= − + ⇔ = − +

Phương trình hoành độ giao điểm của

và (C) là:

kx k

= − +

−

2 3 0 (1).

kx kx k⇔ − + − = Để

cắt (C) tại hai điểm phân biệt

1 1 2 2

( ; ), ( ; )

A x y B x y

thì (1) có 2

nghiệm phân biệt

1 0

≠ ⇔ >

Áp dụng định lý Viet ta có:

1 2

x x





+ =





−





Do đó:

1 2

1 1

2 2

1 2 1 2 1 2

( 1)( ) ( 1) 1 3

y y

y kx k

y y k x x k k x x k k





+ =



= − +



⇒

 

 

= − +

= − − + + − = −

 







Để

thì:

2 2 2 2

1 2 1 2 1 2 1 2 1 2 1 2

( ) ( ) 30 ( ) ( ) 4 4 30

x x y y x x y y x x y y− + − = ⇔ + + + − − =

12 30 12 0 2

k k k k

⇔ − + = ⇔ = ∨ =

Vậy,

1 2

: 2 1 0; : 2 1 0

d x y d x y

− − = − + =

hoặc ngược lại

HT 183. Cho hàm số

1 (1),

y x mx m m

= − + − là tham số. Tìm

để tiếp tuyến của đồ thị

hàm số (1) tại M có hoành độ

= −

cắt đường tròn (C) tâm

(2;3)

bán kính

theo 1 dây

cung AB có độ dài nhỏ nhất.

Giải

Ta có:

'( 1) 3

y m

− = −

Phương trình tiếp tuyến tại

( 1;2 2)

M m

− −

là:

: (3 )( 1) 2 2 (3 ) 1 (3 ) 1 0

y m x m m x m m x y m

∆ = − + + − = − + + ⇔ − − + + =

Để

( )

∆ ∩

thì

( , ) 2.

d I

∆ <

Nhận thấy dây cung AB nhỏ nhất khi

( , )

d I

∆

lớn nhất

( , )

(3 ) 1

d I

−

∆ =

− +

Ta có:

2 2 2

4 (3 ) 1

2 (3 ) 1

( , )

(3 ) 1 (3 ) 1 (3 ) 1

m m

d I

m m m

− − +

− +

∆ = = ≤

− + − + − +

( , ) 2

d I R

∆ ≤ <

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 116

Ta có tiếp tuyến luôn cắt đường tròn (C) hai điểm phân biệt.

AB min

( , ) 2 2

d I m

⇔ ∆ = ⇔ =

Kết luận:

HT 184. Cho hàm số

( ).

2 1

y C

−

Tìm các giá trị của tham số

để đường thẳng

d y x m

= +

cắt đồ thị (C) tại các điểm A, B phân biệt sao cho trọng tâm G của tam giác OAB cách

đường thẳng

một khoảng bằng

(với O là gốc tọa độ).

Giải

Phương trình hoành độ giao điểm:

2 1

( ) 2 2( 1) 2 0,

2 1 2

x m g x x m x m x

= + ⇔ = + − − − = ≠

−

Đường thẳng

cắt (C) tại A, B phân biệt khi và chỉ khi phương trình

( ) 0

g x

có hai nghiệm phân

biệt khác

2 2

' 0

( 1) 2( 2) 5 0

( ) 0

1 2 0

m m m

m m





∆ >

− + + = + >



 

⇔ ⇔ ∀ ∈

 

 

≠

+ − − − ≠

 









ℝ

Gọi

1 2

x x

là các nghiệm của

1 1

( ) 0 ( ; )

g x A x x m

= ⇒ +

và

2 2

( ; )

B x x m

Điều kiện

O d m

∉ ⇒ ≠ ⇒

trọng tâm

1 1

;

3 3

m m

 

− +

















 

Ta có:

1 1

3 3

( , ) 2

2 3 2

m m

d G d

− +





= = = ⇔



= −





HT 185. Cho hàm số

3 2

3 ( 1) 1(1)

y x x m x= − + + + . Tìm

để đường thẳng

: 1

d y x

= +

cắt đồ

thị hàm số (1) tại 3 điểm phân biệt

(0;1), ,

P M N

sao cho bán kính đường tròn ngoại tiếp tam giác

OMN bằng

5 2

với

(0;0).

Giải

(1;1), (2; 0) 2.

A B AB

⇒ =

Phương trình đường thẳng

: 2 0

AB x y

+ − =

( , ). 3 ( , ) 3 2

ABN

S d N AB AB d N AB

∆

= = ⇔ =

Gọi

là đường thẳng đi qua N và

/ / .

d AB

Phương trình đường thẳng

có dạng:

4 (0; 4)( )

0 ( , ) ( , ) 3 2

8 (3;5)

c N l

x y c d A d d N AB

c N

 

= −

 

+ + = ⇒ = ⇔ = ⇔ ⇒

 

= −

 

 

Với

(3;5)

giả sử

0 0

( ; )

M x y

. Phương trình tiếp tuyến với (C) tại M là:

0 0 0

'( )( )

y y x x x y

= − +

Do tiếp tuyến đi qua N nên ta có:

2 3 2

0 0 0 0 0 0

5 (6 18 12)(3 ) 2 9 12 4

x x x x x x

= − + − + − + −

0 0

3( , )

( 3) (4 3) 0

x loai vi N M

x x



= ≠



⇔ − − = ⇔





Vậy,

3 25

;

4 32

 

















 

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 117

TUYỂN TẬP ĐỀ THI ĐẠI HỌC TỪ NĂM 2009

HT 186. (ĐH A – 2009) Cho hàm số

(1)

2 3

. Viết phương trình tiếp tuyến của đồ thị hàm

số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B sao cho tam

giác OAB cân tại gốc tọa độ O.

Giải

Ta có,

OAB

∆

vuông cân tại

suy ra hệ số góc của tiếp tuyến bằng

Gọi tọa độ tiếp điểm là

( ; )

o o

M x y

, ta có:

(2 3)



= −

−



= ± ⇔



= −





TH1: Với

0 0

1, 1

x y

= − =

Phương trình tiếp tuyến

y x

= −

(loại vì đi qua gốc tọa độ O nên không

tồn tại

OAB

∆

)

TH2:

0 0

2; 0

x y

= − =

Phương trình tiếp tuyến

2( / )

y x t m

= − −

KL:

y x

= − −

HT 187. (ĐH B – 2009) Cho hàm số:

4 2

2 4 (1)

y x x= −

.Với giá trị nào của

phương trình

2 2

x x m

− =

có đúng 6 nghiệm thực phân biệt. Đ/s:

0 1

< <

HT 188. (ĐH D – 2009) Cho hàm số

4 2

(3 2) 3

y x m x m

= − + +

có đồ thị là

( )

với

là tham số. Tìm

để đường thẳng

= −

cắt đồ thị

( )

tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2.

Giải

Phương trình hoành độ giao điểm của

( )

và đường thẳng

4 2

1; (3 2) 3 1

y x m x m

= − − + + = −

Đặt

, 0

t x t

= ≥

Phương trình trở thành:

(3 2) 3 1 0

t m t m

− + + + =

⇔ =

hoặc

3 1

t m

= +

Yêu cầu bài toán tương đương với:

0 3 1 4

3 1 1





< + <







+ ≠





1, 0

m m

⇔ − < < ≠

HT 189.

(ĐH A – 2010) Cho hàm số

3 2

2 (1 ) (1),

y x x m x m= − + − +

với

là tham số thực. Tìm

để đồ thị (1) cắt trục hoành tại 3 điểm phân biệt có hoành độ

1 2 3

, ,

x x x

thỏa mãn điều kiện:

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 118

2 2 2

1 2 3

x x x

+ + <

Giải

Phương trình hoành độ giao điểm:

3 2

2 (1 ) 0

x x m x m

− + − + =

( 1)( ) 0

0(*)

x x x m

x x m





⇔ − − − = ⇔



− − =





Đồ thị hàm số (1) cắt trục hoành tại 3 điểm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm

phân biệt, khác 1.

Kí hiệu,

1 2

( ) ; 1;

g x x x m x x

= − − =

và

là các nghiệm của (*).

Yêu cầu bài toán khi và chỉ khi:

2 2

2 3

(1) 0

x x





∆ >



≠





+ <





1 4 0

0 1

1 2 3

m m





+ >



⇔ − ≠ ⇔ − < <





+ <





và

≠

HT 190. (ĐH B – 2010) Cho hàm số

2 1

( )

y C

. Tìm

để đường thẳng

y x m

= − +

cắt đồ thị

( )

tại hai điểm A và B sao cho tam giác OAB có diện tích bằng

(O là gốc tọa độ).

Giải

Phương trình hoành độ giao điểm:

2 1

x m

= − +

2 1 ( 1)( 2 )

x x x m

⇔ + = + − +

(do

= −

không là nghiệm của phương trình)

2 (4 ) 1 0 (1)

x m x m⇔ + − + − =

8 0

∆ = + >

với mọi

suy ra đường thẳng

y x m

= − +

luôn cắt đồ thị (C) tại hai điểm

phân biệt A, B với mọi

Gọi

1 2 2 2

( ; ), ( ; )

A x y B x y

trong đó

1 2

x x

là các nghiệm của (1):

1 1

y x m

= − +

và

2 2

y x m

= − +

Ta có:

( , )

O AB

d = và

2 2 2

1 2 1 2 1 2 1 2

5( 8)

( ) ( ) 5( ) 20

AB x x y y x x x x

= − + − = + − =

( , )

2 4

OAB O AB

m m

S AB d

∆

= =

, suy ra:

3 2

m m

= ⇔ = ±

HT 191. (D – 2010) Cho hàm số

4 2

6 ( )

y x x C

= − − +

. Viết phương trình tiếp tuyến của đồ

thị (C) biết tiếp tuyến vuông góc với đường thẳng

y x

= −

Đ/s:

6 10

y x

= − +

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 119

HT 192. (A – 2011) Cho hàm số

( )

2 1

y C

− +

−

. Chứng minh rằng với mọi

đường thẳng

y x m

= +

luôn cắt đồ thị

( )

tại hai điểm phân biệt A và B. Gọi

1 2

k k

lần lượt là hệ số góc của tiếp

tuyến với

( )

tại A và B. Tìm

để tổng

1 2

k k

đạt giá trị lớn nhất.

Giải

Hoành độ giao điểm của

d y x m

= +

và (C) là nghiệm của phương trình:

2 1

x m

− +

+ =

−

( )(2 1) 1

x m x x

⇔ + − = − +

(vì

không là nghiệm của phương trình)

2 2 1 0 (*)

x mx m⇔ + − − =

' 2 2 0, .

m m m

∆ = + + > ∀

Suy ra

luôn cắt (C) tại hai điểm phân biệt với mọi

Gọi

1 2

x x

là các nghiệm của (*), ta có:

1 2 1 2 1 2

1 2

2 2 2

1 2

1 2 1 2

4( ) 8 4( ) 2

1 1

(2 1) (2 1)

4 2( ) 1

x x x x x x

k k

x x

x x x x

+ − − + +

+ = − − = −

− −

 

− + +

 

 

Theo định lý Viet, suy ra:

2 2

1 2

4 8 6 4( 1) 2 2

k k m m m

+ = − − − = − + − ≤ −

Suy ra:

1 2

k k

lớn nhất bằng

−

, khi và chỉ khi

= −

HT 193. (B – 2011) Cho hàm số

4 2

2( 1) (1)

y x m x m= − + +

(với

là tham số). Tìm

để đồ

thị hàm số (1) có ba điểm cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị

thuộc trục tung, B và C là hai điểm cực trị còn lại.

Giải

3 2

( )

' 4 4( 1) 4 ( 1)

y x m x x x m

= − + = − −

( ) 2

' 0

1 (1)

x m





= ⇔



= +





Đồ thị hàm số có 3 điểm cực trị khi và chỉ khi (1) có hai nghiệm phân biệt khác 0

1 (*)

⇔ > −

Khi đó:

(

)

(

)

2 2

(0; ), 1; 1 , 1; 1

A m B m m m C m m m

− + − − − + − − −

Suy ra:

2 2

4( 1) 4 4 0

OA BC m m m m

= ⇔ = + ⇔ − − =

2 2 2

⇔ = ±

(thỏa mãn (*)). Vậy giá trị cần tìm:

2 2 2

= ±

HT 194. (D – 2011) Cho hàm số

2 1

( )

y C

. Tìm

để đường thẳng

2 1

y kx k

= + +

cắt đồ thị

( )

tại hai điểm phân biệt

A B

sao cho khoảng cách từ A và B đến trục hoành bằng nhau.

Giải

Gọi

: 2 1,

d y kx k

= + +

suy ra hoành độ giao điểm của

với (C) là nghiệm của phương trình:

2 1

2 1 2 1 ( 1)( 2 1)

kx k x x kx k

+ + = ⇔ + = + + +

(do

= −

không là nghiệm)

(3 1) 2 0 (1).

kx k x k⇔ + − + =

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 120

cắt (C) tại hai điểm phân biệt khi và chỉ khi (1) có hai nghiệm phân biệt

Khi đó, và , là nghiệm của (1).

(do )

Áp dụng định lý Viet đối với (1), suy ra: (thỏa mãn (*))

Vậy giá trị cần tìm:

HT 195. (A,A1 – 2012) Cho hàm số

4 2 2

2( 1) (1)

y x m x m= − + +

, với

là tham số thực. Tìm

để

đồ thị hàm số (1) có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác vuông.

Giải

Ta có:

3 2

' 4 4( 1) 4 ( 1)

y x m x x x m

= − + = − −

Đồ thị hàm số có 3 điểm cực trị khi và chỉ khi

1 0 1 (*)

m m

+ > ⇔ > −

Các điểm cực trị của đồ thị hàm số

(

)

(

)

(0; ), 1; 2 1 , 1; 2 1

A m B m m C m m

− + − − + − −

Suy ra:

(

)

1; ( 1)

AB m m= − + − +



và

(

)

1; ( 1)

AC m m= + − +



Ta có:

AB AC

nên tam giác

ABC

vuông khi và chỉ khi:

. 0

AB AC

 

( 1) ( 1) 0.

m m

⇔ + − + =

Kết hợp (*), ta được

Đ/s:

HT 196. (B – 2012) Cho hàm số

3 2 3

3 3 (1),

y x mx m= − +

là tham số thực. Tìm

để đồ thị

hàm số (1) có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 48.

Giải

Ta có:

' 3 6 ; ' 0 0 2

y x mx y x x m

= − = ⇔ = ∨ =

Đồ thị hàm số có 2 điểm cực trị khi và chỉ khi

≠

Các điểm cực trị của đồ thị hàm số:

(

)

(

)

3 3

0;3 ; 2 ;

A m B m m

−

Suy ra:

OA m

= và

( , )

B OA

d m

48 3 48 2( / (*))

OAB

S m m t m

∆

= ⇔ = ⇔ = ±

Đ/s:

= ±

HT 197. (D – 2012) Cho hàm số

3 2 2

2 2

2(3 1) (1),

3 3

y x mx m x m

= − − − + là tham số thực. Tìm

để hàm số (1) có hai điểm cực trị

1 2

;

x x

sao cho:

1 2 1 2

2( ) 1.

x x x x

+ + =

Giải

Ta có:

2 2

' 2 2 2(3 1)

y x mx m

= − − −

, ,

A B

3 2 2

(*)

6 1 0

3 2 2

k k





≠











≠



≠







 

< −

⇔ ⇔ ⇔

  



  

∆ >

− + >



  











> +









1 1

( ; 2 1)

A x kx k

+ +

2 2

( ; 2 1)

B x kx k

+ +

1 2

x x

( , ) ( , ) 1 2

2 1 2 1

A Ox B Ox

d d kx k kx k

= ⇔ + + = + +

1 2

( ) 4 2 0

k x x k

⇔ + + + =

1 2

x x

≠

(1 3 ) 4 2 0 3

k k k

− + + = ⇔ = −

= −

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 121

Đồ thị hàm số có hai điểm cực trị khi và chỉ khi phương trình

' 0

có hai nghiệm phân biệt

2 13 2 13

13 4 0

13 13

m m m⇔ − > ⇔ > ∨ < −

Ta có:

1 2

x x m

+ =

và

1 2

1 3 ;

x x m

= − Do đó,

1 2 1 2

2( ) 1 1 3 2 1

x x x x m m

+ + = ⇔ − + =

m m

⇔ = ∨ =

So sánh điều kiện (*) ta được:

Đ/s:

HT 198. (A,A1 – 2013) Cho hàm số

3 2

3 3 1 (1)

y x x mx= − + + −

, với

là tham số thực. Tìm

để

hàm số (1) nghịch biến trên khoảng

(0; )

+∞

Giải

Ta có:

' 3 6 3

y x x m

= − + +

Hàm số (1) nghịch biến trên khoảng

(0; )

+∞

khi và chỉ khi

' 0, 0

y x

≤ ∀ >

2 , 0

m x x x

⇔ ≤ − ∀ >

Xét:

( ) 2

f x x x

= −

với

. Ta có:

'( ) 2 2; '( ) 0 1

f x x f x x

= − = ⇔ =

Lập bảng biến thiên (nhớ lập nhé) ta được giá trị

thỏa mãn yêu cầu bài toán:

≤ −

Đ/s:

≤ −

HT 199. (B – 2013) Cho hàm số

3 2

2 3( 1) 6 (1),

y x m x mx= − + +

với

là tham số thực. Tìm

để

đồ thị hàm số (1) có hai điểm cực trị A, B sao cho đường thẳng AB vuông góc với đường thẳng

y x

= +

Giải

Ta có:

' 6 6( 1) 6 ; ' 0 1

y x m x m y x x m

= − + + = ⇔ = ∨ =

Điều kiện để đồ thị hàm số có hai điểm cực trị là

≠

Ta có: 2 điểm cực trị của đồ thị hàm số khi đó

3 2

(1;3 1); ( ; 3 ).

A m B m m m

− − +

Hệ số góc của đường thẳng

là

( 1)

k m

= − −

Đường thẳng

vuông góc với đường thẳng

y x

= +

khi và chỉ khi

= −

0 2

m m

⇔ = ∨ =

. Vậy giá trị

cần tìm

0; 2

m m

= =

HT 200. (D – 2013) Cho hàm số

3 2

2 3 ( 1) 1 (1),

y x mx m x= − + − +

với

là tham số thực. Tìm

để đường thẳng

y x

= − +

cắt đồ thị hàm số (1) tại ba điểm phân biệt.

Giải

Phương trình hoành độ giao điểm của đồ thị hàm số (1) với đường thẳng

y x

= − +

là:

3 2

2 3 ( 1) 1 1

x mx m x x

− + − + = − +

2 3 0 (*)

x mx m





⇔



− + =





Yêu cầu của bài toán

⇔

phương trình (*) có hai nghiệm phân biệt khác 0.

GV.Lưu Huy Thưởng 0968.393.899

BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 122

9 8 0

m m









− >





⇔ ⇔







≠











Đ/s:

m m

< >

UPDATING………………

Bấm Tải xuống để xem toàn bộ.

| 1/122

| | Tải xuống

Preview text:

GV.Lưu Huy Thưởng 0968.393.899
LÝ THUYẾT KHẢO SÁT HÀM SỐ
I. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ 1. Định nghĩa:
Hàm số f đồng biến trên K ⇔ x
∀ ,x ∈ K,x < x ⇒ f (x ) < f (x ) 1 2 1 2 1 2
Hàm số f nghịch biến trên K ⇔ x
∀ ,x ∈ K,x < x ⇒ f (x ) > f (x ) 1 2 1 2 1 2
2. Điều kiện cần:
Giả sử f có đạo hàm trên khoảng I.
a) Nếu f đồng biến trên khoảng I thì f '(x ) ≥ 0, ∀x ∈ I
b) Nếu f nghịch biến trên khoảng I thì f '(x ) ≤ 0, ∀x ∈ I
3. Điều kiện đủ:
Giả sử f có đạo hàm trên khoảng I.
a) Nếu f '(x ) ≥ 0, ∀x ∈ I ( f '(x ) = 0 tại một số hữu hạn điểm) thì f đồng biến trên I.
b) Nếu f '(x ) ≤ 0, ∀x ∈ I ( f '(x ) = 0 tại một số hữu hạn điểm) thì f nghịch biến trên I.
c) Nếu f '(x ) = 0 thì f không đổi trên I.
Chú ý: Nếu khoảng I được thay bởi đoạn hoặc nửa khoảng thì f phải liên tục trên đó.
4. Điều kiện hàm số luôn đồng biến trên một miền xác định.
Cho hàm số y = f (x,m), m là tham số, có tập xác định D.
• Hàm số f đồng biến trên D ⇔ y ' ≥ 0, ∀x ∈ D
• Hàm số f nghịch biến trên D ⇔ y ' ≤ 0, ∀x ∈ D .
Từ đó suy ra điều kiện của m. Chú ý:
● y ' = 0 chỉ xảy ra tại một số hữu hạn điểm. ●Nếu 2
y ' = ax + bx + c thì:  a  = b = 0    a  = b = 0      c  ≥ 0   c  ≤ 0  • y ' 0, x R  ≥ ∀ ∈ ⇔  • y ' 0, x R  ≤ ∀ ∈ ⇔   a  > 0    a  < 0       ∆ ≤ 0    ∆ ≤ 0    
●Định lí về dấu của tam thức bậc hai 2
g(x) = ax + bx + c :
♣ Nếu ∆ < 0 thì g(x) luôn cùng dấu với a . b
♣ Nếu ∆ = 0 thì g(x) luôn cùng dấu với a (trừ x = − ) 2a
♣ Nếu ∆ > 0 thì g(x) có hai nghiệm x ,x và trong khoảng hai nghiệm thì g(x) khác dấu 1 2
vớia , ngoài khoảng hai nghiệm thì g(x ) cùng dấu với a .
●So sánh các nghiệm x ,x của tam thức bậc hai 2
g(x) = ax + bx + c với số 0: 1 2 ∆ > 0   ∆ > 0   ♣ x x 0 P  < < ⇔  > 0 ♣ 0 x x P  < < ⇔  > 0
♣x < 0 < x ⇔ P < 0 1 2  1 2  1 2 S  < 0   S  > 0   ●Để hàm số 3 2
y = ax + bx + cx + d có độ dài khoảng đồng biến (nghịch biến) (x ;x ) bằng d thì 1 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 1
GV.Lưu Huy Thưởng 0968.393.899
ta thực hiện các bước sau:
Bước 1: Tính y ' .
Bước 2: Tìm điều kiện để hàm số có khoảng đồng biến và nghịch biến: a  ≠ 0   ∆ > 0  (1)
Bước 3: Biến đổi x − x = d thành 2 2
(x + x ) − 4x x = d 1 2 1 2 1 2 (2)
Bước 4: Sử dụng định lí Viet đưa (2) thành phương trình theo m.
Bước 5: Giải phương trình, so với điều kiện (1) để chọn nghiệm.
II. CỰC TRỊ CỦA HÀM SỐ
1. Khái niệm cực trị của hàm số
Giả sử hàm số f xác định trên tập D (D ⊂ R) và x ∈ D . 0
a) x – điểm cực đại của f nếu tồn tại khoảng (a;b) ∈ D và x ∈ (a;b) sao cho 0 0
f (x) < f (x ), x
∀ ∈ (a;b) \ {x } . 0 0
Khi đó f (x ) được gọi là giá trị cực đại (cực đại) của f. 0
b) x – điểm cực tiểu của f nếu tồn tại khoảng (a;b) ∈ D và x ∈ (a;b) sao cho 0 0
f (x) > f (x ), x
∀ ∈ (a;b) \ {x } . 0 0
Khi đó f (x ) được gọi là giá trị cực tiểu (cực tiểu) của f. 0
c) Nếu x là điểm cực trị của f thì điểm (x ; f (x ) được gọi là điểm cực trị của đồ thị hàm số f. 0 0 ) 0
2. Điều kiện cần để hàm số có cực trị
Nếu hàm số f có đạo hàm tại x và đạt cực trị tại điểm đó thì f '(x ) = 0 . 0 0
Chú ý: Hàm số f chỉ có thể đạt cực trị tại những điểm mà tại đó đạo hàm bằng 0 hoặc không có đạo hàm.
3. Điểu kiện đủ để hàm số có cực trị
1. Định lí 1: Giả sử hàm số f liên tục trên khoảng (a;b) chứa điểm x và có đạo hàm trên 0
(a;b) \ {x } 0
a) Nếu f '(x) đổi dấu từ âm sang dương khi x đi qua x thì f đạt cực tiểu tại x . 0 0
b) Nếu f '(x) đổi dấu từ dương sang âm khi x đi qua x thì f đạt cực đại tại x . 0 0
2. Định lí 2: Giả sử hàm số f có đạo hàm trên khoảng (a; b) chứa điểm x , f '(x ) = 0 và có đạo 0 0
hàm cấp hai khác 0 tại điểm x . 0
a) Nếu f ' (x ) < 0 thì f đạt cực đại tại x . 0 0
b) Nếu f ' (x ) > 0 thì f đạt cực tiểu tại x . 0 0
4. Quy tắc tìm cực trị
Qui tắc 1: Dùng định lí 1.
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 2
GV.Lưu Huy Thưởng 0968.393.899
• Tìm f '(x) .
• Tìm các điểm x (i = 1, 2, …) mà tại đó đạo hàm bằng 0 hoặc không có đạo hàm. i
• Xét dấu f '(x) . Nếu f '(x) đổi dấu khi x đi qua x thì hàm số đạt cực trị tại x . i i
Qui tắc 2: Dùng định lí 2.
• Tính f '(x) .
• Giải phương trình f '(x) = 0 tìm các nghiệm x (i = 1, 2, …). i
• Tính f ' (x)và f ' (x )(i = 1, 2, …). i
Nếu f ' (x ) < 0 thì hàm số đạt cực đại tại x . i i
Nếu f ' (x ) > 0 thì hàm số đạt cực tiểu tại x . i i
III. SỰ TƯƠNG GIAO CỦA CÁC ĐỒ THỊ
1. Cho hai đồ thị (C ) : y = f (x) và (C ) : y = g(x) . Để tìm hoành độ giao điểm của (C 1 2 1) và (C2) ta
giải phương trình: f (x) = g(x) (*) (gọi là phương trình hoành độ giao điểm).
Số nghiệm của phương trình (*) bằng số giao điểm của hai đồ thị.
2. Đồ thị hàm số bậc ba 3 2
y = ax + bx + cx + d (a ≠ 0) cắt trục hoành tại 3 điểm phân biệt ⇔ Phương trình 3 2
ax + bx + cx + d = 0 có 3 nghiệm phân biệt. ⇔ Hàm số 3 2
y = ax + bx + cx + d có cực đại, cực tiểu và y .y < 0 . CÑ CT
IV. TOÁN TIẾP TUYẾN
Bài toán 1: Viết phương trình tiếp tuyến ∆ của (C ) : y = f (x) tại điểm M x ;y : 0 ( 0 0 )
• Nếu cho x thì tìm y = f(x ). 0 0 0
Nếu cho y thì tìm x là nghiệm của phương trình f (x) = y . 0 0 0
• Tính y ' = f '(x) . Suy ra y '(x ) = f '(x ). 0 0
• Phương trình tiếp tuyến ∆ là: y −y = f '(x ).(x − x ) 0 0 0
Bài toán 2: Viết phương trình tiếp tuyến ∆ của (C ) : y = f (x) , biết ∆ có hệ số góc k cho trước.
Cách 1: Tìm toạ độ tiếp điểm.
• Gọi M x ;y là tiếp điểm. Tính f '(x ). 0 ( 0 0 ) 0
• ∆ có hệ số góc k ⇒ f '(x ) = k (1) 0
• Giải phương trình (1), tìm được x và tính y = f(x ). Từ đó viết phương trình của ∆. 0 0 0
Cách 2: Dùng điều kiện tiếp xúc.
• Phương trình đường thẳng ∆ có dạng: y = kx + m .
• ∆ tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:
f (x) = kx + m   (*)
f '(x) = k 
• Giải hệ (*), tìm đượcm . Từ đó viết phương trình của ∆.
Chú ý: Hệ số góc k của tiếp tuyến ∆ có thể được cho gián tiếp như sau:
+ ∆ tạo với chiều dương trục hoành góc α thì k tan α =
+ ∆ song song với đường thẳng d : y = ax + b thì k = a
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 3
GV.Lưu Huy Thưởng 0968.393.899 1
+ ∆ vuông góc với đường thẳng d : y = ax + b (a ≠ 0) thì k = − a k − a
+ ∆ tạo với đường thẳng d : y = ax + b một góc α thì = tan α 1 + ka
Bài toán 3: Viết phương trình tiếp tuyến ∆ của (C): y = f (x), biết ∆ đi qua điểm ( A x ;y ) . A A
Cách 1: Tìm toạ độ tiếp điểm.
• Gọi M x ;y là tiếp điểm. Khi đó: y = f(x );y ' f '(x ). 0 ( 0 0 ) 0 0 0 0
• Phương trình tiếp tuyến ∆ tại M : y −y = f '(x )(x − x ) 0 0 0 • ∆ đi qua (
A x ;y ) nên: y = y −
= f '(x )(x − x ) (2) A A A 0 0 A 0
• Giải phương trình (2), tìm được x . Từ đó viết phương trình của ∆. 0
Cách 2: Dùng điều kiện tiếp xúc.
• Phương trình đường thẳng ∆ đi qua (
A x ;y ) và có hệ số góc k : y − y = k(x − x ) A A A A
• ∆ tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:
f (x) = k(x − x ) + y  A A 
f '(x) = k  (*)
• Giải hệ (*), tìm được x (suy rak ). Từ đó viết phương trình tiếp tuyến ∆.
V. ĐIỀU KIỆN TIẾP XÚC
1. Điều kiện cần và đủ để hai đường (C ) : y = f (x) và (C ) : y = g(x) tiếp xúc nhau là hệ phương 1 2 trình sau có nghiệm:
 f (x) = g(x)   (*)
f '(x) = g '(x) 
Nghiệm của hệ (*) là hoành độ của tiếp điểm của hai đường đó.
2. Nếu (C ) : y = px + q và 2
(C ) : y = ax + bx + c thì 1 2
(C1) và (C2) tiếp xúc nhau ⇔ phương trình 2
ax + bx + c = px + q có nghiệm kép. VI. KHOẢNG CÁCH
1. Khoảng cách giữa hai điểm A, B: AB = 2 2
(x − x ) + (y − y ) B A B A
2. Khoảng cách từ điểm M(x0; y0) đến đường thẳng ∆ : ax + by + c = 0
ax + by + c d(M, ∆) = 0 0 2 2 a + b
VII. ĐỒ THỊ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI
Cách 1: Khảo sát sự biến thiên và vẽ đồ thị.
• Xét dấu biểu thức có chứa dấu giá trị tuyệt đối.
• Chia miền xác định thành nhiều khoảng, trong mỗi khoảng ta bỏ dấu giá trị tuyệt đối.
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 4
GV.Lưu Huy Thưởng 0968.393.899
• Vẽ đồ thị hàm số tương ứng trong các khoảng của miền xác định.
Cách 2: Thực hiện các phép biến đổi đồ thị.
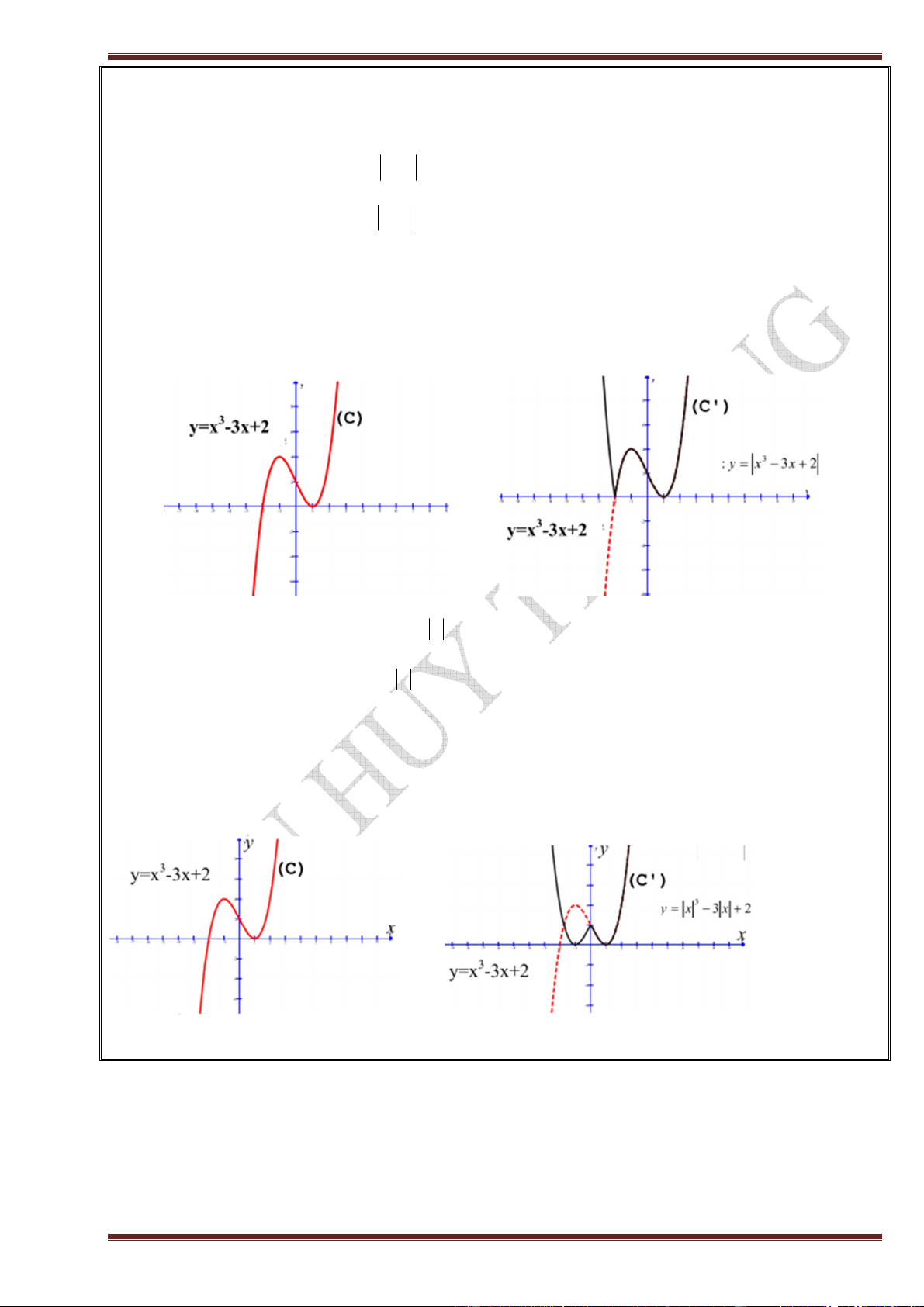
Dạng 1: Vẽ đồ thị hàm số y = f (x) .
Đồ thị (C′) của hàm số y = f (x) có thể được suy từ đồ thị (C) của hàm số y = f(x) như sau:
+ Giữ nguyên phần đồ thị (C) ở phía trên trục hoành.
+ Lấy đối xứng phần đồ thị của (C) ở phía dưới trục hoành qua trục hoành.
+ Đồ thị (C′) là hợp của hai phần trên.
Dạng 2: Vẽ đồ thị của hàm số y = f ( x ).
Đồ thị (C′) của hàm số y = f ( x ) có thể được suy từ đồ thị (C) của hàm số y = f(x) như sau:
+ Giữ nguyên phần đồ thị (C) ở bên phải trục tung, bỏ phần bên trái trục tung.
+ Lấy đối xứng phần bên phải trục tung qua trục tung.
+ Đồ thị (C′) là hợp của hai phần trên.
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 5
GV.Lưu Huy Thưởng 0968.393.899
PHẦN I: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ 1 HT 1. Cho hàm số 3 2 y =
(m − 1)x + mx + (3m − 2)x (1). Tìm tất cả các giá trị của tham số m để 3
hàm số (1) đồng biến trên tập xác định của nó. Giải
• Tập xác định: D = R. 2
y ′= (m − 1)x + 2mx + 3m − 2 .
(1) đồng biến trên R ⇔ y ′≥ 0, ∀x 2
⇔ (m − 1)x + 2mx + 3m − 2 ≥ 0, ∀x  m  − 1 = 2m = 0   m  > 1    3  m − 2 ≥ 0 m  > 1       1 ⇔  ⇔  ⇔  m  ≤ ⇔ m ≥ 2 2  m  − 1 > 0
−2m + 5m − 2 ≤ 0     2     2  m   ≥ 2
m − (m − 1)(3m − 2) ≤ 0      HT 2. Cho hàm số 3 2
y = x + 3x − mx − 4 (1). Tìm tất cả các giá trị của tham số m để hàm số (1)
đồng biến trên khoảng (− ; ∞ 0) . Giải
• Tập xác định: D = ℝ ; 2
y ' = 3x + 6x − m ,
(1) đồng biến trên khoảng (-∞;0) ⇔ y’ ≥ 0, ∀x ∈ (-∞;0) ⇔ 2
3x + 6x − m ≥ 0 ∀x ∈ (-∞;0) x -∞ -1 0 +∞ ⇔ 2 f’(x) - 0 +
3x + 6x ≥ m ∀x ∈ (-∞;0) x + - f(x) Xét hàm số f(x) = 2
3x + 6x − m trên (-∞;0] -3
Có f’(x) = 6x + 6; f’(x) = 0 ⇔ x = -1
Từ bảng biến thiên: ⇒ m ≤ −3
HT 3. Cho hàm số y = x3 2 2
− 3(2m + 1)x + 6m(m + 1)x + 1 có đồ thị (Cm). Tìm m để hàm số đồng biến trên khoảng (2;+ ) ∞ Giải
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 6
GV.Lưu Huy Thưởng 0968.393.899
• Tập xác định: D = ℝ 2
y ' = 6x − 6(2m + 1)x + 6 ( m m + 1) có 2 2
∆ = (2m + 1) − 4(m + m) = 1 > 0 x = m y ' 0  = ⇔  x = m + 1 
Ta có: y’ ≥ 0, ∀x (-∞;m) và (m + 1; +∞)
Do đó: hàm số đồng biến trên (2;+ )
∞ ⇔ m + 1 ≤ 2 ⇔ m ≤ 1 HT 4. Cho hàm số 3 2
y = x + (1 − 2m)x + (2 − m)x + m + 2 . Tìm m để hàm đồng biến trên (0;+∞). Giải
• Tập xác định: D = ℝ 2 y ′= 3x + (
2 1 − 2m)x + (2 − m)
Hàm đồng biến trên (0;+ ) ∞ 2
⇔ y ′= 3x + (
2 1 − 2m)x + (2 − m) ≥ 0 với ∀x ∈ 0 ( ;+ ) ∞ 2 3x + 2x + 2 ⇔ f (x) =
≥ m với ∀x ∈ 0 ( ;+ ) ∞ 4x + 1  2 x = −1 2(2x + x − 1)  Ta có: 2 f ( ′ x) =
= 0 ⇔ 2x + x − 1 = 0 ⇔  2 1 (4x + ) 1 x =  2
Lập bảng biến thiên của hàm f (x) trên (0;+ )
∞ , từ đó ta đi đến kết luận: 1 5 f     ≥ m ⇔ ≥ m 2 4 HT 5. Cho hàm số 4 2
y = x − 2mx − 3m + 1 (1), (m là tham số). Tìm m để hàm số (1) đồng biến trên khoảng (1; 2). Giải
• Tập xác định: D = ℝ Ta có 3 2
y ' = 4x − 4mx = 4x(x − m)
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 7
GV.Lưu Huy Thưởng 0968.393.899
+ m ≤ 0 , y ′≥ 0, ∀x ∈ (1;2) ⇒ m ≤ 0 thoả mãn.
+ m > 0 , y ′= 0 có 3 nghiệm phân biệt: − m, 0, m .
Hàm số (1) đồng biến trên (1; 2) khi chỉ khi m ≤ 1 ⇔ 0 < m ≤ 1 . Vậy m ( ;1 ∈ −∞  .  mx + 4
HT 6. Cho hàm số y =
(1). Tìm tất cả các giá trị của tham số m để hàm số (1) nghịch x + m biến trên khoảng (− ; ∞ 1). Giải 2 • m − 4
Tập xác định: D = R \ {–m}. y ′= . 2 (x + m)
Hàm số nghịch biến trên từng khoảng xác định ⇔ y ′< 0 ⇔ 2 − < m < 2 (1)
Để hàm số (1) nghịch biến trên khoảng(− ;
∞ 1)thì ta phải có m −
≥ 1 ⇔ m ≤ −1 (2)
Kết hợp (1) và (2) ta được: −2 < m ≤ −1.   π
HT 7. Chứng minh rằng, hàm số 2
y = sin x + cos x đồng biến trên đoạn 0;  và nghịch biến trên  3      π đoạn  ; π  3    Giải
Hàm số đã cho xác định trên 0;  π    Ta có: y ' sin x(2 cos x 1), x (0; π = − ∈ ) 1 π Vì x (0; π ∈
) ⇒ sin x > 0 nên trên (0; π) : y ' = 0 ⇔ cos x = ⇔ x = 2 3     π π
+ Trên khoảng0;  : y ' > 0 nên hàm số đồng biến trên đoạn    0;  3  3        π π + Trên khoảng ; 
π : y ' < 0 nên hàm số nghịch biến trên đoạn    ; π  3   3   
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 8
GV.Lưu Huy Thưởng 0968.393.899 HT 8. Cho hàm số 3 2
y = x + 3x + mx + m . Tìm m để hàm số nghịch biến trên đoạn có độ dài bằng 1 Giải
Hàm số đã cho xác định trên ℝ Ta có: 2
y ' = 3x + 6x + m có ∆ ' = 9 − 3m
+ Nếu m ≥ 3 thì y’ ≥ 0, ∀x ∈ ℝ , khi đó hàm số đồng biến trên ℝ , do đó m ≥ 3 không thỏa mãn.
+ Nếu m < 3, khi đó: y’ = 0 có hai nghiệm phân biệt x , x (x < x )và hàm số nghịch biến 1 2 1 2
trong đoạn: x ;x  
với độ dài l = x − x 1 2   2 1 m
Theo Vi-ét ta có: x + x = −2,x x = 1 2 1 2 3
Hàm số nghịch biến trên đoạn có độ dài bằng 1 ⇔ l = 1 ⇔ 4 9 (x − x )2 2
= 1 ⇔ (x + x ) − 4x x = 1 ⇔ 4 − m = 1 ⇔ m = 2 1 1 2 1 2 3 4
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 9
GV.Lưu Huy Thưởng 0968.393.899
PHẦN 2: CỰC TRỊ CỦA HÀM SỐ HT 9. Cho hàm số 3 2
y = x + (1 – 2m)x + (2 – m)x + m + 2 (m là tham số) (1). Tìm các giá trị của
m để đồ thị hàm số (1) có điểm cực đại, điểm cực tiểu, đồng thời hoành độ của điểm cực tiểu nhỏ hơn 1. Giải
• Tập xác định: D = ℝ 2
y ′= 3x + 2(1 − 2m)x + 2 − m = g(x)
YCBT ⇔ phương trình y ′= 0 có hai nghiệm phân biệt x , x thỏa mãn: x < x < 1 . 1 2 1 2  2 ′ ∆ 
= 4m − m − 5 > 0  5 7 ⇔ g  (1) = 5 − m + 7 > 0 ⇔  < m < .  4 5 S 2m − 1  = < 1 2 3 HT 10. Cho hàm số 3 2
y = (m + 2)x + 3x + mx − 5 , m là tham số. Tìm các giá trị của m để các điểm
cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương. Giải
• Các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương ⇔ PT 2
y ' = 3(m + 2)x + 6x + m = 0 có 2 nghiệm dương phân biệt a  = (m + 2) ≠ 0 ∆
 ' = 9 − 3m(m + 2) > 0  2   ∆ ' = m − − 2m + 3 > 0
−3 < m < 1       m  m  = >  0 m  ⇔ ⇔ < ⇔  < 0
⇔ −3 < m < −2 P 0  3(m 2)   +  m  2 0 m  + <  < −2  −3   S  = > 0  m  + 2 HT 11. Cho hàm số 3 2 3
y = 2x − 3(m + 2)x + 6(5m +1)x − (4m + 2). Tìm m để hàm số đạt cực tiểu tại x ∈  0 (1;2 Giải
Vì hàm số bậc 3 nên để hàm số có hai điểm cực trị ⇔ y ' = 0 có 2 nghiệm phân biệt. Do hệ số của 3
x là dương nên khi đó: x > x CT CD
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 10
GV.Lưu Huy Thưởng 0968.393.899 Ta có 2 2
y ' = 6[x − (m + 2)x + 5m +1], y ' = 0 ⇔ m(x − 5) = x − 2x +1 (1) 2 x − 2x +1
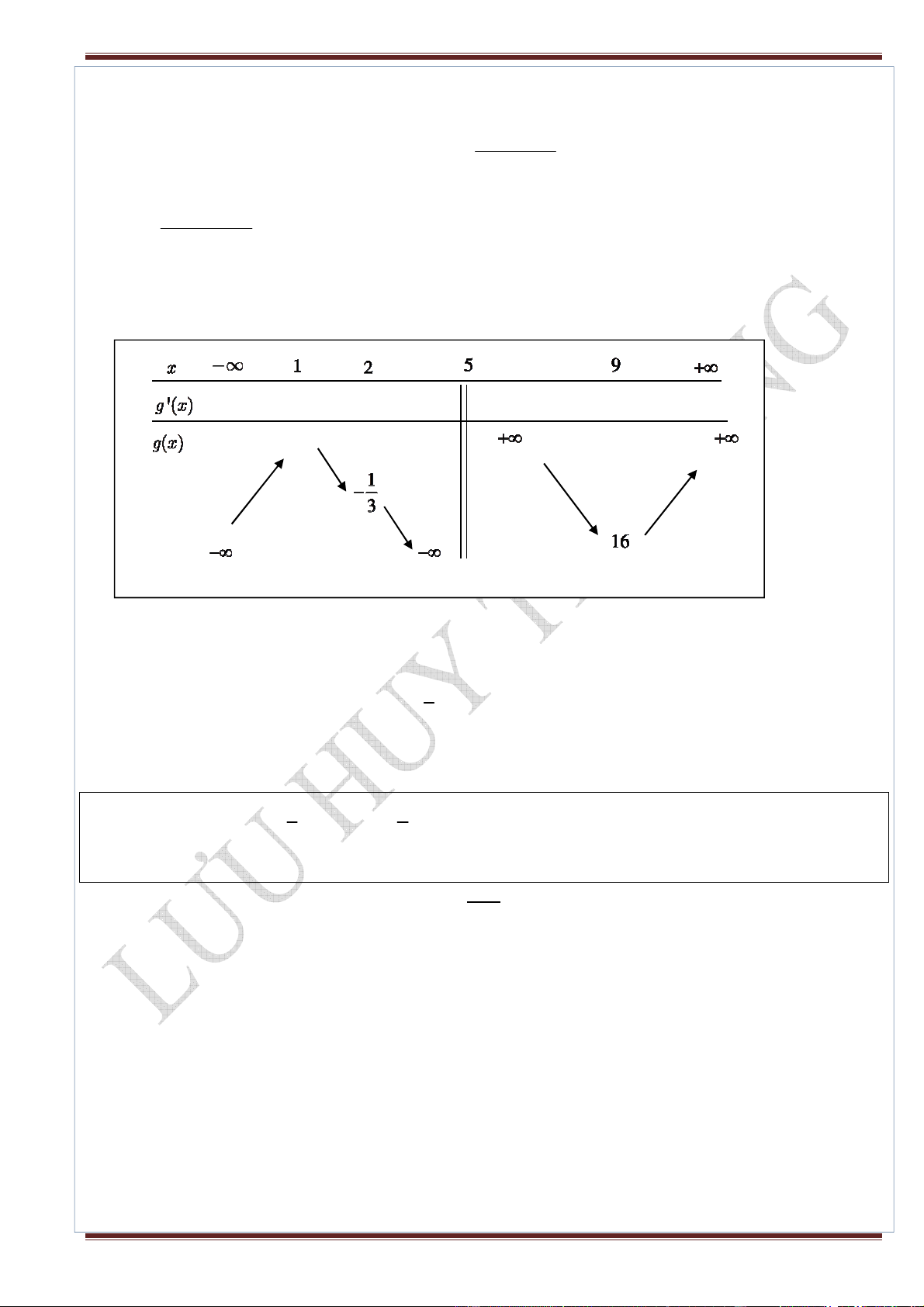
Do x = 5 không là nghiệm của (1) ⇒ (1) ⇔ m = = ( g x) x − 5 2 x −10x + 9 x = 1 g '(x) = = 0 ⇔ 2 x = 9 (x − 5) Bảng biến thiên: + 0 - - - 0 + 0
Từ bảng biến thiên và kết hợp với nhận xét trên 1
⇒ Hàm số đạt cực tiểu tại x0 ∈(1;2] ⇔ − ≤ m < 0 3 1 3 HT 12. Cho hàm số 4 2 y = x − mx +
(1). Xác định m để đồ thị của hàm số (1) có cực tiểu mà 2 2 không có cực đại. Giải
• Tập xác định: D = ℝ x = 0 3 2
y ′= 2x − 2mx = 2x(x − m) . y 0  ′= ⇔  2 x = m 
Đồ thị của hàm số (1) có cực tiểu mà không có cực đại ⇔ PT y ′= 0 có 1 nghiệm ⇔ m ≤ 0
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 11
GV.Lưu Huy Thưởng 0968.393.899 HT 13. Cho hàm số 4 2 y = x − + 2mx − 4
(C ). Tìm các giá trị của m để tất cả các điểm cực trị m
của (C ) đều nằm trên các trục tọa độ. m Giải x  = 0 Ta có: 3 y ' 4x 4mx;y ' 0  = − + = ⇔  2 x = m 
Nếu m ≤ 0 ⇒ đồ thị hàm số có 1 điểm cực trị duy nhất và điểm đó nằm trên trục tung.
Nếu m > 0 thì đồ thị hàm số khi đó có 3 điểm cực trị. Một điểm cực trị nằm trên trục tung và
hai điểm cực trị còn lại có tọa độ: 2
(± m;m − 4) ⇒ Các điểm này chỉ có thể nằm trên trục hoành. m  > 0
⇒ Điều kiện các điểm nằm trên trục hoành là  ⇔ m = 2 2 m  − 4 = 0  m  = 2 Kết luận:  m  ≤ 0  HT 14. Cho hàm số 3 2 2 y = x −
+ (2m + 1)x − (m − 3m + 2)x − 4 (m là tham số) có đồ thị là (Cm).
Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía của trục tung. Giải
•Tập xác định: D = ℝ 2 2 y ′= 3
− x + 2(2m + 1)x − (m − 3m + 2) .
(Cm) có các điểm CĐ và CT nằm về hai phía của trục tung ⇔ PT y′ = 0 có 2 nghiệm trái dấu ⇔ 2
3(m − 3m + 2) < 0 ⇔ 1 < m < 2 . 1 HT 15. Cho hàm số 3 2 y =
x − mx + (2m − 1)x − 3 (m là tham số) có đồ thị là (Cm). Xác định m để 3
(Cm) có các điểm cực đại, cực tiểu nằm về cùng một phía đối với trục tung. Giải • TXĐ: D = ℝ ; 2
y ′= x – 2mx + 2m – 1 .
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 12
GV.Lưu Huy Thưởng 0968.393.899
Đồ thị (Cm) có 2 điểm CĐ, CT nằm cùng phía đối với trục tung ⇔ y ′= 0 có 2 nghiệm phân biệt    2 ′ m  ≠ 1 ∆ 
= m − 2m + 1 > 0  cùng dấu ⇔    ⇔  1 2  m − 1 > 0  m  >   2 HT 16. Cho hàm số 3 2
y = x + 3x + mx + m – 2 (m là tham số) có đồ thị là (Cm). Xác định m để
(Cm) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành. Giải
• PT hoành độ giao điểm của (C) và trục hoành: 3 2
x + 3x + mx + m – 2 = 0 (1) x  = 1 − ⇔  2
g(x) = x + 2x + m − 2 = 0 (2) 
(Cm) có 2 điểm cực trị nằm về 2 phía đối với trục 0x ⇔ PT (1) có 3 nghiệm phân biệt  ′ ∆  = 3 − m > 0
⇔ (2) có 2 nghiệm phân biệt khác –1 ⇔  ⇔ m < 3 g
 (−1) = m − 3 ≠ 0  1 4 HT 17. Cho hàm số 3 2 3 y =
x − (m + 1)x +
(m + 1) (C ). Tìm m để các điểm cực trị của hàm số 3 3
(C) nằm về hai phía (phía trong và phía ngoài) của đường tròn có phương trình: 2 2
x + y − 4x + 3 = 0. Giải Ta có: 2
y ' = x − 2(m + 1)x x  = 0 y ' 0  =
⇔ x = 2(m +1)  4 3 y(0) =
(m + 1) ;y(2m + 2) = 0 3
Đề hàm số có cực trị thì m ≠ −1.  4 
Gọi hai điểm cực trị của đồ thị hàm số là:  3
A0; (m + 1) ;B(2m + 2; 0)  3 
Gọi I là tâm đường tròn, khi đó I (2; 0) và R = 1.
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 13
GV.Lưu Huy Thưởng 0968.393.899
A và B nằm về hai phía của đường tròn khi và chỉ khi: ( 2 2 IA − R )( 2 2
IB − R ) < 0 16 6 2 IA = 4 +
(m + 1) ;IB = 4m 9 (   2 2 IA − R )( 2 2 IB − R ) 16  6  2 < 0 ⇔ 3  +
(m + 1) (4m − 1) < 0 (*)  9   16  Ta có:  6 3 +
(m + 1)  > 0 ∀x  9  Suy ra: 2 1
(*) ⇔ 4m − 1 < 0 ⇔ m < 2 1
Kết hợp điều kiện ta có: m < 2 HT 18. Cho hàm số 3 2 3
y = x − 3mx + 4m (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có
các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng y = x. Giải
• Tập xác định: D = ℝ x = 0 Ta có: 2
y′ = 3x − 6mx ; y′ = 0  ⇔ 
. Để hàm số có cực đại và cực tiểu thì m ≠ 0. x = 2m 
Đồ thị hàm số có hai điểm cực trị là: A(0; 4m3), B(2m; 0) ⇒ 3
AB = (2m;−4m )
Trung điểm của đoạn AB là I(m; 2m3) A  B ⊥ d  3 2  m − 4m = 0 2
A, B đối xứng nhau qua đường thẳng d: y = x ⇔    ⇔  ⇔ m = ± I  ∈ d 3   2  2m = m  HT 19. Cho hàm số 3 2 y = x −
+ 3mx − 3m − 1. Với giá trị nào của m thì đồ thị hàm số có điểm cực
đại và điểm cực tiểu đối xứng với nhau qua đường thẳng d : x + 8y − 74 = 0 . Giải
• Tập xác định: D = ℝ 2 y ′= 3
− x + 6mx ; y ′= 0 ⇔ x = 0 ∨ x = 2m .
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 14
GV.Lưu Huy Thưởng 0968.393.899
Hàm số có CĐ, CT ⇔ PT y ′= 0 có 2 nghiệm phân biệt ⇔ m ≠ 0 .
Khi đó 2 điểm cực trị là: 3 (
A 0;−3m − 1), B(2m; 4m − 3m − 1) ⇒ 3
AB(2m; 4m )
Trung điểm I của AB có toạ độ: 3 I ( ;
m 2m − 3m − 1)
Đường thẳng d: x + 8y − 74 = 0 có một VTCP u = (8;−1) . I  ∈ d  3 m 
+ 8(2m − 3m − 1) − 74 = 0 
A và B đối xứng với nhau qua d ⇔  ⇔  ⇔ m = 2 A  B ⊥ d    AB  .u = 0  HT 20. Cho hàm số 3 2 2 3 2 y = x −
+ 3mx + 3(1 − m )x + m − m (1). Viết phương trình đường thẳng
qua hai điểm cực trị của đồ thị hàm số (1). Giải
• Tập xác định: D = ℝ 2 2 y ′= 3
− x + 6mx + 3(1 − m ).
PT y ′= 0 có ∆ = 1 > 0, ∀m ⇒ Đồ thị hàm số (1) luôn có 2 điểm cực trị (x ;y ), (x ;y ) . 1 1 2 2 1 m  Chia y cho y′ ta được:   2 y =  x −
y ′+ 2x − m + m  3 3  Khi đó: 2
y = 2x − m + m ; 2
y = 2x − m + m 1 1 2 2
PT đường thẳng qua hai điểm cực trị của đồ thị hàm số (1) là 2
y = 2x − m + m . HT 21. Cho hàm số 3 2
y = x − 3x + mx + 2 (C ). Tìm m để (C ) có cực đại và cực tiểu, đồng thời m m
các điểm cực trị của hàm số cách đều đường thẳng d : x − y − 1 = 0. Giải Ta có : 2 2
y ' = 3x − 6x + m;y ' = 0 ⇔ 3x − 6x + m = 0 (1).
Hàm số (C ) có cực đại, cực tiểu khi và chỉ khi (1) có 2 nghiệm phân biệt ⇔ m < 3. m Giả sử (
A x ;y ), B x ;y
là hai điểm cực trị của hàm số (C ),(x ,x là 2 nghiệm của (1). 1 1 ( 2 2) m 1 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 15
GV.Lưu Huy Thưởng 0968.393.899 x 1 m  m
Ta có : y = y '   − + 2   − 1x + 2 + và 
y '(x ) = y '(x ) = 0  3 3     3  3 1 2 m  m
Nên phương trình đường thẳng đi qua ,
A B là : d ' : y = 2 − 1x + 2 + .  3  3 Do đó, các điểm ,
A B cách đều đường thẳng (d) trong hai trường hợp sau : m  9
Trường hợp 1 : (d’) cùng phương với (d) ⇔ 2 − 1 = 1 ⇔ m = (Không thỏa mãn)  3  2
Trường hợp 2 : Trung điểm I của ,
A B nằm trên (d). Do (I) là trung điểm của AB nên tọa độ (I)  x + x  1 2 x  = = 1  là :  2 
Vì I nằm trên (d) nên ta có 1 − m −1 = 0 ⇔ m = 0 (thỏa mãn)  y + y  1 2 y  = = m  2 KL :m = 0 HT 22. Cho hàm số 3 2
y = x − 3x − mx + 2 (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có
các điểm cực đại và cực tiểu cách đều đường thẳng y = x − 1 . Giải
• Tập xác định: D = ℝ Ta có: 2
y ' = 3x − 6x − m . Hàm số có CĐ, CT 2
⇔ y ' = 3x − 6x − m = 0 có 2 nghiệm phân biệt x ;x 1 2
⇔ ∆' = 9 + 3m > 0 ⇔ m > 3 − (*)
Gọi hai điểm cực trị là A(x ;y ;B x ;y 1 1 ) ( 2 2) 1 1 2m   m 
Thực hiện phép chia y cho y′ ta được: y  =  x  − y '  −  + 2x + 2    −  3 3  3        3  2m   m  2m   m  ⇒ y = y x  = − + 2x + 2    − ; y = y x  = − + 2x + 2    −  1 ( 1)   1     2 ( 2)     2 3 3  3          3 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 16
GV.Lưu Huy Thưởng 0968.393.899 2m   m 
⇒ Phương trình đường thẳng đi qua 2 điểm cực trị là ∆:y  = − + 2x + 2    −   3      3 
Các điểm cực trị cách đều đường thẳng y = x − 1 ⇔ xảy ra 1 trong 2 trường hợp:
TH1: Đường thẳng đi qua 2 điểm cực trị song song hoặc trùng với đường thẳng y = x − 1 2m  3  ⇔ −
+ 2 = 1 ⇔ m = − (thỏa mãn)  3    2
TH2: Trung điểm I của AB nằm trên đường thẳng y = x − 1 y + y x + x 2m   m  1 2 1 2
⇔ y = x − 1 ⇔ = − 1  ⇔ − + 2 x + x   +  −  = x + x − I I  ( 2 2 2 1 2 )     ( 1 2 ) 2 2 3     3   2m  2m  ⇔  + 3.2 = 6 − ⇔ m = 0  3  3  3
Vậy các giá trị cần tìm của m là: m 0  ;  = −   2   HT 23. Cho hàm số 3 2
y = x − 3x + mx (1). Với giá trị nào của m thì đồ thị hàm số (1) có các
điểm cực đại và điểm cực tiểu đối xứng với nhau qua đường thẳng d : x – 2y – 5 = 0 . Giải
• Tập xác định: D = ℝ Ta có 3 2 2
y = x − 3x + mx ⇒ y ' = 3x − 6x + m
Hàm số có cực đại, cực tiểu ⇔ y ′= 0 có hai nghiệm phân biệt ⇔ ′
∆ = 9 − 3m > 0 ⇔ m < 3 1 1 2  1 Ta có: y  =  x  − y ′ 
+  m − 2x + m 3 3    3  3
Tại các điểm cực trị thì y ′= 0 , do đó tọa độ các điểm cực trị thỏa mãn phương trình: 2  1 y 
=  m − 2x + m 3  3 2  1
Như vậy đường thẳng ∆ đi qua các điểm cực trị có phương trình y 
=  m − 2x + m 3  3
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 17
GV.Lưu Huy Thưởng 0968.393.899 2
nên ∆ có hệ số góc k = m − 2 . 1 3 1 5 1
d: x – 2y – 5 = 0 ⇔ y = x − ⇒ d có hệ số góc k = 2 2 2 2
Để hai điểm cực trị đối xứng qua d thì ta phải có d ⊥ ∆ 1 2  ⇒ k k = 1  − ⇔
 m − 2 = −1 ⇔ m = 0 1 2 2 3 
Với m = 0 thì đồ thị có hai điểm cực trị là (0; 0) và (2; –4), nên trung điểm của chúng là I(1; –2).
Ta thấy I ∈ d, do đó hai điểm cực trị đối xứng với nhau qua d. Vậy: m = 0 HT 24. Cho hàm số 3 2
y = x − 3(m + 1)x + 9x + m − 2 (1) có đồ thị là (Cm). Với giá trị nào của m thì 1
đồ thị hàm số có điểm cực đại và điểm cực tiểu đối xứng với nhau qua đường thẳng d : y = x . 2 Giải
• Tập xác định: D = ℝ 2
y ' = 3x − 6(m + 1)x + 9 Hàm số có CĐ, CT ⇔ 2
∆' = 9(m + 1) − 3.9 > 0 ⇔ m ∈ (− ;
∞ −1 − 3) ∪ (−1 + 3; + ) ∞ 1 m 1 + Ta có   2 y =  x −
y ′− 2(m + 2m − 2)x + 4m + 1 3 3 
Giả sử các điểm cực đại và cực tiểu là (
A x ;y ), B(x ;y ) , I là trung điểm của AB. 1 1 2 2 2
⇒ y = −2(m + 2m − 2)x + 4m + 1 ; 2
y = −2(m + 2m − 2)x + 4m + 1 1 1 2 2 x
 + x = 2(m + 1) và:  1 2  x  .x = 3  1 2 
Vậy đường thẳng đi qua hai điểm cực đại và cực tiểu là 2 y = 2
− (m + 2m − 2)x + 4m + 1 1 A  B ⊥ d
A, B đối xứng qua (d): y = x ⇔  ⇔ m = 1. 2 I  ∈ d 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 18
GV.Lưu Huy Thưởng 0968.393.899 1 1 HT 25. Cho hàm số 3 2 y =
x − (m − 1)x + 3(m − 2)x +
, với m là tham số thực. Xác định m để 3 3
hàm số đã cho đạt cực trị tại x , x sao cho x + 2x = 1. 1 2 1 2 Giải
• Tập xác định: D = ℝ Ta có: 2
y ′= x − 2(m − 1)x + 3(m − 2)
Hàm số có cực đại và cực tiểu ⇔ y ′= 0 có hai nghiệm phân biệt x , x 1 2 ⇔ 2 ′
∆ > 0 ⇔ m − 5m + 7 > 0 (luôn đúng với ∀m) x
 + x = 2(m − 1) x  = 3 − 2m Khi đó ta có:  1 2  2  ⇔  x
 x = 3(m − 2)  x  1 − 2x = 3(m − 2)  2 ( 2 ) 1 2   − ± 2 4 34
⇔ 8m + 16m − 9 = 0 ⇔ m = . 4 HT 26. Cho hàm số 3 2
y = x − 3(m + 1)x + 9x − m , với m là tham số thực. Xác định m để hàm số
đã cho đạt cực trị tại x ,x sao cho x − x ≤ 2 . 1 2 1 2 Giải
• Tập xác định: D = ℝ Ta có 2
y ' = 3x − 6(m + 1)x + 9.
+ Hàm số đạt cực đại, cực tiểu tại x , x ⇔ PT y ' = 0 có hai nghiệm phân biệt x , x 1 2 1 2 ⇔ PT 2
x − 2(m + 1)x + 3 = 0 có hai nghiệm phân biệt là x , x . 1 2 m  > −1 + 3 2 
⇔ ∆ ' = (m + 1) − 3 > 0 ⇔  (1) m  < −1 − 3 
+ Theo định lý Viet ta có x + x = 2(m + 1); x x = 3. Khi đó: 1 2 1 2 2 2
x − x ≤ 2 ⇔ x + x
− 4x x ≤ 4 ⇔ 4 m + 1 − 12 ≤ 4 1 2 ( 1 2 ) 1 2 ( )
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 19
GV.Lưu Huy Thưởng 0968.393.899 2 ⇔ (m + 1) ≤ 4 ⇔ 3 − ≤ m ≤ 1 (2)
+ Từ (1) và (2) suy ra giá trị của m cần tìm là 3 − ≤ m < 1 − − 3 và 1 − + 3 < m ≤ 1. HT 27. Cho hàm số 3 2
y = x + (1 − 2m)x + (2 − m)x + m + 2 , với m là tham số thực. Xác định m 1
để hàm số đã cho đạt cực trị tại x , x sao cho x − x > . 1 2 1 2 3 Giải
• Tập xác định: D = ℝ Ta có: 2 y ' = 3x + (
2 1 − 2m)x + (2 − m)
Hàm số có CĐ, CT ⇔ y ' = 0 có 2 nghiệm phân biệt x , x (giả sử x < x ) 1 2 1 2  5 m  > 2 2
⇔ ∆ ' = (1 − 2m) − 3(2 − m) = 4m − m − 5 > 0 ⇔  4 (*) m  < −1   ( 2 1 − 2m) x  + x = − 1 2
Hàm số đạt cực trị tại các điểm 
x , x . Khi đó ta có: 3 1 2   2 − m x  x  = 1 2  3 1 2 2 1 x − x > ⇔ x − x = x + x − 4x x > 1 2 ( 1 2 ) ( 1 2 ) 1 2 3 9 + − 2 2 3 29 3 29
⇔ 4(1 − 2m) − 4(2 − m) > 1 ⇔ 16m − 12m − 5 > 0 ⇔ m > ∨ m < 8 8 3 + 29
Kết hợp (*), ta suy ra m > ∨ m < −1 8 2 4 HT 28. Cho hàm số 3 2 y =
x + (m + 1)x + (m + 1)(m + 3)x +
(1),m là tham số. Tìm m để hàm 3 3 1
số (1) đạt cực đại, cực tiểu tại x x sao cho x + x − x x đạt giá trị lớn nhất. 1 2 1 2 1 2 2 Giải Ta có : 2
y ' = 2x + 2(m + 1)x + (m + 1)(m + 3) ;
Hàm số đạt cực đại, cực tiểu khi và chỉ khi y ' = 0 có hai nghiệm phân biệt 2
⇔ (m + 1) − 2(m + 1)(m + 3) > 0
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 20
GV.Lưu Huy Thưởng 0968.393.899 ⇔ (
− m + 1)(m + 5) > 0 ⇔ −5 < m < −1 (m + 1)(m + 3)
Khi đó : x + x = m − − 1;x x = 1 2 1 2 2 1 1 1 Nên 2
x + x − x x = m
− − 1 − (m + 1)(m + 3) = ( − m + 8m + 7) 1 2 1 2 2 4 4 1 2 1 2 9 9
= − (m + 8m + 7) = − (m + 4) + ≤ , ∀m 4 4 4 4 1 9
Suy ra : x + x − x x đạt giá trị lớn nhất bằng khi m = −4(t / m) 1 2 1 2 2 4 HT 29. Cho hàm số 3 2
y = 4x + mx – 3x . Tìm m để hàm số có hai điểm cực trị x , x thỏa 1 2 x = 4 − x . 1 2 Giải
• Tập xác định: D = ℝ 2
y ′= 12x + 2mx – 3 . Ta có: 2 ′
∆ = m + 36 > 0, m ∀
⇒ hàm số luôn có 2 cực trị x , x . 1 2
x = −4x 1 2  m 9 Khi đó: x
 + x = − ⇒ m = ± 1 2  6  2  1 x  x = −  1 2  4 Câu hỏi tương tự: a) 3 2
y = x + 3x + mx + 1; x + 2x = 3 1 2 ĐS: m = 1 − 5 0 . 1 1
HT 30. Tìm các giá trị của m để hàm số 3 2 2 y =
x − mx + (m − 3)x có cực đại x , cực tiểu x đồng 3 2 1 2 5
thời x ; x là độ dài các cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 1 2 2 Giải
Cách 1: Miền xác định: D = ℝ có 2 2 2 2
y ' = x − mx + m − 3;y ' = 0 ⇔ x − mx + m = 0
Hàm số đạt cực đại tại x cực tiểu tại x thỏa mãn yêu cầu bài toán khi và chỉ khi pt y’= 0 có hai 1 2
nghiệm dương phân biệt, triệt tiêu và đồi dấu qua hai nghiệm đó:
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 21
GV.Lưu Huy Thưởng 0968.393.899   2  ∆ > 0 4    − m > 0 −  2 < m < 2       S  0 m  0 m  > ⇔ > ⇔  > 0
⇔ 3 < m < 2 (*)      2 P  0  > m  − 3 > 0 m  < − 3 ∨ m > 3      x  + x = m Theo Vi-ét ta có:  1 2  2 x  x = m − 3  1 2  5 14 Mà 2 2 2 2 2 x + x =
⇔ 2(x + x ) − 4x x = 5 = 5 ⇔ 2m − 4(m − 3) = 5 ⇔ m = ± 1 2 1 2 1 2 2 2 14
Đối chiếu điều kiện (*) ta được: m = 2 2 HT 31. Cho hàm số 3 2 2 y =
x + (m + 1)x + (m + 4m + 3)x + 1. Tìm m để hàm số có cực trị. Tìm 3
giá trị lớn nhất của biểu thức A = x x − 2(x + x ) với x ,x là các điểm cực trị cửa hàm số. 1 2 1 2 1 2 Giải Ta có: 2 2
y ' = 2x + 2(m + 1)x + m + 4m + 3
Hàm số có cực trị ⇔ y ' = 0 có hai nghiệm phân biệt. 2
⇔ m + 6m + 5 < 0 ⇔ −5 < m < −1 x
 + x = −1 − m  1 2  1 Khi đó ta có:  2  ⇒ A = m + 8m + 7 1 2 x
 x = (m + 4m + 3) 2  1 2  2 1 9 Xét 2 t =
(m + 8m + 7) trên (−5;−1) ⇒ − ≤ t < 0 2 2 9 Từ đó ta có A ≤ khi m = −4 2 HT 32. Cho hàm số 3 2
y = x − 3(m + 1)x + 9x − m (1) với m là tham số thực. Xác định m để hàm
số (1) đạt cực đại , cực tiểu sao cho y + y = 2 CD CT Giải Ta có: 2
y ' = 3x − 6(m + 1)x + 9
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 22
GV.Lưu Huy Thưởng 0968.393.899
Hàm số đạt cực đại, cực tiểu tại x ,x ⇔ y ' = 0 có 2 nghiệm phân biệt x ,x 1 2 1 2 2
⇔ x − 2(m + 1)x + 3 = 0 có hai nghiệm phân biệt x ,x 1 2 m  > −1 + 3 2 
⇔ ∆ ' = (m + 1) − 3 > 0 ⇔  (*) m  < −1 − 3  x
 + x = 2(m + 1) Theo Viet ta có:  1 2  x  x = 3  1 2  3 2 3 2 y + y
= 2 ⇔ x − 3(m + 1)x + 9x − m + x − 3(m + 1)x + 9x − m = 2 CD CT 1 1 1 2 2 2 3 3 2 2
⇔ x + x − 3(m + 1)(x + x ) + 9(x + x ) − 2m − 2 = 0 1 2 1 2 1 2 2
⇔ (m + 1)(m + 2m − 3) = 0 m  = 1 − (l)  m  ⇔ = 1(t / m)  m  = 3 − (t / m)  1 HT 33. Cho hàm số 3 2 2 y =
x − mx + (m − 1)x + 1 (C ). Tìm m để hàm số có cực đại cực tiểu và: 3 m y D + y > 2 C CT Giải Ta coù: 2 2
y ' = x − 2mx + (m − 1) 2 2
∆ ' = m − m + 1 = 1 > 0 y ' x = m + 1 y ' 0  ⇒ =
⇔ x = m −1  ⇒ y + y = y + y CD CT (m +1) (m 1 − ) 3 3 [ (m + 1) 2 2 m − =
− m(m + 1) + (m − 1)(m + 1) + 1] + [ ( 1) 2 2
− m(m − 1) + (m − 1)(m − 1) + 1] 3 3 −1 < m < 0 3 2 2m 2m 2 2 m(m 1) 0  = − + > ⇔ − > ⇔ m  > 1  −1 < m < 0 KL: m > 1 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 23
GV.Lưu Huy Thưởng 0968.393.899 3 HT 34. Cho hàm số 3 2
y = x − (m − 2)x − 3(m − 1)x + 1 (1),m là tham số. Tìm m > 0 để đồ thị 2
hàm số (1) có giá trị cực đại, cực tiểu lần lượt là y ,y thỏa mãn: 2y + y = 4 . CD CT CD CT Giải Ta có: 2
y ' = 3x − 3(m − 2)x − 3(m − 1), ∀x ∈ ℝ x = x = −1 2  1
y ' = 0 ⇔ x − (m − 2)x − m + 1 = 0 ⇔ 
x = x = m − 1  2 
Chú ý rằng với m > 0 thì x < x . Khi đó hàm số đạt cực đại tại x = 1
− và đạt cực tiểu tại 1 2 1 3m 1
x = m − 1. Do đó: 2 y = y(−1) = ,y
= y(m − 1) = − (m + 2)(m − 1) + 1 2 CD 2 CT 2 3m 1 Từ giả thiết ta có: 2 2 2.
− (m + 2)(m − 1) + 1 = 4 ⇔ 6m − 6 − (m + 2)(m − 1) = 0 2 2 m  = 1  2
⇔ (m − 1)(m + m − 8) = 0 ⇔   −1 ± 33 m =   2 −1 + 33
Đối chiếu điều kiện m > 0 ta có giá trị của m là m = 1,m = 2 HT 35. Cho hàm số 3 2
y = x – 3x + 2 (1). Tìm điểm M thuộc đường thẳng d : y = 3x − 2 sao tổng
khoảng cách từ M tới hai điểm cực trị nhỏ nhất. Giải
• Các điểm cực trị là: A(0; 2), B(2; –2).
Xét biểu thức g(x,y) = 3x − y − 2 ta có:
g(x ,y ) = 3x − y − 2 = −4 < 0; g(x ,y ) = 3x − y − 2 = 6 > 0 A A A A B B B B
⇒ 2 điểm cực đại và cực tiểu nằm về hai phía của đường thẳng d: y = 3x − 2 .
Do đó MA + MB nhỏ nhất ⇔ 3 điểm A, M, B thẳng hàng ⇔ M là giao điểm của d và AB.
Phương trình đường thẳng AB: y = −2x + 2  4   = 3 − 2 x y x  = 4 2
Tọa độ điểm M là nghiệm của hệ:   5    ⇔  ⇒ M  ;  y  = −2x + 2  2    5 5   y  =  5
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 24
GV.Lưu Huy Thưởng 0968.393.899 HT 36. Cho hàm số 3 2 2 3
y = x − 3mx + 3(m − 1)x − m + m (1). Tìm m để hàm số (1) có cực trị
đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng
cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O. Giải
• Tập xác định: D = ℝ Ta có 2 2
y ′= 3x − 6mx + 3(m − 1)
Hàm số (1) có cực trị thì PT y ′= 0 có 2 nghiệm phân biệt 2 2
⇔ x − 2mx + m − 1 = 0 có 2 nhiệm phân biệt ⇔ ∆ = 1 > 0, ∀m
Khi đó: điểm cực đại (
A m − 1;2 − 2m) và điểm cực tiểu B(m + 1;−2 − 2m) m  = −3 + 2 2 Ta có 2 
OA = 2OB ⇔ m + 6m + 1 = 0 ⇔  . m  = −3 − 2 2  HT 37. Cho hàm số 3 2
y = x − 3(m + 1)x + 3m(m + 2)x − 2 + m (C ) .Tìm m để đồ thị hàm số (C)
có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số (C) tới trục Ox bằng khoảng
cách từ điểm cực tiểu của đồ thị hàm số (C) tới trục Oy. Giải x = m Ta có: 2 y ' 3x 6(m 1)x 3m(m 2);y ' 0  = + + + + = ⇔  x = m + 2 
Hàm số có cực trị với mọi m . Hai điểm cực trị của đồ thị hàm số (C) là: 3 2 3 2 (
A m;m + 3m + m − 2),B(m + 2;m + 3m + m − 6)
Ta có hàm số là hàm bậc ba với hệ số a = 1 > 0 ⇒ điểm cực đại nhỏ hơn điểm cực tiểu.
Vậy A là điểm cực đại, B là điểm cực tiểu. Ta có: 3 d( ;
A Ox) = m + 3m + m − 2 ,d( , B Oy) = m + 2 m  = −2  m  = −1 Theo giả thiết ta có: 3
m + 3m + m − 2 = m + 2  ⇔ m  = 1  m = 0 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 25
GV.Lưu Huy Thưởng 0968.393.899 HT 38. Cho hàm số 3 2
y = x − 3x − mx + 2 có đồ thị là (Cm). Tìm m để (Cm) có các điểm cực đại,
cực tiểu và đường thẳng đi qua các điểm cực trị song song với đường thẳng d : y = −4x + 3 . Giải
• Tập xác định: D = ℝ Ta có: 2
y ' = 3x − 6x − m . Hàm số có CĐ, CT 2
⇔ y ' = 3x − 6x − m = 0 có 2 nghiệm phân biệt x ;x 1 2
⇔ ∆ ' = 9 + 3m > 0 ⇔ m > 3 − (*)
Gọi hai điểm cực trị là A(x ;y ;B x ;y 1 1 ) ( 2 2) 1 1 2m   m 
Thực hiện phép chia y cho y′ ta được: y  =  x  − y '  −  + 2x + 2    −  3 3  3        3  2m   m  2m   m  ⇒ y = y x  = − + 2x + 2    − ; y = y x  = − + 2x + 2    −  1 ( 1)   1     2 ( 2)     2 3 3  3          3  2m   m 
⇒ Phương trình đường thẳng đi qua 2 điểm cực trị là d:y  = − + 2x + 2    −   3      3 
Đường thẳng đi qua các điểm cực trị song song với d: y = −4x + 3  2m    −   + 2 = −4     3   ⇔ 
⇔ m = 3 (thỏa mãn)   m  2      −  ≠ 3    3   HT 39. Cho hàm số 3 2
y = x − 3x − mx + 2 có đồ thị là (Cm). Tìm m để (Cm) có các điểm cực đại,
cực tiểu và đường thẳng đi qua các điểm cực trị tạo với đường thẳng d : x + 4y – 5 = 0 một góc 0 45 . Giải
• Tập xác định: D = ℝ Ta có: 2
y ' = 3x − 6x − m . Hàm số có CĐ, CT 2
⇔ y ' = 3x − 6x − m = 0 có 2 nghiệm phân biệt x ;x 1 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 26
GV.Lưu Huy Thưởng 0968.393.899
⇔ ∆ ' = 9 + 3m > 0 ⇔ m > 3 − (*)
Gọi hai điểm cực trị là A(x ;y ;B x ;y 1 1 ) ( 2 2) 1 1 2m   m 
Thực hiện phép chia y cho y′ ta được: y  =  x  − y '  −  + 2x + 2    −  3 3  3        3  2m   m  2m   m  ⇒ y = y x  = − + 2x + 2    − ; y = y x  = − + 2x + 2    −  1 ( 1)   1     2 ( 2)     2 3 3  3          3  2m   m 
⇒ Phương trình đường thẳng đi qua 2 điểm cực trị là ∆:y  = − + 2x + 2    −   3      3  2m  1 Đặt k  = −
+ 2. Đường thẳng d: có hệ số góc bằng  x + 4y – 5 = 0 − .  3  4 1  1 1  3  39 k + k  + = 1 − k k  = m  = − Ta có: 4  4 4  5  10 tan 45 = ⇔  ⇔  ⇔  1  1 1  5  1 1 − k k + = −1 + k k = − m = −    4  4 4  3  2 1
Kết hợp điều kiện (*), suy ra giá trị m cần tìm là: m = − 2 HT 40. Cho hàm số 3 2
y = x + 3x + m (1). Xác định m để đồ thị của hàm số (1) có hai điểm cực trị A, B sao cho 0 AOB = 120 . Giải
• Tập xác định: D = ℝ
x = −2 ⇒ y = m + 4 Ta có: 2
y ′= 3x + 6x ; y ′= 0  ⇔ 
x = 0 ⇒ y = m 
Vậy hàm số có hai điểm cực trị A(0 ; m) và B(−2 ; m + 4) 1
OA = (0;m), OB = (−2;m + 4) . Để 0
AOB = 120 thì cos AOB = − 2  4 − < m < 0 ( m m + 4) 1 2  m ( 2 4 (m 4) ) 2m(m 4) ⇔ = − ⇔ + + = − + ⇔   m (4 + (m + 4) ) 2 2 2 2
3m + 24m + 44 = 0 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 27
GV.Lưu Huy Thưởng 0968.393.899  4 − < m < 0  1 − 2 + 2 3  ⇔  1 − 2 ± 2 3 ⇔ m = m  = 3  3 HT 41. Cho hàm số 3 2 2 3
y = x − 3mx + 3(m − 1)x − m + 4m − 1 (1),m là tham số thực. Tìm các giá
trị của m để đồ thị hàm số (1) có hai điểm cực trị ,
A B sao cho tam giác OAB vuông tại O, với O là gốc tọa độ. Giải Ta có: 2 3
y ' = 3(x − 2mx + m − 1). Hàm số có cực trị khi và chỉ khi phương trình y ' = 0 có hai nghiệm phân biệt. ' ∆ > 0 ⇔ m ∀ ∈ ℝ y ' x = m + 1 y ' 0  = ⇔  ⇒ Hai điểm cực trị: (
A m − 1;m + 1), B(m + 1;m − 3) x = m − 1 
OA = (m − 1;m + 1),OB = (m + 1;m − 3).
∆OAB vuông tại O khi O, A, B phân biệt và O . AOB = 0 m  = −1 2 2(m m 2) 0  ⇔ − − = ⇔ m  = 2  HT 42. Cho hàm số 3 2 2 3
y = x – 3mx + 3(m – 1)x – m (Cm). Chứng minh rằng (Cm) luôn có điểm
cực đại và điểm cực tiểu lần lượt chạy trên mỗi đường thẳng cố định. Giải
• Tập xác định: D = ℝ x = m + 1 2 2
y ′= 3x − 6mx + 3(m − 1) ; y ′= 0  ⇔  x = m − 1  x  = −1 + t
Điểm cực đại M (m – 1;2 – 3m) chạy trên đường thẳng cố định:  y  = 2 − 3t  x  = 1 + t
Điểm cực tiểu N (m + 1;−2 – m)chạy trên đường thẳng cố định:  y  = 2 − − 3t  HT 43. Cho hàm số 3 2 3 2
y = x + 3(m + 1)x + 3 (
m m + 2)x + m + 3m . Chứng minh rằng với mọi m
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 28
GV.Lưu Huy Thưởng 0968.393.899
hàm số luôn có 2 cực trị và khoảng cách giữa hai điểm này không phụ thuộc vào vị trí của m. Giải x  = −2 − m Ta có: 2 y ' 3x 6(m 1)x 6m(m 2);y ' 0  = + + + + = ⇔ x  = m − 
Hàm số đồng biến trên các khoảng (-∞;-2 - m) và (-m;+∞), nghịch biến trên khoảng (-2 - m;-m) và x = 2 − − m;y = 4;x = m − ;y = 0 CD CD CT CT
Khi đó, khoảng cách giữa hai điểm cực trị là: 2 2
(−2 − m + m) + (4 − 0) = 2 5
⇒ Điều phải chứng minh. HT 44. Cho hàm số 3 2
y = x − 3x − mx + 2 (1) với m là tham số thực. Định m để hàm số (1) có
cực trị, đồng thời đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tạo với hai trục tọa độ một tam giác cân. Giải Ta có: 2
y ' = 3x − 6x − m
Hàm số có cực trị khi và chỉ khi y’ = 0 có 2 nghiệm phân biệt
⇔ ∆ ' = 9 + 3m > 0 ⇔ m > 3 − (1)
Lấy y chia cho y’ ta được: 3 2 1 2m m
y = x − 3x − mx + 2 =
(x − 1).y '+ (− − 2)x + 2 − 3 3 3
Đường thẳng qua hai điểm cực trị của đồ thị hàm số có phương trình 2m m y = (− − 2)x + 2 − 3 3  m 6   6 m  − −
Đường thẳng này cắt 2 trục Ox và Oy lần lượt tai A ; 0, B 0    ;  2(  +    m 3)    3  m − 6 6 − m
Tam giác OAB cân khi và chỉ khi OA = OB ⇒ = 2(m + 3) 3 9 3
⇒ m = 6; m = − ; m = − 2 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 29
GV.Lưu Huy Thưởng 0968.393.899 3
Với m = 6 thì A ≡ B ≡ O do đó so với điều kiện ta nhận m = − 2 1 1 HT 45. Cho hàm số 3 2 y =
x − (m − 1)x + (m − 2)x + 1. Tìm m để đồ thị hàm số có hai điểm 3 2  7
cực trị A, B đồng thời các điểm cực trị tạo với hai điểm D 3;  và gốc tọa độ O tạo thành hình  2 bình hành OADB . Giải x = 1 Ta có: 2 y ' x (m 1)x m 2, y ' 0  = − + + − = ⇔  x = m − 2 
Hàm số có cực trị ⇔ y ' = 0 có hai nghiệm phân biệt ⇔ m − 2 ≠ 1 ⇔ m ≠ 3
Ta có OADB là hình bình hành nên trung điểm của AB cũng chính là trung điểm của OD. x + x x  A B D  =  Từ đó, ta có hệ:  2 2  y + y y  A B D  =  2 2
Giả sử: x = 1,x = m − 2. Từ phương đầu tiên của hệ ta có: m − 1 = 3 ⇔ m = 4. A B  11  5
Với m = 4 ta có: A A 1  ; ;B 2    ;   6      3
Thay vào phương trình thứ hai của hệ ta thấy thỏa mãn.
Kết hợp điều kiện m ≠ 3 ta đi đến kết luận: m = 4 là giá trị cần tìm. HT 46. Cho hàm số 4 2 2
y = f (x) = x + 2(m − 2)x + m − 5m + 5 (C ). Tìm các giá trị của m để đồ m
thị (C ) của hàm số có các điểm cực đại, cực tiểu tạo thành 1 tam giác vuông cân. m Giải
• Tập xác định: D = ℝ x = 0 Ta có f (x) 3 4x 4(m 2)x 0  ′ = + − = ⇔  2 x = 2 − m 
Hàm số có CĐ, CT ⇔ PT f (
′ x) = 0 có 3 nghiệm phân biệt ⇔ m < 2 (*)
Khi đó toạ độ các điểm cực trị là: A( 2
0;m − 5m + 5), B ( 2 − m;1 − m), C (− 2 − m;1 − m) ⇒ AB = ( 2 − m m − + m − ) AC = ( 2 2 ; 4 4 , − 2 − m; m − + 4m − 4)
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 30
GV.Lưu Huy Thưởng 0968.393.899
Do ∆ABC luôn cân tại A, nên bài toán thoả mãn khi ∆ABC vuông tại A
⇔ AB AC = ⇔ (m − )3 . 0 2 = −1 ⇔ m = 1 (thoả (*)) HT 47. Cho hàm số 4 2 2
y = x + 2(m − 2)x + m − 5m + 5
(C ). Với những giá trị nào của m m
thì đồ thị (Cm) có điểm cực đại và điểm cực tiểu, đồng thời các điểm cực đại và điểm cực tiểu lập
thành một tam giác đều. Giải
• Tập xác định: D = ℝ x = 0 Ta có f (x) 3 4x 4(m 2)x 0  ′ = + − = ⇔  2 x = 2 − m 
Hàm số có CĐ, CT ⇔ PT f (
′ x) = 0 có 3 nghiệm phân biệt ⇔ m < 2 (*)
Khi đó toạ độ các điểm cực trị là: A( 2
0;m − 5m + 5), B ( 2 − m;1 − m), C (− 2 − m;1 − m) ⇒ AB = ( 2 − m m − + m − ) AC = ( 2 2 ; 4 4 , − 2 − m; m − + 4m − 4) 1
Do ∆ABC luôn cân tại A, nên bài toán thoả mãn khi 0
A = 60 ⇔ cos A = 2 AB.AC 1 ⇔ = ⇔ 3 m = 2 − 3 . 2 AB . AC
Câu hỏi tương tự đối với hàm số: 4 2
y = x − 4(m − 1)x + 2m − 1 HT 48. Cho hàm số 4 2 2
y = x + 2mx + m + m có đồ thị (Cm) . Với những giá trị nào của m thì đồ
thị (Cm) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có một góc bằng 0 120 . Giải
• Tập xác định: D = ℝ  x = 0 Ta có 3
y′ = 4x + 4mx ; 2 y 0 4x(x m) 0  ′ = ⇔ + = ⇔  (m < 0) x  = ± m − 
Khi đó các điểm cực trị là: 2 (
A 0;m + m), B ( m − ;m), C (− m − ;m)
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 31
GV.Lưu Huy Thưởng 0968.393.899 2 AB = ( m − ; m − ) ; 2 AC = (− m − ; m −
). ∆ABC cân tại A nên góc 120 chính là A . 4 1 AB.AC 1 − m − . m − + m 1
A = 120 ⇔ cos A = − ⇔ = − ⇔ = − 4 2 2 m − m 2 AB . AC m  = 0 (loaïi) 4 m m 1  + 4 4 4 2m 2m m m 3m m 0  ⇔ = − ⇒ + = − ⇔ + = ⇔ 1 4 − 2 m m m  = −  3  3 1 Vậy m = − . 3 3 HT 49. Cho hàm số 4 2
y = x − 2mx + m − 1 có đồ thị (Cm) . Với những giá trị nào của m thì đồ thị
(Cm) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có bán kính đường
tròn ngoại tiếp bằng 1 . Giải
• Tập xác định: D = ℝ x  = 0 Ta có 3 2 y 4x 4mx 4x(x m) 0  ′= − = − = ⇔  2 x = m 
Hàm số đã cho có ba điểm cực trị ⇔ PT y ′= 0 có ba nghiệm phân biệt và y ′ đổi dấu khi x đi
qua các nghiệm đó ⇔ m > 0 . Khi đó ba điểm cực trị của đồ thị (Cm) là: A m − B ( 2 − m m − + m − ) C ( 2 (0; 1), ; 1 , m; m − + m − ) 1 1 2 S =
y − y . x − x = m m ; 4
AB = AC = m + m, BC = 2 m A △ BC 2 B A C B m  = 1 4 AB.AC.BC (m m)2 m  + 3 R = = 1 ⇔
= 1 ⇔ m − 2m + 1 = 0 ⇔  2  5 − 1 4S A △ BC 4m m m =   2 Câu hỏi tương tự: −1 + 5 a) 4 2
y = x − 2mx + 1 ĐS: m = 1, m = 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 32
GV.Lưu Huy Thưởng 0968.393.899 HT 50. Cho hàm số 4 2 4
y = x − 2mx + 2m + m có đồ thị (Cm) . Với những giá trị nào của m thì đồ
thị (Cm) có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có diện tích bằng 4. Giải
• Tập xác định: D = ℝ x = 0 Ta có 3 y ' 4x 4mx 0  = − = ⇔  2
g(x) = x − m = 0 
Hàm số có 3 cực trị ⇔ y ' = 0 có 3 nghiệm phân biệt ⇔ ∆ = m > 0 ⇔ m > 0 (*) g
Với điều kiện (*), phương trình y ′= 0 có 3 nghiệm x = − m; x = 0; x = m . Hàm số đạt 1 2 3
cực trị tại x ;x ;x . Gọi 4 A m + m B ( 4 2
m m − m + m) C ( 4 2 (0;2 ); ; 2 ;
− m;m − m + 2m) là 3 1 2 3
điểm cực trị của (Cm) . Ta có: 2 2 4 2
AB = AC = m + m;BC = 4m ⇒ A ∆ BC cân đỉnh A
Gọi M là trung điểm của BC 4 2 2 2
⇒ M(0;m − m + 2m) ⇒ AM = m = m
Vì ∆ABC cân tại A nên AM cũng là đường cao, do đó: 5 1 1 2 5 5 2 S = AM.BC =
.m . 4m = 4 ⇔ m = 4 ⇔ m = 16 ⇔ m = 16 A ∆ BC 2 2 Vậy 5 m = 16 . Câu hỏi tương tự: a) 4 2 2
y = x − 2m x + 1 , S = 32 ĐS: m = ±2 HT 51. Cho hàm số 4 2
x − 2mx + 2 có đồ thị (C ). Tìm tất cả các giá trị của tham số m để đồ thị m 3 9
(C )có ba điểm cực trị tạo thành một tam giác có đường tròn ngoại tiếp đi qua điểm D ;  m 5 5 Giải x = 0 3 y ' 4x 4mx 0  = − = ⇔ (m > 0) 
Vậy các điểm thuộc đường tròn (P) ngoại tiếp các điểm x  = ± m 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 33
GV.Lưu Huy Thưởng 0968.393.899   cực trị là: A (0;2); 2 2 3 9
B(− m; m −
+ 2);C( m; m −
+ 2);D  ;  . Gọi I(x;y) là tâm đường tròn (P) 5 5   2 2 I  A = ID 3
 x − y + 1 = 0    x  = 0        2 2 I  B IC 2  x m 2x m y  = ⇔ = − ⇔  = 1     2 2  2 2 2 2 2  I  B = IA (
 x + m) + (y + m − 2) = x + (y − 2)  m  = 0(l)       m   = 1(t / m)   Kết luận: m = 1
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 34
GV.Lưu Huy Thưởng 0968.393.899
PHẦN 3: SỰ TƯƠNG GIAO HT 52. Cho hàm số 3 2
y = x − 6x + 9x − 6 có đồ thị là (C). Định m để đường thẳng
(d) : y = mx − 2m − 4 cắt đồ thị (C) tại ba điểm phân biệt. Giải
• PT hoành độ giao điểm của (C) và (d): 3 2
x − 6x + 9x − 6 = mx − 2m − 4 x  = 2 ⇔ 2 
(x − 2)(x − 4x + 1 − m) = 0 ⇔  2 g
 (x) = x − 4x + 1 − m = 0 
(d) cắt (C) tại ba điểm phân biệt ⇔ PT g(x) = 0 có 2 nghiệm phân biệt khác 2 ⇔ m > 3 − HT 53. Cho hàm số 3 2
y = x − 3m x − 2m (Cm). Tìm m để (Cm) và trục hoành có đúng 2 điểm chung phân biệt. Giải x  = 0 Ta có: 2 y ' 3x 6mx y ' 0  = − ⇒ = ⇔ x  = 2m 
y coù CÑ, CT (C 
m) và Ox có đúng 2 điểm chung phân biệt ⇔  y = 0 hoaëc y = 0  CÑ CT 
Hàm số có cực đại, cực tiểu ⇔ 2m ≠ 0 ⇔ m ≠ 0 x = 0 Ta có: 3 3 y .y 0 2m(8m 6m 2m) 0  = ⇔ − − − = ⇔ CD CT x = ±1 
Kết hợp điểu kiện ta có: m = ±1 HT 54. Cho hàm số 3 2 y = 2
− x + 6x + 1. Tìm m để đường thẳng y = mx + 1cắt (C) tại 3 điểm phân
biệt A, B, C sao cho A(0;1) và B là trung điểm của AC. Giải
Phương trình hoành độ giao điểm của đường thẳng y = mx + 1 với đồ thị (C): x = 0 3 2 2  2
− x + 6x + 1 = mx + 1 ⇔ x(2x − 6x + m) = 0 ⇔  2
2x − 6x + m = 0 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 35
GV.Lưu Huy Thưởng 0968.393.899
Với x = 0 ⇒ y = 1 ⇒ A(0;1)
Đường thẳng y = mx + 1 cắt (C) tại ba điểm phân biệt A, B, C ⇔ 2
2x − 6x + m = 0 có hai nghiệm phân biệt x , x khác 0 1 2    9 ∆ ' > 0 9  − 2m > 0  ⇔   m  <   ⇔  ⇔  2 m  ≠ 0 m  ≠ 0   m  ≠ 0 
Khi đó: B(x ;mx + 1);C(x ;mx + 1). Vì trung điểm của AC nên x = 2x (1) 1 1 2 2 2 1 x  + x = 3  1 2
Mà x , x là nghiệm của phương trình: 2 
2x − 6x + m = 0 nên  1 2 m x  x  = (2) 1 2  2 Từ (1) và (2) ⇒ m = 4 HT 55. Cho hàm số 3 2 2 2
y = x − 3mx + 3(m − 1)x − (m − 1) (m là tham số) (1). Tìm các giá trị
của m để đồ thị hàm số (1) cắt trục hoành tại 3 điểm phân biệt có hoành độ dương.
• Để ĐTHS (1) cắt trục hoành tại 3 điểm phân biệt có hoành độ dương, ta phải có: (  1) coù 2  cöïc trò
y .y < 0  CÑ CT (*) x > 0, x > 0  CÑ CT  .a ( y 0) < 0  Trong đó: + 3 2 2 2
y = x − 3mx + 3(m − 1)x − (m − 1) ⇒ 2 2
y′ = 3x − 6mx + 3(m − 1) + 2 2
∆ = m − m + 1 = 0 > 0, ∀m y ′
x = m −1 = x + y ′= 0  CÑ ⇔ 
x = m + 1 = x  CT  m  −1 > 0 m  + 1 > 0 Suy ra: (*)  ⇔ 
⇔ 3 < m < 1 + 2 2 2 2 (
 m − 1)(m − 3)(m − 2m − 1) < 0  2  ( − m − 1) < 0 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 36
GV.Lưu Huy Thưởng 0968.393.899 HT 56. 1 2 Cho hàm số 3 2
y = x − mx − x + m + có đoQ thị
(C ). Tı̀m m đeU (C )caVt trục hoành tạ i 3 3 3 m m đieUm phân biệ
t có toUng bı̀nh phương các hoành độ lớn hơn 15. Giải • 1 2 YCBT ⇔ 3 2
x − mx − x + m +
= 0 (*) có 3 nghiệm phân biệt thỏa 2 2 2
x + x + x > 15 . 3 3 1 2 3 x  = 1 Ta có: (*) 2 ⇔ 
(x − 1)(x + (1 − 3m)x − 2 − 3m) = 0 ⇔  2 g
 (x) = x + (1 − 3m)x − 2 − 3m = 0 
Do đó: YCBT ⇔ g(x) = 0 có 2 nghiệ
m x , x phân biệ t khác 1 và thỏ a 2 2 x + x > 14 . 1 2 1 2 ⇔ m > 1
Câu hỏi tương tự đối với hàm số: 3 2
y = x − 3mx − 3x + 3m + 2 HT 57. Cho hàm số 3 2
y = x − 3x − 9x + m , trong đó m là tham số thực. Tìm tất cả các giá trị của
tham số m để đồ thị hàm số đã cho cắt trục hoành tại 3 điểm phân biệt có hoành độ lập thành cấp số cộng. Giải
• Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt có hoành độ lập thành cấp số cộng ⇔ Phương trình 3 2
x − 3x − 9x + m = 0 có 3 nghiệm phân biệt lập thành cấp số cộng ⇔ Phương trình 3 2
x − 3x − 9x = m
− có 3 nghiệm phân biệt lập thành cấp số cộng
⇔ Đường thẳng y = m
− đi qua điểm uốn của đồ thị (C) ⇔ m − = 1 − 1 ⇔ m = 11. HT 58. Cho hàm số 3 2
y = x − 3mx + 9x − 7 có đồ thị (Cm), trong đó m là tham số thực. Tìm m để
(Cm) cắt trục hoành tại 3 điểm phân biệt có hoành độ lập thành cấp số cộng. Giải
• Hoành độ các giao điểm là nghiệm của phương trình: 3 2
x − 3mx + 9x − 7 = 0 (1)
Gọi hoành độ các giao điểm lần lượt là x ;x ;x ta có: x + x + x = 3m 1 2 3 1 2 3
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 37
GV.Lưu Huy Thưởng 0968.393.899
Để x ;x ;x lập thành cấp số cộng thì x = m là nghiệm của phương trình (1) 1 2 3 2 m = 1    −1 + 15 ⇒ 3
−2m + 9m − 7 = 0 ⇔ m =   2  −1 − 15 m  =  2 −1 − 15 Thử lại ta có m = là giá trị cần tìm. 2 HT 59. Cho hàm số 3 2
y = x − 3mx − mx có đồ thị (Cm), trong đó m là tham số thực. Tìm m để
(Cm) cắt đường thẳng d : y = x + 2 tại 3 điểm phân biệt có hoành độ lập thành cấp số nhân. Giải
• Xét phương trình hoành độ giao điểm của (Cm) và d: 3 2
x − mx − mx = x + ⇔ g (x) 3 2 3 2
= x − 3mx − (m + ) 1 x − 2 = 0
Đk cần: Giả sử (C) cắt d tại 3 điểm phân biệt có hoành độ x ;x ;x lần lượt lập thành cấp số 1 2 3
nhân. Khi đó ta có: g (x) = (x − x x − x x − x 1 )( 2 )( 3 ) x
 + x + x = 3m  1 2 3  Suy ra: x
 x + x x + x x = m − − 1 1 2 2 3 1 3
x x x = 2  1 2 3  5 Vì 2 3 3
x x = x ⇒ x = 2 ⇒ x = 2 nên ta có: 3 m
− − 1 = 4 + 2.3m ⇔ m = − 1 3 2 2 2 3 3 2 + 1 5
Đk đủ: Với m = −
, thay vào tính nghiệm thấy thỏa mãn. 3 3 2 + 1 5 Vậy m = − 3 3 2 + 1 HT 60. Cho hàm số: 3 2
y = 2x − 3x + 1 (1) . Tìm trên (C) những điểm M sao cho tiếp tuyến của (C)
tại M cắt trục tung tại điểm có tung độ bằng 8. Giải
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 38
GV.Lưu Huy Thưởng 0968.393.899
Giả sử M (x0; y0) ∈(C) ⇒ y0 = 2x03 - 3x02 + 1 Ta có : 2
y ' = 3x − 6x
Tiếp tuyến ( ∆ ) của (C) tại M:
y = (6x02 - 6x0) (x - x0) + 2x03 - 3x02 + 1
( ∆ ) đi qua điểm P(0 ; 8) ⇔ 8 = -4x03 + 3x02 + 1
⇔ (x0 + 1) (4x02 - 7x0 + 7) = 0
⇔ x0 = -1 ; (4x02 - 7x0 + 7 > 0, ∀ x0)
Vậy, có duy nhất điểm M (-1 ; -4) cần tìm. HT 61. Cho hàm số 3 2
y = x + 2mx + (m + 3)x + 4 có đồ thị là (Cm) (m là tham số). Cho đường
thẳng (d): y = x + 4 và điểm K(1; 3). Tìm các giá trị của m để (d) cắt (Cm) tại ba điểm phân biệt
A(0; 4), B, C sao cho tam giác KBC có diện tích bằng 8 2 . Giải
• Phương trình hoành độ giao điểm của (Cm) và d là: 3 2 2
x + 2mx + (m + 3)x + 4 = x + 4 ⇔ x(x + 2mx + m + 2) = 0 x = 0 (y = 4)  ⇔  2 g
 (x) = x + 2mx + m + 2 = 0 (1) 
(d) cắt (Cm) tại ba điểm phân biệt A(0; 4), B, C ⇔ (2) có 2 nghiệm phân biệt khác 0.  / 2 ∆ 
= m − m − 2 > 0 m  ≤ 1 − ∨ m ≥ 2   ⇔  ⇔  (*) g  (0) = m + 2 ≠ 0 m  ≠ 2 −    
Khi đó: x + x = −2m; x .x = m + 2 . B C B C 1 − 3 + 4
Mặt khác: d(K,d) = = 2 . Do đó: 2 1 2 S
= 8 2 ⇔ BC.d(K,d) = 8 2 ⇔ BC = 16 ⇔ BC = 256 K ∆ BC 2 2 2
⇔ (x − x ) + (y − y ) = 256 2 2
⇔ (x − x ) + ((x + 4) − (x + 4)) = 256 B C B C B C B C
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 39
GV.Lưu Huy Thưởng 0968.393.899 2 2
⇔ 2(x − x ) = 256 ⇔ (x + x ) − 4x x = 128 B C B C B C ± 2 2 1 137
⇔ 4m − 4(m + 2) = 128 ⇔ m − m − 34 = 0 ⇔ m = (thỏa (*)). 2 1 ± 137 Vậy m = . 2 HT 62. Cho hàm số 3 2
y = x − 3x + 4 có đồ thị là (C). Gọi d là đường thẳng đi qua điểm A − k ( 1; 0)
với hệ số góc k (k ∈ ℝ) . Tìm k để đường thẳng d cắt đồ thị (C) tại ba điểm phân biệt A, B, C và k
2 giao điểm B, C cùng với gốc toạ độ O tạo thành một tam giác có diện tích bằng 1 . Giải
• Ta có: d : y = kx + k ⇔ kx − y + k = k 0
Phương trình hoành độ giao điểm của (Cm) và d là: 3 2  2 x 3x 4 kx k (x 1) (  x 2) k − + = + ⇔ + − −   = 0 ⇔ x = −1  hoặc 2 (x − 2) = k k  > 0
d cắt (C) tại 3 điểm phân biệt  ⇔ k k  ≠ 9 
Khi đó các giao điểm là ( A 1
− ;0),B (2 − k;3k − k k ),C (2 + k;3k + k k ). k 2
BC = 2 k 1 + k , d(O,BC ) = d(O,d ) = k 2 1 + k 1 k 2 3 S = .
.2 k . 1 + k = 1 ⇔ k k = 1 ⇔ k = 1 ⇔ k = 1 O ∆ BC 2 2 1 + k HT 63. Cho hàm số 3 2
y = x − 3x + 2 có đồ thị là (C). Gọi E là tâm đối xứng của đồ thị (C). Viết
phương trình đường thẳng qua E và cắt (C) tại ba điểm E, A, B phân biệt sao cho diện tích tam giác OAB bằng 2 . Giải
• Ta có: E(1; 0). PT đường thẳng ∆ qua E có dạng y = k(x −1).
PT hoành độ giao điểm của (C) và ∆: 2
(x − 1)(x − 2x − 2 − k) = 0
∆ cắt (C) tại 3 điểm phân biệt ⇔ PT 2
x − 2x − 2 − k = 0 có hai nghiệm phân biệt khác 1
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 40
GV.Lưu Huy Thưởng 0968.393.899 ⇔ k > 3 −  1 k = 1 −  S = d(O, )
∆ .AB = k k + 3 ⇒ k k + 3 = 2 ⇔ O ∆ AB  2 k  = 1 − ± 3 
Vậy có 3 đường thẳng thoả YCBT: y = x − + 1; y = ( 1 − ± 3)(x −1) . HT 64. 4 1 Cho hàm số 3 2
y = x − (2m + 1)x + (m + 2)x + có đồ thị (C ),m là tham số. Gọi A là 3 3 m
giao điểm của (C ) với trục tung. Tìm m sao cho tiếp tuyến của (C ) tại A tạo với hai trục tọa độ m m 1
một tam giác có diện tích bằng . 3 Giải  1  Ta có: A  0; và 2 y = x −
m + x + m + Suy ra y = m + 3  ' 4 2(2 1) 2. '(0) 2   1  1 − 
Tiếp tuyến của đồ thị tại A là d  
: y = (m + 2)x + . Đường thẳng d cắt Ox tại B  ; 0   3 3m + 6 
Khi đó diện tích tam giác tạo bởi d với hai trục tọa độ là: 1 1 1 −1 1 S = O . AOB = . . = 2 2 3 3m + 6 18 m + 2  13 m  = − 1 1 1  Theo giả thiết ta có: 6 = ⇔ m + 2 = ⇔  18 m + 2 3 6  11 m = −   6 HT 65. Cho hàm số 3
y = x + mx + 2 có đồ thị (Cm). Tìm m để đồ thị (Cm) cắt trục hoành tại một điểm duy nhất. Giải
• Phương trình hoành độ giao điểm của (Cm) với trục hoành: 3 x + mx + 2 = 0 2 2 ⇔ m = x − − (x ≠ 0) x 3 2 2 −2x + 2 Xét hàm số: 2 f (x) = x
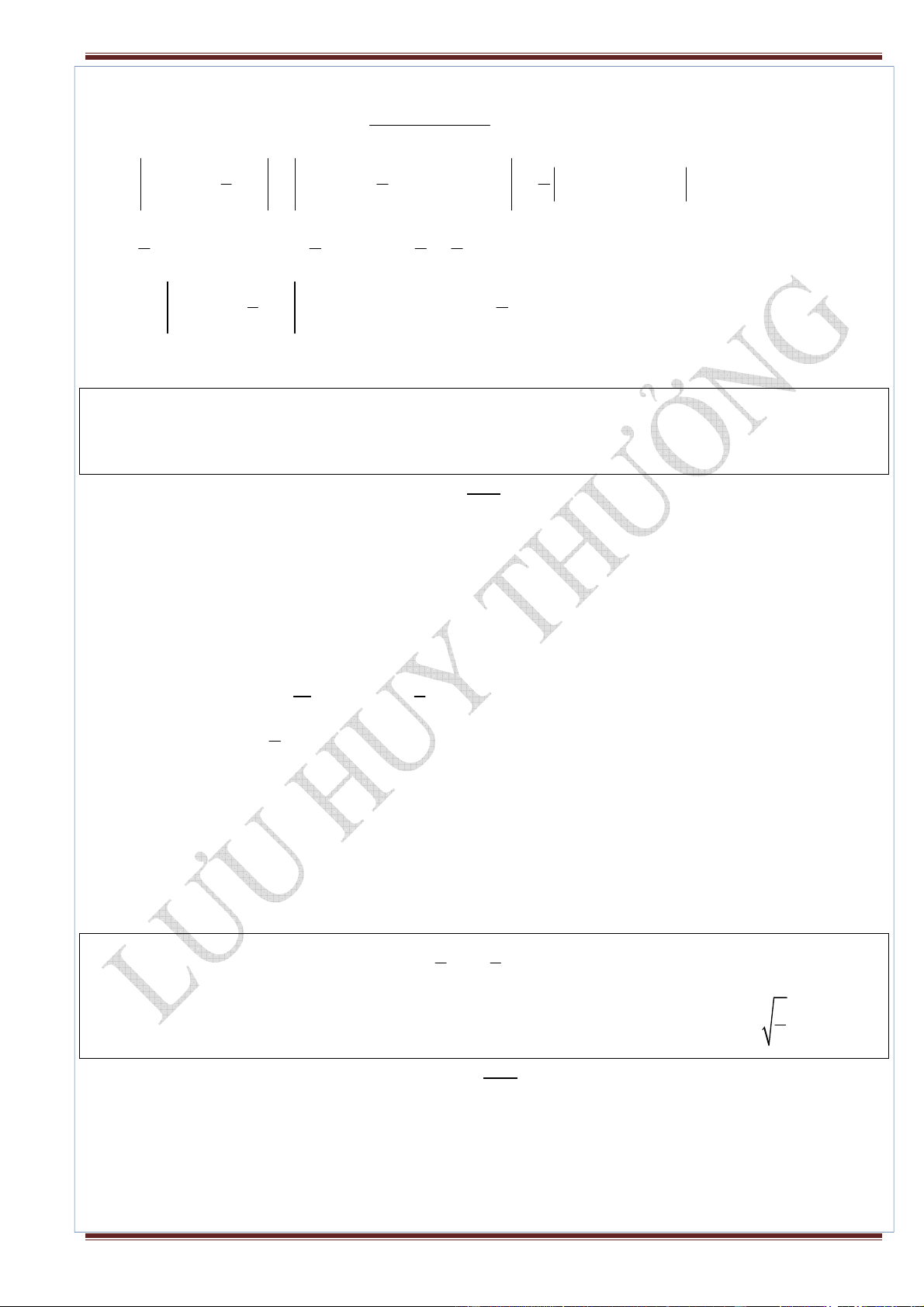
− − ⇒ f '(x) = −2x + = 2 2 x x x Ta có bảng biến thiên:
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 41
GV.Lưu Huy Thưởng 0968.393.899 −∞ +∞ f ′(x) f (x) +∞ −∞ −∞ −∞
Đồ thị (Cm) cắt trục hoành tại một điểm duy nhất ⇔ m > 3 − . HT 66. Cho hàm số 3 2
y = 2x − 3(m + 1)x + 6mx − 2 có đồ thị (Cm). Tìm m để đồ thị (Cm) cắt trục
hoành tại một điểm duy nhất. Giải
• Tập xác định: D = ℝ 2
y ' = 6x − 6(m +1)x + 6m 2 2
∆' = 9(m + 1) − 36m = 9(m − 1) y '
Th1: m = 1⇒ hàm số đồng biến trên ℝ ⇒ đồ thị hàm số cắt trục hoành tại 1 điểm duy nhất. ⇒ m = 1(thỏa mãn)
Th2: m ≠ 1 ⇒ Hàm số có cực đại và cực tiểu. Gọi x , x là các điểm cực trị của hàm số 1 2
⇒ x , x là các nghiệm của phương trình y’ = 0 1 2 x
 + x = m + 1  Theo Viet ta có: 1 2 x .x = m  1 2  x m + 1
Lấy y chia cho y’ ta được: 2 y = ( −
)y '− (m − 1) x − 2 + m(m + 1) 3 6
⇒ Phương trình đi qua điểm cực đại và cực tiểu của hàm số 2 y = (
− m − 1) x − 2 + m(m + 1)
Để hàm số cắt trục hoành tại 1 điểm duy nhất ⇔ y .y < 0 CD CT
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 42
GV.Lưu Huy Thưởng 0968.393.899 [ 2
− (m − 1) x − 2 + m(m + 1 ] ) [ 2
− (m − 1) x − 2 + m(m + 1 ] ) > 0 1 2 4 2 2 2 2
⇔ (m − 1) x x − (m − 1) (m + m − 2)(x + x ) + (m + m − 2) > 0 1 2 1 2 4 2 2 2 2
⇔ (m − 1) m − (m − 1) (m + m − 2)(m + 1) + (m + m − 2) > 0 2 ⇔ (m − 1) [ 2 2 2
(m − 1) m − (m + m − 2)(m + 1) + (m + 2) ] > 0 3 2 3 2 2
⇔ m − 2m + m − m − 2m + m + 2 + m + 4m + 4 > 0(V ì m ≠ 1) 2
⇔ m − 2m − 2 < 0
⇔ 1 − 3 < m < 1 + 3
Kết luận: 1 − 3 < m < 1 + 3 HT 67. Cho hàm số 3 2
y = x – 3x + 1. Tìm m để đường thẳng (∆): y = (2m − 1)x – 4m – 1 cắt đồ thị
(C) tại đúng hai điểm phân biệt. Giải
• Phương trình hoành độ giao của (C) và (∆): 3 2
x – 3x – (2m – 1)x + 4m + 2 = 0 x = 2 ⇔ 2 
(x − 2)(x – x – 2m – 1) = 0 ⇔  2 f
 (x) = x − x − 2m − 1 = 0 (1)  2 ≠ x = x
(∆) cắt (C) tại đúng 2 điểm phân biệt ⇔ (1) phải có nghiệm x , x thỏa mãn:  1 2 1 2 x = 2 ≠ x  1 2  ∆ = 0    8  m + 5 = 0       b   5   − 1   ≠ 2  ≠ 2 m = −  ⇔   2a  ⇔ 2 ⇔ 8    ∆ >  1 0     8m + 5 > 0 m =       f  2 (2) = 0      − m + =  2 1 0    5 1
Vậy: m = − ; m = . 8 2 HT 68. Cho hàm số 3 2
y = x − 6x + 9x (1).Tìm m để đường thẳng (d):y = mx cắt (C) tại ba điểm O
(0;0), A và B. Chứng tỏ rằng khi m thay đổi, trung điểm I của đoạn AB luôn nằm trên một đường thẳng song song với Oy. Giải
Phương trình hoành độ giao điểm của đường thẳng (d) với đồ thị (C) là:
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 43
GV.Lưu Huy Thưởng 0968.393.899 x = 0 3 2 x 
− 6x + 9x = mx (1) ⇔  2 x
 − 6x + 9 − m = 0 (2) 
(d) cắt (C) tại 3 điểm phân biệt O(0;0), A, B
⇔ (1) có 3 nghiệm phân biệt ⇔ (2) có 2 nghiệm phân biệt khác x ≠ 0 ∆' > 0 ⇔  ⇔ 0 < m ≠ 9 (*) 9  − m ≠ 0 
Với điều kiện (*), A, B là 2 điểm có hoành độ lần lượt là x ;x là 2 nghiệm của phương trình A B (2) x + x
I là trung điểm của đoạn thẳng AB nên hoành độ I: A B x = = 3 I 2
⇒ I ∈ ∆ có phương trình là x = 3, ∆ song song với Oy khi m thay đổi (0 < m ≠ 9) HT 69. Cho hàm số 3 2
y = x − 3mx + (m − 1)x + m + 1có đồ thị là (C ). Tìm tất cả các giá trị của m
m để d: y = 2x − m − 1 cắt đồ thị (C )tại ba điểm phân biệt có hoành độ lớn hơn hoặc bằng 1. m Giải
Phương trình hoành độ giao điểm của (C ) với đường thẳng (d): m 3 2
x − 3mx + (m − 1)x + m + 1 = 2x − m − 1 3 2
⇔ x − 3mx + (m − 3)x + 2m + 2 = 0  2 (x 1) x (1 3m)x 2m 2 ⇔ − + − − − = 0 (1)     x = 1  ⇔  2 x 
+ (1 − 3m)x − 2m − 2 = 0 (2) 
(C ) cắt (d) tại 3 điểm phân biệt có hoành độ lớn hơn hoặc bằng 1 m
⇔ (1) có 3 nghiệm phân biệt lớn hơn hoặc bằng 1
⇔ (2) có hai nghiệm phân biệt lớn hơn 1.
Xét phương trình (2); Ta có: 2 2
∆ = (1 − 3m) + 8m + 8 = 9m + 2m + 9 > 0, m ∀ ⇒ m
∀ (2) luôn có 2 nghiệm phân biệt x ;x 1 2
(1) có 2 nghiệm lớn hơn 1 ⇔ 1 < x < x ⇔ 0 < x − 1 < x − 1 1 2 1 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 44
GV.Lưu Huy Thưởng 0968.393.899
Đặt t = x - 1 ⇔ x = t + 1⇒ (2) ⇔ 2
(t + 1) + (1 − 3m)(t + 1) − 2m − 2 = 0 ⇔ 2
t + 3(1 − m)t − 5m = 0 (3)
(2) có 2 nghiệm thỏa mãn: 1 < x < x ⇔ (3) có 2 nghiệm dương phân biệt: 1 2 ∆ > 0  ⇔ S
 = 3(m −1) > 0 ⇔ vn
p = −5m > 0 
Kết luận: không có giá trị m HT 70. Cho hàm số 3
y = x − 3x + 2 (C). Viết phương trình đường thẳng cắt đồ thị (C) tại 3 điểm
phân biệt A, B, C sao cho x = 2 và BC = A 2 2 Giải
Với x = 2 ⇒ y = 4 Phương trình đường thẳng (d) đi qua điểm A(2;4) là: A A
y = k(x − x ) + y ⇒ d : y = k(x − 2) + 4 A A
Phương trình hoành độ giao điểm của (C) với đường thẳng (d) 3 2
x − 3x + 2 = k(x − 2) + 4 ⇔ (x − 2)(x + 2x − k + 1) = 0 x = 2  ⇔  2
g(x) = x + 2x − k + 1  ∆' > 0 k  > 0
Điều kiện để có BC:   ⇔  g  (2) ≠ 0 k  ≠ 9  
Khi đó. Tọa độ của B(x ;y );C(x ;y ) thỏa mãn hệ phương trình: 1 1 2 2  2 x
 + 2x −k +1 = 0 (1)  y
 = kx − 2k + 4 (2) 
(1) ⇔ x − x = 2 ∆ ' = 2 k Ta có: 2 1
(2) ⇔ y − y = k(x − x = 2k k 2 1 2 1
Theo giả thiết ta có: BC = 2 2 ⇔ 3 3
4k + 4k = 2 2 ⇔ 4k + 4k − 8 = 0 ⇔ k = 1
Vậy: d : y = x + 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 45
GV.Lưu Huy Thưởng 0968.393.899 HT 71. Cho hàm số 3 2
y = 4x − 6mx + 1 (C), m là tham số. Tìm m để đường thẳng d : y = x − + 1
cắt đồ thị hàm số tại 3 điểm A(0;1), B, C với B, C đối xứng nhau qua đường phân giác thứ nhất. Giải
Giao của (C) và (d) có hoành độ là nghiệm của phương trình: 3 2 2
4x − 6mx + 1 = x
− + 1 ⇔ x(4x − 6mx + 1) = 0
Để phương trình có 3 nghiệm phân biệt thì 2
4x − 6mx + 1 = 0 có hai nghiệm phân biệt. − ⇒ 2 2 2
∆' = 9m − 4 > 0 ⇔ m > ;m < 3 3
GọiB(x ; x
− + 1),C(x ; x
− + 1)Để B, C đối xứng qua đường phân giác thứ nhất thì: 1 1 2 2 x  = y x  = x − + 1  1 2  1 2 3 2  ⇔ 
⇔ x + x = 1 ⇔ m = 1 ⇔ m = 1 2 y  = x x  = x − + 1 2 3  1 2   2 1 
So sánh điều kiện ta thấy không có giá trị m thỏa mãn. HT 72. Cho hàm số 3 2
y = x + 3x + mx + 1(m là tham số) (1). Tìm m để đường thẳng d : y = 1 cắt
đồ thị hàm số (1) tại ba điểm phân biệt A(0; 1), B, C sao cho các tiếp tuyến của đồ thị hàm số (1)
tại B và C vuông góc với nhau. Giải
• PT hoành độ giao điểm của (1) và d: 3 2 2
x + 3x + mx + 1 = 1 ⇔ x(x + 3x + m) = 0 9
d cắt (1) tại 3 điểm phân biệt A(0; 1), B, C ⇔ m < , m ≠ 0 4
Khi đó: x , x là các nghiệm của PT: 2
x + 3x + m = 0 ⇒ x + x = −3; x .x = m B C B C B C
Hệ số góc của tiếp tuyến tại B là 2
k = 3x + 6x + m và tại C là 2
k = 3x + 6x + m 1 B B 2 C C
Tiếp tuyến của (C) tại B và C vuông góc với nhau ⇔ k .k = 1 − ⇔ 2
4m − 9m + 1 = 0 1 2 9 − 65 9 + 65 ⇔ m = ∨ m = 8 8
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 46
GV.Lưu Huy Thưởng 0968.393.899 HT 73. Cho hàm số 3
y = x – 3x + 1 có đồ thị (C) và đường thẳng (d): y = mx + m + 3 . Tìm m để
(d) cắt (C) tại M(–1; 3), N, P sao cho tiếp tuyến của (C) tại N và P vuông góc với nhau. Giải
• Phương trình hoành độ giao điểm của (C) và (d): 3
x – (m + 3)x – m – 2 = 0 x  = −1 (y = 3) ⇔ 2 
(x + 1)(x – x – m – 2) = 0 ⇔  2 g
 (x) = x − x − m − 2 = 0  9
d cắt (1) tại 3 điểm phân biệt M(–1; 3), N, P ⇔ m > − , m ≠ 0 4
Khi đó: x , x là các nghiệm của PT: 2
x − x − m − 2 = 0 ⇒ x + x = 1; x .x = m − − 2 N P N P N P
Hệ số góc của tiếp tuyến tại N là 2
k = 3x − 3 và tại P là 2 k = 3x − 3 1 N 2 P
Tiếp tuyến của (C) tại N và P vuông góc với nhau ⇔ k .k = 1 − ⇔ 2
9m + 18m + 1 = 0 1 2 ⇔ −3 + 2 2 −3 − 2 2 m = ∨ m = 3 3 HT 74. Cho hàm số 3 2
y = x − 3x + 4 (C). Gọi (d) là đường thẳng đi qua điểm A(2; 0) có hệ số góc
k. Tìm k để (d) cắt (C) tại ba điểm phân biệt A, M, N sao cho hai tiếp tuyến của (C) tại M và N vuông góc với nhau. Giải
• PT đường thẳng (d): y = k(x − 2)
+ PT hoành độ giao điểm của (C) và (d): 3 2
x − 3x + 4 = k(x − 2) x  = 2 = x ⇔ 2  A
(x − 2)(x − x − 2 − k) = 0 ⇔  2 g
 (x) = x − x − 2 − k = 0 
+ (d) cắt (C) tại 3 điểm phân biệt A, M, N ⇔ PT g(x) = 0 có 2 nghiệm phân biệt, khác 2 ∆ > 0  9 ⇔  ⇔ − < k ≠ 0 (*) f (2) ≠ 0 4 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 47
GV.Lưu Huy Thưởng 0968.393.899 x  + x = 1
+ Theo định lí Viet ta có:  M N  x  x = k − − 2  M N 
+ Các tiếp tuyến tại M và N vuông góc với nhau ⇔ y (
′ x ).y (′x ) = 1 − M N − ± ⇔ 2 2 (3x
− 6x )(3x − 6x ) = −1 ⇔ 2 9k + 18k + 1 = 3 2 2 0 ⇔ k = (thoả (*)) M M N N 3 HT 75. Cho hàm số 3
y = x − 3x (C). Chứng minh rằng khi m thay đổi, đường thẳng (d):
y = m(x + 1) + 2 luôn cắt đồ thị (C) tại một điểm M cố định và xác định các giá trị của m để (d)
cắt (C) tại 3 điểm phân biệt M, N, P sao cho tiếp tuyến của (C) tại N và P vuông góc với nhau. Giải x  + 1 = 0
• PT hoành độ giao điểm 2 
(x + 1)(x − x − 2 − m) = 0 (1) ⇔  2 x
 − x − 2 − m = 0 (2) 
(1) luôn có 1 nghiệm x = −1 (y = 2 ) ⇒ (d) luôn cắt (C) tại điểm M(–1; 2).  9 m > −
(d) cắt (C) tại 3 điểm phân biệt ⇔ (2) có 2 nghiệm phân biệt, khác –1 ⇔  4 (*) m ≠ 0 −3 ± 2 2
Tiếp tuyến tại N, P vuông góc ⇔ y '(x ).y '(x ) = 1 − N P ⇔ m = (thoả (*)) 3 HT 76. Cho hàm số 3
y = x − mx + m − 1
(C ). Tìm m để tiếp tuyến của đồ thị hàm số đã cho m
tại điểm x = −1 cắt đường tròn (C): 2 2
(x − 2) + (y − 3) = 4 theo một dây cung có độ dài nhỏ nhất. Giải Cách 1: Ta có: 2
y ' = 3x − m ⇒ y ' = 1 − m (−1)
Phương tình tiếp tuyến tại điểm có hoành độ x = -1 là:
y = (3 − m)x + m + 1 ⇔ (3 − m)x − y + m + 1 (d)
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 48
GV.Lưu Huy Thưởng 0968.393.899 2 4 − m 1 + (3 − m) 2 (3 − m) + 1
d I,(d) = = ≤ = 2   2 2 2 (3 − m) + 1 (3 − m) + 1 (3 − m) + 1
Tiếp tuyến cắt đường tròn tại hai điểm A, B sao cho AB min ⇔ d(I,(d)) max.
Dấu = xảy ra khi m = 2. Khi đó, phương trình tiếp tuyến là x - y + 3 = 0
Cách 2: Phương trình tiếp tuyến tại điểm x = -1 là: y = (3 - m)x + m + 1
⇒ Tiếp tuyến luôn đi qua điểm cố định là M(1;4)
Ta có đường tròn có tâm I(2;3), bán kính R = 2
⇒ IM = 2 < R ⇒ M nằm trong đường tròn
Gọi H là hình chiếu của I lên tiếp tuyến. Giả sử tiếp tuyến cắt đường tròn theo dây cung AB ⇒ AB = 2AH = 2 2 2 R − IH
⇒ AB min khi IH max. Tức là H trùng với M. Khi đó, tiếp tuyến nhận IM làm véc tơ pháp tuyến
Ta có: IM (-1;1) ⇒ m = 2. Khi đó, phương trình tiếp tuyến là: y = x + 3 HT 77. Cho hàm số 3
y = x − 3mx + 2(C ). Tìm m để đường thẳng đi qua điểm cực đại, cực tiểu m
của(C cắt đường tròn tâm I (1; )
1 , bán kính bằng 1 tại hai điểm phân biệt A, B sao cho diện tích m )
tam giác IAB đạt giá trị lớn nhất Giải Ta có 2
y ' = 3x − 3m
Để hàm số có cực đại, cực tiểu thì phương trình y ' = 0 có hai nghiệm phân biệt ⇔ m > 0 1
Vì y = x.y '− 2mx + 2 nên đường thẳng ∆ đi qua cực đại, cực tiểu của đồ thị hàm số có phương 3
trình là y = −2mx + 2 2m − 1
Ta có d (I,∆) =
< R = 1 (vì m > 0), chứng tỏ đường thẳng ∆ luôn cắt đường tròn tâm 2 4m + 1
I(1; 1), bán kính R = 1 tại 2 điểm A, B phân biệt
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 49
GV.Lưu Huy Thưởng 0968.393.899 1 1 1 1
Với m ≠ , đường thẳng ∆ không đi qua I, ta có: 2 S = I .
A IB.sin AIB ≤ R = 2 A ∆ BI 2 2 2 Nên S
đạt giá trị lớn nhất bằng ½ khi sinAIB = 1 hay tam giác AIB vuông cân tại I I ∆ AB R 1 2m − 1 ± ⇔ IH = = 1 2 3
(H là trung điểm của AB) ⇔ = ⇔ m = 2 2 2 2 4m + 1 2 HT 78. Cho hàm số 4 2
y = x − mx + m − 1 có đồ thị là (C Định m để đồ thị (C cắt trục trục m ) m )
hoành tại bốn điểm phân biệt. Giải
• Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành: 4 2
x − mx + m − 1 = 0 (1) t = 1 Đặt: t = 2
x (t ≥ 0) ⇒ (1) ⇔ 2 t mt m 1 0  − + − = ⇔ t = m − 1 
Đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt
⇔ (1) có 4 nghiệm phân biệt m  > 1
⇔ 0 < m - 1 ≠ 1⇔  m  ≠ 2  HT 79. Cho hàm số 4 2
y = x − 2(m + 1)x + 2m + 1 (C ). Tìm tất cả các giá trị của tham số m ∈ ℝ m
để đồ thị hàm số đã cho cắt trục hoành tại 4 điểm phân biệt ,
A B,C,D lần lượt có hoành độ
x ,x ,x ,x (x < x < x < x ) sao cho tam giác ACK có diện tích bằng 4 biết K(3;−2). 1 2 3 4 1 2 3 4 Giải
Phương trình hoành độ giao điểm của (C ) với trục hoành: m 4 2
x − 2(m + 1)x + 2m + 1 = 0 (1) Đặt: 2
t = x (t ≥ 0) Khi đó: 2
(1) ⇔ t − 2(m + 1)t + 2m + 1 = 0 (2).
Để đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt thì phương trình (1) có 4 nghiệm phân biệt
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 50
GV.Lưu Huy Thưởng 0968.393.899
⇔ Phương trình (2) có nghiệm dương phân biệt  2 ∆
 ' = (m + 1) − (2m + 1) > 0 m  ≠ 0   S    2(m 1) 0 ⇔ = + > ⇔  1  m    > − P  = 2m + 1 > 0    2  1
Với − < m ≠ 0 thì đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt có hoành độ theo thứ tự 2
− t ;− t ; t ; t với t > t 1 2 2 1 1 2 1 Theo giả thiết: S
= AC.d(K;AC ) (3) với d(K;AC ) = y ACK 2 K
Khi đó: (3) ⇔ t + t = 4 ⇔ t + t + 2 t t = 16 1 2 1 2 1 2
Theo Viet ta có: 2(m + 1) + 2 2m + 1 = 16 ⇔ 2m + 1 = 7 − m 7  −m ≥ 0  ⇔  ⇔ m = 4 2 m  − 16m + 48 = 0  HT 80. Cho hàm số 4
y = x − (m + ) 2 2
1 x + 2m + 1 có đồ thị là (C
. Định m để đồ thị (C cắt m ) m )
trục hoành tại 4 điểm phân biệt có hoành độ lập thành cấp số cộng. Giải
• Xét phương trình hoành độ giao điểm: 4 x − (m + ) 2 2
1 x + 2m + 1 = 0 (1) Đặt 2
t = x ,t ≥ 0 thì (1) trở thành: 2
f (t) = t − 2(m + )
1 t + 2m + 1 = 0 .
Để (Cm) cắt Ox tại 4 điểm phân biệt thì f (t) = 0 phải có 2 nghiệm dương phân biệt  2 ∆  ' = m > 0  1  m    > − S  2(m )1 0  ⇔ = + > ⇔  2 (*)  m    ≠ 0 P  = 2m + 1 > 0    
Với (*), gọi t < t là 2 nghiệm của f (t) = 0 , khi đó hoành độ giao điểm của (C 1 2 m) với Ox lần lượt
là: x = − t ;x = − t ;x = t ;x = t 1 2 2 1 3 1 4 2
x , x , x , x lập thành cấp số cộng ⇔ x − x = x − x = x − x ⇔ t = 9t 1 2 3 4 2 1 3 2 4 3 2 1
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 51
GV.Lưu Huy Thưởng 0968.393.899 m   = 4 5m = 4m + 4 
⇔ m + 1 + m = 9(m + 1− m ) ⇔ 5 m = 4(m + ) 1  ⇔ ⇔   4 −5m = 4m + 4 m   = −   9  4 Vậy m 4  ;  = −   9   13
Câu hỏi tương tự đối với hàm số 4 2 y = x
− + 2(m + 2)x − 2m − 3 ĐS: m = 3,m = − . 9 HT 81. Cho hàm số 4 2
y = x – (3m + 2)x + 3m có đồ thị là (Cm), m là tham số. Tìm m để đường
thẳng y = −1 cắt đồ thị (Cm) tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2. Giải
• Phương trình hoành độ giao điểm của (Cm) và đường thẳng y = −1: x  = ± 1 4 2 x 
– (3m + 2)x + 3m = 1 − ⇔ 4 2
x – (3m + 2)x + 3m + 1 = 0 ⇔  2 x  = 3m + 1 (*) 
Đường thẳng y = −1 cắt (Cm) tại 4 điểm phân biệt có hoành độ nhỏ hơn 2 khi và chỉ khi phương
trình (*) có hai nghiệm phân biệt khác ±1 và nhỏ hơn 2  0
 < 3m + 1 < 4 1  −  < m < 1 ⇔  ⇔  3 3  m + 1 ≠ 1   m  ≠ 0  HT 82. Cho hàm số 4 2 2 2
y = x − (m + 2)x + m + 1
(Cm) . Tìm các giá trị của m để (C ) cắt m
trục hoành tại 4 điểm phân biệt sao cho hình phẳng giới hạn bởi(C ) với trục hoành phần phía m 96
trên Ox có diện tích bằng . 15 Giải Có 4 2 2 2 2 2 2
y = x − (m + 2)x + m + 1 = (x − 1)(x − m − 1) . Phương trình 2 2 2
y = 0 ⇔ (x − 1)(x − m − 1) = 0 có 4 nghiệm phân biệt là 2 ±1; ± m + 1 khi m ≠ 0 .
Diện tích phần hình phẳng giới hạn bởi (C ) với trục hoành phần phía trên trục hoành là: m
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 52
GV.Lưu Huy Thưởng 0968.393.899 1 +
S = ∫ (x − m + x + m + ) 2 m 4 2 2 2 20 16 96 2 ( 2) 1 dx = = ⇔ m = ±2 15 15 0
Vậy m = ±2 là giá trị cần tìm
HT 83. Cho hàm số y = x3 – 3x2 + 3mx + 3m + 4 đồ thị là ( Cm). Tìm m để diện tích hình phẳng giới
hạn bởi đồ thị ( Cm) và trục hoành có phần nằm phía trên trục hoành bằng phần nằm phía dưới trục hoành
Hàm số bậc 3 nhận điểm uốn làm tâm đối xứng C  où hai cöïc trò ⇒ ycbt ⇔ 
Ñieåm uoán thuoäc truïc Ox 
*Hàm số có cực trị khi phương trình y' = 0 có 2 nghiệm phân biệt <=> 3x2-6x+3m=0 có 2
nghiệm phân biệt <=> '
∆ = 9(1 − m) > 0 ⇔ m < 1
*y''=6x-6 = 0 <=> x = 1 => y = 6m + 2 => đồ thị hàm số nhận điểm U(1; 6m+2) làm điểm uốn −1
Điểm uốn thuộc Ox khi yU = 0 <=> 6m+2 = 0 <=> m = 3 −1 Vậy m = là giá trị cần tìm 3 HT 84. Cho hàm số 4
y = x − (m + ) 2 2
1 x + 2m + 1 có đồ thị là (Cm), m là tham số. Tìm m để đồ thị
(Cm) cắt trục hoành tại 3 điểm phân biệt đều có hoành độ nhỏ hơn 3. Giải
• Xét phương trình hoành độ giao điểm: 4 x − (m + ) 2 2
1 x + 2m + 1 = 0 (1) Đặt 2
t = x ,t ≥ 0 thì (1) trở thành: 2
f (t) = t − 2(m + )
1 t + 2m + 1 = 0 .
(Cm) cắt Ox tại 3 điểm phân biệt có hoành độ nhỏ hơn 3
0 = t < t < 3
⇔ f (t) có 2 nghiệm phân biệt t , t sao cho:  1 2 1 2
0 < t < 3 ≤ t  1 2 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 53
GV.Lưu Huy Thưởng 0968.393.899  2 ∆   ' = m > 0 2 ∆  ' = m > 0   f 
 (3) = 4 − 4m ≤ 0 1
⇔ f (0) = 2m + 1 = 0
⇔ m = − ∨ m ≥ 1  S  = m + > S    = 2  (m + ) 2( )1 0 2 1 < 3   P  = 2m + 1 > 0  1
Vậy: m = − ∨ m ≥ 1. 2 HT 85. Cho hàm số 4 2 2 4
y = x − 2m x + m + 2m (1), với m là tham số. Chứng minh đồ thị hàm số
(1) luôn cắt trục Ox tại ít nhất hai điểm phân biệt, với mọi m < 0 . Giải
• Phương trình hoành độ giao điểm của đồ thị (1) và trục Ox: 4 2 2 4
x − 2m x + m + 2m = 0 (1) Đặt 2
t = x (t ≥ ) 0 , (1) trở thành : 2 2 4
t − 2m t + m + 2m = 0 (2) Ta có : ∆ ' = 2 − m > 0 và 2
S = 2m > 0 với mọi m > 0 . Nên (2) có nghiệm dương
⇒ (1) có ít nhất 2 nghiệm phân biệt ⇒ đồ thị hàm số (1) luôn cắt trục Ox tại ít nhất hai điểm phân biệt. HT 86. Cho hàm số: 4 2
y = x − 5x + 4 . Tìm tất cả các điểm M trên đồ thị (C) của hàm số sao cho
tiếp tuyến của (C) tại M cắt (C) tại hai điểm phân biệt khác M. Giải Gọi 4 2
M(m;m − 5m + 4)∈ (C )
Phương trình tiếp tuyến của (C) tại 3 4 2
M : y = (4m − 10m)(x − m) + m − 5m + 4 (d)
Hoành độ giao điểm của (d) và (C ) là nghiệm của phương trình: 4 2 3 4 2
x − 5x + 4 = (4m − 10m)(x − m) + m − 5m + 4 (d) 2 2 2
⇔ (x − m) (x + 2mx + 3m − 5) = 0 (1)  2 5  − 2m > 0 Yêu cầu bài toán 2 2
⇔ x + 2mx + 3m − 5 = 0 có hai nghiệm phân biệt khác m  ⇔  2 6  m − 5 ≠ 0 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 54
GV.Lưu Huy Thưởng 0968.393.899  10 10 − < m <  2 2 ⇔   30 m  ≠ ±  6 x + HT 87. 2 1
Cho hàm số y =
có đồ thị là (C). Chứng minh rằng đường thẳng d : y = x − + m x + 2
luôn cắt đồ thị (C) tại hai điểm phân biệt A, B. Tìm m để đoạn AB có độ dài nhỏ nhất. Giải • 2x + 1
PT hoành độ giao điểm của (C) và d: = x − + m x + 2 x  ≠ −2  ⇔  2
f(x) = x + (4 − m)x + 1 − 2m = 0 (1)  Do (1) có 2 ∆ = m + 1 > 0 và 2
f (−2) = (−2) + (4 − m).(−2) + 1 − 2m = −3 ≠ 0, ∀m
nên đường thẳng d luôn luôn cắt đồ thị (C ) tại hai điểm phân biệt A, B.
Ta có: y = m − x ; y = m − x nên 2 2 2 2
AB = (x − x ) + (y − y ) = 2(m + 12) A A B B B A B A Suy ra AB ngắn nhất ⇔ 2
AB nhỏ nhất ⇔ m = 0 . Khi đó: AB = 24 .
Câu hỏi tương tự đối với hàm số: x − 2 x − 1 1 a) y = ĐS: m = 2 b) y = ĐS: m = x − 1 2x 2 x − HT 88. 3
Cho hàm số y =
(C). Viết phương trình đường thẳng d qua điểm I(−1;1) và cắt đồ thị x + 1
(C) tại hai điểm M, N sao cho I là trung điểm của đoạn MN. Giải
• Phương trình đường thẳng d : y = k (x + ) 1 + 1 x − 3
d cắt (C) tại 2 điểm phân biệt M, N ⇔
= kx + k + 1 có 2 nghiệm phân biệt khác −1 . x + 1 ⇔ 2
f (x) = kx + 2kx + k + 4 = 0 có 2 nghiệm phân biệt khác −1
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 55
GV.Lưu Huy Thưởng 0968.393.899 k  ≠ 0  ⇔ ∆
 = −4k > 0 ⇔ k < 0
f(−1) = 4 ≠ 0  Mặt khác: x + x = 2
− = 2x ⇔ I là trung điểm MN với k ∀ < 0 . M N I
Kết luận: Phương trình đường thẳng cần tìm là y = kx + k + 1 với k < 0 . x + HT 89. 2 4
Cho hàm số y =
(C). Gọi (d) là đường thẳng qua A(1; 1) và có hệ số góc k. Tìm k để 1 − x
(d) cắt (C) tại hai điểm M, N sao cho MN = 3 10 .
• Phương trình đường thẳng (d) : y = k(x − 1) + 1.
Bài toán trở thành: Tìm k để hệ phương trình sau có hai nghiệm (x ;y ), (x ;y ) phân biệt sao 1 1 2 2 2 2 cho (x − x + y − y = 90 (a) 2 1 ) ( 2 1) 2x + 4    = k(x − 1) + 1 2 k  x 
−(2k − 3)x + k + 3 = 0  x − +  1 (I). Ta có: I ⇔  ( )   y = k  y = k x − + (x − 1) + 1 ( 1) 1    
(I) có hai nghiệm phân biệt ⇔ PT 2
kx − (2k − 3)x + k + 3 = 0 (b) có hai nghiệm phân biệt. 3
⇔ k ≠ 0,k < . 8 2  2 
Ta biến đổi (a) trở thành: 2
(1 + k )(x − x ) 2
= 90 ⇔ (1 + k )  x + x − 4x x  = 90 2 1 ( 2 1) 2 1   (c) 2k − 3 k + 3
Theo định lí Viet cho (b) ta có: x + x = , x x =
, thế vào (c) ta có phương 1 2 1 2 k k trình: 3 2 2
8k + 27k + 8k − 3 = 0 ⇔ (k + 3)(8k + 3k − 1) = 0 −3 + 41 −3 − 41
⇔ k = −3; k = ; k = . 16 16
Kết luận: Vậy có 3 giá trị của k thoả mãn như trên. x − HT 90. 2 2
Cho hàm số y =
(C). Tìm m để đường thẳng (d): y = 2x + m cắt (C) tại hai điểm x + 1
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 56
GV.Lưu Huy Thưởng 0968.393.899
phân biệt A, B sao cho AB = 5 . Giải • 2x − 2
PT hoành độ giao điểm: = 2x + m ⇔ 2
2x + mx + m + 2 = 0 (x ≠ −1) (1) x + 1
d cắt (C) tại 2 điểm phân biệt A, B ⇔ (1) có 2 nghiệm phân biệt x , x khác –1 1 2 ⇔ 2
m − 8m − 16 > 0 (2)  m x  + x = − 1 2  Khi đó ta có: 2 
. Gọi A(x ;2x + m) , B (x ;2x + m . 1 1 2 2 )  m + 2 x  x = 1 2  2 AB2 = 5 ⇔ 2 2
(x − x ) + 4(x − x ) = 5 ⇔ 2
(x + x ) − 4x x = 1 ⇔ 2
m − 8m − 20 = 0 1 2 1 2 1 2 1 2 m  = 10 ⇔  (thoả (2)) m  = −2 
Vậy: m = 10; m = 2 − . x − HT 91. 1
Cho hàm số y =
(1). Tìm các giá trị của tham số m sao cho đường thẳng (d): x + m
y = x + 2 cắt đồ thị hàm số (1) tại hai điểm A và B sao cho AB = 2 2 . Giải x  − ≠ m − • x 1 
PT hoành độ giao điểm: x 2 = + ⇔  2 x + m x
 + (m + 1)x + 2m + 1 = 0 (*) 
d cắt đồ thị hàm số (1) tại hai điểm A, B phân biệt ⇔ (*) có hai nghiệm phân biệt khác m −   2 ∆ > 0 m     − 6m − 3 > 0 m  
 < 3 − 2 3 ∨ m > 3 + 2 3  ⇔  ⇔  ⇔  (**) x  ≠ m − m  ≠ −1 m  ≠ −1      x  + x = ( − m + 1) Khi đó gọi x 
, x là các nghiệm của (*), ta có 1 2  1 2 x  .x = 2m + 1  1 2 
Các giao điểm của d và đồ thị hàm số (1) là ( A x ; x + 2), ( B x ; x + 2). 1 1 2 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 57
GV.Lưu Huy Thưởng 0968.393.899 Suy ra 2 2  2  2
AB = 2(x − x ) = 2 (x + x ) − 4x x = 2(m − 6m − 3) 1 2  1 2 1 2    m  = −1
Theo giả thiết ta được 2 2 2(m 6m 3) 8 m 6m 7 0  − − = ⇔ − − = ⇔ m  = 7 
Kết hợp với điều kiện (**) ta được m = 7 là giá trị cần tìm. x + HT 92. 2
Cho hàm số y =
(C ). Tìm tất cả các giá trị của tham số m ∈ ℝ để đường thẳng 2x − 2
d : y = x + m cắt đồ thị (C) tại hai điểm phân biệt , A B sao cho 2 2 37 OA +OB = 2 Giải
Phương trình hoành độ giao điểm của d và (C) là : x + 2 2
= x + m ⇔ g(x) = 2x + (2m − 3)x − 2(m + 1) = 0,x ≠ 1 2x − 2  2 ∆ 
= 4m + 4m + 25 > 0 Vì  g 
∀m ∈ ℝ nên d cắt (C) tại hai điểm phân biệt với mọim ∈ . ℝ g  (1) = 3 ≠ 0  Gọi (
A x ;x + m),B(x ;x + m) là tọa độ giao điểm của d và (C). 1 1 2 2 2m − 3
Theo định lý Viet ta có : x + x = − ;x x = ( − m + 1) 1 2 1 2 2 Ta có : 2 2 2 2 2 2
OA + OB = x + (x + m) + x + (x + m) 2 2
= 2(x + x ) − 4x x + 2m(x + x ) + 2m 1 1 2 2 1 2 1 2 1 2 2  2m 3    2m 3 − −   2 1 2 = 2 − 
 + 4(m + 1) + 2m −   
 + 2m = (4m + 2m + 17)      2   2  2 37 1 37 Giả thiết : 2 2 2 OA +OB =
⇔ (4m + 2m + 17) = 2 2 2 2 5
⇔ 2m + m − 10 = 0 ⇔ m = − hoặc m = 2 2 5
Kết luận : m = − ∨ m = 2 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 58
GV.Lưu Huy Thưởng 0968.393.899 x
HT 93. Cho hàm số y =
(C ). Tìm tất cả các giá trị của tham số m ∈ ℝ để đường thẳng 1 − x
d : y = mx − m − 1 cắt đồ thị (C) tại hai điểm phân biệt , A B sao cho 2 2
MA + MB đạt giá trị nhỏ
nhất. Với M(−1;1) Giải x
Phương trình hoành độ giao điểm của d và (C) là :
= mx − m − 1 (1) 1 − x
Với điều kiện x ≠ 1 thì ta có : (1) ⇔ x = (mx − m − 1)(1 − x) 2
⇔ mx − 2mx + m + 1 = 0 (2)
d cắt (C) tại hai điểm phân biệt khi và chỉ khi (1) có 2 nghiệm phân biệt.
Điều này tương đương với (2) có 2 nghiệm phân biệt khác 1. Đặt : 2
f (x) = mx − 2mx + m + 1 m  ≠ 0   m  ≠ 0     ⇔ ∆   ' > 0 2 2 ⇔ m  − m − m > ⇔ m <  0 0   f (1) ≠ 0   m
 − 2m + m + 1 ≠ 0 
Khi đó, tọa độ hai điểm A(x ;mx − m − 1 ;B x ;mx − m − 1 1 1 ) ( 2 2 )
Với x ,x là 2 nghiệm của (2) 1 2 Ta có : 2 2 2
MA = (x + 1) + (mx − m − 2) ; 2 2 2
MB = (x + 1) + (mx − m − 2) 1 1 2 2 2 2 2 2 2 2
⇒ MA + MB = (x + 1) + (mx − m − 2) + (x + 1) + (mx − m − 2) 1 1 2 2 2 2 2 2 2 2 2 2
= x + 2x + 1 + m x − 2(m + 2) + (m + 2) + x + 2x + 1 + m x − 2(m + 2) + (m + 2) 1 1 1 2 2 2 2 2 2 2
= (m + 1)(x + x ) + 2(x + x ) − 2m(m + 2)(x + x ) + 2(m + 2) + 2 1 2 1 2 1 2 2  2  2
= (m + 1) (x + x ) − 2x x + 2(x + x ) − 2m(m + 2)(x + x ) + 2(m + 2) + 2  1 2 1 2  1 2 1 2   m + 1
Theo Viet ta có : x + x = 2 ∨ x x = 1 2 1 2 m 2 2 2
⇒ MA + MB = 16 − − 2m m 2
Xét hàm số : f (m) = 16 − − 2m trên (− ; ∞ 0) m
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 59
GV.Lưu Huy Thưởng 0968.393.899
Ta được : min f (m) = 20 tại m = −1
Kết luận : m = −1 x − HT 94. 2
Cho hàm số y =
(C ) . Tìm giá trị của m để đường thẳng d : y = x
− + m cắt đồ thị (C) x − 1
tại hai điểm phân biệt A, B sao cho : 2 2 2
OA +OB + AB đạt giá trị nhỏ nhất. (O là gốc tọa độ) Giải
Hoành độ giao điểm của d và (C) là nghiệm phương trình : x − 2 = x − + m;x ≠ 1 x − 1 2
⇔ g(x) = x − mx + m − 2 = 0 (1)
d cắt (C) tại hai điểm phân biệt ⇔ phương trình (1) có 2 nghiệm phân biệt khác 1  2 ∆
 = m − 4m + 8 > 0  ⇔  ⇔ ∀m g  (1) = −1 ≠ 0 
Vậy d ∩ (C ) tại hai điểm phân biệt với ∀m
Gọi các giao điểm lần lượt là : ( A x ; x
− + m),B(x ; x
− + m) với x ,x là các nghiệm của phương 1 1 2 2 1 2 trình (1) Ta có : 2 2 2 2 2 2 2 2 2
OA +OB + AB = x + ( x
− + m) + x + ( x
− + m) + (x − x ) + (x − x ) 1 1 2 2 1 2 1 2 2 2
= 4(x + x ) − 12x x − 2m(x + x ) + 2m 1 2 1 2 1 2 2 2
= 4m − 12m + 24 = (2m − 3) + 15 ≥ 15∀m 3 Vậy, 2 2 2
OA +OB + AB đạt giá trị nhỏ nhất bằng 15 khi m = 2 x + HT 95. 1
Cho hàm số y =
(C ). Gọi d là đường thẳng qua M (2; 0) và có hệ số góc là k . Tìm k x − 2
để d cắt (C) tại hai điểm phân biệt ,
A B sao cho : MA = −2MB Giải
Phương trình đường thẳng d : y = kx − 2k x + 1
Phương trình hoành độ giao điểm của d và (C) là : = kx − 2k (1) x − 2 Với x ≠ 2 thì (1) 2
⇔ f (x) = kx − (4k + 1)x + 4k − 1 = 0 (2)
d cắt (C) tại hai điểm phân biệt ,
A B ⇔ (1) có hai nghiệm phân biệt.
⇔ (2) có 2 nghiệm phân biệt khác 2.
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 60
GV.Lưu Huy Thưởng 0968.393.899 k  ≠ 0  k  ≠ 0      12k 1 0 ⇔ ∆ = + > ⇔  (*) 1  k    > − f (2) = −3 ≠ 0    12  Đặt (
A x ;y ),B(x ;y ) với x ,x là hai nghiệm của (2) và y = kx − 2k;y = 2x − 2k 1 1 2 2 1 2 1 1 2 2 x
 − 2 = −2(x − 2) Khi đó :  1 2
MA = −2.MB ⇔ 
⇔ x + 2x = 6 (3) 1 2 y
 − 2 = −2(y − 2)  1 2   4k + 1 x  + x = (4) 1 2 
Theo định lý Viet ta có : k   4k − 1 x  x = (5) 1 2  k 2k + 2 4k − 1
Từ (3) và (4) suy ra : x = ;x = (6) 1 2 k k 2k + 2 2k − 1 4k − 1 2
Từ (5) và (6) ta được : . =
⇔ k = thỏa mãn (*) k k k 3 2 KL : k = 3 x + HT 96. 3
Cho hàm số y =
có đồ thị (H). Tìm m để đường thẳng d :y = 2x + 3m cắt (H) tại hai x + 2
điểm phân biệt sao cho O .
AOB = −4 với O là gốc tọa độ. Giải
Phương trình hoành độ giao điểm của (H) với (d) : x + 3 2
= 2x + 3m ⇒ 2x + 3(1 + m)x + 6m − 3 = 0 (1)(x ≠ −2) x + 2
(H) cắt (d) tại hai điểm phân biệt A và B ⇔ (1) có hai nghiệm phân biệt khác -2  2 ∆  = m − m + > ⇔ 9 30 33 0  ⇔ ∀m 8
 − 6(1 + m) + 6m − 3 ≠ 0 
Gọi 2 nghiệm của pt (1) là x ; x thì A( x ;2x +3m) ; B( x ;2 x +3m) 1 2 1 1 2 2 12m − 15 7 Có : O .
AOB = −4 ⇒ x x +(2x +3m)(2 x +3m) = - 4 ⇒ = −4 ⇒ m = 1 2 1 2 2 12
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 61
GV.Lưu Huy Thưởng 0968.393.899 x − + HT 97. 1
Tìm trên (H) : y =
các điểm A, B sao cho độ dài đoạn thẳng AB bằng 4 và đường x − 2
thẳng AB vuông góc với đường thẳng y = x. Giải
Do AB ⊥ d : y = x ⇒ pt AB: y = -x + m
Phương trình hoành độ giao điểm của (H) với đường thẳng AB : x − + 1 2 = x
− + m ⇔ g(x) = x − (m + 3)x + 2m + 1 = 0 (x ≠ 2) (1) x − 2
Để tồn tại 2 điểm A, B thì pt (1) cần có hai nghiệm phân biệt x ;x và khác 2 A B   2 ∆ > 0 (  m  
+ 3) − 4(2m + 1) > 0 g(x )  2 ⇔  ⇔ 
⇔ (m − 1) + 4 > 0; ∀m g  (2) ≠ 0 4
 − (m + 3).2 + 2m + 1 ≠ 0   x
 + x = m + 3
Theo Viets ta có :  A B 
Mặt khác : y = x − + m;y = x − + m x  .x = 2m + 1 A A B B  A B  2 2 2 2
Maø : AB = 4 ⇔ AB = 16 ⇔ (x − x ) + (y − y ) = 16 ⇔ (x + x ) − 4x .x = 8 B A B A B A A B m  = −1 2 2 (m 3) 4(2m 1) 0 m 2m 3 0  ⇔ + − + = ⇔ − − = ⇔ m  = 3 
+) Với m = 3 thay vào pt (1) ta có : 2
x − 6x + 7 = 0 ⇔ x = 3 ± 2 ⇒ y = ± 2 ⇒ (
A 3 + 2;− 2);B(3 − 2; 2)hoaëc (
A 3 + 2;− 2);B(3 − 2; 2)
+) Với m = -1 thay vào (1) ta có : 2
x − 2x − 1 = 0 ⇔ x = 1 ± 2 ⇒ y = −2 ± 2 ⇒ (
A 1 + 2;−2 − 2);B(1 − 2;−2 + 2)hoaëc (
A 1 − 2;−2 + 2);B(1 + 2;−2 − 2) Kết luận: ... x − HT 98. 2 3
Cho hàm số y =
(C ). Tìm m để đường thẳng d : 2x − y + m = 0 cắt đồ thị (C) tại x + 1
hai điểm phân biệt có tung độ dương. Giải
Phương trình hoành độ giao điểm của (C) và d là: 2x − 3 2
= 2x + m ⇔ 2x + mx + m + 3 = 0 (1) x + 1
Đường thẳng d cắt (C) tại hai điểm phân biệt khi và chỉ khi: (1) có hai nghiệm phân biệt khác -1
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 62
GV.Lưu Huy Thưởng 0968.393.899  2 ∆  = m  − 8m − 24 > 0 m > 4 + 40   ⇔  ⇔  2
 − m + m + 3 ≠ 0  m  < 4 − 40  
Hai giao điểm có tung độ dương khi và chỉ khi: 2
 x + m + 2x + m > 0 x
 + x + m > 0  1 2  1 2  ⇔  2 (
 2x + m)(2x + m) > 0 4
 x x + 2m(x + x ) + m > 0  1 2   1 2 1 2   m −  + m > 0  2 ⇔  ⇔ m >  0. m 2 2
 (m + 3) + 2m(− ) + m > 0  2
Kết hợp điều kiện ta có: m > 4 + 40 x + HT 99. 3
Cho hàm số y =
có đồ thị (H). Tìm m để đường thẳng d : y = x
− + m + 1tại hai điểm x − 2
phân biệt A, B sao cho AOB nhọn. Giải
Phương trình hoành độ giao điểm của (H) với d : x + 3 2 = x
− + m + 1 ⇔ x − (m + 2)x + 2m + 5 = 0 (x ≠ 2) x − 2
Để phương trình trên có hai nghiệm phân biệt thì :  2 m
 − 4m +16 > 0 0;x 2  ∆ > ≠ ⇔  ⇔ ∀m 2 2
 − 2(m + 2) + 2m + 5 ≠ 0  Gọi ( A x ; x
− + m + 1);B(x ; x
− + m + 1) là 2 giao điểm của (H) và d 1 1 2 2 Để AOB nhọn thì 2 2 2 2 2 2
AB < OA + AB ⇔ 2(x − x ) < ( x
− + m + 1) + ( x − + m + 1) 2 1 1 2 2
⇔ −2x x + (m + 1)(x + x ) − (m + 1) < 0 ⇔ m > −3 1 2 1 2 Kết luận : m > -3 x + HT 100. 3 2 Cho hàm sốy =
(C ). Đường thẳng y = x cắt (C) tại hai điểm x + 2
A, B. Tìm m để đường thẳng y = x + m cắt (C) tại hai điểm C, D sao cho ABCD là hình bình hành. Giải
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 63
GV.Lưu Huy Thưởng 0968.393.899
Hoành độ điểm A, B là nghiệm của phương trình:  3x + 2 x = −1 x  = ⇔ ⇒ (
A −1;−1);B(2;2) ⇒ AB = 3 2 x  + 2 x = 2 
Ta có: C, D thuộc đường thẳng y = x + m và C D AB nên m ≠ 0 và CD = AB = 3 2
Phương trình hoành độ giao điểm của d và (C): 3x + 2 2
= x + m ⇔ x + (m − 1)x + 2m − 2 = 0 (*) x + 2 m  > 9
Để d cắt (C) tại hai điểm phân biệt phải có: 2 m 10m 9 0  ∆ = − + > ⇔ m  < 1 
Gọi C(a;a+m); D(b;b+m) với a, b là nghiệm của phương trình (*) m  = 0 (loai) CD = 3 2 ⇔ 2
2(a −b) = 3 2 ⇔ 2 m 10m 9 9  − + = m  = 10 (t / m)  KL: m = 10 x − HT 101. 2 1 Cho hàm số y =
(C). Tìm m để đường thẳng d: y = x + m cắt x − 1
(C) tại hai điểm phân biệt A, B sao cho ∆OAB vuông tại O. Giải
• Phương trình hoành độ giao điểm của (C) và d: 2
x + (m − 3)x + 1 − m = 0, x ≠ 1 (*) (*) có 2
∆ = m − 2m + 5 > 0, ∀m ∈ R và (*) không có nghiệm x = 1. x
 + x = 3 − m
⇒ (*) luôn có 2 nghiệm phân biệt là x 
, x . Theo định lí Viét: A B  A B x  .x = 1 − m  A B 
Khi đó: A(x ; x + m B x x + m A A ), ( ; B B )
∆OAB vuông tại O thì O .
AOB = 0 ⇔ x x + (x + m)(x + m) = 0 A B A B
⇔ x x + m (x + x ) 2 2
+ m = 0 ⇔ m = 2 − A B A B Vậy: m = –2.
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 64
GV.Lưu Huy Thưởng 0968.393.899 x + 2 HT 102. Cho hàm số: y =
. Chứng minh rằng với mọi giá trị m thì trên (C) x − 2 x
 − y + m = 0
luôn có cặp điểm A, B nằm về hai nhánh của (C) và thỏa  A A  . x  − y + m = 0  B B  Giải x
 − y + m = 0 y  = x + m • Ta có:  A A  A A  ⇔  ⇒ ,
A B ∈ (d) : y = x + m x  − y + m = 0 y  = x + m  B B   B B 
⇒ A, B là giao điểm của (C) và (d). Phương trình hoành độ giao điểm của (C) và (d): x + 2 2 x + m =
⇔ f (x) = x + (m − 3)x − (2m + 2) = 0 (x ≠ 2) (*). x − 2 (*) có 2
∆ = m + 2m + 17 > 0, ∀m ⇒ (d) luôn cắt (C) tại hai điểm phân biệt A, B. Và 1.f (2) = 4
− < 0 ⇒ x < 2 < x hoặc x < 2 < x (đpcm). A B B A x − m HT 103. 2 Cho hàm số y =
(1). Chứng minh rằng với mọi m ≠ 0 đồ thị mx + 1
hàm số (1) cắt (d) : y = 2x − 2m tại hai điểm phân biệt A, B thuộc một đường (H) cố định. Đường
thẳng (d) cắt trục Ox, Oy lần lượt tại các điểm M, N. Tìm m để S = 3S OAB OMN Giải
Phương trình hoành độ giao điểm của đồ thị hàm số (1) và đường thẳng d : 2x − m   2 2 1  
= 2x − 2m ⇔ 2mx − 2m x − m = 0 x  ≠ −  (2) mx   + 1  m    Do m ≠   0 nên 2 1
(2) ⇔ f (x) = 2mx − 2mx − 1 = 0 x  ≠ −  (*)   m  1
Để tồn tại hai điểm A, B thì phương trình (*) phải có 2 nghiệm phân biệt x ;x khác − A B m  2 ∆  ' = m + 2 > 0  ⇔   1     2 ⇔ ∀m ≠ 0 f −    = + 1 ≠ 0    2
 m  m 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 65
GV.Lưu Huy Thưởng 0968.393.899 1
Mặt khác, ta có : x .x = nên A, B luôn nằm trên một đường (H) cố định. A B 2 −2m
Kẻ OH ⊥ AB⇒ OH= d = . Lại có A, B ∈ d ⇒ (O,d ) 5 x + HT 104. 2 1 Cho hàm số
(C). Tìm trên hai nhánh của đồ thị điểm M và N sao x − 1
cho tiếp tuyến tại M và N cắt hai đường tiệm cận tại 4 điểm lập thành một hình thang. Giải
Gọi M, N là 2 điểm thuộc hai nhánh của đồ thị.
Tiếp tuyến tại M cắt hai tiệm cận tại hai điểm A, B.
Tiếp tuyến tại N cắt hai tiệm cận tại hai điểm C, D
Phương trình tiếp tuyến tại M có dạng : f (x) = f '
(x − m) + f (m) (m)  m +  ⇒ 2 4
Tọa độ điểm A  1  ; ,B   (2m −1;2)  m −1   2n + 1
Tương tự ta có: C   1  ; ,D   (2n −1; )2  n −1  −3
6(2m + 4)(2n − 1)
Phương trình đương thẳng AD: y = x +
(m − 1)(n − 1)
(2m − 2)(n − 1) −3
AD có hệ số góc: k =
(m − 1)(n − 1) −3
Tương tự ta cũng có BC có hệ số góc: k =
(m − 1)(n − 1)
⇒ BC AD ⇒ Mọi điểm M, N thuộc 2 nhánh của đồ thị đều thỏa mãn yêu cầu bài toán. mx − m + HT 105. 4 3
Cho hàm số: y =
. Chứng tỏ rằng với mọi m ≠ 1, đồ thị hàm số luôn đi qua x − m
điểm cố định A và B . Từ hai điểm A và B hãy lập phương trình của hai đường thẳng có hệ số
góc bằng 1,5. Tính diện tích hình thang giới hạn bởi AB, hai đường thẳng này và trục Ox. Giải
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 66
GV.Lưu Huy Thưởng 0968.393.899
Gọi (x ;y ) là điểm cố định của đồ thị hàm số 0 0
⇒ phương trình: (x + y − 4)m + 3 − x y = 0 đúng với m ∀ ≠ 1 0 0 0 0  x  = 1   0  x  + y   − 4 = 0 x  + y − 4 = 0 y  = 3  0 0  0 0  ∆  ⇔  ⇔  ⇔  2 3  − x y = 0 x  − 4x + 3 = 0  x  = 3  0 0   0 0   0 y  = 1  0  
Vậy đồ thị có hai điểm cố định là: ( A 1; 3),B(3;1). 3 3 3 3
Phương trình đường thẳng đi qua A có hệ số góc bằng lày − 3 = (x − 1) ⇔ y = x + (d ) 2 1 2 2 2 3
Phương trình đường thẳng qua B có hệ số góc là là: 2 3 3 7
y − 1 = (x − 3) ⇔ y = x − (d ) 2 2 2 2 7  Giao điểm của  
(d ) với Ox là C (−1; 0), của (d ) với Ox là D  ; 0 1 2   3 
Khoảng cách giữa (d ),(d ) cũng chính là chiều cao của hình thang 1 2 3  7   − −   10   2  2 10 2 h = = = 2   13 3 3   1 +     3 2 h    13  5 4 5 20
Vậy diện tích hình thang phải tìm là: S = (AC + BD) =  13  +  . = . 13. = 2  3  3 3   13 13 x − HT 106. 2 1
Cho hàm số y =
(C ). Gọi I là giao điểm của hai tiệm cận của (C). Với giá trị nào của x − 1
m thì đường thẳng y = x
− + m cắt đồ thị (C) tại hai điểm phân biệt A, B và tam giác IAB đều. Giải
Đường thẳng y = x
− + m cắt đồ thị (C) tại hai điểm phân biệt khi và chỉ khi phương trình sau có
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 67
GV.Lưu Huy Thưởng 0968.393.899 x x  − ≠ 1 2 1  2 nghiệm phân biệt: x m = − + ⇔  2 x − 1 x
 + (1 − m)x + m − 1 = 0   2 ∆
 = (1 − m) − 4(m − 1) > 0 m  > 5   ⇔  ⇔ (*)
1 + 1 − m + m − 1 ≠ 0 m   < 1    
Ta có: I (1;2),x + x = m − 1 & x x = m − 1 1 2 1 2 Gọi (
A x ;y ),B(x ;y ) và H là trung điểm của AB. 1 1 2 2 Khi đó: y = x − + ; m y = x − + m và 1 1 2 2
m −1 m + 1 m   − 3 m − 3 H    ; ;IH =    ;
;AB(x − x ;x − x )     2 1 1 2 2 2   2 2   =  2 2 IA IB  I  A  = IB  ∆  IAB đều ⇔  ⇔  (**) 3 2 3 2 I  H = AB I  H = AB  2  4 Ta có: 2 2 IA IB (x x ) x  x (m 1) = ⇔ − + − − = 0 1 2  1 2 
Do x + x = m − 1 nên đẳng thức này đúng với mọi m thỏa mãn (*) 1 2 2 (m − 3) 3 Ta có:  2   2 (**) (x x ) 4x x 3 (m 1) 4(m 1) ⇔ = − − = − − −  2 1 1 2    2 2     2
⇔ m − 6m + 3 = 0 ⇔ m = 3 ± 6 Các giá trị này thỏa mãn (*) KL: m = 3 ± 6 x
HT 107. Cho hàm số y =
(C ) . Tìm các giá trị của m để đường thẳng y = x
− + m cắt đồ thị x − 1
(C) tại hai điểm phân biệt , A B sao cho O , A OB bằng 0
60 . Với O là gốc tọa độ. Giải x
Phương trình hoành độ giao điểm: 2 = x
− + m ⇔ g(x) = x − mx + m = 0 (1) với x ≠ 1 x − 1
Đường thẳng y = x
− + m cắt đồ thị (C) tại hai điểm phân biệt:
⇔ Phương trình (1) có hai nghiệm phân biệt x ≠ 1
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 68
GV.Lưu Huy Thưởng 0968.393.899  m  < 0  2 ∆  = m  − 4m > 0  m  < 0   ⇔  ⇔  m  4  > ⇔ (*) g   (1) ≠ 0  m  > 4     1  ≠ 0   x  + x = m  1 2 
Gọi x ,x là hai nghiệm của (¡), ta có: x  .x = m (**) 1 2 1 2
g(x ) = g(x ) = 0  1 2  O
 A = (x ; x − + m) Các giao điểm là ( A x ; x
− + m),B(x ; x − + m) và  1 1  1 1 2 2 O
 B = (x ; x − + m) 2 2  x x + ( x − + m)( x − + m) Khi đó: 0 1 2 1 2 cos 60 = cos(O ; A OB = 2 2 2 2
2x − 2mx + m
2x − 2mx + m 1 1 2 2 2 2
2x x − m(x + x ) + m 2x x − (
m x + x ) + m m 1 2 1 2 1 2 1 2 2 1 ⇔ = = = 2 2 2 2 2 2
g x + m − m
g x + m − m
m − m m − m m − 2 2 ( ) 2 2 ( ) 2 2 2 m 1 2 m  = −  2 2 m 2m 4m  − =  m  ⇔  ⇔ = 0 2  m  − 2m = −4m m    = 6 
Kết hợp điều kiện (*) ta có: m = 2 − ∨ m = 6
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 69
GV.Lưu Huy Thưởng 0968.393.899
PHẦN 4: TIẾP TUYẾN HT 108. Cho hàm số 3 2
y = x − 3x + 1 (C ). Chứng minh rằng mỗi tiếp tuyến của (C) chỉ tiếp xúc với
(C) tại đúng một điểm. Giải
Giả sử tiếp tuyến tiếp xúc với đồ thị hàm số tại hai điểm M(x ;y ),M (x ;y ) 0 0 1 1 1
Khi đó, phương trình tiếp tuyến là: 2 3 2
y = (3x − 6x )x − 2x + 3x + 1 và 2 3 2
y = (3x − 6x )x − 2x + 3x + 1 0 0 0 0 1 1 1 1
Hai phương trình trên cùng là phương trình của 1 tiếp tuyến nên:  2 2 3
 x − 6x = 3x − 6x  0 0 1 1  3 2 3 2
−2x + 3x + 1 = −2x + 3x + 1  0 0 1 1 
Giải hệ trên ta được: x = x Suy ra điều phải chứng minh. 0 1 2x − 1
HT 109. Cho hàm so> y =
. Viết phương trình tiếp tuyến của (C), biết khoảng cách từ điểm x − 1
I (1;2) đến tiếp tuyến bằng 2 . Giải
• Tiếp tuyến của (C) tại điểm M(x ; f(x )) ∈ (C) có phương trình: 0 0
y = f '(x )(x − x ) + f (x ) ⇔ 2 2
x + (x − 1) y − 2x + 2x − 1 = 0 (*) 0 0 0 0 0 0 2 − 2x x  = 0
Khoảng cách từ điểm I(1; 2) đến tiếp tuyến (*) bằng 2 0 ⇔ = 2 ⇔  0  4 1 + (x − 1) x = 2  0 0 
Các tiếp tuyến cần tìm : x + y − 1 = 0 và x + y − 5 = 0 HT 110. Cho hàm số 3 2
y = x + (1 − 2m)x + (2 − m)x + m + 2 (1) (m là tham số). Tìm tham số
m để đồ thị của hàm số (1) có tiếp tuyến tạo với đường thẳng d: x + y + 7 = 0 góc α , biết 1 cos α = . 26
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 70
GV.Lưu Huy Thưởng 0968.393.899 Giải
• Gọi k là hệ số góc của tiếp tuyến ⇒ tiếp tuyến có VTPT n = (k; 1 − ) 1
Đường thẳng d có VTPT n = (1;1) . 2  3 .  1 1 k n n k = − Ta có 1 2 2  α 2 cos = ⇔ =
⇔ 12k − 26k + 12 = 0 ⇔  2 n . n  2 1 2 26 2 k + 1 k =   3
YCBT thoả mãn ⇔ ít nhất một trong hai phương trình sau có nghiệm:  3  3 y  ′= 2
3x + 2(1 − 2m)x + 2 − m =  / ∆ ≥ 0  2
8m − 2m − 1 ≥ 0  2   1   ⇔ 2  ⇔  ⇔   2  2 / ∆ ≥ 0 2
4m − m − 3 ≥ 0 y ′= 2 
3x + 2(1 − 2m)x + 2 − m =  2    3  3  1 1 m  ≤ − ;m ≥ 1 1 ⇔  4 2 
⇔ m ≤ − hoặc m ≥  3 4 2
m ≤ − ;m ≥ 1   4 HT 111. Cho hàm số 3 2 y = x −
+ 2x − x (C ). Tìm tọa độ các điểm trên trục hoành sao cho qua điểm
đó kẻ được hai tiếp tuyến với đồ thị (C) và góc giữa hai tiếp tuyến này bằng 0 45 . Giải
Qua điểm M trên Ox, ta luôn kẻ được tiếp tuyến với (C) là y = 0.
Góc của hai tiếp tuyến là 0
45 , mà y = 0 có hệ số góc là 0 nên hệ số góc của tiếp tuyến d còn lại có
hệ số góc bằng -1 hoặc 1. x  = 0  0
Gọi M(x ;y ) là tiếp điểm của d và (C) 2 y ' 3x 4x 1 1  ⇒ = − + − = ± ⇔ 0 0 0 0  4 x  =  0  3
Khi x = 0 ⇒ y = 0 ⇒ d : y = x
− ⇒ M ≡ O 0 0 4 4  4 32 32  Khi x = ⇒ y = −
⇒ d : y = − x    − = x − + ⇒ M    ; 0 0 0 3 27  3 27    27 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 71
GV.Lưu Huy Thưởng 0968.393.899 HT 112. Cho hàm số 3 2
y = x − 3x + 1 có đồ thị (C). Tìm hai điểm A, B thuộc đồ thị (C) sao cho tiếp
tuyến của (C) tại A và B song song với nhau và độ dài đoạn AB = 4 2 . Giải • Giả sử 3 2 3 2 (
A a;a − 3a + 1), B(b;b − 3b + 1) thuộc (C), với a ≠ b .
Vì tiếp tuyến của (C) tại A và B song song với nhau nên: y ( ′ a) = y ( ′ b) ⇔ 2 2 2 2
3a − 6a = 3b − 6b ⇔ a −b − 2(a −b) = 0 ⇔ (a −b)(a + b − 2) = 0
⇔ a +b − 2 = 0 ⇔ b = 2 −a . Vì a ≠ b nên a ≠ 2 −a ⇔ a ≠ 1 Ta có: AB 2 3 2 3 2 2 2 3 3 2 2 2
= (b − a) + (b − 3b + 1 − a + 3a − 1) = (b − a) + (b − a − 3(b − a )) 2 2  3 (b a) (b a  ) 3ab(b a) 3(b a)(b a) = − + − + − − − +   2 2 2  2 (b a) (b a) (b a  ) 3ab 3.2 = − + − − + −   2 2 2  2 (b a) (b a) (b a  ) ab 6 = − + − + − −   2 2 2
= (b − a) + (b − a) (−2 − ab) 2 AB 2  2  2  2 2 (b a) 1  ( 2 ab)   (2 2a) 1   (a 2a 2)  = − + − − = − + − −    2  2  2  2  4 2
= 4(a − 1) 1 + (a  − 1) − 3    = 4(a − 1) (a  
− 1) − 6(a − 1) + 10      6 4 2
= 4(a − 1) − 24(a − 1) + 40(a − 1) Mà AB = 4 2 nên 6 4 2
4(a − 1) − 24(a − 1) + 40(a − 1) = 32 6 4 2
⇔ (a − 1) − 6(a − 1) + 10(a − 1) − 8 = 0 (*) Đặt 2
t = (a − 1) , t > 0 . Khi đó (*) trở thành: 3 2 2
t − 6t + 10t − 8 = 0 ⇔ (t − 4)(t − 2t + 2) = 0 ⇔ t = 4 ⇒ a  = 3 ⇒ b = −1 2 (a 1) 4  − = ⇔ a  = −1 ⇒ b = 3 
Vậy 2 điểm thoả mãn YCBT là: ( A 3;1), ( B 1 − ; 3 − ).
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 72
GV.Lưu Huy Thưởng 0968.393.899 x + 1
HT 113. Cho hàm số y =
(C). Tìm trên Oy tất cả các điểm từ đó kẻ được duy nhất một tiếp x − 1 tuyến tới (C). Giải
• Gọi M(0;y ) là điểm cần tìm. PT đường thẳng qua M có dạng: y = kx + y (d) o o x + 1  2  = kx + y (
 y − 1)x − 2(y + 1)x + y + 1 = 0 (1)  o o o o  
(d) là tiếp tuyến của (C) x − 1  ⇔  ⇔  − (*)  − x  ≠ 2 2 1; = k  = k  2  2  (x − 1) (  x − 1)  
YCBT ⇔ hệ (*) có 1nghiệm ⇔ (1) có 1 nghiệm khác 1 y  = 1   1  o y  ≠ 1    o x =
;y = 1 ⇒ k = −8  ⇔  1 o ∨  ⇔  2 2 x   =
∆ ' = (y + 1) − (y − 1)(y + 1) = 0    o o o x  
 = 0;y = −1 ⇒ k = −2  2 o 
Vậy có 2 điểm cần tìm là: M(0; 1) và M(0; –1). HT 114. Cho hàm số 3
y = 3x − x (C). Tìm trên đường thẳng d : y = x
− các điểm mà từ đó kẻ
được đúng 2 tiếp tuyến phân biệt với đồ thị (C). Giải
• Gọi M(m; m − ) ∈ (d) .
PT đường thẳng ∆ đi qua điểm M và có hệ số góc k có dạng : y = k(x − m) − m  3 3
 x − x = k(x − m) − m (1)
∆ là tiếp tuyến của (C) ⇔ hệ PT sau có nghiệm  (*). 2 3  − 3x = k (2)  3 2
3x − x − (3 − 3x )(x − m) + m = 0 Thay (2) và (1) ta được: 3 2
⇔ 2x − 3mx + 4m = 0 3 2x ⇔ m = (**) 2 3x − 4 3 2x 2 3 2 3
Xét hàm số : f (x) =
. Tập xác định : D = ℝ \ { ;− } 2 3x − 4 3 3 4 2 6x − 24x x  = 0 Có: f’(x) = ; f’(x) = 0 ⇔  2  3x − 4 x = ± 2 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 73
GV.Lưu Huy Thưởng 0968.393.899 x -∞ -2 0 2 - +∞ f’(x) + 0 - - 0 - - 2 + -2 +∞ +∞ +∞ f(x) -∞ -∞ 2 -∞
Từ M kẻ được đúng hai tiếp tuyến tới đồ thị hàm số
⇔ (**) có hai nghiệm phân biệt. m  = 2
Dựa vào bảng biến thiên ta có: (**) có 2 nghiệm phân biệt ⇔  m  = −2 
⇒ Các điểm cần tìm là: A(2; –2) và B(–2; 2). HT 115. Cho hàm số: 3
y = x − 3x + 2 . Tìm tất cả điểm trên đường thẳng y = 4 , sao cho từ đó kẻ
được đúng 2 tiếp tuyến tới đồ thị (C). Giải
Gọi M(x ;4) là điểm cần tìm. 0
Phương trình đường thẳng (d) qua M với hệ số góc k là: y=k(x-xo)+4
(d) là tiếp tuyến của đồ thị hàm số ⇔ hệ sau có nghiệm:  3 k
 (x − x ) + 4 = x − 3x + 2 (1)  0  2 k  = 3x − 3 (2) 
Thay (2) vào (1) ta được: 2 3
(3x − 3)(x − x ) + 4 = x − 3x + 2 o 3 2 3
⇔ 3x − 3x x − 3x + 3x = x − 3x + 2 o o 3 2
⇔ 2x − 3x x + 3x − 2 = 0 o o (x ) 2 1 2x (3x 2)x 3x 2 ⇔ + − + + + = 0 (3)  0 0   
Để kẻ được 2 tiếp tuyến tới đồ thị hàm số khi và chỉ khi (3) có đúng 2 nghiệm.
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 74
GV.Lưu Huy Thưởng 0968.393.899 ⇔ 2
⇔ 2x − (3x + 2)x + 3x + 2 = 0 có : 0 0
+)2 nghiệm trong đó 1 nghiệm bằng-1; +)Có nghiệm kép khác -1.
Giải tìm đúng 3 điểm: (-1;4);(-2/3;4);(2;4) HT 116. Cho hàm số 3 2 y = x −
+ 3x − 2 (C). Tìm trên đường thẳng d : y = 2 các điểm mà từ đó
kẻ được 3 tiếp tuyến phân biệt với đồ thị (C). Giải
• Gọi M(m;2) ∈ (d) .
PT đường thẳng ∆ đi qua điểm M và có hệ số góc k có dạng : y = k(x − m) + 2  3 2  x −
+ 3x − 2 = k(x − m) + 2 (1)
∆ là tiếp tuyến của (C) ⇔ hệ PT sau có nghiệm  (*). 2
−3x + 6x = k (2)  Thay (2) và (1) ta được: 3 2  2 2x 3(m 1)x 6mx 4 0 (x 2) 2x (3m 1)x 2 − + + − = ⇔ − − − +   = 0  x  = 2 ⇔  2
f (x) = 2x − (3m − 1)x + 2 = 0 (3) 
Từ M kẻ được 3 tiếp tuyến đến đồ thị (C) ⇔ hệ (*) có 3 nghiệm x phân biệt  ∆ > m    < − hoÆc 5 0 1 m >
⇔ (3) có hai nghiệm phân biệt khác 2  ⇔  ⇔  3 . f (2) ≠ 0   m  ≠ 2  m  < − hoÆc 5 1 m >
Vậy từ các điểm M(m; 2) ∈ (d): y = 2 với 
3 có thể kẻ được 3 tiếp tuyến đến đồ m  ≠ 2  thị (C). 2 2
HT 117. Cho hàm số y = ( x + ) 1 .( x − ) 1 (C). Cho điểm (
A a; 0). Tìm a để từ A kẻ được 3 tiếp tuyến
phân biệt với đồ thị (C). Giải • Ta có 4 2
y = x − 2x + 1.
Phương trình đường thẳng d đi qua (
A a; 0) và có hệ số góc k : y = k(x − a)
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 75
GV.Lưu Huy Thưởng 0968.393.899  4 2 x 
− 2x + 1 = k(x − a)
d là tiếp tuyến của (C) ⇔ hệ phương trình sau có nghiệm:  (I ) 3 
4x − 4x = k  k  = 0  2 4
 x(x − 1) = k Ta có:   (I )  ⇔  ( ) A hoặ c  (B) 2 x  − 1 = 0 2   
f (x) = 3x − 4ax + 1 = 0 (1)   + Từ hệ
(A), chỉ cho ta một tiếp tuyến duy nhất là d : y = 0 . 1
+ Vậy để từ A kẻ được 3 tiếp tuyến phân biệt với (C) thì điều kiện cawn và đủ là hệ (B) phả i có 2 nghiệ
m phân biệt (x;k) với x ≠ ±1 , tức là phương trı̀nh (1) phải có 2 nghiệm phân biệt khác  2 ′ ∆  = 4a − 3 > 0 3 3 ±1 ⇔ 
⇔ −1 ≠ a < − hoÆc 1 ≠ a > f (±1) ≠ 0  2 2  HT 118. Cho hàm số 3 2
y = x − 3x + 2. Tìm trên đường thẳng y = 2 các điểm mà từ đó có thể kẻ
được 2 tiếp tuyến tới đồ thị hàm số và 2 tiếp tuyến đó vuông góc với nhau. Giải
Gọi điểm cần tìm là M(m;2).
Nhận xét: đường thẳng x = m đi qua M cắt đường cong và song song với trục tung và nó không
thể là tiếp tuyến nên mọi tiếp tuyến qua M đều có dạng: y = k(x − m) + 2.
Vậy, hệ sau phải có nghiệm:  3 2
x − 3x + 2 = k(x − m) + 2  3 2 2 
⇒ x − 3x + 2 = (x − m)(3x − 6x) + 2 2 3  x − 6x =  k 
x = 0 ⇒ k = 0 3 2 2x (3m 3)x 6mx 0  ⇔ − − + = ⇔  2
2x − 3(m + 1)x + 6m = 0 (1) 
Trường hợp 1: k = 0 Tiếp tuyến là y = 2, đường thẳng vuông góc với nó có dạng: x = c. Vậy
không có tiếp tuyến nào của đường cong vuông góc với tiếp tuyến này.
Vậy, để đường cong có hai tiếp tuyến vuông góc thì phương trình (1) phải có 2 nghiệm x ,x sao 1 2
cho: y '(x ).y '(x ) = −1 (2). 1 2
Phương trình (1) có 2 nghiệm phân biệt khi ∆ > 0 m > 3  2 2
⇔ 9m + 18m + 9 − 48m > 0 ⇔ 9m − 30m + 9 > 0 ⇔  (2) 1 m <  3
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 76
GV.Lưu Huy Thưởng 0968.393.899 3m + 3
Theo định lý Viet ta có: x + x =
;x .x = 3m 1 2 1 2 2 3 3 Ta có: 2  2 3x 6x 2x 3(m 1)x 6  − = − +
+ m + (3m − 1)x − 9m 2     2 2 3 2 3
⇒ y '(x ) = 3x − 6x =
(3m − 1)x − 9 ,
m y '(x ) = 3x − 6x =
(3m − 1)x − 9m 1 1 1 1 1 2 2 2 2 2  3   3 
(2) ⇔ y '(x ).y '(x ) = 1
− ⇔  (3m − 1)x − 9m  (3m − 1)x − 9m = −1 1 2 1 2  2  2      9 2 27 2 ⇔
(3m − 1) x x −
m(3m − 1).(x + x ) + 81m = −1 1 2 1 2 4 2 9 2 27 3m + 3 2 ⇔
(3m − 1) .3m − m(3m − 1). + 81m = −1 4 2 2 1
⇔ 27m + 1 = 0 ⇔ m = −
(thỏa mãn điều kiện (2)) 27  1  KL: M 2  ;  −   27 1 HT 119. Cho hàm số 3 2
y = f (x) =
mx + (m − 1)x + (4 − 3m)x + 1 có đồ thị là (Cm). Tìm các giá trị 3
m sao cho trên đồ thị (Cm) tồn tại một điểm duy nhất có hoành độ âm mà tiếp tuyến tại đó
vuông góc với đường thẳng d : x + 2y − 3 = 0 . Giải 1
• (d) có hệ số góc − ⇒ tiếp tuyến có hệ số góc k = 2 . Gọi x là hoành độ tiếp điểm thì: 2 2 2
f '(x) = 2 ⇔ mx + 2(m − 1)x + (4 − 3m) = 2 ⇔ mx + 2(m − 1)x + 2 − 3m = 0 (1)
YCBT ⇔ (1) có đúng một nghiệm âm.
+ Nếu m = 0 thì (1) ⇔ 2 − x = 2 − ⇔ x = 1 (loại) − m
+ Nếu m ≠ 0 thì dễ thấy phương trình (1) có 2 nghiệm là x = hay x= 2 3 1 m
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 77
GV.Lưu Huy Thưởng 0968.393.899 m < 0 2 − 3m 
Do đó để (1) có một nghiệm âm thì < 0 ⇔  2 m m  >  3 Vậy m < hay 2 0 m > . 3
HT 120. Tìm tất cả các giá trị m sao cho trên đồ thị 1 (C ): 3 2 y =
mx + (m − 1)x + (4m − 3)x + 1 tồn tại đúng hai điểm có hoành độ dương mà tiếp m 3
tuyến tại đó vuông góc với đường thẳng (L): x + 2y − 3 = 0 Giải Cách 1: Có y’ = 2
mx + 2(m − 1)x + 4 − 3m  1
Từ yêu cầu bài toán ta có: y '.  −   = 1
− có đúng hai nghiệm dương phân biệt  2 ⇔ 2
mx + 2(m − 1)x + 2 − 3m = 0 có hai nghiệm phân biệt. m  ≠ 0 m  ≠ 0   m  ≠ 0     2  4
 m − 4m + 1 > 0  1  1   m  ≠ 0  ' 0 < m < ∆ >     ⇔  ⇔ m 1  − 2  2  ⇔  ⇔  S  >  > 0 0 0  < m < 1 1 2   m     < m <  P  0 2 − 3m  >  2 2 3   > 0 0  < m <   m    3  1 1 2 Vậy m ∈ 0  ;  
 ∪  ; là các giá trị cần tìm  2    2 3 Cách 2: Có 2
y ' = mx + 2(m − 1)x + 4 − 3m  1
Từ yêu cầu bài toán ta có: y '.  −   = 1
− có đúng hai nghiệm dương phân biệt  2 ⇔ 2
mx + 2(m − 1)x + 2 − 3m = 0 (1) có hai nghiệm phân biệt.
+) TH1: m = 0 từ (1) ta có: x = -1 (loại) 1
+) TH2: m = từ (1) ta có x = ± 1(loại) 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 78
GV.Lưu Huy Thưởng 0968.393.899 1 2 − 3m
+) Th3: m ≠ 0;m ≠ Từ pt (1) có 2 nghiệm x = 1 ∨ x = 2 m 2 − 3m 2 Điều kiện bài toán ⇒
> 0 ⇔ 0 < m < m 3  1 1 2
Kết hợp cả 3 trường hợp trên ta có giá trị của m cần tìm là: m ∈ 0  ;    ∪  ;   2    2 3 HT 121. Cho hàm số 4 2
y = f (x) = x − 2x . Trên (C) lấy hai điểm phân biệt A và B có hoành độ lần
lượt là a và b. Tìm điều kiện đối với a và b để hai tiếp tuyến của (C) tại A và B song song với nhau. Giải • Ta có: 3
f '(x) = 4x − 4x
Hệ số góc tiếp tuyến của (C) tại A và B là 3 3
k = f '(a) = 4a − 4a, k = f '(b) = 4b − 4b A B
Tiếp tuyến tại A, B lần lượt có phương trình là: y = f (
′ a)(x −a) + f(a) ⇔ y = f (′a)x + f (a) − af ( ′ a) y = f (
′ b)(x −b) + f (b) ⇔ y = f (
′ b)x + f(b) −bf ( ′ b)
Hai tiếp tuyến của (C) tại A và B song song hoặc trùng nhau khi và chỉ khi: 3 3
k = k ⇔ a − a = 4b 2 2 4 4
− 4b ⇔ (a − b)(a + ab + b − 1) = 0 (1) A B
Vì A và B phân biệt nên a ≠ b , do đó (1) ⇔ 2 2
a + ab + b − 1 = 0 (2)
Mặt khác hai tiếp tuyến của (C) tại A và B trùng nhau khi và chỉ khi:  2 2   2 2
a + ab + b − 1 = 0  a 
+ ab + b − 1 = 0   (a b)  ⇔ ≠ ⇔  4 2 4 2 f  (a) − af (
′ a) = f (b) −bf ( ′ b)
−3a + 2a = −3b + 2b   
Giải hệ này ta được nghiệm là (a;b) = (−1;1) hoặc (a;b) = (1;−1) , hai nghiệm này tương ứng với
cùng một cặp điểm trên đồ thị là (−1;−1) và (1;−1)
Vậy điều kiện cần và đủ để hai tiếp tuyến của (C) tại A và B song song với nhau là:
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 79
GV.Lưu Huy Thưởng 0968.393.899  2 2 a 
+ ab + b − 1 = 0   a  ≠ 1 ± ; a ≠ b  2x
HT 122. Cho hàm số y =
(C). Viết phương trình tiếp tuyến của đồ thị (C), biết rằng khoảng x + 2
cách từ tâm đối xứng của đồ thị (C) đến tiếp tuyến là lớn nhất. Giải
• Tiếp tuyến (d) của đồ thị (C) tại điểm M có hoành độ a ≠ −2 thuộc (C) có phương trình: 4 2a 2 2 y = (x − a) +
⇔ 4x − (a + 2) y + 2a = 0 2 (a + 2) a + 2
Tâm đối xứng của (C) là I (−2;2). Ta có: 8 a + 2 8 a + 2 8 a + 2 d(I,d) = ≤ = = 2 2 4 2 16 + (a + 2) 2.4.(a + 2) 2 2 a + 2 a  = 0
d(I,d) lớn nhất khi 2 (a 2) 4  + = ⇔ . a  = −4 
Từ đó suy ra có hai tiếp tuyến y = x và y = x + 8 . x + 2
HT 123. Cho hàm số y =
(1). Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp 2x + 3
tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. Giải • −1
Gọi (x ;y ) là toạ độ của tiếp điểm ⇒ y ( ′ x ) = < 0 0 0 0 2 (2x + 3) 0
∆OAB cân tại O nên tiếp tuyến ∆ song song với đường thẳng y = x
− (vì tiếp tuyến có hệ số góc  −1
x = −1 ⇒ y = 1  0 0 âm). Nghĩa là: y ( ′ x ) = = −1 ⇒ 0  2 (2x + 3) x  = −2 ⇒ y = 0 0  0 0 
+ Với x = −1; y = 1 ⇒ ∆: y − 1 = (
− x + 1) ⇔ y = x − (loại) 0 0
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 80
GV.Lưu Huy Thưởng 0968.393.899
+ Với x = −2; y = 0 ⇒ ∆: y − 0 = (
− x + 2) ⇔ y = x − − 2 (nhận) 0 0
Vậy phương trình tiếp tuyến cần tìm là: y = x − − 2 . 2x − 1
HT 124. Cho hàm số y =
. Lập phương trình tiếp tuyến của đồ thị (C) sao cho tiếp tuyến này x − 1
cắt các trục Ox, Oy lần lượt tại các điểm A và B thoả mãn OA = 4OB. Giải
• Giả sử tiếp tuyến d của (C) tại M(x ;y ) ∈ (C) cắt Ox tại A, Oy tại B sao cho OA = 4OB . 0 0 OB 1 1 1
Do ∆OAB vuông tại O nên tan A = =
⇒ Hệ số góc của d bằng hoặc − . OA 4 4 4  3  1 1 1 x = −1 (y = ) 0 0 Hệ số góc của d là  y ( ′ x ) = − < 0 ⇒ − = − ⇔ 2 0  2 2 (x − 1) (x − 1) 4  5 0 0 x = 3 (y = )  0 0  2  1 3  1 5 y  = − (x + 1) + y  = − x +
Khi đó có 2 tiếp tuyến thoả mãn là:  4 2  4 4  ⇔  .  1 5  1 13
y = − (x − 3) + y = − x +    4 2  4 4 2x
HT 125. Viết phương trình tiếp tuyến của đồ thị hàm số y =
biết tiếp tuyến cắt Ox, Oy lần lượt x − 2
tại A và B mà tam giác OAB thỏa mãn: AB = OA 2 Giải
Cách 1: Gọi M(x ;y ), (x ≠ 2) thuộc đồ thị hàm số. Phương trình tiếp tuyến tại M có dạng: o o o 2x −4 o y − = (x − x ) 2 x − 2 (x − 2) o o o
Do tam giác cắt trục Ox, Oy tại các điểm A, B và tam giác OAB có AB = OA 2 nên tam giác
OAB vuông cân tại O. Lúc đố tiếp tuyến d vuông góc với một trong 2 đường phân giác y = x hoặc y = -x
+ TH1: d vuông góc với đường phân giác y = x
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 81
GV.Lưu Huy Thưởng 0968.393.899 −4
x = 2 ⇒ pt d : y = x − (loai) Có: 2 1 (x 2) 4 o  = − ⇔ − = ⇔ 2 o
x = 4 ⇒ pt d : y = x − + 8 (x − 2)  o o 
+ TH2: d vuông góc với đường phân giác y = -x −4 Có:
(−1) = −1 ⇔ ptvn 2 (x − 2) o
Kết luận: Vậy có 1 tiếp tuyến thỏa mãn yêu cầu bài toán d: y= -x + 8 Cách 2: OA 1 π
Nhận xét tam giác AOB vuông tại O nên ta có: sin(ABO) = = = sin nên tam giác AOB AB 4 2
vuông cân tại O, phương trình tiếp tuyến của (C) tại điểm M(x ;y )có dạng: o o −4 2x y = (x − x ) o + 2 (x − 2) o x − 2 o o  2   2 x   2x    Dễ dàng tính được: o =   o 3 A ; 0  ;B 0  ;   
 ⇔ x (x − 4) = 0 2  2     (    x − 2) o o  o 
+) Với x = 0 ta có phương trình tiếp tuyến là: y = -x (loại) o
+) Với x = 4 ta có phương trình tiếp tuyến là: y = -x + 8 o 2x − 3
HT 126. Cho hàm số y =
có đồ thị (C). Tìm trên (C) những điểm M sao cho tiếp tuyến tại M x − 2
của (C) cắt hai tiệm cận của (C) tại A, B sao cho AB ngắn nhất.  1  1 • Lấy điểm M m  ; 2  +  . Ta có: ′   ∈ (C ) y (m) = −  m − 2 2 (m − 2) 1 1
Tiếp tuyến (d) tại M có phương trình: y = − (x − m) + 2 + 2 (m − 2) m − 2  2 
Giao điểm của (d) với tiệm cận đứng là: A 2  ;2  +     m − 2
Giao điểm của (d) với tiệm cận ngang là: B(2m – 2;2)
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 82
GV.Lưu Huy Thưởng 0968.393.899  1  m  = 3 Ta có: 2 2 AB 4 (  m 2)  = − + ≥ 8   . Dấu “=” xảy ra ⇔ 2    (m − 2) m = 1   
Vậy điểm M cần tìm có tọa độ là: M (3; 3) hoặc M(1;1) 2x − 3
HT 127. Cho hàm số y =
. Cho M là điểm bất kì trên (C). Tiếp tuyến của (C) tại M cắt các x − 2
đường tiệm cận của (C) tại A và B. Gọi I là giao điểm của các đường tiệm cận. Tìm toạ độ điểm
M sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Giải   • 2x − 3 1 − Giả sử  0  M x  ; , x ≠ 2  , y '(x ) = 0  0  x 0  − 2  2 0  (x − 2 0 ) −1 2x − 3
Phương trình tiếp tuyến (∆) với ( C) tại M: 0 y = (x − x ) + 2 0 (x − ) x − 2 2 0 0  2x 2 −
Toạ độ giao điểm A, B của (∆) với hai tiệm cận là:  0  A 2  ; ; B   (2x − 2;2 0 )  x  − 2  0  x + x 2 + 2x − 2 y + y 2x − 3 Ta thấy A B 0 =
= x = x , A B 0 =
= y suy ra M là trung điểm 0 2 2 M 2 x − 2 M 0 của AB.
Mặt khác I(2; 2) và ∆IAB vuông tại I nên đường tròn ngoại tiếp tam giác IAB có diện tích  2    2x − 3      1  S = 2 2 0  2 I  π M π = (  x − 2) +  − 2 π    = (x − 2) + ≥ 2π 0  0    2  x  − 2   0   (x − 2)     0    1 x = 1 Dấu “=” xảy ra khi 2  0 (x − 2) = ⇔ 0 2 x = 3 (x − 2)  0 0 
Do đó điểm M cần tìm là M(1; 1) hoặc M(3; 3) HT 128. Cho hàm số 3 2 2
y = x − 2mx + m x − m + 1 (C ). Tìm m để đồ thị hàm số tiếp xúc với trục m hoành. Giải Đồ thị hàm số 3 2 2
y = x − 2mx + m x − m + 1 tiếp xúc với trục hoành
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 83
GV.Lưu Huy Thưởng 0968.393.899  3 2 2 x 
− 2mx + m x − m + 1 = 0  ⇔  có nghiệm. 2 2 3
 x − 4mx + m = 0   3 2 2 x 
− 2mx + m x − m + 1 = 0(1)  ⇔  x = m    3x = m  
Với x = m thế vào (1) ta được: m = 1
Với x = 3m thế vào (1) ta được: 3 3 3 3
x − 6x + 9x − 3x + 1 = 0 ⇔ 4x − 3x + 1 = 0 x  = −1 ⇒ m = −3  ⇔  1 3 x  = ⇒ m =  2 2 3
Kết luận: m = 1 ∨ m = −3 ∨ m = 2 2x + 1
HT 129. Cho hàm số y =
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận. Tìm điểm M x − 1
thuộc (C) sao cho tiếp tuyến của (C) tại M cắt 2 tiệm cận tại A và B với chu vi tam giác IAB đạt giá trị nhỏ nhất. Giải   •  3
Giao điểm của 2 tiệm cận là 
I (1;2). Gọi M x  ;2 +  ∈  (C). 0   x  − 1 0  −3 3
+ PTTT tại M có dạng: y = (x − x ) + 2 + 2 0 (x − 1) x − 1 0 0   6 
+ Toạ độ các giao điểm của tiếp tuyến với 2 tiệm cận: A  1  ;2 +    , B(2x − 1;2)  x 0  − 1 0  1 1 6 + Ta có: S = I . A IB = ⋅
⋅ 2 x − 1 = 2.3 = 6 (đvdt) I ∆ AB 0 2 2 x − 1 0
+ ∆IAB vuông có diện tích không đổi ⇒ chu vi ∆IAB đạt giá trị nhỏ nhất khi IA= IB
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 84
GV.Lưu Huy Thưởng 0968.393.899  6 x = 1 + 3 ⇔  0 = 2 x − 1 ⇒ 0  x − 1 x  = 1 − 3 0 0 
Vậy có hai điểm M thỏa mãn điều kiện M (1 + 3;2 + 3) , M (1 − 3;2 − 3) 1 2
Khi đó chu vi ∆AIB = 4 3 + 2 6 .
Chú ý: Với 2 số dương a, b thoả ab = S (không đổi) thì biểu thức P = 2 2
a + b + a + b nhỏ nhất khi và chỉ khi a = b. Thật vậy: P = 2 2
a + b + a + b ≥ 2 ab + 2ab = (2 + 2) ab = (2 + 2) S . Dấu "=" xảy ra ⇔ a = b. x + 2 HT 130. Cho hàm số: y = (C). Cho điểm (
A 0;a). Tìm a để từ A kẻ được 2 tiếp tuyến tới đồ x − 1
thị (C) sao cho 2 tiếp điểm tương ứng nằm về 2 phía của trục hoành. Giải
• Phương trình đường thẳng d đi qua (
A 0;a) và có hệ số góc k: y = kx + a x + 2  = kx + a 
d là tiếp tuyến của (C) ⇔ Hệ PT x − 1  có nghiệm  3 − k  =  2  (x − 1)  ⇔ PT: 2
(1 −a)x + 2(a + 2)x − (a + 2) = 0 (1) có nghiệm x ≠ 1 .
Để qua A có 2 tiếp tuyến thì (1) phải có 2 nghiệm phân biệt x , x 1 2 a  ≠ 1 a  ≠ 1 ⇔    ⇔  (*) ∆′ = 3a + 6 > 0 a  > −2     2(a + 2) a + 2 3 3
Khi đó ta có: x + x = ; x x = và y = 1 + ; y = 1 + 1 2 1 2 a − 1 a − 1 1 2 x − 1 x − 1 1 2
Để 2 tiếp điểm nằm về 2 phía đối với trục hoành thì y .y < 0 1 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 85
GV.Lưu Huy Thưởng 0968.393.899  3   3 
x .x + 2(x + x ) + 4 2 ⇔ 1    + . 1    +  < 0 ⇔ 1 2 1 2
< 0 ⇔ 3a + 2 > 0 ⇔     a > −  x  − 1  x   − 1
x .x − (x + x ) + 1 3 1 2  1 2 1 2  2 a  > −
Kết hợp với điều kiện (*) ta được:  3 . a  ≠ 1  x + 3
HT 131. Cho hàm số y =
. Cho điểm M (x ;y ) thuộc đồ thị (C). Tiếp tuyến của (C) tại M0 cắt x − 1 o o o
các tiệm cận của (C) tại các điểm A và B. Chứng minh Mo là trung điểm của đoạn thẳng AB. Giải • 4
M (x ;y ) ∈ (C) ⇒ y = 1 + . o o o 0 x − 1 0 4
Phương trình tiếp tuyến (d) tại M0 : y − y = − (x − x ) 0 2 0 (x − 1) 0
Giao điểm của (d) với các tiệm cận là: (
A 2x − 1;1), B(1;2y − 1) . 0 0 x + x y + y ⇒ A B = x ; A B = y ⇒ M 0 0 0 là trung điểm AB. 2 2 x + 2
HT 132. Cho hàm số : y =
(C). Chứng minh rằng mọi tiếp tuyến của đồ thị (C) đều lập với x − 1
hai đường tiệm cận một tam giác có diện tích không đổi. Giải   • a + 2 Giả sử M a  ;  ∈ (C).    a − 1 a + 2 2 −3 a + 4a − 2
PTTT (d) của (C) tại M: y y ( ′ =
a).(x − a) + ⇔ y = x + a − 1 2 2 (a − 1) (a − 1)  a 5 +
Các giao điểm của (d) với các tiệm cận là: A 1  ;  
 , B(2a − 1;1) .  a − 1 →  6  6 → IA  = 0;  IA = ; IB = a   ⇒
IB = (2a − 2; 0) ⇒ 2 − 1  a − 1 a − 1
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 86
GV.Lưu Huy Thưởng 0968.393.899 1 Diện tích ∆IAB : S = I .
A IB = 6 (đvdt) ⇒ ĐPCM. I ∆ AB 2 2x − 4
Câu hỏi tương tự đối với hàm số y = ĐS: S = 12. x + 1 x + 2
HT 133. Cho hàm số y =
. Gọi I là giao điểm của 2 đường tiệm cận, ∆ là một tiếp tuyến bất kỳ x + 1
của đồ thị (C). d là khoảng cách từ I đến ∆ . Tìm giá trị lớn nhất của d. Giải   • 1 − x + 2   y′ =
. Giao điểm của hai đường tiệm cận là I(–1; 1). Giả sử 0 M x  ;  ∈ (C ) 2   ( 0 x + 1)  x  + 1 0 
Phương trình tiếp tuyến ∆ với đồ thi hàm số tại M là: x + 2 1 − 2 0 y = (x − x ) +
⇔ x + (x + 1 y − x − x + 1 x + 2 = 0 0 ) 0 ( 0 )( 0 ) 2 0 (x + ) x + 1 1 0 0 2 x + 1 2 Khoảng cách từ I đến 0 ∆ là d = = ≤ 2 1 1 + (x + )4 1 + x + 1 2 ( 0 )2 0 (x +1 0 )
Vậy GTLN của d bằng 2 khi x = 0 hoặc x = 2 − . 0 0 2x + 1
HT 134. Cho hàm số y =
. Viết phương trình tiếp tuyến của đồ thị (C), biết rằng tiếp tuyến x + 1
cách đều hai điểm A(2; 4), B(−4; −2). Giải
• Gọi x0 là hoành độ tiếp điểm (x ≠ 1 − ). 0 1 2x + 1 PTTT (d) là 0 y = (x − x ) + ⇔ 2 2
x − (x + 1) y + 2x + 2x + 1 = 0 2 0 ( 0 0 0 x + 1) x + 1 0 0 Ta có: d( ,
A d) = d(B,d) ⇔ 2 2 2 2
2 − 4(x + 1) + 2x + 2x + 1 = −4 + 2(x + 1) + 2x + 2x + 1 0 0 0 0 0 0
⇔ x = 1 ∨ x = 0 ∨ x = −2 0 0 0
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 87
GV.Lưu Huy Thưởng 0968.393.899 1 5
Vậy có ba phương trình tiếp tuyến: y = x + ; y = x + 1; y = x + 5 4 4 2x − 1
HT 135. Cho hàm số y =
. Gọi I là giao điểm của hai đường tiệm cận, A là điểm trên (C) có 1 − x
hoành độ là a. Tiếp tuyến tại A của (C) cắt hai đường tiệm cận tại P và Q. Chứng tỏ rằng A là
trung điểm của PQ và tính diện tích tam giác IPQ. Giải   • 2a − 1 1 2a − 1 I(1; 2 − ), A a  ;  
. PT tiếp tuyến d tại A: y = (x − a) +  1  − a  2 (1 − a) 1 − a  2a 
Giao điểm của tiệm cận đứng và tiếp tuyến d: P 1  ;    1  − a 
Giao điểm của tiệm cận ngang và tiếp tuyến d: Q(2a – 1;−2)
Ta có: x + x = 2a = 2x . Vậy A là trung điểm của PQ. P Q A 2a 2 IP = + 2 = ; IQ = 2(a − 1) 1 − a 1 − a 1 SIPQ = IP.IQ = 2 (đvdt) 2 2x − 3
HT 136. Cho hàm số y =
(C). Viết phương trình tiếp tuyến tại điểm M thuộc (C) biết tiếp x − 2
tuyến đó cắt tiệm cận đứng và tiệm cận ngang lần lượt tại A, B sao cho côsin góc ABI bằng
4 , với I là giao 2 tiệm cận. 17 Giải   • 2x − 3 I(2; 2). Gọi  0  M x  ;  ∈ (C )  , x ≠ 2 0   x 0  − 2  0  1 2x − 3
Phương trình tiếp tuyến ∆ tại M: 0 y = − (x − x ) + 2 0 (x − 2) x − 2 0 0  2x 2 −
Giao điểm của ∆ với các tiệm cận:  0  A 2  ;  
, B(2x − 2;2) .  x 0  − 2  0 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 88
GV.Lưu Huy Thưởng 0968.393.899 4 1 IA x  = 0 Do cos ABI = nên tan ABI = = ⇔ 2 2 IB = 16.IA ⇔ 4
(x − 2) = 16 ⇔  0 0  17 4 IB x = 4  0   3 1 3 Kết luận: Tại M 0  ;  
phương trình tiếp tuyến: y = − x +  2 4 2  5 1 7 Tại M 4  ;  
phương trình tiếp tuyến: y = − x +  3 4 2 x + 1
HT 137. Cho hàm số y =
(C). Tìm giá trị nhỏ nhất của m sao cho tồn tại ít nhất một điểm M 2x − 1
∈(C) mà tiếp tuyến tại M của (C) tạo với hai trục tọa độ một tam giác có trọng tâm nằm trên
đường thẳng y = 2m − 1 Giải
Gọi M(x ;y )là tọa độ tiếp điểm o o 3
⇒ Phương trình tiếp tuyến tại điểm M(x ;y )là y = −
(x − x ) + y o o 2 (2x − 1) o o o
Gọi A, B là giao điểm của tiếp tuyến với trục hoành, trục tung tương ứng 2 2x + 4x − 1 2 2x + 4x − 1 Nên ta có: o o y =
và trọng tâm G của tam giác OAB có o o y = B 2 (2 G x − 1) 2 3(2x − 1) o o 2 2x + 4x − 1
Theo giả thiết trọng tâm nằm trên đường thẳng y = 2m + 1 nên o o = 2m − 1 2 3(2x − 1) o 2 2 2 2 2x + 4x − 1
6x − (2x − 1) 6x Ta lại có: o o o o o = = − 1 ≥ −1 2 2 3(2x − 1) (2x − 1) (2x − 1) o o o 1 1
Vậy, tồn tại ít nhất một điểm M thỏa mãn điều kiện bài toán 2m - 1≥ − ⇒ m ≥ 3 3 HT 138. Cho hàm số 3
y = x + 3x − 10 (C ). Viết phương trình tiếp tuyến chung của đồ thị hàm số (C) với Parabol 2
(P) : y = x − 5x + 6. Giải
Gọi y = ax + b là tiếp tuyến chung. Gọi x ,x là hai tiếp điểm ta có hệ phương trình: 1 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 89
GV.Lưu Huy Thưởng 0968.393.899  2 a
 x + b = x − 5x + 6 (1)  1 1 1 a  = 2x − 5 (2)  1  3 a
 x + b = x + 3x − 10 (3)  2 2 2  2 a  = 3x + 3 (4)  2  2 3x + 8 Từ (2) và (4) 2 2
⇒ 2x − 5 = 3x + 3 ⇔ x = (5) 1 2 1 2 Từ (1), (2) 2 2
⇒ x − 5x + 6 = x (2x − 5) + b ⇒ b = 6 − x (6) 1 1 1 1 1 Thay (5), (6) vào (2), (3) 2  2  ( 3x + 8 2  9 3x + 3 .x + 6 −   
 = x + 3x − 10 ⇔ − x + 2x − 12x = 0 22 ) 2 3 4 3 2 2  2 2 2 2 2  2  4   x  = 0 1 2 2  2
⇔ − x (9x − 8x + 48) = 0 ⇔ 2 2 2  2 4
9x − 8x + 48 = 0 (vn)  2 2 
⇒ y = 3x − 10 là phương trình tiếp tuyến chung cần tìm 2x − 1
HT 139. Cho hàm số y =
(C ). Tìm các giá trị của m để đồ thị hàm số (C) tiếp xúc với đường x − 1
thẳng y = mx + 5. Giải
Gọi x là hoành độ tiếp điểm A, suy ra phương trình tiếp tuyến tại A là: 0
y = y '(x )(x − x ) + y(x ) = y '(x )x + y(x ). 0 0 0 0 0 0 1
Tức là ta có: m = y '(x ) = − và y
− '(x )x + y(x ) = 4 0 2 0 0 0 (x − 1) 0 1 2x − 1 2 Từ đó ta có: 0 2 x +
= 5 ⇔ 3x − 8x + 4 = 0 ⇔ x = 2 hoặc x = 2 0 0 0 0 ( 0 x − 1) x − 1 3 0 0
KL: m = −1 hoặc m = −9 HT 140. Cho hàm số 4 2
y = x − 6x + 5 (C ). Tìm m để đường thẳng y = mx − m tiếp xúc với đồ
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 90
GV.Lưu Huy Thưởng 0968.393.899 thị (C). Giải
Đường thẳng y = mx − m tiếp xúc với đồ thị hàm số  4 2 x 
− 6x + 5 = mx − m  ⇔  có nghiệm 3 4
 x − 12x = m  x = 1
x = 1 ⇒ m = 8    3 2  3 2 ⇔ x x  5x 5 m  ⇔ x  + − − = 
+ x − 5x − 5 = m     (I )  3 3 4
 x − 12x = m  4
 x − 12x = m       3 2 x 
+ x − 5x − 5 = m Giải hệ (I):  3 4
 x − 12x = m  Ta có: 3 2 3 3 2
x + x − 5x − 5 = 4x − 12x ⇔ 3x − x − 7x + 5 = 0 x  = 1 ⇒ m = −8  ⇔  5 40 x  = − ⇒ m =  3 27 m  = −8  KL:  40 m  =  27
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 91
GV.Lưu Huy Thưởng 0968.393.899
PHẦN 5: BIỆN LUẬN SỐ NGHIỆM CỦA PHƯƠNG TRÌNH HT 141. Cho hàm số 3 2 y = x − + 3x + 1 .
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Tìm m để phương trình 3 2 x − x = 3 2 3
m − 3m có ba nghiệm phân biệt. • PT 3 2 x − x = 3 2 3 m − 3m ⇔ 3 2 3 2 x − + 3x + 1 = m − + 3m + 1. Đặt 3 2 k = m − + 3m + 1
Số nghiệm của PT bằng số giao điểm của đồ thị (C) với đường thẳng d: y = k
Dựa vào đồ thị (C) ta có PT có 3 nghiệm phân biệt ⇔ 1 < k < 5 ⇔ m ∈ (−1; 3) \ {0;2} HT 142. Cho hàm số 4 2
y = x − 5x + 4 có đồ thị (C).
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Tìm m để phương trình 4 2
| x − 5x + 4 |= log m có 6 nghiệm. 2 9 9
• Dựa vào đồ thị ta có PT có 6 nghiệm ⇔ 4 4 log m = ⇔ m = 12 = 144 12 . 12 4 HT 143. Cho hàm số: 4 2
y = x − 2x + 1.
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Biện luận theo m số nghiệm của phương trình: 4 2
x − 2x + 1 + log m = 0 (m > 0) 2 • 4 2
x − 2x + 1 + log m = 0 ⇔ 4 2
x − 2x + 1 = − log m (*) 2 2
+ Số nghiệm của (*) là số giao điểm của 2 đồ thị 4 2
y = x − 2x + 1 và y = −log m 2 + Từ đồ thị suy ra: 1 0 < m < 1 m = 1 < m < 1 m = 1 m > 1 2 2 2 2 nghiệm 3 nghiệm 4 nghiệm 2 nghiệm vô nghiệm HT 144. Cho hàm số 4 2
y = f (x) = 8x − 9x + 1.
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 92
GV.Lưu Huy Thưởng 0968.393.899
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Dựa vào đồ thị (C) hãy biện luận theo m số nghiệm của phương trình: 4 2
8 cos x − 9 cos x + m = 0 với x [0; π ∈ ] • Xét phương trình: 4 2
8 cos x − 9 cos x + m = 0 với x [0; π ∈ ] (1)
Đặt t = cos x , phương trình (1) trở thành: 4 2
8t − 9t + m = 0 (2) Vì x [0; π ∈
] nên t ∈ [−1;1], giữa x và t có sự tương ứng một đối một, do đó số nghiệm của
phương trình (1) và (2) bằng nhau. Ta có: 4 2
(2) ⇔ 8t − 9t + 1 = 1 − m (3) Gọi (C1): 4 2
y = 8t − 9t + 1 với t ∈ [−1;1] và (d): y = 1 − m . Phương trình (3) là phương trình
hoành độ giao điểm của (C1) và (d).
Chú ý rằng (C1) giống như đồ thị (C) trong miền −1 ≤ x ≤ 1 .
Dựa vào đồ thị ta có kết luận sau: m < 0 m = 0 0 < m < 1 81 1 ≤ m < 81 m = 81 m > 32 32 32 vô nghiệm 1 nghiệm 2 nghiệm 4 nghiệm 2 nghiệm vô nghiệm HT 145. 3x − 4
Cho hàm số y = (C). x − 2
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.  2  π
2) Tìm các giá trị của m để phương trình sau có 2 nghiệm trên đoạn 0;  :  3    6 6 x + x = m ( 4 4 sin cos sin x + cos x) • Xét phương trình: 6 6 x + x = m ( 4 4 sin cos
sin x + cos x) (*) 3  1  2  2
⇔ 1 − sin 2x = m 1  − sin 2x  ⇔ 2 2 4 − 3 sin 2x = 2 ( m 2 − sin 2x) (1) 4  2   2  π Đặt 2
t = sin 2x . Với x ∈ 0;  thì t 0;1 ∈  
 . Khi đó (1) trở thành: 3   
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 93
GV.Lưu Huy Thưởng 0968.393.899 3t − 4 2m = với t 0;1 ∈    t − 2  sin2x = − t Nhận xét : với mỗi  t 0;1 ∈  ta có :  ⇔ sin 2x = t   sin 2x = t   2      π 3  3
Để (*) có 2 nghiệm thuộc đoạn 0;  thì t  ∈
;1 ⇒ t ∈  ;1  3        2   4     3 7 1 7
Dưa vào đồ thị (C) ta có: y(1) < 2m ≤ y  
  ⇔ 1 < 2m ≤  ⇔ < m ≤ . 4 5 2 10 HT 146. x + 1
Cho hàm số y = . x − 1
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. x + 1
2) Biện luận theo m số nghiệm của phương trình = m. x − 1 x + 1 x + 1 • Số nghiệm của
= m bằng số giao điểm của đồ thị (C′): y = và y = m. x − 1 x − 1
Dựa vào đồ thị ta suy ra được:
m < −1;m > 1 m = −1
−1 < m ≤ 1
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 94
GV.Lưu Huy Thưởng 0968.393.899
PHẦN 6: ĐIỂM ĐẶC BIỆT CỦA ĐỒ THỊ HT 147. Cho hàm số 3 y = x −
+ 3x + 2 (C). Tìm 2 điểm trên đồ thị hàm số sao cho chúng đối xứng nhau qua tâm M(–1; 3). Giải
• Gọi A(x ;y , B là điểm đối xứng với A qua điểm M(−1;3) ⇒ B (−2 − x ;6 − y 0 0 ) 0 0 )  3 y  = x − + 3x + 2  ,
A B ∈ (C ) ⇔  0 0 0  3 6  − y = (
− −2 − x ) + 3(−2 − x ) + 2  0 0 0  3 3 ⇔ 6 = x −
+ 3x + 2 − (−2 − x ) + 3(−2 − x ) 2
+ 2 ⇔ 6x + 12x + 6 = 0 0 0 0 0 0 0 ⇔ x = 1 − ⇒ y = 0 0 0
Vậy 2 điểm cần tìm là: (−1;0) và (−1;6) HT 148. Cho hàm số 3 y = x −
+ 3x + 2 (C). Tìm trên (C) hai điểm đối xứng nhau qua đường thẳng
d : 2x – y + 2 = 0 . Giải
• Gọi M (x ;y ;N x ;y thuộc (C) là hai điểm đối xứng qua đường thẳng d 1 1 ) ( 2 2) x x y y  + +
I là trung điểm của AB nên  1 2 1 2  I  ;  
, ta có I ∈ d  2 2  y + y ( 3 x − + 3x + 2) + ( 3 x − + 3x + 2 1 1 2 2 ) x + x Có: 1 2 1 2 = = 2. + 2 2 2 2  3 x + x = 0 (x x 3x x x x 3 x x 2 x x  ⇒ − + + + + + = + ⇒ 1 2 ) 1 2 ( 1 2 ) ( 1 2 ) ( 1 2 ) 1 2  2 2
x − x x + x = 1  1 1 2 2 
Lại có: MN ⊥ d ⇒ (x − x .1 + y − y .2 = 0 2 1 ) ( 2 1 ) 7
⇒ 7 (x − x ) − 2(x − x )( 2 2
x + x x + x ) 2 2
= 0 ⇒ x + x x + x = 2 1 2 1 1 1 2 2 1 1 2 2 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 95
GV.Lưu Huy Thưởng 0968.393.899 - Xét 7 7
x + x = 0 ⇒ x = ± ;x = ∓ 1 2 1 2 2 2  2 2   2 2 9 x  − x x + x = 1  x  + x = 1 1 2 2 - Xét 1 2   4  ⇔  ⇒ vô nghiệm 2 2 7   5 x  + x x + x = 1 1 2 2   2 x x  = 1 2  4   7 1 7   7 1 7   
Vậy 2 điểm cần tìm là:  ;2  −  ;− ;2  +     2 2 2   2 2 2         3 x 11 HT 149. Cho hàm số 2 y = − + x + 3x −
. Tìm trên đồ thị (C) hai điểm phân biệt M, N đối 3 3 xứng nhau qua trục tung. Giải x  = x − ≠ 0
• Hai điểm M(x ;y ), N(x ;y ) ∈ (C ) đối xứng nhau qua Oy ⇔  2 1 1 1 2 2   y = y  1 2   x = x − ≠ 0  2 1  x = 3 x  = −3 ⇔  3 3    x x ⇔ 1  hoặc 1   1 2 11 2 3 11 −  + x + 3x − = − + x + 3x − x  = −3  x = 3 2 1 1 2   2   2   3 3 3 3  16  16
Vậy hai điểm thuộc đồ thị (C) và đối xứng qua Oy là: M 3  ; , N    3 − ;   .  3   3  x − HT 150. Cho hàm số 2 1 y =
(C). Tìm điểm M thuộc đồ thị (C) để tiếp tuyến của (C) tại M với x + 1
đường thẳng đi qua M và giao điểm hai đường tiệm cận có tích các hệ số góc bằng –9. Giải
• Giao điểm 2 tiệm cận là I(−1;2).   y − y Gọi 3 −3 M x  ;2  −  ∈ (C ) M I ⇒ k = = 0   IM 2  x  + 1 x  − x 0 M I (x + 1) 0 3
+ Hệ số góc của tiếp tuyến tại M: k = y ( ′ x ) = M 0 (x + )2 1 0
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 96
GV.Lưu Huy Thưởng 0968.393.899 x  = 0 + YCBT ⇔ k .k = −9 ⇔  0
. Vậy có 2 điểm M thỏa mãn: M(0; –3) và M(–2; 5) M IM x  = 2 −  0  x + HT 151. Cho hàm số 2 1 y =
(C). Tìm trên (C) những điểm có tổng khoảng cách đến hai tiệm x + 1 cận của (C) nhỏ nhất. Giải • 2x + 1 1
Gọi M(x ;y )∈ (C), (x ≠ 1 − ) y = = 2 − 0 0 0 thì 0 0 x + 1 x + 1 0 0
Gọi A, B lần lượt là hình chiếu của M trên TCĐ và TCN thì: 1
MA = x + 1 , MB = y − 2 = 0 0 x + 1 0 1
Áp dụng BĐT Cô-si ta có: MA + MB ≥ 2 M . A MB = 2 x + 1 . = 2 0 x + 1 0 1 x = 0
⇒ MA + MB nhỏ nhất bằng 2 khi  0 x + 1 = ⇔ . 0  x + 1 x = −2  0 0 
Vậy ta có hai điểm cần tìm là (0; 1) và (–2; 3). Câu hỏi tương tự: x a) 2 − 1 y = ĐS: x = 1 − ± 3 x + 1 0 3x − 4
HT 152. Cho hàm số y =
(C). Tìm các điểm thuộc (C) cách đều 2 tiệm cận. x − 2 Giải
• Gọi M(x;y)∈ (C) và cách đều 2 tiệm cận x = 2 và y = 3. 3x − 4 x Ta có:
x − 2 = y − 3 ⇔ x − 2 = − 2 ⇔ x − 2 = x − 2 x − 2 x x = 1 (x 2)  ⇔ = ± − ⇔ x − 2 x = 4 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 97
GV.Lưu Huy Thưởng 0968.393.899
Vậy có 2 điểm thoả mãn đề bài là : M1( 1; 1) và M2(4; 6) 1 1 HT 153. Cho hàm số 4 2 y =
x − x + 1 (C ). Tìm điểm M thuộc (C) sao cho tổng khoảng cách từ 4 2
điểm M đến hai trục tọa độ là nhỏ nhất. Giải
Đồ thị (C) cắt Oy tại (
A 0;1) , nên tổng khoảng cách từ A đến hai trục tọa độ bằng 1. Đồ thị hàm số  3  3
có hai điểm cực tiểu: −  1; ; 1 
  ;  và nhận trục Oy làm trục đối xứng nên ta chỉ cần xét  4     4
M(x ;y ) ∈ (C ) và 0 ≤ x ≤ 1 0 0 0
Tổng khoảng cách từ M đến hai trục tọa độ là: 1 4 1 2 1 4 1
x + y = x + y = x + x − x + 1 = x +
x (2 − x ) + 1 ≥ 1 0 0 0 0 0 0 0 0 0 0 4 2 4 2
Với mọi x : 0 ≤ x ≤ 1, đẳng thức xảy ra khi và chỉ khi x = 0 ⇒ y = 1. Vậy điểm M(0;1) 0 0 0 0 HT 154. Cho hàm số 4 2
y = 2x − 3x + 2x + 1 có đồ thị là (C) và đường thẳng ( ) ∆ = 2x − 1.Tìm 0 0 0 0
trên đồ thị (C) điểm A có khoảng cách đến ( ) ∆ là nhỏ nhất Giải Giả sử (
A x ,y ) ∈ (C ) ,ta có: 4 2
y = 2x − 3x + 2x + 1 0 0 0 0 0 0
Khoảng cách từ A đến ( ∆ ) là : 4 2
| 2x − 3x + 2x + 1 − 2x + 1 | 4 2
| 2x − 3x + 2 | 4 2 2x − 3x + 2 0 0 0 0 d( , A ) ∆ = 0 0 = 0 0 = 5 5 5  2  2      4 2 3 2  3 7    7 = x  − 2x + 1 2 = x   −  + ≥ 0 0       4  0 5    4 16 5   8 5   3 ⇒ Mind= 7 khi x = ± 0 8 5 2     3 1   3 1 
Vậy có hai điểm cần tìm: A − ;− − 3     ;A ;− + 3   1  2 8    2     2 8    x + HT 155. Cho hàm số 1 y =
. Tìm trên đồ thị hàm số điểm M sao cho tồng khoảng cách từ M đến x − 2
hai trục tọa độ là nhỏ nhất.
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 98
GV.Lưu Huy Thưởng 0968.393.899 Giải
Giả sử M(x ;y ) ∈ (C ) ;d | = x | + | y | 0 0 0 0  1 1 Ta có : M 0  ;  −  và  ∈ (C ) d =  2 M 2
Dựa vào đồ thị ta có: 1 1
i) | x |> thì d > 0 2 2 1 1 1
ii) 0 < x < thì y < − ⇒ d > 0 2 0 2 2 x + 1 2 x − + x − 1 0 d = x − − y = x − − 0 0 = 0 0 0 x − 2 x − 2 0 0 2 x − + x − 1  1  Tìm GTNN của y = trên − ;0 x − 2  2    2    1  Ta có: ' x − + 4x − 1 1 y =
< 0, ∀x ∈ − ; 0 ⇒ y giảm trên − ; 0 2 (x 2)  2  −     2   1  1
Vậy miny=y(0) = và điểm M cần tìm là M 0  ;  −  2  2 x − HT 156. Cho hàm số 2 4 y =
. Tìm trên (C) hai điểm đối xứng nhau qua đường thẳng MN biết x + 1 M(–3; 0) và N(–1; –1). Giải
• MN = (2;−1) ⇒ Phương trình MN: x + 2y + 3 = 0 .
Phương trình đường thẳng (d) ⊥ MN có dạng: y = 2x + m .
Phương trình hoành độ giao điểm của (C) và (d): x
2 − 4 = 2x + m ⇔ 2
2x + mx + m + 4 = 0 (x ≠ −1) (1) x + 1
(d) cắt (C) tại hai điểm phân biệt A, B ⇔ 2
∆ = m – 8m – 32 > 0 (2) Khi đó (
A x ;2x + m), B(x ;2x + m) với x , x là các nghiệm của (1) 1 1 2 2 1 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 99
GV.Lưu Huy Thưởng 0968.393.899 x x  +  m m 
Trung điểm của AB là  1 2  I 
;x + x + m ≡    I −  ;  (theo định lý Vi-et) 1 2      2   4 2 
A, B đối xứng nhau qua MN ⇔ I ∈ MN ⇔ m = −4 x = 0 Suy ra (1) ⇔ 2 2x 4x 0  − = ⇔  ⇒ A(0; –4), B(2; 0). x = 2  x HT 157. Cho hàm số 2 y =
. Tìm trên đồ thị (C) hai điểm B, C thuộc hai nhánh sao cho tam giác x − 1
ABC vuông cân tại đỉnh A với A(2; 0). Giải     • 2 2 Ta có 2 (     C ) : y = 2 + . Gọi B  ; b 2 + , C  ; c 2 +   
với b < 1 < c .     x − 1 b − 1  c − 1
Gọi H, K lần lượt là hình chiếu của B, C lên trục Ox. Ta có: 0 0
AB = AC; BAC = 90 ⇒ CAK + BAH = 90 = CAK + ACK ⇒ BAH = ACK và: C B H A K A  H = CK 0
BHA = CKA = 90 ⇒ A ∆ BH = C ∆ AK ⇒   H  B = AK   2 2  −b = 2 +  b  = −1 Hay:  c − 1  ⇔   .  2 c  = 3  2 + = c − 2   b − 1 
Vậy B(−1;1), C(3;3) x − HT 158. Cho hàm số 2 1 y =
. Tìm tọa độ điểm M ∈ (C) sao cho khoảng cách từ điểm I(−1; 2) x + 1
tới tiếp tuyến của (C) tại M là lớn nhất. Giải
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 100
GV.Lưu Huy Thưởng 0968.393.899   • Giả sử  3  M x  ; 2 −  ∈ (C ) 
. PTTT ∆ của (C) tại M là: 0   x  + 1 0  3 3 y − 2 + = (x − x ) ⇔ 2
3(x − x ) − (x + 1) (y − 2) − 3(x + 1) = 0 2 0 x + 1 0 0 0 0 (x + 1) 0
Khoảng cách từ I(−1;2) tới tiếp tuyến ∆ là:
3(−1 − x ) − 3(x + 1) 6 x + 1 6 0 0 0 d = = = . 9 + (x + )4 4 9 + (x + 1) 9 2 1 0 0 + (x + 1) 2 0 (x + 1) 0 9 Theo BĐT Cô–si: 2
+ (x + 1) ≥ 2 9 = 6 ⇒ d ≤ 6 . 2 0 (x + 1) 0 9
Khoảng cách d lớn nhất bằng 6 khi
= (x + 1) ⇔ (x + )2 2
1 = 3 ⇔ x = −1 ± 3 . 2 0 0 0 (x + 1) 0
Vậy có hai điểm cần tìm là: M (−1 + 3;2 − 3) hoặc M (−1− 3;2 + 3) x + 2
HT 159. Cho hàm số y =
. Tìm những điểm trên đồ thị (C) cách đều hai điểm A(2; 0) và 2x − 1 B(0; 2). Giải
• PT đường trung trực đọan AB: y = x .
Những điểm thuộc đồ thị cách đều A và B có hoành độ là nghiệm của PT:  1 − 5  x + 2 x =  = x ⇔ 2 2
x − x − 1 = 0 ⇔  2x − 1  1 + 5 x  =  2  1 5 1 5  1 5 1 5  − −  + + 
Hai điểm cần tìm là:  ,  ;    ,      2 2   2 2         x − HT 160. Cho hàm số 3 y =
. Tìm trên hai nhánh của đồ thị (C) hai điểm A và B sao cho AB x + 1
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 101
GV.Lưu Huy Thưởng 0968.393.899 ngắn nhất. Giải
• Tập xác định D = R \ {− 1} . Tiệm cận đứng x = −1.  4  4 Giả sử A 1 − − a;1  + , B    1 − + ; b 1  −   
(với a > 0,b > 0 ) là 2 điểm thuộc 2 nhánh của (C)     a  b  2 1 1  16   16  64 2 2   2
AB = (a + b) + 16 +  = (a + b) 1  +  ≥ 4ab 1  +  = 4ab + ≥ 32      2 2   2 2 a b  a b   a b  ab  a  = b  a  = b AB nhỏ nhất ⇔   4 AB = 4 2 ⇔  ⇔  ⇔ a = b = 4 16 4 4  ab = a  = 4    ab  Khi đó: A( 4 4 − − + ) B( 4 4 1 4;1 64 , 1 − + 4;1 − 64). HT 161. Cho hàm số 4 2
y = x − 2x + 1 Tìm tọa độ hai điểm P. Q thuộc (C) sao cho đường thẳng PQ
song song với trục hoành và khoảng cách từ điểm cực đại của (C) đến đường thẳng PQ bằng 8 Giải
Phương trình đường thẳng PQ có dạng: y = m (m ≥ 0)
Vì điểm cực đại A(0;1) cách PQ một khoảng bằng 8 nên m = 9
Khi đó, hoành độ P, Q là nghiệm của phương trình: 4 2
x − 2x − 8 = 0 ⇔ x = ±2
Vậy, P(-2;9), Q(2;9) hoặc P(2;9); Q(-2;9) 1 5 HT 162. Cho hàm số 3 2 y =
x + x − 3x +
(C). Gọi A và B là giao điểm của (C) và trục Ox. Chứng 3 3
minh rằng, trên đồ thị tồn tại hai điểm cùng nhìn đoạn AB dưới một góc vuông. Giải
Phương trình hoành độ giao điểm của đồ thị với trục hoành: 1 5 x  = 1 3 2 x x 3x 0  + − + = ⇔ ⇒ A(-5;0) và B(1;0) 3 3 x  = −5   1 5 Gọi M thuộc (C)   ⇒ 3 2 M a
 ; a + a − 3a + khác A, B  3 3
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 102
GV.Lưu Huy Thưởng 0968.393.899  1     3 2 5 1   3 2 5 AM a
 + 5; a + a − 3a + ;BM a
 − 1; a + a − 3a  +   3 3     3 3  1 
Theo giả thiết: AM ⊥ BM ⇔ AM.BM = 0 ⇔ 2 2
(a + 5)(a − 1) +  (a − 1) (a + 5)  = 0  3   
Do M khác A, B nên a khác -5 và a khác 1 nên phương trình tương đương: 1 3 4 3 2
1 + (a − 1) (a + 5) = 0hay a + 2a − 12a + 14a + 4 = 0 (*) 9 Đặt: 4 3 2
y = a + 2a − 12a + 14a + 4 có tập xác định là ℝ 3 2 7 −2043
y ' = 4a + 6a − 12a + 14;y ' = 0 có 1 nghiệm thực a ≈ − ⇒ y ≈ o 2 o 16 a -∞ 1 +∞ y’ - 0 + + + - - +∞ y 9
Từ bảng biến thiên ta có: (*) luôn có hai nghiệm khác 1 và -5
Vậy luôn tồn tại 2 điểm cùng nhìn đoạn AB dưới một góc vuông mx + HT 163. Cho hàm số 8 y =
. Chứng minh rằng mọi điểm không nằm trên đường phân giác 3x + m
thứ nhất của mặt phẳng luôn có duy nhất một đồ thị của hàm số đi qua. Giải
Gọi M(x ;y ) ∉ d;y = x ⇔ x ≠ y 0 0 0 0
Điều kiện để đồ thị hàm số đi qua M(x ;y ) là phương trình sau có nghiệm : 0 0 mx + 8 0 y =
⇔ 3x y + y m = x m + 8 0 0 0 0 0 3x + m 0
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 103
GV.Lưu Huy Thưởng 0968.393.899 3x y − 8 0 0
⇔ (x − y )m = 3x y − 8 ⇔ m = (*) 0 0 0 0 x − y 0 0
Nhìn vào biểu thức (*) ta thấy, ứng với mỗi cặp điểm (x ;y ta luôn có 1 giá trị của m duy nhất 0 0 )
tương ứng. Suy ra điều phải chứng minh. 2
(3m + 1)x − m + m
HT 164. Cho hàm số y =
. Tìm các điểm thuộc đường thẳng x = 1 mà không x + m có đồ thị đi qua. Giải
Gọi điểm M(1;a) là điểm thỏa mãn yêu cầu bài toán. 2
3m + 1 − m + m
Vì không có đồ thị nào đi qua điểm M(1;a) ⇒ Phương trình : a = (1)không có 1 + m nghiệm m.
Với điều kiện m ≠ −1 ta có 2
(1) ⇔ m + (a − 4)m + a − 1 = 0 (2)
Để (1) vô nghiệm thì phương trình (2) xảy ra 1 trong hai trường hợp : - (2) vô nghiệm
- (2) có nghiệm kép m = −1 1,2
Trường hợp 1 : (2) vô nghiệm 2 2
⇔ ∆ < 0 ⇔ (a − 4) − 4(a − 1) < 0 ⇔ a − 12a + 20 < 0 ⇔ 2 < a < 10
Trường hợp 2 : (2) có nghiệm kép bằng -1    a  = 2 ∆ = 0       ⇔  ⇔ a  −  = 10 4 ⇔ vn a   = −1     2 a  = 6 
Kết luận : Như vậy tập hợp các điểm thuộc đường thẳng x = 1 có tung độ bằng a với a thỏa mãn : 2 < a < 10 HT 165. Cho hàm số 4 2 2
y = x − 2mx + m + 1. Chứng minh rằng mỗi điểm thuộc đường thẳng
y = 1 luôn có duy nhất một đồ thị của hàm số đi qua.
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 104
GV.Lưu Huy Thưởng 0968.393.899 Giải Gọi (
A a;1) ∈ d : y = 1 Đồ thị hàm số qua A 4 2 2 4 2 2
⇔ a − 2ma + m + 1 = 1 ⇔ a − 2ma + m = 0 2 2 2
⇔ (m − a ) = 0 ⇔ m = a (*)
Dựa vào (*) ta có, ứng với mỗi giá trị của a ta luôn có 1 giá trị m tương ứng.
Suy ra, mỗi điểm trên y = 1 luôn có duy nhất 1 giá trị m để đồ thị hàm số đi qua.
Suy ra điều phải chứng minh. HT 166. Cho hàm số 3
y = x − 3mx + 2m. Chứng minh rằng với mọi m thì đồ thị hàm số luôn đi
qua điểm cố định duy nhất. Giải Giả sử (
A a;b) là điểm cố định của đồ thị hàm số. 3
⇒ b = a − 3ma + 2m 3
⇔ m(−3a + 2) + a −b = 0 (1)
Đề đồ thị hàm số luôn qua A với mọi m thì phương trình (1) có nghiệm với m ∀  2 −3 + 2 = 0 a   a  =   3 ⇔  ⇔ 3  a  −b = 0  8  b  =  27 2 8 
Vậy đồ thị hàm số luôn đi qua điểm cố định duy nhất : A ;
. Suy ra điều phải chứng minh. 3 27 HT 167. Cho hàm số 3 2
y = (m + 2)x + 2(m + 2)x − (m + 3)x − 2m + 1. Chứng minh rằng đồ thị
hàm số luôn đi qua 3 điểm cố định thẳng hàng. Giải Xét họ đường cong: 3 2
y = (m + 2)x + 2(m + 2)x − (m + 3)x − 2m + 1.
Gọi M(x ;y ) là điểm cố định cần tìm. Khi đó ta có: 0 0 3 2
y = (m + 2)x + 2(m + 2)x − (m + 3)x − 2m + 1 ∀m 0 0 0 0
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 105
GV.Lưu Huy Thưởng 0968.393.899 3 2 3 2
⇔ (x + 2x − x − 2)m + (2x + 4x − 3x + 1 − y ) = 0 ∀m 0 0 0 0 0 0 0  3 2 x 
+ 2x − x − 2 = 0 (1)  0 0 0 ⇔  3 2 2
 x + 4x − 3x + 1 − y = 0 (2)  0 0 0 0  x = 2 − ⇒ y = 7  0 0 2 (1) (x 2)(x 1) 0  ⇔ + − = ⇔ x = 1 − ⇒ y = 6 0 0  0 0
x = 1 ⇒ y = 4 0 0 
Vậy ta được 3 điểm cố định là: (
A −2; 7),B(−1; 6),C (1; 4)
AB = (1;−1),AC = (3;−3) ⇒ AC = 3AB Suy ra A, B, C thẳng hàng. HT 168. Cho hàm số 3
y = (m + 1)x − (2m − 1)x − m + 1. Chứng minh rằng đồ thị hàm số luôn đi
qua 3 điểm cố định thẳng hàng. Giải Xét họ đường cong: 3
y = (m + 1)x − (2m − 1)x − m + 1
Gọi M(x ;y ) là điểm cố định cần tìm. Tương tự bài trước ta có hệ phương trình sau: 0 0  3 x  − 2x − 1 = 0 (1)  0 0  3 y 
− x + x − 1 = 0 (2)  0 0 0  (2) ⇔ y = ( 3
x − 2x − 1 + x + 2 = x + 2 0 0 0 ) 0 0 2
(1) ⇔ (x + 1)(x − x − 1) = 0 ⇒ (1) có 3 nghiệm phân biệt. 0 0 0
Nên 3 điểm đều thỏa mãn: y = x + 2. Vậy 3 điểm thuộc đường thẳng y = x + 2. 0 0 HT 169. Cho hàm số 3 2
y = (m − 3)x − 4(m − 3)x − (m + 1)x + m. Chứng minh rằng đồ thị hàm số
luôn đi qua 3 điểm cố định thẳng hàng. Giải Xét họ đường cong 3 2
y = (m − 3)x − 4(m − 3)x − (m + 1)x + m.
Gọi M(x ;y ) là điểm cố định cần tìm. Tương tự bài trên ta có hệ sau để xác định x ,y 0 0 0 0
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 106
GV.Lưu Huy Thưởng 0968.393.899  3 2 x 
− 4x − x + 1 = 0 (1)  0 0 0  3 2 y 
+ 3x − 12x + x = 0 (2)  0 0 0 0  3 2 3 2
(2) ⇔ y = −3x − 12x − x = −3(x − 4x − x + 1) − 4x + 3 = −4x + 3 0 0 0 0 0 0 0 0 0
Ta chứng minh (1) có 3 nghiệm phân biệt: Xét hàm số: 3 2
f (x) = x − 4x − x + 1 Hàm số liên tục trên ℝ
Có: f (−1) = −3, f (0) = 1, f (1) = −3, f (5) = 21 f ( 1 − ).f (0) = 3
− < 0 ⇒ ∃x ∈ ( 1
− ; 0) : f (x ) = 0 1 1 f (0).f (1) = 3 − < 0 ⇒ x ∃
∈ (0;1) : f (x ) = 0 2 2
f (1).f (5) = −63 < 0 ⇒ ∃x ∈ (1;5) : f (x ) = 0 3 3
Vì x < x < x nên phương trình có 3 nghiệm phân biệt. 1 2 3
Vậy 3 điểm cố định thẳng hàng đều nằm trên đường thẳng y = −4x + 3 HT 170. Cho hàm số 3
y = mx + (1 − m)x. Tìm các điểm trên mặt phẳng tọa độ sao cho không có
đường cong nào của họ đồ thị đi qua. Giải
Gọi M(x ;y ) là điểm cần tìm. Khi đó phương trình sau với m là ẩn: 0 0 3
y = mx + (1 − m)x (1) vô nghiệm. 0 0 0 Dễ thấy (1) 3
⇔ y − x = m(x − x ) (2). 0 0 0 0
Ta có: (2) vô nghiệm khi và chỉ khi hệ sau thỏa mãn:  x = 0  3    0 x − x = 0   0 0   ⇔ x   = 1 ±  0 y  − x ≠ 0   0 0 y    ≠ x  0 0 
Vậy các điểm cần tìm nằm trên 3 đường thẳng: x = 0,x = −1,x = 1 bỏ đi 3 điểm (
A 0; 0), B(1;1),C (−1;−1) HT 171. Cho hàm số 3 3 2 2
y = x − m x + 2mx + m − 1. Tìm các điểm trên mặt phẳng tọa độ mà đồ
thị hàm số không qua với mọi m.
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 107
GV.Lưu Huy Thưởng 0968.393.899 Giải
Gọi M(x ;y ) là điểm cần tìm. Khi đó phương trình sau với m là ẩn: 0 0 3 3 2 2
y = x − m x + 2mx + m − 1 (1) vô nghiệm 0 0 0 0 Ta viết lại: 3 2 2 3
m x − m − 2mx + y + 1 − x = 0 (2) vô nghiệm 0 0 0 0
Nếu x ≠ m thì (2) là phương trình bậc 3. Ta biết rằng mọi phương trình bậc 3 đều có ít nhất 1 0
nghiệm. Vì thế để (2) vô nghiệm thì x = 0 0
Với x = 0 thì (2) trở thành: 2 2 m −
+ y + 1 = 0 ⇔ m = y + 1 (3) 0 0 0
Để (3) vô nghiệm y + 1 < 0 ⇔ y < 1
− . Vậy tập hợp các điểm là nửa đường thẳng: x = 0 với 0 0 y < −1. HT 172. Cho hàm số 3 2 2 2
y = x + 2(m − 1)x + (m − 4m + 1)x − 2(m + 1). Tìm các điểm trên mặt
phẳng tọa độ sao cho đồ thị không qua với mọi m. Giải
Gọi M(x ;y ) là điểm cần tìm. Khi đó phương trình sau với m là ẩn: 0 0 3 2 2 2
y = x + 2(m − 1)x + (m − 4m + 1)x − 2(m + 1) (1) vô nghiệm. 0 0 0 0 Viết lại (1) thành: 2 3 2
(x − 2)m + 2x (x − 2)m + x − 2x + x − 2 − y = 0 (2). 0 0 0 0 0 0 0 Xét các khả năng sau:
Trường hợp 1: x ≠ 2. Khi đó (2) vô nghiệm khi: 0 2 2 3 2
∆ ' = x (x − 2) − (x − 2x + x − 2 − y )(x − 2) < 0 0 0 0 0 0 0 0 3 2 3 2
⇔ (x − 2)(x − 2x − x + 2x − x + 2 + y ) < 0 0 0 0 0 0 0 0  x  − 2 < 0   0   x − + y + 2 > 0  0 0 (x 2)( x y 2) 0  ⇔ − − + + < ⇔ 0 0 0   x  − 2 > 0  0  x − + y + 2 < 0  0 0  
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 108
GV.Lưu Huy Thưởng 0968.393.899 2x − 1
HT 173. Cho hàm số y =
(C ). Tìm trên đồ thị (C) hai điểm ,
A B phân biệt sao cho ba điểm x − 1 ,
A B,I (0;−1) thẳng hàng đồng thời thỏa mãn: I . A IB = 4. Giải Do ,
A B,I (0;−1) thẳng hàng nên ,
A B nằm trên đường thẳng ∆ qua I (0;−1). Do , A B thuộc đồ thị hàm số (C) nên ,
A B là giao điểm của đồ thị hàm số (C) với đường thẳng ∆ : y = kx − 1
Xét phương trình hoành độ giao điểm của (C) và ∆ ta có: 2x − 1 2
= kx − 1 ⇔ kx − (k + 3)x + 2 = 0 (*);(x ≠ 1) x − 1
∆ cắt (C) tại hai điểm phân biệt ,
A B ⇔ phương trình (*) có hai nghiệm phân biệt khác 1 k  ≠ 0  2 ⇔ ∆ 
= k − 2k + 9 > 0 ⇔ k ≠ 0 k
 −(k + 3) + 2 ≠ 0  Gọi (
A x ;y );B(x ;y ) do ,
A B thuộc ∆ nên y = kx − 1;y = kx − 1 1 1 2 2 1 1 2 2 Ta có: 2 2 2 2 2 I . A IB = 4 ⇔
x + kx . x + kx = 4 ⇔ x x (k + 1) = 4 1 1 2 2 1 2 2 2
Theo Viet ta có: x x = thay vào ta được: 2
(k + 1) = 4 ⇔ k = ±1 1 2 k k
Với k = 1 ta được: A(2 − 2;1− 2);B (2 + 2;1 + 2)
Với k = −1 ta được: A(1− 3;−2 + 3);B (1 + 3;−2 − 3) 2x − 4 HT 174. Cho hàm số y =
(C ) . Tìm trên đồ thị (C ) hai điểm A, B đối xứng nhau qua đường x + 1
thẳng MN, biêt M(−3; 0),N(−1;−1) . Giải
Phương trình đường thẳng MN: x + 2y + 3 = 0  6   6 
Xét hai điểm A, B trên đồ thị (C), ta có: A a  ;2  − , B    ; b 2  −
,a,b ≠ −1    +    a 1  b + 1 a b 3 3  + Gọi I  ;2  − −
 là trung điểm của đoạn AB  2  a + 1 b + 1
Theo yêu cầu bài toán ta có:
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 109
GV.Lưu Huy Thưởng 0968.393.899   a  = 2  3 3       b    − a − + = 0  AB ⊥ MN A   B.MN = 0  b  = 0   a + 1 b + 1   ⇔  ⇔  ...  ⇔ ⇔  I  ∈ MN I  ∈ MN b  + a 6 6    a  = 0      − − = −7     2 a + 1 b + 1 b   = 2   Vậy, (
A 2; 0);B(0;−4) hoặc B(2; 0); ( A 0;−4)
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 110
GV.Lưu Huy Thưởng 0968.393.899 CÁC BÀI TỔNG HỢP HT 175. 2x + 3
Cho hàm số y =
(C ). Tìm m để đường thẳng d : y = 2x + m cắt đồ thị tại hai điểm x − 2
phân biệt sao cho tiếp tuyến tại hai điểm đó của đồ thị hàm số song song với nhau. Giải
Phương trình hoành độ giao điểm của d với đồ thị (C) là: 2x + 3 2
= 2x + m ⇔ 2x + (m − 6)x − 2m − 3 = 0(1) (x = 2 không là nghiệm của phương trình) x − 2
d cắt (C) tại hai điểm phân biệt mà tiếp tuyến tại đó song song với nhau
⇔ (1) có hai nghiệm phân biệt x ;x thỏa mãn: y '(x ) = y '(x ) hay x + x = 4 1 2 1 2 1 2  2
∆ = (m − 6) + 8(2m + 3) > 0  ⇔  ⇔ m = −2 6 − m  = 4  2 HT 176. 4 1 Cho hàm số 3 2 y =
x − (2m + 1)x + (m + 2)x +
(C ). Gọi A là giao điểm của (C ) với 3 3 m m
trục tung. Tìm m sao cho tiếp tuyến của (C ) tại A tạo với hai trục tọa độ một tam giác có diện m 1 tích bằng . 3 Giải  1
Ta có: A0;  và 2 Suy ra 
y ' = 4x − 2(2m + 1)x + m + 2. y '(0) = m + 2.  3 1  1  −
Tiếp tuyến của đồ thị tại A là d : y = (m + 2)x + . Đường thẳng d cắt Ox tại B  ; 0. 3 3  m + 6 
Khi đó, diện tích tam giác tạo bởi d với hai trục tọa độ là: 1 1 1 1 − 1 S = O . AOB = . = 2 2 3 3m + 6 18 m + 2  13 m  = − Theo giả thiết ta có: 1 1 1  6 = ⇔ m + 2 = ⇔  18 m + 2 3 6  11 m = −   6
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 111
GV.Lưu Huy Thưởng 0968.393.899 HT 177. Cho hàm số 3 2
y = x − 2mx + 2mx − 1 (C ). Tìm m để đồ thị hàm số (C) cắt trục hoành tại 3 điểm phân biệt (
A 1; 0), B và C sao cho k + k = BC. 5 trong đó k ,k lần lượt là hệ số góc tiếp 1 2 1 2
tuyến tại B, C của đồ thị hàm số (C). Giải
Phương trình hoành độ giao điểm của đồ thị với Ox : x  = 1 3 2  2 x 2mx 2mx 1 0 (x 1) x (1 2m)x 1 − + − = ⇔ − + − + = 0    ⇔    2
x + (1 − 2m)x + 1 = 0 (*) 
Đề đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt khác 1. Tức là phương trình: 2
x + (1 − 2m)x + 1 = 0 có 2 nghiệm phân biệt khác 1  1  m  ≤ −    1  2  2  ∆ = 4 − 4 − 3 > 0  m m m ≤ −   3  2 ⇔  ⇔  m ≥ ⇔ 
1 + (1 − 2m) + 1 ≠ 0       3 2  m  ≥ 3    2 m  ≠  2
Giả sử B(x ; 0),C(x ;0) 1 2
Vì x ,x là 2 nghiệm phân biệt của phương trình (*) nên theo định lý Viet ta có: 1 2
x + x = 2m − 1 và x .x = 1 1 2 1 2 Ta có: 2 2 2
BC = (x − x ) = (x + x ) − 4x .x = 4m − 4m − 3 2 1 1 2 1 2 Mặt khác: 2 2
k + k = 3x − 4mx + 2m + 3x − 4mx + 2m 1 2 1 1 2 2 2 2
= 3(x + x ) − 6x x − 4m(x + x ) + 4m = 4m − 4m − 3 1 2 1 2 1 2
Theo giả thiết ta có: k + k = BC 5 1 2 2 2
⇔ 4m − 4m − 3 = 5(4m − 4m − 3) 2
⇒ 4m − 4m − 3 = 5 Vì 2
4m − 4m − 3 > 0 m  = −1 (t / m) 2 m m 2 0  ⇔ − − = ⇔ m  = 2 (t / m) 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 112
GV.Lưu Huy Thưởng 0968.393.899 m  = −1 KL:  m  = 2  HT 178. Cho hàm số 3 2
y = x − 3x + mx + 2 − m (C ). Tìm m để (C ) cắt trục hoành tại 3 điểm m m phân biệt ,
A B,C sao cho tổng các hệ số góc của tiếp tuyến của (C ) tại ,
A B,C bằng 3. m Giải
Phương trình hoành độ giao điểm của (C ) với trục hoành là: m x = 1 3 2 2 x 3x mx 2 m 0 (1) (x 1)(x 2x m 2) 0  − + + − = ⇔ − − + − = ⇔  2
x − 2x + m − 2 = 0 (2) 
(C ) cắt trục Ox tại 3 điểm phân biệt ⇔ (1) có 3 nghiệm phân biệt ⇔ (2) có 2 nghiệm phân biệt m ∆ > 0 3  − m > 0 khác 1   ⇔  ⇔  ⇔ m < 3(*) 2
f (1) ≠ 0, f (x) = x − 2x + m − 2 m  ≠ 3     x  + x = 2
Khi đó, gọi x ,x là hai nghiệm của (2). Theo Viet ta có:  1 2 2 
(**), f '(x) = 3x − 6x + m 1 2 x  x = m − 2  1 2  ⇔ 3 − m = 6
− ⇔ m = 2 (thỏa mãn (*)) KL: m = 2 HT 179. x + 3 Cho hàm số y =
(C ) Lập phương trình tiếp tuyến d với đồ thị (C) biết tiếp x − 1
tuyến cắt hai đường tiệm cận của (C) tại hai điểm phân biệt A, B sao cho diện tích đường tròn
ngoại tiếp tam giác IAB bằng 17π , với I là giao điểm của hai đường tiệm cận. Giải  x 3 + Gọi  0  M x  ;  ∈ (C )  là tiếp điểm 0   x  − 1  0  −4 x + 3
Phương trình tiếp tuyến của d tại M là 0 y = (x − x ) + 2 0 (x − 1) x − 1 0 0  x 7  + Tiếp tuyến  
d cắt với tiệm cận đứng tại 0 A 1  ;     x  − 1  0 
Tiếp tuyến d cắt với tiệm cận ngang tại B (2x −1;1 0 )
Vì tam giác IAB vuông tại I nên bán kính đường tròn ngoại tiếp tam giác IAB: AB 2 16 R = = (x − 1) + 0 2 2 (x − 1) 0 Theo giả thiết ta có: 2 4 2 S 17π R π 17π = ⇔ =
⇔ (x − 1) − 17(x − 1) + 16 = 0 0 0
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 113
GV.Lưu Huy Thưởng 0968.393.899 x = −1   y = x − − 2 0  x = 0   y = −4x − 3 0 ⇔ ⇒   4 tiếp tuyến: x = 2   y = −4x + 13 0    x = 3  y = x − + 6 0   HT 180. x + m Cho hàm số y =
(m ≠ 1) (1). Gọi k là hệ số góc của tiếp tuyến tại giao điểm x + 1 1
của đồ thị hàm số (1) với trục hoành. Gọi k là hệ số góc của tiếp tuyến với đồ thị hàm số (1) tại 2
điểm có hoành độ x = 1. Tìm tất cả các giá trị của tham số m sao cho k + k đạt giá trị nhỏ nhất. 1 2 Giải 1 − m Ta có: y ' = 2 (x + 1)
Hoành độ giao điểm của đồ thị hàm số (1) với trục hoành là x = m −
Hệ số góc của tiếp tuyến: 1
Tại điểm có hoành độ x = m − là k = 1 − m 1 − m
Tại điểm có hoành độ x = 1 là k = 2 4 1 1 − m 1 1 − m Ta có: k + k = + = + ≥ 1, ∀m ≠ 1 1 2 1 − m 4 1 − m 4 1 1 − m 1  − m = 2 m  = −1 Đẳng thức xảy ra khi:   = ⇔ ⇔ 1   − m 4 1 − m = −2 m = 3    
Vậy: k + k đạt giá trị nhỏ nhất bằng 1 khi m ∈ { − 1; 3} 1 2 HT 181. 1 2 Cho hàm số 3
y = − x + x −
(C ).Gọi M là điểm thuộc đồ thị (C) có hoành độ x = 2 3 3
. Tìm các giá trị của tham số m để tiếp tuyến với (C) tại M song song với đường thẳng 2 9m + 5
d : y = (m − 4)x + 3 Giải 4  4
Ta có y(2) = − ⇒ M 2  ;  −  3  3
Tiếp tuyến ∆ với (C) tại M có phương trình: 4 4 14
y = y '(2)(x − 2) −
⇔ y = −3(x − 2) − ⇔ y = −3x + 3 3 3  2 m  − 4 = −3   2 m  = 1 Ta có:   / /d  ∆ ⇔ 9m + 5 14 ⇔  ⇔ m = −1.  ≠ m  ≠ 1    3 3  Kết luận: m = −1
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 114
GV.Lưu Huy Thưởng 0968.393.899 HT 182. x + 2 Cho hàm số: y =
(C ) Viết phương trình đường thẳng d ;d đi qua giao điểm I x − 1 1 2
của hai tiệm cận và cắt đồ thị (C) tại 4 điểm phân biệt là các đỉnh của một hình chữ nhật biết
đường chéo hình chữ nhật có độ dài bằng 30. Giải
Do I(1;1) là tâm đối xứng của đồ thị hàm số. Giả sử d cắt (C) tại A, B; d cắt (C) Tại C và D thì I là 1 2
trung điểm của AB và CD. Do đó, ACBD là hình bình hành. Để ACBD là hình chữ nhật thỏa mãn đề
bài thì AB = CD = 30
Gọi d là đường thẳng qua I có hệ số góc là k 1
Phương trình đường thẳng d : y = k(x − 1) + 1 ⇔ y = kx − k + 1 1 x + 2
Phương trình hoành độ giao điểm của d và (C) là: = kx − k + 1 1 x − 1 2
⇔ kx − 2kx + k − 3 = 0 (1). Để d cắt (C) tại hai điểm phân biệt (
A x ;y ),B(x ;y ) thì (1) có 2 1 1 1 2 2
nghiệm phân biệt ≠ 1 ⇔ k > 0 x  + x = 2  1 2
Áp dụng định lý Viet ta có:  k − 3 x  x =  1 2  k y
 = kx − k + 1 y  + y = 2 Do đó:  1 1  1 2   ⇒  2 2 y  = kx − k + 1 y
 y = k x x − k(k − 1)(x + x ) + (k − 1) = 1 − 3k  2 2   1 2 1 2 1 2  Để AB = 30 thì: 2 2 2 2
(x − x ) + (y − y ) = 30 ⇔ (x + x ) + (y + y ) − 4x x − 4y y = 30 1 2 1 2 1 2 1 2 1 2 1 2 2 1
⇔ 12k − 30k + 12 = 0 ⇔ k = 2 ∨ k = 2
Vậy, d : 2x − y − 1 = 0;d : x − 2y + 1 = 0 hoặc ngược lại 1 2 HT 183. Cho hàm số 3
y = x − mx + m − 1 (1),m là tham số. Tìm m để tiếp tuyến của đồ thị
hàm số (1) tại M có hoành độ x = −1, cắt đường tròn (C) tâm I(2; 3) bán kính R = 2 theo 1 dây
cung AB có độ dài nhỏ nhất. Giải
Ta có: y '(−1) = 3 − m
Phương trình tiếp tuyến tại M(−1;2m − 2) là:
∆ : y = (3 − m)(x + 1) + 2m − 2 = (3 − m)x + m + 1 ⇔ (3 − m)x − y + m + 1 = 0
Để ∆ ∩ (C ) thì d(I, )
∆ < 2. Nhận thấy dây cung AB nhỏ nhất khi d(I, ) ∆ lớn nhất 4 − m d(I, ) ∆ = 2 (3 − m) + 1 2 4 − m (3 − m) + 1 2 (3 − m) + 1 Ta có: d(I, ) ∆ = = ≤ 2 2 2 (3 − m) + 1 (3 − m) + 1 (3 − m) + 1 d(I, ) ∆ ≤ 2 < R
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 115
GV.Lưu Huy Thưởng 0968.393.899
Ta có tiếp tuyến luôn cắt đường tròn (C) hai điểm phân biệt.
AB min ⇔ d(I, ) ∆ = 2 ⇔ m = 2 Kết luận: m = 2 HT 184. x + 2 Cho hàm số y =
(C ).Tìm các giá trị của tham số m để đường thẳng 2x − 1
d : y = x + m cắt đồ thị (C) tại các điểm A, B phân biệt sao cho trọng tâm G của tam giác OAB cách
đường thẳng d một khoảng bằng 2 (với O là gốc tọa độ). Giải x + 2 1
Phương trình hoành độ giao điểm: 2
= x + m ⇔ g(x) = 2x + 2(m − 1)x − m − 2 = 0,x ≠ 2x − 1 2
Đường thẳng d cắt (C) tại A, B phân biệt khi và chỉ khi phương trình g(x) = 0 có hai nghiệm phân   2 2 ∆ ' > 0 (
 m − 1) + 2(m + 2) = m + 5 > 0 1   biệt khác   ⇔  1 ⇔ 1 ∀m ∈ ℝ 2 g  ( ) 0  ≠ 
 + m − 1 − m − 2 ≠ 0  2   2
Gọi x ,x là các nghiệm của g(x) = 0 ⇒ (
A x ;x + m) và B(x ;x + m) 1 2 1 1 2 2 1 m 1 m  − +
Điều kiện O ∉ d ⇒ m ≠ 0 ⇒ trọng tâm G  ;   3 3  1 − m 1 + m − + m 3 3 m m  = 6
Ta có: d(G,d) 2  = = = ⇔ m  = −6 2 3 2  HT 185. Cho hàm số 3 2
y = x − 3x + (m + 1)x + 1(1) . Tìm m để đường thẳng d : y = x + 1 cắt đồ
thị hàm số (1) tại 3 điểm phân biệt P(0;1),M,N sao cho bán kính đường tròn ngoại tiếp tam giác 5 2 OMN bằng với O(0; 0). 2 Giải
(C) có hai điểm cực trị (
A 1;1), B(2; 0) ⇒ AB = 2.Phương trình đường thẳng 1
AB : x + y − 2 = 0 . S
= d(N, AB).AB = 3 ⇔ d(N, AB) = 3 2 A ∆ BN 2
Gọi d là đường thẳng đi qua N và d / /AB. Phương trình đường thẳng d có dạng: c + 2 c  = 4 N  (0;−4)(l) x y c 0 d( , A d) d(N, AB) 3 2   + + = ⇒ = ⇔ = ⇔ ⇒ c  8 N  = − (3; 5) 2    
Với N(3;5)giả sử M(x ;y ). Phương trình tiếp tuyến với (C) tại M là: 0 0
y = y '(x )(x − x ) + y 0 0 0
Do tiếp tuyến đi qua N nên ta có: 2 3 2
5 = (6x − 18x + 12)(3 − x ) + 2x − 9x + 12x − 4 0 0 0 0 0 0
x = 3(loa ,ivi N ≠ M )  0   2 3 25
⇔ (x − 3) (4x − 3) = 0 ⇔  Vậy, M  ;  0 0 3    x = 4 32   0  4
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 116
GV.Lưu Huy Thưởng 0968.393.899
TUYỂN TẬP ĐỀ THI ĐẠI HỌC TỪ NĂM 2009 HT 186. x +
(ĐH A – 2009) Cho hàm số 2 y =
(1) . Viết phương trình tiếp tuyến của đồ thị hàm 2x + 3
số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B sao cho tam
giác OAB cân tại gốc tọa độ O. Giải Ta có, O
∆ AB vuông cân tại O suy ra hệ số góc của tiếp tuyến bằng 1 ± −1 x  = −2
Gọi tọa độ tiếp điểm là M(x ;y ), ta có:  0 = ±1 ⇔ o o 2 x  = −1 (2x + 3)  0 o  TH1: Với x = 1
− ,y = 1 Phương trình tiếp tuyến y = x
− (loại vì đi qua gốc tọa độ O nên không 0 0 tồn tại O ∆ AB ) TH2: x = 2
− ;y = 0 Phương trình tiếp tuyến y = x
− − 2(t / m) 0 0 KL: y = x − − 2
HT 187. (ĐH B – 2009) Cho hàm số: 4 2
y = 2x − 4x (1) .Với giá trị nào của , m phương trình 2 2
x x − 2 = m có đúng 6 nghiệm thực phân biệt. Đ/s: 0 < m < 1
HT 188. (ĐH D – 2009) Cho hàm số 4 2
y = x − (3m + 2)x + 3m có đồ thị là (C ) với m là tham số. Tìm m
m để đường thẳng y = 1
− cắt đồ thị (C ) tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2. m Giải
Phương trình hoành độ giao điểm của (C )và đường thẳng 4 2 y = 1
− ;x − (3m + 2)x + 3m = 1 − m Đặt 2
t = x ,t ≥ 0 Phương trình trở thành: 2
t − (3m + 2)t + 3m + 1 = 0
⇔ t = 1 hoặc t = 3m + 1 0
 < 3m + 1 < 4
Yêu cầu bài toán tương đương với:  1  ⇔ −
< m < 1,m ≠ 0 3  m + 1 ≠ 1  3
HT 189. (ĐH A – 2010) Cho hàm số 3 2
y = x − 2x + (1 − m)x + m (1), với m là tham số thực. Tìm
m để đồ thị (1) cắt trục hoành tại 3 điểm phân biệt có hoành độ x , x , x thỏa mãn điều kiện: 1 2 3
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 117
GV.Lưu Huy Thưởng 0968.393.899 2 2 2
x + x + x < 4 1 2 3 Giải
Phương trình hoành độ giao điểm: 3 2
x − 2x + (1 − m)x + m = 0 x = 1 2 (x 1)(x x m) 0  ⇔ − − − = ⇔  2
x − x − m = 0(*) 
Đồ thị hàm số (1) cắt trục hoành tại 3 điểm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt, khác 1. Kí hiệu, 2
g(x) = x − x − m;x = 1;x và x là các nghiệm của (*). 1 2 3   ∆ > 0 1 + 4m > 0   1
Yêu cầu bài toán khi và chỉ khi:   g  (1) ≠ 0 ⇔  m − ≠ 0 ⇔ −
< m < 1 và m ≠ 0   4 2 2  x  + x < 3 1  + 2m < 3 2 3   HT 190. 2x + 1
(ĐH B – 2010) Cho hàm số y =
(C ) . Tìm m để đường thẳng y = 2 − x + m x + 1
cắt đồ thị (C )tại hai điểm A và B sao cho tam giác OAB có diện tích bằng 3 (O là gốc tọa độ). Giải
Phương trình hoành độ giao điểm: 2x + 1 = −2x + m x + 1
⇔ 2x + 1 = (x + 1)( 2
− x + m) (do x = 1
− không là nghiệm của phương trình) 2
⇔ 2x + (4 − m)x + 1 − m = 0 (1) 2
∆ = m + 8 > 0 với mọi ,
m suy ra đường thẳng y = 2
− x + m luôn cắt đồ thị (C) tại hai điểm
phân biệt A, B với mọi m Gọi (
A x ;y ),B(x ;y ) trong đó x ,x là các nghiệm của (1): y = −2x + m và y = −2x + m 1 2 2 2 1 2 1 1 2 2 m 2 Ta có: 5(m + 8) d = và 2 2 2
AB = (x − x ) + (y − y ) = 5(x + x ) − 20x x = (O,AB) 1 2 1 2 1 2 1 2 5 2 2 m m + 8 2 1 m m + 8 S = AB.d = , suy ra: = 3 ⇔ m = ±2 O ∆ AB (O,AB) 2 4 4 HT 191.
(D – 2010) Cho hàm số 4 2 y = x −
− x + 6 (C ) . Viết phương trình tiếp tuyến của đồ
thị (C) biết tiếp tuyến vuông góc với đường thẳng 1 y = x − 1 Đ/s: y = 6 − x + 10 6
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 118
GV.Lưu Huy Thưởng 0968.393.899 HT 192. x − +
(A – 2011) Cho hàm số 1 y =
(C ) . Chứng minh rằng với mọi m đường thẳng 2x − 1
y = x + m luôn cắt đồ thị (C ) tại hai điểm phân biệt A và B. Gọi k ,k lần lượt là hệ số góc của tiếp 1 2
tuyến với (C )tại A và B. Tìm m để tổng k + k đạt giá trị lớn nhất. 1 2 Giải x
Hoành độ giao điểm của − +
d : y = x + m và (C) là nghiệm của phương trình: 1 x + m = 2x − 1
⇔ (x + m)(2x − 1) = x − + 1 (vì 1 x =
không là nghiệm của phương trình) 2 2
⇔ 2x + 2mx − m − 1 = 0 (*) 2
∆ ' = m + 2m + 2 > 0, ∀m. Suy ra d luôn cắt (C) tại hai điểm phân biệt với mọi m
Gọi x ,x là các nghiệm của (*), ta có: 1 2 2 1 1
4(x + x ) − 8x x − 4(x + x ) + 2 1 2 1 2 1 2 k + k = − − = − 1 2 2 2 2 (2x − 1) (2x − 1)   1 2
4x x − 2(x + x ) + 1  1 2 1 2  
Theo định lý Viet, suy ra: 2 2
k + k = −4m − 8m − 6 = −4(m + 1) − 2 ≤ −2 1 2
Suy ra: k + k lớn nhất bằng −2 , khi và chỉ khi m = −1. 1 2
HT 193. (B – 2011) Cho hàm số 4 2
y = x − 2(m + 1)x + m (1) (với m là tham số). Tìm m để đồ
thị hàm số (1) có ba điểm cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị
thuộc trục tung, B và C là hai điểm cực trị còn lại. Giải 3 2 y '
= 4x − 4(m + 1)x = 4x(x − m − 1) (x ) x = 0  y ' = 0 ⇔ (x )  2 x = m + 1 (1) 
Đồ thị hàm số có 3 điểm cực trị khi và chỉ khi (1) có hai nghiệm phân biệt khác 0 ⇔ m > 1 − (*) Khi đó: A m B ( 2 − m + m − − m − ) C ( 2 (0; ), 1; 1 , m + 1; m − − m − ) 1 Suy ra: 2 2
OA = BC ⇔ m = 4(m + 1) ⇔ m − 4m − 4 = 0
⇔ m = 2 ± 2 2 (thỏa mãn (*)). Vậy giá trị cần tìm: m = 2 ± 2 2 HT 194. 2x + 1
(D – 2011) Cho hàm số y =
(C ) . Tìm k để đường thẳng y = kx + 2k + 1 cắt đồ thị x + 1
(C ) tại hai điểm phân biệt ,
A B sao cho khoảng cách từ A và B đến trục hoành bằng nhau. Giải
Gọi d : y = kx + 2k + 1, suy ra hoành độ giao điểm của d với (C) là nghiệm của phương trình: 2x + 1 kx + 2k + 1 =
⇔ 2x + 1 = (x + 1)(kx + 2k + 1) (do x = 1 − không là nghiệm) x + 1 2
⇔ kx + (3k − 1)x + 2k = 0 (1).
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 119
GV.Lưu Huy Thưởng 0968.393.899
d cắt (C) tại hai điểm phân biệt ,
A B, khi và chỉ khi (1) có hai nghiệm phân biệt k  ≠ 0  k  ≠ 0 k  ≠ 0       ⇔  ⇔  ⇔ k  < 3 − 2 2  2 ∆ > 0 k  − 6k + 1 > 0     (*)   k  > 3 + 2 2  Khi đó, (
A x ;kx + 2k + 1) và B(x ;kx + 2k + 1) , x , x là nghiệm của (1). 1 1 2 2 1 2 d = d
⇔ kx + 2k + 1 = kx + 2k + 1 ( , A Ox ) (B,Ox ) 1 2
⇔ k(x + x ) + 4k + 2 = 0 (do x ≠ x ) 1 2 1 2
Áp dụng định lý Viet đối với (1), suy ra: (1 − 3k) + 4k + 2 = 0 ⇔ k = −3 (thỏa mãn (*))
Vậy giá trị cần tìm: k = −3
HT 195. (A,A1 – 2012) Cho hàm số 4 2 2
y = x − 2(m + 1)x + m (1), với m là tham số thực. Tìm m để
đồ thị hàm số (1) có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác vuông. Giải Ta có: 3 2
y ' = 4x − 4(m + 1)x = 4x(x − m − 1)
Đồ thị hàm số có 3 điểm cực trị khi và chỉ khi m + 1 > 0 ⇔ m > −1 (*)
Các điểm cực trị của đồ thị hàm số 2 (
A 0;m ),B (− m + 1; 2 − m − )
1 ,C ( m + 1;−2m − ) 1 Suy ra: AB = ( 2 − m + 1; (
− m + 1) ) và AC = ( 2 m + 1; ( − m + 1) )
Ta có: AB = AC nên tam giác ABC vuông khi và chỉ khi: AB.AC = 0 4
⇔ (m + 1) − (m + 1) = 0.Kết hợp (*), ta được m = 0
Đ/s: m = 0
HT 196. (B – 2012) Cho hàm số 3 2 3
y = x − 3mx + 3m (1), m là tham số thực. Tìm m để đồ thị
hàm số (1) có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 48. Giải Ta có: 2
y ' = 3x − 6mx;y ' = 0 ⇔ x = 0 ∨ x = 2m
Đồ thị hàm số có 2 điểm cực trị khi và chỉ khi m ≠ 0
Các điểm cực trị của đồ thị hàm số: A( 3 m ) B ( 3 0; 3 ; 2m; m − ) Suy ra: 3
OA = 3 m và d = 2 m (B,O ) A 4 S
= 48 ⇔ 3m = 48 ⇔ m = 2 ± (t / m (*)) O ∆ AB Đ/s:m = 2 ± HT 197. 2 2
(D – 2012) Cho hàm số 3 2 2 y =
x − mx − 2(3m − 1)x +
(1),m là tham số thực. Tìm m 3 3
để hàm số (1) có hai điểm cực trị x ;x sao cho: x x + 2(x + x ) = 1. 1 2 1 2 1 2 Giải Ta có: 2 2
y ' = 2x − 2mx − 2(3m − 1)
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 120
GV.Lưu Huy Thưởng 0968.393.899
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi phương trình y ' = 0 có hai nghiệm phân biệt 2 2 13 2 13
⇔ 13m − 4 > 0 ⇔ m > ∨ m < − 13 13
Ta có: x + x = m và 2
x x = 1 − 3m ; Do đó, 2
x x + 2(x + x ) = 1 ⇔ 1 − 3m + 2m = 1 1 2 1 2 1 2 1 2 2
⇔ m = 0 ∨ m =
So sánh điều kiện (*) ta được: 2 m = 3 3 Đ/s: 2 m = 3
HT 198. (A,A1 – 2013) Cho hàm số 3 2 y = x −
+ 3x + 3mx − 1 (1), với m là tham số thực. Tìm m để
hàm số (1) nghịch biến trên khoảng (0;+ ) ∞ Giải Ta có: 2 y ' = 3
− x + 6x + 3m
Hàm số (1) nghịch biến trên khoảng (0;+ )
∞ khi và chỉ khi y ' ≤ 0, x ∀ > 0 2
⇔ m ≤ x − 2x, ∀x > 0 Xét: 2
f (x) = x − 2x với x > 0 . Ta có: f '(x) = 2x − 2; f '(x) = 0 ⇔ x = 1
Lập bảng biến thiên (nhớ lập nhé) ta được giá trị m thỏa mãn yêu cầu bài toán: m ≤ −1 Đ/s: m ≤ 1 −
HT 199. (B – 2013) Cho hàm số 3 2
y = 2x − 3(m + 1)x + 6mx (1), với m là tham số thực. Tìm m để
đồ thị hàm số (1) có hai điểm cực trị A, B sao cho đường thẳng AB vuông góc với đường thẳng y = x + 2. Giải Ta có: 2
y ' = 6x − 6(m + 1)x + 6m;y ' = 0 ⇔ x = 1 ∨ x = m
Điều kiện để đồ thị hàm số có hai điểm cực trị là m ≠ 1
Ta có: 2 điểm cực trị của đồ thị hàm số khi đó 3 2 (
A 1; 3m − 1);B( ; m m − + 3m ).
Hệ số góc của đường thẳng AB là 2 k = ( − m − 1)
Đường thẳng AB vuông góc với đường thẳng y = x + 2 khi và chỉ khi k = 1 −
⇔ m = 0 ∨ m = 2 . Vậy giá trị m cần tìm m = 0;m = 2
HT 200. (D – 2013) Cho hàm số 3 2
y = 2x − 3mx + (m − 1)x + 1 (1), với m là tham số thực. Tìm m
để đường thẳng y = x
− + 1 cắt đồ thị hàm số (1) tại ba điểm phân biệt. Giải
Phương trình hoành độ giao điểm của đồ thị hàm số (1) với đường thẳng y = x − + 1 là: x = 0 3 2
2x − 3mx + (m − 1)x + 1 = x − + 1  ⇔  2
2x − 3mx + m = 0 (*) 
Yêu cầu của bài toán ⇔ phương trình (*) có hai nghiệm phân biệt khác 0.
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 121
GV.Lưu Huy Thưởng 0968.393.899   2 m < 0 9
 m − 8m > 0   ⇔  ⇔  8 m  ≠ 0 m  >   9 Đ/s: 8 m < 0;m > 9
UPDATING………………
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ ĐẾN BẾN Page 122

Phân dạng bài tập và lời giải chi tiết chuyên đề hàm số – Lưu Huy Thưởng Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số