Phân dạng các bài toán tích phân – Phạm Minh Tứ Toán 12

Phân dạng các bài toán tích phân – Phạm Minh Tứ Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

82 41 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

42 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
TÍCH PHÂN
I. Khái niệm tích phân
1. Diện tích hình thang cong .
• Giới thiệu cho học sinh về cách tính diện tích của một hình thang cong
• Từ đó suy ra công thức :
( ) ( )
( )
0
0
0
0
lim
xx
Sx Sx
fx
xx
→
−
=
−
2. Định nghĩa tích phân
• Cho hàm f liên túc trên một khoảng K và a, b là hai số bất kỳ thuộc K. Nếu F
là một nguyên hàm của f trên K thì hiệu số : F(b)-F(a) được gọi là tích phân
của f đi từ a đến b , ký hiệu là :
()
b
a
f x dx
∫
• Có nghĩa là :
( ) ( )
()
b
a
f x dx F b F a= −
∫
• Gọi F(x) là một nguyên hàm của f(x) và
( ) ( ) ( )
b
Fx Fb Fa
a
= −
thì :
( ) ( ) ( )
()
b
a
b
f x dx F x F b F a
a
= = −
∫
• Trong đó :
- a : là cận trên , b là cận dưới
- f(x) gọi là hàm số dưới dấu tích phân
- dx : gọi là vi phân của đối số
-f(x)dx : Gọi là biểu thức dưới dấu tích phân
II. Tính chất của tích phân
Giả sử cho hai hàm số f và g liên tục trên K , a,b,c là ba số bất kỳ thuộc K . Khi đó ta
có :
1.
() 0
a
a
f x dx =
∫
2.
() ()
ba
ab
f x dx f x dx= −
∫∫
. ( Gọi là tích chất đổi cận )
3.
() () ()
b cb
a ac
f x dx f x dx f x dx= +
∫∫∫
4.
. ( Tích phân củ một tổng hoặc hiệu hai tích
phân bằng tổng hoặc hiệu hai tích phân ) .
5.
() . ()
bb
aa
kf x dx k f x dx=
∫∫
. ( Hằng số k trong dấu tích phân , có thể đưa ra ngoài dấu
tích phân được )
Ngoài 5 tính chất trên , người ta còn chứng minh được một số tính chất khác như :
6 . Nếu f(x)
[ ]
0;x ab≥∀∈
thì :
[ ]
() 0 ;
b
a
f x dx x a b≥∀∈
∫
7. Nếu :
[ ]
; : () () () ()
bb
aa
x a b f x g x f x dx g x dx∀∈ ≥ ⇒ ≥
∫∫
. ( Bất đẳng thức trong tích
phân )
8. Nếu :
[ ]
;x ab∀∈
và với hai số M,N ta luôn có :
()M fx N≤≤
. Thì :
( ) ( )
()
b
a
Mb a fxdx Nb a−≤ ≤ −
∫
. ( Tính chất giá trị trung bình của tích phân )
III. CÁC PHƯƠNG PHÁP TÍNH TÍCH PHÂN
A. PHƯƠNG PHÁP PHÂN TÍCH
1.Trong phương pháp này , chúng ta cẩn :
• Kỹ năng : Cần biết phân tích f(x) thành tổng , hiệu , tích , thương của nhiều
hàm số khác , mà ta có thể sử dụng được trực tiếp bảng nguyên hàm cơ bản
tìm nguyên hàm của chúng .
• Kiến thức : Như đã trình bày trong phần " Nguyên hàm " , cần phải nắm trắc
các kiến thức về Vi phân , các công thức về phép toán lũy thừa , phép toán căn
bậc n của một số và biểu diễn chúng dưới dạng lũy thừa với số mũ hữu tỷ .
2. Ví dụ áp dụng
Ví dụ 1: Tính các tích phân sau
a/
(
)
4
2
2
1
2 11
1
xx
dx
x
−+
+
∫
b/
( )
1
2
3
0
1
x
dx
x +
∫
c/
( )
( )
3
1
2 2 ln 1
21
xx x x
dx
xx
− ++
+
∫
d/
2
32
42
2
1
21
xxx
dx
xx
+ −+
−+
∫
Giải
a/
(
)
4
22 2
22
2
2 22 2
11 1
2 11
2 11
21
1 11 1
xx
xx x x x
dx dx x x dx
x xx x
−+


−+
= + = −+



+ ++ +


∫∫ ∫
(
)
(
)
(
)
22
2
22 2 2 2
11
22
13
1 1 1 1 1 52
11
22
x dx dx x x⇒ − −+ += − + + =+ −
∫∫
b/
( )
( )
( )
( )
( )
( ) ( ) ( ) ( )
22
11 1 1
2
3 3 3 33 23
00 0 0
11 1
11 1 1 1
22
1
1 1 1 11 11
xx
xx
dx dx dx dx
x
x x x xx xx

+− +
+
= = −+ =−+

+
+ + + ++ +
+


∫∫ ∫ ∫
( ) ( )
( )
( )
( )
( )
1 11
23 2
0 00
11 1
1 11
1 11 3
2 ln 1 2 ln 2
00 0
1 12 8
11 1
dx dx dx
Ix
xx
xx x
+ ++
⇒= − + = + + − = +
++
++ +
∫ ∫∫
c/
( )
( ) ( )
( )
( )
( )
( )
( )
33 3
11 1
2 2 ln 1 ln 1 ln 1
11
1
2
21 1 1 1 2
xx x x x x
x
dx dx x dx
x
x x x x xx

− ++ + +
−

= + = −+

+ ++ +

∫∫ ∫
( )
( )
( ) ( ) ( )
33
3
2
11
ln 1
33
2
1 1 ln 1
11
3
1
x
I x dx d
x x x x
x
+

⇒= − + + = − + + =

+

∫∫
( )
22
2 3 4 ln 1 3 ln 2= −+ + −
d/
( )
( )
( )
3
2 2 22
32
2
42 4
2
2
2
2 2 22
4
11 1 2
21 4 21
1
1
x x dx
x x x dx
dx dx
xx xx
x
x

−
+ −+

= ++
−+ −+
−

−

∫ ∫ ∫∫
( )
( )
42
2
22 2
42
22 2
21
1 111 111
2
4 2 11 411
21
dx x
dx dx
xx xx
xx
−+

= + −+ −

−+ −+
−+

∫∫ ∫
=
( )
2
2
22 2
1 1 1 11 1 1
ln 1 ln ln
4 2 1 2 11 1
22 2
xx
x
x xx x
− −
− + +− − − =

+ −+ +

Ví dụ 2. Tính các tích phân sau
a/
( )
2
2
0
2sin sin 1
1 osx
xx
dx
c
π
−
+
∫
b/
3
22
0
sin 2
2sin 3cos
x
dx
xx
π
+
∫
c/
1
2
1
12
ln
42
x
dx
xx
−
+


−−

∫
d/
4
2
0
sinx+ 1+tanx
os
dx
cx
π
∫
Ví dụ 3. Tính các tích phân sau
a/
2
3
3
ln 1
ln
e
e
x
dx
xx
+
∫
b/
( )
2
2
2
1
1
21
x
dx
xx
−
+
∫
c/
3
4
2
6
4 sin 2
sin 2
x
dx
x
π
π
+
∫
d/
3
0
sin3 . osxdxxc
π
∫
B. PHƯƠNG PHÁP ĐỔI BIẾN SỐ
I. Phương pháp đổi biến số dạng 1.
Để tính tích phân dạng này , ta cần thực hiện theo các bước sau
1/ Quy tắc :
• Bước 1: Đặt x=v(t)
• Bước 2: Tính vi phân hai vế và đổi cận
• Bước 3: Phân tích f(x)dx=f(v(t))v'(t)dt
• Bước 4: Tính
()
()
()
( ) () ()
()
vb
b
a va
vb
f x dx g t dt G t
va
= =
∫∫
• Bước 5: Kết luận : I=
()
()
()
vb
Gt
va
2/ Nhận dạng : ( Xem lại phần nguyên hàm )
* Chú ý :
a. Các dấu hiệu dẫn tới việc lựa chọn ẩn phụ kiểu trên thông thường là :
Dấu hiệu
Cách chọn
22
ax−
sin
22
ost 0 t
xa t t
x ac
ππ
π
= ↔− ≤ ≤
= ↔ ≤≤
22
xa−
[ ]
;
sin 2 2
0; \
ost 2
a
xt
t
a
xt
c
ππ
π
π

= ↔∈−



= ↔∈


22
ax+
( )
tan ;
22
cot 0;
xa t t
xa t t
ππ
π

= ↔∈−


= ↔∈
ax ax
ax ax
+−
∨
−+
x=a.cos2t
( )( )
xabx−−
x=a+
( )
2
sin
ba t
−
b. Quan trọng nhất là các em phải nhận ra dạng :
- Ví dụ : Trong dạng phân thức hữu tỷ :
*
( )
22
2
2
1 1 11
0
ax
b
a x+
2a 2
dx dx du
bx c a u k
a
ββ β
αα α
∆< = =
++ +


−∆


+






∫∫ ∫
Với :
b
x+ , ,
2a 2
u k du dx
a

−∆
= = =



.
* áp dụng để giải bài toán tổng quát :
( )
( )
21
22
k
dx
kZ
ax
β
α
+
∈
+
∫
.
*
( )
( )
22
2
11
22
31
dx dx
xx
x
ββ
αα
=
+−
−−
∫∫
. Từ đó suy ra cách đặt :
1 3sinxt−=
3/ Một số ví dụ áp dụng :
Ví dụ 1: Tính các tích phân sau
a/
1
2
0
1 x dx−
∫
b/
1
2
2
0
1
12
dx
x−
∫
c/
2
2
1
1
32
dx
xx+−
∫
Giải
a/ Đặt x=sint với :
;
22
t
ππ

∈−


• Suy ra : dx=costdt và :
0sin0 0
1 sin 1
2
x tt
x tt
π
= ↔ = →=
=↔ =→=
• Do đó : f(x)dx=
( )
2 22
1
1 1 sin ostdt=cos 1 os2t
2
x dx tc tdt c dt−=− =+
• Vậy :
( )
1
2
00
1 os2t
11 1 1 1
( ) sin 2
2
2 2 2 22 2 4
0
c dt
f x dx t
t
π
π
ππ
+
−

= = + = −=


∫∫
b/ Đặt : x =
1
sin ;
22
2
tt
ππ

∈−


• Suy ra : dx =
x=0 sint=0 t=0
1
ostdt
1 11
x= sin
2
2
2 22
c
tt
π
↔→
⇒
↔ = →=
• Do đó :
11
22
22
2
2
00 0 0
2
1 11 1 1 1 1 1
ostdt
2
1
2 2 2 2 2 22
1
12
1 sin
0
2
2
dx dx c dt t
x
t
x
ππ
π
π
= = = = =
−

−
−


∫∫ ∫ ∫
c/ Vì :
( )
2
2
32 4 1xx x+ −=−−
. Cho nên :
• Đặt :
( )
1
1 2sin ; sin *
22 2
x
x tt t
ππ
−

−= ∈− ↔ =


• Suy ra : dx= 2 costdt và :
11
1 sin 0 0
2
0; ost>0
21 1
6
2 sin
22 6
xt t
tc
xt t
π
π
−
=↔ = = →=

⇒∈ →

−

= ↔ = = →=
• Do đó : f(x)dx=
( )
( )
22
2
11 1
2cos
32
4 1 sin
41
dx dx tdt dt
xx
t
x
= = =
+−
−
−−
• Vậy :
2
6
10
()
6
6
0
f x dx dt t
π
π
π
= = =
∫∫
Ví dụ 2: Tính các tích phân sau
a/
2
2
1
12 4 5x x dx−−
∫
b/
1
2
0
1
1
dx
xx++
∫
c/
5
2
2
1
47
dx
xx−+
∫
d/
( )
2
2
2
0
b
ax
dx
ax
−
+
∫
* Chú ý : Để tính tích phân dạng có chứa
(
)
2 22
,x aa x+−
, ta còn sử dụng phương
pháp đổi biến số : u(x)=g(x,t)
Ví dụ 1 : Tính tích phân sau
1
2
0
1
1
dx
x +
∫
Giải :
• Đặt :
2
2
1
1
2
t
x xt x
t
−
+= −⇒ =
• Khi đó :
2
2
0 1; 1 1 2
1
2
x tx t
t
dx
t
= →=− =→=−
+
=
• Do vậy :
( )
1 12 12
2
22
2
01 1
1 21
12
. ln ln 2 1
12
1
1
t t dt
dx dt t
tt t
x
−−
−−
−+
−
= == =−−
+
−
+
∫∫ ∫
Ví dụ 2: Tính tích phân :
1
22
0
1I x x dx= −
∫
Giải
• Đặt : t=sinx , suy ra dt=cosxdx và khi x=0,t=0 ; Khi x=1 , t=
2
π
• Do đó : f(x)dx=
2 2 2 2 22
1 1 os4t
1 sin . 1 sin ostdt=sin cos
42
c
x x dx t tc t tdt dt
−

−= − =


• Vậy : I=
( )
1
2
00
1 11 1
( ) 1 os4t sin 4
2
8 8
4 8 2 16
0
f x dx c dt t t
π
π
ππ

=−=− ==


∫∫
II. Đổi biến số dạng 2
1. Quy tắc : ( Ta tính tích phân bằng phương pháp đổi biến số dạng 2 theo các bước
sau : )
• Bước 1: Khéo léo chọn một hàm số u(x) và đặt nó bằng t : t=u(x) .
• Bước 2: Tính vi phân hai vế và đổi cận : dt=u'(x)dx
• Bước 3: Ta phân tích f(x)dx = g[u(x)]u'(x)dx = g(t)dt .
• Bước 4: Tính
()
()
()
( ) () ()
()
ub
b
a ua
ub
f x dx g t dt G t
ua
= =
∫∫
• Kết luận : I=
()
()
()
ub
Gt
ua
2. Nhận dạng :
TÍCH PHÂN HÀM PHÂN THỨC HỮU TỶ
A. DẠNG : I=
( )
()
0
ax+b
Px
dx a
β
α
≠
∫
* Chú ý đến công thức :
ln ax+b
ax+b
mm
dx
a
β
α
β
α
=
∫
. Và nếu bậc của P(x) cao hơn hoắc
bằng 2 thì ta chia tử cho mẫu dẫn đến
() 1
() ()
ax+b ax+b ax+b
Px m
dx Q x dx Q x dx m dx
ββ β β
αα α α
=+= +
∫∫ ∫ ∫
Ví dụ 1 : Tính tích phân : I=
2
3
1
23
x
dx
x +
∫
Giải
Ta có :
3
2
1 3 9 27 1
()
232 4 8823
x
fx x x
xx
= = − +−
++
Do đó :
22
3
2 32
11
2
1 3 9 27 1 1 3 9 27 13 27
ln 2 3 ln35
1
2 3 2 4 8 8 2 3 3 8 8 16 6
16
x
dx x x dx x x x x
xx

= − +− = − + − + =− −

++

∫∫
Ví dụ 2: Tính tích phân : I=
3
2
5
5
1
x
dx
x
−
+
∫
Giải
Ta có : f(x)=
2
54
1
11
x
x
xx
−
= −−
++
.
Do đó :
33
2
2
55
3
5 4 1 51
1 4ln 1 5 1 4ln
1 12 4
5
x
dx x dx x x x
xx

−+

= −− = − − + = −+



++


∫∫
B. DẠNG :
2
()
ax
Px
dx
bx c
β
α
++
∫
1. Tam thức :
2
( ) axf x bx c= ++
có hai nghiệm phân biệt
Công thức cần lưu ý :
'( )
ln ( )
()
ux
dx u x
ux
β
α
β
α
=
∫
Ta có hai cách
Cách 1: ( Hệ số bất định )
Cách 2: ( Nhẩy tầng lầu )
Ví dụ 3: Tính tích phân : I=
1
2
0
4 11
56
x
dx
xx
+
++
∫
.
Giải
Cách 1: ( Hệ số bất định )
Ta có : f(x)=
( ) ( )
2
32
4 11 4 11
5 6 ( 2)( 3) 2 3 ( 2)( 3)
Ax Bx
x x AB
xx xx x x xx
++ +
++
= =+=
++ ++ + + ++
Thay x=-2 vào hai tử số : 3=A và thay x=-3 vào hai tử số : -1= -B suy ra B=1
Do đó : f(x)=
31
23xx
+
++
Vậy :
( )
11
2
00
1
4 11 3 1
3ln 2 ln 3 2ln3 ln 2
0
56 2 3
x
dx dx
x x
xx x x
+

= + = ++ + = −

++ + +

∫∫
Cách 2: ( Nhẩy tầng lầu )
Ta có : f(x)=
( )
( )( )
22 2
22 5 1
25 1 25 1 1
2. 2.
56 56 2 3 56 2 3
x
xx
xx xx x x xx x x
++
++
= + = +−
++ ++ + + ++ + +
Do đó :
I=
11
2
2
00
1
25 1 1 2
( ) 2. 2ln 5 6 ln 2ln3 ln 2
0
56 2 3 3
xx
f x dx dx
x x
xxxx x
+ +

= + − = + ++ = −


++++ +


∫∫
2. Tam thức :
2
( ) axf x bx c= ++
có hai nghiệm kép
Công thức cần chú ý :
( )
'( )
ln ( )
()
u x dx
ux
ux
β
α
β
α
=
∫
Thông thừơng ta đặt (x+b/2a)=t .
Ví dụ 4 : Tính tích phân sau : I=
3
3
2
0
21
x
dx
xx++
∫
Giải
Ta có :
( )
33
33
2
2
00
21
1
xx
dx dx
xx
x
=
++
+
∫∫
Đặt : t=x+1 suy ra : dx=dt ; x=t-1 và : khi x=0 thì t=1 ; khi x=3 thì t=4 .
Do đó :
( )
( )
3
3 44
3
2
2
22
0 11
4
1
31 1 1 3
3 3 ln 2ln 2
1
22
1
t
x
dx dt t dt t t t
t tt t
x
−

= = −+ − = − + + = −


+
∫ ∫∫
Ví dụ 5: Tính tích phân sau : I=
1
2
0
4
4 41
x
dx
xx−+
∫
Giải
Ta có :
( )
2
2
44
4 41
21
xx
xx
x
=
−+
−
Đặt : t= 2x-1 suy ra :
01
1
2;
11
2
xt
dt dx dx dt
xt
= ↔=−
= →=
=↔=
Do đó :
( )
( )
1 11 1
2
2 22
0 01 1
1
4. 1
1
4 4 1 11 1
2
ln 2
1
4 41 2
21
t
xx
dx dx dt dt t
x x t tt t
x
−−
+

= = =+ =−=−

−
−+

−
∫ ∫∫ ∫
3. Tam thức :
2
( ) axf x bx c= ++
vô nghiệm :
Ta viết : f(x)=
( )
2
22
2
() ()
2
;
2
22
b
ux
Px Px
a
au k
b
k
ax
a
aa
= +
=

+
−∆

−∆

=

++






Khi đó : Đặt u= ktant
Ví dụ 6: Tính tích phân : I=
2
2
0
45
x
dx
xx++
∫
Giải
• Ta có :
( )
22
2
2
00
45
21
xx
dx dx
xx
x
=
++
++
∫∫
• Đặt : x+2=tant , suy ra : dx=
2
0 tan 2
1
;
2 tan 4
os
xt
dt
xt
ct
=↔=
⇒
=↔=
• Do đó :
( )
( )
( )
22
11
2
2
2
22
1
0
tan 2 sin
2 ln ost 2 1
1 tan os ost
21
tt
tt
t
x t dt t
dx dt c t
t
tc t c
x
−

= = −=− −

+

++
∫∫ ∫
Từ :
22
1
22
2
11
tan 2 1 tan 5 os ost
5
5
11
tan 4 1 tan 17 os ost
17
17
t t ct c
t t ct c
= ↔+ = ↔ = → =
= ↔+ = ↔ = → =
• Vậy :
( ) ( ) ( )
( )
2
2
2 2 1
1 21
1
1
ost
ln ost 2 ln ost 2 ln cos 2 ln 2
cost
t
c
c t c t t t tt
t

− − =− −− − =− +−

•
( ) ( ) ( )
2
21
1
ost
1 15
ln 2 2 arctan4-arctan2 ln . 5 2 arctan4-arctan2 ln
cost 2 17
17
c
tt⇔− + − = − = −
Ví dụ 7: Tính tích phân sau : I=
2
32
2
0
2 49
4
xxx
dx
x
+ ++
+
∫
Giải
• Ta có :
32
22
2 49 1
2
44
xxx
x
xx
+ ++
=++
++
• Do đó :
22 2
32
2
22 2
00 0
2
2 49 1 1
2 26
0
4 42
4
x x x dx
dx x dx x x J
xx x
+ ++

= ++ = + + =+

++ +

∫∫ ∫
(1)
Tính tích phân J=
2
2
0
1
4
dx
x +
∫
• Đặt : x=2tant suy ra : dx =
2
00
2
; 0; ost>0
os 4
2
4
xt
dt t c
ct
xt
π
π
= →=

↔∈ →

= →=

• Khi đó :
2
44
2 22
00 0
1 112 1 1
4
4 4 1 tan os 2 2 8
0
dx dt
dt t
x tc t
ππ
π
π
= = = =
++
∫∫ ∫
• Thay vào (1) :
6
8
I
π
= +
C. DẠNG :
32
()
ax
Px
dx
bx cx d
β
α
+ ++
∫
1. Đa thức : f(x)=
( )
32
ax 0bx cx d a+ ++ ≠
có một nghiệm bội ba
Công thức cần chú ý :
1
1 11
.
1
mm
dx
x mx
β
α
β
α
−
=
−
∫
Ví dụ 8: Tính tích phân : I=
( )
1
3
0
1
x
dx
x +
∫
Giải
Cách 1:
• Đặt : x+1=t , suy ra x=t-1 và : khi x=0 thì t=1 ; khi x=1 thì t=2
• Do đó :
( )
1 22
3
3 23 2
0 11
2
1 1 1 1 11 1
1
28
1
xt
dx dt dt
t tt t t
x
−

= = − =−+ =


+
∫ ∫∫
Cách 2:
• Ta có :
( )
( )
( )
( ) ( )
3 3 23
11
11
1 1 11
x
x
x x xx
+−
= = −
+ + ++
• Do đó :
( ) ( ) ( ) ( )
11
3 23 2
00
1
1 1 111 1
0
12 8
1 11 1
x
dx dx
x
x xx x

= − =−+ =

+
+ ++ +


∫∫
Ví dụ 9 : Tính tích phân : I=
( )
0
4
3
1
1
x
dx
x
−
−
∫
.
Giải
• Đặt : x-1=t , suy ra : x=t+1 và : khi x=-1 thì t=-2 và khi x=0 thì t=-1 .
• Do đó :
( )
( )
4
0 11 1
4 432
3
3 3 23
1 22 2
1
4 6 41 641
4
1
t
x tttt
dx dt dt t dt
t t tt t
x
−− −
− −− −
+
+ + ++

= = = ++ + +


−
∫ ∫∫ ∫
•
1
2
23 2
2
1
6 4 1 1 4 1 1 33
4 4 6ln 6ln 2
2
2 28
t dt
t t t
tt t t t
−
−
−

⇔ +++ + = + + −− = −

−

∫
2. Đa thức : f(x)=
( )
32
ax 0bx cx d a+ ++ ≠
có hai nghiệm :
Có hai cách giải : Hệ số bất định và phương pháp nhẩy tầng lầu
Ví dụ 10 : Tính tích phân sau : I=
( )( )
3
3
2
1
11
dx
xx−+
∫
Giải
Cách 1. ( Phương pháp hệ số bất định )
• Ta có :
( )( )
( )
( )
( ) ( )( ) ( )
( )( )
2
22 2
1 11 1
1
11
11 1 11
Ax Bx x Cx
AB C
xx
xx x xx
+ + − ++ −
=++ =
−+
−+ + −+
• Thay hai nghiệm mẫu số vào hai tử số :
1
14
4
12 1
2
A
A
C
C
=
=
⇔

= −
= −
. Khi đó (1)
( ) ( )
( )( )
2
2
2
11 1
1 11
42 4
11
A Bx A Cx A B C
ABC B AC
xx
+ + + +−−
⇔ ⇒ − − =⇔ = − −= + −=−
−+
• Do đó :
( )( )
( )
( )
33
22
22
1 11 1 1 1 1
..
4 14 1 2
11 1
dx dx
xx
xx x

= +−


−+
−+ +

∫∫
( )( )
( )
3
1 11 1 3
ln 1 1 . ln8 ln 2
2
4 21 4 4
I xx
x

⇔= − ++ = =

+

Cách 2:
• Đặt : t=x+1, suy ra : x=t-1 và khi x=2 thì t=3 ; khi x=3 thì t=4 .
• Khi đó : I=
( )( )
( )
( )
( )
( )
3 4 4 44
2
22
2 3 3 23
2
1 1 11 1
22 2 2 2
11
tt
dt
dx dt dt dt
tt tt tt t
xx

−−
= = = −


−− −
−+

∫ ∫ ∫ ∫∫
44
23
4
11 1 1 1 1 2 1 3
ln ln ln 2
3
22 2 4 2 4
t
I dt dt t
tt t t

−

⇔= − − = − =



−



∫∫
Hoặc :
( )
( )
2
22 2
32 32 32 32 2 32 2
34
32
1 1344 341 34132
2 2 4 2 24 24
tt
t
tt tt tt
tt tt tt tt t tt tt
−
+


−− − −

= − = − = −+



−− − − −



• Do đó : I=
4
2
32
32 2
3
4
3 4 13 2 1 2 3
ln 2 3ln ln 2
3
24 4 4
tt
dt t t t
t t tt t

−

− + = −− − =



−



∫
Hoặc :
( )
( )
( )
22
22 2 2
4
1 1 11 2 11 12
24 2 42 42
tt
t
tt tt t t t tt

−−
+


= = − = −−


− −− −


• Do đó :
I=
4
2
3
4
1 1 12 1 2 2 1 11 12 1 1
ln ln ln ln3 ln 2
3
4 2 4 4
22 33 4 6
t
dt
t tt t t
−

−− = + = + − − = − −


−


∫
Ví dụ 11: Tính tích phân sau : I=
( ) ( )
3
2
2
2
12
x
dx
xx−+
∫
Giải
Đặt : x-1=t , suy ra : x=t+1 , dx=dt và : khi x=2 thì t=1 ; x=3 thì t=2 .
Do đó :
( ) ( )
( )
( )
( )
2
3 22
22
2
22
2 11
1
21
33
12
t
x tt
dx dt dt
tt tt
xx
+
++
= =
++
−+
∫ ∫∫
Cách 1; ( Hệ số bất định )
Ta có :
( )
( )( )
( )
( ) ( )
( )
22
2
22 2 2
3 33
21
3 33 3
At B t Ct A C t A B t B
t t At B C
tt t t tt tt
+ ++ + + + +
++ +
= += =
+ ++ +
Đồng nhất hệ số hai tử số :
( )
2
22
1
3
1
5 2 1 1 3 41
32
9 3 9 93
31
4
9
B
AC
tt t
AB A
tt t t
B
C
=
+=
++ +

+=⇔ =⇒ = +

++

=
=
Do đó :
( )
22
2
22
11
2
2 1 1 1 3 4 1 1 3 4 17 4 7
ln ln 3 ln5 ln 2
1
3 9 9 3 9 9 69 9
tt
dt dt
t t
tt tt t t
++

= + + = −+ + =+ −


++


∫∫
Cách 2:
• Ta có :
( ) ( )
( )
( )
22
22 2 2
2 32 322 32 2
9
211363136 3 136 1
33 3 3 3 3 3 3 9 3
tt
tt tt tt tt
tt t t t t tt t t tt


−−


++ ++ + +


= = += +



+ + ++ + +





22
32 2 32 2
13 6 11 1 3 1 3 6 11 11 3
3 3 9 39 3 3 9 39
tt t tt
tt t t tt t tt


+ −+

= +−= +−−



++ ++

 

• Vậy :
( )
22
22
32
2 32 2
11
2
2 1 13 6 1 1 1 3 1 1 3 3
ln 3 ln
1
3 3 3 9 3 3 27
tt tt t
dt dt
t t
tt t t t tt t t



++ +
+

= + −+ = + + −





+ ++





∫∫
• Do đó I=
17 4 7
ln5 ln 2
69 9
+−
3. Đa thức : f(x)=
( )
32
ax 0bx cx d a+ ++ ≠
có ba nghiệm :
Ví dụ 12: Tính tích phân sau : I=
( )
3
2
2
1
1
dx
xx−
∫
Cách 1: ( Hệ số bất định )
• Ta có :
f(x)=
( )
( )( )
( )
( ) ( )
( )( )
2
2
111
11
11 11 11
1
Ax Bxx Cxx
AB C
xx x x x x xx x
xx
−+++−
= =++=
−+ − + −+
−
• Đồng nhất hệ số hai tử số bằng cách thay các nghiệm : x=0;x=1 và x=-1 vào
hai tử ta có :
1
01
1 11 1 1 1
1 1 2 ()
2 2 12 1
1 12
1
2
A
xA
x C B fx
xx x
xB
C
= −
= →=−


=−→= ⇔ = ⇒ =− + +


−+


=→=
=
• Vậy :
( )
( )( )
( )
33
2
22
3
1 11 1 1 1 5 3
ln 1 1 ln ln 2 ln3
2
21 1 2 2 2
1
dx dx x x x
xx x
xx


= + − = − +− = −



−+
−


∫∫
Cách 2: ( Phương pháp nhẩy lầu )
Ta có :
( )
( )
( )
22
22
22
1
1 1 12 1
1 21
11
xx
xx
xxxx
xx xx
−−
= = −= −
−−
−−
Do đó :
( )
( )
3 33
2
2
2
2 22
3
1 12 1 1 5 3
ln 1 ln ln 2 ln3
2
21 2 2
2
1
xdx
dx dx
x x
xx
xx

= − = −− = −

−
−

∫ ∫∫
Ví dụ 13: Tính tích phân sau : I=
( )
4
2
3
1
4
x
dx
xx
+
−
∫
Cách 1:
Ta có :
( )
( )( )
( )
( ) ( )
( )
2
22
422
11
22 22
44
Ax Bxx Cxx
x x AB C
xx x x x x
xx xx
−+++−
++
= =++=
−+ − +
−−
Thay các nghiệm của mẫu số vào hai tử số :
Khi x=0 : 1= -4A suy ra : A=-1/4
Khi x=-2 : -1= 8C suy ra C=-1/8
Khi x=2 : 3= 8B suy ra : B=3/8 .
Do đó : f(x) =
11 1 1 3 1
4 8 28 2xx x

−− +

−+

Vậy :
( )
4 33 3
2
3 22 2
3
1 11 1 1 3 1 1 1 3
ln ln 2 ln 2
2
4 8282 4 8 8
4
x
dx dx dx dx x x x
xx x
xx
+

=− − + =− − −+ + =

−+
−

∫ ∫∫ ∫
531
ln3 ln5 ln 2
884
=−−
Cách 2:
Ta có :
( ) ( ) ( )
( )
( )
22
2
22 2 2
4
1 1 1 11 1 1 11 1 12 1
42 24 42 224
44 4 4
xx
xx
xx xx
x x
xx x xx xx

−−
+


= + = − + = −+ −


−+ −+ −
−− − −


Do đó :
( )
( )
44
2
2
2
33
4
1 1 1 1 12 1 1 2 1
ln ln 4 ln
3
4 2 22 4 4 22
4
x xx
dx dx x x
xx x x x
xx
+ −

= − + − = + −−


−+ − +
−


∫∫
Ví dụ 14: Tính tích phân sau :
( )
( )
3
2
2
2
12
x
dx
xx−+
∫
Giải
Cách 1: ( Hệ số bất định )
( )
( )
( )( )( )
( )( ) ( )( )
( )
( )
( )
2
22
22
12 12 1
112 1 1 2
12 12
Ax x Bx x Cx
x x ABC
xxx xx x
xx xx
+ ++ − ++ −
= =++ =
−++ − + +
−+ −+
Thay lần lượt các nghiệm mẫu số vào hai tử số :
Thay : x=1 Ta cớ : 1=2A , suy ra : A=1/2
Thay : x=-1 ,Ta có :1=-2B, suy ra : B=-1/2
Thay x=-2 ,Ta có : 4= -5C, suy ra : C=-5/4
Do đó :
I=
( )
( )
33
2
2
22
3
11 11 51 1 1 5 1 3
ln ln 2 ln
2
2 12 14 2 2 1 4 2 2
12
xx
dx dx x
xxx x
xx
−

= − − = − +=


−++ +
−+


∫∫
Cách 2.( Nhẩy tầng lầu )
Ta có :
( )
( )
( )
( )
( )( )( )
( ) ( )( )
( )( )( )
22
22
1 12
11 1 1 1 1
2 112 22 112
12 12
xx x x
xx
x xxx x xxx
xx xx
+− − +
−+
==+=+
+ −++ + −++
−+ −+
( )( )
11 1 1111 1 1
1
22 1 2 1 22 3 1 2 1
x
x xx x x xx x



= + −
= ++ − −



+ −+ + + − + +



Từ đó suy ra kết quả .
D. DẠNG
( )
42
ax
Rx
dx
bx c
β
α
++
∫
Những dạng này , gần đây trong các đề thi đại học ít cho ( Nhưng không hẳn là
không cho ) , nhưng tôi vẫn đưa ra đây một số đề thi đã thi trong những năm các
trường ra đề thi riêng , mong các em học sinh khá ,giỏi tham khảo để rút kinh
nghiệm cho bản thân .
Sau đây tôi lấy một số ví dụ minh họa
Ví dụ 1. Tính các tích phân sau :
a.
( )
1
2
2
0
1
32
dx
xx++
∫
b.
1
2
3
1
2
1
1
x
dx
x
+
+
∫
Giải
a.
( )
1
2
2
0
1
32
dx
xx++
∫
Ta có :
( )( )
( )
( )( )
( ) ( )
2
2
22
2
1 1 11
3 2 1 2 ()
12
12
32
x x x x fx
xx
xx
xx

+ += + + ⇒ = = =
−

++
++

++


( ) ( )
( )( )
( ) ( )
22 22
11 2 11 11
2
12 12
12 12
xx xx
xx xx

=+− =+−−

++ ++

++ ++
. Vậy :
( )
( ) ( )
11
2 22
2
00
1
1 1 1 11 11 12
2 2ln 2ln3
0
12 12 23
12
32
x
dx dx
xx xx x
xx
xx

+

= + − − =−− − =+



++ ++ +

++


++

∫∫
b.
1
2
3
1
2
1
1
x
dx
x
+
+
∫
Ta có :
( )
( )
( )
( )
( )
( )
22 2
3
2 22
11 1
()
1
11 11 11
x xx x xx x
fx
x
x xx x xx x xx
+ −+ + −+
= = = +
+
+ −+ + −+ + −+
1
33
1
2
1 1 12
()
1 1 1 21
xx
f x dx
xx x x

⇔=+ ⇒ +

++ + +

∫
Ví dụ 2. Tính các tích phân sau
a.
3
2
42
1
1
1
x
dx
xx
−
−+
∫
b.
1
4
6
0
1
1
x
dx
x
+
+
∫
Giải
a.
3
2
42
1
1
1
x
dx
xx
−
−+
∫
. Chia tử và mẫu cho
2
0x ≠
, ta có :
( )
33
2
2
2
2
11
2
2
1
1
1
1
() () 1
1
1
1
1
dx
x
x
fx fx
dx
x
x
x
x

−
−


= ⇒=

+−
+−


∫∫
Đặt :
22
22
12
11 1
2, 1
4
3
3
xt
t x x t dt dx
xt
xx x
=→=

=+⇒ + =− = − ↔

= →=

Vậy :
( )( )
44 4
3
33 3
2
1 22 2
1 1 11
()
3
23 3 3
33
dt
f x dx dt dt
t
tt
tt

= = = −

−
−+
−+

∫ ∫∫ ∫
( )
4
1 3 1 1 7 43 1
ln ln ln ln 7 4 3
3
77
23 3 23 23
2
t
I
t

−−
= =−=+


+

)
b.
1
4
6
0
1
1
x
dx
x
+
+
∫
. Vì :
( ) ( )( )
( ) ( )
3
6 2 2 42
2
63 2 3
1 11 1
1 11
x x x xx
x x t tx
−= −= − + +
−= −= − =
Cho nên :
( )( )
( )
( )
11
4 42 2 2
22
62
2 42
33
00
1 1 1 13
() ()
1 13
11
11
x xx x x
f x f x dx dx
xx
x xx
xx

+ −+

== −⇒ =−

++
+ −+
++

∫∫
Vậy :
( )
2
11
1 11
arctan arctan 3x arctan1- arctan3 arctan3
00
3 3 43
Ix
π
=−= =−
Ví dụ 3. Tính các tích phân sau
a.
11
22
44
00
11
11
xx
dx dx
xx
+−
∨
++
∫∫
b.
2
4
1
1
1
dx
x +
∫
Giải
a.
11
22
44
00
11
11
xx
dx dx
xx
+−
∨
++
∫∫
. Ta có :
22
22
44
22
22
11
11
11
() , ()
11
11
xx
xx
fx gx
xx
xx
xx
+−
+−
= = =
=
++
++
. Cho nên
Đặt :
22
22
22
22
1 11 5
1 , 2, 1 2, 2
2
1 11 3
1 , 2,
1 0, 2
2
t x dt dx x t x t x t
x xx
t x dt dx x t x t x t
x xx

= + ⇒ = − + = − =→= = →=



= − ⇒ = + + = + =→= = →=


. Vậy :
( )( )
55 5
2
22 2
2
12 2 2
5
1 111 1 2
( ) ln
2
2
22 2 2 22 2
22
2
dt t
f x dx dt dt
t
tt t
tt
−


⇔= = = − =


−
−+ +


−+
∫∫ ∫ ∫
( )
3
2
2
2
10
1
() 1
2
g x dx dt
t
⇔=
+
∫∫
.
Đặt :
1
2
1 3 32
2 tan 2 0 0, arctan
os 2 4
t u dt du t u t u u
cu
= → = ↔=→= =→= =
Do đó (1)
( )
11
1
1
22
00
2 22 2
0
22 2
os 2 2tan
uu
u
du
du u u
cu u
⇔===
+
∫∫
b.
2
4
1
1
1
dx
x +
∫
. Ta có :
( )
22 2 2
4 4 44
1 11 1 1 1 1 1
() () ()
12 1 2 1 1 2
xx x x
Fx fx gx
x x xx

+ +− + −
== = −= −

+ + ++

Đã tính ở trên ( phần a)
Ví dụ 4. Tính các tích phân sau
a.
( )( )
2
2
22
1
1
51 31
x
dx
xx xx
−
−+ −+
∫
b.
5
2
42
3
2
43
dx
xx−+
∫
c.
15
2
2
42
1
1
1
x
dx
xx
−
+
−+
∫
d. I =
7
3
84
2
x
dx
1 x 2x+−
∫
Giải
a.
( )( )
2
2
22
1
1
51 31
x
dx
xx xx
−
−+ −+
∫
. Ta có :
( )( )
( )
22
2
2
2
22
11
1
1
1
1
1
() () 1
1 1 11
51 31
5 53
3
dx
x
x
x
fx fxdx
xx xx
xx x
x
xx xx

−
−

−

= = ⇒=
 
−+ −+
+− + +
− +−
 
−
 
∫∫
Đặt :
2
11 5
1 , 1 2, 2
2
t x dt dx x t x t
xx

= + → = − =→= = →=


Vậy (1) trở thành :
( )( )
( )
55
22
22
5
1 1 1 1 5 1 15
ln ln5 ln3 ln
2
5 3 2 5 3 2 3 2 23
2
dt t
dt
tt tt t
−

= − = = −=

−− −− −

∫∫
b.
5
2
42
3
2
43
dx
xx−+
∫
. Ta có :
( )( )
42 2 2
22
1 1 11 1
()
43 2 3 1
13
fx
xx x
x
xx

= = =
−

−+ − −
−−

Do đó :
( )
55
22
22
33
22
11
() 1
31
f x dx dx I J
xx

=−=−

−−

∫∫
Với :
( )
( ) ( )
55 5
22 2
2
33 3
22 2
5
1 1 1 1 1 1 3 1 37 20 3
2
ln ln
3
3
23 3 3 23 3 23
3 3 65 7 4 3
2
x
I dx dx dx
x
xx x
xx
−−

== = −= =

−
−+ +
−+ −

∫∫ ∫
( )( )
5
11
2
2
3
00
2
5
1 1 1 1 1 1 1 1 3 1 1 15
2
ln ln ln ln
3
1 112112127527
2
x
J dx dx dx
x xx xx x
−

= = = − = = −=

− −+ − + +

∫∫ ∫
c.
15
2
2
42
1
1
1
x
dx
xx
−
+
−+
∫
.
Học sinh xem lại cách giải ví dụ 2-a . Chỉ khác là đặt :
1
tx
x
= −
, sẽ ra kết quả .
d.
I =
( )
( )
74
33
3
84 2
4
22
xx
dx x dx 1
1 x 2x
x1
=
+−
−
∫∫
Đặt :
( )
( )
3
4
4
3
22
4
3 , 2 15; 3 80
1
1
1 1
11 1
() 3
3 33
1
dt x dx x t x t
t
tx
x
f x dx x dx dt dt
t tt
x
= = →= =→=
+
= −⇒

= =
= +

−

Vậy :
80
2
15
80
1 1 1 1 1 1 16 13
ln ln
15
3 3 3 3 720
I dt t
tt t

= + = −= +


∫
E. TRƯỜNG HỢP :
( )
()
Rx
dx
Qx
β
α
∫
( Với Q(x) có bậc cao hơn 4 )
Ở đây tôi chỉ lưu ý : Đối với hàm phân thức hữu tỷ có bậc tử thấp hơn bậc mẫu tới
hai bậc hoặc tinh ý nhận ra tính chất đặc biệt của hàm số dưới dấu tích phân mà có
cách giải ngắn gọn hơn . Phương pháp chung là như vậy , nhưng chúng ta khéo léo
hơn thì cách giải sẽ hay hơn .
Sau đay tôi minh họa bằng một số ví dụ
Ví dụ 1. Tính các tích phân sau .
a.
( )
2
4
1
1
dx
xx+
∫
b.
( ) ( )
1
2
2
2
0
1
13
x
dx
xx
+
−+
∫
Giải
a.
( )
2
4
1
1
dx
xx+
∫
. Nếu theo cách phân tích bằng đồng nhất hệ số hai tử số thì ta có :
( )
( ) ( )
( )
4 32
32
4
44
1
1
()
1
11
A x x Bx Cx Dx E
A Bx Cx Dx E
fx
xx
xx xx
++ + + +
+ ++
==+= =
+
++
( )
( )
43 2
3
4
4
01
0, 0 1
Ex+A
1
() ()
0 0, 0,
1
1
10
AB A
CD B
A B x Cx Dx
x
fx fx
E CD
xx
xx
AE
+= =


= = = −
+ ++ +

⇔= ⇒ ⇔ ⇒=−

= = =
+
+


= =

Nhưng nếu ta tinh ý thì cách làm sau sẽ hay hơn .
Vì x và
3
x
cách nhau 3 bậc , mặt khác
[ ]
1; 2 0xx∈ ⇒≠
. Cho nên ta nhân tử và mẫu với
3
0x ≠
. Khi đó
( )
3
44
()
1
x
fx
xx
=
+
. Mặt khác
( ) ( )
43 3 4
44d x x dx dt x dx t x= ⇔= =
, cho nên :
( )
( )
3
44
1 3 1 11 1
( ) ()
3 3 13 1
1
x dx dt
f x dx f
t
tt t t
xx

= = =−=

++
+

. Bài toán trở nên đơn giản hơn rất
nhiều . ( Các em giải tiếp )
b.
( ) ( )
1
2
2
2
0
13
x
dx
xx−+
∫
Nhận xét :
* Nếu theo cách hướng dẫn chung ta làm như sau :
-
( ) ( ) ( ) ( )
2
3 32
1
()
13
13 1 1
x A B CD
fx
xx
xx x x
+
= = + ++
−+
−+ − −
- Sau đó quy đồng mẫu số , đồng nhất hệ số hai tử số , ta có :
13 5
,,
2 8 32
A B CD= = =−=
Do vậy :
( ) ( )
( ) ( )
1
2
32
0
1355
32 1 32 3
2181
I dx
xx
xx

= ++−


−+
−−

∫
( )
( )
2
1
1 3 5 5 51
ln 1 ln 3 ln
2
8 1 32 32 32
28
81
0
xx
x
x

=− − + −− + =

−
−


Ví dụ 2. Tính các tích phân sau :
a.
3
4
6
2
1
1
x
dx
x
−
−
∫
b.
2
2
6
1
1
1
x
dx
x
+
+
∫
c.
( )
2
4
1
1
dx
xx+
∫
d.
( )
1
3
3
2
0
1
x
dx
x+
∫
e.
( )
1
42
3
2
0
31
1
xx
dx
x
++
+
∫
f.
( )
1
3
1
3
4
1
3
xx
dx
x
−
∫
Giải
a.
( )( )
( )
( )
2 2 33
4 42 2 2
6 2 33
22
2 42
33
1 1 22
1 1 2 1 11
1 1 11
11
11
x xx
x x
dx dx dx dx
x x xx
x xx
xx

− ++ +

= − = + +−

− − −+
 
− ++
−−

 
 

∫∫ ∫∫
Tính J : J= artanx
3
artan3-artan2
2
=
.
Tính K . Đặt
( )
2
3
2
3
2
3 , 2 8; 3 27
1 11 1 1
()
1 3 32 1 1
1
dt x dx x t x t
tx
x dt
g x dx dx dt
x tt
t
= = →= =→=
= ⇒

= = = −

− −+
−

Do đó : K=
( )
3 27
28
27 27
1 1 1 1 1 1 1 117
( ) ln 1 ln 1 ln ln
88
6 1 1 6 6
1 6 98
t
g x dx dt t t
tt t
−

= − = −− + = =

−+ +

∫∫
Tính E=
( )
( )
33
3
2
22
11
1
11
dx dx
x
x xx
=
−
− ++
∫∫
Ta có :
( )
( )
( )
( )
( )
( )
( )
22
22
3
22 2
1
11
()
1
1111 11
xx
xx
hx
x
x xx x xx x xx
−−
−
= = = −
−
− ++ − ++ − ++
( )( )
( )
( )
2 22
3 32 3 2 2
2
11
1 121 1
1 1 1 12 1 1
11
xx
x xx
x x
x x xx x xx xx
x xx
−+
++

=− =−=− +

− −
++ − ++ ++
− ++

Vậy :
( )
33 3
2
2
32
2
22 2
21
13 1 1
3 12 1
13
22
x
x
I dx dx dx
x xx
x
+
=−−
− ++


++




∫∫ ∫
( ) ( )
( )
32
33
1 1 1 28 1 13
ln 1 ln 1 ln ln 2
22
3 2 3
926
x xx F F= − − ++ − = − −
Tính F : Đặt :
2
31
13
2 os
tan
22
5 10
2 tan ; 3 tan
33
dx dt
ct
xt
x ttax ttb
=
+= ⇒
= → = →= =→ = →=
Do đó F=
( )
2
2
31
5 5 10
2 os
t ant= artan ; artan
3 3 33
1 tan
2
bb
aa
dt
b
ct
dt t b a t a b
a
t

= = =− →= = =


+
∫∫
Thay vào (2) ta có kết quả .
b.
( )( )
( )
( )( )
21 2 2
22
2
6
2 42 2 2
22
10 1 1
11 1 1
1
1 1 11
1
xx
dx dx dx dx
x
x xx xx xx
xx
++
= = =
+
+−+ ++−+
−−
∫∫ ∫ ∫
Ta có :
( )( )
22
22
1 Ax+B
11
11
Cx D
xx xx
xx xx
+
= +
++ −+
++ −+
( ) ( ) ( ) ( )
32
42
1
A Cx B A C Dx A B C Dx B D
xx
+ +−++ +−++ ++
=
−+
Đồng nhất hệ số hai tử số ta có hệ :
1
2
0
1
0 12 0
2
0 01
2
11
1
2
A
AC A
C
C
BACD C
ABCD BD
D
BD BD
B
= −
+= =
−

=

−++ = − =

⇔⇔

−++= −+=

=

+= +
=

=
Vậy :
( )( )
22
22
11
11 1 1
1
2 1 12
xx
I dx dx J K
xx xx

−+
= +=+

++ −+

∫∫
Tính J=
( )
2222
2
2
222
2
1111
2
1 1213 1 21 3 1 1
ln 1 2
1
12 12 12 2
13
22
xx x
dx dx dx dx x x E
xx xx xx
x
−+ +− +
=− =− + =− ++ +
++ ++ ++


++




∫∫∫∫
Tính E =
2
2
2
1
31
2
13
22
dx
x


++




∫
, học sinh tự tính bằng cách đặt :
13
tan
22
xt+=
Tính K
( )
2 2 21
2
2
222
2
1 1 10
2
1 1213 1 21 3 1 1
ln 1 2
1
12 12 12 2
13
22
xx x
K dx dx dx dx x x F
xx xx xx
x
+ −+ −
= = = + = −+ +
−+ −+ −+


−+




∫∫∫∫
Tính F=
2
2
2
1
31
2
13
22
dx
x


−+




∫
, học sinh tự tính bằng cách đặt :
13
tan
22
xt−=
c.
( ) ( )
( )
( )
44
22 2
34
44 4
4 44
11 1
2
1 3 1 1 1 32
ln ln
1
3 3
1 3 1 3 17
11
dx dx
dx x x
dx
xx x
xx x x



= = −= =


++
++


∫∫ ∫
d.
( ) ( )
( )
11
32
33
22
00
1
21
2
11
xx
dx x
dx
xx
=
++
∫∫
. Đặt :
2
2
1; 2
1
0 1, 1 2
x t dt xdx
tx
x tx t
=−=
=+⇒
= →= =→=
Do đó
22
3 23 2
11
2
1 1 1 1 1 13
1
4 16
t
I dt dt
t tt tt
−

= = − =−+ =


∫∫
e.
( )
( )
( )
( ) ( )
( )
2
2
1 1 11
42 2 2
3 33 3
2
2 22 2
0 0 00
1
31 1
1
1
1 11 1
x
xx x x
dx dx dx dx J K
x
x xx x

+
++

=+=+=+

+
+ ++ +

∫ ∫ ∫∫
Tính J : Bằng cách đặt
tan
4
x tJ
π
= ⇒=
Tính K=
( ) ( )
( )
1
23
22
0
11
2
11
dx E F
xx


−=+

++

∫
Tính E : Bằng cách đặt
2
1
os
tan
0 0; 1
4
dx dt
ct
xt
x tx t
π
=
= ↔
= →= =→=
Vậy :
22
1
4 44
2
2 22 2
00 0 0
4
1 1 1 1 1 111 1
os
1
2 1 2 1 tan os 2 os 2
os
E dx dt dt
c tdt
x tct ct
ct
π ππ

= = = =

++

∫∫ ∫ ∫
( )
4
0
1 11 1 1 2
1 os2t sin 2
4
4 4
2 4 4 2 16
0
c dt t t
π
π
ππ
+

= + = + = +=


∫
Tính F. Tương tự như tính E ;
Bằng cách đặt
2
1
os
tan
0 0; 1
4
dx dt
ct
xt
x tx t
π
=
= ↔
= →= =→=
Vậy :
33
1
4 44
4
2 22 2
00 0 0
6
1 1 1 1 1 111 1
os
1
2 1 2 1 tan os 2 os 2
os
F dx dt dt c tdt
x tct ct
ct
π ππ

= = = =

++

∫∫ ∫ ∫
( )
44
2
00
1 1 1 os4t
1 os2t 1 2 os2
4
88 2
0
c
c dt c t dt
ππ
π
+

=+ =++ =


∫∫
( )
4
0
1 1 1138
3 4cos2 os4t 3 2sin 2 sin 4 3 2
4
16 16 4
16 4 64
0
t c dt t t t
π
π
ππ
+

+ + = + + = +=


∫
f.
( )
1
1
1
3
11 1
3
3
3
3
4 33
2 2
11 1
33 3
1 11
1.
xx
x x dx
dx dx
x x x x xx
−

−

= =
−




∫∫ ∫
Đặt :
22
11
11
1
8; 1 0
3
dx
dt
x
tt
xx
x tx t
= −

= − ⇒+= ⇔


= →= =→=
Khi đó
( )
08
1 41 7 4
74
3 33 3 3
80
8
3 3 3 3 24 3 468
1 .2 .2 16
0
7 4 7 4 74 7
I t t dt t t dt t t


=− + = + = + = + = +=




∫∫
* Chú ý : Còn có cách khác
Vì :
1
;1 0
3
xx

∈ →≠


. Đặt
( )
1
3
1
23
3
3
4
22
11
11 1
; ()
1
tt t
tt
x dx dt f x dx dt dt
tt t
t
t

−

−


=⇒=− = − =−





( )
1
1
3
32
3
2
1
1t t t dt dt t dt
t

=−− ==− −


(2) . Đặt :
22
11 1
1 1;u u du dt
tt t
=−⇔=− =
Ví dụ 3. Tính các tích phân sau
a.
1
2
2
2
1
1
p
p
e
p
x
dx
x
+
+
+
∫
b.
( )
3
3
22
0
2
a
x dx
xa+
∫
c.
1
0
x
xe
e dx
+
∫
d.
2
2
0
2
a
x ax x dx−
∫
Giải
a..
1
2
2
2
1
1
p
p
e
p
x
dx
x
+
+
+
∫
( ĐHTNguyên-98) : Ta có :
2
2
2
2
()
1
p
p
x dx
f x dx
x
+
=

+


.
- Đặt :
2
2
1
22
2
1
1
2
1
1 1;
p
e
pp
p
dt x dx
dt
tx x I
t
x t xe t e
+
+
+
=
= = ⇒ ⇔=
+
=→= = →=
∫
- Đặt :
( )
11
2
1
1
22
2
1
44
os
tan
4
os 1 tan
1,
4
uu
du
dt
du
cu
t u I du u
cu u
t u te uu
ππ
π
π
=
= ⇒ ⇔= = = −
+
=→= = →=
∫∫
- Từ :
1
tan artan e artan e
4
u e uu I
π
= ⇒= = ⇔= −
b.
( )
3
3
22
0
2
a
x dx
xa+
∫
. Đặt :
( )
2
3 33
3
33
2
22
22
3
2
dt
dx=a ; 0 0,
cos 4
tan dt
atant
( ) cos .tan
cos
1
os
x t xa t
t
x dx a t
x
f x a a t tdt
t
xa
a
ct
π
= →= = →=
= ⇒
= = =

+


Vậy :
( )
2
33
4 4 44
3
32 2
00 0 0
0
1 os sin
sin sin
( ) cos .tan cos . .
os os os
a
ct t
tt
I f x dx a t tdt a t dt a dt a dt
ct ct ct
π π ππ
−
= = = = = =
∫∫ ∫ ∫ ∫
- Đặt :
( )
( )
2
22
1
sintdt;t= ; 0 1
4
2
ost=u
1
1
() 1
du u t u
c
u
f t dt du du
uu
π
=− →= =→=
⇒
−

= −=−


Vậy :
2
2
2
1
2
1 1 2 2 3 32 32 4
1 2
2 2
2
2 22
22
1
I du
u
uu
−

= − = + = + −= −= −=


∫
c.
11
00
xx
xe x e
e dx e e dx
+
=
∫∫
. Đặt :
; 0 1; 1
()
x
x
x
xe t
dt e dx x t x t e
te
f x dx e e dx e dt
= = →= =→=
= ⇒
= =
Vậy :
1
01
()
1
e
tte
e
I f x dx e dt e e e= = = = −
∫∫
d.
( )
22
2
22
00
2
aa
x ax x dx x a x a dx− = −−
∫∫
Đặt :
( )
22
. ostdt,x=0 t=- ;x=2a t=
22
.sin
( ) .sin os . . ostdt
dx a c
xaa t
f x dx a a t a c t a c
ππ
= →→
−= ⇒
= +
Vậy :
( ) ( )
2 22 2 2
3 23 2 2 3 2
2 22 2 2
1 os2
1 sin os os os sin os os
2
ct
I a t c tdt a c tdt c t tdt a dt c td c t
π ππ π π
π ππ π π
− −− − −

+

=+= + = −



∫ ∫∫ ∫ ∫
3 33 3
11 1 1
22
sin 2 cos
2 2 3 22 2 2
22
at t t a a
ππ
ππ π
ππ





= + − = +=





−−


Ví dụ 4. Tính các tích phân sau
a.
3
52
2
dx
xx−
∫
b.
( )
1
7
2
4
0
1
x dx
x+
∫
c.
( )
1
3
2
2
0
2
1
xx
dx
x
−
+
∫
d.
2
3
4
1
1 x
dx
x
+
∫
Giải
a.
( )
( )
( )
33
52
22
22
1
1
11
dx
dx
xx
xx x x
=
−
− ++
∫∫
Xét :
( )
( )
22
22
1
()
11
11
A B Cx D E
fx
x xx x x
xx x x
+
= =
++ +
++ −
− ++
( )
( ) ( )
( )
( ) ( )
( )
( )
2 2 2 22
22
1 1 1 1 1 ( 1)
11
Axx x Bxx xx CxDxx Exx x
xx x x
++ − + − ++ + + − + ++
=
− ++
( ) ( ) ( )
( )
( )
4 32
22
11
B C Ex A D C Ex E Dx Bx A
xx x x
++ + +−+ + − − −
=
− ++
.
Đồng nhất hệ số hai tử số ta có hệ :
22
1
3
0
1
111
01
3
1
333
0 0 0
()
11
01
3
11
1
D
BCE C E
C
ADCE EEE
x
E D B B
fx
xxx x
B ED
E
AA
A
=
++= =−

= −

+−+= ++=
−+


−= ⇔= ⇔=⇒ =−+ +

++ −

= =

=
=−=−


= −
Vậy :
( )
33
22 2 2
22
111
1 11 1 11
333
1 1 3 13 1
x
x
I dx dx
xxx x x xx x

−+


−

=−+ + =−− +




++ − ++
−




∫∫
( )
2
3
2
2
2
2
2
33
1
1 1 1 1 1 1 2x+1
ln 1 ln 1 ln arctan
22
6 3 61
33
13
22
x
dx
xx x
x x xx
x

−

= − +++ − − = + +



++




++




∫
11 7 5
arctan arctan
6
33 3

=+−


b.
( ) ( )
( )
11
74
3
22
44
00
1
31
3
11
x dx x
x dx
xx
=
++
∫∫
.
Đặt :
3
4
22
3 , 0 1; 1 2
1
1 1 11 1
()
33
dt x dx x t x t
tx
t
f x dx dt dt
t tt
= = →= =→=
=+⇒
−

= = −


Vậy :
2
2
0
2
11 1 1 1 1 1
ln ln 2
1
3 3 32
I dt t
tt t

= − = += −


∫
c.
( )
( )
( )
( )
2
11
3
22
22
00
2
21
21
2
11
x
xx
dx xdx
xx
−
−
=
++
∫∫
Đặt :
22
22
2 ; 0 1; 1 2
1 23
1 3 11 3
()
22
dt xdx x t x t
t xx t
t
f x dx dt dt
t tt
= = →= =→=
=+ ⇔ −=−⇒
−

= = −


Vậy :
2
2
1
2
11 3 1 3 1 3
ln ln 2
1
2 2 22
I dt
t
tt t

= − = += −


∫
d.
( )
22
33
2
46
11
11
1
xx
dx x dx
xx
++
=
∫∫
.
Đặt :
( ) ( )
2
32 3
32
2
22
6
22
2 3 ; 1 2, 2 3
11
11 1 2
() 3 2
3 33
11
tdt x dx x t x t
t xt x
xtt
f x dx x
dx tdt dt
x
tt
= =→= = →=
= + ↔=+↔
+
= = =
−−
Vậy :
( ) ( )
2
2
3 33
22
2 22
21111 2111 1 1 1 11
3 1211 3411 6 11
11
I dt dt
t tt tt tt
tt



  
= + − = − = + −−


  


+ −+ +
− −+
  
+−




∫ ∫∫
( )
( )
2
33
1 1 1 1 1 2 1 82 3 1
ln ln ln 2 2 2
6 1 1 1 6 1 24 3
1
22
t tt
tt t t
t

−
− − −

=−−− = − = + −


+− + +
−


Ví dụ 5. Tính các tích phân sau :
a.
4
2
7
9
dx
xx+
∫
b.
( )
2
1
2
0
1
x x dx
x
−
+
∫
c.
3
53
2
0
2
1
xx
dx
x
−
+
∫
d.
( )
1
3
2
0
1 x dx−
∫
Giải
a.
( )
44
2 22
77
1
99
dx xdx
xx x x
=
++
∫∫
.
Đặt :
2 2 22
2
9 ,9
9
7 4, 4 5
t x tdt xdx x t
tx
x tx t
= +↔ = = −
= +⇒
= →= = →=
. Do đó :
( )
( )( )
55
2
44
33
9
dt dt
I
tt t
tt
= =
−+
−
∫∫
Ta có :
( )( )
( )
( ) ( )
( )
2
2
9 33
1
()
33 33
9
A t Bt t C t t
AB C
ft
tt t t t t
tt
−+ ++ −
= =++=
−+ − +
−
Đồng nhất hệ số hai tử số bằng cách thay lần lượt các nghiệm vào hai tử số ta có :
- Với x=0 : -9A=1
1
9
A→=−
- Với x=-3 : 9C=1
1
9
C→=
- Với x=3 : 9B=1
1
9
B→=
Vậy :
( )
5
2
2
4
55
1 1 1 1 1 1 9 1 144
ln 9 ln ln ln
44
9 3
3 9 9 9 35
t
I dt t t
tt t t

−


= −+ + = − − = =



−+


∫
* Chú ý : Nếu theo phương pháp chung thì đặt :
3sin 3cosx t dx tdt= →=
.
Khi :
7
7 7 3sin sin
3
4
4 4 3sin sin 1
3
x tt
x tt
=→= ↔ =
=→= ↔ = >
. Như vậy ta không sử dụng được phương pháp
này được .
b.
( )
( )
2
1 11
2
22 2
0 00
1
11 1
x x dx
xx
dx dx J K
xx x
−
=−=−
++ +
∫ ∫∫
* Để tính J :
Đặt :
2
2
2
2
2
1
, 0 0; 1
os 4
tan
1
tan .
tan
os
()
ost
1 tan
dx dt x t x t
ct
xt
t dt
t
ct
f x dx dt
c
t
π
= = →= =→=
= ⇒
= =
+
. Tính tích phân này không đơn
giản , vì vậy ta phải có cách khác .
- Từ :
11 1
22
22
22 2 2
00 0
11 1 1
() 1 () 1
11 1 1
xx
g x x g x dx x dx dx
xx x x
+−
= = = +− ⇒ = + −
++ + +
∫∫ ∫
- Hai tích phân này đều tính được .
+/ Tính :
1 1 11
2
22 2
22
0 0 00
1
1
11 21
0
11
x
E x dx x x dx x dx dx
xx

= + = +− =− +−

++

∫ ∫ ∫∫
( ) ( )
2
1
21
2 ln 1 2 2 ln 1 2 ln 1 2
0
22
E xx E E= −+ + + ⇒ = + + ⇔ = + +
* Tính K=
1
2
2
0
1
1 21
0
1
x
dx x
x
= +=−
+
∫
;
( )
1
2
2
0
1
1
ln 1 ln 1 2
0
1
dx x x
x
= + += +
+
∫
Do vậy : I=
( ) ( ) ( )
21 23
ln 1 2 ln 1 2 ln 1 2
22 22
++++=++
c.
( )
333
53 5 3
22 2
000
2
21
11 1
xx x x
dx dx dx J K
xx x
−
=−=−
++ +
∫∫∫
- Tính J: Đặt
( )
( )
22
2
2
2
4
42
2
1; ; 0 1, 3 2
1
1
() 2 1
1
x t xdx tdt x t x t
tx
t tdt
x xdx
f x dx t t dt
t
x
= − = = →= = →=
= +⇒
−
= = =−+
+
Suy ra : J=
( )
2
42 5 3
1
2
1 2 38
21
1
5 3 15
t t dt t t t

−+ = − + =


∫
- Tính K: Đặt
( )
( )
22
2
2
2
2
2
1; ; 0 1, 3 2
1
1
() 1
1
x t xdx tdt x t x t
tx
t tdt
x xdx
f x dx t dt
t
x
= − = = →= = →=
= +⇒
−
= = = −
+
Suy ra : K=
( )
2
23
1
2
14
1
1
33
t dt t t

−= −=


∫
Vậy : I=
28 4 48 16
15 3 15 5
+= =
d.
( )
1
3
2
0
1 x dx−
∫
. Đặt :
( )
3
2 64
ostdt. x=0 t=0;x=1 t=
2
sin
( ) 1 os ostdt=cos
dx c
xt
f x dx x dx c tc tdt
π
= →→
= →
=−=
Do đó I=
2
22 2
00 0
1 os2t 1 1 os4t 3 1 1
1 2cos2 os2t+ os4t
2 4 2 42 8
cc
dt t dt c c dt
ππ π
−+

=−+ =−


∫∫ ∫
31 1 3
sin 2 sin 4
2
4 4 32 8
0
tt t
π
π

=−+ =


TÍCH PHÂN CHỨA CÁC HÀM SỐ LƯỢNG GIÁC
I. KIẾN THỨC
1. Thuộc các nguyên hàm :
a/
( ) ( )
1
sin ax+b os ax+bdx c
a
β
α
β
α
= −
∫
b/
( )
( )
( )
sin ax+b
ln os ax+b
os ax+b
dx c
c
β
α
β
α
= −
∫
c /
( ) ( )
1
os ax+b sin ax+bc dx
a
β
α
β
α
=
∫
d/
( )
( )
( )
os ax+b
ln sin ax+b
sin ax+b
c
dx
β
α
β
α
=
∫
2. Đối với :
()I f x dx
β
α
=
∫
a/ Nếu f(x)=
( )
n
sin ; os
m
R xc x
thì ta chú ý :
- Nếu m lẻ , n chẵn : đặt cosx=t ( Gọi tắt là lẻ sin )
- Nếu n lẻ , m chẵn : đặt sinx=t ( Gọi tắt là lẻ cos )
- Nếu m,n đều lẻ thì : đặt cosx=t hoặc sinx =t đều được ( gọi tắt lẻ sin hoặc lẻ cos )
- Nếu m,n đề chẵn : đặt tanx=t ( gọi tắt là chẵn sinx , cosx )
b/ Phải thuộc các công thức lượng giác và các công thức biến đổi lượng giác , các
hằng đẳng thức lượng giác , công thức hạ bậc , nhân đôi , nhân ba , tính theo tang góc
chia đôi ....
3. Nói chung để tính được một tích phân chứa các hàm số lượng giác , học sinh đòi
hỏi phải có một số yếu tố sau :
- Biến đổi lượng giác thuần thục
- Có kỹ năng khéo léo nhận dạng được cách biến đỏi đưa về dạng đã biết trong
nguyên hàm .
II. MỘT SỐ VÍ DỤ MINH HỌA
Ví dụ 1. Tính các tích phân sau :
a. (ĐH, CĐ Khối A – 2005)
∫
+
+
=
2
0
cos31
sin2sin
π
dx
x
xx
I
b.. ĐH, CĐ Khối B – 2005 .
dx
x
xx
I
∫
+
=
2
0
cos1
cos2sin
π
KQ:
2ln2 1−
Giải
a.
( )
( )
22
00
2cos 1 sinx
sin 2 sin
1
1 3cos 1
3cos
x
xx
I dx dx
xx
ππ
+
+
= =
++
∫∫
Đặt :
2
t1 2
osx= ;sinxdx=-
33
1 3cos
0 2; 1
2
c tdt
tx
x tx t
π
−
=+⇒
= →= = →=
Khi đó :
2
12
2
3
21
1
21
2
3
2 2 1 2 1 34
2
1
3 9 9 3 27
t
t
I tdt dt t t
t

−
+

+


= − = = +=



∫∫
b.
( )
22
22 2
00 0
sin 2 cos 2sin cos os
2 sinxdx 1
1 cos 1 cos osx+1
x x x x cx
I dx dx
x xc
ππ π
= = =
++
∫∫ ∫
Đặt :
( )
2
dt=-sinxdx, x=0 t=2;x= 1
2
1 osx
1
1
() 2
t
tc
t
f x dx dt t dt
tt
π
→ →=
=+⇒
−

= = −+


Do đó :
1
2
2
02
2
11
2 ( ) 2 2 2 2 ln 2ln 2 1
1
2
I f x dx t dt t t t
t
π

= =− −+ = − + = −


∫∫
Ví dụ 2. Tính các tích phân sau
a. ĐH- CĐ Khối A – 2006 .
2
22
0
si n 2x
I dx
cos x 4si n x
π
=
+
∫
KQ:
2
3
b. CĐ Bến Tre – 2005 .
∫
+
=
2
0
1sin
3cos
π
dx
x
x
I
KQ:
2 3ln2−
Giải
a.
2
22
0
si n 2x
I dx
cos x 4si n x
π
=
+
∫
. Đặt :
22222
os 4sin os 4sint cx x t cx x= + ⇒= +
Do đó :
( )
2
2 2sin cos 8sin cos 3sin 2 sin 2
3
0 1; 2
2
tdt x x x x dx xdx xdx tdt
x tx t
π
=− + = →=
= →= = →=
Vậy :
22
2
0 11
2
2 2 22
()
1
3 3 33
tdt
I f x dx dt
t
t
π
= = = = =
∫ ∫∫
b.
∫
+
=
2
0
1sin
3cos
π
dx
x
x
I
.
Ta có :
( ) ( ) ( )
32 2 2
os3x=4cos 3cos 4cos 3 osx= 4-4sin 3 osx= 1-4sin osxc x x xc xc xc−= − −
Cho nên :
( )
( )
2
1 4sin
os3x
( ) osxdx 1
1+sinx 1 sinx
x
c
f x dx dx c
−
= =
+
Đặt :
( )
2
dt=cosxdx,x=0 t=1;x= 2
2
1 sinx
14 1
3
() 8 4
t
t
t
f x dx dt t dt
tt
π
→ →=
=+⇒

−−


= = −−


Vậy :
( )
2
2
2
01
2
3
( ) 8 4 8 2 3ln 2 3ln 2
1
I f x dx t dt t t t
t
π

= = −− = − − =−


∫∫
Ví dụ 3. Tính các tích phân sau
a. CĐSP Sóc Trăng Khối A – 2005 .
2
22
0
sin
sin 2cos .cos
2
xdx
I
x
xx
π
=
+
∫
b. CĐ Y Tế – 2006 .
2
4
si n x cosx
I dx
1 si n 2x
π
π
−
=
+
∫
KQ:
ln 2
Giải
a.
( )
22 2
2
22
00 0
sin sin sinx
ln 1 osx ln 2
2
sin cos . 1 osx 1+cosx
sin 2cos .cos
0
2
xdx x
dx
I dx c
x
x xc
xx
ππ π
π
= = = =−+ =
++
+
∫∫ ∫
b.
( )
( )
ππ π
ππ π
−−−
= = =
+
∫∫ ∫
22 2
2
44 4
si n x cosx si n x cosx si n x cosx
I dx dx dx 1
si nx+cosx
1 si n 2x
si nx+cosx
Vì :
sinx+cosx= 2 sin ; 3 sin 0
44 2 2 4 4 4
xx x x
ππ π π π π π
 
+ ≤≤ ⇒ ≤+ ≤ ⇔ + >
 
 
Do đó :
sinx+cosx sinx+cosx=
Mặt khác :
( ) ( )
sinx+cosx osx-sinxd c dx=
Cho nên :
( )
2
4
sinx+cosx
1
2
ln sinx+cosx ln1 ln 2 ln 2
sinx+cosx 2
4
d
I
π
π
π
π

=− =− =−− =

∫
Ví dụ 4. Tính các tích phân sau
a. CĐ Sư Phạm Hải Dương – 2006 .
( )
2
3
0
cos2x
I dx
si n x cosx 3
π
=
−+
∫
KQ:
1
32
b. CĐ KTKT Đông Du – 2006 .
4
0
cos2x
I dx
1 2 si n 2x
π
=
+
∫
KQ:
1
ln3
4
Giải
a.
( )
2
3
0
cos2x
I dx
si n x cosx 3
π
=
−+
∫
. Vì :
( )( )
22
cos2 os sin osx+sinx osx-sinxxc x x c c=−=
Cho nên :
( )
( )
( )
( )
33
osx-sinx
os2x
( ) osx+sinx
sinx-cosx+3 sinx-cosx+3
c
c
f x dx dx c dx= =
Đặt :
( )
3 23
dt= cosx+sinx ; 0 2, 4
2
sinx-cosx+3
3 11
() 3
dx x t x t
t
t
f x dx dt dt
t tt
π
= →= = →=
= ⇒
−

= = −


Vậy :
4
2
23 2
02
4
1 1 1 31 1
() 3
2
4 32
I f x dx dt
t t tt
π

= = − =−+ =


∫∫
b.
4
0
cos2x
I dx
1 2 si n 2x
π
=
+
∫
. Đặt :
1
4cos2 os2xdx=
4
1 2sin2
0 1; 3
4
dt xdx c dt
tx
x tx t
π
= →
=+⇒
= →= = →=
Vậy :
π
= = = =
+
∫∫
3
4
01
3
cos2x 1 dt 1 1
I dx ln t ln3
1 2 si n 2x 4 t 4 1 4
Ví dụ 5. Tính các tích phân sau :
a. CĐ Sư Phạm Quảng Ngãi – 2006 .
3
2
0
4 si n x
I dx
1 cosx
π
=
+
∫
KQ: 2
b. CĐ Bến Tre – 2006 .
3
6
0
si n 3x sin 3x
I dx
1 cos3x
π
−
=
+
∫
Giải
a.
( )
( ) ( )
ππ π
π
−
= = − −=
++
∫∫ ∫
2
3
22 2
2
00 0
1 cos x
4 si n x 1
I dx 4 sinxdx=4 1 cosx sinxdx=4. 1 cosx 2
2
1 cosx 1 cosx 2
0
b.
3
6
0
si n 3x sin 3x
I dx
1 cos3x
π
−
=
+
∫
.
Ta có :
( )
3 22
sin3 sin 3 sin3 1 sin 3 sin3 . os 3x x x x xc x−= − =
.
Đặt :
1
dt=-3sin3xdx sin3xdx=-
3
1 os3x
0 2; 1
6
dt
tc
x tx t
π
→
=+⇒
= →= = →=
Vậy :
( )
2
12
6
2
02 1
2
1
1 1 1 11 1 1
( ) 2 2 ln ln 2
1
3 3 32 6
3
t
f x dx dt t dt t t t
tt
π
−

=− = −+ = − + =−+


∫∫∫
Ví dụ 6. Tính các tích phân sau
a. I =
3
3
2
3
sin x sin x
cotgxdx
sin x
π
π
−
∫
b. I =
2
2
sin( x)
4
dx
sin( x)
4
π
−π
π
−
π
+
∫
c. I =
2
4
0
sin xdx
π
∫
d. I =
dxxxnsix )cos(2cos
44
2
0
+
∫
π
Giải
a.
I =
3
3
3
2
22
33
1
sinx 1
sin x sin x
sin x
cotgxdx cot xdx
sin x sinx
ππ
ππ

−

−

=
∫∫
22
3
2
3
2
33
1
1 cot xdx cot x cot xdx
sin x
ππ
ππ

=−=−


∫∫
b. I =
22
22
sin( x)
cosx-sinx
4
dx dx
cosx+sinx
sin( x)
4
ππ
−π π
−
π
−
=
π
+
∫∫
( )
2
2
d cosx+sinx
2
ln cosx+sinx 0
cosx+sinx
2
π
π
−
π
= = =
π
−
∫
c. I =
2
22 2
4
00 0
1 cos2x 1 1 cos4x
sin xdx dx 1 2cos2x dx
24 2
ππ π
−+

= =−+


∫∫ ∫
2
0
31 1 3 1 1 3
cos2x+ cos4x dx x sin 2x sin 4x
2
8 2 8 8 4 32 16
0
π
π
π

=− =−+ =


∫
d. I =
dxxxnsix )cos(2cos
44
2
0
+
∫
π
. Vì :
44 2
1
sin os 1 sin 2
2
xc x x+=−
Cho nên :
2 22
223
0 00
1 1 11
1 sin 2 os2xdx= os2xdx- sin 2 cos2 sin 2 sin 2 0
22
2 2 23
00
I x c c x xdx x x
π ππ
ππ

=− =−=


∫ ∫∫
Ví dụ 7. Tính các tích phân sau
a. I =
2
5
0
sin xdx
π
∫
b. I =
4
2
6
1
dx
sin x cotgx
π
π
∫
c. I =
3
22
6
tg x cotg x 2dx
π
π
+−
∫
d. */I =
2
33
0
( cosx sin x)dx
π
−
∫
Giải
a. I =
( )
( )
22 2
2
5 2 24
00 0
sin xdx 1 cos x sinxdx=- 1 2cos x cos x d cosx
ππ π

=− −+

∫∫ ∫
35
21 2
cosx+ cos x cos x
2
3 5 15
0
π

=− −=


b. I =
4
2
6
1
dx
sin x cotgx
π
π
∫
.
Đặt :
22
2
11
22
sin sin
cot cot
3; 1
64
tdt dx dx tdt
xx
t xt x
xtxt
ππ
=−→=−
= ⇒= ↔
= →= = →=
Vậy :
( )
13
1
3
2
3
2 2 2 31
1
tdt
I dt t
t
=−===−
∫∫
c. I =
( )
3 33
2
22
6 66
tg x cotg x 2dx tanx-cotx dx tanx-cotx dx
π ππ
π ππ
+ −= =
∫ ∫∫
Vì :
22
sinx osx sin os os2x
tanx-cotx= 2 2cot 2
cosx sinx sinxcosx sin2x
c xc x c
x
−
−= =− =−
Cho nên :
tanx-cotx<0;x ;
64
33
; 2 ;2 cot 2 ;
63 3 3 3
3
tanx-cotx>0;x ;
43
xx x
ππ
ππ π π
ππ

∈




∈ ↔ ∈ ⇒ ∈− ⇔






∈


Vậy :
( ) ( )
33
44
6 4 64
os2x os2x 1
tanx-cotx t anx-cotx
sin2x sin2x 2
cc
I dx dx dx dx
ππ
ππ
π π ππ
=− + =−+ =
∫ ∫ ∫∫
( ) ( )
1
43
ln sin 2 ln sin 2 ln 2
2
6
4
xx
ππ
π
π
−=
d. I =
2
33
0
( cosx sin x)dx
π
−
∫
(1)
Đặt :
,0 ; 0
2 22
x t dx dt x t x t
π ππ
= −→ =− = →= = →=
Do đó :
( )
( ) ( )
( )
0
22
33 3 3
33
00
2
os sin sin ost sin osx 2
22
I c t t dt t c dt x c dx
ππ
π
ππ


= −− − = − = −





∫ ∫∫
Lấy (1) +(2) vế với vế :
20 0II=⇒=
Ví dụ 8 . Tính các tích phân sau
a.
3
4
4
tan xdx
π
π
∫
(Y-HN-2000) b.
( )
4
0
os2x
sinx+cosx+2
c
dx
π
∫
(NT-2000) c.
6
2
4
4
os
sin
cx
dx
x
π
π
∫
(NNI-2001)
d.
2
4
6
0
sin
os
x
dx
cx
π
∫
( GTVT-2000) e.
2
2
0
sin 2
4 os
x
dx
cx
π
−
∫
f.
2
4
0
1 2sin
1 sin2
x
dx
x
π
−
+
∫
(KB-03)
Giải
a.
3
4
4
tan xdx
π
π
∫
. Ta có :
( )
2
2
4
4
4 4 42
1 os
sin 1 1
( ) tan 2 1
os os os os
cx
x
fx x
cx cx cx cx
−
=== =−+
Do đó :
( )
[ ]
33 3
2
42 2
44 4
11
3
( ) 2 1 1 tan 2tan
os os os
4
dx
I f x dx dx x x x
cx cx cx
ππ π
ππ π
π
π

= = − +=+ − +


∫∫ ∫
3
1 42
3
tanx+ tan 23 2 23 23 2
3 12 3 12 3 12
4
x
π
π ππ
π

= − −+ = − − −+ = +


* Chú ý : Ta còn có cách phân tích khác :
( ) ( ) ( ) ( )
422 2 2 22 2 2
( ) tan tan tan 1 1 tan 1 tan tan tan 1 tan tan 1 1fx xxx x x xx x x== +−= +−= +−++
Vậy :
( ) ( )
3 3 33
222 2
22
4 4
44
tan 1 tan tan 1 1 tan .
os os
dx dx
I x x x dx x dx
cx cx
π π ππ
π π ππ

= + − ++ = − +

∫ ∫ ∫∫
3
1 1 12
3
tan t anx+x 3 3 3 1
3 3 3 3 4 3 12
4
Ix
π
π ππ
π

= − = − + − −+ = +


b.
( )
4
0
os2x
sinx+cosx+2
c
dx
π
∫
.
Ta có :
( )
( )
( )
( )( )
( )
22
33 3
os sin
osx-sinx osx+sinx
os2x
()
sinx+cosx+9 sinx+cosx+9 sinx+cosx+9
cx x
cc
c
fx
−
= = =
Do đó :
( )
( )
( ) ( )
44
3
00
osx+sinx
( ) osx-sinx 1
sinx+cosx+2
c
I f x dx c dx
ππ

= =



∫∫
Đặt :
( )
3 23
cosx+sinx=t-2.x=0 t=3;x= 2 2,
4
sinx+cosx+2
2 11
osx-sinx ( ) 2
t
t
t
dt c dx f x dx dt dt
t tt
π
→ →= +
= ⇒
−

= ⇒==−


Vậy :
( ) ( )
22
22
23 2
3
1 1 11 1 1 11 2 1 2
22
2
39 3
22
3
22 22
I dt
t t tt
+

+
+


= − =−+ =− + −− + = −


+


++

∫
( )
( )
( )( )
( )
( )
( )
sin ost sin ost
sin ost os sin t ( )
sin ost+9 sin ost+9
tc tc
t c dt c t dt f x
tc tc
++
= − −= − =
++
c.
6
2
4
4
os
sin
cx
dx
x
π
π
=
∫
Ta có :
( )
3
2
6 2 46
2
4 4 4 42
1 sin
os 1 3sin 3sin sin 1 1
( ) 3 3 sin
sin sin sin sin sin
x
cx x x x
fx x
x x x xx
−
−+−
= = = = − +−
Vậy :
( )
2 2 22
2
22
4 4 44
1 os2x
1 cot 3 3
sin sin 2
dx dx c
I x dx dx
xx
π π ππ
π π ππ
−

=+ − +−


∫ ∫ ∫∫
3
1 11 523
2
cot 3cot 3 sin 2
3 2 4 8 12
4
x xx x x
π
π
π

=− + +− + = +


d.
( )
22
44 4 4 4
2
6 6 6 4 42 2
00 0 0 0
sin 1 os 1 1 1 1
1 tan
os os os os os os os
x c x dx
dx dx dx dx x
cx cx cxcx cxcx cx
ππ π π π
−

= = − = −+


∫∫ ∫ ∫ ∫
( ) ( ) ( )
( )
( )
( )
4 44 4
2
2 2 24 2
22
0 00 0
11
1 tan 1 tan 1 2tan tan tan 1 tan t anx
os os
x dx x dx x x d x x d
cx cx
π ππ π
=+ −+ =+ + −+
∫ ∫∫ ∫
35 3 35
21 1 11 8
t anx+ tan tan t anx- tan tan tan
44
3 5 3 3
5 15
00
xx x xx
ππ

= +− = + =


e.
( )
22 2 2
2
00 0 0
7 os2x
sin 2 sin 2 2sin2 3
ln 7 os2x ln
2
1 os2x
4 os 7
os2x 7 os2x 4
4
0
2
dc
xx x
dx dx dx c
c
cx c c
ππ π π
π
−
= = =− =−− =
+
− −−
−
∫∫ ∫ ∫
f.
( )
2
444
000
1 sin2
1 2sin os2 1 1 1
ln 1 sin 2 ln 2
4
1 sin2 1 sin2 2 1 sin 2 2 2
0
dx
x cx
dx dx x
xx x
πππ
π
+
−
= = =+=
++ +
∫∫∫
Ví dụ 9. Tính các tích phân sau :
a.
2
34
0
sin cosx xdx
π
∫
b.
2
0
sin3
1 2 os3x
x
dx
c
π
+
∫
c.
5
22
66 3
00
3
2
sin os os2x
sinx+ 3 osx sinx+ 3 osx cosx- 3sinx
x cx c
I dx J dx K dx
cc
ππ π
π
= ∨= ⇒ =
∫∫ ∫
Giải
a.
( ) ( )
( )
22 2
34 2 4 6 4
00 0
sin cos 1 os os .sinxdx os os osxx xdx cxcx cxcxdc
ππ π
=−=−
∫∫ ∫
75
11 2
os os
2
7 5 35
0
cx cx
π

=−=


b.
( )
( )
22 2
00 0
1 2cos3
sin3 1 3sin3 1 1 1
ln 1 2cos3 ln3
2
1 2 os3x 6 1 2cos3 6 1 2cos3 6 6
0
dx
xx
dx dx x
c xx
ππ π
π
+
−
=− =− =−+ =
++ +
∫∫∫
c. Ta có :
22
66 6
00 0
sin os 1 1 1 1
22
sinx+ 3 osx 1 3
sin
sinx+ osx
3
22
xc x
I J dx dx dx
c
x
c
ππ π
π
+
+= = =

+


∫∫ ∫
Do :
2
tan
26
1 1 11
.
sin 2sin os x+ tan 2 os tan
3 26 6 26 26 26
x
d
x xx x
xc c
π
π ππ π π π


+




= = =
  
+ + ++ +
  
  
Vậy :
6
0
tan
26
1 1 11
ln tan ln 3 ln 3
6
2 2 26 2 4
tan
0
26
x
d
x
I
x
π
π
π
π
π


+





= = += =



+


∫
(1)
- Mặt khác :
( )( )
22
66
00
sin 3 os sin 3 os
sin 3 os
3
sinx+ 3 osx sinx+ 3 osx
x cx x cx
xcx
I J dx dx
cc
ππ
−+
−
−= =
∫∫
Do đó :
( ) ( )
6
0
3 sinx- 3 osx osx- 3sinx 1 3
6
0
I J c dx c
π
π
−= =− =−
∫
(2)
Từ (1) và (2) ta có hệ :
( )
3 31
1
ln3
ln3
16 4
4
3
1 31
313
ln3
16 4
I
IJ
IJ
J
−
= −
+=

⇔

−

−=−
= +
Để tính K ta đặt
3 3 ; 0. 5
2 2 36
t x dt dx x t x t
π π ππ
= − → = ⇔ = = = →=
Vậy :
( )
66
00
os 2t+3
os2t 1 3 1
ln3
82
sint+ 3 ost
os t+3 3sin t+3
22
c
c
K dt dt I J
c
c
ππ
π
ππ
−
= =− =−= −
 
−
 
 
∫∫
Ví dụ 10. Tính các tích phân sau .
a.
4
0
1
1 sin2
dx
x
π
+
∫
( CĐ-99) b.
2
0
2 sinx+cosx
dx
π
+
∫
(ĐH-LN-2000)
c.
( )
2
10 10 4 4
0
sin os sin cosx c x x x dx
π
+−
∫
(SPII-2000) d.
3
6
1
sinxsin x+
6
dx
π
π
π



∫
(MĐC-2000)
Giải
a.
( )
44 4
2
2
00 0
11 1
tan 1
4
1 sin2 4
sinx+cosx
2cos
0
4
dx dx dx
x
x
x
ππ π
π
π
π

= = =−=

+


−


∫∫ ∫
b.
2
0
2 sinx+cosx
dx
π
+
∫
.
Đặt :
2
2
2
11 2
tan 1 tan ; ; 0 0, 1
2 22 1 2
2cos
2
x x dt
t dt dx dx dx x t x t
x
t
π

= ⇔ = = + ⇔ = = →= = →=

+

Vậy :
( )
( )
( )
1 11
22
2
2
0 0
0
22
12 2 2
.2
21
23
1
12
2
11
dt dt
I dt
tt
tt
t
t
tt
= =
= =
−
++
+
++
++
++
∫ ∫∫
Đặt :
( )
( )
2
2
2
2
12
2 ; 0 tan ; 1 tan 2
os 2
1 2 tan
2 22
() 2
os
2 1 tan
12
dt du t u t u
cu
tu
dt
f t dt du
du
cu
u
t
= =→= =→=
+= ⇒
= = =
+
++
Vậy :
( )
2
1
2
21
1
2
2 2 2 2 arxtan arctan 2
2
u
u
u
I du u u u
u

= = = −= −



∫
c.
( )
2
10 10 4 4
0
sin os sin cosx c x x x dx
π
+−
∫
Ta có :
( ) ( )( )
10 10 4 4 2 2 4 4 6 6
sin os sin cos sin os os sin os sinxc x x x xc x c x xc x x+− + = − −
( )( )( )
22 22 44 22
os sin os sin os sin os sincx xcx xcx xcx x=−−++
2 22 2
1 1 1 os4x 1 os8x 15 1 1
os 2 1 sin 2 os 2 sin 4 os4x+ os8x
4 16 2 32 32 2 32
cc
cx xcx x c c
+−

=− =− =−=+


Vậy :
2
0
15 1 1 15 1 1 15
os4x+ os8x sin 4 sin8
22
32 2 32 32
2 8 32.8 64
00
I c c dx x x
π
ππ
ππ

=+ =++ =


∫
d.
3
6
1
sinxsin x+
6
dx
π
π
π



∫
.
Ta có :
( )
1
sin sin osx-sinxco = *
6 6 6 6 62
xx xx xc x
ππ π π π

   
+−=⇒ +−= + +
   

   

Do đó :
1
sin osx-sinxco
1
66
2
() 2 2
sinxsin x+ sinxsin x+ s
inxsin x+
66 6
xc x
fx
ππ
ππ π
 
++
 
 
= = =
  
  
  
33
66
os x+ os x+
osx osx
66
3
( ) 2 2 ln sinx ln sin x+
sinx sinx 6
sin sin
66
6
cc
cc
I f x dx dx
xx
ππ
ππ
ππ
π
π
ππ
π

 
 





= − ⇒= = − = −


 



++
 

 

∫∫
sinx 3 1 2 3
3
2ln ln
ln . 2ln
22 2
3
sin x+
6
6
I
π
π
π
= =−=



* Chú ý : Ta còn có cách khác
f(x)=
( )
2
11 2
31
sin 3 cot
sinxsin x+
sinx sinx+ osx
6
22
xx
c
π
= =

+




Vậy :
( )
( )
33
2
66
2 3 cot
21 3
3
2ln 3 cot 2ln
sin 2
3 cot
3 cot
6
dx
I dx x
x
x
x
ππ
ππ
π
π
+
= =− =−+ =
+
+
∫∫
Ví dụ 11. Tính các tích phân sau
a.
3
2
2
0
sinxcos
1 os
x
dx
cx
π
+
∫
(HVBCVT-99) b.
2
22
0
os cos 2c x xdx
π
∫
( HVNHTPHCM-98)
c.
4
66
0
sin 4
os sin
x
dx
cx x
π
+
∫
(ĐHNT-01) d.
4
4
0
os
dx
cx
π
∫
(ĐHTM-95)
Giải
a.
( )
32
22
22
00
sinxcos 1 os
(sin 2 ) 1
1 os 2 1 os
x cx
dx x dx
cx cx
ππ
=
++
∫∫
Đặt :
2
2
2sin cos sin 2
1 os
os 1; 0 2; 1
2
dt x xdx xdx
t cx
c xt x t x t
π
=−=−
=+⇒
=− = →= = →=
Vậy :
( )
( )
( )
12
21
2
1
1 1 1 1 ln 2 1
1 ln
1
2 22 2
t
I dt dt
t t
tt
−
−

= −= − = − =


∫∫
b.
2
22
0
os cos 2c x xdx
π
∫
.
Ta có :
( )
22
1 os2x 1 os4x 1
( ) os cos 2 . 1 os2x+cos4x+cos4x.cos2x
2 24
cc
fx c x x c
++
= = = +
( )
1 1 13 1 1
1 os2x+cos4x+ os6x+cos2x os2x+ os4x+ os6x
4 2 48 4 8
c c ccc

=+=+


Vậy :
2
0
13 1 1 1 3 1 1
os2x+ os4x+ os6x sin 2 sin 4 sin 6
2
4 8 4 8 4
16 16 48 8
0
I cccdxxxxx
π
π
π

=+ =+++ =


∫
c.
4
66
0
sin 4
os sin
x
dx
cx x
π
+
∫
.
Vì :
( ) ( ) ( )
66 5 5 44
sin os 6sin cos 6 os sin 6sin cos sin osd xcx xxcxxdx xx xcx+= − = −
( ) ( )( )
6 6 2 22 2
sin os 3sin 2 sin os sin os 3sin 2 cos2d x c x x x c x x c x dx x xdx⇔ += − + =−
( )
66
32
sin 4 sin 4 sin os
23
xdx xdx d x c x=− ⇒=− +
Vậy :
( )
( )
( )
66
44
66
66
66
00
sin os
sin 4 2 2 4
ln sin os ln 2
4
os sin 3 3 3
sin os
0
d xc x
x
dx x c x
cx x
xc x
ππ
π
+
=− =− +=
+
+
∫∫
d.
( )
( )
44 4
23
4 22
00 0
1 14
1 tan t anx t anx+ tan
4
os os os 3 3
0
dx dx
xd x
cx cxcx
ππ π
π

==+= =


∫∫ ∫
Ví dụ 12. Tính các tích phân sau .
a.
11
0
sin xdx
π
∫
( HVQHQT-96) b.
4
24
0
sin cosx xdx
π
∫
(NNI-96)
c.
4
2
0
os cos4c x xdx
π
∫
(NNI-98 ) d.
0
1 os2xc dx
π
+
∫
(ĐHTL-97 )
Giải
a.
11
0
sin xdx
π
∫
Ta có :
( ) ( )
5
11 10 2 2 3 4 5 6
sin sin .sinx= 1-cos sinx= 1-5cos 10cos 10cos 5cos os sinxx x x x x x xc x= + − +−
Cho nên :
( )
2 3 4 56
0
1-5cos 10cos 10cos 5cos os sinxdxI x x x xc x
π
= + − +−
∫
7 65 4 3
1 5 5 5 118
os os 2cos os os osx
0
7 6 2
3 21
c x c x x c x c xc
π
−

= −+−+− =


b.
4
24
0
sin cosx xdx
π
∫
Hạ bậc :
( )
( )
2
24 2
1 os2x 1 os2x 1
sin cos 1 os2x 1 2cos2 os 2
2 28
cc
x x c xc x
−+

= =− ++


( )
2 23
1
1 2cos2 os 2 os2x-2cos 2 os 2
8
xc xc xc x=+ +− −
( )
23
1 1 1+cos4x 1+cos4x
1 os2x-cos 2 os 2 1 os2x- os2x
8 82 2
c xc x c c


=+ −=+ −




( )
1 1 cos6x+cos2x
1 os2x-cos4x+cos4x.cos2x 1 os2x-cos4x+
16 16 2
cc

=+=+


( )
1
2 3cos2 os6x-cos4x
32
xc++
Vậy
( )
4
0
1 13 1 1
2 3cos2 os6x-cos4x sin 2 sin6 sin 4
4
32 32
64 32.6 32.4
0
I xc dxxxxx
π
π

=++ =+ + − =


∫
d.
2
2
00 00
2
1 os2x 2cos 2 osx 2 osxdx osxdxc dx xdx c dx c c
π
ππ π π
π


+= = = −



∫ ∫ ∫ ∫∫
( )
2 sinx sinx 2 1 1 2 2
2
0
2
ππ
π


= − = +=



III. MỘT SỐ CHÚ Ý QUAN TRỌNG
1. Trong phương pháp đổi biến số dạng 2.
* Sử dụng công thức :
00
() ( )
bb
f x dx f b x dx= −
∫∫
Chứng minh :
• Đặt : b-x=t , suy ra x=b-t và dx=-dt ,
0
0
x tb
xb t
= →=
⇒
= →=
• Do đó :
0
0 00
() ()() () ( )
b bb
b
f x dx f b t dt f b t dt f b x dx= −− = − = −
∫∫ ∫ ∫
. Vì tích phân không
phụ thuộc vào biến số
Ví dụ : Tính các tích phân sau
a/
( )
2
3
0
4sin
sinx+cosx
xdx
π
∫
b/
( )
2
3
0
5cos 4sin
sinx+cosx
xx
dx
π
−
∫
c/
( )
4
2
0
log 1 t anx dx
π
+
∫
d/
6
2
66
0
sin
sin os
x
dx
xc x
π
+
∫
e/
( )
1
0
1
n
m
x x dx−
∫
f/
4
2
33
0
sin cos
sin os
xx
dx
xc x
π
+
∫
Giải
a/
( )
2
3
0
4sin
sinx+cosx
xdx
I
π
=
∫
.(1) . Đặt :
( )
( )
33
,0 ; 0
22
4sin
4cos
2
22
( ) ()
cost+sint
sin os
22
dt dx x t x t
t
t xx t
t
f x dx dt dt
f t dt
tc t
ππ
π
ππ
ππ
=− = →= = →=

−
= − ⇒ = −↔


= =−=


−+ −




Nhưng tích phân không phụ thuộc vào biến số , cho nên :
( )
( )
0
2
3
0
2
4 osx
() 2
sinx+cosx
c
I f t dt dx
π
π
= =
∫∫
Lấy (1) +(2) vế với vế ta có :
( )
( )
( )
22
32
00
4 sinx+cosx
1
22
sinx+cosx sinx+cosx
I dx I dx
ππ
= ⇒=
∫∫
2
2
0
1
2 tan 2
2
4
2cos
0
4
I dx x
x
π
π
π
π

⇔= = − =



−


∫
b/
( )
2
3
0
5cos 4sin
sinx+cosx
xx
I dx
π
−
=
∫
. Tương tự như ví dụ a/ ta có kết quả sau :
( ) ( )
( )
( )
0
22
3 33
00
2
5cos 4sin 5sin 4cos 5sin 4 os
2
sinx+cosx ost+sint sinx+cosx
x x t t x cx
I dx dt dx
c
ππ
π
− −−
= =−=
∫ ∫∫
Vậy :
( )
22
2
2
00
1 11 1
2 tan 1
2
24 2
sinx+cosx
2cos
0
4
I dx dx
x I
x
ππ
π
π
π

= = = − =⇒=



−


∫∫
c/
( )
4
2
0
log 1 t anx dx
π
+
∫
. Đặt :
( ) ( )
22
,0 ; 0
44
44
( ) log 1 t anx log 1 tan
4
dx dt x t x t
t xx t
f x dx dx t dt
ππ
ππ
π
=− = →= = →=
= − → = −⇔


= + = + −−




Hay:
( ) ( )
2 2 22
1 tan 2
( ) log 1 log log 2 log
1 tan 1 tan
t
f t dt dt t
tt
−

= + −= −= −

++

Vậy :
0
44
2
00
4
( ) log 2
4
48
0
I f t dt dt tdt I t I
ππ
π
π
ππ
= = − ⇒ = = ⇔=
∫ ∫∫
d/
6
2
66
0
sin
sin os
x
I dx
xc x
π
=
+
∫
(1)
( )
6
0
6
2
66
66
0
2
sin
os
2
os sin
sin os
22
t
cx
d t dx I
cx x
tc t
π
π
π
ππ

−


−= =
+
 
−+ −
 
 
∫∫
(2)
Cộng (1) và (2) ta có :
66
22
66
00
os sin
2
2
os sin 2
4
0
cx x
I dx dx x I
cx x
ππ
π
ππ
+
= = = = ⇒=
+
∫∫
e/
( )
1
0
1
n
m
x x dx−
∫
. Đặt : t=1-x suy ra x=1-t . Khi x=0,t=1;x=1,t=0; dt=-dx
Do đó :
( )
0 11
1 00
1 ( ) (1 ) (1 )
m
n nm n m
I t t dt t t dt x x dx= − −= − = −
∫ ∫∫
MỘT SỐ BÀI TẬP TỰ LUYỆN
1.
2
2
0
4sin
1 osx
x
dx
c
π
+
∫
2.
4
0
osx+2sinx
4cos 3sin
c
dx
xx
π
+
∫
(XD-98 )
3.
3
2
2
0
sinxcos
1 os
x
dx
cx
π
+
∫
4.
3
2
0
sinx
cos
x
dx
x
π
+
∫
( HVNHTPHCM-2000 )
5.
( )
1
6
53
0
1x x dx−
∫
(ĐHKT-97 ) 6.
2
0
sin
2 os
xx
dx
cx
π
+
∫
( AN-97 )
7.
4
0
sinx+2cosx
3sin osx
dx
xc
π
+
∫
( CĐSPHN-2000) 8.
2
0
1 sinx
ln
1+cosx
dx
π
+



∫
( CĐSPKT-2000 )
9.
2
0
sin
9 4cos
xx
dx
x
π
+
∫
(ĐHYDTPHCM-2000 ) 10.
4
2
33
0
sin cos
sin os
xx
dx
xc x
π
+
∫
* Dạng :
asinx+bcosx+c
'sinx+b'cosx+c'
I dx
a
β
α
=
∫
Cách giải :
Ta phân tích :
( )
' osx-b'sinx
asinx+bcosx+c
'sinx+b'cosx+c' 'sinx+b'cosx+c' 'sinx+b'cosx+c'
Bac
C
dx A
a aa
β
α
=++
∫
- Sau đó : Quy đồng mẫu số
- Đồng nhất hai tử số , để tìm A,B,C .
- Tính I :
( )
( )
' osx-b'sinx
Ax+Bln 'sinx+b'cosx+c'
'sinx+b'cosx+c' 'sinx+b'cosx+c' 'sinx+b'cosx+c'
Bac
C dx
I A dx a C
aa a
ββ
αα
β
α

=++ = +


∫∫
VÍ DỤ ÁP DỤNG
Ví dụ . Tính các tích phân sau :
a.
2
0
sinx-cosx+1
sinx+2cosx+3
dx
π
∫
( Bộ đề ) b.
4
0
osx+2sinx
4cos 3sin
c
dx
xx
π
+
∫
( XD-98 )
c.
2
0
sinx+7cosx+6
4sin 3cos 5
dx
xx
π
++
∫
d. I =
2
0
4cosx 3sin x 1
dx
4sin x 3cosx 5
π
−+
++
∫
Giải
a.
2
0
sinx-cosx+1
sinx+2cosx+3
dx
π
∫
. Ta có :
( )
( )
osx-2sinx
sinx-cosx+1
() 1
sinx+2cosx+3 sinx+2cosx+3 sinx+2cosx+3
Bc
C
fx A==++
Quy đồng mẫu số và đồng nhất hệ số hai tử số :
( ) ( )
1
5
21
2 sinx+ 2A+B osx+3A+C
3
() 2
1
sinx+2cosx+3 5
31
4
5
A
AB
AB c
fx A
B B
AC
C
= −
−=
−

⇔ = ⇒ + =−⇔ =−


+=
=
. Thay vào (1)
( )
22 2
00 0
sinx+2cosx+3
13 4 1 3 4
ln sinx+2cosx+3
2
5 5 sinx+2cosx+3 5 sinx+2cosx+3 10 5 5
0
d
I dx dx J
ππ π
π
π

=− − + =−− −


∫∫ ∫
( )
344
ln 2
10 5 5 5
IJ
π
=−− −
- Tính tích phân J :
Đặt :
( )
2
1
2
0
2
22
22
1
; 0 0, 1
22
os
2
2
tan
1 22
2
12
()
21
1 23
23
11
dx
dt x t x t
x
c
x dt
tJ
dt dt
t
f x dx
tt
tt t
tt
π
= = →= = →=
= ⇒ ⇔=
++
= =
−
+ ++
++
++
∫
. (3)
Tính (3) : Đặt :
12
2
2
2
2
2 . 0 tan ; 1 tan 2
os 2
1 2 tan
12 2
()
2
os 2
os
du
dt t u u t u u
cu
tu
du
f t dt du
cu
cu
= =→===→==
+= ⇒
= =
Vậy :
( ) ( )
2
1
21 21
u
2
2
tan
2 2 3 442
j= ln
2
2 2 10 5 5 5 2
tan 2
u
u
du uu II uu
u
π
=
= − ⇒==− − − −
=
∫
b.
( )
( )
4
0
3cos 4sin
osx+2sinx osx+2sinx
; () 1
4cos 3sin 4cos 3sin 4cos 3sin 4cos 3sin
Bx x
cc C
dx f x A
xx xx xx xx
π
−
==+ +→
+ + ++
∫
Giống như phàn a. Ta có :
21
;
55
AB= = −
;C=0
Vậy :
( )
4
0
3cos 4sin
2 1 2 1 1 42
ln 4cos 3sin ln
4
5 5 4cos 3sin 5 5 10
5 7
0
xx
I dx x x x
xx
π
π
π
−


=− =− +=+


+


∫
| 1/42
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TÍCH PHÂN
I. Khái niệm tích phân
1. Diện tích hình thang cong .
• Giới thiệu cho học sinh về cách tính diện tích của một hình thang cong
• Từ đó suy ra công thức :
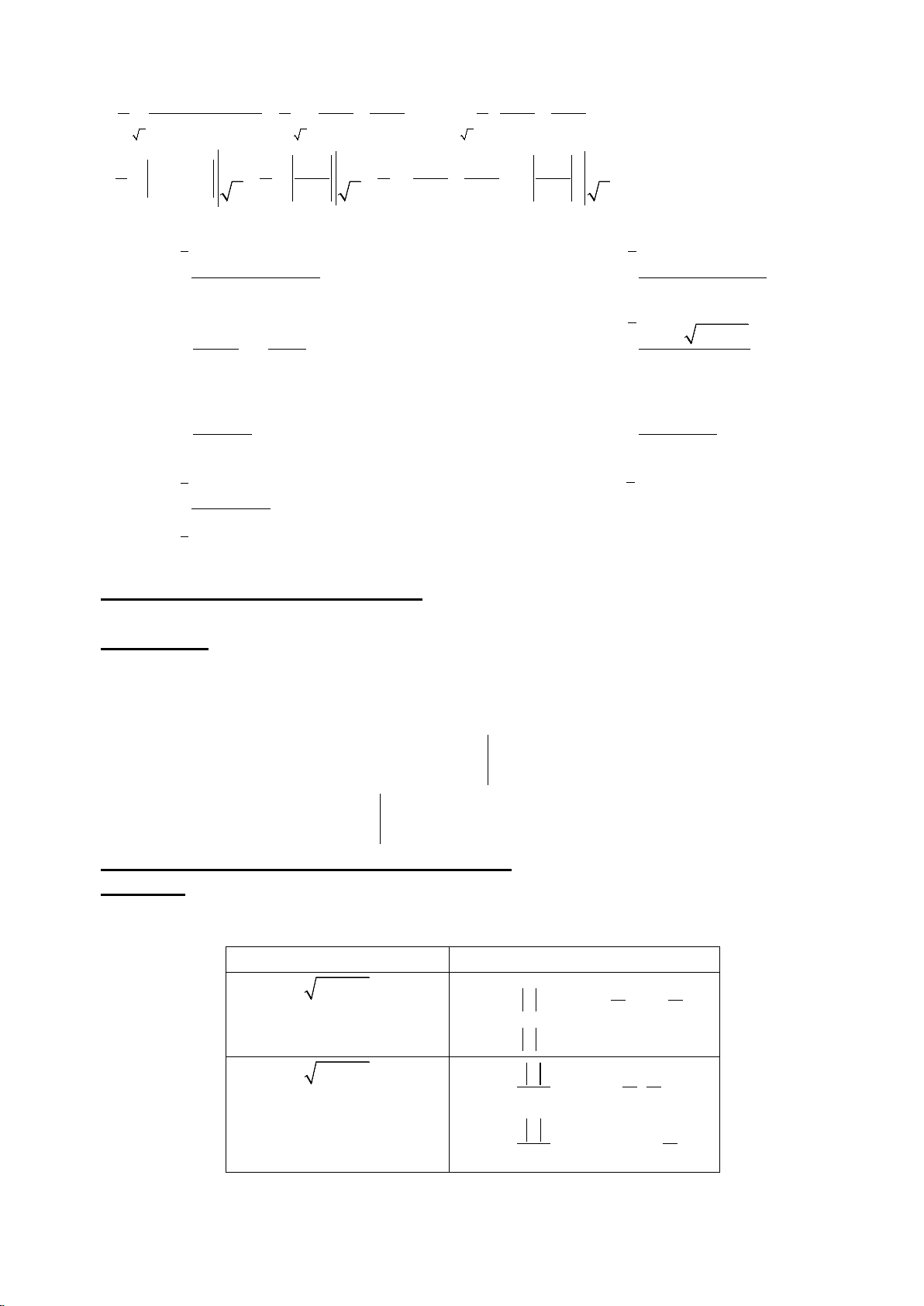
S ( x) − S ( x0 ) lim = f (x0 ) x→ − 0 x x x0
2. Định nghĩa tích phân
• Cho hàm f liên túc trên một khoảng K và a, b là hai số bất kỳ thuộc K. Nếu F
là một nguyên hàm của f trên K thì hiệu số : F(b)-F(a) được gọi là tích phân b
của f đi từ a đến b , ký hiệu là : f (x)dx ∫a b
• Có nghĩa là : f (x)dx = F ∫
(b)− F (a) a
• Gọi F(x) là một nguyên hàm của f(x) và b
F ( x) = F (b) − F (a) thì : a b b
f (x)dx = F ∫
(x) = F (b)− F (a) a a • Trong đó :
- a : là cận trên , b là cận dưới
- f(x) gọi là hàm số dưới dấu tích phân
- dx : gọi là vi phân của đối số
-f(x)dx : Gọi là biểu thức dưới dấu tích phân
II. Tính chất của tích phân
Giả sử cho hai hàm số f và g liên tục trên K , a,b,c là ba số bất kỳ thuộc K . Khi đó ta có : a 1.
f (x)dx = 0 ∫ a b a 2.
f (x)dx = − f (x)dx ∫ ∫
. ( Gọi là tích chất đổi cận ) a b b c b 3. f (x)dx = f (x)dx + f (x)dx ∫ ∫ ∫ a a c b b b
4. ∫[ f (x) ± g(x)]dx = f (x)dx ± g(x)dx ∫ ∫
. ( Tích phân củ một tổng hoặc hiệu hai tích a a a
phân bằng tổng hoặc hiệu hai tích phân ) . b b 5.
kf (x)dx = k. f (x)dx ∫ ∫
. ( Hằng số k trong dấu tích phân , có thể đưa ra ngoài dấu a a tích phân được )
Ngoài 5 tính chất trên , người ta còn chứng minh được một số tính chất khác như : b 6 . Nếu f(x) ≥ 0 x ∀ ∈[ ;
a b] thì : f (x)dx ≥ 0 x ∀ ∈ ∫ [ ;ab] a b b 7. Nếu : x ∀ ∈[ ;
a b] : f (x) ≥ g(x) ⇒ f (x)dx ≥ g(x)dx ∫ ∫
. ( Bất đẳng thức trong tích a a phân ) 8. Nếu : x ∀ ∈[ ;
a b] và với hai số M,N ta luôn có : M ≤ f (x) ≤ N . Thì : b
M (b − a) ≤ f (x)dx ≤ N ∫
(b − a). ( Tính chất giá trị trung bình của tích phân ) a
III. CÁC PHƯƠNG PHÁP TÍNH TÍCH PHÂN
A. PHƯƠNG PHÁP PHÂN TÍCH
1.Trong phương pháp này , chúng ta cẩn :
• Kỹ năng : Cần biết phân tích f(x) thành tổng , hiệu , tích , thương của nhiều
hàm số khác , mà ta có thể sử dụng được trực tiếp bảng nguyên hàm cơ bản
tìm nguyên hàm của chúng .
• Kiến thức : Như đã trình bày trong phần " Nguyên hàm " , cần phải nắm trắc
các kiến thức về Vi phân , các công thức về phép toán lũy thừa , phép toán căn
bậc n của một số và biểu diễn chúng dưới dạng lũy thừa với số mũ hữu tỷ . 2. Ví dụ áp dụng
Ví dụ 1: Tính các tích phân sau x ( 4 2 2 x −1 + ) 1 1 2 x a/ dx ∫ b/ dx ∫ 2 + x +1 0 ( )3 1 x 1
3 2x x − 2 x + ln (1+ x ) 2 3 2
x + x − x +1 c/ dx ∫ d/ dx ∫ + 4 2 x − 2x +1 1 2 x (1 x ) 2 Giải x ( 4 2 2 x −1 + ) 1 2 2 2 2
 2x x −1 x +1 x   x  a/ 2 dx =  +  dx = ∫ ∫ ∫2x x −1+  dx 2  2 2  2 + + +    +  1 x 1 1 x 1 x 1 1 x 1 2 ⇒ x −1d ∫
( x −1) 2+d∫( x +1) 1 = ( x −1)2 2 2 3 2 2 2 2 2 + x +1 = + 5 − 2 2 1 1 2 1 1 b/ 2 x (x +1− )2 1 (x + )2 1 1 1 1 1 x +1 1   1 1 1  = =  − +  =  − +  ∫ ( ∫ ∫ ∫ x + ) dx dx 2 dx 2 dx 3 1 (x + )3 1 (x + )3 1 (x + )3 1 (x + )3 1   x +1   (x + )2 1 (x + )3 1  0 0 0 0  1 d ( x + ) 1 1 d ( x + ) 1 1 d ( x + ) 1 1 1 1 1 1 1 3 ⇒ I = − 2 + = x + + − = + ∫ ∫ ∫ x +1 (x + ) ln 1 2 ln 2 2 1 (x + )3 1 0 x +1 0 2 ( x + )2 1 0 8 0 0 0 c/ − + +  +   +  3 2x x 2 x ln (1 x ) 3 ln − (1 x) 3 ln 1 1 1 x x dx =  +
dx =  x −1 +  dx ∫ ∫ ∫ 2 x 1+ x  1+ x 1+ x 2 x   +  1 ( ) 1 ( ) ( ) ( ) ( ) 1   (1 x)2 x 3 +  
⇒ I = ∫( x − ) 3 ln (1 x ) dx + d ∫ ( + x) 2 1 1 = ( x)3 3 3 2 − x + ln (1+ x) =   1+ x 3  1 1 1 1 2 = − + ( + ) 2 2 3 4 ln 1 3 − ln 2 3 2  + − + 4 −  1 1 ( 3 2 2 x x) 2 2 dx x x x 1 2dx d/ dx =   + dx + ∫ ∫ ∫ ∫ 4 2 4 2 x − 2x +1
4 x − 2x +1    ( 2x − )1 ( 2 − 2 2 2 2 x )2 1 2 d ( 4 2 x − 2x + ) 2 2 2 1 1 1  1 1  1  1 1  = + − dx + − dx ∫ ∫   ∫   4 ( 2 4 2 x − 2x +1 2
x −1 x +1
4  x −1 x +1 2 ) 2 2 2 − 2  −  2 1 1 x 1 1 1 1 x 1 = ln ( x − )2 2 1 + ln + − − − ln =   4 2 2 x +1 2
2  x −1 x +1 x +1  2
Ví dụ 2. Tính các tích phân sau π π 2 sin x ( 2 2 sin x − ) 1 3 sin 2x a/ dx ∫ b/ dx ∫ 1+ os c x 2 2 2 sin x + 3cos x 0 0 π 1 1  2 + x  4 s inx+ 1+tanx c/ ln dx ∫   d/ dx ∫ 2 4 − x  2 − x  2 os c x 1 − 0
Ví dụ 3. Tính các tích phân sau 2 e 3 ln x +1 2 2 x −1 a/ dx ∫ b/ dx ∫ 3 x ln x 2x ( 2 x +1 1 ) e π π 4 3 4 + sin 2x 3 c/ dx ∫ d/ sin 3 . x os c xdx ∫ 2 π sin 2x 0 6
B. PHƯƠNG PHÁP ĐỔI BIẾN SỐ
I. Phương pháp đổi biến số dạng 1.
Để tính tích phân dạng này , ta cần thực hiện theo các bước sau 1/ Quy tắc : • Bước 1: Đặt x=v(t)
• Bước 2: Tính vi phân hai vế và đổi cận
• Bước 3: Phân tích f(x)dx=f(v(t))v'(t)dt b v(b) • v(b)
Bước 4: Tính f (x)dx =
g(t)dt = G(t) ∫ ∫ v(a) a v(a) • v b Bước 5: Kết luận : I= ( ) G(t) v(a)
2/ Nhận dạng : ( Xem lại phần nguyên hàm ) * Chú ý :
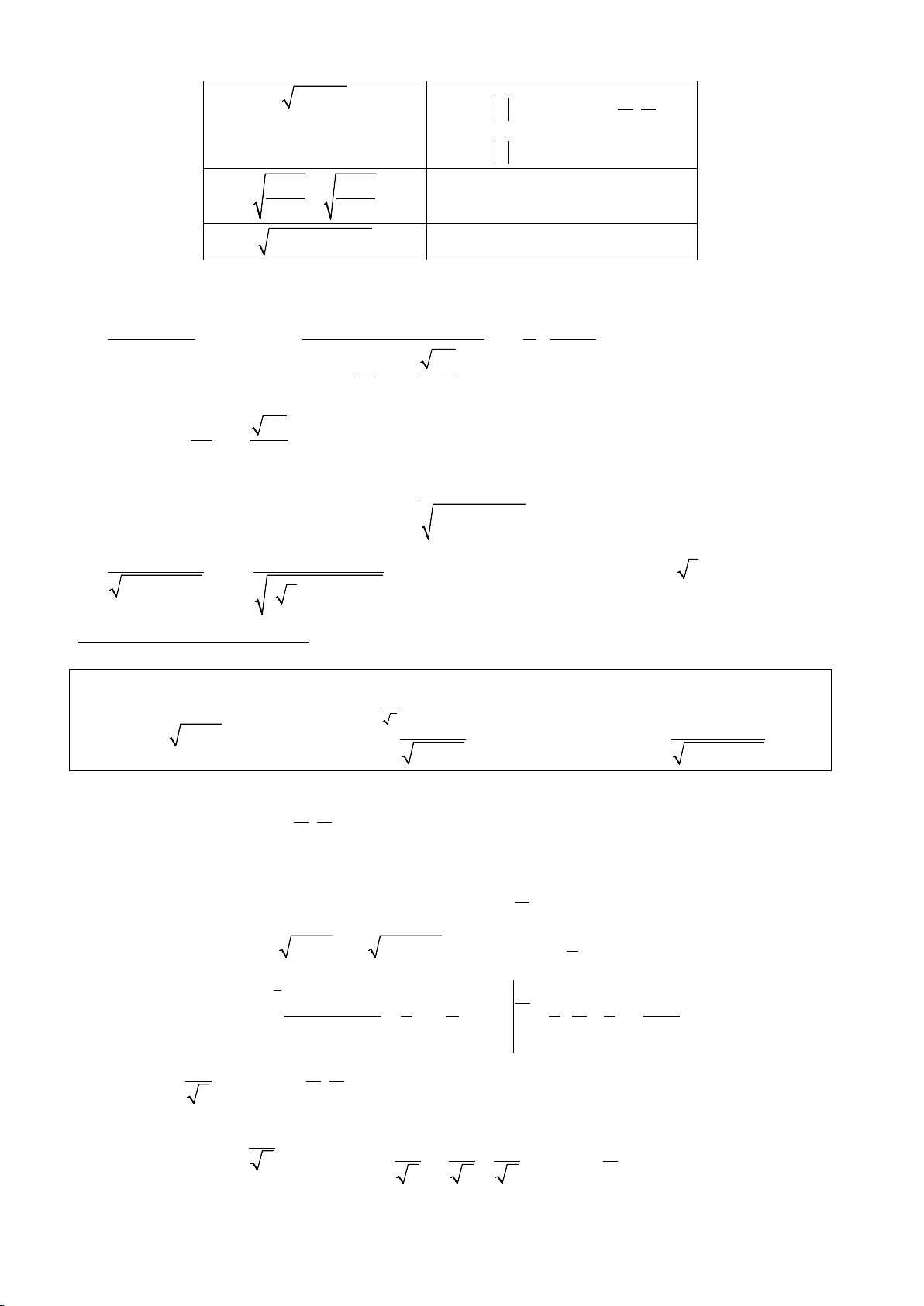
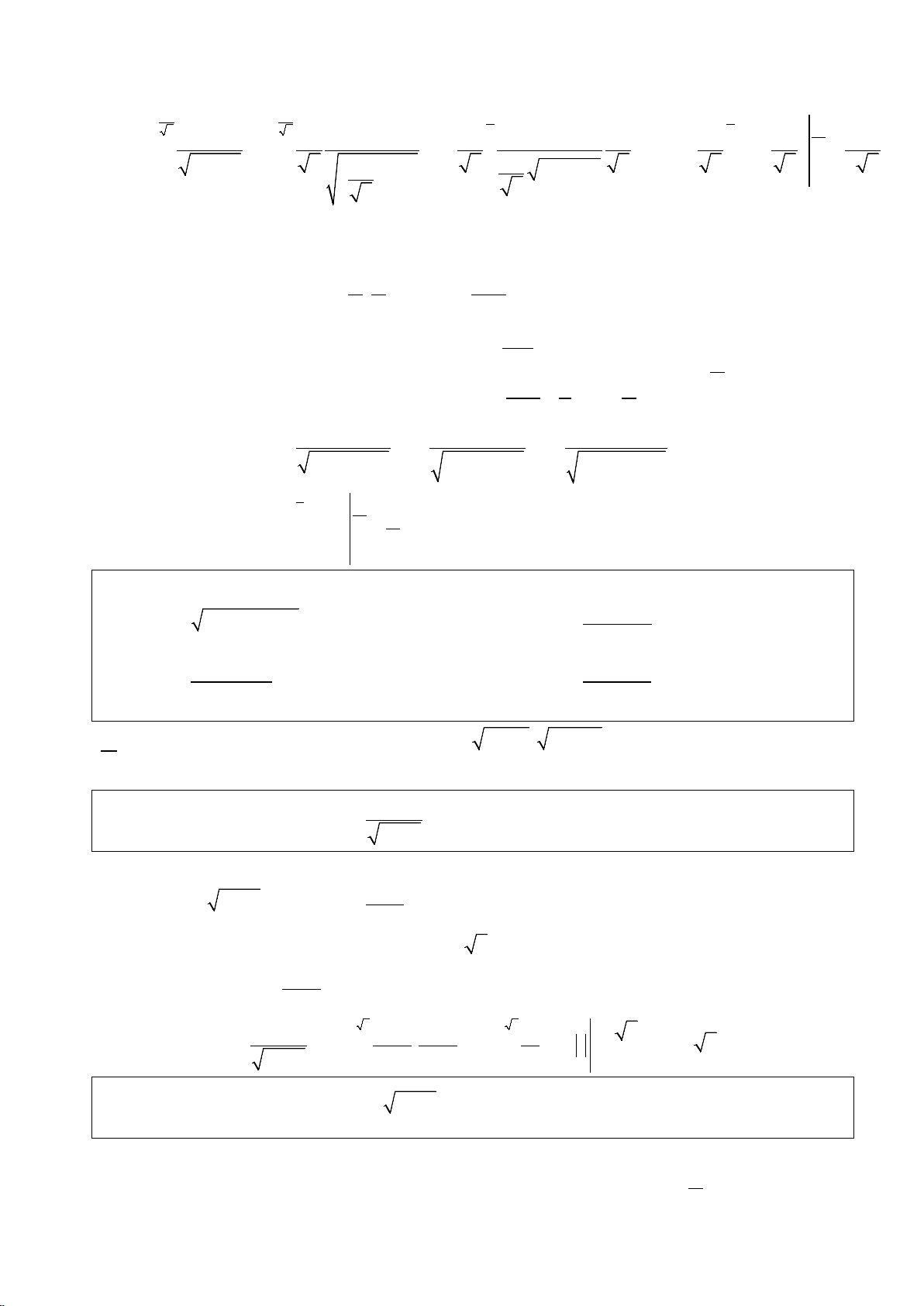
a. Các dấu hiệu dẫn tới việc lựa chọn ẩn phụ kiểu trên thông thường là : Dấu hiệu Cách chọn 2 2 a − x  π π
x = a sin t ↔ − ≤ t ≤  2 2  x = a os c t ↔ 0 ≤ t ≤ π  2 2 x − a a  π π  x = ↔ t ∈ − ;   sin t  2 2    a π  x =
↔ t ∈[0;π ] \    os c t  2  2 2 a + x   π π 
x = a tan t ↔ t ∈ − ;     2 2  
x = a cot t ↔ t ∈  (0;π ) a + x a − x x=a.cos2t ∨ a − x a + x
(x − a)(b − x) x=a+ (b − a) 2 sin t
b. Quan trọng nhất là các em phải nhận ra dạng :
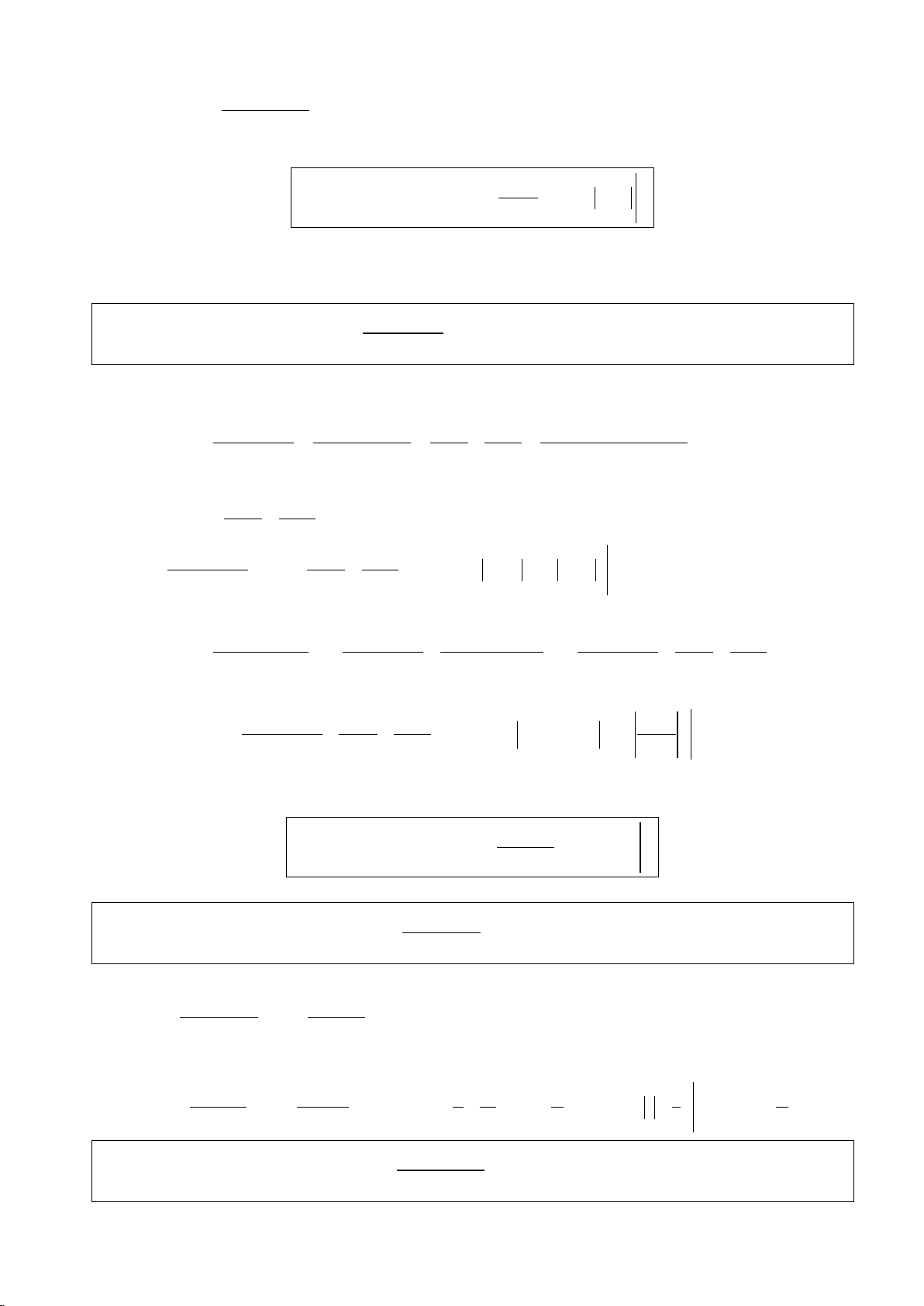
- Ví dụ : Trong dạng phân thức hữu tỷ : β β β 1 1 1 1 * dx ∆ < 0 = dx = du ∫ ∫ ∫ 2 ( ) 2 2 2 ax + bx + c   + α α  b a u k   −∆  α a  x+ +       2a  2a      Với :  b −∆  u = x+ , k = , du = dx    . 2a 2a   β
* áp dụng để giải bài toán tổng quát : dx ∫ (k ∈Z ). + α
(a + x )2k 1 2 2 β β 1 1 * dx = dx ∫ ∫
. Từ đó suy ra cách đặt : x −1= 3sint 2 α 2 + 2x − x α ( 3)2 −(x− )2 1
3/ Một số ví dụ áp dụng :
Ví dụ 1: Tính các tích phân sau 1 1 2 1 2 1 a/ 2 1− x dx ∫ b/ dx ∫ c/ dx ∫ 2 − 2 + − 0 0 1 2x 1 3 2x x Giải
a/ Đặt x=sint với :  π π  t ∈ − ;    2 2 
x = 0 ↔ sin t = 0 → t = 0 •  Suy ra : dx=costdt và :  π
x = 1 ↔ sin t = 1 → t =  2 • 1 Do đó : f(x)dx= 2 2 2
1− x dx = 1− sin t os c tdt=cos tdt = (1+ os c 2t ) dt 2 π π 1 2 • 1+ os c 2t dt 1  1  1  π 1  π −1 Vậy : ( ) f (x)dx = = t + sin 2t 2 = − = ∫ ∫     2 2  2  2  2 2  4 0 0 0 b/ Đặt : x = 1  π π  sin t t ∈ − ;   2  2 2  x=0 ↔ sint=0 → t=0 • 1  Suy ra : dx = os c tdt ⇒  1 1 1 π 2 x= ↔ = sin t → t =  2 2 2 2 • Do đó : 1 1 π π π 2 2 2 2 1 1 1 1 1 1 1 1 π dx = dx = os c tdt = dt = t 2 = ∫ ∫ ∫ ∫ 2 1 1− 2x 2  1  2 2 2 2 2 2 2 0 0 2 0 0 1− sin t − 0 x   2  2 
c/ Vì : + x − x = − ( x − )2 2 3 2 4 1 . Cho nên : •  π π  x −1
Đặt : x −1 = 2sin t t ∈ − ; ↔ sin t = (*)    2 2  2  1−1
x = 1 ↔ sin t = = 0 → t = 0  •   π  Suy ra : dx= 2 costdt và : 2  ⇒ t ∈ 0; → o c st>0   2 −1 1 π   6 
x = 2 ↔ sin t = = → t =  2 2 6 • 1 1 1 Do đó : f(x)dx= dx = dx = 2 cos tdt = dt 2 3 + 2x − x 4 − ( x − )2 1 4 ( 2 1− sin t ) π π 2 6 • π
Vậy : f (x)dx = dt = t 6 = ∫ ∫ 6 1 0 0
Ví dụ 2: Tính các tích phân sau 2 1 1 a/ 2
12x − 4x − 5dx ∫ b/ dx ∫ 2 x + x +1 1 0 5 1 b 2 a − x c/ dx ∫ d/ dx ∫ 2 x − 4x + 7 + 0 (a x )2 2 2
* Chú ý : Để tính tích phân dạng có chứa ( 2 2 2
x + a , a − x ) , ta còn sử dụng phương
pháp đổi biến số : u(x)=g(x,t) 1 Ví dụ 1
1 : Tính tích phân sau dx ∫ 2 0 x +1 Giải : 2 • t −1 Đặt : 2
x +1 = x − t ⇒ x = 2t
x = 0 → t = 1
− ; x = 1 → t = 1− 2 •  Khi đó : 2  t +1 dx = 2  2t 1 1− 2 2 1− 2 • 1 2 − t t +1 dt 1− 2 Do vậy : dx = . dt = = ln t = −ln 2 −1 ∫ ∫ ∫ 2 2 2 ( ) + t +1 2 1 t t x − − − 1 0 1 1 1
Ví dụ 2: Tính tích phân : 2 2 I = x 1− x dx ∫ 0 Giải • π
Đặt : t=sinx , suy ra dt=cosxdx và khi x=0,t=0 ; Khi x=1 , t= 2 • 1  1− os c 4t  Do đó : f(x)dx= 2 2 2 2 2 2 x
1− x dx = sin t. 1− sin t o
c stdt=sin t cos tdt = dt   4  2  π π 1 2 • 1 1  1  1 π π
Vậy : I= f (x)dx = ∫ ∫(1− os c 4t ) dt = t − sin 4t 2 = =   8 8  4  8 2 16 0 0 0
II. Đổi biến số dạng 2
1. Quy tắc : ( Ta tính tích phân bằng phương pháp đổi biến số dạng 2 theo các bước sau : )
• Bước 1: Khéo léo chọn một hàm số u(x) và đặt nó bằng t : t=u(x) .
• Bước 2: Tính vi phân hai vế và đổi cận : dt=u'(x)dx
• Bước 3: Ta phân tích f(x)dx = g[u(x)]u'(x)dx = g(t)dt . b u (b) • u(b)
Bước 4: Tính f (x)dx =
g(t)dt = G(t) ∫ ∫ u(a) a u (a) • u b Kết luận : I= ( ) G(t) u(a)
2. Nhận dạng : TÍCH PHÂN HÀM PHÂN THỨC HỮU TỶ β
A. DẠNG : I= P(x) dx ∫ (a ≠ 0) ax+b α β
* Chú ý đến công thức : m m β dx = ln ax+b ∫
. Và nếu bậc của P(x) cao hơn hoắc ax+b a α α
bằng 2 thì ta chia tử cho mẫu dẫn đến β β β β P(x) m 1
dx = Q(x) +
dx = Q(x)dx + m dx ∫ ∫ ∫ ∫ ax+b ax+b ax+b α α α α 2 Ví dụ 1 : 3 x Tính tích phân : I= dx ∫ 2x + 3 1 Giải 3 x 1 3 9 27 1 Ta có : 2 f (x) = = x − x + − 2x + 3 2 4 8 8 2x + 3 Do đó : 2 3 2 x  1 3 9 27 1   1 3 9 27  2 13 27 2 3 2 dx = x − x + − dx = x − x + x − ln 2x + 3 = − − ln 35 ∫ ∫    2x + 3  2 4 8 8 2x + 3   3 8 8 16  1 6 16 1 1 3 Ví dụ 2: 2 x − 5 Tính tích phân : I= dx ∫ x +1 5 Giải 2 x − 5 4 Ta có : f(x)= = x −1− . x +1 x +1 3 2 3 Do đó : − 3 x 5  4   1   5 +1 2 dx = x −1− dx =
x − x − 4 ln x +1 = 5 −1+ 4ln ∫ ∫         x +1  x +1   2  5 4   5 5 β B. DẠNG : P(x) dx ∫ 2 ax + bx + c α 1. Tam thức : 2
f (x) = ax + bx + c có hai nghiệm phân biệt β u '(x) β Công thức cần lưu ý :
dx = ln u(x) ∫ u(x) α α Ta có hai cách
Cách 1: ( Hệ số bất định )
Cách 2: ( Nhẩy tầng lầu ) 1 Ví dụ 3: 4x +11 Tính tích phân : I= dx ∫ . 2 x + 5x + 6 0 Giải
Cách 1: ( Hệ số bất định ) 4x +11 4x +11 A B
A( x + 3) + B ( x + 2) Ta có : f(x)= = = + = 2 x + 5x + 6 (x + 2)(x + 3) x + 2 x + 3 (x + 2)(x + 3)
Thay x=-2 vào hai tử số : 3=A và thay x=-3 vào hai tử số : -1= -B suy ra B=1 Do đó : f(x)= 3 1 + x + 2 x + 3 1 1 Vậy : 4x +11  3 1  1 dx = +
dx = 3ln x + 2 + ln x + 3 = 2ln 3 − ln 2 ∫ ∫  2 ( ) x + 5x + 6
x + 2 x + 3  0 0 0
Cách 2: ( Nhẩy tầng lầu ) 2 (2x + 5) +1 2x + 5 1 2x + 5 1 1 Ta có : f(x)= = 2. + = 2. + − 2 2 x + 5x + 6 x + 5x + 6 (x + 2)(x +3) 2 x + 5x + 6 x + 2 x + 3 Do đó : 1 1  2x + 5 1 1   x + 2  1 I= 2 f (x)dx = 2. + −
dx = 2 ln x + 5x + 6 + ln = 2ln 3 − ln 2 ∫ ∫    2
x + 5x + 6 x + 2 x + 3   x + 3  0 0 0 2. Tam thức : 2
f (x) = ax + bx + c có hai nghiệm kép
β u '(x)dx β Công thức cần chú ý : = ln ∫
(u(x)) u(x) α α
Thông thừơng ta đặt (x+b/2a)=t . 3 Ví dụ 4 : 3 x Tính tích phân sau : I= dx ∫ 2 x + 2x +1 0 Giải 3 3 3 3 x x Ta có : dx = dx ∫ ∫ 2 x + 2x +1 x +1 0 0 ( )2
Đặt : t=x+1 suy ra : dx=dt ; x=t-1 và : khi x=0 thì t=1 ; khi x=3 thì t=4 . Do đó 3 x (t − )3 3 4 4 1  3 1   1 1  4 3 : 2 = = − + − = − + + = − ∫ ( ∫ ∫    x + ) dx dt t 3 dt t 3t ln t 2 ln 2 2 2 2 1 tt t   2 t  1 2 0 1 1 1 Ví dụ 5: 4x Tính tích phân sau : I= dx ∫ 2 4x − 4x +1 0 Giải 4x 4x Ta có : = 2 4x − 4x +1 (2x − )2 1 Đặt : t= 2x 1
x = 0 ↔ t = 1 −
-1 suy ra : dt = 2dx → dx = dt;  2
x = 1 ↔ t = 1 1 1 1 1 4. (t + ) 1 1 Do đó : 4x 4x 1 1 1   1  1 2 dx = dx = dt = + dt = ln t − = 2 − ∫ ∫ ∫ ∫     2 4x − 4x +1 (2x − )2 2 2 1 t 2  t t   t  1 − 0 0 1 − 1 − 3. Tam thức : 2
f (x) = ax + bx + c vô nghiệm : b u = x +  Ta viết : f(x)= P(x) P(x)  2a = ;  2      −∆  a ( 2 2 2 u + k −∆ b ) k = a x + +       2  2  2 a a a      Khi đó : Đặt u= ktant 2 Ví dụ 6: x Tính tích phân : I= dx ∫ 2 x + 4x + 5 0 Giải 2 2 • x x Ta có : dx = dx ∫ ∫ 2 x + 4x + 5 x + 2 +1 0 0 ( )2 • 1
x = 0 ↔ tan t = 2
Đặt : x+2=tant , suy ra : dx= dt; ⇒  2 os c t
x = 2 ↔ tan t = 4 2 t t • 2 2 x tan t − 2 dt  sin tt Do đó : dx = = − 2 dt = ∫ ∫ ∫  (−ln o
c st − 2t ) 2 1 2 2 2 ( ) x + 2 +1 1+ tan t os c t  os c t  t 0 ( ) t t 1 1 1  1 1 2 2
tan t = 2 ↔ 1+ tan t = 5 ↔ o c s t = → o c st =  1 Từ : 5 5   1 1 2 2
tan t = 4 ↔ 1+ tan t = 17 ↔ os c t = → os c t = 2  17 17 • t os c t Vậy : (−ln o
c st − 2t ) 2 = − (ln o
c st − 2t ) − (ln cost − 2t ) 2  = −ln + 2 t − t 2 2 1 1 ( 2 1)  t cost 1 1 • os c t 1 1 5 2 ⇔ − ln
+ 2(t − t = 2 arctan4-arctan2 − ln . 5 = 2 arctan4-arctan2 − ln 2 1 ) ( ) ( ) cost 17 2 17 1 2 Ví dụ 7: 3 2
x + 2x + 4x + 9 Tính tích phân sau : I= dx ∫ 2 x + 4 0 Giải 3 2 •
x + 2x + 4x + 9 1 Ta có : = x + 2 + 2 2 x + 4 x + 4 2 3 2 2 2 •
x + 2x + 4x + 9  1   1  2 dx Do đó : 2 dx = x + 2 + dx = x + 2x + = 6 + J ∫ ∫    ∫ (1) 2 2 2 x + 4  x + 4   2  0 x + 4 0 0 0 2 1 Tính tích phân J= dx ∫ 2 x + 4 0
x = 0 → t = 0 • 2   π 
Đặt : x=2tant suy ra : dx = dt;  π ↔ t ∈ 0; → o c st>0 2   os c t x = 2 → t =   4   4 π π π 2 4 4 • 1 1 1 2 1 1 π Khi đó : dx = dt = dt = t 4 = ∫ ∫ ∫ 2 2 2 x + 4 4 1+ tan t o c s t 2 2 8 0 0 0 0 • π
Thay vào (1) : I = 6 + 8 β C. DẠNG : P(x) dx ∫ 3 2
ax + bx + cx + d α
1. Đa thức : f(x)= 3 2
ax + bx + cx + d (a ≠ 0) có một nghiệm bội ba β Công thức cần chú ý : 1 1 1 β dx = . ∫ m m 1 x 1− m x − α α 1 Ví dụ 8: x Tính tích phân : I= ∫ ( x + ) dx 3 1 0 Giải Cách 1:
• Đặt : x+1=t , suy ra x=t-1 và : khi x=0 thì t=1 ; khi x=1 thì t=2 1 2 2 • x t −1  1 1   1 1 1  2 1 Do đó : = = − = − + = ∫ ( ∫ ∫    x + ) dx dt dt 3 3 2 3 2 1 tt t
t 2 t  1 8 0 1 1 Cách 2: • x (x + ) 1 −1 1 1 Ta có : = = − ( x + )3 1 (x + )3 1 (x + )2 1 (x + )3 1 1 1     • x 1 1 1 1 1 1 1 Do đó : =  −  = − +  = ∫ ( ∫ x + ) dx dx 3 1 (x + )2 1 (x + )3 1   x +1 2   (x + )2 1  0 8 0 0  0 Ví dụ 9 : 4 x Tính tích phân : I= ∫ . − ( x − ) dx 3 1 1 Giải
• Đặt : x-1=t , suy ra : x=t+1 và : khi x=-1 thì t=-2 và khi x=0 thì t=-1 . 4 − − 4 3 2 − • x (t + )4 0 1 1 1 1
t + 4t + 6t + 4t +1  6 4 1  Do đó : = = = + + + + ∫ ∫ ∫ ∫   − ( x − ) dx dt dt t 4 dt 3 3 3 2 3 1 t tt t t  1 2 − 2 − 2 − 1 − •  6 4 1   1 4 1 1  1 − 33 2 ⇔ t + 4 + + + dt =
t + 4t + 6 ln t − − = − 6ln 2 ∫     2 3 2  t t t   2 t 2 t  2 − 8 2 −
2. Đa thức : f(x)= 3 2
ax + bx + cx + d (a ≠ 0) có hai nghiệm :
Có hai cách giải : Hệ số bất định và phương pháp nhẩy tầng lầu 3 Ví dụ 10 : 1
Tính tích phân sau : I= ∫ ( − ) dx x 1 ( x + )3 1 2 Giải
Cách 1. ( Phương pháp hệ số bất định ) 2 • 1 A B C A( x + ) 1 + B ( x − ) 1 ( x + ) 1 + C ( x − ) 1 Ta có : = + + = ( x − ) 1 ( x + )2 1 x −1 (x + )1 (x + )2 1 (x − )1(x + )2 1  1 A =  =  • 1 4 A
Thay hai nghiệm mẫu số vào hai tử số : 4  ⇔  . Khi đó (1) 1  = 2 − C 1 C  = −  2
( A+ B) 2x +(2A+C) x + A− B −C 1 1 1 ⇔
⇒ − − = ⇔ = − − = + − = − ( − ) A B C B A C x 1 ( x + ) 1 1 1 2 1 4 2 4 3 3   • 1 1 1 1 1 1 1 Do đó : =  + −  ∫ ( ∫ x − ) dx dx 1 ( x + ) . . 2 1
 4 x −1 4 (x + ) 1 2 ( x +  )2 1  2 2  1 1 1  3 1 3
⇔ I =  ln (x − ) 1 ( x + ) 1 + .  = = 4 2 ( x +  ) ln 8 ln 2 1 2 4 4  Cách 2:
• Đặt : t=x+1, suy ra : x=t-1 và khi x=2 thì t=3 ; khi x=3 thì t=4 . 3 4 4 4 4 • 1 dt
1 t − (t − 2) 1  1 1  Khi đó : I= = = = ∫ ∫ ∫  − ( ∫ ∫    x − ) dx dt dt dt 1 ( x + )2 2 1 t (t − 2) 2 2 t t − 2 2 t t − 2 t 2 3 3 ( )  2 ( ) 3  4 4 1  1  1 1  1   1 t − 2 1  4 3 ⇔ I =  − dt − dt ∫  ∫  = ln − ln t = ln 2   2 2 
t − 2 t t   4 t 2  3 4 2 3 1 ( 2 3t − 4t ) 2 2 2 Hoặc
1  3t − 4t − 4 
3t − 4t 1 (3t + 2) 3t − 4t 1  3 2  : = −   = − = − +     3 2 3 2 3 2 3 2 2 3 2 2 t − 2t t − 2t 4  t − 2tt − 2t 4 t t − 2t 4    t t  4 2 •
 3t − 4t 1  3 2   1  2   4 3 Do đó : I= 3 2 ∫ − + 
 dt = ln t − 2t − 3ln t − = ln 2    3 2 2  t − 2t 4  t t    4  t   3 4 3 2
t − ( 2t − 4  1 1 ) Hoặc : 1  1 t + 2  1  1 1 2  =   = − = − −     2 t (t − 2) 2
4  t (t − 2) 2 2  4  t − 2 t
 4  t − 2 t t    • Do đó : 4 1  1 1 2  1  t − 2 2  4 1  1 1 1 2  1  1  I= − − dt = ln + = ln + − ln − = ln 3 − ln 2 − ∫        2 4  t − 2 t t  4  t t  3 4  2 2 3 3  4  6  3 3 2 x
Ví dụ 11: Tính tích phân sau : I= ∫ ( x − ) dx 2 1 x + 2 2 ( ) Giải
Đặt : x-1=t , suy ra : x=t+1 , dx=dt và : khi x=2 thì t=1 ; x=3 thì t=2 . 2 3 2 2 2 Do đó : x (t + ) 2 1 t + 2t +1 = = ∫ ( ∫ ∫ x − ) dx dt dt 2 1 ( x + 2) 2 t (t + 3) 2 t t + 3 2 1 1 ( )
Cách 1; ( Hệ số bất định ) 2 t + 2t +1 At + B C
( At + B)(t +3) 2 + Ct
( A+C) 2t +(3A+ B)t +3B Ta có : = + = = 2 t (t + 3) 2 2 t t + 3 t (t + 3) 2 t (t + 3)  1 B =  3 A + C = 1  Đồng nhất hệ số hai 2   5 t + 2t +1 1 t + 3 4 1 tử số : 3
A + B = 2 ⇔ A = ⇒ = + 2 9 t   (t +3) 2 9 t 9 t + 3 3B = 1   4 C =  9 Do đó : 2 2 2 t + 2t +1
 1 1 3  4  1   1  3  4  2 17 4 7 dt = + + dt = ln t − + ln t + 3 = + ln 5 − ln 2 ∫ ∫         2 t (t + 3) 2
 9  t t  9  t + 3   9  t  9  1 6 9 9 1 1 Cách 2: • Ta có : 2  + +  + +   +    +  t − −  t t t t t t t t ( 2 2 2 2 2 t 9 2 1 1 3 6 3 1 3 6 3 1 3 6 1 ) =   =  +  =   +   2 t (t + 3) 3 2 3 2 2 3  t + 3t  3 t + 3t t  (t +3) 3 2 2 3  
t + 3t  9  t (t + 3)     2 2
1  3t + 6t  1 1 1 t − 3
1  3t + 6t  1 1 1  1 3  =   + − =   + − −   3 2 2 3 2 2
3  t + 3t  9 t + 3 9 t
3  t + 3t  9 t + 3 9  t t  • Vậy : 2 2 2 2 t + 2t +1
 1  3t + 6t  1  1 1 3   1 1  t + 3 3  2 3 2 dt = ∫ ∫   + − +   dt = ln t + 3t + ln −    2 t (t + 3) 3 2 2 3
  t + 3t  9  t + 3 t t  3 27    t t  1  1 1 • Do đó I= 17 4 7 + ln 5 − ln 2 6 9 9
3. Đa thức : f(x)= 3 2
ax + bx + cx + d (a ≠ 0) có ba nghiệm : 3 Ví dụ 12: 1
Tính tích phân sau : I= ∫ x ( dx 2 x −1 2 )
Cách 1: ( Hệ số bất định ) • Ta có : A( 2 x − ) 1 + Bx ( x + ) 1 + Cx ( x A B C − ) 1 1 1 f(x)= = = + + = x ( 2 x − ) 1 x ( x − ) 1 ( x + ) 1 x x −1 x +1 x ( x − ) 1 ( x + ) 1
• Đồng nhất hệ số hai tử số bằng cách thay các nghiệm : x=0;x=1 và x=-1 vào  A = 1 −
x = 0 →1 = −A  hai tử ta có :   1 1 1  1  1  1  x = 1
− →1 = 2C ⇔ B = ⇒ f (x) = − + +     2 x 2  
x −1 2  x +1 x = 1 → 1 = 2B   1 C =  2 • Vậy : 3 3 1  1  1 1  1  1  3 5 3 = + − = − + − = − ∫ ∫      x ( dx dx ln x 1 x 1 ln x ln 2 ln 3 2 x −1
 2  x −1 x +1 x  2  2 2 2 2 ) ( ( )( )) 2
Cách 2: ( Phương pháp nhẩy lầu ) 2 x − ( 2 x − ) 1 1 x 1 1 2x 1 Ta có : = = − = − x ( 2 x − ) 1 x ( 2 x − ) 2 2 1 x −1 x 2 x −1 x 3 3 3 Do đó : 1 1 2xdx 1  1  3 5 3 = − = − − = − ∫ ∫ ∫   x ( dx dx ln x 1 ln x ln 2 ln 3 2 x −1 2 x −1 x  2  2 2 2 2 ) ( 2 2 ) 2 2 4 Ví dụ 13: x +1
Tính tích phân sau : I= ∫ x ( dx 2 x − 4 3 ) Cách 1: + + A x x A B C
( 2x −4)+ Bx(x+2)+Cx(x−2 1 1 ) Ta có : = = + + = x ( 2 x − 4)
x ( x − 2)( x + 2) x x − 2 x + 2 x ( 2 x − 4)
Thay các nghiệm của mẫu số vào hai tử số :
Khi x=0 : 1= -4A suy ra : A=-1/4
Khi x=-2 : -1= 8C suy ra C=-1/8
Khi x=2 : 3= 8B suy ra : B=3/8 .
Do đó : f(x) = 1  1  1 1  3 1  − − +      
4  x  8  x − 2  8  x + 2  Vậy : 4 3 3 3 x +1 1 1 1 1 3 1  1 1 3  3 = − − + = − − − + + = ∫ ∫ ∫ ∫   x ( dx dx dx dx ln x ln x 2 ln x 2 2 x − 4 4 x 8 x − 2 8 x + 2  4 8 8  2 3 ) 2 2 2 5 3 1 = ln 3 − ln 5 − ln 2 8 8 4 Cách 2: Ta có : 2  + x − −  x   ( 2x 4 1 1 1 1 1 1 1 ) 1 1 1 1 2x 1  = + = − +   = − + −     x ( 2 x − 4) ( 2 x − 4) x ( 2 x − 4) 4  x − 2
x + 2  4  x ( 2 x − 4) 2
 4  x − 2 x + 2 2 x − 4 x    4 4 Do đó : x +1 1  1 1 1 2x 1  1 x − 2 1  4 = − + − = + − − ∫ ∫    x ( dx dx ln ln x 4 ln x 2 x − 4 4  x − 2 x + 2 2 x − 4 x  4 x + 2 2  3 3 ) ( 2 2 ) 3 3 Ví dụ 14: 2 x Tính tích phân sau : ∫ ( dx 2 x −1 x + 2 2 )( ) Giải
Cách 1: ( Hệ số bất định ) A( x + )
1 ( x + 2) + B ( x − )
1 ( x + 2) + C ( 2 2 2 x x x A B C − ) 1 ( = = + + = 2 x − ) 1 ( x + 2) (x − ) 1 ( x + ) 1 ( x + 2) x −1 x +1 x + 2 ( 2x − )1(x+2)
Thay lần lượt các nghiệm mẫu số vào hai tử số :
Thay : x=1 Ta cớ : 1=2A , suy ra : A=1/2
Thay : x=-1 ,Ta có :1=-2B, suy ra : B=-1/2
Thay x=-2 ,Ta có : 4= -5C, suy ra : C=-5/4 Do đó : 3 2 3 x  1 1 1 1 5 1  1 x −1 5  3 1 3 I= ∫ ( dx = − − dx = ln − ln x + 2 = ln ∫    2 x −1 x + 2
 2 x −1 2 x +1 4 x + 2  2 x +1 4  2 2 2 2 )( ) 2
Cách 2.( Nhẩy tầng lầu ) Ta có : 2 2 x x −1+1 1 1 1 1 x ( x + ) 1 − ( x − ) 1 ( x + 2) ( = = + = + 2 x − ) 1 ( x + 2)
( 2x − )1(x+2) x+2 (x− )1(x+ )1(x+2) x+2 2 (x− )1(x+ )1(x+2) 1 1  x 1  1 1  1  1 1  1  = +  −  = + + − −     x +
( x − )( x + ) 1 2 2 1 2 x +1 x + 2 2  
3  x −1 x + 2  x +1
Từ đó suy ra kết quả . β D. DẠNG R ( x) dx ∫ 4 2 ax + bx + c α
Những dạng này , gần đây trong các đề thi đại học ít cho ( Nhưng không hẳn là
không cho ) , nhưng tôi vẫn đưa ra đây một số đề thi đã thi trong những năm các
trường ra đề thi riêng , mong các em học sinh khá ,giỏi tham khảo để rút kinh nghiệm cho bản thân .
Sau đây tôi lấy một số ví dụ minh họa
Ví dụ 1. Tính các tích phân sau : 1 1 1 2 1+ x a. ∫ ( dx b. dx ∫ 3 x + 3x + 2)2 2 1+ x 0 1 2 Giải 1 1 a. ∫ ( dx x + 3x + 2)2 2 0 Ta có : 2 1 1  1 1  2
x + 3x + 2 = ( x + )
1 ( x + 2) ⇒ f (x) = ( = =  −  x + 3x + 2)2
(x + )(x + ) 2 2  (x + ) 1 (x + 2 1 2 ) 1 1 2 1 1  1 1  = + − = + − − . Vậy : (   x + ) 2 2 1 (x + 2)2 (x + ) 1 ( x + 2) (x + )2 1 (x + 2)2
x +1 x + 2  1 1 1  1 1  1 1    1 1 x +1  1 2 ∫ ( dx =  + − − ∫   dx = − − − = +   x + 3x + 2) 2 2 ln 2 ln 3 2 (x + )2 1 (x + 2)2 2
x +1 x + 2   x +1 x + 2 x + 2  0 3 0 0  1 2 1+ x b. dx ∫ 3 1+ x 1 2 2 2 2 1+ x
1− x + x + x 1− x + x x Ta có : f (x) = = = + 3 1+ x (1+ x)( 2
1− x + x ) (1+ x)( 2
1− x + x ) (1+ x)( 2 1− x + x ) 1 1 x  1 1 2x  ⇔ f (x) = + ⇒ + dx ∫  3 3 1+ x 1+ x
x +1 2 1+ x  1 2
Ví dụ 2. Tính các tích phân sau 3 2 x −1 1 4 x +1 a. dx ∫ b. dx ∫ 4 2 x − x +1 6 x +1 1 0 Giải 3 2 x −1 a. dx ∫ . Chia tử và mẫu cho 2 x ≠ 0 , ta có : 4 2 x − x +1 1 1  1  1− 1− dx 3 3   2 2 xx f (x) = ⇒ f (x)dx = ∫ ∫ ( )1 1   2 1 2 1 1 x + −1 x + −1 2   2 xx
x = 1 → t = 2 Đặt : 1 1  1  2 2  t = x + ⇒ x +
= t − 2, dt = 1− dx ↔   4 2 2 x xx   x = 3 → t =  3 4 4 4 3 3 3 3 Vậy : dt 1 1  1 1  f (x)dx = = dt = − dt ∫ ∫ ∫ ∫   2 t − 3 t − 3 t + 3 2 3
t − 3 t + 3  1 2 2 ( )( ) 2 4 1 t − 3 1  1 7 − 4 3  1 I = ln 3 = ln − ln  = ln   (7+4 3)) 2 3 t + 3 2 3 7 7 2 3   2 3  6 2 2 4 2 1 4
x −1 = ( x ) −1 = ( x − ) 1 ( x + x + ) x +1 1 b.  dx ∫ . Vì : 6 x +1 x −1=  (x )2 6 3 2 −1 = t −1( 3 t = x ) 0 Cho nên :   4 4 2 2 1 1 2 x +1 x − x +1 x 1 1 3x f (x) = = −
⇒ f (x)dx =  − dx  ∫ ∫ 6 x +1 ( 2x + )1( 4 2 x − x + ) 1 ( 3  +  x )2 2 x 1 3 +1  ( 3 + 0 0 x )2 1 Vậy : 1 1 π I = arctan x − arctan ( 1 1 1 2 3x ) = arctan1- arctan3 = − arctan3 0 3 0 3 4 3
Ví dụ 3. Tính các tích phân sau 1 2 1 2 x +1 x −1 2 1 a. dx ∨ dx ∫ ∫ b. dx ∫ 4 4 x +1 x +1 4 x +1 0 0 1 Giải 1 2 1 2 x +1 x −1 a. dx ∨ dx ∫ ∫ . Ta có : 4 4 x +1 x +1 0 0 1 1 + − 2 1 2 1 2 2 x +1 x −1 ( ) x = = , ( ) x f x g x = = . Cho nên 4 4 x +1 1 x +1 1 2 2 x + x + 2 2 x x  1  1  1 5 2 2 t = x + ⇒ dt = 1− dx, x +
= t − 2, x = 1 → t = 2, x = 2 → t =    2 2 Đặt : xx x 2  . Vậy :  1  1  1 3 2 2 t = x − ⇒ dt = 1+ dx, x +
= t + 2, x =1 → t = 0, x = 2 → t =    2 2  xx x 2 5 5 5 5 2 2 2 2  dt  1 1  1 1  1 t − 2
⇔ f (x)dx = = dt = − dt = ln ∫ ∫  ∫ ∫  2 2  t − 2  t − 2 t + 2 2 2  t − 2 t + 2  2 2 t + 2 1 2 2 ( )( ) 2 2 3 2 2 1
⇔ g(x)dx = dt 1 ∫ ∫ . 2 ( ) t + 2 1 0 Đặt : 1 3 3 2 t = 2 tan u → dt = 2
du ↔ t = 0 → u = 0, t = → u = arctan = u 2 1 os c u 2 4 u u Do đó (1) 1 1 2du 2 2 u 2 ⇔ = du = u = u ∫ ∫ o
c s u (2 + 2 tan u) 1 1 2 2 2 2 0 2 0 0 2 1 2 2 2 2 1
1  1+ x +1− x  1  x +1 x −1  1 b. dx ∫
. Ta có : F (x) = =   =  −  =
f (x) − g(x) 4 4 4 4 ( ) 4 x +1 x +1 2  x +1
 2  x +1 x +1 2 1
Đã tính ở trên ( phần a)
Ví dụ 4. Tính các tích phân sau 5 2 2 x −1 2 dx a. ∫ ( dx b. ∫ 2 x − 5x + ) 1 ( 2 x − 3x +1 4 2 x − 4x + 3 1 ) 3 2 1− 5 3 7 2 2 x +1 x c. dx ∫ d. I = ∫ dx 4 2 x − x +1 8 4 + − 1 2 1 x 2x Giải 2 2 x −1 a. ∫ ( dx . Ta có : 2 x − 5x + ) 1 ( 2 x − 3x +1 1 ) 1  1  1− 1− dx   2 2 2 2 2 x −1 xx f (x) = ( =
⇒ f (x)dx = 1 ∫ ∫ 2 x − 5x + ) 1 ( 2 x − 3x + ) ( ) 1  1  1   1  1  1 1 x + − 5 x + x + − 5 x + − 3        x  x − 3   x  x  Đặt : 1  1  5 t = x + → dt = 1−
dx , x = 1 → t = 2, x = 2 → t =   2 xx  2 Vậy (1) trở thành : 5 5 5 2 2 dt 1  1 1  1 t − 5 1 1 5 = − dt = ln ∫ ∫  2 = ln 5 − ln 3 = ln t − 5 t − 3
2  t − 5 t − 3  2 t − 3 2 2 3 2 ( )( ) ( ) 2 2 5 2 dx 1 1 1  1 1  b. ∫
. Ta có : f (x) = = = −   4 2 x − 4x + 3 4 2 x − 4x + 3
( 2x − )1( 2x −3) 2 2 2  x − 3 x −1  3 2 5 5 Do đó : 2 2  1 1  f (x)dx = −
dx = I − J 1 ∫ ∫  Với : 2 2 ( )
x − 3 x −1 3 3 2 2 5 5 5 5 2 2 2 1 1 1  1 1  1 x − 3 2 1 37 − 20 3 I = dx = dx = − dx = ln = ln ∫ ∫ ∫  2 x − 3 x − 3 x + 3 2 3  x − 3 x + 3  2 3 x + 3 3 − 3 3 ( )( ) 3 2 3 65(7 4 3) 2 2 2 2 5 5 1 1 2 1 1 1  1 1  1 x −1 2 1  3 1  1 15 J = dx = dx = − dx = ln = ln − ln = ln ∫ ∫ ∫    2 x −1 x −1 x +1
2  x −1 x +1 2 x +1 3 2  7 5  2 7 0 0 ( )( ) 3 2 2 1− 5 2 2 x +1 c. dx ∫ . 4 2 x − x +1 1
Học sinh xem lại cách giải ví dụ 2-a . Chỉ khác là đặt : 1 t = x − , sẽ ra kết quả . x 3 7 3 4 x x d. 3 I = ∫ dx = ∫ x dx ( ) 1 8 4 1+ x − 2x (x − )2 4 2 2 1 3
dt = 3x dx, x = 2 → t =15; x = 3 → t = 80 Đặt :  4 4
t = x −1 ⇒  1 x 1 t +1 1  1 1  3 ( ) f (x)dx = x dx = dt = + dt    3 ( 3 4 x − ) 2 2 1 3 t 3  t t   80 Vậy : 1  1 1  1  1  80 1 16 13 I = + dt = ln t − = ln + ∫     2 3  t t  3  t  15 3 3 720 15 β
E. TRƯỜNG HỢP : R(x) dx ∫
( Với Q(x) có bậc cao hơn 4 ) Q(x) α
Ở đây tôi chỉ lưu ý : Đối với hàm phân thức hữu tỷ có bậc tử thấp hơn bậc mẫu tới
hai bậc hoặc tinh ý nhận ra tính chất đặc biệt của hàm số dưới dấu tích phân mà có
cách giải ngắn gọn hơn . Phương pháp chung là như vậy , nhưng chúng ta khéo léo
hơn thì cách giải sẽ hay hơn .
Sau đay tôi minh họa bằng một số ví dụ
Ví dụ 1. Tính các tích phân sau . 1 2 dx 2 2 x +1 a. ∫ b. dx ∫ x ( 4 x +1 (x − )2 1 x + 3 0 ( ) 1 ) Giải 2 dx a. ∫
. Nếu theo cách phân tích bằng đồng nhất hệ số hai tử số thì ta có : x ( 4 x +1 1 ) + + + A( 4 x + ) 1 1 + x( 3 2 3 2
Bx + Cx + Dx + E A Bx Cx Dx E ) f (x) = = + = = x ( 4 x + ) 4 1 x x +1 x ( 4 x + ) 1 A + B = 0 A = 1 (   A + B) 4 3 2 3
x + Cx + Dx + Ex+A C  = 0, D = 0 B = 1 − 1 x ⇔ f (x) = ⇒  ⇔  ⇒ = − x ( f (x) 4 x + ) 4 1 E = 0 C = 0, D = 0, x x +1   A =1 E = 0
Nhưng nếu ta tinh ý thì cách làm sau sẽ hay hơn . Vì x và 3
x cách nhau 3 bậc , mặt khác x ∈[1; 2] ⇒ x ≠ 0 . Cho nên ta nhân tử và mẫu với 3 x 3
x ≠ 0 . Khi đó f (x) =
. Mặt khác d ( 4x) 3 3
= x dx ⇔ dt = x dx ( 4 4 4
t = x ) , cho nên : 4 x ( 4 x + ) 1 3 1 3x dx 1 dt 1  1 1  f (x)dx = = = − = f (t)  
. Bài toán trở nên đơn giản hơn rất 4 3 x ( 4 x + ) 1 3 t (t + ) 1 3  t t +1 
nhiều . ( Các em giải tiếp ) 1 2 2 x b. ∫ ( x − ) dx 2 1 x + 3 0 ( ) Nhận xét :
* Nếu theo cách hướng dẫn chung ta làm như sau : 2 x +1 A B C D - f (x) = = + + + ( x − )3 1 ( x + 3) (x − )3 1 (x − )2 1 x −1 x + 3
- Sau đó quy đồng mẫu số , đồng nhất hệ số hai tử số , ta có : 1 3 5 A = , B = , C = −D = 2 8 32 1   Do vậy : 2 1 3 5 5 I =  + + −  dx ∫ 2 ( x − )3 1 8( x −  )2 1 32 x −1 32 x + 3  0 ( ) ( )  1  1 3 5 5  5 1 = − − + x − − x +  =  8  (x − ) ln 1 ln 3 2 ln 2 1 8( x − ) 1 32 32  32 28  0
Ví dụ 2. Tính các tích phân sau : 3 4 x −1 2 2 x +1 2 dx a. dx ∫ b. dx ∫ c. ∫ 6 x −1 6 x +1 x ( 4 1+ x 1 ) 2 1 1 3 1 ( x − x )1 3 x 1 4 2 x + 3x +1 3 d. ∫ ( e. dx ∫ f. dx ∫ + 3 4 x ) dx 3 2 ( 2 + x 0 1 x ) 0 1 1 3 Giải a.     2 4 2 4 2 2 3 3 2 x −1  x + x +1 x + 2  1  x 1 1  dx = − dx = dx + + − dx ∫ ∫ ∫ ∫ 6     x −1  ( 2 x − ) 1 ( 4 2 x + x + ) 1 ( 3  −   − + x )2 2 x 1 −1   ( 3 x 1 x 1 1 1 2 2 x )2 3 3 −1            3
Tính J : J= artanx = artan3-artan2 . 2 2
dt = 3x dx, x = 2 → t = 8; x = 3 → t = 27 Tính K . Đặt  3 2 t = x ⇒  x 1 dt 1 1  1 1  g(x)dx = dx = = − dt    3 x −1 3 ( 2 t − ) 1
3 2  t −1 t +1  3 27 Do đó : K= 1  1 1  1 − g x dx = − dt = ∫ ∫  
( t − − t + ) 27 1 t 1 27 1 117 ( ) ln 1 ln 1 = ln = ln 6
t −1 t +1 6 8 6 t +1 8 6 98 2 8 3 3 1 1 Tính E= dx = dx ∫ ∫ 3 x −1
(x − )1( 2x + x +1 2 2 ) 2 x − ( 2 x − ) 2 2 1 1 x x −1
Ta có : h(x) = ( = = − x − ) 1 ( 2 x + x + ) 1 (x − ) 1 ( 2 x + x + ) 3 1 x −1 (x − ) 1 ( 2 x + x + ) 1 2 x (x − ) 1 ( x + ) 2 2 1 x x +1 x 1  2x +1 1  = − = − = − +   3 x −1 (x − ) 1 ( 2 x + x + ) 3 2 3 2 2 1 x −1 x + x +1 x −1
2  x + x +1 x + x +1 3 2 3 3 Vậy : 1 3x 1 (2x + ) 1 1 I = dx − dx − dx ∫ ∫ ∫ 3 2 2 2 3 x −1 2 x + x +1     2 2 2 1 3 x + +      2  2   1 = ln ( 3 1 3 1 28 1 13 3 x − ) 1 − ln ( 2 x + x + ) 1 − F = ln − ln − F (2) 3 2 2 2 3 9 2 6  3 1 dx = dt Tính F : Đặt : 2 1 3  2 os c t x + = tan t ⇒  2 2 5 10
x = 2 → tant =
→ t = a; x = 3 → tan t = → t = b  3 3 3 1 b dt b Do đó F= 2 b  5 5 10 2 os c t
= dt = t = b − a t ant=
→ t = a = artan ;b = artan ∫ ∫   3 a   a ( 3 3 3 2 1+ tan t ) a 2
Thay vào (2) ta có kết quả . 2 2 1 2 2 2 x +1 x +1 1 1 b. dx = dx = dx = dx ∫ ∫ ∫ ∫ 6 x +1 ( 2x + )1( 4 2 x − x + ) 1 (x − )2 1 − x ( 2x + x+ )1( 2 2 2 x − x +1 1 0 1 1 ) 1 Ax+B Cx + D Ta có : ( = + 2 x + x + ) 1 ( 2 x − x + ) 2 2 1 x + x +1 x − x +1
( A+C) 3x +(B − A+C + D) 2x +( A− B +C + D) x +(B + D) = 4 2 x − x +1  1 A = −  2  A + C = 0 A = C − 1    C =
Đồng nhất hệ số hai tử số ta có hệ : B − A+C + D = 0 1  − 2C = 0  2  ⇔  ⇔ 
A − B + C + D = 0 −B + D = 0 1   D = B + D =1 B + D =1  2  1 B =  2 2 2 Vậy : 1  1− x x +1  1 I =  dx + dx ∫ ∫  = J + K 1 2 2 ( )( ) 2 x + x +1 x − x +1 2  1 1  Tính J= 2 2 2 2 −x +1 1 2x +1− 3 1 2x +1 3 1 1 2 2 dx = − dx = − dx + dx = − ln x + x +1 + E 2 ∫ ∫ ∫ ∫ 2 2 2 2 ( ) 2 x + x +1 2 x + x +1 2 x + x +1 2     2 1 1 1 1 1 1 3 x + +      2  2   2 3 1 Tính E = dx ∫
, học sinh tự tính bằng cách đặt : 1 3 x + = tan t 2 2 2     2 2 1 1 3 x + +      2  2   Tính K 2 2 2 1 x +1 1 2x −1+ 3 1 2x −1 3 1 1 2 2 K = dx = dx = dx + dx = ln x − x +1 + F 2 ∫ ∫ ∫ ∫ 2 2 2 2 ( ) 2 x − x +1 2 x − x +1 2 x − x +1 2     2 1 1 1 1 0 1 3 x − +      2  2   2 3 1 Tính F= dx ∫
, học sinh tự tính bằng cách đặt : 1 3 x − = tan t 2 2 2     2 2 1 1 3 x − +      2  2   3   1 3 1 d ( 4 x ) d ( 4 2 2 2 x dx x ) 4 1  x  2 1 32 c. = =  −  = ∫ ∫ ∫   = x ( dx ln ln 4 1+ x ) 4 3 x ( 4 1+ x 3  x 1+ x  3 1+ x 1  3 17 1 1 ) 4 4 4 1   1 3 1 2 x 1 x 2
x = t −1;dt = 2xdx d. dx = 2xdx 1 ∫ ∫ . Đặt : 2 t = 1+ x ⇒  3 3 ( ) ( 2 + x ) 2 1 ( 2 +
x = 0 → t =1, x =1 → t = 2 0 0 1 x ) 2 2 Do đó t −1  1 1   1 1  2 13 I = dt = − dt = − + = ∫ ∫    3 2 3 2 tt t
t 4t  1 16 1 1   4 2 + + (1 3 1 + x x x )2 2 1 1 2 1 1 2 x 1 x e. dx   = + dx = dx +
dx = J + K 1 ∫ ∫ ∫ ∫ 3 3 3 2 3 ( ) ( 2 + )   ( 2 + ) ( 2 + )  1 1 1 1 + x x x x  ( 2 + 0 0 0 0 1 x ) Tính J : Bằng cách đặt π
x = tan t ⇒ J = 4   1 1 1 Tính K=   −
dx = E + F 2 ∫ 2 3 ( )   ( 2  1+ x ) ( 2 + 0 1 x )   1 dx = dt  2  os c t
x = tan t ↔  Tính E : Bằng cách đặt π 
x = 0 → t = 0; x = 1 → t =  4 π π π 1 2 2 Vậy : 4 4 4 1  1  1  1  1 1 1 1 1 2 E = dx = dt = dt = os c tdt ∫  ∫  ∫ ∫ 2 2 2 2 2  1+ x  2  1+ tan t  os c t 2 1 os c t 2 0 0 0 0 4 os c t π π 4 1 = ∫(    π  π + + c ) 1 1 1 1 2 1 os2t dt = t + sin 2t 4 = + =     4 4  2  4  4 2  16 0 0
Tính F. Tương tự như tính E ;  1 dx = dt  2  os c t
Bằng cách đặt x = tant ↔  π 
x = 0 → t = 0; x = 1 → t =  4 π π π 1 3 3 Vậy : 4 4 4 1  1  1  1  1 1 1 1 1 4 F = dx = dt = dt = os c tdt ∫  ∫  ∫ ∫ 2 2 2 2 2  1+ x  2  1+ tan t  os c t 2 1 os c t 2 0 0 0 0 6 os c t π π π 4 1 ∫(  +  = + c ) 4 2 1 1 os c 4t 1 os2t dt = 1+ 2 os c 2t + dt 4 = ∫  8 8  2  0 0 0 π π 4 1 ∫(    π  π + + t + c ) 1 1 1 3 8 3 4 cos 2 os4t dt = 3t + 2 sin 2t + sin 4t 4 = 3 + 2 =     16 16  4  16  4  64 0 0 (x− x )1 1 1 3 1 3 1 3 1 3  −  3 x x 1  1  1 dx f. dx = dx ∫ ∫  = −1 . ∫  4 3 3 2 2 xxxxx x 1 1 1 3 3 3  dx dt = −  Đặt :  1  1  x t = −1 ⇒ t +1 = ⇔    2 2  xx 1
x = → t = 8; x =1→ t = 0  3 0 1 8 4 1 7 4 Khi đó       I = − t ∫ (t + ) 3 3 8 3 3 24 3 468 7 4 3 3 3 3 3
1 dt = ∫t + t dt =  t + t  = .2 + .2 =16 + =   7 4 0 7 4      7 4  7 8 0
* Chú ý : Còn có cách khác 1 3 1 1  1 −  2   1 1    1 t  ( 3t −t t t ) 1  3 3 Vì : x ∈ ;1 → x ≠ 0  
. Đặt x = ⇒ dx = − dt; f (x)dx = − dt = − dt   3  2 4 2 t t 1  t t    t  1   = 1 1 1 t − (t −t)1 3 1 3 2
3 dt = dt = t − 1− dt  
(2) . Đặt : u =1− ⇔ =1−u;du = dt 2  t  2 2 t t t
Ví dụ 3. Tính các tích phân sau 1 p p+2 e 2 x a 3 x dx a. dx ∫ b. ∫ p+2 x +1 3 1 ( 2 2 0 x + a )2 1 2a x c. x+e e dx ∫ d. 2
x 2ax − x dx ∫ 0 0 Giải 1 p p p+2 e 2 x 2 x dx a.. dx ∫
( ĐHTNguyên-98) : Ta có : f (x)dx = . p+2 x +1 2 p+2   1 2  x  +1   pp+2 p 2 e = 1 + dt x dxdt - Đặt : 2 2 t = x = x ⇒ ⇔ I =  ∫ 1 2 t +1 + 1 p 2
x =1→ t =1;x = e → t = edu dt =  2 1 u 1 u os c u du π
- Đặt : t = tan u ⇒  ⇔ I = = du = − u ∫ ∫  π π o
c s u (1+ tan u) 1 1 2 2 π 4 2 t = 1 → u =
, t = e → u = u1  4 4  4 π
- Từ : tan u = e ⇒ u = u = artan e ⇔ I = − artan e 1 4  dt π dx=a
; x = 0 → t = 0, x = a → t =  2 cos t 4 a 3  x dx  b. ∫ . Đặt : 3 3 3 = ⇒ x dx a tan t dt x atant 3  ( f (x) = = a
= a cost.tan tdt 3 3 2 x + a )3 2 2 0 2   ( cos t 2 2 x + a )2 2  1  3 a   2   os c t  π π π π a 4 4 4 4 1− os c t sin sin sin t t t 3 ( 2 3 3 )
Vậy : I = f (x)dx = acost.tan tdt = acost. dt = . a dt a = dt = ∫ ∫ ∫ ∫ ∫ 3 2 2 os c t os c t os c t 0 0 0 0 0  π 1 du = − s intdt;t= → u = ;t = 0 → u = 1  4  2 - Đặt : o c st=u ⇒   ( 2 1− u )  1  f (t)dt = −du = 1− du    2 ( ) 2  uu  2 2 Vậy : 2  1   1  2 2 3 3 2 3 2 − 4 I = 1− du = u + = + − 2 = − 2 = − 2 = ∫     2 2  u   u  2 2 2 2 2 1 1 1 1 x
dt = e dx x = → t = x = → t = e x x c. x+e x e e dx = e e dx ∫ ∫ . Đặt : ; 0 1; 1 x t = e ⇒  x x e t  = = 0 0 f (x)dx e e dx e dt 1 e Vậy : e I = f (x) t t e
dx = e dt = e = e − e ∫ ∫ 1 0 1 2a 2a
d. x 2ax − x dx = x a − ∫ ∫ (x − a)2 2 2 dx 0 0  π π = → → Đặt : dx . a os c tdt,x=0 t=- ;x=2a t=  x − a = . a sin t ⇒ 2 2 
f (x)dx = 
(a + .asint) 2 2 a os c t . . a os c tdt Vậy : π π π π π     2 = ∫ (    + c tI a 1+ sin t ) 2 2 2 2 1 os2 3 2 3 2 2 3 2 os c tdt = a os c tdt + os c
t sin tdt = a dt − os c td ∫ ∫ ∫ ∫ ( os c t )     π π π π 2 π − − −  − −  2  2 2   2 2   π π    1  1  2 1 2 1  π π  π 3 3 3 3 = a t + sin 2t − cos t  = a + = a      2  2  π 3 π  2  2 2  2 − −    2 2 
Ví dụ 4. Tính các tích phân sau 3 dx 1 7 x dx a. ∫ b. ∫ 5 2 x − x + 0 (1 x )2 4 2 1 3 x − 2x 2 3 1+ x c. ∫ ( d. dx ∫ 4 x + ) dx 2 2 x 0 1 1 Giải 3 3 dx 1 a. = dx 1 ∫ ∫ 5 2 2 x − x x ( x − ) 1 ( 2 x + x +1 2 2 ) ( ) 1 A B Cx + D E Xét : f (x) = = + + + 2 x ( x − ) 1 ( 2 x + x + ) 2 2 1 x x x + x +1 x −1 A( 2 x + x + ) 1 ( x − ) 1 + Bx ( x − ) 1 ( 2 x + x + ) 1 + (Cx + D) 2 x ( x − ) 2 2
1 + E(x + x +1)x = 2 x ( x − ) 1 ( 2 x + x + ) 1
(B +C + E) 4x +( A+ D −C + E) 3x +(E − D) 2x − Bx − A = . 2 x ( x − )( 2 1 x + x + ) 1
Đồng nhất hệ số hai tử số ta có hệ :  1 D =  3 
B + C + E = 0 C  = −E 1    C = − 1 1 1
A + D − C + E = 0
E + E + E = 1  3   − x +    1 3 3 3 E − D = 0 ⇔ B = 0
⇔ B = 0 ⇒ f (x) = − + + 2 2 x x + x +1 x −1    B = 0 E = D 1   E = A = 1 −  A = 1 −   3 A = 1 −    1 1 1  − + 3 x 3  1 
 1 1  x −1  1 1  Vậy : 3 3 3 I = ∫− + +  dx = ∫− − +     dx 2 2 2 2 x x x 1 x 1 x 3     x
x 1  3 x 1  + + − + + − 2 2 ( )     1 1 1  3 dx  1 1 (x − )2 3 1 1 2x+1  3 2 =
− ln x + x +1 + ln x −1 − =  + ln + arctan    ∫ 2 2 2  x 6 3  2      x 6 x + x +1 3 3  2 2 1 3   x + +      2  2   1 1  7 5  = + arctan − arctan   6 3  3 3  1 7 1 4 x dx 1 x b. 3 = 3x dx 1 ∫ ∫ . 2 2 ( ) ( 4 + x ) 3 1 ( 4 + 0 0 1 x ) 3
dt = 3x dx, x = 0 → t =1; x =1→ t = 2 Đặt :  4 t = 1+ x ⇒  1  t −1  1  1 1  f (x)dx = dt = − dt      2 2  3  t  3  t t  2 Vậy : 1  1 1  1  1  2 1  1  I = − dt = ln t + = ln 2 − ∫       2 3  t t  3  t  1 3  2  0 3 x − x ( 2 1 1 x − 2 2 1 ) c. dx = 2xdx 1 ∫ ∫ 2 2 ( ) ( 2x + ) 2 1 ( 2 + 0 0 x )1 dt = 2x ;
dx x = 0 → t = 1; x = 1 → t = 2 Đặt :  2 2
t = 1+ x ⇔ x − 2 = t − 3 ⇒  1  t − 3  1  1 3  f (x)dx = dt = − dt      2 2  2  t  2  t t  2 Vậy 1  1 3  1  3  2 1  3  : I = − dt = ln t + = ln 2 − ∫       2 2  t t  2  t  1 2  2  1 2 3 2 3 1+ x 1+ x d. 2 dx = x dx 1 ∫ ∫ . 4 6 ( ) x x 1 1 2 2tdt = 3x ; dx x = 1 → t =
2, x = 2 → t = 3  Đặt :  3 2 3 3 2
t = 1+ x ↔ t = 1+ x ↔  1 1+ x 1 t 2 t 2 f (x)dx = 3x dx = 2tdt = dt  6 3 x 3 ( 2t − )2 3 1 ( 2t −  )2 1 Vậy : 2 3 3 2 3 2  1 1  1 1   2  1  1 1   1  1 1  1 1   I = + − dt = ∫     − ∫    =  + − −  dt ∫   3
t +1 2  t −1 t +1
3  4  t +1 t −1   6    (t + )2 1 (t − )2 1
t −1 t +1   2 2 2  3    −  − − 3 1 1 1 t 1 1 2t t 1 8 2 − 3 1 = − − − ln =  −  = + −  
6  t +1 t −1 t +1  2 6  ( ln ln 2 2 2 2 t − ) ( ) 1 t +1  2 24 3 
Ví dụ 5. Tính các tích phân sau : 4 ( 2 1 x − x) dx dx a. ∫ b. ∫ 2 2 + 7 x x + 9 0 x 1 3 5 3 x − 2x 1 3 c. dx ∫ d. ∫ ( 2 1− x ) dx 2 + 0 x 1 0 Giải 4 4 dx xdx a. = ∫ ∫ ( ) 1 . 2 2 2 + + 7 x x 9 7 x x 9 2 2 2 2  5 5 Đặt : t
 = x + 9 ↔ tdt = xdx, x = t − 9 dt dt 2 t = x + 9 ⇒  . Do đó : I = = ∫ ∫
x = 7 → t = 4, x = 4 → t = 5 t ( 2 t − 9 t t − 3 t + 3 4 ) 4 ( )( ) A( 2
t − 9) + Bt (t + 3) + C (t − 3 1 )t A B C Ta có : f (t) = = + + =
t (t − 3)(t + 3) t t − 3 t + 3 t ( 2 t − 9)
Đồng nhất hệ số hai tử số bằng cách thay lần lượt các nghiệm vào hai tử số ta có : 1
- Với x=0 : -9A=1 → A = − 9 1
- Với x=-3 : 9C=1 → C = 9 - Với x=3 : 9B=1 1 → B = 9 5 Vậy : 1   1 1 1   1 t − I =  − + + dt ∫   = ln  (t − 9) 2 5 1 9 5 1 144 2 − ln t = ln = ln 
9   t t − 3 t + 3  9 4 9 t 4 9 35 4 
* Chú ý : Nếu theo phương pháp chung thì đặt : x = 3sint → dx = 3costdt .  7
x = 7 → 7 = 3sin t ↔ sin t =  Khi : 3 
. Như vậy ta không sử dụng được phương pháp 4
x = 4 → 4 = 3sint ↔ sint = >1  3 này được . ( 2 1 x − x) 1 2 1 dx x x b. = dx −
dx = J − K ∫ ∫ ∫ ( ) 1 2 2 2 + + + 0 x 1 0 x 1 0 x 1 * Để tính J :  1 π dx =
dt, x = 0 → t = 0; x = 1 → t =  2 os c t 4 Đặt : 
x = tan t ⇒  1
. Tính tích phân này không đơn 2 tan t. dt 2  2 tan os t ( ) c t f x dx = = dt  2  + os c t 1 tan t
giản , vì vậy ta phải có cách khác . 2 2 1 1 1 x x +1−1 1 1 - Từ : 2 2 g(x) = = = x +1 −
⇒ g(x)dx = x +1dx − dx ∫ ∫ ∫ 2 2 2 2 x +1 x +1 x +1 + 0 0 0 x 1
- Hai tích phân này đều tính được . 1 1 2 1 1 1 x  1  +/ Tính : 2 2 2 E = x +1dx x = x +1 − dx = 2 − ∫ ∫  x +1dx − dx ∫ ∫  2 2 0 +  + 0 0 x 1 0 0 x 1  1 2 1 2
= 2 − E + ln x + x +1 ⇒ 2E = 2 + ln (1+ 2) ⇔ E = + ln (1+ 2) 0 2 2 1 x 1 1 1 1 * Tính K= 2 dx = x +1 = 2 −1 ∫ ; 2 dx = ln x + x +1 = ln 1+ 2 ∫ 2 ( ) 2 + 0 + 0 0 x 1 0 x 1 Do vậy : I= 2 1 + ( + )+ ( + ) 2 3 ln 1 2 ln 1 2 = + ln (1+ 2) 2 2 2 2 3 5 3 3 5 3 3 x − 2x x x c. dx = dx − 2
dx = J − K ∫ ∫ ∫ ( ) 1 2 2 2 + + + 0 x 1 0 x 1 0 x 1 2 2
x = t −1; xdx = tdt; x = 0 → t =1, x = 3 → t = 2  - Tính J: Đặt 2 t = x +1 ⇒  ( 2 4 t − )2 1 tdt x xdx
f (x)dx = = = ( 4 2 t − 2t + ) 1 dt 2  +1 t x 2  1 2  2 38 Suy ra : J= ∫( 4 2 t − 2t + ) 5 3 1 dt = t − t + t =    5 3  1 15 1 2 2
x = t −1; xdx = tdt; x = 0 → t =1, x = 3 → t = 2  - Tính K: Đặt 2 t = x +1 ⇒  ( 2 2 t − ) 1 tdt x xdx
f (x)dx = = = ( 2t − ) 1 dt 2  +1 t x 2  1  2 4
Suy ra : K= ∫( 2t − ) 3 1 dt = t − t =    3  1 3 1 Vậy : I= 28 4 48 16 + = = 15 3 15 5  π = → → 1 dx os c tdt. x=0 t=0;x=1 t=  3 d. ∫ ( 2
1− x ) dx . Đặt : 2
x = sin t →  0
f (x)dx = (1− x )3 2 6 4 dx = os c t os c tdt=cos tdt  π π π 2 Do đó I= 2 2 2 1− os c 2t  1  1+ os c 4t   3 1 1  dt = 1− 2 cos 2t + dt = − os c 2t+ os c 4t dt ∫  ∫  ∫   2  4  2   4 2 8  0 0 0 π  3 1 1  3π = t − sin 2t + sin 4t 2 =    4 4 32  8 0
TÍCH PHÂN CHỨA CÁC HÀM SỐ LƯỢNG GIÁC I. KIẾN THỨC
1. Thuộc các nguyên hàm : β β 1 β sin (ax+b) β a/ sin ∫ (ax+b)dx = − os c (ax+b) b/ dx = − ln os c ax+b ∫ a α os c α α (ax+b) ( ) α β β 1 β os c (ax+b) β c / os c
∫ (ax+b)dx = sin(ax+b) d/ dx = ln sin ax+b ∫ a α sin α α (ax+b) ( ) α β
2. Đối với : I = f (x)dx ∫ α
a/ Nếu f(x)= R( m n sin ; x os c x) thì ta chú ý :
- Nếu m lẻ , n chẵn : đặt cosx=t ( Gọi tắt là lẻ sin )
- Nếu n lẻ , m chẵn : đặt sinx=t ( Gọi tắt là lẻ cos )
- Nếu m,n đều lẻ thì : đặt cosx=t hoặc sinx =t đều được ( gọi tắt lẻ sin hoặc lẻ cos )
- Nếu m,n đề chẵn : đặt tanx=t ( gọi tắt là chẵn sinx , cosx )
b/ Phải thuộc các công thức lượng giác và các công thức biến đổi lượng giác , các
hằng đẳng thức lượng giác , công thức hạ bậc , nhân đôi , nhân ba , tính theo tang góc chia đôi ....
3. Nói chung để tính được một tích phân chứa các hàm số lượng giác , học sinh đòi
hỏi phải có một số yếu tố sau :
- Biến đổi lượng giác thuần thục
- Có kỹ năng khéo léo nhận dạng được cách biến đỏi đưa về dạng đã biết trong nguyên hàm .
II. MỘT SỐ VÍ DỤ MINH HỌA
Ví dụ 1. Tính các tích phân sau : π 2 sin 2x + sin x
a. (ĐH, CĐ Khối A – 2005) I = ∫ dx 1 + 3cos x 0 π 2 sin 2x cos x
b.. ĐH, CĐ Khối B – 2005 . I = dx ∫ KQ: 2ln2 −1 1 + cos x 0 Giải π π 2 2 sin 2x + sin x (2cos x + ) 1 s inx a. I = dx = dx ∫ ∫ ( ) 1 1+ 3cos x 1+ 3cos x 0 0 2  t −1 2 os c x= ;s inxdx=- tdt  Đặt :  3 3
t = 1+ 3cos x ⇒  π
x = 0 → t = 2; x = → t =1  2 2  t −1  2 +1   1 2 Khi đó : 2  3   2  2t +1 2 1  2 34 3 I = − tdt = 2 dt = t + t = ∫   ∫   t  3  9 9 3  1 27 2 1 π π π 2 2 2 2 2 sin 2x cos x 2 sin x cos x os c x b. I = dx = dx = 2 s inxdx ∫ ∫ ∫ ( )1 1+ cos x 1+ cos x os c x+1 0 0 0  π dt=-sinxdx, x=0 → t=2;x= → t = 1  Đặt :  2 t = 1+ os c x ⇒   (t − )2 1  1  f (x)dx = dt = t − 2 + dt    tt  π 2 1 Do đó :  1   1  2 2
I = 2 f (x)dx = 2 − t − 2 + dt = 2
t − 2t + ln t = 2ln 2 −1 ∫ ∫     t   2  1 0 2
Ví dụ 2. Tính các tích phân sau π 2 sin2x 2
a. ĐH- CĐ Khối A – 2006 . I = dx ∫ KQ: 2 2 + 3 0 cos x 4sin x π 2 cos 3x
b. CĐ Bến Tre – 2005 . I = ∫ dx KQ: 2 − 3ln2 sin x + 1 0 Giải π 2 sin2x a. I = dx ∫ . Đặt : 2 2 2 2 2 t = os c
x + 4 sin x ⇒ t = os c x + 4 sin x 2 2 + 0 cos x 4sin x  tdt = (− x x + x x) 2 2 2 sin cos 8sin cos
dx = 3sin 2xdx → sin 2xdx = tdt  Do đó :  3  π
x = 0 → t =1; x = → t = 2  2 π 2 2 2 Vậy : 2 tdt 2 2 2 2 I = f (x)dx = = dt = t = ∫ ∫ ∫ 3 t 3 3 1 3 0 1 1 π 2 cos 3x b. I = ∫ dx . sin x + 1 0 Ta có : 3 c x − x = ( 2 x − )c ( 2 x − )c ( 2 os3x=4cos 3cos 4 cos 3 osx= 4-4sin 3 osx= 1-4sin x) o c sx ( 2 1− 4 sin os3x x c )
Cho nên : f (x)dx = dx = os c xdx ( ) 1 1+sinx 1+ s inx  π dt=cosxdx,x=0 → t=1;x= → t = 2  Đặt : 2  t = 1+ s inx ⇒  1  − 4(t − )2 1      3  f (x)dx =
dt = 8 − 4t − dt     tt  π 2 2 Vậy :  3  I = f (x)dx = 8 − 4t − dt = ∫ ∫  ( 2 2
8t − 2t − 3ln t ) = 2 − 3ln 2  t  1 0 1
Ví dụ 3. Tính các tích phân sau π 2 sin xdx
a. CĐSP Sóc Trăng Khối A – 2005 . I = ∫ x 2 2 0 sin x + 2 cos . x cos 2 π 2 sinx − cosx
b. CĐ Y Tế – 2006 . I = dx ∫ KQ: ln 2 π 1+ sin2x 4 Giải π π π π 2 2 2 sin xdx sin xdx s inx a. I = = = dx = − ln 1+ o c sx 2 = ln 2 ∫ ∫ ∫ 2 x + + 2 2 sin x cos . x 1 os c x 1+cosx 0 0 ( ) 0 sin x + 2 cos . x cos 0 2 π π π 2 sinx − 2 cosx sinx − 2 cosx sinx − cosx b. I = dx = dx = ∫ ∫ dx 1 2 ∫ ( ) π 1+ sin2x π (sinx+cosx) π sinx+cosx 4 4 4  π  π π π π π  π 
Vì : s inx+cosx= 2 sin x + ; ≤ x ≤ ⇒
≤ x + ≤ 3 ⇔ sin x + > 0      4  4 2 2 4 4  4 
Do đó : sinx+cosx = sinx+cosx
Mặt khác : d (sinx+cosx) = ( os c x-sinx ) dx π π 2 d (s inx+cosx) 2 1 Cho nên : I = − = −ln sinx+cosx = − ln1− ln 2 = ln 2 ∫ π   π sinx+cosx 2 4 4
Ví dụ 4. Tính các tích phân sau π 2 cos2x 1
a. CĐ Sư Phạm Hải Dương – 2006 . I = ∫ ( KQ: sin x − cosx + ) dx 3 32 0 3 π 4 cos2x 1
b. CĐ KTKT Đông Du – 2006 . I = dx ∫ KQ: ln3 1+ 2sin2x 4 0 Giải π 2 cos2x a. I = ∫ 2 2 = − = ( . Vì : cos 2x os c x sin x ( os c x+sinx )( os c x-sinx ) sin x − cosx + ) dx 3 0 3 os c 2x ( os c x-sinx )
Cho nên : f (x)dx = dx = os c x+sinx dx 3 3 ( ) (sinx-cosx+3) (sinx-cosx+3)  π dt= (cosx+sinx) ;
dx x = 0 → t = 2, x = → t = 4  Đặt :  2
t = s inx-cosx+3 ⇒  t − 3  1 1 
f (x)dx = dt = − 3 dt   3 2 3  tt t  π 2 4 Vậy :  1 1   1 3 1  4 1 I = f (x)dx = − 3 dt = − + = ∫ ∫    2 3 2  t t
t 4 t  2 32 0 2 π  1
dt = 4 cos 2xdx → os c 2xdx= dt 4 cos2x  b. 4 I = dx ∫
. Đặt : t = 1+ 2sin 2x ⇒  1+ 2sin2x π 0
x = 0 → t =1; x = → t = 3  4 π 4 3 Vậy : = cos2x = 1 dt = 1 3 = ∫ ∫ 1 I dx ln t ln3 1+ 2sin2x 4 t 4 1 4 0 1
Ví dụ 5. Tính các tích phân sau : π 2 3 4sin x
a. CĐ Sư Phạm Quảng Ngãi – 2006 . I = dx ∫ KQ: 2 1+ cosx 0 π 6 3 sin3x − sin 3x
b. CĐ Bến Tre – 2006 . I = dx ∫ 1+ cos3x 0 Giải π π 2 2 ( 2 3 1 cos x 4sin x ) π π − 2 1 a. I = dx = ∫ 4∫
sinxdx=4∫(1− cosx)sinxdx=4. (1− cosx)2 2 = 2 1+ cosx 1+ cosx 2 0 0 0 0 π 6 3 sin3x − sin 3x b. I = dx ∫ . 1+ cos3x 0 Ta có : 3 x − x = x ( 2 − x) 2 sin 3 sin 3 sin 3 1 sin 3 = sin 3 . x o c s 3x .  1
dt=-3sin3xdx → sin3xdx=- dt  Đặt :  3 t = 1+ os c 3x ⇒  π
x = 0 → t = 2; x = → t =1  6 π Vậy : 6 1 (t − )2 1 2 1 1  1  1  1  2 1 1 2
f (x)dx = − dt = t − 2 + dt =
t − 2t + ln t = − + ln 2 ∫ ∫ ∫    3 t 3  t  3  2  1 6 3 0 2 1
Ví dụ 6. Tính các tích phân sau π π π 3 3 2 − sin( − x) a. sin x sin x I = ∫ cot gx dx b. I = 2 4 ∫ dx π sin x π − π sin( + x) 3 2 4 π π 2 2 4 4 c. I = 4 ∫ sin xdx d. I = cos 2x( n si
x + cos x)dx ∫ 0 0 Giải π π  1  s inx 3 1− 3  3 2 2 2 a. − I = sin x sin x  sin x  ∫ cot gx dx = ∫ cot xdx π sin x π s inx 3 3 π π 2 2  1  3 2 = 3 ∫ 1−
cot xdx = ∫ − cot x cot xdx   2 π  sin x  π 3 3 π π π sin( − x) b. 2 2 I = cosx-sinx 4 ∫ dx = ∫ dx π − π π cosx+sinx sin( + x) − 2 2 4 π π 2 d (cosx+sinx) 2 = ∫ = ln cosx+sinx = 0 π cosx+sinx π − − 2 2 π π π 2 2 2 2 1− cos2x  1  1+ cos4x  c. I = 4 ∫ sin xdx = ∫ dx = ∫ 1− 2cos2x + dx      2  4  2  0 0 0 π π 2  3 1 1   3 1 1  3π
= ∫ − cos2x+ cos4x dx = x − sin 2x + sin 4x 2 =      8 2 8   8 4 32  16 0 0 π 2 4 4 1 d. I = cos 2x( n si
x + cos x)dx ∫ . Vì : 4 4 2 sin x + o c s x = 1− sin 2x 2 0 Cho nên : π π π π π 2 2 2  1  1 1 1 2 2 3 I = 1− sin 2x os c 2xdx= os c 2xdx-
sin 2x cos 2xdx = sin 2x ∫  2 − sin 2x 2 = 0 ∫ ∫  2  2 2 3 0 0 0 0 0
Ví dụ 7. Tính các tích phân sau π π 2 4 1 a. I = 5 ∫ sin xdx b. I = ∫ dx 2 0 π sin x cot gx 6 π π 3 2 c. I = 2 2 ∫ tg x + cotg x − 2dx d. */I = 3 3 ∫ ( cosx − sin x)dx π 0 6 Giải π π π 2 2 2 2 a. I = 5 ∫ sin xdx = ∫ ( 2 1− cos x ) 2 4 s inxdx=-∫ 1
 − 2cos x + cos x d(cosx)   0 0 0 π  2  3 1 5 2 = −cosx+ cos x − cos x 2 =    3 5  15 0 π 4 1 b. I = ∫ dx . 2 π sin x cot gx 6  1 1 2tdt = − dx → dx = 2 − tdt  Đặt : 2 2 2 sin x sin x
t = cot x ⇒ t = cot x ↔  π π
x = → t = 3; x = → t =1  6 4 1 3 Vậy : 2tdt 3 I = − = 2 dt = 2t = 2( 3 − ∫ ∫ )1 t 1 3 1 π π π 3 3 3 2 2 2
c. I = ∫ tg x + cot g x − 2dx = ∫ (t anx-cotx) dx = ∫ t anx-cotx dx π π π 6 6 6 2 2 sinx os c x sin x − os c x os c 2x Vì : tanx-cotx= − = = 2 − = 2 − cot 2x cosx sinx s inxcosx sin2x  π π  t anx-cotx<0;x ∈ ;  π π   π π      3 3   6 4  Cho nên : x ∈ ; ↔ 2x ∈ ; 2 ⇒ cot 2x ∈      − ;  ⇔     6 3   3 3  3 3    π π  t anx-cotx>0;x ∈ ;      4 3  π π π π Vậy : 4 3 4 3 os c 2x os c 2x 1
I = − (t anx-cotx) dx + (t anx-cotx) dx = − dx + dx = ∫ ∫ ∫ ∫ π π π sin2x π sin2x 2 6 4 6 4 π π ( x ) 4 1 − ( x ) 3 ln sin 2 ln sin 2 = ln 2 π 2 π 6 4 π 2 d. I = 3 3 ∫ ( cosx − sin x)dx (1) 0 Đặt : π π π x =
− t → dx = −dt, x = 0 → t = ; x = → t = 0 2 2 2 Do đó : π π 0  π π      I =  o c s − t − sin t ∫     (−dt) 2 =   ∫( sint − o c st ) 2 3 3 dt = ∫ ( 3 3 3 3 sin x − o c sx )dx (2) π  2   2    0 0 2
Lấy (1) +(2) vế với vế : 2I = 0 ⇒ I = 0
Ví dụ 8 . Tính các tích phân sau π π π 3 4 os c 2x 2 6 os c x a. 4 tan xdx ∫ (Y-HN-2000) b. dx ∫ (NT-2000) c. dx ∫ (NNI-2001) sinx+cosx+2 4 π sin x 0 ( ) π 4 4 π π π 4 2 sin x 2 sin 2x 4 2 1− 2 sin x d. dx ∫ ( GTVT-2000) e. dx ∫ f. dx ∫ (KB-03) 6 os c x 2 4 − os c x 1+ sin 2x 0 0 0 Giải π 3 1− os sin c x x 1 1 4 ( )2 2 4 a. 4 tan xdx ∫
. Ta có : f (x) = tan x = = = − 2 +1 4 4 4 2 π os c x os c x os c x os c x 4 π π π π Do đó : 3 3 3  1 1  I = f x dx = − + dx = ∫ ∫  ∫( dx 2 3 ( ) 2 1 1+ tan x − 2 tan x + x 4 2 ) 2 [ ]   π π π os c x os c x π os c x 4 4 4 4 π  1  3  π   4   π  2 π 3 = t anx+ tan x − 2 3 − 2 + = 2 3 − − 2 3 − 2 + = +          3  π  12   3   12  3 12 4
* Chú ý : Ta còn có cách phân tích khác : 4 2 f x = x = x ( 2 x + − ) 2 = x ( 2 + x) 2 2 − x = x ( 2 + x) − ( 2 ( ) tan tan tan 1 1 tan 1 tan tan tan 1 tan tan x + ) 1 +1 π π π π Vậy : 3 dx dx I = tan x ∫ 
(1+ tan x)−(tan x+ ) 3 3 3 2 2 2 2 1 +1 dx = tan . x − + dx  ∫ ∫ ∫ 2 2 π π os c x π os c x π 4 4 4 4 π  1  3  1 π   1 π  2 π 3 I = tan x − t anx+x = 3 3 − 3 + − −1+ = +        3  π  3 3   3 4  3 12 4 π 4 os c 2x b. dx ∫ . sinx+cosx+2 0 ( ) os c 2x ( 2 2 os c x − sin x) ( os c x-sinx )( os c x+sinx ) Ta có : f (x) = = = ( sinx+cosx+9)3 (sinx+cosx+9)3 (sinx+cosx+9)3 π π   Do đó : 4 4 ( os c x+sinx ) I =
f (x)dx =   os c x-sinx dx 1 ∫ ∫ 3 ( ) ( )  sinx+cosx+2  0 0  ( )   π cosx+sinx=t-2.x=0 → t=3;x= → t = 2 + 2,  Đặt :  4
t = s inx+cosx+2 ⇒  −   dt = (c ) t 2 1 1
osx-sinx dx ⇒ f (x)dx = dt = − 2 dt   3 2 3  tt t  Vậy :   2 +2  1 1   1 1  2 + 2  1 1   1 1  2 1+ 2 I = − 2 dt = − + = − + − − + = − ∫         2 3 2  t t   t t  3  2 + 2 +   3 9  3 3  (2 2)2  (2+ 2)2 (sint + o c st ) sin t + o c st = ( − − = − = t + c ) (sint o c st )( dt ) ( ) ( t + c ) ( o c st sin t ) dt f (x) sin ost+9 sin ost+9 π 2 6 os c x c. dx = ∫ 4 π sin x 4 (1−sin os x c x )3 2 6 2 4 6
1− 3sin x + 3sin x − sin x 1 1 Ta có : 2 f (x) = = = = − 3 + 3 − sin x 4 4 4 4 2 sin x sin x sin x sin x sin x π π π π Vậy : 2 = ∫( dx dx  − cI 1+ cot x) 2 2 2 1 os2x 2 − 3 + 3 dx − dx ∫ ∫ ∫  2 2 π sin x π sin x π π  2  4 4 4 4 π  1 1 1  2 5π 23 3
= − cot x + 3cot x + 3x − x + sin 2x = +    3 2 4  π 8 12 4 π π π π π 4 2 4 2 4 4 4 sin x 1− os c x  1 1  1 1 dx d. dx = dx = − dx = dx − ∫ ∫ ∫  ∫ ∫( 2 1+ tan x 6 6 6 4 4 2 ) 2 os c x os c x  os c x os c x  os c x os c x os c x 0 0 0 0 0 π π π π 4 = ∫( + x) 4 1 dx − ∫ ( + x) 4 1 1 tan 1 tan
dx = ∫ (1+ 2 tan x + tan x)d (tan x) 4 2 2 2 2 4 − ∫( 2 1+ tan x d t anx 2 2 ) ( ) os c x os c x 0 0 0 0 π π  2 1 1   1 1  8 3 5 3 3 5
= t anx+ tan x + tan x − t anx- tan x 4 = tan x + tan x 4 =      3 5 3   3 5  15 0 0 π π π π π 2 2 2 2 sin 2x sin 2x 2 sin 2x d (7 − os c 2x ) 3 e. dx = dx = dx = − = − ln 7 − o c s2x 2 = ln ∫ ∫ ∫ ∫ 2 4 − os c x 1+ os c 2x 7 − os c 2x 7 − os c 2x 4 0 0 0 0 4 − 0 2 π π π π 4 2 4 4 1− 2 sin x os c 2x 1 d (1+ sin 2x) 1 1 f. dx = dx = = ln 1+ sin 2x 4 = ln 2 ∫ ∫ ∫ 1+ sin 2x 1+ sin 2x 2 1+ sin 2x 2 2 0 0 0 0
Ví dụ 9. Tính các tích phân sau : π π 2 2 sin 3x a. 3 4 sin x cos xdx ∫ b. dx ∫ 1+ 2 os c 3x 0 0 π π π 5 6 2 6 2 3 sin x os c x os c 2x c. I = dx ∨ J = dx ⇒ K = dx ∫ ∫ ∫ s inx+ 3 os c x s inx+ 3 os c x π cosx- 3 s inx 0 0 3 2 Giải π π π 2 2 2 a. 3 4 sin x cos xdx = ∫ ∫( 2 1− os c x) 4 os c . x s inxdx = ∫ ( 6 4 os c x − os c x) d ( os c x ) 0 0 0 π  1 1  2 7 5 = os c x − os c x 2 =    7 5  35 0 π π π π 2 2 2 sin 3x 1 3 − sin 3x
1 d (1+ 2 cos 3x) 1 1 b. dx = − dx = − = − ∫ ∫ ∫
(ln 1+ 2cos3x ) 2 = ln3 1+ 2 os c 3x 6 1+ 2 cos 3x 6 1+ 2 cos 3x 6 6 0 0 0 0 π π π 6 2 2 6 6 sin x + os c x 1 1 1 1
c. Ta có : I + J = dx = dx = dx ∫ ∫ ∫ s inx+ 3 os c x 2 1 3 2  π  0 0 0 s inx+ os c x sin x +   2 2  3    x π  d tan +    1 1 1 1   2 6  Do : = = . =  π   x π   π   x π   x π   x π  2 sin x + 2 sin + o c s x+ tan + 2 o c s + tan +              3   2 6   6   2 6   2 6   2 6  π   x π  d tan +    π Vậy : 6 1   2 6  1  x π  1 1 I = = ln tan + ∫   6 = ln 3 = ln 3 (1) 2  x π  2  2 6  2 4 0 tan +   0  2 6  π π 6 2 2 6 − (sinx− 3 os
c x)(sin x + 3 os sin 3 os c x x c x )
- Mặt khác : I − 3J = dx = dx ∫ ∫ s inx+ 3 os c x s inx+ 3 os c x 0 0 π π Do đó : 6
I − 3J = ∫ (sinx- 3 os
c x )dx = (− os
c x- 3 s inx ) 6 =1− 3 (2) 0 0  3 3 −1  1 I = ln 3 −
Từ (1) và (2) ta có hệ : I + J = ln3  16 4  4 ⇔  (3)   1 3 −1
I − 3J =1− 3 J = ln 3 +  16 4 Để tính K ta đặt π π π π t = x − 3
→ dt = dx ⇔ x = 3 ;t = 0.x = 5 → t = 2 2 3 6 π π Vậy : 6 os c (2t+3π ) 6 os c 2t 1 3 −1 K = dt = −
dt = I − J = ln 3 − ∫ ∫  π   π  sint+ 3 os c t 8 2 0 0 o c s t+3 − 3 sin t+3      2   2 
Ví dụ 10. Tính các tích phân sau . π π 4 1 2 dx a. dx ∫ ( CĐ-99) b. ∫ (ĐH-LN-2000) 1+ sin 2x 2 + s inx+cosx 0 0 π π 2 3 1 c. ∫( 10 10 4 4 sin x + os c
x − sin x cos x) dx (SPII-2000) d. dx ∫ (MĐC-2000)  π  0 π sinxsin x+   6  6  Giải π π π π 4 4 4 1 1 1  π  a. dx = dx = dx = x − = ∫ ∫ ∫   1+ sin 2x (sinx+cosx) tan 4 1 2  π  2  4  0 0 0 2 cos x −   0  4  π 2 dx b. ∫ . 2 + s inx+cosx 0 Đặt : x 1 1  x  2dt π 2 t = tan ⇔ dt = dx = 1+ tan ; dx ⇔ dx =
; x = 0 → t = 0, x = → t = 1   2 2 x   + 2 2 2 1 t 2 2 cos 2 1 1 1 Vậy : 1 2 2dt 2dt I = . dt = = = 2 ∫ ∫ ∫ 2 2t 1− t ( 2 1+ t t + 2t + 3 t +1 + 2 0 ) 2 2 ( ) 0 0 ( ) 2 + + 2 2 1+ t 1+ t  1 2 dt = 2
du;t = 0 → tan u =
;t = 1 → tan u = 2 2 Đặt :  os c u 2 t +1 = 2 tan u ⇒  2dt 2 2
f (t)dt = = =  (t + ) du 2du 2 1 + 2 2  ( 2 1+ tan u ) 2 os c u u Vậy : 2 u   2 I = du = u = ∫ ( 2 2 2 2 u − u = 2 arxtan − arctan 2  2 1 ) u   2 u 1   1 π 2 c. ∫( 10 10 4 4 sin x + os c
x − sin x cos x) dx 0 Ta có : 10 10 4 4 x + c x − x x ( 2 2 x + c x) = ( 4 4 c x − x)( 6 6 sin os sin cos sin os os sin os c x − sin x) = ( 2 2 c x − x)( 2 2 c x − x)( 4 4 2 2 os sin os sin os c x + sin x + os c x sin x)  1  1 1+ os c 4x 1− os c 8x 15 1 1 2 2 2 2 = os c 2x 1− sin 2x = os c 2x − sin 4x = − = + os c 4x+ os c 8x    4  16 2 32 32 2 32 π π π Vậy : 2  15 1 1  15 π 1 1 15π I = + os c 4x+ os c 8x dx = + sin 4x 2 + sin 8x 2 = ∫   32 2 32  32 2 8 32.8 64 0 0 0 π 3 1 d. dx ∫ .  π π  s inxsin x+   6  6   π  π  π    π   π  1 Ta có : x +
− x = ⇒ sin x + − x = sin x + os c x-sinxco x + =          (*)  6  6  6    6   6  2 1  π   π  sin x + os c x-sinxco x +     Do đó : 1  6   6 2  f (x) = = 2 = 2  π   π   π  s inxsin x+ s inxsin x+ s inxsin x+        6   6   6   π  π π   π   π os c x+ os c x+      3 3  os c x  6  os c x  6    π   3 = −
⇒ I = f (x)dx = 2  −  dx = 2 ∫ ∫ ln sinx − ln sin x+    sinx  π    π      π π π sinx 6 sin x sin x  + +       6 6  6    6   6 π s inx 3 3 1 2 3 I = 2 ln = ln − ln . = 2ln  π  π 2 2 3 2 sin x+    6  6
* Chú ý : Ta còn có cách khác 1 1 2 f(x)= = = 2  π   3 1  sin x( 3 +cot s inxsin x+ x)   sinx  s inx+ os c x   6  2 2   π π π 3 3 2d ( 3 + cot 2 1 x) Vậy : 3 3 I = dx = − = 2 − ln 3 + cot x = 2ln ∫ ∫ 2 + + π π 3 cot x sin x π ( 3 cot x) 2 6 6 6
Ví dụ 11. Tính các tích phân sau π π 2 3 s inxcos x 2 a. dx ∫ (HVBCVT-99) b. 2 2 os c x cos 2xdx ∫ ( HVNHTPHCM-98) 2 1+ os c x 0 0 π π 4 sin 4x 4 dx c. dx ∫ (ĐHNT-01) d. ∫ (ĐHTM-95) 6 6 os c x + sin x 4 os c x 0 0 Giải π π 2 3 2 2 s inxcos x 1 os c x a. dx = (sin 2x)dx 1 ∫ ∫ 2 2 ( ) 1+ os c x 2 1+ os c x 0 0 dt = 2
− sin x cos xdx = −sin 2xdx Đặt :  2 t = 1+ os c x ⇒  π 2 o
c s x = t −1; x = 0 → t = 2; x = → t =1  2 1 2 Vậy : 1 (t − ) 1   − I = ∫ (−dt) 1 1 1 = − dt = ∫
( t −t) 2 ln2 1 1 ln =   2 t 2  t  2 1 2 2 1 π 2 b. 2 2 os c x cos 2xdx ∫ . 0 1+ os c 2x 1+ os c 4x 1 Ta có : 2 2 f (x) = os c x cos 2x = . = (1+ os
c 2x+cos4x+cos4x.cos2x ) 2 2 4 1  1  = + c  (c ) 1 3 1 1 1 os2x+cos4x+ os6x+cos2x = + os c 2x+ os c 4x+ os c 6x  4  2  4 8 4 8 π π Vậy : 2  1 3 1 1   1 3 1 1  π I = + os c 2x+ os c 4x+ os c 6x dx = x + sin 2x + sin 4x + sin 6x 2 = ∫     4 8 4 8   4 16 16 48  8 0 0 π 4 sin 4x c. dx ∫ . 6 6 os c x + sin x 0 Vì : d ( 6 6 x + c x) = ( 5 5 x x − c x x) dx = x x ( 4 4 sin os 6 sin cos 6 os sin 6 sin cos sin x − os c x) ⇔ d ( 6 6 x + c x) = x ( 2 2 x − c x)( 2 2 sin os 3sin 2 sin os sin x + o
c s x) dx = 3
− sin 2x cos 2xdx 3 2
= − sin 4xdx ⇒ sin 4xdx = − d ( 6 6 sin x + o c s x) 2 3 π π π d ( 6 6 4 4 sin x + os sin 4 2 c x x ) Vậy : 2 4 dx = − = − ln sin x + o c s x 4 = ln 2 ∫ ∫ os c x + sin x 3 sin x + os c x 3 3 0 0 ( ) ( 6 6 6 6 6 6 ) 0 π π π π 4 4 4 dx 1 dx  1  4 d. = = ∫ ∫ ∫( 2
1+ tan x) d (t anx) 3 = t anx+ tan x 4 =   4 2 2 os c x os c x os c x  3  3 0 0 0 0
Ví dụ 12. Tính các tích phân sau . π π 4 a. 11 sin xdx ∫ ( HVQHQT-96) b. 2 4 sin x cos xdx ∫ (NNI-96) 0 0 π 4 π c. 2 os c x cos 4xdx ∫ (NNI-98 ) d. 1+ os c 2xdx ∫ (ĐHTL-97 ) 0 0 Giải π a. 11 sin xdx ∫ 0 Ta có : x = x ( x)5 11 10 2 ( 2 3 4 5 6 sin sin .s inx= 1-cos
s inx= 1-5cos x +10 cos x −10 cos x + 5 cos x − os c x)sinx π Cho nên : I = ∫( 2 3 4 5 6
1-5cos x +10 cos x −10 cos x + 5 cos x − os c x)sinxdx 0  1 5 5 5  π 118 − 7 6 5 4 3 = os c x − os c x + 2 cos x − os c x + os c x − os c x =    7 6 2 3  0 21 π 4 b. 2 4 sin x cos xdx ∫ 0 Hạ bậc : 2 1− os c 2x   1+ os c 2x  1 2 4 sin x cos x = =    (1− os c 2x )( 2 1+ 2 cos 2x + os c 2x)  2  2  8 1 = ( 2 2 3 1+ 2 cos 2x + os c 2x − os
c 2x-2cos 2x − os c 2x) 8 1 = ( 1  1+cos4x 1+cos4x  2 3 1+ os
c 2x-cos 2x − os c 2x) = 1+ os c 2x- − os c 2x    8 8  2  2  1 (   = + c ) 1 cos6x+cos2x 1 os2x-cos4x+cos4x.cos2x = 1+ os c 2x-cos4x+   16 16  2  1 (2+3cos2x + os c 6x-cos4x ) 32 π π Vậy 4 1   I = ∫ ( + x + c ) 1 3 1 1 2 3cos 2 os6x-cos4x dx = x + sin 2x + sin 6x − sin 4x 4 =   32  32 64 32.6 32.4  0 0 π   π π π 2 π   d. 2 1+ os c 2xdx = 2 cos xdx = 2 os c x dx = 2 os c xdx − os c xdx ∫ ∫ ∫  ∫ ∫  0 0 0  0 π   2   π π   
= 2 sinx 2 − sinx π = 2 (1+ ) 1 = 2 2    0   2 
III. MỘT SỐ CHÚ Ý QUAN TRỌNG
1. Trong phương pháp đổi biến số dạng 2. b b
* Sử dụng công thức : f (x)dx = f (b − x)dx ∫ ∫ 0 0 Chứng minh : •
x = 0 → t = b
Đặt : b-x=t , suy ra x=b-t và dx=-dt , ⇒ 
x = b → t = 0 b 0 b b
• Do đó : f (x)dx = f (b −t)(−dt) = f (b −t)dt = f (b − x)dx ∫ ∫ ∫ ∫ . Vì tích phân không 0 b 0 0
phụ thuộc vào biến số
Ví dụ : Tính các tích phân sau π π 2 4 sin xdx
2 5cos x − 4sin x a/ ∫ ( b/ dx ∫ 3 s inx+cosx )3 s inx+cosx 0 ( ) 0 π π 4 2 6 sin x c/ log 1+ t anx dx ∫ d/ dx ∫ 2 ( ) 6 6 sin x + os c x 0 0 π 1 2 4 sin x cos x e/ ∫ ( n m x 1− x) dx f/ dx ∫ 3 3 sin x + os c x 0 0 Giải π 2 4 sin xdx a/ I = ∫ .(1) . Đặt : (sinx+cosx)3 0  π π
dt = −dx, x = 0 → t = ; x = → t = 0  2 2  π π   π  t =
− x ⇒ x = − t ↔ 4 sin − t     2  4 cos 2 2 t
f (x)dx = dt = −
dt = f (t)dt 3 ( )    π   π  (cost+sint)3 sin − t + os c − t          2   2 
Nhưng tích phân không phụ thuộc vào biến số , cho nên : π 0 2 4 os c x I = f (t)dt = dx 2 ∫ ∫ 3 ( ) π sinx+cosx 0 ( ) 2 π π
Lấy (1) +(2) vế với vế ta có : 2 4(s inx+cosx) 2 1 2I = ⇒ = ∫ ( dx I dx ∫ s inx+cosx ) 2 3 (sinx+cosx)2 0 0 π π 2 1  π  ⇔ I = 2 dx = tan x − ∫   2 = 2  π  2  4  0 2 cos x −   0  4  π
2 5cos x − 4sin x b/ I = ∫
. Tương tự như ví dụ a/ ta có kết quả sau : ( dx s inx+cosx )3 0 π π 2 0 2
5 cos x − 4 sin x
5sin t − 4 cos t 5sin x − 4 os c x I = dx = − dt = dx 2 ∫ ∫ ∫ 3 3 3 ( ) s inx+cosx π os c t+sint s inx+cosx 0 ( ) ( ) 0 ( ) 2 π π π Vậy : 2 2 1 1 1  π  1 2I = = = − = ⇒ = ∫ ( dx dx x I ∫   s inx+cosx ) tan 2 1 2  π  2 2  4  2 0 0 2 cos x −   0  4  π 4 c/ log 1+ t anx dx ∫ . Đặt : 2 ( ) 0  π π
dx = −dt, x = 0 → t = ; x = → t = 0 π π  4 4 t =
− x → x = − t ⇔  4 4   π 
f (x)dx = log 1+ t anx dx = log 1+ tan − t −dt 2 ( ) 2   ( )    4   1− tan t  2
Hay: f (t) = log 1+ −dt = log
−dt = log 2 − log t 2  ( ) 2 ( ) 2 2  1+ tan t  1+ tan t π π π 0 Vậy : 4 4 π π I =
f (t)dt = dt − log tdt ⇒ 2I = t 4 = ⇔ I = ∫ ∫ ∫ 2 π 4 8 0 0 0 4 π 2 6 sin x d/ I = dx ∫ (1) 6 6 sin x + os c x 0  π  6 π sin − t 0    2  ∫ (− ) 2 6 os c x d t = dx = I ∫ (2) 6 6  π   π  + π 6 6 os c x sin x 0 sin − t + os c − t     2  2   2  π π π Cộng (1) và (2) ta có : 2 6 6 2 os c x + sin x π π 2I =
dx = dx = x 2 = ⇒ I = ∫ ∫ 6 6 os c x + sin x 2 4 0 0 0 1 e/ ∫ ( n m x
1− x) dx . Đặt : t=1-x suy ra x=1-t . Khi x=0,t=1;x=1,t=0; dt=-dx 0 0 1 1 Do đó : = ∫( m 1− ) n (− ) n = (1− )m n = (1− )m I t t dt t t dt x x dx ∫ ∫ 1 0 0
MỘT SỐ BÀI TẬP TỰ LUYỆN π π 2 2 4 sin x 4 os c x+2sinx 1. dx ∫ 2. dx ∫ (XD-98 ) 1+ os c x 4 cos x + 3sin x 0 0 π π 2 3 s inxcos x 3 x + s inx 3. dx ∫ 4. dx ∫ ( HVNHTPHCM-2000 ) 2 1+ os c x 2 cos x 0 0 1 π 6 x sin x 5. 5 x ∫ ( 3
1− x ) dx (ĐHKT-97 ) 6. dx ∫ ( AN-97 ) 2 2 + os c x 0 0 π π 4 s inx+2cosx 2 1+ sinx  7. dx ∫ ( CĐSPHN-2000) 8. ln dx ∫   ( CĐSPKT-2000 ) 3sin x + o c sx  1+cosx  0 0 π π x sin x 2 4 sin x cos x 9. dx ∫ (ĐHYDTPHCM-2000 ) 10. dx ∫ 2 9 + 4 cos x 3 3 sin x + os c x 0 0 β * Dạng : asinx+bcosx+c I = dx ∫ a 's inx+b'cosx+c' α Cách giải : β asinx+bcosx+c B (a ' os c x-b'sinx ) C Ta phân tích : dx = A + + ∫ a 's inx+b'cosx+c' a 's inx+b'cosx+c' ' a s inx+b'cosx+c' α
- Sau đó : Quy đồng mẫu số
- Đồng nhất hai tử số , để tìm A,B,C . - Tính I : β β  B (a ' os c x-b'sinx ) C  = ∫ + +  = ( β dx I A dx
Ax+Bln a 's inx+b'cosx+c' ) + C∫ a 's inx+b'cosx+c' ' a s inx+b'cosx+c' α a 's inx+b'cosx+c' α   α VÍ DỤ ÁP DỤNG
Ví dụ . Tính các tích phân sau : π π 2 s inx-cosx+1 4 os c x+2sinx a. dx ∫ ( Bộ đề ) b. dx ∫ ( XD-98 ) s inx+2cosx+3 4 cos x + 3sin x 0 0 π 2 s inx+7cosx+6 π c. dx ∫ d. I = 2 4 cos x − 3sin x +1
4 sin x + 3cos x + 5 ∫ dx 0 4 sin x + 3 cos x + 5 0 Giải π 2 s inx-cosx+1 s inx-cosx+1 B ( os c x-2sinx ) C a. dx ∫
. Ta có : f (x) = = A + + ( )1 s inx+2cosx+3 s inx+2cosx+3 s inx+2cosx+3 s inx+2cosx+3 0
Quy đồng mẫu số và đồng nhất hệ số hai tử số :  1 A = −  5 (  − =  A − B) ( ) A 2B 1 2 s inx+ 2A+B os c x+3A+C   3 ⇔ f (x) = ⇒ 2A+ B = 1
− ⇔ B = − . Thay vào (1) s inx+2cosx+3 5   3A + C = 1   4 C =  5 π π π π 2 2  1  3 d (s inx+2cosx+3) 2 4 1 π 3 4 I = − dx − + dx = − − ln sinx+2cosx+3 ∫  2 − J ∫ ∫  5  5 s inx+2cosx+3 5 s inx+2cosx+3 10 5 5 0 0 0 0 π 3 4 4 I = − − ln − J (2) 10 5 5 5 - Tính tích phân J :  1 dx π dt =
; x = 0 → t = 0, x = → t = 1  2 x 2 2  os c 1 Đặt : x  2 2dt t = tan ⇒  ⇔ J = ∫ . (3) 2 1 2dt 2dt  (t + )2 1 + 2 0 f (x)dx = = 2 2 2  2t 1− t 1+ t t + 2t + 3 + 2 + 3  2 2  1+ t 1+ t Tính (3) : Đặt :  du 2 dt = 2
.t = 0 → tan u =
= u ;t = 1 → tan u = 2 = u 2 1 2 os c u 2  t +1 = 2 tan u ⇒  1 2du 2
f (t)dt = = du 2 2 os c u 2  2  os c uu 2 Vậy : 2 2 2 π  = du = ∫ (u −u ) 3 4 4 2 u j= ⇒ I = I = − − ln − (u −u ) tan 1  2 2 1 2 1 2 2 10 5 5 5 2 u tanu = 2  2 π 4 os c x+2sinx os c x+2sinx
B (3cos x − 4sin x) C b. ; dx f (x) = = A + + → ∫ ( )1 4 cos x + 3sin x 4 cos x + 3sin x 4 cos x + 3sin x 4 cos x + 3sin x 0
Giống như phàn a. Ta có : 2 1 A = ; B = − ;C=0 5 5 π π Vậy :
4  2 1 (3cos x − 4sin x)   2 1  π 1 4 2 I = ∫  −  dx =
x − ln 4 cos x + 3sin x   4 = + ln 5
5 4 cos x + 3sin x    5 5  10 5 7 0 0