


























































































Preview text:
2
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Chûúng
HÀM SỐ VÀ ĐỒ THỊ 5
HÀM SỐ VÀ ĐỒ THỊ Baâi 1 KHÁI NIỆM HÀM SỐ A
TRỌNG TÂM KIẾN THỨC
1 Khái niệm hàm số
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ
một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.
2 Giá trị của hàm số
2.1. Cách cho một hàm số
Hàm số có thể cho bằng bảng, biểu đồ hoặc bằng công thức, . . .
Nếu y là hàm số của x ta có thể viết y = f (x), y = g(x), . . . Chẳng hạn, với hàm số được cho bởi công thức
y = 4x + 1, ta có thể viết y = f (x) = 4x + 1.
2.2. Giá trị của hàm số
Cho hàm số y = f (x), nếu ứng với x = a ta có y = f (a) thì f (a) được gọi là giá trị của hàm số y = f (x) tại x = a.
Bảng số liệu sau đây được gọi là một bảng giá trị của hàm số y = f (x). x a b c · · · · · · y = f (x) f (a) f (b) f (c) · · · · · · A B CÁC DẠNG BÀI TẬP
Dạng 1. Hàm số, bảng giá trị của hàm số
c Ví dụ 1. Các giá trị tương ứng của hai đại lượng x và y được cho bởi các bảng sau. Đại lượng y có phải
là một hàm số của đại lượng x không? x −3 −2 2 4 6 x −2 −1 0 1 −2 a) b) y −4 −6 6 3 2 y −1 0 1 2 1 Lời giải.
a) Đại lượng y là hàm số của x vì với mỗi giá trị của x (x ∈ {−3; −2; 2; 4; 6}), ta luôn xác định được chỉ một
giá trị tương ứng của y.
b) Đại lượng y không phải là một hàm số của x vì với x = −2 ta xác định được hai giá trị tương ứng của y (y = −1 và y = 1). 2/119 2/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 3
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO □
c Ví dụ 2. Đại lượng y có phải là hàm số của đại lượng x hay không nếu bảng giá trị tương ứng của chúng được cho bởi bảng sau? x 1 2 3 4 5 y 6 6 6 6 6 Lời giải.
Đại lượng y là hàm số của đại lượng x vì mỗi giá trị của x chỉ xác định đúng một giá trị của y. □
c Ví dụ 3. Viết công thức tính thể tích V (cm3) của hình lập phương có độ dài cạnh là x (cm). Hỏi V có
phải là hàm số của x không? Vì sao? Lời giải. Ta có V = x3 (cm3).
Nhận thấy mỗi giá trị của x chỉ xác định đúng một giá trị của V . Vậy V là hàm số của x. □
c Ví dụ 4. Viết công thức tính thời gian di chuyển t (giờ) của một ô tô chuyển động trên quãng đường dài
150 km với vận tốc không đổi v (km/h). Thời gian di chuyển t có phải là một hàm số của vận tốc v không?
Tính giá trị của t khi v = 60 (km/h). Lời giải. 150 Ta có vt = 150 ⇒ t =
. Do đó thời gian di chuyển t là một hàm số theo vận tốc v. v 150 5 Với v = 60 thì t = = (giờ). □ 60 2
c Ví dụ 5. Viết công thức tính thể tích V (cm3) của hình lập phương có độ dài cạnh là x (cm). Hỏi V có
phải là hàm số của x không? Vì sao? Lời giải. Ta có V = x3 (cm3).
Nhận thấy mỗi giá trị của x chỉ xác định đúng một giá trị của V . Vậy V là hàm số của x. □
c Ví dụ 6. Gọi C = f (d) là hàm số mô tả mối quan hệ giữa chu vi C và đường kính d của một đường tròn.
Tìm công thức f (d) và lập bảng giá trị của hàm số ứng với d bằng 1; 2; 3; 4 (theo đơn vị cm). Lời giải.
− Mối quan hệ giữa chu vi C và đường kính d theo công thức C = f (d) = πd. − Bảng giá trị x 1 2 3 4 C = f (d) = πd π 2π 3π 4π □
c Ví dụ 7. Nhiệt độ N của một máy ấp trứng gà được cài đặt luôn bằng 37, 5◦C không thay đổi theo thời
gian t. Em hãy viết công thức xác định hàm số N(t) của nhiệt độ theo thời gian. Lời giải.
Vì nhiệt độ không đổi và luôn bằng 37, 5◦C với mọi giá trị của biến số t nên ta có hàm hằng N(t) = 37,5. □
c Ví dụ 8. Cho hàm số y = f (x) = 3x. Lập bảng các giá trị tương ứng của y khi x nhận các giá trị lần lượt là −2; −1; 0; 1; 2. Lời giải. 3/119 3/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 4 1. KHÁI NIỆM HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Bảng các giá trị tương ứng của y: x −2 −1 0 1 2 y = f (x) = 3x −6 −3 0 3 6 □
c Ví dụ 9. Cho hàm số y = f (x) = −2x + 1. a) Tính f (10); f (−10).
b) Lập bảng giá trị của hàm số với x lần lượt bằng −2; −1; 0; 1; 2. Lời giải.
a) Thay x bằng 10 hoặc −10 vào f (x), ta có:
f (10) = −2 · 10 + 1 = −20 + 1 = −19 f (−10) = −2 · (−10) = 20 + 1 = 21
b) Cho x lần lượt bằng −2; −1; 0; 1; 2, ta có bảng giá trị của hàm số: x −2 −1 0 1 2 y = f (x) = −2x + 1 5 3 1 −1 −3 □ c Ví dụ 10.
a) Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau x −3 −2 −1 1 2 3 y −6 −4 −2 2 4 6
Đại lượng y có phải là hàm số của đại lượng x không?
b) Cho hàm số y = f (x) = x2 − Tính f (2); f (−3).
− Lập bảng giá trị của hàm số với x lần lượt bằng −3; −2; −1; 0; 1; 2; 3. Lời giải.
a) Đại lượng y là một hàm số. Hàm số y = f (x) = 2x, x ̸= 0 b) Hàm số y = f (x) = x2
− Ta có y = f (x) = x2, f (2) = 22 = 4; f (−3) = (−3)2 = 9. − Bảng giá trị x −3 −2 −1 0 1 2 3 y = x2 9 4 1 0 1 4 9 □
Dạng 2. Tính giá trị của hàm số khi biết giá trị của biến số, và ngược lại
Tìm tập xác định D của hàm số y = f (x).
○ Thế giá trị x = x0 ∈ D vào thức của hàm số rồi tính giá trị biểu thức (đôi khi ta rút gọn biểu thức, biến
đổi x0 rồi mới thay vào để tính toán).
○ Thế giá trị y = y0 ta được y0 = f(x). Giải phương trình f(x) = y0 để tìm giá trị biến số x (chọn x ∈ D). 4/119 4/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 5
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Ví dụ 11. Cho hàm số y = f (x) = x + 5. Tính f (−2), f (0). Lời giải. Ta có f (−2) = (−2) + 5 = 3; f (0) = 0 + 5 = 5. □ 3 1
c Ví dụ 12. Tính giá của hàm số y = f (x) = − x2 − tại x = 1; x = −1. 4 4 Lời giải. Ta có 3 1 3 1 f (1) = − · 12 − = − − = −1 4 4 4 4 3 1 3 1 3 1 4 f (−1) = − · (−1)2 − = − · 1 − = − − = − = −1. 4 4 4 4 4 4 4 □ x2 − 9
c Ví dụ 13. Cho hàm số y = f (x) =
. Khi đó f (−3) bằng bao nhiêu? x + 3 Lời giải.
Vì x = −3 không thỏa mãn điều kiện nên không tồn tại f (−3). □
c Ví dụ 14. Cho hàm số y = f (x) = mx + m − 1, biết f (3) = 8. Tính f (3). Lời giải. TXĐ: R. Ta có
f (2) = 8 ⇔ m · 2 + m − 1 = 8 ⇔ 3m = 9 ⇔ m = 3.
⇒ f (x) = 3x + 2 ⇒ f (3) = 3 · 3 + 2 = 11. □ √ √
c Ví dụ 15. Cho hàm số y = f (x) = x + 1 − x. a) Tìm x, biết f (x) = 1; b) Tìm x sao cho f (x) = 0,5;
c) Tìm m để có giá trị của x thỏa mãn f (x) = m. Lời giải.
a) Điều kiện: 0 ≤ x ≤ 1. Ta có √ √ f (x) = 1 ⇔ x + 1 − x = 1 √ √ ⇔ ( x + 1 − x)2 = 12 √ √ √ √ ⇔ x + 2 x · 1 − x + x = 1 ⇔ 2 x · 1 − x = 0 √ √ ⇔ x = 0 hoặc 1 − x = 0
⇔ x = 0 hoặc x = 1 (thỏa mãn điều kiện). b) Ta có √ √ f (x) = 0,5 ⇔ x + 1 − x = 0,5 5/119 5/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 6 1. KHÁI NIỆM HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO √ √ Ä ä2 ⇔ x + 1 − x = 0,52 √ √ ⇔ x + 2 x · 1 − x + 1 − x = 0,25 √ √ √ √ ⇔ 2 x ·
1 − x = −0,75 không xảy ra vì 2 x · 1 − x ≥ 0).
Do đó không có giá trị nào của x để f (x) = 0,5. √ √ √ √ Ä ä2 c) Ta có f (x) = x + 1 − x ⇔ f 2(x) = x + 1 − x √ √
⇔ f 2(x) = x + 2 x 1 − x + 1 − x √ √ √ √ ⇔ f 2(x) = 2 x · 1 − x + 1 ≥ 1 (vì 2 x · 1 − x ≥ 0).
Suy ra f (x) ≥ 0 (dấu bằng xảy ra khi và chỉ khi x = 0 và x = 1).
Do đó chỉ khi m ≥ 1 thì có giá trị thỏa mãn f (x) = m. □ Dạng 3. Vận dụng
c Ví dụ 16. Nhà bác học Galileo Galilei (1564 − 1642) là người đầu tiên phát hiện ra quan hệ giữa quãng
đường chuyển động y (m) và thời gian chuyển động x (giây) của một vật được biểu diễn gần đúng bởi hàm số
y = 5x2. Tính quãng đường mà vật đó chuyển động được sau 2 giây. Lời giải. Xét hàm số y = f (x) = 5x2
Quãng đường mà vật đó chuyển động được sau 2 giây là f (2) = 5 · 22 = 20 (m). □ c Ví dụ 17.
Để xem dự báo nhiệt độ (T ◦C) tại một số thời điểm t (h) trong cùng một ngày, chúng
ta có thể truy cập trang https://accuweather.com. Hình bên là nhiệt độ dự báo ở Thành 10 30◦
phố Hồ Chí Minh tại một số thời điểm trong ngày 15/3/2022. Khi biểu diễn các dữ liệu
lên bảng, ta có bảng giá trị sau: 11 32◦ t (h) 10 11 12 13 14 12 33◦ T (◦C) 30 32 33 34 34 13 34◦ 14 34◦
a) Nhiệt độ T có phải là hàm số của thời điểm t không? Vì sao?
b) Thời điểm t có phải là hàm số của nhiệt độ T không? Vì sao? Lời giải.
a) Nhiệt độ T là hàm số của thời điểm t vì mỗi giá trị của t chỉ xác định đúng một giá trị của T .
b) Thời điểm t không phải là hàm số của nhiệt độ T . Lí do: Nhiệt độ T = 34(◦C) tương ứng với hai thời điểm
khác nhau là t = 13 (h) và t = 14 (h). □
c Ví dụ 18. Hình sau là biểu đồ đoạn thẳng mô tả sản lượng tiêu thụ ô tô của thị trường Việt Nam trong 5
tháng đầu năm 2020. Em hãy cho biết: 6/119 6/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 7
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Sản lượng tiêu thụ ô tô trong 5 tháng đầu năm 2020 25 000 19 154 19 081 20 000 17 616 15 787 15 000 hiếc) 11 761 (c tô ô 10 000 Số 5 000 0 Tháng 1 Tháng 2 Tháng 3 Tháng 4 Tháng 5 Tháng
(Theo Hiệp hội các nhà sản xuất ô tô Việt Nam (VAMA))
a) Tháng nào thì số lượng ô tô tiêu thụ là ít nhất và số lượng ô tô tiêu thụ trong tháng đó là bao nhiêu?
b) Nếu gọi y là số lượng ô tô tiêu thụ trong tháng x (x ∈ {1; 2; 3; 4; 5}) thì y có phải là một hàm số của x
không? Tính giá trị của y khi x = 5. Lời giải.
a) Tháng 4 có số lượng ô tô tiêu thụ là ít nhất và có số lượng ô tô tiêu thụ là 11 761 chiếc.
b) Đại lượng y là hàm số của x vì với mỗi giá trị của x (x ∈ {1; 2; 3; 4; 5}), ta luôn xác định được chỉ một giá trị tương ứng của y. Khi x = 5 thì y = 19 081. □
c Ví dụ 19. Số tiền điện phải trả trong tháng khi lượng điện sử dụng x (kWh) trong khoảng từ 51 kWh đến
100 kWh được cho bởi công thức sau
T (x) = 1 734x − 2 800 (đồng).
a) Tính số tiền điện phải trả khi lượng điện tiêu thụ trong tháng là 90 kWh.
b) Nếu số tiền điện phải trả trong tháng là 144 590 đồng thì gia đình đó đã sử dụng bao nhiêu kWh điện? Lời giải.
a) Khi x = 90 ta có T (90) = 1 734 · 90 − 2 800 = 153 260 đồng.
Vậy khi lượng điện tiêu thụ trong tháng là 90 kWh thì số tiền điện phải trả là 153 260 đồng.
b) Ta phải tìm x sao cho T (x) = 144 590, tức là 1 734x − 2 800 = 144 590 1 734x = 147 390 x = 85 (thỏa mãn).
Vậy trong tháng đó gia đình đó đã sử dụng 85 kWh. □ 7/119 7/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 8 1. KHÁI NIỆM HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO A C BÀI TẬP VẬN DỤNG
c Bài 1. Các giá trị tương ứng của hai đại lượng x và y cho bởi các bảng sau. Đại lượng y có phải là một hàm số của x không? x −3 −1 0 2 4 x −2 1 0 1 2 a) b) y 1 1 1 1 1 y −2 1 0 2 2 Lời giải.
a) Đại lượng y là một hàm số của x vì với mỗi giá trị của x (x ∈ {−3; −1; 0; 2; 4}), ta luôn xác định được chỉ
một giá trị tương ứng của y.
b) Đại lượng y không là hàm số của đại lượng x vì với x = 1 ta xác định được hai giá trị tương ứng của y (y = 1 và y = 2). □
c Bài 2. Các giá trị tương ứng của hai đại lượng x và y được cho trong các bảng sau. Trong mỗi trường hợp,
hãy cho biết đại lượng y có phải là hàm số của đại lượng x không? Giải thích. x 0 1 2 3 4 5 6 7 x −3 −2 −1 1 2 2 a) b) 1 1 1 1 y 1 2 3 4 5 6 7 8 y − − −1 1 3 2 2 3 Lời giải. a) Hàm số y = x + 1. 1 1
b) Không là hàm số. Khi x = 2 thì y = và y = . 2 3 □
c Bài 3. Đại lượng y có phải là hàm số của đại lượng x hay không nếu bảng giá trị tương ứng của chúng
được cho bởi mỗi trường hợp sau: x 1 2 3 4 5 6 x 1 2 3 4 1 5 a) b) y −2 −2 −2 −2 −2 −2 y −2 −3 −4 −5 −6 −7 Lời giải.
○ Đại lượng y là hàm số của đại lượng x vì mỗi giá trị của x chỉ xác định đúng một giá trị của y.
○ Đại lượng y không là hàm số của đại lượng x vì giá trị x = 1 xác định đến hai giá trị y = −2 và y = −6. □ c Bài 4.
○ Cho hàm số y = 2x + 10. Tìm giá trị của y tương ứng với mỗi giá trị sau của x: 1 x = −5; x = 0; x = . 2
○ Cho hàm số y = −2x2 + 1. Tìm giá trị của y tương ứng với mỗi giá trị sau của x: 1 x = −1; x = 0; x = 1; x = . 3 Lời giải. 8/119 8/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 9
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
○ f (−5) = 2 · (−5) + 10 = 0. f (0) = 2 · 0 + 10 = 10. Å 1 ã Å 1 ã f = 2 · + 10 = 11. 2 2
○ f (−1) = −2 · (−1)2 + 1 = −1. f (0) = −2 · (0)2 + 1 = 1.
f (1) = −2 · (1)2 + 1 = −1. Å 1 ã Å 1 ã2 7 f = −2 · + 1 = . 3 3 9 □
c Bài 5. Cho hàm số y = f (x) = 3x. Å 1 ã a) Tính f (1); f (−2); f . 3
b) Lập bảng các giá trị tương ứng của y khi x lần lượt nhận các giá trị −3; −2; −1; 0; 1; 2; 3. Lời giải. Hàm số y = f (x) = 3x Å 1 ã 1
a) Ta có f (1) = 1 · 3 = 3; f (−2) = −2 · 3 = −6; f = · 3 = 1. 3 3 b) Bảng giá trị x −3 −2 −1 0 1 2 3 y = 3x −9 −6 −3 0 3 6 9 □
c Bài 6. Cho hàm số y = f (x) = x2 + 4. Tính f (−3); f (−2); f (−1); f (0); f (1). Lời giải.
Hàm số y = f (x) = x2 + 4. Tính f (−3) = (−3)2 + 4 =13 □ f (−2) = (−2)2 + 4 =8 f (−1) = (−1)2 + 4 =5 f (0) = 02 + 4 =4 f (1) = 12 + 4 =5 4
c Bài 7. Cho hàm số y = f (x) = . x a) Tính f (−4); f (8).
b) Hoàn thành bảng sau vào vở: x −2 ? 2 3 ? y = f (x) ? −4 ? ? 8 Lời giải. 4 4 1 a) Ta có: f (−4) = = −1; f (8) = = . −4 8 2 9/119 9/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 10 1. KHÁI NIỆM HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO 1 x −2 −1 2 3 2 b) 4 y = f (x) −2 −4 2 8 3 □
c Bài 8. Khối lượng m (g) của một thanh sắt có khối lượng riêng là 7, 8 kg/dm3 tỉ lệ thuận với thể tích
V (cm3) theo công thức m = 7, 8V. Đại lượng m có phải là hàm số của đại lượng V không? Nếu có, tính
m(10); m(20); m(30); m(40); m(50). Lời giải.
Hàm số y = m(V ) = 7,8V . Tính m(10) = 7,8 · 10 = 78 □ m(20) = 7,8 · 20 = 156 m(30) = 7,8 · 30 = 234 m(40) = 7,8 · 40 = 312 m(50) = 7,8 · 50 = 390.
c Bài 9. Thời gian t (giờ) của một vật chuyển động đều trên quãng đường 20 km tỉ lệ nghịch với tốc độ v 20
(km/h) của nó theo công thức t =
. Tính và lập bảng các giá trị tương ứng của t khi v lần lượt nhận các v giá trị 10; 20; 40; 80. Lời giải. 20 Hàm số y = t(v) = . v Bảng giá trị v 10 (km/h) 20 (km/h) 40 (km/h) 80 (km/h) 20 1 1 t = 2 (giờ) 1 (giờ) (giờ) (giờ) v 2 4 □
c Bài 10. Khối lượng m (g) của một thanh sắt có khối lượng riêng là 7, 8 kg/dm3 tỉ lệ thuận với thể tích
V (cm3) theo công thức m = 7, 8V. Đại lượng m có phải là hàm số của đại lượng V không? Nếu có, tính
m(10); m(20); m(30); m(40); m(50). Lời giải.
Hàm số y = m(V ) = 7,8V . Tính m(10) = 7,8 · 10 = 78 □ m(20) = 7,8 · 20 = 156 m(30) = 7,8 · 30 = 234 m(40) = 7,8 · 40 = 312 m(50) = 7,8 · 50 = 390.
c Bài 11. Thời gian t (giờ) của một vật chuyển động đều trên quãng đường 20 km tỉ lệ nghịch với tốc độ v 20
(km/h) của nó theo công thức t =
. Tính và lập bảng các giá trị tương ứng của t khi v lần lượt nhận các v giá trị 10; 20; 40; 80. Lời giải. 20 Hàm số y = t(v) = . v Bảng giá trị 10/119 10/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 11
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO v 10 (km/h) 20 (km/h) 40 (km/h) 80 (km/h) 20 1 1 t = 2 (giờ) 1 (giờ) (giờ) (giờ) v 2 4 □
c Bài 12. Cho một thanh kim loại đồng chất có khối lượng riêng là 7,8 g/cm3.
○ Viết công thức tính khối lượng m (g) theo thể tích V (cm3). Hỏi m có phải là hàm số của V hay không? Vì sao?
○ Tính khối lượng của thanh kim loại đó khi biết thể tích của thanh kim loại đó là V = 1000 cm3. Lời giải.
○ Công thức tính khối lượng m (g) theo thể tích V (cm3) là m = 7,8 · V .
m là hàm số của V vì mỗi giá trị của V chỉ xác định được duy nhất giá trị m.
○ m = 7,8 · 1000 = 7800 (g). □
c Bài 13. Dừa sáp là một trong những đặc sản lạ, quý hiếm và có giá trị dinh dưỡng cao, thường được trồng
ở Bến Tre hoặc Trà Vinh. Giá bán mỗi quả dừa sáp là 200 000 đồng.
○ Viết công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (quả) dừa sáp. Hỏi y có phải
là hàm số của x hay không? Vì sao?
○ Hãy tính số tiền mà người đó phải trả khi mua 10 quả dừa sáp. Lời giải.
○ Công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (quả) dừa sáp là y = 200000 · x.
y là hàm số của x vì mỗi giá trị của x chỉ xác định được duy nhất giá trị y.
○ y = 200000 · 10 = 2000000 (đồng). □
c Bài 14. Bác Ninh gửi tiết kiệm 10 triệu đồng ở ngân hàng với kì hạn 12 tháng và không rút tiền trước kì
hạn. Lãi suất ngân hàng quy định cho kì hạn 12 tháng là r%/năm.
○ Viết công thức biểu thị số tiền lãi y (đồng) theo lãi suất r%/năm mà bác Ninh nhận được khi hết kì
hạn 12 tháng. Hỏi y có phải là hàm số của r hay không? Vì sao?
○ Tính số tiền lãi mà bác Ninh nhận được khi hết kì hạn 12 tháng, biết r = 5,6. Lời giải.
○ Công thức biểu thị số tiền lãi y (đồng) theo lãi suất r%/năm mà bác Ninh nhận được khi hết kì hạn 12 tháng là y = 100000 · r.
y là hàm số của r vì mỗi giá trị của r chỉ xác định được duy nhất giá trị y.
○ y = 100000 · 5,6 = 560000 (đồng). □
c Bài 15. Giá cước taxi của một hãng xe taxi khi quãng đường di chuyển x km trong khoảng từ 1 km đến
30 km được cho bởi công thức sau:
T (x) = 10 000 + 13 600 · (x − 1) (đồng).
a) Tính số tiền phải trả khi xe di chuyển 20 km. 11/119 11/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 12 1. KHÁI NIỆM HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
b) Nếu một hành khách phải trả 200 400 đồng thì hành khách đó đã di chuyển bao nhiêu kilômét? Lời giải.
a) Khi x = 20 thì T (20) = 10 000 + 13 600 · (20 − 1) = 268 400. Vậy khi xe di chuyển 20 km thì số tiền phải trả là 268 400 đồng.
b) Ta phải tìm x sao cho T (x) = 200 400, tức là
T (x) = 200 400 ⇒ 10 000 + 13 600 · (x − 1) = 200 400
⇒ 13 600 · (x − 1) = 190 400 ⇒ x − 1 = 14 ⇒ x = 15.
Vậy nếu một hành khách phải trả 200 400 đồng thì hành khách đó đã di chuyển 15 kilômét. □
c Bài 16. Cho hai hàm số √x − 2 √ √ y = f (x) = vày = g(x) = x + 1 − x. 3 Å 1 ã Å 1 ã Tính f (2), f , g(0), g(1), g . 2 2 Lời giải. Å 1 ã Ta có f (2) = 0; f không xác định; 2 Å 1 ã 1 1 2 √ g(0) = 1; g(1) = 1; g = √ + √ = √ = 2. □ 2 2 2 2
c Bài 17. Cho hàm số y = f (x) = −mx + m − 3. Biết f (−2) = 6, tính f (−3). Lời giải.
f (−2) = 6 ⇔ −m(−2) + m − 3 = 6 ⇔ 3m = 9 ⇔ m = 3 ⇒ f (x) = −3x ⇒ f (−3) = 9. □
c Bài 18. Cho hàm số y = f (x) = −mx + m − 3. Biết f (−2) = 6, tính f (−3). Lời giải. √ √ √ √ √ √ √ √ Ä ä − 2 f (x) = 3 ⇔ 3 − 2 x + 2 + 3 = 3 ⇔ x = √ √ = − 6 − 2. Ä ä 3 − 2 □
c Bài 19. Chứng minh rằng không tồn tại đa thức f (x) bậc ba với hệ số nguyên sao cho f (7) = 2010 và f (11) = 2012. Lời giải.
Giả sử có đa thức f (x) = ax3 + bx2 + cx + d; a, b, c, d ∈ Z, a ̸= 0 thỏa mãn f (7) = 2010, f (11) = 2012. Ta có f (11) − f (7) =
a · 113 + b · 112 + c · 11 + d − a · 73 + b · 72 + c · 7 + d . =
a · 113 − 73 + b · 112 − 72 + c · (11 − 7) .. 4 (do mỗi số hạng chia hết cho 4). 12/119 12/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 13
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO .
Từ đó suy ra f (11) − f (7) .. 4. (1)
Mặt khác f (11) = 2012, f (7) = 2010 nên f (11) − f (7) = 2. (2) .
Từ (1) và (2) suy ra 2 .. 4 vô lí, vậy điều giả sử sai. □ 13/119 13/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 14
2. KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Baâi 2
KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ A
TRỌNG TÂM KIẾN THỨC
1 Tọa độ của một điểm
1.1. Mặt phẳng tọa độ
Trên mặt phẳng, ta vẽ hai trục số Ox và Oy vuông góc với nhau y
tại gốc O của mỗi trục, khi đó ta có hệ trục tọa độ Oxy. 4
Các trục Ox, Oy gọi là các trục tọa độ. Ox gọi là trục hoành và
thường được vẽ nằm ngang, Oy gọi là trục tung và thường được vẽ 3 II I
thẳng đứng. Giao điểm O được gọi là gốc tọa độ. 2
Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.
Hai trục Ox, Oy chia mặt phẳng tọa độ thành bốn góc: góc phần 1 tư thứ I, II, III, IV . x
Các đơn vị dài trên hai trục tọa độ thường được chọn bằng nhau −4 −3 −2 −1O 1 2 3 4 −1 (nếu không nói gì thêm). −2 III IV −3 −4
1.2. Tọa độ của một điểm trên mặt phẳng tọa độ
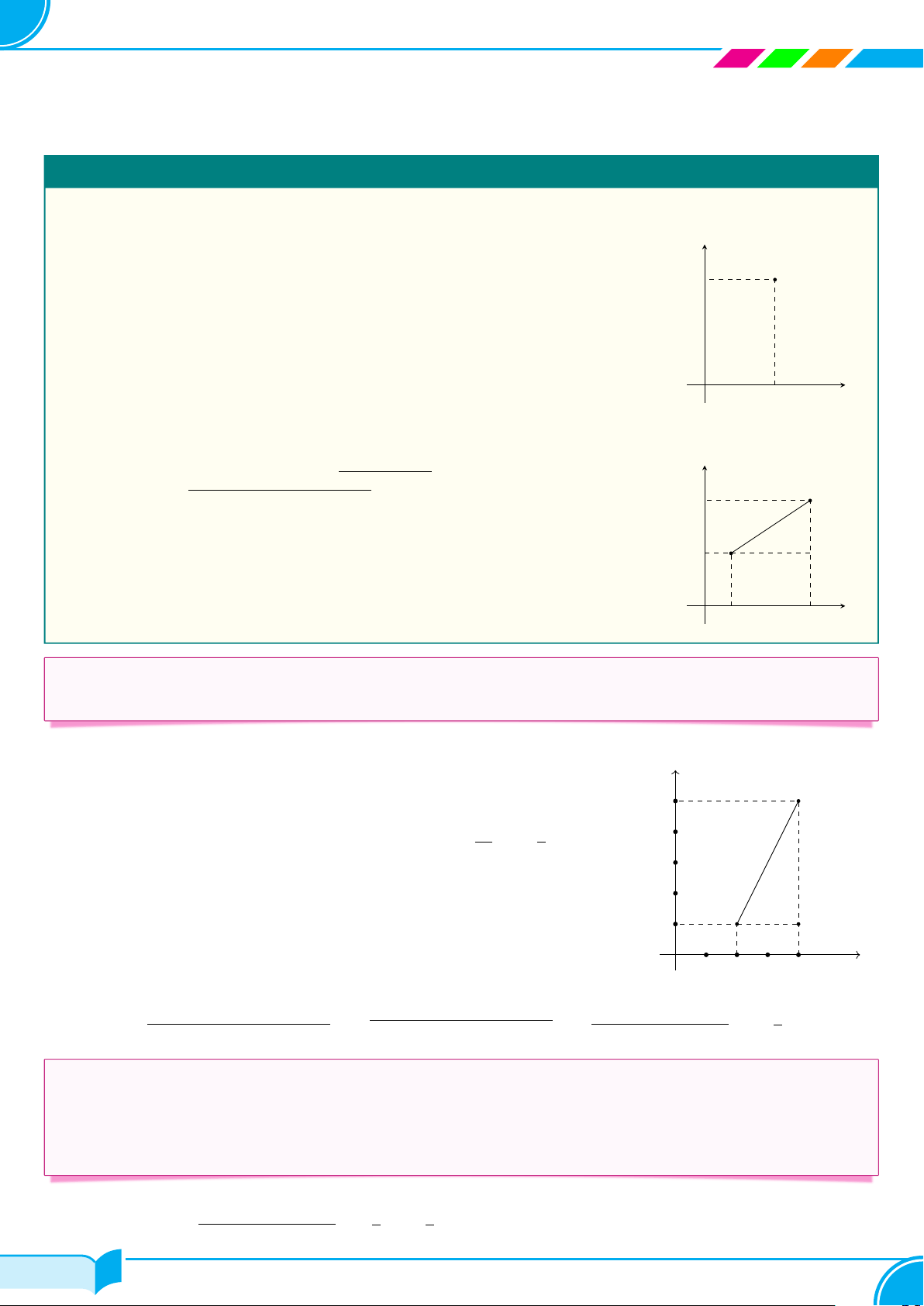
Ta xác định vị trí một điểm P trong mặt phẳng tọa độ Oxy bằng cách dùng hai số y thực như sau: P b
Từ P vẽ các đường vuông góc với các trục tọa độ cắt trục hoành tại điểm a và trục tung tại điểm b.
Khi đó cặp số (a; b) gọi là tọa độ của điểm P và kí hiệu là P (a; b). Số a gọi là hoành a x O
độ và số b gọi là tung độ của điểm P .
Gốc tọa độ O có tọa độ là (0; 0).
Trên mặt phẳng tọa độ, mỗi điểm P xác định đúng một cặp số (a; b).
2 Xác định một điểm trên mặt phẳng tọa độ khi biết tọa độ của nó
Để xác định một điểm P có tọa độ là (a; b), ta thực hiện các bước sau: y 3 P (a; b)
− Tìm trên trục hoành điểm a và vẽ đường thẳng vuông góc với trục b này tại điểm a. 2
− Tìm trên trục tung điểm b và vẽ đường thẳng vuông góc với trục này 1 tại điểm b. a x −3 −2 −1O 1 2 3
− Giao điểm của hai đường thẳng vừa vẽ cho ta điểm P cần tìm. −1 −2 −3 14/119 14/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 15
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Trên mặt phẳng tọa độ, mỗi cặp số (a; b) xác định một điểm P duy nhất.
3 Đồ thị của hàm số
Đồ thị của hàm số y = f (x) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm M (x; f (x)). A B CÁC DẠNG BÀI TẬP
Dạng 1. Đọc, biểu diễn toạ độ điểm trên mặt phẳng toạ độ
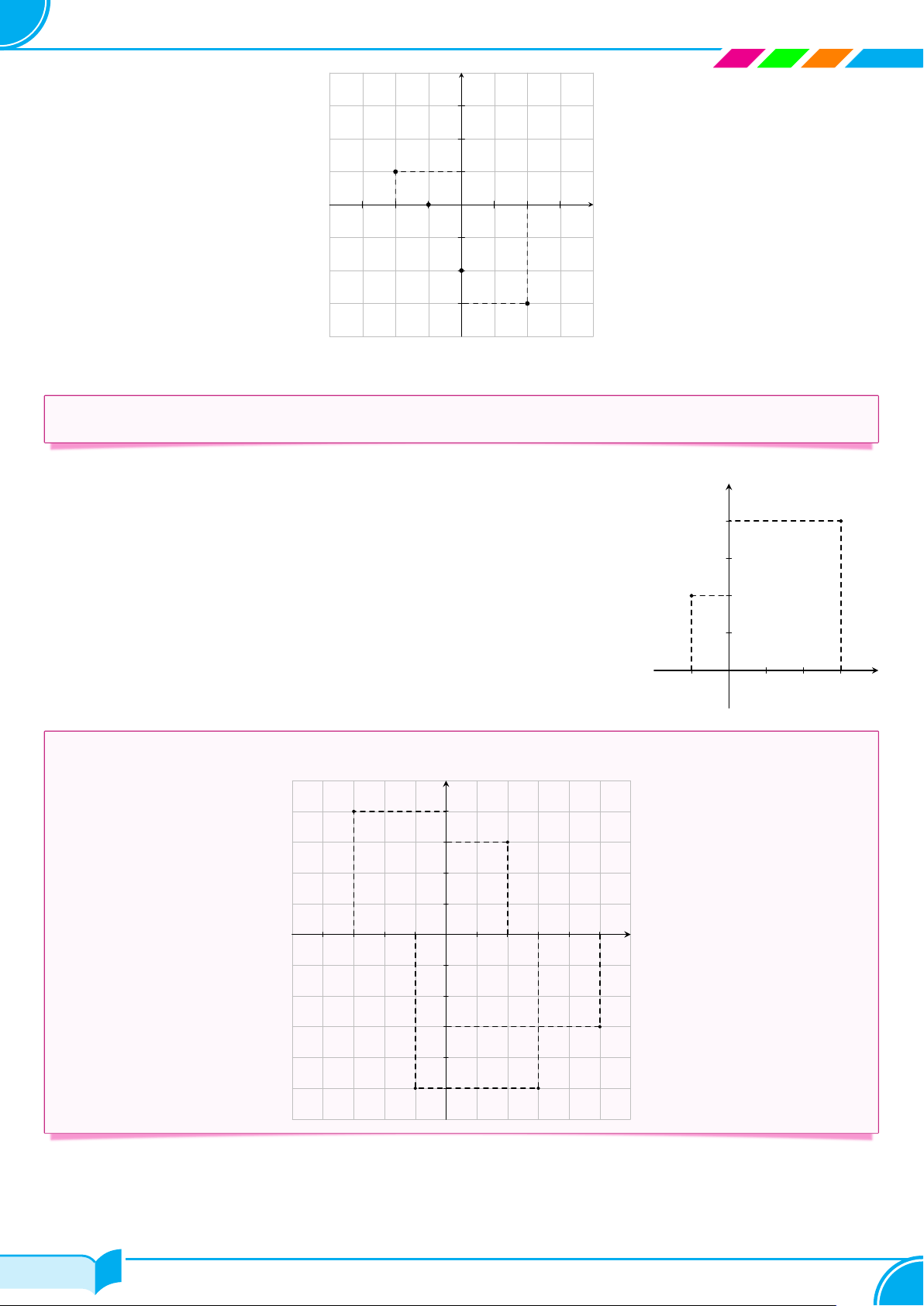
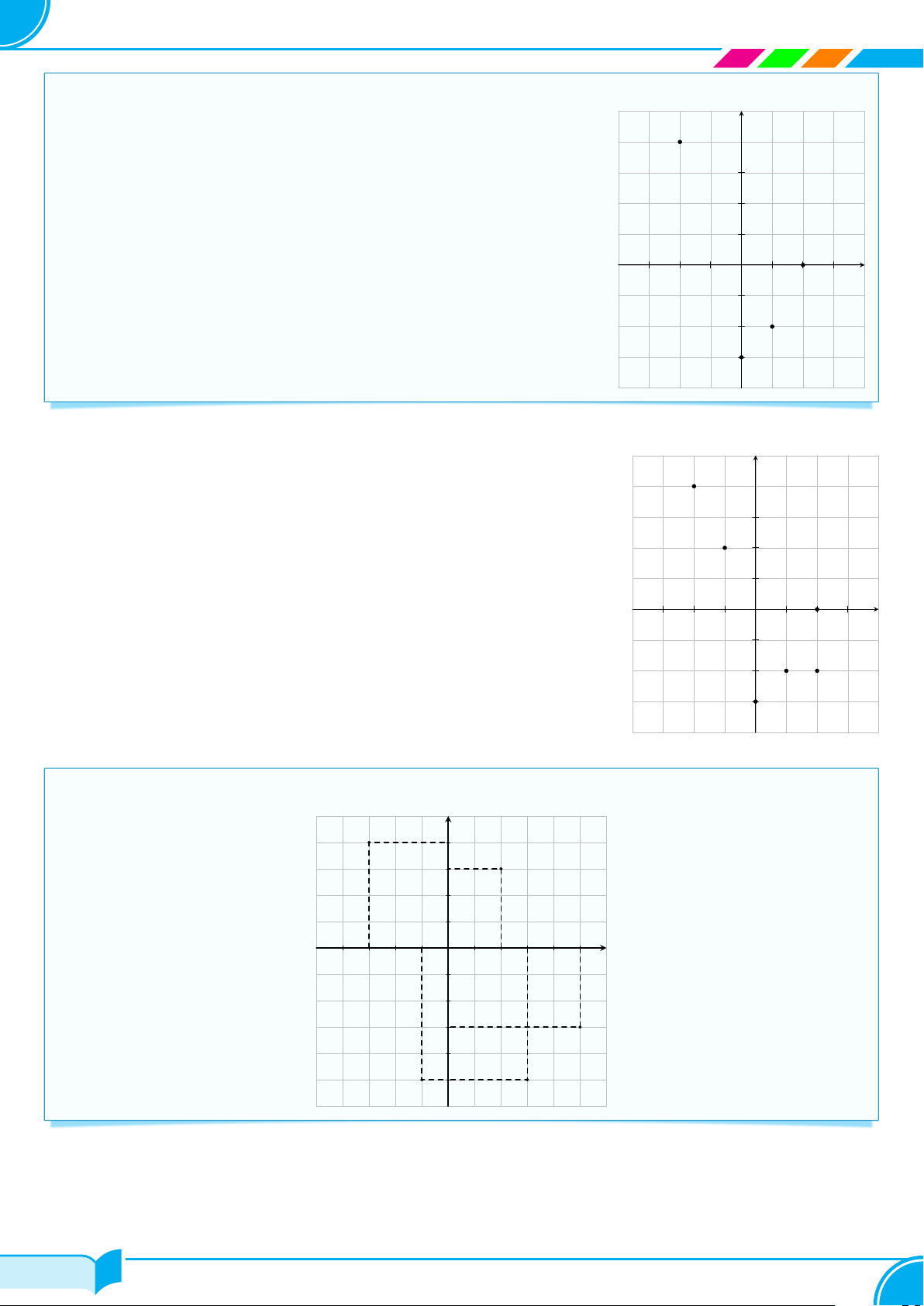
c Ví dụ 1. Cho mặt phẳng toạ độ Oxy như dưới đây. Xác định toạ độ các điểm D, E, F , G, O. y 3 2 E 1 G x −3 −2 −1 1 2 3 −1 −2 D −3 F Lời giải.
Toạ độ các điểm D, E, F , G, O lần lượt là: D(1; −2); E(−2; 1) ; F (0; −3) ; G(−3; 0) ; O(0; 0). □ c Ví dụ 2.
a) Viết toạ độ của các điểm A, B trong hình dưới.
b) Xác định các điểm C(0; −2) và D(−1; 0) trong hình dưới. y 1 B x −2 O 2 −3 A Lời giải.
a) Ta có tọa độ của hai điểm A, B là A(2; −3), B(−2; 1).
b) Các điểm C(0; −2), D(−1; 0) được xác định như hình. 15/119 15/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 16
2. KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO y B 1 D x −2 −1 O 2 −2 C −3 A □
c Ví dụ 3. Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm A(−1; 2) và B(3; 4). Lời giải.
Các điểm A(−1; 2) và B(3; 4) được xác định trên mặt phẳng tọa độ Oxy như y hình bên. B 4 3 A 2 1 x −1 O 1 2 3 □
c Ví dụ 4. Tìm tọa độ của các điểm A, B, C trong hình sau: y E 4 A 3 2 1 −1 3 5 x −4 −3 −2 O 1 2 4 −1 −2 −3 B −4 C −5 F Lời giải.
Qua A kẻ các đường thẳng vuông góc với hai trục tọa độ, các đường này cắt Ox tại điểm 2 và cắt Oy tại điểm 3.
Ta được tọa độ điểm A là (2; 3).
Tương tự, ta có B(5; −3) và C(−1; −5). □ 16/119 16/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 17
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Ví dụ 5. Tìm tọa độ vị trí A của con thuyền và B của hòn đảo trong hình sau: Bắc (km) y 8 A 7 B 6 5 Tây Đông 4 3 2 1 Vị trí gốc x −4 −3 −2 − O 1 1 2 3 4 (km) −1 Nam Lời giải. Bắc (km) y 8 A 7 B 6 5 Tây Đông 4 3 2 1 Vị trí gốc x −4 −3 −2 − O 1 1 2 3 4 (km) −1 Nam
Qua A kẻ các đường thẳng vuông góc với hai trục tọa độ, các đường này cắt Ox tại điểm 4 và cắt Oy tại điểm 8.
Ta được tọa độ điểm A là (4; 8).
Tương tự, ta có B(−3; 7). □
Dạng 2. Vẽ đồ thị hàm số cho bởi bảng giá trị
c Ví dụ 6. Vẽ đồ thị của hàm số y = f (x) cho bởi bảng sau 3 x −2 −1 3 2 7 y − −2 2 4 2 Lời giải. 17/119 17/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 18
2. KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Đồ thị của hàm số y = f (x) gồm bốn điểm như hình vẽ bên. y 4 2 −2 −1 x O 3 3 2 −2 7 − 2 □
c Ví dụ 7. Vẽ đồ thị của hàm số y = f (x) cho bởi bảng sau x −3 −1 1 2,5 y 4 3,5 1 0 Lời giải.
Đồ thị của hàm số y = f (x) gồm bốn điểm như hình bên. y 4 3,5 1 x −3 −1O 1 2,5 □
c Ví dụ 8. Lập bảng giá trị của hàm số có đồ thị như hình sau: y Q 16 14 P 12 10 N 8 6 M 4 2 x O 1 2 3 4 Lời giải.
Ta có bảng giá trị của hàm số đã cho như sau: x 1 2 3 4 y 4 8 12 16 □ 18/119 18/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 19
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Ví dụ 9. Vẽ đồ thị của hàm số y = f (x) cho bằng bảng sau: x −2 −1 0 1 2 y 2 1 0 −1 −2 Lời giải.
Đồ thị hàm số là tập hợp các điểm có tọa độ (−2; 2), (−1; 1), (0; 0), (1; −1), y
(2; −2) được vẽ trên mặt phẳng tọa độ như hình bên. 2 1 1 2 x −2 −1 O −1 −2 □ c Ví dụ 10.
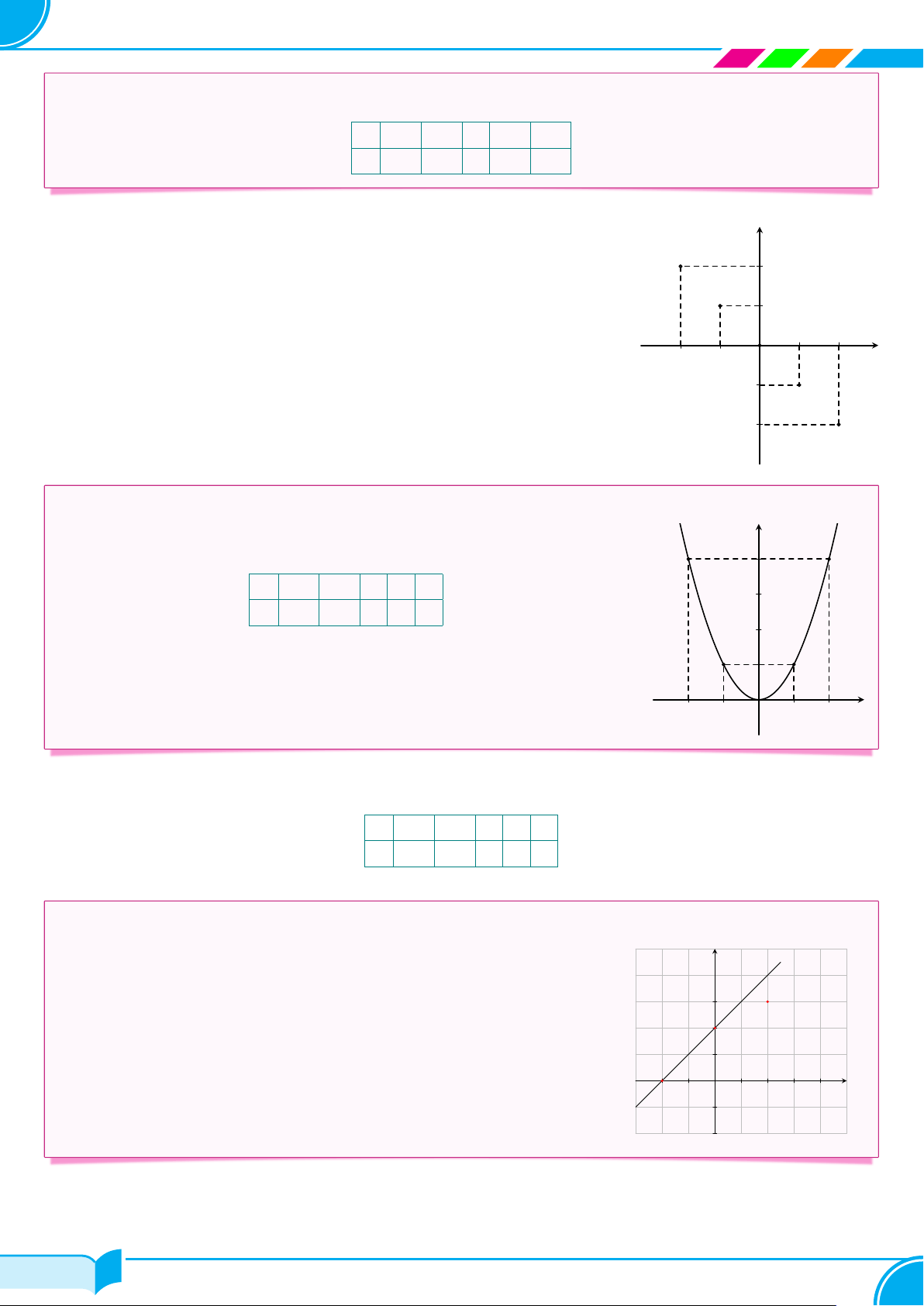
Cho hàm số y = f (x) có đồ thị như hình bên. Hãy hoàn thành bảng giá trị y của hàm số sau đây: 4 x −2 −1 0 1 2 3 y ? ? ? ? ? 2 1 x −2 −1 O 1 2 Lời giải.
Dựa vào đồ thị, ta có bảng giá trị của hàm số như sau: x −2 −1 0 1 2 y 4 1 0 1 4 □ c Ví dụ 11.
Trong mặt phẳng toạ độ Oxy, cho đồ thị của hàm số y = x + 2 (Hình bên). y y = x + 2
a) Quan sát đồ thị của hàm số và cho biết trong ba điểm: A(0; 2), C
B(−2; 0), C(2; 3), điểm nào thuộc đồ thị của hàm số, điểm nào không 3
thuộc đồ thị của hàm số. 2 A
b) Điểm D(2022; 2023) có thuộc đồ thị của hàm số hay không? Vì sao? 1 B x −2 −1 1 2 3 4 −1 −2 Lời giải.
a) Quan sát đồ thị của hàm số y = x + 2 , ta thấy hai điểm A(0; 2), B(−2; 0) thuộc đồ thị của hàm số, điểm
C(2; 3) không thuộc đồ thị của hàm số. 19/119 19/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 20
2. KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
b) Đối với hàm số y = x + 2, giá trị của y tương ứng vởi giá trị x = 2022 là y = 2022 + 2 = 2024 ̸= 2023. Vì
vậy, điểm D(2022; 2023) không thuộc đồ thị của hàm số. □
Dạng 3. * Xác định khoảng cách giữa hai điểm trên mặt phẳng tọa độ
○ Để biểu diễn điểm M (a; b) trên mặt phẳng tọa độ ta làm như sau:
— Kẻ đường thẳng vuông góc với trục Ox tại điểm a; y M (a; b)
— Kẻ đường thẳng vuông góc với trục Oy tại điểm b; b
— Hai đường thẳng cắt nhau tại một điểm đó là M . a x O
○ Để xác định khoảng cách giữa hai điểm A(xA; yB) và B(xB; yB), ta làm như sau:
Ta có AH = |xA − xB|; BH = |yA − yB|. √ y AB2 = AH2 + BH2 ⇒ AB = AH2 + BH2 » ⇒ AB = (x yB B B − xA)2 + (yB − yA)2 (*) y A A H x O A x
c Ví dụ 12. Biểu diễn hai điểm A(2; 1) và B(4; 5) trên cùng một mặt phẳng tọa độ. Tính khoảng cách giữa hai điểm đó. Lời giải.
Biểu diễn các điểm A, B như hình bên. y Trong △ABH ta có “
H = 90◦; AH = 4 − 2 = 2; BH = 5 − 1 = 4. 5 B
Áp dụng định lí Py - ta - go vào △ABH vuông tại H ta có √ √ 4
AB2 = AH2 + BH2 = 22 + 42 = 20 ⇒ AB = 20 = 2 5. 3 2 A 1 H x O 1 2 3 4 □
Sau này trong thực hành ta sẽ vận dụng ngay công thức (*) » √
Ta có p(yB − xA)2 + (yB − xA)2 =
(xB − xA)2 + (yB − yA)2 = p(4 − 2)2 + (5 − 1)2 = 2 5.
c Ví dụ 13. Cho tam giác ABC có A(1; 1); B(3; 3) và C(5; 1). a) Tính chu vi tam giác ABC;
b) Chứng minh rằng tam giác ABC vuông cân. Lời giải. √ √
a) Ta có AB = p(3 − 1)2 + (3 − 1)2 = 8 = 2 2; 20/119 20/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 21
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO √ √
AC = p(5 − 1)2 + (1 − 1)2 = 4; BC = p(5 − 3)2 + (1 − 3)2 = 4 + 4 = 2 2. √ √ √ Ä ä
Chu vi tam giác ABC là AB + BC + AC = 2 2 + 2 2 + 4 = 4 2 + 1 (đvđd). √
b) Ta có AB = BC = 2 2, suy ra △ABC cân tại B. (1) √
®AB2 = BC2 = (2 2)2 = 8 ⇒ AB2 + BC2 = AC2 AC2 = 42 = 16 ⇒ △ABC vuông tại B. (2)
Từ (1) và (2) suy ra △ABC vuông cân tại B. □
c Ví dụ 14. Cho các điểm A(2; 4), B(−1; 0) và C(0; 4).
a) Biểu diễn trên các điểm A, B, C trên mặt phẳng tọa độ.
b) Tính chu vi và diện tích của tam giác ABC. Lời giải. y
a) Biểu diễn các điểm A(2; 4), B(−1; 0) và C(0; 4) như hình bên.
b) Ta thấy A, B, C không thẳng hàng nên A, B, C là ba đỉnh của một tam giác. H 4 C A » Áp dụng công thức M N =
(xN − xM )2 + (yN − yM )2, ta tính được √ AB = 5; AC = 2; BC = 17. √ √
Chu vi tam giác ABC là 5 + 2 + 17 = 7 + 17 (đvđd). Diện tích tam giác ABC là B 1 1 −1 2 x O SABC =
· BH · CA = , 4.2 = 4 (đvdt). 2 2 □
c Ví dụ 15. Cho hai điểm A(2; 4) và B(−1; 0) trên hệ trục tọa độ Oxy.
a) Biểu diễn các điểm A, B trên mặt phẳng tọa độ.
b) Tìm các điểm C trên trục hoành sao cho △ABC cân tại A. Lời giải. y
a) Biểu diễn các điểm A(2; 4), B(−1; 0) như hình bên. A 4
b) Vì C nằm trên trục hoành nên tung độ của điểm C bằng 0, do đó C(x; 0) với x ̸= −1. Áp dụng công thức » M N =
(xN − xM )2 + (yN − yM )2, ta tính được
AB = 5; AC = p(x − 2)2 + (0 − 4)2. B H C −1 2 x x O » Ta có △ABC cân tại A ⇔ (x − 2)2 + (0 − 4)2 = 5 ⇔ (x − 2)2 + 16 = 25 ⇔ (x − 2)2 = 9
⇔ x = 5 hoặc x = −1 (loại). 21/119 21/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 22
2. KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Vậy C(5; 0) thì △ABC cân tại A.
a) Ta có thể giải cách khác như sau
△ABC cân tại A ⇔ HB = HC ⇔ HC = 3 (vì HB = 3) ⇔ x − 2 = 3 ⇔ x = 5.
Do đó, nếu kết hợp với kiến thức hình học thì chúng ta có thể giải bài toán đơn giản hơn, nhanh hơn.
b) Ta có thể thay đổi yêu cầu bài toán thành “Tìm điểm C trên trục hoành sao △ABC cân”. Với yêu cầu
mới ta phải giải bài toán trong ba trường hợp
○ Trường hợp 1: △ABC cân tại A.
○ Trường hợp 2: △ABC cân tại B.
○ Trường hợp 3: △ABC cân tại C. □
Dạng 4. * Điểm thuộc đồ thị, điểm không thuộc đồ thị của hàm số
Cho hàm y = f (x) có miền xác định D và có đổ thị G, Khi đó ®x0 ∈ D
○ M (x0; y0) thuộc đổ thị G khi và chỉ khi . y0 = f (x0)
○ M (x0; y0) không thuộc đồ thị G khi và chỉ khi y0 ̸= f(x0) hoặc x0 / ∈ D. √
c Ví dụ 16. Cho hàm số y = f (x) =
x. Trong các điểm A(9; 3), B(4; −2), M (−1; 1) điểm nào thuộc đồ thị (G) của hàm số cho? Lời giải. Ta có M /
∈ (G) vì khi x = −1 thì hàm số không xác định, √ B(4; −2) / ∈ (G) vì 4 = 2 ̸= −2, √ A(9; 3) ∈ (G) vì f (9) = 9 = 3, □
c Ví dụ 17. Điểm M (−1; −1) thuộc đồ thị của hàm số nào trong các hàm số dưới dây? A y = x2. B y = x4. C y = 3x + 2. D y = −x3. Lời giải.
Loại (A), (B) vì tung độ của M âm.
Loại (D) vì hoành độ và tung độ của M cùng dấu. Chọn đáp án C □
c Ví dụ 18. Cho hàm số y = f (x) = (m + 1)x − 2m.
a) Tìm m để đồ thị của hàm số đã cho đi qua điểm A(1; 1).
b) Chứng minh rằng đồ thị của hàm số đã cho luôn đi qua một điểm cố định với mọi m. Lời giải.
a) A(1; 1) ∈ d : y = (m + 1)x − 2m ⇔ 1 = (m + 1) · 1 − 2m ⇔ m = 0.
b) M (x0; y0) ∈ d : y = (m + 1)x − 2m ⇔ y0 = (m + 1)x0 − 2m ⇔ m (x0 − 2) + (x0 − y0) = 0. (1) 22/119 22/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 23
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
d đi qua M với mọi m khi (1) đúng với mọi m, tức là ®x ® 0 − 2 = 0 x0 = 2 ⇔ x0 − y0 = 0 y0 = 2.
Vậy d luôn đi qua điểm M (2; 2) cố định với mọi m. □
c Ví dụ 19. Khi m thay đổi, tìm tập hợp các điểm M có tọa độ như sau a) M (m; 3); b) M (2; m). Lời giải. a)
Ta có f (m) = 3. Khi m thay đổi f (m) luôn nhận một giá trị không đổi. y
Hàm số y = f (m) = 3 là một hàm hằng.
Đồ thị của một hàm số y = 3 là đường thẳng song song với trục hoành và cắt y = 3 M
trục tung tại điểm có tung độ bằng 3. 3
Tập hợp các điểm M (m; 3) là đường thẳng song song với trục hoành và cắt
trục tung tại điểm có tung độ bằng 3. m x O b)
Tập hợp các điểm M (2; m) là đường thẳng song song với trục tung và cắt trục y
hoành tại điểm có hành độ bằng 2. x = 2 2 M (2; m) x O □ A C BÀI TẬP VẬN DỤNG
c Bài 1. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Điểm thuộc trục hoành có tung độ bằng 0.
b) Điểm thuộc trục hoành có hoành độ bằng 0.
c) Điểm thuộc trục tung có tung độ bằng 0.
d) Điểm thuộc trục tung có hoành độ bằng 0. Lời giải. Phát biểu đúng: a, d Phát biểu sai: b, c. □
c Bài 2. Điểm M (a; b) thuộc góc phần tư nào trong mỗi trường hợp sau? a) a > 0, b > 0. b) a > 0, b < 0. c) a < 0, b > 0. d) a < 0, b < 0. 23/119 23/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 24
2. KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Lời giải. a) Góc phần tư thứ I. b) Góc phần tư thứ IV. c) Góc phần tư thứ II. d) Góc phần tư thứ III. □
c Bài 3. Xác định toạ độ điểm A trong mỗi trường hợp sau:
a) Hoành độ bằng −3 và tung độ bằng 5;
b) Hoành độ bằng −2 và nằm trên trục hoành;
c) Tung độ bằng −4 và nằm trên trục tung. Lời giải.
Tọa độ điểm A lần lượt là a) A (−3; 5); b) A (−2; 0); c) A (0; −4). □
c Bài 4. Trong mặt phẳng toạ độ Oxy, nêu cách xác định điểm A(−3; −5). Lời giải.
Qua điểm −3 trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.
Qua điểm −5 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.
Hai đường thẳng trên cắt nhau tại điểm A(−3; −5). □
c Bài 5. Vẽ một hệ trục toạ độ Oxy và đánh dấu các điểm A(−2; 0), B(3; 0) và C(4; 0).
a) Em có nhận xét gì về các điểm A, B và C?
b) Em hãy cho biết một điểm bất kì trên trục hoành có tung độ bằng bao nhiêu? Lời giải. y 1 A B C x −2 O 1 2 3 4 −1
a) Các điểm A, B và C đều có tung độ bằng 0.
b) Một điểm bất kì trên trục hoành có tung độ bằng 0. □
c Bài 6. Vẽ một hệ trục toạ độ Oxy và đánh dấu các điểm M (0; −2), N (0; 1) và P (0; 4).
a) Em có nhận xét gì về các điểm M , N và P ?
b) Em hãy cho biết một điểm bất kì trên trục tung có tung độ bằng bao nhiêu? Lời giải. 24/119 24/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 25
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
a) Các điểm M , N và P đều có hoành độ bằng 0.
b) Một điểm bất kì trên trục tung có hoành độ bằng 0. y 4 P 3 2 1 N x −1O 1 −2 M □
c Bài 7. Vẽ một hệ trục tọa độ Oxy và đánh đấu các điểm A(−3; 3), B(3; 3), C(3; −3) và D(−3; −3). Nêu
nhận xét về các cạnh và các góc của tứ giác ABCD. Lời giải. y A 3 B 2 1 O x −3 −2 −1 1 2 3 −1 −2 −3 D C
Tứ giác ABCD trong hình trên có AB = BC = CD = AD và b A = “ B = “ C = “ D = 90◦. □
c Bài 8. Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm C(3; 0), D(0; −2) và E(−3; −4). Lời giải.
Các điểm C(3; 0), D(0; −2) và E(−3; −4) được xác định trên mặt phẳng y
tọa độ Oxy như hình bên. −3 O C x −2 −1 1 2 3 −1 −2 D −3 E −4 □ 25/119 25/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 26
2. KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO c Bài 9. y M
a) Xác định tọa độ của các điểm M , N , P , Q trong hình bên. 3
b) Xác định các điểm R(2; −2) và S(−1; 2) trong hình bên. 2 1 O P x −3 −2 −1 1 2 3 −1 −2 N −3 Q Lời giải. y M
a) Tọa độ của các điểm M , N , P , Q là M (−2; 4), N (1; −2), P (2; 0), Q(0; −3). 3
b) Các điểm R(2; −2) và S(−1; 2) được xác định như hình bên. S 2 1 O P x −3 −2 −1 1 2 3 −1 −2 R N −3 Q □
c Bài 10. Tìm tọa độ của các điểm O, E, F trong hình sau: y E 4 A 3 2 1 −1 3 5 x −4 −3 −2 O 1 2 4 −1 −2 −3 B −4 C −5 F Lời giải.
Qua O kẻ các đường thẳng vuông góc với hai trục tọa độ, các đường này cắt Ox tại điểm 0 và cắt Oy tại điểm 0.
Ta được tọa độ điểm O là (0; 0).
Tương tự, ta có E(−3; 4) và F (3; −5). □ 26/119 26/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 27
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO c Bài 11. y A
a) Xác định toạ độ của các điểm A; B; C; D trong hình.
b) Xác định các điểm E(0; −2) và F (2; −1) trong hình. D x O B C Lời giải. y A
a) Ta có tọa độ của các điểm A, B, C, D là A(−3; 4), B(−2; −2), C(1; −3), D(3; 0).
b) Các điểm E, F được xác định như bình bên. D x O F E B C □
c Bài 12. Hàm số y = f (x) được cho bởi bảng sau x −2 −1 0 1 2 y = f (x) −5 −2,5 0 2,5 5
Vẽ đồ thị của hàm số y = f (x). Lời giải.
Đồ thị của hàm số y = f (x) gồm năm điểm như hình bên. y 5 2,5 −2 −1 x O 1 2 −2,5 −2 27/119 27/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 28
2. KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO □
c Bài 13. Cân nặng và tuổi của bốn bạn An, Bình, Hưng, Việt được biểu diễn trên mặt phẳng tọa độ như hình sau. y Cân nặng (kg) Hưng 50 Bình 45 Việt 40 An 35 30 25 20 15 10 5 Tuổi x O 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
(Do số liệu về tuổi và cân nặng rất chênh lệch nên trong Hình 7.9 , ta đã lấy một đơn vị dài trên trục tung
bằng 5 lần đơn vị dài trên trục hoành). Hãy cho biết:
a) Ai là người nặng nhất và nặng bao nhiêu?
b) Ai là người ít tuổi nhất và bao nhiêu tuổi?
c) Bình và Việt ai nặng hơn và ai nhiểu tuổi hơn?
d) Thay dấu “?” bằng số thích hợp để hoàn thành bảng sau vào vở: Tên An Bình Hưng Việt Tuổi ? ? ? ? Cân nặng (kg) ? ? ? ?
Theo bảng đã hoàn thành, cân nặng có phải là hàm số của tuổi không? Vì sao? Lời giải.
a) Hưng là người nặng nhất và nặng 50 kg.
b) An là người ít tuổi nhất và tuổi của An là 11.
c) Bình nặng hơn Việt và Bình ít tuổi hơn Việt. d) Tên An Bình Hưng Việt Tuổi 11 13 14 14 Cân nặng (kg) 35 45 50 40 28/119 28/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 29
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Theo bảng đã hoàn thành, cân nặng không là hàm số của tuổi (vì với tuổi là 14 thì ta có 2 giá trị cân nặng là 40 kg và 50kg). □
c Bài 14. Hình sau là đồ thị của hàm số mô tả nhiệt độ T (◦C) tại các thời điểm t (giờ) của một thành phố
ở châu Âu từ giữa trưa đến 6 giờ tối.
a) Tìm T (1), T (2), T (5) và giải thích ý nghĩa của các số này.
b) Trong hai giá trị T (1) và T (4), giá trị nào lớn hơn? c) Tìm t sao cho T (t) = 5.
d) Trong khoảng thời gian nào thì nhiệt độ cao hơn 5◦C ? y T (◦C) 8 7 6 5 4 3 2 1 (giờ) x O 1 2 3 4 5 6 Lời giải.
a) Ta có T (1) = 6, T (2) = 8, T (5) = 4. Nghĩa là nhiệt độ vào lúc 1 giờ, 2 giờ, 5 giờ ở thành phố đó lần lượt là 6◦C, 8◦C, 4◦C
b) Ta có T (1) = 6 và T (4) = 5 nên T (1) < T (4).
c) Dựa vào đồ thị, ta có T (t) = 5 khi t = 0 hoặc t = 4.
d) Dựa vào đồ thị, trong khoảng thời gian từ sau 12 giờ trưa đến trước 4 giờ chiều thì nhiệt độ ở thành phố đó cao hơn 5◦C. □
c Bài 15. Vẽ một hệ trục toạ độ Oxy và đánh dấu các điểm A(−2; 0), B(3; 0) và C(4; 0).
a) Em có nhận xét gì về các điểm A, B và C?
b) Em hãy cho biết một điểm bất kì trên trục hoành có tung độ bằng bao nhiêu? 29/119 29/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 30
2. KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Lời giải. y 1 A B C x −2 O 1 2 3 4 −1
a) Các điểm A, B và C đều có tung độ bằng 0.
b) Một điểm bất kì trên trục hoành có tung độ bằng 0. □
c Bài 16. Vẽ một hệ trục toạ độ Oxy và đánh dấu các điểm M (0; −2), N (0; 1) và P (0; 4).
a) Em có nhận xét gì về các điểm M , N và P ?
b) Em hãy cho biết một điểm bất kì trên trục tung có tung độ bằng bao nhiêu? Lời giải. y 4 P 3 2 1 N x −1 O 1 −2 M
a) Các điểm M , N và P đều có hoành độ bằng 0.
b) Một điểm bất kì trên trục tung có hoành độ bằng 0. □
c Bài 17. Vẽ một hệ trục tọa độ Oxy và đánh đấu các điểm A(−3; 3), B(3; 3), C(3; −3) và D(−3; −3). Nêu
nhận xét về các cạnh và các góc của tứ giác ABCD. Lời giải. 30/119 30/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 31
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO y A 3 B 2 1 x −3 −2 −1 O 1 2 3 −1 −2 −3 D C
Tứ giác ABCD trong hình trên có AB = BC = CD = AD và b A = “ B = “ C = “ D = 90◦. □
c Bài 18. Vẽ đồ thị hàm số được cho bởi bảng sau: x −3 −1 0 1 2 y −6 −2 0 2 4 Lời giải.
Đồ thị hàm số là tập hợp các điểm có tọa độ (−3; −6), (−1; −2), y
(0; 0), (1; 2), (2; 4) được vẽ trên mặt phẳng tọa độ như hình bên. 4 3 2 1 −3 −1 x −2 O 1 2 3 −1 −2 −3 −4 −5 −6 □
c Bài 19. Trong những điểm sau, tìm điểm thuộc đồ thị của hàm số y = 4x: M (−1; −4); N (1; −4) và Å 1 ã P ; 1 . 4 Lời giải.
Thay tọa độ điểm M vào hàm số y = 4x, ta được −4 = 4 · (−1): đúng
Suy ra điểm M thuộc đồ thị của hàm số y = 4x. 31/119 31/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 32
2. KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Thay tọa độ điểm N vào hàm số y = 4x, ta được −4 = 4 · 1: sai
Suy ra điểm N không thuộc đồ thị của hàm số y = 4x. 1
Thay tọa độ điểm P vào hàm số y = 4x, ta được 1 = 4 · : đúng 4
Suy ra điểm P thuộc đồ thị của hàm số y = 4x. □
c Bài 20. Cho y là hàm số của biến số x. Giá trị tương ứng của x, y được cho trong bảng sau: x −2 −1 0 1 2 y −6 −3 0 3 6
a) Vẽ hệ trục tọa độ Oxy và xác định các điểm biểu diễn các cặp giá trị (x; y) tương ứng có trong bảng trên.
b) Em có nhận xét gì về các điểm vừa xác định trong câu a? Lời giải. a) y 6 5 4 3 2 1 −2 −1 x O 1 2 −1 −2 −3 −4 −5 −6
b) Các điểm vừa xác định trong câu a) là các điểm thẳng hàng. □ c Bài 21. 32/119 32/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 33
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Cho tam giác ABC như bên. y
a) Xác định toạ độ các điểm A, B, C. A 3
b) Tam giác ABC có là tam giác vuông hay không? 2
c) Xác định toạ độ điểm D để tứ giác ABCD là hình chữ nhật. 1 B C x −2 −1 1 2 3 4 −1 Lời giải.
a) Ta có A(−2; 3), B(−2; 0), C(2; 0).
b) Tam giác ABC là tam giác vuông.
c) Tọa độ điểm D (2; 3) thì ABCD là hình chữ nhật. □ c Bài 22.
Nhập địa điểm “chợ Bến Thành ”trên trang https://google.com/maps, sau đó
nháy chuột phải vào địa điểm đó trên bản đồ ta được thông tin về kinh độ, vĩ
độ như hình bên. Hãy viết toạ độ địa lí của chợ Bến Thành thuộc Thành phố Hồ Chí Minh. Lời giải.
Tọa độ địa lí TPHCM là (10.77258; 106.69804). □
c Bài 23. Nhiệt độ dự báo tại một số thời điểm trong ngày 25/5/2022 ở Thành phố Hồ Chí Minh được cho bởi hình dưới đây.
a) Viết hàm số dạng bảng biểu thị nhiệt độ dự báo y (◦C) tại thời điểm x (h) ở Thành phố Hồ Chí Minh.
b) Trong mặt phẳng toạ độ Oxy, biểu diễn các điểm có toạ độ là các cặp số (x; y) tương ứng ở bảng trên.
c) Trong mặt phẳng toạ độ Oxy, điểm M (15; 24) có thuộc đồ thị của hàm số cho bởi bảng trên hay không? Vì sao? 13:00 14:00 15:00 16:00 33◦ 28◦ 28◦ 28◦ Lời giải. a) x(h) 13 14 15 16 y (◦C) 33 28 28 28 33/119 33/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 34
2. KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO b) y◦C A 33 B C D 28 x(h) O 13 14 15 16
c) Điểm M (15; 24) không thuộc đồ thị cho bởi bảng trên. Vì theo đồ thị trong bảng trên thì điểm B có hoành
độ 15 thì tung độ của nó là 28. □ c Bài 24.
Số quyển vở x đã mua và số tiền y (nghìn đồng) phải trả của ba bạn Hùng, Dũng, y
Mạnh được biểu diễn lần lượt bởi ba điểm H, D, M trong mặt phẳng tọa độ Oxy như D hình bên. 12
a) Tìm tọa độ của các điểm H, D và M . 10 H
b) Hỏi ai mua nhiều quyển vở nhất? 8 M 6 4 2 x O 1 2 3 4 Lời giải.
a) Ta có H(3; 9), D(4; 12) và M (2; 6).
b) Vì điểm H có hoành độ bằng 3, điểm D có hoành độ bằng 4 và điểm M có hoành độ bằng 2 nên bạn Dũng
mua nhiều quyển vở nhất. □
c Bài 25. Mai trông coi một cửa hàng bán kem, em nhận thấy có mối quan hệ giữa số que kem S bán ra
mỗi ngày và nhiệt độ cao nhất t (◦C) của ngày hôm đó. Mai đã ghi lại các giá trị tương ứng của t và S trong bảng sau: t 18 20 21 25 28 30 S 36 40 42 50 56 60
Vẽ đồ thị của hàm số S theo biến số t. Lời giải. 34/119 34/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 35
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Đồ thị hàm số là tập hợp các điểm có tọa độ (18; 36), (20; 40), S
(21; 42), (25; 50), (28; 56) và (30; 60) được vẽ trên mặt phẳng tọa độ như hình bên. 60 56 50 42 40 36 20 O 18 21 25 2830 t □
c Bài 26. Cho các điểm A(2; 3), B(−2; 0) và C(4; 3).
a) Biểu diễn các điểm A, B, C trên mặt phẳng tọa độ.
b) Tính chu vi và diện tích của tam giác ABC.
c) Tìm điểm M trên trục hoành sao cho tam giác ABM cân tại A.
d) Tìm điểm N trên trục tung sao cho tam giác ABN cân tại B. Lời giải. a)
Biểu diễn các điểm A(2; 3), B(−2; 0), C(4; 3) như hình vẽ. y
b) Ta thấy A, B, C không thẳng hàng nên ba đỉnh này tạo thành 3 A C H một tam giác. » Áp dụng công thức M N = (xN − xM )2 + (yN − yM )2 √
ta tính được AB = 5; AC = 2; BC = 3 5. √ √
Chu vi tam giác ABC là 5 + 2 + 3 5 = 7 + 3 5. B −2 2 4 x O c) M (6; 0). √ √ Ä ä Ä ä d) N 0; 21 hoặc N 0; − 21 . □ 35/119 35/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 36
2. KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 27. Cho hàm số y = f (x) = −mx + 4.
a) Tìm m để đồ thị của hàm số đã cho đi qua điểm A(−1; −1).
b) Chứng minh rằng đồ thị của hàm số đã cho luôn đi qua một điểm cố định với mọi m Lời giải.
a) A(−1; −1) ∈ d : y = −mx + 4 ⇔ −1 = −m(−1) + 4 ⇔ m = −5.
b) Cho x = 0 suy ra y = 4. Ta tìm được điểm M (0; 4) là điểm cố định mà d luôn đi qua. □ 36/119 36/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 37
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Baâi 3
HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0) A
TRỌNG TÂM KIẾN THỨC
1 Hàm số bậc nhất, bảng giá trị
Hàm số bậc nhất là hàm số cho bởi công thức y = ax + b, trong đó a, b là các số cho trước và a ̸= 0.
Để lập bảng giá trị của hàm số bậc nhất y = ax + b ta lần lượt cho x nhận các giá trị x1, x2, x3, . . . (x1, x2, x3, . . .
tăng dần) và tính các giá trị tương ứng của y rồi ghi vào bảng có dạng sau: x x1 x2 x3 . . . y = ax + b y1 y2 y3 . . .
2 Đồ thị của hàm số bậc nhất
Đồ thị của hàm số y = ax + b (a ̸= 0) là một đường thẳng.
Đồ thị của hàm số y = ax + b (a ̸= 0) còn được gọi là đường thẳng y = ax + b.
Cách vẽ đồ thị của hàm số bậc nhất
Ta đã biết đồ thị của hàm số bậc nhất y = ax + b (a ̸= 0) là một đường thẳng. Do y
đó , để vẽ đồ thị này, ta chỉ cần xác định được hai điểm phân biệt nào đó thuộc
đồ thị rồi vẽ đường thẳng đi qua hai điểm đó. Ta xét hai trường hợp: ○ a
Khi b = 0 thì y = ax. Đồ thị của hàm số y = ax là đường thẳng đi qua gốc A
tọa độ O(0; 0) và điểm A(1; a) như hình bên. x O 1
○ Khi b ̸= 0 ta thường xác định hai điểm đặc biệt trên đồ thị là y
giao của đồ thị với hai trục tọa độ như sau y = ax + b
— Cho x = 0 thì y = b, ta được điểm P (0; b) thuộc trục tung Oy. b Å b ã P b
— Cho y = 0 thì x = − , ta được điểm Q − ; 0 thuộc trục Q a a x hoành Ox. b O − a
— Vẽ đường thẳng đi qua hai điểm P , Q ta được đồ thị của
hàm số y = ax + b như hình bên. A B CÁC DẠNG BÀI TẬP
Dạng 1. Hàm số bậc nhất, giá trị của hàm số bậc nhất
Hàm số bậc nhất làm hàm số có dạng y = ax + b, trong đó a và b là các số cho trước và a ̸= 0. 37/119 37/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 38
3. HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0)
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Ví dụ 1. Tìm các hàm số bậc nhất trong các hàm số sau đây và chỉ ra các hệ số a, b của các hàm số đó: √ √
y = 2x + 5; y = −7x; s = 2v + 8; P = 9,8m + 2,3; y = 2x + 3; y = 2x2 + 9. Lời giải.
Các hàm số sau là hàm số bậc nhất:
○ y = 2x + 5 với a = 2 và b = 5.
○ y = −7x với a = −7 và b = 0.
○ s = 2v + 8 với a = 2 và b = 8.
○ P = 9,8m + 2,3 với a = 9,8 và b = 2,3. √ √ √ √ ○ y = 2x + 3 với a = 2 và b = 3. □
c Ví dụ 2. Trong các hàm số sau, hàm số nào là hàm số bậc nhất a) y = 1 − 3x; b) y = 2x2 + x − 5; √ √ Ä ä Ä ä2 c) y = x2 + x 2 − x + 3; d) y = 3 − 1 x + 1. Lời giải.
a) Hàm số y = 1 − 3x hay y = −3x + 1 có dạng y = ax + b, trong đó a = −3 ̸= 0, nên y = −3x + 1 là hàm số bậc nhất.
b) Hàm số y = 2x2 + x − 5 không phải là hàm số bậc nhất vì sau khi rút gọn không có dạng y = ax + b. √ √ √ Ä ä c) Hàm số y = x2 + x 2 − x + 3 = x2 + 2x − x2 + 3 =
2x + 3 là hàm số bậc nhất vì hàm số có dạng √ y = ax + b, trong đó a = 2 ̸= 0. √ √ Ä ä2 Ä ä2 d) Hàm số y = 3 − 1
x + 1 là hàm số bậc nhất vì hàm số có dạng y = ax + b, trong đó a = 3 − 1 ̸= 0. □
c Ví dụ 3. Trong các hàm số sau, những hàm số nào là hàm số bậc nhất? a) y = 3x − 2; b) y = −2x; c) y = 2x2 + 3; d) y = 3(x − 1); e) y = 0x + 1. Lời giải.
Hàm số bậc nhất là y = 3x − 2; y = −2x; y = 3(x − 1). □
c Ví dụ 4. Cho hàm số bậc nhất y = −2x + 5.
a) Hoàn thành bảng giá trị sau x −2 −1 0 1 2 y = −2x + 5 ? ? ? ? ? b) Tìm x sao cho y = 12. Lời giải.
a) Ta có bảng giá trị sau 38/119 38/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 39
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO x −2 −1 0 1 2 y = −2x + 5 9 7 5 3 1 7
b) Ta phải tìm x sao cho y = 12, tức là −2x + 5 = 12 hay −2x = 7, suy ra x = − . 2 □
c Ví dụ 5. Lập bảng giá trị của các hàm số bậc nhất y = f (x) = 5x + 3 và y = g(x) = −2x + 3 với x lần
lượt bằng −2; −1; 0; 1; 2. Lời giải.
Bảng giá trị của hàm số y = f (x) = 5x + 3 là x −2 −1 0 1 2 y = f (x) = 5x + 3 −7 −2 3 8 13
Bảng giá trị của hàm số y = g(x) = −2x + 3 là x −2 −1 0 1 2 y = g(x) = −2x + 3 7 5 3 1 −1 □
c Ví dụ 6. Cho hàm số y = f (x) = (1 − 2m)x + m2 + 2. Tìm m để hàm số đã cho là hàm số bậc nhất. Lời giải. 1
Hàm số y = f (x) = (1 − 2m)x + m2 + 2 là hàm số khi và chỉ khi 1 − 2m ̸= 0 ⇔ m ̸= . □ 2
c Ví dụ 7. Cho hàm số y = f (x) = m2 − m x2 + mx + 2. Tìm m để hàm số đã cho là hàm số bậc nhất. Lời giải.
Hàm số y = f (x) = m2 − m x2 + mx + 2 là hàm số bậc nhất khi và chỉ khi ®m2 − m = 0 ®m(m − 1) = 0 ⇔ ⇔ m − 1 = 0 ⇔ m = 1. m ̸= 0 m ̸= 0
Khi m = 1 ta có hàm số y = x + 2 là hàm số bậc nhất. □
Dạng 2. Vẽ đồ thị hàm số bậc nhất
Tìm hai điểm thuộc đồ thị hàm số bằng cách cho x nhận hai giá trị xác định rồi tính hai giá trị tương ứng
của y (thông thường ta lấy hai điểm đó là giao điểm của đồ thị với trục hoành và trục tung). Đường thẳng đi
qua hai điểm vừa tìm được là đồ thị hàm số cần vẽ. c Ví dụ 8.
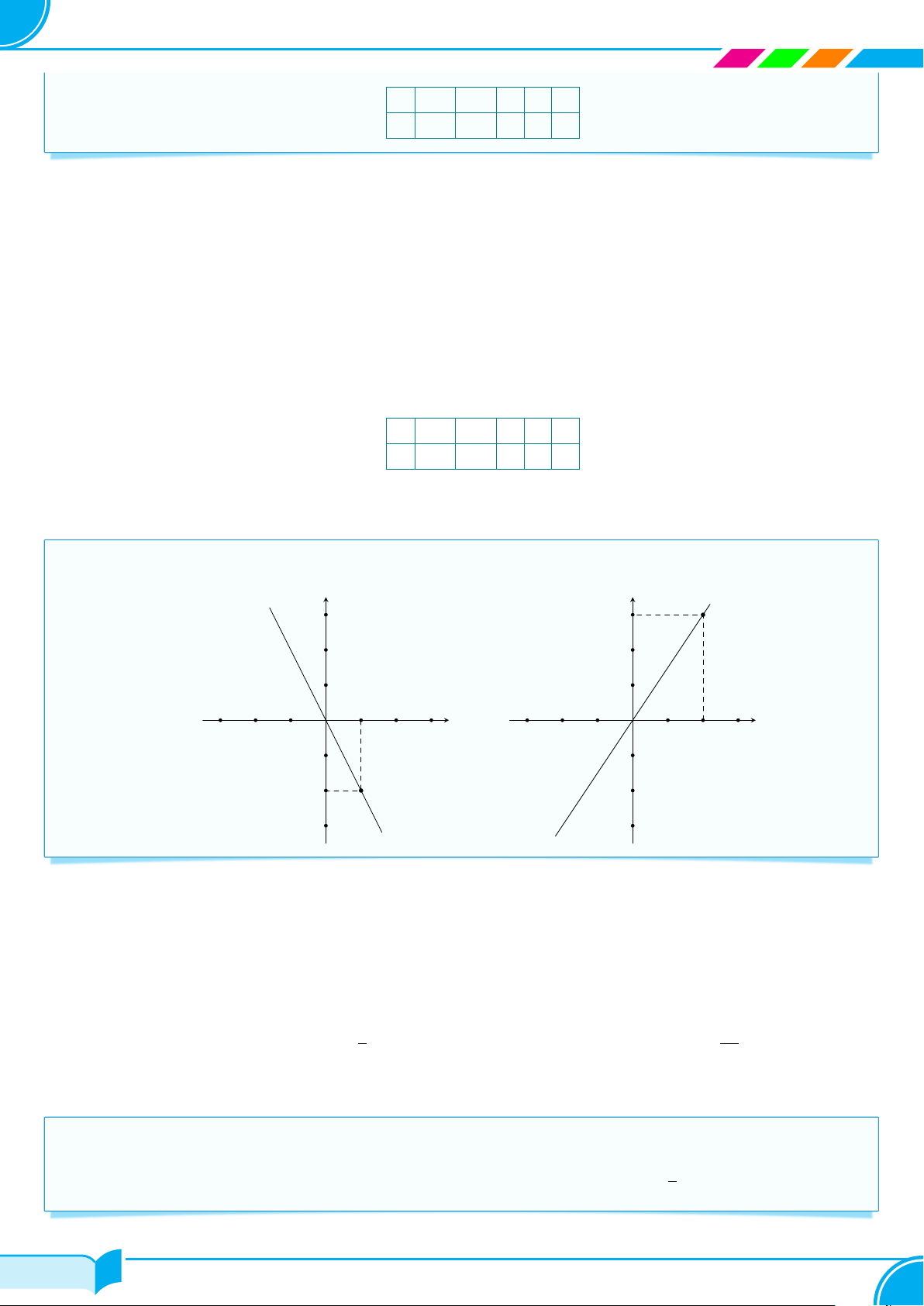
a) Vẽ đồ thị của các hàm số: y = 0,5x; y = −3x; y = x.
b) Các đồ thị sau đây là đồ thị của hàm số nào? 39/119 39/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 40
3. HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0)
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO y 3 y y 3 3 2 A B 2 2 1 1 1 −3 −2 −1 x O O 1 2 3 −3 −2 −1 O 1 2 3 −1 x −3 −2 −1 1 2 3 x C −1 −1 −2 −2 −2 −3 −3 −3 a) b) c) Lời giải.
a) Vẽ đồ thị của các hàm số: y = 0,5x; y = −3x; y = x. Cho x = 2 ta có y = 1. Ta vẽ điểm A(2; 1). Đồ thị hàm
số y = 0,5x là đường thẳng đi qua các điểm O(0; 0) và A(2; 1). y 2 1 A x −3 −2 −1 O 1 2 3 −1 −2
Cho x = 1 ta có y = −3. Ta vẽ điểm B(1; −3). Đồ thị hàm số y = −3x là đường thẳng đi qua các điểm O(0; 0) và B(1; −3). y 3 2 1 −3 −2 −1 1 2 3 x O −1 −2 −3 B
Cho x = 1 ta có y = 1. Ta vẽ điểm C(1; 1). Đồ thị hàm số y = −3x là đường thẳng đi qua các điểm O(0; 0) và C(1; 1). 40/119 40/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 41
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO y 3 2 1 C x −3 −2 −1 O 1 2 3 −1 −2 −3 b)
(a) Đường thẳng trong hình a) đi qua các điểm O(0; 0) và A(1; 22) nên là đồ thị của hàm số y = ax. Cho
x = 1 ta có y = a nên a = 2. Vậy đồ thị ở câu a) là đồ thị của hàm số y = 2x.
(b) Đường thẳng trong câu b) đi qua các điểm O(0; 0) và B(−2; 2) nên là đồ thị của hàm số y = ax. Cho
x = −2 ta có y = −2a nên −2a = 2, suy ra a = −1. Vậy đồ thị ở câu b) là đồ thị của hàm số y = −2x.
(c) Đường thẳng trong câu c) đi qua các điểm O(0; 0) và C(2; 1) nên là đồ thị của hàm số y = ax. Cho
x = 2 ta có y = 2a nên −1a = 2, suy ra a = −0,5. Vậy đồ thị ở câu c) là đồ thị của hàm số y = −0,5x. y 3 y y 3 3 2 A B 2 2 1 1 1 −3 −2 −1 x O O 1 2 3 −3 −2 −1 O 1 2 3 −1 x −3 −2 −1 1 2 3 x C −1 −1 −2 −2 −2 −3 −3 −3 a) b) c) □
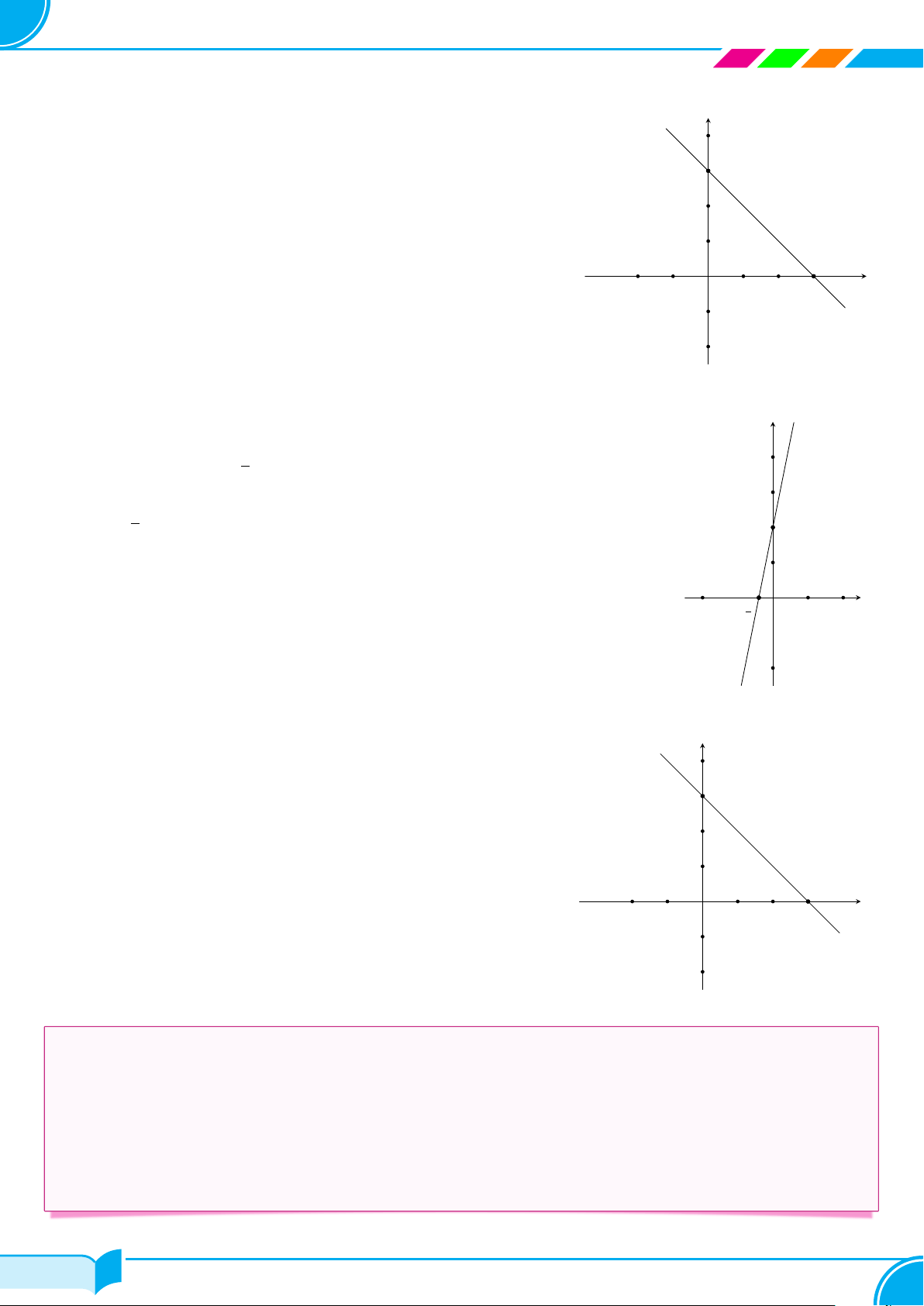
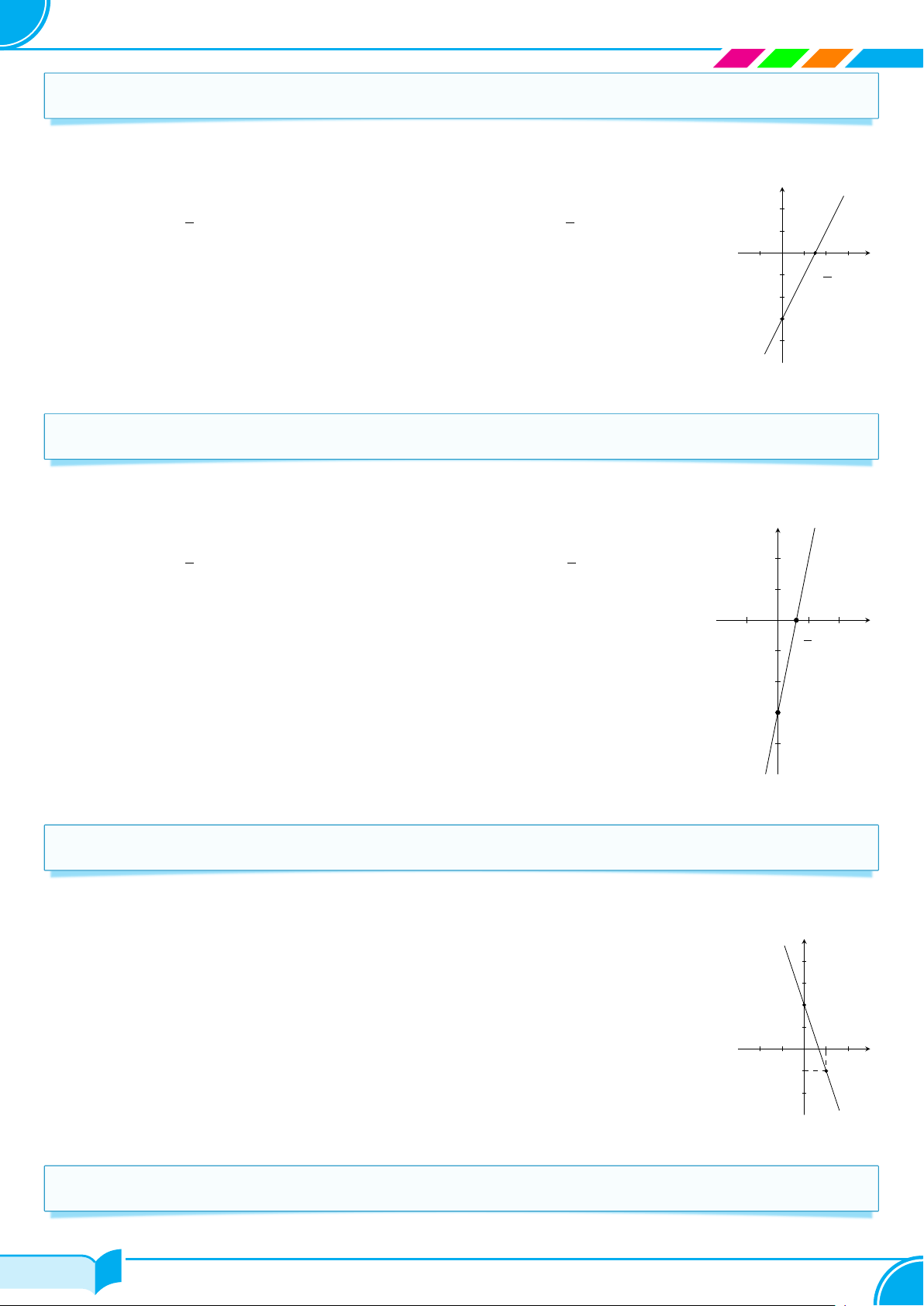
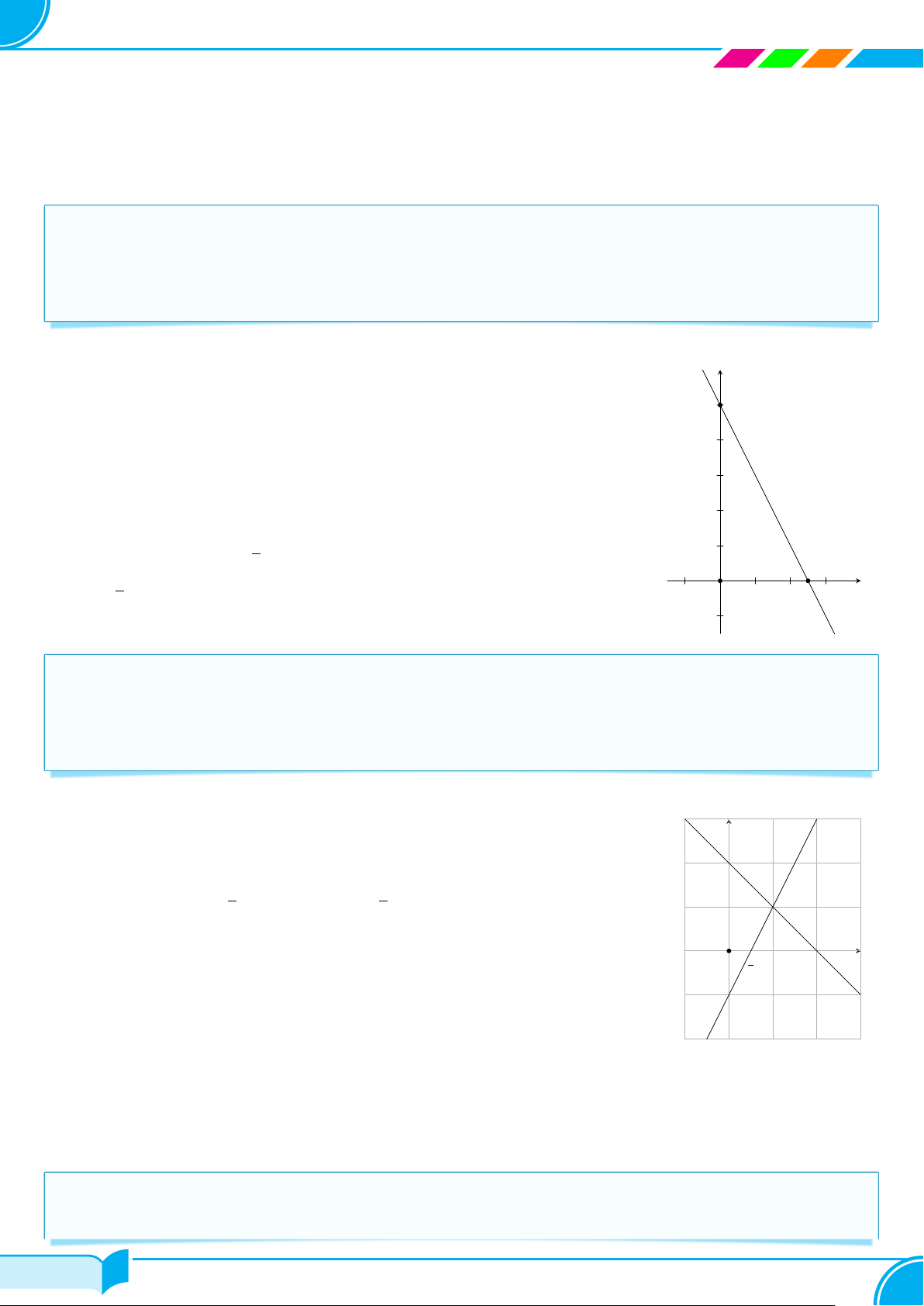
c Ví dụ 9. Vẽ đồ thị của các hàm số sau: a) y = 2x − 4; b) y = −x + 3; c) y = 5x + 2; d) y = −2x − 6. Lời giải. a) Với hàm số y = 2x − 4. y Cho x = 0 thì y = −4; 2 Cho y = 0 thì x = 2.
Đồ thị của hàm số y = 2x−4 là đường thẳng đi qua hai điểm M (0; −4) 1 và N (2; 0). −2 −1 O 1 2 3 x M −1 −2 −3 −4 N 41/119 41/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 42
3. HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0)
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO b) Với hàm số y = −x + 3. y Cho x = 0 thì y = 3; 4 Cho y = 0 thì x = 3. P
Đồ thị của hàm số y = −x + 3 là đường thẳng đi qua hai điểm 3 P (0; 3) và Q(3; 0). 2 1 −2 −1 O 1 2 3 x Q −1 −2 c) Với hàm số y = 5x + 2. y Cho x = 0 thì y = 2; 2 4 Cho y = 0 thì x = − . 5
Đồ thị của hàm số y = 5x + 2 là đường thẳng đi qua hai điểm M (0; 2) và 3 Å 2 ã N − ; 0 . 5 2 M 1 N O 2 x −2 1 2 5 −2 d) Với hàm số y = −x + 3. y Cho x = 0 thì y = 3; 4 Cho y = 0 thì x = 3. P
Đồ thị của hàm số y = −x + 3 là đường thẳng đi qua hai điểm 3 P (0; 3) và Q(3; 0). 2 1 −2 −1 O 1 2 3 x Q −1 −2 □
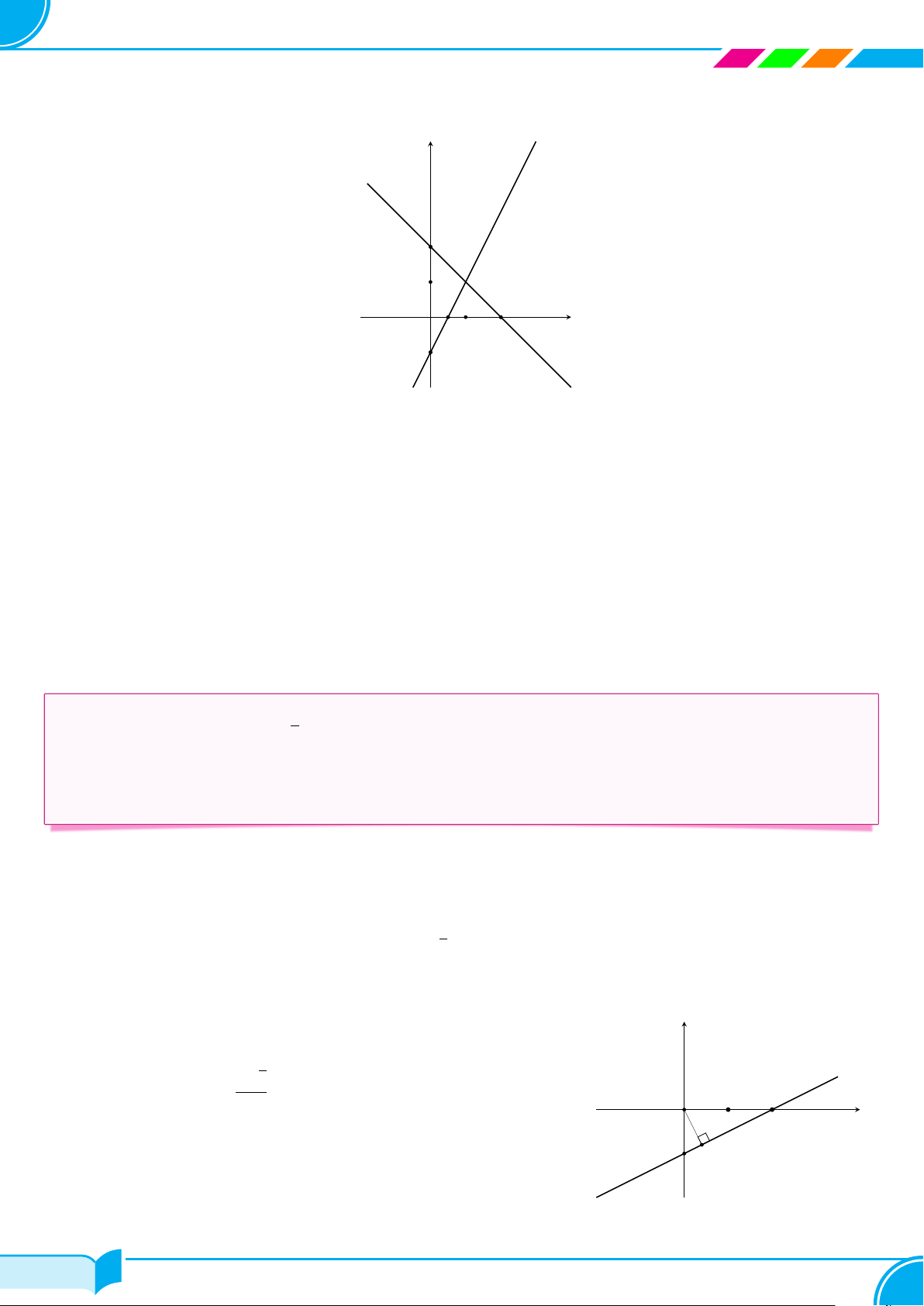
c Ví dụ 10. Cho các hàm số sau y = −x + 2 (1) y = 2x − 1 (2)
a) Vẽ đồ thị các hàm số (1), (2) trên cùng một mặt phẳng tọa độ.
b) Xác định tọa độ giao điểm I của (1) và (2). Lời giải. 42/119 42/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 43
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
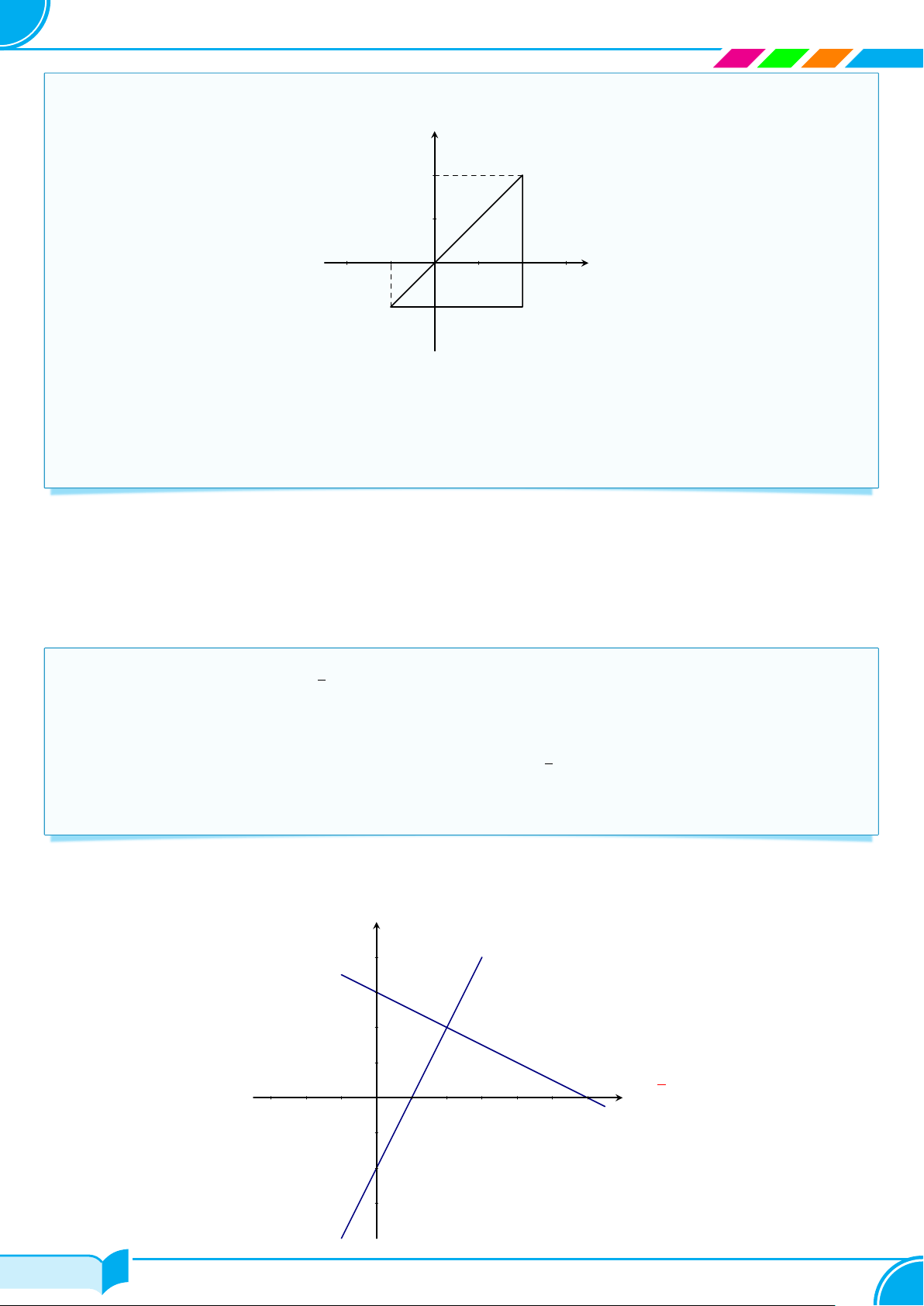
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO a) y 1 − x2 = y 2 A 1 D B x O 1 2 y = −1 C −x +2
b) Cách 1. Từ giao điểm I của đồ thị ta vẽ đường thẳng vuông góc với trục hoành, cắt trục này tại điểm có hoành độ là 1.
Vẽ đường thẳng vuông góc với trục tung, cắt trục này tại điểm có tung độ là 1.
Vậy tọa độ giao điểm là I(1; 1).
Cách 2. Gọi tạo độ giao điểm I là (x1; y1).
Vì I là giao điểm của AB và CD nên I vừa thuộc AB, vừa thuộc CD.
Vì I(x1; y1) ∈ AB : y = −x + 2 nên y1 = −x1 + 2.
Vì I(x1; y1) ∈ CD : y = 2x − 1 nên y1 = 2x1 − 1.
Suy ra ta có −x1 + 2 = 2x1 − 1 ⇔ 3x1 = 3 ⇔ x1 = 1 ⇒ y1 = −x1 + 2 = −1 + 2 = 1.
Vậy tọa độ giao điểm I là I(1; 1). □ 1
c Ví dụ 11. Cho hàm số y = x − 1 (d). 2
a) Vẽ đồ thị (d) của hàm số đã cho.
b) Tính khoảng cách từ gốc O của hệ trục tọa độ đến đường thẳng (d). Lời giải.
a) Cho x = 0 ⇒ y = −1 ⇒ A(0; −1) ∈ Oy.
Cho y = 0 ⇒ x = 2 ⇒ B(2; 0) ∈ Ox. 1
Đường thẳng AB là đồ thị (d) của hàm số y = x − 1. 2 b)
Kẻ OH vuông góc với (d) tại H. Khi đó OH là khoảng cách từ O y đến đường thẳng (d).
Trong tam giác vuông OAB ta có OA·OB = AB·OH(= 2·S△OAB). √ 2 5 Từ đó ta tính được . 5 B x O H 2 A −1 □ 43/119 43/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 44
3. HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0)
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Ví dụ 12. Cho các hàm số sau: y = 2 (1) y = |x + 1| (2) y = 2mx + m − 1 (3)
a) Vẽ đồ thị các hàm số (1), (2) trên cùng một mặt phẳng tọa độ.
b) Tìm m để đồ thị của hàm số (3) đi qua giao điểm của hai đồ thị (1) và (2). Lời giải. a)
Vẽ đồ thị của hàm số (1). y
Đồ thị hàm số y = 2 là đường thẳng song song với trục hoành
và cắt trục tung tại điểm có tung độ bằng 2. N 2 M
Vẽ đồ thị của hàm số y = |x + 1| (2). Ta có ®x + 1 khi x ≥ −1 y = |x + 1| = − (x + 1) khi x ≤ −1 −3 −2 −1 1 x O
Từ đó, ta được đồ thị có hình chữ V như hình bên.
Từ hình vẽ ta thấy đồ thị của hai hàm số (1) và (2) cắt nhau tại hai điểm M (1; 2) và N (−3; 2).
b) Đồ thị (d) của hàm số y = 2mx + m˘1 đi qua giao điểm của hai đồ thị hàm số (1) và (2) khi và chỉ khi (d)
đi qua hai điểm M hoặc N . c)
○ Trường hợp (d) đi qua M (1; 2). Khi đó
2 = 2m · 1 + m˘1 ⇔ 3m = 3 ⇔ m = 1.
○ Trường hợp (d) đi qua N (−3; 2). Khi đó 3
2 = 2m · (−3) + m˘1 ⇔ 5m = −3 ⇔ m = − . 5 3
Vậy với m = 1 hoặc m = −
thì đồ thị hàm số (3) đi qua giao điểm của đồ thị hàm số (1) và hàm số 5 (2). □
c Ví dụ 13. Cho hàm số y = mx + 3 (d). Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) là lớn nhất. Lời giải. a)
Xét m = 0 khi đó (d) có phương trình y = 0 · x + 3 = 3 hay y y = 3. A y = 3
Đồ thị hàm số y = 3 là đường thẳng song song với trục hoành 3
và cắt trục tung tại điểm có tung độ bằng 3 nên khoảng cách từ O đến (d) bằng 3. H x O d 44/119 44/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 45
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
b) Xét m ̸= 0. Khi đó (d) : y = mx + 3 luôn đi qua điểm A(0; 3) nằm trên trục tung. Kẻ OH vuông góc với (d) tại H.
Khi đó OH ≤ OA hay OH ≤ 3 (dấu “=” không xảy ra vì m ̸= 0 nên H không trùng A).
Do đó OH < 3. Kết hợp hai trường hơp ta có khi m = 0 thì khoảng cách từ O đến đường thẳng (d) là lớn nhất. □
Dạng 3. Điểm thuộc đường thẳng. Điểm không thuộc đường thẳng
Cho điểm M (x0; y0) và đường thẳng (d) có phương trình y = ax + b. Khi đó
M ∈ (d) ⇔ y0 = ax0 + b; M / ∈ (d) ⇔ y0 ̸= ax0 + b. Å 1 ã
c Ví dụ 14. Cho đường thẳng (d) : y = −3x + 1. Trong các điểm M (−1; 2), N (0; 1), P ; 0 , hãy xác định 3
các điểm thuộc và không thuộc đường thẳng (d). Lời giải. Ta có ○ M (−1; 2) /
∈ (d), vì khi x = −1 thì −3 · (−1) + 1 = 3 + 1 = 4 ̸= 2.
○ N (0; 1) ∈ (d), vì khi x = 0 thì −3 · 0 + 1 = 0 + 1 = 1 . Å 1 ã 1 ○ P ; 0
∈ (d), vì khi x = 0 thì −3 · + 1 = −1 + 1 = 0. 3 3 □ √ Ä ä
c Ví dụ 15. Điểm M
2; 1 thuộc đường thẳng nào trong các đường thẳng dưới dây? √ √ √ √ √ A y = x + 1 − 2. B x + y − 2 + 1. C y = 2x + 1 − 2. D x + y − 2 = 0. Lời giải.
Kí hiệu các đường thẳng ở các trường hợp (A), (B), (C), (D) lần lượt là (d1), (d2), (d3), (d4). Ta có √ √ √ √ Ä ä ○ M 2; 1 ∈ (d1), vì khi x = 2 thì 2 + 1 − 2 = 1. √ √ √ √ Ä ä ○ M 2; 1 / ∈ (d2), vì khi x = 2 thì − 2 + 2 − 1 = −1 ̸= 1. √ √ √ √ √ √ Ä ä ○ M 2; 1 / ∈ (d3), vì khi x = 2 thì 2 · 2 + 1 − 2 = 3 − 2 ̸= 1. √ √ √ √ Ä ä ○ M 2; 1 / ∈ (d4), vì khi x = 2 thì − 2 + 2 = 0 ̸= 1. Chọn đáp án A □
c Ví dụ 16. Cho đường thẳng (d) : y = −2x + 3. Tìm m để đường thẳng (d) đi qua điểm A(−m; −3). Lời giải.
Đường thẳng (d) : y = −2x + 3 đi qua điểm A(−m; −3) khi
−3 = (−2) · (−m) + 3 ⇔ 2m = −6 ⇔ m = −3.
Vậy đường thẳng (d) : y = −2x + 3 đi qua điểm A(−m; −3) khi m = −3. □
c Ví dụ 17. Cho đường thẳng (d) : y = (m+2)x+3m−1. Tìm m để đường thẳng (d) đi qua điểm M (−2; 3). Lời giải. 45/119 45/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 46
3. HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0)
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Đường thẳng (d) : y = (m + 2)x + 3m − 1 đi qua điểm M (−2; 3) khi
3 = (m + 2) · (−2) + 3m − 1 ⇔ 3 = −2m − 4 + 3m − 1 ⇔ m = 8.
Vậy đường thẳng (d) : y = (m + 2)x + 3m − 1 đi qua điểm M (−2; 3) khi m = 8. □
c Ví dụ 18. Chứng minh rằng đường thẳng (m + 2)x + y + 4m − 3 = 0 luôn đi qua một điểm cố định với mọi giá trị của m. Lời giải.
Gọi M (x0; y0) là điểm cố đinh thuộc (d), ta có
(m + 2)x0 + y0 + 4m − 3 = 0 ⇔ m(x0 + 4) + (2x0 + y0 − 3) = 0.
Đường thẳng (d) luôn đi qua điểm M (x0; y0) với mọi m khi và chỉ khi ®x ® 0 + 4 = 0 x0 = −4 ⇔ 2x0 + y0 − 3 = 0 y0 = 11.
Vậy đường thẳng (d) luôn đi qua điểm M (−4; 11) với mọi giá trị của m. □
Dạng 4. Xác định đường thẳng
Gọi hàm số cần tìm là y = ax + b (a ̸= 0), ta phải tìm a và b.
○ Với điều kiện của bài toán ta xác định được các hệ thức liên hệ giữa a và b.
○ Giải phương trình để tìm a, b.
c Ví dụ 19. Cho hàm số bậc nhất y = −2x + b. Xác định b nếu
a) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2.
b) Đồ thị hàm số đi qua điểm A(−1; 2). Lời giải.
a) Đồ thị hàm số y = −2x + b cắt trục tung tại điểm có tung độ bằng 2 nên b = 2.
b) Đồ thị hàm số y = −2x + b đi qua điểm A(−1; 2) khi
2 = (−2) · (−1) + b ⇔ 2 = 2 + b ⇔ b = 0.
Vậy b = 0 thì y = −2x đi qua điểm A(−1; 2). □
c Ví dụ 20. Xác định đường thẳng (d), biết (d) có dạng y = ax − 4 và đi qua điểm A(−3; 2). Lời giải.
Đường thẳng (d) : y = ax − 4 đi qua điểm A(−3; 2) khi
2 = a · (−3) − 4 ⇔ −3a = 2 + 4 ⇔ a = −2.
Vậy (d) có phương trình y = −2x − 4 đi qua điểm A(−3; 2). □
c Ví dụ 21. Xác định đường thẳng (d), biết (d) có dạng y = ax − 4 và đi qua điểm A(−3; 2). Lời giải.
Đường thẳng (d) : y = ax − 4 đi qua điểm A(−3; 2) khi
2 = a · (−3) − 4 ⇔ −3a = 2 + 4 ⇔ a = −2.
Vậy (d) có phương trình y = −2x − 4 đi qua điểm A(−3; 2). □ 46/119 46/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 47
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Ví dụ 22. Cho hàm số y = (m − 2)x + m + 2. Xác định m, biết
a) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng −2.
b) Đồ thị hàm số đi qua gốc tọa độ. Lời giải.
a) Đồ thị (d) của hàm số y = (m − 2)x + m + 2 cắt trục hoành độ bằng −2 nên A(−2; 0) thuộc (d). Do đó
0 = (m − 2) · (−2) + m + 2 ⇔ −2m + 4 + m + 2 = 0 ⇔ m = 6.
b) Đồ thị (d) của hàm số y = (m − 2)x + m + 2 đi qua gốc tọa độ nên O(0; 0) thuộc (d). Do đó
0 = (m − 2) · 0 + m + 2 ⇔ m + 2 = 0 ⇔ m = −2. □
c Ví dụ 23. Xác định đường thẳng đi qua hai điểm A(−3; 0) và B(0; 2). Lời giải.
Gọi phương trình đường thẳng AB là y = ax + b. y
Ta có A(−3; 0) ∈ AB ⇒ 0 = a · (−3) + b hay b = 3a. 2
B(0; 2) ∈ AB ⇒ 2 = a · 0 + b hay b = 2. Từ đó suy ra a = . 3 2 B 2
Vậy phương trình đường thẳng AB là y = x + 2. 3 A −3 x O □
c Ví dụ 24. Cho đường thẳng (d1) : y = 2012x + 2. Xác định đường thẳng (d2) sao cho (d1) và (d2) cắt nhau
tại một điểm nằm trên trục tung. Lời giải.
Đồ thị hàm số y = 2012x + 2 cắt trục tung tại điểm có tung độ bằng 2 vì có tung độ gốc là b = 2 nên đường thẳng
(d1) luôn đi qua điểm A(0; 2) nằm trên trục tung.
Vì (d1) và (d2) cắt nhau tại một điểm nằm trên trục tung nên A(0; 2) thuộc (d2).
Do đó (d2) có phương trình y = 2 hoặc x = 0 (trục tung) hoặc y = ax + 2 (với a ̸= 0, a ̸= 2012).
Có vô số đường thẳng đi qua điểm A(0; 2). □ Dạng 5. Vận dụng
c Ví dụ 25. Một hình chữ nhật có các kích thước là 2 m và 3 m. Gọi y là chu vi của hình chữ nhật này sau
khi tăng chiều dài và chiều rộng thêm x (m). Hãy chứng tỏ y là một hàm số bậc nhất theo biến số x. Tìm các
hệ số a, b của hàm số này. Lời giải.
Chiều dài và chiều rộng của hình chữ nhật sau khi tăng thêm x (m) lần lượt là 3 + x (m) và 2 + x (m).
Khi đó chu vi là y = 2[(3 + x) + (2 + x)] = 4x + 10 (m).
Do đó y = 4x + 10 là hàm số bậc nhất với a = 4 và b = 10. □ 47/119 47/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 48
3. HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0)
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Ví dụ 26. Trong hệ đo lường Anh - Mỹ, quãng đường thường được đo bằng dặm (mile) và 1 dặm bằng khoảng 1,609 km.
a) Viết công thức để chuyển đổi x km sang y dặm. Công thức tính y theo x này có phải là một hàm số bậc nhất của x không?
b) Một ô tô chạy với vận tốc 55 dặm/giờ trên một quãng đường có hạn chế tốc độ tối đa là 80 km/h. Hỏi
ô tô đó có vi phạm luật giao thông không? Lời giải.
a) Vì 1 dặm bằng khoảng 1,609 km nên công thức để chuyển đổi x km sang y dặm có dạng hàm số bậc nhất là y = 1,609x.
b) Thay x = 55, ta được y = 1,609 · 55 = 88,495 > 80. Vậy ô tô đó đã vi phạm luật giao thông. □
c Ví dụ 27. Một xe khách khởi hành từ bến xe phía Bắc bưu điện thành phố Nha Trang để đi ra thành phố
Đà Nẵng với tốc độ 40 km/h (Hình 2).
a) Biết rằng bến xe cách bưu điện thành phố Nha Trang 6 km. Sau x giờ, xe khách cách bưu điện thành
phố Nha Trang y km. Tính y theo x.
b) Chứng minh rằng y là một hàm số bậc nhất theo biến số x.
c) Hoàn thành bảng giá trị của hàm số ở câu b) và giải thích ý nghĩa của bảng giá trị này: x 0 1 2 3 y ? ? ? ? Lời giải.
a) Sau x giờ, xe khách đi được quãng đường là 40x (km), do đó y = 40x + 6 (km).
b) y = 40x + 6 là mà số bậc nhất vì có a = 40, b = 6.
c) Bảng giá trị theo yêu cầu đề bài x 0 1 2 3 y 6 46 86 126
Tại thời điểm chưa đi, xe khách cách bưu điện 6 km.
Sau 1 giờ, xe khách cách bưu điện 46 km.
Sau 2 giờ, xe khách cách bưu điện 86 km.
Sau 3 giờ, xe khách cách bưu điện 126 km. □ c Ví dụ 28. 48/119 48/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 49
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
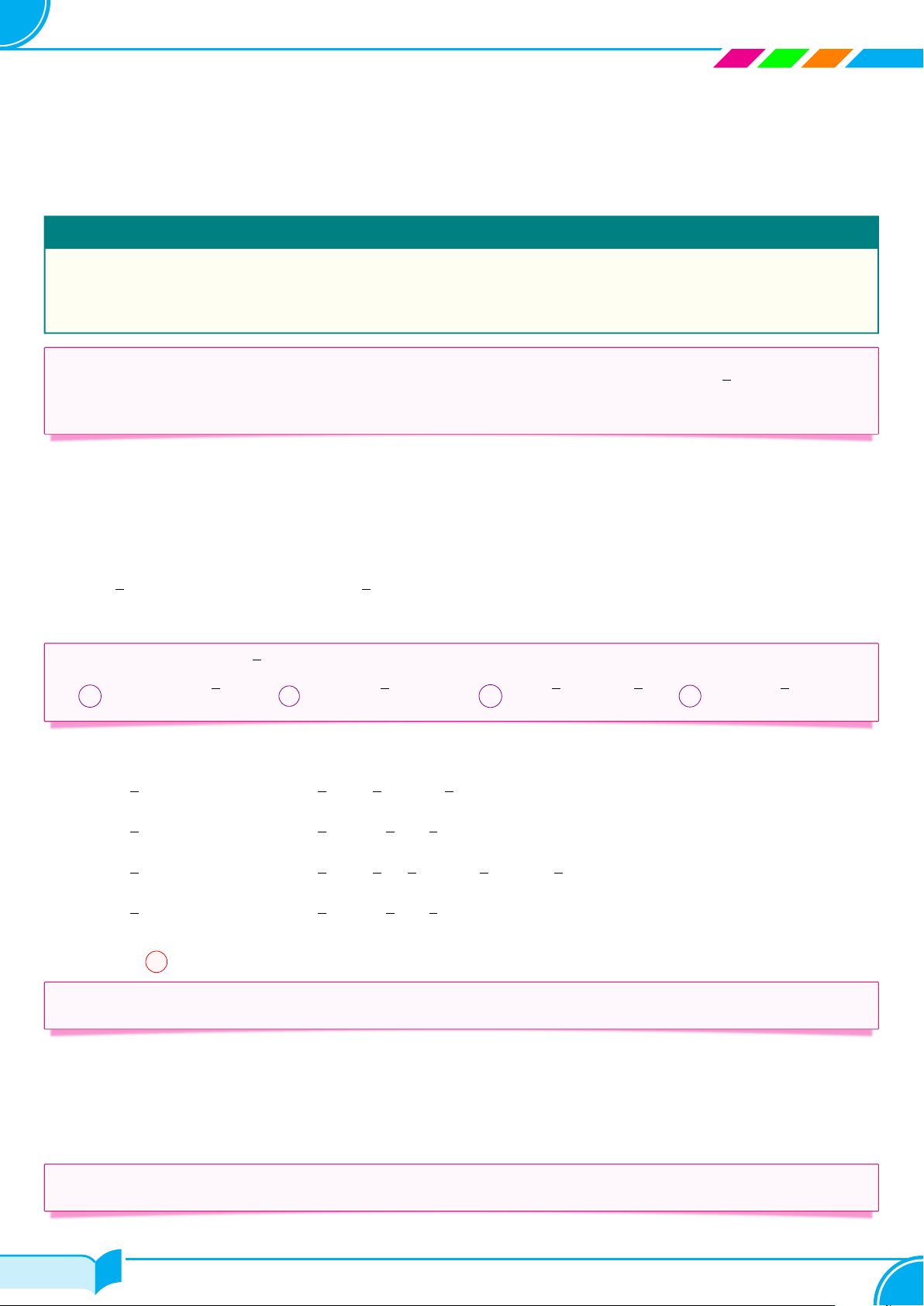
Một lò xo có chiều dài ban đầu khi chưa treo vật nặng là 10 cm. Cho biết khi treo thêm
vào lò xo một vật nặng 1 kg thì chiều dài lò xo tăng thêm 3 cm.
a) Tính chiều dài y (cm) của lò xo theo khối lượng x (kg) của vật. 10 cm
b) Vẽ đồ thị của hàm số y theo biến số x. Lời giải. 10 cm 3x cm x kg y
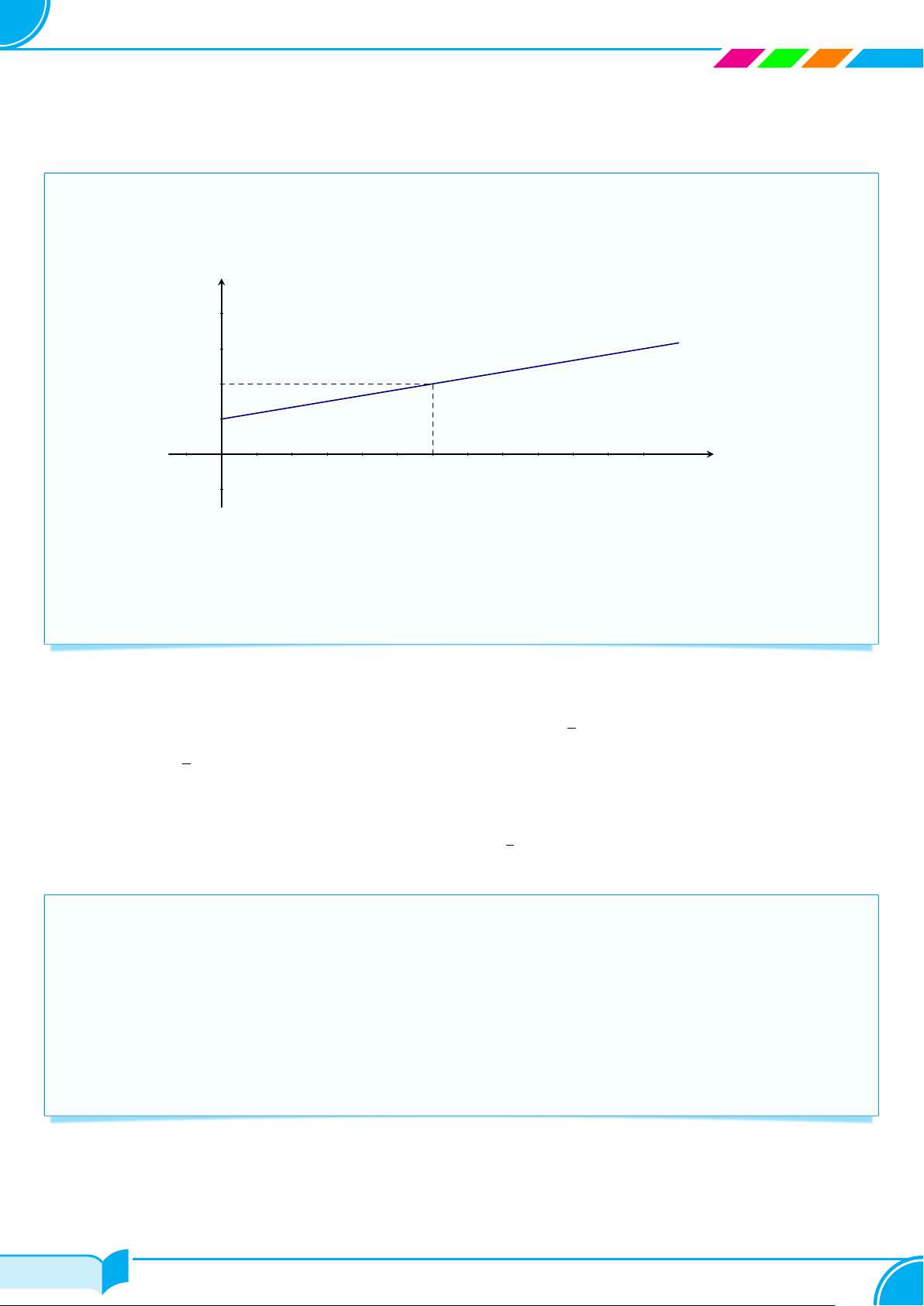
a) Chiều dài của lò xo tăng thêm khi treo vật có khối lượng x (kg) là 3x. Vậy y = 3x + 10 (cm). 10 A b) Cho x = 0 thì y = 10; 10 Cho y = 0 thì x = − . 10 3 − 3 O
Đồ thị của hàm số y = 3x + 10 là đường thẳng đi qua hai điểm A(0; 10) Å x 10 ã B và B − ; 0 . 3 □ A C BÀI TẬP VẬN DỤNG
c Bài 1. Tìm các hàm số bậc nhất trong các hàm số sau đây và chỉ ra các hệ số a, b của các hàm số đó: 3
y = 4x − 7; y = x2; y = −6x − 4; y = 4x; y = ; s = 5v + 8; m = 30n − 25. x Lời giải.
Các hàm số sau là hàm số bậc nhất:
○ y = 4x − 7 với a = 4 và b = −7.
○ y = −6x − 4 với a = −6 và b = −4.
○ y = 4x với a = 4 và b = 0.
○ s = 5v + 8 với a = 5 và b = 8.
○ m = 30n − 25 với a = 30 và b = −25. □ 49/119 49/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 50
3. HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0)
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 2. Trong các hàm số sau, những hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số a, b của chúng. a) y = 0x − 5; b) y = 1 − 3x; c) y = −0,6x; √ √ d) y = 2(x − 1) + 3; e) y = 2x2 + 1; f) y = −3 x + 2. Lời giải. √
y = −3 x + 2 không phải là hàm số bậc nhất.
Các hàm số bậc nhất là
○ y = 1 − 3x có hệ số a = −3, b = 1.
○ y = −0,6x có hệ số a = −0,6, b = 0. √ √ √ ○ y =
2(x − 1) + 3 có hệ số a = 2, b = 3 − 2. □
c Bài 3. Tìm các hàm số bậc nhất trong các hàm số sau đây và xác định các hệ số a, b của chúng. √ a) y = 4x + 2 b) y = 5 − 3x y = 2 + x2 c) d) y = −0,2x e) y = 5x − 1. Lời giải.
○ y = 4x + 2 với a = 4 và b = 2.
○ y = 5 − 3x với a = −3 và b = 5.
○ y = −0,2x với a = 0,2 và b = 0. √ √ ○ y = 5x − 1. với a = 5 và b = −1. □
c Bài 4. Lập bảng giá trị của mỗi hàm số bậc nhất sau: y = f (x) = 4x − 1 và y = h(x) = −0,5x + 8, với x
lần lượt bằng −3; −2; −1; 0; 1; 2; 3. Trong mỗi bảng vừa lập, khi x tăng thì y tăng hay giảm? Lời giải.
Bảng giá trị của hàm số y = f (x) = 4x − 1 là x −3 −2 −1 0 1 2 3 y = f (x) = 4x − 1 −13 −9 −5 −1 3 7 11
Từ bảng giá trị ta thấy khi x tăng thì y tăng.
Bảng giá trị của hàm số y = h(x) = −0,5x + 8 là x −3 −2 −1 0 1 2 3 y = h(x) = −0,5x + 8 9,5 9 8,5 8 7,5 7 6,5
Từ bảng giá trị ta thấy khi x tăng thì y giảm. □
c Bài 5. Cho hàm số bậc nhất y = ax + 3.
a) Tìm hệ số a, biết rằng khi x = 1 thì y = 5.
b) Với giá trị a tìm được, hãy hoàn thành bảng giá trị sau vào vở: 50/119 50/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 51
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO x −2 −1 0 1 2 y ? ? ? ? ? Lời giải.
a) Thay x = 1, y = 5 vào hàm số y = ax + 3, ta được a + 3 = 5 ⇒ a = 2.
b) Với giá trị a = 2, ta có hàm số y = 2x + 3. x −2 −1 0 1 2 y −1 1 3 5 7 □
c Bài 6. Tìm a để hàm số y = ax có đồ thị như trong hình sau: y y 3 3 B 2 2 1 1 −3 −2 −1 1 2 3 a) b) x O x −3 −2 −1 O 1 2 3 −1 −1 −2 A −2 −3 −3 Lời giải.
a) Đường thẳng trong câu a) đi qua các điểm O(0; 0) và A(1; −2) nên là đồ thị của hàm số y = ax. Cho x = 1
ta có y = a nên a = −2. Vậy đồ thị ở câu a) là đồ thị của hàm số y = −2x.
b) Đường thẳng trong câu b) đi qua các điểm O(0; 0) và B(2; 3) nên là đồ thị của hàm số y = ax. Cho x = 2 3 3x
ta có y = 2a nên 2a = 3, suy ra a =
. Vậy đồ thị ở câu b) là đồ thị của hàm số y = . 2 2 □
c Bài 7. Vẽ đồ thị của các hàm số sau 3 a) y = 2x − 6; b) y = −3x + 5; c) y = x. 2 Lời giải. 51/119 51/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 52
3. HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0)
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
a) Vẽ đồ thị hàm số y = 2x + 6. y
Cho x = 0 thì y = 6, ta được giao điểm của đồ thị với trục Oy là P (0; 6).
Cho y = 0 thì x = −3, ta được giao điểm của đồ thị với trục Ox là Q (−3; 0). 6 P
Đồ thị của hàm số y = 2x + 6 là đường thẳng P Q. 5 4 3 2 1 Q x −3 −2 −1 O 1 2 −1
b) Vẽ đồ thị hàm số y = −3x + 5. y
Cho x = 0 thì y = 5, ta được giao điểm của đồ thị với trục Oy là P (0; 6).
Cho x = 1 thì y = 2, ta được điểm Q (1; 2).
Đồ thị của hàm số y = −3x + 5 là đường thẳng P Q. 5 P 4 3 Q 2 1 x −3 −2 −1 O 1 2 3 −1 3
c) Vẽ đồ thị hàm số y = x. y 2 A
Cho x = 0 thì y = 0, ta được điểm O(0; 0). 3
Cho x = 2 thì y = 3, ta được điểm A(2; 3). 2 3
Đồ thị của hàm số y = x là đường thẳng OA. 2 1 x −2 −1 O 1 2 3 −1 □
c Bài 8. Vẽ đồ thị của các hàm số sau: 1 a) y = 3x; b) y = x; c) y = 2x + 4. 3 Lời giải.
a) Cho x = 1 ta có y = 3. Ta vẽ điểm A(1; 3). Đồ thị hàm số y = 3x là đường thẳng đi qua các điểm O(0; 0) và A(1; 3) 52/119 52/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 53
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO y 3 A 2 1 x −3 −2 −1 O 1 2 3 −1 −2 −3 1
b) Cho x = 3 ta có y = 1. Ta vẽ điểm B(3; 1). Đồ thị hàm số y =
x là đường thẳng đi qua các điểm O(0; 0) 3 và B(3; 1). y 2 1 B x −3 −2 −1 O 1 2 3 −1 −2
c) Cho x = 0 thì y = 4, ta được giao điểm của đồ thị với trục Oy là P (0; 4).
Cho y = 0 thì x = −2, ta được giao điểm của đồ thị với trục Ox là Q(−2; 0).
Đồ thị của hàm số y = 2x + 4 là đường thẳng P Q. y 5 4 P 3 2 1 Q x −3 −2 −1 O 1 2 3 −1 □ 1
c Bài 9. Vẽ đồ thị của các hàm số bậc nhất y = −2x + 3 và y = x. 2 Lời giải. 53/119 53/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 54
3. HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0)
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Vẽ đồ thị hàm số y = −2x + 3. y
Cho x = 0 thì y = 3, ta được giao điểm của đồ thị với trục Oy là 5 P (0; 3). 3 Cho y = 0 thì x =
, ta được giao điểm của đồ thị với trục Ox là 4 2 Å 3 ã Q ; 0 . 2 3 P
Đồ thị của hàm số y = −2x + 3 là đường thẳng P Q. 2 1 Q x −2 −1 O 1 2 3 −1 1 Vẽ đồ thị hàm số y = x. y 2
Cho x = 0 thì y = 0, ta được điểm O(0; 0). 3
Cho x = 2 thì y = 1, ta được điểm A(2; 1). 1
Đồ thị của hàm số y = x là đường thẳng OA. 2 2 A 1 x −2 −1 O 1 2 3 −1 □ c Bài 10.
a) Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng toạ độ: y = x; y = x + 2; y = −x; y = −x + 2.
b) Bốn đồ thị nói trên cắt nhau tại các điểm O(0; 0), A, B, C. Tứ giác có 4 đỉnh O, A, B, C là hình gì? Giải thích. Lời giải. a) ○ Với hàm số y = x. Cho x = 1 thì y = 1. y
Đồ thị của hàm số y = x là đường thẳng đi qua hai điểm O(0; 0) và C (1; 1). 4 3 ○ Với hàm số y = −x. Cho x = −1 thì y = 1. 2 B
Đồ thị của hàm số y = −x là đường thẳng đi qua hai điểm 1 A C O(0; 0) và A (−1; 1). x −4 −3 −2 −1 1 2 3 4 O ○ Với hàm số y = x + 2. Cho x = 0 thì y = 2; −2 Cho x = −2 thì y = 0. −3
Đồ thị của hàm số y = x + 2 là đường thẳng đi qua hai điểm B(0; 2) và N (−2; 0).
○ Với hàm số y = −x + 2. Cho x = 0 thì y = 2; Cho x = 2 thì y = 0.
Đồ thị của hàm số y = x là đường thẳng đi qua hai điểm B(0; 2) và Q (2; 0). 54/119 54/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 55
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
b) Dựa vào đồ thị trên ta có các điểm O(0; 0), A(−1, 1), B(0, 2), C(1, 1). Do đó OB và AD vuông góc và cắt
nhau tại trung điểm mỗi đường là I(0, 1), ngoài ra ta có OB = AD = 2. Suy ra OABC là hình vuông (dấu
hiệu nhận biết hình vuông). □
c Bài 11. Vẽ đồ thị của các hàm số sau trên cùng một hệ trục tọa độ: 1 y = x + 2; y = −2x + 2; y = −2x + 4. 2 Lời giải. 1
Vẽ đồ thị của hàm số y = x + 2 (d1) y 2
Cho x = 0 ⇒ y = 2 ⇒ A(0; 2).
Cho y = 0 ⇒ x = −4 ⇒ B(−4; 0). (d1) 4
Biểu diễn các điểm A, B trên mặt phẳng tọa độ.
Vẽ đường thẳng AB ta được đồ thị d1. Tương tự ta vẽ được: A 2
(d2) : y = −2x + 2; (d3) : y = −2x + 4. B −4 x O (d2) (d3) □ √ √
c Bài 12. Đồ thị của hàm số y = 2x + 1 −
2 đi qua điểm nào sau đây? √ A Ä ä M (−1; 1). B N(1; 1). C P(1; −1). D Q 2; 1 . Lời giải. √
Ta thử cặp giá trị mà triệt tiêu
2 trước. Thử N (1; 1) thấy đúng. Chọn đáp án B □
c Bài 13. Điểm E(−2; 0) thuộc đường thẳng nào trong các đường thẳng sau đây? 2 4 (d1) : y = x + 2; (d2) : y = −2x − 4; (d3) : y = 3x + 6; (d4) : y = x + . 3 3 A Chỉ thuộc (d1).
B Chỉ thuộc (d2) và (d4).
C Chỉ thuộc (d2) và (d3).
D Thuộc cả bốn đường thẳng trên. Lời giải.
Thử trực tiếp ta thấy tọa độ E(−2; 0) thỏa mãn cả bốn hàm số. Chọn đáp án D □ 1
c Bài 14. Cho hai đường thẳng (d1) : y = 2x + 2012 và d2 : y = − x + 2012. Đường thẳng nào dưới đây 2
không đi qua giao điểm của (d1) và (d2)? A y = 2012x. B y = x + 2012. C y = 2012x + 2012. D y = −x + 2012. Lời giải.
(d1) và (d2) có cùng tung độ gốc là 2012, hệ số a khác nhau. Các đường thẳng có cùng tung độ gốc 2012 sẽ đi qua
giao điém của (d1) và (d2). Do đó ta loại (B), (C), (D) vì có tung độ gốc là 2012. Chọn đáp án A □
c Bài 15. Xác định đường thẳng đi qua hai điểm A(−2; 0) và B(0; 3). 55/119 55/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 56
3. HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0)
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Lời giải.
Gọi phương trình đường thẳng AB là y = ax + b. Ta có
A(−2; 0) ∈ AB ⇒ 0 = a · (−2) + b hay b = 2a. 3
B(0; 3) ∈ AB ⇒ 3 = a · 0 + b hay b = 3. Từ đó suy ra a = . 2 3
Vậy phương trình đường thẳng AB là y = x + 3. □ 2
c Bài 16. Cho (d1) : y = x, (d2) : y = 0,5x; đường thẳng (d) song song với trục Ox và cắt trục tung Oy tại
điểm C có tung độ bằng 2. Đường thảng (d) lần lượt cắt (d1) , (d2) tại D và E. Khi đó, tính diện tích tam giác ODE. Lời giải.
Từ đồ thị ta thấy DE = 2, OC = 2. 1 1
Do đó diện tích tam giác cần tìm là S△ODE = OC · DE = · 2 · 2 = 2 (đvdt). □ 2 2
c Bài 17. Với giá trị nào của m thì mỗi hàm số sau đây là hàm số bậc nhất? a) y = (m − 1)x + m; b) y = 3 − 2mx. Lời giải.
y = ax + b là hàm số bậc nhất khi a ̸= 0. Do đó
a) Với m − 1 ̸= 0 ⇔ m ̸= 1 thì y = (m − 1)x + m;
b) Với −2m ̸= 0 ⇔ m ̸= 0 thì y = 3 − 2mx. □
c Bài 18. Với giá trị nào của m thì đồ thị của các hàm số y = 2x + 4 − m và y = 3x + m − 2 cắt nhau lại
một điểm nằm trên trục tung. Lời giải.
Hai đường thẳng cắt nhau trên trục tung khi và chỉ khi
4 − m = m − 2 ⇔ 2m = 6 ⇔ m = 3.
Vậy m = 3 thì đồ thị của hai hàm số trên cắt nhau tại một điểm trên trục tung. □
c Bài 19. Cho hai đường thẳng (d1) : (m − 2)x + 4my + 1 = 0 và (d2) : (m − 2)x + 2012y + 5 − m = 0 (m là tham số).
a) Chứng minh rằng (d1) luôn đi qua một điểm cố định khi m thay đổi.
b) Tìm m để hai dường thẳng (d1), (d2) cắt nhau tại mội điểm thuộc trục hoành. Lời giải. Å 1 1 ã a) M ; − . 2 8
b) Giao điểm thuộc trục hoành, nên tung độ y = 0.
Vậy (m − 2)x + 4m · 0 + 1 = 0 và (m − 2)x + 2012 · 0 + 5 − m = 0.
Suy ra m − 5 = −1 ⇔ m = 4 (thỏa mãn). □
c Bài 20. Cho hàm số y = f (x) = (m − 2)x + 2 có đồ thị là đường thẳng (d). 56/119 56/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 57
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
a) Tìm m để (d) đi qua điểm M (−1; 1).
b) Xác định m để khoảng cách từ điểm O(0; 0) đến (d) có giá trị lớn nhất. Lời giải. y (d) a) m = 3.
b) Khi m = 2, y = 2 khoảng cách từ O đến (d) là OH = 2. H y = 2
Khi m ̸= 2, y = (m − 2)x + 2. 2 −2 Å −2 ã Cho y = 2 ⇒ x = ⇒ A ; 0 . K m − 2 m − 2
Vẽ OK ⊥ (d). Ta có H(0; 2) ∈ (d) : y = (m − 2)x + 2 với mọi m. x A O
Suy ra OK < OH hay OK < 2.
Vậy khoảng cách từ điểm O đến (d) lớn nhất bằng 2 khi m = 2. □ 5
c Bài 21. Để đổi nhiệt độ từ độ F (Fahrenheit) sang độ C (Celsius), ta dùng công thức C = (F − 32). 9
a) C có phải là hàm số bậc nhất theo biến số F không?
b) Hãy tính C khi F = 32 và tính F khi C = 100. Lời giải. 5 5 160 a) Ta có C = (F − 32) = F − . 9 9 9 5 160
Do đó C là hàm số bậc nhất theo biến F với a = và b = − . 9 9 5 b) F = 32 ⇒ C = (32 − 32) = 0. 9 5
C = 100 ⇒ 100 = (F − 32) = 0 ⇔ F = 212. 9 □
c Bài 22. Gọi C và r lần lượt là chu vi và bán kính của một đường tròn. Hãy chứng tỏ C là một hàm số
bậc nhất theo biến số r. Tìm hệ số a, b của hàm số này. Lời giải.
Theo công thức tính chu vi đường tròn ta có C = 2πr. Do đó C là hàm số bậc nhất theo biến số r với a = 2π và b = 0. □
c Bài 23. Một người đi bộ trên đường thẳng với tốc độ v (km/h). Gọi s (km) là quãng đường đi được trong t (giờ).
a) Lập công thức tính s theo t.
b) Vẽ đồ thị của hàm số s theo biến số t khi v = 4. Lời giải. 57/119 57/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 58
3. HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0)
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO s
a) Theo công thức tính quãng đường theo vận tốc và thời gian ta có s = vt. 4 A 3
b) Khi v = 4, ta có s = 4t, trong đó t ≥ 0. 2 Cho t = 1 thì y = 4.
Đồ thị của hàm số s = 4t là đường thẳng đi qua hai điểm O(0; 0) và A (1; 4). 1 1 2 t O □
c Bài 24. Đồng euro (EUR) là đơn vị tiền tệ chính thức ở một số quốc gia thành viên của Liên minh châu
Âu. Vào một ngày, tỉ giá hối đoái giữa đồng euro và đồng đô la Mỹ (USD) là 1 EUR = 1, 1052 USD.
a) Viết công thức để chuyển đổi x euro sang y đô la Mỹ. Công thức tính y theo x này có phải là một hàm
số bậc nhất của x không?
b) Vào ngày đó, 200 euro có giá trị bằng bao nhiêu đô la Mỹ?
c) Vào ngày đó, 500 đô la Mỹ có giá trị bằng bao nhiêu euro? Lời giải.
a) Công thức để chuyển đổi x euro sang y đô la Mỹ là y = 1, 1052x. Công thức tính y theo x này là một hàm số bậc nhất của x.
b) 200 euro có giá trị là 1, 1052 · 200 = 210, 4 đô la Mỹ.
c) 500 đô la Mỹ có giá trị là 500 : 1, 1052 ≈ 475, 3 euro. □
c Bài 25. Giá cước điện thoại cố định của một hãng viễn thông bao gồm cước thuê bao là 22 000 đồng/tháng
và cước gọi là 800 đồng/phút.
a) Lập công thức tính số tiền cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút.
b) Tính số tiền cước điện thoại phải trả khi gọi 75 phút.
c) Nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi bao nhiêu phút? Lời giải.
a) Công thức tính số tiền cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút là y = 800x + 22 000.
b) Số tiền cước điện thoại phải trả khi gọi 75 phút là 800 · 75 + 22 000 = 82 000 (đồng).
c) Thay y = 94 000 vào y = 800x + 22 000, ta được
800x + 22 000 = 94 000 ⇒ x = 90.
Vậy nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi 90 phút. □
c Bài 26. Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất y = ax + b, trong đó b biểu thị chi phí cố
định của hoạt động kinh doanh và hệ số a biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một
xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 36 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là 1, 8 triệu đồng. 58/119 58/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 59
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
a) Viết công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày.
b) Vẽ đồ thị của hàm số thu được ở câu a.
c) Chi phí để sản xuất 15 chiếc xe đạp trong một ngày là bao nhiêu?
d) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngày, nếu chi phí trong ngày đó là 72 triệu đồng? Lời giải.
a) Công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày là y = 1,8x + 36. b)
Vẽ đồ thị hàm số y = 1,8x + 36. y
Cho x = 0 thì y = 36, ta được điểm A(0; 36). 40 A
Cho y = 0 thì y = −20, ta được điểm B(−20; 0).
Đồ thị của hàm số y = 1,8x + 36 là đường thẳng AB. 30 20 10 B x −30 −20 −10 O 10 20 30 −10
c) Chi phí để sản xuất 15 chiếc xe đạp trong một ngày là
1, 8 · 15 + 36 = 63 (triệu đồng).
d) Thay y = 72 vào hàm số y = 1,8x + 36, ta được 1,8x + 36 = 72 ⇒ x = 20.
Vậy nếu chi phí trong ngày đó là 72 triệu đồng thì có thể sản xuất 20 chiếc xe đạp trong ngày. □
c Bài 27. Với các giá trị nào của m thì hàm số sau là hàm số bậc nhất? √ a) y = 4m2 − 1 x; b) y = 5 − m(x − 2);
c) y = m2x2 + m x + 2 − 4x2 + 1 − 2x. Lời giải. 1 a) m ̸= ± . b) m < 5. c) m = 0 hoặc m = 4. 2 □ 59/119 59/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 60
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Baâi 4
HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG A
TRỌNG TÂM KIẾN THỨC
1 Hệ số góc của đường thẳng
○ Đường thẳng y = ax + b, trong đó a là hệ số góc của đường thẳng.
○ Ý nghĩa hình học của hệ số góc a.
Gọi α là góc kẻ từ tia Ox theo ngược chiều kim đồng hồ đến đường thẳng. Khi đó hệ số góc a = tan α. b + y ax y = y y = ax + b α α x x
Chú ý rằng 0◦ < α < 180◦ (hình vẽ).
Ta gọi a là hệ số góc của đường thẳng y = ax + b (a ̸= 0).
○ Góc α nhọn (0 < α < 90◦) khi a > 0.
○ Góc α tù (90◦ < α < 180◦) khi a < 0. Nhận xét.
○ Khi hệ số góc a dương, đường thẳng y = ax + b đi lên từ trái sang phải. Góc tạo bởi đường thẳng này và
trục Ox là góc nhọn (H.7.14a).
○ Khi hệ số góc a âm, đường thẳng y = ax + b đi xuống từ trái sang phải. Góc tạo bởi đường thẳng này và trục Ox là góc tù.
2 Đường thẳng song song và đường thẳng cắt nhau
Cho hai đường thẳng d : y = ax + b (a ̸= 0) và d′ : y = a′x + b′ (a′ ̸= 0). ®a = a′ ®a = a′ a) d ∥ d′ ⇔ b) d trùng d′ ⇔ b ̸= b′. b = b′.
c) d cắt d′ ⇔ a ̸= a′.
d) d ⊥ d′ ⇔ a · a′ = −1. A B CÁC DẠNG BÀI TẬP
Dạng 1. Nhận diện hệ số góc. Xác định đường thẳng biết hệ số góc
c Ví dụ 1. Tìm hệ số góc của đường thẳng y = ax + b (a ̸= 0). 2 a) y = 0,7x; b) y = −2x + 2022; c) y = − x − 2023. 3 60/119 60/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 61
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Lời giải.
a) Đường thẳng y = 0,7x có hệ số góc a = 0,7.
b) Đường thẳng y = −2x + 2022 có hệ số góc a = −2. 2 2
c) Đường thẳng y = − x − 2023 có hệ số góc a = − . 3 3 □
c Ví dụ 2. Tìm hệ số góc của các đường thẳng sau đây: √ √ √ a) y = −5x − 5; b) y = 3x + 3; c) y = 11x + 7. Lời giải.
a) Đường thẳng y = −5x − 5 có hệ số góc là a = −5. √ √ b) Đường thẳng y =
3x + 3 có hệ số góc là a = 3. √ √ √ c) Đường thẳng y = 11x + 7 có hệ số góc là a = 11. □
c Ví dụ 3. Trong các đường thẳng sau đây, đường thẳng nào tạo với Ox một góc nhọn, đường thẳng nào tạo với Ox một góc tù? a) y = 3x + 6; b) y = −4x + 1; c) y = −3x − 6. Lời giải.
a) Đường thẳng y = 3x + 6 có hệ số góc a = 3 > 0 nên tạo với Ox một góc nhọn.
b) Đường thẳng y = −4x + 1 có hệ số góc a = −4 < 0 nên tạo với Ox một góc tù.
c) Đường thẳngy = −3x − 6 có hệ số góc a = −3 < 0 nên tạo với Ox một góc tù. □
c Ví dụ 4. Xác định đường thẳng (d) đi qua điểm A(−2; 3) và có hệ số góc bằng −2. Lời giải.
Gọi phương trình đường thẳng (d) là y = ax + b.
Vì (d) có hệ số góc là −2 nên a = −2 ⇒ (d) : y = −2x + b.
Vì A(−2; 3) ∈ (d) nên 3 = −2 · (−2) + b ⇔ b = −1.
Do đó phương trình đường thẳng (d) là y = −2x − 1. □
c Ví dụ 5. Tìm hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc a = −2 và đi qua điểm (1; 2). Lời giải.
Hàm số bậc nhất cần tìm có dạng y = −2x + b.
Vì đường thẳng đi qua điểm (1; 2) nên ta có
2 = −2 · 1 + b suy ra b = 4.
Vậy hàm số cần tìm là y = −2x + 4. □
c Ví dụ 6. Tìm hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc là 3 và cắt trục tung tại điểm có tung độ bằng −1. 61/119 61/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 62
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Lời giải.
Hàm số bậc nhất có dạng y = 3x + b.
Hàm số này cắt trục tung tại M (0; −1) nên ta có
−1 = 3 · 0 + b ⇒ b = −1.
Vậy hàm số cần tìm là y = 3x − 1. □
Dạng 2. Nhận dạng cặp đường thẳng song song với nhau, cặp
đường thẳng cắt nhau, cặp đường thẳng vuông góc với nhau
c Ví dụ 7. Hãy chỉ ra hai cặp đường thẳng song song với nhau trong các đường thẳng sau: x + 3 1 (d1) : y = 2x + 1; (d2) : y = ; (d3) : y = − x + 2; 2 2 (d4) : y = 0,5x − 1; (d5) : y = 4 + 2x; (d6) : y = 1 − 2x. Lời giải.
Hai cặp đường thẳng song song với nhau là
○ (d1) ∥ (d5) vì a = a′ (= 2); b ̸= b′ (1 ̸= 4);
○ (d2) ∥ (d4) vì a = a′ (= 0,5); b ̸= b′ (1,5 ̸= −1). □
c Ví dụ 8. Hãy chỉ ra các cặp đường thẳng vuông góc với nhau trong các đường thẳng sau: x + 3 1 (d1) : y = 2x + 1; (d2) : y = ; (d3) : y = − x + 2; 2 2 (d4) : y = 0,5x − 1; (d5) : y = 4 + 2x; (d6) : y = 1 − 2x. Lời giải.
Bốn cặp đường thẳng vuông góc với nhau là (d1) ⊥ (d3); (d2) ⊥ (d6); (d3) ⊥ (d5); (d4) ⊥ (d6) vì đều có a·a′ = −1. □
c Ví dụ 9. Tìm các cặp đường thẳng cắt nhau hay song song trong các đường thẳng sau: a) d1 : y = 3x + 2; b) d2 : y = 3x − 6; c) d3 : y = 4x + 2. Lời giải.
Hai đường thẳng d1 và d2 song song vì có hệ số góc bằng nhau.
Hai đường thẳng d1 và d3 cắt nhau vì có hệ số góc khác nhau.
Hai đường thẳng d2 và d3 cắt nhau vì có hệ số góc khác nhau. □
c Ví dụ 10. Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong các đường thẳng sau: a) d1 : y = 3x; b) d2 : y = −7x + 9; c) d3 : y = 3x − 0,8; √ √ √ d) d4 : y = −7x − 1; e) d5 : y = 2x + 10; f) d6 : y = 2x + 10. Lời giải.
Các đường thẳng song song là d1 và d3 vì a1 = a3 = 3.
Các đường thẳng song song là d2 và d4 vì a2 = a4 = −7. √
Các đường thẳng song song là d5 và d6 vì a5 = a6 = 2. 62/119 62/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 63
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Các đường thẳng cắt nhau là d1 và d2.
Các đường thẳng cắt nhau là d1 và d5.
Các đường thẳng cắt nhau là d2 và d5. □
c Ví dụ 11. Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong ba đường thẳng
sau: y = 2x + 1; y = 2x + 3 ; y = 3x − 1. Lời giải.
○ Hai đường thẳng y = 2x + 1; y = 2x + 3 có hệ số góc bằng nhau và hệ số tự do khác nhau nên hai đường thẳng đó song song.
○ Hai đường thẳng y = 2x + 1; y = 3x − 1 có hệ số góc khác nhau nên hai đường thẳng đó cắt nhau.
○ Hai đường thẳng y = 2x + 3; y = 3x − 1 có hệ số góc khác nhau nên hai đường thẳng đó cắt nhau. □
c Ví dụ 12. Xét vị trí tương đối của hai đường thẳng y = −5x và y = −5x + 2. Lời giải.
Hai đường thẳng y = −5x và y = −5x + 2 có hệ số góc bằng nhau (−5 = −5) và hai hệ số tự do khác nhau (0 ̸= 2)
nên hai đường thẳng trên song song với nhau. □ c Ví dụ 13.
a) Nêu nhận xét về vị trí giữa hai đường thẳng d1 : y = −x và d2 : y = −x − 2.
b) Tìm phương trình đường thẳng d3 song song với đường thẳng d1 và cắt trục Oy tai điểm (0; 3). Lời giải.
a) Hai đường thẳng d1 và d2 phân biệt (cắt Oy tại hai điểm khác nhau) và có hệ số góc bằng nhau (cùng bằng −1 ), suy ra d1 ∥ d2.
b) Đường thẳng d3 song song với d1, suy ra d3 phải có hệ số góc bằng −1. Ta lại có d3 đi qua điểm (0; 3). Vậy
d3 có phương trình y = −x + 3. □ c Ví dụ 14.
a) Tìm các cặp đường thẳng cắt nhau trong các đường thẳng sau: d1 : y = 5x + 4; d2 : y = −2x − 3; d3 : y = 5x.
b) Cho đường thẳng d4 : y = mx + n. Tìm điều kiện của m để d4 cắt d1 và cắt d2. Lời giải.
a) Ta có các cặp đường thằng cắt nhau là: d1 và d2; d2 và d3 vì hai đường thằng trong mỗi cặp có hệ số góc khác nhau.
b) Điều kiện của m để d4 cắt d1 và cắt d2 là m ̸= 5 và m ̸= −2. □
c Ví dụ 15. Chứng tỏ rằng hai đường thẳng sau luôn cắt nhau với mọi giá trị của m: −x + m
a) (d1) : y = (m2 − m + 1)x + 1 và (d2) : y = . 2 63/119 63/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 64
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
b) (d3) : y = (m2 + 1)x + 2012 và (d4) : y = −mx + 2012. Lời giải. Å 1 ã2 3 3 1
a) Xét (d1) có a = m2 − m + 1 = m − + ≥
> 0; (d2) có a′ = − < 0. 2 4 4 2
Suy ra a ̸= a′ với mọi m nên (d1) luôn cắt (d2). Å 1 ã2 3 3
b) Ta có a − a′ = m2 + 1 − (−m) = m2 + m + 1 = m + + ≥
> 0 nên a ̸= a′ với mọi m, suy ra (d3) 2 4 4 luôn cắt (d4). □
Dạng 3. Bài toán tham số liên quan đến hệ số góc của đường thẳng
c Ví dụ 16. Đường thẳng y = (m + 1)x + 5 đi qua điểm F (−1; 3) có hệ số góc bằng bao nhiêu? Lời giải.
Kí hiệu (d) là đường thẳng y = (m + 1)x + 5.
Vì F (−1; 3) ∈ (d) nên 3 = (m + 1)(−1) + 5 ⇔ m = 1.
Hệ số góc của đường thẳng (d) là a = m + 1 = 1 + 1 = 2. □
c Ví dụ 17. Tìm giá trị của m để đường thẳng y = (m + 1)x + 2 (m ̸= −1) song song với đường thẳng y = −2x + 1. Lời giải.
Hai đường thẳng đã cho song song với nhau khi m + 1 = −2, tức là m = −3.
Giá trị này thỏa mãn điều kiện m ̸= −1. Vậy giá trị m cần tìm là m = −3. □
c Ví dụ 18. Tính hệ số góc của đường thẳng (d) : y = (m − 2)x + 3, biết nó song song với đường thẳng
(d′) : 2x − y − 1 = 0. Vẽ đồ thị (d) vừa tìm được. Lời giải. y
○ Đường thẳng (d′) có phương trình 2x − y − 1 = 0 hay y = 2x − 1.
Vì (d) ∥ (d′) ⇔ a = a′ và b ̸= b′ nên m − 2 = 2 và 3 ̸= −1. A 3
Do đó hệ số góc của đường thẳng (d) là 2. Å 3 ã
○ Ta có (d) : y = 2x + 3. Vẽ đường thẳng đi qua hai điểm A(0; 3) và B − ; 0 2 B
là đường thẳng (d) cần vẽ (hình bên). 3 x O − 2 □
c Ví dụ 19. Tính hệ số góc của đường thẳng (d) : y = (1 − m)x + 1, biết nó vuông góc với đường thẳng
(d′) : x − 2y − 4 = 0. Vẽ đồ thị (d) vừa tìm được. Lời giải. 64/119 64/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 65
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO y 1
○ Đường thẳng (d′) có phương trình x − 2y − 4 = 0 hay y = x − 2. 2 1
Vì (d) ⊥ (d′) ⇔ a · a′ = −1 nên (1 − m) · = −1 ⇒ 1 − m = −2. 1 2
Do đó hệ số góc của đường thẳng (d) là −2. Å 1 ã
○ Ta có (d) : y = −2x + 1. Vẽ đường thẳng đi qua hai điểm A(0; 1) và B ; 0 là 2 1 x O
đường thẳng (d) cần vẽ (hình bên). 2 □
c Ví dụ 20. Tính hệ số góc của đường thẳng đi qua hai điểm A(−1; 1) và B(2; −3). Lời giải.
Giả sử phương trình đường thẳng đi qua hai điểm A(−1; 1) và B(2; −3) là AB : y = ax + b.
○ A ∈ AB nên 1 = a · (−1) + b ⇔ −a + b = 1 ⇔ b = a + 1 (1)
○ B ∈ AB nên −3 = a · 2 + b ⇔ b = −2a − 3 (2) 4
Từ (1) và (2) ta có −2a − 3 = a + 1 ⇔ a = − . 3 4
Vậy hệ số góc của đường thẳng AB là a = − . □ 3
Dạng 4. Xác định đường thẳng với quan hệ song song
Viết phương trình đường thẳng đi qua một điểm và song song với một đường thẳng cho trước:
○ Gọi phương trình đường thẳng cần tìm là y = ax + b.
○ Sử dụng điều kiện hai đường thẳng song song với nhau để xác định hệ số a.
○ Với a vừa tìm được, sử dụng điều kiện còn lại để xác định tung độ gốc b.
c Ví dụ 21. Tìm m để đường thẳng (d1) : y = (2 − m2)x − m − 5 song song với đường thẳng (d2) : y = −2x + 2m + 1. Lời giải. ®2 − m2 = 2 (1) (d1) ∥ (d2) ⇔ − m − 5 ̸= 2m + 1. (2) ñm = 2
Giải (1): 2 − m2 = −2 ⇔ m2 = 4 ⇔ m = −2.
Giải (2): −m − 5 ̸= 2m + 1 ⇔ 3m ̸= −6 ⇔ m ̸= −2.
Vậy với m = 2 thì (d1) ∥ (d2). □
c Ví dụ 22. Cho đường thẳng (d) : 2x + y − 3 = 0 và điểm M (−1; 1). Viết phương trình đường thẳng (d′) đi
qua điểm M và song song với (d). Lời giải.
Gọi phương trình đường thẳng (d′) là y = ax + b.
Ta có (d) : 2x + y − 3 = 0 hay y = −2x + 3.
Vì (d′) ∥ (d) nên a = −2 và b ̸= 3. Mặc khác, (d′) đi qua điểm M (−1; 1) nên
1 = a · (−1) + b ⇔ −a + b = 1 ⇔ −(−2) + b = 1 (vì a = −2) ⇔ b = −1 (̸= 3).
Vậy phương trình đường thẳng cần tìm là y = −2x − 1. □ 65/119 65/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 66
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Ví dụ 23. Cho M (0; 2), N (1; 0), P (−1; −1) lần lượt là trung điểm của các cạnh BC, CA và AB của tam
giác ABC. Viết phương trình đường thẳng AB. Lời giải.
Gọi phương trình đường thẳng M N là y = ax + b. Ta có
○ N (1; 0) ∈ M N ⇒ 0 = a · 1 + b hay a = −b;
○ M (0; 2) ∈ M N ⇒ 2 = a · 0 + b hay b = 2 ⇒ a = −2.
Do đó phương trình đường thẳng M N là y = −2x + 2. Vì M, N lần lượt là trung điểm của CB, CA nên M N là
đường trung bình của △ABC ⇒ M N ∥ AB.
Vì AB ∥ M N nên phương trình đường thẳng AB có dạng y = −2x + b′ (b′ ̸= 2).
Vì P (−1; −1) là trung điểm của đoạn thẳng AB nên đường thẳng AB đi qua P (−1; −1)
⇒ −1 = −2 · (−1) + b′ ⇔ b′ = −3 (thỏa mãn).
Vậy phương trình đường thẳng AB là y = −2x − 3.
Ta có thể viết phương trình đường thẳng chứa các cạnh của △ABC. □
c Ví dụ 24. Cho ba điểm không thẳng hàng A(−2; −2), B(0; 4), C(2; 0). Xác định điểm D trên mặt phẳng
tọa độ sao cho ABCD là hình bình hành. Lời giải.
Dễ thấy BC : y = −2x + 4. y
Giả sử có D để ABCD là hình bình hành. 4 Khi đó AD B
∥ BC nên đường thẳng AD có phương trình: y = −2x − 6 (vì đường thẳng AD qua A).
Vì D thuộc AD nên D(x0; −2x0 − 6).
Tứ giác ABCD là hình bình hành nên −2 C AD = BC ⇔ AD2 = BC2 2 x O ñx0 = 0
⇔ (x0 + 2)2 + (−2x0 − 4)2 = 22 + (−4)2 ⇔ x0 = −4. A −2
⇒ D1(−4; 2), D2(0; −6). Từ hình trên suy ra loại D1 vì không đúng thứ tự các đỉnh
của tứ giác ABCD. Vậy D(0; −6). D □
Dạng 5. Xác định đường thẳng với quan hệ vuông góc
Viết phương trình đường thẳng đi qua một điểm và vuông góc với một đường thẳng cho trước:
○ Gọi phương trình đường thẳng cần tìm là y = ax + b.
○ Sử dụng điều kiện hai đường thẳng vuông góc để xác định hệ số a.
○ Với a vừa tìm được, sử dụng điều kiện điểm thuộc đường thẳng để xác định tung độ gốc b. 1
c Ví dụ 25. Tìm m để đường thẳng (d) : y = m2x + 1 − m vuông góc với đường thẳng (d′) : y = − x + 2012. 4 Lời giải. ñ 1 m = 2
(d) ⊥ (d′) ⇔ a · a′ = −1 ⇔ − · m2 = −1 ⇔ m2 = 4 ⇔
. Vậy m = ±2 thì (d) ⊥ (d′). □ 4 m = −2 66/119 66/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 67
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO 1
c Ví dụ 26. Tìm a và b, biết đường thẳng (d1) : y = ax + b vuông góc với đường thẳng (d2) : y = − x và 3
(d1) đi qua điểm P (1; −1). Lời giải. 1
Vì (d1) ⊥ (d2) nên a · a′ = −1 ⇔ − · a = −1 ⇔ a = 3 ⇒ (d1) : y = 3x + b. 3
Vì (d1) đi qua điểm P (1; −1) nên 3 · 1 + b = −1 ⇔ b = −4. Vậy a = 3 và b = −4. □
c Ví dụ 27. Cho ba điểm A(1; 2), B(3; 0), C(0; 1).
a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác.
b) Viết phương trình đường thẳng chứa đường cao AH của △ABC. Lời giải.
a) Gọi phương trình đường thẳng đi qua B(3; 0) và C(0; 1) là BC : y = ax + b. B ∈ BC nên 0 = a · 3 + b ⇔ 3a + b = 0 (1)
C ∈ BC nên 1 = a · 0 + b ⇔ b = 1 (2) 1 1
Từ (1) và (2) suy ra 3a + 1 = 0 ⇔ a = − ⇒ BC : y = − x + 1. 3 3
Vì A ̸∈ BC nên ba điểm A, B, C không thẳng hàng. Vậy ba điểm A, B, C là ba đỉnh của một tam giác.
b) Gọi phương trình đường cao AH là (d′) : y = a′x + b′.
Vì AH là đường cao của tam giác ABC nên Å 1 ã
AH ⊥ BC ⇔ d′ ⊥ BC ⇔ a · a′ = −1 ⇔ a′ · − = −1 ⇔ a′ = 3. 3
Mặt khác A(1; 2) ∈ (d′) nên 2 = a′ · 1 + b′ ⇔ 2 = 3 · 1 + b′ ⇔ b′ = −1.
Vậy phương trình đường cao AH của △ABC là y = 3x − 1. □
c Ví dụ 28. Cho M (0; 2), N (1; 0), P (−1; −1) lần lượt là trung điểm của các cạnh BC, CA, AB của tam
giác ABC. Viết phương trình đường trung trực của đoạn thẳng AB. Lời giải.
Gọi phương trình đường trung trực của đoạn AB là (d) : y = mx + n. C
Gọi phương trình đường thẳng M N là y = ax + b.
○ N (1; 0) ∈ M N ⇒ 0 = a · 1 + b hay a = −b; M
○ M (0; 2) ∈ M N ⇒ 2 = a · 0 + b hay b = 2 ⇒ a = −2. N
Do đó phương trình đường thẳng M N là y = −2x + 2.
Vì M, N lần lượt là trung điểm của BC và CA nên M N là đường trung B
bình của △ABC ⇒ M N ∥ AB. P (−1; −1) A
Vì (d) là đường trung trực của đoạn AB nên (d) ⊥ AB 1 1
⇒ (d) ⊥ M N ⇒ m(−2) = −1 ⇒ m = . Suy ra (d) : y = x + n. 2 2
Vì P (−1; −1) là trung điểm của đoạn AB nên đường thẳng (d) đi qua P (−1; −1) 1 1 ⇒ −1 = · (−1) + n ⇔ n = − . 2 2 1 1
Vậy phương trình đường trung trực của đoạn thẳng AB là y = x − . □ 2 2 67/119 67/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 68
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO A C BÀI TẬP VẬN DỤNG
c Bài 1. Hãy chỉ ra các cặp đường thẳng song song với nhau và các cặp đường thẳng cắt nhau trong các đường thẳng sau a) y = −x + 1; b) y = −2x + 1; c) y = −2x + 2; d) y = −x. Lời giải. ®a ® 1 = −1 a2 = −2 a) d1 : y = −x + 1 ⇒ ; b) d2 : y = −2x + 1 ⇒ ; b1 = 1 b2 = 1 ®a ® 3 = −2 a4 = −1 c) d3 : y = −2x + 2 ⇒ ; d) d4 : y = −x ⇒ . b3 = 2 b4 = 0 ®a1 = a4 Ta thấy ⇒ d1 ∥ d4. b1 ̸= b4 ®a2 = a3 Ta thấy ⇒ d2 ∥ d3. b2 ̸= b3
Ta thấy a1 ̸= a2; a3 ⇒ d1 cắt d2; d3.
Ta thấy a4 ̸= a2; a3 ⇒ d4 cắt d2; d3. □
c Bài 2. Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong các đường thẳng sau: d1 : y = 0,2x; d2 : y = −2x + 4; d3 : y = 0,2x − 0,8; √ √ √ d4 : y = −2x − 5; d5 : y = 3x + 3; d6 : y = 3x − 5. Lời giải.
○ Ba cặp đường thẳng cắt nhau là d1 và d2; d1 và d5; d2 và d5.
○ Các cặp đường thẳng song song là d1 và d3; d2 và d4; d5 và d6. □
c Bài 3. Cho đường thẳng d : y = x + 2023. Hãy viết phương trình hai đường thẳng song song với d. Lời giải.
Gọi y = ax + b và y = a′x + b′ là phương trình hai đường thẳng song song với đường thẳng y = x + 2023. ®a = a′ = 1 Suy ra b ̸= b′ ̸= 2023.
Ta chọn b và b′ bất kì ∈ R sao cho khác 2023.
Suy ra hai đường thẳng cần tìm có phương trình là y = x + 1 và y = x + 2. □
c Bài 4. Đường thẳng (d) đi qua giao điểm của hai đường thẳng y = x + 1, y = 2x và song song với đường √ √ thẳng y = 2x + 2 + 2 là √ √ √ √ √ √ A y = 4x + 2 − 2. B y = (2 + 2)x + 1. C y = 2x + 2 − 2. D y = x + 2. Lời giải. √ √ √
Đường thẳng (d) : y = ax + b song song với đường thẳng y = 2x + 2 + 2 nên có dạng y = 2x + b.
Giao điểm của hai đường thẳng y = x + 1, y = 2x là điểm A(1; 2). √ √ √ √ A(1; 2) ∈ (d) : y = 2x + b ⇒ b = 2 − 2. Vậy (d) : y = 2x + 2 − 2. Chọn đáp án C □ 68/119 68/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 69
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO 1 3
c Bài 5. Đường thẳng y = x +
vuông góc với đường thẳng nào dưới đây? 2 2 A 1 3 3 3 1 3 y = − x − . B y = 2x − . C y = −2x + . D y = x − . 2 2 2 2 2 2 Lời giải. 1 1 3 3 Ta có
· (−2) = −1 nên đường thẳng y = x +
vuông góc với đường thẳng y = −2x + . 2 2 2 2 Chọn đáp án C □ 1
c Bài 6. Đường thẳng y = (m + 1)x − 2 vuông góc với đường thẳng y = x + 2011 thì m bằng 2 A −2. B −3. C −1. D 1. Lời giải. 1 (m + 1) · = −1 ⇒ m = −3. 2 Chọn đáp án B □
c Bài 7. Xác định đường thẳng (d) biết nó có hệ số góc bằng 2 và đi qua điểm A(−3; 2). Lời giải. y = 2x + 8 □
c Bài 8. Tìm hàm số bậc nhất có đồ thị là đường thẳng đi qua điểm (1; −2) và có hệ số góc là 3. Lời giải.
Hàm số bậc nhất có dạng d : y = ax + b có hệ số góc là 3 ⇒ a = 3.
d qua (1; −2) nên ta có −2 = 3 · 1 + b ⇒ b = 5.
Vậy hàm số cần tìm là d : y = 3x + 5. □
c Bài 9. Tìm hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc là −2 và cắt trục hoành tại điểm có hoành độ bằng 3. Lời giải.
Hàm số bậc nhất có dạng d : y = ax + b có hệ số góc là −2 ⇒ a = −2.
d cắt trục hoành tại điểm có hoành độ bằng 3 nên ta có A(3; 0) ∈ d ⇒ 0 = −2 · 3 + b ⇒ b = 6.
Vậy hàm số cần tìm là d : y = −2x + 6. □
c Bài 10. Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng y = −3x + 1 và đi qua điểm (2; 6). Lời giải.
Hàm số bậc nhất có dạng d : y = ax + b song song với y = −3x + 1 suy ra a = −3.
d qua điểm (2; 6) suy ra 6 = −3 · 2 + b ⇔ b = 12 ̸= 1.
Vậy hàm số cần tìm là d : y = −3x + 12. □
c Bài 11. Tìm hệ số góc a để hai đường thẳng y = ax + 2 và y = 9x − 9 song song với nhau. Lời giải.
Vì hai đường thẳng song song nhau nên a = a′ ⇒ a = 9.
Vậy a = 9 thoả mãn yêu cầu bài toán. □ 69/119 69/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 70
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 12. Cho hàm số bậc nhất y = ax − 4.
a) Tìm hệ số góc a biết rằng đồ thị hàm số đi qua điểm M (1; −2).
b) Vẽ đồ thị của hàm số. Lời giải.
a) Vì đồ thị hàm số y = ax − 4 đi qua điểm M (1; −2) nên thay x = 1, y = −2 vào hàm số ta có 1 · a − 4 = −2 ⇒ a = 2.
Vậy hàm số có phương trình là y = 2x − 4 b) x 0 1 Bảng giá trị: y y = 2x − 4 −4 −2
đồ thị hàm số đi qua các điểm (0; −4); (1; −2). 3 2 1 −4 −3 −2 −1 O 1 2 3 4 x −1 −2 −3 −4 □
c Bài 13. Cho hai hàm số bậc nhất y = mx − 5 và y = (2m + 1)x + 3. Tìm các giá trị của m để đồ thị của hai hàm số là
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau. Lời giải. ®a = m ®a′ = 2m + 1 Ta có d : y = mx − 5 ⇒
và d′ : y = (2m + 1)x + 3 ⇒ b = −5 b′ = 3. ®m = 2m + 1 a) d song song d′ khi ⇔ m = −1. − 5 ̸= 3
b) d cắt d′ khi m ̸= 2m + 1 ⇔ m ̸= −1. □
c Bài 14. Tính hệ số góc của đường thẳng đi qua hai điểm A(1; 2) và B(3; 4). Lời giải.
AB : y = x + 1 ⇒ đường thẳng AB có hệ số góc a = 1. □
c Bài 15. Cho hai hàm số bậc nhất y = 2mx − 5 và y = 2x + 1. Với giá trị nào của m thì đồ thị của hai hàm số đã cho là
a) Hai đường thẳng song song với nhau?
b) Hai đường thẳng cắt nhau? 70/119 70/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 71
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Lời giải.
a) Hai đường thẳng song song suy ra a = a′ ⇒ 2m = 2 ⇔ m = 1.
Vậy m = 1 thì hai đường thẳng song song nhau.
b) Hai đường thẳng cắt nhau suy ra a ̸= a′ ⇒ 2m ̸= 2 ⇔ m ̸= 1.
Vậy m ̸= 1 thì hai đường thẳng cắt nhau. □
c Bài 16. Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong số các đường thẳng
sau: y = −2x + 5; y = −2x; y = 4x − 1. Lời giải.
Vì hai đường thẳng y = −2x + 5 và y = −2x có hệ số góc giống nhau và hệ số tự do khác nhau nên hai đường thẳng này song song.
Vì hai đường thẳng y = −2x + 5 và y = 4x − 1 có hệ số góc khác nhau nên hai đường thẳng này cắt nhau.
Vì hai đường thẳng y = −2x và y = 4x − 1 có hệ số góc khác nhau nên hai đường thẳng này cắt nhau. □
c Bài 17. Xác định đường thẳng y = ax + b (a ̸= 0) có hệ số góc bằng −1 và đi qua điểm M (1; 2). Sau đó
vẽ đường thẳng tìm được trên mặt phẳng toạ độ. Lời giải.
Vì đường thẳng cần tìm có hệ số góc là −1 nên a = −1 ⇒ y = −x + b. y
Điểm M (1; 2) thuộc đường thẳng cần tìm nên ta có 2 = −1 · 1 + b ⇒ b = 3. 4
Suy ra đường thẳng cần tìm là y = −x + 3.
Với x = 0 thì y = 3. Ta được điểm N (0; 3) thuộc đồ thị hàm số N 3 y = −x + 3.
Vậy đồ thị hàm số đã cho là đường thẳng đi qua hai điểm M (1; 2) và M 2 N (0; 3). y = − 1 x + 3 −1 O 1 2 3 4 x −1 □
c Bài 18. Tìm các giá trị của m để đường thẳng y = mx − 2 (m ̸= 0) cắt đường thẳng y = −2x + 1. Lời giải.
Hai đường thẳng đã cho cắt nhau khi m ̸= −2.
Kết hợp với điều kiện đã cho, ta được các giá trị m cần tìm là m ̸= 0 và m ̸= −2. □
c Bài 19. Cho hai hàm số bậc nhất y = 2mx + 1 và y = (m − 1)x + 2. Tìm các giá trị của m để đồ thị của hai hàm số đã cho là
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau. Lời giải. ®a = 2m ®a′ = m − 1
Ta có d có hệ số góc là ; d′ có hệ số góc là b = 1 b′ = 2. ®2m = m − 1
a) d song song d′ khi và chỉ khi ⇔ m = −1. 1 ̸= 2 71/119 71/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 72
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
b) d cắt d′ khi và chỉ khi 2m ̸= m − 1 ⇔ m ̸= −1. □
c Bài 20. Cho đường thẳng (d) : y = ax + b. Tìm giá trị của a và b trong mỗi trường hợp sau: a) (d) ∥ (d1) : y = 2x + 3;
b) (d) trùng (d2) : y = −x + 1; 1 1 c) (d) cắt (d3) : y = x; d) (d) ⊥ (d4) : y = − x. 2 2 Lời giải.
a) (d) ∥ (d1) ⇔ a = 2; b ̸= 3.
b) (d) trùng (d2) ⇔ a = −1; b = 1. 1 c) (d) cắt (d3) ⇔ a ̸= ; b ∈ R.
d) (d) ⊥ (d4) ⇔ a · a′ = −1 ⇔ a = 2; b ∈ R. 2 □
c Bài 21. Viết phương trình đường thẳng (d′) song song với đường thẳng (d) : y = −4x + 5 và đi qua điểm M (1; −1). Lời giải.
Gọi phương trình đường thẳng (d′) là y = ax + b.
Vì (d′) ∥ (d) : y = −4x + 5 nên a = −4; b ̸= 5.
Mặt khác (d′) đi qua M (1; −1) nên −1 = a · 1 + b ⇔ a + b = −1 ⇔ −4 + b = −1 ⇔ b = 3 (thỏa mãn). Vậy (d′) : y = −4x + 3. □ 1
c Bài 22. Xác định a và b để đường thẳng (d1) : y = ax + b vuông góc với đường thẳng (d2) : y = − x và 2 đi qua điểm P (−1; 2). Lời giải. 1
Vì (d1) ⊥ (d2) nên a · a′ = −1 ⇔ − a = −1 ⇔ a = 2. Do đó (d1) : y = 2x + b. 2
Vì (d1) đi qua điểm P (−1; 2) nên 2 · (−1) + b = 2 ⇔ b = 4. □
c Bài 23. Đường thẳng (d) : y = −ax + 2011 song song với đường phân giác của góc phần tư (I) và (III) thì hệ số a của (d) bằng: A 1 1. B −1. C 0. D − . 2011 Lời giải.
(d′) : y = x là đường phân giác của góc phần tư (I) và (III).
(d) ∥ (d′) ⇔ −a = 1 ⇔ a = −1. Chọn đáp án B □ 1 1
c Bài 24. Cho bốn đường thẳng (d1) : y = x − 2; (d2) : y = −3x; (d3) : y = −3x + 4 và (d4) : y = x + 2 3 3
cắt nhau tại bốn điểm phân biệt M, N, P, Q.
Khi đó bốn điểm M, N, P, Q là bốn đỉnh của: A Một hình thang.
B Một hình bình hành.
C Một hình chữ nhật.
D Một tứ giác không có gì đặc biệt. Lời giải. 1 1 (d1) ∥ (d4) vì a =
= a′; b = −2 ̸= 2 = b′; tương tự (d2) ∥ (d3); (d2) ⊥ (d4) vì (−3) = −1. 3 3
Do đó bốn giao điểm M, N, P, Q là bốn đỉnh của một hình chữ nhật. Chọn đáp án C □ 72/119 72/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 73
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 25. Trong mặt phẳng toạ độ Oxy, cho hai đường thẳng y = x và y = −x + 2.
a) Vẽ hai đường thẳng đã cho trên cùng mặt phẳng toạ độ.
b) Tìm giao điểm A của hai đường thẳng đã cho.
c) Gọi B là giao điểm của đường thẳng y = −x + 2 và trục Ox. Chứng minh tam giác OAB vuông tại A,
tức là hai đường thẳng y = x và y = −x + 2 vuông góc với nhau.
d) Có nhận xét gì về tích hai hệ số góc của hai đường thẳng đã cho? Lời giải. a) Vẽ đồ thị.
Hàm số y = x qua điểm O(0; 0) và A(1; 1).
Hàm số y = −x + 2 qua điểm B(0; 2) và C(2; 0). Đồ thị y y = x C A 1 x O 1 B y = −x + 3
b) Phương trình hoành độ giao điểm của hai đường thẳng y = x và y = −x + 2 là
x = −x + 2 ⇔ x = 1 ⇒ y = 1 ⇒ A(1; 1).
c) Gọi B là giao điểm của đường thẳng y = −x + 2 và trục Ox.
Suy ra yB = 0 ⇒ 0 = −xB + 2 ⇔ xB = 2. Vậy B(2; 0). √ √ Ta có OA = 2; OB = 2; AB = 2 ⇒ OB2 = OA2 + AB2.
Suy ra △OAB vuông tại A. Vậy hai đường thẳng vuông góc nhau.
d) Do hai đường thẳng vuông góc nhau nên tích hai hệ số góc a1 · a2 = −1. □
c Bài 26. Cho tam giác ABC có A(1; 5), B(−3; 1), C(5; 3).
a) Viết phương trình đường trung trực của cạnh BC.
b) Viết phương trình đường trung bình M N của tam giác ABC (M N ∥ BC). Lời giải.
a) Gọi phương trình đường thẳng BC là y = ax + b.
Vì B(−3; 1) ∈ BC nên 1 = −3a + b ⇒ b = 1 + 3a (1) C(5; 3) ∈ BC nên 3 = 5a + b (2) 1 7 1 7
Thay (1) vào (2) ta được a = , b = . Do đó BC : y = x + . 4 4 4 4
Trung trực của BC là đường thẳng (d) vuông góc với BC tại trung điểm I của BC. xB + xC yB + yC
Tọa độ của điểm I là x1 = = 1; y1 = = 2 hay I(1; 2). 2 2
Do đường trung trực (d) : y = −4x + m đi qua I(1; 2) nên ta được m = 6.
Vậy đường thẳng (d) là y = −4x + 6. 73/119 73/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 74
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
b) Gọi M, N lần lượt là trung điểm của AB, AC. Khi đó ta có M (−1; 3). 1 Å 7 ã
Vì M N ∥ BC nên M N có dạng y = x + n n ̸= . 4 4 13 1 13
Do M (−1; 3) thuộc M N nên n =
(thỏa mãn). Vậy M N có phương trình: y = x + . 4 4 4 □
c Bài 27. Cho M (0; 4), N (2; 0), P (−1; −2) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác
ABC. Viết phương trình đường thẳng AB. Lời giải.
Phương trình đường thẳng M N là y = −2x + 4.
Vì AB ∥ M N nên phương trình đường thẳng AB có dạng y = −2x + b′ (b ̸= 2).
Vì đường thẳng AB đi qua P (−1; −2) nên −2 = −2 · (−1) + b′ ⇔ b′ = −4.
Vậy phương trình đường thẳng AB là y = −2x − 4. □ √ √
c Bài 28. Cho hai đường thẳng (d1) : y = mx + m và (d2) : y = 3x + m2 + 3.
Chứng minh rằng (d1) và (d2) không trùng nhau với mọi giá trị của m. Lời giải. √ ® ( a = a′ m = 3 (1) Cách 1. (d1) ≡ (d2) ⇔ ⇔ √ b = b′ m = m2 + 3. (2)
Thay (1) vào (2) ta được 0 = 3 (vô lí). Do đó (d1) không trùng (d2) với mọi m. √ 1 √ 1 Å 1 ã2 Å√ 1 ã
Cách 2. Giả sử b = b′ ⇔ m = m2 + 3 ⇔ m2 − m + + 3 − = 0 ⇔ m − + 3 − = 0 (vô lí). Do 4 4 2 4
đó điều giả sử là sai. Vậy (d1) không trùng (d2) với mọi m.
Chỉ cần a ̸= a′ hoặc b ̸= b′ thì (d1) : y = ax + b không trùng (d2) : y = a′x + b′. □
c Bài 29. Lan phụ giúp mẹ bán nước chanh, em nhận thấy số li nước chanh y bán được trong ngày và nhiệt
độ trung bình x (◦C) của ngày hôm đó có mối tương quan. Lan ghi lại các giá trị tương ứng của hai đại lượng x và y trong bảng sau: x (◦C) 20 22 24 26 28 30 y (li nước chanh) 10 11 12 13 14 15
a) So sánh các giá trị x và y tương ứng trong bảng dữ liệu trên với toạ độ (x; y) của các điểm A, B, C, D,
E, F trên mặt phẳng toạ độ trong Hình 6. 74/119 74/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 75
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO y F 15 E D C B A 10 5 O 5 10 15 20 25 30 x Hình 6
b) Cho biết đường thẳng d : y = mx đi qua các điểm A, B, C, D, E, F ở câu a. Tìm hệ số góc của d. Lời giải.
a) Dựa vào đồ thị ta có A(20; 10), B(22; 11), C(24; 12), D(26; 13), E(28; 14), F (20; 15).
Suy ra xA < xB < xC < xD < xE < xF ; yA < yB < yC < yD < yE < yF .
b) Vì đường thẳng d đi qua A(20; 10) nên ta thay x = 20, y = 10 vào phương trình y = mx suy ra 20 · m = 1 10 ⇒ m = . 2 1
Vậy hệ số góc của đường thẳng d là m = . 2 □
c Bài 30. Một xe khách khởi hành từ bến xe phía Nam bưu điện thành phố Huế để đi vào thành phố Quy
Nhơn với tốc độ 50 km/h. Thành Phố Bến xe Bưu điện Quy Nhơn thành phố Huế Hình 7
a) Cho biết bến xe cách bưu điện thành phố Huế 4 km. Sau x giờ, xe khách cách bưu điện thành phố Huế y (km). Tính y theo x.
b) Tìm hệ số góc của đường thẳng là đồ thị của hàm số y ở câu a. Lời giải.
a) Vì ban đầu xe khách cách bưu điện là 4 km nên ta có phương trình y theo x là y = 4 + 50x (km).
b) hệ số góc của đồ thị hàm số y = 50x + 4 là a = 50. □
c Bài 31. Một người bắt đầu mở một vòi nước vào một cái bể đã chứa sẵn 3 m3 nước, mỗi giờ chảy được 1 m3.
a) Tính thể tích y m3 của nước có trong bể sau x giờ.
b) Vẽ đồ thị của hàm số y theo biến số x. 75/119 75/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 76
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Lời giải.
a) Vì ban đầu bể chứa sẵn 3 m3 và mỗi giờ chảy được 1 m3 nên ta có thể tích nước có trong bể sau x giờ là y = x + 3 (m3). b) x 0 1 Bảng giá trị y y 3 4 3
Đồ thị hàm số đi qua các điểm 4 + x = 3 y 2 1 O −4 −3 −2 −1 1 2 3 4 x −1 −2 −3 −4 □ 76/119 76/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 77
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO LUYỆN TẬP CHUNG A HÀM SỐ BẬC NHẤT
c Bài 1. Trong các hàm số sau, hàm số nào là hàm số bậc nhất? a) y = −3x. b) y = x − 99. c) y = 6 − 0x. √ √ √ Ä ä d) y = 2 + 3 x − 5. e) y = 2 · x − 1. f) y = 3(1 − x) − x. 2 1 x + 4 x 1 g) y = x − . h) y = . i) y = − . −3 2 −3 5 5 √ 1 5 1 j) y = x. k) y = 3 − √ x. l) y = x + . 6 − 3 x 2 6 x − 3 m) y = . n) y = − 3. o) y = . 2x + 1 x x + 2 2x − 5 x p) y = √ . q) y = . r) y = 3 − (−3x). 5 x − 1 Lời giải.
Ta có các hàm số bậc nhất: √ √ Ä ä a) y = −3x. b) y = x − 99. c) y = 2 + 3 x − 5. √ 2 1 d) y = 2 · x − 1. e) y = 3(1 − x) − x. f) y = x − . −3 2 x + 4 x 1 1 g) y = . h) y = − . i) y = x. −3 5 5 6 √5 2x − 5 j) y = 3 − √ x. k) y = √ . l) y = 3 − (−3x). − 3 5 □
c Bài 2. Cho hàm số y = f (x) = (2a − 3)x + x + 4.
a) Tìm hệ số a để hàm số y = f (x) là hàm số bậc nhất.
b) Tìm hệ số a biết f (2) = 3. Lời giải.
a) Ta có: y = f (x) = (2a − 3)x + x + 4 = (2a − 2)x + 4.
Để y = f (x) là hàm số bậc nhất thì 2a − 2 ̸= 0 ⇔ a ̸= 1. 3
b) Ta có f (2) = 3 ⇔ 3 = (2a − 2) · 2 + 4 ⇔ a = . 4 □
c Bài 3. Cho hàm số bậc nhất y = (a + 1)x + 5 với a là một số cho trước và a ̸= −1.
a) Tìm a để đồ thị hàm số đi qua điểm A(5; 2).
b) Tìm a để đồ thị hàm số đi qua điểm B(3; 6). Lời giải. 77/119 77/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 78
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO 8
a) Đồ thị hàm số đi qua điểm A(5; 2) ⇒ 2 = (a + 1) · 5 + 5 ⇔ a = − . 5 2
b) Đồ thị hàm số đi qua điểm B(3; 6) ⇒ 6 = (a + 1) · 3 + 5 ⇔ a = − . 3 □
c Bài 4. Cho hàm số bậc nhất y = (m − 3)x.
a) Xác định hệ số a, b của hàm số trên.
b) Xác định m để đồ thị hàm số đi qua A(1; 2).
c) Xác định m để đồ thị hàm số đi qua B(1; −2). Lời giải.
a) Hàm số y = (m − 3)x có hệ số a = m − 3, b = 0.
b) Đồ thị hàm số đi qua A(1; 2) ⇒ 2 = (m − 3) · 1 ⇔ m = 5.
c) Đồ thị hàm số đi qua B(1; −2) ⇒ −2 = (m − 3) · 1 ⇔ m = 1. □
c Bài 5. Cho hàm số y = f (x) = (6 − 3m)x + m − 6. a) Tìm m để f (2) = 0.
b) Biết f (−1) = 8. Xác định hệ số a, b của hàm số trên. Lời giải. 6
a) Ta có f (2) = 0 ⇒ 0 = (6 − 3m) · 2 + m − 6 ⇔ m = . 5
b) Với f (−1) = 8, ta có 8 = (6 − 3m) · (−1) + m − 6 ⇔ m = 5.
Khi đó y = f (x) = −9x − 1. Hàm số có hệ số a = −9, b = −1. □
c Bài 6. Cho hàm số y = (3 − 2m)x − 1.
a) Xác định m để đồ thị hàm số đi qua điểm A(−2; −3).
b) Vẽ đồ thị hàm số với giá trị m vừa tìm được. Lời giải.
a) Đồ thị hàm số đi qua điểm A(−2; −3) ⇒ −3 = (3 − 2m) · (−2) − 1 ⇔ m = 1.
b) Với m = 1, ta có y = f (x) = x − 1.
Vẽ đồ thị của hàm số y = x − 1. y
Cho x = 0 thì y = −1, ta được giao điểm của đồ thị với trục Oy là A(0; −1).
Cho y = 0 thì x = 1, ta được giao điểm của đồ thị với trục Ox là B (1; 0).
Đồ thị hàm số y = x − 1 là đường thẳng AB. (Hình bên) O B 1 x A −1 □ 78/119 78/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 79
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 7. Cho hàm số y = (a − 1)x + a. Xác định a để đồ thị hàm số cắt trục tung tại điểm có tung độ 2. Lời giải.
Đồ thị hàm số cắt trục tung tại điểm có tung độ 2 nên đi qua điểm A(0; 2).
Thay tọa độ điểm A(0; 2) vào hàm số ta được: 2 = (a − 1) · 0 + a ⇔ a = 2. □
c Bài 8. Cho hàm số y = (a − 1)x + a. Xác định a để đồ thị hàm số cắt trục hoành tại điểm có hoành độ −3. Lời giải.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ −3 nên đi qua điểm A(−3; 0). 3
Thay tọa độ điểm A(−3; 0) vào hàm số ta được: 0 = (a − 1) · (−3) + a ⇔ a = . □ 2
c Bài 9. Cho hàm số y = 2x + b. Tìm b trong các trường hợp sau:
a) Đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng −3.
b) Đồ thị của hàm số đi qua điểm A(1; 5). Lời giải.
a) Đồ thị hàm số cắt trục tung tại điểm có tung độ −3 nên đi qua điểm A(0; −3),
Thay tọa độ A(0; −3) vào hàm số ta được −3 = 2 · 0 + b ⇔ b = −3.
b) Thay tọa độ điểm A(1; 5) vào hàm số ta được 5 = 2 · 1 + b ⇔ b = 3 □
c Bài 10. Cho hàm số bậc nhất y = (k − 2)x + k2 − 2k.
a) Vẽ đồ thị hàm số khi k = 3.
b) Tìm k để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2. Lời giải.
a) Khi k = 3 hàm số trở thành y = x + 3.
Vẽ đồ thị của hàm số y = x + 3. y
Cho x = 0 ⇒ y = 3. Đồ thị hàm số đi qua điểm A(0; 3).
Cho y = 0 ⇒ x = −3. Đồ thị hàm số đi qua điểm B(−3; 0).
Đồ thị hàm số y = x + 3 là đường thẳng AB. (Hình bên) A 3 −3 O x B
b) Hàm số đã cho là hàm số bậc nhất khi k − 2 ̸= 0 ⇔ k ̸= 2.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ 2 nên đi qua điểm M (2; 0).
Thay tọa độ M (2; 0) vào hàm số ta được 0 = (k − 2) · 2 + k2 − 2k ⇔ k2 = 4 ⇔ k = ±2.
Kết hợp với điều kiện k ̸= 2, suy ra k = −2. □
c Bài 11. Cho hàm số bậc nhất y = m2 + 1 x + m + 2 với m là tham số.
a) Vẽ đồ thị hàm số khi m = 1.
b) Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng −3. 79/119 79/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 80
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Lời giải.
a) Khi m = 1 thì hàm số trở thành y = 2x + 3.
Vẽ đồ thị của hàm số y = 2x + 3. y
Cho x = 0 ⇒ y = 3. Đồ thị hàm số đi qua điểm M (0; 3).
Cho y = 1 ⇒ x = −1. Đồ thị hàm số đi qua điểm N (−1; 1).
Đồ thị hàm số y = 2x + 3 là đường thẳng M N . (Hình bên) M 3 N 1 −1 x O
b) Đồ thị hàm số cắt trục tung tại điểm có tung độ −3 nên đi qua điểm A(0; −3).
Thay toạ độ điểm A vào hàm số ta được −3 = m + 2 ⇔ m = −5. □
c Bài 12. Cho hàm số y = ax + b.
a) Xác định a, b biết đồ thị hàm số đi qua A(2; 5) và cắt trục tung tại điểm có tung độ là 3.
b) Vẽ đồ thị hàm số với a, b vừa tìm được. Lời giải.
a) Đồ thị hàm số cắt trục tung tại điểm có tung độ 3 nên đi qua điểm M (0; 3).
Thay toạ độ điểm M vào hàm số ta được 3 = a · 0 + b ⇔ b = 3.
Khi đó hàm số trở thành y = ax + 3.
Thay toạ độ điểm A(2; 5) vào hàm số ta được 5 = a · 2 + 3 ⇔ a = 1. Vậy a = 1, b = 3.
b) Với a = 1, b = 3 thì hàm số là y = x + 3.
Vẽ đồ thị của hàm số y = x + 3. y
Cho x = 0 ⇒ y = 3. Đồ thị hàm số đi qua điểm A(0; 3).
Cho y = 0 ⇒ x = −3. Đồ thị hàm số đi qua điểm B(−3; 0).
Đồ thị hàm số y = x + 3 là đường thẳng AB. (Hình bên) A 3 −3 O x B □
c Bài 13. Vẽ đồ thị hàm số y = 3x − 4. Lời giải.
Cho x = 0 thì y = −4, ta được giao điểm của đồ thị với trục Oy là P (0; −4). y 4 Å 4 ã Cho y = 0 thì x =
, ta được giao điểm của đồ thị với trục Ox là Q ; 0 . Q 3 3 4 x O
Đồ thị hàm số y = 3x − 4 là đường thẳng P Q. (Hình bên) 3 P −4 □ 80/119 80/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 81
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 14. Vẽ đồ thị hàm số y = 2x − 3. Lời giải.
Cho x = 0 thì y = −3, ta được giao điểm của đồ thị với trục Oy là A(0; −3). y 3 Å 3 ã Cho y = 0 thì x =
, ta được giao điểm của đồ thị với trục Ox là B ; 0 . 2 2 B
Đồ thị hàm số y = 2x − 3 là đường thẳng AB. (Hình bên) O 3 x 2 A −3 □
c Bài 15. Vẽ đồ thị hàm số y = 5x − 3. Lời giải.
Cho x = 0 thì y = −3, ta được giao điểm của đồ thị với trục Oy là M (0; −3). y 3 Å 3 ã Cho y = 0 thì x =
, ta được giao điểm của đồ thị với trục Ox là N ; 0 . 5 5
Đồ thị hàm số y = 5x − 3 là đường thẳng M N . (Hình bên) N 3 x O 5 M −3 □
c Bài 16. Vẽ đồ thị hàm số y = −3x + 2. Lời giải.
Cho x = 0 thì y = 2, ta được giao điểm của đồ thị với trục Oy là C(0; 2). y
Cho x = 1 thì y = −1. Đồ thị hàm số đi qua điểm D(1; −1).
Đồ thị hàm số y = −3x + 2 là đường thẳng CD. (Hình bên) C 2 O 1 x −1 D □
c Bài 17. Vẽ đồ thị hàm số y = −3x + 4. Lời giải. 81/119 81/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 82
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Cho x = 0 thì y = 2, ta được giao điểm của đồ thị với trục Oy là H(0; 4). y
Cho x = 1 thì y = 1. Đồ thị hàm số đi qua điểm K(1; 1).
Đồ thị hàm số y = −3x + 4 là đường thẳng HK. (Hình bên) H 4 1 K 1 x O □ A B
TÌM HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
c Bài 18. Tìm hệ số góc của đường thẳng (d) : y = 2x − 5. Lời giải.
Hệ số góc của đường thẳng (d) : y = 2x − 5 là a = 2. □
c Bài 19. Tìm hệ số góc của đường thẳng (d) : y = −3x − 7. Lời giải.
Hệ số góc của đường thẳng (d) : y = −3x − 7 là a = −3 □
c Bài 20. Tìm hệ số góc của đường thẳng (d) : y = ax + 3 biết (d) đi qua điểm A(2; 6). Lời giải. 3
Đường thẳng (d) : y = ax + 3 đi qua điểm A(2; 6) nên 6 = a.2 + 3 ⇔ a = . 2 3
Vậy hệ số góc của đường thẳng (d) là a = . □ 2
c Bài 21. Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2; 1). Lời giải.
Đường thẳng đi qua gốc tọa độ có dạng y = ax. 1
Do đường thẳng đi qua điểm A(2; 1) nên 1 = a.2 ⇔ a = . 2 1
Vậy hệ số góc của đường thẳng trên là a = . □ 2
c Bài 22. Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm B(1; −2). Lời giải.
Đường thẳng đi qua gốc tọa độ có dạng y = ax.
Do đường thẳng đi qua điểm B(1; −2) nên −2 = a.1 ⇔ a = −2.
Vậy hệ số góc của đường thẳng trên là a = −2. □
c Bài 23. Tìm giá trị của b để đường thẳng (d) : y = ax + b đi qua điểm A(2; 5) và có hệ số góc bằng −3. Lời giải.
Đường thẳng (d) : y = ax + b có hệ số góc bằng −3 nên a = −3.
Mặt khác (d) đi qua điểm A(2; 5) nên ta được 5 = −3.2 + b ⇔ b = 11. □ 82/119 82/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 83
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 24. Cho đường thẳng y = (1 − 4m)x + m − 2.
a) Tìm m để đồ thị hàm số tạo với trục Ox một góc nhọn.
b) Tìm m để đồ thị hàm số tạo với trục Ox một góc tù. Lời giải. 1
a) Để đồ thị hàm số tạo với trục Ox một góc nhọn thì 1 − 4m > 0 ⇔ m < . 4 1
b) Để đồ thị hàm số tạo với trục Ox một góc tù thì 1 − 4m < 0 ⇔ m > . 4 □
c Bài 25. Cho đường thẳng y = (2m − 1)x + m2 + 2.
a) Tìm m để đồ thị hàm số tạo với trục Ox một góc nhọn.
b) Tìm m để đồ thị hàm số tạo với trục Ox một góc tù. Lời giải. 1
a) Để đồ thị hàm số tạo với trục Ox một góc nhọn thì 2m − 1 > 0 ⇔ m > . 2 1
b) Để đồ thị hàm số tạo với trục Ox một góc tù thì 2m − 1 < 0 ⇔ m < . 2 □ A C
XÁC ĐỊNH VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG
c Bài 26. Cho các đường thẳng sau: 3 3 1 (d1) : y = x + 2; (d2) : y = x − 1; (d3) : y = x − 3; 2 2 2 1 (d4) : y = x − 3; (d5) : y = x + 3; (d6) : y = x + 2. 2
a) Chỉ ra các cặp đường thẳng song song.
b) Chỉ ra vị trí tương đối của (d2) và (d5). Lời giải.
a) Các cặp đường thẳng song song là: (d1)//(d2); (d3)//(d5); (d4)//(d6).
b) (d2) và (d5) có hệ số góc khác nhau nên chúng cắt nhau. □
c Bài 27. Cho các đường thẳng sau: (d1) : y = 2x + 1; (d2) : y = 5 + 2x; (d3) : y = 3 − 2x; x + 3 −3 1 (d4) : y = ; (d5) : y = x + 4; (d6) : y = x − 9. 2 2 2
a) Chỉ ra các cặp đường thẳng song song.
b) Đường thẳng nào cắt đường thẳng (d5)? 83/119 83/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 84
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Lời giải.
a) Các cặp đường thẳng song song là (d1)//(d2); (d4)//(d6).
b) Tất cả các đường thẳng còn lại đều cắt đường thẳng (d5). □
c Bài 28. Tìm các giá trị của tham số m để các cặp đường thẳng sau song song với nhau.
a) (d) : y = mx − 7 và (d′) : y = 2x với m ̸= 0 ;
b) (d) : y = (m + 2)x + 4 và (d′) : y = x − 3 với m ̸= −2;
c) (d) : y = (1 − m2)x + 2 và (d′) : y = −3x − m với m ̸= ±1; ß 2 ™
d) (d) : y = (5m − 2)x − 1 và (d′) : y = m(m + 2)x + 2 với m ̸= 0; −2; ; 5 √ √ ¶ ©
e) (d) : y = (2 − m2)x + m − 5 và (d′) : y = mx + 3m − 7 với m ̸= 2; − 2; 0 ;
f) (d) : y = (m − 1)x + 2 và (d′) : y = (3 − m)x + 1 với m ̸= {1; 3};
g) (d) : y = (m2 + m)x + 2 và (d′) : y = (m + 1)x − m với m ̸= {0; 1};
h) (d) : y = mx + m − 2 và (d′) : y = (5 − m)x + 4 − m với m ̸= {0; 5}. Lời giải.
a) Hai đường thẳng đã cho song song với nhau khi m = 2.
Giá trị này thỏa mãn điều kiện m ̸= 0.
Vậy giá trị m cần tìm là m = 2.
b) Hai đường thẳng đã cho song song với nhau khi m + 2 = 1, tức là m = −1.
Giá trị này thỏa mãn điều kiện m ̸= −2.
Vậy giá trị m cần tìm là m = −1. ®1 − m2 = −3
c) Hai đường thẳng song song với nhau khi ⇔ m = 2. 2 ̸= −m
Giá trị này thỏa mãn điều kiện m ̸= ±1.
Vậy giá trị m cần tìm là m = 2. ñm = 1
d) Hai đường thẳng song song với nhau khi 5m − 2 = m(m + 2) ⇔ m = 2.
Hai giá trị này thỏa mãn điều kiện đã cho. Vậy hai giá trị m cần tìm là m = 1 hoặc m = 2. ®2 − m2 = m
e) Hai đường thẳng song song với nhau khi ⇔ m = −2. m − 5 ̸= 3m − 7
Giá trị này thỏa mãn điều kiện đã cho. Vậy giá trị m cần tìm là m = −2.
f) Hai đường thẳng song song với nhau khi m − 1 = 3 − m ⇔ m = 2.
Giá trị này thỏa mãn điều kiện đã cho. Vậy giá trị m cần tìm là m = 2. ®m2 + m = m + 1
g) Hai đường thẳng song song với nhau khi ⇔ m = ±1. 2 ̸= −m
Kết hợp với điều kiện đã cho ta được một giá trị của m thỏa mãn là m = −1. ®m = 5 − m 5
h) Hai đường thẳng song song với nhau khi ⇔ m = . m − 2 ̸= 4 − m 2 5
Giá trị này thỏa mãn điều kiện đã cho. Vậy giá trị m cần tìm là m = . 2 □ 84/119 84/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 85
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 29. Cho đường thẳng (d) : y = 2mx + 3 và (d′) : y = (m + 1)x + 2. Tìm m để:
a) (d) và (d′) là hai đường thẳng cắt nhau.
b) (d) và (d′) là hai đường thẳng song song. Lời giải.
a) (d) và (d′) cắt nhau khi 2m ̸= m + 1, tức là m ̸= 1.
b) (d) và (d′) song song với nhau khi 2m = m + 1, tức là m = 1. □
c Bài 30. Cho đường thẳng (d) : y = mx + 3 và (d′) : y = (2m + 1)x − 5. Tìm m để:
a) (d) và (d′) là hai đường thẳng cắt nhau.
b) (d) và (d′) là hai đường thẳng song song. Lời giải.
a) (d) và (d′) cắt nhau khi m ̸= 2m + 1, tức là m ̸= −1.
b) (d) và (d′) song song với nhau khi m = 2m + 1, tức là m = −1. □
c Bài 31. Cho đường thẳng (d) : y = (m − 2)x − 3 và (d′) : y = 2x − (m − 1). Tìm m để:
a) (d) và (d′) là hai đường thẳng cắt nhau.
b) (d) và (d′) là hai đường thẳng song song.
c) (d) và (d′) là hai đường thẳng trùng nhau. Lời giải.
a) (d) và (d′) là hai đường thẳng cắt nhau khi m − 2 ̸= 2 ⇔ m ̸= 4. ®m − 2 = 2 ®m = 4
b) (d) và (d′) là hai đường thẳng song song khi ⇔ − 3 ̸= −(m − 1) m ̸= 4.
Vậy không có giá trị nào của m thỏa mãn để (d) và (d′) song song với nhau. ®m − 2 = 2 ®m = 4
c) (d) và (d′) là hai đường thẳng trùng nhau ⇔ ⇔ m = 4. − 3 = −(m − 1) m = 4
Vậy giá trị m cần tìm là m = 4. □
c Bài 32. Cho đường thẳng (d) : y = 2x + 3m và (d′) : y = (2m + 1)x + 2m − 3 (với m là tham số). Tìm m để:
a) (d) và (d′) là hai đường thẳng cắt nhau.
b) (d) và (d′) là hai đường thẳng song song.
c) (d) và (d′) là hai đường thẳng trùng nhau. Lời giải. 1
a) (d) và (d′) là hai đường thẳng cắt nhau khi 2m + 1 ̸= 2 ⇔ m ̸= . 2 85/119 85/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 86
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO ®2 = 2m + 1 1
b) (d) và (d′) là hai đường thẳng song song khi ⇔ m = . 3m ̸= 2m − 3 2 1 ®2 = 2m + 1 m =
c) (d) và (d′) là hai đường thẳng trùng nhau khi ⇔ 2 3m = 2m − 3 m = −3.
Vậy không có giá trị nào của m thỏa mãn. □
c Bài 33. Cho đường thẳng (d) : y = (m + 1)x + 3 và (d′) : y = (3 − 2m)x + 1 (với m là tham số). Tìm m để:
a) (d) và (d′) là hai đường thẳng cắt nhau.
b) (d) và (d′) là hai đường thẳng song song.
c) (d) và (d′) là hai đường thẳng trùng nhau. Lời giải. 2
a) (d) và (d′) là hai đường thẳng cắt nhau khi m + 1 ̸= 3 − 2m ⇔ m ̸= . 3 2
b) (d) và (d′) là hai đường thẳng song song khi m + 1 = 3 − 2m ⇔ m = . 3 ®m + 1 = 3 − 2m
c) (d) và (d′) là hai đường thẳng trùng nhau khi 3 = 1.
Vậy không có giá trị nào của m thỏa mãn. □
c Bài 34. Cho đường thẳng (d) : y = ax + 2. Tìm a để đường thẳng (d):
a) cắt đường thẳng y = 4x − 5.
b) song song với đường thẳng y = −3x + 1. Lời giải.
a) Đường thẳng (d) : y = ax + 2 cắt đường thẳng y = 4x − 5 khi a ̸= 4.
b) Đường thẳng (d) : y = ax + 2 song song với đường thẳng y = −3x + 1 khi a = −3. □
c Bài 35. Cho đường thẳng (d) : y = (m + 3)x + m + 1 và (d′) : y = (2 − m)x − m.
a) Tìm m để (d) và (d′) song song.
b) Chứng minh khi m = −1 thì (d) cắt (d′). Lời giải. 1 ®m + 3 = 2 − m m = −
a) (d) và (d′) song song với nhau khi ⇔ 2 m + 1 ̸= −m 1 m ̸= − . 2
Vậy không có giá trị nào của m thỏa mãn.
b) Khi m = −1 thì (d) : y = 2x cắt (d′) : y = 3x + 1. Do đó (d) và (d′) là hai đường thẳng cắt nhau. □ 86/119 86/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 87
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 36. Cho đường thẳng (d) : y = (m + 6)x + 2 và (d′) : y = m(3m + 4)x − 5.
a) Tìm m để (d) và (d′) song song.
b) Chứng minh khi m = −2 thì (d) song song (d′). Lời giải. ñm = −2
a) (d) và (d′) song song với nhau khi m + 6 = m(3m + 4) ⇔ m = 1.
b) Khi m = −2 thì (d) : y = 4x + 2, (d′) : y = 4x − 5 nên (d) và (d′) song song với nhau. □
c Bài 37. Tìm a, b để đường thẳng (d) : y = ax + b đi qua điểm A(2; 1) và song song với đường thẳng (d′) : y = 3x − 1. Lời giải.
Vì (d) song song với (d′) nên a = 3.
Vì đường thẳng (d) : y = 3x + b đi qua điểm A(2; 1) nên 1 = 3.2 + b, suy ra b = −5.
Khi đó (d) : y = 3x − 5 song song với (d′) : y = 3x − 1. Vậy a = 3, b = −5. □
c Bài 38. Tìm a, b để đường thẳng (d) : y = ax + b đi qua điểm A(4; −5) và song song với đường thẳng (d′) : y = 3x + 1. Lời giải.
Vì (d) song song với (d′) nên a = 3.
Vì đường thẳng (d) : y = 3x + b đi qua điểm A(4; −5) nên −5 = 3.4 + b, suy ra b = −17.
Khi đó (d) : y = 3x − 17 song song với (d′) : y = 3x + 1. Vậy a = 3, b = −17. □
c Bài 39. Tìm a, b để đường thẳng (d) : y = ax + b đi qua điểm A(−4; 5) và song song với đường thẳng (d′) : y = 2x + 1. Lời giải.
Vì (d) song song với (d′) nên a = 2.
Vì đường thẳng (d) : y = 2x + b đi qua điểm A(−4; 5) nên 5 = 2.(−4) + b, suy ra b = 13.
Khi đó (d) : y = 2x + 13 song song với (d′) : y = 2x + 1. Vậy a = 2, b = 13. □
c Bài 40. Tìm a, b để đường thẳng (d) : y = ax + b đi qua điểm A(1; −2) và song song với đường thẳng (d′) : y = −x − 2. Lời giải.
Vì (d) song song với (d′) nên a = −1.
Vì đường thẳng (d) : y = −x + b đi qua điểm A(1; −2) nên −2 = −1 + b, suy ra b = −1.
Khi đó (d) : y = −x − 1 song song với (d′) : y = −x − 2. Vậy a = −1, b = −1. □
c Bài 41. Tìm a, b để đường thẳng (d) : y = ax + b đi qua điểm A(1; −8) và song song với đường thẳng (d′) : y = −3x + 9. Lời giải. 87/119 87/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 88
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Vì (d) song song với (d′) nên a = −3.
Vì đường thẳng (d) : y = −3x + b đi qua điểm A(1; −8) nên −8 = −3.1 + b, suy ra b = −5.
Khi đó (d) : y = −3x − 5 song song với (d′) : y = −3x + 9. Vậy a = −3, b = −5. □
c Bài 42. Xác định hàm số (d) : y = ax + b trong các trường hợp sau:
a) Hệ số góc bằng 3 và đồ thị hàm số đi qua điểm A(2; 2).
b) Đồ thị hàm số đi qua điểm A(1; 5) và song song với đường thẳng y = −3x. Lời giải.
a) Đường thẳng (d) : y = ax + b có hệ số góc bằng 3 suy ra a = 3. Khi đó (d) : y = 3x + b.
Đồ thị hàm số đi qua điểm A(2; 2) nên 2 = 3.2 + b, suy ra b = −4.
Vậy hàm số cần tìm là y = 3x − 4.
b) Vì đường thẳng (d) : y = ax + b song song với đường thẳng y = −3x nên a = −3. Khi đó (d) : y = −3x + b.
Đồ thị hàm số đi qua điểm A(1; 5) nên 5 = −3.1 + b, suy ra b = 8.
Vậy hàm số cần tìm là y = −3x + 8. □
c Bài 43. Cho đường thẳng (d) : y = −3x và đường thẳng (d′) : y = x + 2.
a) Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ.
b) Tìm a, b để đường thẳng (d′′) : y = ax + b đi qua điểm A(−1; 3) và song song với (d′). Lời giải. a)
Đường thẳng (d) : y = 3x đi qua gốc tọa độ O(0; 0) và điểm P (1; 3). y
Đường thẳng (d′) : y = x + 2 cắt trục hoành tại điểm M (−2; 0) và cắt trục tung tại điểm N (0; 2). 3 P N 2 M O x −2 1 (d′) (d)
b) Vì đường thẳng (d′′) : y = ax + b song song với đường thẳng (d′) : y = x + 2 nên a = 1. Khi đó (d) : y = x + b.
Đồ thị hàm số đi qua điểm A(−1; 3) nên 3 = −1 + b, suy ra b = 4.
Vậy hàm số cần tìm là y = x + 4. □
c Bài 44. Xác định hàm số y = ax + b trong các trường hợp sau:
a) Hệ số góc bằng 3 và đồ thị hàm số cắt trục tung tại điểm có tung độ bằng −2.
b) Hệ số góc bằng −5 và đồ thị hàm số đi qua điểm A(−2; 3).
c) Đồ thị hàm số đi qua điểm B(1; 7) và song song với đường thẳng y = 7x. 88/119 88/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 89
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Lời giải.
a) Đường thẳng y = ax + b có hệ số góc bằng 3 suy ra a = 3. Khi đó y = 3x + b.
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng −2 nên đi qua điểm M (0; −2).
Suy ra −2 = 3.0 + b ⇔ b = −2. Vậy y = 3x − 2.
b) Đường thẳng y = ax + b có hệ số góc bằng −5 suy ra a = −5. Khi đó y = −5x + b.
Đồ thị hàm số đi qua điểm A(−2; 3) nên 3 = −5.(−2) + b, suy ra b = −7. Vậy y = −5x − 7.
c) Đường thẳng y = ax + b song song với đường thẳng y = 7x suy ra a = 7 và b ̸= 0. Khi đó y = 7x + b.
Đồ thị hàm số đi qua điểm B(1; 7) nên 7 = 7.1 + b, suy ra b = 0 (loại).
Vậy không tồn tại hàm số thỏa mãn. □
c Bài 45. Cho hàm số (d) : y = (m − 2)x + 3.
a) Xác định m để (d) đi qua điểm A(1; −1). Vẽ đồ thị hàm số với m vừa tìm được.
b) Tìm hàm số bậc nhất có đồ thị đi qua điểm B(−2; 2) và song song với đường thẳng (d). Lời giải. a)
Đường thẳng (d) : y = (m − 2)x + 3 đi qua điểm A(1; −1) nên −1 = (m − 2).1 + 3, suy y ra m = −2. Khi đó (d) : y = −4x + 3. B 3
Theo giả thiết, đồ thị hàm số đi qua điểm A(1; −1).
Cho x = 0 ⇔ y = 3 suy ra đồ thị hàm số đi qua điểm B(0; 3).
Đường thẳng đi qua hai điểm A, B là đồ thị của hàm số y = −4x + 3 (hình vẽ bên). O 1 x −1 A
b) Hàm số bậc nhất có dạng y = ax + b.
Do đồ thị của hàm số trên song song với đường thẳng (d) : y = −4x + 3 nên a = −4 và b ̸= 3.
Khi đó hàm số có dạng y = −4x + b.
Đồ thị hàm số đi qua điểm B(−2; 2) nên 2 = −4.(−2) + b ⇒ b = −6.
Vậy hàm số cần tìm là y = −4x − 6. □ 3
c Bài 46. Cho hàm số (d) : y = x và (d′) : y = 3x − 3. 2
a) Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ.
b) Tìm a, b để đường thẳng (∆) : y = ax + b song song với (d) và cắt trục hoành tại điểm có hoành độ bằng −6. Lời giải. a) 89/119 89/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 90
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Cho x = 0 ⇒ y = 0 nên đường thẳng (d) đi qua gốc tọa độ O. y
Cho x = 2 ⇒ y = 3 nên đường thẳng (d) đi qua điểm B(2; 3). 3 3 B
Đường thẳng đi qua hai điểm O, B là đồ thị hàm số (d) : y = x. 2
Cho y = 0 ⇒ x = 1 nên đường thẳng (d′) đi qua điểm C(1; 0).
Cho x = 0 ⇒ y = −3 nên đường thẳng (d′) đi qua điểm D(0; −3).
Đường thẳng đi qua hai điểm C, D là đồ thị hàm số (d′) : y = 3x − 3. O C x 1 2 (d) −3 D (d′) 3
b) Đường thẳng (∆) : y = ax + b song song với (d) nên a = và b ̸= 0. 2 3 Khi đó (∆) : y = x + b. 2
Do đường thẳng (∆) cắt trục hoành tại điểm có hành độ bằng −6 nên đi qua điểm M (−6; 0). 3 Suy ra 0 = .(−6) + b ⇒ b = 9. 2 3 Vậy (∆) : y = x + 9. 2 □
c Bài 47. Cho hàm số y = (2a − 5)x + a − 2 có đồ thị là đường thẳng (d).
a) Tìm a để đường thẳng (d) cắt trục Oy tại điểm có tung độ bằng 2.
b) Tìm a để đường thẳng (d) song song với đường thẳng y = 3x + 1. Lời giải.
a) Đường thẳng y = (2a − 5)x + a − 2 cắt trục Oy tại điểm có tung độ bằng 2 nên đi qua điểm A(0; 2).
Suy ra 2 = (2a − 5).0 + a − 2 ⇒ a = 4.
b) Đường thẳng y = (2a − 5)x + a − 2 song song với đường thẳng y = 3x + 1 khi ®2a − 5 = 3 ®a = 4 ⇒ ⇒ a = 4. a − 2 ̸= 1 a ̸= 3 □ A D
TÌM m ĐỂ ĐỒ THỊ HÀM SỐ THOẢ MÃN ĐIỀU KIỆN VỀ VỊ TRÍ TƯƠNG ĐỐI
c Bài 48. Cho hàm số (d) : y = (m−1)x+2m−3 với m là tham số. Tìm m để (d) cắt đường thẳng y = 2x+1
tại 1 điểm nằm trên trục tung. Lời giải.
Nhận thấy đường thẳng y = 2x + 1 luôn cắt trục tung tại điểm cố định có tung độ bằng 1.
Hơn nữa, đồ thị hàm số (d) : y = (m − 1)x + 2m − 3 luôn cắt trục tung tại điểm có tung độ là 2m − 3.
Do đó, để hàm số (d) cắt đường thẳng y = 2x + 1 tại một điểm trên trục tung thì 1 = 2m − 3 ⇔ m = 2. □ 90/119 90/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 91
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 49. Cho đường thẳng y = (1 − 4m)x + m − 2. 3
a) Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ . 2 1
b) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ . 2 Lời giải.
a) Đồ thị hàm số y = (1 − 4m)x + m − 2 cắt trục tung tại điểm có tung độ là m − 2. 3 3 7
Để đồ thị hàm số cắt trục tung tại điểm có tung độ thì m − 2 = ⇔ m = . 2 2 2 1 Å 1 ã
b) Đồ thị hàm số y = (1 − 4m)x + m − 2 cắt trục hoành tại điểm có hoành độ là nên đi qua điểm A ; 0 . 2 2 1 Thay tọa độ x =
và y = 0 vào y = (1 − 4m)x + m − 2, ta được 2 1 3 0 = (1 − 4m) · + m − 2 ⇔ m = − . 2 2 □
c Bài 50. Cho hàm số (d) : y = mx + 5 với m là tham số. Tìm giá trị của m để (d) cắt đường thẳng
y = −3x + m + 1 tại một điểm trên trục tung. Lời giải.
Nhận thấy đường thẳng (d) : y = mx + 5 luôn cắt trục tung tại điểm cố định có tung độ bằng 5.
Hơn nữa, đường thẳng y = −3x + m + 1 luôn cắt trục tung tại điểm có tung độ là m + 1.
Do đó, để hàm số (d) cắt đường thẳng y = −3x + m + 1 tại một điểm trên trục tung thì 5 = m + 1 ⇔ m = 4. □
c Bài 51. Cho hàm số bậc nhất y = ax − 4. Xác định a trong các trường hợp sau
a) Đồ thị của hàm số cắt đường thẳng y = 2x − 1 tại điểm có hoành độ bằng 2.
b) Đồ thị của hàm số cắt đường thẳng y = −3x + 2 tại điểm có tung độ bằng 5. Lời giải.
a) Vì đồ thị của hàm số cắt đường thẳng y = 2x − 1 tại điểm có hoành độ bằng 2 nên ta thay x = 2 vào đường
thẳng y = 2x − 1, ta được y = 2 · 2 − 1 = 3. 7
Thay x = 2 và y = 3 vào hàm số y = ax − 4, ta được 3 = a · 2 − 4 ⇔ a = . 2
b) Vì đồ thị của hàm số cắt đường thẳng y = −3x + 2 tại điểm có tung độ bằng 5 nên ta thay y = 5 vào
y = −3x + 2, ta được 5 = −3x + 2 ⇔ x = −1.
Thay x = −1 và y = 5 vào hàm số y = ax − 4, ta được 5 = a · (−1) − 4 ⇔ a = −9. □
c Bài 52. Tìm m để hai đường thẳng
a) (d) : y = 2x + (m − 1) và (d′) : y = 3x − 5 cắt nhau tại 1 điểm thuộc trục hoành.
b) (d) : y = 2x + (3 + m) và (d′) : y = 3x + (5 − m) cắt nhau tại 1 điểm thuộc trục tung. Lời giải. 91/119 91/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 92
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO 5
a) Vì (d) và (d′) cắt nhau tại 1 điểm thuộc trục hoành nên thay y = 0 vào (d′) : y = 3x − 5, ta được x = . 3 Å 5 ã
Do đó (d) và (d′) cắt nhau tại điểm có tọa độ ; 0 . 3 5 Thay x =
và y = 0 vào (d) : y = 2x + (m − 1), ta được 3 5 7 0 = 2 · + m − 1 ⇔ m = − . 3 3 7 Vậy m = −
thỏa mãn yêu cầu bài toán. 3
b) Đường thẳng (d) : y = 2x + (3 + m) luôn cắt trục tung tại điểm có tung độ là 3 + m.
Hơn nữa, đường thẳng (d′) : y = 3x + (5 − m) luôn cắt trục tung tại điểm có tung độ là m − 5.
Do đó để (d) cắt (d′) tại 1 điểm thuộc trục tung thì 3 + m = 5 − m ⇔ m = 1. □
c Bài 53. Cho hàm số (d) : y = (m − 2)x + m với m ̸= 2.
a) Tìm giá trị của m để đường thẳng (d) đi qua A(0; 5).
b) Tìm m để (d) cắt đường thẳng y = 2x + 3 tại 1 điểm trên trục tung. Lời giải.
a) Vì đường thẳng (d) đi qua A(0; 5) nên thay x = 0 và y = 5 vào (d) : y = (m − 2)x + m, ta được 5 = (m − 2) · 0 + m ⇔ m = 5.
b) Đường thẳng y = 2x + 3 luôn cắt trục tung tại điểm cố định có tung độ là 3.
Hơn nữa, đường thẳng (d) : y = (m − 2)x + m luôn cắt trục tung tại điểm có tung độ là m.
Để (d) cắt đường thẳng y = 2x + 3 tại 1 điểm trên trục tung thì m = 3. □
c Bài 54. Cho đường thẳng (d) : y = ax + b. Tìm a, b để (d) song song với đường thẳng y = 2x và cắt trục
hoành tại điểm có hoành độ là 3. Lời giải. Gọi (d′) : y = 2x.
Để (d) ∥ (d′) thì a = 2 và b ̸= 0. Khi đó (d) : y = 2x + b.
Vì (d) cắt trục hoành tại điểm có hoành độ là 3 nên (d) đi qua điểm (3; 0).
Thay x = 3 và y = 0 vào (d) : y = 2x + b, ta được 0 = 2 · 3 + b ⇔ b = −6. Vậy a = 2 và b = −6. □
c Bài 55. Cho hàm số (d) : y = (3 − m)x + m − 1.
a) Tìm m để (d) song song với đồ thị hàm số y = 2x + 3.
b) Tìm m để (d) cắt đường thẳng y = x + 3m − 2 tại điểm trên trục tung. Lời giải.
a) Để (d) song song với đồ thị hàm số y = 2x + 3 thì ®3 − m = 2 ®m = 1 ⇔ ⇔ m = 1. m − 1 ̸= 3 m ̸= 4
b) Đường thẳng (d) luôn cắt trục tung tại điểm có tung độ m − 1.
Hơn nữa, đường thẳng y = x + 3m − 2 luôn cắt trục tung tại điểm có tung độ 3m − 2.
Do đó, để (d) cắt đường thẳng y = x + 3m − 2 tại điểm trên trục tung thì 1 m − 1 = 3m − 2 ⇔ m = . 2 92/119 92/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 93
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO □
c Bài 56. Cho hàm số (d) : y = (m − 3)x + 5 − m.
a) Tìm m để đường thẳng (d) đi qua A(2; 5).
b) Tìm m để (d) cắt đường thẳng y = 2x − 4 tại 1 điểm nằm trên Oy. Lời giải.
a) Để đường thẳng (d) đi qua A(2; 5), thay x = 2 và y = 5 vào (d) : y = (m − 3)x + 5 − m, ta được 5 =
(m − 3) · 2 + 5 − m ⇔ m = 6.
b) Đường thẳng (d) luôn cắt trục Oy tại điểm có tung độ −4.
Hơn nữa, đường thẳng y = 2x − 4 luôn cắt trục Oy tại điểm có tung độ 5 − m.
Do đó, để (d) cắt đường thẳng y = 2x − 4 tại 1 điểm nằm trên Oy thì −4 = 5 − m ⇔ m = 9. □
c Bài 57. Cho hàm số (d) : y = (2 − m)x + 3m − 1.
a) Tìm m để hàm số trên là hàm bậc nhất. Vẽ đồ thị với m = −1.
b) Tìm m để (d) song song với (d′) : y = −x + m − 3.
c) Tìm m để (d) cắt đường thẳng (d′′) : y = −x + 2 tại một điểm thuộc trục tung. Lời giải. y (d)
a) Để hàm số (d) : y = (2 − m)x + 3m − 1 là hàm bậc nhất thì 2 − m ̸= 0 ⇔ m ̸= 2.
Cho x = 0 ⇒ y = −4, đồ thị hàm số đi qua A(0; −4). 1
Cho y = −1 ⇒ x = 1, đồ thị hàm số đi qua B(1; −1). O x
Đường thẳng đi qua hai điểm A, B là độ thị ham số của (d) khi m ̸= 2. Đồ thị −1 B
b) Để (d) song song với (d′) : y = −x + m − 3 thì ®2 − m = −1 ®m = 3 ⇔ ⇔ m = 3. 3m − 1 ̸= m − 3 m ̸= −1 −4 A
c) Đường thẳng (d′′) : y = −x + 2 luôn cắt trục tung tại điểm có tung độ là 2.
Đường thẳng (d) luôn cắt trục tung tại điểm có tung độ là 3m − 1.
Do đó, để (d) cắt đường thẳng (d′′) : y = −x + 2 tại một điểm thuộc trục tung thì 2 = 3m − 1 ⇔ m = 1. □
c Bài 58. Cho hàm số (d) : y = (m + 1)x + 2m và (d′) : y = (2m + 1)x + 3m.
a) Tìm m để đồ thị hai hàm số trên song song với nhau.
b) Tìm m để (d) cắt (d′) tại 1 điểm trên trục hoành. Lời giải. ®m + 1 = 2m + 1 ®m = 0 a) Để (d) ∥ (d′) ⇒ ⇔ . 2m ̸= 3m m ̸= 0
Vậy không có giá trị m thỏa mãn yêu cầu bài toán. 93/119 93/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 94
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO −2m
b) Đường thẳng (d) : y = (m + 1)x + 2m luôn cắt trục hoành tại điểm có hoành độ là . m + 1 −3m
Đường thẳng (d′) : y = (2m + 1)x + 3m luôn cắt trục hoành tại điểm có hoành độ là . 2m + 1
Để (d) cắt (d′) tại 1 điểm trên trục hoành thì − ñ 2m −3m m = 0 = ⇒ m2 − m = 0 ⇒ m + 1 2m + 1 m = 1.
Khi m = 0 thì (d) : y = x và (d′) : y = x, hai đường thẳng trùng nhau nên loại m = 0.
Vậy m = 1 thỏa mãn yêu cầu bài toán. □ 2
c Bài 59. Cho hai đường thẳng (d) : y = 3x − 7 và (d′) : y = x + m. 3
a) Vẽ (d) và (d′) trên cùng một mặt phẳng tọa độ khi m = 2.
b) Tìm m để (d) cắt (d′) tại 1 điểm trên trục hoành. Lời giải. (d) 2 y a) Khi m = 2 thì (d′) : y = x + 2. (d′) 3 D
Vẽ đường thẳng (d) : y = 3x − 7. 4
Cho x = 0 ⇒ y = −7, đồ thị của (d) đi qua A(0; −7).
Cho x = 2 ⇒ y = −1, đồ thị của (d) đi qua B(2; −1).
Đường thẳng đi qua hai điểm A, B là đường thẳng (d). 2 2 C
Vẽ đường thẳng (d′) : y = x + 2. 3
Cho x = 0 ⇒ y = 2, đồ thị của (d′) đi qua C(0; 2). 2
Cho x = 3 ⇒ x = 4, đồ thị của (d′) đi qua D(3; 4). O x 3
Đường thẳng đi qua hai điểm C, D là đường thẳng (d′). −1 B 7
b) Đường thẳng (d) luôn cắt trục hoành tại điểm có hoành độ . 3
Đường thẳng (d′) luôn cắt trục hoành tại điểm có hoành độ −3m . 2
Do đó, để (d) cắt (d′) tại 1 điểm trên trục hoành thì 7 −3m 14 = ⇒ m = − . 3 2 9 −7 A □
c Bài 60. Cho hàm số (d) : y = 2x + 4 và (d′) : y = (m − 2)x + m + 2.
a) Khi m = 0 vẽ (d) và (d′) trên cùng một mặt phẳng tọa độ.
b) Tìm giao điểm (d) và (d′) khi m = 0.
c) Tìm m để (d) song song với (d′).
d) Tìm m để (d) cắt (d′) tại 1 điểm thuộc trục hoành. Lời giải. 94/119 94/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 95
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO a)
Khi m = 0 thì (d′) : y = −2x + 2. y (d)
Vẽ đường thẳng (d) : y = 2x + 4.
Cho x = 0 ⇒ y = 4, đồ thị của (d) đi qua A(0; 4). 4 A
Cho y = 0 ⇒ x = −2, đồ thị của (d) đi qua B(−2; 0).
Đường thẳng đi qua hai điểm A, B là đường thẳng (d).
Vẽ đường thẳng (d′) : y = −2x + 2.
Cho x = 0 ⇒ y = 2, đồ thị của (d′) đi qua C(0; 2). 2 C
Cho y = 0 ⇒ x = 1, đồ thị của (d′) đi qua D(0; 1).
Đường thẳng đi qua hai điểm C, D là đường thẳng (d′). −2 D B O x 1 3 (d′)
b) Khi m = 0 thì phương trình hoành độ giao điểm của (d) và (d′) là 1
2x + 4 = −2x + 2 ⇒ x = − . 2 1 Å 1 ã Thay x = −
vào (d) : y = 2x + 4, ta được y = 2 − + 4 = 3. 2 2 Å 1 ã
Vậy (d) cắt (d′) tại điểm M − ; 3 . 2 ®m − 2 = 2 ®m = 4 c) Để (d) ∥ (d′) ⇔ ⇔ ⇔ m = 4. m + 2 ̸= 4 m ̸= 2.
d) Đường thẳng (d) luôn cắt trục hoành tại điểm cố định có hoành độ −2.m + 2
Đường thẳng (d′) luôn cắt trục hoành tại điểm cố định có hoành độ − . m − 2
Do đó, để (d) cắt (d′) tại 1 điểm trên trục hoành thì m + 2 −2 = − ⇒ m = 6. m − 2 □
c Bài 61. Cho hàm số bậc nhất (d) : y = (m − 1)x − 4 với m ̸= 1.
a) Vẽ đồ thị hàm số khi m = 2.
b) Tìm m để (d) song song với đường thẳng y = −3x + 2.
c) Tìm m để (d) cắt (d′) : y = x − 7 tại một điểm nằm bên trái trục tung. Lời giải. a)
Khi m = 2 thì (d) : y = x − 4. y (d)
Vẽ đường thẳng (d) : y = x − 4. B
Cho x = 0 ⇒ y = −4, đồ thị của (d) đi qua A(0; −4). O x 4
Cho y = 0 ⇒ x = 4, đồ thị của (d) đi qua B(4; 0).
Đường thẳng đi qua hai điểm A, B là đường thẳng (d).
b) Gọi (d′) : y = −3x + 2. ®m − 1 = −3 Để (d) ∥ (d′) ⇔ ⇔ m = −2. − 4 ̸= 2 −4 A 95/119 95/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 96
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c) Xét phương trình hoành độ giao điểm của (d) và (d′) là −3
(m − 1)x − 4 = x − 7 ⇒ x = (m ̸= 2). m − 2
Để (d) cắt (d′) tại tại một điểm nằm bên trái trục tung thì hoành độ giao điểm thỏa mãn −3 ®x < 0 ® ® < 0 m − 2 > 0 m > 2 ⇔ m − 2 ⇔ ⇔ ⇔ m > 2. m − 2 ̸= 0 m ̸= 2 m ̸= 2 m ̸= 2 □
c Bài 62. Cho hai đường thẳng (d) : y = 4x + m và (d′) : y = −3x + 2 − m.
a) Vẽ hai đường thẳng trên cùng một mặt phẳng tọa độ khi m = −4.
b) Tìm tọa độ giao điểm của (d) và (d′) khi m = −4.
c) Tìm m để (d) cắt (d′) tại 1 điểm nằm bên phải trục tung. Lời giải. a)
Khi m = −4 thì (d) : y = 4x − 4 và (d′) : y = −3x + 6. y (d)
Vẽ đường thẳng (d) : y = 4x − 4.
Cho x = 0 ⇒ y = −4, đường thẳng (d) đi qua A(0; −4). 6 C
Cho y = 0 ⇒ x = 1, đường thẳng (d) đi qua B(1; 0).
Đường thẳng đi qua hai điểm A, B là đường thẳng (d).
Vẽ đường thẳng (d′) : y = −3x + 6.
Cho x = 0 ⇒ y = 6, đường thẳng (d′) đi qua C(0; 6).
Cho y = 0 ⇒ x = 2, đường thẳng (d′) đi qua D(2; 0).
Đường thẳng đi qua hai điểm C, D là đường thẳng (d′).
b) Khi m = −4, ta có phương trình hoành độ giao điểm của (d) và (d′) là 10 4x − 4 = −3x + 6 ⇒ x = . 7 B D O x 1 2 10 10 12 Thay x =
vào (d) : y = 4x − 4, ta được y = 4 · − 4 = . 7 7 7 Å 10 12 ã
Vậy khi m = −4 thì (d) cắt (d′) tại điểm có tọa độ là ; . 7 7 (d′) −4 A
c) Xét phương trình hoành độ giao điểm của (d) và (d′) là 2(1 − m)
4x + m = −3x + 2 − m ⇒ x = . 7
Để (d) cắt (d′) tại tại một điểm nằm bên phải trục tung thì x > 0 hay
2(1 − m) > 0 ⇒ 1 − m > 0 ⇒ m < 1. 7 □ 96/119 96/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 97
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 63. Cho hàm số (d) : y = x − 2.
a) Vẽ đường thẳng (d) trên mặt phẳng tọa độ Oxy.
b) Tìm a, b để y = ax + b để đường thẳng này đi qua A(1; −5) và song song với (d).
c) Tìm m để (d′) : y = (m − 3)x + 5 với m ̸= 3 cắt (d) tại một điểm nằm bên phải trục tung. Lời giải. a)
Cho x = 0 ⇒ y = −2, đồ thị của (d) đi qua A(0; −2). y
Cho y = 0 ⇒ x = 2, đồ thị của (d) đi qua B(2; 0).
Đường thẳng đi qua hai điểm A, B là đường thẳng (d). (d) b) Gọi (d B 1) : y = ax + b. ®a = 1 O x 2 Để (d1) ∥ (d) ⇔
. Khi đó (d1) : y = x + b với b ̸= −2. b ̸= −2
Vì (d1) đi qua A(1; −5) nên thay x = 1 và y = −5 vào (d1) : y = x + b, ta được −2 A
−5 = 1 + b ⇒ b = −6 (thỏa mãn). Vậy a = 1 và b = −6.
c) Xét phương trình hoành độ giao điểm của (d) và (d′) là −7
x − 2 = (m − 3)x + 5 ⇒ x = . m − 4
Để (d) cắt (d′) tại tại một điểm nằm bên phải trục tung thì m − 3 ̸= 1 ® m ̸= 4 −7 ⇒ ⇒ m < 4. > 0 m < 4 m − 4 □
c Bài 64. Cho đường thẳng (d) : y = x + 4 và (d′) : y = −2x − 2.
a) Vẽ đồ thị của (d) và (d′) trên cùng một mặt phẳng tọa độ.
b) Tìm a, b để (d′′) : y = ax + b song song với (d) và (d′′) cắt (d′) tại A có hoành độ −3. Lời giải. a)
Vẽ đường thẳng (d) : y = x + 4. y (d)
Cho x = 0 ⇒ y = 4, đồ thị hàm số của (d) đi qua A(0; 4).
Cho y = 0 ⇒ x = −4, đồ thị hàm số của (d) đi qua B(−4; 0). 4 A
Đường thẳng đi qua hai điểm A, B là đồ thị hàm số của (d).
Vẽ đường thẳng (d′) : y = −2x − 2.
Cho x = 0 ⇒ y = −2, đồ thị hàm số của (d′) đi qua C(0; −2).
Cho y = 0 ⇒ x = −1, đồ thị hàm số của (d′) đi qua D(−1; 0).
Đường thẳng đi qua hai điểm C, D là đồ thị hàm số của (d′). B D −4 −1 O x −2 C (d′) 97/119 97/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 98
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO ®a = 1 b) Để d′′ ∥ d ⇔
. Khi đó (d′′) : y = x + b với b ̸= 4. b ̸= 4
Xét phương trình hoành độ giao điểm của (d′′) và (d), ta có x + b = −2x − 2. (1)
Để (d′′) cắt (d) tại A có hoành độ −3 thì
−3 + b = −2 · (−3) − 2 ⇒ b = 7 (thỏa mãn). Vậy a = 1 và b = 7. □ −1
c Bài 65. Cho hàm số (d) : y =
x và hàm số (d′) : y = 2x + 3. 2
a) Vẽ hai hàm số trên cùng một hệ tọa độ Oxy.
b) Tìm a, b để (d′′) : y = ax + b song song với (d) và cắt (d′) tại 1 điểm trên trục tung. Lời giải. a) −1
Vẽ đường thẳng (d) : y = x. 2 y (d′)
Cho x = 0 ⇒ y = 0, đồ thị hàm số của (d) đi qua O(0; 0).
Cho x = 2 ⇒ y = −1, đồ thị hàm số của (d) đi qua A(2; −1). 3 B
Đường thẳng đi qua hai điểm O, A là đồ thị hàm số của (d).
Vẽ đường thẳng (d′) : y = 2x + 3.
Cho x = 0 ⇒ y = 3, đồ thị hàm số của (d′) đi qua B(0; 3). C 1
Cho x = −1 ⇒ y = 1, đồ thị hàm số của (d′) đi qua C(−1; 1). 2
Đường thẳng đi qua hai điểm B, C là đồ thị hàm số của (d′). −1 O x −1 A (d) −1 a = −1 b) Để d′′ ∥ d ⇒ 2 . Khi đó (d′′) : y = x + b với b ̸= 0. 2 b ̸= 0
Mà (d′) luôn cắt trục tung tại điểm có tung độ 3.
Do đó, để (d′′) cắt (d′) tại 1 điểm trên trục tung thì (d′′) cũng cắt trục tung tại điểm có tung độ bằng 3 nên −1
thay x = 0 và y = 3 vào (d′′) : y =
x + b, ta được b = 3 (thỏa mãn). 2 −1 Vậy a = và b = 3. 2 □
c Bài 66. Cho hàm số (d) : y = −2x + 3 và hàm số (d′) : y = x + 1.
a) Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ.
b) Tìm a, b để (d′′) : y = ax + b song song với (d) và cắt trục hoành tại điểm có hoành độ −4. Lời giải. a) 98/119 98/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 99
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Vẽ đường thẳng (d) : y = −2x + 3. y
Cho x = 0 ⇒ y = 3, đồ thị hàm số của (d) đi qua A(0; 3).
Cho x = 2 ⇒ y = −1, đồ thị hàm số của (d) đi qua B(2; −1). (d′) 3 A
Đường thẳng đi qua hai điểm A, B là đồ thị hàm số của (d).
Vẽ đường thẳng (d′) : y = x + 1.
Cho x = 0 ⇒ y = 1, đồ thị hàm số của (d′) đi qua C(0; 1). 1 C
Cho y = 0 ⇒ x = −1, đồ thị hàm số của (d′) đi qua D(−1; 0).
Đường thẳng đi qua hai điểm C, D là đồ thị hàm số của (d′). D 2 −1 O x −1 B (d) ®a = −2 b) Để d′′ ∥ d ⇒
. Khi đó (d′′) : y = −2x + b với b ̸= 3. b ̸= 3
Điểm trên trục hoành có hoành độ −4 có tọa độ là (−4; 0).
Do đó, để (d′′) cắt trục hoành tại điểm có hoành độ bằng −4 thì thay x = −4 và y = 0 vào (d′′) : y = −2x+b,
ta được 0 = −2 · (−4) + b ⇒ b = −8 (thỏa mãn). Vậy a = −2 và b = −8. □
c Bài 67. Cho hàm số (d) : y = 3x − 2 và hàm số (d′) : y = −2x + 3.
a) Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ.
b) Tìm a, b để (d′′) : y = ax + b song song với (d) và cắt (d′) tại điểm có hoành độ bằng 2. Lời giải. a)
Vẽ đường thẳng (d) : y = 3x − 2. y
Cho x = 0 ⇒ y = −2, đồ thị hàm số của (d) đi qua A(0; −2).
Cho x = 1 ⇒ y = 1, đồ thị hàm số của (d) đi qua B(1; 1). 3 C (d)
Đường thẳng đi qua hai điểm A, B là đồ thị hàm số của (d).
Vẽ đường thẳng (d′) : y = −2x + 3.
Cho x = 0 ⇒ y = 3, đồ thị hàm số của (d′) đi qua C(0; 3). 1 B
Cho x = 2 ⇒ y = −1, đồ thị hàm số của (d′) đi qua D(2; −1). 2
Đường thẳng đi qua hai điểm C, D là đồ thị hàm số của (d′). O x 1 −1 D (d′) −2 A ®a = 3 b) Để d′′ ∥ d ⇒
. Khi đó (d′′) : y = 3x + b với b ̸= −2. b ̸= −2
Xét phương trình hoành độ giao điểm của (d′′) và (d′) : − 2x + 3 = 3x + b.
Để (d′′) cắt (d′) tại điểm có hoành độ bằng 2 thì
−2 · 2 + 3 = 3 · 2 + b ⇒ b = −7 (thỏa mãn). Vậy a = 3 và b = −7. □ −1
c Bài 68. Cho hàm số (d) : y = x và (d′) : y = x + 2. 2
a) Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ. 99/119 99/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 100
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
b) Tìm a, b để (d′′) : y = ax + b song song với (d) và cắt (d′) tại 1 điểm có tung độ bằng −3. Lời giải. a) −1
Vẽ đường thẳng (d) : y = x. y 2 (d′)
Cho x = 0 ⇒ y = 0, đồ thị hàm số của (d) đi qua O(0; 0).
Cho x = 2 ⇒ y = −1, đồ thị hàm số của (d) đi qua A(2; −1). 2
Đường thẳng đi qua hai điểm O, A là đồ thị hàm số của (d). B
Vẽ đường thẳng (d′) : y = x + 2.
Cho x = 0 ⇒ y = 2, đồ thị hàm số của (d′) đi qua B(0; 2). C 2
Cho y = 0 ⇒ x = −2, đồ thị hàm số của (d′) đi qua C(−2; 0). −2 O x
Đường thẳng đi qua hai điểm B, C là đồ thị hàm số của (d′). −1 (d) A −1 a = −1 b) Để d′′ ∥ d ⇒ 2 . Khi đó (d′′) : y = x + b với b ̸= 0. 2 b ̸= 0
Thay tung độ y = −3 vào (d′) : − 3 = x + 2 ⇒ x = −5.
Để (d′′) cắt (d′) tại 1 điểm có tung độ bằng −3 thì (d′′) phải đi qua D(−5; −3). −1
Thay x = −5 và y = −3 vào (d′′) : y = x + b, ta được 2 −1 −11 −3 = · (−5) + b ⇒ b = (thỏa mãn). 2 2 −1 −11 Vậy a = và b = . 2 2 □
c Bài 69. Cho hai đường thẳng (d) : y = 2x − 4 và (d′) : y = −3x + 5.
a) Đường thẳng (d) và (d′) có cắt nhau không? Vì sao?
b) Vẽ (d) trên mặt phẳng tọa độ.
c) Tìm a, b để (d′′) : y = ax + b cắt (d) tại một điểm trên trục tung và đi qua A(1; −1). Lời giải. y (d)
a) Đường thẳng (d) có hệ số góc a = 2 khác với hệ số góc a′ = −3 của đường thẳng C
(d′) nên (d) và (d′) cắt nhau. O x 2
b) Vẽ đường thẳng (d) : y = 2x − 4.
Cho x = 0 ⇒ y = −4, đồ thị hàm số của (d) đi qua B(0; −4).
Cho y = 0 ⇒ x = 2, đồ thị hàm số của (d) đi qua C(2; 0).
Đường thẳng đi qua hai điểm B, C là đồ thị hàm số của (d).
c) Vì (d) luôn cắt trục tung tại điểm cố định có tung độ −4. −4 B
Hơn nữa, (d′′) luôn cắt trục tung tại điểm có tung độ b.
Nên để (d′′) cắt (d) tại một điểm trên trục tung thì b = −4. Khi đó (d′′) : y = ax − 4.
Vì (d′′) đi qua A(1; −1) nên thay x = 1 và y = −1 vào (d′′) : y = ax − 4, ta được −1 = a − 4 ⇒ a = 3. Vậy a = 3 và b = −4. □ 100/119 100/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 101
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 70. Cho đường thẳng (d) : y = (3 − m)x − m + 5 với m là tham số. Xác định m để (d)
a) Cắt đường thẳng y = 2mx + 8.
b) Song song với đường thẳng y = 2x − 1.
c) Cắt đường thẳng y = −x + 9 tại điểm có tung độ là 5.
d) Cắt đường thẳng y = −3x + 12 tại 1 điểm trên trục hoành. Lời giải.
a) Để (d) cắt y = 2mx + 8 thì 2m ̸= 3 − m ⇒ m ̸= 1. ®3 − m = 2 ®m = 1
b) Để (d) ∥ y = 2x − 1 thì ⇒ ⇒ m = 1 thỏa mãn. − m + 5 ̸= −1 m ̸= 6
c) Thay y = 5 vào y = −x + 9, ta được 5 = −x + 9 ⇒ x = 4.
Để (d) cắt y = −x + 9 tại điểm có tung độ là 5 thì (d) đi qua A(4; 5).
Thay x = 4 và y = 5 vào (d) : y = (3 − m)x − m + 5, ta được 12
5 = (3 − m) · 4 − m + 5 ⇒ m = . 5
d) Đường thẳng y = −3x + 12 luôn cắt trục hoành tại điểm cố định có hoành độ là 4. m − 5
Đường thẳng (d) luôn cắt trục hoành tại điểm có hoành độ là x = (m ̸= 3). 3 − m
Để (d) cắt y = −3x + 12 tại 1 điểm trên trục hoành thì m − 5 17 = 4 ⇒ m = (thỏa mãn). 3 − m 5 □ 101/119 101/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 102
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO ÔN TẬP CHƯƠNG V A
BÀI TẬP TRẮC NGHIỆM
c Câu 1. Đại lượng y gọi là hàm số của x khi nào?
A Khi mỗi giá trị của x ta luôn xác định được chỉ một giá trị của y.
B Khi mỗi giá trị của x ta phải xác định được 2 giá trị của y.
C Khi hai giá trị của x ta luôn xác định được 3 giá trị của y.
D Khi nhiều giá trị của x ta luôn xác định được chỉ một giá trị của y. Lời giải. Chọn đáp án A □
c Câu 2. Trong mặt phẳng tọa độ, có mấy trục tọa độ A 1. B 2. C 3. D 4. Lời giải. Chọn đáp án B □
c Câu 3. Cho điểm M (x0; y0). Hỏi tọa độ y0 gọi là gì của điểm M ? A Hoành độ. B Tung độ. C Gốc tọa độ. D Giao điểm. Lời giải. Chọn đáp án B □
c Câu 4. Hệ trục tọa độ Oxy chia mặt phẳng tọa độ thành bao nhiêu phần? A 1 phần. B 2 phần. C 3 phần. D 4 phần. Lời giải. Chọn đáp án D □
c Câu 5. Cho hàm số y = f (x) = 2x − 1. Giá trị của f (0) là A f (0) = 0. B f (0) = x. C f (0) = 2. D f (0) = −1. Lời giải. Chọn đáp án D □
c Câu 6. Điểm nằm trên trục hoành sẽ có tung độ là bao nhiêu? A −1. B 1. C 0. D 5. Lời giải. Chọn đáp án C □
c Câu 7. Điểm trong mặt phẳng tọa độ có hoành độ âm và tung độ dương sẽ nằm ở góc phần tư thứ mấy? A I. B II. C III. D IV . Lời giải. Chọn đáp án B □ 102/119 102/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 103
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Câu 8. Cho hàm số y = f (x) = x + 5, điểm nào sau đây thuộc đồ thị hàm số đã cho? A A (0; 3). B (1; 5). C (5; 1). D (2; 7). Lời giải. Chọn đáp án D □
c Câu 9. Điểm A (3; −2) trên mặt phẳng tọa độ, nối điểm A tới gốc O và một điểm B bất kì nằm trên trục
hoành (B ̸= O). Khi đó chiều cao của ∆ABC ứng với đáy BO là A 3. B −2. C 2. D 0. Lời giải. Chọn đáp án C □
c Câu 10. Để đồ thị hàm số y = f (x) = mx + 2 đi qua điểm A (−3; −4) thì giá trị của m là A −3. B 2. C −4. D 0. Lời giải. Chọn đáp án B □
c Câu 11. Hàm số bậc nhất được cho bởi công thức nào sau đây A y = ax + b (a ̸= 0).
B y = ax2 + bx + c (a ̸= 0). C 1 1 y = (a ̸= 0). D y = . ax + b ax Lời giải. Chọn đáp án A □
c Câu 12. Đồ thị của hàm số y = ax + b với a ̸= 0 là
A một đường thẳng.
B một đoạn thẳng. C một đường cong. D một Parabol. Lời giải. Chọn đáp án A □
c Câu 13. Khi b = 0 thì đồ thị của hàm số y = ax + b (a ̸= 0) luôn đi qua điểm nào trong các điểm sau đây? A O(0; 0). B A(1; 1). C M(1; −1). D N(−1; 1). Lời giải. Chọn đáp án A □
c Câu 14. Trong các hàm số sau, hàm số nào là hàm số bậc nhất? A −1 1 6 y = . B y = x − 3. C y = x2 − 1. D y = 5 − . x + 2 2 x Lời giải. Chọn đáp án B □
c Câu 15. Đồ thị của hàm số y = 3x − 1 giao với trục tung tại điểm A có tọa độ là A A(3; −1). B (0; 3). C (−1; 0). D (0; −1). Lời giải. Chọn đáp án D □ 103/119 103/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 104
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO 1
c Câu 16. Đồ thị của hàm số y = x giao với trục hoành tại điểm nào trong các điểm sau đây? 2 A O(0; 0). B A(1; 1). C N(2; −2). D M(2; 1). Lời giải. Chọn đáp án A □
c Câu 17. Cho hàm số y = −2x + 3. Đồ thị của hàm số đi qua điểm nào sau đây? Å ã Å ã Å ã A 1 3 9 (−5; 4). B ; 0 . C ; −3 . D ; −6 . 2 4 2 Lời giải. Chọn đáp án D □
c Câu 18. Cho hàm số bậc nhất y = (a + 1)x + 5 với a + 1 là hệ số của x. Để đồ thị của hàm số đi qua điểm
A(5; 2) thì giá trị của a là A −1 −8 −5 a = . B a = . C a = 5. D a = . 5 5 8 Lời giải. Chọn đáp án B □ x − 4
c Câu 19. Đồ thị của hàm số bậc nhất y =
cắt trục tung tại điểm có tung độ là 5 A 1. B −4. C −4. D 1. 5 5 Lời giải. Chọn đáp án C □
c Câu 20. Hệ số b của đường thẳng y = 2(3x − 5) − 7 là A −7. B −5. C 6. D −17. Lời giải. Chọn đáp án D □
c Câu 21. Hệ số góc của đường thẳng y = ax + b (a ̸= 0) là A b. B a. C −a. D −b. Lời giải. Chọn đáp án B □
c Câu 22. Hai đường thẳng y = ax + b (a ̸= 0) và y = a′x + b′ (a′ ̸= 0) song song với nhau khi nào? A a = a′; b = b′. B a ̸= a′; b = b′.
C a ̸= a′; b ̸= b′. D a = a′; b ̸= b′. Lời giải. Chọn đáp án D □
c Câu 23. Hai đường thẳng y = ax + b (a ̸= 0) và y = a′x + b′ (a′ ̸= 0) có a ̸= a′. Vậy hai đường thẳng này có vị trí như thế nào? A Song song. B Cắt nhau. C Trùng nhau.
D Cả ba đáp án trên đều sai. 104/119 104/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 105
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Lời giải. Chọn đáp án B □
c Câu 24. Gọi α là góc tạo bởi đường thẳng y = 3x − 4 với trục hoành. Khẳng định nào sau đây đúng?
A α là một góc nhọn.
B α là một góc vuông.
C α là một góc tù.
D α là một góc bẹt. Lời giải. Chọn đáp án A □
c Câu 25. Góc tạo bởi trục Ox với đường thẳng nào sau đây là góc tù? A y = 3x − 1. B y = −3 + x. C y = −2(x − 1). D y = 4x. Lời giải. Chọn đáp án C □
c Câu 26. Cho ba đường thẳng (d1) : y = 3x − 2, (d2) : y = x − 2, (d3) : y = 2(x − 2) + x. Trong các khẳng
định sau, khẳng định nào sai? A (d1) song song (d3). B (d1) cắt (d2). C (d2) cắt (d3).
D Ba đường thẳng (d1), (d2), (d3) song song. Lời giải. Chọn đáp án D □
c Câu 27. Đường thẳng có hệ số góc bằng 2 và đi qua điểm A(−1; 2) là A y = 2x + 2. B y = 2x − 1. C y = −x + 2. D y = 2x + 4. Lời giải. Chọn đáp án D □
c Câu 28. Giá trị của m để đường thẳng y = (m + 1)x + 2 song song với đường thẳng y = −2x là A m = −3. B m = −2. C m = 2. D m = 1. Lời giải. Chọn đáp án A □
c Câu 29. Hai đường thẳng (d) : y = 2x + 4 và (d′) : y = −x + 1 cắt nhau tại điểm có tọa độ là A (2; −1). B (4; 1). C (−1; 4). D (−1; 2). Lời giải. Chọn đáp án D □
c Câu 30. Giá trị của a để đường thẳng y = ax − 4 cắt đường thẳng y = 2x − 1 tại điểm có hoành độ bằng 2 là A 7. B 1. C −2. D −4. 2 4 7 Lời giải. Chọn đáp án A □
c Câu 31. Giá trị m để đường thẳng y = (m + 1)x + 2 song song với đường thẳng y = −2x là A m = −3. B m = −2. C m = 2. D m = 1. Lời giải. 105/119 105/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 106
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
Do đường thẳng y = (m + 1)x + 2 song song với đường thẳng y = −2x nên m + 1 = −2 hay m = −3. Chọn đáp án A □
c Câu 32. Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm M (1; 1), N (4; 1), P (2; −1), Q(−1; −1). Tứ giác M N P Q là hình gì? A Hình bình hành. B Hình thang cân. C Hình vuông. D Hình chữ nhật. Lời giải. y M N x Q P
Tứ giác ABCD là hình bình hành. Chọn đáp án A □
c Câu 33. Tứ giác M N P Q có M (1; 1), N (4; 1), P (2; −1), Q(−1; −1). Độ dài cạnh M N của tứ giác là √ √ A 3. B 5. C 3. D 5. Lời giải. Độ dài cạnh M N = 3. Chọn đáp án A □
c Câu 34. Một người bắt đầu mở một vòi nước vào một cái bể đã chứa sẵn 2 m3 nước, mỗi giờ chảy được
3 m3 nước. Thể tích y (m3) của nước có trong bể sau x giờ bằng A y = 2x + 3. B y = 3x + 2. C y = 6x. D y = x + 6. Lời giải.
Thể tích y = 2 + 3 · x = 3x + 2. Chọn đáp án B □
c Câu 35. Trong các điểm sau, điểm nào thuộc đồ thị của hàm số y = 2 − 4x? A (1; 1). B (2; 0). C (1; −1). D (1; −2). Lời giải.
○ Vì 2 − 4 · 1 = −2 ̸= 1 nên điểm (1; 1) không thuộc đồ thị hàm số y = 2 − 4x.
○ Vì 2 − 4 · 2 = −6 ̸= 0 nên điểm (2; 0) không thuộc đồ thị hàm số y = 2 − 4x.
○ Vì 2 − 4 · 1 = −2 ̸= −1 nên điểm (1; −1) không thuộc đồ thị hàm số y = 2 − 4x.
○ Vì 2 − 4 · 1 = −2 nên điểm (1; −2) thuộc đồ thị hàm số y = 2 − 4x. Chọn đáp án D □
c Câu 36. Trong các điểm sau, điểm nào thuộc đồ thị của hàm số y = −5x + 5? A (1; 1). B (2; 0). C (0; 4). D (2; −5). Lời giải. 106/119 106/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 107
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
○ Vì −5 · 1 + 5 = 0 ̸= 1 nên điểm (1; 1) không thuộc đồ thị hàm số y = −5x + 5.
○ Vì −5 · 2 + 5 = −5 ̸= 0 nên điểm (2; 0) không thuộc đồ thị hàm số y = −5x + 5.
○ Vì −5 · 0 + 5 = 5 ̸= 4 nên điểm (0; 4) không thuộc đồ thị hàm số y = −5x + 5.
○ Vì −5 · 2 + 5 = −5 nên điểm (2; −5) thuộc đồ thị hàm số y = −5x + 5. Chọn đáp án D □
c Câu 37. Đường thẳng song song với đường thẳng y = 2x và cắt trục tung tại điểm có tung độ bằng 1 là A y = 2x−1. B y = −2x − 1. C y = 2x + 1. D y = 6 − 2(1 − x). Lời giải.
Đường thẳng cần tìm có dạng y = 2x + a (a ̸= 0) vì đường thẳng cần tìm song song với đường thẳng y = 2x.
Vì đường thẳng cần tìm cắt trục tung tại điểm có tung độ bằng 1 nên điểm (0; 1) thuộc đồ thị của đường thẳng cần tìm.
Do đó 2 · 0 + a = 1 ⇒ a = 1.
Vậy đường thẳng cần tìm là y = 2x + 1. Chọn đáp án C □ 1 1
c Câu 38. Cho hai đường thẳng y = x + 3 và y = − x + 3. Hai đường thẳng đã cho 2 2
A cắt nhau tại điểm có hoành độ là 3. B song song với nhau.
C cắt nhau tại điểm có tung độ là 3. D trùng nhau. Lời giải.
Vì hai đường thẳng trên có hệ số góc khác nhau nên hai đường thẳng trên cắt nhau.
Gọi x là hoành độ giao điểm của hai đường thẳng trên. Khi đó ta có 1 1 x + 3 = − x + 3 2 2 1 1 x + x = 0 2 2 x = 0. 1 1 Thay x = 0 vào y = x + 3, ta được y = · 0 + 3 = 3. 2 2
Vậy (0; 3) là giao điểm của hai đường thẳng trên. Chọn đáp án A □ 1 1
c Câu 39. Cho các hàm số bậc nhất y =
x + 2; y = − x + 2; y = −3x + 2. Kết luận nào sau đây là 3 3 đúng?
A Đồ thị của các hàm số trên là các đường thẳng song song với nhau.
B Đồ thị của các hàm số trên là các đường thẳng đi qua gốc tọa độ.
C Đồ thị của các hàm số trên là các đường thẳng trùng nhau.
D Đồ thị của các hàm số trên là các đường thẳng cắt nhau tại một điểm. Lời giải.
○ Vì ba đường thẳng trên có các hệ số góc khác nhau nên ba đường thẳng trên không song song với nhau.
○ Vì ba đường thẳng trên đều có b ̸= 0 nên các đường thẳng trên không đi qua gốc tọa độ.
○ Vì ba đường thẳng trên có các hệ số a và b đôi một khác nhau nên ba đường thẳng trên không trùng nhau. Chọn đáp án D □ 107/119 107/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 108
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO −x + 10
c Câu 40. Đồ thị hàm số y = 5
A là một đường thẳng có hệ số góc là −1.
B không phải là một đường thẳng.
C cắt trục hoành tại điểm có hoành độ là 10.
D đi qua điểm (200; 50). Lời giải. −x + 10 1 Ta có y = = − x + 2. 5 5 1 Vì −
· 10 + 2 = 0 nên đồ thị hàm số trên cắt trục hoành tại điểm có hoành độ là 10. 5 Chọn đáp án C □ A B BÀI TẬP TỰ LUẬN
c Bài 1. Cho hàm số bậc nhất y = (m + 2)x + 3.
a) Tìm m để đồ thị hàm số song song với đường thẳng y = −x.
b) Vẽ đồ thị hàm số với giá trị m tìm được ở câu a. Lời giải. a) Theo đề bài ta có m + 2 = −1 ⇒ m = −3
b) Với m = −3 ta có hàm số y = −x + 3 Lập bảng giá trị y 3 x 0 3 y = −x + 3 3 0
Đồ thị hàm số (hình bên). 3 x O □ 5
c Bài 2. Cho hàm số f (x) = . 4x Å 1 ã Å 4 ã a) Tính f ; f (−5); f . 5 5
b) Hãy tìm các giá trị tương ứng của hàm số trong bảng sau: 1 1 x −3 −2 −1 − 1 2 2 4 5 y = f (x) = ? ? ? ? ? ? ? 4x Lời giải. 108/119 108/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 109
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO a) Ta có Å 1 ã 5 25 ○ f = = . 5 4 · 1 4 5 5 −1 ○ f (−5) = = . 4 · (−5) 4 Å 4 ã 5 ○ f = = 1. 5 4 · 45 b) Ta có 1 1 x −3 −2 −1 − 1 2 2 4 5 −5 −5 −5 −5 5 5 y = f (x) = 5 4x 12 8 4 2 4 2 □
c Bài 3. Cho hàm số y = f (x) = −x2 + 1. Tính f (−3); f (−2); f (−1); f (0); f (1). Lời giải. Ta có:
○ f (−3) = −(−3)2 + 1 = −8
○ f (−2) = −(−2)2 + 1 = −3
○ f (−1) = −(−1)2 + 1 = 0 ○ f (0) = −(0)2 + 1 = 1 ○ f (1) = −(1)2 + 1 = 0 □
c Bài 4. Vẽ một hệ trục tọa độ Ox và đánh dấu các điểm A(−2; 0), B(0; 4), C(5; 4), D(3; 0). Tứ giác ABCD là hình gì? Lời giải. y B C x A D
Dựa vào hình vẽ, ta có tứ giác ABCD là hình bình hành. □ 109/119 109/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 110
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO Å 4 ã
c Bài 5. Cho biết đồ thị của hàm số y = ax đi qua điểm P 1; − . 5 a) Xác định hệ số a.
b) Vẽ điểm trên đồ thị có hoành độ bằng −5.
c) Vẽ điểm trên đồ thị có tung độ bằng 2. Lời giải. Å 4 ã
a) Vì đồ thị của hàm số y = ax đi qua điểm P 1; − . 5 4 −4 Nên − = a · 1 ⇒ a = . 5 5 4
b) Ta có hàm số đã cho là y = − x. 5 4
Với x = −5 thì y = − · (−5) = 4. 5
Điểm trên đồ thị có hoành độ bằng 5 là điểm A(−5; 4) như đồ thị dưới đây y A 4 y = −4 5 x 0 x −5 4 5
c) Với y = 2 ta có 2 = − x ⇒ x = − . 5 2 Å 5 ã
Điểm trên đồ thị có tung độ bằng 2 là điểm B − ; 2 như đồ thị dưới đây 2 y B y 2 = −4 5 x 5 0 x − 2 □
c Bài 6. Tìm hàm số có đồ thị là đường thẳng song song với đồ thị hàm số y = −2x + 10. Lời giải.
Hàm số có đồ thị là đường thẳng song song với đồ thị hàm số y = −2x + 10 có dạng y = −2x + a với a ̸= 10. □ 110/119 110/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 111
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 7. Một người đi bộ với tốc độ không đổi 3 km/h. Gọi s (km) là quãng đường đi được trong t (giờ).
a) Lập công thức tính s theo t.
b) Vẽ đồ thị của hàm số s theo biến số t. Lời giải. a) Ta có s = 3t. b) Bảng giá trị t 0 1 s = 3t 0 3
Dựa vào bảng giá trị trên, đồ thị của hàm số s theo biến số t là đường thẳng như hình dưới đây s s = 3t 3 O 1 t □
c Bài 8. Tìm m để các hàm số bậc nhất y = 2mx − 2 và y = 6x + 3 có đồ thị là những đường thẳng song song với nhau. Lời giải.
Để hai hàm số trên có đồ thị là những đường thẳng song song với nhau thì 2m = 6 ⇒ m = 3. □
c Bài 9. Tìm n để các hàm số bậc nhất y = 3nx + 4 và y = 6x + 4 có đồ thị là những đường thẳng trùng nhau. Lời giải.
Để hai hàm số trên có đồ thị những đường thẳng trùng nhau thì 3n = 6 và 4 = 4 (luôn đúng). ⇒ n = 2.
Vậy n = 2 thì hai hàm số bậc nhất trên có đồ thị là hai đường thẳng trùng nhau. □
c Bài 10. Tìm k để các hàm số bậc nhất y = kx − 1 và y = 4x + 1 có đồ thị là những đường thẳng cắt nhau. Lời giải.
Để hai hàm số bậc nhất trên có đồ thị là các đường thẳng cắt nhau thì k ̸= 4. □
c Bài 11. Cho hai hàm số y = x + 3, y = −x + 3 có đồ thị lần lượt là các đường thẳng d1 và d2.
a) Bằng cách vẽ hình, tìm toạ độ giao điểm A của hai đường thẳng nói trên và tìm các giao điểm B, C lần
lượt của d1 và d2 với trục Ox.
b) Dùng thước đo góc để tìm góc tạo bởi d1 và d2 lần lượt với trục Ox. 111/119 111/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 112
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c) Tính chu vi và diện tích của tam giác ABC. Lời giải. a) Bảng giá trị x 0 1 x 0 1 y = x + 3 3 4 y = −x + 3 3 2 y A y 3 = + − x x = + y 3 x O B C
Dựa vào hình đồ thị trên, điểm A(0; 3) là tọa độ giao điểm của d1 và d2.
Giao điểm của d1 và Ox là B(−3; 0).
Giao điểm của d2 và Ox là C(3; 0).
b) Góc tạo bởi d1 và Ox là 135◦.
Góc tạo bởi d2 và Ox là 45◦.
c) Ta có OA = OB = OC = 3, BC = 6. 1 1 Diện tích tam giác ABC là · OA · BC = · 3 · 6 = 9 (đvdt). 2 2
Tam giác OAC vuông tại O có OA2 + OC2 = AC2 (Định lí Pytago) √ √
⇒ AC2 = 32 + 32 = 18 ⇒ AC = 18 = 3 2.
Tam giác OAB vuông tại O có OA2 + OB2 = AB2 (Định lí Pytago) √ √
⇒ AB2 = 32 + 32 = 18 ⇒ AB = 18 = 3 2. √ √ √
Chu vi tam giác ABC là AB + BC + CA = 3 2 + 6 + 3 2 = 6 + 6 2. □
c Bài 12. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai về hai đường thẳng:
d : y = ax + b (a ̸= 0), d′ : y = a′x + b′ (a′ ̸= 0)?
a) Nếu hai đường thẳng d và d′ song song với nhau thì a = a′, b ̸= b′.
b) Nếu hai đường thẳng d và d′ song song với nhau thì a = a′, b = b′.
c) Nếu hai đường thẳng d và d′ cắt nhau thì a ̸= a′.
d) Nếu hai đường thẳng d và d′ cắt nhau thì a ̸= a′, b ̸= b′. Lời giải. Phát biểu a), c) đúng. □ 112/119 112/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 113
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
c Bài 13. Cho tam giác ABC như hình vẽ. y C 2 1 −2 −1 O x 1 2 3 A B
a) Xác định tọa độ các điểm A, B, C.
b) △ABC có là tam giác vuông cân hay không?
c) Gọi D là điểm để ABCD là hình vuông. Xác định tọa độ điểm D. Lời giải.
a) Tọa độ các điểm A(−1; −1), B(2; −1), C(2; 2).
b) △ABC là tam giác vuông cân vì CB ⊥ AB và CB = AB = 3. c) Điểm D(−1; 2). □ 1
c Bài 14. Cho hai hàm số y = − x + 3; y = 2x − 2. 2
a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ. 1
b) Gọi A, B lần lượt là giao điểm của hai đường thẳng y = − x + 3; y = 2x − 2 với trục hoành và C là 2
giao điểm của hai đường thẳng đó. Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là centimet). Lời giải. a) Vẽ đồ thị. y 4 y = 2x − 2 3 C 2 1 1 B A y = − x + 3 2 −3 −2 −1 O x 1 2 3 4 5 6 −1 −2 −3 113/119 113/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 114
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO b) Ta có A(6; 0), B(1; 0).
Hoành độ giao điểm C là nghiệm của phương trình 1 1 5
− x + 3 = 2x − 2 ⇔ 2x + x = 3 + 2 ⇔ x = 5 ⇔ x = 2 ⇒ y = 2 · 2 − 2 = 2. 2 2 2 Vậy C(2; 2). □ c Bài 15.
a) Biết rằng với x = 3 thì hàm số y = 2x + b có giá trị là 11. Tìm b và vẽ đồ thị của hàm số với giá trị b vừa tìm được.
b) Biết rằng đồ thị của hàm số y = ax + 6 đi qua điểm A(−2; 2). Tìm a và vẽ đồ thị của hàm số với giá trị a vừa tìm được. Lời giải.
a) Khi x = 3 thì y = 11 ⇒ b = 11 − 2 · 3 = 5.
Khi đó ta có hàm số y = 2x + 5.
b) Vì hàm số đã cho đi qua A(−2; 2) ⇒ 2 = −2a + 6 ⇒ a = 2.
Vậy ta có hàm số y = 2x + 6. y y = 2x + 6 7 6 5 4 3 2 1 −4 −3 −2 −1 O x 1 2 3 −1 −2 □
c Bài 16. Tìm hàm số bậc nhất y = ax + b (a ̸= 0) trong mỗi trường hợp sau:
a) Đồ thị của hàm số đó đi qua điểm M (1; 3) và có hệ số góc bằng −2;
b) Đồ thị của hàm số đó đi qua điểm N (−1; 4) và song song với đường thẳng y = −3x − 1. Lời giải.
a) Gọi hàm số có dạng y = ax + b, ta có a = −2 nên y = −2x + b.
Lại vì đồ thị hàm số đi qua M (1; 3) nên b = 3 + 2 = 5.
Vậy hàm số có dạng y = −2x + 5. 114/119 114/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 115
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
b) Gọi hàm số có dạng y = ax + b, ta có a = −3 nên y = −3x + b.
Lại vì đồ thị hàm số đi qua N (−1; 4) nên b = 4 − 3 = 1.
Vậy hàm số có dạng y = −3x + 1. □
c Bài 17. Một kho chứa 60 tấn xi măng, mỗi ngày đều xuất đi m (tấn) với 0 < m < 60. Gọi y (tấn) là khối
lượng xi măng còn lại trong kho sau x ngày xuất hàng. y (tấn) 70 60 A 50 40 30 B 20 t 10 O 10 20 30 x (ngày)
a) Chứng tỏ rằng y là hàm số bậc nhất của biến x, tức là y = ax + b (a ̸= 0).
b) Trong hình bên, tia At là một phần đường thẳng y = ax + b. Tìm a, b. Từ đó hãy cho biết trong kho
còn lại bao nhiêu tấn xi măng sau 15 ngày. Lời giải.
a) Ta thấy x = 0; y = 60 ⇒ b = 60; x = 10; y = 30 ⇒ a = −3 Do đó y = −3x + 60.
b) Khi x = 15 ⇒ y = 3 · 15 + 60 = 15. Vậy trong kho còn 15 tấn xi măng sau 15 ngày. □ c Bài 18.
Cho đồ thị hàm số bậc nhất y = f (x) như hình vẽ. Hãy giải các phương y trình sau (55; 95) a) f (x) = 70. (30; 70) b) f (x) = 95. c) f (x) = 0. f(x) = y (−40; 0) O x Lời giải.
Đồ thị hàm số y = f (x) là đường thẳng △.
a) Từ đồ thị hàm số y = f (x), ta thấy A(30; 70) ∈ △ ⇒ f (30) = 70.
Vậy phương trình f (x) = 70 có nghiệm là x = 30. 115/119 115/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 116
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
b) Từ đồ thị hàm số y = f (x), ta thấy B(55; 95) ∈ △ ⇒ f (55) = 95.
Vậy phương trình f (x) = 95 có nghiệm là x = 55.
c) Từ đồ thị hàm số y = f (x), ta thấy C(−40; 0) ∈ △ ⇒ f (−40) = 0.
Vậy phương trình f (x) = 0 có nghiệm là x = −40. □
c Bài 19. Cho hàm số bậc nhất y = ax + 5.
a) Xác định hệ số a, biết đồ thị hàm số đi qua điểm A(1; 3).
b) Vẽ đồ thị hàm số đã cho với giá trị a tìm được. Lời giải. y
a) Vì đồ thị hàm số đi qua điểm A(1; 3) nên ta có P 5 3 = a + 5 ⇒ a = −2. 4 3
b) Với a = −2 ta có hàm số y = −2x + 5. Đồ thị của hàm số này là một đường thẳng. 2
Cho x = 0 thì y = 5, ta được giao điểm của đồ thị với trục tung là P (0; 5). 5 Cho y = 0 thì x =
, ta được giao điểm của đồ thị với trục hoành là 1 2 Q Å 5 ã Q ; 0 . − x 2 1 O 1 2 3
Đồ thị hàm số y = −2x + 5 là đường thẳng P Q như hình vẽ. −1 □
c Bài 20. Cho hai hàm số y = 2x − 1 và y = −x + 2.
a) Trong cùng mặt phẳng tọa độ Oxy, vẽ đồ thị của hai hàm số đã cho.
b) Tìm tọa độ giao điểm của hai đồ thị trên. Lời giải. y d1
a) Đồ thị hàm số y = 2x − 1 là đường thẳng d1. Cho x = 0 thì y = −1 nên d 2 1 đi qua A(0; −1). 1 Å 1 ã Cho y = 0 thì x = nên d1 đi qua B ; 0 . 2 2
Đồ thị hàm số y = −x + 2 là đường thẳng d2.
Cho x = 0 thì y = 2 nên d2 đi qua M (0; 2). 1 x O 2 Cho y = 0 thì x = 2 nên d 2 2 đi qua N (2; 0). −1 d2
b) Cách 1: Dựa vào đồ thị hai hàm số y = 2x − 1 và y = −x + 2 đã vẽ trên hình,
ta nhận thấy tọa độ giao điểm của hai đường thẳng là (1; 1).
Cách 2: Phương trình hoành độ giao điểm của hai đồ thị hàm số y = 2x − 1 và y = −x + 2
2x − 1 = −x + 2 ⇔ 3x = 3 ⇔ x = 1.
Với x = 1, suy ra y = 2 · 1 − 1 = 1.
Vậy tọa độ giao điểm của hai đồ thị hàm số y = 2x − 1 và y = −x + 2 là (1; 1). □
c Bài 21. Trong lí thuyết tài chính, giá trị sổ sách là giá trị một tài sản mà công ty sử dụng để xây dựng
bảng cân đối kế toán của mình. Một công ty khấu hao tài sản của họ bằng sử dụng phương pháp khấu hao 116/119 116/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 117
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
đường thẳng để giá trị của tài sản giảm một lượng cố định mỗi năm. Mức suy giảm phụ thuộc vào thời gian
sử dụng hữu ích mà công ty đặt vào tài sản đó.
Giả sử công ty vừa mua một chiếc máy photocopy mới với giá 18 triệu đồng. Công ty lựa chọn cách tính khấu
hao chiếc máy photocopy này theo phương pháp khấu hao đường thẳng trong thời gian 3 năm, tức là mỗi năm
giá trị của chiếc máy photocopy sẽ giảm 18 : 3 = 6 triệu đồng.
a) Viết hàm số bậc nhất biểu thị giá trị sổ sách V (x) của máy photocopy dưới dạng một hàm số theo thời
gian sử dụng x (năm) của nó.
b) Vẽ đồ thị của hàm số bậc nhất V (x).
c) Giá trị sổ sách của máy photocopy sau 2 năm sử dụng là bao nhiêu?
d) Sau thời gian sử dụng là bao lâu thì máy photocopy có giá trị sổ sách là 9 triệu đồng? Lời giải. y
a) Vì mỗi năm giá trị của chiếc máy photocopy sẽ giảm 18 : 3 = 6 triệu đồng nên nếu
thời gian sử dụng x (năm) thì giá trị sổ sách V (x) của máy photocopy là 18
V (x) = 18 − 6x (triệu đồng).
Vậy hàm số bậc nhất biểu thị giá trị sổ sách V (x) của máy photocopy là V (x) = 18 − 6x với 0 ≤ x ≤ 3.
b) Đồ thị hàm số bậc nhất V (x) = 18 − 6x là đường thẳng △.
Cho x = 0 thì V (0) = 18 nên △ đi qua điểm A(0; 18).
Cho V (x) = 0 thì x = 3 nên △ đi qua điểm B(3; 0).
Đồ thị hàm số V (x) = 18 − 6x là đường thẳng △ đi qua AB.
c) Sau 2 năm sử dụng tức là x = 2 thì giá trị sổ sách của máy photocopy là V (2) =
18 − 6 · 2 = 6 triệu đồng.
d) Ta phải tìm x với 0 ≤ x ≤ 3 để V (x) = 9, tức là V (x) = 9 ⇒ 18 − 6x = 9 ⇒ −6x = −9 ⇒ x = 1,5. x O 3
Vậy sau 1,5 năm sử dụng thì giá trị sổ sách của máy photocopy là 9 triệu đồng. □
c Bài 22. Cho hàm số y = (3 − m)x + 2m + 1. Tìm các giá trị của m để đồ thị hàm số đã cho là
a) Đường thẳng đi qua điểm (1; 2).
b) Đường thẳng cắt đường thẳng y = x + 1 tại một điểm nằm trên trục tung. Lời giải.
a) Đường thẳng đi qua điểm (1; 2) khi
2 = (3 − m) · 1 + 2m + 1 ⇒ 2 = 4 + m ⇒ m = −2.
Vậy với m = −2 thì đường thẳng đi qua điểm (1; 2).
b) Đường thẳng y = x + 1 tại một điểm nằm trên trục tung tại điểm A(0; 1).
Đường thẳng y = (3 − m)x + 2m + 1 cắt đường thẳng y = x + 1 tại một điểm nằm trên trục tung, tức là 117/119 117/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 118
4. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
chúng đồng qui tại A(0; 1).
Khi đó 1 = (3 − m) · 0 + 2m + 1 ⇒ 2m = 0 ⇒ m = 0.
Vậy với m = 0 thì thỏa mãn bài toán. □
c Bài 23. Để sử dụng dịch vụ truyền hình cáp, người dùng phải trả một khoản phí ban đầu và phí thuê bao
hằng tháng. Một phần đường thẳng d ở hình bên biểu thị tổng chi phí (đơn vị: triệu đồng) để sử dụng dịch
vụ truyền hình cáp theo thời gian sử dụng của một gia đình (đơn vị: tháng). y (triệu đồng) 4 d 3 2 1 −1 O 1 2 3 4 5 6 7 8 9 10 11 12 x (tháng) −1
a) Tìm hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng d.
b) Giao điểm của đường thẳng d với trục tung trong tình huống này có ý nghĩa gì?
c) Tính tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng. Lời giải.
a) Gọi hàm số bậc nhất cần tìm là y = ax + b (a ̸= 0). 1
Theo giả thiết ta có x = 0; y = 1 ⇒ b = 1 và x = 6; y = 2 ⇒ a = . 6 1 Vậy d : y = x + 1. 6
b) Giao điểm của d với Oy có ý nghĩa là chi phí ban đầu người dùng phải trả cho nhà mạng là 1 triệu đồng. 1
c) Trong thời gian 12 tháng người dùng phải trả số tiền là
· 12 + 1 = 3 (triệu đồng). 6 □
c Bài 24. Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Chẳng hạn, các khu vực của
thành phố Hồ Chí Minh đều có độ cao sát mực nước biển nên có áp suất khí quyển là p = 760 mmHg; thành
phố Puebla (Mexico) có độ cao h = 2 200 m so với mực nước biển nên có áp suất khí quyển là p = 550, 4 mmHg.
Người ta ước lượng được áp suất khí quyển p (mmHg) tương ứng với độ cao h (m) so với mực nước biển là
một hàm số bậc nhất có dạng p = ah + b (a ̸= 0).
a) Xác định hàm số bậc nhất đó.
b) Cao nguyên Lâm Đồng có độ cao 650 m so với mực nước biển thì áp suất khí quyển là bao nhiêu mmHg
(làm tròn đến hàng phần mười)? Lời giải. a) Theo giả thiết ta có:
h = 0, p = 760 ⇒ a · 0 + b = 760 ⇒ b = 760.
h = 2 200, p = 550, 4 ⇒ a · 2 200 + 760 = 550, 4 ⇒ a ≈ −0, 095.
Vậy hàm số bậc nhất là y = −0, 095x + 760. 118/119 118/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 119
Chương 5. HÀM SỐ VÀ ĐỒ THỊ
SÁCH TOÁN 8 CHÂN TRỜI SÁNG TẠO
b) Với h = 650 ⇒ p = −0, 095 · 650 + 760 = 698, 25 ≈ 698, 3 (mmHg). □ 119/119 119/119
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Document Outline
- I SỐ VÀ ĐẠI SỐ
- HÀM SỐ VÀ ĐỒ THỊ
- KHÁI NIỆM HÀM SỐ
- Trọng tâm kiến thức
- Khái niệm hàm số
- Giá trị của hàm số
- Các dạng bài tập
- blue!80124 Dạng 1. Hàm số, bảng giá trị của hàm số
- blue!80124 Dạng 2. Tính giá trị của hàm số khi biết giá trị của biến số, và ngược lại
- blue!80124 Dạng 3. Vận dụng
- Bài tập vận dụng
- Trọng tâm kiến thức
- KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ CỦA HÀM SỐ
- Trọng tâm kiến thức
- Tọa độ của một điểm
- Xác định một điểm trên mặt phẳng tọa độ khi biết tọa độ của nó
- Đồ thị của hàm số
- Các dạng bài tập
- blue!80124 Dạng 1. Đọc, biểu diễn toạ độ điểm trên mặt phẳng toạ độ
- blue!80124 Dạng 2. Vẽ đồ thị hàm số cho bởi bảng giá trị
- blue!80124 Dạng 3. * Xác định khoảng cách giữa hai điểm trên mặt phẳng tọa độ
- blue!80124 Dạng 4. * Điểm thuộc đồ thị, điểm không thuộc đồ thị của hàm số
- Bài tập vận dụng
- Trọng tâm kiến thức
- HÀM SỐ BẬC NHẤT y=ax+b (a=0)
- Trọng tâm kiến thức
- Hàm số bậc nhất, bảng giá trị
- Đồ thị của hàm số bậc nhất
- Các dạng bài tập
- blue!80124 Dạng 1. Hàm số bậc nhất, giá trị của hàm số bậc nhất
- blue!80124 Dạng 2. Vẽ đồ thị hàm số bậc nhất
- blue!80124 Dạng 3. Điểm thuộc đường thẳng. Điểm không thuộc đường thẳng
- blue!80124 Dạng 4. Xác định đường thẳng
- blue!80124 Dạng 5. Vận dụng
- Bài tập vận dụng
- Trọng tâm kiến thức
- HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
- Trọng tâm kiến thức
- Hệ số góc của đường thẳng
- Đường thẳng song song và đường thẳng cắt nhau
- Các dạng bài tập
- blue!80124 Dạng 1. Nhận diện hệ số góc. Xác định đường thẳng biết hệ số góc
- blue!80124 Dạng 2. Nhận dạng cặp đường thẳng song song với nhau, cặp đường thẳng cắt nhau, cặp đường thẳng vuông góc với nhau
- blue!80124 Dạng 3. Bài toán tham số liên quan đến hệ số góc của đường thẳng
- blue!80124 Dạng 4. Xác định đường thẳng với quan hệ song song
- blue!80124 Dạng 5. Xác định đường thẳng với quan hệ vuông góc
- Bài tập vận dụng
- Trọng tâm kiến thức
- magenta LUYỆN TẬP CHUNG
- Hàm số bậc nhất
- Tìm hệ số góc của đường thẳng
- Xác định vị trí tương đối giữa hai đường thẳng
- Tìm m để đồ thị hàm số thoả mãn điều kiện về vị trí tương đối
- magenta ÔN TẬP CHƯƠNG V
- Bài tập trắc nghiệm
- Bài tập tự luận
- Bài tập trắc nghiệm
- Hàm số bậc nhất
- KHÁI NIỆM HÀM SỐ
- HÀM SỐ VÀ ĐỒ THỊ






