Phân dạng và bài tập trắc nghiệm chuyên đề hàm số – Trần Hiền Toán 12

Phân dạng và bài tập trắc nghiệm chuyên đề hàm số – Trần Hiền Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

47 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
1
CHUYÊN ĐỀ 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
DẠNG 1: TÌM KHOẢNG ĐỒNG BIẾN – NGHỊCH BIẾN CỦA HÀM SỐ
Loại 1: Hàm số bậc ba
Mẫu 1. Tìm khong bin ca hàm s
32
3x 1yx
0;2
;2
;0
và
0;
Mẫu 2. Tìm khong bin ca hàm s
32
4
2x 3
3
y x x
0;1
0;
R
;0
Mẫu 3. Tìm khong nghch bin ca hàm s
3
1
4x 1
3
yx
;0
và
; 
2;
;2
--------------------------------------------------------------------------------------------------------------------
Loại 2: Hàm số trùng phƣơng
Mẫu 4. Tìm khong bin ca hàm s
42
2x 1yx
1;0
và
1; 
1;0
1;1
1; 
Mẫu 5. Tìm khong nghch bin ca hàm s
42
2x 5yx
0;
;0
R
1;1
--------------------------------------------------------------------------------------------------------------------
Loại 3: Hàm phân thức.
Mẫu 6. Hàm s
2x 3
1
y
x
nghch bin trên khong nào
R
1; 
;1
và
1; 
;1
Mẫu 7. Tìm khong bin ca hàm s
2
2x 2
1
x
y
x

2;0
2; 
;2
và
;0
--------------------------------------------------------------------------------------------------------------------
Loại 4: Hàm số khác.
Mẫu 8. Tìm khong nghch bin ca hàm s
4
yx
x

2;2
2;
2;0
và
0;2
;2
Mẫu 9. Tìm khong nghch bin c th hàm s
2
25yx
5;0
0;5
5;5
0;
Mẫu 10. Hàm s
4 3 2
1 5 7
3x 2018
4 3 2
y x x x
nghch bin trên khong nào
Dạng 1: Tìm kho NB ca hàm s
Dạng 2:   NB trên R
Dạng 3:   NB trên khong (a ; b)
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
2
0;3
0;
3; 
1;3
DẠNG 2: TÌM M ĐỂ HÀM SỐ ĐB – NB TRÊN R.
Mẫu 11. Tìm tt c giá tr thc ca tham s  hàm s
32
x x 1y m m x m
ng bin trên R
Mẫu 12. Cho hàm s
32
1
3 2 1
3
y x mx m x
. Tìm giá tr ca m  hàm s nghch bin
trên
R
.
Mẫu 13. Vi giá tr nào ca m thì hàm s
x3
2
m
y
xm

nghch bin trên tng khonh.
Mẫu 14. Tìm tt c giá tr thc ca tham s
m
 hàm s

2
2
1
x mx
y
x
ng bin trên tng
khonh.
10.
03m
11.
21m
12.
31m
13.
3m
.
DẠNG 3: TÌM M ĐỂ HÀM SỐ ĐB – NB TRÊN KHOẢNG
;ab
Mẫu 15.  hàm s
3
3 x 2018y x m
nghch bin trên khong
1;1
31m
1m
0m
3m
Mẫu 16. Tp hp giá tr c hàm s
32
x 3x 2y m x m
ng bin trên khong
3;0
1
;
3


1
;
3



1
;
3




1
;0
3


Mẫu 17. Tìm tham s
m
 hàm s
32
31y x x mx
ng bin trên khong
0;
.
0m
.
3m
.
3m
.
0m
.
Mẫu 18.  hàm s
x4m
y
xm
nghch bin trên khong
1; 
12m
12m
22m
21m
Mẫu 19. Tìm tt c giá tr thc ca tham s  hàm s
x9m
y
xm
ng bin trên khong
2;
32m
32m
2m
23m
PHẦN MỞ RỘNG - CASIO
Mẫu 20. 
32
3x 1 2 3f x x m x m
ng bin trên mt kho dài l
1.
0m
0m
5
0
4
m
5
4
m 
Mẫu 21. Tìm giá tr thc ca tham s   hàm s
tanx
tanx 1
m
y
m
nghch bin trên khong
0;
4



;0 1; 
; 1 1;
0;
1; 
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
3
PHẦN 2. BÀI TẬP RÈN LUYỆN
DẠNG 1
Câu 1. Hàm s
32
7y x x x
ng bin trên R
Luôn nghch bin trên R
Có khong bin và nghch bin. Nghch bin trên khong
.1;3
Câu 2. Hàm s
32
y x x x
có khong bin là
1;3
1
;1
3


1
( ; ) (1; )
3
 
1;3
Câu 3. Hàm s
42
23y x x
ng bin trên kho
;1
và
0;1
1;0
và
1; 
;0
1;1
Câu 4. Hàm s ng bin trên R?
1
3
x
y
x
32
21y x x x
42
23y x x
3
2y x x
Câu 5. Tìm khong nghch bin c th hàm s
2
1
1
xx
y
x

0;1
và
1;2
0;2
;1
và
1; 
;0
và
Câu 6. Khong bin ca hàm s
42
81y x x
là:
;2
và
0;2
;0
và
0;2
;2
và
2;0
và
Câu 7.  th ca hàm s nào luôn nghch bin trên R
42
21y x x
2
3 4 1y x x
2
21yx
3
3 2 1y x x
Câu 8. Hàm s

1
.yx
x
Nghch bin trên kho
 ;1
và
1;
.
1;0
và
0;1
.
. Không có.
Câu 9. Hàm s

1
2
1
yx
x
ng bin trên kho
 ;1
.
1;
. . Không có.
Câu 10.Hàm s

2
2y x x
ng bin trên kho
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
4
;1
.
0;1
.
1;2
.
1;
.
DẠNG 2
Câu 1.Hàm s
32
1
( 1) ( 1) 1
3
y x m x m x
ng bin trên tnh ca nó khi :
1m 
21m
21m
2m 
Câu 2. Hàm s
2
1
mx m
y
x

ng khonh ca nó khi :
0m
0m
1m
0m
Câu 3. Tìm tt c giá tr thc ca tham s
m
 hàm s
2
xm
y
x
nghch bin trên tng khong xác
nh.
2m
.
.
2m
.
2m
.
Câu 4.Hàm s
2
2
1
x mx
y
x
gim trên tng khonh khi:
3m 
3m
3m 
m
Câu 5. Tìm tt c giá tr thc ca tham s
m
 hàm s

78mx m
y
xm
ng bin trên tng khong
nh.
81m
.
81m
.
41m
.
41m
.
Câu 6. Tìm tt c giá tr thc ca tham s
m
 hàm s

2
2
1
x mx
y
x
ng bin trên tng khong
nh.
3m
.
3m
.
2 2 2 2m
.
22m
hoc
22m
.
Câu 7. Tìm tham s
m
 hàm s
3
1
17
3
y x m x
luôn nghch bin trên .
1m
.
2m
.
1m
.
2m
.
Câu 8. Cho
32
1
3 2 1
3
y x mx m x
. Tìm giá tr ca m  hàm s nghch bin trên
R
.
1
2
m
m


21m
1
2
m
m


21m
Câu 9. Có bao nhiêu tham s  hàm s
3
2
x
x 3 2
3
m
y m m x m
ng bin trên
R
1 Vô s Không có 2
==================================================================
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
5
DẠNG 3
Câu 1. Tìm
m
 hàm s
32
1
1 3 10
3
y x m x m x
ng bin trên khong
0;3
.
12
7
m
.
.
m
.
7
12
m
.
Câu 2. Cho hàm s
42
2 x 3 1y x m m
.  th hàm s ng bin trên khong
1;2
1m
0m
01m
0m
Câu 3. Tìm các giá tr ca tham s  hàm s
32
2x x 2xym
ng bin trên khong
2;0
13
2
m 
23m 
23m
13
2
m
Câu 4. Tìm giá tr ca tham s  hàm s
32
2x x 2xym
ng bin trên khong
2;0
A.
13
2
m 
B.
23m 
C.
23m
D.
13
2
m
Câu 5. Tìm s
m
 hàm s
32
3 ( 1) 4y x x m x m
nghch bin trên khong
1;1
.
10m
.
10m
.
10m
.
5m
.
Câu 6. Tìm tt c giá tr ca tham s
m
 hàm s
x
y
xm
ng bin trên khong
2;
.
0m
.
0m
.
2m
.
2m
.
Câu 7. Vi giá tr nào ca m thì hàm s
1 2 2m x m
y
xm
ng bin trên khong
1; 
1m
2m
1
2
m
m
12m
Câu 8. Tìm giá tr ca tham s  hàm s
3x
y
xm
nghch bin trên khong
4;16
4m
3m
33
16
m
34m
Câu 9.Tìm giá tr ca  hàm s
3 2 2
1
1 2 3
3
y x m x m m x
nghch bin trên
0;1
1; 
;0
0;1
1;0
Câu 10.  hàm s
2
4x
2x
x
y
m
ng bin trên na khong
1; 
1
;
3




1
;
3



1
; \ 0
3



1
;
3



==================================================================
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
6
PHẦN MỞ RỘNG – CASIO
Câu 1.Tìm tt c giá tr c hàm s
32
2x 3 1 6 2 3y m x m x
nghch bin trên
kho dài l
0
6
m
m
06m
0
6
m
m
06m
Câu 2. Tìm tt c giá tr thc ca tham s   th hàm s
sinx sx xy co m
ng bin
trên R
22m
2m 
22m
2m
Câu 3. ng thi bu kin c hàm s
sin x sx 3xy m nco
nghch bin trên R.
33
9mn
33
9mn
2, 1mn
22
9mn
Câu 4.   th hàm s
2 2 2
2
1 tan 1
tan 3
m x m
y
x
ng bin trên khong
0;
4



11
22
m
1
2
m 
hoc
1
2
m
11
22
m
1
0
2
m
Câu 5. Tìm giá tr ca tham s  hàm s
x sinxym
ng bin trên R
1m
1m 
1m
0m
Câu 6.Có tt c bao nhiêu giá tr nguyên c hàm s
32
2 2 1y x m x m x m
ng
bin trên R
7 8 9 10
Câu 7.
Tìm giá tr thc ca tham s
m
 hàm s
2
21y x x mx
ng bin trên
2m
.
0m
.
1m
.
1m
.
Câu 8. Hàm s
2
2x 3
1
y
x
nghch bin trên kho
;1
và
3
1;
2



3
;
2




3
1;
2



;1
Câu 9. Tp giá tr c hàm s
32
2
2 3 1 7
3
m
y x m x m x
ng bin trên R
1
2
4
m
1
2
4
m
1
2
4
m
1
2
4
m
Câu 10. Tìm tp giá tri c hàm s
2
x
s
m sin
y
co x
nghch bin trên khong
0;
6



1m
2m
5
4
m
0m
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
7
CHUYÊN ĐỀ 2: CỰC TRỊ CỦA HÀM SỐ
DẠNG 1: TÌM ĐIỂM CỰC TRỊ CỦA HÀM SỐ
Mẫu 1. Hàm s
3
34y x x
có cc tiu ti
Mẫu 2. Tìm giá tr cc tiu ca hàm s
42
21y x x
.
Mẫu 3. Tìm
CT
y
ca hàm s
2
3
1yx
Mẫu 4. Cho hàm s
fx
o hàm
2 3 4
' 1 2 3f x x x x x
. Hi hàm s
y f x
m cc tr ?
1.
1x
. 2.
0
CT
y
. 3.
1
CT
y
4. 2
DẠNG 2: TÌM M KHI BIẾT HS CÓ MỘT CĐ HOẶC CT
Mẫu 5.  hàm s
3
2 x + m + 1y x m
t cc tiu ti
2x
Mẫu 6. Hàm s
32
. 2 4 1
32
xx
y m m x
t cc i ti
2x
.
9.
10m
10.
4m
.
DẠNG 3: TÌM M ĐỂ HS CÓ 1 – 2 – 3 CỰC TRỊ
Mẫu 7. Cho hàm s
32
1
1 2 x
3
y m x m x m
 hàm s có ci, cc tiu
4
1
5
m
4
5
m 
1m
Mẫu 8. Tìm tt c giá tr c  th hàm s
4 2 2
2 x 1y x m m
m cc tr
1m
1m
0m
0m
Mẫu 9. Tìm tt c giá tr ca tham s  hàm s
4
x 1 1 2y m m x m
ch có mt cc tr
0m
0m
01m
0
1
m
m
Dạng 1: Tìm cc tr ca hàm s
Dạng 2: Tìm m khi bit Hs có mc CT
Dạng 3:  Hs có 1 2 3 cc tr
Dạng 4:  Hs có 2 cc tr th bài
Dạng 5:  Hs có 3 cc tr tha 
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
8
DẠNG 4: TÌM M ĐỂ HS CÓ 2 CỰC TRỊ THỎA ĐIỀU KIỆN VIET
Mẫu 10.     th hàm s
32
31y x x mx
  m cc tr
12
,xx
tho 

22
12
3xx
2m
.
3
2
m
.
1m
.
1
2
m
.
Mẫu 11. Mu  th hàm s
3 2 3
34y x mx m
  th hàm s m cc tr
A
và
B
sao cho
20AB
.
1m
.
2m
.
1; 2mm
.
1m
.
DẠNG 5: PHƢƠNG TRÌNH ĐƢỜNG THẲNG QUA CÁC ĐIỂM CỰC TRỊ
Mẫu 12. Cho hàm s
32
2x 1y x x
. Ving thm cc tr ca
hàm s trên.
Mẫu 13. Cho hàm s
32
6x 9x 2yx
ng th-1; 1) và vuông góc vi
ng thm cc tr ca (C ) là.
12.
14 7
99
yx
13.
13
22
yx
DẠNG 6: TÌM M ĐỂ HS CÓ 3 CỰC TRỊ THỎA ∆ ĐỀU, VUÔNG, …
Mẫu 14. Tìm các giá tr thc ca tham s   th hàm s
42
21y x mx
m cc tr
lp thành mt tam giác vuông.
1m
3
2 2.m
3
2m
2m
Mẫu 15. Tìm tham s   th hàm s
4 2 4
22y x mx m m
m cc tr to thành
mu.
1m
3m
3m
3
3.m
Mẫu 16.   th hàm s
42
2 x 2y x m
có 3 cc tr to thành mt tam giác có din tích
bng 1.
1m
2m
3m
4m
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
9
PHẦN 2: BÀI TẬP TỰ LUYỆN
DẠNG 1
Câu 1. Tìm giá tr ci
CĐ
y
ca hàm s
32
3 3 2y x x x
.
3 4 2
.
3 4 2
.
3 4 2
.
3 4 2
.
Câu 2. Tìm giá tr cc tiu
CT
y
ca hàm s
42
21y x x
.
2
CT
y
.
1
CT
y
.
1
CT
y
.
0
CT
y
.
Câu 3. Hàm s o hàm
2
'2
1 2x 1f x x x
s m cc tr c th hàm s là
1 2 3 0
Câu 4. Cho hàm s
y f x
nh và liên tc trên R có bng bii. Hãy chn
kh
Hàm s giá tr cc tiu bng 1
Hàm s có giá tr ln nht bng 0 và giá tr bé nht bng -1
Hàm s t cc tr
Hàm s t ci ti
0x
t cc tiu ti
1x
Câu 5. S m cc tiu ca hàm s
2016
16yx
0 1 2016 2015
Câu 6. m ci c th hàm s
36y x x
D
3
C
x
D
6
C
x
Không có
Câu 7. Cho hàm s
3
3x 1yx
. Tng l cc i và giá tr cc tiu ca hàm s 
cho
27 26 -8 28
Câu 8.  th hàm s
32
3x xy x a b
m cc tiu
2; 2A
thì tng
ab
có giá tr bng
-2 2 -3 3
Câu 9. H thc liên h gia giá tr ci và giá tr cc tiu c th hàm s
3
2xyx
là
D
0
C CT
yy
D
23
CT C
yy
DCT C
yy
D
2
CT C
yy
Câu 10. Khong cách gim ci và cc tiu c th hàm s
32
3xyx
bng
2
25
4
45
=================================================================
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
10
DẠNG 2 - 3
Câu 1. hàm s
32
3y x x mx
t ci ti
2x
.
0m
.
0m
.
0m
.
0m
.
Câu 2.  hàm s
32
3 2 1y x mx x
t ci ti
1x
.
Không tn ti
.m
Có vô s
.m
6.m
5
.
2
m
Câu 3. Tìm tt c giá tr ca tham s  hàm s
2
x1
1
xm
y
x

t cc tiu ti
0x
1m 
1m
1m 
Không có m
Câu 4. Tìm giá tr c hàm s
3 2 2
1
x 1 1
3
y x m m m x
t ci ti
1x
2m 
1m 
2m
1m
Câu 5.Hàm s
32
2 3 1 6 2y x m x m x
 hàm s có ci và cc tiu.
3m
.
3m
. Không có giá tr
m
.
m
.
Câu 6. Hàm s
32
23y m x x mx m
 hàm s có ci và cc tiu.
3;1 \{ 2} m
.
3;1m
.
; 3 1; m
.
3m
.
Câu 7. Tìm tt c giá tr ca tham s  hàm s
42
x 1 1 2y m m x m
ch có mt cc tr
0m
0m
01m
0
1
m
m
Câu 8. Tìm tt c giá tr thc ca tham s  hàm s
42
x 1 2 1y m m x m
m cc
tr?
1m 
1m 
10m
1
0
m
m

Câu 9. Tìm tt c giá tr c hàm s
32
1 3x 3x 5y m x
có cc tr
1m
1m 
01m
0m
Câu 10. Tìm các giá tr ca tham s   th hàm s
42
x 2 1 2y m m x m
ch có ci và
không có cc tiu.
1m
0m
0m
1m
==================================================================
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
11
DẠNG 4 – 5 - 6
Câu 1. ng thm cc tr c th hàm s
32
4x 1y x x
là
38 5
99
yx
38 5
99
yx
38 5
99
yx

Câu 2.  nh h s góc c ng th    m cc tr c  th hàm s
32
3x 2x 1yx
1
3
10
3
10
3
1
3
Cho hàm s
32
2x 3 1 6 2 1y m x m x
 ng thm cc tr
ca hàm s (1) song song vng thng
4x 1y
1
5
m
m
1m
5m
3m
Câu 3. Tìm tt c các giá tr thc ca tham s m sao cho hàm s
32
1
1
3
y x mx x m
có 2 cc
tr
12
,xx
tha mãn
22
1 2 1 2
42x x x x
3m 
2m
0m
1m 
Câu 4.  hàm s
3 2 2
1
x 1 1
3
y x m m m x
t cc tr tm x
1
; x
2
tha
12
4xx
2m 
2m 
Không tn ti m
2m
Câu 5. Tính khong cách gia 2 m cc tr c th hàm s

2
1
x mx m
y
x
.
25
.
52
.
45
.
5
.
Câu 6.  th hàm s
42
2 x 1y x m m
m cc tr to thành mt tam giác có din tích
bng 243 là
3
3m
1m
2m
9m
Câu 7. Gi
,,A B C
m cc tr c th hàm s
42
2 4 1y x x
. Tính din tích
S
ca tam
giác
ABC
.
4S
.
3S
.
2S
.
1S
.
Câu 8. Cho hàm s
3
3 x 1y x m
  th hàm s m cc tr B và C sao cho tam
giác ABC cân ti A, vi
2;3A
1
2
m 
3
2
m 
1
2
m
3
2
m
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
12
Câu 9.   th hàm s
42
21y x m x m
m cc tr lp thành mt tam giác
vuông cân.
0m
1m 
2m
1m
Câu 10. Tìm các giá tr c  th hàm s
42
2 x 3y x m m
có 3 cc tr lp thành mt tam
giác cân
0m
1m
0m
3m
==================================================================
PHẦN MỞ RỘNG – CASIO
Câu 1. Hàm s

32
(1 )y x x
m cc tr?
1 2 3 4
Câu 2. Cho hàm s
32
1
1 15x
3
y x m x
 hàm s có hai cc tr
12
;xx
tha
12
21xx
0
2
3
m
m
2m
0m
2
3
m
Câu 3. Tìm các giá tr c hàm s
42
1
2 1 5
6
y m x m x
t cc tiu
21m
2 m
1m
1m
Câu 4. Vi giá tr nào ca  th hàm s
3 2 2 2016
2 2017 2018y x m m x m x
có hai
m cc tr u trc tung
1m
1
2
m
m

2m
1m 
Câu 5.   th hàm s
4 2 2
81y x m x
m cc tr nm trên các trc t
1m 
1
2
m 
1
2
m
1
2
m 
Câu 6.Tìm tt c giá tr ca tham s   th hàm s
4 2 2
22y x m x m
m cc tr A, B,
nh ca hình thoi
1m 
1m
2m
3m
Câu 7.   th hàm s
42
3
1x
2
y m x m
ch có cc tiu mà không có ci
0m
10m
2m
1m 
Câu 8. Tìm tt c giá tr ca tham s   th
32
1
12
3
y x x m x
m cc tr nm
bên trái trc tung
12m
1m
2m
1m
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
13
Câu 9. Tìm tt c giá tr ca tham s   th hàm s
3 2 2
4x 1 1y x m x
m cc tr
nm v i vi trc tung
11
33
m
11m
11m
Câu 10.   th hàm s
32
1
( 2) (5 4) 3 1
3
y x m x m x m
t cc tr ti
12
,xx
sao cho

12
2.xx
0m
.
1m
.
0m
.
1m
.
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
14
CHUYÊN ĐỀ 3: GTLN – GTNN CỦA HÀM SỐ
DẠNG 1: TÌM GTLN – GTNN CỦA HÀM SỐ
Mẫu 1. Tìm giá tr ln nht ca hàm s

2
31
1
xx
y
x
n


2;5 .



2;5
max 1y
.


2;5
11
max
4
y
.


2;5
max 1y
.



2;5
11
max
4
y
Mẫu 2. Tìm giá tr nh nht m ca hàm s
2
25y x x
n


1;3
.
22m
.
5
2
m
.
2m
.
23m
.
Mẫu 3. Tìm giá tr ln nht
M
ca hàm s
2 1 6y x x
trên tnh.
2M
.
5M
.
3M
.
4M
.
Mẫu 4. Tìm giá tr nh nht ca hàm s
2
1
1
xx
y
x

trên
1; 
3m
2m
1m
0m
Mẫu 5. Giá tr ln nht ca hàm s
2
4xy x m
n
1;3
 ca m
bng bao nhiêu?
3 -15 -6 -7
Mẫu 6. Tìm giá tr c giá tr nh nht ca hàm s
2x 1
()
1
m
fx
x

n
1;2
bng 1
1m
2m
3m
0m
DẠNG 2: BÀI TOÁN THỰC TẾ
Mẫu 7. Mt nhà máy sn xut sa cn thit k mt loi bao bì mi có dng hình hng vi th tích
1 dm
3
nh x. Tìm x sao cho nguyên vt liu làm bao bì nh nht
:
1x
Mẫu 8. Cho mt tm bìa hình vuông có ci ta ct bn góc cn hình
vuông bng nhau, mi hình vuông có cnh x, ri gp t c mt cái hp không np. Tìm x
 hình hp nhc th tích ln nht ?
:
2x
====================================================================
Dạng 1: Tìm GTLN GTNN ca hàm s
Dạng 2: Bài toán thc t.
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
15
PHẦN MỞ RỘNG - CASIO
Câu 1. Tìm GTNN ca hàm s
3 2xy 
n
1;1
Min 1y
Min 2y
Min 3y
Min 4y
Câu 2. Tìm giá tr ln nht ca hàm s
2
4x 3yx
n
0;3
Maxy = 3 Maxy = 4 Maxy = 5 Maxy = 6
Câu 3. Tìm giá tr ln nht ca hàm s
3
3sinx 4sin xy 
trên
;
22




xy 1Ma
xy 2Ma
xy 3Ma
xy 4Ma
Câu 4. Tìm giá tr nh nht ca hàm s
4
2sin cos2 5y x x
trên tnh.
11
min
4
y
.
11
min
2
y
.
min 2y
.
min 3y
.
Câu 5. Tìm giá tr nh nht ca hàm s
3
11
32
xx
y
xx




3Miny
4Miny
5Miny
6Miny
Câu 6. Tìm giá tr ln nht
M
ca hàm s
44
sin cos sin cosy x x x x
trên tnh.
1
2
M
.
9
8
M
.
1
4
M
.
3
4
M
.
Câu 7. Tính din tích ln nht
max
S
ca mt tam giác vuông có cnh huyn bng
52
.
max
25
8
S
.
max
25
4
S
.
max
25
2
S
.
max
25S
.
Câu 8. Chu vi ca mt tam giác là
16cm
, bi dài mt cnh ca tam giác là
6a cm
 dài hai
cnh còn li
,bc
cn tích ln nht.
4 ; 6b cm c cm
.
3 ; 7b cm c cm
.
2 ; 8b cm c cm
.
5b c cm
.
Câu 9. Cho mt hình ch nht có din tích
100S
. Tính chiu rng
x
và chiu dài
y
ng tha
u kin chu vi hình ch nht là nh nht.
25; 4xy
.
10; 10xy
.
20; 5xy
.
50; 2xy
Câu 10. Giá tr nh nht ca hàm s
66
64y x x
bng
66
3 61
6
1 63
2
6
2 32
====================================================================
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
16
PHẦN 2: BÀI TẬP TỰ LUYỆN
Câu 1. Gi
M
và
m
lt là giá tr ln nht và giá tr nh nht ca hàm s
3
2
2 3 4
3
x
y x x
n


4;0 .
Tính tng
Mm
.
28
3
.
28
3
.
28
3
.
35
.
Câu 2. Tìm giá tr ln nht
M
ca hàm s
31
3
x
y
x
n
[0;2]
.
1
3
M
.
5M
.
5M
.
1
3
M
.
Câu 3. Tìm giá tr ln nht ca hàm s
4
1
2
yx
x
n

1; 5 .


1;5
max 3y
.


1;5
max 4y
.


1;5
46
max
7
y
.



1;5
max 5y
.
Câu 4. Tìm giá tr nh nht ca hàm s
3
31y x x
trên khong
;1
.

;1
min 3y
.


;1
min 1y
.

;1
min 2y
.


;1
min 3y
.
Câu 5.Tìm giá tr nh nht ca hàm s
2
2
x
y
x
n


1;4
.



1;4
min 1y
.


1;4
min 0y
.


1;4
min 6y
.


1;4
min 8y
.
Câu 6. Cho hàm s

2
4
1
xx
y
x
. M đúng?
 
4; 2 4; 2
16
max ,min 6
3
yy
.
 
4; 2 4; 2
max 6,min 5yy
.

4; 2 4; 2
max 5,min 6yy
.
 
4; 2 4; 2
max 4,min 6yy
.
Câu 7. Tìm giá tr ln nht
M
ca hàm s
12y x x
n



1
4;
2
.
1M
.
1
2
M
.
0M
.
1M
.
Câu 8.Tìm giá tr ln nht M ca hàm s

2
1y x x
trên tnh.
1
2
M
.
1
2
M
.
2
2
M
.
1M
.
Câu 9. Tìm các giá tr ca
m
 giá tr nh nht ca hàm s

2
1
x m m
y
x
trên


0;1
bng
2
.

1
2
m
m
.

1
2
m
m
.


1
2
m
m
.
1
2
m
m
Câu 10.  hàm s
x5m
y
xm
t giá tr nh nhn
0;1
bng -7
2m
0m
1m
5m
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
17
CHUYÊN ĐỀ 4: ĐƢỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
DẠNG 1: TÌM ĐƢỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
Mẫu 1. Tìm tim cng và tim cn ngang c th hàm s
1.
2x 3
8
y
x

8x
; TCN:
2y 
2.
2
2x 1
1
y
x
: TCN:
0y

1x 
3.
2
2
5x 1
2x 2
x
y
x


5
2
y 
4.
2
2
2x 3
1
x
y
x


1x 
; TCN:
1y
5.
3x 2
5
y
x

25x
; TCN:
3y
6.
2x 1 3
3
y
x


0y
7.
2
3x 2
1
x
y
x

1x 
; Không có tim cn ngang
8.
2
1
4x 3
y
x


1x
và
x3
; TCN:
0y
9.
2
3y
x


0x
; TCN:
3y
10.
2
23x
y
x

0x
; TCN:
2y 
DẠNG 2: BÀI TOÁN THAM SỐ M
Mẫu 2. Cho hàm s
2
x 3x
1
m
y
x
vi giá tr nào ca m thì
1x
là tim cng c th hàm
s
3m
3m 
3m
3m 
Mẫu 3. Tìm tt c các giá tr thc ca tham s
m
  th hàm s

2
1x
y
x x m
ng
tim cng.
Mi
m
.
1
.
4
2

m
m
1
.
4
2

m
m
2.m
Mẫu 4. Tìm tt c giá tr thc c  th hàm s
2
4
2
x3
x
y
m
có mt tim cn ngang
Dạng 1: ng tim cn c th hàm s
Dạng 2:   th Hs có tim cn tha ycbt
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
18
0m
0m
0m
3m
PHẦN MỞ RỘNG – CASIO
Câu 1. Cho hàm s
3x 1
3
y
x
 th m M thuc (C ) sao cho khong cách t n
tim cng bng hai ln khong cách t n tim cn ngang
12
(1; 1); (7;5)MM
12
(1;1); ( 7;5)MM
12
( 1;1); (7;5)MM
12
(1;1); (7; 5)MM
Câu 2. Cho hàm s
2
xm
y
xm

Giá tr nào c th có tim cng và tim cn ngang
cùng vi hai tr to thành hình ch nht có din tích bng 1
1
3
m
m
1m 
1m
3m
Câu 3. Tìm tt c các giá tr thc ca tham s
m
  th hàm s
2
:
1
m
xm
Cy
mx
có tim cn
ng, tim cn ngang và các tim cn cùng vi hai trc t to thành mt hình ch nht
có din tích bng
8
.
1
4
m
.
1
2
m
.
1
8
m
. Không có
m
Câu 4.S tim cn ngang c th hàm s
2
23y x x x
là :
0
2
1
3
Câu 5.  th hàm s
2
1
43
x
y
xx

ng tim cng?
1 2 3 4
Câu 6. Hàm s
1
4 3x 1 3x 5
x
y
có bao nhiêu tim cng ?
Không có 1 2 3
Câu 7. Tim cn ngang c th hàm s
20 30
50
2x 3 . 2x 2
2x 1
y

0y
1y
1
2
y 
Không có
Câu 8. Tìm tt c các tim cng c th hàm s
2
2
2 6 2
.
6
x x x
y
xx

3.x 
và
2.x
3.x
3.x
và
2.x 
3.x 
Câu 9. Tìm giá tr c  th hàm s
2
1
2x x 4
x
y
m

t tim cn ngang là
A.
0m
B.
0
4
m
m
C.
4m
D.
04m
Câu 10. Tp hp giá tr ca tham s   th hàm s
2
21
x3
x
y
x m m


m cng
11
;
42



1
0;
2



; 12 0;
0;
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
19
==================================================================
PHẦN 2: BÀI TẬP TỰ LUYỆN
DẠNG 1
Câu 1. Tim cng c th hàm s
2x 1 1
1
y
x

1
2
x
1y 
1x 
Không có
Câu 2. Tim cn ngang c th hàm s
7
7
x
y
x

1x 
1y 
7x 
7x
Câu 3. Tim cn ngang c th hàm s
2
2x 3
1
x
y
x

Không có
1y 
2y 
1x 
Câu 4.Tim cn ngang c th hàm s
2
1
1
xx
y
xx

0y
1y
0x
Không có
Câu 5. Tim cn ngang c th hàm s
2
3
1
x
y
x
1y
1y 
1y 
Không có
Câu 6. S ng tim cn c th hàm s
2
2
1
3 2x 5x
xx
y


1 2 3 4
Câu 7. Hàm s
2
2
3x 2
1
x
y
x

có my tim cng
Không có 1 2 3
Câu 8.  th hàm s
2
2x 1
1
y
xx

có bao nhiêu tim cn?
Không có 1 2 3
Câu 9. Tìm s tim cn c th hàm s
2
2
3x 1
3x 4
x
y
x


Không có 1 2 3
Câu 10.  th hàm s
2
5x 6
x
y
x

có my tim cn?
1 2 3 4
==================================================================
DẠNG 2
Câu 1. Cho hàm s
x
,( )
x
ab
yC
cd
vi
0c
và
ad 0bc
. M 
 th luôn có tim cng
 th luôn có tim cn ngang
 th i xng
Trc tung không th là tim cng ca (C )
Câu 2. Cho hàm s
2
2x 3x
y
xm

vi giá tr nào ca m thì hàm s có tim cng?
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
20
1m 
13m
1
3
m
m

3m
Câu 3. Cho hàm s
2
2x 2x
y
xm
 th (C ). Tìm tt c giá tr c (C ) không có tim cn
ng.
0m
1m
0m
hoc
1m
2m
Câu 4. Tìm tt c các giá tr thc ca tham s
m
  th hàm s

2
1
2
m m x
y
x
ng tim
cm
–3; 2A
.
12 mm
.
12 mm
.
12 mm
.
12 mm
.
Câu 5. Tìm tt c các giá tr thc ca tham s
m
  th hàm s
1
2
mx
y
xm
có tim c
m
1; 2A
.
2m
.
2m
.
1
2
m
.
1
2
m
Câu 6. Cho hàm s
2
23x x m
y
xm

 th
C
. Tìm tt c các giá tr ca m  (C) không có
tim cng.
2m
1m
0m
hoc
1m
0m
Câu 7. Tìm tt c các giá tr thc ca tham s   th hàm s
2
x1
y
x mx m

t tim
cng.
m0
m0
m 0;4
m4
Câu 8. Tìm tt c các giá tr ca m   th hàm s
2
2
32
xm
y
xx

ng tim cn?
1m
và
4m
.
1m
.
4m
.
0m
.
Câu 9.   th hàm s
1 2 1
1
m x m
y
x
không có tim cng
2m
1m
1m 
1
2
m
Câu 10. Tp hp các giá tr ca tham s   th hàm s
2
2
3x 2
xm
y
x

t tim cn
ng
1; 4m
1m 
4m
1;4m
==================================================================
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
21
CHUYÊN ĐỀ 5 – ĐỒ THỊ CỦA HÀM SỐ
DẠNG 1: HÀM BẬC BA
32
( x x x , 0)y a b c d a
Mẫu 1. Bng bia mt trong
4 hàm s c li
nào?
32
32y x x
32
32y x x
32
32y x x
32
32y x x
Mẫu 2. Bng bia mt trong
4 hàm s c li
nào?
xxxy 33
23
xxxy 33
23
xxxy 33
23
xxxy 33
23
Mẫu 3.  th hàm s
32
x x xy a b c d
 th
. M 
0; 0; 0; 0a b c d
.
0; 0; 0; 0a b c d
.
0; 0; 0; 0a b c d
.
0; 0; 0; 0a b c d
.
Dạng 1:  th Hs
Dạng 2: 
Dạng 3: Hàm phân thc
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
22
Mẫu 4. Cho hàm s
32
x x ,( 0)y a b cx d a
có
 th  
du ct ?
,0ad
0, 0, 0a b c
, , , 0a b c d
, 0, 0a d c
Mẫu 5. ng cong trong hình bên  i là th ca
mt hàm s trong bn hàm s c lit kê bn png
án A, B, C, D di ây. Hi hàm s ó là hàm s nào?
133
23
xxxy
.
13
23
xxy
.
13
3
xxy
.
13
23
xxy
.
====================================================================
DẠNG 2: HÀM SỐ TRÙNG PHƢƠNG
42
x x , 0y a b c a
Mẫu 6.  th ca mt hàm
s trong bn hàm s c lit kê b
i hàm s  nào ?
42
2y x x
42
2y x x
42
31y x x
42
2y x x
Mẫu 10.  th hình bên là ca m th ca các hàm
s 
Hãy ch
A.
42
5y x x
. B.
42
1
5
4
y x x
.
C.
4
1
5
4
yx

. D.
42
1
27
4
y x x
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
23
Mẫu 11. Cho hàm s
42
x x , 0y a b c a
 th 
nh du ca a, b, c.
0, 0, 0a b c
0, 0, 0abc
0, 0, 0abc
0, 0, 0a b c
Mẫu 12. Cho hàm s
42
x x , 0y a b c a
 th 
hình bên
Trong các kt lut lu
0, 0, 0a b c
0, 0, 0a b c
0, 0, 0abc
0, 0, 0abc
====================================================================
DẠNG 3: HÀM PHÂN THỨC
x
x
ab
y
cd
Mẫu 13.  th ca mt hàm
s trong bn hàm s c lit kê b án A, B, C,
i hàm s  nào?
21
;
1
x
y
x
21
;
1
x
y
x
21
;
1
x
y
x
12
.
1
x
y
x
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
24
Mẫu 15.  hàm s
x2
x
a
y
cb
 th 
bên.
2, 2, 1a b c
1, 1, 1a b c
1, 2, 1a b c
1, 2, 1a b c
====================================================================
PHẦN 2: BÀI TẬP RÈN LUYỆN
Câu 1.Bng bia mt trong 4
hàm s c li
hàm s nào?
13
23
xxy
13
23
xxy
13
23
xxy
13
23
xxy
Câu 2.ng cong trong hình bên  i là  th ca mt hàm
s trong bn hàm s c lit kê bn png án A, B, C,
D di ây. Hi hàm s ó là hàm s nào?
3
31y x x
.
3
31y x x
.
42
1y x x
.
2
1y x x
.
Câu 1.Cho hàm s
42
x x , 0y a b c a
 th 
nh các h s a, b, c.
12
, , 0
33
a b c
12
, , 1
33
a b c
1, 2, 1a b c
1, 2, 0a b c
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
25
Câu 1.
42
y ax bx c


a 0,b 0,c 0
a 0,b 0,c 0
a 0,b 0,c 0
a 0,b 0,c 0
Câu 1. th ca hàm s 
42
22y x x
.
42
22y x x
.
42
22y x x
.
3
32y x x
.
Câu 1.
Xét các phát biu sau:
1.
1a 
2.
0ad
3.
0ad
4.
1d 
5.
1a c b
S phát biu sai là:
2
.
3
.
1
.
4
.
Câu 1.ng cong  th 

42
2x 2x 3y
2
2x 3x 2y
32
3xy x x
42
2x 4x 3y
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
26
x
y
-2
2
-1
0
1
Câu 1.nh a, b, c ca hàm s
42
xxy a b c

th 
4; 2; 2a b c
1
; 2; 2
4
a b c
4; 2; 2abc
1
; 2; 0
4
a b c
Câu 2. Cho hàm s
32
0y ax bx cx d a
 th .
Khđúng ?
0; 0; 0; 0.a d b c
0; 0; 0; 0.a b c d
0; 0; 0; 0.a c d b
0; 0; 0; 0a b d c
Câu 1. Cho hàm s
()y f x

th
()C
.
Hi
()C
 th ca hàm s nào?
3
( 1)yx
.
3
1yx
.
3
1yx
.
3
( 1)yx
.
==================================================================
DẠNG 3
Câu 1. th ca mt hàm s
trong bn hàm s c lit kê b
i hàm s  nào?
25
;
1
x
y
x
32
3 1;y x x
42
1;y x x
21
.
1
x
y
x
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
27
x
y
-2
1
-1
0
1
Câu 2. Cho hàm s
y f x
có bng bin thiên sau. Kh
x

1

y
y
1


1
 th hàm s có tim cng
1x
, tim cn ngang
1y 
;
 th hàm s có tim cng
1x 
, tim cn ngang
1y
;
 th hàm s ng tim cn ng;
 th hàm s ng tim cn ngang.
Câu 3.  th hàm s
y f x
ng

 th hàm s có tim cng
0x
, tim cn ngang
1y
;
 th hàm s ch có mt tim cn;
Hàm s có hai cc tr;
Hàm s ng bin trong khong
;0
và
0; 
.
Câu 4.Cho hàm s có
ax b
y
x1
 th i. Khng

b 0 a
0ba
b a 0
0 a b
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
28
Câu 5. Cho hàm s
x
xb
y
cd
 th .
Kh
0, 0, 0b c d
0, 0, 0b c d
0, 0, 0b c d
0, 0, 0b c d
Câu 6. Cho hàm s
x
x
ab
y
cd
 th .
M  là

. 0, . 0c d b d
a. 0, .c 0db
.a 0,a.b 0c 
a. 0, .c 0db
Câu 7. Cho hàm s
ax b
xd
y
c
vi
0a
 th 
v bên. M 
0, 0, 0b c d
0, 0, 0b c d
0, 0, 0b c d
0, 0, 0b c d
Câu 8. Cho hàm s
ax b
y
cx d
có
 th  bên.
Kh nh nào sau
   nh

.
0
0
ad
bc
.
.
0
0
ad
bc
.
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
29
x
y
-2
2
-1
0
1
Câu 9.  th hàm s
y f x
nh
 sai?
Hàm s có hai cc tr;
Hàm s ng bin trong khong
;1
và
1; ; 
 th hàm s có hai tim cn;
 th hàm s có tim cng
1x 
, tim cn ngang
2y
.
Câu 10. Cho hàm số
x
1
ab
y
x
có đồ thị như hình vẽ bên.
Tìm khẳng định đúng trong các khẳng định sau?
0ab
0ba
0 ba
0 ab
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
30
CHUYÊN ĐỀ 6 – SỰ TƢƠNG GIAO CỦA HAI ĐỒ THỊ
DẠNG 1: TÌM TỌA ĐỘ GIAO ĐIỂM
Mẫu 1.  th hàm s
3
32y x x
ct trc hoành t
12
;.xx
Tính tng
12
xx

12
2xx
.

12
0xx
.

12
–1xx
.

12
–2xx
.
Mẫu 2. Tìm t m c th hàm s
1
21
x
y
x
và
1yx
.
1;1 , 1; 2
.
1;0 , 1; 2
.
1;0 , 1;2
.
1; 2
.
Mẫu 3.  th hàm s
32
3x 2x 1yx
c th hàm s
2
3x 1yx
tm phân
bi dài AB bng bao nhiêu ?
3AB
22AB
2AB
1AB
DẠNG 2: BÀI TOÁN CHỨA THAM SỐ M
Mẫu 4. Tìm tt c giá tr c  th hàm s
32
2 1 4xy x m x
ct trc Ox tm

2x
2m
3m
1m 
4m
Mẫu 5.  ng thng
( ):d y x m
c th
2
( ):
1
x
Hy
x
tm phân
bit.
22m
2
2
m
m

0
2
m
m
02m
Mẫu 7. Tìm tt c giá tr ca tham s   th
22
2 x 3y x x m m
ct trc Ox ti
m phân bit
22m
21m
12m
22
1
m
m
--------------------------------------------------------------------------------------------------------------------
Mẫu 8. Tìm tt c giá tr c 
3
3x 0xm
có 3 nghim phân bit
22m
23m
13m
12m
Mẫu 9. Tìm tt c giá tr thc ca tham s  
42
2xxm
có 4 nghim
phân bit
0m
01m
01m
1m
Mẫu 10.  th ca hàm s
42
2xyx

tt c các giá tr thc ca tham s  
42
x 2x m
có 6 nghim thc phân bit.
01m
11m
02m
1m
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
31
PHẦN 2: BÀI TẬP RÈN LUYỆN
Câu 1. Tìm s m c th hàm s
32
21y x x x
ng thng
12yx
.
0
.
1
.
2
.
3
.
Câu 2. Tìm tt các giá tr ca
m
 ng thng
y x m
c th hàm s
21
2
x
y
x
ti hai
m phân bit .
1m
.
1m
.
1m
.
m
.
Câu 3. Bit r th ca hàm s
32
32 y x x x
cng thng
22 yx
tm
phân bit. Kí hi
11
;A x y
,
22
;B x y
và
33
;C x y
. Tính tng
1 2 3
S x x x
.
2S
.
3S
.
1S
.
23S
.
Câu 4. Tìm tt c các giá tr thc ca tham s
m
  th hàm s
ym
c th hàm s
3
32 y x x
tm phân bit.
0 4.m
4.m
0 4.m
0 4.m
Câu 5. Tìm tt c các giá tr thc ca tham s
m
  th hàm s
32
4 y x mx mx
ct
ng thng
4yx
tm phân bit.
2m
.
1m
.
4m
.
2m
.
Câu 6.  th ca hàm s
3
3.y x x
Tìm tt
c giá tr thc ca tham s
m
 
32
3x x m
m phân bit.
2;0 0; 2 m
.
0; 2m
.
2;0 0;2 m
.
0;2m
.
Câu 7. Tìm tt c giá tr thc ca tham s
m
  th hàm s
42
21 y x mx m
ct trc tung t bng
2
.
3m
.
3m
. Không có m
2m
.
Câu 8. Tìm tt c giá tr thc ca tham s
m
 ng thng
ym
c th hàm s
42
– 2 3y x x
ti bm phân bit.
11 m
.
23m
.
01m
.
– 1 0m
.
Câu 9. Tìm tt c giá tr thc ca tham s
m
  th hàm s
42
:1
m
C y x mx m
ct
trc hoành ti bm phân bit.
1
.
2

m
m
Không có
.m
1.m
2.m
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
32
Câu 10.Gi
,MN
m cng thng
1yx
ng cong
24
1
x
y
x
. Tìm hoành
 m
I
cn thng
MN
.
5
2
.
1
.
2
.
5
2
.
Câu 11. Tìm các giá tr thc ca tham s
m
ng thng
yx
c th hàm s
5
x
y
xm
tm
A
và
B
sao cho
42AB
.
2. 5. 7. 
Câu 12.  th ca hàm s
21
1
x
y
x
. Tìm tt c
các giá tr thc ca tham s
m
 
21
2
1
x
m
x
có hai nghim phân bit.
Vi mi
m
. Không có giá tr ca
m
.
0m
.
0; \ 1 m
.
Câu 13. Cho hàm s
32
2x 1yx
 th (C ). Tìm tt c giá tr c ng thng
:xd y m m
C th (C ) tm phân bit ?
5
4
1
m
m


5
4
1
m
m

5
4
1
m
m

5
4
1
m
m


Câu 14. Tìm t m
M
thuc  th hàm s
2
33
1


xx
y
x
sao cho
M
u hai trc
t.
1
;2
2



M
.
33
;
22



M
.
33
;
22



M
.
1
;2
2



M
.
Câu 15. Tìm t m
M
thuc  th hàm s
3
1
x
y
x
m
M
u hai trc ta
.
2;5M
.
1; 1M
.
3; 3M
.
1
2;
3



M
.
Câu 16. Cho hàm s
3
3x 2yx
 th (C ). Gng th
s góc là m. Giá tr c ng thng d ct (C ) tm phân bit
15
, 24
4
mm
15
4
m
15
, 24
4
mm
15
4
m
8
6
4
2
2
4
6
15
10
5
5
10
15
1
1
-1
I
O
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
33
Câu 17. Tìm giá tr c ng thng
( ):d y x m
c th
32
3 1 x 1y x m x m
()
m
C
tm phân bit?
5
; 1 ;
9
m




1;m 
mR
\0mR
Câu 18. Các giá tr ca tham s   th hàm s
32
3x 9xy x m
ct trc hoành ti 3
m phân bi lp thành cp s cng là
11m
11m 
11m
D.
11m 
Câu 19. Cho hàm s
()fx
nh trên
\0R
và có bng bi. Tìm tt c giá
tr ca tham s  
( ) 1f x m
có 3 nghim thc phân bit
4m
Không tn ti m
3m
3m
Câu 20. Cho hàm s
fx
 th  nh tt
c giá tr ca tham s  
f x m
có
6 nghim phân bit
4m
04m
34m
03m
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
34
CHUYỀN ĐỀ 7: PHƢƠNG TRÌNH TIẾP TUYẾN
PHẦN 1: BÀI TẬP MẪU
DẠNG 1: VIẾT PHƢƠNG TRÌNH TIẾP TUYẾN
Mẫu 1. p tuyn c th
32
( ): 2xC y x
tm
(1;3)M
là:
7x 4y 
7x 4y 
7x 4y
7x 4y
Mẫu 2. m M thu th
2x 1
( ):
1
Cy
x
 bng -p
tuyn ca (C ) tm M là:
31
44
yx
31
44
yx
31
44
yx
31
44
yx
Mẫu 3. p tuyn c th
3
( ): 3x 2C y x
có h s góc bng 9 là:
9x 18; 9x 22yy
9x 14; 9x - 18yy
9x + 8; 9x 22yy
9x 18; 9x 22yy
Mẫu 4. Tip tuyn c th
2x 1
( ):
2
Cy
x
song song vng thng
:3x 2 0y
có

3x 4y 
3x 2y 
3x 14y 
3x 4y 
Mẫu 5. Tip tuyn c th
3
( ): 4x 3x 1Cy
m
( 1;2)A

9x 7; 2y y x
9x 11; 2y y x
9x 11; 2yy
9x 7; 2yy
DẠNG 2: BÀI TOÁN CHỨA THAM SỐ M
Mẫu 6. Cho hàm s
32
3xyx
 th (C ). Gm thu th 
bng 1. Vi giá tr nào ca m thì tip tuyn ca (C ) ti M song song vng thng
2
: ( 4) 2 1d y m x m
1m
1m 
2m
2m 
Mẫu 7. Vi giá tr nào cng thng
8xym
là tip tuyn c th hàm s
42
2x 3yx
8m
8m 
18m
18m 
====================================================================
PHẦN 2: BÀI TẬP RÈN LUYỆN
Câu 1. Cho hàm s
32
5x 1y x x
p tuyn t th có hoành

2x
10x 9y 
11x 19y 
11x 10y 
10x 8y 
Câu 2. Tip tuyn c th hàm s
32
4x 4x 1yx
Tm
( 3; 2)A 
c th ti
m th m B có t là
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
35
1;0B
(1;10)B
2;33B
2;1B
Câu 3. Hai tip tuyn tm cc tr c th hàm s
3
3x 1yx
cách nhau mt
khong bng
1 4 3 2
Câu 4. Cho hàm s
32
1y x x x
ng tip tuyn c th hàm s ti
m ca nó vi trc hoành là
0; 1y y x
1; 4y x y x
0; 4x 4yy
1; 1y x y x
Câu 5.  th hàm s
42
2x 1yx
có bao nhiêu tip tuyn song song vi trc hoành
1 2 3 4
Câu 6. Tip tuyn c th hàm s
3
2
3x 2
3
x
y
có h s góc
9k 

16 9 3yx
16 9 3yx
9 3yx
16 9 3yx
Câu 7. Cho hàm s
32
3x 2yx
 th (C ). S tip tuyn c th ( C ) mà song song
vng thng
9x 7y
là:
0 1 3 2
Câu 8. Tip tuyn c th hàm s
2
1
x
y
x
song song vng thng
3x 2y
có

3x 10y 
3x 2; 3x 10yy
3x 10y
3x 2y
Câu 9. Cho hàm s
42
6y x x
 th (C ). Vip tuyn c th (C ),
Bit tip tuyn vuông góc vng thng
1
1
6
yx
.
6x 6y
6x 8y
6x 10y
6x 12y
Câu 10. Cho hàm s
32
4x 6x 1y
 th ( C). Vip tuyn vi (C ) bit
rng tip tuym M(-1; -9)
15 21
24x 25;
4 24
y y x
15 21
24x 15;
44
y y x
15 21
24x 5;
4 24
y y x
15 21
24x 25;
44
y y x
Câu 11. ng thng
6xym
là tip tuyn cng cong
3
3x 1yx
khi m bng
3
1
m
m

3
1
m
m
3
1
m
m

3
1
m
m


ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
36
Câu 12. Cho hàm s
x2
xb
y
a
 th ( C ). Bit rng a, b là các giá tr thc sao cho tip
tuyn ca ( C) tm M(1; -2) song song vng thng
:3x 4 0dy

giá tr ca
ab
bng
0 -1 2 1
Câu 13. Tp hp các giá tr thc ca tham s   th (C ) ca hàm s
2x 3
1
y
x
cng
thng
2
2xym
tm phân bit mà hai tip tuyn ca ( C) t
song song vi nhau là
2
2; 2
1;1
2;2
Câu 14. Cho hàm s
2x 1
1
y
x
 thì (C). Gm thu bng 5. Tip
tuyn ca (C ) tm M ct các trc Ox, Oy lt ti A và B. Tính din tích tam
giác
OAB
S
112
6
121
6
122
6
113
6
Câu 15. Cho hàm s
42
2 x 2 1y x m m
 tip tuyn c th (Cm) ti
m A(1; 0), B(-1; 0) vuông góc vi nhau.
53
;
44
mm
53
;
44
mm
53
;
44
mm
53
;
44
mm
Câu 16. Cho
2x 3
1
y
x
(C). Vip tuyn ca (C) bit tip tuyn ct Ox, Oy ti
m A, B sao cho OB = 5OA.
5x 3, 5x 17yy
5x + 3, 5x 17yy
5x 3, 5x - 17yy
5x + 3, 5x - 17yy
Câu 17.  tip tuyn c th hàm s y = (2m 1)x
4
m +
5
4
t x =
1 vuông góc vng thng 2x y 3 = 0
2
3
1
6
1
6
5
6
Câu 18. Cho hàm s y =
1
ax b
x
 th ct trc tung ti A(0; 1), tip tuyn ti A có h s góc
3k 
. Các giá tr ca a, b là:
a = 1; b=1 a = 2; b=1 a = 1; b=2 a = 2; b=2
Câu 19. Cho hàm s y =

2
2
1
x mx m
x
. Giá tr   th hàm s ct trc Ox tm và
tip tuyn c th t
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
37
3 4 5 7
Câu 20. Cho hàm s
42
2 1 2y x m x m
 th (C ). Gm thu th hàm
s  bng 1. Vi giá tr nào ca m thì tip tuyn c th (C ) ti A vuông
góc vng thng
: 2 4 0xy
2m 
1m 
0m
4m
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
38
ÔN TẬP CHƢƠNG HÀM SỐ
Câu 1. Giá tr ca tham s  hàm s
32
6x 2 x 1y x m
m cc tr x
1
, x
2
tha
22
12
12xx
A.
1m 
B.
3m
C.
1m
D.
3m 
Câu 2. Giá tr nh nht ca hàm s
2
1y x x
là
A. -1 B.
2
C. 1 D.
2
Câu 3. Tìm Tt c giá tr c  th hàm s
2
1
2x x 4
x
y
m

t tim cn
ngang là
A.
0m
B.
0
4
m
m
C.
4m
D.
04m
Câu 4. Tìm tt c giá tr c 
32
3x 2xm
có 2 nghim thc phân bit
A.
2
2
m
m

B.
22m
C.
20m
D.
02m
Câu 5.  th ca hàm s
32
3x 5x 3yx
p tuyn ca (C ) có h
s góc nh nhm nào thu
A.
(0;3)M
B.
1;2N
C.
3;0P
D.
2; 1Q
Câu 6.  th hàm s
32
3x 2x 1yx
c th hàm s
2
3x 1yx
tm
phân bi dài AB bng bao nhiêu ?
A.
3AB
B.
22AB
C.
2AB
D.
1AB
Câu 7. Tìm tt c giá tr thc c  th hàm s
2
4
2
x3
x
y
m
có mt tim cn ngang
A.
0m
B.
0m
C.
0m
D.
3m
Câu 8. Tìm tt c giá tr c hàm s
32
2x 3 1 6 2 3y m x m x
nghch bin
trên kho dài l
A.
6m
B.
9m
C.
0m
hoc
6m
D.
0m
Câu 9. Tìm tt c giá tr c hàm s
3 2 2
1
x 1 1
3
y x m m m x
t ci ti
1x
A.
2m 
B.
1m 
C.
2m
D.
1m
Câu 10. Tìm tt c giá tr c hàm s
12mx
y
xm

ng bin trên khonh
A.
21m
B.
1
2
m
m

C.
21m
D.
1
2
m
m

Câu 11. Cho hàm s
32
1
x 3 2 1
3
y x m m x
. Tìm tt c giá tr c hàm s
nghch bin trên R
A.
1
2
m
m


B.
1
2
m
m


C.
21m
D.
21m
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
39
Câu 12. Cho hàm s
2x 1
1
y
x
 th (C ). Tìm tt c giá tr c ng thng (d):
1y x m
ct (C ) tm phân bit A, B sao cho
23AB
A.
43m 
B.
4 10
C.
23m 
D.
2 10m 
Câu 13. Cho hàm s
2
2
x
y
x
 th (C ). Tìm t  c (C
) sao cho tng khong cách t n hai tim cn nh nht.
A.
(0; 1)M
B.
2;2M
C.
(1; 3)M
D.
(4;3)M
Câu 14. Cho hàm s
2
2x 3x
y
xm
 th (C ). Tìm tt c giá tr c (C ) không có
tim cng.
A.
0m
B.
1m
C.
0m
hoc
1m
D.
2m
Câu 15. Tìm t c giá tr c giá tr nh nht ca hàm s
2x 1
()
1
m
fx
x

n
1;2
bng 1
A.
1m
B.
2m
C.
3m
D.
0m
Câu 16. Cho hàm s
32
1
x1
3
y x m x m
Tìm tt c giá tr c hàm s m
cc tr là A, B tha mãn
22
2
AB
xx
A.
0m
B.
1m 
C.
3m 
D.
2m
Câu 17.  hàm s
32
3 x 1y x m
m cc tr A, B sao cho tam giác OAB
có din tích bng 1.
A.
3m 
B.
1m 
C.
5m 
D.
2m 
Câu 18. Tìm các giá tr ca tham s   th hàm s
42
x 2 1 2y m m x m
ch có
ci và không có cc tiu.
A.
0
1
2
m
m
B.
0m
C.
0
1
2
m
m
D.
1
2
m
Câu 19.  th hàm s
2x 1
1
y
x
nhm M sao cho khong cách t n
tim cng bng 3 ln khong cách t n tim cn ngang c th
A.
4;3M
hoc
(2;5)M
B. .
7
4;
5
M



hoc
(2;5)M
C.
4;3M
hoc
( 2;1)M
D.
7
4;
5
M



hoc
( 2;1)M
Câu 20. Cho hàm s
32
2x 1yx
 th (C ). Tìm tt c giá tr c ng thng
:xd y m m
C th (C ) tm phân bit ?
A.
5
4
1
m
m


B.
5
4
1
m
m

C.
5
4
1
m
m

D.
5
4
1
m
m


ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
40
Câu 21. Tp tt c giá tr c hàm s
32
2
2 3 1 7
3
m
y x m x m x
ng bin
trên R
A.
1
2
4
m
B.
1
2
4
m
C.
1
2
4
m
D.
1
2
4
m
Câu 22. Tìm tt c giá tr c  th hàm s
4 2 2
2 x 1y x m m
m cc tr,
ng thm cc tr này cùng vi gc t O to thành mt t giác ni tip
c
A.
3
3m
B.
1m 
C.
1m 
D.
1m
Câu 23. Tìm các giá tr c hàm s
42
1
2 1 5
6
y m x m x
t cc tiu
A.
21m
B.
2m 
C.
1m
D.
2m 
Câu 24.  th ca hàm s ng tim cn ngang
A.
2
2
2x 3
x
y
x

B.
2
2
4
2
x
y
x
C.
32
2x 7yx
D.
2
2x 2
4
y
x

Câu 25. Giá tr ln nht và giá tr nh nht ca hàm s
2
4y x x
lt là
A.
22
và 2 B.
22
và -2 C.
22
và
22
D. 2 và -2
Câu 26. Tìm tt c giá tr c hàm s
32
1 3x 3x 5y m x
có cc tr
A.
1m
B.
1m 
C.
01m
D.
0m
Câu 27. Tìm tt c giá tr c hàm s
2
2
x
y x x m
ng bin trên khong
;2
A.
1
4
m
B.
1
4
m
C.
2m
D.
7m
Câu 28. Tim cn ngang c th hàm s
2
2x 17y x x
khi
x 

trình là
A.
1y 
B.
1y
C.
2y
D.
2y 
Câu 29. Tìm tt c giá tr ca tham s   th hàm s
4 2 2
22y x m x m
m cc
tr nh ca hình thoi
A.
1m 
B.
1m
C.
2m
D.
3m
Câu 30. Gm bt k  th (C ) ca hàm s
4
1
y
x
. Tng khong cách t M
n hai tim cn ct giá tr nh nht là
A.
22
B. 4 C.
42
D. 2
Câu 31. Tìm tt c giá tr ca tham s  m
(2; )Mm
k c ba tip tuyn phân bit
 th hàm s
32
3xyx
là
A.
4;5m
B.
2;3m
C.
5; 4m
D.
5;4m
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
41
Câu 32. G khác 1, thu th (C ) ca hàm s
32
3xyx
. Tip
tuyn ca (C ) ti M ct (C ) tm th hai là N ( N không trùng M). Kí hiu
;
MN
xx
th t  ca M và N. Kt lu
A.
2
MN
xx
B.
3
MN
xx
C.
23
MN
xx
D.
23
MN
xx
Câu 33. Tìm giá tr c hàm s
32
12
1 2 3
33
y x m x m x
ng bin trên
1; 
A.
2m
B.
1m
C.
1m
D.
2m
Câu 34. Cho hàm s
3
3x 2yx
 th (C ). Gng th
h s góc là m. Giá tr c ng thng d ct (C ) tm phân bit
A.
15
, 24
4
mm
B.
15
4
m
C.
15
, 24
4
mm
D.
15
4
m
Câu 35. Tìm tt c giá tr ca tham s  
42
2x 3 2 0xm
có 4 nghim
phân bit?
A.
3
2
2
m
B.
34m
C.
3
2
2
m
D.
3
2
2
m
Câu 36. Cho hàm s
32
6x 9x 2yx
ng th-1; 1) và vuông góc vi
ng thm cc tr ca (C ) là
A.
13
22
yx
B.
13
22
yx
C.
3yx
D.
2 3 0xy
Câu 37.  th hàm s
32
3 9 1y x x x
có hai cc tr
A
và
B
c
ng thng
AB
?
A.
0;2N
. B.
1;1P
. C.
1; 8Q 
. D.
0; 1M
.
Câu 38. Gi
S
là tng tt c các giá tr   a tham s
m
sao cho hàm s
2
2
4
xm
y
xm

ng bin trên khong
2021;
 ca
S
bng
A.
2035144
. B.
2035145
. C.
2035146
. D.
2035143
Câu 39.  th
2
2
4
x
y
x
có bao nhiêu tim cn?
A. 2. B. 4. C. 3. D. 1.
Câu 40. Tìm các giá tr ca tham s
m
 hàm s
3
22
3 2 3
3
x
y x m x m
ng bin trên
R
.
A.
3
3
m
m

. B.
33m
. C.
33m
. D.
3
3
m
m

.
Câu 41. Cho hàm s
y f x
có bng xét d
M 
A. Hàm s nghch bin trên khong
;2
. B. Hàm s nghch bin trên khong
;2
.
+
0
0
2
0
2
+
y'
x
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
42
C. Hàm s nghch bin trên khong
;0
. D. Hàm s nghch bin trên khong
2;0
Câu 42. Cho hàm s
2
,
8
xm
fx
x
vi
m
là tham s. Giá tr ln nht ca
m

0;3
min 2fx
là
A.
5m
. B.
6m
. C.
4m
. D.
3m
.
Câu 43. Giá tr ln nht ca hàm s
4
2
x
y
x
n
3,4
.
A.
4
. B.
10
. C.
7
. D.
8
.
Câu 44. Cho hàm s
y = ax
3
+ bx
2
+cx + d
. Hi hàm s ng bin trên R khi nào?
A.
a = b = 0,c > 0
a > 0;b
2
- 3ac £ 0
é
ë
ê
. B.
a = b = 0,c > 0
a > 0;b
2
- 3ac ³ 0
é
ë
ê
.
C.
a = b = 0,c > 0
a < 0;b
2
- 3ac £ 0
é
ë
ê
.
D.
a = b = c = 0
a < 0;b
2
- 3ac < 0
é
ë
ê
.
Câu 45. Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
y = (m-3)x -(2m+1)cosx
luôn nghch bin trên
R
?
A.
m Î -4;
2
3
é
ë
ê
ù
û
ú
. B.
m ³ 2
. C.
m > 3
m ¹ 1
ì
í
î
ï
. D.
m Î -¥;2
(
ù
û
.
Câu 46. Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
y =
mx + 4
x + m
gim trên
khong
-¥;1
( )
?
A.
-2 < m £ -1
. B.
-2 £ m £ -1
. C.
-2 < m < 2
. D.
-2 £ m £ 2
.
Câu 47. Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
y = x
3
-6x
2
+ mx +1
ng
bin trên khong
0;+¥
( )
?
A.
m ³12
. B.
m £12
. C.
m ³ 0
. D.
m £ 0
.
Câu 48. Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
y = x
4
-2(m-1)x
2
+ m -2
ng bin trên khong
(1;3)
?
A.
m Î -¥;2
(
ù
û
. B.
m Î -5;2
é
ë
)
. C.
m Î 2,+¥
( )
. D.
m Î -¥;-5
( )
.
Câu 49. Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
y =
1
3
x
3
-
1
2
mx
2
+ 2mx - 3m + 4
nghch bin trên m dài là 3?
A.
m = -1;m = 9
. B.
m = -1
. C.
m = 9
. D.
m =1;m = -9
.
Câu 50. Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
y =
1- sinx
sinx - m
nghch bin
trên khong
0;
p
6
æ
è
ç
ö
ø
÷
?
A.
m £ 0;
1
2
£ m <1
. B.
m £ 0;
1
2
£ m £1
. C.
m <1
. D.
m £1
.
Câu 51. Tìm tt c các giá tr thc ca tham s
m
sao cho hàm s
3
2
( ) 7 14 2
3
mx
y f x mx x m
gim trên na khong
[1;+¥)
?
A.
-¥;-
14
15
(
ù
û
. B.
-¥;-
14
15
( )
. C.
-2;-
14
15
é
ë
ù
û
. D.
-
14
15
;+¥
é
ë
)
.
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
43
Câu 52. Cho hàm s
32
1
3 2 1
3
y x mx m x
. Tìm các giá tr ca m  hàm s nghch
bin trên
R
.
A.
1
2
m
m


B.
21m
C.
1
2
m
m


D.
21m
Câu 53. Tìm tt c các giá tr ca m  hàm s :
12mx
y
xm

ng bin trên tng khong
nh.
A.
21m
B.
21m
C.
1
2
m
m

D.
1
2
m
m

Câu 54. Tìm tt c các giá tr ca m  hàm s:
32
2 3 1 6 2 3y x m x m x
nghch bin
trên kho dài l
A.
0m
hoc
6m
B.
6m
C.
0m
D.
9m
Câu 55. 
2
1 mx
y x 2x 2017
32

R
A.
2 2 m 2 2
B.
m 2 2
C.
2 2 m
D.
2 2 m 2 2
Câu 56. Giá tr ca tham s thc
m
 hàm s
sin2y x mx
ng bin trên là
A.
2m 
B.
2m 
C.
2m 
D.
2m 
.
Câu 57. 
32
11
y x m 5 x mx
32


CD CT
x x 5
A.
m0
B.
m6
C.
m 6;0
D.
m 6;0
Câu 58. 
x1

3 2 2
1
x mx m m 1 x
3
A.
m 2; 1
B.
m2
C.
m1
D. 
Câu 59. Tìm tt c các giá tr ca tham s  hàm s
4 2 2
y x 2 m 1 x m 1
t cc tiu
ti
x0
A.
x1
B.
m 1 1 hoaëc m
C.
m1
D.
m1
Câu 60. Các giá tr thc ca tham s m sao cho hàm s
3 2 2
f x 4x 2 m 2 x m 1
có
t cc tr ?
A.
m2
B.
m2
C.
m2
D.
m2
Câu 61. Gm cc tr c th hàm s
42
y x 2x 3
. Tính din tích ca
tam giác ABC.
A. 2 B. 1 C.
2
D.
22
Câu 62. Cho hàm s
42
y mx m 1 x 1 2m
. Tìm tt c các giá tr c hàm s có 3
m cc tr.
A.
1 m 2
B.
0 m 1
C.
1 m 0
D.
m1
Câu 63. Cho hàm s
32
1
1
3
y x mx x m
. Tìm tt c các giá tr ca m   th hàm s có
m cc tr là
; , ;
A A B B
A x y B x y
tha mãn
22
2
AB
xx
A.
3m 
B.
0m
C.
2m
D.
1m 
Câu 64. 
32
y x 6x 9x 2 C

A 1;1


ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
44
A.
13
yx
22

B.
13
yx
22

C.
y x 3
D.
x 2y 3 0
Câu 65. Tính khong cách d gim cc tr c th hàm s
32
y x 3x 2
.
A.
d4
B.
d 2 5
C.
d 2 2
D.
d 10
Câu 66. Cho hàm s
y f x
liên tc trên o hàm
23
1 1 .f x x x x
Hàm s 
m cc tr?
A. m cc tr. B. Không có cc tr.
C. m cc tr. D. Ch m cc tr.
Câu 67. Trong khong (
0;2 )
hàm s
cos
2
x
yx
m cc tr
A. 1 B. 2 C. 3 D. 4
Câu 68. Cho hàm s
3
32y x x
. Gi
A
m cc tiu c th hàm s và
d
ng
thm
0; 2M
có h s góc
k
. Tìm
k
 khong cách t
A
n
d
bng
1
.
A.
3
4
k 
. B.
3
4
k
. C.
1k
. D.
1k
.
Câu 69. Vi
m
là mt tham s th th hàm s
42
21y x mx
m cc tr
to thành mt tam giác vuông. M 
A.
2m
. B.
20m
. C.
2m 
. D.
02m
.
Câu 70. Cho hàm s
y x 2
. Chn khng 
A. Hàm s t cc tiu ti x = 0 B. Hàm s t ci ti x = -2
C. Hàm s t cc tiu ti x = -2 D. Hàm s không có cc tr.
Câu 71. Tìm các giá tr thc ca tham s   th hàm s
32
y x 3x mx 2
m
cc tr ng thng AB song song vng thng
d: y 4x 1
A.
m1
B.
m3
C.
m0
D. không có m
Câu 72. Tìm tt c các giá tr ca tham s
m
  th hàm s
42
1 2017y m x mx
có
t cc tiu.
A.
0;1m
B.
1;m
C.
0;m 
D.
0;1 1;m 
Câu 73. Tính khong cách d gim cc tiu c th hàm s
42
4 1.y x x
A.
22d
. B.
3d
. C.
2d
. D.
1d
.
Câu 74.  hàm s
32
6 3 2 6y x x m x m
có ci, cc tiu lt ti
1
x
và
2
x
sao
cho
12
1xx
thì giá tr ca tham s
m
là
A.
1.m 
B.
1.m
C.
1.m
D.
1.m 
Câu 75. Tìm các s thc p và q sao cho hàm s
()
1
q
f x x p
x
t ci ti
2x 
và
22f
A.
1; 1pq
B.
1; 1pq
C.
1; 1pq
D.
1; 1pq
Câu 76. Tìm tt c các giá tr ca m  giá tr nh nht ca hàm s
21
1
xm
fx
x

n
1;2
bng 1
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
45
A.
1m
B.
2m
C.
3m
D.
0m
Câu 77. Gng là GTNN và GTLN ca hàm s
y 1 x 1 x
, tính tng
mM
A. 2 B.
22
C.
2 1 2
D.
12
Câu 78. Gi
M
và
m
 ng là giá tr ln nht và giá tr nh nht ca hàm s
32
22
(x 1)
x x x
y


Mm
bng:
A.
1
2
. B.
2
. C.
3
2
. D.
1
.
Câu 79. Gi
,Mm
l t là giá tr ln nht và giá tr nh nht ca hàm s
3 1 4 5 .y x x
Tính
.Mm
A.
16Mm
. B.
18Mm
.
C.
12 3 6 4 10
2
Mm


. D.
16 3 6 4 10
2
Mm


.
Câu 80. Cho hàm s
1
()
mx
fx
xm
. Giá tr ln nht ca hàm s trên
[1;2]
bng
3

m
bng:
A.
1
2
m 
B.
1
2
m
C.
1m
D.
2m
Câu 81. 
2
x
y
x1

A. 0 B. 1 C. 2 D. 3
Câu 82. Cho hàm s
y f x
nh và liên tc trên tp
\1D
và có bng bin thiên:
Câu 83. Da vào bng bin thiên ca hàm s
y f x
. Khnh
sai?
A. Giá tr nh nht ca hàm s n
1;8
bng
2
.
B. Hàm s t cc tiu ti
3x
.
C. 
f x m
có
3
nghim thc phân bit khi
2m 
.
D. Hàm s nghch bin trên khong
;3
.
Câu 84. Tìm t ca tt c  th (C) ca hàm s
x1
y
x1
sao cho tip
tuyn ca (C) ti M song song vng thng
17
d : y x
22

A.
0;1
và
2; 3
B.
1;0
và
3;2
C.
3;2
D.
1;0
Câu 85. 
3
y x x 1


A.
y 2x 2
B.
y x 1
C.
y x 1
D.
y 2x 1
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
46
Câu 86. Tip tuyn ca parabol
2
4yx
tm (1 ; 3) to vi hai trc t mt tam giác
vuông. Tính din tích
S

A.
25
.
4
S
B.
5
.
4
S
C.
25
.
2
S
D.
5
.
2
S
Câu 87. Bit r th các hàm s
3
5
2
4
y x x
và
2
2y x x
tip xúc nhau tm
00
( ; )M x y
. Tìm
0
.x
A.
0
1
2
x
. B.
0
5
.
2
x
C.
0
3
.
4
x
D.
0
3
2
x
.
Câu 88. Tìm tt c các giá tr ca tham s  
22
x 1 4 x m 0
có
nghim.
A.
2 m 2
B.
m2
C.
0 m 2
D.
2 m 0
Câu 89. Cho hàm s
2
y x 1 x mx 1
 th (C). Tìm s  nh
 th (C) ct trc hoành tm phân bit.
A.
m4
B.
m3
C.
m1
D.
m2
Câu 90. Tìm tt c các giá tr c 
32
x 3x m 0
có 3 nghim thc phân
bit.
A.
4 m 0
B.
m0
C.
m4
D.
0 m 4
Câu 91. Cho hàm s
21
1
x
y
x
 th (C). Tìm tt c các giá tr c ng thng
:1d y x m
ct (C) tm phân bit A, B sao cho
23AB
.
A.
4 10m 
B.
43m 
C.
2 10m 
D.
23m 
Câu 92. Tìm tt c các giá tr ca m  
2
4
1x x m
có nghim.
A.
1; 
B.
0;1
C.
;0
D.
0;1
Câu 93. 
3
y x 3x 2

A 3;20


A.
15
m ,m 24
4

B.
15
m
4
C.
15
m ,m 24
4

D.
15
m
4
Câu 94. 
42
x 2x 3 2m 0


A.
3
2m
2
B.
3 m 4
C.
3
2m
2
D.
3
m2
2

Câu 95. Cho hàm s
4 2 2
y x 2mx m 1
 th ng thng
d: y x 1
. Tìm tt c
giá tr thc ca tham s   th hàm s ng thm nm
trên trc hoành.
A.
m2
B.
m2
C.
m0
D.
m 0;2
Câu 96.
Tìm tt c các giá tr ca tham s
m
   th ca hai hàm s
32
y x x
và
2
3y x x m
ct nhau ti nhim nht.
A.
22m
B.
22m
C.
2m
D.
02m
Câu 97. Bit r ng thng
22yx
c  th hàm s
3
2y x x
t m duy
nht; kí hiu
00
;xy
là t c
0
y
:
A.
0
4y
B.
0
0y
C.
0
2y
D.
0
1y 
ĐẠI SỐ 12
[Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Trên bước đường thành công không có dấu chân của kẻ lười biếng.
47
Câu 98. Tìm tt c các giá tr c ng thng y = m c th hàm s
42
2y x x
ti
6
m phân bit.
A.
01m
B.
10m
C.
11m
D.
11m
Câu 99. 
:d y x m

21
( ):
2
x
Cy
x


,AB

AB

A.
6.
B.
2 6.
C.
3 6.
D.
4.
Câu 100. Hình v  ca hàm s
3
31y x x
giá tr ca m
 
3
3x 1xm
có 3 nghit khác
nhau là
A.
1 3.m
B.
0.m
C.
0, 3.mm
D.
3 1.m
| 1/47
| | Tải xuống

Có thể bạn quan tâm:

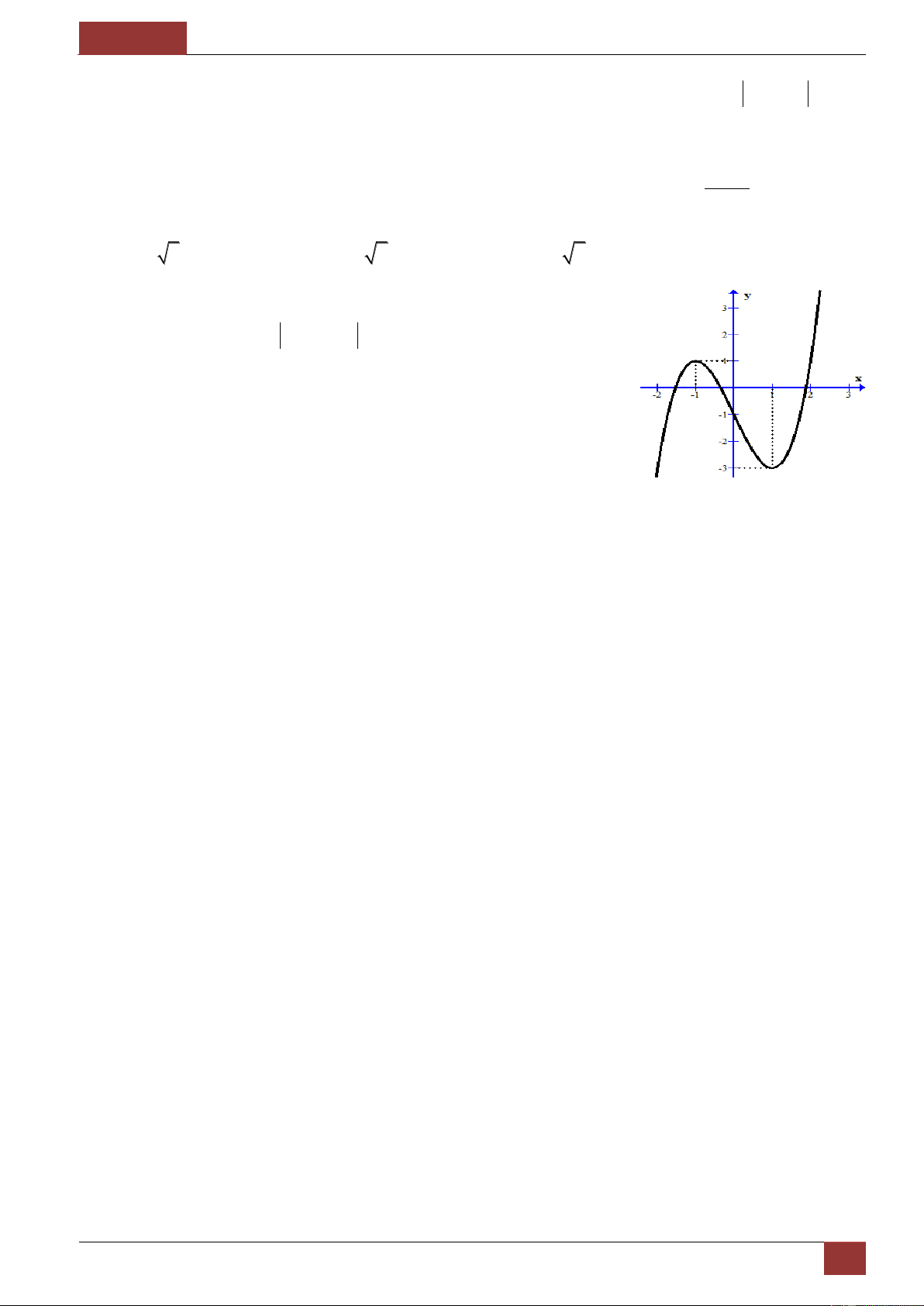
Preview text:

ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
CHUYÊN ĐỀ 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Dạng 1: Tìm khoảng ĐB – NB của hàm số
Dạng 2: Tìm m để Hs ĐB – NB trên R
Dạng 3: Tìm m để Hs ĐB – NB trên khoảng (a ; b)
DẠNG 1: TÌM KHOẢNG ĐỒNG BIẾN – NGHỊCH BIẾN CỦA HÀM SỐ
Loại 1: Hàm số bậc ba
Mẫu 1. Tìm khoảng đồng biến của hàm số 3 2
y x  3x 1  0;2   ;  2   ;0
  và 2;  0; 4
Mẫu 2. Tìm khoảng đồng biến của hàm số 3 2 y
x  2x  x  3 3  0  ;1  0;  R   ;  0 1
Mẫu 3. Tìm khoảng nghịch biến của hàm số 3 y   x  4x 1 3   ;0
  và 2;  ;    2;   ;  2
--------------------------------------------------------------------------------------------------------------------
Loại 2: Hàm số trùng phƣơng
Mẫu 4. Tìm khoảng đồng biến của hàm số 4 2
y x  2x 1   1  ;0 và 1;   1  ;0   1   ;1   1  ;
Mẫu 5. Tìm khoảng nghịch biến của hàm số 4 2
y  x  2x  5  0;   ;  0  R   1   ;1
--------------------------------------------------------------------------------------------------------------------
Loại 3: Hàm phân thức. 2x  3
Mẫu 6. Hàm số y x  nghịch biến trên khoảng nào 1  R  1;    ;1  và 1;     ;1  2 x  2x  2
Mẫu 7. Tìm khoảng đồng biến của hàm số y x 1   2  ;0   2;     ;  2
  và 0;   ;  0
--------------------------------------------------------------------------------------------------------------------
Loại 4: Hàm số khác. 4
Mẫu 8. Tìm khoảng nghịch biến của hàm số y x x   2  ;2  2;   2
 ;0 và 0;2   ;  2
Mẫu 9. Tìm khoảng nghịch biến của đồ thị hàm số 2 y  25  x   5  ;0  0;5   5  ;5  0; 1 5 7 Mẫu 10. Hàm số 4 3 2 y x x
x  3x  2018 nghịch biến trên khoảng nào 4 3 2
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 1
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]  0;3  0;  3;  1;3
DẠNG 2: TÌM M ĐỂ HÀM SỐ ĐB – NB TRÊN R.
Mẫu 11. Tìm tất cả giá trị thực của tham số m để hàm số 3 2 y  x m  x m
x m 1 đồng biến trên R 1
Mẫu 12. Cho hàm số 3 2
y   x mx  3m  2 x 1 . Tìm giá trị của m để hàm số nghịch biến 3 trên R . x m  3
Mẫu 13. Với giá trị nào của m thì hàm số y x m  nghịch biến trên từng khoảng xác định. 2 2 x mx  2
Mẫu 14. Tìm tất cả giá trị thực của tham số m để hàm số y  đồng biến trên từng x  1 khoảng xác định.
10. 0  m  3 11. 2   m  1  12. 3
  m 1 13. m  3.
DẠNG 3: TÌM M ĐỂ HÀM SỐ ĐB – NB TRÊN KHOẢNG  ; a b
Mẫu 15. Tìm m để hàm số 3 y x  3 x
m  2018 nghịch biến trên khoảng  1  ;  1  3   m 1  m 1  m  0  m  3
Mẫu 16. Tập hợp giá trị của m để hàm số 3 2 y  x m
x  3x  m  2 đồng biến trên khoảng  3  ;0  1   1   1   1    ;     ;     ;       ;0    3   3   3   3 
Mẫu 17. Tìm tham số m để hàm số y  3 x  2
3x mx  1 đồng biến trên khoảng 0; . m  0 .  m  3 .  m  3 .  m  0 . x m  4
Mẫu 18. Tìm m để hàm số y  1; x
nghịch biến trên khoảng   m  1   m  2  1   m  2  2   m  2  2   m 1 x m  9
Mẫu 19. Tìm tất cả giá trị thực của tham số m để hàm số y
đồng biến trên khoảng 2;  x m  3   m  2  3   m  2  m  2  2  m  3
PHẦN MỞ RỘNG - CASIO
Mẫu 20. Tìm m để f x 3 2
 x  3x  m  
1 x  2m  3 đồng biến trên một khoảng có độ dài lớn hơn 1. 5 5  m  0  m  0    m  0  m   4 4 tan x  m   
Mẫu 21. Tìm giá trị thực của tham số m để để hàm số y
nghịch biến trên khoảng 0;   m tan x 1  4    ;  01;   ;    1  1;  0;  1;
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 2
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
PHẦN 2. BÀI TẬP RÈN LUYỆN DẠNG 1 Câu 1. Hàm số 3 2
y x x  7x
 Luôn đồng biến trên R
 Luôn nghịch biến trên R
 Có khoảng đồng biến và nghịch biến.
 Nghịch biến trên khoảng  1  ;3. Câu 2. Hàm số 3 2
y  x x x có khoảng đồng biến là  1 1  1;3    ;1    ( ;
  )  (1;)   1  ;3  3  3 Câu 3. Hàm số 4 2
y  x  2x  3 đồng biến trên khoảng nào sau đây?   ;    1 và 0;  1   1  ;0 và 1;    ;0     1  ;  1
Câu 4. Hàm số nào sau đây đồng biến trên R? x 1  y
y x x x x   3 2 2 1 3  4 2
y x  2x  3  3
y  x x  2 2 x x  1
Câu 5. Tìm khoảng nghịch biến của đồ thị hàm số y x  1  0;  1 và 1;2  0;2    ;1  và 1;   ;0  và 2;
Câu 6. Khoảng đồng biến của hàm số 4 2
y  x  8x 1 là:   ;  2   và 0;2   ;0   và 0;2   ;  2  và 2;   2  ;0 và 2;
Câu 7. Đồ thị của hàm số nào luôn nghịch biến trên R  4 2
y x  2x 1  2
y  3x  4x 1
y   x  2 2 1  3 y  3
x  2x 1
Câu 8. Hàm số y x  1 . Nghịch biến trên khoảng nào dưới đây? x ;   1 và 1; .
1;0 và 0;1.  .  Không có. 1
Câu 9. Hàm số y   
2x đồng biến trên khoảng nào dưới đây? x 1 ;   1 .
1;  .  .  Không có.
Câu 10.Hàm số y x  2 2
x đồng biến trên khoảng nào dưới đây?
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 3
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]   ;1 .  0;1.  1; 2 .  1; . DẠNG 2 1 Câu 1.Hàm số 3 2 y
x  (m 1)x  (m 1)x 1 đồng biến trên tập xác định của nó khi : 3  m  1   2   m  1   2   m  1
m  2  2  mx m
Câu 2. Hàm số y
tăng trên từng khoảng xác định của nó khi : x 1  m  0 m  0  m  1  m  0 x m
Câu 3. Tìm tất cả giá trị thực của tham số m để hàm số y
nghịch biến trên từng khoảng xác x  2 định.
m  2 .
m  2 .
m  2 .
m  2 . 2
x mx  2
Câu 4.Hàm số y
giảm trên từng khoảng xác định khi: x 1  m  3   m  3  m  3   m  mx  7m  8
Câu 5. Tìm tất cả giá trị thực của tham số m để hàm số y
đồng biến trên từng khoảng x m xác định.
8  m  1.
8  m  1.
4  m  1.
4  m  1. 2 x mx  2
Câu 6. Tìm tất cả giá trị thực của tham số m để hàm số y
đồng biến trên từng khoảng x  1 xác định.  m  3.  m  3.
2 2  m  2 2 .
m  2 2 hoặc m  2 2 . 1
Câu 7. Tìm tham số m để hàm số y   3
x  m  
1 x  7 luôn nghịch biến trên . 3 m  1.  m  2 .  m  1.  m  2 . 1 Câu 8. Cho 3 2
y   x mx  3m  2 x 1 . Tìm giá trị của m để hàm số nghịch biến trên R . 3 m  1  m  1       m      2   m  1   2 1 m  2  m  2  3 x m
Câu 9. Có bao nhiêu tham số nguyên m để hàm số 2 y   x m
 3 2mx m đồng biến trên 3 R  1  Vô số  Không có  2
==================================================================
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 4
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] DẠNG 3 1
Câu 1. Tìm m để hàm số y   3
x  m   2
1 x  m  3 x  10 đồng biến trên khoảng 0; 3 . 3 m  12 .  m  12 .  m .  m  7 . 7 7 12 Câu 2. Cho hàm số 4 2 y x  2 x m
 3m 1 .Tìm m để đồ thị hàm số đồng biến trên khoảng 1;2
m  1
m  0
0  m  1
m  0
Câu 3. Tìm các giá trị của tham số m để hàm số 3 2 y  2x  x m
 2x đồng biến trên khoảng  2  ;0 13 13  m    m  2  3  m  2 3  m  2 2
Câu 4. Tìm giá trị của tham số m để hàm số 3 2 y  2x  x m
 2x đồng biến trên khoảng  2  ;0 13 13 A. m   B. m  2  3 C. m  2 3 D. m  2 2
Câu 5. Tìm số m để hàm số y  3 x  2
3x  (m  1)x  4m nghịch biến trên khoảng 1;  1 . m  10.  m  10 .
m  10 .  m  5 . x
Câu 6. Tìm tất cả giá trị của tham số m để hàm số y
đồng biến trên khoảng 2;  . x m m  0 .  m  0 .  m  2 .  m  2 . m  1 x  2m  2
Câu 7. Với giá trị nào của m thì hàm số y
đồng biến trên khoảng  1  ; x mm  1  m 1  m  2    1 m  2 m  2 x  3
Câu 8. Tìm giá trị của tham số m để hàm số y
nghịch biến trên khoảng 4;16 x m 33  m  4
m  3 m
3  m  4 16 1
Câu 9.Tìm giá trị của m để hàm số 3 y
x  m   2 1 x   2
m  2mx  3 nghịch biến trên 0  ;1 3   1  ;   ;  0 0  ;1  1  ;0 2 x  4x
Câu 10. Tìm m để hàm số y
đồng biến trên nữa khoảng 1; 2x  m  1   1   1   1    ;     ;      ; \     0   ;     3   3  3   3 
==================================================================
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 5
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
PHẦN MỞ RỘNG – CASIO
Câu 1.Tìm tất cả giá trị của m để hàm số 3 y   m   2 2x 3
1 x  6m  2 x  3 nghịch biến trên
khoảng có độ dài lớn hơn 3 m  0 m  0    0  m  6    m m  6   0 6 m  6
Câu 2. Tìm tất cả giá trị thực của tham số m để đồ thị hàm số y  sin x  c s o x  x m đồng biến trên R
 2  m  2
m   2
 2  m  2
m  2
Câu 3. Cho m, n không đồng thời bằng 0. Tìm điều kiện của m, n để hàm số
y msin x  nc s
o x  3x nghịch biến trên R. 3 3 m n  9       3 3 m n 9
m 2, n 1  2 2 m n 9  2 1 m  2 2 tan x m 1   
Câu 4. Tìm m để đồ thị hàm số y
đồng biến trên khoảng 0;   2 tan x  3  4  1 1 1 1    m   m   hoặc m  2 2 2 2 1 1 1    m   0  m  2 2 2
Câu 5. Tìm giá trị của tham số m để hàm số y  x
m  sin x đồng biến trên R  m 1  m  1   m 1  m  0
Câu 6.Có tất cả bao nhiêu giá trị nguyên của m để hàm số 3
y x  m   2
2 x  2m  
1 x m đồng biến trên R  7  8  9  10 2
Câu 7. Tìm giá trị thực của tham số m để hàm số y
x  2x  1  mx đồng biến trên
m  2 .  m  0 .  m  1.  m  1. 2x  3
Câu 8. Hàm số y
nghịch biến trên khoảng nào dưới đây 2 x 1  3   3   3    ;    1 và 1;    ;     1;     ;    1  2   2   2  m  2
Câu 9. Tập giá trị của m để hàm số 3 y
x  m  2 2
x  3m  
1 x  7 đồng biến trên R 3 1 1 1 1  2   m    2   m    2   m    2   m   4 4 4 4 m s x in   
Câu 10. Tìm tập giá tri của m để hàm số y
nghịch biến trên khoảng 0;   2 c s o x  6  5
m  1 m  2 m
m  0 4
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 6
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
CHUYÊN ĐỀ 2: CỰC TRỊ CỦA HÀM SỐ
Dạng 1: Tìm cực trị của hàm số
Dạng 2: Tìm m khi biết Hs có một CĐ hoặc CT
Dạng 3: Tìm m để Hs có 1 – 2 – 3 cực trị
Dạng 4: Tìm m để Hs có 2 cực trị thỏa đề bài
Dạng 5: Tìm m để Hs có 3 cực trị thỏa ∆ đều,…
DẠNG 1: TÌM ĐIỂM CỰC TRỊ CỦA HÀM SỐ
Mẫu 1. Hàm số y   3
x  3x  4 có cực tiểu tại
Mẫu 2. Tìm giá trị cực tiểu của hàm số y  4 x  2 2x  1. Mẫu 3. Tìm y của hàm số 3 2 y x 1 CT 2 3 4
Mẫu 4. Cho hàm số f x có đạo hàm f 'x  xx  
1 x  2 x  3 . Hỏi hàm số y f x
có bao nhiêu điểm cực trị ?
1. x  1. 2. y  0 . 3. y 1 4. 2 CT CT
DẠNG 2: TÌM M KHI BIẾT HS CÓ MỘT CĐ HOẶC CT
Mẫu 5. Tìm m để hàm số 3
y x  m  2 x + m + 1 đạt cực tiểu tại x  2 3 2 x x
Mẫu 6. Hàm số y   . m
 2m 4x 1 đạt cực đại tại x  2. 3 2
9. m  10 10. m  4 .
DẠNG 3: TÌM M ĐỂ HS CÓ 1 – 2 – 3 CỰC TRỊ 1
Mẫu 7. Cho hàm số y  m   3
1 x  m  2 2 x  x
m . Tìm m để hàm số có cực đại, cực tiểu 3 4 4 4    m  1  m    m    m 1 5 5 5
Mẫu 8. Tìm tất cả giá trị của m để đồ thị hàm số 4 2 2 y x  2 x m
m 1 có 3 điểm cực trị  m 1  m 1  m  0  m  0
Mẫu 9. Tìm tất cả giá trị của tham số m để hàm số 4 y  x m  m  
1 x 1 2m chỉ có một cực trị m  0  m  0  m  0  0  m 1   m 1
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 7
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
DẠNG 4: TÌM M ĐỂ HS CÓ 2 CỰC TRỊ THỎA ĐIỀU KIỆN VIET
Mẫu 10. Tìm m để Đồ thị hàm số y  3 x  2
3x mx  1 có hai điểm cực trị x , x thoả m n 1 2 2 x  2 x  3 1 2
m  2 . m  3 .  m  1.  m  1 . 2 2
Mẫu 11. Mẫu Đồ thị hàm số y  3 x  2 mx  3 3
4m . Tìm m để đồ thị hàm số có hai điểm cực trị A
và B sao cho AB  20 . m  1.
m  2 .
m  1; m  2 .  m  1.
DẠNG 5: PHƢƠNG TRÌNH ĐƢỜNG THẲNG QUA CÁC ĐIỂM CỰC TRỊ
Mẫu 12. Cho hàm số 3 2
y x  2x  x 1. Viết phương trình đường thẳng đi qua hai điểm cực trị của hàm số trên.
Mẫu 13. Cho hàm số 3 2
y x  6x  9x  2 (C ). Đường thẳng đi qua A(-1; 1) và vuông góc với
đường thẳng đi qua hai điểm cực trị của (C ) là. 14 7 1 3 12. y   x  13. y x  9 9 2 2
DẠNG 6: TÌM M ĐỂ HS CÓ 3 CỰC TRỊ THỎA ∆ ĐỀU, VUÔNG, …
Mẫu 14. Tìm các giá trị thực của tham số m để đồ thị hàm số y  4 x  2 2
mx 1 có ba điểm cực trị
lập thành một tam giác vuông.  m 1  m  3 2 2.  3 m  2  m  2
Mẫu 15. Tìm tham số m để đồ thị hàm số y  4 x  2 mx  4 2
m 2m có ba điểm cực trị tạo thành một tam giác đều.  m 1  m  3  m  3  m  3 3.
Mẫu 16. Tìm m để đồ thị hàm số 4 2 y x  2 x m
 2 có 3 cực trị tạo thành một tam giác có diện tích bằng 1.  m 1  m  2  m  3  m  4
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 8
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
PHẦN 2: BÀI TẬP TỰ LUYỆN DẠNG 1
Câu 1. Tìm giá trị cực đại y
của hàm số y  3 x  2
3x  3x  2 . CĐ 3  4 2 .  3  4 2 .  3  4 2 .  3  4 2 .
Câu 2. Tìm giá trị cực tiểu y
của hàm số y  4 x  2 2x  1. CT y  2 .  y  1.  y  1.  y  0 . CT CT CT CT 2
Câu 3. Hàm số f có đạo hàm ' f x 2
x x   1 2x  
1 số điểm cực trị của đồ thị hàm số là  1  2 3 0
Câu 4. Cho hàm số y f x xác định và liên tục trên R có bảng biến thiên như hình dưới. Hãy chọn khẳng định đúng
Hàm số giá trị cực tiểu bằng 1
Hàm số có giá trị lớn nhất bằng 0 và giá trị bé nhất bằng -1
Hàm số có đúng một cực trị
Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1
Câu 5. Số điểm cực tiểu của hàm số 2016 y  16  x  0  1  2016  2015
Câu 6. Tìm điểm cực đại của đồ thị hàm số y
x  3  6  x x  3  x  6 x  6  Không có D C D C D C Câu 7. Cho hàm số 3
y x  3x 1. Tổng lập phương giá trị cực đại và giá trị cực tiểu của hàm số đ cho  27  26  -8  28
Câu 8. Đồ thị hàm số 3 2
y x  3x  x
a b có điểm cực tiểu A2; 2
  thì tổng a b có giá trị bằng  -2  2  -3  3
Câu 9. Hệ thức liên hệ giữa giá trị cực đại và giá trị cực tiểu của đồ thị hàm số 3
y x  2x là  yy  0  2y  3y yy y  2y D C CT CT D C CT D C CT D C
Câu 10. Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số 3 2
y x  3x bằng  2  2 5  4  4 5
=================================================================
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 9
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] DẠNG 2 - 3
Câu 1.Tìm m để hàm số y  3 x  2
3x mx đạt cực đại tại x  2 . m  0 .  m  0 .  m  0 .  m  0 .
Câu 2. Tìm m để hàm số y  3 x  2
3mx  2x  1 đạt cực đại tại x  1.
Không tồn tại . m Có vô số . m m  6.  m  5 . 2 2 x  x m 1
Câu 3. Tìm tất cả giá trị của tham số m để hàm số y x x  đạt cực tiểu tại 0 1  m  1   m  1  m  1   Không có m 1
Câu 4. Tìm giá trị của m để hàm số 3 2 y x  x m   2 m m  
1 x 1 đạt cực đại tại x  1 3  m  2    m  1  m  2  m  1
Câu 5.Hàm số y  3
x  m   2 2 3
1 x  6m  2x . Tìm m để hàm số có cực đại và cực tiểu.  m  3 .  m  3 .
Không có giá trị m .  m .
Câu 6. Hàm số y  m   3 x  2 2
3x mx m . Tìm m để hàm số có cực đại và cực tiểu.  m  3   ;1 \ { 2  }.  m  3   ;1 .  m ;    3  1;  .  m  3  .
Câu 7. Tìm tất cả giá trị của tham số m để hàm số 4 y m  m   2 x
1 x 1 2m chỉ có một cực trị m  0  m  0  m  0  0  m 1   m  1
Câu 8. Tìm tất cả giá trị thực của tham số m để hàm số 4 y m  m   2 x
1 x  2m 1 có 3 điểm cực trị? m  1   m  1   m  1   1   m  0   m  0
Câu 9. Tìm tất cả giá trị của m để hàm số y    m 3 2 1
x  3x  3x  5 có cực trị  m  1  m  1   0  m  1  m  0
Câu 10. Tìm các giá trị của tham số m để đồ thị hàm số 4 y m   m   2 x 2
1 x m  2 chỉ có cực đại và không có cực tiểu.  m 1  m  0  m  0  m 1
==================================================================
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 10
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] DẠNG 4 – 5 - 6
Câu 1. Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  4x  x 1 là 38 5 38 5 38 5  y   x   y x   y x   Đáp án khác 9 9 9 9 9 9
Câu 2. Xác định hệ số góc của đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  3x  2x 1 1 10 10 1       3 3 3 3 Cho hàm số 3 y   m   2 2x 3
1 x  6m  2 x 1. Tìm m để đường thẳng đi qua hai điểm cực trị
của hàm số (1) song song với đường thẳng y  4  x 1 m 1    m 1  m  5  m  3 m  5 1
Câu 3. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2 y
x mx x m 1 có 2 cực 3
trị x , x thỏa mãn 2 2
x x  4x x  2 1 2 1 2 1 2  m  3   m  2  m  0  m  1  1
Câu 4. Tìm m để hàm số 3 2 y x  x m   2 m m  
1 x 1 đạt cực trị tại hai điểm x1; x2 thỏa 3 x x  4 1 2  m  2   m  2 
Không tồn tại m  m  2 2
x mx m
Câu 5. Tính khoảng cách giữa 2 điểm cực trị của đồ thị hàm số y  . x  1 2 5 .  5 2 .  4 5 .  5 .
Câu 6. Đồ thị hàm số 4 2 y x  2 x m
m 1 có 3 điểm cực trị tạo thành một tam giác có diện tích bằng 243 là  3 m  3  m  1  m  2  m  9
Câu 7. Gọi A, B, C là 3 điểm cực trị của đồ thị hàm số y  4 x  2 2
4x  1. Tính diện tích S của tam giác ABC . S  4 .  S  3 .  S  2 .  S  1. Câu 8. Cho hàm số 3 y x  3 x
m 1. Tìm m để đồ thị hàm số có hai điểm cực trị B và C sao cho tam
giác ABC cân tại A, với A2;3 1 3 1 3  m    m    m   m  2 2 2 2
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 11
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Câu 9. Tìm m để đồ thị hàm số 4
y x  m   2 2
1 x m có 3 điểm cực trị lập thành một tam giác vuông cân.  m  0  m  1   m  2  m  1
Câu 10. Tìm các giá trị của m để đồ thị hàm số 4 2 y x  2 x m
m  3 có 3 cực trị lập thành một tam giác cân  m  0  m  1  m  0  m  3
==================================================================
PHẦN MỞ RỘNG – CASIO
Câu 1. Hàm số y  3 x  2
(1 x) có bao nhiêu điểm cực trị?  1  2  3  4 1 Câu 2. Cho hàm số 3 y
x  m   2
1 x 15x . Tìm m để hàm số có hai cực trị x ; x thỏa x  2x  1 1 2 3 1 2 m  0  2  2   m  2  m  0  m m  3  3 1
Câu 3. Tìm các giá trị của m để hàm số y
m 2 4x m  2
1 x  5 có đúng một cực tiểu 6  2   m 1  2   m m 1  m 1
Câu 4. Với giá trị nào của m thì đồ thị hàm số 3
y x   2
m m   2 x   2016 2 m
 2017 x  2018 có hai
điểm cực trị cách đều trục tung m  1   m  1    m  2  m  1  m  2
Câu 5. Tìm m để đồ thị hàm số 4 2 2
y x  8m x 1 có 3 điểm cực trị nằm trên các trục tọa độ 1 1 1  m  1   m    m   m   2 2 2
Câu 6.Tìm tất cả giá trị của tham số m để đồ thị hàm số 4 2 2
y x  2m x  2m có ba điểm cực trị A, B,
C sao cho O, A, B, C là các đỉnh của hình thoi  m  1   m  1  m  2  m  3 3
Câu 7. Tìm m để đồ thị hàm số y  m   4 2 1 x  x m
 chỉ có cực tiểu mà không có cực đại 2 m  0  1   m  0  m  2  m  1  1
Câu 8. Tìm tất cả giá trị của tham số m để đồ thị 3 2 y
x x  m  
1 x  2 có hai điểm cực trị nằm 3 bên trái trục tung  1  m  2  m  1  m  2  m  1
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 12
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Câu 9. Tìm tất cả giá trị của tham số m để đồ thị hàm số 3 2 y x    2 4x
1 m x 1 có hai điểm cực trị
nằm về hai phía khác nhau đối với trục tung 1 1 m 1
   m     1   m 1  1   m 1 3 3 m  1  1
Câu 10. Tìm m để đồ thị hàm số y  3 x  (m  2
2)x  (5m  4)x  3m  1 đạt cực trị tại x , x sao cho 3 1 2 x  2  x . 1 2 m  0 .
m  1. m  0 .  m  1.
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 13
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
CHUYÊN ĐỀ 3: GTLN – GTNN CỦA HÀM SỐ
Dạng 1: Tìm GTLN – GTNN của hàm số
Dạng 2: Bài toán thực tế.
DẠNG 1: TÌM GTLN – GTNN CỦA HÀM SỐ 2 x  3x  1
Mẫu 1. Tìm giá trị lớn nhất của hàm số y  trên đoạn 2; 5  . x  1 11 11  max y  1.  max y  .  max y  1.  max y   2;5   2;5   4 2;5   2;5   4
Mẫu 2. Tìm giá trị nhỏ nhất m của hàm số y  2
x  2x  5 trên đoạn 1; 3   .  m  2 2 .  m  5 .  m  2 .  m  2 3 . 2
Mẫu 3. Tìm giá trị lớn nhất M của hàm số y  2 x  1  6  x trên tập xác định.  M  2 .  M  5 .  M  3 .  M  4 . 2 x x 1
Mẫu 4. Tìm giá trị nhỏ nhất của hàm số y  1;  x  trên   1  m  3  m  2  m 1  m  0
Mẫu 5. Giá trị lớn nhất của hàm số 2
y  x  4x  m trên đoạn  1  ; 
3 là 10. Khi đó giá trị của m bằng bao nhiêu?  3  -15  -6  -7 2x  m 1
Mẫu 6. Tìm giá trị của m để giá trị nhỏ nhất của hàm số f (x) 
trên đoạn 1;2 bằng 1 x 1  m  1  m  2  m  3  m  0
DẠNG 2: BÀI TOÁN THỰC TẾ
Mẫu 7. Một nhà máy sản xuất sữa cần thiết kế một loại bao bì mới có dạng hình hộp đứng với thể tích
1 dm3, đáy là hình vuông cạnh x. Tìm x sao cho nguyên vật liệu làm bao bì nhỏ nhất
14. Đáp số: x  1
Mẫu 8. Cho một tấm bìa hình vuông có cạnh là 12cm. Người ta cắt ở bốn góc của tâm bìa đó bốn hình
vuông bằng nhau, mỗi hình vuông có cạnh x, rồi gấp tấm nhôm để được một cái hộp không nắp. Tìm x
để hình hộp nhận được thể tích lớn nhất ?
15. Đáp số: x  2
====================================================================
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 14
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
PHẦN MỞ RỘNG - CASIO
Câu 1. Tìm GTNN của hàm số y  3  2x trên đoạn  1  ;  1  Min y 1  Min y  2  Min y  3  Min y  4
Câu 2. Tìm giá trị lớn nhất của hàm số 2
y x  4x  3 trên đoạn 0;  3  Maxy = 3  Maxy = 4  Maxy = 5  Maxy = 6    
Câu 3. Tìm giá trị lớn nhất của hàm số 3
y  3sin x  4sin x trên  ;    2 2   x Ma y  1  x Ma y  2     x Ma y 3 x Ma y 4
Câu 4. Tìm giá trị nhỏ nhất của hàm số y  4
2 sin x  cos 2x  5 trên tập xác định.  y  11 min .  y  11 min .  min y  2 .  min y  3 . 4 2 3 1 x  1 x
Câu 5. Tìm giá trị nhỏ nhất của hàm số y   3  2    x xMiny  3  Miny  4  Miny  5  Miny  6
Câu 6. Tìm giá trị lớn nhất M của hàm số y  4 x  4 sin
cos x  sin xcos x trên tập xác định.  M  1 .  M  9 .  M  1 .  M  3 . 2 8 4 4
Câu 7. Tính diện tích lớn nhất S
của một tam giác vuông có cạnh huyền bằng 5 2 . max 25 25 25  S  .  S  . S  . S  25 . max 8 max 4 max 2 max
Câu 8. Chu vi của một tam giác là 16cm , biết độ dài một cạnh của tam giác là a  6cm . Tìm độ dài hai cạnh còn lại ,
b c của tam giác sao cho tam giác đó có diện tích lớn nhất.  b  4c ; m c  6cm .  b  3c ; m c  7cm .  b  2c ; m c  8cm .
b c  5cm .
Câu 9. Cho một hình chữ nhật có diện tích S  100 . Tính chiều rộng x và chiều dài y tương ứng thỏa
điều kiện chu vi hình chữ nhật là nhỏ nhất.
x  25; y  4.
x  10; y  10.
x  20; y  5.
x  50; y  2
Câu 10. Giá trị nhỏ nhất của hàm số 6 6 y
x  64  x bằng  6 6 3  61  6 1 63  2  6 2 32
====================================================================
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 15
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
PHẦN 2: BÀI TẬP TỰ LUYỆN 3 x
Câu 1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y   2 2x  3x  4 3 trên đoạn 4;0 
. Tính tổng M m. 28   28 .  .   28 .  35 . 3 3 3 3x  1
Câu 2. Tìm giá trị lớn nhất M của hàm số y  trên đoạn [0; 2]. x  3   M  1 .  M  5 .  M  5 .  M  1 . 3 3 4
Câu 3. Tìm giá trị lớn nhất của hàm số y x  1  trên đoạn 1; 5  . x  2 46  max y  3 .  max y  4 .  max y  .  max y  5 . 1;5   1;5   1;5   7 1;5  
Câu 4. Tìm giá trị nhỏ nhất của hàm số y   3
x  3x  1 trên khoảng   ;1 .  min y  3 .  min y  1 .  min y  2 .  min y  3 .   ;1   ;1   ;1   ;1 2 x
Câu 5.Tìm giá trị nhỏ nhất của hàm số y  trên đoạn 1; 4   . x  2  min y  1.  min y  0 .  min y  6 .  min y  8 . 1;4   1;4   1;4   1;4   2 x x  4
Câu 6. Cho hàm số y
. Mệnh đề nào dưới đây là đúng? x  1 16  max y   ,min y  6 .
 max y  6,min y  5 . 4;2 3 4;2     4;2 4;2    
 max y  5,min y  6 .
 max y  4,min y  6 . 4;2 4;2     4;2 4;2      1 
Câu 7. Tìm giá trị lớn nhất M của hàm số y x  1  2x trên đoạn   4;  .  2   M  1.  M  1 .  M  0 .  M  1 . 2
Câu 8.Tìm giá trị lớn nhất M của hàm số y x  2
1 x trên tập xác định. 1  M  1 .  M   .  M  2 .  M  1. 2 2 2 x  2 m m
Câu 9. Tìm các giá trị của m để giá trị nhỏ nhất của hàm số y  trên 0;    1 bằng 2  . x  1 m  1 m  1 m  1 m  1   .   .   .  m    2 m   2 m    2 m   2 x m  5
Câu 10. Tìm m để hàm số y
đạt giá trị nhỏ nhất trên đoạn 0;  1 bằng -7 x mm  2  m  0  m  1  m  5
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 16
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
CHUYÊN ĐỀ 4: ĐƢỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
Dạng 1: Tìm đường tiệm cận của đồ thị hàm số
Dạng 2: Tìm m để đồ thị Hs có tiệm cận thỏa ycbt
DẠNG 1: TÌM ĐƢỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
Mẫu 1. Tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 2x  3 1. y
x  ; TCN: y  2  8  Đáp số: TCĐ: 8 x 2x 1 2. y
Đáp số: TCN: y  0 ; TCĐ: x  1  2 x 1 2 5  x  x 1 5 3. y
Đáp số: Không có TCĐ, TCN: y   2 2x  x  2 2 2 x  2x  3 4. y
Đáp số: TCĐ: x  1  ; TCN: y 1 2 x 1 3x  2 5. y
Đáp số: TCĐ: x  25 ; TCN: y  3  x 5 2x 1  3 6. y y x
Đáp số: Không có TCĐ và TCN: 0 3 2 x  3x  2 7. y
Đáp số: TCĐ: x  1
 ; Không có tiệm cận ngang x 1 1 8. y
Đáp số: TCĐ: x  1 và x  3; TCN: y  0 2 x  4x  3 2   9. y 3
Đáp số: TCĐ: x  0 ; TCN: y  3 x 2 2x  3 10. y
Đáp số: TCĐ: x  0 ; TCN: y   2 x
DẠNG 2: BÀI TOÁN THAM SỐ M 2 x m  3x
Mẫu 2. Cho hàm số y
với giá trị nào của m thì x  1 là tiệm cận đứng của đồ thị hàm x 1 số  m  3  m  3   m  3  m  3  x  1
Mẫu 3. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y  có hai đường 2
x x m tiệm cận đứng.  1   1 m   m    Mọi m .   4 .   4 .  m  2. m   2 m   2 2 x  2
Mẫu 4. Tìm tất cả giá trị thực của m để đồ thị hàm số y  có một tiệm cận ngang 4 x m  3
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 17
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]m  0  m  0  m  0  m  3
PHẦN MỞ RỘNG – CASIO 3x 1
Câu 1. Cho hàm số y
có đồ thị (C ). Tìm điểm M thuộc (C ) sao cho khoảng cách từ M đến x  3
tiệm cận đứng bằng hai lần khoảng cách từ M đến tiệm cận ngang  M (1; 1  );M (7;5)
M (1;1);M ( 7  ;5) 1 2 1 2  M ( 1  ;1);M (7;5)
M (1;1);M (7; 5  ) 1 2 1 2 x m
Câu 2. Cho hàm số y x m  Giá trị nào của m thì đồ thị có tiệm cận đứng và tiệm cận ngang 2
cùng với hai trục toa độ tạo thành hình chữ nhật có diện tích bằng 1 m  1    m  1  m   m  3   1 m  3 2x m
Câu 3. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C y có tiệm cận m   :  mx1
đứng, tiệm cận ngang và các tiệm cận cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8 .  1 m   .  1 m   .  1 m   .  Không có m 4 2 8
Câu 4.Số tiệm cận ngang của đồ thị hàm số 2 y
x  2x  3  x là :  0  2 1  3 x 1
Câu 5. Đồ thị hàm số y  2
x  4 x  có bao nhiêu đường tiệm cận đứng? 3  1  2  3  4 x 1
Câu 6. Hàm số y
có bao nhiêu tiệm cận đứng ? 4 3x 1  3x  5  Không có  1  2  3
2x 320.2x  230
Câu 7. Tiệm cận ngang của đồ thị hàm số y   2x  50 1 1  y  0  y  1  y    Không có 2 2
2x  6  x x  2
Câu 8. Tìm tất cả các tiệm cận đứng của đồ thị hàm số y  . 2 x x 6  x  3.
và x  2.  x  3.
x  3. và x  2.   x  3.  x 1
Câu 9. Tìm giá trị của m để đồ thị hàm số y
có đúng một tiệm cận ngang là 2 2x  x m  4 m  0 A. m  0 B.  C. m  4 D. 0  m  4 m  4 2  x 1
Câu 10. Tập hợp giá trị của tham số m để đồ thị hàm số y
có đúng hai tiệm cận đứng 2 x  x m  3m 1 1   1   ;    0;     ;  1
 2 0;  0;  4 2  2 
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 18
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
==================================================================
PHẦN 2: BÀI TẬP TỰ LUYỆN DẠNG 1 2x 1 1
Câu 1. Tiệm cận đứng của đồ thị hàm số y x  1 1  x   y  1   x  1   Không có 2 x  7
Câu 2. Tiệm cận ngang của đồ thị hàm số y x  7  x  1   y  1   x  7   x  7 2 x  2x  3
Câu 3. Tiệm cận ngang của đồ thị hàm số y x 1  Không có  y  1   y  2   x  1  x x 1
Câu 4.Tiệm cận ngang của đồ thị hàm số y  2 x x  1  y  0  y  1  x  0  Không có x  3
Câu 5. Tiệm cận ngang của đồ thị hàm số y  2 x 1  y  1  y  1   y  1   Không có 2 x x 1
Câu 6. Số đường tiệm cận của đồ thị hàm số y  2 3  2x  5x  1  2  3  4 2 x  3x  2
Câu 7. Hàm số y
có mấy tiệm cận đứng 2 x 1  Không có  1  2  3 2x 1
Câu 8. Đồ thị hàm số y  2
x x  có bao nhiêu tiệm cận? 1  Không có  1  2  3 2 x  3x 1
Câu 9. Tìm số tiệm cận của đồ thị hàm số y  2 x  3x  4  Không có  1  2  3 x
Câu 10. Đồ thị hàm số y  có mấy tiệm cận? 2 x  5x  6  1  2  3  4
================================================================== DẠNG 2 x a b
Câu 1. Cho hàm số y  ,(C)
c  và ad  bc  0 . Mệnh đề nào sau đây sai? x c  với 0 d
 Đồ thị luôn có tiệm cận đứng
 Đồ thị luôn có tiệm cận ngang
 Đồ thị luôn có tâm đối xứng
 Trục tung không thể là tiệm cận đứng của (C ) 2 x  2x  3
Câu 2. Cho hàm số y x
với giá trị nào của m thì hàm số có tiệm cận đứng? m
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 19
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]m  1   m  1   1   m  3    m  3 m  3 2 2x  2x
Câu 3. Cho hàm số y
có đồ thị (C ). Tìm tất cả giá trị của m để (C ) không có tiệm cận x m đứng.  m  0  m  1
m  0 hoặc m  1  m  2  2
m mx 1
Câu 4. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y  có đường tiệm x  2
cận ngang qua điểm A –3; 2 .  m  1   m  2  .
m  1 m  2  .
m  1 m  2.  m  1   m  2. mx  1
Câu 5. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y
có tiệm cận đứng đi qua 2x m điểm A 1  ; 2.  m  2  .  m  2 .  1 m  .  1 m   2 2 2
2x  3x m
Câu 6. Cho hàm số y
có đồ thị C  . Tìm tất cả các giá trị của m để (C) không có x m tiệm cận đứng.  m  2  m 1
m  0 hoặc m 1  m  0 x 1
Câu 7. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y  2 x  mx  có đúng một tiệm m cận đứng.  m  0  m  0  m0;  4  m  4 2 x m
Câu 8. Tìm tất cả các giá trị của m để đồ thị hàm số y
có đúng hai đường tiệm cận? 2 x  3x  2
m 1 và m  4 .  m 1.  m  4 .  m  0.
m  1x  2m 1
Câu 9. Tìm m để đồ thị hàm số y x
không có tiệm cận đứng 1 1  m  2  m  1  m  1   m  2 2 x m
Câu 10. Tập hợp các giá trị của tham số m để đồ thị hàm số y  2 x  3x 
có đúng một tiệm cận 2 đứng  m  1  ;  4  m  1   m  4  m 1;  4
==================================================================
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 20
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
CHUYÊN ĐỀ 5 – ĐỒ THỊ CỦA HÀM SỐ
Dạng 1: Đồ thị Hs
Dạng 2: Hàm trùng phương
Dạng 3: Hàm phân thứ c DẠNG 1: HÀM BẬC BA 3 2 ( y  x a  x b  x
c d, a  0)
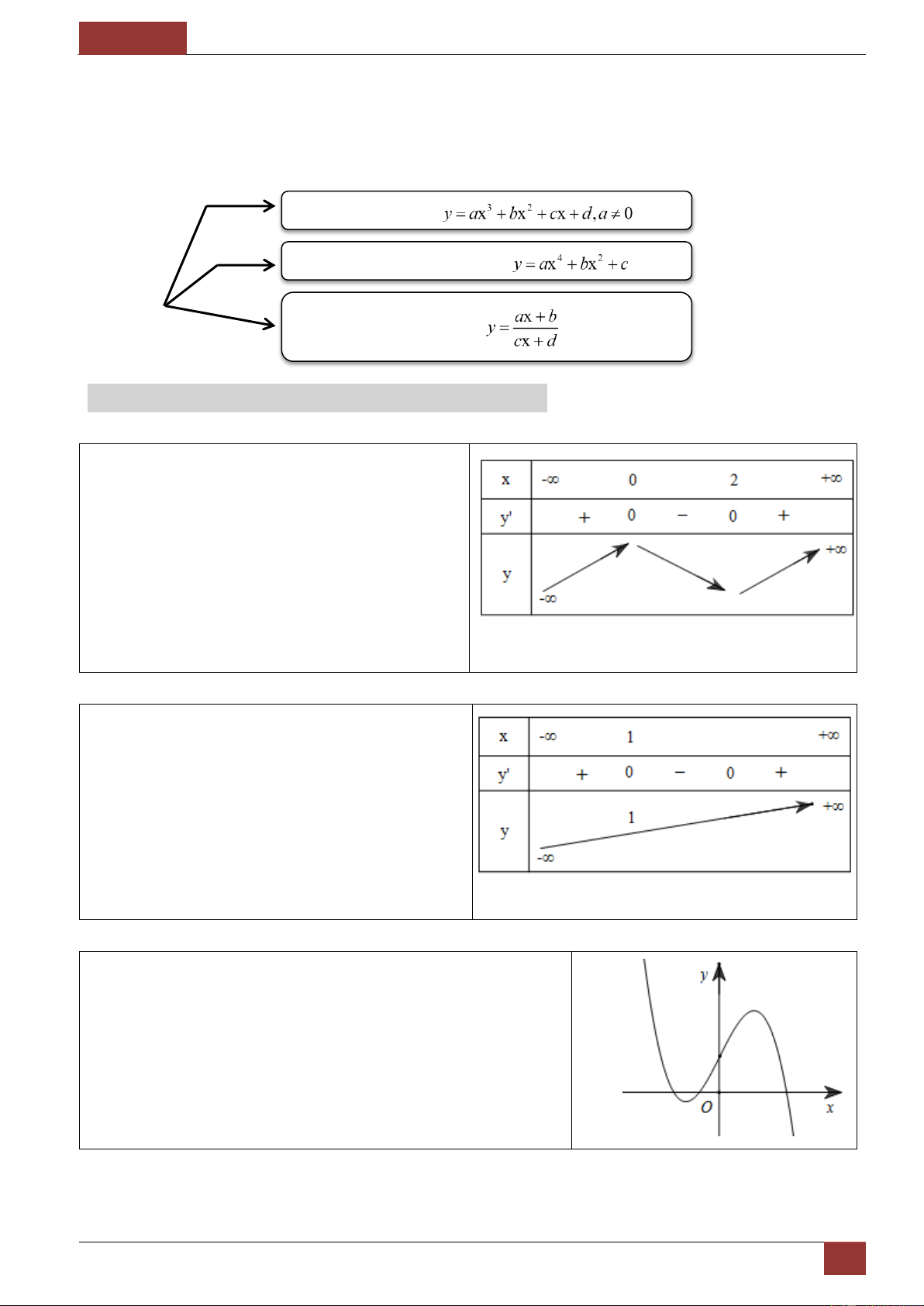
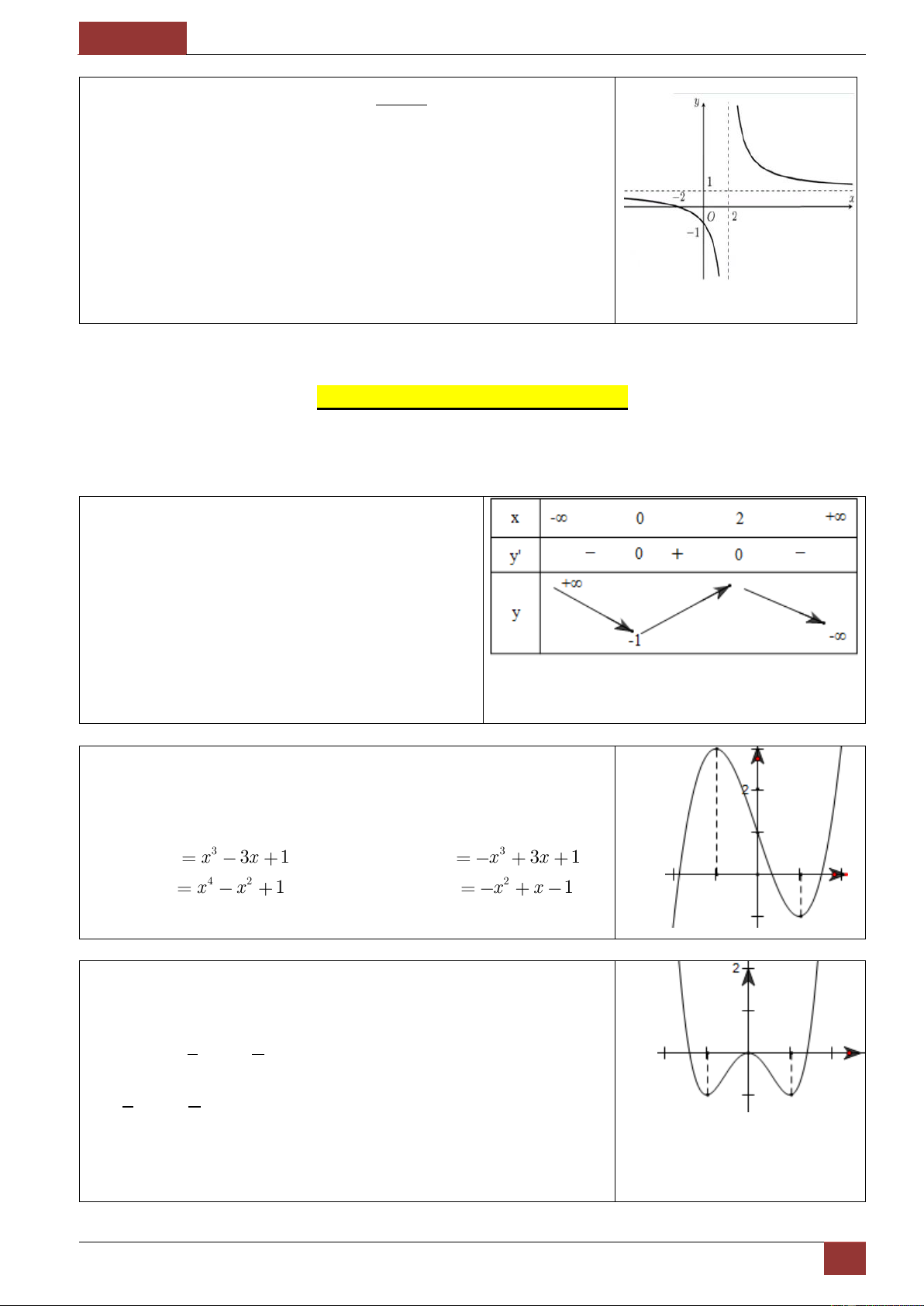
Mẫu 1. Bảng biến thiên sau đây là của một trong
4 hàm số được liệt kê dưới đây. Hỏi đó là hàm số nào?  3 2
y x 3x  2  3 2
y  x 3x  2  3 2
y x 3x  2  3 2
y  x 3x  2
Mẫu 2. Bảng biến thiên sau đây là của một trong
4 hàm số được liệt kê dưới đây. Hỏi đó là hàm số nào?
y x3  3x2  3x
y  x3  3x2  3x
y x3  3x2  3x
y  x3  3x2  3x
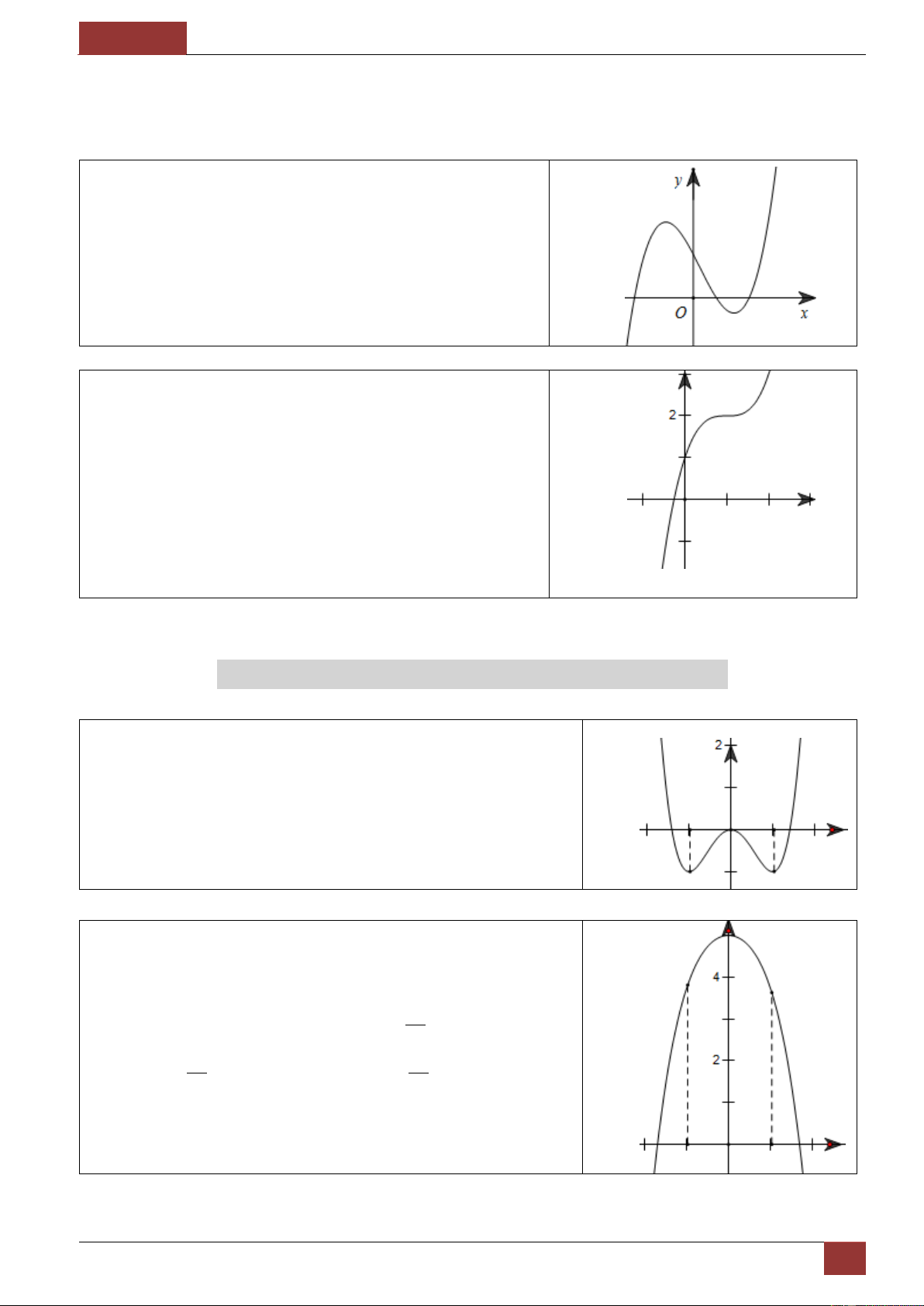
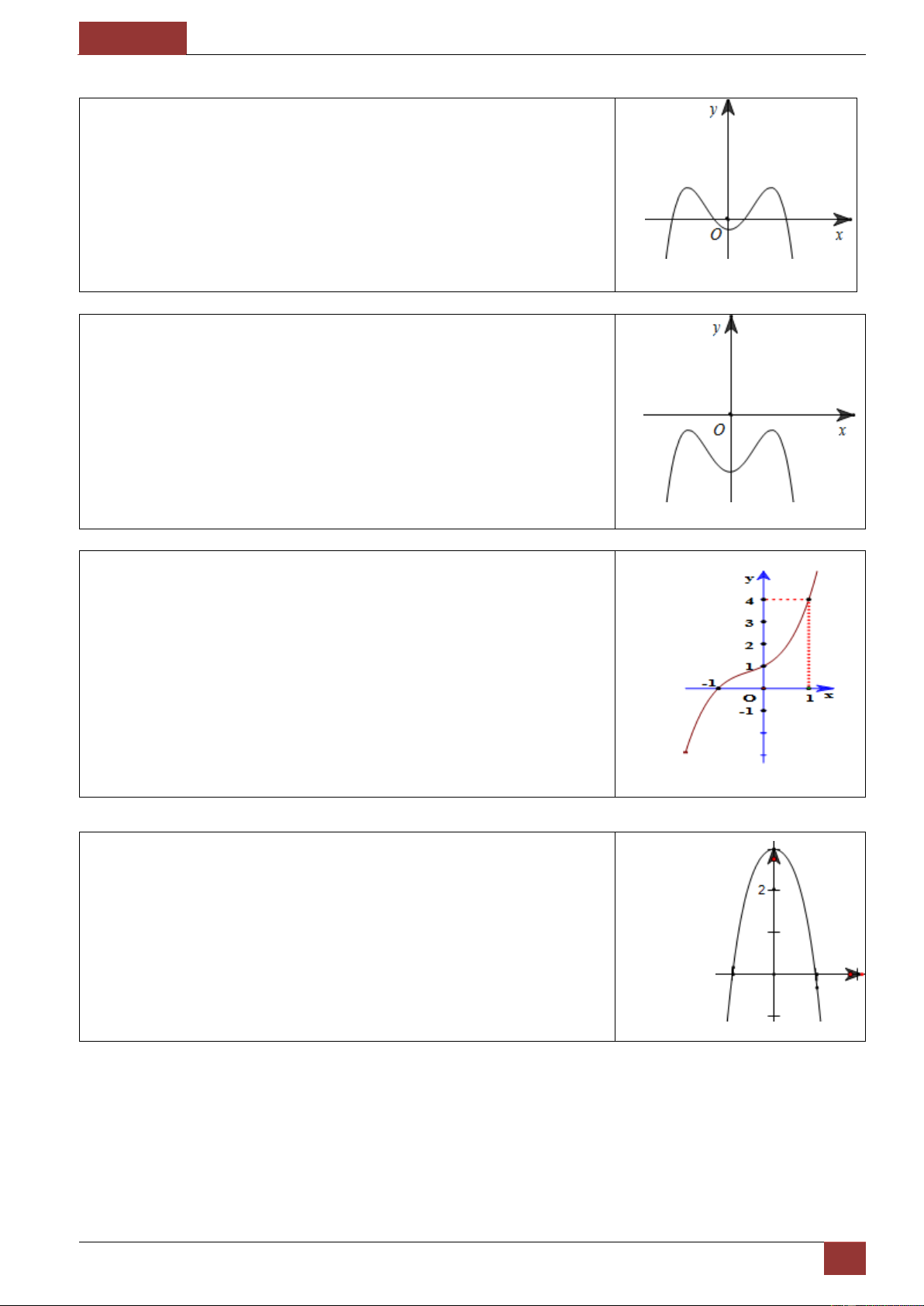
Mẫu 3. Cho đồ thị hàm số 3 2 y  x a  x b  x
c d có đồ thị
như hình vẽ. Mệnh đề nào sau đây là đúng?
a  0;b  0;c  0;d  0 .
a  0;b  0;c  0;d  0.
a  0;b  0;c  0;d  0.
a  0;b  0;c  0;d  0.
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 21
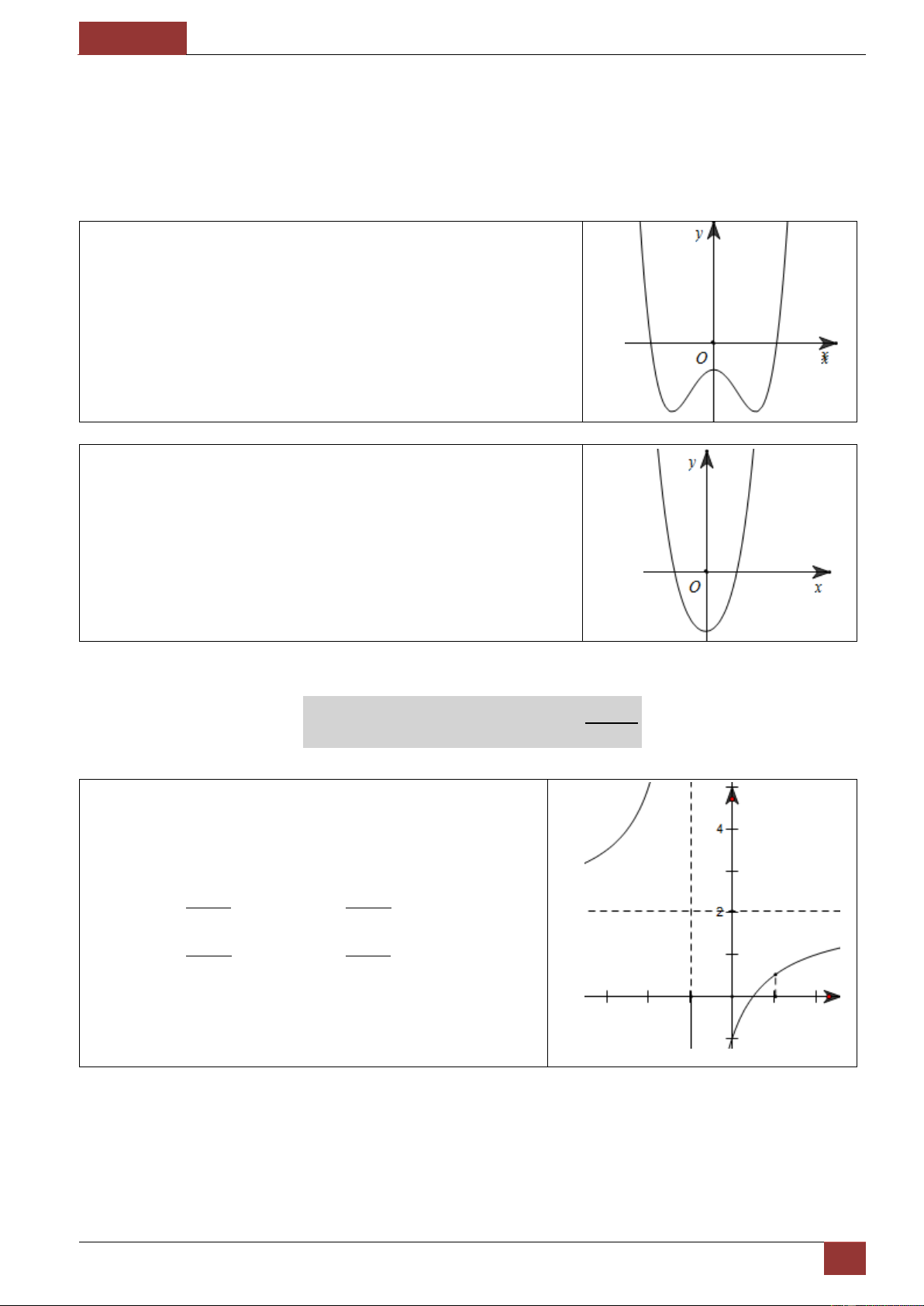
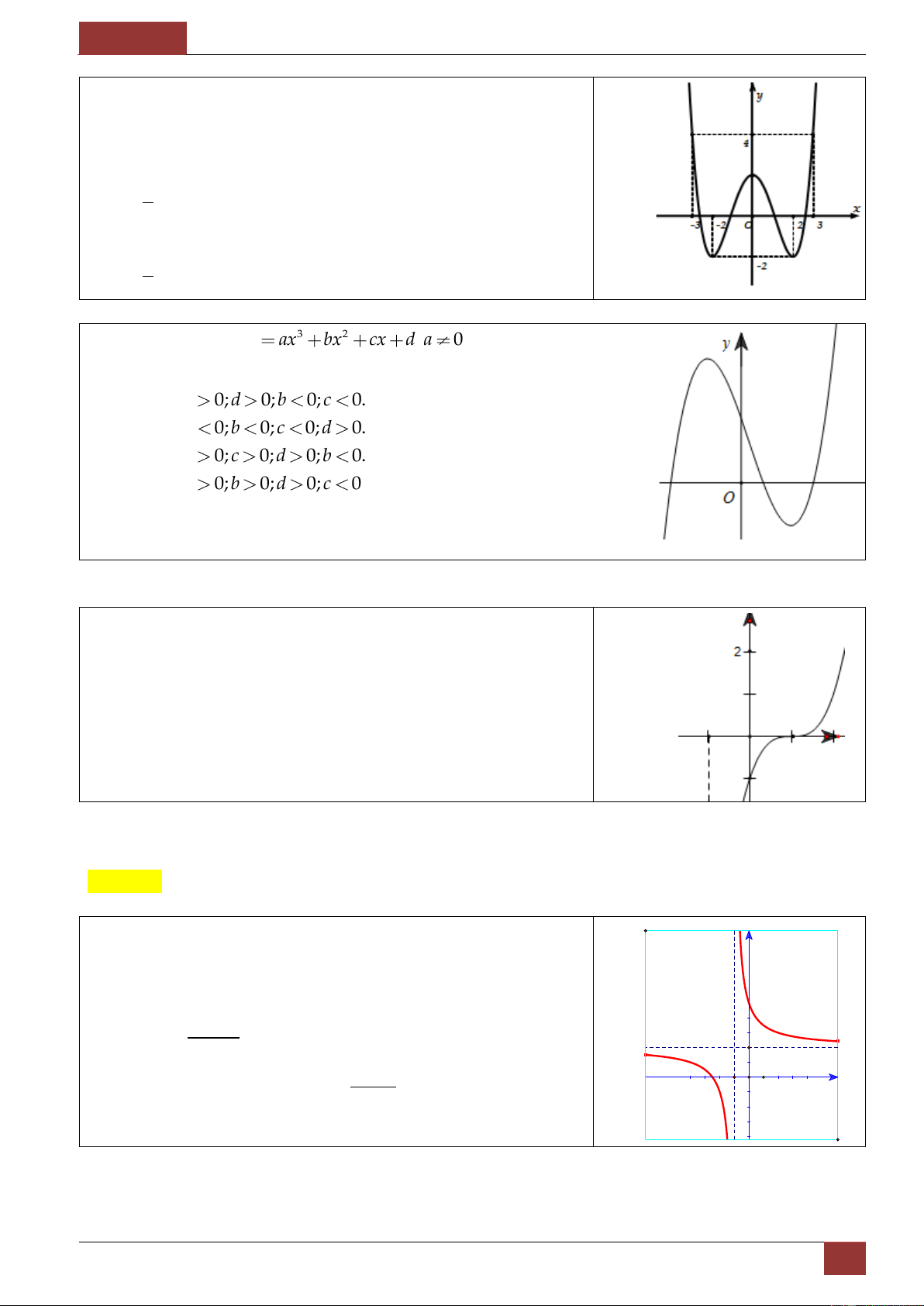
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] Mẫu 4. Cho hàm số 3 2 y  x a  x b
cx d,(a  0) có
đồ thị như hình vẽ dưới đây. Khẳng định nào sau đây về
dấu của a, b, c, d là đúng nhất ?  a,d  0
a  0,b  0,c  0  , a , b , c d  0  ,
a d  0,c  0
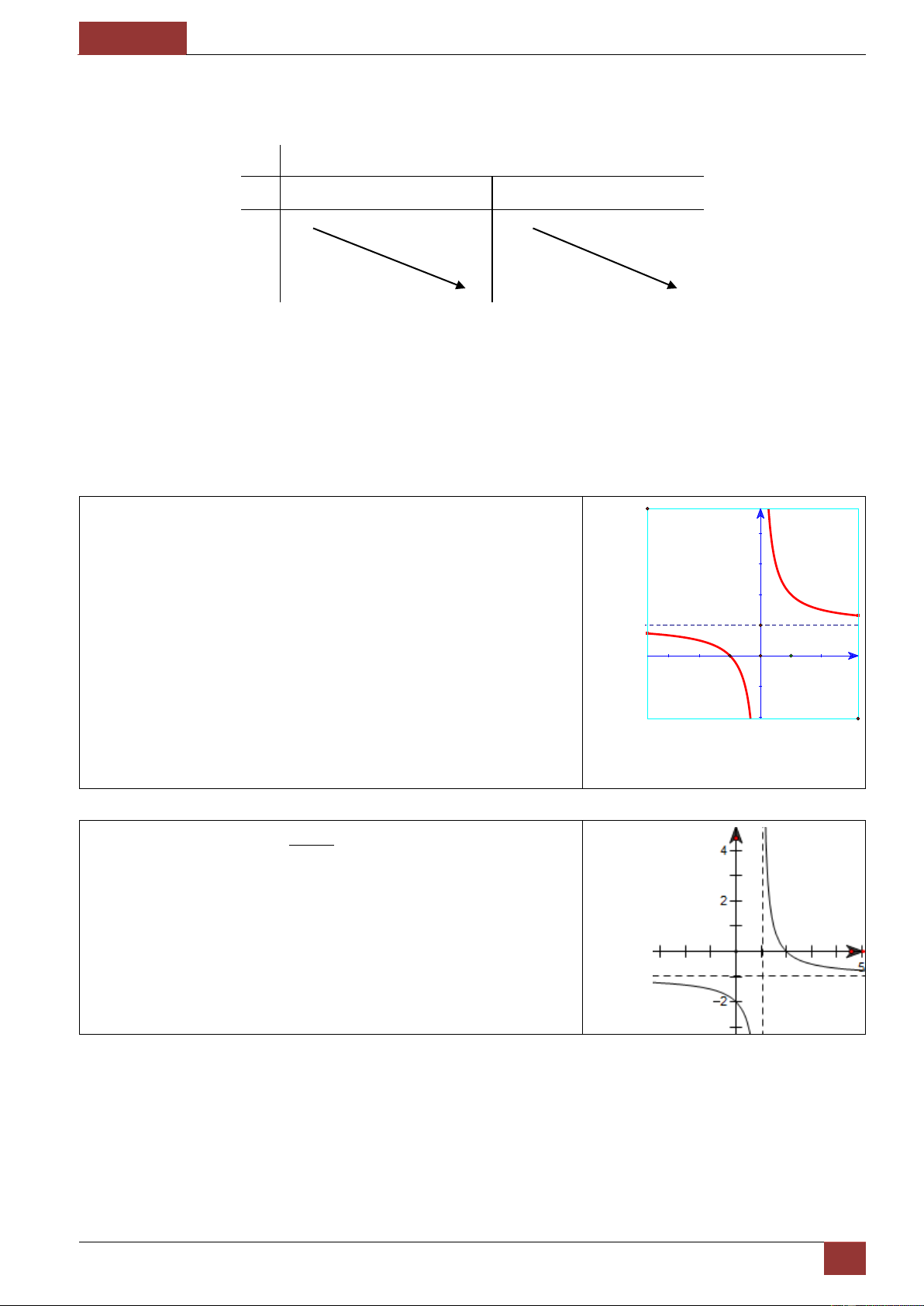
Mẫu 5. Đường cong trong hình bên d ư ớ i là đồ thị của
một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?  3 y x  3 2 x  3x 1.  3
y  x  3 2 x 1.  3
y x  3x 1.  3
y  x  3 2 x 1.
====================================================================
DẠNG 2: HÀM SỐ TRÙNG PHƢƠNG 4 2 y  x a  x b  , c a  0
Mẫu 6. Đường cong trong hình bên là đồ thị của một hàm
số trong bốn hàm số được liệt kê ở bốn phương án A, B, C,
D dưới đây. Hỏi hàm số đó là hàm số nào ?  4 2
y x  2x  4 2
y x  2x  4 2
y x  3x 1  4 2
y  x  2x
Mẫu 10. Đồ thị hình bên là của một trong 4 đồ thị của các hàm
số ở các phương án A, B, C, D dưới đây.
Hãy chọn phương án đúng. 1  A. 4 2
y x x  5 . B. 4 2 y x x  5 . 4 1  1  C. 4 y x  5 . D. 4 2 y
x  2x  7 4 4
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 22
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Mẫu 11. Cho hàm số 4 2 y  x a  x b  ,
c a  0 có đồ thị như
hình bên. Xác định dấu của a, b, c.
a  0,b  0,c  0
a  0,b  0,c  0
a  0,b  0,c  0
a  0,b  0,c  0
Mẫu 12. Cho hàm số 4 2 y  x a  x b  ,
c a  0 có đồ thị như hình bên
Trong các kết luận sau, đâu là kết luận đúng?
a  0,b  0,c  0
a  0,b  0,c  0
a  0,b  0,c  0
a  0,b  0,c  0
==================================================================== x a b
DẠNG 3: HÀM PHÂN THỨC y  x c d
Mẫu 13. Đường cong trong hình bên là đồ thị của một hàm
số trong bốn hàm số được liệt kê ở bốn phương án A, B, C,
D dưới đây. Hỏi hàm số đó là hàm số nào? 2x 1 x   y  ;  2 1 y  ; x 1 x 1 2x 1  xy  ;  1 2 y  . x 1 x 1
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 23
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] x a  2
Mẫu 15. Tìm a, b, c để hàm số y  có đồ thị như hình x c b bên.
a  2,b  2  ,c  1 
a 1,b  1  ,c  1 
a 1,b  2,c 1
a 1,b  2  ,c 1
====================================================================
PHẦN 2: BÀI TẬP RÈN LUYỆN
Câu 1.Bảng biến thiên sau đây là của một trong 4
hàm số được liệt kê dưới đây. Hỏi đó là hàm số nào?  3
y  x  3 2 x 1  3 y x  3 2 x 1  3 y x  3 2 x 1  3
y  x  3 2 x 1
Câu 2.Đường cong trong hình bên d ư ớ i là đồ thị của một hàm
số trong bốn hàm số được liệt kê ở bốn phương án A, B, C,
D dưới đây. Hỏi hàm số đó là hàm số nào?  3 y x 3x 1.  3 y x 3x 1.  4 2 y x x 1.  2 y x x 1. Câu 1.Cho hàm số 4 2 y  x a  x b  ,
c a  0 có đồ thị như hình bên.
Xác định các hệ số a, b, c. 1 2
a  ,b   ,c  0  3 3 1 2 a
,b   ,c  1  3 3
a 1,b  2  ,c  1 
a 1,b  2  ,c  0
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 24
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] Câu 1.Cho hàm số 4 2
y  ax  bx  c có đồ thị như hình vẽ bên. Mệnh
đề nào dưới đây đúng?
a  0,b  0,c  0
a  0, b  0,c  0
a  0,b  0,c  0
a  0,b  0,c  0
Câu 1.Đường cong như hình bên là đồ thị của hàm số nào sau đây?  4 2
y  x  2x  2 .  4 2
y  x  2x  2 .  4 2
y  x  2x  2 .  3
y  x  3x  2 . Câu 1. Xét các phát biểu sau: 1. a  1  2. ad  0 3. ad  0 4. d  1 
5. a c b 1
Số phát biểu sai là:
2 .  3 .  1.  4 .
Câu 1.Đường cong trong hình bên có đồ thị là phương án nào trong các phương án sau.  4 2 y  2  x  2x  3  2 y  2x  3x  2  3 2
y x  3x  x  4 2 y  2  x  4x 3
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 25
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Câu 1.H y xác định a, b, c của hàm số 4 2 y  x a  x bc có đồ thị như hình vẽ
a  4;b  2  ;c  2  1 a  ;b  2  ;c  2 4
a  4;b  2;c  2  1 a  ;b  2  ;c  0 4 Câu 2. Cho hàm số 3 2 y ax bx cx d a
0 có đồ thị như hình vẽ.
Khẳng định nào sau đây đúng ?
a 0;d 0;b 0;c 0.
a 0;b 0;c 0;d 0.
a 0;c 0;d 0;b 0.
a 0;b 0;d 0;c 0 Câu 1.
Cho hàm số y f (x) có đồ
thị (C) như hình vẽ.
Hỏi (C) là đồ thị của hàm số nào?  3
y  (x 1) .  3 y x 1.  3 y x 1.  3
y  (x 1) .
================================================================== DẠNG 3 y
Câu 1.Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A,
B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? 2x  5  y  ;  3 2
y x  3x 1; 2 x  1 x    2x 1  -2 -1 0 1  4 2 y x x 1;  y . x 1
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 26
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Câu 2. Cho hàm số y f x có bảng biến thiên sau. Khẳng định nào sau đây là đúng? x  1  y – – 1   y  1 
 Đồ thị hàm số có tiệm cận đứng x  1, tiệm cận ngang y  1  ;
 Đồ thị hàm số có tiệm cận đứng x  1
 , tiệm cận ngang y  1;
 Đồ thị hàm số có hai đường tiệm cận đứng;
 Đồ thị hàm số có hai đường tiệm cận ngang. y
Câu 3. Cho đồ thị hàm số y f x như hình bên. Khẳng
định nào sau đây là đúng?
 Đồ thị hàm số có tiệm cận đứng x  0 , tiệm cận ngang 1 y  1; x -2 -1 0 1
 Đồ thị hàm số chỉ có một tiệm cận;
Hàm số có hai cực trị;
 Hàm số đồng biến trong khoảng  ;0
  và 0; . ax  b
Câu 4.Cho hàm số có y 
đồ thị như hình dưới. Khẳng x 1
định nào dưới đây là đúng?  b  0  a  0  b  a b  a  0  0  a  b
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 27
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] x b
Câu 5. Cho hàm số y
có đồ thị như hình vẽ. x c d
Khẳng định nào sau đây là đúng?
b  0,c  0,d  0
b  0,c  0,d  0
b  0,c  0,d  0
b  0,c  0,d  0 x a b
Câu 6. Cho hàm số y
có đồ thị như hình vẽ. x c d
Mệnh đề nào sau đây trong các mệnh đề là đúng?  . c d  0, . b d  0  a.d  0, . b c  0  . c a  0,a.b  0  a.d  0, . b c  0 ax b
Câu 7. Cho hàm số y
với a  0 có đồ thị như hình x c d
vẽ bên. Mệnh đề nào dưới đây đúng?
b  0,c  0,d  0  b  0,c  0,d  0
b  0,c  0,d  0  b  0,c  0,d  0 ax b
Câu 8. Cho hàm số y  có cx d
đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng? ad  0 ad  0   .   . bc  0 bc  0 ad  0 ad  0   .   . bc  0 bc  0
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 28
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] Câu 9.
Cho đồ thị hàm số y f x như hình bên. Khẳng định y
nào sau đây là sai?
Hàm số có hai cực trị; 2
 Hàm số đồng biến trong khoảng  ;    1 và  1  ;; x
 Đồ thị hàm số có hai tiệm cận; -2 -1 0 1
 Đồ thị hàm số có tiệm cận đứng x  1  , tiệm cận ngang y  2 . x a b
Câu 10. Cho hàm số y x
có đồ thị như hình vẽ bên. 1
Tìm khẳng định đúng trong các khẳng định sau?
a b  0
b  0  a
 0  b a
 0  a b
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 29
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
CHUYÊN ĐỀ 6 – SỰ TƢƠNG GIAO CỦA HAI ĐỒ THỊ
DẠNG 1: TÌM TỌA ĐỘ GIAO ĐIỂM
Mẫu 1. Đồ thị hàm số y  3
x  3x  2cắt trục hoành tại 2 điểm có hoành độ x ; x . Tính tổng 1 2 x x 1 2
x x  2 .
x x  0 .
x x  –1.
x x  –2. 1 2 1 2 1 2 1 2 x  1
Mẫu 2. Tìm tọa độ giao điểm của đồ thị hàm số y
và y  x  1. 2x  1  1;  1 , 1  ; 2.  1;0 , 1  ; 2.   1  ; 0 ,1; 2.  1; 2  .
Mẫu 3. Đồ thị hàm số 3 2
y x  3x  2x 1 cắt đồ thị hàm số 2
y x  3x 1 tại hai điểm phân
biệt A, B. Khi đó độ dài AB bằng bao nhiêu ?  AB  3  AB  2 2  AB  2  AB 1
DẠNG 2: BÀI TOÁN CHỨA THAM SỐ M
Mẫu 4. Tìm tất cả giá trị của m để đồ thị hàm số 3
y x  m   2 2
1 x  4x cắt trục Ox tại điểm
có hoành độ x  2  m  2  m  3  m  1   m  4 x  2
Mẫu 5. Xác định m để đường thẳng (d) : y x m cắt đồ thị (H ) : y  tại hai điểm phân x 1 biệt. m  2  m  0  2   m  2      0  m  2 m  2 m  2
Mẫu 7. Tìm tất cả giá trị của tham số m để đồ thị y   x   2 2 2 x  x
m m  3 cắt trục Ox tại 3 điểm phân biệt  2   m  2  2   m  2  2   m  1   1   m  2   m  1
--------------------------------------------------------------------------------------------------------------------
Mẫu 8. Tìm tất cả giá trị của m để phương trình 3
x  3x  m  0 có 3 nghiệm phân biệt  2   m  2  2   m  3  1   m  3  1   m  2
Mẫu 9. Tìm tất cả giá trị thực của tham số m để phương trình 4 2
x  2x  m có 4 nghiệm phân biệt  m  0  0  m 1  0  m 1  m 1
Mẫu 10. Cho đồ thị của hàm số 4 2
y x  2x như hình bên. Tìm
tất cả các giá trị thực của tham số m để phương trình 4 2 x  2x  m
có 6 nghiệm thực phân biệt.
0  m 1  1   m 1  0  m  2  m 1
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 30
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
PHẦN 2: BÀI TẬP RÈN LUYỆN
Câu 1. Tìm số giao điểm của đồ thị hàm số y  3 x  2
2x x  1 và đường thẳng y  1  2x .  0 .  1 .  2 .  3 . 2x  1
Câu 2. Tìm tất các giá trị của m để đường thẳng y x
m cắt đồ thị hàm số y  tại hai x  2 điểm phân biệt .  m  1.  m  1 .  m  1.  m .
Câu 3. Biết rằng đồ thị của hàm số 3 2
y x  3x  2x cắt đường thẳng y  2
x  2 tại ba điểm
phân biệt. Kí hiệu ba điểm đó là A x ; y , Bx ; y và C x ; y . Tính tổng 3 3  2 2  1 1 
S x x x . 1 2 3 S  2 . S  3 . S  1 .  S  2 3 .
Câu 4. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y m cắt đồ thị hàm số 3
y x  3x  2 tại ba điểm phân biệt.
0  m  4.  m  4.  0  m  4.  0  m  4.
Câu 5. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 3 2
y x mx mx  4 cắt
đường thẳng y x  4 tại ba điểm phân biệt. m  2 .  m  1.  m  4 .  m  2 .
Câu 6. Hình bên dưới là đồ thị của hàm số 3 y x  3 . x Tìm tất
cả giá trị thực của tham số m để phương trình 3 2
x  3x m có năm nghiệm phân biệt.
m 2;0 0; 2.  m0; 2 . m 2
 ; 0 0; 2.  m0; 2 .
Câu 7. Tìm tất cả giá trị thực của tham số m để đồ thị hàm số 4 2
y x  2mx m  1 cắt trục tung tại điểm có tung độ bằng 2 . m  3  .  m  3 .
Không có m m  2 .
Câu 8. Tìm tất cả giá trị thực của tham số m để đường thẳng y m cắt đồ thị hàm số 4 2
y x – 2x  3 tại bốn điểm phân biệt.  1   m  1.  2  m  3.  0  m  1.
 – 1  m  0 .
Câu 9. Tìm tất cả giá trị thực của tham số m để đồ thị hàm số C y x mx m cắt m  4 2 :     1
trục hoành tại bốn điểm phân biệt. m  1   .  Không có . m m  1.  m  2. m   2
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 31
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] 2x  4
Câu 10.Gọi M, N là giao điểm của đường thẳng y x  1 và đường cong y  . Tìm hoành x  1
độ trung điểm I của đoạn thẳng MN .  5  5 .  1 .  2 .  . 2 2
Câu 11. Tìm các giá trị thực của tham số m sao cho đường thẳng y x cắt đồ thị hàm số x  5 y
tại hai điểm A và B sao cho AB  4 2 . x m 2.  5.  7.  Đáp án khác. 2x  1 8
Câu 12. Hình bên là đồ thị của hàm số y  . Tìm tất cả x  1 6
các giá trị thực của tham số m để phương trình 4
2x  1  2m có hai nghiệm phân biệt. 2 I x  1 1 15 10 5 1 5 10 15 O -1
Với mọi m .
Không có giá trị của m . 2  m  0 .
m0;   \  1 . 4 6 Câu 13. Cho hàm số 3 2
y x  2x 1 có đồ thị (C ). Tìm tất cả giá trị của m để đường thẳng d : y  x
m m Cắt đồ thị (C ) tại ba điểm phân biệt ?  5     5 5 5 m   m  m  m     4   4   4   4 m  1  m  1  m  1  m  1  2 x  3x  3
Câu 14. Tìm tọa độ điểm M thuộc đồ thị hàm số y
sao cho M cách đều hai trục x  1 tọa độ.          1 M  ; 2 .  3 3 M ;    .  3 3 M   ;  .  1 M   ; 2  .  2   2 2   2 2   2  x  3
Câu 15. Tìm tọa độ điểm M thuộc đồ thị hàm số y
sao cho điểm M cách đều hai trục tọa x  1 độ.   M  2;  5 .  M 1;  1  .  M 3; 3   .  1 M 2;    .  3  Câu 16. Cho hàm số 3
y x  3x  2 có đồ thị (C ). Gọi d là đường thẳng đi qua A(3; 20) và có hệ
số góc là m. Giá trị của m để đường thẳng d cắt (C ) tại 3 điểm phân biệt  15 m  , m  24  15 m   15 m  , m  24  15 m  4 4 4 4
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 32
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Câu 17. Tìm giá trị của m để đường thẳng (d ) : y x m cắt đồ thị 3
y x  m   2 3 1 x  x m 1
(C ) tại 3 điểm phân biệt? m  
m    5 ; 1  ;    m 1
 ;  mR m R \ 0     9 
Câu 18. Các giá trị của tham số m để đồ thị hàm số 3 2
y x  3x  9x  m cắt trục hoành tại 3
điểm phân biệt có hoành độ lập thành cấp số cộng là  m 11  m  11   m 11 D. m  11 
Câu 19. Cho hàm số f (x) xác định trên R \  
0 và có bảng biến thiên như hình vẽ. Tìm tất cả giá
trị của tham số m để phương trình f (x) 1  m có 3 nghiệm thực phân biệt  m  4  Không tồn tại m  m  3  m  3
Câu 20. Cho hàm số f x có đồ thị như hình vẽ bên. Xác định tất
cả giá trị của tham số m để phương trình f x  m có 6 nghiệm phân biệt  m  4  0  m  4  3  m  4  0  m  3
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 33
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
CHUYỀN ĐỀ 7: PHƢƠNG TRÌNH TIẾP TUYẾN PHẦN 1: BÀI TẬP MẪU
DẠNG 1: VIẾT PHƢƠNG TRÌNH TIẾP TUYẾN
Mẫu 1. Phương trình tiếp tuyến của đồ thị 3 2
(C) : y x  2x tại điểm M (1;3) là:  y  7x  4  y  7x  4  y  7  x  4  y  7  x  4 2x 1
Mẫu 2. Cho điểm M thuộc đồ thị (C) : y
và có hoành độ bằng -1. Phương trình tiếp x 1
tuyến của (C ) tại điểm M là:  3 1 y x   3 1 y x   3 1 y   x   3 1 y x  4 4 4 4 4 4 4 4
Mẫu 3. Phương trình tiếp tuyến của đồ thị 3
(C) : y x  3x  2 có hệ số góc bằng 9 là:
y  9x 18; y  9x  22
y  9x 14; y  9x - 18
y  9x + 8; y  9x  22
y  9x 18; y  9x  22 2x 1
Mẫu 4. Tiếp tuyến của đồ thị (C) : y
song song với đường thẳng  : 3x  y  2  0 có x  2 phương trình là  y  3x  4  y  3x  2  y  3x 14  y  3x  4
Mẫu 5. Tiếp tuyến của đồ thị 3 (C) : y  4
 x  3x 1 đi qua điểm ( A 1
 ;2) có phương trình là  y  9
 x  7; y  x  2  y  9x 
11; y  x  2  y  9  x 11; y  2  y  9  x  7; y  2
DẠNG 2: BÀI TOÁN CHỨA THAM SỐ M Mẫu 6. Cho hàm số 3 2
y x  3x có đồ thị (C ). Gọi M là điểm thuộc đồ thị (C ) có hoành độ
bằng 1. Với giá trị nào của m thì tiếp tuyến của (C ) tại M song song với đường thẳng 2
d : y  (m  4)x  2m 1  m 1  m  1   m  2  m  2 
Mẫu 7. Với giá trị nào của m thì đường thẳng y  8x  m là tiếp tuyến của đồ thị hàm số 4 2
y  x  2x  3  m  8  m  8   m 18  m  18 
====================================================================
PHẦN 2: BÀI TẬP RÈN LUYỆN Câu 1. Cho hàm số 3 2
y x x  5x 1, phương trình tiếp tuyến tại điểm trên đồ thị có hoành độ x  2  y 10x  9  y  11x 19  y 11x 10  y 10x  8
Câu 2. Tiếp tuyến của đồ thị hàm số 3 2
y x  4x  4x 1 Tại điểm ( A 3  ; 2  ) cắt đồ thị tại
điểm thứ hai là B. Điểm B có tọa độ là
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 34
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]B 1  ;0  B(1;10)  B2;33  B 2  ;  1
Câu 3. Hai tiếp tuyến tại hai điểm cực trị của đồ thị hàm số 3
y x  3x 1 cách nhau một khoảng bằng  1  4  3  2 Câu 4. Cho hàm số 3 2
y x x x 1. Phương trình các đường tiếp tuyến của đồ thị hàm số tại
giao điểm của nó với trục hoành là
y  0; y x 1
y x 1; y x  4
y  0; y  4x  4
y x 1; y x 1
Câu 5. Đồ thị hàm số 4 2
y x  2x 1 có bao nhiêu tiếp tuyến song song với trục hoành  1  2  3  4 3 x
Câu 6. Tiếp tuyến của đồ thị hàm số 2 y
 3x  2 có hệ số góc k  9  có phương trình là: 3
y 16  9  x 3  y 16  9  x  3  y  9  x  3  y 16  9  x  3 Câu 7. Cho hàm số 3 2
y  x  3x  2 có đồ thị (C ). Số tiếp tuyến của đồ thị ( C ) mà song song
với đường thẳng y  9  x  7 là:  0  1  3  2 x  2
Câu 8. Tiếp tuyến của đồ thị hàm số y
song song với đường thẳng y  3  x  2 có x 1 phương trình là:
y  3x 10  y  3  x  2; y  3  x 10  y  3  x 10  y  3  x  2 Câu 9. Cho hàm số 4 2
y  x x  6 có đồ thị (C ). Viết phương trình tiếp tuyến của đồ thị (C ), 1
Biết tiếp tuyến vuông góc với đường thẳng y x 1 . 6  y  6  x  6  y  6  x 8  y  6  x 10  y  6  x 12 Câu 10. Cho hàm số 3 2
y  4x  6x 1 có đồ thị ( C). Viết phương trình tiếp tuyến với (C ) biết
rằng tiếp tuyến đi qua điểm M(-1; -9) 15 21
y  24x  25; y x   15 21
y  24x 15; y x  4 24 4 4 15 21 15 21
y  24x  5; y x
y  24x  25; y x  4 24 4 4
Câu 11. Đường thẳng y  6x  m là tiếp tuyến của đường cong 3
y x  3x 1 khi m bằng m  3  m  3 m  3 m  3          m  1 m  1 m  1  m  1 
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 35
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] x b
Câu 12. Cho hàm số y
có đồ thị ( C ). Biết rằng a, b là các giá trị thực sao cho tiếp x a  2
tuyến của ( C) tại điểm M(1; -2) song song với đường thẳng d : 3x  y  4  0 . Khi đó
giá trị của a b bằng  0  -1  2  1 2x  3
Câu 13. Tập hợp các giá trị thực của tham số m để đồ thị (C ) của hàm số y  cắt đường x 1 thẳng 2
y  2x  m tại hai điểm phân biệt mà hai tiếp tuyến của ( C) tại hai điểm đó song song với nhau là    2   2; 2   1  ;  1  2  ;  2 2x 1
Câu 14. Cho hàm số y
có độ thì (C). Gọi M là điểm thuộc (C ) có tung độ bằng 5. Tiếp x 1
tuyến của (C ) tại điểm M cắt các trục Ox, Oy lần lượt tại A và B. Tính diện tích tam giác S OAB  112 122   121   113 6 6 6 6 Câu 15. Cho hàm số 4 2
y  x  2 x m
 2m 1 (Cm). Tìm m để tiếp tuyến của đồ thị (Cm) tại
hai điểm A(1; 0), B(-1; 0) vuông góc với nhau. 5 3 5 3
m  ;m
m   ;m   4 4 4 4 5 3 5 3
m   ;m
m  ;m   4 4 4 4 2x  3
Câu 16. Cho y x  (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến cắt Ox, Oy tại 1
hai điểm A, B sao cho OB = 5OA. y  5  x  3, y  5  x 17  y  5  x + 3, y  5  x 17  y  5  x  3, y  5  x - 17  y  5  x + 3, y  5  x - 17
Câu 17. Tìm m để tiếp tuyến của đồ thị hàm số y = (2m – 1)x4 – m + 5 tại điểm có hoành độ x = 4
–1 vuông góc với đường thẳng 2x – y – 3 = 0 2 1 5  1  3 6 6 6 ax b
Câu 18. Cho hàm số y =
có đồ thị cắt trục tung tại A(0; –1), tiếp tuyến tại A có hệ số góc x  1 k  3
 . Các giá trị của a, b là: a = 1; b=1  a = 2; b=1  a = 1; b=2  a = 2; b=2 2
x  2mx m
Câu 19. Cho hàm số y =
. Giá trị m để đồ thị hàm số cắt trục Ox tại hai điểm và x  1
tiếp tuyến của đồ thị tại hai điểm đó vuông góc là:
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 36
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] 3  4  5  7 Câu 20. Cho hàm số 4
y x  m   2 2
1 x m  2 có đồ thị (C ). Gọi A là điểm thuộc đồ thị hàm
số có hoành độ bằng 1. Với giá trị nào của m thì tiếp tuyến của đồ thị (C ) tại A vuông
góc với đường thẳng  : x  2y  4  0  m  2   m  1   m  0  m  4
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 37
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
ÔN TẬP CHƢƠNG HÀM SỐ
Câu 1. Giá trị của tham số m để hàm số 3 2
y x  6x  2 x
m 1 có hai điểm cực trị x1, x2 thỏa 2 2 x x 12 1 2 A. m  1  B. m  3 C. m  1 D. m  3 
Câu 2. Giá trị nhỏ nhất của hàm số 2
y x  1 x là A. -1 B.  2 C. 1 D. 2 x 1
Câu 3. Tìm Tất cả giá trị của m để đồ thị hàm số y
có đúng một tiệm cận 2 2x  x m  4 ngang là m  0 A. m  0 B.  C. m  4 D. 0  m  4 m  4
Câu 4. Tìm tất cả giá trị của m để phương trình 3 2
x  3x  2  m có 2 nghiệm thực phân biệt m  2 A.  B. 2   m  2 C. 2   m  0  m   D. 0 2 m  2 
Câu 5. Cho (C ) là đồ thị của hàm số 3 2
y x  3x  5x  3 và ∆ là tiếp tuyến của (C ) có hệ
số góc nhỏ nhất. Trong các điểm sau đây điểm nào thuộc ∆ A. M (0;3) B. N  1  ;2 C. P 3;0 D. Q 2;  1
Câu 6. Đồ thị hàm số 3 2
y x  3x  2x 1 cắt đồ thị hàm số 2
y x  3x 1 tại hai điểm
phân biệt A, B. Khi đó độ dài AB bằng bao nhiêu ? A. AB  3 B. AB  2 2 C. AB  2 D. AB  1 2 x  2
Câu 7. Tìm tất cả giá trị thực của m để đồ thị hàm số y  có một tiệm cận ngang 4 x m  3 A. m  0 B. m  0 C. m  0 D. m  3
Câu 8. Tìm tất cả giá trị của m để hàm số 3 y   m   2 2x 3
1 x  6m  2 x  3 nghịch biến
trên khoảng có độ dài lớn hơn 3 A. m  6 B. m  9
C. m  0 hoặc m  6 m  D. 0 1
Câu 9. Tìm tất cả giá trị của m để hàm số 3 2 y x  x m   2 m m  
1 x 1 đạt cực đại tại 3 x  1 A. m  2   B. m  1 C. m  2 D. m  1
m  1x  2
Câu 10. Tìm tất cả giá trị của m để hàm số y x
đồng biến trên khoảng xác định mm  1 m  1 A. 2   m 1 B.  C. 2   m 1   D. m  2  m  2  1
Câu 11. Cho hàm số 3 2 y   x  x m
 3m  2 x 1. Tìm tất cả giá trị của m để hàm số 3 nghịch biến trên R m  1  m  1  A.  B.  C. 2   m  1  D. 2   m  1  m  2  m  2 
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 38
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] 2x 1
Câu 12. Cho hàm số y
có đồ thị (C ). Tìm tất cả giá trị của m để đường thẳng (d): x 1
y x m 1 cắt (C ) tại hai điểm phân biệt A, B sao cho AB  2 3 A. m  4  3 B. 4  10 C. m  2  3 D. m  2  10 x  2
Câu 13. Cho hàm số y
có đồ thị (C ). Tìm tọa độ điểm M có hoành độ dương thuộc (C x  2
) sao cho tổng khoảng cách từ M đến hai tiệm cận nhỏ nhất. A. M (0; 1  ) B. M 2;2 C. M (1; 3  ) D. M (4;3) 2 2x  3x
Câu 14. Cho hàm số y x
có đồ thị (C ). Tìm tất cả giá trị của m để (C ) không có m tiệm cận đứng. A. m  0 B. m  1
C. m  0 hoặc m  1 D. m  2 2x  m 1
Câu 15. Tìm tấ cả giá trị của m để giá trị nhỏ nhất của hàm số f (x)  trên đoạn x 1 1;2 bằng 1 A. m  1 B. m  2 C. m  3 D. m  0 1
Câu 16. Cho hàm số 3 2 y x  x m
x m 1 Tìm tất cả giá trị của m để hàm số có hai điểm 3
cực trị là A, B thỏa mãn 2 2 xx  2 A B A. m  0 B. m  1   C. m  3 D. m  2
Câu 17. Tìm m để hàm số 3 2 y x  3 x m
1 có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 1. A. m  3  B. m  1  C. m  5  D. m  2 
Câu 18. Tìm các giá trị của tham số m để đồ thị hàm số 4 y m   m   2 x 2
1 x m  2 chỉ có
cực đại và không có cực tiểu. m  0 m  0   1 A. 1  B. m  0 C. 1 D. m m  m  2  2  2 2x 1
Câu 19. Tìm trên đồ thị hàm số y
những điểm M sao cho khoảng cách từ điểm M đến x 1
tiệm cận đứng bằng 3 lần khoảng cách từ điểm M đến tiệm cận ngang của đồ thị  7 
A. M 4;3 hoặc M (2;5) B. . M 4;    hoặc M (2;5)  5   7 
C. M 4;3 hoặc M ( 2  ;1) D. M 4;    hoặc M ( 2  ;1)  5 
Câu 20. Cho hàm số 3 2
y x  2x 1 có đồ thị (C ). Tìm tất cả giá trị của m để đường thẳng d : y  x
m m Cắt đồ thị (C ) tại ba điểm phân biệt ?  5     5 5 5 m   m  m  m   A.  4 B.  4 C.  4 D.  4 m  1  m  1  m  1  m  1 
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 39
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] m  2
Câu 21. Tập tất cả giá trị của m để hàm số 3 y
x  m  2 2
x  3m  
1 x  7 đồng biến 3 trên R 1 1 1 1 A. 2   m   B. 2   m   C. 2   m   D. 2   m   4 4 4 4
Câu 22. Tìm tất cả giá trị của m để đồ thị hàm số 4 2 2 y x  2 x m
m 1 có 3 điểm cực trị,
đồng thời 3 điểm cực trị này cùng với gốc tọa độ O tạo thành một tứ giác nội tiếp được A. 3 m  3 B. m  1  C. m  1  D. m  1 1
Câu 23. Tìm các giá trị của m để hàm số y
m  2 4x m   2
1 x  5 có đúng một cực tiểu 6 A. 2   m 1 B. m  2  C. m  1 D. m  2 
Câu 24. Đồ thị của hàm số nào sau đây có đường tiệm cận ngang x  2 2 x  4 A. y  B. y  2 x  2x  3 2 x  2 2 2  x  2 C. 3 2
y x  2x  7 D. y x  4
Câu 25. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y x  4  x lần lượt là A. 2 2 và 2 B. 2 2 và -2 C. 2 2 và 2  2 D. 2 và -2
Câu 26. Tìm tất cả giá trị của m để hàm số y    m 3 2 1
x  3x  3x  5 có cực trị A. m  1 B. m  1  C. 0  m  1 D. m  0 x
Câu 27. Tìm tất cả giá trị của m để hàm số 2 y
x x m đồng biến trên khoảng 2  ;2   1 1 A. m  B. m  C. m  2 D. m  7 4 4
Câu 28. Tiệm cận ngang của đồ thị hàm số 2 y
x  2x 17  x khi x   có phương trình là A. y  1  B. y  1 C. y  2  D. y  2
Câu 29. Tìm tất cả giá trị của tham số m để đồ thị hàm số 4 2 2
y x  2m x  2m có ba điểm cực
trị A, B, C sao cho O, A, B, C là các đỉnh của hình thoi A. m  1  B. m  1 C. m  2 D. m  3 4
Câu 30. Gọi M là điểm bất kỳ trên đồ thị (C ) của hàm số y
. Tổng khoảng cách từ M x 1
đến hai tiệm cận của (C ) đạt giá trị nhỏ nhất là A. 2 2 B. 4 C. 4 2 D. 2
Câu 31. Tìm tất cả giá trị của tham số m để qua điểm M (2; )
m kẻ được ba tiếp tuyến phân biệt đến đồ thị hàm số 3 2
y x  3x là A. m  4;5 B. m   2  ;3 C. m  5  ; 4   D. m   5  ;4
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 40
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Câu 32. Gọi M là điểm có hoành độ khác 1, thuộc đồ thị (C ) của hàm số 3 2
y x  3x . Tiếp
tuyến của (C ) tại M cắt (C ) tại điểm thứ hai là N ( N không trùng M). Kí hiệu x ; x M N
thứ tự là hoành độ của M và N. Kết luận nào sau đây là đúng? A. x x  2  B. x x  3
C. x  2x  3 D. M N M N M N 2x x  3 M N 1 2
Câu 33. Tìm giá trị của m để hàm số 3 y
x  m   2
1 x  2m  3 x  đồng biến trên 3 3 1; A. m  2 B. m  1 C. m  1 D. m  2
Câu 34. Cho hàm số 3
y x  3x  2 có đồ thị (C ). Gọi d là đường thẳng đi qua A(3; 20) và có
hệ số góc là m. Giá trị của m để đường thẳng d cắt (C ) tại 3 điểm phân biệt 15 15 15 15 A. m  , m  24 B. m  C. m  , m  24 D. m  4 4 4 4
Câu 35. Tìm tất cả giá trị của tham số m để phương trình 4 2
x  2x  3 2m  0 có 4 nghiệm phân biệt? 3 3 3 A. 2   m   B. 3  m  4 C. 2   m   D.   m  2 2 2 2
Câu 36. Cho hàm số 3 2
y x  6x  9x  2 (C ). Đường thẳng đi qua A(-1; 1) và vuông góc với
đường thẳng đi qua hai điểm cực trị của (C ) là 1 3 1 3 A. y   x  B. y x
C. y x  3
D. x  2y  3  0 2 2 2 2
Câu 37. Đồ thị hàm số 3 2
y x  3x  9x 1 có hai cực trị A và B . Điểm nào dưới đây thuộc đường thẳng AB ? P  1  ;  1 Q  1  ;8 M 0;  1 A. N 0; 2 . B. . C. . D. .
Câu 38. Gọi S là tổng tất cả các giá trị nguyên dương của tham số m sao cho hàm số 2 2x m y
đồng biến trên khoảng 2021; . Khi đó, giá trị của S bằng x m  4 A. 2035144 . B. 2035145 . C. 2035146 . D. 2035143 x 2
Câu 39. Đồ thị y có bao nhiêu tiệm cận? 2 x 4 A. 2. B. 4. C. 3. D. 1. 3 x
Câu 40. Tìm các giá trị của tham số m để hàm số 2 2 y
 3x m x  2m  3 đồng biến trên R . 3 m  3  m  3  A.  . B. 3   m  3 . C. 3   m  3 . D.  . m  3 m  3
Câu 41. Cho hàm số y f x có bảng xét dấu đạo hàm như sau x  2 0 2 + y' + 0 0
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng  ;  2 .
B. Hàm số nghịch biến trên khoảng  ;  2  .
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 41
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
C. Hàm số nghịch biến trên khoảng  ;  0.
D. Hàm số nghịch biến trên khoảng  2  ;0 x m
Câu 42. Cho hàm số f x 2 
, với m là tham số. Giá trị lớn nhất của m để x  8
min f x  2  là 0;  3 A. m  5 . B. m  6 . C. m  4 . D. m  3 . x  4
Câu 43. Giá trị lớn nhất của hàm số y  trên đoạn 3, 4 . x  2 A. 4  . B. 10 . C. 7 . D. 8 .
Câu 44. Cho hàm số y = ax3 + bx2 + cx + d. Hỏi hàm số luôn đồng biến trên R khi nào?
éa = b = 0,c > 0
éa = b = 0,c > 0 A. ê . B. ê .
ëa > 0;b2 - 3ac £ 0
ëa > 0;b2 - 3ac ³ 0
éa = b = 0,c > 0
éa = b = c = 0 C. ê . D. ê .
ëa < 0;b2 - 3ac £ 0
ëa < 0;b2 - 3ac < 0
Câu 45. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = (m- 3)x - (2m+1)cosx
luôn nghịch biến trên R ? é 2 ù ìm > 3 A. m Îê-4; ú. B. m ³ 2. C. í . D. m Î(-¥;2ù ë û. 3 û îïm ¹ 1
Câu 46. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = mx + 4 giảm trên x + m khoảng (-¥;1)? A. -2 < m £ -1. B. -2 £ m £ -1. C. -2 < m < 2. D. -2 £ m £ 2.
Câu 47. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x3 - 6x2 + mx +1 đồng
biến trên khoảng (0;+¥)? A. m ³ 12 . B. m £ 12 . C. m ³ 0. D. m £ 0 .
Câu 48. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x4 - 2(m-1)x2 + m- 2
đồng biến trên khoảng (1;3)? A. m Î(-¥;2ùû. B. m Îé-5;2 ë ). C. m Î(2,+¥). D. m Î(-¥;-5).
Câu 49. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y = 1 x3 - 1 mx2 + 2mx - 3m + 4 nghịch biến trên một đoạn có độ dài là 3? 3 2
A. m = -1;m = 9. B. m = -1. C. m = 9. D. m = 1;m = -9 .
Câu 50. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = 1- sin x nghịch biến sin x - m æ p ö trên khoảng 0; èç 6 ø÷ ? 1 1
A. m £ 0; £ m < 1.
B. m £ 0; £ m £ 1. C. m < 1. D. m £ 1. 2 2
Câu 51. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 mx 2
y f (x) 
 7mx 14x m  2 giảm trên nữa khoảng 3 [1;+¥)? A. (-¥;- 14 ù (-¥;-14). C. é-2;- 14 é- 14 ;+¥ 15 û. B. 15 ë ù 15 û . D. ë ). 15
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 42
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] 1
Câu 52. Cho hàm số 3 2
y   x mx  3m  2 x 1 . Tìm các giá trị của m để hàm số nghịch 3 biến trên R . m  1  m  1  A.B. 2   m  1  C.D. 2   m  1  m  2  m  2  m  1 x  2
Câu 53. Tìm tất cả các giá trị của m để hàm số : y
đồng biến trên từng khoảng x m xác định.  m 1  m 1 A. 2   m 1 B. 2   m 1 C.D.  m  2  m  2 
Câu 54. Tìm tất cả các giá trị của m để hàm số: 3
y x  m   2 2 3
1 x  6m  2 x  3 nghịch biến
trên khoảng có độ dài lớn hơn 3
A. m  0 hoặc m  6 B. m  6 C. m  0 D. m  9 2 1 mx
Câu 55. Tìm tất cả các giá trị m để hàm số y  x 
 2x  2017 đồng biến trên R 3 2 A. 2  2  m  2 2 B. m  2 2 C. 2  2  m D. 2  2  m  2 2
Câu 56. Giá trị của tham số thực m để hàm số y  sin 2x mx đồng biến trên là A. m  2  B. m  2  C. m  2  D. m  2  . 1 1
Câu 57. Tìm tất cả các giá trị của tham số thực m để hàm số 3 y  x  m5 2 x  mx có cực 3 2
đại, cực tiểu và x  x  5 CD CT A. m  0 B. m  6  C. m 6;  0 D. m  6  ;  0 1
Câu 58. ới giá trị nào của m thì x  1 là điểm cực tiểu của hàm số 3 2 x  mx   2 m  m   1 x 3 A. m  2  ;  1 B. m  2  C. m  1  D. Không có m
Câu 59. Tìm tất cả các giá trị của tham số m để hàm số 4      2 2 y x
2 m 1 x  m 1 đạt cực tiểu tại x  0 A. x  1 
B. m 1 hoaëc m  1  C. m  1  D. m  1 
Câu 60. Các giá trị thực của tham số m sao cho hàm số   3      2 2 f x 4x 2 m 2 x  m 1 có đúng một cực trị ? A. m  2 B. m  2 C. m  2 D. m  2
Câu 61. Gọi A, B, C là các điểm cực trị của đồ thị hàm số 4 2
y  x  2x  3 . Tính diện tích của tam giác ABC. A. 2 B. 1 C. 2 D. 2 2
Câu 62. Cho hàm số 4      2 y mx
m 1 x 1 2m . Tìm tất cả các giá trị của m để hàm số có 3 điểm cực trị. A. 1  m  2 B. 0  m  1 C. 1   m  0 D. m  1 1
Câu 63. Cho hàm số 3 2 y
x mx x m 1 . Tìm tất cả các giá trị của m để đồ thị hàm số có 3
hai điểm cực trị là Ax ; y , Bx ; y thỏa mãn 2 2 x x  2 A A B B A B A. m  3  B. m  0 C. m  2 D. m  1 
Câu 64. Cho hàm số 3 2
y  x  6x  9x  2C . Đường thẳng đi qua điểm A 1  ;  1 và vuông góc
với đường thẳng đi qua hai điểm cực trị của (C) là:
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 43
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] 1  3 1 3 A. y  x  B. y  x  C. y  x  3
D. x  2y  3  0 2 2 2 2
Câu 65. Tính khoảng cách d giữa hai điểm cực trị của đồ thị hàm số 3 2 y  x  3x  2 . A. d  4 B. d  2 5 C. d  2 2 D. d  10
Câu 66. Cho hàm số 2 3
y f x liên tục trên
, có đạo hàm f x  xx   1 x   1 . Hàm số đ
cho có bao nhiêu điểm cực trị?
A. Có 3 điểm cực trị.
B. Không có cực trị.
C. Có 2 điểm cực trị.
D. Chỉ có 1 điểm cực trị. x
Câu 67. Trong khoảng ( 0; 2 ) hàm số y
 cos x có bao nhiêu điểm cực trị 2 A. 1 B. 2 C. 3 D. 4
Câu 68. Cho hàm số 3
y  x  3x  2 . Gọi A là điểm cực tiểu của đồ thị hàm số và d là đường
thẳng đi qua điểm M 0; 2 có hệ số góc k . Tìm k để khoảng cách từ A đến d bằng 1 . 3 3 A. k   . B. k  . C. k 1. D. k  1. 4 4
Câu 69. Với m là một tham số thực sao cho đồ thị hàm số 4 2
y x  2mx 1 có ba điểm cực trị
tạo thành một tam giác vuông. Mệnh đề nào dưới đây đúng? A. m  2 . B. 2   m  0 . C. m  2  .
D. 0  m  2 .
Câu 70. Cho hàm số y  x  2 . Chọn khẳng định đúng?
A. Hàm số đạt cực tiểu tại x = 0
B. Hàm số đạt cực đại tại x = -2
C. Hàm số đạt cực tiểu tại x = -2
D. Hàm số không có cực trị.
Câu 71. Tìm các giá trị thực của tham số m để đồ thị hàm số 3 2
y  x  3x  mx  2 có hai điểm
cực trị A và B sao cho đường thẳng AB song song với đường thẳng d : y  4  x 1 A. m  1  B. m  3 C. m  0 D. không có m
Câu 72. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y  m   4 2
1 x mx  2017 có đúng một cực tiểu.
A. m 0;  1
B. m 1;
C. m 0;
D. m 0;  1  1; 
Câu 73. Tính khoảng cách d giữa hai điểm cực tiểu của đồ thị hàm số 4 2
y x  4x 1. A. d  2 2 . B. d  3 . C. d  2 .
D. d  1 .
Câu 74. Để hàm số 3 2
y x  6x  3m  2 x m  6 có cực đại, cực tiểu lần lượt tại x và x sao 1 2 cho x  1
  x thì giá trị của tham số m là 1 2 A. m  1.  B. m  1. C. m  1. D. m  1.  q
Câu 75. Tìm các số thực p và q sao cho hàm số f (x)  x p
đạt cực đại tại x  2  và x 1 f  2    2 
A. p  1; q  1  B. p  1  ;q 1
C. p  1; q  1 D. p  1  ;q  1  x m
Câu 76. Tìm tất cả các giá trị của m để giá trị nhỏ nhất của hàm số f x 2 1  trên đoạn x 1 1;2 bằng 1
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 44
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN] A. m  1 B. m  2 C. m  3 D. m  0
Câu 77. Gọi m, M tương ứng là GTNN và GTLN của hàm số y  1 x  1 x , tính tổng m  M A. 2 B. 2  2 C. 21 2 D. 1 2
Câu 78. Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
x x x y
. Khi đó M m bằng: 2 2 (x 1) 1 3 A. . B. 2 . C. . D. 1. 2 2
Câu 79. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y  3 x 1  4 5  x. Tính M  . m
A. M m  16 .
B. M m  18 . 12  3 6  4 10 16  3 6  4 10
C. M m  .
D. M m  . 2 2 mx 1
Câu 80. Cho hàm số f (x) 
. Giá trị lớn nhất của hàm số trên [1; 2] bằng 3 . Khi đó giá trị x m m bằng: 1 1 A. m   B. m C. m  1 D. m  2 2 2 x
Câu 81. ố tiệm cận ngang của hàm số y  là: 2 x 1 A. 0 B. 1 C. 2 D. 3
Câu 82. Cho hàm số y f x xác định và liên tục trên tập D  \  
1 và có bảng biến thiên:
Câu 83. Dựa vào bảng biến thiên của hàm số y f x . Khẳng định nào sau đây là khẳng định sai?
A. Giá trị nhỏ nhất của hàm số trên đoạn 1;8 bằng 2  .
B. Hàm số đạt cực tiểu tại x  3.
C. Phương trình f x  m có 3 nghiệm thực phân biệt khi m  2  .
D. Hàm số nghịch biến trên khoảng  ;3   . x 1
Câu 84. Tìm tọa độ của tất cả các điểm M trên đồ thị (C) của hàm số y  sao cho tiếp x 1
tuyến của (C) tại M song song với đường thẳng   1 7 d : y  x  2 2 A. 0  ;1 và 2; 3   B. 1;0 và  3  ;2 C.  3  ;2 D. 1;0
Câu 85. Cho hàm số 3
y  x  x 1 có đồ thị (C). Phương trình tiếp tuyến của (C) tại giao điểm
của (C) với trục tung là: A. y  2x  2 B. y  x 1 C. y  x 1 D. y  2x 1
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 45
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Câu 86. Tiếp tuyến của parabol 2
y  4  x tại điểm (1 ; 3) tạo với hai trục tọa độ một tam giác
vuông. Tính diện tích S tam giác vuông đó. 25 5 25 5 A. S  . B. S  . C. S  . D. S  . 4 4 2 2 5
Câu 87. Biết rằng đồ thị các hàm số 3 y x x  2 và 2
y x x  2 tiếp xúc nhau tại điểm 4
M (x ; y ) . Tìm x . 0 0 0 1 5 3 3 A. x  .
B. x   . C. x  . D. x  . 0 2 0 2 0 4 0 2
Câu 88. Tìm tất cả các giá trị của tham số m để phương trình  2   2 x 1 4  x  m  0 có nghiệm. A. 2   m  2 B. m  2 C. 0  m  2 D. 2   m  0
Câu 89. Cho hàm số     2 y x 1 x  mx  
1 có đồ thị (C). Tìm số nguyên dương nhỏ nhất m để
đồ thị (C) cắt trục hoành tại ba điểm phân biệt. A. m  4 B. m  3 C. m  1 D. m  2
Câu 90. Tìm tất cả các giá trị của m để phương trình 3 2
x  3x  m  0 có 3 nghiệm thực phân biệt. A. 4   m  0 B. m  0 C. m  4 D. 0  m  4 2x 1
Câu 91. Cho hàm số y
có đồ thị (C). Tìm tất cả các giá trị của m để đường thẳng x 1
d: y x m1 cắt (C) tại hai điểm phân biệt A, B sao cho AB  2 3 .
A. m  4  10
B. m  4  3
C. m  2  10
D. m  2  3
Câu 92. Tìm tất cả các giá trị của m để phương trình: 4 2
x 1  x m có nghiệm. A. 1;  B. 0  ;1 C.  ;  0 D. 0  ;1
Câu 93. Cho hàm số 3
y  x  3x  2 có đồ thị (C). ọi d là đường thẳng đi qua A 3; 20 và có
hệ số góc m. iá trị của m để đường thẳng d cắt (C) tại 3 điểm phân biệt 15 15 15 15 A. m  , m  24 B. m  C. m  , m  24 D. m  4 4 4 4
Câu 94. Tìm tất cả các giá trị của tham số m để phương trình 4 2
x  2x  3 2m  0 có 4 nghiệm phân biệt: 3  3  3  A. 2   m  B. 3  m  4 C. 2   m  D.  m  2 2 2 2
Câu 95. Cho hàm số 4 2 2
y  x  2mx  m 1 có đồ thị (C) và đường thẳng d : y  x 1. Tìm tất cả
giá trị thực của tham số m để đồ thị hàm số (C) và đường thẳng d có giao điểm nằm trên trục hoành. A. m  2 B. m  2 C. m  0 D. m 0;  2  
Câu 96. Tìm tất cả các giá trị của tham số m sao cho đồ thị của hai hàm số 3 2 y x x và 2
y x  3x m cắt nhau tại nhiều điểm nhất. A. 2   m  2 B. 2   m  2 C. m  2
D. 0  m  2
Câu 97. Biết rằng đường thẳng y   2x  2 cắt đồ thị hàm số 3
y x x  2 tại điểm duy nhất; kí hiệu  0 x ; 0
y  là tọa độ của điểm đó. Tìm 0 y : A. 0 y  4 B. 0 y  0 C. 0 y  2 D. 0 y  1
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 46
ĐẠI SỐ 12 [Lớp Toán Thầy Hiền – 0164 968 6263 Đ/c: 77/11 Thái Phiên – Hải Châu - ĐN]
Câu 98. Tìm tất cả các giá trị của m để đường thẳng y = m cắt đồ thị hàm số 4 2
y x  2x tại 6 điểm phân biệt.
A. 0  m  1 B. 1
  m  0 C. 1   m 1 D. 1   m  1 2x 1
Câu 99. Biết rằng đường thẳng d : y  x m luôn cắt đường cong (C) : y  tại hai điểm x  2 phân biệt ,
A B . Độ dài đoạn AB đạt giá trị nhỏ nhất bằng bao nhiêu ? A. 6. B. 2 6. C. 3 6. D. 4.
Câu 100. Hình vẽ bên là đồ của hàm số y  3
x 3x 1 giá trị của m để phương trình 3
x  3x 1  m có 3 nghiệm đôi một khác nhau là
A. 1  m  3. B. m  0.
C. m  0,m  3.   m D. 3 1.
Trên bước đường thành công không có dấu chân của kẻ lười biếng. 47