Phân dạng và kỹ thuật giải toán hàm số và đồ thị – Trần Thanh Hiền Toán 12

Phân dạng và kỹ thuật giải toán hàm số và đồ thị – Trần Thanh Hiền Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

27 14 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

PHÂN DẠNG DỄ NHỚ VÀ KỸ THUẬT GIẢI NHANH

CHỦ ĐỀ 1: ỨNG DỤNG ĐẠO HÀM KHẢO SÁT HÀM SỐ

BÀI TOÁN 1

Tìm khoảng ĐB - NB của hàm số.

Đồng biến trên D



' 0,y x D  

Nghịch biến trên D



' 0,y x D  

Chú ý: Hàm phân thức

ax b

cx d



Đồng biến:

'0y 



Ngịch biến:

'0y 

1: Lập bảng biến thiên

 Tính

 ( Xét dấu

)

PP xét dấu: Hàm thường gặp:



y ax b

: Phải cùng, trái khác



y ax bx c  

2 nghiệm

Trong trái, ngoài cùng

1 hoặc vô nghiệm

Cùng dấu với a,

xR



y ax bx cx d   

3 nghiệm

Phải cùng, tiếp theo xen dấu

2 nghiệm

Xét dấu nghiệm đơn (nghiệm

casio)

1 nghiệm

Phải cùng, trái khác

2: Casio: Dùng Mode 7

Nhập hàm

 

?fx

 Start: … End … là khoảng

trong đáp án A, B, C, D.

Kiểm tra giá trị

 

trong máy tính.

 Nếu

 

tăng thì đồng biến

 Nếu

 

giảm thì nghịch biến

BÀI TOÁN 2

Tìm m để hàm số ĐB –NB trên khoảng

 

;ab

Loại 

x x xy a b c d   

 ĐB trên R

a 











 NB trên R

a 











Loại 







ĐB trên TXĐ

. . 0a d bc  

NB trên TXĐ

. . 0a d bc  

Loại 

x x xy a b c d   

ĐB trên

 

;ab

 

' 0, ;y x a b   

NB trên

 

;ab

 

' 0, ;y x a b   

PP Cô lập m:

     

, ; x

m g x x a b m Ming x

m g x x a b m Ma g x

    





    





Loại 







 ĐB trên

 

;





. . 0a d b c



















 NB trên

 

;





. . 0a d b c



















BÀI TOÁN 3

Tìm điểm cực trị của đồ thị hàm số

ĐK cần: Cực trị là nghiệm của

'0y 

hoặc

không xác định.

ĐK đủ:

Dấu hiệu 1: Xét dấu

a là cực tiểu a là cực đại

Dấu hiệu 2:

 

'' 0 D

'' 0

y a a C

y a a CT

  





  





ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

BÀI TOÁN 5

Tìm GTLN – GTNN của hàm số

Loại 1: Trên

 

;ab

: Tìm

 

;

x a b

và

 

fx

     

 

     

 

min ; ;

x x ; ;

Min f a f b f x

Ma ma f a f b f x



2: Casio: Mode 7

Loại 2: Trên khong

 

;ab

hoc R: Lp bng bin

thiên.

Chú ý: Hàm









'0y 

trên

 

;ab

   

,Min f a Max f b



'0y 

trên

 

;ab

   

,Min f b Max f a

BÀI TOÁN 4

Bài toán cực trị có chứa tham số m

Loại 1: Tìm m biết trƣớc CĐ hoặc CT





 

'' 0



















là CT

 

'' 0

















Loại 2: Tìm m để HS có 1 – 2 – 3 cực trị



x x xy a b c d   

 2 cc tr

'0y

có 2 nghim phân bit

 Ko có cc tr khi

'0y 

có 1 nghim hoc vô N



xxy a b c  

 có 3 cc tr khi

.0ab

 có 1 cc tr khi

.0ab

Loại 3: Tìm m

x x xy a b c d   

có 2 CT thỏa



'0y 

có 2 nghim phân bit

a 











Áp dng viet:

1 2 1 2

x x x x

   

Loại 4: Tìm m để

xxy a b c  

có 3 cực trị

thỏa tính chất tam giác.

Chú ý: m

     

1 1 2 2

0;c , ; , ;A B x y C x y

luôn có

tính cht cân ti A.

Loại 5: Phƣơng trình qua các điểm cực trị



x x xy a b c d   

'0y 

m

   

1 1 2 2

; , ;A x y B x y

Ving thng AB có

vtpt n AB

qua A













2: Dùng Casio

: vào CMPLX

: Nhp công thc:

'. ''



: CALC vi X = i, Y = 1000

BÀI TOÁN 6

Ứng dụng GTLN – GTNN vào bài toán thực tế

Ý tƣởng:

: Da vào gi thuyt lp hàm s

 

y f x

: Tìm Min  Max ca

 

Đây là bài tập Vận dụng và vận dung cao. Yêu cầu

các em phải liên kết được các giả thuyết của bài toán

BÀI TOÁN 7

Tìm tiệm cận của hàm số

 Nếu

lim





và

lim





thì hàm s 2 tim cn ngang.

ya

và

yb

 Nếu

lim





 

hoc

lim





 

( Chỉ cần thỏa một trong 4 kết quả trên là ok)

thì hàm s có tim cng là:

xx

Chú ý:

 

...

g x b x







 Bc t = bc mu



TCN



 Bc t < bc mu



TCN

0y 

 Bc t > bc mu



Ko có tim cn ngang.

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

BÀI TOÁN 8

Bài toán tiệm cận có chứa tham số m

Loại 1: Tìm m để HS có tiệm cận đứng

 Hàm

 



( Xét

là nghiệm của mẫu)



xx



 















hoc

 

0gx 

và

thu kin ca hàm s.

Loại 2: Tìm m để HS có tiệm cận ngang

 Bc t phi nh c bng bc mu

BÀI TOÁN 9

Nhận dạng đồ thị hàm số



xxy ax b c d   

A hướng

B Điểm uốn



0a 

: Đi lên



0a 

: Đi xuống



.0ab

Lệch phải



.0ab

Lệch trái



0b 

trùng gốc O

C cực trị

D giao Oy



.0ac

hai phía Oy



.0ac

cùng phía Oy



0c 

CT thuộc Oy



0d 

: phía trên Oy.



0d 

: phía dưới Oy



0d 

: trùng gốc O



xy ax b c

A hướng



0a 

Đi lên



0a 

Đi xuống



.0ab

Hình dạng chữ

W hoặc M



.0ab

Hình dạng



0c 

phía trên Oy.



0c 

phía dưới Oy



0c 

trùng gốc O



ax b







: Tính

 

a d b c

cx d







và xem hàm s 

: Xét tim cng và tim cn ngang.

: m c th vi Ox, Oy.

BÀI TOÁN 10

Bài toán đồ thị của hàm

 

'fx

Loại 1: Khoảng ĐB – NB của hàm hợp

 

y f u

: o hàm:

 

' '. 'y u f u

: Lp bng xét du:

 

'fu

' '. '( )y u f u

Loại 2: Tìm cực trị của hàm hợp

 

y f u

: Tính

 

' '. 'y u f u

và tìm nghim

 

'. ' 0u f u 

: Da vào du hiu kim cc tr

Loại 3: Tìm GTLN - GTNN của hàm

 

y f u

Ý tƣởng: T  th hàm

 

'fx

ta bic các

khong (a, b) mà

     

'0f x f a f b  

BÀI TOÁN 11

Tìm tọa độ giao điểm thỏa yêu cầu bài toán

Tìm tọa độ giao điểm của

 

y f x

và

 

y g x

:  m:

   

f x g x

: Thay

vào mt trong hai hàm s c

BÀI TOÁN 12

Bài toán tƣơng giao có chứa tham số m

Loại 1: Biện luận nghiệm PT:

 

f x m

 

: Chuyn tham s v bên phi PT (1)

: D th hàm

 

y f x

. Bin lun s

nghing s m c th

 

y f x

ng thng

ym

Loại 2: Bin lun s m c th

 

y f x

Cách vẻ đồ thị:

: Gi nguyên ph th

 

y f x

i Oy

: Li xng ph th

()y f x

i lên

trên Oy

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

BÀI TOÁN 13

Viết phƣơng trình tiếp tuyến

p tuyn c th

 

y f x

Ti

 

;M x y

   

0 0 0

'.y y f x x x  

 H s góc k:

 

'f x k



 

;M x y

là t tim

PP chung: Muốn viết PT tiếp tuyến ta cần tìm điểm

 

;M x y

Chú ý:

:d y a x b

 Nếu

//dd

thì

 

2 1 1

:,d y a x c c b  

 Nếu

dd

thì

:d y x c

  

BÀI TOÁN 14

Bài toán tiếp tuyến có chứa m

Điệu kiện tiếp xúc

 

y f x

và

 

y g x

tip xúc

   

f x g x

















ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

CHỦ ĐỀ 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

BÀI TOÁN 1: TÌM KHOẢNG ĐỒNG BIẾN – NGHỊCH BIẾN

Loại 1: Hàm bậc 3

1. Hàm s

y x x x   

có khong bin là

 

1;3











( ; ) (1; )

   

 

1;3

2. Tìm khong bin ca hàm s

3x 1yx  

 

0;2

 

;2

 

;0

và

 

2;

 

0;

3. Tìm khong bin ca hàm s

2x 3

y x x   

 

0;1

 

0;

C. R D.

 

;0

4. Tìm khong nghch bin ca hàm s

4x 1

yx   

 

;0

và

 

2;

 

; 

 

2;

 

;2

Loại 2: Hàm bậc 4

5. Tìm khong bin ca hàm s

2x 1yx  

 

1;0

và

 

1; 

 

1;0

 

1;1

 

1; 

6. Tìm khong nghch bin ca hàm s

2x 5yx   

 

0;

 

;0

C. R D.

 

1;1

7. Hàm s

4 3 2

1 5 7

3x 2018

4 3 2

y x x x    

nghch bin trên khong nào

 

0;3

 

0;

 

3; 

 

1;3

Loại 3: Hàm phân thức.

8. Hàm s

2x 3







nghch bin trên khong nào

A. R B.

 

1; 

 

;1

và

 

1; 

 

;1

9. Tìm khong bin ca hàm s

2x 2







 

2;0

 

2; 

 

;2 

và

 

0;

 

;0

Loại 4: Hàm số khác.

10. Tìm khong nghch bin ca hàm s



 

2;2

 

2;

 

2;0

và

 

0;2

 

;2

11. Tìm khong nghch bin c th hàm s

25yx

 

5;0

 

0;5

 

5;5

 

0;

Loại 5: Dựa vào đồ thị và bảng biến thiên

12. Cho hàm s

 

y f x

 th . Chn m 

A. Hàm s ng

 

0;

B. Hàm s ng

 

2;2

C. Hàm s ng

 

1;1

D. Hàm s ng

 

2;1

-2

-1

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

13. Cho hàm s

 

y f x

liên tc trên o hàm

      

2 2017

1 2 3f x x x x



   

.Khnh



A. Hàm s ng bin trên các khong

 

1;2

và

 

3; 

B. Hàm s m cc tr.

C. Hàm s nghch bin trên khong

 

1;3

D. Hàm s t ci ti

2x 

t cc tiu ti

1x 

và

3x 

14. Cho hàm s

 

y f x

có bng bi bên.

M sai?

A. Hàm s ng bin trên khong

 

;1

B. Hàm s ng bin trên khong

 

2;

C. Hàm s ch bin trên khong

 

0;3

D. Hàm s ng bin trên khong

 

3; 

BÀI TOÁN 2: TÌM M ĐỂ HÀM SỐ ĐỒNG BIẾN – NGHỊCH BIẾN TRÊN (A; B)

DẠNG 1: HÀM BẬC BA

x x xy a b c d   

ĐỒNG BIẾN – NGHỊCH BIẾN TRÊN R.

15. Hàm s

( 1) ( 1) 1

y x m x m x     

ng bin trên tnh ca nó khi :

1m 

21m   

21m   

2m 

16. Cho hàm s

 

x 4 9 5y x m m x     

có bao nhiêu giá tr  hàm s nghch bin trên

khong

 

; 

A. 7 B. 4 C. 6 D. 5

DẠNG 2: HÀM PHÂN THỨC ĐB – NB TRÊN TẬP XÁC ĐỊNH

17. Tìm tt c giá tr ca tham s

 hàm s







78mx m

ng bin trên tng khonh.

  81m

. B.

  81m

. C.

  41m

. D.

  41m

18. Tìm tt c giá tr thc ca tham s

 hàm s





 2

nghch bin trên tng khonh.

2m

. B.

2m

. C.

2m

. D.

2m

DẠNG 3: HÀM ĐA THỨC ĐỒNG BIẾN – NGHỊCH BIẾN TRÊN (A; B)

19. Tp hp giá tr c hàm s

x 3x 2y m x m    

ng bin trên khong

 

3;0

;



 







;



 





;



 















20. Tìm tham s  hàm s

   

31y x x mx

ng bin trên khong

 

0;

 0m

. B.

 3m

. C.

 3m

. D.

 0m

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

21. Tìm giá tr c hàm s

 

3 2 2

1 2 3

y x m x m m x     

nghch bin trên

 

0;1





1; 





;0

 

0;1

 

1;0

DẠNG 4: HÀM PHÂN THỨC ĐỒNG BIẾN – NGHỊCH BIẾN TRÊN (A; B).

22. Tìm tt c giá tr ca tham s  hàm s





ng bin trên khong

 

2;

 0m

. B.

 0m

. C.

 2m

. D.

 2m

23. Vi giá tr nào ca m thì hàm s

 

1 2 2m x m

  





ng bin trên khong

 

1; 

1m 

2m 











12m

24. Có bao nhiêu giá tr nguyên ca tham s  hàm s







nghch bin trên khong

 

0;2

A. 4 B. 5 C. 6 D. 9

===============HẾT CHUYÊN ĐỀ 1================

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

CHUYÊN ĐỀ 2: CỰC TRỊ

BÀI TOÁN 3: TÌM CỰC TRỊ CỦA HÀM SỐ.

DẠNG 1: TÌM ĐIỂM CỰC TRỊ.

25. Tìm giá tr ci

CĐ

ca hàm s

   

3 3 2y x x x

3 4 2

. B.

3 4 2

. C.

3 4 2

. D.

3 4 2

26. Tìm giá tr cc tiu

ca hàm s

  

21y x x

 2

. B.

1

. C.

 1

. D.

 0

27. m ci c th hàm s

36y x x   

x 

D. Không có

28. Khong cách gim ci và cc tiu c th hàm s

3xyx

bng

A. 2 B.

C. 4 D.

29. Tính khong cách d gim cc tiu c th hàm s

4 1.y x x  

22d 

. B.

3d 

. C.

2d 

. D.

1d 

30. Cho hàm s

()y f x

liên tc trên và có bng xét du c.

Hàm s

()y f x

m cc tr?

. B.

. C.

. D.

31. Hàm s

()y f x

liên tc trên R và có bng bi. M 



1 2





+ 0 - || +





A. Hàm s m cc tr. B. Hàm s m cc tr.

C. Hàm s  cc tiu. D. Hàm s  ci.

32. Cho hàm s

 

y f x

có bng bi. Hi hàm s m cc tr?



1







1

A. Có mm B. m C. m D. Có bm





(

)











ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

BÀI TOÁN 4: BÀI TOÁN CỰC TRỊ CHỨA THAM SỐ M

DẠNG 2: ĐƢỜNG THẲNG QUA HAI ĐIỂM CỰC TRỊ.

33. ng thm cc tr c th hàm s

4x 1y x x   

là

38 5

yx  

38 5

yx

38 5

yx

 

34.  th ca hàm s

3x 9x 1yx   

m cc tr ng

thng AB.

 

1;0P

 

0; 1M 

 

1; 10N 



 

1;10

35. Cho hàm s

   

2x 3 1 6 2 1y m x m x     

 ng thm cc tr ca

hàm s (1) song song vng thng

4x 1y   











1m 

5m 



3m 

DẠNG 3: TÌM M BIẾT HÀM SỐ CÓ 1 CỰC TRỊ CHO TRƢỚC.

36. Tìm giá tr c hàm s

 

3 2 2

x 1 1

y x m m m x     

t ci ti

1x 

2m 

1m 

2m 



1m 

37. Tìm tt c giá tr ca tham s  hàm s







t cc tiu ti

0x 

1m 

1m 

1m 

 Không có m

DẠNG 4: TÌM M ĐỂ

x x xy a b c d   

KHÔNG CÓ HOẶC 2 CỰC TRỊ.

38. Hàm s

 

    

23y m x x mx m

 hàm s có ci và cc tiu.

 

3;1 \{ 2}m  

. B.

 

3;1m

   

; 3 1;m    

. D.

3m 

DẠNG 5: TÌM M ĐỂ

xxy a b c  

CÓ 1 HOẶC 3 CỰC TRỊ.

39. Tìm tt c giá tr thc ca tham s  hàm s

 

x 1 2 1y m m x m    

m cc tr?

1m 

1m 

10m  











40. Tìm tt c giá tr ca tham s  hàm s

 

x 1 1 2y m m x m    

ch có mt cc tr

0m 

0m 

01m











41. Tìm các giá tr ca tham s   th hàm s

 

x 2 1 2y m m x m    

ch có ci và không

có cc tiu.

1m 

0m 

0m 

1m 

42.   th hàm s

 

y m x m   

ch có cc tiu mà không có ci

0m 

10m  

10m  

1m 

DẠNG 6: TÌM M ĐỂ

x x xy a b c d   

CÓ 2 CỰC TRỊ THỎA ĐIỀU KIỆN CHO TRƢỚC.

43. Tìm tt c các giá tr thc ca tham s m sao cho hàm s

y x mx x m    

có 2 cc tr

,xx

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM



-1



tha mãn

1 2 1 2

42x x x x  

3m 

2m 

0m 

1m 

44.  hàm s

 

3 2 2

x 1 1

y x m m m x     

t cc tr tm x

; x

tha

4xx

2m 

2m 

C. Không tn ti m D.

2m 

45. M th hàm s

  

3 2 3

34y x mx m

  th hàm s m cc tr

và

sao

cho

 20AB

1m

. B.

2m

. C.

1; 2mm

. D.

 1m

46.   th hàm s

4 2 2

81y x m x  

m cc tr nm trên các trc t

1m 

m 

m 

m 

DẠNG 7: TÌM M ĐỂ

xxy a b c  

CÓ 3 CỰC TRỊ THỎA ĐIỀU KIỆN CHO TRƢỚC.

47. Tìm tt c các giá tr c  th hàm s

4 2 2

21y x m x  

m cc tr nh ca

mt tam giác vuông cân.

1m 

 

1;1m

 

1;0;1m

 

0;1m

48.   th hàm s

   

4 2 4

22y x mx m m

m cc tr to thành mu.

1m 

3m 



3.m

49.   th hàm s

2 x 2y x m  

có 3 cc tr to thành mt tam giác có din tích bng 1

1m 

2m 

3m 



4m 

DẠNG 8: TÍNH CHẤT CỰC TRỊ HÀM SỐ.

50. Cho hàm s

 

o hàm

       

' 1 2 2 3f x x x x   

. Tìm s m cc tr ca

 

A. 3 B. 2 C. 0 D. 1

51. Bit hàm s

 

f x x ax bx c   

t cc tiu tm

 

1, 1 3xf  

 th ca hàm s ct

trc tung t bng 2. Tính giá tr ca hàm s ti

3x 

 

3 81f 

 

3 27f 

 

3 29f 

 

3 29f 

52. Cho hàm s

x+b







t

,2A a b B a b   

 hàm s t ci tm

 

0; 1A 

thì tng

giá tr ca

2AB

bng

A. 6 B. 1 C. 3 D. 0

DẠNG 9: TÌM SỐ CỰC TRỊ CỦA HÀM SỐ.

53. Cho hàm s

 

y f x

có bng bi

 th ca hàm s

 

y f x

m cc tr?

A.4 B. 2

C. 3 D. 5

===============HẾT CHUYÊN ĐỀ 2================

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

CHUYÊN ĐỀ 3: GIÁ TRỊ LỚN NHẤT – NHỎ NHẤT CỦA HÀM SỐ.

BÀI TOÁN 5: TÌM GIÁ TRỊ LỚN NHẤT – NHỎ NHẤT

DẠNG 1: TÌM GTLN – GTNN

54. Gi

và

lt là giá tr ln nht và giá tr nh nht ca hàm s

   

2 3 4

y x x

trên

n





4;0 .

Tính tng

Mm



. B.

. C.



. D.

35

55. Tìm giá tr ln nht M ca hàm s







n

[0;2]





. B.

5M

. C.

 5M

. D.



56. Tìm giá tr nh nht ca hàm s

   

31y x x

trên khong

 

;1

 





min 3y

. B.

 





min 1y

. C.

 





min 2y

. D.

 





min 3y

57. Giá tr ln nht ca hàm s

( ) 1 4f x x x  

n







.là:

15

13

1 2 3

D. 3

58. Cho hàm s

 

y f x

liên tn [- th  bên. Gi M và m lt là

giá tr ln nht và nh nht ca hàm s n [-1;3]. Giá tr ca M  m bng

A. 0 B. 1

C. 4 D. 5

BÀI TOÁN 6: BÀI TOÁN GTLN – GTNN CHỨA THAM SỐ M

DẠNG 2: TÌM M ĐỂ HÀM SỐ CÓ GTLN – GTNN.

59. Giá tr ln nht ca hàm s

4xy x m   

n

 

1;3

 ca m bng bao

nhiêu?

A. 3 B. -15 C. -6 D. -7

60.  hàm s

x5m







t giá tr nh nhn

 

0;1

bng -7

 

1;0m

 

0;2m

 

1;3m

 

2;4m

61. Cho hàm s







thõa mãn

 

0;1

min max

yy

. m thuc khong nào trong các khoi



 

;1 

 

2;0

 

0;2

 

2;

DẠNG 3: BÀI TOÁN THỰC TẾ.

===============HẾT CHUYÊN ĐỀ 3================

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

CHUYÊN ĐỀ 4: ĐƢỜNG TIỆM CẬN

BÀI TOÁN 7: TÌM ĐƯỜNG TIỆM CẬN

DẠNG 1: TÌM ĐƢỜNG TIỆM CẬN.

62. Tim cn ngang c th hàm s







1y 

1y 

1y 

D. Không có

63. Tim cn ngang c th hàm s







1x 

1y 

7x 

7x 

64. Tim cn ngang c th hàm s

2x 3







A. Không có B.

1y 

2y 

1x 

65. Hàm s

3x 2







có my tim cng

A. Không có B. 1 C. 2 D. 3

66. Tim cng c th hàm s

2x 1 1







x 

1y 

1x 

D. Không có

67.  th hàm s

5x 6







có my tim cn?

A. 1 B. 2 C. 3 D. 4

68. S ng tim cn c th hàm s

3 2x 5x







A. 1 B. 2 C. 3 D. 4

DẠNG 2: DỰA VÀO BẢNG BIẾN THIÊN TÌM TIỆM CẬN.

69. Cho hàm s

y f(x)

có bng bin thiên



2



 

'fx



 



S ng tim cng và ngang c th hàm s 

A. 4 B. 2 C. 3 D. 1

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

70. Cho hàm s

 

y f x

có bng bi



1 +



 



2 3

Tng s tim cn ngang và tim cng c th hàm s 

A. 4. B. 1. C. 3. D. 2.

BÀI TOÁN 8: BÀI TOÁN TIỆM CẬN CÓ CHỨA THAM SỐ M

DẠNG 3: TÌM M ĐỂ HÀM SỐ CÓ TIỆM CẬN ĐỨNG.

71. Cho hàm s

x 3x







vi giá tr nào ca m thì

1x 

là tim cng c th hàm s

3m 

3m 

3m 

3m 

72. Tìm tt c các giá tr thc ca tham s

  th hàm s







x x m

ng tim cn

ng.

m

. B.





























2.m

73. Cho hàm s

2x 3x







vi giá tr nào ca m thì hàm s có tim cng?

1m 

13m  











3m 

74. Cho hàm s

2x 2x







 th (C ). Tìm tt c giá tr c (C ) không có tim cng.

0m 

1m 

0m 

hoc

1m 

2m 

DẠNG 4: TÌM M ĐỂ HÀM SỐ CÓ TIỆM CẬN NGANG.

75. Tìm tt c giá tr thc c  th hàm s







có mt tim cn ngang

0m 

0m 

0m 

3m 

76. Tìm Tt c giá tr c  th hàm s

2x x 4







t tim cn ngang là

0m 











4m 

04m

===============HẾT CHUYÊN ĐỀ 4================

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

-1

-3

-2

-3

-2

-1

CHỦ ĐỀ 5: ĐỒ THỊ HÀM SỐ

BÀI TOÁN 9: NHẬN DẠNG ĐỒ THỊ

DẠNG 1: NHẬN DẠNG ĐỒ THỊ HÀM

x x xy a b c d   

77.  th a hàm s 

y x x  

31y x x   

31y x x  

y x x  

78.

 th a hàm s nào ? Ch

34y x x   

 xxy

 xxy

y x x   

79. Cho hàm s

0y ax bx cx d a

 th . Khnh

đúng ?

0; 0; 0; 0.a d b c

0; 0; 0; 0.a b c d

0; 0; 0; 0.a c d b

0; 0; 0; 0a b d c

80. Cho hàm s

y ax bx cx d   

 th nh

 sau, m nào đúng?

0, 0, 0ab bc cd  

0, 0, 0ab bc cd  

0, 0, 0.ab bc cd  

0, 0, 0.ab bc cd  

81. ng cong trong hình bên  i là  th ca mt hàm s trong bn hàm s c lit kê  bn

png án A, B, C, D di ây. Hi hàm s ó là hàm s nào?

133

 xxxy

. B.

31y x x   

31y x x  

. D.

31y x x   

DẠNG 2: NHẬN DẠNG ĐỒ THỊ HÀM

xxy a b c  

82.  th ca mt hàm s trong bn hàm s c lit kê  b

Hi hàm s là hàm s nào ?

2y x x

2y x x

31y x x  

2y x x  

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

83.  th hình bên là ca m th ca các hàm s  

Hãy ch

5y x x  

. B.

y x x



  





. D.

y x x



  

84. nh a, b, c ca hàm s

xxy a b c  

 th 

4; 2; 2a b c   

; 2; 2

a b c   

4; 2; 2abc  

; 2; 0

a b c   

85. 

y ax bx c  





a 0,b 0,c 0  

a 0,b 0,c 0  

a 0,b 0,c 0  

a 0,b 0,c 0  

DẠNG 3: NHẬN DẠNG ĐỒ THỊ HÀM PHÂN THỨC.

86.  th ca hàm s 





















87. Bng bii là ca hàm s nào trong các hàm s 







1





1

























88.

Bng bia hàm s nào?

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM





















89. Cho hàm s

x1a







kh

0ab

0ab

90. Cho hàm s







 th  bên. Tìm khnh sau?

0ab

0ba

0 ba

0 ab

91. Cho hàm s

ax b







vi

0a 

 th  bên. M 

0, 0, 0b c d  

0, 0, 0b c d  

0, 0, 0b c d  

0, 0, 0b c d  

DẠNG 4: NHẬN DẠNG ĐỒ THỊ HÀM TRỊ TUYỆT ĐỐI

92. Cho hàm s

()y f x

 th hàm s

 

y f x

:

Chn kt lun đúng trong các kt lun sau:

( ) 4 4f x x x x    

( ) 4 4f x x x x   

( ) 4 4f x x x x    

( ) 4 4f x x x x   



-1



ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

93.  th ca mt trong bn hàm s   nào?

y x 3 x

y x 3x

y x 3x

y x 3 x

DẠNG 10: BÀI TOÁN 10 HÀM ẨN

 

'fx

94. Cho hàm s

()y f x

o hàm liên t th hàm s

()y f x





. Khng

sai?

A. Hàm s ng bin trên khong

(1; )

B. Hàm s ng bin trên khong

( 2; 1)

C. Hàm s y = f(x) nghch bin trên khong

( 1;1)

D. Hàm s y = f(x) nghch bin trên khong

( ; 2) 

95. Cho hàm s

 

y f x

 th ca hàm s

 

'y f x

. Xét hàm s

 

2g x f x

M 

A. Hàm s

 

nghch bin trên

 

0;2

B. Hàm s

 

ng bin trên

 

2;

C. Hàm s

 

nghch bin trên

 

;2 

D. Hàm s

 

nghch bin trên

 

1;0

96. Cho hàm s

y f(x)

. Hàm s

y f '(x)

có bng xét d



2



 

'fx



Hàm s

 

y f x 2x

nghch bin trên kho

(0;1)

( 2; 1)

( 2;1)

( 4; 3)

97. Cho hàm s

 

y f x

o hàm là

 

'fx

liên tc trên và hàm s

 

'fx

 th 



ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

Hi hàm s

 

y f x

có bao nhiêu cc tr?

A. 1. B. 0.

C. 3. D. 2.

98. Cho hàm s

 

y f x

o hàm trên  th  bên. H th ca hàm s

 

y f x

m ci, cc tiu?

A. m ci, m cc tiu.

B. m cm cc tiu.

C. m cm cc tiu.

D. m cm cc tiu.

99. Cho hàm s o hàm trên  th  bên. Hàm s có bao

m cc tr?

A. 5 B. 3

C. 4 D. 5

100. Cho hàm s

 

y f x

o hàm

 

'y f x

liên tc trên  th ca hàm s

 

'fx

trên

n

 

2;6

 bên. Tìm khnh đúng trong các khnh sau.

 

   

2;6

max 2f x f





 

   

2;6

max 6f x f





 

     

 

2;6

max max 1 , 6f x f f





 

   

2;6

max 1f x f





===============HẾT CHUYÊN ĐỀ 5================

()y f x

-1

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

CHỦ ĐỀ 6: SỰ TƢƠNG GIAO CỦA HAI ĐỒ THỊ

BÀI TOÁN 11: TỌA ĐỘ GIAO ĐIỂM

DẠNG 1: TÌM TỌA ĐỘ GIAO ĐIỂM.

101. Gi M, N m cng thng

1yx

ng cong









m I cn thng MN bng



B. 1 C. 2 D.

102. Cho hàm s







 th (C). Tìm tt c các giá tr c ng thng

 

:1d y x m  

ct (C) tm phân bit A, B sao cho

23AB 

4 10m 

43m 

2 10m 

23m 

103. Tìm tt c giá tr c  th hàm s

 

2 1 4xy x m x   

ct trc Ox tm có hoành



2x 

2m 

3m 

1m 

4m 

BÀI TOÁN 12: BÀI TOÁN TƯƠNG GIAO CÓ CHỨA THAM SÓ M

DẠNG 2: BIỆN LUẬN SỐ GIAO ĐIỂM CỦA HAI ĐỒ THỊ

104. Tìm tt c giá tr thc ca tham s

 ng thng

ym

c th hàm s

– 2 3y x x

ti bm phân bit.

11  m

. B.

23m

. C.

01m

. D.

– 1 0m

105. Tìm tt c giá tr c 

3x 0xm  

có 3 nghim phân bit

22m  

23m  

13m  

12m  

DẠNG 3: TÌM M ĐỂ HÀM SỐ CÓ SỐ GIAO ĐIỂM CHO TRƢỚC

106.  ng thng

( ):d y x m

c th

( ):







tm phân bit.

22m  





















02m

107. Tìm tt c các giá tr thc ca tham s

  th hàm s

   

4y x mx mx

cng thng

4yx

tm phân bit.

 

1;1m

. B.

 

 1; 3m

. C.

 

 3; 5m

. D.

 

 4;6m

108. Tìm tt c giá tr thc ca tham s

  th hàm s

 

:1   

C y x mx m

ct trc hoành

ti bm phân bit.









B. Không có

1.m

2.m

109. Cho hàm s

( ) :







ng thng

d y x m  

 d ct (C) tm nm

v i vi trc tung :

1m 

2m 

3m 

4m 

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

DẠNG 4: TÌM SỐ GIAO ĐIỂM CỦA HÀM TRỊ TUYỆT ĐỐI.

110. Cho hàm s

 

 th  nh tt c giá tr ca tham s  

trình

 

f x m

có 6 nghim phân bit

4m 

04m

34m

03m

111.  th ca hàm s



3.y x x

Tìm tt c giá tr thc ca

tham

s

 



3x x m

m phân bit.

   

  2;0 0; 2m

. B.

 

 0; 2m

   

  2;0 0; 2m

. D.

 

 0; 2m

112.  th ca hàm s







. Tìm tt c các giá tr thc ca

tham s

 







có hai nghim phân bit.

A. Vi mi

B. Không có giá tr ca

0m

   

0; \ 1 m

DẠNG 5: TÌM SỐ GIAO ĐIỂM CỦA HÀM ẨN.

113. Cho hàm s

()y f x

liên tn

 

2;2

 th :

S nghim c

3 ( 2) 4 0fx  

n

 

2;2

là?

A. 4. B. 2.

C. 3. D. 1.

-1

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

DẠNG 6: TÌM SỐ GIAO ĐIỂM DỰA VÀO BẢNG BIẾN THIÊN.

114. Cho hàm s

 

y f x

có bng bin thiên sau



1









1

Tìm s nghim c

 

2 1 0fx

A. 0 B. 3 C. 4 D. 6

115. Cho hàm s

 

y f x

nh và liên tc trên mi na khong





;2 

và





2;

, có bng

bi



2







Tìm tp hp các giá tr ca m  

 

f x m

có hai nghim phân bit.

 

;2 22;



 









22;

;













;2 22;



 







===============HẾT CHUYÊN ĐỀ 6================

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

CHỦ ĐỀ 7: ĐƢỜNG TIẾP TUYẾN

BÀI TOÁN 13: VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN

DẠNG 1: VIẾT PHƢƠNG TRÌNH TIẾP TUYẾN.

116. Cho hàm s

5x 1y x x   

p tuyn t th 

2x 

10x 9y 

11x 19y 

11x 10y 

10x 8y 

117. Tip tuyn c th hàm s







song song vng thng

3x 2y   



là:

3x 10y 

3x 2; 3x 10yy     

3x 10y   

3x 2y   

118. Cho hàm s

6y x x   

 th (C ). Vip tuyn c th (C ), Bit tip

tuyn vuông góc vng thng

yx

6x 6y   

6x 8y   

6x 10y   

6x 12y   

119. Cho hàm s

4x 6x 1y   

 th ( C). Vip tuyn vi (C ) bit rng tip

tuym M(-1; -9)

15 21

24x 25;

4 24

y y x   

15 21

24x 15;

y y x   

15 21

24x 5;

4 24

y y x   

15 21

24x 25;

y y x   

120. Cho hàm s

2x 1







 thì (C). Gm thu bng 5. Tip tuyn ca

(C ) tm M ct các trc Ox, Oy lt ti A và B. Tính din tích tam giác

OAB



112

121

122

113

BÀI TOÁN 14: BÀI TOÁN TIẾP TUYẾN CHỨA THAM SỐ M

DẠNG 2: TÌM M ĐỒ THỊ CÓ TIẾP TUYẾN THỎA ĐK CHO TRƢỚC

121. Cho hàm s

2 x 2 1y x m m    

 tip tuyn c th (Cm) tm

   

1;0 , 1;0AB

vuông góc vi nhau.

;

mm

;

mm   

;

mm  

;

mm  

122. Cho hàm s







 th ( C ). Bit rng a, b là các giá tr thc sao cho tip tuyn ca (

C) tm

 

1; 2M 

song song vng thng

:3x 4 0dy  

 ca

ab

bng

A. 0 B. -1 C. 2 D. 1

123. Cho hàm s

 

2 1 2y x m x m    

 th (C ). Gm thu th hàm s có

 bng 1. Vi giá tr nào ca m thì tip tuyn c th (C ) ti A vuông góc vng thng

: 2 4 0xy   

 

3;0m

 

2;2m

 

2;5m

 

5;9m

ĐS 12 – CHƯƠNG I

[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN. DI ĐỘNG: 0364 968 6263]

FANPAGE: NHÓM LUYỆN THI MPEC WEBSITE: TRUNGTAMMPECDANANG.COM

DẠNG 3: ĐIỆU KIỆN TIẾP XÚC

124. Bit r th các hàm s

y x x  

và

2y x x  

tip xúc nhau tm

( ; )M x y

Tìm

x 

. B.

x

x

125. Tìm tt c giá tr ca tham s  m

(2; )Mm

k c ba tip tuyn phân bi th

hàm s

3xyx

là

 

4;5m

 

2;3m

 

5; 4m  

 

5;4m

===============HẾT CHUYÊN ĐỀ 7================

ĐÁP ÁN 125 CÂU TRẮC NGHIỆM

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

Mua file Word: Giá 100K.

Liên hệ: Di động: 0349.686.263 – Thầy Hiền – Nhóm luyện thi MPEC tại Đà Nẵng.

Nhằm ủng hộ cho Team có kinh phí để biên soạn nhiều tài liệu chất lượng hơn - giúp giáo viên tiết kiệm

thời gian soạn tài liệu và học sinh dễ ôn tập nhé.

Bấm Tải xuống để xem toàn bộ.

| 1/23

| | Tải xuống

Preview text:

ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
PHÂN DẠNG DỄ NHỚ VÀ KỸ THUẬT GIẢI NHANH
CHỦ ĐỀ 1: ỨNG DỤNG ĐẠO HÀM KHẢO SÁT HÀM SỐ BÀI TOÁN 1 BÀI TOÁN 2
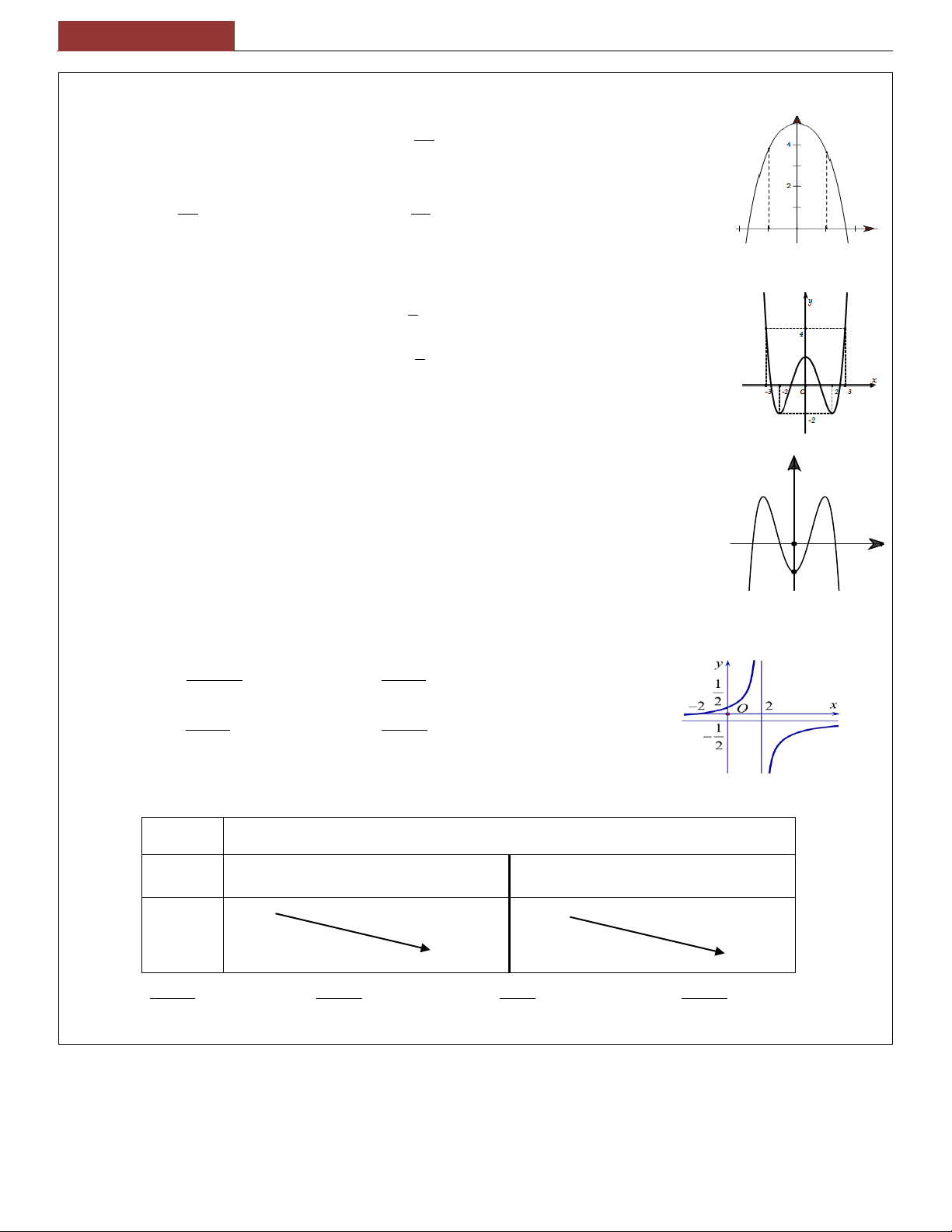
Tìm khoảng ĐB - NB của hàm số.
Tìm m để hàm số ĐB –NB trên khoảng  ; a b
Đồng biến trên D  y '  0, x   D Loại  3 2 y  x a  x b  x c  d
Nghịch biến trên D  y '  0, x   D a  0 a  0 ax  b  
Chú ý: Hàm phân thức  ĐB trên R   NB trên R    0   0 cx  d
Đồng biến: y '  0   Ngịch biến: y ' 0 x a  b
Loại  y 
P2 1: Lập bảng biến thiên x c  d  Tính y ' ĐB trên TXĐ  . a d  . b c  0
 ( Xét dấu y ' ) NB trên TXĐ  . a d  . b c  0
PP xét dấu: Hàm thường gặp:
 y  ax  b : Phải cùng, trái khác Loại  3 2 y  x a  x b  x c  d  2
y  ax  bx  c : ;
a b  y '  0, x   ; a b 2 nghiệm Trong trái, ngoài cùng ĐB trên   1 hoặc vô nghiệm Cùng dấu với a, x   R NB trên  ;
a b  y '  0, x   ; a b  3 2
y  ax  bx  cx  d :
m  g x, x   ;
a b  m  Ming  x
3 nghiệm Phải cùng, tiếp theo xen dấu
PP Cô lập m: m  g  x, x   ;
a b  m  M x a g  x
2 nghiệm Xét dấu nghiệm đơn (nghiệm x casio) 1
1 nghiệm Phải cùng, trái khác x a  b
Loại  y 
P2 2: Casio: Dùng Mode 7 x c  d
Nhập hàm f  x  ?  Start: … End … là khoảng  . a d  . b c  0  trong đáp án A, B, C, D.
 ĐB trên ;   d   
Kiểm tra giá trị f  x trong máy tính.  c
 Nếu f  x tăng thì đồng biến  . a d  . b c  0     
Nếu f  x giảm thì nghịch biến NB trên  ;   d     c BÀI TOÁN 3
Tìm điểm cực trị của đồ thị hàm số
ĐK cần: Cực trị là nghiệm của  y ' a
y '  0 hoặc y '  0  a  D C Dấu hiệu 2:  không xác định.  y '
 a  0  a  CT ĐK đủ:
Dấu hiệu 1: Xét dấu y ' _ a + + a _ a là cực tiểu a là cực đại
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263] BÀI TOÁN 5 BÀI TOÁN 4
Tìm GTLN – GTNN của hàm số
Bài toán cực trị có chứa tham số m Loại 1: Trên  ; a b :
Loại 1: Tìm m biết trƣớc CĐ hoặc CT y '   x  0 0  B  1: Tìm x
 ;ab và f 'x  i  0 i   x là CĐ   0 y '   x  0 0 
Min  min f a; f b; f  xi  B2: M x a  m x
a  f a; f b; f  x y '   x  0 0  i   x là CT  
P2 2: Casio: Mode 7 0 y '   x  0 0 
Loại 2: Trên khoảng  ;
a b hoặc R: Lập bảng biến thiên.
Loại 2: Tìm m để HS có 1 – 2 – 3 cực trị x a  b     
Chú ý: Hàm y  3 2 y x a x b x c d x c  d
 2 cực trị  y '  0 có 2 nghiệm phân biệt
 y '  0 trên  ;
a b : Min  f a, Max  f b
 Ko có cực trị khi y '  0 có 1 nghiệm hoặc vô N0
 y '  0trên  ;
a b : Min  f b, Max  f a  4 2 y  x a  x b  c  có 3 cực trị khi . a b  0  có 1 cực trị khi . a b  0 BÀI TOÁN 6
Ứng dụng GTLN – GTNN vào bài toán thực tế Loại 3: Tìm m 3 2 y  x a  x b  x
c  d có 2 CT thỏa YC Ý tƣởng: a  0 B y  f x .
 y '  0 có 2 nghiệm phân biệt 
1: Dựa vào giả thuyết lập hàm số      0
B2: Tìm Min – Max của f  x b c
Áp dụng viet: x  x   ; x .x  1 2 1 2
Đây là bài tập Vận dụng và vận dung cao. Yêu cầu a a
các em phải liên kết được các giả thuyết của bài toán Loại 4: Tìm m để 4 2 y  x a  x b
 c có 3 cực trị
thỏa tính chất tam giác.
Chú ý: Ba điểm A0;c, B x ; y ,C x ; y luôn có 1 1   2 2 BÀI TOÁN 7
Tìm tiệm cận của hàm số tính chất cân tại A.
 Nếu lim y  a và lim y  b
Loại 5: Phƣơng trình qua các điểm cực trị x x  3 2 y  x a  x b  x c  d
thì hàm số 2 tiệm cận ngang. y  a và y  b
P2 1: y '  0 tìm 2 điểm A x ; y , B x ; y 1 1   2 2
 Nếu lim y   hoặc lim y     xx xx 0 0
vtpt : n  AB
Viết pt đường thẳng AB có
( Chỉ cần thỏa một trong 4 kết quả trên là ok)  qua : A
thì hàm số có tiệm cận đứng là: x  x0 P2 2: Dùng Casio B1: vào CMPLX f  x m a x  ... 1 y '.y ' Chú ý: y   n B 
2: Nhập công thức: y g  x b x  ... 1 18a
B3: CALC với X = i, Y = 1000  a
Bậc tử = bậc mẫu  TCN 1 y  b1
 Bậc tử < bậc mẫu  TCN y  0
 Bậc tử > bậc mẫu  Ko có tiệm cận ngang.
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263] BÀI TOÁN 8 BÀI TOÁN 9
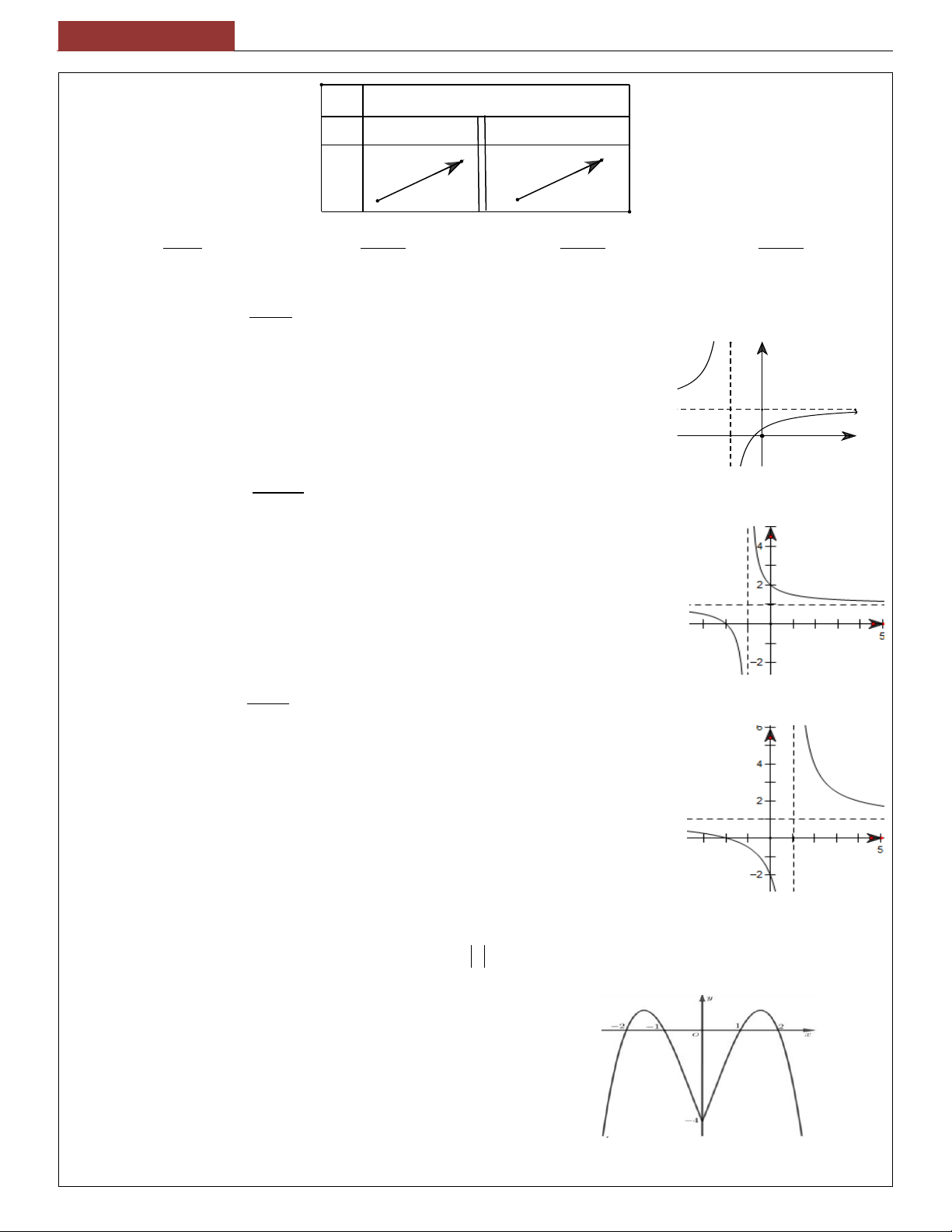
Bài toán tiệm cận có chứa tham số m
Nhận dạng đồ thị hàm số
Loại 1: Tìm m để HS có tiệm cận đứng  3 2 y  ax  x b  x c  d f  x  Hàm y 
( Xét x là nghiệm của mẫu) A hướng B Điểm uốn g  x 0  a  0 : Đi lên  .
a b  0 Lệch phải    g   x  0 a  0 : Đi xuống . a b  0 Lệch trái 0 
Để x  x là TCĐ khi 
hoặc g  x  0 và
 b  0 trùng gốc O 0  0  f   x  0 0  C cực trị D giao Oy
x thỏa điều kiện của hàm số.  . a c  0 hai phía Oy
 d  0 : phía trên Oy. 0
Loại 2: Tìm m để HS có tiệm cận ngang  .
a c  0 cùng phía Oy
 d  0 : phía dưới Oy
 c  0 CT thuộc Oy
 d  0 : trùng gốc O
 Bậc tử phải nhỏ hơn hoặc bằng bậc mẫu  4 2 y  ax  x b  c BÀI TOÁN 10 A hướng B C
Bài toán đồ thị của hàm f ' x  a  0  . a b  0  c  0
Loại 1: Khoảng ĐB – NB của hàm hợp y  f u Đi lên Hình dạng chữ phía trên Oy. W hoặc M  c  0 B 
1: Tính đạo hàm: y '
u '. f 'u  a  0  . a b  0 phía dưới Oy
B2: Lập bảng xét dấu: Đi xuống Hình dạng  c  0 trùng gốc O u ' + - + f 'u - - + 
y '  u '. f '(u) - + +  ax b y  x c  d . a d  . b c B   1: Tính y '
Loại 2: Tìm cực trị của hàm hợp y f u  và xem hàm số ĐB hay NB cx  d 2 B   1: Tính y '
u '. f 'u và tìm nghiệm u '. f 'u 0
B2: Xét tiệm cận đứng và tiệm cận ngang.
B2: Dựa vào dấu hiệu kiểm tra điểm cực trị
B3: Xét giao điểm của đồ thị với Ox, Oy.
Loại 3: Tìm GTLN - GTNN của hàm y  f u
Ý tƣởng: Từ đồ thị hàm f ' x ta biết được các
khoảng (a, b) mà f ' x  0  f a  f b BÀI TOÁN 11 BÀI TOÁN 12
Tìm tọa độ giao điểm thỏa yêu cầu bài toán
Bài toán tƣơng giao có chứa tham số m
Loại 1: Biện luận nghiệm PT: f  x  m   1
Tìm tọa độ giao điểm của y  f  x và y  g  x
B1: Chuyển tham số về bên phải PT (1) B  
1: Pt hoành độ giao điểm: f  x g  x
B2: Dựa vào đồ thị hàm y
f  x . Biện luận số B
nghiệm phương trình bằng số giao điểm của đồ thị 2: Thay x
vào một trong hai hàm số ta được y 1 1
y  f  x và đường thẳng y  m
Loại 2: Biện luận số giao điểm của đồ thị y  f  x
Cách vẻ đồ thị: B  bên dướ
1: Giữ nguyên phần đồ thị y f  x i Oy B  bên dướ
2: Lấy đối xứng phần đồ thị y f (x) i lên trên Oy
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263] BÀI TOÁN 13 BÀI TOÁN 14
Viết phƣơng trình tiếp tuyến
Bài toán tiếp tuyến có chứa m
Phương trình tiếp tuyến của đồ thị y  f x
Điệu kiện tiếp xúc
y  f  x và y  g  x tiếp xúc
Tại M  x ; y : y  y  f ' x . x  x 0  0  0  0 0  Trong đó:   f
  x  g x
Hệ số góc k: f ' x  k 0      f '
 x  g 'x
M  x ; y là tọa độ tiếp điểm 0 0 
PP chung: Muốn viết PT tiếp tuyến ta cần tìm điểm
M  x ; y 0 0 
Chú ý: d : y  a x  b 1 1
 Nếu d / /d thì d : y  a x  , c c  b 2 1  1  2 1  1
Nếu d  d thì d : y   x  c 2 1 2 a1
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
CHỦ ĐỀ 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
BÀI TOÁN 1: TÌM KHOẢNG ĐỒNG BIẾN – NGHỊCH BIẾN Loại 1: Hàm bậc 3 1. Hàm số 3 2
y  x  x  x có khoảng đồng biến là  1 1 A. 1;3 B.   ;1   C. ( ;   ) (1;) D.  1  ;3  3  3
2. Tìm khoảng đồng biến của hàm số 3 2
y  x  3x 1 A. 0;2 B.  ;  2 C.  ;  0 và 2; D. 0; 4
3. Tìm khoảng đồng biến của hàm số 3 2 y 
x  2x  x  3 3 A. 0  ;1 B. 0; C. R D.  ;  0 1
4. Tìm khoảng nghịch biến của hàm số 3
y   x  4x 1 3 A.  ;  0 và 2; B.  ;   C. 2;  D.  ;  2 Loại 2: Hàm bậc 4
5. Tìm khoảng đồng biến của hàm số 4 2
y  x  2x 1 A.  1  ;0 và 1; B.  1  ;0 C.  1   ;1 D.  1  ;
6. Tìm khoảng nghịch biến của hàm số 4 2
y  x  2x  5 A. 0;  B.  ;  0 C. R D.  1   ;1 1 5 7 7. Hàm số 4 3 2 y  x  x 
x  3x  2018 nghịch biến trên khoảng nào 4 3 2 A. 0;3 B. 0; C. 3; D. 1;3
Loại 3: Hàm phân thức.  8. Hàm số 2x 3 y 
nghịch biến trên khoảng nào x 1 A. R B. 1; C.   ;1  và 1; D.   ;1  2 x  2x  2
9. Tìm khoảng đồng biến của hàm số y  x 1 A.  2  ;0 B.  2;   C.  ;  2
  và 0; D.  ;0  
Loại 4: Hàm số khác.
10. Tìm khoảng nghịch biến của hàm số 4
y  x  x A.  2  ;2 B. 2; C.  2  ;0 và 0;2 D.  ;  2
11. Tìm khoảng nghịch biến của đồ thị hàm số 2 y  25  x A.  5  ;0 B. 0;5 C.  5  ;5 D. 0;
Loại 5: Dựa vào đồ thị và bảng biến thiên
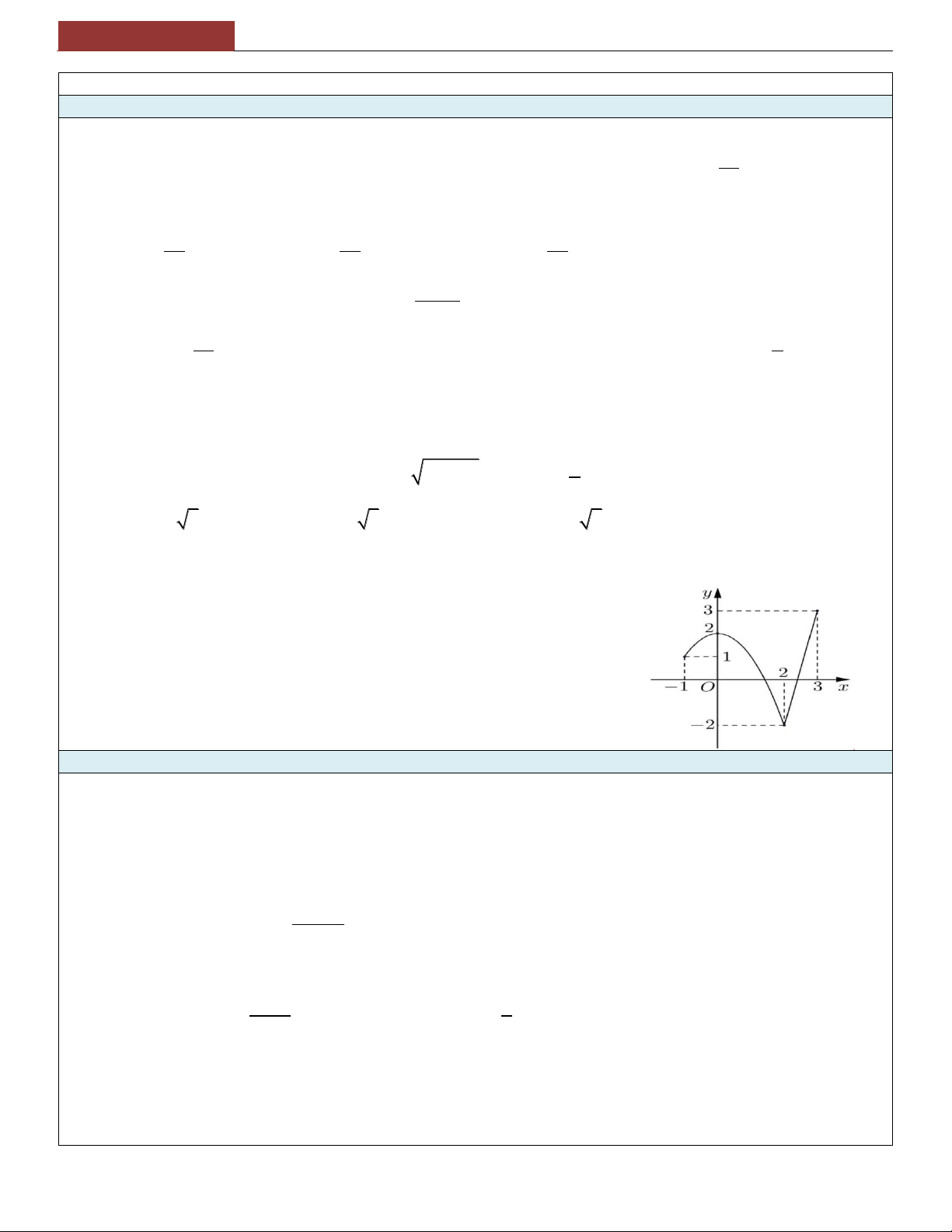
12. Cho hàm số y  f  x có đồ thị như hình vẽ. Chọn mệnh đề đúng.
A. Hàm số tăng trên khoảng 0; y 2
B. Hàm số tăng trên khoảng  2  ;2 1 -1 O
C. Hàm số tăng trên khoảng  1   ;1 1 x 2 -1
D. Hàm số tăng trên khoảng  2   ;1 -2
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263] 2 2017
13. Cho hàm số y  f  x liên tục trên
và có đạo hàm f  x   x  
1  x  2  x  3 .Khẳng định nào dưới đây đúng?
A. Hàm số đồng biến trên các khoảng 1; 2 và 3; .
B. Hàm số có ba điểm cực trị.
C. Hàm số nghịch biến trên khoảng 1;3 .
D. Hàm số đạt cực đại tại x  2 và đạt cực tiểu tại x  1 và x  3 .
14. Cho hàm số y  f  x có bảng biến thiên như hình vẽ bên.
Mệnh đề nào sau đây là sai?
A. Hàm số đã cho đồng biến trên khoảng   ;1 
B. Hàm số đã cho đồng biến trên khoảng 2;  
C. Hàm số đã cho nghịch biến trên khoảng 0;3
D. Hàm số đã cho đồng biến trên khoảng 3;   .
BÀI TOÁN 2: TÌM M ĐỂ HÀM SỐ ĐỒNG BIẾN – NGHỊCH BIẾN TRÊN (A; B) DẠNG 1: HÀM BẬC BA 3 2     ĐỒ y x a x b x c d
NG BIẾN – NGHỊCH BIẾN TRÊN R. 1 15. Hàm số 3 2 y 
x  (m 1)x  (m 1)x 1 đồng biến trên tập xác định của nó khi : 3 A. m  1  B. 2   m  1  C. 2   m  1  D. m  2  16. Cho hàm số 3 2 y  x  x m
 4m9 x 5 có bao nhiêu giá trị nguyên m để hàm số nghịch biến trên khoảng  ;   A. 7 B. 4 C. 6 D. 5
DẠNG 2: HÀM PHÂN THỨC ĐB – NB TRÊN TẬP XÁC ĐỊNH mx  7m  8
17. Tìm tất cả giá trị của tham số m để hàm số y 
đồng biến trên từng khoảng xác định. x  m
A. 8  m  1.
B. 8  m  1.
C. 4  m  1.
D. 4  m  1. x  m
18. Tìm tất cả giá trị thực của tham số m để hàm số y 
nghịch biến trên từng khoảng xác định. x  2 A. m  2 . B. m  2 . C. m  2 . D. m  2 .
DẠNG 3: HÀM ĐA THỨC ĐỒNG BIẾN – NGHỊCH BIẾN TRÊN (A; B)
19. Tập hợp giá trị của m để hàm số 3 2 y  x m
 x  3x  m  2 đồng biến trên khoảng  3  ;0  1   1   1   1  A.  ;    B.  ;    C.  ;     D.  ; 0    3   3   3   3 
20. Tìm tham số m để hàm số y  3 x  2
3x  mx  1 đồng biến trên khoảng 0; . A. m  0 . B. m  3 . C. m  3 . D. m  0 .
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263] 1
21. Tìm giá trị của m để hàm số 3 y 
x  m   2 1 x   2
m  2m x  3 nghịch biến trên 0  ;1 3 A.  1  ; B.  ;  0 C. 0  ;1 D.  1  ;0
DẠNG 4: HÀM PHÂN THỨC ĐỒNG BIẾN – NGHỊCH BIẾN TRÊN (A; B). x
22. Tìm tất cả giá trị của tham số m để hàm số y 
đồng biến trên khoảng 2;  . x  m A. m  0 . B. m  0 . C. m  2 . D. m  2 . m  1 x  2m  2
23. Với giá trị nào của m thì hàm số y 
đồng biến trên khoảng  1  ; x  m m  1 A. m  1 B. m  2 C.  D. 1  m  2 m  2 mx 
24. Có bao nhiêu giá trị nguyên của tham số m để hàm số 10 y 
nghịch biến trên khoảng 0; 2 ? 2x  m A. 4 B. 5 C. 6 D. 9
===============HẾT CHUYÊN ĐỀ 1================
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
CHUYÊN ĐỀ 2: CỰC TRỊ
BÀI TOÁN 3: TÌM CỰC TRỊ CỦA HÀM SỐ.
DẠNG 1: TÌM ĐIỂM CỰC TRỊ.
25. Tìm giá trị cực đại y của hàm số y  3 x  2
3x  3x  2 . CĐ A. 3  4 2 . B. 3  4 2 . C. 3  4 2 . D. 3  4 2 .
26. Tìm giá trị cực tiểu y
của hàm số y  4 x  2 2x  1. CT A. y  2 . B. y  1. C. y  1. D. y  0 . CT CT CT CT
27. Tìm điểm cực đại của đồ thị hàm số y 
x  3  6  x A. x  3 B. x  6 C. x  6 D. Không có D C D C D C
28. Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số 3 2
y  x  3x bằng A. 2 B. 2 5 C. 4 D. 4 5
29. Tính khoảng cách d giữa hai điểm cực tiểu của đồ thị hàm số 4 2
y  x  4x 1. A. d  2 2 . B. d  3 . C. d  2 . D. d  1.
30. Cho hàm số y  f (x) liên tục trên
và có bảng xét dấu của đạo hàm như hình vẽ. x  1 0 2 4  f'(x)  0   0  0 
Hàm số y  f (x) có bao nhiêu điểm cực trị? A. 4 . B. 1. C. 2 . D. 3 .
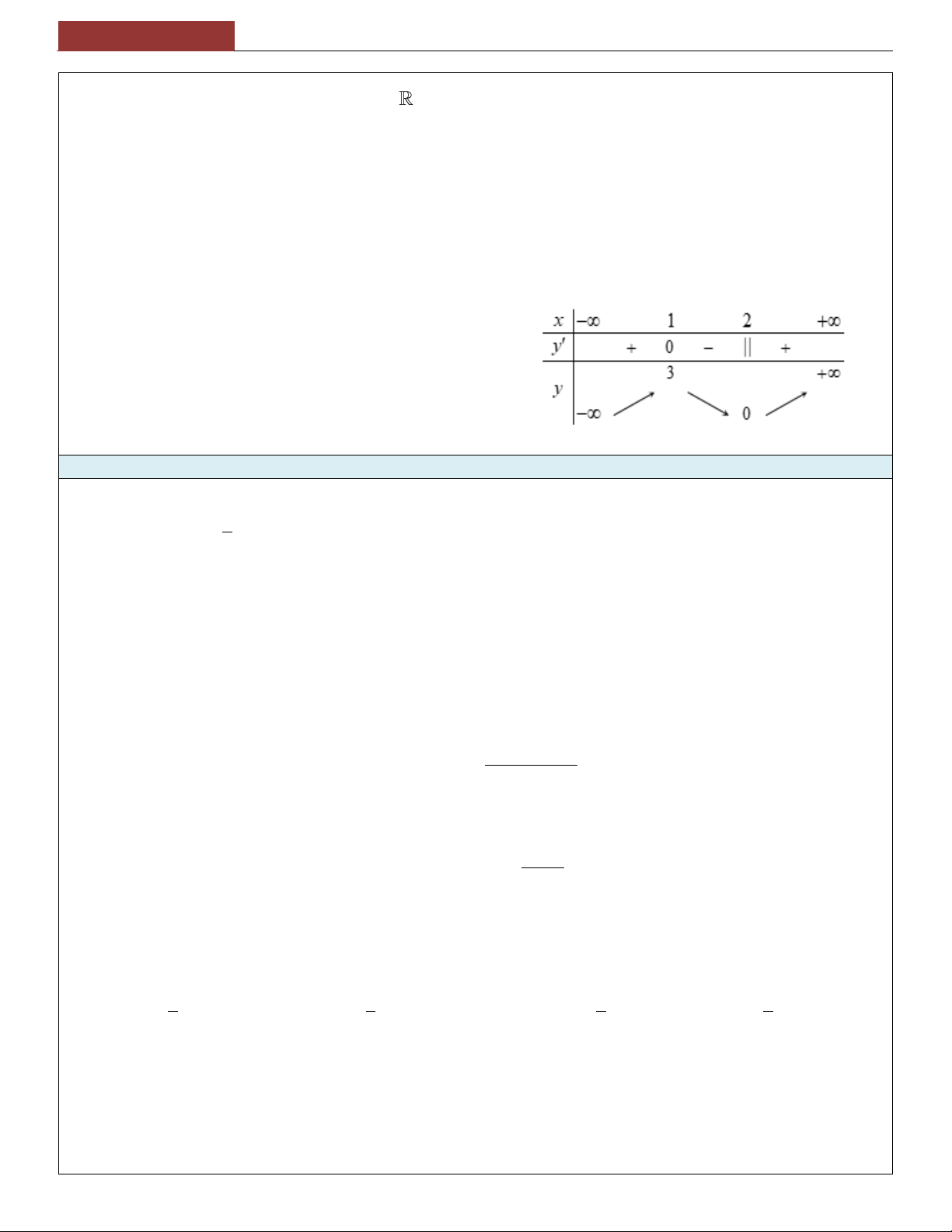
31. Hàm số y  f (x) liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là đúng? x  1 2  y + 0 - || + y 3   0
A. Hàm số đã cho có hai điểm cực trị.
B. Hàm số đã cho có đúng một điểm cực trị.
C. Hàm số đã cho không có giá trị cực tiểu.
D. Hàm số đã cho không có giá trị cực đại.
32. Cho hàm số y  f  x có bảng biến thiên như hình vẽ. Hỏi hàm số có bao nhiêu điểm cực trị? x  1  0 1  y ' + 0  + 0  y 2 3  1  1  2 A. Có một điểm B. Có ba điểm C. Có hai điểm D. Có bốn điểm
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
BÀI TOÁN 4: BÀI TOÁN CỰC TRỊ CHỨA THAM SỐ M
DẠNG 2: ĐƢỜNG THẲNG QUA HAI ĐIỂM CỰC TRỊ.
33. Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y  x  4x  x 1 là 38 5 38 5 38 5 A. y   x  B. y  x  C. y  x   Đáp án khác 9 9 9 9 9 9
34. Đồ thị của hàm số 3 2
y  x  3x  9x 1 có hai điểm cực trị A, B. Điểm nào dưới đây thuộc đường thẳng AB. A. P 1;0
B. M 0;   1 C. N 1; 1  0   1  ;10 35. Cho hàm số 3 y   m  2 2x 3
1 x  6m  2 x 1. Tìm m để đường thẳng đi qua hai điểm cực trị của
hàm số (1) song song với đường thẳng y  4  x 1 m  1 A.  B. m  1 C. m  5  m  3 m  5
DẠNG 3: TÌM M BIẾT HÀM SỐ CÓ 1 CỰC TRỊ CHO TRƢỚC. 1
36. Tìm giá trị của m để hàm số 3 2 y  x  x m   2 m  m  
1 x 1 đạt cực đại tại x  1 3 A. m  2  B. m  1  C. m  2  m  1 2 x  x m 1
37. Tìm tất cả giá trị của tham số m để hàm số y  x  x  đạt cực tiểu tại 0 1 A. m  1  B. m  1 C. m  1   Không có m DẠNG 4: TÌM M ĐỂ 3 2 y  x a  x b  x
c  d KHÔNG CÓ HOẶC 2 CỰC TRỊ.
38. Hàm số y  m   3 x  2 2
3x  mx  m . Tìm m để hàm số có cực đại và cực tiểu. A. m  3  ;  1 \{ 2  }. B. m  3  ;  1 . C. m  ;  3  1;. D. m  3  . DẠNG 5: TÌM M ĐỂ 4 2 y  x a  x b
 c CÓ 1 HOẶC 3 CỰC TRỊ.
39. Tìm tất cả giá trị thực của tham số m để hàm số 4 y  m m  2 x
1 x  2m 1 có 3 điểm cực trị? m  1  A. m  1  B. m  1  C. 1   m  0
D. m  0
40. Tìm tất cả giá trị của tham số m để hàm số 4 y  m  m  2 x
1 x 1 2m chỉ có một cực trị m  0 A. m  0 B. m  0
C. 0  m  1 D. m 1
41. Tìm các giá trị của tham số m để đồ thị hàm số 4 y  m   m  2 x 2
1 x  m  2 chỉ có cực đại và không có cực tiểu. A. m  1 B. m  0 C. m  0 D. m  1 3
42. Tìm m để đồ thị hàm số y  m   4 2 1 x  x m
 chỉ có cực tiểu mà không có cực đại 2 A. m  0 B. 1   m  0 C. 1   m  0 D. m  1  DẠNG 6: TÌM M ĐỂ 3 2 y  x a  x b  x
c  d CÓ 2 CỰC TRỊ THỎA ĐIỀU KIỆN CHO TRƢỚC. 1
43. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2 y 
x  mx  x  m 1 có 2 cực trị x , x 3 1 2
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263] thỏa mãn 2 2
x  x  4x x  2 1 2 1 2 A. m  3  B. m  2 C. m  0 D. m  1  1
44. Tìm m để hàm số 3 2 y  x  x m   2 m  m  
1 x 1 đạt cực trị tại hai điểm x   1; x2 thỏa x x 4 3 1 2 A. m  2  B. m  2  C. Không tồn tại m D. m  2
45. Mẫu Đồ thị hàm số y  3 x  2 mx  3 3
4m . Tìm m để đồ thị hàm số có hai điểm cực trị A và B sao cho AB  20 . A. m  1. B. m  2 .
C. m  1; m  2 . D. m  1.
46. Tìm m để đồ thị hàm số 4 2 2
y  x  8m x 1 có 3 điểm cực trị nằm trên các trục tọa độ 1 1 1 A. m  1  B. m   C. m  D. m   2 2 2 4 2
DẠNG 7: TÌM M ĐỂ y  x a  x b
 c CÓ 3 CỰC TRỊ THỎA ĐIỀU KIỆN CHO TRƢỚC.
47. Tìm tất cả các giá trị của m để đồ thị hàm số 4 2 2
y  x  2m x 1 có ba điểm cực trị là ba đỉnh của một tam giác vuông cân. A. m  1 B. m  1  ;  1 C. m  1  ;0;  1
D. m 0;  1
48. Tìm m để đồ thị hàm số y  4 x  2 mx  4 2
m  2m có ba điểm cực trị tạo thành một tam giác đều. A. m  1 B. m  3 C. m  3 D. m  3 3.
49. Tìm m để đồ thị hàm số 4 2 y  x  2 x m
 2 có 3 cực trị tạo thành một tam giác có diện tích bằng 1 A. m  1 B. m  2 C. m  3  m  4
DẠNG 8: TÍNH CHẤT CỰC TRỊ HÀM SỐ. 2 3
50. Cho hàm số f  x có đạo hàm f ' x   x  
1  x  2 2x  3 . Tìm số điểm cực trị của f  x . A. 3 B. 2 C. 0 D. 1 51. Biết hàm số   3 2
f x  x  ax  bx  c đạt cực tiểu tại điểm x  1, f   1  3
 và đồ thị của hàm số cắt
trục tung tại điểm có tung độ bằng 2. Tính giá trị của hàm số tại x  3 .
A. f 3  81
B. f 3  27
C. f 3  29
D. f 3  2  9 2 x  x a +b
52. Cho hàm số y 
. Đặt A  a  ,
b B  a  2b . Để hàm số đạt cực đại tại điểm A0;  1 thì tổng x 1
giá trị của A  2B bằng A. 6 B. 1 C. 3 D. 0
DẠNG 9: TÌM SỐ CỰC TRỊ CỦA HÀM SỐ.
53. Cho hàm số y  f  x có bảng biến thiên như sau:
Đồ thị của hàm số y  f x có bao nhiêu điểm cực trị? -∞ -1 x 3 +∞ _ A.4 B. 2 y' 0 + 0 + 5 +∞ C. 3 D. 5 y 1 -∞
===============HẾT CHUYÊN ĐỀ 2================
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
CHUYÊN ĐỀ 3: GIÁ TRỊ LỚN NHẤT – NHỎ NHẤT CỦA HÀM SỐ.
BÀI TOÁN 5: TÌM GIÁ TRỊ LỚN NHẤT – NHỎ NHẤT
DẠNG 1: TÌM GTLN – GTNN 3 x
54. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y   2
2x  3x  4 trên 3 đoạn 4;0 
. Tính tổng M  m. 28 A.  28 . B. . C.  28 . D. 35 . 3 3 3 3x  1
55. Tìm giá trị lớn nhất M của hàm số y  trên đoạn [0;2]. x  3  A. M  1 . B. M  5 . C. M  5 . D. M  1 . 3 3
56. Tìm giá trị nhỏ nhất của hàm số y   3
x  3x  1 trên khoảng   ;1 .
A. min y  3 .
B. min y  1 .
C. min y  2 .
D. min y  3 .   ;1   ;1   ;1   ;1 1 
57. Giá trị lớn nhất của hàm số 2
f (x)  1 4x  x trên đoạn ;3   .là: 2  A. 1 5 B. 1 3 C. 1 2 3 D. 3
58. Cho hàm số y  f  x liên tục trên đoạn [-1;3] và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là
giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [-1;3]. Giá trị của M – m bằng A. 0 B. 1 C. 4 D. 5
BÀI TOÁN 6: BÀI TOÁN GTLN – GTNN CHỨA THAM SỐ M
DẠNG 2: TÌM M ĐỂ HÀM SỐ CÓ GTLN – GTNN.
59. Giá trị lớn nhất của hàm số 2
y  x  4x  m trên đoạn  1  ; 
3 là 10. Khi đó giá trị của m bằng bao nhiêu? A. 3 B. -15 C. -6 D. -7 m 
60. Tìm m để hàm số x 5 y 
đạt giá trị nhỏ nhất trên đoạn 0  ;1 bằng -7 x  m A. m  1  ;0
B. m 0; 2
C. m 1;3
D. m 2; 4 x  m 7
61. Cho hàm số y 
min y  max y 
. m thuộc khoảng nào trong các khoảng dưới x  thõa mãn 2 0; 1 0; 1 6 đây? A.  ;    1 B.  2  ;0 C. 0; 2 D. 2; 
DẠNG 3: BÀI TOÁN THỰC TẾ.
===============HẾT CHUYÊN ĐỀ 3================
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
CHUYÊN ĐỀ 4: ĐƢỜNG TIỆM CẬN
BÀI TOÁN 7: TÌM ĐƯỜNG TIỆM CẬN
DẠNG 1: TÌM ĐƢỜNG TIỆM CẬN. x  3
62. Tiệm cận ngang của đồ thị hàm số y  2 x 1 A. y  1 B. y  1  C. y  1  D. Không có x 
63. Tiệm cận ngang của đồ thị hàm số 7 y  x7 A. x  1  B. y  1  C. x  7  D. x  7 2 x  2x  3
64. Tiệm cận ngang của đồ thị hàm số y  x 1 A. Không có B. y  1  C. y  2  D. x  1  2 x  3x  2
65. Hàm số y  2 x 
có mấy tiệm cận đứng 1 A. Không có B. 1 C. 2 D. 3  
66. Tiệm cận đứng của đồ thị hàm số 2x 1 1 y  x 1 1 A. x  B. y  1  C. x  1  D. Không có 2 x
67. Đồ thị hàm số y  có mấy tiệm cận? 2 x  5x  6 A. 1 B. 2 C. 3 D. 4 2 x  x 1
68. Số đường tiệm cận của đồ thị hàm số y  2 3  2x  5x A. 1 B. 2 C. 3 D. 4
DẠNG 2: DỰA VÀO BẢNG BIẾN THIÊN TÌM TIỆM CẬN.
69. Cho hàm số y  f (x) có bảng biến thiên x  2  2  f ' x 2  + 0  f  x 5 1  
Số đường tiệm cận đứng và ngang của đồ thị hàm số đã cho là A. 4 B. 2 C. 3 D. 1
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
70. Cho hàm số y  f  x có bảng biến thiên như sau x  1 +  f  x +  5 2 3
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4. B. 1. C. 3. D. 2.
BÀI TOÁN 8: BÀI TOÁN TIỆM CẬN CÓ CHỨA THAM SỐ M
DẠNG 3: TÌM M ĐỂ HÀM SỐ CÓ TIỆM CẬN ĐỨNG. 2 x m  3x
71. Cho hàm số y 
với giá trị nào của m thì x  1 là tiệm cận đứng của đồ thị hàm số x 1 A. m  3 B. m  3  C. m  3 D. m  3  x  1
72. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y 
có hai đường tiệm cận 2
x  x  m đứng.  1   1 m   m   A. m  . B.  4 . C.  4 . D. m  2. m   2 m   2 2 x  2x  3
73. Cho hàm số y  x 
với giá trị nào của m thì hàm số có tiệm cận đứng? m m  1  A. m  1  B. 1   m  3 C.  D. m  3 m  3 2 2x  2x
74. Cho hàm số y 
có đồ thị (C ). Tìm tất cả giá trị của m để (C ) không có tiệm cận đứng. x  m A. m  0 B. m  1
C. m  0 hoặc m  1 D. m  2
DẠNG 4: TÌM M ĐỂ HÀM SỐ CÓ TIỆM CẬN NGANG. 2 x  2
75. Tìm tất cả giá trị thực của m để đồ thị hàm số y  có một tiệm cận ngang 4 x m  3 A. m  0 B. m  0 C. m  0 D. m  3 x 1
76. Tìm Tất cả giá trị của m để đồ thị hàm số y 
có đúng một tiệm cận ngang là 2 2x  x m  4 m  0 A. m  0 B.  C. m  4 D. 0  m  4 m  4
===============HẾT CHUYÊN ĐỀ 4================
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
CHỦ ĐỀ 5: ĐỒ THỊ HÀM SỐ
BÀI TOÁN 9: NHẬN DẠNG ĐỒ THỊ
DẠNG 1: NHẬN DẠNG ĐỒ THỊ HÀM 3 2 y  x a  x b  x c  d
77. Đồ thị như hình bên là của hàm số nào sau đây? 1 y A. 3 y  x  3x 1 3 3 2 B. 3 2
y  x  3x 1 C. 3
y  x  3x 1 -3 -2 -1 1 2 3 1 x -1 D. 3 y  x  x 1 3 -2 -3 78.
Đồ thị sau đây là của hàm số nào ? Chọn câu đúng. A. 3 2
y  x  3x  4 y B. 3
y  x  3 2 x  4 1 x C. 3
y  x  3x  4 1 D. 3 2
y   x  x  4 3 79. Cho hàm số 3 2 y ax bx cx d a
0 có đồ thị như hình vẽ. Khẳng định
nào sau đây đúng ? A. a 0; d 0; b 0; c 0. B. a 0; b 0; c 0; d 0. C. a 0; c 0; d 0; b 0. D. a 0; b 0; d 0; c 0 80. Cho hàm số 3 2
y  ax  bx  cx  d có đồ thị như hình bên. Trong các mệnh
đề sau, mệnh đề nào đúng?
A. ab  0,bc  0,cd  0 .
B. ab  0,bc  0,cd  0 .
C. ab  0,bc  0, cd  0.
D. ab  0,bc  0, cd  0.
81. Đường cong trong hình bên d ư ớ i là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. 3 y  x  3 2 x  3x 1. B. 3 2
y  x  3x 1. C. 3
y  x  3x 1. D. 3 2
y  x  3x 1.
DẠNG 2: NHẬN DẠNG ĐỒ THỊ HÀM 4 2 y  x a  x b  c
82. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án
A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? A. 4 2
y  x  2x B. 4 2
y  x  2x C. 4 2
y  x  3x 1 D. 4 2
y  x  2x
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
83. Đồ thị hình bên là của một trong 4 đồ thị của các hàm số ở các phương án A, B, C, D dưới đây.
Hãy chọn phương án đúng. 1  4 2    4 2    y x x 5 A. y x x 5 . B. 4 . 1  1  4 y  x  5 4 2 y  x  2x  7 C. 4 . D. 4
84. Hãy xác định a, b, c của hàm số 4 2 y  x a  x b
 c có đồ thị như hình vẽ 1
A. a  4;b  2  ;c  2
B. a  ;b  2  ;c  2 4 1
C. a  4;b  2;c  2
D. a  ;b  2  ;c  0 4 85. Cho hàm số 4 2
y  ax  bx  c có đồ thị như hình vẽ bên. ệnh đề nào dưới đây đúng?
A. a  0, b  0,c  0
B. a  0, b  0,c  0
C. a  0, b  0,c  0
D. a  0, b  0,c  0
DẠNG 3: NHẬN DẠNG ĐỒ THỊ HÀM PHÂN THỨC.
86. Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? x  2 x 1 A. y  y  2  x  B. 4 x  2 2x  3 x  3 C. y  y  x  D. 2 2x  4
87. Bảng biến thiên trong hình dưới là của hàm số nào trong các hàm số đã cho? x  1  y '   y 1    1  x  3 x  3 x  3 x  2 A. y  y  y  y  x  B. 1 x  C. 1 x  D. 1 x 1
88. Bảng biến thiên sau đây là của hàm số nào?
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263] x -∞ -1 +∞ y' + + +∞ 2 y 2 -∞ x  2 x 1 2x  1 2x  1 A. y  B. y  C. y  D. y  1  x 2x  1 x 1 x  1 a  89. Cho hàm số x 1 y 
khẳng định nào sau đây đúng? x  b y
A. a  0  b
B. a  b  0
C. a  0  b
D. a  b  0 x x a  b y  90. Cho hàm số
x 1 có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau?
A. a  b  0
B. b  0  a
C. 0  b  a
D. 0  a  b  91. Cho hàm số ax b y 
với a  0 có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? x c  d
A. b  0, c  0, d  0
B. b  0, c  0, d  0
C. b  0, c  0, d  0
D. b  0, c  0, d  0
DẠNG 4: NHẬN DẠNG ĐỒ THỊ HÀM TRỊ TUYỆT ĐỐI
92. Cho hàm số y  f (x) có đồ thị hàm số y  f  x  như hình vẽ:
Chọn kết luận đúng trong các kết luận sau: A. 3 2
f (x)  x  x  4x  4 B. 3 2
f (x)  x  x  4x  4 C. 3 2
f (x)  x  x  4x  4 D. 3 2
f (x)  x  x  4x  4
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
93. Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. 3 y  x  3 x B. 3 y  x  3x C. 3 y  x  3x 3 D. y  x  3 x
DẠNG 10: BÀI TOÁN 10 HÀM ẨN f 'x
94. Cho hàm số y  f (x) có đạo hàm liên tục trên R và đồ thị hàm số y  f (
 x) như hình vẽ. Khẳng
định sau đây là sai?
A. Hàm số y = f(x) đồng biến trên khoảng (1; )
B. Hàm số y = f(x) đồng biến trên khoảng ( 2  ; 1  )
C. Hàm số y = f(x) nghịch biến trên khoảng ( 1  ;1)
D. Hàm số y = f(x) nghịch biến trên khoảng ( ;  2  )
95. Cho hàm số y  f  x có đạo hàm trên R và có đồ thị của hàm số y  f ' x như hình vẽ. Xét hàm số
g  x  f  2 x  2 .
Mệnh đề nào sau đây sai?
A. Hàm số g  x nghịch biến trên 0; 2 .
B. Hàm số g  x đồng biến trên 2; 
C. Hàm số g  x nghịch biến trên  ;  2  
D. Hàm số g  x nghịch biến trên  1  ;0 .   96. Cho hàm số y
f (x) . Hàm số y f '(x) có bảng xét dấu như sau: x  2  1 3  f ' x  0 + 1 + 0  Hàm số   2 y
f x  2x  nghịch biến trên khoảng nào dưới đây? A. (0;1) B. ( 2  ; 1  ) C. ( 2  ;1) D. ( 4  ; 3  )
97. Cho hàm số y  f  x , có đạo hàm là f ' x liên tục trên
và hàm số f ' x có đồ thị như hình dưới đây.
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
Hỏi hàm số y  f  x có bao nhiêu cực trị? A. 1. B. 0. C. 3. D. 2.
98. Cho hàm số y  f  x có đạo hàm trên và có đồ thị như hình vẽ bên. Hỏi đồ thị của hàm số 2
y  f  x có bao nhiêu điểm cực đại, cực tiểu?
A. 1 điểm cực đại, 2 điểm cực tiểu.
B. 2 điểm cực đại, 3 điểm cực tiểu.
C. 3 điểm cực đại, 2 điểm cực tiểu.
D. 2 điểm cực đại, 2 điểm cực tiểu. 2
99. Cho hàm số y
f (x) có đạo hàm trên
và có đồ thị như hình vẽ bên. Hàm số y f (x) có bao nhiêu điểm cực trị? A. 5 B. 3 y C. 4 D. 5 1 x -1 0 1 2 3 100.
Cho hàm số y  f  x có đạo hàm y  f ' x liên tục trên
và đồ thị của hàm số f 'x trên đoạn  2
 ;6 như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau.
A. max f  x  f  2  
B. max f  x  f 6   2;6  2;6  
C. max f  x  max f   1 , f 6
D. max f  x  f   1   2;6   2;6
===============HẾT CHUYÊN ĐỀ 5================
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
CHỦ ĐỀ 6: SỰ TƢƠNG GIAO CỦA HAI ĐỒ THỊ
BÀI TOÁN 11: TỌA ĐỘ GIAO ĐIỂM
DẠNG 1: TÌM TỌA ĐỘ GIAO ĐIỂM. 2x  4 101.
Gọi M, N là giao điểm của đường thẳng y  x 1 và đường cong y  . Khi đó hoành độ x 1
trung điểm I của đoạn thẳng MN bằng 5 5 A.  B. 1 C. 2 D. 2 2 x  102. Cho hàm số 2 1 y 
có đồ thị (C). Tìm tất cả các giá trị của m để đường thẳng x 1
d: y  x  m1 cắt (C) tại hai điểm phân biệt A, B sao cho AB  2 3 .
A. m  4  10 B. m  4  3
C. m  2  10 D. m  2  3 103.
Tìm tất cả giá trị của m để đồ thị hàm số 3
y  x  m   2 2
1 x  4x cắt trục Ox tại điểm có hoành độ x  2 A. m  2 B. m  3 C. m  1  D. m  4
BÀI TOÁN 12: BÀI TOÁN TƯƠNG GIAO CÓ CHỨA THAM SÓ M
DẠNG 2: BIỆN LUẬN SỐ GIAO ĐIỂM CỦA HAI ĐỒ THỊ
104. Tìm tất cả giá trị thực của tham số m để đường thẳng y  m cắt đồ thị hàm số 4 2
y  x – 2x  3
tại bốn điểm phân biệt. A. 1   m  1.
B. 2  m  3.
C. 0  m  1.
D. – 1  m  0 .
105. Tìm tất cả giá trị của m để phương trình 3
x  3x  m  0 có 3 nghiệm phân biệt A. 2   m  2 B. 2   m  3 C. 1   m  3 D. 1   m  2
DẠNG 3: TÌM M ĐỂ HÀM SỐ CÓ SỐ GIAO ĐIỂM CHO TRƢỚC x  2
106. Xác định m để đường thẳng (d) : y  x  m cắt đồ thị (H ) : y 
tại hai điểm phân biệt. x 1 m  2  m  0 A. 2   m  2 B.  C.  D. 0  m  2 m  2 m  2
107. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y  3 x  2
mx  mx  4 cắt đường thẳng
y  x  4 tại ba điểm phân biệt.
A. m1;  1 .
B. m1; 3 .
C. m3; 5 .
D. m4; 6 .
108. Tìm tất cả giá trị thực của tham số m để đồ thị hàm số C y x mx m cắt trục hoành m  4 2 :     1
tại bốn điểm phân biệt. m  1 A.  . B. Không có . m C. m  1. D. m  2. m   2 x  1 109. Cho hàm số 2 (C) : y 
và đường thẳng d : y  
x  m . Tìm m để d cắt (C) tại 2 điểm nằm x  1 2
về 2 phía đối với trục tung : A. m  1 B. m  2 C. m  3 D. m  4
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
DẠNG 4: TÌM SỐ GIAO ĐIỂM CỦA HÀM TRỊ TUYỆT ĐỐI. 110.
Cho hàm số f  x có đồ thị như hình vẽ bên. Xác định tất cả giá trị của tham số m để phương
trình f  x  m có 6 nghiệm phân biệt y A. m  4 B. 0  m  4 x 1 C. 3  m  4 D. 0  m  3 111.
Hình bên dưới là đồ thị của hàm số y  3 x  3 .
x Tìm tất cả giá trị thực của tham số 3 2 x 3x
m có năm nghiệm phân biệt. y
m để phương trình  
A. m 2;00; 2 .
B. m 0; 2  .
C. m2;0 0; 2 .
D. m0; 2 . x 1 x  112.
Hình bên là đồ thị của hàm số 2 1 y 
. Tìm tất cả các giá trị thực của tham số x  1 2x  1
m để phương trình
 2m có hai nghiệm phân biệt. x  1
A. Với mọi m . 8 6
B. Không có giá trị của m . 4 C. m  0 . 2 I 1 15 10 5 1 5 10 15 O -1
D. m  0;   \  1 . 2 4 6
DẠNG 5: TÌM SỐ GIAO ĐIỂM CỦA HÀM ẨN. 113.
Cho hàm số y  f (x) liên tục trên đoạn  2
 ;2 và có đồ thị như hình vẽ:
Số nghiệm của phương trình 3 f (x  2)  4  0 trên đoạn  2  ;2 là? A. 4. B. 2. C. 3. D. 1.
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
DẠNG 6: TÌM SỐ GIAO ĐIỂM DỰA VÀO BẢNG BIẾN THIÊN. 114.
Cho hàm số y  f  x có bảng biến thiên sau x  1  1  y ' + 0  0 + y 3   1 
Tìm số nghiệm của phương trình 2 f  x 1  0 . A. 0 B. 3 C. 4 D. 6 115.
Cho hàm số y  f  x xác định và liên tục trên mỗi nửa khoảng  ;  2
  và 2; , có bảng
biến thiên như hình trên. 5 x  2  2  2 y '   0 + y   22 2 7 4
Tìm tập hợp các giá trị của m để phương trình f  x  m có hai nghiệm phân biệt.  7  A. ; 2  22;     B. 22;  4   7   7  C. ;    D. ; 2 22;      4   4 
===============HẾT CHUYÊN ĐỀ 6================
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
CHỦ ĐỀ 7: ĐƢỜNG TIẾP TUYẾN
BÀI TOÁN 13: VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN
DẠNG 1: VIẾT PHƢƠNG TRÌNH TIẾP TUYẾN. 116. Cho hàm số 3 2
y  x  x  5x 1, phương trình tiếp tuyến tại điểm trên đồ thị có hoành độ x  2
A. y  10x  9
B. y  11x 19
C. y  11x 10
D. y  10x  8 x  117.
Tiếp tuyến của đồ thị hàm số 2 y 
song song với đường thẳng y  3
 x  2 có phương trình x 1 là:
A. y  3x 10 B. y  3  x  2; y  3  x 10 C. y  3  x 10 D. y  3  x  2 118. Cho hàm số 4 2
y  x  x  6 có đồ thị (C ). Viết phương trình tiếp tuyến của đồ thị (C ), Biết tiếp 1
tuyến vuông góc với đường thẳng y  x 1. 6 A. y  6  x  6 B. y  6  x 8 C. y  6  x 10 D. y  6  x 12 119. Cho hàm số 3 2
y  4x  6x 1 có đồ thị ( C). Viết phương trình tiếp tuyến với (C ) biết rằng tiếp
tuyến đi qua điểm M(-1; -9) 15 21 15 21
A. y  24x  25; y  x 
B. y  24x 15; y  x  4 24 4 4 15 21 15 21
C. y  24x  5; y  x 
D. y  24x  25; y  x  4 24 4 4 2x 1 120. Cho hàm số y 
có độ thì (C). Gọi là điểm thuộc (C ) có tung độ bằng 5. Tiếp tuyến của x 1
(C ) tại điểm M cắt các trục Ox, Oy lần lượt tại A và B. Tính diện tích tam giác S OAB  112 121 122 113 A. B. C. D. 6 6 6 6
BÀI TOÁN 14: BÀI TOÁN TIẾP TUYẾN CHỨA THAM SỐ M
DẠNG 2: TÌM M ĐỒ THỊ CÓ TIẾP TUYẾN THỎA ĐK CHO TRƢỚC 121. Cho hàm số 4 2
y  x  2 x m
 2m 1 (Cm). Tìm m để tiếp tuyến của đồ thị (Cm) tại hai điểm
A1;0, B 1
 ;0 vuông góc với nhau. 5 3 5 3 A. m  ; m 
B. m   ; m   4 4 4 4 5 3 5 3
C. m   ; m  D. m  ; m   4 4 4 4 x  b 122. Cho hàm số y 
có đồ thị ( C ). Biết rằng a, b là các giá trị thực sao cho tiếp tuyến của ( x a  2
C) tại điểm M 1; 2
  song song với đường thẳng d :3x  y 4  0. Khi đó giá trị của a  b bằng A. 0 B. -1 C. 2 D. 1 123. Cho hàm số 4
y  x  m   2 2
1 x  m  2 có đồ thị (C ). Gọi A là điểm thuộc đồ thị hàm số có
hoành độ bằng 1. Với giá trị nào của m thì tiếp tuyến của đồ thị (C ) tại A vuông góc với đường thẳng
 : x  2y  4  0 A. m  3  ;0 B. m  2  ;2
C. m 2;5
D. m 5;9
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM ĐS 12 – CHƯƠNG I
[LỚP TOÁN THẦY HIỀN – 77/11 THÁI PHIÊN – ĐN.
DI ĐỘNG: 0364 968 6263]
DẠNG 3: ĐIỆU KIỆN TIẾP XÚC 5 124.
Biết rằng đồ thị các hàm số 3 y  x  x  2 và 2
y  x  x  2 tiếp xúc nhau tại điểm M (x ; y ) . 4 0 0 Tìm x . 0 1 5 3 3 A. x  . B. x   . C. x  . D. x  . 0 2 0 2 0 4 0 2 125.
Tìm tất cả giá trị của tham số m để qua điểm M (2; )
m kẻ được ba tiếp tuyến phân biệt đến đồ thị hàm số 3 2
y  x  3x là
A. m 4;5 B. m  2  ;3 C. m  5  ; 4   D. m  5  ;4
===============HẾT CHUYÊN ĐỀ 7================
ĐÁP ÁN 125 CÂU TRẮC NGHIỆM 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 B C C B A A C C C C B C C C B 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 D A C A C D A B C A D D B A A 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 A C A C A C B A D D B B D B A 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 B B D A B C A C A D B D D C C 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 B C B A B D D C B C A B C C C 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 B C B D A A B B B B A B D C D 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 A A A C D B C B D C B A B B A 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 B C A B C A D D D D B C C B B 121 122 123 124 125 A D A A C
Mua file Word: Giá 100K.
Nhằm ủng hộ cho Team có kinh phí để biên soạn nhiều tài liệu chất lượng hơn - giúp giáo viên tiết kiệm
thời gian soạn tài liệu và học sinh dễ ôn tập nhé.
Liên hệ: Di động: 0349.686.263 – Thầy Hiền – Nhóm luyện thi MPEC tại Đà Nẵng.
FANPAGE: NHÓM LUYỆN THI MPEC
WEBSITE: TRUNGTAMMPECDANANG.COM

Phân dạng và kỹ thuật giải toán hàm số và đồ thị – Trần Thanh Hiền Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số