Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số – Nguyễn Vũ Minh (Tập 3)

Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số – Nguyễn Vũ Minh (Tập 3) được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

96 48 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

96 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Phân dạng và phương pháp giải
trắc nghiệm Toán 12
Tập 3
Biện luận
Trị tuyệt đối
Tổng hợp
Tịnh tiến
BIÊN HÒA – Ngày 15 tháng 07 năm 2017
TÀI LIỆU LƯU HÀNH NỘI BỘ
1
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
◙ Lý Thuyết : Ta xét bài toán sau đây :
Vẽ đồ thị (C) của hàm số
()y f x
sau đó biện luận
theo tham số m số nghiệm của phương trình :
( ; m) 0hx
(♥)
☻ Ta đưa (♥) về dạng
Trong đó
()fm
là biểu thức theo m, không chứa x
Số nghiệm của (♥) chính là số giao điểm của (C) và đường thẳng (D)
()y f m
mà ta nhìn thấy
qua đồ thị ((D) ............................. Ox )
VD như hình bên, ta thấy (♥) có :
☻ 3 nghiệm khi ............................................
☻ 2 nghiệm khi .......................
hoặc ...............................
☻ 1 nghiệm khi .......................
hoặc ...............................
Ví dụ 01 : Cho hàm số
(có đồ thị là (C))
a/ Khảo sát và vẽ đồ thị hàm số.
b/ Biện luận theo
m
số nghiệm của phương trình
32
30x x m
.
PHẦN 8 : BIỆN LUẬN NGHIỆM BẰNG ĐỒ THỊ
_
x
_
,
_
_
y
_ =
_
f
_
(
_
m
_
)
_
y
_
-4
_
3
_
2
_
-
1
_
O
2
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
a/ ► Tập xác định
D
.
► Đạo hàm
2
' 3 6 3 2y x x x x
;
0
'0
2
x
y
x


.
► Hàm số đồng biến trên khoảng
2;0
;
nghịch biến trên các khoảng
;2
và
0;
.
► Hàm số đạt cực đại tại
0x
,
CD
4y
; đạt cực tiểu tại
2x 
,
CT
0y
.
► Giới hạn tại vô cực
lim
x
y


; và
lim
x
y


.
► Bảng biến thiên
► Đồ thị hàm số đi qua các điểm
3;4
,
1;0
.
b/ Ta có
32
30x x m
32
3 4 4 *x x m
.
Phương trình
*
là phương trình hoành độ
giao điểm của đồ thị và đường thẳng
4ym
.Do đó số nghiệm của phương trình
*
là số giao điểm của đồ thị và đường thẳng
d:
4ym
. (d cùng phương Ox)
Dựa vào đồ thị, ta có
♥ Với
4 4 0
4 0 4
mm
mm



: Phương trình có
duy nhất
1
nghiệm.
♥ Với
4 4 0
4 0 4
mm
mm



: Phương trình có
2
nghiệm.
♥ Với
0 4 4 4 0mm
: Phương trình có
3
nghiệm.
y
x
'y
2
4
0
0
0
0
3
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
0
-4
-∞
+∞
m
☻Toán nếu trắc nghiệm thì đề sẽ bắt chúng ta “suy luận và hiểu” nhiều hơn là phương pháp
“Casio thần chưởng”
☻Vậy phải làm sao ???
☻Thật ra thì “bảng biến thiên đã nói lên tất cả”rồi
Chúng ta bắt tay vào làm !!! Ở đây thầy không dùng bảng biến thiên cũ (nếu dùng vẫn
được) để cho các em biết là đưa về hàm nào cũng được ☺
Phương trình
32
30x x m
ta viết lại
32
3m x x
Lập BBT đi
“phác thảo” đồ thị
Từ đồ thị “phác thảo” này ta thấy rõ ràng
ở đây thầy ví dụ có 3 nghiệm !!!thì m chạy từ - 4 đến 0
x

2
0

'y
0
0
y

0
4

2 con số đáng yêu !!!
(biện luận ko cần vẽ đồ thị)
Đây không phải là công thức giải nhanh –
chỉ là hướng tư duy giúp giải bài toán
nhanh hơn cho trắc nghiệm !!
Vẽ đồ thị mất 15 phút rồi
Nhìn hàm g(x) này nè !!!
4
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
Ứng dụng 01 : Biện luận theo
m
số nghiệm của phương trình
3
2
2 2 0
3
x
xm
.
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Ứng dụng 02 : Tìm
m
để phương trình
32
3 2 2 0x x m
có 3 nghiệm phân biệt.
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Ứng dụng 03 : Tìm
m
để phương trình
3
3 7 5 0x x m
có 2 nghiệm.
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
5
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
Ứng dụng 04 (Đề giữa kì- Chuyên Lê Hồng Phong-TP. HCM): Tìm tất cả các giá trị của tham
số sao cho phương trình
32
30x x k
có nghiệm phân biệt.
A. B. . C. D.
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Ứng dụng 05 (Đề An Nhơn 3- Bình Định):Tìm tất cả các giá trị của tham sốđể đường thẳng
4ym
cắt đồ thị hàm số
42
83y x x
tại bốn điểm phân biệt
A. B. C. D.
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Ứng dụng 06 : Tìm giá trị của tham số m để phương trình sau có 4 nghiệm phân biệt
42
4 3 2 0x x m
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
k
3
0 k 4.
k0
k 4.
0 k 4.
13 3
.
44
m
3
.
4
m
13
.
4
m 
13 3
.
44
m
6
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
Ứng dụng 07: Tìm giá trị của tham số m để phương trình sau có 3 nghiệm
4
2
3 3 3 0
4
x
xm
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Ứng dụng 08 : Tìm giá trị của tham số m để phương trình sau có 3 nghiệm phân biệt
3
2
3 3 2 0
3
x
xm
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Ứng dụng 09 : Tìm giá trị của tham số m để phương trình sau có 2 nghiệm
3
2
90
3
x
xm
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
7
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
Ví dụ 02 : (C):
32
3y x x
.Tìm
m
để phương trình
32
3 2 1 0x x m
có ba nghiệm phân biệt,
trong đó có đúng hai nghiệm không nhỏ hơn 1.
Đồ thị được vẽ :
Ta có
32
3 2 1 0x x m
.
*
....................................................
♠ Phương trình
*
là phương trình
hoành độ giao điểm của đồ thị và đường
thẳng..............................................
♠ Do đó số nghiệm của phương trình
*
là số giao điểm của đồ thị và đường thẳng
......................................................................
♠ Dựa vào đồ thị, ta thấy phương trình
*
có ba nghiệm phân biệt, trong đó có đúng hai
nghiệm không nhỏ hơn
1
khi và chỉ khi.................................................................................
Vậy .................................................. thỏa mãn yêu cầu bài toán.
Ví dụ 03 : Cho hàm số
24
1
x
y
x
.
a/ Khảo sát sự biến thiên và vẽ đồ thị
C
của hàm số đã cho.
b/ Biện luận theo
m
số nghiệm của phương trình
24
1
x
m
x
.
a/ ► Tập xác định:
\1D
.► Đạo hàm
2
2
' 0,
1
y x D
x
.
► Hàm số đồng biến trên từng khoảng
;1
và
1; 
.
► Giới hạn và tiệm cận:
8
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
►
1
lim
x
y

và
1
lim
x
y

;
tiệm cận đứng:
1x
.
►
lim lim 2
xx
yy
 

; tiệm cận ngang:
2y
.
► Bảng biến thiên
► Đồ thị
C
cắt
Ox
tại
2;0
, cắt
Oy
tại
0;4
và nhận giao điểm
1;2I
của hai đường tiệm cận làm
tâm đối xứng
b/ Ta có
24
1
x
m
x
là phương trình hoành độ giao điểm của đồ thị và đường thẳng d:
ym
.
Do đó số nghiệm của phương trình là số giao điểm của đồ thị và đường thẳng d:
ym
.(d
cùng phương Ox)
Dựa vào đồ thị, ta có ☻ Với
2
2
m
m

: phương trình có duy nhất một nghiệm.
☻ Với
2m
: phương trình vô nghiệm.
Ví dụ 04 : Cho hàm số
42
8 9 1y x x
.
a/ Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
b/ Dựa vào đồ thị, hãy biện luận theo
m
số nghiệm của phương trình
42
8 9 0x x m
.
c/ Viết phương trình tiếp tuyến của đồ thị tại điểm có tung độ bằng
1
, hoành độ dương.
y
x
'y
1
2
2
9
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
a/ ► Tập xác định:
D
.
► Đạo hàm
32
' 32 18 2 16 9y x x x x
;
0
'0
3
4
x
y
x


.
► Hàm số đồng biến trên các khoảng
3
;
4




và
3
0;
4



;
nghịch biến trên các khoảng
3
;0
4



và
3
;
4




.
► Hàm số đạt cực tiểu tại
3
4
x 
,
CT
49
32
y 
; đạt cực đại tại
0x
,
CD
1y
.
► Giới hạn tại vô cực
lim lim
xx
yy
 

.
► Bảng biến thiên
► Đồ thị hàm số đi qua các điểm
1;0
,
1;0
và nhận
Oy
làm trục đối
xứng.
b/ Ta có
4 2 4 2
8 9 0 8 9 1 1x x m x x m
.
*
Phương trình
*
là pthđgđ của đồ thị
và đường thẳng d:
1ym
.
Do đó số nghiệm của phương trình
*
là số giao điểm của (C) và đường thẳng
d:
1ym
.(d cùng phương Ox)
y
x
y'
3
4
49
32
1
0
0
0
3
4
0
49
32
x
y
y
1
1
1
O
1ym
49
32
1
3
4
3
4
10
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
Dựa vào đồ thị, ta thấy : ♥ Với :
49 81
1
32 32
mm
: phương trình vô nghiệm.
♥ Với :
49 81
1
32 32
1 1 0
mm
mm




: phương trình có hai nghiệm.
♥ Với :
1 1 0mm
: phương trình có ba nghiệm.
♥ Với :
49 81
1 1 0
32 32
mm
: phương trình có bốn nghiệm.
c/ Với
0
1y
, ta được
4 2 2 2
0 0 0 0
0
1 8 9 1 8 9 0
32
4
x
x x x x
x

Vì tiếp điểm có hoành độ dương nên ta chọn
32
;1
4
M




.
Đạo hàm
3
' 32 18y x x
. Suy ra hệ số góc của tiếp tuyến là
3 2 27 2
'
42
ky





.
Vậy phương trình tiếp tuyến cần tìm là
27 2 3 2
:1
24
d y x




hay
27 2 77
:
24
d y x
Ví dụ 05 : Cho hàm số:
42
43y x x
a/ Khảo sát sự biến thiên và vẽ đồ thị
()C
của hàm số đã cho.
b/ Dựa vào
()C
, hãy biện luận số nghiệm của phương trình:
42
4 3 2 0x x m
► Ta có phương trình :
42
4 3 2 0x x m
42
4 3 2x x m
(*)
► Số nghiệm phương trình (*) bằng với số giao điểm
của
42
( ): 4 3C y x x
và d: y = 2m (d cùng phương Ox)
x
y
y
= 2m
2
-
2
-
3
3
1
2m
-3
-1
O
1
11
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
Giá trị m
2m
Số giao điểm của
(C) và d
Số nghiệm
của pt (*)
m> 0,5
2m> 1
0
0
m = 0,5
2m = 1
2
2
–1,5 <m< 0,5
–3 < 2m< 1
4
4
m = –1,5
2m = –3
3
3
m< –1,5
2m< –3
2
2
BÀI TẬP TRẮC NGHIỆM PHẦN BIỆN LUẬN
Câu 1 : Giá trị tham số m để phương trình sau
32
19
30
22
x x x m
có nghiệm duy nhất là
A.
0
2
m
m
B.
1
4
m
m
C.
4m
D.
2m
Câu 2 : Giá trị tham số m để phương trình sau
42
2 2 0x x m
có 4 nghiệm phân biệt là
A.
0
2
m
m
B.
1
2
m
m
C.
12m
D.
1m
Câu 3 : Giá trị tham số k để phương trình sau
32
30x x k
có đúng 3 nghiệm phân biệt là
A.
04k
B.
03k
C.
13k
D.
1k
12
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
Câu 4 : Đồ thị hàm số
y f x
xác định trên
\D
như hình vẽ bên.
4.1 :Giao điểm của đồ thị hàm số này và đường
thẳng y = x + 1 là
A.
0;2
B.
6; 2
C.
2;0
D.
4; 3
4.2 : Giá trị của α là
A.
1
B.
1
C.
2
D.
2
4.3 :Đồ thị hàm số cắt
trục Ox tại .........................
trục Oy tại .........................
Câu 5 : Giá trị tham số m để phương trình sau
32
3x x m
có 2 nghiệm là
A.
04m hay m
B.
13m hay m
C.
13m
D.
03m hay m
Câu 6 : Hàm số
y f x
xác định trên
D
có bảng biến thiên như sau :
x

2
0

'y
0
0
y
3


1
Giá trị của tham số m để phương trình
20f x m
có 3 nghiệm phân biệt là
A.
0
1
m
m
B.
1
3
2
m
m
C.
1
2
2
m
D.
13
22
m
13
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
Câu 7 : Giá trị tham số a để phương trình sau
3
2 1 0
3
x
xa
có đúng 3 nghiệm phân biệt là
A.
15
66
a
B.
17
66
a
C.
15
66
a hay a
D.
5
1
6
a
Câu 8 : Hàm số
y f x
xác định trên
D
có bảng biến thiên như sau :
Giá trị tham số m để phương trình
0
2
m
fx
có 3 nghiệm phân biệt là
A.
5
1
m
m
B.
2 10m
C.
1 10m
D.
2
10
m
m
Câu 9 : Hàm số
y f x
xác định trên
D
có bảng biến thiên như sau :
x

1
0
1

y’
0
0
0
y

0

1
1
Giá trị tham số m để phương trình
1f x m
có đúng 2 nghiệm phân biệt là
A.
1m
B.
1m 
C.
1
8
m
m

D.
1
0
m
m

Câu 10 : Với giá trị nào của tham số m thì đường cong có phương trình
42
2 1 2y f x x x m
và đường thẳng
1ym
cắt nhau tại 4 điểm phân biệt
A.
m
B.
12
33
m
C.
10m
D.
2
0
3
m
x

0
2

y’
0
0
y
5


1
14
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
_
y
_
_
_
x
-4
_
3
_
2
_
-
1
_
O
-2
1
Câu 11 : Với giá trị nào của tham số m thì đường cong có phương trình
32
39y f x x x x m
cắt Ox nhau tại 3 điểm phân biệt
A.
m
B.
2
1
3
m
C.
30m
D.
27 5m
Câu 12 : Giá trị của tham số m thì phương trình
32
30x x m
có nghiệm duy nhất
A.
m
B.
04m hay m
C.
30m
D.
04m
Câu 13 : Giá trị của tham số m thì phương trình
32
3 2 0x x m
có nghiệm duy nhất
A.
m
B.
04m hay m
C.
22m
D.
04m
Câu 14 : Cho hàm số :
()y f x C
xác định trên D.
Có đồ thị (C) được vẽ như hình bên dưới.
Số giao điểm của (C) và đường thẳng y = k ,
1k 
A. 1
B. 2
C. 3
D. 0
Câu 15 : Cho hàm số :
()y f x C
xác định trên D.
Có đồ thị (C) được vẽ như hình bên.
15.1 Số giao điểm của (C)
và đường thẳng y = k ,
40k
A. 1 B. 2
C. 3 D. 0
15.2 Số giao điểm của (C)
và đường thẳng y = k,
0k
A. 1 B. 2
C. Cả A hoặc B D. 3
15.3 Giá trị lớn nhất K của hàm số trên
1;2
là
-1
x
y
1
3
-2
-1
2
O
1
15
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
A. 0 B. 1
C. Cả A hoặc B D. 2
15.4 Giá trị của a để phương trình
12f x m
có đúng 3 nghiệm phân biệt trong đó có đúng 2
nghiệm không nhỏ hơn 1
A.
35
22
m
B.
35
22
m
C. Cả A hoặc B D. Không có giá trị m thỏa yêu cầu
Câu 16 : Hàm số
42
21y x x
có đồ thị
C
. Xác định m để phương trình
42
2
2 1 logx x m
có 2
nghiệm
A.
1
0; 1
2
m




B.
1
;1
2
m



C.
1m
D.
1;m 
Câu 17 : Hàm số
42
21y x x
có đồ thị
C
. Xác định m để phương trình
42
2
2 1 logx x m
có 4
nghiệm
A.
1
0; 1
2
m




B.
1
;1
2
m



C.
1m
D.
1;m 
Câu 18 : Hàm số
42
21y x x
có đồ thị
C
. Xác định m để phương trình
42
2
2 1 logx x m
vô
nghiệm
A.
1
0; 1
2
m




B.
1
;1
2
m



C.
1m
D.
1;m 
Câu 19 (Trích đề thi THPTQG – 2017) : Cho hàm số có đồ thị như hình bên.
Tìm tất cả các giá trị thực của tham số để phương trình
có bốn nghiệm thực phân biệt.
A. .
B. .
C.
D. .
Câu 20 : Tìm m để phương trình có 3 nghiệm
3
3 1 0x x m
là:
A. 1 < m < 3 B. 2 < m < 3
C. m = 1 D. m = 3
42
2y x x
m
42
2x x m
0m
01m
01m
1m
x
y
1
-1
0
1
16
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
Câu 21 : Cho hàm số :
()y f x C
xác định trên D. Có đồ thị (C) được vẽ như hình bên dưới .
Giá trị tham số m để phương trình
42
2x x m
có đúng 4
nghiệm phân biệt là
A.
10m
B.
1m 
C.
1
0
m
m

D.
1
0
m
m

Câu 22 : Xác định giá trị của tham sốm để phương trình
32
3 9 0x x x m
có ba nghiệm phân biệt
A.
;27m
B.
; 27 5;m 
C.
; 27 1;m 
D.
27;5m
Câu 23 (THPT Chuyên Bến Tre – 2017) : Cho hàm số
y f x
xác định trên , liên tục trên
khoảng xác định và có bảng biến thiên như sau:
x

1
2

y
0
0
y

2
3

Tìm tập hợp tất cả các giá trị của tham số
m
sao cho phương trình
1f x m
có một nghiệm
thực?
A.
; 2 3;m 
. B.
; 3 2;m  
.
C.
3;2m
. D.
; 2 3;m  
.
Câu 24 : Hàm số
32
31y x x
có đồ thị
C
. Xác định m để phương trình
3 3 2 2
33x m x m
có ba
nghiệm phân biệt
A.
1;3 \ 0;2m
B.
1;3 \ 0;2m
C.
1;3 \ 2m
D.
1;3 \ 0m
17
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
Câu 25 : Đường thẳng y = m không cắt đồ thị hàm số (C):
42
242y x x
khi :
A.
04m
B.
4m
C.
0m
D.
4m
Câu 26 : Cho hàm số
3
1yx
có đồ thị là (C). Với giá trị nào của tham số m thì đồ thị hàm số cắt
đường thẳng d : y = 3x + m tại ba điểm phân biệt
A.
m
B.
13m
C.
13
0
m
m
D.
13
1
m
m
Câu 27 (Đề thi thử nghiệm 2017) : Cho hàm số xác định trên , liên tục trên mỗi
khoảng xác định và có bảng biến thiên như sau
Tìm tập hợp tất cả các giá trị của tham số thực msao cho phương trình có ba nghiệm
thực phân biệt.
A. . B. . C. . D. .
Câu 28 : Tìm m để phương trình có 1 nghiệm
32
3 2 2 0x x m m
là:
A.
2, 6mm
B.
62m
C.
40m
D.
0
2
m
m

Câu 29 : Tìm m để phương trình có 2 nghiệm
3
3 4 0x x m
là:
A.
20m
B.
0
2
m
m

C.
0
2
m
m

y f x
\0
x

0
1

y
0
y

1

2

f x m
1;2
1;2
1;2
;2
18
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
D. m = 2 ; m = 6
Câu 30 : Tìm m để phương trình có 2 nghiệm
42
4 4 2 0x x m
là:
A. m < 1
B. m > 1
C. m < 2
D. m > 2
Câu 31 : Tìm m để phương trình có 3 nghiệm
42
2 2 0x x m
là:
A. m = 2
B. m = 1
C.
12m
D.
2m
Câu 32 : (THPT CHUYÊN HÀ NỘI – AMSTERDAM) Tìm các giá trị của tham số m để phương
trình
32
3x x m m
có 3 nghiệm phân biệt ?
A.
21m
B.
12m
C.
1m
D.
21m 
Câu 33 (THPT Phả Lại – Hải Dương) : Cho hàm số
y f x
có bảng biến thiên sau:
x
–∞
1
0
1
+∞
y
–
0
+
0
–
0
+
y
+∞
1
0
1
+∞
Với giá trị nào của
m
thì phương trình
( ) 1f x m
có đúng 2 nghiệm
A.
1m
.
B.
1m 
.
C.
1m 
hoặc
2m 
. D.
1m 
hoặc
2m 
.
Câu 34 (THPT chuyên Biên Hòa – Hà Nam) : Cho hàm số
y f x
có bảng biến thiên như hình vẽ:
x
1
0 1
'fx
- 0 + 0 - 0 +
fx
5
3 3
Tìm m để phương trình:
23f x m
có bốn nghiệm phân biệt.
A.
1m 
. B.
1
3
m 
.
19
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
C.
1
1
3
m
. D.
1m 
hoặc
1
3
m 
.
Câu 35 (THPT Hà Uy Tập – Hà Tĩnh) : Tìm tất cả các giá trị của m để đồ thị hàm số
32
31 y x x
cắt đường thẳng
23ym
tại 3 điểm phân biệt ?
A.
04m
B.
02m
C.
31 m
D.
02m
Câu 36 (THPT chuyên Lê Hồng Phong ) : Cho hàm số
()y f x
xác định trên , và có bảng biến
thiên như sau
x
-1 0 1
,
y
- 0 + 0 - 0 +
y
3
1
1
Tìm tập hợp tất cả các giá trị của tham số m sao cho phương trình
()f x m
có bốn nghiệm thực
phân biệt?
A.
1;3
. B.
( 1; ) 
. C.
1;3
. D.
(3; )
.
Câu 37 (THPT Hồng Quang – Hải Dương) : Cho hàm số có đồ thị như hình vẽ bên
Mệnh đề nào sau đây đúng:
A. Phương trình
f x m
luôn có nghiệm.
B. Phương trình
f x m
có 2 nghiệm phân biệt khi
0m
.
C. Phương trình
f x m
có 4 nghiệm phân biệt khi
10m
.
D. Phương trình
f x m
vô nghiệm khi
1m 
Câu 38 (THPT Ngô Sĩ Liên – Bắc Giang) :
Cho hàm số
y f x
xác định trên
\3
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như bên.
20
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN
2017
Phương trình
f x m
có đúng hai nghiệm thực phân biệt khi và chỉ khi
A.
1m
hoặc
2.m 
B.
1.m
C.
2.m 
D.
2.m 
Câu 39 (THPT chuyên Nguyễn Quang Diệu) : Tìm tất cả các giá trị thực của tham số
m
sao cho đường
thẳng
ym
cắt đồ thị hàm số
3
31y x x
tại ba điểm phân biệt, trong đó có đúng hai điểm phân biệt có
hoành độ dương
A.
1 3.m
B.
1 3.m
C.
1 1.m
D.
1.m
Câu 40 : Đồ thị hình bên là của hàm số
32
34y x x
. Tìm tất cả giá trị của m để
phương trình
32
30x x m
có hai nghiệm phân
biệt? Chọn một khẳng định ĐÚNG
A.
4m
hoặc
0m
.
B.
4m
.
C.
04m
.
D.
0m
.
Câu 41: Cho hàm số
()y f x
xác định trên
\ 1;1
, liên tục trên mỗi khoảng xác định và có
bảng biến thiên như sau:.
Tìm tập hợp tất cả các giá trị của thàm số
m
sao cho phương trình
f x m
có ba nghiệm thực
phân biệt
A.
2;2
.
B.
2;2
.
C.
; 
.
D.
2;
.
21
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
t v n : 
y f(x)
 th 
 th  sau :
☻ Li xng (C) qua Ox ta s  th (C1) :
y f(x)
☻ Li xng (C) qua Oy ta s  th (C2) :
y f( x)
Phương pháp : u tr tuyi r tr tuy
tng phn ri
khi A 0
khi A 0
A
A
A

TIẾN HÀNH VÀO DẠNG CỤ THỂ
◙ Dạng 1 :  th  
y f(x)
khi f x 0 1
khi f x 0 2
fx
fx
fx

Đồ thị (C’) gồm 2 phần :
► Gi  th
C

► Li xng qua Ox ph th
C
ni trc Ox (do (2))
► B ph th
C
ni trc Ox ta s  th
'.C
Ví dụ :
PHẦN 9 : BIẾN ĐỔI ĐỒ THỊ TRỊ TUYỆT ĐỐI
22
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
◙ Dạng 2 :  th  
y f( x )
f(x) khi x 0
y f( x )
f( x) khi x 0


Đồ thị (C’) gồm 2 phần :
► Gi 
► Li xng qua Oy ph phn (C) n
Ví dụ :
◙ Dạng 3 :  th  
y f(x)
;
f(x) 0
y f(x)
y f(x) ; (1)
y f(x) ; (2)


Đồ thị (C’) gồm 3 phần :
► Gi n (C) n(do (1))
► B phn (C) ni Ox
► Li xng qua Ox phn (C) n
23
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
Ví dụ :
◙ Dạng 4 : T  th
C y u x v x:.
 th
C y u x v x:.
.

. khi 0
.
. khi 0
u x v x f x u x
y u x v x
u x v x f x u x


Đồ thị (C’) gồm 2 phần :
► Gi  phần đồ thị trên miền
0ux
của đồ thị
:C y f x
.
► B phần đồ thị trên miền
0ux
của
C
, lấy đối xứng phần đồ thị b b qua Ox.
Ví dụ :
Bài 01 : T  th
32
: 2 3 1C y f x x x
 th
2
: 1 2 1C y x x x
Bài 02 : T  th
:
1
x
C y f x
x

suy ra
 th
:
1
x
Cy
x
2
khi 1
1 2 1
khi 1
f x x
y x x x
f x x

Đồ thị (C’) gồm 2 phần :
► Gi i
1x
.
► B (C) vi
1x
. Ly đối xứng phần đồ thị
khi 1;
1
.
1
khi ;1
1
x
x
x
x
y
x
x
x
x



Đồ thị (C’) gồm 2 phần :
► B ph th ca
C
vi
1x
, gi
 th 
3
32y x x
 th 
3
32y x x
24
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
bị bỏ qua Ox.

C
vi
1.x
► Li xng ph th b b qua
Ox.
BÀI TẬP TRẮC NGHIỆM PHẦN BIẾN ĐỔI ĐỒ THỊ
Câu 1 : 
()y f x C
 th c v i. 
 
42
2
5 4 logx x m
m
A.
4
42m
B.
4
44m
C.
4
42m 
D.
4
44m 
x
y
(C)
(C')
1
O
1
x
y
1
O
1
25
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
Câu 2 : 
()y f x C
 th c v i. 
 
3
33x x m
4 nghim
A.
4m
B.
1
2
m
C.
6m
D.
1
2
m 
Câu 3 : 
()y f x C
 th c v i. 
nh tham s k  
3
30x x k
3.1 2 nghim 
A.
0k
B.
0k
C.
2k
D.
2k
3.2 2 nghim 
A.
0k
B.
0k
C.
2k
D.
2k
3.3 3 nghim  A.
0k
B.
0k
C.
2k
D.
2k
3.4 m A.
0k
B.
0k
C.
2k
D.
2k
26
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
Câu 4 : 
42
2 ( )y f x x x C

 th c v 
 th
42
2 ( ')y f x x x C

A. B.
C. D.
Câu 5 : 
32
2 9 12 3 ( )y f x x x x C

 th c v .
D th   th 
3
2
2 9 12 3y x x x

 m 
 th  h  theo)
27
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
Câu 6 : 
3
3 1 ( )y f x x x C

 th c v . D th  
th 
3
31y x x
 
chm  th  h 
theo)
28
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
Câu 7 : 
3
3 1 ( )y f x x x C
nh
 th c v . D th
  th 
3
31y x x

 m 
 th  h  theo)
Câu 8 : 
42
()y f x x x C
 th c v . Da
 th   th 
42
y x x
 m 
 th  h  theo)
29
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
Câu 9 : 
y f x

 th c v . D th (C),
  th 
3
2
69y x x x

m 
 th  h  theo)
30
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
Câu 10 : D th  câu 9  
3
2
6 9 3 0x x x m
10.1 m
A.
0m
B.
3m
C.
1m
D.
2m
10.2 6 nghim t
A.
13m
B.
3m
C.
1m
D.
1m 
10.3 4 nghim
A.
13m
B.
3m
C.
1m 
D.
1m 
10.4 m
A.
13m
B.
3m
C.
1m 
D.
1m 
Câu 11 : 
3
31y x x

 th c v . D th 
 th 
3
31y x x
 
31
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
m  th  h  theo)
Câu 12 : 
y f x
 th c
v . D th   th 
y f x
 m 
th  h  theo)
32
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
Câu 13 : 
y f x
 th c v  th 
c 
A.
3
2
69y x x x
B.
32
69y x x x
C.
3
2
69y x x x
D.
32
69y x x x
Câu 14 : 
32
32y x x
 th c v  th 
s 
A.
32
32y x x
B.
3
2
32y x x
C.
32
32y x x
D.
32
32y x x
Câu 15 : 
32
32y x x
 th c v . V 
t
32
3 2 0x x m
A.
22m
B.
20m
C.
22m
D.
02m
33
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
Câu 16 : 
21
x
y
x
 th c v
 th   
A.
21
x
y
x
B.
21
x
y
x
C.
21
x
y
x
D.
21
x
y
x
Câu 17 : 
2
21
x
y
x
 th c v
 th   
A.
2
21
x
y
x
B.
2
21
x
y
x
C.
2
21
x
y
x
D.
2
21
x
y
x
34
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
Câu 18 :  th ca m trong b c li bn
H 
 ?
A.
32
1
23
3
y x x x
. B.
3
2
23y x x x
.
C.
32
23y x x x
. D.
3
2
1
23
3
y x x x
.
Câu 19 :  th ca m trong b c li bn
 
 ?
A.
3
3y x x
. B.
3
3y x x
.
C.
3
3y x x
. D.
3
3y x x
.
x
y
3
O
1
x
y
-1
O
2
-2
1
35
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
Câu 20 :   th 

m
 
f x m

m
A.
31m
.
B.
0m
.
C.
0m
,
3m
.
D.
13m
.
Câu 21 p  : t c  c ng thng y = m c th

42
2y x x
ti
6
t.
A.
01m
B.
10m
C.
11m
D.
11m
Câu 22  :  th 
42
43y x x
nh hnh v d
t c  ca m  phng trnh
42
4 3 1x x m
m tht
A.
0 2 1m;
.
B.
1 0 2m;
.
C.
02m
.
D.
13m
.
Câu 23  Trng nh) : 
3
y x 3x 1
 th nh hnh v t
c  thc c phng trnh
3
x 3 x m 0
t.
A.
m 0;2
B.
m 1;1
36
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ
2017
C.
m 0;2
D.
m 1;1
Câu 24 (THPT  ) :

3
31y x x
.

m

3
31x x m
i m
A.
1 3.m
B.
0.m
C.
0, 3.mm
D.
3 1.m
Câu 25  : 
32
32f x x x

th 
m

3
2
32x x m

A.
22m
.
B.
02m
.
C.
22m
.
D.
02m
.
37
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
◙ Trung điểm
( ; )
II
I x y
cn thng AB :
2
2
AB
I
AB
I
xx
x
yy
y
◙ Trọng tâm G
c :
3
3
A B C
G
A B C
G
xxx
x
yyy
y


◙ Khoảng cách giữa 2 điểm A,B là
22
( ) ( )
B A B A
AB x x y y
◙ Khoảng cách t m
MM
M(x ;y )
ng thng (D):
0Ax By C
:
MM
22
Ax By C
d[M; D]
AB

vi
n (A; B)

◙ Điểm cố định :
2
0
( ; ) ( ; ) 0 . . 0 0
0
A
f x m y f x m y Am B m C B m
C
◙ Tọa độ nguyên :    chia ht
◙ Bất đăng thức Cachy :
2.a b ab
,dy ra
ab
◙ Góc giữa 2 đƣờng thẳng: ng thng
1 1 1 1
2 2 2 2
:a 0
:a 0
d x b y c
d x b y c
.
Gi
00
φ (0 φ 90 )
a d1 2  :
1 2 1 2
2 2 2 2
1 1 2 2
cosφ.
.
a a b b
a b a b

Ví dụ 01 : 
1
1
x
y
x

 th 
C
m
MC
sao cho kho
ng thng
: 2 1yx
bng
3
.
5
PHẦN 10 : TỔNG ÔN
38
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
◙ Phân tích :
Khoảng cách t m
MM
M(x ;y )
ng thng (D):
0Ax By C
:
MM
22
Ax By C
d[M; D]
AB

vi
n (A; B)

♥ Giải: Gi
0
00
0
1
;.
1
x
M x y C
x





ng thc vit li
2 1 0xy
 :
3
,
5
dM
0
0
0
2 2 2 2
1
21
2 1 1
33
55
1 2 1 2
MM
x
x
x y x



0
0
0
1
2 1 3
1
x
x
x
2
0 0 0
2 2 2 3 1x x x
2
0 0 0
2
0 0 0
2 2 2 3 1
2 2 2 3 1
x x x
x x x
2
0
00
2
0
00
1
2 5 5 0 ( )
1
2 1 0
2
x
x x vn
x
xx


► Vi
0
1x 

0
0y

1; 0M
► Vi
0
1
2
x

0
3y

1
;3
2
M



Vy
1
1; 0 ; 3
2
M hay M



m c
Ví dụ 02 (THPT Chuyên Bến Tre) :  th ca m c
li bn phng n
, , ,A B C D
di y. H   
A.
32
3 3 1y x x x
. B.
3
1
31
3
y x x
.
C.
32
3 3 1y x x x
. D.
3
31y x x
.
◙ Phân tích : Đây là dạng nhìn đồ thị
♥ Giải: Chọn D.
Nhìn nhánh ngoài cùng bên phải thấy ĐI LÊN suy ra a > 0
ab
ab
ab


39
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Lại có :
0y
1
1
x
x

(Hai điểm cực trị của ĐTHS) nên D là thỏa mãn
Ví dụ 03 (Chuyên Bến Tre) :  nh nht ca hm s
4
yx
x

ng
0;
.
A.
0;
min 2y

. B.
0;
min 4y

. C.
0;
min 0y

. D.
0;
min 3y

.
◙ Phân tích : Đây là dạng tìm GTLN – GTNN ( đã có chuyên đề riêng – CĐ3)
♥ Giải: Chọn B.

2
22
44
1,
x
y
xx
.
02yx
Lp bng bia hm s ng
0;
.
Nhn thy hm s ch t cc tiu ti im
2x
v
4
CT
y

0;
min 4y

.
Ví dụ 04 (Chuyên Bến Tre) : p hp tt c cc gi tr ca tham s thc
m
 hm s
32
1
4
3
y x mx x m
ng bin trn khong
; 
.
A.
;2
. B.
2;
. C.
2;2
. D.
;2
.
◙ Phân tích : Đây là dạng đơn điệu của hàm số ( đã có chuyên đề riêng – CĐ1 )
♥ Giải: Chọn C.; Ta có:
2
24y x mx
.
Hàm số đồng biến trên khoảng
; 
khi v ch khi
0, ;yx
 
.
2
4 0 2 2mm
.
Ví dụ 05 (SGDĐT Phú Thọ) : Hình vẽ dưới đây là đồ thị của hàm số nào?
A.
1
1
x
y
x

. B.
42
4y x x
. C.
3
3y x x
. D.
42
4y x x
.
40
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
♥ Giải: Chọn B.
+ Hàm số đã cho là hàm TRÙNG PHƢƠNG nên loại A, C
+ Nhìn vào nhánh phải ngoài cùng đi xuống nên a < 0 (Đơn giản thế thôi)
Cách khác: 
42
4:y x x
3
0
0 4 8 0
2
x
y x x
x

.
Ví dụ 06 (THPT chuyên Lê Thánh Tông – Quảng Nam) : T
m
 
32
1
41
3
y x mx x
t cc tr ti
2x
.
A.
0.m
B.
2.m
n ti
.m
D.
2.m 
♥ Giải: Chọn C.
2
24y x mx
.
22y x m


.
 t cc tr ti
2x
20
20
y
y

4 4 4 0
4 2 0
m
m

.
2
2
m
m
m
. Vn ti
m
th
Chú ý : hc sinh hay ch  ng hp
20y
t
20y

 nhm v
Ví dụ 07 (THPT chuyên Thái Bình) : 
3
1
y
x

C

mnh  sai ?
A.  B. 
C
m cn ngang.
C. 
C

( 1;0)I
ng. D. n trn m
♥ Giải: Chọn B.
41
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
☻  
2
3
0
1
y
x
,
\1x
 nghch bin ng kho
nh c tr

Hay chú ý : hàm số nhất biến
ax b
y
cx d
c gic tr
☻ Do
11
lim 0; lim ; lim
x
xx
y y y


 
 th  m cng ln l
0; 1yx

Ví dụ 08 (THPT chuyên Thái Bình) : i y khng tim cn ?
A.
2
1
4
x
y
x
. B.
3
1
x
y
x
. C.
4
2016yx
. D.
2
23
1
xx
y
x

.
♥ Giải: Chọn C.

2
1
lim 1
4
x
x
x


 th  m cn ngang
1; 1.yy

11
3 3 3
lim 1; lim ; lim
1 1 1
x
xx
x x x
x x x



 
 th  m cn ngang
1,y
tim
cng
1.x

4
lim 2016
x
x


 th  m cm cn
ng).
Ví dụ 09 (THPT chuyên Thái Bình) : i n thi

A.
42
23y x x
. B.
42
23y x x
. C.
42
3y x x
. D.
42
23y x x
.
x

1
0
1

y
0
0
0
y

4
3
4

♥ Giải: Chọn B.
 phng
42
0y ax bx c a
.
T bng bi 
2
cc ti
1
c
0a
,
0b
.
Cách khác :
☻ c tr 
42
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Ví dụ 10 (Trƣờng Quốc Học Quy Nhơn – Bình Định) : 
31
3
x
y f x
x

 th
C
. Vit phng trnh tip tuyn c th
C
, bi tim ca phng
trnh
7 11 . 10x f x

.
A.
2 1 5 1
;
5 5 2 2
y x y x
. B.
2 1 5 1
;
5 5 2 2
y x y x
.
C.
2 9 5 9
;
5 5 2 2
y x y x
. D.
2 9 5 1
;
5 5 2 2
y x y x
.
♥ Giải: Chọn A. M
\3D

2
10
3
fx
x
.
Gi
A
 tim ca tip tuy th  m
A
thng
trnh:
2
2
10
7 11 . 10 7 11 10 7 11 6 9
3
x f x x x x x
x
2
1
20
2
x
xx
x

Vi
5
1 1 2, 1
2
x f f

51
22
yx

Vi
2
2 2 1, 2
5
x f f

21
55
yx

Vp tuyn c
2 1 5 1
;
5 5 2 2
y x y x
Ví dụ 10 (Trƣờng Quốc Học Quy Nhơn – Bình Định) : t c m cng c th

2
2
2 16 2
3 10
x x x
y
xx

.
A.
2; 5yy
. B.
2x 
. C.
2; 5xx
. D.
2, 5xx
.
♥ Giải: Chọn C.
m
\ 2,5D
22
22
22
22
22
55
2 16 2 2 16 2
lim , lim
3 10 3 10
2 16 2 2 16 2
lim , lim
3 10 3 10
xx
xx
x x x x x x
x x x x
x x x x x x
x x x x


 

 
 
 th  ng tim c
2; 5xx
43
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Ví dụ 11 : 
1 sin 2
sin
mx
y
xm

t c  ca tham s
m
  nghch
bing
0;
2



A.
12m
. B.
1
2
m
m

. C.
1
2
m
m

. D.
0
1
m
m
.
♥ Giải: Chọn B.
Cách 1: Dùng casio: Dùng chức năng mode 7.
+ Th
0m
sin 2
sin
x
y
x


.
Nhnh
t
FX
ta thấy giá trị tăng dần khi
X
tăng vậy hàm đồng biến khi
0m
Vy ta long n cha
0m
Loi A, D.
☻ Th vi
2m
sin 2
1
sin 2
x
y
x
i
loi C. Nên ta chọn B.
Cách 2: t
sin xt

0; 0;1
2
xt



. 
12mt
y
tm

ng ng v
m
 
12mt
y
tm

nghch bing
0;1
.
Ta có
2
2
2
2
mm
y
t
.

0;2
2
0
20
1
0;2
0;2
2
0;2
y
mm
m
t
m
m
m



.
44
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Bài tập tại lớp
Bài 01 (THPT Vi ) :  tr ln nht c
42
31y x x

A. 1. B. 29. C. 3. D.
13
4
.
♥ Giải :



Bài 02 (THPT Vi ) : Mt chm chuyng theo quy lut
23
13s t t
. Vn
tc
/v m s
ca chuy ln nht khi
t
bng:
A.
1 .s
B.
3 .s
C.
4 .s
D.
2 .s
♥ Giải :


Bài 03 (THPT Vi ) : S m cng cong
32
23y x x x
ng
thng
3yx
bng
A. 0. B. 1. C. 2. D. 3.
♥ Giải :


Bài 04 (THPT Vi ) : Tip tuyn c th 
32
32y x x
 s 
3k 
nh l
A.
3 3yx
. B.
3 3yx
. C.
3 3.yx
D.
3 3yx
.
♥ Giải :

45
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Bài 05 (THPT Vi ) : 
32
1
( ) 2 1 5
3
f x x x m x
. Vu ki
ca
m
 ng bi ?
A.
3.m
B.
3.m
C.
3.m 
D.
3.m
♥ Giải :




Bài 06 (THPT Vi ) : Tip tuyn tm cc tiu c th 
32
1
2 3 5
3
y x x x
A. Song song vi tr  s ng 1.
 s  D. Song song vng thng y = x - 1.
♥ Giải :
Chú ý : 
Bài 07 (THPT Vi ) :  th 
1
1
x
y
x

I
II
III
IV
-2 -1 1 2 3
-3
-2
-1
1
2
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
46
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
A. II. B. IV. C. III. D. I.
Bài 08 (THPT Vi ) :  
32
3 2 1 5y x mx m x m
i, cc tiu
u kin c
A.
1
; 1; .
3
m




B.
1
;1 .
3
m




C.
1
; 1; .
3
m

 

D.
1
;1 .
3
m




♥ Giải :




Bài 09 (THPT Vi ) :  s
2sin 1
sinx 2
x
y
 ln nh
A. 1. B. -1. C. -3. D.
1
3
.
♥ Giải :



Bài 10 (THPT Vi ) :   th 
2
1 2 1y x x m x m


ct trc
t
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
47
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
A.
m
. B.
1
0
2
m
. C.
02m
. D.
0m
.
♥ Giải :




Bài 11 (THPT Vi ) :  th 
:
A.
3
2
1.
3
x
yx
B.
32
3 1.y x x
C.
32
3 1.y x x
D.
32
3 1.y x x
♥ Giải :
 i thym vi Oy
Lại có ......................................................................
Bài 12 (THPT Phng ) :  th 
32
+c +y ax bx x d
m cc ti
0;0O
m c
1;1M
 ca
, , ,a b c d
ln l
A.
3;0; 2;0
. B.
2;3;0;0
. C.
3;0;2;0
. D.
2;0;0;3
♥ Giải :




-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
48
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Bài 13 (THPT Phng ) : 
32
y ax bx cx d
 th nh 
 
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
♥ Giải :



Bài 13 (THPT SPHN ln 02) : khong cch gia hai im cc tiu ca  th hm s
42
2 3 1y x x
A.
4
23
B.
3
C.
23
D.
4
3
♥ Giải :


Bài 14 (THPT SPHN ln 02) : t c cc gi tr ca tham s
m
 hm s
32
11
5
32
y x m x mx
c i, cc tiu v
5
CD CT
xx
.
A.
0m
B.
6m 
C.
6;0m
D.
0; 6m
♥ Giải :



Bài 15 (THPT p ) : t c  ca m   th 
3
32y x x
ct
ng thng
1ym
ti 3 t
c :
49
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
x
y
0
A.
15m
B.
15m
C.
15m
D.
04m
♥ Giải :



Bài 16 (THPT p ) : 
32
y ax bx cx d
 th nh hnh v 
M 
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
♥ Giải :



Bài 17 (THPT  c) : 
32
y ax bx cx d
 th nh
hnh bn. Kh
A.
, , 0; 0a b c d
B.
, , 0; 0a b d c
C.
, , 0; 0a c d b
D.
, 0; , 0a d b c
♥ Giải :



Bài 18 (THPT  c) : 
y f x
  th
c
'y f x
nh hnh v . Chn kh ?
50
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
a b c
A.
f b f a f c
B.
f b f c f a
C.
f c f a f b
D.
f c f b f a
♥ Giải :



Bài 19 (THPT ) : Gm M, N ln lm cng thng
1yx
ng cong
24
1
x
y
x
 m cn thng MN:
A. 1. B. 8. C.
5
2
. D.
5
2
.
♥ Giải :


Bài 20 (THPT ) : 
fx
  th 
fx
ct trc Ox t ln l
a b c
nh hnh v. Chn khnh sai 
khnh sau:
A.
f c f a f b
B.
f c f b f a
. C.
f a f b f c
. D.
f b f a f c .
♥ Giải :

51
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Bài 21 (THPT HN Ln 04) :  bc ba
32
y ax bx cx d
 th nh
: Du ca
; ; ;a b c d

A.
0; 0; 0; 0a b c d
. B.
0; 0; 0; 0a b c d
.
C.
0; 0; 0; 0a b c d
. D.
0; 0; 0; 0a b c d
.
♥ Giải :



Bài 22 n 04) : 
42
y ax bx c
 th nh . Du
ca
,,abc

A.
0, 0, 0.abc
B.
0, 0, 0.abc
C.
0, 0, 0.a b c
D.
0, 0, 0.a b c
♥ Giải :



Bài 23 n 04) : t c  thc ca tham s   th 
s
21
3
x
y
xm
ng tim cng
A.
1m
B.
1m
C.
mR
D.
3
2
m
♥ Giải :

52
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Bài 24 y) : 
y f x


'fx
  th c
'fx

S m cực trị c
fx
 A. 0 B. 1 C. 3 D. 2
♥ Giải :



Bài 25 y) : S tim cn c th 
2
1
x
y
x

A. 1 B. 2 C. 4 D. 3
Bài 26 y) : Tp h  
32
13y mx mx m x
ng bi 
A.
3
0;
2


B.
3
;
2



C.
3
0;
2



D.
3
;0 ;
2

 


♥ Giải :



Bài 27 y) :   
3 2 2
3 3 1y x x m x
t cc tiu
ti
2x

A.
1m 
B.
1m 
C.
1m 
D.
1m
♥ Giải :


53
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Bài 28 y) :  th d th c
32
34y x x
V ng trnh
32
30x x m
t ?
A.
40mm
B.
40mm
C.
44mm
D. mt kt qu 
♥ Giải :

Bài 29 (THPT ng H) : 
x
ax b
d
y
c
vi
0a
 th nh hnh
v  
A.
0, 0, 0b c d
B.
0, 0, 0b c d
C.
0, 0, 0b c d
D.
0, 0, 0b c d
♥ Giải :



Bài 30 (THPT ) :  th c
31
1
x
y
x
 th c
45yx

tt c m chung ?
A. 0. B. 1. C. 2 . D. 3.
♥ Giải :

x
O
y
54
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Bài 31 (THPT ) : Tip tuyn ca parabol
2
4yx
tm (1 ; 3) to vi hai trc
t m
S

A.
25
.
4
S
B.
5
.
4
S
C.
25
.
2
S
D.
5
.
2
S
♥ Giải :



Bài 32 (THPT ) : 
()y f x
n
2;2

 th  nh tt c  ca tham s m  phng trnh
f x m
 nghim thc nhiu nht.
A.
02m
. B.
02m
. C.
2m
. D.
0m
.
♥ Giải :



Bài 33 (THPT ) : Bit r th 
3
5
2
4
y x x

2
2y x x
tip
m
00
( ; )M x y

0
.x
A.
0
1
2
x
. B.
0
5
.
2
x
C.
0
3
.
4
x
D.
0
3
2
x
.
♥ Giải :


55
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017


Bài 34 ng) :  s
43
2
mx m
y
x
. V a
m
ng tim
cng, tim cn ngang c th  c t t nh
ding
2016
.
A.
m 
. B.
504m 
. C.
252m 
. D.
1008m 
.
♥ Giải :



Bài 35 (THPT Tro nh) : 
4 2 2
22y x mx m

m
 
m cc tr m cc tr c th  nh ca mt  ?
A.
1.m
B.
1.m 
C.
2.m
D.
2.m 
♥ Giải :



Bài 36 c : 
y f x

2
' 1 2 3 1f x x x x
. S m cc tr c 
A. 4 B. 3 C. 1 D. 2
♥ Giải :

Chú ý cho bài 33 :
56
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Bài 37 : 
y f x
 th 
'fx
nh sau
-4 -2 2 4
-1
1
2
3
x
y
nh s m cc tr c
y f x
 A.3 B. 2 C.1 D.0
♥ Giải :


Bài 38 : 
()y f x
n
2;2
 th ng cong
 
()fx
t ci t
A. x = 2.
B. x = 0.
C. x = 1.
D. x = 2.
Bài 39 (THPT  HN) : 
2
2
1
x
y
x
n
01x
 ln nh
 nh nht thng thc
A.
44
max min
y +y 1
. B.
44
max min
y +y 4
. C.
44
max min
y +y 16
. D.
44
max min
y +y 8
.
♥ Giải :


-2
-1
1
2
3
-1
-2
y
x
0
57
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Bài 40  HN) : 
32
51y x x x
p tuyn ti
 th 
2x

A.
10 9yx
. B.
11 19yx
. C.
11 10yx
. D.
10 8yx
.
♥ Giải :

Chú ý công thức giải nhanh hàm trùng phƣơng
Tổng quát:
b
a
3
2
cot
28
Dữ kiện
Công thức thỏa mãn
0ab

ABC
i
A
3
80ba

ABC
u
3
24 0ba

ABC

0ABC
SS
a S b
3 2 5
0
32 ( ) 0
Vận dụng 01 : t c  thc ca
m
m s
42
23y x mx m
n.
A.
0m
. B.
1m
. C.
0m
. D.
3m
.
♥ Giải :


x
y
O
A
B
C
58
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Vận dụng 02 :
t c  thc ca tham s  th 
4 2 4
22y x mx m m
m cc tr tu.
A.
3
3m
B.
3
13m 
C.
3
13m 
D.
3
3m 
♥ Giải :



Vận dụng 03 :

m
  th 
42
21y x mx
m cc tr t
ng
42

A.
2m
B.
4m 
C.
2m 
D.
1m
♥ Giải :


Vận dụng 04
(S GD nh) :    th 
4 2 2
2 2 4y x mx m m

m cc tr
A
,
B
,
C
sao cho
1
ABC
S
.
A.
4m
. B.
1m
C.
3m
.
D.
2m
.
♥ Giải :



Vận dụng 05
(T nh) :  ca tham s
m
  th 
42
13
42
y x mx
m cc tr t
A.
3
2
6
3
m
. B.
3
6m
. C.
3
3
6
2
m
. D.
26m
m
59
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
♥ Giải :


Vận dụng 06 :

42
22y x mx m

m
  s m ci, cc tiu to
ng 32.
A.
4m
. B.
5m
. C.
3m 
. D.
1m
.
♥ Giải :



Vận dụng 07 :
 th 
4 2 4
22y x mx m m
m cc tr tnh ca mt

m
nh
A.
3m 
. B.
1m 
. C.
3m
. D.
1.m
♥ Giải :



Vận dụng 08 :

4 2 2
21y x m x
 th
m
C

m
  th
m
C
m
cc tr tu.
A.
6
3m 
B.
23
2
m
C.
1m 
D.
3
3m 
♥ Giải :


60
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Vận dụng 09 :

42
3 2016 10.y x a x a

a
  th  m cc tr
lnh ca mu.
A.
1a
B.
1a 
C.
3
23a
-3 D.
3
2 3 3a 
♥ Giải :


Vận dụng 10
(Minh ha ln 01- BGD-) : t c  thc ca tham s
m

th c
42
21y x mx
m cc tr t
A.
3
1
9
m 
B.
1m 
C.
3
1
9
m
D.
1m
♥ Giải :


Vận dụng 11 :
t c  tham s
m
 
4 2 2 9 4
2( 1) 2017y x m m x m m

3
cc
tr sao cho khong a hai cc tiu bng
3
.
A.
0,5m
B.
0,5m 
C.
0,5m
hoc
0,5m 
D.
2m
♥ Giải :




Vận dụng 12 :
t c  tham s
m
 
4 2 2 4
2(1 ) 2017 2016y x m x m

3
cc
tr sao cho khoa hai cc tiu nh nht.
A.
1m
B.
0m
C.
1m
hoc
1m 
D.
1m 
61
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
♥ Giải :


Vận dụng 13 :
t c  tham s thc
m
 
42
( 2015) 2017y x m x

3
cc tr
ti
A
.
A.
2017m
B.
2014m
C.
2016m
D.
2015m
♥ Giải :



Vận dụng 14 :
t c  tham s thc
m
 
42
2( 2016) 2017 2016y x m x m

3
cc tr ti
A
.
A.
2017m 
B.
2017m
C.
2018m 
D.
2015m
♥ Giải :



Vận dụng 15 :
t c  tham s
m
 
42
9
3( 2017) 2016
8
y x m x

3
cc tr to
u.
A.
2015m
B.
2016m
C.
2017m
D.
2017m 
♥ Giải :


62
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
CÂU HỎI TRẮC NGHIỆM PHẦN TỔNG ÔN
Câu 01 : Bi th ca

32
0y ax bx cx d a
 s
b
a
.
A.
1
b
a
.
B.
1
b
a

.
C.
3
b
a
.
D.
3
b
a

.
Câu 02 : t c  thc ca tham s
m
  nh nht c
3 2 2
12y x m x m
n
0;2
bng
7
.
A.
3m 
.
B.
7m 
.
C.
m
.
D.
1m 
.
Câu 03 : t c  thc ca tham s
m
  th 
2
2
4
x
y
x x m

m
cng.
A.
12m 
B.
4m
.
C.
4m
.
D.
12 4m
.
Câu 04 (THPT Lý Tự Trong – Khánh Hòa) : 
32
1
4 5 17
3
y x x x
. Phng trnh
'0y
m
12
,xx
ng
12
xx
bng :
A.
5
. B.
8
.
C.
5
. D.
8
.
Câu 05 (THPT Nguyễn Văn Trỗi – Khánh Hòa) : 
s
ax b
xd
y
c
vi
0a
 th nh hnh v bn. Mnh 
no di y ng?
O
x
y
63
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
A.
0b
,
0c
,
0d
.
B.
0b
,
0c
,
0d
.
C.
0b
,
0c
,
0d
.
D.
0, 0, 0b c d
.
Câu 06 (THPT Đoàn Thị Điểm – Khánh Hòa) : nh phng tim cn ngang ca
 th 
81
12
x
y
x
A.
1
2
x
. B.
4x 
. C.
4y 
. D.
8y
.
Câu 07 (THPT Đoàn Thị Điểm – Khánh Hòa) :  th 
42
22y x x
 th 
2
4yx
t c m chung?
A.
0
.
B.
1
.
C.
2
.
D.
4
.
Câu 08 (THPT Lạc Long Quân – Khánh Hòa) :   
y f x
    
1;3
   th  ng
 
fx
t cc tiu t

A.
1x 
.
B.
0x
.
C.
2x
.
D.
3x 
.
Câu 09 (THPT Lạc Long Quân – Khánh Hòa) : 
32
– 6 – 9 4y x x x
ng bi
khong
A.
1; 3
. B.
3; 
. C.
;3
. D.
1; 
.
Câu 10 (THPT Lạc Long Quân – Khánh Hòa) : 
y f x
 

2
3
12f x x x x
. 
y f x
m cc tr?
A. 
3
m cc tr.
B. 
1
m cc tr.
C. c tr.

2
m cc tr.
Câu 11 (THPT Lạc Long Quân – Khánh Hòa) : Cho bit

32
y ax bx cx d
 th i. Trong
nh sau, kh?
-3
3
2
1
O
1
-1
x
y
64
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
A.
2
0
30
a
b ac

. B.
2
0
30
a
b ac

. C.
2
0
30
a
b ac

. D.
2
0
30
a
b ac

.
Câu 12 (THPT Trần Hƣng Đạo – Khánh Hòa) :  th  m c
A. . B. .
C. . D. .
Câu 13 (THPT Trần Hƣng Đạo – Khánh Hòa):  th
 ng v:
A. .
B. .
C. .
D. .
Câu 14 (THPT Trần Hƣng Đạo – Khánh Hòa):  ng bing:
A. . B.
1; 
. C. . D. .
Câu 15 (THPT Trần Hƣng Đạo – Khánh Hòa):  ln nht  nh nht c
s n 
A.
2, 3Mm
. B.
9
,4
4
Mm
.
C.
9
,3
4
Mm
. D.
9
3,
4
Mm
.
Câu 16 (THPT Trần Hƣng Đạo – Khánh Hòa): 
2
32
23
x
y
xx


?
A. 
B. 
3y
C. 
3; 3yy
.
D. 
3y 
.
Câu 17 (THPT Chuyên Phan Bội Châu – Nghệ An):  ca tham s
m
 tim cng
c th 
3
1
x
y
xm

m
5;2A
.
A.
4m 
. B.
1m 
. C.
6m
. D.
4m
.
32
31y x x
(0; 1)
( 1;0)
( 2;3)
( 3;2)
31
2
x
y
x
31
2
x
y
x
21
2
x
y
x
21
2
x
y
x
42
2 4 2y x x
( ;1)
( ;0)
(0; )
M
m
23
1
x
y
x
3;0
65
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 18 (THPT Chuyên Phan Bội Châu – Nghệ An): 
y f x

ng bi
M 
A.  ng bing
;1
.  th  m cn ngang.
C.  t cc tr ti
2x 
. D.   ln nht bng 1.
Câu 19 (THPT Chuyên Hoàng Văn Thụ – Hòa Bình): 
()y f x
ng bi
 th  m cng thng trnh
A.
2x 

1x
.
B.
1x
.
C. m cn ng.
D.
2x 
.
Câu 20 (THPT Chuyên Hoàng Văn Thụ – Hòa Bình): 
42
y ax bx c
 th nh
hnh v sau Kh
A.
0, 0, 0abc
.
B.
0, 0, 0a b c
.
C.
0, 0, 0a b c
.
D.
0, 0, 0abc
.
y
x
O
x

2
1

y
y
4
1

2
2

x
–∞
2
1
1
+∞
y
0
0
0
y

1
1

66
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 21 (THPT Chuyên Hoàng Văn Thụ – Hòa Bình): S m cc tr ca 
2
12y x x

A.
2
.
B.
1
.
C.
4
.
D.
3
.
Câu 22 (THPT Chuyên Quốc Học Huế): Cho  s
1
ax b
y
x
 th nh hnh v 
khnh đúng nh sau?
A.
0ab
.
B.
0ba
.
C.
0 ba
.
D.
0 ab
.
Câu 23 (THPT Chuyên Quốc Học Huế): tr ln nh nh nht c
3
2cos cos2f x x x
p hp
;
33
D





.
A.
19
max 1, min
27
xD
xD
f x f x

.
B.
3
max , min 3
4
xD
xD
f x f x
.
C.
3 19
max , min
4 27
xD
xD
f x f x

.
D.
max 1, min 3
xD
xD
f x f x
.
Câu 24 (THPT Chuyên Quốc Học Huế) :  m c th 
2
45yx

ng thng
?yx
A.
3
.
B.
0
.
C.
2
.
D.
1
.
Câu 25 (SGD Nam Định) : t c ng bin c
2
1
x
y
x
.
A.
1;1
. B.
0;
.
C.
;1

1; 
. D.
; 
.
O
x
y
Chú ý :
67
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 26 (SGD Nam Định) : m cn ngang c th 
22
1
1
x
y
x

.
A.
1x
. B.
2y
. C.
3y
. D.
1y
.
Câu 27 (SGD Nam Định) : th  th ca m th c 
phng n A, B, C, D dn phng n ng.
A.
42
1
5
4
y x x
.
B.
42
1
5
4
y x x
.
C.
4
1
5
4
yx
.
D.
42
1
25
4
y x x
.
Câu 28 (SGD Nam Định) : Gi
M
,
m
ln l ln nht, nh nht c
32
3y x x
n
2;1
 ca
T M m
.
A.
20T 
.
B.
4T 
.
C.
2T
.
D.
24T 
.
Câu 29 (Trích đề THPTQG – 2017 ) : 
2
21y x x
 th
C
. M 
d
A.
C
ct trm.
B.
C
ct tri mm.
C.
C
t tr
D.
C
ct trm.
Câu 30 (Trích đề THPTQG – 2017 ) : s
y f x

2
1f x x

,
x
.
M 
A.  nghch bing
;0
. B.  nghch bing
1; 
.
C.  nghch bing
1;1
.  ng bing
; 
.
Câu 31 (Trích đề THPTQG – 2017 ) : 
y f x
ng bi sau
O
1
1
2
2
x
y
1
2
3
4
5
68
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
M 
A.  m cc tr.  t cc tiu ti
2x
.
C.  i. D.  t cc tiu ti
5x 
.
Câu 32 (Trích đề THPTQG – 2017 ) :  nh nht
m
c
42
13y x x
n
2;3 .
A.
51
.
4
m
B.
49
.
4
m
C.
13.m
D.
51
.
2
m
Câu 33 (Trích đề THPTQG – 2017 ) : t c  thc ca tham s
m
  th c
s
42
2y x mx
m cc tr t hn 1.
A.
0.m
B.
1.m
C.
3
0 4.m
D.
0 1.m
Câu 34 (Trích đề THPTQG – 2017 ) : ng cong
 th c
ax b
y
cx d
vi
a
,
b
,
c
,
d
 thc. M 

A.
0, 2yx
.
B.
0, 1yx
.
C.
0, 2yx
.
D.
0, 1yx
.
Câu 35 (Trích đề THPTQG – 2017 ) :  th cs  dm cn
ng?
A.
1
y
x
. B.
2
1
1
y
xx

. C.
4
1
1
y
x
. D.
2
1
1
y
x
.
Câu 36 (Trích đề THPTQG – 2017 ) : 
42
2y x x
. M 
A.  ng bing
;2
.  nghch bing
;2
.
C.  ng bing
1;1
. D. ch bing
1;1
.
Câu 37 (Trích đề THPTQG – 2017 ) : 
23mx m
y
xm

vi m . Gi
S
p
hp tt c  a
m
  ng bi phn t
ca
S
.
A.
5
. B.
4
. C. . D.
3
.
69
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 38 (Trích đề THPTQG – 2017 ) :  th ca  s
32
35y x x
m cc tr
A

B

S
c
OAB
vi
O
c t..
A.
9S
. B.
10
3
S
.
C.
5S
. D.
10S
.
Câu 39 (Trích đề THPTQG – 2017 ) : Mt vt chuyn ng theo quy lut
32
1
6
2
s t t
vi
t

ng th khi vt bu chuy
s
ng vt di chuyn
c trong khong thi trong khong thi gian
6
 t khi bu chuyn
ng, vn tc ln nht ca vc b
A.
24( / ).ms
B.
108( / ).ms
C.
18( / ).ms
D.
64( / ).ms
Câu 40 (Trích đề THPTQG – 2017 ) : 
y f x
 sau :
x

1
0
2

y
0
||
0
M 
A.  ng bing
2;0
.
B.  ng bing
;0
.
 nghch bing
0;2
.
D.  ng bing
;2
.
Câu 41 (Trích đề THPTQG – 2017 ) :  th
ca mt trong b d  
A.
3
32y x x
.
B.
42
1y x x
.
C.
42
1y x x
.
D.
3
32y x x
.
Câu 42 (Trích đề THPTQG – 2017 ) : 
23
1
x
y
x
m cc tr ?
A.
3.
B.
0.
C.
2
. D.
1
.
Câu 43 (Trích đề THPTQG – 2017 ) :  th 
2
2
4
x
y
x
y tim cn.
x
y
O
70
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
A. 1 B. 2 C. 3 D. 4
Câu 44 (Trích đề THPTQG – 2017 ) : GTNN
m
c
2
2
yx
x

n
1
;2
2



.
A.
17
4
m
.
B.
10m
.
C.
5m
.
D.
3m
Câu 45 (Trích đề THPTQG – 2017 ) : 
2
21yx
. Mnh  no di y ng?
A.  nghch bin trn khong
1;1
.
B.  ng bin trn khong
0;
.
C.  ng bin trn khong
;0
.
D.  nghch bin trn khong
0;
.
Câu 46 (Trích đề THPTQG – 2017 ) :  thc ca tham s
m
 ng thng
: 2 1 3d y m x m
ng thm cc tr c th 
32
3 1.y x x
A.
3
.
2
m
B.
3
.
4
m
C.
1
.
2
m 
D.
1
.
4
m
Câu 47 (Trích đề THPTQG – 2017 ) : 
4mx m
y
xm
vi
m

S
p
t
m
n tr s phn t

S
.
A.
5
.
B.
4
.
C. 
D.
3
.
Câu 48 (Trích đề THPTQG – 2017 ) : 
m

s
3 2 3
34y x mx m

A

B

OAB
ng
4
vi
O
.
A.
4
1
2
m 
;
4
1
2
m
.
71
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
B.
1m 
;
1m
.
C.
1m
.
D.
0m
.
Câu 49 (Trích đề THPTQG – 2017 ) : Mt vt chuyng theo quy lut
32
1
6
3
s t t
vi
t

ng th khi vt bu chuy
s
ng vt di chuyn
c trong khong thi trong khong th t khi bu chuyng,
vn tc ln nht ca vc b ?
A.
144
(m/s). B.
36
(m/s).
C.
243
(m/s). D.
27
(m/s).
Câu 50 (Trích đề THPTQG – 2017 ) :  th c
32
3 9 1y x x x
m cc tr A
Bng thng
AB
?
A.
(1;0)P
B.
(0; 1)M
C.
(1; 10)N
D.
( 1;10)Q
Câu 51 (Trích đề THPTQG – 2017 ) : 
32
(4 9) 5y x mx m x
vi m 
 a m   nghch bing
( ; ) 
?
A.
7
B.
4
C.
6
D.
5
Câu 52 (Trích đề THPTQG – 2017 ) :  tim cng c th 
2
2
34
16
xx
y
x

.
A. 2.
B. 3.
C. 1.
D. 0.
Câu 53 (Trích đề THPTQG – 2017 ) : 
2
2
1
y
x
nghch bi
A.
(0; )
B.
( 1;1)
C.
( ; ) 
D.
( ;0)
Câu 54 (Trích đề THPTQG – 2017 ) : 
3
32y x x
. M 
 ng bing
( ;0)
ch bing
(0; )
.
 nghch bing
( ; ) 
.
 ng bing
( ; ) 
.
 nghch bing
( ;0)
ng bing
(0; )
.
72
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 55 (Trích đề THPTQG – 2017 ) : ng cong  th
ca mt trong b di   
A.
32
1y x x
.
B.
42
1y x x
.
C.
32
1y x x
.
D.
42
1y x x
.
Câu 56 : 
3
1f x x

2
3g x x
. Chsai
A. 
fx

B. 
f x g x

C. 
gx

D. 
fx

Câu 57 : nh t m c th 
21
1
x
y
x
vng thng
7yx
A.
2;5 , 4;3
B.
2;5 , 4;3
C.
2;5 , 4;4
D.
2;5 , 3;4
Câu 58 (THPT Chuyên ĐHSPHN – lần 04 ) : 
42
21y x x
. Khoa hai
m cc tiu c th  bng:
A.
2
B.
4
C.
1
D.
3
Câu 59 (THPT Chuyên ĐHSPHN – lần 04 ) : t c  thc ca tham s
m
 
32
21y mx m x x
c tiu:
A.
1m
B.
2m 
C.
0m
D.
m
Câu 60 (THPT Tử Đà – Phú Thọ ) : 
y f x
p s thc  th nh hnh
bn. Hm s
y f x
t cc tiu tm 
A.
1x
B.
2x 
C.
2x 

0x
D.
0x
73
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 61 (THPT chuyên Vị Thanh – Hậu Giang) : 
()y f x

0
lim ( )
x
fx


2
.lim ( )
x
fx

Kh
 th  m cng.
 th  t tim cng.
 th  m cng thng
0y

2y
.
 th  m cng thng
0x

2x
.
Câu 62 (THPT chuyên Lê Thánh Tông – Quảng Nam) : 
()y f x
 vi
b sau:
x

3
1
2

()fx
0
0
+
0
S m cc tr ca 
()y f x

A.
2
. B.
1
. C.
3
. D.
0
.
Câu 63 : H
21
1
x
y
x
 th
C
. Vit p tuyn ca
C
tm
2;5P
A.
3 11yx
B.
3 11yx
C.
1 13
33
yx
D.
1 13
33
yx
Câu 64 : H
21
1
x
y
x
 th
C
. Vip tuyn ca
C
tm
4;3Q
A.
3 11yx
B.
3 11yx
C.
1 13
33
yx
D.
1 13
33
yx
Câu 65 :  ln nht c
32
3 4, 2;1y x x x
t c t ?
A.
0x
B.
1x
C.
2x 
D.
2x
Câu 66 (THPT Trần Hƣng Đạo – Ninh Bình) : Cho hm s
4 2 4
2 2 .y x mx m m
V no
ca
m
 th
m
C
im cc tr, ng thi 3 im cc tr  to thnh mn
ng 2.
A.
5
4m
.
B.
16m
.
C.
5
16m
.
D.
3
16m 
.
Câu 67 : Bng bi  sau:
74
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
x
-
-1
+
y’
+
0
+
y
-
1
+
A.
32
3 3 2y x x x
B.
32
34y x x
C.
32
3 4 2y x x x
D.
42
22y x x
Câu 68 : Cho 
3
3 ( )
4
x
y x C
. H s p truyn tm
()KC

23
K
x

A.
5
B.
7
C.
6
D.
8
Câu 69 : Cho 
2
44
()
1
xx
yC
x

. H s p truyn tm
()KC

2
K
x

A.
0
B.
7
C.
3
D.
1
2
Câu 70 : Cho 
3
2
22
3
x
y x mx
  s 
nh
A.
0
B.
13
3
C.
11
3
D.
1
2
Câu 71 (I AMSTERDAM) :  ca tham s m   th

4 3 2
2016y mx m x
m cc tr?
A.
0m
B.
0m
C.
\{0}m
n t ca m
Câu 72 (I AMSTERDAM) : Trong tt c  ca tham s m  
s
32
1
3
y x mx mx m
ng bi
,
 nh nht ca m 
A. 4
B. 1
C. 0
D. 1
75
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 73 (I AMSTERDAM) : Trong 
21
( ).
1
x
yC
x
H s 
ca tip tuyn v th (C) sao cho tip tuyc Ox, Oy ln lt tm A, B
tho 
4OA OB

A.
1
4
B.
1
4
C.
1
4
hoc
1
4
D. 1
Câu 74 (I AMSTERDAM) : Trong gm cng tim cn ca
 th  ng thng
( ): ?d y x
A.
21
3
x
y
x
B.
4
1
x
y
x
C.
21
2
x
y
x
D.
1
3
y
x
Câu 75 : 
42
1 ( )y x mx m C
. Vi m ca tham s  th 
qua mm K c 
A.
3;0
B.
1;2
C.
0;2
D.
1;0
Câu 76 :  (C) :
24
1
x
y
x

 th  

A. 4 B. 6
C. 8 D. 2
Câu 77 :  (C) :
32
3 9 3y x x x
. Trong mi tip tuyn v th p tuy
h s  nhkmin
A. 1 B. 6
C. 12 D. 9
Câu 78 :  (C) :
21
1
x
y
x
m H thu th   H
n tim cng bng 3 ln kho n tim c
A.
4;2
hay
0;2
B.
5;2
hay
2; 1
C.
4;3
hay
2; 1
D.
4;3
hay
0;2
Câu 79 :  (C) :
21
1
x
y
x
. Gm thu th   bng 2.
Di th Vi A(0;1), B(3;2)
A. 1 B. 6
C. 12 D. 9
76
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 80 :  (C) :
21
1
x
y
x
. Gm thu th  
bDi  th i A(1;1), B(3;2)
A. 1 B. 3
C. 4 D. 5
Câu 81 :  (C) :
1
2
mx
y
xm
 tham s   ng kho

A. 1 B. Vi mi s thc m
C. 2 D. 3
Câu 82 :  (C) :
1
2
mx
y
xm
 tham s   th  m hai
ng tim cn c th 
21
( ')
1
x
yC
x
A. 5  m.
C. 1 D. 3
Câu 83 :  (C) :
2
2 6 4
2
x m x
y
mx
 tham s   th  
m A(1;1)
A. 1 B. 0
C. 2 D. 3
Câu 84 : Cho  (C) :
32
3 2 ( )y x x C
. H s p tuyn tm A thu th 
th
'' 0
A
yx

A. 3 B. 0
C. 4 D. 3
Câu 85 :  (C) :
32
3 9 2 ( )y x x x C
. H s p tuyn tm M thu th
 th
'' 0
M
yx

A. 6 B. 8
C. 10 D. 12
Câu 86  c) : m c th
4
:
1
x
Cy
x

ng thng
:1yx
.
A.
0;1
. B.
2;3
.
C.
1;2
. D.
1;3
.
Câu 87  c) : 
2
41
21
xx
y
x

. Tim cn ngang
c th  ng trnh l
77
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
A.
2.y
B.
1
.
2
y 
C.
1.y
D.
1, 1.yy
Câu 88 : Cho chuyn ca mt chnh b
32
3 9 2 , ;S t t t m s
. Vn tc ca ch t u chuyng.
A.
9/ms
B.
8/ms
C.
9/ms
D.
8/ms
Câu 89 : Cho chuyn ca mt chnh b
32
3 9 2 , ;S t t t m s
. Gia tc ca ch t u chuyng.
A.
2
12 /ms
B.
2
12 /ms
C.
2
10 /ms
D.
2
10 /ms
Câu 90 : Cho chuyn ca mt chnh b
32
3 9 2 , ;S t t t m s
. Thm tmax  vn tc chm ci ?
A. 1 B. 2
C. 3 D. 4
Câu 91 (THPT Phng :  th c
42
2y x x
ct tri bao
m?
A. 0. B. 2.
C. 4. D. 3.
Câu 92 (THPT Phng : 
()y f x
nh   th ng cong trong
 m cc tiu c th 
()y f x

A.
(0; 2)M
B.
0x
C.
2y 
D.
2x 
Câu 93 (THPT Phng :

3
3y x x
. M 
 ng bing
1;1
.
 nghch bi .
 ng bi .
 th  i xng qua gc t.
Câu 94 : Gm M thu th 
21
()
1
x
y f x C
x

 x0 0 
nghim c
0
4. ' 3 0fx
 x0 :
A. 1 B. 2
C. 3 D. 4
x
y
2
2
-2
-1
1
-2
O
78
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 95 : Cho 
32
3 2 ( )y f x x x C
. Gm cc tr c
S∆HAB i H(1;1) ?
A.  B. 2 
C. 3  D. 4 
Câu 96 : Cho 
21
()
4
x
y f x C
x

.Gm hai tim cn c th B(0;-3)
C(2;m)   S∆ABC = 2
A.
1
2
B.
3
2
C.
2
D.
2
3
Câu 97 : Cho 
3
2y f x x x

 
 th  ct Oy t bng 2
C.  th  ct Ox t bng 1
D. C 
Câu 98 ng Quc H nh):
 d th 
0, 0
ax b
y ac ad bc
cx d
M 
A.
0ad

0bd
.
B.
0ad

0ab
.
C.
0bd

0ab
.
D.
0ad

0ab
.
Câu 99 : Cho 
32
2 12 13y x ax x
 th  
th m cm cc tiu u trc tung ?
A.
0a
B.
1a
C.
1a 
D. C u sai.
Câu 100 : Gm ci, cc tiu c th  (C) :
32
32y x x

an th nh nhvới I(a;2a)) :
79
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
A.
3
B.
6
5
C.
5
6
D.
8
Câu 101 (THPT  HN ) : t c  ca tham s thc
m
  th 
2
2
2
2
xx
y
x x m


m cng.
A.
1m

8m 
.
B.
1m 

8m
.
C.
1m

8m 
.
D.
1m

8m 
.
Câu 102 (THPT  HN ) :

ax b
y
xc
 th nh hnh v 
 ca
2.a b c
A.
1
.
B.
2
.
C.
0
.
D.
3
.
Câu 103 : Gm ci, cc tiu c th  (C) :
32
32y x x

an thng IB đạt giá trị nhỏ nhất khi (với I(a;2a)) :
A.
2
5
a 
B.
3
5
a
C.
1a
D.
4a
Câu 104 : V a tham s  th 
4 2 2
22y x m x
m cc tr ?
A.
2m 
B.
2m 
C.
0m
D.
1m
Câu 105 : Gi s  th  (C) :
4 2 2 6
22y x m x m
m cc tr
A (n
A. ng

C. Khom cc ti
2
BC B
dx
 u
Câu 106 : Gi s  th  (C) :
4 2 2 6
22y x m x m
m cc tr
3
2
O
1
3
2
x
y
80
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
A (n
ng

C. Khom cc ti
BC C B
d x x
 u
Câu 107 :  sau (C) :
42
x 10x 3y
. Khom cc ti
 M
2

A.
5
B.
1
2
C.
20
D.
55
Câu 108 :  sau (C) :
42
x 2 2 x 6, 2y m m
. Khom cc tiu
 tham s 
A.
6
B.
3
C.
10
D.
5
Câu 109 :  sau (C) :
3
2
2 3 5
3
x
y x x
. Tip truyn tm cc tiu c th 
A. Song song vng thng x = 1
B. Song song vi tr
 s 
 s 
Câu 110 : Ch sai.  sau (C) :
32
69y x x x
. Gp truyn tm cc
tiu c th .
A. d song song vng thng y = 3
B. d song song vi tr
ng thng x = 5
D. d ct Oy ti O
Câu 111 :  
32
22y x x x
(C). Gi
12
,xx
 m M, N 
p tuyn ca (C) vuông góc vng thng
2017yx
. 
22
12
xx
A.
4
3
B.
4
9
C.
10
3
D.
10
9
Câu 112 :  
32
32y f x x x
(C). Gi
12
,xx
 m A, B 
p tuyn ca (C) h s  3.
81
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017

12
xx
A.
5
B.
1
C.
2
D.
3
Câu 113 (SGDĐT Phú Thọ) : 
y f x
ng
; 

bng bi sau:
M sai?
A. 
y f x
m cc tr.
B. 
y f x
m cc tr.
C.  ng bing
;1
.
D.  nghch bing
1;1
.
Câu 114 (THPT  Vinh HN ) : 
y f x

\0

mi khong bi sau
M 
A.  ln nht c 
2
.  th  ng tim cng.
 c tr.  t cc tiu ti
0x
.
Câu 115 (THPT  Vinh HN ) : Hiu s gi c cc tiu c
32
31y x x

A.
2
.
B.
6
.
x

0
1

y
0
y
2


1

x

1
1

fx
0
0
fx

2
1

82
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
C.
4
.
D.
8
.
Câu 116 : 
32
34y x x
ng thm cc tr c 

A.
1;6M
B.
1;5M
C.
2;8M
D.
0;6M
Câu 117 : ng thng y = m ct   (C):
42
242y x x
tt khi :
A.
04m
B.
4m
C.
0m
D.
4m
Câu 118 :  nh nh ln nht c
3
33f x x x
n
3
3;
2




A. 6
B. -10
C. 4
D. -35
Câu 119 : 
21
1
x
y
x
 th ng thng
:3d y x m
. V a m
t (C) tt A, B sao cho trOAB nng thng
2 2 0xy
A.
m
B.
2m
C.
11
5
m
D.
11m
Câu 120 : 
42
2 1 1 (1)y x m x m
. V  m
cc tr ?
A.
m
B.
m
C.
1m 
D.
8m 
Câu 121 : 
21
2
x
y
x
 th ng thng
:d y x m
. V a m
t (C) tt A, B ?
A.
m
83
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
B.
m
C.
4 12 4 12m
D.
4 12
4 12
m
m


Câu 122 : 
23
2
x
y
x
 th (C). Gi M, N lm n th 
 lm ca hai tim c
MIN
A.
2
51
B.
2
51
C.
1
3
D.
1
17
Câu 123 : 
3
2
x
y
x
 th ng thng
:d y x m
. V a m
t (C) tt A, B nm v 2 c tung
A.
m
B.
m
C.
3
2
m 
D.
3
2
m 
Câu 124 : 
2
3
x
y
x
 th  th  n
tim cn ngang bng 5 ln kho n tim c
A.
4;6
B.
5;6
C.
2; 4
D. C 
Câu 125 : 
32
31y x x
p tuyn c th (C) tm thuc
 b
A.
32yx
B.
3 11yx
C.
1 13
33
yx
D.
1 13
33
yx
Câu 126 : 
21
1
x
y
x
 th m thu bng 2. Gi
p tuyn vi (C) ti M. Ch
A. ng thi IM
B. ng thng d song song vi IM
84
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Cu sai
D. , B sai
Câu 127 : 
3
35y x x
ng thm cc tr c th  
 
A.
2
B.
1
C.
2
D.
5
Câu 128 : 
3
( ) :
21
x
Cy
x
. Vip tuyn vi (C) bit tip tuyn ct
trc Ox, Oy lt tng trung trc cc t
A.
3
2
yx
B.
5
4
yx
C. C 

Câu 129 : 
1
1
x
y f x
x

 th  s p tuyn t
  ca k + 1 
A.
1
B.
0
C.
3
D.
1
Câu 130 : 
31
2
x
y
x
 th m thu n
ng thng
( ):3 4 1 0xy
bng
12
5

A.
(1; 2)A
B.
26 15
;
34
B



C.
7
2;
4
C



D. C A, B, C
Câu 131 : 
32
94y x mx x
 a tham s   th tn ti mt cp
i xng nhau qua gc t ?
A.
0m
B.
0m
C.
0m
D.
m
Câu 132 (THPT Nguyễn Diêu – Bình Định) :  ca tham s  
x
y
xm
ng bi
2 ( ; )
A.
0m
B.
0m
C.
2m 
85
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
D.
2m 
Câu 133 (THPT Nguyễn Diêu – Bình Định) : S ng tim cn c th 
2
1
4
x
y
x

A.
1
B.
2
C.
3
D.
4
Câu 134 (THPT Nguyễn Diêu – Bình Định) : 
32
1
1
3
y x mx x m
m 

,AB

22
2
AB
xx
A.
1m 
B.
2m
C.
3m 
D.
0m
Câu 135 (THPT Nguyễn Diêu – Bình Định) :  
bng bi ng
nh sai ?
A.  
2
cc tr.
B.   ci bng
3
.
  ln nht b nh nht bng
1
.
D.  t cc tiu ti
0x
.
Câu 136 : 
3
2
x
y
x
 th m thuhoành độ là 3 m
I(1; - 2). T m N ni xng v
A.
(1; 2)
B.
26 15
;
34



C.
5;2C
D.
1; 4
Câu 137 : 
3 2 2 3
3 3 1y x mx m x m
 ca tham s   c tr

A.
m
B.
11m
C.
21m
D.
11m
Câu 138 : 
31
2
x
y
x
 th m thu bng 6. Kho
ng thng
( ):3 4 1 0xy

A.
12
5
B.
13
5
--
+
∞
-
∞
3
+
--
+
∞
-1
-
∞
0
0
2
0
y
y'
x
86
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
C.
14
5
D. C A, B, C
Câu 139 : 
3
2
2 1 3
3
x
y mx m x
. V a tham s  c
tr
A.
1m
B.
11m
C.
21m
D.
11m
Câu 140 : 
21
1
x
y
x
(C). Gi M, N thu l1 2 
tip tuyn v th (C) ct Ox, Oy lt t
1 2 
A.
10
B.
16
C.
18
D.
36
Câu 141 : 
32
6 9 ( )y f x x x x C
ng thm cc
tr c s 
A.
2
3
B.
3
2
C.
2
D.
3
Câu 142 (THPT Nguyễn Đình Chiểu – Bình Định) :  th  
A.
42
23y x x
. B.
42
2y x x
. C.
42
21y x x
. D.
42
21y x x
.
Câu 143 (THPT Nguyễn Đình Chiểu – Bình Định) : 
32
32y x x
 cc
tiu
CT
y

A.
2
CT
y
.
B.
2
CT
y 
.
C.
4
CT
y 
.
D.
6
CT
y
.
y
x
-1
-1
2
1
O
1
87
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 144 (THPT Nguyễn Đình Chiểu – Bình Định) : ng thng
31yx
c th 
s
32
2 1y x x
t
00
( ; )xy

A.
0
1y
.
B.
0
2y
.
C.
0
2y 
.
D.
0
1y 
.
Câu 145 :  c 
42
3
2018
7
y mx x
m cc tr 
A.
0m
B.
0m
C.
0m
D.
0m
Câu 146 :  th 
A.
3
yx
B.
3
1yx
C.
3
1y x x
D.
3
1yx
Câu 147 :  th 
A.
32
32y x x
B.
32
32y x x
C.
32
22y x x
D.
32
22y x x
Câu 148 :  th 
A.
32
69y x x x
B.
32
69y x x x
C.
32
69y x x x
D.
32
69y x x x
Câu 149 :  th 
A.
2
11y x x
B.
2
11y x x
C.
2
12y x x
88
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
D.
2
12y x x
Câu 150 :  th 
A.
42
23y x x
B.
42
23y x x
C.
42
23y x x
D.
42
3y x x
Câu 151 : 
42
y ax bx c
 th 
151.1  c
A. 0 B. 3/2 C. -3/2 D. 1
151.2 H s p tuyn t
A. 0 B. 3/2 C. -3/2 D. 1
Câu 152 : Nhn bi s
3
3y x x
 th 
Hình 1 Hình 2 Hình 3 Hình 4
   
89
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 153 (THPT Chuyên Lê Khiết – Quảng Nam) :  th di  
A.
1
21
x
y
x
.
B.
3
21
x
y
x
.
C.
21
x
y
x
.
D.
1
21
x
y
x
.
Câu 154 : Nhn bi th  
A.
32
22y x x
B.
32
32y x x
C.
2
32y x x
D.
32
32y x x
Câu 155 : Nhn bi
1
2
x
y
x
 th 
Hình 1 Hình 2 Hình 3 Hình 4
   D. 
Câu 156 : Nhn bi
42
2y x x
 th 
Hình 1 Hình 2 Hình 3 Hình 4
   
x
y
1
2
1
2
90
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 157 : Nhn bi th 

A.
2
1
x
y
x
B.
1
x
y
x
C.
2
1
x
y
x
D.
2
1
x
y
x
Câu 158 : T  th 
y f x
cho 
nhn bit 2 tim cn:
A. Tim cng
1,x 
tim cn ngang
2y
B. Tim cng
0,x
tim cn ngang
1y
C. Tim cng
2,x
tim cn ngang
1.y 
D. Tim cng
1,y 
tim cn ngang
2.x
Câu 159 :  th ca m trong b c li bn
phng n A, B, C, D d  
A.
23
1
x
y
x
.
B.
21
1
x
y
x

.
C.
21
1
x
y
x
.
D.
21
1
x
y
x
.
Câu 160 : s
78mx m
y
xm


m
  ng bing khonh ca

A.
81m
. B.
0
1
m
m
.
C.
30m
. D.
30m
.
91
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN
2017
Câu 161 : 
y f x
n
2;2
 th 
n
2;2
nh sau: Kh
A.
2;2
max 2f x f
. B.
2;2
max 2f x f

.
C.
2;2
min 1f x f
. D.
2;2
min 0f x f
.
Câu 162 : t c  ca
m

3 2 2
1
11
3
y x mx m m x
c 
1x
A.
2m 
. B.
1m 
.
C.
2m
. D.
1m
.
Câu 163 : t c  ca
m
 
12mx
y
xm

ng bing kho nh
A.
21m
. B.
1
2
m
m

.
C.
21m
. D.
1
2
m
m

.
Câu 164 :  th  
Chn mt kh
A.
32
31y x x
.
B.
3
2
1
3
x
yx
.
C.
32
2 6 1y x x
.
D.
32
31y x x
.
Câu 165 : t c  ca
m
  th 
42
2 2 1y x mx m
m
2;0N
A.
5
2
. B.
17
6
. C.
17
6
. D.
3
2
.
Câu 166 :  th ca m
trong b c li bn phng n A, B, C, D di
  
A.
42
81y x x
.
B.
42
81y x x
.
C.
32
31y x x
.
D.
3
2
31y x x
.
O
1
1
2
2
x
y
2
2
O
2
2
1
x
y
3
92
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – PHÉP TỊNH TIẾN
2017
KIẾN THỨC CĂN BẢN
Trong mặt phẳng Oxy, cho hàm số
y f x
có đô thị là (C) và x0, y0 là hai số dương tùy ý.
► Tịnh tiến (C) lên trên y0 đơn vị thì ta được đồ thị
0
y f x y
► Tịnh tiến (C) xuống dưới y0 đơn vị thì ta được đồ thị
0
y f x y
► Tịnh tiến (C) sang trái x0 đơn vị thì ta được đồ thị
0
y f x x
► Tịnh tiến (C) sang phải x0 đơn vị thì ta được đồ thị
0
y f x x
Ví dụ : Cho hàm số y = f(x) có đồ thị như hình
► Thì đồ thị hàm số y = f(x) + 1 ( lên trên 1 đơn vị )
PHẦN 11 : PHÉP TỊNH TIẾN
y = f(x)+1
93
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – PHÉP TỊNH TIẾN
2017
► Thì đồ thị hàm số y = f(x) - 1 ( xuống dưới 1 đơn vị )
► Thì đồ thị hàm số y = f(x - 1) ( sang phải 1 đơn vị )
► Thì đồ thị hàm số y = f(x + 1) ( sang trái 1 đơn vị )
y = f(x) -1
y = f(x - 1)
y = f(x + 1)
94
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – PHÉP TỊNH TIẾN
2017
BÀI TẬP TRẮC NGHIỆM PHẦN TỊNH TIẾN ĐỒ THỊ
Câu 1 : Cho đường cong (C) có phương trình :
3
yx
. Tịnh tiến (C) lên trên 2 đơn vị thì ta được đồ
thị của hàm số nào sau đây ?
A.
3
1yx
B.
3
2yx
C.
3
2yx
D.
3
2 2yx
Câu 2 : Cho đường cong (C) có phương trình :
3
2yx
. Tịnh tiến (C) sang trái 3 đơn vị thì ta
được đồ thị của hàm số nào sau đây ?
A.
3
32yx
B.
3
32yx
C.
3
3yx
D.
3
1 3yx
Câu 3 : Cho đường cong (C) có phương trình :
2
yx
. Tịnh tiến (C) lên trên 5 đơn vị, sau đó tịnh
tiến đồ thị nhận được sang trái 1 đơn vị thì ta nhận được đồ thị của hàm số nào sau đây ?
A.
2
26y x x
B.
2
12yx
C.
2
2 5yx
D.
2
2 4yx
Câu 4 : Cho đường cong (C) có phương trình :
21
3
x
y f x
x

. Tịnh tiến (C) sang trái 3 đơn vị
sau đó tịnh tiến xuống dưới 2 đơn vị thì ta được đồ thị hàm số nào sau đây ?
A.
2 3 1
2
x
y
x

B.
31
32
x
y
x

C.
7
y
x
D.
7
2
y
x
Câu 5 : Cho đường cong (C) có phương trình :
y f x
. Tịnh tiến (C) sang trái 1 đơn vị ta được
đồ thị hàm số
A.
1y f x
B.
1y f x
C.
1y f x
D.
1y f x
Câu 6 : Cho đường cong (C) có phương trình :
y f x
. Tịnh tiến (C) sang phải 3 đơn vị ta được
đồ thị hàm số
A.
3y f x
B.
3y f x
C.
3y f x
D.
3y f x
95
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – PHÉP TỊNH TIẾN
2017
Câu 7 : Cho đường cong (C) có phương trình :
y f x
. Tịnh tiến (C) lên trên 4 đơn vị ta được đồ
thị hàm số
A.
34y f x
B.
34y f x
C.
3y f x
D.
4y f x
Câu 8 : Cho đường cong (C) có phương trình :
y f x
. Tịnh tiến (C) xuống dưới 4 đơn vị ta được
đồ thị hàm số
A.
4y f x
B.
34y f x
C.
4y f x
D.
4y f x
Câu 9 : Cho đường cong (C) có phương trình :
y f x
. Tịnh tiến (C) xuống dưới 4 đơn vị sau đó
tịnh tiến lên trên 2 đơn vị ta được đồ thị hàm số
A.
4y f x
B.
32y f x
C.
4y f x
D.
2y f x
Câu 10 : Cho đường cong (C) có phương trình :
y f x
. Tịnh tiến (C) xuống dưới 4 đơn vị sau đó
tịnh tiến sang trái 2 đơn vị ta được đồ thị hàm số
A.
4y f x
B.
24y f x
C.
4y f x
D.
24y f x
Câu 11 : Hàm số
y f x
liên tục và nghịch biến trên
0;2
thì hàm số
3y f x
nghịch biến
trên
A.
3; 1
B.
3;4
C.
3;0
D.
3;5
Câu 12 : (THPT Cẩm Bình – HN) Nếu hàm số
y f x
đồng biến trên khoảng
1;2
thì hàm số
2y f x
đồng biến trên khoảng nào sau đây ?
A.
3;0
.
B.
2;4
.
C.
1;2
.
D.
1;4
.
| 1/96
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Phân dạng và phương pháp giải
trắc nghiệm Toán 12 Tập 3
Biện luận
Trị tuyệt đối
Tổng hợp
Tịnh tiến
BIÊN HÒA – Ngày 15 tháng 07 năm 2017
TÀI LIỆU LƯU HÀNH NỘI BỘ
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
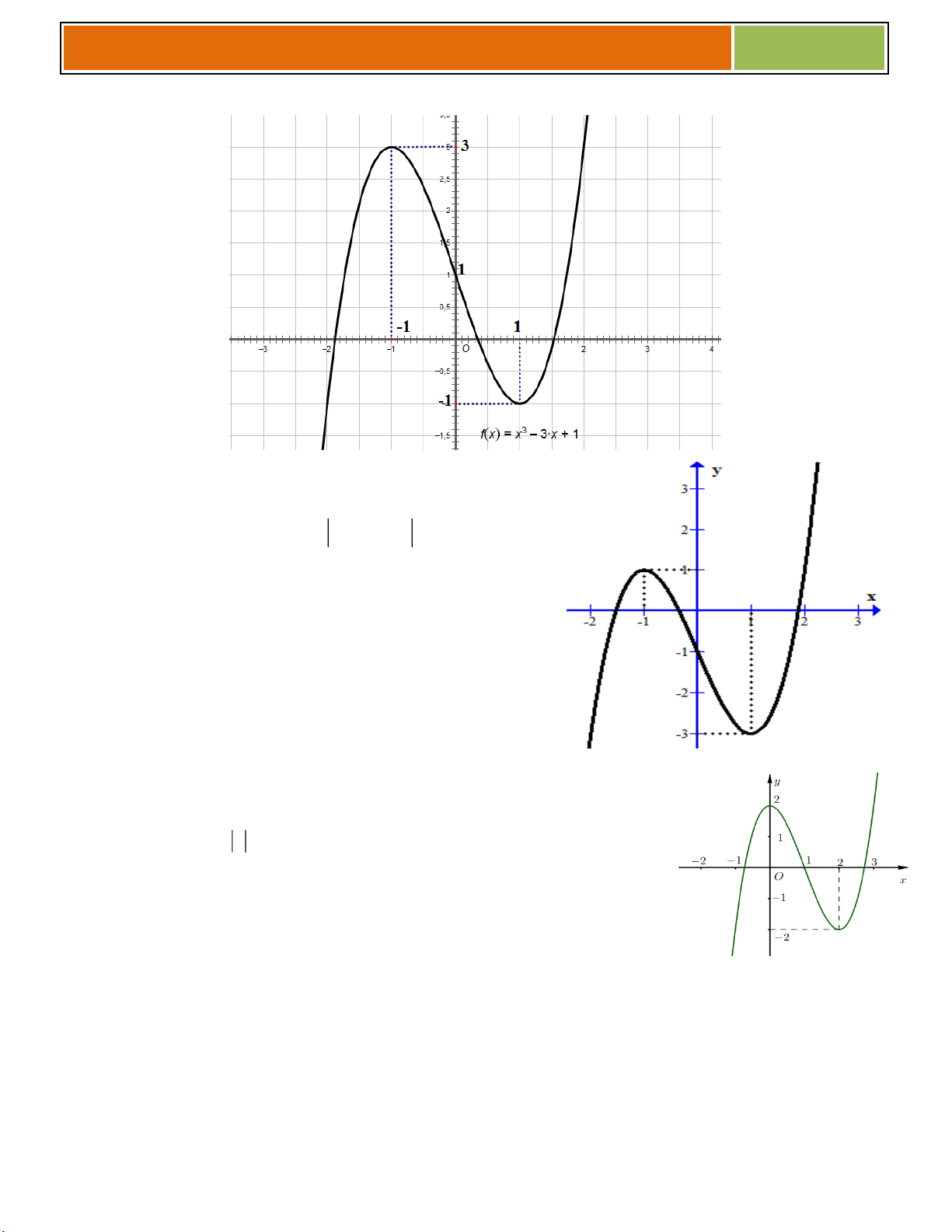
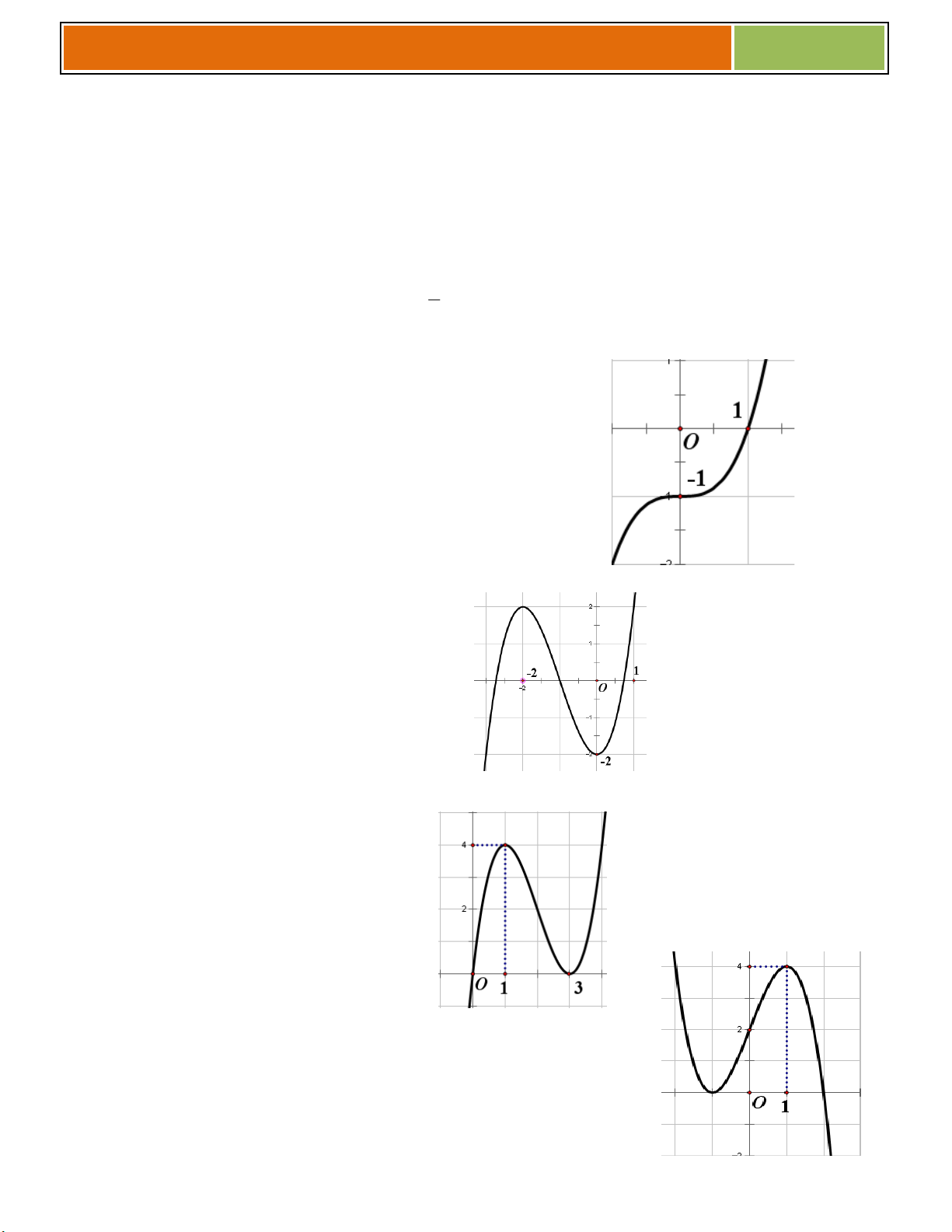
PHẦN 8 : BIỆN LUẬN NGHIỆM BẰNG ĐỒ THỊ
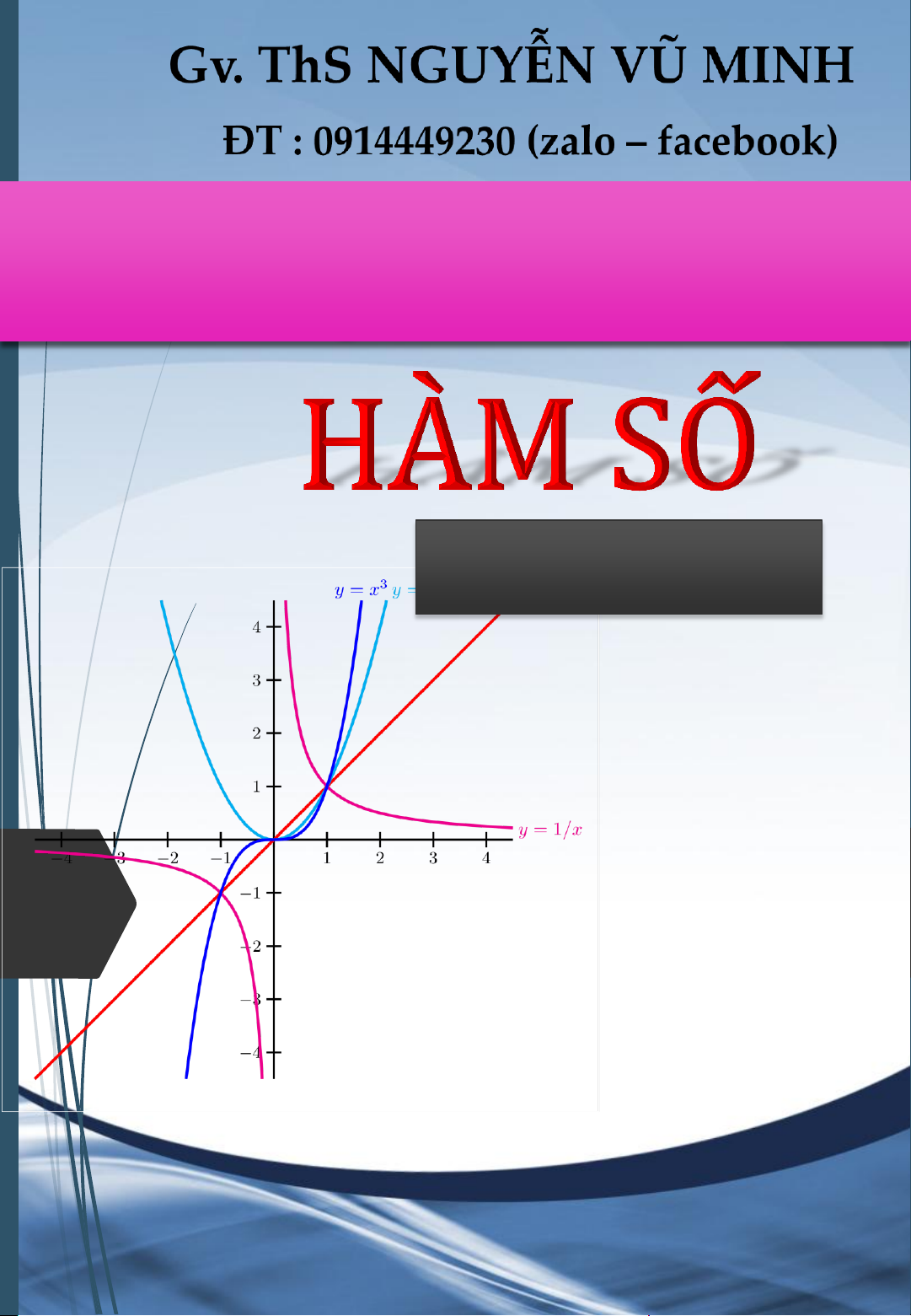
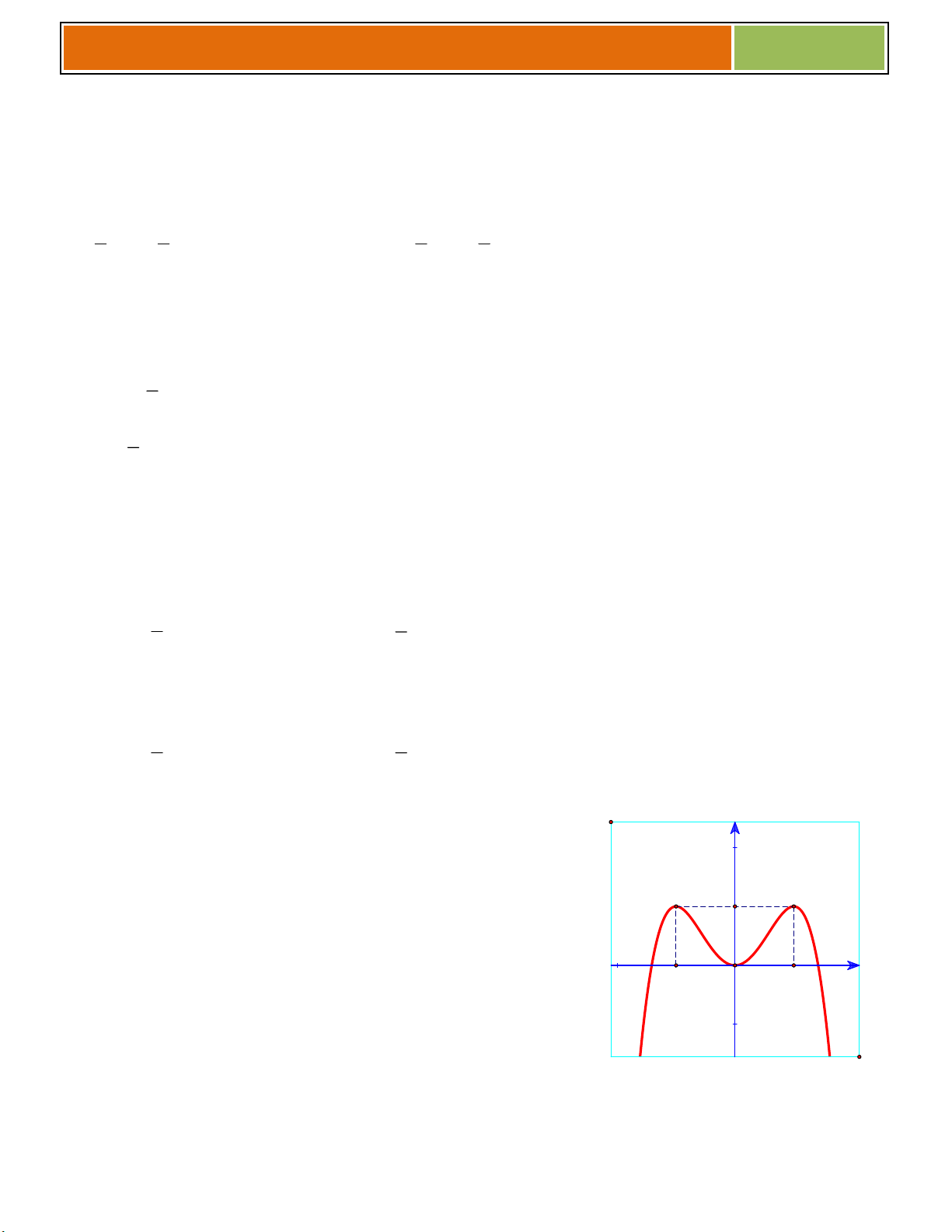
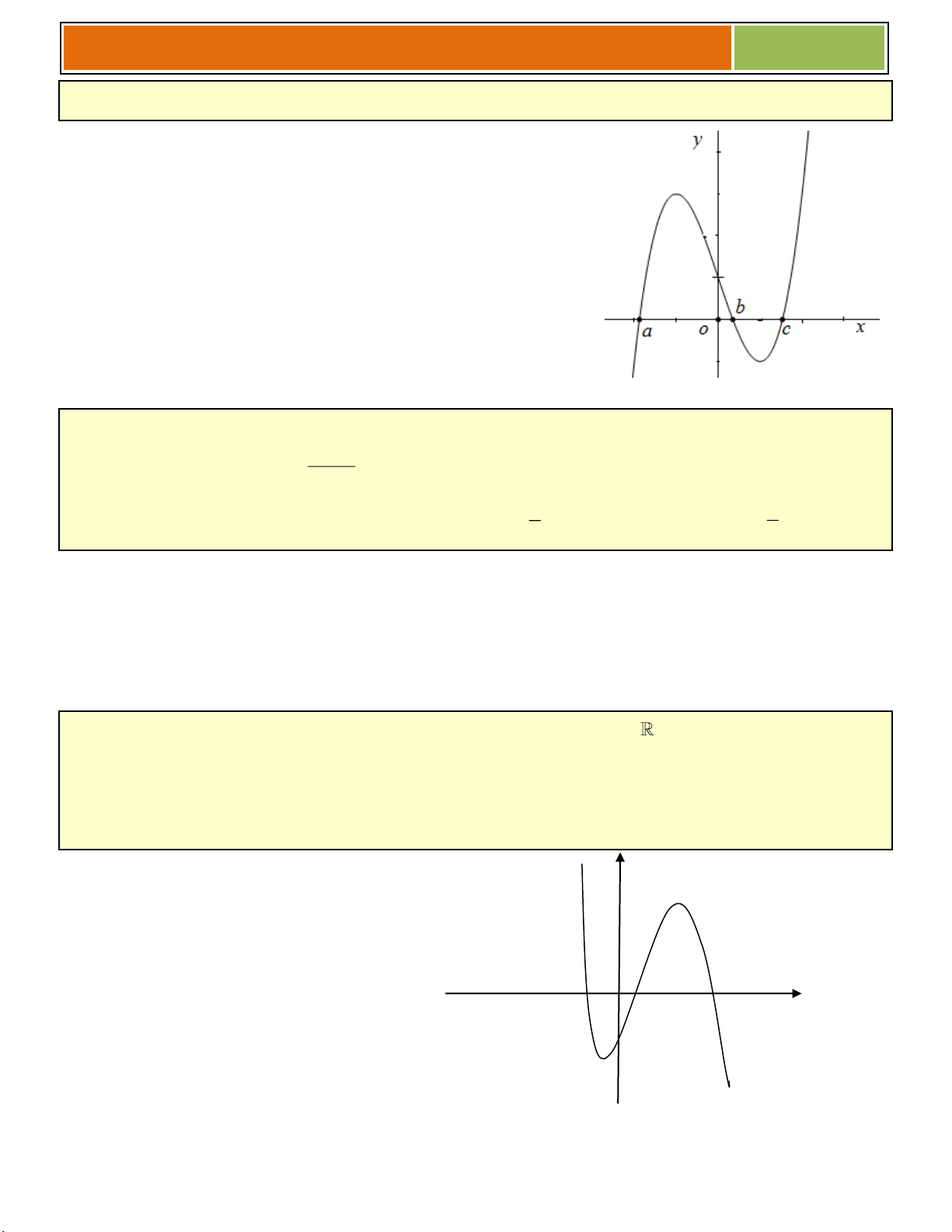
◙ Lý Thuyết : Ta xét bài toán sau đây :
Vẽ đồ thị (C) của hàm số y f (x) sau đó biện luận
theo tham số m số nghiệm của phương trình : ( h ; x m)  0 (♥)
☻ Ta đưa (♥) về dạng Trong đó f ( )
m là biểu thức theo m, không chứa x
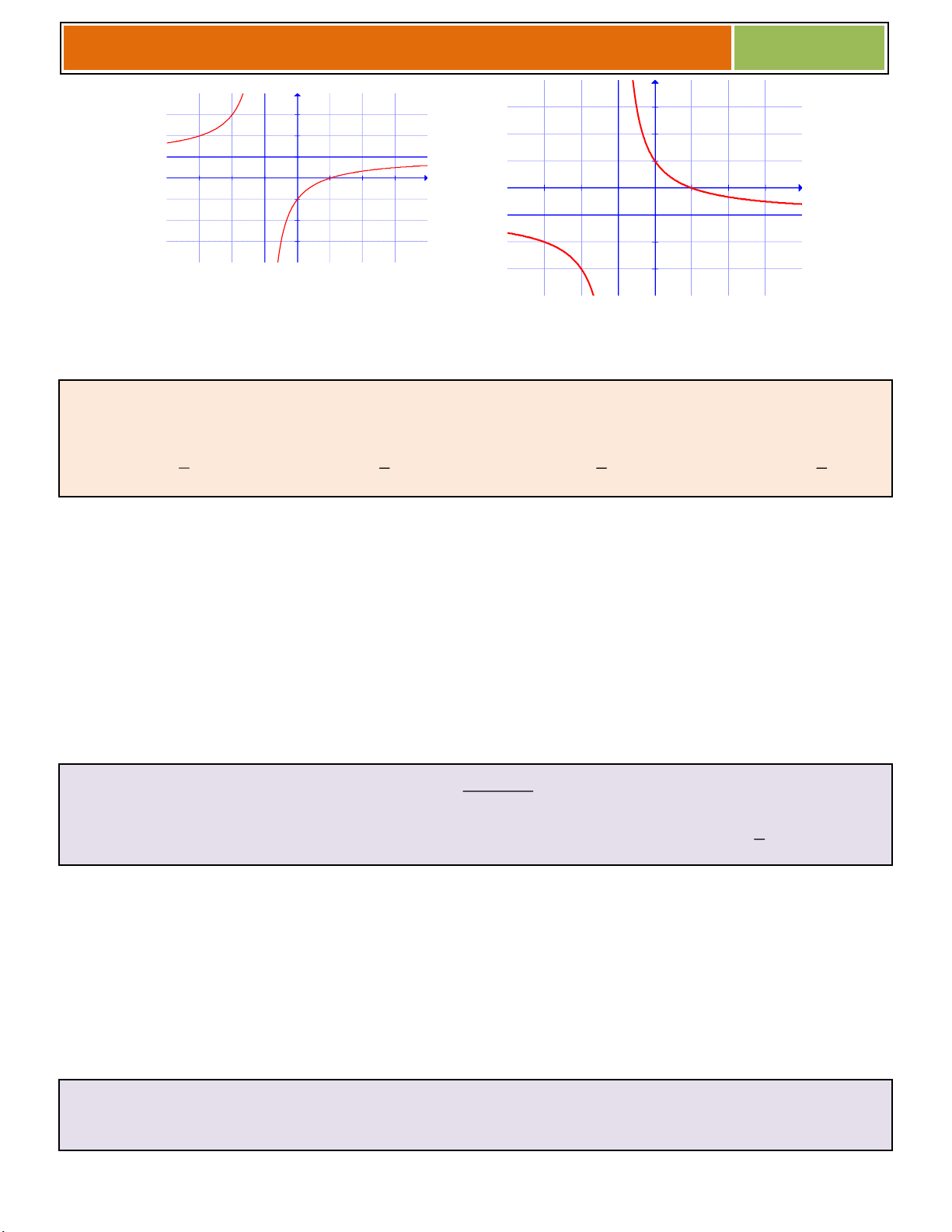
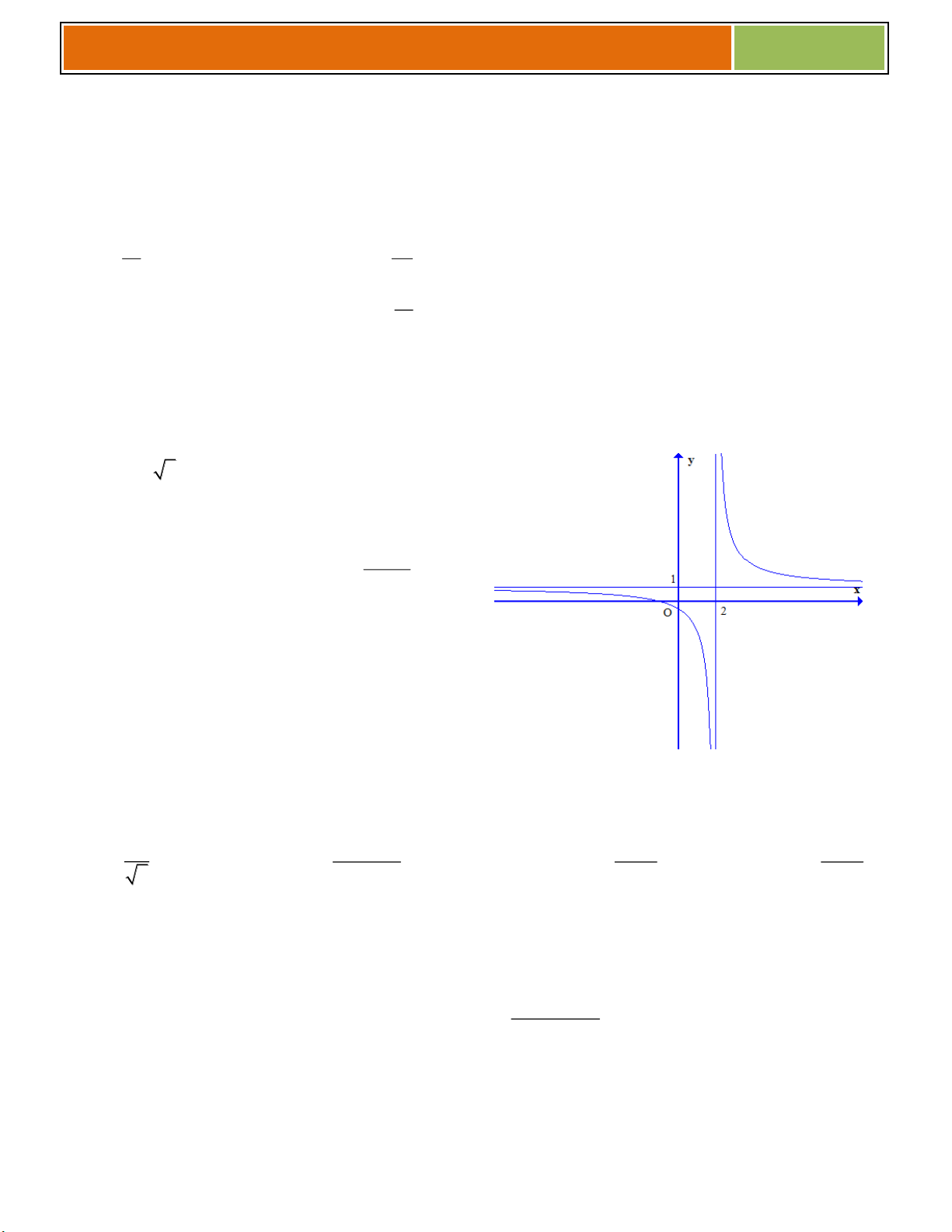
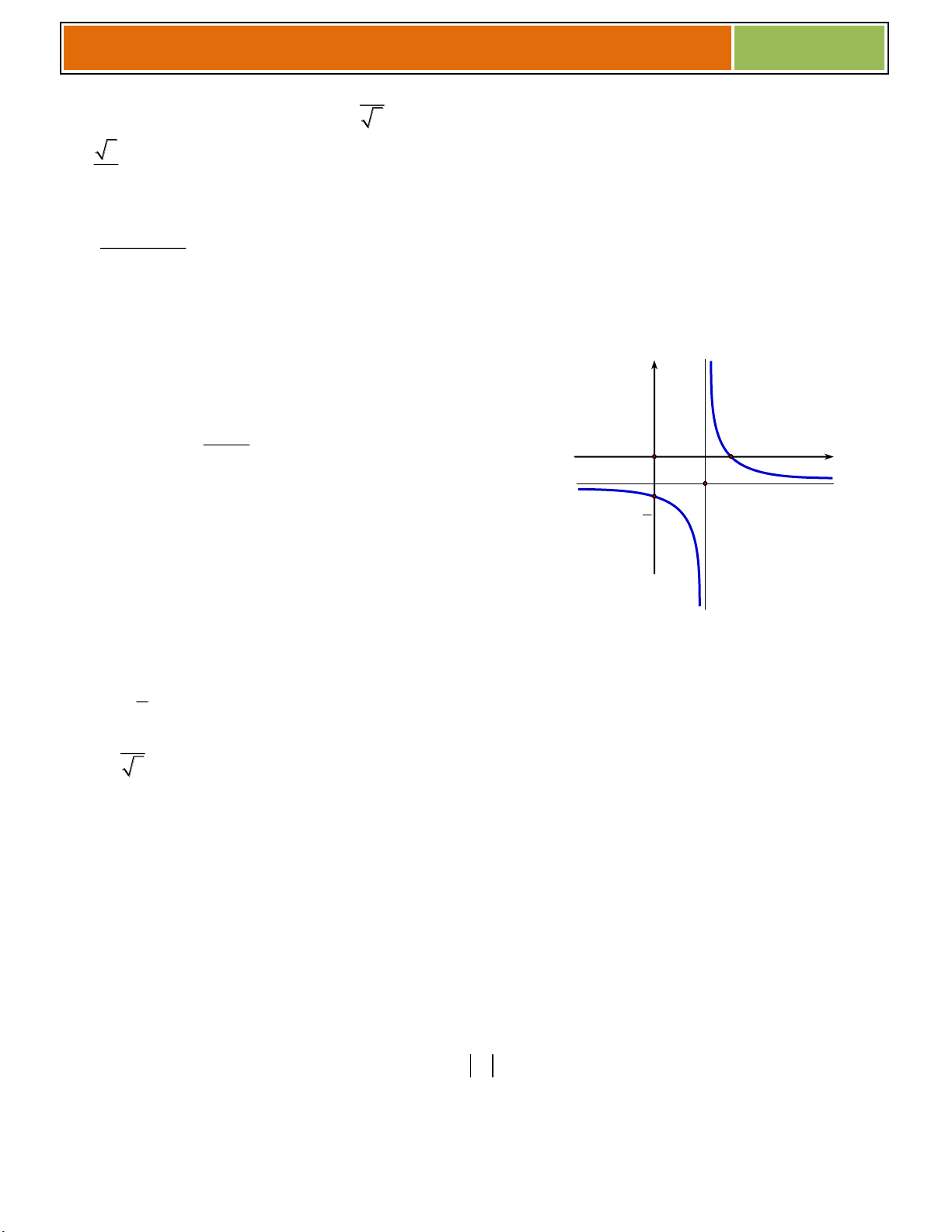
Số nghiệm của (♥) chính là số giao điểm của (C) và đường thẳng (D) y f ( ) m mà ta nhìn thấy
qua đồ thị ((D) ............................. Ox ) _y
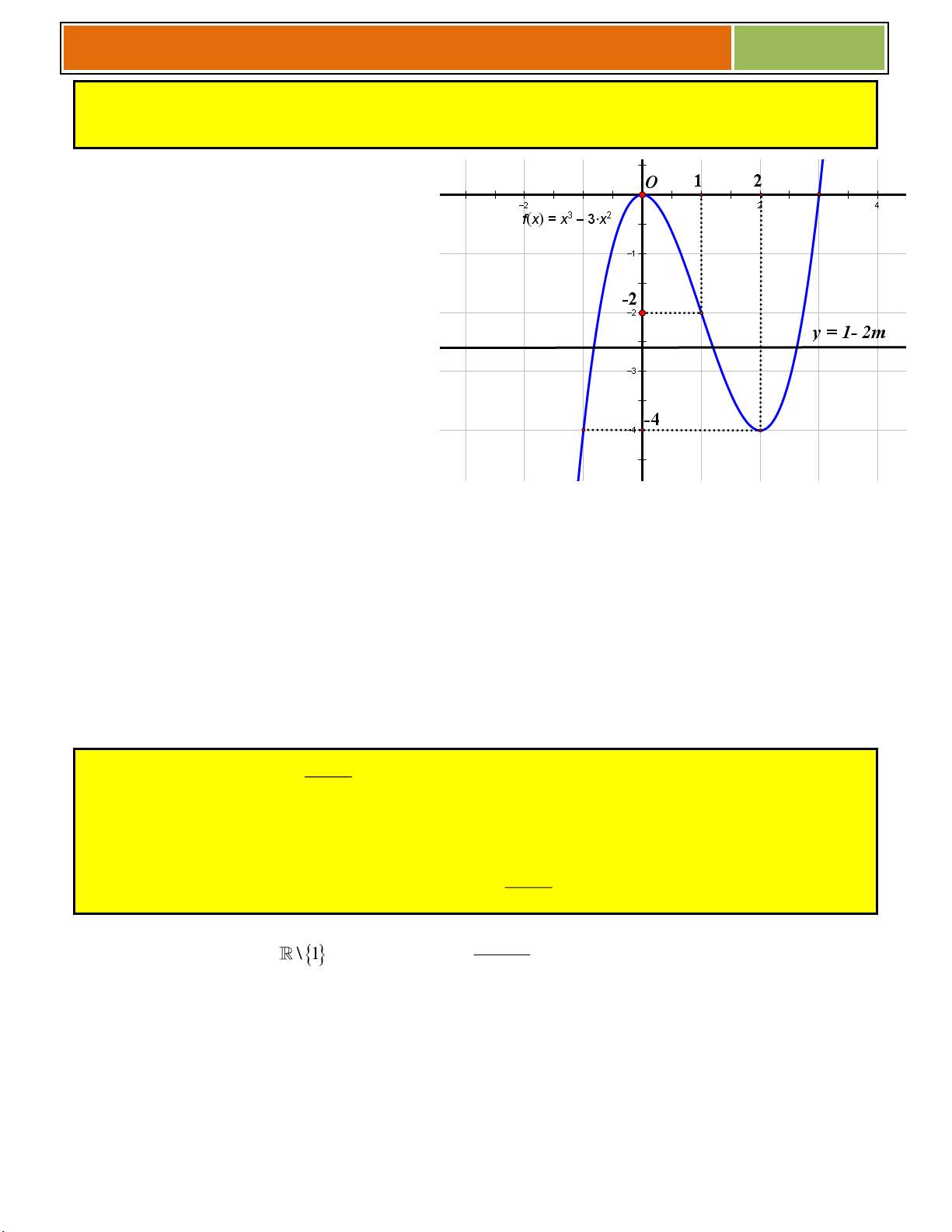
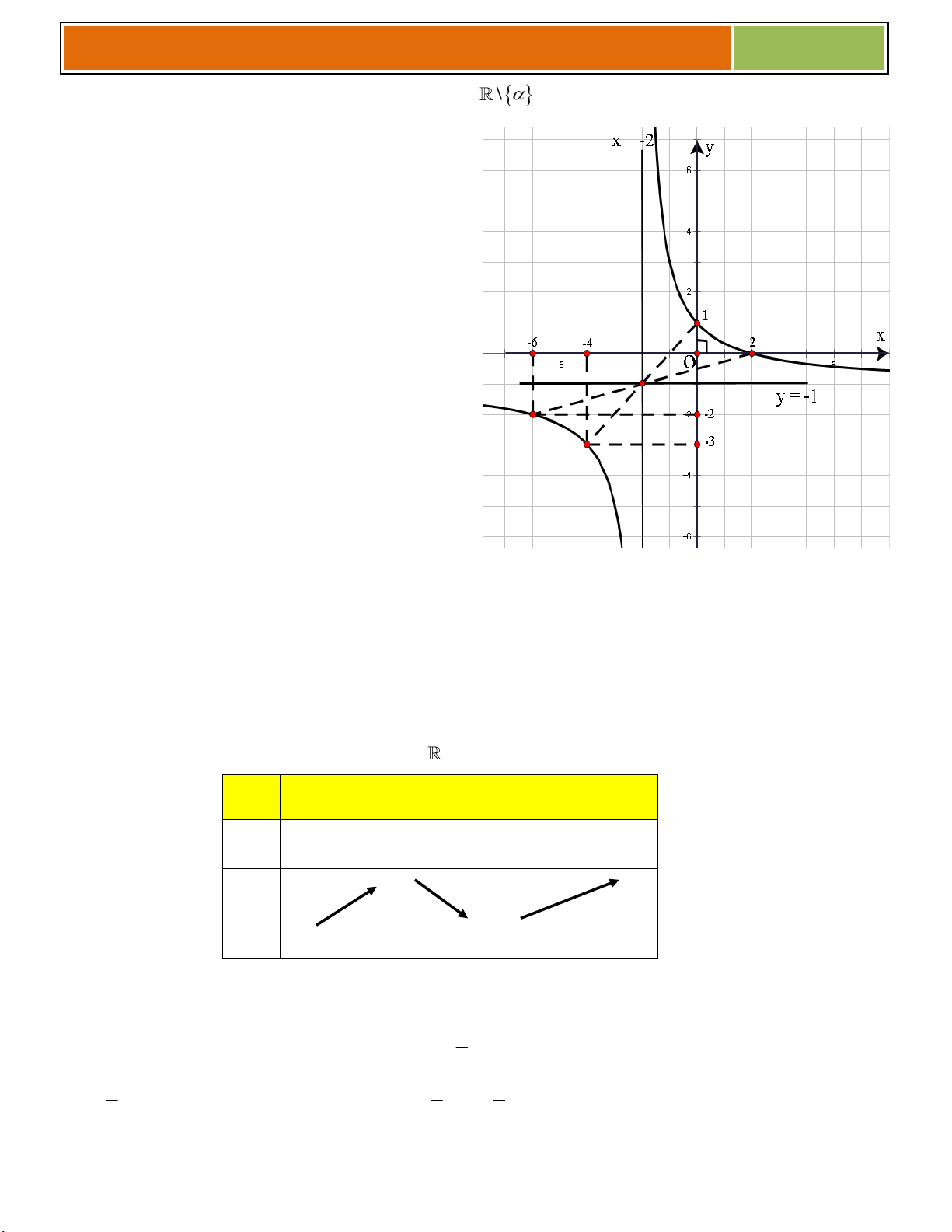
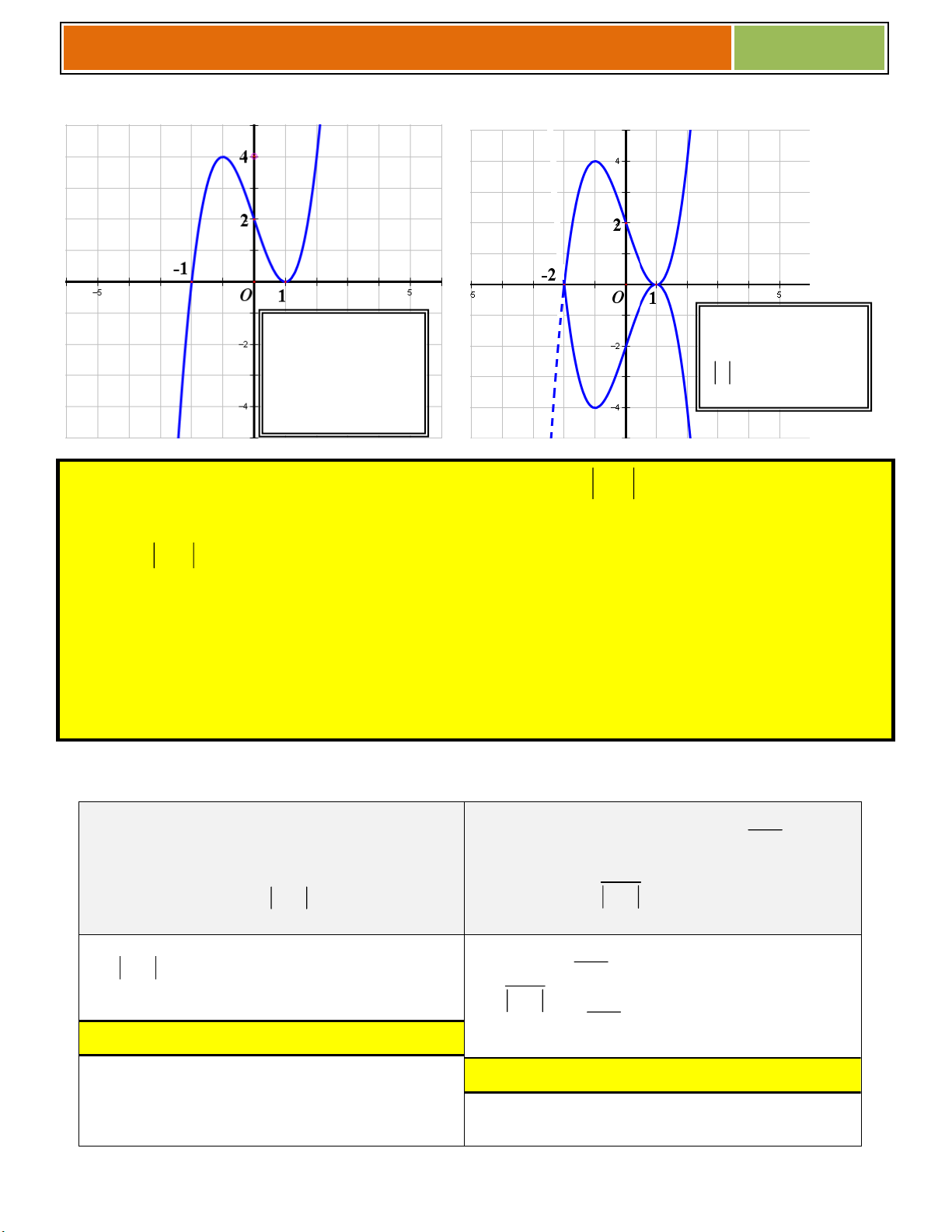
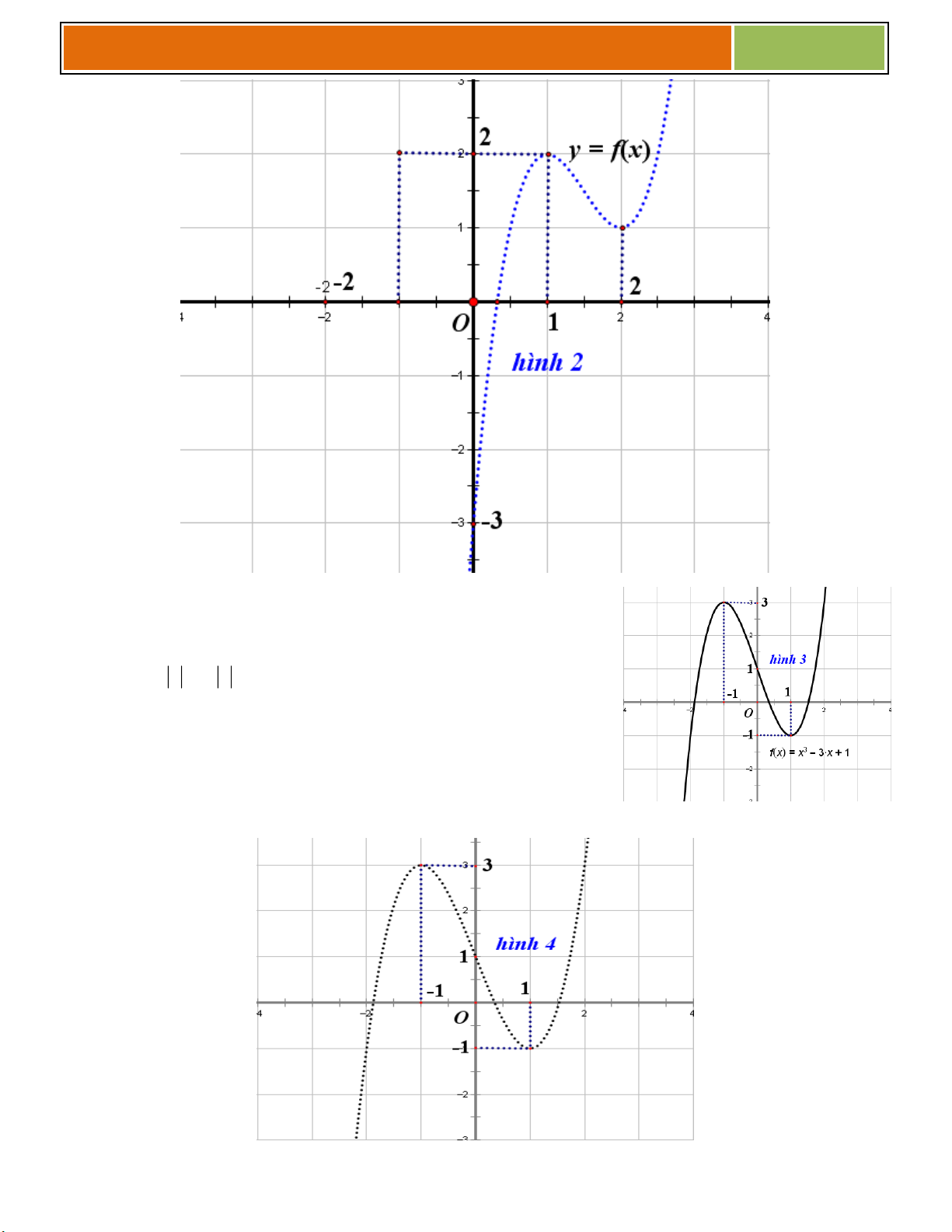
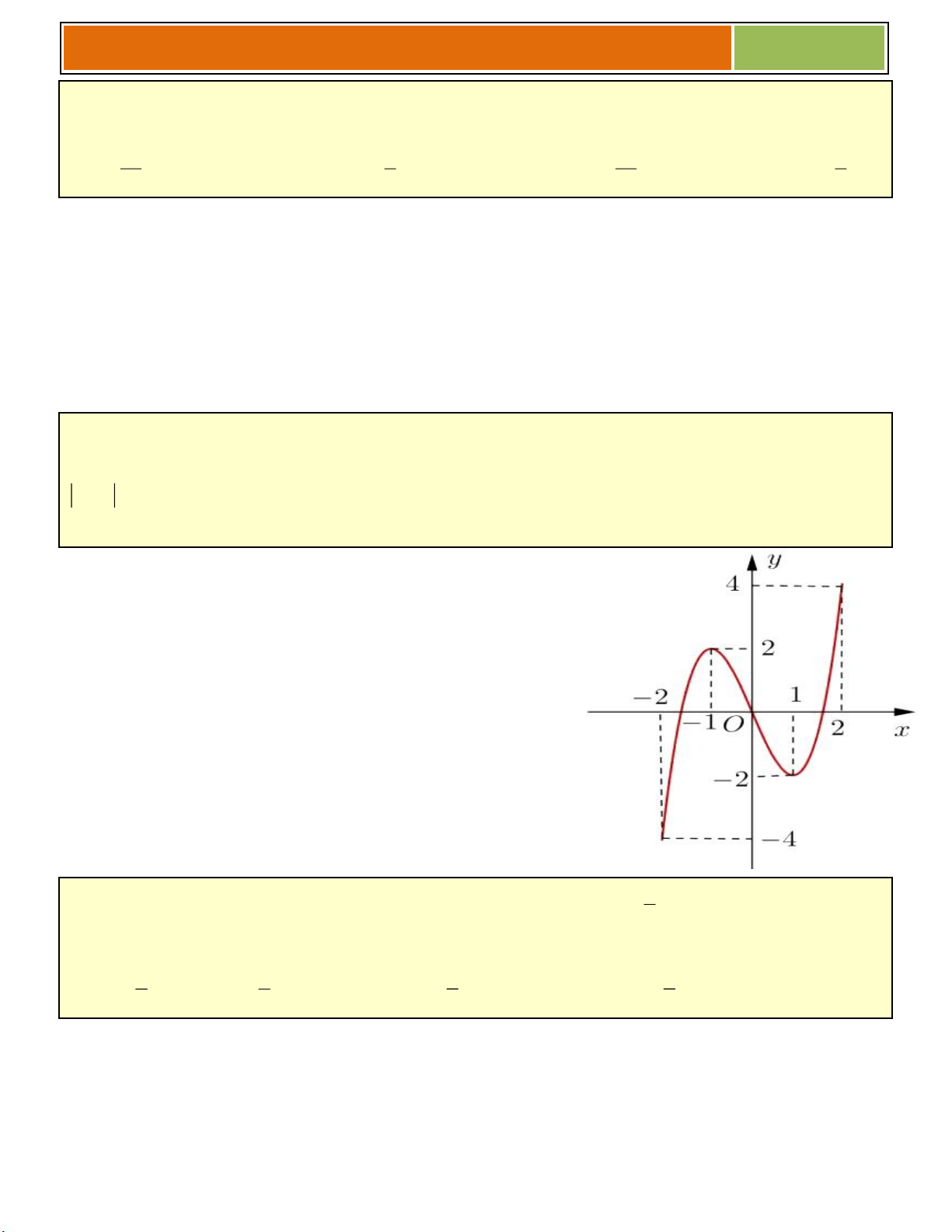
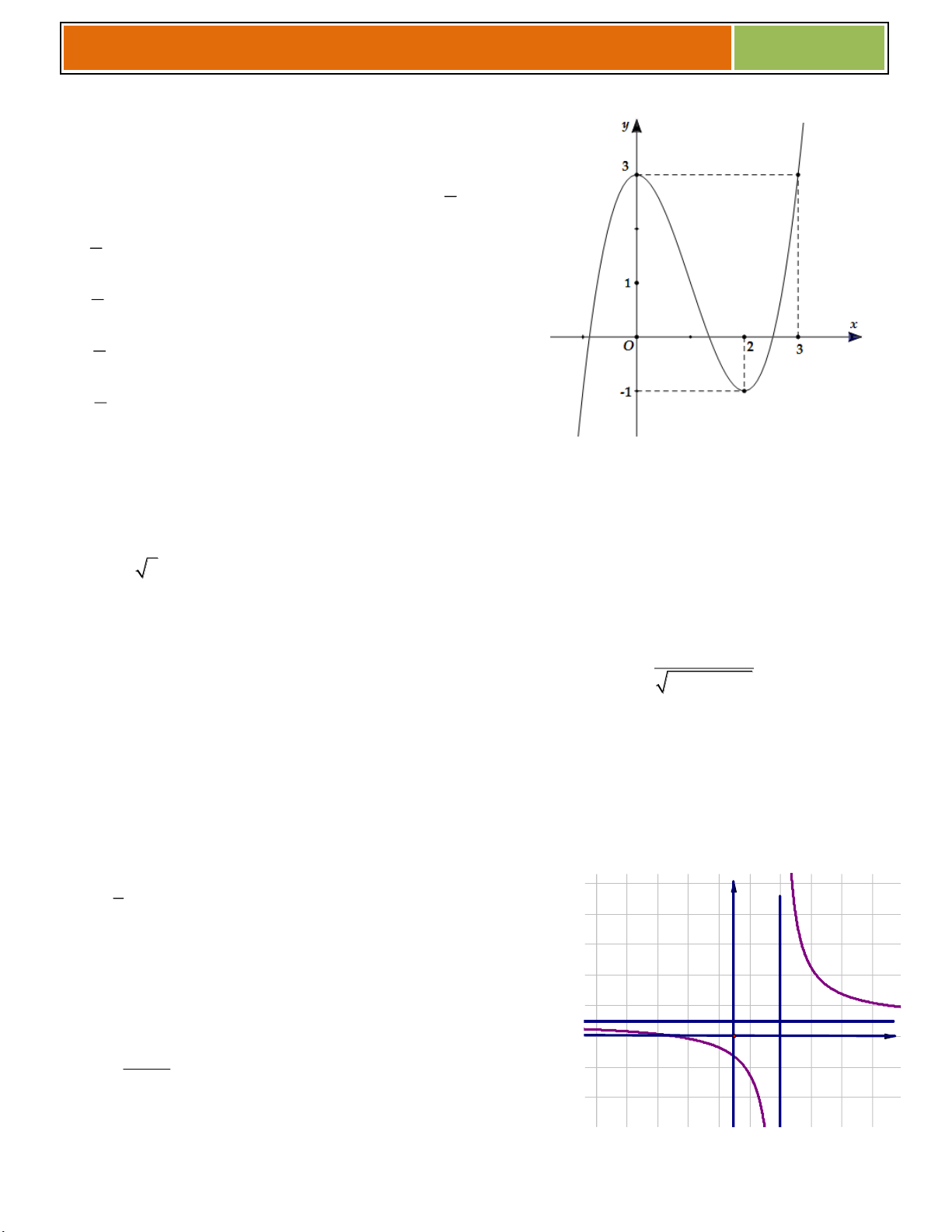
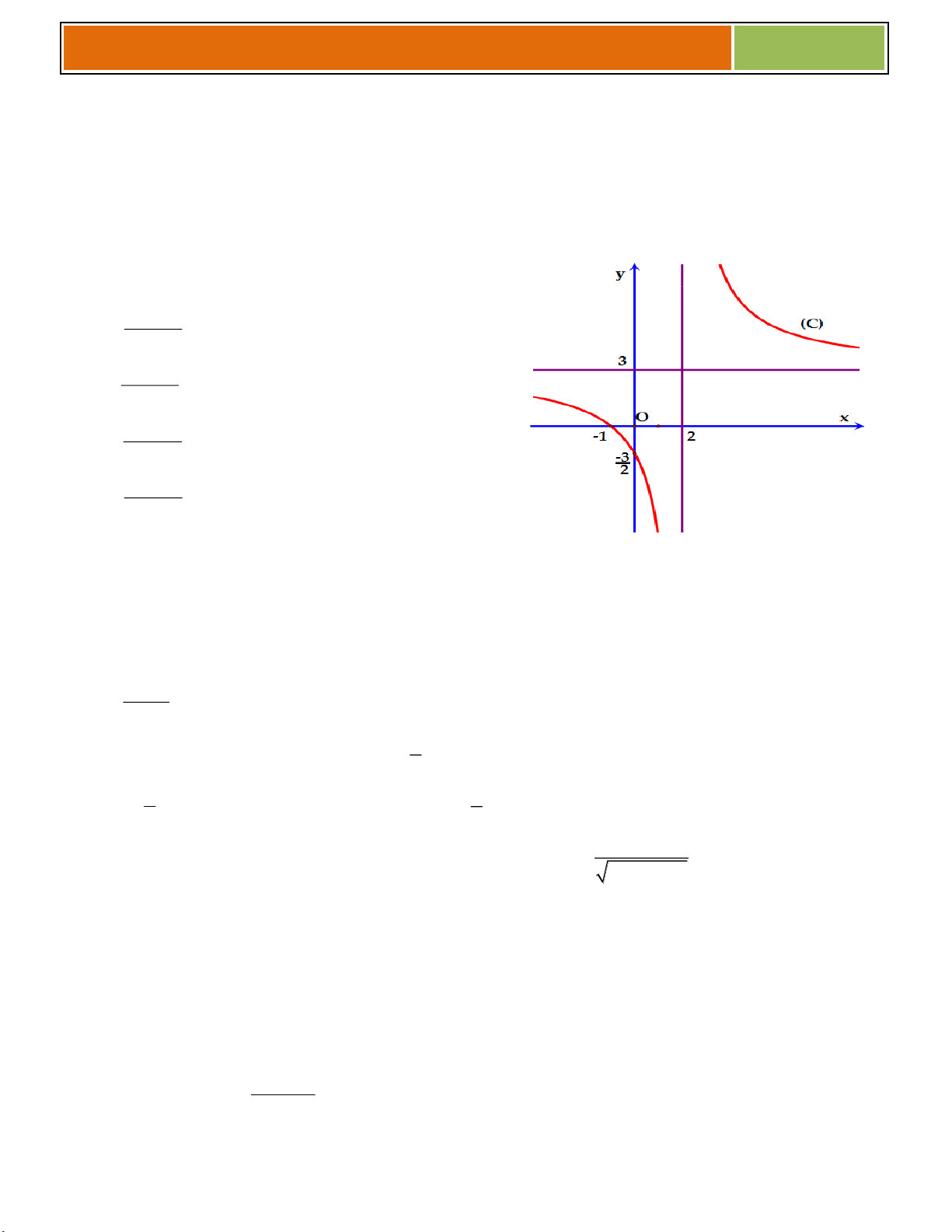
VD như hình bên, ta thấy (♥) có :
☻ 3 nghiệm khi ............................................
_- 1 _ O _ 2 _ x _ , _ _ 3
☻ 2 nghiệm khi .......................
_y _= _f _( _
m _ )
hoặc ...............................
☻ 1 nghiệm khi .......................
hoặc ...............................
_ -4
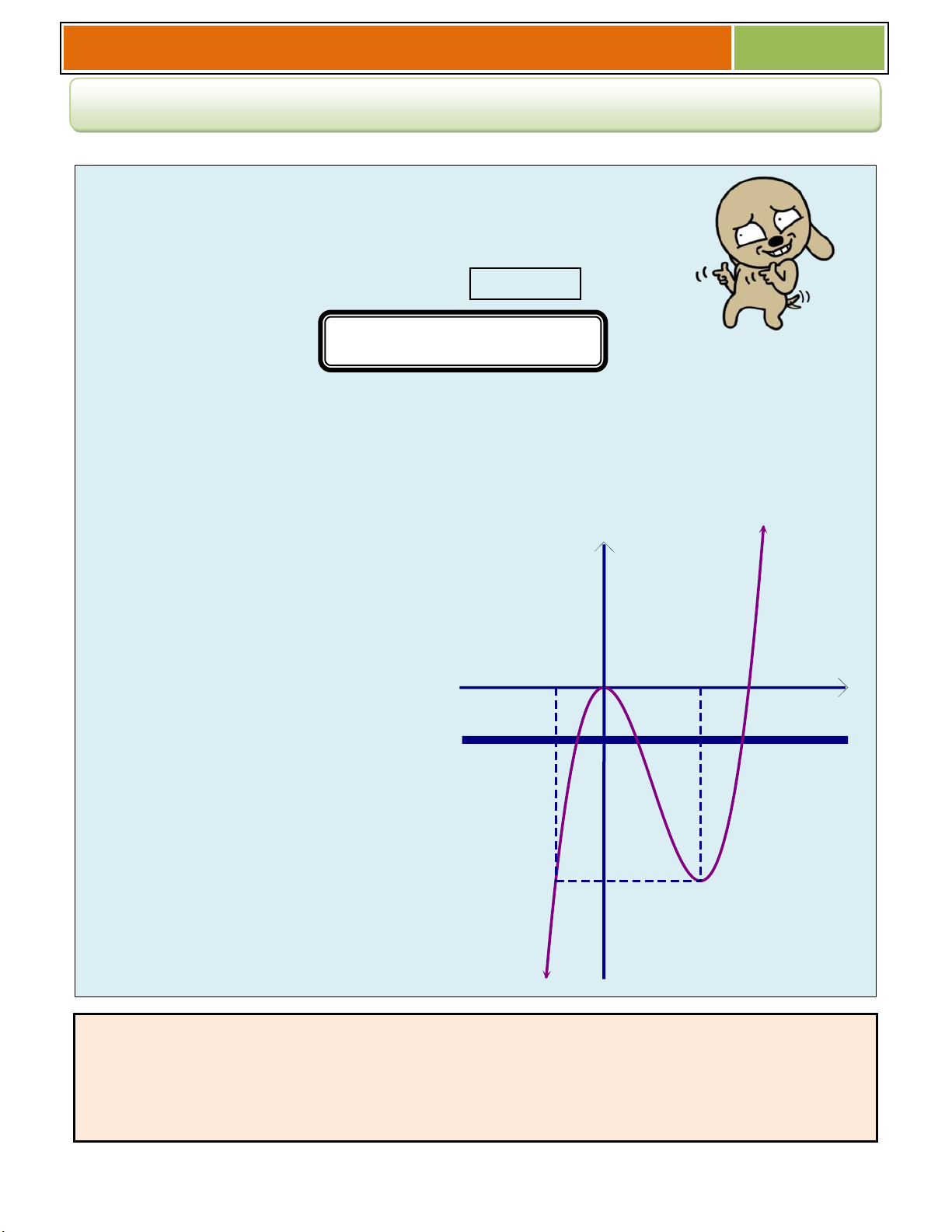
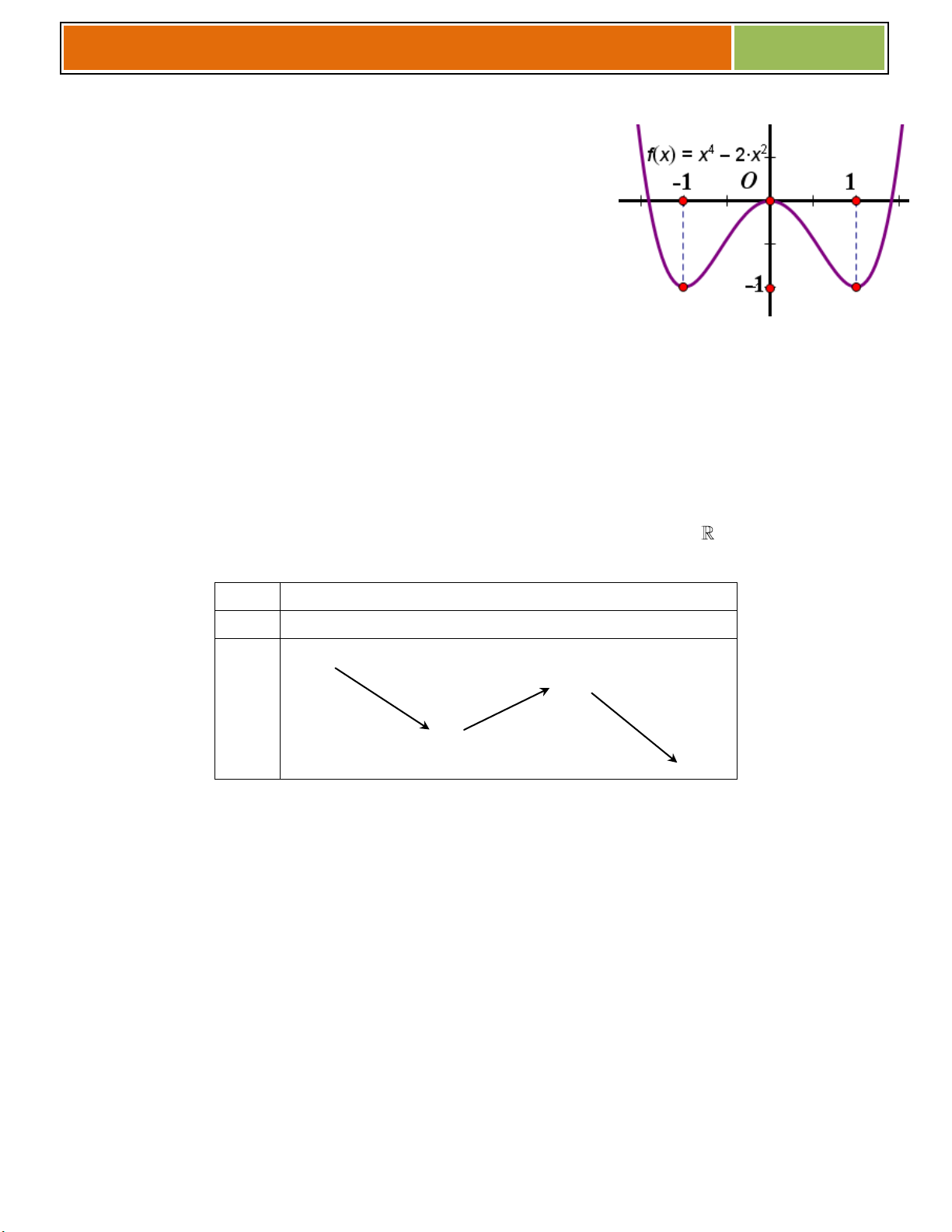
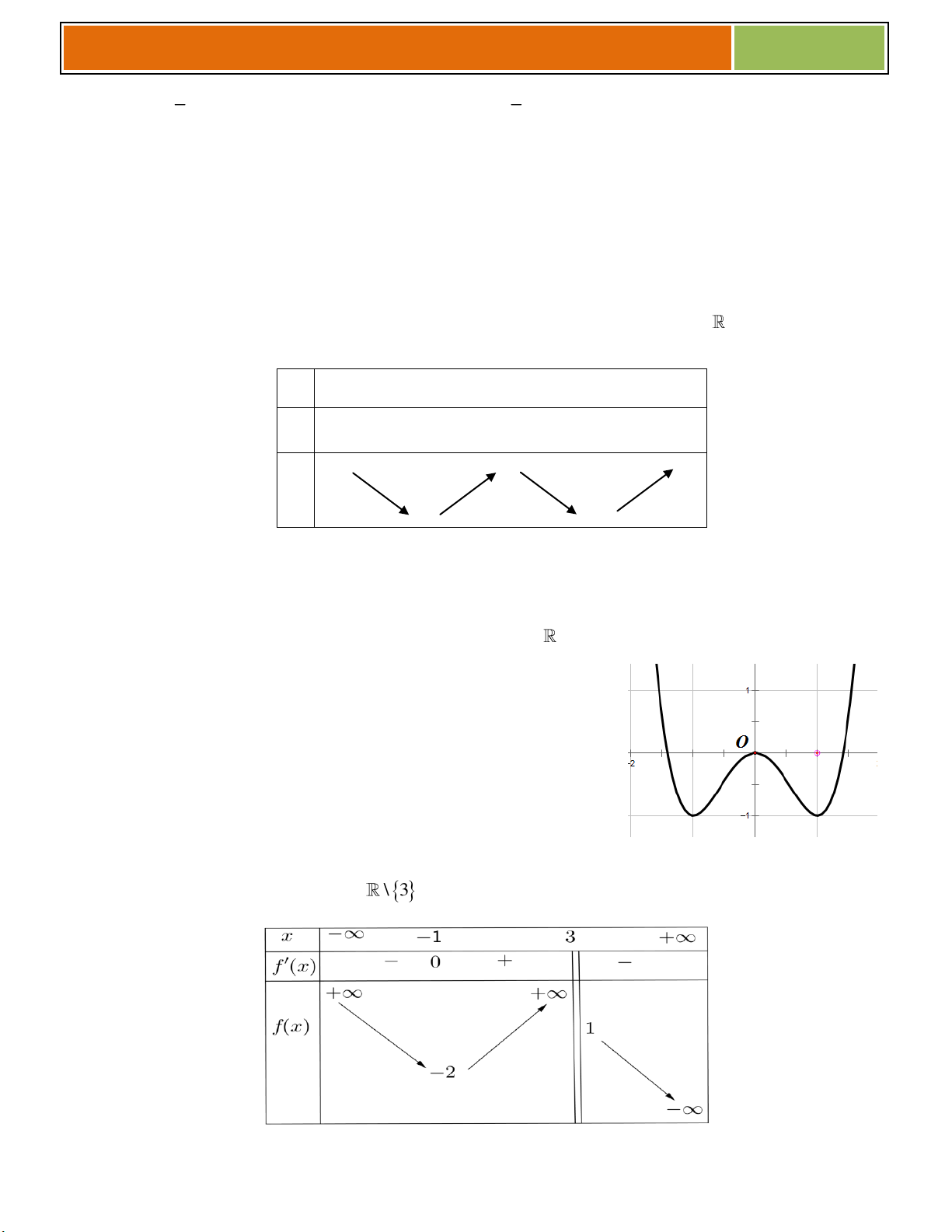
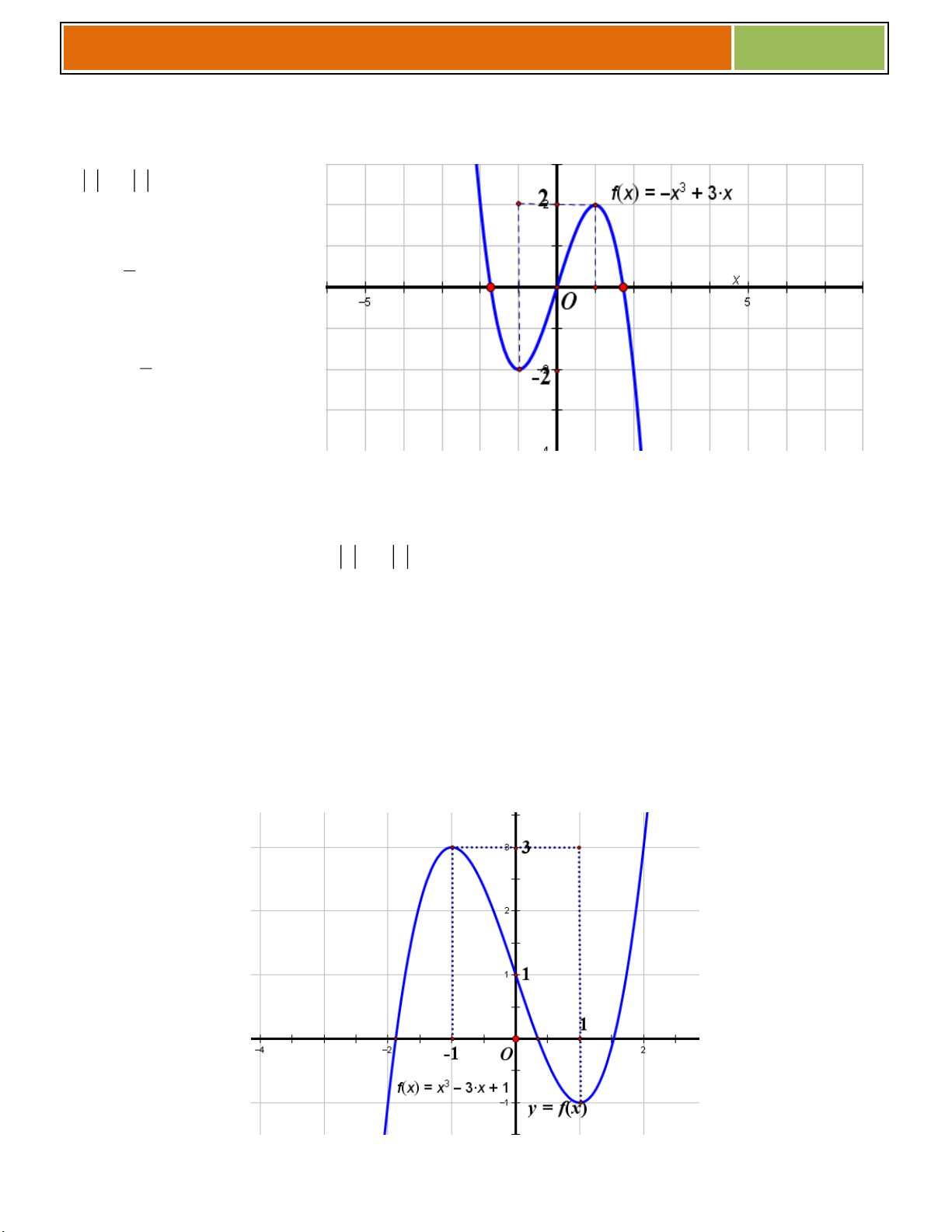
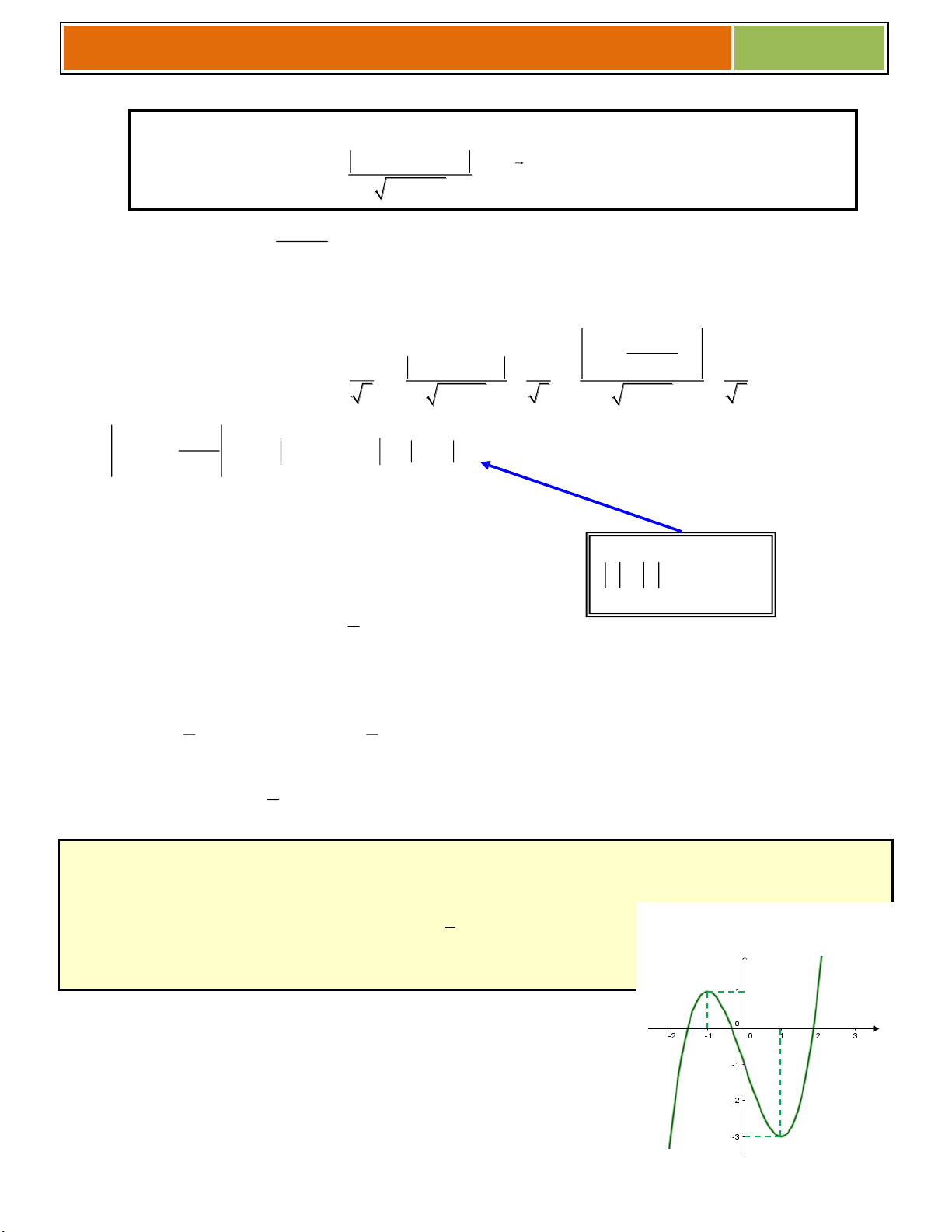
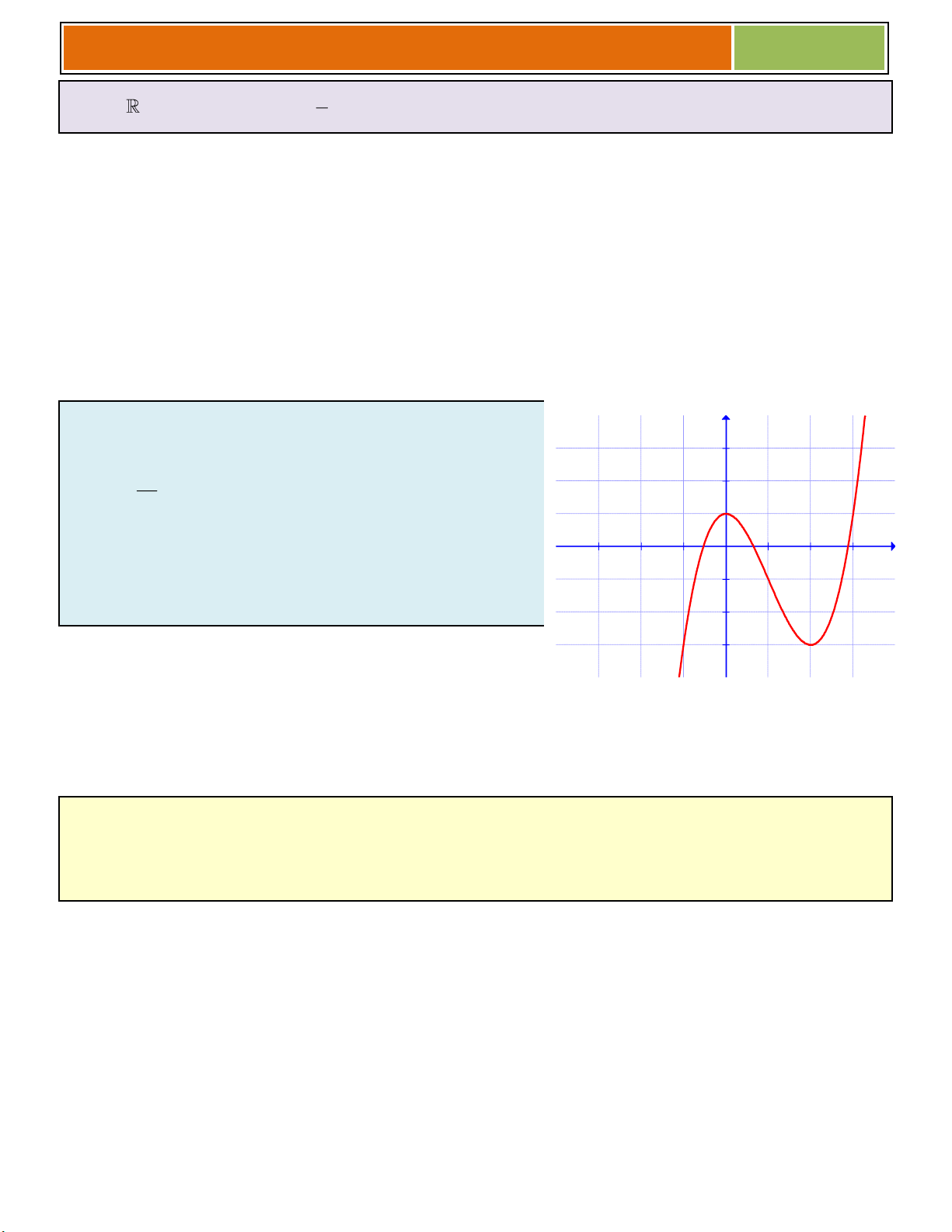
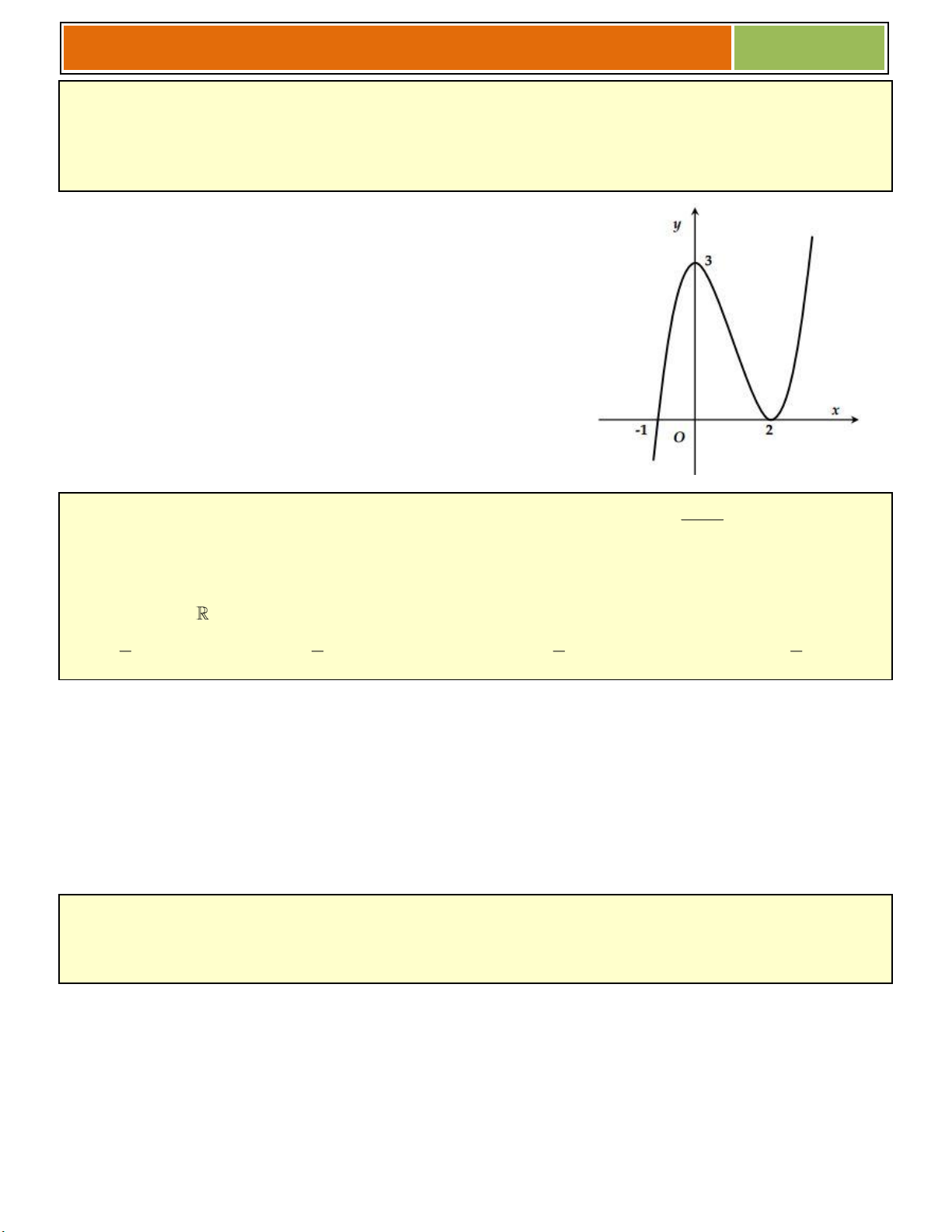
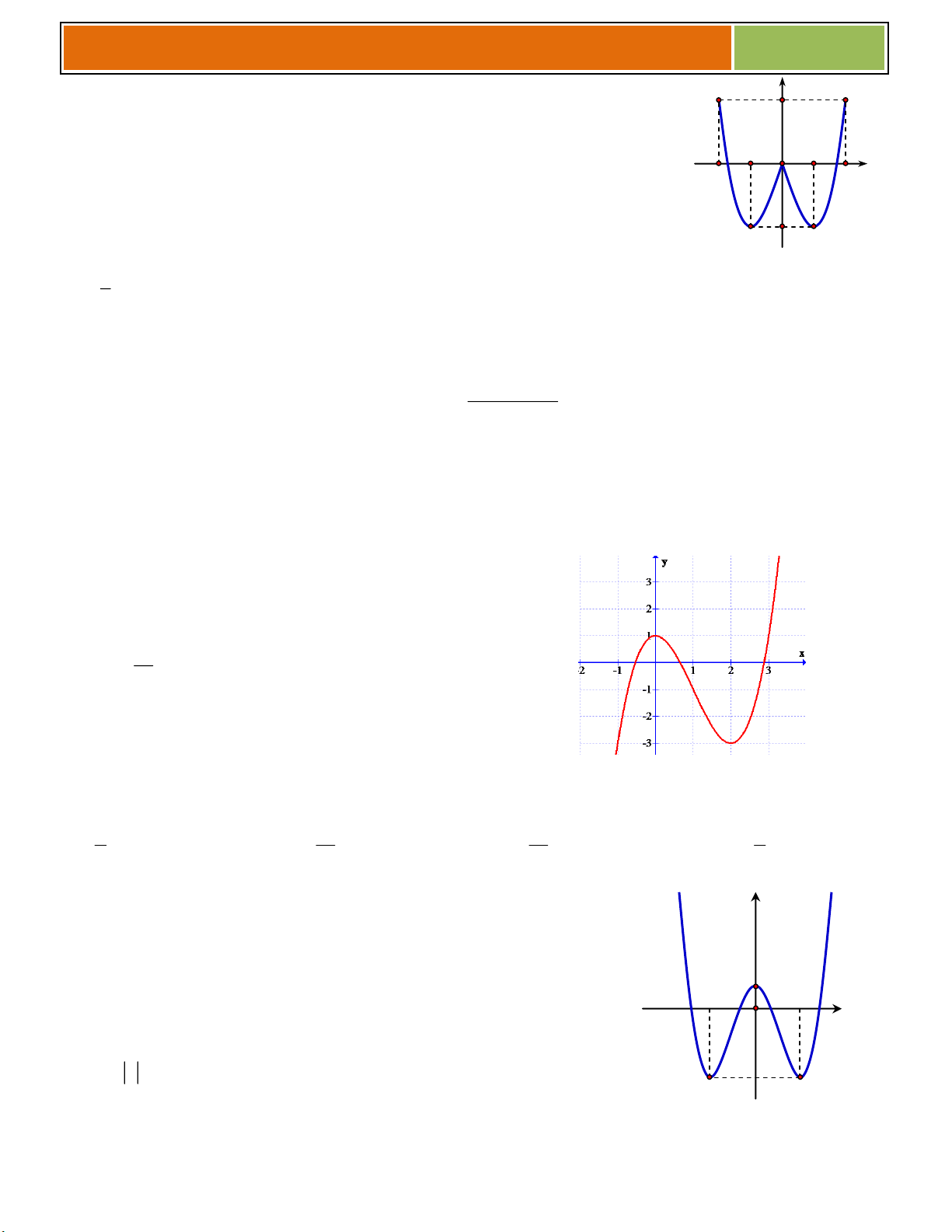
Ví dụ 01 : Cho hàm số 3 2
y  x  3x  4 (có đồ thị là (C))
a/ Khảo sát và vẽ đồ thị hàm số.
b/ Biện luận theo m số nghiệm của phương trình 3 2
x  3x m  0 . 1
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
a/ ► Tập xác định D  . x  0 ► Đạo hàm 2 y '  3
x  6x  3
xx  2; y '  0   . x  2 
► Hàm số đồng biến trên khoảng  2  ;0 ;
nghịch biến trên các khoảng  ;  2   và 0;.
► Hàm số đạt cực đại tại x  0 , y  4 ; đạt cực tiểu tại x  2  , y  0. CD CT
► Giới hạn tại vô cực lim y   ; và lim y   . x x x 2 0 ► Bảng biến thiên y ' 0 0 y 4 0
► Đồ thị hàm số đi qua các điểm  3  ;4, 1;0 . b/ Ta có 3 2
x  3x m  0 3 2
 x 3x  4  m  4   * .
Phương trình * là phương trình hoành độ
giao điểm của đồ thị và đường thẳng
y m  4 .Do đó số nghiệm của phương trình
* là số giao điểm của đồ thị và đường thẳng
d: y m  4 . (d cùng phương Ox)
Dựa vào đồ thị, ta có m  4  4 m  0 ♥ Với    : Phương trình có m  4  0 m  4 
duy nhất 1 nghiệm. m  4  4 m  0 ♥ Với   
: Phương trình có 2 nghiệm.m  4  0 m  4 
♥ Với 0  m  4  4  4
  m  0 : Phương trình có 3 nghiệm. 2
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
☻Toán nếu trắc nghiệm thì đề sẽ bắt chúng ta “suy luận và hiểu” nhiều hơn là phương pháp
“Casio thần chưởng”
☻Vậy phải làm sao ???
☻Thật ra thì “bảng biến thiên đã nói lên tất cả”rồi
Chúng ta bắt tay vào làm !!! Ở đây thầy không dùng bảng biến thiên cũ (nếu dùng vẫn
được) để cho các em biết là đưa về hàm nào cũng được ☺
Vẽ đồ thị mất 15 phút rồi
Nhìn hàm g(x) này nè !!! 3 2 Phương trình 3 2
x  3x m  0 ta viết lại m
  x 3x Lập BBT đi x  2  0  y '  0  0   y 0 4  2 con số đáng yêu !!! 
“phác thảo” đồ thị +∞ 0
Từ đồ thị “phác thảo” này ta thấy rõ ràng
ở đây thầy ví dụ có 3 nghiệm !!!thì m chạy từ - 4 đến 0 m
(biện luận ko cần vẽ đồ thị)
Đây không phải là công thức giải nhanh – -4
chỉ là hướng tư duy giúp giải bài toán
nhanh hơn cho trắc nghiệm !! -∞ 3
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 3 x
Ứng dụng 01 : Biện luận theo m số nghiệm của phương trình 2
 2x  2m  0 . 3
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Ứng dụng 02 : Tìm m để phương trình 3 2
x  3x  2  2m  0 có 3 nghiệm phân biệt.
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Ứng dụng 03 : Tìm m để phương trình 3
x  3x  7 5m  0 có 2 nghiệm.
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
....................................................................................................................................... 4
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
Ứng dụng 04 (Đề giữa kì- Chuyên Lê Hồng Phong-TP. HCM): Tìm tất cả các giá trị của tham
số k sao cho phương trình 3 2
x  3x k  0 có 3 nghiệm phân biệt.
A. 0 k 4. B. k 0 . C. k 4.
D. 0 k 4.
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Ứng dụng 05 (Đề An Nhơn 3- Bình Định):Tìm tất cả các giá trị của tham sốđể đường thẳng
y  4m cắt đồ thị hàm số 4 2
y x  8x  3 tại bốn điểm phân biệt 13 3 A.   m  3 . B. m  13 . C. m   13 3 . D.   m  . 4 4 4 4 4 4
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Ứng dụng 06 : Tìm giá trị của tham số m để phương trình sau có 4 nghiệm phân biệt 4 2
x  4x  3  2m  0
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
....................................................................................................................................... 5
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
Ứng dụng 07: Tìm giá trị của tham số m để phương trình sau có 3 nghiệm 4 x 2
 3x  3 3m  0 4
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Ứng dụng 08 : Tìm giá trị của tham số m để phương trình sau có 3 nghiệm phân biệt 3 x 2 
 3x  3 2m  0 3
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Ứng dụng 09 : Tìm giá trị của tham số m để phương trình sau có 2 nghiệm 3 x 2 
 9x m  0 3
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
....................................................................................................................................... 6
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
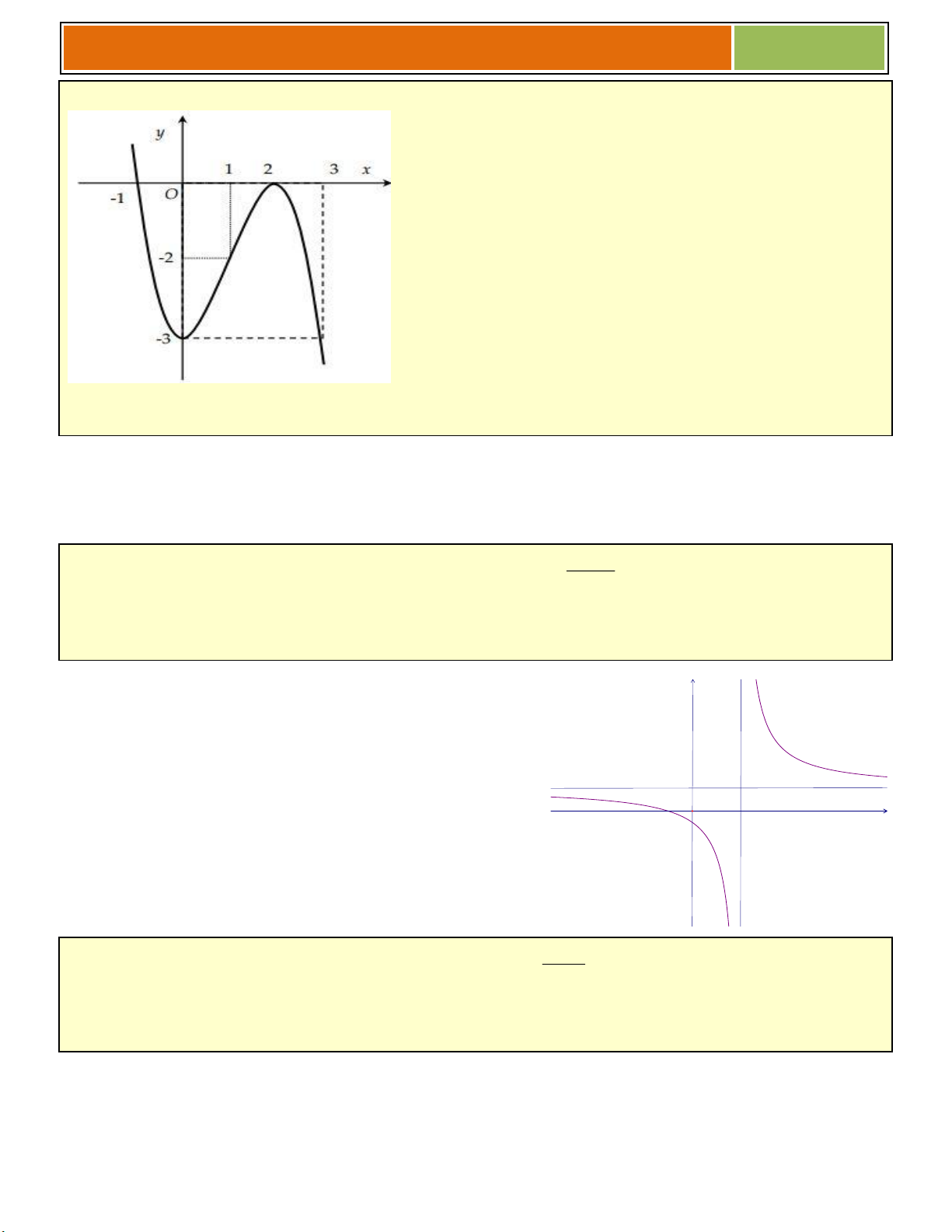
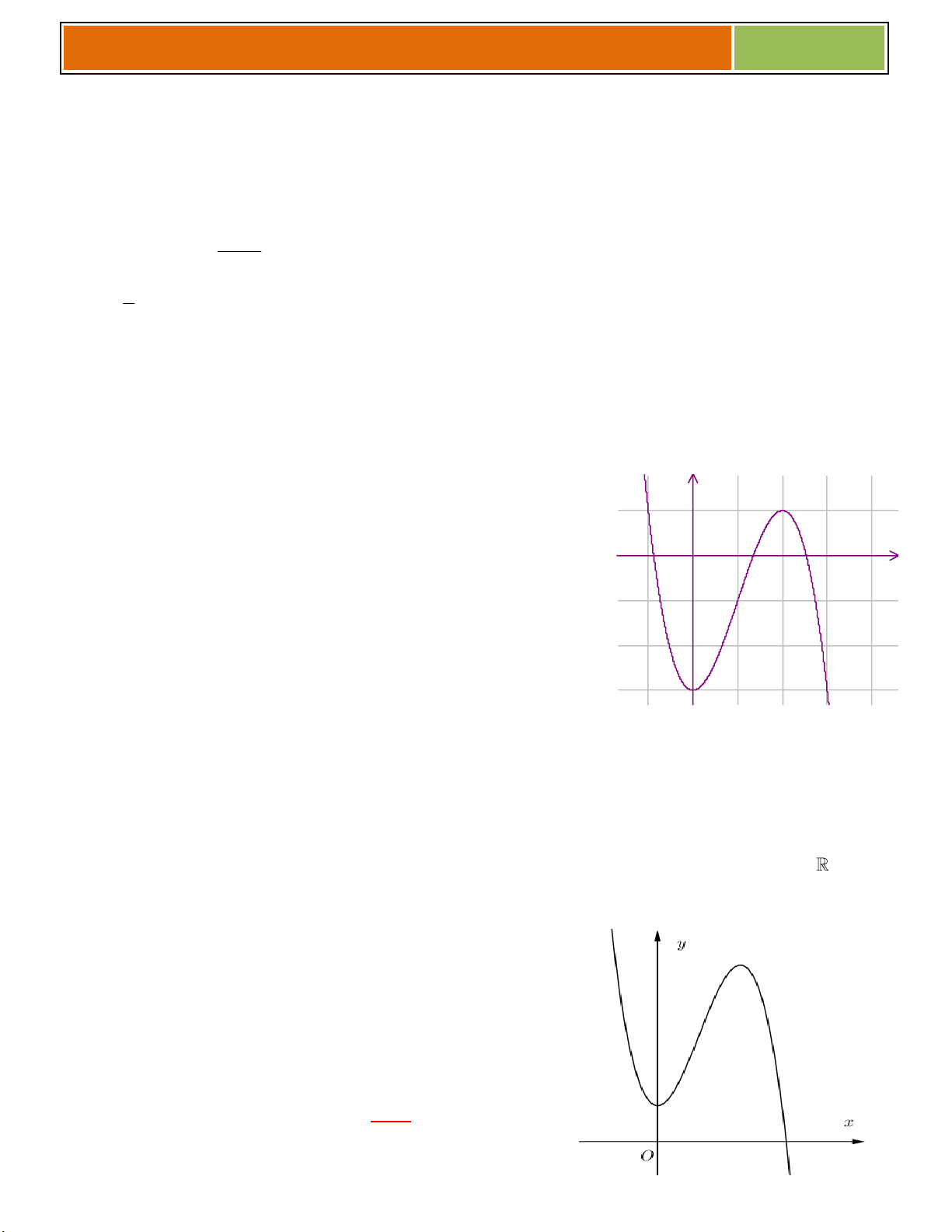
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 Ví dụ 02 : (C): 3 2
y x  3x .Tìm m để phương trình 3 2
x  3x  2m 1  0 có ba nghiệm phân biệt,
trong đó có đúng hai nghiệm không nhỏ hơn 1.
Đồ thị được vẽ : Ta có 3 2
x  3x  2m 1  0 . *
 ....................................................
♠ Phương trình * là phương trình
hoành độ giao điểm của đồ thị và đường
thẳng..............................................
♠ Do đó số nghiệm của phương trình * là số giao điểm của đồ thị và đường thẳng
......................................................................
♠ Dựa vào đồ thị, ta thấy phương trình * có ba nghiệm phân biệt, trong đó có đúng hai
nghiệm không nhỏ hơn 1 khi và chỉ khi.................................................................................
Vậy .................................................. thỏa mãn yêu cầu bài toán. 2x  4
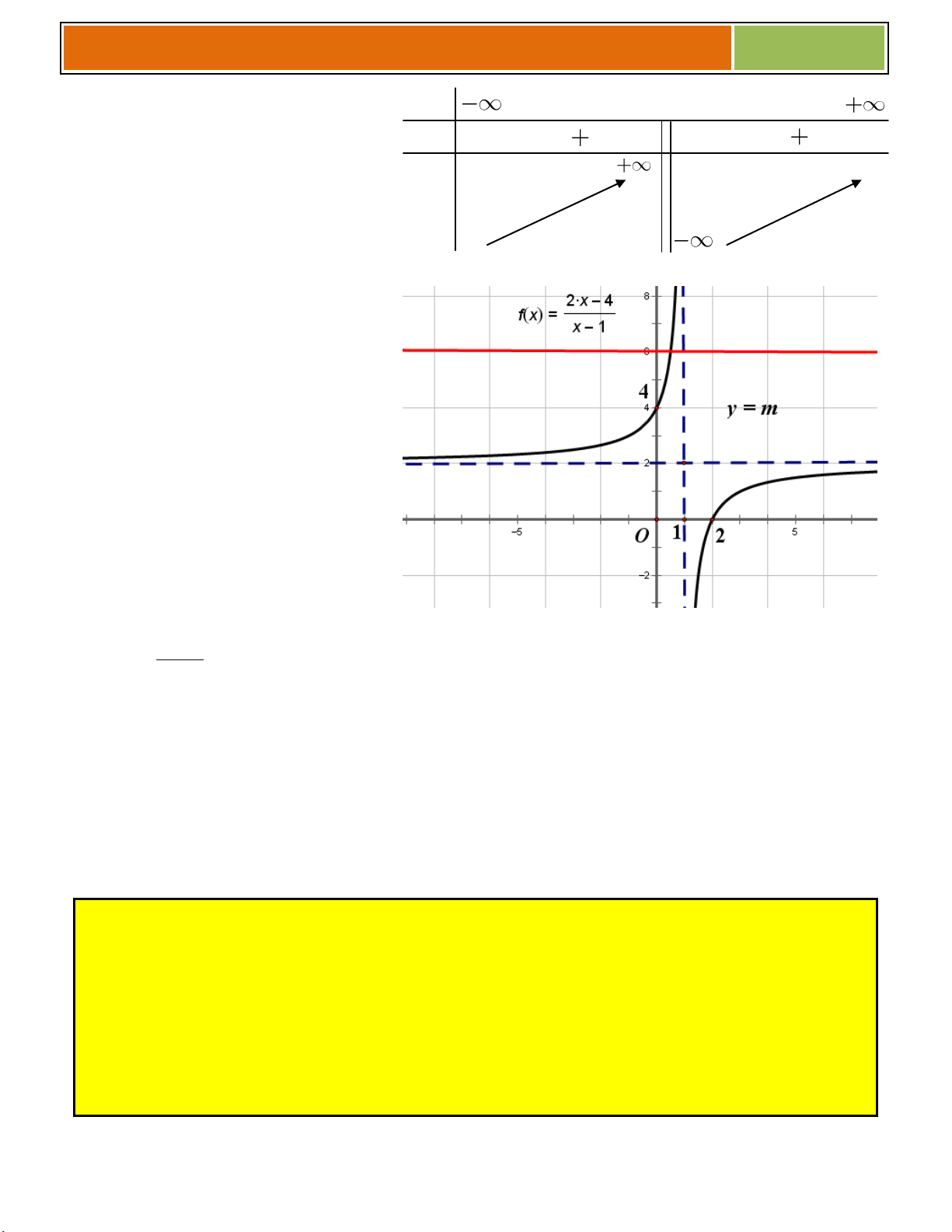
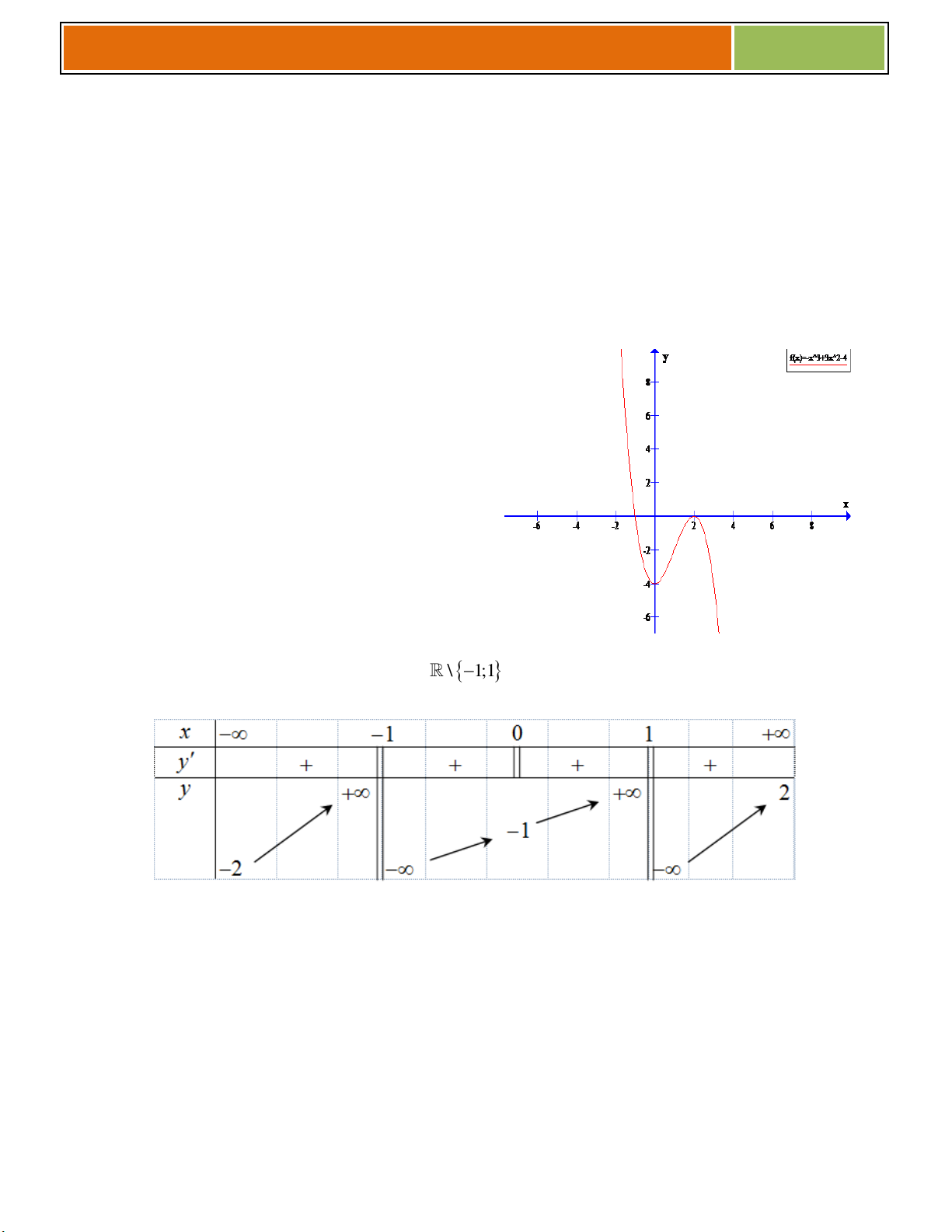
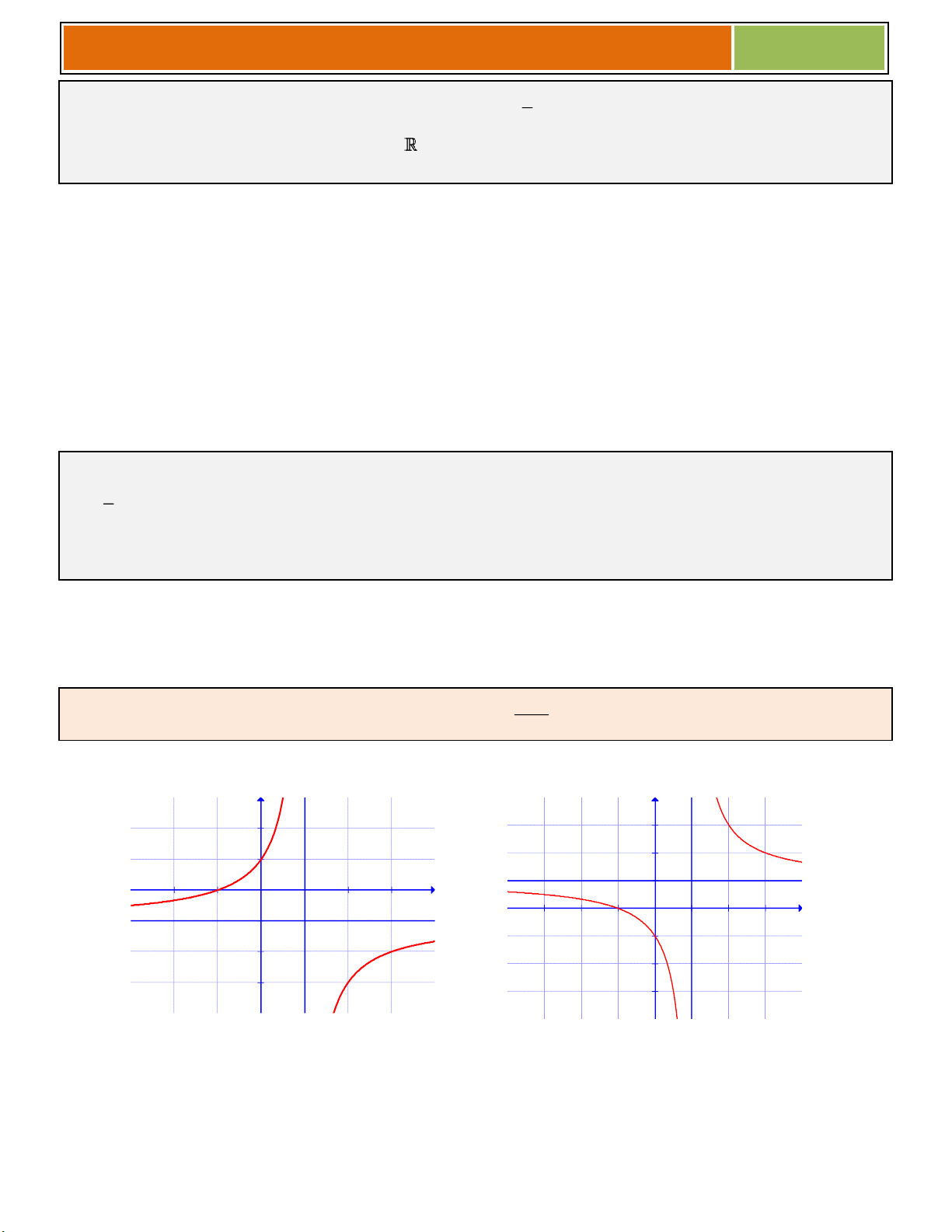
Ví dụ 03 : Cho hàm số y x  . 1
a/ Khảo sát sự biến thiên và vẽ đồ thị C  của hàm số đã cho. 2x  4
b/ Biện luận theo m số nghiệm của phương trình  m x  . 1 2
a/ ► Tập xác định: D  \  
1 .► Đạo hàm y '      . x   0, x D 2 1
► Hàm số đồng biến trên từng khoảng   ;1  và 1;.
► Giới hạn và tiệm cận: 7
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
► lim y   và lim y   ;   x 1  x 1  x 1 y '
tiệm cận đứng: x  1. 2 y ►
lim y  lim y  2 ; tiệm cận ngang: x x y  2 . 2 ► Bảng biến thiên
► Đồ thị C cắt Ox tại 2;0 , cắt
Oy tại 0;4 và nhận giao điểm
I 1; 2 của hai đường tiệm cận làm tâm đối xứng 2x  4 b/ Ta có  m  . x
là phương trình hoành độ giao điểm của đồ thị và đường thẳng d: y m 1
Do đó số nghiệm của phương trình là số giao điểm của đồ thị và đường thẳng d: y m .(d cùng phương Ox)m  2
Dựa vào đồ thị, ta có ☻ Với 
: phương trình có duy nhất một nghiệm. m  2 
☻ Với m  2 : phương trình vô nghiệm.
Ví dụ 04 : Cho hàm số 4 2
y  8x  9x 1.
a/ Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
b/ Dựa vào đồ thị, hãy biện luận theo m số nghiệm của phương trình 4 2
8x  9x m  0 .
c/ Viết phương trình tiếp tuyến của đồ thị tại điểm có tung độ bằng 1, hoành độ dương. 8
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
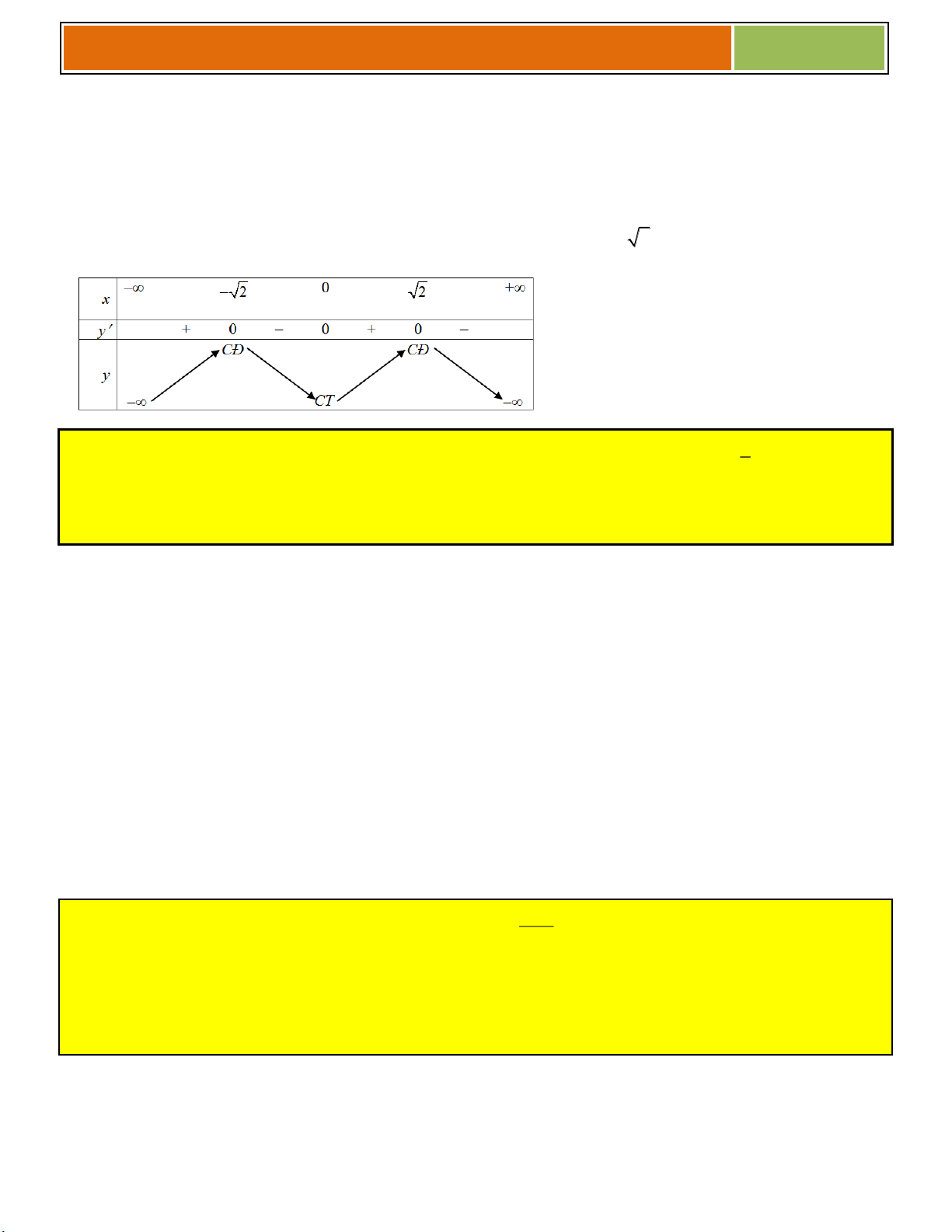
a/ ► Tập xác định: D  . x  0 ► Đạo hàm 3  y x x x  2 ' 32 18 2
16x  9 ; y '  0  3  . x    4     ► 3 3
Hàm số đồng biến trên các khoảng  ;     và 0;   ;  4   4   3   3 
nghịch biến trên các khoảng  ;0   và ;    .  4   4  ► 3 49
Hàm số đạt cực tiểu tại x   , y  
; đạt cực đại tại x  0 , y 1. 4 CT 32 CD
► Giới hạn tại vô cực lim y  lim y   . x x y ► Bảng biến thiên 3 3 x 4 0 4 y ' 0 0 0 y 1 49 49 32 32
► Đồ thị hàm số đi qua các điểm  1
 ;0 , 1;0 và nhận Oy làm trục đối y xứng. b/ Ta có 4 2 4 2
8x  9x m  0  8x  9x 1  m 1. *
Phương trình * là pthđgđ của đồ thị 1
và đường thẳng d: y  m 1. 3 3 x
Do đó số nghiệm của phương trình * 4 4 1
là số giao điểm của (C) và đường thẳng 1 O 1
d: y  m 1.(d cùng phương Ox) 49 y m 1 32 9
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 49 81
Dựa vào đồ thị, ta thấy : ♥ Với : m 1    m
: phương trình vô nghiệm. 32 32  49  81 m 1   m  ♥ Với :   32  32  
: phương trình có hai nghiệm. m 1 1 m  0 ♥ Với : m
 11 m  0: phương trình có ba nghiệm. ♥ 49 81 Với : 
 m 11  0  m
: phương trình có bốn nghiệm. 32 32 x  0 
c/ Với y  1, ta được 4 2 2
1  8x  9x 1  x  2 8x  9  0  0 0 0 0  0 3 2 x    4  3 2 
Vì tiếp điểm có hoành độ dương nên ta chọn M  ;1   . 4    3 2  27 2 Đạo hàm 3
y '  32x 18x . Suy ra hệ số góc của tiếp tuyến là k y '     . 4 2   27 2  3 2  27 2 77
Vậy phương trình tiếp tuyến cần tìm là d : y   x   1  
hay d : y x  2 4   2 4
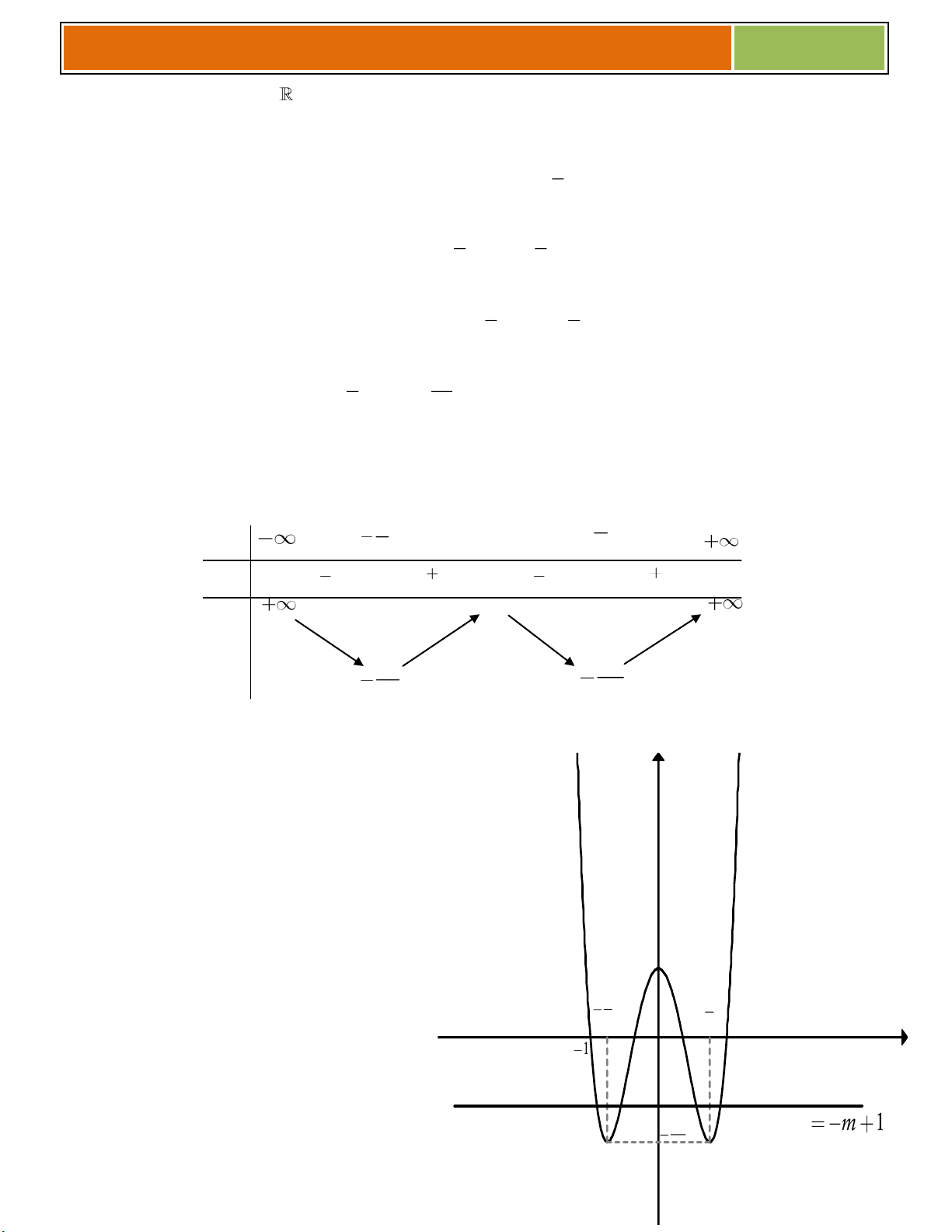
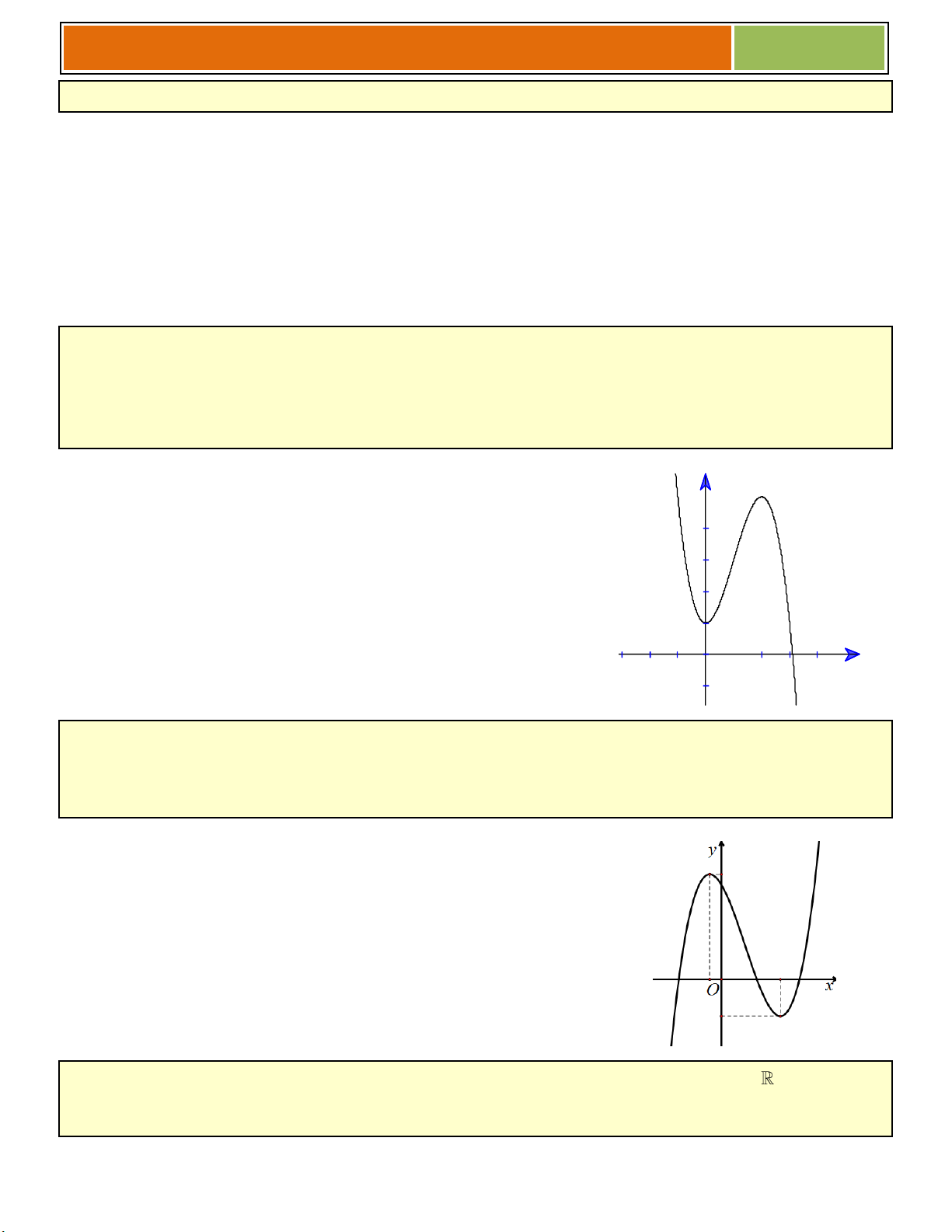
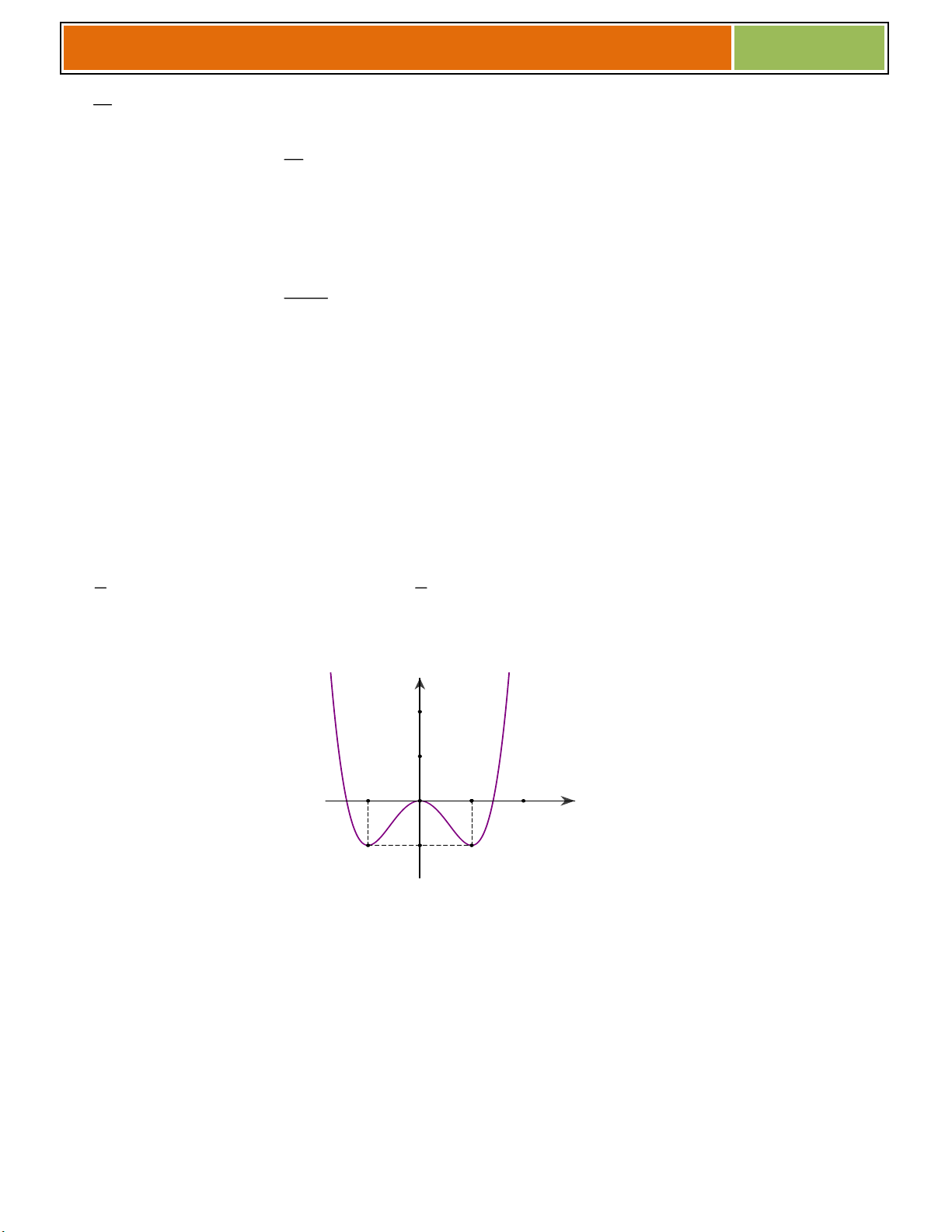
Ví dụ 05 : Cho hàm số: 4 2
y  x  4x  3
a/ Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b/ Dựa vào (C) , hãy biện luận số nghiệm của phương trình: 4 2
x  4x  3  2m  0 ► Ta có phương trình : 4 2
x  4x  3  2m  0 y 4 2
 x  4x 3  2m(*) 1
► Số nghiệm phương trình (*) bằng với số giao điểm - 3 3 -1 1 của 4 2
(C) : y  x  4x  3 O x - 2 2
và d: y = 2m (d cùng phương Ox) -3 y = 2m 2m 10
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
Giá trị m 2m
Số giao điểm của Số nghiệm
(C) và d của pt (*)
m> 0,5 2m> 1 0 0 m = 0,5 2m = 1 2 2
–1,5 <m< 0,5
–3 < 2m< 1 4 4
m = –1,5
2m = –3 3 3
m< –1,5
2m< –3 2 2
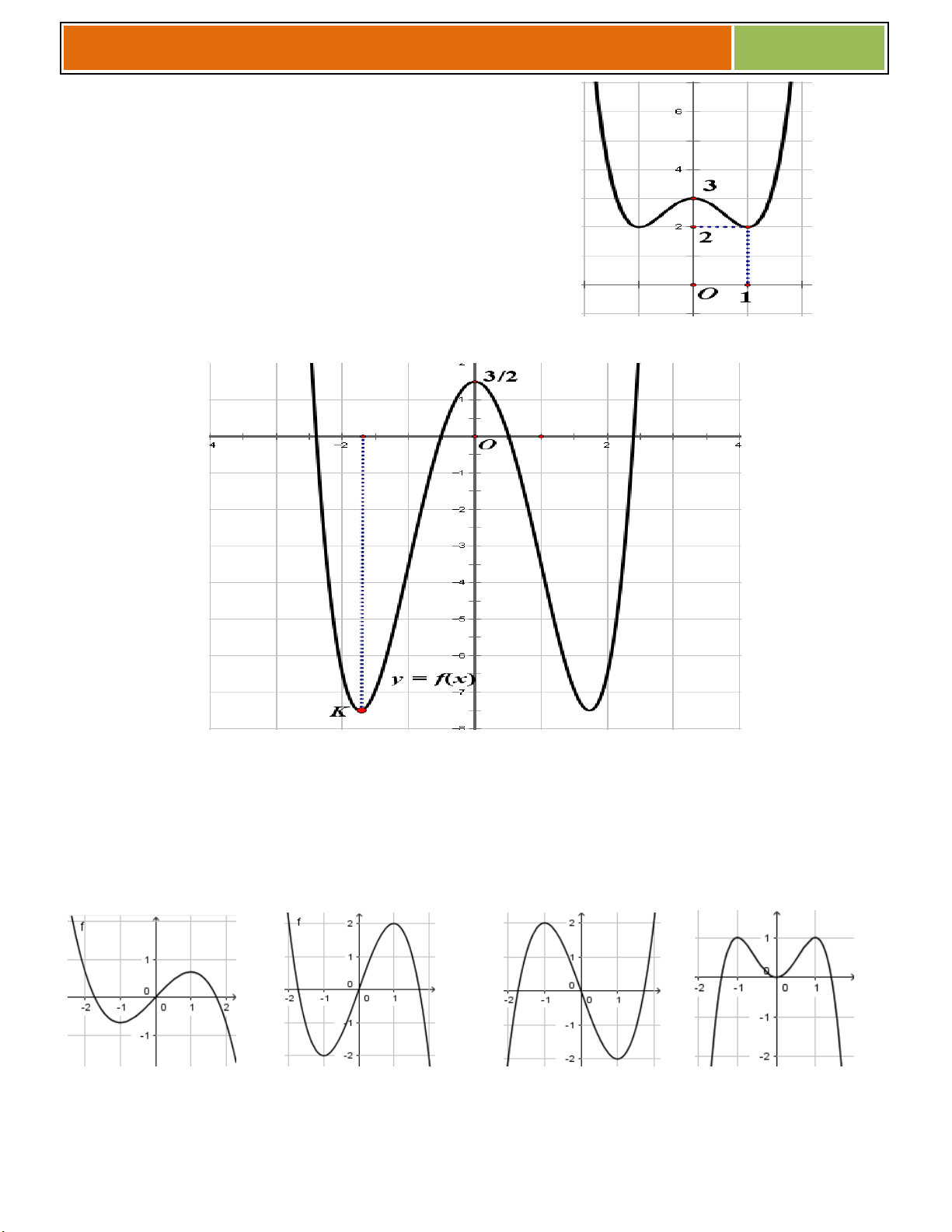
BÀI TẬP TRẮC NGHIỆM PHẦN BIỆN LUẬN 1 9
Câu 1 : Giá trị tham số m để phương trình sau 3 2 x  3x
x m  0 có nghiệm duy nhất là 2 2 m  0 A.  m  2 m  1 B.  m  4 C. m  4 D. m  2
Câu 2 : Giá trị tham số m để phương trình sau 4 2
x  2x m  2  0 có 4 nghiệm phân biệt là m  0 A.  m  2 m  1 B.  m  2 C. 1 m  2 D. m  1
Câu 3 : Giá trị tham số k để phương trình sau 3 2
x  3x k  0 có đúng 3 nghiệm phân biệt là A. 0  k  4 B. 0  k  3 C. 1   k  3 D. k  1 11
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
Câu 4 : Đồ thị hàm số y f x xác định trên D
\ như hình vẽ bên.
4.1 :Giao điểm của đồ thị hàm số này và đường thẳng y = x + 1 là A. 0;2 B.  6  ; 2   C. 2;0 D.  4  ; 3  
4.2 : Giá trị của α là A. 1  B. 1 C. 2  D. 2
4.3 :Đồ thị hàm số cắt
trục Ox tại .........................
trục Oy tại .........................
Câu 5 : Giá trị tham số m để phương trình sau 3 2
x  3x m có 2 nghiệm là
A. m  0 hay m  4 B. m  1  hay m  3 C. 1   m  3
D. m  0 hay m  3
Câu 6 : Hàm số y f x xác định trên D
có bảng biến thiên như sau : x  2  0  y '  0  0  y 3   1 
Giá trị của tham số m để phương trình f x  2m  0 có 3 nghiệm phân biệt là    m 1 m  0 A.  B.  3 m  1 m   2 1 1 3 C.   m  2 D.   m  2 2 2 12
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 3 x
Câu 7 : Giá trị tham số a để phương trình sau
x  2a 1  0 có đúng 3 nghiệm phân biệt là 3 1 5 A.  a  6 6 1 7 B.  a  6 6 1 5 C. a hay a  6 6 5 D. 1  a  6
Câu 8 : Hàm số y f x xác định trên D
có bảng biến thiên như sau : m
Giá trị tham số m để phương trình f x 
 0 có 3 nghiệm phân biệt là 2 m  5 A.  x  0 2  m  1 B. 2  m 10 y’  0  0  C. 1 m 10 y  5  m  2 D. m 10  1
Câu 9 : Hàm số y f x xác định trên D
có bảng biến thiên như sau : x  1  0 1  y’  0  0  0   0  y 1  1 
Giá trị tham số m để phương trình f x 1  m có đúng 2 nghiệm phân biệt là A. m  1 B. m  1  m  1  m  1  C.  D.  m  8 m  0
Câu 10 : Với giá trị nào của tham số m thì đường cong có phương trình y f x 4 2
x  2x 1 2m
và đường thẳng y m 1 cắt nhau tại 4 điểm phân biệt 1 2 A. m B.  m  3 3 2 C. 1   m  0 D.   m  0 3 13
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
Câu 11 : Với giá trị nào của tham số m thì đường cong có phương trình y f x 3 2
x  3x  9x m
cắt Ox nhau tại 3 điểm phân biệt A. m 2 B.1  m  3 C. 3   m  0 D. 2  7  m  5
Câu 12 : Giá trị của tham số m thì phương trình 3 2
x  3x m  0 có nghiệm duy nhất A. m
B. m  0 hay m  4  C. 3   m  0 D. 0  m  4
Câu 13 : Giá trị của tham số m thì phương trình 3 2
x  3x  2  m  0 có nghiệm duy nhất A. m y
B. m  0 hay m  4  C. 2   m  2 3 D. 0  m  4
Câu 14 : Cho hàm số : y f x (C) xác định trên D. 1
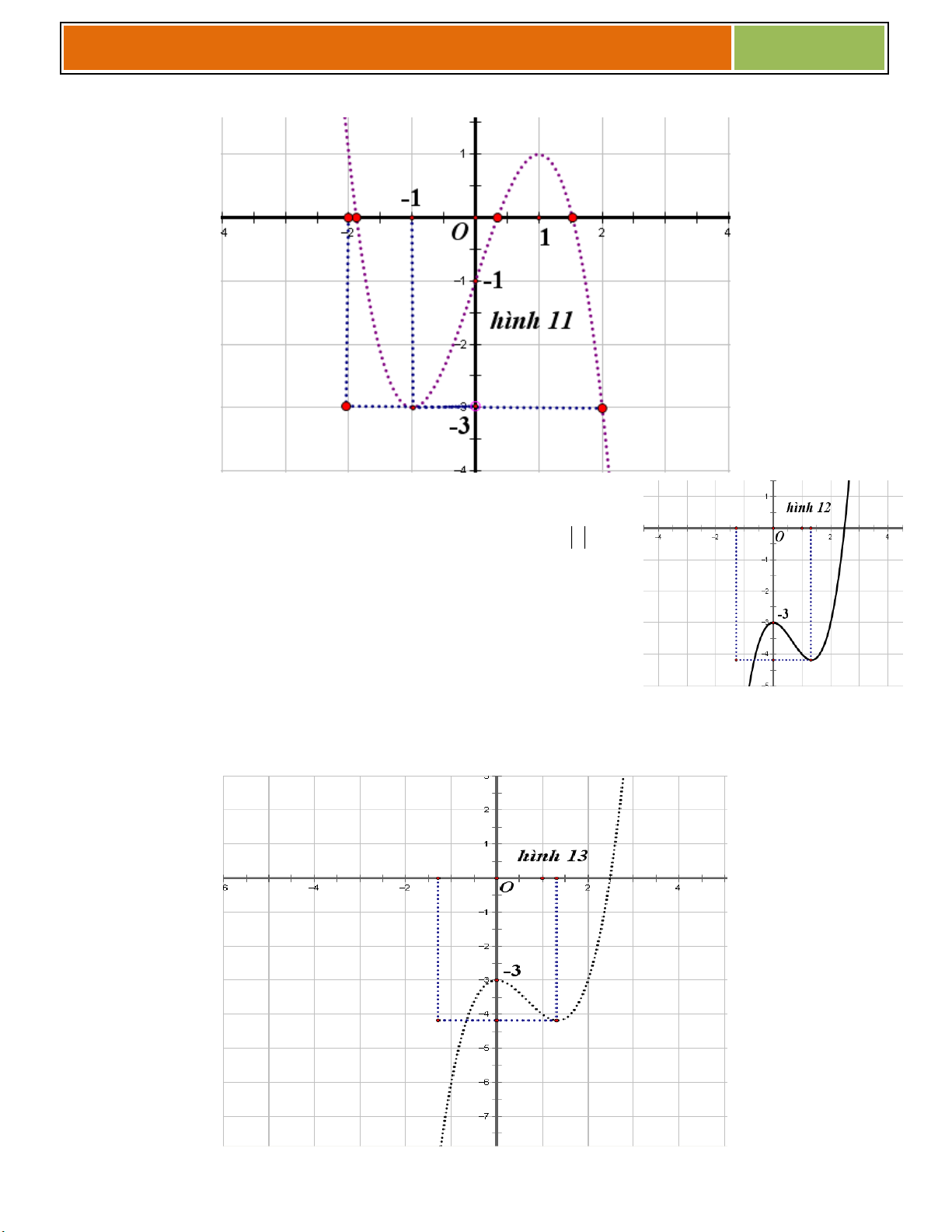
Có đồ thị (C) được vẽ như hình bên dưới. -2 -1 O x
Số giao điểm của (C) và đường thẳng y = k , 1 k  1  2 A. 1 -1 B. 2 C. 3 _y D. 0
Câu 15 : Cho hàm số : y f x (C) xác định trên D.
Có đồ thị (C) được vẽ như hình bên.
15.1 Số giao điểm của (C)
_- 1 _ O 1 _ 2 _
_ x _ _ 3
và đường thẳng y = k , 4   k  0 A. 1 B. 2 C. 3 D. 0 -2
15.2 Số giao điểm của (C)
và đường thẳng y = k, k  0 A. 1 B. 2 C. Cả A hoặc B D. 3 -4
15.3 Giá trị lớn nhất K của hàm số trên  1  ;2 là 14
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 A. 0 B. 1 C. Cả A hoặc B D. 2
15.4 Giá trị của a để phương trình f x 1 2m có đúng 3 nghiệm phân biệt trong đó có đúng 2
nghiệm không nhỏ hơn 1 3 5 3 5 A.  m  B.  m  2 2 2 2 C. Cả A hoặc B
D. Không có giá trị m thỏa yêu cầu Câu 16 : Hàm số 4 2 y x 2
x 1có đồ thịC. Xác định m để phương trình 4 2 x 2
x 1 log m có 2 2 nghiệm  1  A. m  0;      1  2   1  B. m  ;1    2  C. m  1 D. m1; Câu 17 : Hàm số 4 2 y x 2
x 1có đồ thịC. Xác định m để phương trình 4 2 x 2
x 1 log m có 4 2 nghiệm  1   1  A. m  0;      1 B. m  ;1   C. m  1 D. m1;  2   2  Câu 18 : Hàm số 4 2 y x 2
x 1có đồ thịC. Xác định m để phương trình 4 2 x 2
x 1 log m vô 2 nghiệm  1   1  A. m  0;      1 B. m  ;1   C. m  1 D. m1;  2   2 
Câu 19 (Trích đề thi THPTQG – 2017) : Cho hàm số 4 2
y  x  2x có đồ thị như hình bên.
Tìm tất cả các giá trị thực của tham số m để phương trình y 4 2
x  2x m có bốn nghiệm thực phân biệt. A. m  0 . B. 0  m 1. 1 C. 0  m 1 -1 1 D. m  1. 0 x 3
Câu 20 : Tìm m để phương trình có 3 nghiệm x  3x 1 m  0 là: A. 1 < m < 3 B. 2 < m < 3 C. m = 1 D. m = 3 15
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
Câu 21 : Cho hàm số : y f x (C) xác định trên D. Có đồ thị (C) được vẽ như hình bên dưới .
Giá trị tham số m để phương trình 4 2
x  2x m có đúng 4
nghiệm phân biệt là A. 1   m  0 B. m  1  m  1  C.  m  0 m  1  D. m  0
Câu 22 : Xác định giá trị của tham sốm để phương trình 3 2
x  3x  9x m  0 có ba nghiệm phân biệt A. m ;  27 B. m ;  2  75; C. m ;  2  71; D. m 2  7;5
Câu 23 (THPT Chuyên Bến Tre – 2017) : Cho hàm số y f x xác định trên , liên tục trên
khoảng xác định và có bảng biến thiên như sau: x  1  2  y  0  0   2 y 3  
Tìm tập hợp tất cả các giá trị của tham số m sao cho phương trình f x  m 1 có một nghiệm thực? A. m ;  2  3;. B. m ;  3  2; . C. m 3  ;2. D. m ;  2  3; . Câu 24 : Hàm số 3 2
y  x  3x 1có đồ thị C  . Xác định m để phương trình 3 3 2 2
x m  3x  3m có ba nghiệm phân biệt A. m 1  ;  3 \ 0;  2 B. m 1  ;  3 \ 0;  2 C. m 1  ;3 \  2 D. m 1  ;3 \  0 16
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
Câu 25 : Đường thẳng y = m không cắt đồ thị hàm số (C): 4 2 y  2
x  4x  2 khi : A. 0  m  4 B. m  4 C. m  0 D. m  4 Câu 26 : Cho hàm số 3
y x 1 có đồ thị là (C). Với giá trị nào của tham số m thì đồ thị hàm số cắt
đường thẳng d : y = 3x + m tại ba điểm phân biệt A. m B. 1   m  3  1   m  3 C.  m  0  1   m  3 D.  m  1
Câu 27 (Đề thi thử nghiệm 2017) : Cho hàm số y f x xác định trên \   0 , liên tục trên mỗi
khoảng xác định và có bảng biến thiên như sau x   0 1 y  0   2 y 1   
Tìm tập hợp tất cả các giá trị của tham số thực msao cho phương trình f x  m có ba nghiệm thực phân biệt. A.  1  ;2. B.  1  ;2 . C.  1  ;2. D. ; 2 .
Câu 28 : Tìm m để phương trình có 1 nghiệm 3 2
x  3x m  2m  2  0 là: A. m  2  ,m  6  B. 6   m  2  C. 4   m  0 m  0 D.  m  2 
Câu 29 : Tìm m để phương trình có 2 nghiệm 3
x  3x m  4  0 là: A. 2   m  0 m  0 B.  m  2  m  0 C.  m  2  17
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 D. m = 2 ; m = 6
Câu 30 : Tìm m để phương trình có 2 nghiệm 4 2
x  4x  4  2m  0 là: A. m < 1 B. m > 1 C. m < 2 D. m > 2
Câu 31 : Tìm m để phương trình có 3 nghiệm 4 2
x  2x m  2  0 là: A. m = 2 B. m = 1 C. 1 m  2 D. m  2
Câu 32 : (THPT CHUYÊN HÀ NỘI – AMSTERDAM) Tìm các giá trị của tham số m để phương trình 3 2
x  3x m m có 3 nghiệm phân biệt ? A. 2   m 1 B. 1   m  2 C. m  1 D. m  21 
Câu 33 (THPT Phả Lại – Hải Dương) : Cho hàm số y f x có bảng biến thiên sau: x –∞ 1  0 1 +∞ y – 0 + 0 – 0 + +∞ 0 +∞ y 1  1 
Với giá trị nào của m thì phương trình f (x) 1  m có đúng 2 nghiệm A. m  1. B. m  1  . C. m  1  hoặc m  2  . D. m  1  hoặc m  2  .
Câu 34 (THPT chuyên Biên Hòa – Hà Nam) : Cho hàm số y f x có bảng biến thiên như hình vẽ: x   1 0 1   f ' x- 0 + 0 - 0 +   5   f x 3 3
Tìm m để phương trình: f x  2  3m có bốn nghiệm phân biệt. 1 A. m  1  . B. m   . 3 18
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 1 1 C. 1   m   . D. m  1  hoặc m   . 3 3
Câu 35 (THPT Hà Uy Tập – Hà Tĩnh) : Tìm tất cả các giá trị của m để đồ thị hàm số 3 2
y x  3x 1 cắt đường thẳng y  2m  3 tại 3 điểm phân biệt ? A. 0  m  4 B. 0  m  2 C. 3   m 1 D. 0  m  2
Câu 36 (THPT chuyên Lê Hồng Phong ) : Cho hàm số y f (x) xác định trên , và có bảng biến thiên như sau x   -1 0 1   , y - 0 + 0 - 0 +   3   y 1 1
Tìm tập hợp tất cả các giá trị của tham số m sao cho phương trình f (x)  m có bốn nghiệm thực phân biệt? A.  1  ;  3 . B. ( 1  ; )  . C.  1  ;3 . D. (3; )  .
Câu 37 (THPT Hồng Quang – Hải Dương) : Cho hàm số
có đồ thị như hình vẽ bên
Mệnh đề nào sau đây đúng:
A. Phương trình f x  m luôn có nghiệm.
B. Phương trình f x  m có 2 nghiệm phân biệt khi m  0 .
C. Phương trình f x  m có 4 nghiệm phân biệt khi 1   m  0 .
D. Phương trình f x  m vô nghiệm khi m  1 
Câu 38 (THPT Ngô Sĩ Liên – Bắc Giang) :
Cho hàm số y f x xác định trên \  
3 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như bên. 19
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017
Phương trình f x  m có đúng hai nghiệm thực phân biệt khi và chỉ khi
A. m  1 hoặc m  2.  B. m 1. C. m  2.  D. m  2. 
Câu 39 (THPT chuyên Nguyễn Quang Diệu) : Tìm tất cả các giá trị thực của tham số m sao cho đường
thẳng y m cắt đồ thị hàm số 3
y x  3x 1 tại ba điểm phân biệt, trong đó có đúng hai điểm phân biệt có hoành độ dương A. 1   m  3. B. 1  m  3. C. 1   m 1. D. m  1.
Câu 40 : Đồ thị hình bên là của hàm số 3 2
y  x  3x  4 . Tìm tất cả giá trị của m để phương trình 3 2
x  3x m  0 có hai nghiệm phân
biệt? Chọn một khẳng định ĐÚNG
A. m  4 hoặc m  0 . B. m  4 . C. 0  m  4 . D. m  0 .
Câu 41: Cho hàm số y f (x) xác định trên \  1  ; 
1 , liên tục trên mỗi khoảng xác định và có
bảng biến thiên như sau:.
Tìm tập hợp tất cả các giá trị của thàm số m sao cho phương trình f x  m có ba nghiệm thực phân biệt A.  2  ;2. B.  2  ;2 . C.  ;   . D. 2; . 20
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
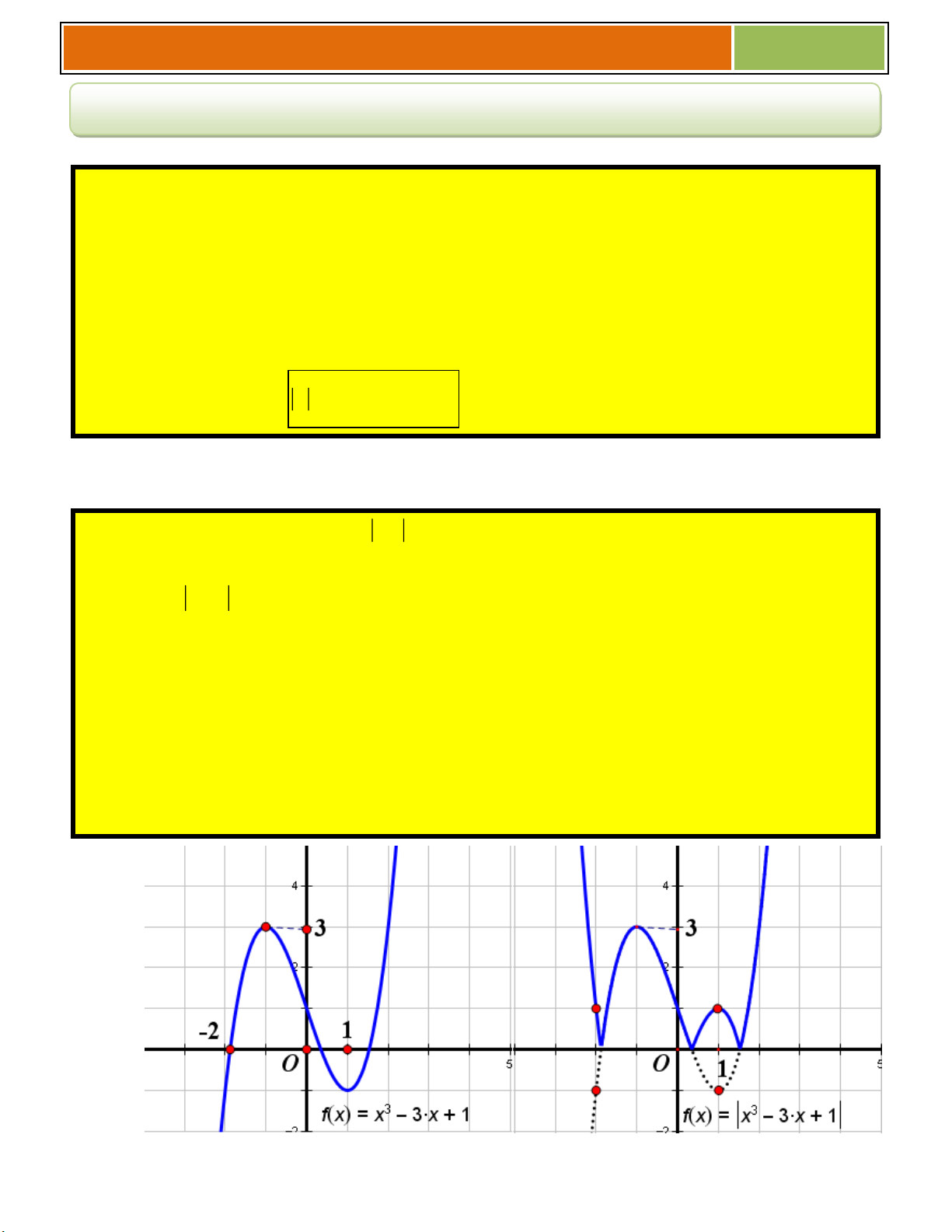
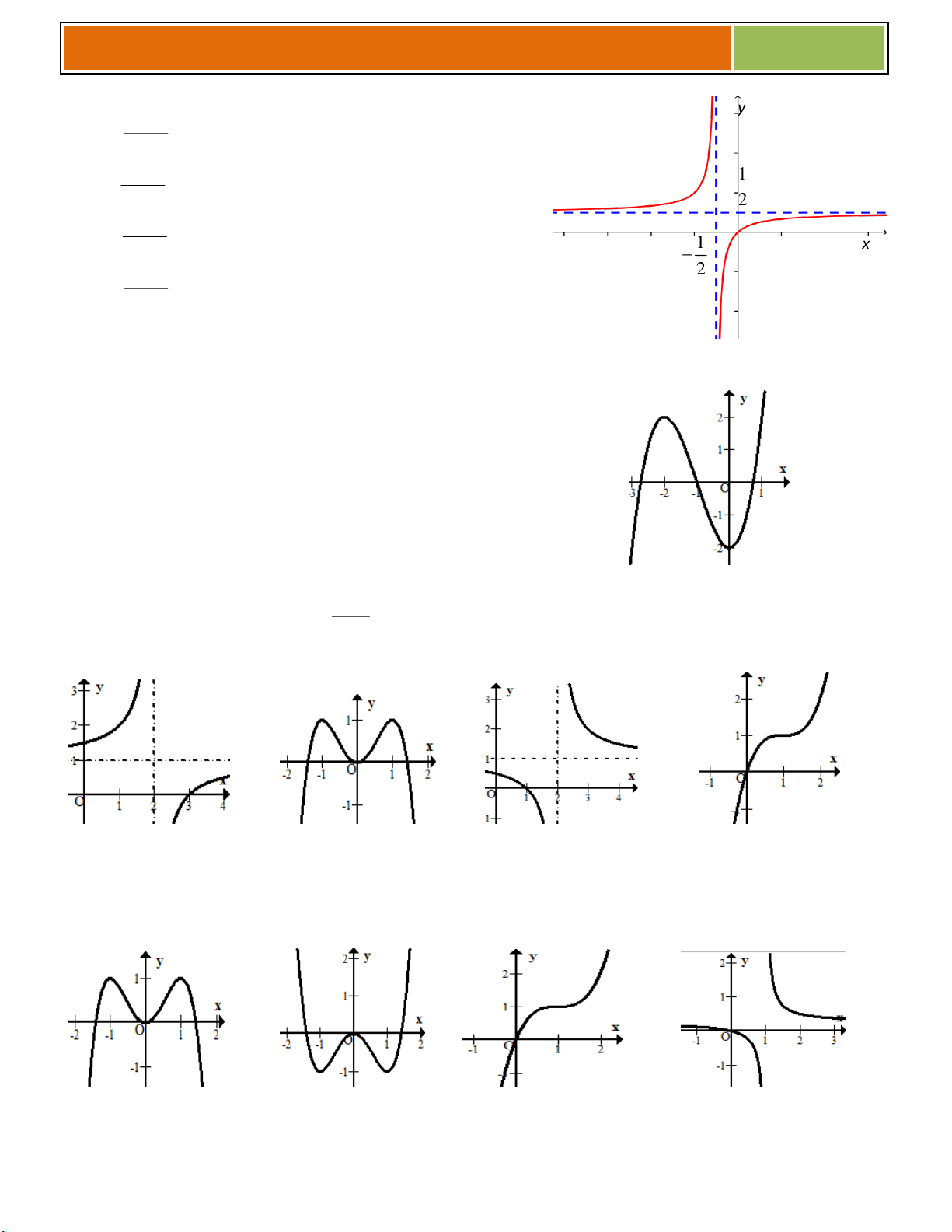
PHẦN 9 : BIẾN ĐỔI ĐỒ THỊ TRỊ TUYỆT ĐỐI
Lý Thuyết về các phép biến đổi cơ bản : Cho hàm số y  f(x) có đồ thị là (C) ta suy ra được các đồ thị hàm số sau :
☻ Lấy đối xứng (C) qua Ox ta sẽ được đồ thị (C1) : y  f  (x)
☻ Lấy đối xứng (C) qua Oy ta sẽ được đồ thị (C2) : y  f(  x)
Phương pháp : Xét dấu trị tuyệt đối rồi đưa thành các hàm không chứ trị tuyệt đối sau đó vẽ A khi A  0
từng phần rồi ghép lại A   A khi A  0
TIẾN HÀNH VÀO DẠNG CỤ THỂ
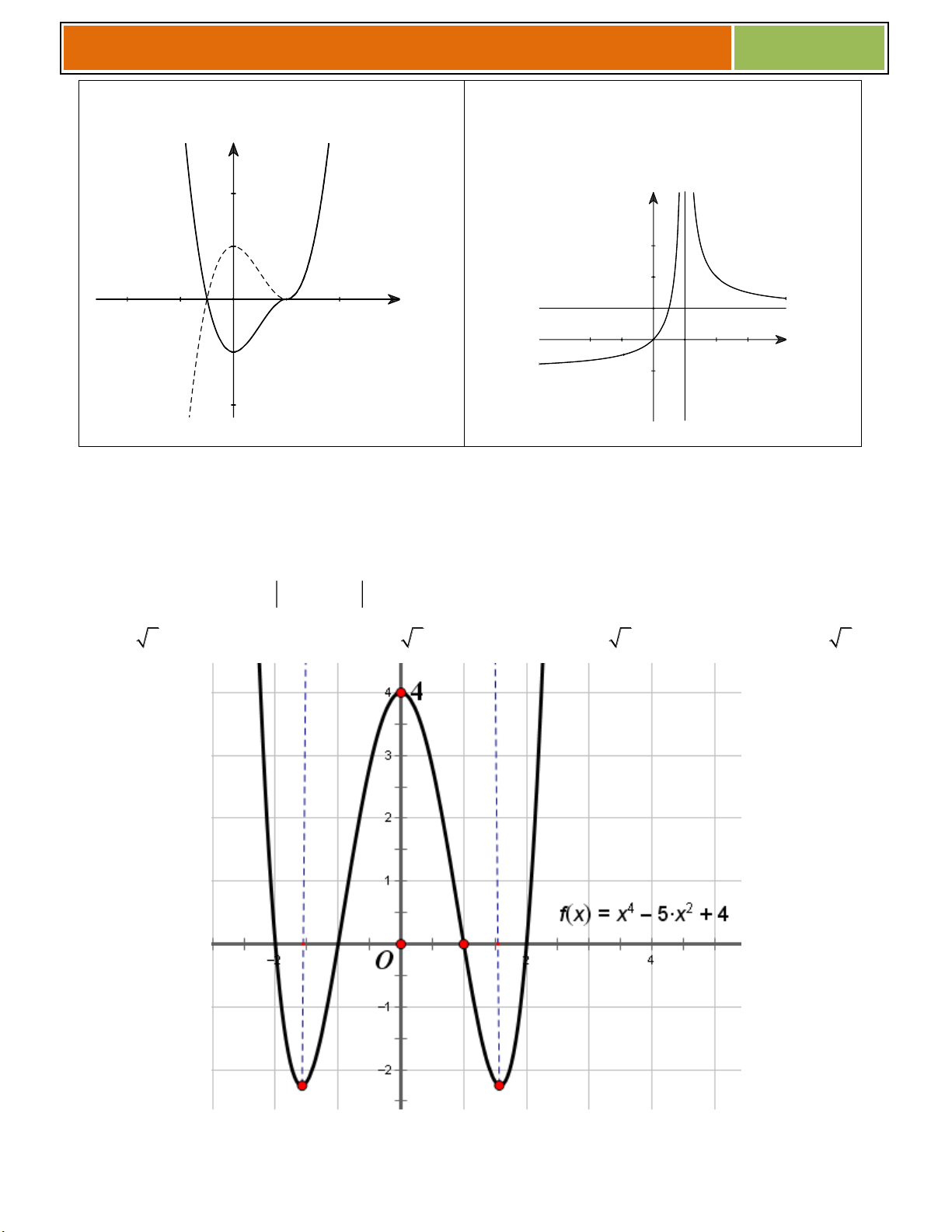
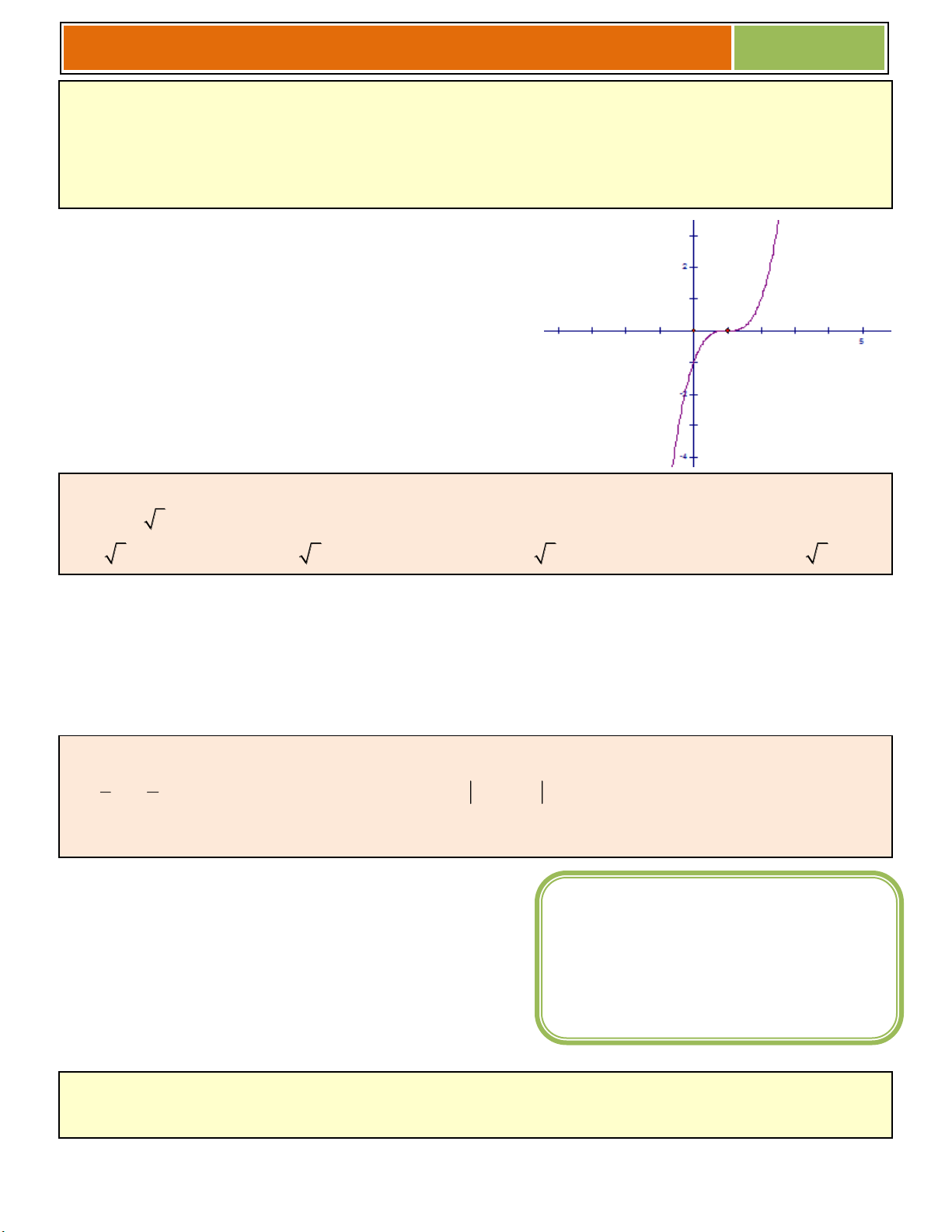
◙ Dạng 1 : Đồ thị hàm số (C’) : y  f(x)  f
  x khi f x  0   1
f x    f
x khi f x  0 2
Đồ thị (C’) gồm 2 phần :
► Giữ nguyên phần đồ thị C phía trên trục hoành Ox (do (1))
► Lấy đối xứng qua Ox phần đồ thị C nằm phía dưới trục Ox (do (2))
► Bỏ phần đồ thị C nằm phía dưới trục Ox ta sẽ được đồ thị C '. Ví dụ : 21
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
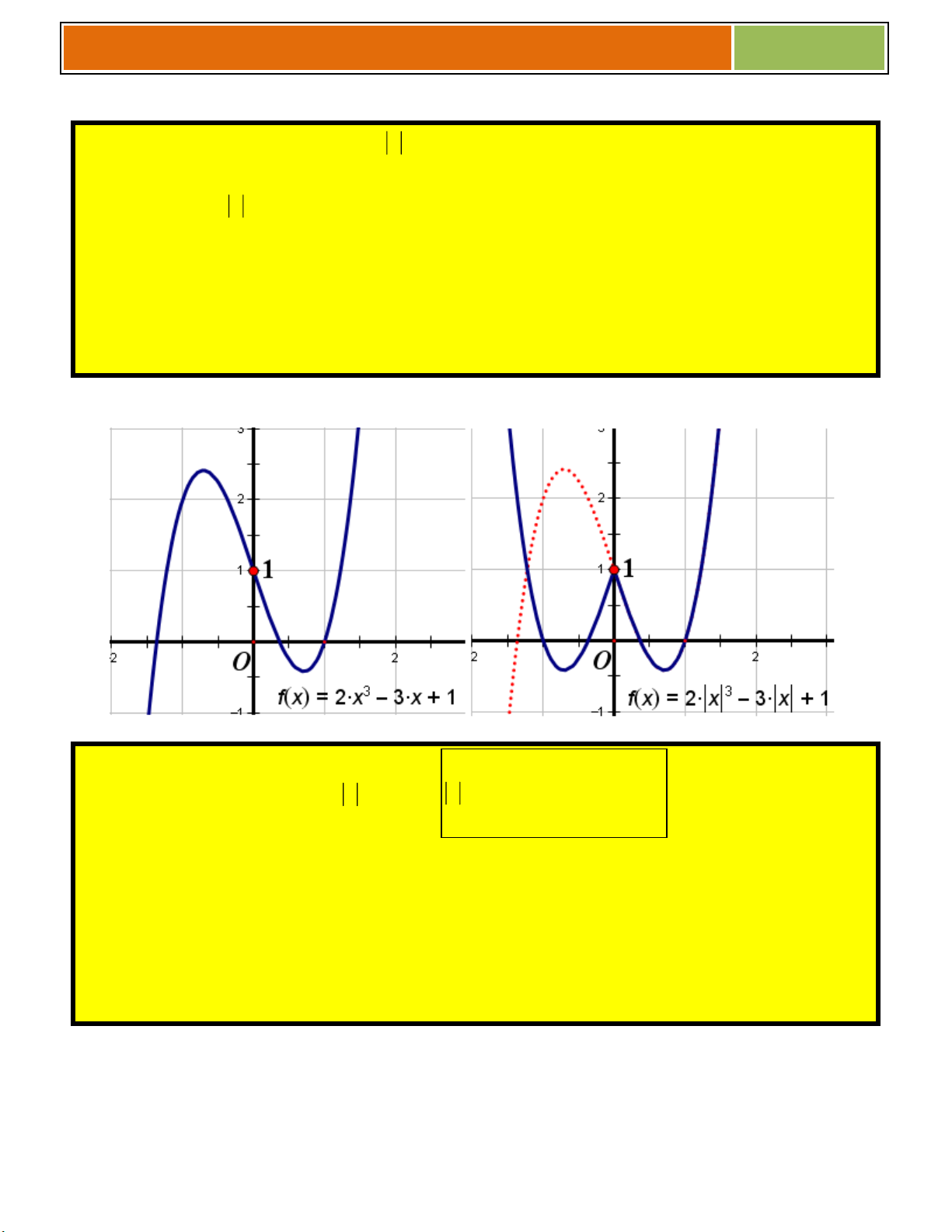
◙ Dạng 2 : Đồ thị hàm số (C’) : y  f( x ) f(x) khi x  0 y  f( x )   f(  x) khi x  0
Đồ thị (C’) gồm 2 phần :
► Giữ nguyên phần (C) phía bên phải Oy ( x ≥ 0 )
► Lấy đối xứng qua Oy phần (C) trên và bỏ phần (C) nằm bên trái Oy Ví dụ : f(x)  0 
◙ Dạng 3 : Đồ thị hàm số (C’) : y  f(x) ; y  f(x)  y  f(x) ; (1)  y  f(x) ; (2)
Đồ thị (C’) gồm 3 phần :
► Giữ nguyên phần (C) nằm phía trên Ox (do (1))
► Bỏ phần (C) nằm dưới Ox
► Lấy đối xứng qua Ox phần (C) nằm phía trên 22
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
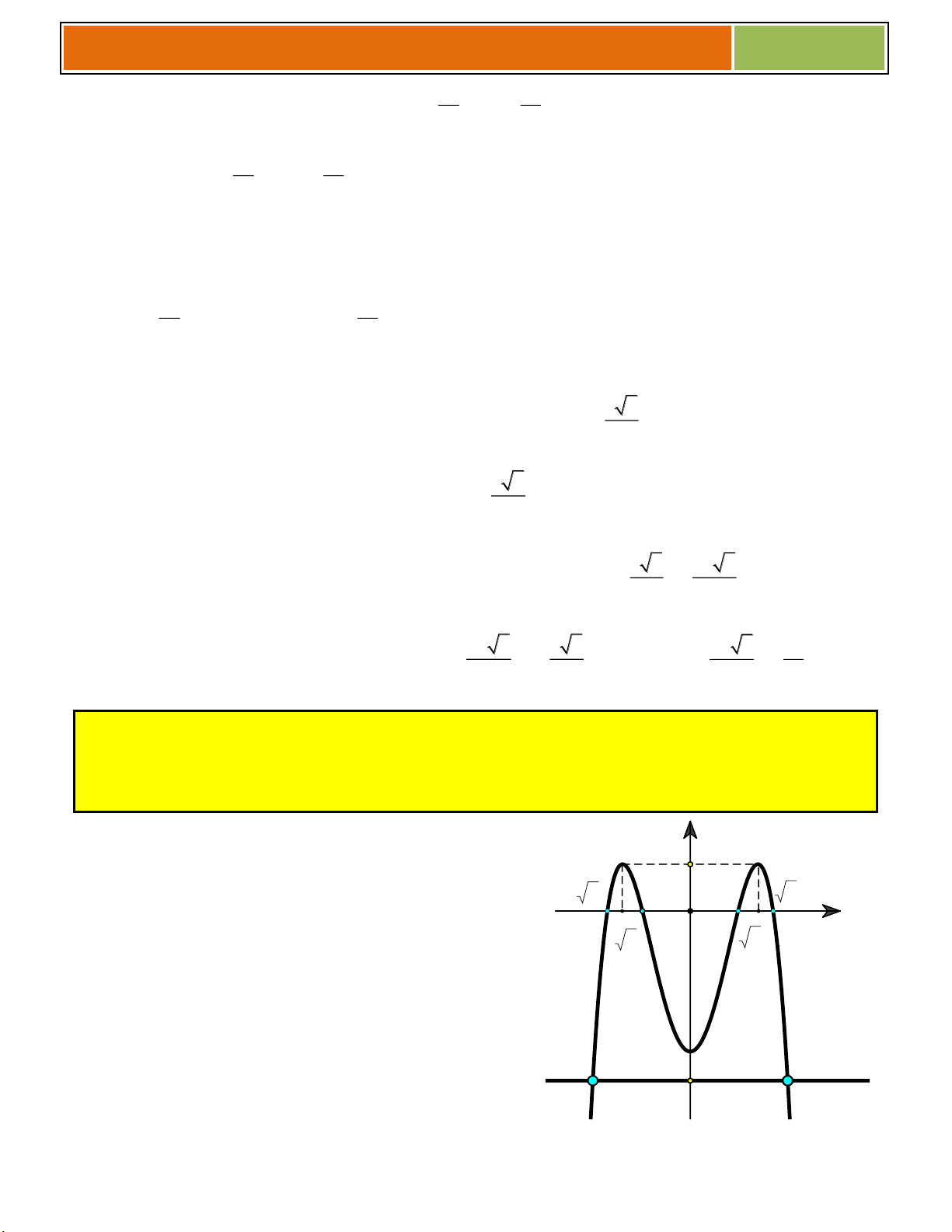
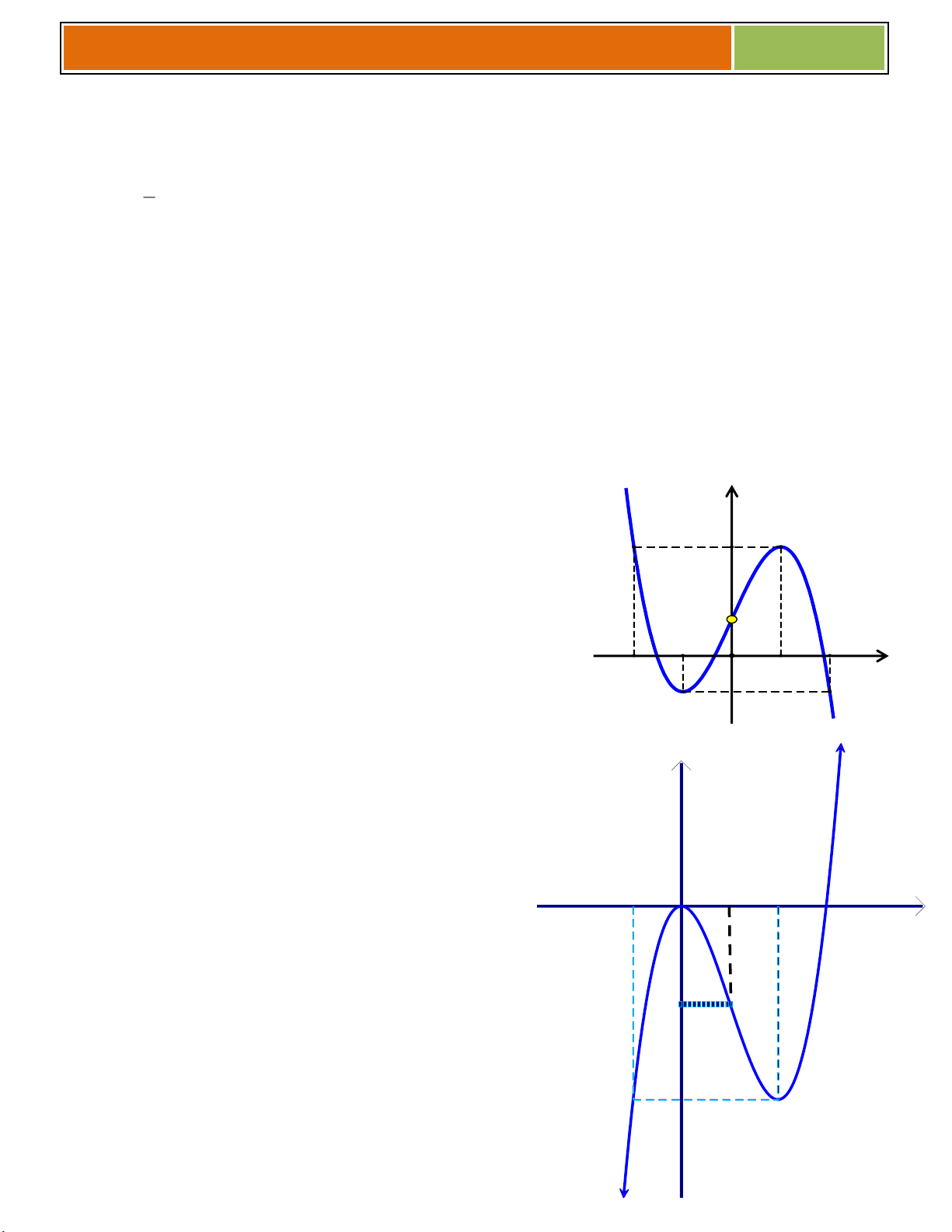
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017 Ví dụ : Đồ thị hàm số Đồ thị hàm số 3 3   
y x  3x  2 y x 3x 2
◙ Dạng 4 : Từ đồ thị C  : y u x v. x  suy ra đồ thị C : y u x v. x  . u
 x.vx  f x khi ux  0
Ta có: y u x .v x    u
  x.vx  f x khi u x  0
Đồ thị (C’) gồm 2 phần :
► Giữ nguyên phần đồ thị trên miền u x  0 của đồ thị C : y f x.
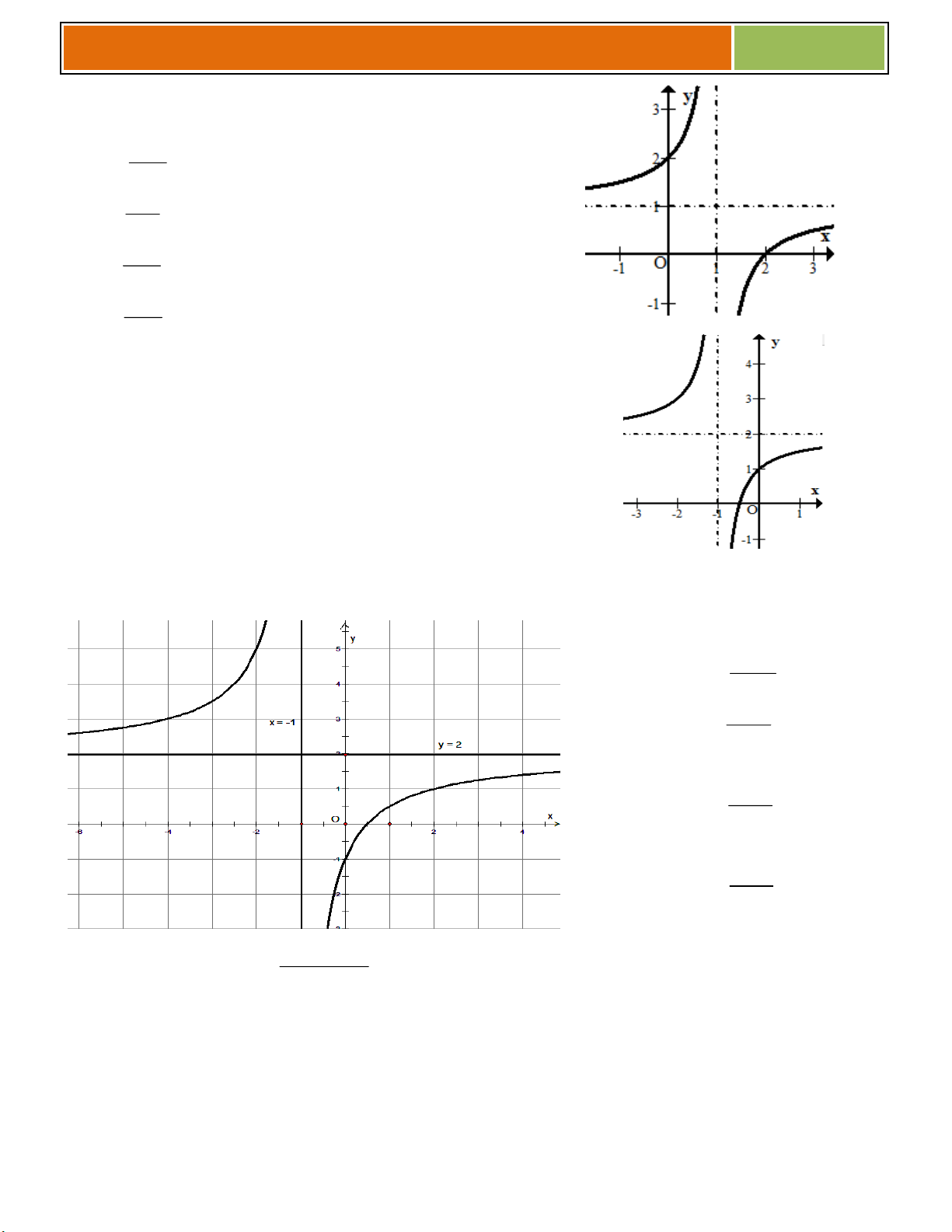
► Bỏ phần đồ thị trên miền u x  0của C, lấy đối xứng phần đồ thị bị bỏ qua Ox. Ví dụ :
Bài 01 : Từ đồ thị x   
Bài 02 : Từ đồ thị C : y f x
C y f x 3 2 :
 2x 3x 1 x  suy ra 1 x
đồ thị C : y
suy ra đồ thị C y x   2 :
1 2x x   1 x  1  f x x  
x khi x1; y x 1  khi 1 2 2x x     1     xf
x khi x 1 x 1 y    . x 1 x 
khi x    ;1  x 1
Đồ thị (C’) gồm 2 phần : ►
Đồ thị (C’) gồm 2 phần :
Giữ nguyên (C) với x  1. ► ►
Bỏ (C) với x  1. Lấy đối xứng phần đồ thị
Bỏ phần đồ thị của C  với x 1, giữ 23
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
bị bỏ qua Ox.
nguyên C  với x 1. y
► Lấy đối xứng phần đồ thị bị bỏ qua Ox. (C') y 1 1 O 1 x O 1 x (C)
BÀI TẬP TRẮC NGHIỆM PHẦN BIẾN ĐỔI ĐỒ THỊ
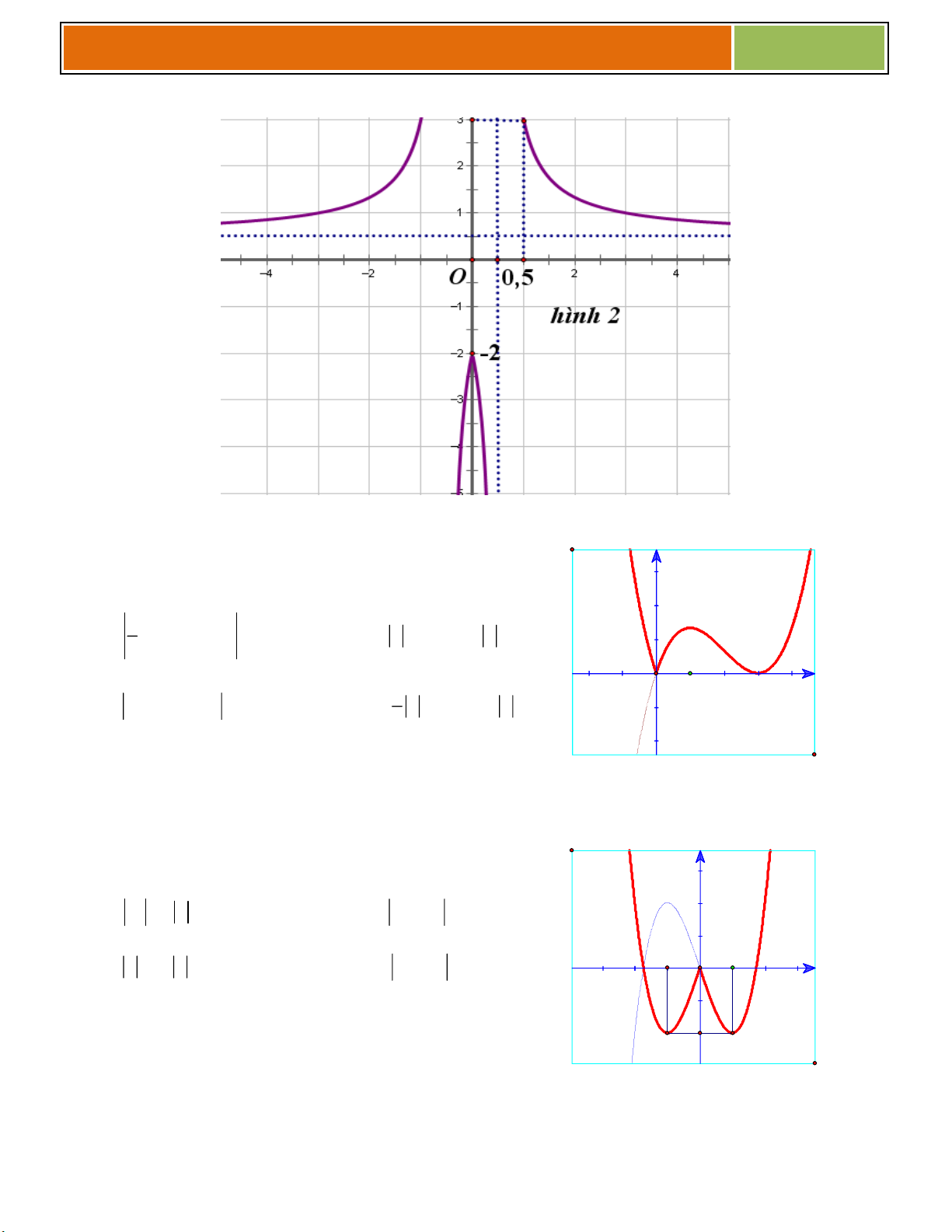
Câu 1 : Cho hàm số : y f x (C) xác định trên D. Có đồ thị (C) được vẽ như hình bên dưới. Xác
định m để phương trình 4 2 x 5
x  4  log m có 6 nghiệm 2 A. 4 m  4 2 B. 4 m  4 4 C. 4 m  4  2 D. 4 m  4  4 24
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
Câu 2 : Cho hàm số : y f x (C) xác định trên D. Có đồ thị (C) được vẽ như hình bên dưới. Xác
định m để phương trình 3
x  3 x  3m có 4 nghiệm A. m  4 1 B. m  2 C. m  6 1 D. m   2
Câu 3 : Cho hàm số : y f x (C) xác định trên D. Có đồ thị (C) được vẽ như hình bên dưới. Xác 3
định tham số k để phương trình x  3 x k  0
3.1 có 2 nghiệm đơn A. k  0 B. k  0 C. k  2 D. k  2
3.2 có 2 nghiệm kép A. k  0 B. k  0 C. k  2 D. k  2
3.3 có 3 nghiệm đơn A. k  0 B. k  0 C. k  2 D. k  2
3.4 vô nghiệm A. k  0 B. k  0 C. k  2 D. k  2 25
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
Câu 4 : Cho hàm số : y f x 4 2
x  2x (C) xác định trên D.
Có đồ thị (C) được vẽ như hình bên.
Đồ thị y f x 4 2
x  2x (C ') là hình nào ? A. B. C. D.
Câu 5 : Cho hàm số : y f x 3 2
 2x 9x 12x 3 (C) xác
định trên D. Có đồ thị (C) được vẽ như hình 1.
Dựa vào đồ thị (C), hãy vẽ đồ thị (C’): 3 2
y  2 x  9x 12 x  3 vào
hình 2 được trình bày bên dưới (nét chấm ở đây chính là
đồ thị (C) để học sinh có thể so sánh và vẽ theo) 26
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
Câu 6 : Cho hàm số : y f x 3
x 3x 1 (C) xác định trên D.
Có đồ thị (C) được vẽ như hình 3. Dựa vào đồ thị (C), hãy vẽ đồ thị (C’): 3
y x  3 x 1 vào hình 4 được trình bày bên dưới (nét
chấm ở đây chính là đồ thị (C) để học sinh có thể so sánh và vẽ theo) 27
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
Câu 7 : Cho hàm số : y f x 3
x 3x 1 (C) xác định
trên D. Có đồ thị (C) được vẽ như hình 3. Dựa vào đồ thị
(C), hãy vẽ đồ thị (C’): 3
y x  3x 1 vào
hình 5 được trình bày bên dưới (nét chấm ở đây chính là
đồ thị (C) để học sinh có thể so sánh và vẽ theo)
Câu 8 : Cho hàm số : y f x 4 2
x x (C) xác định trên D. Có đồ thị (C) được vẽ như hình 6. Dựa
vào đồ thị (C), hãy vẽ đồ thị (C’): 4 2
y x x
vào hình 7 được trình bày bên dưới (nét chấm ở đây
chính là đồ thị (C) để học sinh có thể so sánh và vẽ theo) 28
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
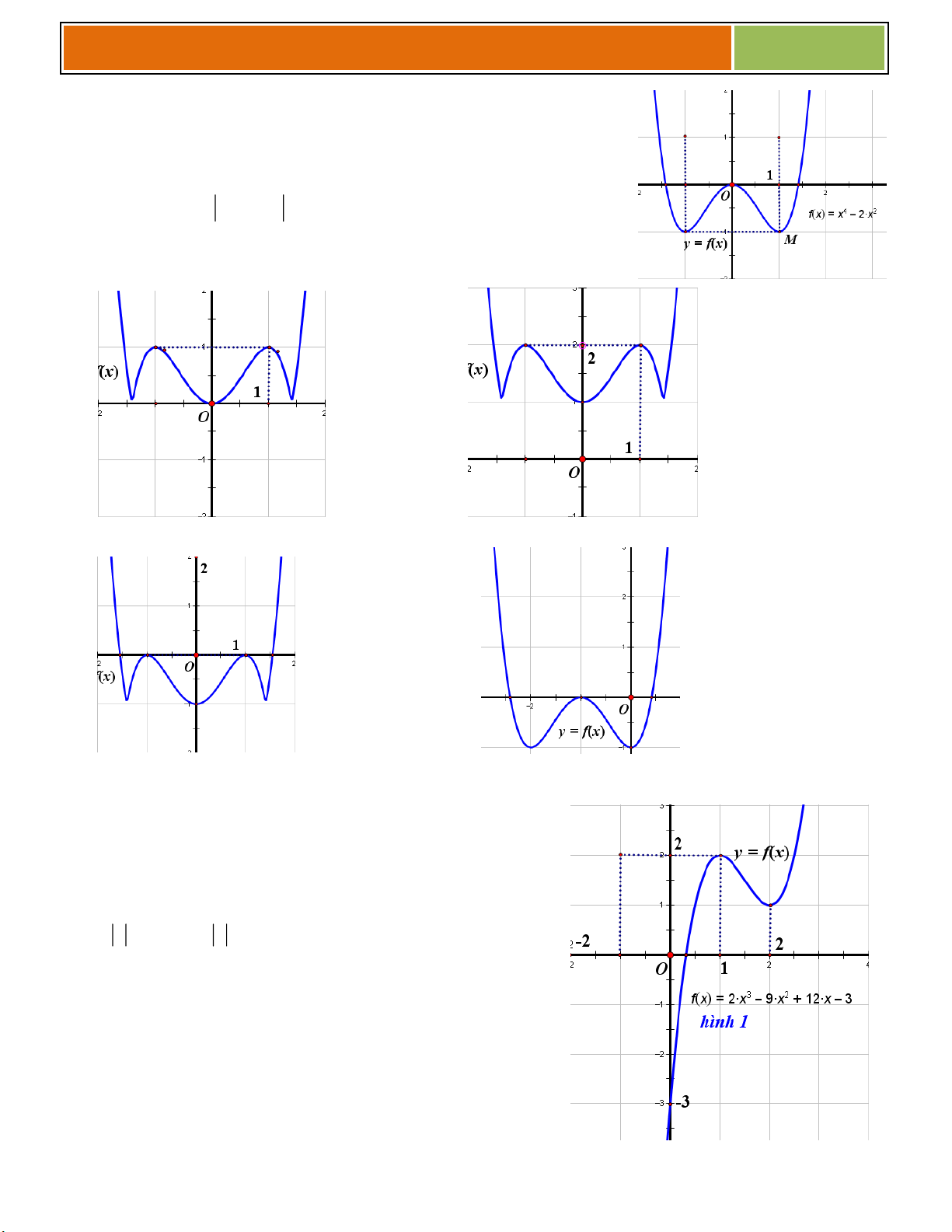
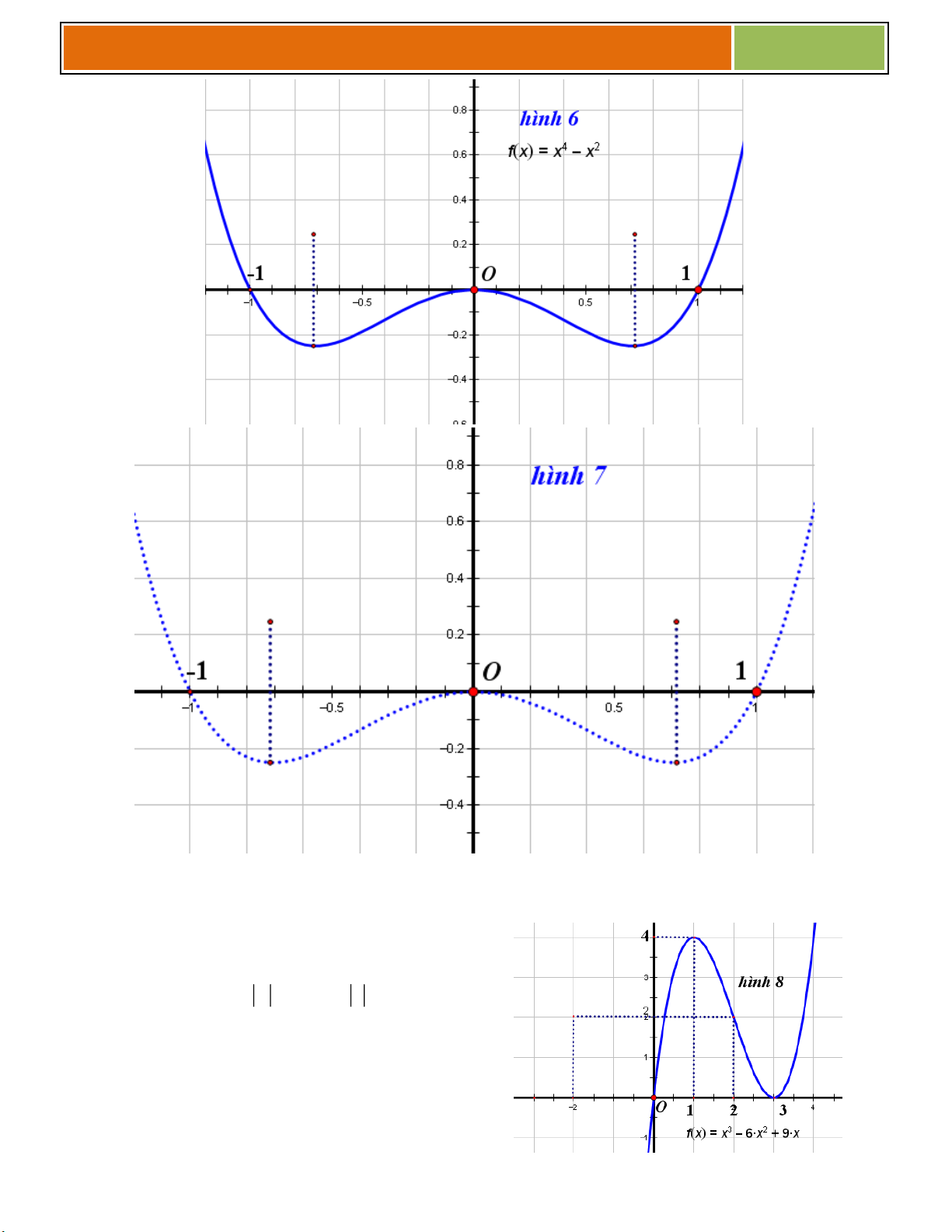
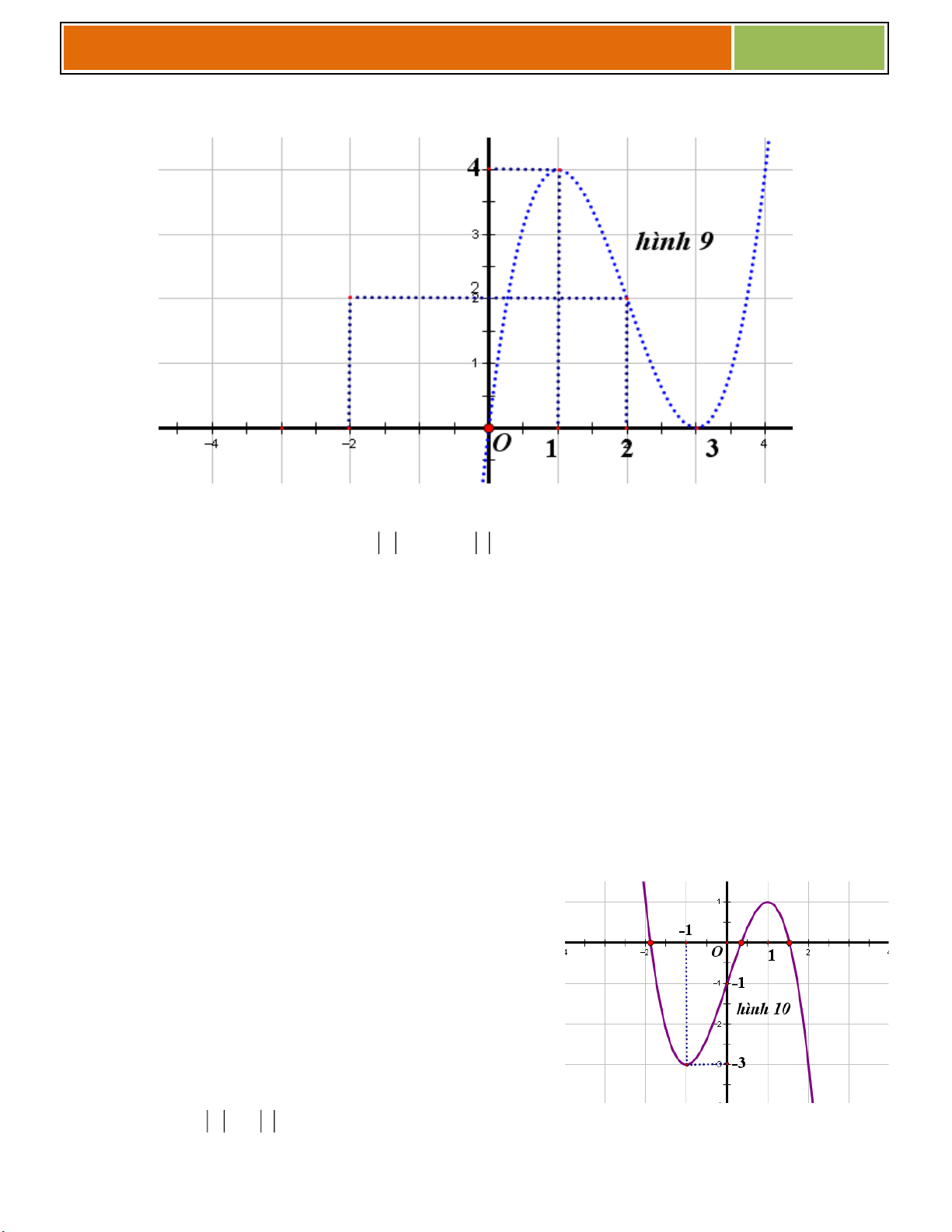
Câu 9 : Cho hàm số : y f x xác định trên D. Có
đồ thị (C) được vẽ như hình 8. Dựa vào đồ thị (C), hãy vẽ đồ thị (C’): 3 2 y x
 6x  9 x vào hình 9
được trình bày bên dưới (nét chấm ở đây chính là
đồ thị (C) để học sinh có thể so sánh và vẽ theo) 29
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
Câu 10 : Dựa vào đồ thị (C’) ở câu 9, hãy tìm giá trị m để phương trình : 3 2 x
 6x  9 x 3 m  0 10.1 vô nghiệm A. m  0 B. m  3 C. m  1 D. m  2
10.2 có 6 nghiệm phân biệt A. 1   m  3 B. m  3 C. m  1 D. m  1  10.3 có 4 nghiệm A. 1   m  3 B. m  3 C. m  1  D. m  1  10.4 có 3 nghiệm A. 1   m  3 B. m  3 C. m  1  D. m  1 
Câu 11 : Cho hàm số : 3
y  x  3x 1xác định trên D. Có
đồ thị (C) được vẽ như hình 10. Dựa vào đồ thị (C), hãy vẽ đồ thị (C’): 3 y   x
 3 x 1 vào hình 11 được trình bày 30
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
bên dưới (nét chấm ở đây chính là đồ thị (C) để học sinh có thể so sánh và vẽ theo)
Câu 12 : Cho hàm số : y f x xác định trên D. Có đồ thị (C) được
vẽ như hình 12. Dựa vào đồ thị (C), hãy vẽ đồ thị (C’): y f x
vào hình 13 được trình bày bên dưới (nét chấm ở đây chính là đồ
thị (C) để học sinh có thể so sánh và vẽ theo) 31
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
Câu 13 : Cho hàm số : y f x xác định trên D. Có đồ thị (C) được vẽ như hình 1. Đồ thị hình 2 là
của hàm số nào dưới đây ? A. 3 2
y x  6x  9 x B. 3 2
y x  6x  9x C. 3 2
y x  6x  9 x D. 3 2
y x  6 x  9 x
Câu 14 : Cho hàm số : 3 2
y x  3x  2 . Có đồ thị (C) được vẽ như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây A. 3 2
y x  3 x  2 B. 3 2
y x  3x  2 C. 3 2
y x  3x  2 D. 3 2
y x  3x  2
Câu 15 : Cho hàm số : 3 2
y x  3x  2 . Có đồ thị (C) được vẽ như hình 1. Với giá trị nào của m thì
phương trình sau có 6 nghiệm phân biệt 3 2
x  3x  2  m  0 A. 2   m  2 B. 2   m  0 C. 2   m  2 D. 0  m  2 32
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017 x
Câu 16 : Cho hàm số : y
. Có đồ thị (C) được vẽ 2x 1
như hình 1. Đồ thị hình 2 là của hàm số sau đây ? x A. y  2x 1 x B. y  2 x 1 x
C. y  2 x  1 x D. y  2 x 1 x  2
Câu 17 : Cho hàm số : y
. Có đồ thị (C) được vẽ 2x 1
như hình 1. Đồ thị hình 2 là của hàm số sau đây x  2
A. y  2 x  1 x  2 B. y  2x 1 x  2 C. y  2 x 1 x  2
D. y  2 x  1 33
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
Câu 18 : Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số y nào ? 1 A. 3 2 y
x  2x  3x . B. 3 2
y x  2x  3 x . 3 x O 1 3 1 C. 3 2
y x  2x  3x . D. 3 2 y
x  2x  3 x . 3
Câu 19 : Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? y 2 A. 3
y x  3 x . B. 3
y x  3x . -1 1 C. 3
y x  3 x . D. 3
y x  3x . O x -2 34
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017
Câu 20 : Hình vẽ bên là đồ thị hàm trùng phương.
Giá trị m để phương trình f x  m có 4 nghiệm đôi một khác nhau là: A. 3   m 1. B. m  0 .
C. m  0 , m  3 . D. 1 m  3.
Câu 21 (THPT Hà Uy Tập – Hà Tĩnh) : Tìm tất cả các giá trị của m để đường thẳng y = m cắt đồ thị hàm số 4 2
y x  2x tại 6 điểm phân biệt. A. 0  m 1 B. 1   m  0 C. 1   m 1 D. 1   m  1
Câu 22 (THPT chuyên Thái Nguyên) : Cho đồ thị hàm số 4 2
y  x  4x  3 như hình vẽ dưới đây:
Tìm tất cả các giá trị của m để phương trình 4 2
x  4x  3  m 1 có đúng 4 nghiệm thực phân biệt A. m 0; 2   1. B. m  1  ;0    2 . C. 0  m  2 . D. 1 m  3.
Câu 23 (THPT Lý tự Trọng – Nam Định) : Hàm số 3
y  x  3x 1 có đồ thị như hình vẽ bên. Tìm tất 3
cả các giá trị thực của m để phương trình x  3 x  m  0 có 4 nghiệm phân biệt. A. m 0;2 B. m  1  ;  1 35
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIẾN ĐỔI ĐỒ THỊ 2017 C. m 0;2 D. m  1  ;  1
Câu 24 (THPT chyên Nguyễn Quang Diêu – Đồng Tháp) :
Hình vẽ bên là đồ thị của hàm số 3
y x  3x 1.
Giá trị của m để phương trình 3
x  3x 1  m
có 3 nghiệm đôi một khác nhau là: A. 1 m  3. B. m  0.
C. m  0, m  3. D. 3   m 1.
Câu 25 (THPT chyên Thái Bình) : Cho hàm số f x 3 2
x 3x  2 có đồ
thị là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m đ phương trình 3 2
x  3x  2  m c nhiều nghi m thực nhất A. 2   m  2 . B. 0  m  2 . C. 2   m  2 . D. 0  m  2 . 36
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 PHẦN 10 : TỔNG ÔN x x A B x   I
◙ Trung điểm I(x ; y ) của đoạn thẳng AB : 2  I I y yA B y I  2 
x x x A B C x   G  3 ◙ Trọng tâm G  của ∆ABC :
y y yA B C y G  3
◙ Khoảng cách giữa 2 điểm A,B là 2 2
AB  (x x )  ( y y ) B A B A
◙ Khoảng cách từ điểm M(x ;y ) đến đường thẳng (D): Ax By C  0 : M M Ax  By  C M M d[M; D] 
với n  (A; B) là pháp vectơ 2 2 A  B A  0 
◙ Điểm cố định : 2 f ( ; x )
m y f ( ; x )
m y  0  . A m  .
B m C  0  B  0 m   C  0 
◙ Tọa độ nguyên : Chia hàm số ra , sau đó cho mẫu là các số mà tử chia hết
◙ Bất đăng thức Cachy : a b  2 .
a b ,dấu “ = “ xảy ra  a b
d : a x b y c  0
◙ Góc giữa 2 đƣờng thẳng: Cho 2 đường thẳng 1 1 1 1  .
d : a x b y c  0  2 2 2 2 a a b b Gọi 0 0
φ (0  φ  90 ) là góc giữa d1 và d2 thì : 1 2 1 2 cos φ  . 2 2 2 2
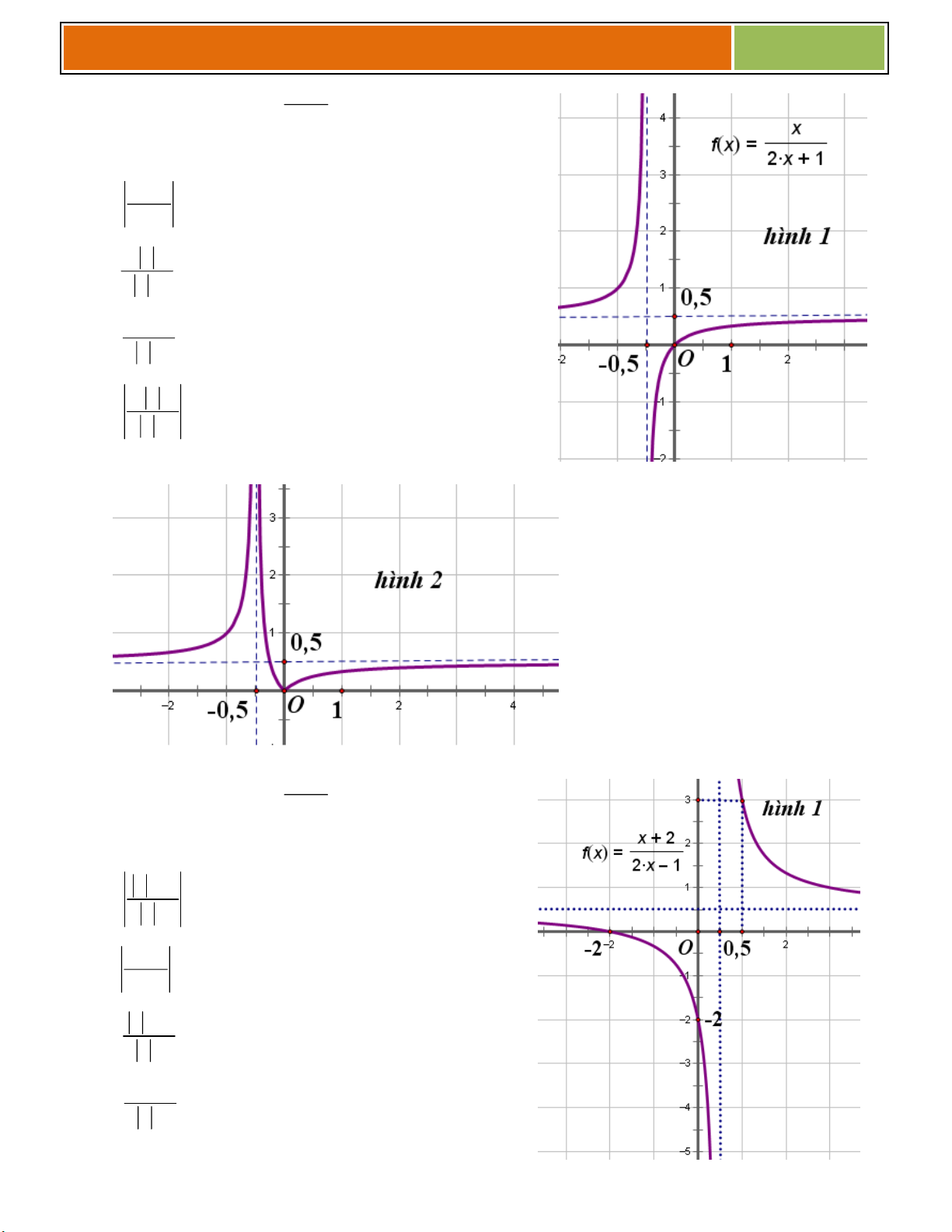
a b . a b 1 1 2 2 x 1
Ví dụ 01 : Cho hàm số y
có đồ thị là C  . Tìm điểm M C sao cho khoảng cách từ x 1 3
điểm M đến đường thẳng  : y  2x 1 bằng . 5 37
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 ◙ Phân tích :
Khoảng cách từ điểm M(x ;y ) đến đường thẳng (D): Ax By C  0 : M M Ax  By  C M M d[M; D] 
với n  (A; B) là pháp vectơ 2 2 A  B     ♥ x 1 Giải: Gọi 0
M x ; y   C . 0 0   x 1  0 
Phương trình đường thẳng (∆) được viết lại 2x y 1  0 x 1 0 2x  1 0 2x y 1 x M M 3 1 3
Khi đó theo đề ta có: d M  3 ,  0     5 2 2 2 2 1  2 5 1  2 5 x 1 0  2x 1  3 2
 2x  2x  2  3 x 1 0 x 1 0 0 0 0 2
2x  2x  2  3 x 1 0 0  0    2
2x  2x  2  3  x 1  0 0  0  a  b      a b  2 x 1 0    
2x  5x  5  0 (vn) a b 0 0     1 2
2x x 1  0 x   0 0 0  2 ► Với x  1
 thì y  0 , ta có M  1  ; 0 0 0   ► 1 1 Với x
thì y  3, ta có M ; 3 0   2 0  2    Vậy M   1 1; 0 hay M ; 3   là điểm cần tìm  2 
Ví dụ 02 (THPT Chuyên Bến Tre) : Đường cong trong hình bên là đồ thị của một hàm số được
liệt kê ở bốn phương án , A ,
B C, D dưới đây. Hỏi hàm số đố là hàm số nào? 1 A. 3 2
y x  3x  3x 1. B. 3 y x  3x 1 . 3 C. 3 2
y x  3x  3x 1. D. 3
y x  3x 1.
◙ Phân tích : Đây là dạng nhìn đồ thị
♥ Giải: Chọn D.
Nhìn nhánh ngoài cùng bên phải thấy ĐI LÊN suy ra a > 0 38
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 x 1
Lại có : y  0  
(Hai điểm cực trị của ĐTHS) nên D là thỏa mãnx  1  4
Ví dụ 03 (Chuyên Bến Tre) : Tìm giá trị nhỏ nhất của hàm số y x
trên khoảng 0; . x A. min y  2 . B. min y  4 . C. min y  0 . D. min y  3 . 0; 0; 0; 0;
◙ Phân tích : Đây là dạng tìm GTLN – GTNN ( đã có chuyên đề riêng – CĐ3)
♥ Giải: Chọn B. 2 4 x  4 Ta có y  1  , . 2 2 x x
y  0  x  2 
Lập bảng biến thiên của hàm số trên khoảng 0; .
Nhận thấy hàm số chỉ đạt cực tiểu tại điểm x  2 và y
 4 nên min y  4. CT 0;
Ví dụ 04 (Chuyên Bến Tre) : Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số 1 3 2 y
x mx  4x m đồng biến trên khoảng  ;   . 3 A.  ;  2  . B. 2; . C.  2  ;2. D.  ;  2 .
◙ Phân tích : Đây là dạng đơn điệu của hàm số ( đã có chuyên đề riêng – CĐ1 )
♥ Giải: Chọn C.; Ta có: 2
y  x  2mx  4 .
Hàm số đồng biến trên khoảng  ;
  khi và chỉ khi y  0, x   ;   . 2  
  m  4  0  2
  m  2 .
Ví dụ 05 (SGDĐT Phú Thọ) : Hình vẽ dưới đây là đồ thị của hàm số nào? x 1 A. y  . B. 4 2
y  x  4x . C. 3
y  x  3x . D. 4 2
y x  4x . x 1 39
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
♥ Giải: Chọn B.
+ Hàm số đã cho là hàm TRÙNG PHƢƠNG nên loại A, C
+ Nhìn vào nhánh phải ngoài cùng đi xuống nên a < 0 (Đơn giản thế thôi) x  0
Cách khác: Xét hàm số 4 2
y  x  4x : 3 y  0  4
x  8x  0   . x   2 1
Ví dụ 06 (THPT chuyên Lê Thánh Tông – Quảng Nam) : Tìm m để hàm số 3 2 y
x mx  4x 1 3
đạt cực trị tại x  2 . A. m  0. B. m  2. C. Không tồn tại . m D. m  2. 
♥ Giải: Chọn C. 2
y  x  2mx  4 .
y  2x  2m . y  2  0 4  4m  4  0
Hàm số đạt cực trị tại x  2     . y  2  0 4  2m  0 m  2  
m. Vậy không tồn tại m thỏa yêu cầu bài toán. m  2
Chú ý : học sinh hay chỉ để ý đến trường hợp y2  0
mà quên mất y 2  0 nên dễ nhầm với đáp án B !!! 3
Ví dụ 07 (THPT chuyên Thái Bình) : Cho hàm số y
có đồ thị C  . Mệnh đề nào sau đây là x 1 m nh sai ?
A. Hàm số không có điểm cực trị.
B. Đồ thị C  không có tiệm cận ngang.
C. Đồ thị C  nhận I( 1
 ;0) làm tâm đối x ng. D. Hàm số nghịch biến trên m i khoảng xác định.
♥ Giải: Chọn B. 40
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 ☻ 3
Hàm số đã cho có y      , x   \  
1 nên hàm số nghịch biến trên từng khoảng xác x   0 2 1
ịnh và không có cực trị  A và D đúng.  Hay chú ý : ax b
hàm số nhất biến y
luôn đơn điệu tăng hoặc giảm và không có cực trị cx d
☻ Do lim y  0; lim y   ;
 lim y   nên đồ thị hàm số có tiệm cận ngang và đ ng lần lượt là x    x 1  x 1  y  0; x  1   C đúng, B sai.
Ví dụ 08 (THPT chuyên Thái Bình) : Đồ thị của hàm số nào dưới đây không có đường tiệm cận ? x 1 x  3 2 x  2x  3 A. y  . B. y  . C. 4
y x  2016 . D. y  . 2 x  4 x 1 x 1
♥ Giải: Chọn C. x 1 Ta có lim  1
 nên đồ thị hàm số có hai tiệm cận ngang y 1; y  1  . x 2 x  4 x  3 x  3 x  3 Ta có lim 1; lim   ;  lim
  nên đồ thị hàm số có tiệm cận ngang y 1, tiệm x     x 1   x 1 x 1 x 1  x 1 cận đ ng x  1. Ta có  4
lim x  2016   nên đồ thị hàm số không có tiệm cận ngang (và cũng không có tiệm cận x đ ng).
Ví dụ 09 (THPT chuyên Thái Bình) : Bảng biến thiên trong hình v dưới đây là bảng biến thiên của hàm số nào? A. 4 2
y  x  2x  3 . B. 4 2
y x  2x  3 . C. 4 2
y  x x  3 . D. 4 2
y x  2x  3 . x  1  0 1  y  0  0  0   3   y 4  4 
♥ Giải: Chọn B.
Hàm số phải tìm có dạng 4 2
y ax bx c a  0 .
Từ bảng biến thiên suy ra hàm số có 2 cực tiểu và 1 cực đại nên a  0 , b  0 . Cách khác :
☻ nhìn nhánh phải ngoài cùng đi lên nên a > 0 , mà có 3 cực trị thì a.b < 0 nên suy ra b < 0 41
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 x
Ví dụ 10 (Trƣờng Quốc Học Quy Nhơn – Bình Định) : Cho hàm số y f x 3 1  có đồ thị x  3
C. Viết phương trình tiếp tuyến của đồ thị C, biết hoành độ tiếp điểm là nghiệm của phương trình 7x 1 
1 . f  x 10 . 2 1 5 1 2 1 5 1
A. y   x  ; y   x  .
B. y   x  ; y x  . 5 5 2 2 5 5 2 2 2 9 5 9 2 9 5 1
C. y   x  ; y   x  .
D. y   x  ; y   x  . 5 5 2 2 5 5 2 2  ♥ 10
Giải: Chọn A. MXĐ: D  \  
3 Ta có: f  x   . x  32
Gọi A là tọa độ tiếp điểm của tiếp tuyến và đồ thị hàm số.Hoành độ điểm A thỏa mãn phương 10  trình: 7x 1 
1 . f  x  10  7x 1  2 1         x x x x  3 10 7 11 6 9 2 x 1 2
x x  2  0   x  2   5  1
Với x   f     f   5 1 1 2, 1 
. Ta được PTTT là: y x  2 2 2  2  1
Với x    f    f   2 2 2 1, 2 
. Ta được PTTT là: y x  5 5 5 2 1 5 1
Vậy có hai tiếp tuyến cần tìm: y   x  ; y   x  5 5 2 2
Ví dụ 10 (Trƣờng Quốc Học Quy Nhơn – Bình Định) : Tìm tất cả các tiệm cận đ ng của đồ thị 2
x  2x 16  2  x hàm số y  2 x  3x  . 10 A. y  2  ; y  5 . B. x  2  . C. x  2  ; x  5.
D. x  2, x  5  .
♥ Giải: Chọn C. mXĐ: D  \  2  ,  5 2 2
x  2x 16  2  x
x  2x 16  2  x lim   ,  lim    2  2 x 2    x 2 x 3x 10  x  3x 10 2 2
x  2x 16  2  x
x  2x 16  2  x lim   ,  lim    2  2 x5   x5 x 3x 10 x  3x 10
nên đồ thị hàm số có hai đường tiệm cận đ ng là x  2  ; x  5 42
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 m  1 sin x  2
Ví dụ 11 : Cho hàm số y
. Tìm tất cả các giá trị của tham số m để hàm số nghịch sin x m    biến trên khoảng 0;    2  m  1  m  1  m  0 A. 1   m  2 . B.  . C.  . D.  . m  2 m  2 m  1
♥ Giải: Chọn B.
Cách 1: Dùng casio: Dùng chức năng mode 7. sin x  2
+ Thừ m  0  y  . sin x Nhập vào máy tính lệnh
Nhìn vào cột F X  ta thấy giá trị tăng dần khi X tăng vậy hàm đồng biến khi m  0
Vậy ta loại các phương án ch a m  0  Loại A, D.  ☻ sin x 2
Thử với m  2  y
1 là hàm không đổi  loại C. Nên ta chọn B. sin x  2    m  1 t  2
Cách 2: Đặt sin x t khi đó x  0;  t    0  ;1 . Khi đó y   2  t mm  1 t  2
Yêu cầu bài toán tương đương với tìm m để hàm số y
nghịch biến trên khoảng 0  ;1 . t m 2    Ta có m m 2 y  . t  22 2 y  0 
m m  2  0 m  1 
Hàm số nghịch biến trên khoảng 0;2   .     t       m 0; 2 0;2 m  0;2 m  2 43
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 Bài tập tại lớp
Bài 01 (THPT Vi t Trì – Phú Thọ) : Giá trị lớn nhất của hàm số 4 2
y  x  3x 1 trên *0; 2+ là: 13 A. 1. B. 29. C. – 3. D. . 4 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Bài 02 (THPT Vi t Trì – Phú Thọ) : Một chất điểm chuyển động theo quy luật 2 3
s  1 3t t . Vận
tốc vm / s của chuyển động đạt giá trị lớn nhất khi t bằng: A.1s. B. 3 s. C. 4s. D. 2s. ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Bài 03 (THPT Vi t Trì – Phú Thọ) : Số giao điểm của đường cong 3 2
y x x  2x  3 và đường
thẳng y x  3 bằng A. 0. B. 1. C. 2. D. 3. ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Bài 04 (THPT Vi t Trì – Phú Thọ) : Tiếp tuyến của đồ thị hàm số 3 2
y x 3x  2 có hệ số góc k  3  có phương trình là A. y  3  x  3. B. y  3  x 3 .
C. y  3x  3.
D. y  3x  3 . ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 44
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 1
Bài 05 (THPT Vi t Trì – Phú Thọ) : Cho hàm số 3 2 f (x) 
x  2x  m  
1 x  5 . Với điều kiện nào 3
của m thì hàm số đã cho đồng biến trên ? A. m  3. B. m  3. C. m   3. D. m  3. ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Bài 06 (THPT Vi t Trì – Phú Thọ) : Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số 1 3 2 y
x  2x  3x  5 3
A. Song song với trục hoành.
B. Có hệ số góc bằng – 1.
C. Có hệ số góc dương.
D. Song song với đường thẳng y = x - 1. ♥ Giải :
Chú ý : <<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. x 1
Bài 07 (THPT Vi t Trì – Phú Thọ) : Đồ thị hàm số y  là hình nào: 1 x I II y y 2 3 2 1 x 1 -2 -1 1 2 3 x -1 -3 -2 -1 1 2 3 -1 -2 -2 -3 -3 III IV 45
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 y y 3 3 2 2 1 1 x x -3 -2 -1 1 2 3 -1 -3 -2 -1 1 2 3 -1 -2 -3 -2 -3 A. II. B. IV. C. III. D. I.
Bài 08 (THPT Vi t Trì – Phú Thọ) : Để hàm số 3 2
y x  3mx  2m  
1 x m  5 có cực đại, cực tiểu điều kiện của m là:  1   1   1  1  A. m   ;   1;  
. B. m  ;1 . C. m  ;   1;  . D. m  ;1 .       3   3   3  3  ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 2sin x 1
Bài 09 (THPT Vi t Trì – Phú Thọ) : Hàm số y
có giá trị lớn nhất là s inx  2 1 A. 1. B. -1. C. -3. D. . 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Bài 10 (THPT Vi t Trì – Phú Thọ) : Tìm m để đồ thị hàm số y   x   2
1 x  2m   1 x m   cắt trục
hoành tại ba điểm phân biệt 46
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 1 A. m . B.   m  0 . C. 0  m  2 . D. m  0 . 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Bài 11 (THPT Vi t Trì – Phú Thọ) : Đồ thị hình bên y là của hàm số: 3 3 x A. 2 2 y    x 1. 3 1 B. 3 2
y x  3x 1. x -3 -2 -1 1 2 3 C. 3 2
y  x  3x 1. -1 D. 3 2
y x  3x 1. -2 -3 ♥ Giải :
Nhìn vào nhánh ngoài cùng bên phải thấy<<<<<<<là ............................, Lại có ......................................................................
Bài 12 (THPT Phạm Văn Đồng – Phú Yên) : Đồ thị hàm số 3 2
y ax bx +cx+d có điểm cực tiểu là
O 0;0 và điểm cực đại là M 1  ;1 . Giá trị của , a , b ,
c d lần lượt là: A. 3;0; 2  ;0 . B. 2  ;3;0;0 . C. 3;0;2;0 . D. 2  ;0;0;3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 47
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Bài 13 (THPT Phạm Văn Đồng – Phú Yên) : Cho hàm số 3 2
y ax bx cx d có đồ thị như hình v
bên. Mệnh đề nào dưới đây đúng?
A. a  0,b  0,c  0,d  0 .
B. a  0,b  0,c  0, d  0 .
C. a  0,b  0,c  0,d  0 .
D. a  0,b  0,c  0, d  0 . ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Bài 13 (THPT SPHN – lần 02) : Tính khoảng cách giữa hai điểm cực tiểu của đồ thị hàm số 4 2
y  2x  3x 1 A. 4 2 3 B. 3 C. 2 3 D. 4 3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Bài 14 (THPT SPHN – lần 02) : Tìm tất cả các giá trị của tham số m để hàm số 1 1 3 y
x  m  5 2
x mx có cực đại, cực tiểu và xx  5 . 3 2 CD CT A. m  0 B. m  6  C. m6;  0 D. m0;  6 ♥ Giải :
Ta chú ý công thức :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Bài 15 (THPT Hà Uy Tập– Hà Tĩnh) : Tìm tất cả các giá trị của m để đồ thị hàm số 3
y x  3x  2 cắt
đường thẳng y m 1 tại 3 điểm phân biệt 48
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
A. 1  m  5 B. 1  m  5 C. 1  m  5 D. 0  m  4 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Bài 16 (THPT Hà Uy Tập– Hà Tĩnh) : Cho hàm số 3 2
y ax bx cx d có đồ thị như hình v bên.
Mệnh đề nào dưới đây đúng?
A. a  0,b  0, c  0, d  0 .
B. a  0,b  0, c  0, d  0 .
C. a  0,b  0, c  0, d  0 .
D. a  0,b  0, c  0, d  0 . ♥ Giải : y
<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<< x 0
Bài 17 (THPT chuyên Bình Long – Bình Phước) : Cho hàm số 3 2
y ax bx cx d có đồ thị như
hình bên. Khẳng định nào sau đây đúng? A. , a ,
b c  0; d  0 B. , a ,
b d  0;c  0 C. , a ,
c d  0;b  0 D. , a d  0; , b c  0 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 18 (THPT chuyên Bình Long – Bình Phước) : Cho hàm số y f x liên tục trên và có đồ thị
của hàm số y f ' x như hình v . Chọn khẳng định đúng ? 49
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
A. f b  f a  f c
B. f b  f c  f a C. f c  f a  f b D. f c  f b  f a♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 19 (THPT chuyên Thái Nguyên) : Gọi hai điểm M, N lần lượt là giao điểm của đường thẳng 2x  4
y  x 1 và đường cong y  x . Tìm hoành độ trung điểm của đoạn thẳng MN: 1 5 5 A. 1. B. 8. C. . D.  . 2 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Bài 20 (THPT chuyên Thái Nguyên) : Cho hàm số f x xác định trên và có đồ thị hàm số fx
cắt trục Ox tại 3 điểm có hoành độ lần lượt là a  b  c như hình v . Chọn khẳng ịnh sai trong các khẳng định sau:
A. f c  f a  f b B. f c  f b  f a . C. f a  f b  f c . D. f b  f a  f c. ♥ Giải : a b c
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 50
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Bài 21 (THPT chuyên ĐHSPHN Lần 04) : Cho hàm số bậc ba 3 2
y ax bx cx d có đồ thị như hình v : Dấu của ; a ; b ; c d là:
A. a  0;b  0;c  0;d  0 .
B. a  0;b  0;c  0;d  0 .
C. a  0;b  0;c  0;d  0 .
D. a  0;b  0;c  0;d  0 . ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<
Bài 22 (THPT chuyên ĐHSPHN Lần 04) : Cho hàm số 4 2
y ax bx c có đồ thị như hình v . Dấu của a, , b c là:
A. a  0,b  0,c  0.
B. a  0,b  0,c  0. C. a  0,b  0,c  0. D. a  0,b  0,c  0. ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<
Bài 23 (THPT chuyên ĐHSPHN Lần 04) : Tìm tất cả các giá trị thực của tham số m để đồ thị hàm 2x 1 số y
có đường tiệm cận đ ng 3x m 3 A. m  1 B. m  1 C. m   R D. m  2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 51
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Bài 24 (THPT chuyên Lương Văn Tụy) : Hàm số y f x xác định liên tục trên khoảng K và có
đạo hàm là f ' x trên K. Biết hình v sau đây là đồ thị của hàm số f ' x trên K.
Số điểm cực trị của hàm số f x trên K là: A. 0 B. 1 C. 3 D. 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<< x
Bài 25 (THPT chuyên Lương Văn Tụy) : Số tiệm cận của đồ thị hàm số y  là 2 x 1 A. 1 B. 2 C. 4 D. 3
Bài 26 (THPT chuyên Lương Văn Tụy) : Tập hợp giá trị m để hàm số 3 2
y mx mx  m   1 x  3 đồng biến trên là:  3 3   3   A. 0;   B. ;    C. 0; D.   3 ; 0  ;       2  2   2  2  ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Bài 27 (THPT chuyên Lương Văn Tụy) : Giá trị m để hàm số 3 2
y x x   2 3 3 m  
1 x đặt cực tiểu tại x  2 là A. m  1  B. m  1  C. m  1  D. m  1 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 52
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Bài 28 (THPT chuyên Lương Văn Tụy) : Đồ thị dưới đây là đồ thị của hàm số 3 2
y  x  3x  4
Với giá trị nào của m thì phương trình 3 2
x  3x m  0 có hai nghiệm phân biệt ?
A. m  4  m  0 B. m  4   m  0 C. m  4
  m  4 D. một kết quả khác ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. ax b
Bài 29 (THPT Đoàn Thượng – Hải Dương) : Cho hàm số y
với a  0 có đồ thị như hình x c d
v bên. Mệnh đề nào dưới đây đúng
A. b  0,c  0, d  0 B. b  0,c  0, d  0 C. b  0,c  0, d  0
D. b  0,c  0, d  0 ♥ Giải : y
<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<< O x
<<<<<<<<<<<<<<<<<<<<<<<< 3x 1
Bài 30 (THPT chuyên Hưng Yên) : Đồ thị của hàm số y
và đồ thị của hàm số y  4  x  5 có x 1
tất cả bao nhiêu điểm chung ? A. 0. B. 1. C. 2 . D. 3. ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 53
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Bài 31 (THPT chuyên Hưng Yên) : Tiếp tuyến của parabol 2
y  4  x tại điểm (1 ; 3) tạo với hai trục
tọa độ một tam giác vuông. Tính diện tích S tam giác vuông đó. 25 5 25 5 A. S  . B. S  . C. S  . D. S  . 4 4 2 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Bài 32 (THPT chuyên Hưng Yên) : Cho hàm số y f (x) xác định và liên tục trên đoạn  2  ;2 và có
đồ thị là đường cong trong hình v bên. Xác định tất cả các giá trị của tham số m để phương trình
f x  m có số nghiệm thực nhiều nhất. A. 0  m  2 . B. 0  m  2 . C. m  2 . D. m  0 . ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<< 5
Bài 33 (THPT chuyên Hưng Yên) : Biết rằng đồ thị các hàm số 3 y x x  2 và 2
y x x  2 tiếp 4
xúc nhau tại điểm M (x ; y ) . Tìm x . 0 0 0 1 5 3 3 A. x
. B. x   . C. x  . D. x  . 0 2 0 2 0 4 0 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 54
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<< Chú ý cho bài 33 : 4mx  3m
Bài 34 (THPT Đoàn Thượng) : Cho hàm số y
. Với giá trị nào của m thì đường tiệm x  2
cận đ ng, tiệm cận ngang của đồ thị hàm số cùng hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 2016 . A. m  . B. m  504  . C. m  252  . D. m  1008  . ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Bài 35 (THPT Trần Hưng Đạo – Nam Định) : Cho hàm số 4 2 2
y x  2mx m  2 . Tìm m để hàm số
có 3 điểm cực trị và các điểm cực trị của đồ thị hàm số là ba đỉnh của một tam giác vuông ? A. m  1. B. m  1.  C. m  2. D. m  2.  ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Bài 36 (THPT Yên Lạc – Vĩnh Phúc) : Cho hàm số y f x có đạo hàm
f x   x  2 '
1  x  23x  
1 . Số điểm cực trị của hàm số là: A. 4 B. 3 C. 1 D. 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<< 55
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Bài 37 : Cho hàm số y f x có đồ thị hàm số f ' x như sau y 3 2 1 x -4 -2 2 4 -1
Xác định số điểm cực trị của hàm số y f x là A.3 B. 2 C.1 D.0 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Bài 38 : Cho hàm số y f (x) xác định và liên tục trên đoạn  2
 ;2và có đồ thị là đường cong
trong hình v bên. Hàm số f (x) đạt cực đại tại điểm nào dưới đây? y A. x =  2. 3 B. x = 0. C. x = 1. D. x = 2. 1 2 x -2 -1 0 -1 -2 2x
Bài 39 (THPT chuyên KHTN – HN) : Hàm số y
trên đoạn 0  x 1 có giá trị lớn nhất và 2 x 1
giá trị nhỏ nhất thỏa mãn đẳng th c A. 4 4 y +y 1. B. 4 4 y +y  4 . C. 4 4 y +y 16 . D. 4 4 y +y  8 . max min max min max min max min ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<. 56
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Bài 40 (THPT chuyên KHTN – HN) : Cho hàm số 3 2
y x x  5x 1 , phương trình tiếp tuyến tại
điểm trên đồ thị có hoành độ x  2 là:
A. y  10x  9 .
B. y  11x 19 .
C. y  11x 10 .
D. y  10x  8 . ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
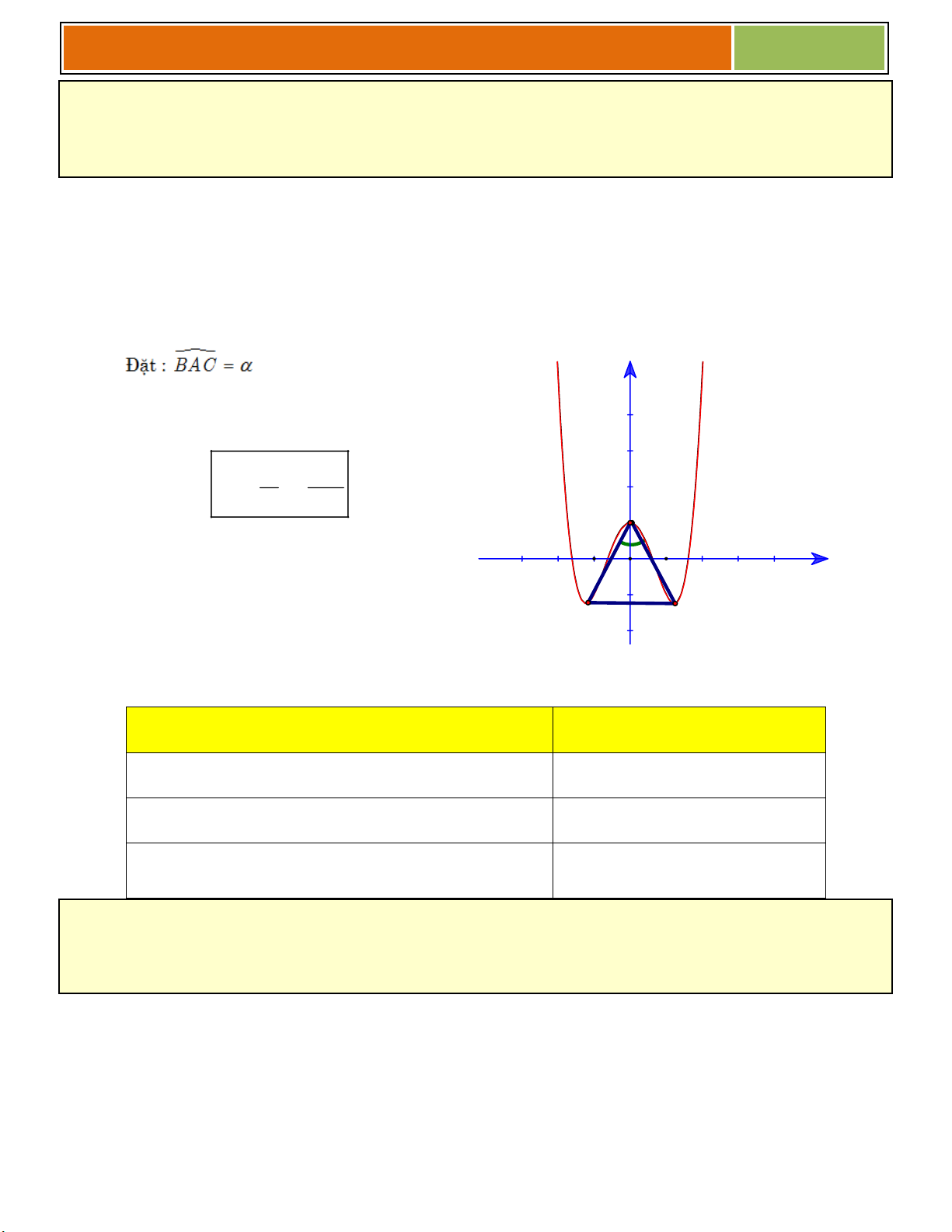
Chú ý công thức giải nhanh hàm trùng phƣơng yb3  2 Tổng quát: cot  2 a 8 A O x B C Dữ kiện
Công thức thỏa mãn ab  0
Tam giác ABC vuông cân tại A 3 b  8a  0 Tam giác ABC đều 3 b  24a  0
Tam giác ABC có diện tích SS 3 a3 2 S 2 ( )  b5  0 ABC  0 0
Vận dụng 01 (THPT chuyên Thái Bình) : Tìm tất cả các giá trị thực của m để đồ thị hàm số 4 2
y x  2mx m  3 có ba điểm cực trị tạo thành một tam giác cân. A. m  0 . B. m  1. C. m  0 . D. m  3 . ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<< 57
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Vận dụng 02 : Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số 4 2 4
y x  2mx  2m m có ba điểm cực trị tạo thành một tam giác đều. A. 3 m  3 B. 3 m  1 3 C. 3 m  1 3 D. 3 m   3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Vận dụng 03 : Giá trị m để đồ thị hàm 4 2
y x  2mx 1 có ba điểm cực trị tạo thành một tam giác
có diện tích bằng 4 2 là: A. m  2 B. m  4  C. m  2  D. m  1 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Vận dụng 04 (Sở GD – ĐT Nam Định) : Tìm m để đồ thị hàm số 4 2 2
y x  2mx  2m  4m có ba
điểm cực trị A , B , C sao cho S 1 . ABC A. m  4 . B. m  1 C. m  3 . D. m  2 . ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Vận dụng 05 (THPT Phù Cát 1 – Bình Định) : Các giá trị của tham số m để đồ thị hàm số 1 3 4 2 y   x
mx có ba điểm cực trị tạo thành một tam giác đều là: 4 2 2 3 A. 3 m  6 . B. 3 m  6 . C. 3 m  6 . D. m  2 6 3 2 58
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Vận dụng 06 : Cho hàm số 4 2
y x  2mx  2m . Tìm m để hàm số có các điểm cực đại, cực tiểu tạo
thành tam giác có diện tích bằng 32. A. m  4 . B. m  5 . C. m  3  . D. m  1. ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Vận dụng 07 : Đồ thị hàm số 4 2 4
y x  2mx  2m m có 3 điểm cực trị tạo thành 3 đỉnh của một
tam giác vuông khi m nhận giá trị A. m   3 . B. m  1  . C. m  3 . D. m  1. ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Vận dụng 08 : Cho hàm số 4 2 2
y x  2m x 1 , có đồ thị C
.Tìm m để đồ thị C có ba điểm m m
cực trị tạo thành một tam giác đều. 2  3 A. 6 m   3   B. m C. m  1 D. 3 m   3 2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<< 59
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Vận dụng 09 : Cho hàm số 4
y x  a   2
3 x  2016a 10. Tìm a để đồ thị hàm số có 3 điểm cực trị
lập thành 3 đỉnh của một tam giác đều. A. a  1 B. a  1  C. 3 a  2 3 -3 D. 3 a  2 3  3 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Vận dụng 10 (Minh họa lần 01- BGD-ĐT) : Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 4 2
y x  2mx 1 có ba điểm cực trị tạo thành một tam giác vuông cân. 1 1 A. m   B. m  1  C. m  D. m  1 3 9 3 9 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Vận dụng 11 : Tìm tất cả giá trị tham số m để hàm số 4 2 2 9 4
y x  2(m m 1)x  2017m m có 3 cực
trị sao cho khoảng cách giữa hai cực tiểu bằng 3 . A. m  0,5 B. m  0  ,5
C. m  0,5 hoặc m  0  ,5 D. m  2 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Vận dụng 12 : Tìm tất cả giá trị tham số m để hàm số 4 2 2 4
y x  2(1 m )x  2017m  2016 có 3 cực
trị sao cho khoảng cách giữa hai cực tiểu nhỏ nhất. A. m  1 B. m  0
C. m  1hoặc m  1  D. m  1  60
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
Vận dụng 13 : Tìm tất cả giá trị tham số thực m để hàm số 4 2
y  x  (m  2015)x  2017 có 3 cực trị
tạo thành tam giác vuông cân tại A . A. m  2017 B. m  2014 C. m  2016 D. m  2015 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
Vận dụng 14 : Tìm tất cả giá trị tham số thực m để hàm số 4 2
y x  2(m  2016)x  2017m  2016 có
3 cực trị tạo thành tam giác vuông cân tại A . A. m  2017  B. m  2017 C. m  2018  D. m  2015 ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<< 9
Vận dụng 15 : Tìm tất cả giá trị tham số m để hàm số 4 2 y
x  3(m  2017)x  2016 có 3 cực trị tạo 8 thành tam giác đều. A. m  2015 B. m  2016 C. m  2017 D. m  2017  ♥ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<<<<.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<....<<<<<<<<< 61
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
CÂU HỎI TRẮC NGHIỆM PHẦN TỔNG ÔN
Câu 01 : Biết đường cong trong hình bên là đồ thị của b hàm số 3 2
y ax bx cx d a  0 . Tính tỉ số . a b A.  1. a b B.  1  . a b C.  3. a b D.  3  . a
Câu 02 : Tìm tất cả các giá trị thực của tham số m ể giá trị nhỏ nhất của hàm số 3
y x   2 m   2
1 x m  2 trên đoạn 0; 2 bằng 7 . A. m  3  . B. m   7 . C. m . D. m  1  . x  2
Câu 03 : Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y  có hai tiệm 2
x  4x m cận đ ng. A. m  12  B. m  4 . C. m  4 . D. 1  2  m  4.
Câu 04 (THPT Lý Tự Trong – Khánh Hòa) : Cho hàm số 1 3 2 y
y   x  4x  5x 17 . Phương trình y '  0 có hai nghiệm 3
x , x . Khi đó tổng x x bằng : 1 2 1 2 A. 5 . B. 8  . C. 5  . D. 8 .
Câu 05 (THPT Nguyễn Văn Trỗi – Khánh Hòa) : Cho hàm O ax b x số y
với a  0 có đồ thị như hình v bên. Mệnh đề x c d nào dưới đây đúng? 62
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
A. b  0 , c  0 , d  0 .
B. b  0 , c  0 , d  0 .
C. b  0 , c  0 , d  0 .
D. b  0,c  0, d  0 .
Câu 06 (THPT Đoàn Thị Điểm – Khánh Hòa) : Xác định phương trình đường tiệm cận ngang của 8x 1
đồ thị hàm số y  1 2x 1 A. x  . B. x  4  . C. y  4  . D. y  8 . 2
Câu 07 (THPT Đoàn Thị Điểm – Khánh Hòa) : Đồ thị hàm số 4 2
y x  2x  2 và đồ thị hàm số 2
y  x  4 có tất cả bao nhiêu điểm chung? A. 0 . B. 1. C. 2 . D. 4 . y 1
Câu 08 (THPT Lạc Long Quân – Khánh Hòa) : Cho hàm số x
y f x xác định, liên tục trên  1  ; 
3 và có đồ thị là đường O -1 1 2 3
cong trong hình v bên. Hàm số f x đạt cực tiểu tại điểm nào dưới đây? A. x  1  . B. x  0 . -3 C. x  2 . D. x  3  .
Câu 09 (THPT Lạc Long Quân – Khánh Hòa) : Hàm số 3 2
y  –x  6x – 9x  4 đồng biến trên khoảng A. 1; 3 . B. 3;  . C.  ;3   . D. 1;  .
Câu 10 (THPT Lạc Long Quân – Khánh Hòa) : Hàm Cho hàm số y f x liên tục trên và có
đạo hàm f  x  x x  2 3
1  x  2 . Hàm số y f x có bao nhiêu điểm cực trị? A. Có 3 điểm cực trị. B. Có 1 điểm cực trị. C. Không có cực trị. D. Có 2 điểm cực trị.
Câu 11 (THPT Lạc Long Quân – Khánh Hòa) : Cho biết hàm số 3 2
y ax bx cx d có đồ thị như hình dưới. Trong
các khẳng định sau, khẳng định nào úng? 63
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  . 2 b   3ac  0 2 b   3ac  0 2 b   3ac  0 2 b   3ac  0
Câu 12 (THPT Trần Hƣng Đạo – Khánh Hòa) : Đồ thị hàm số 3 2
y x  3x 1 có điểm cực đại là: A. (0; 1  ) . B. ( 1  ;0) . C. ( 2  ;3) . D. ( 3  ;2) .
Câu 13 (THPT Trần Hƣng Đạo – Khánh Hòa): Đồ thị
hàm số tương ng với hình bên là: 3x   1 A. y  . x  2 3x   1 B. y  . x  2 2x   1 C. y  . x  2 2x   1 D. y  . x  2
Câu 14 (THPT Trần Hƣng Đạo – Khánh Hòa): Hàm số 4 2
y  2x  4x  2 đồng biến trên khoảng: A. ( ;  1) . B.  1  ;. C. ( ;  0) . D. (0; )  .
Câu 15 (THPT Trần Hƣng Đạo – Khánh Hòa): Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm 2x  3 số y  trên đoạn  3  ;0 là: 1 x 9 A. M  2  ,m  3  .
B. M   , m  4  . 4 9 9
C. M   , m  3  . D. M  3,  m   . 4 4 3x  2
Câu 16 (THPT Trần Hƣng Đạo – Khánh Hòa): Cho hàm số y  . Khẳng định nào sau 2 x  2x  3 đây đúng?
A. Đồ thị hàm số không có đường tiệm cận ngang.
B. Đồ thị hàm số chỉ có một đường tiệm cận ngang là y  3
C. Đồ thị hàm số có hai đường tiệm cận ngang y  3  ; y  3.
D. Đồ thị hàm số chỉ có một đường tiệm cận ngang là y  3  .
Câu 17 (THPT Chuyên Phan Bội Châu – Nghệ An): Tìm giá trị của tham số m để tiệm cận đ ng x  3
của đồ thị hàm số y
đi qua điểm A5;2 . x m 1 A. m  4  . B. m  1  . C. m  6 . D. m  4 . 64
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Câu 18 (THPT Chuyên Phan Bội Châu – Nghệ An): Cho hàm số y f x xác định, liên tục trên
và có bảng biến thiên: x –∞ 2  1  1 +∞ y  0  0  0  1  y  1 
Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng   ;1  .
B. Đồ thị hàm số không có tiệm cận ngang.
C. Hàm số đạt cực trị tại x  2  .
D. Hàm số có giá trị lớn nhất bằng 1.
Câu 19 (THPT Chuyên Hoàng Văn Thụ – Hòa Bình): Cho hàm số y f (x) có bảng biến thiên x  2  1  y    4   y 1 2 2
Đồ thị hàm số có tiệm cận đ ng là đường thẳng có phương trình A. x  2  và x 1. B. x  1.
C. không tồn tại tiệm cận đ ng. D. x  2  .
Câu 20 (THPT Chuyên Hoàng Văn Thụ – Hòa Bình): Cho hàm số 4 2
y ax bx c có đồ thị như
hình v sau Khẳng định nào sau đây đúng? y x O
A. a  0,b  0,c  0 .
B. a  0,b  0,c  0 .
C. a  0,b  0,c  0 .
D. a  0,b  0,c  0 . 65
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Câu 21 (THPT Chuyên Hoàng Văn Thụ – Hòa Bình): Số điểm cực trị của hàm số
y   x   x  2 1 2 là: Chú ý : A. 2 . B. 1. C. 4 . D. 3 . ax b
Câu 22 (THPT Chuyên Quốc Học Huế): Cho hàm số y
có đồ thị như hình v bên. Tìm x 1
khẳng định đúng trong các khẳng định sau? y
A. a b  0.
B. b  0  a .
C. 0  b a .
D. 0  a b . O x
Câu 23 (THPT Chuyên Quốc Học Huế): Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số     f x 3
 2cos x  cos 2x   trên tập hợp D ;   .  3 3  A. f x  f x 19 max 1, min  . x Dx D  27 3
B. max f x  , min f x  3  . x D  4 x D  3 19
C. max f x  , min f x  . x D  4 x D  27
D. max f x 1, min f x  3  . x Dx D
Câu 24 (THPT Chuyên Quốc Học Huế) : Tìm số giao điểm của đồ thị hàm số 2 y x  4  5 và
đường thẳng y x ? A. 3 . B. 0 . C. 2 . D. 1. x
Câu 25 (SGD Nam Định) : Tìm tất cả các khoảng đồng biến của hàm số y  . 2 x 1 A.  1   ;1 . B. 0;  . C.  ;   
1 và 1; . D.  ;   . 66
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 2x  2
Câu 26 (SGD Nam Định) : Tìm tiệm cận ngang của đồ thị hàm số y  1 . x 1 A. x  1. B. y  2 . C. y  3 . D. y  1.
Câu 27 (SGD Nam Định) :Đồ thị hình bên là đồ thị của một trong 4 đồ thị của các hàm số ở các y
phương án A, B, C, D dưới đây. Hãy chọn phương án đúng. 5 1 A. 4 2 y x x  5 . 4 4 3 1 B. 4 2 y   x x  5. 4 2 1 C. 4 y   x  5 . 1 4 1 2  1  O 1 2 x D. 4 2 y  
x  2x  5 . 4
Câu 28 (SGD Nam Định) : Gọi M , m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số 3 2
y x  3x trên đoạn  2  
;1 . Tính giá trị của T M m . A. T  20  . B. T  4  . C. T  2 . D. T  24  .
Câu 29 (Trích đề THPTQG – 2017 ) : Cho hàm số y   x   2 2 x  
1 có đồ thị C  . Mệnh đề nào dưới đây đúng ?
A. C  cắt trục hoành tại hai điểm.
B. C  cắt trục hoành tại một điểm.
C. C  không cắt trục hoành.
D. C  cắt trục hoành tại ba điểm.
Câu 30 (Trích đề THPTQG – 2017 ) : Cho hàm số y f x có đạp hàm f  x 2  x 1, x   .
Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng  ;
 0. B. Hàm số nghịch biến trên khoảng 1;.
C. Hàm số nghịch biến trên khoảng  1   ;1 .
D. Hàm số đồng biến trên khoảng  ;   .
Câu 31 (Trích đề THPTQG – 2017 ) : Cho hàm số y f x có bảng biến thiên như sau 67
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Mệnh đề nào dưới đây đúng ?
A. Hàm số có bốn điểm cực trị.
B. Hàm số đạt cực tiểu tại x  2 .
C. Hàm số không có cực đại.
D. Hàm số đạt cực tiểu tại x  5  .
Câu 32 (Trích đề THPTQG – 2017 ) : Tìm giá trị nhỏ nhất m của hàm số 4 2
y x x 13 trên đoạn  2  ;  3 . 51 49 A. m  . B. m  . 4 4 51 C. m 13. D. m  . 2
Câu 33 (Trích đề THPTQG – 2017 ) : Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 4 2
y x  2mx có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1. A. m  0. B. m 1. C. 3 0  m  4. D. 0  m 1.
Câu 34 (Trích đề THPTQG – 2017 ) : Đường cong ax b
ở hình bên là đồ thị của hàm số y  với a , cx d
b , c , d là các số thực. Mệnh đề nào dưới đây đúng? A. y  0, x   2 . B. y  0, x  1. C. y  0, x   2. D. y  0, x  1.
Câu 35 (Trích đề THPTQG – 2017 ) : Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đ ng? 1 1 1 1 A. y  . B. y  . C. y  . D. y  . x 2 x x 1 4 x 1 2 x 1
Câu 36 (Trích đề THPTQG – 2017 ) : Cho hàm số 4 2
y x  2x . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng  ;  2
  . B. Hàm số nghịch biến trên khoảng  ;  2   .
C. Hàm số đồng biến trên khoảng  1  
;1 . D. Hàm sô nghịch biến trên khoảng  1   ;1 . mx  2m  3
Câu 37 (Trích đề THPTQG – 2017 ) : Cho hàm số y
với m là tham số. Gọi S là tập x m
hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S . A. 5 . B. 4 . C. Vô số. D. 3 . 68
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Câu 38 (Trích đề THPTQG – 2017 ) : Đồ thị của hàm số 3 2
y  x  3x  5 có hai điểm cực trị A và
B . Tính diện tích S của tam giác OAB với O là gốc tọa độ.. 10 A. S  9 . B. S  . 3 C. S  5. D. S 10 . 1
Câu 39 (Trích đề THPTQG – 2017 ) : Một vật chuyển động theo quy luật 3 2
s   t  6t với t (giây) 2
là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển
được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 6 giây, kể từ khi bắt đầu chuyển
động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? A. 24(m / s). B. 108(m / s). C. 18(m / s). D. 64(m / s).
Câu 40 (Trích đề THPTQG – 2017 ) : Cho hàm số y f x có bảng xét dấu đạo hàm như sau : x  1  0 2  y  0  ||  0 
Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng  2  ;0 .
B. Hàm số đồng biến trên khoảng  ;  0.
C. Hàm số nghịch biến trên khoảng 0; 2 .
D. Hàm số đồng biến trên khoảng  ;  2   . y
Câu 41 (Trích đề THPTQG – 2017 ) : Đường cong hình bên là đồ thị
của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ? A. 3
y x  3x  2 . B. 4 2
y x x 1. C. 4 2
y x x 1. O x D. 3
y  x  3x  2 . 2x  3
Câu 42 (Trích đề THPTQG – 2017 ) : Hàm số y
có bao nhiêu điểm cực trị ? x 1 A. 3. B. 0. C. 2 . D. 1. x  2
Câu 43 (Trích đề THPTQG – 2017 ) : Đồ thị hàm số y  có mấy tiệm cận. 2 x  4 69
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 A. 1 B. 2 C. 3 D. 4 2 1 
Câu 44 (Trích đề THPTQG – 2017 ) : Tìm GTNN m của hàm số 2 y x  trên đoạn ; 2   . x 2  17 A. m  . 4 B. m 10 . C. m  5 . D. m  3
Câu 45 (Trích đề THPTQG – 2017 ) : Cho hàm số 2
y  2x 1 . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng  1   ;1 .
B. Hàm số đồng biến trên khoảng 0; .
C. Hàm số đồng biến trên khoảng  ;  0.
D. Hàm số nghịch biến trên khoảng 0; .
Câu 46 (Trích đề THPTQG – 2017 ) : Tìm giá trị thực của tham số m để đường thẳng
d : y  2m  
1 x  3  m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  3x 1. 3 A. m  . 2 3 B. m  . 4 1 C. m   . 2 1 D. m  . 4 mx  4m
Câu 47 (Trích đề THPTQG – 2017 ) : Cho hàm số y
với m là tham số. Gọi S là tập hợp x m
tất cả các giá trị nguyên của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S . A. 5 . B. 4 . C. Vô số. D. 3 .
Câu 48 (Trích đề THPTQG – 2017 ) : Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 3 2 3
y x  3mx  4m có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa độ. 1 1 A. m   ; m  . 4 2 4 2 70
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 B. m  1  ; m 1. C. m  1. D. m  0 . 1
Câu 49 (Trích đề THPTQG – 2017 ) : Một vật chuyển động theo quy luật 3 2
s   t  6t với t (giây) 3
là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển
được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây kể từ khi bắt đầu chuyển động,
vận tốc lớn nhất của vật đạt được bằng bao nhiêu ? A. 144 (m/s). B. 36 (m/s). C. 243 (m/s). D. 27 (m/s).
Câu 50 (Trích đề THPTQG – 2017 ) : Đồ thị của hàm số 3 2
y x  3x  9x 1 có hai điểm cực trị A
và B. Điểm nào dưới đây thuộc đường thẳng AB ? A. P(1;0) B. M (0; 1  ) C. N(1; 1  0) D. ( Q 1  ;10)
Câu 51 (Trích đề THPTQG – 2017 ) : Cho hàm số 3 2
y  x mx  (4m  9)x  5 với m là tham số. Có
bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng ( ;   )  ? A. 7 B. 4 C. 6 D. 5 2 x  3x  4
Câu 52 (Trích đề THPTQG – 2017 ) : Tìm số tiệm cận đ ng của đồ thị hàm số y  . 2 x 16 A. 2. B. 3. C. 1. D. 0. 2
Câu 53 (Trích đề THPTQG – 2017 ) : Hàm số y
nghịch biến trên khoảng nào dưới đây ? 2 x 1 A. (0; )  B. ( 1  ;1) C. ( ;   )  D. ( ;  0)
Câu 54 (Trích đề THPTQG – 2017 ) : Cho hàm số 3
y x  3x  2 . Mệnh đề nào dưới đây là đúng ?
A. Hàm số đồng biến trên khoảng ( ;
 0) và nghịch biến trên khoảng (0; )  .
B. Hàm số nghịch biến trên khoảng ( ;   )  .
C. Hàm số đồng biến trên khoảng ( ;   )  .
D. Hàm số nghịch biến trên khoảng ( ;
 0) và đồng biến trên khoảng (0; )  . 71
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Câu 55 (Trích đề THPTQG – 2017 ) : Đường cong ở hình bên là đồ thị
của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào ? A. 3 2
y  x x 1. B. 4 2
y x x 1. C. 3 2
y x x 1 . D. 4 2
y  x x 1.
Câu 56 : Cho các hàm số f x 3
x 1 và g x 2
 3x . Chọn đáp án sai
A. Hàm số f x không có cực trị
B. Hàm số f x  g x có hai điểm cực trị
C. Hàm số g x là hàm số chẵn
D. Hàm số f x là hàm số lẻ 2x 1
Câu 57 : Xác định tọa độ giao điểm của đồ thị hàm số y
với đường thẳng y x  7 x 1 A.  2  ;5, 4  ;  3 B. 2;5, 4  ;3 C.  2  ;5, 4  ;4 D.  2  ;5,3;4
Câu 58 (THPT Chuyên ĐHSPHN – lần 04 ) : Cho hàm số 4 2
y x  2x 1. Khoảng cách giữa hai
điểm cực tiểu của đồ thị hàm số bằng: A. 2 B. 4 C. 1 D. 3
Câu 59 (THPT Chuyên ĐHSPHN – lần 04 ) : Tìm tất cả các giá trị thực của tham số m để hàm số 3
y mx  m   2
2 x x 1 có cực đại và cực tiểu: A. m  1 B. m  2  C. m  0 D. m  
Câu 60 (THPT Tử Đà – Phú Thọ ) : Cho hàm số y f x
xác định, liên tục trên tập số thực
và có đồ thị như hình
bên. Hàm số y f x đạt cực tiểu tại điểm nào dưới đây ? A. x  1 B. x  2  C. x  2  và x  0 D. x  0 72
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Câu 61 (THPT chuyên Vị Thanh – Hậu Giang) : Cho hàm số y
f (x) có lim f (x)    và x 0 
lim f (x)   .  
Khẳng định nào sau đây là khẳng định đúng ? x 2 
Đồ thị hàm số đã cho không có tiệm cận đ ng.
Đồ thị hàm số đã cho có đúng một tiệm cận đ ng.
Đồ thị hàm số đã cho có hai tiệm cận đ ng là các đường thẳng y 0 và y 2 .
D. Đồ thị hàm số đã cho có hai tiệm cận đ ng là các đường thẳng x 0 và x 2 .
Câu 62 (THPT chuyên Lê Thánh Tông – Quảng Nam) : Cho hàm số y f (x) liên tục trên với
bảng xét dấu đạo hàm như sau: x  3  1 2  f (  x)  0  0 + 0 
Số điểm cực trị của hàm số y f (x) là A. 2 . B. 1. C. 3 . D. 0 . 2x 1
Câu 63 : Hàm số y
có đồ thị C  . Viết phương trình tiếp tuyến của C  tại điểm P 2  ;5 x 1
A. y  3x 11
B. y  3x 11 1 13 1 13 C. y x  D. y x  3 3 3 3 2x 1
Câu 64 : Hàm số y
có đồ thị C  . Viết phương trình tiếp tuyến của C  tại điểm Q 4  ;3 x 1
A. y  3x 11
B. y  3x 11 1 13 1 13 C. y x  D. y x  3 3 3 3
Câu 65 : Giá trị lớn nhất của hàm số 3 2
y x  3x  4, x   2  ; 
1 đạt được tại đâu ? A. x  0 B. x  1 C. x  2  D. x  2
Câu 66 (THPT Trần Hƣng Đạo – Ninh Bình) : Cho hàm số 4 2 4
y x  2mx  2m m . Với giá trị nào
của m thì đồ thị C có 3 điểm cực trị, đồng thời 3 điểm cực trị đó tạo thành một tam giác có diện m  tích bằng 2. A. 5 m  4 . B. m 16 . C. 5 m  16 . D. 3 m   16 .
Câu 67 : Bảng biến thiên bên dưới là của hàm số nào trong các hàm số sau: 73
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 x -  -1 +  y’ + 0 + +  1 y -  A. 3 2
y x  3x  3x  2 B. 3 2
y x  3x  4 C. 3 2
y  x  3x  4x  2 D. 4 2
y x  2x  2 3 x
Câu 68 : Cho hàm số y
 3x (C) . Hệ số góc tiếp truyến tại điểm K  (C) có hoành độ 4 x  2 3 là K A. 5 B. 7 C. 6 D. 8 2 x  4x  4
Câu 69 : Cho hàm số y
(C) . Hệ số góc tiếp truyến tại điểm K  (C) có hoành độ x 1 x  2 là K 1 A. 0 B. 7 C. 3 D. 2 3 x
Câu 70 : Cho hàm số 2 y
 2x mx  2 . Giá trị m nào sau đây thì hàm số s tăng trên miền xác 3 định 13 11 1 A. 0 B. C. D. 3 3 2
Câu 71 (THPT CHUYÊN HÀ NỘI – AMSTERDAM) : Xác định các giá trị của tham số m để đồ thị hàm số 4 3 2
y mx m x  2016 có 3 điểm cực trị? A. m  0 B. m  0 C. m   \{0}
D. Không tồn tại giá trị của m
Câu 72 (THPT CHUYÊN HÀ NỘI – AMSTERDAM) : Trong tất cả các giá trị của tham số m để hàm 1 số 3 2 y
x mx mx m đồng biến trên , giá trị nhỏ nhất của m là: 3 A. –4 B. –1 C. 0 D. 1 74
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 2x 1
Câu 73 (THPT CHUYÊN HÀ NỘI – AMSTERDAM) : Trong Cho hàm số y  (C). x  Hệ số góc 1
của tiếp tuyến với đồ thị (C) sao cho tiếp tuyến đó cắt các trục Ox, Oy lần lượt tại các điểm A, B
thoả mãn OA  4OB là: 1 1 1 1 A.  B. C.  hoặc D. 1 4 4 4 4
Câu 74 (THPT CHUYÊN HÀ NỘI – AMSTERDAM) : Trong giao điểm của hai đường tiệm cận của
đồ thị hàm số nào dưới đây nằm trên đường thẳng (d) : y x? 2x 1 x  4 2x 1 1 A. y y y y x  B. 3 x  C. 1 x  D. 2 x  3
Câu 75 : Cho hàm số 4 2
y x mx 1 m (C) . Với mọi giá trị của tham số m thì đồ thị (C) luôn đi
qua một điểm K cố định có tọa độ A.  3;0 B. 1;2 C. 0; 2 D. 1;0 2  x  4
Câu 76 : Cho hàm số (C) : y
.Trên đồ thị (C) có bao nhiêu điểm mà tại đó tọa độ là các số x 1 nguyên A. 4 B. 6 C. 8 D. 2
Câu 77 : Cho hàm số (C) : 3 2
y x  3x  9x  3 . Trong mọi tiếp tuyến với đồ thị (C) thì tiếp tuyến có
hệ số góc nhỏ nhất là kmin A. 1 B. 6 C. – 12 D. – 9 2x 1
Câu 78 : Cho hàm số (C) : y
. Các điểm H thuộc đồ thị hàm số (C) mà khoảng cách từ H x 1
đến tiệm cận đ ng bằng 3 lần khoảng cách từ H đến tiệm cận ngang có tọa độ A. 4; 2 hay 0; 2 B. 5; 2 hay 2;  1  C. 4;3 hay 2;  1  D. 4;3 hay 0; 2 2x 1
Câu 79 : Cho hàm số (C) : y
. Gọi R là điểm thuộc đồ thị hàm số (C) có hoành độ bằng 2. x 1
Di n tích tam giác ∆RAB thỏa mãn giá trị nào sau đây. Với A(0;1), B(3;2) A. 1 B. 6 C. 12 D. 9 75
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 2x 1
Câu 80 : Cho hàm số (C) : y
. Gọi M và N là điểm thuộc đồ thị hàm số (C) có hoành độ x 1
bằng 2 và 0. Di n tích tứ giác AMBN thỏa mãn giá trị nào sau đây. Với A(1;1), B(3;2) A. 1 B. 3 C. 4 D. 5 mx 1
Câu 81 : Cho hàm số (C) : y
. Giá trị tham số m để hàm số luôn tăng trên từng khoảng xác 2x m định là A. 1 B. Với mọi số thực m C. 2 D. 3 mx 1
Câu 82 : Cho hàm số (C) : y
. Giá trị tham số m để đồ thị hàm số (C) đi qua giao điểm hai 2x m 2x 1
đường tiệm cận của đồ thị hàm số y  (C ') x 1 A. 5 B. Không có giá trị m. C. 1 D. 3 2
2x  6  mx  4
Câu 83 : Cho hàm số (C) : y
. Giá trị tham số m để đồ thị hàm số (C) đi qua mx  2
điểm A(–1;1) A. 1 B. 0 C. 2 D. 3
Câu 84 : Cho hàm số (C) : 3 2
y x  3x  2 (C) . Hệ số góc tiếp tuyến tại điểm A thuộc đồ thị hàm số
thỏa mãn y '  x   0 là A A. 3 B. 0 C. 4 D. –3
Câu 85 : Cho hàm số (C) : 3 2
y  x  3x  9x  2 (C) . Hệ số góc tiếp tuyến tại điểm M thuộc đồ thị
hàm số thỏa mãn y '  x   0 là M A. 6 B. 8 C. 10 D. 12 x
Câu 86 (THPT Chuyên Quang Trung – Bình Phước) : Tìm giao điểm của đồ thị C  4 : y  và x 1
đường thẳng  : y x 1. A. 0  ;1 . B. 2;3 . C. 1; 2 . D. 1;3 . 2 4x x 1
Câu 87 (THPT Chuyên Quang Trung – Bình Phước) : Cho hàm số y  2x  . Tiệm cận ngang 1
của đồ thị hàm số có phương trình là 76
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 1 A. y  2. B. y   . C. y  1.
D. y 1, y  1  . 2
Câu 88 : Cho chuyển của một chất điểm xác định bởi phương trình dưới đây 3 2
S t  3t  9t  2 , ;
m s . Vận tốc của chất điểm khi sau 2 giây kể từ lúc bắt đầu chuyển động.
A. 9 m / s
B. 8 m / s C. 9  m / s D. 8  m / s
Câu 89 : Cho chuyển của một chất điểm xác định bởi phương trình dưới đây 3 2
S t  3t  9t  2 , ;
m s . Gia tốc của chất điểm khi sau 3 giây kể từ lúc bắt đầu chuyển động. A.  2 12 m / s  B.   2 12 m / s  C.  2 10 m / s  D.   2 10 m / s
Câu 90 : Cho chuyển của một chất điểm xác định bởi phương trình dưới đây 3 2
S t  3t  9t  2 , ;
m s . Thời điểm tmax (s) để vận tốc chất điểm cực đại ? A. 1 B. 2 C. 3 D. 4
Câu 91 (THPT Phạm Văn Đồng – Phú Yên) : Đồ thị của hàm số 4 2
y x  2x cắt trục hoành tại bao nhiêu điểm? A. 0. B. 2. C. 4. D. 3. y
Câu 92 (THPT Phạm Văn Đồng – Phú Yên) : Cho hàm số y f (x) xác định trên
và liên tục trên và có đồ thị là đường cong trong 2
hình v bên. Điểm cực tiểu của đồ thị hàm số y f (x) là: A. M (0; 2  ) B. x  0 x O 2 -2 -1 1 C. y  2  D. x  2  -2
Câu 93 (THPT Phạm Văn Đồng – Phú Yên) : Cho hàm số 3
y x  3x . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng  1   ;1 .
B. Hàm số nghịch biến trên .
C. Hàm số đồng biến trên .
D. Đồ thị hàm số đối x ng qua gốc tọa độ. x
Câu 94 : Gọi điểm M thuộc đồ thị hàm số y f x 2 1 
(C) có hoành độ x0 không âm và x0 là x 1
nghiệm của phương trình 4. f ' x  3  0 thì giá trị x 0  0 : A. 1 B. 2 C. 3 D. 4 77
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Câu 95 : Cho hàm số y f x 3 2
x 3x  2 (C) . Gọi A và B là hai điểm cực trị của (C). Khi đó
S∆HAB là bao nhiêu, với H(1;1) ? A. 1 (đvdt) B. 2 (đvdt) C. 3 (đvdt) D. 4 (đvdt) x
Câu 96 : Cho hàm số y f x 2 1 
(C) .Gọi A là giao điểm hai tiệm cận của đồ thị (C) và B(0;-3) x  4
và C(2;m), m là tham số dương. Giá trị m để S∆ABC = 2 1 A. 2 3 B.  2 C. 2 2 D. 3
Câu 97 : Cho hàm số y f x 3
 x x  2 . Phát biểu nào sau đây là đúng ?
A. Hàm số luôn giảm trên
B. Đồ thị hàm số cắt Oy tại điểm có tung độ bằng 2
C. Đồ thị hàm số cắt Ox tại điểm có hoành độ bằng 1
D. Cả ba đáp án đều đúng.
Câu 98 (Trường Quốc Học Quy Nhơn – Bình Định):
Hình v dưới đây là đồ thị hàm số ax b y
ac  0, ad bc  0 cx d
Mệnh đề nào dưới đây đúng?
A. ad  0 và bd  0.
B. ad  0 và ab  0 .
C. bd  0 và ab  0 .
D. ad  0 và ab  0 .
Câu 99 : Cho hàm số 3 2
y  2x ax 12x 13 có đồ thị là (C) và a là tham số. Giá trị nào của a thì đồ
thị (C) có điểm cực đại, điểm cực tiểu cách u trục tung ? A. a  0 B. a  1 C. a  1 
D. Cả ba đáp án đều sai.
Câu 100 : Gọi A và B lần lượt là điểm cực đại, cực tiểu của đồ thị hàm số (C) : 3 2
y x  3x  2 . Độ
dài đọan thẳng IB đạt giá trị nhỏ nhất là (với I(a;2a)) : 78
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 6 A. 3 B. 5 5 C. D. 8 6
Câu 101 (THPT Kim Liên – HN ) : Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số 2 x x  2 y
có hai tiệm cận đ ng. 2
x  2x m
A. m  1 và m  8  . B. m  1  và m  8.
C. m  1 và m  8  . y
D. m  1 và m  8  .
Câu 102 (THPT Kim Liên – HN ) : ax b Cho hàm số y
có đồ thị như hình v bên. O 2 3 x x c 1 
Tính giá trị của a  2b  . c 3 A. 1  .  2 B. 2  . C. 0 . D. 3 .
Câu 103 : Gọi A và B lần lượt là điểm cực đại, cực tiểu của đồ thị hàm số (C) : 3 2
y x  3x  2 . Độ
dài đọan thẳng IB đạt giá trị nhỏ nhất khi (với I(a;2a)) : 2 A. a   5 3 B. a  5 C. a  1 D. a  4
Câu 104 : Với giá trị nào của tham số m thì đồ thị hàm số 4 2 2
y x  2m x  2 có ba điểm cực trị ? A. m  2  B. m  2  C. m  0 D. m  1
Câu 105 : Giả sử đồ thị hàm số (C) : 4 2 2 6
y x  2m x  2m có ba điểm cực trị
A (nằm trên Oy), B, C. Chọn đáp án sai ?
A. ∆ABC là tam giác thường B. ∆ABC là tam giác cân
C. Khoảng cách giữa hai điểm cực tiểu là d  2 x BC B
D. B và C có hoành độ trái dấu
Câu 106 : Giả sử đồ thị hàm số (C) : 4 2 2 6
y x  2m x  2m có ba điểm cực trị 79
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
A (nằm trên Oy), B, C. Chọn đáp án đúng ?
A. ∆ABC là tam giác thường B. ∆ABC là tam giác cân
C. Khoảng cách giữa hai điểm cực tiểu là dx x BC C B
D. B và C có hoành độ cùng dấu
Câu 107 : Cho hàm số sau (C) : 4 2
y  x 10x  3 . Khoảng cách giữa hai điểm cực tiểu là M. Khi đó giá trị M2 là 1 A. 5 B. 2 C. 20 D. 5 5
Câu 108 : Cho hàm số sau (C) : 4 y   m  2 x 2
2 x  6, m  2 . Khoảng cách giữa hai điểm cực tiểu
là 4. Khi đó giá trị tham số m là A. 6 B. 3 C. 10 D. 5 3 x
Câu 109 : Cho hàm số sau (C) : 2 y
 2x  3x  5 . Tiếp truyến tại điểm cực tiểu của đồ thị hàm số 3
A. Song song với đường thẳng x = 1
B. Song song với trục hoành C. Có hệ số góc là 1 D. Có hệ số góc âm
Câu 110 : Chọn đáp án sai. Cho hàm số sau (C) : 3 2
y x  6x  9x . Gọi d là tiếp truyến tại iểm cực
tiểu của đồ thị hàm số.
A. d song song với đường thẳng y = 3
B. d song song với trục hoành
C. d vuông góc với đường thẳng x = 5 D. d cắt Oy tại O
Câu 111 : Cho đồ thi hàm số 3 2
y x  2x  2x (C). Gọi x , x là hoành độ các điểm M, N trên (C), 1 2
mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y  x  2017 . Khi đó 2 2 x x  1 2 4 4 A. B. 3 9 10 10 C. D. 3 9
Câu 112 : Cho đồ thi hàm số y f x 3 2
x 3x  2 (C). Gọi x , x là hoành độ các điểm A, B trên 1 2
(C), mà tại đó tiếp tuyến của (C) có h số góc là – 3. 80
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Khi đó x x  1 2 A. 5 B. 1  C. 2 D. 3
Câu 113 (SGDĐT Phú Thọ) : Cho hàm số y f x xác định và liên tục trên khoảng  ;   , có
bảng biến thiên như hình v sau: x  1  1  f  x  0  0  2 f x 1  
Mệnh đề nào sau đây sai?
A. Hàm số y f x có hai điểm cực trị.
B. Hàm số y f x có một điểm cực trị.
C. Hàm số đồng biến trên khoảng  ;    1 .
D. Hàm số nghịch biến trên khoảng  1   ;1 .
Câu 114 (THPT Lương Thế Vinh – HN ) : Cho hàm số y f x xác định trên \  0 , liên tục trên
m i khoảng xác định và có bảng biến thiên như sau x  0 1  y   0  2 1 y   
Mệnh đề nào sau đây là úng?
A. Giá trị lớn nhất của hàm số là 2 .
B. Đồ thị hàm số có 1 đường tiệm cận đ ng.
C. Hàm số không có cực trị.
D. Hàm số đạt cực tiểu tại x  0 .
Câu 115 (THPT Lương Thế Vinh – HN ) : Hiệu số giữa giá trị cực đại và giá trị cực tiểu của hàm số 3 2
y x  3x 1 là A. 2 . B. 6 . 81
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 C. 4 . D. 8 . Câu 116 : Hàm số 3 2
y x  3x  4 . Đường thẳng đi qua 2 điểm cực trị của hàm số đi qua điểm nào sau đây A. M  1  ;6 B. M  1  ;5 C. M  2  ;8 D. M 0;6
Câu 117 : Đường thẳng y = m cắt đồ thi hàm số (C): 4 2 y  2
x  4x  2 tại 4 điểm phân biệt khi : A. 0  m  4 B. m  4 C. m  0 D. m  4  3 
Câu 118 : Tích giá trị nhỏ nhất và giá trị lớn nhất của hàm số f x 3
x 3x  3 trên đoạn 3;    là  2  A. 6 B. -10 C. 4 D. -35 2x 1
Câu 119 : Cho hàm số y
có đồ thị (C) và đường thẳng d : y  3
x m . Với giá trị nào của m x 1
thì d cắt (C) tại 2 điểm phân biệt A, B sao cho trọng tâm ∆OAB nằm trên đường thẳng
x  2y  2  0 A. m B. m  2 11  C. m  5 D. m 11
Câu 120 : Cho hàm số 4
y x  m   2 2
1 x m 1 (1) . Với giá trị nào của m thì hàm số (1) có 3 điểm cực trị ? A. m B. m C. m  1  D. m  8  2x 1
Câu 121 : Cho hàm số y
có đồ thị (C) và đường thẳng d : y  x m . Với giá trị nào của m x  2
thì d cắt (C) tại 2 điểm phân biệt A, B ? A. m82
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 B. m
C. 4  12  m  4  12 m  4  12 D.  m  4  12 2x  3
Câu 122 : Cho hàm số y
có đồ thị (C). Gọi M, N lần lượt là hai điểm nằm trên đồ thị (C) có x  2
hoành độ lần lượt là 0 và 4. (C) có giao điểm của hai tiệm cận là I. Tính cosin của góc MIN 2 2 A. B. 51 51 1 1 C. D. 3 17 x  3
Câu 123 : Cho hàm số y
có đồ thị (C) và đường thẳng d : y  x m . Với giá trị nào của m x  2
thì d cắt (C) tại 2 điểm phân biệt A, B nằm về 2 phía trục tung A. m B. m 3 C. m   2 3 D. m   2 x  2
Câu 124 : Cho hàm số y
có đồ thị (C). Điểm trên đồ thị mà khoảng cách từ điểm đó đến x  3
tiệm cận ngang bằng 5 lần khoảng cách từ điểm đó đến tiệm cận đ ng có tọa độ A. 4;6 B. 5;6 C. 2; 4   D. Cả A và C
Câu 125 : Cho hàm số 3 2
y  x  3x 1 (1). Phương trình tiếp tuyến của đồ thị (C) tại điểm thuộc
(C) có hoành độ bằng 1 là
A. y  3x  2
B. y  3x 11 1 13 1 13 C. y x  D. y x  3 3 3 3 2x 1
Câu 126 : Cho hàm số y
có đồ thị là (C). Gọi M là điểm thuộc (C) có hoành độ bằng 2. Gọi x 1
d là tiếp tuyến với (C) tại M. Chọn đáp án đúng
A. Đường thẳng d vuông góc với IM
B. Đường thẳng d song song với IM 83
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 C. A và B đều sai D. A đúng, B sai
Câu 127 : Cho hàm số 3
y x  3x  5 . Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số có tung độ góc là A. 2  B. 1 C. 2 D. 5 x  3
Câu 128 : Cho hàm số (C) : y
. Viết phương trình tiếp tuyến với (C) biết tiếp tuyến cắt 2 x   1
trục Ox, Oy lần lượt tại A và B sao cho ường trung trực của AB i qua gốc tọa ộ 3
A. y  x  2 5
B. y  x  4 C. Cả A và B D. Không có x
Câu 129 : Cho hàm số y f x 1 
có đồ thị là (C). Hệ số góc tiếp tuyến tại điểm M có hoành x 1
độ x = 2 là k, giá trị của k + 1 là A. 1 B. 0 C. 3 D. 1  3x 1
Câu 130 : Cho hàm số y
có đồ thị là (C). Điểm thuộc (C) mà có khoảng cách từ đó đến x  2 12 đường thẳng ( )
 :3x  4y 1 0 bằng là 5  26 15   7  A. ( A 1; 2  ) B. B ;   C. C 2;    D. Cả A, B, C  3 4   4 
Câu 131 : Cho hàm số 3 2
y x mx  9x  4 .Giá trị nào của tham số m để trên đồ thị tồn tại một cặp
điểm đối x ng nhau qua gốc tọa độ ? A. m  0 B. m  0 C. m  0 D. mx
Câu 132 (THPT Nguyễn Diêu – Bình Định) : Tìm giá trị của tham số m để hàm số y x m đồng biến trên ( 2  ;) A. m  0 B. m  0 C. m  2  84
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 D. m  2  x  1
Câu 133 (THPT Nguyễn Diêu – Bình Định) : Số đường tiệm cận của đồ thị hàm số y  là 2 x  4 A.1 B. 2 C. 3 D. 4 1
Câu 134 (THPT Nguyễn Diêu – Bình Định) : Cho hàm số 3 2 y
x mx x m  1. Tìm m để 3
hàm số có 2 cực trị tại , A B thỏa 2 2 x x  2 A B A. m  1  B. m  2 C. m  3  x -∞ D. m  0 0 2 +∞ y' -- 0 + 0 --
Câu 135 (THPT Nguyễn Diêu – Bình Định) : Cho hàm số có +∞ 3
bảng biến thiên ở hình bên. Khẳng định nào sau đây là khẳng y định sai ? -1 -∞
A. Hàm số có 2 cực trị.
B. Hàm số có giá trị cực đại bằng 3 .
C. Hàm số có giá trị lớn nhất bằng 3, giá trị nhỏ nhất bằng 1  .
D. Hàm số đạt cực tiểu tại x  0 . x  3
Câu 136 : Cho hàm số y
có đồ thị là (C). Gọi M là điểm thuộc (C) có hoành độ là 3 và điểm x  2
I(1; - 2). Tọa độ điểm N nằm trên (C) và đối x ng với M qua I là  26 15  A. (1; 2  ) B. ;    3 4  C. C 5;2 D.  1  ; 4  
Câu 137 : Cho hàm số 3 2
y x mx   2 m   3 3 3
1 x m . Giá trị của tham số m để hàm số có hai cực trị trái dấu là A. m B. 1   m 1 C. 2   m 1 D. 1   m 1 3x 1
Câu 138 : Cho hàm số y
có đồ thị là (C). Điểm thuộc (C) có tung độ bằng 6. Khoảng cách từ x  2
điểm đó đến đường thẳng ( )
 :3x  4y 1 0 là 12 13 A. B. 5 5 85
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 14 C. D. Cả A, B, C 5 3 x
Câu 139 : Cho hàm số 2 y
mx  2m  
1 x  3 . Với giá trị nào của tham số m thì hàm số có cực 3 trị A. m  1 B. 1   m 1 C. 2   m 1 D. 1   m 1 2x 1
Câu 140 : Cho hàm số y
(C). Gọi M, N thuộc (C) có hoành độ lần lượt là x1 và x2 mà tại đó x 1
tiếp tuyến với đồ thị (C) cắt Ox, Oy lần lượt tại A và B sao cho OA = 4OB. Khi đó tổng bình phương x1 và x2 là A. 10 B. 16 C. 18 D. 36
Câu 141 : Cho hàm số y f x 3 2
x  6x  9x (C) . Phương trình đường thẳng đi qua hai điểm cực
trị của (C) có hệ số góc là 2 3 A. B. 3 2 C. 2  D. 3
Câu 142 (THPT Nguyễn Đình Chiểu – Bình Định) : Đồ thị bên dưới là của hàm số nào? y 2 1 -1 O 1 x -1 A. 4 2
y  x  2x  3 . B. 4 2
y  x  2x . C. 4 2
y x  2x 1. D. 4 2
y x  2x 1.
Câu 143 (THPT Nguyễn Đình Chiểu – Bình Định) : Hàm số 3 2
y  x  3x  2 có giá trị cực tiểu y là CT A. y  2 . CT B. y  2  . CT C. y  4  . CT D. y  6 . CT 86
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Câu 144 (THPT Nguyễn Đình Chiểu – Bình Định) : Đường thẳng y  3
x 1 cắt đồ thị hàm số 3 2
y x  2x 1 tại điểm có tọa độ (x ; y ) thì 0 0 A. y  1. 0 B. y  2 . 0 C. y  2  . 0 D. y  1  . 0 3
Câu 145 : Giá trị của m để hàm số 4 2 y mx
x  2018 có ba điểm cực trị là 7 A. m  0 B. m  0 C. m  0 D. m  0
Câu 146 : Đồ thị sau đây là của hàm số A. 3 y  x B. 3 y x 1 C. 3
y x x 1 D. 3 y  x 1
Câu 147 : Đồ thị sau đây là của hàm số A. 3 2
y x  3x  2 B. 3 2
y x  3x  2 C. 3 2
y x  2x  2 D. 3 2
y x  2x  2
Câu 148 : Đồ thị sau đây là của hàm số A. 3 2
y x  6x  9x B. 3 2
y x  6x  9x C. 3 2
y x  6x  9x D. 3 2
y x  6x  9x
Câu 149 : Đồ thị sau đây là của hàm số
A. y   x  2 1 1 x
B. y   x  2 1 1 x
C. y   x  2 1 2  x87
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
D. y   x  2 1 2  x
Câu 150 : Đồ thị sau đây là của hàm số A. 4 2
y  x  2x  3 B. 4 2
y  x  2x  3 C. 4 2
y x  2x  3 D. 4 2
y  x x  3
Câu 151 : Cho hàm số 4 2
y ax bx c có đồ thị như hình dưới đây
151.1 Giá trị của c là A. 0 B. 3/2 C. -3/2 D. 1
151.2 Hệ số góc tiếp tuyến tại K là A. 0 B. 3/2 C. -3/2 D. 1
Câu 152 : Nhận biết hàm số 3
y  x  3x có đồ thị nào trong các hình dưới đây ? Hình 1
Hình 2 Hình 3 Hình 4 A. Hình 2 B. Hình 4 C. Hình 3 D. Hình 1 88
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Câu 153 (THPT Chuyên Lê Khiết – Quảng Nam) : Đồ thị dưới đây là của hàm số nào? y x 1 A. y  . 2x 1 x  3 1 B. y  . 2x 1 2 x C. y  . 2x 1 1 x x 1 2 D. y  . 2x 1
Câu 154 : Nhận biết đồ thị ở hình bên là của hàm số nào: A. 3 2
y x  2x  2 B. 3 2
y  x  3x  2 C. 2
y  3x x  2 D. 3 2
y x  3x  2 x 1
Câu 155 : Nhận biết hàm số y
có đồ thị nào trong các hình dưới đây ? x  2 Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 3 B. Hình 1 C. Hình 4 D. Hình 2
Câu 156 : Nhận biết hàm số 4 2
y x  2x có đồ thị nào trong các hình dưới đây ? Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 3 B. Hình 1 C. Hình 4 D. Hình 2 89
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017
Câu 157 : Nhận biết đồ thị ở hình bên dưới là của hàm số nào ? x  2 A. y x 1 x B. y x 1 x  2 C. y x 1 x  2 D. y x 1
Câu 158 : Từ đồ thị hàm số y f x cho ở hình bên dưới, hãy nhận biết 2 tiệm cận:
A. Tiệm cận đ ng x  1
 , tiệm cận ngang y  2
B. Tiệm cận đ ng x  0, tiệm cận ngang y  1
C. Tiệm cận đ ng x  2, tiệm cận ngang y  1. 
D. Tiệm cận đ ng y  1
 , tiệm cận ngang x  2.
Câu 159 : Đường cong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hàm số đó là hàm số nào?. 2x  3 A. y  . x 1 2x 1 B. y  . x 1 2x 1 C. y  . x 1 2x 1 D. y  . x 1 mx  7m  8
Câu 160 : Cho hàm số y
. Tìm m để hàm số đồng biến trên từng khoảng xác định của x m nó. m  0 A. 8   m 1. B.  . m  1 C. 3   m  0. D. 3   m  0. 90
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TỔNG ÔN 2017 y
Câu 161 : Cho hàm số y f x liên tục trên đoạn  2
 ;2 và có đồ thị trên 2 đoạn  2
 ;2 như sau: Khẳng định nào sau đây là sai? 1  O 1
A. max f x  f 2 .
B. max f x  f  2  .  2  ;2  2  ;2 2  2 x
C. min f x  f   1 .
D. min f x  f 0 .  2  ;2  2  ;2 2 
Câu 162 : Tìm tất cả giá trị của m để hàm số 1 3 2 y
x mx   2 m m  
1 x 1 đạt cực đại tại x  1 3 A. m  2  . B. m  1  . C. m  2 . D. m  1. m  1 x  2
Câu 163 : Tìm tất cả giá trị của m để hàm số y
đồng biến trên từng khoảng xác định x mm 1 A. 2   m 1. B.  . m  2  m 1 C. 2   m 1. D.  . m  2 
Câu 164 : Đồ thị hình bên là của hàm số nào?.
Chọn một khẳng định ĐÚNG. A. 3 2
y x  3x 1. 3 x B. 2 y    x 1. 3 C. 3 2
y  2x  6x 1. D. 3 2
y  x  3x 1.
Câu 165 : Tìm tất cả giá trị của m để đồ thị hàm số 4 2
y x  2mx  2m 1 đi qua điểm N  2  ;0 5 17 17 3 A. . B.  . C. . D. . 2 6 6 2
Câu 166 : Đường cong trong hình bên là đồ thị của một hàm số y
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào? A. 4 2
y  x  8x 1. 1 B. 4 2
y x  8x 1 . 2  2 O x C. 3 2
y  x  3x 1. D. 3 2
y x  3x 1. 3  91
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – PHÉP TỊNH TIẾN 2017
PHẦN 11 : PHÉP TỊNH TIẾN
KIẾN THỨC CĂN BẢN
Trong mặt phẳng Oxy, cho hàm số y f x có đô thị là (C) và x0, y0 là hai số dương tùy ý.
► Tịnh tiến (C) lên trên y0 đơn vị thì ta được đồ thị y f x  y 0
► Tịnh tiến (C) xuống dưới y0 đơn vị thì ta được đồ thị y f x  y 0
► Tịnh tiến (C) sang trái x0 đơn vị thì ta được đồ thị y f x x 0 
► Tịnh tiến (C) sang phải x0 đơn vị thì ta được đồ thị y f x x 0 
Ví dụ : Cho hàm số y = f(x) có đồ thị như hình
► Thì đồ thị hàm số y = f(x) + 1 ( lên trên 1 đơn vị ) y = f(x)+1 92
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – PHÉP TỊNH TIẾN 2017
► Thì đồ thị hàm số y = f(x) - 1 ( xuống dưới 1 đơn vị ) y = f(x) -1
► Thì đồ thị hàm số y = f(x - 1) ( sang phải 1 đơn vị ) y = f(x - 1)
► Thì đồ thị hàm số y = f(x + 1) ( sang trái 1 đơn vị ) y = f(x + 1) 93
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – PHÉP TỊNH TIẾN 2017
BÀI TẬP TRẮC NGHIỆM PHẦN TỊNH TIẾN ĐỒ THỊ
Câu 1 : Cho đường cong (C) có phương trình : 3
y x . Tịnh tiến (C) lên trên 2 đơn vị thì ta được đồ
thị của hàm số nào sau đây ? A. 3 y x 1 B. 3 y x  2
C. y   x  3 2
D. y   x  3 2  2
Câu 2 : Cho đường cong (C) có phương trình : 3
y x  2 . Tịnh tiến (C) sang trái 3 đơn vị thì ta
được đồ thị của hàm số nào sau đây ?
A. y   x  3 3  2
B. y   x  3 3  2
C. y   x  3 3
D. y    x  3 1 3
Câu 3 : Cho đường cong (C) có phương trình : 2
y x . Tịnh tiến (C) lên trên 5 đơn vị, sau đó tịnh
tiến đồ thị nhận được sang trái 1 đơn vị thì ta nhận được đồ thị của hàm số nào sau đây ? A. 2
y x  2x  6
B. y   x  2 1  2
C. y   x  2 2  5
D. y   x  2 2  4 x
Câu 4 : Cho đường cong (C) có phương trình : y f x 2 1 
. Tịnh tiến (C) sang trái 3 đơn vị x  3
sau đó tịnh tiến xuống dưới 2 đơn vị thì ta được đồ thị hàm số nào sau đây ? 2 x  3 1 A. y x  2 x 31 B. y  3x  2 7 C. y x 7 D. y  2x
Câu 5 : Cho đường cong (C) có phương trình : y f x . Tịnh tiến (C) sang trái 1 đơn vị ta được đồ thị hàm số
A. y f x   1
B. y f x   1
C. y f x 1
D. y f x 1
Câu 6 : Cho đường cong (C) có phương trình : y f x . Tịnh tiến (C) sang phải 3 đơn vị ta được đồ thị hàm số
A. y f x  3
B. y f x  3
C. y f x  3
D. y f x  3 94
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – PHÉP TỊNH TIẾN 2017
Câu 7 : Cho đường cong (C) có phương trình : y f x . Tịnh tiến (C) lên trên 4 đơn vị ta được đồ thị hàm số
A. y f x  3  4
B. y f x  3  4
C. y f x  3
D. y f x  4
Câu 8 : Cho đường cong (C) có phương trình : y f x . Tịnh tiến (C) xuống dưới 4 đơn vị ta được đồ thị hàm số
A. y f x  4
B. y f x  3  4
C. y f x  4
D. y f x  4
Câu 9 : Cho đường cong (C) có phương trình : y f x . Tịnh tiến (C) xuống dưới 4 đơn vị sau đó
tịnh tiến lên trên 2 đơn vị ta được đồ thị hàm số
A. y f x  4
B. y f x  3  2
C. y f x  4
D. y f x  2
Câu 10 : Cho đường cong (C) có phương trình : y f x . Tịnh tiến (C) xuống dưới 4 đơn vị sau đó
tịnh tiến sang trái 2 đơn vị ta được đồ thị hàm số
A. y f x  4
B. y f x  2  4
C. y f x  4
D. y f x  2  4
Câu 11 : Hàm số y f x liên tục và nghịch biến trên 0; 2 thì hàm số y f x  3 nghịch biến trên A.  3  ;  1 B. 3;4 C.  3  ;0 D. 3;5
Câu 12 : (THPT Cẩm Bình – HN) Nếu hàm số y f x đồng biến trên khoảng  1  ;2 thì hàm số
y f x  2 đồng biến trên khoảng nào sau đây ? A.  3  ;0. B.  2  ;4 . C.  1  ;2 . D. 1;4 . 95
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook