Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số – Nguyễn Vũ Minh (Tập 2) Toán 12

Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số – Nguyễn Vũ Minh (Tập 2) Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

107 54 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

86 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Phân dạng và phương pháp giải
trắc nghiệm Toán 12
Tập 2
Đồ thị
Tiếp tuyến
Sự tương giao
BIÊN HÒA – Ngày 07 tháng 07 năm 2017
TÀI LIỆU LƯU HÀNH NỘI BỘ
1
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
1/ Tập x{c định
2/ Sự biến thiên
2.1 Xét chiều biến thiên của hàm số

+ ng 0 honh
u bi.
2.2 Tìm cực trị
2.3 Tìm các giới hạn tại vô cực (
x
)
2.4 Lập bảng biến thiên.
Th hi  ng bi
3/ Đồ thị
- Giao c th vi trc Oy: x=0 =>y= ? => (0;?)
- Giao c th vi trc Ox:
y 0 f(x) 0 x ? (?;0)
- m CĐ; CT n
(Chú ý:nếu nghiệm bấm máy tính được thì OK, nghiệm lẻ giải tay được thì phải giải ra- chẳng hạn phương
trình bậc 2, còn nghiệm lẻ mà không giải được thì ghi ra giấy nháp cho biết giá trị để khi vẽ cho chính xác-
không ghi trong bài- chẳng hạn hàm bậc 3)
- Lt s m (nếu cần)
- Nh  th. Điều này sẽ cụ thể hơn khi đi vẽ từng đồ thị hàm số. D{ng điệu của
đồ thị l| d{ng điệu của bảng biến thiên.
I- SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM BẬC BA:
y = ax
3
+ bx
2
+ cx + d (a 0) .
1/ Tập x{c định. D = R
2/ Sự biến thiên
2.1 Xét chiều biến thiên của hàm số

2
y' 3ax 2bx c
+
2
y' 0 3ax 2bx c 0
 CHUNG KH  TH .
2
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
(Bấm máy tính nu nghim chn, gii
;'
nu nghim l - không được ghi nghiệm gần đúng)
u bia .
2.2 Tìm cực trị
2.3 Tìm các giới hạn tại vô cực (
x
)
(Hàm bậc ba và các hàm đa thức không có TCĐ và TCN.)
2.4 Lập bảng biến thiên.
Th hi  ng bi
3/ Đồ thị
- Giao c th vi trc Oy: x=0 =>y= d =>(0; d)
- Giao c th vi trc Ox:
32
y 0 ax +bx +cx+d 0 x ?
- m ci, cc tiu (nếu có).
(Chú ý: nc tr ng HÌNH CHỮ NHẬT CƠ SỞ)
Các dạng đồ thị hàm số bậc 3:y = ax
3
+ bx
2
+ cx + d (a
0)
Dấu của a
Dấu ∆
a > 0
a < 0
Pt y’ = 0 có
hai nghiệm
ph}n biệt
2
-2
O
2
-2
3
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
Pt y’ = 0 có
nghiệm kép
Pt y’ = 0 vô nghiệm
VÍ DỤ MINH HỌA : Kh bi  th 
32
31y x x
.
Tập x{c định:
.
Sự biến thiên:Chiu bi
2
36y x x

;
0
0
2
x
y
x

.
0, ; 0 2;yx
 ng bing
;0

2; 
.
0, 0; 2yx
 nghch bing
0; 2
.
Cc tr t ci ti
0; 6
CD
xy
 t cc tiu ti
2; 2
CT
xy
.
+ Gii hn:
lim ; lim
xx
yy
 
.
Bảng biến thiên
2
2
2
4
2
4
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
x

0
2

y
0
0
y

1
3

Đồ thị:
 th  ct trc
Oy
tm
0; 1
.
 th  m
1; 3 , 1; 1 , 3;1
Vẽ đồ thị:
II - SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM TRÙNG PHƯƠNG:
y = ax
4
+ bx
2
+ c (a 0) .
1/ Tập x{c định. D=R
2/ Sự biến thiên
2.1 Xét chiều biến thiên của hàm số
3
' 4ax +2bxy

32
' 0 4ax 2bx 0 2x.(2ax b) 0y
2
2
0
0
...
2ax b 0
2a
x
x
b
x

u bi.
5
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
2.2 Tìm cực trị
2.3 Tìm các giới hạn tại vô cực (
x
). (Hàm trùng phương không có TCĐ và TCN.)
2.4 Lập bảng biến thiên.Th hi  ng bi
3. Đồ thị- Giao c th vi trc Oy: x=0 =>y= c => (0;c)
- Giao c th vi trc Ox:
42
0 ax +bx +c 0 ? (?;0)yx
- 
-  th ci xng.
(Chú ý:giải phương trình trùng phương- các bạn bấm máy tính như giải pt bậc 2 nhưng chỉ lấy
nghiệm không âm, sau đó giải để tìm ra x)
- Lt s m (nu cn)- (điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu
bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)
Các dạng đồ thị hàm số trùng phương:y = ax
4
+ bx
2
+ c (a 0)
Dấu a
y’=0
a > 0
a < 0
Pt y’ = 0 có ba
nghiệm ph}n biệt
Pt y’ = 0 có một
nghiệm
-2
2
2
-2
6
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
VÍ DỤ MINH HỌA : Kh bi  th 
42
23y x x
.
Tập x{c đinh:
.
Sự biến thiên:Chiu bi
3
44y x x

;
0
0
1
x
y
x


.
0, 1; 0 1;yx
 ng bing
1; 0

1; 
.
0, ; 1 0; 1yx

 nghch bing
3; 2I

0; 1
.
Cc tr t ci ti
0; 3
CD
xy
.  t cc tiu ti
1; 2
CT
xy
.
Gii hn:
lim ; lim
xx
yy
 

.
Bảng biến thiên
x

0
2

y
0
0
y

1
3

Đồ thị :  th  ct trc
Oy
tm
0; 3
.
 th  m
2; 11 , 2; 11
.
 th  nhn trc
Oy
i xng.
7
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
III - SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM NHẤT BIẾN:
( 0, 0)
ax b
y c ad bc
cx d
1/ Tập x{c định.
\
d
DR
c



2/ Sự biến thiên
2.1 Xét chiều biến thiên của hàm số

2
d bc
''
(cx d)
ax b a
y
cx d






i mi
d
x
c
 ng bin (nghch bing
( ; )
d
c


( ; )
d
c

2.2 Tìm cực trị: Hàm số đã cho không có cực trị
2.3 Tiệm cận:

ax+b
lim lim
cx+d
xx
a
y
c
 


a
y
c
tiệm cận ngang
ax+b
lim lim ( )
cx+d
dd
xx
cc
y



;
ax+b
lim lim ( )
cx+d
dd
xx
cc
y




d
x
c
tiệm cận đứng
2.4 Lập bảng biến thiên.
Th hi  ng bi
3/ Đồ thị
8
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
- Giao c th vi trc Oy: x=0 =>y=
b
d
=> (0;
b
d
)
- Giao c th vi trc Ox:
ax b
0 0 0 ( ;0)
cx d
bb
y ax b x
aa
- Lt s m (nu cn)
- Nh  th th nhm
( ; )
da
I
cc
ng tim c
tâm đối xứng
Các dạng đồ thị hàm số:
( 0, 0)
ax b
y c ad bc
cx d
D = ad bc > 0
D = ad bc < 0
VÍ DỤ MINH HỌA : Kh bi  th 
3x 2
y
x2
.
Tập x{c định:
\2
.
Sự biến thiên: Chiu bi
2
4
2
y
x
.
0, ; 2 2;yx

 ng bing
;2

2;
.
Cc tr c tr.
Gii hn:
lim 3; lim 3
xx
yy
 

 th  nhng thng
3y
tiệm cận ngang
4
2
4
2
-2
9
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
22
lim ; lim
xx
yy

 
 th  nhng thng
2x 
tiệm cận đứng
Bảng biến thiên
x

2

y
y
3


3
 th  ct trc
Ox
tm
2
;0
3



, ct trc
Oy
tm
0; 1
.
 th  m
4; 5 , 3; 7 , 1; 1 , 2; 2
.
 th  nhm
2; 3I
ca hai tim ctâm đối xứng.
BÀI TẬP TỰ LUẬN PHẦN HÀM SỐ
B|i 01 : Kh  th  sau:
a/
32
y 3 1xx
b/
32
34y x x
c/
3
y 3 1xx
d/
32
6 9 4.y x x x
ii :
...

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
...

...

...

...

...

...

...

...

...

...

...

...

...

10
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
...

...

...

...

...

...

...

...

...

...

...

...

...

11
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
B|i 02 : Kh  th  sau:
a/
21
1
x
y
x
b/
1
1
x
y
x
c/
1
2
x
y
x
d/
22
1
x
y
x
ii :
...

...

...

...

...

...

...

...

...

...

...

12
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
...

...

...

...

...

...

...

...

...

...

...

...

...

13
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
B|i 03 : Kh  th  sau:
a/
42
2y x x
b/
42
21y x x
c/
42
41y x x
ii :

...

...


...

...


...

...


...

...


...

14
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
...


...

...


...

...


...

...

15
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
16
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
BÀI TẬP TRẮC NGHIỆM PHẦN ĐỒ THỊ HÀM SỐ
C}u 1 :Dựa vào đồ thịc 
bit:
1.1 ng bin, nghch bin c.
.................................................................
.................................................................
1.2 Cc tr c.
.................................................................
..................................................................
1.3  ln nh nht c n
1; 2
........................................................................................................
1.4 ng thng
, 2;2y

c  th   ti
m
C}u 2 :Dựa vào đồ thịc t:
2.1 ng bin, nghch bin c.
.............................................................................
2.2 Cc tr c.
....................................................................................................
2.3  ln nh nht c n
1; 2
....................................................................................................
2.4 ng thm cc tr c th  ...........................
C}u 3 :Dựa vào đồ thịc 
 ng v th 
A.
2
1
x
y
x
B.
2
1
x
y
x
2
2
O
1
2
I
x
y
y
x
O
2
1
1
–2
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
C.
2
1
x
y
x
D. Tt c u sai
C}u 4 :Dựa vào đồ thịc t:
ng bin, nghch bin c.
.....................................................................................................
B/ Cc tr c.
.......................................................................................
 ln nh nht c
n
1; 1
.............................................................................
D/ Khong m c........................
ng thng
, ; 6y


c th  ti ..............................m
F/ Dia tam o bm cc tr ...........................................
C}u 5 :Dựa vào đồ thịc
1
xa
y
bx

t

A.
1; 2ab
B.
1; 2ab
C.
1; 2ab
D.
1; 2ab
C}u 6 : 
2
4
x
y
x
 th  :
 m c
 m c
 ng tim cI(1;4)
A. Ch 
B. Ch 
O
1
x
1
y
2
1
1
O
x
y
1
1
I
1
18
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017

 u sai.
C}u 7 : 
y f x

 th 
 li sau :
7.1 Tim c
7.2 Minh D =...........................
7.3 
A.
' 0,y x D
B.
' 0,y x D
C.
' 0,y x D
D.
' 0,y x D
7.4 m c th vi
Oy   Ox 
C}u 8 : 
y f x
 th  l
hi sau :
8.1 Tim c
8.2 Minh D =.........................
8.3 
A.
' 0,y x D
B.
' 0,y x D
C.
' 0,y x D
D.
' 0,y x D
8.4 m c th vi
Oy 

Ox 
4
2
2
5
1
-0,5
O
6
4
2
2
5
5
1
3
y
x
5
-2
-1
4
2
1
O
19
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
-1
-2
-5
-1
3
2
1
O
x
y
C}u 9 : 
4
2
2
x
y f x bx c
 th  .
 ca c 
A.
1
B.
0
C.
3
2
D.
2
C}u 10 : Bng bing v th
 
A.
3
2
x
y
x
B.
22
2
x
y
x
C.
2
2
x
y
x
D.
2
1
x
y
x
C}u 11 :  th 
4
6 2 7
2
x
y f x k m x n

 th c biu di  s k trong
 
A.
0k
B.
0k
C.
0k
D.
0k
C}u 13 :  th 
3
2
34
xm
y f x a x nx k
 th c biu di
  th
A.
2k
B.
2k 
C.
0k
D.
1k
C}u 14 :  th  c v ng vi

A.
21
3
x
y
x
y
x
-2
0
1
2
2
1
-1
-1
4
20
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
B.
2x 1
y
x3

C.
2x
y
x2
D.
2 2x
y
x3
C}u 15 : 
4
6 2 7
x
y f x k m x n
2

Kt lu
 
bit 
 m duy
nh
 
bi
 m duy nh
C}u 16 : 
y f x
 th c v 
D th  li sau :
16.1 Điểm cực tiểu c th  n
  nht
 ph hai
 
 u sai
16.2 Chsai
 m ci c th  
M 1;3
  ng bi
1;1
 nh ca hình chữ nhật cơ sở
x 2; y 3; y 1
 
x 2;1
Miny 2


C}u 17 (Đề minh họa lần 03):  th ca m trong bn
 c li b 
x

0

'y
0
y
M


-1
x
y
1
3
-2
-1
2
O
1
21
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
f(x)=(2x-1)/(x+1)
x(t)=-1 , y(t)=t
f(x)=2
0
-1
2
x
y
A.
23
1
x
y
x
. B.
21
1
x
y
x
. C.
22
1
x
y
x
. D.
21
1
x
y
x
.
C}u 18 :  th .
Tr li sau :
18.1  ln nht c 
4 3 2 1
18.2  c
A.
7
B.
7
C.
1
D.
1
18.3 Khom c........................
16.4 ng thng
, 0;4y

c th  ti ...........m
C}u 19 : th c  th c 
A.
32
y x 3x 3x 2
B.
32
y x 3x 4
C.
32
y x 3x 4x 2
D.
42
y x 2x 2
C}u 20 : th c 
 th c 
A.
32
y x 3x 3x 2
7
M
22
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
B.
32
y x 3x 4
C.
3
y x 1
D.
32
y x 2x 2
C}u 21 :Bng bi  sau:
A.
32
y x 3x 3x 2
B.
32
y x 3x 4
C.
32
y x 3x 4x 2
D.
42
y x 2x 2
C}u 22 :Bng bi  sau:
x

1
0
1

y
0
0
0
y


A.
32
y x 3x 3x 2
B.
32
y x 3x 4
C.
4
2
x3
yx
22
D.
42
y x 2x 2
C}u 25 :Bng bi  sau:
A.
32
y x 3x 3x 2
B.
32
y x 3x 4
C.
2x 4
y
x1

D.
3x
y
x2
C}u 26 : th c 
 th (C) c 
A.
42
y x 4x 2
B.
42
y x 4x 1
C.
4
2
x3
yx
22
x
-
+

-
y
+
-
x
-
2
- +

-
-
y
-1
-
+
-1
23
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
D.
42
y x 2x 2
C}u 27 : th c 
 th (C) c 
A.
42
y x 4x 2
B.
42
1
y x x 1
2
C.
4
2
x3
yx
22
D.
42
y x 2x 2
C}u 28 :  th . Cho bi th ca m
s sau.

A.
32
y ax bx cx d
B.
ax b
y
cx d
C.
2
ax bx c
y
dx e

D.
42
y ax bx c
C}u 29 :  th . Cho bi th ca m
s sau.
29.1 
A.
32
y ax bx cx d
B.
42
y ax bx c
C.
2
ax bx c
y
dx e

D.
ax b
y
cx d
29.2 s  chn l
29.3 Giá trị nhỏ nhất c 
7;9
.........................
C}u 30 : 
3
1f x x

2
3g x x
 th 
f x g x

A. B.
-1
24
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
C. D.
C}u 31 : ng cong (C) :
32
y ax bx cx d
 th .
Ch
 
 m
 
 m
C}u 32 : ng cong (C) :
32
y ax bx cx d
 th . Ch
 
 m
 
 m
C}u 33 : ng cong (C) :
y f x
 th . Gi S (đơn vị diện tích)
o bm cc tr ca
 th  
A. 0,5
B. 1
C. 2
D. 3
C}u 34 :  :
32
31
m
y f x x x mx C
. V a tham s  th  m
hai tim cn c th 
2
2
x
y r x H
x

25
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
A. 0,5 B. 1
C. 2 D. 3
C}u 35 :  :
32
31
m
y f x x x mx C

32
27y g x x x C
Kt lu
  th  
B. Minh ca c   .
  th t nhau.
D. Vi m = -mc tr.
C}u 36 :  :
32
32y f x x x C
m
c
A.
1 2;0 , 1;0 , C 1 2;0AB
B.
1;0 , 2;0 , C 1;0AB
C.
1 3;0 , 2;0 , C 1 3;0AB
D.
1 3;0 , 1;0 , C 1 3;0AB
C}u 37 :  :
42
65y f x x x C
m c

A.
2;0 , 1;0 , C 1;0 , 2;0A B D
B.
5;0 , 1;0 , C 1;0 , 5;0A B D
C.
7;0 , 2;0 , C 2;0 , 7;0A B D
D.
5;0 , 1;0 , C 2;0 , 5;0A B D
C}u 38 :  :
4
2
9
2
44
x
y f x x C
. Gm c
  s p tuyn t
A.
15
B.
15
C.
9
4
D.
9
4
C}u 39 : 
42
1 ( )y x mx m C
. Vi m ca tham s  th 
qua mm K c 
A.
3;0
B.
1;2
C.
0;2
D.
1;0
C}u 40 : Cho  (C) :
32
1
x
y
x
 th  

26
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
A. 4 B. 3
C. 2 D. 1
C}u 41 :  (C) :
27
3
x
y
x
 th  

A. 4 B. 3
C. 2 D. 1
C}u 42 :  (C) :
8
1
x
y
x
 th  

A. 4 B. 6
C. 8 D. 2
C}u 43 :  (C) :
32
2
x
y
x
 th 
  
A. 4
B. 6
C. 8
D. 2
C}u 44 :  (C) :
y f x
 th c v
m A(2;1).
Di∆AMD bng
A. 4
B. 3/2
C. 5/2
D. 2
C}u 45 :  th  m cc tr :
A.
42
2 4 1y x x
B.
42
21y x x
C.
42
21y x x
D.
42
21y x x
C}u 46 :  th   m cc tr :
A.
42
2 4 2y x x
B.
42
91y x x
C.
42
21y x x
D.
4 2 2
11y x m x
C}u 47 : Kh 
42
42y x x
:
 t cc tiu ti x = 0
27
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
 c tiu
 c tiu
 c tr.
C}u 48 :  (C) :
y f x
 th c v 
hình 1  th c
1y f x
A. B.
C. D.
C}u 49 : Kh 
ax b
y
cx d
:
  
\
d
D
c



B.
0ad bc
  c tr
D. C 
C}u 50 : 
,0
ax b
y ad bc
cx d
.
Kh
  ng khonh.

28
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
  
2
bc ad
y
cx d
 m cn.
  th  hình
C}u 51 :  th 
A.
42
22y x x
B.
42
22y x x
C.
42
22y x x
D.
42
2y x x
C}u 52 :  th 
A.
42
1y x x
B.
42
21y x x
C.
42
21y x x
D.
42
1y x x
C}u 53 : Bng bi 
 
A.
32
33y x x x
B.
32
33y x x x
C.
32
33y x x x
D.
32
33y x x x
C}u 54 : Bng bi a
 
A.
42
33y x x
B.
42
1
33
4
y x x
C.
42
23y x x
D.
42
23y x x
29
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
C}u 55 : Bng bi 

A.
42
31y x x
B.
42
31y x x
C.
42
31y x x
D.
42
31y x x
C}u 56 : (Sở GD&ĐT B| Rịa – Vũng
T|u, lần 1) 
     



A.
B. .
C. .
D. .
C}u 57 : Bng bi a
 
A.
42
33y x x
B.
42
3y x x
C.
42
23y x x
D.
42
23y x x
C}u 58 : Bng bi a
 
A.
21
1
x
y
x
B.
1
21
x
y
x
C.
21
1
x
y
x
D.
2
1
x
y
x
3
3 2.y x x
3
45y x x
3
32y x x
3
32y x x
x
y
4
2
2
-1
O
1
30
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
C}u 59 : Bng bi a
 
A.
21
2
x
y
x
B.
1
21
x
y
x
C.
1
2
x
y
x
D.
3
2
x
y
x
C}u 60 :  th 

A.
3
3y x x
B.
3
3y x x
C.
3
2y x x
D.
3
2y x x
C}u 61 :  th 

A.
3
1yx
B.
32
2y x x
C.
2
31yx
D.
3
41yx
C}u 62 :  th  
A.
42
31y x x
B.
42
21y x x
C.
42
21y x x
D.
42
31y x x
C}u 63 :  th  
A.
42
2y x x
B.
42
2y x x
C.
42
2y x x
D.
42
2y x x
31
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
C}u 64 :  th  
A.
21
21
x
y
x

B.
1
x
y
x
C.
1
1
x
y
x

D.
2
1
x
y
x

C}u 65 :  th  
A.
1
1
x
y
x
B.
1
1
x
y
x
C.
21
22
x
y
x
D.
1
x
y
x
C}u 66 :  th  
A.
32
3 4 2y x x x
B.
2
3 4 2y x x x
C.
32
3 4 2y x x x
D.
32
32y x x
C}u 67 :  th  
A.
32
2 3 1y x x
B.
32
2 3 1y x x
C.
32
2 3 1y x x
D.
22
2 3 1y x x
32
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
C}u 68 :  th  
A.
3
3y x x
B.
3
3y x x
C.
3
31y x x
D.
3
31y x x
C}u 69 :  th  
A.
42
2y x x
B.
42
2y x x
C.
42
2y x x
D.
42
3y x x
C}u 70 :  th  
A.
32
1
3
y x x x
B.
32
1
1
3
y x x x
C.
32
33y x x x
D.
32
3 3 2y x x x
C}u 71 :  th  
A.
42
41y x x
B.
42
21y x x
C.
42
21y x x
D.
42
41y x x
33
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
C}u 72 :  th  
A.
42
21y x x
B.
42
21y x x
C.
42
21y x x
D.
42
21y x x
C}u 73 :  th  
A.
3
34y x x
B.
32
34y x x
C.
3
34y x x
D.
32
34y x x
C}u 74 :  th  
A.
32
3 3 1y x x x
B.
32
31y x x
C.
3
31y x x
D.
32
31y x x
C}u 75 :  th  
A.
42
33y x x
B.
42
1
33
4
y x x
C.
42
23y x x
D.
42
23y x x
34
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
C}u 76 :  th  
A.
42
3y x x
B.
42
1
3
4
y x x
C.
42
2y x x
D.
42
4y x x
C}u 77 :  th  
A.
42
31y x x
B.
42
1
31
4
y x x
C.
42
21y x x
D.
42
21y x x
C}u 78 :  th  ?
A.
21
1
x
y
x
B.
1
1
x
y
x
C.
2
1
x
y
x
D.
3
1
x
y
x
C}u 79:  th  
A.
21
1
x
y
x
B.
2
1
x
y
x
C.
1
1
x
y
x
D.
2
1
x
y
x
35
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
C}u 80:  th  
A.
3
31y x x
B.
32
31y x x
C.
3
31y x x
D.
32
31y x x
C}u 81:  th 
32
32y x x
ng:
A.
B.
C.
D.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
C}u 82:  th 
3
32y x x
ng:
A.
B.
C.
D.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-4
-3
-2
-1
1
2
x
y
-3 -2 -1 1 2 3
-2
-1
1
2
3
4
x
y
C}u 83:  th 
42
21y x x
ng:
A.
B.
C.
D.
-2 -1 1 2
-2
-1
1
2
x
y
-2 -1 1 2
-2
-1
1
2
x
y
-2 -1 1 2
-2
-1
1
2
x
y
-2 -1 1 2
-2
-1
1
2
x
y
36
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
C}u 84:  th 
4
2
21
4
x
yx
ng:
A.
B.
C.
D.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
C}u 85:  th 
2
1
x
y
x
ng:
A.
B.
C.
D.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
C}u 86:  th 
1
1
x
y
x
ng:
A.
B.
C.
D.
-2 -1 1 2 3
-3
-2
-1
1
2
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
C}u 87:  th  ng
1/
32
31y x x
 th 
2/
32
31y x x
 th 
37
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
3/
32
9
32
4
y x x x
 th 
4/
32
1
1
3
y x x x
 th 
C}u 88: 
42
y f x ax bx c a 0
 th 
v sau:

y f x
  sau:
A.
2
2
y x 2 1
B.
2
2
y x 2 1
C.
42
y x 2x 3
D.
42
y x 4x 3
C}u 89: 
32
y f x x ax bx 4
 th 

y f x
  sau:
A.
32
y x 3x 2
38
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
B.
32
y x 3x 2
C.
32
y x 6x 9x 4
D.
32
y x 6x 9x 4
C}u 90:  th ca m
trong b c li b i
  
A.
3
y x 3x 2
B.
3
y x 3x 1
C.
42
y x x 1
D.
3
y x 3x 1
C}u 91:  th ca m
trong b c li bn phng n A, B, C, D
d  
A.
42
21y x x
.
B.
42
21y x x
.
C.
42
21y x x
.
D.
4
2
1
2
x
yx
.
C}u 92:  +
42
x0y ax b c c
 th
u
,,abc
A.
0, 0, 0a b c
.
B.
0, 0, 0abc
.
C.
0, 0, 0a b c
.
D.
0, 0, 0a b c
.
C}u 93:  n
 th ng cong  
n ?
A.   ln nht ti .
B t cc tiu tm .
C  nghch bing .
D  nghch bing
y f x
3;3
3;3
y f x
2x
y f x
1x 
y f x
1;2
y f x
1;3
4
2
-2
39
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
C}u 94: (THPT Trung Giã – H| Nội)  
   
 
A. m cm cc tiu.
B. m cm cc tiu.
C. m cm cc tiu.
D.  m cm cc tiu.
C}u 95: (SGD – B| Rịa Vũng T|u 2017 lần 2) ng cong
 th ca m trong bn
 c li b
  
A . B. .
C. . D.
C}u 96: (THPT Đa Phúc – H| Nội, lần 1) 
 
M sai?
A. .
B. .
C. .
D. .
C}u 97: (THPT Ngô Sĩ Liên – H| Nội, lần 3) 
          

A.
B.
C.
D.
y f x
y f x
y f x
21
1
x
y
x
21
1
x
y
x
21
1
x
y
x
12
.
1
x
y
x
ax b
y
cx d
0ac
0ab
0cd
0bd
42
y ax bx c
0; 0; 0.a b c
0; 0; 0.a b c
0; 0; 0.a b c
0; 0; 0.a b c
40
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
x
y
-1
1
3
-1
O
1
x
y
1
1
-2
-
1
2
O
C}u 98:  th  ?
A.
3
3 1.y x x
B.
32
3 1.y x x
C.
3
3 1.y x x
D.
3
3 1.y x x
C}u 99 :  th 
32
4 6 1y x x
 

A.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
. B.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
.
C.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
. D.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
.
C}u 100:   th ?
A.
21
1
x
y
x
.
B.
21
1
x
y
x
.
C.
21
12
x
y
x
.
D.
23
1
x
y
x
.
C}u 101:  th  
A.
42
21y x x
. B.
42
21y x x
. C.
42
21y x x
. D.
42
21y x x
.
41
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ
2017
C}u 102:  th 
42
2y x x
ng:
A.
-4 -3 -2 -1 1 2 3 4
-3
-2
-1
1
2
3
4
5
x
y
B.
-4 -3 -2 -1 1 2 3 4
-3
-2
-1
1
2
3
4
5
x
y
C.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
D.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
C}u 103: 
y f x
 th
'g x f x
 sau:
S m cc tr c th 
A.
2
m.
B.
1
m.
C.
3
m.
D. 
x
y
-1
-2
O
2
1
-2
-1
1
42
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
Định lý : Đạo hàm của hàm số
y f(x)
tại điểm x0 là hệ số góc của tiếp tuyến với đồ thị tại
điểm M(x0;y0 = f(x0)) :
Yêu cầu bài toán
Phương trình tiếp tuyến
Tiếp tuyến tại
00
M(x ; y ) (C)
(1)
0
'( )k f x
: hệ số góc tiếp tuyến tại M
Tiếp tuyến có hệ số góc k cho trước
► Gọi
00
M(x ; y ) (C)
là tiếp điểm
► Giải pt :
0
'( )f x k
00
xy
► Áp Dụng (1)
phương trình tiếp tuyến
Tiếp tuyến song song với đường
thẳng (d) cho trước :
d
y k x b
► Gọi
oo
M(x ; y ) (C)
là tiếp điểm
► Giải pt :
0
'( )
d
f x k
00
xy
► Áp Dụng (1)
phương trình tiếp tuyến
Tiếp tuyến vuông góc với đường
thẳng (d) trước :
d
y k x b
► Gọi
00
M(x ; y ) (C)
là tiếp điểm
► Giải pt :
0
1
'( )
d
fx
k

00
xy
► Áp Dụng (1)
phương trình tiếp tuyến
Tiếp tuyến đi qua điểm
( ; ) ( )
AA
A x y C
cho trước
► Gọi
00
M(x ; y ) (C)
là tiếp điểm
► Tiếp tuyếm tại M là
()
:
0 0 0
y f '(x ).(x x )y
(1)
►
()
qua A: thay tọa độ A vào (1)
00
xy
phương trình tiếp tuyến
◙ Lưu ý : hai đường thẳng :
11
22
y k x c
y k x c


☻ vuông góc với nhau
12
.1kk
,
☻ song song
12
kk
và
12
cc
(Với
12
,kk
là hệ số góc)
43
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
Bài 01 : Viết phương trình tiếp tuyến của đồ thị hàm số
32
32y x x
a/ Tại điểm
(2; 2)M
. b/ Tại điểm có hoành độ
1x 
.
c/ Tại điểm có tung độ
2y 
. d/ Tại giao điểm của đồ thị với đường thẳng
1yx
.
e/ Tại giao điểm của đồ thị với trục tung.
f/ Tại giao điểm của đồ thị với trục hoành.
g/ Tiếp tuyến có hệ số góc nhỏ nhất
● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
44
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 02 : Viết phương trình tiếp tuyến của đồ thị hàm số
1
2
x
y
x
tại điểm
1;0M
A.
1
1
3
yx
B.
31yx
C.
1
1
3
yx
D.
1
1
9
yx
● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 03 : Cho hàm số
3
1y x x
có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại giao
điểm của (C) với trục tung.
A.
1yx
B.
1yx
C.
22yx
D.
21yx
● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
Bài 04 : Cho hàm số
32
1
2 3 1 (1)
3
y x x x
. Phương trình tiếp tuyến của đồ thị hàm số
(1)
song
song với đường thẳng
31yx
có dạng
y ax b
. Tìm giá trị
S a b
A.
29
3
B.
20
3
C.
19
3
D.
20
3
● Giải :
45
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 05 : Tiếp tuyến của đồ thị hàm số
42
6y x x
song song với đường thẳng
:6x 0dy
là:
A.
6x 10y 
B.
67yx
C.
6 10yx
D.
67yx
● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 06 : Tiếp tuyến của đồ thị hàm số
32
32y x x
tại điểm
1; 2A 
là:
A.
92yx
B.
97yx
C.
24 7yx
D.
24 2yx
● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 07 : Tiếp tuyến của đồ thị hàm số
3
32y x x
tại các giao điểm với trục hoành có phương
trình là
A.
0y
và
9 18yx
B.
0y
và
9 18yx
C.
0y
và
9 18yx
D.
0y
và
9 18yx
● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
Bài 08 : Gọi A là giao điểm của đồ thị hàm số
2
21
x
y
x
với trục Ox. Tiếp tuyến tại A của đồ thị
hàm số đã cho có hệ số góc k là:
A.
5
9
k 
B.
1
3
k
C.
1
3
k 
D.
5
9
k
● Giải :
46
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 09 : Viết phương trình tiếp tuyến của đồ thị hàm số
3
32y x x
, biết tiếp tuyến đó tiếp xúc
với đồ thị hàm số tại điểm
2;4M
.
A.
3 10yx
B.
9 14yx
C.
9 14yx
D.
32yx
● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………….……………………………………………
Bài 10 : Cho hàm số
:2C y x
. Viết phương trình tiếp tuyến với đồ thị
C
tại điểm có tung độ
bằng
2
.
A.
4 3 0xy
. B.
4 1 0xy
. C.
4 2 0xy
. D.
4 6 0xy
● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………….……………………………………………
Bài 11 : Có bao nhiêu tiếp tuyến của đồ thị hàm số
32
6 6 2016y x x x
song song với đường
thẳng
3 2016yx
.
A. 0 B. 1 C. 2 D. 3
● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………….……………………………………………
Bài 12 : Trong các phương trình sau, phương trình nào là phương trình tiếp tuyến của đồ thị
1
2yx
x

tại điểm có hoành độ
1x
A.
1yx
B.
22yx
C.
2yx
D.
2yx
● Giải :
47
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 13 : Cho hàm số
32
1
2 3 1
3
y x x x C
. Tiếp tuyến của đồ thị (C) song song với đường
thẳng
: 3 1d y x
có phương trình là:
A.
31yx
B.
26
3
3
yx
C.
32yx
D.
29
3
3
yx
● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 14 : Phương trình tiếp tuyến của
:C
2
1
x
y
x
tại điểm có hoành độ bằng
2
có là phương
trình nào sau đây
A.
3 10yx
. B.
3 10yx
. C.
3 10yx
. D.
3 10yx
.
● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Ví dụ 01 : Cho hàm số
42
2y x x
. Viết phương trình tiếp tuyến của đồ thị tại điểm có hoành
độ
2x
.
♥ Giải : Đạo hàm
3
' 4 4y x x
; Ta có
28xy
Suy ra hệ số góc của tiếp tuyến tại điểm đang xét là
' 2 24.ky
Phương trình tiếp tuyến của đồ thị là
: 8 24 2d y x
hay
: 24 40.d y x
Vậy tiếp tuyến cần tìm
: 24 40.d y x
Ví dụ 02 : Cho hàm số
32
31y x x
. Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp
tuyến đó vuông góc với đường thẳng
1
( ): 2009
9
d y x
.
♥ Giải :
1
( ): 2009
9
d y x
có hệ số góc là
1
9
; Gọi M(x0; y0) thuộc (C) là tiếp điểm
Suy ra hệ số góc của tiếp tuyến của đồ thị tại điểm
M
là
2
0 0 0
' 3 6k f x x x
48
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
Tiếp tuyến vuông góc với (d) suy ra
00
1
f'(x ) 1 f'(x ) 9
9
00
2
00
00
13
3 6 9 0
31
xy
xx
xy
Vậy có hai phương trình tiếp tuyến của (C) thoả điều kiện là:
9 6 9 26y x hay y x
Ví dụ 03 : Cho hàm số
1
1
x
y
x
. Viết phương trình tiếp tuyến của đồ thị hàm số, biết rằng tiếp
tuyến có hệ số góc bằng
2
.
♥ Giải : Gọi
00
;M x y
với
0
1x 
là điểm thuộc đồ thị. Ta có đạo hàm
2
2
'
1
y
x
.
Suy ra hệ số góc của tiếp tuyến của đồ thị tại điểm
M
là
0
2
0
2
'
1
k y x
x

.
Theo giả thiết, ta có
2
0
0
2
0
0
0
2
2 1 1 .
2
1
x
x
x
x

●Với
0
0x
, suy ra
0; 1M
. Phương trình tiếp tuyến là
1
: 2 0 1d y x
.
●Với
0
2x 
, suy ra
2;2M
. Phương trình tiếp tuyến là
2
: 2 2 2d y x
.
Vậy có hai phương trình tiếp tuyến cần tìm là
1
: 2 1d y x
,
2
: 2 6d y x
.
Ví dụ 04 : Cho hàm số
: 3 1 2d y x
. Viết phương trình tiếp tuyến với đồ thị tại giao điểm
của đồ thị và đường thẳng
: 3 5d y x
♥ Giải : Ta có
2
1
'
2
y
x
Gọi
00
;2A x y
,
0
2x 
là giao điểm của đồ thị với đường thẳng
2y
Suy ra tọa độ điểm
00
1; 2A x y
; Suy ra hệ số góc của tiếp tuyến
0
' ' 1 1.k y x y
Phương trình tiếp tuyến cần tìm là
: 1 1 2d y x
hay
:1d y x
.
49
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
Ví dụ 05 : Cho hàm số
32
3 1 1y x mx m x
(
m
là tham số thực). Tìm
m
để tiếp tuyến
của đồ thị hàm số đã cho tại điểm có hoành độ
0
1x 
đi qua điểm
1;2A
.
♥ Giải : Ta có
2
' 3 6 1y x mx m
Với
0
1x 
, suy ra
32
0
1 3 1 1 1 1 2 1.y m m m
Suy ra hệ số góc của tiếp tuyến
' 1 4 5 .k y m
Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ bằng
0
1x 
là:
: 4 5 . 1 2 1d y m x m
.
Theo giả thiết, tiếp tuyến đi qua
1;2A
nên
5
2 4 5 . 1 1 2 1 .
8
m m m
Vậy
5
8
m
là giá trị cần tìm thỏa yêu cầu bài toán.
Ví dụ 06 : Cho hàm số
22
()
1
x
y f x
x

. Viết phương trình tiếp tuyến của đồ thị tại giao điểm
của đồ thị với trục tung.
♥ Giải : Đạo hàm
2
4
'
1
fx
x
. Gọi
A
là giao điểm của
C
với trục tung (Oy : x = 0)
Suy ra tọa độ điểm
A
là nghiệm của hệ phương trình
22
0
0; 2
1
2
0
x
x
y
A
x
y
x


Suy ra hệ số góc của tiếp tuyến
' 0 4kf
Phương trình tiếp tuyến của đồ thị tại
A
là
: 4 0 2d y x
hay
: 4 2.d y x
Ví dụ 07 : Cho hàm số
32
32y x x
. Viết phương trình tiếp tuyến của đồ thị biết tiếp tuyến
song song với đường thẳng
: 9 25yx
.
♥ Giải : Đạo hàm
2
' 3 6y x x
; Đường thẳng
: 9 25yx
có hệ số góc là – 9
Gọi
00
;M x y
là điểm thuộc đồ thị hàm số (hay tiếp điểm)
50
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
Suy ra hệ số góc của tiếp tuyến của đồ thị tại điểm
M
là
2
0 0 0
' 3 6k f x x x
Do tiếp tuyến song song với đường thẳng
: 9 25yx
(có hệ số góc là – 9)
nên
0
2
0 0 0
0
1
' 9 3 6 9 .
3
x
y x x x
x

Với
0
1x 
, suy ra phương trình tiếp tuyến:
1
: 9 1 2d y x
hay
1
: 9 7d y x
.
Với
0
3x
, suy ra phương trình tiếp tuyến:
2
: 9 3 2d y x
hay
2
: 9 25d y x
(loại (d2) vì đường thẳng này có phương trình trùng với ∆)
Vậy tiếp tuyến cần tìm là
1
: 9 7d y x
☻ Chú ý : đối với tiếp tuyến song song – chúng ta nên loại đi những phương trình trùng với
phương trình đường thẳng đề cho !!!
Ví dụ 08 : Cho hàm số
32
34y x x
. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm
có hoành độ
0
x
, biết
0
x
thỏa mãn
00
'' 1 2 4.y x x
♥ Giải : Gọi
32
0 0 0 0
;y 3 4M x x x
là điểm thuộc đồ thị hàm số (tiếp điểm)
Ta có đạo hàm
2
' 3 6y x x
;
'' 6 6yx
.
Theo đề bài, ta có
0 0 0 0 0 0
'' 1 2 4 6 1 6 2 4 4 4 1.y x x x x x x
Với
0
1x
, suy ra
1;2M
và hệ số góc của tiếp tuyến
0
' ' 1 3.k y x y
Vậy phương trình tiếp tuyến cần tìm là
: 3 1 2d y x
hay
: 3 5d y x
.
Ví dụ 09 : Cho hàm số
3
12
33
y x x
có đồ thị là
C
. Gọi
M
là điểm thuộc đồ thị
C
có
hoành độ
2x
.Tìm các giá trị của tham số
m
để tiếp tuyến với
C
tại M song song với
đường thẳng
2
95
:4
3
m
d y m x
.
♥ Giải : Ta có
0
4
(x 2)
3
y
tọa độ tiếp điểm
4
2;
3
M



; Tiếp tuyến
với
C
tại
M
có
phương trình :
4 4 14
'(2). 2 3 2 3
3 3 3
y y x y x y x
51
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
Ta có
2
43
//
9 5 14
33
m
d
m

2
1
1
1
m
m
m
. Vậy
1m 
là giá trị cần tìm
Ví dụ 10 : Cho hàm số
32
1
3
y x x
.Tìm tọa độ điểm M thuộc
C
sao cho tiếp tuyến của
C
tại
M
tạo với hai trục tọa độ một tam giác cân.
♥ Giải : Gọi
00
;M x y
thuộc (C) là tiếp điểm
Tiếp tuyến của (C) tại M tạo với các trục tọa độ một tam giác cân
OB OA
tiếp tuyến có hệ số góc
1
OB
k
OA
.
Theo đề ta có :
0
'1yx
2
00
2
00
2 1 0
2 1 0
xx
xx
0
0
12
1
x
x

2 2 2
1 2; 1;
3 3 3
M hay M





◙ Lưu ý : Tiếp tuyến với (C) và cắt Ox, Oy lần lượt tại 2 điểm A, B.
Gọi α là góc nhọn hợp bởi tiếp tuyến và Ox thì
22
k tan tan
OB AB OA
BAO
OA OA
♦ Tam giác OAB luôn vuông
♦
1
.
2
OAB
S OAOB
♦ Không kể 2 đường thẳng y = kx và y
=
kx (vì 2 đường này qua O, không
cắt 2 trục được )
52
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
Ví dụ 11 : Cho hàm số:
.
1
x
yC
x
Tìm tọa độ điểm
M
thuộc
C
sao cho tiếp tuyến của
C
tại
M
tạo với hai trục tọa độ một tam giác cân.
♥ Giải : Gọi
00
;M x y
thuộc (C) là tiếp điểm
Đạo hàm
2
1
' 0, 1
1
yx
x
Tiếp tuyến tạo với các trục tọa độ một tam giác cân, thì hệ số góc của tiếp tuyến bằng
1.
OB
k
OA
; Suy ra:
2
0
0
2
0
1
1
1
0
1
1 ( )
1
x
x
vn
x



hoặc
0
2.x 
► Với
0
0x
, suy ra
0
0;y
tiếp tuyến là
yx
đi qua gốc tọa độ, không thỏa mãn yêu cầu.
► Với
0
2,x 
suy ra
0
2;y
tiếp tuyến là
4,yx
thỏa mãn yêu cầu.
Vậy, điểm cần tìm là:
2;2M
Ứng dụng (Ví dụ 12 ): Cho hàm số
3
( ) :
21
x
Cy
x
. Phương trình tiếp tuyến với (C) biết tiếp
tuyến cắt trục Ox, Oy lần lượt tại A và B sao cho đường trung trực của AB đi qua gốc tọa độ có
hệ số góc là
A.
1k
B.
1k 
C. Cả A và B D. Không có
♥ Giải :
Đường trung trực của AB đi qua gốc tọa độ
là gì vậy ?????
Ý nói đó là tam giác vuông
cân Nên : OA = OB
đó bạn !
Ồ ! Vậy hệ số góc tiếp tuyến là
k1
OB
OA
Mà y’ < 0 có nghĩa k < 0 ; Chọn B !
53
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
BÀI TẬP TRẮC NGHIỆM PHẦN TIẾP TUYẾN
Câu 1 : Hệ số góc tiếp tuyến của đồ thị hàm số
2
2 10
21
xx
y
x

tại điểm có hoành độ
0
1x 
là
A.
7
8
B.
3
8
C.
5
8
D. Đáp án khác
Câu 2 : Cho hàm số
3
1
3
x
yx
. Trong tất cả các tiếp tuyến với đồ thị hàm số tại điểm M nằm
trên đồ thị hàm số thì hệ số góc tiếp tuyến nhỏ nhất là
A.
1
B.
2
C.
3
D. Đáp án khác
Câu 3 : Cho hàm số (C) :
32
1
3
y x x
. Phương trình tiếp tuyến với (C) tại điểm có hoành độ
0
1x
là
A.
1yx
B.
1
3
yx
C.
1
3
3
yx
D.
yx
Câu 4 : Cho hàm số (C) :
32
3 3 2y x x x
. Phương trình tiếp tuyến với (C) tại giao điểm của
(C) và trục tung có phương trình
A.
1yx
B.
22yx
C.
31yx
D.
32yx
Câu 5 : Cho hàm số (C) :
3
43y x x
. Phương trình tiếp tuyến với (C) tại giao điểm của (C) và
trục tung có tung độ góc là
A.
1
B. 2
C. 3 D. 4
Câu 6 : Các tiếp tuyến của đồ thị hàm số
21
2
x
y
x
có hệ số góc bằng
5
lần lượt tiếp xúc đồ thị
hàm số tại A và B
6.1 : tọa độ A và B là
A.
(0;2), (1;3)AB
B.
(1;7), (1; 2)AB
C.
(3;7), (1; 3)AB
D.
2
( 1;7), (1; )
3
AB
6.2 : độ dài AB là
A.
2 26
B.
2 13
C.
26
D.
2 21
54
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
Câu 7 : Cho hàm số :
23
()
1
x
yC
x
. Phương trình tiếp tuyến của đồ thị (C) tại điểm có tung độ
bằng 1 là
A.
11
54
yx
B.
11
55
yx
C.
13
55
yx
D.
1
5
5
yx
Câu 8 : Cho hàm số :
32
3 2 ( )y x x C
. Phương trình tiếp tuyến với đồ thị (C) và vuông góc
với đường thẳng
: 3 3 0yx
có phương trình
A.
3 2 0yx
B.
3 2 0yx
C.
3 3 0yx
D.
1
3
2
yx
Câu 9 : Cho hàm số :
32
3 ( )y x x C
. Chọn phát biểu sai :
A. Hàm số nghịch biến trên khoảng
0;2
B. Hàm số đạt cực tiểu tại
2x
C. Hệ số góc tiếp tuyến tại điểm có hoành độ
0
1x
là
2
D. Đồ thị hàm số đi qua điểm
1; 2I
Câu 10 : Cho hàm số :
32
3 2 ( )y x x C
. Phương trình tiếp tuyến với đồ thị (C) và vuông góc
với đường thẳng
: 9 3 0d x y
có tung độ góc lần lượt là m và n. Tổng của m và n là
A.
18
B.
19
C.
20
D.
21
Câu 11 : Cho hàm số :
21
()
1
x
yC
x
. Phương trình tiếp tuyến với đồ thị (C) và vuông góc với
đường thẳng
: 3 2 0yx
có phương trình
A.
3 2 0xy
B.
3 13 0xy
C.
3 3 0yx
D.
1
3
7
yx
Câu 12 : Cho hàm số :
()y f x C
. Gọi (d) là tiếp tuyến với (C) và cắt Ox, Oy lần lượt tại 2
điểm A, B sao cho tam giác OAB cân tại O thì hệ số góc của (d) lúc này là
A.
1k
B.
1k 
C.
0k
55
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
D.
1k 
Câu 13 : Cho hàm số :
()y f x C
. Gọi (d) là tiếp tuyến với (C) và cắt Ox, Oy lần lượt tại 2
điểm A, B sao cho OB = 4OA thì hệ số góc của (d) lúc này là
A.
4k
B.
1
4
k 
C.
4k 
D.
4k 
Câu 14 : Cho hàm số :
2x 1
()
x1
y f x C

. Gọi (d) là tiếp tuyến với (C) và cắt Ox, Oy lần lượt
tại 2 điểm A, B sao cho tam giác OA = 4OB thì hệ số góc của (d) lúc này là
A.
4k
B.
1
4
k 
C.
4k 
D.
1
4
k 
Câu 15 : Cho hàm số :
()y f x C
. Gọi (d) là tiếp tuyến với (C) và cắt Ox, Oy lần lượt tại 2
điểm A, B sao cho tam giác OA = k.OB
0k
thì phương trình (d) không thể là :
A.
2y kx
B.
4y kx
C.
y kx
D.
2
k
y x k
Câu 16 : Xác định hệ số góc của d biết d làtiếp tuyến của đồ thị hàm số
2
1
x
y
x
và d cắt hai trục
Ox, Oy lần lượt tại các điểm A, B phân biệt thỏa mãn điều kiệu OB = 3OA.
A. 0 B. 3
C.
2
D.
3
Câu 17 : Có bao nhiêu đường thẳng d thỏa mãn d là tiếp tuyến của đồ thị hàm số
2
1
x
y
x
và d
cắt hai trục Ox, Oy lần lượt tại các điểm A, B phân biệt sao cho OB = 3OA.
A. 0 B. 3
C. 2 D. 1
Câu 18 : Viết phương trình đường thẳng của dbiết d là tiếp tuyến của đồ thị hàm số
2
1
x
y
x
và
d cắt hai trục Ox, Oy lần lượt tại các điểm A, B phân biệt , OB = 3OA.
A.
: 3 10d y x
B.
: 3 9d y x
C.
: 3 10d y x
D.
: 3 9d y x
Câu 19 : Cho đường cong (C) :
x2
x2
y f x

. Khi đó tiếp tuyến của (C) và song song với
đường phân giác của góc phần tư thứ nhất là
A.
1; 7y x y x
B.
1; 7y x y x
C.
1; 7y x y x
D.
1; 7y x y x
56
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
Câu 20 : Cho đường cong (C) :
x2
x1
y f x

. Tìm các điểm thuộc (C) sao cho tiếp tuyến tại đó
có hệ số góc
1
3
k 
A.
4;2A
B.
2;0A
C.
4;2 ; 2;0AB
D. Không tồn tại
Câu 21 : Cho đường cong (C) :
3
1y f x x
và điểm A thuộc (C) có hoành độ xA = 2. Tiếp
tuyến của (C) tại M cắt Oy tại điểm nào sau đây
A.
0;1M
B.
0;9M
C.
0; 1M
D.
0; 15M
Câu 22 : Cho đường cong (C) :
32
4y f x x x
và đường thẳng (d) :
3yx
. Có bao nhiêu
tiếp tuyến với (C) vuông góc (d)
A. 0 B. 1
C. 2 D. 3
Câu 23 : Cho hàm số :
32
3 1 ( )y x x C
. Phương trình tiếp tuyến với (C) có hệ số góc k = 9 có
phương trình
A.
94yx
hay
9 29yx
B.
94yx
hay
9 28yx
C.
97yx
hay
9 28yx
D.
92yx
hay
9 29 0yx
Câu 24 : Cho hàm số :
32
4 1 ( )y x mx C
. Phương trình tiếp tuyến với (C) tại điểm có hoành
độ x0 = 2 có hệ số góc k = 24. Giá trị m là
A. 6 B. 3
C. 8 D. 0
Câu 25 : Cho hàm số :
()y f x C
xác định trên D
có đạo hàm cấp 1 tại điểm x = 0 là k = 3.
Phương trình tiếp tuyến với đồ thị hàm số (C)
tại điểm A trên hình vẽ của đồ thị hàm số (C) là
A.
31yx
B.
32yx
C.
31yx
D.
32yx
Câu 26 : Cho hàm số
2
x
y
x
(C). Tiếp tuyến tại điểm M thuộc (C) có tung độ
1
A.
31yx
B.
22yx
-1
x
y
1
3
-2
-1
2
O
1
A
57
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
C.
31yx
D.
21yx
Câu 27 : Cho hàm số
1
2
x
y
x
(C). Tiếp tuyến tại điểm M thuộc (C) có hoành độ bằng 3
A.
3 13yx
B.
22yx
C.
31yx
D.
31yx
Câu 28 : Cho hàm số
4
2
23
4
x
yx
(C). Tiếp tuyến tại điểm M thuộc (C) có hoành độ bằng
1
A.
3 13yx
B.
17
3
4
yx
C.
17
3
4
yx
D.
31yx
Câu 29 : Cho hàm số
3
2
33
x
yx
(C). Số tiếp tuyến với (C) và vuông góc với đường thẳng
30xy
là
A. 1 B. 2
C. 3 D. 4
Câu 30 : Cho hàm số
32
32y x x
(C). Hệ số góc tiếp tuyến với (C) tại điểm có hoành độ x = - 3
là
A. 12 B. 21
C. 45 D. 54
Câu 31 : Cho hàm số
32
32y x x
(C). Trong tất cả các tiếp tuyến với (C) tại điểm M thuộc (C)
thì tiếp tuyến có hệ số góc nhỏ nhất là
A. - 3 B. 3
C. 4 D. - 4
Câu 32 : Cho hàm số
3
31y x x
(C). Số tiếp tuyến với (C) và vuông góc với đường thẳng
9 15 0xy
là
A. 1 B. 2
C. 3 D. 4
Câu 33 : Cho hàm số :
4
2
9
2
44
x
y f x x C
. Gọi M là giao điểm của (C) và trục hoành có
hoành độ dương. Hệ số góc tiếp tuyến tại M là
A.
15
B.
15
C.
9
4
D.
9
4
Câu 34 : Cho hàm số
42
1 ( )y x mx m C
. Với mọi giá trị của tham số m thì ta nhận thấy đồ
thị (C) luôn đi qua một điểm K(1;0) cố định . Khi đó tiếp tuyến tại K song song với đường thẳng
2yx
ứng với giá trị
58
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
A.
0m
B.
3m
C.
1m
D.
1m 
Câu 35 : Cho hàm số
32
3y x x
(C). Tiếp tuyến với (C) và vuông góc với đường thẳng
1
9
yx
tại các tiếp điểm
A. (-1; 4), (3;0) B. (-1; 4), (2;0)
C. (-1; 3), (2;0) D. (0; 4), (2;0)
Câu 36 : Gọi điểm M thuộc đồ thị hàm số
21
()
1
x
y f x C
x

có hoành độ x0 không âm và x0 là
nghiệm của phương trình
0
4. ' 3 0fx
thì phương trình tiếp tuyến tại M là :
A.
3 23
44
yx
B.
3
1
4
yx
C.
1yx
D.
1yx
Câu 37 : Cho hàm số
32
32y f x x x x
có đồ thị là (C). Phương trình tiếp tuyến tại điểm
I(x0;y0) thuộc (C) thỏa mãn
0
'' 0fx
là
A.
yx
B.
1yx
C.
1yx
D.
yx
Câu 38 : Cho hàm số
32
32y f x x x x
có đồ thị là (C). Phương trình tiếp tuyến tại điểm có
hoành độ bằng -1 là
A.
11 2yx
B.
11 3yx
C.
4yx
D.
11 5yx
Câu 39 : Cho hàm số
32
32y f x x x x
có đồ thị là (C). Phương trình tiếp tuyến tại điểm có
tung độ bằng 6 là
A.
11 12yx
B.
11 3yx
C.
11 4yx
D.
11 27yx
Câu 40 : Cho hàm số
32
32y f x x x x
có đồ thị là (C). Trong các phương trình tiếp tuyến
tại giao điểm (C) và trục hoành thì ∆ là tiếp tuyến có hệ số góc nhỏ nhất. Phương trình ∆ là
A.
24yx
B.
1yx
C.
4yx
D.
2yx
Câu 41 : Cho hàm số
3
2
2
3
x
y f x x x
có đồ thị là (C). Trong các phương trình tiếp tuyến
với (C) thì ∆ là tiếp tuyến có hệ số góc nhỏ nhất. Phương trình ∆ là
A.
4
2
x
y
59
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
B.
7
2 12
x
y
C.
4yx
D.
2yx
Câu 42 : Cho hàm số
2
2
2.y f x x x
có đồ thị là (C). Hệ số góc tiếp tuyến tại gốc tọa độ O
là.
A. 0 B.
1
C.
2
D.
3
Câu 43 : Cho hàm số
2
2
2.y f x x x
có đồ thị là (C). Hệ số góc tiếp tuyến tại điểm có
hoành độ x = 3 là.
A.
20
B.
22
C.
24
D.
26
Câu 44 : Cho hàm số
2
2
2.y f x x x
có đồ thị là (C). Hệ số góc tiếp tuyến tại điểm có
hoành độ x = 4/3 là.
A.
4
3
B.
0
C.
32
27
D.
15
17
Câu 45 : Cho hàm số
2
2
2.y f x x x
có đồ thị là (C). Hệ số góc tiếp tuyến tại điểm có
hoành độ x = 2 là.
A.
4
3
B.
0
C.
32
27
D.
15
17
Câu 46 : Cho hàm số
1
1
x
y f x
x

có đồ thị là (C). Hệ số góc tiếp tuyến tại điểm có hoành độ
x = 2 là.
A.
1
B.
0
C.
3
D.
2
Câu 47 : Cho hàm số
1
2
mx
y f x
xm


có đồ thị là (C). Với giá trị nào của tham số m thì tiếp
tuyến với (C) tại điểm có hoành độ x = 1 vuông góc với đường phân giác của góc phần tư thứ
nhất.
A.
0
B.
2
C. Cả A và B đều đúng
D. Cả A và B đều sai
60
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
Câu 48 : Cho hàm số
3
2
1
3 2 3
xm
y f x x
có đồ thị là (C). Với giá trị nào của tham số m thì
tiếp tuyến với (C) tại điểm có hoành độ x = -1 song song với đường thẳng y = 5x
A.
0
B.
2
C.
4
D.
6
Câu 49 : Cho hàm số
y f x
có đồ thị là (C) như hình 1.
Hệ số góc tiếp tuyến tại điểm A là
A.
0
B.
2
C.
4
D.
6
Câu 50 : Cho hàm số sau (C) :
3
2
2 3 5
3
x
y x x
. Tiếp
truyến tại điểm cực tiểu của đồ thị hàm số
A. Song song với đường thẳng x = 1
B. Có hệ số góc là dương
C. Có hệ số góc là 1
D. Vuông góc với Oy
Câu 51 : Cho đồ thị hàm số
32
22y x x x
(C) . Gọi
12
,xx
là hoành độ các điểm M, N trên (C),
mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng
2017yx
. Khi đó
12
xx
A.
4
3
B.
4
3
C.
1
3
D.
1
Câu 52 : Cho đồ thị hàm số
32
32y f x x x
(C). Gọi
12
,xx
là hoành độ các điểm A, B trên
(C), mà tại đó tiếp tuyến của (C) có hệ số góc là – 3.
Khi đó
22
12
xx
A.
5
B.
1
C.
2
D.
3
Câu 53 : Cho đồ thị hàm số
32
32y f x x x
(C). Gọi
12
,xx
là hoành độ các điểm H, I trên
(C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng
1
2017
24
yx
. Khi đó
33
12
xx
A.
55
B.
56
C.
57
D.
58
Câu 54 : Cho đồ thị hàm số
21
1
x
y f x
x

(C).
61
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
Gọi
12
,xx
là hoành độ các điểm H, F trên (C), mà tại đó tiếp tuyến của (C) song song với đường
thẳng
1 13
37
yx
. Khi đó
2
12
xx
A.
7
B.
2
C.
20
D.
4
Câu 55 : Cho đồ thị hàm số
3
31y f x x x
(C). Gọi
12
,xx
là hoành độ các điểm E, F trên
(C), mà tại đó tiếp tuyến của (C) song song với đường thẳng
94yx
. Khi đó
33
12
xx
A.
0
B.
56
C.
5
D.
5
Câu 56 : Cho đồ thị hàm số
1
x
y
x
(C). Gọi
12
,xx
là hoành độ các điểm A, B trên (C), mà tại đó
tiếp tuyến của (C) có hệ số góc là – 1. Khi đó
33
12
xx
A.
8
B.
6
C.
5
D.
5
Câu 57 : Cho đồ thị hàm số
1
x
y
x
(C). Gọi
12
,yy
là tung độ các điểm A, B trên (C), mà tại đó
tiếp tuyến của (C) có hệ số góc là – 1. Khi đó
33
12
yy
A.
8
B.
6
C.
5
D.
5
Câu 58 : Cho hàm số
32
31y x x
(1). Hệ số góc tiếp tuyến k của đồ thị (C) tại điểm thuộc
(C) có hoành độ bằng 1 có giá trị đối là
A.
3
B.
3
C.
1
3
D.
1
3
Câu 59 : Cho hàm số
32
2 3( 1) 6 (1)y x m x mx
, với m là tham số thực. Với giá trị nào của tham
số m thì đồ thị hàm số (1) có hai điểm cực trị A và B sao cho đường thẳng AB vuông góc với
đường thẳng y = x + 2
A.
0m
B.
2m
C. Cả A và B đều sai D. Cả A và B đều đúng
Câu 60 : Cho hàm số
21
1
x
y
x
có đồ thị là (C). Gọi M là điểm thuộc (C) có tung độ bằng 5. Tiếp
tuyến của (C) tại M cắt các trục tọa độ Ox và Oy lần lượt tại A và B thì diện tích tam giác OAB là
A.
3
B.
121
6
C.
2
3
D.
12
7
62
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
Câu 61 : Cho hàm số
42
1y x mx m
có đồ thị là (C) với m là tham số. Gọi A là điểm thuộc
(C) có hoành độ là 1. Tiếp tuyến của (C) tại A có hệ số góc là 2 ứng với giá trị m bằng
A.
3
B.
1
C.
2
D.
0
Câu 62 : Cho hàm số
21
1
x
y
x
có đồ thị là (C). Gọi M là điểm thuộc (C) có hoành độ bằng 0. Gọi
d là tiếp tuyến với (C) tại M. Chọn đáp án đúng
A. Đường thẳng d vuông góc với IM
B. Đường thẳng d song song với IM
C. A và B đều sai
D. A đúng - B sai
Câu 63 : Cho hàm số
3
21
x
y
x
có đồ thị là (C). Gọi M là điểm thuộc (C) mà tại đó tiếp tuyến
với đồ thị (C) cắt Ox, Oy lần lượt tại A và B sao cho đường trung trực của AB đi qua gốc O.
Phương trình tiếp tuyến tại M là
A.
3
2
yx
B.
4
5
yx
C. A đúng, B sai D. A và B đều đúng
Câu 64 : Cho hàm số
2
2
x
y
x
có đồ thị là (C). Gọi M là điểm thuộc (C) mà tại đó tiếp tuyến với
đồ thị (C) cắt Ox, Oy lần lượt tại A và B sao
2AB OA
Khi đó hệ số góc tiếp tuyến tại M là :
A.
1
B.
1
C. A đúng, B sai D. A sai, B đúng
Câu 65 : Cho hàm số
21
1
x
y
x
(C). Tiếp tuyến với đồ thị (C) cắt Ox, Oy lần lượt tại A và B sao
cho OA = 4OB có phương trình là :
A.
15
44
yx
B.
1 13
44
yx
C. A, B đều sai D. A, B đều đúng.
Câu 66 : Cho hàm số
32
2 3 1y x x
có đồ thị
C
. Điểm trên
C
có hệ số góc tiếp tuyến tại đó
nhỏ nhất là
A.
0;1
. B.
1;0
. C.
1
;0
2



. D.
11
;
22



.
Câu 67 : Cho đường cong (C) :
32
3 3 1y x x x
. Phương trình tiếp tuyến của (C) tại giao điểm
của (C) và Oy là
A.
81yx
B.
31yx
63
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN
2017
C.
81yx
D.
31yx
Câu 68 : Cho đường cong (C) :
42
21y x x
. Phương trình tiếp tuyến của (C) tại điểm cực đại
là
A.
1y
B.
31yx
C.
2y
D.
1yx
Câu 69 : Cho đường cong (C) :
1
1
x
y f x
x

. Tiếp tuyến với đường cong (C) tại điểm M
thuộc (C) có hoành độ xM = 2 chắn trên hai trục tọa độ một tam giác có diện tích bằng
A.
49
2
(đvdt) B.
9
4
(đvdt)
C.
1
2
(đvdt) D.
49
4
(đvdt)
Câu 70 : Cho hàm số :
3
2
31
3 ( )
2 4 2
x
y x x C
. Phương trình tiếp tuyến với đồ thị (C) và vuông
góc với đường thẳng
8
:1
27
yx
có phương trình
A.
27 9
8 16
yx
B.
27 9
8 17
yx
C.
8
3
27
yx
D.
1
8 27
2
yx
Câu 71 : Cho hàm số
3
2
2x
y x 4x 2
3
, gọi đồ thị của hàm số là (C). Viết phương trình tiếp
tuyến của (C) có hệ số góc lớn nhất
A.
9 25
yx
2 12

B.
9
17
yx
C.
2
3
9
yx
D.
1
29
2
yx
Câu 72 : Phương trình tiếp tuyến với đồ thị :
2
1
x
y
x
và có hệ số góc của tiếp tuyến bằng
2.
A.
25
y 2x
12
B.
28yx
C.
2yx
D. Cả B và C
Câu 73 : Phương trình tiếp tuyến với đồ thị :
2
1
x
y
x
và vuông góc với đường thẳng
(
): 9x
2y +1=0 có phương trình
A.
2 25
yx
9 12
B.
24
99
yx
C.
2 32
99
yx
D. Cả B và C
64
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
☺ Lý Thuyết : 
()y f x
 th 
()y g x
 th 
 th  m
(*)
s nghim csố giao điểm c th 
Phương pháp chi tiết : Cho
y f x
1
C

y g x
2
C
.
 m ca
1
C

2
C

♥ Bước 1:   m ca
1
C

2
C
m c

f x g x
.
*

*
c g m ca
1
C

2
C
.
♥ Bước 2: m. Nu
0
x
 
00
;x f x
(hoc
00
;x g x

mm ca
1
C

2
C
.
☻Chú ý:  git hay s dVi-ét đảo:
Nếu
1
x
,
2
x
 m cc hai
2
0ax bx c
(
0a
)
thì
12
b
xx
a

12
.
c
xx
a

☻Nhận xét:
 th  m
 m.
+ S m c th  bng s nghim c m.
☻Chú ý : s không l| nghiệm c
g( ) 0

Ví dụ 01 : Cho
32
25y x x x
1
C

7yx
2
C
  m ca hai
 th
1
C

2
C
.
65
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
♠ Giải : phương trình hoành độ giao điểm ca
1
C

2
C
:
32
2 5 7x x x x
2
1 3 5 0x x x
1
3 29
2
3 29
2
x
x
x


( lƣu ý : thay tọa độ x v|o (C2) :
7yx
)
V th ba giao điểm:
1
1;7M
,
2
3 29 21 7 29
;
22
M




,
3
3 29 21 7 29
;
22
M




.
Ví dụ 02 : Cho
3
42y x mx
1
C

2
34y x m
2
C
.
Bin lun s m ca
1
C

2
C
.
♠ Giải :  m ca
1
C

2
C
32
4 2 3 4x mx x m
1
2
( 1)( 2 4 2) 0x x x m
2
1
2 4 2 0 2 ; ' 4 3
x
x x m m
.
S m ca
1
C

2
C
bng s nghim c
1
.
Do đó :
♥ Vi :
3
0
4
m
:
2
m
1
m duy nht (
1x
)
1
C

2
C
m.
♥ Vi :
3
0
4
m
:
2
tr 
2
2
2 1 0 1 0 1x x x x
.
ng h
1
m duy nht (
1x
)
1
C

2
C
t giao
m.
66
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
♥ Vi :
3
0
4
m
:
2
t. Ta thy
1 4 3 0tm
3
4
m
1
m ca
2
1
t
1
C

2
C
m.
Kết luận:
3
4
m 
:
1
C

2
C
có một giao điểm.
3
4
m 
:
1
C

2
C
có ba giao điểm.
Ví dụ 03 (Trích đề thi ĐH Khối A - 2010 : 
32
21y x x m x m
C

m

C
ct tri
3
 
1
x
,
2
x
,
3
x
sao cho
222
1 2 3
4xxx
♠ Giải :  m c th
C
c vi tr
0y
):
32
2 1 0x x m x m
1
2
10x x x m
3
2
()
1
0
tx
xx
x x m

C
ct trt
1
t
tx

1
0
10t

1 4 0
0
m
m


1
4
0
m
m
.(*) Vi-ét
12
12
1
b
xx
a
c
x x m
a
.

2
222
1 2 3 1 2 1 2
2 2 21x x x x x x x m
;
222
1 2 3
4 2 2 4 1x x x m m
(thỏa mãn điều kiện (*))
Vậy  th  ct tri
3

1
x
,
2
x
,
3
x
sao cho
222
1 2 3
4xxx
 khi
1
1
4
m
,
0m
.
Ví dụ 04 : 
3
1
x
y
x
C
.Chng minh rng vi m ca
m
ng thng
2y x m
t
C
tt
M

N
nh
m
 
MN

nht.
♠ Giải :  m ca
C
ng thng
2y x m
:
67
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
3
2 ; 1
1
x
x m x
x
3 1 2x x x m
(vì
1x 
không là nghiệm của phương trình)
2
2 1 3 0x m x m
*

22
2
1 8 3 6 25 3 16 0,m m m m m m
Vng thng
2y x m
t
C
tt
M

N
.

M

N
m chung cng th
C
i
11
;2M x x m
,
22
;2N x x m
trong

12
, xx
m c
*
.
-
12
1
2
m
xx

12
3
2
m
xx
.

22
2 1 2 1
4MN x x x x
22
2 1 2 1 1 2
5 5 4x x x x x x


2
1
5 2 3
2
m
m







2
5
3 20 2 5.
4
m
Du
'' ''
x khi
3m
.
Vy
3m

MN
  nht bng
25
.
Khi gp h|m số bậc 1/1 giao vng thng y = kx + r
Ta xét nhanh phương trình hoành độ giao điểm tính đƣợc ∆ = b
2
– 4ac
m t thầy Cƣờng (H| Nội) ng minh li !
Cách giải trên quá hay !
Nhưng để làm tự luận thôi
Khi làm trắc nghiệm chắc em chết
Thì giải cách khác thôi
Bình tĩnh !!!!!
68
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
2
2
1
.
k
AB
a

k  sng thng y = kx + r
a   ax
2
+ bx + c = 0
Vy ABmin khi ∆min
Hay ta s 
2
min min
2
1
.
k
AB
a

Vô l|m liền !!
♠ Ta đi từ chỗ n|y :  m ca
C
ng thng
2y x m
:
x3
2x m; x 1
x1
x 3 x 1 2x m
2
2x m 1 x m 3 0
*

2
2
2
m 1 8 m 3 m 6m 25
m 3 16 16 0, m
∆
min
= 16 khi m = 3
Khi đó ta
LIỆT KÊ CÁC CON SỐ VI DIỆU
Suy ra
22
min min
22
1 2 1
. .16 2 5
2
k
MN
a

Chú ý em
này nha!
Hệ số a = 2
∆
min
= 16
k = 2
Gi{o viên cần file word hoặc học sinh cần file đ{p
{n xin vui lòng liên hệ trực tiếp
Qua facebook/zalo/ đt : 0914449230
69
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
☻ Ứng dụng 1: 
2
2
x
y f x
x

 th  ng thng (d) : y = x
+ m ct (C) t n AB ngn nht.
♠ Ta đi từ chỗ n|y :
 
2
2
x
xm
x


2
4 2 0x m x m

2
2
4 8 16 16 0, m m m m
∆
min
= 16 khi m = 0
Khi đó ta
LIỆT KÊ CÁC CON SỐ VI DIỆU
22
min min
22
1 1 1
. .16 4 2
1
k
AB
a

☻ Ứng dụng 2 (học sinh tự l|m) : 
21
1
x
y f x
x

 th 
ng thng (d) : y = – x + m ct (C) t n AB
ngn nht.
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Đ{p số
2
min min
2
1
. 2 2
k
AB
a
Khi m = 1
☻ Ứng dụng 3 (học sinh tự l|m) : 
2x 1
x2
y f x

 th 
ng thng (d) : y = – x + m ct (C) t n AB
ngn nht.
Hệ số a = 1
∆
min
= 16
k = 1
70
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
Đ{p số
2
min min
2
1
. 2 6
k
AB
a
Khi m = 0
☻ Ứng dụng 3 (học sinh tự l|m) : 
x2
x1
y f x

 th  tham s
 ng thng (d) : y = – x + m ct (C) t n
AB ngn nh
A. m = 2 B. m = 0 C. m = 1 D. m = 4
---------------------------------------------------------------
Ví dụ 05 : 
32
31y x x
nh
m
 ng thng
1y mx
c th ti ba
t.
♠ Giải :  m cng th th 
3 2 2
2
0
3 1 1 (1) 3 0
30
x
x x mx x x x m
g x x x m
ng thng
1y mx
c th ti
3
t
t
0gx

0
0
0
0
9
9 4 0
00
4
g
m
m
m
m
g




.
Vy
9
0
4
m
 c
Ví dụ 06 : 
32
31y x x

m
 ng thng
:1d y mx
c th c
s tt.
♠ Giải :  m cng thng
d
 th 
32
3 1 1x x mx
3 2 2
2
0
3 0 3 0 .
30
x
x x mx x x x m
g x x x m
ng thng
d
c th c tt  khi p
0gx

2
nghi
0
0
9 4 0
9
0
0
4
00
g
m
m
m
g



.
71
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
Vy vi
9
0
4
m
th
Ví dụ 07 : 
2
1
x
y
x
C

m
 ng thng
:d y x m
c th
C
ti
t.
♠ Giải :  m ca
C

d

2
; 1
1
x
x m x
x
21x x m x

1x
m c
2
2 2 0. *g x x m x m
ng thng
d
ct
C
tt khi và chỉ khi 
*

nghit
2
2
0 4 0 .
2
g
m
m
m

Vy
2m 
hoc
2m
th
Lƣu ý : “vì
1x
không là nghiệm của phương trình” 
 c
hai nghit.
Ví dụ 08 : 
22
21
x
y
x
C

m
 ng thng
: 2 1d y mx m
c th
C
tt.
♠ Giải :  m ca
C

d

2 2 1
2 1 ;
2 1 2
x
mx m x
x



2 2 2 1 . 2 1x mx m x

1
2
x 
m c
2
4 4 1 0 *g x mx mx m
ng thng
d
ct
C
tt khi và chỉ khi 
*
t
0
0
' 4 0
g
m
m
m
Vy
0m
th
Ví dụ 9 : 
42
1 (1)y x mx m
. V a tham s  th  (1)
ct trt ?
A.
m
B.
1m
C.
1; \ 2m 
D.
1m
72
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
Tuy nhiên để l|m đƣợc c}u n|y ngo|i ch}m ngôn đó ra c{c em
còn phải nắm kiến thức cơ bản của h|m số n|y đã !!!
Ví dụ nhƣ b|i n|y ta phải đặt
2
0tx
  m vi Ox :
2
01t mt m
 cc ti có 4 nghiệm đối với phương trình theo x
hai nghiệm phân biệt dương đối với phương trình theo t
► Bóc đại m = 1 ca đ{p {n B ra th 
2
0 1.tt
Bu thm bng 0 !!! (bỏ qua)
► Bóc đại m = 0 < 1 ca đ{p {n D ra th 
2
0 t
Bu thm bng 0 !!! (bỏ qua)
► Bóc đại m = 3 ca đ{p {n C ra th 
2
0 3 2tt
Bu th
(không bỏ qua nữa (^.^)!) Đ{p {n C nhé
B|i 01 :  m c th
2
21
( ):
21
x
Cy
x

ng thng
( ): 1yx
A.
( 1;1)
. B.
(0;1)
. C.
( 1;2)
. D.
(2;3)
.
i :



B|i 02 :  th (C):
1
2
x
y
x
ng thng
:2d y x m
t c   d ct (C)
tt.
A.
1m 
. B.
\ 1;0m
. C.
m
. D.
10m
i :
Ch}m ngôn “sống TẠM” khi l|m b|i
trắc nghiệm l| :
◙ ĐÁP ÁN LÀ ĐỀ
◙ phƣơng ph{p BÓC ĐẠI
73
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017





B|i 03 :  th 
42
2 2 2 3y x m x m
ct trti
4
t khi
A.
3
2
m 
. B.
3
2
1
m
m


. C.
3
2
1
m
m

. D.
1m 
.
i :






B|i 04 : m ca ng thng
23yx
 th 
32
6 7 1y x x x
 a
A.
1; 1

4;5
. B.
1;0

0;4
. C.
1;1

4; 5
. D.
1;4

4;1
.
i :




B|i 05 : 
3
y x x
 th 
C
. S m ca
C
vi tr
A.
2
. B.
1
. C.
3
. D.
4
.
i :


74
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
B|i 06 : 
42
: 2 1 2 1
m
C y x m x m
. 
m

m
C
ct
Ox
t 
bit. A.
1
0
2
m
. B.
1
2
m 
. C.
0m
. D.
1m 
.
i :




B|i 07 : S m cng cong
42
10y x x
tr
A.
1
. B.
2
. C.
3
. D.
0
.
i :


B|i 08 : 
m

2y mx

32
: 3 2 C y x x

A.
9
0
4
m
B.
9
4
m
. C.
9
4
m
. D. Kt qu 
i :







B|i 09 : T m c th
5: 2d yx

32
31: xC yx

A.
0
. B.
1
. C.
2
. D.
3
.
i :
75
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017



B|i 10 : 
32
23y x x x

2
1y x x
.
A.
0
. B.
1
. C.
3
. D.
2
.
i :



B|i 11 :  ca
m
 ng thng
2y x m
cng cong
1
1
x
y
x
tm t
 A.
1m
. B.
0m
. C.
0m
. D. Mt kt qu 
i :





B|i 12 : S m chung c th h
42
41y x x
ng thng
3y 

A.
4
. B.
2
. C.
0
. D.
3
.
i :



B|i 13 : m cng thng
23yx
 th 
1
31
x
y
x

m
M

N
. Khi
 m
I
ca
MN
 bng
A.
0
. B.
5
6
. C.
2
3
. D.
1
.
i :
76
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017





B|i 14 : 
m
 ng thng
12y m x
c th 
21
1
x
y
x
tt.
A.
0m
. B.
0m
. C.
0m
hoc
3
2
m
. D.
03m
.
i :





B|i 15 : t c  thc ca
m

42
: yxC x

2
:2P y x m
ct nhau ti bn
t
A.
31m
. B.
11m
. C.
12m
. D.
1
0
4
m
.
i :





B|i 16 : T vi ng thng 
21
21
x
y
x
2yx
77
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
A. B. C. D.
i :


B|i 17 : G vi ng thng  
bng:
A. B. C. D.
i :



B|i 18 : Gm cng thng ng cong 
 m cn MN bng:
A. 1 B. 2 C. D.
i :



B|i 19 : Bi vi ng thng ct nhau tm
 n th
A. B. C. D.
i :


31
; & 1;3
22



1
;0 & 1;3
2



5
0;2 & 2;
3



5
1;1 & 2;
3



21
2
x
y
x
2yx
1AB
42AB
2AB
22
1yx
24
1
x
y
x
5
2
5
2
32
31y x x
41yx
0;1 , ,A B C
15
5 17
20
5 33
78
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
B|i 20 : Bi vi ng thng ct nhau tm
 bit .
A. B. C. D.
i :

B|i 21 : G vi ng thng  
OA: A. B. C. D.
i :



B|i 22 : Bi vi ng thng ct nhau tm .

OBC
.
A.
1
 B.
2
 C.
4
 D.
6

i :



BÀI TẬP TRẮC NGHIỆM PHẦN SỰ TƢƠNG GIAO
C}u 1 : 
32
1y f x x x
ng thng (d) :
yx
. (C)
t nhau tm ?
A.
0
B.
1
C.
2
D.
3
C}u 2 : 
21
1
x
y
x
 th m cng th
A.
2;5
B.
6;5
C.
7;5
D.
2;5
C}u 3 : 
2
3
x
y f x
x

.
3
31y x x
1yx
0;1 , ,A B C
MBC
2; 1M
4
42
8
16
2
23
1
xx
y
x

1yx
1
2
5
13
42
43y x x
3y
0;3 , ,A B C
79
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
T m M c
A.
0;2
B.
6; 2
C.
2;0
D.
2;0
C}u 4 : 
22
43
x
y f x
x

. T m N c
tr
A.
2
0;
3



B.
2
0;
3



C.
2;0
D.
2;0
C}u 5 : S m c
42
y f x x x

A.
0
B.
1
C.
2
D.
3
C}u 6 : 
32
34y x x
. T m A c
ng th
A.
1;4
3;4
A
A
B.
0;4
3;4
A
A
C.
0;4
1;4
A
A
D.
1;4
2;4
A
A
C}u 7 : 
2
2
x
y f x
x


( ): 7 10d y x


A.
55
7
AB
B.
55 2
7
AB
C.
55 2
3
AB
D.
55 3
7
AB
C}u 8 : 
2
2
2.y f x x x
 th 
S m c
2
yx

A.
0
B.
1
C.
2
D.
3
C}u 9 : ng cong (C) (hình vẽ bên)

y f x
ng thng
(d) :
2y
9.1 t nhau tm ?
A.
0
B.
1
80
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
C.
2
D.
3
9.2 T 
C}u 10 : 
2
1
x
y
x
 th 
   tng khonh.
  th  ct trm
2;0J
 m
0;2M
n
 
\2D
C}u 11 : 
21
1
x
y
x
 ng thng (d) :
y x m

  ng khonh.
 m
C. H s p tuyn t
 t (d) ti hai 
C}u 12 : 
2
x
y
x
 ng thng (d) :
1y 

  ng khonh.
 
1; 1M
 
3; 1M
 m
C}u 13 : T m c th  sau (C) :
21
21
x
y
x

y x 2
 :
A.
31
; ; N 1;3
22
M



 m
C.
1
1; ; N 1;2
2
M



D.
3
;0 ; N 1;4
2
M



C}u 14 : T m c th  sau (C) :
23
1
x
y
x


y x 3
 :
A.
0; 2 ; N 1; 2M 
 m
C.
1; 4 ; N 1;2M 
D.
0; 3 ; N 2; 1M 
C}u 15 :  sau (C) :
3
4x 3x 1y
ng thng (d) :
y m x 1 2
 tham s m
 m :
A.
0 m 9
  m th
81
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
C.
0m
D.
0m
C}u 16 :  sau (C) :
1
1
x
y
x
ng thng (d) :
y mx
 tham s  
 m :
  m th B.
0;4m
C.
m 0 4hay m
D.
0m
C}u 17 :  sau (C) :
3
y x 3x 2
ng thA(3;20)  hệ số góc m .
Tr li sau :
17.1 ng th
17.2   (C) ct (d) ti
A.
15
m 21
4

 m th
C.
15
m 24
4

D.
0m
C}u 18 :  sau (C) :
2x 1
y
x1
ng thA(–2; 2) hệ số góc  m .
Tr li sau :
18.1 ng th
18.2  t
18.3 ng bich bin c
và .....................................
18.4  th  ct trục hoành trục tung lt ti ............và ...................
18.5   (C) ct (d) t
A.
0 m 12
B.
0 m 12
C.
m 0 hay m 12
D.
m 0haym 12
C}u 19 :  sau (C) :
42
x 10x 6 3ym
 tham s  (C) ct tri 4
t  :
A.
1
0m
2

B.
1
m
2
C.
1
0m
2

D.
0m
C}u 20* :
4 2 2 4
m
(C ) : y x 2( 2) 3m x m
.  th  t Ox ti bt
1 2 3 4
, , ,x x x x
sao cho
2 2 2 2
1 2 3 4 1 2 3 4
. . . 11x x x x x x x x
ng v tham s 
A.
0m
B.
1m
C.
2m
D.
3m
C}u 21* : 
32
2( 2) (8 5 ) 5y x m x m x m
 th (Cmng thng
:1d y x m
  d ct (Cm) tt ?
82
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
A.
2
1
m
m

B.
2
2
m
m

C.
2;2m
D.
0m
C}u 22* : 
2
11y x x mx
 th (Cm). V m) ct Ox ti
t ?
A.
2
1
m
m

B.
2
2
m
m

C.
2
1
m
m

D.
0m
C}u 23 : 
32
3y x x
ng thng (d)
3 1 0yx
. Trả
lời c{c c}u hỏi sau
23.1 m c
A.
1; 2K
B.
1; 2K 
  D.
0;1K
23.2  th 
A. B.
C. D.
83
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
C}u 24* : 
21
2
x
y
x
 th ng thng
:d y x m
. V a m
t (C) tt ?
A.
m
B.
m
C.
2m 
D.
2 12m
C}u 25* : 
21
1
x
y
x
 th ng thng
:3d y x m
. V a m
t (C) tm t ?
A.
m
B.
m
C.
11
1
m
m

D.
1 11m
C}u 26 : 
21
2
x
y
x
 th ng thng
:d y x m
. V a m
t (C) t 1, x2 thu thc sau
2
1 2 1 2
44x x x x
A.
m
B.
m
C.
0m
D.
8m
C}u 27 : 
42
2 1 2 1y x m x m
 th ng thng
:1dy
. V
t (C) tt A, B
A.
m
B.
m
C.
0m
D.
0m
C}u 28 : 
1
1
x
y
x
 th m cng thng
1
:
6
d y x
 
A.
(2; 2), (1; 2)
B.
11
(2; ), (3; )
32
C.
(0; 2), (1; 2)
D.
( 1; 4), (3; 2)
C}u 29 : 
2
43
2
xx
y
x
 th m c
 
A.
(1;0), (3;0)
B.
(2;0), (3;0)
C.
(0;0), (2;0)
D.
( 1;0), (3;0)
C}u 30 : 
22
13y x x mx m
 th m). V a tham s 
 th  ct trt
A.
m
B.
22
1
m
m

84
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
C.
11
1
m
m

D.
32
1
m
m

C}u 31 : 
32
2y x x x
 th  a tham s  th 
s cng thng d : y = mx tt
A.
m
B.
02
1
m
m

C.
0
1
m
m
D.
03
1
m
m

C}u 32 : 
3
1yx
 th  a tham s  th  ct
ng thng d : y = 3x + m tt
A.
m
B.
13m
C.
13
0
m
m
D.
13
1
m
m
C}u 33 : p tuyn v th (C) c
32
6 11 1y x x x
tm ca
 ng thng y = 5
A.
0
B.
1
C.
2
D.
3
C}u 34 : 
21
1
x
y
x
. Tip tuyn c th (C) tại M(2; 5) ct trc Ox, Oy lt ti A,
B. Di
A.
121
6
OAB
S
B.
123
6
OAB
S
C.
13
6
OAB
S
D.
11
6
OAB
S
C}u 35 : 
32
2
x
y
x
 th  m ca
 nh
A. M
0;2
B. M
1;2
C. M
1; 2
D. M
2;2
C}u 36 : 
35
2
x
y
x
 th 
sai ?
5
2
K
y
 m
1; 1M 
n th  (C)
D. Minh c 
\2D
  ging khonh.
  th  ct trc tung t
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO
2017
C}u 37 : 
2
1
x
y
x
 th    th (C) cng thng d : y
= x + 2m tt
A.
m
B.
1 3 1 3m
C.
1 3 1 3
0
m
m
D.
13
13
m
m


C}u 38 : 
42
1 2 1y m x mx m
 ca tham s   th  ct trc
t
A.
m
B.
m
C.
1
1
2
2
3
m
m

D.
1
3
2
2
3
m
m
C}u 39 : 
4 2 2
2 1 3y x m x m
 ca tham s   th  
i tr
A.
3m
B.
m
C.
3m
D.
3m
C}u 40 : Nh ca
m
 ng thng
1y x m
c th 
21
1
x
y
x
tm
t
,AB
sao cho
23AB

A.
4 10m 
. B.
43m 
.
C.
23m 
. D.
2 10m 
.
C}u 41 : Bing thng
2yx
c th
21
1
x
y
x
t
ln lt
,
AB
xx
ng
AB
xx
A.
2
AB
xx
. B.
1
AB
xx
.
C.
5
AB
xx
. D.
3
AB
xx
.
C}u 42 : S m cng cong
32
2 2 1y x x x
ng thng
1yx
bng
A. 1. B. 2. C. 3. D. 0.
“Học vấn do người siêng năng đạt được, tài sản do người tinh tế sở hữu, quyền lợi do người dũng
cảm nắm giữ, thiên đường do người lương thiện xây dựng”.
Franklin (Mỹ)
Gi{o viên cần file word hoặc học sinh cần file đ{p
{n xin vui lòng liên hệ trực tiếp
Qua facebook/zalo/ đt : 0914449230
| 1/86
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Phân dạng và phương pháp giải
trắc nghiệm Toán 12 Tập 2 Đồ thị
Tiếp tuyến
Sự tương giao
BIÊN HÒA – Ngày 07 tháng 07 năm 2017
TÀI LIỆU LƯU HÀNH NỘI BỘ
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
PHẦN 5 : KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
SƠ ĐỒ CHUNG KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ. 1/ Tập x{c định 2/ Sự biến thiên
2.1 Xét chiều biến thiên của hàm số + Tính đạo hàm y’
+ Tìm các điểm mà tại đó đạo hàm y’ bằng 0 hoặc không xác định
+ Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
2.2 Tìm cực trị
2.3 Tìm các giới hạn tại vô cực ( x   )
2.4 Lập bảng biến thiên.
Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên. 3/ Đồ thị
- Giao của đồ thị với trục Oy: x=0 =>y= ? => (0;?)
- Giao của đồ thị với trục Ox: y  0  f (x)  0  x  ?  (?;0)
- Các điểm CĐ; CT nếu có.
(Chú ý:nếu nghiệm bấm máy tính được thì OK, nghiệm lẻ giải tay được thì phải giải ra- chẳng hạn phương
trình bậc 2, còn nghiệm lẻ mà không giải được thì ghi ra giấy nháp cho biết giá trị để khi vẽ cho chính xác-
không ghi trong bài- chẳng hạn hàm bậc 3)
- Lấy thêm một số điểm (nếu cần)
- Nhận xét về đặc trưng của đồ thị. Điều này sẽ cụ thể hơn khi đi vẽ từng đồ thị hàm số. D{ng điệu của
đồ thị l| d{ng điệu của bảng biến thiên.
I- SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM BẬC BA:
y = ax3 + bx2 + cx + d (a 0) .
1/ Tập x{c định. D = R 2/ Sự biến thiên
2.1 Xét chiều biến thiên của hàm số 2
+ Tính đạo hàm: y'  3ax  2bx  c 2
+ y'  0  3ax  2bx  c  0 1
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
(Bấm máy tính nếu nghiệm chẵn, giải ;
  ' nếu nghiệm lẻ - không được ghi nghiệm gần đúng)
+ Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
2.2 Tìm cực trị
2.3 Tìm các giới hạn tại vô cực ( x   )
(Hàm bậc ba và các hàm đa thức không có TCĐ và TCN.)
2.4 Lập bảng biến thiên.
Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên. 3/ Đồ thị
- Giao của đồ thị với trục Oy: x=0 =>y= d =>(0; d) 3 2
- Giao của đồ thị với trục Ox: y  0  ax +bx +cx+d  0  x  ?
- Các điểm cực đại, cực tiểu (nếu có).
(Chú ý: nếu có 2 cực trị thì nhìn bằng HÌNH CHỮ NHẬT CƠ SỞ)
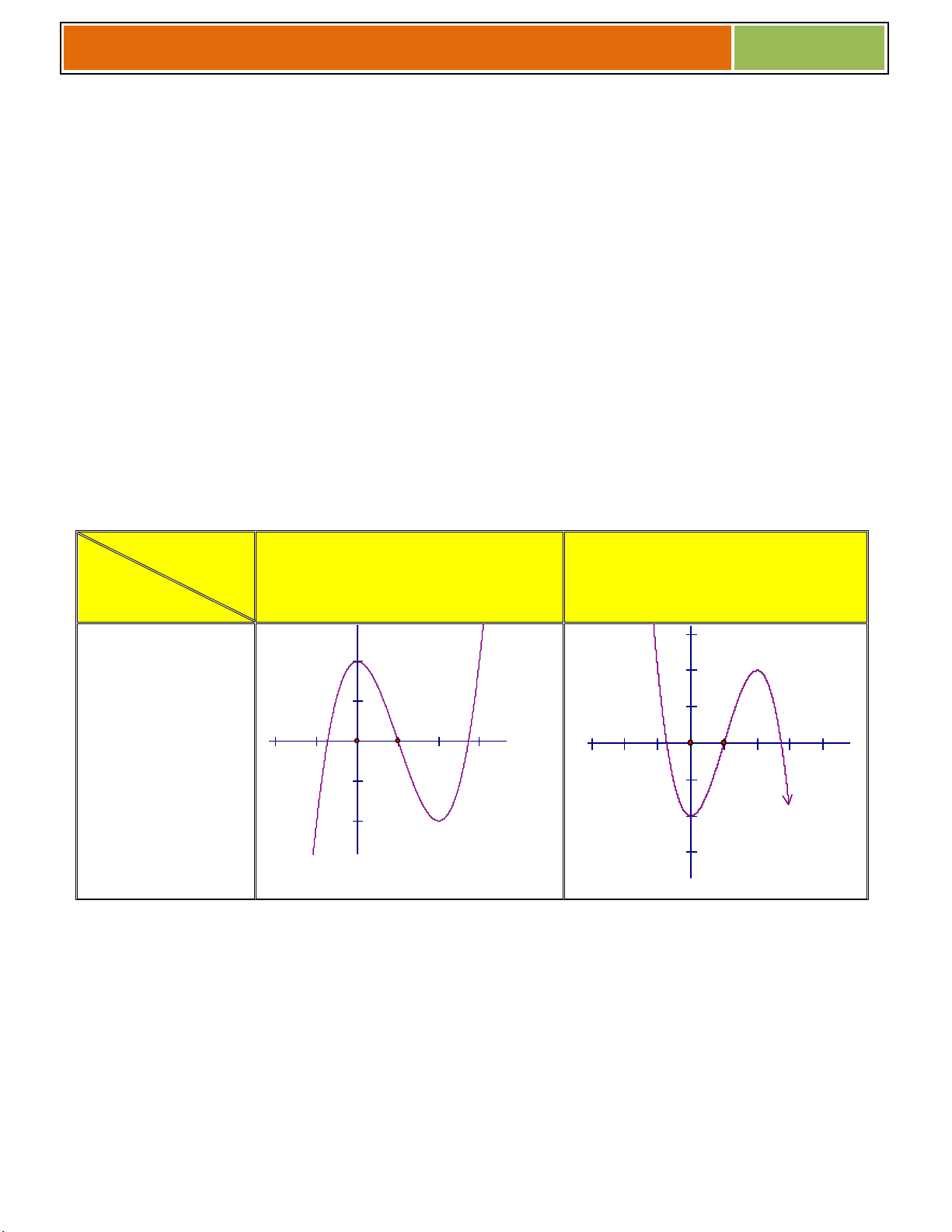
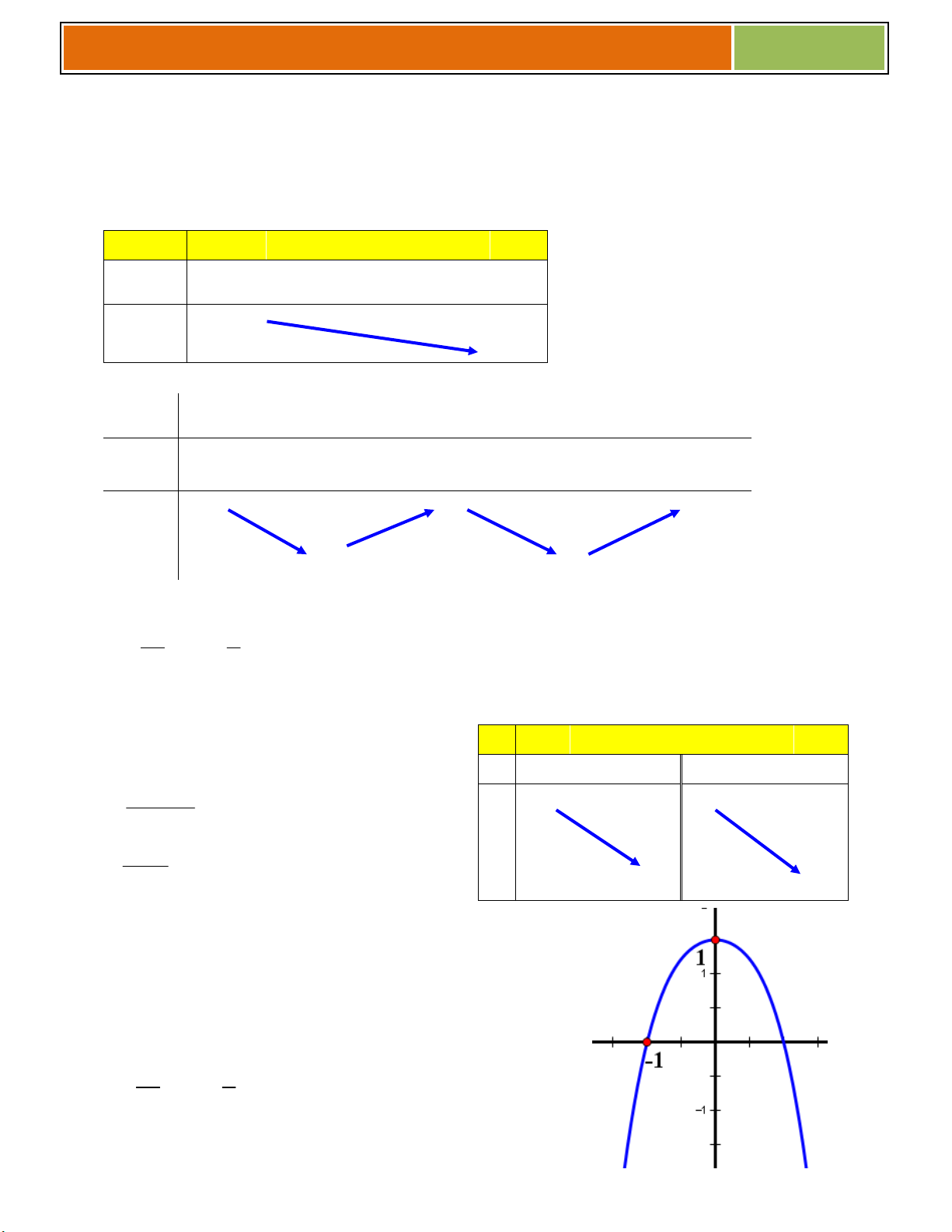
Các dạng đồ thị hàm số bậc 3:y = ax3 + bx2 + cx + d (a 0) Dấu của a a > 0 a < 0 Dấu ∆ Pt y’ = 0 có 2 2 hai nghiệm ph}n biệt O -2 -2 2
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 2 2 Pt y’ = 0 có nghiệm kép 4 2 2
Pt y’ = 0 vô nghiệm
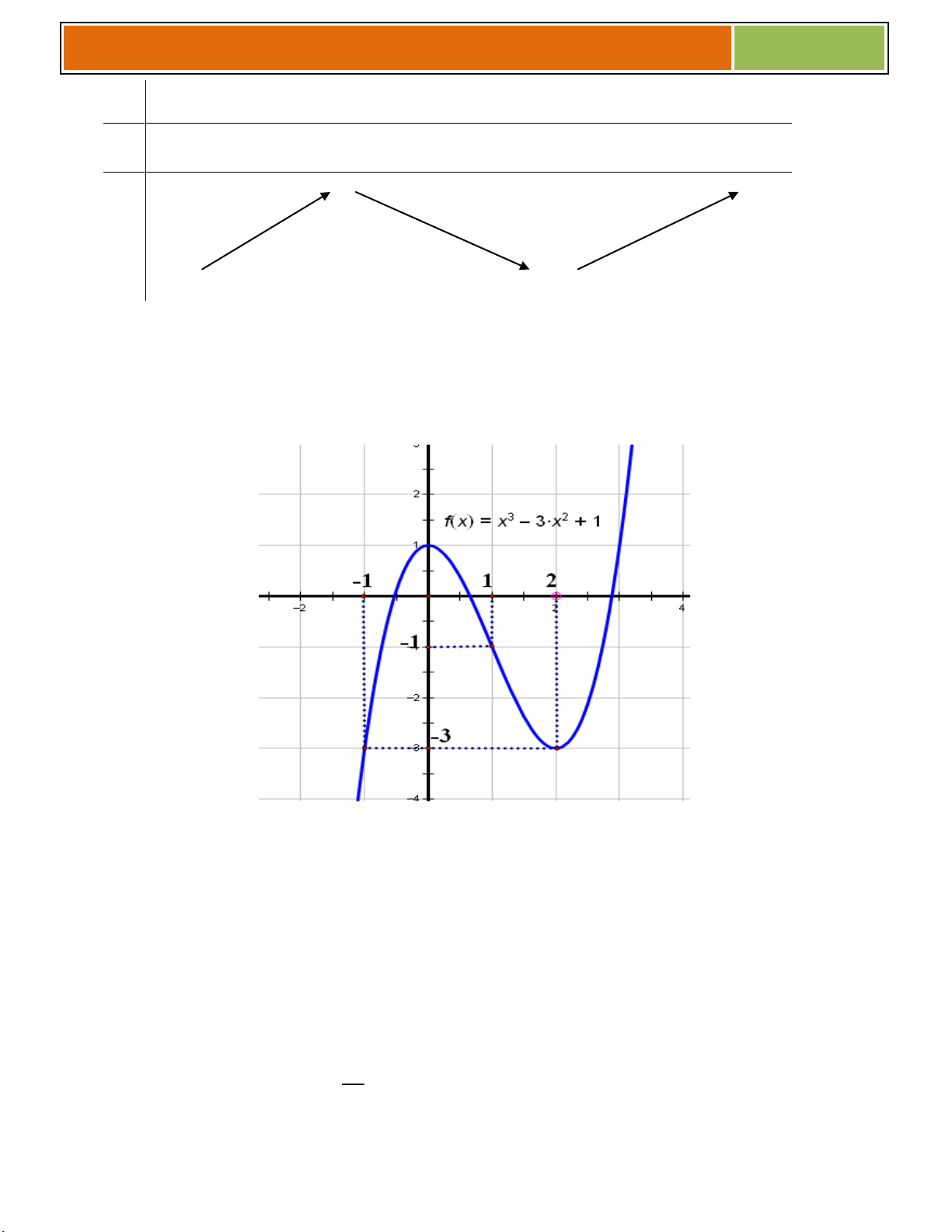
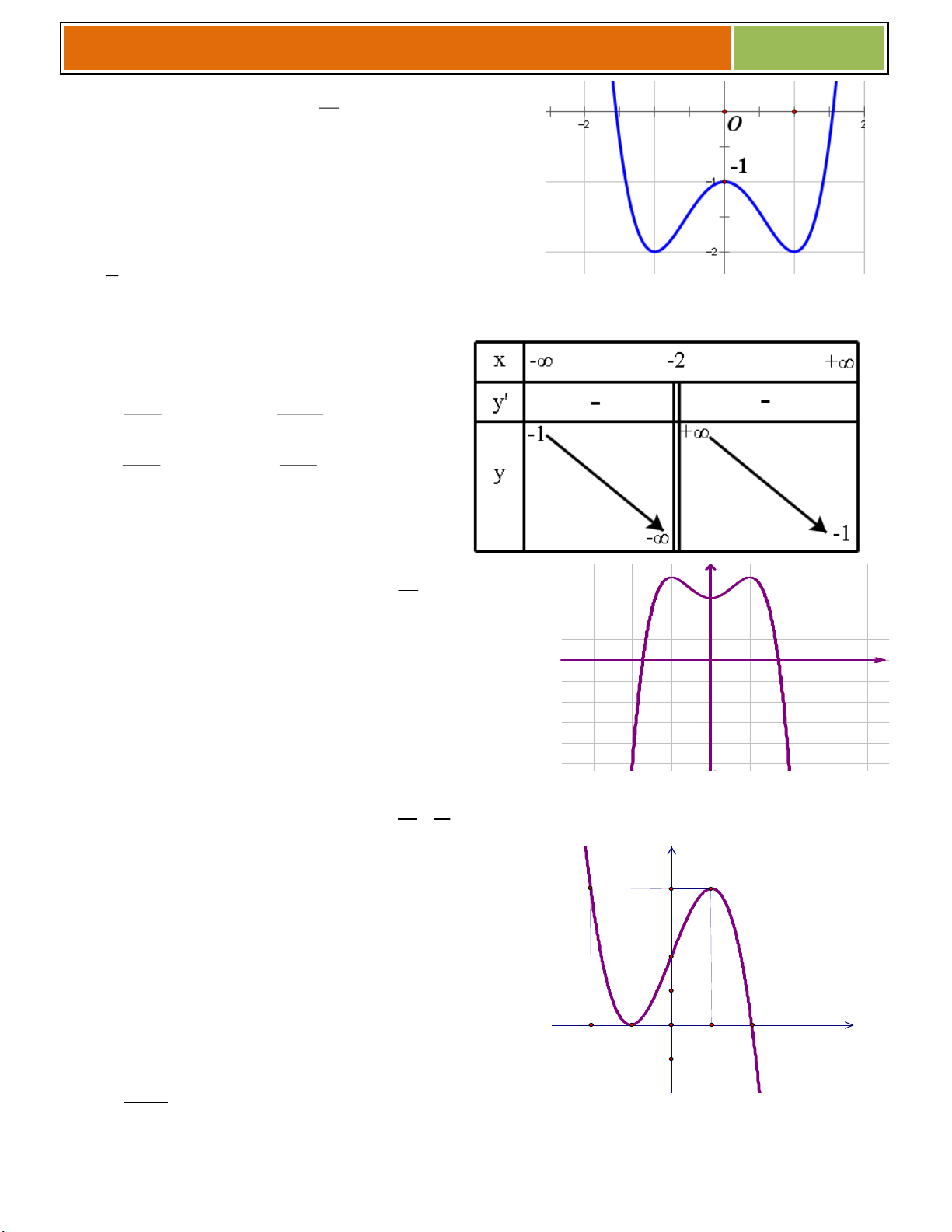
VÍ DỤ MINH HỌA : Khảo sát sự biến thiên và vẽ đồ thị hàm số 3 2
y x  3x 1. Tập x{c định:  . x  0
Sự biến thiên:Chiều biến thiên: 2
y  3x  6x ; y  0   . x  2 y  0, x   ;
 0 2;  , suy ra hàm số đồng biến trên các khoảng  ;
 0 và 2;   . y  0, x
 0; 2 , suy ra hàm số nghịch biến trên khoảng 0; 2.
Cực trị: Hàm số đạt cực đại tại x  0; y
 6 . Hàm số đạt cực tiểu tại x  2; y  2 . CD CT
+ Giới hạn: lim y   ;  lim y   . x x Bảng biến thiên 3
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
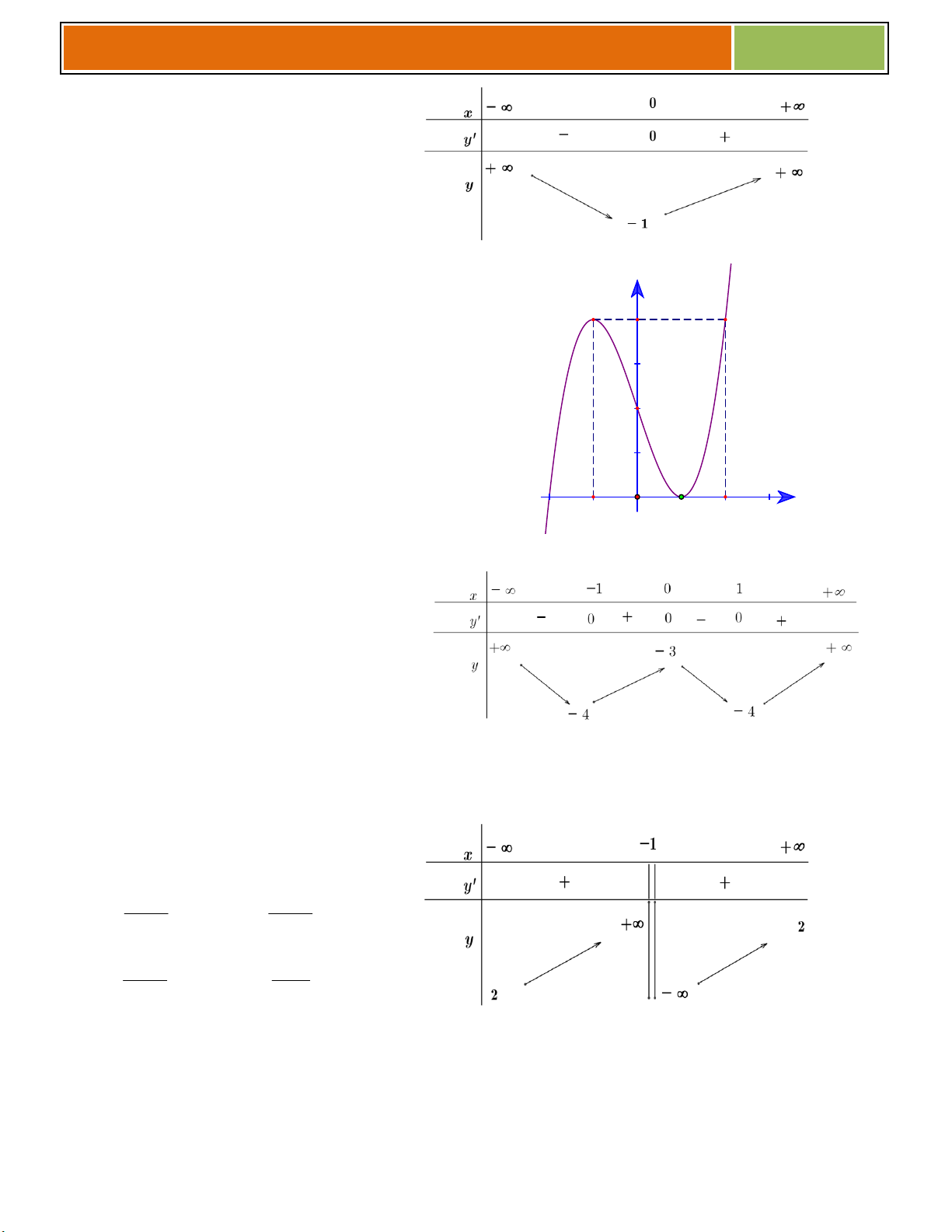
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 x  0 2  y  0  0  y 1   3  Đồ thị:
+ Đồ thị hàm số cắt trục Oy tại điểm 0;  1 .
+ Đồ thị hàm số đi qua các điểm  1  ; 3, 1;   1 , 3;  1 Vẽ đồ thị:
II - SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM TRÙNG PHƯƠNG:
y = ax4 + bx2 + c (a 0) .
1/ Tập x{c định. D=R 2/ Sự biến thiên
2.1 Xét chiều biến thiên của hàm số+ Tính đạo hàm 3 y '  4ax +2bx + Ta có: 3 2
y '  0  4ax  2bx  0  2x.(2ax  b)  0 x  0 x  0     b   ... 2 2 2ax  b  0 x   2a
+ Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số. 4
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
2.2 Tìm cực trị
2.3 Tìm các giới hạn tại vô cực ( x   ). (Hàm trùng phương không có TCĐ và TCN.)
2.4 Lập bảng biến thiên.Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.
3. Đồ thị- Giao của đồ thị với trục Oy: x=0 =>y= c => (0;c)
- Giao của đồ thị với trục Ox: 4 2
y  0  ax +bx +c  0  x  ?  (?;0)
- Các điểm CĐ; CT nếu có.
- Đồ thị của nó nhận Oy làm trục đối xứng.
(Chú ý:giải phương trình trùng phương- các bạn bấm máy tính như giải pt bậc 2 nhưng chỉ lấy
nghiệm không âm, sau đó giải để tìm ra x)
- Lấy thêm một số điểm (nếu cần)- (điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu
bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)
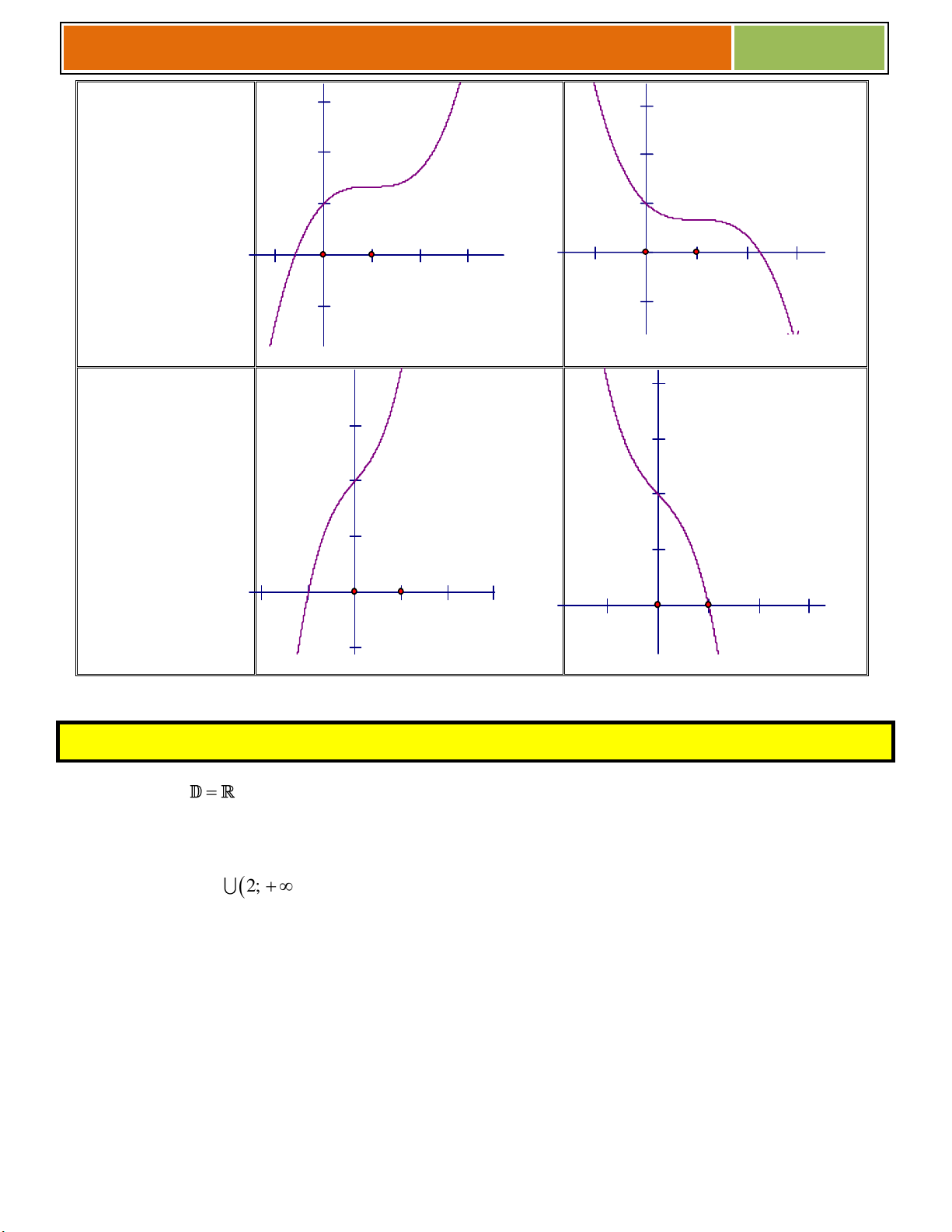
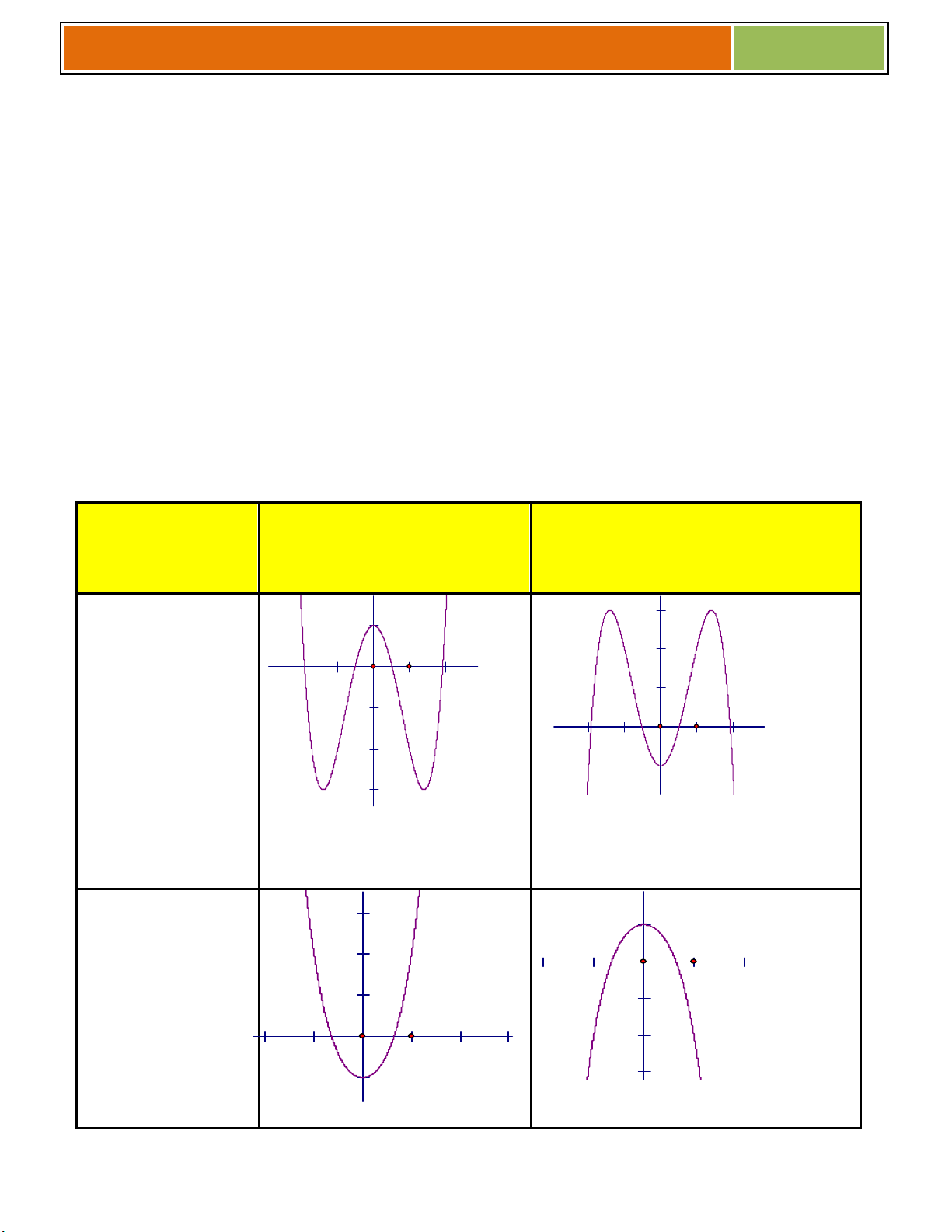
Các dạng đồ thị hàm số trùng phương:y = ax4 + bx2 + c (a 0) Dấu a a > 0 a < 0 y’=0 2 Pt y’ = 0 có ba nghiệm ph}n biệt -2 2 Pt y’ = 0 có một nghiệm -2 5
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
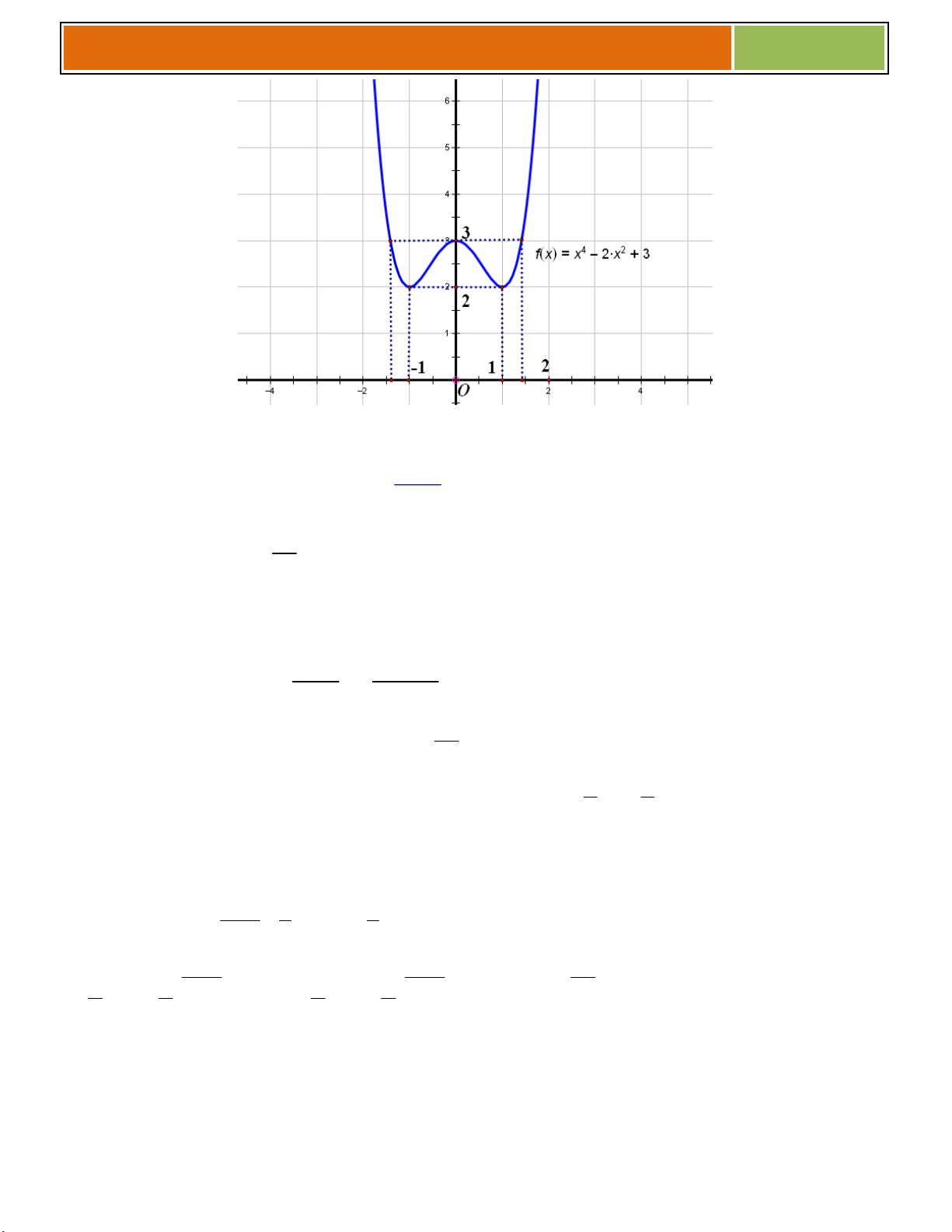
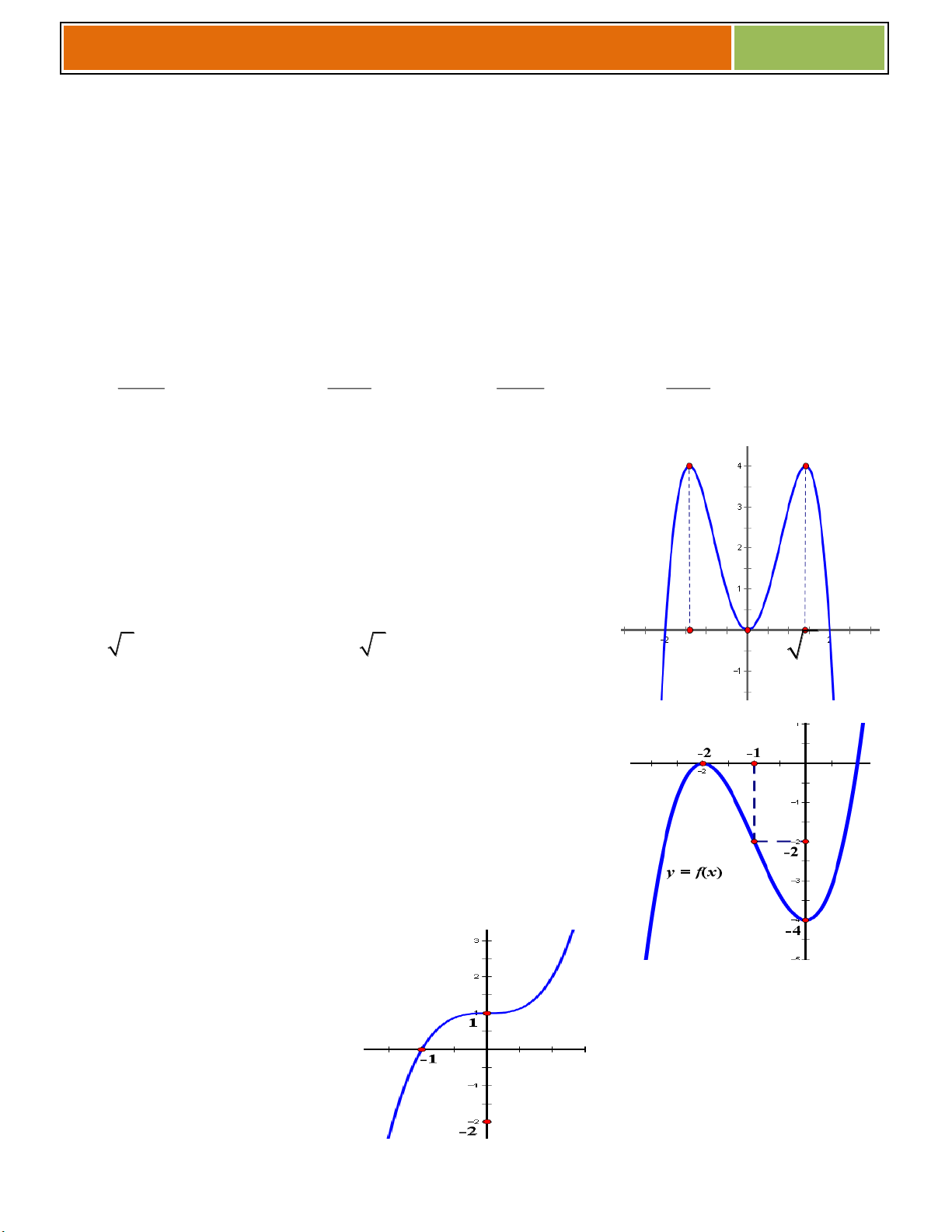
VÍ DỤ MINH HỌA : Khảo sát sự biến thiên và vẽ đồ thị hàm số 4 2
y x  2x  3 . Tập x{c đinh:  . x  0
Sự biến thiên:Chiều biến thiên: 3
y  4x  4x ; y  0   . x  1  y  0, x   1
 ; 0 1;  , suy ra hàm số đồng biến trên các khoảng  1
 ; 0 và 1;   . y  0, x   ;    1 0; 
1 , suy ra hàm số nghịch biến trên các khoảng I 3; 2 và 0;  1 .
Cực trị: Hàm số đạt cực đại tại x  0; y
 3 . Hàm số đạt cực tiểu tại x  1  ; y  2 . CD CT
Giới hạn: lim y   ;  lim y   . x x Bảng biến thiên x  0 2  y  0  0  y 1   3 
Đồ thị : + Đồ thị hàm số cắt trục Oy tại điểm 0; 3 .
+ Đồ thị hàm số đi qua điểm  2  ; 1  1 , 2; 1  1 .
+ Đồ thị hàm số nhận trục Oy làm trục đối xứng. 6
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
III - SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM NHẤT BIẾN: ax b y
(c  0, ad bc  0) cx d d
1/ Tập x{c định. D R \    c 2/ Sự biến thiên
2.1 Xét chiều biến thiên của hàm số ax b  d a  bc
+ Tính đạo hàm y '  '    2  cx d  (cx  d) d
+ y’ luôn âm (hoặc dương) với mọi x c d d
+ Hàm số đồng biến (nghịch biến) trên các khoảng ( ;   ) và ( ;) c c
2.2 Tìm cực trị: Hàm số đã cho không có cực trị
2.3 Tiệm cận: ax+b a a Ta có: lim y  lim  nên y  là tiệm cận ngang x x cx+d c c ax+b ax+b d lim y  lim
 () ; lim y  lim  () nên x
là tiệm cận đứng      dd cx+d dd cx+d c xxxxc c c c
2.4 Lập bảng biến thiên.
Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên. 3/ Đồ thị 7
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 b b
- Giao của đồ thị với trục Oy: x=0 =>y= => (0; ) d d ax  b bb
- Giao của đồ thị với trục Ox: y  0 
 0  ax b  0  x   ( ;0) cx  d a a
- Lấy thêm một số điểm (nếu cần) d a
- Nhận xét về đặc trưng của đồ thị. Đồ thị nhận điểm I (
; ) là giao hai đường tiệm cận làm c c
tâm đối xứng   ax b
Các dạng đồ thị hàm số: y
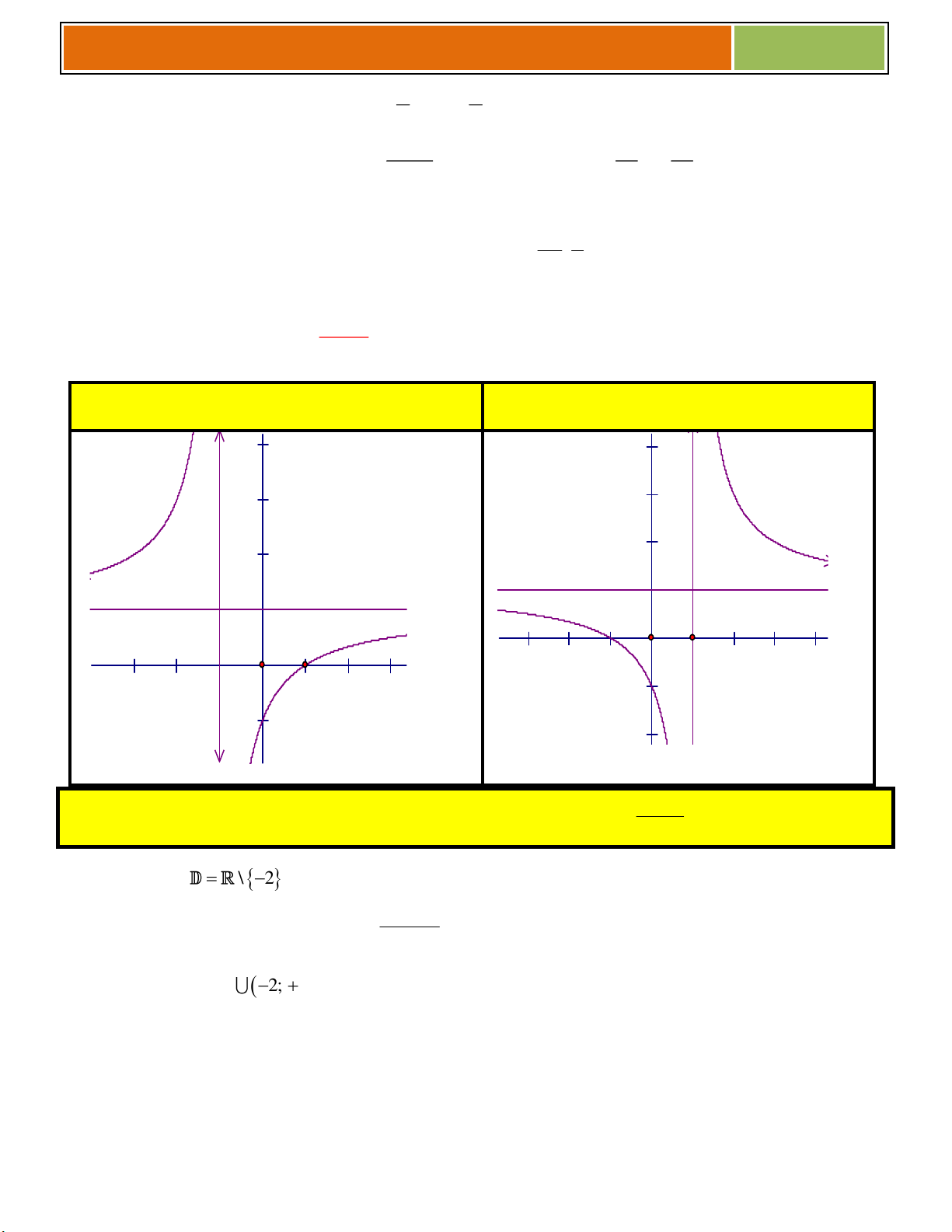
(c  0, ad bc  0) cx d D = ad – bc > 0 D = ad – bc < 0 4 4 2 2 -2 3x  2
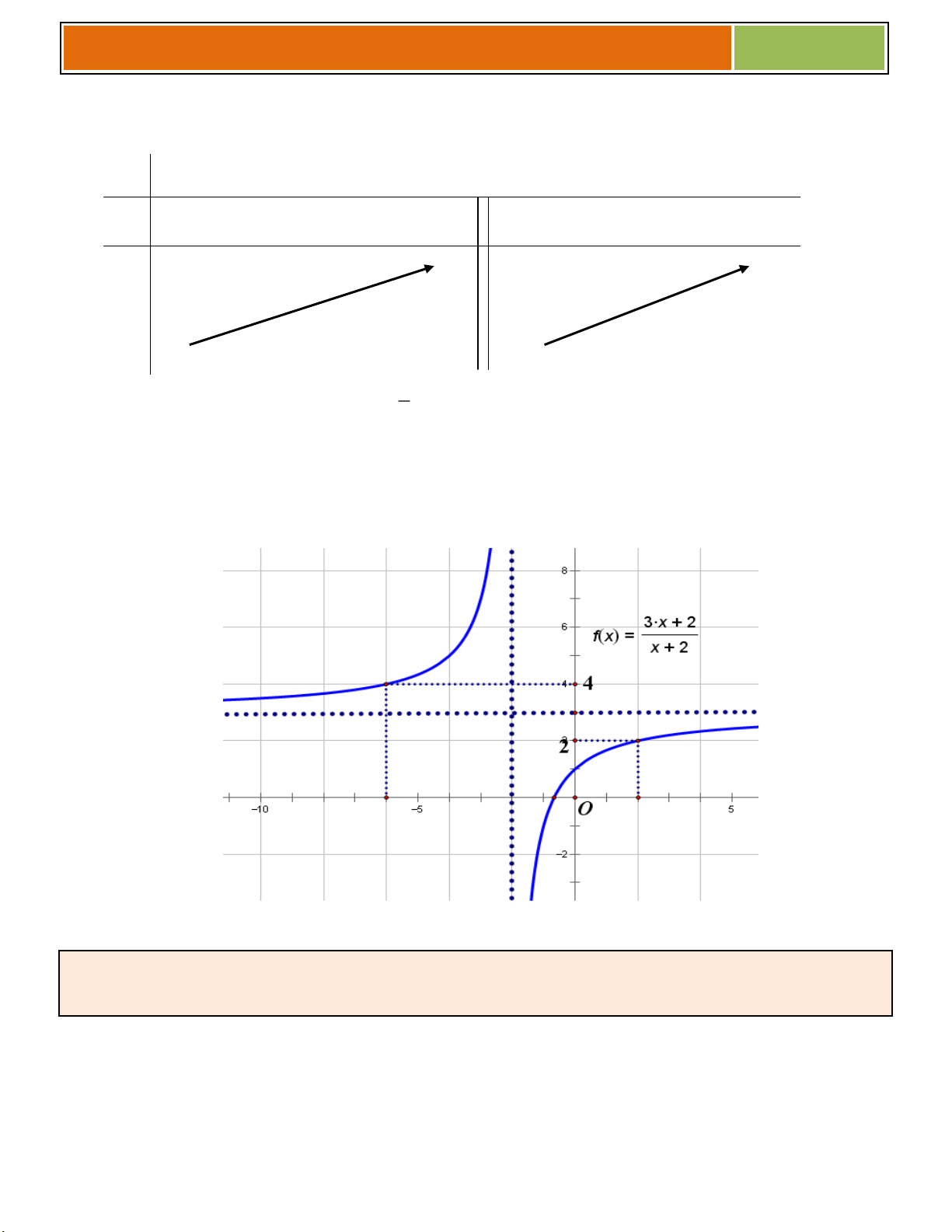
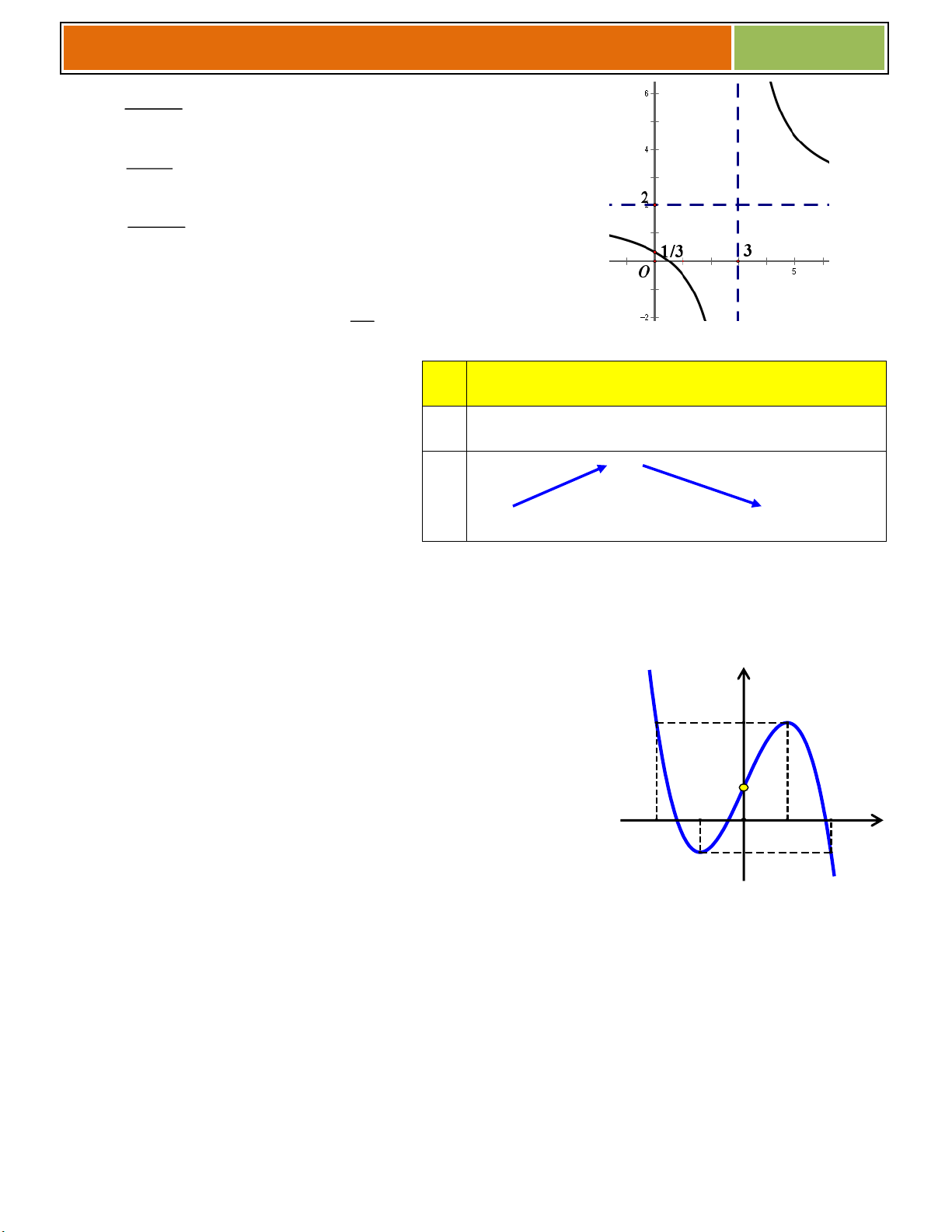
VÍ DỤ MINH HỌA : Khảo sát sự biến thiên và vẽ đồ thị hàm số y  . x  2 Tập x{c định:  \  2 . 4
Sự biến thiên: Chiều biến thiên: y   . x  22 y  0, x   ;   2  2
 ;   , suy ra hàm số đồng biến trên các khoảng  ;   2 và  2;   .
Cực trị: Hàm số không có cực trị. Giới hạn:
lim y  3; lim y  3 đồ thị hàm số nhận đường thẳng y  3 là tiệm cận ngang x x 8
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 lim y   ;
 lim y   đồ thị hàm số nhận đường thẳng x  2
 là tiệm cận đứng   x 2  x 2  Bảng biến thiên x  2   y    y  3 3   2 
+ Đồ thị hàm số cắt trục Ox tại điểm  ; 0 
 , cắt trục Oy tại điểm 0;  1 .  3 
+ Đồ thị hàm số đi qua các điểm  4  ; 5,  3  ; 7,  1  ;   1 , 2; 2 .
+ Đồ thị hàm số nhận giao điểm I  2
 ; 3 của hai tiệm cận làm tâm đối xứng.
BÀI TẬP TỰ LUẬN PHẦN HÀM SỐ
B|i 01 : Khảo sát và vẽ các đồ thị hàm số sau: a/ 3 2
y  x  3x 1 b/ 3 2
y  x  3x  4 c/ 3
y  x  3x 1 d/ 3 2
y  x  6x  9x  4. ● Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<< 9
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<< 10
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<< 11
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
B|i 02 : Khảo sát và vẽ các đồ thị hàm số sau: 2x 1 x 1 x 1 2x  2 a/ y  b/ y  c/ y  d/ y x 1 x 1 x  2 x 1 ● Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<< 12
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<< 13
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
B|i 03 : Khảo sát và vẽ các đồ thị hàm số sau: a/ 4 2
y  x  2x b/ 4 2
y x  2x 1 c/ 4 2
y x  4x 1 ● Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<< 14
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<...<..<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<.<<<<<<<<<<<<<<<<< 15
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
BÀI TẬP TRẮC NGHIỆM PHẦN ĐỒ THỊ HÀM SỐ
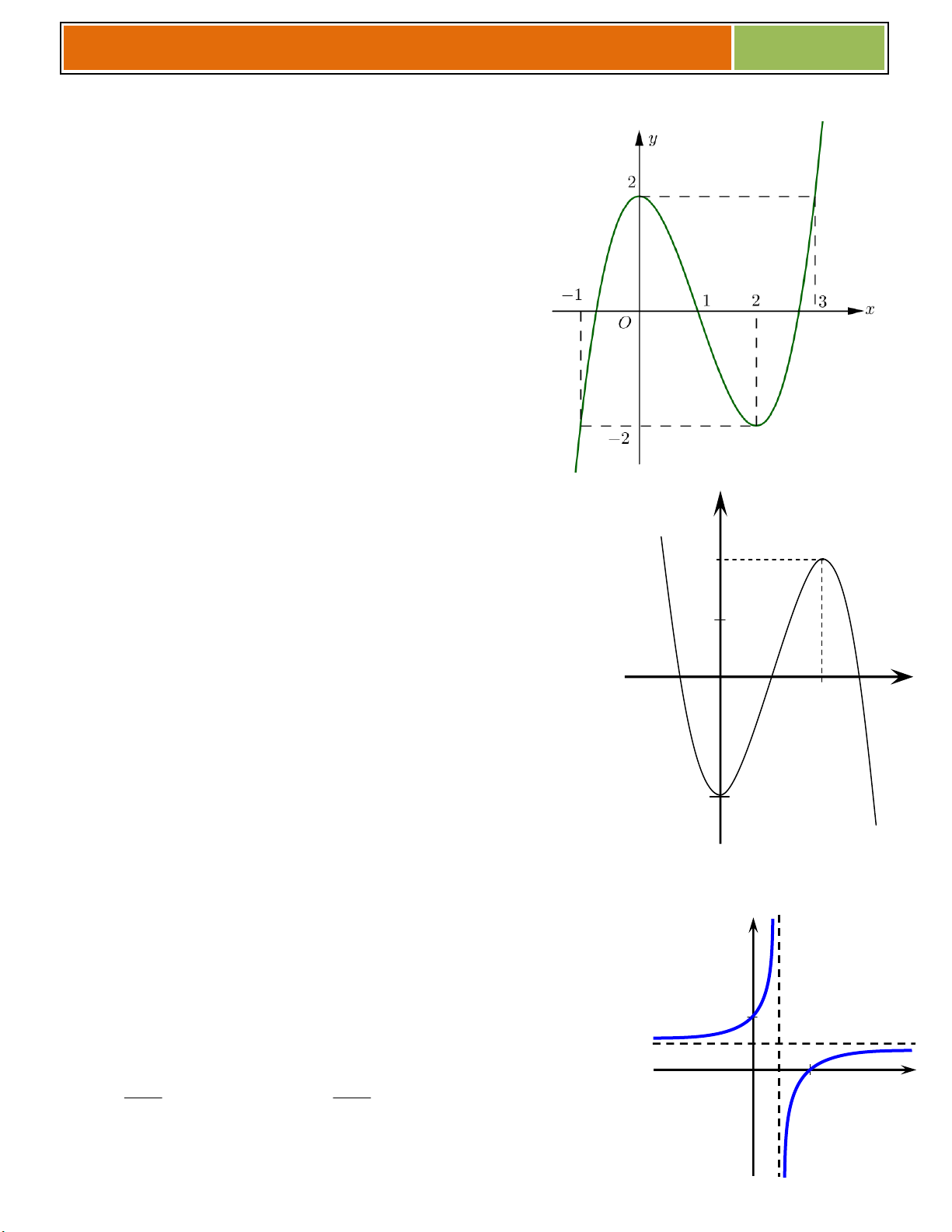
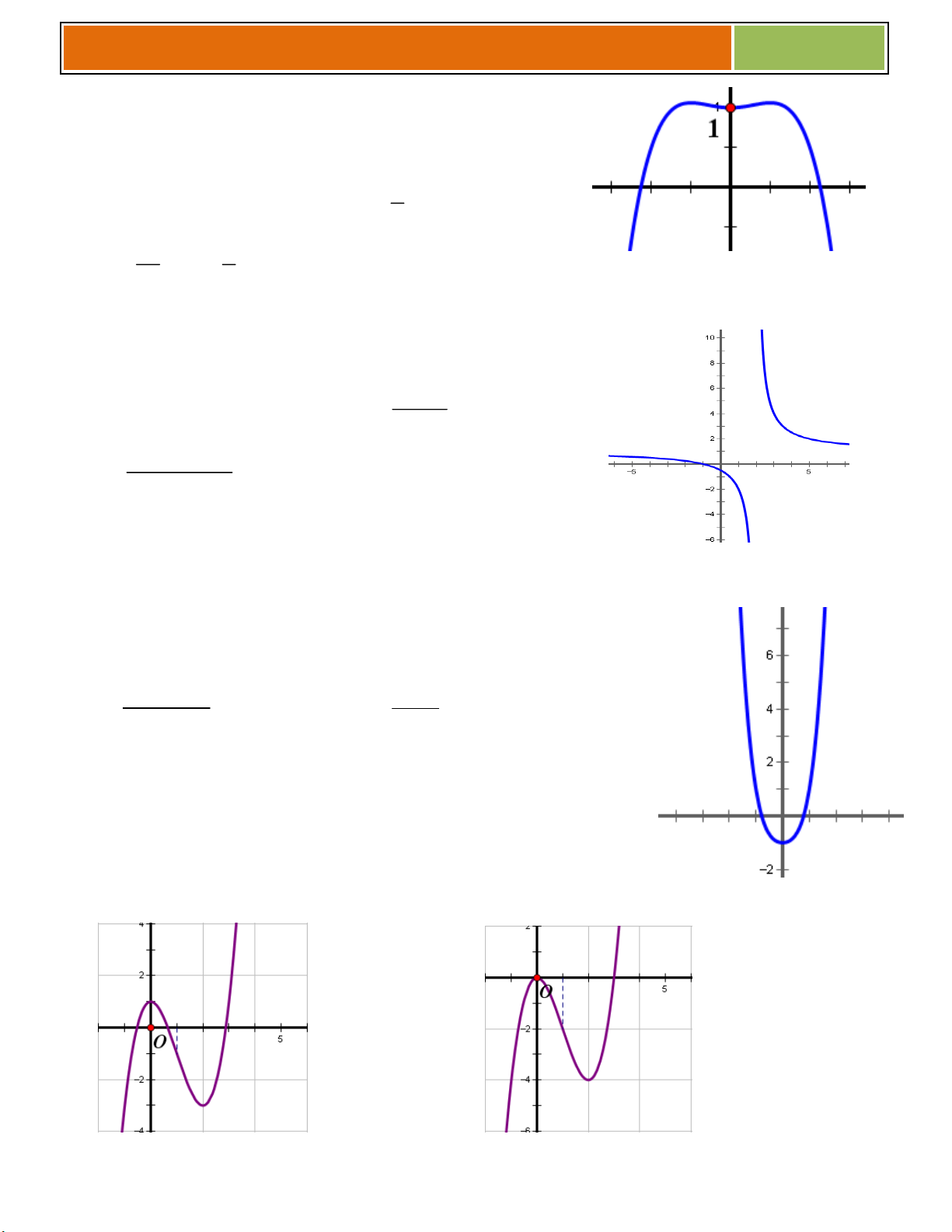
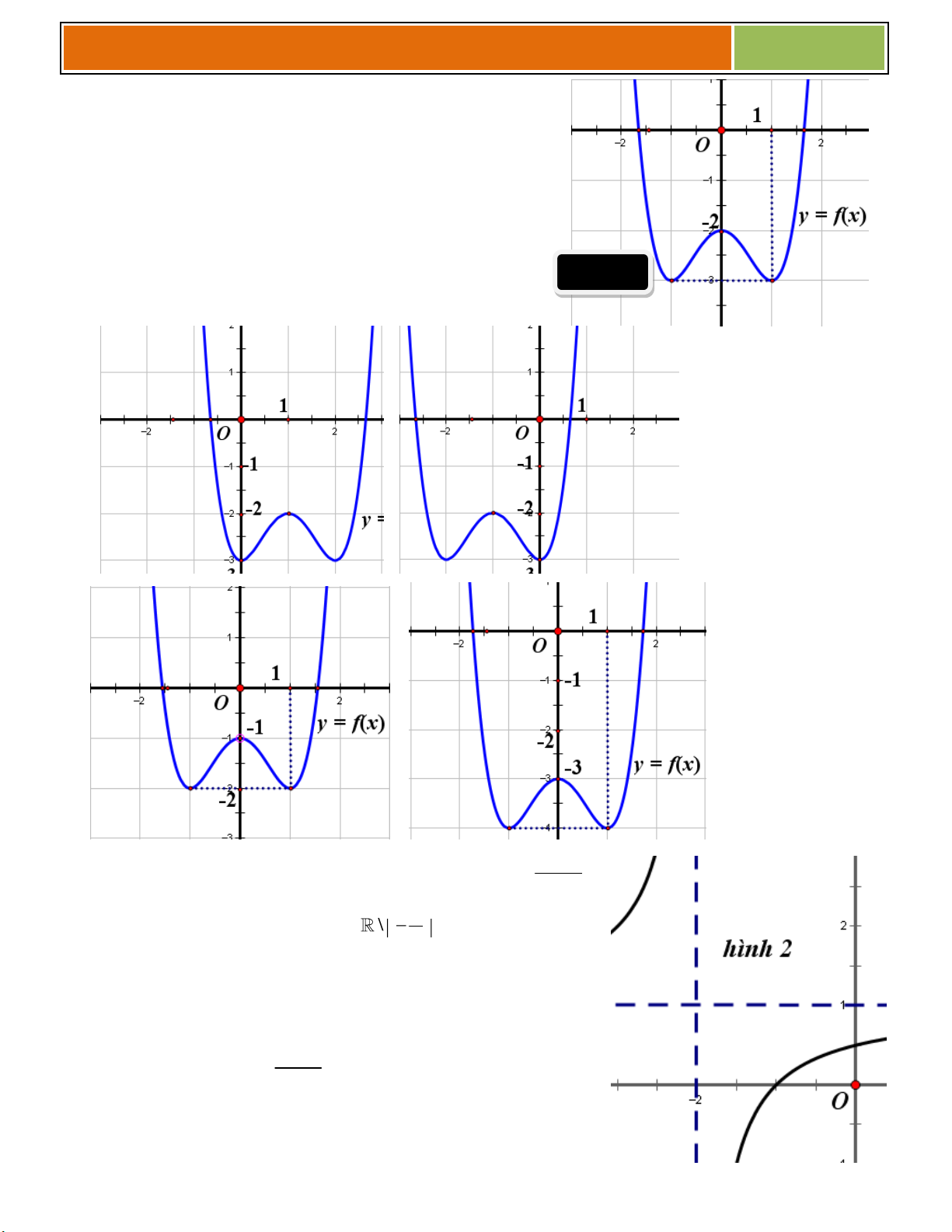
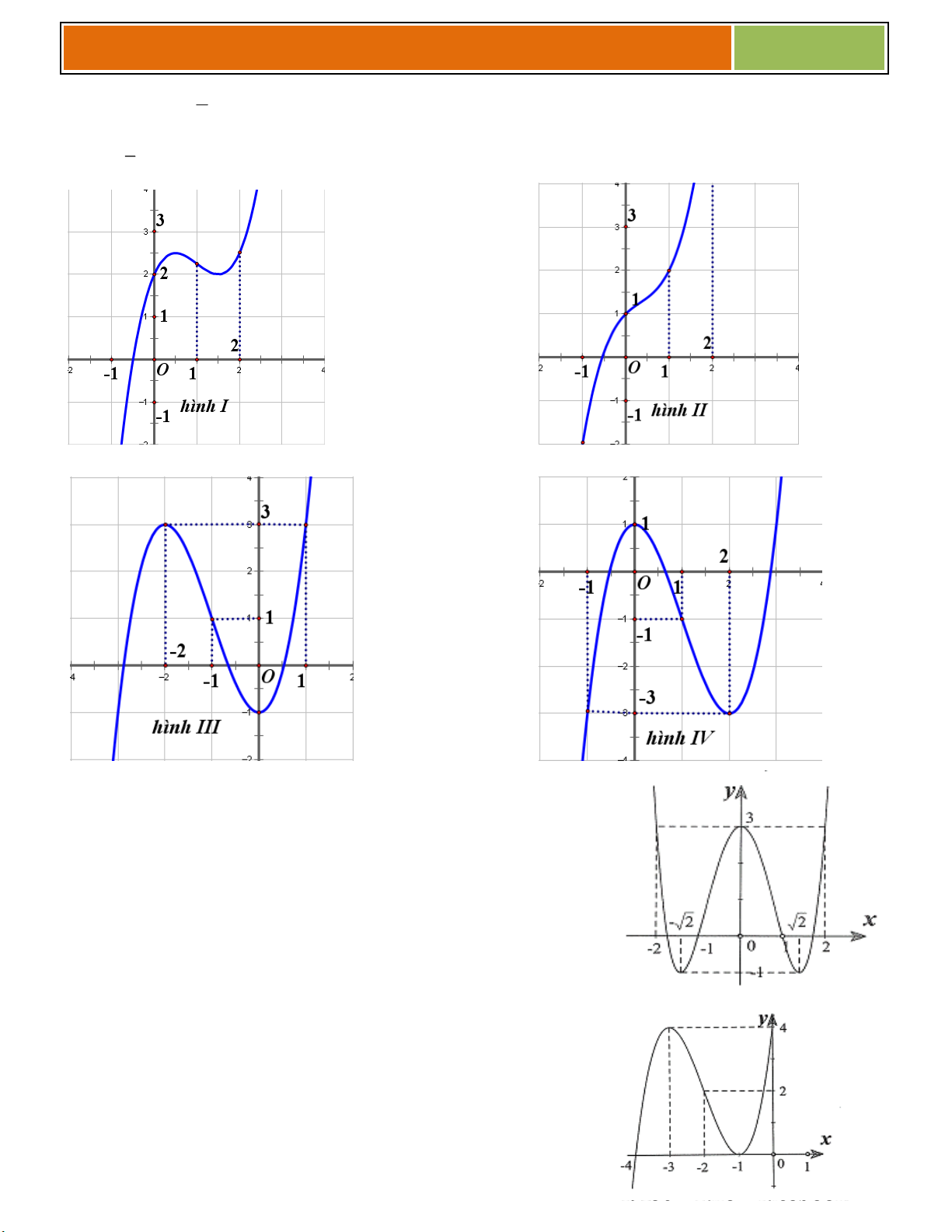
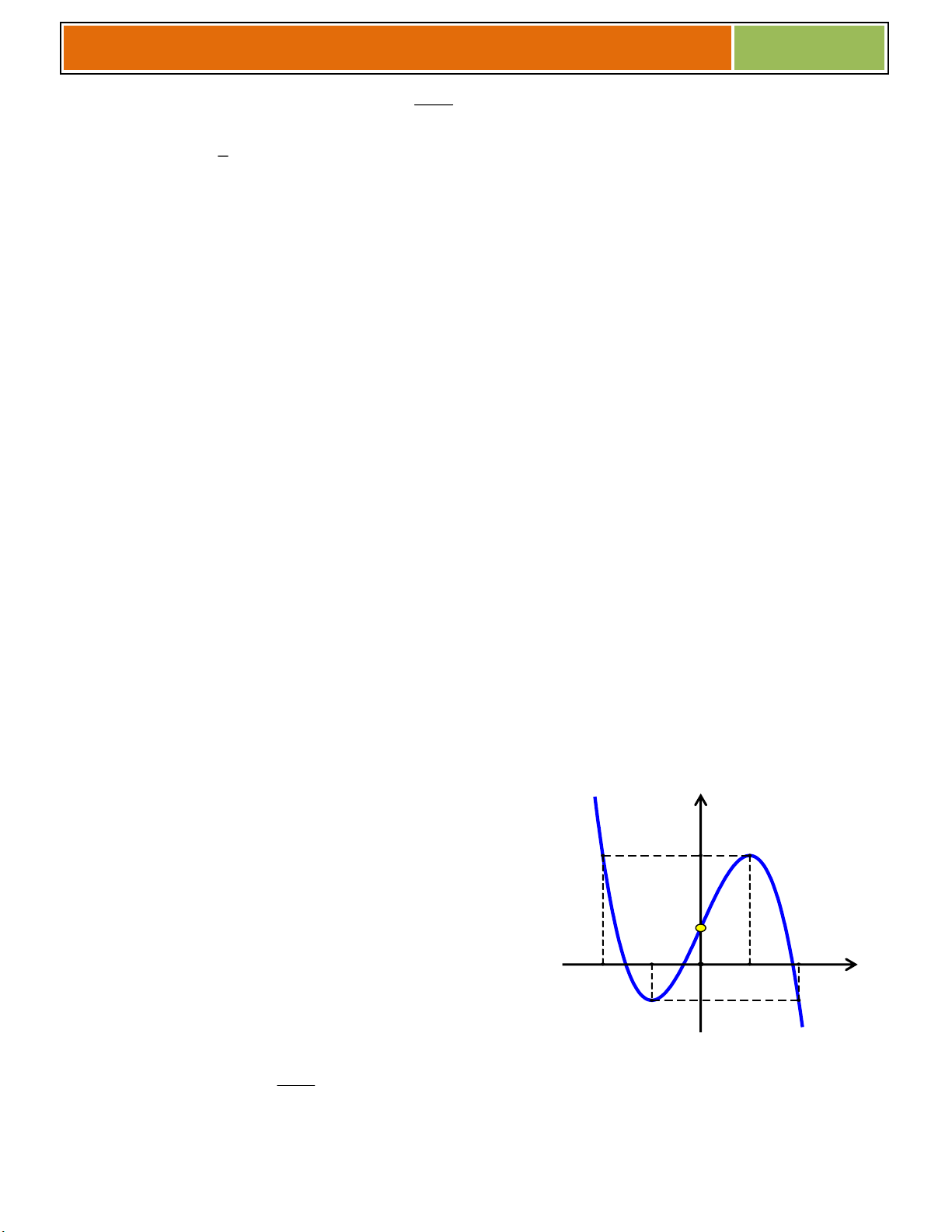
C}u 1 :Dựa vào đồ thịcủa hàm số ở hình bên, hãy cho biết:
1.1 Các khoảng đồng biến, nghịch biến của hàm số.
.................................................................
.................................................................
1.2 Cực trị của hàm số.
.................................................................
..................................................................
1.3 Giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn  1  ; 2 y
........................................................................................................ 2
1.4 Đường thẳng y  ,    2
 ;2 cắt đồ thị hàm số tại .............. điểm 1
C}u 2 :Dựa vào đồ thịcủa hàm số ở hình bên, hãy cho biết: 1 O x
2.1 Các khoảng đồng biến, nghịch biến của hàm số.
............................................................................. 2
2.2 Cực trị của hàm số. –2
....................................................................................................
2.3 Giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn 1; 2 y
....................................................................................................
2.4 Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là ........................... 2
C}u 3 :Dựa vào đồ thịcủa hàm số ở hình bên, I
hàm số ứng với đồ thị đó là: x  2 x  2 O 1 2 x A. y  B. y x 1 x 1 16
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 x  2 C. y
D. Tất cả đáp án đều sai y x 1 1 –1
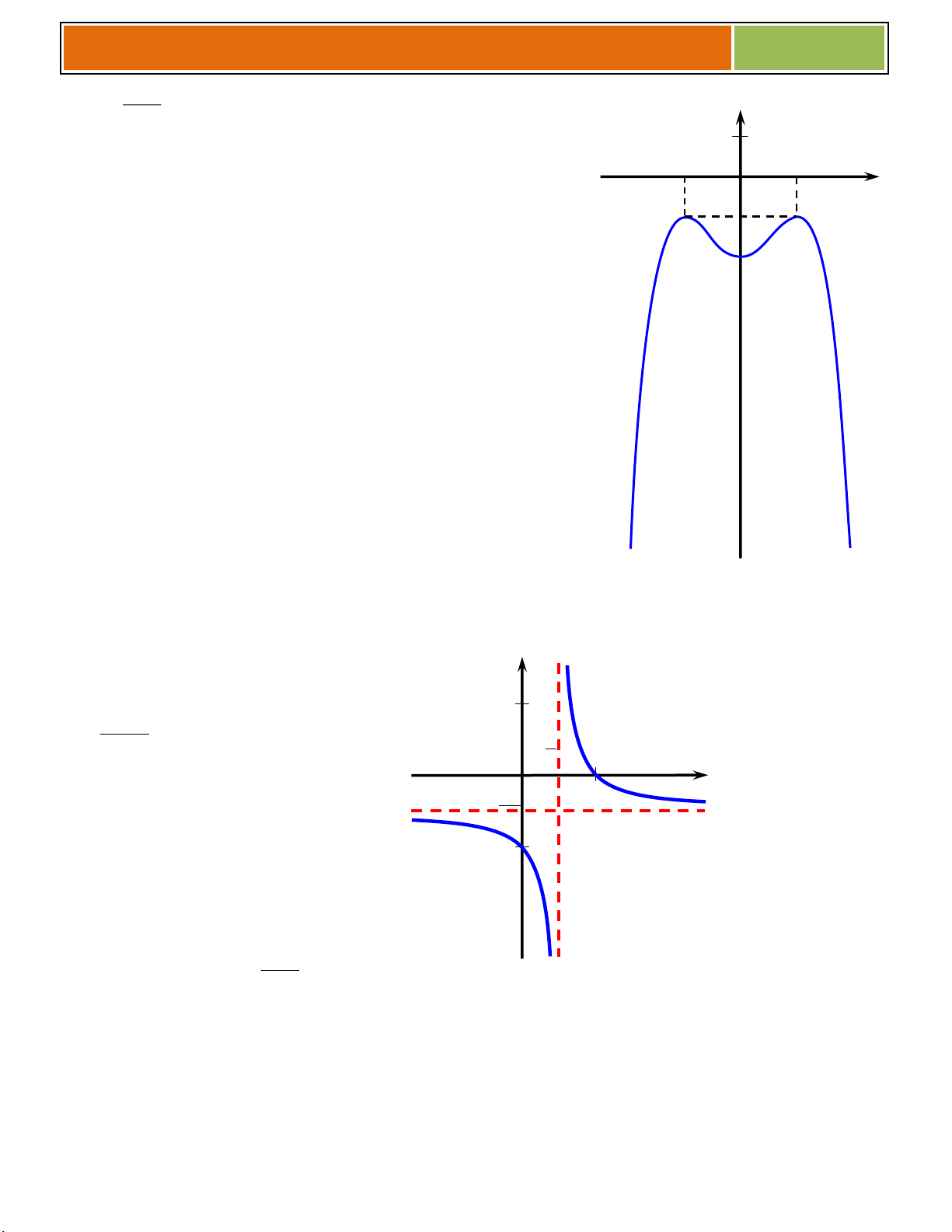
C}u 4 :Dựa vào đồ thịcủa hàm số ở hình bên, hãy cho biết: O x 1 –1
A/ Các khoảng đồng biến, nghịch biến của hàm số.
..................................................................................................... –2
B/ Cực trị của hàm số.
.......................................................................................
C/ Giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn  1  ; 
1 .............................................................................
D/ Khoảng cách giữa hai điểm cực đại là................................
E/ Đường thẳng y  ,    ;  6
  cắt đồ thị hàm số tại ......................................... điểm
F/ Diện tích của tam giác tạo bởi 3 điểm cực trị là S =.........................................................(đvdt) y
C}u 5 :Dựa vào đồ thịcủa hàm số 1 x a y
ở hình bên, hãy cho biết bx 1 O 1 x a và b trong hàm số I
A. a 1;b  2
B. a 1;b  2  –1 C. a  1  ;b  2 D. a  1  ;b  2  x  2
C}u 6 : Cho hàm số y
có đồ thị là (C). Xét các mệnh đề : x  4
(I) (C) có tiệm cận đứng là x = 1
(II) (C) có tiệm cận ngang là y = 4
(III) (C) có giao điểm 2 đường tiệm cận là I(1;4) A. Chỉ (I) đúng. B. Chỉ (II) đúng.
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
C.(I), (II), (III) đều đúng.
D. (I), (II), (III) đều sai.
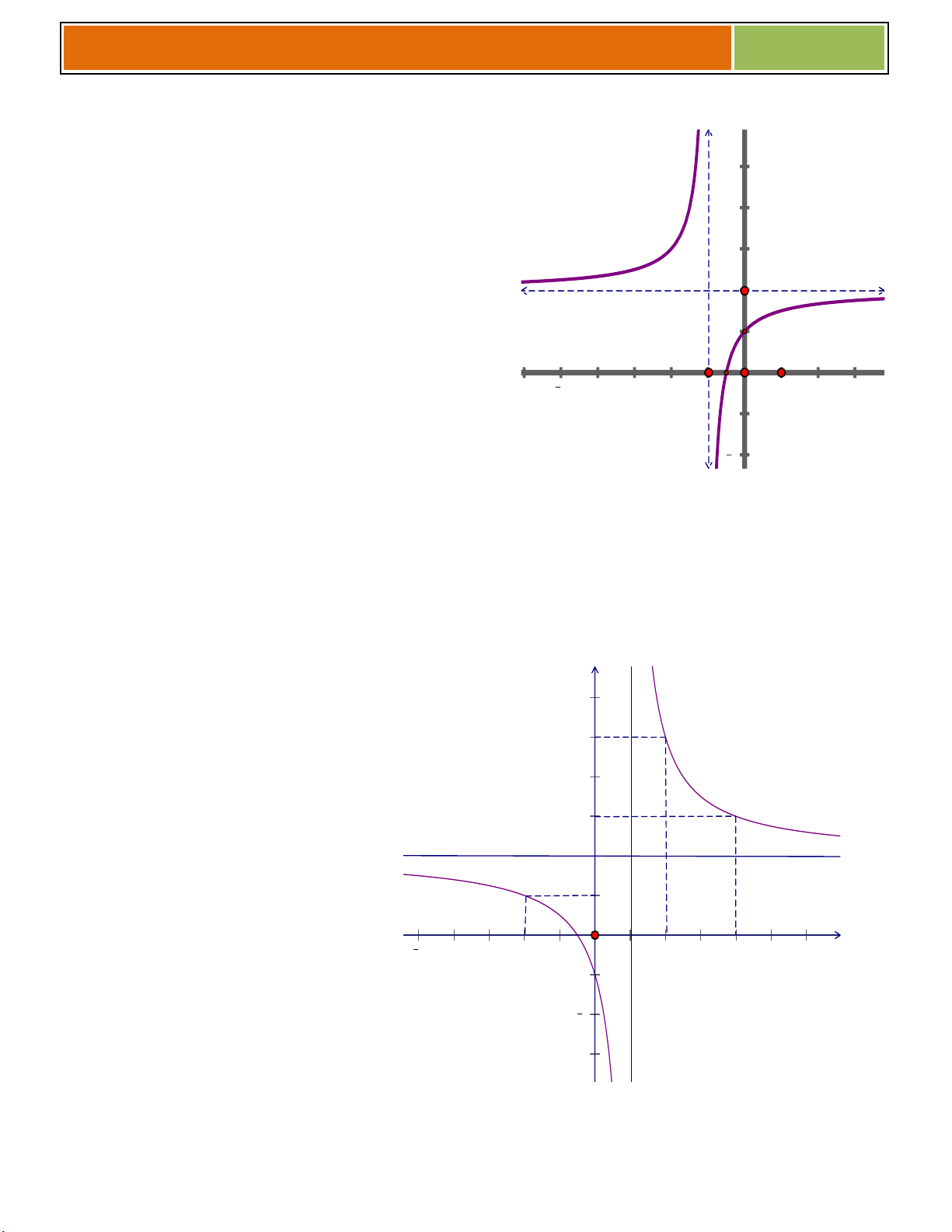
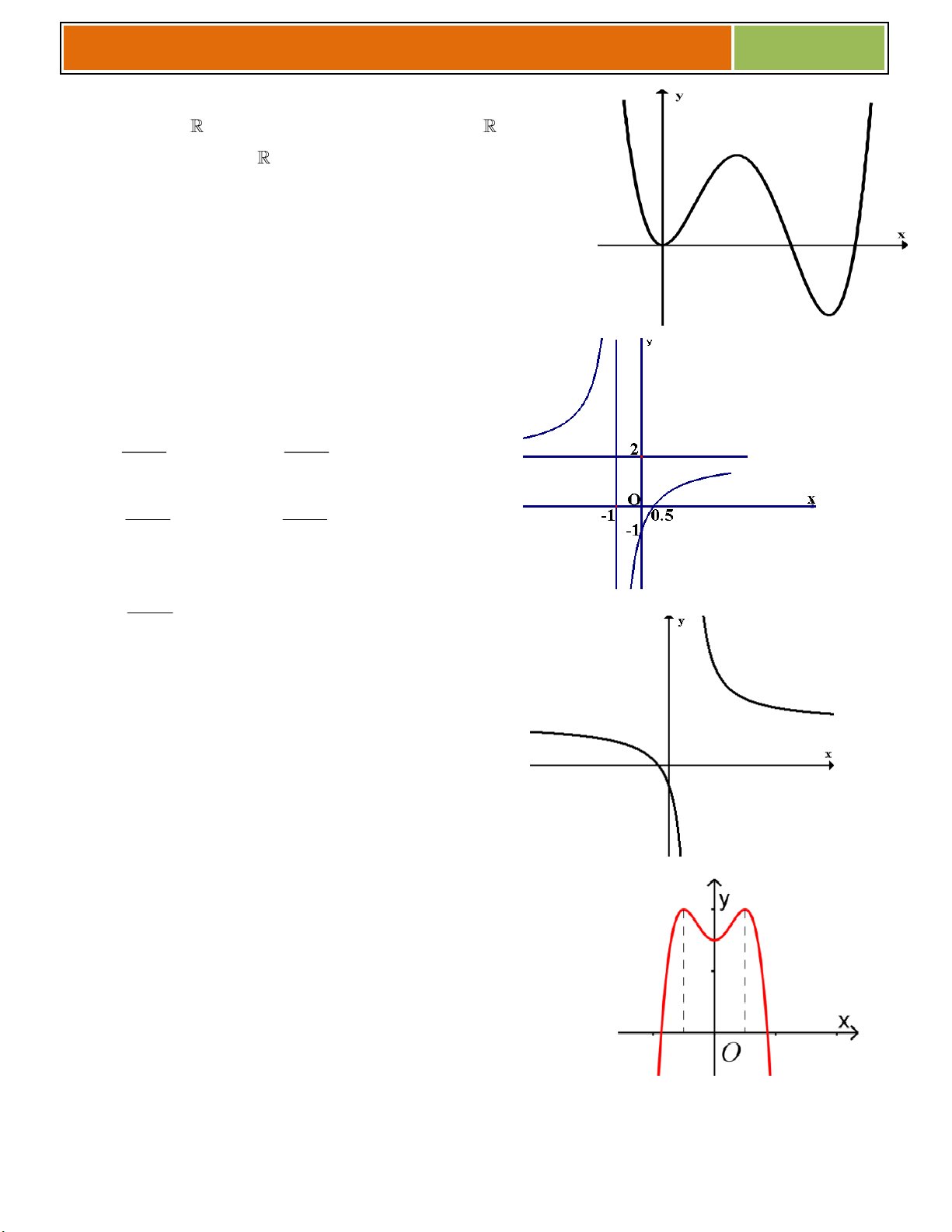
C}u 7 : Cho hàm số y f x có tập xác định là D và
đồ thị là (C) như hình vẽ
Hãy trả lời các câu hỏi sau : 4
7.1 Tiệm cận ngang là ........................... 2
7.2 Miền xác định D =........................... 1 7.3 Đạo hàm -0,5 5 O A. y '  0, x   D B. y '  0, x   D 2 C. y '  0, x   D D. y '  0, x   D
7.4 Giao điểm của đồ thị với
Oy là........................... và Ox là...........................
C}u 8 : Cho hàm số y f x có tập xác định là D và đồ thị là (C) như hình vẽ. Hãy trả lời các câu hỏi sau : y
8.1 Tiệm cận ngang là.......................... 6 5
8.2 Miền xác định D =......................... 8.3 Đạo hàm 4 A. y '  0, x   D 3 B. y '  0, x   D 2 C. y '  0, x   D 1 D. y '  0, x   D
8.4 Giao điểm của đồ thị với O 2 4 x 5 -2 1 5 -1
Oy là........................... 2 và
Ox là.......................... 18
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 x
C}u 9 : Cho hàm số y f x 4 2   bx c 2
có tập xác định là D và đồ thị là (C) như hình vẽ. Giá trị của c là A. 1  B. 0 3 C.  2 D. 2 
C}u 10 : Bảng biến thiên sau ứng với đồ thị hàm số nào 3  x 2  2x A. y  B. y x  2 x  2 2  x 2  x C. y  D. y x  2 x 1 y x
C}u 11 : Cho đồ thị hàm số y f x 4 6 2 7  k
m x n có 2
đồ thị được biểu diễn như hình bên. Khi đó hệ số k trong O x hàm số thõa mãn: -2 -1 1 2 3 -1 A. k  0 B. k  0 C. k  0 -5 D. k  0 x m
C}u 13 : Cho đồ thị hàm số y f x 3 2  a
x nx k có đồ thị được biểu diễn như hình bên. 3 4
Khi đó giá trị k trong hàm số thỏa mãn: y A. k  2 4 B. k  2  C. k  0 2 D. k  1 1
C}u 14 : Đồ thị hàm số được vẽ bên đây ứng với -2 -1 0 x 1 2 hàm số -1 2x 1 A. y x 3 19
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 2x 1 B. y  x  3 2  x C. y  x  2 2  2x D. y  x 3 x
C}u 15 : Cho hàm số y  f x 4 6 2 7  k  m x  n 2
có tập xác định là D và có BBT như sau : x  0 
Kết luận nào sau đây là đúng :
A. Phương trình y’ = 0 có 3 nghiệm phân y '  0  biệt và k < 0 y M
B. Phương trình y’ = 0 có 1 nghiệm duy nhất và k < 0  
C. Phương trình y’ = 0 có 3 nghiệm phân biệt và k > 0
D. Phương trình y’ = 0 có 1 nghiệm duy nhất và k > 0
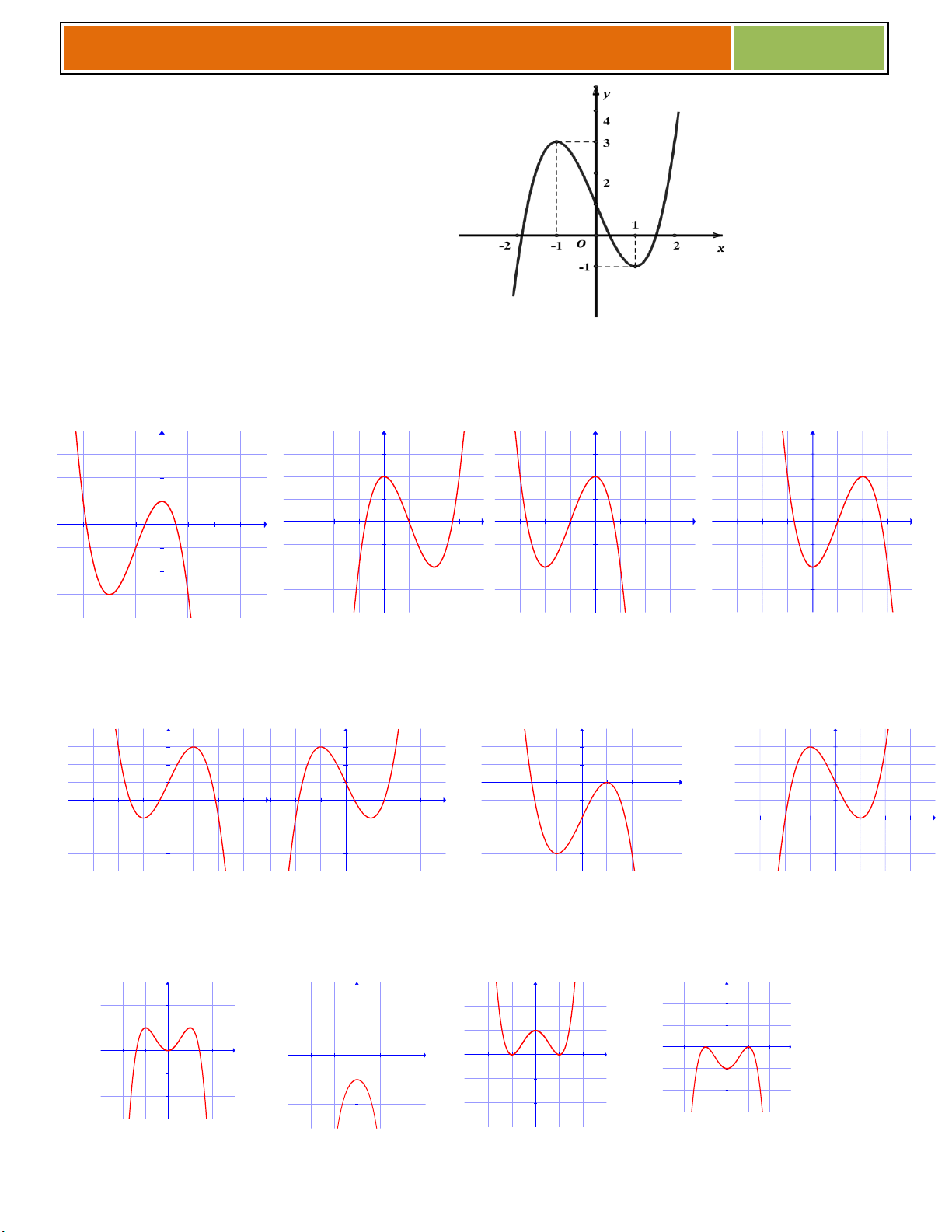
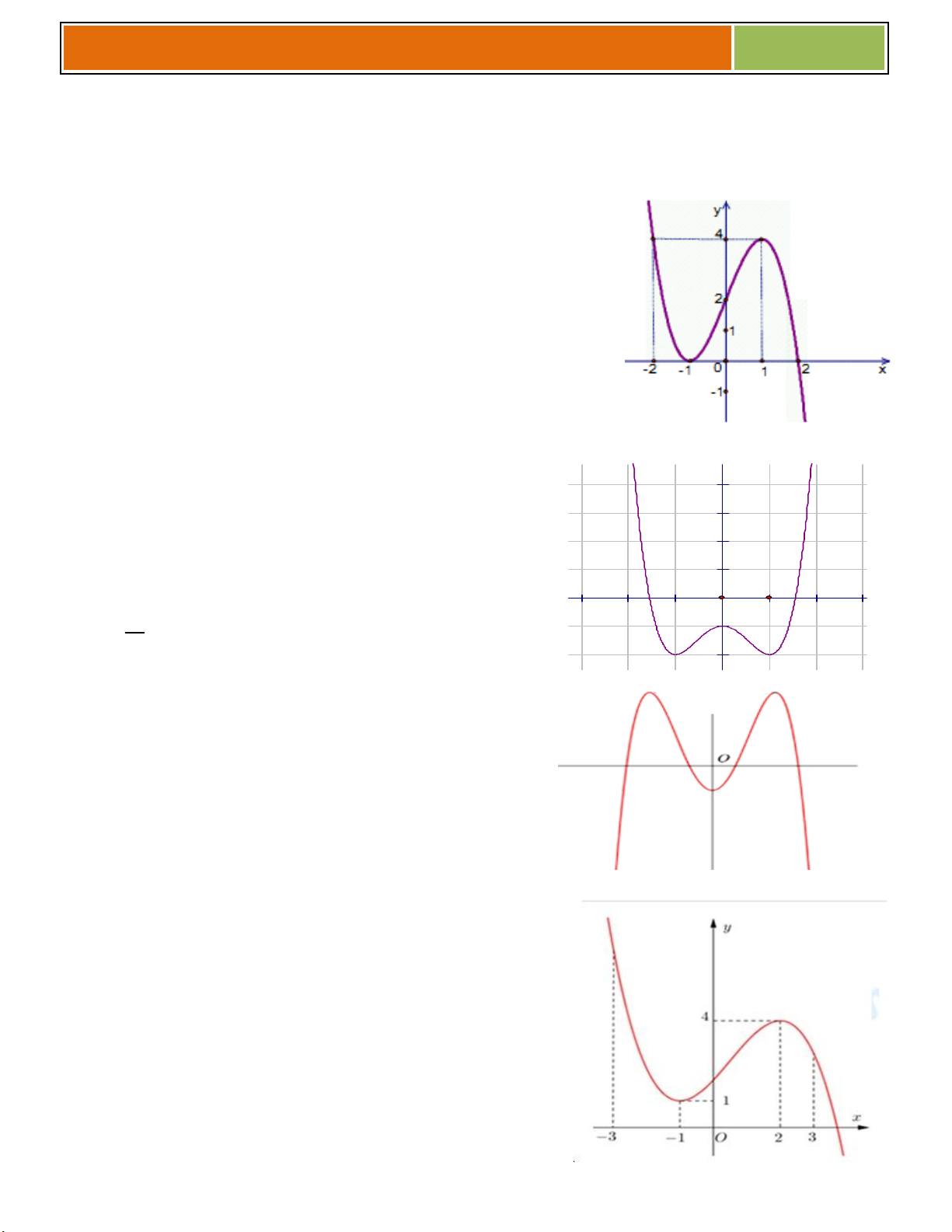
C}u 16 : Cho hàm số y  f x có đồ thị là (C) được vẽ như hình bên.
Dựa vào đồ thị (C) hãy trả lời các câu hỏi sau : y
16.1 Điểm cực tiểu của đồ thị hàm số nằm trên
A. Đường phân giác của góc phần tư thứ nhất 3
B. Đường phân giác của góc phần tư thứ hai C. A và B đều đúng 1 D. A và B đều sai -2 -1 O 1 x 2
16.2 Chọn câu sai
A. Điểm cực đại của đồ thị hàm số là M1;3 -1
B. Hàm số đồng biến trên  1  ;  1
C. Phương trình các cạnh của hình chữ nhật cơ sở x  2  ; y  3; y  1  D. Giá trị Miny  2  x   2  ;  1
C}u 17 (Đề minh họa lần 03):Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn
hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? 20
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook f(x)=(2x-1)/(x+1)
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ x(t)=-1 , y(t)=t f(x)=2 2017 y 2 -1 0 x 2x  3 2x 1 2x  2 2x 1 A. y y y y x  . B. 1 x  . C. 1 x  . D. 1 x  . 1
C}u 18 : Cho đường cong (C) có đồ thị như hình vẽ.
Trả lời các câu hỏi sau :
18.1 Giá trị lớn nhất của hàm số là □ 4 □ 3 □ 2 □ 1
18.2 Giá trị của M là A.  7 B. 7 M 7 C. 1 D. 1 
18.3 Khoảng cách giữa hai điểm cực đại là ...........................
16.4 Đường thẳng y  ,   0;4
cắt đồ thị hàm số tại .............điểm
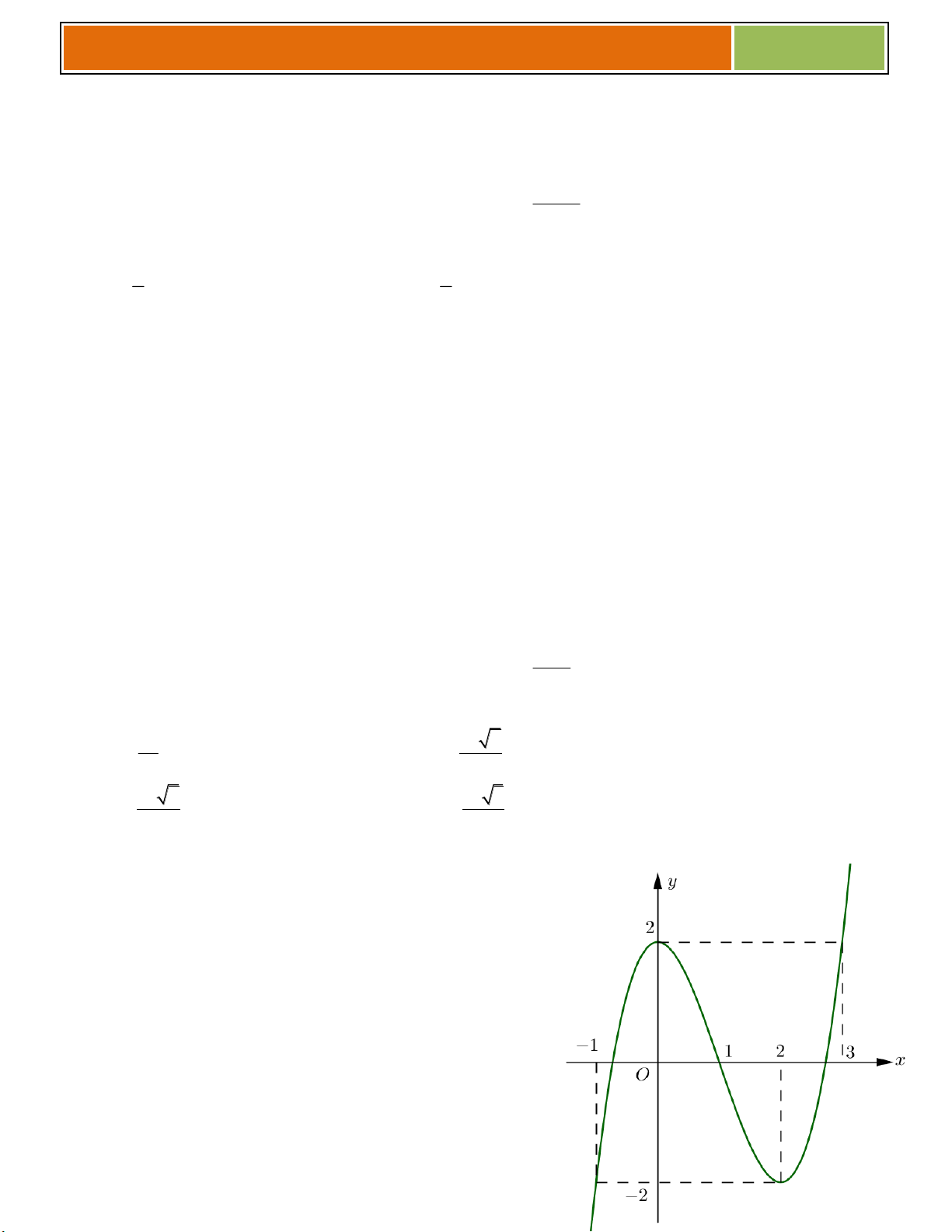
C}u 19 :Đồ thị của hình vẽ bên là đồ thị của hàm số nào sau đây A. 3 2 y  x  3x  3x  2 B. 3 2 y  x  3x  4 C. 3 2
y  x  3x  4x  2 D. 4 2 y  x  2x  2
C}u 20 :Đồ thị của hình vẽ bên
là đồ thị của hàm số nào sau đây A. 3 2 y  x  3x  3x  2 21
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 B. 3 2 y  x  3x  4 C. 3 y  x 1 D. 3 2 y  x  2x  2
C}u 21 :Bảng biến thiên bên dưới là của hàm số nào trong các hàm số sau: A. 3 2 y  x  3x  3x  2 x -  +  B. 3 2 y  x  3x  4 y’ - C. 3 2 y  x  3x  4x  2 +  y -  D. 4 2 y  x  2x  2
C}u 22 :Bảng biến thiên bên dưới là của hàm số nào trong các hàm số sau: x  1  0 1  y  0  0  0  y   A. 3 2 y  x  3x  3x  2 B. 3 2 y  x  3x  4 4 x 3 C. 2 y    x  D. 4 2 y  x  2x  2 2 2
C}u 25 :Bảng biến thiên bên dưới là của hàm số nào trong các hàm số sau: A. 3 2 y  x  3x  3x  2 x -  2 - +  B. 3 2 y  x  3x  4 y’ - - 2  x  4 C. y  -1 +  x 1 3  x y D. y  x  2 -  -1
C}u 26 :Đồ thị của hình vẽ bên
là đồ thị (C) của hàm số nào sau đây A. 4 2 y  x  4x  2 B. 4 2 y  x  4x 1 4 x 3 C. 2 y    x  2 2 22
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 D. 4 2 y  x  2x  2
C}u 27 :Đồ thị của hình vẽ bên
là đồ thị (C) của hàm số nào sau đây 1 A. 4 2 y  x  4x  2 B. 4 2 y  x  x 1 2 4 x 3 C. 2 y    x  D. 4 2 y  x  2x  2 2 2
C}u 28 : Cho đường cong (C) có đồ thị như hình vẽ. Cho biết (C) là đồ thị của một trong các hàm số sau. Hãy chọn đáp án đúng ax  b A. 3 2 y  ax  bx  cx  d B. y  cx  d 2 ax  bx  c C. y     dx  D. 4 2 y ax bx c e
C}u 29 : Cho đường cong (C) có đồ thị như hình vẽ. Cho biết (C) là đồ thị của một trong các hàm số sau.
29.1 Hãy chọn đáp án đúng A. 3 2
y ax bx cx d B. 4 2
y ax bx c 2
ax bx c ax b C. y y dx  D. e cx d
29.2 Hàm số này là hàm số □ chẵn □ lẻ
29.3 Giá trị nhỏ nhất của hàm số trên  7
 ;9 là ............................. -1
C}u 30 : Cho các hàm số f x 3
x 1 và g x 2
 3x . Đồ thị hàm số
f x  g x là A. B. 23
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 C. D.
C}u 31 : Cho đường cong (C) : 3 2
y ax bx cx d có đồ thị như hình vẽ. Chọn đáp án đúng :
A. a < 0 và y’ = 0 có nghiệm kép
B. a < 0 và y’ = 0 vô nghiệm
C. a > 0 và y’ = 0 có nghiệm kép
D. a > 0 và y’ = 0 vô nghiệm
C}u 32 : Cho đường cong (C) : 3 2
y ax bx cx d
có đồ thị như hình vẽ. Chọn đáp án đúng :
A. a < 0 và y’ = 0 có nghiệm kép
B. a < 0 và y’ = 0 vô nghiệm
C. a > 0 và y’ = 0 có nghiệm kép
D. a > 0 và y’ = 0 vô nghiệm
C}u 33 : Cho đường cong (C) : y f x
có đồ thị như hình vẽ. Gọi S (đơn vị diện tích)
là diện tích tam giác tạo bởi 3 điểm cực trị của
đồ thị hàm số. Khi đó giá trị S là A. 0,5 B. 1 C. 2 D. 3
C}u 34 : Cho hàm số :
y f x 3 2
x  3x mx 1 C . Với giá trị nào của tham số m thì đồ thị hàm số đi qua giao điểm m  2  x
hai tiệm cận của đồ thị hàm số y r x  H x  2 24
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 A. 0,5 B. 1 C. 2 D. 3
C}u 35 : Cho hàm số : y f x 3 2
x  3x mx 1 C và y g x 3 2
x  2x  7 Cm
Kết luận nào sau đây là sai ?
A. Đồ thị hàm số (C) như hình bên.
B. Miền xác định của cả hai hàm số là .
C. Hai đồ thị không cắt nhau.
D. Với m = -2 thì (Cm) có hai cực trị.
C}u 36 : Cho hàm số : y f x 3 2
 x  3x  2 C . Giao điểm
của (C) và trục hoành là các điểm nào dưới đây :
A. A1 2;0, B1;0, C1 2;0
B. A1;0, B2;0, C 1  ;0
C. A1 3;0, B2;0, C1 3;0
D. A1 3;0, B1;0, C1 3;0
C}u 37 : Cho hàm số : y f x 4 2
x  6x  5 C . Giao điểm của (C) và trục hoành là các điểm nào dưới đây :
A. A 2;0, B 1
 ;0, C1;0, D 2;0
B. A 5;0, B 1
 ;0, C1;0, D 5;0
C. A 7;0, B 2
 ;0, C2;0, D 7;0
D. A 5;0, B 1
 ;0, C2;0, D 5;0 4 x 9
C}u 38 : Cho hàm số : y f x 2 
 2x  C . Gọi M là giao điểm của (C) và trục hoành có 4 4
hoành độ âm. Hệ số góc tiếp tuyến tại M là A. 15 B. 15  9 9 C. D.  4 4 C}u 39 : Cho hàm số 4 2
y x mx 1 m (C) . Với mọi giá trị của tham số m thì đồ thị (C) luôn đi
qua một điểm K cố định có tọa độ A.  3;0 B. 1;2 C. 0; 2 D.  1  ;0 3x  2
C}u 40 : Cho hàm số (C) : y
.Trên đồ thị (C) có bao nhiêu điểm mà tại đó tọa độ là các số x 1 nguyên 25
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 A. 4 B. 3 C. 2 D. 1 2x  7
C}u 41 : Cho hàm số (C) : y
.Trên đồ thị (C) có bao nhiêu điểm mà tại đó tọa độ là các số x  3 nguyên A. 4 B. 3 C. 2 D. 1 x  8
C}u 42 : Cho hàm số (C) : y
.Trên đồ thị (C) có bao nhiêu điểm mà tại đó tọa độ là các số x 1 nguyên A. 4 B. 6 C. 8 D. 2 3x  2
C}u 43 : Cho hàm số (C) : y  .Trên đồ thị (C) có x  2
bao nhiêu điểm mà tại đó tọa độ là các số nguyên A. 4 B. 6 C. 8 D. 2
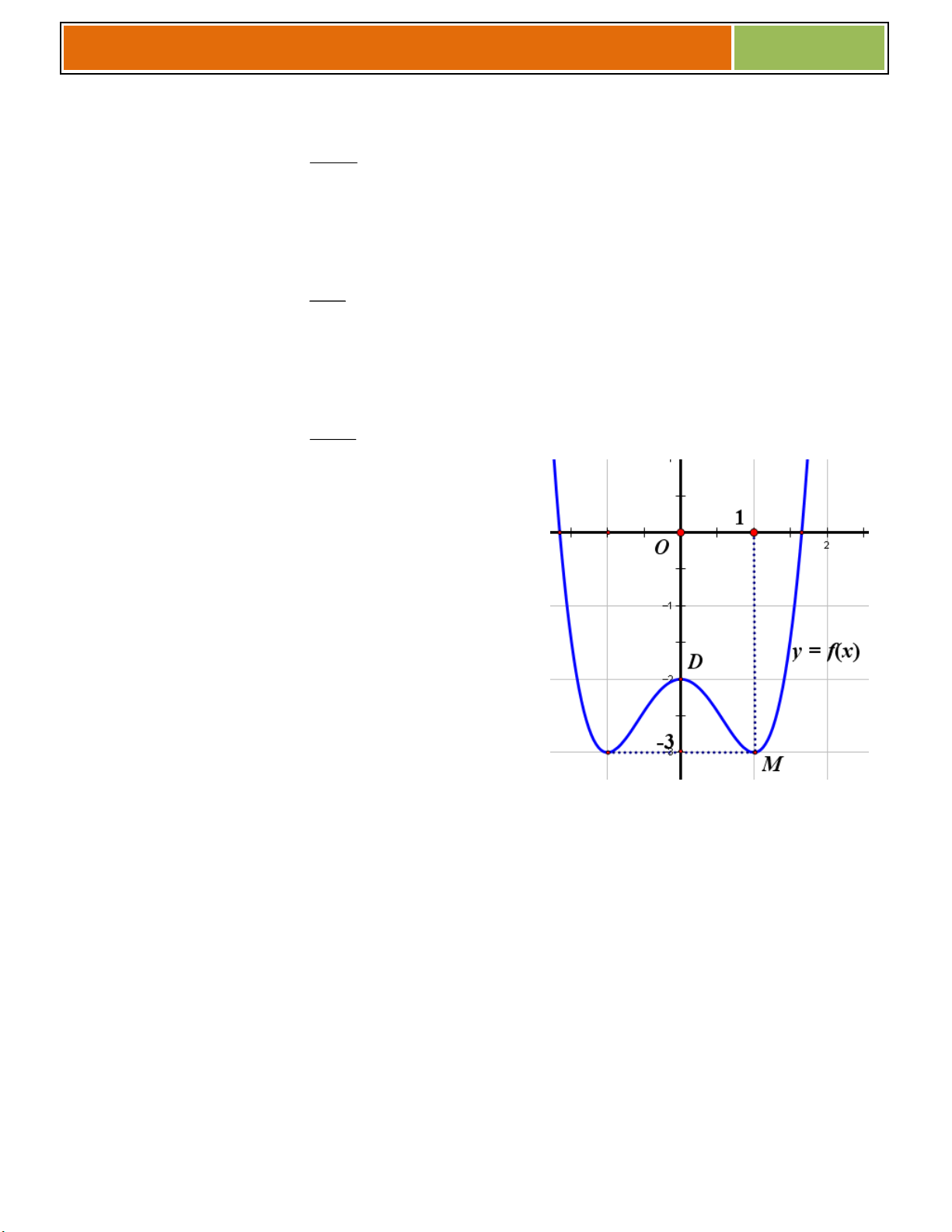
C}u 44 : Cho hàm số (C) : y f x có đồ thị được vẽ
như hình bên và điểm A(2;1).
Diện tích tam giác ∆AMD bằng A. 4 B. 3/2 C. 5/2 D. 2
C}u 45 : Đồ thị hàm số nào sau đây có 3 điểm cực trị : A. 4 2
y  2x  4x 1 B. 4 2
y x  2x 1 C. 4 2
y x  2x 1 D. 4 2
y  x  2x 1
C}u 46 : Đồ thị hàm số nào sau đây chỉ có 1 điểm cực trị : A. 4 2
y  2x  4x  2 B. 4 2
y x  9x 1 C. 4 2
y  x  2x 1 D. 4
y  x   2 m   2 1 x 1
C}u 47 : Khẳng định nào sau đây là đúng về hàm số 4 2
y x  4x  2 :
A. Đạt cực tiểu tại x = 0 26
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
B. Có cực đại và cực tiểu
C. Có cực đại và không có cực tiểu D. Không có cực trị.
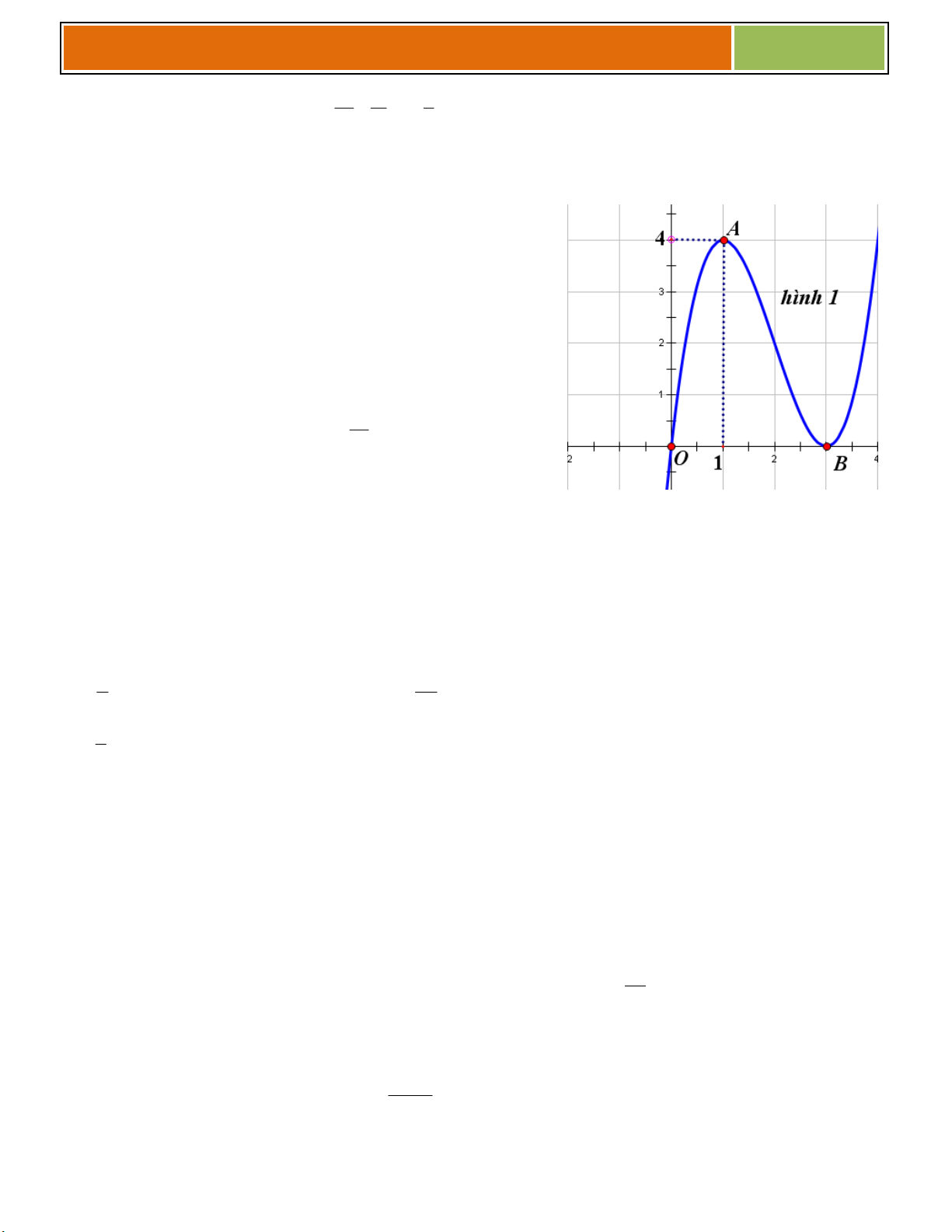
C}u 48 : Cho hàm số (C) : y f x có đồ thị được vẽ như
hình 1 . Hình nào dưới đây là đồ thị của (C’) : y f x 1 Hình A. B. C. D. ax b
C}u 49 : Khẳng định nào sau đây là đúng về hàm số y  : cx dd
A. Hàm số có miền xác định là D  \     c
B. ad bc  0
C. Hàm số không có cực trị D. Cả A, B, C đều đúng ax b
C}u 50 : Cho hàm số y
, ad bc  0 . cx d
Khẳng định nào sau đây là đúng
A. Hàm số luôn giảm trên từng khoảng xác định. 27
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 bc ad
B. Hàm số có đạo hàm y  cxd2 C. Không có tiệm cận.
D. Đồ thị hàm số là hình
C}u 51 : Đồ thị sau đây là của hàm số A. 4 2
y  x  2x  2 B. 4 2
y  x  2x  2 C. 4 2
y x  2x  2 D. 4 2
y  x x  2
C}u 52 : Đồ thị sau đây là của hàm số A. 4 2
y  x x 1 B. 4 2
y x  2x 1 C. 4 2
y  x  2x 1 D. 4 2
y x x 1
C}u 53 : Bảng biến thiên ở bên là của hàm số nào? A. 3 2
y x  3x  3x B. 3 2
y  x  3x  3x C. 3 2
y x  3x  3x D. 3 2
y  x  3x  3x
C}u 54 : Bảng biến thiên ở bên là của hàm số nào ? A. 4 2
y x  3x  3 1 B. 4 2 y   x  3x  3 4 C. 4 2
y x  2x  3 D. 4 2
y x  2x  3 28
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
C}u 55 : Bảng biến thiên ở bên là của hàm số nào ? A. 4 2
y x  3x 1 B. 4 2
y  x  3x 1 C. 4 2
y x  3x 1 D. 4 2
y  x  3x 1
C}u 56 : (Sở GD&ĐT B| Rịa – Vũng y
T|u, lần 1) Đường cong hình bên (Hình
1) là đồ thị của một hàm số trong bốn 4
hàm số được liệt kê trong bốn phương
án A, B, C, D dưới đây. Hỏi đó là hàm số nào? A. y   3 x  3x  2. 2 B. y  3
x  4x  5 . x C. y  3
x  3x  2 . -1 O 1 2 D. y   3
x  3x  2 .
C}u 57 : Bảng biến thiên ở bên là của hàm số nào ? A. 4 2
y  x  3x  3 B. 4 2
y x x  3 C. 4 2
y x  2x  3 D. 4 2
y x  2x  3
C}u 58 : Bảng biến thiên ở bên là của hàm số nào ? 2x 1 x 1 A. y B. y x 1 2x 1 2x 1 x  2 C. y D. y x 1 1 x 29
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
C}u 59 : Bảng biến thiên ở bên là của hàm số nào ? 2x 1 x 1 A. y B. y x  2 2x 1 x 1 x  3 C. y D. y x  2 2  x
C}u 60 : Đồ thị hình bên là của hàm số nào ? A. 3
y x  3x B. 3
y x  3x C. 3
y  x  2x D. 3
y  x  2x
C}u 61 : Đồ thị hình bên là của hàm số nào ? A. 3 y  x 1 B. 3 2 y  2  x x C. 2 y  3x 1 D. 3 y  4  x 1
C}u 62 : Đồ thị hình bên là của hàm số nào ? A. 4 2
y  x  3x 1 B. 4 2
y x  2x 1 C. 4 2
y  x  2x 1 D. 4 2
y x  3x 1
C}u 63 : Đồ thị hình bên là của hàm số nào ? A. 4 2
y x  2x B. 4 2
y x  2x C. 4 2
y  x  2x D. 4 2
y x  2x 30
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
C}u 64 : Đồ thị hình bên là của hàm số nào ? 2  x 1 x A. y B. y  2x 1 x 1 x 1 x  2 C. y D. y x 1 x 1
C}u 65 : Đồ thị hình bên là của hàm số nào ? x 1 x 1 A. y B. y x 1 x 1 2x 1 x C. y D. y  2x  2 1 x
C}u 66 : Đồ thị hình bên là của hàm số nào ? A. 3 2
y  x  3x  4x  2 B.  2
y  x  3x  4x  2 C. 3 2
y x  3x  4x  2 D. 3 2
y x  3x  2
C}u 67 : Đồ thị hình bên là của hàm số nào ? A. 3 2
y  2x  3x 1 B. 3 2
y  2x  3x 1 C. 3 2 y  2  x 3x 1 D. 2 2 y  2
x  3x 1 31
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
C}u 68 : Đồ thị hình bên là của hàm số nào ? A. 3
y x  3x B. 3
y x  3x C. 3
y  x  3x 1 D. 3
y x  3x 1
C}u 69 : Đồ thị hình bên là của hàm số nào ? A. 4 2
y x  2x B. 4 2
y x  2x C. 4 2
y  x  2x D. 4 2
y x  3x
C}u 70 : Đồ thị hình bên là của hàm số nào ? 1 A. 3 2 y
x x x 3 1 B. 3 2 y
x x x 1 3 C. 3 2
y  x  3x  3x D. 3 2
y x  3x  3x  2
C}u 71 : Đồ thị hình bên là của hàm số nào ? A. 4 2
y  x  4x 1 B. 4 2
y x  2x 1 C. 4 2
y x  2x 1 D. 4 2
y x  4x 1 32
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
C}u 72 : Đồ thị hình bên là của hàm số nào ? A. 4 2
y x  2x 1 B. 4 2
y  x  2x 1 C. 4 2
y x  2x 1 D. 4 2
y  x  2x 1
C}u 73 : Đồ thị hình bên là của hàm số nào ? A. 3
y x  3x  4 B. 3 2
y  x  3x  4 C. 3
y x  3x  4 D. 3 2
y  x  3x  4
C}u 74 : Đồ thị hình bên là của hàm số nào ? A. 3 2
y x  3x  3x 1 B. 3 2
y  x  3x 1 C. 3
y x  3x 1 D. 3 2
y  x  3x 1
C}u 75 : Đồ thị hình bên là của hàm số nào ? A. 4 2
y x  3x  3 1 B. 4 2 y   x  3x  3 4 C. 4 2
y x  2x  3 D. 4 2
y x  2x  3 33
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
C}u 76 : Đồ thị hình bên là của hàm số nào ? A. 4 2
y x  3x 1 B. 4 2 y   x  3x 4 C. 4 2
y  x  2x D. 4 2
y  x  4x
C}u 77 : Đồ thị hình bên là của hàm số nào ? 1 A. 4 2
y x  3x 1 B. 4 2 y   x  3x 1 4 C. 4 2
y x  2x 1 D. 4 2
y x  2x 1
C}u 78 : Đồ thị hình bên là của hàm số nào ? 2x 1 x 1 A. y B. y x 1 x 1 x  2 x  3 C. y D. y x 1 1 x
C}u 79: Đồ thị hình bên là của hàm số nào ? 2x 1 x  2 A. y B. y x 1 x 1 x 1 x  2 C. y D. y x 1 1 x 34
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
C}u 80: Đồ thị hình bên là của hàm số nào ? A. 3
y x  3x 1 B. 3 2
y  x  3x 1 C. 3
y x  3x 1 D. 3 2
y  x  3x 1
C}u 81: Đồ thị hàm số 3 2
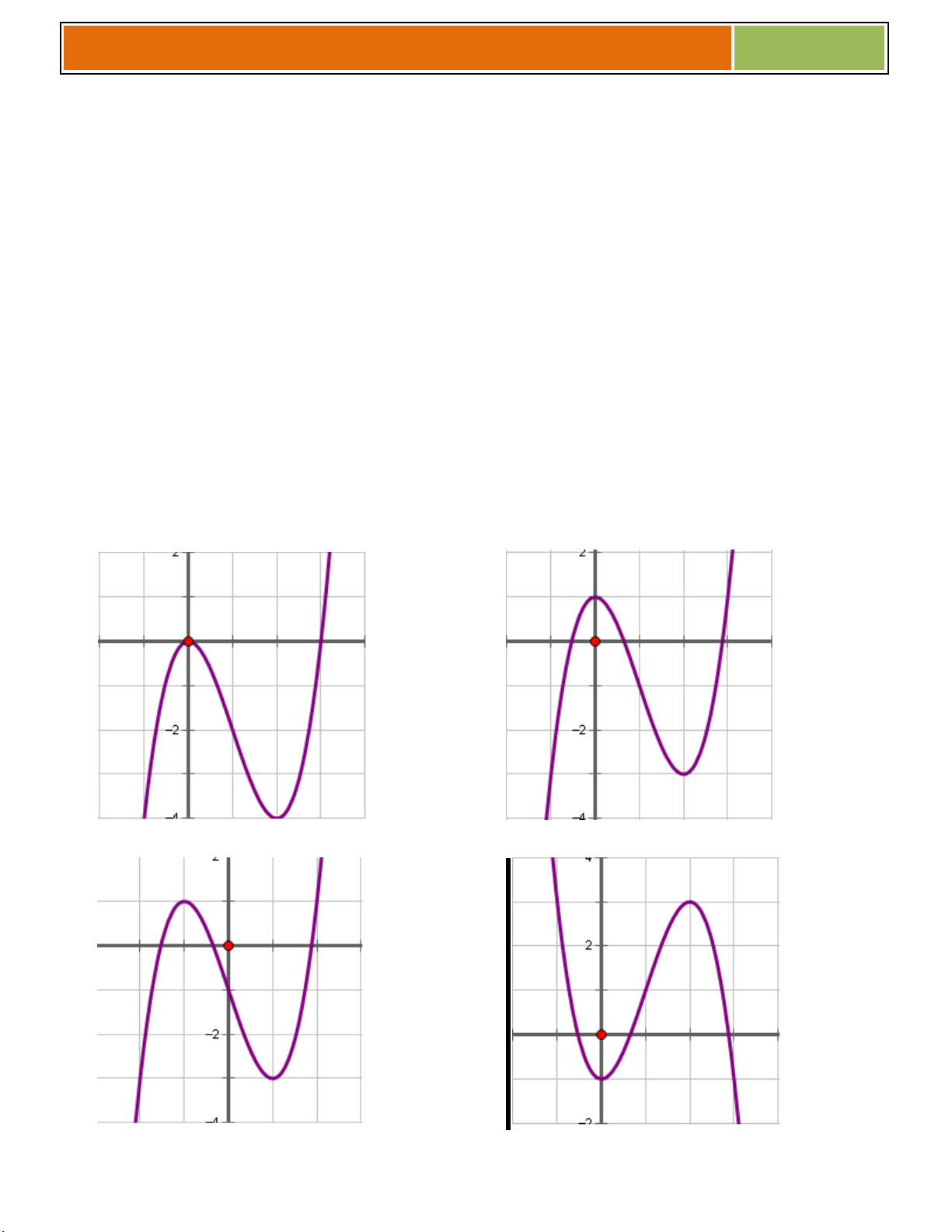
y  x  3x  2 có dạng: A. B. C. D. y y y y 3 3 3 3 2 2 2 2 1 1 1 1 x x x x -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -1 -1 -2 -2 -2 -2 -3 -3 -3 -3
C}u 82: Đồ thị hàm số 3
y x  3x  2 có dạng: A. B. C. D. y y y y 3 3 2 4 2 2 1 3 x 1 1 2 -3 -2 -1 1 2 3 x x -1 1 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 x -1 -1 -2 -3 -2 -1 1 2 3 -2 -2 -3 -1 -3 -3 -4 -2
C}u 83: Đồ thị hàm số 4 2
y  x  2x 1 có dạng: A. B. C. D. y y y y 2 2 2 2 1 1 1 1 x x x x -2 -1 1 2 -2 -1 1 2 -2 -1 1 2 -2 -1 1 2 -1 -1 -1 -1 -2 -2 -2 -2 35
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 4 x
C}u 84: Đồ thị hàm số 2 y  
 2x 1 có dạng: 4 A. B. C. D. y y y y 3 3 3 3 2 2 2 2 1 1 1 1 x x x x -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -1 -1 -2 -2 -2 -2 -3 -3 -3 -3 x  2
C}u 85: Đồ thị hàm số y  có dạng: 1 x A. B. C. D. y y y y 3 3 3 3 2 2 2 2 1 1 1 1 x x x x -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -1 -1 -2 -2 -2 -2 -3 -3 -3 -3 x 1
C}u 86: Đồ thị hàm số y  có dạng: 1 x A. B. C. D. y y y y 2 3 3 3 2 2 2 1 x 1 1 1 -2 -1 1 2 3 x x x -1 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -1 -2 -2 -2 -2 -3 -3 -3 -3
C}u 87: Điền hình đồ thị thích hợp vào hàm số tương ứng 1/ 3 2
y x  3x 1
có đồ thị là hình .............. 2/ 3 2
y x  3x 1
có đồ thị là hình .............. 36
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 9 3/ 3 2
y x  3x x  2
có đồ thị là hình .............. 4 1 4/ 3 2 y
x x x 1
có đồ thị là hình .............. 3 C}u 88: Hàm số    4 2 y
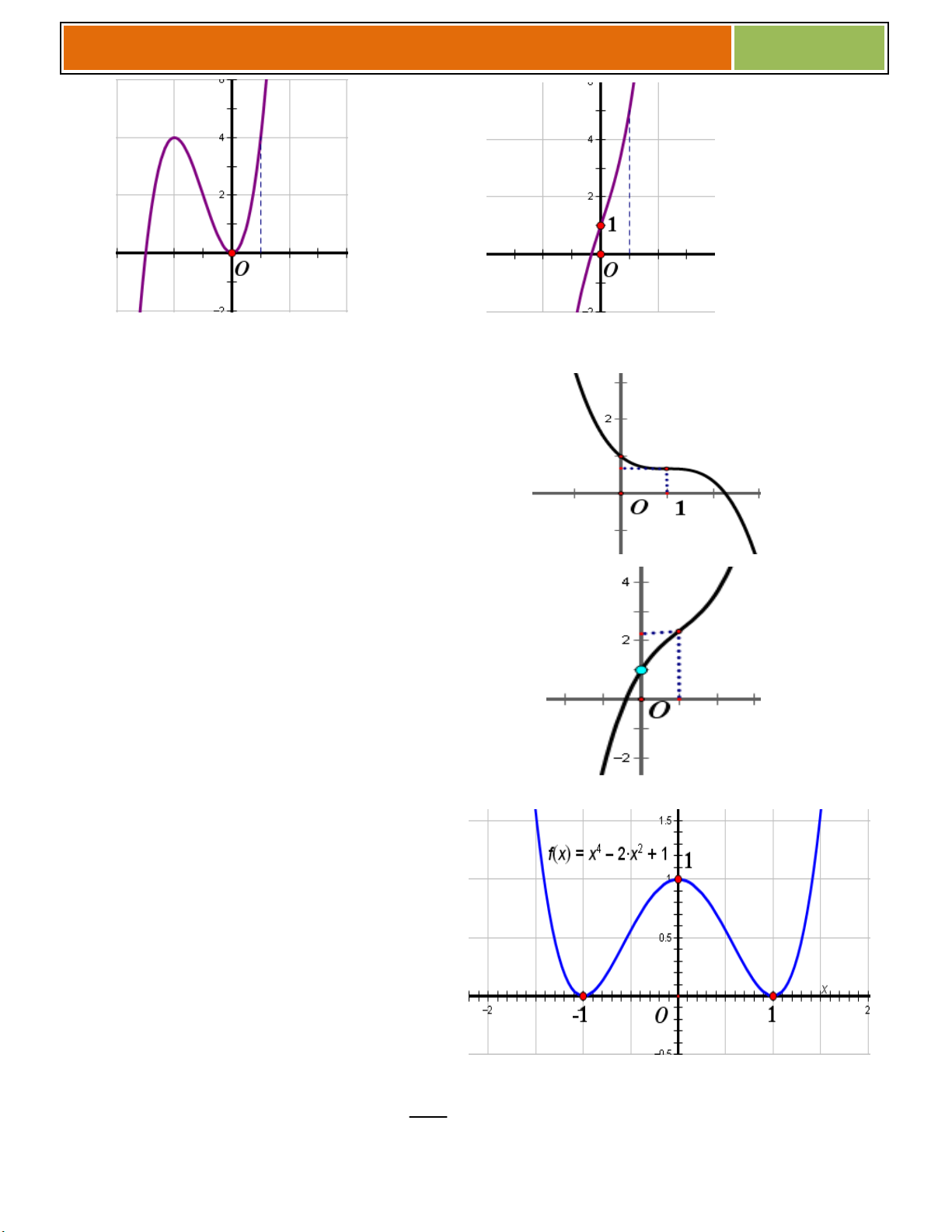
f x  ax  bx  ca  0 có đồ thị như hình vẽ sau:
Hàm số y  f x là hàm số nào trong bốn hàm số sau: A.    2 2 y x 2 1 B.    2 2 y x 2 1 C. 4 2 y  x  2x  3 D. 4 2 y  x  4x  3
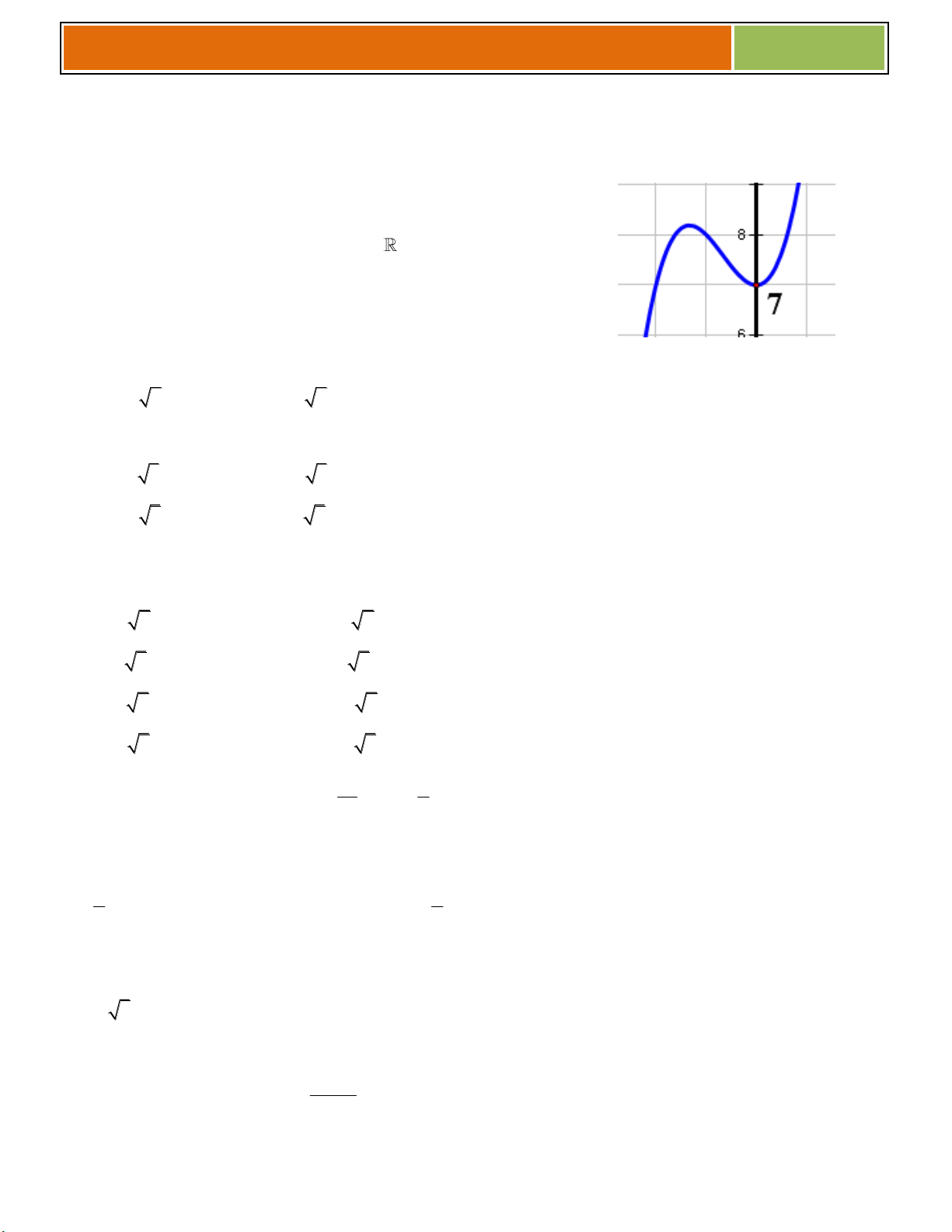
C}u 89: Cho hàm số    3 2 y
f x  x  ax  bx  4 có đồ thị như
hình vẽ:Hàm số y  f x là hàm số nào trong bốn hàm số sau: A. 3 2 y  x  3x  2 37
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 B. 3 2 y  x  3x  2 C. 3 2 y  x  6x  9x  4 D. 3 2 y  x  6x  9x  4
C}u 90: Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào? A. 3 y  x  3x  2 B. 3 y  x  3x 1 C. 4 2 y  x  x 1 D. 3 y  x  3x 1
C}u 91: Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D
dưới đây. Hỏi hàm số đó là hàm số nào? 4 A. 4 2
y x  2x 1. 2 B. 4 2
y  x  2x 1. C. 4 2
y x  2x 1. 4 x D. 2 y   x 1 2 . -2 C}u 92: Cho hàm số + 4 2 y ax  x b
cc  0 có đồ thị sau:.Xét dấu a, , b c
A. a  0,b  0,c  0 .
B. a  0,b  0,c  0 .
C. a  0,b  0,c  0 .
D. a  0,b  0,c  0 .
C}u 93: Cho hàm số y f x xác định, liên tục trên đoạn  3  ; 
3 và có đồ thị đường cong ở hình vẽ bên. Mệnh đề
nào dưới đây đúng trên đoạn  3  ;  3 ?
A. Hàm số y f x đạt giá trị lớn nhất tại x  2 .
B. Hàm số y f x đạt cực tiểu tại điểm x  1  .
C. Hàm số y f x nghịch biến trên khoảng  1  ;2.
D. Hàm số y f x nghịch biến trên khoảng  1  ;3 38
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
C}u 94: (THPT Trung Giã – H| Nội) Cho hàm số y f x có đạo hàm trên
và đồ thị hàm số y f  x trên như hình bên dưới. Khi đó trên
hàm số y f x
A. có 1 điểm cực đại và 1 điểm cực tiểu.
B. có 2 điểm cực đại và 2 điểm cực tiểu.
C. có 1 điểm cực đại và 2 điểm cực tiểu.
D. có 2 điểm cực đại và 1 điểm cực tiểu.
C}u 95: (SGD – B| Rịa Vũng T|u 2017 lần 2) Đường cong
trong hình bên là đồ thị của một hàm số trong bốn
hàm số được liệt kê ở bốn phương án A, B, C, D
dưới đây. Hỏi hàm số đó là hàm số nào? 2x 1 2x 1 A y  . B. y  . x 1 x 1 2x 1 1 2x C. y  . D. y  . x 1 x 1
C}u 96: (THPT Đa Phúc – H| Nội, lần 1) Đồ thị hàm ax b số y
có dạng như hình bên dưới. cx d
Mệnh đề nào sau đây là sai? A. ac  0 . B. ab  0 . C. cd  0 . D. bd  0 .
C}u 97: (THPT Ngô Sĩ Liên – H| Nội, lần 3) Hàm số  4  2 y ax
bx c có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
A. a  0; b  0; c  0.
B. a  0; b  0; c  0.
C. a  0; b  0; c  0.
D. a  0; b  0; c  0. 39
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017 y
C}u 98: Đồ thị sau là của hàm số nào? 3 A. 3
y  x  3x 1. B. 3 2
y x  3x 1. C. 3
y x  3x 1. 1 D. 3
y x  3x 1. 1 x -1 O -1
C}u 99 : Đồ thị hàm số 3 2
y  4x  6x 1 là hình vẽ nào sau đây? y y 3 3 2 2 1 1 x x -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -2 -2 -3 -3 A. . B. . y y 3 3 2 2 1 1 x x -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -2 -2 -3 -3 C. . D. .
C}u 100: Hàm số nào sau đây có đồ thị như hình vẽ? y 2x 1 A. y  . 1 x 2x 1 B. y  . 1 x 1 1 - 2x 1 2 1 x O C. y  . 1 2x 2x  3 D. y  . -2 1 x
C}u 101: Đồ thị sau đây là của hàm số nào ? A. 4 2
y x  2x 1 . B. 4 2
y x  2x 1. C. 4 2
y  x  2x 1. D. 4 2
y  x  2x 1. 40
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – KHẢO SÁT VÀ VẼ 2017
C}u 102: Đồ thị hàm số 4 2
y  x x  2 có dạng: y y 5 5 4 4 3 3 2 2 1 1 x x -4 -3 -2 -1 1 2 3 4 -4 -3 -2 -1 1 2 3 4 -1 -1 -2 -2 -3 -3 A. B. y y 3 3 2 2 1 1 x x -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -2 -2 -3 -3 C. D. y
C}u 103: Cho hàm số y f x có đồ thị g x  f ' x như hình vẽ sau:
Số điểm cực trị của đồ thị trên là 2 A. 2 điểm. 1 B. 1 điểm. C. 3 điểm. O x -2 -1 1 D. Không có -1 -2 41
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017
PHẦN 6 : TIẾP TUYẾN VỚI ĐỒ THỊ HÀM SỐ
Định lý : Đạo hàm của hàm số y  f(x) tại điểm x0 là hệ số góc của tiếp tuyến với đồ thị tại
điểm M(x0;y0 = f(x0)) :
Yêu cầu bài toán
Phương trình tiếp tuyến
Tiếp tuyến tại M(x ; y ) (C) 0 0 (1)
k f '(x ) : hệ số góc tiếp tuyến tại M 0
Tiếp tuyến có hệ số góc k cho trước
► Gọi M(x ; y )(C) là tiếp điểm 0 0
► Giải pt : f '(x )  k x y 0 0 0
► Áp Dụng (1)  phương trình tiếp tuyến
Tiếp tuyến song song với đường
► Gọi M(x ; y )(C) là tiếp điểm o o
thẳng (d) cho trước : y k x b    d
► Giải pt : f '(x ) k x y 0 d 0 0
► Áp Dụng (1)  phương trình tiếp tuyến
Tiếp tuyến vuông góc với đường
► Gọi M(x ; y )(C) là tiếp điểm 0 0
thẳng (d) trước : y k x b d ► 1
Giải pt : f '(x )    x y 0 k 0 0 d
► Áp Dụng (1)  phương trình tiếp tuyến
Tiếp tuyến đi qua điểm
► Gọi M(x ; y )(C) là tiếp điểm 0 0 (
A x ; y ) (C) cho trước A A ► Tiếp tuyếm tại M là
() : y  y  f '(x ).(x  x ) (1) 0 0 0
► () qua A: thay tọa độ A vào (1) x y  0 0
phương trình tiếp tuyến
y k x c
◙ Lưu ý : hai đường thẳng : 1 1
y k xc  2 2
☻ vuông góc với nhau  k .k  1  , 1 2
☻ song song k k và c c
(Với k , k là hệ số góc) 1 2 1 2 1 2 42
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017
Bài 01 : Viết phương trình tiếp tuyến của đồ thị hàm số 3 2
y x  3x  2
a/ Tại điểm M (2; 2  ) .
b/ Tại điểm có hoành độ x  1  .
c/ Tại điểm có tung độ y  2  .
d/ Tại giao điểm của đồ thị với đường thẳng y x 1.
e/ Tại giao điểm của đồ thị với trục tung.
f/ Tại giao điểm của đồ thị với trục hoành.
g/ Tiếp tuyến có hệ số góc nhỏ nhất ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….…………………………………………… 43
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….…………………………………………… x 1
Bài 02 : Viết phương trình tiếp tuyến của đồ thị hàm số y
tại điểm M 1;0 x  2 1 1 1
A. y    x   1
B. y  3 x   1
C. y   x   1
D. y   x   1 3 3 9 ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 03 : Cho hàm số 3
y x x 1 có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại giao
điểm của (C) với trục tung.
A. y  x 1
B. y  x 1
C. y  2x  2
D. y  2x 1 ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..………………………… 1
Bài 04 : Cho hàm số 3 2 y
x  2x  3x 1 (1) . Phương trình tiếp tuyến của đồ thị hàm số (1) song 3
song với đường thẳng y  3x 1 có dạng y ax b . Tìm giá trị S a b 29 20 19 20 A. B. C. D. 3 3 3 3 ● Giải : 44
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 05 : Tiếp tuyến của đồ thị hàm số 4 2
y  x x  6 song song với đường thẳng d : 6x  y  0 là:
A. y  6x 10 B. y  6  x  7 C. y  6  x 10
D. y  6x  7 ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 06 : Tiếp tuyến của đồ thị hàm số 3 2
y x  3x  2 tại điểm A 1  ; 2   là:
A. y  9x  2
B. y  9x  7
C. y  24x  7
D. y  24x  2 ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 07 : Tiếp tuyến của đồ thị hàm số 3
y x  3x  2 tại các giao điểm với trục hoành có phương trình là
A. y  0 và y  9  x 18
B. y  0 và y  9  x 18
C. y  0 và y  9x 18
D. y  0 và y  9x 18 ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..………………………… x  2
Bài 08 : Gọi A là giao điểm của đồ thị hàm số y
với trục Ox. Tiếp tuyến tại A của đồ thị 2x 1
hàm số đã cho có hệ số góc k là: 5 1 1 5 A. k   B. k C. k   D. k  9 3 3 9 ● Giải : 45
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Bài 09 : Viết phương trình tiếp tuyến của đồ thị hàm số 3
y x  3x  2 , biết tiếp tuyến đó tiếp xúc
với đồ thị hàm số tại điểm M 2;4 . A. y  3  x 10 B. y  9  x 14
C. y  9x 14
D. y  3x  2 ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………….……………………………………………
Bài 10 : Cho hàm số C : y x  2 . Viết phương trình tiếp tuyến với đồ thị C  tại điểm có tung độ bằng 2 .
A. x  4y  3  0 .
B. 4x y 1  0 .
C. x  4y  2  0 .
D. x  4y  6  0 ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………….……………………………………………
Bài 11 : Có bao nhiêu tiếp tuyến của đồ thị hàm số 3 2
y x  6x  6x  2016 song song với đường thẳng y  3  x  2016 . A. 0 B. 1 C. 2 D. 3 ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………….……………………………………………
Bài 12 : Trong các phương trình sau, phương trình nào là phương trình tiếp tuyến của đồ thị 1 y  2x
tại điểm có hoành độ x  1 x
A. y x 1
B. y  2x  2
C. y x  2
D. y x  2 ● Giải : 46
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….…………………………………………… 1
Bài 13 : Cho hàm số 3 2 y
x  2x  3x 1 C  . Tiếp tuyến của đồ thị (C) song song với đường 3
thẳng d : y  3x 1 có phương trình là: 26 29
A. y  3x 1
B. y  3x
C. y  3x  2
D. y  3x  3 3 ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….…………………………………………… x  2
Bài 14 : Phương trình tiếp tuyến của C  : y
tại điểm có hoành độ bằng 2 có là phương x 1 trình nào sau đây
A. y  3x 10 . B. y  3  x 10 . C. y  3  x 10.
D. y  3x 10. ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
Ví dụ 01 : Cho hàm số 4 2
y  x  2x . Viết phương trình tiếp tuyến của đồ thị tại điểm có hoành độ x  2 .
♥ Giải : Đạo hàm 3 y '  4  x  4x ;
Ta có x  2  y  8 
Suy ra hệ số góc của tiếp tuyến tại điểm đang xét là k y '2  2  4.
Phương trình tiếp tuyến của đồ thị là d : y  8  2
 4x  2 hay d : y  2  4x  40.
Vậy tiếp tuyến cần tìm d : y  2  4x  40.
Ví dụ 02 : Cho hàm số 3 2
y  x  3x 1. Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp 1
tuyến đó vuông góc với đường thẳng (d) : y x  2009 . 9 ♥ 1 1
Giải : (d) : y
x  2009 có hệ số góc là ; Gọi M(x0; y0) thuộc (C) là tiếp điểm 9 9
Suy ra hệ số góc của tiếp tuyến của đồ thị tại điểm M là k f ' x  2  3  x  6x 0 0 0 47
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017 1
Tiếp tuyến vuông góc với (d) suy ra f'(x )  1   f'(x )  9  0 0 9 x  1   y  3 2 0 0  3
x  6x  9  0  0 0
x  3  y  1   0 0
Vậy có hai phương trình tiếp tuyến của (C) thoả điều kiện là: y  9
x  6 hay y  9  x  26 x 1
Ví dụ 03 : Cho hàm số y
. Viết phương trình tiếp tuyến của đồ thị hàm số, biết rằng tiếp x 1
tuyến có hệ số góc bằng 2 . ♥ 2
Giải : Gọi M x ; y với x  1
 là điểm thuộc đồ thị. Ta có đạo hàm y '  . 0 0  0 x  2 1 2
Suy ra hệ số góc của tiếp tuyến của đồ thị tại điểm M là k y ' x  . 0  x  2 1 0 2 x  0 Theo giả thiết, ta có
 2  x 1 1  .  2  0 2 0 x   1 x  2   0 0
●Với x  0 , suy ra M 0; 
1 . Phương trình tiếp tuyến là d : y  2 x  0 1. 1   0 ●Với x  2  , suy ra M  2
 ;2. Phương trình tiếp tuyến là d : y  2 x  2  2. 2   0
Vậy có hai phương trình tiếp tuyến cần tìm là d : y  2x 1, d : y  2x  6 . 1 2
Ví dụ 04 : Cho hàm số d : y  3  x  
1  2 . Viết phương trình tiếp tuyến với đồ thị tại giao điểm
của đồ thị và đường thẳng d : y  3  x  5  ♥ 1
Giải : Ta có y '  x22
Gọi Ax ; y  2 , x  2
 là giao điểm của đồ thị với đường thẳng y  2 0 0  0
Suy ra tọa độ điểm Ax  1
 ; y  2 ; Suy ra hệ số góc của tiếp tuyến k y 'x y ' 1   1  . 0    0 0 
Phương trình tiếp tuyến cần tìm là d : y    1 x  
1  2 hay d : y  x 1. 48
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017
Ví dụ 05 : Cho hàm số 3 2
y x  3mx  m  
1 x 1 ( m là tham số thực). Tìm m để tiếp tuyến
của đồ thị hàm số đã cho tại điểm có hoành độ x  1
 đi qua điểm A1;2 . 0 ♥ Giải : Ta có 2
y '  3x  6mx  m   1 Với 3 2 x  1  , suy ra y  1   3m 1   m 1 1  1 2m 1. 0        0
Suy ra hệ số góc của tiếp tuyến k y '  1  4  5 . m
Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ bằng x  1  là: 0
d : y  4  5m. x   1  2m 1.
Theo giả thiết, tiếp tuyến đi qua A1;2 nên    m    5 2 4 5
. 1 1  2m 1  m  . 8 5 Vậy m
là giá trị cần tìm thỏa yêu cầu bài toán. 8 2x  2
Ví dụ 06 : Cho hàm số y f (x) 
. Viết phương trình tiếp tuyến của đồ thị tại giao điểm x 1
của đồ thị với trục tung.  ♥ 4
Giải : Đạo hàm f ' x  
. Gọi A là giao điểm của C  với trục tung (Oy : x = 0) x  2 1  2x  2 y  x  0
Suy ra tọa độ điểm A là nghiệm của hệ phương trình  x 1    A0; 2    y  2  x  0
Suy ra hệ số góc của tiếp tuyến k f '0  4 
Phương trình tiếp tuyến của đồ thị tại A là d : y  4
 x 0  2 hay d : y  4  x  2.
Ví dụ 07 : Cho hàm số 3 2
y  x  3x  2 . Viết phương trình tiếp tuyến của đồ thị biết tiếp tuyến
song song với đường thẳng  : y  9  x  25 .
♥ Giải : Đạo hàm 2 y '  3
x  6x ; Đường thẳng  : y  9
x  25 có hệ số góc là – 9
Gọi M x ; y
là điểm thuộc đồ thị hàm số (hay tiếp điểm) 0 0  49
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017
Suy ra hệ số góc của tiếp tuyến của đồ thị tại điểm M là k f ' x  2  3  x  6x 0 0 0
Do tiếp tuyến song song với đường thẳng  : y  9
x  25 (có hệ số góc là – 9) x  1 
nên y ' x  9   3
x  6x  9   . 0  2 0 0 0 x  3  0 Với x  1
 , suy ra phương trình tiếp tuyến: d : y  9
x 1  2 hay d : y  9  x  7 . 1   0 1
Với x  3, suy ra phương trình tiếp tuyến: d : y  9
x 3  2 hay d : y  9  x  25 2   0 2
(loại (d2) vì đường thẳng này có phương trình trùng với ∆)
Vậy tiếp tuyến cần tìm là d : y  9  x  7 1
☻ Chú ý : đối với tiếp tuyến song song – chúng ta nên loại đi những phương trình trùng với
phương trình đường thẳng đề cho !!!
Ví dụ 08 : Cho hàm số 3 2
y x  3x  4 . Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm
có hoành độ x , biết x thỏa mãn y '  x 1  2x  4. 0  0 0 0
♥ Giải : Gọi M  3 2
x ; y  x  3x  4 là điểm thuộc đồ thị hàm số (tiếp điểm) 0 0 0 0  Ta có đạo hàm 2
y '  3x  6x ; y '  6x  6 .
Theo đề bài, ta có y '  x 1  2x  4  6 x 1  6  2x  4  4x  4  x 1. 0  0  0  0 0 0
Với x  1, suy ra M 1;2 và hệ số góc của tiếp tuyến k y ' x y ' 1  3  . 0    0
Vậy phương trình tiếp tuyến cần tìm là d : y  3  x  
1  2 hay d : y  3  x  5 . 1  2
Ví dụ 09 : Cho hàm số 3 y x x
có đồ thị là C  . Gọi M là điểm thuộc đồ thị C  có 3 3
hoành độ x  2 .Tìm các giá trị của tham số m để tiếp tuyến với C  tại M song song với 9m  5
đường thẳng d : y   2 m  4 x  . 3     ♥ 4 4
Giải : Ta có y(x  2) 
 tọa độ tiếp điểm M 2;
; Tiếp tuyến  với C  tại M có 0   3  3  4 4 14
phương trình : y y '(2). x  2   y  3
 x  2   y  3  x  3 3 3 50
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017 2 m  4  3   2 m 1
Ta có  / /d  9m  5 14    m  1  . Vậy m  1  là giá trị cần tìm   m  1  3 3 1
Ví dụ 10 : Cho hàm số 3 2 y
x x .Tìm tọa độ điểm M thuộc C  sao cho tiếp tuyến của C  3
tại M tạo với hai trục tọa độ một tam giác cân.
♥ Giải : Gọi M x ; y thuộc (C) là tiếp điểm 0 0 
Tiếp tuyến của (C) tại M tạo với các trục tọa độ một tam giác cân  OB
OB OA  tiếp tuyến có hệ số góc k    1  . OA 2
x  2x 1  0 x 1 2
Theo đề ta có : y ' x  1  0 0   0   0  2
x  2x 1  0  x 1  0 0 0  2 2   2   M 1 2;  hay M 1;     3 3    3 
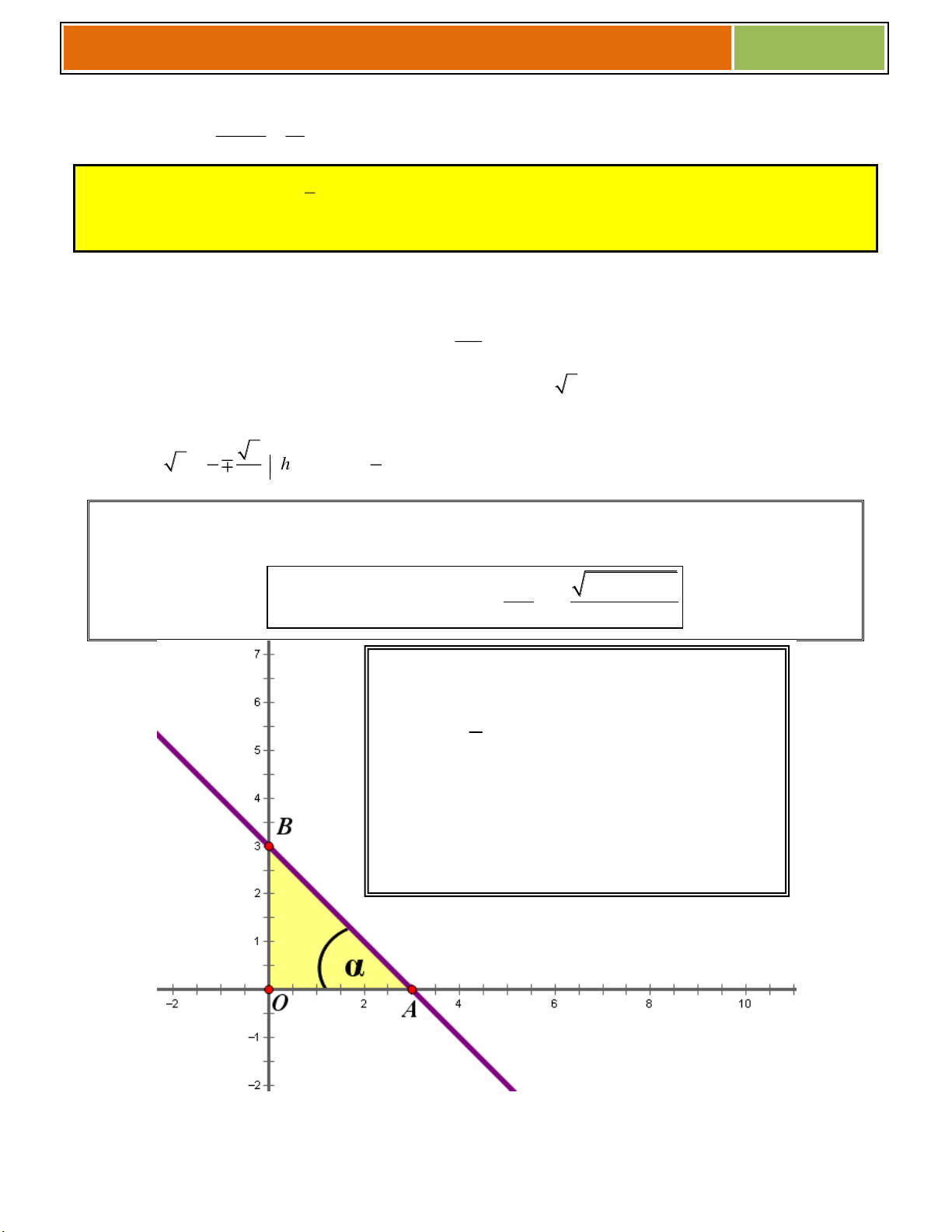
◙ Lưu ý : Tiếp tuyến với (C) và cắt Ox, Oy lần lượt tại 2 điểm A, B.
Gọi α là góc nhọn hợp bởi tiếp tuyến và Ox thì 2 2 OB AB OA k tan      tan BAO     OA OA ♦ Tam giác OAB luôn vuông ♦ 1 SO . A OB OAB 2
♦ Không kể 2 đường thẳng y = kx và y
= kx (vì 2 đường này qua O, không cắt 2 trục được ) 51
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017 x
Ví dụ 11 : Cho hàm số: y
C. Tìm tọa độ điểm M thuộc C sao cho tiếp tuyến của x 1
C tại M tạo với hai trục tọa độ một tam giác cân.
♥ Giải : Gọi M x ; y thuộc (C) là tiếp điểm 0 0  1 Đạo hàm y '      x   0, x 1 2 1
Tiếp tuyến tạo với các trục tọa độ một tam giác cân, thì hệ số góc của tiếp tuyến bằng  1  1   2 OBx 1 0   k    1.  ; Suy ra:
x  0 hoặc x  2.  OA 0  1 0    x   1 (vn) 2 1 0
► Với x  0 , suy ra y  0; tiếp tuyến là y x đi qua gốc tọa độ, không thỏa mãn yêu cầu. 0 0 ► Với x  2,
 suy ra y  2; tiếp tuyến là y x  4, thỏa mãn yêu cầu. 0 0
Vậy, điểm cần tìm là: M  2  ;2 x  3
Ứng dụng (Ví dụ 12 ): Cho hàm số (C) : y
. Phương trình tiếp tuyến với (C) biết tiếp 2 x   1
tuyến cắt trục Ox, Oy lần lượt tại A và B sao cho đường trung trực của AB đi qua gốc tọa độ có hệ số góc là A. k  1 B. k  1  C. Cả A và B D. Không có ♥ Giải :
Đường trung trực của AB đi qua gốc tọa độ
là gì vậy ?????
Ồ ! Vậy hệ số góc tiếp tuyến là OB k    1  OA
Ý nói đó là tam giác vuông
Mà y’ < 0 có nghĩa k < 0 ; Chọn B ! cân Nên : OA = OB đó bạn ! 52
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017
BÀI TẬP TRẮC NGHIỆM PHẦN TIẾP TUYẾN 2 x  2x 10
Câu 1 : Hệ số góc tiếp tuyến của đồ thị hàm số y
tại điểm có hoành độ x  1  là 2 x   1 0 7 3 A.  B.  8 8 5 C.  D. Đáp án khác 8 3 x
Câu 2 : Cho hàm số y
x 1 . Trong tất cả các tiếp tuyến với đồ thị hàm số tại điểm M nằm 3
trên đồ thị hàm số thì hệ số góc tiếp tuyến nhỏ nhất là A. 1  B. 2  C. 3 D. Đáp án khác 1
Câu 3 : Cho hàm số (C) : 3 2 y
x x . Phương trình tiếp tuyến với (C) tại điểm có hoành độ 3 x  1 là 0 1
A. y  x 1
B. y  x  3 1 C. y  3  x  D. y  x 3
Câu 4 : Cho hàm số (C) : 3 2
y x  3x  3x  2 . Phương trình tiếp tuyến với (C) tại giao điểm của
(C) và trục tung có phương trình
A. y  x 1 B. y  2  x  2 C. y  3  x 1 D. y  3  x  2
Câu 5 : Cho hàm số (C) : 3
y x  4x  3. Phương trình tiếp tuyến với (C) tại giao điểm của (C) và
trục tung có tung độ góc là A. 1 B. 2 C. 3 D. 4 2x 1
Câu 6 : Các tiếp tuyến của đồ thị hàm số y  có hệ số góc bằng 5
 lần lượt tiếp xúc đồ thị x  2 hàm số tại A và B
6.1 : tọa độ A và B là A. ( A 0; 2), ( B 1;3) B. ( A 1;7), B(1; 2  ) 2 C. ( A 3;7), B(1; 3  ) D. ( A 1  ;7), B(1; ) 3
6.2 : độ dài AB là A. 2 26 B. 2 13 C. 26 D. 2 21 53
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017 2x  3
Câu 7 : Cho hàm số : y
(C) . Phương trình tiếp tuyến của đồ thị (C) tại điểm có tung độ x 1 bằng 1 là 1 1 1 1 A. y x  B. y x  5 4 5 5 1 3 1 C. y x  D. 5y x  5 5 5
Câu 8 : Cho hàm số : 3 2
y x  3x  2 (C) . Phương trình tiếp tuyến với đồ thị (C) và vuông góc
với đường thẳng  : 3
y x  3  0 có phương trình
A. y  3x  2  0
B. y  3x  2  0 1
C. y  3x  3  0
D. 3y x  2
Câu 9 : Cho hàm số : 3 2
y x  3x (C) . Chọn phát biểu sai :
A. Hàm số nghịch biến trên khoảng 0; 2
B. Hàm số đạt cực tiểu tại x  2
C. Hệ số góc tiếp tuyến tại điểm có hoành độ x  1 là 2  0
D. Đồ thị hàm số đi qua điểm I 1; 2  
Câu 10 : Cho hàm số : 3 2
y x  3x  2 (C) . Phương trình tiếp tuyến với đồ thị (C) và vuông góc
với đường thẳng d : x  9y  3  0 có tung độ góc lần lượt là m và n. Tổng của m và n là A. 18 B. 19 C. 20 D. 21 2x 1
Câu 11 : Cho hàm số : y
(C) . Phương trình tiếp tuyến với đồ thị (C) và vuông góc với x 1
đường thẳng  : y  3x  2  0 có phương trình
A. x  3y  2  0
B. x  3y 13  0
C. y  3x  3  0 1
D. 3y x  7
Câu 12 : Cho hàm số : y f x (C) . Gọi (d) là tiếp tuyến với (C) và cắt Ox, Oy lần lượt tại 2
điểm A, B sao cho tam giác OAB cân tại O thì hệ số góc của (d) lúc này là A. k  1 B. k  1  C. k  0 54
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017 D. k  1 
Câu 13 : Cho hàm số : y f x (C) . Gọi (d) là tiếp tuyến với (C) và cắt Ox, Oy lần lượt tại 2
điểm A, B sao cho OB = 4OA thì hệ số góc của (d) lúc này là 1 A. k  4 B. k   4 C. k  4  D. k  4  
Câu 14 : Cho hàm số : y f x 2x 1 
(C) . Gọi (d) là tiếp tuyến với (C) và cắt Ox, Oy lần lượt x 1
tại 2 điểm A, B sao cho tam giác OA = 4OB thì hệ số góc của (d) lúc này là 1 A. k  4 B. k   4 1 C. k  4  D. k   4
Câu 15 : Cho hàm số : y f x (C) . Gọi (d) là tiếp tuyến với (C) và cắt Ox, Oy lần lượt tại 2
điểm A, B sao cho tam giác OA = k.OB k  0 thì phương trình (d) không thể là :
A. y kx  2
B. y  kx  4 k C. y kx
D. y   x k 2 x  2
Câu 16 : Xác định hệ số góc của d biết d làtiếp tuyến của đồ thị hàm số y  và d cắt hai trục x 1
Ox, Oy lần lượt tại các điểm A, B phân biệt thỏa mãn điều kiệu OB = 3OA. A. 0 B. 3 C. 2 D. 3  x  2
Câu 17 : Có bao nhiêu đường thẳng d thỏa mãn d là tiếp tuyến của đồ thị hàm số y  và d x 1
cắt hai trục Ox, Oy lần lượt tại các điểm A, B phân biệt sao cho OB = 3OA. A. 0 B. 3 C. 2 D. 1 x  2
Câu 18 : Viết phương trình đường thẳng của dbiết d là tiếp tuyến của đồ thị hàm số y  và x 1
d cắt hai trục Ox, Oy lần lượt tại các điểm A, B phân biệt , OB = 3OA. A. d : y  3  x 10 B. d : y  3  x  9 C. d : y  3  x 10 D. d : y  3  x 9 
Câu 19 : Cho đường cong (C) : y f x x 2 
. Khi đó tiếp tuyến của (C) và song song với x  2
đường phân giác của góc phần tư thứ nhất là
A. y x 1; y x  7
B. y x 1; y x  7
C. y x 1; y x  7
D. y x 1; y x  7 55
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017
Câu 20 : Cho đường cong (C) : y f x x 2 
. Tìm các điểm thuộc (C) sao cho tiếp tuyến tại đó x 1 1
có hệ số góc k   3 A. A4;2 B. A 2  ;0
C. A4;2; B 2  ;0 D. Không tồn tại
Câu 21 : Cho đường cong (C) : y f x 3
x 1 và điểm A thuộc (C) có hoành độ xA = 2. Tiếp
tuyến của (C) tại M cắt Oy tại điểm nào sau đây A. M 0;  1 B. M 0;9 C. M 0;  1 D. M 0; 1  5
Câu 22 : Cho đường cong (C) : y f x 3 2
x x  4 và đường thẳng (d) : y x  3. Có bao nhiêu
tiếp tuyến với (C) vuông góc (d) A. 0 B. 1 C. 2 D. 3
Câu 23 : Cho hàm số : 3 2
y x  3x 1 (C) . Phương trình tiếp tuyến với (C) có hệ số góc k = 9 có phương trình
A. y  9x  4 hay y  9x  29
B. y  9x  4 hay y  9x  28
C. y  9x  7 hay y  9x  28
D. y  9x  2 hay y  9x  29  0
Câu 24 : Cho hàm số : 3 2
y  4x mx 1 (C) . Phương trình tiếp tuyến với (C) tại điểm có hoành
độ x0 = 2 có hệ số góc k = 24. Giá trị m là A. 6 B. 3 C. 8 D. 0 y
Câu 25 : Cho hàm số : y f x (C) xác định trên D 3
có đạo hàm cấp 1 tại điểm x = 0 là k = 3.
Phương trình tiếp tuyến với đồ thị hàm số (C) A
tại điểm A trên hình vẽ của đồ thị hàm số (C) là 1 A. y  3x 1 -2 -1 O x 1 2
B. y  3x  2 C. y  3x 1 -1
D. y  3x  2 x
Câu 26 : Cho hàm số y
(C). Tiếp tuyến tại điểm M thuộc (C) có tung độ 1  x  2 A. y  3x 1
B. y  2x  2 56
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017 C. y  3x 1 D. y  2  x 1 x 1
Câu 27 : Cho hàm số y
(C). Tiếp tuyến tại điểm M thuộc (C) có hoành độ bằng 3 x  2 A. y  3  x 13
B. y  2x  2 C. y  3x 1 D. y  3  x 1 4 x
Câu 28 : Cho hàm số 2 y
 2x  3 (C). Tiếp tuyến tại điểm M thuộc (C) có hoành độ bằng 1  4 17 A. y  3  x 13
B. y  3x  4 17 C. y  3x  D. y  3  x 1 4 3 x 2
Câu 29 : Cho hàm số y
x  (C). Số tiếp tuyến với (C) và vuông góc với đường thẳng 3 3
x  3y  0 là A. 1 B. 2 C. 3 D. 4
Câu 30 : Cho hàm số 3 2
y x  3x  2 (C). Hệ số góc tiếp tuyến với (C) tại điểm có hoành độ x = - 3 là A. 12 B. 21 C. 45 D. 54
Câu 31 : Cho hàm số 3 2
y x  3x  2 (C). Trong tất cả các tiếp tuyến với (C) tại điểm M thuộc (C)
thì tiếp tuyến có hệ số góc nhỏ nhất là A. - 3 B. 3 C. 4 D. - 4
Câu 32 : Cho hàm số 3
y x  3x 1(C). Số tiếp tuyến với (C) và vuông góc với đường thẳng
9x y 15  0 là A. 1 B. 2 C. 3 D. 4 4 x 9
Câu 33 : Cho hàm số : y f x 2 
 2x  C . Gọi M là giao điểm của (C) và trục hoành có 4 4
hoành độ dương. Hệ số góc tiếp tuyến tại M là A. 15 B. 15  9 9 C. D.  4 4
Câu 34 : Cho hàm số 4 2
y x mx 1 m (C) . Với mọi giá trị của tham số m thì ta nhận thấy đồ
thị (C) luôn đi qua một điểm K(1;0) cố định . Khi đó tiếp tuyến tại K song song với đường thẳng
y  2x ứng với giá trị 57
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017 A. m  0 B. m  3 C. m  1 D. m  1  1
Câu 35 : Cho hàm số 3 2
y  x  3x (C). Tiếp tuyến với (C) và vuông góc với đường thẳng y x 9 tại các tiếp điểm A. (-1; 4), (3;0) B. (-1; 4), (2;0) C. (-1; 3), (2;0) D. (0; 4), (2;0) x
Câu 36 : Gọi điểm M thuộc đồ thị hàm số y f x 2 1 
(C) có hoành độ x0 không âm và x0 là x 1
nghiệm của phương trình 4. f ' x  3  0 thì phương trình tiếp tuyến tại M là 0  : 3 23 3
A. y   x
B. y   x 1 4 4 4
C. y  x 1 D. y x 1
Câu 37 : Cho hàm số y f x 3 2
x 3x  2x có đồ thị là (C). Phương trình tiếp tuyến tại điểm
I(x0;y0) thuộc (C) thỏa mãn f '  x  0 là 0  A. y  x
B. y  x 1 C. y x 1 D. y x
Câu 38 : Cho hàm số y f x 3 2
x 3x  2x có đồ thị là (C). Phương trình tiếp tuyến tại điểm có
hoành độ bằng -1 là
A. y 11x  2
B. y 11x  3 C. y x  4
D. y 11x  5
Câu 39 : Cho hàm số y f x 3 2
x 3x  2x có đồ thị là (C). Phương trình tiếp tuyến tại điểm có
tung độ bằng 6 là
A. y 11x 12
B. y 11x  3
C. y 11x  4
D. y 11x  27
Câu 40 : Cho hàm số y f x 3 2
x 3x  2x có đồ thị là (C). Trong các phương trình tiếp tuyến
tại giao điểm (C) và trục hoành thì ∆ là tiếp tuyến có hệ số góc nhỏ nhất. Phương trình ∆ là
A. y  2x  4
B. y  x 1
C. y  x  4 D. y  2x 2x
Câu 41 : Cho hàm số y f x 3 2 
x x có đồ thị là (C). Trong các phương trình tiếp tuyến 3
với (C) thì ∆ là tiếp tuyến có hệ số góc nhỏ nhất. Phương trình ∆ là x A. y    4 2 58
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017 x 7 B. y    2 12
C. y  x  4 D. y  2x
Câu 42 : Cho hàm số y f x    x2 2 2
.x có đồ thị là (C). Hệ số góc tiếp tuyến tại gốc tọa độ O là. A. 0 B. 1 C. 2 D. 3
Câu 43 : Cho hàm số y f x    x2 2 2
.x có đồ thị là (C). Hệ số góc tiếp tuyến tại điểm có hoành độ x = 3 là. A. 20 B. 22 C. 24 D. 26
Câu 44 : Cho hàm số y f x    x2 2 2
.x có đồ thị là (C). Hệ số góc tiếp tuyến tại điểm có hoành độ x = 4/3 là. 4 A. B. 0 3 32 15 C.  D. 27 17
Câu 45 : Cho hàm số y f x    x2 2 2
.x có đồ thị là (C). Hệ số góc tiếp tuyến tại điểm có hoành độ x = 2 là. 4 A. B. 0 3 32 15 C.  D. 27 17 x
Câu 46 : Cho hàm số y f x 1 
có đồ thị là (C). Hệ số góc tiếp tuyến tại điểm có hoành độ x 1 x = 2 là. A. 1 B. 0 C. 3 D. 2  mx
Câu 47 : Cho hàm số y f x 1 
có đồ thị là (C). Với giá trị nào của tham số m thì tiếp x m  2
tuyến với (C) tại điểm có hoành độ x = 1 vuông góc với đường phân giác của góc phần tư thứ nhất. A. 0 B. 2 C. Cả A và B đều đúng D. Cả A và B đều sai 59
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017 x m 1
Câu 48 : Cho hàm số y f x 3 2 
x  có đồ thị là (C). Với giá trị nào của tham số m thì 3 2 3
tiếp tuyến với (C) tại điểm có hoành độ x = -1 song song với đường thẳng y = 5x A. 0 B. 2 C. 4 D. 6
Câu 49 : Cho hàm số y f x có đồ thị là (C) như hình 1.
Hệ số góc tiếp tuyến tại điểm A là A. 0 B. 2 C. 4 D. 6 3 x
Câu 50 : Cho hàm số sau (C) : 2 y
 2x  3x  5 . Tiếp 3
truyến tại điểm cực tiểu của đồ thị hàm số
A. Song song với đường thẳng x = 1
B. Có hệ số góc là dương C. Có hệ số góc là 1 D. Vuông góc với Oy
Câu 51 : Cho đồ thị hàm số 3 2
y x  2x  2x (C) . Gọi x , x là hoành độ các điểm M, N trên (C), 1 2
mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y  x  2017 . Khi đó x x  1 2 4 4 A. B. 3 3 1 C. D. 1  3
Câu 52 : Cho đồ thị hàm số y f x 3 2
x 3x  2 (C). Gọi x , x là hoành độ các điểm A, B trên 1 2
(C), mà tại đó tiếp tuyến của (C) có hệ số góc là – 3. Khi đó 2 2 x x  1 2 A. 5 B. 1  C. 2 D. 3
Câu 53 : Cho đồ thị hàm số y f x 3 2
x 3x  2 (C). Gọi x , x là hoành độ các điểm H, I trên 1 2 1
(C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y   x  2017 . Khi đó 3 3 x x  24 1 2 A. 55 B. 56 C. 57 D. 58 x
Câu 54 : Cho đồ thị hàm số y f x 2 1  (C). x 1 60
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017
Gọi x , x là hoành độ các điểm H, F trên (C), mà tại đó tiếp tuyến của (C) song song với đường 1 2 1 13
thẳng y   x
. Khi đó  x x  1 2 2 3 7 A. 7 B. 2 C. 20 D. 4
Câu 55 : Cho đồ thị hàm số y f x 3
x 3x 1 (C). Gọi x , x là hoành độ các điểm E, F trên 1 2
(C), mà tại đó tiếp tuyến của (C) song song với đường thẳng y  9x  4 . Khi đó 3 3 x x  1 2 A. 0 B. 56 C. 5 D. 5 x
Câu 56 : Cho đồ thị hàm số y
(C). Gọi x , x là hoành độ các điểm A, B trên (C), mà tại đó x 1 1 2
tiếp tuyến của (C) có hệ số góc là – 1. Khi đó 3 3 x x  1 2 A. 8 B. 6 C. 5 D. 5 x
Câu 57 : Cho đồ thị hàm số y
(C). Gọi y , y là tung độ các điểm A, B trên (C), mà tại đó x 1 1 2
tiếp tuyến của (C) có hệ số góc là – 1. Khi đó 3 3 y y  1 2 A. 8 B. 6 C. 5 D. 5
Câu 58 : Cho hàm số 3 2
y  x  3x 1 (1). Hệ số góc tiếp tuyến k của đồ thị (C) tại điểm thuộc
(C) có hoành độ bằng 1 có giá trị đối là A. 3 B. 3  1 1 C. D.  3 3
Câu 59 : Cho hàm số 3 2
y  2x  3(m 1)x  6mx (1) , với m là tham số thực. Với giá trị nào của tham
số m thì đồ thị hàm số (1) có hai điểm cực trị A và B sao cho đường thẳng AB vuông góc với đường thẳng y = x + 2 A. m  0 B. m  2 C. Cả A và B đều sai D. Cả A và B đều đúng 2x 1
Câu 60 : Cho hàm số y
có đồ thị là (C). Gọi M là điểm thuộc (C) có tung độ bằng 5. Tiếp x 1
tuyến của (C) tại M cắt các trục tọa độ Ox và Oy lần lượt tại A và B thì diện tích tam giác OAB là 121 A. 3 B. 6 2 12 C. D. 3 7 61
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017
Câu 61 : Cho hàm số 4 2
y x mx  m  
1 có đồ thị là (C) với m là tham số. Gọi A là điểm thuộc
(C) có hoành độ là 1. Tiếp tuyến của (C) tại A có hệ số góc là 2 ứng với giá trị m bằng A. 3 B. 1  C. 2 D. 0 2x 1
Câu 62 : Cho hàm số y
có đồ thị là (C). Gọi M là điểm thuộc (C) có hoành độ bằng 0. Gọi x 1
d là tiếp tuyến với (C) tại M. Chọn đáp án đúng
A. Đường thẳng d vuông góc với IM
B. Đường thẳng d song song với IM C. A và B đều sai D. A đúng - B sai x  3
Câu 63 : Cho hàm số y
có đồ thị là (C). Gọi M là điểm thuộc (C) mà tại đó tiếp tuyến 2 x   1
với đồ thị (C) cắt Ox, Oy lần lượt tại A và B sao cho đường trung trực của AB đi qua gốc O.
Phương trình tiếp tuyến tại M là 3 4
A. y  x
B. y  x  2 5 C. A đúng, B sai D. A và B đều đúng 2x
Câu 64 : Cho hàm số y
có đồ thị là (C). Gọi M là điểm thuộc (C) mà tại đó tiếp tuyến với x  2
đồ thị (C) cắt Ox, Oy lần lượt tại A và B sao AB OA 2
Khi đó hệ số góc tiếp tuyến tại M là : A. 1  B. 1 C. A đúng, B sai D. A sai, B đúng 2x 1
Câu 65 : Cho hàm số y
(C). Tiếp tuyến với đồ thị (C) cắt Ox, Oy lần lượt tại A và B sao x 1
cho OA = 4OB có phương trình là : 1 5 1 13
A. y   x
B. y   x  4 4 4 4 C. A, B đều sai D. A, B đều đúng.
Câu 66 : Cho hàm số 3 2
y  2x  3x 1 có đồ thị C  . Điểm trên C  có hệ số góc tiếp tuyến tại đó nhỏ nhất là  1   1 1  A. 0  ;1 . B. 1;0 . C.  ;0   . D. ;   .  2   2 2 
Câu 67 : Cho đường cong (C) : 3 2
y x  3x  3x 1 . Phương trình tiếp tuyến của (C) tại giao điểm của (C) và Oy là A. y  8x 1 B. y  3x 1 62
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIẾP TUYẾN 2017 C. y  8  x 1 D. y  3x 1
Câu 68 : Cho đường cong (C) : 4 2
y x  2x 1. Phương trình tiếp tuyến của (C) tại điểm cực đại là A. y  1 B. y  3x 1 C. y  2 D. y x 1 x
Câu 69 : Cho đường cong (C) : y f x 1 
. Tiếp tuyến với đường cong (C) tại điểm M x 1
thuộc (C) có hoành độ xM = 2 chắn trên hai trục tọa độ một tam giác có diện tích bằng 49 9 A. (đvdt) B. (đvdt) 2 4 1 49 C. (đvdt) D. (đvdt) 2 4 3 x 3 1
Câu 70 : Cho hàm số : 2 y
x  3x  (C) . Phương trình tiếp tuyến với đồ thị (C) và vuông 2 4 2
góc với đường thẳng  8 : y x 1 27 có phương trình 27 9 27 9 A. y   x  B. y   x  8 16 8 17 8 1 C. y x  3
D. 8y  27x  27 2 3 2x Câu 71 : Cho hàm số 2 y  
 x  4x  2 , gọi đồ thị của hàm số là (C). Viết phương trình tiếp 3
tuyến của (C) có hệ số góc lớn nhất 9 25 9 A. y  x 
B. y  x  2 12 17 2 1 C. y x  3 D. 2y  9x  9 2 2x
Câu 72 : Phương trình tiếp tuyến với đồ thị : y
và có hệ số góc của tiếp tuyến bằng  2. x 1 25 A. y  2  x  B. y  2  x 8 12 C. y  2  x D. Cả B và C 2x
Câu 73 : Phương trình tiếp tuyến với đồ thị : y
và vuông góc với đường thẳng x 1
(  ): 9x  2y +1=0 có phương trình 2 25 2 4 A. y   x 
B. y   x  9 12 9 9 2 32
C. y   x  D. Cả B và C 9 9 63
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017
PHẦN 7 : SỰ TƯƠNG GIAO ĐỒ THỊ HÀM SỐ
☺ Lý Thuyết : Cho hai hàm số y f (x) có đồ thị là (C) và y g(x) có đồ thị là (C’). Muốn xét sự
tương giao của 2 đồ thị trên ta xét phương trình hoành độ giao điểm (*)
số nghiệm của (*) là số giao điểm của 2 đồ thị C) và (C’)
Phương pháp chi tiết : Cho y f x C và y g x C . 2  1 
Để tìm giao điểm của C và C , ta làm như sau: 2  1 
♥ Bước 1: Tìm hoành độ giao điểm. Hoành độ giao điểm của C và C là nghiệm của phương 2  1  trình
f x  g x . *
Phương trình * được gọi là phương trình hoành độ giao điểm của C và C . 2  1 
♥ Bước 2: Tìm giao điểm. Nếu x là một hoành độ giao điểm thì x ; f x
(hoặc  x ; g x ) là 0  0 0  0 0
một giao điểm của C và C . 2  1 
☻Chú ý: Để giải các bài toán loại này, ta rất hay sử dụng định lý Vi-ét đảo:
Nếu x , x là các nghiệm của phương trình bậc hai 2
ax bx c  0 ( a  0 ) 1 2 b c
thì x x   x .x   1 2 và a 1 2 a ☻Nhận xét:
+ Hai đồ thị hàm số có giao điểm  phương trình hoành độ giao điểm có nghiệm.
+ Số giao điểm của hai đồ thị hàm số bằng số nghiệm của phương trình hoành độ giao điểm.
☻Chú ý : số α không l| nghiệm của phương trình g(x) = 0  g()  0 Ví dụ 01 : Cho 3 2
y x  2x x  5 C
và hàm số y  7x C . Hãy xác định các giao điểm của hai 2  1 
đồ thị C và C . 2  1  64
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017
♠ Giải : Xét phương trình hoành độ giao điểm của C và C : 2  1   x 1   3   29 3 2
x  2x x  5  7x   x   2
1 x  3x  5  0  x   2   3   29 x   2
( lƣu ý : thay tọa độ x v|o (C2) : y  7x )
Vậy hai đồ thị đã cho có ba giao điểm:  3   29 2  1 7 29   3   29 2  1 7 29  M 1;7 , M  ;  , M  ;  . 1   2     2 2   3 2 2   Ví dụ 02 : Cho 3
y x  4mx  2 C và 2
y  3x  4m C . 2  1 
Biện luận số giao điểm của C và C . 2  1 
♠ Giải : Xét phương trình hoành độ giao điểm của C và C 2  1  3 2
x  4mx  2  3x  4m   1 x 1  2
(x 1)(x  2x  4m  2)  0   . 2
x  2x  4m  2  0 
2 ; '  4m3
Số giao điểm của C và C
bằng số nghiệm của phương trình   1 . 2  1  Do đó : ♥ 3
Với :   0  m   : 2 vô nghiệm   
1 có nghiệm duy nhất ( x  1) 4
 C và C có một giao điểm. 2  1  ♥ 3
Với :   0  m   : 2 trở thành x x     x  2 2 2 1 0 1  0  x 1 . 4
Trong trường hợp này,  
1 cũng có nghiệm duy nhất ( x  1)  C và C có một giao 2  1  điểm. 65
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017 ♥ 3 3
Với :   0  m   : 2 có hai nghiệm phân biệt. Ta thấy t   1  4
m  3  0 m     1 4 4
không phải là nghiệm của 2   
1 có ba nghiệm phân biệt  C và C có ba giao điểm. 2  1  Kết luận: 3 m   : C và C
có một giao điểm. 2  1  4 3 m   : C và C có ba giao điểm. 2  1  4
Ví dụ 03 (Trích đề thi ĐH Khối A - 2010 : Cho hàm số 3 2
y x  2x  1 mx m C  . Tìm m để
C cắt trục hoành tại 3 điểm phân biệt có hoành độ là x , x , x sao cho 2 2 2
x x x  4 1 2 3 1 2 3
♠ Giải : Xét phương trình hoành độ giao điểm của đồ thị C của hàm số với trục hoành ( y  0): 3 2
x  2x  1 mx m  0   1 x 1  x3  x   2
1 x x m  0   2
x x m  0   t ( x)
C cắt trục hoành tại ba điểm phân biệt   
1 có ba nghiệm phân biệt   0  
t x có hai nghiệm phân biệt khác 1  t 1  0     b       1   x x 1  1 2  1 4m 0 m   a  
4 .(*) Theo định lý Vi-ét, ta có:  . m  0  cm  0
x x   m 1 2  a
Do đó: x x x   x x 2 2 2 2
 2x x 1 2  2m ; 2 2 2
x x x  4  2  2m  4  m  1 1 2 3 1 2 1 2 1 2 3
(thỏa mãn điều kiện (*))
Vậy đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt có hoành độ x , x , x sao cho 1 2 3 1 2 2 2
x x x  4 khi và chỉ khi 
m 1, m  0 . 1 2 3 4 x  3
Ví dụ 04 : Cho hàm số y
C.Chứng minh rằng với mọi giá trị của m , đường thẳng x 1
y  2x m luôn cắt C  tại hai điểm phân biệt M và N . Xác định m sao cho độ dài MN là nhỏ nhất.
♠ Giải : Phương trình hoành độ giao điểm của C và đường thẳng y  2x m : 66
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017
x  3  2x  ;
m x    1
x  3  x  
1 2x m(vì x  1
không là nghiệm của phương trình) x 1 2
 2x  m  
1 x m  3  0 *
Ta có   m  2  m    m m   m  2 2 1 8 3 6 25 3 16  0, m  
Vậy đường thẳng y  2x m luôn cắt C  tại hai điểm phân biệt M và N .
Vì M và N là điểm chung của đường thẳng và C  nên ta gọi M x ;2x m , N x ;2x m trong 2 2  1 1 
đó x , x là hai nghiệm của phương trình * . 1 2 m 1 m  3
Theo định lý Vi-et, ta có x x   và x x  . 1 2 2 1 2 2 2 2 Ta có 2 2
MN   x x  4 x x  5x x  5 x x  4x x  2 1   2 1 2 1   2 1 1 2   2  m 1    5 5   2   m3 
m32  20  2 5.  2    4
Dấu '  ' xảy ra khi và chỉ khi m  3 .
Vậy m  3 thì MN có độ dài nhỏ nhất bằng 2 5 .
Cách giải trên quá hay !
Nhưng để làm tự luận thôi
Khi làm trắc nghiệm chắc em chết
Thì giải cách khác thôi Bình tĩnh !!!!!
Khi gặp h|m số bậc 1/1 giao với đường thẳng y = kx + r
Ta xét nhanh phương trình hoành độ giao điểm và tính đƣợc ∆ = b2 – 4ac
Đây là công thức sưu tầm từ thầy Cƣờng (H| Nội) và chứng minh lại ! 67
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017  2k  1 AB  . 2 a
k là hệ sốc góc của đường thẳng y = kx + r
a là của phương trình hoành độ giao điểm khi đã đưa về ax2 + bx + c = 0
Vậy ABmin khi ∆min  2k  1 AB  . Hay ta sẽ có min 2 min a Vô l|m liền !!
♠ Ta đi từ chỗ n|y : Phương trình hoành độ giao điểm của C và đường thẳng y  2x m : x  3  Chú ý em 2x  m; x    1  x  3  x   1 2x  m x 1 này nha! 2  2x  m   1 x  m  3  0 *
Gi{o viên cần file word hoặc học sinh cần file đ{p
{n xin vui lòng liên hệ trực tiếp Ta có   m  2 1  8m  3 2
 m  6m  25Qua facebook/zalo/ đt : 0914449230
 m  32 16 16  0, m  
∆min = 16 khi m = 3 Hệ số a = 2 Khi đó ta ∆min = 16
LIỆT KÊ CÁC CON SỐ VI DIỆU k = 2  2k  1  22  1 Suy ra MN  .  .16  2 5 min 2 min 2 a 2 68
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017 ☻ x
Ứng dụng 1: Cho hàm số y f x 2 
có đồ thị là (C). Tìm m để đường thẳng (d) : y = x x  2
+ m cắt (C) tại hai điểm phân biệt A và B sao cho độ dài đoạn AB ngắn nhất.
♠ Ta đi từ chỗ n|y : 2x
Phương trình hoành độ giao điểm (C) và (d) :  x m x  2 Đưa về 2
x  m  4 x  2m  0
Ta có   m  2 2 4
8m m 16 16  0, m  
∆min = 16 khi m = 0 Hệ số a = 1 Khi đó ta ∆min = 16
LIỆT KÊ CÁC CON SỐ VI DIỆU k = 1 2 k   1  21  1 AB  .  .16  4 2 min 2 min 2 a 1  ☻ x
Ứng dụng 2 (học sinh tự l|m) : Cho hàm số y f x 2 1 
có đồ thị là (C). Tìm m để x 1
đường thẳng (d) : y = – x + m cắt (C) tại hai điểm phân biệt A và B sao cho độ dài đoạn AB ngắn nhất.
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................  2k  1 Đ{p số AB  .  2 2 min 2 min a Khi m = 1
☻ Ứng dụng 3 (học sinh tự l|m) : Cho hàm số y f x 2x 1 
có đồ thị là (C). Tìm m để x  2
đường thẳng (d) : y = – x + m cắt (C) tại hai điểm phân biệt A và B sao cho độ dài đoạn AB ngắn nhất. 69
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................
.......................................................................................................................................  2k  1 Đ{p số AB  .  2 6 min 2 min a Khi m = 0
☻ Ứng dụng 3 (học sinh tự l|m) : Cho hàm số y f x x 2 
có đồ thị là (C). Giá trị tham số x 1
m để đường thẳng (d) : y = – x + m cắt (C) tại hai điểm phân biệt A và B sao cho độ dài đoạn AB ngắn nhất là A. m = 2 B. m = 0 C. m = 1 D. m = 4
---------------------------------------------------------------
Ví dụ 05 : Cho hàm số 3 2
y x  3x 1 Xác định m để đường thẳng y mx 1 cắt đồ thị tại ba điểm phân biệt.
♠ Giải : Phương trình hoành độ giao điểm của đường thẳng và đồ thị là: x  0 3 2
x  3x 1  mx 1 (1)  x  2
x  3x m  0  g   x 2
x  3x m  0
Đường thẳng y mx 1 cắt đồ thị tại 3 điểm phân biệt
 phương trình (1) có 3 nghiệm phân biệt m  0   0     g m 0 
g x  0 có hai nghiệm phân biệt khác 0       . g  0 9  0 9   4m  0 m    4 9
Vậy   m  0 là giá trị cần tìm. 4
Ví dụ 06 : Cho hàm số 3 2
y x  3x 1. Tìm m để đường thẳng d : y  1 mx cắt đồ thị của hàm
số tại ba điểm phân biệt.
♠ Giải : Phương trình hoành độ giao điểm của đường thẳng d và đồ thị hàm số x  0 3 2
x  3x 1  1 mx 3 2
x  3x mx  0  x 2
x  3x m  0  g   x . 2
x  3x m  0
Đường thẳng d cắt đồ thị của hàm số tại ba điểm phân biệt khi và chỉ khi phương trình   0     g 9 4m 0 9
g x  0 có 2 nghiệm phân biệt khác 0        . g   m 0 0  0 m  0 4 70
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017 9 Vậy với 0  m
thỏa mãn yêu cầu bài toán. 4 x  2
Ví dụ 07 : Cho hàm số y
C. Tìm m để đường thẳng d: y x m cắt đồ thị C tại x 1 hai điểm phân biệt.  ♠ x 2
Giải : Phương trình hoành độ giao điểm của C  và d  là
x m ;x   1 x 1
x  2  x mx  
1 (vì x  1 không là nghiệm của phương trình)  g x 2
x 2 mx m  2  0.   *
Đường thẳng d  cắt C  tại hai điểm phân biệt khi và chỉ khi phương trình * có hai m  2 nghiệm phân biệt 2
  0  m  4  0  . g  m  2  Vậy m  2
 hoặc m  2 thỏa mãn yêu cầu bài toán.
Lƣu ý : vì đã có câu “vì x  1 không là nghiệm của phương trình” nên ta
không cần xét phương trình (*) có hai nghiệm khác 1 nữa mà chỉ cần có hai nghiệm phân biệt. 2x  2
Ví dụ 08 : Cho hàm số y
C. Tìm m để đường thẳng 2x 1
d: y  2mx m1 cắt đồ thị C tại hai điểm phân biệt.
♠ Giải : Phương trình hoành độ giao điểm của C và d  là 2x  2  1 
 2mx m 1 ; x     2x 1  2   1
2x  2  2mx m   1 .2x   1 (vì x  
không là nghiệm của phương trình) 2  g x 2
 4mx  4mx m 1 0   *
Đường thẳng d  cắt C  tại hai điểm phân biệt khi và chỉ khi phương trình * m  0
có hai nghiệm phân biệt    m  0  '  4m  0  g
Vậy m  0 thỏa mãn yêu cầu bài toán.
Ví dụ 9 : Cho hàm số 4 2
y x mx m 1 (1) . Với giá trị nào của tham số m thì đồ thị hàm số (1)
cắt trục hoành tại 4 điểm phân biệt ? A. m B. m  1
C. m1; \  2 D. m  1 71
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017
Ch}m ngôn “sống TẠM” khi l|m b|i trắc nghiệm l| : ◙ ĐÁP ÁN LÀ ĐỀ
◙ phƣơng ph{p BÓC ĐẠI
Tuy nhiên để l|m đƣợc c}u n|y ngo|i ch}m ngôn đó ra c{c em
còn phải nắm kiến thức cơ bản của h|m số n|y đã !!!
Ví dụ nhƣ b|i n|y ta phải đặt 2 t x  0
Đưa về phương trình hoành độ giao điểm với Ox : 2
0  t mt m 1
Và để cắt được tại 4 điểm thì phải có 4 nghiệm đối với phương trình theo x
và hai nghiệm phân biệt dương đối với phương trình theo t
► Bóc đại m = 1 của đ{p {n B ra thế vào thì 2 0  t 1.t
Bấm máy hay nhẫm đều thấy phương trình này có nghiệm bằng 0 !!! (bỏ qua)
► Bóc đại m = 0 < 1 của đ{p {n D ra thế vào thì 2 0  t
Bấm máy hay nhẫm đều thấy phương trình này có 1 nghiệm bằng 0 !!! (bỏ qua)
► Bóc đại m = 3 của đ{p {n C ra thế vào thì 2
0  t  3t  2
Bấm máy hay nhẫm đều thấy phương trình này có 2 nghiệm dương là 1 và 2
(không bỏ qua nữa (^.^)!) Đ{p {n C nhé 2 2  x 1
B|i 01 : Tìm tọa độ giao điểm của đồ thị (C) : y
y  x  2x  và đường thẳng ( ) : 1 1 A. ( 1  ;1) . B. (0;1) . C. ( 1  ;2) . D. (2;3) . ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..………………………… x 1
B|i 02 : Cho đồ thị (C): y
d y x m . Tìm tất cả các giá trị m để d cắt (C)
x  và đường thẳng : 2 2
tại 2 điểm A, B phân biệt. A. m  1  . B. m \  1  ;  0 . C. m . D. 1   m  0 ● Giải : 72
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
B|i 03 : Đồ thị hàm số 4
y  x  m   2 2
2 x  2m  3 cắt trục hoành tại 4 điểm phân biệt khi  3  3 3 m   m  A. m   . B.  2 . C.  2 . D. m  1  . 2 m  1  m  1  ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
B|i 04 : Giao điểm của đường thẳng y  2
x  3 và đồ thị hàm số 3 2
y x  6x  7x 1 là hai điểm có tọa độ A. 1;  1  và 4;5 . B. 1;0 và 0;4 . C. 1  ;1 và 4; 5   . D. 1;4 và 4  ;1 . ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
B|i 05 : Cho hàm số 3
y x x có đồ thị là C  . Số giao điểm của C  với trục hoành là A. 2 . B. 1. C. 3 . D. 4 . ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….…………………………………………… 73
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017
B|i 06 : Cho hàm số   4      2 : 2 1  2 1 m C y x m x m
. Tìm m để  m
C  cắt Ox tại bốn điểm phân 1 1
biệt. A.   m  0 . B. m   . C. m  0 . D. m  1  . 2 2 ● Giải :
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
B|i 07 : Số giao điểm của đường cong 4 2
y x 10x trục hoành là A. 1. B. 2 . C. 3 . D. 0 . ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
B|i 08 : Xác định tất cả các giá trị của tham số m để đường thẳng y mx  2 cắt đồ thị C 3 2
: y x  3x  2 tại ba điểm phân biệt 9 9 9 A.   m  0 B.   m . C.   m . D. Kết quả khác. 4 4 4 ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
B|i 09 : Tổng các hoành độ giao điểm của đồ thị d  : y  2x  5 và C 3 2
: y x  3x 1 là A. 0 . B. 1. C. 2 . D. 3  . ● Giải : 74
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
B|i 10 : ố giao điểm của hai đường cong 3 2
y x x  2x  3 và 2
y x x 1. A. 0 . B. 1. C. 3 . D. 2 . ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….…………………………………………… x 1
B|i 11 : Giá trị của m để đường thẳng y  2x m cắt đường cong y
tại hai điểm phân biệt x 1 là A. m  1. B. m  0 . C. m  0 . D. Một kết quả khác. ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
B|i 12 : Số điểm chung của đồ thị hàm số 4 2
y x  4x 1 và đường thẳng y  3  là A. 4 . B. 2 . C. 0 . D. 3 . ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….…………………………………………… x 1
B|i 13 : Giao điểm của đường thẳng y  2x  3 và đồ thị hàm số y
là điểm M và N . Khi 3x 1
đó hoành độ trung điểm I của MN có giá trị bằng 5 2 A. 0 . B. . C. . D. 1. 6 3 ● Giải : 75
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….…………………………………………… 2x 1
B|i 14 : Tìm m để đường thẳng y mx  
1  2 cắt đồ thị hàm số y
tại hai điểm phân biệt. x 1 3 A. m  0 . B. m  0 .
C. m  0 hoặc m  . D. 0  m  3. 2 ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
B|i 15 : Tìm tất cả các giá trị thực của m để C 4 2
: y x x và P 2
: y x m  2 cắt nhau tại bốn điểm phân biệt 1 A. 3   m  1  . B. 1   m 1. C. 1 m  2 . D.  m  0 . 4 ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………
………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….…………………………………………… 2x 1
B|i 16 : Tọa độ giao điểm của đồ thị hàm số y
với đường thẳng y x  2 là: 2x 1 76
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017  3 1   1      A.  ; &   1;3 B.  ;0 &   1;3 C.   5 0; 2 & 2;   D.   5 1;1 & 2;    2 2   2   3   3  ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..………………………… 2x 1
B|i 17 : Gọi A, B là giao điểm của đồ thị hàm số y
với đường thẳng y x  2 . Độ dài AB x  2 bằng: A. AB 1 B. AB  4 2 C. AB  2 D. 2 2 ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….…………………………………………… 2x  4
B|i 18 : Gọi M, N là giao điểm của đường thẳng y x 1và đường cong y  . Khi đó hoành x 1
độ trung điểm của đoạn MN bằng: 5 5 A. 1 B. 2 C. D.  2 2 ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
B|i 19 : Biết đồ thị hàm số 3 2
y x  3x 1 với đường thẳng y  4x 1 cắt nhau tại 3 điểm A0;  1 , ,
B C . Độ dài đoạn thẳng BC là: A. 15 B. 5 17 C. 20 D. 5 33 ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..………………………… 77
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017
B|i 20 : Biết đồ thị hàm số 3
y x  3x 1 với đường thẳng y x 1 cắt nhau tại 3 điểm A0;  1 , , B C
. Tính diện tích tam giác MBC biết M 2;  1 . A. 4 B. 4 2 C. 8 D. 16 ● Giải :
…………………………………………………………………………………………….…………………………………………… 2 x  2x  3
B|i 21 : Gọi A là giao điểm của đồ thị hàm số y
với đường thẳng y x 1 Tính độ dài x 1 OA: A. 1 B. 2 C. 5 D. 13 ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
B|i 22 : Biết đồ thị hàm số 4 2
y x  4x  3 với đường thẳng y  3 cắt nhau tại 3 điểm A0;3, , B C .
Tính diện tích tam giác OBC . A. 1 (đvdt) B. 2 (đvdt) C. 4 (đvdt) D. 6 (đvdt) ● Giải :
…………………………………………………………………………………………….……………………………………………
…………………………………………………………………………………
………………………...…..…………………………
…………………………………………………………………………………………….……………………………………………
BÀI TẬP TRẮC NGHIỆM PHẦN SỰ TƢƠNG GIAO
C}u 1 : Cho đường cong (C) có phương trình y f x 3 2
x x 1 và đường thẳng (d) : y  x . (C)
và (d) cắt nhau tại bao nhiêu điểm ? A. 0 B. 1 C. 2 D. 3 2x 1
C}u 2 : Cho hàm số y
có đồ thị là (C). Giao điểm của (C) và đường thẳng y = 5 có tọa độ x 1 A. 2;5 B.  6  ;5 C. 7;5 D.  2  ;5 x
C}u 3 : Cho đường cong (C) có phương trình y f x 2  . x  3 78
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017
Tọa độ giao điểm M của (C) và trục hoành là A. 0; 2 B.  6  ; 2   C. 2;0 D.  2  ;0 x
C}u 4 : Cho đường cong (C) có phương trình y f x 2 2 
. Tọa độ giao điểm N của (C) và 4x  3 trục tung là  2   2  A. 0;    B. 0;    3   3  C. 2;0 D.  2  ;0
C}u 5 : Số giao điểm của đường cong (C) có phương trình    4 2 y
f x  x x và trục hoành là A. 0 B. 1 C. 2 D. 3
C}u 6 : Cho đường cong (C) có phương trình 3 2
y  x  3x  4 . Tọa độ giao điểm A của (C) và đường thẳng y = 4 là A1;4 A0;4 A.  B.  A   3  ;4 A   3  ;4 A0;4 A1;4 C.  D.  A   1  ;4 A  2;4  x
C}u 7 : Cho đường cong (C) có phương trình y f x 2 
. Đường thẳng (d) : y  7x 10 cắt đồ x  2
thị (C) tại hai điểm phân biệt A, B. Độ dài AB 55 55 2 A. AB  B. AB  7 7 55 2 55 3 C. AB  D. AB  3 7
C}u 8 : Cho hàm số y f x    x2 2 2
.x có đồ thị là (C).
Số giao điểm của (C) và parabol (P) : 2 y x là A. 0 B. 1 C. 2 D. 3
C}u 9 : Cho đường cong (C) (hình vẽ bên)
có phương trình y f x và đường thẳng (d) : y  2
9.1 (C) và (d) cắt nhau tại bao nhiêu điểm ? A. 0 B. 1 79
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017 C. 2 D. 3
9.2 Tọa độ giao điểm đó là....................và..................... x  2
C}u 10 : Cho hàm số y
có đồ thị là (C). Phát biểu nào sau đây là sai ? x 1
A. Hàm số luôn tăng trên từng khoảng xác định.
B. Đồ thị hàm số cắt trục hoành tại điểm J 2;0
C. Điểm M 0;2 nằm trên hàm số D. Đạo hàm D  \   2 2x 1
C}u 11 : Cho hàm số y
(C) và đường thẳng (d) : y  x m . Tìm khẳng định đúng. x 1
A. Hàm số luôn giảm trên từng khoảng xác định.
B. (C) và (d) không có giao điểm
C. Hệ số góc tiếp tuyến tại giao điểm (C) và Oy là k = 9
D. (C) luôn cắt (d) tại hai điểm phân biệt A và B x
C}u 12 : Cho hàm số y
(C) và đường thẳng (d) : y  1
 . Tìm khẳng định đúng. x  2
A. Hàm số luôn tăng trên từng khoảng xác định.
B. (C) và (d) có giao điểm là M 1;  1
C. (C) và (d) có giao điểm là M 3;  1
D. (C) và (d) không có giao điểm 2x 1
C}u 13 : Tọa độ giao điểm của hai đồ thị hàm số sau (C) : y  2x 1 và (d) : y  x  2 là :  3 1  A. M  ; ; N   1;3 B. Không có giao điểm  2 2   1   3  C. M 1  ; ; N   1;2 D. M  ;0 ; N   1;4  2   2  2  x  3
C}u 14 : Tọa độ giao điểm của hai đồ thị hàm số sau (C) : y x 1 và (d) : y  x  3 là : A. M 0; 2  ; N1; 2   B. Không có giao điểm C. M  1  ; 4  ; N1;2 D. M 0; 3  ; N2;  1
C}u 15 : Cho hàm số sau (C) : 3
y  4x  3x 1 và đường thẳng (d) : y  mx  
1  2 Giá trị tham số m
để (C) và (d) có 3 giao điểm : A. 0  m  9
B. Không có giá trị m thỏa mãn. 80
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017 C. 0  m D. m  0 x 1
C}u 16 : Cho hàm số sau (C) : y
và đường thẳng (d) : y  m x .Giá trị tham số m để (C) và x 1 (d) có 2 giao điểm :
A. Không có giá trị m thỏa mãn. B. m0;4 C. m  0 hay m  4 D. m  0
C}u 17 : Cho hàm số sau (C) : 3
y  x  3x  2 và đường thẳng (d) đi qua A(3;20) và có hệ số góc m .
Trả lời các câu hỏi sau :
17.1 Phương trình đường thẳng (d) là..................................................................
17.2 Giá trị m để (C) cắt (d) tại 3 điểm phân biệt là : 15 A.  m  21
B. Không có giá trị m thỏa mãn. 4 15 C.  m  24 D. m  0 4 2x 1
C}u 18 : Cho hàm số sau (C) : y 
và đường thẳng (d) đi qua A(–2; 2) và có hệ số góc là m . x 1
Trả lời các câu hỏi sau :
18.1 Phương trình đường thẳng (d) là..................................................................
18.2 Đạo hàm của hàm số tại x = 3 là ..................................................................
18.3 Các khoảng □ đồng biến, □ nghịch biến của hàm số
là ..................................... và .....................................
18.4 Đồ thị hàm số cắt trục hoành và trục tung lần lượt tại ............và ...................
18.5 Giá trị m để (C) cắt (d) tại 2 điểm phân biệt là : A. 0  m  12 B. 0  m 12 C. m  0 hay m 12 D. m  0hay m  12
C}u 19 : Cho hàm số sau (C) : 4 2
y  x 10x  6m  3 . Giá trị tham số m để (C) cắt trục hoành tại 4 điểm phân biệt là : 1 1 A. 0  m  B. m  2 2 1 C. 0  m  D. m  0 2 C}u 20* : 4 2 2 4
(C ) : y  x  2(m  2)x m  3. Đồ thị hàm số luôn cắt Ox tại bốn điểm phân biệt m
x , x , x , x sao cho 2 2 2 2
x x x x x .x .x .x  11 ứng với giá trị tham số m là 1 2 3 4 1 2 3 4 1 2 3 4 A. m  0 B. m  1 C. m  2 D. m  3
C}u 21* : Cho hàm số 3 2
y x  2(m  2)x  (8  5 )
m x m  5 có đồ thị (Cm) và đường thẳng
d : y x m 1. Giá trị m để d cắt (Cm) tại 3 điểm phân biệt ? 81
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017 m  2 m  2 A.  B.  m  1  m  2  C. m 2  ;2 D. m  0
C}u 22* : Cho hàm số y   x   2
1 x mx  
1 có đồ thị (Cm). Với giá trị nào của m thì (Cm) cắt Ox tại 3 điểm phân biệt ? m  2 m  2 A.  B.  m  1  m  2  m  2 C.  D. m  0 m  1 
C}u 23 : Cho đường cong (C) có phương trình : 3 2
y x  3x và đường thẳng (d) y  3x 1  0 . Trả
lời c{c c}u hỏi sau
23.1 Giao điểm của (C) và (d) là A. K 1; 2   B. K  1  ; 2   C. Không có D. K 0  ;1
23.2 Đồ thị (C) là hình nào dưới đây A. B. C. D. 82
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017 2x 1
C}u 24* : Cho hàm số y
có đồ thị (C) và đường thẳng d : y  x m . Với giá trị nào của m x  2
thì d cắt (C) tại 2 điểm phân biệt ? A. m B. m C. m  2  D. 2   m 12 2x 1
C}u 25* : Cho hàm số y
có đồ thị (C) và đường thẳng d : y  3
x m . Với giá trị nào của m x 1
thì d cắt (C) tại 2 điểm phân biệt ? A. m B. m m  11 C.  D. 1   m 11 m  1  2x 1
C}u 26 : Cho hàm số y
có đồ thị (C) và đường thẳng d : y  x m . Với giá trị nào của m x  2
thì d cắt (C) tại 2 điểm phân biệt A, B có hoành độ là x1, x2 thỏa mãn biểu thức sau
x x 2 4x x  4 1 2 1 2 A. m B. m C. m  0 D. m  8 C}u 27 : Cho hàm số 4
y x  m   2 2
1 x  2m 1 có đồ thị (C) và đường thẳng d : y  1  . Với giá trị
nào của m thì d cắt (C) tại 2 điểm phân biệt A, B A. m B. m C. m  0 D. m  0 x 1
C}u 28 : Cho hàm số y
có đồ thị là (C). Gọi M, N là giao điểm của (C) và đường thẳng x 1 1 d : y
x . Khi đó tọa độ M, N là 6 1 1 A. (2; 2  ), (1; 2  ) B. (2; ), (3; ) 3 2 C. (0; 2  ), (1; 2  ) D. ( 1  ; 4  ), (3; 2  ) 2
x  4x  3
C}u 29 : Cho hàm số y x
có đồ thị là (C). Gọi M, N là giao điểm của (C) và trục hoành. 2 Khi đó tọa độ M, N là A. (1;0), (3;0) B. (2;0), (3;0) C. (0;0), (2;0) D. ( 1  ;0), (3;0)
C}u 30 : Cho hàm số y   x   2 2
1 x mx m  3 có đồ thị là (Cm). Với giá trị nào của tham số m thì
đồ thị hàm số cắt trục hoành tại ba điểm phân biệt  2   m  2 A. m B. m  1  83
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017 m  11  3   m  2 C.  D.  m  1  m  1  C}u 31 : Cho hàm số 3 2
y x  2x x có đồ thị là (C). Với giá trị nào của tham số m thì đồ thị hàm
số cắt đường thẳng d : y = mx tại ba điểm phân biệt 0  m  2 A. m B. m 1 0  m 0  m  3 C.  D.  m  1 m  1 C}u 32 : Cho hàm số 3
y x 1 có đồ thị là (C). Với giá trị nào của tham số m thì đồ thị hàm số cắt
đường thẳng d : y = 3x + m tại ba điểm phân biệt A. m B. 1   m  3  1   m  3  1   m  3 C.  D.  m  0 m  1
C}u 33 : Có bao nhiêu tiếp tuyến với đồ thị (C) của hàm số 3 2
y x  6x 11x 1 tại giao điểm của
(C) và đường thẳng y = 5 A. 0 B. 1 C. 2 D. 3 2x 1
C}u 34 : Cho hàm số y
. Tiếp tuyến của đồ thị (C) tại M(2; 5) cắt trục Ox, Oy lần lượt tại A, x 1
B. Diện tích tam giác OAB là 121 123 A. S  B. SOAB  6 OAB 6 13 11 C. S  D. SOAB  6 OAB 6 3x  2
C}u 35 : Cho hàm số y
có đồ thị là (C). Tọa độ giao điểm của (C) và đường phân giác của x  2
góc phần tư thứ nhất là A. M 0; 2 B. M  1  ;2 C. M  1  ; 2   D. M 2; 2 3x  5
C}u 36 : Cho hàm số y  có đồ thị là (C). x  2
Phát biểu nào sau đây là sai ?
A. Hàm số luôn giảm trên từng khoảng xác định. 5
B. Đồ thị hàm số cắt trục tung tại điểm K có tung độ y K 2 C. Điểm M  1  ; 
1 nằm trên đồ thị hàm số (C)
D. Miền xác định của hàm số là D  \   2 84
Đăng kí học thêm To{n tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – SỰ TƢƠNG GIAO 2017 x  2
C}u 37 : Cho hàm số y
có đồ thị là (C). Tìm tham số m để đồ thị (C) cắt đường thẳng d : y x 1
= x + 2m tại hai điểm phân biệt A. m
B. 1 3  m 1 3 1
  3  m 1 3 m 1 3 C.  D.  m  0 m 1 3
C}u 38 : Cho hàm số y    m 4 2 1
x mx  2m 1. Giá trị của tham số m để đồ thị hàm số cắt trục
hoành tại 3 điểm phân biệt A. m B. m 1   1 m  1      m 3  2  2 C.  D.  2  2 m     m  3  3 C}u 39 : Cho hàm số 4
y x    m 2 2 2 1
x m  3. Giá trị của tham số m để đồ thị hàm số không có
điểm chung nào với trục hoành . A. m  3 B. m C. m  3 D. m  3 2x 1
C}u 40 : Những giá trị của m để đường thẳng y x m 1 cắt đồ thị hàm số y  tại hai điểm x 1 phân biệt ,
A B sao cho AB  2 3 là A. m  4  10 . B. m  4  3 . C. m  2  3 . D. m  2  10 . 2x 1
C}u 41 : Biết đường thẳng y x  2 cắt đồ thị y
tại hai điểm phân biệt A, B có hoành độ x 1
lần lượt x , x hãy tính tổng x x A B A B
A. x x  2 .
B. x x  1. A B A B
C. x x  5.
D. x x  3. A B A B
C}u 42 : Số giao điểm của đường cong 3 2
y x  2x  2x 1 và đường thẳng y  1 x bằng A. 1. B. 2. C. 3. D. 0.
“Học vấn do người siêng năng đạt được, tài sản do người tinh tế sở hữu, quyền lợi do người dũng
cảm nắm giữ, thiên đường do người lương thiện xây dựng”. Franklin (Mỹ)
Gi{o viên cần file word hoặc học sinh cần file đ{p
{n xin vui lòng liên hệ trực tiếp
Qua facebook/zalo/ đt : 0914449230