Phân loại dạng và phương pháp giải nhanh nguyên hàm – tích phân – Nguyễn Vũ Minh (Tập 1) Toán 12

Phân loại dạng và phương pháp giải nhanh nguyên hàm – tích phân – Nguyễn Vũ Minh (Tập 1) Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

30 15 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

PHÂN LOI DNG V

PHƯƠNG PHP GII NHANH

BIÊN HO – Ngy 27 thng 11 năm 2017

TI LIỆU LƯU HNH NỘI BỘ

Chuyeân ñeà

TẬP 1

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

1) Định nghĩa :  



................................

2) Họ nguyên hàm : , v

3) Bảng nguyên hàm :

Hàm cơ bản :

Hàm chứa (ax + b)

dx x C



α1

x .dx C

α1









 

α1

1 (ax b)

ax b dx C

a α1



  





ln x C





dx 1

ln ax b C

ax b a

  





dx 1

C  



dx 1 1

(ax b) a ax b

  





2 x C





dx 2

ax b C

ax b

  





a dx C

lna





ax b

a dx C

a lna







e dx e C



ax b ax b

e dx e C







sinx.dx cosx C  



sin(ax b).dx cos(ax b) C

    



cosx.dx sinx C



cos(ax b).dx sin(ax b) C

   



tanx C

cos x





dx 1

tan(ax b) C

cos (ax b) a

  





cotx C

sin x

  



dx 1

cot(ax b) C

sin (ax b) a

   





Phần 01 : NGUYÊN HÀM (TÍCH PHÂN BẤT ĐỊNH)

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

dx 1 x a

ln C

x a 2a x a









Công thức chú ý :

4) Cách tìmnguyên hàm : Bii tích hoc , tng, bạ bậc, khai triển lũy thừy, chia đa

thức a :

m n m n

x x ; x ; x



  

5) Công thức thường dùng :

1 cos2u

cos u

1 cos2u

sin u









1 tan u

cos u

1 cot u

sin u



3cosu cos3u

cos u

3sinu sin3u

sin u









sin2u 2sinu.cosu

cos2u cos u sin u

cos2u 2cos u 1

cos2u 1 2sin u





Ví dụ 01:   SAU:

f(x) (2x 1)

f(x) (tanx cotx)

2x 5x 2

f(x)





2x x

e 3e 2

f(x)







♥ Giải : a/   dc :

α1

x .dx C

α1











6 4 2

f(x) 8x 12x 6x 1   

Suy ra :

6 4 2

f(x)dx 8 x dx 12 x dx 6 x dx 1dx   

    

7 5 3

8 12

x x 2x x C

    

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018



f(x) tan x cot x 2 1 1 2

cos x sin x

   

       

   

   

cos x sin x



Suy ra:

f(x)dx dx dx tan x cotx C

cos x sin x

    

  



f(x) 2x .

  

Suy ra:

f(x)dx 2 xdx 5 dx 2 x dx x 5ln x C



      

   



2x x x x x x

e e 2(e 1) e (e 1) 2(e 1)

f(x)

e 1 e 1

     





(e 1)(e 2)



  



Suy ra:

f(x)dx e dx 2dx e 2x C    

  

Ví dụ 02 (THPT chuyên Phan Bội Châu lần 2):

Bi

     

21      F x ax a b x a b c x



 

3 6 2  f x x x

. Tng

abc



. B.

. C.

. D.

♥ Giải : 

     

3 2 2



     F x ax a b x a b c



     

2 6 2









     







  



F x f x a b b

a b c

5   abc

. Ch

Ví dụ 03 (Cụm 1 – Tp.HCM): Bit mt 

 

y f x



 

41F x x x  

 c

 

y f x

ti

3x 



 

3 30f 

. B.

 

3 22f 

. C.

 

3 10f 

. D.

 

36f 

♥ Giải :

Cách 1 : 

     

 

4 1 2 4F x f x f x x x x



      

 

3 2.3 4 10f   

. Ch

Cách 2 : s d Casio.

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Bài Tập 1:   sau

f(x) x 3x 5

   

5 4 3 2

3 7 9 20

f(x)

x x x x

   

5 7 9

x 4x 2x 8 7x

f(x)

   



f(x) x x 4 x  

f(x) ( x 1)(x x 1)   

f(x) e 2

sin x











♥ Giải :

.................................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Bài Tập 2 (SỞ GD ĐT HÀ TĨNH): Bit rng

 

.2F x m x



 

f x x

 ca

A.

. B. 1. C. 0. D. 4.

♥ Giải :

.................................................................................................................................................................................

Bài Tập 3: a/ 

( ) 3f x x x

  



xC  

  

3 lnx x x C  

xC  

b/ H a

( ) 2 1f x x x  



( ) 2

F x x x C   

( ) 2 2F x x C  

()

F x x x x C   

( ) 2

F x x x x C   

c/ 

()fx





ln lnx x C

B. lnx 

+ C C. ln|x| +

+ C D.

ln xC



♥ Giải :

.................................................................................................................................................................................

Bài Tập 4:  sau

f(x) e (7 3e )

cos x



  

 

x x 2x 1

f(x) 2 3 .2





f(x) e (5 3e )





♥ Giải :

.................................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

.................................................................................................................................................................................

Bài Tập 5:   s sau

f(x) 2sinx 3cosx

  

f(x) tan x 3cot x

f(x) (2tanx cotx)

f(x)

sin x.cos x



 

f(x) x 3x x 1  

f(x) 3sinx 7cosx

15 4 6

3x 7x 2x 8 10x

f(x)

   



f(x) 2 x 3e 4sin x 8/ x   

f(x)

sin x.cos x



♥ Giải :

.................................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

.................................................................................................................................................................................

Bài Tập 6: a/ 

 







 

F x 3 C









 

F x C









 

F x C



 

F x 3 C









2x x x

2 .3 .7 dx





ln84



2x x x

2 .3 .7

ln4.ln3.ln7



84 C

84 ln84 C

♥ Giải :

.................................................................................................................................................................................

Bài Tập 6:   sau

f(x) x 3x 4x 3   

; 2/

f(x) 2x(x 3x)

f(x) 4sin cos



f(x) 2sin x 3cosx 5e  

f(x) tan x 3

f(x) (2 )



( x 2)

f(x)





2x 1 3x 2

f(x) 2 .3





f(x) (3 2)

♥ Giải :

.................................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

.................................................................................................................................................................................

Bài Tập 7: Chng minh

()Fx



()fx

ng hp sau:

( ) 5 4 7 120F x x x x   



( ) 15 8 7.f x x x  

( ) ln( 3)F x x x  



( ) .





( ) (4 5)

F x x e  



( ) (4 1) .

f x x e  

Phng php: 

()Fx



( ),fx

ta cn chng minh:

♥ Giải :

.................................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Ví dụ 03: H  C SAU:

f(x) (2x 1)

; b/

 

f(x) cos 3x 2

; c/

f(x)

7x 1





; d/

f(x) e





; e/

f(x) (7 3x)

Giải : a/ s dc

 

α1

1 (ax b)

ax b dx C

a α1



  





1 (2x 1)

f(x)dx (2x 1) dx . C



   



b/ s dc

cos(ax b).dx sin(ax b) C

   



   

f(x)dx cos 3x 2 dx .sin 3x 2 C

    



c/ s dc

dx 1

ln ax b C

ax b a

  





2 dx 2

f(x)dx dx 2 .ln 3x 2 C

7x 1 7x 1 7

    



  

d/ s dc

ax b ax b

e dx e C







x x x

f(x)dx e dx e C e C

  

     





(  s -1 )

e/ gi

1 (7 3x)

f(x)dx (7 3x) dx . C

3 11



   





Điền vào ô trống

(7 4x) dx=



27



 

41



8x 7

e dx=





e dx =





 

cos







Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Bài tập 01 (THPT Hoàng Văn Thụ - Khánh Hòa): 

 

2017x

f x e





 

2017

f x x e C







. B.

 

2017

d .ln2017

f x x e C



  



 

2017

f x x e C



  



. D.

 

2017

d 2017.

f x x e C



  



♥ Giải :

.................................................................................................................................................................................

Bài tập 02 (THPT Trần Hưng Đạo – Nam Định): 

 





 

d 3 ln3

f x x C







. B.

 

ln3

f x x C







 

ln9

f x x C







. D.

   

d 2 1 3

f x x x C  



♥ Giải :

.................................................................................................................................................................................

Bài tập 03 (THPT chuyên Lê Hồng Phong – Nam Định): 

c

1000 .

1000

F x C

3.10 ln10

1000

F x C

3ln10

F x C

♥ Giải :

.................................................................................................................................................................................

Bài tập 04 (Sở GD-ĐT Long An): 

 

ca 

 

cos2

f x x e x  

 

sin2

5 3 2

x e x

F x C   

 

sin2

F x x C   

 

sin2

5 3 2

x e x

F x C   

 

sin2

F x e C   

♥ Giải :

.................................................................................................................................................................................

Bài tập 05 :   sau

f(x) sin x

2 /

f(x) sin 7x

f(x) cos 4x

f(x) cos x

f(x) sin 2x

f(x) 7sin x.cos x

♥ Giải : Lưu ý các công thức sử dụng cho phần này là : HẠ BẬC

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

..............................................................................................................................................................................

Bài tập 06:   sau

f(x) sin2x.cosx

f(x) sin4x.sin6x

3 /

f(x) cos6x.cos2x

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

♥ Giải : Lưu ý các công thức sử dụng cho phần này là :TÍCH THÀNH TỔNG

♥ Giải :

.................................................................................................................................................................................

Bài tập 07:   sau

1 /

x 3x 6x 5

f(x)

  





f(x)

x 9 x





3x 6x 5

f(x)

2x 1







f(x)

cos 2x











5 /

6x 5

f(x)

2x 5







f(x) cos x sin x

♥ Giải :

.................................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

.................................................................................................................................................................................

Bài tập 08:   sau

1/ (ĐH Ngoại Thương – 1998- Khối A)

x x 1

f(x)

x x 1







Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

2/ (ĐH Ngoại Thương – 1998- Khối D)

x 2x 2 x

f(x)

x x 1

  





3/ (ĐH Ngoại Thương – 2000 - Khối D)

cos2x

f(x)

sinx cosx





4 /

f(x)













♥ Giải :

.................................................................................................................................................................................

Bài tập 09 (THPT chuyên Hưng Yên lần 2):  ca

 

   

2 3 2

3 2 4 3F x m x m x x    



 

3 10 4.f x x x  

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

2m 

1m 

1m 

1m 

♥ Giải :

.................................................................................................................................................................................

Bài tập 10 (THPT chuyên Thái Bình):  

 

cos

f x e











 

2 tan

F x e x

 

2 tan

F x e x C  

 

2 cot

F x e x C  

 

2 tan

F x e x C  

♥ Giải :

.................................................................................................................................................................................

Bài tập 11: 

 

F x e

:

 

f x x e

 



 

f x e

 

f x xe

♥ Giải :

.................................................................................................................................................................................

Bài tập 12 (Cụm 1 HCM): 

 

f x x



 

2 ln2

f x x C  



 

ln2

f x x C  



 

f x x C  



 

2 ln2

f x x C  



♥ Giải :

.................................................................................................................................................................................

Bài tập 13: a/ 

 

1 3x

f x e







 

1 3x

F x C





 

1 3x

F x C





 

F x C

  

 

F x C

  

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

b/ 

 

2 5x







 

2 5x

F x C





 

2 5x

F x C



  

 

2 5x

F x C



  

 

F x C



♥ Giải :

.................................................................................................................................................................................

Bài tập minh họa cho phương pháp :

a/ 

3x 7 A B

x 4x 3 x 1 x 3





   

(

x 1; 3

)

b/ 

3x 7

I dx

x 4x 3









Giải : a/

   

3x 7 A B

3x 7 A x 3 B x 1

x 4x 3 x 1 x 3



       

   

 

A B 3 A 2

3x 7 A B .x 3A B

3A B 7 B 1

  



       



  



Phương pháp Xê Hắc E :

c c

PHC E

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

3x 7 2 1

I dx dx 2ln x 1 ln x 3 C

x 4x 3 x 1 x 3





       



   





Bài tập 7 :  sau ( s dng pp Xê Hắc E )

3x 4

A dx

x 4x 5









;

B dx

x 8x 9









;

C dx

x x 2







 

x x 1







;

F dx

x x 6









;

G dx

x 7x 12







;

F dx

x 10x 9









♥ Giải :

.................................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

.................................................................................................................................................................................

Trắc nghiệm bổ sung

TN1 (THPT Hà Huy Tập): y sai?

ln dx x C





d lnx x C





d tan

cos

x x C





sin2 d cos2

x x x C  



TN2 :  f(x) bit

()











 







 

ln 1 3ln 3

   x x C

(2 3)ln 4 3   x x x C

TN3 : :

(I) cot

sin





(II)



   





dx e e x C

Kh

 B. 

C. C  D. C u sai

TN4 : a f(x) = cos 2x.

u s

( ) (0)



FF

bng:

A. 15 B.

C. 2 D.

TN5 (THPT Chuyên Tuyên Quang): 

 

7f x x

 :

 

5F x x C

 

35F x x C

 

35F x x C

 

F x x C

TN6 (THPT Lý Nhân Tông): nh sau khsai ?

0dxC



(

ng s). B.

x x x C













(

ng s).

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

d lnx x C





(

ng s). D.

dx x C



(

ng s).

TN7 (THPT chuyên Vĩnh Phúc lần 5):  

x



log 1 xC

. B.

 

ln 1 xC

. C.

ln 1 xC

. D.

 





TN8: 

23x









32x





2017



TN9 (THPT chuyên LTV):  s

 

y f x

  

 

d 4 3 2f x x x x x C   





 



 

4 3 2

f x x x x Cx C



    

 

12 6 2f x x x C   

 

4 3 2

f x x x x Cx   

 

12 6 2f x x x  

TN10 (THPT chuyên Lê Thánh Tông): Bit

 



nh biu thc

 

.17

f x x





. B.

 

17 ln17

f x C

 

ln17

fx

. D.

 

17 ln17

fx

TN11 (THPT Tiên Du 1): 

 

f x x 



2 .ln2

  

. B.

4 ln2

  

. D.

3ln 2 .ln2

xC  

TN12 (Sở GDĐT Lâm Đồng lần 04): 

 

f x x



Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

C

. B.

xC

. C.

xC

. D.

xC

TN13 (THPT Nguyễn Khuyến –NĐ): 

 

a

 

f x e x

p s

th

 

F x e x

. B.

 

F x e x  

 

F x e x  

. D.

 

F x e x  

TN14 (THPT Hùng Vương–PT): 

 

2f x x



 

d lnf x x x x C  



. B.

 

df x x x C

  



 

df x x x C

  



. D.

 

d lnf x x x x C  



TN15 (THPTQG – 2017):  

 

2sinf x x

2sin 2cosxdx x C



. B.

2sin sinxdx x C



2sin sin2xdx x C



. D.

2sin 2cosxdx x C  



TN16 (THPT chuyên Phan Bội Châu):  

 





 

ln( 2 1) 5

F x x x   

. B.

 

ln 2 2 4F x x   

 

ln 1 2F x x  

. D.

 

ln 4 4 3

F x x   

TN17 :  

(I) F(x) = G(x) + C (II) G(x) = F(x) + C

Vt hng s  ?

  B. 

C. C  D. C u sai

TN18 (THPT chuyên Nguyễn Trãi lần 2): 











Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

ln 2 3

xC

ln 2 3xC

 

ln 2 3

xC

2ln 2 3xC

TN19 (THPT Nguyễn Tất Thành):  

 









. B.









. D.







TN20 (THPT chuyên LHP): Cho

 



 















 

ln 6 3

F x C





. B.

 

ln 2 1

F x C





 

ln 2 1

F x C





. D.

 

ln 2 1F x x C  

TN21 (THPT chuyên Bến Tre): 

 





 

d 2ln 1 2f x x x C  



. B.

 

d ln 1 2

f x x x C



  



 

d ln 1 2f x x x C  



. D.

 

d ln 1 2

f x x x C  



TN22 (Sở GD-ĐT Đồng Nai): 

 





 

ln 4 3

g x dx x C  



. B.

 

ln 4 3

g x dx x C



  



 

5ln 4 3g x dx x C  



. D.

   

5ln 4 3g x dx x C  



TN23 (Cụm 7 – Tp.HCM): 

x 



c:

 

ln 2 1

xC

. B.

ln 2 1

xC

 





. D.

ln 2 1xC

TN24 (THPT chuyên LTV): 

 

f x e







Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

 

f x x e C







. B.

 

f x x e C



  



 

f x x e C



  



. D.

 

f x x e C



  



TN25 (THPT Tiên Lãng): 

 

I e x



I x e e C   

I x e e C   

. D.

I x e e C   

TN26 (Sở GD-ĐT Đồng Nai): 

   

15 12h x x



 

dh x x



   

d 12 15

108

h x x x C  



. B.

   

d 8 15 12h x x x C  



   

d 96 15 12h x x x C   



. D.

   

d 15 12

h x x x C   



TN27 (Sở GDĐT Lâm Đồng lần 05): 

 

( ) 3 1f x x

 

( ) 3 1

f x dx x C  



 

( ) 3 1

f x dx x C  



 

( ) 3 1

f x dx x C  



. D.

 

( ) 3 1

f x dx x C  



TN28 (THPT Nguyễn Thị Minh Khai – KH):  

ye

y e x

. B.

y e x  

y e x  

. D.

y e x

TN29 (Cụm 1 – Tp.HCM): 

 

f x x



 

2 ln2

f x x C  



. B.

 

ln2

f x x C  



 

f x x C  



. D.

 

d 2 ln2

f x x C  



TN30 (THPT chuyên Nguyễn Trãi lần 2): 

 

sin2f x x

2cos2xC

. B.

cos2

xC

. C.

2cos2xC

. D.

cos2

xC

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

TN31 (THPT chuyên Nguyễn Trãi lần 1): 

sinyx



?

cosyx

. B.

tanyx

. C.

cotyx

. D.

sin 1yx

TN32 (THPT chuyên Nguyễn Trãi lần 1):  sau, m 

e e C



. B.

sinxdx cos xC



2 dxx x C



. D.

dx ln xC





TN33 (THPT Nguyễn Tất Thành): 

 

cos 4 3 dI x x



 

sin 4 3I x C  

. B.

 

sin 4 3I x C   

 

4sin 4 3I x C  

. D.

 

sin 4 3

I x C  

TN34 (Đề Minh Họa lần 2): 

 

cos2f x x

 

d sin2

f x x x C



. B.

 

d 2sin2f x x x C  



 

d sin2

f x x x C  



. D.

 

d 2sin2f x x x C



TN35 (THPT chuyên Võ Nguyên Giáp): Kt qu 

cos2 d 2cosx x x C  



. B.

cos2 d sin cosx x x x C



cos2 d sin2x x x C



. D.

cos2 d 2sin2x x x C



TN36:

x 



bng:

2ln 2 5xC

ln 2 5

xC

3ln 2 5xC

ln 2 5

xC

TN37:

 

x 



bng:

 

5 5 3





 

5 5 3





 





 

5 5 3





TN38:







bng:

3 7ln 2x x C  

3 ln 2x x C  

3 ln 2x x C  

3 7ln 2x x C  

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

TN39:

  

xx



bng:

ln 1 ln 2x x C   



ln 1xC

ln 2xC

TN40:







bng:

3ln 2 2ln 1x x C   

3ln 2 2ln 1x x C   

2ln 2 3ln 1x x C   

2ln 2 3ln 1x x C   

TN41:

xx



bng:





6ln















TN42: 

( 3)

xx













TN43:

xx



bng:















TN44: 

 







 

f x dx C









 

f x dx C









 

f x dx C









 

f x dx C









TN45: 

()







( ) ln | |

F x C







( ) ln | |

F x C







Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

( ) ln| 4 3|F x x x C   

( ) ln | |

F x C







TN46: 

2x 3

x 



















TN47: H a f(x) =

( 1)xx



A. F(x) = ln



B. F(x) = ln



C. F(x) =



D. F(x) = ln

( 1)x x C

TN48:  f(x) bit

()







 







(2 3)ln 4 3x x x C   





 

ln 1 3ln 3

x x C   

TN49: 

 





 

c g

 



nu:

   

’,F x f x x K  

   

’,F x f x x K 

   

,f x F x x K  

   

,f x F x x K 

TN50: sai?

'( ) ( )f x dx f x C



 

( ) ( ) 0Kf x dx K f x dx K



 

( ) ( ) ( ) ( )f x g x dx f x dx g x dx  

  

( ) ( )F x dx f x C



TN51:  m  sai

()

'( ) ( )

f x f x dx C



 

( ). ( ) ( ) . ( )f x g x dx f x dx g x dx

  

 

( ) ( ) ( ) ( )f x g x dx f x dx g x dx  

  

( ) ( )kf x dx k f x dx



(

ng s)

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

TN52: Cho

   

f x dx F x C



i

0a 



 

f ax b dx



bng

 

F ax b C



 

F ax b C



 

F ax b C

 

.a F ax b C

Bài tập minh họa :  ( sử dụng pp đổi biến số )

sinx

A e .cosxdx



2x 4

B dx

x 4x 5









ln x

C dx





D dx







Giải : a/

sinx

A e .cosxdx



t

t sinx dt cosxdx  

; Vy

t t sinx

A e .dt e C e C    



2x 4

B dx

x 4x 5









t

 

t x 4x 5 dt 2x 4 dx     

Vy

B ln t C ln x 4x 5 C

      



ln x

C dx





t

t ln x dt

  

Vy

t ln x

C t .dt C C

    



D dx







t

t e 1 dt e dx   

Vy :

D ln t C ln e 1 C

     



Dạng Tích Phân

Cách Giải

f(x)

.dx

g(x)



+ Nu bc t



bc mu ta chia đa thức

+ Nu bc t



bc mu ta xem t 

CÁCH ĐỔI BIẾN SỐ CẦN NHỚ

PHI BIN S

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

ca mu hay ko ? nt t = mẫu số

+ Nng h ng

  ph

........dx



t

....... t .......  



f(lnx).



t

t lnx C dt

   

f(cosx).sinxdx



f(sinx).cosxdx



f(tanx)

cos x



f(cotx)

sin x



t

cos sin    t x C dt xdx

t

sin cos   t x C dt xdx

t

tan

cos

   

t x C dt

t

cot

sin

    

t x C dt

f(e ).e dx



t

t e C dt e dx   

dx dx

sin x cos x



vi n chn



2 4 2 2 4 2

1 1 1 1 1 1

. ... , . ...

sin sin sin cos cos cos

   



n n n n

dx dx

x x x x x

t

tan

cos

   

t x C dt

sin xdx



hay

cos xdx



vi n chẵn

c h bc

1 cos2u 1 cos2u

cos u ; sin u





sin xdx



hay



n n 1

sin xdx sin x.sinxdx







t t = cosx

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

cos xdx



vi n lẻ

n n 1

cos xdx cos x.cosxdx







t t = sinx

Ax B

ax bx c







+ Nu mm

x , x



Ax B

a(x x )(x x )







 s bnh

+ Nu m

, 

Ax B

a(x x )







+ Nu m

Ax B





t X = D.tant











R(x, x )a

t x = sint

R(x, x )a

t x = atant

Bài tập 01 : 

2 12

A x(2 x ) dx



8xdx







C 3 1 4sinx.cosx.dx



♥ Giải :

.................................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

.................................................................................................................................................................................

Bài tập 02 (THPT Thuận Thành 2):

 

F x



 

21f x x



 

.

 

d 2 1

f x x x C  



 

d 2 1

f x x x C   



 

( )d 2 1 2 1

f x x x x C   



   

d 2 1 2 1

f x x x x C   



♥ Giải :

.................................................................................................................................................................................

................................................................................................................................................................................

Bài tập 03: a/

3cosx

2 sin x



bng:

 

3ln 2 sinx C

3ln 2 sinx C  

 

3sin x

2 sin x



 

3sin x

ln 2 sin x











bng:

ln e e C





ln e e C



  

ln e e C



  

ln e e C





♥ Giải :

.................................................................................................................................................................................

................................................................................................................................................................................

.................................................................................................................................................................................

................................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

.................................................................................................................................................................................

Bài tập 04: a/

4x 1

4x 2x 5







bng:

4x 2x 5





4x 2x 5



ln 4x 2x 5 C   

ln 4x 2x 5 C

  

b/ a

sin x cosx







ln sin x cosx C

ln sin x cosx





ln sin x cosx C

sinx cosx



 

x 2x 3

x 1 e dx







bng:

x 2x 3

x e C











 

x x 3x

x 1 e C



x 2x





x 2x 3





♥ Giải :

.................................................................................................................................................................................

................................................................................................................................................................................

.................................................................................................................................................................................

................................................................................................................................................................................

.................................................................................................................................................................................

Bài tập 05: a/

x.ln x



bng:

ln x



ln x



4ln x



4ln x



lnx



bng:

 

lnx C



 

2 ln x C

 

lnx C



 

3 ln x C

2x 3



bng:

3x 2 C



2x 3 C



2x 3 C

2 2x 3 C

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

♥ Giải :

.................................................................................................................................................................................

................................................................................................................................................................................

.................................................................................................................................................................................

................................................................................................................................................................................

.................................................................................................................................................................................

................................................................................................................................................................................

Bài tập 06: a/

x.e dx





bng:



2e C



2 x 1

x .e C



 

x1



bng:

ln x 1 x 1 C   

ln x 1 C



ln x 1 C

  



♥ Giải :

.................................................................................................................................................................................

................................................................................................................................................................................

.................................................................................................................................................................................

Bài tập 07: a/



bng: A.

eC

eC



Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

e1



bng: A.

e x C

ln e 1 C



ln e 1



♥ Giải :

.................................................................................................................................................................................

................................................................................................................................................................................

.................................................................................................................................................................................

Bài tập 08: 

D x. x 1.dx



E x . 1 x.dx



3dx

2x. 2 ln x







♥ Giải :

.................................................................................................................................................................................

Bài tập 09: 

e .dx







I dx

3x 1









x dx

2x e







Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

♥ Giải :

.................................................................................................................................................................................

Bài tập 10(THPT An Lão lần 2): 

2 15

( 7) dx x x

. B.

. C.

. D.

♥ Giải :

.................................................................................................................................................................................

................................................................................................................................................................................

Bài tập 11: a/ Nu

 

F x x











 

F x x x C   

 

F x C







 

ln 2 3

F x x x C   

 

23F x x x C   

b/ (THPT Lý Thái Tổ): 

x



, kt qu .





21 xC  

x

1 xC

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

♥ Giải :

.................................................................................................................................................................................

Bài tập 12(THPT Hoàng Quốc Việt): 

x



bng.

2 2ln | 1|x x C  

2 xC

2ln| 1|xC

2 2ln | 1|x x C  

♥ Giải :

.................................................................................................................................................................................

Bài tập 13(TTGDTX Cam Ranh - Khánh Hòa): Bit

 



()

f x xe



 

F 



 

. A.

e 

e 

2e 

2e

♥ Giải :

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

..............................................................................................................................................................................

Bài tập 14(Cụm 6 – Tp.HCM): 

 

43I x x dx



. Bt

43ux

, khnh

. A.

I u du



. B.

I u du



. C.

I u du



. D.

I u du



♥ Giải :

..............................................................................................................................................................................

Bài tập 15: 

K x 2 x .dx



2 3ln x

L dx







cosx

P dx

sin x





cotx

Q .dx

sin x





♥ Giải :

.................................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

.................................................................................................................................................................................

Bài tập 16: 

7 4 5

R 2x .(x 1) .dx



xdx

2x 1







xdx

(2x 1)













.................................................................................................................................................................................

Bài tập 17: 

N cos xdx



 

S dx

x. 4lnx 7







T sin xdx



♥ Giải :

.................................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

..............................................................................................................................................................................

Bài tập 18: 

A cotx.dx



B tanx.dx



 

C 2 sin x .sin2x.dx



 

sin2x

D .dx

3 cos x







♥ Giải :

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

..............................................................................................................................................................................

.............................................................................................................................................................................

Bài tập 19: 

3sin2

N .dx

cos x 5sin x







♥ Giải :

..............................................................................................................................................................................

Bài tập 20: 

A .dx







(HV CNBCVT – 1999)

♥ Giải :

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

..............................................................................................................................................................................

Bài tập minh họa 01:



f(x) tan x

, bit

F( ) 0



b/ 

( ) sin cos2f x x x



()Fx

c

()fx

bit











☻ Giải : a/

f(x)dx tan xdx 1 dx tanx x C F(x)

cos x



      





  

π π π π π

F( ) tan C 1 C 0 C 1

4 4 4 4 4

         

; Vy

F(x) tan x x 1

   

 

sin cos2 sin 2 cos

   



x x dx x x C

;

()

2 2 2

  

  FC

. Vy

 

sin2 cos



  F x x x

Bài tập minh họa 02 (THPT Ngô Sĩ Liên lần 3) : Bit

 

a c

 

2 3cosf x x x















 





 





 





 





 





☻ Giải :

   

d 2 3cos d 3sinf x x x x x x x C    



2 2 2

3sin 3

2 4 4 2 4

F C C

    



      





. Suy ra:

 





. Ch

Bài tập tương tự

Bài 01 (TTGDTX Nha Trang - Khánh Hòa): 

 

c

 

sinf x x x

tha



 

0 19F 



cos 2

x

. B.

cos 20

x

cos 20

x

. D.

cos

x

♥ Giải :

.................................................................................................................................................................................

NG S C)

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Bài 02 (THPTQG – 2017): Cho

 

a 

 

f x e x

th

 

F 



 

.Fx

 

F x e x  

. B.

 

F x e x  

. C.

 

F x e x  

. D.

 

F x e x  

♥ Giải :

.................................................................................................................................................................................

Bài 03 (THPT Chuyên Nguyễn Bỉnh Khiêm – QN): Bit

 

a

 

fx



 

ln2

F 

 ca

 

bng. A.

ln 2

. B.

ln 2

. C.

ln 2

. D.

ln 2

♥ Giải :

.................................................................................................................................................................................

Bài 04: Tìm một nguyên hàm của các hàm số sau

x 3x 3x 1

f(x)

x 2x 1

  





bit

F(1) 1/3

(TN THPT – 2003) b/

f(x) x sinx

bit

π 2 2

F( )



♥ Giải :

.................................................................................................................................................................................

Bài 05: Tìm một nguyên hàm của các hàm số sau

2x 1

f(x) e cos2x 3



  

bit

F(0)



1 2x

f(x)





bit

F( 1) 3

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

♥ Giải :

.................................................................................................................................................................................

Bài 06: Tìm một nguyên hàm của các hàm số sau

 

f(x) cosx. 2 3tan x

bit

F(π) 1

♥ Giải :

.................................................................................................................................................................................

................................................................................................................................................................................

Câu hỏi trắc nghiệm :

Câu 01(THPT Chuyên Phan Bội Châu): Bit

 



 





 

13F 

. 

 

45F 

 

43F 

 

4 3 ln2F 

 

44F 

Câu 02(THPT Trần Hưng Đạo – NĐ): Bit

 



 







 

01F 

 ca

 

ln5

F 

 

2 1 ln5F 

 

ln5

F 

 

ln5

F 

Câu 03(THPT Chuyên Vĩnh Phúc): :

cos .siny x x



cos

xC

. B.

cos xC

sin

xC

. D.

cos

xC

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Câu 04(THPT Hoàng Văn Thụ - Khánh Hòa): Cho

 

31f x x x   



 





 



 

12F 



 

4 3 2

3 2 2F x x x x    

 

F x x x    

 

F x x x    

 

4 3 2

3F x x x x    

Câu 05(THPT Chuyên Vinh): Cho

 

a

 

f x e

tha

 

01F 

. Mnh

 ?

 

F x e

 

F x e

 

F x e

 

F x e  

Câu 06(THPT Chuyên Vinh): t c 

 





 





 

41F x x

 

21F x x

 

1F x x

Câu 07: Bit

 



 







 

21F 

. 

 

bng.

ln2

. B.

ln2 1

. D.

Câu 08(THPT Hoàng Văn Thụ - Hòa Bình): 

 



 

3 2 1

f x x e  

, bit

 

01F 

 

F x x e x   

 

F x x x

   

 

F x x e x  

 

F x x e x   

Câu 09(Sở GD-ĐT Hải Dương): 

 

2 sin 2cosf x x x x  



 

F x

ca



 

th

 

01F 

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

cos 2sinx x x

2 cos 2sinxx

cos 2sin 2x x x  

cos 2sin 2x x x  

Câu 10: H 

()  f x x x x

234

()

3 4 5

   F x x x x C

234

()

3 4 5

   F x x x x C

2 4 5

()

334

   F x x x x C

234

()

3 4 5

   F x x x x C

Câu 11:  f(x) bit

()





 

  x x C

 

  x x C

 

3( 9 )





 

Câu 12: 

( ) tanf x x



tan



sin cos

cos





x x x

tan 1xC

 

Câu 13: 

( ) tan  

F x e x C

 

()

sin



f x e

()

sin



f x e

( ) 1

cos











f x e

 

Câu 14:  f(x) =

2



3ln 2 .ln2

  

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

  

4 ln2

  

2 .ln2

  

Câu 15: : y =

cos2

sin .cos



A. tanx  cotx + C

B. tanx  cotx + C

C. tanx + cotx + C

D. cotx tanx + C

Câu 16: : y =

cos













2 tan

e x C

cos



cos



2 tan

e x C

Câu 17: : y = cos

x.sinx 

cos

xC

cosxC

C. -

cos

xC

sin

xC

Câu 18: M: y = cos5x.cosx 

A. F(x) =

1 1 1

cos6 cos4

2 6 4









B. F(x) =

sin5x.sinx

1 1 1

sin6 sin4

2 6 4









1 sin6 sin4

2 6 4









Câu 19: M: y = sin5x.cos3x 

1 cos6 cos2

2 8 2









1 cos6 cos2

2 8 2









1 cos6 cos2

2 8 2









Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

1 sin6 sin2

2 8 2









Câu 20:

sin 2



xdx

sin4

x x C

sin 2

xC

sin4

x x C

sin4

x x C

Câu 21:

sin .cos



2tan2 xC



cot2 xC

C. 4

cot2 xC

D. 2

cot2 xC

Câu 22:

 

1



2ln

  

2ln

  

2ln

  

2ln

  

Câu 23:

 

2017





x x e dx

2017

2 2017



x x C

2017

5 2017



x x C

2017

5 2017



x x C

2017

5 2017



x x C

Câu 24(Sở GDĐT Lâm Đồng lần 01): Cho

0a 



1a 

ng s



d .ln

a x a a C



a x a C



2ln

a x C





d .ln

a x a a C



Câu 25(THPT Hoàng Hoa Thám - Khánh Hòa): M







 

ln 1xx

ln 1x 

 





ln 1xx

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Câu 26(THPT Kim Liên – Hà Nội): a hm s

 

f x x



 

d ln

f x x x C  



 

d3f x x x C

  



 

d ln

f x x x C  



 

d3f x x x C

  



Câu 27(Cụm 7 – Tp.HCM): Cho bit

 



 



 

3 1 dI f x x







 

31I F x C  

 

3I F x x C  

 

31I xF x C  

 

3I xF x x C  

Câu 28:

45















Câu 29: M:







( ) 2F x x x

 

  xx

xx

 

  xx

Câu 30: M:

( ) 1f x x x







( ) 1

F x x x





( ) 1

F x x





( ) 1



F x x





( ) 1

F x x x

Câu 31:

tan2



xdx

A. 2

ln cos2 xC

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018



ln cos2 xC

ln sin 2

xC

Câu 32: a (vi C hngs

















ln 1xC

Câu 33: Nu

()Fx



( ) , (0) 0







f x F

ng s C bng

ln3



ln3



Câu 34(THPT chuyên Biên Hòa lần 2): 

   

sin dF x x x x



bit

 

0 19F 

 

cos 20

F x x x  

. B.

 

cos 20

F x x x  

 

cos 20F x x x  

. D.

 

cos 20F x x x  

Câu 35(Chuyên ĐH Vinh): t c 

 

cos2f x x



 

sin2

F x x C

. B.

 

sin2

F x x C  

 

sin2F x x C  

. D.

 

sin2F x x

Câu 36(Sở GD – ĐT Đồng Nai): 

 

cos4f x x

 

4sin4f x dx x C



. B.

 

4sin4f x dx x C  



 

sin4

f x dx x C



. D.

 

sin4

f x dx x C  



Câu 37(THPT Hàm Long): :

cos











.

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

2 tan

e x C

cos



2 tan

e x C

cos



Câu 38(Cụm 4 – Tp.HCM): 

 

2sin 3cosF x x x

.

 

2cos 3sinf x x x  

 

2cos 3sinf x x x  

 

2cos 3sinf x x x

 

2cos 3sinf x x x

Câu 39(Sở GD – ĐT Hà Tĩnh lần 2): Bit

( ) sinxd ; (0) 1F x x F





( ) 1 cosF x x

( ) cosF x x

( ) cosF x x

( ) 2 cosF x x

Câu 40(THPT Lý Nhân Tông): 

 

sin2017F x x

.

 

2017cos2017f x x

 

cos2017f x x

 

2017cos2017f x x

 

cos2017

2017

f x x

Câu 41(THPT Lương Tài): Kh

sin sin







d tan

sin

x x C





d cot

sin

x x C

  



d cot

sin

x x C





Câu 42(Sở GDĐT Lâm Đồng lần 2): M

 

c

 

2 3 1 sin2f x x x x   

khi

 

01F 



 

2 3 .cos2

4 3 2 2

F x x x    

 

2 3 .cos2

4 3 2 2

F x x x    

 

2 3 .cos2

4 3 2 2

F x x x    

 

2 3 .cos2

4 3 2 2

F x x x    

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Câu 43(TT Tân Hồng Phong): 

 

sin2f x x

cos2

xC

cos2

xC

cos2xC

cos2xC

Câu 44(Sở GDĐT Lâm Đồng lần 07): 

( ) sin3 . os5f x x c x



( ) os2 os8

4 16

f x dx c x c x C   



( ) os2 sin8

4 16

f x dx c x x C  



( ) sin2 os8

4 16

f x dx x c x C  



( ) os2 os8

4 16

f x dx c x c x C  



Câu 45: 

()Fx

c

sin2

sin 3





khi

(0) 0F



ln 1 sin x

ln 2 sin

 x

sin

ln 1



ln cos x

Câu 46: Nu

()Fx









(2) 1F



(3)F

bng

ln2

ln2 1

Câu 47: :

 







ln 3 1

xC

ln 3 1

xC

 

ln 3 1

xC

ln 3 1xC

Câu 48: :

   

cos 5 2f x x



 

sin 5 2

xC

 

5sin 5 2xC

 

sin 5 2

xC

 

5sin 5 2  xC

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Câu 49: :

 

41



f x e



41







Câu 50: :

 

tanf x x



tan xC

tanx xC

2tan xC

tanx xC

Câu 51: :

 





















 







Câu 52: M

 

os3x.cos2xf x c



sin sin5xx

sin sin5

2 10

xx

cos cos5

2 10

xx

cos sin5

2 10

xx

Câu 53: 

 

y f x



 







 

11f



 

bng:

A. ln2 B. ln3

C. ln2 + 1 D. ln3 + 1

Câu 54: 

 





vi

 

13F



2 2 1x

2 1 2x

2 2 1 1x

2 2 1 1x

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Câu 55: 

   

.cos 0F x a bx b



 

sin2f x x



tr l

A.  

 

C. 1

D.   1

Câu 56: Cho

()





(ln )

()

f x dx C



( ) lnf x dx x C



( ) (ln )f x dx x C



()

f x dx C



Câu 57: 

 



  

F x e e x

:

 



  

f x e e

 



  

xf x e e

 





f x e e

 



  

xf x e e

Câu 58: 

 

c

 

4 3 2 2   f x x x x

th

 

19F



 

4 3 2

2   x x xfx

 

4 3 2

10   x x xfx

 

4 3 2

2   x x x xfx

 

4 3 2

2 10    x x x xfx

Câu 59: :

 













e e C





e e C









Câu 60: 

 

c

 

sinxf x x

th

 

0 19F



Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

 

osx

  

F x c

 

osx 2

   

F x c

 

osx 20

  

F x c

 

osx 20

   

F x c

Câu 61: Cho

 

' 3 5sinxfx



 

0 10f



 

3 5 osx+2f x x c











 



f

 

3 5 osx+2f x x c

Câu 62: : y = sin

x.cos

x 

sin sin

x x C

sin sin

  x x C

C. sin

x sin

x + C



Câu 63: : y = cos

x.sinx 

cos

xC

cosxC

sin

xC

 

Câu 64: M: y = cos5x.cosx 

A. F(x) = cos6x

B. F(x) = sin6x

1 1 1

sin6 sin4

2 6 4









Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

1 sin6 sin4

2 6 4









Câu 65: M: y = sin5x.cos3x 

1 cos6 cos2

2 8 2









1 cos6 cos2

2 8 2









C. cos8x + cos2x



Câu 66: M:

( ) 1f x x x







( ) 1

F x x





( ) 1

F x x





( ) 1



F x x





( ) 1

F x x

Câu 67: : y =











a x a





a x a





a x a





a x a

Câu 68: : y =











a a x

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018





a a x





a x a





a x a

Câu 69: : y =

1





ln 1

    x x x x C

ln 1

    x x x x C

ln 1

    x x x x C

ln 1

    x x x x C

Câu 70: : y =

4 7 dx





   

1 2 2

4 7 7 4 7

20 5 3



    





x x C

   

1 2 2

4 7 7 4 7

18 5 3



    





x x C

   

1 2 2

4 7 7 4 7

14 5 3



    





x x C

   

1 2 2

4 7 7 4 7

16 5 3



    





x x C

Câu 71: M

sin3yx

3 os3cx

3 os3 cx

os3

 cx

Câu 72: Cho

(x)

cos 4

f



(x)



f dx

bng:

tan4

xC

tan4

xC

cot 4

xC

cot 4

xC

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Câu 73: Cho

()







()



f x dx

bng:













Câu 74(Cụm 6 Tp.HCM):  

 

c

 

f x e e





 

F x e e C



  

. B.

 

F x e e C



  

 

F x e e C



  

. D.

 

F x e e C



  

Câu 75: Cho

log

()



()f x dx



bng:

(log )



ln10.(ln )

xC

(ln )

2ln10

xC

(log ) xC

Câu 76: Bi

()fx

th

'( ) .

f x a x

vi

,0ab

( 1) 2; (1) 4; '(1) 0   f f f



1 1 11

()

   f x x

1 1 5

()

  f x x

( ) 4 2  f x x

( ) 2 2  f x x

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Định lý:

()u u x



()v v x





( ) ( ) ( ) ( ) ( ) ( )I u x v x dx u x v x u x v x dx



       



hay

I udv uv vdu   



Vận dụng giải toán:

Nhận dạng:

.sin . ,....

e x dx





Vi phân

Nguyên ha m

u du dx

dv dx v



    







    





Suy ra:

.I udv uv vdu  





u:  và

dv 

.



log

n

lnu 

hay

log .ln

u x x





dv 

i. Nu



ln; log

n

u 



dv 

i.



u 



Lưu ý: 

Bài tập : 

Câu 01:

sinI x x dx   



:

sin cos .I x x C  

♥ Giải :

.................................................................................................................................................................................

Câu 02:

(1 2 )

I x e dx    



:

(3 2 ) .

I x e C   

♥ Giải :

.................................................................................................................................................................................

NG PHNG PHP TNG PHN

NGUYN HM TNG PHN

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

.................................................................................................................................................................................

Câu 03:

cos

I e x dx   



:

(sin cos ) .

I x x C  

♥ Giải :

.................................................................................................................................................................................

Câu 04:

(2 1) lnI x x dx    



:

( )ln .

I x x x x C    

♥ Giải :

.................................................................................................................................................................................

Câu 05:

I x e dx   



:

xe e

IC  

♥ Giải :

.................................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

.................................................................................................................................................................................

Câu 06:

lnI x dx  



:

ln .I x x x C  

♥ Giải :

.................................................................................................................................................................................

Câu 07:

( 1) sin2I x x dx    



:

cos2 sin2 .

I x x C



   

♥ Giải :

.................................................................................................................................................................................

Câu 08:

I x e dx



   



:

(1 ) .

I x e C



    

♥ Giải :

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

.................................................................................................................................................................................

Câu 09:

cosI x x dx   



:

sin cos .I x x x C  

♥ Giải :

.................................................................................................................................................................................

Câu 10:

I x e dx   



:

I xe e C  

♥ Giải :

.................................................................................................................................................................................

I TRC NGHIM

Câu 01: M

()

f x xe



eC

 

e x C

 

e x C

eC

Câu 02: M

( ) ( 2 ).

f x x x e



Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

(2 2).

xe

2 x

( ).

x x e

( 2 ).

x x e

Câu 03: 

( ) .

f x x e





. M

()Fx

ca

()fx

tha

(0) 1F 



( 1) 1



  

( 1) 2



  

( 1) 1





( 1) 2





Câu 04: Cho

( ) sinf x x x

a

()fx



cosx x C

sin cosx x x C

cos sinx x x C  

Câu 05: 

()

f x xe

:

( ) 2

F x e

()

F x e

( ) 2

F x x e

()

F x e xe

Câu 06: Cho

( ) ln

f x tdt





'( )fx

 

ln x

Câu 07: Ma

()

f x x e



( 3 6 6)

x x x e  

( 6 6)

x x e

( 3 6)

x x e

Câu 08: M

 

f x x e



 

F x e

 

F x x e

 

F x e

 

F x xe e

Câu 09: 

( ) ( 1)sinf x x x



( ) ( 1)cos sinF x x x x C   

( ) ( 1)cos sinF x x x x C    

( ) ( 1)cos sinF x x x x C    

( ) ( 1)cos sinF x x x x C   

Câu 10: 

( ) lnf x x



( ) (ln 1)F x x x C  

()F x C



()

F x C

( ) (ln 1)F x x x C  

Câu 11: 

( ) cos

cos

f x x x











Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

( ) sin

sin 2

F x x x C



  





( ) (1 sin ) cosF x x x x C   

( ) (1 sin ) cosF x x x x C   

( ) (1 sin ) cosF x x x x C   

Câu 12: G

()Fx

a

( ) cos3f x x x

, bit

(0) 1F 

. Vy

()Fx



( ) sin3 cos3

F x x x x C  

( ) sin3 cos3 1

F x x x x  

( ) sin3

F x x x

1 1 8

( ) sin3 cos3

3 9 9

F x x x x  

Câu 13: 

xe dx



c kt qu 

 

–

F x e xe C

 

F x e xe C

 

–

F x e xe C  

 

F x e xe C  

Câu 14: 

cosx xdx



c kt qu 

 

sin cosF x x x x C  

 

sin cosF x x x x C  

 

sin cosF x x x x C   

 

sin cosF x x x x C   

Câu 15: 

cos2x xdx





sin2 cos2

x x x C

sin2 cos2

x x x C

sin2

C

sin2xC

Câu 16: M

 

( ) 2

f x x x e



( ) (2 2).

F x x e

()

F x x e

( ) ( ).

F x x x e

( ) ( 2 ).

F x x x e

Câu 17: Ma

()

f x x e



( ) ( 2 2)

F x x x e  

()

F x e

( ) ( 2 2)

F x x x e  

( ) 2

F x xe

Câu 18: 

 

ca

()

f x xe





tha

 

01F 



 

( ) 1 1

F x x e



   

   

F x x e



   

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

 

( ) 1 1

F x x e



  

 

( ) 1 2

F x x e



  

Câu 19: Kt qu t qu sau ?

.cos

sin

x xdx C







sin cos sinx xdx x x x C   



cos sin cosx xdx x x x C  



cos2 1

sin2 sin2

x xdx x C



  



Câu 20: Kt qu t qu sau ?

xe dx e C  



x x x

xe dx xe e C  



xe dx e C



x x x

dx C

e e e



  



Câu 21: Kt qu t qu sau ?

ln lnxdx x x x C  



ln xdx C





ln ln

x xdx x C  



ln .ln

x xdx x C  



Câu 22: Kt qu t qu sau ?

 

ln ln 2 lnxdx x x x x x C   



xdx C



ln ln 1xx

dx C

x x x



  



3 2 2

ln ln 1

dx C

x x x



  



Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Câu 01 : 

 

y f x



Kh

A. Nu

 

0fx







 

t cc tr

B. S nghim ca phng trnh

 

0fx





bng s m cc tr c

 

.fx

C. Nu

 



i du t ng khi qua

 t ci ti

D. N

 

t cc tr

xa



 

0.fa





Câu 02 : ng nghch bin c

3 2.y x x  

 

1;1 .

   

; 1 1; .   

 

;. 

 

;1 



 

1; .

Câu 03 : m ci c

2sin 1?yx







1.

Câu 04 : 

 

y f x

  th

nh hnh bn. Tm s m cc tr c

 

.y f x

Câu 05 : ng tim cn c th 







1; 2.xx

1; 2.yx

1; 2.xy

1; 2.xx  

Câu 06 : 

()

f x e e



e e C

( ) .

e e x C

D. Kt qu 

Câu 07 : Gi



ln l ln nh nh nht c

x m m

  







1; 2 .



 nh nht ca biu thc

2 3 .MN

 P H

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Câu 08 : t c  thc ca tham s

  th 







ng tim

cn.





0; .

 

;0 .

 

0; .





;0 .

Câu 09 : Vit tt c ng trnh tip tuyn c th

 

: 2 1,C y x x  

bit tip tuyn song

song vng thng

1.yx  

1; 1.y x y x    

; 1.

y x y x     

yx  

3; 1.y x y x     

Câu 10 : 

 

y f x

ng bi





 

'yx







Khsai?

 ng thng

2x 

m cng c th .

  ng bi

 

;1 .

 

   

3;10

max 10 .

f x f





D. Phng trnh

 

50fx

m thc.

Câu 11 : ng cong   th ca mt trong b

s c cho d  























Câu 12 :   không c tr?

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

.yx







Câu 13 : 

3 3 1y x x x   

ng bi















































Câu 14 : 

 

y f x



 

lim 2







 

lim 2.





Kh 

A.  th 

 

y f x

ng tim c

2x 



2.x 

  th 

 

y f x

ch t mng tim cn ngang.

  th 

 

y f x

ng tim c

2y 



2.y 

  th 

 

y f x

ng tim cn ngang.

Câu 15 :  ng tim cn c th 







Câu 16 : Bi

 

y f x

 ln nhn

 

1;4

bng

 ln nht ca



 

2y f x



 

1;4

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Câu 17 : (Trích câu 15, đề tham khảo Bộ GD&ĐT) 

 

21y x x  

 th nh 

 th c

 

21y x x  

       

Câu 18 :  m c th 







vi tr

 

0; 1 .

 

1;0 .

 

2;1 .

 

0;1 .

Câu 19 : t c  thc ca tham s

 phng trnh

3 4 0x x k   

m

tht.

2 6.k

2 6.k

1 3.k

1 3.k

Câu 20 : Cho h

 

0y ax bx c a   

 th nh hnh v



0, 0, 0.abc  

0, 0, 0.a b c  

0, 0, 0.abc  

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

0, 0, 0.abc  

Câu 21 : Gi s

, ab

 dng b

, .





ng thsai?

..a a a

   



 

. . .ab a b



























Câu 22 : nh c

 

1.yx





 

0; .D  

   

0; \ 1 .D  

 

1; .D  

 

\ 1 .D 

Câu 23 : Cho

log 4, log 5

xx

vi,

01x

a, b  thc ln hn 1. Tnh

log

Px

P 

20.P 

P 

Câu 24 : s

()f x x



xC



x x C

Câu 25 : ba s thc dng

, , .a b c

 th 

, ,

a b c

y x y x y x  

c cho nh hnh v



1.abc  

1; 0.c b a  

1 0; 0.c b a   

1; 0.b c a  

Câu 26 :  a tham s



phng trnh

log log 1 2 1 0x x k    

m thuc

1;3 ?





 .

Câu 27 : nh

c

 

log 6 9 .

y x x



  

 

1; .D  

   

1; \ 2 .D  

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

   

1; \ 2, 3 .D  

.D 

Câu 28 : 

 

log10 , 0 .y x x

10 ln10





ln10





ln10





ln10





Câu 29 : Vi

 thc dng khc 1. Xt cc m sau:

 th 

ya











i xng nhau qua Oy.

 th 

log

yx



log

yx

i xng nhau qua Ox.

 th 

ya



log

yx

i xng thng

.yx

 m 

A. 0. B. 1. C. 2. D. 3.

Câu 30 : Cho

0.a 

Vit da ca biu thc

.aaaa

. C.

. D.

Câu 31 : Phng trnh no sau y vô nghiệm?

2 4.



2 1.



2 1.







Câu 32 : p nghim

ca bt phng trnh

 

log 4 2 1.x   



 

































Câu 33 :  

 

0;10

nghit phng trnh

   

log 3 4 log 1 ?

xx  

10.

11.

Câu 34 : 

 





Khsai?

   

1 2 log 3.f x x x   

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

 

1 log 3 1 log 7



  



   

1 log7 2 log3.f x x x   

   

1 log 7 2 log 3.f x x x   

Câu 35 : Bi phng trnh

5 .8 500





c sau:

Bước 1: u kin:

0x 

. Phng trnh tng ng vi

5 .8 5 .2





5 .2 1





Bước 2: L s 2 hai v phng trnh (1):

 

3 log 5 0



  

 

3 log 5 0x



   





Bước 3:

 

log 2

log 5 0





















(thu kin).

Vy phng trnh  cho c hai nghim:

3, log 2xx

Hi bu t b

  B. Sai t bc 1. C. Sai t bc 2. D. Sai t bc 3.

Câu 36 : Mm mt s hu hng (k c m trong c

n li.









Câu 37 : 

(cos6 cos4 )x x dx





sin6 sin4

x x C  

6sin6 5sin4x x C

sin6 sin4

x x C

6sin6 sin4x x C  

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

Câu 38 : M ng v 

cc cho nh hnh v  

khn tng ng.

 

2960

V cm

 

2560 .V cm

 

2960 .V cm

 

2590 .V cm

Câu 39 : 

.S ABCD

i



SBD

Mt phng

 

cha

i

, ct

, , SB SC SD

ln lt ti

', ', 'B C D

 s

th a khi

. ' ' 'S AB C D

i

..S ABCD

k 

Câu 40 : 

.S ABC

u cnh

 ng

u cao

c

h 

3.ha

Câu 41 : p

.ABCD A B C D

   

nh

n c

thoi bng

60 .

 

ca khi hp

..ABCD A B C D

   

3 cm

40 cm

7 cm

5 cm

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

V 

3.Va

V 

Câu 42 : Bt micng

. Bn

Lan ct mt mit vi

30AOB 



mii tt xung quanh ca m

 



di

c

 

















Câu 43 : Cho  ng

.ABC A B C

  

u cnh

bit t 

BCC B





 

ca kh

..ABC A B C

  

V 

Câu 44 : 

ABCD



; 3 ; 45AD a AB a BAD  

(nh hnh bn). Tnh th 

kh nh

ABCD

quanh trc

.AB

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

5.Va





6.Va













Câu 45 :  chun b cho T ng hoa Nguyn Hu, qun 1,

 H  ng mt khi cng

 trng by hoa

ti xung quanh,  tit kim di ni tip mt c



c sao cho khi tr  n nht.

r 

32 3





r 

Câu 46 : N nh c

 

bng

a

 

b

30 .

45 .

60 .

90 .

Câu 47 :  ng

.ABC A B C

  



ABC

i

, 120 ,A B AC a BAC  

mt phng

 

AB C



to v

60 .

 

ca khi

 

V 

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

V 

Câu 48 : 

()C

ngoi tip mu

ABC

nh bng

m

.BC



()C

xung quanh trc

c mt khi c 



Câu 49 : T din

OABC



, , OA OB OC



1.OA OB OC  

t

cu ngoi tip t din

.OABC

. C.

Câu 50 : 

 

 t phng qua trc

ca

 

ct

 

theo thit dii tip bng





ca khi hn bi

 

9 3 .V





9.V





3 3 .V





3.V





HẾT

Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Gv. ThS Nguy N

2018

BẢNG ĐÁP ÁN:





















Bấm Tải xuống để xem toàn bộ.

| 1/75

| | Tải xuống

Preview text:

PHÂN LOẠI DẠNG VÀ
PHƯƠNG PHÁP GIẢI NHANH Chuyeân ñeà TẬP 1
BIÊN HOÀ – Ngày 27 tháng 11 năm 2017
TÀI LIỆU LƯU HÀNH NỘI BỘ
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
Phần 01 : NGUYÊN HÀM (TÍCH PHÂN BẤT ĐỊNH)
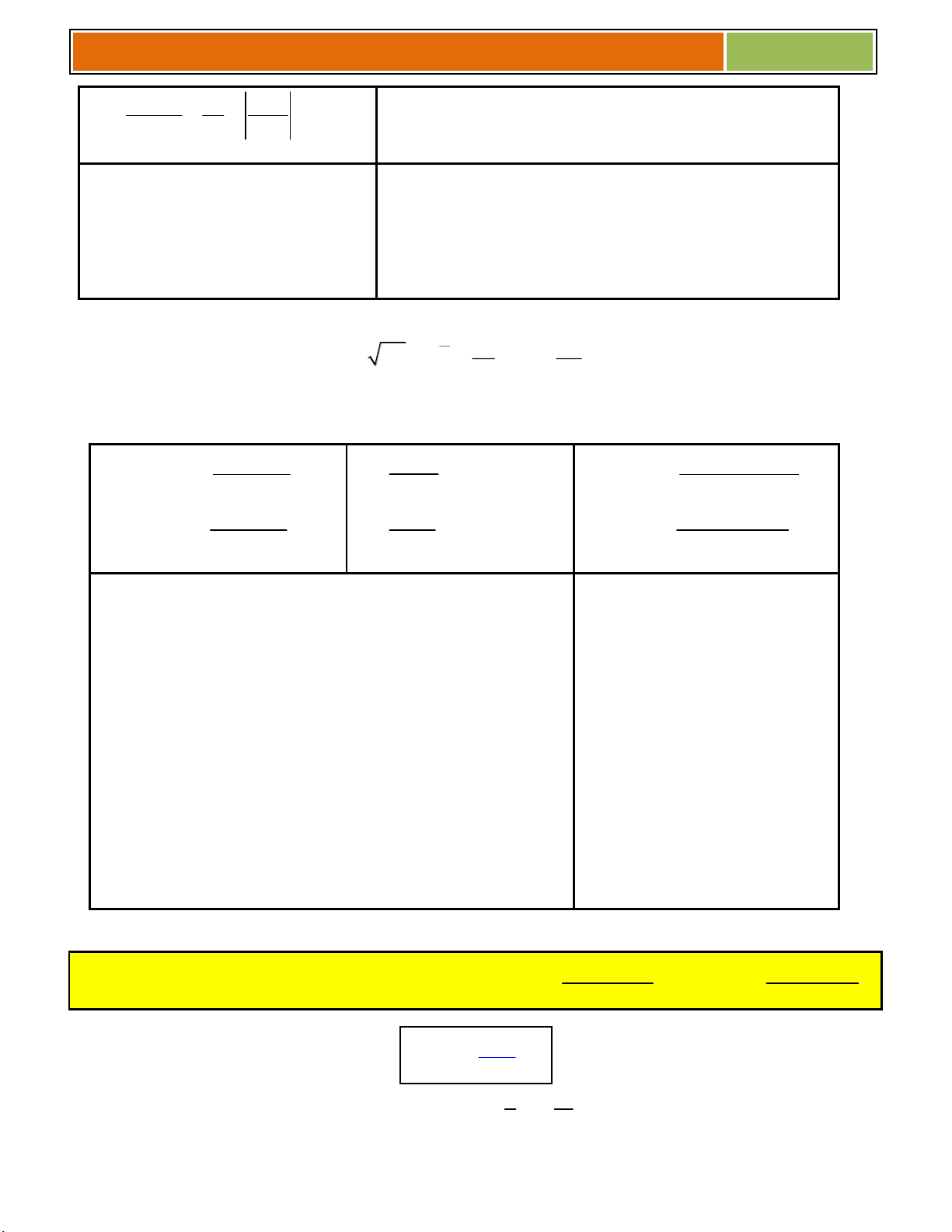
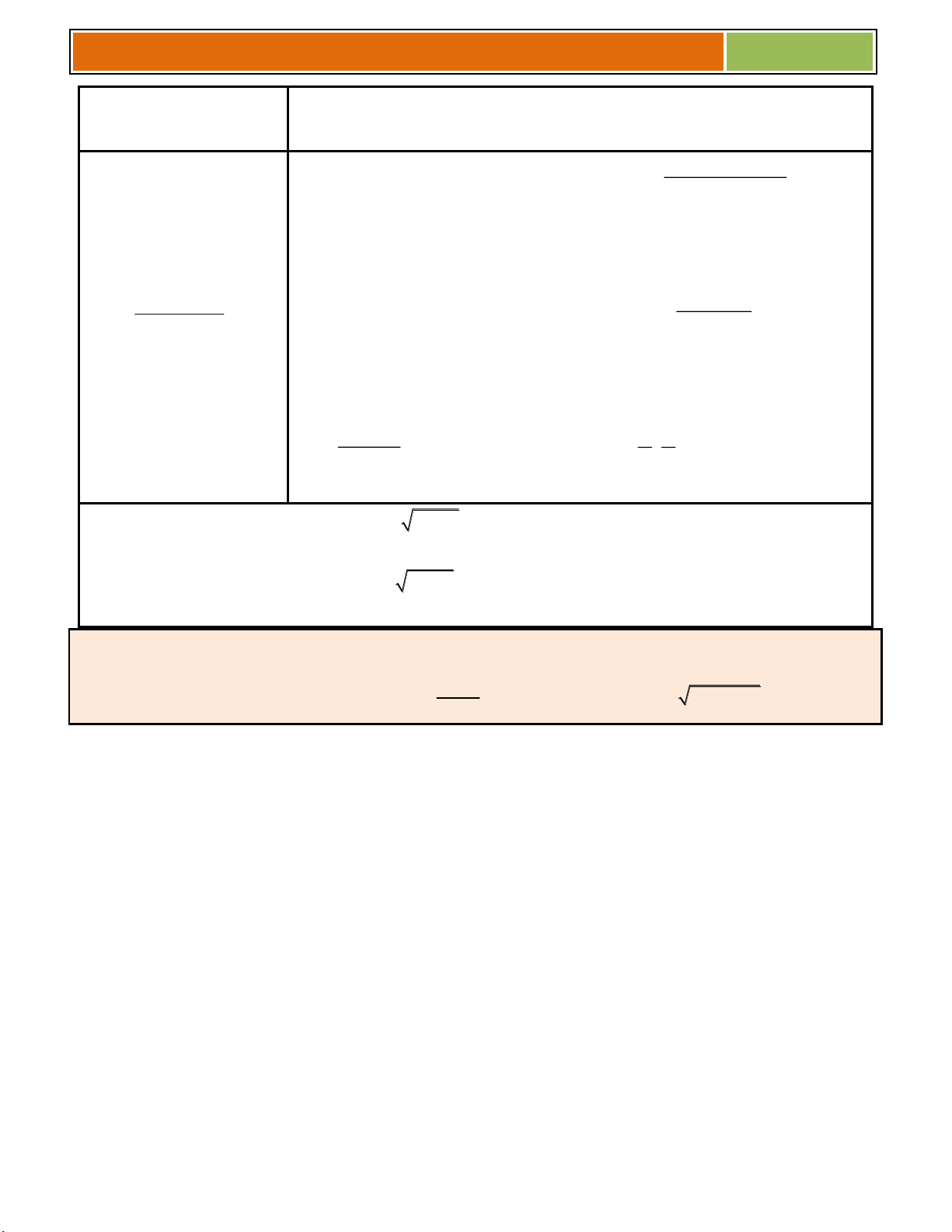
1) Định nghĩa : F(x) là nguyên hàm của hàm số f(x) trên (a; b)  ................................ 2) Họ nguyên hàm :
, với C là ............................
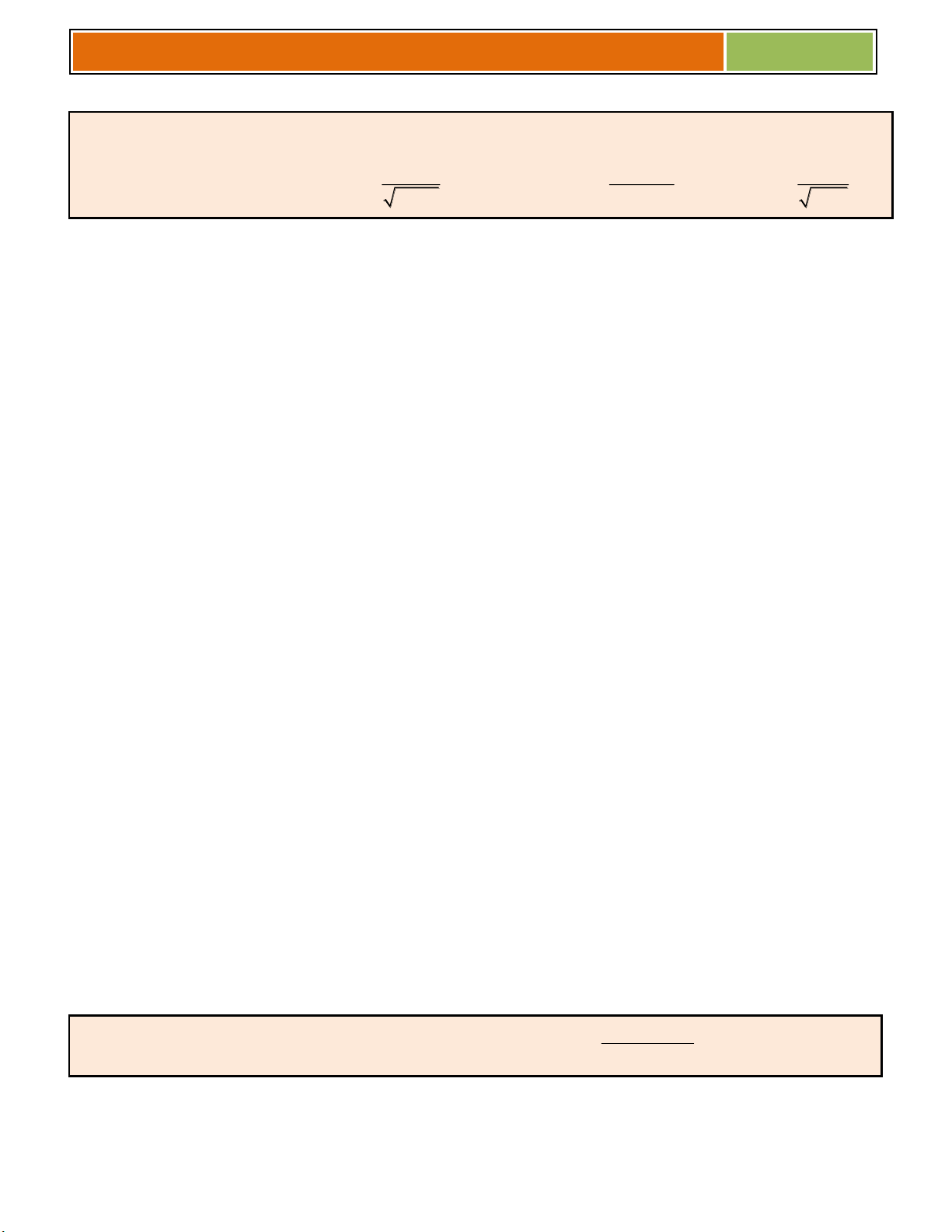
3) Bảng nguyên hàm : Hàm cơ bản : Hàm chứa (ax + b) dx  x  C  α 1  α 1   α x α 1 (ax b) x .dx   C  ax b dx   C α 1 a α 1 dx  ln x  C  dx 1  ln ax  b  C  x ax  b a dx 1    dx 1 1 C    .  C  2 x x 2 (ax  b) a ax  b dx  dx 2 2 x  C   ax  b  C  x ax  b a x a axb  1 a x a dx   C  ax b a dx   C  lna a lna x x  1 e dx  e  C  ax b axb e dx  e  C  a sinx.dx  c  osx  C  1
sin(ax  b).dx   cos(ax  b)  C  a cosx.dx  sinx  C  1 cos(ax  b).dx  sin(ax  b)  C  a dx  dx 1 tanx  C   tan(ax  b)  C  2 cos x 2 cos (ax  b) a dx   dx 1 cotx  C    cot(ax  b)  C  2 sin x 2 sin (ax  b) a 1
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
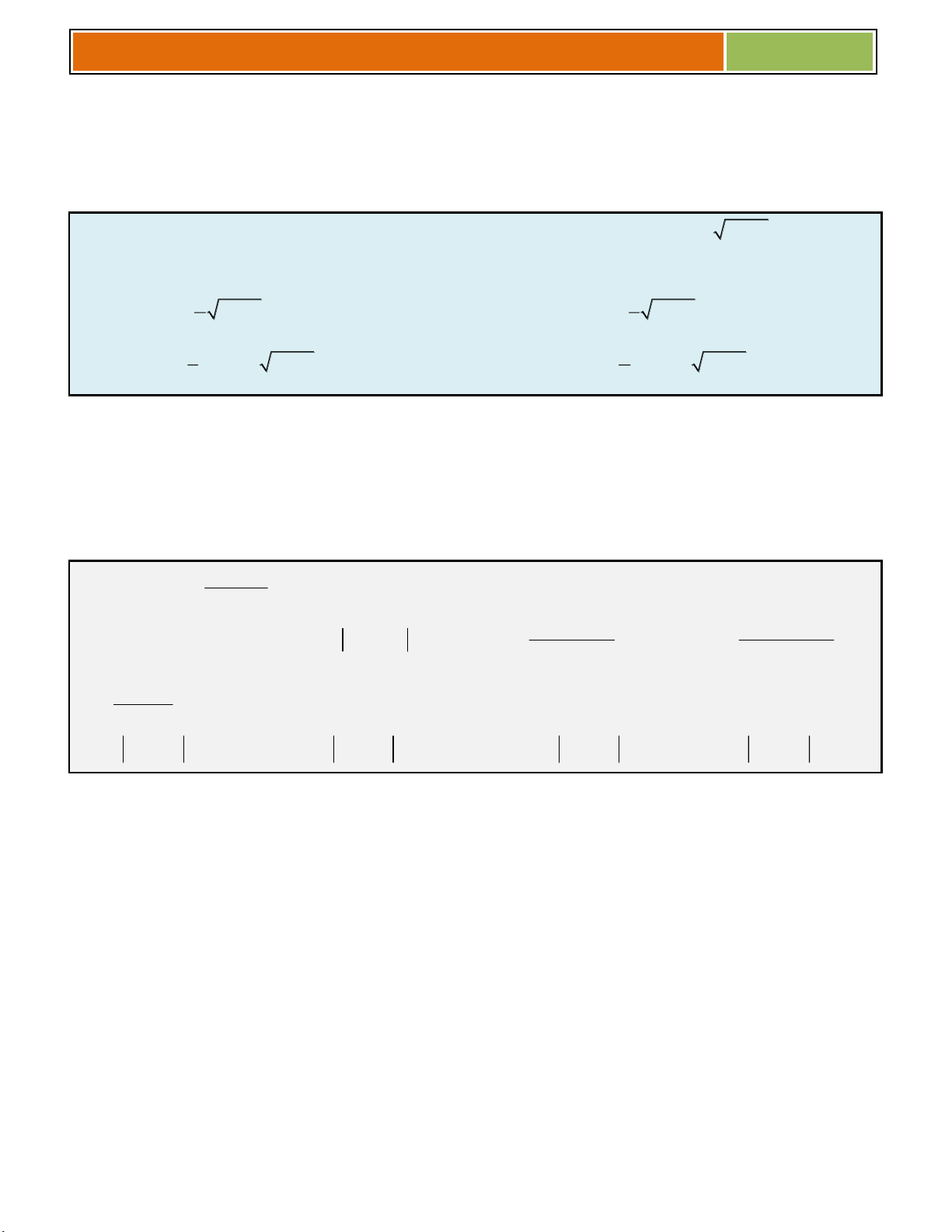
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 dx 1 x  a  ln  C  2 2 x  a 2a x  a Công thức chú ý :
4) Cách tìmnguyên hàm : Biến đổi tích hoặc thƣơng, tổng, bạ bậc, khai triển lũy thừy, chia đa m m 1  x 
thức<.. Căn thức thành lũy thừa : n m n m n n x  x ;  x ;  x n n x x
5) Công thức thường dùng : 1 cos2u 1 3cosu  cos3u 2 cos u  2 1 tan u 3 cos u  2 2 cos u 4 1 cos2u 1 3sinu  sin3u 2 sin u  2 1 cot u 3 sin u  2 2 sin u 4 sin2u  2sinu.cosu 2 2 cos2u  cos u  sin u 2 cos2u  2cos u 1 2 cos2u  1 2sin u
Ví dụ 01: TÌM HỌ NGUYÊN HÀM CỦA CÁC HÀM SỐ SAU: 3 2x  5x  2 2x x e  3e  2 a/ 2 3 f(x)  (2x 1) b/ 2 f(x)  (tan x  cot x) c/ f(x)  d/ f(x)  2 x x e 1 α 1  ♥ α x
Giải : a/ Ở đây ta sử dụng công thức : x .dx   C      α 1 Ta có 6 4 2 f(x) 8x 12x 6x 1, 8 12 Suy ra : 6 4 2
f(x)dx  8 x dx 12 x dx  6 x dx  1dx      7 5 3  x  x  2x  x  C 7 5 2
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018  1   1  1 1 b/ Ta có 2 2
f(x)  tan x  cot x  2  1  1  2       2 2  cos x   sin x  2 2 cos x sin x 1 1 Suy ra: f(x)dx  dx  dx  tan x  cot x  C    2 2 cos x sin x 5 2 1  2 c/ Ta có f(x)  2x   . Suy ra: 2 2 f(x)dx  2 xdx  5
dx  2 x dx  x  5ln x   C     2 x x x x 2x x x x x x e
 e  2(e 1) e (e 1)  2(e 1) x x (e 1)(e  2) d/ Ta có f(x)   x   e  2 x x e 1 e 1 x e 1 Suy ra: x x
f(x)dx  e dx  2dx  e  2x  C   
Ví dụ 02 (THPT chuyên Phan Bội Châu lần 2):
Biết hàm số F  x 3
 ax  a b 2
x  2a  b  c x 1 là một nguyên hàm của hàm số f  x 2
 3x  6x  2 . Tổng a b  c là: A. 3 . B. 2 . C. 4 . D. 5 .
♥ Giải : Đạo hàm : Fx 2
 3ax  2a b x 2a b  c. 3  a  3 a 1  
Ta có: F x  f  x  2a  b  6  b  2  a  b  c  5. Chọn đáp án D  
2a  b  c  2 c  2 
Ví dụ 03 (Cụm 1 – Tp.HCM): Biết một nguyên hàm của hàm số y  f  x là F  x 2
 x  4x 1.
Khi đó, giá trị của hàm số y  f  x tại x  3 là. A. f   3  30 . B. f   3  22 . C. f   3  10 . D. f   3  6 . ♥ Giải : 
Cách 1 : Ta có: F x  f  x  f  x   2 x  4x   1  2x  4 .
f 3  2.3  4 10 . Chọn đáp án C
Cách 2 : sử dụng máy tính Casio. 3
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
Bài Tập 1: Tìm họ nguyên hàm các hàm số sau 1 3 7 9 20 1/ 5 2 f(x)  x  3x  5  2/ f(x)     x 5 4 3 2 x x x x 5 7 9 x  4x  2x  8  7x 3/ f(x)  4/ 3 4 f(x)  x  x  4 x 2 x x  e 
5/ f(x)  ( x 1)(x  x 1) 6/ x f(x)  e  2   2  sin x  ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 4
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
Bài Tập 2 (SỞ GD ĐT HÀ TĨNH): Biết rằng F  x 4  .
m x  2 là một nguyên hàm của hàm số   3 1
f x  x , giá trị của m là. A. . B. 1. C. 0. D. 4. 4 ♥ Giải :
.................................................................................................................................................................................
................................................................................................................................................................................. 1
Bài Tập 3: a/ Nguyên hàm của hàm số 2
f (x)  x  3x  là: x 3 2 x 3x 3 2 x 3x 1 3 2 x 3x A.   ln x  C B.    C C. 3 2
x  3x  ln x  C . D.   ln x  C 3 2 2 3 2 x 3 2 b/ Họ nguyên hàm của 2
f (x)  x  2x 1 là 1 A. 3 F (x) 
x  2  x  C
B. F(x)  2x  2  C 3 1 1 C. 3 2 F (x) 
x  x  x  C D. 3 2 F (x) 
x  2x  x  C 3 3 1 1
c/ Nguyên hàm của hàm số f (x)   là : 2 x x 1 1 1 A. 2
ln x  ln x  C B. lnx – + C C. ln|x| + + C
D. ln x   C x x x ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài Tập 4: Tìm nguyên hàm của các hàm số sau x  e a/ x x  f(x)  e (7  3e  ) b/  x x 2x 1 f(x) 2 3 .2    c/ x x f(x)  e (5  3e ) 2 cos x ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 5
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài Tập 5: Tìm họ nguyên hàm các hàm số sau 7
1/ f(x)  2sinx  3cosx  2/ 2 2 f(x)  tan x  3cot x 3/ 2 f(x)  (2tanx  cotx) x 1 2 4/ f(x)  5/   5 f(x) x  3x x   1 6/ f(x)  3sinx  7cosx 2 2 sin x.cos x 15 4 6 3x  7x  2x  8 10x 6 8/ f(x)  7/ x 3
f(x)  2 x  3e  4sin x  8 / x 9/ f(x)  3 x 2 2 sin x.cos x ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 6
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 3 
Bài Tập 6: a/ Nguyên hàm của hàm số f x x 1  là: x 4 x  x x 4   3   3         3   4   4  A. Fx  3  C B. Fx   C C.   x F x   C D. Fx  3  C 3 3 2 3 ln ln ln 4 4 4 b/ 2x x x 2 .3 .7 dx  là x 84 2x x x 2 .3 .7 A.  C B.  C C. x 84  C D. x 84 ln 84  C ln 84 ln 4.ln 3.ln 7 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài Tập 6: Tìm họ nguyên hàm các hàm số sau x x 1/ 3 2
f(x)  x  3x  4x  3; 2/ 2 2 f(x)  2x(x  3x) 3/ f(x)  4sin cos 2 2 1 4/ x
f(x)  2sin x  3cos x  5e 5/ 2 f(x)  tan x  3 6/ 2 f(x)  (2  ) x 3 ( x  2) 7/   f(x)  8/ 2x 1 3x 2 f(x)  2 .3 9/ x 2 f(x)  (3  2) x ♥ Giải :
................................................................................................................................................................................. 7
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài Tập 7: Chứng minh F(x) là một nguyên hàm của hàm số f (x) trong các trường hợp sau: a/ 3 2
F(x)  5x  4x  7x 120 và 2
f (x)  15x  8x  7. 1 b/ 2
F(x)  ln(x  x  3) và f (x)  . c/ ( )  (4  5) x F x x
e và ( )  (4 1) x f x x e . 2 x  3
Phƣơng pháp: Đ F(x) à t nguyên hà c a hà s f (x), ta cần chứng minh: ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 8
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
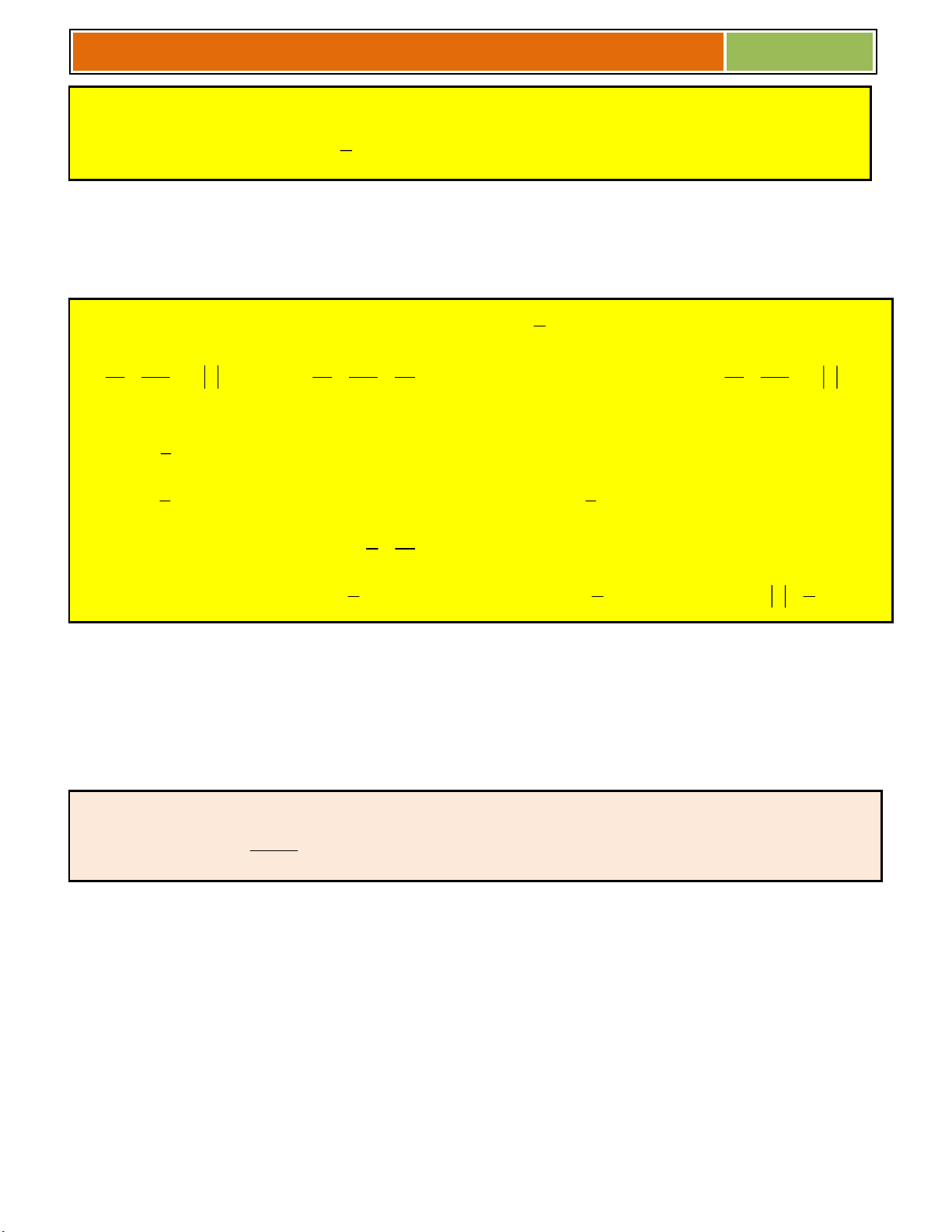
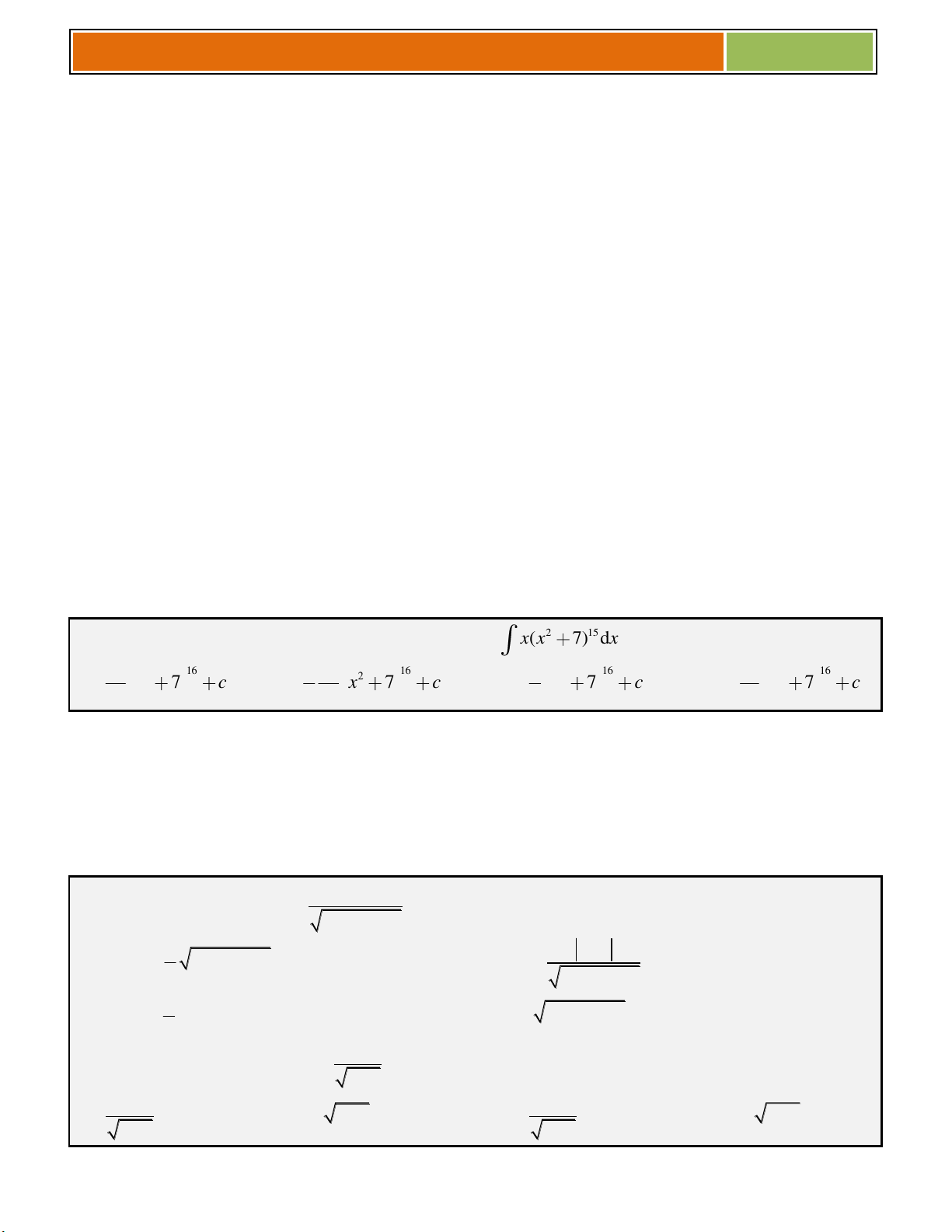
Ví dụ 03: TÌM HỌ NGUYÊN HÀM CỦA CÁC HÀM SỐ SAU: 2 a/ 3
f(x)  (2x 1) ; b/ f(x)  cos 3x  2 ; c/ f(x)    7x  ; d/ x f(x) e  ; e/ 10 f(x) (7 3x) 1 α 1  α 1 (ax  b)
Giải : a/ sử dụng công thức ax  b dx   C a α 1 4 1 (2x 1) 3 f(x)dx  (2x 1) dx  .  C   2 4 1 1
b/ sử dụng công thức cos(ax  b).dx  sin(ax  b)  C  f(x)dx  cos 
 3x 2dx  .sin3x 2C a 3 dx 1
c/ sử dụng công thức  ln ax  b  C  axb a 2 dx 2 f(x)dx  dx  2  .ln 3x  2  C    7x 1 7x 1 7  1 
d/ sử dụng công thức ax b ax b e dx  e  C  a  1 x x x f(x)dx  e dx  e  C  e   C  
( chú ý hệ số a trong bài này là -1 ) 1  11 1 (7  3x) e/ giống bài a/ 10 f(x)dx  (7  3x) dx  .  C   3  11
Điền vào ô trống dx a/ 5 (7  4x) dx =  b/ =  2x7 dx c/    d/ 8x 7 e dx =  4x   = 5 1  dx e/ x e dx =  f/ =  2 cos    x 9
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
Bài tập 01 (THPT Hoàng Văn Thụ - Khánh Hòa): Tìm nguyên hàm của hàm số   2017  x f x  e . A.    2017   d x f x x  e  C . B.    2017 d x f x x  e  .ln 2017  C . 1 C.    2017   d x f x x   e  C . D.    2017 d  2  017. x f x x e  C . 2017 ♥ Giải :
.................................................................................................................................................................................
Bài tập 02 (THPT Trần Hưng Đạo – Nam Định): Tìm nguyên hàm của hàm số   2 1 3 x f x   . x A. f  x 2 x 1 dx 3   ln 3  C . B. f  x 2 1 3 dx   C . ln 3 x C. f  x 2 1 3 dx   C .
D.        2 d 2 1 3 x f x x x  C . ln 9 ♥ Giải :
.................................................................................................................................................................................
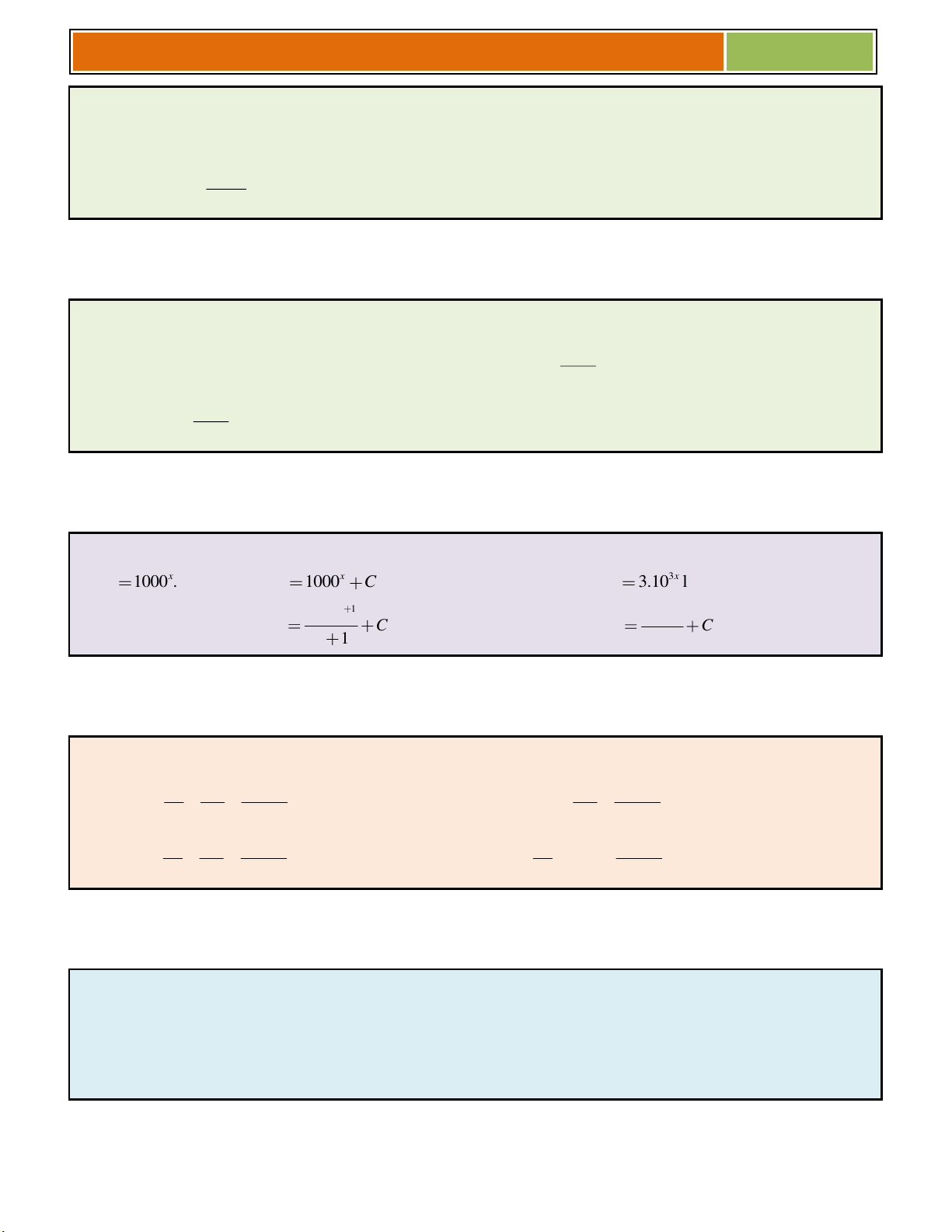
Bài tập 03 (THPT chuyên Lê Hồng Phong – Nam Định): Tìm nguyên hàm F x của hàm số 1000 . x f x A. 1000x F x C B. 3 3.10 x F x ln10 x 1 1000 3 10 x C. F x C D. F x C x 1 3ln10 ♥ Giải :
.................................................................................................................................................................................
Bài tập 04 (Sở GD-ĐT Long An): Tìm nguyên hàm F  x của hàm số   4 3x
f x  x  e  cos 2x . x x e x x e sin 2x A. F  x 5 3 sin 2     C B. F  x 3 3  4x    C 5 3 2 3 2 x x e x x x x sin 2 C. F  x 5 3 sin 2     C D. F  x 5 3   3e   C 5 3 2 5 2 ♥ Giải :
.................................................................................................................................................................................
Bài tập 05 : Tìm họ nguyên hàm các hàm số sau 1/ 2 f(x)  sin x 2 / 2 f(x)  sin 7x 3/ 2 f(x)  cos 4 x 4/ 4 f(x)  cos x 5/ 4 f(x)  sin 2 x 6/ 2 2 f(x)  7sin x.cos x
♥ Giải : Lưu ý các công thức sử dụng cho phần này là : HẠ BẬC 10
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài tập 06: Tìm họ nguyên hàm các hàm số sau 1/ f(x)  sin 2 x.cos x 2/ f(x)  sin 4 x.sin 6x 3 / f(x)  cos 6 x.cos 2 x 11
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
♥ Giải : Lưu ý các công thức sử dụng cho phần này là :TÍCH THÀNH TỔNG ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài tập 07: Tìm họ nguyên hàm các hàm số sau 3 2 x  3x  6x  5 1 2 3x  6x  5 1 / f(x)  f(x)  3/ f(x)  x  2/ 1 x  9  x 2x 1 3 6  x  5 4/ f(x)  5 / f(x)     π   6/ 4 4 f(x) cos x sin x 2 2x 5 cos 2x     4  ♥ Giải :
................................................................................................................................................................................. 12
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài tập 08: Tìm họ nguyên hàm các hàm số sau 4 2 x  x 1
1/ (ĐH Ngoại Thương – 1998- Khối A) f(x)  2 x  x 1 13
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 4 2 x  2x  2  x
2/ (ĐH Ngoại Thương – 1998- Khối D) f(x)  2 x  x 1 2 cos2x  x 1 
3/ (ĐH Ngoại Thương – 2000 - Khối D) f(x)  f(x)    sinx  4 / cosx  x  2  ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài tập 09 (THPT chuyên Hưng Yên lần 2): Tìm giá trị của m để hàm số F  x 2 3
 m x   m   2 3
2 x  4x  3 là một nguyên hàm của hàm số f  x 2
 3x 10x  4.. 14
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 A. m  2 B. m  1 C. m  1  D. m  1  ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. x  e 
Bài tập 10 (THPT chuyên Thái Bình): Tìm nguyên hàm của hàm số f  x x  e 2  ? 2  cos x  A.    2 x F x e  tan x B.    2 x F x
e  tan x  C C.    2 x F x
e  cot x  C D.    2 x F x
e  tan x  C ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài tập 11: Hàm số   2 x F x  e
là một nguyên hàm của hàm số: 2 x e A.   2 2 x f x  x e 1
B. f  x  C.   2 x f x  e D.   2  2 x f x xe 2x ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài tập 12 (Cụm 1 HCM): Nguyên hàm của hàm số     2x f x x là: x x x A. f  x 2 2 x d    C B. f  x 2 x d 1  C 2 ln 2 ln 2 x x C. f  x 2 x d   2x  C D. f  x 2 x d 
 2x ln 2  C 2 2 ♥ Giải :
.................................................................................................................................................................................
Bài tập 13: a/ Nguyên hàm của hàm số   1 3x f x e   là:  3 3e e A. Fx   C B.   1 3x e F x   C C. Fx    C D. Fx    C 1 3x e  3 3x e 3x 3e 15
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 1
b/ Nguyên hàm của hàm số f x  là: 2 5x e   5 5 e A. Fx   C B. Fx    C C.   2 5x e F x    C D. Fx 5x   C 2 5x e  2 5x e  5 2 5e ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
PHƢƠNG PHÁP XÊ HẮC E
Bài tập minh họa cho phương pháp : 3x  7 A B a/ Tìm A, B sao cho     ) 2 x  4x  3 x 1 x  (x 1; 3 3 3x  7 b/ Tính I  dx  2x 4x3 3x  7 A B Giải : a/  
 3x  7  A x  3  B x 1 2     x  4x  3 x 1 x  3       A  B  3 A  2 3x 7 A B .x  3A  B     3  A  B  7 B 1
Phương pháp Xê Hắc E :
Hai công thức cần chú ý cho dạng này 16
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 3x  7  2 1  b/ I  dx  
dx  2 ln x 1  ln x  3  C    2 x  4x  3  x 1 x  3 
Bài tập 7 : Tính các nguyên hàm số sau ( sử dụng pp Xê Hắc E ) 3x  4 x  7 1 A  dx  ; B  dx  ; C  dx  2 x  4x  5 2 x  8x  9 2 x  x  2 dx x 3 8  D   ; F  dx  ; G  dx  ; F  dx  x x   1 2 x  x  6 2 x  7x 12 2 x 10x  9 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 17
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
.................................................................................................................................................................................
.................................................................................................................................................................................
Trắc nghiệm bổ sung
TN1 (THPT Hà Huy Tập): Công thức nào sau đây sai? 1 1 1 1 A. ln d x x   C  B.
dx  ln x  C  C.
dx  tan x  C  D. sin 2 d
x x   cos 2x  C  x x 2 cos x 2 2x  3
TN2 : Tìm nguyên hàm của hàm số f(x) biết f (x)  2 x  4x  3 2 x  3x 2 x  3x A.  C B.   C 2 x  4x  3
x 4x32 2 1 C.
ln x1 3ln x3C D. 2
(2x  3) ln x  4x  3  C 2 3x e 1 1
TN3 : Xét các mệnh đề: (I)  cot   dx x C 2 (II) dx  x e  x e  x   C 2 sin x x e 1 2
Khẳng định nào sau đây là đúng? A.(I) đúng , (II) sai B. (I) sai, (II) đúng
C. Cả (I) và (II) đều đúng
D. Cả (I) và (II) đều sai
TN4 : Cho F(x) là một nguyên hàm của f(x) = cos 2x. 
Khi đó, hiệu số F( )  F(0) bằng: 4 1 2 A. 15 B. C. 2 D. 2 4
TN5 (THPT Chuyên Tuyên Quang): Nguyên hàm của hàm số f  x 5  7x là : A. F  x 6  5x  C B. F  x 6  35x  C 7 C. F  x 4  35x  C D. F  x 6  x  C 6
TN6 (THPT Lý Nhân Tông): Trong các khẳng định sau khẳng định nào sai ?  1 A.   0dx  C  ( C là hằng số). B. 1 x dx  x  C    ( C là hằng số). 1 18
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 1 C.
dx  ln x  C  ( C là hằng số).
D. dx  x  C  ( C là hằng số). x 1
TN7 (THPT chuyên Vĩnh Phúc lần 5): Tính nguyên hàm dx  . 1 x 1
A. log 1 x  C .
B. ln 1 x  C .
C. ln 1 x  C . D.    C . 1 x2 4 2x  3
TN8: Hàm số y  có một nguyên hàm là 2 x 3 2x 3 3 3 2x 3 3 x 3 A.   3 B. 3 3  x  2 C.  1 D.   2017 3 x x 3 x 3 x
TN9 (THPT chuyên LTV): Cho hàm số y  f  x liên tục trên và thoả mãn f  x 3 2
dx  4x  3x  2x  C . Hàm số f  x là: A.   4 3 2
f x  x  x  x  Cx  C . B. f  x 2
12x  6x  2  C . C.   4 3 2
f x  x  x  x  Cx . D. f  x 2
12x  6x  2 .
TN10 (THPT chuyên Lê Thánh Tông): Biết f  x có một nguyên hàm là 17x .
Xác định biểu thức f  x . A.   1 .17x f x x   . B.   17x f x ln17  C . x C. f  x 17  . D.   17x f x  ln17 . ln17 3
TN11 (THPT Tiên Du 1): Nguyên hàm của hàm số f  x 3  x   2x là. 2 x 4 x 3 4 3 2x x A.
  2 .xln 2  C . B.    C . 4 x 4 x ln 2 3 x 1 4 x C.   2x  C . D. 2
 3ln x  2 .xln 2  C . 3 3 x 4 x
TN12 (Sở GDĐT Lâm Đồng lần 04): Nguyên hàm của hàm số f  x 2  3x  là: 2 19
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 3 2 x x 2 x 2 x 2 x A.   C . B. 3 x   C . C. 3 x   C . D. 3 x   C 3 4 4 2 2
TN13 (THPT Nguyễn Khuyến –NĐ): Hàm số F  x là nguyên hàm của f  x x 2
 e 3x trên tập số
thực. Tìm F  x . x 3 A. F  x 3  e  x . B. F  x x 2
 e  x 1. 2 C. F  x x 3
 e  x 1. D. F  x x 3
 e  x 1.
TN14 (THPT Hùng Vương–PT): Tìm nguyên hàm của hàm số f  x 1  2x  . x 1 A. f  x 2
dx  x  ln x  C . B. f  x 2 dx  x   C . 2 x 1 C. f  x 2 dx  x   C . D. f  x 2
dx  x  ln x  C . 2 x
TN15 (THPTQG – 2017): Tìm nguyên hàm của hàm số f  x  2sin x .
A. 2sin xdx  2cos x  C  . B. 2
2sin xdx  sin x  C  .
C. 2sin xdx  sin 2x  C  . D. 2sin xdx  2  cos x  C  .
TN16 (THPT chuyên Phan Bội Châu): Hàm số nào dưới đây là nguyên hàm của hàm số f  x 1  ? 1 . x 1 A. F  x 2
 ln(x  2x 1)  5.
B. F  x  ln 2x  2  4 . 2
C. F  x  ln 1 x  2 . D. F  x 1
  ln 4  4x  3 . 4
TN17 : Cho F(x) và G(x) là các nguyên hàm của hàm số f(x) trên khoảng (a,b). Khi đó (I) F(x) = G(x) + C (II) G(x) = F(x) + C
Với C là một hằng số nào đó. Khẳng định nào sau đây là đúng ? A. (I) đúng, (II) sai B. (I) sai, (II) đúng
C. Cả (I) và (II) đều đúng
D. Cả (I) và (II) đều sai  1 
TN18 (THPT chuyên Nguyễn Trãi lần 2): Tính nguyên hàm dx   .  2x  3  20
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 1 1
A. ln 2x  3  C
B. ln 2x  3  C C.
ln 2x  3  C
D. 2ln 2x  3  C 2 2 1
TN19 (THPT Nguyễn Tất Thành): Tìm họ nguyên hàm của hàm số f  x  2 x  4x  . 3 1 x  3 1 x  3 A. ln  C . B. ln  C . 2 x 1 2 x 1 1 x  3 1 x  3 C.  ln  C . D. ln  C . 2 x 1 2 x 1 1 
TN20 (THPT chuyên LHP): Cho F  x là một nguyên hàm của hàm số f  x 1  \   . 2x  trên 1 2
Phát biểu nào sau đây sai ? x  x 
A. F  x ln 6 3   C .
B. F  x ln 2 1   C . 2 2 x  C. F  x  2 ln 2 1   C .
D. F  x  ln 2x 1  C . 4
TN21 (THPT chuyên Bến Tre): Tìm nguyên hàm của hàm số f  x 1  1 . 2x  A. f
 xdx  2ln 12x C . B. f  x 1 dx 
ln 1 2x  C . 2 C. f
 xdx ln 12x C . D. f  x 1 dx 
ln 1 2x  C . 2
TN22 (Sở GD-ĐT Đồng Nai): Tìm nguyên hàm của hàm số g  x 5  4 . 3x  A. g  x 5 dx 
ln 4  3x  C . B. g  x 5 dx 
ln 4  3x  C . 3 3 C. g
 xdx 5ln 43x C. D. g
 xdx 5ln43xC . dx
TN23 (Cụm 7 – Tp.HCM): Tìm  , ta được: 2x 1 1 1 A. ln 2x   1  C .
B. ln 2x 1  C . 2 2 2 C.      C . D. ln 2x 1 C . 2x  2 1
TN24 (THPT chuyên LTV): Nguyên hàm của hàm số   2 x f x e  là: 21
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 1 1 A.    2 d  x f x x  e  C . B.    2 d  x f x x   e  C . 2 2 C.    2 d  2  x f x x  e  C . D.    2 d  x f x x  e   C .
TN25 (THPT Tiên Lãng): Tìm nguyên hàm   x I  e 2 3 2 dx  . 4 4 x 5 x 1 A. 3 6  4 x I x  e  e  C B. 3 6  4 x I x  e  e  C . 3 6 3 6 4 4 x 1 x 1 C. 3 6  4 x I x  e  e  C . D. 3 6  3 x I x  e  e  C . 3 6 3 6
TN26 (Sở GD-ĐT Đồng Nai): Cho hàm số h x    x8 15 12
. Tìm h xdx  . 1 A. h
 xdx  12x159 C . B. h
 x x    x7 d 8 15 12  C . 108 1 C. h
 x x     x7 d 96 15 12  C . D. h
 xdx   1512x9 C . 96
TN27 (Sở GDĐT Lâm Đồng lần 05): Tìm nguyên hàm của hàm số f x   x  5 ( ) 3 1 . 1 1 A.
f (x)dx   3x  5 1  C . B.
f (x)dx   3x  6 1  C . 18 6 1 1 C.
f (x)dx   3x  6 1  C . D.
f (x)dx   3x  6 1  C . 18 3
TN28 (THPT Nguyễn Thị Minh Khai – KH): Hàm số nào sau đây là một nguyên hàm của hàm số x y  e  2 ? A. 2 x
y  e  2x . B. x
y  e  2x 1. C. x
y  e  2x 1. D. x
y  e  x .
TN29 (Cụm 1 – Tp.HCM): Nguyên hàm của hàm số     2x f x x là: x x x A. f  x 2 2 dx    C . B. f  x 2 dx  1  C . 2 ln 2 ln 2 x x C. f  x 2 dx   2x  C . D. f  x 2 dx 
 2x ln 2  C . 2 2
TN30 (THPT chuyên Nguyễn Trãi lần 2): Tìm nguyên hàm của hàm số f  x  sin 2x . 1 1 A. 2
 cos2x  C .
B. cos 2x  C .
C. 2cos 2x  C .
D.  cos 2x  C . 2 2 22
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
TN31 (THPT chuyên Nguyễn Trãi lần 1): Hàm số y  sin x là nguyên hàm của hàm nào trong các hàm sau ?
A. y  cos x .
B. y  tan x .
C. y  cot x .
D. y  sin x 1.
TN32 (THPT chuyên Nguyễn Trãi lần 1): Trong các mệnh đề sau, mệnh đề nào sai? A. xdx x e  e C  .
B. sin xdx  cos x  C  . 1 C. 2 2 d
x x  x  C  . D.
dx  ln x  C  . x
TN33 (THPT Nguyễn Tất Thành): Tính I  cos
 4x3dx.
A. I  sin 4x  3  C .
B. I  sin 4x  3  C . 1
C. I  4sin 4x  3  C .
D. I  sin 4x  3  C . 4
TN34 (Đề Minh Họa lần 2): Tìm nguyên hàm của hàm số f  x  cos 2x . A. f  x 1 dx  sin 2x  C . B. f
 xdx  2
 sin 2x  C . 2 C. f  x 1
dx   sin 2x  C . D. f
 xdx  2sin2xC . 2
TN35 (THPT chuyên Võ Nguyên Giáp): Kết quả nào đúng trong các phép tính sau? A. 2 cos 2 d x x  2  cos x  C  . B. cos 2 d
x x  sin x cos x  C  . C. cos 2 d
x x  sin 2x  C  . D. cos 2 d
x x  2sin 2x  C  . 3 TN36: dx  bằng: 2x  5 3 3
A. 2ln 2x  5  C
B. ln 2x  5  C
C. 3ln 2x  5  C
D. ln 2x  5  C 2 2 1 TN37:   dx bằng: 5x  32 1 1 1 1 A.   C  C   C   C 55x  B. 3 55x  C. 3 5x  D. 3 55x  3 3x 1 TN38: dx  bằng: x  2
A. 3x  7 ln x  2  C
B. 3x  ln x  2  C
C. 3x  ln x  2  C
D. 3x  7 ln x  2  C 23
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 1 TN39:     dx bằng:
x 1  x  2 x 1
A. ln x 1  ln x  2  C B. ln  C x  2
C. ln x 1  C
D. ln x  2  C x 1 TN40: dx  bằng: 2 x  3x  2
A. 3ln x  2  2ln x 1  C
B. 3ln x  2  2ln x 1  C
C. 2ln x  2  3ln x 1  C
D. 2ln x  2  3ln x 1  C 1 TN41: dx  bằng: 2 x  4x  5 x  5 x  5 1 x  5 1 x  5 A. ln  C B. 6 ln  C C. ln  C D.  ln  C x 1 x 1 6 x 1 6 x 1 1
TN42: Tìm nguyên hàm: dx  . x(x  3) 1 x 1 x  3 1 x 1 x  3 A. ln  C B. ln  C C. ln  C D. ln  C 3 x  3 3 x 3 x  3 3 x 1 TN43: dx  bằng: 2 x  6x  9 1 1 1 1 A.   C  C   C  C x  B. 3 x  C. 3 x  D. 3 3  x 1
TN44: Cho hàm f  x  2 x  3x  . Khi đó: 2 x  x  A. f  x 1 dx  ln  C B. f  x 1 dx  ln  C x  2 x  2 x  x  C. f  x 2 dx  ln  C D. f  x 2 dx  ln  C x 1 x 1 1
TN45: Họ nguyên hàm F(x) của hàm số f (x)  2
x  4x  là 3 1 x  3 1 x 1 A. F(x)  ln | | C  F (x)  ln | | C  2 x  B. 1 2 x  3 24
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 x  3 C. 2
F(x)  ln | x  4x  3 | C  D. F(x)  ln | | C  x 1 x d TN46: Tính  2 x  2x  3 1  x 1 1  x  3 1 x  3 1 x 1 A. ln  C B. ln  C C. ln  C D. ln  C 4 x  3 4 x 1 4 x 1 4 x  3 1
TN47: Họ nguyên hàm của f(x) = x(x  là: 1) x 1 x A. F(x) = ln  C B. F(x) = ln  C x x 1 1 x C. F(x) = ln  C
D. F(x) = ln x(x 1)  C 2 x 1 2x  3
TN48: Tìm nguyên hàm của hàm số f(x) biết f (x)  2 x  4x  3 2 x  3x A.    C B. 2
(2x  3) ln x  4x  3  C
x  4x  32 2 2 x  3x 1 C.  C
ln x 1  3ln x  3  C 2 x  4x  D.   3 2
TN49: Cho hàm số f  x xác định trên K . Hàm số F  x được gọi là nguyên hàm của hàm số
f  x trên K nếu:
A. F’ x  f  x, x   K
B. F’ x  f  x, x   K
C. f  x  F  x, x   K
D. f  x  F  x, x   K
TN50: Các tính chất nguyên hàm sau đây tính chất nào sai? A.
f '(x)dx  f (x)  C  B.
Kf (x)dx  K f (x)dx   K  0
C.  f (x)  g(x)dx  f (x)dx  g(x)dx   D.
F(x)dx  f (x)  C 
TN51: Trong các mệnh đề sau, tìm mệnh đề sai 3 f (x) A. 2
f '(x) f (x)dx   C 
B.  f (x).g(x)dx  f (x)d .x g(x)dx   3
C.  f (x)  g(x)dx  f (x)dx  g(x)dx  
D. kf (x)dx k  f (x)dx   ( k là hằng số) 25
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 TN52: Cho f
 xdx  F xC . Khi đó, với a  0, ta có f
 axbdx bằng 1 1 A.
F ax  b  C
B. F ax  b  C 2a a
C. F ax  b  C D. .
a F ax  b  C
PHƢƠNG PHÁP ĐỔI BIẾN SỐ
Bài tập minh họa : Tính các nguyên hàm sau ( sử dụng pp đổi biến số ) 2x  4 5 ln x x e a/ sinx A  e .cosxdx  b/ B  dx  c/ C  dx  d/ D  dx  2 x  4x  5 x x e 1 Giải : a/ sinx A  e .cosxdx 
; đặt t  sinx  dt  cosxdx ; Vậy t t sinx A  e .dt  e  C  e  C  2x  4 b/ B  dx  Đặt 2
t  x  4x  5  dt  2x  4 dx 2 x  4x  5 dt Vậy 2 B 
 ln t  C  ln x  4x  5  C  t 5 ln x dx c/ C  dx 
; đặt t  ln x  dt  x x 6 6 t ln x Vậy 5 C  t .dt   C   C  6 6 x e d/ D  dx  ; đặt x x t  e 1 dt  e dx x e 1 dt Vậy : x D 
 ln t  C  ln e 1  C  t
CÁCH ĐỔI BIẾN SỐ CẦN NHỚ Dạng Tích Phân Cách Giải
+ Nếu bậc tử  bậc mẫu ta chia đa thức f(x) .dx  g(x)
+ Nếu bậc tử  bậc mẫu ta xem tử có phải là đạo hà 26
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
c a mẫu hay ko ? nếu có đặt t = mẫu số
+ Nếu ko có 2 trường hợp này ta sẽ làm theo dạng
khác sẽ trình bày ở phần khác n ........dx  Đặt n n
t  .......  t  .......sau đó lấy đạo hàm 2 vế dx dx f(lnx). 
Đặt t  lnx  C  dt  x x f(cosx).sinxdx 
Đặt t  cos x  C  dt  sin xdx f(sinx).cosxdx 
Đặt t  sin x  C  dt  cos xdx dx  tan    dx t x C dt f(tanx)  Đặt 2 2 cos x cos x dx  cot     dx t x C dt f(cotx)  Đặt 2 2 sin x sin x x x f(e ).e dx  Đặt x x t  e  C  dt  e dx 1 1 1 1 1 1 dx dx Đưa về . ... d , x . ...  dx n n  ,   2 4 2 n2 n4 2 sin x sin sin x cos x cos x cos x n n sin x cos x với n chẵn Và Đặt  tan    dx t x C dt 2 cos x n sin xdx  hay Dùng công thức hạ bậc n cos xdx  1 cos2u 1 cos2u 2 2 cos u  ; sin u  2 2 với n chẵn n sin xdx  hay Tách n n 1 sin xdx sin   x.sinxdx   , đặt t = cosx 27
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 n cos xdx  với n lẻ n n 1 cos xdx cos   x.cosxdx   , đặt t = sinx Ax  B
+ Nếu mẫu có 2 nghiệm x , x , ta đưa về dx  1 2 a(x  x )(x  x ) 1 2
Sau đó dùng pp hệ số bất định Ax  B Ax  B dx 
+ Nếu mẫu có nghiệm kép x , ta đưa về dx  2 0 2 ax  bx  c a(x  x ) 0
+ Nếu mẫu vô nghiệm ,đưa về Ax  B     dx 
và đặt X = D.tant t   ;   2 2 X  D  2 2  1/ 2
R(x, a  x ) thì đặt x = sint 2/ 2
R(x, a  x ) thì đặt x = atant
Bài tập 01 : Tính các nguyên hàm sau 8xdx 2 12 A  x(2  x ) dx  B   C  3 1 4sin x.cos x.dx  2 x 1 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 28
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài tập 02 (THPT Thuận Thành 2): F  x là nguyên hàm của hàm số f  x  2x 1 .
Khi đó, F  x là hàm số. A. f  x 1 dx  2x 1  C B. f  x 1 dx   2x 1  C 2 3 1 2 C.
f (x)dx   2x   1 2x 1  C D. f
 xdx  2x 1 2x1C 3 3 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................ 3cos x Bài tập 03: a/ dx  bằng: 2  sin x 3sin x 3sin x A. 3ln 2  sin x  C B. 3  ln 2  sin x  C C.     D. C 2  sin x  C 2 ln 2  sin x x x e  e b/ dx  bằng: x x e  e A. x x ln e  e  C B. x x ln e  e  C C. x x ln e  e  C D. x x ln e  e  C ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................ 29
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
................................................................................................................................................................................. 4x 1 Bài tập 04: a/ dx  bằng: 2 4x  2x  5 1 1 1 A.  C B.   C C. 2
ln 4x  2x  5  C D. 2 ln 4x  2x  5  C 2 4x  2x  5 2 4x  2x  5 2 sin x  cos x b/ Nguyên hàm của là: sin x  cos x 1 1 A. ln sin x  cos x  C B.  C   D.  C ln sin x  C. ln sin x cos x C cos x sin x  cos x c/     2x2x3 x 1 e dx bằng: 2   1 2 x x x 3x 2 1 2 1 A. x 2x3   x e  C B.    3 2 3 x 1 e  C C. x 2x e  C D. x 2x3 e  C  2  2 2 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................. 1 Bài tập 05: a/ dx  bằng: 5 x.ln x 4 ln x 4 1 1 A.   C B.   C C.  C D.   C 4 4 ln x 4 4 ln x 4 4 ln x ln x b/ dx  bằng: x 3 2 A. ln x3 C B.  3 2 ln x  C C. ln x3 C D.  3 3 ln x  C 2 3 x c/ dx  bằng: 2 2x  3 1 1 A. 2 3x  2  C B. 2 2x  3  C C. 2 2x  3  C D. 2 2 2x  3  C 2 2 30
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................ 2 Bài tập 06: a/ x 1 x.e  dx  bằng: 2 1 2 2 2 A. x 1    e   C B. x 1 e  C C. x 1 2e  C D. 2 x 1 x .e  C 2 x b/   bằng: x   dx 2 1 1 1 A. ln x 1  x 1 C B. ln x 1  C C.  C D. ln x 1   C x 1 x 1 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 1 x e 1 1 1 Bài tập 07: a/ dx  bằng: A. x e  C B. x e   C C. x e  C D.  C 2 x 1 x e 31
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 x e x e 1 b/ dx  bằng: A. x e  x  C B. x ln e 1  C C.  C  C x e 1 x e  D. x x ln e 1 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài tập 08: Tính các nguyên hàm sau 2 D  x. x 1.dx  3 4 E  x . 1 x.dx  3dx F   2x. 2ln x ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. x e .dx  2 x dx
Bài tập 09: Tính các nguyên hàm sau G   x 1 I  dx  J   x 3 1 e 3x 1 2x  e 32
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài tập 10(THPT An Lão lần 2): Tìm nguyên hàm 2 15 x(x 7) dx . 16 1 16 1 16 1 16 1 A. 2 x 7 c . B. 2 x 7 c . C. 2 x 7 c . D. 2 x 7 c . 32 32 2 16 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................ x 1
Bài tập 11: a/ Nếu F  x    dx  thì : 2 x  2x  3 1 x 1 A. F  x 2 
x  2x  3  C
B. F  x  ln  C 2 2 x  2x  3 1
C. F  x  ln  2
x  2x  3  C D. F  x 2
 x  2x  3  C 2 dx
b/ (THPT Lý Thái Tổ): Tính  , kết quả là. 1 x 2 C A.  C B. 2  1 x  C C. D. 1 x  C 1 x 1 x 33
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 1
Bài tập 12(THPT Hoàng Quốc Việt): Nguyên hàm dx  bằng. 1 x
A. 2 x  2ln | x 1 | C  B. 2 x  C
C. 2ln | x 1| C 
D. 2 x  2ln | x 1| C  ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài tập 13(TTGDTX Cam Ranh - Khánh Hòa): Biết F  x là một nguyên hàm của hàm số 2 e  2 e  2 ( ) x
f x  xe và F   3 0  . Tính F   1 . A. B. C. e  2 D. e  2 2 2 2 ♥ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 34
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
..............................................................................................................................................................................
Bài tập 14(Cụm 6 – Tp.HCM): Xét I  x  x   5 3 4 4
3 dx . Bằng cách đặt 4
u  4x  3 , khẳng định 1 1 1 nào sau đây đúng. A. 5 I  u du  . B. 5 I  u du  . C. 5 I  u du  . D. 5 I  u du  12 16 4 ♥ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài tập 15: Tính các nguyên hàm sau  cos x cot x e 5 3 K  x 2  x .dx  2 3ln x L  dx  P  dx  Q  .dx  x 2 sin x 2 sin x ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 35
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
.................................................................................................................................................................................
Bài tập 16: Tính các nguyên hàm sau xdx dx 7 4 5 R  2x .(x 1) .dx  xdx O   M   V   2x 1 3 (2x 1) 3 x  5
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 1
Bài tập 17: Tính các nguyên hàm sau 5 N  cos xdx  S   3    dx T sin xdx  x. 4lnx 7 ♥ Giải : 36
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài tập 18: Tính các nguyên hàm sau sin2x A  cot x.dx  B  tanx.dx      2 2 C 2 sin x .sin2x.dx D   3cos x .dx 4 2 ♥ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 37
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
............................................................................................................................................................................. 3sin 2
Bài tập 19: Tính các nguyên hàm sau N  .dx  x 4 2 2 cos x  5sin x ♥ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. x
Bài tập 20: Tính các nguyên hàm sau A  .dx  (HV CNBCVT – 1999) 10 x 1 ♥ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 38
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
TÌM MỘT NGUYÊN HÀM (TÌM HẰNG SỐ C)
Bài tập minh họa 01: π
a/ Tìm một nguyên hàm của hàm số 2
f(x)  tan x , biết F( )  0 4    
b/ Cho hàm số f (x)  sin x  cos 2x . Tìm nguyên hàm F(x) của hàm số f (x) biết F     2  2   ☻ 1 Giải : a/ 2 f(x)dx  tan xdx 
1 dx  tan x  x  C  F(x)     2  cos x  π π π π π π F( )  tan
  C 1  C  0  C  1; Vậy F(x)  tan x  x  1 4 4 4 4 4 4     b/    1 sin cos 2  sin 2  cos   x x dx x x C ; F( ) 
 C  . Vậy F x 1
 sin 2x  cos x  2 2 2 2 2 2
Bài tập minh họa 02 (THPT Ngô Sĩ Liên lần 3) : Biết F  x là một nguyên hàm của của hàm số 2    
f  x  2x  3cos x và F   
. Giá trị F    2  4 là. A. F   2    3
B. F      3 C. F   2   3
D. F      3 ☻ Giải : f
 x x   x x 2 d 2 3cos
dx  x  3sin x  C . 2 2 2        F    3sin  C   C  3   . Suy ra: F   2
   3. Chọn đáp án A  2  4 4 2 4
Bài tập tương tự
Bài 01 (TTGDTX Nha Trang - Khánh Hòa): Nguyên hàm F  x của hàm số f  x  x  sin x thỏa
mãn F 0 19 là. 2 x 2 x 2 x 2 x A.  cos x  2 . B.  cos x  20 C.  cos x  20 . D.  cos x . 2 2 2 2 ♥ Giải :
................................................................................................................................................................................. 39
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
Bài 02 (THPTQG – 2017): Cho F  x là một nguyên hàm của hàm số   x
f x  e  2x thỏa mãn F   3 0 
. Tìm F  x. 2 x 3 x 1 x 5 x 1 A. F  x 2
 2e  x  . B. F  x 2
 e  x  . C. F x 2
 e  x  . D. F  x 2
 e  x  . 2 2 2 2 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài 03 (THPT Chuyên Nguyễn Bỉnh Khiêm – QN): Biết F  x là nguyên hàm của   4x f x  và 9 8 3 7 F   3 1 
. Khi đó giá trị của F 2 bằng. A. . B. . C. . D. . ln 2 ln 2 ln 2 ln 2 ln 2 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài 04: Tìm một nguyên hàm của các hàm số sau 3 2 x  3x  3x 1 π 2 2 a/ f(x)  
(TN THPT – 2003) b/ f(x)  x  sin x biết F( )  2 x  2x  biết F(1) 1/ 3 1 4 3 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài 05: Tìm một nguyên hàm của các hàm số sau 3 2 1 2x a/ 2x 1 f(x) e  
 cos2x  3 biết F(0)  b/ f(x)  biết F( 1)  3 e x 40
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Bài 06: Tìm một nguyên hàm của các hàm số sau f(x)  cos x.2  3tan x biết F(π) 1 ♥ Giải :
.................................................................................................................................................................................
................................................................................................................................................................................
Câu hỏi trắc nghiệm :
Câu 01(THPT Chuyên Phan Bội Châu): Biết F  x là một nguyên hàm của hàm số   1 f x  và x F  
1  3. Tính F 4 . A. F 4  5 B. F 4  3
C. F 4  3 ln 2 D. F 4  4
Câu 02(THPT Trần Hưng Đạo – NĐ): Biết F  x là một nguyên hàm của hàm số f  x 1  2x và 1
F 0  1. Tính giá trị của F 2 . A. F   ln 5 2 
B. F 2 1 ln 5 2 C. F   ln 5 2  1 D. F   ln 5 2  1 2 2
Câu 03(THPT Chuyên Vĩnh Phúc): Nguyên hàm của hàm số: 2 y  cos . x sin x là: 1 A. 3
 cos x  C . B. 3
cos x  C . 3 1 1 C. 3 sin x  C . D. 3 cos x  C . 3 3 41
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
Câu 04(THPT Hoàng Văn Thụ - Khánh Hòa): Cho f  x 3 2
 x  3x 1. Một nguyên hàm F x
của hàm số f  x thỏa mãn F   1  2 là. x 9 A. F  x 4 3 2
 x  3x  2x  2 B. F  x 4 3    x  x  4 4 x 1 C. F  x 4 3 2    x  x  D. F  x 4 3 2
 x  x  x  3 4 4
Câu 05(THPT Chuyên Vinh): Cho F  x là một nguyên hàm của   3x f x  e
thỏa F 0 1. Mệnh
đề nào sau đây là đúng? 1 1 A.   3x F x  e B.   3x F x  e 1 3 3 1 1 x 4 x 2 C. F  x 3  e  D. F  x 3   e  3 3 3 3
Câu 06(THPT Chuyên Vinh): Tìm tất cả các nguyên hàm của hàm số f  x 2  . x 1 A. F  x 1 
B. F  x  4 x 1 x 1
C. F  x  2 x 1
D. F  x  x 1
Câu 07: Biết F  x là nguyên hàm của hàm số f  x 1 
F 2  1. Khi đó F 3 bằng. x  và   1 1 A. ln 2 . B. . 2 3 C. ln 2 1. D. ln . 2
Câu 08(THPT Hoàng Văn Thụ - Hòa Bình): Tìm một nguyên hàm F  x cùa hàm số   2  3  2 x f x x
e 1, biết F 0  1. 2 A.   3   2 x F x x e  x  3 B. F  x 3  x   x 1 x e C.   3   2 x F x x e  x D.   3   2 x F x x e  x 1
Câu 09(Sở GD-ĐT Hải Dương): Cho hàm số f  x  2x  sin x  2cos x . Tìm nguyên hàm F  x của
hàm số f  x thỏa mãn F 0  1. 42
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 A. 2
x  cos x  2sin x
B. 2  cos x  2sin x C. 2
x  cos x  2sin x  2 D. 2
x  cos x  2sin x  2
Câu 10: Họ nguyên hàm của hàm số 3 4 f (x) 
x  x  x 2 4 5 2 3 4 A. 3 3 4 F (x)  x  x  x  C 3 4 5 2 4 5 2 3 4 B. 3 3 4 F (x)  x  x  x  C 3 4 5 2 4 5 2 4 5 C. 3 3 4 F (x)  x  x  x  C 3 3 4 3 4 5 2 3 4 D. 2 3 4 F (x)  x  x  x  C 3 4 5 1
Câu 11: Tìm nguyên hàm của hàm số f(x) biết f (x)  x  9  x 2 3 2 3 A. x   x  C B. x   x  C 27   9 3  27   9 3  2 C.  C D. Đáp án khác 3(  x  93 3  x )
Câu 12: Nguyên hàm của hàm số 2
f (x)  tan x là 3 tan x
sin x  x cos x A.  C B.  C 3 cos x
C. tan x 1 C D. Đáp án khác
Câu 13: Hàm số ( )  x F x
e  tan x  C là nguyên hàm của hàm số f(x) nào x 1 x 1
A. f (x)  e 
B. f (x)  e  2 sin x 2 sin x   x e 
C. f (x)  x e 1  D. Đáp án khác 2  cos x  3
Câu 14: Nguyên hàm của hàm số f(x) = 3   2x x là: 2 x 4 x A. 2
 3ln x  2 .xln 2  C 4 43
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 3 x 1 B.   2x  C 3 3 x 4 3 2x x C.    C 4 x ln 2 4 x 3 D.
  2 .xln 2  C 4 x cos 2x
Câu 15: Nguyên hàm của hàm số: y = là: 2 2 sin . x cos x
A. tanx  cotx + C
B. tanx  cotx + C
C. tanx + cotx + C
D. cotx tanx + C   x e 
Câu 16: Nguyên hàm của hàm số: y = x e  2   là: 2  cos x  x 1 x 1 A. 2 x
e  tan x  C B. 2e   C C. 2e   C D. 2 x
e  tan x  C cos x cos x
Câu 17: Nguyên hàm của hàm số: y = cos2x.sinx là: 1 1 1 A. 3 cos x  C B. 3 cos x  C C. - 3 cos x  C D. 3 sin x  C . 3 3 3
Câu 18: Một nguyên hàm của hàm số: y = cos5x.cosx là: 1  1 1  1 A. F(x) = cos 6x  cos 4  x  B. F(x) = sin5x.sinx 2  6 4  5 1  1 1  1  sin 6x sin 4x  C. sin 6x  sin 4  x  D.     2  6 4  2  6 4 
Câu 19: Một nguyên hàm của hàm số: y = sin5x.cos3x là: 1  cos 6x cos 2x  A.     2  8 2  1  cos 6x cos 2x  B.    2  8 2  1  cos 6x cos 2x  C.    2  8 2  44
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 1  sin 6x sin 2x  D.    . 2  8 2  Câu 20: 2 sin 2  xdx = 1 1 1
A. x  sin 4x  C B. 3 sin 2x  C 2 8 3 1 1 1 1
C. x  sin 4x  C
D. x  sin 4x  C 2 8 2 4 1 Câu 21:  dx = 2 2 sin . x cos x
A. 2 tan 2x  C
B.  2 cot 2x  C
C. 4 cot 2x  C
D. 2 cot 2x  C   2 2 1 Câu 22:  x dx = 3 x 3 x 1 3 x 1 A.  2ln x   C B.  2ln x   C 2 3 2x 2 3 x 3 x 1 3 x 1 C.  2ln x   C D.  2ln x   C 2 3 2x 2 3 3x Câu 23:  2017   x x x e dx = 2017 5 x e 2017 2 x e A. 2 x x   C B. 3 x x   C 2 2017 5 2017 2017 3 x e 2017 2 x e C. 2 x x   C D. 2 x x   C 5 2017 5 2017
Câu 24(Sở GDĐT Lâm Đồng lần 01): Cho a  0 và a  1. C là hằng số. Phát biểu nào sau đây đúng ? A. xd x
a x  a .ln a  C  B. 2 x 2 d x a x  a  C  2 x a C. 2 x a dx   C  D. 2 x 2 d x a
x  a .ln a  C  2 ln a 1
Câu 25(THPT Hoàng Hoa Thám - Khánh Hòa): Một nguyên hàm của hàm số y  x  là : 1 1 A. ln  x   1  x B. ln x 1 C.     D. ln x 1 x x  2 1 45
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 1
Câu 26(THPT Kim Liên – Hà Nội): Tìm nguyên hàm của hàm số f  x 3  x  ? x x 1 A. f  x 4 dx   ln x  C B. f  x 2 dx  3x   C 4 2 x x 1 C. f  x 4 dx   ln x  C D. f  x 2 dx  3x   C 4 2 x
Câu 27(Cụm 7 – Tp.HCM): Cho biết F  x là một nguyên hàm của hàm số f  x . Tìm I  3  f
 x1dx  .
A. I  3F  x 1 C
B. I  3F  x  x  C
C. I  3xF  x 1 C
D. I  3xF  x  x  C Câu 28:  dx = 2 x  4x  5 1 x 1 1 x  5 A. ln  C B. ln  C 6 x  5 6 x 1 1 x 1 1 x 1 C. ln  C D. ln  C 6 x  5 6 x  5 3 x
Câu 29: Một nguyên hàm của hàm số: y  là: 2 2  x 1 A. 2
F(x)  x 2  x B.   2 x  4 2 2  x 3 1 1 C. 2 2  x 2  x D.   2 x  4 2 2  x 3 3
Câu 30: Một nguyên hàm của hàm số: 2
f (x)  x 1 x là: 1 1
A. F(x)   2 2 x 1 x 
B. F(x)   1 x 3 2 2 3 2 3 x 1 C. F x   2 ( ) 1 x 
D. F(x)  x  1 x 3 2 2 3 3 Câu 31: tan 2  xdx = 1
A. 2 ln cos 2x  C B. ln cos 2x  C 2 46
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 1 1 C.  ln cos 2x  C
D. ln sin 2x  C 2 2 2 
Câu 32: Nguyênhàmcủa (với C hằngsố) là  x dx 2 1 x 1 x A.  C B.  C 1 x 1 x 1 x C.  C D. 2 ln 1 x  C 1 x x  3
Câu 33: Nếu F(x) là một nguyên hàm của hàm f (x) 
, F (0)  0 thì hằng số C bằng 2 x  2x  3 3 A. ln 3 2 2 B. ln 3 3 3 C.  ln 3 2 2 D.  ln 3 3
Câu 34(THPT chuyên Biên Hòa lần 2): Tìm nguyên hàm F  x  x sin xdx biết F 0 19 . 1 1 A. F  x 2
 x  cos x  20 . B. F  x 2
 x  cos x  20 . 2 2 C. F  x 2
 x  cos x  20 . D. F  x 2
 x  cos x  20 .
Câu 35(Chuyên ĐH Vinh): Tìm tất cả các nguyên hàm của hàm số f  x  cos 2x là. A. F  x 1
 sin2x  C . B. F  x 1
  sin2x  C . 2 2
C. F  x  sin2x  C .
D. F  x  sin2x .
Câu 36(Sở GD – ĐT Đồng Nai): Tìm nguyên hàm của hàm số f  x  cos 4x . A. f
 xdx  4sin4xC . B. f
 xdx  4
 sin 4x  C . C. f  x 1 dx  sin 4x  C . D. f  x 1
dx   sin 4x  C . 4 4 x  e 
Câu 37(THPT Hàm Long): Nguyên hàm của hàm số: x
y  e  2   là. 2  cos x  47
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 x 1 A. 2 x
e  tan x  C B. 2e   C cos x x 1 C. 2 x
e  tan x  C D. 2e   C cos x
Câu 38(Cụm 4 – Tp.HCM): Hàm số F  x  2sin x  3cos x là một nguyên hàm của hàm số.
A. f  x  2
 cos x 3sin x
B. f  x  2
 cos x  3sin x
C. f  x  2cos x  3sin x
D. f  x  2cos x  3sin x
Câu 39(Sở GD – ĐT Hà Tĩnh lần 2): Biết F(x)  sin xd ; x F (0)  1  khi đó.
A. F(x) 1 cos x
B. F(x)  cos x
C. F(x)  cos x
D. F(x)  2  cos x
Câu 40(THPT Lý Nhân Tông): Hàm số F  x  sin 2017x là nguyên hàm của hàm số.
A. f  x  2  017cos 2017x
B. f  x  cos 2017x
C. f  x  2017cos 2017x D. f  x 1   cos 2017x 2017
Câu 41(THPT Lương Tài): Khẳng định nào sau đây là khẳng định đúng? 1 1  1 A. dx   C  B.
dx  tan x  C  2 2 sin x sin x 2 sin x 1 1 C.
dx   cot x  C  D.
dx  cot x  C  2 sin x 2 sin x
Câu 42(Sở GDĐT Lâm Đồng lần 2): Một nguyên hàm F  x của hàm số f  x 3 2
 2x 3x 1sin 2x
khi F 0  1 là: x x A. F  x 4 3 1 1  2  3
 x  .cos 2x  4 3 2 2 x x B. F  x 4 3 1 1  2  3
 x  .cos 2x  4 3 2 2 x x C. F  x 4 3 1 1  2  3
 x  .cos 2x  4 3 2 2 x x D. F  x 4 3 1 1  2  3
 x  .cos 2x  4 3 2 2 48
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
Câu 43(TT Tân Hồng Phong): Tìm nguyên hàm của hàm số f  x  sin 2x . 1 1 A. cos 2x  C
B.  cos 2x  C 2 2
C. cos 2x  C D. cos 2x  C
Câu 44(Sở GDĐT Lâm Đồng lần 07): Nguyên hàm của hàm số f (x)  sin 3 . x o c s5x là. 1 1
A. f (x)dx   o c s2x  o
c s8x  C  4 16 1 1
B. f (x)dx  o c s2x  sin 8x  C  4 16 1 1
C. f (x)dx  sin 2x  o
c s8x  C  4 16 1 1
D. f (x)dx  o c s2x  o
c s8x  C  4 16 sin 2x
Câu 45: Nguyênhàm F(x) củahàmsố y  khi F(0)  0 là 2 sin x  3 2 ln 2  sin x A. 2 ln 1 sin x B. 3 2 sin C. ln 1 x D. 2 ln cos x 3 1
Câu 46: Nếu F(x) là một nguyên hàm của hàm số y 
và F(2) 1 thì F(3) bằng x 1 A. ln 2 B. ln 2 1 3 1 C. ln D. 2 2
Câu 47: Nguyên hàm của hàm số: f  x 1  là: 3x 1 1 1 1
A. ln 3x 1  C
B. ln 3x 1  C C. ln 3x   1  C
D. ln 3x 1  C 2 3 3
Câu 48: Nguyên hàm của hàm số: f  x  cos5x  2 là: 1 A.
sin 5x  2  C
B. 5sin 5x  2  C 5 1 C.
sin 5x  2  C D. 5
 sin5x  2 C 5 49
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
Câu 49: Nguyên hàm của hàm số:   4  1   x f x e là: A. 4  x 1  e  C B. 4x 1 4    e  C 1 1 C. 4  x 1   e  C D. 4  x 1  e  C 4 4
Câu 50: Nguyên hàm của hàm số: f  x 2  tan x là: A. tan x  C B. tanx  x  C C. 2 tan x  C D. tanx  x  C 1
Câu 51: Nguyên hàm của hàm số: f  x   là: 2x  2 1 1  1  A.  C B.  C 2x 1 2  4x 1 1  C.  C D.  C 4x  2 2x  3 1
Câu 52: Một nguyên hàm của hàm số f  x  o c s3x.cos2x là:
A. sin x  sin 5x 1 1 B. sin x  sin 5x 2 10 1 1 C. cosx  co s 5x 2 10 1 1 D. cosx  sin 5x 2 10
Câu 53: Cho hàm số y  f  x có đạo hàm là f  x 1  và f  
1  1 thì f 5 bằng: 2x 1 A. ln2 B. ln3 C. ln2 + 1 D. ln3 + 1
Câu 54: Nguyên hàm của hàm f  x 2  với F   1  3 là: 2x 1 A. 2 2x 1 B. 2x 1  2 C. 2 2x 1 1 D. 2 2x 1 1 50
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
Câu 55: Để F  x 2  .
a cos bx b  0 là một nguyên hàm của hàm số f  x  sin 2x thì a và b có giá trị lần lượt là: A. – 1 và 1 B. 1 và 1 C. 1 và –1 D. – 1 và – 1 ln x
Câu 56: Cho f (x)  . Khi đó: x 2 (ln x)
A. f (x)dx   C 
B. f (x)dx  ln x  C  2 ln x C. 2
f (x)dx  (ln x)  C 
D. f (x)dx   C  2 Câu 57: Hàm số   x    x F x e e
 x là nguyên hàm của hàm số:  x x 1 A.    x  x f x e e 1 B. f  x 2
 e e  x 2 x  x x 1 C.     x f x e e 1 D. f  x 2
 e  e  x 2
Câu 58: Nguyên hàm F  x của hàm số f  x 3 2
 4x 3x  2x  2 thỏa mãn F   1  9 là: A. f  x 4 3 2
 x  x  x  2 B. f  x 4 3 2
 x  x  x 10 C. f  x 4 3 2
 x  x  x  2x D. f  x 4 3 2
 x  x  x  2x 10 x  e  x e
Câu 59: Nguyên hàm của hàm số: f  x   là: x e  x e A. ln x   x e e  C C. ln x   x e e  C 1 B.  C x  e  x e 1 D.  C x  e  x e
Câu 60: Nguyên hàm F  x của hàm số f  x  x  sinx thỏa mãn F 0 19 là: 51
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 x A.   2   osx  x F x c B. F  x 2   o c sx   2 2 2 x x C. F  x 2  o c sx   20 D. F  x 2   o c sx   20 2 2
Câu 61: Cho f ' x  3 5sinx và f 0 10 . Trong các khẳng định sau đây, khẳng định nào đúng:
A. f  x  3x  5 o c sx+2    3 B. f     2  2
C. f    3
D. f  x  3x  5 o c sx+2
Câu 62: Nguyên hàm của hàm số: y = sin2x.cos3x là: 1 1 A. 3 5
sin x  sin x  C 3 5 1 1 B. 3 5
 sin x  sin x  C 3 5
C. sin3x sin5x + C D.Đáp án khác.
Câu 63: Nguyên hàm của hàm số: y = cos2x.sinx là: 1 A. 3 cos x  C 3 B. 3 cos x  C 1 C. 3 sin x  C 3 D. Đáp án khác.
Câu 64: Một nguyên hàm của hàm số: y = cos5x.cosx là: A. F(x) = cos6x B. F(x) = sin6x 1  1 1  C. sin 6x  sin 4  x  2  6 4  52
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 1  sin 6x sin 4x  D.     2  6 4 
Câu 65: Một nguyên hàm của hàm số: y = sin5x.cos3x là: 1  cos 6x cos 2x  A.     2  8 2  1  cos 6x cos 2x  B.    2  8 2  C. cos8x + cos2x D.Đáp án khác.
Câu 66: Một nguyên hàm của hàm số: 2
f (x)  x 1 x là: 1
A. F(x)   1 x 2 2 2 1
B. F(x)   1 x 3 2 3 2 2 x C. F x   2 ( ) 1 x  2 1
D. F(x)   1 x 2 2 3 dx
Câu 67: Nguyên hàm của hàm số: y =  là: 2 2 x  a 1 x  a A. ln +C 2a x  a 1 x  a B. ln +C 2a x  a 1 x  a C. ln +C a x  a 1 x  a D. ln +C a x  a dx
Câu 68: Nguyên hàm của hàm số: y =  là: 2 2 a  x 1 a  x A. ln +C 2a a  x 53
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 1 a  x B. ln +C 2a a  x 1 x  a C. ln +C a x  a 1 x  a D. ln +C a x  a 3
Câu 69: Nguyên hàm của hàm số: y = dx  x là: x 1 1 1 A. 3 2 x 
x  x  ln x 1  C 3 2 1 1 B. 3 2 x 
x  x  ln x 1  C 3 2 1 1 C. 3 2 x 
x  x  ln x 1  C 6 2 1 1 D. 3 2 x 
x  x  ln x 1  C 3 4
Câu 70: Nguyên hàm của hàm số: y = 4  7 dx  x x là: 5 3 1  2 2  A.
4x  72  7 4x  72    C 20  5 3  5 3 1  2 2  B.
4x  72  7 4x  72    C 18  5 3  5 3 1  2 2  C.
4x  72  7 4x  72    C 14  5 3  5 3 1  2 2  D.
4x  72  7 4x  72    C 16  5 3 
Câu 71: Một nguyên hàm của hàm số y  sin 3x 1 1 A. 3 o c s3x B. 3  o c s3x C. o c s3x D.  o c s3x 3 3 1
Câu 72: Cho f (x)  . Khiđó (x)  f dxbằng: 2 cos 4x 1 1 A. tan 4x  C
B.  tan 4x  C 4 4 1 1 C. cot 4x  C
D.  cot 4x  C 4 4 54
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 1
Câu 73: Cho f (x)  . Khiđó ( )  f x dx bằng: 2 x  9 x  3 x  3 A. ln  C B. ln  C x  3 x  3 1 x  3 1 x  3 C. ln  C D. ln  C 6 x  3 6 x  3
Câu 74(Cụm 6 Tp.HCM): Tìm nguyên hàm F  x của hàm số   x  2 1 3 x f x e e   . A.   x 2   3  x F x e e  C . B.   x   3 x F x e e  C . C.   x 3  3  x F x e e  C . D.   x  3 x F x e e  C . log Câu 75: Cho ( )  x f x
. Khi đó f (x)dx  bằng: x 2 (log x) A.  C 2 1 B. 2
ln10.(ln x)  C 2 1 C. 2 (ln x)  C 2 ln10 D. 2 (log ) x  C
Câu 76: Biết hàm số f (x) thỏa mãn '( )  .  b f x a x với ,
a b  0 , f ( 1
 )  2; f (1)  4; f '(1)  0 . Khi đó: 2 x 1 1 11 A. 2 f (x)   x   2 x 2 1 1 5 B. 2 f (x)  x   2 x 2 4 C. 2
f (x)  4x   2 x 2 D. 2
f (x)  2x   2 x 55
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
TÍNH NGUYÊN HÀM BẰNG PHƢƠNG PHÁP TỪNG PHẦN
NGUYÊN HÀM TỪNG PHẦN
Định lý: Nếu hai hàm số u  u(x) và v  v(x) có đạo hàm và liên tục trên K thì
I  u(x)  v (
 x)dx  u(x)v(x)  u (x)v(x)dx  
hay I  udv  uv  vdu   
Vận dụng giải toán:
Nhận dạng: Tích 2 hàm khác loại nhân nhau, chẳng hạn: mũ nhân lượng giác x e .sin . x d , x ....  Vi u
   phân
 du   dx Đặt: 
 Suy ra: I  udv  uv  vd . u   Nguyên ha m
dv  dx 
 v   Thứ tự ưu tiên
chọn u: og – đa – ƣ ng – ũ và dv  phần c n ại. 1
Nghĩa là nếu có ln hay log x thì chọn u  ln hay u  log x 
.ln x và dv  còn lại. Nếu a a ln a
không có ln; log thì chọn u  đa thức và dv  còn lại.
Nếu không có log, đa thức, ta chọn u  lượng giác,<.
Lưu ý: bậc của đa thức và bậc của ln tư ng ứng với số lần lấy nguyên hàm.
Bài tập : Tính các nguyên hàm sau:
Câu 01: I  x sin x  dx  
ĐS: I  sin x  cos x  . C ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. Câu 02:  (1 2 ) x I
x  e  dx   ĐS:  (3 2 ) x I x  e  . C ♥ Giải :
................................................................................................................................................................................. 56
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. x e Câu 03: x
I  e  cos x  dx   ĐS: I 
(sin x  cos x)  C. 2 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 2 x
Câu 04: I  (2x 1) ln x  dx   ĐS: 2
I  (x  x) ln x   x  C. 2 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. 3x 3x xe e Câu 05: 3x
I  x  e  dx   ĐS: I    C. 3 9 ♥ Giải :
.................................................................................................................................................................................
................................................................................................................................................................................. 57
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Câu 06: I  ln x  dx  
ĐS: I  x ln x  x  . C ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. x 1 1
Câu 07: I  (x 1) sin 2x  dx   ĐS: I   cos 2x  sin 2x  C. 2 4 ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. Câu 08: x 
I  x  e dx  ĐS:  (  1 ) x I x  e  . C ♥ Giải : 58
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
Câu 09: I  x cos x  dx  
ĐS: I  xsin x  cos x  . C ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
................................................................................................................................................................................. Câu 10: x
I  x  e  dx   ĐS: x x
I  xe  e  . C ♥ Giải :
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
.................................................................................................................................................................................
CÂU HỎI TRẮC NGHIỆM
Câu 01: Một nguyên hàm của hàm số ( ) x f x  xe là: 2 x A. x e  C B. x e  x   1  C C. x e  x   1  C D. x e  C 2
Câu 02: Một nguyên hàm của hàm số 2 ( )  (  2 ). x f x x x e là: 59
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 A. (2  2). x x e B. 2 x x e C. 2 (  ). x x x e D. 2 (  2 ). x x x e
Câu 03: Cho hàm số ( ) . x f x x e 
. Một nguyên hàm F(x) của f (x) thỏa F(0) 1 là: A. ( 1) x x e   1 B. ( 1) x x e    2 C. ( 1) x x e  1 D. ( 1) x x e   2
Câu 04: Cho f (x)  xsin x . Nguyên hàm của f (x) là:
A. x cos x  C
B. xsin x  cos x  C
C. sin x  x cos x  C
D. x cos x  sin x  C 2
Câu 05: Nguyên hàm của hàm số ( ) x f x  xe là hàm số: 2 2 1 2 2 2 A. ( )  2 x F x e B. ( ) x F x  e C. 2 ( )  2 x F x x e D. ( ) x x
F x  e  xe 2 x
Câu 06: Cho f (x)  ln tdt 
. Đạo hàm f '(x) là hàm số nào dưới đây? 0 1 1 A. B. ln x C. 2 ln x D. 2 ln x x 2
Câu 07: Một nguyên hàm của 3 ( ) x
f x  x e là: A. 3 2 ( 3  6  6) x x x x e B. 3 (  6  6) x x x e C. 3 2 (  3  6) x x x e D. 2 3 x x e
Câu 08: Một nguyên hàm của hàm số   2  . x f x x e là : A.   2  2 x F x e B.   2 2  2 x F x x e C.   2 1 x F x  e D.   2 2 x x
F x  xe  e 2
Câu 09: Hàm số f (x)  (x 1)sin x có các nguyên hàm là: A. F( )
x  (x 1) cos x  sinx  C B. F( ) x  (
 x 1)cos x sinx C C. F( ) x  (
 x 1)cos x sinx C D. F( )
x  (x 1) cos x  sinx  C
Câu 10: Hàm số f (x)  ln x có các nguyên hàm là: 1
A. F(x)  x(ln x 1)  C B. F(x)   C x 2 ln x C. F(x)   C
D. F(x)  x(ln x 1)  C 2  1 
Câu 11: Hàm số f (x)  cos x  x 
 có các nguyên hàm là:  cos x  60
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018  x 1  A. 2
F (x)  sin x  x  C   B. F( ) x  ( x 1 sin )
x  cos x  C  sin x 2  C. F( ) x  ( x 1 sin )
x  cos x  C D. F( ) x  ( x 1 sin )
x  cos x  C
Câu 12: Gọi hàm số F(x) là một nguyên hàm của f (x)  x cos3x , biết F(0)  1. Vậy F(x) là: 1 1 1 1
A. F(x)  x sin 3x  cos3x  C
B. F(x)  x sin 3x  cos3x 1 3 9 3 9 1 1 1 8 C. 2 F (x)  x sin 3x
D. F(x)  x sin 3x  cos3x  6 3 9 9 Câu 13: Tính x xe dx 
, ta được kết quả là: A.   x  – x F x e xe  C B.   x x
F x  e  xe  C C.   x   – x F x e xe  C D.   x x F x  e   xe  C
Câu 14: Tính x cos xdx  , ta được kết quả là:
A. F  x  xsin x  cos x  C
B. F  x  xsin x  cos x  C
C. F  x  xsin x  cos x  C
D. F  x  xsin x  cos x  C
Câu 15: Tìm x cos 2xdx  là: 1 1 1 1
A. x sin 2x  cos 2x  C
B. x sin 2x  cos 2x  C 2 4 2 2 2 x sin 2x C.  C D. sin 2x  C 4
Câu 16: Một nguyên hàm của hàm số   2 ( )  2  x f x x x e là A. ( )  (2  2). x F x x e B. 2 ( ) x F x  x e C. 2 ( )  (  ). x F x x x e D. 2 ( )  (  2 ). x F x x x e
Câu 17: Một nguyên hàm của 2 ( ) x f x  x e là 3 x A. 2 ( )  (  2  2) x F x x x e B. F(x) x  e 3 C. 2 ( )  (  2  2) x F x x x e D. ( )  2 x F x xe
Câu 18: Nguyên hàm F  x của ( ) x f x xe 
thỏa F 0  1 là A. ( )   1 x F x x e    1 B.     1 x F x x e     2 61
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 C. ( )   1 x F x x e   1 D. ( )   1 x F x x e    2
Câu 19: Kết quả nào sai trong các kết quả sau ? 2 x .cos x A. x sin xdx   C  B.
x sin xdx  x cos x  sin x  C  2 xcos 2x 1
C. x cos xdx  x sin x  cos x  C  D. x sin 2xdx   sin 2x  C  2 4
Câu 20: Kết quả nào sai trong các kết quả sau ? 3x xe x 1 A. 3 3x xe dx   e  C  B. x x x
xe dx  xe  e  C  3 9 2 x x x 1 C. x xe dx  . x e  C  D. dx    C  2 x x x e e e
Câu 21: Kết quả nào sai trong các kết quả sau ? 1
A. ln xdx  x ln x  x  C  B. ln xdx   C  x 2 2 x x 3 3 x x C. x ln xdx  ln x   C  D. 2 x ln xdx  .ln x   C  2 4 3 9
Câu 22: Kết quả nào sai trong các kết quả sau ? A. 2 2
ln xdx  x ln x  2 
xln x  xC 3 ln x B. 2 ln xdx   C  3 ln x ln x 1 C. dx    C  2x x x ln x ln x 1 D. dx    C  3 2 2 x 2x 4x 62
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
ĐỀ ÔN TẬP HỌC KÌ I
Câu 01 : Cho hàm số y  f x xác định và có đạo hàm trên . Khẳng định nào sau đây đúng?
A. Nếu f x  0 thì hàm số f x đạt cực trị x . 0  0
B. Số nghiệm của phư ng trình f x  0 bằng số điểm cực trị của hàm số f x.
C. Nếu f x đổi dấu từ âm sang dư ng khi qua x thì hàm số đạt cực đại tại x . 0 0
D. Nếu hàm số f x đạt cực trị x  a thì f a  0.
Câu 02 : Tìm khoảng nghịch biến của hàm số 3
y  x  3x  2. A.  1  ;  1 . B.  ;    1 1; . C. ; . D. ;   1 và 1; .
Câu 03 : Điểm nào sau đây là điểm cực đại của hàm số y  2sin x  1?    y A. . B. . 2 2 C. 3. D. 1. 
Câu 04 : Cho hàm số y  f x xác định, liên tục trên và có đồ thị O x
như hình bên. Tìm số điểm cực trị của hàm số y  f x . A. 4. B. 6. C. 5. D. 7. 2x  1
Câu 05 : Tìm các đường tiệm cận của đồ thị hàm số y  . x  1
A. x  1; x  2.
B. y  1; x  2.
C. x  1; y  2.
D. x  1; x  2  .
Câu 06 : Nguyên hàm của hàm số 2 ( ) x x
f x  e  e là: 1 A. 2 x x e  e  C. B. 2 2 x x e  e  . C 2 C. x ( x e e  x)  . C D. Kết quả khác . 2
x  m  2m  3
Câu 07 : Gọi M và N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  x  1 trên 1  ; 2. 
 Tìm giá trị nhỏ nhất của biểu thức 2M  3 . N 19 A. 7. B. . 2 63
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 9 C. 5. D. . 5 2 mx  4
Câu 08 : Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y  có 3 đường tiệm x  1 cận. A. 0;. B.  ;  0. C. 0;. D.  ;  0.
Câu 09 : Viết tất cả các phư ng trình tiếp tuyến của đồ thị C 3 2
: y  x  2x 1, biết tiếp tuyến song
song với đường thẳng y  x 1.
A. y  x 1; y  x 1. 31
B. y  x 
; y  x 1. 27 31
C. y  x  . 27
D. y  x  3; y  x 1.
Câu 10 : Cho hàm số y  f x có bảng biến thiên sau: x  2  y'x    3 y 3 
Khẳng định nào sau đây sai?
A. Đường thẳng x  2 là tiệm cận đứng của đồ thị hàm số.
B. Hàm số đồng biến trên  ;   1 .
C. max f  x  f 10. x   3;10
D. Phư ng trình f  x  5  0 có hai nghiệm thực. y
Câu 11 : Đường cong ở hình bên là đồ thị của một trong bốn hàm
số được cho dưới đây. Hỏi hàm số đó là hàm số nào? 2 2x  3 2x 1 A. y  . y  . x  B. 1 x 1 O 1 x x 1 x 1 C. y  . y  . x  D. 1 x 1
Câu 12 : Trong các hàm số sau, hàm số nào không có cực trị? 64
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 A. 2 y  x . B. y  x . x 1 C. 4 y  x . D. y  . x 1 Câu 13 : Hàm số 3 2
y  x  3x  3x 1 có bảng biến thiên nào dưới đây? A. B. x   x  1  y  y  0    y  y 0  C. D. x  1  x  1  y  0  y  0    y 1 y 0  
Câu 14 : Cho hàm số y  f  x có lim f  x  2 và lim f  x  2
 . Khẳng định nào sau đây đúng? x x
A. Đồ thị hàm số y  f  x có hai đường tiệm cận ngang là x  2 và x  2. 
B. Đồ thị hàm số y  f  x chỉ có duy nhất một đường tiệm cận ngang.
C. Đồ thị hàm số y  f  x có hai đường tiệm cận ngang là y  2 và y  2. 
D. Đồ thị hàm số y  f  x không có đường tiệm cận ngang. 2x  7
Câu 15 : Tìm số đường tiệm cận của đồ thị hàm số y  . 2 x 1 A. 0. B. 4. C. 1. D. 3.
Câu 16 : Biết hàm số y  f  x đạt giá trị lớn nhất trên đoạn 1;4 bằng 5 . Tìm giá trị lớn nhất của
hàm số y  f  x  2 trên 1;4 A. 5. B. 7. C. 3. D. 8. 65
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
Câu 17 : (Trích câu 15, đề tham khảo Bộ GD&ĐT) Hàm số y   x   2 2 x  
1 có đồ thị như hình vẽ
bên. Hình nào dưới đây là đồ thị của hàm số y  x   2 2 x   1 ? A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. x 1
Câu 18 : Tìm tọa độ giao điểm của đồ thị hàm số y  x  với trục hoành. 1 A. 0;  1 . B. 1;0. C. 2  ;1 . D. 0  ;1 .
Câu 19 : Tìm tất cả các giá trị thực của tham số k để phư ng trình 3
x  3x  4  k  0 có ba nghiệm thực phân biệt. A. 2  k  6. B. 2  k  6. C. 1 k  3. y D. 1 k  3.
Câu 20 : Cho hàm số 4 2
y  ax  bx  c a  0 có đồ thị như hình vẽ
bên. Khẳng định nào dưới đây đúng? O x
A. a  0, b  0, c  0.
B. a  0, b  0, c  0.
C. a  0, b  0, c  0. 66
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
D. a  0, b  0, c  0.
Câu 21 : Giả sử a, b là các số dư ng bất kì khác 1, ,   . Đẳng thức nào sau đây sai?      a  a a A.   .
a .a  a . B.      .
a b  a .b . C.  .     D. a .   b  b a 
Câu 22 : Tìm tập xác định của hàm số y   x   2 1 .
A. D  0;.
B. D  0; \  1 .
C. D  1;. D. D  \   1 .
Câu 23 : Cho log x  4, log x  5 với, 0  x  1 và a, b là các số thực lớn h n 1. Tính 2 P  log x . a b ab 9 1 40 A. P  . B. P  . C. P  20. D. P  . 40 20 9
Câu 24 : Nguyên hàm của hàm số f (x)  x là 1 2 3 A. x  C B.  C C. x x  C D. x x  C 2 x 3 2
Câu 25 : ba số thực dư ng , a , b .
c Đồ thị các hàm số a  , b  , c y x y x
y  x được cho như hình vẽ
bên. Khẳng định nào sau đây đúng? y xc xb
A. 1 a  b  . c
B. c  b 1; a  0. C. 1
1  c  b  0; a  0. xa
D. b  c 1; a  0. O 1 x
Câu 26 : Có bao nhiêu giá trị nguyên của tham số k để phư ng trình 2 2
log x  log x 1  2k 1  0 có nghiệm thuộc 3 1  ;3 ? 3 3   A. 0. B. 4. C. 3. D. Vô số.
Câu 27 : Tìm tập xác định D của hàm số y  log     2 x 6x 9 . x 1 
A. D  1;.
B. D  1; \  2 . 67
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
C. D  1; \2,  3 . D. D  .
Câu 28 : Tính đạo hàm của hàm số y  log10 ,
x  x  0. 1 10 A. y  . B. y  . 10x ln10 x ln10 1 ln10 C. y  . D. y  . x ln10 x
Câu 29 : Với a là số thực dư ng khác 1. Xét các mệnh đề sau: x  1  (I): Đồ thị hàm số x
y  a và y    đối xứng nhau qua Oy.  a 
(II): Đồ thị hàm số y  log x và y  log x đối xứng nhau qua Ox. a 1 a (III): Đồ thị hàm số x
y  a và y  log x đối xứng nhau qua đường thẳng y   . x a
Tìm số mệnh đề đúng. A. 0. B. 1. C. 2. D. 3.
Câu 30 : Cho a  0. Viết dạng lũy thừa của biểu thức 3 3 3 3 a a a a . 40 20 40 1 A. 27 a B. 81 a . C. 81 a . D. 81 a .
Câu 31 : Phư ng trình nào sau đây vô nghiệm? A. 2x  4. B. 2x  1. C. 2x  1  . D. 2x  .
Câu 32 : Tìm tập nghiệm T của bất phư ng trình log 4x  2  1  . 1   4 3   1 3  1 3  1 3 A. T  ;  .   B. T  ; .   C. T  ; . D. T  ; .      2   2 2  2 2  2 2
Câu 33 : Có bao nhiêu số nguyên trên 0;10 nghiệm đúng bất phư ng trình
log 3x  4  log  x   1 ? e e A. 10. B. 11. C. 9. D. 8. 7x
Câu 34 : Cho hàm số f  x 
. Khẳng định nào sau đây sai? x2 3
A. f  x 1  x   x  2log 3. 7 68
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 x x  2
B. f  x 1   . 1 log 3 1 log 7 7 3
C. f  x 1  x log 7   x  2log3.
D. f  x 1  x log 7  x  2 log 3. 1   5 5 1 1
Câu 35 : Bạn Hùng giải phư ng trình 5 .
x 8 x  500 theo các bước sau: 1 x3 1
Bước 1: Điều kiện: x  0 . Phư ng trình tư ng đư ng với x 3 2 5 .8 x  5 .2 x3  5 .2 x 1 x  3
Bước 2: Lấy lôgarit c số 2 hai vế phư ng trình (1):  x  3log 5   0 2 x     x   1 3 log 5   0  2   x  x  3  0 x  3 Bước 3:   2  1   
(thỏa mãn điều kiện). log 5   0 x  log 2  2 5  x
Vậy phư ng trình đã cho có hai nghiệm: x  3, x  log 2 . 5
Hỏi bài giải bạn Hùng đúng hay sai? Nếu sai thì sai bắt đầu từ bước nào? A. Đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ bước 3.
Câu 36 : Mỗi hình sau gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), tìm số hình đa diện lồi. Hình 1 Hình 4 Hình 2 Hình 3 A. 1. B. 2. C. 3. D. 4.
Câu 37 : Tìm (cos 6x  cos 4x)dx  là: 1 1
A.  sin 6x  sin 4x  C
B. 6sin 6x 5sin 4x  C 6 4 1 1
C. sin 6x  sin 4x  C D. 6
 sin6x sin 4x C 6 4 69
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018
Câu 38 : Một khúc gỗ có dạng với độ dài các
cạnh được cho như hình vẽ bên. Tính thể tích 40 cm
khối đa diện tư ng ứng. 2960 A.V   3 cm . 3 7 cm 3 cm B. V   3 2560 cm . 5 cm 7 cm C. V   3 2960 cm . D. V   3 2590 cm .
Câu 39 : Cho hình chóp S.ABCD , có đáy là hình bình hành. Gọi G là trọng tâm tam giác SBD .
Mặt phẳng  P chứa AG và song song với BD , cắt S ,
B SC, SD lần lượt tại B ', C ', D' . Tính tỉ số
thể tích giữa khối S.AB 'C 'D ' và khối S.ABC . D 1 A. k  . 9 2 B. k  . 9 1 C. k  . 3 8 D. k  . 27
Câu 40 : Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng 3 a . Tính chiều cao
h của hình chóp đã cho. 3a A. h  . 6 3a B. h  . 2 3a C. h  . 3 D. h  3 . a
Câu 41 : Cho hình hộp ABC . D A B  C  D
  có sáu mặt đều là hình thoi cạnh a và góc nhọn của hình thoi bằng 0
60 . Tính thể tích V của khối hộp ABC . D A B  C  D  . 70
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 3 2a A. V  . 6 B. 3 V  3a . 3 a C. V  . 3 3 2a D. V  . 2
Câu 42 : Bạn Lan có một miếng bìa cứng hình tròn có bán kính bằng 2 . Bạn
Lan cắt một góc một miếng bìa hình quạt với 0
AOB  30 , sau đó bạn dán O
miếng bìa còn lại tạo thành mặt xung quanh của một hình nón  N . Tính 300
diện tích xung quanh S của hình nón  N . 2 xq A B 23 A. S  . 2 23 B. S  . xq 3 11 C. S  . xq 3 11 D. S  . xq 2
Câu 43 : Cho hình lăng trụ đứng AB . C A B  C
  có đáy là tam giác đều cạnh a, biết tứ giác BCC B   là
hình vuông. Tính thể tích V của khối lăng trụ AB . C A B  C  . 3 3a A. V  . 6 3 3a B. V  . 2 3 3a C. V  . 12 3 3a D. V  . 4
Câu 44 : Cho hình bình hành ABCD có 0 AD  ; a AB  3 ;
a BAD  45 (như hình bên). Tính thể tích
khối tròn xoay nhận được khi quay hình bình hành ABCD quanh trục . AB 71
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 A. 3 V  5 a . D C B. 3 V  6 a . 2a 3 9 a C. V  . 2 450 A B 3 3a 5 a D. V  . 2
Câu 45 : Để chuẩn bị cho Tết Nguyên Đán 2017, ban dự án đường hoa Nguyễn Huệ, quận 1,
Thành phố Hồ Chí Minh dự định xây dựng một khối cầu có bán kính bằng 2 m để trưng bày hoa
tư i xung quanh, để tiết kiệm diện tích Ban quản lý xây một hình trụ nội tiếp mặt cầu. Tính bán
kính đáy r của hình trụ sao cho khối trụ có thể tích lớn nhất. 4 3 A. r  . 3 32 3 B. r  . 9 2 6 C. r  . 3 8 D. r  . 3
Câu 46 : Nếu góc ở đỉnh của hình nón  N  bằng 0
60 thì góc giữa đường sinh và mặt đáy của  N  bằng bao nhiêu? A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Câu 47 : Cho hình lăng trụ đứng AB . C A B  C
  có đáy ABC là tam giác cân với 0
AB  AC  a, BAC  120 , mặt phẳng  AB C
  tạo với đáy một góc 0
60 . Tính thể tích V của khối lăng trụ đã cho. 3 3a A. V  . 8 72
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 3 9a B. V  . 8 3 a C. V  . 8 3 3a D. V  . 4
Câu 48 : Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a , M là trung điểm
BC. Quay hình tròn (C) xung quanh trục AM , ta được một khối cầu có thể tích bằng bao nhiêu? 3  a 3 A. . 54 3 4 a B. . 9 3 4 a 3 C. . 27 3 4 a D. . 3
Câu 49 : Tứ diện OABC có O , A O ,
B OC đôi một vuông góc, OA  OB  OC 1. Tính bán kính mặt
cầu ngoại tiếp tứ diện OAB . C 1 3 2 A. 1. B. . C. . D. . 2 2 2
Câu 50 : Cho hình nón  N  có đường sinh có độ dài gấp đôi bán kính đáy. Mặt phẳng qua trục
của  N  cắt  N  theo thiết diện là một tam giác có bán kính đường tròn nội tiếp bằng 1. Tính thể
tích V của khối nón giới hạn bởi  N . A. V  9 3. B. V  9. C. V  3 3. D. V  3. HẾT 73
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƢU TẦM và BIÊN SOẠN 2018 BẢNG ĐÁP ÁN: Câu 1 2 3 4 5 6 7 8 9 10 Đáp án D A B D C A A C C D Câu 11 12 13 14 15 16 17 18 19 20 Đáp án A D B C D C A B B D Câu 21 22 23 24 25 26 27 28 29 30 Đáp án A D D C B C C C C C Câu 31 32 33 34 35 36 37 38 39 40 Đáp án C D C D D B C C C D Câu 41 42 43 44 45 46 47 48 49 50 Đáp án D C D B C C A C C D 74
Đăng kí học thêm Toán tại Biên Hòa – Đồng nai qua sđt 0914449230 (Zalo – facebook)

Phân loại dạng và phương pháp giải nhanh nguyên hàm – tích phân – Nguyễn Vũ Minh (Tập 1) Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề nguyên hàm – tích phân Toán 12

Gắn hệ tọa độ Oxyz để giải các bài toán hình học không gian – Phương Nguyễn Toán 12

20 kĩ thuật chinh phục vận dụng cao số phức – Hoàng Xuân Nhàn Toán 12

Phân dạng bài tập và lời giải chi tiết chuyên đề Tích phân – Lưu Huy Thưởng Toán 12

Phương pháp giải các bài toán Tích phân – Trung tâm LTĐH Vĩnh Viễn Toán 12