Phân Tích Chiết Khấu và Ác Cảm Rủi Ro | Microeconomics | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

δu(c), trong đó c là số tiền mà cô ấy thường tiêu dùng trong một ngày và δ là hệ số
chiết khấu của cô ấy. Công thức này thừa nhận rằng cô ấy sẽ chi tiêu thêm 100 đô
la vào ngày hôm nay. Nếu cô ấy đợi đến ngày mai thì độ thỏa dụng kỳ vọng đã
chiết khấu của cô ấy sẽ là u(c) δu(c 110). Trong trường hợp này, cô ấy phải chi thêm $110 vào ngày mai.
Maria nên chọn số tiền ngày hôm nay nếu
u(c 100) δu(c) > u(c) δu(c 110).
Vậy cô nên chọn cái gì? Nếu cô ấy trung lập với rủi ro thì hàm thỏa dụng của cô ấy
là tuyến tính và vì vậy chúng ta có điều kiện đơn giản là cô ấy nên chọn số tiền
ngày hôm nay nếu c 100 δc > c δ (c 110), điều này đơn giản hóa thành điều kiện δ
< 10/11. Bây giờ, giả sử rằng Maria không thích rủi ro. Cụ thể hơn, giả sử rằng
u(x) = x. Bảng 4.13 trình bày chi tiết độ thỏa dụng kỳ vọng được chiết khấu của cô
ấy nếu cô ấy nhận tiền hôm nay hoặc ngày mai cho bốn giá trị khác nhau của hệ số
chiết khấu. Trong cả hai trường hợp, chúng tôi đặt c = $100. Để so sánh, chúng ta
cũng có lợi ích kỳ vọng đã chiết khấu đối với trường hợp cô ấy không quan tâm
đến rủi ro. Điều quan trọng cần rút ra từ Bảng 4.13 là tâm lý e ngại rủi ro có nghĩa
là Maria có xu hướng nhận tiền nhiều hơn vào ngày hôm nay. Chẳng hạn, nếu δ =
0,92 thì Maria trung lập với rủi ro sẽ đợi đến ngày mai nhưng Maria không thích
rủi ro sẽ nhận tiền ngay hôm nay.
Ác cảm với rủi ro khiến Maria ít sẵn sàng chờ đợi hơn vì điều đó có nghĩa là cô ấy
đánh giá thấp hơn số tiền 10 đô la mà cô ấy nhận được từ việc chờ đợi. Để giải
thích điểm này, hãy nhớ lại rằng ác cảm rủi ro có nghĩa là hàm thỏa dụng là lõm.
Điều đó có nghĩa là Maria định giá ít hơn khi tăng từ 100 đô la lên 110 đô la (hoặc
200 đô la lên 210 đô la) so với việc cô ấy đánh giá từ 0 đô la lên 10 đô la. Nếu cô
ấy đánh giá thấp hơn 10 đô la mà cô ấy nhận được từ việc chờ đợi thì không có gì
ngạc nhiên khi cô ấy ít sẵn sàng chờ đợi hơn. Do đó, ác cảm rủi ro có thể khiến
mọi người tỏ ra thiếu kiên nhẫn hơn thực tế.
Nếu chúng ta bỏ qua rủi ro, như thường lệ khi xem xét thời gian, thì về cơ bản,
chúng ta cho rằng mọi người trung lập với rủi ro. Điều này có nghĩa là các yếu tố
chiết khấu 'lớn đến mức khó tin' mà chúng tôi quan sát được trong phòng thí
nghiệm (xem phần 4.1.1) có thể một phần là do ngại rủi ro hơn là do thiếu kiên
nhẫn. Một nghiên cứu của Andersen và các đồng tác giả (2008) cho phép chúng tôi
định lượng hiệu ứng này. Họ đã đo lường cả sở thích rủi ro và sở thích thời gian
cho một mẫu đại diện của dân số Đan Mạch. Họ thấy rằng, nếu các đối tượng được
giả định là không có rủi ro, thì hệ số chiết khấu ước tính sẽ là 0,80. Tuy nhiên, các
đối tượng không trung lập với rủi ro. Sau khi tính đến sự e ngại rủi ro, hệ số chiết
khấu thay đổi thành 0,91 hợp lý hơn một chút. Hệ số chiết khấu này dường như
vẫn còn quá thấp. Tuy nhiên, mọi thứ không tệ như vẻ ngoài của chúng khi chúng
ta không tính đến thái độ đối với rủi ro.
Chúng ta vừa thấy rằng sự e ngại rủi ro có thể ảnh hưởng đến sự lựa chọn theo thời
gian ngay cả khi sự lựa chọn đó không liên quan đến rủi ro. Bây giờ chúng ta hãy
bắt đầu thêm rủi ro vào sự lựa chọn. Một nghiên cứu của Andreoni
Risk- neutral: bàng quan với rủi ro Risk-averse: ngại rủi ro Today: hôm nay Tomorrow: ngày mai Choice: sự lựa chọn
và Sprenger (2012) thể hiện một cách độc đáo các vấn đề có thể phát sinh. Trong
nghiên cứu, các phân nhóm đã được đưa ra một loạt các lựa chọn trong đó họ phải
phân bổ 100 mã thông báo giữa hai ngày. Ngày đầu tiên là bảy ngày và ngày thứ
hai là 35 hoặc 63 ngày. Do đó, trong cả hai trường hợp, thanh toán sẽ bị trì hoãn,
nhưng trong ngày thứ hai, nó bị trì hoãn nhiều hơn (xem Phương pháp nghiên cứu
4.3). Điều này cho phép đo lường trước theo thời gian.
Phương pháp nghiên cứu 4.3 đã chậm trễ trong phòng thí nghiệm
Thí nghiệm trong phòng thí nghiệm điển hình liên quan đến các đối tượng được trả
tiền vào cuối thời gian. Nếu chúng ta muốn nghiên cứu các ưu tiên theo thời gian
thì cần phải trì hoãn thanh toán. Chẳng hạn, trong nghiên cứu của Andersen và
đồng tác giả thanh toán đã bị trì hoãn đến hai năm. Điều này đặt ra một số vấn đề
hậu cần phức tạp, bởi vì người thí nghiệm cần theo dõi xem một chủ đề đã thắng
bao nhiêu và sau đó sắp xếp cho khoản thanh toán phù hợp để đến vào ngày đã đặt.
Và điều này cần phải được thực hiện theo cách bảo tồn càng nhiều ẩn danh càng
tốt. Tuy nhiên, một mối quan tâm lớn hơn là các đối tượng có thể nghi ngờ tiền sẽ
được trả như đã hứa. Những nghi ngờ như vậy sẽ thêm một ảnh hưởng bổ sung,
không mong muốn đối với sự lựa chọn.
Để đối phó với những vấn đề này đòi hỏi một thiết kế thử nghiệm cẩn thận, và hai
nghiên cứu của Andersen và đồng tác giả và Andreoni và Sprenger là những ví dụ
tuyệt vời về cách làm điều này có thể được thực hiện. Trong cả hai nghiên cứu
không bao giờ có sự lựa chọn để lấy tiền ngày hôm nay. Thay vào đó, các đối
tượng phải lựa chọn giữa việc lấy tiền trong một tháng hoặc một tuần so với việc
nhận được, nói, sáu tháng hoặc chín tuần. Cách tiếp cận này hoàn toàn loại trừ sự
cám dỗ cho các đối tượng lấy tiền ngay bây giờ. Điều này được gọi là độ trễ phía trước.
Tuy nhiên, chúng tôi vẫn cần phải thấm nhuần trong các đối tượng rằng tiền sẽ
được trả như đã hứa. Trong nghiên cứu của Andersen và các đồng tác giả, thanh
toán được Bộ Kinh tế và Kinh doanh Đan Mạch đảm bảo đã được thực hiện bằng
chuyển nhượng ngân hàng tự động. Điều này nên thấm nhuần sự tự tin. Trong
nghiên cứu của Andreoni và Sprenger, tất cả các đối tượng tham gia sống trên máy
ảnh, nơi họ có quyền truy cập vào hộp thư cá nhân. Các đối tượng đã được cung
cấp hai phong bì, trên đó họ đã viết địa chỉ của họ, khoản thanh toán họ đến hạn và
ngày đáo hạn. Thanh toán sau đó được gửi bằng séc thông qua dịch vụ thư. Một lần
nữa, điều này sẽ giúp các đối tượng tự tin tiền sẽ đến như đã hứa.
Sự thay đổi quan trọng đối với nghiên cứu là thanh toán phải chịu rủi ro. Chẳng
hạn, trong một bộ lựa chọn, chỉ có 50 % cơ hội mà mỗi khoản thanh toán sẽ được
gửi. Thanh toán sau, đến hạn sau 35 hoặc 63 ngày, sẽ được gửi. Đối với các lựa
chọn khác, các xác suất khác nhau. Để đưa ra một ví dụ thứ hai, đối với một số lựa
chọn, có 80 % cơ hội, khoản thanh toán trước đó sẽ được gửi và cơ hội 100 %,
khoản thanh toán sau này sẽ được gửi. Cái kịch bản cụ thể đấy rất thú vị bởi vì nó
đảo ngược các chủ đề logic trực quan có thể có rằng các khoản thanh toán sớm hơn
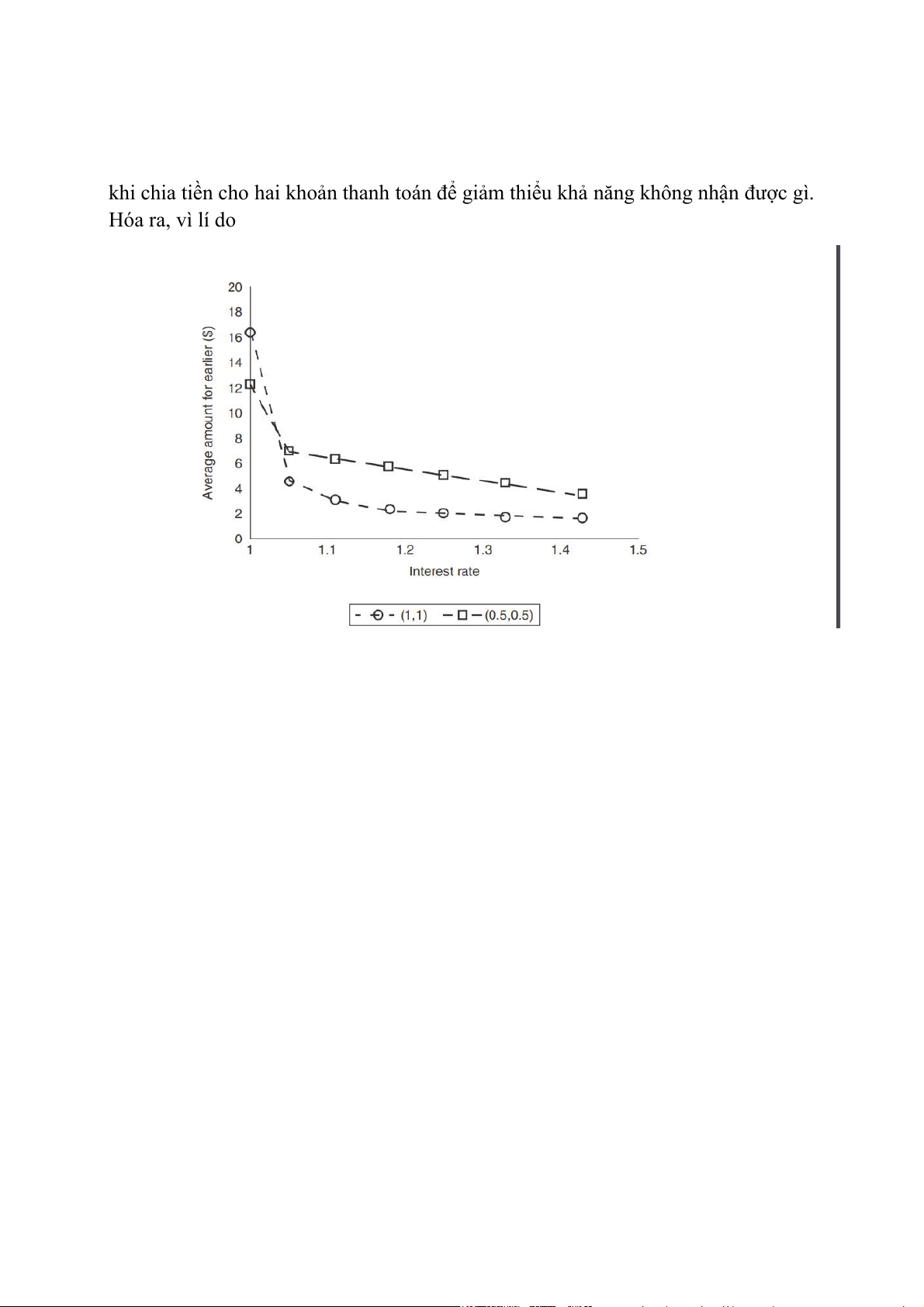
an toàn hơn các khoản thanh toán bị trì hoãn. Hình 4.5 so sánh lựa chọn trong bối
cảnh không có rủi ro, (1, 1), với trường hợp mỗi khoản thanh toán có 50% cơ hội
được gửi, (0,5, 0,5). Hình này biểu thị số tiền, tối đa là 20 đô la, được phân bổ cho
khoản thanh toán trước đó như là một chức năng của lợi nhuận từ sự chậm trễ. Như
chúng ta mong đợi, lợi nhuận thu được từ sự chậm trễ càng cao thì càng ít chủ thể
phân bổ cho khoản thanh toán sớm hơn. Thú vị hơn cho mục đích của chúng tôi là
so sánh giữa cài đặt (0,5, 0,5) và (1, 1). Có hai điều quan trọng cần chọn ra từ Hình
4.5. Đầu tiên, nếu một đối tượng đang tối đa hóa tiện ích dự kiến động thì chúng ta
sẽ mong đợi các lựa chọn của họ giống hệt nhau trong cài đặt (0,5, 0,5) với cài đặt
(1, 1). Rõ ràng là không. Đối với hầu hết các đối tượng ít sẵn sàng trì hoãn hơn khi
chỉ có 50% cơ hội nhận được khoản thanh toán. Nói cách khác, khi thanh toán
được đối tượng nào đó tỏ ra kiên nhẫn hơn để nhận được số tiền cao hơn, bị chậm
thanh toán. Điều này có vẻ tương tự như hiệu ứng chắc chắn mà chúng ta đã xem
xét trong phần 3.1.1 khi thảo luận về nghịch lý Allais. Điều thứ hai rút ra từ Hình
4.5 là hiệu ứng chéo đối với các giá trị nhỏ của lãi suất. Nếu không có khoản thanh
toán thêm cho việc chờ đợi – tức là lãi suất bằng 0 – thì các đối tượng sẵn sàng trì
hoãn hơn khi chỉ có 50% cơ hội nhận được khoản thanh toán. Ở mức độ trực quan,
điều này có thể được giải thích như một hình thức đa dạng hóa. Cho rằng cả hai
khoản thanh toán sớm hơn và sau đó xảy ra độc lập với 50% cơ hội, có vẻ hợp lý
khi chia tiền cho hai khoản thanh toán để giảm thiểu khả năng không nhận được gì. Hóa ra, vì lí do
Hình 4.5 Số tiền được phân bổ cho khoản thanh toán sớm hơn, với các mức lãi suất
khác nhau, so sánh khoản thanh toán nhất định (1, 1) với 50% cơ hội thanh toán (0,5, 0,5).
Nguồn: Andreoni và Sprenger (2012).
Tôi sẽ không đi sâu vào ở đây, rằng hiệu ứng chéo mà chúng ta quan sát được
trong Hình 4.5 khó có thể dung hòa với các mô hình lựa chọn tiêu chuẩn có rủi ro.
Trước khi tôi giải thích chi tiết hơn về điểm này, chúng ta hãy xem xét thêm một số
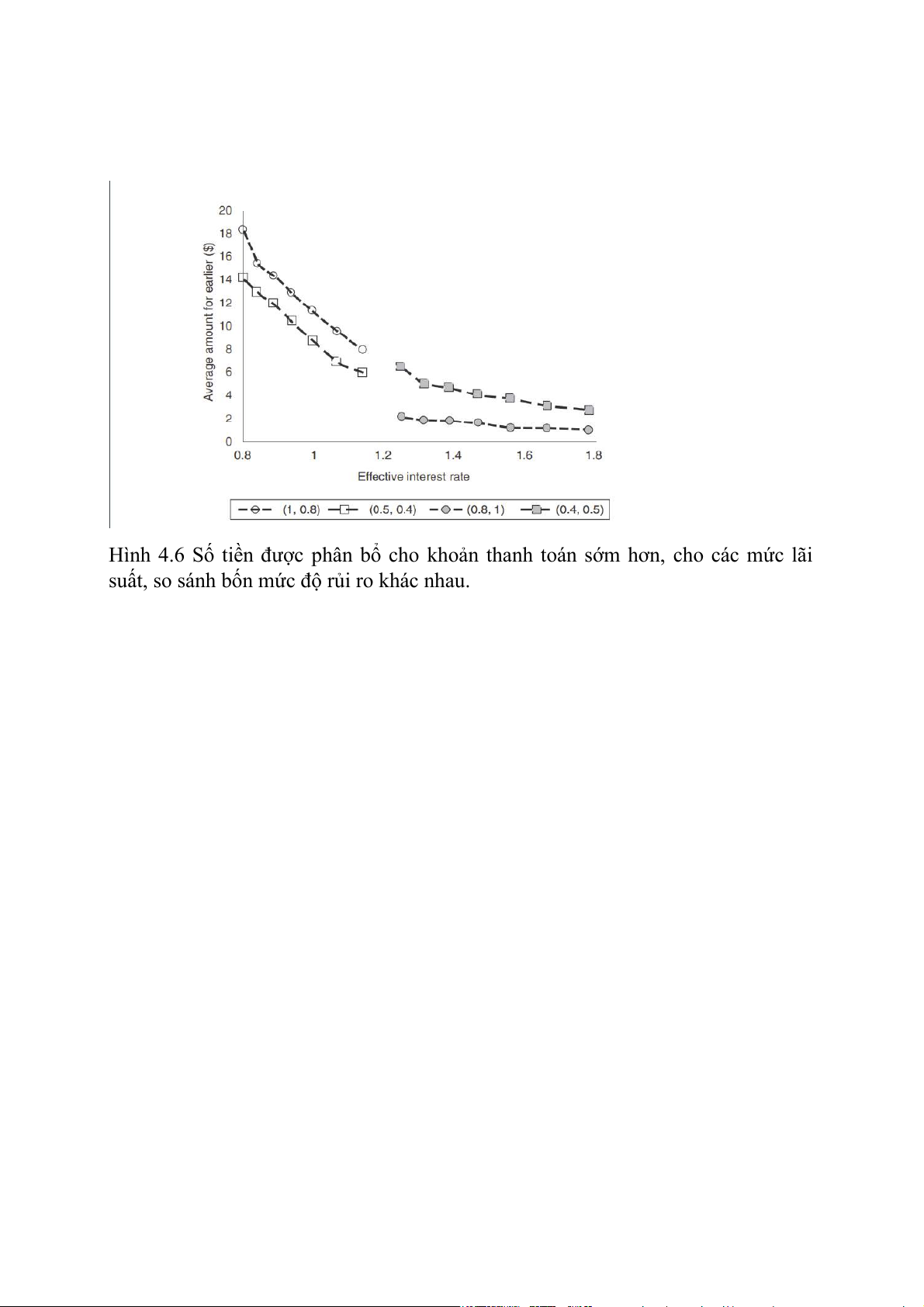
dữ liệu. Hình 4.6 biểu thị số tiền mà các đối tượng phân bổ cho lựa chọn trước đó
cho bốn tổ hợp rủi ro khác nhau. Đầu tiên, hãy xem xét vế trái của hình, trong đó
khoản thanh toán sớm hơn có nhiều khả năng được gửi hơn khoản thanh toán sau.
Cụ thể, chúng tôi so sánh cài đặt trong đó khoản thanh toán sớm hơn là chắc chắn
và khoản thanh toán sau được gửi với 80 phần trăm cơ hội, (1, 0,8), với cài đặt
trong đó khoản thanh toán sớm hơn được gửi với 50 phần trăm cơ hội và khoản
thanh toán sau đó với 40 phần trăm cơ hội, (0,5, 0,4). Ở đây, chúng ta thấy rằng các
đối tượng ít kiên nhẫn hơn khi có cơ hội nhận được khoản thanh toán cao hơn.
Điều này phù hợp với điểm cực bên trái trên Hình 4.5.
Bây giờ hãy nhìn vào phía bên phải của Hình 4.6. Ở đây, khoản thanh toán trước ít
có khả năng được gửi hơn khoản thanh toán sau. Cụ thể, chúng tôi đang so sánh cài
đặt trong đó khoản thanh toán sau là chắc chắn (0,8, 1) với cài đặt trong đó có 50
phần trăm cơ hội thanh toán được gửi (0,4, 0,5). Ở đây, chúng tôi thấy các đối
tượng kiên nhẫn hơn khi có cơ hội nhận được khoản thanh toán cao hơn. Điều này
phù hợp với vế phải của Hình 4.5. Điều quan trọng là, điều này củng cố ý tưởng
rằng các đối tượng dường như có xu hướng thích sự chắc chắn hơn.
Như tôi đã đề cập ở trên, các kết quả trong Hình 4.5 và 4.6 khó phù hợp với độ
thỏa dụng kỳ vọng đã chiết khấu. Tuy nhiên, xét đến những khó khăn của việc lập
mô hình lựa chọn với rủi ro và lựa chọn với thời gian mà chúng ta đã xem xét trong
hai chương trước, không có gì ngạc nhiên khi việc lập mô hình lựa chọn với rủi ro
và thời gian rất phức tạp. Công trình gần đây của Epper và Fehr-Duda (2015) cung
cấp một bước đột phá trong việc chỉ ra rằng một dạng trọng số xác suất phụ thuộc vào thứ hạng
Hình 4.6 Số tiền được phân bổ cho khoản thanh toán sớm hơn, cho các mức lãi
suất, so sánh bốn mức độ rủi ro khác nhau.