Thông tin
Quiz

Phiếu bài tập tích phân hàm ẩn có đáp án và lời giải Toán 12

Phiếu bài tập tích phân hàm ẩn có đáp án và lời giải Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề:

Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn:

Toán 12 3.8 K tài liệu

Thông tin:

65 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Phiếu bài tập tích phân hàm ẩn có đáp án và lời giải Toán 12

49 25 lượt tải Tải xuống

Ả

ờ

ặ

ứ

ế

ọ

ị

ỉ

ễ

ộ

ạ

ế

ặ

TÝCH PH¢N – øng dông

HµM ÈN

Cè lªn c¸c em nhÐ!

HuÕ, th¸ng 02/2021

Phiªn b¶n 2020

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU ÔN TẬP SỐ 01

CHUY£N §Ò

TÝCH PH¢N – øng dông

TÝch ph©n _ Hµm Èn

Líp To¸n thÇy L£ B¸ B¶O

Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o

116/04 NguyÔn Lé Tr¹ch

, TP HuÕ

Trung t©m KM 10 H-¬ng Trµ

, HuÕ.

NỘI DUNG ĐỀ BÀI

Câu 1: Cho hàm số

()fx

liên tục trên

thỏa mãn

( ) (2020 )f x f x

và

2016

( ) 2.



f x dx

Tính

2016

( )d .



xf x x

16160

. B.

2020

. C.

4040

. D.

8080

Câu 2: Cho hàm số

 

liên tục trên





0;

và thoả mãn

 





4 2 7 1, 0;f x x x x x       

Biết

 

58f 

, tính

 

. d .







I x f x x

I 

. B.

I 

. C.

I 

. D.

I 

Câu 3: Cho

()y f x

là hàm số đa thức bậc ba có đồ thị như hình vẽ. Tính diện tích hình phẳng được

tô đậm.

. B.

. C.

. D.

Câu 4: Cho hàm số

 

0fx

và có đạo hàm liên tục trên , thỏa mãn

   

 

x f x







và

 

ln2









. Giá trị

 

bằng

 

4ln2 ln5



. B.

 

4 4ln 2 ln5

. C.

 

4ln2 ln5



. D.

 

2 4ln 2 ln5

Câu 5: Cho hàm số f(x) liên tục trên và thỏa mãn

 

tan . cos d 2







x f x x

và

 





. Tính

 



. B.

. C.

. D.

Câu 6: Cho hàm số

()y f x

có đạo hàm, nhận giá trị dương trên

(0; )

và thoả mãn

2 ( ) 9 ( )f x x f x





với mọi

(0; ).x  

Biết









tính







. B.

. C.

. D.

Câu 7: Cho hàm số

 

có đạo hàm liên tục trên , đồ thị của

 

y f x

đi qua điểm

 

1;0A

và

nhận điểm

 

2;2I

làm tâm đối xứng. Tính tích phân

     

 

2I x x f x f x dx  





. B.

. C.



. D.

Câu 8: Cho hàm số

 

thỏa mãn

   

. sin .sin 2f x f x x x









với mọi

x

và











. Giá trị

của

 







bằng



. B.

. C.

. D.

Câu 9: Cho hàm số

()fx

xác định, có đạo hàm, liên tục và đồng biến trên

[1;4]

thỏa mãn

[

2 ( ) ( ) , 1;4], (1)

x xf x f x x f





    



. Giá trị

(4)f

bằng

391

. B.

361

. C.

381

. D.

371

Câu 10: Cho hàm số

 

liên tục trên đoạn

0;1





thỏa mãn

 

f x x f x





. Tính

 

.f x x



1.

Câu 11: Cho hàm số

 

liên tục trên

0;1





thỏa

 

4 . 3 1 1x f x f x x   

. Tính

 

.f x x





Câu 12: Cho hàm số

 

y f x

xác định và liên tục trên

 

và thỏa mãn

       

2 1 1x f x x f x xf x



   

với

 

\0x

và

 

12f 

. Tính

 

.f x x



ln2



. B.

ln2



. C.

ln2



. D.

3 ln2



Câu 13: Cho hàm số

 

có

 

20f 

và

 

f x x









    







. Biết rằng











(

, , 0,

a b b



là phân số tối giản). Khi đó

ab

bằng

250

. B.

251

. C.

133

. D.

221

Câu 14: Cho hàm số

 

y f x

liên tục trên

thỏa mãn

 

4 3 2 1f x x x   

với mọi

x

. Giá trị

của

 

df x x





bằng

. B.

. C.

. D.

Câu 15: Cho hàm số

 

liên tục trên và

   

2 1 3 0 0ff

 

d7f x x 



. Tính

 

6 d .













I x f x

40I 

. B.

28I 

. C.

18I 

. D.

42I 

Câu 16: Xt hàm số

()fx

liên tục trên

 

1;2

và thỏa mn

 

( ) 2 2 3 1 4f x xf x f x x    

. Tnh giá

trị của tch phân

()I f x x







3I 

. B.

5I 

. C.

15I 

. D.

6I 

Câu 17: Cho

 

là hàm số liên tục trên đoạn

 

0;1

thoả mãn

 

14f 

và

 

d 2.



f x x

Tính

 

' d .



x f x x

16.

Câu 18: Cho hàm số

 

y f x

có đạo hàm liên tục trên

 

0;1

thỏa mãn

 

 

1 0, ( ) d 7f f x x







và

( )d

x f x x 



. Tính

( )d .



f x x

Câu 19: Cho hàm số

 

y f x

liên tục trên thỏa mãn

 

2 2 2 ,xf x f x x x x    

. Tính giá

trị

 

dI f x x



25I 

. B.

21I 

. C.

27I 

. D.

23I 

Câu 20: Cho hàm số

()fx

liên tục trên

 

0; ,

thỏa mãn

 

f 

và

 

3 ( ) ( ) 2 ( )



xf x x f x f x

( ) 0fx

với

x

 

0;

. Gọi

,Mm

lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số

()fx

trên đoạn

 

1;2

. Tổng

Mm

bằng

. B.

. C.

. D.

_________________HẾT_________________

Huế, ngày 07 tháng 02 năm 2021

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU ÔN TẬP SỐ 01

CHUY£N §Ò

TÝCH PH¢N – øng dông

TÝch ph©n _ Hµm Èn

LỜI GIẢI CHI TIẾT

Câu 1: Cho hàm số

()fx

liên tục trên

thỏa mãn

( ) (2020 )f x f x

và

2016

( ) 2.



f x dx

Tính

2016

( )d .



xf x x

16160

. B.

2020

. C.

4040

. D.

8080

Lời giải:

Xét

2016

( ) .



I xf x dx

Đặt

2020t x dt dx    

và

4 2016

2016 4

  

Do đó

2016 4 2016

4 2016 4

( ) (2020 ) (2020 )( ) (2020 ) (2020 )       

  

I xf x dx t f t dt x f x dx

2016 2016 2016

4 4 4

(2020 ) ( ) 2020 ( ) ( ) 2020.2

4040 2 4040 2020.

     

      

  

x f x dx f x dx xf x dx I

I I I I



Chọn đáp án B.

Câu 2: Cho hàm số

 

liên tục trên





0;

và thoả mãn

 





4 2 7 1, 0;f x x x x x       

Biết

 

58f 

, tính

 

. d .







I x f x x

I 

. B.

I 

. C.

I 

. D.

I 

Lời giải:

Ta có

 

   

 

2 2 2 2

4 2 7 1 2 4 4 2 7 1 2 4f x x x x x f x x x x x            

Lấy tích phân cận chạy từ

01

hai vế ta được:

 

   

 

2 4 4 2 7 1 2 4

x f x x dx x x x dx        



Xét

 

2 4 4x f x x dx



. Đặt

 

4 2 4

0 0, 1 5

t x x dt x dx

x t x t



    





     





. Khi đó ta có

 

   

1 5 5

0 0 0

2 4 4

x f x x dx f t dt f x dx     

  

Xét

     

52 68

. 40

I x f x dx xf x f x dx





        









Chọn đáp án A.

Câu 3: Cho

()y f x

là hàm số đa thức bậc ba có đồ thị như hình vẽ. Tính diện tích hình phẳng được

tô đậm.

. B.

. C.

. D.

Lời giải:

Giả sử

()f x ax bx cx d   

có đồ thị

()C

như hình vẽ trên.

Điểm

(0;0) ( ) d 0 ( )O C f x ax bx cx      

Các điểm

(1;0), (2;2), (3;0) (C) 4 2 1 4 ( ) 4 3

9 3 0 3

a b c a

A B D a b c b f x x x x

a b c c

    





           





    



Diện tích hình phẳng cần tìm là

   

1 3 1 3

3 2 3 2

0 1 0 1

0 ( ) ( ) 0 ( 4 3 ) ( 4 3 )

S f x dx f x dx x x x dx x x x dx           

   



Chọn đáp án B.

Câu 4: Cho hàm số

 

0fx

và có đạo hàm liên tục trên , thỏa mãn

   

 

x f x







và

 

ln2









. Giá trị

 

bằng

 

4ln2 ln5



. B.

 

4 4ln 2 ln5

. C.

 

4ln2 ln5



. D.

 

2 4ln 2 ln5

Lời giải:

Với

 

0;3x

ta có:

   

 

x f x







 

  







 





  









 

2 ln







   

 

2 3 0 ln ln

ff   

 

ln2 1 8

3 ln

2 2 5



  





   

1 8 1

3 ln ln2 4ln2 ln5

2 5 2



    





   

3 4ln2 ln5

f  



Chọn đáp án C.

Câu 5: Cho hàm số f(x) liên tục trên và thỏa mãn

 

tan . cos d 2







x f x x

và

 





. Tính

 



. B.

. C.

. D.

Lời giải:

Xét

 

tan . cos 2I x f x dx







Đặt

2sin cos 2tan .cos tan

cos

0 1;

dt x xdx x xdx xdx

x t x t





      









     





Suy ra

     

f t f t f t

I dt dt dt

t t t

     

  

Xét

 

I dx





Đặt

2ln 1 1

2ln

ln 2 ln

1; 4

x dt

dt dx xdx dx

x x x t x x

x e t x e t



   









     



Suy ra

   

f t f t

I dt dt

   



Xét

 

2fx

I dx





. Đặt

; 2 4

x dt

dt dx dx dx

x x t

x t x t



   









     





Suy ra

     

4 1 4

4 4 8

f t f t f t

I dt dt dt

t t t

     

  



Chọn đáp án D.

Câu 6: Cho hàm số

()y f x

có đạo hàm, nhận giá trị dương trên

(0; )

và thoả mãn

2 ( ) 9 ( )f x x f x





với mọi

(0; ).x  

Biết









tính







. B.

. C.

. D.

Lời giải:

Ta có

2 ( ) 9 ( )f x x f x

 

2 2 2 2

9 9 9

2 2 2

xf x

x x f x x

f x f x











     





Do đó

 

2 2 3

f x x x x C  



. Mà

2 2 2 3 2 2

. . 0

3 3 3 2 3 3

f C C

Suy ra

 

2 6 3

9 9 1 9 1 1

4 4 3 4 3 12

f x x f x x f

   

     

   

   



Chọn đáp án C.

Câu 7: Cho hàm số

 

có đạo hàm liên tục trên , đồ thị của

 

y f x

đi qua điểm

 

1;0A

và

nhận điểm

 

2;2I

làm tâm đối xứng. Tính tích phân

     

 

2I x x f x f x dx  





. B.

. C.



. D.

Lời giải:

+ Từ giả thiết, suy ra đẳng thức

   

4 4,f x f x x   

(*).

+ Ta có

     

 

3 3 3

1 1 1

2 d 2 d 2 dI x x f x f x x x x f x x x x f x



      

  

 

     

2 d 2 2 2 dx x f x x x x f x x f x x



     





 

     

4 2 d 3 3 1x x f x x f f    



+ Từ giả thiết và (*) suy ra

 

10f 

và

 

34f 

+ Kí hiệu

 

42J x x f x dx  



, dùng php đổi biến

4tx

dẫn đến

   

 

4 4 4 2 4 4 2 4J x x f x dx x x f x dx         



Suy ra

 

   

 

40 20

2 4 2 4 4 4 2

J x x f x f x dx x x dx J            



Vậy

20 16

3.4 0

I     

Cách dự đoán đáp số: Chọn

   

2 2 2f x x  

thỏa mn các đk đề bài, thu được

I 



Chọn đáp án B.

Câu 8: Cho hàm số

 

thỏa mãn

   

. sin .sin 2f x f x x x









với mọi

x

và











. Giá trị

của

 







bằng



. B.

. C.

. D.

Lời giải:

Ta có

 

1 1 1 1

sin .sin 2 sin 1 cos4 sin sin5 sin3

2 2 4 4

x x x x x x x    

Vậy

       

. sin .sin 2 . d sin .sin 2 df x f x x x f x f x x x x x



  

   

   



   

 

1 1 1

d sin sin5 sin3 d

2 4 4

1 1 1

cos cos5 cos3 .

5 2 20 12

f x f x x x x x

x x x C



   





     







  





. Vậy

 

1 1 1 1 11

5 cos cos5 cos3

2 20 12 5 3

   



     







Chọn đáp án D.

Câu 9: Cho hàm số

()fx

xác định, có đạo hàm, liên tục và đồng biến trên

[1;4]

thỏa mãn

[

2 ( ) ( ) , 1;4], (1)

x xf x f x x f





    



. Giá trị

(4)f

bằng

391

. B.

361

. C.

381

. D.

371

Lời giải:

Ta có

[]

[ ] [ ]

( ) ( )

2 ( ) ( ) (1 2 ( )) ( )

1 2 ( )

f x f x

x xf x f x x f x f x x x



        



()

14 14 391

1 2 ( ) 1 2 (4) 2 (4) .

3 3 18

1 2 ( )

dx xdx f x f f



          







Chọn đáp án A.

Câu 10: Cho hàm số

 

liên tục trên đoạn

0;1





thỏa mãn

 

f x x f x





. Tính

 

.f x x



1.

Lời giải:

 

2 3 2 3

6 . 2 3 .

3 1 3 1

f x x f x I f x dx x f x dx A B



       









Gọi

 

2 3 . .A x f x dx



Đặt

3.t x dt x dx  

Đổi cận

0 0; 1 1x t x t     

Ta có:

   

2 2 2A f t dt f x dx I  



   

2 6 6 3 1 . . 3 1 2.2. 3 1 4.

I I B I B dx x d x x



          







Chọn đáp án B.

Câu 11: Cho hàm số

 

liên tục trên

0;1





thỏa

 

4 . 3 1 1x f x f x x   

. Tính

 

.f x x





Lời giải:

 

4 . 3 1 1x f x f x x   

 

   

1 1 1 1

2 2 2

0 0 0 0

2. 2 . 3 1 1 2 3 1 *x f x dx f x dx x dx A B x dx        

   

 

2.A x f x dx



Đặt

2t x dt xdx  

;

0 0; 1 1x t x t     

   

A f t dt f x dx



 

1B f x dx



Đặt

1 ; 0 1, 1 0t x dt dx x t x t          

   

B f t dt f x dx



       

1 1 1 1 1

0 0 0 0 0

* 2 3 1 5. 1f x dx f x dx x dx f x dx x dx      

    

Đặt:

sin , ; ; 0 0, 1

2 2 2

x t dx costdt t x t x t

  



          





0 0 0

1 2 1 1

1 1 sin .cos . sin2

2 2 2 4

cos t

x dx t tdt dt t t









       





  

Vậy

 

f x dx









Chọn đáp án C.

Câu 12: Cho hàm số

 

y f x

xác định và liên tục trên

 

và thỏa mãn

       

2 1 1x f x x f x xf x



   

với

 

\0x

và

 

12f 

. Tính

 

.f x x



ln2



. B.

ln2



. C.

ln2



. D.

3 ln2



Lời giải:

Biến đổi

         

 

    

2 1 1x f x xf x f x xf x xf x f x xf x



        

Đặt

         

1.h x xf x h x f x x f x



    

, Khi đó

 



có dạng:

   

 

   

 

2 2 2

1 1 1

1 2 1 0.

h x h x dh x

h x h x dx dx x C x C

h x h x h x

h x xf x C

x C x C C







           

            

  

  

Khi đó

   

1 1 1

1.xf x f x

      

Suy ra:

 

1 1 1

ln2

f x dx dx

     





Chọn đáp án A.

Câu 13: Cho hàm số

 

có

 

20f 

và

 

f x x









    







. Biết rằng











(

, , 0,

a b b



là phân số tối giản). Khi đó

ab

bằng

250

. B.

251

. C.

133

. D.

221

Lời giải:

Lấy nguyên hàm hai vế của

 









ta được

 

, ; .

















Đặt

u x x



   

suy ra

ddx u u

Suy ra

 

17d 2 3 .

2 2 3

f x x Cu u







    











Theo giả thiết ta có

 

20f 

suy ra

C 

Do đó

 

1 26

17 2 3 .

2 3 3

f x x







   





Ta có









. Đặt

d 2dt

tx  

.Đổi cận với

42xt  

, với

xt  

Suy ra

   

4 2 2

d 2 dt 2

f x f t f x x









  

Vậy

 

13 236

2 17 2 3

3 3 1

f x x x x







    







Suy ra

236, 15ab

nên

236 15 251ab   



Chọn đáp án B.

Câu 14: Cho hàm số

 

y f x

liên tục trên

thỏa mãn

 

4 3 2 1f x x x   

với mọi

x

. Giá trị

của

 

df x x





bằng

. B.

. C.

. D.

Lời giải:

Ta có

     

 

4 5 4

5 4 . 4 3 5 4 2 1x f x x x x     

Đặt

43t x x  

ta có

 

d 5 4 dt x x

và

 

21f t x

Đổi cận

2 4 5 0t x x     

1x  

8 4 5 0t x x    

1x

Do đó

   

 

d 2 1 5 4 d 10f t t x x x



   





Chọn đáp án B.

Câu 15: Cho hàm số

 

liên tục trên và

   

2 1 3 0 0ff

 

d7f x x 



. Tính

 

6 d .













I x f x

40I 

. B.

28I 

. C.

18I 

. D.

42I 

Lời giải:

Xét

 

I x f x













Đặt

v f x













































Khi đó:

 

2 6 2 d

I x f f x

   

  

   

   



   

4 2 1 3 0 2 2f f J J   





Xét

J f x











+ Đặt

t t x  

+ Đổi cận :

0 0; 2 1x t x t     

Lúc này:

 

2 d 2 7 14J f t t   



. Vậy

2 2 14 28IJ   



Chọn đáp án B.

Câu 16: Xt hàm số

()fx

liên tục trên

 

1;2

và thỏa mn

 

( ) 2 2 3 1 4f x xf x f x x    

. Tnh giá

trị của tch phân

()I f x x







3I 

. B.

5I 

. C.

15I 

. D.

6I 

Lời giải:

Lấy nguyên hàm hai vế giả thiết ta có

2 2 4

( ) 2 ( 2) 3 (1 ) 4

( ) ( 2) ( 2) 3 (1 ) (1 )

f x xf x f x dx x dx

f x dx f x d x f x d x x C



    



        



  

Đặt

( ) ( ) ( ) ( 2) 3 (1 )f t dx F t F x F x F x x C       



Ta có

1 ( 1) ( 1) 3 (2) 1 2 ( 1) 3 (2) 1

2 (2) (2) 3 ( 1) 16 2 (2) 3 ( 1) 16

x F F F C F F C

           







          



Trừ từng vế thu được

5 (2) 5 ( 1) 15 (2) ( 1) 3 ( ) 3F F F F I f x dx



         





Chọn đáp án A.

Câu 17: Cho

 

là hàm số liên tục trên đoạn

 

0;1

thoả mãn

 

14f 

và

 

d 2.



f x x

Tính

 

' d .



x f x x

16.

Lời giải:

Đặt

2.x t xdx dt  

Khi đó ta có

xdx 

Suy ra:

 

     

1 1 1

0 0 0

x f x dx tf t dt t f t f t dt



  





  

   

1 1.

f f t  





Chọn đáp án C.

Câu 18: Cho hàm số

 

y f x

có đạo hàm liên tục trên

 

0;1

thỏa mãn

 

 

1 0, ( ) d 7f f x x







và

( )d

x f x x 



. Tính

( )d .



f x x

Lời giải:

Đặt

   

u f x du f x dx



  

dv x dx v  

Ta có

     

3 3 3

f x f x dx x f x dx



    



Ta có

 

 

1 1 1 1

6 3 3

0 0 0 0

49 d 7, ( ) d 7, 2.7 . 14 7 ( ) d 0x x f x x x f x dx x f x x

  



      



   

 

7 ( ) 0

x f x f x C



      

, mà

 

fC  

7 7 7

( )d d

4 4 5

f x x x



    









Chọn đáp án A.

Câu 19: Cho hàm số

 

y f x

liên tục trên thỏa mãn

 

2 2 2 ,xf x f x x x x    

. Tính giá

trị

 

dI f x x



25I 

. B.

21I 

. C.

27I 

. D.

23I 

Lời giải:

Ta có:

 

2 3 2 3

2 2 2 2 d 2 2 dxf x f x x x xf x f x x x x x



      





 

2 2 2 2

2 2 2

1 1 1 1

d 2 d d 2 d

xf x x f x x x xf x x f x x



   

      



   



   

. (*)

+ Tính

 

dxf x x







Đặt

d 2 d d

u x u x x x x    

;

1 1; 2 4x u x u     

Suy ra

 

2 4 4

1 1 1

d d d

xf x x u f x x







  

+ Tính

 

2df x x





. Đặt

2 d 2d d

t x t x x    

;

1 2; 2 4x t x t     

Suy ra

 

2 4 4

1 2 2

2 d d d

f x x t f x x





  

Thay vào (*) ta được

         

4 4 2 4 4

1 2 1 2 2

1 1 21 1 1 1 21

d d d d d

2 2 2 2 2 2 2

f x x f x x f x x f x x f x x     

    

   

1 21

d d 21

f x x f x x   





Chọn đáp án B.

Câu 20: Cho hàm số

()fx

liên tục trên

 

0; ,

thỏa mãn

 

f 

và

 

3 ( ) ( ) 2 ( )



xf x x f x f x

( ) 0fx

với

x

 

0;

. Gọi

,Mm

lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số

()fx

trên đoạn

 

1;2

. Tổng

Mm

bằng

. B.

. C.

. D.

Lời giải:

+) Xét hàm số

()fx

trên

 

0;

ta có:

3 ( ) ( ) 2 ( )xf x x f x f x





2 3 2

3 ( ) ( ) 2 ( )x f x x f x xf x



  

 

( ) ( )

x f x x f x

f x f x







   





 

Lấy nguyên hàm hai vế của

 

ta được :

d 2 d

( ) ( )

x x x x C

f x f x





   







Mà

 

f 

nên

(1)

   

. Suy ra

 





+) Xét hàm số

 





trên

 

1;2

Xét hàm số

 

   

2 2 3

2 2`

3 1 2 .

x x x x





  



với

 

1;2x

Suy ra

 

   

 

   

1;2

max 2 ; min 1 .

M f x f m f x f     

Vậy

1 8 21

2 5 10

Mm   



Chọn đáp án A.

_________________HẾT_________________

Huế, ngày 07 tháng 02 năm 2021

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU ÔN TẬP SỐ 02

CHUY£N §Ò

TÝCH PH¢N – øng dông

TÝch ph©n _ Hµm Èn

Líp To¸n thÇy L£ B¸ B¶O

Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o

116/04 NguyÔn Lé Tr¹ch

, TP HuÕ

Trung t©m KM 10 H-¬ng Trµ

, HuÕ.

NỘI DUNG ĐỀ BÀI

Câu 1: Cho hàm số

 

có đạo hàm liên tục trên đoạn

 

2;4

và thỏa mãn

   

2 2, 4 2020ff

Tính tích phân

 

2dI f x x







1009I 

. B.

2022I 

. C.

2018I 

. D.

1011I 

Câu 2: Cho

là hằng số thực và hàm số

 

liên tục trên thỏa mãn

 

2021f x a dx



. Giá trị

của tích phân

 

I f x dx







là

2021.I 

2021.I 

2021 .Ia

2021 .Ia

Câu 3: Cho hàm số

 

liên tục trên khoảng

 

0;

và thỏa mãn

 

1 .ln 1

f x x



   

. Biết

 

d ln5 2lnf x x a b c  



với

,,abc

. Giá trị

của

2a b c

bằng

. B.

. C.

. D.

Câu 4: Cho hàm số

 

y f x

có đạo hàm liên tục trên . Biết

 

e1f 

và

     

2x f x xf x x



  

x

. Tính

 

4 4 4

4 2 1

2 2 2

4 4 4

Câu 5: Cho

 

là hàm số liên tục trên thoả mãn

 

11f

và

 





f t t

, tính

 

sin 2 . sin d .









I x f x x

I 

. B.

I 

. C.

I 

. D.

I 

Câu 6: Cho hàm số

 

có đạo hàm xác định trên . Biết

 

12f 

và

 

d 2 d 4

x f x x f x x





  



. Giá trị của

 

df x x



bằng

. B.

. C.

. D.

Câu 7: Cho hàm số

 

y f x

đồng biến và có đạo hàm liên tục trên thỏa mãn

 

f x f x e x



  

và

 

0 2.f 

Khi đó

 

thuộc khoảng nào sau đây?

 

12;13

. B.

 

9;10

. C.

 

11;12

. D.

 

13;14

Câu 8: Cho hàm số

 

liên tục trên và thỏa mãn

( ) ( ) 2cos2 ,f x f x x x    

. Khi đó

 

df x x







bằng

2

. B.

. C.

. D.

Câu 9: Cho

 

là hàm số liên tục trên tập số thực và thỏa mãn

 

3 1 2f x x x   

. Tính

 

d.



I f x x

. B.

527

. C.

. D.

464

Câu 10: Cho hàm số

 

2 khi 0 2

5 khi 2 5



  









   



. Khi đó

 





d 1 d

x xf x x





bằng

. B.

. C.

. D. 5.

Câu 11: Cho hàm số

 

có đạo hàm liên tục trên . Biết

 

. ' 10x f x dx 



và

 

13f 

, tính

 

f x dx



. B.

. C.

. D.

7

Câu 12: Cho hàm số

()fx

liên tục trên đoạn

0;1





và thỏa mãn

 

. 3 1 1x f x f x x   

. Tính

 

f x x





. B.



. C.



. D.



Câu 13: Cho hàm số

 

thỏa mãn

   

. sin .sin 2f x f x x x









với mọi

x

và











. Giá trị

của

 







bằng



. B.

. C.

. D.

Câu 14: Cho hàm số

()fx

liên tục trên thỏa mãn

( ) ( )d ,   



f x e tf t t x

. Tính

(ln(5620))f

A. 5622. B. 5621. C. 5620. D. 5619.

Câu 15: Cho hàm số

 

có đạo hàm liên tục trên và thỏa mãn

 

d 10f x x 



 

1 cot1f 

. Tính tích

phân

   

tan tan dI f x x f x x x











 

1 ln 1cos

. B.

1

. C.

9

. D.

1 cot1

Câu 16: Cho hàm số

 

y f x

liên tục và thỏa mãn

 

23f x f x









với mọi









. Tính

 



. B.

. C.



. D.



Câu 17: Cho hàm số

 

y f x

xác định và liên tục trên

 

0;

sao cho

   

x xf e f e  

với mọi

 

0;x  

. Tính tích phân

   

x f x





I 

. B.

I 

. C.

I 

. D.

I 

Câu 18: Cho hàm số

()y f x

liên tục trên có đồ thị như hình vẽ . Biết

có diện tích bằng 7

(đvdt) ,

có diện tích bằng 3 (đvdt).

Tính

 

2 6 6 7 d .



   



I x f x x x

(đvdt). B.

(đvdt). C.

(đvdt). D.

(đvdt).

Câu 19: Cho hàm số

 

y f x

liên tục trên và thỏa mãn

   

,.f x f x x x



   



Tính

 

.I f x x



I 

I 

I 

I 

Câu 20: Cho hàm số

()fx

liên tục trên thỏa

   

3 2 10 6

1 2 ,xf x f x x x x x       

. Khi đó

()f x x





bằng



. B.



. C.

. D.

1

_________________HẾT_________________

Huế, ngày 07 tháng 02 năm 2021

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU ÔN TẬP SỐ 02

CHUY£N §Ò

TÝCH PH¢N – øng dông

TÝch ph©n _ Hµm Èn

LỜI GIẢI CHI TIẾT

Câu 1: Cho hàm số

 

có đạo hàm liên tục trên đoạn

 

2;4

và thỏa mãn

   

2 2, 4 2020ff

Tính tích phân

 

2dI f x x







1009I 

. B.

2022I 

. C.

2018I 

. D.

1011I 

Lời giải:

Đặt

2 d d

t x x t  

. Đổi cận:

1 2; 2 4x t x t     

Do đó, ta có

         

 

1 1 1

2 d d 4 2 1009.

2 2 2



     



I f x x f t t f t f f



Chọn đáp án A.

Câu 2: Cho

là hằng số thực và hàm số

 

liên tục trên thỏa mãn

 

2021f x a dx



. Giá trị

của tích phân

 

I f x dx







là

2021.I 

2021.I 

2021 .Ia

2021 .Ia

Lời giải:

Đặt:

t x a dt dx   

Đổi cận: Với

1x 

ta có

1ta

; với

2x 

ta có

2ta

     

2 2 2

1 1 1

2021.

I f t dt f x dx f x a dx



     

  



Chọn đáp án A.

Câu 3: Cho hàm số

 

liên tục trên khoảng

 

0;

và thỏa mãn

 

1 .ln 1

f x x



   

. Biết

 

d ln5 2lnf x x a b c  



với

,,abc

. Giá trị

của

2a b c

bằng

. B.

. C.

. D.

Lời giải:

Cách 1:

 

liên tục trên khoảng

 

0;

nên tồn tại

   

dF x f x x



0x

Với

0x 

, ta có:

 

1 .ln 1

f x x



   



 

   

2 . 1 2 1 .ln 1

x f x x x

    

Xét vế trái:

 

2 . 1

g x x f x

  



 

d1g x x F x F x C   



Xét vế phải:

     

2 1 .ln 1h x x x  



     

d 2 1 ln 1 dh x x x x x  



 

ln 1 dx x x  



 

ln 1 d

x x x x x x

    





 

ln 1 dx x x x x   



 

ln 1

x x x C    

Suy ra

 

   

1 ln 1 1

F x F x x x x C      

Thay

4x 

vào

 

ta có:

   

17 2 20ln5 8F F C   

Thay

1x 

vào

 

ta có:

   

2 1 2ln2

F F C   

Nên

     

d 17 1 20ln5 2ln2

f x x F F    



, suy ra

20a 

2b 

c 

Vậy:

2 20 2 15 7a b c     

Cách 2:

 

liên tục trên khoảng

 

0;

nên tồn tại

   

dF x f x x



0x

Với

0x 

, ta có:

 

1 .ln 1

f x x



   



 

   

2 . 1 2 1 .ln 1

x f x x x

    

Lấy tích phân hai vế cận từ

đến

ta được:

   

 

   

4 4 4

1 1 1

1 1 2 1 .ln 1f x d x f x d x x x dx     

  

   

 

17 2 4

2 1 1

ln 1

f t dt f t dt x x x dx



     



  

   

17 4 17

1 1 1

20ln5 2ln2 20ln5 2ln2

f t dt xdx f x dx       

  

Vậy:

2 20 2 15 7a b c     



Chọn đáp án C.

Câu 4: Cho hàm số

 

y f x

có đạo hàm liên tục trên . Biết

 

e1f 

và

     

2x f x xf x x



  

x

. Tính

 

4 4 4

4 2 1

2 2 2

4 4 4

Lời giải:

Ta có:

     

2x f x xf x x



  

     

xf x x f x







 













 

d e d















   





    



   



   

   

ee2 4 1 1ff



   



4 4 4ee  



Chọn đáp án D.

Câu 5: Cho

 

là hàm số liên tục trên thoả mãn

 

11f

và

 





f t t

, tính

 

sin 2 . sin d .









I x f x x

I 

. B.

I 

. C.

I 

. D.

I 

Lời giải:

Đặt

sin cos dt x dt x x  

. Đổi cận

0 0; 1.

x t x t



     

Khi đó

   

sin 2 . sin d 2 . d .I x f x x t f t t









Đặt

   

2 d 2d

u t u t

v f t t v f t



















Vậy

     

2 . 2 d 2 1 2

I t f t f t t f    









Chọn đáp án A.

Câu 6: Cho hàm số

 

có đạo hàm xác định trên . Biết

 

12f 

và

 

d 2 d 4

x f x x f x x





  



. Giá trị của

 

df x x



bằng

. B.

. C.

. D.

Lời giải:

Ta có:

   

 

1 1 1

2 2 2

0 0 0

4 d d 2 d

x f x x x f x x f x xf x x



   

  

     

4 1 2 d 4 2 2 df xf x x xf x x     



 

d1xf x x  



Xét

 

f x x







. Đặt

2 d d

t x t x

    

Với

11xt  

và

40xt  

Khi đó

 

   

4 2 d 1 3 2 d

f x x t f t t



     







       

1 1 1

0 0 0

4 7 3 d 4 7 d 3 dt f t t f t t tf t t     

  

     

4 7 d 3 1 d

f t t f t t     



Vậy

 

f x x 





Chọn đáp án D.

Câu 7: Cho hàm số

 

y f x

đồng biến và có đạo hàm liên tục trên thỏa mãn

 

f x f x e x



  

và

 

0 2.f 

Khi đó

 

thuộc khoảng nào sau đây?

 

12;13

. B.

 

9;10

. C.

 

11;12

. D.

 

13;14

Lời giải:

Hàm số đồng biến trên nên ta có

 

   

0 , 0

f x f x











  





 

     

 

f x f x e f x f x e e





     

 

     

dx dx 2 0 1

e f x e f f e



       



 

2 2 1 9;10fe    



Chọn đáp án B.

Câu 8: Cho hàm số

 

liên tục trên và thỏa mãn

( ) ( ) 2cos2 ,f x f x x x    

. Khi đó

 

df x x







bằng

2

. B.

. C.

. D.

Lời giải:

Với

( ) ( ) 2cos2 ,f x f x x x    

     

2 2 2 2 2

( ) ( ) 2cosd 2 dd 2 osd c d2x x f xfx x f x xfxxxx

    

    

     

    

(*)

Tính

 

dI f x x









. Đặt

d d .    t x t x

Đổi cận:



   

;



   

Khi đó

     

2 2 2

d d dI f t t f t t f x x

  



  



   



Từ (*), ta được:

 

2 d d sin 22cos2 0f x x x xx











  



 

d0f x x











Chọn đáp án D.

Câu 9: Cho

 

là hàm số liên tục trên tập số thực và thỏa mãn

 

3 1 2f x x x   

. Tính

 

d.



I f x x

. B.

527

. C.

. D.

464

Lời giải:

Đặt

31x t t  

. Đổi cận:

10xt  

51xt  

Ta có:

 

d d 3 1x t t  

 

3 3 dtt

Khi đó:

 

dI f x x



  

3 1 3 3 df t t t t   



 

2 3 3 dt t t  







Chọn đáp án A.

Câu 10: Cho hàm số

 

2 khi 0 2

5 khi 2 5



  









   



. Khi đó

 





d 1 d

x xf x x





bằng

. B.

. C.

. D. 5.

Lời giải:

Xét

 





Đặt

ln d d .  t x t x

Đổi cận

x e t

  





  



Suy ra

 

   

2 2 2

1 0 0 0

d d = d 2 d 2 5.

I x f t t f x x x x x



      





   

Xét





1dI xf x x



Đặt

2 2 2

1 1 d d .t x t x t t x x      

Đổi cận

2 6 5



  





  





Suy ra





     

2 6 5 5 5

2 2 2

1 d d d 5 d 5 .

I xf x x f t t f x x x x x





         





   

Vậy

 





9 19

d 1 d 5 .

x xf x x

    





Chọn đáp án A.

Câu 11: Cho hàm số

 

có đạo hàm liên tục trên . Biết

 

. ' 10x f x dx 



và

 

13f 

, tính

 

f x dx



. B.

. C.

. D.

7

Lời giải:

Xét tích phân

 

. ' 10x f x dx 



. Đặt

   

u x du dx

dv f x dx v f x

















Do đó,

         

1 1 1

0 0 0

. ' 10 . 10 1 10x f x dx x f x f x dx f f x dx      

  

Suy ra

 

3 10 7f x dx    





Chọn đáp án D.

Câu 12: Cho hàm số

()fx

liên tục trên đoạn

0;1





và thỏa mãn

 

. 3 1 1x f x f x x   

. Tính

 

f x x





. B.



. C.



. D.



Lời giải:

Từ giả thiết

4 . ( ) 3 (1 ) 1x f x f x x   

, lấy tích phân hai vế ta được:





1 1 1

0 0 0

[4 . ( )]d 3 (1 )d 1 dx f x x f x x x x   

  

(*)

Tính

[4 . ( )]d .



A x f x x

Đặt

dt 2 .dt x x x  

. Đổi cận:

x 0 0t  

;

11xt  

1 1 1 1

0 0 0 0

[4 . ( )]d 2 ( )2 .d 2 ( )dt =2 ( )dx A x f x x f x x x f t f x   

   

Tính

3 (1 )dB f x x



Đặt

1 dt dt x x    

. Đổi cận:

x 0 1t  

;

10xt  

1 0 1 1

0 1 0 0

3 ( 1)]d 3 ( )dt 3 ( )dt =3 ( )dx B f x x f t f t f x     

   

Tính





1dC x x



Đặt

sin dx cos .dtx t t  

. Đổi cận:

x 0 0t  

;



  





0 0 0

1 os2t 1 1

1 d cos .dt = .dt = sin 2

2 2 4 4

C x x t t t









     





  

Thay

,,A B C

vào (*) ta được:

5 ( )dx ( )dx

4 20

f x f x



  





Chọn đáp án C.

Câu 13: Cho hàm số

 

thỏa mãn

   

. sin .sin 2f x f x x x









với mọi

x

và











. Giá trị

của

 







bằng



. B.

. C.

. D.

Lời giải:

Ta có

 

1 1 1 1

sin .sin 2 sin 1 cos4 sin sin5 sin3

2 2 4 4

x x x x x x x    

Vậy

       

. sin .sin 2 . d sin .sin 2 df x f x x x f x f x x x x x



  

   

   



   

 

1 1 1

d sin sin5 sin3 d

2 4 4

1 1 1

cos cos5 cos3 .

5 2 20 12

f x f x x x x x

x x x C



   





     







  





. Vậy

 

1 1 1 1 11

5 cos cos5 cos3

2 20 12 5 3

   



     







Chọn đáp án D.

Câu 14: Cho hàm số

()fx

liên tục trên thỏa mãn

( ) ( )d ,   



f x e tf t t x

. Tính

(ln(5620))f

A. 5622. B. 5621. C. 5620. D. 5619.

Lời giải:

Theo giả thiết, ta có:

()

f x e c

, với

()c tf t dt



là hằng số.

Khi đó:

 

1 1 1

0 0 0

c t e c dt te dt ctdt I I     

  

, với

I te dt



I ctdt



Vì

1 1 1

1 0 0

0 0 0

( ) ( ) ( ) ( 1) 1

t t t t t

I te dt td e te e dt e e e e         

  

()

ct c

I ctdt  



nên

c I I c c      

. Vậy

( ) 2,

f x e x   

Do đó

ln(5620)

(ln(5620)) 2 5620 2 5622fe    



Chọn đáp án A.

Câu 15: Cho hàm số

 

có đạo hàm liên tục trên và thỏa mãn

 

d 10f x x 



 

1 cot1f 

. Tính tích

phân

   

tan tan dI f x x f x x x











 

1 ln 1cos

. B.

1

. C.

9

. D.

1 cot1

Lời giải:

Cách 1:

   

tan tan dI f x x f x x x











     

tan d tan d 1f x x x f x x x







+ Tính

 

tan dJ f x x x







Đặt

 

tan

















v f x x

, ta có

 

d 1 tan d















u x x

v f x

   

 

.tan . 1 tan d   



J f x x f x x x

       

1 .tan1 0 .tan0 .tan d df f f x x x f x x   



 

cot1.tan1 .tan d 10f x x x  



   

1 .tan d 10 9 .tan df x x x f x x x     



Thay

vào

 

ta được:

   

tan d 9 .tan d 9I f x x x f x x x



     







Cách 2:

Ta có:

 

   

 

     

tan tan tan 1 tan tanf x x f x x f x x f x x f x x f x





     

       

tan tan tanf x x f x x f x x f x





   



       

tan tan d tan dI f x x f x x x f x x f x x







    









     

tan d 1 tan1 10 cot1.tan1 10 9       



f x x f x x f



Chọn đáp án C.

Câu 16: Cho hàm số

 

y f x

liên tục và thỏa mãn

 

23f x f x









với mọi









. Tính

 



. B.

. C.



. D.



Lời giải:

Ta có

   

1 1 3

2 3 2f x f x f f x

x x x

   

    

   

   

Từ đó ta có hệ phương trình:

 

f x f x

f x x

f x f













  

















 

  

. Do đó

 

d 1 d

I x x



   









Chọn đáp án A.

Câu 17: Cho hàm số

 

y f x

xác định và liên tục trên

 

0;

sao cho

   

x xf e f e  

với mọi

 

0;x  

. Tính tích phân

   

x f x





I 

. B.

I 

. C.

I 

. D.

I 

Lời giải:

Với

 

0;x  

ta có

     

x x x

x xf e f e f e x



      



Đặt

ln d

x t t

  

 

d 1 d

    



I tf e t t t t



Chọn đáp án C.

Câu 18: Cho hàm số

()y f x

liên tục trên có đồ thị như hình vẽ . Biết

có diện tích bằng 7

(đvdt) ,

có diện tích bằng 3 (đvdt).

Tính

 

2 6 6 7 d .



   



I x f x x x

(đvdt). B.

(đvdt). C.

(đvdt). D.

(đvdt).

Lời giải:

Dựa vào đồ thị ta thấy

 

( )d ( )d 7

( ) d ( )d 3















   







S f x x f x x

Xét

(2 6) ( 6 7)dI x f x x x



   



Đặt

6 7 dt (2 6)dt x x x x     

.Đổi cận :

    





   



Khi đó

2 2 1 2

1 1 1 1

( )dt ( )d ( )d ( )d 7 ( 3) 4I f t f x x f x x f x x

  

       

   

(đvdt).



Chọn đáp án B.

Câu 19: Cho hàm số

 

y f x

liên tục trên và thỏa mãn

   

,.f x f x x x



   



Tính

 

.I f x x



I 

I 

I 

I 

Lời giải:

Đặt

 

u f x

, ta thu được

.u u x

Suy ra

 

3 1 .u u x

Từ

u u x

, ta đổi cận



  







Khi đó

 

3 1 .

I u u u  



Cách khác: Nếu bài toán cho

 

có đạo hàm liên tục thì ta làm như sau:

Từ giả thiết

   

 

0 0 0 0 0

2 2 2

f f f

f x f x x



  



   











 

Cũng từ giả thiết

   

f x f x x

, ta có

         

' . ' . . ' .f x f x f x f x x f x

Lấy tích phân hai vế

         

' . ' . . 'f x f x f x f x x x f x x









   

     

4 2 4

f x f x

xf x f x x f x x



   

   



     









Chọn đáp án D.

Câu 20: Cho hàm số

()fx

liên tục trên thỏa

   

3 2 10 6

1 2 ,xf x f x x x x x       

. Khi đó

()f x x





bằng



. B.



. C.

. D.

1

Lời giải:

Với

x

ta có :

3 2 10 6

( ) (1 ) 2xf x f x x x x     

2 3 2 11 7 2

( ) (1 ) 2 (*)x f x xf x x x x      

 

d d d

1 1 1

2 3 2 11 7 2

0 0 0

( ) (1 ) 2x f x x xf x x x x x x      

  

3 3 2 2

1 1 5

( ) ( ) (1 ) (1 )

3 2 8

f x x f x x     



d d d

1 1 1

0 0 0

1 1 5 3

( ) ( ) ( )

3 2 8 4

f x x f x x f x x      

  

Mặt khác :

 

d d d

0 0 0

2 3 2 11 7 2

1 1 1

(*) ( ) (1 ) 2x f x x xf x x x x x x

  

      

  

 





3 3 2

1 1 17

(*) ( ) (1 ) 1

3 2 24

f x x f x x



     



d d d

0 1 0

1 0 1

1 1 17 1 3 17 13

( ) ( ) ( ) 3 .

3 2 24 2 4 24 4

f x x f x x f x x







        





  

Cách khác tham khảo câu 48: Chọn hàm

Từ giả thiết :

3 2 10 6

( ) (1 ) 2 ,xf x f x x x x x       

ta suy ra

 

là bậc ba có

1a 

. Nên

 

f x x bx cx d    

Cho

 

0 1 0 1x f b c d      

Cho

     

1 1 0 2 0 2 2x f f f d          

Cho

     

1 1 0 2 1 4 1 4x f f f b c d                

Suy ra

0; 3bc  

. Từ đó có

 

32f x x x   

 

( ) 3 2 .

f x x x x x



      





Chọn đáp án B.

_________________HẾT_________________

Huế, ngày 07 tháng 02 năm 2021

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU ÔN TẬP SỐ 03

CHUY£N §Ò

TÝCH PH¢N – øng dông

TÝch ph©n _ Hµm Èn

Líp To¸n thÇy L£ B¸ B¶O

Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o

116/04 NguyÔn Lé Tr¹ch

, TP HuÕ

Trung t©m KM 10 H-¬ng Trµ

, HuÕ.

NỘI DUNG ĐỀ BÀI

Câu 1: Cho hàm số

 

liên tục trên và thỏa mãn

   

10 ,f x f x x   

. Biết

 

d4f x x 



Tính

 

dI xf x x



40I 

. B.

80I 

. C.

60I 

. D.

20I 

Câu 2: Cho hàm số

 

y f x

có đạo hàm và liên tục trên thỏa mãn

   

2 ' 2 1f x f x x  

và

 

01f 

. Tính

 



f x x



. C.



. D.



Câu 3: Cho hàm số

 

y f x

liên tục và có đạo hàm trên thỏa mãn:

   

5 7 1 4 6 ,f x f x x x x     

. Biết rằng

 

f x x











(

là phân số tối giản). Tính

143ab

. B.

. C.

. D.

Câu 4: Cho hàm số

()y f x

liên tục, có đạo hàm trên thỏa mãn

(1) 0f 

 





và

 

xf x x







. Khi đó

( )df x x



bằng

. B.

. C.

. D.

Câu 5: Cho hàm số

 

liên tục trên thỏa mãn

 

khi



















(

là hằng số). Biết

 

.f x x a b e







trong đó

,ab

là các số hữu tỷ. Tính

.ab

. B.

. C.

. D.

Câu 6: Giả sử hàm số

 

liên tục và dương trên ; thảo mãn

 

01f 

và

 

   

1 . .x f x x f x





Khi đó

 

d



I f x x

thuộc khoảng nào sau đây?

 

1;4 .

 

72;74 .

 

8;10 .

 

4;6 .

Câu 7: Cho hàm số

 

có đạo hàm và đồng biến

 

1;4

thỏa mãn

   

2x xf x f x









với mọi

 

1;4x 

. Biết rằng

 

f 

, tính

 

d



I f x x

1183

I 

. B.

1187

I 

. C.

1186

I 

. D.

I 

Câu 8: Cho hàm số

 

liên tục trên và thoả mãn

   

21  





f x f x x

với mọi

x

Tính

 





f x x



. B.



. C.

. D.

Câu 9: Cho hàm số

 

xác định và dương trên

 

0;

, thỏa mãn

     

12 .f x x f x f x

 







với

mọi

 

0;x 

và

   

1 1; 1 4ff





. Giá trị của

 

bằng

. B.

. C.

. D.

2 10

Câu 10: Cho hàm số

 

y f x

xác định trên đọan

 

0,5

và thoả mãn điều kiện

   

'' '' 5f x f x

 

0,5x

 

01f





 

57f





.Tính

 

d4f x x







. B.

. C.

. D.

Câu 11: Cho hàm số

   

, ; ; .f x x ax bx c a b c    

Nếu phương trình

 

0fx

có ba nghiệm thực

phân biệt thì phương trình

     

2.f x f x f x



 





có nhiều nhất bao nhiêu nghiệm thực?

. B.

. C.

. D.

Câu 12: Cho hàm số

 

có đạo hàm trên thỏa mãn

   

2018 2019

2019 2019. .

f x f x x e





x

và

 

0 2019f 

. Giá trị của

 

là

 

2019

1 2019.fe





. B.

 

2019

1 2019.fe

. C.

 

2019

1 2020.fe

. D.

 

2019

1 2020.fe





Câu 13: Biết rằng hàm số

 

f x ax bx c  

thỏa mãn

   

d , d 2

f x x f x x   



và

 

f x x 



(với

,,abc

). Tính

.  P a b c

P 

. B.

P 

. C.

P 

. D.

P 

Câu 14: Giả sử hàm

có đạo hàm cấp 2 trên thỏa mãn

 

' 1 1f 

và

   

1 '' 2f x x f x x  

với mọi

x 

. Tính

 

' d .



xf x x

A. 1. B. 0. C. 2. D.

Câu 15: Cho hàm số

 

liên tục trên

thỏa mãn

   

4 2 2 1 8 ,     f x f x x x

. Biết rằng

 

d3



f x x

. Tính

 

d



I f x x

36I 

. B.

21I 

. C.

33I 

. D.

39I 

Câu 16: Cho hàm số

()y f x

liên tục trên

[ 1;2]

có đồ thị như hình vẽ dưới đây:

Biết

,SS

có diện tích lần lượt là

và

Tích phân

( 1) ( )x f x x









bằng

2.

12.

4.

Câu 17: Cho hàm số

 

liên tục trên thỏa mãn

   

23f x f x

x

. Biết rằng

 

1f x x 



. Tính

 

I f x x



5.I 

6.I 

3.I 

2.I 

Câu 18: Cho hàm số

 

y f x

xác định trên

 

và thỏa mãn

   

3,f x xf x x x



   

và

 

28f 

Viết phương trình tiếp tuyến của đồ thị hàm số

 

y f x

tại giao điểm với trục hoành.

1.yx

2 4.yx

4.yx

6 12.yx  

Câu 19: Cho hàm số

 

y f x

liên tục trên

0;1





và thỏa mãn

   

1 2 .x f x f x x x   

Tính tích

phân

 

.I f x x



I 

Câu 20: Cho hàm số

 

có đạo hàm liên tục trên









thỏa mãn

     

0 0, sin .

f f x x xf x x









  





Tính

 

.f x x







. B.



. C.

. D.

_________________HẾT_________________

Huế, ngày 07 tháng 02 năm 2021

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU ÔN TẬP SỐ 03

CHUY£N §Ò

TÝCH PH¢N – øng dông

TÝch ph©n _ Hµm Èn

LỜI GIẢI CHI TIẾT

Câu 1: Cho hàm số

 

liên tục trên và thỏa mãn

   

10 ,f x f x x   

. Biết

 

d4f x x 



Tính

 

dI xf x x



40I 

. B.

80I 

. C.

60I 

. D.

20I 

Lời giải:

Ta có

         

7 7 7

3 3 3

10 d 10 d d 40 1x f x x f x x xf x x I    

  

Theo bài ra

   

10 ,f x f x x   

suy ra:

       

10 d 10 10 dx f x x x f x x   



     

1 40 10 10 dI x f x x    



 

40 dtI tf t  



40 I

 

dxf x x



40 20I I I    



Chọn đáp án D.

Câu 2: Cho hàm số

 

y f x

có đạo hàm và liên tục trên thỏa mãn

   

2 ' 2 1f x f x x  

và

 

01f 

. Tính

 



f x x



. C.



. D.



Lời giải:

Ta có:

   

2 ' 2 1f x f x x  

     

2 2 2

2 . . ' 2 1 .

x x x

e f x e f x x e   

 

. ' 2 1 .

e f x x e  

   

. 2 1 .

e f x x e dx  



(*)

Xét

 

2 1 . .



I x e dx

Đặt

2 1 2u x d u dx   

;

dv e dx v e  

 

2 1 . .2

I x e e dx  



 

2 1 .

x e e C   

Thay vào (*) ta có:

   

2 2 2

. 2 1 .

x x x

e f x x e e C   

   

f x x

    

 

01f 

CC     

   

1 1 1

f x x x e



      

Vậy

 

2 2 1

1 1 1 1 1

2 2 2 2 2 2

f x dx x e dx e





        









Chọn đáp án A.

Câu 3: Cho hàm số

 

y f x

liên tục và có đạo hàm trên thỏa mãn:

   

5 7 1 4 6 ,f x f x x x x     

. Biết rằng

 

f x x











(

là phân số tối giản). Tính

143ab

. B.

. C.

. D.

Lời giải:

Theo giả thiết:

   

5 7 1 4 6 ,f x f x x x x     

Thay

bởi

1 x

ta được:

       

5 1 7 4 1 6 1f x f x x x     

6 8 2xx   

Ta được hệ:

   

5 7 1 4 6

7 5 1 6 8 2

f x f x x x



   





      





   

25 49 5 4 6 7 6 8 2f x f x x x x x       

 

24 72 76 14f x x x     

 

19 7

6 12

f x x x   

 

f x x



  

Khi đó:

 

19 5149

d 6 d

6 36

f x x x x





  











. Vậy

5149, 36ab

nên

143 1ab



Chọn đáp án D.

Câu 4: Cho hàm số

()y f x

liên tục, có đạo hàm trên thỏa mãn

(1) 0f 

 





và

 

xf x x







. Khi đó

( )df x x



bằng

. B.

. C.

. D.

Lời giải:

Xét

 





   

2 d 5f x x



   

f t t



Xét

 

I xf x x







. Đặt

2 d 2dt x t x  

 

I tf t t







Đặt

   

u t u t

v f t t v f t dt



















Do đó:

   

I tf t f t t



  







 

d2f t t  



Vậy

3 1 3

0 0 1

( )d ( )d ( )d 2

f x x f x x f x x     

  



Chọn đáp án B.

Câu 5: Cho hàm số

 

liên tục trên thỏa mãn

 

khi



















(

là hằng số). Biết

 

.f x x a b e







trong đó

,ab

là các số hữu tỷ. Tính

.ab

. B.

. C.

. D.

Lời giải:

Do hàm số liên tục trên

nên hàm số liên tục tại

0x 

   

lim lim (0)

f x f x f





  

1m

Khi đó ta có

     

d d d

2 0 2

1 1 0

f x x f x x f x x





  

 

e x x x



  







  





1 9 1

2 2 2 2



    

Do đó :

ab  

Vậy

4ab



Chọn đáp án B.

Câu 6: Giả sử hàm số

 

liên tục và dương trên ; thảo mãn

 

01f 

và

 

   

1 . .x f x x f x





Khi đó

 

d



I f x x

thuộc khoảng nào sau đây?

 

1;4 .

 

72;74 .

 

8;10 .

 

4;6 .

Lời giải:

Ta có

 

   

 

x f x x f x

f x x



   



 

ln ln 1 ln ln 1

f x x f x x C



      

Mà

 

0 1 0fC  

 

ln ln 1 1

f x x f x x     

Vậy

 

d 1 d .

   



I f x x x x



Chọn đáp án A.

Câu 7: Cho hàm số

 

có đạo hàm và đồng biến

 

1;4

thỏa mãn

   

2x xf x f x









với mọi

 

1;4x 

. Biết rằng

 

f 

, tính

 

d



I f x x

1183

I 

. B.

1187

I 

. C.

1186

I 

. D.

I 

Lời giải:

Vì

 

đồng biến

 

1;4

và

 

f 

nên

 

 

0, 1;4f x x  

Ta có

   

2x xf x f x









   

. 1 2f x x f x



  

 







 

dx xdx









 

f x x x C   

. Mà

 

f 

nên

C 

Suy ra

 

f x x x  

 











 

4 16 7

x x x





Do đó

 

I f x dx



4 16 7 1186

18 45

x x x









Chọn đáp án C.

Câu 8: Cho hàm số

 

liên tục trên và thoả mãn

   

21  





f x f x x

với mọi

x

Tính

 





f x x



. B.



. C.

. D.

Lời giải:

Đặt

 

t f x

thì

21t t x  

, suy ra

 

3 2 d dt t x  

Với

2x 

ta có

2 3 0tt  

, suy ra

1t 

Với

1x 

ta có

20tt

, suy ra

0t 

Vậy

 

   

1 0 1

2 3 4 2

2 1 0

d 3 2 d = 3 2 d =

f x x t t t t t t t t





     





  



Chọn đáp án D.

Câu 9: Cho hàm số

 

xác định và dương trên

 

0;

, thỏa mãn

     

12 .f x x f x f x

 







với

mọi

 

0;x 

và

   

1 1; 1 4ff





. Giá trị của

 

bằng

. B.

. C.

. D.

2 10

Lời giải:

Ta có:

           

12 . . 12f x x f x f x f x f x f x x

   

    

   

   

       

. 12 . 4f x f x x f x f x x C





    





Thay

1x 

ta được:

       

1 . 1 4 4 4 0 . 4f f C C C f x f x x



        

   

 

. d 4 d

f x f x x x x x C



    



Thay

1x 

ta được:

 

1 8 1 7 2 7

C C C f x x

  

         

 

2 2 2 7 46f   



Chọn đáp án A.

Câu 10: Cho hàm số

 

y f x

xác định trên đọan

 

0,5

và thoả mãn điều kiện

   

'' '' 5f x f x

 

0,5x

 

01f





 

57f





.Tính

 

d4f x x







. B.

. C.

. D.

Lời giải:

Cách 1.

Ta có

         

d 4 . . d 4 4 4 1 4f x x f x x x f x x f f I

    

       







Xét

             

4 4 1 4

1 1 4 1

. d . d 5 5 . 5 d 5 . 5 dI x f x x x f x x t f t t t f t t

   

          

   

Suy ra

       

5 . 5 d 5 . dI x f x x x f x x

 

    



Khi đó

             

4 4 4

1 1 1

2 . d 5 . d 5 d 5 5 4 5 1I x f x x x f x x f x x f x f f

     

      

  

Do đó

         

5 5 3

4 1 d 4 4 1 4

2 2 2

I f f f x x f f

    

      







Lại có

           

'' '' 5 ' ' 5 ' ' 5f x f x f x f x C C f x f x          

Thay

0x 

và

1x 

ta được

       

1 4 0 5 8C f f f f

   

    

Vậy

     

d 4 4 1 4 .8 4 8

f x x f f

  

      







Cách 2.

Ta có

       

d 4 4 4 1 4.f x x f x f f



     



Vì

           

'' '' 5 ' ' 5 ' ' 5f x f x f x f x C C f x f x          

Thay

0x 

ta được

   

' 0 ' 5 8C f f  

Khi đó

           

8 ' ' 5 8d ' ' 5 d 5f x f x x f x f x x f x f x         

   

   



Suy ra

             

8 4 1 1 4 4 1 12x f f f f f f      





Vậy

       

d 4 4 4 1 4 12 4 8f x x f x f f



        





Chọn đáp án B.

Câu 11: Cho hàm số

   

, ; ; .f x x ax bx c a b c    

Nếu phương trình

 

0fx

có ba nghiệm thực

phân biệt thì phương trình

     

2.f x f x f x



 





có nhiều nhất bao nhiêu nghiệm thực?

. B.

. C.

. D.

Lời giải:

Ta có:

 

f x x ax bx c   

     

3 2 ; 6 2 ; 6.f x x x b f x x a f x

  

     

Gọi ba nghiệm của phương trình

 

0fx

lần lượt là

;;a b c

Đặt

       

 

2.h x f x f x f x

 



                   

   

2 . 2 . 2 . 2 . 12.

h x f x f x f x f x f x f x f x f x f x

h x f x x b

      

    









    







Ta có bảng biến thiên của hàm số

 

Lại có phương trình

 

0fx

có ba nghiệm thực phân biệt

     

 

; ; 0 0 0a b c f b f b f b



      

Khi đó ta có bảng biến thiên của hàm số

 

Từ bảng biến thiên phương trình

 

0hx

có hai nghiệm phân biệt hay

     

2.f x f x f x



 





có hai nghiệm phân biệt.



Chọn đáp án B.

Câu 12: Cho hàm số

 

có đạo hàm trên thỏa mãn

   

2018 2019

2019 2019. .

f x f x x e





x

và

 

0 2019f 

. Giá trị của

 

là

 

2019

1 2019.fe





. B.

 

2019

1 2019.fe

. C.

 

2019

1 2020.fe

. D.

 

2019

1 2020.fe





Lời giải:

Từ giả thiết

   

2018 2019

2019 2019. .

f x f x x e





     

 

     

   

 

2019 2019 2018 2019 2018

2019 2018 2019 2019 2019

2019 2019

. 2019. . 2019. 2019.

. 2019. . . 1 0 1

1 1 0 . 2020. .

x x x

f x e f x e x e f x x

e f x x x x e f x x e f f

f f e e

  



    



      

   





Chọn đáp án C.

Câu 13: Biết rằng hàm số

 

f x ax bx c  

thỏa mãn

   

d , d 2

f x x f x x   



và

 

f x x 



(với

,,abc

). Tính

.  P a b c

P 

. B.

P 

. C.

P 

. D.

P 

Lời giải:

 

+bx+c d

3 2 3 2 2

ax bx a b

ax x cx c



       







 

+bx+c d 2 2

3 2 3 2

ax bx a b

ax x cx c



       







 

27 9 13

+bx+c d 3

3 2 3 2 2

ax bx a b

ax x cx c



      







Suy ra :

3 2 2

2 2 3

27 9 13

3 2 2



   









     







  







P a b c     



Chọn đáp án B.

Câu 14: Giả sử hàm

có đạo hàm cấp 2 trên thỏa mãn

 

' 1 1f 

và

   

1 '' 2f x x f x x  

với mọi

x 

. Tính

 

' d .



xf x x

A. 1. B. 0. C. 2. D.

Lời giải:

Ta có

     

1 '' 2 1f x x f x x  

Thay

0x 

vào (1) ta được

 

10f 

Mặt khác , lấy tích phân hai vế cận từ 0 đến 1 của (1) ta có:

   

         

1 1 1

0 0 0

1 1 1 1

0 0 0 0

1 '' 2

1 (1 ) ' 1 2 ' 1 2 ' 0 (2)

  

         

  

   

f x dx x f x dx xdx

f x d x f xf x dx f x dx xf x dx

Vì

     

1 1 1

0 0 0

' (1) (3)xf x dx f f x dx f x dx   

  

Thay (3) vào (2) ta được

   

3 ' 0.  



f x dx xf x dx



Chọn đáp án B.

Câu 15: Cho hàm số

 

liên tục trên

thỏa mãn

   

4 2 2 1 8 ,     f x f x x x

. Biết rằng

 

d3



f x x

. Tính

 

d



I f x x

36I 

. B.

21I 

. C.

33I 

. D.

39I 

Lời giải:

Ta có:

   

4 2 2 1 8f x f x x   

   

2 1 4 8 2f x f x x    

     

1 1 1

0 0 0

2 1 4 8 2 4.3 6 18f x dx f x dx x dx       

  

Đặt

t x dx   

;

0 1;  xt

13xt  

Ta có

       

1 3 3 3

0 1 1 1

2 1 18 36 36

f x dx f t dt f t dt f x dx      

   

Do đó

     

3 1 3

0 0 1

3 36 39f x dx f x dx f x dx    

  

. Vậy

39I 



Chọn đáp án D.

Câu 16: Cho hàm số

()y f x

liên tục trên

[ 1;2]

có đồ thị như hình vẽ dưới đây:

Biết

,SS

có diện tích lần lượt là

và

Tích phân

( 1) ( )x f x x









bằng

2.

12.

4.

Lời giải:

Đặt

( ) ( )

u x u x

v f x x v f x



   







  



 

( 1) ( ) ( 1) ( )x f x x x f x f x x







   



3 (2) 0 ( 1) ( ) 3.0 (6 2) 4.f f S S         



Chọn đáp án D.

Câu 17: Cho hàm số

 

liên tục trên thỏa mãn

   

23f x f x

x

. Biết rằng

 

1f x x 



. Tính

 

I f x x



5.I 

6.I 

3.I 

2.I 

Lời giải:

Ta có:

         

d d d d

1 1 1 1

0 0 0 0

3 3.1 3. 3 2 2 2 ,

f x x f x x f x x f x x x      

   

Đặt

 

dd22x t x t  

, với

00xt  

;

12xt  

       

d d d

1 2 2

0 0 0

1 1 1

3 2 2 ,

2 2 2

f x x f t t f x x x     

  

(do hàm số

 

liên tục trên ).



 

6,f x x x  



   

6,f x x f x x x    



 

1 6,f x x x    



 

5,f x x x   





Chọn đáp án A.

Câu 18: Cho hàm số

 

y f x

xác định trên

 

và thỏa mãn

   

3,f x xf x x x



   

và

 

28f 

Viết phương trình tiếp tuyến của đồ thị hàm số

 

y f x

tại giao điểm với trục hoành.

1.yx

2 4.yx

4.yx

6 12.yx  

Lời giải:

Ta có:

     

 

2 2 2 3

3 3 3f x xf x x xf x x xf x dx x dx xf x x C





        



Vì

 

28f 

nên

 

C f x



  

Gọi

là giao điểm của đồ thị hàm số

 





với trục hoành, suy ra

 

2;0M 

    

: 0 2 2 6 2 0 6 12.pttt y f x x x



          



Chọn đáp án D.

Câu 19: Cho hàm số

 

y f x

liên tục trên

0;1





và thỏa mãn

   

1 2 .x f x f x x x   

Tính tích

phân

 

.I f x x



I 

Lời giải:

Từ giả thiết, thay

bằng

1 x

ta được

         

1 1 2 1 1x f x f x x x      

 

   

2 2 3 4

2 1 1 1 2 6 4 .x x f x f x x x x x         

 

Ta có

       

2 4 4 2

1 2 1 2x f x f x x x f x x x x f x        

Thay vào

 

ta được:

 

   

2 4 2 2 3 4

2 1 2 1 2 6 4x x x x x f x f x x x x x



         



 

2 3 4 6 5 3 2

1 2 2 2 2 1x x x f x x x x x        

 

  

 

2 3 4 2 2 3 4 2

1 2 1 1 2 1 .x x x f x x x x x f x x           

Vậy

 

I f x x x x x x



     









Chọn đáp án C.

Câu 20: Cho hàm số

 

có đạo hàm liên tục trên









thỏa mãn

     

0 0, sin .

f f x x xf x x









  





Tính

 

.f x x







. B.



. C.

. D.

Lời giải:

     

sin cos cosxf x dx xf x x f x dx









  





. Suy ra

 

cos

x f x dx









Hơn nữa ta tính được

1 cos2 2 sin2

cos

2 4 4

x x x

xdx dx









  







Do đó

     

2 2 2 2

0 0 0 0

2. cos cos 0 cos 0f x dx xf x dx xdx f x x dx

   

   

  

     

   

   

Suy ra

 

cosf x x





, do đó

 

sinf x x C

. Vì

 

10f 

nên

0C 

Ta được

 

sin 1f x dx xdx









Chọn đáp án D.

_________________HẾT_________________

Huế, ngày 07 tháng 02 năm 2021

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU ÔN TẬP SỐ 04

CHUY£N §Ò

TÝCH PH¢N – øng dông

TÝch ph©n _ Hµm Èn

Líp To¸n thÇy L£ B¸ B¶O

Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o

116/04 NguyÔn Lé Tr¹ch

, TP HuÕ

Trung t©m KM 10 H-¬ng Trµ

, HuÕ.

NỘI DUNG ĐỀ BÀI

Câu 1: Cho hàm số

()fx

có

(2) 0f 

( ) ln( 1) 1

f x x x



    



. Giá trị

( )df x x



thuộc khoảng nào

sau đây?

( ; 1) 

. B.

(2;4)

. C.

(1;2)

. D.

( 1;1)

Câu 2: Cho hàm số

 

liên tục trên



thỏa mãn

   

, 0;f x x x



    

và

 

11f 

. Giá trị

nhỏ nhất của

 

là

. B.

. C.

ln2



. D.

Câu 3: Cho hàm số

 

y f x

có

 

01f 

và

 

tan tan ,f x x x x



   

. Biết

 









f x x

với

,ab

. Khi đó hiệu

ba

bằng

. B.

. C.

4

. D.

Câu 4: Cho hàm số

 

y f x

có đạo hàm liên tục trên và có đồ thị như hình vẽ bên dưới:

Giá trị của

( 2)d ( 2)d



  



f x x f x x

bằng

A. 2 B. -

C. 6 D. 4

Câu 5: Cho hàm số

 

y f x

liên tục trên và thỏa mãn

   

sin cos cos sin sin2 sin 2

xf x xf x x x  

với mọi

x

. Tính tích phân

 

dI f x x



. B.

. C.

. D.

Câu 6: Cho hàm số

 

y f x

có đạo hàm liên tục trên thỏa mãn

   

' . 0f x x f x

 

0,fx

x

và

 

0 1.f 

Giá trị của

 

bằng

. B.

. C.

. D.

Câu 7: Cho hàm số

 

liên tục trên thỏa

 

d 10



f x x

và

 

d6



f x x

. Tính

3 2 d .







I f x x

A. 16. B. 3. C. 15. D. 8.

Câu 8: Cho

 

liên tục trên và thỏa mãn

 

2 16f 

 

2 d 2f x x 



. Tính

 





xf x x

. B.

. C.

. D.

Câu 9: Cho hàm số

 

y f x

có đạo hàm liên tục trên









thỏa

 

sin , 0;

cos 2

f x x







  





và









. Khi đó,

 



f x x

bằng

5 3 8



. B.

8 5 3



. C.

. D.



Câu 10: Cho hàm số

 

xác định trên







thỏa mãn

 







 

01f 

và

 

12f 

. Giá trị

biểu thức

   

13ff

bằng

4 ln15

. B.

2 ln15

. C.

3 ln15

. D.

ln15

Câu 11: Cho hàm số

 

liên tục trên đoạn

 

0;1

và thỏa mãn

 

f x x f x





. Giá trị

 



f x x

bằng

. B.

. C.

. D.

1

Câu 12: Cho hàm số

 

y f x

có đạo hàm liên tục trên

 

0;1

, thỏa mãn

 

' 4 8 4f x f x x  

 

0;1x

và

 

12f 

. Tính

 



f x x

. B.

. C.

. D.

Câu 13: Cho hàm số

 

y f x

xác định và liên tục trên

 

thỏa mãn:

       

2 1 1x f x x f x xf x



   

 

\0x

đồng thời

 

12f 

. Tính

 



f x x

ln2

. B.

ln2

. C.

ln2 3

. D.

ln2

Câu 14: Cho hàm số

 

có

   

cos cos 2 ,f x f x x x x    

. Khi đó

 







f x x

bằng

. B.

. C.

. D.

Câu 15: Cho hàm số

 

đồng biến trên , có

     

cos .cos 2 4 2cos .cos 2f x f x x x x x







   



x

và

 

00f 

. Khi đó

 

df x x





bằng

242

225





. B.

242

225

. C.

149 225

225





. D.

242

225





Câu 16: Cho hàm

: 0;











là hàm liên tục thỏa mãn điều kiện:

 

  

2 sin cos 1

f x f x x x dx





   







. Tính

 

f x x





 

1f x dx







. B.

 

1f x dx







. C.

 

2.f x dx







 

0.f x dx







Câu 17: Cho hàm số

 

có đạo hàm liên tục và không âm trên

 

1;4

đồng thời thỏa mãn điều kiện

   

2'x xf x f x





và

 

f 

. Tính

 



f x x

1186

2507

. C.

848

. D.

1831

Câu 18: Cho hàm số

 

y f x

liên tục trên thoả mãn

( ) 2 . ( ) ,





   

f x x f x e x

và

(0) 0f 

. Tính

(1)f

(1) .



f

(1) .f

(1) .fe

Câu 19: Cho hàm số

 

y f x

có đạo hàm liên tục trên thỏa mãn

 

3 1 3 2f x x x   

với mọi

.x

Tính

 

. d .x f x x





. B.

. C.

. D.

Câu 20: Cho hàm số

 

thỏa mãn

 

0fx

và

   

 

0;1

f x f x x

e x x x







    



. Biết









, khẳng định nào sau đây đúng?









. B.

1 1 1

5 5 4









. C.









. D.

1 1 1

6 5 5









_________________HẾT_________________

Huế, ngày 07 tháng 02 năm 2021

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU ÔN TẬP SỐ 04

CHUY£N §Ò

TÝCH PH¢N – øng dông

TÝch ph©n _ Hµm Èn

LỜI GIẢI CHI TIẾT

Câu 1: Cho hàm số

()fx

có

(2) 0f 

( ) ln( 1) 1

f x x x



    



. Giá trị

( )df x x



thuộc khoảng nào

sau đây?

( ; 1) 

. B.

(2;4)

. C.

(1;2)

. D.

( 1;1)

Lời giải:

Ta có

( ) ln( 1) d ln( 1) d d ln( 1)

1 1 1

x x x

f x x x x x x C x x x C

x x x



          



  



  

Lại có

(2) 0 2ln1 0 0 ( ) ln( 1)f C C f x x x        

Lúc đó

3 3 3 3

2 2 2

2 2 2 2

1 1 1 1

( )d ln( 1)d ln( 1)d .ln( 1) . d

2 2 2 1

x x x

f x x x x x x x x



  

      







   

4ln 2 d 4ln2 4ln2 (1;2)

2 4 2 4

x x x





       









Chọn đáp án C.

Câu 2: Cho hàm số

 

liên tục trên



thỏa mãn

   

, 0;f x x x



    

và

 

11f 

. Giá trị

nhỏ nhất của

 

là

. B.

. C.

ln2



. D.

Lời giải:

Ta có

   

, 0;f x x x



    

 

f x dx x dx





  







   

2 1 ln ln 2

f f x



     





 

2 ln2

f  

Vậy giá trị nhỏ nhất của

 

là

ln2





Chọn đáp án C.

Câu 3: Cho hàm số

 

y f x

có

 

01f 

và

 

tan tan ,f x x x x



   

. Biết

 









f x x

với

,ab

. Khi đó hiệu

ba

bằng

. B.

. C.

4

. D.

Lời giải:

Có

   

 

tan tan 1 tan tan tan

f x f x dx x x dx x d x x C



     

  

 

01f 

nên

1C 

 

1 1 1 1 1

tan 1 tan 1 1

2 2 2 2

cos

f x x



       





 

tan 1

f x dx x dx













 

1 1 1 1 4

1 tan 1

2 2 2 4 8

cos

dx x x







   

      

   

   



Vậy

4; 8 4a b b a    



Chọn đáp án D.

Câu 4: Cho hàm số

 

y f x

có đạo hàm liên tục trên và có đồ thị như hình vẽ bên dưới:

Giá trị của

( 2)d ( 2)d



  



f x x f x x

bằng

A. 2 B. -

C. 6 D. 4

Lời giải:

Ta có

2 4 2 4

0 0 0 0

( 2) ( 2) ( 2) ( 2) ( 2) ( 2)f x dx f x dx f x d x f x d x

   

        

   

) ( 2) ( 2).



   



I f x d x

Đặt:

2tx

. Đổi cận:

02xt  

;

24xt  

 

( )dt (4) (2) 4 2 2I f t f t f f



      



   

) 2 2 .



   



K f x d x

Đặt:

2ux

. Đổi cận:

02xu   

;

42xu  

( 2) ( 2) ( ) ( ) (2) ( 2) 2 ( 2) 4K f x d x f u du f u f f





           



Vậy

( 2) ( 2) 2 4 6f x dx f x dx



     





Chọn đáp án C.

Câu 5: Cho hàm số

 

y f x

liên tục trên và thỏa mãn

   

sin cos cos sin sin2 sin 2

xf x xf x x x  

với mọi

x

. Tính tích phân

 

dI f x x



. B.

. C.

. D.

Lời giải:

Ta có:

   

sin cos cos sin d sin 2 sin 2 d

xf x xf x x x x x





  











   

 

2 2 2

0 0 0

sin cos d cos sin d sin 2 1 cos 2 d

xf x x xf x x x x x

  

   

  

* Tính

 

sin cos d .







I xf x x

Đặt

cos d sin d d sin dt x t x x t x x      

Đổi cận:

0 1 ; 0

x t x t



     

Ta có:

   

ddI f t t f x x



* Tương tự , ta tính được:

   

cos sin d dI xf x x f x x







* Tính

   

 

sin 2 1 cos 2 1 cos 2 cos2

I x x dx x d x



    



1 1 1 4 1 4 2

cos2 cos 2 . .

4 3 4 3 4 3 3







      





Do đó

   

 

2 2 2

0 0 0

sin cos cos sin sin2 1 cos 2

xf x dx xf x dx x x dx

  

  

  

trở thành:

   

2 d d

f x x f x x  





Chọn đáp án D.

Câu 6: Cho hàm số

 

y f x

có đạo hàm liên tục trên thỏa mãn

   

' . 0f x x f x

 

0,fx

x

và

 

0 1.f 

Giá trị của

 

bằng

. B.

. C.

. D.

Lời giải:

Từ

     

' . 0, 0f x x f x f x x    

ta có:

 

   

 

d d ln ln 1

ln 2 ln 0 1 1 2 e.



      



     



f x f x

x x x x f x f x

f x f x

f f f



Chọn đáp án A.

Câu 7: Cho hàm số

 

liên tục trên thỏa

 

d 10



f x x

và

 

d6



f x x

. Tính

3 2 d .







I f x x

A. 16. B. 3. C. 15. D. 8.

Lời giải:

Ta có

3 2 ,

2 3 ,



















. Nên

   

3 2 d 3 2 d 2 3 d



       

  

I f x x f x x f x x I I

+) Tính

Đặt

3 2 d 2d    t x t x

. Với

27   xt

;

  xt

     

0 7 7

7 0 0

111

d d d 5

222

    



I f t t f t t f x x

+) Tính

Đặt

2 3 d 2d   t x t x

. Với

  xt

;

33  xt

   

d d 3

  



I f t t f x x

Vậy

3 2 d 5 3 8



    



I f x x



Chọn đáp án D.

Câu 8: Cho

 

liên tục trên và thỏa mãn

 

2 16f 

 

2 d 2f x x 



. Tính

 





xf x x

. B.

. C.

. D.

Lời giải:

Ta có

       

1 1 2

0 0 0

2 2 d 2 d 2 d

f x x f x x f t t  

  

 

d4f x x



Đặt

   

u x u x

v f x x v f x



















Khi đó

     

d . d 2.16 4 28xf x x x f x f x x



    





Chọn đáp án B.

Câu 9: Cho hàm số

 

y f x

có đạo hàm liên tục trên









thỏa

 

sin , 0;

cos 2

f x x







  





và









. Khi đó,

 



f x x

bằng

5 3 8



. B.

8 5 3



. C.

. D.



Lời giải:

+) Ta có:

   

' sin cos ' sin 0;

cos cos

f x x f x x





    





. Lấy nguyên hàm hai vế ta

được:

     

   

cos sin sin sin tan

cos

sin tan 1 , 0;

xf x dx dx f x d x x c

f x x c x





   



    





  

+) Thay





vào

 

ta có:

 

1 3 3 3

0 sin tan

2 3 3 3

f c c c f x x



        





Đặt

sin cos 1 sin 1u x x x u     

vì

cos 0 0;





  





Khi đó có:

     

3 3 3

5 5 5

1 1 1

2 2 2

f u f x dx f u du du

   



  

Đặt

2 2 2

11t u t u udu tdt       

và

1 3 3 4

;

2 2 5 5

u t u t     

   

3 3 3 4 4

5 5 5 5 5

1 1 1

2 2 2

5 3 8

u tdt

f x dx f u du du dt



      



    



Chọn đáp án A.

Câu 10: Cho hàm số

 

xác định trên







thỏa mãn

 







 

01f 

và

 

12f 

. Giá trị

biểu thức

   

13ff

bằng

4 ln15

. B.

2 ln15

. C.

3 ln15

. D.

ln15

Lời giải:

Cách 1. Ta có:

 

2. ln 2 1 ln 2 1 .

2 1 2

f x x x x C x C



      





Do đó

 

ln 2 1f x x C  

Suy ra:

 

ln 2 1 ,

ln 1 2 ,

x C x



  









  





Với

x 

, ta có:

   

0 1 ln 1 2.0 1 1.f C C      

Với

x 

, ta có:

   

1 2 ln 2.1 1 2 2.f C C      

Khi đó:

 

ln 2 1 2,

ln 1 2 1,



  









  





Suy ra:

   

1 ln 1 2. 1 1 1 ln 3

3 ln 2.3 1 2 2 ln5





      







    





Vậy:

   

1 3 1 ln3 2 ln5 3 ln15.ff       

Cách 2. Ta có

         

0 1 ln 2 1 0 1f x x f f x f f





       



 

1 1 ln3.f   

Mà

         

3 1 ln 2 1 3 1f x x f f x f f



     



 

3 2 ln5.f  

Vậy

   

1 3 3 ln3 ln5 3 ln15.ff      



Chọn đáp án C.

Câu 11: Cho hàm số

 

liên tục trên đoạn

 

0;1

và thỏa mãn

 

f x x f x





. Giá trị

 



f x x

bằng

. B.

. C.

. D.

1

Lời giải:

Từ giả thiết ta có

 

1 1 1

0 0 0

f x dx x f x dx dx





  

 Xét

 

6I x f x dx



Đặt

3t x dt x dx  

. Với

00xt  

;

11xt  

Suy ra

 

   

1 1 1

0 0 0

6 2 2I x f x dx f t dt f x dx  

  

 Xét

 

4 3 1 4 3 1 4

dx d x x

    





       

1 1 1

0 0 0

* 2 4 4f x dx f x dx f x dx    

  

Vậy

 

4f x dx 





Chọn đáp án B.

Câu 12: Cho hàm số

 

y f x

có đạo hàm liên tục trên

 

0;1

, thỏa mãn

 

' 4 8 4f x f x x  

 

0;1x

và

 

12f 

. Tính

 



f x x

. B.

. C.

. D.

Lời giải:

Ta có

 

1 1 1

0 0 0

20 20

' 8 4 4 4 4

f x dx x f x dx f x dx I      

  

Đặt

( ) '( )u f x du f x dx

dx dv v x













Nên

   

( ) ' 2 'I xf x xf x dx xf x dx   



Suy ra

 

   

1 1 1

0 0 0

20 20

' 4 2 ' 8 4 '

f x dx xf x dx xf x dx



     





  

 

' 4 ' 0

f x dx xf x dx   



 

   

' 2 0 ' 2f x x f x x f x x C       



Mà

 

1 2 1.  fC

Vậy

 

( 1) .

  



f x dx x dx



Chọn đáp án A.

Câu 13: Cho hàm số

 

y f x

xác định và liên tục trên

 

thỏa mãn:

       

2 1 1x f x x f x xf x



   

 

\0x

đồng thời

 

12f 

. Tính

 



f x x

ln2

. B.

ln2

. C.

ln2 3

. D.

ln2

Lời giải:

Ta có:

       

2 1 1x f x x f x xf x



   

       

21x f x xf x f x xf x



    

       

21x f x xf x xf x f x



    

     

1xf x xf x f x



   





 

Xét

 

10xf x 

 

  

 

11f  

(không thỏa mãn).

Xét

 

10xf x 

, ta có

 

   

 

xf x f x

xf x













 

xf x

















 

xf x



















 

xf x

   



Cho

1x 

ta được :

 

1 1 1

  



CC     



 

xf x

  



 

1xf x

   

(vì

0x 

)

 

   

Vậy

 

ddf x x x



  







ln x



ln2

  



Chọn đáp án A.

Câu 14: Cho hàm số

 

có

   

cos cos 2 ,f x f x x x x    

. Khi đó

 







f x x

bằng

. B.

. C.

. D.

Lời giải:

Ta có

     

d d df x x f x x f x x







  

Với

 

J f x dx









ta đặt

x t dx dt    

Đổi cận :

Khi đó

      

dt dt dJ f t f t f x x





      

  

         

2 2 2 2 2

0 0 0 0

d d d d cos cos 2 df x x f x x f x x f x f x x x x x

    





       





    

   

 

2 2 4

cos 1 2sin d 1 4sin 4sin d sinx x x x x x



    



4 4 4 4 7 14

sin sin sin 1

3 5 3 5 15 30

x x x





       







Chọn đáp án C.

Câu 15: Cho hàm số

 

đồng biến trên , có

     

cos .cos 2 4 2cos .cos 2f x f x x x x x







   



x

và

 

00f 

. Khi đó

 

df x x





bằng

242

225





. B.

242

225

. C.

149 225

225





. D.

242

225





Lời giải:

Ta có:

     

cos .cos 2 4 2cos .cos 2f x f x x x x x







   



   

.cos .cos 2 4 2cos .cos 2f x f x x x x x



   





   

4 .cos .cos 2 2cos .cos 2 0f x f x x x x x



    





     

2 . 2 cos .cos 2 . 2 0f x f x x x f x

  

     

     

     

   

2 . 2 cos .cos 2 0f x f x x x





    





   

2 cos .cos 2

f x L

f x x x tm



















(vì hàm số đồng biến trên ).

Với

 

1 cos4 cos cos5 cos3

2 cos .cos 2 2 cos . 2

2 2 4 4

x x x x

f x x x x





       

 

cos cos5 cos3 sin sin5 sin3

2 d 2

2 4 4 2 20 12

x x x x x x

f x x x C



         







Vì

 

0 0 0fC  

.Do đó

 

sin sin5 sin3

2 20 12

x x x

f x x   

Khi đó

 

sin sin5 sin3 cos cos5 cos3 242

d 2 d

2 20 12 2 100 36 225

x x x x x x

f x x x x x







   

         

   

   





Chọn đáp án A.

Câu 16: Cho hàm

: 0;











là hàm liên tục thỏa mãn điều kiện:

 

  

2 sin cos 1

f x f x x x dx





   







. Tính

 

f x x





 

1f x dx







. B.

 

1f x dx







. C.

 

2.f x dx







 

0.f x dx







Lời giải:

Có

   

sin cos 1 sin 2 cos2 1

x x dx x dx x x







      







Khi đó:

 

        

2 sin cos sin cos 0 sin cos 0f x f x x x x x dx f x x x dx





        









     

sin cos 0 sin cosf x x x f x x x      

Vậy

     

sin cos sin cos 0f x dx x x dx x x





    





Chọn đáp án D.

Câu 17: Cho hàm số

 

có đạo hàm liên tục và không âm trên

 

1;4

đồng thời thỏa mãn điều kiện

   

2'x xf x f x





và

 

f 

. Tính

 



f x x

1186

2507

. C.

848

. D.

1831

Lời giải:

Vì có đạo hàm liên tục và không âm trên

 

1;4

nên Ta có :

   

2'x xf x f x





Vì

 

có đạo hàm liên tục và không âm trên

 

1;4

 

   

1 2 1 2 d

x f x x f x x x





       







 

f x x C   

. Do

 

f 

nên suy ra

 

1 2 1

f C C    

 

f x x   

 





 





 

3 3 3 3

4 2 1 2 8 7

1 2 2 2

9 9 2 9 9 18

f x x f x x f x x x           

 

2 8 7 1186

9 9 18 45

f x x x x x



    









Chọn đáp án A.

Câu 18: Cho hàm số

 

y f x

liên tục trên thoả mãn

( ) 2 . ( ) ,





   

f x x f x e x

và

(0) 0f 

. Tính

(1)f

(1) .



f

(1) .f

(1) .fe

Lời giải:

Ta có

2 2 2

'( ) 2 . ( ) 1

'( ) 2 . ( ) 1 ( ) ' 1:

x x x

f x x f x

x f x x f x e f x

e e e



  



        





Suy ra

2 2 2

1 1 1 1

( ) 1 (1) (0) 1 (1) 1 (1)

f x dx f f ef f

e e e

  

       





Chọn đáp án C.

Câu 19: Cho hàm số

 

y f x

có đạo hàm liên tục trên thỏa mãn

 

3 1 3 2f x x x   

với mọi

.x

Tính

 

. d .x f x x





. B.

. C.

. D.

Lời giải:

Ta có

 

3 1 3 2f x x x   

với

x

   

0 1 2; 1 5 5x f x f     

Đặt

ddu x u x  

;

 

ddv f x x





, ta chọn

 

v f x

Suy ra

       

5 5 5

1 1 1

. d . d 23 d

x f x x x f x f x x f x x



   





  

Đặt

 

3 1 d 3 1 dt x x t x x     

 

32f t x  

Đổi cận

0 1; 1 5x t x t     

Do đó

   

5 1 1

2 3 2

1 0 0

d 3 2 3 3 d 3 3 2 3 2 d

f t t x x x x x x x       

  

hay

 

f x x 



Vậy

 

59 33

. d 23 .

x f x x



  





Chọn đáp án C.

Câu 20: Cho hàm số

 

thỏa mãn

 

0fx

và

   

 

0;1

f x f x x

e x x x







    



. Biết









, khẳng định nào sau đây đúng?









. B.

1 1 1

5 5 4









. C.









. D.

1 1 1

6 5 5









Lời giải:

Ta có:

   

 

0;1

f x f x x

e x x x







    



   

 

e f x e f x

x x x





  







 

x x x















   

dx dx dx

f x f x

x x x







   









  

 

Xét

I dx









. Đặt

1 1 1

1 1 2t t tdt dx

x x x

       

4 4 1

I dt t C C



        



Từ

 

1 4 1

C f x

f x x

      

  

1 1 1

2 2 4 2

f C e



     







 

4 1 2 2



   

Vậy

0,33











Chọn đáp án A.

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU ÔN TẬP SỐ 05

CHUY£N §Ò

TÝCH PH¢N – øng dông

Líp To¸n thÇy L£ B¸ B¶O

Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o

116/04 NguyÔn Lé Tr¹ch

, TP HuÕ

, HuÕ.

NỘI DUNG ĐỀ BÀI

Câu 1: Cho hàm số

 

thỏa mãn

   

1 ' d 10x f x x



và

   

2 1 0 2ff

. Tính

 

dI f x x



8I 

. B.

8I 

. C.

1.I 

12I 

Câu 2: Cho hàm số

 

0fx

thỏa mãn điều kiện

     

23f x x f x









và

 

f 

. Biết rằng tổng

         

1 2 3 ... 2017 2018

f f f f f

     

với

 

, , 0a b b

và

là phân số tối giản. Khẳng

định nào sau đây đúng?



. B.



. C.

1010ab

. D.

3029ba

Câu 3: Cho hàm số

()fx

thỏa mãn

(1) 4f 

và

 

3 ( ) 2 . ( ); ( ) 0,x f x x f x f x x



    

. Giá trị của

(3)f

bằng

. B.

. C.

2019

. D.

Câu 4: Cho hàm số

()fx

liên tục trên và thỏa mãn

( ) ( ) 2 2cos2 ,f x f x x x     

. Tính

( )d









I f x x

6I 

. B.

0I 

. C.

2I 

. D.

6I 

Câu 5: Cho hàm số

()y f x

liên tục trên

 

\ 0; 1

(1) 2ln2f 

và

( 1). ( ) ( ) .



   x x f x f x x x

Giá

trị

(2) ln3f a b

, với

, , ,a b a b

là phân số tối giản. Tính

.ab

. B.

. C.

. D.

Câu 6: Cho hàm số

 

có đạo hàm liên tục trên đoạn

 

0;2

và thỏa mãn

   

 

 

2 3 2 , 0;2f x f x x x x     

. Biết

 

2 10f 

, tính













I xf x

A. 72. B. 96. C. 32. D. 88.

Câu 7: Cho hàm số

 

liên tục trên và thỏa mãn





5 d 1f x x x



  



 





. Tính

 



f x x

15

. B.

2

. C.

13

. D.

Câu 8: Cho hàm số

 

có











và

 

sin .sin 2 , .f x x x x



  

Khi đó

 

df x x





bằng

104

225



121

225

104

225

167

225

Câu 9: Cho hàm số

 

y f x

liên tục trên thỏa

 

d1



f x x

và

 

d 16



f x x

. Tính

   

4 d sin cos d .







I f x x f x x x

5.I

I

9.I

I

Câu 10: Cho hàm số

 

có đạo hàm

 



liên tục trên và thỏa mãn điều kiện

   

2f x xf x





x

. Biết

 

02f 

và

 

0,f x x  

. Tính

 

dI x f x x



1I 

. B.

Ie

. C.





. D.

1Ie

Câu 11: Cho hàm số

 

liên tục trên thỏa mãn

   

7 4 4 2020 9f x f x x x   

x

.Tính

 

d.



I f x x

197960

. B.

7063

. C.

197960

. D.

2020

Câu 12: Cho hàm số

 

liên tục, có đạo hàm trên thỏa mãn

   

3 0, .     





x f x f x x

Tính

 









I xf x x

. B.

. C.

. D.

Câu 13: Cho hàm số

()fx

có

()

( 1) 1

x x x x





  

0x

và

(1) 2 2f 

. Khi đó

( )df x x



bằng



. B.



. C.

4 2 10



. D.



Câu 14: Cho hàm số

 

y f x

có đồ thị như hình vẽ, biết

 

d 12







f x x

.Tính

 

2mf

. B.

. C.

. D.

Câu 15: Cho hàm số

 

y f x

liên tục trên và thỏa mãn

(2 ) ( ) (1 )

f x f x f x

    



. Biết tích

phân

( ) .lnI f x dx a b



(

là số hữu tỉ,

là số nguyên tố). Hãy chọn mệnh đề đúng.

ab 

. B.

1ab 

. C.

13ab 

. D.

ab 

Câu 16: Cho hàm số

()fx

liên tục trên đoạn

0;2





và thỏa mãn điều kiện

3 ( ) 7 (2 )f x f x x  

0;2x







. Tính

()f x x



7 2 6



. B.

4 2 2



. C.

. D.

7 2 5



Câu 17: Cho hàm số

 

y f x

xác định và liên tục trên thỏa

mãn:

   

 

3 2 2 3

3 3 1 0, .      f x xf x x f x x x

Tính

 

d.



I f x x



. B.

. C.

. D.



Câu 18: Cho hàm số

 

y f x

có đạo hàm liên tục trên khoảng

;



 





. Biết

 

13f 

và

     

2 1 2 ,

f x x f x x K



    



. Giá trị

 

gần với số nào nhất trong các số sau ?

1,2

. B.

1,1

. C.

. D.

1,3

Câu 19: Cho hàm số

   

, , , , , 0y f x ax bx cx d a b c d a      

có đồ thị là

 

Biết đồ thị

 

đi qua gốc toạ độ và có đồ thị

 

'y f x

cho bởi hình vẽ.Tính giá trị

   

4 2 .H f f

45H 

. B.

64H 

. C.

51H 

. D.

58H 

Câu 20: Cho hàm số

 

có đạo hàm liên tục trên

 

0;1

và thỏa mãn

 

1 1;f 

 

f x x











 

f x x 



Tính

 

d.I f x x



I 

_________________HẾT_________________

Huế, ngày 07 tháng 02 năm 2021

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU ÔN TẬP SỐ 05

CHUY£N §Ò

TÝCH PH¢N – øng dông

LỜI GIẢI CHI TIẾT

Câu 1: Cho hàm số

 

thỏa mãn

   

1 ' d 10x f x x



và

   

2 1 0 2ff

. Tính

 

dI f x x



8I 

. B.

8I 

. C.

1.I 

12I 

Lời giải:

Đặt

   

1 du d

dv d

u x x

f x x v f x

  













   

1 ' dx f x x 



   

( 1). dx f x f x x  



     

1 1 1

0 0 0

2 (1) (0) d 2 d 10 d 8.f f f x x f x x I f x x         

  



Chọn đáp án A.

Câu 2: Cho hàm số

 

0fx

thỏa mãn điều kiện

     

23f x x f x









và

 

f 

. Biết rằng tổng

         

1 2 3 ... 2017 2018

f f f f f

     

với

 

, , 0a b b

và

là phân số tối giản. Khẳng

định nào sau đây đúng?



. B.



. C.

1010ab

. D.

3029ba

Lời giải:

Ta có

     

23f x x f x





 



  

 

x x x



  



 

3x x C

    

. Vì

 

fC   

Vậy

 

  

1 1 1

   



Do đó

         

1 1 1009

1 2 3 ... 2017 2018

2020 2 2020

f f f f f        

Vậy

1009a 

;

2020b 

. Do đó

3029ba



Chọn đáp án D.

Câu 3: Cho hàm số

()fx

thỏa mãn

(1) 4f 

và

 

3 ( ) 2 . ( ); ( ) 0,x f x x f x f x x



    

. Giá trị của

(3)f

bằng

. B.

. C.

2019

. D.

Lời giải:

Vì

2 2 2

( 3) ( ) 2 . ( ); ( ) 0,x f x x f x f x x



    

nên

3 3 3 3

2 2 2 2 2 2 2 2 2

1 1 1 1

( ) ( ) ( )

2 2 3)

( ) ( 3) ( ) ( 3) ( ) ( 3)

f x f x f x

x x x

f x x f x x f x x





     

  

   

1 1 1 1 1 1 1 1 1 1

( ) (1) (3) 4 12 4 (3) 4 12

f x f f f

           



(3) 12f



Chọn đáp án D.

Câu 4: Cho hàm số

()fx

liên tục trên và thỏa mãn

( ) ( ) 2 2cos2 ,f x f x x x     

. Tính

( )d









I f x x

6I 

. B.

0I 

. C.

2I 

. D.

6I 

Lời giải:

Tính

 







f x x

Đặt

ddt x t x    

       

3 3 3 3

2 2 2 2

3 3 3 3

2 2 2 2

d d d df x x f t t f t t f x x

   



  

     

   

 

2 ( ) ( ) d 2 2cos2 dI f x f x x x x





     



4cos d 2 cos d 12x x x x





  



6I



Chọn đáp án D.

Câu 5: Cho hàm số

()y f x

liên tục trên

 

\ 0; 1

(1) 2ln2f 

và

( 1). ( ) ( ) .



   x x f x f x x x

Giá

trị

(2) ln3f a b

, với

, , ,a b a b

là phân số tối giản. Tính

.ab

. B.

. C.

. D.

Lời giải:

 

\ 0; 1x  

ta có

()

( ). ( ) ( ) ( ) 1

( 1)

()

( ) ( ).

1 ( 1) 1 1 1



      









    



    



x x f x f x x x f x

x f x x x x

f x f x

x x x x x

Nên

( ).















f x dx dx

do đó

2 1 2 2 1 2

(2). (1). 1 ln ( ln3) ( 2ln2) 1 ln

3 2 3 3 2 3

2 2 9

ln3 1 ln3 .

3 3 2

        







       













f f a b

a b a b



Chọn đáp án D.

Câu 6: Cho hàm số

 

có đạo hàm liên tục trên đoạn

 

0;2

và thỏa mãn

   

 

 

2 3 2 , 0;2f x f x x x x     

. Biết

 

2 10f 

, tính













I xf x

A. 72. B. 96. C. 32. D. 88.

Lời giải:

Cách 1: Ta có:

   

 

     

       

   

         

 

2 2 2 2

0 0 0 0

2 0 2 2

0 2 0 0

4 2 2

0 0 0

2 d 3 2 d d 2 d 2 4

d d 4 d d 4

2 d 4 d 2

d 4 d 4 d 4 2 2 2 88

          

       

     





       





   



  

f x f x x x x x f x x f x x

f x x f t t f x x f x x

f x x f x x

I xf x xf x x xf x f x x f

Cách 2:

Xét

   

0f x ax bx c a   

;

   

2 4 2 1f a b c  

       

     

2 2 2 4 4 2

2 4 4 2

2 2 4 4 2 2 2

f x a x b x c ax a b x a b c

f x f x ax bx c ax a b x a b c

f x f x ax ax a b c

           

           

       

Mà

   

 

2 3 2f x f x x x   

 

Từ

   

1 , 2

và

 

ta có hệ phương trình:

4 2 10

4 2 2 0

a b c

abc



  







  







  







 

7 10

f x x x   

         

 

4 2 2

0 0 0

d 4 d 4 d 4 2 2 2 88

I xf x xf x x xf x f x x f





       





  



Chọn đáp án D.

Câu 7: Cho hàm số

 

liên tục trên và thỏa mãn





5 d 1f x x x



  



 





. Tính

 



f x x

15

. B.

2

. C.

13

. D.

Lời giải:

Xét:





5dI f x x x



  



Đặt :

5 d 1 d d

x x x

t x x t x x





       







Với

 

51t x x  

 

t x x

     



   

5 5 5

1 , 2 2 5 5

x t x

t t t



       

2 2 2

2 5 1 5

d d d d 1 d

5 2 2

t x x t t

t t t





        







Đổi cận:

2

     

 

1 5 5 5

2 2 2

5 1 1 1

1 5 1 5 1 5

. . 1 d . 1 d d d

2 2 2 2

I f t t f t t f t t t

t t t

     

       

     

     

   

 

   

5 5 5 5

1 1 1 1

1 5 1 5

d d 1 d .3 d 13.

2 2 2 2

        

   

I f x x x f x x f x x



Chọn đáp án C.

Câu 8: Cho hàm số

 

có











và

 

sin .sin 2 , .f x x x x



  

Khi đó

 

df x x





bằng

104

225



121

225

104

225

167

225

Lời giải:

Ta có:

 

3 2 2 2 4 2

d 4sin cos d 4 1 cos cos d cos 4cos 4cos d cosf x x x x x x x x x x x



     

   

4cos 4cos

C  











nên

0C 

. Suy ra

 

4cos 4cos

fx

Vậy

 

   

 

2 2 2

0 0 0

4cos 4cos 4 4

d d . 1 sin . 1 sin d sin

5 3 5 3

f x x x x x x

  



     





  

3 5 3

4 2sin sin 4 sin 104

sin sin

5 3 5 3 3 225

x x x





   

      



   

   





Chọn đáp án A.

Câu 9: Cho hàm số

 

y f x

liên tục trên thỏa

 

d1



f x x

và

 

d 16



f x x

. Tính

   

4 d sin cos d .







I f x x f x x x

5.I

I

9.I

I

Lời giải:

Đặt

t x dt dx dx    

; đổi cận:

0 0; 2

x t x t     

Khi đó:

     

0 0 0

1 1 16

4 4 4

f x dx f t dt f x dx   

  

Đặt

sin cost x dt xdx  

; Đổi cận:

0 0; 1

x t x t



     

Khi đó:

     

0 0 0

sin cos 1f x xdx f t dt f x dx



  

  

. Vậy

1 4 5I   



Chọn đáp án A.

Câu 10: Cho hàm số

 

có đạo hàm

 



liên tục trên và thỏa mãn điều kiện

   

2f x xf x





x

. Biết

 

02f 

và

 

0,f x x  

. Tính

 

dI x f x x



1I 

. B.

Ie

. C.





. D.

1Ie

Lời giải:

Ta có:

   

 

f x xf x x



  

 

d 2 d 2 d

f x f x

x x x x x

f x f x



   

   

   

ln ln 0 ln 2f x x C f C C      

     

2 ln2

ln ln2 2

f x x f x e f x e



      

Vì vậy,

 

1 1 1 1

3 3 2 2

0 0 0 0

d 2 d d d

x x t

I x f x x x e x x e x te t   

   

Đặt











v e x

Ta có











 

t t t t

I te e t te e     





Chọn đáp án A.

Câu 11: Cho hàm số

 

liên tục trên thỏa mãn

   

7 4 4 2020 9f x f x x x   

x

.Tính

 

d.



I f x x

197960

. B.

7063

. C.

197960

. D.

2020

Lời giải:

 

liên tục trên và

x

   

7 4 4 2020 9f x f x x x   

   

7 4 4 d 2020 9df x f x x x x x    







   

4 4 4

0 0 0

7 d 4 4 d 2020 9df x x f x x x x x    

  

Đặt

2020 9dK x x x



;

 

4dH f x x



+ Tính

2020 9dK x x x



Đặt

2 2 2

99u x u x    

ddu u x x

. Với

03xu  

;

45xu  

Khi đó

 

2 2 3 3

2020 197960

2020 9d 2020 du= 5 3

K x x x u    



+ Tính

 

4dH f x x



. Đặt

4 d du x u x    

. Với

04xu  

;

40xu  

Khi đó

     

4 0 4

0 4 0

4 d du = duH f x x f u f u I    

  

Vậy

   

4 4 4

0 0 0

7 d 4 4 d 2020 9df x x f x x x x x   

  

197960

II  

197960

I

197960

I



Chọn đáp án C.

Câu 12: Cho hàm số

 

liên tục, có đạo hàm trên thỏa mãn

   

3 0, .     





x f x f x x

Tính

 









I xf x x

. B.

. C.

. D.

Lời giải:

Từ giả thiết ta có:

   

30x f x f x   

     

7 7 7 7 3 0 7 2x f f f       

     

1 1 1 1 3 0 1 1x f f f            

           

3 0 3x f x f x xf x f x f x f x





       



             

3 4 2

d 3 d 3

xf x x f x f x f x x f x f x f x











      









           

4 2 4 2

1 1 1 1 9 9

7 7 3 7 1 1 3 1 0

4 2 4 2 4 4

f f f f f f

   

            





   



Chọn đáp án C.

Câu 13: Cho hàm số

()fx

có

()

( 1) 1

x x x x





  

0x

và

(1) 2 2f 

. Khi đó

( )df x x



bằng



. B.



. C.

4 2 10



. D.



Lời giải:

Ta có

 

( ) ( )d d d

( 1) 1

f x f x x x x

x x x x



  

  

  

  

1 1 1

( ) d d 2 1 2

( 1) 1

f x x x x x C

x x x x





      









Vì

(1) 2 2f 

nên

2C 

và

( ) 2 1 2 2f x x x   

Khi đó

 

4 4 10

( )d 2 1 2 2 d ( 1) 1 2 4 3

3 3 3

f x x x x x x x x x x



          









Chọn đáp án A.

Câu 14: Cho hàm số

 

y f x

có đồ thị như hình vẽ, biết

 

d 12







f x x

.Tính

 

2mf

. B.

. C.

. D.

Lời giải:

Từ đồ thị, ta có

   

1 4 0ff

và bảng xét dấu

 



như sau:

Do đó ta có

         

4 2 4 2 4

1 1 2 1 2

12 12 12f x dx f x dx f x dx f x dx f x dx

    

      

    

                 

12 12 2 1 4 2 12 2 2 1 4f x f x f f f f f f f



           



12 2 0 0 6.mm     

Vậy

 

2 6.mf



Chọn đáp án A.

Câu 15: Cho hàm số

 

y f x

liên tục trên và thỏa mãn

(2 ) ( ) (1 )

f x f x f x

    



. Biết tích

phân

( ) .lnI f x dx a b



(

là số hữu tỉ,

là số nguyên tố). Hãy chọn mệnh đề đúng.

ab 

. B.

1ab 

. C.

13ab 

. D.

ab 

Lời giải:

Ta có:

(2 ) ( ) (1 )

f x f x f x

    



 

(2 ) ( ) (1 ) d d ln2

f x f x f x x x



      





3 3 3

2 2 2

( 2)d ( )d (1 )d ln2

f x x f x x f x x

  

     

  

 

5 3 3 5

0 2 2 0

( )d ( )d ( )d ( )d ln2 2; 1

f t t f x x f u u f x x t x u x



        

   

5 3 3

0 2 2

( )d ( )d ( )df x x f x x f x x



  

  

( )d ln2

I f x x  



. Do đó,

; 2 1

a b ab   



Chọn đáp án B.

Câu 16: Cho hàm số

()fx

liên tục trên đoạn

0;2





và thỏa mãn điều kiện

3 ( ) 7 (2 )f x f x x  

0;2x







. Tính

()f x x



7 2 6



. B.

4 2 2



. C.

. D.

7 2 5



Lời giải:

Thay

bởi

2 x

vào đẳng thức

3 ( ) 7 (2 )f x f x x  

(1) được:

3 (2 ) 7 ( ) 2f x f x x   

(2)

Từ (1) và (2) tính được

 

( ) 7 2 3

f x x x  

 

( ) 7 2 3

f x dx x x dx  



7 1 7 2 5

(2 ) 2

60 20 30

x x x x



      



Chọn đáp án D.

Câu 17: Cho hàm số

 

y f x

xác định và liên tục trên thỏa

mãn:

   

 

3 2 2 3

3 3 1 0, .      f x xf x x f x x x

Tính

 

d.



I f x x



. B.

. C.

. D.



Lời giải:

Theo đề bài ta có

 

         

.          f x x f x f x x f x x f x f x

Đặt

   

  u f x u f x

ta có

 

31      x u u dx u du

Với

0 0; 2 1.      x u x u

Nên

 

   

2 1 0

3 2 5 3 0

0 0 1

3 1 3 .

2 4 4





         





  

I f x dx u u du u u du



Chọn đáp án A.

Câu 18: Cho hàm số

 

y f x

có đạo hàm liên tục trên khoảng

;



 





. Biết

 

13f 

và

     

2 1 2 ,

f x x f x x K



    



. Giá trị

 

gần với số nào nhất trong các số sau ?

1,2

. B.

1,1

. C.

. D.

1,3

Lời giải:

Ta có:

     

2 d 1 2 d

f x x x f x x





  









     

2 2 2

1 1 1

2 d 1 2 d d

f x x x f x x x



   



  

       





2 2 2

1 1 1

2 d 1 2 2 d d 3f x x x f x f x x x     

  

   





   

3 2 1 3 0 3 2 3 7 2 0 2 1,2



              f f x f f



Chọn đáp án A.

Câu 19: Cho hàm số

   

, , , , , 0y f x ax bx cx d a b c d a      

có đồ thị là

 

Biết đồ thị

 

đi qua gốc toạ độ và có đồ thị

 

'y f x

cho bởi hình vẽ.Tính giá trị

   

4 2 .H f f

45H 

. B.

64H 

. C.

51H 

. D.

58H 

Lời giải:

Dựa vào đồ thị

   

' ' 3 1f x f x ax  

Do đồ thị

 

'y f x

qua điểm

 

0;1

và

   

1;4 ' 3 1f x x  

   

'f x f x dx x x C    



 

qua gốc toạ độ nên

     

0 4 2 58.C f x x x f f      



Chọn đáp án D.

Câu 20: Cho hàm số

 

có đạo hàm liên tục trên

 

0;1

và thỏa mãn

 

1 1;f 

 

f x x











 

f x x 



Tính

 

d.I f x x



I 

Lời giải:

Xét

 

I f x x



Đặt

d d d 2 d

x t t x x t t

    

Đổi cận

  





  



. Khi đó

   

2 d 2 d

I f t t t xf x x   



Khi đó đặt

 

   

2 d d

u f x x

f x u

I x f x x f x x

x x v













   











     

1 1 1

2 2 2

0 0 0

2 3 18

1 d d 6 d

5 5 5

x f x x x f x x x f x x

  

      

  

Ta có

 

f x x











 

x f x x







;

xx



     

 

     

1 1 1 1

2 4 2 4

0 0 0 0

2 2 3

d 6 d 9 d 0 6 9 d 0

3 d 0 3 0

f x x x f x x x x f x x f x x x

f x x x f x x f x x C



   

       









        



   



Mà

     

1 1 0 d d .

f C f x x f x x x x       





Chọn đáp án D.

_________________HẾT_________________

Huế, ngày 07 tháng 02 năm 2021

Bấm Tải xuống để xem toàn bộ.

| 1/65

| | Tải xuống

Preview text:

Giáo viên: LÊ BÁ BẢO_ Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115
Đăng kí học theo địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
Hoặc Trung tâm Km 10 Hương Trà TÝCH PH¢N – øng dông HµM ÈN Phiªn b¶n 2020 Cè lªn c¸c em nhÐ! HuÕ, th¸ng 02/2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông TÝch ph©n _ Hµm Èn
PHIẾU ÔN TẬP SỐ 01 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI 2016
Câu 1: Cho hàm số f (x) liên tục trên
, thỏa mãn f (x)  f (2020  x) và ( )  2.  f x dx 4 2016 Tính ( )d .  xf x x 4 A. 16160 . B. 2020 . C. 4040 . D. 8080 .
Câu 2: Cho hàm số f  x liên tục trên 0;  và thoả mãn f  2 x  x 2 4  2
 x  7x 1, x  0; . 5 Biết f 5  8  , tính I  . x f   xd .x 0 68 35 52 62 A. I   . B. I   . C. I   . D. I   . 3 3 3 3
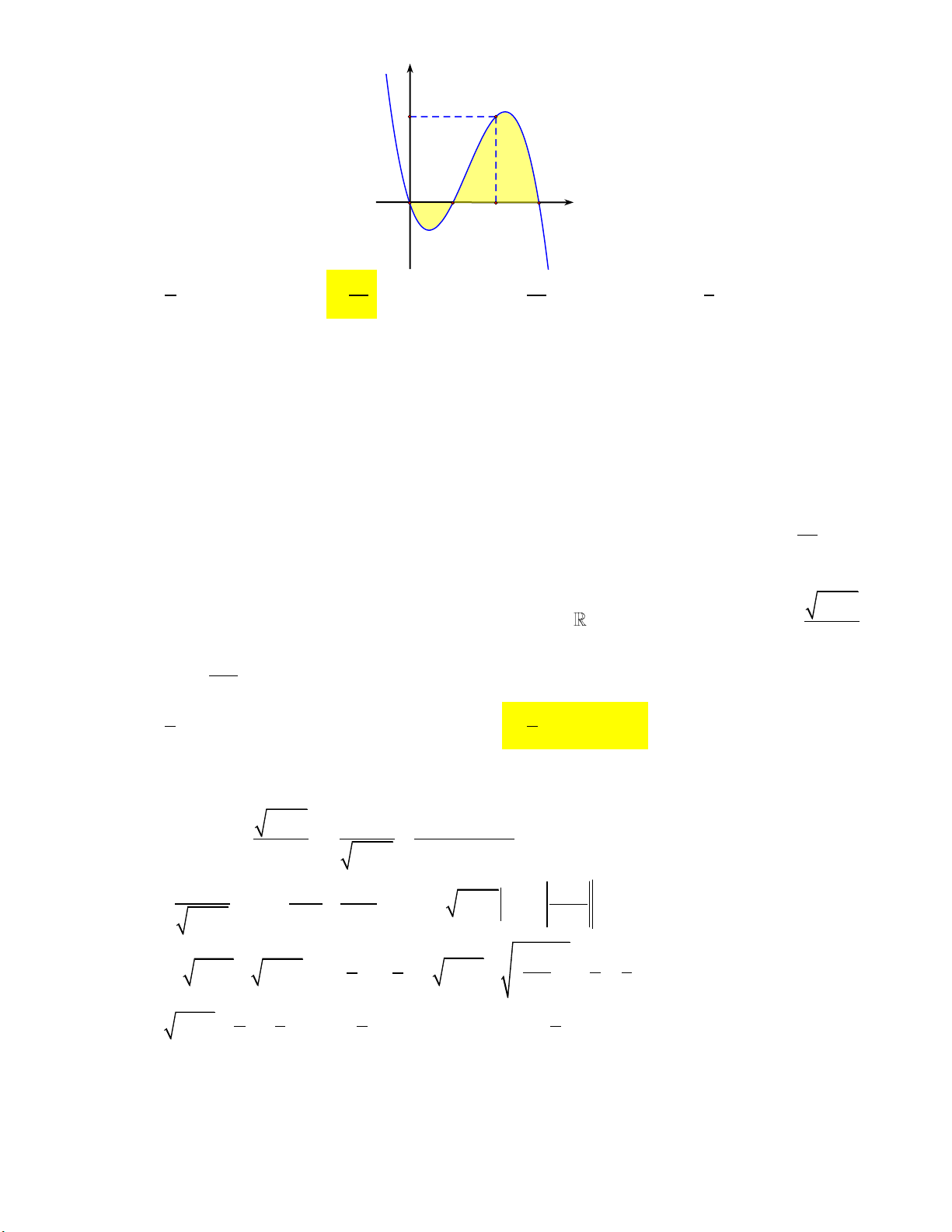
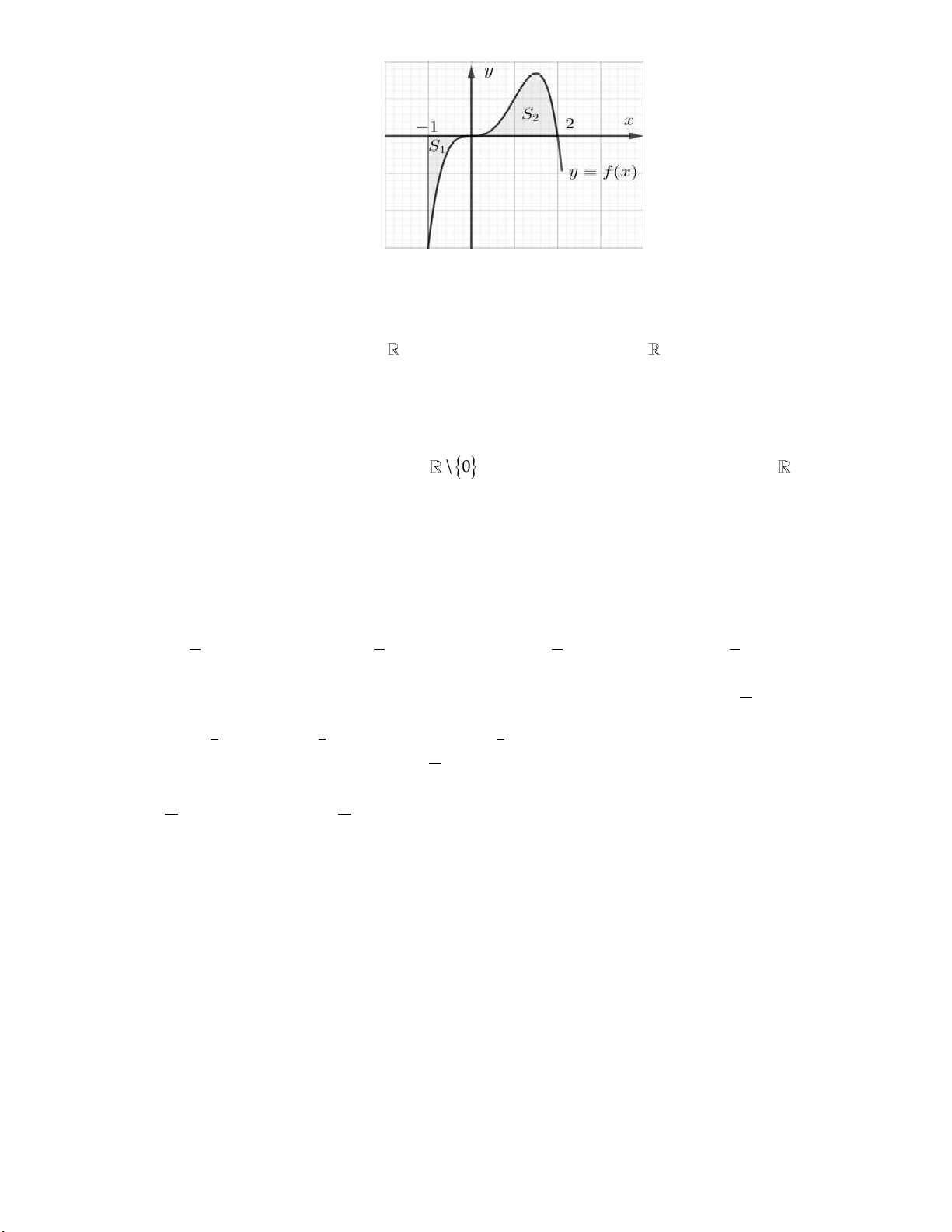
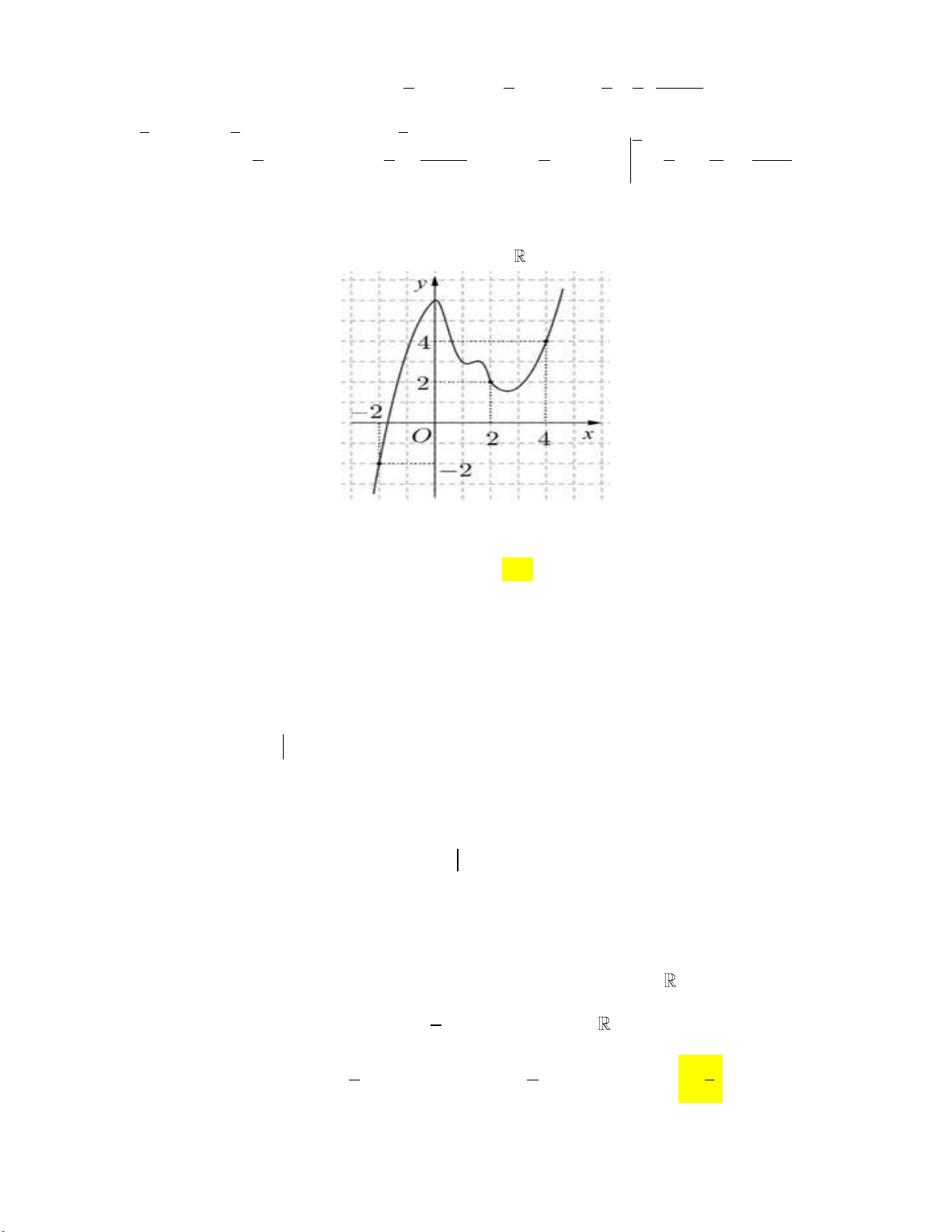
Câu 3: Cho y  f (x) là hàm số đa thức bậc ba có đồ thị như hình vẽ. Tính diện tích hình phẳng được tô đậm. y 2 O 1 2 3 x 9 37 5 8 A. . B. . C. . D. . 4 12 12 3 f x
Câu 4: Cho hàm số f  x  0 và có đạo hàm liên tục trên
, thỏa mãn  x   f  x   1  x và 2 2   f   ln 2 0  
 . Giá trị f 3 bằng  2  1 1 A. 4ln 2  ln 52 . B.   2 4 4 ln 2 ln 5 . C. 4ln 2  ln 52 . D.   2 2 4 ln 2 ln 5 . 2 4  4 2 e f  2 ln x
Câu 5: Cho hàm số f(x) liên tục trên và thỏa mãn tan .  x f  2
cos xdx  2 và dx  2  . Tính x ln x 0 e 2 2  d  f x x. x 1 4 A. 4 . B. 1. C. 0 . D. 8 .
Câu 6: Cho hàm số y  f (x) có đạo hàm, nhận giá trị dương trên (0;  ) và thoả mãn  2  2  1  2 2 2 f (
 x )  9x f (x ) với mọi x (0;  ). Biết f  ,   tính f .    3  3  3  1 1 1 1 A. . B. . C. . D. . 4 3 12 6
Câu 7: Cho hàm số f  x có đạo hàm liên tục trên
, đồ thị của y  f  x đi qua điểm A1;0 và 3
nhận điểm I 2; 2 làm tâm đối xứng. Tính tích phân I  x
 x2 f x /
 f xdx . 1 16 16 8 8 A.  . B. . C.  . D. . 3 3 3 3   
Câu 8: Cho hàm số f  x thỏa mãn f  x  f   x 4 2 .   sin . x sin 2x  với mọi x  và f 1   . Giá trị  2  của    5 f     bằng 11 11 23 11 A.  . B. . C. . D. . 3 5 15 3
Câu 9: Cho hàm số f (x) xác định, có đạo hàm, liên tục và đồng biến trên [1; 4] thỏa mãn 2 3
x  2xf (x)   f (  x) , x  [1;4], f (1)   
. Giá trị f (4) bằng 2 391 361 381 371 A. . B. . C. . D. . 18 18 18 18 6 1
Câu 10: Cho hàm số f x liên tục trên đoạn 0;1 
 thỏa mãn f x 2  6x . f  3 x  
. Tính f xd . x  3x  1 0 A. 2. B. 4. C. 1. D. 6. 1
Câu 11: Cho hàm số f x liên tục trên 0;1   thỏa x f  2
x   f   x 2 4 . 3 1
 1  x . Tính f xd . x  0     A. . B. . C. . D. . 4 6 20 16 Câu 12: Cho hàm số
y  f x xác định và liên tục trên  \  0 và thỏa mãn 2 2 2
x f x  2x  1 f x  xf x  1 với x    \  0 và f 1  2
 . Tính f xd . x  1 1 3 ln 2 3 ln 2 A.   ln 2 . B.   ln 2 . C. 1   . D.   . 2 2 2 2 2 x  7   7  x  a
Câu 13: Cho hàm số f  x có f 2  0 và f  x 3  , x   ;     . Biết rằng f dx     2x  3  2  4  2  b a
( a, b  , b  0,
là phân số tối giản). Khi đó a  b bằng b A. 250 . B. 251 . C. 133 . D. 221 .
Câu 14: Cho hàm số y  f  x liên tục trên thỏa mãn f  5
x  4x  3  2x 1 với mọi x  . Giá trị 8 của f
 xdx bằng 2  32 A. 2 . B. 10 . C. . D. 72 . 3 1 Câu 15: Cho hàm số
f  x liên tục trên và 2 f  
1  3 f 0  0 , f
 xdx  7. Tính 0 2 I    x  6  x f  d .   x  2  0 A. I  40 . B. I  28 . C. I  18 . D. I  42 .
Câu 16: Xét hàm số f (x) liên tục trên  1
 ;2 và thỏa mãn f x  xf  2x    f   x 3 ( ) 2 2 3 1  4x . Tính giá 2
trị của tích phân I  f (x d ) x  . 1  A. I  3 . B. I  5 . C. I  15 . D. I  6 . 1
Câu 17: Cho f  x là hàm số liên tục trên đoạn 0;  1 thoả mãn f  
1  4 và  f xdx  2. Tính 0 1 3 ' 2 d .  x f x x 0 A. 16. B. 5. C. 1. D. 2. 1 2
Câu 18: Cho hàm số y  f  x có đạo hàm liên tục trên 0;  1 thỏa mãn f  
1  0,  f (x) dx  7 và 0 1 1 1 2
x f (x)dx   . Tính ( )d .  f x x 3 0 0 7 7 A. D. 4 5 B. 1 C. 4
Câu 19: Cho hàm số y  f  x liên tục trên thỏa mãn xf  2
x   f  x 3 2
 2x  2x, x   . Tính giá 2 trị I  f  xdx . 1 A. I  25 . B. I  21 . C. I  27 . D. I  23 .
Câu 20: Cho hàm số f (x) liên tục trên 0; , thỏa mãn f   1 1 
và xf x  x f  x   f x 2 2 3 ( ) ( ) 2 ( ) , 2
f (x)  0 với x  0;  . Gọi M , m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số f (x)
trên đoạn 1; 2 . Tổng M  m bằng 21 7 9 6 A. . B. . C. . D. . 10 5 10 5
_________________HẾT_________________
Huế, ngày 07 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông TÝch ph©n _ Hµm Èn
PHIẾU ÔN TẬP SỐ 01
LỜI GIẢI CHI TIẾT 2016
Câu 1: Cho hàm số f (x) liên tục trên
, thỏa mãn f (x)  f (2020  x) và ( )  2.  f x dx 4 2016 Tính ( )d .  xf x x 4 A. 16160 . B. 2020 . C. 4040 . D. 8080 . Lời giải: 2016
x  4  t  2016 Xét I  xf (x)d . 
x Đặt t  2020  x  dt  dx và
x  2016  t  4 4 2016 4 2016 Do đó I 
xf (x)dx 
(2020  t) f (2020  t)(dt) 
(2020  x) f (2020  x)    dx 4 2016 4 2016 2016 2016 
(2020  x) f (x)dx  2020
f (x)dx 
xf (x)dx  2020.2     I 4 4 4
 I  4040  I  2I  4040  I  2020.
Chọn đáp án B.
Câu 2: Cho hàm số f  x liên tục trên 0;  và thoả mãn f  2 x  x 2 4  2
 x  7x 1, x  0; . 5 Biết f 5  8  , tính I  . x f   xd .x 0 68 35 52 62 A. I   . B. I   . C. I   . D. I   . 3 3 3 3 Lời giải: Ta có f  2 x  x 2
  x  x    x   f  2
x  x   2 4 2 7 1 2 4 4 2
 x  7x   1 2x  4 .
Lấy tích phân cận chạy từ 0  1 hai vế ta được: 1 1
2x  4f  52 2
x  4x dx   2 2
 x  7x  
1 2x  4dx     . 3 0 0 1 2 t
  x  4x  dt  2x  4 dx
Xét 2x  4f  2
x  4x dx . Đặt  . Khi đó ta có
x  0  t  0, x 1 t  5 0 1 5 5
2x  4f  52 2
x  4x dx  f t dt  f  xdx      . 3 0 0 0 5 5 5  52  68 Xét I  . x f  
xdx  xf x  f
 xdx  4  0       . 0  3  3 0 0
Chọn đáp án A.
Câu 3: Cho y  f (x) là hàm số đa thức bậc ba có đồ thị như hình vẽ. Tính diện tích hình phẳng được tô đậm. y 2 O 1 2 3 x 9 37 5 8 A. . B. . C. . D. . 4 12 12 3 Lời giải: Giả sử 3 2
f (x)  ax  bx  cx  d có đồ thị (C) như hình vẽ trên. Điểm 3 2
O(0; 0)  (C)  d  0  f (x)  ax  bx  cx .
a  b  c  0 a  1    Các điểm 3 2 (
A 1; 0), B(2; 2), D(3; 0)  (C)  4a  2b  c  1  b
  4  f (x)  x  4x  3x .  
9a  3b  c  0 c  3   
Diện tích hình phẳng cần tìm là 1
S  0  f (x) 3
dx   f (x)  0 1 3 37 3 2 3 2
dx  (x  4x  3x)dx  (x  4x  3x)dx      12 0 1 0 1
 Chọn đáp án B. f x
Câu 4: Cho hàm số f  x  0 và có đạo hàm liên tục trên
, thỏa mãn  x   f  x   1  x và 2 2   f   ln 2 0  
 . Giá trị f 3 bằng  2  1 1 A. 4ln 2  ln 52 . B.   2 4 4 ln 2 ln 5 . C. 4ln 2  ln 52 . D.   2 2 4 ln 2 ln 5 . 2 4 Lời giải:
Với x 0;  3 ta có:  f  x 1
x   f  x f  x 1    x  2 f  x
x  1x  2 3 3 f  x 3  1 1  3  x 1 dx   dx   
 2 f x  ln f x
 x 1 x  2  0 x  2 0   0 0 2    ln 2  1 8
f    f    4 1 2 3 0
 ln  ln  f 3   ln   5 2  2  2 5    1 f   1 8 1 3  ln  ln 2   
4ln 2ln5  f 3  4ln 2ln52. 2  5  2 4
Chọn đáp án C.  4 2 e f  2 ln x
Câu 5: Cho hàm số f(x) liên tục trên và thỏa mãn tan .  x f  2
cos xdx  2 và dx  2  . Tính x ln x 0 e 2 2  d  f x x. x 1 4 A. 4 . B. 1. C. 0 . D. 8 . Lời giải:  4 Xét I  tan . x f   2 cos x dx  2 . 1  0  dt 2 dt  2
 sin x cos xdx  2 tan x.cos xdx    tanxdx  2t Đặt 2
t  cos x    . 1
x  0  t 1; x   t   4 2 1 2 f t  1 f t  1 f t  Suy ra I   dt  dt  2  dt  4    . 1 2t 2t t 1 1 1 2 2 2 e f  2 ln x Xét I  dx  2  . 2 x ln x e  2 ln x 1 dt 1 2 dt  dx  2 ln xdx   dx Đặt 2
t  ln x   x x ln x 2t x ln x . 2
x  e  t 1; x  e  t  4 4 f t 4 f t Suy ra I  dt  2  dt  4   . 2 2t t 1 1  2x 1 dt dt  2dx  dx  dx  2 f 2x  x x t Xét I  dx 
. Đặt t  2x   . x 1 1 1
x   t  ; x  2  t  4 4  4 2 4 f t  1 f t  4 f t  Suy ra I  dt  dt  dt  4  4  8    . t t t 1 1 1 2 2
Chọn đáp án D.
Câu 6: Cho hàm số y  f (x) có đạo hàm, nhận giá trị dương trên (0;  ) và thoả mãn  2  2  1  2 2 2 f (
 x )  9x f (x ) với mọi x (0;  ). Biết f  ,   tính f .    3  3  3  1 1 1 1 A. . B. . C. . D. . 4 3 12 6 Lời giải:    2   9 f  2 x xf x  9    9   Ta có 2 2 2f (x ) 9x f (x ) 2 2   x   x  f  2 x  2    f  x 2 x  2 f  2 x  2 2 2 2 9 3 2 2 2 3 2 2 Do đó f  2 x  2 3  x dx  x  C  . Mà f . . C C 0 . 2 2 3 3 3 2 3 3 3 9 9  1  9  1  1 Suy ra f  2 x  6
 .x  f x 3  x  f  .      . 4 4  3  4  3  12
Chọn đáp án C.
Câu 7: Cho hàm số f  x có đạo hàm liên tục trên
, đồ thị của y  f  x đi qua điểm A1;0 và 3
nhận điểm I 2; 2 làm tâm đối xứng. Tính tích phân I  x
 x2 f x /
 f xdx . 1 16 16 8 8 A.  . B. . C.  . D. . 3 3 3 3 Lời giải:
+ Từ giả thiết, suy ra đẳng thức f  x  f 4  x  4, x  (*). 3 3 3 + Ta có I  x
 x2 f x f xdx   2x 2x f xdx  2x 2xdf x 1 1 1 3
 x 2x 3
f  x dx  x  2x f x 3 2 2
  2x2 f xdx  1 1 1 3
  2x 4x  2 f xdx 3f 3 f  1. 1
+ Từ giả thiết và (*) suy ra f  
1  0 và f 3  4 . 3
+ Kí hiệu J   2
x  4x  2 f  x dx , dùng phép đổi biến t  4  x dẫn đến 1 3 J   3
4 x2  44 x 2 f 4 xdx   2x 4x2 f 4 xdx. 1 1 Suy ra 3
2J   x  4x  2 3 40 20 2
f  x  f 4  xdx  4  2
x  4x  2dx    J     . 3 3 1 1 20 16 Vậy I    3.4  0  . 3 3 16
Cách dự đoán đáp số: Chọn f  x   x  3 2 2
 2 thỏa mãn các đk đề bài, thu được I  . 3
Chọn đáp án B.   
Câu 8: Cho hàm số f  x thỏa mãn f  x  f   x 4 2 .   sin . x sin 2x  với mọi x  và f 1   . Giá trị  2  của    5 f     bằng 11 11 23 11 A.  . B. . C. . D. . 3 5 15 3 Lời giải: 1 1 1 1 Ta có 2 sin . x sin 2x 
sin x 1 cos 4x  sin x  sin 5x  sin 3x . 2 2 4 4 4 4
Vậy f  x  f   x 2   x x  f  
 x  f x 2 . sin .sin 2 .  dx  sin . x sin 2 d x x    1 1 1  4  f
 xdf x  sin x  sin 5x  sin 3x dx    2 4 4  5 f  x 1 1 1    cos x  cos 5x  cos 3x  C. 5 2 20 12    1  1 1 1 1  11 Do f 1  C    . Vậy 5
f    5  cos  cos 5  cos 3   .    2  5  2 20 12 5  3
Chọn đáp án D.
Câu 9: Cho hàm số f (x) xác định, có đạo hàm, liên tục và đồng biến trên [1; 4] thỏa mãn 2 3
x  2xf (x)   f (  x) , x  [1;4], f (1)   
. Giá trị f (4) bằng 2 391 361 381 371 A. . B. . C. . D. . 18 18 18 18 Lời giải: [f (  x ]2 ) f (  x)
Ta có x  2xf (x)  [f (  x ]2 )  (
x 1  2 f (x))  [f (  x ]2 )   x   x 1  2 f (x) 1  2 f (x) 4 4  4 f (x) 14 14 391  dx 
xdx  1  2 f (x) 
 1 2 f (4)  2   f (4)  .   1 1  2 f (x) 3 3 18 1 1
Chọn đáp án A. 6 1
Câu 10: Cho hàm số f x liên tục trên đoạn 0;1 
 thỏa mãn f x 2  6x . f  3 x  
. Tính f xd . x  3x  1 0 A. 2. B. 4. C. 1. D. 6. Lời giải:  
f x  x f x  1 6   I  f  x 1 2 3 2
dx   x f  3 x  3 6 . 2 3 .  d
 x  A  B 3x  1    0 0 3x 1 1 Gọi 2
A  2 3x . f 
 3xd .x Đặt 3 2
t  x  dt  3x .
dx Đổi cận x  0  t  0; x  1  t  1 0 1 1
Ta có: A  2 f
 tdt  2 f
 xdx  2I 0 0 1 1 1 
I  2I  B  I  B  6 dx  6  3x   1 1 1 2 1
. .d3x  1  2.2. 3x  1  4. 3x  1 3 0 0 0
Chọn đáp án B. 1
Câu 11: Cho hàm số f x liên tục trên 0;1   thỏa x f  2
x   f   x 2 4 . 3 1
 1  x . Tính f xd . x  0     A. . B. . C. . D. . 4 6 20 16 Lời giải: x f  2
x   f   x 2 4 . 3 1  1  x 1  2. 2 . x f  x  1 dx  3 f  1 x 1 1 2 2 2 dx 
1  x dx  2A  3B  1  x dx   * 0 0 0 0 1 A  2 . x f 
 2xdx Đặt 2
t  x  dt  2xdx ; x  0  t  0; x  1  t  1 0 1 A  f  t 1 dt  f  xdx 0 0 1 B  f
 1 xdx Đặt t 1 x  dt   ;
dx x  0  t  1, x  1  t  0 0 1 B  f  t 1 dt  f  xdx 0 0 * 1  2 f  x 1 dx  3 f  x 1 1 dx 
1  x dx  5. f   x 1 2 2 dx  1  x dx  0 0 0 0 0     
Đặt: x  sint  dx  costdt, t  ;
; x  0  t  0, x  1 t     2 2  2    1 2 2     2 2 1 cos2t 1 1  1  x dx 
1  sin t .costdt 
dt  . t  sin 2t    2    2 2  2  4 0 0 0 0 1  Vậy f
 xdx  . 20 0
Chọn đáp án C. Câu 12: Cho hàm số
y  f x xác định và liên tục trên  \  0 và thỏa mãn 2 2 2
x f x  2x  1 f x  xf x  1 với x    \  0 và f 1  2
 . Tính f xd . x  1 1 3 ln 2 3 ln 2 A.   ln 2 . B.   ln 2 . C. 1   . D.   . 2 2 2 2 2 Lời giải: 2 Biến đổi 2 2
x f x  2xf x  1  f x  xf x  xf x  1  f x  xf x .
Đặt hx  xf x  1  hx  f x  .
x f x , Khi đó  có dạng: h x h x dh x 2
h x  hx       1   1 dx  dx 
 x  C    x  C.    2 h x 2 h x 2 h x hx   hx 1    xf x 1 f   1 2 1  1    2  1    C  0. x  C x  C 1  C 1 1 1
Khi đó xf x  1    f x    . 2 x x x 2 2 1 1 1 Suy ra: f
 xdx    dx  ln2  . 2 x x 2 1 1
Chọn đáp án A. x  7   7  x  a
Câu 13: Cho hàm số f  x có f 2  0 và f  x 3  , x   ;     . Biết rằng f dx     2x  3  2  4  2  b a
( a, b  , b  0,
là phân số tối giản). Khi đó a  b bằng b A. 250 . B. 251 . C. 133 . D. 221 . Lời giải: x  x   3 
Lấy nguyên hàm hai vế của f  x 7 
ta được f  x 7  dx, x   ;   .    2x  3  2x 3  2  2 u  3
Đặt u  2x  3  x 
suy ra dx  udu . 2 3   1 1 2x  3 Suy ra  
f  x   2 u 17   du 
17 2x  3  C. 2 2  3    3   26 1 2x  3 26
Theo giả thiết ta có f 2  0 suy ra   C  
. Do đó f  x   
17 2x  3  . 3 2  3  3   7  x  x 7 Ta có f dx
   . Đặt  t  dx  2dt .Đổi cận với x  4  t  2 , với x  7  t  . 4  2  2 2 7 7 7  x  Suy ra 2 f dx  2 f     t 2 dt  2 f  xdx. 4 2 2  2  3   7 7 2x  3 13 236 Vậy 2   2 f  x   2 dx  17  2x 3  dx  . 2 2  3 3  15  
Suy ra a  236,b  15 nên a  b  236 15  251.
Chọn đáp án B.
Câu 14: Cho hàm số y  f  x liên tục trên thỏa mãn f  5
x  4x  3  2x 1 với mọi x  . Giá trị 8 của f
 xdx bằng 2  32 A. 2 . B. 10 . C. . D. 72 . 3 Lời giải: Ta có  4
x   f  5
x  x     4 5 4 . 4 3
5x  42x   1 . Đặt 5
t  x  4x  3 ta có t   4 d
5x  4dx và f t   2x 1. Đổi cận + 5 t  2
  x  4x  5  0  x  1. + 5
t  8  x  4x  5  0  x  1. 8 1 Do đó f
 tdt   2x 1 4
5x  4dx 10 . 2  1 
Chọn đáp án B. 1 Câu 15: Cho hàm số
f  x liên tục trên và 2 f  
1  3 f 0  0 , f
 xdx  7. Tính 0 2 I    x  6  x f  d .   x  2  0 A. I  40 . B. I  28 . C. I  18 . D. I  42 . Lời giải: 2  x 
Xét I  6  x f  dx    2  0 u   6  x du  dx   Đặt   x     x  . dv  f  dx    v  2 f      2    2  2 2  x   x 
Khi đó: I  26  x f  2 f dx       42 f   
1  3 f 0  2J  2J   . 2   2  0 0 2  x  Xét J  f dx     2  0 x 1 + Đặt t   dt  dx . 2 2
+ Đổi cận : x  0  t  0; x  2  t  1 . 1
Lúc này: J  2 f
 tdt  27 14. Vậy I  2J  214  28 . 0
Chọn đáp án B.
Câu 16: Xét hàm số f (x) liên tục trên  1
 ;2 và thỏa mãn f x  xf  2x    f   x 3 ( ) 2 2 3 1  4x . Tính giá 2
trị của tích phân I  f (x d ) x  . 1  A. I  3 . B. I  5 . C. I  15 . D. I  6 . Lời giải:
Lấy nguyên hàm hai vế giả thiết ta có 2 3
 f (x)  2xf (x  2)  3 f (1 x) dx   4x dx    2 2 4
 f (x)dx  f (x  2)d(x  2)  3 f (1 x)d(1 x)  x  C    Đặt 2 4
f (t)dx  F (t)  F (x)  F (x  2)  3F (1 x)  x  C  .
x 1 F( 1  )  F( 1
 )  3F(2) 1 C 2F( 1
 )  3F(2) 1 C Ta có   
x  2  F(2)  F(2)  3F( 1  ) 16  C
2F(2)  3F( 1  ) 16  C 2
Trừ từng vế thu được 5F (2)  5F ( 1
 ) 15  F(2)  F( 1
 )  3  I  f (x)dx  3  . 1 
Chọn đáp án A. 1
Câu 17: Cho f  x là hàm số liên tục trên đoạn 0;  1 thoả mãn f  
1  4 và  f xdx  2. Tính 0 1 3 ' 2 d .  x f x x 0 A. 16. B. 5. C. 1. D. 2. Lời giải: dt Đặt 2
x  t  2xdx  dt. Khi đó ta có xdx  . 2 1 1 1 1 1   1 1 1 1 Suy ra: 3 x f ' 
 2xdx  tf '
 tdt  t f t  f
 tdt  f  1 f  t 1. 0 2 2 2 2 0 0  0  0
Chọn đáp án C. 1 2
Câu 18: Cho hàm số y  f  x có đạo hàm liên tục trên 0;  1 thỏa mãn f  
1  0,  f (x) dx  7 và 0 1 1 1 2
x f (x)dx   . Tính ( )d .  f x x 3 0 0 7 7 A. D. 4 5 B. 1 C. 4 Lời giải: 3 x
Đặt u  f  x  du  f  x dx , 2
dv  x dx  v  . 3 1 3 1 3 1 1 x x Ta có  f  x  f  x 3
dx  x f  xdx  1    3 3 3 0 0 0 1 1 1 1 2 2 Ta có 6 49x dx  7, 
 f (x) 3
dx  7, 2.7x . f   x 3 dx  1
 4  7x  f (x) dx  0   0 0 0 0 x
 7x  f (x)  0  f x 4 7 3  
 C , mà f   7 1  0  C  4 4 1 1 4  7x 7  7
 f (x)dx     dx  .  4 4  5 0 0
Chọn đáp án A.
Câu 19: Cho hàm số y  f  x liên tục trên thỏa mãn xf  2
x   f  x 3 2
 2x  2x, x   . Tính giá 2 trị I  f  xdx . 1 A. I  25 . B. I  21 . C. I  27 . D. I  23 . Lời giải: 2 2 Ta có: xf  2
x   f 2x 3
 2x  2x  xf
  2x f 2x dx    3
2x  2xdx 1 1 2    xf   x 2 21 2 x  2 4 2 2 d  x   f   2x 2 d  x   
 x   xf
  2x dx  f 
 2x dx   . (*)  2 1  2 1 1 1 1 2 + Tính xf
  2x dx  : 1 du Đặt 2
u  x  du  2 d x x  d x x 
; x  1  u  1; x  2  u  4 . 2 2 4 4 f u 1 Suy ra xf   2x   d  x  du  f   xdx  . 2 2 1 1 1 2 dt + Tính  f
 2x dx
 . Đặt t  2x  dt  2dx  dx 
; x  1  t  2; x  2  t  4 . 2 1 2 4 4 f t 1 Suy ra  f  2x   d  x  dt  f    xdx . 2 2 1 2 2 4 4 2 4 4 1 1 21 1 1 1 21 Thay vào (*) ta được
f  xdx 
f  x dx  
f  x dx 
f  x dx 
f  x dx       2 2 2 2 2 2 2 1 2 1 2 2 2 2 1  f  x 21 dx   f
 xdx  21. 2 2 1 1
Chọn đáp án B.
Câu 20: Cho hàm số f (x) liên tục trên 0; , thỏa mãn f   1 1 
và xf x  x f  x   f x 2 2 3 ( ) ( ) 2 ( ) , 2
f (x)  0 với x  0;  . Gọi M , m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số f (x)
trên đoạn 1;2 . Tổng M  m bằng 21 7 9 6 A. . B. . C. . D. . 10 5 10 5 Lời giải:
+) Xét hàm số f (x) trên 0;  ta có: 2 2    3xf (x) x f (x) 2 f (x)  3 x  3    3 f (x) x f (x)  x  2 3 2
 3x f (x)  x f (x)  2xf (x)       2x 2x   1 2 f (x)  f (x)  .  3 3  x  x 2      
Lấy nguyên hàm hai vế của   1 ta được : dx 2 d x x x C   f (x)  f (x) . 3 1 x Mà f   1 1  nên 2
1  C  C 1. Suy ra f x 3  2 2 f (1) x  . 1 x
+) Xét hàm số f  x 3  1; 2 . 2 x  trên  1 2 3x x 1  2 . x x x  3x '  2  3 4 2
Xét hàm số f  x    0 với x  1;2 . 2 2  2x  1  2` x   1 8 1
Suy ra M  max f  x  f 2  ;m  min f  x  f   1  . 1;2 1;2 5 2 1 8 21
Vậy M  m    . 2 5 10
Chọn đáp án A. _________________HẾT_________________
Huế, ngày 07 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông TÝch ph©n _ Hµm Èn
PHIẾU ÔN TẬP SỐ 02 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Câu 1: Cho hàm số f  x có đạo hàm liên tục trên đoạn 2; 4 và thỏa mãn f 2  2, f 4  2020 . 2 Tính tích phân I  f 
 2xdx . 1 A. I  1009 . B. I  2022 . C. I  2018 . D. I  1011. 2
Câu 2: Cho a là hằng số thực và hàm số f  x liên tục trên thỏa mãn f
 xadx  2021. Giá trị 1 2a của tích phân I  f
 xdx là 1a A. I  2021. B. I  2021. C. I  2021 . a D. I  2021 . a Câu 3: Cho hàm số f  x liên tục trên khoảng
0; và thỏa mãn f x 17 2x 1 2   f  x   1   .ln  x   1 . Biết f
 xdx  aln52lnbc với a, ,bc . Giá trị 4x x 2x 1
của a  b  2c bằng 29 A. . B. 5 . C. 7 . D. 37 . 2
Câu 4: Cho hàm số y  f x có đạo hàm liên tục trên
. Biết f 1  e và x   f x  xf x 3 2  x ,
x  . Tính f 2 . A. e2 4  4e  4 B. e2 4  2e  1 C. e3 2  2e  2 D. e2 4  4e  4 1 1
Câu 5: Cho f  x là hàm số liên tục trên thoả mãn f   1  1 và  d   f t t , tính 3 0  2 I  sin 2 . x f  
sin xd .x 0 4 2 2 1 A. I  . B. I  . C. I   . D. I  . 3 3 3 3 Câu 6: Cho hàm số
f  x có đạo hàm xác định trên . Biết f   1  2 và 1 4 1 3 x 1 2 x f   xdx  f 
2 xdx 4. Giá trị của f xdx  bằng 2 x 0 1 0 5 3 1 A. 1. B. . C. . D. . 7 7 7
Câu 7: Cho hàm số y  f  x đồng biến và có đạo hàm liên tục trên thỏa mãn
  2   . x f x f x e , x
  và f 0  2. Khi đó f 2 thuộc khoảng nào sau đây? A. 12;13 . B. 9;10 . C. 11;12 . D. 13;14 .
Câu 8: Cho hàm số f  x liên tục trên
và thỏa mãn f (x)  f (x)  2 cos 2x, x   . Khi đó  2 f
 xdx bằng   2 A. 2  . B. 4 . C. 2 . D. 0 .
Câu 9: Cho f  x là hàm số liên tục trên tập số thực
và thỏa mãn f  3 x  3x   1  x  2 . Tính 5
I   f xd .x 1 41 527 61 464 A. . B. . C. . D. . 4 3 6 3 1  2
x  2 khi 0  x  2 e f ln x 2 6
Câu 10: Cho hàm số f  x  2 . Khi đó dx  xf 
  2x 1dx bằng  x
x  5 khi 2  x  5 1 3 19 37 27 A. . B. . C. . D. 5. 2 2 2 1 1
Câu 11: Cho hàm số f x có đạo hàm liên tục trên . Biết . x f ' 
xdx  10 và f 1  3, tính f xdx  . 0 0 A. 30 . B. 7 . C. 13 . D. 7 .
Câu 12: Cho hàm số f (x) liên tục trên đoạn 0;1 
 và thỏa mãn 4x f  2
x   f   x 2 . 3 1  1 x . Tính 1
f xdx  . 0     A. . B. . C. . D. . 16 4 20 6   
Câu 13: Cho hàm số f  x thỏa mãn f  x  f   x 4 2 .   sin . x sin 2x  với mọi x  và f 1   . Giá trị  2  của    5 f     bằng 11 11 23 11 A.  . B. . C. . D. . 3 5 15 3 1
Câu 14: Cho hàm số f (x) liên tục trên thỏa mãn ( )  x f x
e  tf (t)dt, x   . Tính f (ln(5620)) . 0 A. 5622. B. 5621. C. 5620. D. 5619. 1
Câu 15: Cho hàm số f  x có đạo hàm liên tục trên và thỏa mãn f
 xdx 10, f  1  cot1. Tính tích 0 1
phân I   f  x 2
tan x  f  x tan x d  x   . 0 A. 1 ln cos  1 . B. 1  . C. 9  . D. 1 cot1.   1 
Câu 16: Cho hàm số y  f  x liên tục và thỏa mãn f  x 1  2 f  3x   với mọi x  ; 2 . Tính    x  2 
2 f  x dx  . x 1 2 3 9 9 3 A. . B. . C.  . D.  . 2 2 2 2
Câu 17: Cho hàm số y  f  x xác định và liên tục trên 0;  sao cho 2 
 x  x x xf e
f e   1 với mọi
e ln x f  x
x  0; . Tính tích phân I  dx  . x e 1 2 1 3 A. I   . B. I   . C. I  . D. I  . 8 3 12 8
Câu 18: Cho hàm số y  f (x) liên tục trên
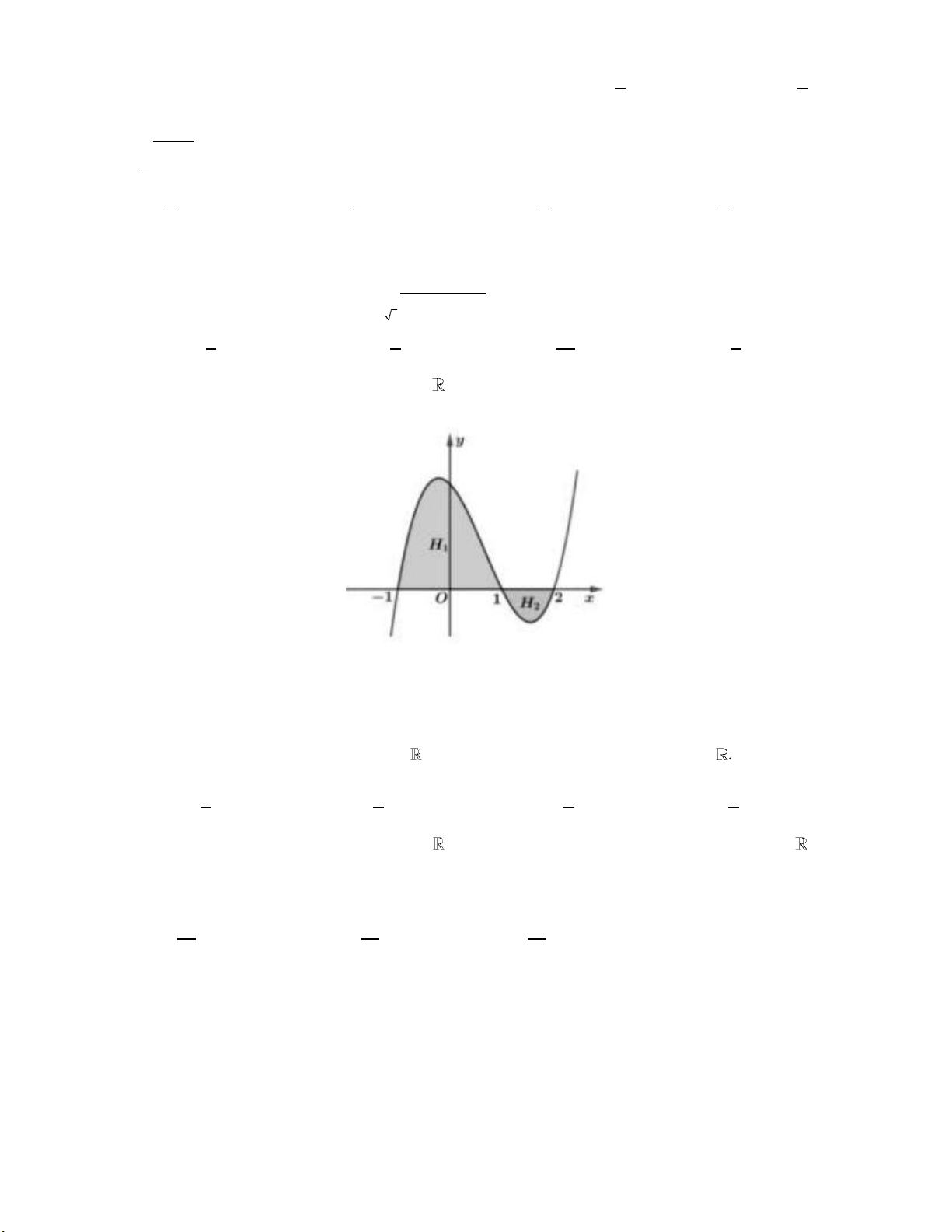
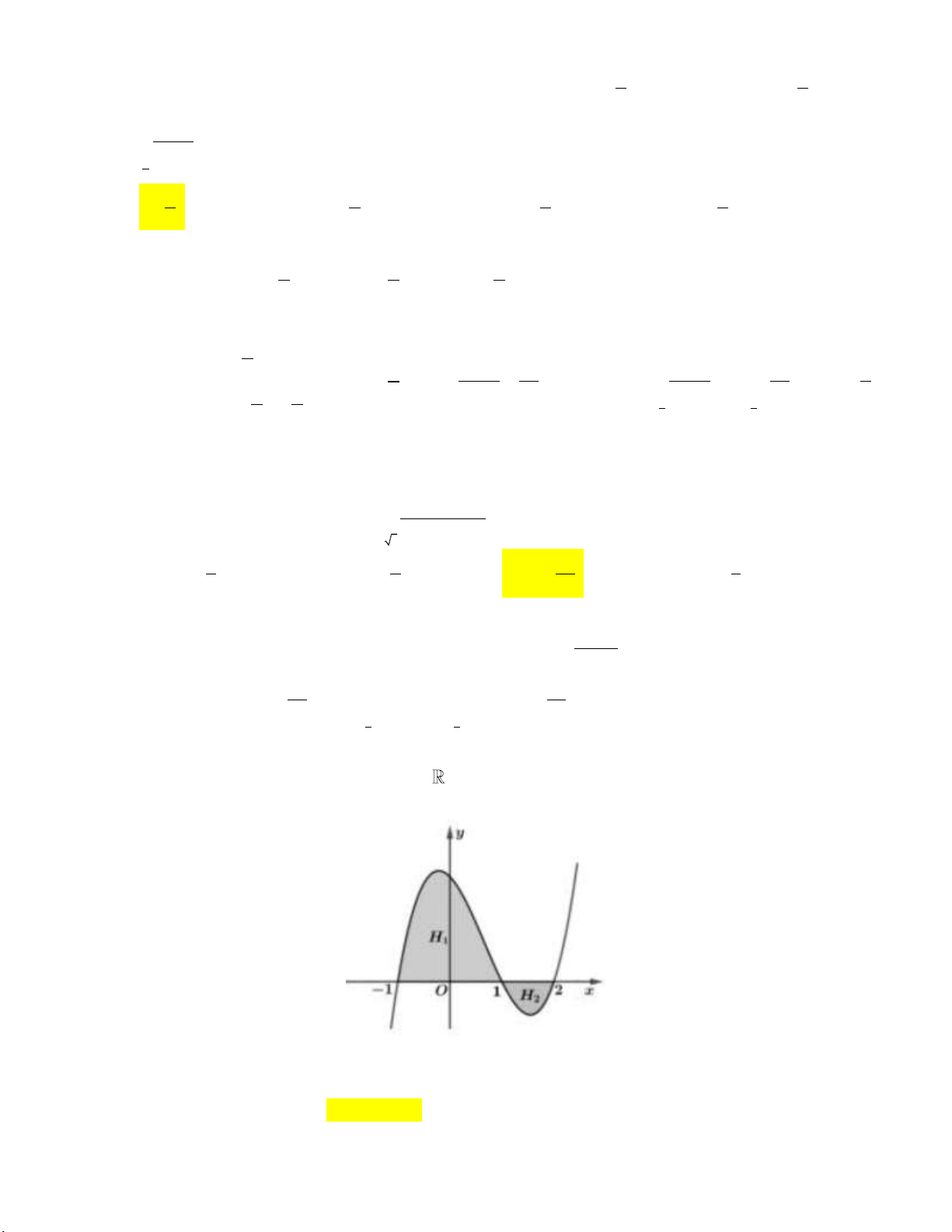
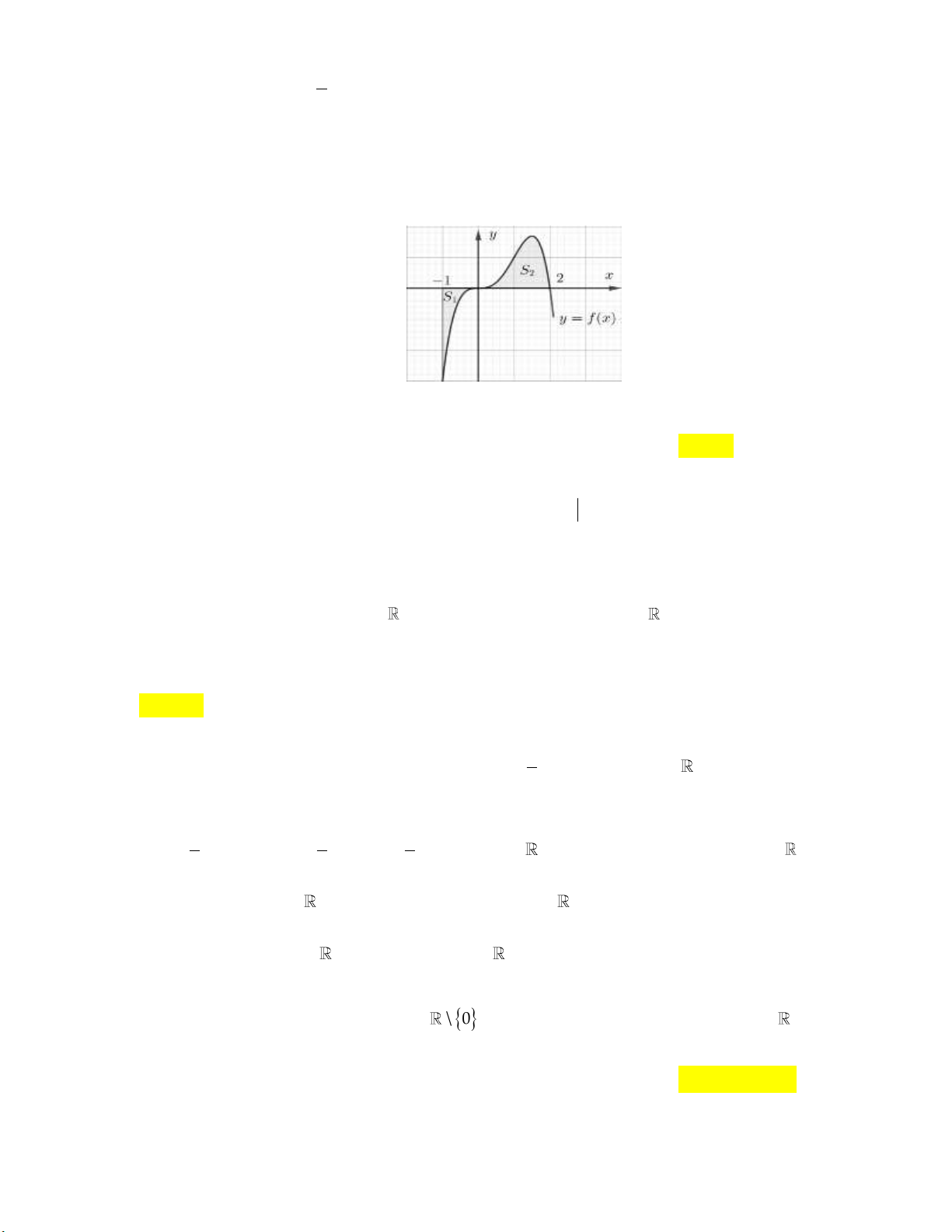
có đồ thị như hình vẽ . Biết H có diện tích bằng 7 1
(đvdt) , H có diện tích bằng 3 (đvdt). 2 1 
Tính I   2x  6 f  2
x  6x  7d . x 2  A. 11 (đvdt). B. 4 (đvdt). C. 1 (đvdt). D. 10 (đvdt). 2 3
Câu 19: Cho hàm số y  f x liên tục trên và thỏa mãn  f
 x  f 
x  x, x
  . Tính I  f
 xd .x 0 4 4 5 5 A. I   . B. I  . C. I   . D. I  . 5 5 4 4
Câu 20: Cho hàm số f (x) liên tục trên thỏa xf  3 x   f  2  x  10 6 1
 x  x  2x, x   . Khi đó 0 f (x d ) x  bằng 1  17 13 17 A.  . B.  . C. . D. 1  . 20 4 4
_________________HẾT_________________
Huế, ngày 07 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông TÝch ph©n _ Hµm Èn
PHIẾU ÔN TẬP SỐ 02
LỜI GIẢI CHI TIẾT
Câu 1: Cho hàm số f  x có đạo hàm liên tục trên đoạn 2; 4 và thỏa mãn f 2  2, f 4  2020 . 2 Tính tích phân I  f 
 2xdx . 1 A. I  1009 . B. I  2022 . C. I  2018 . D. I  1011. Lời giải: 1
Đặt t  2x  dx  dt . Đổi cận: x  1  t  2; x  2  t  4 . 2 2 4 4 1 1 1 Do đó, ta có I  f 
 2xdx  f 
 tdt  f t   f 4 f 2 1009. 2 2 2 1 2 2
Chọn đáp án A. 2
Câu 2: Cho a là hằng số thực và hàm số f  x liên tục trên thỏa mãn f
 xadx  2021. Giá trị 1 2a của tích phân I  f
 xdx là 1a A. I  2021. B. I  2021. C. I  2021 . a D. I  2021 . a Lời giải:
Đặt: t  x  a  dt  dx .
Đổi cận: Với x  1 ta có t  1 a ; với x  2 ta có t  2  a . 2a 2a 2  I  f
 tdt  f
 xdx  f
 xadx  2021. 1a 1a 1
Chọn đáp án A. Câu 3: Cho hàm số f  x liên tục trên khoảng
0; và thỏa mãn f x 17 2x 1 2   f  x   1   .ln  x   1 . Biết f
 xdx  aln52lnbc với a, ,bc . Giá trị 4x x 2x 1
của a  b  2c bằng 29 A. . B. 5 . C. 7 . D. 37 . 2 Lời giải: Cách 1:
Do f  x liên tục trên khoảng 0;  nên tồn tại F  x  f
 xdx , x  0.
Với x  0 , ta có: f x f x 2   2x 1 2   f  x   1   .ln  x   1  2 .
x f  x   1   2x   1 .ln  x   1 . 4x x 2x 2 x f x 2  
Xét vế trái: g  x  2 .
x f  x   1   g
 xdx  F  2x  1 F  xC . 1 2 x
Xét vế phải: h  x  2x   1 .ln  x   1  1
h  xdx  2x   1 ln  x    
1 dx   x    2 ln
1 d x  x   2
x  xln  x   1   2 x  x dx x 1   2 x
x  xln  x   1  d x x 
 x  xlnx   2 2 1   C . 2 2 2 x Suy ra F  2
x    F  x    2 1
x  xln  x   1   C   1 . 2
Thay x  4 vào  
1 ta có: F 17  F 2  20ln 5  8  C .
Thay x  1 vào  
1 ta có: F    F   1 2 1  2 ln 2   C . 2 17 15 15 Nên
f  xdx F
 17  F   1  20 ln 5  2 ln 2  
, suy ra a  20 , b  2 , c   . 2 2 1
Vậy: a  b  2c  20  2 15  7 . Cách 2:
Do f  x liên tục trên khoảng 0;  nên tồn tại F  x  f
 xdx , x  0.
Với x  0 , ta có: f x f x 2   2x 1 2   f  x   1   .ln  x   1  2 .
x f  x   1   2x   1 .ln  x   1 . 4x x 2x 2 x
Lấy tích phân hai vế cận từ 1 đến 4 ta được: 4 f  x  
1 d  x   4 1  f  x  4 2 2
d x  2x   1 .ln  x     1dx 1 1 1 17 2 4
            x  x f t dt f t dt x
x ln  x   2 4 2 1  dx  1 x 1 2 1 1 17 4 17
 f tdt  
 xdx  f x 15 20 ln 5 2 ln 2
dx 20 ln 5  2 ln 2     . 2 1 1 1
Vậy: a  b  2c  20  2 15  7 .
Chọn đáp án C.
Câu 4: Cho hàm số y  f x có đạo hàm liên tục trên
. Biết f 1  e và x   f x  xf x 3 2  x ,
x  . Tính f 2 . A. e2 4  4e  4 B. e2 4  2e  1 C. e3 2  2e  2 D. e2 4  4e  4 Lời giải:
xf x  x  2 f x
Ta có: x   f x  xf x 3 2  x   1 3 x   
ex f x 
2  ex f x 2  e 2
 f 2 e 1 f   1     ex  
 dx  exdx       e 2  e 1   2    x    2  x  2 2 2 1 1   1 e 2
 f 2 e 1 f 1 e 1 e 2    
 f 2  4ef 2
 1  e  1  4e  4e  4 . 4 1
Chọn đáp án D. 1 1
Câu 5: Cho f  x là hàm số liên tục trên thoả mãn f   1  1 và  d   f t t , tính 3 0  2 I  sin 2 . x f  
sin xd .x 0 4 2 2 1 A. I  . B. I  . C. I   . D. I  . 3 3 3 3 Lời giải: 
Đặt t  sin x  dt  cos xdx . Đổi cận x  0  t  0; x   t 1. 2  2 1 u   2t  du  2dt  Khi đó I  sin 2 . x f  
sin xdx  2t.f  
tdt. Đặt    dv  f  
tdt v  f  t 0 0 1 1 1 4
Vậy I  2t. f 
t 2 f 
 tdt  2 f  12  . 0 3 3 0
Chọn đáp án A. Câu 6: Cho hàm số
f  x có đạo hàm xác định trên . Biết f   1  2 và 1 4 1 3 x 1 2 x f   xdx  f 
2 xdx 4. Giá trị của f xdx  bằng 2 x 0 1 0 5 3 1 A. 1. B. . C. . D. . 7 7 7 Lời giải: 1 1 1 1 Ta có: 2 4  x f   x 2 dx  x d
  f x   2x f x  2xf  xdx 0 0 0 0 1 1 1  4  f   1  2 xf
 xdx  4  22 xf
 xdx  xf xdx  1   . 0 0 0 4 1 3 x 1 Xét f 
2 xdx. Đặt t  2 x dt   dx. 2 x 2 x 1
Với x  1  t  1 và x  4  t  0 . 4 0 1 3 x Khi đó 4  f 
2 xdx   13
 2t f  tdt 2 x 1 1 1 1 1 1 1  1
4  7 3t f tdt  4  7 f
 tdt 3 tf
 tdt  4  7 f tdt 3 1  f tdt    . 7 0 0 0 0 0 1 1
Vậy f  xdx   . 7 0
Chọn đáp án D.
Câu 7: Cho hàm số y  f  x đồng biến và có đạo hàm liên tục trên thỏa mãn
  2   . x f x f x e , x
  và f 0  2. Khi đó f 2 thuộc khoảng nào sau đây? A. 12;13 . B. 9;10 . C. 11;12 . D. 13;14 . Lời giải:  f    x  0
Hàm số đồng biến trên nên ta có   f
  x  f 0, x   0   x x    2    f x f x f x . x
e  f  x  f  x   1 2 2 .e   e 2 f  x 2   2 2 2 1 x x f x  dx  e dx  f  x 2 2 2  e
 f 2  f 0  e    2 f  x 1 0 2 0 0 0
 f    e  2 2 2 1  9;10 .
Chọn đáp án B.
Câu 8: Cho hàm số f  x liên tục trên
và thỏa mãn f (x)  f (x)  2 cos 2x, x   . Khi đó  2 f
 xdx bằng   2 A. 2  . B. 4 . C. 2 . D. 0 . Lời giải:
Với f (x)  f (x)  2 cos 2x, x        2
   f (x) f (x) 2 2 dx  2 cos 2 d x x  f   x 2 dx  f  x 2 dx  2 os c 2 d x x  (*)           2 2 2 2 2  2     Tính I  f
 xdx . Đặt t  x  dt  d  .
x Đổi cận: x 
 t   ; x    t  .  2 2 2 2  2     2 2 2 Khi đó I   f
 tdt  f
 tdt  f  xdx .      2 2 2    2 2  2 Từ (*), ta được: 2 f  x 2 dx  2 cos 2 d x x  sin 2x  0     f
 xdx 0.    2     2 2 2
Chọn đáp án D.
Câu 9: Cho f  x là hàm số liên tục trên tập số thực
và thỏa mãn f  3 x  3x   1  x  2 . Tính 5
I   f xd .x 1 41 527 61 464 A. . B. . C. . D. . 4 3 6 3 Lời giải: Đặt 3
x  t  3t  1 . Đổi cận: x  1  t  0 , x  5  t  1. Ta có: x   3 d
d t  3t   1   2 3t  3dt . 5 1 1 41 Khi đó: I  f
 xdx  f
  3t 3t  1 2
3t  3dt  t  2 2
3t  3dt  . 4 1 0 0
Chọn đáp án A. 1  2
x  2 khi 0  x  2 e f ln x 2 6
Câu 10: Cho hàm số f  x  2 . Khi đó dx  xf 
  2x 1dx bằng  x
x  5 khi 2  x  5 1 3 19 37 27 A. . B. . C. . D. 5. 2 2 2 Lời giải: 2 e f ln x 1
x 1 t  0 Xét I  d . x 
Đặt t  ln x  dt  d . x Đổi cận  1 x x 2
x  e  t  2 1 2 e f ln x 2 2 2 2  1   x  2 Suy ra I  dx 
f t dt= f x dx  x  2 dx         2x  5. 1     x  2   4 0  1 0 0 0 2 6 Xét I  xf
  2x 1 dx Đặt 2 2 2 t 
x 1  t  x 1  d t t  d x . x 2  3
x  3  t  2 Đổi cận 
x  2 6  t  5 2 6 5 5 5 2  x  5 9 Suy ra I  xf
  2x 1 dx  f t dt  f x dx  x5 dx       5x   . 2         2 2  2 3 2 2 2 2 e f ln x 2 6 9 19 Vậy dx  xf 
  2x 1dx  5  . x 2 2 1 3
Chọn đáp án A. 1 1
Câu 11: Cho hàm số f x có đạo hàm liên tục trên . Biết . x f ' 
xdx  10 và f 1  3, tính f xdx  . 0 0 A. 30 . B. 7 . C. 13 . D. 7 . Lời giải: 1 u   x du    dx Xét tích phân . x f ' 
xdx 10. Đặt    . dv  f '  xdx v    f  x 0 1 1 1 1 Do đó, . x f ' 
xdx 10  .xf x  f
 xdx 10  f 110  f  xdx . 0 0 0 0 1
Suy ra f xdx  3  10  7   . 0
Chọn đáp án D.
Câu 12: Cho hàm số f (x) liên tục trên đoạn 0;1 
 và thỏa mãn 4x f  2
x   f   x 2 . 3 1  1 x . Tính 1
f xdx  . 0     A. . B. . C. . D. . 16 4 20 6 Lời giải: 2 2 Từ giả thiết 4 .
x f (x )  3 f (1 x)  1 x , lấy tích phân hai vế ta được: 1 1 1 2 [4 .
x f (x )]dx  3 f (1 x)dx     2
1 x dx (*) 0 0 0 1 Tính 2 A  [4 . x f (x )]d .  x Đặt 2
t  x  dt  2 .
x dx . Đổi cận: x  0  t  0 ; x  1  t  1. 0 1 1 1 1 2 2  A  [4 .
x f (x )]dx  2 f (x )2 .
x dx  2 f (t)dt =2 f (x)dx     0 0 0 0 1
Tính B  3 f (1 x)dx  0
Đặt t  1 x  dt  dx . Đổi cận: x  0  t  1 ; x  1  t  0 . 1 0 1 1
 B  3 f (x 1)]dx  3 
f (t)dt  3 f (t)dt =3 f (x)dx     0 1 0 0 1 Tính C   2 1 x dx 0 
Đặt x  sin t  dx  cost.dt . Đổi cận: x  0  t  0 ; x  1  t  . 2    1     c    C 1 x  2 2 2 1 os2t 1 1 2 2
dx  cos t.dt = .dt = t  sin 2t      2  2 4  4 0 0 0 0 1 1   Thay ,
A B,C vào (*) ta được: 5 f (x)dx   f (x)dx    . 4 20 0 0
Chọn đáp án C.   
Câu 13: Cho hàm số f  x thỏa mãn f  x  f   x 4 2 .   sin . x sin 2x  với mọi x  và f 1   . Giá trị  2  của    5 f     bằng 11 11 23 11 A.  . B. . C. . D. . 3 5 15 3 Lời giải: 1 1 1 1 Ta có 2 sin . x sin 2x 
sin x 1 cos 4x  sin x  sin 5x  sin 3x . 2 2 4 4 4 4
Vậy f  x  f   x 2   x x  f  
 x  f x 2 . sin .sin 2 .  dx  sin . x sin 2 d x x    1 1 1  4  f
 xdf x  sin x  sin 5x  sin 3x dx    2 4 4  5 f  x 1 1 1    cos x  cos 5x  cos 3x  C. 5 2 20 12    1  1 1 1 1  11 Do f 1  C    . Vậy 5
f    5  cos  cos 5  cos 3   .    2  5  2 20 12 5  3
Chọn đáp án D. 1
Câu 14: Cho hàm số f (x) liên tục trên thỏa mãn ( )  x f x
e  tf (t)dt, x   . Tính f (ln(5620)) . 0 A. 5622. B. 5621. C. 5620. D. 5619. Lời giải: 1
Theo giả thiết, ta có: ( ) x
f x  e  c , với c  tf (t)dt  là hằng số. 0 1 1 1 1 1
Khi đó:    t   t c t e
c dt  te dt  ctdt  I  I   , với t I  te dt  , I  ctdt  . 1 2 1 2 0 0 0 0 0 1 1 1 1 2 ct c Vì t t t 1 t t 1
I  te dt  td (e )  (te )
 e dt  e  (e )  e  (e 1) 1    , 1 I  ctdt  ( )   nên 1 0 0 2 0 2 2 0 0 0 0 c
c  I  I  c  1  c  2 . Vậy ( ) x
f x  e  2, x   . 1 2 2 Do đó ln(5620)
f (ln(5620))  e
 2  5620  2  5622 .
Chọn đáp án A. 1
Câu 15: Cho hàm số f  x có đạo hàm liên tục trên và thỏa mãn f
 xdx 10, f  1  cot1. Tính tích 0 1
phân I   f  x 2
tan x  f  x tan x d  x   . 0 A. 1 ln cos  1 . B. 1  . C. 9  . D. 1 cot1. Lời giải: Cách 1: 1 1 1 + I   f  x 2
tan x  f  x tan x d  x 2    f
 xtan dxx f 
 xtan dxx  1. 0 0 0 1 + Tính J  f 
 xtan dxx. 0 u  tan  x  u    2 d 1 tan xdx Đặt  , ta có  . dv  f   xdx v   f  x 1 1 1
 J  f x 1
.tan x   f x. 2
1 tan xdx  f  
1 .tan1 f 0.tan 0  f  x 2 .tan d x x  f  xdx 0 0 0 0 1 1 1  cot1.tan1 f  x 2 .tan d x x 10  1 f  x 2 .tan d x x 10  9   f  x 2 .tan d x x . 0 0 0 1 1   Thay J vào   1 ta được: I  f  x 2 tan d x x   9   f  x 2 .tan d x x   9  . 0  0  Cách 2:   f  x
x  f  x
x  f  x
2 x    f x
x  f  x 2 tan tan tan 1 tan
tan x  f  x Ta có:   f x
x  f  x 2 tan tan x   f
 x tan x  f  x . 1 1     I   f  x 2
tan x  f  x tan x dx   
 f xtan x  f  xdx   0 0 1  f x 1 tan x 
f  xdx  f  
1 tan110  cot1.tan110  9   . 0 0
Chọn đáp án C.   1 
Câu 16: Cho hàm số y  f  x liên tục và thỏa mãn f  x 1  2 f  3x   với mọi x  ; 2 . Tính    x  2 
2 f  x dx  . x 1 2 3 9 9 3 A. . B. . C.  . D.  . 2 2 2 2 Lời giải:  1   1  3
Ta có f  x  2 f  3x  f
 2 f x       x   x  x
Từ đó ta có hệ phương trình:    f   x 1  2 f  3x     f  x 2 f  x 2 x  2  2  3   f x 2   x   1 . Do đó I  dx  1 dx     .     1  6 2 2 x  x  2 4  2 x f x f    x x 1 1   x  x 2 2
Chọn đáp án A.
Câu 17: Cho hàm số y  f  x xác định và liên tục trên 0;  sao cho 2 
 x  x x xf e
f e   1 với mọi
e ln x f  x
x  0; . Tính tích phân I  dx  . x e 1 2 1 3 A. I   . B. I   . C. I  . D. I  . 8 3 12 8 Lời giải:  x x x x 1
Với x  0; ta có x  xf e   f e   1  f e  2 2   1 x 1  x dx 1 1 t 1
Đặt ln x  t  dt 
 I  tf e dt  t 1tdt    . x 12 1 1 2 2
Chọn đáp án C.
Câu 18: Cho hàm số y  f (x) liên tục trên
có đồ thị như hình vẽ . Biết H có diện tích bằng 7 1
(đvdt) , H có diện tích bằng 3 (đvdt). 2 1 
Tính I   2x  6 f  2
x  6x  7d . x 2  A. 11 (đvdt). B. 4 (đvdt). C. 1 (đvdt). D. 10 (đvdt). Lời giải: 1 1  
S  f (x)dx f x x H   ( )d  7  1   
Dựa vào đồ thị ta thấy 1 1    . 2 S f x x f x x H     ( ) 2 d ( )d  3    2   1 1 1  Xét 2 I 
(2x  6) f (x  6x  7)dx  . 2  x  2   t  1  Đặt 2
t  x  6x  7  dt  (2x  6)dx .Đổi cận :  . x  1   t  2 2 2 1 2 Khi đó I  f (t)dt 
f (x)dx 
f (x)dx 
f (x)dx  7  ( 3  )  4     (đvdt). 1  1  1  1
Chọn đáp án B. 2 3
Câu 19: Cho hàm số y  f x liên tục trên và thỏa mãn  f
 x  f 
x  x, x
  . Tính I  f
 xd .x 0 4 4 5 5 A. I   . B. I  . C. I   . D. I  . 5 5 4 4 Lời giải:
Đặt u  f x , ta thu được 3 u  u  . x Suy ra  2
3u  1du  d . x
x  0  u  0 1 5 Từ 3
u  u  x , ta đổi cận 
. Khi đó I  u   2
3u  1du  .
x  2  u   1 4 0
Cách khác: Nếu bài toán cho f x có đạo hàm liên tục thì ta làm như sau: 3
 f 0  f 0  0  f 0    0 Từ giả thiết 3
f x  f x      x     . * 3 f
 2  f 2   2  f  2  1 Cũng từ giả thiết 3
f x  f  x  x , ta có f x 3 '
. f x  f 'x. f x  . x f 'x. 2 2
Lấy tích phân hai vế  f '  x 3
. f x  f 'x. f x dx  . x f '   xdx 0 0    f   x 4   f   x 2  2    
 xf x 2 2  f  x 2 5 dx  f
 xdx  .  4 2    0 0 4 0 0  
Chọn đáp án D.
Câu 20: Cho hàm số f (x) liên tục trên thỏa xf  3 x   f  2  x  10 6 1
 x  x  2x, x   . Khi đó 0 f (x d ) x  bằng 1  17 13 17 A.  . B.  . C. . D. 1  . 20 4 4 Lời giải:
Với x  ta có : 3 2 10 6
xf (x )  f (1  x )  x  x  2x 2 3 2 11 7 2
 x f (x )  xf (1 x )  x  x  2x (*) 1 1 1 2 3  x f (x d 2
) x  xf (1  x d ) x     11 7 2
x  x  2x dx 0 0 0 1 1 1 1 1 1 3 1 5  1 1 5 3 f (x d 3 2 ) (x )  f (1  x )d 2 (1  x )      f (x d ) x  f (x d
) x    f (x d ) x      3 2 8 3 2 8 4 0 0 0 0 0 0 0 0 Mặt khác : 2 3 (*)  x f (x d 2
) x  xf (1  x d ) x     11 7 2
x  x  2x dx 1  1  1  0 0 1 1 2 3 17 (*)  f (x d )  3 x  2  f (1  x d
) 1 x      3  2  24 1 1 0 1 0 1 1 17  1 3  17  13  f (x d ) x  f (x d ) x    f (x d ) x  3 .         . 3  2 24   2 4 24  4 1 0 1
Cách khác tham khảo câu 48: Chọn hàm Từ giả thiết : 3 2 10 6
xf (x )  f (1  x )  x  x  2x, x  
ta suy ra f x là bậc ba có a  1 . Nên   3 2
f x  x  bx  cx  d
Cho x  0  f 1  0  b  c  d  1 .
Cho x  1  f 1  f 0  2   f 0  2   d  2  Cho x  1    f  1
   f 0  2  f  1    4
  1 b  c  d  4  . 0 0 13
Suy ra  b  0; c  3 . Từ đó có f x 3
 x  3x  2  f (x d ) x    3
x  3x  2dx   .   4 1 1
Chọn đáp án B.
_________________HẾT_________________
Huế, ngày 07 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông TÝch ph©n _ Hµm Èn
PHIẾU ÔN TẬP SỐ 03 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI 7
Câu 1: Cho hàm số f  x liên tục trên
và thỏa mãn f  x  f 10  x, x   . Biết f
 xdx  4. 3 7 Tính I  xf  xdx 3 A. I  40 . B. I  80 . C. I  60 . D. I  20 .
Câu 2: Cho hàm số y  f  x có đạo hàm và liên tục trên
thỏa mãn 2 f  x  f ' x  2x 1và 1 f 0  1. Tính  d .  f x x 0 1 1 1 1 A.1 B. . C.1 . D.  . 2 2e 2 2 2 2e 2e 2e Câu 3: Cho hàm số
y  f  x liên tục và có đạo hàm trên thỏa mãn: 3 2 a a
f  x  f   x 2 5 7 1
 4x  6x , x
  . Biết rằng  f 
 x dx   (
là phân số tối giản). Tính b b 2 a 143b . A. 3 . B. 2 . C. 0 . D. 1. 9 f  x 
Câu 4: Cho hàm số y  f (x) liên tục, có đạo hàm trên
thỏa mãn f (1)  0 , dx  5  và x 1 1 2 3 xf  x 1 dx  
. Khi đó f (x)dx  bằng 2 0 0 1 9 A. 7 . B. . C. 3 . D. . 2 2 x  m x  0
Câu 5: Cho hàm số f x liên tục trên
thỏa mãn f x khi  
( m là hằng số). Biết 2x e khi x  0 2 f  xd 2 x  a  .
b e trong đó a,b là các số hữu tỷ. Tính a  . b 1  A. 1 . B. 4 . C. 3 . D. 0 .
Câu 6: Giả sử hàm số f  x liên tục và dương trên
; thảo mãn f 0  1 và  2 x  
1 f  x  . x f  x. 2 Khi đó 2
I   f xdx thuộc khoảng nào sau đây? 1 A. 1;4. B. 72;74. C. 8;10. D. 4;6.
Câu 7: Cho hàm số f  x có đạo hàm và đồng biến 1; 4 thỏa mãn x  xf  x   f  x 2 2    với mọi 4
x 1;4. Biết rằng f   3 1 
, tính I   f xdx . 2 1 1183 1187 1186 9 A. I  . B. I  . C. I  . D. I  . 45 45 45 2 3
Câu 8: Cho hàm số f  x liên tục trên
và thoả mãn  f  x  2 
f  x  1 x với mọi x  . 1
Tính  f xd .x 2  7 17 17 7 A.  . B.  . C. . D. . 4 4 4 4 2
Câu 9: Cho hàm số f  x xác định và dương trên 0;  , thỏa mãn  f    x 2  12x  f 
x.f  x với
mọi x 0;  và f   1  1; f  
1  4 . Giá trị của f 2 bằng A. 46 . B. 7 . C. 3 5 . D. 2 10 . Câu 10: Cho hàm số
y  f  x xác định trên đọan 0,5 và thoả mãn điều kiện 4
f '  x  f ' 5 x , x
 0,5, f 0 1, f 5  7 .Tính f 
 xdx4. 1 A. 12 . B. 8 . C. 24 . D. 20 .
Câu 11: Cho hàm số f x 3 2
 x  ax  bx  c, a;b;c . Nếu phương trình f x  0 có ba nghiệm thực
phân biệt thì phương trình f x f  x   f   x 2 2 .
 có nhiều nhất bao nhiêu nghiệm thực? A. 1 . B. 2 . C. 4 . D. 3 .
Câu 12: Cho hàm số f  x có đạo hàm trên thỏa mãn      2018 2019 2019  2019. . x f x f x x e , x 
và f 0  2019 . Giá trị của f   1 là A. f   2019 1 2019.e  . B. f   2019 1  2019.e . C. f   2019 1  2020.e . D. f   2019 1 2020.e  . 1 2 7
Câu 13: Biết rằng hàm số   2
f x  ax  bx  c thỏa mãn
f  x dx   ,
f  x dx  2    và 2 0 0 3 f  x 13 dx   (với a, , b c 
). Tính P  a  b  . c 2 0 3 4 4 3 A. P   . B. P   . C. P  . D. P  . 4 3 3 4
Câu 14: Giả sử hàm f có đạo hàm cấp 2 trên thỏa mãn f '  
1  1 và f   x 2 1
 x f ' x  2x với mọi 1 x  . Tính '  d .  xf x x 0 2 A. 1. B. 0. C. 2. D. . 3
Câu 15: Cho hàm số f  x liên tục trên
4 f x  2  f 2x 1  8x, x  . Biết rằng thỏa mãn     1 3
 f xdx  3. Tính I   f xdx . 0 0 A. I  36 . B. I  21. C. I  33 . D. I  39 .
Câu 16: Cho hàm số y  f (x) liên tục trên [1; 2] có đồ thị như hình vẽ dưới đây: 2
Biết S , S có diện tích lần lượt là 2 và 6. Tích phân (x  1) f (  x d ) x  bằng 1 2 1  A. 2. B. 12. C. 6. D. 4. 1
Câu 17: Cho hàm số f x liên tục trên thỏa mãn f 2x  3 f x , x  . Biết rằng f
 xdx 1. Tính 0 2 I  f  xdx . 1 A. I  5. B. I  6. C. I  3. D. I  2.
Câu 18: Cho hàm số y  f x xác định trên  \ 
0 và thỏa mãn f x  xf x 2  3x , x
  và f 2  8 .
Viết phương trình tiếp tuyến của đồ thị hàm số y  f x tại giao điểm với trục hoành.
A. y  x  1.
B. y  2x  4. C. y  4 . x
D. y  6x  12.
Câu 19: Cho hàm số y  f x liên tục trên 0;1   và thỏa mãn 2
x f x  f   x 4 1
 2x  x . Tính tích 1 phân I  f  xd .x 0 1 3 2 4 A. I  . B. I  . C. I  . D. I  . 2 5 3 3    Câu 20: Cho hàm số f x có đạo hàm liên tục trên 0;   thỏa mãn  2      2 f 0 2  0,  f   x 2 2
 dx  sin xf  
xdx  . Tính f  xd .x 4 0 0 0   A. . B. . C. 2 . D. 1 . 4 2
_________________HẾT_________________
Huế, ngày 07 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông TÝch ph©n _ Hµm Èn
PHIẾU ÔN TẬP SỐ 03
LỜI GIẢI CHI TIẾT 7
Câu 1: Cho hàm số f  x liên tục trên
và thỏa mãn f  x  f 10  x, x   . Biết f
 xdx  4. 3 7 Tính I  xf  xdx 3 A. I  40 . B. I  80 . C. I  60 . D. I  20 . Lời giải: 7 7 7
Ta có 10  x f xdx  10 f 
xdx  xf
 xdx  40 I  1. 3 3 3 7 7
Theo bài ra f  x  f 10  x, x
  suy ra: 10 x f xdx  10 x f 10 xdx . 3 3 7 7  
1  40  I  10  x f 10  xdx  40  I  tf  tdt 3 3 7
 40  I  xf
 xdx  40 I  I  I  20. 3
Chọn đáp án D.
Câu 2: Cho hàm số y  f  x có đạo hàm và liên tục trên
thỏa mãn 2 f  x  f ' x  2x 1và 1 f 0  1. Tính  d .  f x x 0 1 1 1 1 A.1 B. . C.1 . D.  . 2 2e 2 2 2 2e 2e 2e Lời giải:
Ta có: 2 f  x  f ' x  2x 1 2 x    2x        2 2 . . ' 2 1 . x e f x e f x x e
  2x       2 . ' 2 1 . x e f x x e 2 x         2 . 2 1 . x e f x x e dx (*) x 1 Xét      2 2 1 . x I x e d .
x Đặt u  2x 1  du  2dx ; 2 2 x
dv  e dx  v  e 2   1 x 1 2   1 x 1 2 2 1 . x I x e  e .2dx   2   2 2 1 . x x e  e  C 2 2 2 2 1 1 C x 1 x 1
Thay vào (*) ta có: 2 .    2   2 2 1 . x e f x x e
 e  C  f x  2x   1   2 2 2 2 2 x e 1 1 1 1 1  f 0  1 
  C 1  C 1  f x  2x   2 1 x    x  e 2 2 2 2 2 x e 1 1 2    x x 1  x 1 1 1 1 Vậy f
 xdx   2 x  e  2 1 dx    e     1 . 0 2 2  2 2  2 2e 2 2e 0 0
Chọn đáp án A. Câu 3: Cho hàm số
y  f  x liên tục và có đạo hàm trên thỏa mãn: 3 2 a a
f  x  f   x 2 5 7 1
 4x  6x , x
  . Biết rằng  f 
 x dx   (
là phân số tối giản). Tính b b 2 a 143b . A. 3 . B. 2 . C. 0 . D. 1. Lời giải:
Theo giả thiết: f  x  f   x 2 5 7 1
 4x  6x , x   . Thay 2
x bởi 1 x ta được: f   x  f  x    x    x2 5 1 7 4 1 6 1
 6x  8x  2 . 5  f 
x7 f 1 x 2  4x  6x Ta được hệ:   7  f 
x5 f 1 x 2  6
 x  8x  2  f  x 
f  x   2
x  x    2 25 49 5 4 6 7 6
 x  8x  2   f x 2 24  72
 x  76x 14  f x 19 7 2  3x  x   f x 19  6x  . 6 12 6 3 3 2 2  19  5149 Khi đó:  f 
 x dx  6x dx    
. Vậy a  5149, b  36 nên a 143b  1 .  6  36 2 2
Chọn đáp án D. 9 f  x 
Câu 4: Cho hàm số y  f (x) liên tục, có đạo hàm trên
thỏa mãn f (1)  0 , dx  5  và x 1 1 2 3 xf  x 1 dx  
. Khi đó f (x)dx  bằng 2 0 0 1 9 A. 7 . B. . C. 3 . D. . 2 2 Lời giải: 9 f  x  9 3 5 Xét I  dx   2 f
  xd x  5  f tdt   . 1 x 2 1 1 1 1 2 1 1 1
Xét I  xf  2x dx  
. Đặt t  2x  dt  2dx  I 
tf  t dt  . 2   2   2 4 0 0 u   t d   u  dt  Đặt    dv  f   tdt v   f  tdt 1 1   1 1
Do đó: I  tf t  1  f t dt 
   f tdt  2   . 2 0   4 2  0  0 3 1 3 5 1
Vậy f (x)dx 
f (x)dx 
f (x)dx  2       . 2 2 0 0 1
Chọn đáp án B. x  m x  0
Câu 5: Cho hàm số f x liên tục trên
thỏa mãn f x khi  
( m là hằng số). Biết 2x e khi x  0 2 f  xd 2 x  a  .
b e trong đó a,b là các số hữu tỷ. Tính a  . b 1  A. 1 . B. 4 . C. 3 . D. 0 . Lời giải:
Do hàm số liên tục trên
nên hàm số liên tục tại x  0  lim f   
x lim f x f(0) x0 x0  m  1 2 0 2 0 2 Khi đó ta có f
 xdx  f
 xdx  f  xdx 2x
 e dx  x    1dx 1  1  0 1  0 0 2 2 x 2 e  x  2 1 e 9 1     x 2 4 e      2  2  2 2 2 2 1  0 9 1
Do đó : a  ;b   . Vậy a  b  4 . 2 2
Chọn đáp án B.
Câu 6: Giả sử hàm số f  x liên tục và dương trên
; thảo mãn f 0  1 và  2 x  
1 f  x  . x f  x. 2 Khi đó 2
I   f xdx thuộc khoảng nào sau đây? 1 A. 1;4. B. 72;74. C. 8;10. D. 4;6. Lời giải: f  x x Ta có  2 x  
1 f  x  . x f  x     f  x 2 x  1  1  1
 ln f x  ln 2 x  
1   ln  f x  ln  2 x   1  C 2 2 1
Mà f 0  1  C  0  ln  f  x  ln  2 x   1  f  x 2  x 1 2 2 2 10 Vậy 2
I   f xdx   2 x   1 dx  . 3 1 1
Chọn đáp án A.
Câu 7: Cho hàm số f  x có đạo hàm và đồng biến 1; 4 thỏa mãn x  xf  x   f  x 2 2    với mọi 4
x 1;4. Biết rằng f   3 1 
, tính I   f xdx . 2 1 1183 1187 1186 9 A. I  . B. I  . C. I  . D. I  . 45 45 45 2 Lời giải:
Vì f  x đồng biến 1; 4 và f   3 1 
nên f  x  0, x  1;4. 2 f  x
Ta có x  xf  x   f  x 2 2  
  f  x  x. 1 2 f  x   x .
1 2 f  x f  x  4 dx  xdx     f x 2 1 2
 x x  C . Mà f   3 1  nên C  .
1 2 f  x 3 2 3 2  2 4  x x  1    3 3  x  x x  Suy ra  f x 2 4 1 2
 x x   f  x   f x 3 4 16 7  . 3 3 2 18 4 4 3
4x 16x x  7 1186 Do đó I 
f  x dx   dx   . 18 45 1 1
Chọn đáp án C. 3
Câu 8: Cho hàm số f  x liên tục trên
và thoả mãn  f  x  2 
f  x  1 x với mọi x  . 1
Tính  f xd .x 2  7 17 17 7 A.  . B.  . C. . D. . 4 4 4 4 Lời giải:
Đặt t  f  x thì 3
t  2t  1 x , suy ra  2
3t  2dt  dx .
Với x  2 ta có 3
t  2t  3  0 , suy ra t  1. Với x  1 ta có 3
t  2t  0 , suy ra t  0 .  3  7 Vậy f
 xdx   t3t 2dt=3t 2t 1 1 0 1 2 3 4 2 dt= t  t    .  4  4 2  1 0 0
Chọn đáp án D. 2
Câu 9: Cho hàm số f  x xác định và dương trên 0;  , thỏa mãn  f    x 2  12x  f 
x.f  x với
mọi x 0;  và f   1  1; f  
1  4 . Giá trị của f 2 bằng A. 46 . B. 7 . C. 3 5 . D. 2 10 . Lời giải: 2 2 Ta có:  f    x 2   x  f 
x f  x   f 
 x  f 
x f  x 2 12 . . 12x    f
  x f  x 2   x  f 
x f x 3 . 12 .  4x  C .
Thay x  1 ta được: f   f     C    C  C   f  x f  x 3 1 . 1 4 4 4 0 .  4x 2  f
 x f x f x 3   4 .
dx  4x dx   x  C  . 2 2 f   1
Thay x  1 ta được: 2
1 C  8 1 C  C  7  f x  2 4 x  7 2  f     4 2 2 2  7  46 .
Chọn đáp án A. Câu 10: Cho hàm số
y  f  x xác định trên đọan 0,5 và thoả mãn điều kiện 4
f '  x  f ' 5 x , x
 0,5, f 0 1, f 5  7 .Tính f 
 xdx4. 1 A. 12 . B. 8 . C. 24 . D. 20 . Lời giải: Cách 1. 4 4 4 Ta có f 
 xdx4   f 
 x.x  . x f   
xdx 4  4 f 4 f   1  4  I . 1 1 1 1 4 4 1 4 Xét I  .
x f  x dx   .
x f  x d 5  x  
5  t . f  5  t dt 
5  t . f  5  t dt     . 1               1 1 4 1 4 4 Suy ra I 
5  x . f  5  x dx 
5  x . f  x dx   . 1         1 1 4 4 4 4 Khi đó 2I  .
x f  x dx 
5  x . f  x dx  5 f  x dx  5 f  x
 5 f  4  5 f  1    . 1               1 1 1 1 4 5 5 3 Do đó I  f  4  f  1 
f  x dx  4 
 f  4  f  1   4  . 1            2 2 2 1
Lại có f '  x  f ' 5  x  f ' x   f '5  x  C  C  f ' x  f '5  x .
Thay x  0 và x  1 ta được C  f  
1  f 4  f 0  f 5  8 . 4 3 3 Vậy f 
 xdx4   f 
 4  f   1   4  .8  4  8  . 2 2 1 Cách 2. 4 4 Ta có f 
 xdx4  f x 4  f 4 f  14. 1 1
Vì f '  x  f ' 5  x  f ' x   f '5  x  C  C  f ' x  f '5  x .
Thay x  0 ta được C  f '0  f '5  8 . 4 4 4
Khi đó 8  f ' x  f '5  x  8dx   f ' 
 x f '5 x dx   f x f 5 x     . 1 1 1 4
Suy ra 8x   f
 4  f   1  f  
1  f 4  f  4 f   1  12 . 1 4 4 Vậy f 
 xdx4  f x 4  f 4 f  14 124 8. 1 1
Chọn đáp án B.
Câu 11: Cho hàm số f x 3 2
 x  ax  bx  c, a;b;c . Nếu phương trình f x  0 có ba nghiệm thực
phân biệt thì phương trình f x f  x   f   x 2 2 .
 có nhiều nhất bao nhiêu nghiệm thực? A. 1 . B. 2 . C. 4 . D. 3 . Lời giải: Ta có:   3 2
f x  x  ax  bx  c f x 2
 3x  2ax  b; f  x  6x  2a; f  x  6.
Gọi ba nghiệm của phương trình f x  0 lần lượt là a;b;c
Đặt hx  f x f  x   f x2 2 .
hx  2 f x. f  x  2 f x. f  x  2 f x. f  x  2 f x. f  x  12. f x x  a 
hx  0  f x  0  x  b  x  c 
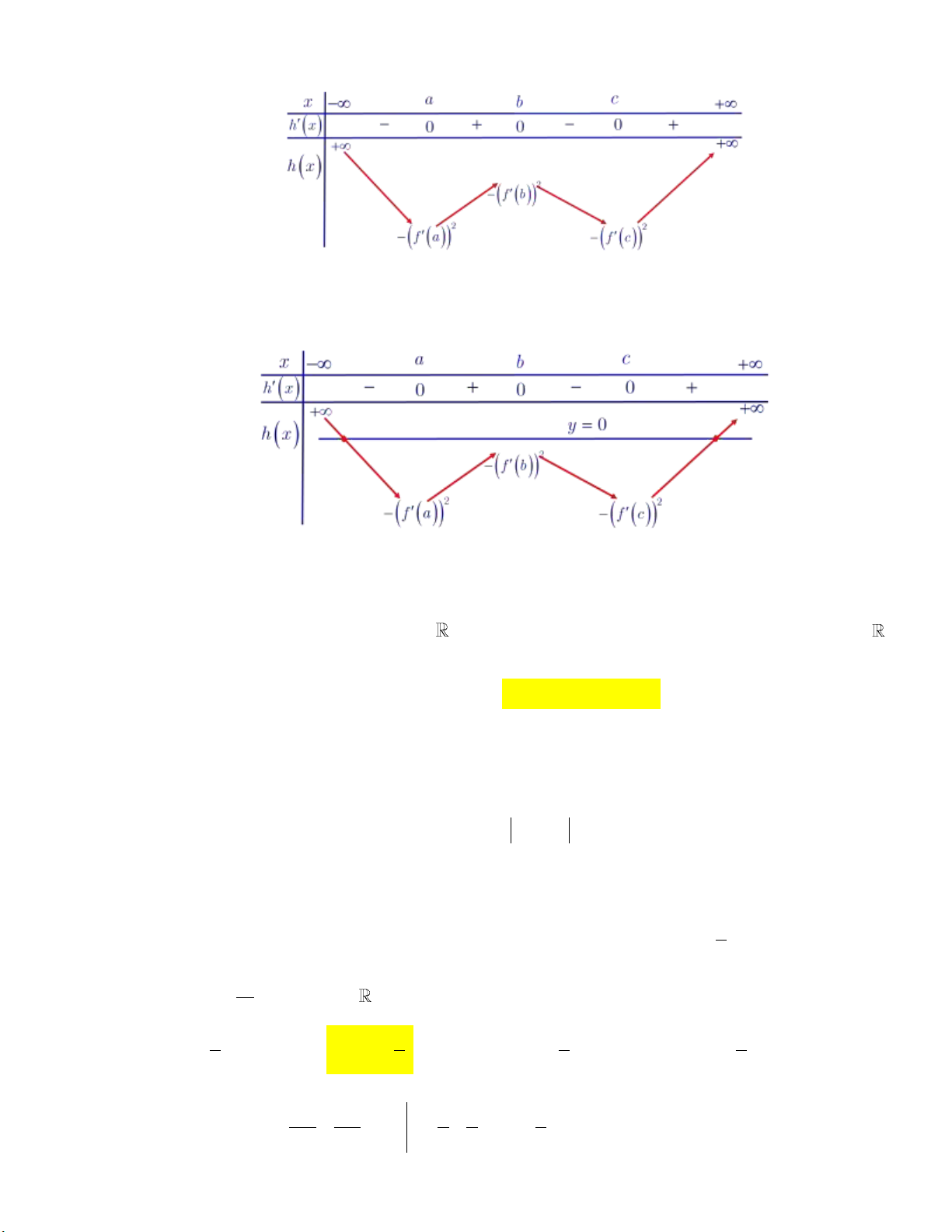
Ta có bảng biến thiên của hàm số hx :
Lại có phương trình f x  0 có ba nghiệm thực phân biệt
a b c  f b   f b    f  b 2 ; ; 0 0  0
Khi đó ta có bảng biến thiên của hàm số hx :
Từ bảng biến thiên phương trình hx  0 có hai nghiệm phân biệt hay f x f  x   f   x 2 2 . 
có hai nghiệm phân biệt.
Chọn đáp án B.
Câu 12: Cho hàm số f  x có đạo hàm trên thỏa mãn      2018 2019 2019  2019. . x f x f x x e , x 
và f 0  2019 . Giá trị của f   1 là A. f   2019 1 2019.e  . B. f   2019 1  2019.e . C. f   2019 1  2020.e . D. f   2019 1 2020.e  . Lời giải:
Từ giả thiết      2018 2019 2019  2019. . x f x f x x e . 
 f x 2019 .  x e
 2019. f x 2019  x 2018 .e  2019.x   2019  x e f x 2018  2019.x 1 1 1 1    2019  x e . f x d 2018 x  2019.x d 2019  x x  e . f  x 2019 2019  x
 e . f 1  f 0  1 0 0 0 0
 f 1  1 f 0 2019 2019 .e  2020.e .
Chọn đáp án C. 1 2 7
Câu 13: Biết rằng hàm số   2
f x  ax  bx  c thỏa mãn
f  x dx   ,
f  x dx  2    và 2 0 0 3 f  x 13 dx   (với a, , b c 
). Tính P  a  b  . c 2 0 3 4 4 3 A. P   . B. P   . C. P  . D. P  . 4 3 3 4 Lời giải: 1   ax bx  a b ax +bx+c 3 2 1 7 2 dx   
 cx    c    3 2 0  3 2 2 0 2 3 2  ax bx  2 8a 4b  2
ax +bx+cdx     cx    2c  2   3 2 0  3 2 0 3   ax bx  a b ax +bx+c 3 2 3 27 9 13 2 dx     cx    3c   3 2 0  3 2 2 0 a b 7   c     3 2 2   a  1 8a 4b  4 Suy ra :  
 2c  2  b   3
 P  a  b  c   . 3 2   3 16 27a 9b 13 z     3c    3  3 2 2
Chọn đáp án B.
Câu 14: Giả sử hàm f có đạo hàm cấp 2 trên thỏa mãn f '  
1  1 và f   x 2 1
 x f ' x  2x với mọi 1 x  . Tính '  d .  xf x x 0 2 A. 1. B. 0. C. 2. D. . 3 Lời giải:
Ta có f   x 2 1
 x f ' x  2x  1
Thay x  0 vào (1) ta được f   1  0 .
Mặt khác , lấy tích phân hai vế cận từ 0 đến 1 của (1) ta có: 1 1 1
 f 1 x 2 dx  x f '  xdx  2  xdx 0 0 0 . 1 1 1 1
  f 1 xd(1 x) f ' 1 2 xf '
 xdx 1  f xdx 2 xf '
 xdx  0 (2) 0 0 0 0 1 1 1 Vì xf '
 xdx  f (1) f
 xdx   f  xdx (3) 0 0 0 1 1
Thay (3) vào (2) ta được  f xdx  3  xf '
 xdx 0. 0 0
Chọn đáp án B.
Câu 15: Cho hàm số f  x liên tục trên
4 f x  2  f 2x 1  8x, x  . Biết rằng thỏa mãn     1 3
 f xdx  3. Tính I   f xdx . 0 0 A. I  36 . B. I  21. C. I  33 . D. I  39 . Lời giải:
Ta có: 4 f  x  2  f 2x  
1  8x  f 2x  
1  4 f  x  8x  2 . 1 1 1  f
 2x  1 dx  4 f
 xdx  8x  2dx  4.3 6 18. 0 0 0 dt
Đặt t  2x 1  dx 
; x  0  t  1; x  1  t  3 . 2 1 3 3 3 1 Ta có f
 2x  1dx  f
 tdt 18  f
 tdt  36  f
 xdx  36. 2 0 1 1 1 3 1 3 Do đó f
 xdx  f
 xdx  f
 xdx  336  39. Vậy I  39. 0 0 1
Chọn đáp án D.
Câu 16: Cho hàm số y  f (x) liên tục trên [1; 2] có đồ thị như hình vẽ dưới đây: 2
Biết S , S có diện tích lần lượt là 2 và 6. Tích phân (x  1) f (  x d ) x  bằng 1 2 1  A. 2. B. 12. C. 6. D. 4. Lời giải: u
  x  1 du  dx 2 2 2 Đặt 
 (x  1) f (x d
) x  (x  1) f (x)  f   xdx dv  f (  x d ) x  v   f (x) 1  1  1 
 3 f (2)  0 f ( 1
 )  (S  S )  3.0  (6  2)  4.  2 1
Chọn đáp án D. 1
Câu 17: Cho hàm số f x liên tục trên thỏa mãn f 2x  3 f x , x  . Biết rằng f
 xdx 1. Tính 0 2 I  f  xdx . 1 A. I  5. B. I  6. C. I  3. D. I  2. Lời giải: 1 1 1 1 1
Ta có: 3  3.1  3. f xdx  3 f xdx  f 2xdx 
f 2xd2x, x       . 2 0 0 0 0
Đặt 2x  t  d2x  dt , với x  0  t  0 ; x  1  t  2 . 1 1   f  x 2 2 1 1 3 2 d 2x 
f tdt 
f xdx , x     
(do hàm số f x liên tục trên ). 2 2 2 0 0 0 2 1 2
 f xdx  6, x   
 f xdx  f xdx  6, x     . 0 0 1 2 2
 1 f xdx  6, x   
 f xdx  5, x    . 1 1
Chọn đáp án A.
Câu 18: Cho hàm số y  f x xác định trên  \ 
0 và thỏa mãn f x  xf x 2  3x , x
  và f 2  8 .
Viết phương trình tiếp tuyến của đồ thị hàm số y  f x tại giao điểm với trục hoành.
A. y  x  1.
B. y  2x  4. C. y  4 . x
D. y  6x  12. Lời giải:  
Ta có: f x  xf x 2
 x  xf x 2
 x  xf x 2 dx  x dx  xf  x 3 3 3 3  x  C x 
Vì f 2  8 nên C   f x 3 8 8  . x x 
Gọi M là giao điểm của đồ thị hàm số f x 3 8 
với trục hoành, suy ra M 2;0 x
pttt : y  0  f  2
 x  2  6
 x  2  0  6  x  12.
Chọn đáp án D.
Câu 19: Cho hàm số y  f x liên tục trên 0;1   và thỏa mãn 2
x f x  f   x 4 1
 2x  x . Tính tích 1 phân I  f  xd .x 0 1 3 2 4 A. I  . B. I  . C. I  . D. I  . 2 5 3 3 Lời giải: 2 4
Từ giả thiết, thay x bằng 1  x ta được 1  x f 1  x  f x  21  x  1  x   2
x  x   f   x  f x 2 3 4 2 1 1
 1 2x  6x  4x  x . 1 Ta có 2
x f x  f   x 4
 x  x  f   x 4 2 1 2 1
 2x  x  x f x.
Thay vào 1 ta được:  2 x  x   4 2
 x  x  x f  x  f  x 2 3 4 2 1 2
 1 2x  6x  4x  x   2 3 4
 x  x  x  f x 6 5 3 2 1 2
 x  2x  2x  2x  1   2 3 4
 x  x  x  f x   2  x  2 3 4
 x  x  x   f x 2 1 2 1 1 2  1 x . 1 1 1  1  2 Vậy I  f
 xdx   2 1  x d 3
x  x  x   
.  Chọn đáp án C.  3  3 0 0 0    Câu 20: Cho hàm số f x có đạo hàm liên tục trên 0;   thỏa mãn  2      2 f 0 2  0,  f   x 2 2
 dx  sin xf  
xdx  . Tính f  xd .x 4 0 0 0   A. . B. . C. 2 . D. 1 . 4 2 Lời giải:    2  2  sin xf 
xdx  cosxf  x 2 2   cos xf   
xdx. Suy ra cosxfxdx   . 0 4 0 0 0    2 2 2 1  cos 2x
 2x  sin 2x   Hơn nữa ta tính được 2 cos xdx  dx       . 2  4  4 0 0 0     2 2 2 2 2 2 Do đó  f 
 x dx  2. cosxf   x 2
dx  cos xdx  0   f  
 xcosx dx  0  . 0 0 0 0
Suy ra f x  cos x , do đó f x  sin x  C . Vì f 1  0 nên C  0 .   2 2 Ta được f
 xdx  sinxdx 1 
Chọn đáp án D. 0 0
_________________HẾT_________________
Huế, ngày 07 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông TÝch ph©n _ Hµm Èn
PHIẾU ÔN TẬP SỐ 04 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI 3 x
Câu 1: Cho hàm số f (x) có f (2)  0 , f (
 x)  ln(x 1)  x
 1. Giá trị f (x)dx  thuộc khoảng nào x 1 2 sau đây? A. ( ; 1) . B. (2; 4) . C. (1; 2) . D. (1;1) . 1
Câu 2: Cho hàm số f  x liên tục trên  thỏa mãn f  x  x  , x 0; và f   1  1. Giá trị x
nhỏ nhất của f 2 là 5 A. 2 . B. 4 . C.  ln 2 . D. 3 . 2  4  
Câu 3: Cho hàm số y  f  x có f 0  1và f  x 3
 tan x  tan x, x   . Biết  d   a f x x với b 0 a, b 
. Khi đó hiệu b  a bằng A. 0 . B. 12 . C. 4  . D. 4 .
Câu 4: Cho hàm số y  f  x  có đạo hàm liên tục trên
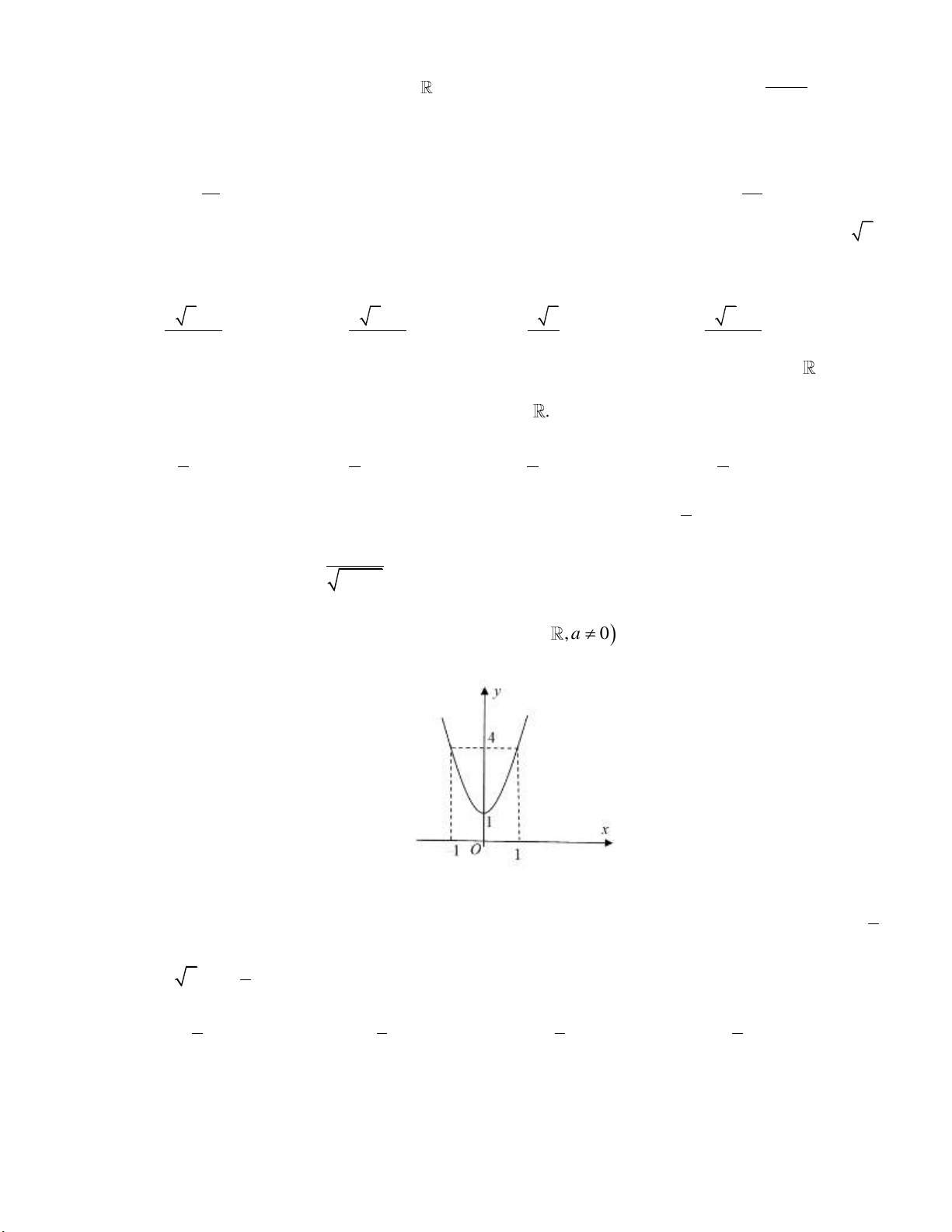
và có đồ thị như hình vẽ bên dưới: 2 4 Giá trị của f (
 x  2)dx  f (x  2)d   x bằng 0 0 A. 2 B. - 4. C. 6 D. 4 Câu 5: Cho hàm số
y  f  x liên tục trên và thỏa mãn 1
sin xf cos x  cos xf sin x 1 3
 sin 2x  sin 2x với mọi x  . Tính tích phân I  f  xdx . 2 0 1 2 1 A. 1. B. . C. . D. . 6 3 3
Câu 6: Cho hàm số y  f  x có đạo hàm liên tục trên
thỏa mãn f ' x  .
x f  x  0 ,
f  x  0, x 
và f 0  1. Giá trị của f  2  bằng 1 A. e . B. . C. 2 e . D. e . e 7 3 3
Câu 7: Cho hàm số f  x liên tục trên
thỏa  f xdx 10 và  f xdx  6 . Tính I  f 3 2xd .  x 0 0 2  A. 16. B. 3. C. 15. D. 8. 1 2
Câu 8: Cho f  x liên tục trên và thỏa mãn f 2  16 , f
 2xdx  2. Tính 
 xf xd .x 0 0 A. 30 . B. 28 . C. 36 . D. 16 .    1   
Câu 9: Cho hàm số y  f  x có đạo hàm liên tục trên 0; 
 thỏa f sin x  , x   0;   và  2  3 cos x  2  3  1  3 5 f    . Khi đó,  d
 f x x bằng  2  3 1 2 5 3  8 8  5 3 3 3 A. . B. . C. . D.  . 10 10 10 10 1
Câu 10: Cho hàm số f x xác định trên \  thỏa mãn f x 2 
, f 0  1 và f 1  2 . Giá trị 2  2x  1 biểu thức f  1
   f 3 bằng A. 4  ln15 . B. 2  ln15 . C. 3  ln15 . D. ln15 . 6
Câu 11: Cho hàm số f  x liên tục trên đoạn 0; 
1 và thỏa mãn f  x 2  6x f  3 x   . Giá trị 3x 1 1  d  f x x bằng 0 A. 2 . B. 4 . C. 6 . D. 1  . 2
Câu 12: Cho hàm số y  f  x có đạo hàm liên tục trên 0; 
1 , thỏa mãn  f  x  f  x 2 ' 4  8x  4 , 1 x  0;  1 và f   1  2 . Tính  d .  f x x 0 4 1 21 A. . B. . C. . D. 2 . 3 3 4 Câu 13: Cho hàm số
y  f  x xác định và liên tục trên \   0 thỏa mãn: 2 2 2
x f  x  2x  
1 f  x  xf  x 1 x   \ 
0 đồng thời f   1  2  . Tính  d .  f x x 1 1 3 ln 2 3 ln 2 A. ln 2 . B. ln 2 . C. . D. 1 . 2 2 2 2 2  2
Câu 14: Cho hàm số f  x có f  x  f x 2
 cos x cos 2x, x
  . Khi đó  f xdx bằng   2 14 28 14 30 A. . B. . C. . D. . 15 15 30 14
Câu 15: Cho hàm số f  x đồng biến trên
, có f  x  f  x 2  x x     x 2 cos .cos 2 4 2 cos .cos 2x   , 
x  và f 0  0. Khi đó f
 xdx bằng 0 242 242 2 149  225 2 242   A. 2  . B. . C. . D. . 225 225 225 225    Câu 16: Cho hàm f : 0;    là hàm liên tục thỏa mãn điều kiện:  2    2  2    
f x2  2 f xsin x  cos x dx  1    . Tính f  xdx . 2 0 0     2 2 2 2 A. f
 xdx  1. B. f
 xdx 1. C. f
 xdx  2. D. f
 xdx  0. 0 0 0 0
Câu 17: Cho hàm số f  x có đạo hàm liên tục và không âm trên 1;4 đồng thời thỏa mãn điều kiện 4
x  xf  x   f  x 2 2 '    và f   3 1  . Tính  d .  f x x 2 1 1186 2507 848 1831 A. . B. . C. . D. . 45 90 45 90 2
Câu 18: Cho hàm số y  f  x liên tục trên thoả mãn ( ) 2 . ( )     x f x x f x e , x 
và f (0)  0 . Tính f (1) . 1  1 1 A. f (1)  . B. f (1)  . C. f (1)  . D. 2 f (1)  e . e 2 e e
Câu 19: Cho hàm số y  f  x có đạo hàm liên tục trên thỏa mãn f  3 x  3x  
1  3x  2 với mọi 5 x  . Tính . x f   xd .x 1 17 5 33 29 A. . B. . C. . D. . 4 4 4 4 2 2  f x   
Câu 20: Cho hàm số f  x thỏa mãn f  x  0 và f  x  f  x     x  0  ;1 . Biết x 2 e . . x x  x  1  1 f   
, khẳng định nào sau đây đúng?  2  2  1  1 1  1  1  1  1 1  1  1 A. f    . B.  f    . C. f    . D.  f    .  5  4 5  5  4  5  6 6  5  5
_________________HẾT_________________
Huế, ngày 07 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông TÝch ph©n _ Hµm Èn
PHIẾU ÔN TẬP SỐ 04
LỜI GIẢI CHI TIẾT 3 x
Câu 1: Cho hàm số f (x) có f (2)  0 , f (
 x)  ln(x 1)  x
 1. Giá trị f (x)dx  thuộc khoảng nào x 1 2 sau đây? A. ( ; 1) . B. (2; 4) . C. (1; 2) . D. (1;1) . Lời giải:  x  x x Ta có f (x)  ln(x 1) 
dx  x ln(x 1)  dx  C 
dx  x ln(x 1)  C      x 1 x 1 x 1
Lại có f (2)  0  2 ln1 C  0  C  0  f (x)  x ln(x 1) 3 3 3 3 2 2 3 2
 x 1 x 1 x 1 1
Lúc đó f (x)dx  x ln(x 1)dx  ln(x 1)d       .ln(x 1)  . dx   2  2 2 x 1 2 2 2 2 2 3 3 2 x 1  x x  7  4ln 2  dx  4 ln 2   
   4ln 2  (1;2) 2  4 2  4 2 2
Chọn đáp án C. 1
Câu 2: Cho hàm số f  x liên tục trên  thỏa mãn f  x  x  , x 0; và f   1  1. Giá trị x
nhỏ nhất của f 2 là 5 A. 2 . B. 4 . C.  ln 2 . D. 3 . 2 Lời giải: 2 2 1  1 
Ta có f  x  x  , x
 0;  f 
 xdx  x dx   x  x  1 1 2  
 f    f   2 x 3 2 1  
 ln x    ln 2  f   5 2   ln 2  2  2 2 1 5
Vậy giá trị nhỏ nhất của f 2 là  ln 2 . 2
Chọn đáp án C.  4  
Câu 3: Cho hàm số y  f  x có f 0  1và f  x 3
 tan x  tan x, x   . Biết  d   a f x x với b 0 a, b 
. Khi đó hiệu b  a bằng A. 0 . B. 12 . C. 4  . D. 4 . Lời giải: 1
Có f  x  f 
 xdx  tan x   2 tan x   1 dx  tanx d  tan x 2
 tan x  C 2 1 1 1 1  1 
Do f 0  1 nên C  1  f  x 2
 tan x 1   2 tan   1   1   2 2 2 2 2  cos x      4   4 1  1  1 4 1    4  f  x 4 1 2 dx  tan x 1 dx    1 dx  
tan x  x  1       2  2 2  cos x  2 2  4  8 0 0 0 0
Vậy a  4;b  8  b  a  4 .
Chọn đáp án D.
Câu 4: Cho hàm số y  f  x  có đạo hàm liên tục trên và có đồ thị như hình vẽ bên dưới: 2 4 Giá trị của f (
 x  2)dx  f (x  2)d   x bằng 0 0 A. 2 B. - 4. C. 6 D. 4 Lời giải: 2 4 2 4 Ta có f (
 x  2)dx  f (x  2)dx  f (x  2)d(x  2)  f (x  2)d(x  2)     . 0 0 0 0 2
) I  f (x  2)d(x  2). 
Đặt: t  x  2 . Đổi cận: x  0  t  2 ; x  2  t  4 0 4 I  f (  t)dt  f 
t 4  f (4) f (2)  4 2  2. 2 2 4 ) K  f 
 x 2dx 2. Đặt: u  x 2 . Đổi cận: x  0  u  2 ; x  4  u  2. 0 4 2 2 K  f (
 x  2)d(x  2)  f (u)du  f (u)  f (2)  f ( 2  )  2 ( 2  )  4   . 2  0 2  2 4 Vậy f (
 x  2)dx  f (x  2)dx  2  4  6   . 0 0
Chọn đáp án C. Câu 5: Cho hàm số
y  f  x liên tục trên và thỏa mãn 1
sin xf cos x  cos xf sin x 1 3
 sin 2x  sin 2x với mọi x  . Tính tích phân I  f  xdx . 2 0 1 2 1 A. 1. B. . C. . D. . 6 3 3 Lời giải:   2 2  1  Ta có: sin xf  
cos x cos xf sin x 3  dx  sin 2x  sin 2x dx     2  0 0    2  xf   x 2 x  xf   x 2 1 sin cos d cos sin dx  sin 2x   2
1 cos 2xdx 2 0 0 0  2
* Tính I  sin xf cos x d . 
x Đặt t  cos x  dt   sin xdx  dt  sin xdx 1   0 
Đổi cận: x  0  t  1 ; x   t  0 . 2 1 1 Ta có: I  f t dt  f x dx   . 1     0 0  2 1
* Tương tự , ta tính được: I  cos xf sin x dx  f x dx   . 2     0 0   2 2 1 1 * Tính I  sin 2x   2
1 cos 2x dx     2
1 cos 2x d cos 2x 3    2 4 0 0  2 1  1  1 4  1 4 2 3  
cos 2x  cos 2x   .  .    . 4  3  4 3 4 3 3 0    2 2 2 1 Do đó sin xf 
cos xdx  cos xf 
sin xdx  sin 2x   2
1 cos 2x dx trở thành: 2 0 0 0 1 1 f  x 2 x   f x 1 2 d dx    . 3 3 0 0
Chọn đáp án D.
Câu 6: Cho hàm số y  f  x có đạo hàm liên tục trên
thỏa mãn f ' x  .
x f  x  0 ,
f  x  0, x 
và f 0  1. Giá trị của f  2  bằng 1 A. e . B. . C. 2 e . D. e . e Lời giải:
Từ f ' x  .
x f  x  0, f  x  0 x   ta có: f ' x f ' x 2 2 2 2 2   x x dx  d
x x  ln f x    ln       f x  2  f  x  1  f x 2 0       0 0 0 0
 ln  f  2  ln f 011 f  2  e.
Chọn đáp án A. 7 3 3
Câu 7: Cho hàm số f  x liên tục trên
thỏa  f xdx 10 và  f xdx  6 . Tính I  f 3 2xd .  x 0 0 2  A. 16. B. 3. C. 15. D. 8. Lời giải:  3 3 3  2x , x   3 2 3 2 Ta có 3  2x   . Nên I 
f 3  2x dx 
f 3  2xdx  f 2x  3dx  I     I . 3 1 2
2x 3 , x  2  2  3  2 2 +) Tính I 1 3
Đặt t  3  2x  dt  2d
 x . Với x  2  t  7 ; x   t  0 . 2 0 7 7 1 1 1 I   f t dt  f t dt  f x dx  5    . 1       2 2 2 7 0 0 +) Tính I 2 3
Đặt t  2x  3  dt  2dx . Với x 
 t  0 ; x  3  t  3 . 2 3 3 1 1 I  f t dt  f x dx  3   2     2 2 0 0 3 Vậy I 
f 3  2x dx  5  3  8  . 2 
Chọn đáp án D. 1 2
Câu 8: Cho f  x liên tục trên và thỏa mãn f 2  16 , f
 2xdx  2. Tính 
 xf xd .x 0 0 A. 30 . B. 28 . C. 36 . D. 16 . Lời giải: 1 1 2 1 1 2 Ta có 2  f
 2xdx  f
 2xd2x  f
 tdt  f
 xdx  4. 2 2 0 0 0 0 u   x  du  dx  Đặt    . dv  f   xdx v   f  x 2 2 2 Khi đó xf 
 xdx  .xf x  f
 xdx  2.164  28. 0 0 0
Chọn đáp án B.    1   
Câu 9: Cho hàm số y  f  x có đạo hàm liên tục trên 0; 
 thỏa f sin x  , x   0;   và  2  3 cos x  2  3  1  3 5 f    . Khi đó,  d
 f x x bằng  2  3 1 2 5 3  8 8  5 3 3 3 A. . B. . C. . D.  . 10 10 10 10 Lời giải: 1 1   
+) Ta có: f 'sin x 
 cos x f 'sin x  x   0; 
 . Lấy nguyên hàm hai vế ta 3 2 cos x cos x  2  được: xf    x 1 cos sin dx  dx 
f  sin x d sin x  tan x  c   2     cos x   
 f sin x  tan x  c   1 , x   0;    2    1  3 3 3 +) Thay x  vào   1 ta có: f   c  
 c  c  0  f  
sin x  tan x. 6  2  3 3 3    Đặt 2 2
u  sin x  cos x  1  sin x  1  u vì cos x  0 x   0;   .  2  3 3 3 5 5 5 u u
Khi đó có: f u   f
 xdx  f
 udu  du  2 2 1  u 1 1 1 1  u 2 2 2 1 3 3 4 Đặt 2 2 2
t  1  u  t  1  u  udu  tdt  và u   t  ;u   t  2 2 5 5 3 3 3 4 4 5    f  x 5 dx  f  u 5 5 5 u tdt 5 3 8 du  du   dt     . 2  t 10 1 1 1 1 u 3 3 2 2 2 2 2
Chọn đáp án A. 1
Câu 10: Cho hàm số f x xác định trên \  thỏa mãn f x 2 
, f 0  1 và f 1  2 . Giá trị 2  2x  1 biểu thức f  1
   f 3 bằng A. 4  ln15 . B. 2  ln15 . C. 3  ln15 . D. ln15 . Lời giải: 2 1
Cách 1. Ta có: f 
 xdx 
dx  2. ln 2x  1  C  ln 2x  1  C.  2x1 2
Do đó f x  ln 2x  1  C .   x  1 ln 2 1  C , x   1 
Suy ra: f x 2   .    x 1 ln 1 2  C ,x  2  2 1
Với x  0  , ta có: f 0  1  ln1  2.0  C  1  C  1. 2 2 2 1
Với x  1  , ta có: f 1  2  ln2.1  1  C  2  C  2. 2 1 1   x  1 ln 2 1  2 , x  
Khi đó: f x 2   .    x 1 ln 1 2  1,x   2
 f 1  ln 1   2.  1 1 1  ln 3  Suy ra:  Vậy: f  1
   f 3  1 ln3  2  ln5  3  ln15.  f        . 3 ln 2.3 1  2  2  ln 5 0 0
Cách 2. Ta có f xdx  f 0  f   1  ln 2x  1
 f 0  f  1     f  1    1 ln3. 1  1  3 3 Mà f 
 xdx  f 3 f  1  ln 2x 1  f 3 f 1  f 3  2  ln5. 1 1 Vậy f  1
   f 3  3  ln3  ln5  3 ln15.
Chọn đáp án C. 6
Câu 11: Cho hàm số f  x liên tục trên đoạn 0; 
1 và thỏa mãn f  x 2  6x f  3 x   . Giá trị 3x 1 1  d  f x x bằng 0 A. 2 . B. 4 . C. 6 . D. 1  . Lời giải: 1 1 1 6
Từ giả thiết ta có f  x 2 dx  6x f   3xdx dx    * . 3x 1 0 0 0 1  Xét 2 I  6x f   3xdx 0 Đặt 3 2
t  x  dt  3x dx . Với x  0  t  0 ; x  1  t  1 1 1 1 Suy ra 2 I  6x f 
 3xdx  2f
 tdt  2f  xdx . 0 0 0 1 1  1 6 Xét dx  4d 
  3x1 4 3x1  4. 0 3x 1 0 0 1 1 1   *  f
 xdx  2 f
 xdx4  f
 xdx  4 0 0 0 1 Vậy f
 xdx  4. 0
Chọn đáp án B. 2
Câu 12: Cho hàm số y  f  x có đạo hàm liên tục trên 0; 
1 , thỏa mãn  f  x  f  x 2 ' 4  8x  4 , 1 x  0;  1 và f   1  2 . Tính  d .  f x x 0 4 1 21 A. . B. . C. . D. 2 . 3 3 4 Lời giải: 1 1 1 2 20 20
Ta có  f 'x dx   2
8x  4  4 f  xdx   4 f
 xdx  4I 3 3 0 0 0 u   f (x)
du  f '(x)dx   
Đặt dx  dv v  x 1 1 1
I  xf (x)  xf '
 xdx  2 xf '  xdx Nên 0 0 0 1 1 1   2 20 20
Suy ra  f ' x dx   42  xf '
 xdx  8 4 xf '  xdx 3 3 0  0  0 1 1   1 2
f  x2dx  xf  x 4 ' 4 ' dx 
 0   f 'x 2x  0  f 'x  2x  f x 2  x  C 3 0 0 0 1 1 4 Mà f  
1  2  C  1. Vậy  f x 2
dx  (x 1)dx  .  3 0 0
Chọn đáp án A. Câu 13: Cho hàm số
y  f  x xác định và liên tục trên \   0 thỏa mãn: 2 2 2
x f  x  2x  
1 f  x  xf  x 1 x   \ 
0 đồng thời f   1  2  . Tính  d .  f x x 1 1 3 ln 2 3 ln 2 A. ln 2 . B. ln 2 . C. . D. 1 . 2 2 2 2 2 Lời giải: Ta có: 2 2
x f  x  2x  
1 f  x  xf  x 1 2 2
 x f x  2xf x  f x  xf x 1 2 2  2
x f  x  2xf  x 1  xf  x  f  x  xf
  x 1  xf  
x f x * .
Xét xf  x 1  0    1 f x    f  
1  1 (không thỏa mãn). x 
xf  x  f x
xf x 1  
Xét xf  x 1  0 , ta có       *     1. xf x 1 2 1   xf x 2 1   
xf x 1   1        x  C . xf x dx dx 2 1   xf  x 1 1 1
Cho x  1 ta được :     
1 C  C  0 . f   1 C 1 1 1 2  1 1 1 1  
   x  xf x 1
1   (vì x  0 )  f x    xf x 1 x 2 x x 2 2  2 1 1  1 2 Vậy f
 xdx    dx     1 ln x    ln 2 . 2  x x  1 x 2 1 1 1
Chọn đáp án A.  2
Câu 14: Cho hàm số f  x có f  x  f x 2
 cos x cos 2x, x
  . Khi đó  f xdx bằng   2 14 28 14 30 A. . B. . C. . D. . 15 15 30 14 Lời giải:   2 0 2 Ta có f
 xdx  f
 xdx  f  xdx .   0   2 2 0 Với J  f
 xdx ta đặt x  t  dx  dt.   2 Đổi cận :   0 2 2 Khi đó J  f
  tdt  f
  tdt  f
 xdx.  0 0 2      2  f  x 2 dx  f  x 2 dx  f  x 2 dx   f
  x f x 2 2 d
 x  cos x cos 2 d x x   .  0 0 0 0  2   2  cos x  12sin x 2 2 2 dx    2 4
1 4 sin x  4 sin xd sin x . 0 0   4 4  4 4 7 14 3 5
 sin x  sin x  sin x 2 1      .  3 5  3 5 15 30 0
Chọn đáp án C.
Câu 15: Cho hàm số f  x đồng biến trên
, có f  x  f  x 2  x x     x 2 cos .cos 2 4 2 cos .cos 2x   , 
x  và f 0  0. Khi đó f
 xdx bằng 0 242 242 2 149  225 2 242   A. 2  . B. . C. . D. . 225 225 225 225 Lời giải:
Ta có: f  x  f  x 2  x x     x 2 cos .cos 2 4 2 cos .cos 2x     f    x 2   f   x 2 2 .cos .
x cos 2x  4  2 cos . x cos 2x   f    x 2    f   x 2 2 4 .cos .
x cos 2x  2 cos . x cos 2x  0   f 
  x    f     x 2 2 .  2  cos . x cos 2 . x  f  
 x  2  0    f 
  x    f   x 2 2 .  2  cos .
x cos 2x  0  
 f  x  2L  
(vì hàm số đồng biến trên ).  f    x 2  2  cos .
x cos 2x tm 1 cos 4x cos x cos 5x cos 3x
Với f  x 2  2  cos .
x cos 2x  2  cos . x  2    2 2 4 4     cos x cos 5x cos 3x  sin x sin 5x sin 3x f x  2    dx  2x     C   .  2 4 4  2 20 12 x x x
Vì f 0  0  C  0 .Do đó f  x sin sin 5 sin 3  2x    . 2 20 12     sin x sin 5x sin 3x   cos x cos 5x cos 3x  242 Khi đó f  x 2 2 dx  2x    dx  x          .  2 20 12   2 100 36  225 0 0 0
Chọn đáp án A.    Câu 16: Cho hàm f : 0;    là hàm liên tục thỏa mãn điều kiện:  2    2  2    
f x2  2 f xsin x  cos x dx  1    . Tính f  xdx . 2 0 0     2 2 2 2 A. f
 xdx  1. B. f
 xdx 1. C. f
 xdx  2. D. f
 xdx  0. 0 0 0 0 Lời giải:    2 2 2 2  1  
Có sin x  cosx dx  1 sin2xdx  x  cos2x     1 .  2  2 0 0 0   2 2 2 2 2  
Khi đó:   f x  2 f xsin x  cosx  sin x  cosx dx  0   f  
 xsinx cosx dx  0   0 0
 f x  sin x  cosx  0  f x  sin x  cosx .   2 2  Vậy f
 xdx  sinx cosxdx  sinx cosx 2  0 . 0 0 0
Chọn đáp án D.
Câu 17: Cho hàm số f  x có đạo hàm liên tục và không âm trên 1;4 đồng thời thỏa mãn điều kiện 4
x  xf  x   f  x 2 2 '    và f   3 1  . Tính  d .  f x x 2 1 1186 2507 848 1831 A. . B. . C. . D. . 45 90 45 90 Lời giải: 1;4
Vì có đạo hàm liên tục và không âm trên nên Ta có :
x  xf  x   f  x 2 2 '   
Vì f  x có đạo hàm liên tục và không âm trên 1;4 f  x  
 x   1 2 f x  x  1 2 f x      f x xdx 1 2
 1 2 f x 2 3 
x  C . Do f   3 1  nên suy ra  f   2 4 1 2 1 
 C  C  . 3 2 3 3
 1 2 f x 2 4 3  x  . 3 3
1 2 f x 4
  x  22  f x 2   x  22 1 2 8 7 3 3
  f x 3 3  x  x  9 9 2 9 9 18 4 4    f  x 2 8 7 1186 3 3 dx  x  x  dx    .  9 9 18  45 1 1
Chọn đáp án A. 2
Câu 18: Cho hàm số y  f  x liên tục trên thoả mãn ( ) 2 . ( )     x f x x f x e , x 
và f (0)  0 . Tính f (1) . 1  1 1 A. f (1)  . B. f (1)  . C. f (1)  . D. 2 f (1)  e . e 2 e e Lời giải: 2  f x x f x   x '( ) 2 . ( ) 1 Ta có x
  : f '(x)  2 .
x f (x)  e   1 f (x) '  1   2 2 2 x x x e e  e  1 1 1 1 1 Suy ra f (x)
dx  1  f (1)  f (0)
1 ef (1) 1 f (1)   . 2 2 2 0 x 1  0 e e e e
Chọn đáp án C.
Câu 19: Cho hàm số y  f  x có đạo hàm liên tục trên thỏa mãn f  3 x  3x  
1  3x  2 với mọi 5 x  . Tính . x f   xd .x 1 17 5 33 29 A. . B. . C. . D. . 4 4 4 4 Lời giải: Ta có f  3 x  3x  
1  3x  2 với x 
x  0  f  
1  2; x  1  f 5  5
Đặt u  x  du  dx ; dv  f  x dx , ta chọn v  f  x 5 5 5 5 Suy ra . x f  
xdx   .xf  x  f 
 xdx  23 f  xdx 1 1 1 1 Đặt 3
t  x  x   t   2 3 1 d 3 x  
1 dx  f t   3x  2
Đổi cận x  0  t  1; x  1  t  5 5 1 1 5 59 59
Do đó f t dt  3x  2 2
3x  3dx  3  3 2
3x  2x  3x  2dx     hay f
 xdx  . 4 4 1 0 0 1 5 59 33 Vậy . x f 
 xdx  23  . 4 4 1
Chọn đáp án C. 2 2  f x   
Câu 20: Cho hàm số f  x thỏa mãn f  x  0 và f  x  f  x     x  0  ;1 . Biết x 2 e . . x x  x  1  1 f   
, khẳng định nào sau đây đúng?  2  2  1  1 1  1  1  1  1 1  1  1 A. f    . B.  f    . C. f    . D.  f    .  5  4 5  5  4  5  6 6  5  5 Lời giải: 2 2  f x    x   x
e f x  e . f  x 2
Ta có: f  x  f  x     x  0  ;1    x 2 e . . x x  x  f   x 2 2  x x  x    x  e  2  x x      e 2 e 2        dx  dx   dx     1 f   x 2  x x  x f   x 2   f  x x x x  1 2 x 1 x 2  1 1 1 Xét I  dx  . Đặt 2 t 
1  t  1  2tdt   dx 1 2 x x x 2 x 1 x 4  t 1 x x  e 1 e I  dt  4
 t  C  4  1  C  Từ   1   4 
1  C  f x  t x f  x   x 1 4  1  C x 1 1 2  1  1 e 1 x e Do 2 f  
  C  2e  2  
 f  x  .  2  2 4   C 2 1 1 2 4  1  2e  2 x  1  1 Vậy f  0,33    .  5  4
Chọn đáp án A.
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông TÝch ph©n _ Hµm Èn
PHIẾU ÔN TẬP SỐ 05 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI 1 1
Câu 1: Cho hàm số f  x thỏa mãn x  
1 f ' xdx  10 và 2 f  
1  f 0  2 . Tính I  f  xdx. 0 0 A. I  8 . B. I  8 . C. I  1. D. I  12 .
Câu 2: Cho hàm số f x  0 thỏa mãn điều kiện f x   x    f  x 2 2 3  và f   1
0   . Biết rằng tổng 2   a a
f 1  f 2  f 3  ...  f 2017  f 2018  với a,b , b  0 và là phân số tối giản. Khẳng b b
định nào sau đây đúng? a a A.  1  . B.  1 .
C. a  b  1010 .
D. b  a  3029 . b b
Câu 3: Cho hàm số f (x) thỏa mãn f (1)  4 và x  2 2 2 3 f (  x)  2 .
x f (x); f (x)  0, x   . Giá trị của f (3) bằng A. 9 . B. 6 . C. 2019 . D. 12 .
Câu 4: Cho hàm số f (x) liên tục trên
và thỏa mãn f (x)  f (x)  2  2cos 2x, x   . Tính 3 2 I  f (x)d  x . 3  2 A. I  6 . B. I  0 . C. I  2 . D. I  6 .
Câu 5: Cho hàm số y  f (x) liên tục trên \ 0;  1
 , f (1)  2ln 2 và 2
x(x 1). f (
 x)  f (x)  x  . x Giá
trị f (2)  a  b ln 3 , với a,b  , a,b là phân số tối giản. Tính 2 2
a  b . 25 13 5 9 A. . B. . C. . D. . 4 4 2 2 Câu 6: Cho hàm số
f  x có đạo hàm liên tục trên đoạn 0; 2 và thỏa mãn 4  
f  x  f   x   2 2
3 x  2x, x
 0;2 . Biết f 2  10 , tính   d .  x I xf   x  2  0 A. 72. B. 96. C. 32. D. 88. 2 5 f  x
Câu 7: Cho hàm số f  x liên tục trên và thỏa mãn f
  2x 5  xdx 1, dx  3  . Tính 2 x 2  1 5  d .  f x x 1 A. 15 . B. 2  . C. 13 . D. 0 .     2
Câu 8: Cho hàm số f  x có f  0  
và f  x 2  sin .
x sin 2x, x   . Khi đó f
 xdx bằng  2  0 104 121 104 167 A.  . B. . C. . D. . 225 225 225 225 1 2
Câu 9: Cho hàm số y  f  x liên tục trên
thỏa  f xdx 1 và  f xdx 16 . Tính 0 0 1  2 I  f 4x 2 dx  
 f sin xcos d x . x 0 0 31 33 A. I  5. B. I  . C. I  9. D. I  . 2 2
Câu 10: Cho hàm số f  x có đạo hàm f  x liên tục trên
và thỏa mãn điều kiện f  x  2xf  x , 1
x  . Biết f 0  2 và f x  0, x   . Tính 3 I  x f
 xdx. 0 1 e A. I  1. B. I  e . C. I  .
D. I  e 1. 2
Câu 11: Cho hàm số f  x liên tục trên thỏa mãn
f  x  f   x 2 7 4 4
 2020x x  9 ,x  .Tính 4
I   f xd .x 0 197960 7063 197960 2020 A. . B. . C. . D. . 99 3 33 11 3
Câu 12: Cho hàm số f  x liên tục, có đạo hàm trên
thỏa mãn x   f  x  
f  x  3  0, x  . 7 Tính I  xf   xd .x 1  5 3 9 51 A. . B. . C. . D. . 4 4 4 4 1 2
Câu 13: Cho hàm số f (x) có f (  x) 
, x  0 và f (1)  2 2 . Khi đó f (x)dx  bằng
(x 1) x  x x 1 1 10 10 4 2 10 14 A. 4 3  . B. 4 3  . C. 4 3   . D. 4 3  . 3 3 3 3 3 4
Câu 14: Cho hàm số y  f  x có đồ thị như hình vẽ, biết 
 f x dx 12.Tính m  f 2 . 1 A. 6 . B. 5 . C. 12 . D. 3 . x
Câu 15: Cho hàm số y  f  x liên tục trên
và thỏa mãn f (2  x)  f (x)  f (1 x)  2 1 . Biết tích x 5 phân I 
f (x)dx  . a ln b 
( a là số hữu tỉ, b là số nguyên tố). Hãy chọn mệnh đề đúng. 0 13 26 A. ab  . B. ab  1 . C. ab  13 . D. ab  . 2 3
Câu 16: Cho hàm số f (x) liên tục trên đoạn 0; 2 
 và thỏa mãn điều kiện 3 f (x)  7 f (2  x)  x , 1 x   0;2 
 . Tính f (x d ) x  . 0 7 2  6 4 2  2 4 2 7 2  5 A. . B. . C. . D. . 30 15 15 30 Câu 17: Cho hàm số
y  f  x xác định và liên tục trên thỏa 2 mãn: 3 f  x 2
 xf x   2
x   f  x 3 3 3 1
 x  0, x  . Tính I   f xd .x 0 3 5 3 5 A.  . B. . C. . D.  . 4 4 4 4  1 
Câu 18: Cho hàm số y  f  x có đạo hàm liên tục trên khoảng K  ;    . Biết f   1  3 và  2  x
2 f  x  1 2x f  x  , x
  K . Giá trị f 2 gần với số nào nhất trong các số sau ? 2 x  3 A. 1, 2 . B. 1,1. C. 1. D. 1,3 .
Câu 19: Cho hàm số y  f  x 3 2
 ax  bx  cx  d,a,b,c,d  ,a  0 có đồ thị là C. Biết đồ thị C
đi qua gốc toạ độ và có đồ thị y  f ' x cho bởi hình vẽ.Tính giá trị H  f 4  f 2. A. H  45 . B. H  64 . C. H  51. D. H  58 . 1 2 9
Câu 20: Cho hàm số f  x có đạo hàm liên tục trên 0; 
1 và thỏa mãn f   1  1;  f 
 x dx  ;  5 0 1 1 f   x 2 dx  . Tính I  f  xd .x 5 0 0 3 1 3 1 A. I  . B. I  . C. I  . D. I  . 4 5 5 4
_________________HẾT_________________
Huế, ngày 07 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông TÝch ph©n _ Hµm Èn
PHIẾU ÔN TẬP SỐ 05
LỜI GIẢI CHI TIẾT 1 1
Câu 1: Cho hàm số f  x thỏa mãn x  
1 f ' xdx  10 và 2 f  
1  f 0  2 . Tính I  f  xdx. 0 0 A. I  8 . B. I  8 . C. I  1. D. I  12 . Lời giải:  u  x 1  du  dx 1 1 1 Đặt     x   
1 f ' x dx  (x 1). f  x  f  xdx dv  f   xdx v  f  x 0 0 0 1 1 1
 2 f (1)  f (0)  f
 xdx  2 f
 xdx 10  I  f
 xdx  8  . 0 0 0
Chọn đáp án A.
Câu 2: Cho hàm số f x  0 thỏa mãn điều kiện f x   x    f  x 2 2 3  và f   1
0   . Biết rằng tổng 2   a a
f 1  f 2  f 3  ...  f 2017  f 2018  với a,b , b  0 và là phân số tối giản. Khẳng b b
định nào sau đây đúng? a a A.  1  . B.  1 .
C. a  b  1010 .
D. b  a  3029 . b b Lời giải: f x
Ta có f x   x   2 2 3 f x   2x  3 2 f x f x      1 2  
 x  3x  C . Vì f   1
0    C  2 .
f xdx 2x 3dx 2 f x 2 1 1 1
Vậy f x      . x  
1 x  2 x  2 x  1
Do đó f    f    f     f   f   1 1 1009 1 2 3 ... 2017 2018     . 2020 2 2020 Vậy a  1009 
; b  2020 . Do đó b  a  3029 .
Chọn đáp án D.
Câu 3: Cho hàm số f (x) thỏa mãn f (1)  4 và x  2 2 2 3 f (  x)  2 .
x f (x); f (x)  0, x   . Giá trị của f (3) bằng A. 9 . B. 6 . C. 2019 . D. 12 . Lời giải: Vì 2 2 2 (x  3) f (  x)  2 .
x f (x); f (x)  0, x   nên 3 3 3 f (  x) 2x f (  x) 2x d 3 f (x) d( 2 x  3)    dx  dx       2 2 2 2 2 2 2 2 2 f (x) (x  3) f (x) (x  3) f ( ) x (x  3) 1 1 1 1 1 3 1 3 1 1 1 1 1 1 1 1              f (3)  12 . 2 f (x) 1 x  3 1 f (1) f (3) 4 12 4 f (3) 4 12
Chọn đáp án D.
Câu 4: Cho hàm số f (x) liên tục trên
và thỏa mãn f (x)  f (x)  2  2cos 2x, x   . Tính 3 2 I  f (x)d  x . 3  2 A. I  6 . B. I  0 . C. I  2 . D. I  6 . Lời giải: 3 2 Tính 
 f xd .x Đặt t  x  dt  dx 3  2 3 3 3 3  2  f  x 2 dx   f  t 2 dt  f  t 2 dt  f  xdx 3 3 3 3    2 2 2 2 3 3 3 3 2 2 2
 2I    f (x) f (x) 2 dx  2  2 cos 2xdx  2  4 cos xdx 
2 cos x dx  12    I  6 . 3 3     3 3   2 2 2 2
Chọn đáp án D.
Câu 5: Cho hàm số y  f (x) liên tục trên \ 0;  1
 , f (1)  2ln 2 và 2
x(x 1). f (
 x)  f (x)  x  . x Giá
trị f (2)  a  b ln 3 , với a,b  , a,b là phân số tối giản. Tính 2 2
a  b . 25 13 5 9 A. . B. . C. . D. . 4 4 2 2 Lời giải: x   \0;  1 ta có f (x) 2 2
(x  x). f (
 x)  f (x)  x  x  f (x)  1 x(x 1)  x f (x) x  x   x f (  x)    f (x).  2   x 1 (x 1) x 1  x 1 x 1 2  2  x  x Nên f (x). dx     dx do đó  x 1 x 1 1 1 2 1 2 2 1 2
f (2).  f (1).
 1 ln  (a  b ln 3)  (2ln 2)  1 ln 3 2 3 3 2 3  3 a  2 2  2 9 2 2
 a  b ln 3  1 ln 3  
 a  b  . 3 3 3  2 b   2
Chọn đáp án D. Câu 6: Cho hàm số
f  x có đạo hàm liên tục trên đoạn 0; 2 và thỏa mãn 4  
f  x  f   x   2 2
3 x  2x, x
 0;2 . Biết f 2  10 , tính   d .  x I xf   x  2  0 A. 72. B. 96. C. 32. D. 88. Lời giải: Cách 1: Ta có: 2   2 2 2
f  x  f 2  xdx  3
  2x 2xdx   f xdx   f 2 xd2 x  4 0 0 0 0 2 0 2 2
  f xdx   f tdt  4   f xdx   f xdx  4 0 2 0 0 2 2
 2 f xdx  4   f xdx  2 0 0 4 2 2  x    I  xf  dx  4 xf    
 xdx  4xf x 2   f xdx  42 f 2 2    88 0  2  0 0  0  Cách 2:
Xét f  x 2
 ax  bx  c a  0 ; f 2  4a  2b  c  1
f 2  x  a 2  x2  b 2  x 2
 c  ax  4a  b x  4a  2b  c
 f x  f 2  x 2 2
 ax  bx  c  ax  4a  b x  4a  2b  c
 f x  f 2  x 2
 2ax  4ax  4a  2b  2c2
Mà f  x  f   x   2 2
3 x  2x 3 Từ  
1 , 2 và 3 ta có hệ phương trình:  3
4a  2b  c  10 a    3  2  3 a   b   7  f  x 2
 x  7x 10 2  c  10  2
4a  2b  2c  0   4 2 2  x    I  xf  dx  4 xf    
 xdx  4xf x2  f
 xdx  42f 2 2    88 0  2  0 0  0 
Chọn đáp án D. 2 5 f  x
Câu 7: Cho hàm số f  x liên tục trên và thỏa mãn f
  2x 5  xdx 1, dx  3  . Tính 2 x 2  1 5  d .  f x x 1 A. 15 . B. 2  . C. 13 . D. 0 . Lời giải: 2 Xét: I  f
  2x 5  xdx . 2  2  x  x  5  x Đặt : 2 t 
x  5  x  dt   1dx   dx . 2 2  x  5  x  5 5 5 Với 2 t 
x  5  x   1 2  t 
 x  5  x  2 . 2  5  t x x 5 t  5 t  5  1,2 2 2 2 2
 2 x  5  t    x  5  . t t 2t 2 2 2t t  5 1  5   dt  
dx  dx   dt   1 dt   . 2 2 2 t  5 2t 2  t  Đổi cận: x 2  2 t 5 1 1 5 5 5  1   5  1  5  1 5 f t  I  f
 t.  . 1 dt  f t . 1 dt  f t dt  dt          . 2   2     2  2   t  2  t  2 2 t 5 1 1 1 5 5 5 5 1 5 f x 1 5
 I   f x   dx  dx  1 
f x dx  .3  f x dx  1  3.    2     2 2 x 2 2 1 1 1 1
Chọn đáp án C.     2
Câu 8: Cho hàm số f  x có f  0  
và f  x 2  sin .
x sin 2x, x   . Khi đó f
 xdx bằng  2  0 104 121 104 167 A.  . B. . C. . D. . 225 225 225 225 Lời giải: Ta có: f   x 3 2 x  x x x      2  x 2 x  x   4 2 d 4sin cos d 4 1 cos cos d cos
4 cos x  4 cos xd cos x 5 3 4 cos x 4 cos x    C . 5 3    x x Do f  0  
nên C  0 . Suy ra f  x 5 3 4 cos 4 cos   .  2  5 3    2 2 5 3 2   2 4 cos x 4 cos x  4 4  Vậy f
 xdx    dx  .   2 1 sin x  . 2 1 sin x d  sin x  5 3   5 3  0 0 0  3 5 3 2  4  2 sin x sin x  4  sin x  104   sin x     sin x     . 5   3 5  3  3  225  0
Chọn đáp án A. 1 2
Câu 9: Cho hàm số y  f  x liên tục trên
thỏa  f xdx 1 và  f xdx 16 . Tính 0 0 1  2 I  f 4x 2 dx  
 f sin xcos d x . x 0 0 31 33 A. I  5. B. I  . C. I  9. D. I  . 2 2 Lời giải: dt 1
Đặt t  4x  dt  4dx  dx 
; đổi cận: x  0  t  0; x   t  2 . 4 2 1 1 2 2 2 1 1 16 Khi đó: f
 4xdx  f
 tdt  f
 xdx   4. 4 4 4 0 0 0 
Đặt t  sin x  dt  cos xdx ; Đổi cận: x  0  t  0; x   t 1. 2  2 1 1 Khi đó: f
 sin xcosxdx  f
 tdt  f
 xdx 1. Vậy I 1 4  5. 0 0 0
Chọn đáp án A.
Câu 10: Cho hàm số f  x có đạo hàm f  x liên tục trên
và thỏa mãn điều kiện f  x  2xf  x , 1
x  . Biết f 0  2 và f x  0, x   . Tính 3 I  x f
 xdx. 0 1 e A. I  1. B. I  e . C. I  .
D. I  e 1. 2 Lời giải: f  x f  x df  x
Ta có: f  x  2xf  x       2x  dx  2 d x x   2 d x x     f x f  x f  x  f  x 2 ln
 x  C  ln f 0  C  ln 2  C     2 x          2 2 ln 2 ln ln 2  2 x f x x f x e f x e . 1 1 1 1 2 2 Vì vậy, 3     3 x 2 d  2 d x  d    2 t I x f x x x e x x e x  te dt  . 0 0 0 0 u  t du  dt 1 1 1 Đặt  . Ta có  t t    d    t t I te e t
te  e   1. dv  x e dx x v  e 0 0 0
Chọn đáp án A.
Câu 11: Cho hàm số f  x liên tục trên thỏa mãn
f  x  f   x 2 7 4 4
 2020x x  9 ,x  .Tính 4
I   f xd .x 0 197960 7063 197960 2020 A. . B. . C. . D. . 99 3 33 11 Lời giải:
Do f  x liên tục trên và x 
, f  x  f   x 2 7 4 4
 2020x x  9 4 4 4 4 4  7 f
 x4 f 4 x 2 d
 x  2020x x  9dx    7 f
 xdx4 f  4 x 2
dx  2020x x  9dx  . 0 0 0 0 0 4 4 Đặt 2
K  2020x x  9dx  ; H  f
 4 xdx. 0 0 4 + Tính 2
K  2020x x  9dx  . 0 Đặt 2 2 2 u 
x  9  u  x  9  udu  d
x x . Với x  0  u  3 ; x  4  u  5 . 4 5 2020 197960 Khi đó 2 2
K  2020x x  9dx  2020 u du=  3 3 5  3     . 3 3 0 3 4 + Tính H  f
 4 xdx. Đặt u  4 x  du  dx. Với x  0  u  4; x  4  u  0. 0 4 0 4 Khi đó H  f
 4 xdx   f
 udu = f
 udu  I . 0 4 0 4 4 4 197960 Vậy 7 f
 xdx4 f  4 x 2
dx  2020x x  9dx 
 7I  4I  3 0 0 0 197960  197960 11I   I  . 3 33
Chọn đáp án C. 3
Câu 12: Cho hàm số f  x liên tục, có đạo hàm trên
thỏa mãn x   f  x  
f  x  3  0, x  . 7 Tính I  xf   xd .x 1  5 3 9 51 A. . B. . C. . D. . 4 4 4 4 Lời giải: Từ giả thiết ta có: 3
x  f  x  f  x  3  0 3
x  7  7  f 7  f 7  3  0  f 7  2 3 x  1   1   f   1  f  
1  3  0  f   1  1 . 3
x  f  x  f  x    xf  x 3 3 0
  f x  f x  3 f x   7 7 7    xf   x 1 1 3 dx   f
 x f x3 f x 4 dx  f  x 2
 f x 3 f x     4 2  1  1  1  1 1 1 1   9  9 4  f 7 2
 f 7 3 f 7 4  f   2 1  f   1  3 f   1  0        . 4 2 4 2   4  4
Chọn đáp án C. 1 2
Câu 13: Cho hàm số f (x) có f (  x) 
, x  0 và f (1)  2 2 . Khi đó f (x)dx  bằng
(x 1) x  x x 1 1 10 10 4 2 10 14 A. 4 3  . B. 4 3  . C. 4 3   . D. 4 3  . 3 3 3 3 3 Lời giải: 1 1 Ta có f (x)  f (  x)dx  dx     x  x  x x  x x 
 x  xdx ( 1) 1 ( 1) 1 x 1  x  1 1  f (x)  dx  
dx  2 x 1  2 x  C    x(x 1)  x 1 x 
Vì f (1)  2 2 nên C  2 và f (x)  2 x 1  2 x  2 . 4 4  10
Khi đó f (x)dx  
2 x12 x 2 2 2 2 dx 
(x 1) x 1  x x  2x  4 3    . 3 3  3 1 1 1
Chọn đáp án A. 4
Câu 14: Cho hàm số y  f  x có đồ thị như hình vẽ, biết 
 f x dx 12.Tính m  f 2 . 1 A. 6 . B. 5 . C. 12 . D. 3 . Lời giải:
Từ đồ thị, ta có f  
1  f 4  0 và bảng xét dấu f  x như sau: 4 2 4 2 4 Do đó ta có 12  f 
 xdx 12  f 
 xdx f 
 xdx 12  f 
 xdx f   xdx 1 1 2 1 2
 12  f x 2  f x 4 12  f 2  f   1   f
 4  f 2  12  2 f  2 f   1  f 4 1 2
 12  2m  0  0  m  6. Vậy m  f 2  6.
Chọn đáp án A. x
Câu 15: Cho hàm số y  f  x liên tục trên
và thỏa mãn f (2  x)  f (x)  f (1 x)  2 1 . Biết tích x 5 phân I 
f (x)dx  . a ln b 
( a là số hữu tỉ, b là số nguyên tố). Hãy chọn mệnh đề đúng. 0 13 26 A. ab  . B. ab  1 . C. ab  13 . D. ab  . 2 3 Lời giải: x
f (2  x)  f (x)  f (1 x)  2 Ta có: 1 x 3
   f  x  f x  f  x  3 x 1 (2 ) ( ) (1 ) dx  dx  ln 2  2 1 x 2 2  2  3 3 3 1
 f (x  2)dx  f (x)dx  f (1 x)dx  ln 2    2 2  2  2  5 3 3 5 1
 f (t)dt  f (x)dx  f (u)du  f (x)dx  ln 2    
t  x  2; u 1 x 2 0 2  2  0 5 3 3 5  1 1
f (x)dx 
f (x)dx  f (x)dx   
 I  f (x)dx  ln 2 
. Do đó, a  ;b  2  ab  1. 2 2 0 2  2  0
Chọn đáp án B.
Câu 16: Cho hàm số f (x) liên tục trên đoạn 0; 2 
 và thỏa mãn điều kiện 3 f (x)  7 f (2  x)  x , 1 x   0;2 
 . Tính f (x d ) x  . 0 7 2  6 4 2  2 4 2 7 2  5 A. . B. . C. . D. . 30 15 15 30 Lời giải:
Thay x bởi 2  x vào đẳng thức 3 f (x)  7 f (2  x)  x (1) được:
3 f (2  x)  7 f (x)  2  x (2) 1
Từ (1) và (2) tính được f (x) 
7 2x 3 x 40 1 1 1 7 1 7 2  5
f (x)dx  
 7 2  x 3 xdx 1 1  
(2  x) 2  x   x x  . 40 0 0 60 20 30 0 0
Chọn đáp án D. Câu 17: Cho hàm số
y  f  x xác định và liên tục trên thỏa 2 mãn: 3 f  x 2
 xf x   2
x   f  x 3 3 3 1
 x  0, x  . Tính I   f xd .x 0 3 5 3 5 A.  . B. . C. . D.  . 4 4 4 4 Lời giải:
Theo đề bài ta có
 f x x3   f x  f x 3
 x   f x 3
 x   f x  f x. Đặt u f  x 3 3 
 u  f  x ta có 3
x  u  u  dx    2 3u   1 du .
Với x  0  u  0; x  2  u  1.  2 1  0 6 4  u u  3
Nên I   f x 3
dx    u  2 3u   1 du    5 3 3u  u  0 du       . 1   2 4  4 0 0 1 
Chọn đáp án A.  1 
Câu 18: Cho hàm số y  f  x có đạo hàm liên tục trên khoảng K  ;    . Biết f   1  3 và  2  x
2 f  x  1 2x f  x  , x
  K . Giá trị f 2 gần với số nào nhất trong các số sau ? 2 x  3 A. 1, 2 . B. 1,1. C. 1. D. 1,3 . Lời giải: 2 2  x  Ta có: 2 f
 xdx  12x f x  dx 2   1 1 x 3  2 2 2 x  2 f
 xdx  12x f xdx dx  2  1 1 1 x 3 2 2 2  2 f
 xdx  12x f x2  2 f
 xdx d   2x 3 1  1 1 1   3
 f 2  f   1   x  3 2 1 7 2  0  3
 f 2  3 7  2  0  f 2  1,2 1 3
Chọn đáp án A.
Câu 19: Cho hàm số y  f  x 3 2
 ax  bx  cx  d,a,b,c,d  ,a  0 có đồ thị là C. Biết đồ thị C
đi qua gốc toạ độ và có đồ thị y  f ' x cho bởi hình vẽ.Tính giá trị H  f 4  f 2. A. H  45 . B. H  64 . C. H  51. D. H  58 . Lời giải:
Dựa vào đồ thị f  x  f  x 2 ' '  3ax 1
Do đồ thị y  f ' x qua điểm 0;  1 và 
  f x 2 1; 4 '  3x 1
 f x  f  x 3 '
dx  x  x  C
Do C  qua gốc toạ độ nên C   f  x 3 0
 x  x  f 4  f 2  58.
Chọn đáp án D. 1 2 9
Câu 20: Cho hàm số f  x có đạo hàm liên tục trên 0; 
1 và thỏa mãn f   1  1;  f 
 x dx  ;  5 0 1 1 f   x 2 dx  . Tính I  f  xd .x 5 0 0 3 1 3 1 A. I  . B. I  . C. I  . D. I  . 4 5 5 4 Lời giải: 1 2 1 Xét I  f x dx  . 
Đặt x  t  dt 
dx  dx  2 d t t 1   5 2 x 0
x  0  t  0 1 1 2 2 Đổi cận  . Khi đó I 
f t 2tdt   2xf x dx    1    
x 1 t 1 5 5 0 0
 f x  u
du  f x 1 dx 1 Khi đó đặt 2   
 I  x f x 2
 x f  x dx  1   2 0 2 d x x  dv v  x 0 1 1 1 2 3 18 2
 1 x f x 2 dx 
 x f x 2 dx 
 6x f xdx     5 5 5 0 0 0 1 1 1 2 9 6 9 Ta có  f 
 x dx  ;  2
2x f  x dx   ; 4 9x dx   5 5 5 0 0 0 1 1 1 1   f 
 x 2 dx 6x f   
xdx  9x dx  0   
  f x2 2 4 2
 6x f x 4
 9x  dx  0   0 0 0 0 1   f   x 2 2
 3x  dx  0  f x 2
 3x  0  f x 3  x  C   0 1 1 1 Mà f  
1  1  C  0  f  x 3  x  f  x 3
dx  x dx  .  4 0 0
Chọn đáp án D.
_________________HẾT_________________
Huế, ngày 07 tháng 02 năm 2021