Phiếu bài tập Toán 8 chủ đề đa thức, hằng đẳng thức đáng nhớ và ứng dụng

Tài liệu gồm 58 trang, phân dạng và tuyển chọn các bài tập Toán 8 chủ đề đa thức, hằng đẳng thức đáng nhớ và ứng dụng. Mời các bạn theo dõi và đón đọc!

62 31 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 8

Môn: Toán 8

Thông tin:

58 trang 9 tháng trước

Tác giả:

Profile Mai Nguyệt
PHIẾU BÀI TẬP TOÁN 8
Trang 1/10
A. KIẾN THỨC TRỌNG TÂM
I/ Đơn nhất nhiều biến.
1. Khái niệm.
Đơn thức nhiều biến là biểu thức đại số chỉ gồm một số, hoặc một biến hoặc một tích giữa các số và các
biến.
2. Đơn thức thu gọn.
Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến đã được nâng lên lũy
thừa với số mũ nguyên dương.
Trong đơn thức thu gọn có hai phần: phần hệ số và phần biến.
Ta cũng coi một số là một đơn thức thu gọn chỉ có phần hệ số.
Trong đơn thức thu gọn, mỗi biến chỉ được viết một lần.
3. Đơn thức đồng dạng.
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
Các số khác 0 được coi là những đơn thức đồng dạng.
4. Cộng trừ đơn thức đồng dạng.
Để cộng (trừ) các đơn thức đồng dạng, ta cộng (trừ) các hệ số với nhau và giữ nguyên phần biến.
II/ Đa nhất nhiều biến.
1. Định nghĩa.
Đa thức nhiều biến (hay đa thức) là tổng của những đơn thức. Mỗi đơn thức được coi là một đa thức.
Mỗi đơn thức trong tổng gọi là hạng tử của đa thức đó.
2. Đa thức thu gọn.
Thu gọn đa thức nhiều biến là làm cho trong đa thức đó không còn hai đơn thức nào đồng dạng.
3. Giá trị của đa thức .
Để tính giá trị của một đa thức tại những giá trị cho trước của các biến, ta thay những giá trị cho trước
đó vào biểu thức xác định đa thức rồi thực hiện các phép tính .
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
ĐƠN THỨC NHIỀU BIẾN.
ĐA THỨC NHIỀU BIẾN
PHIẾU BÀI TẬP TOÁN 8
Trang 2/10
Dạng 1: Nhận biết các đơn thức nhiều biến, đa thức nhiều biến.
Ví dụ 1. Trong các biểu thức sau, biểu thức nào là đơn thức?
a)
2
12xy
; b)
; c)
12
x
−
; d)
18
; e)
5
2
x
.
Bài giải
2
12xy
; 18 là đơn thức.
Ví dụ 2. Biểu thức nào dưới đây không phải là đơn thức?
a)
22
xy−
; b)
x y xy−+
; c)
2
2xy
; d)
3
4xy
; e)
1
()
xy+
.
Bài giải
22
xy−
;
x y xy−+
;
1()
xy
+
;
3
4xy
không phải là đơn thức.
Ví dụ 3. Cho biết phần hệ số, phần biến của mỗi đơn thức sau
a)
2
2
xy
; b)
3
1
2
xy
−
.
Bài giải
a)
2
2xy
: Hệ số là 2, phần biến là x
2
y.
b)
3
1
2
xy
−
: Hệ số là
1
2
−
, phần biến là
3
xy
.
Ví dụ 4. Biểu thức nào là đa thức trong các biểu thức sau?
a)
22
23x y xy−+
; b)
2
2
x
x
y
−
; c)
2018
; d)
()xx y+
.
Bài giải
22
23x y xy−+
;
2018
;
()xx y+
là đa thức.
Ví dụ 5. Biểu thức nào không phải là đa thức trong các biểu thức sau?
a)
3
2x
x
−+
; b)
2
2
xy x−
; c)
2
4x −
; d)
2
1x
xy
+
.
Bài giải
3
2x
x
−+
;
2
1x
xy
+
không phải là đa thức.
Dạng 2: Nhận biết các đơn thức đồng dạng
Ví dụ 1. Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng
22
3 135 5
73
2 346 6
; ; ;; ; ; .xy x z xyz xy xyz x z xy−−
PHIẾU BÀI TẬP TOÁN 8
Trang 3/10
Bài giải
Nhóm các đơn thức đồng dạng là :
Nhóm 1 :
35
3
26
−;; .xy xy xy
Nhóm 2:
3
7
4
;.
xyz xyz
Nhóm 3:
22
15
36
− ;xz xz
Ví dụ 2. Trong các đơn thức sau, đơn thức nào đồng dạng với đơn thức
2
3x yz−
?
a)
3
xyz−
; b)
2
2
3
x yz
; c)
2
3
2
yzx
; d)
2
4xy
.
Bài giải
2
2
3
x yz
đồng dạng với đơn thức
2
3x yz−
.
Câu b đúng .
Dạng 3: Cộng, trừ các đơn thức đồng dạng
Ví dụ 1. Tính tổng, hiệu các biểu thức sau
a)
22
1
3
3
xy xy+
; b)
22 22 22
23
xy xy xy
++
;
c)
22 22
34x yz x yz−
; d)
22 2
21
2
33
xy xy xy

+ +−


.
Bài giải
a)
2222
1
3
3
1 10
3
33

=+=


+ xyy xy xyx
b)
( )
22 2 22 2 2222
23 231 6=+=+ ++ xyxy xy xy yx
c)
( )
2 22 222 22
34 43 =− −=−x yz xyz x yz yzx
d)
22 2 2 2
2 1 21 7
22
3 3 33 3

+ +− = + − =


xy xy xy xy xy
Ví dụ 2. Tính giá trị biểu thức
22 2
2011 12 2015P xy xy xy= +−
tại
1x = −
;
2y =
.
Bài giải
( )
2 2 2 22
2011 12 2015 2011 12 2015 8= + − = +− =P xy xy xy xy xy
.
Thay x = -1; y = 2 vào
2
8xy
ta được :
( )
2
2
8 8 1 2 812 16=−= =. . ..xy
Dạng 4: Tìm đơn thức thỏa mãn đẳng thức
Dùng quy tắc chuyển vế giống như đối với với số.
Nếu
MBA+=
thì
M AB= −
.
Nếu
MBA−=
thì
M AB= +
.
Nếu
BM A−=
thì
M BA= −
.
Ví dụ 1. Xác định đơn thức
M
để
PHIẾU BÀI TẬP TOÁN 8
Trang 4/10
a)
43 43
23xy M xy
+=−
; b)
33 33
24xy M xy
−=
.
Bài giải
a)
43 43
23
xy M xy
+=−
b)
33 33
24xy M xy−=
.
( )
43
4
4
43
3
3
3
2
5
3
2
−
= −
=
−
−
=
−
M xy
M
M xy
x
x
y
y
( )
3
3
33
3
3
33
2
24
4
2
= −
= −
= −M xy
y
M
x
Mx
xy
y
Dạng 5: Tính giá trị của đa thức
Thay giá trị của biến vào đa thức rồi thực hiện phép tính.
Ví dụ 1. Tính giá trị của đa thức sau:
a)
22
4 +xy xy
tại
2x = −
,
1
2
y =
; b)
23
1
2
− +xy x
tại
3x =
,
2
y = −
.
Bài giải
a)
22
4 +xy xy
tại
2x = −
,
1
2
y =
.
Thay
2
x = −
,
1
2
y =
vào
22
4 +xy xy
ta được :
( )
( ) ( )
2
2
1 11
4 2 2 16 1 4 1 3
2 24

− +− = +− = − =


.. . .
.
b)
23
1
2
− +xy x
tại
3x =
,
2
y = −
.
Thay
3x =
,
2y = −
vào
23
1
2
− +xy x
ta được :
( ) ( )
( )
23
1 1 72 78
3 2 3 9 8 3 3 39
2 2 22
− − +=− −+= += =. . ..
Dạng 6: Thu gọn đa thức
Bước 1: Nhóm các hạng tử đồng dạng với nhau;
Bước 2: Cộng, trừ các đơn thức đồng dạng trong từng nhóm.
Ví dụ 1. Thu gọn các đa thức sau
a)
22
22 52=−− + + +y x
yA x y x xy
; b)
22
31
2
22
B xy xy xy xy=−+++
;
c)
222222222
Cx yzxyzxyz=+++−+++−
; d)
2 2 22
23D xy z xy z xyz xy z xy z= + −− +
.
Bài giải
a)
PHIẾU BÀI TẬP TOÁN 8
Trang 5/10
(
)
( )
( )
(
)
2 2 22
22
22 52 2 2 5 2
12 25 2 3 2


=− − + + +=− + +− + +



= −+ + −+ + = + +

A x xy x xy x y x y xy xy
x y xy x y xy
yy
b)
( )
( )
22 22
22
31 31
22
22 22
31
21 2
22


=−+++= + +−+






= + + −+ = −





B xy xy xy xy xy xy xy xy
xy xy xy xy
c)
( ) ( ) ( )
22 222 222
2
222 22 22
22
22
2
=++
=+++
−+ + +−
=
−
++
+++−Cx y z x
xx yyy zzz
x
yz
y
xy
z
z
d)
( )
2 2 22
2 2 22
2
23
23
= + −− +
=+−+−
= −
D xy z xy z xyz xy z xy z
xy z xy z xy z xy z xyz
xy z xyz
Ví dụ 2. Thu gọn các đa thức sau :
a)
22
2 46= +− + +yz yzA x xy x xy
; b)
22
13
4
22
B xy x y xy x y= + −+
;
c)
222222222
Cxyzxyzxyz=−+−+−+++
; d)
2 22 2
245D x yz xy z x yz xy z xyz= + − +−
.
e)
23 4 2 4 23
2 376= +−+−
E xy x x x xy
.
Bài giải
a) b)
( )
( )
22
22
2
2 46
2 46
56
= +− + +
= − ++ +
= ++
A x xy x xy
x yz x yz xy xy
x yz
yz
xy
yz
( )
22
22
2
13
4
22
13
4
22
32
= + −+

= −+ +


= +
B xy x y xy x y
xy xy x y x y
xy x y
c)
( ) ( ) ( )
222 222 222
2
222222222
22
=−+−+−++
= − + +− + + +
+
+
+−
= +
xx
Cx y z x y z x
x
y
yyy zzz
x yz
z
d) e)
PHIẾU BÀI TẬP TOÁN 8
Trang 6/10
( ) ( )
2 22 2
2 2 22
22
245
25 4
35
= + − +−
= − + +−
=−+ −
D x yz xy z x yz xy z xyz
x yz x yz xy z xy z xyz
x yz xy z xyz
(
) (
)
234242
23 23 4 4 2
23 4 2
3
2 376
2 36 7
97
= − ++−
= +−
= +−+−
xy xy x x x
xy x
Exyxxxx
x
y
C. BÀI TẬP VẬN DỤNG
Bài 1. Trong các biểu thức sau, biểu thức nào là đơn thức?
a)
2 xy+
;
2
3xy z
;
1
3
2
;
22
3
1
2
xy

−


;
10
3
x
y
. b)
2
4
3
x yz
;
2018
;
2
3
xy
;
2xy
z
;
xy+
.
Bài giải
a) Đơn thức là :
2
3
xy z
;
1
3
2
;
22
3
1
2
xy

−


.
b) Đơn thức là :
2
4
3
x yz
;
2018
.
Bài 2. Biểu thức nào là đa thức trong các biểu thức sau?
a)
2
23
x y xy++
; b)
2
xy+
; c)
2()
xx y
+
; d)
1
2
1
x
x
+
−
−
.
Bài giải
Đa thức là
2()
xx y+
;
2
23
x y xy++
.
Bài 3. Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng
2 2 2 22 2 22
1 25
83 5
3 37
;; ; ; ; .xyz xyz xyz xyz xyz xyz− −−
Bài giải
Nhóm các đơn thức đồng dạng là :
Nhóm 1:
22
1
8
3
− ;.x yz x yz
Nhóm 2 :
22
2
3
3
−;.xy z xy z
Nhóm 3 :
22 22
5
5
7
−;.xyz xyz
Bài 4. Thu gọn mỗi đơn thức sau:
a)
22
23x y xy⋅
; b)
23
4
2 10
5
xy x y xyz⋅⋅
; c)
2 32
10 2( )( )y xy x− ⋅ ⋅−
.
d)
2 23
4
26
3
xy x y x⋅⋅
; e)
222
43
34
x y z xyz⋅
;
f)
2 2 23
1
42
4
()a x bxy x y

− ⋅− ⋅ −


với
a
,
b
là hằng số.
PHIẾU BÀI TẬP TOÁN 8
Trang 7/10
Bài giải
a)
( )
( ) ( )
2 32 2 23
23 623= =⋅ .. .x y xy x x yy x y
b)
(
) ( )
23 2 3 45
44
2 10 2 10 16
55

⋅ ⋅= =


.. . .xy x y xyz xx x yy y x y
c)
( )
( ) ( )
2 33 22 32
3 2 2 3 55
1
10 8 10 8 1 80
02

=−=−
−⋅ ⋅
−
− =
. . .. . . .() )
.(
y xy x x x y yxy x
y
yx
d)
(
)
( )
2 23 2 2 3 45
44
2 6 2 6 16
33

⋅ ⋅= =


...... .
xy xy x xx x y y xy
e)
( ) ( ) ( )
222 2 2 2 333
4 3 43
3 4 34

⋅= =


.. . .
xyz xyz xx yy zz xyz
f)
( )
( ) ( )
2 2 23 2 222 23 2 2 2 2 2 3
22 55
1 11
4 2 44 44
4 44
4

 
−⋅−⋅−=− −=− −

 
 

=
( ) . . . b. . . . . .ax bxy xy ax bxy xy a xx x y y
abxy
với
a
,
b
là hằng số.
Bài 5. Thu gọn các đa thức sau
a)
22
31
2
22
=−+++A xy xy xy xy
;
b)
2 2 22
23= + −− +B xy z xy z xyz xy z xy z
.
c)
23 4 2 4 23
4 26= +−+−C xy x x x xy
.
d)
22
31
23
42
= −− +D xy xy xy xy
;
e)
2 34 2 3 4
23 423= − −− + +E x yz x y z
;
f)
22 2
3 23= + −+ −F xy z xy z xyz xy z xyz
.
Bài giải
a)
( )
22 22 2
31 31
2 22
22 22

=−+ + += + +−+ = −


A xy xy xy xy xy xy xy xy xy xy
;
b)
( )
2 2 22 2 2 22 2
2 3 23
=+−−+=+−+−=−B xy z xy z xyz xy z xy z xy z xy z xy z xy z xyz xy z xyz
.
c)
( ) ( )
23 23 4 4 2234242 23 23
4
4 6 2326 724 = −
= +− + ++ − = −− +C xy x x xy xy x x x xy xxy x
x
.
PHIẾU BÀI TẬP TOÁN 8
Trang 8/10
d)
( )
2 2 22 2
3 1 31 1
2 3 23
4 2 42 4

= − − + = − +− + = +


D xy xy xy xy xy xy xy xy xy xy
;
e)
(
) ( ) ( )
2 34 2 3 4
2 2 3 3 4 4 23 4
24 32 3 2
23 423 2= − +− + +− +
= − −− =−−+
++
xxE x yz x y z
y y z z xy z
f)
(
)
( )
22 2 22 2 2
3 233 2 364= +−+ −= ++ +−− = −F xy z xy z xyz xy z xyz xy z xy z xy z xyz xyz xy z xyz
.
Bài 6. Tính giá trị mỗi đa thức sau :
a)
2 3 23
678A xy xy x y=++
; tại x = 2 ; y =
1
2
b)
6 23 5 5 6
2B x x y x xy xy x=+ −+− −
; tại x =0 ; y =
1
4
c)
2 62 6
7 43 4C xy x yz x= −+ +
; tại x = 2 ; y = 1
Bài giải
a)
2 3 23
678A xy xy x y
=++
; tại x = 2 ; y =
1
2
Thay x = 2 ; y =
1
2
vào
2 3 23
678
A xy xy x y=++
ta được :
( )
23 3
2
1 1 1 35
62 72 8 2
2 2 24
  
++ =
  
  
.. .. . .
b)
3 3 52 2
2=+ −+−
B x x y x xy xy
; tại x =
1
4
; y = 0.
Thay x =
1
4
; y = 0 vào
6 23 5 5 6
2B x x y x xy xy x
=+ −+− −
ta được :
23
1 13
4 4 64
 
−=
 
 
c)
2 62 6
7 43 4
C xy x yz x= −+ +
; tại x = 2 ; y = 1; z = 4
Thay x = 2 ; y = 1 vào
2 62 6
7 43 4C xy x yz x= −+ +
ta được :
2 62 6
72 1 42 31 4 42 40−+ +=.. . .. .
D. BÀI TẬP TỰ LUYỆN.
Bài 1. Trong các biểu thức sau, biểu thức nào là đơn thức?
a)
43x−
; b)
6
5x
; c)
2xy
; d)
9
5
; e)
32()xy−
.
Bài 2. Biểu thức nào dưới đây không phải là đơn thức?
PHIẾU BÀI TẬP TOÁN 8
Trang 9/10
a)
2
2
3
xy−
; b)
; c)
22
xy+
; d)
3
4xy
; e)
x y xy
++
.
Bài 3. Cho biết phần hệ số, phần biến của mỗi đơn thức sau
a)
3
1
3
xy
; b)
22
3
4
xy−
.
Bài 4. Thực hiện phép tính :
a)
2
1
2
xy−
+
2
2
xy
; b)
3
2xy
-
3
1
4
xy
.
c)
2 22
2
3
3
xy xy xy++
; d)
2 222
1
42
5
−+ + −xxy yyxxy
;
e)
222
111
236
xy xy xy++
; f)
333
19 15 12xy xy xy+−
.
g)
22 2
11
3
42
xy xy xy

+ +−


.
Bài 5. Thu gọn mỗi đơn thức sau:
a)
22
11
42
x yx

⋅− ⋅


; b)
23
13
32
x y xy−⋅
;
c)
( )
2
32
3
4
xy
⋅
; d)
2
2
1
2
()
x by

−


(
b
là hằng số).
Bài 6. Tính giá trị của đơn thức sau
a)
2
2
xy
tại
1x = −
,
1
4
y =
; b)
32
1
2
xy
−
tại
1
2
x = −
,
4y = −
.
Bài 7. a/ Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng
2 2 2 22 2 22
1 25
83 5
3 37
;; ; ; ; .xyz xyz xyz xyz xyz xyz− −−
b/ Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng
2 22 2 2 2 2 22
51 2
26
42 5
; ; ; ;; ; .xyxy xy xy xy xy xy−− −
Bài 8. Tính giá trị biểu thức
a)
2 22
2
3
3
xy xy xy++
tại
3x =
,
;
b)
222
111
236
xy xy xy++
tại
3
4
x =
,
;
PHIẾU BÀI TẬP TOÁN 8
Trang 10/10
c)
33
2xy
+
33 33
10 20xy xy
−
tại
1
x
=
,
1y = −
.
d)
22 2
2018 16 2016+−
xy xy xy
tại
2x = −
;
.
Bài 9. Tính giá trị của biểu thức
M
biết rằng
a)
24 24 24
15 10 6
xy M xy xy−= +
tại
1
2
x
= −
,
2y =
;
b)
3 33
40 20 15xy M xy xy+= +
tại
2x = −
,
1
5
y =
.
Bài 10. Xác định đơn thức
M
để
a)
44 44 44
2 33 2xy M xy xy+= −
; b)
22
23x Mx−=
.
c)
23 23
3xy M xy+=−
; d)
22 22
73xy M xy−=
.
PHIẾU BÀI TẬP TOÁN 8
Trang 1/22
A. KIẾN THỨC TRỌNG TÂM
1/ Cộng hai đa thức nhiều biến.
Để cộng hai đa thức theo hàng ngang, ta có thể làm như sau:
• Viết tổng hai đa thức theo hàng ngang ;
• Nhóm các đơn thức đồng dạng với nhau;
• Thực hiện phép tính theo trong từng nhóm , ta được tổng cần tìm.
2/ Trừ hai đa thức nhiều biến.
Để trừ đa thức P cho đa thức Q theo hàng ngang, ta có thể làm như sau:
• Viết hiệu P - Q theo hàng ngang, trong đó đa thức Q được đặt trong dấu ngoặc;
• Sau khi bỏ dấu ngoặc và đổi dấu một đơn thức của đa thức Q, nhóm các đơn thức đồng dạng
với nhau;
Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
3/ Nhân hai đa thức nhiều biến.
a/ Nhân hai đơn thức:
Tương tự như đối với đơn thức một biến, để nhân hai đơn thức nhiều biến ta có thể làm như sau:
• Nhân các hệ số với nhau và nhân các phần biến với nhau;
• Thu gon đơn thức nhận được ở tích .
b/ Nhân đơn thức với đa thức:
Tương tự như trường hợp một biến, ta có quy tắc sau:
Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức đó với từng đơn thức của đa thức rồi
cộng các kết quả với nhau.
c/ Nhân hai đa thức:
Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức
của đa thức kia rồi cộng các kết quả với nhau.
4/ Nhân hai đa thức nhiều biến.
a/ Phép chia hết một đơn thức cho một đơn thức
CÁC PHÉP TÍNH VỚI ĐA THỨC
NHIỀU BIẾN
PHIẾU BÀI TẬP TOÁN 8
Trang 2/22
Đơn thức A chia hết cho đơn thức B (
0
B ≠
) khi mỗi biến của B đều là biến của A với số mũ không
lớn hơn số mũ của nó trong A.
Quy tắc : Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B), ta có thể làm như sau
:
- Chia hệ số của đơn thức A cho hệ số của đơn thức B
- Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
- Nhân các kết quả vừa tìm được với nhau.
b/ Phép chia hết một đa thức cho một đơn thức
Đa thức A chia hết cho đơn thức (
0B
≠
) khi mỗi đơn thức của A chia hết cho B.
Quy tắc : Muốn chia đa thức A cho đơn thức B ( trường hợp A chia hết cho B), ta chia mỗi đơn thức
của A cho B rồi cộng các kết quả với nhau.
--------------------------------------------
PHIẾU BÀI TẬP TOÁN 8
Trang 3/22
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI.
Dạng 1: Tính tổng (hay hiệu) đa thức nhiều biến.
Ví dụ 1. Tính tổng
AB+
và hiệu
AB−
của hai đa thức
A
,
B
trong các trường hợp sau:
a)
2Ax y= +
và
2Bx y= −
.
b)
232
21A x y x xy= −− +
và
32
22
B x xy
=+−
.
c)
22
2A x yz z=−+
và
22
35B yz x z=+−
.
d)
2 3 32 3
15
22
A x y xy x y x
= +− +
và
32 2 3
71
22
B x y x y xy
= −+
.
Bài giải
a)
2 2 2 2 22 2+=+ +− =+ +− =++ − =( )( ) ( )( )ABxy xyxyx yxx yy x
2 2 2 2 22 4
−=+ −− =+ −+ =−+ + =
( )( ) ( )( )ABxyxyxyxyxx yy y
b)
232 3 2
2 3 2 3 2 2 2 2 33
22
232 3 2
2 3 2 3 2 2 2 2 33
2 1 22
2 1 2 2 2 2 12
21
2 1 22
2 1 2 2 2 2 12
+ = − − ++ + −

= − − ++ + −= +− + +− + +−

= +−
− = − − +− + −

= − − +− − += +− − +− − ++

( )( )
( ) () ( )
( )( )
( ) () (
A B x y x xy x xy
x y x xy x xy x y xy xy x x
x y xy
A B x y x xy x xy
x y x xy x xy x y xy xy x x
2 23
2 3 23= − −+
)
x y xy x
c)
22 2 2 22
2 2 22 2
22 22
2 2 22 2
2
22 2
2
2
2
2 35 2 35
5 23 6
35 35
5 23 4 2
22
5
+ +−=−+++−

= + +− + + − = +

−=
+= − +
−+− + −= −− +

= − +− − + + =− − +
−+

)( )
( )( ) ( )
)( )
( )( ) (
(
)
( yz x zA B x yz z
xy
x yz z yz x z
x x yz yz z z x yz
A B yz x z yz x z
x x yz yz z z x y
yz z
z
zz
z
x
d)
PHIẾU BÀI TẬP TOÁN 8
Trang 4/22
( )
2 3 32 3 32 2 3
2 3 32 3 32 2 3
32 32 3 3 2 2 3
32 3 3
2 3 32 3 32 2
1 5 71
2 2 22
1 5 71
2 2 22
5 7 11
2 2 22
2
1 5 71
2 2 22

+= + − + + − +


= +− + − +


=− + +++ − +




=++

−= + − + − −


+
A B x y xy x y x x y x y xy
x y xy x y x x y x y xy
x y x y xy xy x y x y x
x y xy x
A B xy xy xy x xy xy
( )
3
2 3 32 3 32 2 3
32 32 3 3 2 2 3
32 2 3
1 5 71
2 2 22
5 7 11
2 2 22
6

+


= +− + + −


=− − +−+
−
++




=− ++
xy
x y xy x y x x y x y xy
x y x y xy xy x y x y x
xy xy x
Ví dụ 2. Thực hiện phép tính sau:
22 2 2
22
( )( )A x y xy x xy y
= +− + + +
.
22
11
3 23
22
()B xy xy xy xy xy

= − + +−


.
Bài giải
22 2 2 2
22 22
2
2
22
2
2 2 22
2 2 22
= +− + + + =+− ++ +

=++++− + = +

( )(
( )( ) ( )
)
x x y y xy x
A x y xy x xy y x y xy y
x
x xy
yy
2 2 22
22 2
1 11 1
3 23 323
2 22 2
1 17 1
3 32
2 22 2

= − + + − = − + +−




= + +− + − = − −



()
()
B xy xy xy xy xy xy xy xy xy xy
xy xy xy xy xy xy xy xy
Ví dụ 3.
Cho các đa thức
32
3 23
M x x y xy=−++
;
2
22N x y xy
=−−
và
32
32 3P x x y xy= − −+
. Tính:
a)
. b)
MP−
. c)
2MP−
. d)
MNP++
.
Bài giải
a/
32 2 2 2 3
3
3 23 22 22 3 32
31

+ = − + ++ − −=− + + − + +−

= +
( )( ) ( )( ) ( ) ( )M N x x y xy x y xy x y x y xy xy x
x
b/
PHIẾU BÀI TẬP TOÁN 8
Trang 5/22
( )
32 3 2 32 3 2
33 2 2 2
3 2332 33 2332 3
3 3 2 2 33 3
−= −++− − −+=−++−+ +−

= − +− + + + + − = +

( )( )
( ) ( )( )
M P x x y xy x x y xy x x y xy x x y xy
x x x y x y xy xy x y xy
c/
32 3 2
32 3 2
33 2 2 32
2 3 2 3 23 2 3
3 2 36 4 2 6
36 4 22 3695 9
− = − + ++ − − +
= − + ++ − − +

= + +− − + − + + = − +

( )( )
( ) ( ) ( )( )
M P x x y xy x x y xy
x x y xy x x y xy
x x xy xy xy xy x xy
d/
32 2 3 2
32 2 3 2
33 2 2 2
32
3 2 3 2 23 2 3
3 2 3 2 23 2 3
3 3 2 2 2 323
62 4
= − + ++ − −+ − − +
= − + ++ − −+ − − +

= + +− + − + − − + −+

= − −+
( )( )( )
( ) ( ) ( )( )
M x x y xy x y xy x x y xy
x x y xy x y xy x x y xy
x x x y x y x y xy xy xy
x x y xy
Dạng 2: Tìm đa thức thỏa mãn đẳng thức cho trước
Ví dụ 4. Tìm đa thức
A
,
B
biết:
a)
22 2 2
232A x y x y xy+−=− + −
. b)
22
52 22 1()B x xyz x xyz−− =+ +
.
Bài giải
a/
(
)
22 2 2
2 2 22 2 2 22
22 2 2 2
232
232 232
2 32332
+−=− + −
=−+−−−=−+−−−

=−+−−+−=−+−

()
( )( )
A x y x y xy
A x y xy x y x y xy x y
x x y y xy y xy
b/
22
22
2 2 22 2
52 22 1
2 2 15 2
22 152 25 2 2 171
−− =+ +
= + ++ −
= + ++ − = + + − += +
()
( )( )
( )( )
B x xyz x xyz
B x xyz x xyz
x xyz x xyz x x xyz xyz x
Ví dụ 5. Cho các đa thức
22
435A x y xy= +−
;
2 2 22
322B x y xy=++
. Tìm đa thức
C
sao cho:
a)
C AB= +
. b)
CAB+=
.
Bài giải
a/
2 2 2 2 22
22 2 2 2 2 22 2 2
435 322
2543322575
=+= + − + + +
= −+ + + + = −++
( )( )
( )( )
C A B x y xy x y x y
x y xy x x y y x y xy x y
b/
PHIẾU BÀI TẬP TOÁN 8
Trang 6/22
( )
2 2 22 2 2
2 2 22 2 2 22 2 2 2 2
22 2 2
322 435
322 435 2 5 34 23
25
=−= + + − + −
=++ −−+ = ++ − + −
= + −−
()
( )( )
C B A x y x y x y xy
x y x y x y xy x y xy x x y y
x y xy x y
Dạng 3: Thực hiện phép tính nhân đơn thức với đa thức
Quy tắc:
A B C AB AC

(với A, B, C là các đơn thức).
Ví dụ 6. Làm tính nhân
a)
32
(2 ).( 2 1)M xy x y 
b)
3
1
(2 4 8 )
2
N xy y x y



c)
2 22 3
1
2
P x y xy x y



Bài giải
a/
32 323 3 5 323
(2 ).( 2 1) 2 . 2 .( 2 ) 2 .1 2 4 2M xy x y xyx xy y xy xy xy xy 
b/
3 3 42
11 1 1
(2 4 8 ) 2 . ( 4 ). ( 8 ). 2 4
22 2 2
N xy y x y xy y y y x y xy y xy
   



 





   
c/
2 2 2 3 2 2 2 2 2 3 33 4 24
1 11
.( ) .( ) .
2 22
P xy xy x y xy xy xy x xy y xy xy xy











Ví dụ 7. Nhân đơn thức
A
với đa thức
B
biết rằng
2
2
1
2
A xy



và
22
44 3B x xy
.
Bài giải
22 4222
42 2 42 2 42 62 54 2
2
2
4
1
.(4 4 3) .(4 4 3)
4
11 1 3
.4 .4 .( 3)
44 4
1
.
2
4
x xy x y x xy
xy x xy xy x
A
y xy x
B xy
y xy

 

  












  
Dạng 4: Thực hiện phép tính nhân đa thức với đa thức
Sử dụng quy tắc:
( )( )
ABCD ACADBCBD 
Ví dụ 8. Thực hiện phép nhân
a)
2
( )( )x yxy x
; b)
2
( 2 )( 2 4 )x yx y z 
; c)
22
( 2 )( 2 4 )x y x xy y 
.
Bài giải
a/
2 2 2 3 2 22
( )( ) . .( ) . .( )x y x x xxy x x yxy y x xy x xy xyy  
PHIẾU BÀI TẬP TOÁN 8
Trang 7/22
b/
22 2
3 22
( 2 )( 2 4 ) .( 2 ) .4 2 . 2 .( ) 2 .4
242 28
x yx y z xx x y xz yx y y yz
x xy xz x y y yz


Ví dụ 9. Rút gọn rồi tính giá trị của biểu thức
a)
11
22
22
M x yx y











tại
1
2
x
và
4y
b)
22 24
(2 )(4 2 )
N x y x xy y

tại
1
2
x
và
2
y
.
Bài giải:
a/
2 22 2
1 1 1 1 11
2 2 2 .2 2 . .2 .
2 2 2 2 22
11
44
44
M x y x y xx x y y x y y
x xy xy y x y
 










 

Thay
1
2
x
và
4y
vào
22
1
4
4
xy
ta được :
2
2
11
4. . 4 1 4 3
24



b/
22 24
2 2 4222224
3 22 4 22 4 6 3 6
(2 )(4 2 )
2 .4 2 .2 2 . ( ).4 ( ).2 ( ).
84 2 4 2 8
N x y x xy y
x x x xy x y y x y xy y y
x x y xy x y xy y x y

  

Thay
1
2
x
và
2y
vào
36
8xy
ta được :
3
6
36
1
8 8. 2 1 64 63
2
xy



Dạng 5: Thực hiện phép tính chia đơn thức với đa thức
Ví dụ 10: Làm phép tính chia:
a)
53
:xx
. b)
74
18 : 6xx
.
c)
672 47
8 :4xyz xy
. d)
( )
95 44
65 : 13xy xy
−
.
e)
35 2
27 9
:
15 5
x yz xz
.
Bài giải:
a)
53 2
:xx x=
. b)
74 3
18 : 6 3xx x=
.
c)
672 47 22
8 :4 2xyz xy xz=
. d)
( )
95 44 5
65 : 13 5xy xy xy
−=−
.
e)
35 2 22
27 9
:
15 5
x yz xz x yz=
.
Dạng 6: Thực hiện phép tính chia đa thức với đa thức
Ví dụ 11: Làm phép tính chia:
PHIẾU BÀI TẬP TOÁN 8
Trang 8/22
a)
( )
32
12 5 :x x xx+−
b)
(
)
43 22 3 2
3 9 15 :x y x y xy xy−+
c)
5 4 4 23 32 2
11
5 2:
24
xyz xyz xyz xyz

+−


Bài
giải:
a)
(
)
32 2
12 5 : 12 5.x x xxx x+ − =+−
b)
( )
43 22 3 2 3
3 9 25 : 3 9 25
x y x y xy xy x y x y
− + = −+
c)
5 4 4 23 32 2 4 2 32
11
5 2 : 20 2 8
24
x y z x y z xy z xy z x y x z yz

+ − = +−


C. BÀI TẬP VẬN DỤNG
Bài 1: Tính tổng các đa thức
a)
232
3A x y x xy= +− +
và
32
6.B x xy xy=+ −−
b)
11
2;
33
C a b ab



và
11
.
33
D a b ab



Bài giải:
a)
+= + − + + + − −

= +− +++ −−= + +− + + −+−

= + −−
232 32
2 3 2 3 2 33 2 2 2
32
( 3) ( 6)
3 6 ( ) ( ) (3 6)
23
A B x y x xy x xy xy
x y x xy x xy xy x x xy xy x y xy
x x y xy
b)
11 11
( 2) ( )
33 33
11 11
2
33 33
1 1 11
2
33 3 3
2
2
3
CD a bab a bab
a ba b a bab
a a b b aa bb
a ab





















 







PHIẾU BÀI TẬP TOÁN 8
Trang 9/22
Bài 2: Cho hai đa thức:
2
3 3 5 1;
M xyz x xy= −+−
và
2
5 5 3.N x xyz xy y= + − +−
Tính
.
NM−
Bài giải:
( ) ( )
− = − + − − + − +−
= −+−−−+−+
= − +− − + + + +−−
= − + +−
22
22
22
2
3 3 5 15 5 3
3 3 5 15 5 3
(3 ) ( 3 5 ) (5 5 ) ( 1 3)
2 8 10 4
M N xyz x xy x xyz xy y
xyz x xy x xyz xy y
xyz xyz x x xy xy y
xyz x xy y
− =− − =− − + +− =− + − −+
22
( ) (2 8 10 4) 2 8 10 4
N M M N xyz x xy y xyz x xy y
Bài 3: Cho các đa thức :
3 2 22
546A x y xy x y
;
3222
84B xy xy x y
3 3 3 2 22
4645C x x y xy xy x y
Hãy tính:
a)
ABC−−
b)
B AC+−
c)
C AB−−
Bài giải:
a)
3 2 22 3 2 22 3 3 3 2 22
(5 4 6 )(8 4 )( 4 6 4 5 )A B C x y xy x y xy xy x y x x y xy xy x y

3 2 22 3 2 22 3 3 3 2 22
546 8 4 4645x y xy x y xy xy x y x x y xy xy x y  
3 2 22 3 3
7 14x y xy x y xy x

b)
3 2 22 3 2 22 3 3 3 2 22
(8 4)(5 4 6)( 4 6 4 5)B A C xy xy x y x y xy x y x x y xy xy x y 
3 2 22 3 2 22 3 3 3 2 22
8 4 546 4645xy xy x y x y xy x y x x y xy xy x y
3 2 22 3 3
2 15xy xy x y x y x
c)
3 3 3 2 22 3 2 22 3 2 22
( 4 6 4 5 )(5 4 6 )(8 4 )C A B x x y xy xy x y x y xy x y xy xy x y 
3 3 3 2 22 3 2 22 3 2 22
4645 546 8 4x x y xy xy x y x y xy x y xy xy x y
3 3 3 2 22
2 15
x x y xy xy x y
Bài 4: Cho đa thức
22
ax xM by c y 
(
,xy
là biến). Tìm
,,abc
biết:
Khi
0, 1xy
thì
3M 
. Khi
2, 0xy
thì
8.M
Khi
1, 1
xy 
thì
0.M
Bài giải:
Khi
0; 1; 3x yM 
thì:
22
3 .0 .1 .0.1 3.abc b 
Khi
2; 0; 8x yM
thì:
2
2
8 . 2 .0 . 2 .0 4 8 2.a bc a a 
Khi
1; 1; 0xy M 
thì:
2
2
0 2.1 3 . 1 .1. 1 1cc 
.
Vậy
22
23 .M x y xy
Bài 5: Tìm đa thức M biết:
PHIẾU BÀI TẬP TOÁN 8
Trang 10/22
a)
2 2 22 2
6x 3x 2x ;
y Mx y y 
b)
2 22
2x 4 5x 7 .
M y y yx y

Bài giải:
a/
2 2 22 2
22 2 2 2 22 2 2 2
2 2 2 2 2 22 2
6x 3x 2x
( 2x ) 6x 3x 2x 6x 3x
( 6 ) (2 3 ) 5
y Mx y y
Mxy y y xy y y
x x y xy xy x y xy

 
 
b/
2 22
22 2 22 2
2 22 2 2
2x 4 5x 7
(5x 7 ) (2x 4 ) 5 7 2 4
( 7 4 ) (5 2 ) 11 7
M y y yx y
M y x y y y xy x y xy y
x y y xy xy x y xy

 

Bài 6: Thực hiện phép tính
a)
22 32 23 5
1
2
2
xy xy xy y



b)
32 2 2
1
(3 6 )
3
xy x y x y 
c)
22 2
23
24
32
xy y xy xy



. d)
2
2 3( )x xy xy 
e)
23 2
12
21
25
x y x xy



f)
22 2
( ) ( 2 1)xy x x 
.
Bài giải:
a/
22 32 23 5 22 32 22 23 22 5
54 45 27
11
2 2. 2.( )2.
22
22
xy xy xy y xy xy xy xy xy y
xy xy xy












b/
32 2 2 32 2 2
43 3 3
1 1 11
(3 6 ) . 3 . 6 .
3 333
1
2
3
xy x y x y xy x y xy x xy y
x y x y xy
  










  

c/
22 2 2 2 2
23 3 23
2 3 3 32 3
2 4 . 2 . .4
3 2 2 23 2
36
xy y xy xy xy xy xy y xy xy
xy xy xy
 









 

d/
22
3 22
2 3()(). ().2 ().(3)
23
x xy xy xy x xy xy xy
x y x y xy
 

e/
PHIẾU BÀI TẬP TOÁN 8
Trang 11/22
2 3 2 23 2 2 2
5 33 2
1 2 1 12 1
2 1 .2 . . 1
2 5 2 25 2
11
52
xy x xy xy x xy xy xy
xy xy xy












f/
22 2 24 2 24 2 24 24
44 34 24
( ) ( 2 1) .( 2 1) . .( 2 ) .1
2
xy x x xy x x xy x xy x xy
xy xy xy
 

Bài 7: Rút gọn các biểu thức sau
a)
22 3
( ) (1 )A x x y xy yx x

b)
( 3 1) 2 ( 1) ( 1)B xx y yx y x x 
Bài giải:
a/
2 22
3
22 3
22 22 3
. .( ) ( ).1 (( )( ).(1) )xx x y xA x x y xy y xy yx
x x y xy x y x xy
yx x  



b/
22
22
( 3 1) 2 ( 1) ( 1)
. .3 .1 ( 2 ). ( 2 ).( 1) ( ). ( ). ( ).1
3 22
( )(3 2 )( )2 2
B xx y yx y x x
xx x y x y x y x y x x x
x xy x xy y xy x x
x x xy xy xy x x y y

    


Bài 8: Rút gọn rồi tính giá trị biểu thức
a)
22
()()P xx y yx y 
tại
1
2
x 
và
1
2
y

;
b)
2 3 2 22
( ) ( 1)
Q x y xy y x x y 
tại
10x 
và
10y 
.
Bài giải:
a/
Thay
1
2
x 
và
1
2
y 
vào P ta được :
33
1 1 1 1 21
2 2 8 8 84
− − − − −−

+ =+==


2 22 2
3 3 33
( ) ( ) . .( ) . .( )Pxxyyxy xx xyyxyy
x xy xy y x y


PHIẾU BÀI TẬP TOÁN 8
Trang 12/22
b/
2 3 2 22
2 3 2 2 22 22 22
23 32 23 32 22
22
.. . . .
(
1
) ( 1)
x y x xy xy y xy x xy
xy xy
Q x y xy y x
xy xy x
x
y
y
x
y




Thay
10
x 
và
10y 
vào Q ta được :
( ) ( )
22
10 . 10 100.100 10000− −= =
Bài 9: Chứng tỏ rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến
x
a)
23
(3 2) ( 3 ) 2 3P x x xx x x x 
;
b)
11
(2 3) 6 1
23
Q xx x x



.
Bài giải:
a/
23 2 3
2 3 23
(3 2) ( 3 ) 2 3 .3 .2 . .3 2 3
3 2 3 2 33
P xx xx x x x xx x xx xx x x
x xx x x x
 
 
Vậy giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến
x
.
b/
22
11 1 1
(2 3) 6 1 .2 .( 3) 6 . 6 .
23 2 3
2 332 0
Q xx x x xx x x x x
x xxx












Vậy giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến
x
.
Bài 10: Nhân các đa thức sau
a)
(2 3)( 2 )xy x y
; b)
2
( 2 )( 2 4)yxy y x xy 
; c)
22
11
4
22
x yx y











.
Bài giải:
a)
22
(2 3)( 2) 2 . 2 .( 2) 3. 3.( 2)
2 4 36
xy x y xy x xy y x y
x y xy x y


b)
PHIẾU BÀI TẬP TOÁN 8
Trang 13/22
22 2
32 22 22 2
32 2
( 2 )( 2 4) . .( 2 ) .4 2 . 2 .( 2 ) 2 .4
2 42 4 8
44 8
xy y x xy xy x y xy xy xy y x y y xy y
x y x y xy x y xy y
x y xy
y
xy y
 


Bài 11: Chứng minh rằng với mọi
,xy
ta luôn có
22 3 3 3 3
( 1)( 1) ( 1)(1 )xy x y xy x y x y 
.
Bài giải:
22 3 3
22 22 3 33 3
33 2 22 3 33 3
33
VT ( 1)( 1) ( 1)(1 )
( . . .1 1. 1. 1.1) ( . 1 1.1 1. )
11
xy x y xy x y
xy x y xy xy xy x y xy x x y y
x y x y xy x y xy x x y y
x y VP




Bài 12: Cho biểu thức
(2 1)(2 3) (4 5)( 1) 3
Qn n n n 
. Chứng minh
Q
luôn chia hết cho
5
với mọi số nguyên
n
.
Bài giải:
22
22
(2 1)(2 3) (4 5)( 1) 3
(4 n 6 2 3) (4 4 5 5) 3
4n 6 2 3 4 4 5 5 3
5 5 5,
Qn n n n
nn n nn
nn n nn
nn

 
 

Bài 13: Làm tính chia:
a)
88 55 33 22
( 2 7 ):( )xy x y xy xy
;
b)
53 35 33
32
25 :
43
xy xy xy xy



;
c)
24 324 32
(9 12 4 ) :x y z x y z xy z xyz

.
Bài giải:
a)
88 55 33 22
88 22 5 5 22 33 22
66 33
( 2 7 ):( )
:( ) 2 :( ) 7 :( )
27
xy xy xy xy
xy xy xy xy xy xy
x y x y xy

 

b)
PHIẾU BÀI TẬP TOÁN 8
Trang 14/22
53 35 33
53 35 33
42 24 22
32
25 :
43
2 2 32
2: 5: :
3 3 43
15 9
3
28
xy xy xy xy
x y xy x y xy x y xy
xy xy xy



 









 

c)
24 32 4 32
24 324 32
3 23 2
(9 12 4 ) :
(9 :)(12 :)(4 :)
9 12 4
x y z x y z xy z xyz
x y z xyz x y z xyz xy z xyz
xy x yz y z

 

Bài 14: Tính giá trị biểu thức:
a)
( )
53 32 44 22
15 10 20 : 5A xy xy xy xy= −+
tại
1; 2.xy=−=
b)
( )
( )
2
2
2 43 32
2 3 6:B xy xy xy xy

= +−


tại
2.xy= = −
c)
( )
=− +−
22 3
2
2 46:
3
C x y xy xy xy
tại
1
; 4.
2
xy= =
d)

= −


25 52 22
12
:2
33
D xy xy xy
tại
3; 3.xy=−=
e)
( )
54 32 23 2
20 10 5 : 5
E xy xy xy xy= +−
tại
1; 1xy= = −
.
f)
( )
5 43 4 2 2 2 2
7 3 2:G xyz xyz xyz xyz= −+
tại
1; 1; 2x yz=−==
.
Bài giải:
a)
( )
( ) (
) ( )
= −+
= +− +
= −+
53 32 44 22
53 22 32 22 44 22
3 22
15 10 20 : 5
15 : 5 10 : 5 20 : 5
3 2 4 (*)
A xy xy xy xy
xy xy xy xy xy xy
xyxxy
Thay
=−=1; 2xy
vào (*) ta được :
3 22
3.( 1) .2 2.( 1) 4.( 1) .2 ( 6) 2 16 12− −−+− =−++=
b)
( )
( )
( )
( ) ( )

= +−


= +−
= + +−
=+−
2
2
2 43 32
42 43 32 22
42 22 43 22 32 22
22
2 3 6:
4 3 6:
4 : 3 : (6 : )
4 3 6 (*)
B xy xy xy xy
xy xy xy xy
xy xy xy xy xy xy
x xy x
PHIẾU BÀI TẬP TOÁN 8
Trang 15/22
Thay
=−=−2; 2xy
vào (*) ta được :
22
4.( 2) 3.( 2) .( 2) 6.( 2)
4.4 3.4.( 2) 12 16 24 12 4
− +− −−−
= + −+=−+=
c)
( )
=− +−
 
=− + +−
 
 
=− +−
22 3
23
2
2
2 46:
3
22 2
2 : 4: 6 :
33 3
3 6 9 (*)
C x y xy xy xy
x y xy xy xy xy xy
xy
Thay
1
; 4.
2
xy= =
vào (*) ta được :
2
1 3 279
( 3). 6 9.(4) 6 9.16
22 2
−−
− +− = +− =
d)

=−= − =−


25 52 22 25 22 52 22 3 3
1 2 1 2 11
:2 :2 :2 (*)
3 3 3 3 63
D xy xy xy xy xy xy xy y x
Thay
3; 3.xy=−=
vào (*) ta được :
33
1 1 9 27
.(3) .( 3) 9
63 22
− − = +=
e)
( )
( )
( )
( )
54 32 23 2
54 2 32 2 23 2
33 2
20 10 5 :5
20 :5 10 :5 5 :5
4 2 (*)
E xy xy xy xy
xy xy xy xy xy xy
x y xy y
= +−
= +−
= +−
Thay
1; 1
xy= = −
vào (*) ta được :
33 2
4.(1) .( 1) 2.1.( 1) ( 1)
( 4) 2 1 7
− + − −−
=− −−=−
f)
( )
5 43 4 2 2 2 2 5 43 2 4 2 2 2 2 2
332 2
7 3 2 : (7 :)(3 :)(2 :)
7 3 2 (*)
G xyz xyz xyz xyz xyz xyz xyz xyz xyz xyz
xyz xz y
= −+ = − +
= −+
Thay
1; 1; 2x yz=−==
vào (*) ta được :
332 2
7.( 1) .1 .2 3.( 1) .2 2.1 ( 28) 6 2 32− − − + =− −+=−
PHIẾU BÀI TẬP TOÁN 8
Trang 16/22
Bài 15:
Hình ảnh bên dưới mô tả cách có thể làm để có một hình hộp chữ nhật có ba kích thước là x; y; z.
(cm). Các kích thước và tỉ lệ của hộp phụ thuộc vào các giá trị của x; y; z. Tính diện tích của các mặt
của hình hộp chữ nhật được thể hiện qua hình đó.
Lời giải
Diện tích của các mặt của hình hộp chữ nhật là :
222xz xz xy xy yz yz xz xy yz+++++= + +
(cm
2
)
Bài 16:
Bác Nam có một mảnh vườn hình chữ nhật. Bác chia
mảnh vườn này ra làm hai khu đất hình chữ nhật: Khu
thứ nhất dùng để trồng cỏ. Khu thứ hai dùng để trồng
hoa. (Với các kích thước có trong hình vẽ).
a/ Tính diện tích khu đất dùng để trồng hoa theo x,y.
b/ Tính diện tích khu đất dùng để trồng cỏ theo x,y.
c/ Tính diện tích mảnh vườn hình chữ nhật của bác
Nam với x = 4 và y = 4.
Lời giải
a/ Diện tích khu đất dùng để trồng hoa là :
( )
2. 1 2 2x y xy x+= +
(m
2
)
b/
Chiều dài khu đất dùng để trồng cỏ là :
(2 12) ( 1) 2 12 1 (2 ) (12 1) 11y y y y yy y+ −+= +−−= −+ −=+
(m)
Diện tích khu đất dùng để trồng cỏ là :
( )
2 . 11 2 2 .11 2 22x y xy x xy x+= + = +
(m
2
)
c/ Học sinh có thể trình bày hai cách như sau :
Cách 1:
Diện tích mãnh vườn hình chữ nhật theo x,y là :
z
x
x
y
x
x
z
PHIẾU BÀI TẬP TOÁN 8
Trang 17/22
( )
2 . 2 12 2 .2 2 .12 4 24x y x y x xy x+= + = +
(m
2
)
Thay x = 4 và y = 4 vào
4 24xy x+
ta được : 4.4.4 + 24.4 = 160 (m
2
)
Vậy với x = 4 và y = 4 thì diện tích mảnh vườn hình chữ nhật đó là 160 (m
2
)
Cách 2:
Diện tích mãnh vườn hình chữ nhật theo x,y là :
(22)(222)424
xy x xy x xy x
++ + = +
(m
2
)
Thay x = 4 và y = 4 vào
4 24xy x
+
ta được : 4.4.4 + 24.4 = 160 (m
2
)
Vậy với x = 4 và y = 4 thì diện tích mảnh vườn hình chữ nhật đó là 160 (m
2
).
Bài 17:
Khu vườn trồng mía của nhà bác Minh ban đầu có dạng một hình
vuông biết chu vi hình vuông là 20 (m) sau đó được mở rộng bên
phải thêm y (m), phía dưới thêm 10x (m) nên mảnh vườn trở thành
một hình chữ nhật (hình vẽ bên)
a/ Tính diện tích khu vườn bác Minh sau khi được mở rộng theo x,
y.
b/ Tính diện tích khu vườn bác Minh sau khi được mở rộng khi
x = 1 ; y = 2
Lời giải
a/
Cạnh của mảnh vườn hình vuông ban đầu là 20 : 4 = 5 (m)
Chiều rộng của khu vườn sau khi được mở rộng là : y + 5 (m)
Chiều dài của khu vườn sau khi được mở rộng là : 8x + 5 (m)
Diện tích của khu vườn bác Minh sau khi được mở rộng là :
(y +5).(8x + 5) = y.8x + y.5 + 5.8x + 5.5 = 8xy + 5y + 40x + 25 (m
2
)
b/ Khi x = 1 ; y = 2 thì diện tích khu vườn bác Minh sau khi được mở rộng là :
8.1.2 + 5.2 + 40.1 + 25 = 91 (m
2
)
PHIẾU BÀI TẬP TOÁN 8
Trang 18/22
Bài 18:
Một cửa hàng buổi sáng bán được
xy
bao gạo thì cửa hàng đó thu được số
tiền là
65 54
xy xy−
nghìn đồng.
a/ Tính số tiền mỗi bao gạo mà của cửa hàng đó đã bán theo x,y.
b/ Tính số tiền mỗi bao gạo mà của cửa hàng đó đã bán khi x = 2; y = 2.
Lời giải
a/ Số tiền mỗi bao gạo mà của cửa hàng đó đã bán theo x,y là :
( ) (
)
65 54 65 54 54 43
( ): : :x y x y xy x y xy x y xy x y x y−= − =−
(nghìn đồng).
b/ Số tiền mỗi bao gạo mà của cửa hàng đó đã bán khi x = 2; y = 2 là :
54 43
2 .2 2 .2 384−=
(nghìn đồng)
Bài 19:
Một tấm bìa cứng hình chữ nhật có chiều dài là x + 43 (cm) và chiều rộng là x + 30 (cm). Người ta
cắt ở mỗi góc của tấm bìa một hình vuông cạnh
2
1y
+
(cm) ( phần tô màu) và xếp phần còn lại thành
một cái hộp không nắp.
a/ Tính diện tích xung quanh của hình hộp chữ nhật trên theo x; y.
b/ Tính diện tích xung quanh của hình hộp chữ nhật trên với x = 16 ; y = 4.
Lời giải
a/ Chiều cao của hình hộp chữ nhật bằng cạnh của hình vuông cắt đi và bằng
2
1y +
(cm).
Chiều dài của hình hộp chữ nhật là :
2 22
( 43) (y 1).2 43 2 2 2 41x x y xy
+−+=+−−=−+
(cm).
Chiều rộng của hình hộp chữ nhật là:
2 22
( 30) (y 1).2 30 2 2 2 28x x y xy+−+=+−−=−+
(cm).
Diện tích xung quanh của hình hộp chữ nhật trên theo x, y là :
( )
2 2 2 22
2 2 2 22 2 2
24 2 2
2 2 41 ( 2 28) .( 1) 2(2 4 69).( 1)
(4 x 8 y 138).( 1) 4 . 8 . 138 4 8 138
4 8 130 4 138( )
xy xy y xy y
y xy y y y x y
xy y y x cm

−++−+ += −+ +

= − + += − + + − +
= − + ++
PHIẾU BÀI TẬP TOÁN 8
Trang 19/22
b/ Diện tích xung quanh của hình hộp chữ nhật trên với x = 16 ; y = 4 là :
24 2 2
4.16.(4) 8.(4) 130.(4) 4.16 138 1258( )cm− + + +=
D. BÀI TẬP TỰ LUYỆN.
Bài 1. Tính tổng của hai đa thức
a)
22
23
Ax y= +
và
22
34Bx y= −
.
b)
22
235A x xy y=−+
và
22
32B x xy y= +−
.
Bài 2. Tính tổng và hiệu của hai đa thức
M
và
N
với:
a)
22
2M x y xy=++
và
22
2N x y xy=+−
.
b)
23 32 10,,M xy=+−
và
03 22 5,,N xy=−+ −
.
PHIẾU BÀI TẬP TOÁN 8
Trang 20/22
Bài 3: Tính tổng
AB+
và hiệu
AB−
của hai đa thức
A
,
B
trong các trường hợp sau:
a)
23
Axy
= +
và
2B xy= −
.
b)
232
2
A x y x xy
= +− +
và
3 22
7
B x xy x y=+−−
.
c)
22
21
A x yz z
= −−+
và
22
43 2
B yz x z= + +−
.
d)
2 3 32 3
3 11
22
A x y xy x y x=+− +
và
3 2 32
19
22
B xy x y x y
= −+
.
Bài 4: Thực hiện phép tính sau:
a)
2 22 2
75( )( )A x xy y x xy y= − + −− + −
.
b)
22 22 2 2
3 25 3()( )()
B xy x y xy x y x y xy= − −− − + −
.
Bài 5: Cho các đa thức
32
22 1M x x y xy= − ++
;
2
3 22
N x y xy
= +−
và
32
31P x x y xy=−−+
. Tính:
a)
. b)
MP−
. c)
2MP−
. d)
MNP++
.
Bài 6: Cho các đa thức
2
22M xy= −−
;
2
31N xy= ++
và
2
15Px= −
. Tính
a)
. b)
MP−
. c)
2MP−
. d)
MNP++
.
Bài 7: Tìm đa thức
A
,
B
biết
a)
2 2 22 2
63 2x xy A x y xy− += + −
. b)
2 22
24 5 7()B xy y xy x y− − = +−
.
Bài 8: Tìm đa thức
M
biết:
a)
2 22
32 45()M x xy x xy y+ − =+−
. b)
22 2 2
5 376
()M x y x xy y−− = − +
.
c)
32 3 2
2 1 32()
M x xy x xy+ − +=−+ +
. d)
2
690
()Mx x− − +=
.
Bài 9: Cho các đa thức
22
21A x y xy
=− ++
;
2 2 22
1B x y xy=+− −
. Tìm đa thức
C
sao cho:
C AB= +
.
CAB+=
.
Bài 10: Tính giá trị của các đa thức sau:
a)
3 3 3 33
2222
A x xy x y x y=+−++−
tại
2x =
,
3y = −
.
b)
22 44 66 88
B xy xy xy xy xy=+−+−
tại
1x =
,
1y = −
.
c)
2 2 3 3 10 10
C xy x y x y x y= + + ++
tại
1x = −
,
1
y =
.
Bài 11: Thực hiện phép tính
a)
22
2 (1 3 2 )M x xx 
; b)
2
1
(2 3 4)
2
Nxx x



;
c)
32
1
( 2 4)
2
P xy x xy y 
. d)
23 2
12
21
25
x y x xy

−−


PHIẾU BÀI TẬP TOÁN 8
Trang 21/22
Bài 12: Nhân đa thức
A
với đơn thức
B
biết rằng
3 23
11
42
A xy x y

và
2
(2 )B xy

.
Bài 13: Rút gọn các biểu thức sau
a)
22 3
3 (6 1) 9 (2 )
A x x xx x

; ĐS:
2
12Ax
b)
22
1
( 2) 2 ( ) (6 3)
3
B x x y xy x y y x y 
. ĐS:
33
Bx y
Bài 14: Tính giá trị của biểu thức
a)
22 3 2
2 ( 5) ( 2 4 ) (6 )M x x x x x xx 
tại
4x 
; ĐS:
64M 
b)
32 2
( 1) ( 2 1) ( 2 3 )N x y xy x x x x xy y  
tại
8x
và
. ĐS:
80Q 
Bài 15: Cho biểu thức
23 4
(1 2 ) 2 ( 2) ( 4)P x x xx x xx

. Chứng tỏ giá trị của
P
không phụ
thuộc vào giá trị của
x
.
Bài 16: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của các biến:
( ) ( ) ( )
2 73 72 5 .A xx x xx x= +− +− +−
Bài 17: Cho biểu thức
10 5 ( 1,2) 2 (2,5 3)B xx x x
=− −+ −
. Chứng minh rằng giá trị của biểu thức này
luôn luôn không đổi.
Bài 18: Chứng tỏ rằng các biểu thức sau không phụ thuộc vào giá trị của biến
x
:
a)
( )
22
(5 3) ( 1) 6 10 3
x x x x xx x x
−− −+ − − +
;
b)
(
)
22
1 ( 1) 5xx x x x x++ − + −+
.
c)

22 1 2 3 1 2x x xx  
Bài 19: Tính giá trị của biểu thức
a)
(
)
22 2
5 3 (7 5 ) 7P xx x x x= −+ − −
tại
5x = −
;
b)
()()Qxxy yxy= −+ −
tại
1, 5x =
và
10y =
.
c)
22
(3 )(9 3 )Q yxy xyx
tại
3x
và
1
3
y
.
Bài 20: Chứng minh đẳng thức
32 23 44
()x y x x y xy y x y 
.
Bài 21: Chứng minh đẳng thức
22
( )( ) 2( 1)( 1) 2xyxyz x y x y  
.
Bài 22: Chứng minh đẳng thức
22 44
( )( )( )
x yx yx y x y 
Bài 23: Chứng minh đẳng thức
2 2 33
( )( )x y x xy y x y  
Bài 24: Cho
1ab
. Chứng minh đẳng thức
( 1) ( 1) ( 1)( 1)ab ba a b
.
PHIẾU BÀI TẬP TOÁN 8
Trang 22/22
Bài 25: Làm tính nhân: a)
(2 7)(3 1)xx
; b)
2
(5 2 ) 1x y x xy

;
c)
( 1)( 1)( 2)xxx
; d)
22
5 42 9 3
x xx x

.
Bài 26: Thực hiện phép tính:
a)
(7)(5)xx
; b)
1
1 (2 3)
2
xx



; c)
11
(4 1)
22
xx x











.
d)
22
( )( )x y y xy x 
Bài 27:
Làm tính chia:
a)
5 6 32
(357):5xxxx
; ĐS:
34
37
55
xx x
b)
67 56 45 32
(5 4 3 ) : ( )xy xy xy xy
; ĐS:
35 24 3
543x y x y xy
c)
58 42 79 3
5 75
5:
8 93
xy xy xy xy



; ĐS:
27 48
37
3
8 15
x y xy x y
d)
342 424 523 222
( 2 7 ):xyz xyz xyz xyz
. ĐS:
2 22 3
27xy x z x z
Bài 28: Làm tính chia:
a)
5 7 43
(3 2 4 ) : 6yyyy
; ĐS:
24
112
233
yyy

b)
24 56 72
(2 3 5 ) : ( )x y x y x y xy

; ĐS:
3 45 6
23 5xy x y x y

c)
46 24 42 22
2 14
2:
5 55
xy xy xy xy



; ĐS:
24 2 2
1 51
2 24
xy y x

d)
322 453 647 3 2
(3 5 6 ) :xyz xyz xyz xyz
. ĐS:
4 335
35 6
y xy z x y z
PHIẾU BÀI TẬP TOÁN 8
Trang 1/12
A. KIẾN THỨC TRỌNG TÂM.
1. Bình phương một tổng.
Quy tắc: Bình phương của một tổng gồm hai số bằng tổng bình phương mỗi số với 2 lần
tích hai số đó.
2
22
2a b a ab b 
.
Ví dụ:
22 2
( 2) 2 2 4 4 4x x x xx 
.
2. Bình phương một hiệu.
Quy tắc: Bình phương của một hiệu gồm hai số bằng hiệu của tổng bình phương mỗi số
với 2 lần tích hai số đó.
2
22
2a b a ab b 
.
Ví dụ:
22 2
( 3) 2 3 9 6 9x x x xx 
.
3. Hiệu hai bình phương.
Quy tắc: Hiệu hai bình phương bằng tích của tổng với hiệu của hai số đó.
22
a b a ba b a ba b
.
Ví dụ:
2 22
4 2 ( 2)( 2)x x xx
.
4. Lập phương của một tổng.
3
3 2 23
33a b a a b ab b 
.
Ví dụ:
33 2 233 2
( 1) 3 1 3 1 1 3 3 1x x x x xxx  
.
5. Lập phương của một hiệu.
3
3 2 23
33a b a a b ab b 
.
Ví dụ:
33 2 233 2
( 2) 3 2 3 2 2 6 12 8x x x x xx x  
.
6. Tổng hai lập phương.
Quy tắc: Tổng của hai lập phương bằng tích của tổng hai số với bình phương thiếu của
hiệu hai số đó.
33 2 2
a b a b a ab b
.
Chú ý: biểu thức
22
a ab b
được gọi là bình phương thiếu của hiệu.
Ví dụ:
33 2 2 2
2 ( 2) 2 2 ( 2) 2 4
x x xx x xx 
.
7. Hiệu hai lập phương.
NHỮNG HẰNG ĐẲNG THỨC ĐÁNG NHỚ
PHIẾU BÀI TẬP TOÁN 8
Trang 2/12
Quy tắc: Hiệu của hai lập phương bằng tích của hiệu hai số với bình phương thiếu của
tổng hai số đó.
33 2 2
a b a b a ab b

.
Chú ý: biểu thức
22
a ab b
được gọi là bình phương thiếu của tổng.
Ví dụ:
3 22 2
3
3 ( 3) 3 3 ( 3) 3 9
x x xx x xx 
.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Thực hiện phép tính
Vận dụng linh hoạt các hằng đẳng thức ở phần trọng tâm kiến thức.
Ví dụ 1. Thực hiện phép tính
a)
2
( 1)x
; b)
2
(2 1)x
; c)
( 3)(3 )xx
; d)
22
( 2)
x
.
Ví dụ 2. Khai triển các biểu thức sau
a)
2
(2 3 )xy
; b)
2
( 3)xy
;
c)
(2 1)(2 1)xy xy
; d)
22
1
2 ( 2)
2
x yx y



.
Ví dụ 3. Khai triển các biểu thức sau
a)
2
()A xyz 
; ĐS:
222
222A x y z xy yz zx 
b)
2
()B abc 
. ĐS:
222
222B a b c ab ac bc 
Ví dụ 4. Thực hiện phép tính:
a)
3
( 3)x
; b)
3
1
3
x


; c)
3
( 3)xy
; d)
3
2
3
y
x


.
Ví dụ 5. Thực hiện phép tính
a)
2
( 2) 2 4
x xx 
; b)
2
(21)4 21x xx 
;
c)
2
11
2 24
x xx





; d)
2
2
2
xx
y yx
y
y





.
Ví dụ 6. Thực hiện phép tính
a)
2
( 3) 3 9Mx x x
; b)
2
(1 3 ) 1 3 9N x xx

;
c)
2
11
2 24
x
Px x











; d)
22
(2 3 ) 4 6 9Q x y x xy y
.
Dạng 2: Viết biểu thức dưới dạng tích
PHIẾU BÀI TẬP TOÁN 8
Trang 3/12
Sử dụng cách viết ngược lại của các hằng đẳng thức đã nêu ở phần trọng tâm
kiến thức.
Lưu ý:
2
aa a

. Như vậy bình phương của một số cũng gọi là dạng tích của
số đó.
Ví dụ 7. Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu
a)
2
69xx
; b)
2
9 61
xx

;
c)
22
1
4
x y xy
; d)
2
()6()9xy xy 
.
Ví dụ 8. Điền các đơn thức vào chỗ “...” để hoàn thành các hằng đẳng thức sau
a)
22
6 ()xx x  
; b)
22
4 4 (2 )xx x 
;
c)
22
9 (3 2 )x xy
; d)
2
()
39
yy
x



.
Ví dụ 9. Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc hiệu:
a)
32
3 31
xxx

; b)
32
11
3 27
xx x
;
c)
6 4 22 3
33x xy xy y
; d)
32
11
()() ()
3 27
xy xy xy 
.
Ví dụ 10. Viết các biểu thức sau dưới dạng tích:
a)
3
27x
; b)
3
1
8
x
; c)
33
8xy
; d)
33
8 27xy
.
Dạng 3: Tính giá trị của biểu thức
Bước 1: Rút gọn biểu thức (nếu cần).
Bước 2: Thay giá trị của biến vào biểu thức rồi thực hiện phép tính.
Ví dụ 14. Tính giá trị biểu thức:
a)
32
6 12 8Ax x x
tại
28x 
; ĐS: 27000
b)
32
8 12 6 1Bx x x 
tại
1
2
x
; ĐS: 8
c)
32
( 2) 6( 2) 12( 2) 8Cxy xy xy
tại
20
x
,
1y
. ĐS: 8000
Ví dụ 15. Tính bằng cách hợp lí:
a) Tính
3
11 1
; ĐS: 1330
b) Tính giá trị biểu thức
33
xy
biết
6xy

và
9xy
. ĐS: 378
Ví dụ 16. Tính giá trị biểu thức:
PHIẾU BÀI TẬP TOÁN 8
Trang 4/12
a)
22
(3) 39(32)4 69M x x x xx x 
tại
20
x
; ĐS: 72000
b)
2 23
( 2 ) 2 4 16
N x y x xy y y
biết
20xy
. ĐS: 0
Dạng 4: Tính nhanh
Áp dụng các hằng đẳng thức một cách linh hoạt cho các số tự nhiên.
Ví dụ 17. Tính nhanh
a)
2
101
; b)
22
75 50 75 25
; c)
103 97
.
Ví dụ 18. Tính nhanh:
a)
3
101
; ĐS: 1030301 b)
32
98 6 98 12 98 8
; ĐS: 1000000
c)
3
99
; ĐS: 970299 d)
32
13 9 13 27 13 27
. ĐS: 1000
Ví dụ 19. Tính giá trị của biểu thức
2
9 12 4Px x
trong mỗi trường hợp sau
a)
34x
; ĐS:
10000P
b)
2
3
x
; ĐS:
0P
c)
8
3
x
. ĐS:
100
P
Dạng 5: Chứng minh đẳng thức. Rút gọn biểu thức
Áp dụng các hằng đẳng thức một cách linh hoạt để biến đổi vế này thành vế
kia trong một đẳng thức.
Ví dụ 20. Chứng minh các đẳng thức sau
a)
22
( )( )4a b a b ab 
; b)
2 2 22
( ) ( ) 2( )xy xy x y 
.
Ví dụ 21. Rút gọn các biểu thức sau
a)
22
( 3) ( 3)Mxy xy 
; ĐS:
12M xy
b)
22
( ) 4( )( 2 ) 4( 2 )
Q xy xyx y x y
. ĐS:
2
( 5)Q xy
Ví dụ 22. Rút gọn biểu thức:
a)
3 32
( 2) ( 2) 2 12A x x xx 
;
b)
32
( 2) 6( 2) 12( 2) 8B xy xy xy 
.
Ví dụ 23. Rút gọn các biểu thức:
a)
23
( 3) 3 9 3Ax x x x 
;
b)
22
1 11
(21)4 218
2 24
Bx xx x x x











;
PHIẾU BÀI TẬP TOÁN 8
Trang 5/12
c)
22 22
( 2 ) 2 4 (2 3 ) 4 6 9
C x y x xy y y x y xy x
.
Dạng 6****: Chứng minh bất đẳng thức; tìm GTLN hoặc GTNN của biểu thức
Bước 1: Đưa các biểu thức về dạng bình phương của một tổng hoặc một hiệu.
Bước 2: Đánh giá dựa vào kết quả
2
0A
và
2
0A
.
Bước 3: Kết luận GTLN hoặc GTNN
MA
thì biểu thức A có GTLN là M.
Am
thì biểu thức A có GTNN là
m
.
Ví dụ 24. Chứng minh
a) Biểu thức
2
4 43xx
luôn dương với mọi
x
.
b) Biểu thức
2
1yy
luôn âm với mọi
y
.
Ví dụ 25. Tìm giá trị nhỏ nhất của các biểu thức sau
a)
2
45
Mx x
; ĐS:
12
min
Mx
b)
2
3Ny y 
; ĐS:
13 1
42
min
Ny

c)
22
47Px y xy 
. ĐS:
2
11
1
4
2
min
x
P
y

Ví dụ 26. Tìm giá trị lớn nhất của biểu thức
2
61Ax x

. ĐS:
10 3
max
Ax

C. BÀI TẬP VẬN DỤNG
Bài 1. Khai triển biểu thức sau
a)
2
( 3)x
; b)
2
1
3
x


; c)
2
(3 )xy
;
d)
2
2
1
2
x xy


; e)
22
(2 1)(1 2 )xy xy
; f)
2
( 2)xy
.
Bài 8. Thực hiện phép tính
b)
2
(3 1)x
; c)
11
22
xx











; d)
2
2
1
3
x


.
Bài 9. Khai triển các biểu thức sau
a)
2
(2 )xy
; b)
2
(2 )xy
;
c)
(3 2 )(3 2 )x yx y
; d)
22
1
2 (2 )
2
x yx y



.
PHIẾU BÀI TẬP TOÁN 8
Trang 6/12
Bài 2. Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu
a)
2
8 16xx
; b)
2
9 24 16xx
;
c)
2
9
3
4
xx
; d)
24 3 2
44x y xy y
;
e)
2
( 2) 4( 2) 4xy xy 
; f)
2
( 3 ) 12x y xy
.
Bài 1. Tính:
a)
3
( 2)x
; b)
3
(2 3 )xy
; c)
3
y
x
x


; d)
3
2
23
xy
.
Bài 2. Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu:
a)
32
9 27 27xx x
; b)
3
2
33
1
84 2
x
xx

; c)
6 4 22 3
33 1
24 8
x xy xy y
.
Bài 3. Rút gọn biểu thức:
a)
32
6 12 8Ax x x
; b)
23
33
1
248
x xx
B

;
c)
3 2 23
(2 ) 6(2 ) 12(2 ) 8C xy xyx xyx x 
.
Bài 4. Tính giá trị biểu thức:
a)
32
8 12 6 1
Mx x x 
tại
25, 5x
; ĐS: 125000
b)
23
1
3 27
xx
Nx

tại
27
x 
; ĐS: 1000
c)
32
32
6 12 8
xx x
Q
y
yy

tại
36x
,
2y
. ĐS: 8000
Bài 5. Tính nhanh:
a)
3
51
; ĐS: 132651
b)
32 3
89 33 89 3 121 89 11 
; ĐS: 1000000
c)
32
23 9 23 27 23 27
. ĐS: 8000
Bài 1. Đơn giản biểu thức:
a)
2
( 3) 3 9x xx 
; b)
2
(3 1) 9 3 1x xx 
;
c)
2
11
2 24
x xx





; d)
2
2
3 93
x x xy
yy





.
Bài 3. Tính nhanh
a)
2
103
; ĐS:
10609
b)
22
96 8 96 4
; ĐS:
10000
PHIẾU BÀI TẬP TOÁN 8
Trang 7/12
c)
99 101
. ĐS:
9999
Bài 4. Rút gọn biểu thức
a)
22
(2 3) (2 3)Ax x 
; ĐS:
24Ax

b)
22
( 1) 2(2 1)(1 ) 4 4 1Bx x x x x 
. ĐS:
2
( 2)Bx
Bài 1. Tính:
a)
2
(4 7)x
; b)
2
1
6
3
xy


; c)
2 32 3
35 35x xy x xy
.
Bài 2. Viết các đa thức sau dưới dạng bình phương của một tổng hoặc hiệu.
a)
22
69x xy y
; b)
2
4 41xx
.
Bài 5. Tính giá trị của biểu thức
a)
2
10 25Nx x
tại
55x
; ĐS:
2500
N
b)
4
22
4
x
P xy y
tại
1
4;
2
xy
. ĐS:
225
9
P
Bài 6. Tìm giá trị nhỏ nhất của các biểu thức sau
a)
2
46Ax x
; ĐS:
22
min
Ax
b)
2
1By y

; ĐS:
31
42
min
Bx

c)
22
45
C x xy y 
. ĐS:
2
3
1
4
2
min
x
C
y

Bài 7. Tìm giá trị lớn nhất của các biểu thức sau
a)
2
42
Ax x
; ĐS:
62
max
Ax
b)
2
2B xx
. ĐS:
91
42
max
Bx 
Bài 10. Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu
a)
2
44xx
; b)
2
4 41xx
;
c)
2
1
4
xx
; d)
2
4( ) 4( ) 1xy xy 
.
Bài 11. Hoàn thiện các hằng đẳng thức sau
a)
2
10 25 ( )xx 
; b)
2 4 22
4 ()xx x 
;
c)
22 2
9( )x yx 
; d)
2 24
(2 )( ) 4x y xy 
.
PHIẾU BÀI TẬP TOÁN 8
Trang 8/12
Bài 12. Chứng minh các đẳng thức sau
a)
22 2 22
( 1) 4 ( 1)a aa
. b)
2 2 22 2
( ) ( ) 2( ) 4xy xy x y x 
.
Bài 13. Rút gọn các biểu thức
a)
22
(2 ) (2 )A xy xy 
; ĐS:
8M xy
b)
22
( 2) 4( 2) 4Bxy xyyy
. ĐS:
22
8 16Q x xy y
Bài 14. Khai triển các biểu thức sau
a)
2
()C xyz 
; ĐS:
222
222C x y z xy yz zx
b)
2
( 1)Da b 
. ĐS:
22
1 22 2D a b a ab b 
Bài 3. Rút gọn các biểu thức:
a)
2
(7 4) (7 4)(7 4)x xx
; b)
2
( 2) 6 ( 2)xy xyxy

.
Bài 17. Tính: a)
2
1
4
2
x


; b)
2
(7 5 )xy
; c)
2 22 2
66x yy x

;
d)
2
( 2)xy
; e)
( 3)( 3)
x yx y
; f)
2
(5 )x
.
Bài 15. Tính nhanh
a)
2
501
; b)
22
88 24 88 12
; c)
52 48
.
Bài 16. Tính giá trị của biểu thức
2
9 61Qx x 
trong mỗi trường hợp sau
a)
33x
; ĐS:
10000Q
b)
1
3
x
; ĐS:
0Q
c)
11
3
x
. ĐS:
100Q
Bài 18. Thực hiện phép tính
a)
2
( 1)x
; b)
2
(3 )y
; c)
2
1
2
x


.
Bài 19. Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu
a)
2
10 25xx
; b)
2
49 14
xx
; c)
2
1
4
xx
.
Bài 2. Rút gọn biểu thức:
a)
22
(2 1) 4 2 1 ( 1) 1P x x x x xx 
;
PHIẾU BÀI TẬP TOÁN 8
Trang 9/12
b)
2 2 2 23
() () 2Q x y x xy y x y x xy y y

.
Bài 3. Chứng minh giá trị của các biểu thức sau không phụ thuộc vào giá trị của
x
a)
23
6( 2) 2 4 6 2Ax xx x 
;
b)
23
2(31)9 3154B x xx x 
.
Bài 4. Tính giá trị biểu thức:
a)
33
()
A xy x

biết
20
xy
; ĐS: 0
b)
33
3B x y xy 
biết
1xy
. ĐS: 1
Bài 5. Viết các biểu thức sau dưới dạng tích:
a)
3
1
x
; b)
3
1
27
x
; c)
33
27xy
; d)
33
27 8xy
.
Bài 6. Rút gọn các biểu thức:
a)
23
( 2) 2 4 2Ax x x x

;
b)
22
( 1) 1 ( 1) 1Bx xx x xx
;
c)
22 2 2
(2 ) 4 2 ( 3 ) 3 9C x y x xy y y x y xy x 
.
Bài 8.
a) Chứng minh
33 3
()3()
A B AB ABAB 
và
33 3
()3()
A B AB ABAB 
b) Áp dụng để tính
3
101 1
. ĐS: 1030300
c) Tính giá trị biểu thức
33
xy
biết
2xy
và
3xy 
. ĐS: 26
Bài 9. Tính giá trị biểu thức:
a)
23
( 4) 4 16 64Px x x x
tại
100x
; ĐS: 2000000
b)
2 23
(2 ) 4 2 2Q x y x xy y y 
biết
20xy
. ĐS: 0
Bài 1. Tính: a)
3
2
25xy
; b)
3
3
34x xy
;
c)
2
11
6 36 3
24
x xx











; d)
22 2 4
5 5 25x y x xy y 
.
Bài 8. Tính: a)
3
(5 1)x
; b)
3
( 2)xy
;
PHIẾU BÀI TẬP TOÁN 8
Trang 10/12
c)
2
(4 5) 16 20 25
x xx 
; d)
2
11
6 36 2
39
x xx











.
Bài 2. Viết các đa thức sau dưới dạng bình phương hay lập phương của một tổng hoặc hiệu.
a)
22
1
25 5
4
x xy y
; b)
3 2 23
8 12 6
x x y xy y 
.
Bài 3. Điền các đơn thức thích hợp vào ô trống
a)
2
2
2
11
xx
x
x



;
b)
2 233
1 1 1 11
2 4 9 8 27
x x yxy











.
Bài 4. Rút gọn các biểu thức:
2 2 32
(3 ) 9 3 (3 ) 27x y x xy y x y x y

.
Bài 20. Rút gọn biểu thức:
a)
22
( )( )xy xy 
; b)
22
2()()()()xyxy xy xy  
.
Bài. Tính nhanh (không dùng MTBT)
a)
2
98
; b)
22
63 37
; c)
2
105
; d)
2
97 9
.
Bài 22. Rút gọn rồi tính giá trị của biểu thức sau với
19x 
.
22
(3 2) (2 7) 2(3 2)(2 5).Ax x x x 
Bài 23. Rút gọn rồi tính giá trị của biểu thức sau với
1
5
x
.
22
(3 1) ( 7) 2(2 5)(2 5).Bx x x x 
Bài 4. Cho biểu thức
22
5( 3)( 3) (2 3) ( 6)Ax x x x 
. Rút gọn rồi tính giá trị của biểu
thức
A
với
1
5
x 
.
Bài 5. Cho biết
15xy
và
100xy 
. Tính giá trị của biểu thức
22
Bx y
.
Bài 6. Tính nhanh giá trị của biểu thức
a)
22
39 78 61 61C

; b)
2
50 49 51D 
.
Bài 7. Chứng minh đẳng thức
22
( )( ) 4x y x y xy 
.
Bài 8. Chứng minh đẳng thức
222 2 2 2 2
3 ( )( )( ) ( ).x y z xy yz zx xyz 
PHIẾU BÀI TẬP TOÁN 8
Trang 11/12
Bài 17. Chứng tỏ
a)
2
6 10 0
xx
với mọi
x
; b)
2
4 50yy 
với mọi
y
.
Bài 18. Tìm giá trị nhỏ nhất của các biểu thức sau
a)
2
6 11
Px x
; ĐS:
23
min
Px

b)
2
Qy y
; ĐS:
11
42
min
Qx


c)
22
6 10K x y xy 
. ĐS:
3
3
1
4
2
min
x
K
y


Bài 19. Tìm giá trị lớn nhất của biểu thức
2
45B xx 
. ĐS:
92
max
Bx
.
Bài 12. Chứng minh giá trị của biểu thức
2
23Px x
luôn luôn dương với mọi
x
.
Bài 13. Chứng minh giá trị của biểu thức
2
6 10Q xx 
luôn luôn âm với mọi giá trị của
x
.
Bài 14. Tìm giá trị nhỏ nhất của biểu thức
2
10 28
Px x
.
Bài 15. Tìm giá trị nhỏ nhất của biểu thức
2
5 10
Qx x
.
Bài 16. Tìm giá trị lớn nhất của biểu thức
2
1P xx
.
Bài 24. Chứng minh rằng
22
(2 3) (2 1)nn
chia hết cho
8
với
n
.
Bài 25. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức sau:
a)
2
4 12 10Ax x
; b)
2
22B xx 
.
Bài. Cho
222
a b c ab bc ca
. Chứng minh rằng
abc
.
Bài 5. Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến
23
(3 2) 9 6 4 3 9 2 .Ax xx x 
Bài 6. Giá trị của biểu thức sau có phụ thuộc vào giá trị của biến không?
32
( 1) ( 1) 1 3 ( 1).B x x x x xx 
Bài 7. Chứng minh đẳng thức:
33 2
( )( )a b a b a b ab




.
Bài. Rút gọn các biểu thức sau:
3 33
( 2) ( 2) 3 ( 2)( 2)x x x xx x 
.
PHIẾU BÀI TẬP TOÁN 8
Trang 12/12
Bài. Chứng minh đẳng thức
3 3 22
( ) ( ) 23
x y x y yx y

.
Bài. Cho
1xy

, tính giá trị của biểu thức
33 22
23M xy xy 
.
PHIẾU BÀI TẬP TOÁN 8
Trang 1/7
A. KIẾN THỨC TRỌNG TÂM.
1. Phân tích đa thức thành nhân tử.
Phân tích đa thức thành nhân tử là viết đa thức dưới dạng tích của những đa thức.
2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức.
Ngoài cách đặt nhân tử chung ta còn sử dụng bảy hằng đẳng thức đáng nhớ để phân tích
đa thức thành nhân tử. Cụ thể :
(1)
2
22
2a ab b a b 
; (2)
2
22
2a ab b a b 
.
(3)
22
a b a ba b
; (4)
3
3 2 23
33
a a b ab b a b

;
(5)
3
3 2 23
33a a b ab b a b

; (6)
33 2 2
a b a b a ab b
;
(7)
33 2 2
a b a b a ab b
.
Ví dụ: Phân tích thành nhân tử các biểu thức
a)
2 22
4 2 ( 2)( 2)
x x xx
.
b)
3 2 3 2 23 3
6 12 8 3 2 3 2 2 ( 2)xx x xx x x 
.
c)
32 3
6 12 9 6 12 8 1xx x xxx
3
( 2) 1
x
2
(21)(2)(2)1x xx




2
( 3) 3 3
x xx
.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Phân tích đa thức thành nhân tử bằng phương pháp vận dụng trực tiếp hằng
đẳng thức
Bước 1: Biến đổi đa thức đã cho về đúng dạng hằng đẳng thức cần sử dụng.
Bước 2: Phân tích thành nhân tử.
Ví dụ 1. Phân tích các đa thức sau thành nhân tử:
a)
2
44xx
. b)
2
4 41xx
. c)
2
21xx
. d)
2
1
4
xx
.
Ví dụ 2. Phân tích các đa thức sau thành nhân tử:
PHÂN TÍCH ĐA THỨC THÀNH NHÂN
TỬ BẰNG PHƯƠNG PHÁP DÙNG
HẰNG ĐẲNG THỨC .
Phân
thức đại
PHIẾU BÀI TẬP TOÁN 8
Trang 2/7
a)
2
3
x
. b)
2
31x
. c)
2
2
54xx
. d)
22
1 21xx
.
Ví dụ 3. Phân tích các đa thức sau thành nhân tử:
a)
22
69x xy y
. ĐS:
2
3xy
b)
22
9
xy
. ĐS:
33x yx y

c)
22
44
x y xy
. ĐS:
2
2xy
d)
22
21yx x 
. ĐS:
11yx yx 
Ví dụ 4. Phân tích các đa thức sau thành nhân tử:
a)
3
81x
. ĐS:
2
2 14 2 1x xx 
b)
3
8 21x 
. ĐS:
2
2 3 4 18 21x xx 
c)
32
6 12 8xx x
. ĐS:
3
2
x
d)
3 2 23
8 12 6x x y xy y 
. ĐS:
3
2xy
Dạng 2: Phân tích đa thức thành nhân tử bằng phương pháp vận dụng hằng đẳng
thức thông qua nhóm số hạng và đặt nhân tử chung.
Nhóm các số hạng xuất hiện hằng đẳng thức thành một nhóm , các số hạng
còn lại thành một nhóm
Dùng hằng đẳng thức để viết nhóm các số hạng xuất hiện hằng đẳng thứ
c
thành tích
Đặt nhân tử chung ở các nhóm ra ngoài để viết thành tích
Ví dụ 5. Phân tích các đa thức sau thành nhân tử:
a/
22
44xx y− +−
ĐS:
22xyxy 
b/
22
2x xy y x y+ + −−
ĐS:
1xyxy 
c/
22
29x xy y
− +−
ĐS:
33xy xy 
Dạng 3**: Phân tích đa thức thành nhân tử bằng cách áp dụng nhiều hằng đẳng thức
Sử dụng các phép phân tách hoặc thêm bớt hợp lý để đưa biểu thức về dạng
hằng đẳng thức cần sử dụng và phân tích thành nhân tử.
Lưu ý: có thể áp dụng nhiều hằng đẳng thức trong một bài toán.
Ví dụ 6. Phân tích các đa thức sau thành nhân tử:
PHIẾU BÀI TẬP TOÁN 8
Trang 3/7
a)
2
21xx
. ĐS:
2
1
x
b)
2
23
xx

. ĐS:
31xx

c)
2
22
xx
. ĐS:
13 13xx
d)
22
44
x xy y
. ĐS:
2 22 2xy yxy y 
Ví dụ 7. Phân tích các đa thức sau thành nhân tử:
a)
3
21x 
. ĐS:
2
( 3) 3 3x xx 
b)
32
6 12 9xx x
. ĐS:
2
( 3) 3 3
x xx

c)
32
6 12 7xx x
. ĐS:
2
( 1) 5 7x xx

d)
32
2 6 12 8xx x
. ĐS:
2
22 24x xx 
Dạng 4: Chứng minh các bài toán chia hết
Biểu thức A chia hết cho biểu thức B khi và chỉ khi có biểu thức Q khác 0 sao
cho
A QB
.
Ví dụ 8. Chứng minh:
a)
2
21 9k 
chia hết cho
4
. b)
2
4 13k
chia hết cho
3
.
C. BÀI TẬP VẬN DỤNG
Bài 1. Phân tích các đa thức sau thành nhân tử:
1)
2
8 16xx
. ĐS:
2
( 4)x
2)
2
9 61xx
. ĐS:
2
(3 1)x
3)
2
10 25xx
. ĐS:
2
( 5)x
4)
2
25
5
4
xx
. ĐS:
2
5
2
x


5)
2
16 x
. ĐS:
(4 )(4 )xx
6)
2
16 3 1x
. ĐS:
(3 3)(5 3)xx

7)
2
2
259xx
. ĐS:
(5 )(5 5)xx
PHIẾU BÀI TẬP TOÁN 8
Trang 4/7
8)
22
21 31xx
. ĐS:
52
xx

9)
22
44x xy y

. ĐS:
2
(2 )
xy
10)
22
( 1) 9xy
. ĐS:
( 3 1)( 3 1)
xy xy 
11)
44 22
44xy xy
. ĐS:
2
22
2xy
12)
22
44yy x 
. ĐS:
22y xy x 
13)
3
1 27x
. ĐS:
2
(1 3 ) 1 3 9x xx 
14)
3
3 27x 
. ĐS:
2
9 27xx x

15)
32
27 27 9 1x xx 
. ĐS:
3
(3 1)x
16)
64
23
27 3
x xy
xy y

. ĐS:
3
2
3
x
y


17)
3
21 8x 
. ĐS:
2
(2 1) 4 8 7x xx 
18)
32
8 12 6 1x xx 
. ĐS:
3
(2 1)x
19)
32
8 12 6 2x xx 
. ĐS:
2
(2 2) 4 2 1x xx

20)
32
9 12 6 1x xx 
. ĐS:
2
(3 1) 3 3 1x xx 
21)
2
69xx
. 22)
2
9 61xx
. 23)
2
44xx
. 24)
2
1
4
xx
.
25)
2
9x
. 26)
2
19x 
. 27)
2
2
41 9xx
. 28)
22
2 31xx
.
Bài 2. Phân tích các đa thức sau thành nhân tử:
1)
22
44x xy y

. ĐS:
2
2x
2)
22
9xy
. ĐS:
33xy xy
3)
22
9 61x y xy
. ĐS:
2
31
xy
4)
22
44xy y 
. ĐS:

22xy xy
 
5)
3
8x
. ĐS:
2
2 24x xx

6)
3
3
3xx
. ĐS:
2
33 9 9
xx 
PHIẾU BÀI TẬP TOÁN 8
Trang 5/7
7)
32
8 12 6 1x xx 
. ĐS:
3
2x
8)
32 23
6 12 8
x x y xy y
. ĐS:
3
2xy
9)
2
4 41xx
. ĐS:
2
21x
10)
2
4 43xx
. ĐS:
2321xx
11)
2
4 41
xx

. ĐS:
212212xx

12)
22
45
x xy y
. ĐS:
5
x yx y

13)
3
11x 
. ĐS:
2
( 2) 1x xx 
14)
32
3 32xxx 
. ĐS:
2
( 2) 1x xx 
15)
32
3 37xxx 
. ĐS:
2
( 1) 4 7x xx 
16)
32
2 3 31xxx 
. ĐS:
2
21 1
x xx 
Bài 3. Phân tích đa thức thành nhân tử
1)
; 2)
22
1
9
16
xy
; 3)
64
xy
.
4)
2
(2 5) 64x 
; 5)
2
81 (3 2)x
; 6)
22
9( 5 ) 16( )x y xy
.
7)
3
8x
; 8)
33
27 125xy
; 9)
6
216x
.
10)
2
8 16xx

; 11)
22
9 12 4x xy y
; 12)
22
25 10 1
x y xy 
.
13)
32
6 12 8xx x
; 14)
3 2 23
8 12 6x x y xy y 
.
15)
7
1x
; 16)
10
1x
.
17)
2
9x
; 18)
2
4 25
x
; 19)
44
xy
.
20)
22
96x xy y
; 21)
2
69xx
; 22)
22
44x y xy
.
23)
22
( )( )
xy xy 
; 24)
22
( )4xyz z
; 25)
22
(3 1) ( 1)xx 
.
26)
33
125xy
; 27)
33
8 6 (2 )x y xy x y
;
28)
22
(3 2) 2( 1)(3 2) ( 1)x xx x 
.
Bài 4. Phân tích đa thức thành nhân tử
a)
3 3 22
224 2x y xy x y xy
; b)
22
2 44x y xy x y

;
PHIẾU BÀI TẬP TOÁN 8
Trang 6/7
c)
33 22
33
x xy
x xy y y

; d)
2 22
24
x xy y z 
;
e/
22
xy
x
y

; f)
2 22
2xyx yz 
;
Bài 5. Tính giá trị của biểu thức
a)
22
(2 1) 2(2 1)(3 1) (3 1)Mx x x x
 
với
1
5
x 
;
b)
22 2
(3 1) 2(9 1) (3 1)Nx x x

với
x
.
Bài 6. Tính giá trị của biểu thức
a)
23
27 27 9P x xx
với
17x 
;
b)
32
33
Qx x x

với
99x
.
Bài 7. Chứng minh:
a)
2
23 5k 
chia hết cho
4
. b)
2
9 25k
chia hết cho
5
.
Bài 8. Chứng minh:
a)
2
32 4k 
chia hết cho
3
. b)
2
9 14k
chia hết cho
8
.
Bài 9. Chứng minh rằng
12
21
chia hết cho
17
.
Bài 10. Chứng minh rằng hiệu các bình phương của hai số lẻ liên tiếp thì chia hết cho
8
.
Bài 11. Chứng minh rằng
173 73
nn
chia hết cho
100
với mọi
n
.
Bài 12. Tìm
n
để biểu thức
22 2
( 10) 36An n
có giá trị là một số nguyên tố.
Bài 13 Chia một hình vuông thành các hình vuông và hình chữ
nhật (hình vẽ). Tính diện tích mỗi hình vuông và mỗi hình chữ
nhật được chia theo x và y rồi tính tổng của chúng và phân tích
kết quả vừa tìm được thành nhân tử.
Bài 14 Một cánh cửa sổ có dạng như hình ảnh bên . Ô cửa sổ
được cấu tạo bao gồm 1 hình vuông cạnh x (m) và một nữa
hình tròn.
a/ Tính diện tích S của cánh cửa đó.
b/ Phân tích S thành nhân tử sau đó tính diện tích của cánh của đó
với x = 1,2 m.
PHIẾU BÀI TẬP TOÁN 8
Trang 7/7
Bài 15 Một khối gỗ dạng hình lập phương
có cạnh là x (cm). Người ta cắt bỏ đi một
phần gỗ cũng có dạng hình lập phương có
thể tích là 1728 (cm
3
).
a/ Tính thể tích V của phần gỗ còn lại rồi
sau đó phân tích V thành nhân tử.
b/ Tính thể tích V của phần gỗ còn lại biết
x = 26 (cm).
Bài 16 Bác Lan gửi tiết kiệm với số tiền
400 triệu đồng vào một ngân hàng, kì hạn 12 tháng và theo thể thức lãi kép. Nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập làm vốn ban đầu để tính
lãi cho năm tiếp theo. Giả sử lãi xuất cố định là x% /năm, x > 0. Tính x biết rằng sau 2 năm
gửi tiết kiệm , bác Hoa nhận được số tiền (bao nhiêu gồm cả gốc lẫn lãi) là 449,44 triệu đồng.
PHIẾU BÀI TẬP TOÁN 8
Trang 1/7
I/ BÀI TẬP TRẮC NGHIỆM :
Câu 1: Trong các biểu thức sau, biểu thức nào không phải là đơn thức ?
A.
1
4
. B.
2xy
+
.
C.
23
3xy z−
. D.
x
.
Câu 2: Trong những đơn thức sau, đơn thức nào không phải là đơn thức thu gọn ?
A.
2
. B.
x
.
C.
23
xy
. D.
32
2xyx
.
Câu 3: Trong các biểu thức đại số sau, biểu thức nào là đơn thức
A.
2
2
xy+
. B.
45
1
5
xy
−
.
C.
3
3
xy
y
+
. D.
3
3
7
4
xy x−+
.
Câu 4: Sau khi thu gọn đơn thức
22
3x yxy
ta được đơn thức :
A.
23
3xy
. B.
33
3xy
.
C.
32
3
xy
. D.
24
3
xy
.
Câu 5: Thu gọn đơn thức
22
x xyz
ta được
A.
32
xz
. B.
32
x yz
.
C.
22
x yz
. D.
2
xyz
.
Câu 6: Kết quả của phép tính
23 23
34xy xy+
là :
A.
23
7xy
. B.
23
12xy
. C.
46
12xy
. D.
46
7xy
.
Câu 7: Cho các biểu thức
2 23 2 2
1
2 ;3 ;
2
xy
x y xy xyz xyz
xy
+
++ − +
−
. Có bao nhiêu đa thức trong các
biểu thức trên ?
A.0 . B.1 . C.2 . D.3 .
Câu 8: Thu gọn đa thức
2 32 2 32
4 6 10 4
xy xy xy xy+−+
ta được
A.
2 32
14 10xy xy+
. B.
2 32
14 10xy xy−+
.
C.
2 32
6 10xy xy−
. D.
2 32
6 10xy xy−+
.
Câu 9: Thu gọn đa thức
4545224
2 45 7 2xy y xy y xy xy−+ −+ −
ta được :
A.
4 5 22
5 11xy y xy++
. B.
4 5 22
9 11xy y xy−+
.
C.
4 5 22
5 11xy y xy−−+
. D.
4 5 22
5 11xy y xy−+
.
Câu 10: Giá trị của đa thức
22 4
2
xy xy xy+−
tại x = y = -1 là :
A.3 . B.1 . C.-1 . D. 0.
Câu 11: Giá trị của đa thức
3 32
14 6 2x y y xy y− − ++
tại x = -1 ; y = 0,5 là :
A. 1 . B.0,75.
BÀI TẬP TỔNG HỢP CHƯƠNG
ĐA THỨC NHIỀU BIẾN
PHIẾU BÀI TẬP TOÁN 8
Trang 2/7
C.2,5. D.1,75.
Câu 12: Trong giờ học Mỹ Thuật, bạn Hạnh dán lên
trang vở hai hình vuông và một tam giác vuông
có độ dài hai cạnh góc vuông là
x (cm), y (cm) như hình bên. Tổng diện tích của
hai hình vuông và tam giác vuông đó tại x = 3
và y = 5 là :
A.41,5cm
2
. B. 40,5cm
2
.
C.44cm
2
. D. 47,2cm
2
.
Câu 13: Bác Huỳnh muốn sơn bề mặt của hai khối gỗ có dạng hình hộp chữ nhật . Hình hộp
chữ nhật thứ nhất có ba kích thước x (cm), 2y (cm), z (cm). Hình hộp chữ nhật thứ hai
có ba kích thước là 2x (cm), 2y (cm), 3z (cm). Viết đa thức biểu thị tổng diện tích bề
mặt của hai khối gỗ mà bác Huỳnh cần phải sơn :
A.
12 16 14xy yz zx++
. B.
10 5 4
xy yz zx++
.
C.
2 4 10xy yz zx++
. D.
2 10 13xy yz zx++
.
Câu 14: Cho
32 2
32A x y x y xy= +−
và
2 32 2
43 2B xy x y x y y=−+ +
. Kết quả của
AB−
là :
A.
32 2 2
53
x y x y xy y−−+
. B.
32 2 2
5 53x y x y xy y+ ++
.
C.
32 2 2
5 53x y x y xy y+ −+
. D.
32 2 2
53x y x y xy y−++
.
Câu 15: Cho
42 3
42 35
A x yx z= + −+
và
3 24
4 83 5B z yx x
=− ++ −
. Kết quả của
AB−
là :
A.
42 3
93x yx z+ +−
. B.
4 23
5 13x yx z−+ ++
.
C.
42 3
93x yx z
− +−
. D.
42 3
93x yx z− ++
.
Câu 16: Kết quả của tích
23 46
3 .8
xy xy
là :
A.
69
24
xy
. B.
23
24xy
. C.
69
5xy
−
. D.
69
11xy
.
Câu 17: Kết quả của tích
( )
22
1
5.
5
x y xy−
là :
A.
33
5xy
. B.
33
5xy−
. C.
33
xy−
. D.
32
xy
.
Câu 18: Kết quả của tích
( )
3
2
1
2.
4
xy x−
là :
A.
45
2xy−
. B.
54
1
2
xy
. C.
54
2xy
. D.
54
2
xy−
.
Câu 19: Kết quả thương của phép chia
2
42 2
1
6:
2
xy xy



là :
A.
12
. B.
24
. C.
2
24xy
. D.
2
12xy
.
Câu 20: Kết quả thương của phép chia
( )
2
23
1
:3
9
x y xy−
là :
A.
1
81
y
. B.
1
27
y−
. C.
1
81
xy
. D.
1
81
y
−
.
PHIẾU BÀI TẬP TOÁN 8
Trang 3/7
Câu 21: Kết quả của tích
( )
2
62 3xy x y
−
là :
A.
22
12 18x y xy+
. B.
32
12 18x y xy−
. C.
32
12 18x y xy+
. D.
22
12 18x y xy−
.
Câu 22: Kết quả của tích
( )( )
22xy xy+−
là :
A.
4
xy
−
. B.
4
xy
+
. C.
22
4xy
−
. D.
22
4xy+
.
Câu 23: Kết quả của tích
( )( )
22xy xy+−
là :
A.
4xy−
. B.
4xy+
. C.
22
4
xy
−
. D.
22
4xy+
.
Câu 24: Kết quả của tích
( )( )
15xy xy−+
là :
A.
22
45x y xy+−
. B.
22
45x y xy++
. C.
2
45xy xy−−
. D.
22
45x y xy−−
.
Câu 25: Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
Cột A
Cột B
a.
(
)
(
)
22
x y x xy y
+ ++
1.
33
xy−
b.
( )
(
)
22
x y x xy y− ++
2.
3 2 23
22x x y xy y+++
c.
( )
( )
22
x y x xy y+ −+
3.
33
xy−
4.
Câu 26: Kết quả
( )
2
2
2
xy−
là :
A.
2
2xy−
. B.
2
2xy+
. C.
( )
( )
22x yx y−+
. D.
( )( )
22xyxy++
.
Câu 27: Kết quả
2
1x −
là :
A.
( )( )
11xx−+
. B.
(
)( )
11xx++
. C.
2
21xx++
. D.
2
21xx+−
.
Câu 28: Kết quả
là :
A.
( )
2
2
7 x−
. B.
2
14 49xx−+
. C.
2
2 49xx−+
. D.
2
14 7xx
−+
.
Câu 29: Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
A
B
a.
22
69x xy y++
1.
( )
2
31x +
b.
( )(
)
2323xyxy−+
2.
( )
2
3xy+
c.
2
9 61xx−+
3.
22
49xy−
PHIẾU BÀI TẬP TOÁN 8
Trang 4/7
4.
( )
2
9xy−
Câu 30: Kết quả
32
3 31xxx+ ++
là :
A.
3
1x +
. B.
( )
3
1
x −
. C.
( )
3
1x
+
. D.
(
)
3
3
1
x
+
.
Câu 31: Kết quả
32
11
3 27
xx x−+ −
là :
A.
3
1
3
x −
. B.
3
1
3
x

−


. C.
3
1
3
x

+


. D.
3
3
1
3
x

−


.
Câu 32: Kết quả
3 2 23
8 12 6x x y xy y+ ++
là :
A.
( )
3
3
2xy+
. B.
( )
3
3
2xy+
. C.
( )
3
2xy+
. D.
( )
3
2xy−
.
Câu 33: Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
A
B
a.
32
3 31
xxx− +−
1.
( )
3
1x +
b.
2
8 16xx++
2.
( )
3
1x −
c.
23
3 31xx x+ ++
3.
4.
( )
2
1x −
Câu 34 Khai triển
( )
3
51x −
được kết quả là
A.
( )
(
)
2
5 1 25 5 1
x xx− −+
. B.
( )
( )
2
5 1 25 10 1x xx− ++
.
C.
( )
( )
2
5 1 25 10 1x xx− −+
. D.
( )
(
)
2
5 1 25 10 1
x xx+ −+
.
Câu 35: Rút gọn biểu thức
( ) (
)
22
ab ab+ −−
được kết quả là
A.
4ab
. B.
4
ab−
. C.
0
. D.
2
2
b
.
Câu 36
( )
( )
2
3 39x xx+ −+=
A.
33
3x −
. B.
3
27
x +
. C.
9x −
. D.
(
)
3
3x
+
.
Câu 37 Điền đơn thức vào chỗ trống:
( )
( )
2 33
3 ....... 3 27x y xy y x y+ −+= +
A.
9x
. B.
2
6x
. C.
9xy
. D.
2
9x
.
Câu 38 Đẳng thức:
( ) ( )
3
33
3x y xy xyxy+=+ − +
Đúng. B. Sai.
Câu 39 Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
A
B
PHIẾU BÀI TẬP TOÁN 8
Trang 5/7
1.
( )
(
)
xyxy+−
a.
33
xy
+
2.
22
2x xy y−+
b.
22
2x xy y++
3.
( )
2
xy+
c.
22
xy−
4.
( )
(
)
22
x y x xy y
+ −+
d.
( )
2
xy−
e.
22
xy+
Câu 40 Thương
(
)
532 2
3 2 4 :2xxxx
−+
bằng
A.
3
3 24xx−+
. B.
3
3
2
2
xx−+
. C.
3
3
2
2
xx++
. D.
53 2
3
2
2
xx x−+
.
Câu 41 Thương
(
) ( )
4 3 22 4
12 4 8 : 4
xy x xy x− +− −
bằng
A.
22
32
xy x y− +−
. B.
4 3 22
32
xy x xy
+−
. C.
22
12 4 2xy x y− +−
. D.
22
32xy x y−+
.
Câu 42 Thương
( )
223
1
32 :
2
xy x y x x

−+ −


bằng
A.
22
31
22
y xy x− +−
. B.
22
32
y xy x++
. C.
22
642y xy x−+ −
. D.
22
64y xy x−+
.
Câu 43 Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
A
B
a.
(
)
3 2 22
2 :2xx x y xy−+
1.
2
245xy x
−+−
b.
( )
2 3 22
15 19 16 : 6xy xy y y++
2.
5 19 8
26 3
x xy++
c.
( )
22 3
4 8 10 : 2x y x y xy xy− +−
3.
2
13
22
x xy y−+
4.
2
45xy x+−
Câu 44 Đa thức
2
12 9 4xx−−
được phân tích thành
A.
( )( )
2 32 3xx−+
. B.
( )
2
23x
−−
. C.
( )
2
32x−
. D.
( )
2
23x−+
.
Câu 45 Phân tích đa thức
32 23
6 12 8x x y xy x−+ −
được kết quả là
PHIẾU BÀI TẬP TOÁN 8
Trang 6/7
A.
. B.
(
)
3
2xy
−
. C.
(
)
3
3
2
xy−
. D.
( )
3
2xy−
.
Câu 46 Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
A
B
a.
( )( )
xyxy−+
1.
(
)
2
5
x−−
b.
2
10 25xx−−
2.
22
xy−
c.
3
1
8
8
x −
3.
2
11
24
24
x xx

− ++


4.
(
)
2
xy
−
II/ BÀI TẬP TỰ LUẬN :
Bài 1. Cho hai đa thức
3 2 32
235 2A x y x y xy xy= − + −+
và
2 33 2
5 3 6 52A x y xy x y xy
= − + ++
a/ Tính giá trị của mỗi đa thức A, B tại x = 1; y = -1.
b/ Tính
;.A BA B
+−
Bài 2. Thực hiện phép tính :
a/
23
13
.6 1
22
xy xy x y

+−


b/
11
22
22
xyxy

−+


c/
5 36 4 23
24 : 6xyz xyz
d/
( )
6 76 5 37 5 38 3 36
3 2 6 : 42xyz xyz xyz xyz+−
Bài 3. Viết mỗi biểu thức sau dưới dạng bình phương, lập phương của một tổng hoặc
một hiệu.
a/
42
44xx++
b/
4 22 4
9 24 16x xy y++
c/
32
27 27 3 1x xx− ++
d/
32
3 31xxx− +−
PHIẾU BÀI TẬP TOÁN 8
Trang 7/7
Bài 4. :Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của
biến.
a/
( ) ( )
1
2 .2 4 4 2
2
A xy x x y x x= + − +− +
b/
( ) ( ) ( )
2
2 1 . 2 1 2 3 12
Bx x x
= − +− − −
c/
( )
(
)
22
2 3 10
xx x+ −− −
d/
( ) ( )
( )
( )( )
3
2
1 2 1 22x x x x xx x− − + ++ − − +
Bài 5. Phân tích các đa thức sau thành nhân tử.
a/
22
6 91a ab b++−
b/
( )( )
2
4 25 2 7 5 2xxx−+ + −
c/
( ) ( )
5 3 15 3xy xxy+− +
d/
( ) ( )
22
2
xxy yxy xyx+− ++−
e/
22
69a ab−−+
f/
33 2
3 31xy x x−− +−
| 1/58
| | Tải xuống

Có thể bạn quan tâm:

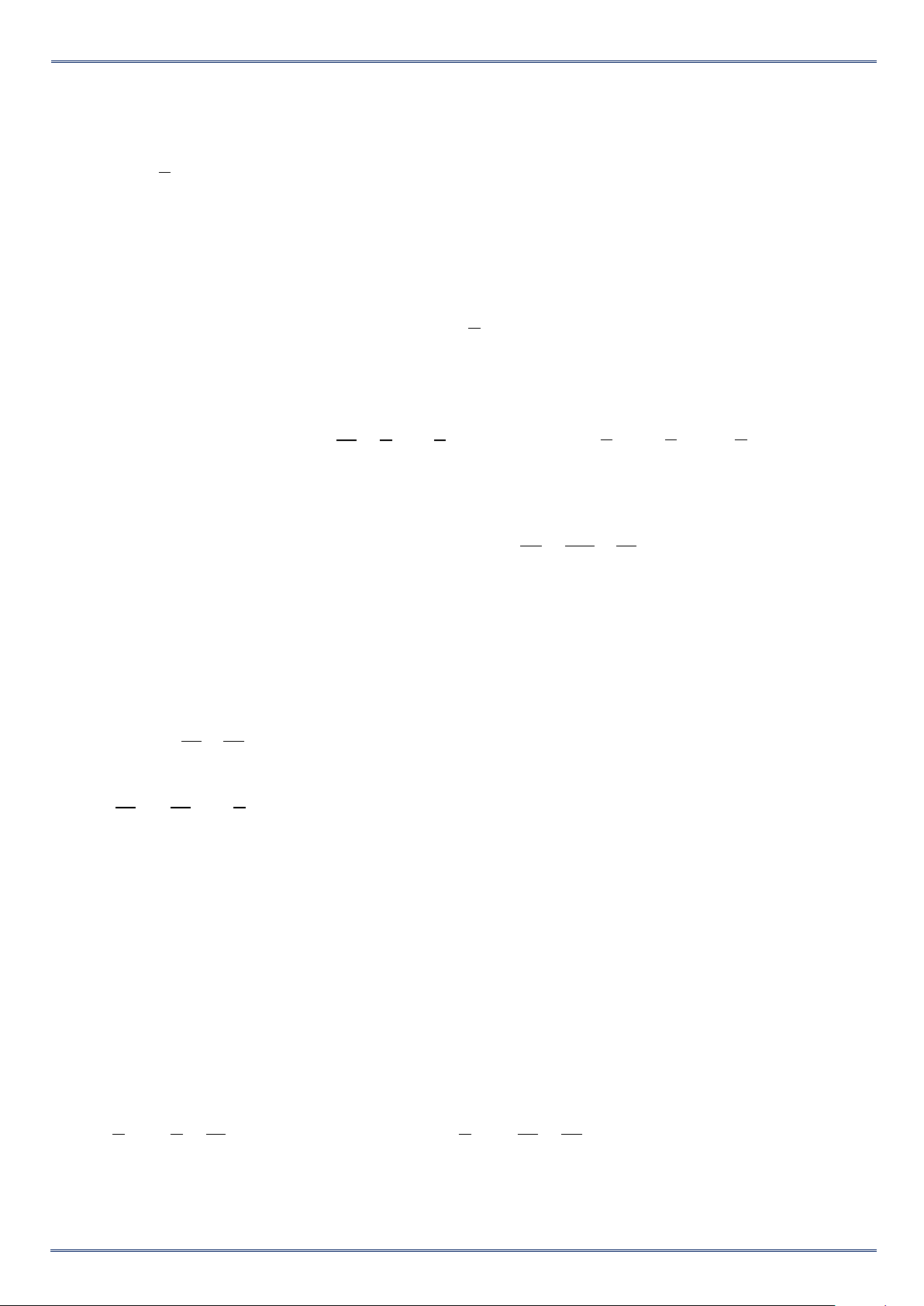
Preview text:

PHIẾU BÀI TẬP TOÁN 8 Trang 1/10 ĐƠN THỨC NHIỀU BIẾN. ĐA THỨC NHIỀU BIẾN A. KIẾN THỨC TRỌNG TÂM
I/ Đơn nhất nhiều biến. 1. Khái niệm.
 Đơn thức nhiều biến là biểu thức đại số chỉ gồm một số, hoặc một biến hoặc một tích giữa các số và các biến.
2. Đơn thức thu gọn.
 Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến đã được nâng lên lũy
thừa với số mũ nguyên dương.
 Trong đơn thức thu gọn có hai phần: phần hệ số và phần biến.
 Ta cũng coi một số là một đơn thức thu gọn chỉ có phần hệ số.
 Trong đơn thức thu gọn, mỗi biến chỉ được viết một lần.
3. Đơn thức đồng dạng.
 Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
 Các số khác 0 được coi là những đơn thức đồng dạng.
4. Cộng trừ đơn thức đồng dạng.
 Để cộng (trừ) các đơn thức đồng dạng, ta cộng (trừ) các hệ số với nhau và giữ nguyên phần biến.
II/ Đa nhất nhiều biến. 1. Định nghĩa.
 Đa thức nhiều biến (hay đa thức) là tổng của những đơn thức. Mỗi đơn thức được coi là một đa thức.
 Mỗi đơn thức trong tổng gọi là hạng tử của đa thức đó.
2. Đa thức thu gọn.
 Thu gọn đa thức nhiều biến là làm cho trong đa thức đó không còn hai đơn thức nào đồng dạng.
3. Giá trị của đa thức .
 Để tính giá trị của một đa thức tại những giá trị cho trước của các biến, ta thay những giá trị cho trước
đó vào biểu thức xác định đa thức rồi thực hiện các phép tính .
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
PHIẾU BÀI TẬP TOÁN 8 Trang 2/10
Dạng 1: Nhận biết các đơn thức nhiều biến, đa thức nhiều biến.
Ví dụ 1. Trong các biểu thức sau, biểu thức nào là đơn thức? a) 2 12x y ; b) x(y + 1); c) 1 − 2x ; d) 18; e) 5 . 2x Bài giải 2
12x y ; 18 là đơn thức.
Ví dụ 2. Biểu thức nào dưới đây không phải là đơn thức? a) 2 2 x − y ;
b) x − y + xy ; c) 2 2x y ; d) 3 ; e) x(y + 1). 4xy Bài giải 2 2
x − y ; x − y + xy ; x(y + 1); 3 không phải là đơn thức. 4xy
Ví dụ 3. Cho biết phần hệ số, phần biến của mỗi đơn thức sau a) 2 2 1 x y ; b) 3 − xy . 2 Bài giải a) 2
2x y : Hệ số là 2, phần biến là x 2 y. b) 1 3
− xy : Hệ số là 1 − , phần biến là 3 xy . 2 2
Ví dụ 4. Biểu thức nào là đa thức trong các biểu thức sau? a) 2 2 x
x y − 2 + 3xy ; b) 2 − 2x ; c) 2018 ;
d) x(x + y). y Bài giải 2 2
x y − 2 + 3xy ; 2018 ;x(x + y)là đa thức.
Ví dụ 5. Biểu thức nào không phải là đa thức trong các biểu thức sau? 2 a) 3 x + 1 x − 2 + ; b) 2 xy − 2x ; c) 2 x − 4 ; d) . x xy Bài giải 3 2 x + 1 x − 2 + ;
không phải là đa thức. x xy
Dạng 2: Nhận biết các đơn thức đồng dạng
Ví dụ 1. Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng 3 1 2 3 5 5 2
xy; − x z; xyz; xy;7xyz; x z; 3 − xy. 2 3 4 6 6
PHIẾU BÀI TẬP TOÁN 8 Trang 3/10 Bài giải
Nhóm các đơn thức đồng dạng là : Nhóm 1 : 3 5 1 5 xy; xy; 3
− xy. Nhóm 2: 3 xyz;7xyz. Nhóm 3: 2 2 − x z; x z 2 6 4 3 6
Ví dụ 2. Trong các đơn thức sau, đơn thức nào đồng dạng với đơn thức 2 3 − x yz ? a) 3 2 3 − xyz ; b) 2 x yz ; c) 2 yzx ; d) 2 4x y . 3 2 Bài giải 2 2
x yz đồng dạng với đơn thức 2 3 − x yz . 3 Câu b đúng .
Dạng 3: Cộng, trừ các đơn thức đồng dạng
Ví dụ 1. Tính tổng, hiệu các biểu thức sau a) 2 1 2 3xy + xy ; b) 2 2 2 2 2 2
2x y + 3x y + x y ; 3   c) 2 2 2 2 2 1
3x yz − 4x yz ; d) 2 2 2
2x y + x y + − x y . 3  3  Bài giải   a) 2 1 2 1 2 10 2
3xy + xy = 3 + xy = xy b) 2 2 2 2 2 2
2x y + 3x y + x y = (2 + 3 + ) 2 2 2 2 1 x y = 6x y 3  3  3     c) 2 2 2 2 3 2 1 2 1 7
x yz − 4x yz = (3 − 4) 2 2 2 2
x yz = −x yz d) 2 2 2 2 2
2x y + x y + − x y = 2 + − x y = x y 3  3   3 3  3
Ví dụ 2. Tính giá trị biểu thức 2 2 2
P = 2011x y + 12x y − 2015x y tại x = 1 − ; y = 2 . Bài giải 2 2 2 P = x y + x y − x y = ( + − ) 2 2 2011 12 2015
2011 12 2015 x y = 8x y . Thay x = -1; y = 2 vào 2
8x y ta được : x y = .(− )2 2 8 8 1 .2 = 8.1.2 = 16
Dạng 4: Tìm đơn thức thỏa mãn đẳng thức
Dùng quy tắc chuyển vế giống như đối với với số.
 Nếu M + B = A thì M = A − B .
 Nếu M − B = A thì M = A + B .
 Nếu B − M = A thì M = B − A .
Ví dụ 1. Xác định đơn thức M để
PHIẾU BÀI TẬP TOÁN 8 Trang 4/10 a) 4 3 4 3 2x y + M = 3 − x y ; b) 3 3 3 3
2x y − M = 4x y . Bài giải 4 3 4 3 a) 2x y + M = 3 − x y b) 3 3 3 3
2x y − M = 4x y . 4 3 4 3 M = 3 − x y − 2x y 3 3 3 3
M = 2x y − 4x y M = ( 3 − − 2) 4 3 x y M = (2 − 4) 3 3 x y 4 3 M = 5 − x y 3 3 M = 2 − x y
Dạng 5: Tính giá trị của đa thức
 Thay giá trị của biến vào đa thức rồi thực hiện phép tính.
Ví dụ 1. Tính giá trị của đa thức sau: a) 2 2 4 1
x y + xy tại x = 2 − , 1 y = ; b) 2 3
− x y + x tại x = 3 , y = 2 − . 2 2 Bài giải a) 2 2
4x y + xy tại x = 2 − , 1 y = . 2 2   Thay 2 1 1 1 x = 2 − , 1 y = vào 2 2
4x y + xy ta được : 4.( 2 − ) .  + ( 2 − ). = 16. + (− ) 1 = 4 − 1 = 3. 2  2  2 4 b) 1 2 3
− x y + x tại x = 3 , y = 2 − . 2 Thay 1 x = 3 , y = 2 − vào 2 3
− x y + x ta được : 2 1 − .( )2 .(− )3 1 + = − . .(− ) 72 78 3 2 3 9 8 + 3 = + 3 = = 39 2 2 2 2
Dạng 6: Thu gọn đa thức
 Bước 1: Nhóm các hạng tử đồng dạng với nhau;
 Bước 2: Cộng, trừ các đơn thức đồng dạng trong từng nhóm.
Ví dụ 1. Thu gọn các đa thức sau a) 2 2 3 1
A = −x y − 2xy + 2x y + 5xy + 2 ; b) 2 2 B = 2
− xy + xy + xy + xy ; 2 2 c) 2 2 2 2 2 2 2 2 2
C = x + y + z + x − y + z + x + y − z ; d) 2 2 2 2
D = xy z + 2xy z − xyz − 3xy z + xy z . Bài giải a)
PHIẾU BÀI TẬP TOÁN 8 Trang 5/10 2 2
A = −x y − 2xy + 2x y + 5xy + 2 = ( 2 −x y ) 2 + 2  x y +   ( 2
− xy ) + 5xy + 2  = ( 1 − + 2) 2 x y  +   ( 2 − + 5) 2
xy  + 2 = x y + 3xy + 2  b) 3   2 1 2 3 2 1 2 B = 2
− xy + xy + xy + xy =  xy + xy  + ( 2 − xy ) + xy 2 2  2 2     3 1   2
=  + xy  + ( 2 − + ) 2
1 xy = 2xy − xy 2 2     c) 2 2 2 2 2 2 2 2 2
C = x + y + z + x − y + z + x + y − z = ( 2 2 x + x ) + ( 2 2 2
y − y + y ) + ( 2 2 2
z + z − z ) 2 2 2
= 2x + y + z d) 2 2 2 2
D = xy z + 2xy z − xyz − 3xy z + xy z = ( 2 2 2 2
xy z + 2xy z − 3xy z + xy z ) − xyz 2 = xy z − xyz
Ví dụ 2. Thu gọn các đa thức sau : a) 2 2 1 3
A = 2x yz + xy − x yz + 4xy + 6 ; b) 2 2
B = 4xy + x y − xy + x y ; 2 2 c) 2 2 2 2 2 2 2 2 2
C = x − y + z − x + y − z + x + y + z ; d) 2 2 2 2
D = 2x yz + 4xy z − 5x yz + xy z − xyz . e) 2 3 4 2 4 2 3
E = 2x y + 3x − 7x + 6x − x y . Bài giải a) b) 1 2 3 2
B = 4xy + x y − xy + x y 2 2
A = 2x yz + xy − x yz + 4xy + 6 2 2  1 3  = ( 2 2
2x yz − x yz ) + (xy + 4xy) + 6 = (4xy − xy) 2 2
+  x y + x y  2 2  2 =  x yz + 5xy + 6 2 = 3xy + 2x y c) 2 2 2 2 2 2 2 2 2
C = x − y + z − x + y − z + x + y + z = ( 2 2 2
x − x + x ) + ( 2 2 2
−y + y + y ) + ( 2 2 2
z − z + z ) 2 2 2
= x + y + z d) e)
PHIẾU BÀI TẬP TOÁN 8 Trang 6/10 2 2 2 2
D = 2x yz + 4xy z − 5x yz + xy z − xyz 2 3 4 2 4 2 3
E = 2x y + 3x − 7x + 6x − x y = ( 2 2
2x yz − 5x yz ) + ( 2 2
4xy z + xy z ) − xyz = ( 2 3 2 3
2x y − x y ) + ( 4 4 3x + 6x ) 2 − 7x 2 2 = 3
− x yz + 5xy z − xyz 2 3 4 2
= x y + 9x − 7x C. BÀI TẬP VẬN DỤNG
Bài 1. Trong các biểu thức sau, biểu thức nào là đơn thức?   2 a) 3 2 4 + x xy xy ; 2 3xy z ; 1 3 ; 2 2
1 − x y ; 10 . b) 2 x yz ; 2018 ;
; 2xy ; x + y . 2  2  3y 3 3 z Bài giải   a) Đơn thức là : 2 3 3xy z ; 1 3 ; 2 2 1 − x y . 2  2  b) Đơn thức là : 4 2 x yz ; 2018 . 3
Bài 2. Biểu thức nào là đa thức trong các biểu thức sau? a) + 2 2 x x y + 3 + xy ; b) 2 ;
c) x(x + 2y); d) 1 2 − . x + y x − 1 Bài giải
Đa thức là x(x + 2y) ; 2 2x y + 3 + xy .
Bài 3. Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng 2 2 1 2 2 2 2 2 5 2 2 8
− x yz;3xy z; x yz;5x y z;− xy z;− x y z. 3 3 7 Bài giải
Nhóm các đơn thức đồng dạng là : Nhóm 1: 2 1 2 8 − 2 5
x yz; x yz. Nhóm 2 : 2 2
3xy z;− xy z. Nhóm 3 : 2 2 2 2
5x y z;− x y z. 3 3 7
Bài 4. Thu gọn mỗi đơn thức sau: a) 2 2 2 4 x y ⋅ 3xy ; b) 2 3
2xy ⋅ x y ⋅10xyz ; c) 2 3 2 10
− y ⋅ (2xy) ⋅ ( x − ) . 5 d) 2 4 2 3 2 4 3
xy ⋅ x y ⋅ 6x ; e) 2 2 2 x y z ⋅ xyz ; 3 3 4   f) 2 2 1 2 3 4 − a x ⋅ ( 2
− bxy) ⋅ − x y với a , b là hằng số. 4   
PHIẾU BÀI TẬP TOÁN 8 Trang 7/10 Bài giải a) 2 2
2x y ⋅ 3xy = (2.3).( 2 x x ).( 2 yy ) 3 3 = 6x y   b) 4 2 3 4
2xy ⋅ x y ⋅10xyz = 2. .10.( 2 xx x ).( 3 yy y ) 4 5 = 16x y 5  5  c) 2 3 2 2 3 3 2
− 0y ⋅ (2xy) ⋅ (−x) = − y . x y .x = (−  ). . .( 3 2 x .x ).( 2 3 y .y ) 5 5 1 10 8 10 8 1 = 80 − x y   d) 2 4 2 3 4
2xy ⋅ x y ⋅ 6x = 2. .6.( 2
x.x .x ).( 2 3 y .y ) 4 5 = 16x y 3  3    e) 4 2 2 2 3 4 3
x y z ⋅ xyz =  . .( 2 x x ).( 2 y y ).( 2 z z ) 3 3 3 = x y z 3 4  3 4         2 2 1 2 3 2 2 2 2 1 2 3
− a x ⋅ (− bxy) ⋅ − x y  = − a x. b x y .− x y  = (− ) 2 2 1 4 2 4 4
4 a .4 b .− .( 2 2
x.x .x ).( 2 3 y .y ) f)  4   4    4  với 2 2 5 5 = 4a b x y
a , b là hằng số.
Bài 5. Thu gọn các đa thức sau a) 3 2 1 2 A = 2
− xy + xy + xy + xy ; 2 2 b) 2 2 2 2
B = xy z + 2xy z − xyz − 3xy z + xy z . c) 2 3 4 2 4 2 3
C = 4x y + x − 2x + 6x − x y . d) 3 2 1 2
D = xy − 2xy − xy + 3xy ; 4 2 e) 2 3 4 2 3 4
E = 2x − 3y − z − 4x + 2y + 3z ; f) 2 2 2
F = 3xy z + xy z − xyz + 2xy z − 3xyz . Bài giải   a) 3 2 1 2 3 2 1 2 A = 2
− xy + xy + xy + xy =  xy + xy  + ( 2 − xy + xy ) 2 = 2xy − xy ; 2 2  2 2  b) 2 2 2 2
B = xy z + xy z − xyz − xy z + xy z = ( 2 2 2 2
xy z + xy z − xy z + xy z ) 2 2 3 2 3
− xyz = xy z − xyz . c) 2 3 4 2 4 2 3
C = 4x y + x − 2x + 6x − x y = ( 2 3 2 3
4x y − x y ) + ( 4 4 x + 6x ) 2 2 3 4 2
− 2x = 3x y + 7x − 2x .
PHIẾU BÀI TẬP TOÁN 8 Trang 8/10   d) 3 2 1 2 3 2 1 2
D = xy − 2xy − xy + 3xy =  xy − xy  + ( 2
− xy + 3xy) 1 2 = xy + xy ; 4 2  4 2  4 e) 2 3 4 2 3 4
E = 2x − 3y − z − 4x + 2y + 3z = ( 2 2 x − x ) + ( 3 3
− y + y ) + ( 4 4 −z + z ) 2 3 4 2 4 3 2 3 = 2
− x − y + 2z f) 2 2 2
F = xy z + xy z − xyz + xy z − xyz = ( 2 2 2
xy z + xy z + xy z ) + (−xyz − xyz ) 2 3 2 3 3 2 3
= 6xy z − 4xyz .
Bài 6. Tính giá trị mỗi đa thức sau : a) 2 3 2 3
A = 6xy + 7xy + 8x y ; tại x = 2 ; y = 1 2 b) 6 2 3 5 5 6
B = x + 2x y − x + xy − xy − x ; tại x =0 ; y = 1 4 c) 2 6 2 6
C = 7x y − 4x + 3y z + 4x ; tại x = 2 ; y = 1 Bài giải a) 2 3 2 3
A = 6xy + 7xy + 8x y ; tại x = 2 ; y = 1 2 2 3 3      
Thay x = 2 ; y = 1 vào 2 3 2 3 1 1 2 1 35
A = 6xy + 7xy + 8x y ta được : 6.2.  + 7.2.  + 8.(2) .  = 2  2   2   2  4 b) 2 2 3 3 5
B = x + 2x y − x + xy − xy ; tại x = 1 ; y = 0. 4
Thay x = 1 ; y = 0 vào 6 2 3 5 5 6
B = x + 2x y − x + xy − xy − x ta được : 4 2 3  1   1  3   −   =  4   4  64 c) 2 6 2 6
C = 7x y − 4x + 3y z + 4x ; tại x = 2 ; y = 1; z = 4
Thay x = 2 ; y = 1 vào 2 6 2 6
C = 7x y − 4x + 3y z + 4x ta được : 2 6 2 6
7.2 .1 − 4.2 + 3.1 .4 + 4.2 = 40
D. BÀI TẬP TỰ LUYỆN.
Bài 1. Trong các biểu thức sau, biểu thức nào là đơn thức? a) 4 − 3x ; b) 6 ; c) 2xy ; d) 9 ; e) 3x(y − 2). 5x 5
Bài 2. Biểu thức nào dưới đây không phải là đơn thức?
PHIẾU BÀI TẬP TOÁN 8 Trang 9/10 a) 2 2 − x y ; b) x(y − 1); c) 2 2 x + y ; d) 3 ;
e) x + y + xy . 3 4xy
Bài 3. Cho biết phần hệ số, phần biến của mỗi đơn thức sau a) 1 3 3 xy ; b) 2 2 − x y . 3 4
Bài 4. Thực hiện phép tính : a) 1 2 − 1 x y + 2 2x y ; b) 3 2x y - 3 x y . 2 4 c) 2 2 2 2 1
x y + 3x y + x y ; d) 2 2 2 2
−x y + x y + 4x y − 2x y ; 3 5 e) 1 2 1 2 1 2
xy + xy + xy ; f) 3 3 3
19x y + 15x y − 12x y . 2 3 6   g) 2 1 2 1 2
3xy + xy + − xy . 4  2 
Bài 5. Thu gọn mỗi đơn thức sau:     a) 2 1 1 2 1 3
x ⋅  − y  ⋅  x ; b) 2 3
− x y ⋅ xy ; 4 2      3 2 2   c) 3 1 ⋅ (x y )2 3 2 ; d) 2
 − x  (by) (b là hằng số). 4  2 
Bài 6. Tính giá trị của đơn thức sau a) 2 2 1 x y tại x = 1 − , 1 y = ; b) 3 2 − x y tại 1 x = − , y = 4 − . 4 2 2
Bài 7. a/ Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng 2 2 1 2 2 2 2 2 5 2 2 8
− x yz;3xy z; x yz;5x y z;− xy z;− x y z. 3 3 7
b/ Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng 5 2 2 2 1 2 2 2 2 2 2 2
x y;x y ; − x y; 2
− xy ;x y; − xy ;6x y . 4 2 5
Bài 8. Tính giá trị biểu thức a) 2 2 2 2
x y + 3x y + x y tại x = 3 , 1 y = − ; 3 7 b) 1 2 1 2 1 2
xy + xy + xy tại 3 x = , 1 y = − ; 2 3 6 4 2
PHIẾU BÀI TẬP TOÁN 8 Trang 10/10 c) 3 3 2x y + 3 3 3 3
10x y − 20x y tại x = 1, y = 1 − . d) 2 2 2
2018xy + 16xy − 2016xy tại x = 2 − ; 1 y = − . 3
Bài 9. Tính giá trị của biểu thức M biết rằng a) 2 4 2 4 2 4
15x y − M = 10x y + 6x y tại 1
x = − , y = 2 ; 2 b) 3 3 3
40x y + M = 20x y + 15x y tại x = 2 − , 1 y = . 5
Bài 10. Xác định đơn thức M để a) 4 4 4 4 4 4
2x y + 3M = 3x y − 2x y ; b) 2 2
x − 2M = 3x . c) 2 3 2 3
3x y + M = x − y ; d) 2 2 2 2
7x y − M = 3x y .
PHIẾU BÀI TẬP TOÁN 8 Trang 1/22
CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN A. KIẾN THỨC TRỌNG TÂM
1/ Cộng hai đa thức nhiều biến.
Để cộng hai đa thức theo hàng ngang, ta có thể làm như sau:
• Viết tổng hai đa thức theo hàng ngang ;
• Nhóm các đơn thức đồng dạng với nhau;
• Thực hiện phép tính theo trong từng nhóm , ta được tổng cần tìm.
2/ Trừ hai đa thức nhiều biến.
Để trừ đa thức P cho đa thức Q theo hàng ngang, ta có thể làm như sau:
• Viết hiệu P - Q theo hàng ngang, trong đó đa thức Q được đặt trong dấu ngoặc;
• Sau khi bỏ dấu ngoặc và đổi dấu một đơn thức của đa thức Q, nhóm các đơn thức đồng dạng với nhau;
Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
3/ Nhân hai đa thức nhiều biến. a/ Nhân hai đơn thức:
Tương tự như đối với đơn thức một biến, để nhân hai đơn thức nhiều biến ta có thể làm như sau:
• Nhân các hệ số với nhau và nhân các phần biến với nhau;
• Thu gon đơn thức nhận được ở tích .
b/ Nhân đơn thức với đa thức:
Tương tự như trường hợp một biến, ta có quy tắc sau:
Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức đó với từng đơn thức của đa thức rồi
cộng các kết quả với nhau. c/ Nhân hai đa thức:
Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức
của đa thức kia rồi cộng các kết quả với nhau.
4/ Nhân hai đa thức nhiều biến.
a/ Phép chia hết một đơn thức cho một đơn thức
PHIẾU BÀI TẬP TOÁN 8 Trang 2/22
Đơn thức A chia hết cho đơn thức B ( B ≠ 0 ) khi mỗi biến của B đều là biến của A với số mũ không
lớn hơn số mũ của nó trong A.
Quy tắc : Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B), ta có thể làm như sau :
- Chia hệ số của đơn thức A cho hệ số của đơn thức B
- Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
- Nhân các kết quả vừa tìm được với nhau.
b/ Phép chia hết một đa thức cho một đơn thức
Đa thức A chia hết cho đơn thức ( B ≠ 0 ) khi mỗi đơn thức của A chia hết cho B.
Quy tắc : Muốn chia đa thức A cho đơn thức B ( trường hợp A chia hết cho B), ta chia mỗi đơn thức
của A cho B rồi cộng các kết quả với nhau.
--------------------------------------------
PHIẾU BÀI TẬP TOÁN 8 Trang 3/22
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI.
Dạng 1: Tính tổng (hay hiệu) đa thức nhiều biến.
Ví dụ 1. Tính tổng A + B và hiệu A − B của hai đa thức A , B trong các trường hợp sau:
a) A = x + 2y và B = x − 2y . b) 2 3 2
A = 2x y − x − xy + 1 và 3 2
B = x + 2xy − 2 . c) 2 2
A = x − 2yz + z và 2 2
B = 3yz + 5x − z . d) 1 2 3 5 3 2 3 7 1
A = x y + xy − x y + x và 3 2 2 3
B = x y − x y + xy . 2 2 2 2 Bài giải
a) A + B = (x + 2y) + (x − 2y) = x + 2y + x − 2y = (x + x) + (2y − 2y) = 2x
A − B = (x + 2y) − (x − 2y) = x + 2y − x + 2y = (x − x) + (2y + 2y) = 4y b) 2 3 2 3 2
A + B = (2x y − x − xy + 1) + (x + 2xy − 2) 2 3 2 3 2 2 2 2 3 3
= 2x y − x − xy + 1 + x + 2xy − 2 = 2x y + (−xy ) + 2xy  + (−x ) + x  + 1 ( − 2     ) 2 2
= 2x y + xy − 1 2 3 2 3 2
A − B = (2x y − x − xy + 1) − (x + 2xy − 2) 2 3 2 3 2 2 2 2 3 3
= 2x y − x − xy + 1 − x − 2xy + 2 = 2x y + (−xy ) − 2xy  + (−x ) − x  + 1 ( + 2     ) 2 2 3
= 2x y − 3xy − 2x + 3 c) 2 2 2 2 2 2 2 2
A + B = (x − 2yz + z ) + 3
( yz + 5x − z ) = x − 2yz + z + 3yz + 5x − z 2 2 2 2 2
= (x + 5x ) + ( 2
− yz) + 3yz  + (z − z ) = 6x +   yz 2 2 2 2 2 2 2 2
A − B = (x − 2yz + z ) − 3
( yz + 5x − z ) = x − 2yz + z − 3yz − 5x + z 2 2 2 2 2 2
= (x − 5x ) + ( 2
− yz) − 3yz  + (z + z ) = 4
− x − 5yz + 2   z d)
PHIẾU BÀI TẬP TOÁN 8 Trang 4/22  1    2 3 5 3 2 3 7 3 2 1 2 3
A + B =  x y + xy − x y + x  +  x y − x y + xy 2 2 2 2      1 2 3 5 3 2 3 7 3 2 1 2 3
= x y + xy − x y + x + x y − x y + xy 2 2 2 2  5     3 2 7 3 2
= − x y  + x y  + ( 3 3 xy + xy ) 1 2 1 2 3
+  x y − x y  + x  2  2   2 2  3 2 3 3
= x y + 2xy + x  1    2 3 5 3 2 3 7 3 2 1 2
A − B =  x y + xy − x y + x  −  x y − x y 3 + xy   2 2   2 2  1 2 3 5 3 2 3 7 3 2 1 2 3
= x y + xy − x y + x − x y + x y − xy 2 2 2 2  5     3 2 7 3 2
= − x y  − x y  + ( 3 3 xy − xy ) 1 2 1 2 3
+  x y + x y  + x  2  2   2 2  3 2 2 3 = 6
− x y + x y + x
Ví dụ 2. Thực hiện phép tính sau: 2 2 2 2
A = (x + y − 2xy) + (x + 2xy + y ) .  1  2 2 1
B =  xy − 3xy  + (2xy + 3xy) − xy .  2  2 Bài giải 2 2 2 2 2 2 2 2
A = (x + y − 2xy) + (x + 2xy + y ) = x + y − 2xy + x + 2xy + y 2 2 2 2 2 2
= (x + x ) + (y + y ) + ( 2
− xy) + 2xy = 2x + 2   y  1  2 2 1 1 2 2 1
B =  xy − 3xy  + (2xy + 3xy) − xy = xy − 3xy + 2xy + 3xy − xy  2  2 2 2  1  2 2 1 7 2 1
=  xy + 3xy  + ( 3
− xy ) + 2xy  − xy = xy − xy − xy 2     2 2 2 Ví dụ 3. Cho các đa thức 3 2
M = 3x − x y + 2xy + 3; 2
N = x y − 2xy − 2 và 3 2
P = 3x − 2x y − xy + 3 . Tính: a) M + N . b) M − P . c) M − 2P .
d) M + N + P . Bài giải 3 2 2 2 2 3
M + N = ( x − x y + xy + ) + (x y − xy − ) = (−x y) + (x y  a/ 3 2 3 2 2
) + (2xy − 2xy) + 3x + 3 ( − 2   ) 3 = 3x + 1 b/
PHIẾU BÀI TẬP TOÁN 8 Trang 5/22 3 2 3 2 3 2 3 2 M − P = 3
( x − x y + 2xy + 3) − 3
( x − 2x y − xy + 3) = 3x − x y + 2xy + 3 − 3x + 2x y + xy − 3c/ = ( 3 3 3x − 3x ) 2 2 2
+ (−x y) + 2x y + (2xy + xy) + 3 ( − 3) = x y + 3   xy 3 2 3 2 M − 2P = 3
( x − x y + 2xy + 3) + 2 3
( x − 2x y − xy + 3) 3 2 3 2
= 3x − x y + 2xy + 3 + 6x − 4x y − 2xy + 6 3 3 2 2 3 2 = 3
( x + 6x ) + (−x y) − 4x y + (2xy − 2xy) + 3
( + 6) = 9x − 5x y + 9   d/ 3 2 2 3 2 M = 3
( x − x y + 2xy + 3) + (x y − 2xy − 2) + 3
( x − 2x y − xy + 3) 3 2 2 3 2
= 3x − x y + 2xy + 3 + x y − 2xy − 2 + 3x − 2x y − xy + 3 3 3 2 2 2 = 3
( x + 3x ) + (−x y) + x y − 2x y + (2xy − 2xy − xy) + 3 ( − 2 + 3   ) 3 2
= 6x − 2x y − xy + 4
Dạng 2: Tìm đa thức thỏa mãn đẳng thức cho trước
Ví dụ 4. Tìm đa thức A , B biết: a) 2 2 2 2
A + x − y = x − 2y + 3xy − 2 . b) 2 2 B − 5
( x − 2xyz) = 2x + 2xyz + 1. Bài giải a/ 2 2 2 2
A + x − y = x − 2y + 3xy − 2 A = ( 2 2
x − 2y + 3xy − 2) 2 2 2 2 2 2
− (x − y ) = x − 2y + 3xy − 2 − x − y 2 2 2 2 2
= (x − x ) + ( 2
− y ) − y  + 3xy − 2 = 3
− y + 3xy − 2   b/ 2 2 B − 5
( x − 2xyz) = 2x + 2xyz + 1 2 2
B = (2x + 2xyz + 1) + 5 ( x − 2xyz) 2 2 2 2 2
= 2x + 2xyz + 1 + 5x − 2xyz = (2x + 5x ) + (2xyz − 2xyz) + 1 = 7x + 1
Ví dụ 5. Cho các đa thức 2 2
A = 4x + 3y − 5xy ; 2 2 2 2
B = 3x + 2y + 2x y . Tìm đa thức C sao cho:
a) C = A + B .
b) C + A = B . Bài giải a/ 2 2 2 2 2 2
C = A + B = (4x + 3y − 5xy) + 3
( x + 2y + 2x y ) 2 2 2 2 2 2 2 2 2 2
= 2x y − 5xy + (4x + 3x ) + 3
( y + 2y ) = 2x y − 5xy + 7x + 5y b/
PHIẾU BÀI TẬP TOÁN 8 Trang 6/22
C = B − A = ( 2 2 2 2
3x + 2y + 2x y ) 2 2
− (4x + 3y − 5xy) 2 2 2 2 2 2 2 2 2 2 2 2
= 3x + 2y + 2x y − 4x − 3y + 5xy = 2x y + 5xy + 3
( x − 4x ) + (2y − 3y ) 2 2 2 2
= 2x y + 5xy − x − y
Dạng 3: Thực hiện phép tính nhân đơn thức với đa thức
 Quy tắc: AB C   AB AC (với A, B, C là các đơn thức).
Ví dụ 6. Làm tính nhân     a) 3 2
M  (2x y).(x  2y  1) b) 3 1 1
N  (2xy  4y  8x)    y    c) 2 2 2 3
P x y xy   x y  2   2  Bài giải a/ 3 2 3 2 3 3 5 3 2 3
M  (2x y).(x  2y  1)  2x y.x  2x y.(2y)  2x y.1  2x y  4x y  2x y b/         3 1   3 1   1   1   4 2
N  (2xy  4y  8x)  y  2xy .  
y  (4y).    
y  (8x).     
y  xy  2y  4xy 2 2  2    2  c/        2 2 2 1 3 2 2 2 2 2 1  3  3 3 4 1 2 4
P x y x
y x y   x y.(xy )  x y.( x  )  x y.   
y   x y x y x y  2     2  2 2  
Ví dụ 7. Nhân đơn thức 1
A với đa thức B biết rằng  2 A    x y  và 2 2
B  4x  4xy  3.  2  Bài giải 2  1     2  2 2 1  4 2  2 2 . A B   
x y .(4x  4xy  3)   
x y .(4x  4xy  3)  2    4  1       4 2  2 1  4 2  2 1  4 2  6 2 5 4 3 4 2
  x y .4x   
x y .4xy     
x y .(3)  x y x y x y 4  4    4  4
Dạng 4: Thực hiện phép tính nhân đa thức với đa thức
 Sử dụng quy tắc: (A B)(C D)  AC AD B C B D
Ví dụ 8. Thực hiện phép nhân a) 2
(x y)(x y x); b) 2
(x  2y)(x  2y  4z) ; c) 2 2
(x  2y)(x  2xy  4y ). Bài giải a/ 2 2 2 3 2 2 2
(x y)(x y x)  x.x y x.( x
 )  y.x y y.( x
 )  x y x x y xy
PHIẾU BÀI TẬP TOÁN 8 Trang 7/22 2 2 2
b/ (x  2y)(x  2y  4z)  xx x.(2y)  x.4z  2y.x  2y.( y
 )  2y.4z 3 2 2
x  2xy  4xz  2x y  2y  8yz
Ví dụ 9. Rút gọn rồi tính giá trị của biểu thức    a) 1   1  M  2  x y 2   
 x y tại 1  và y  4  x  2   2  2 b) 2 2 2 4
N  (2x y )(4x  2xy y ) tại 1
x  và y  2 . 2 Bài giải: a/  1    1    1  1     1      1 M  2  x y 2 
 x y  2x.2x  2x. y      y.2x       y. y 2 2  2  2     2  2 2 1 2 2 1 2
 4x xy xy y  4x y 4 4 2   Thay 1 1 1   1 2 x  và y  4 vào 2 2
4x y ta được : 4.   .   4  1 4  3 2 4  2  4 b/ 2 2 2 4
N  (2x y )(4x  2xy y ) 2 2 4 2 2 2 2 2 4
 2x.4x  2x.2xy  2x.y  ( y  ).4x  ( y
 ).2xy  ( y  ).y 3 2 2 4 2 2 4 6 3 6
 8x  4x y  2xy  4x y  2xy y  8x y 3   Thay 1 6
x  và y  2 vào 3 6
8x y ta được : 3 6 1
8x y  8.       2  1 64  63 2 2
Dạng 5: Thực hiện phép tính chia đơn thức với đa thức
Ví dụ 10: Làm phép tính chia: a) 5 3 x : x . b) 7 4 18x :6x . c) 6 7 2 4 7
8x y z : 4x y . d) 9 5 x y ( 4 4 65 : 13 − x y ) . e) 27 3 5 9 2 x yz : xz . 15 5 Bài giải: a) 5 3 2
x : x = x . b) 7 4 3
18x :6x = 3x . c) 6 7 2 4 7 2 2
8x y z : 4x y = 2x z . d) 9 5 x y ( 4 4 − x y ) 5 65 : 13 = 5 − x y . 27 9 e) 3 5 2 2 2
x yz : xz = x yz . 15 5
Dạng 6: Thực hiện phép tính chia đa thức với đa thức
Ví dụ 11: Làm phép tính chia:
PHIẾU BÀI TẬP TOÁN 8 Trang 8/22 a) ( 3 2
x +12x − 5x): x b) ( 4 3 2 2 3
x y − x y + xy ) 2 3 9 15 : xy c)  5 4 1 4 2 3 3 2  1 2
5x y z + x y z − 
2xy z : xy z Bài  2  4 giải: a) ( 3 2
x + x − x) 2 12
5 : x = x +12x − 5. b) ( 4 3 2 2 3
x y − x y + xy ) 2 3 3 9 25
: xy = 3x y − 9x + 25y c)  5 4 1 4 2 3 3 2  1 2 4 2 3 2
5x y z + x y z − 2xy z : xy z = 20x y + 2x z −   8yz  2  4
C. BÀI TẬP VẬN DỤNG
Bài 1: Tính tổng các đa thức a) 2 3 2
A = x y + x − xy + 3 và 3 2
B = x + xy − xy − 6.     b) 1 1 C
  a b  1 1   
 a  2b; và D   a b  
 a b  . 3 3  3 3  Bài giải: a) A + B = 2 (x y + 3 x − 2 xy + 3) + 3 (x + 2 xy − xy − 6) = 2 x y + 3 x − 2 xy + 3 + 3 x + 2
xy − xy − 6 = 3 (x + 3 x ) + (− 2 xy ) + 2 xy  + 2
x y − xy + (3 −   6) = 3 2x + 2 x y − xy − 3 b) 1 1     1 1  
C D   a b  (a  2b)    
a b  (a b) 3 3    3 3       1 1 1 1
a b a  2b a b a b 3 3 3 3 1 1     1 1     a a      
b b       a
 a  2b b 3 3   3 3  2
a  2a b 3
PHIẾU BÀI TẬP TOÁN 8 Trang 9/22
Bài 2: Cho hai đa thức: 2
M = 3xyz − 3x + 5xy −1; và 2
N = 5x + xyz − 5xy + 3 − . y
Tính M − N; N − M. Bài giải:
M − N = (3xyz − 2
3x + 5xy −1)−( 2
5x + xyz − 5xy + 3 − y) = 3xyz − 2
3x + 5xy −1− 2
5x − xyz + 5xy − 3 + y
= (3xyz − xyz) + (− 2 3x − 2
5x ) + (5xy + 5xy) + y + (−1− 3) = 2xyz − 2
8x + 10xy + y − 4
N − M = − M − N = − xyz − 2
x + xy + y − = − xyz + 2 ( ) (2 8 10 4) 2
8x −10xy − y + 4
Bài 3: Cho các đa thức : 3 2 2 2
A  5x y  4xy  6x y ; 3 2 2 2
B  8xy xy  4x y 3 3 3 2 2 2
C x  4x y  6xy  4xy  5x y Hãy tính:
a) A− B −C
b) B + A−C
c) C − A− B Bài giải: a) 3 2 2 2 3 2 2 2 3 3 3 2 2 2
A B C  (5x y  4xy  6x y )  (8xy xy  4x y )  (x  4x y  6xy  4xy  5x y ) 3 2 2 2 3 2 2 2 3 3 3 2 2 2
 5x y  4xy  6x y  8xy xy  4x y x  4x y  6xy  4xy  5x y 3 2 2 2 3 3
x y xy  7x y  14xy x b) 3 2 2 2 3 2 2 2 3 3 3 2 2 2
B A C  (8xy xy  4x y )  (5x y  4xy  6x y )  (x  4x y  6xy  4xy  5x y ) 3 2 2 2 3 2 2 2 3 3 3 2 2 2
 8xy xy  4x y  5x y  4xy  6x y x  4x y  6xy  4xy  5x y 3 2 2 2 3 3
 2xy xy  15x y x y x c) 3 3 3 2 2 2 3 2 2 2 3 2 2 2
C A B  (x  4x y  6xy  4xy  5x y )  (5x y  4xy  6x y )  (8xy xy  4x y ) 3 3 3 2 2 2 3 2 2 2 3 2 2 2
x  4x y  6xy  4xy  5x y  5x y  4xy  6x y  8xy xy  4x y 3 3 3 2 2 2
x x y  2xy xy  15x y Bài 4: Cho đa thức 2 2
M  ax  by  x
c y (x,y là biến). Tìm a, , b c biết:
Khi x  0,y  1 thì M  3. Khi x  2,y  0 thì M  8. Khi x  1,y  1 thì M  0. Bài giải:
Khi x  0; y  1; M  3 thì: 2 2 3  a.0  .1 b  .0
c .1  b  3.
Khi x  2; y  0; M  8 thì:  a  2 2 8 . 2  .0 b  .
c 2.0  4a  8  a  2.
Khi x  1; y  1; M  0 thì:      2 2 0 2.1 3 . 1  . c 1.  1  c  1. Vậy 2 2
M  2x  3y xy.
Bài 5: Tìm đa thức M biết:
PHIẾU BÀI TẬP TOÁN 8 Trang 10/22 a)  2 2  y  2 2 2 6x 3x
M x y  2xy ; b) M  2 y y  2 2 2x 4
 5xy x  7y . Bài giải: a/  2 2 6x  3xy  2 2 2
M x y  2xy 2 2 2
M  (x y  2xy )   2 2 6x  3xy  2 2 2 2 2
x y  2xy  6x  3xy 2 2 2 2 2 2 2 2
 (x  6x )  y  (2xy  3xy )  5x y xy b/ M   2 2xy  4y  2 2
 5xy x  7y 2 2 2 2 2 2
M  (5xy x  7y )  (2xy  4y )  5xy x  7y  2xy  4y 2 2 2 2 2
x  (7y  4y )  (5xy  2xy)  x  11y  7xy
Bài 6: Thực hiện phép tính     a) 2 2  3 2 2 3 1 5 2   3 2x y x 1
y x y y   b) 3 2 2 2    c) 2 2 2 
 2xy y  4xy  xy . d)  xy(3x y 6x y )  2  3  3  2  1  2  2
x  2xy   3 ( xy  ) e) 2  3 2 x y 2
x xy  1 f) 2 2 2 ( xy
)  (x  2x  1) . 2  5  Bài giải: a/        2 2 3 2 2 3 1 5 2 2 3 2 2 2 2 3 2 2 1  5 2x y x
y x y y   2x y .x y  2x y .( x
y )  2x y .    y   2     2  5 4 4 5 2 7
 2x y  2x y x y b/ 1              3 2 2 2 1
xy(3x y  6x y )   xy.    3 2 3x y  1   xy.      2 6x  1   2   xy.y 3 3   3     3  4 3 3 1 3  x
y  2x y xy 3 c/            2 2 2 2  3 3 
 2xy y  4xy  xy      xy.      2 2xy  3   2  2  3   2   xy.       y      
  xy.4xy 3 2 2 2  3    2  2 3 3 2 3
 3x y xy  6x y d/
 2x 2xy   2 3 ( xy  )  ( xy  ).x  ( xy
 ).2xy  ( xy  ).(3) 3 2 2  x
y  2x y  3xy e/
PHIẾU BÀI TẬP TOÁN 8 Trang 11/22 1        2 3 2 2 1 2 3 1 2 2  2  1 2 x y 2
x xy  1  x y.2x x y.    xy   x y.      1 2 5  2 2  5  2 5 1 3 3 1 2
x y x y x y 5 2 f/ 2 2 2 2 4 2 2 4 2 2 4 2 4 ( x
y )  (x  2x  1)  x y .(x  2x  1)  x y .x x y .(2x)  x y .1 4 4 3 4 2 4
x y  2x y x y
Bài 7: Rút gọn các biểu thức sau a) 2 2 3
A x (x y )  xy(1  yx)  x
b) B x(x  3y  1) 2y(x 1)(y x  1)x Bài giải: a/ 2 2 3 2 2 2
A x (x y )  xy(1  yx)  x x .x x .( y  )  ( xy).1  ( xy).( yx  ) 3 2 2 2 2 3
x x y xy x y x xy b/
B x(x  3y  1)  2y(x  1)  (y x  1)x
x.x x.3y x.1  (2y).x  (2y).(1)  ( x  ).y  ( x  ).x  ( x  ).1 2 2
x  3xy x  2xy  2y xy x x 2 2
 (x x )  (3xy  2xy xy)  (x x)  2y  2y
Bài 8: Rút gọn rồi tính giá trị biểu thức a) 2 2
P x(x y)  y(x y ) tại 1 x   và 1 y   ; 2 2 b) 2 3 2 2 2
Q x (y xy )  ( y
  x  1)x y tại x  10 và y  10. Bài giải: a/ 2 2 2 2
P x(x y)  y(x y )  x.x x.( y
 )  y.x y.(y ) 3 3 3 3
x xy xy y x y Thay 1 x   và 1
y   vào P ta được : 2 2 3 3  1 −   1 −   1 −   1 −  2 − 1 − + = + = =  2   2   8   8          8 4
PHIẾU BÀI TẬP TOÁN 8 Trang 12/22 b/ 2 3 2 2 2
Q x (y xy )  ( y
  x  1)x y 2 3 2 2 2 2
x .y x .xy x y . y   2 2 2 2
x y .x x y .1 2 3 3 2 2 3 3 2 2 2
x y x y x y x y x y 2 2  x y
Thay x  10 và y  10 vào Q ta được : (− )2 (− )2
10 . 10 =100.100 =10000
Bài 9: Chứng tỏ rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến x a) 2 3
P x(3x  2)  x(x  3x)  x  2x  3 ;   b) 1 1
Q x(2x  3)  6x   x  1  . 2 3  Bài giải: a/ 2 3 2 3
P x(3x  2)  x(x  3x)  x  2x  3  x.3x x.2  x.x x.3x x  2x  3 2 3 2 3
 3x  2x x  3x x  2x  3  3
Vậy giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến x . b/ 1 1    1  1  
Q x(2x  3)  6x   x  1  x.2x x.(3)  6x.  6x.     x 2 3  2  3  2 2
 2x  3x  3x  2x  0
Vậy giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến x .
Bài 10: Nhân các đa thức sau   
a) (2xy  3)(x  2y); b) 2
(xy  2y)(x y  2xy  4); c)  2 1  2 1 4 x   yx    y.  2   2  Bài giải: a)
(2xy  3)(x  2y)  2xy.x  2xy.(2y)  3.x  3.(2y) 2 2
 2x y  4xy  3x  6y b)
PHIẾU BÀI TẬP TOÁN 8 Trang 13/22 2 2 2
(xy  2y)(x y  2xy  4)  xy.x y xy.(2xy)  xy.4  2y.x y  2y.(2xy)  2y.4 3 2 2 2 2 2 2
x y  2x y  4xy  2x y  4xy  8y 3 2 2
x y  4xy  4xy  8y
Bài 11: Chứng minh rằng với mọi x,y ta luôn có 2 2 3 3 3 3
(xy  1)(x y xy  1)  (x  1)(1  y )  x y . Bài giải: 2 2 3 3
VT  (xy  1)(x y xy  1)  (x  1)(1  y ) 2 2 2 2 3 3 3 3
 (xy.x y xy.xy xy.1  1.x y  1.xy  1.1)  (x .1  x y  1.1  1.y ) 3 3 2 2 2 3 3 3 3
x y x y xy x y xy  1  x x y  1  y 3 3
x y VP
Bài 12: Cho biểu thức Q  (2n 1)(2n  3)(4n  5)(n  1)  3. Chứng minh Q luôn chia hết cho
5 với mọi số nguyên n . Bài giải:
Q  (2n  1)(2n  3)  (4n  5)(n  1)  3 2 2
 (4 n  6n  2n  3)  (4n  4n  5n  5)  3 2 2
 4 n  6n  2n  3  4n  4n  5n  5  3
 5n  55, n  
Bài 13: Làm tính chia: a) 8 8 5 5 3 3 2 2
(x y  2x y  7x y ) : ( xy );   b)  5 3 3 5 3 3 3 2 2
x y  5x y x y  : xy  ;  4  3 c) 2 4 3 2 4 3 2
(9x y z  12x y z  4xy z ) : xyz . Bài giải: a) 8 8 5 5 3 3 2 2
(x y  2x y  7x y ) : ( xy ) 8 8 2 2 5 5 2 2 3 3 2 2  x y : ( x
y )  2x y : ( x
y )  7x y : ( xy ) 6 6 3 3  x
y  2x y  7xy b)
PHIẾU BÀI TẬP TOÁN 8 Trang 14/22    5 3 3 5 3 3 3 2 2
x y  5x y x y  : xy  4  3        5 3 2   3 5 2  3  3 3 2  2
x y : xy   
  5x y : xy    
  x y : xy 3   3    4 3  4 2 15 2 4 9 2 2  3x y x y x y 2 8 c) 2 4 3 2 4 3 2
(9x y z  12x y z  4xy z ) : xyz 2 4 3 2 4 3 2
 (9x y z : xyz)  (12x y z : xyz)  (4xy z : xyz) 3 2 3 2
 9xy  12x yz  4y z
Bài 14: Tính giá trị biểu thức: a) A = ( 5 3 3 2 4 4
x y − x y + x y ) 2 2 15 10 20
: 5x y tại x = 1; − y = 2.
b) B ( x y)2 x y x y  = + − (xy)2 2 4 3 3 2 2 3 6 :
tại x = y = 2. −   c) 2 C = (− 2 2 2x y + 4xy − 3
6xy ) : xy tại 1 x = ; y = 4. 3 2 d)  1 2 5 2 5 2  D = x y −  x y  2 2
: 2x y tại x = 3; − y = 3.  3 3  e) E = ( 5 4 3 2 2 3
x y + x y − x y ) 2 20 10 5
:5x y tại x =1; y = 1 − . f) G = ( 5 4 3 4 2 2 2
x y z − x yz + x y z) 2 7 3 2
: x yz tại x = 1;
− y =1; z = 2 . Bài giải: a) A = ( 5 3 15x y − 3 2 10x y + 4 4 20x y ) 2 2 : 5x y = ( 5 3 2 2
15x y : 5x y )+(− 3 2 2 2 10x y : 5x y )+( 4 4 2 2 20x y : 5x y ) = 3
3x y − 2x + 2 2 4x y (*)
Thay x = −1; y = 2 vào (*) ta được : 3 2 2 3.( 1 − ) .2 − 2.( 1 − ) + 4.( 1 − ) .2 = ( 6) − + 2 +16 =12 b)  2 2 2 4 3 3 2 B (2x y)  =
+ 3x y − 6x y : (xy)   = ( 4 2 4x y + 4 3 3x y − 3 2 6x y ) 2 2 : x y = ( 4 2 2 2
4x y : x y )+( 4 3 2 2
3x y : x y )+(− 3 2 2 2 6x y : x y ) = 2 4x + 2 3x y − 6 (* x )
PHIẾU BÀI TẬP TOÁN 8 Trang 15/22
Thay x = −2; y = −2 vào (*) ta được : 2 2 4.( 2) − + 3.( 2) − .( 2) − − 6.( 2) − = 4.4 + 3.4.( 2) − +12 =16 − 24 +12 = 4 c) 2 C = (− 2 2 2x y + 4xy − 3 6xy ) : xy 3  2 2   2   3 2 
= −2x y : xy + 4xy : xy + −   
  6xy : xy   3   3   3  = −3x + 6 − 2 9y (*) Thay 1
x = ; y = 4. vào (*) ta được : 2 1 2 3 − 279 ( 3). 6 9.(4) 6 9.16 − − + − = + − = 2 2 2 d)  1 2 5 2 5 2  2 2  1 2 5 2 2   2 5 2 2 2  1 1 D =
x y − x y : 2x y = x y : 2x y − x y : 2x y = 3 y −       3 x (*)  3 3   3   3  6 3 Thay x = 3;
− y = 3. vào (*) ta được : 1 3 1 3 9 27 .(3) − .( 3) − = + 9 = 6 3 2 2 e) E = ( 5 4 3 2 2 3
20x y +10x y − 5x y ) 2 :5x y = ( 5 4 2 20x y :5x y) + ( 3 2 2
10x y :5x y) −( 2 3 2 5x y :5x y) 3 3 2
= 4x y + 2xy − y (*) Thay x =1; y = 1 − vào (*) ta được : 3 3 2 4.(1) .( 1 − ) + 2.1.( 1 − ) − ( 1 − ) = ( 4) − − 2 −1 = 7 − f) G = ( 5 4 3 4 2 2 2
7x y z − 3x yz + 2x y z) 2 5 4 3 2 4 2 2 2 2 2
: x yz = (7x y z : x yz) − (3x yz : x yz) + (2x y z : x yz) 3 3 2 2
= 7x y z − 3x z + 2y(*) Thay x = 1;
− y =1; z = 2 vào (*) ta được : 3 3 2 2 7.( 1 − ) .1 .2 − 3.( 1 − ) .2 + 2.1 = ( 28 − ) − 6 + 2 = 32 −
PHIẾU BÀI TẬP TOÁN 8 Trang 16/22 Bài 15:
Hình ảnh bên dưới mô tả cách có thể làm để có một hình hộp chữ nhật có ba kích thước là x; y; z.
(cm). Các kích thước và tỉ lệ của hộp phụ thuộc vào các giá trị của x; y; z. Tính diện tích của các mặt
của hình hộp chữ nhật được thể hiện qua hình đó. z x x z y x x Lời giải
Diện tích của các mặt của hình hộp chữ nhật là :
xz + xz + xy + xy + yz + yz = 2xz + 2xy + 2yz (cm 2 ) Bài 16:
Bác Nam có một mảnh vườn hình chữ nhật. Bác chia
mảnh vườn này ra làm hai khu đất hình chữ nhật: Khu
thứ nhất dùng để trồng cỏ. Khu thứ hai dùng để trồng
hoa. (Với các kích thước có trong hình vẽ).
a/ Tính diện tích khu đất dùng để trồng hoa theo x,y.
b/ Tính diện tích khu đất dùng để trồng cỏ theo x,y.
c/ Tính diện tích mảnh vườn hình chữ nhật của bác Nam với x = 4 và y = 4. Lời giải
a/ Diện tích khu đất dùng để trồng hoa là : 2 .x( y + )
1 = 2xy + 2x (m 2 ) b/
Chiều dài khu đất dùng để trồng cỏ là :
(2y +12) − (y +1) = 2y +12 − y −1= (2y − y) + (12 −1) = y +11 (m)
Diện tích khu đất dùng để trồng cỏ là : 2 .x( y + ) 11 = 2xy + 2 .11
x = 2xy + 22x (m 2 )
c/ Học sinh có thể trình bày hai cách như sau : Cách 1:
Diện tích mãnh vườn hình chữ nhật theo x,y là :
PHIẾU BÀI TẬP TOÁN 8 Trang 17/22
2 .x(2y +12) = 2 .2 x y + 2 .12 x
= 4xy + 24x (m 2 )
Thay x = 4 và y = 4 vào 4xy + 24x ta được : 4.4.4 + 24.4 = 160 (m 2 )
Vậy với x = 4 và y = 4 thì diện tích mảnh vườn hình chữ nhật đó là 160 (m 2 ) Cách 2:
Diện tích mãnh vườn hình chữ nhật theo x,y là :
(2xy + 2x) + (2xy + 22x) = 4xy + 24x (m 2 )
Thay x = 4 và y = 4 vào 4xy + 24x ta được : 4.4.4 + 24.4 = 160 (m 2 )
Vậy với x = 4 và y = 4 thì diện tích mảnh vườn hình chữ nhật đó là 160 (m 2 ). Bài 17:
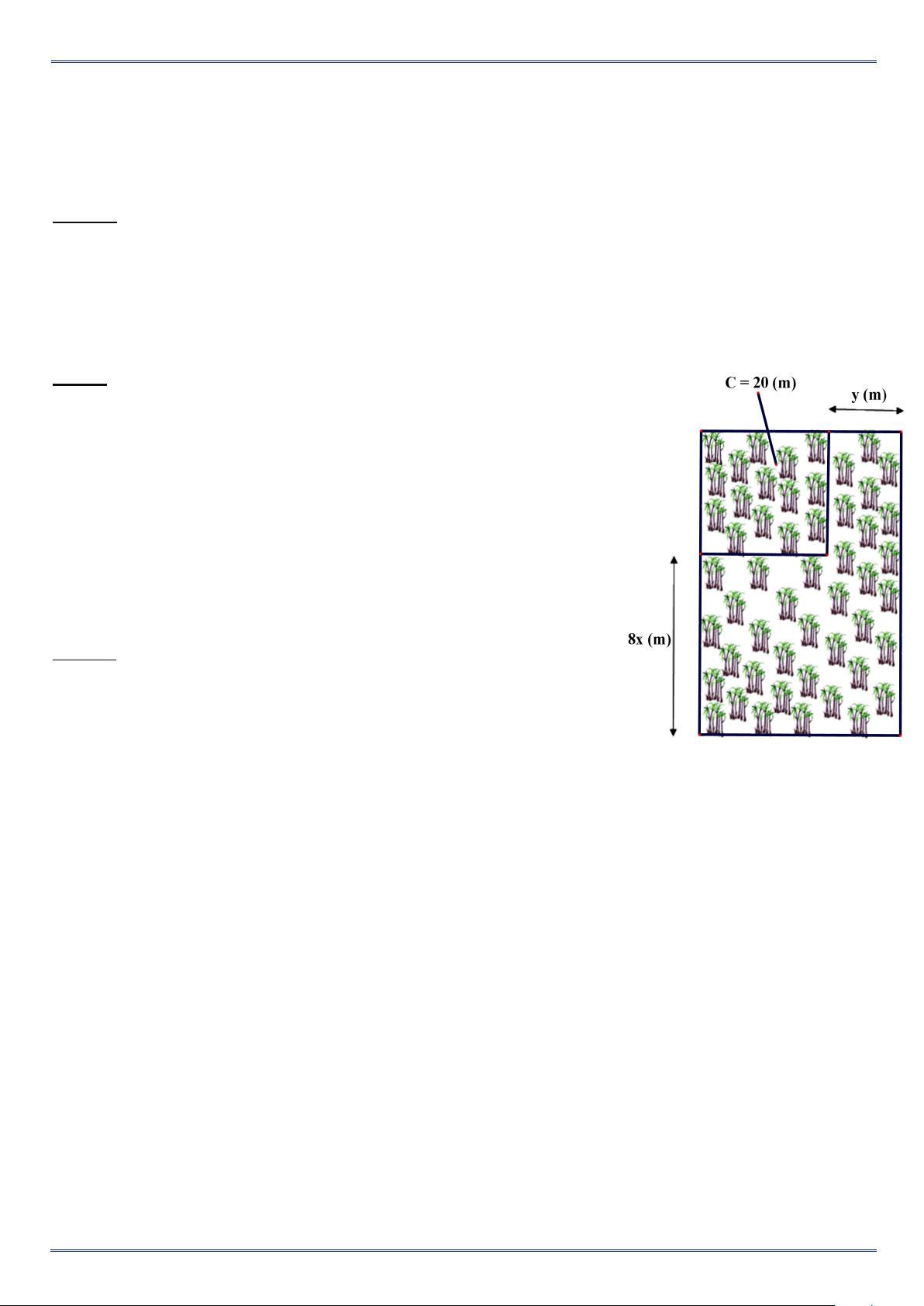
Khu vườn trồng mía của nhà bác Minh ban đầu có dạng một hình
vuông biết chu vi hình vuông là 20 (m) sau đó được mở rộng bên
phải thêm y (m), phía dưới thêm 10x (m) nên mảnh vườn trở thành
một hình chữ nhật (hình vẽ bên)
a/ Tính diện tích khu vườn bác Minh sau khi được mở rộng theo x, y.
b/ Tính diện tích khu vườn bác Minh sau khi được mở rộng khi x = 1 ; y = 2 Lời giải a/
Cạnh của mảnh vườn hình vuông ban đầu là 20 : 4 = 5 (m)
Chiều rộng của khu vườn sau khi được mở rộng là : y + 5 (m)
Chiều dài của khu vườn sau khi được mở rộng là : 8x + 5 (m)
Diện tích của khu vườn bác Minh sau khi được mở rộng là :
(y +5).(8x + 5) = y.8x + y.5 + 5.8x + 5.5 = 8xy + 5y + 40x + 25 (m 2 )
b/ Khi x = 1 ; y = 2 thì diện tích khu vườn bác Minh sau khi được mở rộng là :
8.1.2 + 5.2 + 40.1 + 25 = 91 (m 2 )
PHIẾU BÀI TẬP TOÁN 8 Trang 18/22 Bài 18:
Một cửa hàng buổi sáng bán được xy bao gạo thì cửa hàng đó thu được số tiền là 6 5 5 4
x y − x y nghìn đồng.
a/ Tính số tiền mỗi bao gạo mà của cửa hàng đó đã bán theo x,y.
b/ Tính số tiền mỗi bao gạo mà của cửa hàng đó đã bán khi x = 2; y = 2. Lời giải
a/ Số tiền mỗi bao gạo mà của cửa hàng đó đã bán theo x,y là : 6 5 5 4 x y − x y xy = ( 6 5 x y xy) −( 5 4 x y xy) 5 4 4 3 ( ) : : :
= x y − x y (nghìn đồng).
b/ Số tiền mỗi bao gạo mà của cửa hàng đó đã bán khi x = 2; y = 2 là : 5 4 4 3
2 .2 − 2 .2 = 384 (nghìn đồng) Bài 19:
Một tấm bìa cứng hình chữ nhật có chiều dài là x + 43 (cm) và chiều rộng là x + 30 (cm). Người ta
cắt ở mỗi góc của tấm bìa một hình vuông cạnh 2
y +1 (cm) ( phần tô màu) và xếp phần còn lại thành
một cái hộp không nắp.
a/ Tính diện tích xung quanh của hình hộp chữ nhật trên theo x; y.
b/ Tính diện tích xung quanh của hình hộp chữ nhật trên với x = 16 ; y = 4. Lời giải
a/ Chiều cao của hình hộp chữ nhật bằng cạnh của hình vuông cắt đi và bằng 2 y +1 (cm).
Chiều dài của hình hộp chữ nhật là : 2 2 2
(x + 43) − (y +1).2 = x + 43− 2y − 2 = x − 2y + 41 (cm).
Chiều rộng của hình hộp chữ nhật là: 2 2 2
(x + 30) − (y +1).2 = x + 30 − 2y − 2 = x − 2y + 28 (cm).
Diện tích xung quanh của hình hộp chữ nhật trên theo x, y là : 2 ( 2 x − 2y + ) 2 2 2 2
41 + (x − 2y + 28).(y +1) = 2(2x − 4y + 69).(y +1)  2 2 2 2 2 2 2
= (4 x−8 y +138).(y +1) = 4 .
x y −8y .y +138y + 4x −8y +138 2 4 2 2
= 4xy −8y +130y + 4x +138(cm )
PHIẾU BÀI TẬP TOÁN 8 Trang 19/22
b/ Diện tích xung quanh của hình hộp chữ nhật trên với x = 16 ; y = 4 là : 2 4 2 2
4.16.(4) −8.(4) +130.(4) + 4.16 +138 =1258(cm ) D. BÀI TẬP TỰ LUYỆN.
Bài 1. Tính tổng của hai đa thức a) 2 2
A = 2x + 3y và 2 2
B = 3x − 4y . b) 2 2
A = 2x − 3xy + 5y và 2 2
B = 3x + xy − 2y .
Bài 2. Tính tổng và hiệu của hai đa thức M và N với: a) 2 2
M = x + y + 2xy và 2 2
N = x + y − 2xy .
b) M = 2,3x + 3,2y − 10 và N = 0
− ,3x + 2, 2y − 5.
PHIẾU BÀI TẬP TOÁN 8 Trang 20/22
Bài 3: Tính tổng A + B và hiệu A − B của hai đa thức A , B trong các trường hợp sau:
a) A = 2x + 3y và B = 2x − y . b) 2 3 2
A = x y + x − xy + 2 và 3 2 2
B = x + xy − x y − 7 . c) 2 2
A = 2x − yz − z + 1 và 2 2
B = 4yz + 3x + z − 2. d) 2 3 3 11 3 2 3 1 9
A = x y + xy − x y + x và 3 2 3 2
B = xy − x y + x y . 2 2 2 2
Bài 4: Thực hiện phép tính sau: a) 2 2 2 2
A = (x − xy + y ) − ( x −
+ 7xy − 5y ) . b) 2 2 2 2 2 2
B = (xy − 3x y) − ( 2
− xy − 5x y) + (x y − 3xy ).
Bài 5: Cho các đa thức 3 2
M = 2x − 2x y + xy + 1; 2
N = 3x y + 2xy − 2 và 3 2
P = x − x y − 3xy + 1. Tính: a) M + N . b) M − P . c) M − 2P .
d) M + N + P .
Bài 6: Cho các đa thức 2
M = 2x − y − 2 ; 2
N = 3x + y + 1 và 2
P = 1 − 5x . Tính a) M + N . b) M − P . c) M − 2P .
d) M + N + P .
Bài 7: Tìm đa thức A , B biết a) 2 2 2 2 2
6x − 3xy + A = x + y − 2xy . b) 2 2 2
B − (2xy − 4y ) = 5xy + x − 7y .
Bài 8: Tìm đa thức M biết: a) 2 2 2 M + 3
( x − 2xy) = 4x + 5xy − y . b) 2 2 2 2
M − (x − 5y ) = 3x − 7xy + 6y . c) 3 2 3 2
M + (2x − x y + 1) = x − + 3x y + 2 . d) 2
M − (x − 6x + 9) = 0 .
Bài 9: Cho các đa thức 2 2
A = x − 2y + xy + 1; 2 2 2 2
B = x + y − x y − 1. Tìm đa thức C sao cho:
C = A + B .
C + A = B .
Bài 10: Tính giá trị của các đa thức sau: a) 3 3 3 3 3
A = x + 2xy − 2x + 2y + 2x − y tại x = 2 , y = 3 − . b) 2 2 4 4 6 6 8 8
B = xy + x y − x y + x y − x y tại x = 1, y = 1 − . c) 2 2 3 3 10 10
C = xy + x y + x y +  + x y tại x = 1 − , y = 1.
Bài 11: Thực hiện phép tính   a)  2 2
M  2x (1  3x  2x ) ; b) 2 1
N  (2x  3x  4)    x  ;  2  c) 1 1  2  3 2
P xy( x
  2xy  4y ). d) 2 3 2
x y 2x − xy −  1 2 2  5 
PHIẾU BÀI TẬP TOÁN 8 Trang 21/22
Bài 12: Nhân đa thức 1 1
A với đơn thức B biết rằng 3 2 3 A x y x y và 2
B  (2xy) . 4 2
Bài 13: Rút gọn các biểu thức sau a) 2 2 3
A  3x (6x  1)  9x(2x x); ĐS: 2 A  12x b) 2 1 2
B x (x  2y)  2xy(x y)  y (6x  3y). ĐS: 3 3
B x y 3
Bài 14: Tính giá trị của biểu thức a) 2 2 3 2
M  2x (x  5)  x(2x  4x)  (6  x)x tại x  4 ; ĐS: M  64 b) 3 2 2
N x (y  1)  xy(x  2x  1)  x(x  2xy  3y) tại x  8 và y  5. ĐS: Q  80
Bài 15: Cho biểu thức 2 3 4
P x (1  2x )  2x(x x  2)  x(x  4). Chứng tỏ giá trị của P không phụ
thuộc vào giá trị của x .
Bài 16: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của các biến:
A = 2x(x + 7) −3(x + 7) − 2x(x + 5) − .x
Bài 17: Cho biểu thức B =10 −5x(x −1,2) + 2x(2,5x −3). Chứng minh rằng giá trị của biểu thức này luôn luôn không đổi.
Bài 18: Chứng tỏ rằng các biểu thức sau không phụ thuộc vào giá trị của biến x : a) 2
x x − − x x − + x( 2 (5 3) ( 1)
x − 6x) −10 + 3x ;
b) x( 2x + x + ) 2
1 − x (x +1) − x + 5 .
c) x 22x  
1  2x  3x   1  2
Bài 19: Tính giá trị của biểu thức
a) P = x( 2x − ) 2 2 5
3 + x (7 − 5x) − 7x tại x = 5 − ;
b) Q = x(x − y) + y(x − y) tại x =1,5 và y =10. c) 2 2
Q  (3y x)(9y  3xy x ) tại x  3 và 1 y  . 3
Bài 20: Chứng minh đẳng thức x y  3 2 2 3
x x y xy y  4 4 ( )  x y .
Bài 21: Chứng minh đẳng thức 2 2
(x y)(x y z)  2(x  1)(y  1)  2  x y .
Bài 22: Chứng minh đẳng thức 2 2 4 4
(x y)(x y)(x y )  x y
Bài 23: Chứng minh đẳng thức 2 2 3 3
(x y)(x xy y )  x y
Bài 24: Cho ab  1. Chứng minh đẳng thức a(b  1)  (
b a  1)  (a  1)(b  1).
PHIẾU BÀI TẬP TOÁN 8 Trang 22/22
Bài 25: Làm tính nhân: a) (2x  7)(3x 1); b) x y  2 (5
2 ) x xy   1 ;
c) (x 1)(x  1)(x  2); d)  2 x x 2 5 4
2x  9x   3 .
Bài 26: Thực hiện phép tính:     
a) (x  7)(x  5); b) 1
 x 1(2x  3)     ; c) 1 1 x    x
  (4x  1). 2   2  2 d) 2 2
(x y)(y xy x )
Bài 27: Làm tính chia: a) 5 6 3 2 3 7
(3x  5x  7x ) : 5x ; ĐS: 3 4
x x x 5 5 b) 6 7 5 6 4 5 3 2
(5x y  4x y  3x y ) : ( xy ); ĐS: 3 5 2 4 3
5x y  4x y  3xy   c) 5  5 8 4 2 7 7 9 5 3 3 7
x y  5x y x y  : x y  ; ĐS: 2 7 4 8    x y 3xy x y 8 9  3 8 15 d) 3 4 2 4 2 4 5 2 3 2 2 2
(x y z  2x y z  7x y z ) : x y z . ĐS: 2 2 2 3
xy  2x z  7x z
Bài 28: Làm tính chia: a) 5 7 4 3 1 1 2
(3y  2y  4y ) : 6y ; ĐS: 2 4
y y y 2 3 3 b) 2 4 5 6 7 2
(2x y  3x y  5x y ) : ( xy  ); ĐS: 3 4 5 6
2xy  3x y  5x y   c) 2  4 6 2 4 1 4 2 4 2 2 1 5 1
x y  2x y x y  : x y  ; ĐS: 2 4 2 2    x y y x 5 5  5 2 2 4 d) 3 2 2 4 5 3 6 4 7 3 2
(3x y z  5x y z  6x y z ) : x yz . ĐS: 4 3 3 5
3y  5xy z  6x y z
PHIẾU BÀI TẬP TOÁN 8 Trang 1/12 NHỮNG HẰNG ĐẲ NG THỨC ĐÁNG NHỚ
A. KIẾN THỨC TRỌNG TÂM.
1. Bình phương một tổng.
Quy tắc: Bình phương của một tổng gồm hai số bằng tổng bình phương mỗi số với 2 lần tích hai số đó. a b2 2 2
a  2ab b . Ví dụ: 2 2 2
(x  2)  x  2  x  2  4  x  4x  4 .
2. Bình phương một hiệu.
Quy tắc: Bình phương của một hiệu gồm hai số bằng hiệu của tổng bình phương mỗi số
với 2 lần tích hai số đó. a b2 2 2
a  2ab b . Ví dụ: 2 2 2
(x  3)  x  2  x  3  9  x  6x  9 .
3. Hiệu hai bình phương.
Quy tắc: Hiệu hai bình phương bằng tích của tổng với hiệu của hai số đó. 2 2
a b  a ba b  a ba b. Ví dụ: 2 2 2
x  4  x  2  (x  2)(x  2) .
4. Lập phương của một tổng. a b3 3 2 2 3
a  3a b  3ab b . Ví dụ: 3 3 2 2 3 3 2
(x  1)  x  3  x  1  3  x  1  1  x  3x  3x  1.
5. Lập phương của một hiệu. a b3 3 2 2 3
a  3a b  3ab b . Ví dụ: 3 3 2 2 3 3 2
(x  2)  x  3  x  2  3  x  2  2  x  6x  12x  8 .
6. Tổng hai lập phương.
Quy tắc: Tổng của hai lập phương bằng tích của tổng hai số với bình phương thiếu của hiệu hai số đó. 3 3      2 2 a b a
b a ab b .
Chú ý: biểu thức 2 2
a ab b được gọi là bình phương thiếu của hiệu.
Ví dụ: 3 3 x   x   2 2
x x    x   2 2 ( 2) 2 2 (
2) x  2x  4.
7. Hiệu hai lập phương.
PHIẾU BÀI TẬP TOÁN 8 Trang 2/12
Quy tắc: Hiệu của hai lập phương bằng tích của hiệu hai số với bình phương thiếu của tổng hai số đó. 3 3      2 2 a b
a b a ab b .
Chú ý: biểu thức 2 2
a ab b được gọi là bình phương thiếu của tổng. Ví dụ: 3 3
x  3  (x  3) 2 2
x  3x  3   (x  3) 2 x  3x   9 .
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Thực hiện phép tính
 Vận dụng linh hoạt các hằng đẳng thức ở phần trọng tâm kiến thức.
Ví dụ 1. Thực hiện phép tính a) 2 (x  1) ; b) 2 (2x  1) ;
c) (x  3)(3  x); d) 2 2 (x  2) .
Ví dụ 2. Khai triển các biểu thức sau a) 2 (2x  3y) ; b) 2 (xy  3) ;   c) 1
(2xy  1)(2xy  1); d)  2  2
2 x y(x  2y)  . 2 
Ví dụ 3. Khai triển các biểu thức sau a) 2
A  (x y z) ; ĐS: 2 2 2
A x y z  2xy  2yz  2zx b) 2
B  (a b c) . ĐS: 2 2 2
B a b c  2ab  2ac  2bc
Ví dụ 4. Thực hiện phép tính: 3 3 a)   2   3 1 (x  3) ; b)  y x        ; c) 3 (x  3y) ; d) x    .  3  3 
Ví dụ 5. Thực hiện phép tính a) x   2 (
2) x  2x  4; b) x   2 (2
1) 4x  2x   1 ; 2    2    c) x   x x x   x 1    1      2   ; d) y    y   x   .        2  2 4  2 y  y 
Ví dụ 6. Thực hiện phép tính
a) M x   2 (
3) x  3x   9 ;
b) N   x  2
(1 3 ) 1  3x  9x ;    c) 1   2 x 1 P x    x  2 2     ;
d) Q  (2x  3y)4x 6xy  9y .  2  2 4
Dạng 2: Viết biểu thức dưới dạng tích
PHIẾU BÀI TẬP TOÁN 8 Trang 3/12
 Sử dụng cách viết ngược lại của các hằng đẳng thức đã nêu ở phần trọng tâm kiến thức.  Lưu ý: 2
a a a . Như vậy bình phương của một số cũng gọi là dạng tích của số đó.
Ví dụ 7. Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu a) 2
x  6x  9 ; b) 2
9x  6x  1; c) 2 2 1
x y xy  ; d) 2
(x y)  6(x y)  9. 4
Ví dụ 8. Điền các đơn thức vào chỗ “...” để hoàn thành các hằng đẳng thức sau a) 2 2
x  6x   (x )  ; b) 2 2
4x  4x   (2x )  ; 2   c) 2 2 y   y
9x    (3x  2y) ; d) (x )         .  3 9
Ví dụ 9. Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc hiệu: a) 3 2 x
  3x  3x  1; b) 3 2 1 1
x x x  ; 3 27 c) 6 4 2 2 3
x  3x y  3x y y ; d) 3 2 1 1
(x y)  (x y)  (x y)  . 3 27
Ví dụ 10. Viết các biểu thức sau dưới dạng tích: a) 3 x  27 ; b) 3 1 x  ; c) 3 3 8x y ; d) 3 3 8x  27y . 8
Dạng 3: Tính giá trị của biểu thức
 Bước 1: Rút gọn biểu thức (nếu cần).
 Bước 2: Thay giá trị của biến vào biểu thức rồi thực hiện phép tính.
Ví dụ 14. Tính giá trị biểu thức: a) 3 2 A x
  6x  12x  8 tại x  28 ; ĐS: 27000 b) 3 2
B  8x  12x  6x  1 tại 1 x  ; ĐS: 8 2 c) 3 2
C  (x  2y)  6(x  2y)  12(x  2y)  8 tại x  20 , y  1. ĐS: 8000
Ví dụ 15. Tính bằng cách hợp lí: a) Tính 3 11  1 ; ĐS: 1330
b) Tính giá trị biểu thức 3 3
x y biết x y  6 và x y  9 . ĐS: 378
Ví dụ 16. Tính giá trị biểu thức:
PHIẾU BÀI TẬP TOÁN 8 Trang 4/12
a) M x   2x x    x  2 ( 3) 3 9
(3 2 ) 4x  6x   9 tại x  20 ; ĐS: 72000
b) N x y  2 2
x xy y  3 ( 2 ) 2 4
 16y biết x  2y  0. ĐS: 0 Dạng 4: Tính nhanh
 Áp dụng các hằng đẳng thức một cách linh hoạt cho các số tự nhiên.
Ví dụ 17. Tính nhanh a) 2 101 ; b) 2 2 75  50  75  25 ; c) 103  97.
Ví dụ 18. Tính nhanh: a) 3 101 ; ĐS: 1030301 b) 3 2
98  6  98  12  98  8 ; ĐS: 1000000 c) 3 99 ; ĐS: 970299 d) 3 2
13  9  13  27  13  27 . ĐS: 1000
Ví dụ 19. Tính giá trị của biểu thức 2
P  9x  12x  4 trong mỗi trường hợp sau a) x  34; ĐS: P  10000 b) 2 x  ; ĐS: P  0 3 c) 8 x  . ĐS: P  100 3
Dạng 5: Chứng minh đẳng thức. Rút gọn biểu thức
 Áp dụng các hằng đẳng thức một cách linh hoạt để biến đổi vế này thành vế
kia trong một đẳng thức.
Ví dụ 20. Chứng minh các đẳng thức sau a) 2 2
(a b)  (a b)  4ab ; b) 2 2 2 2
(x y)  (x y)  2(x y ) .
Ví dụ 21. Rút gọn các biểu thức sau a) 2 2
M  (x  3y)  (x  3y) ;
ĐS: M  12xy b) 2 2
Q  (x y)  4(x y)(x  2y)  4(x  2y) . ĐS: 2 Q  ( x   5y)
Ví dụ 22. Rút gọn biểu thức: a) 3 3 A x   x   x  2 ( 2) ( 2) 2 x  1  2 ; b) 3 2
B  (xy  2)  6(xy  2)  12(xy  2)  8 .
Ví dụ 23. Rút gọn các biểu thức:
a) A x   2x x   3 ( 3) 3 9 x   3 ;   
b) B x   2x x   1   2 1 1 (2 1) 4 2 1  8 x    x    x    ;  2  2 4
PHIẾU BÀI TẬP TOÁN 8 Trang 5/12
c) C x y  2 2
x xy y   y x  2 2 ( 2 ) 2 4 (2
3 ) 4y  6xy  9x .
Dạng 6****: Chứng minh bất đẳng thức; tìm GTLN hoặc GTNN của biểu thức
 Bước 1: Đưa các biểu thức về dạng bình phương của một tổng hoặc một hiệu.
 Bước 2: Đánh giá dựa vào kết quả 2 A 0 và 2 A  0.
 Bước 3: Kết luận GTLN hoặc GTNN
A M thì biểu thức A có GTLN là M.
Am thì biểu thức A có GTNN là m .
Ví dụ 24. Chứng minh a) Biểu thức 2
4x  4x  3 luôn dương với mọi x . b) Biểu thức 2
y y  1 luôn âm với mọi y .
Ví dụ 25. Tìm giá trị nhỏ nhất của các biểu thức sau a) 2
M x  4x  5 ;
ĐS: M  1  x  2 min b) 2 
N y y  3 ; ĐS: 13 1 N   y min 4 2 x   2  c) 2 2 11
P x y  4x y  7 . ĐS: P     min 1 4 y    2
Ví dụ 26. Tìm giá trị lớn nhất của biểu thức 2 A x
  6x  1. ĐS: A  10  x  3 max C. BÀI TẬP VẬN DỤNG
Bài 1. Khai triển biểu thức sau 2 a)   2 1 (x  3) ; b) x       ; c) 2 (3x y) ;  3 2 d)  1   2 x   x y  ; e) 2 2
(2xy  1)(1  2xy ) ; f) 2
(x y  2) .  2 
Bài 8. Thực hiện phép tính    2 b)   2 (3x  1) ; c) 1   1 x      2 1 
  x ; d) x    .  2 2   3
Bài 9. Khai triển các biểu thức sau a) 2 (2x y) ; b) 2 (2  xy) ;   c) 1
(3x  2y)(3x  2y); d)  2  2 2 x
  y(2x y)  .  2 
PHIẾU BÀI TẬP TOÁN 8 Trang 6/12
Bài 2. Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu a) 2
x  8x  16 ; b) 2
9x  24x  16 ; c) 2 9 x  3x  ; d) 2 4 3 2
4x y  4xy y ; 4 e) 2
(x  2y)  4(x  2y)  4 ; f) 2
(x  3y)  12xy . Bài 1. Tính: 3 a)   3 y (x  2) ; b) 3 (2x  3y) ; c) x       ;
d)  x y3 2 2 3 .  x 
Bài 2. Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu: 3 a) 3 2 x 3 3 3 3 1
x  9x  27x  27 ; b) 2 
x x  1; c) 6 4 2 2 3
x x y x y y . 8 4 2 2 4 8
Bài 3. Rút gọn biểu thức: 2 3 a) 3 2 3x 3x x
A x  6x  12x  8 ; b) B  1   ; 2 4 8 c) 3 2 2 3
C  (2x y)  6(2x y)  x  12(2x y)x  8x .
Bài 4. Tính giá trị biểu thức: a) 3 2
M  8x  12x  6x  1 tại x  25,5; ĐS: 125000 2 3 b) x x
N  1  x   tại x  27 ; ĐS: 1000 3 27 3 2 c) x x x Q   6
 12  8 tại x  36 , y  2 . ĐS: 8000 3 2 y y y Bài 5. Tính nhanh: a) 3 51 ; ĐS: 132651 b) 3 2 3
89  33  89  3  121 89  11 ; ĐS: 1000000 c) 3 2
23  9  23  27  23  27 . ĐS: 8000
Bài 1. Đơn giản biểu thức: a) x   2 (
3) x  3x   9 ; b) x   2 (3
1) 9x  3x   1 ; 2    2    c) x   x x x  x xy 1    1      2   ; d)  y   y .        2  2 4  3  9 3  Bài 3. Tính nhanh a) 2 103 ; ĐS: 10609 b) 2 2 96  8  96  4 ; ĐS: 10000
PHIẾU BÀI TẬP TOÁN 8 Trang 7/12 c) 99 101. ĐS: 9999
Bài 4. Rút gọn biểu thức a) 2 2
A  (2x  3)  (2x  3) ;
ĐS: A  24x b) 2 2
B  (x  1)  2(2x  1)(1  x)  4x  4x  1. ĐS: 2 B  ( x   2) Bài 1. Tính: 2 a)   2 1 (4x  7) ; b) 6
 x y 2 3 2 3  ;
c) 3x 5xy 3x  5xy .  3 
Bài 2. Viết các đa thức sau dưới dạng bình phương của một tổng hoặc hiệu. a) 2 2
x  6xy  9y ; b) 2
4x  4x  1 .
Bài 5. Tính giá trị của biểu thức a) 2
N x  10x  25 tại x  55 ; ĐS: N  2500 4 b) x 2 2 P
x y y tại 1 x  4;y  . ĐS: 225 P  4 2 9
Bài 6. Tìm giá trị nhỏ nhất của các biểu thức sau a) 2
A x  4x  6 ;
ĐS: A  2  x  2 min b) 2
B y y  1 ; ĐS: 3 1 B   x min 4 2 x   2  c) 2 2 3
C x  4x y y  5 . ĐS: C     min 1 4 y    2
Bài 7. Tìm giá trị lớn nhất của các biểu thức sau a) 2 A x   4x  2 ;
ĐS: A  6  x  2 max b) 2
B x x  2 . ĐS: 9 1 B   x max 4 2
Bài 10. Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu a) 2
x  4x  4 ; b) 2
4x  4x  1; c) 2 1 x x  ; d) 2
4(x y)  4(x y)  1 . 4
Bài 11. Hoàn thiện các hằng đẳng thức sau a) 2
 10x  25  (x )  ; b) 2 4 2 2
 4x x  ( x ) ; c) 2 2 2
x   9y  (x )  ; d) 2 2 4 (2x  )
 ( y )  4x y .
PHIẾU BÀI TẬP TOÁN 8 Trang 8/12
Bài 12. Chứng minh các đẳng thức sau a) 2 2 2 2 2
(a  1)  4a  (a  1) . b) 2 2 2 2 2
(x y)  (x y)  2(x y )  4x .
Bài 13. Rút gọn các biểu thức a) 2 2
A  (2x y)  (2x y) ; ĐS: M  8xy b) 2 2
B  (x  2y)  4(x  2y)y  4y . ĐS: 2 2
Q x  8xy  16y
Bài 14. Khai triển các biểu thức sau a) 2
C  (x y z) ; ĐS: 2 2 2
C x y z  2xy  2yz  2zx b) 2
D  (a  1 b) . ĐS: 2 2
D a  1  b  2a  2ab  2b
Bài 3. Rút gọn các biểu thức: a) 2
(7x  4)  (7x  4)(7x  4); b) 2
(x  2y)  6xy(x  2y). 2 Bài 17. Tính: a) 1   x  4 2 2 2 2  ; b) 2 (7x  5y) ;
c) 6x y y 6x ; 2  d) 2 (x  2y) ;
e) (x  3y)(x  3y); f) 2 (5  x) . Bài 15. Tính nhanh a) 2 501 ; b) 2 2 88  24  88  12 ; c) 52 48 .
Bài 16. Tính giá trị của biểu thức 2
Q  9x  6x  1 trong mỗi trường hợp sau a) x  33; ĐS: Q  10000 b) 1 x  ; ĐS: Q  0 3 c) 11 x  . ĐS: Q  100 3
Bài 18. Thực hiện phép tính 2 a)   2 1 (x  1) ; b) 2 (3  y) ; c) x       .  2
Bài 19. Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu a) 2
x  10x  25 ; b) 2
49  x  14x ; c) 2 1 x x  . 4
Bài 2. Rút gọn biểu thức:
a) P x   2x x   x   2 (2 1) 4 2 1 (
1) x x   1 ;
PHIẾU BÀI TẬP TOÁN 8 Trang 9/12
b) Q x y  2 2
x xy y  x y  2 2
x xy y  3 ( ) ( )  2y .
Bài 3. Chứng minh giá trị của các biểu thức sau không phụ thuộc vào giá trị của x
a) A x   2x x   3 6( 2) 2 4  6x  2 ;
b) B x   2x x   3 2(3 1) 9 3 1  54x .
Bài 4. Tính giá trị biểu thức: a) 3 3
A  (x y)  x biết 2x y  0; ĐS: 0 b) 3 3
B x y  3xy biết x y  1. ĐS: 1
Bài 5. Viết các biểu thức sau dưới dạng tích: a) 3 x  1; b) 3 1 x  ; c) 3 3 x  27y ; d) 3 3 27x  8y . 27
Bài 6. Rút gọn các biểu thức:
a) A x   2x x   3 ( 2) 2 4  x  2 ;
b) B x   2x x   x   2 ( 1) 1 (
1) x x   1 ;
c) C x y  2 2
x xy y   y x  2 2 (2 ) 4 2 (
3 ) y  3xy  9x . Bài 8. a) Chứng minh 3 3 3
A B  (A B)  3AB(A B) và 3 3 3
A B  (A B)  3AB(A B) b) Áp dụng để tính 3 101  1 . ĐS: 1030300
c) Tính giá trị biểu thức 3 3
x y biết x y  2 và x y  3 . ĐS: 26
Bài 9. Tính giá trị biểu thức:
a) P x   2x x   3 ( 4) 4 16
64  x  tại x  100; ĐS: 2000000
b) Q x y  2 2
x xy y  3 (2 ) 4 2
 2y biết 2x y  0. ĐS: 0
Bài 1. Tính: a)  x y3 2 2 5 ;
b)  x xy3 3 3 4 ;    c) 1   2 1 6  x   2 2 2 4  36x  3x   ;
d) x 5y x  5xy  25y .  2  4 Bài 8. Tính: a) 3 (5x  1) ; b) 3 (x  2y) ;
PHIẾU BÀI TẬP TOÁN 8 Trang 10/12    c) 1   1 x   2 (4
5) 16x  20x   25 ; d)  2 6  x    36x  2x    .  3  9
Bài 2. Viết các đa thức sau dưới dạng bình phương hay lập phương của một tổng hoặc hiệu. a) 2 1 2
25x  5xy y ; b) 3 2 2 3
8x  12x y  6xy y . 4
Bài 3. Điền các đơn thức thích hợp vào ô trống 2 a)  1   2 1 x     x     ; 2  x  x    b) 1   1  2 1 2 1 3 1 3  x     x
y   x y . 2  4 9  8 27
Bài 4. Rút gọn các biểu thức: x y  2 2
x xy y  3 2 (3 ) 9 3
 (3x y)  27x y .
Bài 20. Rút gọn biểu thức: a) 2 2
(x y)  (x y) ; b) 2 2
2(x y)(x y)  (x y)  (x y) .
Bài. Tính nhanh (không dùng MTBT) a) 2 98 ; b) 2 2 63  37 ; c) 2 105 ; d) 2 97  9 .
Bài 22. Rút gọn rồi tính giá trị của biểu thức sau với x  19 . 2 2
A  (3x  2)  (2x  7)  2(3x  2)(2x  5).
Bài 23. Rút gọn rồi tính giá trị của biểu thức sau với 1 x  . 5 2 2
B  (3x  1)  (x  7)  2(2x  5)(2x  5).
Bài 4. Cho biểu thức 2 2
A  5(x  3)(x  3)  (2x  3)  (x  6) . Rút gọn rồi tính giá trị của biểu thức A với 1 x   . 5
Bài 5. Cho biết x y  15 và xy  100. Tính giá trị của biểu thức 2 2
B x y .
Bài 6. Tính nhanh giá trị của biểu thức a) 2 2
C  39  78  61  61 ; b) 2
D  50  49  51.
Bài 7. Chứng minh đẳng thức 2 2
(x y)  (x y)  4xy .
Bài 8. Chứng minh đẳng thức  2 2 2
x y z  2 2 2 2 3
 (x y)  (y z)  (z x)  (x y z) .
PHIẾU BÀI TẬP TOÁN 8 Trang 11/12 Bài 17. Chứng tỏ a) 2
x  6x  10  0 với mọi x ; b) 2
4y y  5  0 với mọi y .
Bài 18. Tìm giá trị nhỏ nhất của các biểu thức sau a) 2
P x  6x  11; ĐS: P  2  x  3 min b) 2  
Q y y ; ĐS: 1 1 Q   x min 4 2 x   3  c) 2 2 3
K x y  6x y  10 . ĐS: K     min 1 4 y     2
Bài 19. Tìm giá trị lớn nhất của biểu thức 2
B  4x x  5 . ĐS: B  9  x  2 . max
Bài 12. Chứng minh giá trị của biểu thức 2
P x  2x  3 luôn luôn dương với mọi x .
Bài 13. Chứng minh giá trị của biểu thức 2
Q  6x x  10 luôn luôn âm với mọi giá trị của x .
Bài 14. Tìm giá trị nhỏ nhất của biểu thức 2
P x  10x  28 .
Bài 15. Tìm giá trị nhỏ nhất của biểu thức 2
Q  5x  10x .
Bài 16. Tìm giá trị lớn nhất của biểu thức 2
P x x  1 .
Bài 24. Chứng minh rằng 2 2
(2n  3)  (2n  1) chia hết cho 8 với n   .
Bài 25. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức sau: a) 2
A  4x  12x  10 ; b) 2
B  2x x  2 . Bài. Cho 2 2 2
a b c ab bc ca . Chứng minh rằng a b c .
Bài 5. Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến
A x   2
x x    3 (3 2) 9 6 4 3 9x   2 .
Bài 6. Giá trị của biểu thức sau có phụ thuộc vào giá trị của biến không? 3 B x   x   2 ( 1) (
1) x x  
1  3x(x  1).
Bài 7. Chứng minh đẳng thức: 3 3 2 a b (a b) (a b) ab       .  
Bài. Rút gọn các biểu thức sau: 3 3 3
(x  2)  (x  2)  x  3x(x  2)(x  2) .
PHIẾU BÀI TẬP TOÁN 8 Trang 12/12
Bài. Chứng minh đẳng thức 3 3
x y x y y  2 2 ( ) ( ) 2 3x y .
Bài. Cho x y  1, tính giá trị của biểu thức M   3 3
x y   2 2 2 3 x y .
PHIẾU BÀI TẬP TOÁN 8 Trang 1/7
PHÂN TÍCH ĐA THỨC THÀNH NHÂN Phân thức đại TỬ BẰNG PHƯƠ NG PHÁP DÙNG HẰNG ĐẲ NG THỨC .
A. KIẾN THỨC TRỌNG TÂM.
1. Phân tích đa thức thành nhân tử.
 Phân tích đa thức thành nhân tử là viết đa thức dưới dạng tích của những đa thức.
2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức.
 Ngoài cách đặt nhân tử chung ta còn sử dụng bảy hằng đẳng thức đáng nhớ để phân tích
đa thức thành nhân tử. Cụ thể :
(1) a ab b  a b2 2 2 2 ;
(2) a ab b  a b2 2 2 2 . (3) 2 2
a b  a ba b;
(4) a a b ab b  a b3 3 2 2 3 3 3 ;
(5) a a b ab b  a b3 3 2 2 3 3 3 ; (6) 3 3      2 2 a b a
b a ab b ; (7) 3 3      2 2 a b
a b a ab b .
Ví dụ: Phân tích thành nhân tử các biểu thức a) 2 2 2
x  4  x  2  (x  2)(x  2) . b) 3 2 3 2 2 3 3
x  6x  12x  8  x  3x  2  3x  2  2  (x  2) . c) 3 2
x x x    3 6 12 9
x  6x  12x  81 3  (x  2)  1 2 (x 2 1) (x 2) (x 2) 1            x   2 (
3) x  3x   3 .
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Phân tích đa thức thành nhân tử bằng phương pháp vận dụng trực tiếp hằng đẳng thức
 Bước 1: Biến đổi đa thức đã cho về đúng dạng hằng đẳng thức cần sử dụng.
 Bước 2: Phân tích thành nhân tử.
Ví dụ 1. Phân tích các đa thức sau thành nhân tử: a) 2
x  4x  4 . b) 2
4x  4x  1. c) 2
2x  1  x . d) 2 1 x x  . 4
Ví dụ 2. Phân tích các đa thức sau thành nhân tử:
PHIẾU BÀI TẬP TOÁN 8 Trang 2/7 a) 2 2 2 3  x . b) x  2 3 1 . c) x  2 2 5  4x .
d) x  1 2x  1 .
Ví dụ 3. Phân tích các đa thức sau thành nhân tử: a) 2 2
x  6xy  9y .
ĐS: x y2 3 b) 2 2 x  9y .
ĐS: x  3yx  3y c) 2 2
x y  4xy  4 . ĐS: xy  2 2 d) 2 y   2 x  2x   1 .
ĐS: y x  1y x  1
Ví dụ 4. Phân tích các đa thức sau thành nhân tử: a) 3 8x  1 . ĐS:  x   2 2
1 4x  2x   1 b) x  3 8 2  1 . ĐS:  x   2 2
3 4x  18x   21 c) 3 2
x  6x  12x  8 . ĐS: x  3 2 d) 3 2 2 3
8x  12x y  6xy y . ĐS:   3 2x y
Dạng 2: Phân tích đa thức thành nhân tử bằng phương pháp vận dụng hằng đẳng
thức thông qua nhóm số hạng và đặt nhân tử chung.
 Nhóm các số hạng xuất hiện hằng đẳng thức thành một nhóm , các số hạng còn lại thành một nhóm
 Dùng hằng đẳng thức để viết nhóm các số hạng xuất hiện hằng đẳng thức thành tích
 Đặt nhân tử chung ở các nhóm ra ngoài để viết thành tích
Ví dụ 5. Phân tích các đa thức sau thành nhân tử: a/ 2 2
x − 4x + 4 − y ĐS: x  2 yx  2 y b/ 2 2
x + 2xy + y − x − y ĐS: x yx y   1 c/ 2 2
x − 2xy + y − 9 ĐS: x y  3x y  3
Dạng 3**: Phân tích đa thức thành nhân tử bằng cách áp dụng nhiều hằng đẳng thức
 Sử dụng các phép phân tách hoặc thêm bớt hợp lý để đưa biểu thức về dạng
hằng đẳng thức cần sử dụng và phân tích thành nhân tử.
 Lưu ý: có thể áp dụng nhiều hằng đẳng thức trong một bài toán.
Ví dụ 6. Phân tích các đa thức sau thành nhân tử:
PHIẾU BÀI TẬP TOÁN 8 Trang 3/7 a) 2
x  2x  1 . ĐS: x  2 1 b) 2
x  2x  3 .
ĐS: x  3x  1 c) 2
x  2x  2 .
ĐS: x 1 3x 1 3 d) 2 2
4x  4xy y .
ĐS: 2x y  2y2x y  2y
Ví dụ 7. Phân tích các đa thức sau thành nhân tử: a) x  3 2  1 . ĐS: x   2 (
3) x  3x   3 b) 3 2
x  6x  12x  9 . ĐS: x   2 (
3) x  3x   3 c) 3 2
x  6x  12x  7 . ĐS: x   2 (
1) x  5x  7 d) 3 2
2x  6x  12x  8 . ĐS:  x   2 2
2 x  2x  4
Dạng 4: Chứng minh các bài toán chia hết
Biểu thức A chia hết cho biểu thức B khi và chỉ khi có biểu thức Q khác 0 sao cho
A Q B .
Ví dụ 8. Chứng minh: a)  k  2 2 1  9 chia hết cho 4 . b)   2 4 1 3k chia hết cho 3 . C. BÀI TẬP VẬN DỤNG
Bài 1. Phân tích các đa thức sau thành nhân tử: 1) 2
x  8x  16 . ĐS: 2 (x  4) 2) 2
9x  6x  1. ĐS: 2 (3x  1) 2 3)   2 5
10x  25  x . ĐS: 2 (  x  5) 4) 2 25 x  5x  . ĐS: x      4  2 5) 2 16  x .
ĐS: (4  x)(4  x) 6)  x  2 16 3 1 .
ĐS: (3  3x)(5  3x) 7)  x  2 2 2 5  9x .
ĐS: (5  x)(5x  5)
PHIẾU BÀI TẬP TOÁN 8 Trang 4/7
8)  x  2  x  2 2 1 3 1 . ĐS: x  5x  2 9) 2 2
4x  4xy y . ĐS: 2 (2x y) 10) 2 2
(x  1)  9y .
ĐS: (x  3y  1)(x  3y  1) 11) 4 4 2 2
x y  4x y  4 . ĐS: x y  2 2 2 2 12) 2 2
y  4y  4  x .
ĐS: y 2  xy 2 x 13) 3 1  27x . ĐS:  x  2
(1 3 ) 1  3x  9x  14) x  3 3  27 .
ĐS: x  2x 9x  27 15) 3 2
27x  27x  9x  1. ĐS: 3 (3x  1) 6 4 3 16) x x y 2   2 3   x x y y . ĐS:  y 27 3  3  17)  x  3 2 1  8 . ĐS: x   2 (2
1) 4x  8x  7 18) 3 2
8x  12x  6x  1. ĐS: 3 (2x  1) 19) 3 2
8x  12x  6x  2 . ĐS: x   2 (2
2) 4x  2x   1 20) 3 2
9x  12x  6x  1. ĐS: x   2 (3
1) 3x  3x   1 21) 2
x  6x  9 . 22) 2
9x  6x  1. 23) 2
4x  4  x . 24) 2 1 x x  . 4 25) 2 2 2 x  9 . 26) x  2 1  9 . 27)  x  2 2 4
1  9x . 28) x  2 3x   1 .
Bài 2. Phân tích các đa thức sau thành nhân tử: 1) 2 2
x  4xy  4y . ĐS: x  2 2 2) 2 2 9x y .
ĐS: 3x y3x y 3) 2 2
9x y  6xy  1 . ĐS:  xy  2 3 1 4) 2 x   2
y  4y  4 .
ĐS: x y 2x y  2 5) 3 x  8 . ĐS: x   2
2 x  2x  4
6) x x  3 3 3 . ĐS:   2
3 3x  9x   9
PHIẾU BÀI TẬP TOÁN 8 Trang 5/7 7) 3 2
8x  12x  6x  1 . ĐS: x  3 2 8) 3 2 2 3
x  6x y  12xy  8y . ĐS:   3 2x y 9) 2
4x  4x  1 . ĐS:  x  2 2 1 10) 2
4x  4x  3 .
ĐS: 2x  32x  1 11) 2
4x  4x  1 .
ĐS: 2x 1 22x 1 2 12) 2 2
x  4xy  5y .
ĐS: x  5yx y 13) x  3 1  1 . ĐS: x   2 (
2) x x   1 14) 3 2
x  3x  3x  2 . ĐS: x   2 (
2) x x   1 15) 3 2
x  3x  3x  7 . ĐS: x   2 (
1) x  4x  7 16) 3 2
2x  3x  3x  1 . ĐS:  x   2 2
1 x x   1
Bài 3. Phân tích đa thức thành nhân tử 1) 1 2 x  25 ; 2) 2 2 9x y ; 3) 6 4 x y . 16 4) 2 (2x  5)  64 ; 5) 2 81  (3x  2) ; 6) 2 2
9(x  5y)  16(x y) . 7) 3 x  8 ; 8) 3 3 27x  125y ; 9) 6 x  216 . 10) 2
x  8x  16 ; 11) 2 2
9x  12xy  4y ; 12) 2 2
25x y  10xy  1. 13) 3 2
x  6x  12x  8 ; 14) 3 2 2 3
8x  12x y  6xy y . 15) 7 x  1 ; 16) 10 x  1 . 17) 2 x  9 ; 18) 2 4x  25 ; 19) 4 4 x y . 20) 2 2
9x  6xy y ; 21) 2
6x  9  x ; 22) 2 2
x  4y  4xy . 23) 2 2
(x y)  (x y) ; 24) 2 2
(x y z)  4z ; 25) 2 2
(3x  1)  (x  1) . 26) 3 3 x y  125 ; 27) 3 3
8x y  6xy(2x y) ; 28) 2 2
(3x  2)  2(x  1)(3x  2)  (x  1) .
Bài 4. Phân tích đa thức thành nhân tử a) 3 3 2 2
2x y  2xy  4x y  2xy ; b) 2 2
x y  2xy  4x  4y ;
PHIẾU BÀI TẬP TOÁN 8 Trang 6/7 c) 3 2 2 3
x x  3x y  3xy y y ; d) 2 2 2
x  2xy y  4z ; e/ 2 2
x x y y ; f) 2 2 2
x  2xy y z ;
Bài 5. Tính giá trị của biểu thức a) 2 2
M  (2x  1)  2(2x  1)(3x  1)  (3x  1) với 1 x   ; 5 b) 2 2 2
N  (3x  1)  2(9x  1)  (3x  1) với x   .
Bài 6. Tính giá trị của biểu thức a) 2 3
P  27  27x  9x x với x  17 ; b) 3 2
Q x  3x  3x với x  99 . Bài 7. Chứng minh: a)  k  2 2 3  5 chia hết cho 4 . b)   2 9 2 5k chia hết cho 5. Bài 8. Chứng minh: a)  k  2 3 2  4 chia hết cho 3 . b)   2 9 1
4k chia hết cho 8 .
Bài 9. Chứng minh rằng 12 2  1 chia hết cho 17 .
Bài 10. Chứng minh rằng hiệu các bình phương của hai số lẻ liên tiếp thì chia hết cho 8 .
Bài 11. Chứng minh rằng 173n 73n
chia hết cho 100 với mọi n   .
Bài 12. Tìm n   để biểu thức 2 2 2
A  (n  10)  36n có giá trị là một số nguyên tố.
Bài 13 Chia một hình vuông thành các hình vuông và hình chữ
nhật (hình vẽ). Tính diện tích mỗi hình vuông và mỗi hình chữ
nhật được chia theo x và y rồi tính tổng của chúng và phân tích
kết quả vừa tìm được thành nhân tử.
Bài 14 Một cánh cửa sổ có dạng như hình ảnh bên . Ô cửa sổ
được cấu tạo bao gồm 1 hình vuông cạnh x (m) và một nữa hình tròn.
a/ Tính diện tích S của cánh cửa đó.
b/ Phân tích S thành nhân tử sau đó tính diện tích của cánh của đó với x = 1,2 m.
PHIẾU BÀI TẬP TOÁN 8 Trang 7/7
Bài 15 Một khối gỗ dạng hình lập phương
có cạnh là x (cm). Người ta cắt bỏ đi một
phần gỗ cũng có dạng hình lập phương có thể tích là 1728 (cm3).
a/ Tính thể tích V của phần gỗ còn lại rồi
sau đó phân tích V thành nhân tử.
b/ Tính thể tích V của phần gỗ còn lại biết x = 26 (cm).
Bài 16 Bác Lan gửi tiết kiệm với số tiền
400 triệu đồng vào một ngân hàng, kì hạn 12 tháng và theo thể thức lãi kép. Nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập làm vốn ban đầu để tính
lãi cho năm tiếp theo. Giả sử lãi xuất cố định là x% /năm, x > 0. Tính x biết rằng sau 2 năm
gửi tiết kiệm , bác Hoa nhận được số tiền (bao nhiêu gồm cả gốc lẫn lãi) là 449,44 triệu đồng.
PHIẾU BÀI TẬP TOÁN 8 Trang 1/7
BÀI TẬP TỔNG HỢP CHƯƠNG
ĐA THỨC NHIỀU BIẾN
I/ BÀI TẬP TRẮC NGHIỆM :
Câu 1: Trong các biểu thức sau, biểu thức nào không phải là đơn thức ?
A. 1 . B.2x + y . 4 C. 2 3 3
− xy z . D. x .
Câu 2: Trong những đơn thức sau, đơn thức nào không phải là đơn thức thu gọn ?
A. 2 . B. x . C. 2 3 x y . D. 3 2 2x y x .
Câu 3: Trong các biểu thức đại số sau, biểu thức nào là đơn thức A. 2 2 − + x y . B. 1 4 5 x y . 5 3
C. x + y . D. 3 3 − x y + 7x . 3y 4
Câu 4: Sau khi thu gọn đơn thức 2 2
3x yxy ta được đơn thức : A. 2 3 3x y . B. 3 3 3x y . C. 3 2
3x y . D. 2 4 3x y .
Câu 5: Thu gọn đơn thức 2 2 x xyz ta được A. 3 2 x z . B. 3 2 x yz . C. 2 2
x yz . D. 2 xyz .
Câu 6: Kết quả của phép tính 2 3 2 3
3x y + 4x y là : A. 2 3 7x y . B. 2 3 12x y . C. 4 6 12x y . D. 4 6 7x y .
Câu 7: Cho các biểu thức 2 2 3 1 2 2 2 + + ;− 3 + ; x + y x y x y xy z x y z
. Có bao nhiêu đa thức trong các 2 x − y biểu thức trên ?
A.0 . B.1 . C.2 . D.3 .
Câu 8: Thu gọn đa thức 2 3 2 2 3 2
4x y + 6x y −10x y + 4x y ta được A. 2 3 2
14x y +10x y . B. 2 3 2 14
− x y +10x y . C. 2 3 2
6x y −10x y . D. 2 3 2 6
− x y +10x y .
Câu 9: Thu gọn đa thức 4 5 4 5 2 2 4
2x y − 4y + 5x y − 7y + x y − 2x y ta được : A. 4 5 2 2
5x y +11y + x y . B. 4 5 2 2
9x y −11y + x y . C. 4 5 2 2 5
− x y −11y + x y . D. 4 5 2 2
5x y −11y + x y .
Câu 10: Giá trị của đa thức 2 2 4
xy + 2x y − x y tại x = y = -1 là :
A.3 . B.1 . C.-1 . D. 0.
Câu 11: Giá trị của đa thức 3 3 2
x y −14y − 6xy + y + 2 tại x = -1 ; y = 0,5 là :
A. 1 . B.0,75.
PHIẾU BÀI TẬP TOÁN 8 Trang 2/7
C.2,5. D.1,75.
Câu 12: Trong giờ học Mỹ Thuật, bạn Hạnh dán lên
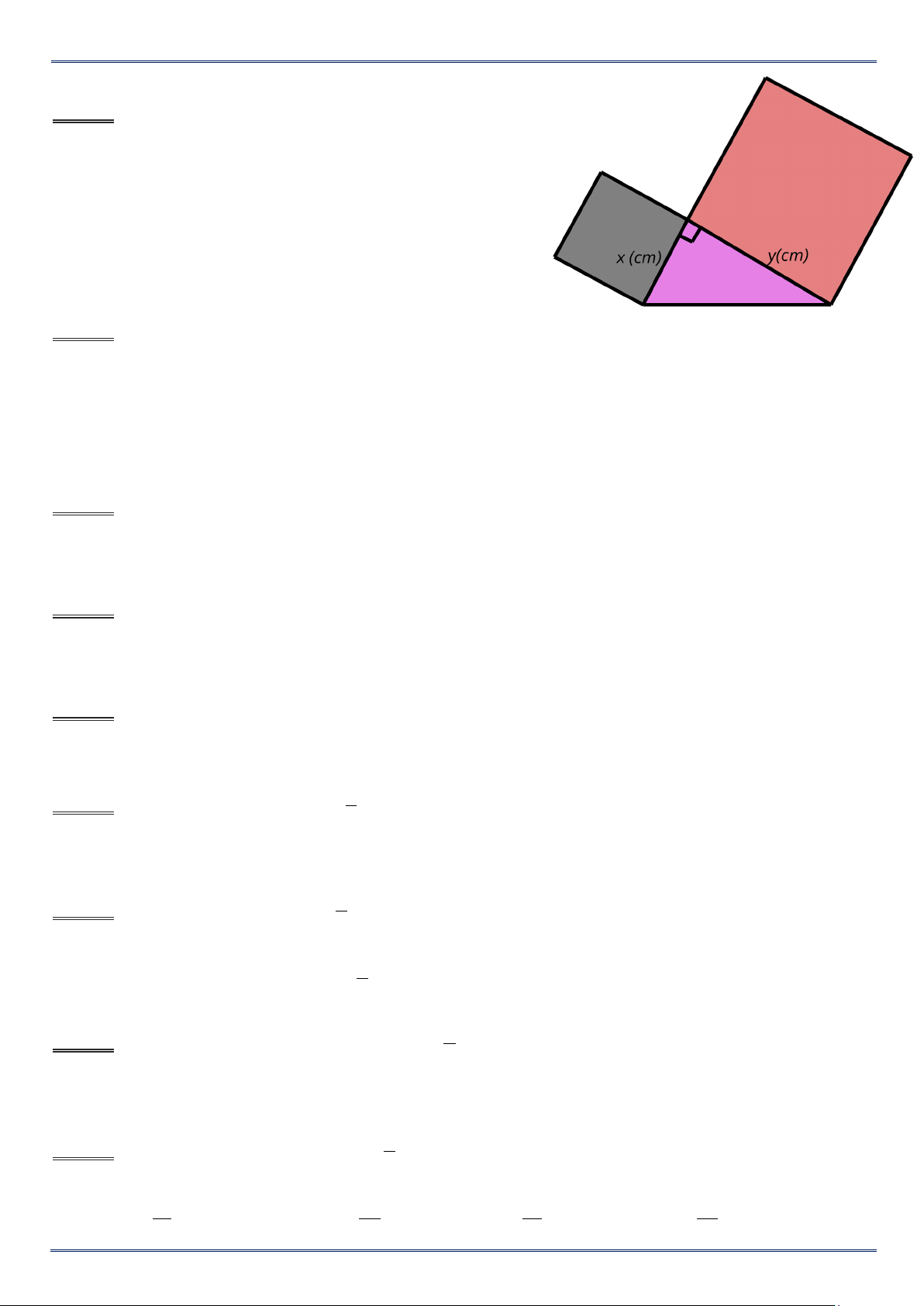
trang vở hai hình vuông và một tam giác vuông
có độ dài hai cạnh góc vuông là
x (cm), y (cm) như hình bên. Tổng diện tích của
hai hình vuông và tam giác vuông đó tại x = 3 và y = 5 là :
A.41,5cm2 . B. 40,5cm2 .
C.44cm2 . D. 47,2cm2 .
Câu 13: Bác Huỳnh muốn sơn bề mặt của hai khối gỗ có dạng hình hộp chữ nhật . Hình hộp
chữ nhật thứ nhất có ba kích thước x (cm), 2y (cm), z (cm). Hình hộp chữ nhật thứ hai
có ba kích thước là 2x (cm), 2y (cm), 3z (cm). Viết đa thức biểu thị tổng diện tích bề
mặt của hai khối gỗ mà bác Huỳnh cần phải sơn :
A.12xy +16yz +14zx . B.10xy +5yz + 4zx .
C.2xy + 4yz +10zx. D.2xy +10yz +13zx . Câu 14: Cho 3 2 2
A = 3x y + 2x y − xy và 2 3 2 2
B = 4xy − 3x y + 2x y + y . Kết quả của A − B là : A. 3 2 2 2
5x y − x y − 3xy + y . B. 3 2 2 2
5x y + 5x y + 3xy + y . C. 3 2 2 2
5x y + 5x y − 3xy + y . D. 3 2 2 2
5x y − x y + 3xy + y . Câu 15: Cho 4 2 3
A = 4x + 2y x − 3z + 5 và 3 2 4 B = 4
− z + 8 + 3y x − 5x . Kết quả của A − B là : A. 4 2 3
9x + y x + z − 3 . B. 4 2 3
−x + 5y x + z +13 . C. 4 2 3
9x − y x + z − 3 . D. 4 2 3
9x − y x + z + 3.
Câu 16: Kết quả của tích 2 3 4 6
3x y .8x y là : A. 6 9 24x y . B. 2 3 24x y . C. 6 9 5 − x y . D. 6 9 11x y .
Câu 17: Kết quả của tích ( 2 − x ) 2 1 5 y . xy là : 5 A. 3 3 5x y . B. 3 3 5 − x y . C. 3 3 −x y . D. 3 2 x y . Câu 18: 1
Kết quả của tích ( 2 − xy)3 2 . x là : 4 A. 4 5 2 1 − x y . B. 5 4 x y . C. 5 4 2x y . D. 5 4 2 − x y . 2 2 Câu 19:  1
Kết quả thương của phép chia 4 2 2 6x y : x y   là : 2   
A.12. B. 24 . C. 2 24x y . D. 2 12x y . Câu 20: 1
Kết quả thương của phép chia 2 3 x y :( 3 − xy)2 là : 9
A. 1 y . B. 1 − −
y . C. 1 xy . D. 1 y . 81 27 81 81
PHIẾU BÀI TẬP TOÁN 8 Trang 3/7
Câu 21: Kết quả của tích xy( 2 6
2x − 3y) là : A. 2 2 12x y +18xy . B. 3 2 12x y −18xy . C. 3 2 12x y +18xy . D. 2 2 12x y −18xy .
Câu 22: Kết quả của tích (2x + y)(2x − y) là :
A. 4x − y .
B. 4x + y . C. 2 2 4x − y . D. 2 2 4x + y .
Câu 23: Kết quả của tích (2x + y)(2x − y) là :
A. 4x − y .
B. 4x + y . C. 2 2 4x − y . D. 2 2 4x + y .
Câu 24: Kết quả của tích (xy − ) 1 (xy + 5) là : A. 2 2
x y + 4xy − 5. B. 2 2 x y + 4xy + 5 . C. 2
xy − 4xy − 5 . D. 2 2
x y − 4xy − 5.
Câu 25: Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng. Cột A Cột B a. ( + )( 2 2
x y x + xy + y ) 1. 3 3 x − y b. ( − )( 2 2
x y x + xy + y ) 2. 3 2 2 3
x + 2x y + 2xy + y c. ( + )( 2 2
x y x − xy + y ) 3. 3 3 x − y 4. ( + )3 x y
Câu 26: Kết quả 2
x − (2y)2 là :
A. 2x − 2y.
B. 2x + 2y .
C. (x − 2y)(x + 2y). D. (x + 2y)(x + 2y).
Câu 27: Kết quả 2 x −1 là :
A. (x − )1(x + )1.
B. (x + )1(x + )1 .
C. 2x + 2x +1.
D. 2x + 2x −1.
Câu 28: Kết quả (x − )2 7 là : A. ( − )2 2 7 x .
B. 2x −14x + 49.
C. 2x − 2x + 49.
D. 2x −14x + 7 .
Câu 29: Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng. A B a. 2 2
x + 6xy + 9y 1. ( x + )2 3 1
b. (2x −3y)(2x +3y) 2. (x + y)2 3 c. 2
9x − 6x +1 3. 2 2 4x − 9y
PHIẾU BÀI TẬP TOÁN 8 Trang 4/7 4. (x − y)2 9
Câu 30: Kết quả 3 2
x + 3x + 3x +1 là : A. 3x +1. B. (x − )3 1 . C. (x + )3 1 . D. (x + )3 3 1 .
Câu 31: Kết quả 3 2 1 1
x − x + x − là : 3 27 3 3 3 A. 3 1 x − . B.  1  1   x  − . C.x + . D. 3 1 x   − . 3 3        3   3 
Câu 32: Kết quả 3 2 2 3
8x +12x y + 6xy + y là : A. ( + )3 3 2x y . B. ( + )3 3 2x y . C. ( + )3 2x y . D. ( − )3 2x y .
Câu 33: Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng. A B a. 3 2
x − 3x + 3x −1 1. (x + )3 1
b. 2x +8x +16 2. (x − )3 1 c. 2 3
3x + 3x +1+ x 3. (x + )2 4 4. (x − )2 1
Câu 34 Khai triển ( x − )3 5 1 được kết quả là A. ( x − )( 2
5 1 25x − 5x + ) 1 . B. ( x − )( 2 5 1 25x +10x + ) 1 . C. ( x − )( 2
5 1 25x −10x + ) 1 . D. ( x + )( 2
5 1 25x −10x + ) 1 .
Câu 35: Rút gọn biểu thức ( + )2 −( − )2 a b
a b được kết quả là A. 4ab. B. 4 − ab . C. 0 . D. 2 2b . (x + )( 2
3 x − 3x + 9) = Câu 36 A. 3 3 x − 3 . B. 3x + 27. C. x −9. D. (x + )3 3 .
Câu 37 Điền đơn thức vào chỗ trống: ( x + y)( 2 − xy + y ) 3 3 3 ....... 3 = 27x + y A. 9x . B. 2 6x . C. 9xy . D. 2 9x . 3 3 3
Câu 38 Đẳng thức: x + y = (x + y) −3xy(x + y) Đúng. B. Sai.
Câu 39 Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng. A B
PHIẾU BÀI TẬP TOÁN 8 Trang 5/7
1. (x + y)(x − y) a. 3 3 x + y 2. 2 2
x − 2xy + y b. 2 2
x + 2xy + y 3. ( + )2 x y c. 2 2 x − y 4. ( + )( 2 2
x y x − xy + y ) d. ( − )2 x y e. 2 2 x + y 5 3 2 2 − +
Câu 40 Thương (3x 2x 4x ) : 2x bằng A. 3 3x − 2x + 4.
B. 3 3x − x + 2.
C. 3 3x + x + 2. D. 3 5 3 2
x − x + 2x . 2 2 2
Câu 41 Thương ( 4 3 2 2
− x y + x − x y ) ( 4 12 4 8 : 4 − x ) bằng A. 2 2 3
− x y + x − 2y . B. 4 3 2 2
3x y + x − 2x y . C. 2 2 12
− x y + 4x − 2y . D. 2 2
3x y − x + 2y .
Câu 42 Thương ( 2 2 3 xy x y x )  1 3 2 : x − + −  bằng 2    A. 3 2 1 2
− y + xy − x . B. 2 2
3y + 2xy + x . C. 2 2 6
− y + 4xy − 2x . D. 2 2
6y − 4xy + x . 2 2
Câu 43 Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng. A B a. ( 3 2 22
x − 2x y + xy ): 2x 1. 2 2
− xy + 4x − 5 b. ( 2 3 2
xy + xy + y ) 2 15 19 16 : 6y 2. 5 19 8 x + xy + 2 6 3 c. ( 1 3 2 2 3 4
− x y + 8x y −10xy): 2xy 3. 2
x − xy + y 2 2 4. 2 xy + 4x − 5
Câu 44 Đa thức 2
12x − 9 − 4x được phân tích thành
A. (2x −3)(2x +3) . B. −( x − )2 2 3 . C. ( − )2 3 2x . D. −( x + )2 2 3 .
Câu 45 Phân tích đa thức 3 2 2 3
x − 6x y +12xy −8x được kết quả là
PHIẾU BÀI TẬP TOÁN 8 Trang 6/7 A. ( − )3 x y . B. ( − )3 2x y .
C. 3x −(2y)3 .
D. (x − y)3 2 .
Câu 46 Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng. A B
a. (x − y)(x + y) 1. −(x − )2 5 b. 2
10x − 25 − x 2. 2 2 x − y  1  1  c. 3 1 8x − 3. 2 2x − 4x + x +    8  2  4  4. ( − )2 x y
II/ BÀI TẬP TỰ LUẬN :
Bài 1. Cho hai đa thức 3 2 3 2
A = 2x y − 3x y + 5xy − xy + 2 và 2 3 3 2
A = 5x y − 3xy + 6x y + 5 + 2xy
a/ Tính giá trị của mỗi đa thức A, B tại x = 1; y = -1.
b/ Tính A+ ;BA− .B
Bài 2. Thực hiện phép tính : a/ 1 2  3 3 xy . 6xy x y 1 + −      b/ 1 1
2x − y 2x +   y  2  2   2  2  c/ 5 3 6 4 2 3
24x y z : 6x y z d/ ( 6 7 6 5 3 7 5 3 8
x y z + x y z − x y z ) 3 3 6 3 2 6 : 42x y z
Bài 3. Viết mỗi biểu thức sau dưới dạng bình phương, lập phương của một tổng hoặc một hiệu. a/ 4 2 x + 4x + 4 b/ 4 2 2 4
9x + 24x y +16y c/ 3 2
27x − 27x + 3x +1 d/ 3 2
x − 3x + 3x −1
PHIẾU BÀI TẬP TOÁN 8 Trang 7/7
Bài 4. :Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến. a/ 1 A = 2xy + .
x (2x − 4y + 4) − x(x + 2) b/ B = ( x − ) ( x + ) − ( x − )2 2 1 . 2 1 2 3 −12 2
c/ (x+ )2 −(x− )2 2
3 −10x d/ (x − )3 −(x + )( 2 1 2 x + x + )
1 − x(x − 2)(x + 2) 
Bài 5. Phân tích các đa thức sau thành nhân tử. a/ 2 2
a + 6ab + 9b −1 b/ 2
4x − 25 + (2x + 7)(5− 2x)
c/5(x +3y) −15x(x +3y) d/ ( + )2 − ( + )2 2 x x y
y x y + xy − x e/ 2 2
a − 6a − b + 9 f/ 3 3 2
x − y − 3x + 3x −1
Document Outline

  • 1 Đơn thức nhiều biến. Đa thức nhiều biến
  • 2 Các phép tính với đa thức nhiều biến
  • 3 Hằng đẳng thức đáng nhớ
  • 4 Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử
  • 5 Bài tập tổng hợp đa thức nhiều biến