Phiếu Bài Tập Toán 9 Căn Bậc Hai Và Căn Bậc Ba Của Số Thực

MÔN : TOÁN
1. Căn bậc hai của số thực không âm.
Định nghĩa . Căn bậc hai của số thực a không âm là số x sao cho x2 = a.
Chú ý : Cho số thực a Với a  0, ta có :
• Nếu a > 0 có đúng hai căn bậc hai là hai số đối nhau :
số dương kí hiệu là a ; số âm kí hiệu là − a . ( )2 a = a
• Nếu a = 0 có đúng một căn bậc hai là 0.
• Nếu a < 0 thì không có căn bậc hai.
Với hai số a, b không âm, ta có:
- Nếu a < b thì a  b .
- Nếu a  b thì a < b.
2. Căn bậc ba của một số
Định nghĩa . Căn bậc ba của số thực a là số thực x sao cho x3 = a. Căn bậc ba c
ủa số thực a được kí hiệu là 3 a ( )3 3 a = a
Chú ý. Mọi số thực a đều có duy nhất một căn bậc ba. BÀI TẬP
Bài tập 1. a / Tính giá trị của : ( )2 16, 1, 44, 5 . b/ Tính giá trị của : 1 27 3 3 3 9; ; . 125 125
Bài tập 2. Chỉ ra phát biểu đúng trong các phát biểu sau : a/ 25 = 5 b/ − 9 = 3 − c/ 1 1 = − 81 9
Bài tập 3. Tính giá trị của các biểu thức sau : a/ 4 1 8 0,16 + b/ 1 3 − 0,36 c/ 3 3 3 8 + 64 + 27 d/ 3 3 + 25 16 125 27
Bài tập 4. Trong các số (− )2 − (− )2 2 2 3 , 3 ,
3 , − 3 số nào là căn bậc hai số học của 9.
Bài tập 5. So sánh : Trang 1
a/ 6 và 37 b/ 3 và 7 c/ 2 và 3 3 2
d/ 17 và 4 e/ 0,7 và 0,8 f/ 0,7 và 0,5
g/ 1 và 3 2 h/ 6 và 3 42 i/ 0,7 và 3 0,5
Bài tập 6. Chứng minh rằng : a/ (2 − 5)(2 + 5) = 1
− b/ ( 2024 − 2023)( 2024 + 2023) =1
Bài tập 7. Chứng minh 2025 − 2024 và 2025 + 2024 là hai số nghịch đảo của nhau. Bài tập 8.
a / Tính cạnh hình vuông biết diện tích hình vuông là 9cm2.
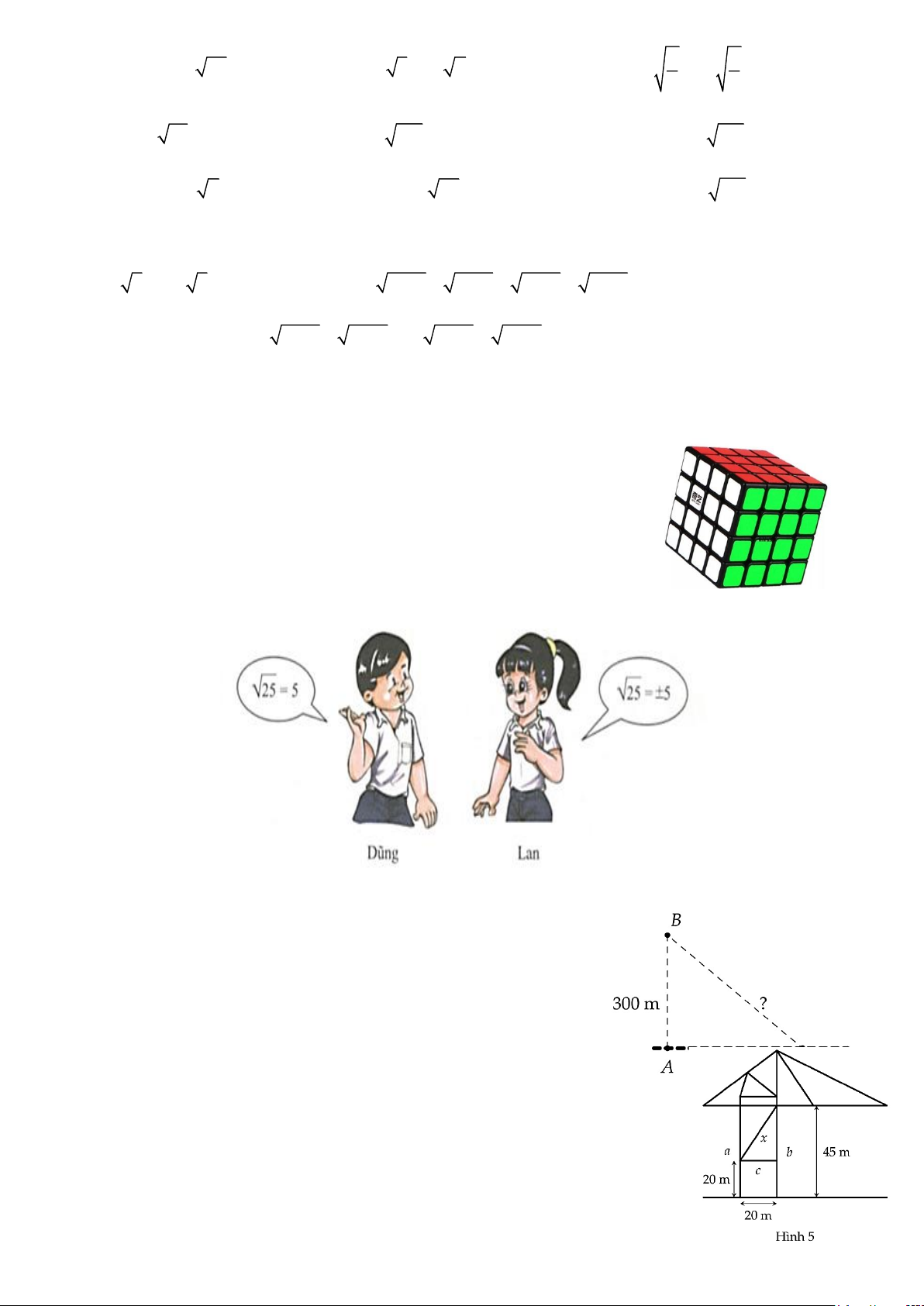
b / Một khối Rubik có thể tích bằng 125 cm3 (như hình bên).
Tính độ dài cạnh của khối Rubik đó.
Bài tập 9. Theo em bạn nào đúng ,bạn nào sai ? Vì sao ?
Bài tập 9. Một trạm phát sóng được đặt ở vi trí B cách
đường tàu một khoảng AB = 300 (m). Đầu tàu đang ở vi trí
C, cách vị trí A một khoảng AC = x (m).
a) Viết biểu thức biểu thi khoảng cách từ trạm phát sóng đến đầu tàu.
b) Tính khoảng cách trên khi x = 400, x = 1000 (kết quả
làm tròn đến hàng đơn vị của mét).
Bài tập 10. Trên cần trục ở Hình 5 , hai trụ a và b đứng cách nhau 20
m, hai xà ngang c và d lần lượt có độ cao 20 m và 45 m so với mặt
đất. Xà chéo x có độ dài bao nhiêu mét (kêt quả làm tròn đến hàng đơn vị)? Trang 2
Bài tập 11. Galilei là người phát hiện ra công thức tính y (giây) là thời gian chuyển động của x
vật rơi tự do theo x (mét) là quảng đường chuyển động của vật đó như sau : y = . 5
a/ Người ta thả vật nặng rơi tự do từ độ cao 55m trên đỉnh của tháp nghiêng Pisa xuống đất.
Bỏ qua lực cản của không khí. Sau bao lâu thì vật nặng đó chạm mặt đất ? (kết quả làm tròn đến hàng phần trăm).
b/ Sau 2 giây kể từ lúc thả thì vật nặng rơi tự do được bao nhiêu mét ?
Bài tập 12. Biết vận tốc của một xe và vết trượt của nó để lại trên nền đường thỏa : v = 2 5s, trong
đó v là vận tốc xe tính bằng m/s,  là hệ số ma sát giữa bánh xe và nền đường, s là độ dài vết trượt
của bánh xe trên nền đường (tính bằng mét).
Một chiếc xe vận tải đang chạy trên đường thì tài xế thắng khẩn cấp làm các bánh xe không lăn mà
trượt tạo thành một vết trượt dài 12m. Giả sử hệ số ma sát giữa bánh xe và mặt đường ở thời điểm đó là 0,6.
a/ Hỏi vận tốc của xe khi tài xế thắng khẩn cấp là bao nhiêu ?
b/ Nếu vận tốc của xe là 10 m/s và hệ số ma sát của mặt đường giữa lúc mưa nặng hạt là 0,2 thì vết
trượt sẽ dài bao nhiêu ?
Bài tập 13*. Cho a ≥ 0 2 a/ Chứng minh rằng  1  3 a − a +1 = a − +    2  4
b/ Tìm giá trị nhỏ nhất của biểu thức sau: A = a − a +1; B = a + a +1
Bài tập 14*. Cho biểu thức M = x − 2 x +1 với x  −1
a/ Đặt y = x +1 . Hãy biểu thị M qua y
b/ Tìm giá trị nhỏ nhất của M. Trang 3