Phiếu Bài Tập Toán 9 Một Số Phép Tính Về Căn Bậc Hai Của Số Thực

MÔN : TOÁN
1. Căn bậc hai của một bình phương.
Định nghĩa . Với mọi số a, ta có 2 a = a .
2. Căn bậc hai của một tích.
Định nghĩa . Với hai số không âm a và b, ta có : .
a b = a. b.
Chú ý. Quy tắc trên có thể mở rộng cho tích có nhiều thừa số không âm.
3. Căn bậc hai của một thương. a a
Định nghĩa . Với a  0 và b > 0, ta có : = . b b
4. Đưa thừa số ra ngoài dấu căn bậc hai.
Định nghĩa . Cho hai số a, b với b  0 . Khi đó 2 a b = a b . Cụ thể ta có : 2
- Nếu a  0,b  0 thì a b = a b; 2
- Nếu a  0,b  0 thì a b = −a b;
5. Đưa thừa số vào trong dấu căn bậc hai.
- Nếu a  0 và b  0 ta có 2
a b = a b.
- Nếu a  0 và b  0 ta có 2
a b = − a b.
Bài tập 1. Áp dụng quy tắc về căn bậc hai của một bình phương , hãy tính. a/ 2 14 b/ ( )2 0,09 c/ ( − )2 3 2 d/ ( − )2 8 5
Bài tập 2. Áp dụng quy tắc về căn bậc hai của một tích , hãy tính.
a/ 25.49 b/ 9.16.36 c/ 27.48 d/ 2 81a
Bài tập 3. Thực hiện phép tính sau :
a/ A = ( 8 + 72 − 2) 2. b/ B = ( + − − )2 4 7 4 7 .
c/ C = (3 5 + 2)(3 5 − 2) d/ D = ( − − + )2 4 3 4 3 . e/ E = ( 5 + 2 + ) 1 ( 5 − )
1 f/ F = ( 2 +1+ 3)( 2 +1− 3) 2 2 g/ G = ( 3 + ) 1 + ( 3 − 2) Bài tập 4. Tính : a/ 49.100 b/ ( )2 4 2 . 9 − c/ 72.32 d/ 12,1.490
Bài tập 5. Áp dụng quy tắc về căn bậc hai của một thương , hãy tính :
a/ 72 : 2 b/ ( 12 − 27 + 3): 3 c/ (5 3 +3 5): 15 49 5 d/ 12,1.490 e/ 0,81: 0,36 f/ g/ 81 80 Bài tập 6. Tính : Trang 1 a/ 2 2 10 − 6 b/ 2 2 17 − 8 c/ 2 2 (2,9) − (2,1) 2 2 13 −12 2 2 (6, 2) − (5,9) 3 3 9 + 7 d/ e/ f/ 81 2, 43 2 2 9 − 9.7 + 7 2 2 61 − 60 2 2 74 − 24 g/ h/ 81 121 Bài tập 7. Tính : 13 32 1 a/ 1,96 b/ 1 .1 c/ .0,09.64 2, 25 36 49 9 10,8 7 2,84 d/ e/ f/ 0,3 175 0,71 Bài tập 8. Tính : 7 6 a/ 2 : b/ ( 12 + 27 − 3): 3 81 150  1 9  2 + 3 99 28 c/  − + 5  : 5  d/ e/ + − 49 5 5    2 11 7 Bài tập 9.
1/ Áp dụng quy tắc đưa thừa số ra ngoài dấu căn bậc hai, hãy rút gọn biểu thức : a/ 2 5 .3 b/ (− )2 12 .2 c/ 75
2/ Rút gọn biểu thức :
a/ 20 − 5 − 125 b/ 25.90 c/ 3 125 − 2 20 − 3 80 + 4 45
d/ 20 − 2 45 − 3 80 + 2 45 e/ ( − )2 2 2 + 32 f/ 1 3 72 +
48 − 162 − 75 g/ 32 − 2 98 2 4 h/ ( − )2 7 2 + 28 i/ 3 12 + 2 27 + 3 75 − 6 48 + 20 12 − 112 k/ l/ 12 + 5 3 − 28 Bài tập 10.
1/ Thực hiện các phép tính sau : a/ 5 12 − 4 3 + 48 b/ 2 1 2 1 3 − 18 + 2 − 12 3 4 5 4  15 4 12  c/  3  12 − 2 3 + 5 2 − 8 .2 6   d/ + − .   ( 16 +1 ) 1  4   6 +1 16 − 2 3 − 16 
2/ Sắp xếp các số sau theo thứ tự giảm dần : 6 2; 4 5 ; 2 13 ; 3 7. 3/ So sánh : 45 a/ 2. 3 và 7 b/
và 3 27 c/ 3 5 và 46 d/ -10 và −4 6 15
Bài tập 11. Khi một quả bóng rổ được thả xuống, nó sẽ nảy trở lại,
nhưng do tiêu hao năng lượng nên nó không đạt được chiều cao
như lúc ban đầu. Hệ số phục hồi của quả bóng rổ được tính theo h công thức C =
trong đó H là độ cao mà quả bóng được thả R H
rơi và h là độ cao mà quả bóng bật lại. Trang 2
(Nguồn: Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby, năm 2017)
Một quả bóng rổ rơi từ độ cao 3,24 m và bật lại độ cao 2,25 m. Tính hệ số phục hồi của quả bóng đó dưới dạng phân số ?
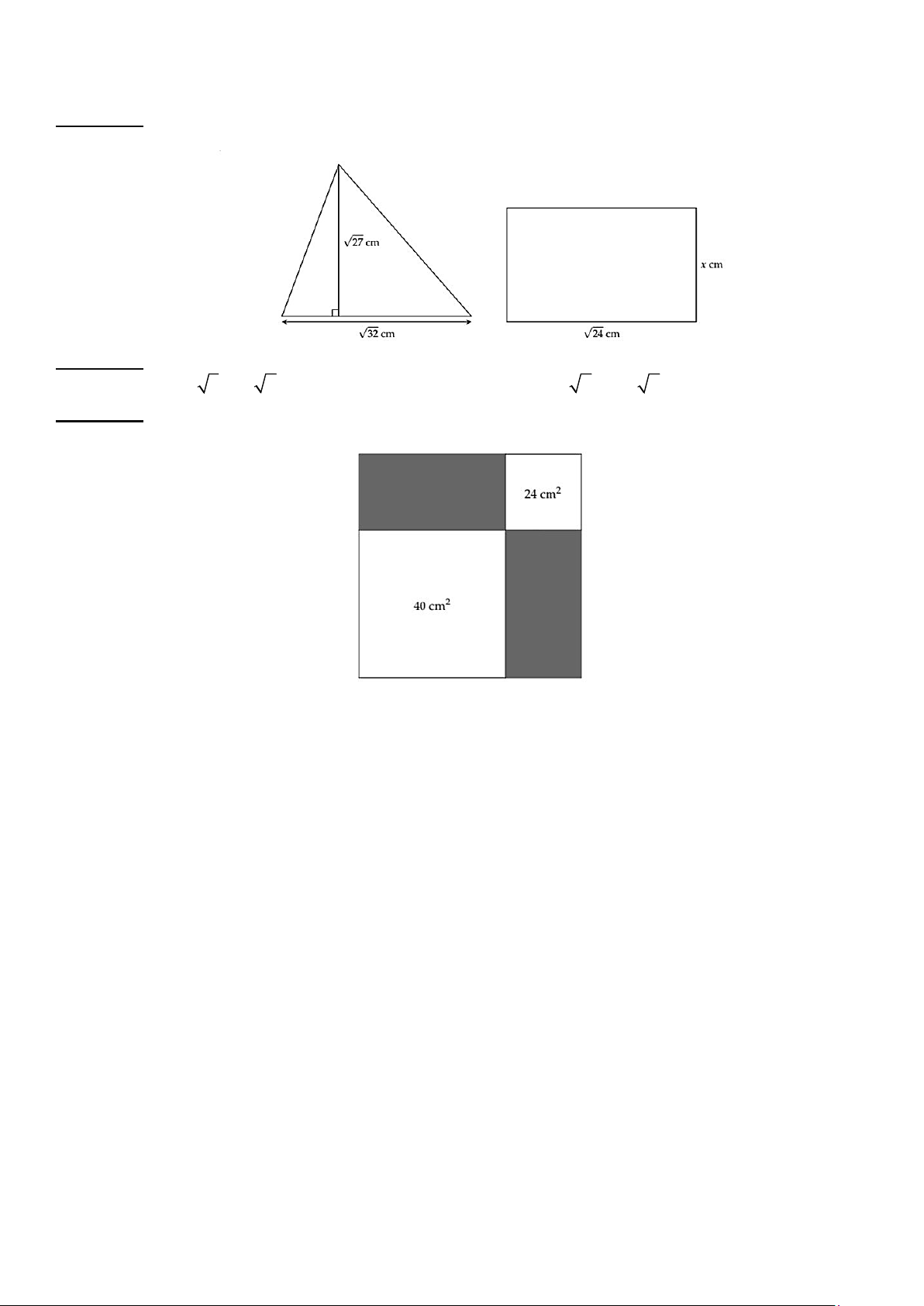
Bài tập 12. Biết rằng hình tam giác và hình chữ nhật ở hình bên có diện tích bằng nhau. Tính chiều
rộng x của hình chữ nhật.
Bài tập 13. Hình chữ nhật có chiều rộng là a cm, chiều rộng b cm và diện tích S cm2.
a/ Tìm S biết a = 8,b = 2. b/ Tìm b, biết S = 3 2, a = 2 7 .
Bài tập 14. Từ một tấm thép hình vuông, người thợ cắt ra làm hai mảnh hình vuông có diện tích lần
lượt là 24cm2 và 40 cm2 như hình bên. Tính diện tích phần còn lại của tấm thép. Trang 3