Phiếu bài tập ứng dụng tích phân có đáp án và lời giải Toán 12

Phiếu bài tập ứng dụng tích phân có đáp án và lời giải được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

21 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

86 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
G
G
i
i
á
á
o
o
v
v
i
i
ê
ê
n
n
:
:
L
L
Ê
Ê
B
B
Á
Á
B
B
Ả
Ả
O
O
_
_
T
T
r
r
ư
ư
ờ
ờ
n
n
g
g
T
T
H
H
P
P
T
T
Đ
Đ
ặ
ặ
n
n
g
g
H
H
u
u
y
y
T
T
r
r
ứ
ứ
,
,
H
H
u
u
ế
ế
S
S
Đ
Đ
T
T
:
:
0
0
9
9
3
3
5
5
.
.
7
7
8
8
5
5
.
.
1
1
1
1
5
5
Đ
Đ
ă
ă
n
n
g
g
k
k
í
í
h
h
ọ
ọ
c
c
t
t
h
h
e
e
o
o
đ
đ
ị
ị
a
a
c
c
h
h
ỉ
ỉ
:
:
1
1
1
1
6
6
/
/
0
0
4
4
N
N
g
g
u
u
y
y
ễ
ễ
n
n
L
L
ộ
ộ
T
T
r
r
ạ
ạ
c
c
h
h
,
,
T
T
P
P
H
H
u
u
ế
ế
H
H
o
o
ặ
ặ
c
c
T
T
r
r
u
u
n
n
g
g
t
t
â
â
m
m
K
K
m
m
1
1
0
0
H
H
ư
ư
ơ
ơ
n
n
g
g
T
T
r
r
à
à
TÝCH PH¢N – øng dông
øng dông tÝch ph©n
Cè lªn c¸c em nhÐ!
HuÕ, th¸ng 02/2021
Phiªn b¶n 2020
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU ÔN TẬP SỐ 01
CHUY£N §Ò
TÝCH PH¢N – øng dông
øng dông tÝch ph©n
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Câu 1: Cho hình phẳng
giới hạn bởi đường cong
2 sinyx
, trục hoành và các đường thẳng
0x
,
x
. Khối tròn xoay tạo thành khi quay
D
quay quanh trục hoành có thể tích
V
bằng
bao nhiêu?
A.
2 1 .
V
B.
2 1 .

V
C.
2
2.
V
D.
2.
V
Câu 2: Gọi
S
là diện tích của hình phẳng giới hạn bởi các đường
2
x
y
,
0y
,
0x
,
2x
. Mệnh đề
nào dưới đây đúng?
A.
2
0
2d
x
Sx
B.
2
2
0
2d
x
Sx
C.
2
2
0
2d
x
Sx
D.
2
0
2d
x
Sx
Câu 3: Cho hình phẳng
H
giới hạn bởi các đường
2
3yx
,
0y
,
0x
,
2x
. Gọi
V
là thể tích
của khối tròn xoay được tạo thành khi quay
H
xung quanh trục
Ox
. Mệnh đề nào dưới đây
đúng?
A.
2
2
2
0
3.

dV x x
B.
2
2
0
3.

dV x x
C.
2
2
2
0
3.
dV x x
D.
2
2
0
3.
dV x x
Câu 4: Gọi
S
là diện tích hình phẳng
H
giới hạn bởi các đường
y f x
, trục hoành và hai đường
thẳng
1x 
,
2x
. Đặt
0
1
da f x x
,
2
0
db f x x
, mệnh đề nào sau đây đúng?
A.
.S b a
B.
.S b a
C.
. S b a
D.
. S b a
Câu 5: Cho hình phẳng
()H
(phần gạch sọc) như hình vẽ bên dưới:
Tính diện tích hình phẳng
( ).H
A.
1.
B.
9
ln3 2.
2
C.
93
ln3 .
22
D.
9
ln3 2.
2
Câu 6: Viết công thức tính thể tích V của vật thể T giới hạn bởi hai mặt phẳng
2019x
và
2020x
,
vật thể T bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ
x
2019 2020x
có thiết diện là một hình vuông độ dài cạnh là
a
.
A.
2020
2
2019
d
V a x
. B.
2020
2019
d
V a x
. C.
2020
2
2019
d
V a x
. D.
2020
2019
d
V a x
.
Câu 7: Gọi
H
là hình phẳng giới hạn bởi các đường
2
3 , 0, 0y x x y x
và
3x
. Quay hình
H
quanh trục
Ox
, ta được khối tròn xoay có thể tích bằng
A.
27
10
. B.
9
2
. C.
81
10
. D.
5
2
.
Câu 8: Cho hàm số
42
3y x x m
có đồ thị là
m
C
(
m
là tham số thực). Giả sử
m
C
cắt trục
Ox
tại 4 điểm phân biệt. Gọi
12
,SS
là diện tích của hai hình phẳng nằm dưới trục
Ox
và
3
S
là diện
tích của hình phẳng nằm trên trục
Ox
được tạo bởi
m
C
với trục
Ox
. Biết rằng tồn tại duy
nhất giá trị của
a
m
b
(với
,*ab
và
a
b
tối giản) để
1 2 3
S S S
. Giá trị của
2ab
bằng
A.
3
. B.
4
. C.
6
. D.
2
.
Câu 9: Diện tích hình phẳng giới hạn bởi hai đường
2
1yx
và
1yx
bằng
A.
6
B.
13
6
C.
13
6
D.
1
6
Câu 10: Cho
H
là hình phẳng giới hạn bởi parabol
2
3yx
, cung tròn có phương trình
2
4yx
và trục hoành . Diện tích của
H
bằng
A.
43
.
12
B.
43
.
6
C.
4 2 3 3
.
6

D.
5 3 2
.
3
Câu 11: Cho hàm số
y f x
liên tục trên . Đồ thị hàm số
y f x
như hình vẽ bên dưới:
Đặt
2
21g x f x x
. Bất phương trình
2
21f x x m
nghiệm đúng với mọi
3;3x
khi và chỉ khi
A.
3mg
. B.
3mg
. C.
1mg
. D.
3mg
.
Câu 12: Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển
động chậm dần đều với vận tốc
5 10 v t t
(m/s), trong đó
t
là khoảng thời gian tính bằng
giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển
bao nhiêu mét?
A. 0,2m. B. 2m. C. 10m. D. 20m.
Câu 13: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
yx
; tiếp tuyến với đồ thị tại
4;2M
và
trục hoành là
A.
3
8
. B.
2
3
. C.
8
3
. D.
1
3
.
Câu 14: Cho hình phẳng
D
giới hạn bởi đường cong
x
ye
, trục hoành và các đường thẳng
0x
,
1x
. Khối tròn xoay tạo thanh khi quay
D
quanh trục hoành có thể tích
V
bằng bao nhiêu?
A.
2
2
e
V
. B.
2
1
2
e
V
. C.
2
1
2
e
V
. D.
2
1
2
e
V
.
Câu 15: Cho hai hàm số
22
2bcf x a xx x
và
2
2xg x dx e
(
a
,
b
,
c
,
d
,
e
). Biết rằng
đồ thị của hàm số
y f x
và
y g x
cắt nhau tại ba điểm có hoành độ lần lượt là
2
;
1
;
1
(tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
A.
37
6
B.
13
2
C.
9
2
D.
37
12
Câu 16: Cho hai hàm số
32
f x ax bx cx d
,
0a
và
2
g x mx nx p
,
0m
có đồ thị cắt
nhau tại 3 điểm có hoành độ
1 2 3
,,x x x
. Kí hiệu
12
,SS
lần lượt là diện tích các hình phẳng giới
hạn bởi đồ thị hàm số
y f x
và
y g x
(tham khỏa hình vẽ)
Biết
1
10S
,
2
7S
. Khi đó,
3
1
d
x
x
g x f x x


bằng
A.
3
. B.
3
. C.
17
. D.
17
.
Câu 17: Cho hàm số
fx
có đồ thị trên đoạn
3;3
là đường gấp khúc
ABCD
như hình vẽ.
x
y
D
3
-2
C
1
B
-2
1
A
Tính
3
3
df x x
.
A.
5
2
. B.
35
6
. C.
5
2
. D.
35
6
.
Câu 18: Một biển quảng cáo có dạng hình elip với bốn đỉnh
1 2 1 2
, , ,A A B B
như hình vẽ bên dưới:
Biết chi phí để sơn phần tô đậm là 200.000 đồng/
2
m
và phần còn lại là 100.000 đồng/
2
m
. Hỏi
số tiền để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết
1 2 1 2
8 , 6A A m B B m
và tứ
giác MNPQ là hình chữ nhật có
3MQ m
.
A.
7322000
đồng. B.
7213000
đồng. C.
5526000
đồng. D.
5782000
đồng.
Câu 19: Trong đợt hội trại “Khi tôi 18” được tổ chức tại trường THPT X. Đoàn trường có thực hiện một
dự án ảnh trưng bày trên một Pano có dạng hình parabol như hình vẽ.
Biết rằng Đoàn trường X sẽ yêu cầu các lớp gửi ảnh dự thi và dán lên khu vực hình chữ nhật
ABCD, phần còn lại sẽ được tranh trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000
đồng cho một
2
m
. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên Pano sẽ là bao nhiêu ?
A.
1.230.000
đồng. B.
900.000
đồng. C.
1.232.000
đồng. D.
902.000
đồng.
Câu 20: Người ta làm một chiếc vòng tròn bằng bạc, biết đường kính ngoài của chiếc vòng bạc là
70cm
, đường kính trong là
50cm
( tham khảo hình vẽ bên dưới).
Thể tích của vòng bạc là
A.
23
1500 .cm
B.
23
9000 .cm
C.
3
1500 .cm
D.
3
1500 .cm
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU ÔN TẬP SỐ 01
CHUY£N §Ò
TÝCH PH¢N – øng dông
øng dông tÝch ph©n
LỜI GIẢI CHI TIẾT
Câu 1: Cho hình phẳng
giới hạn bởi đường cong
2 sinyx
, trục hoành và các đường thẳng
0x
,
x
. Khối tròn xoay tạo thành khi quay
D
quay quanh trục hoành có thể tích
V
bằng
bao nhiêu?
A.
2 1 .
V
B.
2 1 .

V
C.
2
2.
V
D.
2.
V
Lời giải:
Ta có:
2
00
2 sin d 2 sin dV x x x x



0
2 cos 2 1xx
.
Chọn đáp án B.
Câu 2: Gọi
S
là diện tích của hình phẳng giới hạn bởi các đường
2
x
y
,
0y
,
0x
,
2x
. Mệnh đề
nào dưới đây đúng?
A.
2
0
2d
x
Sx
B.
2
2
0
2d
x
Sx
C.
2
2
0
2d
x
Sx
D.
2
0
2d
x
Sx
Lời giải:
22
00
2 d 2 d
xx
S x x

(do
2 0, 0;2
x
x
).
Chọn đáp án A.
Câu 3: Cho hình phẳng
H
giới hạn bởi các đường
2
3yx
,
0y
,
0x
,
2x
. Gọi
V
là thể tích
của khối tròn xoay được tạo thành khi quay
H
xung quanh trục
Ox
. Mệnh đề nào dưới đây
đúng?
A.
2
2
2
0
3.

dV x x
B.
2
2
0
3.

dV x x
C.
2
2
2
0
3.
dV x x
D.
2
2
0
3.
dV x x
Lời giải:
Thể tích của khối tròn xoay được tạo thành khi quay
H
xung quanh trục
Ox
là:
2
2
2
0
3V x dx

.
Chọn đáp án A.
Câu 4: Gọi
S
là diện tích hình phẳng
H
giới hạn bởi các đường
y f x
, trục hoành và hai đường
thẳng
1x 
,
2x
. Đặt
0
1
da f x x
,
2
0
db f x x
, mệnh đề nào sau đây đúng?
A.
.S b a
B.
.S b a
C.
. S b a
D.
. S b a
Lời giải:
Ta có:
2 0 2
1 1 0
d d dS f x x f x x f x x

02
10
ddf x x f x x a b

.
Chọn đáp án A.
Câu 5: Cho hình phẳng
()H
(phần gạch sọc) như hình vẽ bên dưới:
Tính diện tích hình phẳng
( ).H
A.
1.
B.
9
ln3 2.
2
C.
93
ln3 .
22
D.
9
ln3 2.
2
Lời giải:
Ta có: diện tích cần tìm là
3
1
lnS x xdx
Đặt
2
1
ln
2
du dx
ux
x
dv xdx
x
v

khi đó:
3
2 2 2
1
33
1 9 1 9
ln ln3 ln3 2.
11
2 2 2 2 2 2
x x x
S x dx
x
Chọn đáp án B.
Câu 6: Viết công thức tính thể tích V của vật thể T giới hạn bởi hai mặt phẳng
2019x
và
2020x
,
vật thể T bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ
x
2019 2020x
có thiết diện là một hình vuông độ dài cạnh là
a
.
A.
2020
2
2019
d
V a x
. B.
2020
2019
d
V a x
. C.
2020
2
2019
d
V a x
. D.
2020
2019
d
V a x
.
Lời giải:
Hình vuông có độ dài cạnh a có diện tích là
2
S x a
Thể tích của vật thể T là
2020
2
2019
V a dx
.
Chọn đáp án C.
Câu 7: Gọi
H
là hình phẳng giới hạn bởi các đường
2
3 , 0, 0y x x y x
và
3x
. Quay hình
H
quanh trục
Ox
, ta được khối tròn xoay có thể tích bằng
A.
27
10
. B.
9
2
. C.
81
10
. D.
5
2
.
Lời giải:
Khi quay hình
H
quanh trục
Ox
, ta được khối tròn xoay có thể tích bằng
3
33
54
2
2 4 3 2 3
00
0
3 81
3 d 6 9 d 3 .
5 2 10




xx
V x x x x x x x x
Chọn đáp án C.
Câu 8: Cho hàm số
42
3y x x m
có đồ thị là
m
C
(
m
là tham số thực). Giả sử
m
C
cắt trục
Ox
tại 4 điểm phân biệt. Gọi
12
,SS
là diện tích của hai hình phẳng nằm dưới trục
Ox
và
3
S
là diện
tích của hình phẳng nằm trên trục
Ox
được tạo bởi
m
C
với trục
Ox
. Biết rằng tồn tại duy
nhất giá trị của
a
m
b
(với
,*ab
và
a
b
tối giản) để
1 2 3
S S S
. Giá trị của
2ab
bằng
A.
3
. B.
4
. C.
6
. D.
2
.
Lời giải:
Gọi 4 nghiệm của
42
30y x x m
lần lượt là
2 1 1 2
, , ,t t t t
với
12
0 tt
.
Để
1 2 3
S S S
thì
2
2
5
2
4 2 3
2
3 0 0
5
t
t
t
x
x x m dx x mx
t



5
22
3
2
22
2 2 2 2 2 2
0 0 ( 0) 0 (1)
5 5 5



t
tt
t m t t t m do t t m
Vì
2
t
là nghiệm của
42
30x x m
2
22
3 0 (2)t t m
Từ (1) và (2) suy ra:
2
2
2
2 2 2
30
5
t
t t t
2
2 2 2 2 2 2
4 4 5
2 0 . 2 0 0
5 5 2
t t t t t do t




.
Thay
2
5
2
t
vào (2) ta được
25 15 5
0
4 2 4
mm
. Do đó
5; 4 2 6a b a b
.
Chọn đáp án C.
Câu 9: Diện tích hình phẳng giới hạn bởi hai đường
2
1yx
và
1yx
bằng
A.
6
B.
13
6
C.
13
6
D.
1
6
Lời giải:
Phương trình hoành độ giao điểm hai đường là:
2
0
1 1 .
1
x
xx
x
Diện tích hình phẳng giới hạn bởi hai đường là
1
2
0
1
d.
6
S x x x
Chọn đáp án D.
Câu 10: Cho
H
là hình phẳng giới hạn bởi parabol
2
3yx
, cung tròn có phương trình
2
4yx
và trục hoành . Diện tích của
H
bằng
A.
43
.
12
B.
43
.
6
C.
4 2 3 3
.
6

D.
5 3 2
.
3
Lời giải:
Phương trình hoành độ giao điểm giữa parabol và cung tròn ta được
22
3 4 1x x x
với
0 x 2
nên ta có
1x
Ta có diện tích
1
1 2 2 2
2 2 3 2 2
0 1 1 1
0
33
3 4 4 4
33
S x dx x dx x x dx x dx
Đặt :
2sin 2cos ; 1 ; 2
62

   x t dx tdt x t x t
2
6
3 1 4 3
2 sin 2 .
3 2 6



S t t
Chọn đáp án B.
Câu 11: Cho hàm số
y f x
liên tục trên . Đồ thị hàm số
y f x
như hình vẽ bên dưới:
Đặt
2
21g x f x x
. Bất phương trình
2
21f x x m
nghiệm đúng với mọi
3;3x
khi và chỉ khi
A.
3mg
. B.
3mg
. C.
1mg
. D.
3mg
.
Lời giải:
Có
2
21f x x m
,
3;3x
2
2 1 , 3;3m g x f x x x
3;3
minm g x

.
Ta có
0 2 2 1 0g x f x x

1f x x
3, 1, 3x x x
.
Vì kẻ đường thẳng
1yx
cắt đồ thị hàm số
y f x
tại các điểm có hoành độ
3x 
,
1x
,
3x
như sau:
Dựa vào bảng biến thiên ta có
3;3
min min 3 , 3g x g g

.
Quan sát diện tích của hai hình phẳng trên hình vẽ ta có
13
12
31
1 d 1 dS f x x x S f x x x


13
31
1 d 1 df x x x f x x x


1 3 1 3
3 1 3 1
11
d d d d
22
g x x g x x g x x g x x

1 3 1 3 3 3g g g g g g
3;3
min 3g x g
.Vậy
3mg
.
Chọn đáp án B.
Câu 12: Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển
động chậm dần đều với vận tốc
5 10 v t t
(m/s), trong đó
t
là khoảng thời gian tính bằng
giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển
bao nhiêu mét?
A. 0,2m. B. 2m. C. 10m. D. 20m.
Lời giải:
Xét phương trình
5 10 0 2. tt
Do vậy, kể từ lúc người lái đạp phanh thì sau 2s ô tô
dừng hẳn.
Quãng đường ô tô đi được kể từ lúc người lái đạp phanh đến khi ô tô dừng hẳn là
2
2
0
2
5
5 10 10 10 .
0
2



s t dt t t m
Chọn đáp án C.
Câu 13: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
yx
; tiếp tuyến với đồ thị tại
4;2M
và
trục hoành là
A.
3
8
. B.
2
3
. C.
8
3
. D.
1
3
.
Lời giải:
Xét hàm số
yx
ta có
11
' ' 4
4
2
yy
x
.
Phương trình tiếp tuyến của đồ thị tại điểm
4;2M
là
11
4 2 1
44
y x y x
.
Diện tích hình phẳng cần tìm là
4
0
1 1 8
.4.1 1
2 4 3
OAM OMB
S S S x x dx



.
Chọn đáp án C.
Câu 14: Cho hình phẳng
D
giới hạn bởi đường cong
x
ye
, trục hoành và các đường thẳng
0x
,
1x
. Khối tròn xoay tạo thanh khi quay
D
quanh trục hoành có thể tích
V
bằng bao nhiêu?
A.
2
2
e
V
. B.
2
1
2
e
V
. C.
2
1
2
e
V
. D.
2
1
2
e
V
.
Lời giải:
2
1
1
22
0
0
1
1
d
22
xx
e
V e x e

.
Chọn đáp án D.
Câu 15: Cho hai hàm số
22
2bcf x a xx x
và
2
2xg x dx e
(
a
,
b
,
c
,
d
,
e
). Biết rằng
đồ thị của hàm số
y f x
và
y g x
cắt nhau tại ba điểm có hoành độ lần lượt là
2
;
1
;
1
(tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
A.
37
6
B.
13
2
C.
9
2
D.
37
12
Lời giải:
Phương trình hoành độ giao điểm của đồ thị
fx
và
gx
là
3 2 2 3 2
2 3 2 4 0. *bx cx dx x a b d x c e xax
Do đồ thị của hai hàm số cắt nhau tại ba điểm suy ra phương trình
*
có ba nghiệm
2x 
;
1x 
;
1x
. Ta được
32
4 2 1 1ax b d x c e x k x x x
.
Khi đó
4 2 2kk
. Vậy diện tích hình phẳng cần tìm là
1
2
37
d2
6
2 1 1xxxx
.
Chọn đáp án A.
Câu 16: Cho hai hàm số
32
f x ax bx cx d
,
0a
và
2
g x mx nx p
,
0m
có đồ thị cắt
nhau tại 3 điểm có hoành độ
1 2 3
,,x x x
. Kí hiệu
12
,SS
lần lượt là diện tích các hình phẳng giới
hạn bởi đồ thị hàm số
y f x
và
y g x
(tham khỏa hình vẽ)
Biết
1
10S
,
2
7S
. Khi đó,
3
1
d
x
x
g x f x x


bằng
A.
3
. B.
3
. C.
17
. D.
17
.
Lời giải:
Theo đề bài ta có
2
1
1
10 d
x
x
S f x g x x


,
3
2
2
7d
x
x
S g x f x x


.
Suy ra
33
2
1 1 2
12
d d d 10 7 3
xx
x
x x x
g x f x x g x f x x g x f x x S S
Chọn đáp án B.
Câu 17: Cho hàm số
fx
có đồ thị trên đoạn
3;3
là đường gấp khúc
ABCD
như hình vẽ.
x
y
D
3
-2
C
1
B
-2
1
A
Tính
3
3
df x x
.
A.
5
2
. B.
35
6
. C.
5
2
. D.
35
6
.
Lời giải:
x
y
A
3
A
2
A
1
E
D
3
-2
C
1
B
-2
1
A
Phương trình đường thẳng
CD
đi qua
1;1C
và nhận
2; 3CD 
làm véctơ chỉ phương.
Phương trình chính tắc
11
: 3 2 5
23
xy
CD x y

.
Đặt
E CD Ox
. Ta được
5
3 2 5
5
;0
3
0
3
0
xy
x
E
y
y





.
Do đó
3
3
df x x
5
2 1 3
3
5
3 2 1
3
d d d df x x f x x f x x f x x

1 1 2 2 3
ABA A BCA A CE EDA
S S S S
1 1 2 1 4
1 1 3 1 1 2
2 2 3 2 3
5
2
.
Chọn đáp án A.
Câu 18: Một biển quảng cáo có dạng hình elip với bốn đỉnh
1 2 1 2
, , ,A A B B
như hình vẽ bên. Biết chi phí
để sơn phần tô đậm là 200.000 đồng/
2
m
và phần còn lại là 100.000 đồng/
2
m
. Hỏi số tiền để
sơn theo cách trên gần nhất với số tiền nào dưới đây, biết
1 2 1 2
8 , 6A A m B B m
và tứ giác
MNPQ là hình chữ nhật có
3MQ m
.
A.
7322000
đồng. B.
7213000
đồng. C.
5526000
đồng. D.
5782000
đồng.
Lời giải:
Gắn hệ trục tọa độ
Oxy
có
12
AA
trùng với trục
Ox
,
12
BB
trùng với trục
Oy
, gốc tọa độ
1 2 1 2
O A A B B
(như hình vẽ).
Elip có độ dài trục lớn
12
28a A A
4am
, độ dài trục nhỏ
12
26b B B
3bm
.
Suy ra phương trình chính tắc của elip là
22
22
1
43
xy

2
3
16
4
yx
. Trong đó:
Do
3MQ
3
22
M
MQ
y
2
4 1 2 3
9
M
M
y
x
23
N
x
.
Gọi
1
S
là diện tích phần tô đậm của elip,
2
S
là diện tích phần không bị tô đậm của elip và
S
là
diện tích elip. Suy ra
1
S
là diện tích hình phẳng giới hạn bởi các đường
2
3
16
4
yx
,
2
3
16
4
yx
,
23x 
,
23x
Ta có:
+
2
12S ab m


.
+
23
22
1
23
33
16 16 dx
44
S x x



23
2
0
= 3 16 dxx
.
Đặt
4sinxt
dx 4cos dtt
.
Khi
00xt
. Khi
23
3
xt
23
2
1
0
= 3 16 dx =Sx
3
2
0
3 16 16sin .4cost tdt

3
2
0
48cos dtt
3
0
24 1 os2t dtc
3
0
24 12sin 2tt

2
8 6 3 m

.
2
21
4 6 3S S S m
.
Suy ra chi phí để sơn biển quảng cáo là:
12
200000. 100000. 7322416SS
(đồng).
Vậy số tiền để sơn biển quảng cáo gần nhất với
7322000
đồng.
Chọn đáp án A.
Câu 19: Trong đợt hội trại “Khi tôi 18” được tổ chức tại trường THPT X. Đoàn trường có thực hiện một
dự án ảnh trưng bày trên một Pano có dạng hình parabol như hình vẽ.
Biết rằng Đoàn trường X sẽ yêu cầu các lớp gửi ảnh dự thi và dán lên khu vực hình chữ nhật
ABCD, phần còn lại sẽ được tranh trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000
đồng cho một
2
m
. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên Pano sẽ là bao nhiêu ?
A.
1.230.000
đồng. B.
900.000
đồng. C.
1.232.000
đồng. D.
902.000
đồng.
Lời giải:
Chọn hệ trục tọa độ
Oxy
như hình vẽ, khi đó ta được phương trình của parabol là
2
4.yx
Gọi
22
;0 0 2 ;0 , ; 4 , ; 4 .C x x D x B x x A x x
Ta có diện tích của Pano là
2
22
2
32
4 d .
3
x x m
Diện tích hình chữ nhật
ABCD
là
2
. 2 . 4 .
ABCD
S CD BC x x
Chi phí dán hoa văn thấp nhất khi và chỉ khi diện tích hình chữ nhật
ABCD
lớn nhất.
Xét hàm số
2
( ) 2 . 4 , 0;2f x x x x
có
0;2
32 3
max ( ) .
9
x
fx
Chi phí thấp nhất cho việc dán hoa văn là
32 32 3
.200000 902.000
39





.
Chọn đáp án D.
Câu 20: Người ta làm một chiếc vòng tròn bằng bạc, biết đường kính ngoài của chiếc vòng bạc là
70cm
, đường kính trong là
50cm
( tham khảo hình vẽ bên dưới).
Thể tích của vòng bạc là
A.
23
1500 .cm
B.
23
9000 .cm
C.
3
1500 .cm
D.
3
1500 .cm
Lời giải:
Ta có bán kính ngoài của chiếc vòng bạc là
35cm
, bán kính trong là
25cm
.
Để tính thể tích của vòng bạc ta coi nó là hình tròn xoay sinh ra bằng cách quay một hình tròn
xung quanh trục
.Ox
Bán kính của hình tròn này bằng
35 25 :2 5 .R cm
Tâm của hình tròn là
0;30I
.
Phương trình của đường tròn là
2
2
30 25x y C
.
2
30 25yx
.
Khi đó thể tích của vòng bạc được sinh ra bởi hình phẳng tạo bởi 2 đường cong
2
1
30 25f x x
và
2
2
30 25f x x
,
5;5x
quay quanh trục
.Ox
Vậy thể tích của vòng bạc bằng:
5 5 5
22
2 2 2 2
5 5 5
30 25 30 25 120 25 .V y dx x x dx x dx



Đặt
5sin 5cos . .x t dx t dt
Đổi cận :
Khi đó
2 2 2
22
2 2 2
120 25 25sin .5cos .d 120.25 cos .d 60.25 1 cos2 .dV t t t t t t t
23
2
2
sin2
1500 1500 .
2
t
t cm




Chọn đáp án A.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU ÔN TẬP SỐ 02
CHUY£N §Ò
TÝCH PH¢N – øng dông
øng dông tÝch ph©n
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Câu 1: Cho hàm số
fx
liên tục trên . Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
, 0, 1y f x y x
và
4x
. Mệnh đề nào dưới đây là đúng?
A.
14
11
dd

S f x x f x x
. B.
14
11
dd


S f x x f x x
.
C.
14
11
dd


S f x x f x x
. D.
14
11
dd

S f x x f x x
.
Câu 2: Tính thể tích của vật thể nằm giữa hai mặt phẳng
1x 
và
1x
biết rằng thiết diện của vật
thể bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
11xx
là một hình
vuông có cạnh bằng
4
1 x
.
A.
8
5
. B.
2
. C.
4
. D.
1
4
.
Câu 3: Cho hàm số
()y f x
liên tục trên và có đồ thị như hình vẽ sau:
Giá trị của
4
4
( )d
f x x
bằng
A. 10. B. 4. C. 12. D. 8.
Câu 4: Diện tích hình phẳng giới hạn bởi hai đường
2
4yx
và
24yx
bằng
A.
36
. B.
4
3
. C.
4
3
. D.
36
.
Câu 5: Cho hai hàm số
32
f x ax bx cx d
,
0a
và
2
g x mx nx p
,
0m
có đồ thị cắt
nhau tại 3 điểm có hoành độ
1 2 3
,,x x x
.
Kí hiệu
12
,SS
lần lượt là diện tích các hình phẳng giới hạn bởi đồ thị hàm số
y f x
và
y g x
. Biết
1
10S
,
2
7S
. Khi đó,
3
1
d
x
x
g x f x x


bằng
A.
3
. B.
3
. C.
17
. D.
17
.
Câu 6: Cho đường thẳng
3yx
và parabol
2
2y x a
(
a
là tham số thc dương). Gọi
1
S
và
2
S
lần
lượt là diện tch của 2 hình phẳng được gạch cho trong hình vẽ bên. Khi
12
SS
thì
a
thuộc
khong nào dưới đây?
A.
49
;
5 10



. B.
4
0;
5



. C.
9
1;
8



. D.
9
;1
10



Câu 7: Tính diện tích hình phẳng tạo thành bởi Parabol
2
yx
, đường thẳng
2yx
và trục hoành
trên đoạn
0;2
(phần gạch sọc trong hình vẽ).
A.
3
5
. B.
5
6
. C.
2
3
. D.
7
6
.
Câu 8: Một vật chuyển động trong
3
giờ với vận tốc
km/hv
phụ thuộc thời gian
ht
có đồ thị là
một phần của đường parabol có đỉnh
2;9I
và trục đối xứng song song với trục tung như
hình bên. Tnh quãng đường
s
mà vật di chuyển được trong
3
giờ đó.
A.
24,25 km .s
B.
26,75 km .s
C.
24,75 km .s
D.
25,25 km .s
Câu 9: Đường thẳng
d
cắt đường cong
32
f x a x bx cx d
tại ba điểm phân biệt có hoành độ
2x
,
1x
,
2x
như hình vẽ dưới đây:
Diện tích hình phẳng gạch sọc thuộc khong nào dưới đây?
A.
9
;5
2



. B.
13
6;
2



. C.
11
5;
2



. D.
11
;6
2



.
Câu 10: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
khi 1
2 khi 1


xx
y f x
xx
, trục hoành và
các đường thẳng
0, 2xx
. Thể tích của khối tròn xoay tạo thành khi quay
H
quanh trục
hoành bằng
A.
8
15
. B.
9
5
. C.
9
5
. D.
32
15
.
Câu 11: Viết công thức tính thể tích
V
của khối tròn xoay được tạo ra khi quay hình thang cong, giới
hạn bởi đồ thị hàm số
y f x
, trục
Ox
và hai đường thẳng
,x a x b a b
, xung quanh
trục
Ox
.
A.
2
d.
b
a
V f x x
B.
2
d.
b
a
V f x x
C.
d.
b
a
V f x x
D.
d.
b
a
V f x x
Câu 12: Cho hàm số
y f x
có đồ thị
y f x
cắt trục
Ox
tại ba điểm có hoành độ
abc
như
hình vẽ dưới đây:
y
x
c
b
O
a
Khẳng định nào dưới đây đúng?
A.
.f b f a f c
B.
f a f b f c
.
C.
f c f a f b
. D.
f c f b f a
.
Câu 13: Một ô-tô đang dừng và bắt đầu chuyển động theo một đường thẳng với gia tốc
( ) 6 2a t t
2
/ms
, trong đó
t
là khong thời gian tính bằng giây kể từ lúc ô tô bắt đầu chuyển động.
Quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc ô tô đạt giá trị lớn
nhất là
A.
9
m
. B.
20
m
. C.
18
m
. D.
27
2
m
.
Câu 14: Cho
y f x
là hàm số đa thức bậc ba có đồ thị như hình vẽ bên dưới :
2
2
y
x
O
3
1
Tính diện tích hình phẳng được tô đậm.
A.
9
4
. B.
37
12
. C.
5
12
. D.
8
3
.
Câu 15: Cho hàm số
y f x
liên tục và nhận giá trị dương trên . Gọi
1
D
là hình phẳng giới hạn
bởi đồ thị hàm số
y f x
, các đường
0x
,
1x
và trục
Ox
. Gọi
2
D
là hình phẳng giới hạn
bởi đồ thị hàm số
1
3
y f x
, các đường
0x
,
1x
và trục
Ox
. Quay các hình phẳng
1
D
,
2
D
quanh trục
Ox
ta được các khối tròn xoay có thể tích lần lượt là
1
V
,
2
V
. Khẳng định nào
sau đây đúng?
A.
12
9VV
. B.
21
9VV
. C.
12
3VV
. D.
21
3VV
.
Câu 16: Cho hình vuông
ABCD
tâm
O
, độ dài cạnh là
4
cm. Đường cong
BOC
là một phần của
parabol đỉnh
O
chia hình vuông thành hai hình phẳng có diện tích lần lượt là
1
S
và
2
S
(tham
kho hình vẽ).
S
2
S
1
4 cm
A
B
C
D
O
4 cm
Tỉ số
1
2
S
S
bằng
A.
2
5
. B.
1
2
. C.
1
3
. D.
3
5
.
Câu 17: Tính diện tích
S
của hình phẳng (phần gạch sọc) giới hạn bởi đồ thị của các hàm số
2
, 4 4y x y x
và
44yx
như hình vẽ bên.
A.
6
3
S
. B.
16
3
S
. C.
26
3
S
. D.
16
9
S
.
Câu 18: Cho hàm số
()y f x
có đồ thị trên đoạn
[ 2;6]
như hình vẽ bên dưới.
Biết các miền
,,A B C
có diện tch lần lượt là
32, 2
và
3
.
Tính
2
2
2
3
(3 4) 1 2 5 d .
4






I x f x x x
A.
1
2
I
B.
82I 
. C.
66I
. D.
50I
.
Câu 19: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
54y x x
và trục
Ox
. Tính thể tích của
khối tròn xoay sinh ra khi quay hình
H
quanh trục
.Ox
A.
9
2
. B.
81
10
. C.
81
10
. D.
9
2
.
Câu 20: Một cái cổng hình Parabol như hình vẽ sau. Chiều cao
4GH m
, chiều rộng
4AB m
,
0,9AC BD m
. Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật
CDEF
tô đậm có
giá là
1200000
đồng
2
/m
, còn các phần để trắng làm xiên hoa có giá là
900000
đồng
2
/m
(tham
khỏa hình vẽ)
Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?
A.
11445000
đồng. B.
4077000
đồng. C.
7368000
đồng. D.
11370000
đồng.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU ÔN TẬP SỐ 02
CHUY£N §Ò
TÝCH PH¢N – øng dông
øng dông tÝch ph©n
LỜI GIẢI CHI TIẾT
Câu 1: Cho hàm số
fx
liên tục trên . Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
, 0, 1y f x y x
và
4x
. Mệnh đề nào dưới đây là đúng?
A.
14
11
dd

S f x x f x x
. B.
14
11
dd


S f x x f x x
.
C.
14
11
dd


S f x x f x x
. D.
14
11
dd

S f x x f x x
.
Lời giải:
Ta có
4 1 4 1 4
1 1 1 1 1
S f x dx f x dx f x dx f x dx f x dx
Chọn đáp án B.
Câu 2: Tính thể tích của vật thể nằm giữa hai mặt phẳng
1x 
và
1x
biết rằng thiết diện của vật
thể bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
11xx
là một hình
vuông có cạnh bằng
4
1 x
.
A.
8
5
. B.
2
. C.
4
. D.
1
4
.
Lời giải:
Thể tích của vật thể là
1
2
4
1
8
1
5
V x dx
.
Chọn đáp án A.
Câu 3: Cho hàm số
()y f x
liên tục trên và có đồ thị như hình vẽ sau:
Giá trị của
4
4
( )d
f x x
bằng
A. 10. B. 4. C. 12. D. 8.
Lời giải:
Ta có
4 2 0 4
4 4 2 0
( ) ( ) ( ) ( )
11
.2.2 .2.2 2.4 8.
22

ABC COD DOFE
f x dx f x dx f x dx f x dx S S S
Chọn đáp án D.
Câu 4: Diện tích hình phẳng giới hạn bởi hai đường
2
4yx
và
24yx
bằng
A.
36
. B.
4
3
. C.
4
3
. D.
36
.
Lời giải:
Phương trình hoành độ giao điểm của hai đồ thị đã cho là:
22
0
4 2 4 2 0
2
x
x x x x
x
.
Diện tích hình phẳng giới hạn bởi hai đồ thị đã cho là:
2 2 2
3
2 2 2 2
0 0 0
2
4
4 2 4 d 2 d 2 d
0
33
x
S x x x x x x x x x x



.
Chọn đáp án B.
Câu 5: Cho hai hàm số
32
f x ax bx cx d
,
0a
và
2
g x mx nx p
,
0m
có đồ thị cắt
nhau tại 3 điểm có hoành độ
1 2 3
,,x x x
.
Kí hiệu
12
,SS
lần lượt là diện tích các hình phẳng giới hạn bởi đồ thị hàm số
y f x
và
y g x
. Biết
1
10S
,
2
7S
. Khi đó,
3
1
d
x
x
g x f x x


bằng
A.
3
. B.
3
. C.
17
. D.
17
.
Lời giải:
Theo đề bài ta có
2
1
1
10 d
x
x
S f x g x x


,
3
2
2
7d
x
x
S g x f x x


.
Suy ra
33
2
1 1 2
12
d d d 10 7 3.
xx
x
x x x
g x f x x g x f x x g x f x x S S
Chọn đáp án B.
Câu 6: Cho đường thẳng
3yx
và parabol
2
2y x a
(
a
là tham số thc dương). Gọi
1
S
và
2
S
lần
lượt là diện tch của 2 hình phẳng được gạch cho trong hình vẽ bên. Khi
12
SS
thì
a
thuộc
khong nào dưới đây?
A.
49
;
5 10



. B.
4
0;
5



. C.
9
1;
8



. D.
9
;1
10



Lời giải:
Xt phương trình tương giao:
2
32x x a
2
2 3 0x x a
1
Để phương trình
1
có hai nghiệm dương phân biệt
12
,xx
(
21
0)xx
12
12
9 8 0
39
00
28
.0
2
a
x x a
a
xx

.
Ta có:
1
1
2 3 2
1
0
0
23
23
32
x
x
S x x a dx x x ax



32
1 1 1
23
32
x x ax
2
1
2
2
23
x
x
S x x a dx
2
1
32
23
32
x
x
x x ax



3 2 3 2
2 2 2 1 1 1
2 3 2 3
3 2 3 2
x x ax x x ax
Do
32
1 2 2 2 2
23
0
32
S S x x ax
mà
2
x
là nghiệm của
1
nên
22
2 2 2 2
2 3 0 2 3x x a a x x
2
3 2 2
2 2 2 2 2
23
2 3 . 0
32
x x x x x
32
22
43
0
32
xx
2
9
8
x
( loại nghiệm
2
0x
)
Thay vào
2
27 4 9
;
32 5 10
a



.
Chọn đáp án A.
Câu 7: Tính diện tích hình phẳng tạo thành bởi Parabol
2
yx
, đường thẳng
2yx
và trục hoành
trên đoạn
0;2
(phần gạch sọc trong hình vẽ).
A.
3
5
. B.
5
6
. C.
2
3
. D.
7
6
.
Lời giải:
Ta có
2
1
12
32
2
01
0
1
5
d 2 d 2
3 2 6
xx
S x x x x x




.
Chọn đáp án B.
Câu 8: Một vật chuyển động trong
3
giờ với vận tốc
km/hv
phụ thuộc thời gian
ht
có đồ thị là
một phần của đường parabol có đỉnh
2;9I
và trục đối xứng song song với trục tung như
hình bên. Tnh quãng đường
s
mà vật di chuyển được trong
3
giờ đó.
A.
24,25 km .s
B.
26,75 km .s
C.
24,75 km .s
D.
25,25 km .s
Lời giải:
Gọi
2
.v t a t bt c
.
Đồ thị
vt
là một phần parabol có đỉnh
2;9I
và đi qua điểm
0;6A
nên
2
2
3
2
2
4
.2 .2 9 3
6
.0 .0 6
b
a
a
a b c b
c
a b c



. Tìm được
2
3
36
4
v t t t
Vậy
3
2
0
3
36
4
S t t dt



24,75 (km)
Chọn đáp án C.
Câu 9: Đường thẳng
d
cắt đường cong
32
f x a x bx cx d
tại ba điểm phân biệt có hoành độ
2x
,
1x
,
2x
như hình vẽ dưới đây:
Diện tích hình phẳng gạch sọc thuộc khong nào dưới đây?
A.
9
;5
2



. B.
13
6;
2



. C.
11
5;
2



. D.
11
;6
2



.
Lời giải:
Ta có
: d y mx n
Phương trình hoành độ giao điểm
3 2 3 2
a x bx cx d mx n g x a x bx cx d mx n
có
3
nghiệm
2x
;
1x
;
2x
.
Do đó
2 1 2 g x a x x x
.
Do
11
0 3 1 4 2 1 2
22
g d n a a g x x x x
.
Vì vậy
2
2
1 71
2 1 2 d
2 12
S x x x x
.
Chọn đáp án D.
Câu 10: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
khi 1
2 khi 1


xx
y f x
xx
, trục hoành và
các đường thẳng
0, 2xx
. Thể tích của khối tròn xoay tạo thành khi quay
H
quanh trục
hoành bằng
A.
8
15
. B.
9
5
. C.
9
5
. D.
32
15
.
Lời giải:
x
y
2
1
1
O
Thể tích của khối tròn xoay tạo thành khi quay
H
quanh trục hoành là
2
1
3
1 2 1 2
5
2
2 2 4
0 1 0 1
0
1
2
.d .d .d 2 .d
53
x
x
V f x x f x x x x x x
18
0
5 3 15




.
Chọn đáp án A.
Câu 11: Viết công thức tính thể tích
V
của khối tròn xoay được tạo ra khi quay hình thang cong, giới
hạn bởi đồ thị hàm số
y f x
, trục
Ox
và hai đường thẳng
,x a x b a b
, xung quanh
trục
Ox
.
A.
2
d.
b
a
V f x x
B.
2
d.
b
a
V f x x
C.
d.
b
a
V f x x
D.
d.
b
a
V f x x
Lời giải:
Chọn đáp án A.
Câu 12: Cho hàm số
y f x
có đồ thị
y f x
cắt trục
Ox
tại ba điểm có hoành độ
abc
như
hình vẽ dưới đây:
y
x
c
b
O
a
Khẳng định nào dưới đây đúng?
A.
.f b f a f c
B.
f a f b f c
.
C.
f c f a f b
. D.
f c f b f a
.
Lời giải:
Ta có bng biến thiên của hàm số
:y f x
f
b
( )
f
c
( )
f
a
( )
+
-
+
-
0
0
0
c
b
a
+
∞
-
∞
f
x
( )
f
'
x
( )
x
Từ bng biến thiên suy ra trong ba giá trị
, , f a f b f c
thì
fb
lớn nhất.
y
x
S
2
S
1
c
b
O
a
Ta có : diện tích
1
d
b
a
S f x x
, diện tích
2
d
c
b
S f x x

.
Từ hình vẽ ta có:
12
SS
dd
bc
ab
f x x f x x



f b f a f b f c
.f a f c
Vậy
.f b f a f c
Chọn đáp án A.
Câu 13: Một ô-tô đang dừng và bắt đầu chuyển động theo một đường thẳng với gia tốc
( ) 6 2a t t
2
/ms
, trong đó
t
là khong thời gian tính bằng giây kể từ lúc ô tô bắt đầu chuyển động.
Quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc ô tô đạt giá trị lớn
nhất là
A.
9
m
. B.
20
m
. C.
18
m
. D.
27
2
m
.
Lời giải:
Ta có
2
( ) ( ) (6 2 ) 6v t a t dt t dt t t C

Do ban đầu ô tô đang dừng nên
0 0 0. vC
Suy ra
2
( ) 6v t t t
Ta có
max
3vt
Quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc ô tô đạt giá trị lớn
nhất là
3
2
0
6 18 .
S t t m
Chọn đáp án C.
Câu 14: Cho
y f x
là hàm số đa thức bậc ba có đồ thị như hình vẽ bên dưới :
2
2
y
x
O
3
1
Tính diện tích hình phẳng được tô đậm.
A.
9
4
. B.
37
12
. C.
5
12
. D.
8
3
.
Lời giải:
Gi sử
32
()f x ax bx cx d
có đồ thị
()C
như hình vẽ trên.
Điểm
32
(0;0) ( ) d 0 ( )O C f x ax bx cx
.
Các điểm
32
01
(1;0), (2;2), (3;0) (C) 4 2 1 4 ( ) 4 3
9 3 0 3
a b c a
A B D a b c b f x x x x
a b c c





.
Diện tích hình phẳng cần tìm là
1 3 1 3
3 2 3 2
0 1 0 1
37
0 ( ) ( ) 0 ( 4 3 ) ( 4 3 ) .
12
S f x dx f x dx x x x dx x x x dx
Chọn đáp án B.
Câu 15: Cho hàm số
y f x
liên tục và nhận giá trị dương trên . Gọi
1
D
là hình phẳng giới hạn
bởi đồ thị hàm số
y f x
, các đường
0x
,
1x
và trục
Ox
. Gọi
2
D
là hình phẳng giới hạn
bởi đồ thị hàm số
1
3
y f x
, các đường
0x
,
1x
và trục
Ox
. Quay các hình phẳng
1
D
,
2
D
quanh trục
Ox
ta được các khối tròn xoay có thể tích lần lượt là
1
V
,
2
V
. Khẳng định nào
sau đây đúng?
A.
12
9VV
. B.
21
9VV
. C.
12
3VV
. D.
21
3VV
.
Lời giải:
Ta có
1
2
1
0
d
V f x x
và
2
11
2
2
00
11
dd
39






V f x x f x x
. Vậy
21
1
9
VV
hay
12
9VV
.
Chọn đáp án A.
Câu 16: Cho hình vuông
ABCD
tâm
O
, độ dài cạnh là
4
cm. Đường cong
BOC
là một phần của
parabol đỉnh
O
chia hình vuông thành hai hình phẳng có diện tích lần lượt là
1
S
và
2
S
(tham
kho hình vẽ).
S
2
S
1
4 cm
A
B
C
D
O
4 cm
Tỉ số
1
2
S
S
bằng
A.
2
5
. B.
1
2
. C.
1
3
. D.
3
5
.
Lời giải:
x
y
-2
2
-2
2
O
D
C
B
A
1
Gắn hệ trục toạ độ như hình vẽ.
Ta có phương trình parabol
2
1
:
2
P y x
.
Suy ra
2
2
1
2
1 16
2
23
S x dx



(đvdt).
Diện tích hình vuông
ABCD
là
2
4 16
ABCD
S 
(đvdt).
Do đó diện tích
2
S
là
21
16 32
16
33
ABCD
S S S
(đvdt).
Vậy tỉ số
1
2
16 32 1
:
3 3 2
S
S

.
Chọn đáp án B.
Câu 17: Tính diện tích
S
của hình phẳng (phần gạch sọc) giới hạn bởi đồ thị của các hàm số
2
, 4 4y x y x
và
44yx
như hình vẽ bên.
A.
6
3
S
. B.
16
3
S
. C.
26
3
S
. D.
16
9
S
.
Lời giải:
Ta thấy đường thẳng
44yx
và đường thẳng
44yx
lần lượt là hai tiếp tuyến của đồ
thị hàm số
2
yx
tại các tiếp điểm có hoành độ
2x 
và
2x
.
Do tnh đối xứng qua
Oy
của parabol
2
yx
nên diện tch hình phẳng cần tìm bằng 2 lần diện
tch tam giác cạnh
2
OMT
và bằng
22
2
2
00
2 4 4 d 2 2 dS x x x x x



2
3
0
2
16
2.
33

x
Chọn đáp án B.
Câu 18: Cho hàm số
()y f x
có đồ thị trên đoạn
[ 2;6]
như hình vẽ bên dưới.
Biết các miền
,,A B C
có diện tch lần lượt là
32, 2
và
3
.
Tính
2
2
2
3
(3 4) 1 2 5 d .
4






I x f x x x
A.
1
2
I
B.
82I 
. C.
66I
. D.
50I
.
Lời giải:
Đặt
2
33
2 5 2 3 4 2
42
t x x dt x dx x dx dt



Đổi cận: - Với
22xt
-Với
26xt
Ta được:
6 6 6
2 2 2
2 1 2 2 16 2I f t dt dt f t dt M


.
Với
6 2 4 6
2 2 2 4
32 2 3 33M f t dt f t dt f t dt f t dt

.
Vậy:
16 2. 33 50I
.
Chọn đáp án D.
Câu 19: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
54y x x
và trục
Ox
. Tính thể tích của
khối tròn xoay sinh ra khi quay hình
H
quanh trục
.Ox
A.
9
2
. B.
81
10
. C.
81
10
. D.
9
2
.
Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số
2
54y x x
và trục
Ox
ta có:
2
1
5 4 0
4
x
xx
x
Thể tích của khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
44
2
22
11
81
54
10
V f x dx x x dx


.
Chọn đáp án C.
Câu 20: Một cái cổng hình Parabol như hình vẽ sau. Chiều cao
4GH m
, chiều rộng
4AB m
,
0,9AC BD m
. Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật
CDEF
tô đậm có
giá là
1200000
đồng
2
/m
, còn các phần để trắng làm xiên hoa có giá là
900000
đồng
2
/m
(tham
khỏa hình vẽ)
Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?
A.
11445000
đồng. B.
4077000
đồng. C.
7368000
đồng. D.
11370000
đồng.
Lời giải:
Gắn hệ trục tọa độ Oxy sao cho
AB
trùng
Ox
,
A
trùng
O
khi đó parabol có đỉnh
2;4G
và
đi qua gốc tọa độ.
Gi sử phương trình của parabol có dạng
2
0y ax bx c a
.
Vì parabol có đỉnh là
2;4G
và đi qua điểm
0;0O
nên ta có
2
0
2
2
.2 .2 4
c
b
ab
a
c

1
4
0
a
b
c


.
Suy ra phương trình parabol là
2
() 4y f x x x
.
Diện tích của c cổng là
4
4
3
2 2 2
0
0
32
4 d 2 m
33
x
S x x x x



.
Mặt khác chiều cao
0,9 2,79(m)CF DE f
;
4 2.0,9 2,2 mCD
.
Diện tích hai cánh cổng là
2
. 6,138 m
CDEF
S CD CF
.
Diện tích phần xiên hoa là
2
32 6793
6,14 m
3 1500
xh CDEF
S S S
.
Vậy tổng số tiền để làm cổng là
6793
6,138.1200000 .900000 11441400
1500

đồng.
Chọn đáp án A.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU ÔN TẬP SỐ 03
CHUY£N §Ò
TÝCH PH¢N – øng dông
øng dông tÝch ph©n
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Câu 1: Viết công thức tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với
trục
Ox
tại các điểm
,x a x b a b
có thiết diện bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x a x b
là
Sx
.
A.
2
b
a
V S x dx
. B.
b
a
V S x dx
. C.
b
a
V S x dx
. D.
2
b
a
V S x dx
.
Câu 2: Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
e
x
y
,
0y
,
0x
,
2x
. Mệnh đề nào
dưới đây đúng?
A.
2
2
0
e d .
x
Sx
B.
2
0
e d .
x
Sx
C.
2
0
e d .
x
Sx
D.
2
2
0
e d .
x
Sx
Câu 3: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y x x
và đồ thị hàm số
2
.y x x
A.
37
.
12
B.
9
.
4
C.
81
.
12
D.
13.
Câu 4: Cho hình thang cong
H
giới hạn bởi các đường
x
ye
,
0y
,
0x
,
ln 4x
. Đường thẳng
(0 ln 4)x k k
chia
H
thành hai phần có diện tích là
1
S
và
2
S
như hình vẽ bên. Tìm
k
để
12
2SS
.
A.
2
ln4
3
k
. B.
ln 2k
. C.
8
ln
3
k
D.
ln3k
.
Câu 5: Diện tích hình phẳng giới hạn bởi đường
2
41y x x
,
ym
,
3m 
,
0x
,
3x
là
A.
36m
. B.
36m
. C.
36m
. D.
36m
.
Câu 6: Cho hàm số
()y f x
có đồ thị trên đoạn
[-1;4]
như hình vẽ dưới:
O
x
y
1
S
2
S
k
ln 4
Tính tích phân
4
1
( )d .
I f x x
A.
5
.
2
I
B.
11
.
2
I
C.
5.I
D.
3.I
Câu 7: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới
đây?
A.
2
2
1
2 2 4 dx x x

. B.
2
1
2 2 dxx

. C.
2
1
2 2 dxx
. D.
2
2
1
2 2 4 dx x x
.
Câu 8: Cho đồ thị biểu thị vận tốc của hai chất điểm
A
và
B
xuất phát cùng một lúc, bên cạnh nhau
và trên cùng một con đường. Biết đồ thị biểu diễn vận tốc của chất điểm
A
là một đường
Parabol, đồ thị biểu diễn vận tốc của chất điểm
B
là một đường thẳng như hình vẽ sau.
Hỏi sau khi đi được
3
giây, khoảng cách giữa hai chất điểm là bao nhiêu mét?
A.
120 .m
B.
60 .m
C.
270 .m
D.
90 .m
Câu 9: Đường thẳng
4y kx
cắt parabol
2
2yx
tại hai điểm phân biệt và diện tích các hình
phẳng
1
S
,
2
S
bằng nhau như hình vẽ bên.
Mệnh đề nào sau đây đúng?
A.
6; 4k
. B.
1
1;
2
k



. C.
2; 1k
. D.
1
;0
2
k




.
Câu 10: Kí hiệu
H
là hình phẳng giới hạn bởi đồ thị hàm số
2( 1) ,
x
y x e
trục tung và trục hoành.
Tính thể tích
V
của khối tròn xoay thu được khi quay hình
H
xung quanh trục
Ox
.
A.
4 2 .Ve
B.
4 2 .
Ve
C.
2
5.Ve
D.
2
5.
Ve
Câu 11: Cho hai hàm số
32
1
2
f x ax bx cx
và
2
1g x dx ex
, , , ,a b c d e
. Biết rằng đồ
thị hàm số
y f x
và
y g x
cắt nhau tại 3 điểm có hoành độ lần lượt là
3
;
1
;
1
(tham
khảo hình vẽ)
Hình phẳng giới hạn bởi
2
đồ thị đã cho có diện tích bằng
A.
9
.
2
B.
8.
C.
4.
D.
5.
Câu 12: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng
1x
và
3x
, biết rằng khi cắt
vật thể bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
(
13x
) thì được thiết
diện là một hình chữ nhật có độ dài hai cạnh là
3x
và
2
32x
.
A.
32 2 15.V
B.
124
.
3
V
C.
124
.
3
V
D.
32 2 15 .
V
Câu 13: Một chất điểm
A
xuất phát từ
O
, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi
quy luật
2
1 59
/
150 75
v t t t m s
, trong đó
t
(giây) là khoảng thời gian tính từ lúc
a
bắt đầu
chuyển động. Từ trạng thái nghỉ, một chất điểm
B
cũng xuất phát từ
O
, chuyển động thẳng
cùng hướng với
A
nhưng chậm hơn 3 giây so với
A
và có gia tốc bằng
2
/a m s
(
a
là hằng
số). Sau khi
B
xuất phát được 12 giây thì đuổi kịp
A
. Vận tốc của
B
tại thời điểm đuổi kịp
A
bằng
A.
20 / .ms
B.
16 / .ms
C.
13 / .ms
D.
15 / .ms
Câu 14: Cho hàm số
y f x
. Đồ thị của hàm số
y f x
như hình bên dưới :
Đặt
2
21g x f x x
. Mệnh đề nào dưới đây đúng?
A.
3 3 1 . g g g
B.
1 3 3 . g g g
C.
3 3 1 . g g g
D.
1 3 3 . g g g
Câu 15: Cho hình phẳng
H
được giới hạn bởi các đường
1, e, 0x x y
và
lnyx
. Thể tích
V
của khối tròn xoay tạo thành khi quay
H
xung quanh trục
Ox
được tính theo công thức
A.
e
1
ln dV x x
. B.
e
1
ln dV x x
. C.
e
2
1
ln dV x x
. D.
e
2
1
ln dV x x
.
Câu 16: Gọi
1
D
là hình phẳng giới hạn bởi các đường
2 , 0y x y
và
2
2020;xD
là hình phẳng
giới hạn bởi các đường
3 , 0y x y
và
2020x
. Gọi
12
,VV
lần lượt là thể tích khối tròn xoay
tạo thành khi quay
1
D
và
2
D
xung quanh trục
Ox
. Tỉ số
1
2
V
V
bằng
A.
4
3
. B.
23
3
. C.
2
3
. D.
6
3
.
Câu 17: Kí hiệu
St
là diện tích hình phẳng giới hạn bởi các đường
2 1, 0, 1, , 1y x y x x t t
. Tìm
t
để
10St
.
A.
4t
. B.
13t
. C.
3t
. D.
14t
.
Câu 18: Cho hàm số
32
, ; ; ;y ax bx cx d a b c d
có đồ thị như hình vẽ bên dưới:
Biết diện tích hình phẳng tô đậm bằng
1
. Giá trị của
2 3 4a b c d
bằng
A.
8.
B.
1.
C.
1.
D.
8.
Câu 19: Cho hàm số
fx
xác định và liên tục trên đoạn
5;3
có đồ thị như hình vẽ bên dưới:
y=g(x)
y=f(x)
S
2
S
3
S
1
2
-1
5
-2
2
3
-5
O
x
y
Biết rằng diện tích hình phẳng
1 2 3
,,S S S
giới hạn bởi đồ thị hàm số
fx
và đường parabol
2
y g x ax bx c
lần lượt là
,,m n p
. Tích phân
3
5
df x x
bằng
A.
208
.
45
m n p
B.
208
.
45
m n p
C.
208
45
m n p
. D.
208
.
45
m n p
Câu 20: Cho
H
là hình phẳng giới hạn bởi parabol
2
23
3
yx
với cung tròn có phương trình
2
9 , 0 3y x x
và trục hoành (phần tô đậm trong hình vẽ dưới đây). Diện tích
S
của hình
phẳng
H
được tính bằng công thức nào dưới đây?
A.
3
22
0
2
9d
3
S x x x



. B.
3
3
2
22
3
0
2
2
d 9 d
3
S x x x x

.
C.
3
22
0
2
9d
3
S x x x
. D.
33
22
22
03
2
9d
3
S x dx x x

.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU ÔN TẬP SỐ 03
CHUY£N §Ò
TÝCH PH¢N – øng dông
øng dông tÝch ph©n
LỜI GIẢI CHI TIẾT
Câu 1: Viết công thức tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với
trục
Ox
tại các điểm
,x a x b a b
có thiết diện bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x a x b
là
Sx
.
A.
2
b
a
V S x dx
. B.
b
a
V S x dx
. C.
b
a
V S x dx
. D.
2
b
a
V S x dx
.
Lời giải:
Chọn đáp án B.
Câu 2: Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
e
x
y
,
0y
,
0x
,
2x
. Mệnh đề nào
dưới đây đúng?
A.
2
2
0
e d .
x
Sx
B.
2
0
e d .
x
Sx
C.
2
0
e d .
x
Sx
D.
2
2
0
e d .
x
Sx
Lời giải:
Diện tích hình phẳng giới hạn bởi các đường
e
x
y
,
0y
,
0x
,
2x
là:
2
0
d
x
S e x
.
Chọn đáp án B.
Câu 3: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y x x
và đồ thị hàm số
2
.y x x
A.
37
.
12
B.
9
.
4
C.
81
.
12
D.
13.
Lời giải:
Phương trình hoành độ giao điểm
3 2 3 2
0
2 0 1
2
x
x x x x x x x x
x

Diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y x x
và đồ thị hàm số
2
y x x
là:
1 0 1
3 2 3 2 3 2
2 2 0
22

S x x x x dx x x x dx x x x dx
01
4 3 4 3
22
20
16 8 1 1 37
41
4 3 4 3 4 3 4 3 12
x x x x
xx
.
Chọn đáp án A.
Câu 4: Cho hình thang cong
H
giới hạn bởi các đường
x
ye
,
0y
,
0x
,
ln 4x
. Đường thẳng
(0 ln4)x k k
chia
H
thành hai phần có diện tích là
1
S
và
2
S
như hình vẽ bên. Tìm
k
để
12
2SS
.
A.
2
ln4
3
k
. B.
ln 2k
. C.
8
ln
3
k
D.
ln3k
.
Lời giải:
Ta có
0
1
0
d1
k
k
x x k
S e x e e
và
ln4
ln4
2
d4
x x k
k
k
S e x e e
.
Lại có
12
2 1 2 4 ln3
kk
S S e e k
.
Chọn đáp án D.
Câu 5: Diện tích hình phẳng giới hạn bởi đường
2
41y x x
,
ym
,
3m 
,
0x
,
3x
là
A.
36m
. B.
36m
. C.
36m
. D.
36m
.
Lời giải:
Ta có:
22
4 1 4 1 0x x m x x m
1
3 0, 3mm
Ta có diện tích hình phẳng là:
33
22
00
4 1 d 4 1 d 6 3 6 3S x x m x x x m x m m

.
Chọn đáp án D.
Câu 6: Cho hàm số
()y f x
có đồ thị trên đoạn
[-1;4]
như hình vẽ dưới:
Tính tích phân
4
1
( )d .
I f x x
A.
5
.
2
I
B.
11
.
2
I
C.
5.I
D.
3.I
Lời giải:
Ta có:
4 0 1 2 3 4
1 1 0 1 2 3
( ) ( ) ( ) ( ) ( ) ( )I f x dx f x dx f x dx f x dx f x dx f x dx

O
x
y
1
S
2
S
k
ln 4
15
1 2 1 1 .
22
Chọn đáp án A.
Câu 7: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới
đây?
A.
2
2
1
2 2 4 dx x x

. B.
2
1
2 2 dxx

. C.
2
1
2 2 dxx
. D.
2
2
1
2 2 4 dx x x
.
Lời giải:
Phần hình phẳng gạch chéo trong hình vẽ bên được giới hạn bởi hai đồ thị hàm số
2
3yx
và
2
21y x x
nên có diện tích được tính theo công thức:
2 2 2
2 2 2 2 2
1 1 1
3 2 1 d 3 2 1 d 2 2 4 dS x x x x x x x x x x x


.
Chọn đáp án D.
Câu 8: Cho đồ thị biểu thị vận tốc của hai chất điểm
A
và
B
xuất phát cùng một lúc, bên cạnh nhau
và trên cùng một con đường. Biết đồ thị biểu diễn vận tốc của chất điểm
A
là một đường
Parabol, đồ thị biểu diễn vận tốc của chất điểm
B
là một đường thẳng như hình vẽ sau.
Hỏi sau khi đi được
3
giây, khoảng cách giữa hai chất điểm là bao nhiêu mét?
A.
120 .m
B.
60 .m
C.
270 .m
D.
90 .m
Lời giải:
Phương trình vận tốc của chất điểm
A
có dạng
2
v t at bt c
.
Dựa vào đồ thị ta có
00
0 20
3 60 9 3 60 80
16 4 0 0
40
v
ca
v a b c b
a b c c
v



.
2
20 80v t t t
suy ra quãng đường chất điểm
A
đi được sau
3
giây đầu là
33
2
00
d 20 80 d 180
A
S v t t t t t m

.
Vận tốc chất điểm
B
có phương trình là
20v t t
, suy ra sau
3
giây chất điểm
B
đi được
quãng đường là
3
0
20 d 90
B
S t t m
.
Vậy sau khi đi được
3
giây, hai chất điểm cách nhau
180 90 90
m
.
Chọn đáp án D.
Câu 9: Đường thẳng
4y kx
cắt parabol
2
2yx
tại hai điểm phân biệt và diện tích các hình
phẳng
1
S
,
2
S
bằng nhau như hình vẽ bên.
Mệnh đề nào sau đây đúng?
A.
6; 4k
. B.
1
1;
2
k



. C.
2; 1k
. D.
1
;0
2
k




.
Lời giải:
Phương trình hoành độ giao điểm
2
24x kx
2
0
40
4
x
x k x
xk

.
Đường thẳng
4y kx
cắt các trục tọa độ tại các điểm
4
;0A
k



,
0;4B
.
4
42k
k
20k
.
Diện tích hình phẳng
44
23
2
1
00
1
4 2 d 4 d 4
6
kk
S kx x x x k x x k


.
Diện tích hình phẳng
4
4
4
23
2
24
2
1
2 d 4 d 2
32
k
k
k
k
S x x kx x k
k

.
12
SS
4
33
0,457
2
11
42
6 3 2
5,54
k TM
k
kk
k
kL


.
Chọn đáp án D.
Câu 10: Kí hiệu
H
là hình phẳng giới hạn bởi đồ thị hàm số
2( 1) ,
x
y x e
trục tung và trục hoành.
Tính thể tích
V
của khối tròn xoay thu được khi quay hình
H
xung quanh trục
Ox
.
A.
4 2 .Ve
B.
4 2 .
Ve
C.
2
5.Ve
D.
2
5.
Ve
Lời giải:
Phương trình hoành độ giao điểm
2 1 0 1
x
x e x
Thể tích của khối tròn xoay thu được khi quay hình
H
xung quanh trục
Ox
là:
11
2
2
2
00
2 1 4 1
xx
V x e dx x e dx




. Đặt
2
2
2
21
1
2
x
x
du x dx
ux
e
v
dv e dx




11
11
2 2 2
22
2
00
00
4 1 4 2 1 4 1 4 1
2 2 2
x x x
x
e e e
V x x dx x x e dx

Gọi
1
2
1
0
1
x
I x e dx
. Đặt
2
2
1
2
x
x
u x du dx
e
dv e dx v
1
1
22
1
2 2 2
1
0
0
0
4 1 4 2 2 3
22
xx
x
ee
I x dx e e e
Vậy
1
2
2
22
1
0
4 1 2 3 5
2
x
e
V x I e e
.
Chọn đáp án D.
Câu 11: Cho hai hàm số
32
1
2
f x ax bx cx
và
2
1g x dx ex
, , , ,a b c d e
. Biết rằng đồ
thị hàm số
y f x
và
y g x
cắt nhau tại 3 điểm có hoành độ lần lượt là
3
;
1
;
1
(tham
khảo hình vẽ)
Hình phẳng giới hạn bởi
2
đồ thị đã cho có diện tích bằng
A.
9
.
2
B.
8.
C.
4.
D.
5.
Lời giải:
Cách 1:
Xét phương trình
3 2 2
1
1
2
ax bx cx dx ex
( ) ( )
32
3
0
2
ax b d x ecxÛ + - + - - =
có 3
nghiệm lần lượt là
3
;
1
;
1
nên suy ra
3
27 9 3 0
2
3
0
2
3
0
2
a b d c e
a b d c e
a b d c e
3
2
1
2
1
2
bd
a
ce



Vậy
32
1 3 1 3
2 2 2 2
f x g x x x x
.
Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng
11
31
S f x g x dx g x f x dx


11
3 2 3 2
31
1 3 1 3 1 3 1 3
2 2 4
2 2 2 2 2 2 2 2
S x x x dx x x x dx


.
Cách 2:
Ta có:
3 1 1f x g x a x x x
.
Suy ra
32
3
3 1 1
2
a x x x ax b d x c d x
Xét hệ số tự do suy ra:
31
3
22
aa
. Do đó:
1
3 1 1
2
f x g x x x x
.
Diện tích bằng:
11
31
ddS f x g x x g x f x x


11
31
11
3 1 1 d 3 1 1 d
22
S x x x x x x x x


4
.
Chọn đáp án C.
Câu 12: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng
1x
và
3x
, biết rằng khi cắt
vật thể bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
(
13x
) thì được thiết
diện là một hình chữ nhật có độ dài hai cạnh là
3x
và
2
32x
.
A.
32 2 15.V
B.
124
.
3
V
C.
124
.
3
V
D.
32 2 15 .
V
Lời giải:
Diện tích thiết diện là:
2
( ) 3 . 3 2S x x x
Thể tích vật thể là:
3
2
1
124
3 . 3 2
3
V x x dx
Chọn đáp án C.
Câu 13: Một chất điểm
A
xuất phát từ
O
, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi
quy luật
2
1 59
/
150 75
v t t t m s
, trong đó
t
(giây) là khoảng thời gian tính từ lúc
a
bắt đầu
chuyển động. Từ trạng thái nghỉ, một chất điểm
B
cũng xuất phát từ
O
, chuyển động thẳng
cùng hướng với
A
nhưng chậm hơn 3 giây so với
A
và có gia tốc bằng
2
/a m s
(
a
là hằng
số). Sau khi
B
xuất phát được 12 giây thì đuổi kịp
A
. Vận tốc của
B
tại thời điểm đuổi kịp
A
bằng
A.
20 / .ms
B.
16 / .ms
C.
13 / .ms
D.
15 / .ms
Lời giải:
Quãng đường chất điểm
A
đi từ đầu đến khi
B
đuổi kịp là
15
2
0
1 59
96
150 75
S t t dt m



.
Vận tốc của chất điểm
B
là
B
v t adt at C
.
Tại thời điểm
3t
vật
B
bắt đầu từ trạng thái nghỉ nên
3 0 3
B
v C a
.
Lại có quãng đường chất điểm
B
đi được đến khi gặp
A
là
15
15
2
2
3
3
3 3 72
2
at
S at a dt at a m



.
Vậy
4
72 96
3
aa
2
/ms
.
Tại thời điểm đuổi kịp
A
thì vận tốc của
B
là
15 16 /
B
v m s
.
Chọn đáp án B.
Câu 14: Cho hàm số
y f x
. Đồ thị của hàm số
y f x
như hình bên dưới :
Đặt
2
21g x f x x
. Mệnh đề nào dưới đây đúng?
A.
3 3 1 . g g g
B.
1 3 3 . g g g
C.
3 3 1 . g g g
D.
1 3 3 . g g g
Lời giải:
Ta có
2 2 1g x f x x

1
01
3
x
g x f x x
x


.
Bảng biến thiên
Suy ra
31gg
và
31gg
. (1)
Gọi
1
S
là diện tích hình phẳng giới hạn bởi các đường:
'( ), 1, 3, 1y f x y x x x
Gọi
2
S
là diện tích hình phẳng giới hạn bởi các đường:
1, '( ), 1, 3y x y f x x x
Dựa vào hình vẽ, ta thấy:
12
0SS
.
Suy ra:
12
0SS
13
31
1 d 1 d 0f x x x x f x x


13
31
1 d 1 d 0f x x x f x x x


3
3
1 d 0f x x x


.
Khi đó:
33
33
3 3 d 2 1 d 0g g g x x f x x x





(2)
Từ (1) và (2) suy ra:
1 3 3g g g
.
Chọn đáp án D.
Câu 15: Cho hình phẳng
H
được giới hạn bởi các đường
1, e, 0x x y
và
lnyx
. Thể tích
V
của khối tròn xoay tạo thành khi quay
H
xung quanh trục
Ox
được tính theo công thức
A.
e
1
ln dV x x
. B.
e
1
ln dV x x
. C.
e
2
1
ln dV x x
. D.
e
2
1
ln dV x x
.
Lời giải:
Thể tích
V
của khối tròn xoay tạo thành khi quay
H
xung quanh trục
Ox
là:
e
2
1
ln dV x x
.
Chọn đáp án C.
Câu 16: Gọi
1
D
là hình phẳng giới hạn bởi các đường
2 , 0y x y
và
2
2020;xD
là hình phẳng
giới hạn bởi các đường
3 , 0y x y
và
2020x
. Gọi
12
,VV
lần lượt là thể tích khối tròn xoay
tạo thành khi quay
1
D
và
2
D
xung quanh trục
Ox
. Tỉ số
1
2
V
V
bằng
A.
4
3
. B.
23
3
. C.
2
3
. D.
6
3
.
Lời giải:
Xét
1
V
:
Ta có phương trình hoành độ giao điểm là:
2 0 0 0 x x x
Suy ra
2020 2020
2
22
1
00
2020
2 d 4xd 2 2 .2020
0
V x x x x

Xét
2
V
:
Ta có phương trình hoành độ giao điểm là:
3 0 0 0 x x x
Suy ra
2020 2020
2
22
2
00
2020
33
3 d 3xd .2020 .
0
22

V x x x x
Vậy
2
1
2
2
2 .2020 4
3
3
.2020
2
V
V

.
Chọn đáp án A.
Câu 17: Kí hiệu
St
là diện tích hình phẳng giới hạn bởi các đường
2 1, 0, 1, , 1y x y x x t t
. Tìm
t
để
10St
.
A.
4t
. B.
13t
. C.
3t
. D.
14t
.
Lời giải:
Ta có
1
21
t
S t x dx
. Do
1; , 1x t t
nên
2 1 0x 
.
Khi đó:
22
1
1
2 1 | 2
t
t
S t x dx x x t t
.
Để
10St
thì
22
3
2 10 12 0
4
t
t t t t
t

.
Do
1t
nên
3t
thỏa mãn.
Chọn đáp án C.
Câu 18: Cho hàm số
32
, ; ; ;y ax bx cx d a b c d
có đồ thị như hình vẽ bên dưới:
Biết diện tích hình phẳng tô đậm bằng
1
. Giá trị của
2 3 4a b c d
bằng
A.
8.
B.
1.
C.
1.
D.
8.
Lời giải:
Đồ thị hàm số đi qua các điểm có tọa độ lần lượt là
1;0 ; 3;0 ; 5;0
nên ta có
0
27 9 3 0 1
125 25 5 0
a b c d
a b c d
a b c d
Diện tích hình phẳng tô đậm
5 3 5 3 5
1 1 3 1 3
dx=1 dx dx 1 dx- dx=1
3 1 5 3 1 2 3 1 5 1 116 24 4 1. 2
S f x f x f x f x f x
F F F F F F F a b c
với
4 3 2
81 9
dx ; 3 9 3 ; 1
4 3 2 4 2 4 3 2
ax bx cx a b c
f x dx F x F a b c d F d
625 125 25
55
4 3 2
F a b c d
Từ
1
và
2
ta có hệ:
1
8
0
9
27 9 3 0
8
125 25 5 0 23
8
116 24 4 1
15
8
a
a b c d
b
a b c d
a b c d
c
a b c
d



Khi đó
2 3 4 1.a b c d
Chọn đáp án B.
Câu 19: Cho hàm số
fx
xác định và liên tục trên đoạn
5;3
có đồ thị như hình vẽ bên dưới:
y=g(x)
y=f(x)
S
2
S
3
S
1
2
-1
5
-2
2
3
-5
O
x
y
Biết rằng diện tích hình phẳng
1 2 3
,,S S S
giới hạn bởi đồ thị hàm số
fx
và đường parabol
2
y g x ax bx c
lần lượt là
,,m n p
. Tích phân
3
5
df x x
bằng
A.
208
.
45
m n p
B.
208
.
45
m n p
C.
208
45
m n p
. D.
208
.
45
m n p
Lời giải:
Từ đồ thị ta thấy
y=g(x)
y=f(x)
S
2
S
3
S
1
2
-1
5
-2
2
3
-5
O
x
y
2 2 2 2 2
11
5 5 5 5 5
d d d d dS f x g x x f x x g x x f x x S g x x


.
0 0 0 0 0
22
2 2 2 2 2
d d d d dS g x f x x g x x f x x f x x g x x S


.
3 3 3 3 3
33
0 0 0 0 0
d d d d dS f x g x x f x x g x x f x x S g x x


.
Do vậy:
3 3 3
1 2 3
5 5 5
d d d .f x x S S S g x x m n p g x x
Do đó ta loại đáp án A và D.
Từ đồ thị ta thấy
3
5
dg x x
là số dương. Mà 2 đáp án còn lại chỉ có
208
45
là phù hợp, nên ta
chọn
3
5
208
d
45
f x x m n p
.
Chú ý: Có thể tính
3
5
dg x x
như sau:
Từ đồ thị hàm số
y g x
ta thấy nó đi qua các điểm
5;2 , 2;0 , 0;0
nên ta có:
25 5 2
24
4 2 0 , , 0.
15 15
0
a b c
a b c a b c
c
Do đó:
33
2
55
2 4 208
dd
15 15 45
g x x x x x





.
Chọn đáp án B.
Câu 20: Cho
H
là hình phẳng giới hạn bởi parabol
2
23
3
yx
với cung tròn có phương trình
2
9 , 0 3y x x
và trục hoành (phần tô đậm trong hình vẽ dưới đây). Diện tích
S
của hình
phẳng
H
được tính bằng công thức nào dưới đây?
A.
3
22
0
2
9d
3
S x x x



. B.
3
3
2
22
3
0
2
2
d 9 d
3
S x x x x

.
C.
3
22
0
2
9d
3
S x x x
. D.
33
22
22
03
2
9d
3
S x dx x x

.
Lời giải:
Xét phương trình
22
2 3 3
9
32
x x x
(vì
03x
).
Quan sát đồ thị, suy ra
3 3 3
3
2 2 2
2 2 2 2
3
0 0 3
2
2 3 2
d 9 d d 9 d
3
3
S x x x x S x x x x
.
Chọn đáp án D.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU ÔN TẬP SỐ 04
CHUY£N §Ò
TÝCH PH¢N – øng dông
øng dông tÝch ph©n
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Câu 1: Diện tích hình phẳng của hình được tô đen như hình vẽ bên là
A.
d


b
a
f x g x x
. B.
d
b
a
g x f x x


.
C.
d
b
a
f x g x x


. D.
d
b
a
g x f x x


.
Câu 2: Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo
thành được tính theo công thức
A.
22
d.



b
a
V f x g x x
B.
2
d.



b
a
V f x g x x
C.
2
d.


b
a
V f x g x x
D.
d.



b
a
V f x g x x
Câu 3: Cho hai đồ thị hàm số
2
3f x x
và
2
x
gx
có đồ thị như hình vẽ bên dưới:
Diện tích phần hình phẳng gạch chéo trong hình vẽ được tính theo công thức nào dưới đây ?
A.
1
2
2
0
3 4 d
x
xx




. B.
1
2
0
3 2 d
x
xx
.
C.
3
2
2
1
3 2 d
x
xx
. D.
3
2
1
3 2 d
x
xx
.
Câu 4: Cho hàm số
32
32f x x x x
. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
y f x
, trục tung, trục hoành và đường thẳng
3x
A.
10
4
S
. B.
12
4
S
. C.
11
4
S
. D.
9
4
S
.
Câu 5: Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol
2
:P y x
và đường thẳng
:2d y x
quay quanh trục
Ox
bằng
A.
22
24
00
4 d dx x x x


. B.
2
2
2
0
2dx x x
. C.
2
2
0
2dx x x
. D.
22
24
00
4 d dx x x x


.
Câu 6: Gọi
S
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
1
:
1
x
Hy
x
và các trục tọa độ. Khi
đó giá trị của
S
bằng
A.
2ln2 1S 
. B.
ln2 1S 
. C.
ln2 1S 
. D.
1 2ln 2S 
.
Câu 7: Cho hình phẳng
giới hạn bởi các đường
5 , 0, 2, 2
x
y y x x
. Thể tích khối tròn
xoay tạo thành do hình phẳng
D
quay quanh trục hoành được tính theo công thức nào dưới
đây?
A.
2
2
25 d .
x
Vx
B.
2
2
2
5 d .
x
Vx
C.
2
2
5 d .
x
Vx
D.
2
2
0
2 5 d .
x
Vx
Câu 8: Cho hàm số
y f x
có đạo hàm liên tục trên đoạn
0;7
và có đồ thị
y f x
trên đoạn
0;7
như hình vẽ.
Đt
21g x f x
bit rằng diện tch các hình phẳng trong hình vẽ lần lượt là
1 2 3
244 28 2528
,,
15 15 15
S S S
và
01f
. Tnh
4g
.
A.
2744
15
. B.
5518
15
. C.
563
3
. D.
2759
15
.
Câu 9: Tính thể tích của vật thể nằm giữa hai mt phẳng
1x
và
2x
, bit rằng thit diện của vật
thể bị cắt bởi mt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
,
12x
là một
hình chữ nhật có độ dài hai cạnh là
x
và
2
3.x
A.
7 7 8
3
. B.
8 7 7
3
. C.
16 2 7
3
. D.
8 2 4
.
Câu 10: Tính diện tích
S
của hình phẳng (phần gạch sọc) giới hạn bởi hai đồ thị hàm số
f x x
và
2g x x
như trong hình sau:
A.
7
3
S
. B.
10
3
S
. C.
11
3
S
. D.
7
3
S
.
Câu 11: Người ta xây sân khấu với mt sàn có dạng hợp của hai đường tròn giao nhau. Bán kính của
hai hình tròn lần lượt là
20m
và
15m
. Khoảng cách giữa hai tâm của hai hình tròn là
30m
.Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là
300
nghìn đồng và chi
phí làm mỗi mét vuông còn lại là
100
nghìn đồng (tham khảo hình vẽ)
Hỏi số tiền làm mt sàn sân khấu gần với số nào trong các số dưới đây?
A.
202
triệu đồng. B.
208
triệu đồng. C.
218
triệu đồng. D.
200
triệu đồng.
Câu 12: Trong mt phẳng cho Parabol
2
( ):P y x
và đường tròn
22
( ): 2C x y
. Tính diện tích phần
tô đậm (gần đúng đn hàng phần trăm).
A. 1,19. B. 1,90. C. 1,81. D. 1,80.
Câu 13: Diện tch hình phẳng giới hạn bởi hai đồ thị hàm số
3
yx
,
2
44y x x
và trục
Ox
được
tnh theo công thức nào dưới đây?
A.
2
32
0
4 4 dx x x x
. B.
12
32
01
d 4 4 dx x x x x

.
C.
12
32
01
d 4 4 dx x x x x

. D.
12
32
01
d 4 4 dx x x x x

.
Câu 14: Tính diện tích hình phẳng giới hạn bởi các đường
2
yx
,
14
33
yx
và trục hoành.
A.
11
6
. B.
61
3
. C.
343
162
. D.
39
2
.
Câu 15: Đoạn đường thẳng AB có chiều dài 200 km. Hai xe ôtô khởi hành cùng một lúc, xe ôtô thứ
nhất đi từ A đn B với vận tốc
1
8 40 km/hvt
, xe ôtô thứ hai đi từ B đn A với vận tốc
2
2 50km/hvt
. Hỏi sau bao lâu thì hai xe gp nhau?
A. 3 giờ. B. 5 giờ. C. 4 giờ. D. 2 giờ.
Câu 16: Tính diện tích hình phẳng được đánh dấu trên hình dưới:
A.
28
3
S
. B.
1
32
3
S 
. C.
18
3
S
. D.
2
23
3
S 
.
Câu 17: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
2
1yx
,
0y
quanh
trục
Ox
là
πa
V
b
với
a
,
b
là số nguyên và
a
b
là phân số tối giản. Khi đó
ab
bằng
A. 11. B. 17. C. 25. D. 31.
Câu 18: Tính diện tích
S
của hình phẳng (phần gạch sọc) trong hình sau:
x
y
g
x
( )
=
x
2
f
x
( )
=
x
4
2
O
A.
8
3
S
. B.
10
3
S
. C.
11
3
S
. D.
7
3
S
.
Câu 19: Cho chic trống như hình vẽ, có đường sinh là nửa elip được cắt bởi trục lớn với độ dài trục
lớn bằng
80cm
, độ dài trục bé bằng
60cm
và đáy trống là hình tròn có bán knh bằng
60cm
.
Tnh thể tch
V
của chic trống (kt quả làm tròn đn hàng đơn vị).
A.
3
344963V cm
. B.
3
344964V cm
. C.
3
208347V cm
. D.
3
208346V cm
.
Câu 20: Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường
2 0; ; 0x y y x y
quay
quanh trục
Ox
bằng
A.
5
6
. B.
2
3
. C.
6
5
. D.
5
6
.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU ÔN TẬP SỐ 04
CHUY£N §Ò
TÝCH PH¢N – øng dông
øng dông tÝch ph©n
LỜI GIẢI CHI TIẾT
Câu 1: Diện tích hình phẳng của hình được tô đen như hình vẽ bên là
A.
d


b
a
f x g x x
. B.
d
b
a
g x f x x


.
C.
d
b
a
f x g x x


. D.
d
b
a
g x f x x


.
Lời giải:
Diện tích hình phẳng của hình được tô đen như hình vẽ bên là
d
b
a
f x g x x


.
Chọn đáp án C.
Câu 2: Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo
thành được tính theo công thức
A.
22
d.



b
a
V f x g x x
B.
2
d.



b
a
V f x g x x
C.
2
d.


b
a
V f x g x x
D.
d.



b
a
V f x g x x
Lời giải:
Chọn đáp án A.
Câu 3: Cho hai đồ thị hàm số
2
3f x x
và
2
x
gx
có đồ thị như hình vẽ bên dưới:
Diện tích phần hình phẳng gạch chéo trong hình vẽ được tính theo công thức nào dưới đây ?
A.
1
2
2
0
3 4 d
x
xx




. B.
1
2
0
3 2 d
x
xx
.
C.
3
2
2
1
3 2 d
x
xx
. D.
3
2
1
3 2 d
x
xx
.
Lời giải:
Dựa theo hình vẽ trên, diện tích phần gạch chéo tính theo công thức
11
22
00
3 2 d 3 2 d
xx
x x x x

.
Chọn đáp án B.
Câu 4: Cho hàm số
32
32f x x x x
. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
y f x
, trục tung, trục hoành và đường thẳng
3x
A.
10
4
S
. B.
12
4
S
. C.
11
4
S
. D.
9
4
S
.
Lời giải:
Áp dụng công thức ta có:
3
32
0
11
3 2 d
4
S x x x x
.
Chọn đáp án C.
Câu 5: Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol
2
:P y x
và đường thẳng
:2d y x
quay quanh trục
Ox
bằng
A.
22
24
00
4 d dx x x x


. B.
2
2
2
0
2dx x x
. C.
2
2
0
2dx x x
. D.
22
24
00
4 d dx x x x


.
Lời giải:
Phương trình hoành độ giao điểm của: Parabol
2
:P y x
và đường thẳng
:2d y x
là:
2
0
2
2
x
xx
x

Gọi
1
D
là hình phẳng giới hạn bởi đồ thị các đường thẳng:
2 ; 0; 0; 2y x y x x
.
Quay hình phẳng
1
D
quanh
Ox
ta được khối tròn xoay có thể tích
2
2
1
0
4dV x x
.
Gọi
2
D
là hình phẳng giới hạn bởi Parabol
2
:P y x
và các đường thẳng:
0; 0; 2y x x
.
Quay hình phẳng
2
D
quanh
Ox
ta được khối tròn xoay có thể tích
2
4
2
0
dV x x
.
Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol
2
:P y x
và đường thẳng
:2d y x
quay quanh trục
Ox
có thể tích
22
24
12
00
4 d dV V V x x x x


.
Chọn đáp án A.
Câu 6: Gọi
S
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
1
:
1
x
Hy
x
và các trục tọa độ. Khi
đó giá trị của
S
bằng
A.
2ln2 1S 
. B.
ln2 1S 
. C.
ln2 1S 
. D.
1 2ln 2S 
.
Lời giải:
Phương trình hoành độ giao điểm của
H
và
Ox
là
1
01
1
x
x
x
.
Diện tích hình phẳng
S
giới hạn bởi đồ thị hàm số
1
:
1
x
Hy
x
và các trục tọa độ là
11
1
1
0
0
00
1 1 2
d d 1 d 2ln 1 2ln2 1
1 1 1
xx
S x x x x x
x x x



.
Chọn đáp án A.
Câu 7: Cho hình phẳng
giới hạn bởi các đường
5 , 0, 2, 2
x
y y x x
. Thể tích khối tròn
xoay tạo thành do hình phẳng
D
quay quanh trục hoành được tính theo công thức nào dưới
đây?
A.
2
2
25 d .
x
Vx
B.
2
2
2
5 d .
x
Vx
C.
2
2
5 d .
x
Vx
D.
2
2
0
2 5 d .
x
Vx
Lời giải:
Ta có thể tích khối tròn xoay do hình phẳng giới hạn bởi các
đường
, y 0, , y f x x a x b a b
sinh ra khi quay quanh trục
Ox
là
2
d
b
a
V f x x
.
Áp dụng công thức ta có:
22
2
22
5 d 25 d
xx
V x x




.
Chọn đáp án A.
Câu 8: Cho hàm số
y f x
có đạo hàm liên tục trên đoạn
0;7
và có đồ thị
y f x
trên đoạn
0;7
như hình vẽ.
Đt
21g x f x
bit rằng diện tch các hình phẳng trong hình vẽ lần lượt là
1 2 3
244 28 2528
,,
15 15 15
S S S
và
01f
. Tnh
4g
.
A.
2744
15
. B.
5518
15
. C.
563
3
. D.
2759
15
.
Lời giải:
Ta có
2
2
1
0
0
0 2 0
S f x dx f x f f
.
Mà
1
244
15
S
và
01f
suy ra
244 259
21
15 15
f
.
Tương tự
3
3
2
2
2
0 2 3
S f x dx f x f f
Mà
2
28
15
S
và
259
2
15
f
suy ra
259 28 231
3
15 15 15
f
.
7
7
3
3
3
0 7 3
S f x dx f x f f
Mà
3
2528
15
S
và
231
3
15
f
suy ra
2528 231 2759
7
15 15 15
f
.
Do
21g x f x
nên
2759
4 2.4 1 7
15
g f f
.
Chọn đáp án D.
Câu 9: Tính thể tích của vật thể nằm giữa hai mt phẳng
1x
và
2x
, bit rằng thit diện của vật
thể bị cắt bởi mt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
,
12x
là một
hình chữ nhật có độ dài hai cạnh là
x
và
2
3.x
A.
7 7 8
3
. B.
8 7 7
3
. C.
16 2 7
3
. D.
8 2 4
.
Lời giải:
Diện tích thit diện của vật thể bị cắt bởi mt phẳng vuông góc với với trục
Ox
tại điểm có
hoành độ
x
,
12x
là:
2
3S x x
.
Khi đó thể tích của vật thể nằm giữa hai mt phẳng
1x
và
2x
là:
22
2
2 2 2 2 2
1
11
1 1 2 7 7 8
3 3 3 3 3
2 2 3 3

V x x dx x d x x x
.
Chọn đáp án A.
Câu 10: Tính diện tích
S
của hình phẳng (phần gạch sọc) giới hạn bởi hai đồ thị hàm số
f x x
và
2g x x
như trong hình sau:
A.
7
3
S
. B.
10
3
S
. C.
11
3
S
. D.
7
3
S
.
Lời giải:
4
44
3
2
2
00
2
2 10
2 d 2 d 2
3 2 3
x
S x x x x x x x x




.
Chọn đáp án B.
Câu 11: Người ta xây sân khấu với mt sàn có dạng hợp của hai đường tròn giao nhau. Bán kính của
hai hình tròn lần lượt là
20m
và
15m
. Khoảng cách giữa hai tâm của hai hình tròn là
30m
.Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là
300
nghìn đồng và chi
phí làm mỗi mét vuông còn lại là
100
nghìn đồng (tham khảo hình vẽ)
Hỏi số tiền làm mt sàn sân khấu gần với số nào trong các số dưới đây?
A.
202
triệu đồng. B.
208
triệu đồng. C.
218
triệu đồng. D.
200
triệu đồng.
Lời giải:
Gọi
,IJ
lần lượt là tâm của hai đường tròn bán kính
20m
,
15m
.
Gọi
,AB
là giao của hai đường tròn.
Chọn hệ trục tọa độ
Oxy
sao cho
Oy
trùng
IJ
và
Ox
song song với
AB
và
I
là gốc tọa độ
(như hình vẽ).
Khi đó đường tròn tâm
I
bán kính
20Rm
có phương trình
22
400xy
.
Vì khoảng cách giữa hai tâm của hai hình tròn là
30m
nên
0;30J
. Do đó đường tròn
tâm
0;30J
bán kính
15Rm
có phương trình
2
2
30 225xy
.
Khi đó phần chung của hai đường tròn giới hạn bởi
22
400 ; 30 225y x y x
.
Xét hệ
2
2
4 455
400
12
215
30 225
12
x
yx
yx
y





Diện tích phần chung của hai đường tròn là
5 455
12
22
1
5 455
12
400 225 30 60,2S x x dx
.
Diện tích riêng của hai đường tròn là
21
625 2 625 120,4SS

.
Số tiền chi phí là
12
300000 100000 300000.60,2 100000. 625 120,4 202369540SS
.
Vậy số tiền làm mt sàn sân là gần
202
triệu đồng.
Chọn đáp án A.
Câu 12: Trong mt phẳng cho Parabol
2
( ):P y x
và đường tròn
22
( ): 2C x y
. Tính diện tích phần
tô đậm (gần đúng đn hàng phần trăm).
A. 1,19. B. 1,90. C. 1,81. D. 1,80.
Lời giải:
Ta có
2 2 2
22x y y x
. Vì đường cong nửa trên của
()C
tương ứng phần dương của
trục hoành nên có phương trình
2
2 , 0y x y
Phương trình hoành độ giao điểm của đường cong nửa trên của
()C
và Parabol
()P
là :
22
2xx
42
20xx
2
2
1
1
2
x
x
x

Suy ra diện tích hình phẳng
()H
cần tính là :
1
1 1 1
3
2 2 2 2
1 1 1
1
2
2 2 2
33
x
S x x dx x dx x dx
Xét
1
2
1
2I x dx

, đt
2sin 2 cosx t dx tdt
ta được
4
2
4
2 2sin 2 cosI t tdt

4
2
4
2cos tdt
4
4
1 cos2t dt

4
4
sin 2
2
t
t




1
2

.
Do đó
21
1 1,90
2 3 2 3
S

.
Chọn đáp án B.
Câu 13: Diện tch hình phẳng giới hạn bởi hai đồ thị hàm số
3
yx
,
2
44y x x
và trục
Ox
được
tnh theo công thức nào dưới đây?
A.
2
32
0
4 4 dx x x x
. B.
12
32
01
d 4 4 dx x x x x

.
C.
12
32
01
d 4 4 dx x x x x

. D.
12
32
01
d 4 4 dx x x x x

.
Lời giải:
Dựa vào hình vẽ ta thấy hình phẳng cần tính diện tích gồm 2 phần:
Phần 1: Hình phẳng giới hạn bởi đồ thị hàm số
3
yx
, trục
Ox
,
0x
,
1x
.
Phần 2: Hình phẳng giới hạn bởi đồ thị hàm số
2
44y x x
, trục
Ox
,
1x
,
2x
.
Do đó diện tích cần tính là
1 2 1 2
3 2 3 2
0 1 0 1
d 4 4 d d 4 4 dS x x x x x x x x x x
.
Chọn đáp án D.
Câu 14: Tính diện tích hình phẳng giới hạn bởi các đường
2
yx
,
14
33
yx
và trục hoành.
A.
11
6
. B.
61
3
. C.
343
162
. D.
39
2
.
Lời giải:
Phương trình hoành độ giao điểm của các đường
2
yx
,
14
33
yx
là
2
14
33
xx
2
3 4 0xx
1
4
3
x
x

.
Hoành độ giao điểm của đường thẳng
14
33
yx
với trục hoành là
4x
.
Hoành độ giao điểm của parabol
2
yx
với trục hoành là
0x
.
Diện tích hình phẳng cần tìm là
14
2
01
14
dd
33
S x x x x




1
4
3
2
1
0
14
3 6 3
x
xx



11
6
.
Chọn đáp án A.
Câu 15: Đoạn đường thẳng AB có chiều dài 200 km. Hai xe ôtô khởi hành cùng một lúc, xe ôtô thứ
nhất đi từ A đn B với vận tốc
1
8 40 km/hvt
, xe ôtô thứ hai đi từ B đn A với vận tốc
2
2 50km/hvt
. Hỏi sau bao lâu thì hai xe gp nhau?
A. 3 giờ. B. 5 giờ. C. 4 giờ. D. 2 giờ.
Lời giải:
Gọi thời gian kể từ lúc hai xe đi đn lúc hai xe gp nhau là
a
(giờ,
0a
)
Vì hai xe đi ngược chiều nên ta có phương trình:
22
00
00
2 2 2
8 40 2 50 200 4 40 50 200
2
4 40 50 200 5 90 200 0
20


aa
aa
t dt t dt t t t t
a TM
a a a a a a
a KT M
Vậy sau 2 giờ thì hai xe gp nhau.
Chọn đáp án D.
Câu 16: Tính diện tích hình phẳng được đánh dấu trên hình dưới:
A.
28
3
S
. B.
1
32
3
S 
. C.
18
3
S
. D.
2
23
3
S 
.
Lời giải:
Ta có
2
y x x y
, từ hình vẽ ta thấy
0x x y
.
3
33
3
1
11
2 2 2
d d 3 3 1 2 3
3 3 3
S y y x x x

.
Chọn đáp án D.
Câu 17: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
2
1yx
,
0y
quanh
trục
Ox
là
πa
V
b
với
a
,
b
là số nguyên và
a
b
là phân số tối giản. Khi đó
ab
bằng
A. 11. B. 17. C. 25. D. 31.
Lời giải:
Phương trình hoành độ giao điểm giữa
2
( ): 1P y x
và trục
Ox
:
2
10x
1
1
x
x

.
Thể tích của khối tròn xoay thu được khi quay hình phẳng quanh trục
Ox
là:
1
2
2
1
16
1
15
dV x x
. Suy ra:
16, 15ab
. Vậy
31ab
.
Chọn đáp án D.
Câu 18: Tính diện tích
S
của hình phẳng (phần gạch sọc) trong hình sau:
x
y
g
x
( )
=
x
2
f
x
( )
=
x
4
2
O
A.
8
3
S
. B.
10
3
S
. C.
11
3
S
. D.
7
3
S
.
Lời giải:
x
y
g
x
( )
=
x
2
f
x
( )
=
x
4
2
O
Dựa và hình vẽ, ta có hình phẳng được giới hạn bởi các đường:
2
0
yx
yx
y

.
Suy ra
24
02
d 2 dS x x x x x

2
π2a
.
Chọn đáp án B.
Câu 19: Cho chic trống như hình vẽ, có đường sinh là nửa elip được cắt bởi trục lớn với độ dài trục
lớn bằng
80cm
, độ dài trục bé bằng
60cm
và đáy trống là hình tròn có bán knh bằng
60cm
.
Tnh thể tch
V
của chic trống (kt quả làm tròn đn hàng đơn vị).
A.
3
344963V cm
. B.
3
344964V cm
. C.
3
208347V cm
. D.
3
208346V cm
.
Lời giải:
Chọn hệ trục tọa độ như hình vẽ ta thấy elip có tâm
0 ; 6I
, độ dài trục lớn
8dm
và độ dài trục
nhỏ
6dm
.
y
x
6
-4
4
O
Suy ra đường sinh chic trống thuộc elip có phương trình:
2
22
22
6
1 3 1 6
4 3 16
y
xx
y
.
Khối tròn xoay giới hạn bởi
2
3 1 6
16
0
4
4
x
y
y
x
x

.
Ta có thể tích chic trống:
2
4
2
33
4
3 1 6 d 344,9636 344964
16
x
V x dm cm




.
Chọn đáp án B.
Câu 20: Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường
2 0; ; 0x y y x y
quay
quanh trục
Ox
bằng
A.
5
6
. B.
2
3
. C.
6
5
. D.
5
6
.
Lời giải:
Đường thẳng
2yx
cắt đường thẳng
0y
tại
2;0
và cắt đồ thị hàm số
yx
tại
1;1
Đồ thị hàm số
yx
cắt đường thẳng
0y
tại
0;0O
Thể tích khối tròn xoay đó là:
2
1
3
12
2
2
2
01
0
1
2
5
d 2 d
2 3 6
x
x
V x x x x

.
Chọn đáp án A.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU ÔN TẬP SỐ 05
CHUY£N §Ò
TÝCH PH¢N – øng dông
øng dông tÝch ph©n
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Câu 1: Diện tích phần hình phẳng tô đậm trong hình vẽ bên dưới được tính theo công thức nào dưới
đây?
A.
3
2
df x g x x
. B.
3
2
dg x f x x
.
C.
03
20
d g df x g x x x f x x

. D.
03
20
ddg x f x x f x g x x

.
Câu 2: Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
1
2
x
y
x
và hai đường thẳng
2y
,
1yx
. Tính diện tích
S
của hình phẳng
H
.
A.
8 3ln3S 
. B.
8 3ln3S 
. C.
3ln3S
. D.
4 3ln3S
.
Câu 3: Đường thẳng
ym
(
01m
) cắt đường cong
42
21y x x
tại hai điểm thuộc góc phần tư
thứ nhất của hệ tọa độ
Oxy
và chia thành hai hình phẳng có diện tích
1
S
,
2
S
như hình vẽ.
Biết
12
SS
. Mệnh đề nào dưới đây đúng?
A.
2
0;
5
m



. B.
21
;
52
m



. C.
13
;
25
m



. D.
3
;1
5
m



.
Câu 4: Diện tích hình phẳng giới hạn bởi các đường
2
3yx
và
1y
bằng
A.
8
3
. B.
16
3
. C.
32
3
. D.
32
.
Câu 5: Một viên gạch hoa hình vuông cạnh
40cm
được thiết kế như hình bên dưới. Diện tích mỗi
cánh hoa bằng
y
x
20
20
20
20
y =
20
x
y =
1
20
x
2
A.
2
400
cm
3
. B.
2
800
cm
3
. C.
2
250cm
. D.
2
800cm
.
Câu 6: Cho hàm số
y f x
. Hàm số có đồ thị hàm số
'y f x
như hình vẽ dưới đây.
Biết diện tích hình phẳng giới hạn bởi trục
Ox
và đồ thị hàm số
'y f x
trên đoạn
2;1
và
1;4
lần lượt bằng 9 và 12. Cho biết
13f
. Tính giá trị biểu thức
24P f f
.
A. 21. B. 3. C. 9. D. 2.
Câu 7: Tính diện tích hình phẳng giới hạn bởi các đường
2
yx
,
14
33
yx
và trục hoành.
A.
11
6
. B.
61
3
. C.
343
162
. D.
39
2
.
Câu 8: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
44yx x
, trục tung và trục hoành. Xác
định
k
để đường thẳng
d
đi qua điểm
0;4A
có hệ số góc
k
chia
H
thành hai phần có
diện tích bằng nhau.
A.
4k 
. B.
8k 
. C.
6k 
. D.
2k 
.
Câu 9: Cho hàm số đa thức bậc ba
32
( 0)y f x ax bx cx d a
có đồ thị như hình vẽ bên dưới:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
y f x
và trục hoành.
A.
6
. B.
19
4
. C.
27
4
. D. 8.
Câu 10: Cho hình phẳng
H
giới hạn bởi các đường
2
1yx
và
,0 1.y k k
Tìm
k
để diện tích của
hình phẳng
H
gấp hai lần diện tích hình phẳng được kẻ sọc trong hình vẽ bên dưới.
A.
3
4.k
B.
3
2 1.k 
C.
1
.
2
k
D.
3
41k 
.
Câu 11: Gọi
H
là hình phẳng giới hạn bởi đồ thị của hàm số
2
6y x x
và trục hoành. Hai đường
thẳng
, 9y m y n m n
chia hình
H
thành ba phần có diện tích bằng nhau. Tính
33
(9 ) (9 ) .P m n
A.
405P
. B.
409P
. C.
407P
. D.
403P
.
Câu 12: Cho hàm số
y f x
là hàm đa thức bậc bốn có đồ thị là
C
và
d
là tiếp tuyến của đồ thị
C
tại hai điểm như hình vẽ. Biết diện tích hình phẳng giới hạn bởi đồ thị
C
và
d
là
11
3
. Khi đó
tích phân
d
1
1
I f x x
bằng
A.
19
6
. B.
25
6
. C.
23
6
. D.
13
3
Câu 13: Một chất điểm chuyển động trong 3 giây với vận tốc
cosv a t b

(mét/giây) (trong đó
t
là
biến thời gian;
,ab
là các hằng số) có đồ thị là một đường hình sin như hình vẽ bên. Tính tổng
quãng đường mà vật đi được sau 3 giây (kết quả làm tròn đến hàng phần trăm).
A.
29,93m
. B.
15m
. C.
27,93m
. D.
17m
.
Câu 14: Cho hàm số
y f x
liên tục trên đoạn
0;8
và có đồ thị như hình vẽ dưới đây:
Trong các giá trị sau, giá trị nào lớn nhất?
A.
3
0
d.f x x
B.
1
0
d.f x x
C.
8
0
d.f x x
D.
5
0
d.f x x
Câu 15: Cho hàm số
y f x
liên tục trên có đồ thị tạo với trục hoành các miền có diện tích
1 2 3 4
, , ,S S S S
như hình vẽ bên dưới:
y
=
f(x)
S
2
S
3
S
4
S
1
2
1
2
1
-1
y
x
O
Biết
14
10SS
,
23
8SS
. Tích phân
ln3
0
1d
xx
I e f e x
bằng
A.
8
. B.
10
. C.
8
. D.
10
.
Câu 16: Cho parabol
2
:P y x
và một đường thẳng
d
thay đổi cắt
P
tại hai điểm
A
,
B
sao cho
2020AB
. Gọi
S
là diện tích hình phẳng giới hạn bởi
P
và đường thẳng
d
. Tìm giá trị lớn
nhất
max
S
của
A.
3
2020 1
.
6
max
S
B.
3
2020
.
6
max
S
C.
3
2020 1
.
6
max
S
D.
3
2020
.
3
max
S
Câu 17: Cho Parabol
2
:.P y x
Hai điểm A, B di động trên
P
sao cho
2.AB
Gọi S là diện tích
hình phẳng giới hạn bởi Parabol
P
và đoạn thẳng
AB
. Tìm giá trị lớn nhất của S.
A.
4
max
3
S
. B.
7
max
6
S
. C.
5
max
3
S
. D.
5
max
6
S
.
Câu 18: Hình gạch chéo được giới hạn bởi đường tròn
2
22
x y a b
;
0ab
và các đường thẳng
2
b
x 
và
2
b
x
. Thể tích vật tròn xoay tạo bởi hình gạch chéo quay xung quanh trục
Ox
là
A.
22
ab
. B.
22
3
4
ab
. C.
2
2
3
3
ab




. D.
2
3
24
ab



.
Câu 19: Cho hàm số đa thức bậc bốn
y f x
có đồ thị
C
, biết rằng
C
đi qua điểm
1;0A
. Tiếp
tuyến
tại
A
của đồ thị
C
cắt
C
tại hai điểm có hoành độ lần lượt là
0
và
2
. Biết diện
tích hình phẳng giới hạn bởi
, đồ thị
C
và hai đường thẳng
0x
;
2x
có diện tích
bằng
56
.
5
B
A
y
x
O
3
2
1
-1
Diện tích hình phẳng giới hạn bởi , đồ thị
C
và hai đường thẳng
1x
;
0x
bằng
A.
2
5
. B.
1
20
. C.
1
10
. D.
1
5
.
Câu 20: Ông A đi làm lúc 7 giờ và đến cơ quan lúc 7 giờ 12 phút bằng xe gắn máy, trên đường đến cơ
quan ông A gặp một người băng qua đường nên ông phải giảm tốc độ để đảm bào an toàn rồi
sau đó lại từ từ tăng tốc độ để đến cơ quan làm việc. Hỏi quãng đường kể từ lúc ông A giảm
tốc độ để tránh tai nạn cho đến khi tới cơ quan dài bao nhiêu mét? (Độ thị dưới đâu mô tả vận
tốc chuyển động của ông A theo thời gian khi đến cơ quan)
A.
3600
. B.
3200
. C.
3500
. D.
3900
.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU ÔN TẬP SỐ 05
CHUY£N §Ò
TÝCH PH¢N – øng dông
øng dông tÝch ph©n
LỜI GIẢI CHI TIẾT
Câu 1: Diện tích phần hình phẳng tô đậm trong hình vẽ bên dưới được tính theo công thức nào dưới
đây?
A.
3
2
df x g x x
. B.
3
2
dg x f x x
.
C.
03
20
d g df x g x x x f x x

. D.
03
20
ddg x f x x f x g x x

.
Lời giải:
Từ đồ thị hai hàm số
y f x
và
y g x
ta có diện tích phần hình phẳng tô đen trong hình
vẽ bên dưới được tính là
3
2
dS f x g x x

03
20
ddf x g x x f x g x x

03
20
ddf x g x x g x f x x

.
Chọn đáp án C.
Câu 2: Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
1
2
x
y
x
và hai đường thẳng
2y
,
1yx
. Tính diện tích
S
của hình phẳng
H
.
A.
8 3ln3S 
. B.
8 3ln3S 
. C.
3ln3S
. D.
4 3ln3S
.
Lời giải:
Dựa vào đồ thị ta có
3 1 3 1
5 3 5 3
1
2
3
5
3
13
2 d 1 2 d 1 d 1 d
22
3ln 2 3ln3.
2
x
S x x x x x x
xx
x
x x x




Chọn đáp án C.
Câu 3: Đường thẳng
ym
(
01m
) cắt đường cong
42
21y x x
tại hai điểm thuộc góc phần tư
thứ nhất của hệ tọa độ
Oxy
và chia thành hai hình phẳng có diện tích
1
S
,
2
S
như hình vẽ.
Biết
12
SS
. Mệnh đề nào dưới đây đúng?
A.
2
0;
5
m



. B.
21
;
52
m



. C.
13
;
25
m



. D.
3
;1
5
m



.
Lời giải:
Phương trình hoành độ giao điểm
42
21x x m
2
2
11x m x m
.
Vậy các giao điểm thuộc thuộc góc phần tư nhất của hệ tọa độ
Oxy
có hoành độ bằng
1xm
và
1xm
.
Diện tích
1
42
1
0
2 1 d
m
S x x m x
và
1
42
2
1
2 1 d
m
m
S x x m x
.
12
SS
5
3
1
24
1 1 1 0
5 3 9
m
m m m m
.
Chọn đáp án B.
Câu 4: Diện tích hình phẳng giới hạn bởi các đường
2
3yx
và
1y
bằng
A.
8
3
. B.
16
3
. C.
32
3
. D.
32
.
Lời giải:
Xét phương trình
22
2
3 1 4 0
2
x
xx
x

.
Do đó
22
3
22
22
2
32
4d 4 d 4
2
33
x
S x x x x x





.
Chọn đáp án C.
Câu 5: Một viên gạch hoa hình vuông cạnh
40cm
được thiết kế như hình bên dưới. Diện tích mỗi
cánh hoa bằng
y
x
20
20
20
20
y =
20
x
y =
1
20
x
2
A.
2
400
cm
3
. B.
2
800
cm
3
. C.
2
250cm
. D.
2
800cm
.
Lời giải:
Diện tích mỗi cánh hoa là
20
20
3
2
0
0
1 2 20 1 400
20 dx= .
20 3 20 3 3
x x x
xx







2
cm
.
Chọn đáp án A.
Câu 6: Cho hàm số
y f x
. Hàm số có đồ thị hàm số
'y f x
như hình vẽ dưới đây.
Biết diện tích hình phẳng giới hạn bởi trục
Ox
và đồ thị hàm số
'y f x
trên đoạn
2;1
và
1;4
lần lượt bằng 9 và 12. Cho biết
13f
. Tính giá trị biểu thức
24P f f
.
A. 21. B. 3. C. 9. D. 2.
Lời giải:
Ta có:
11
22
| d 9 ' d 9 1 ( 2) 9f x x f x x f f


.
Mà
13f
2 12f
.
Ta có:
44
11
| | d 12 d 12 4 1 12f x x f x x f f

.
Mà
13f
49f
. Vậy
2 4 3P f f
.
Chọn đáp án B.
Câu 7: Tính diện tích hình phẳng giới hạn bởi các đường
2
yx
,
14
33
yx
và trục hoành.
A.
11
6
. B.
61
3
. C.
343
162
. D.
39
2
.
Lời giải:
Phương trình hoành độ giao điểm của các đường
2
yx
,
14
33
yx
là
2
14
33
xx
2
3 4 0xx
1
4
3
x
x

.
Hoành độ giao điểm của đường thẳng
14
33
yx
với trục hoành là
4x
.
Hoành độ giao điểm của parabol
2
yx
với trục hoành là
0x
.
Diện tích hình phẳng cần tìm là
14
2
01
14
dd
33
S x x x x




1
4
3
2
1
0
14
3 6 3
x
xx



11
6
.
Chọn đáp án A.
Câu 8: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
44yx x
, trục tung và trục hoành. Xác
định
k
để đường thẳng
d
đi qua điểm
0;4A
có hệ số góc
k
chia
H
thành hai phần có
diện tích bằng nhau.
A.
4k 
. B.
8k 
. C.
6k 
. D.
2k 
.
Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số
2
44yx x
và trục hoành là:
2
4 0 24x xx
.
Diện tích hình phẳng
H
giới hạn bởi đồ thị hàm số:
2
44yx x
, trục tung và trục hoành
là:
22
3
22
2
00
2
0
8
4 4 4
3
4 4 2
3
x
S xx d xx x xdxx




.
Phương trình đường thẳng
d
đi qua điểm
0;4A
có hệ số góc
k
có dạng:
4y kx
.
Gọi
B
là giao điểm của
d
và trục hoành. Khi đó
4
;0B
k



.
Đường thẳng
d
chia
H
thành hai phần có diện tích bằng nhau khi
B OI
và
14
23
OAB
SS

.
4
02
2
6
1 1 4 4 6
. .4.
2 2 3
OAB
k
k
k
k
S OAOB
k



.
Chọn đáp án C.
Câu 9: Cho hàm số đa thức bậc ba
32
( 0)y f x ax bx cx d a
có đồ thị như hình vẽ bên dưới:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
y f x
và trục hoành.
A.
6
. B.
19
4
. C.
27
4
. D. 8.
Lời giải:
Đồ thị hàm số
y f x
cắt và tiếp xúc trục hoành lần lượt tại tại điểm
2;0
và
1;0
nên hàm
số có dạng
2
3
2 1 3 2y f x a x x a x x
.
Mặt khác đồ thị hàm số lại đi qua điểm
1;4
nên ta có
1a
. Vậy
3
32y f x x x
.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
y f x
và trục hoành là:
1
3
2
27
32
4
S x x dx
.
Chọn đáp án C.
Câu 10: Cho hình phẳng
H
giới hạn bởi các đường
2
1yx
và
,0 1.y k k
Tìm
k
để diện tích của
hình phẳng
H
gấp hai lần diện tích hình phẳng được kẻ sọc trong hình vẽ bên dưới.
A.
3
4.k
B.
3
2 1.k 
C.
1
.
2
k
D.
3
41k 
.
Lời giải:
Do đồ thị nhận trục
Oy
làm trục đối xứng nên yêu cầu bài toán trở thành:
Diện tích hình phẳng giới hạn bởi
2
1 , , 0y x y k x
bằng diện tích hình phẳng giới hạn
bởi :
22
1 , 1, , 0.y x y x y k x
Nghĩa là
1 1 1
2 2 2
01
1
1 d 1 d 1 d .
kk
k
x k x k x x k x x

3 3 3 3 3
2 1 1 1 1
( 1 ) 1 ( 1 ) ( 1 ) ( 1 ) ( 1 ) 1
3 3 3 3 3
k k k k k k k
3
24
( 1 )
33
k
3
12k
3
4 1.k
Chọn đáp án D.
Câu 11: Gọi
H
là hình phẳng giới hạn bởi đồ thị của hàm số
2
6y x x
và trục hoành. Hai đường
thẳng
, 9y m y n m n
chia hình
H
thành ba phần có diện tích bằng nhau. Tính
33
(9 ) (9 ) .P m n
A.
405P
. B.
409P
. C.
407P
. D.
403P
.
Lời giải:
Gọi
2
:6
: : 0
0, 6
P y x x
H Ox y
xx


. Suy ra:
6
2
0
6 36
H
S S x x dx
Ta có:
2
1
2
2
39
6 3 9
39
x y P
y x x x y
x y P
Gọi
1
12
: 3 9
: : 3 9
, 9 9
P x y
H P x y
y n y n
.
Suy ra:
1
99
3
1
4
3 9 3 9 2 9 d 9
3
H
nn
S S y y dy y y n

Mà
1
12
3
S
S 
nên
3
3
4
9 12 9 81
3
nn
Gọi
1
22
: 3 9
: : 3 9
, 9 9
P x y
H P x y
y m y m
. Suy ra:
2
9
3
2
4
2 9 d 9
3
H
m
S S y y m
Mà
2
2
24
3
S
S 
nên
3
3
4
9 24 9 324.
3
nn
Vậy
81 324 405P
.
Chọn đáp án A.
Câu 12: Cho hàm số
y f x
là hàm đa thức bậc bốn có đồ thị là
C
và
d
là tiếp tuyến của đồ thị
C
tại hai điểm như hình vẽ. Biết diện tích hình phẳng giới hạn bởi đồ thị
C
và
d
là
11
3
. Khi đó
tích phân
d
1
1
I f x x
bằng
A.
19
6
. B.
25
6
. C.
23
6
. D.
13
3
Lời giải:
Phương trình đường thẳng đi qua hai điểm




3
1; ; 1; 1
2
là
51
44
g x x





1 1 1
1 1 1
1
1
11 11
33
5 1 11 1 11 25
4 4 3 2 3 6
S f x g x dx f x dx g x dx
I x dx I I
.
Chọn đáp án B.
Câu 13: Một chất điểm chuyển động trong 3 giây với vận tốc
cosv a t b

(mét/giây) (trong đó
t
là
biến thời gian;
,ab
là các hằng số) có đồ thị là một đường hình sin như hình vẽ bên. Tính tổng
quãng đường mà vật đi được sau 3 giây (kết quả làm tròn đến hàng phần trăm).
A.
29,93m
. B.
15m
. C.
27,93m
. D.
17m
.
Lời giải:
Quan sát đồ thị ta có:
0 10
10 5
05
30
v
a b a
a b b
v



. Suy ra
5cos 5vt

.
Vậy quãng đường mà vật đi được sau 3 giây là:
3
0
5cos 5 15S t dt
(m).
Chọn đáp án B.
Câu 14: Cho hàm số
y f x
liên tục trên đoạn
0;8
và có đồ thị như hình vẽ dưới đây:
Trong các giá trị sau, giá trị nào lớn nhất?
A.
3
0
d.f x x
B.
1
0
d.f x x
C.
8
0
d.f x x
D.
5
0
d.f x x
Lời giải:
Ta có
1
3
0
d
S
f x x S
.
13
00
ddf x x f x x

8 3 5 8
0 0 3 5
d d d df x x f x x f x x f x x
12
3
SS
S
S S S
.
12
5 3 5
0 0 3
d d d
SS
f x x f x x f x x S S
.
Từ hình vẽ, ta thấy
2
3
S
S
SS
nên
1 2 1 1 2
3
S S S S S
S
S S S S S S
Suy ra
8
0
df x x
là lớn nhất.
Chọn đáp án C.
Câu 15: Cho hàm số
y f x
liên tục trên có đồ thị tạo với trục hoành các miền có diện tích
1 2 3 4
, , ,S S S S
như hình vẽ bên dưới:
y
=
f(x)
S
2
S
3
S
4
S
1
2
1
2
1
-1
y
x
O
Biết
14
10SS
,
23
8SS
. Tích phân
ln3
0
1d
xx
I e f e x
bằng
A.
8
. B.
10
. C.
8
. D.
10
.
Lời giải:
Đặt
1
t
te
x
dt e dx
;
00xt
và
ln3 2xt
.
ln3
0
1
xx
I e f e dx
2
0
f t dt
1
2
0
f t dt
1
1
2
f t dt
+
2
1
f t dt
234
S S S
8 8 10
10
.
Chọn đáp án B.
Câu 16: Cho parabol
2
:P y x
và một đường thẳng
d
thay đổi cắt
P
tại hai điểm
A
,
B
sao cho
2020AB
. Gọi
S
là diện tích hình phẳng giới hạn bởi
P
và đường thẳng
d
. Tìm giá trị lớn
nhất
max
S
của
A.
3
2020 1
.
6
max
S
B.
3
2020
.
6
max
S
C.
3
2020 1
.
6
max
S
D.
3
2020
.
3
max
S
Lời giải:
Giả sử
2
( ; )A a a
;
2
( ; )( )B b b b a
sao cho
2020AB
.
Phương trình đường thẳng
d
là:
()y a b x ab
. Khi đó
3
22
1
( ) d d
6
bb
aa
S a b x ab x x a b x ab x x b a

.
Vì
2
2 2 2
2 2 2 2
2020 2020 1 2020AB b a b a b a b a
.
2
2
2020ba
3
2020
2020
6
b a b a S
.
Vậy
3
max
2020
6
S
khi
1010a 
và
1010b
.
Chọn đáp án B.
Câu 17: Cho Parabol
2
:.P y x
Hai điểm A, B di động trên
P
sao cho
2.AB
Gọi S là diện tích
hình phẳng giới hạn bởi Parabol
P
và đoạn thẳng
AB
. Tìm giá trị lớn nhất của S.
A.
4
max
3
S
. B.
7
max
6
S
. C.
5
max
3
S
. D.
5
max
6
S
.
Lời giải:
Gọi
22
; , ;A a a B b b P
sao cho
ba
là hai điểm trên Parabol và
2.AB
Khi đó phương trình đường thẳng
AB
là
22
2
.
ba
y a x a y a b x ab
ba
Gọi S là diện tích hình phẳng cần tìm, ta có:
3
2
1
..
6
b
a
S a b x ab x dx b a


Ta có:
3
3
ax
1 2 4 4
2 2 .
6 6 3 3
m
AB b a b a S b a S
Đẳng thức xảy ra khi và chỉ khi
1; 1 1;1 , 1;1 .a b A B
Chọn đáp án A.
Câu 18: Hình gạch chéo được giới hạn bởi đường tròn
2
22
x y a b
;
0ab
và các đường thẳng
2
b
x 
và
2
b
x
. Thể tích vật tròn xoay tạo bởi hình gạch chéo quay xung quanh trục
Ox
là
A.
22
ab
. B.
22
3
4
ab
. C.
2
2
3
3
ab




. D.
2
3
24
ab



.
Lời giải:
Ta có:
2
22
x y a b
22
22
y a b x
y a b x
.
Thể tích vật tròn xoay tạo bởi hình gạch chéo quay xung quanh trục
Ox
là:
2
22
2 2 2 2
2
d
b
b
V a b x a b x x



2
22
2
4d
b
b
a b x x

2
22
2
4d
b
b
a b x x

Đặt
sin , ; d cos d
22
x b t t x b t t







. Đổi cận:
26
b
xt
;
26
b
xt
.
2 2 2
6
4 sin cos d
b
V a b b tb t t

6
22
6
4 cos dab t t
6
2
6
1 cos2
4d
2
t
ab t
6
2
6
sin 2
2
2
t
ab t




2
33
2
6 4 6 4
ab





2
2
3.
3
ab





Chọn đáp án C.
Câu 19: Cho hàm số đa thức bậc bốn
y f x
có đồ thị
C
, biết rằng
C
đi qua điểm
1;0A
. Tiếp
tuyến
tại
A
của đồ thị
C
cắt
C
tại hai điểm có hoành độ lần lượt là
0
và
2
. Biết diện
tích hình phẳng giới hạn bởi
, đồ thị
C
và hai đường thẳng
0x
;
2x
có diện tích
bằng
56
.
5
B
A
y
x
O
3
2
1
-1
Diện tích hình phẳng giới hạn bởi , đồ thị
C
và hai đường thẳng
1x
;
0x
bằng
A.
2
5
. B.
1
20
. C.
1
10
. D.
1
5
.
Lời giải:
Hàm số
42
y ax bx c
. TXĐ:
D
.
Ta có:
3
' 4 2y ax bx
.
Phương trình tiếp tuyến
của đồ thị
C
tại
1;0A
có dạng
4 2 1 y a b x
.
Do tiếp tuyến
tại
A
của đồ thị
C
cắt
C
tại hai điểm có hoành độ lần lượt là 0 và 2 nên
phương trình
42
4 2 1 ax bx c a b x
nhận ba nghiệm là
1x
;
0x
;
2x
.
Suy ra:
3

c a b
ba
2
3

ca
ba
.
Vậy
C
:
4 2 4 2
3 2 3 2 y ax ax a a x x
và
:
21y a x
.
Diện tích hình phẳng giới hạn bởi
, đồ thị
C
và hai đường thẳng
0x
;
2x
bằng
56
5
nên:
2
42
0
56
2 1 3 2 d
5
a x a x x x
2
42
0
56
2 1 3 2 d .
5
a x a x x x
2
42
0
56
3 2 d
5
a x x x x
2
5
32
0
56
.
55



x
a x x
28 56
.
55
a
2a
.
Diện tích hình phẳng giới hạn bởi
, đồ thị
C
và hai đường thẳng
1x
;
0x
là
0
42
1
3 2 2 1 d
S a x x a x x
0
0
5
4 2 3 2
1
1
2
2 6 4 d 2. .
55
x
x x x x x x



Góp ý cách khác.
Phương trình đường thẳng
:1yx
.
Do
và
C
cắt nhau tại các điểm có hoành độ
1;0;2
nên ta có phương
trình
2
1 . . 2 0a x x x
Theo bài ta có phương trình
d
2
2
0
56
1 . 2 2
5
a x x x x a
.
Từ đó ta được



d
0
2
1
2 1 . 2S x x x x
2
5
.
Chọn đáp án A.
Câu 20: Ông A đi làm lúc 7 giờ và đến cơ quan lúc 7 giờ 12 phút bằng xe gắn máy, trên đường đến cơ
quan ông A gặp một người băng qua đường nên ông phải giảm tốc độ để đảm bào an toàn rồi
sau đó lại từ từ tăng tốc độ để đến cơ quan làm việc. Hỏi quãng đường kể từ lúc ông A giảm
tốc độ để tránh tai nạn cho đến khi tới cơ quan dài bao nhiêu mét? (Độ thị dưới đâu mô tả vận
tốc chuyển động của ông A theo thời gian khi đến cơ quan)
A.
3600
. B.
3200
. C.
3500
. D.
3900
.
Lời giải:
Thời gian đi đến cơ quan của ông A là 12 phút bằng 0,2 giờ.
Chọn gốc thời gian từ lúc 7 giờ sáng
0t
.
Lúc ông A giảm tốc độ là 7 giờ 5 phút
51
60 12
t




Ta có:
0,2
1
12
()s v t dt
là diện tích hình phẳng giới hạn bởi trục hoành, đường cong
vt
và hai
đường thẳng
1
12
t
,
0,2t
Diện tích hình phẳng trên được tính bằng cách chia nhỏ các hình đã biết nên
63
11
60 60
36 48 3,9km
2 60 2
s
.
Chọn đáp án D.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
| 1/86
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


Giáo viên: LÊ BÁ BẢO_ Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115
Đăng kí học theo địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
Hoặc Trung tâm Km 10 Hương Trà TÝCH PH¢N – øng dông øng dông tÝch ph©n Phiªn b¶n 2020 Cè lªn c¸c em nhÐ! HuÕ, th¸ng 02/2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông øng dông tÝch ph©n
PHIẾU ÔN TẬP SỐ 01 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
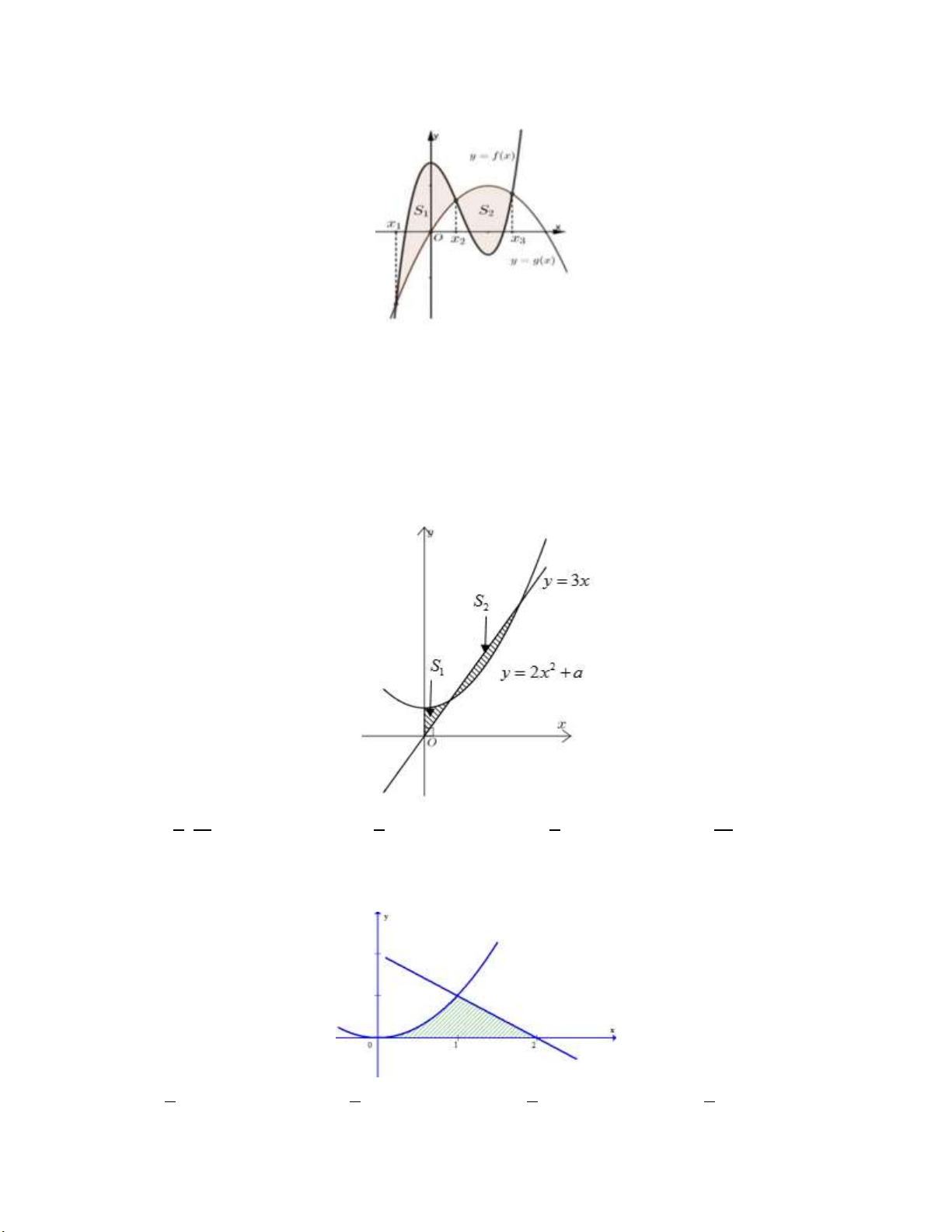
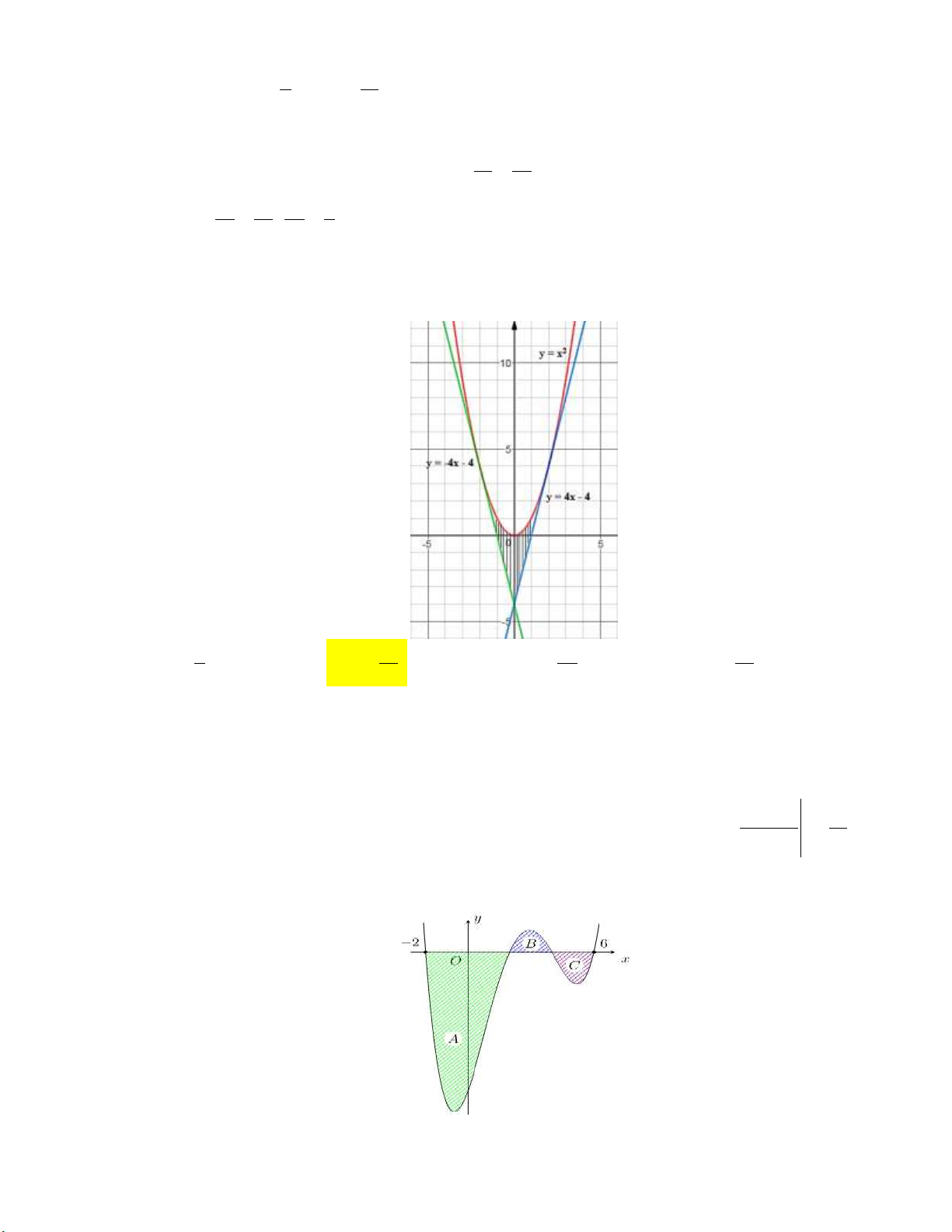
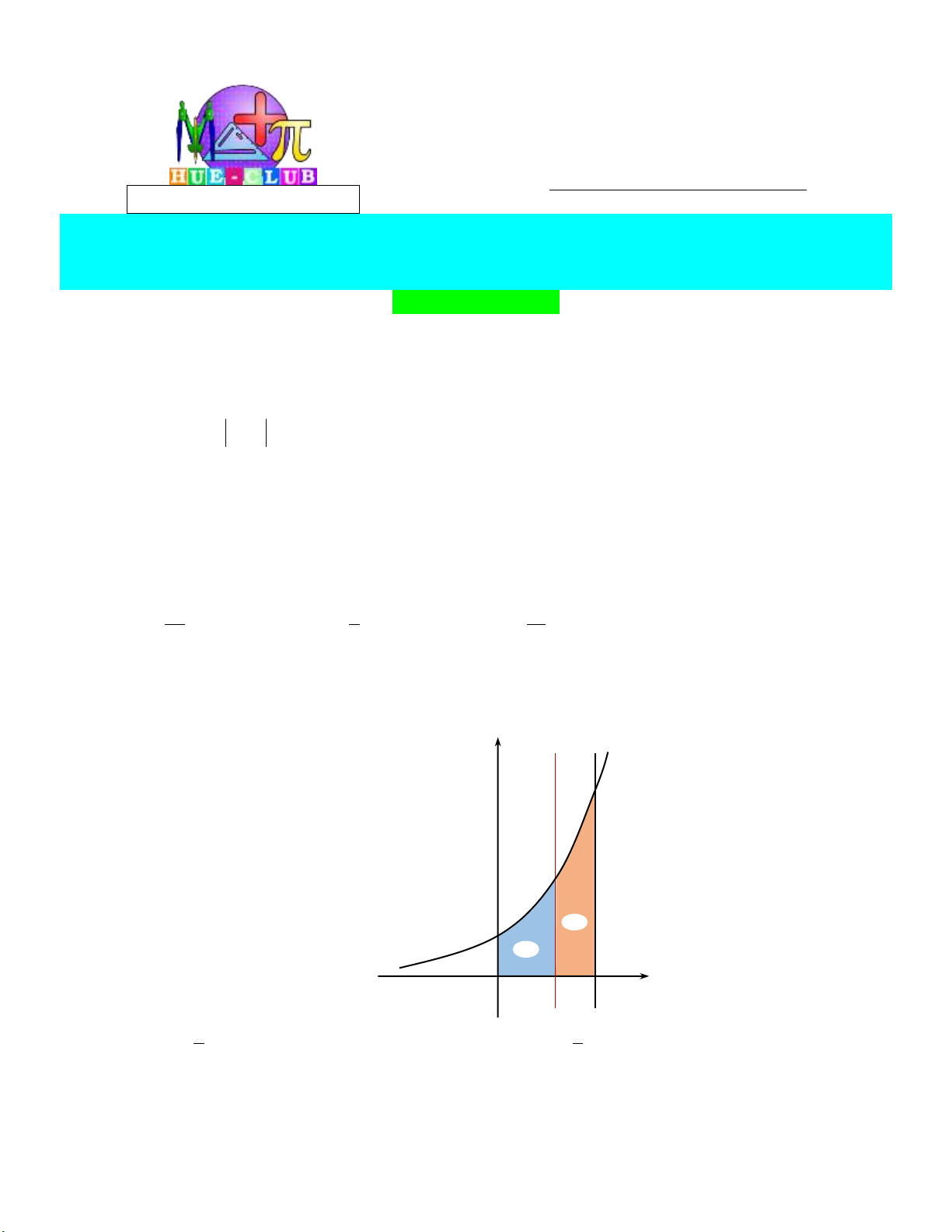
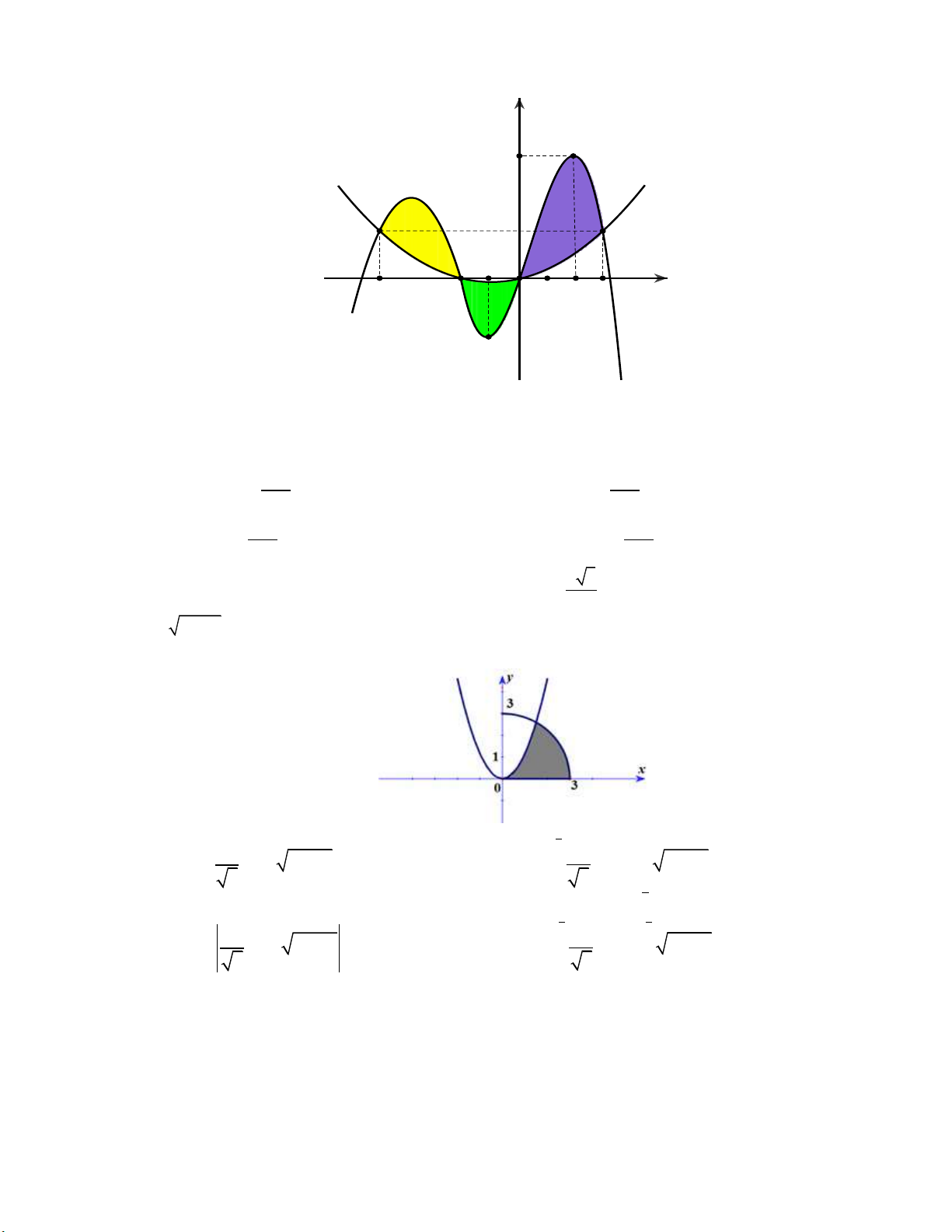
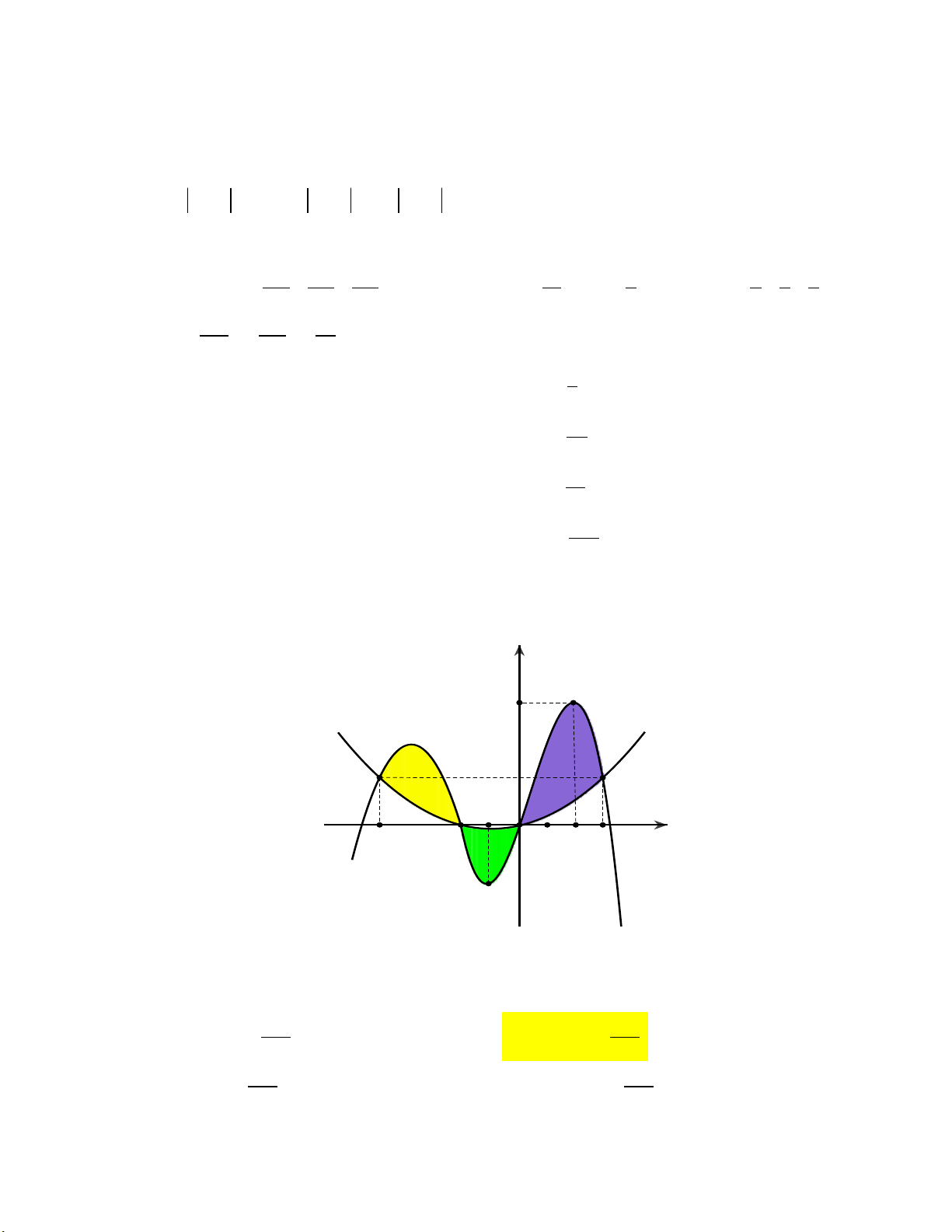
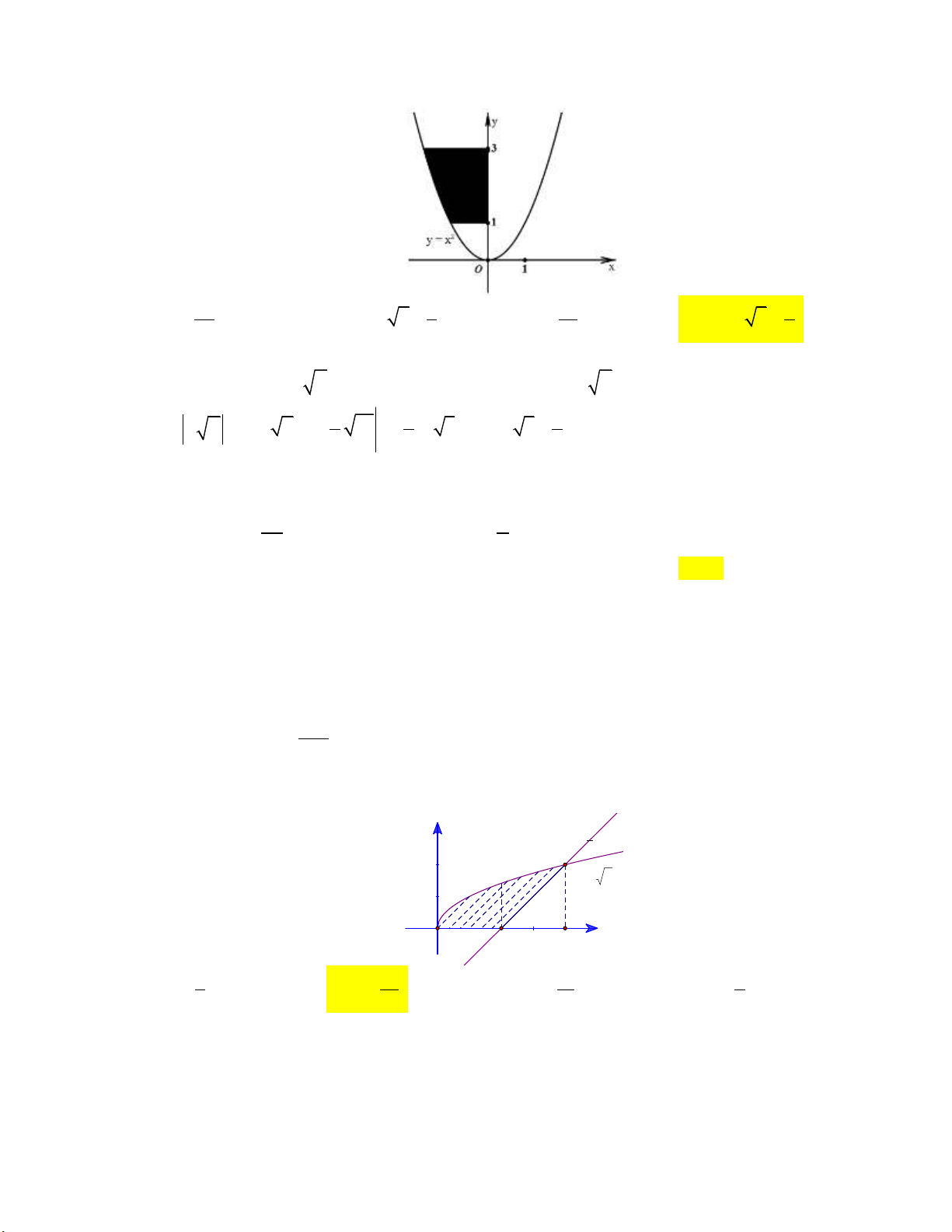
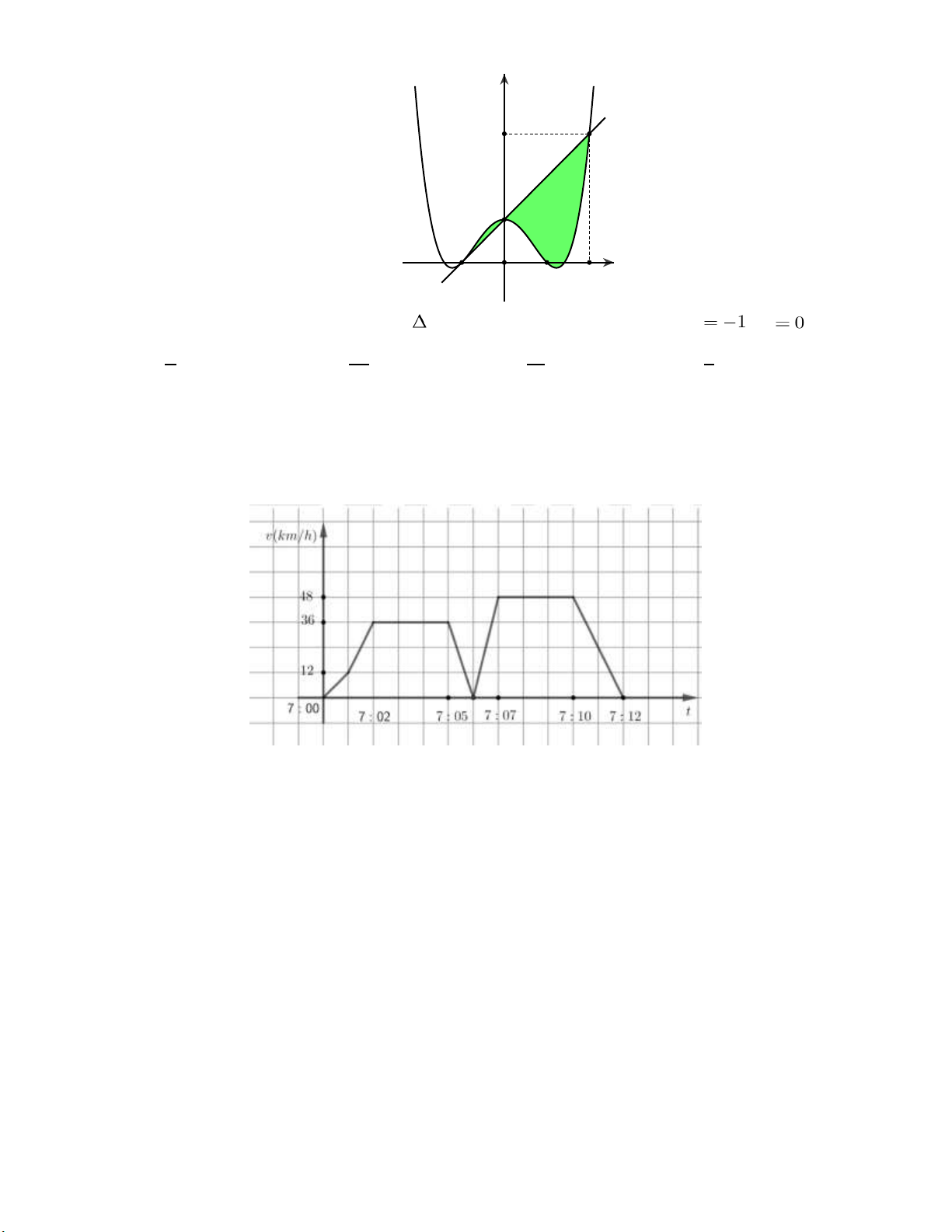
Câu 1: Cho hình phẳng D giới hạn bởi đường cong y  2  sin x , trục hoành và các đường thẳng
x  0 , x   . Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng bao nhiêu?
A. V  2   1 .
B. V  2    1 . C. 2 V  2 . D. V  2 .
Câu 2: Gọi S là diện tích của hình phẳng giới hạn bởi các đường 2x y
, y  0 , x  0 , x  2 . Mệnh đề
nào dưới đây đúng? 2 2 2 2 A.  2x S dx  B. 2   2 x S dx  C. 2  2 x S dx  D.   2x S dx  0 0 0 0
Câu 3: Cho hình phẳng  H  giới hạn bởi các đường 2
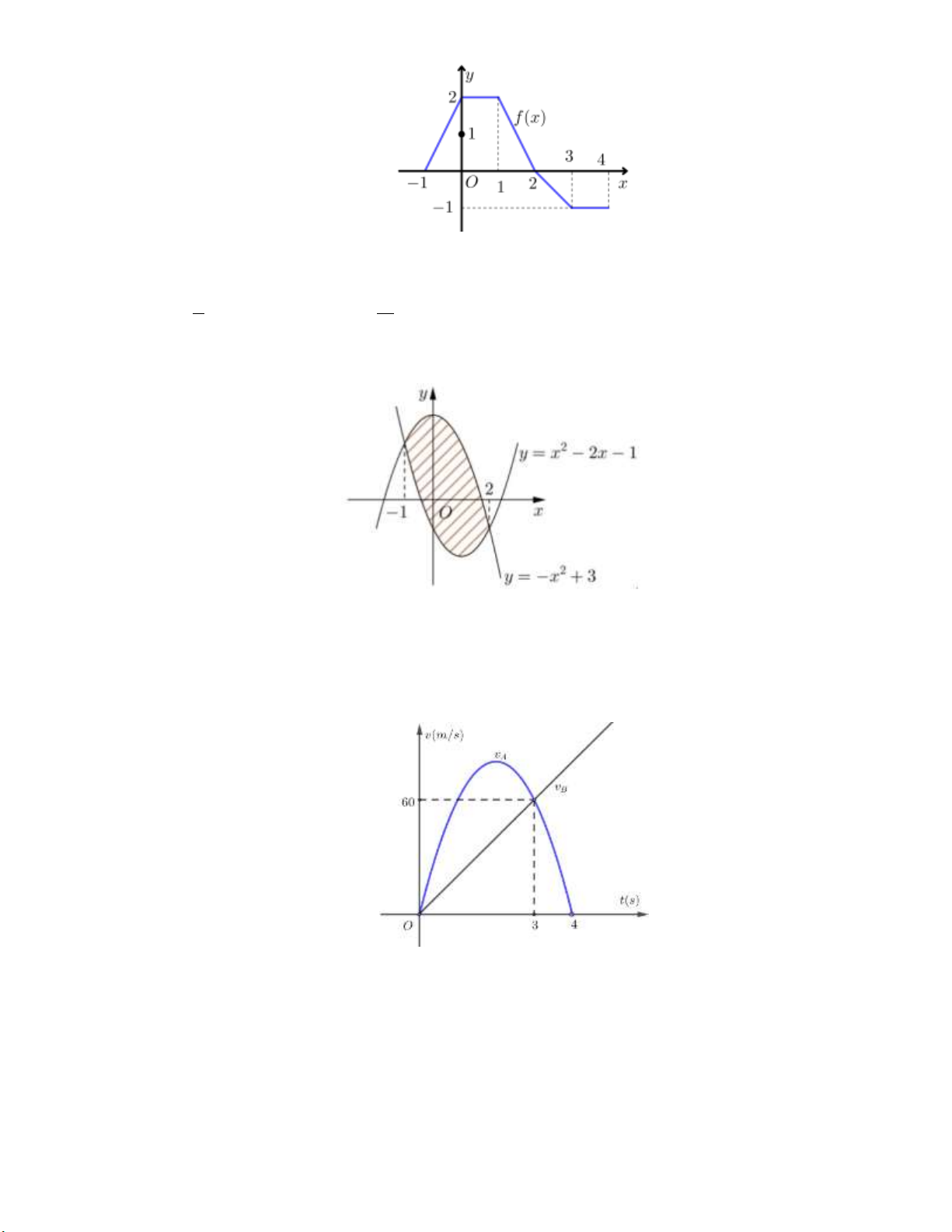
y x  3 , y  0 , x  0 , x  2 . Gọi V là thể tích
của khối tròn xoay được tạo thành khi quay  H  xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2 A. V    2 x  3 d .
x B. V    2 x  3d .
x C. V   2 x  3 d .
x D. V   2 x  3d . x 0 0 0 0
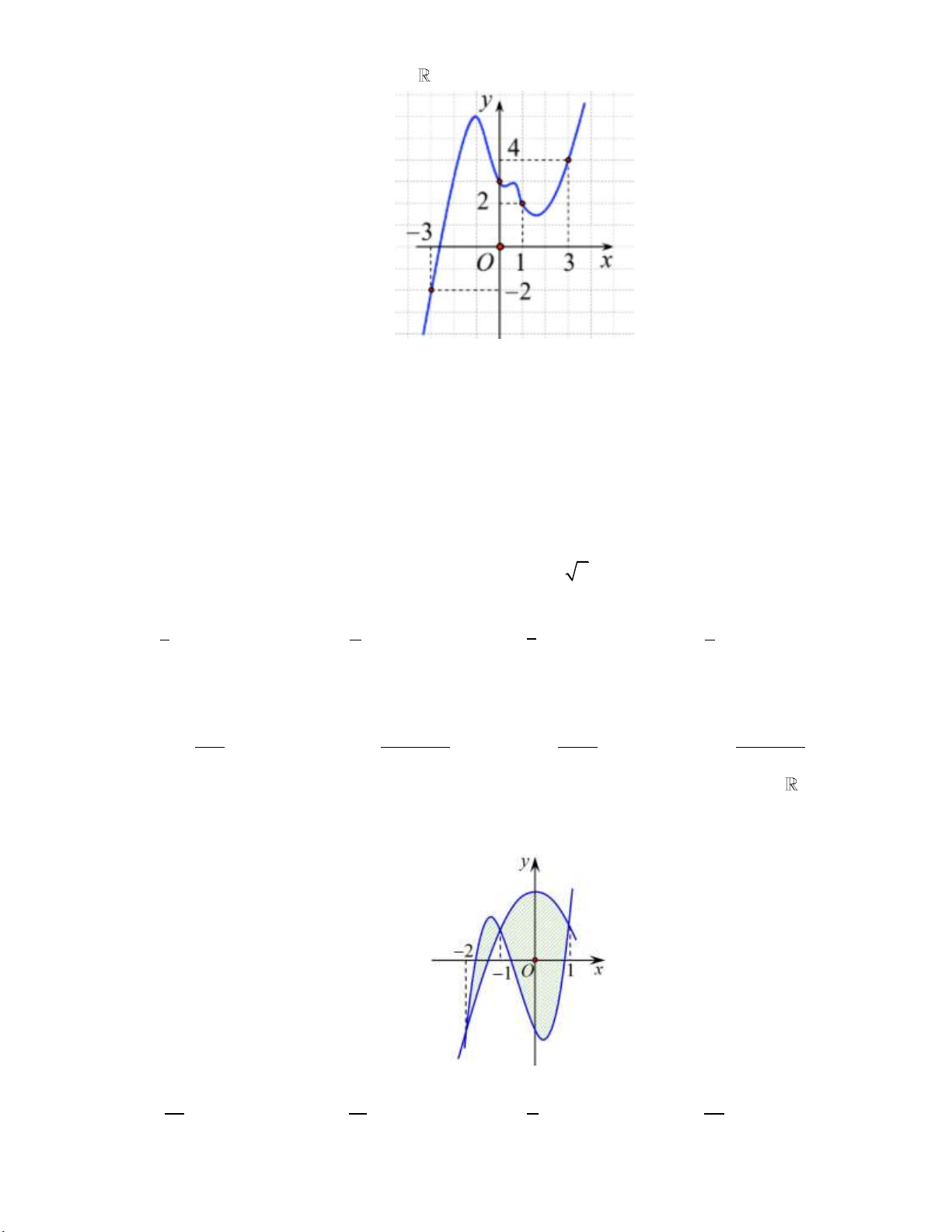
Câu 4: Gọi S là diện tích hình phẳng  H  giới hạn bởi các đường y f x , trục hoành và hai đường 0 2
thẳng x  1 , x  2 . Đặt a f
 xdx,b f
 xdx , mệnh đề nào sau đây đúng? 1  0 A. S b  . a B. S b  . a
C. S  b  . a
D. S  b  . a
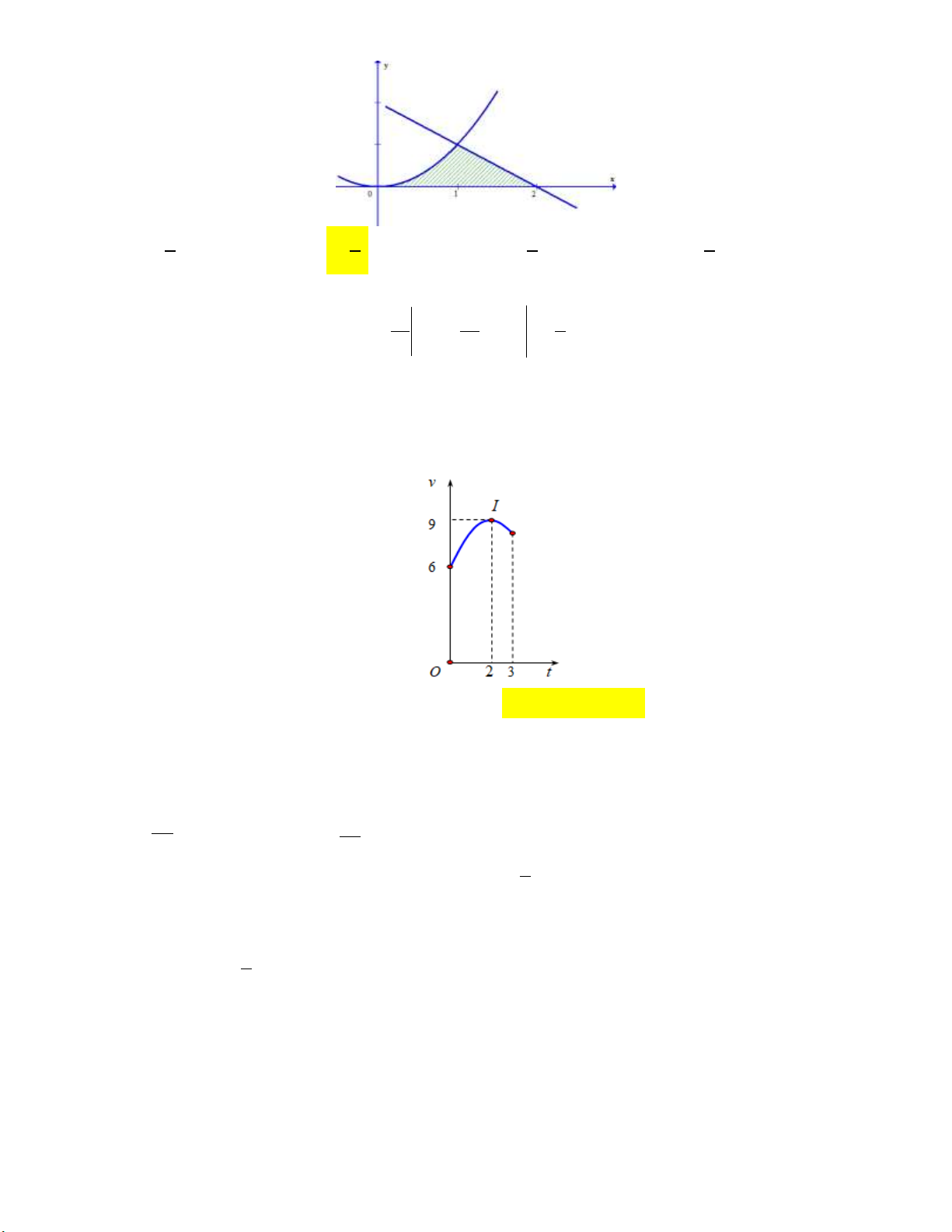
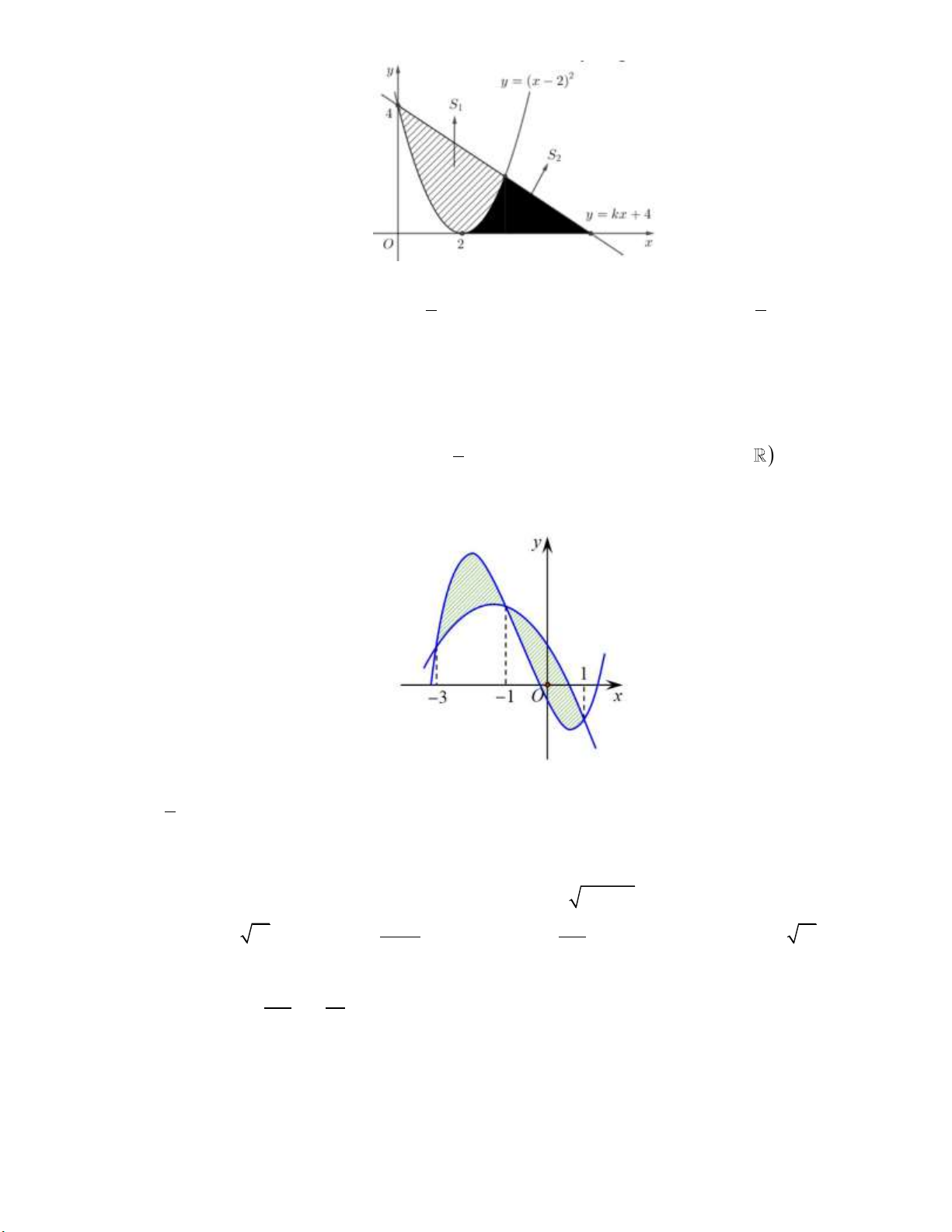
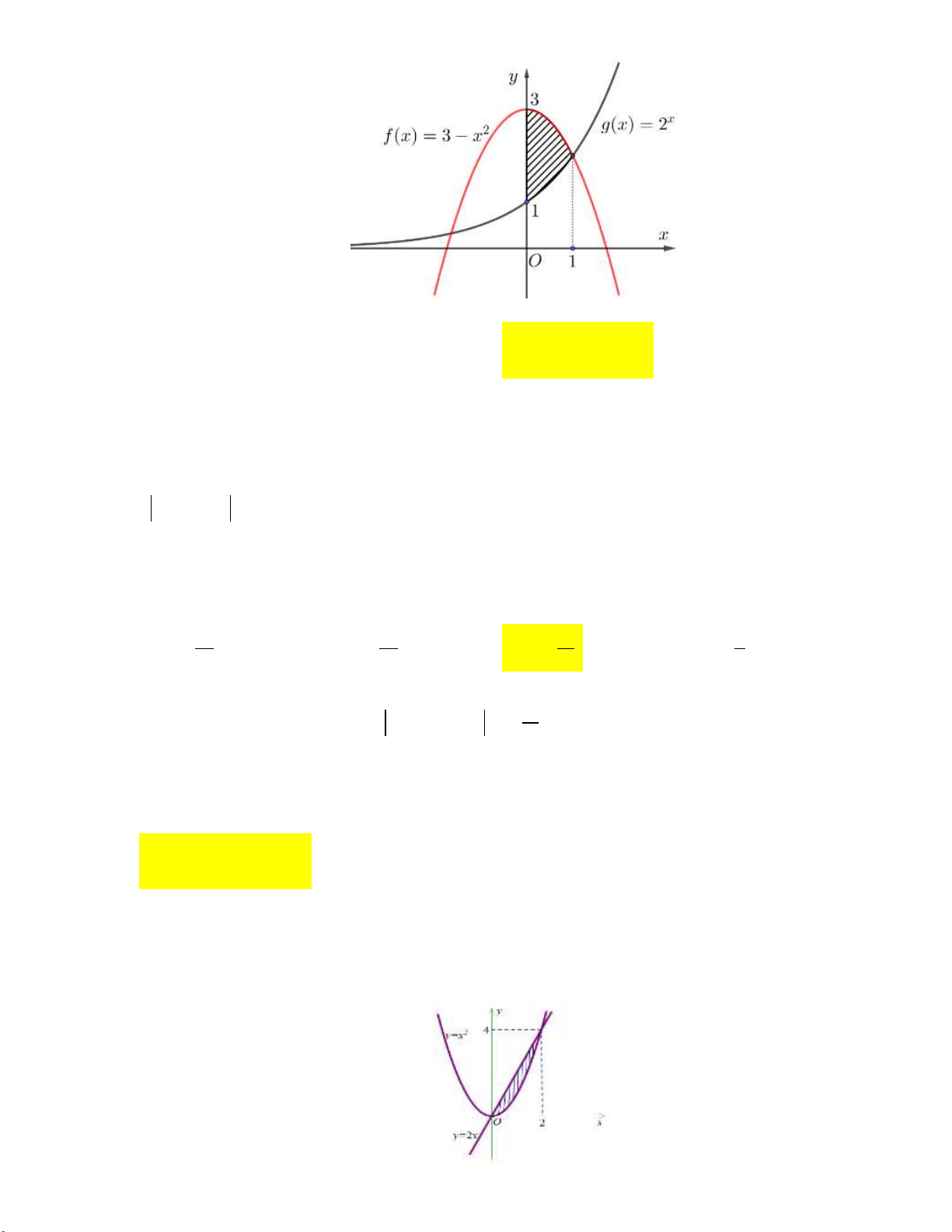
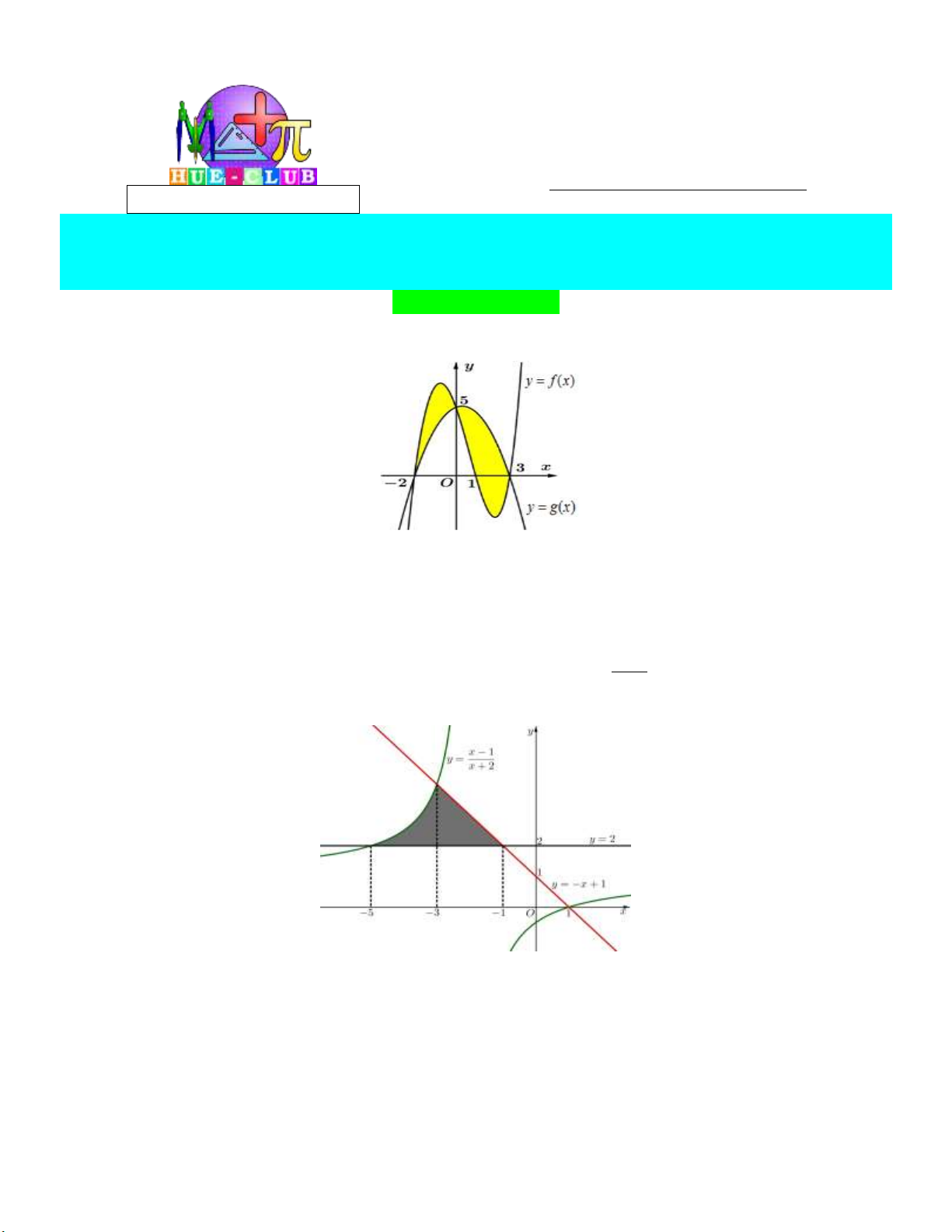
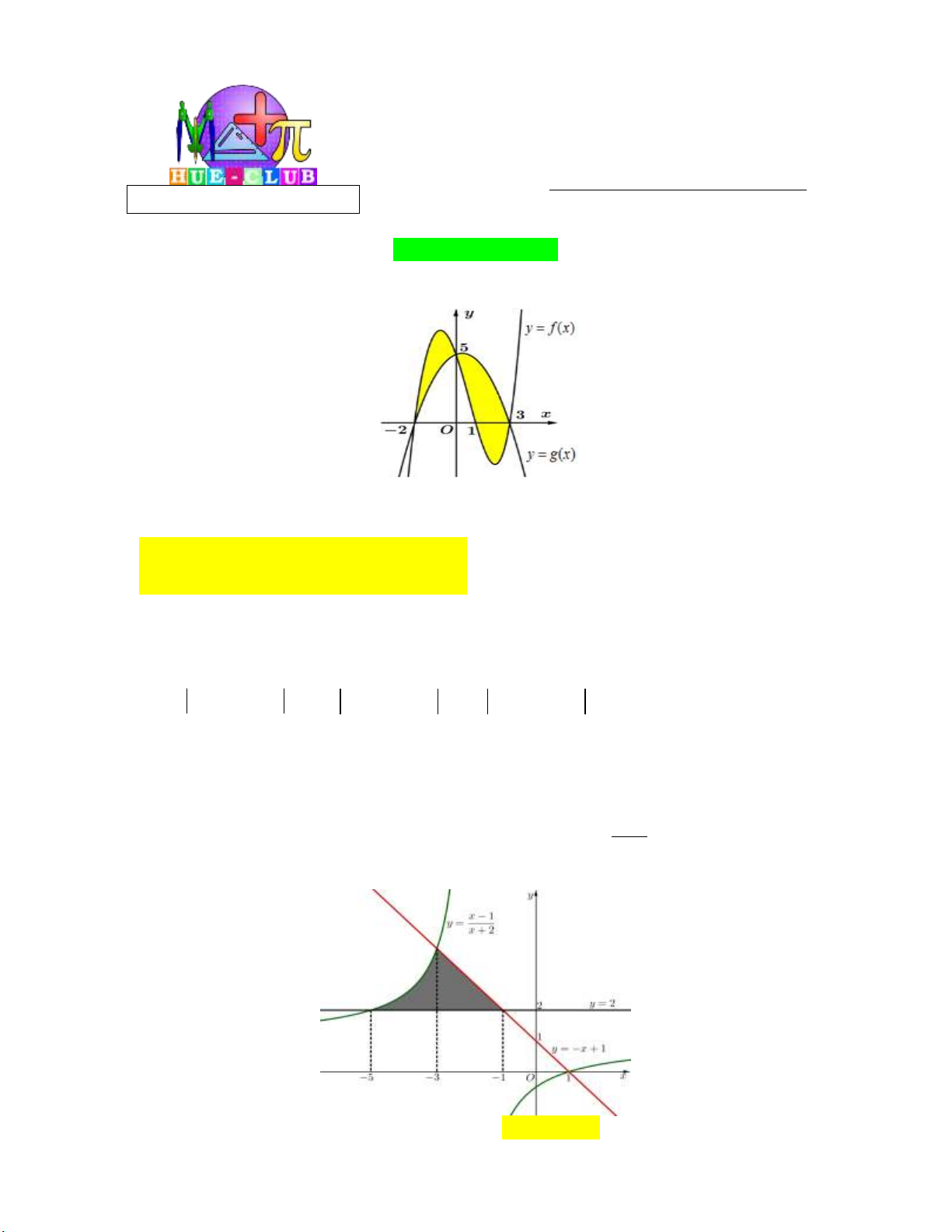
Câu 5: Cho hình phẳng (H ) (phần gạch sọc) như hình vẽ bên dưới:
Tính diện tích hình phẳng (H ). 9 9 3 9 A. 1. B. ln 3  2. C. ln 3  . D. ln 3  2. 2 2 2 2
Câu 6: Viết công thức tính thể tích V của vật thể T giới hạn bởi hai mặt phẳng x  2019 và x  2020 ,
vật thể T bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ
x 2019  x  2020 có thiết diện là một hình vuông độ dài cạnh là a . 2020 2020 2020 2020 A. 2 V   a d  x . B. V   a d  x . C. 2 V a d  x . D. V  d  a x . 2019 2019 2019 2019
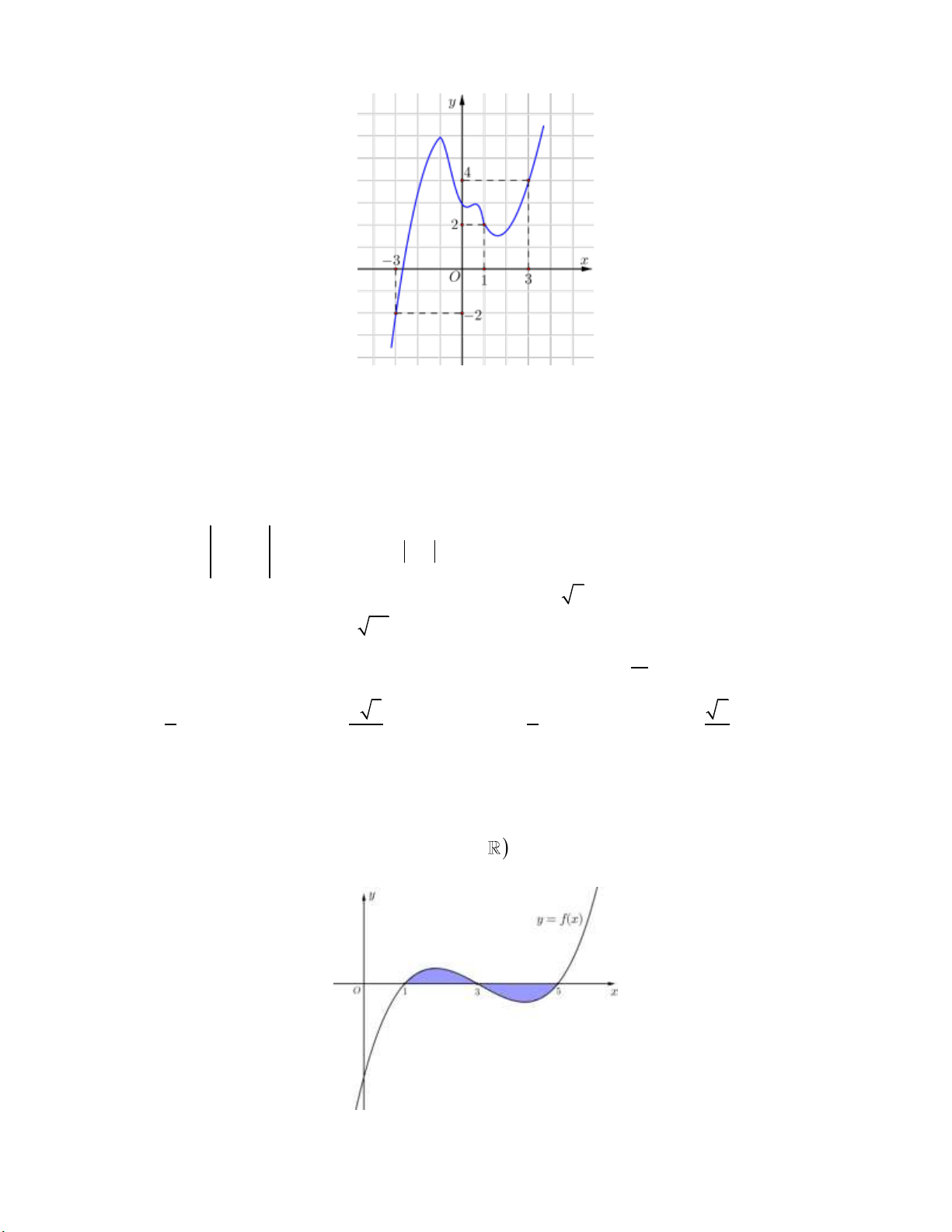
Câu 7: Gọi  H  là hình phẳng giới hạn bởi các đường 2
y  x  3x, y  0, x  0 và x  3 . Quay hình
H  quanh trục Ox , ta được khối tròn xoay có thể tích bằng 27 9 81 5 A. . B. . C. . D. . 10 2 10 2 Câu 8: Cho hàm số 4 2
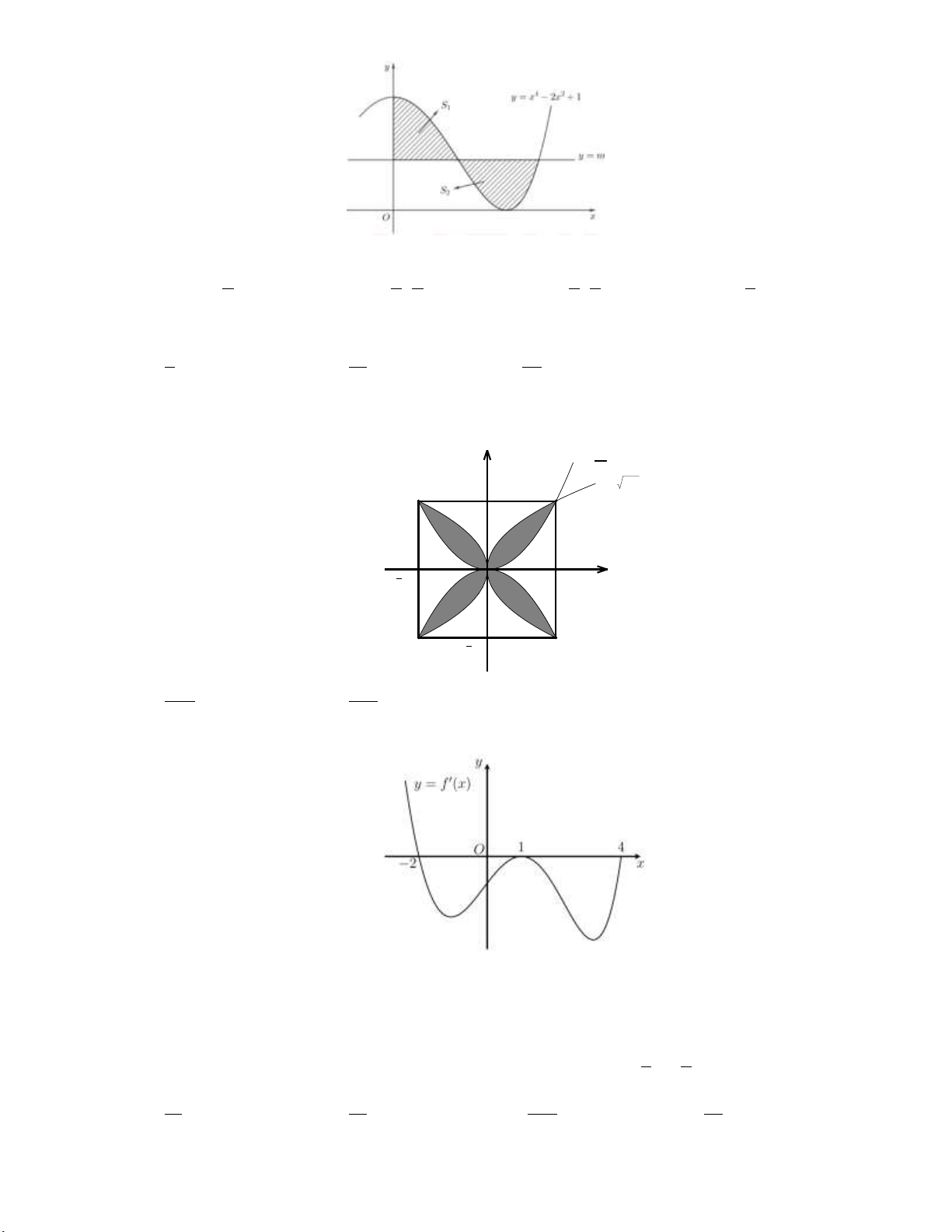
y x  3x m có đồ thị là C
( m là tham số thực). Giả sử C cắt trục Ox m m
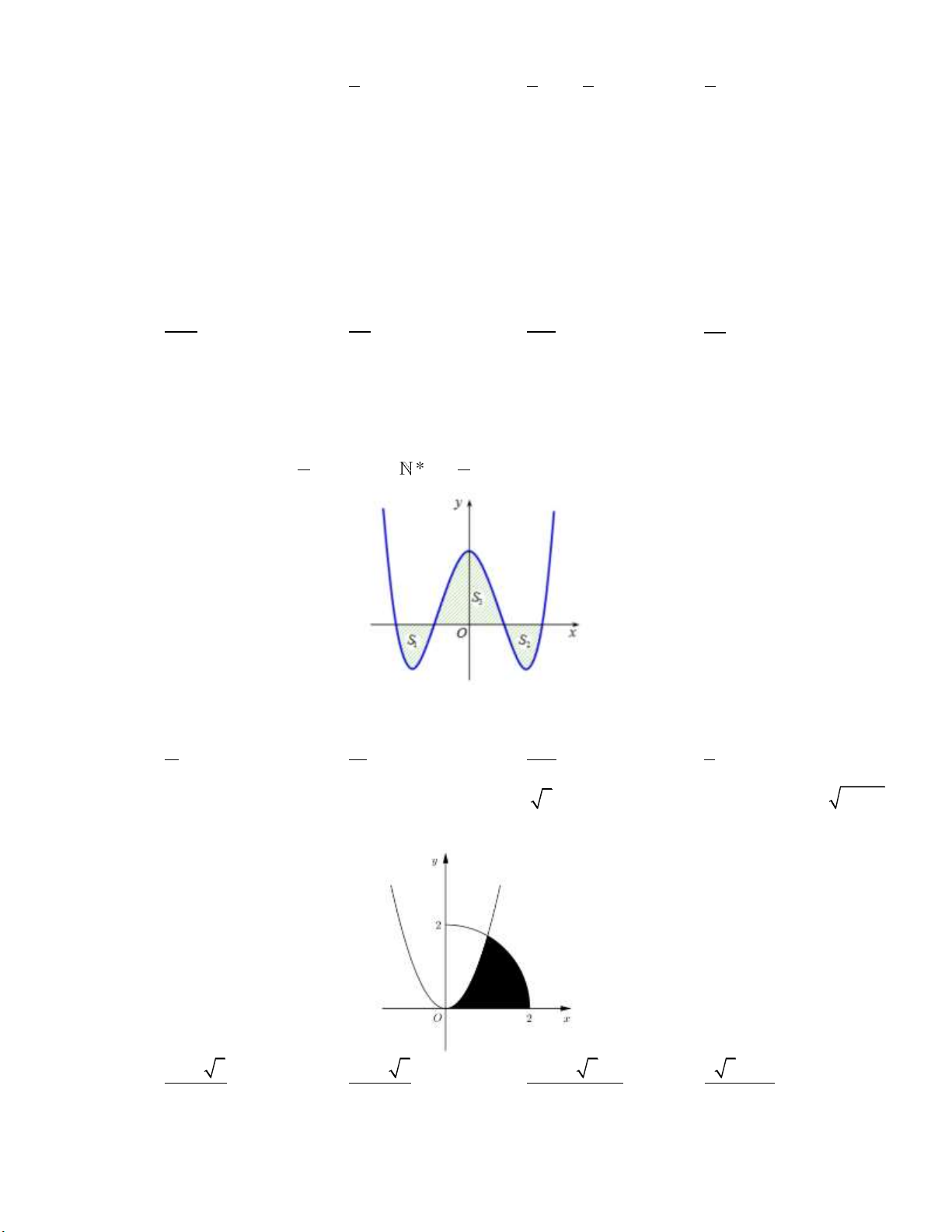
tại 4 điểm phân biệt. Gọi S , S là diện tích của hai hình phẳng nằm dưới trục Ox và S là diện 1 2 3
tích của hình phẳng nằm trên trục Ox được tạo bởi C
với trục Ox . Biết rằng tồn tại duy m a a
nhất giá trị của m
(với a,b  * và
tối giản) để S S S . Giá trị của 2a b bằng b b 1 2 3 A. 3 . B. 4  . C. 6 . D. 2  .
Câu 9: Diện tích hình phẳng giới hạn bởi hai đường 2
y x  1 và y x  1 bằng  13 13 1 A.  B.  C.  D.  6 6 6 6
Câu 10: Cho H là hình phẳng giới hạn bởi parabol 2
y  3x , cung tròn có phương trình 2 y  4  x
và trục hoành . Diện tích của H bằng 4  3 4  3 4  2 3  3 5 3  2 A. . B. . C. . D. . 12 6 6 3
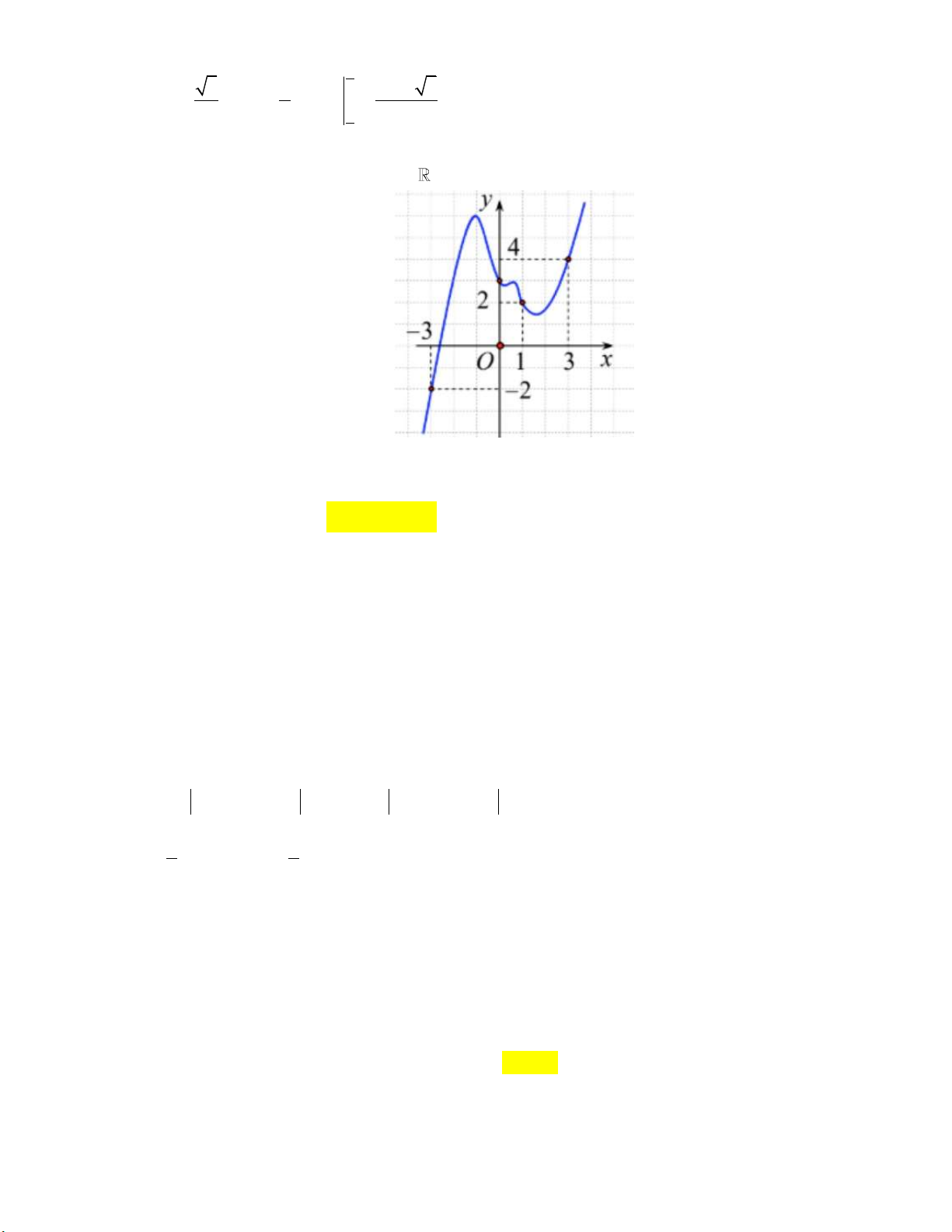
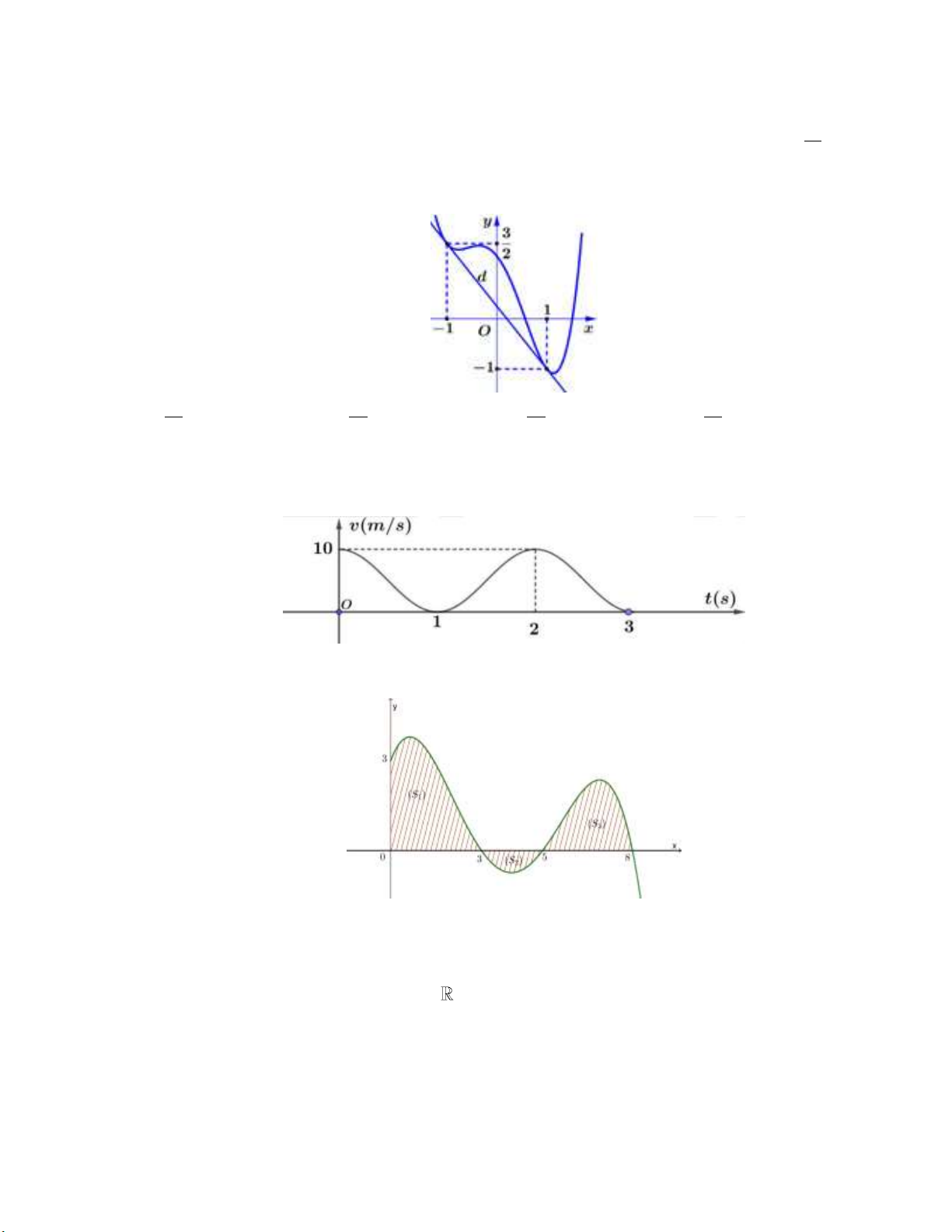
Câu 11: Cho hàm số y f x liên tục trên
. Đồ thị hàm số y f  x như hình vẽ bên dưới:
Đặt g x  f x   x  2 2
1 . Bất phương trình f x   x  2 2
1  m nghiệm đúng với mọi x  3  ;  3 khi và chỉ khi
A. m g 3 . B. m g  3   .
C. m g   1 . D. m g  3   .
Câu 12: Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển
động chậm dần đều với vận tốc v t   5
t 10 (m/s), trong đó t là khoảng thời gian tính bằng
giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 0,2m. B. 2m. C. 10m. D. 20m.
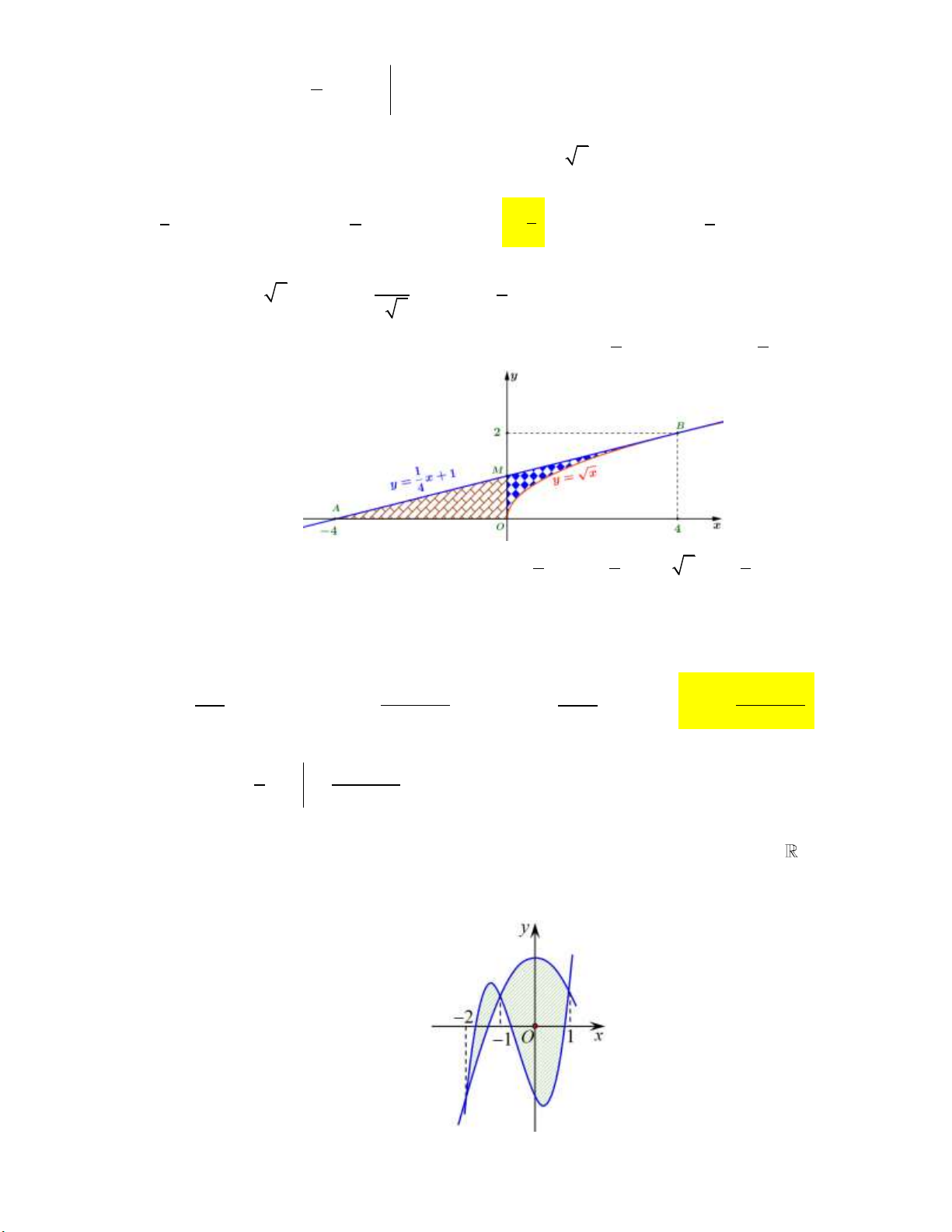
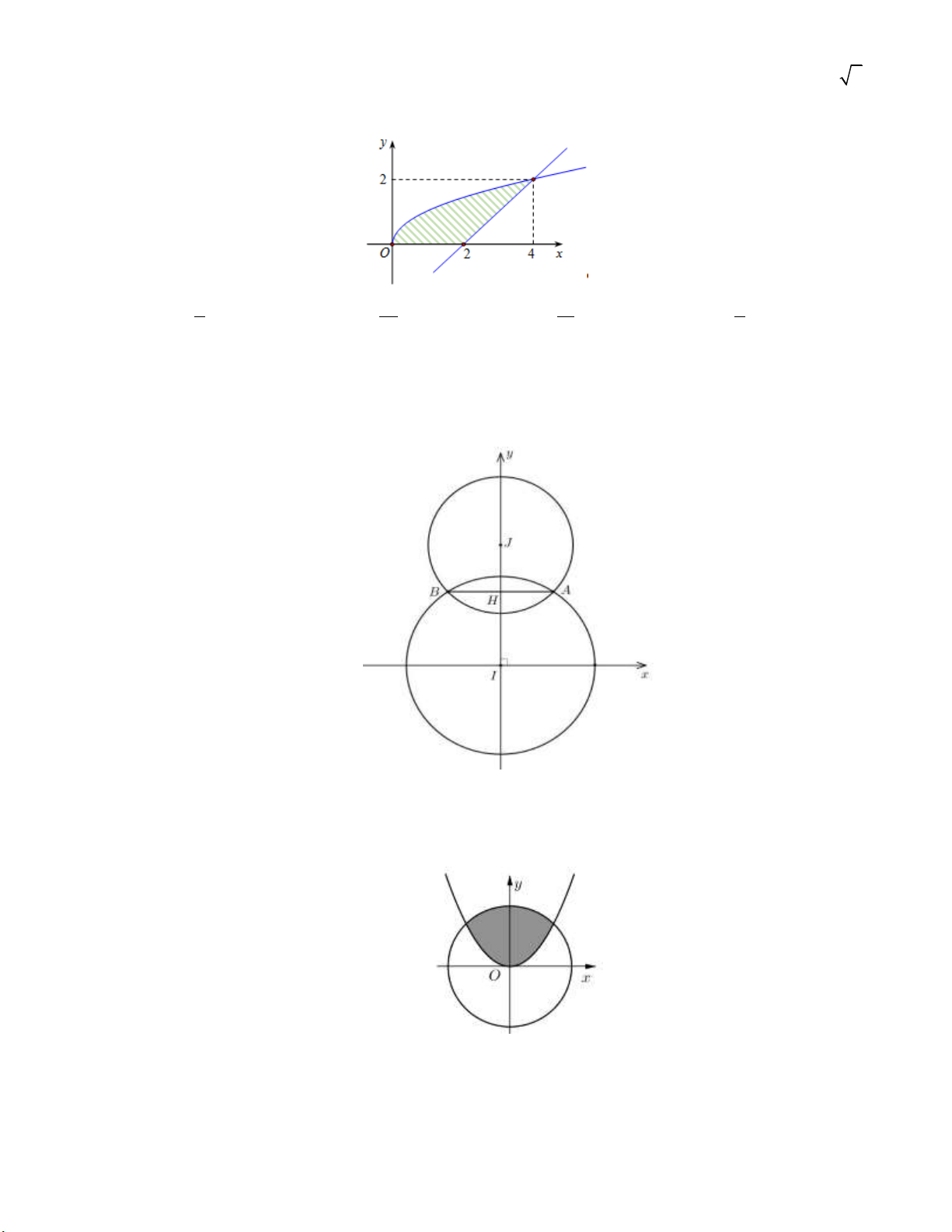
Câu 13: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y
x ; tiếp tuyến với đồ thị tại M 4; 2 và trục hoành là 3 2 8 1 A. . B. . C. . D. . 8 3 3 3
Câu 14: Cho hình phẳng D giới hạn bởi đường cong x
y e , trục hoành và các đường thẳng x  0 ,
x  1 . Khối tròn xoay tạo thanh khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 2    2e     2e   e 1 2 e 1 1 A. V  . B. V  . C. V  . D. V  . 2 2 2 2
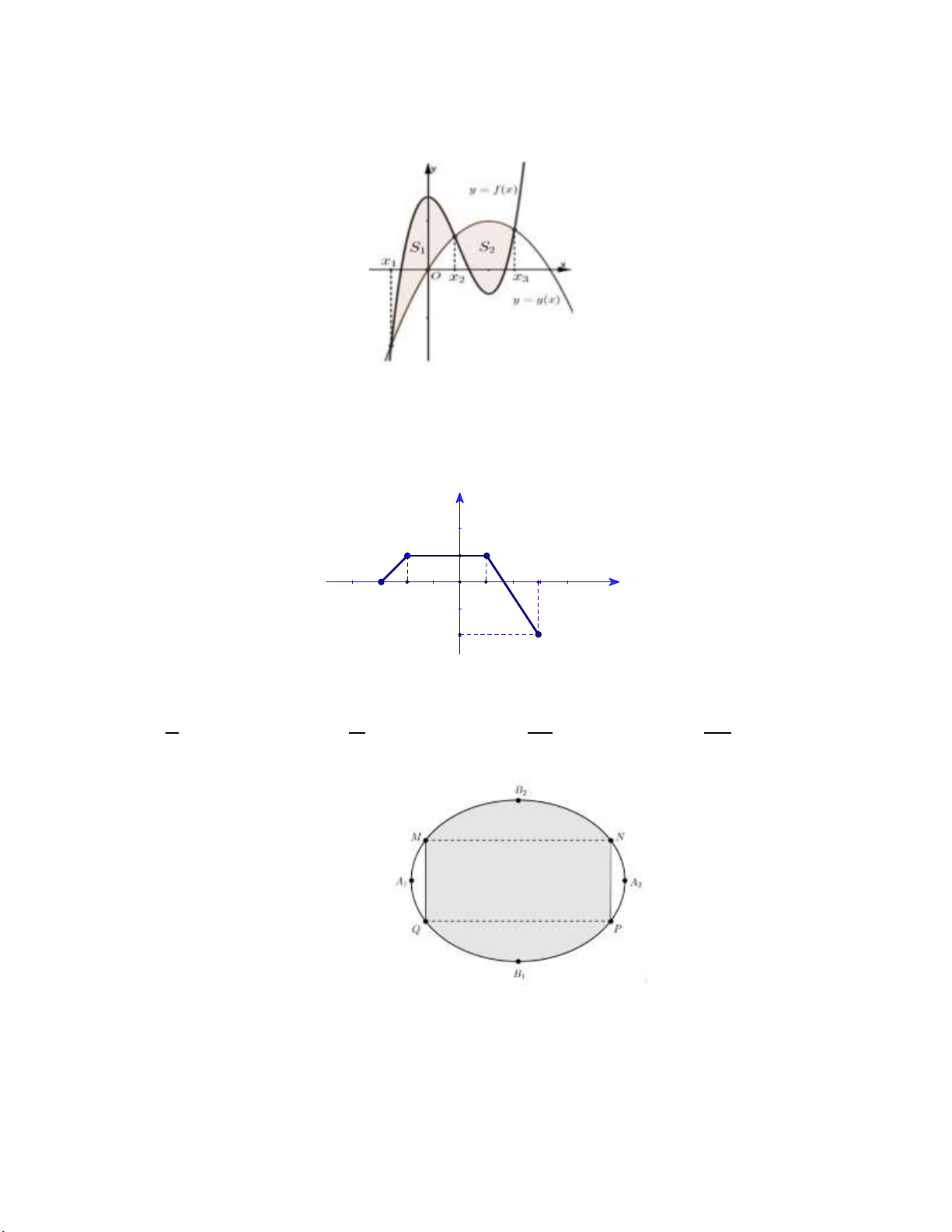
Câu 15: Cho hai hàm số f x 2 2
ax bx cx  2 và g x 2  dx x
e  2 ( a , b , c , d , e  ). Biết rằng
đồ thị của hàm số y f x và y g x cắt nhau tại ba điểm có hoành độ lần lượt là 2  ; 1  ; 1 (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 37 13 9 37 A. B. C. D. 6 2 2 12
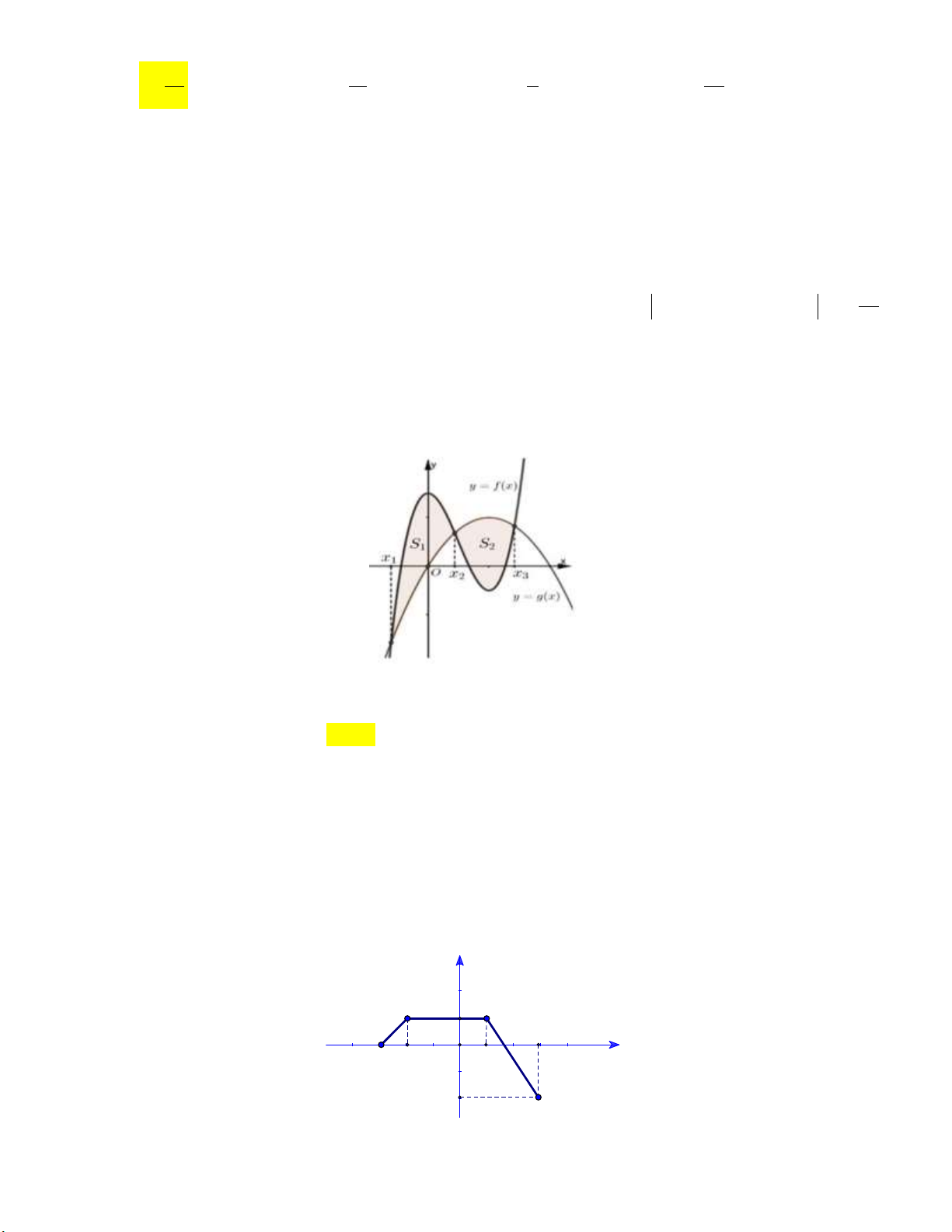
Câu 16: Cho hai hàm số f x 3 2
ax bx cx d , a  0 và g x 2
mx nx p , m  0 có đồ thị cắt
nhau tại 3 điểm có hoành độ x , x , x . Kí hiệu S , S lần lượt là diện tích các hình phẳng giới 1 2 3 1 2
hạn bởi đồ thị hàm số y f x và y g x (tham khỏa hình vẽ) 3 x
Biết S  10 , S  7 . Khi đó, g
  x f xdx bằng 1 2  1 x A. 3 . B. 3  . C. 17 . D. 17 .
Câu 17: Cho hàm số f x có đồ thị trên đoạn 3; 
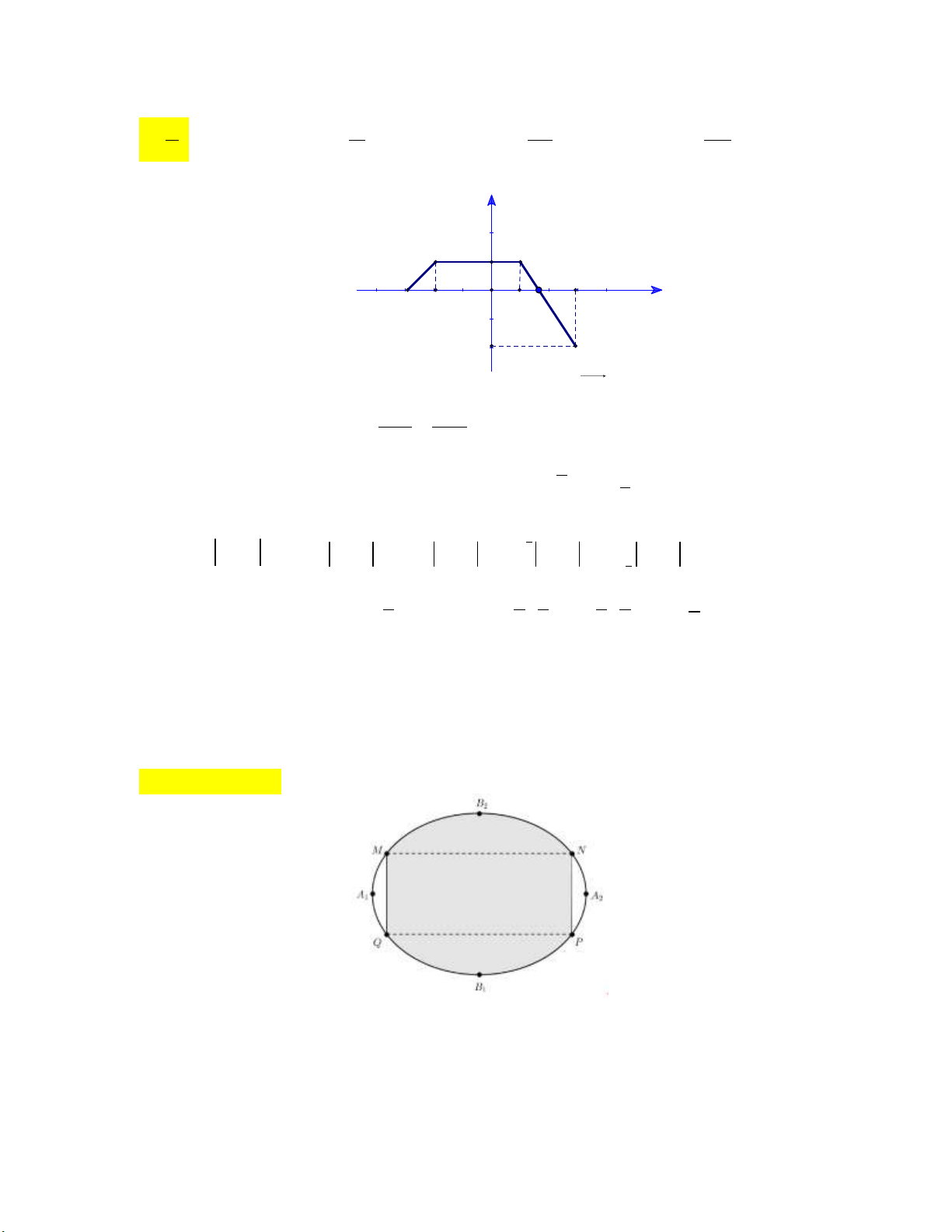
3 là đường gấp khúc ABCD như hình vẽ. y B 1 C 3 A x -2 1 -2 D 3 Tính f  xdx . 3  5 35 5  35  A. . B. . C. . D. . 2 6 2 6
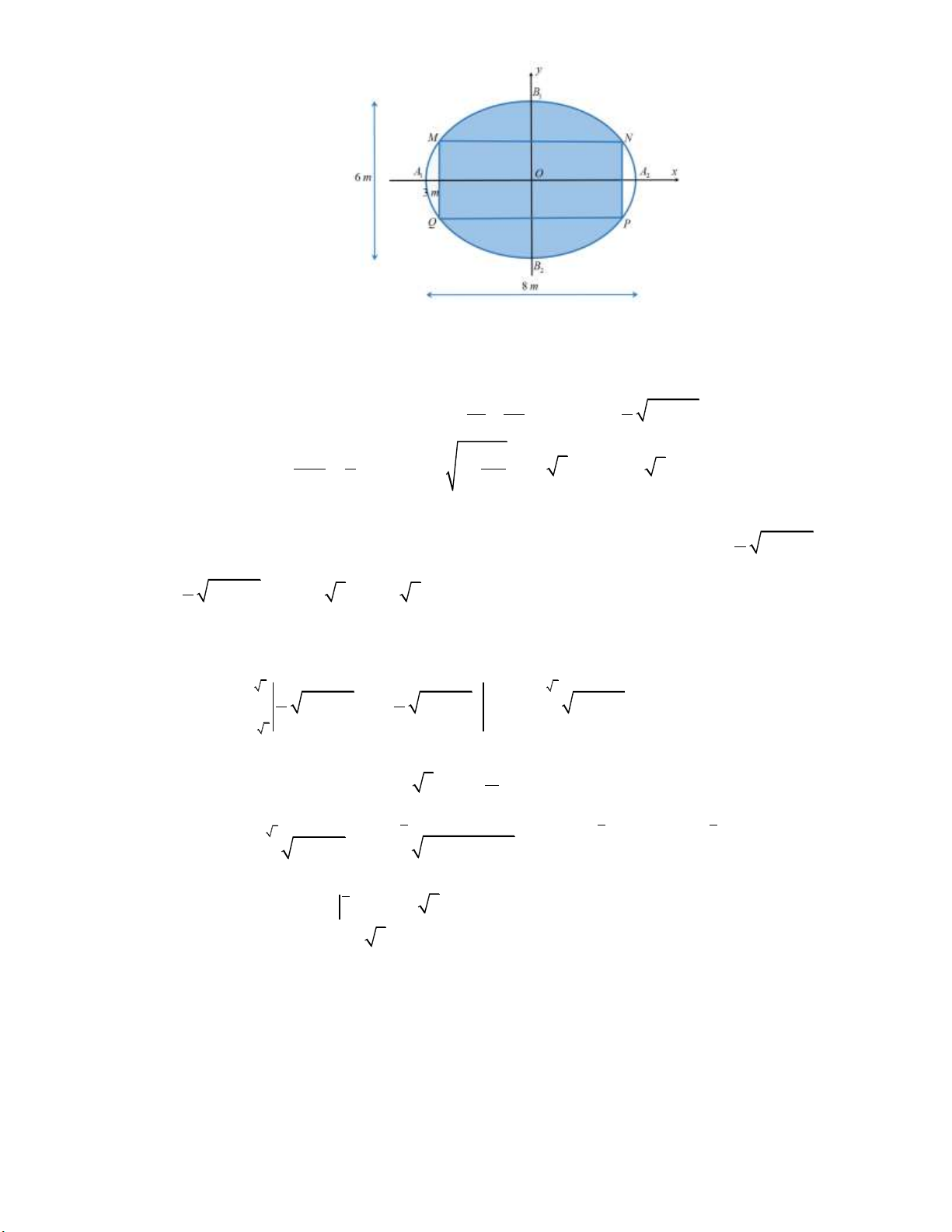
Câu 18: Một biển quảng cáo có dạng hình elip với bốn đỉnh A , A , B , B như hình vẽ bên dưới: 1 2 1 2
Biết chi phí để sơn phần tô đậm là 200.000 đồng/ 2
m và phần còn lại là 100.000 đồng/ 2 m . Hỏi
số tiền để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết A A  8 ,
m B B  6m và tứ 1 2 1 2
giác MNPQ là hình chữ nhật có MQ  3m . A. 7 322 000 đồng. B. 7 213000 đồng. C. 5526 000 đồng. D. 5782 000 đồng.
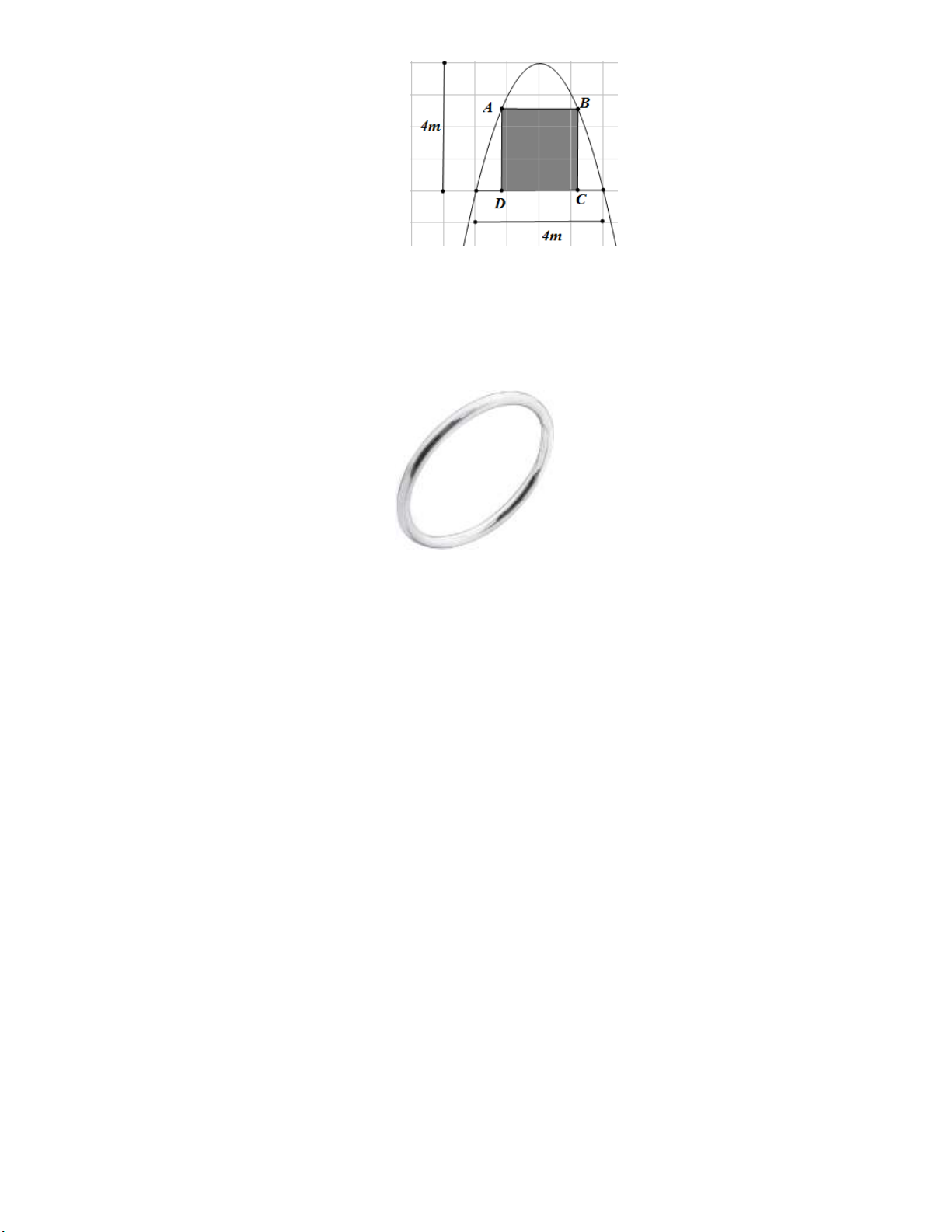
Câu 19: Trong đợt hội trại “Khi tôi 18” được tổ chức tại trường THPT X. Đoàn trường có thực hiện một
dự án ảnh trưng bày trên một Pano có dạng hình parabol như hình vẽ.
Biết rằng Đoàn trường X sẽ yêu cầu các lớp gửi ảnh dự thi và dán lên khu vực hình chữ nhật
ABCD, phần còn lại sẽ được tranh trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000 đồng cho một 2
m . Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên Pano sẽ là bao nhiêu ? A. 1.230.000 đồng. B. 900.000 đồng. C. 1.232.000 đồng. D. 902.000 đồng.
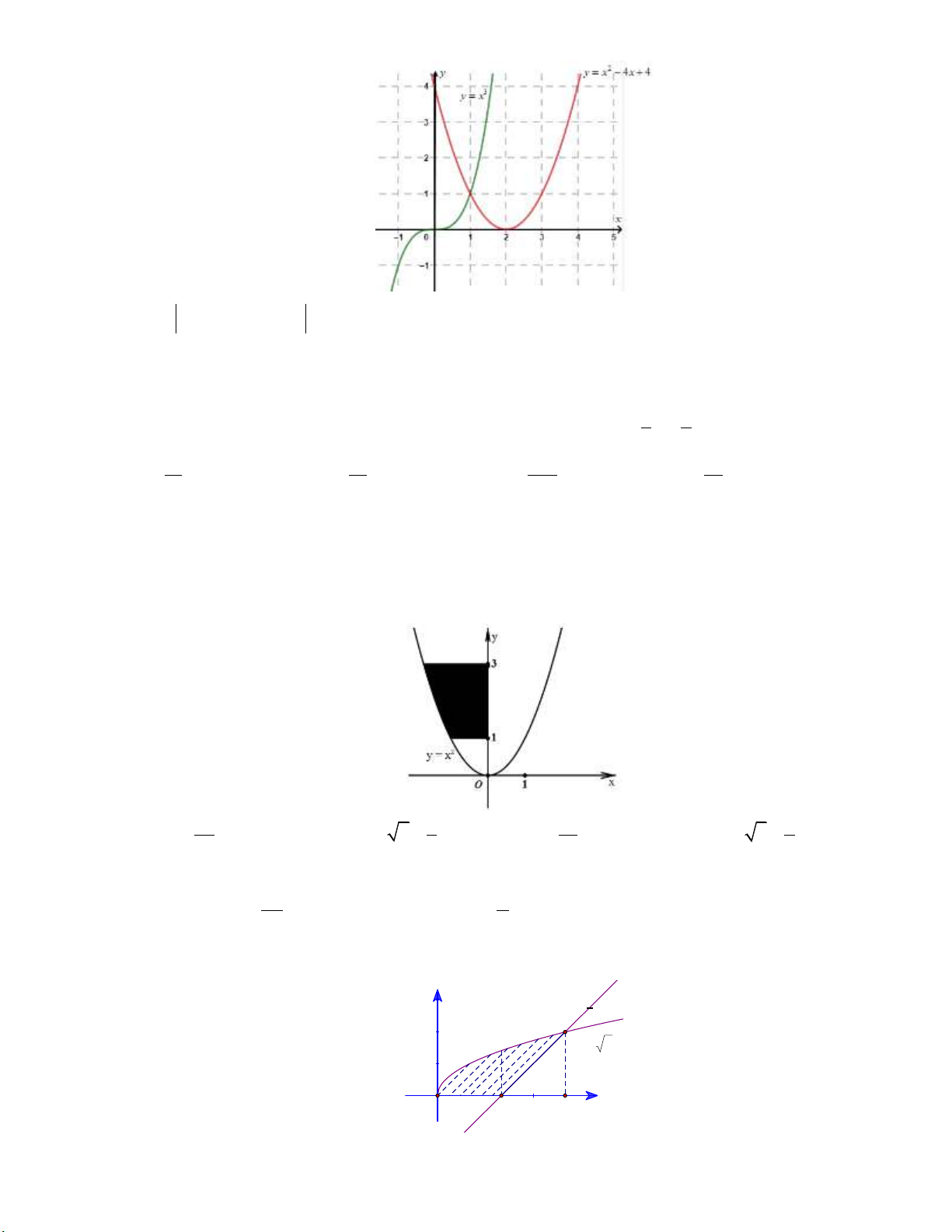
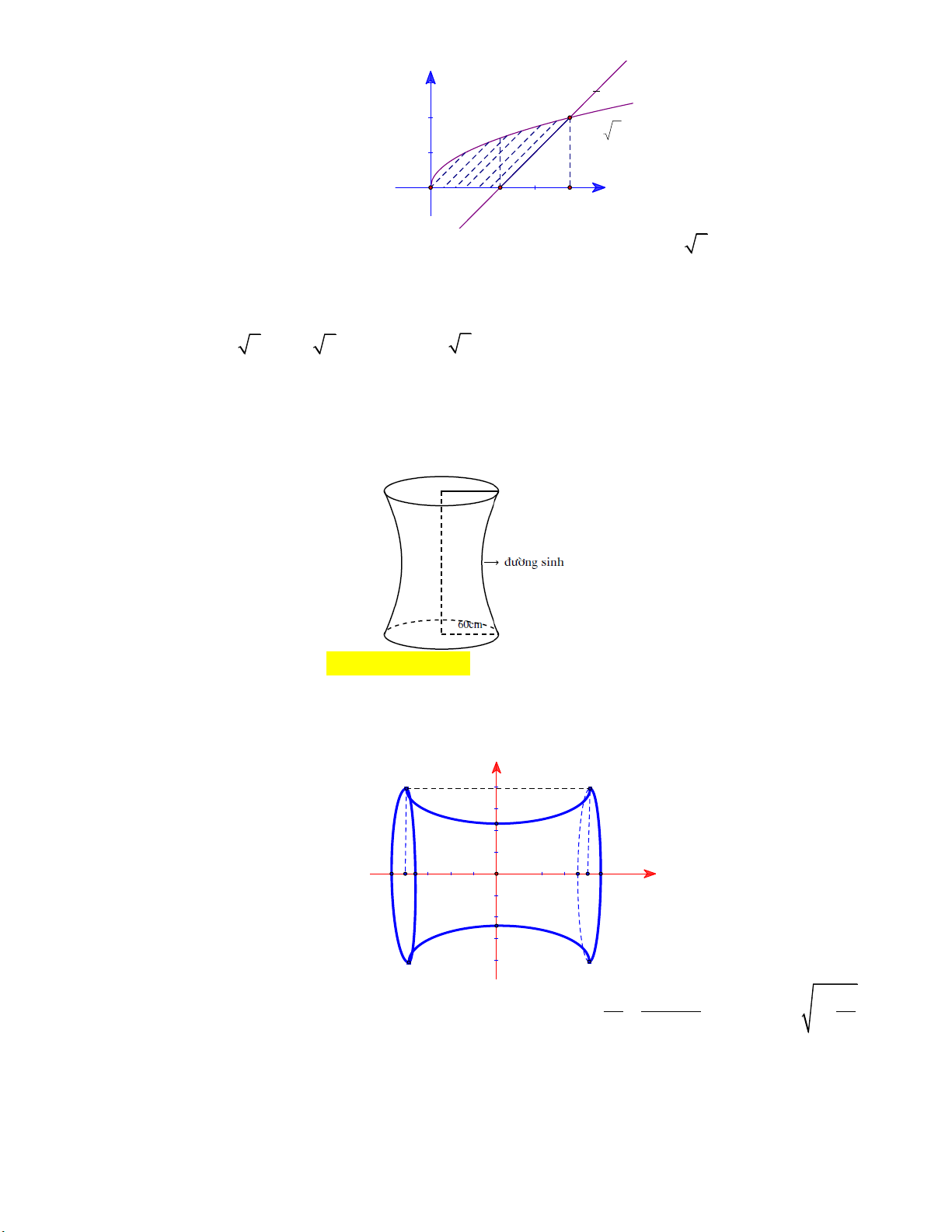
Câu 20: Người ta làm một chiếc vòng tròn bằng bạc, biết đường kính ngoài của chiếc vòng bạc là
70 cm , đường kính trong là 50 cm ( tham khảo hình vẽ bên dưới).
Thể tích của vòng bạc là A. 2 3 1500 cm . B. 2 3 9000 cm . C. 3 1500 cm . D. 3 1500 cm .
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông øng dông tÝch ph©n
PHIẾU ÔN TẬP SỐ 01
LỜI GIẢI CHI TIẾT
Câu 1: Cho hình phẳng D giới hạn bởi đường cong y  2  sin x , trục hoành và các đường thẳng
x  0 , x   . Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng bao nhiêu?
A. V  2   1 .
B. V  2    1 . C. 2 V  2 . D. V  2 . Lời giải:   2 
Ta có: V    2  sin x  dx   2  sin xdx   2x  cos x  2    1 . 0 0 0
Chọn đáp án B.
Câu 2: Gọi S là diện tích của hình phẳng giới hạn bởi các đường 2x y
, y  0 , x  0 , x  2 . Mệnh đề
nào dưới đây đúng? 2 2 2 2 A.  2x S dx  B. 2   2 x S dx  C. 2  2 x S dx  D.   2x S dx  0 0 0 0 Lời giải: 2 2  2x d  2x S x dx   (do 2x  0, x  0;2 ). 0 0
Chọn đáp án A.
Câu 3: Cho hình phẳng  H  giới hạn bởi các đường 2
y x  3 , y  0 , x  0 , x  2 . Gọi V là thể tích
của khối tròn xoay được tạo thành khi quay  H  xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2 A. V    2 x  3 d .
x B. V    2 x  3d .
x C. V   2 x  3 d .
x D. V   2 x  3d . x 0 0 0 0 Lời giải:
Thể tích của khối tròn xoay được tạo thành khi quay  H  xung quanh trục Ox là: 2
V   x  32 2 dx . 0
Chọn đáp án A.
Câu 4: Gọi S là diện tích hình phẳng  H  giới hạn bởi các đường y f x , trục hoành và hai đường 0 2
thẳng x  1 , x  2 . Đặt a f
 xdx,b f
 xdx , mệnh đề nào sau đây đúng? 1  0 A. S b  . a B. S b  . a
C. S  b  . a
D. S  b  . a Lời giải: Ta có: 2 0 2 0 2 S f
 x dx f
 x dxf
 x dx   f
 xdxf
 xdx  ab . 1  1  0 1  0
Chọn đáp án A.
Câu 5: Cho hình phẳng (H ) (phần gạch sọc) như hình vẽ bên dưới:
Tính diện tích hình phẳng (H ). 9 9 3 9 A. 1. B. ln 3  2. C. ln 3  . D. ln 3  2. 2 2 2 2 Lời giải: 3
Ta có: diện tích cần tìm là S x ln xdx  1  1 du dx u   ln x  2 3 x 2 2 x 3 1 x 9 1 x 3 9 Đặt    khi đó: S  ln x dx  ln 3   ln 3 2.  2 dv xdx x  2 1 x 2 2 2 2 1 2 v  1  2
Chọn đáp án B.
Câu 6: Viết công thức tính thể tích V của vật thể T giới hạn bởi hai mặt phẳng x  2019 và x  2020 ,
vật thể T bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ
x 2019  x  2020 có thiết diện là một hình vuông độ dài cạnh là a . 2020 2020 2020 2020 A. 2 V   a d  x . B. V   a d  x . C. 2 V a d  x . D. V  d  a x . 2019 2019 2019 2019 Lời giải:
Hình vuông có độ dài cạnh a có diện tích là   2 S x a 2020
Thể tích của vật thể T là 2 V a dx. 2019
Chọn đáp án C.
Câu 7: Gọi  H  là hình phẳng giới hạn bởi các đường 2
y  x  3x, y  0, x  0 và x  3 . Quay hình
H  quanh trục Ox , ta được khối tròn xoay có thể tích bằng 27 9 81 5 A. . B. . C. . D. . 10 2 10 2 Lời giải:
Khi quay hình  H  quanh trục Ox , ta được khối tròn xoay có thể tích bằng 3 3 3 5 4 2  x 3x  81 V    2
x  3x dx    4 3 2
x  6x  9x  3 dx      3x   .  5 2  10 0 0 0
Chọn đáp án C. Câu 8: Cho hàm số 4 2
y x  3x m có đồ thị là C
( m là tham số thực). Giả sử C cắt trục Ox m m
tại 4 điểm phân biệt. Gọi S , S là diện tích của hai hình phẳng nằm dưới trục Ox và S là diện 1 2 3
tích của hình phẳng nằm trên trục Ox được tạo bởi C
với trục Ox . Biết rằng tồn tại duy m a a
nhất giá trị của m
(với a,b  * và
tối giản) để S S S . Giá trị của 2a b bằng b b 1 2 3 A. 3 . B. 4  . C. 6 . D. 2  . Lời giải:
Gọi 4 nghiệm của 4 2
y x  3x m  0 lần lượt là  t ,  t , t , t với 0  t t . 2 1 1 2 1 2 t2 5   t x Để 2
S S S thì   4 2
x  3x m 3 dx  0    x mx   0 1 2 3  5    t t 2 2  t 5 2 2 3 2  tt    t  2 2
m t  0  t  t m  0 (do t  0) 
t m  0 (1) 2 2 2 2 2 2 5  5  5
Vì t là nghiệm của 4 2
x  3x m  0 2
t  3t m  0 (2) 2 2 2 2 t Từ (1) và (2) suy ra: 2 2
t t  3t  0 2 2 2 5 4   4   5 2  t
 2t  0  t .
t  2  0  t do t  0 . 2 2 2  2  2  2  5  5  2 5 25 15 5 Thay t  vào (2) ta được 
m  0  m  . Do đó a  5;b  4 2a b  6 . 2 2 4 2 4
Chọn đáp án C.
Câu 9: Diện tích hình phẳng giới hạn bởi hai đường 2
y x  1 và y x  1 bằng  13 13 1 A.  B.  C.  D.  6 6 6 6 Lời giải: x  0
Phương trình hoành độ giao điểm hai đường là: 2
x 1  x 1  .  x  1 1 1
Diện tích hình phẳng giới hạn bởi hai đường là 2 S
x x dx  .  6 0
Chọn đáp án D.
Câu 10: Cho H là hình phẳng giới hạn bởi parabol 2
y  3x , cung tròn có phương trình 2 y  4  x
và trục hoành . Diện tích của H bằng 4  3 4  3 4  2 3  3 5 3  2 A. . B. . C. . D. . 12 6 6 3 Lời giải:
Phương trình hoành độ giao điểm giữa parabol và cung tròn ta được 2 2
3x  4  x x  1 
với 0  x  2 nên ta có x  1 1 1 2 2 2 3 3 Ta có diện tích 2 2 3 2 2 S  3x dx  4  x dx x  4  x dx   4      x dx 3 3 0 1 1 1 0  
Đặt : x  2sin t  dx  2costdt; x  1  t
; x  2  t  6 2  2 3  1  4  3  S
 2 t  sin 2t  .   3  2   6 6
Chọn đáp án B.
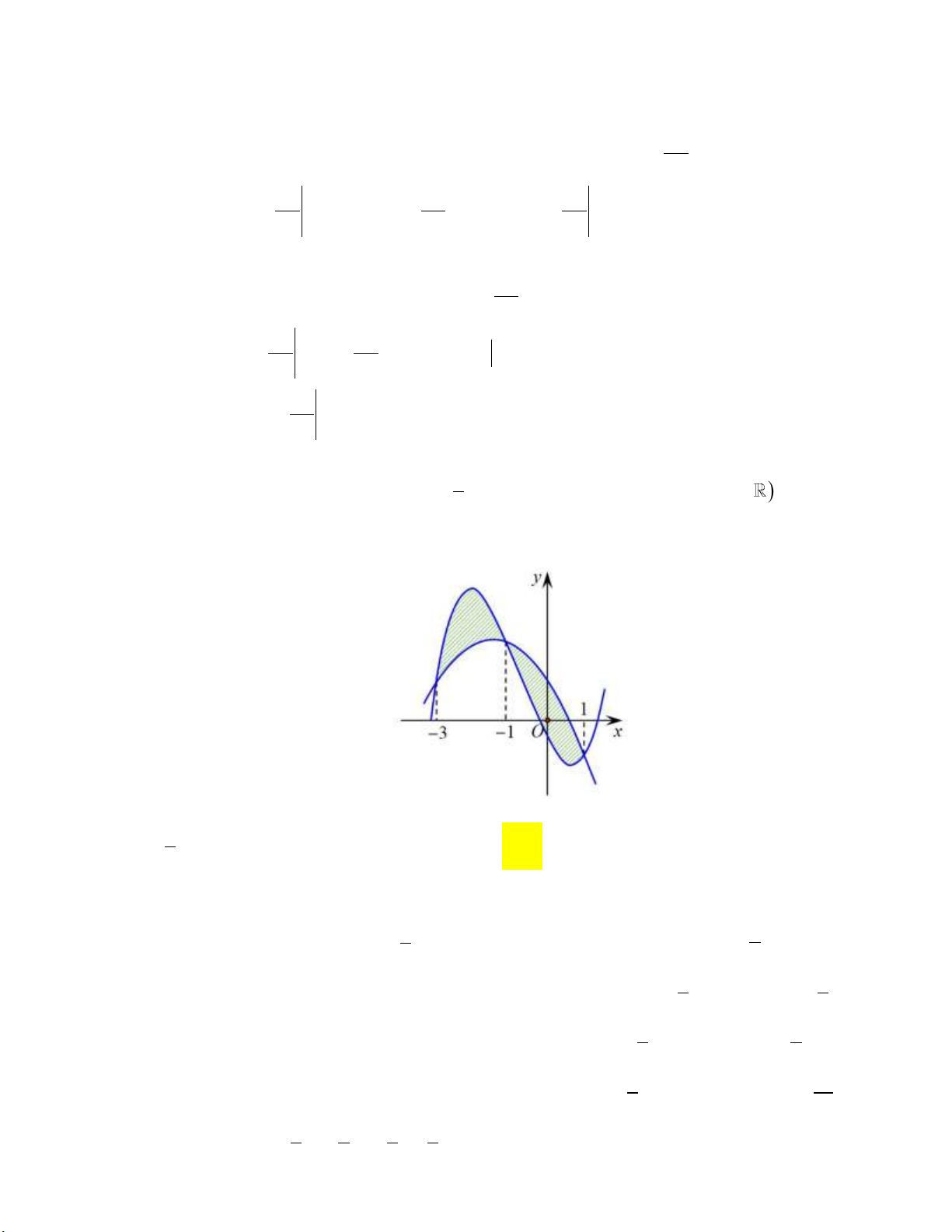
Câu 11: Cho hàm số y f x liên tục trên
. Đồ thị hàm số y f  x như hình vẽ bên dưới:
Đặt g x  f x   x  2 2
1 . Bất phương trình f x   x  2 2
1  m nghiệm đúng với mọi x  3  ;  3 khi và chỉ khi
A. m g 3 . B. m g  3   .
C. m g   1 . D. m g  3   . Lời giải: 2
Có f x   x  2 2 1  m , x   3  ; 
3  m g x  2 f x   x   1 , x   3  ;  3
m  min g x .  3  ;  3
Ta có g x  0  2 f  x  2 x  
1  0  f  x  x 1  x  3, x  1, x  3 .
Vì kẻ đường thẳng y x 1 cắt đồ thị hàm số y f  x tại các điểm có hoành độ x  3 ,
x  1 , x  3 như sau:
Dựa vào bảng biến thiên ta có min g x  ming  3  , g 3.  3  ;  3
Quan sát diện tích của hai hình phẳng trên hình vẽ ta có 1 3 1 3 S
f x x 1 dx S
f x x 1 dx  
  f x x  
1 dx    f  x   x     1 dx 1     2     3  1 3  1 1 3 1 3 1  g  x 1 dx   g
 xdx g
 xdx   g  xdx 2 2 3  1 3  1  g   1  g  3    g  
1  g 3  g  3
   g 3  min g x  g  3
 .Vậy m g  3   .  3   ;3
Chọn đáp án B.
Câu 12: Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển
động chậm dần đều với vận tốc v t   5
t 10 (m/s), trong đó t là khoảng thời gian tính bằng
giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 0,2m. B. 2m. C. 10m. D. 20m. Lời giải:
Xét phương trình 5t 10  0  t  2. Do vậy, kể từ lúc người lái đạp phanh thì sau 2s ô tô dừng hẳn.
Quãng đường ô tô đi được kể từ lúc người lái đạp phanh đến khi ô tô dừng hẳn là 2 s     5  t 10 5 2 2
dt   t 10t 10 .   m  2  0 0
Chọn đáp án C.
Câu 13: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y
x ; tiếp tuyến với đồ thị tại M 4; 2 và trục hoành là 3 2 8 1 A. . B. . C. . D. . 8 3 3 3 Lời giải: 1 1 Xét hàm số y
x ta có y '   y '4  . 2 x 4 1 1
Phương trình tiếp tuyến của đồ thị tại điểm M 4; 2 là y   x  4  2  y x 1 . 4 4 4 1  1  8
Diện tích hình phẳng cần tìm là S SS  .4.1
x 1 x dx   . OAM OMB   2  4  3 0
Chọn đáp án C.
Câu 14: Cho hình phẳng D giới hạn bởi đường cong x
y e , trục hoành và các đường thẳng x  0 ,
x  1 . Khối tròn xoay tạo thanh khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 2    2e     2e   e 1 2 e 1 1 A. V  . B. V  . C. V  . D. V  . 2 2 2 2 Lời giải: 1 1  e 1 x 1 2 2 x  2 
V   e dx  e   . 2 2 0 0
Chọn đáp án D.
Câu 15: Cho hai hàm số f x 2 2
ax bx cx  2 và g x 2  dx x
e  2 ( a , b , c , d , e  ). Biết rằng
đồ thị của hàm số y f x và y g x cắt nhau tại ba điểm có hoành độ lần lượt là 2  ; 1  ; 1 (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 37 13 9 37 A. B. C. D. 6 2 2 12 Lời giải:
Phương trình hoành độ giao điểm của đồ thị f x và g x là 3 2 2 3
ax bx cx
dx x   a  b d  2 2 3 2
x  c ex  4  0. *
Do đồ thị của hai hàm số cắt nhau tại ba điểm suy ra phương trình * có ba nghiệm x  2 ;
x  1; x  1. Ta được 3
ax  b d  2
x  c ex  4  k x  2 x   1  x   1 . 1 37
Khi đó 4  2k k  2 . Vậy diện tích hình phẳng cần tìm là
2 x  2 x   1  x    1 dx  . 6 2 
Chọn đáp án A.
Câu 16: Cho hai hàm số f x 3 2
ax bx cx d , a  0 và g x 2
mx nx p , m  0 có đồ thị cắt
nhau tại 3 điểm có hoành độ x , x , x . Kí hiệu S , S lần lượt là diện tích các hình phẳng giới 1 2 3 1 2
hạn bởi đồ thị hàm số y f x và y g x (tham khỏa hình vẽ) 3 x
Biết S  10 , S  7 . Khi đó, g
  x f xdx bằng 1 2  1 x A. 3 . B. 3  . C. 17 . D. 17 . Lời giải: x 2 x 3
Theo đề bài ta có 10  S   f x g x  dx
, 7  S  g x f x  dx  . 2      1       1 x 2 x 3 x x x 2 3 Suy ra g
  x f xdx  g
  x f xdx g
  x f xdx  S S  1  0  7  3   1 2 1 x 1 x 2 x
Chọn đáp án B.
Câu 17: Cho hàm số f x có đồ thị trên đoạn 3; 
3 là đường gấp khúc ABCD như hình vẽ. y B 1 C 3 A x -2 1 -2 D 3 Tính f  xdx . 3  5 35 5  35  A. . B. . C. . D. . 2 6 2 6 Lời giải: y B 1 C E A A 3 2 1 A A3 x -2 1 -2 D
Phương trình đường thẳng CD đi qua C 1; 
1 và nhận CD  2; 3
  làm véctơ chỉ phương. x y
Phương trình chính tắc CD 1 1 :   3
x  2y  5  . 2 3   5  3
x  2y  5 x   5 
Đặt E  CD  Ox . Ta được    3  E ; 0   .  y  0   3   y  0 3 5 2  1 3 Do đó
f x dx   f
 x dxf  x 3 dx f
 x dxf x dx 5   3  3  2  1 3  1 1  2  1  4  SSSS  5 11  31  1   2  AB         . 1 A 1 A B 2 CA 2 A CE ED 3 A 2 2  3  2  3  2
Chọn đáp án A.
Câu 18: Một biển quảng cáo có dạng hình elip với bốn đỉnh A , A , B , B như hình vẽ bên. Biết chi phí 1 2 1 2
để sơn phần tô đậm là 200.000 đồng/ 2
m và phần còn lại là 100.000 đồng/ 2
m . Hỏi số tiền để
sơn theo cách trên gần nhất với số tiền nào dưới đây, biết A A  8 ,
m B B  6m và tứ giác 1 2 1 2
MNPQ là hình chữ nhật có MQ  3m . A. 7 322 000 đồng. B. 7 213000 đồng. C. 5526 000 đồng. D. 5782 000 đồng. Lời giải:
Gắn hệ trục tọa độ Oxy có A A trùng với trục Ox , B B trùng với trục Oy , gốc tọa độ 1 2 1 2
O A A B B (như hình vẽ). 1 2 1 2
Elip có độ dài trục lớn 2a A A  8  a  4 m , độ dài trục nhỏ 2b B B  6  b  3 m . 1 2 1 2 2 2 x y 3
Suy ra phương trình chính tắc của elip là  1 2  y   16  x . Trong đó: 2 2 4 3 4 MQ 2 y Do MQ  3 3  y    x  4  1 M   2  3  x  2 3 . M 2 2 M 9 N
Gọi S là diện tích phần tô đậm của elip, S là diện tích phần không bị tô đậm của elip và S là 1 2 3
diện tích elip. Suy ra S là diện tích hình phẳng giới hạn bởi các đường 2 y  16  x , 1 4 3 2 y  
16  x , x  2  3 , x  2 3 4 Ta có:
+ S   ab    2 12 m  . 2 3 3  3  2 3 + 2 2 S  16  x   16  x dx  2 = 3 16  x dx  . 1   4  4  2  3 0
Đặt x  4 sin t  dx  4 costdt . 
Khi x  0  t  0 . Khi x  2 3  t  3    2 3 3 3 3 2  S = 3 16  x dx =  2 3
16 16 sin t.4 cos tdt   2 48 cos tdt   24  1 os2 c t  dt 1 0 0 0 0 
 24t  12sin 2t 3     2 8 6 3 m  . 0
S S S  4  6 3  2 m . 2 1 
Suy ra chi phí để sơn biển quảng cáo là: 200000.S 100000.S  7322416 (đồng). 1 2
Vậy số tiền để sơn biển quảng cáo gần nhất với 7 322 000 đồng.
Chọn đáp án A.
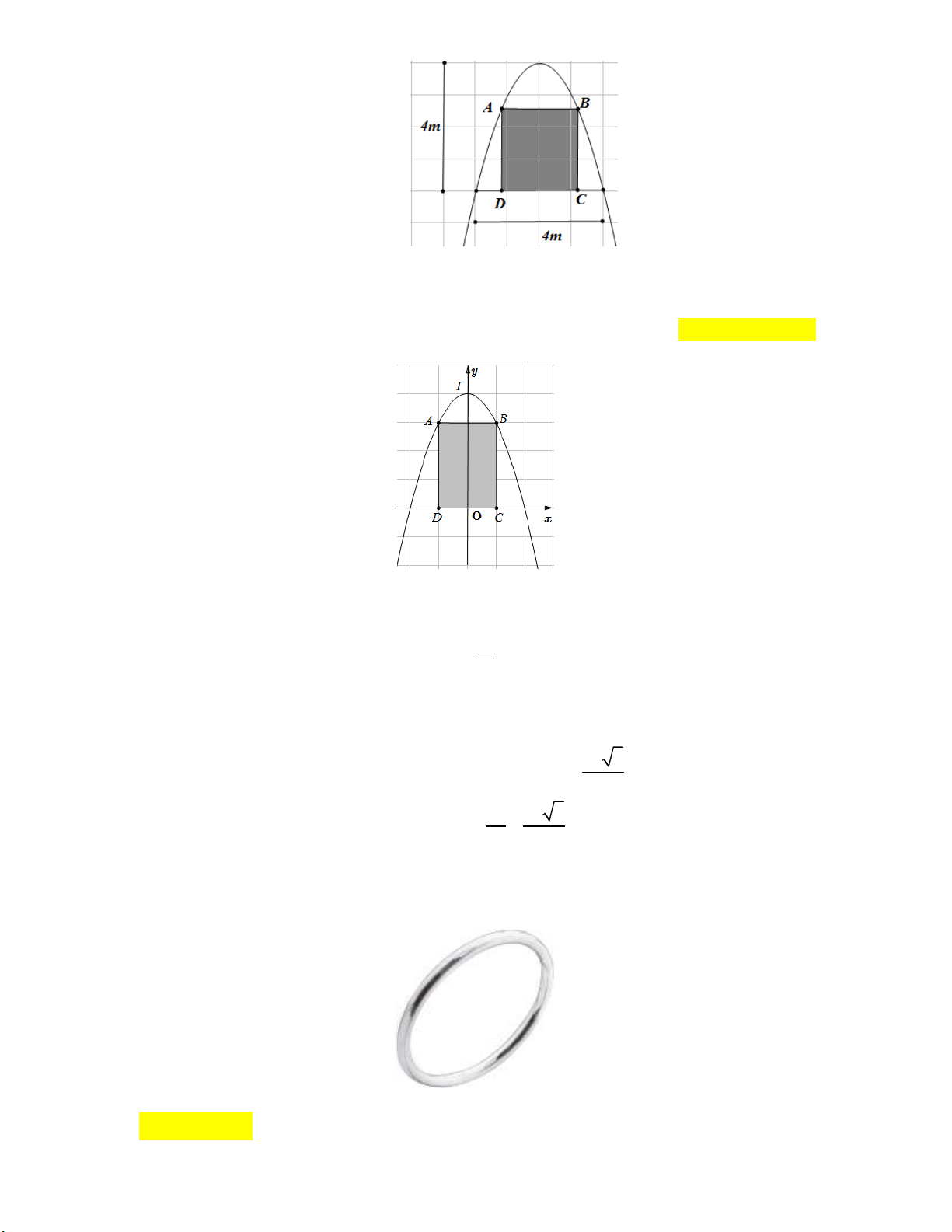
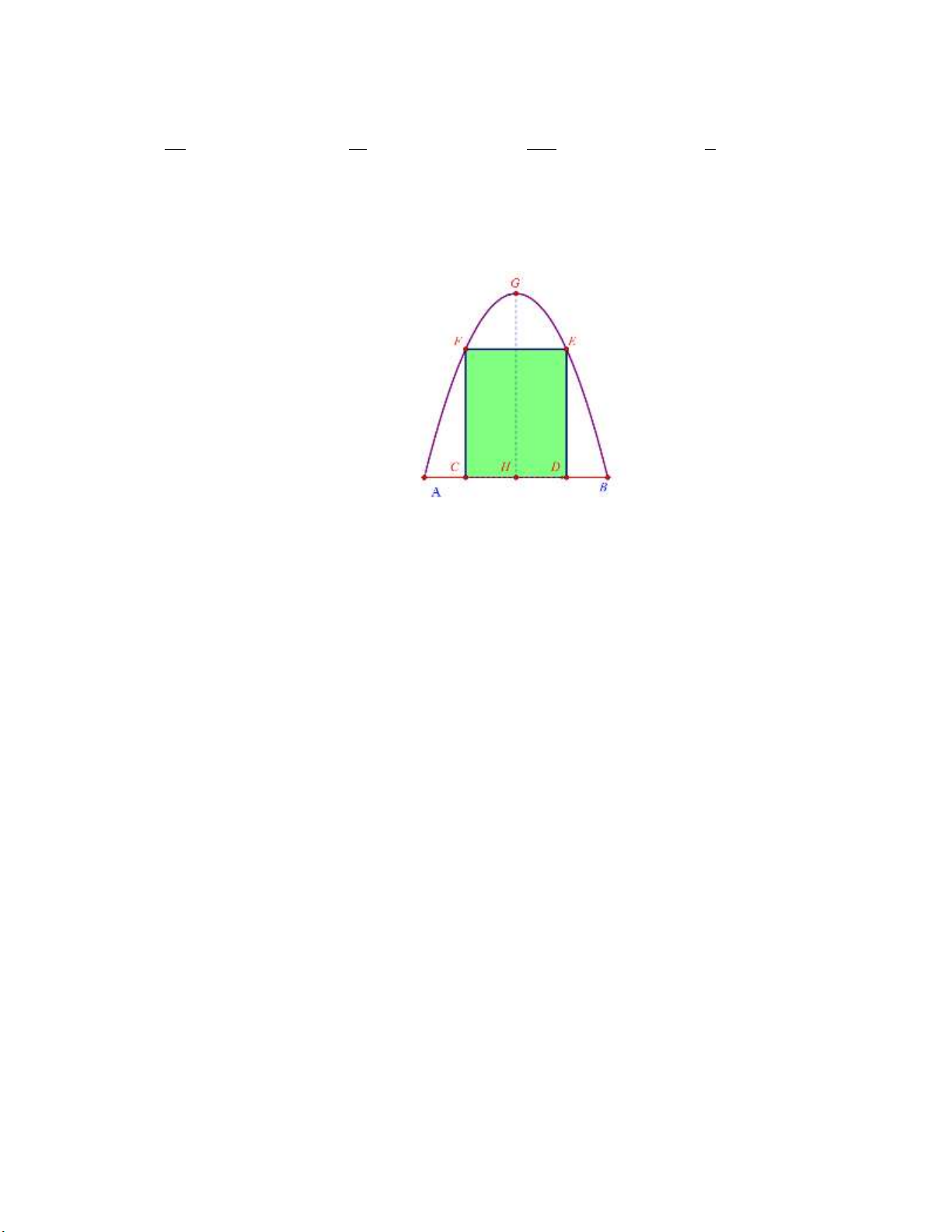
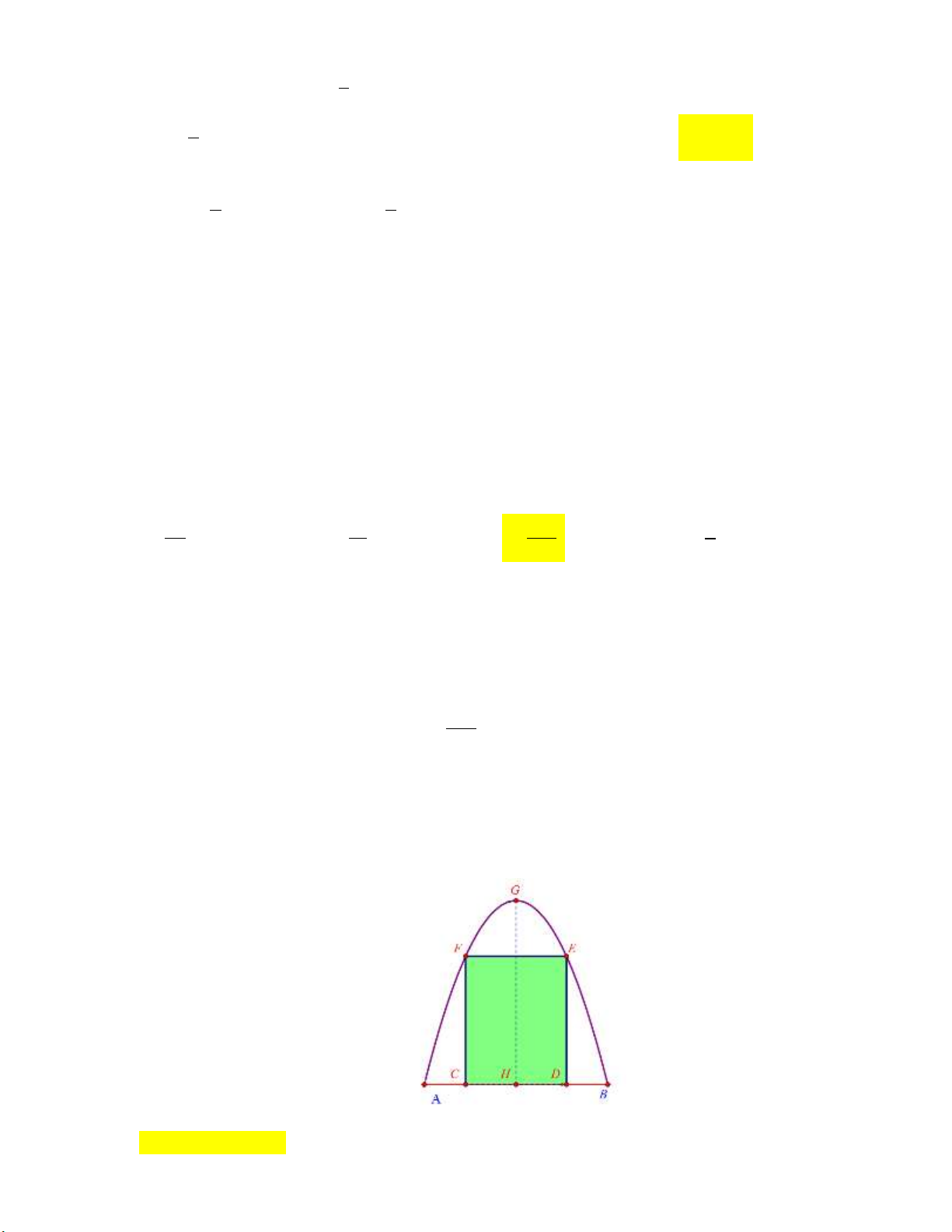
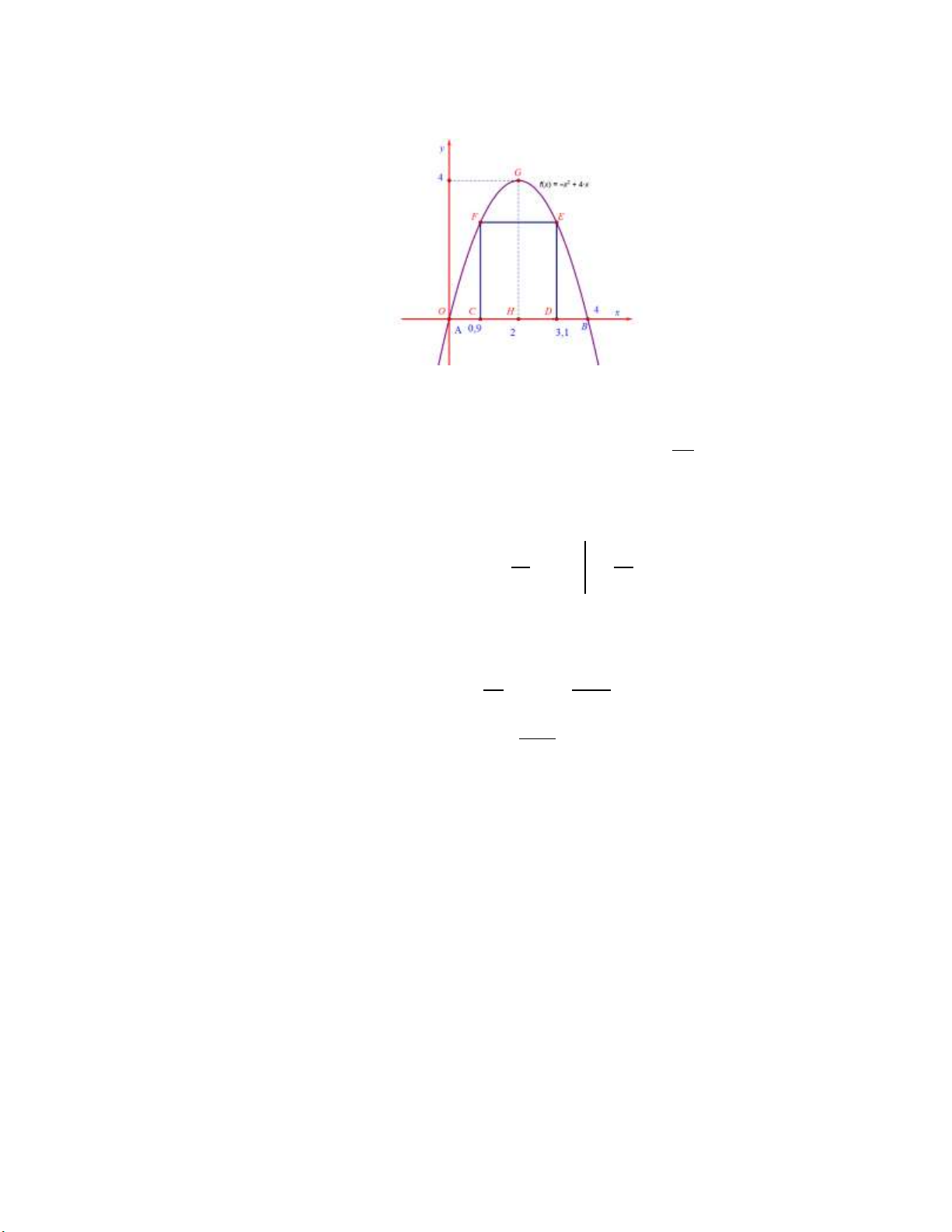
Câu 19: Trong đợt hội trại “Khi tôi 18” được tổ chức tại trường THPT X. Đoàn trường có thực hiện một
dự án ảnh trưng bày trên một Pano có dạng hình parabol như hình vẽ.
Biết rằng Đoàn trường X sẽ yêu cầu các lớp gửi ảnh dự thi và dán lên khu vực hình chữ nhật
ABCD, phần còn lại sẽ được tranh trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000 đồng cho một 2
m . Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên Pano sẽ là bao nhiêu ? A. 1.230.000 đồng. B. 900.000 đồng. C. 1.232.000 đồng. D. 902.000 đồng. Lời giải:
Chọn hệ trục tọa độ Oxy như hình vẽ, khi đó ta được phương trình của parabol là 2
y  x  4.
Gọi C x   x    D x B  2
x x   A 2 ; 0 0 2 ; 0 , ; 4 ,  ;
x x  4. 2 32
Ta có diện tích của Pano là  2
x  4dx    2 m . 3 2 
Diện tích hình chữ nhật ABCD là S
CD BC x  2 . 2 . x  4. ABCD
Chi phí dán hoa văn thấp nhất khi và chỉ khi diện tích hình chữ nhật ABCD lớn nhất. 32 3
Xét hàm số f x x  2 ( )
2 . x  4, x 0;2 có max f (x)  . x   0;2 9  32 32 3 
Chi phí thấp nhất cho việc dán hoa văn là   .200000  902.000   . 3 9  
Chọn đáp án D.
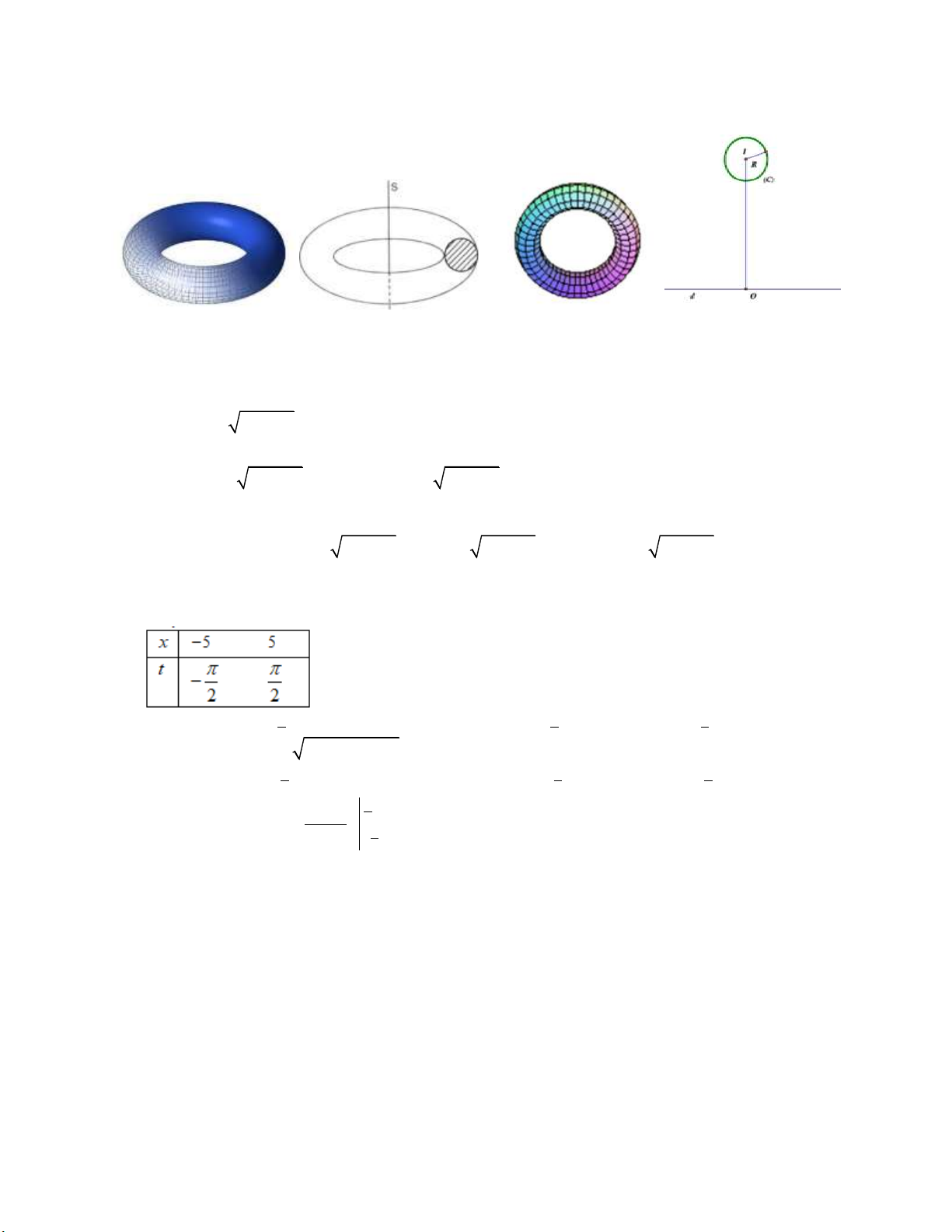
Câu 20: Người ta làm một chiếc vòng tròn bằng bạc, biết đường kính ngoài của chiếc vòng bạc là
70 cm , đường kính trong là 50 cm ( tham khảo hình vẽ bên dưới).
Thể tích của vòng bạc là A. 2 3 1500 cm . B. 2 3 9000 cm . C. 3 1500 cm . D. 3 1500 cm . Lời giải:
Ta có bán kính ngoài của chiếc vòng bạc là 35 cm , bán kính trong là 25 cm .
Để tính thể tích của vòng bạc ta coi nó là hình tròn xoay sinh ra bằng cách quay một hình tròn xung quanh trục . Ox
Bán kính của hình tròn này bằng R  35  25 : 2  5c . m
Tâm của hình tròn là I 0;30 . 2
Phương trình của đường tròn là 2
x   y  30  25 C  . 2
y  30  25  x .
Khi đó thể tích của vòng bạc được sinh ra bởi hình phẳng tạo bởi 2 đường cong f x 2
 30  25  x và f x  30  25  x , x  5  ;5 quay quanh trục . Ox 2   2 1
Vậy thể tích của vòng bạc bằng: 5 5   V   y dx   
 30 25 x  30 25 x  5 2 2 2 2 2 2 dx  120 25  x d . x     5  5  5 
Đặt x  5sin t dx  5 cos t.dt. Đổi cận :    2 2 2 Khi đó 2 2 V  120
25  25sin t .5cos t.dt  120.25
cos t.dt  60.25  
 1cos2t.dt       2 2 2   sin 2t  2 3 2 1500 t  1500 cm .     2   2
Chọn đáp án A.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông øng dông tÝch ph©n
PHIẾU ÔN TẬP SỐ 02 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Câu 1: Cho hàm số f x liên tục trên
. Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x, y  0, x  1
 và x  4 . Mệnh đề nào dưới đây là đúng? 1 4 1 4
A. S   f xdx  
f xdx . B. S
f x dx  
f xdx . 1  1 1  1 1 4 1 4 C. S
f x dx  
f xdx .
D. S   f xdx  
f xdx . 1  1 1  1
Câu 2: Tính thể tích của vật thể nằm giữa hai mặt phẳng x  1 và x  1 biết rằng thiết diện của vật
thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x  1   x   1 là một hình vuông có cạnh bằng 4 1 x . 8 1 A. . B. 2 . C. 4 . D. . 5 4
Câu 3: Cho hàm số y f (x) liên tục trên
và có đồ thị như hình vẽ sau: 4 Giá trị của ( )d  f x x bằng 4  A. 10. B. 4. C. 12. D. 8.
Câu 4: Diện tích hình phẳng giới hạn bởi hai đường 2
y x  4 và y  2x  4 bằng 4 4 A. 36 . B. . C. . D. 36 . 3 3
Câu 5: Cho hai hàm số f x 3 2
ax bx cx d , a  0 và g x 2
mx nx p , m  0 có đồ thị cắt
nhau tại 3 điểm có hoành độ x , x , x . 1 2 3
Kí hiệu S , S lần lượt là diện tích các hình phẳng giới hạn bởi đồ thị hàm số y f x và 1 2 3 x
y g x . Biết S  10 , S  7 . Khi đó, g
  x f xdx bằng 1 2  1 x A. 3 . B. 3  . C. 17 . D. 17 .
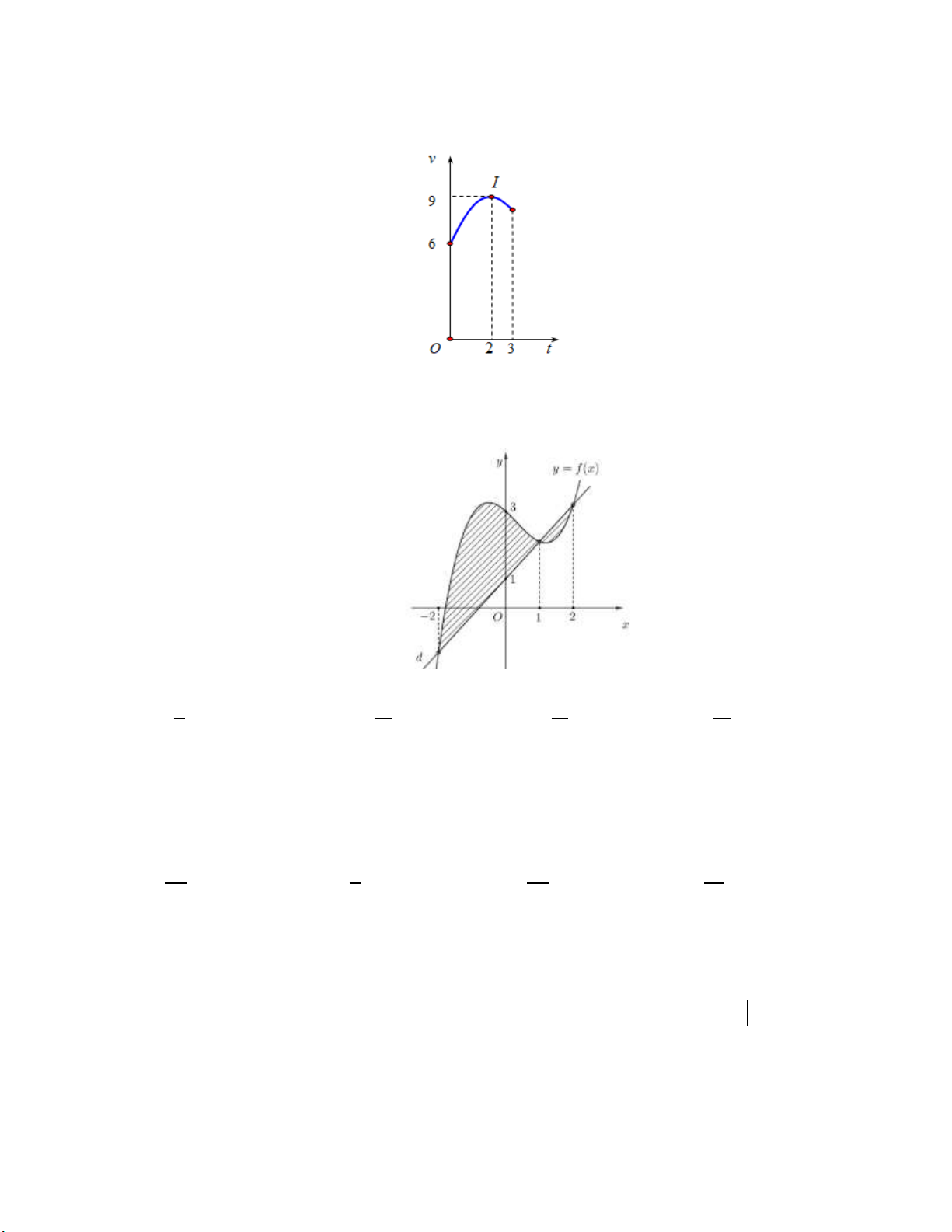
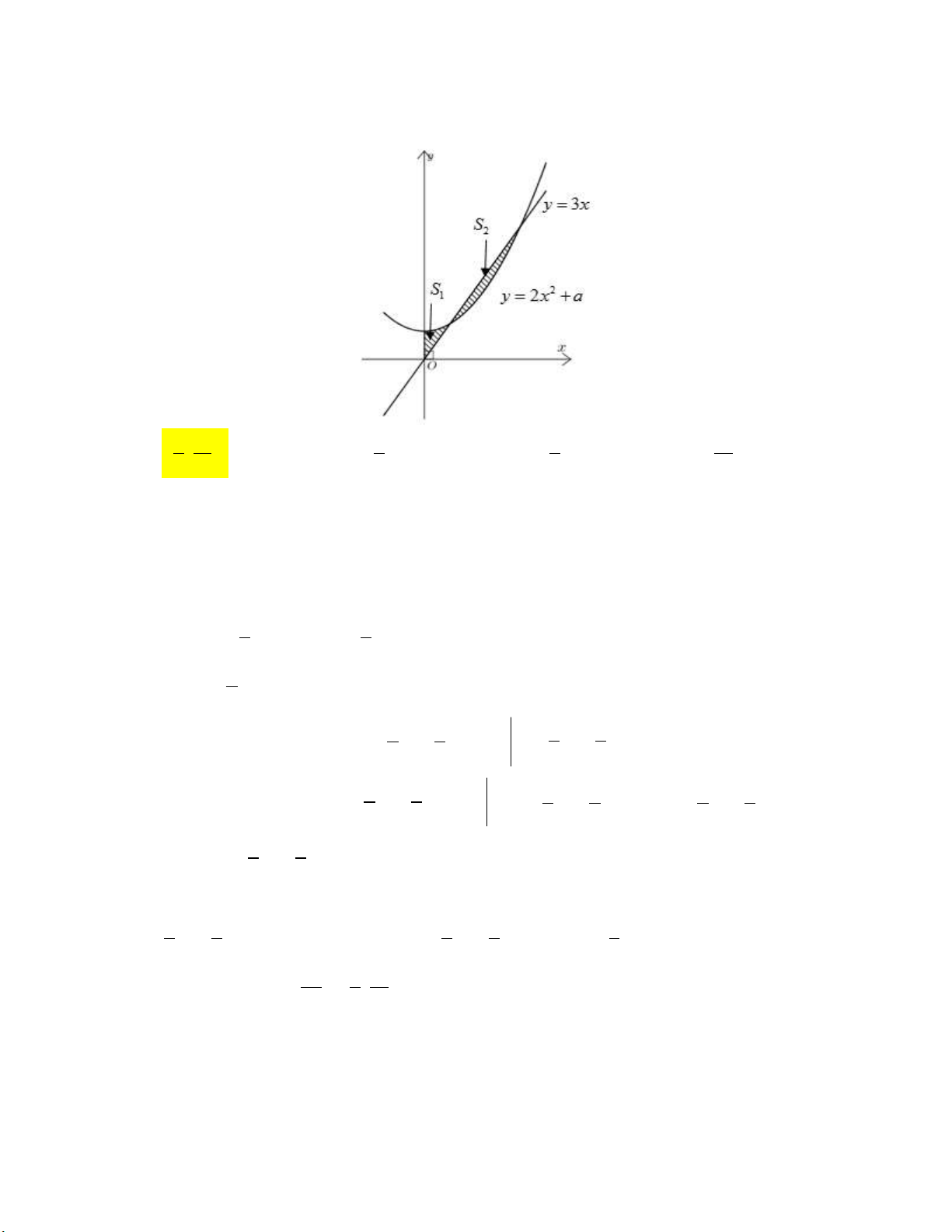
Câu 6: Cho đường thẳng y  3x và parabol 2
y  2x a ( a là tham số thực dương). Gọi S và S lần 1 2
lượt là diện tích của 2 hình phẳng được gạch chéo trong hình vẽ bên. Khi S S thì a thuộc 1 2 khoảng nào dưới đây?  4 9   4   9   9  A. ;   . B. 0;   . C. 1;   . D. ;1    5 10   5   8  10 
Câu 7: Tính diện tích hình phẳng tạo thành bởi Parabol 2
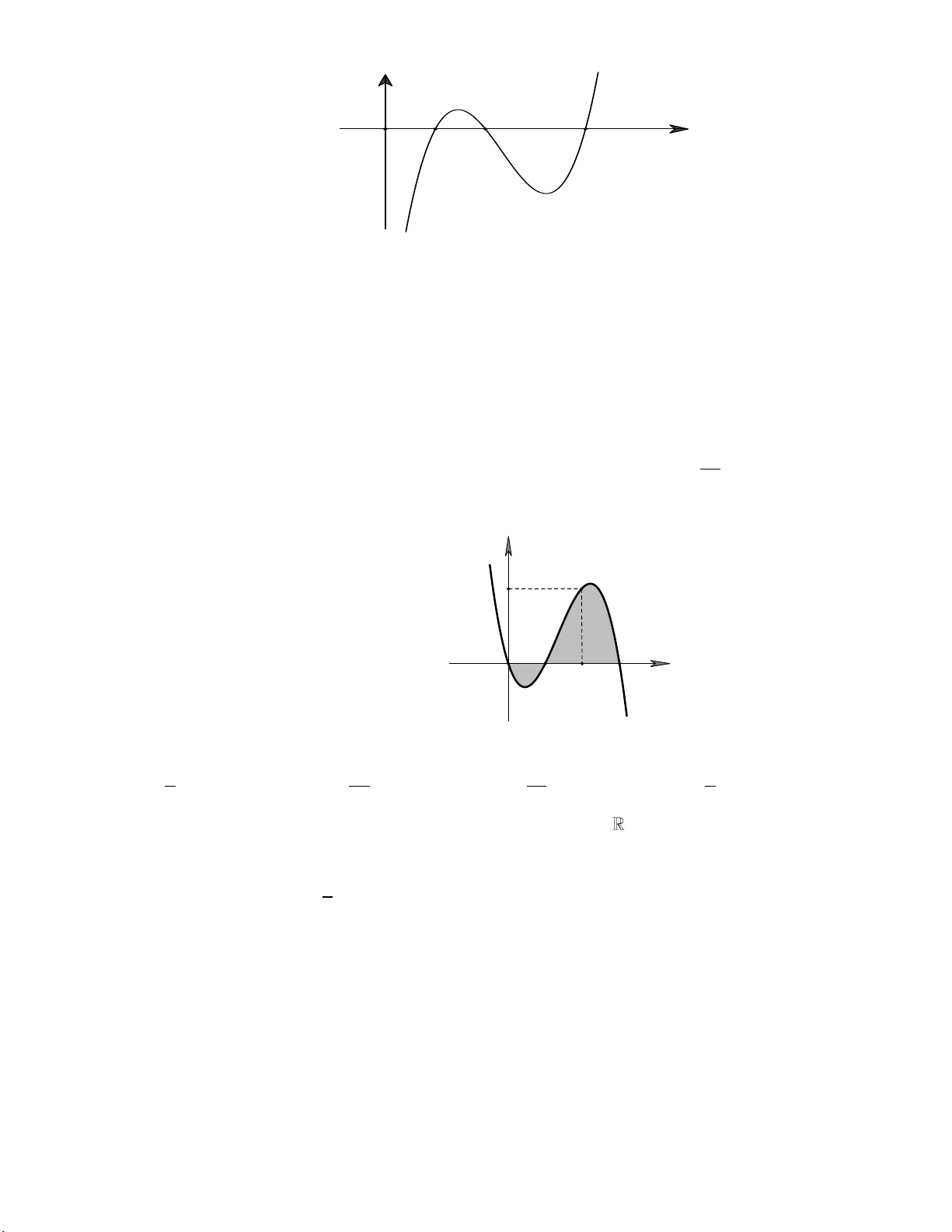
y x , đường thẳng y  x  2 và trục hoành
trên đoạn 0; 2 (phần gạch sọc trong hình vẽ). 3 5 2 7 A. . B. . C. . D. . 5 6 3 6
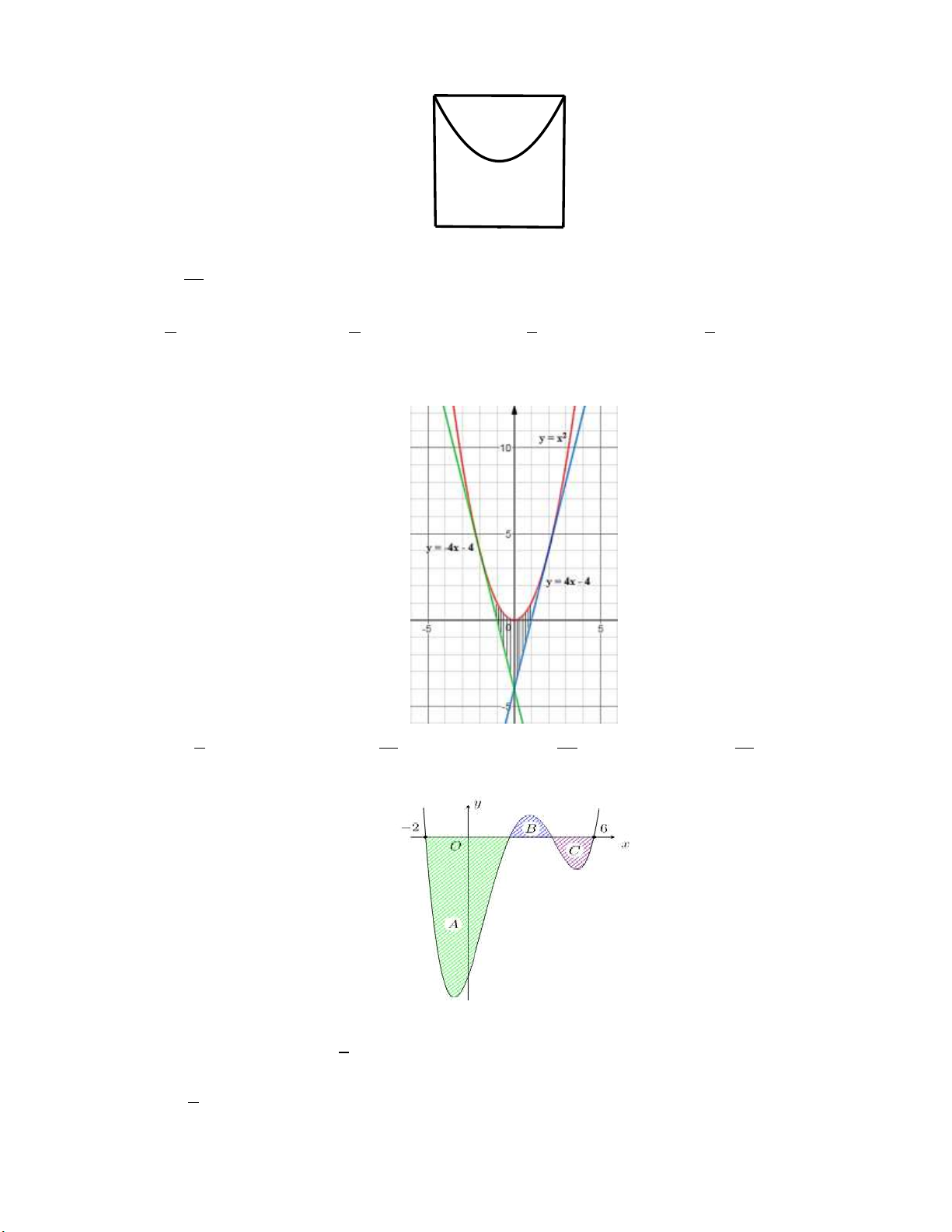
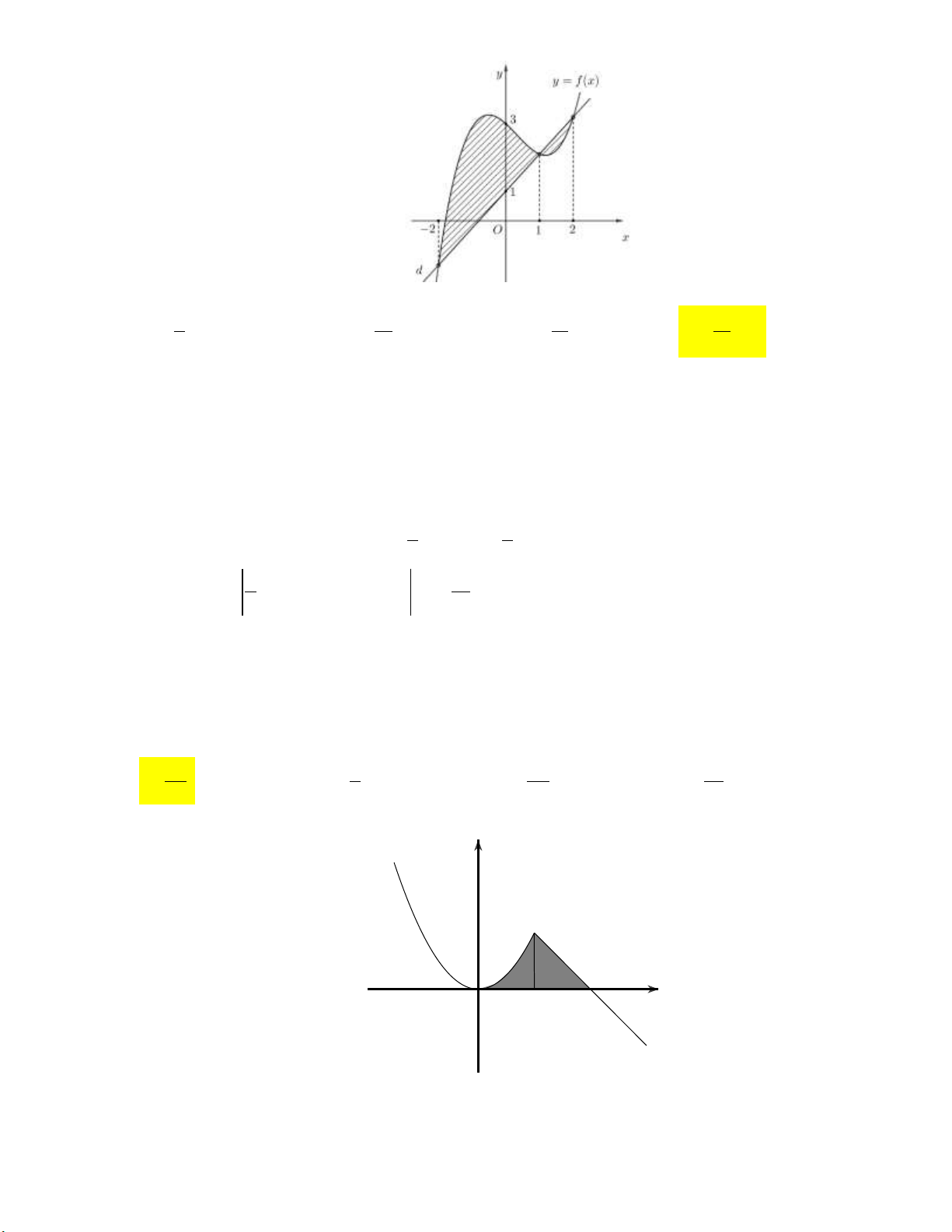
Câu 8: Một vật chuyển động trong 3 giờ với vận tốc v km/h phụ thuộc thời gian t h có đồ thị là
một phần của đường parabol có đỉnh I 2;9 và trục đối xứng song song với trục tung như
hình bên. Tính quãng đường s mà vật di chuyển được trong 3 giờ đó.
A. s  24, 25km.
B. s  26, 75km.
C. s  24, 75km.
D. s  25, 25km.
Câu 9: Đường thẳng d cắt đường cong f x 3 2
a x bx cx d tại ba điểm phân biệt có hoành độ
x  2 , x  1 , x  2 như hình vẽ dưới đây:
Diện tích hình phẳng gạch sọc thuộc khoảng nào dưới đây?  9   13   11 11  A. ;5   . B. 6;   . C. 5;   . D. ; 6   .  2   2   2   2  2 x khi x 1
Câu 10: Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số y f x   , trục hoành và
2  x khi x 1
các đường thẳng x  0, x  2 . Thể tích của khối tròn xoay tạo thành khi quay  H  quanh trục hoành bằng 8 9 9 32 A. . B. . C. . D. . 15 5 5 15
Câu 11: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới
hạn bởi đồ thị hàm số y f x , trục Ox và hai đường thẳng x a, x b a b , xung quanh trục Ox . b b b b A. 2
V    f xd .x B. 2
V   f xd .x
C. V    f xd .x
D. V   f x d .x a a a a
Câu 12: Cho hàm số y f x có đồ thị y f  x cắt trục Ox tại ba điểm có hoành độ a b c như hình vẽ dưới đây: y c x O a b
Khẳng định nào dưới đây đúng?
A. f b  f a  f c.
B. f a  f b  f c .
C. f c  f a  f b .
D. f c  f b  f a .
Câu 13: Một ô-tô đang dừng và bắt đầu chuyển động theo một đường thẳng với gia tốc a(t)  6  2t  2
m / s  , trong đó t là khoảng thời gian tính bằng giây kể từ lúc ô tô bắt đầu chuyển động.
Quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc ô tô đạt giá trị lớn nhất là 27 A. 9 m . B. 20 m . C.18 m . D. m . 2
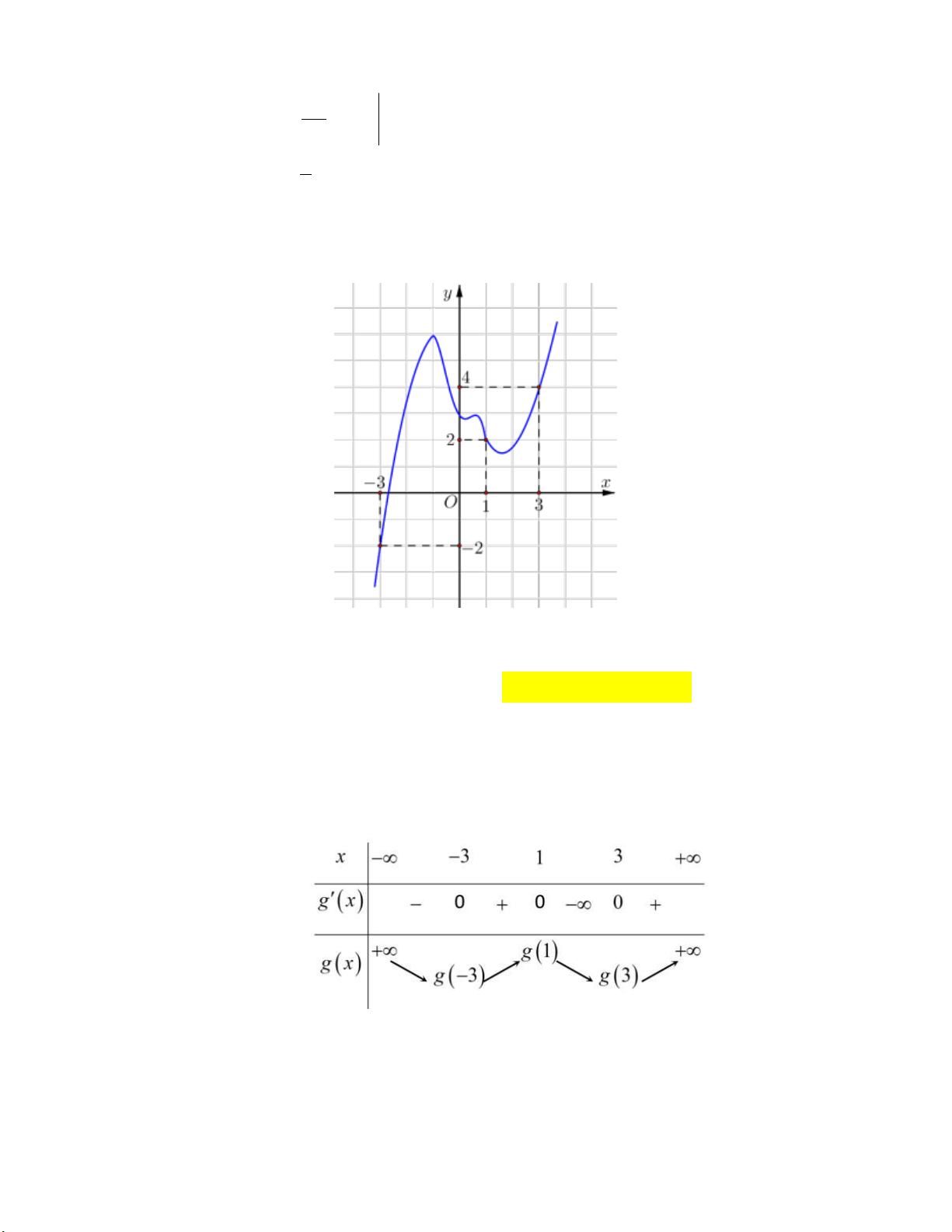
Câu 14: Cho y f x là hàm số đa thức bậc ba có đồ thị như hình vẽ bên dưới : y 2 O 1 2 3 x
Tính diện tích hình phẳng được tô đậm. 9 37 5 8 A. . B. . C. . D. . 4 12 12 3
Câu 15: Cho hàm số y f x liên tục và nhận giá trị dương trên
. Gọi D là hình phẳng giới hạn 1
bởi đồ thị hàm số y f x , các đường x  0 , x  1 và trục Ox . Gọi D là hình phẳng giới hạn 2 1
bởi đồ thị hàm số y
f x , các đường x  0 , x  1 và trục Ox . Quay các hình phẳng D , 3 1
D quanh trục Ox ta được các khối tròn xoay có thể tích lần lượt là V , V . Khẳng định nào 2 1 2 sau đây đúng? A. V  9V . B. V  9V . C. V  3V . D. V  3V . 1 2 2 1 1 2 2 1
Câu 16: Cho hình vuông ABCD tâm O , độ dài cạnh là 4 cm. Đường cong BOC là một phần của
parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S và S (tham 1 2 khảo hình vẽ). 4 cm B C S1 4 cm O S2 A D S Tỉ số 1 bằng S2 2 1 1 3 A. . B. . C. . D. . 5 2 3 5
Câu 17: Tính diện tích S của hình phẳng (phần gạch sọc) giới hạn bởi đồ thị của các hàm số 2
y x , y  4x  4 và y  4
x  4 như hình vẽ bên. 6 16 26 16 A. S  . B. S  . C. S  . D. S  . 3 3 3 9
Câu 18: Cho hàm số y f (x) có đồ thị trên đoạn [  2;6] như hình vẽ bên dưới. Biết các miền ,
A B, C có diện tích lần lượt là 32, 2 và 3 . 2   3  Tính 2 I
(3x  4) 1 f x  2x  5 d .     x   4  2  1 A. I  B. I  82 . C. I  66 . D. I  50 . 2
Câu 19: Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số 2
y x  5x  4 và trục Ox . Tính thể tích của
khối tròn xoay sinh ra khi quay hình  H  quanh trục . Ox 9 81 81 9 A. . B. . C. . D. . 2 10 10 2
Câu 20: Một cái cổng hình Parabol như hình vẽ sau. Chiều cao GH  4m , chiều rộng AB  4m ,
AC BD  0, 9m . Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm có giá là 1200000 đồng 2
/m , còn các phần để trắng làm xiên hoa có giá là 900000 đồng 2 /m (tham khỏa hình vẽ)
Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây? A. 11445000 đồng. B. 4077000 đồng. C. 7368000 đồng. D. 11370000 đồng.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông øng dông tÝch ph©n
PHIẾU ÔN TẬP SỐ 02
LỜI GIẢI CHI TIẾT
Câu 1: Cho hàm số f x liên tục trên
. Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x, y  0, x  1
 và x  4 . Mệnh đề nào dưới đây là đúng? 1 4 1 4
A. S   f xdx  
f xdx . B. S
f x dx  
f xdx . 1  1 1  1 1 4 1 4 C. S
f x dx  
f xdx .
D. S   f xdx  
f xdx . 1  1 1  1 Lời giải: 4 1 4 1 4 Ta có S f
 xdx f
 xdxf
 xdx f
 xdx f  xdx 1  1  1 1  1
Chọn đáp án B.
Câu 2: Tính thể tích của vật thể nằm giữa hai mặt phẳng x  1 và x  1 biết rằng thiết diện của vật
thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x  1   x   1 là một hình vuông có cạnh bằng 4 1 x . 8 1 A. . B. 2 . C. 4 . D. . 5 4 Lời giải: 1 2 8
Thể tích của vật thể là V   4
1 x dx   . 5 1 
Chọn đáp án A.
Câu 3: Cho hàm số y f (x) liên tục trên
và có đồ thị như hình vẽ sau: 4 Giá trị của ( )d  f x x bằng 4  A. 10. B. 4. C. 12. D. 8. Lời giải: Ta có 4 2  0 4
f (x)dx
f (x)dx
f (x)dx
f (x)dx  SS       S ABCCOD DOFE 4  4  2  0 1 1
  .2.2  .2.2  2.4  8. 2 2
Chọn đáp án D.
Câu 4: Diện tích hình phẳng giới hạn bởi hai đường 2
y x  4 và y  2x  4 bằng 4 4 A. 36 . B. . C. . D. 36 . 3 3 Lời giải:
Phương trình hoành độ giao điểm của hai đồ thị đã cho là: x  0 2 2
x  4  2x  4  x  2x  0   . x  2
Diện tích hình phẳng giới hạn bởi hai đồ thị đã cho là: 2     x S x  4 2 2
 2x  4 dx x  2x dx  
2xx  3 2 4 2 2 2 2 dx   x    .  3 0  3 0 0 0
Chọn đáp án B.
Câu 5: Cho hai hàm số f x 3 2
ax bx cx d , a  0 và g x 2
mx nx p , m  0 có đồ thị cắt
nhau tại 3 điểm có hoành độ x , x , x . 1 2 3
Kí hiệu S , S lần lượt là diện tích các hình phẳng giới hạn bởi đồ thị hàm số y f x và 1 2 3 x
y g x . Biết S  10 , S  7 . Khi đó, g
  x f xdx bằng 1 2  1 x A. 3 . B. 3  . C. 17 . D. 17 . Lời giải: x 2 x 3
Theo đề bài ta có 10  S   f x g x  dx
, 7  S  g x f x  dx  . 2      1       1 x 2 x 3 x x x 2 3 Suy ra 
 gx f xdx   
 gx f xdx  
 gx f xdx  S S  1  0  7  3  .  1 2 1 x 1 x 2 x
Chọn đáp án B.
Câu 6: Cho đường thẳng y  3x và parabol 2
y  2x a ( a là tham số thực dương). Gọi S và S lần 1 2
lượt là diện tích của 2 hình phẳng được gạch chéo trong hình vẽ bên. Khi S S thì a thuộc 1 2 khoảng nào dưới đây?  4 9   4   9   9  A. ;   . B. 0;   . C. 1;   . D. ;1    5 10   5   8  10  Lời giải:
Xét phương trình tương giao: 2
3x  2x a 2
 2x  3x a  0   1 Để phương trình  
1 có hai nghiệm dương phân biệt x , x ( x x  0) 1 2 2 1 
  9  8a  0   3 9
 x x   0  0  a  . 1 2 2 8   a x .x   0  1 2  2 x x  2 3  2 3
Ta có: S  2x 3x a 1 1 2 3 2 dx x x ax 3 2
x x ax 1    3 2  1 1 1 3 2 0 0 x 2 x 2  2 3   2 3   2 3  S    2
2x  3x a dx 3 2   x x ax 3 2 3 2   x x axx x ax 2         3 2  2 2 2 1 1 1  3 2   3 2  1 x 1 x 2 3 Do 3 2 S S x x ax  0 1 2 2 2 2 3 2
mà x là nghiệm của   1 nên 2 2
2x  3x a  0  a  2
x  3x 2 2 2 2 2 2 2 3 4 3 9 3 2
x x   2 2
x  3x .x  0 3 2
  x x  0  x  ( loại nghiệm x  0 ) 2 2 2 2  2 3 2 2 2 3 2 2 8 2 27  4 9 
Thay vào 2  a   ;   . 32  5 10 
Chọn đáp án A.
Câu 7: Tính diện tích hình phẳng tạo thành bởi Parabol 2
y x , đường thẳng y  x  2 và trục hoành
trên đoạn 0; 2 (phần gạch sọc trong hình vẽ). 3 5 2 7 A. . B. . C. . D. . 5 6 3 6 Lời giải: 1 2 1 2 3 2 xx  5 Ta có 2
S x dx  
x  2dx
   2x  . 3  2  6 0 1 0 1
Chọn đáp án B.
Câu 8: Một vật chuyển động trong 3 giờ với vận tốc v km/h phụ thuộc thời gian t h có đồ thị là
một phần của đường parabol có đỉnh I 2;9 và trục đối xứng song song với trục tung như
hình bên. Tính quãng đường s mà vật di chuyển được trong 3 giờ đó.
A. s  24, 25km.
B. s  26, 75km.
C. s  24, 75km.
D. s  25, 25km. Lời giải:
Gọi v t  2  .
a t bt c .
Đồ thị v t  là một phần parabol có đỉnh I 2;9 và đi qua điểm A0;6 nên  b   3   2 a  2a  4   2  3 .2 a  .2
b c  9  b
  3 . Tìm được vt 2
  t  3t  6   4 2 .0 a  .0 b c  6 c  6     3  3  Vậy 2 S
t  3t  6 dt    24,75 (km)  4  0
Chọn đáp án C.
Câu 9: Đường thẳng d cắt đường cong f x 3 2
a x bx cx d tại ba điểm phân biệt có hoành độ
x  2 , x  1 , x  2 như hình vẽ dưới đây:
Diện tích hình phẳng gạch sọc thuộc khoảng nào dưới đây?  9   13   11 11  A. ;5   . B. 6;   . C. 5;   . D. ; 6   .  2   2   2   2  Lời giải:
Ta có d : y mx n
Phương trình hoành độ giao điểm 3 2 a x bx cx d mx n g x 3 2      
a x bx cx d  mx n có 3 nghiệm x  2; x 1; x  2 .
Do đó g x  a x  2 x   1  x  2 . 1 1
Do g 0  d n  3 1  4a a
g x  x  2x   1  x  2 . 2 2 2 1 71 Vì vậy S
x  2x  
1  x  2 dx   . 2 12 2 
Chọn đáp án D. 2 x khi x 1
Câu 10: Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số y f x   , trục hoành và
2  x khi x 1
các đường thẳng x  0, x  2 . Thể tích của khối tròn xoay tạo thành khi quay  H  quanh trục hoành bằng 8 9 9 32 A. . B. . C. . D. . 15 5 5 15 Lời giải: y 1 O 1 2 x
Thể tích của khối tròn xoay tạo thành khi quay  H  quanh trục hoành là  V   f  xx x .dx   f
 x.dx  x .dx    2 x 2  2 1 3 1 2 1 2 5 2 2 2 4 .dx    5 3 0 1 0 1 0 1  1 8      0     . 5  3  15
Chọn đáp án A.
Câu 11: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới
hạn bởi đồ thị hàm số y f x , trục Ox và hai đường thẳng x a, x b a b , xung quanh trục Ox . b b b b A. 2
V    f xd .x B. 2
V   f xd .x
C. V    f xd .x
D. V   f x d .x a a a a Lời giải:
Chọn đáp án A.
Câu 12: Cho hàm số y f x có đồ thị y f  x cắt trục Ox tại ba điểm có hoành độ a b c như hình vẽ dưới đây: y c x O a b
Khẳng định nào dưới đây đúng?
A. f b  f a  f c.
B. f a  f b  f c .
C. f c  f a  f b .
D. f c  f b  f a . Lời giải:
Ta có bảng biến thiên của hàm số y f x : x c a b +∞ -∞ f ' x ( ) - 0 + - + 0 0 f b ( ) f x ( ) f a ( ) f c ( )
Từ bảng biến thiên suy ra trong ba giá trị f a, f b, f c thì f b lớn nhất. y c x O a S1 b S2 b c
Ta có : diện tích S   f x dx , diện tích S   f x dx . 2   1   a b b c
Từ hình vẽ ta có: S S   f  xdx   f  xdx 1 2 a b
f b  f a  f b  f c  f a  f c.
Vậy f b  f a  f c.
Chọn đáp án A.
Câu 13: Một ô-tô đang dừng và bắt đầu chuyển động theo một đường thẳng với gia tốc a(t)  6  2t  2
m / s  , trong đó t là khoảng thời gian tính bằng giây kể từ lúc ô tô bắt đầu chuyển động.
Quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc ô tô đạt giá trị lớn nhất là 27 A. 9 m . B. 20 m . C.18 m . D. m . 2 Lời giải: Ta có 2
v(t)  a(t)dt  (6  2t)dt  6t t C  
Do ban đầu ô tô đang dừng nên v 0  0  C  0. Suy ra 2
v(t)  6t t Ta có vt  3 max
Quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc ô tô đạt giá trị lớn 3 nhất là S   2
6t t  18m. 0
Chọn đáp án C.
Câu 14: Cho y f x là hàm số đa thức bậc ba có đồ thị như hình vẽ bên dưới : y 2 O 1 2 3 x
Tính diện tích hình phẳng được tô đậm. 9 37 5 8 A. . B. . C. . D. . 4 12 12 3 Lời giải: Giả sử 3 2
f (x)  ax bx cx d có đồ thị (C) như hình vẽ trên. Điểm 3 2
O(0; 0)  (C)  d  0  f (x)  ax bx cx .
a b c  0 a  1    Các điểm 3 2 (
A 1; 0), B(2; 2), D(3; 0)  (C)  4a  2b c  1  b
  4  f (x)  x  4x  3x .  
9a  3b c  0 c  3   
Diện tích hình phẳng cần tìm là 1
S  0  f (x) 3
dx   f (x)  0 1 3 37 3 2 3 2
dx  (x  4x  3x)dx  (x  4x  3x)dx  .   12 0 1 0 1
Chọn đáp án B.
Câu 15: Cho hàm số y f x liên tục và nhận giá trị dương trên
. Gọi D là hình phẳng giới hạn 1
bởi đồ thị hàm số y f x , các đường x  0 , x  1 và trục Ox . Gọi D là hình phẳng giới hạn 2 1
bởi đồ thị hàm số y
f x , các đường x  0 , x  1 và trục Ox . Quay các hình phẳng D , 3 1
D quanh trục Ox ta được các khối tròn xoay có thể tích lần lượt là V , V . Khẳng định nào 2 1 2 sau đây đúng? A. V  9V . B. V  9V . C. V  3V . D. V  3V . 1 2 2 1 1 2 2 1 Lời giải: 1 1 2 1 1  1 1 Ta có 2 V   f x d 
x và V    f x 2 dx   f x d 
x . Vậy V V hay V  9V . 2   1     3  9 2 1 9 1 2 0 0 0
Chọn đáp án A.
Câu 16: Cho hình vuông ABCD tâm O , độ dài cạnh là 4 cm. Đường cong BOC là một phần của
parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S và S (tham 1 2 khảo hình vẽ). 4 cm B C S1 4 cm O S2 A D S Tỉ số 1 bằng S2 2 1 1 3 A. . B. . C. . D. . 5 2 3 5 Lời giải: y 2 B C -2 1 2 x O D A -2
Gắn hệ trục toạ độ như hình vẽ. 1
Ta có phương trình parabol  P 2 : y x . 2 2  1  16 Suy ra 2 S  2  x dx   (đvdt). 1    2  3 2 
Diện tích hình vuông ABCD là 2 S  4  16 (đvdt). ABCD 16 32
Do đó diện tích S là S SS 16   (đvdt). 2 2 ABCD 1 3 3 S 16 32 1 Vậy tỉ số 1  :  . S 3 3 2 2
Chọn đáp án B.
Câu 17: Tính diện tích S của hình phẳng (phần gạch sọc) giới hạn bởi đồ thị của các hàm số 2
y x , y  4x  4 và y  4
x  4 như hình vẽ bên. 6 16 26 16 A. S  . B. S  . C. S  . D. S  . 3 3 3 9 Lời giải:
Ta thấy đường thẳng y  4
x  4 và đường thẳng y  4x  4 lần lượt là hai tiếp tuyến của đồ thị hàm số 2
y x tại các tiếp điểm có hoành độ x  2 và x  2 .
Do tính đối xứng qua Oy của parabol 2
y x nên diện tích hình phẳng cần tìm bằng 2 lần diện 2 2 x  2 2 3 2 16
tích tam giác cạnh OMT và bằng 2 S  2 x  
4x  4dx  2x2 dx  2  . 2   3 3 0 0 0
Chọn đáp án B.
Câu 18: Cho hàm số y f (x) có đồ thị trên đoạn [  2;6] như hình vẽ bên dưới. Biết các miền ,
A B, C có diện tích lần lượt là 32, 2 và 3 . 2   3  Tính 2 I
(3x  4) 1 f x  2x  5 d .     x   4  2  1 A. I  B. I  82 . C. I  66 . D. I  50 . 2 Lời giải: 3  3  Đặt 2 t  
x  2x  5  dt   x  2 dx   
3x  4dx  2  dt 4  2 
Đổi cận: - Với x  2   t  2 
-Với x  2  t  6 6 6 6 Ta được: I  2  1   f  
tdt  2  dt  2 f  
 tdt  1  6  2M . 2  2  2  6 2 4 6 Với M f
 tdt f
 tdt f
 tdt f
 tdt  3  2  2  3  3  3 . 2  2  2 4 Vậy: I  16   2. 33    50 .
Chọn đáp án D.
Câu 19: Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số 2
y x  5x  4 và trục Ox . Tính thể tích của
khối tròn xoay sinh ra khi quay hình  H  quanh trục . Ox 9 81 81 9 A. . B. . C. . D. . 2 10 10 2 Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số 2
y x  5x  4 và trục Ox ta có: x 1 2
x  5x  4  0   x  4
Thể tích của khối tròn xoay sinh ra khi quay hình  H  quanh trục Ox 4 4  V  
f xdx    x  5x  42 81 2 2 dx    . 10 1 1
Chọn đáp án C.
Câu 20: Một cái cổng hình Parabol như hình vẽ sau. Chiều cao GH  4m , chiều rộng AB  4m ,
AC BD  0, 9m . Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm có giá là 1200000 đồng 2
/m , còn các phần để trắng làm xiên hoa có giá là 900000 đồng 2 /m (tham khỏa hình vẽ)
Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây? A. 11445000 đồng. B. 4077000 đồng. C. 7368000 đồng. D. 11370000 đồng. Lời giải:
Gắn hệ trục tọa độ Oxy sao cho AB trùng Ox , A trùng O khi đó parabol có đỉnh G 2; 4 và đi qua gốc tọa độ.
Giả sử phương trình của parabol có dạng 2
y ax bx ca  0 . c  0  a  1   b
Vì parabol có đỉnh là G 2; 4 và đi qua điểm O 0;0 nên ta có   2  b  4 . 2a  c  0 2    .2 a  .2 b c  4
Suy ra phương trình parabol là 2
y f (x)  x  4x . 4 4 3  x  32
Diện tích của cả cổng là S   2 x  4x 2 dx     2x    2 m  .  3  3 0 0
Mặt khác chiều cao CF DE f 0,9  2,79(m) ; CD  4  2.0,9  2, 2 m . 2
Diện tích hai cánh cổng là S  . CD CF  6,138 m CDEF . 32 6793
Diện tích phần xiên hoa là S S S   6,14  . xh CDEF  2 m  3 1500 6793
Vậy tổng số tiền để làm cổng là 6,138.1200000  .900000  11441400 đồng. 1500
Chọn đáp án A.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông øng dông tÝch ph©n
PHIẾU ÔN TẬP SỐ 03 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Câu 1: Viết công thức tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với
trục O x tại các điểm x a, x b a b có thiết diện bị cắt bởi mặt phẳng vuông góc với trục
O x tại điểm có hoành độ x a x b là S x . b b b b 2 2 A. V   S
 xdx. B. V S  xdx. C. V   S
 xdx. D. V  S  xdx . a a a a
Câu 2: Gọi S là diện tích hình phẳng giới hạn bởi các đường ex y
, y  0 , x  0 , x  2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A. 2   e d .  x S x B.  e d .  x S x C.   e d .  x S x D. 2  e d .  x S x 0 0 0 0
Câu 3: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x x và đồ thị hàm số 2
y x x . 37 9 81 A. . B. . C. . D. 13. 12 4 12
Câu 4: Cho hình thang cong  H  giới hạn bởi các đường x
y e , y  0 , x  0 , x  ln 4 . Đường thẳng
x k (0  k  ln 4) chia  H  thành hai phần có diện tích là S và S như hình vẽ bên. Tìm k 1 2
để S  2S . 1 2 y S 2 S1 x O k ln 4 2 8 A. k  ln 4 . B. k  ln 2 . C. k  ln D. k  ln 3 . 3 3
Câu 5: Diện tích hình phẳng giới hạn bởi đường 2
y x  4x 1, y m , m  3 , x  0 , x  3 là A. 3m  6 . B. 3m  6 . C. 3m  6 . D. 3m  6 .
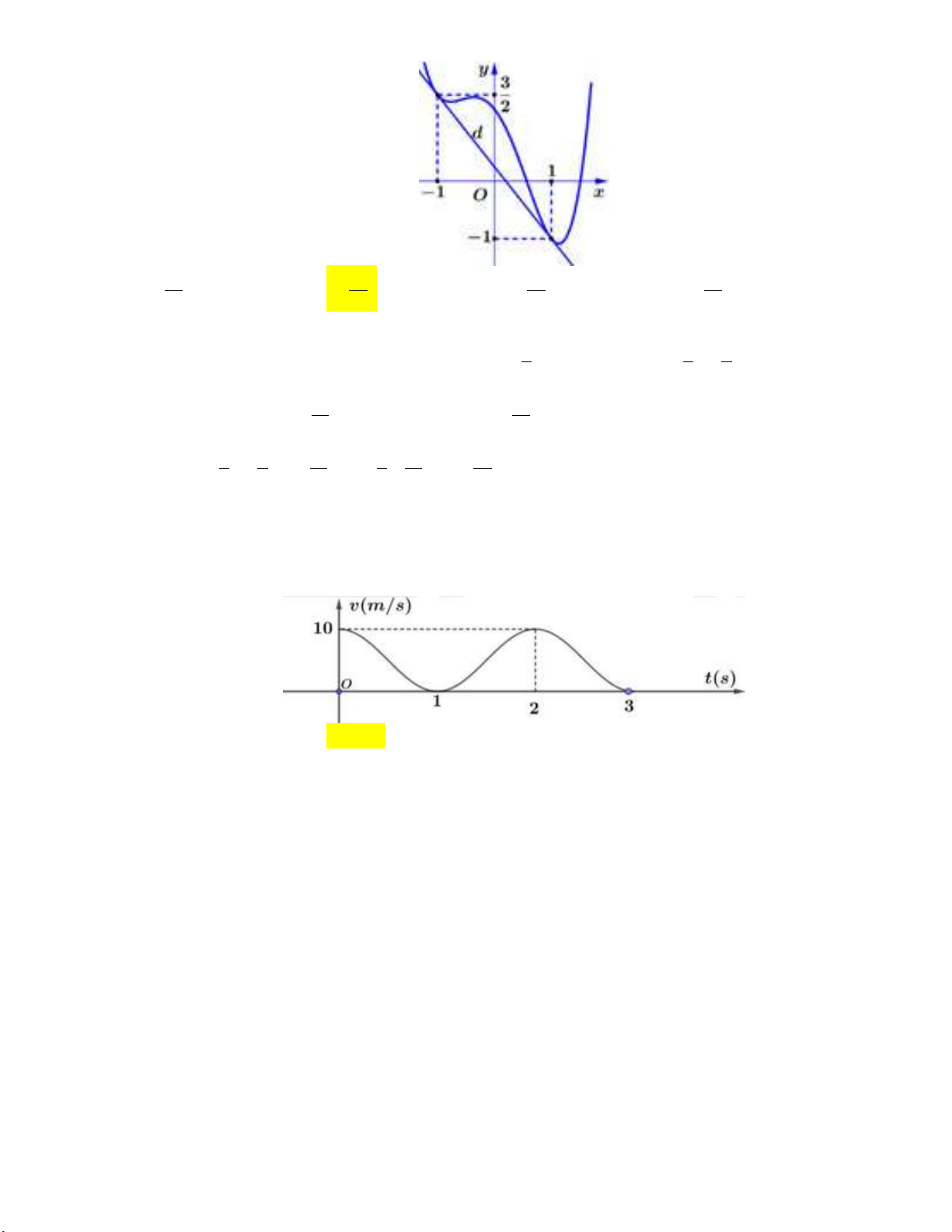
Câu 6: Cho hàm số y f (x) có đồ thị trên đoạn [-1; 4] như hình vẽ dưới: 4 Tính tích phân I f (x)d .  x 1  5 11 A. I  . B. I  . C. I  5. D. I  3. 2 2
Câu 7: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 2 2 2 2 A.   2
2x  2x  4dx . B.   2
x  2dx .
C.  2x  2dx . D.   2 2
x  2x  4dx . 1  1  1  1 
Câu 8: Cho đồ thị biểu thị vận tốc của hai chất điểm A và B xuất phát cùng một lúc, bên cạnh nhau
và trên cùng một con đường. Biết đồ thị biểu diễn vận tốc của chất điểm A là một đường
Parabol, đồ thị biểu diễn vận tốc của chất điểm B là một đường thẳng như hình vẽ sau.
Hỏi sau khi đi được 3 giây, khoảng cách giữa hai chất điểm là bao nhiêu mét? A. 120 . m B. 60 . m C. 270 . m D. 90 . m
Câu 9: Đường thẳng y kx  4 cắt parabol y   x  2 2
tại hai điểm phân biệt và diện tích các hình
phẳng S , S bằng nhau như hình vẽ bên. 1 2
Mệnh đề nào sau đây đúng?  1   1  A. k  6  ; 4   . B. k  1  ;   . C. k   2  ;  1 . D. k   ;0   .  2   2 
Câu 10: Kí hiệu  H  là hình phẳng giới hạn bởi đồ thị hàm số  2( 1) x y x
e , trục tung và trục hoành.
Tính thể tích V của khối tròn xoay thu được khi quay hình  H  xung quanh trục Ox . A. V  4  2 . e
B. V  4  2e. C. 2 V e  5. D. V   2 e  5. 1
Câu 11: Cho hai hàm số f x 3 2
ax bx cx  và g x 2
dx ex 1 a, ,
b c, d, e   . Biết rằng đồ 2
thị hàm số y f x và y g x cắt nhau tại 3 điểm có hoành độ lần lượt là 3  ; 1  ; 1 (tham khảo hình vẽ)
Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng 9 A. . B. 8. C. 4. D. 5. 2
Câu 12: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x  1 và x  3 , biết rằng khi cắt
vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (1  x  3 ) thì được thiết
diện là một hình chữ nhật có độ dài hai cạnh là 3x và 2 3x  2 . 124 124 A. V  32  2 15. B. V  . C. V  .
D. V  32  2 15. 3 3
Câu 13: Một chất điểm A xuất phát từ O , chuyển động thẳng với vận tốc biến thiên theo thời gian bởi 1 59
quy luật v t  2  t
t m / s , trong đó t (giây) là khoảng thời gian tính từ lúc a bắt đầu 150 75
chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O , chuyển động thẳng
cùng hướng với A nhưng chậm hơn 3 giây so với A và có gia tốc bằng a  2
m / s  ( a là hằng
số). Sau khi B xuất phát được 12 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kịp A bằng
A. 20m / s.
B. 16m / s.
C. 13m / s.
D. 15m / s.
Câu 14: Cho hàm số y f x . Đồ thị của hàm số y f  x như hình bên dưới :
Đặt g x  f x   x  2 2
1 . Mệnh đề nào dưới đây đúng? A. g  3
   g 3  g   1 . B. g   1  g  3    g 3.
C. g 3  g  3    g   1 . D. g  
1  g 3  g  3  .
Câu 15: Cho hình phẳng  H  được giới hạn bởi các đường x  1, x  e, y  0 và y  ln x . Thể tích V
của khối tròn xoay tạo thành khi quay  H  xung quanh trục Ox được tính theo công thức e e e e A. V   ln d x x  .
B. V   ln x dx  . C. 2 V   ln d x x  . D. 2 V  ln d x x  . 1 1 1 1
Câu 16: Gọi  D là hình phẳng giới hạn bởi các đường y  2 x, y  0 và x  2020; D là hình phẳng 2  1 
giới hạn bởi các đường y  3x, y  0 và x  2020 . Gọi V ,V lần lượt là thể tích khối tròn xoay 1 2 V
tạo thành khi quay  D và  D xung quanh trục Ox . Tỉ số 1 bằng 2  1  V2 4 2 3 2 6 A. . B. . C. . D. . 3 3 3 3 Câu 17: Kí hiệu S t  là diện tích hình phẳng giới hạn bởi các đường
y  2x 1, y  0, x  1, x t, t  
1 . Tìm t để S t   10 . A. t  4 . B. t  13 . C. t  3 . D. t  14 . Câu 18: Cho hàm số 3 2
y ax bx cx d ,  ; a ; b ; c d
 có đồ thị như hình vẽ bên dưới:
Biết diện tích hình phẳng tô đậm bằng 1. Giá trị của a  2b  3c  4d bằng A. 8. B. 1. C. 1. D. 8.
Câu 19: Cho hàm số f x xác định và liên tục trên đoạn 5; 
3 có đồ thị như hình vẽ bên dưới: y 5 y=g(x) S3 2 S1 -1 -5 -2 O x S 2 3 2 y=f(x)
Biết rằng diện tích hình phẳng S , S , S giới hạn bởi đồ thị hàm số f x và đường parabol 1 2 3 3    2 y
g x ax bx c lần lượt là m , n , p . Tích phân f
 xdx bằng 5  208 208
A. m n p  .
B. m n p  . 45 45 208 208
C. m n p  .
D. m n p  . 45 45 2 3
Câu 20: Cho  H  là hình phẳng giới hạn bởi parabol 2 y
x với cung tròn có phương trình 3 2
y  9  x , 0  x  3 và trục hoành (phần tô đậm trong hình vẽ dưới đây). Diện tích S của hình
phẳng  H  được tính bằng công thức nào dưới đây? 3 3  2  2 3 2 A. 2 2 S x  9  x dx   . B. 2 2 S x dx  9  x dx   .  3  3 0 0 3 2 3 3 3 2 2 2 2 C. 2 2 S  
x  9  x dx  . D. 2 2 S x dx  9  x dx   . 3 3 0 0 3
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông øng dông tÝch ph©n
PHIẾU ÔN TẬP SỐ 03
LỜI GIẢI CHI TIẾT
Câu 1: Viết công thức tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với
trục O x tại các điểm x a, x b a b có thiết diện bị cắt bởi mặt phẳng vuông góc với trục
O x tại điểm có hoành độ x a x b là S x . b b b b 2 2 A. V   S
 xdx. B. V S  xdx. C. V   S
 xdx. D. V  S  xdx . a a a a Lời giải:
Chọn đáp án B.
Câu 2: Gọi S là diện tích hình phẳng giới hạn bởi các đường ex y
, y  0 , x  0 , x  2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A. 2   e d .  x S x B.  e d .  x S x C.   e d .  x S x D. 2  e d .  x S x 0 0 0 0 Lời giải: 2
Diện tích hình phẳng giới hạn bởi các đường ex y
, y  0 , x  0 , x  2 là: x
S e dx  . 0
Chọn đáp án B.
Câu 3: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x x và đồ thị hàm số 2
y x x . 37 9 81 A. . B. . C. . D. 13. 12 4 12 Lời giải: x  0 
Phương trình hoành độ giao điểm 3 2 3 2
x x x x x x  2x  0  x  1  x  2  
Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x x và đồ thị hàm số 2
y x x là: 1 S x x   xx  0
dx   x x  2x 1 3 2 3 2 dx   3 2
x x  2xdx 2  2  0 0 1 4 3 4 3  x x   x x  16 8   1 1  37 2 2
    x      x      4   1      . 4 3 4 3      4 3   4 3  12 2  0
Chọn đáp án A.
Câu 4: Cho hình thang cong  H  giới hạn bởi các đường x
y e , y  0 , x  0 , x  ln 4 . Đường thẳng
x k (0  k  ln 4) chia  H  thành hai phần có diện tích là S và S như hình vẽ bên. Tìm k 1 2
để S  2S . 1 2 y S 2 S1 x O k ln 4 2 8 A. k  ln 4 . B. k  ln 2 . C. k  ln D. k  ln 3 . 3 3 Lời giải: k ln 4 k ln 4 Ta có x  d x k S e x e   x x k     0 e 1  và S e dx e k 4 e  . 1 2 0 k Lại có  2 k  1  24 k S S e
e   k  ln 3 . 1 2
Chọn đáp án D.
Câu 5: Diện tích hình phẳng giới hạn bởi đường 2
y x  4x 1, y m , m  3 , x  0 , x  3 là A. 3m  6 . B. 3m  6 . C. 3m  6 . D. 3m  6 . Lời giải: Ta có: 2 2
x  4x 1  m x  4x 1 m  0  1 
  m  3  0, m   3 
Ta có diện tích hình phẳng là: 3 3 2 S
x  4x 1 m dx  
 2x 4x1mdx  6   3m  6   3m . 0 0
Chọn đáp án D.
Câu 6: Cho hàm số y f (x) có đồ thị trên đoạn [-1; 4] như hình vẽ dưới: 4 Tính tích phân I f (x)d .  x 1  5 11 A. I  . B. I  . C. I  5. D. I  3. 2 2 Lời giải: 4 0 1 2 3 4 Ta có: I
f (x)dx
f (x)dx
f (x)dx
f (x)dx
f (x)dx f (x)dx       1  1  0 1 2 3 1 5 1 2 1 1  . 2 2
Chọn đáp án A.
Câu 7: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 2 2 2 2 A.   2
2x  2x  4dx . B.   2
x  2dx .
C.  2x  2dx . D.   2 2
x  2x  4dx . 1  1  1  1  Lời giải:
Phần hình phẳng gạch chéo trong hình vẽ bên được giới hạn bởi hai đồ thị hàm số 2
y  x  3 và 2
y x  2x 1 nên có diện tích được tính theo công thức: 2
S   x  3 x  2x   2 1 dx  
 x 3x 2x  2 2 2 2 2 1  dx    2 2
x  2x  4dx . 1  1  1 
Chọn đáp án D.
Câu 8: Cho đồ thị biểu thị vận tốc của hai chất điểm A và B xuất phát cùng một lúc, bên cạnh nhau
và trên cùng một con đường. Biết đồ thị biểu diễn vận tốc của chất điểm A là một đường
Parabol, đồ thị biểu diễn vận tốc của chất điểm B là một đường thẳng như hình vẽ sau.
Hỏi sau khi đi được 3 giây, khoảng cách giữa hai chất điểm là bao nhiêu mét? A. 120 . m B. 60 . m C. 270 . m D. 90 . m Lời giải:
Phương trình vận tốc của chất điểm A có dạng   2
v t at bt c . v0  0 c  0 a  2  0   
Dựa vào đồ thị ta có v 3  60  9
a  3b c  60  b   80 .    v   
16a  4b c  0 c  0 4 0     v t 2  20
t  80t suy ra quãng đường chất điểm A đi được sau 3 giây đầu là 3 3 S v
 tdt   2 2
 0t  80tdt 180 m . A   0 0
Vận tốc chất điểm B có phương trình là v t   20t , suy ra sau 3 giây chất điểm B đi được 3
quãng đường là S  20tdt  90 m  . B   0
Vậy sau khi đi được 3 giây, hai chất điểm cách nhau 180  90  90 m .
Chọn đáp án D.
Câu 9: Đường thẳng y kx  4 cắt parabol y   x  2 2
tại hai điểm phân biệt và diện tích các hình
phẳng S , S bằng nhau như hình vẽ bên. 1 2
Mệnh đề nào sau đây đúng?  1   1  A. k  6  ; 4   . B. k  1  ;   . C. k   2  ;  1 . D. k   ;0   .  2   2  Lời giải: x  0
Phương trình hoành độ giao điểm  x  2 2  kx  4 2
x  k  4 x  0   . x k  4  4 
Đường thẳng y kx  4 cắt các trục tọa độ tại các điểm A  ;0   , B 0;4 .  k  4
  k  4  2  2  k  0 . k k 4 k 4 2 1 3
Diện tích hình phẳng S   kx  4 x  2 dx    2
x k  4 x dx k  4 . 1      6 0 0 4  4 k 4 k  2 1 3 k 2
Diện tích hình phẳng S x  2 dx kx  4 dx k  2    . 2         3 2k 2 k 4 4 1 1 k  2 k  0, 457 TM 3 3
S S  k  4  k  2        . 1 2 6 3 2kk  5,54  L
Chọn đáp án D.
Câu 10: Kí hiệu  H  là hình phẳng giới hạn bởi đồ thị hàm số  2( 1) x y x
e , trục tung và trục hoành.
Tính thể tích V của khối tròn xoay thu được khi quay hình  H  xung quanh trục Ox . A. V  4  2 . e
B. V  4  2e. C. 2 V e  5. D. V   2 e  5. Lời giải:
Phương trình hoành độ giao điểm 2   1 x x
e  0  x  1
Thể tích của khối tròn xoay thu được khi quay hình  H  xung quanh trục Ox là:
du  2 x 1 dx 1 1 u
  x  2      1  2     2 1 x   4   2 2 1 x V x e dx x e dx   . Đặt   2 xe 2 x     0 0 dv e dx v  2 1 1 2 x 1 2 x 2 x 1 e e e
V  4 x  2 1  4 2x   1
dx  4  x  2 1  4 x     2 1 x e dx 2 2 2 0 0 0 0 u
  x 1 du dx 1  Gọi      2 1 x I x e dx . Đặt 2 x  1 e 2 x
dv e dx v  0  2 1 2 x 1 x e e
I  4 x   2 1 2 x 2 2 1  4
dx  2   e
 2 e   3 e  1 0 2 2 0 0 1 2 x 2 e
Vậy V  4  x   1  I  2     2
3   e     2 e  5 . 1  2 0
Chọn đáp án D. 1
Câu 11: Cho hai hàm số f x 3 2
ax bx cx  và g x 2
dx ex 1 a, ,
b c, d, e   . Biết rằng đồ 2
thị hàm số y f x và y g x cắt nhau tại 3 điểm có hoành độ lần lượt là 3  ; 1  ; 1 (tham khảo hình vẽ)
Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng 9 A. . B. 8. C. 4. D. 5. 2 Lời giải:
Cách 1: 1 3 Xét phương trình 3 2 2
ax bx cx
dx ex 1 3
Û ax + (b- d ) 2
x + (c- e) x- = 0 có 3 2 2   3
a  b d   c e 3 27 9 3   0  b d   2  2   3  1 nghiệm lần lượt là 3  ; 1
 ; 1 nên suy ra a  b d   c e   0  a  2  2    1 a  
b d  c e 3   0 c e    2  2 1 3 1 3
Vậy f x  g x 3 2
x x x  . 2 2 2 2
Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng 1  S    1
f x  g x dx   g x  f xdx 3  1  1  1  1 3 1 3   1 3 1 3  3 2 3 2  S x x x dx x x x dx  2  2  4      .  2 2 2 2   2 2 2 2  3  1  Cách 2:
Ta có: f x  g x  a x  3 x   1  x   1 . 3
Suy ra a x  3 x   1  x   3
1  ax  b d  2
x  c d x  2 3 1 1
Xét hệ số tự do suy ra: 3
a    a  . Do đó: f x  g x  x  3x   1  x   1 . 2 2 2 1  1
Diện tích bằng: S   f
  x gxdx g
  x f xdx  3  1  1  1 1  S
x  x  x   1 3 1 1 dx
x 3x   1  x     1 dx  4 . 2 2 3  1 
Chọn đáp án C.
Câu 12: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x  1 và x  3 , biết rằng khi cắt
vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (1  x  3 ) thì được thiết
diện là một hình chữ nhật có độ dài hai cạnh là 3x và 2 3x  2 . 124 124 A. V  32  2 15. B. V  . C. V  .
D. V  32  2 15. 3 3 Lời giải:
Diện tích thiết diện là: 2 S (x)  3 . x 3x  2 3  124 Thể tích vật thể là: 2 V  3 .
x 3x  2dx   3 1
Chọn đáp án C.
Câu 13: Một chất điểm A xuất phát từ O , chuyển động thẳng với vận tốc biến thiên theo thời gian bởi 1 59
quy luật v t  2  t
t m / s , trong đó t (giây) là khoảng thời gian tính từ lúc a bắt đầu 150 75
chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O , chuyển động thẳng
cùng hướng với A nhưng chậm hơn 3 giây so với A và có gia tốc bằng a  2
m / s  ( a là hằng
số). Sau khi B xuất phát được 12 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kịp A bằng
A. 20m / s.
B. 16m / s.
C. 13m / s.
D. 15m / s. Lời giải: 15  1 59 
Quãng đường chất điểm A đi từ đầu đến khi B đuổi kịp là 2 S t t dt  96   m . 150 75  0
Vận tốc của chất điểm B là v t adt at C  . B  
Tại thời điểm t  3 vật B bắt đầu từ trạng thái nghỉ nên v 3  0  C  3  a . B Lại có quãng đường chất điểm B đi được đến khi gặp A là 15 15    atS at  3a 2 dt  
 3at   72a m . 2    2  3 3 4
Vậy 72a  96  a   2 m / s  . 3
Tại thời điểm đuổi kịp A thì vận tốc của B là v 15  16m / s . B
Chọn đáp án B.
Câu 14: Cho hàm số y f x . Đồ thị của hàm số y f  x như hình bên dưới :
Đặt g x  f x   x  2 2
1 . Mệnh đề nào dưới đây đúng? A. g  3
   g 3  g   1 . B. g   1  g  3    g 3.
C. g 3  g  3    g   1 . D. g  
1  g 3  g  3  . Lời giải:
Ta có g x  2 f  x  2 x   1  
g x   f  xx 1 0  x 1   . x  3  Bảng biến thiên Suy ra g  3    g  
1 và g 3  g   1 . (1)
Gọi S là diện tích hình phẳng giới hạn bởi các đường: y f '(x), y x 1, x  3  , x 1 1
Gọi S là diện tích hình phẳng giới hạn bởi các đường: y x 1, y f '(x), x  1, x  3 2
Dựa vào hình vẽ, ta thấy: S S  0 . 1 2 1 3
Suy ra: S S  0   f
  xx 1dx  
x 1 f xdx  0 1 2  3  1 1 3 3   f
  xx 1dx  f  
 xx 1dx  0    f
  xx 1dx  0  . 3  1 3  3 3
Khi đó: g 3  g  3    g
 xdx  2  f
  xx 1dx  0  (2) 3  3 
Từ (1) và (2) suy ra: g  
1  g 3  g  3  .
Chọn đáp án D.
Câu 15: Cho hình phẳng  H  được giới hạn bởi các đường x  1, x  e, y  0 và y  ln x . Thể tích V
của khối tròn xoay tạo thành khi quay  H  xung quanh trục Ox được tính theo công thức e e e e A. V   ln d x x  .
B. V   ln x dx  . C. 2 V   ln d x x  . D. 2 V  ln d x x  . 1 1 1 1 Lời giải:
Thể tích V  của khối tròn xoay tạo thành khi quay  H  xung quanh trục Ox là: e 2 V   ln d x x  . 1
Chọn đáp án C.
Câu 16: Gọi  D là hình phẳng giới hạn bởi các đường y  2 x, y  0 và x  2020; D là hình phẳng 2  1 
giới hạn bởi các đường y  3x, y  0 và x  2020 . Gọi V ,V lần lượt là thể tích khối tròn xoay 1 2 V
tạo thành khi quay  D và  D xung quanh trục Ox . Tỉ số 1 bằng 2  1  V2 4 2 3 2 6 A. . B. . C. . D. . 3 3 3 3 Lời giải: Xét V : 1
Ta có phương trình hoành độ giao điểm là:
2 x  0  x  0  x  0 2020 2020 2 2020
Suy ra V    2 x  2 2 dx   4xdx  2 x  2.2020  1 0 0 0 Xét V : 2
Ta có phương trình hoành độ giao điểm là:
3x  0 x  0  x  0 2020 2020 2 3 2020 3 2 V 2 .2020 4
Suy ra V     3x  2 2 dx   3xdx   x  .2020 .  Vậy 1   . 2 2 0 2 V 3 2 3 0 0 2 .2020 2
Chọn đáp án A. Câu 17: Kí hiệu S t  là diện tích hình phẳng giới hạn bởi các đường
y  2x 1, y  0, x  1, x t, t  
1 . Tìm t để S t   10 . A. t  4 . B. t  13 . C. t  3 . D. t  14 . Lời giải: t
Ta có S t   2x 1 dx
. Do x 1;t, t  1 nên 2x 1  0 . 1 t
Khi đó: S t   2x   1 dx   2
x xt 2
|  t t  2 . 1 1 t  3
Để S t   10 thì 2 2
t t  2  10  t t 12  0   . t  4 
Do t  1nên t  3 thỏa mãn.
Chọn đáp án C. Câu 18: Cho hàm số 3 2
y ax bx cx d ,  ; a ; b ; c d
 có đồ thị như hình vẽ bên dưới:
Biết diện tích hình phẳng tô đậm bằng 1. Giá trị của a  2b  3c  4d bằng A. 8. B. 1. C. 1. D. 8. Lời giải:
Đồ thị hàm số đi qua các điểm có tọa độ lần lượt là 1;0;3 ;0;5 ;0 nên ta có
a b c d  0 
27a  9b  3c d  0   1
125a  25b 5c d  0 
Diện tích hình phẳng tô đậm 5 3 5 3 5
S   f xdx=1   f xdx   f xdx 1   f xdx- f xdx=1 1 1 3 1 3
F 3  F  
1  F 5  F 3  1  2F 3  F  
1  F 5  1  1
 16a  24b  4c 1.2 4 3 2 81 9 với  dx       ; 3   9   3 ;   1      ax bx cx a b c f x dx F x F a b c d F d 4 3 2 4 2 4 3 2 F   625 125 25 5  a b c  5d 4 3 2  1 a   8 
a b c d  0 9    b
27a  9b  3c d  0  8 Từ   1 và 2 ta có hệ:   
125a  25b  5c d  0 23  c   116 
a  24b  4c  1  8  15  d   8
Khi đó a  2b  3c  4d  1.
Chọn đáp án B.
Câu 19: Cho hàm số f x xác định và liên tục trên đoạn 5; 
3 có đồ thị như hình vẽ bên dưới: y 5 y=g(x) S3 2 S1 -1 -5 -2 O x S 2 3 2 y=f(x)
Biết rằng diện tích hình phẳng S , S , S giới hạn bởi đồ thị hàm số f x và đường parabol 1 2 3 3    2 y
g x ax bx c lần lượt là m , n , p . Tích phân f
 xdx bằng 5  208 208
A. m n p  .
B. m n p  . 45 45 208 208
C. m n p  .
D. m n p  . 45 45 Lời giải:
Từ đồ thị ta thấy y 5 y=g(x) S3 2 S1 -1 -5 -2 O x S 2 3 2 y=f(x) 2  2  2  2  2  S
f x g x dx f x dx g x dx f x dx S g x dx      . 1            1   5  5  5  5  5  0 0 0 0 0 S
g x f x dx g x dx f x dx f x dx g x dx S      . 2              2 2  2  2  2  2  3 3 3 3 3
S   f x g x  dx
f x dx g x dx
f x dx S g x dx      . 3            3   0 0 0 0 0 3 3 3 Do vậy: f
 xdx S S S g x dx mnp g x d .x   1 2 3     5  5  5 
Do đó ta loại đáp án A và D. 3 208
Từ đồ thị ta thấy g
 xdx là số dương. Mà 2 đáp án còn lại chỉ có là phù hợp, nên ta 45 5  3 208 chọn
f xdx m n p   . 45 5  3
Chú ý: Có thể tính g
 xdx như sau: 5 
Từ đồ thị hàm số y g x ta thấy nó đi qua các điểm  5
 ;2, 2;0, 0;0 nên ta có:
25a  5b c  2  3 3 2 4  2 4  208
4a  2b c  0  a  , b  , c  0. Do đó: g  x 2 dx x x dx     . 15 15  15 15  45 c  0  5  5 
Chọn đáp án B. 2 3
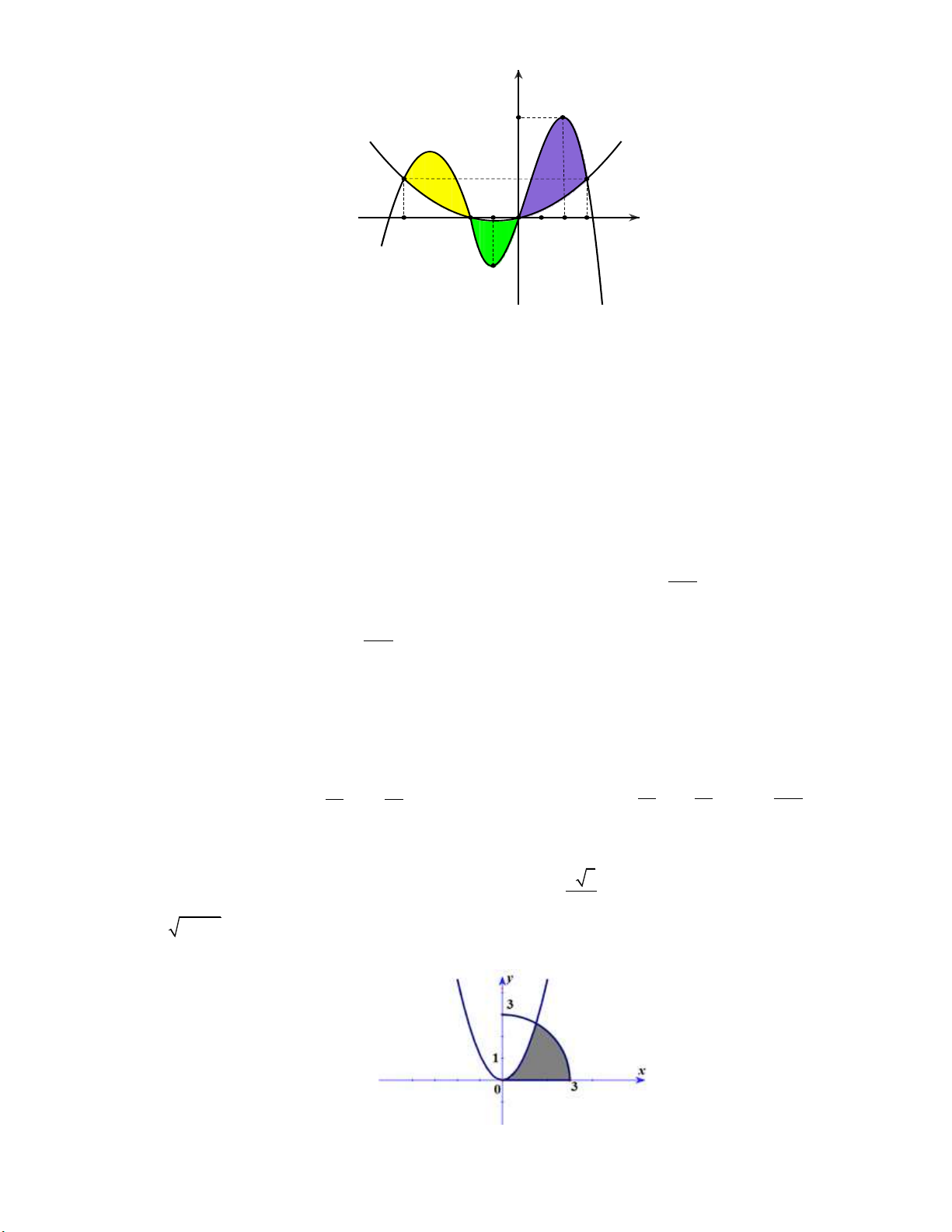
Câu 20: Cho  H  là hình phẳng giới hạn bởi parabol 2 y
x với cung tròn có phương trình 3 2
y  9  x , 0  x  3 và trục hoành (phần tô đậm trong hình vẽ dưới đây). Diện tích S của hình
phẳng  H  được tính bằng công thức nào dưới đây? 3 3  2  2 3 2 A. 2 2 S x  9  x dx   . B. 2 2 S x dx  9  x dx   .  3  3 0 0 3 2 3 3 3 2 2 2 2 C. 2 2 S  
x  9  x dx  . D. 2 2 S x dx  9  x dx   . 3 3 0 0 3 Lời giải: 2 3 3 Xét phương trình 2 2
x  9  x x  (vì 0  x  3 ). 3 2 3 3 3 2 3 2 2 2 3 2 Quan sát đồ thị, suy ra 2 2 2 2 S x dx
9  x dx S x dx  9  x dx     . 3 3 0 3 0 3 2
Chọn đáp án D.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông øng dông tÝch ph©n
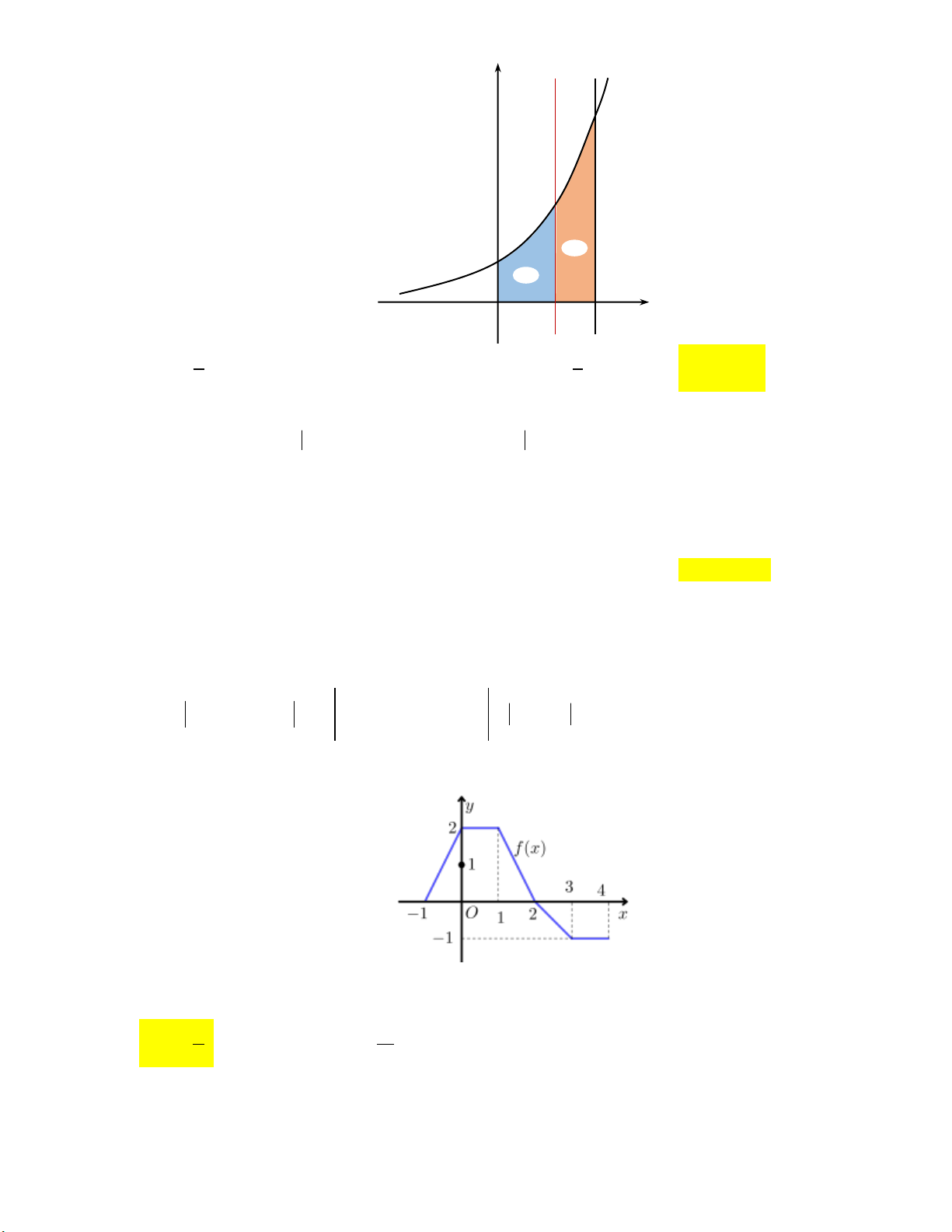
PHIẾU ÔN TẬP SỐ 04 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Câu 1: Diện tích hình phẳng của hình được tô đen như hình vẽ bên là b b
A.   f x  g x d   x . B.  g
  x  f x dx   . a a b b C.  f
  x  g x dx   . D. g
  x  f x dx   . a a
Câu 2: Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo
thành được tính theo công thức b b A. 2 V     f x 2
g x d .   x B. V   
 f x gx 2 d .  x a a b b C. V  
 f x gx 2 d .  x D. V   
 f x gxd .  x a a
Câu 3: Cho hai đồ thị hàm số f x 2
 3 x và   2x g x
có đồ thị như hình vẽ bên dưới:
Diện tích phần hình phẳng gạch chéo trong hình vẽ được tính theo công thức nào dưới đây ? 1 1 2 A.     2  3   4x x dx 2 x      .
B. 3 x 2 dx . 0 0 3 3 2 C.  2 3   2x x  dx . D.  2 3   2x x dx . 1 1
Câu 4: Cho hàm số f x 3 2
x  3x  2x . Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
y f x , trục tung, trục hoành và đường thẳng x  3 10 12 11 9 A. S  . B. S  . C. S  . D. S  . 4 4 4 4
Câu 5: Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol  P 2
: y x và đường thẳng
d : y  2x quay quanh trục Ox bằng 2 2 2 2 2 2 2 A. 2 4
 4x dx  x dx   . B.   2
x  2x dx . C.   2
x  2xdx . D. 2 4
 4x dx  x dx   . 0 0 0 0 0 0 x
Câu 6: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số  H  1
: y x  và các trục tọa độ. Khi 1
đó giá trị của S bằng A. S  2 ln 2 1. B. S  ln 2 1 . C. S  ln 2 1. D. S  1 2 ln 2 .
Câu 7: Cho hình phẳng D giới hạn bởi các đường  5x y
, y  0, x  2, x  2 . Thể tích khối tròn
xoay tạo thành do hình phẳng D quay quanh trục hoành được tính theo công thức nào dưới đây? 2 2 2 2 A.   25x V d . x  B. 2  5 x V d . x  C.  5x V d . x  D. 2  2 5 x V d . x  2  2  2  0
Câu 8: Cho hàm số y f x có đạo hàm liên tục trên đoạn 0;7 và có đồ thị y f  x trên đoạn 0;7 như hình vẽ.
Đặt g x  f 2x  
1 biết rằng diện tích các hình phẳng trong hình vẽ lần lượt là 244 28 2528 S  , S  , S
và f 0  1. Tính g 4 . 1 2 3 15 15 15 2744 5518 563 2759 A. . B. . C. . D. . 15 15 3 15
Câu 9: Tính thể tích của vật thể nằm giữa hai mặt phẳng x  1 và x  2 , biết rằng thiết diện của vật
thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x , 1  x  2 là một
hình chữ nhật có độ dài hai cạnh là x và 2 x  3. 7 7  8 8 7  7 16 2  7 A. . B. . C. . D. 8 2  4 . 3 3 3
Câu 10: Tính diện tích S của hình phẳng (phần gạch sọc) giới hạn bởi hai đồ thị hàm số f x  x và
g x  x  2 như trong hình sau: 7 10 11 7 A. S  . B. S  . C. S  . D. S  . 3 3 3 3
Câu 11: Người ta xây sân khấu với mặt sàn có dạng hợp của hai đường tròn giao nhau. Bán kính của
hai hình tròn lần lượt là 20 m và 15 m . Khoảng cách giữa hai tâm của hai hình tròn là
30 m .Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là 300 nghìn đồng và chi
phí làm mỗi mét vuông còn lại là 100 nghìn đồng (tham khảo hình vẽ)
Hỏi số tiền làm mặt sàn sân khấu gần với số nào trong các số dưới đây? A. 202 triệu đồng. B. 208 triệu đồng. C. 218 triệu đồng. D. 200 triệu đồng.
Câu 12: Trong mặt phẳng cho Parabol 2
(P) : y x và đường tròn 2 2
(C) : x y  2 . Tính diện tích phần
tô đậm (gần đúng đến hàng phần trăm). A. 1,19. B. 1,90. C. 1,81. D. 1,80.
Câu 13: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 3 y x , 2
y x  4x  4 và trục Ox được
tính theo công thức nào dưới đây? 2 1 2 A. 3 x  
 2x 4x4 dx. B. 3  x dx  
 2x 4x4dx . 0 0 1 1 2 1 2 C. 3 x dx  
 2x 4x4dx . D. 3 x dx  
 2x 4x4dx . 0 1 0 1 1 4
Câu 14: Tính diện tích hình phẳng giới hạn bởi các đường 2
y x , y   x  và trục hoành. 3 3 11 61 343 39 A. . B. . C. . D. . 6 3 162 2
Câu 15: Đoạn đường thẳng AB có chiều dài 200 km. Hai xe ôtô khởi hành cùng một lúc, xe ôtô thứ
nhất đi từ A đến B với vận tốc v  8t  40 km/h , xe ôtô thứ hai đi từ B đến A với vận tốc 1
v  2t  50 km/h . Hỏi sau bao lâu thì hai xe gặp nhau? 2 A. 3 giờ. B. 5 giờ. C. 4 giờ. D. 2 giờ.
Câu 16: Tính diện tích hình phẳng được đánh dấu trên hình dưới: 28 1 18 2 A. S  . B. S  3 2  . C. S  . D. S  2 3  . 3 3 3 3
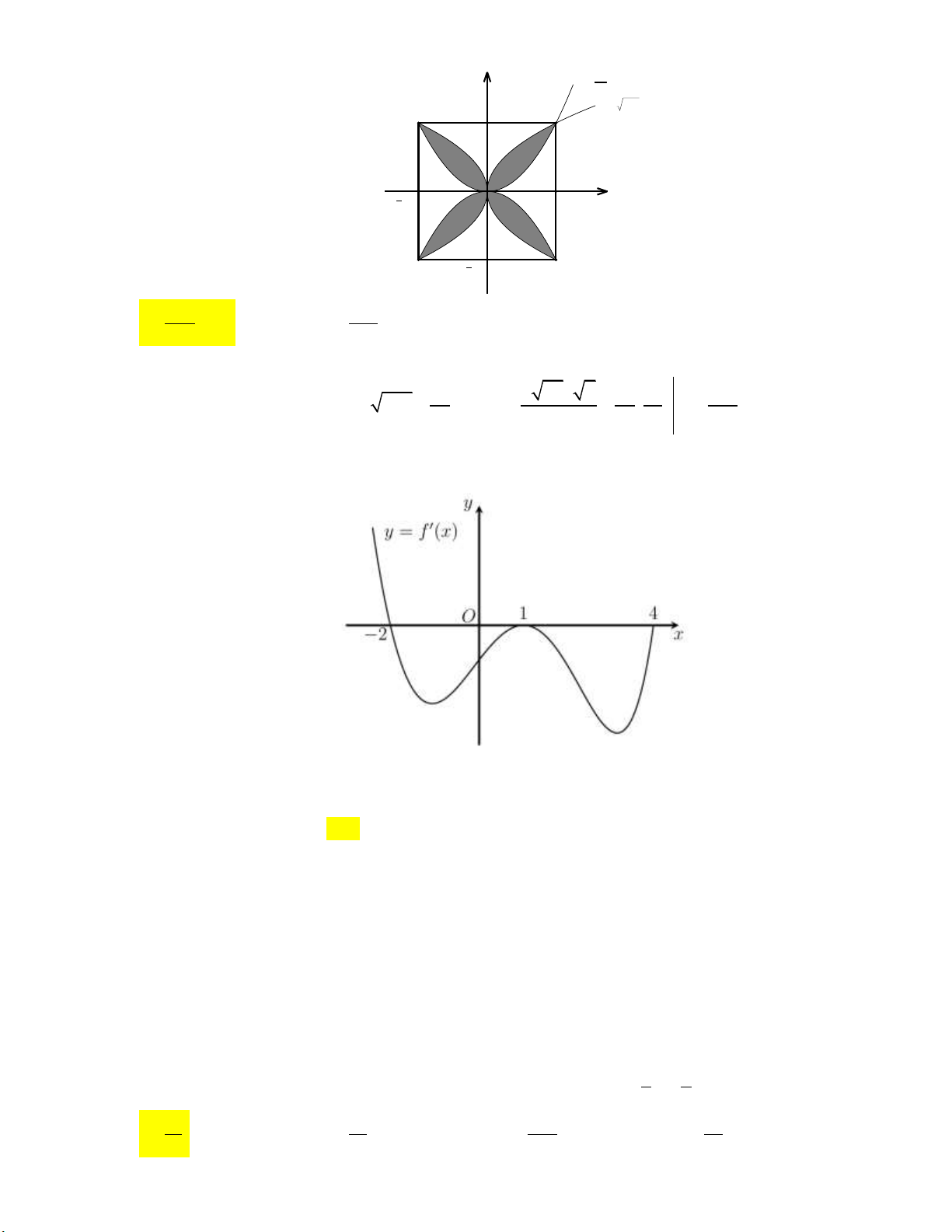
Câu 17: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường 2
y  1 x , y  0 quanh aπ a
trục Ox là V
với a , b là số nguyên và
là phân số tối giản. Khi đó a b bằng b b A. 11. B. 17. C. 25. D. 31.
Câu 18: Tính diện tích S của hình phẳng (phần gạch sọc) trong hình sau: y
g(x) = x 2 f(x) = x O 2 4 x 8 10 11 7 A. S  . B. S  . C. S  . D. S  . 3 3 3 3
Câu 19: Cho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bởi trục lớn với độ dài trục
lớn bằng 80cm , độ dài trục bé bằng 60cm và đáy trống là hình tròn có bán kính bằng 60cm .
Tính thể tích V của chiếc trống (kết quả làm tròn đến hàng đơn vị). A. 3
V  344963cm . B. 3
V  344964cm . C. 3
V  208347cm . D. 3
V  208346cm .
Câu 20: Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường x y  2  0; y x; y  0 quay
quanh trục Ox bằng 5 2 6 5 A. . B. . C. . D. . 6 3 5 6
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông øng dông tÝch ph©n
PHIẾU ÔN TẬP SỐ 04
LỜI GIẢI CHI TIẾT
Câu 1: Diện tích hình phẳng của hình được tô đen như hình vẽ bên là b b
A.   f x  g x d   x . B.  g
  x  f x dx   . a a b b C.  f
  x  g x dx   . D. g
  x  f x dx   . a a Lời giải: b
Diện tích hình phẳng của hình được tô đen như hình vẽ bên là  f
  x  g x dx   . a
Chọn đáp án C.
Câu 2: Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo
thành được tính theo công thức b b A. 2 V     f x 2
g x d .   x B. V   
 f x gx 2 d .  x a a b b C. V  
 f x gx 2 d .  x D. V   
 f x gxd .  x a a Lời giải:
Chọn đáp án A.
Câu 3: Cho hai đồ thị hàm số f x 2
 3 x và   2x g x
có đồ thị như hình vẽ bên dưới:
Diện tích phần hình phẳng gạch chéo trong hình vẽ được tính theo công thức nào dưới đây ? 1 1 2 A.     2  3   4x x dx 2 x      .
B. 3 x 2 dx . 0 0 3 3 2 C.  2 3   2x x  dx . D.  2 3   2x x dx . 1 1 Lời giải:
Dựa theo hình vẽ trên, diện tích phần gạch chéo tính theo công thức 1 1 2 3   2x d    2 3   2x x x x dx. 0 0
Chọn đáp án B.
Câu 4: Cho hàm số f x 3 2
x  3x  2x . Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
y f x , trục tung, trục hoành và đường thẳng x  3 10 12 11 9 A. S  . B. S  . C. S  . D. S  . 4 4 4 4 Lời giải: 3 11
Áp dụng công thức ta có: 3 2 S
x  3x  2x dx   . 4 0
Chọn đáp án C.
Câu 5: Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol  P 2
: y x và đường thẳng
d : y  2x quay quanh trục Ox bằng 2 2 2 2 2 2 2 A. 2 4
 4x dx  x dx   . B.   2
x  2x dx . C.   2
x  2xdx . D. 2 4
 4x dx  x dx   . 0 0 0 0 0 0 Lời giải:
Phương trình hoành độ giao điểm của: Parabol  P 2
: y x và đường thẳng d : y  2x là: x  0 2 x  2x   x  2
Gọi D là hình phẳng giới hạn bởi đồ thị các đường thẳng: y  2 ;
x y  0; x  0; x  2 . 1 2
Quay hình phẳng D quanh Ox ta được khối tròn xoay có thể tích 2
V   4x dx  . 1 1 0
Gọi D là hình phẳng giới hạn bởi Parabol  P 2
: y x và các đường thẳng: y  0; x  0; x  2 . 2 2
Quay hình phẳng D quanh Ox ta được khối tròn xoay có thể tích 4
V   x dx  . 2 2 0
Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol  P 2
: y x và đường thẳng 2 2
d : y  2x quay quanh trục Ox có thể tích 2 4
V V V   4x dx   x dx   . 1 2 0 0
Chọn đáp án A. x
Câu 6: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số  H  1
: y x  và các trục tọa độ. Khi 1
đó giá trị của S bằng A. S  2 ln 2 1. B. S  ln 2 1 . C. S  ln 2 1. D. S  1 2 ln 2 . Lời giải: x 1
Phương trình hoành độ giao điểm của  H  và Ox là  0  x 1 x  . 1 x
Diện tích hình phẳng S giới hạn bởi đồ thị hàm số  H  1
: y x  và các trục tọa độ là 1 1 1    1 x 1 x 1  2  S  dx  dx  1   dx      
x2ln x11 2ln21. 0 0 x 1 x 1  x 1  0 0
Chọn đáp án A.
Câu 7: Cho hình phẳng D giới hạn bởi các đường  5x y
, y  0, x  2, x  2 . Thể tích khối tròn
xoay tạo thành do hình phẳng D quay quanh trục hoành được tính theo công thức nào dưới đây? 2 2 2 2 A.   25x V d . x  B. 2  5 x V d . x  C.  5x V d . x  D. 2  2 5 x V d . x  2  2  2  0 Lời giải:
Ta có thể tích khối tròn xoay do hình phẳng giới hạn bởi các
đường y f x, y  0, x a, x bab sinh ra khi quay quanh trục Ox là b 2 V   f  xdx . a 2 2 2
Áp dụng công thức ta có:
   5x  d  25x V x dx  . 2  2 
Chọn đáp án A.
Câu 8: Cho hàm số y f x có đạo hàm liên tục trên đoạn 0;7 và có đồ thị y f  x trên đoạn 0;7 như hình vẽ.
Đặt g x  f 2x  
1 biết rằng diện tích các hình phẳng trong hình vẽ lần lượt là 244 28 2528 S  , S  , S
và f 0  1. Tính g 4 . 1 2 3 15 15 15 2744 5518 563 2759 A. . B. . C. . D. . 15 15 3 15 Lời giải: 2 2 Ta có S
f x  0 dx f xf 2  f 0  . 1         0 0 244 Mà S
và f 0  1 suy ra f   244 259 2  1  . 1 15 15 15 3 3 Tương tự S
f x  0 dx   f xf 2  f 3  2         2 2 28 Mà S  và f   259 2  suy ra f   259 28 231 3    . 2 15 15 15 15 15 7 S f
 x0 dx f x7  f 7  f 3 3     3 3 2528 Mà S  và f   231 3  suy ra f   2528 231 2759 7    . 3 15 15 15 15 15
Do g x  f 2x  
1 nên g    f
   f   2759 4 2.4 1 7  . 15
Chọn đáp án D.
Câu 9: Tính thể tích của vật thể nằm giữa hai mặt phẳng x  1 và x  2 , biết rằng thiết diện của vật
thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x , 1  x  2 là một
hình chữ nhật có độ dài hai cạnh là x và 2 x  3. 7 7  8 8 7  7 16 2  7 A. . B. . C. . D. 8 2  4 . 3 3 3 Lời giải:
Diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với với trục Ox tại điểm có
hoành độ x , 1  x  2 là: 2
S x x  3 .
Khi đó thể tích của vật thể nằm giữa hai mặt phẳng x  1 và x  2 là: 2 2 2 1 1 2 7 7  8 2 2
V x x  3dx x  3d  2 x  3 
 2x 3 2x 3    . 2 2 3 1 3 1 1
Chọn đáp án A.
Câu 10: Tính diện tích S của hình phẳng (phần gạch sọc) giới hạn bởi hai đồ thị hàm số f x  x và
g x  x  2 như trong hình sau: 7 10 11 7 A. S  . B. S  . C. S  . D. S  . 3 3 3 3 Lời giải: 4 4 4 3      xS x x  2dx x   x  2 2 2 10 2 dx   x   2x   . 3 2 3   0 0 2
Chọn đáp án B.
Câu 11: Người ta xây sân khấu với mặt sàn có dạng hợp của hai đường tròn giao nhau. Bán kính của
hai hình tròn lần lượt là 20 m và 15 m . Khoảng cách giữa hai tâm của hai hình tròn là
30 m .Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là 300 nghìn đồng và chi
phí làm mỗi mét vuông còn lại là 100 nghìn đồng (tham khảo hình vẽ)
Hỏi số tiền làm mặt sàn sân khấu gần với số nào trong các số dưới đây? A. 202 triệu đồng. B. 208 triệu đồng. C. 218 triệu đồng. D. 200 triệu đồng. Lời giải:
Gọi I , J lần lượt là tâm của hai đường tròn bán kính 20 m , 15 m . Gọi ,
A B là giao của hai đường tròn.
Chọn hệ trục tọa độ Oxy sao cho Oy trùng IJ và Ox song song với AB và I là gốc tọa độ (như hình vẽ).
Khi đó đường tròn tâm I bán kính R  20 m có phương trình 2 2
x y  400 .
Vì khoảng cách giữa hai tâm của hai hình tròn là 30 m nên J 0;30 . Do đó đường tròn
tâm J 0;30 bán kính R  15 m có phương trình x   y  2 2 30  225 .
Khi đó phần chung của hai đường tròn giới hạn bởi  2 2 y
400  x ; y  30  225  x  .  4 455  2      400 x yx  Xét hệ 12    2 215
y  30  225  xy   12
Diện tích phần chung của hai đường tròn là 5 455 12 S    2 2
400  x  225  x  30 dx  60, 2 1  . 5  455 12
Diện tích riêng của hai đường tròn là S  625  2S  625 120, 4 2 1 .
Số tiền chi phí là 300000S 100000S  300000.60, 2 100000. 625 120, 4  202369540 1 2   .
Vậy số tiền làm mặt sàn sân là gần 202 triệu đồng.
Chọn đáp án A.
Câu 12: Trong mặt phẳng cho Parabol 2
(P) : y x và đường tròn 2 2
(C) : x y  2 . Tính diện tích phần
tô đậm (gần đúng đến hàng phần trăm). A. 1,19. B. 1,90. C. 1,81. D. 1,80. Lời giải: Ta có 2 2 2
x y  2  y   2  x . Vì đường cong nửa trên của (C) tương ứng phần dương của
trục hoành nên có phương trình 2
y  2  x ,  y  0
Phương trình hoành độ giao điểm của đường cong nửa trên của (C) và Parabol (P) là : 2 x 1 2 2 x  2  x 4 2
x x  2  0    x  1  2 x  2 
Suy ra diện tích hình phẳng (H ) cần tính là : S   x 2 2 2
2  x x  1 1 1 3 1 2 2 dx  2  x dx   2  x dx     3 3 1  1  1  1  1 Xét 2 I  2  x dx
, đặt x  2 sin t dx  2 costdt 1      4 4 4 4  sin 2t   ta được 2 I
2  2 sin t 2 cos tdt  2  2cos tdt
  1cos2tdt t     1.     2   2     4 4 4 4  2  1 Do đó S  1   1,90. 2 3 2 3
Chọn đáp án B.
Câu 13: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 3 y x , 2
y x  4x  4 và trục Ox được
tính theo công thức nào dưới đây? 2 1 2 A. 3 x  
 2x 4x4 dx. B. 3  x dx  
 2x 4x4dx . 0 0 1 1 2 1 2 C. 3 x dx  
 2x 4x4dx . D. 3 x dx  
 2x 4x4dx . 0 1 0 1 Lời giải:
Dựa vào hình vẽ ta thấy hình phẳng cần tính diện tích gồm 2 phần:
Phần 1: Hình phẳng giới hạn bởi đồ thị hàm số 3
y x , trục Ox , x  0 , x  1 .
Phần 2: Hình phẳng giới hạn bởi đồ thị hàm số 2
y x  4x  4 , trục Ox , x  1 , x  2 . 1 2 1 2
Do đó diện tích cần tính là 3 2 3 S x dx
x  4x  4 dx x dx    
 2x 4x4dx . 0 1 0 1
Chọn đáp án D. 1 4
Câu 14: Tính diện tích hình phẳng giới hạn bởi các đường 2
y x , y   x  và trục hoành. 3 3 11 61 343 39 A. . B. . C. . D. . 6 3 162 2 Lời giải: 1 4
Phương trình hoành độ giao điểm của các đường 2
y x , y   x  là 3 3 x  1 1 4 2 x   x  2
 3x x  4  0   4 . 3 3 x    3 1 4
Hoành độ giao điểm của đường thẳng y   x  với trục hoành là x  4 . 3 3
Hoành độ giao điểm của parabol 2
y x với trục hoành là x  0 .
Diện tích hình phẳng cần tìm là 1 4  1 4 1 4  3 x  1 4  11 2
S x d x   x  d x    2    x x    .  3 3  3  6 3  6 0 1 0 1
Chọn đáp án A.
Câu 15: Đoạn đường thẳng AB có chiều dài 200 km. Hai xe ôtô khởi hành cùng một lúc, xe ôtô thứ
nhất đi từ A đến B với vận tốc v  8t  40 km/h , xe ôtô thứ hai đi từ B đến A với vận tốc 1
v  2t  50 km/h . Hỏi sau bao lâu thì hai xe gặp nhau? 2 A. 3 giờ. B. 5 giờ. C. 4 giờ. D. 2 giờ. Lời giải:
Gọi thời gian kể từ lúc hai xe đi đến lúc hai xe gặp nhau là a (giờ, a  0 )
Vì hai xe đi ngược chiều nên ta có phương trình: a a  a a
8t  40 dt  2t  50dt  200   2
4t  40t    2
t  50t   200 0 0 0 0  a  2 TM 2 2 2  
 4a  40a a  50a  200  5a  90a  200  0  a  20   KTM
Vậy sau 2 giờ thì hai xe gặp nhau.
Chọn đáp án D.
Câu 16: Tính diện tích hình phẳng được đánh dấu trên hình dưới: 28 1 18 2 A. S  . B. S  3 2  . C. S  . D. S  2 3  . 3 3 3 3 Lời giải: Ta có 2
y x x   y , từ hình vẽ ta thấy x  0  x   y . 3 3 3 2 2 2 3 S   y dy xdx x  3 3   1  2 3    . 3 3 3 1 1 1
Chọn đáp án D.
Câu 17: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường 2
y  1 x , y  0 quanh aπ a
trục Ox là V
với a , b là số nguyên và
là phân số tối giản. Khi đó a b bằng b b A. 11. B. 17. C. 25. D. 31. Lời giải:
Phương trình hoành độ giao điểm giữa 2
(P) : y  1 x và trục Ox : x 1 2 1 x  0   . x  1 
Thể tích của khối tròn xoay thu được khi quay hình phẳng quanh trục Ox là: 1 
V   1 x 2 16 2 dx  
. Suy ra: a  16, b  15 . Vậy a b  31. 15 1 
Chọn đáp án D.
Câu 18: Tính diện tích S của hình phẳng (phần gạch sọc) trong hình sau: y
g(x) = x 2 f(x) = x O 2 4 x 8 10 11 7 A. S  . B. S  . C. S  . D. S  . 3 3 3 3 Lời giải: y
g(x) = x 2 f(x) = x O 2 4 xy x
Dựa và hình vẽ, ta có hình phẳng được giới hạn bởi các đường:  y x  2 . y  0  2 4 Suy ra S xdx  
 x x2dx 2 πa 2 . 0 2
Chọn đáp án B.
Câu 19: Cho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bởi trục lớn với độ dài trục
lớn bằng 80cm , độ dài trục bé bằng 60cm và đáy trống là hình tròn có bán kính bằng 60cm .
Tính thể tích V của chiếc trống (kết quả làm tròn đến hàng đơn vị). A. 3
V  344963cm . B. 3
V  344964cm . C. 3
V  208347cm . D. 3
V  208346cm . Lời giải:
Chọn hệ trục tọa độ như hình vẽ ta thấy elip có tâm I 0 ; 6 , độ dài trục lớn 8dm và độ dài trục nhỏ 6dm . y 6 x -4 O 4 xy 62 2 2 x
Suy ra đường sinh chiếc trống thuộc elip có phương trình:  1 y  3  1  6 2 2 4 3 16 . 2  xy  3  1  6  16 
Khối tròn xoay giới hạn bởi  y  0 . x  4  x  4  2 4 2  x
Ta có thể tích chiếc trống: 3 3 V    3 1
 6 dx  344,9636dm  344964cm   . 16  4   
Chọn đáp án B.
Câu 20: Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường x y  2  0; y x; y  0 quay
quanh trục Ox bằng 5 2 6 5 A. . B. . C. . D. . 6 3 5 6 Lời giải:
Đường thẳng y  2  x cắt đường thẳng y  0 tại 2;0 và cắt đồ thị hàm số y x tại 1;  1
Đồ thị hàm số y x cắt đường thẳng y  0 tại O 0;0 x 2  x 5
Thể tích khối tròn xoay đó là: V    x  dx  2  x   2 1 3 1 2 2 2 2 dx       . 2 3 6 0 1 0 1
Chọn đáp án A.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông øng dông tÝch ph©n
PHIẾU ÔN TẬP SỐ 05 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
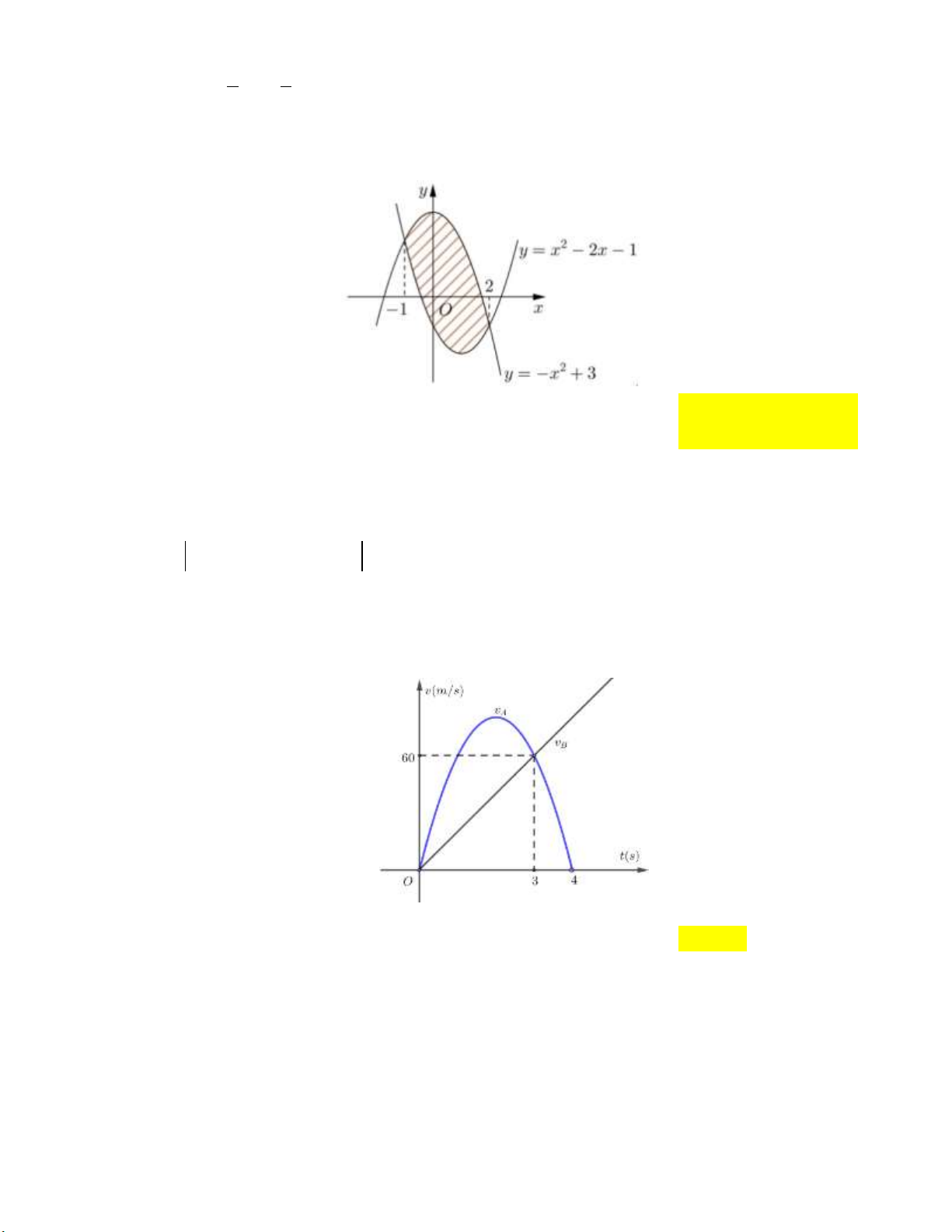
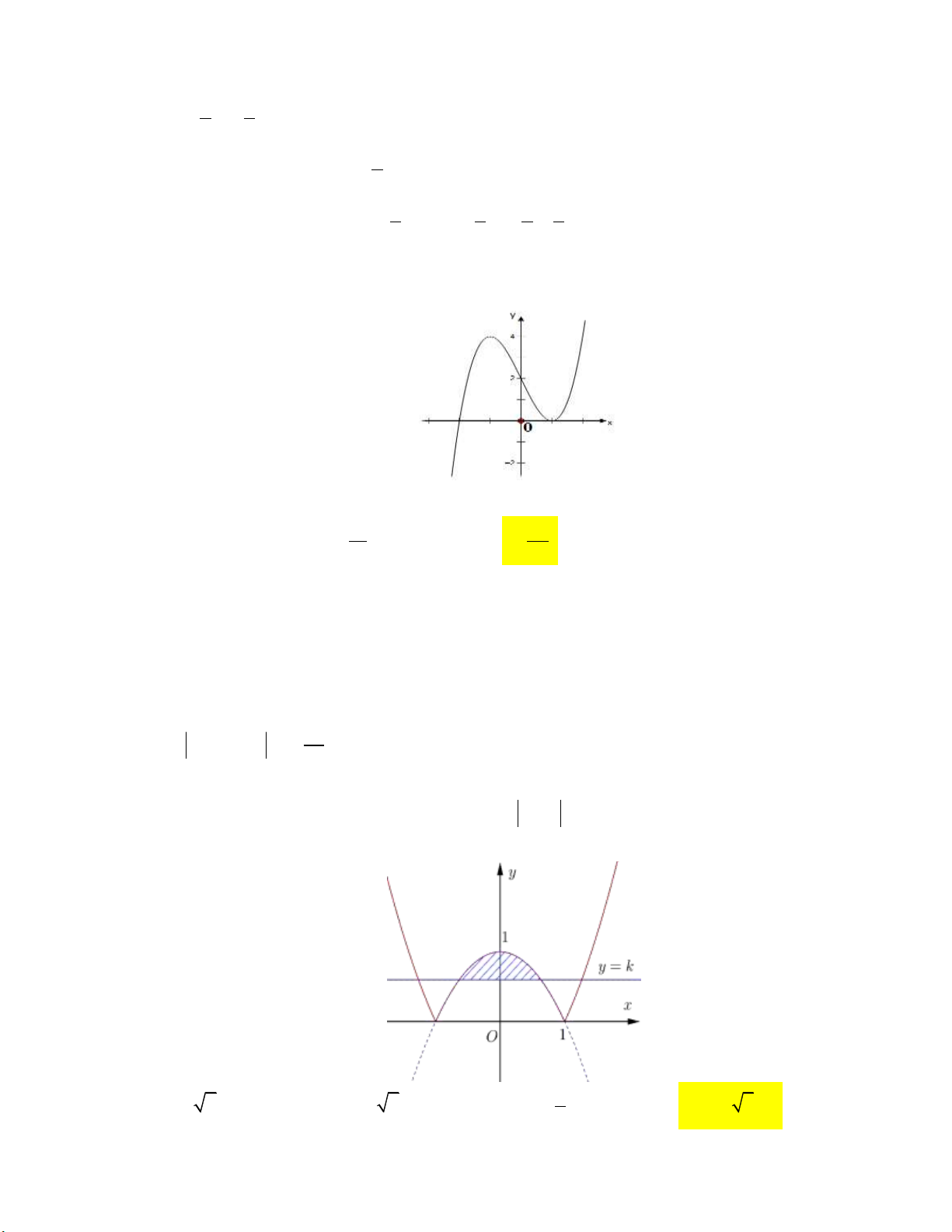
Câu 1: Diện tích phần hình phẳng tô đậm trong hình vẽ bên dưới được tính theo công thức nào dưới đây? 3 3
A.   f x  g xdx .
B.  g x  f xdx . 2  2  0 3 0 3
C.   f x  g xdx  gx  f xdx .
D.  g x  f xdx   f x  g xdx . 2  0 2  0 x 1
Câu 2: Cho hình phẳng  H  giới hạn bởi đồ thị hàm số y y  ,
x  và hai đường thẳng 2 2
y  x 1 . Tính diện tích S của hình phẳng  H  . A. S  8  3ln 3 . B. S  8  3ln 3 . C. S  3ln 3 .
D. S  4  3ln 3 .
Câu 3: Đường thẳng y m ( 0  m  1 ) cắt đường cong 4 2
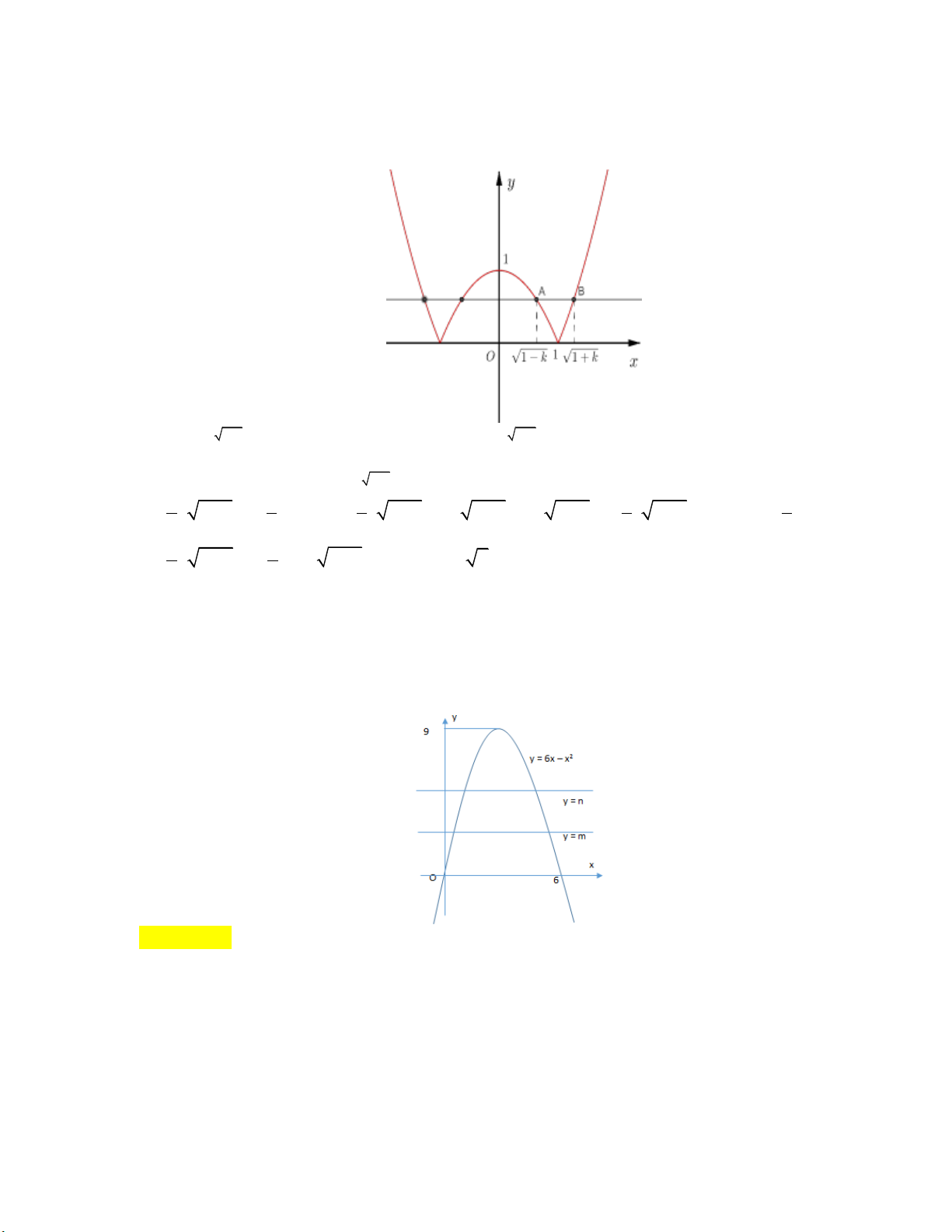
y x  2x 1 tại hai điểm thuộc góc phần tư
thứ nhất của hệ tọa độ Oxy và chia thành hai hình phẳng có diện tích S , S như hình vẽ. 1 2
Biết S S . Mệnh đề nào dưới đây đúng? 1 2  2   2 1   1 3   3  A. m  0;   . B. m  ;   . C. m  ;   . D. m  ;1   .  5   5 2   2 5   5 
Câu 4: Diện tích hình phẳng giới hạn bởi các đường 2
y x  3 và y  1 bằng 8 16 32 A. . B. . C. . D. 32 . 3 3 3
Câu 5: Một viên gạch hoa hình vuông cạnh 40 cm được thiết kế như hình bên dưới. Diện tích mỗi cánh hoa bằng y 1 y = x2 20 y = 20x 20 x 20 20 20 400 800 A. 2 cm . B. 2 cm . C. 2 250 cm . D. 2 800 cm . 3 3
Câu 6: Cho hàm số y f x . Hàm số có đồ thị hàm số y f ' x như hình vẽ dưới đây.
Biết diện tích hình phẳng giới hạn bởi trục Ox và đồ thị hàm số y f ' x trên đoạn 2;  1 và
1;4 lần lượt bằng 9 và 12. Cho biết f  1  3. Tính giá trị biểu thức P f  2
   f 4 . A. 21. B. 3. C. 9. D. 2. 1 4
Câu 7: Tính diện tích hình phẳng giới hạn bởi các đường 2
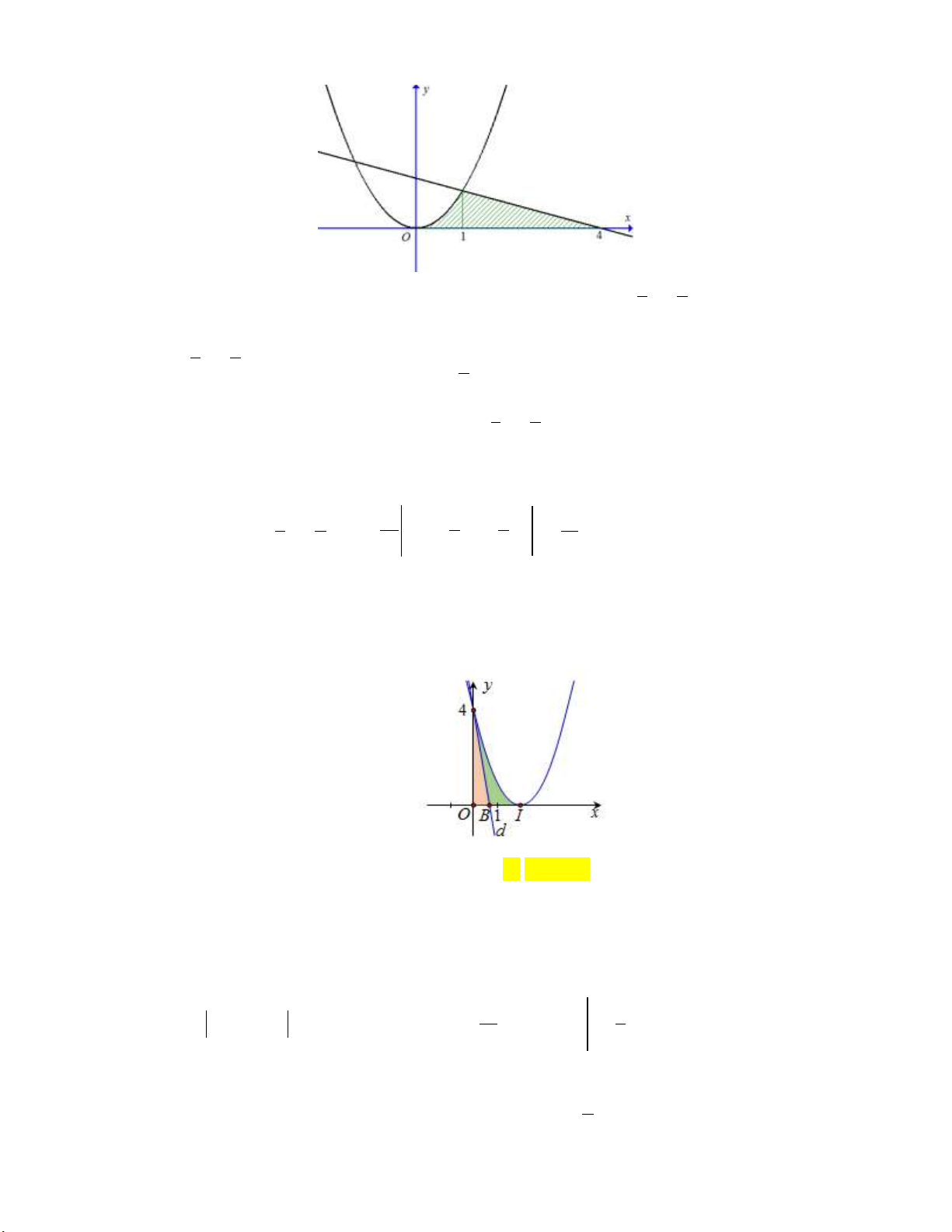
y x , y   x  và trục hoành. 3 3 11 61 343 39 A. . B. . C. . D. . 6 3 162 2
Câu 8: Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số 2
y x  4x  4 , trục tung và trục hoành. Xác
định k để đường thẳng d  đi qua điểm A0; 4 có hệ số góc k chia  H  thành hai phần có diện tích bằng nhau. A. k  4 . B. k  8 . C. k  6 . D. k  2 .
Câu 9: Cho hàm số đa thức bậc ba y f x 3 2
ax bx cx d (a  0) có đồ thị như hình vẽ bên dưới:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x và trục hoành. 19 27 A. 6 . B. . C. . D. 8. 4 4
Câu 10: Cho hình phẳng  H  giới hạn bởi các đường 2
y x 1 và y k, 0  k  1. Tìm k để diện tích của
hình phẳng  H  gấp hai lần diện tích hình phẳng được kẻ sọc trong hình vẽ bên dưới. 1 A. 3 k  4. B. 3 k  2 1. C. k  . D. 3 k  4 1. 2
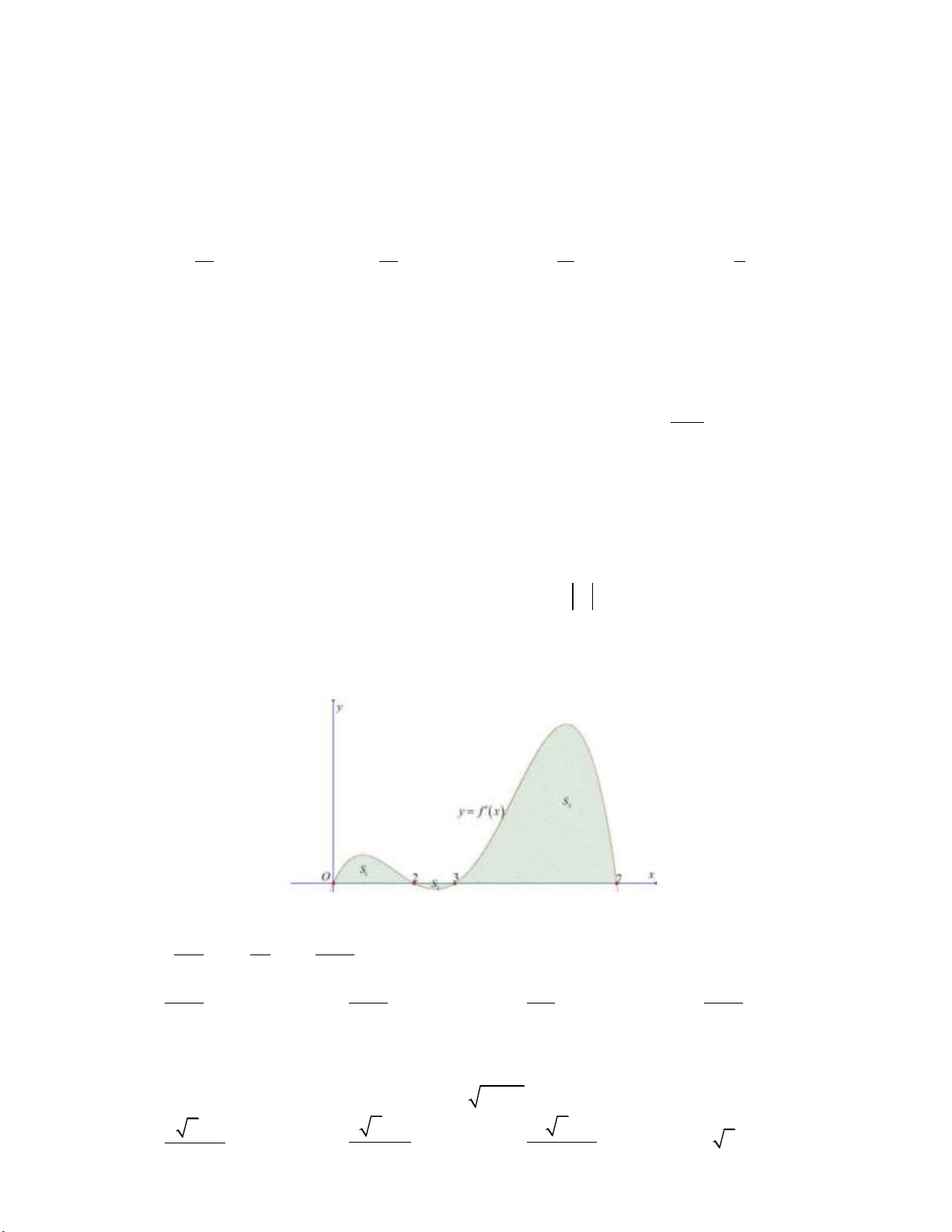
Câu 11: Gọi  H  là hình phẳng giới hạn bởi đồ thị của hàm số 2
y  6x x và trục hoành. Hai đường thẳng y  ,
m y n m n  9 chia hình  H  thành ba phần có diện tích bằng nhau. Tính 3 3
P  (9  m)  (9  n) . A. P  405 . B. P  409 . C. P  407 . D. P  403 .
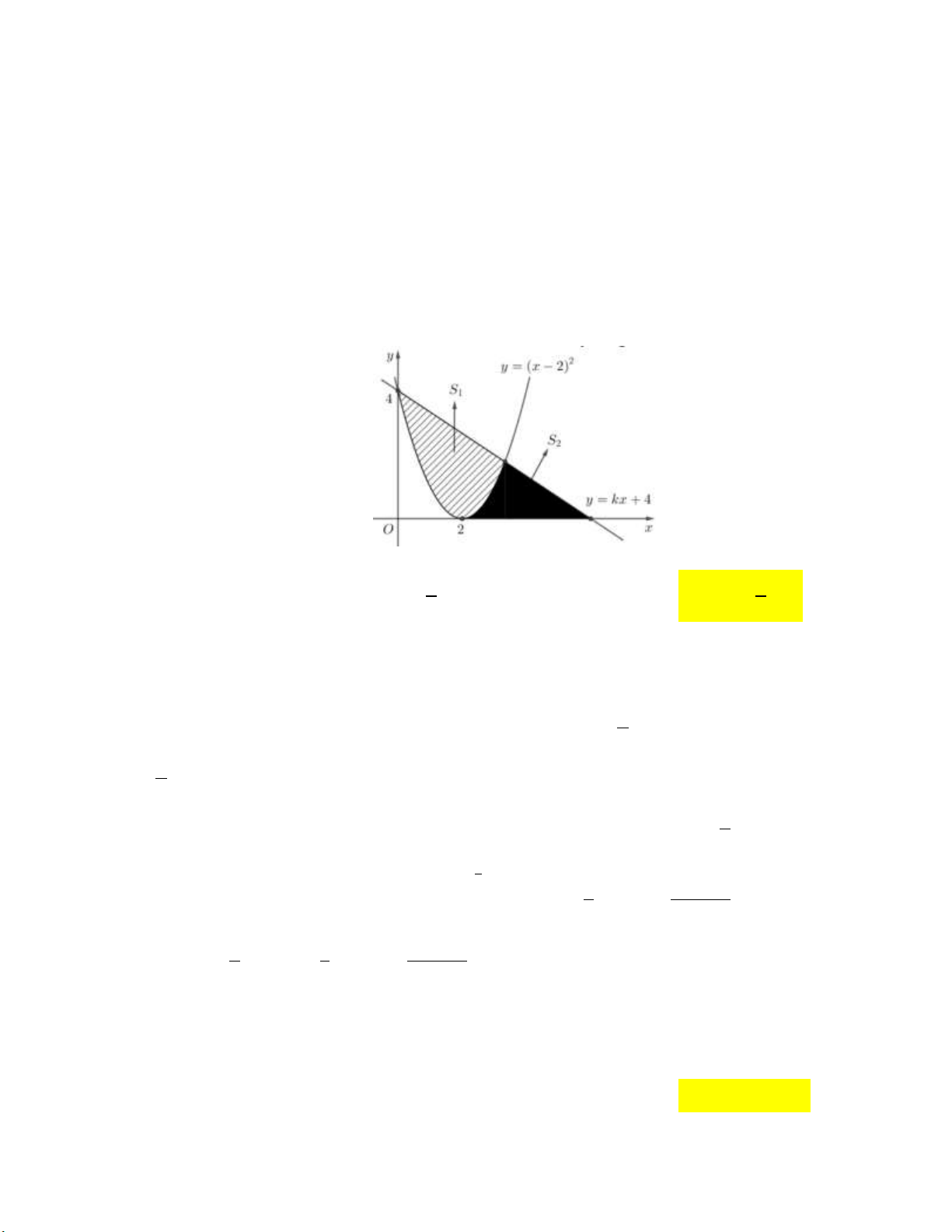
Câu 12: Cho hàm số y f x là hàm đa thức bậc bốn có đồ thị là C và d là tiếp tuyến của đồ thị C 11
tại hai điểm như hình vẽ. Biết diện tích hình phẳng giới hạn bởi đồ thị C và d là . Khi đó 3 1
tích phân I   f xdx bằng 1 19 25 23 13 A. . B. . C. . D. 6 6 6 3
Câu 13: Một chất điểm chuyển động trong 3 giây với vận tốc v a cos  t   b (mét/giây) (trong đó t là
biến thời gian; a,b là các hằng số) có đồ thị là một đường hình sin như hình vẽ bên. Tính tổng
quãng đường mà vật đi được sau 3 giây (kết quả làm tròn đến hàng phần trăm). A. 29, 93m . B. 15m . C. 27,93m . D. 17m .
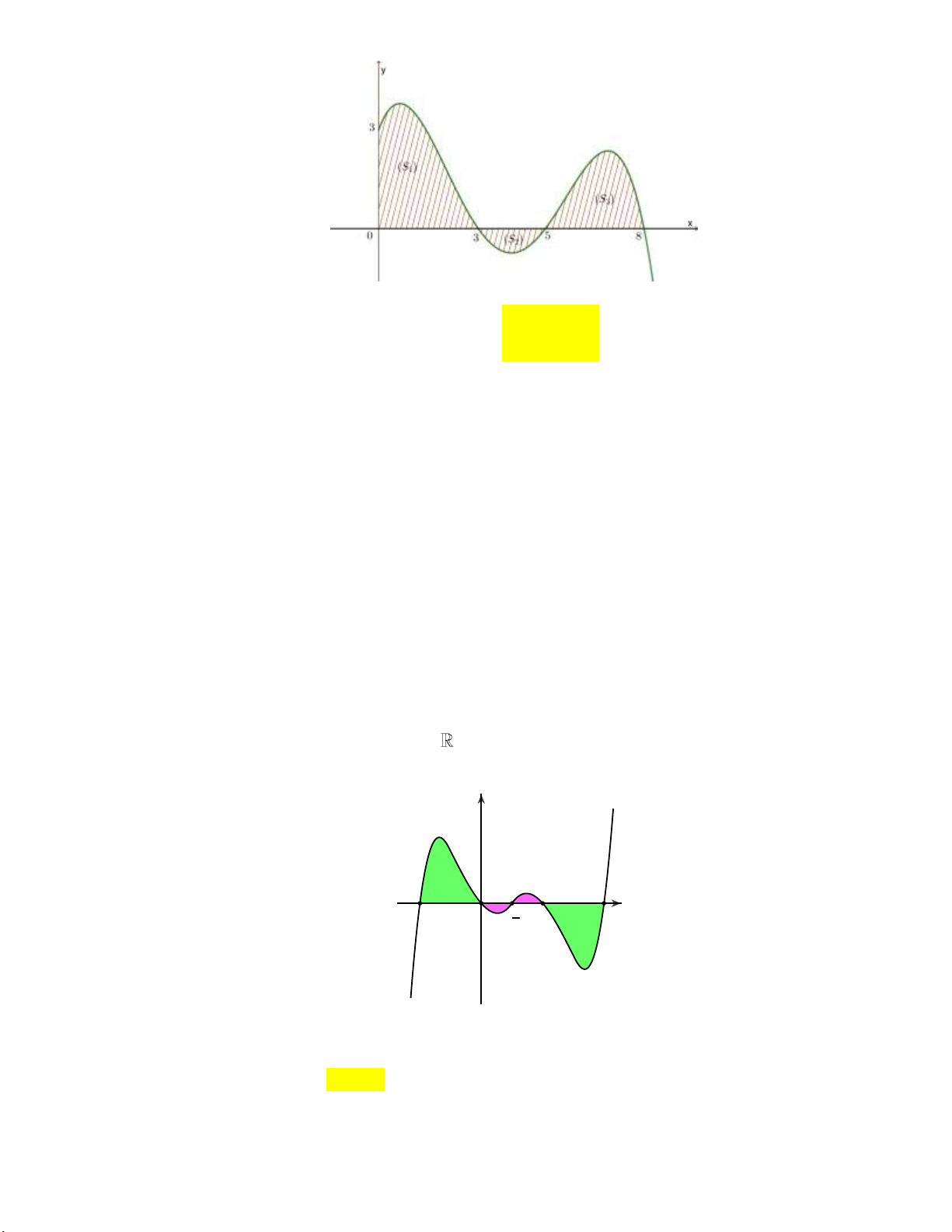
Câu 14: Cho hàm số y f x liên tục trên đoạn 0;8 và có đồ thị như hình vẽ dưới đây:
Trong các giá trị sau, giá trị nào lớn nhất? 3 1 8 5
A. f x d . x
B. f x d . x
C. f x d . x
D. f x d . x  0 0 0 0
Câu 15: Cho hàm số y f x liên tục trên
có đồ thị tạo với trục hoành các miền có diện tích
S , S , S , S như hình vẽ bên dưới: 1 2 3 4 y y=f(x) S1 S S 3 x 2 1 -1 O 1 2 2 S4 ln 3
Biết S S  10 , S S  8 . Tích phân x   x I e f e   1dx bằng 1 4 2 3 0 A. 8  . B. 10 . C. 8 . D. 10 .
Câu 16: Cho parabol  P 2
: y x và một đường thẳng d thay đổi cắt  P tại hai điểm A , B sao cho
AB  2020 . Gọi S là diện tích hình phẳng giới hạn bởi  P và đường thẳng d . Tìm giá trị lớn nhất S của S. max 3 2020 1 3 2020 3 2020 1 3 2020 A. S  . B. S  . C. S  . D. S  . max 6 max 6 max 6 max 3
Câu 17: Cho Parabol  P 2
: y x . Hai điểm A, B di động trên  P sao cho AB  2. Gọi S là diện tích
hình phẳng giới hạn bởi Parabol  P và đoạn thẳng AB . Tìm giá trị lớn nhất của S. 4 7 5 5 A. max S  . B. max S  . C. max S  . D. max S  . 3 6 3 6
Câu 18: Hình gạch chéo được giới hạn bởi đường tròn    2 2 2 x y a
b ; a b  0 và các đường thẳng b b x   và x
. Thể tích vật tròn xoay tạo bởi hình gạch chéo quay xung quanh trục Ox là 2 2 3  2   3 A. 2 2  ab . B. 2 2  ab . C. 2  ab   3   . D. 2    ab    . 4  3   2 4 
Câu 19: Cho hàm số đa thức bậc bốn y f x có đồ thị C , biết rằng C đi qua điểm A1;0 . Tiếp
tuyến  tại A của đồ thị C cắt C tại hai điểm có hoành độ lần lượt là 0 và 2 . Biết diện
tích hình phẳng giới hạn bởi  , đồ thị C và hai đường thẳng x  0 ; x  2 có diện tích 56 bằng . 5 y 3 B 1 A -1 O 2 x
Diện tích hình phẳng giới hạn bởi
, đồ thị C và hai đường thẳng x 1; x 0 bằng 2 1 1 1 A. . B. . C. . D. . 5 20 10 5
Câu 20: Ông A đi làm lúc 7 giờ và đến cơ quan lúc 7 giờ 12 phút bằng xe gắn máy, trên đường đến cơ
quan ông A gặp một người băng qua đường nên ông phải giảm tốc độ để đảm bào an toàn rồi
sau đó lại từ từ tăng tốc độ để đến cơ quan làm việc. Hỏi quãng đường kể từ lúc ông A giảm
tốc độ để tránh tai nạn cho đến khi tới cơ quan dài bao nhiêu mét? (Độ thị dưới đâu mô tả vận
tốc chuyển động của ông A theo thời gian khi đến cơ quan) A. 3600 . B. 3200 . C. 3500 . D. 3900 .
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TÝCH PH¢N – øng dông øng dông tÝch ph©n
PHIẾU ÔN TẬP SỐ 05
LỜI GIẢI CHI TIẾT
Câu 1: Diện tích phần hình phẳng tô đậm trong hình vẽ bên dưới được tính theo công thức nào dưới đây? 3 3
A.   f x  g xdx .
B.  g x  f xdx . 2  2  0 3 0 3
C.   f x  g xdx  gx  f xdx .
D.  g x  f xdx   f x  g xdx . 2  0 2  0 Lời giải:
Từ đồ thị hai hàm số y f x và y g x ta có diện tích phần hình phẳng tô đen trong hình
vẽ bên dưới được tính là 3 0 3 S f
 x gx dx f
 x gx dxf
 x gx dx 2  2  0 0    3
f x  g xdx  g x  f xdx . 2  0
Chọn đáp án C. x 1
Câu 2: Cho hình phẳng  H  giới hạn bởi đồ thị hàm số y y  ,
x  và hai đường thẳng 2 2
y  x 1 . Tính diện tích S của hình phẳng  H  . A. S  8  3ln 3 . B. S  8  3ln 3 . C. S  3ln 3 .
D. S  4  3ln 3 . Lời giải: Dựa vào đồ thị ta có 3  1  3  1   x 1    S   x    x   3 2 d 1 2 dx  1 dx    x      1 dxx  2   x  2  5  3  5  3  1     x
 x  3ln x  2  2
3    x  3ln3. 5   2  3
Chọn đáp án C.
Câu 3: Đường thẳng y m ( 0  m  1 ) cắt đường cong 4 2
y x  2x 1 tại hai điểm thuộc góc phần tư
thứ nhất của hệ tọa độ Oxy và chia thành hai hình phẳng có diện tích S , S như hình vẽ. 1 2
Biết S S . Mệnh đề nào dưới đây đúng? 1 2  2   2 1   1 3   3  A. m  0;   . B. m  ;   . C. m  ;   . D. m  ;1   .  5   5 2   2 5   5  Lời giải:
Phương trình hoành độ giao điểm 4 2
x  2x 1  m   x  2 2 1
m x   1 m .
Vậy các giao điểm thuộc thuộc góc phần tư nhất của hệ tọa độ Oxy có hoành độ bằng
x  1 m và x  1 m . 1 m 1 m
Diện tích S    4 2
x  2x 1 m dx và S    4 2
x  2x 1 m dx . 2  1  0 1 m 1 m5 3 2 4 S S  
1 m 1m 1 m  0  m  . 1 2 5 3 9
Chọn đáp án B.
Câu 4: Diện tích hình phẳng giới hạn bởi các đường 2
y x  3 và y  1 bằng 8 16 32 A. . B. . C. . D. 32 . 3 3 3 Lời giải: x  2 Xét phương trình 2 2
x  3  1  x  4  0   . x  2  2 2 3  x  2 32 Do đó 2 S x  4dx     2
4  x dx   4x    . 3 2    3 2  2 
Chọn đáp án C.
Câu 5: Một viên gạch hoa hình vuông cạnh 40 cm được thiết kế như hình bên dưới. Diện tích mỗi cánh hoa bằng y 1 y = x2 20 y = 20x 20 x 20 20 20 400 800 A. 2 cm . B. 2 cm . C. 2 250 cm . D. 2 800 cm . 3 3 Lời giải: 20 20 3  1 
 2 20x x 1 x  400
Diện tích mỗi cánh hoa là 2 20x x dx=      .     2 cm .  20  3 20 3 3 0   0
Chọn đáp án A.
Câu 6: Cho hàm số y f x . Hàm số có đồ thị hàm số y f ' x như hình vẽ dưới đây.
Biết diện tích hình phẳng giới hạn bởi trục Ox và đồ thị hàm số y f ' x trên đoạn 2;  1 và
1;4 lần lượt bằng 9 và 12. Cho biết f  1  3. Tính giá trị biểu thức P f  2
   f 4 . A. 21. B. 3. C. 9. D. 2. Lời giải: 1 1
Ta có: | f xdx 9
  f 'xdx  9   f   1  f ( 2  )  9    . 2  2  Mà f   1  3  f  2   12. 4 4 Ta có: | f
 x|dx 12  f
 xdx  1
 2  f 4  f   1  1  2 . 1 1 Mà f  
1  3  f 4  9 . Vậy P f 2  f 4  3 .
Chọn đáp án B. 1 4
Câu 7: Tính diện tích hình phẳng giới hạn bởi các đường 2
y x , y   x  và trục hoành. 3 3 11 61 343 39 A. . B. . C. . D. . 6 3 162 2 Lời giải: 1 4
Phương trình hoành độ giao điểm của các đường 2
y x , y   x  là 3 3 x  1 1 4 2 x   x  2
 3x x  4  0   4 . 3 3 x    3 1 4
Hoành độ giao điểm của đường thẳng y   x  với trục hoành là x  4 . 3 3
Hoành độ giao điểm của parabol 2
y x với trục hoành là x  0 .
Diện tích hình phẳng cần tìm là 1 4  1 4 1 4  3 x  1 4  11 2
S x d x   x  d x    2    x x    .  3 3  3  6 3  6 0 1 0 1
Chọn đáp án A.
Câu 8: Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số 2
y x  4x  4 , trục tung và trục hoành. Xác
định k để đường thẳng d  đi qua điểm A0; 4 có hệ số góc k chia  H  thành hai phần có diện tích bằng nhau. A. k  4 . B. k  8 . C. k  6 . D. k  2 . Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số 2
y x  4x  4 và trục hoành là: 2
x  4x  4  0  x  2 .
Diện tích hình phẳng  H  giới hạn bởi đồ thị hàm số: 2
y x  4x  4 , trục tung và trục hoành 2 2 2 3  x  8 là: 2 S
x  4x  4 dx   2
x  4x  4 2 dx    
 2x  4x   .  3  3 0 0 0
Phương trình đường thẳng d  đi qua điểm A0; 4 có hệ số góc k có dạng: y kx  4 .  4 
Gọi B là giao điểm của d  và trục hoành. Khi đó B  ;0   .  k
Đường thẳng d  chia  H  thành hai phần có diện tích bằng nhau khi B OI và 1 4 SS OAB 2 3 .  4 0    2  k  2 k       k  6  . 1 1 4 4  k  6  SO . A OB  .4.   OAB  2 2 k 3
Chọn đáp án C.
Câu 9: Cho hàm số đa thức bậc ba y f x 3 2
ax bx cx d (a  0) có đồ thị như hình vẽ bên dưới:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x và trục hoành. 19 27 A. 6 . B. . C. . D. 8. 4 4 Lời giải:
Đồ thị hàm số y f x cắt và tiếp xúc trục hoành lần lượt tại tại điểm 2;0 và 1;0 nên hàm
số có dạng y f x  a x   x  2  a  3 2 1
x  3x  2 .
Mặt khác đồ thị hàm số lại đi qua điểm 1; 4 nên ta có a  1 . Vậy y f x 3
x  3x  2 .
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x và trục hoành là: 1 27 3 S
x  3x  2dx   . 4 2 
Chọn đáp án C.
Câu 10: Cho hình phẳng  H  giới hạn bởi các đường 2
y x 1 và y k, 0  k  1. Tìm k để diện tích của
hình phẳng  H  gấp hai lần diện tích hình phẳng được kẻ sọc trong hình vẽ bên dưới. 1 A. 3 k  4. B. 3 k  2 1. C. k  . D. 3 k  4 1. 2 Lời giải:
Do đồ thị nhận trục Oy làm trục đối xứng nên yêu cầu bài toán trở thành:
Diện tích hình phẳng giới hạn bởi 2
y  1 x , y k, x  0 bằng diện tích hình phẳng giới hạn bởi : 2 2
y  1 x , y x 1, y k, x  0. 1k 1 1k Nghĩa là  2
1 x k dx   2
k 1 x dx   2 k x     1d .x 0 1k 1 2 3 1 
k     k 1 3 3 3 1 3   k   k   k
k    k  1 ( 1 ) 1 ( 1 ) ( 1 ) ( 1 ) ( 1 ) 1  3 3 3 3 3 2 3 4
 ( 1 k )     k 3 1  2 3  k  4 1. 3 3
Chọn đáp án D.
Câu 11: Gọi  H  là hình phẳng giới hạn bởi đồ thị của hàm số 2
y  6x x và trục hoành. Hai đường thẳng y  ,
m y n m n  9 chia hình  H  thành ba phần có diện tích bằng nhau. Tính 3 3
P  (9  m)  (9  n) . A. P  405 . B. P  409 . C. P  407 . D. P  403 . Lời giải:   P 2
: y  6x x  6
Gọi  H  : Ox : y  0
. Suy ra: S S x x dx   H  2 6  36
x  0, x  6 0 
x  3 9  y P 2  1 Ta có: 2
y  6x x   x  3  9  y  
x  3 9  y  P2  
P : x  3 9  y 1  
Gọi  H :  P : x  3  9  y . 1   2 
y n, y  9n  9  9 9 3 4 Suy ra: S S
 3 9  y  3 9  y dy  2 9  ydy  9  n   1 1 H     3 n n S 3 4 3 Mà S
12 nên  9 n 12  9 n  81 1 3 3
P : x  3 9  y 1   9 3 4
Gọi  H :  P : x  3   9  y . Suy ra: S S  2 9  ydy  9  m  2 H2   2   2   3 m
y m, y  9 m  9  2S 3 4 3 Mà S
 24 nên  9 n  24  9 n  324. Vậy P  81324  405. 2 3 3
Chọn đáp án A.
Câu 12: Cho hàm số y f x là hàm đa thức bậc bốn có đồ thị là C và d là tiếp tuyến của đồ thị C 11
tại hai điểm như hình vẽ. Biết diện tích hình phẳng giới hạn bởi đồ thị C và d là . Khi đó 3 1
tích phân I   f xdx bằng 1 19 25 23 13 A. . B. . C. . D. 6 6 6 3 Lời giải:  3  5 1
Phương trình đường thẳng đi qua hai điểm 1; ;1;   
1 là gx   x   2  4 4 1 1 1 S  
f x gxdx  11   f xdx   gxdx  11    3 3 1 1 1 . 1  5 1   I
x dx  11  I  1  11  I   25    4 4 3 2 3 6 1  
Chọn đáp án B.
Câu 13: Một chất điểm chuyển động trong 3 giây với vận tốc v a cos  t   b (mét/giây) (trong đó t là
biến thời gian; a,b là các hằng số) có đồ thị là một đường hình sin như hình vẽ bên. Tính tổng
quãng đường mà vật đi được sau 3 giây (kết quả làm tròn đến hàng phần trăm). A. 29, 93m . B. 15m . C. 27,93m . D. 17m . Lời giải:
Quan sát đồ thị ta có: v  0  10
a b  10 a  5     
. Suy ra v  5cos t   5 . v  3  0
a b  0 b   5 3
Vậy quãng đường mà vật đi được sau 3 giây là: S  5cost  5dt 15 (m). 0
Chọn đáp án B.
Câu 14: Cho hàm số y f x liên tục trên đoạn 0;8 và có đồ thị như hình vẽ dưới đây:
Trong các giá trị sau, giá trị nào lớn nhất? 3 1 8 5 A. f xd . x  B. f xd . x  C. f xd . x  D. f xd . x  0 0 0 0 Lời giải: 3 Ta có f
 xdx S . S1 0 1 3 f
 xdx f  xdx 0 0 8 3 5 8 f
 xdx f
 xdxf
 xdxf
 xdx S S S . S S 1   2 S3 0 0 3 5 5 3 5 f
 xdx f
 xdxf
 xdx S S . S S 1   2 0 0 3
Từ hình vẽ, ta thấy S  S nên SSSSSS S SS S S S S 1   2  1  1  2 S3 3   2 8
Suy ra f xdx  là lớn nhất. 0
Chọn đáp án C.
Câu 15: Cho hàm số y f x liên tục trên
có đồ thị tạo với trục hoành các miền có diện tích
S , S , S , S như hình vẽ bên dưới: 1 2 3 4 y y=f(x) S1 S S 3 x 2 1 -1 O 1 2 2 S4 ln 3
Biết S S  10 , S S  8 . Tích phân x   x I e f e   1dx bằng 1 4 2 3 0 A. 8  . B. 10 . C. 8 . D. 10 . Lời giải: Đặt t t e 1 x
dt e dx ; x  0  t  0 và x  ln 3  t  2 . 1 ln 3 2 2 1 2 x   x I e f e   1dx f
 tdt f
 tdt f
 tdt + f tdt  0 0 0 1 1 2
 S S S  8  8 10  10 . 2 3 4
Chọn đáp án B.
Câu 16: Cho parabol  P 2
: y x và một đường thẳng d thay đổi cắt  P tại hai điểm A , B sao cho
AB  2020 . Gọi S là diện tích hình phẳng giới hạn bởi  P và đường thẳng d . Tìm giá trị lớn nhất S của S. max 3 2020 1 3 2020 3 2020 1 3 2020 A. S  . B. S  . C. S  . D. S  . max 6 max 6 max 6 max 3 Lời giải: Giả sử 2 ( A a; a ) ; 2 B( ;
b b ) (b a) sao cho AB  2020 .
Phương trình đường thẳng d là: y  (a b)x ab . Khi đó b b S
a b x ab x x  
 abxabx  1 ( ) d dx  b a3 2 2 . 6 a a 2 2 2 2 Vì AB
 b a   2 2 b a  2 
 b a  ba  2 2020 2020 1  2020 . 3   2020 b a2 2
 2020  b a b a  2020  S  . 6 3 2020 Vậy S  khi a  1010  và b  1010 . max 6
Chọn đáp án B.
Câu 17: Cho Parabol  P 2
: y x . Hai điểm A, B di động trên  P sao cho AB  2. Gọi S là diện tích
hình phẳng giới hạn bởi Parabol  P và đoạn thẳng AB . Tìm giá trị lớn nhất của S. 4 7 5 5 A. max S  . B. max S  . C. max S  . D. max S  . 3 6 3 6 Lời giải: Gọi A 2 a a B  2 ; , ;
b b  P sao cho b a là hai điểm trên Parabol và AB  2. 2 2 b a
Khi đó phương trình đường thẳng AB là 2 y a
x a  y  a bx a .b b a b 1
Gọi S là diện tích hình phẳng cần tìm, ta có: S  
 a bx abx .dx  b a3 2 .   6 a 1 2 4 4
Ta có: AB  2  b a b a  2  S  b a 3 3    S  . ax 6 6 3 m 3
Đẳng thức xảy ra khi và chỉ khi a  1
 ;b  1  A 1  ;  1 , B 1;  1 .
Chọn đáp án A.
Câu 18: Hình gạch chéo được giới hạn bởi đường tròn    2 2 2 x y a
b ; a b  0 và các đường thẳng b b x   và x
. Thể tích vật tròn xoay tạo bởi hình gạch chéo quay xung quanh trục Ox là 2 2 3  2   3 A. 2 2  ab . B. 2 2  ab . C. 2  ab   3   . D. 2    ab    . 4  3   2 4  Lời giải: 2 2
y a b x Ta có:    2 2 2 x y ab   . 2 2
y a b x
Thể tích vật tròn xoay tạo bởi hình gạch chéo quay xung quanh trục Ox là: b b b 2   2 2
V    a b x 2  a b x 2 2 2 2 2 dx  2 2
  4a b x dx  2 2  4a
b x dx    bbb  2 2 2       bb
Đặt x b sin t, t   ;
 dx b costdt    
. Đổi cận: x    t  
; x   t  .   2 2   2 6 2 6     b 6 6 1  cos 2t  sin 2t  2 2 2 V  4a
b b sin tb cos tdt  2 2  4ab  cos d t t  2  4ab  dt  6 2
 2ab t       2  2       6 6 6 6   3    3   2  2  2ab          2       ab   3 .   6 4 6 4      3 
Chọn đáp án C.
Câu 19: Cho hàm số đa thức bậc bốn y f x có đồ thị C , biết rằng C đi qua điểm A1;0 . Tiếp
tuyến  tại A của đồ thị C cắt C tại hai điểm có hoành độ lần lượt là 0 và 2 . Biết diện
tích hình phẳng giới hạn bởi  , đồ thị C và hai đường thẳng x  0 ; x  2 có diện tích 56 bằng . 5 y 3 B 1 A -1 O 2 x
Diện tích hình phẳng giới hạn bởi
, đồ thị C và hai đường thẳng x 1; x 0 bằng 2 1 1 1 A. . B. . C. . D. . 5 20 10 5 Lời giải: Hàm số 4 2
y ax bx c . TXĐ: D  . Ta có: 3
y '  4ax  2bx .
Phương trình tiếp tuyến  của đồ thị C  tại A1;0 có dạng y   4
a  2bx   1 .
Do tiếp tuyến  tại A của đồ thị C  cắt C  tại hai điểm có hoành độ lần lượt là 0 và 2 nên phương trình 4 2
ax bx c   4
a  2bx  
1 nhận ba nghiệm là x  1 ; x  0 ; x  2 .
c  a bc  2a Suy ra:    . b  3  ab  3  a Vậy C  : 4 2
y ax ax a a  4 2 3 2
x  3x  2 và  : y  2a x   1 . 56
Diện tích hình phẳng giới hạn bởi  , đồ thị C  và hai đường thẳng x  0 ; x  2 bằng 5 2 56 2 56
nên: 2a x   1  a  4 2
x  3x  2 dx  
 2ax  1a 4 2
x  3x  2 dx  . 5 5 0 0 2 2 5  x   56 28 56 a  56 4 2
x  3x  2xdx   3 2  . a
x x    . a   a  2 . 5  5  5 5 5 0 0
Diện tích hình phẳng giới hạn bởi  , đồ thị C  và hai đường thẳng x  1 ; x  0 là 0 0 0 5  x  2 S a  4 2
x  3x  2  2a x   1 dx   4 2
2x  6x  4x 3 2 dx 2.
x x   .  5  5 1  1  1 
Góp ý cách khác.
Phương trình đường thẳng  : y x  1 .
Do  và C cắt nhau tại các điểm có hoành độ 1;0; 2 nên ta có phương 2
trình ax  1 . .
x x  2  0 2 2 56
Theo bài ta có phương trình a x   1 .
x x  2 x   a   d 2 . 5 0 0 2 Từ đó ta được  S
 2x 1 .xx 2     dx  2 .  5 1
Chọn đáp án A.
Câu 20: Ông A đi làm lúc 7 giờ và đến cơ quan lúc 7 giờ 12 phút bằng xe gắn máy, trên đường đến cơ
quan ông A gặp một người băng qua đường nên ông phải giảm tốc độ để đảm bào an toàn rồi
sau đó lại từ từ tăng tốc độ để đến cơ quan làm việc. Hỏi quãng đường kể từ lúc ông A giảm
tốc độ để tránh tai nạn cho đến khi tới cơ quan dài bao nhiêu mét? (Độ thị dưới đâu mô tả vận
tốc chuyển động của ông A theo thời gian khi đến cơ quan) A. 3600 . B. 3200 . C. 3500 . D. 3900 . Lời giải:
Thời gian đi đến cơ quan của ông A là 12 phút bằng 0,2 giờ.
Chọn gốc thời gian từ lúc 7 giờ sáng t  0 .  5 1 
Lúc ông A giảm tốc độ là 7 giờ 5 phút t    60 12    0,2 Ta có: s v(t)dt
là diện tích hình phẳng giới hạn bởi trục hoành, đường cong v t và hai 1 12 1 đường thẳng t t  12 , 0,2
Diện tích hình phẳng trên được tính bằng cách chia nhỏ các hình đã biết nên 6 3 1 1  60 60 s  36   48  3,9km 2 60 2 .
Chọn đáp án D.
_________________HẾT_________________
Huế, ngày 10 tháng 02 năm 2021