Phương pháp giải các bài toán Tích phân – Trung tâm LTĐH Vĩnh Viễn Toán 12

Phương pháp giải các bài toán Tích phân – Trung tâm LTĐH Vĩnh Viễn Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

86 43 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

33 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
124
Chuyeân ñeà 4: TÍCH PHAÂN
Vaán ñeà 1:
BIEÁN ÑOÅI VEÀ TOÅNG – HIEÄU CAÙC TÍCH PHAÂN CÔ BAÛN
A. PHÖÔNG PHAÙP GIAÛI
Söû duïng ba tích chaát sau ñeå bieán ñoåi tích phaân caàn tính thaønh toång – hieäu caùc
tích phaân cô baûn
1/

bb
aa
k.f(x)dx k f(x)dx
2/
b b b
a a a
f(x) g(x) dx f(x)dx g(x)dx
3/

b c b
a a c
f(x)dx f(x)dx f(x)dx
BAÛNG NGUYEÂN HAØM CÔ BAÛN
Nguyeân haøm cuûa caùc haøm soá sô caáp
Nguyeân haøm cuûa caùc haøm soá hôïp
1.
2.


1
x
x dx c, ( 1)
1
3.

dx
ln x c
x
4.

xx
e dx e c
5.
x
x
a
a dx c (0 a 1)
lna
6.

cosxdx sinx c
7.
sinxdx cosx c
8.

2
dx
tanx c
cos x
9.
2
dx
cotx c
sin x
10.
tanxdx ln cosx c
11.

cotxdx ln sinx c
(u = u(x))
1.


1
u
u u'dx c ; ( 1)
1
2.

u'
dx ln u c
u
3.

uu
e u'dx e c
4.
u
u
a
a u'dx c (0 a 1)
lna
5.

u'cosudx sinu c
6.
u'sinudx cosu c
7.

2
u'
dx tanu c
cos u
8.
2
u'
dx cot u c
sin u
9.
u'tanudx ln cosu c
10.

u'cotudx ln sinu c
TT Luyện Thi Đại Học VĨNH VIỄN
125
Ñaëc bieät: u(x) = ax + b;

1
f(x)dx F(x) c f(ax b)dx F(ax b) c
a
1.


1
1 (ax b)
(ax b) dx c
a1
2.
dx 1
ln ax b c
ax b a
3.

ax b ax b
1
e dx e
a
4.

x
1
a dx ln x c
5.
1
cos(ax b)dx sin(ax b) c
a
6.
1
sin(ax b)dx cos(ax b) c
a
7.
2
dx 1
tan(ax b) c
a
cos (ax b)
2
dx 1
8. cot(ax b) c
a
sin (ax b)
1
9. tan(ax b)dx ln cos(ax b) c
a
1
10. cot(ax b)dx ln sin(ax b) c
a
11.

22
dx 1 x a
ln c
2a x a
xa
B – ÑEÀ THI
Baøi 1: CAO ÑAÚNG KHOÁI A, B, D NAÊM 2011
Tính tích phaân
2
1
2x 1
I dx
x(x 1)
Giaûi
I =
2
1
(x 1) x
dx
x(x 1)

=
2
1
11
dx
x 1 x



=
2
1
6
lnx(x 1) ln ln3
2
.
Baøi 2: CAO ÑAÚNG KHOÁI A, B, D NAÊM 2010
Tính tích phaân:
1
0
2x 1
I dx
x1
Giaûi
1
0
2x 1
I dx
x1
=



1
0
3
2 dx
x1
=

1
0
2x 3ln x 1
= 2 – 3ln2.
Baøi 3: CAO ÑAÚNG GTVT III KHOÁI A NAÊM 2007
Tính caùc tích phaân sau:
2
4 3 2
2
1
x x 3x 2x 2
I dx
xx
Giaûi
Chia töû cho maãu, ta ñöôïc:
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
126

4 3 2
2
22
x x 3x 2x 2 x 2
x3
x x x x
=
2
12
x3
x 1 x



2
2
1
12
I x 3 dx
x 1 x




2
3
1
x
3x ln x 1 2ln x
3
I =
16 3
ln
38
Baøi 4: CAO ÑAÚNG KINH TEÁ – COÂNG NGHIEÄP TPHCM NAÊM 2007
Tính tích phaân:
x
1
dt
I(x)
t(t 1)
, vôùi x > 1. Töø ñoù tìm
x
lim I(x)
Giaûi
I(x) =






xx
11
dt 1 1
dt
t t 1 t t 1
=
x
x
1
1
t
lnt ln t 1 ln
t1
=
x1
ln ln
x 1 2
 



xx
x1
lim I x lim ln ln ln2
x 1 2
Baøi 5: ÑEÀ DÖÏ BÒ 1 - ÑAÏI HOÏC KHOÁI B NAÊM 2005
Tính tích phaân:
4
sinx
0
tanx e cosx dx
Giaûi
4 4 4
sinx sinx
0 0 0
I tanx e .cosx dx tanxdx sinx 'e dx
=
sinx
4
4
0
0
ln cosx + e
2
2
ln 2 e 1
.
Baøi 6: ÑEÀ DÖÏ BÒ 2
Tính tích phaân:
3
3
1
dx
I
xx
Giaûi

22
3 3 3 3
3 2 2 2
1 1 1 1
dx 1 x x 1 x 1 1 2x
I dx dx dx
x x 2
x x x(1 x ) x 1 x 1
TT Luyện Thi Đại Học VĨNH VIỄN
127






22
1
33
ln ln(x 1) lnx ln x 1
x
2
11
2
x 3 1 6
3
ln ln ln ln
22
12
1x
Baøi 7:
Tính tích phaân : I =
2
2
0
x xdx
.
Giaûi
Tính
2 1 2
2 2 2
0 0 1
I x x dx x x dx x x dx
Do : x 0 1 2
x
2
x 0 +
3 2 3 2
12
x x x x
I1
01
3 2 3 2
.
Baøi 8: ÑEÀ DÖÏ BÒ 3
Cho haøm soá: f(x) =
x
3
a
bxe
x1
.
Tìm a vaø b bieát raèng f’(0) = 22 vaø
1
0
f(x)dx 5
Giaûi
Ta coù:

x
3
a
f(x) bx.e
(x 1)

x
4
3a
f (x) be (x 1) f (0) 3a b 22 (1)
(x 1)



1
1 1 1
3 x x x
2
0 0 0
0
a 3a
f(x)dx a(x 1) dx b xe b(xe e ) b 5 (2)
8
2(x 1)
(1) vaø (2) ta coù heä:


3a b 22
a8
3a
b2
b5
8
.
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
128
Vaán ñeà 2:
TÍNH TÍCH PHAÂN BAÈNG PHÖÔNG PHAÙP ÑOÅI BIEÁN SOÁ
A. PHÖÔNG PHAÙP GIAÛI
ÑOÅI BIEÁN SOÁ LOAÏI I
1. Söû duïng coâng thöùc:

b
a
f[u(x)].u (x)dx f(u)du
2. Phöông phaùp: Xeùt tích phaân
b
a
I f(x)du
- Ñaët t = u(x) dt = u'(x)dx
- Ñoåi caän u(a) = t
1 ;
u(b) = t
2
- Suy ra:
t
2
t
2
t
1
t
1
I g(t)dt g(t)
(g(t) f[u(x)].u (x))
Thöôøng ñaët aån phuï t laø
caên thöùc, hoaëc muõ cuûa e, hoaëc maãu soá, hoaëc bieåu thöùc trong ngoaëc.
coù sinxdx ñaët t = cosx, coù cosxdx ñaët t = sinx, coù
dx
x
ñaët t = lnx.
ÑOÅI BIEÁN SOÁ LOAÏI II
Coâng thöùc:
;
x (t); ( ) a, ( ) b
Tính:
b
a
I f(x)dx
Ñaët
x (t) dx (t)dt
Ñoåi caän:
x (t); ( ) a, ( ) b
Khi ñoù:

b
a
I f( (t)). (t)dt f(x)dx
Caùc daïng thöôøng gaëp: 1.

b
22
a
a x dx ñaët x asint
2.
3.
b
22
a
dx
ñaët x atant
ax
B. ÑEÀ THI
Baøi 1: ÑAÏI HOÏC KHOÁI A NAÊM 2011
TT Luyện Thi Đại Học VĨNH VIỄN
129
Tính tích phaân :
4
0
xsinx x 1 cosx
I dx.
xsinx cosx

Giaûi
Ta coù:
4
0
xsinx cosx xcosx
I dx
xsinx cosx

4
0
xcosx
1 dx
xsinx cosx




44
4
0
00
xcosx xcosx
x dx dx
xsinx cosx 4 xsinx cosx



Ñaët t = xsinx + cosx dt = xcosxdx.
Khi x = 0 thì t = 1, x =
4
thì t =
2
1
24



Suy ra:




2
1
24
1
dt
I
4t




2
1
24
1
ln t
4




2
ln 1
4 2 4
.
Baøi 2: ÑAÏI HOÏC KHOÁI D NAÊM 2011
Tính tích phaân:
4
0
4x 1
I dx.
2x 1 2

Giaûi
Ñaët:
t 2x 1 2
2x 1 t 2
2
2x 1 t 4t 4
2
t 4t 3
x
2

dx = (t – 2)dt.
x = 0 t = 3, x = 4 t = 5.
Suy ra:
2
5
3
t 4t 3
41
2
I t 2 dt
t


=
2
5
3
2t 8t 5 t 2
dt
t
=
5
32
3
2t 12t 21t 10
dt
t
=
5
2
3
10
2t 12t 21 dt
t



=
5
3
2
3
2t
6t 21t 10ln t
3




=
34 3
10ln
35
.
Baøi 3: ÑAÏI HOÏC KHOÁI B NAÊM 2010
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
130
Tính tích phaân: I =
e
2
1
lnx
dx
x(2 lnx)
Giaûi
Ñaët
1
u lnx du dx
x
, x = 1 u = 0, x = e u = 1






22
11
00
u 1 2
I du du
2u
2 u 2 u



1
0
2
ln 2 u
2u



2
ln3 ln2 1
3




31
ln
23
.
Baøi 4: ÑAÏI HOÏC KHOÁI D NAÊM 2009
Tính tích phaân:
3
x
1
dx
I
e1
.
Giaûi
Ñaët t = e
x
dx =
dt
t
; x = 1 t = e; x = 3 t = e
3





33
ee
ee
dt 1 1
I dt
t t 1 t 1 t
33
ee
ee
ln t 1 ln t
2
ln e e 1 2
Baøi 3: ÑAÏI HOÏC KHOÁI A NAÊM 2008
Tính tích phaân:
64
0
tan x
I dx
cos2x
Giaûi
Caùch 1: Ñaët t = tanx dt = (1 + tan
2
x)dx
2
dt
dx
1t
2
2
1t
cos2x
1t
Ñoåi caän: x = 0 t = 0;
3
xt
63
Khi ñoù:





33
3 4 3
2
22
00
t1
I dt t 1 dt
1 t 1 t
TT Luyện Thi Đại Học VĨNH VIỄN
131





3
3
t 1 1 t 1 3 1 10
t ln ln
3
3 2 1 t 2
3 1 9 3
0
Caùch 2:
Ta coù:

6 4 6 4 6 4
2 2 2 2
0 0 0
tan x tan x tan x
I dx dx dx
cos2x
cos x sin x cos x(1 tan x)
Ñaët: t = tanx
2
dx
dt
cos x
Ñoåi caän: x = 0 t = 0;
3
xt
63
Khi ñoù:
3
34
2
0
t 1 3 1 10
I dt ln
2
3 1 9 3
1t
Baøi 4: ÑAÏI HOÏC KHOÁI B NAÊM 2008
Tính tích phaân:



4
0
sin x dx
4
I
sin2x 2(1 sinx cosx)
Giaûi
Tính tích phaân:



4
0
sin x dx
4
I
sin2x 2(1 sinx cosx)
Ñaët t = sinx + cosx



dt (cosx sinx)dx 2sin x dx
4
Ñoåi caän: x = 0 t = 1;
x t 2
4
Ta coù: t
2
= sin
2
x + cos
2
x + 2sinxcosx = 1 + sin2x sin2x = t
2
– 1
Khi ñoù:

22
22
11
2 dt 2 dt
I
22
t 1 2(1 t) (t 1)



2 1 2 1 1 4 3 2
2
.
2 t 1 2 2 4
1 2 1
.
Baøi 5: ÑAÏI HOÏC SAØI GOØN KHOÁI B NAÊM 2007
Tính tích phaân:

1
2
0
1
I dx
x x 1
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
132
Giaûi
I =




1
2
0
1
dx
13
x
24
Ñaët
2
1 3 3
x tant, t ; dx 1 tan t dt
2 2 2 2 2




I =
2
3
2
6
3
1 tan t
2
dt
3
33
1 tan t
4
Baøi 6: CAO ÑAÚNG XAÂY DÖÏNG SOÁ 2 NAÊM 2007
Tính tích phaân: I =
e
3
1
dx
x 1 lnx
Giaûi
Ñaët:

3
t 1 lnx
lnx = t
3
– 1,
2
dx
3t dt
x
Ñoåi caän: x = 1 t = 1; x = e
3
t2
3
2
1
I 3tdt
2
3
3
3t 3 4 3
2
22
1
Baøi 7: CAO ÑAÚNG COÂNG NGHIEÄP THÖÏC PHAÅM NAÊM 2007
Tính tích phaân:
1
2
0
x1
dx
x1
Giaûi


11
12
22
00
xdx dx
I I I
x 1 x 1
;
2
1
1
11
I ln(x 1) ln2
0
22
.
Ñaët x = tant,




2
dt
t 0, , dx
4
cos t

4
2
0
I dt
4
. Vaäy

1
I ln2
24
Baøi 8: CAO ÑAÚNG TAØI CHÍNH – HAÛI QUAN NAÊM 2007
Tính tích phaân:
2
3
sinx
I dx
cos2x cosx
TT Luyện Thi Đại Học VĨNH VIỄN
133
Giaûi
Ñaët t = cosx dt = sinxdx
x
3
2
t
1
2
0
I =






11
0
22
22
1
00
2
12
dt 1
dt dt
33
2t t 1 2t t 1
t 1 2t 1
I =


1
2
0
11
ln4
ln ln
t 1 2t 1
33
Baøi 9: ÑEÀ DÖÏ BÒ 1 - ÑAÏI HOÏC KHOÁI A NAÊM 2006
Tính tích phaân: I =
6
2
dx
2x 1 4x 1
Giaûi
Ñaët
2
t 1 1
t 4x 1 x dx tdt
42





5 5 5
2 2 2
3 3 3
t
dt
t 1 1
2
I dt dt
t1
t 1 (t 1) (t 1)
2. 1 t
4



5
1 3 1
ln t 1 ln
3
t 1 2 12
Baøi 10: ÑEÀ DÖÏ BÒ 1 - ÑAÏI HOÏC KHOÁI B NAÊM 2006
Tính tích phaân: I =

10
5
dx
x 2 x 1
Giaûi
Ñaët t =
2
x 1 t x 1 dx 2tdt
vaø x = t
2
+ 1
Ñoåi caän
x 5 10
t 2 3
Khi ñoù: I =







33
22
22
2tdt 1 1
2 dt
t1
t 2t 1
t1
=



3
2
2
2ln t 1 2ln2 1
t1
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
134
Baøi 11: ÑAÏI HOÏC KHOÁI A NAÊM 2006
Tính tích phaân:
2
22
0
sin2x
I dx
cos x 4sin x
Giaûi
Ta coù:
2
22
0
sin2x
I dx
cos x 4sin x
=
2
2
0
sin2x
dx
1 3sin x
Ñaët t = 1 + 3sin
2
x dt = 3sin2xdx.
Vôùi x = 0 thì t = 1, vôùi x =
2
thì t = 4
4
4
1
1
1 dt 2 2
It
3 3 3
t
Baøi 12: ÑAÏI HOÏC KHOÁI B NAÊM 2006
Tính tích phaân:

ln5
xx
ln3
dx
I
e 2e 3
Giaûi


ln5 ln5
x
x x 2x x
ln3 ln3
dx e dx
I
e 2e 3 e 3e 2
Ñaët t = e
x
dt = e
x
dx . Vôùi x = ln3 t = 3 ; vôùi x = ln5 t = 5.




55
33
dt 1 1
I dt
(t 1)(t 2) t 2 t 1
=
5
3
t 2 3
ln ln
t 1 2
Baøi 13: ÑAÏI HOÏC KHOÁI A NAÊM 2005
Tính tích phaân: I =
2
0
sin2x sinx
dx
1 3cosx
Giaûi
2
0
(2cosx 1)sinx
I dx
1 3cosx
.
Ñaët t =


2
t1
cosx
3
1 3cosx
3sinx
dt dx
2 1 3cosx
x = 0 t = 2, x =
2
t = 1.
TT Luyện Thi Đại Học VĨNH VIỄN
135
I =








12
2
2
21
t 1 2 2
2 1 dt 2t 1 dt
3 3 9
=







3
2
2 2t 2 16 2 34
t 2 1 .
9 3 9 3 3 27
1
Baøi 14: ÑAÏI HOÏC KHOÁI B NAÊM 2005
Tính tích phaân:
2
0
sin2xcosx
I dx
1 cosx
.
Giaûi
Ta coù
2
0
sin2xcosx
I 2 dx
1 cosx
. Ñaët t = 1 + cosx dt = sinxdx.
x = 0 t = 2, x =
2
t = 1.




12
2
21
(t 1) 1
I 2 ( dt) 2 t 2 dt
tt
=





2
2
t
2 2t ln t
2
1
= 2






1
(2 4 ln2) 2 2ln2 1
2
.
Baøi 15: ÑEÀ DÖÏ BÒ 1
Tính tích phaân:
3
2
0
I sin x.tanxdx
Giaûi



22
33
00
sinx
I sin xtanxdx sin x dx
cosx
Ñaët t = cosx dt = sinxdx dt = sinxdx, sin
2
x = 1 – t
2
Ñoåi caän
x
0
3
t
1
1
2








1
1
22
1
2
1
1
1
2
2
(1 t ) 1 t 3
I dt t dt lnt ln2
t t 2 8
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
136
Baøi 16: ÑEÀ DÖÏ BÒ 2
Tính tích phaân:
7
3
0
x2
I dx
x1
Giaûi
7
3
0
x2
I dx
x1
Ñaët
3 2 3
3
t x 1 t x 1 3t dt dx x 2 t 1
Ñoåi caän:
x 0 7
t 1 2





2
22
3 5 2
24
11
1
t 1 t t 231
I 3t dt 3 t t dt 3
t 5 2 10
Baøi 17: ÑEÀ DÖÏ BÒ 1
Tính tích phaân:
3
e
2
1
ln x
I dx
x lnx 1
.
Giaûi
2
3
e
1
ln x
I dx
x lnx 1
Ñaët
t lnx 1
t
2
= lnx + 1

2
dx
2tdt
x
lnx 1 t
.
Ñoåi caän
3
x 1 e
t 1 2

22
22
42
11
(t 1)
I 2tdt 2 (t 2t 1)dt
t
=




5
3
2
t 2 76
2 t t
1
5 3 15
Baøi 18:
Tính tích phaân:

2
1
x
I
1 x 1
dx.
Giaûi
Ñaët t =
x1
t
2
= x 1 2tdt = dx. Ñoåi caän

x 1 t = 0
x = 2 t = 1
TT Luyện Thi Đại Học VĨNH VIỄN
137
Vaäy



2
1 1 1
3
2
0 0 0
t 1 2t
t t 2
I dt 2 dt 2 t t 2 dt
1 t t 1 t 1




1
32
0
t t 11
I 2 2t 2ln | t 1| 4ln2
3 2 3
.
Baøi 19:
Tính tích phaân:
e
1
1 3lnx.lnx
I dx
x
.
Giaûi
Ñaët
2
3dx
t 1 3lnx t 1 3lnx 2tdt =
x
Ñoåi caän


x e t = 2
x 1 t = 1

22
2 5 3
42
11
2
t 1 2tdt 2 2 t t 116
I t t t dt
1
3 3 9 9 5 3 135
Baøi 20: ÑEÀ DÖÏ BÒ 2
Tính tích phaân:

2
4
2
0
x x 1
I
x4
dx.
Giaûi
I =




22
4
2
2 2 2
00
x x 1 x 17
dx x 4 dx
x 4 x 4 x 4
=




2
2
3
2
2
0
0
x 1 dx
4x ln x 4 17
32
x4
.
Tính: I
1
=
2
2
0
dx
x4
. Ñaët x = 2tant dx = 2(tan
2
x + 1)dt
Ñoåi caän:
x 0 2
t0
4
I
1
=


2
44
4
2
0
00
tan t 1 1
2 dt dt
2 2 8
4 tan t 1
Vaäy I =




2
3
2
0
x1
4x ln x 4 17.
3 2 8
=
17 16
ln2
83
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
138
Baøi 21:
Tính tích phaân:
23
2
5
dx
I
x x 4
.
Giaûi
Tính tích phaân
23
2
5
dx
I
x x 4
. Ta coù



2 3 2 3
2 2 2
55
dx xdx
I
x x 4 x x 4
Ñaët
2 2 2
2
xdx
t x 4 t 4 x dt =
x4
Ñoåi caän


x 2 3 t = 4
x 5 t = 3
Vaäy



4
2
3
4
dt 1 t 2 1 1 1 1 5
I ln ln ln ln
3
4 t 2 4 3 5 4 3
t4
.
Baøi 22: ÑEÀ DÖÏ BÒ 1
Tính tích phaân:
ln3
2x
x
ln2
e dx
I
e1
.
Giaûi
ln5
2x
x
ln2
e
I dx
e1
. Ñaët t =
x
e1
t
2
= e
x
– 1 2tdt = e
x
dx vaø e
x
= t
2
+ 1
Ñoåi caän:
x ln2 ln5
t 1 2




2
2
2
3
1
1
t 1 .2tdt
t 20
I 2 t
t 3 3
Baøi 23:
Tính tích phaân:
2
4
0
1 2sin x
I dx
1 sin2x
.
Giaûi
Ta coù
44
4
00
d 1 sin2x
cos2x 1 1 1
I dx ln 1 sin2x ln2
1 sin2x 2 1 sin2x 2 2
0



.
Baøi 24: ÑEÀ DÖÏ BÒ 2
Tính tích phaân:
ln3
x
3
x
0
e dx
I
e1
.
TT Luyện Thi Đại Học VĨNH VIỄN
139
Giaûi
ln3
x
3
x
0
e
I dx
e1
. Ñaët
xx
t e 1 dt e dx
; Ñoåi caän:
x 0 ln3
t 2 4
Khi ñoù
4
4
3
2
2
2
dt 2
I 2 1
t
t
Baøi 25: ÑEÀ DÖÏ BÒ 1
Tính tích phaân:

2
6
35
0
I 1 cos x sinxcos xdx
Giaûi


22
66
3 5 3 3 2
00
I 1 cos x sinxcos xdx 1 cos x.cos x.sinx.cos xdx
Ñaët
6
3 6 3 5 2
t 1 cos x t 1 cos x 6t dt 3sinxcos xdx
2t
5
dt = sinxcos
2
xdx vaø cos
3
x = 1 – t
6
Ñoåi caän;
x0
2
t 0 1





1
11
13
6 5 6 12 7
00
0
2 2t 12
I t. 1 t 2t dt 2t 2t dt t
7 13 91
Baøi 26: CAO ÑAÚNG KINH TEÁ TP. HCM
Tính tích phaân:
2
0
I xsin2xdx
Giaûi
u x du dx
cos2x
dv sin2xdx v
2
Vaäy: I =




2
22
00
0
1
xcos2x sin2x
cos2xdx
2 4 2 4
22
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
140
Vaán ñeà 3: TÍNH TÍCH PHAÂN BAÈNG PHÖÔNG PHAÙP
TÍCH PHAÂN TÖØNG PHAÀN
A. PHÖÔNG PHAÙP GIAÛI
Coâng thöùc:



bb
b
a
aa
u(x).v (x)dx u(x).v(x) v(x).u (x)dx
Vieát goïn:
bb
b
a
aa
udv uv vdu

B. ÑEÀ THI
Baøi 1: ÑAÏI HOÏC KHOÁI B NAÊM 2011
Tính tích phaân:
3
2
0
1 xsinx
I dx.
cos x
Giaûi
Ta coù:
3 3 3
2 2 2
0 0 0
1 xsinx 1 xsinx
I dx dx dx
cos x cos x cos x
33
3
0
22
00
xsinx xsinx
tanx dx 3 dx
cos x cos x


.
Tính J =
3
2
0
xsinx
dx
cos x
baèng phöông phaùp tích phaân töøng phaàn.
Ñaët: u = x du = dx
dv =
2
sinx
cos x
dx, choïn v =
1
cosx
Suy ra: J =
3
3
0
0
x1
dx
cosx cosx



=
3
0
21
dx
3 cosx
Tính K =
33
2
00
1 cosx
dx dx
cosx
1 sin x


baèng phöông phaùp ñoåi bieán soá.
Ñaët t = sinx dt = cosxdx.
TT Luyện Thi Đại Học VĨNH VIỄN
141
Suy ra:
3
3
2
2
2
0
0
dt 1 1 t 1 2 3
K ln ln
2 1 t 2
23
1t





2
23
1
ln ln 2 3
2 4 3





.
Vaäy I =
2
3 ln 2 3
3
.
Baøi 2: ÑAÏI HOÏC KHOÁI B NAÊM 2009
Tính tích phaân:
3
2
1
3 lnx
I dx
x1
Giaûi
2
dx 1 1
u 3 lnx dv ; du dx v
x x 1
x1

3
3
1
1
3 lnx dx
I
x 1 x x 1

33
11
3 ln3 3 1 dx
dx
4 2 x x 1



33
11
3 ln3 1 27
ln x ln x 1 3 ln
4 4 16
Baøi 3: ÑAÏI HOÏC KHOÁI D NAÊM 2008
Tính tích phaân:
2
3
1
lnx
I dx
x
.
Giaûi
Tính tích phaân:
2
3
1
lnx
I dx
x
. Ñaët:

3
u lnx
dx
du
dx
dv
x
x
, choïn

2
1
v
2x
2
23
1
2
11
I lnx dx
1
2x 2x
=
2
2
1 1 1 3 3 2ln2
ln2 ln2
1
8 8 16 16
4x
.
Baøi 4: ÑAÏI HOÏC KHOÁI D NAÊM 2007
Tính tích phaân:
e
32
1
I x ln xdx
Giaûi
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
142
Tính tích phaân
Ñaët u = ln
2
x
2lnx
du dx;
x
dv = x
3
dx

4
x
v.
4
Ta coù:

ee
44
e
2 3 3
1
11
x 1 e 1
I .ln x x lnxdx x lnxdx
4 2 4 2
Ñaët u = lnx
dx
du
x
, dv = x
3
dx, choïn
4
x
v.
4
Ta coù

ee
ee
4 4 4
3 3 4
11
11
x 1 e 1 3e 1
x lnxdx lnx x dx x
4 4 4 16 16
.
Vaäy
4
5e 1
I
32
Baøi 5: ÑAÏI HOÏC KHOÁI D NAÊM 2006
Tính tích phaân:

1
2x
0
I (x 2)e dx
.
Giaûi
Tính tích phaân.

1
2x
0
I (x 2)e dx
. Ñaët


2x
2x
u x 2
1
du dx, choïn v = e
2
dv e dx
1
1
2x 2x
0
0
11
I (x 2)e e dx
22
=
22
1
2x
0
e 1 5 3e
1e
2 4 4
Baøi 6: ÑEÀ DÖÏ BÒ 1 - ÑAÏI HOÏC KHOÁI D NAÊM 2006
Tính tích phaân: I =
2
0
(x 1)sin2xdx
Giaûi
Ñaët

u x 1
1
du dx, choïn v cos2x
dv sin2xdx
2

2
2
0
0
x 1 1
I cos2x cos2xdx 1
2 2 4
Baøi 7: ÑEÀ DÖÏ BÒ 2 - ÑAÏI HOÏC KHOÁI D NAÊM 2006
TT Luyện Thi Đại Học VĨNH VIỄN
143
Tính tích phaân: I =
2
1
(x 2)lnxdx
Giaûi
Ñaët

2
u lnx
1x
du dx, choïnv 2x
dv x 2 dx
x2
I =







2
2
2
1
1
x x 5
2x lnx 2 dx 2ln2
2 2 4
Baøi 8: ÑAÏI HOÏC KHOÁI D NAÊM 2005
Tính tích phaân:

2
2
0
I 2x 1 cos xdx
.
Giaûi


22
2
00
1 cos2x
I (2x 1)cos x.dx (2x 1) dx
2


22
00
11
(2x 1)dx (2x 1)cos2x.dx
22
Tính

2
2
2
2
1
0
0
I (2x 1)dx x x
42
Tính

2
2
0
I (2x 1)cos2x.dx
.
Ñaët

u 2x 1
1
du 2dx choïnv sin2x
dv cos2xdx
2

2
22
2
00
0
11
I (2x 1)sin2x sin2xdx cos2x 1
22

2
12
1 1 1
I I I
2 2 8 4 2
.
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
144
Baøi 9:
Tính tích phaân:

3
2
2
I ln x x dx
.
Giaûi

3
2
2
I ln x x dx
Ta coù I =


3 3 3
2
2 2 2
ln x x dx lnx x 1 dx lnx ln x 1 dx
Ñaët

dx
u lnx du =
x
dv dx choïn v = x

33
1
22
33
I lnxdx xlnx dx xlnx x 3ln3 3 2ln2 2
22
3ln3 2ln2 1

32
2
2
1
21
I ln x 1 dx lnudu ulnu u 2ln2 1
Vaäy
3
2
12
2
I ln x x dx I I 3ln3 2ln2 1 2ln2 1
I 3ln3 2
Baøi 10: ÑEÀ DÖÏ BÒ 1
Tính tích phaân:
4
0
x
I dx
1 cos2x
.
Giaûi



44
2
00
x 1 xdx
I dx
1 cos2x 2
cos x
. Ñaët

2
ux
du dx
du
dv
choïn v tanx
cos x
4
4
4
0
0
0
1 1 1 1
I xtanx tanxdx xtanx ln cosx ln2
2 2 2 8 4

Baøi 11: CÑ KINH TEÁ – KYÕ THUAÄT COÂNG NGHIEÄP I
Tính tích phaân:
3
2
1
lnx
I dx
(x 1)
TT Luyện Thi Đại Học VĨNH VIỄN
145
Giaûi
Ñaët u = lnx
dx
du
x
dv = (x + 1)
-2
dx,
choïn

1
v
x1





33
11
3
lnx (x 1) x 1 1 1
I dx ln3 dx
1
x 1 x(x 1) 4 x x 1
=



3
1
1 x 1 3
ln3 ln ln3 ln
4 x 1 4 2
Baøi 12: CAO ÑAÚNG KINH TEÁ ÑOÁI NGOAÏI
Tính tích phaân:
4
3
0
ln 2x 1
I dx
(2x 1)
Giaûi
Ñaët u = ln
2x 1
, dv=
3
2
(2x 1)
dx du = (2x 1)
1
dx, choïn v =
1
2
(2x 1)
I =

1
4
2
0
12
(2x 1) ln3
ln 2x 1
33
Baøi 13: CAO ÑAÚNG KINH TEÁ TP. HCM
Tính tích phaân :
2
0
I xsin2xdx
Giaûi
u x du dx
cos2x
dv sin2xdx, choïnv
2
Vaäy: I =




2
22
00
0
1
xcos2x sin2x
cos2xdx
2 4 2 4
22
Vaán ñeà 4:
TÍNH TÍCH PHAÂN BAÈNG PHÖÔNG PHAÙP PHOÁI HÔÏP
A.ÑEÀ THI
Baøi 1: ÑAÏI HOÏC KHOÁI A NAÊM 2010
Tính tích phaân :

2 x x
x
1
0
x (1 2e ) e
I dx
1 2e
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
146
Giaûi


2 x x x
2
xx
1 1 1
0 0 0
x (1 2e ) e e
I dx x dx dx
1 2e 1 2e
1
3
2
1
0
1
0
x1
I x dx
33
x
2
x
1
0
e
I dx
1 2e
=
x
x
1
0
1 d(1 2e )
2
1 2e
=
1
x
0
1
ln(1 2e )
2
=



1 1 2e
ln
23
Vaäy I =



1 1 1 2e
ln
3 2 3
Baøi 2: ÑAÏI HOÏC KHOÁI D NAÊM 2010
Tính tích phaân:




e
1
3
I 2x lnxdx
x
Giaûi



e e e
1 1 1
31
I 2x lnxdx 2 xlnxdx 3 lnx. dx
xx
Xeùt
1
e
1
I xlnxdx
. Ñaët
dx
u lnx du
x
;
2
x
dv xdx v
2
Do ñoù
2 2 2 2
1
ee
e
1
11
x 1 e 1 x e 1
I lnx xdx
2 2 2 2 2 4
Xeùt I
2
=
e
1
1
lnx. dx
x
.
Ñaët t = lnx
dx
dt .
x
Vôùi x = 1
t = 0; x = e
t = 1 .
Do ñoù




2
1
1
2
0
0
t1
I tdt
22
. Vaäy
2
e2
I
2
Baøi 3: ÑAÏI HOÏC KHOÁI A NAÊM 2009
Tính tích phaân

2
32
0
I cos x 1 cos xdx
.
TT Luyện Thi Đại Học VĨNH VIỄN
147
Giaûi



22
52
00
I cos xdx cos xdx
Ñaët t = sinx dt = cosxdx; x = 0 t = 0,
x t 1
2
1
1
22
22
5 2 2 3 5
1
0
0 0 0
2 1 8
I cos xdx 1 sin x cosxdx 1 t dt t t t
3 5 15









22
2
2
2
0
00
1 1 1
I cos xdx 1 cos2x dx x sin2x
2 2 2 4
Vaäy
12
8
I I I
54
Baøi 4: CAO ÑAÚNG KHOÁI A, B, D NAÊM 2009
Tính tích phaân

1
2x x
0
I e x e dx
Giaûi
Ta coù


11
xx
00
I e dx xe dx
1
x
1
0
I e dx
1
x
0
1
e 1
e
1
x
2
0
I xe dx
.
xx
Ñaët u x du dx; ñaët dv e dx, choïn v e
Suy ra
1
1
xx
2
0
0
I xe e dx 1
. Vaäy
12
1
I I I 2
e
.
Baøi 5: ÑAÏI HOÏC SAØI GOØN KHOÁI A NAÊM 2007
Tính:

1
2
0
2x 1
I dx
x x 1
Giaûi
I =

11
22
00
2x 1 1
dx 2 dx
x x 1 x x 1
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
148
I
1
=

1
1
2
2
0
0
2x 1
dx ln x x 1 ln3
x x 1
; I
2
=




1
2
0
dx
13
x
24
Ñaët x +
13
tant
22
dx =
2
3
1 tan t dt
2
I
2
=
2
3
2
6
3
1 tan t dt
2
2
3
63
1 tan t
4
I =
2
ln3
63
Baøi 6: CAO ÑAÚNG GTVT III KHOÁI A NAÊM 2007
Tính tích phaân :
2
9
0
J sin xdx
Giaûi
Ñaët t =
x
thì dx = 2tdt

3
0
J 2tsintdt
Choïn :




u 2t du 2dt
dv sintdt choïn v cost
J =
3
3 3 3
0
00
0
2t cost 2 costdt 2t cost 2sint
=
3
3
Baøi 7: ÑAÏI HOÏC KHOÁI D NAÊM 2005
Tính tích phaân

2
sinx
0
I 2 e cosx cosxdx
.
Giaûi



22
sinx
00
1 cos2x
I 2 e d sinx 2 dx
2




2
sinx
0
2
11
2e
x sin2x
22
0
e1
2
TT Luyện Thi Đại Học VĨNH VIỄN
149
Baøi 8: ÑEÀ DÖÏ BÒ 2
Tính tích phaân:
2
0
I x sin xdx
.
Giaûi
2
0
I x sin xdx
. Ñaët t =
x
t
2
= x 2tdt = dx
Ñoåi caän
x
0
2
t
0
2
0
I 2 t sintdt
. Ñaët
2
ut
dv sintdt

du 2tdt
v cost
22
1
0
I 2(t cost) 4 tcostdt 2 4I
0
Tính
1
0
I tcostdt
Ñaët
ut
dv costdt
du dt
choïnv sint

1
0
I tsint sintdt cost 2
00
. Vaäy I = 2
2
– 8
Baøi 9: ÑEÀ DÖÏ BÒ 1
Tính tích phaân:
1
2
3x
0
I x e dx
Giaûi
Tính


11
22
3 x 2 x
00
I x e dx x e xdx
Ñaët t = x
2
dt = 2xdx

dt
xdx
2
. Ñoåi caän:
x 0 1
t 0 1







11
1
1
t t t t t
0
0
00
1 1 1 1
I te dt te e dt te e
2 2 2 2
Baøi 10: ÑEÀ DÖÏ BÒ 2
Tính tích phaân:
0
2x
3
1
I x e x 1 dx
.
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
150
Giaûi
Tính
0 0 0
2x 2x
33
1 1 1
I x e x 1 dx x.e .dx x x 1dx
Tính
0
2x
1
1
I xe dx
. Ñaët


2x
2x
du dx
ux
1
choïnv e
dv e dx
2





0
00
0
0
x 2x 2x 2x
1
1
2
1
1
11
1 1 1 1 3 1
I uv vdu x.e e dx x.e .e
2 2 2 4 4
4e
Tính

0
3
2
1
I x x 1dx
Ñaët
32
3
t x 1 t x 1 3t dt dx
. Ñoåi caän:
x 1 0
t 0 1





1
11
74
3 3 6 3
2
00
0
t t 9
I t 1 .t.3t dt 3 t t dt 3
7 4 28
Vaäy I = I
1
+ I
2
=
22
3 1 9 3 4
4 28 7
4e 4e
Baøi 11: CAO ÑAÚNG KYÕ THUAÄT CAO THAÉNG
Tính tích phaân:
4
2
0
1 sin2x
dx
cos x
Giaûi
I =
4
2
0
1 sin2x
dx
cos x
=
44
22
00
1 sin2x
dx dx
cos x cos x


2
4
2
0
4
d(cos x)
tanx dx
cos x
0

.
=

2
tanx ln(cos x)
44
00
= 1 + ln2
TT Luyện Thi Đại Học VĨNH VIỄN
151
Vaán ñeà 5: ÖÙNG DUÏNG CUÛA TÍCH PHAÂN
A. PHÖÔNG PHAÙP GIAÛI
TÍNH DIEÄN TÍCH
Baøi toaùn 1: Cho haøm soá y = f(x) lieân tuïc vaø khoâng aâm treân ñoaïn [a, b]. Dieän tích
hình phaúng giôùi haïn bôûi ñoà thò cuûa haøm soá y = f(x), truïc hoaønh vaø hai ñöôøng
thaúng x = a, x = b laø:


bb
aa
S f(x)dx f(x) dx
Töø baøi toaùn 1 suy ra neáu f(x) khoâng
döông treân ñoaïn [a, b]

bb
aa
S f(x)dx f(x) dx
Baøi toaùn 2: (Toång quaùt)
Cho hai haøm soá y
1
= f(x), y
2
= g(x) lieân tuïc treân ñoaïn [a, b] vaø coù ñoà thò laàn löôït
laø (C1), (C2). Dieän tích hình phaúng giôùi haïn bôûi (C1), (C2) vaø hai ñöôøng x = a,
x = b ñöôïc xaùc ñònh bôûi coâng thöùc:

b
a
S f(x) g(x) dx
(*)
* Phöông phaùp giaûi (*):
Giaûi phöông trình: f(x) = g(x) (1)
Neáu (1) voâ nghieäm thì:

b
a
S (f(x) g(x))dx
Neáu (1) coù nghieäm thuoäc [a, b] giaû söû laø
, ( )
thì

b
a
S (f(x) g(x) dx (f(x) g(x) dx (f(x) g(x) dx
Baøi toaùn 3: Cho
1 1 2 2
(C ):x f(y), (C ): x g(y), f(y),g(y)
lieân tuïc treân ñoaïn [a, b].
Dieän tích hình phaúng S ñöôïc giôùi haïn bôûi (C1); (C2) vaø hai ñöôøng thaúng y = a,
y = b ñöôïc xaùc ñònh bôûi coâng thöùc:

b
a
S f(y) g(y) dy
y
0
x = a
x = b
y = f(x)
y
x = a
x = b
y = f(x)
S
0
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
152
THEÅ TÍCH CAÙC VAÄT THEÅ
I. COÂNG THÖÙC THEÅ TÍCH
Giaû söû vaät theå T ñöôïc xaùc ñònh bôûi 2 maët
phaúng
( ) vaø ( )
song song vôùi nhau. Ta
choïn truïc Ox sao cho noù vuoâng goùc vôùi
caùc maët phaúng ( vaø (). Ta coù Ox ()
= A, Ox () = B. Giaû söû maët phaúng
(
( ) Ox,( ) Ox C,
() caét vaät theå T
coù thieát dieän laø S(x).
Khi ñoù
b
a
V S(x)dx
II. BAØI TOAÙN
Baøi toaùn 1: Giaû söû hình phaúng giôùi haïn bôûi caùc
ñöôøng y = f(x), x = a, x = b vaø y = 0 quay quanh Ox.
Hình troøn S(x) coù baùn kính R = y:

2
S(x) y

b
2
a
V y dx
Baøi toaùn 2: Theå tích do hình phaúng: x = g(y), x = 0,
y = a, y = b quay quanh truïc Oy:

b
2
a
V x dy
Baøi toaùn 3: Tính theå tích vaät theå do hình phaúng
giôùi haïn hai ñöôøng caét nhau quay quanh Ox:
12
21
y f(x), y g(x)
y y 0 x [a, b]

b
22
21
a
V (y y )dx
Baøi toaùn 4: Tính theå tích vaät theå do hình phaúng
giôùi haïn hai ñöôøng caét nhau quay quanh Ox.
12
12
y f(x),y g(x)
y y 0 x [a,b]

b
22
12
a
V (y y )dx
x
y
O
A
C
B
a
b
x
S(x)
x
y
O
y
x
a
y = f(x)
S(x)
b
O
x
y
a
b
x
x = g(y)
x
O
a
b
y
g(x) = y
2
f(x) = y
1
x
y
g(x) = y
2
f(x) = y
1
O
a
b
TT Luyện Thi Đại Học VĨNH VIỄN
153
B. ÑEÀ THI
Baøi 1: CAO ÑAÚNG KHOÁI A, B, D NAÊM 2008
Tính dieän tích hình phaúng giôùi haïn bôûi parabol (P): x = x
2
+ 4x vaø ñöôøng
thaúng d: y = x.
Giaûi
Phöông trình hoaønh ñoä giao ñieåm cuûa (P) vaø d:
2
x 4x x x 0 hayx 3





33
32
33
00
3
x 3x 9
S x 3x dx ( x 3x)dx
0
3 2 2
(ñvdt)
Baøi 2: ÑAÏI HOÏC KHOÁI A NAÊM 2007
Tính dieän tích hình phaúng giôùi haïn bôûi caùc ñöôøng: y = (e + 1)x, y = (1 + e
x
)x
Giaûi
Phöông trình hoaønh ñoä giao ñieåm cuûa hai ñöôøng ñaõ cho laø:
(e + 1)x = (1 + e
x
)x (e
x
e)x = 0 x = 0 hoaëc x = 1
Dieän tích cuûa hình phaúng caàn tìm laø:
1 1 1
x
x
0 0 0
S dx e xdx xe dx
xe ex
Ta coù:
1
1 1 1
2
11
x x x x
00
0 0 0
0
ex e
e xdx , xe dx xe e dx e e 1
22
Vaäy

e
S1
2
(ñvdt).
Baøi 3: ÑAÏI HOÏC KHOÁI B NAÊM 2007
Cho hình phaúng (H) giôùi haïn bôûi caùc ñöôøng: y = xlnx, y = 0, x = e.
Tính theå tích cuûa khoái troøn xoay taïo thaønh khi quay hình (H) quanh truïc Ox.
Giaûi
Phöông trình hoaønh ñoä giao ñieåm cuûa caùc ñöôøng y = xlnx vaø y = 0 laø:
xlnx = 0 x = 1
Theå tích khoái troøn xoay taïo thaønh khi quay hình H quanh truïc hoaønh laø:

ee
22
11
V y dx (xlnx) dx
Ñaët u = ln
2
x, dv = x
2
dx

3
2lnx x
du dx, v .
x3
Ta coù:
e
e e e
33
2 2 2 2
1 1 1
1
x 2 e 2
(xlnx) dx ln x x lnxdx x lnxdx
3 3 3 3
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
154
Ñaët u = lnx, dv = x
2
dx

3
dx x
du , choïnv .
x3
Ta coù:

ee
ee
3 3 3 3
22
11
11
x 1 e x 2e 1
x lnxdx lnx x dx
3 3 3 9 9
Vaäy

3
(5e 2)
V
27
(ñvtt).
Baøi 4: ÑEÀ DÖÏ BÒ 2 - ÑAÏI HOÏC KHOÁI A NAÊM 2006
Tính dieän tích hình phaúng giôùi haïn bôûi paraol y = x
2
– x + 3 vaø ñöôøng thaúng
d: y = 2x + 1.
Giaûi
Phöông trình hoaønh ñoä giao ñieåm cuûa parabol vaø d:
x
2
– x + 3 = 2x + 1 x
2
– 3x + 2 = 0 x = 1 x = 2
Ta coù

22
22
11
S (x x 3) (2x 1)dx x 3x 2 dx




2
32
2
1
2
x 3x 1
( x 3x 2)dx 2x
1
3 2 6
(ñvdt)
Baøi 5: ÑEÀ DÖÏ BÒ 1
Tính theå tích vaät theå troøn xoay sinh ra trong pheùp quay xung quanh truïc Ox,
cuûa hình phaúng giôùi haïn bôûi truïc Ox vaø ñöôøng y =
x
sinx (0 x )
Giaûi
V =


2
2
0 0 0
f x dx x.sin xdx x 1 cos2x dx
2
=






00
xdx x.cos2xdx
2
Tính : I
1
=

22
0
0
x
xdx
22
. Tính : I
2
=
0
xcos2xdx
Ñaët

du dx
ux
1
dv cos2xdx
choïnv sin2x
2
I
2
=



0
0
x 1 x 1
sin2x sin2xdx sin2x cos2x 0
2 2 2 4
V =





23
0
2 2 4
(ñvtt)
TT Luyện Thi Đại Học VĨNH VIỄN
155
Baøi 6:
Tính dieän tích hình phaúng giôùi haïn bôûi caùc ñöôøng:
2
y x 4x 3 vaø y = x + 3
.
Giaûi



53
22
01
S x 3 x 4x 3 dx 2 x 4x 3 dx

53
22
01
S x 5x dx 2 x 4x 3 dx
3 2 3
2
53
x 5x x
S 2 2x 3x
01
3 2 3
109
S
6
(ñvdt)
Baøi 7:
Tính dieän tích cuûa hình phaúng giôùi haïn bôûi caùc ñöôøng:

22
xx
y 4 vaø y =
4
42
Giaûi
Ta coù
2 2 2 2 2
22
x x x x y
y 4 y 4 y 4 1 (E)
4 4 4 16 4
Phöông trình hoaønh ñoä giao ñieåm:
2 2 2 4
x x x x
4 4
4 4 32
42
4 2 2 2
x 8x 128 0 x 8 x 16
(loaïi) x = 2
2
Neân S =




2 2 2 2 2 2
2 2 2 2
00
22
x x x x
4 dx 2 4 dx dx
44
4 2 4 2
Tính

22
2
1
0
x
I 4 dx
4
Ñaët x = 4sint dx = 4costdt
Ñoåi caän
t =
x 2 2
4
x0
t0
x
y
1
1
1
O
1
3
3
8
5
y = x + 3
y =
2
x
42
x
y
2
4
4
O
y =
2
4
x
4
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
156





44
2
4
1
00
1
I 8cos tdt 4 1 cos2t dt 4 t sin2t 2
2
0
22
23
2
0
x x 4
22
I dx
3
4 2 12 2 0
Vaäy
4
S2
ñvdt
3



.
Baøi 8: CAO ÑAÚNG KYÕ THUAÄT CAO THAÉNG
Tính dieän tích hình phaúng giôùi haïn bôûi caùc ñöôøng
(P
1
): y = x
2
2x vaø (P
2
) : y = x
2
+ 4x.
Giaûi
Phöông trình hoaønh ñoä giao ñieåm cuûa (P
1
) vaø (P
2
) laø: x
2
2x = x
2
+ 4x
2x
2
+ 6x = 0
2x(x 3) = 0 x = 0 x = 3.
Dieän tích caàn tìm:

33
2 2 2
00
S (( x 4x) (x 2x))dx ( 2x 6x)dx
=



32
3
2
x 3x
0
3
= 9 (ñvdt)
Baøi 9: CAO ÑAÚNG KYÕ THUAÄT CAO THAÉNG
Tính dieän tích cuûa hình phaúng giôùi haïn bôûi caùc ñöôøng: y = 7 – 2x
2
, y = x
2
+ 4.
Giaûi
Phöông trình hoaønh ñoä giao ñieåm 7 – 2x
2
= x
2
– 4
3x
2
= 3 x = 1 hoaëc x = 1
Dieän tích S caàn tìm


11
2 2 2
11
S (7 2x x 4)dx (3 3x )dx 4
(ñvdt)
| 1/33
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
Chuyeân ñeà 4: TÍCH PHAÂN
Vaán ñeà 1:
BIEÁN ÑOÅI VEÀ TOÅNG – HIEÄU CAÙC TÍCH PHAÂN CÔ BAÛN
A. PHÖÔNG PHAÙP GIAÛI
Söû duïng ba tích chaát sau ñeå bieán ñoåi tích phaân caàn tính thaønh toång – hieäu caùc tích phaân cô baûn b b b b b 1/ k.f(x)dx   kf(x)dx
2/ f(x)  g(x )dx  f(x)dx    g(x)dx a a a a a b c b 3/ f(x)dx  f(x)dx    f(x)dx a a c
BAÛNG NGUYEÂN HAØM CÔ BAÛN
Nguyeân haøm cuûa caùc haøm soá sô caáp
Nguyeân haøm cuûa caùc haøm soá hôïp (u = u(x))
1. dx  x  c; kdx  kx    c 1 1.  u u u'dx   c ;  (    1) 1 1   2.  x x dx   c,  (    1)  1 2.    u'dx ln u c u 3.    dx ln x c x 3.    u u e u'dx e c 4.    x x e dx e c u 4. u a a u'dx   c (0  a   1) x lna 5. x a a dx   c (0  a   1) lna 5.   u'cosudx sinu c 6.   cosxdx sinx c 6.    u'sinudx cosu c 7.    sinxdx cosx c 7. u' dx tanu  c 2 cos u 8. dx  tanx   c 2 cos x u' dx 8. dx   cot u  c 9.   cot x   c  2 2 sin u sin x 9.    10.    tanxdx ln cosx c u'tanudx ln cosu c 10.   11.   cotxdx ln sinx c u'cotudx ln sinu c 124
TT Luyện Thi Đại Học VĨNH VIỄN
Ñaëc bieät: u(x) = ax + b;          1 f(x)dx F(x) c f(ax b)dx F(ax b) c a 1 dx 1 1.  1 (ax  b) (ax  b) dx    c 7.  tan(ax  b)   c a  1 2 cos (ax  b) a 2. dx 1     dx 1 ln ax b c 8.   cot(ax  b)  c ax   b a 2 sin (ax  b) a 3.  1  e dx   ax b ax b e 1  a 9. tan(ax  b)dx  ln cos(ax  b)  c  a 4.         x 1 a dx ln x c       1 10. cot(ax b)dx ln sin(ax b) c a dx 1 x a 5.      1 cos(ax b)dx sin(ax b) c 11.   ln   c a 2 x  2 a 2a x  a 6.       1 sin(ax b)dx cos(ax b) c a B – ÑEÀ THI
Baøi 1: CAO ÑAÚNG KHOÁI A, B, D NAÊM 2011 Tính tích phaân 2 2x  1 I  dx  1 x(x 1) Giaûi 2 2 I = (x 1)  xdx  =  1 1 dx  6  lnx(x  1)  ln  ln3 . x(x  =  2 1)   x 1 x   1 2 1 1 
Baøi 2: CAO ÑAÚNG KHOÁI A, B, D NAÊM 2010 1 Tính tích phaân: 2x 1 I   dx x 1 0 Giaûi 1 2x 1 1  3  1 I   dx 2  dx 2x  3ln x 1 x  = 2 – 3ln2. 1 =    x 1 =  0 0  0
Baøi 3: CAO ÑAÚNG GTVT III KHOÁI A NAÊM 2007 2 4 3 2
Tính caùc tích phaân sau: x  x  3x  2x  2 I   dx 2 x  1 x Giaûi
Chia töû cho maãu, ta ñöôïc: 125
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc – 4 3 2 x  x  3x  2x  2 2 x  2  x  3  = 2 1 2 x  3   2 x  2 x x  x x 1 x 2 x 2 3  2 1 2  I  x  3   dx    
 3x  ln x 1  2ln x   x 1 x  3 1  1 I = 16 3  ln 3 8
Baøi 4: CAO ÑAÚNG KINH TEÁ – COÂNG NGHIEÄP TPHCM NAÊM 2007 Tính tích phaân: dt I(x)  x
, vôùi x > 1. Töø ñoù tìm lim I(x) 1 t(t 1) x Giaûi x x x I(x) = dt 1 1    x t lnt  ln t 1       dt =    ln t t 1  t t 1 1 t 1 1 1 1 = x 1 ln  ln x 1 2 x 1  lim Ix    lim ln  ln  ln2 x x    x 1 2
Baøi 5: ÑEÀ DÖÏ BÒ 1 - ÑAÏI HOÏC KHOÁI B NAÊM 2005  4 Tính tích phaân:  sin x tan x  e cosxdx 0 Giaûi    4 4 4 I  tanx  sinx e .cosxdx  tanxdx    sinx sinx 'e dx 0 0 0 2
=  ln cosx  + e     sin x 4 4   2 ln 2 e 1. 0 0
Baøi 6: ÑEÀ DÖÏ BÒ 2 3 Tính tích phaân: dx I   x  3 1 x Giaûi 2 2 3 dx 3 1 x  x 3 1 x  3 1 1 2x  I   dx   dx    dx 1 3 1 2 1  2   x x x(1 x ) x 1  2     x 1 x 2 x 1 126
TT Luyện Thi Đại Học VĨNH VIỄN  1 2  3  2  3  ln x  ln(x 1)  lnx  ln x    2  1   1   1 x 3 3 1 6  ln  ln  ln  ln 1 2 1 2 2 2 x Baøi 7: 2 Tính tích phaân : I = 2 x   xdx . 0 Giaûi 2 1 2 Tính I  2 x  x dx   2 x  xdx   2 x     xdx 0 0 1 Do : x 0 1 2 x2x  0 + 3 2 1 3 2 2  x x   x x  I          1.  3 2  0  3 2  1
Baøi 8: ÑEÀ DÖÏ BÒ 3 Cho haøm soá: f(x) = a  x bxe . x  3 1 1
Tìm a vaø b bieát raèng f’(0) =  22 vaø f(x)dx   5 0 Giaûi Ta coù: a f(x)   x bx.e (x  3 1) 3a  f(x)    x
be (x 1)  f(0)  3a  b  22 (1) (x  4 1) 1 1 1 1 3 x a 3a    
f(x)dx  a(x 1) dx  b xe       x b(xe  x e )   b  5 (2) 2(x  2 1) 8 0 0 0 0 3a  b  22  a  8
(1) vaø (2) ta coù heä: 3a   .  b   5 b  2  8 127
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
Vaán ñeà 2:
TÍNH TÍCH PHAÂN BAÈNG PHÖÔNG PHAÙP ÑOÅI BIEÁN SOÁ
A. PHÖÔNG PHAÙP GIAÛI
ÑOÅI BIEÁN SOÁ LOAÏI I b 
1. Söû duïng coâng thöùc: f[u(x)].  u (x)dx   f(u)du a  b
2. Phöông phaùp: Xeùt tích phaân I  f(x)du a
- Ñaët t = u(x)  dt = u'(x)dx
- Ñoåi caän u(a) = t1 ; u(b) = t2 t2 t - Suy ra: 2 I  g(t)dt  g(t)  (g(t) f[u(x)].  u (x)) t1 t1
Thöôøng ñaët aån phuï t laø
 caên thöùc, hoaëc muõ cuûa e, hoaëc maãu soá, hoaëc bieåu thöùc trong ngoaëc.
 coù sinxdx  ñaët t = cosx, coù cosxdx  ñaët t = sinx, coù dx ñaët t = lnx. x
ÑOÅI BIEÁN SOÁ LOAÏI II  b  Coâng thöùc: f  ( (t) / ) (t)dt  
f(x)dx ; x  (t);   ( )  a,  ( )  b  a b  Tính: I  f(x)dx a
Ñaët x  (t)  dx    (t)dt
Ñoåi caän: x  (t);   ( )  a,  ( )  b  b Khi ñoù: I  f  ( (t)).   (t)dt   f(x)dx  a b
Caùc daïng thöôøng gaëp: 1. 2 a  2 x dx ñaët x   asint a b b 2. dx dx ñaët x   asin t 3. ñaët x  atan t  2 a  2 2 2 a x a a  x B. ÑEÀ THI
Baøi 1: ÑAÏI HOÏC KHOÁI A NAÊM 2011 128
TT Luyện Thi Đại Học VĨNH VIỄN  4 xsinx  x   1 cosx Tính tích phaân : I  dx.  xsinx  cosx 0 Giaûi   4 4 Ta coù: xsin x  cosx  x cosx I  x cosx  dx  1    dx xsin x   cosx   xsin x cosx   0 0     4 4 4 xcosx  xcosx  x  dx   dx 0  xsinx   cosx 4 xsinx  cosx 0 0
Ñaët t = xsinx + cosx  dt = xcosxdx. 
Khi x = 0 thì t = 1, x = thì t = 2   1  4 2  4    2     1 2  4  2     dt  1   2    Suy ra: I    2  4    ln t   ln  1 . 4 t 4  1 4 2 4 1  
Baøi 2: ÑAÏI HOÏC KHOÁI D NAÊM 2011 4 Tính tích phaân: 4x 1 I  dx.  2x 1  2 0 Giaûi
Ñaët: t  2x 1  2  2x 1  t  2 2 2x 1 t  4t  4 2 t  4t  3  x   dx = (t – 2)dt. 2
x = 0  t = 3, x = 4  t = 5. 2 t  4t  3 5 4 1  2
5 2t  8t  5t 2 Suy ra: 2 I   t  2dt = dt t  t 3 3 5 3 2 5 = 2t 12t  21t 10  10 dt  = 2 2t 12t 21     dt t  t  3 3  5 3   = 2t 2   6t  21t 10ln t   = 34 3 10ln . 3    3 5 3
Baøi 3: ÑAÏI HOÏC KHOÁI B NAÊM 2010 129
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc – e Tính tích phaân: ln x I =  dx x(2  2 1 ln x) Giaûi Ñaët 1
u  lnx  du  dx , x = 1  u = 0, x = e  u = 1 x 1 1   u 1 2 1  2  I  du      du  ln 2  u  2    2 u 2 u  2  u 0      0 2  2  u   0  2   3  1  ln 3   ln2     1  ln     3   2  3 .
Baøi 4: ÑAÏI HOÏC KHOÁI D NAÊM 2009 3 Tính tích phaân: dx I   . x e  1 1 Giaûi
Ñaët t = ex  dx = dt ; x = 1  t = e; x = 3  t = e3 t 3 3 e e 3 3 dt  1 1 I   e e 2       dt  ln t 1  ln t  lne  e   1  2 t t 1  t 1 t  e e e e
Baøi 3: ÑAÏI HOÏC KHOÁI A NAÊM 2008  6 4 tan x Tính tích phaân: I   dx cos2x 0 Giaûi Caùch 1: dt
 Ñaët t = tanx  dt = (1 + tan2x)dx   dx 1 2 t 2 1 t cos2x  1 2 t 3
 Ñoåi caän: x = 0  t = 0;  x   t  6 3 3 3 3 4 3 t 1  Khi ñoù:  2  I  dt  t 1  dt 2   2  1 t  1 t  0 0 130
TT Luyện Thi Đại Học VĨNH VIỄN  3 3 t 1 1 t  1 3 1 10    t  ln  3  ln   3 2 1  t  2 3   1 9 3 0 Caùch 2:    6 4 6 4 6 4 Ta coù: tan x tan x tan x I  dx  dx    dx 2 2  cos2x cos x  2 sin x cos x(1 2 0 0 0 tan x) Ñaët: t = tanx dx  dt  2 cos x Ñoåi caän: x = 0 3  t = 0;  x   t  6 3 3 3 4 Khi ñoù: t 1 3 1 10 I  dt  ln   1 2 t 2 3 1 9 3 0
Baøi 4: ÑAÏI HOÏC KHOÁI B NAÊM 2008     sin x  4  dx Tính tích phaân:  4  I  
sin2x  2(1 sinx  cosx) 0 Giaûi     sin x  4  dx Tính tích phaân:  4  I  
sin2x  2(1 sinx  cosx) 0 Ñaët t = sinx + cosx    
dt  (cosx  sinx)dx   2 sin x   dx  4 
Ñoåi caän: x = 0  t = 1;  x   t  2 4
Ta coù: t2 = sin2x + cos2x + 2sinxcosx = 1 + sin2x  sin2x = t2 – 1 2 2 Khi ñoù: 2 dt 2 dt I      2  2 t 1 2(1 t) 2 (t  2 1 1 1) 2 1 2 2 1 1 4 3 2     .      . 2 t 1 1 2  2 1 2  4
Baøi 5: ÑAÏI HOÏC SAØI GOØN KHOÁI B NAÊM 2007 1 Tính tích phaân: 1 I   dx 2 x  x  0 1 131
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc – Giaûi 1 I =  1 dx  1 2 0 3 x      2  4 Ñaët 1 3     3 x   tant, t   ;  dx     2 1 tan tdt 2 2  2 2  2  3 1 2 3 tan t I = 2  dt   3    2  3 3 1 tan t 6 4
Baøi 6: CAO ÑAÚNG XAÂY DÖÏNG SOÁ 2 NAÊM 2007
Tính tích phaân: I = e dx 1 3 x 1 lnx Giaûi Ñaët: dx  3 t 1 lnx  lnx = t3 – 1,  2 3t dt x
Ñoåi caän: x = 1  t = 1; x = e   3 t 2 3 2 3 3 2 3t 2 3 4 3  I   3tdt    1 2 1 2
Baøi 7: CAO ÑAÚNG COÂNG NGHIEÄP THÖÏC PHAÅM NAÊM 2007 Tính tích phaân: x  1 1 dx 0 2 x 1 Giaûi 1 1 1 xdx 1 dx I 1    I   I ; I  2 ln(x 1)  ln2 . 0  x  0 1 x  1 2 2 2 1 1 2 0 2 Ñaët x = tant,   dt t  0, , dx     4  2 cos t   1 I  dt  4 2 . Vaäy  I  ln2  0 4 2 4
Baøi 8: CAO ÑAÚNG TAØI CHÍNH – HAÛI QUAN NAÊM 2007  2 Tính tích phaân: sin x I   dx cos2x cosx   3 132
TT Luyện Thi Đại Học VĨNH VIỄN Giaûi
Ñaët t = cosx  dt = sinxdx  x  3 2 1 t 0 2 1 1 0 2 2  1 2  I = dt 1  dt     3 3 dt 2  2  1 2t  t  1 2t  t 1    0 0  t 1 2t 1 2 1 1 1
 I = ln t 1  ln 2t 1  2   ln4 0 3 3
Baøi 9: ÑEÀ DÖÏ BÒ 1 - ÑAÏI HOÏC KHOÁI A NAÊM 2006 6 Tính tích phaân: I =  dx 2x 1 4x 1 2 Giaûi 2 Ñaët t 1 1 t  4x 1  x   dx  tdt 4 2 t 5 dt 5 5 2 t  1 1   I   dt   dt 2  2     2  t 1 (t 1) t 1 3 3 3  (t 1)  2. 1 t 4 1 5   3 1  ln t 1   ln     t 1 3 2 12
Baøi 10: ÑEÀ DÖÏ BÒ 1 - ÑAÏI HOÏC KHOÁI B NAÊM 2006 10 Tính tích phaân: I =  dx x  2 x 1 5 Giaûi  Ñaët t =   2 x 1
t  x 1 dx  2tdt vaø x = t2 + 1 x 5 10  Ñoåi caän t 2 3 3 3   Khi ñoù: I = 2tdt 1 1  2     dt 2  t  2t 1  t 1 t  2 2 2    1  3 =  2  2ln t 1   2ln2    1  t 1 2 133
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
Baøi 11: ÑAÏI HOÏC KHOÁI A NAÊM 2006  2 Tính tích phaân: sin2x I   dx 2 cos x  2 0 4sin x Giaûi   2 2 Ta coù: sin2x I sin2x   dx =  dx 2 cos x  2 2 0 4sin x 0 1  3sin x
Ñaët t = 1 + 3sin2x  dt = 3sin2xdx. 4 4
Vôùi x = 0 thì t = 1, vôùi x =  thì t = 4 1 dt 2 2  I   t  2  3 t 3 3 1 1
Baøi 12: ÑAÏI HOÏC KHOÁI B NAÊM 2006 ln5 Tính tích phaân: dx I   x  e  x 2e  ln3 3 Giaûi ln5 ln5 x dx e dx I    x x  e  2e  2x 3 e  x 3e  ln3 ln3 2
Ñaët t = ex  dt = ex dx . Vôùi x = ln3  t = 3 ; vôùi x = ln5  t = 5. 5 5 5 dt 1 1 t 2 3    I      dt =  ln  ln (t 1)(t  2)  t  2 t 1 t 1 2 3 3 3
Baøi 13: ÑAÏI HOÏC KHOÁI A NAÊM 2005  2
Tính tích phaân: I = sin2x   sin x dx 1 3cosx 0 Giaûi  2 (2cosx 1)sin x I   dx . 1 3cosx 0  2 t 1 cosx  Ñaët t =    3 1 3cosx   3sin x dt   dx  2 1 3cosx
x = 0  t = 2, x =   t = 1. 2 134
TT Luyện Thi Đại Học VĨNH VIỄN 1  2 t 1  2 I =  2  2 2 1  dt   2     2t  1dt 3  3  9 2   1 2 2  3 2t  = 2 16   2  34   t    2  1   3      . 9   9  3   3  27 1
Baøi 14: ÑAÏI HOÏC KHOÁI B NAÊM 2005  2 Tính tích phaân: sin2x cosx I   dx . 1 cosx 0 Giaûi  2 Ta coù sin2x cosx I  2
dx . Ñaët t = 1 + cosx  dt = sinxdx. 1 cosx 0
x = 0  t = 2, x =   t = 1. 2 1 2 2 (t 1)  1 I  2 (dt)  2 t  2    dt t  t  2 1 2  2 t  = 2  1    2t  ln t   = 2   (2  4  ln2)   2  2ln2 1. 2       2 1   
Baøi 15: ÑEÀ DÖÏ BÒ 1  3
Tính tích phaân: I   2 sin x.tan xdx 0 Giaûi   sinx I  2 sin xtanxdx    2 3 3 sin x dx 0 0 cosx
Ñaët t = cosx  dt = sinxdx  dt = sinxdx, sin2x = 1 – t2 Ñoåi caän x 0  3 t 1 1 2 1 1 (1 2t) 1  2 1 t    3 I   2 dt  1  t dt   lnt ln2 1         t  t   2 1 8 2 2 135
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
Baøi 16: ÑEÀ DÖÏ BÒ 2 7 Tính tích phaân: x  2 I   dx 3 x  0 1 Giaûi 7 x  2 I   dx 3 x  0 1 Ñaët  3 t x 1  3 t  x 1 2 3t dt  dx  x  2  3 t 1 x 0 7 Ñoåi caän: t 1 2 2 2 3 2 5 2 t 1 t t 231 I  2 3t dt   3 4t  t   dt  3      t 5 2 10 1 1  1
Baøi 17: ÑEÀ DÖÏ BÒ 1 3 e 2 Tính tích phaân: ln x I   dx . x lnx  1 1 Giaûi 3 2 e ln x I   dx 1 x lnx 1 dx  2tdt
Ñaët t  lnx 1  t2 = lnx + 1   x . lnx 1 2t 3 x 1 e Ñoåi caän t 1 2 2 2  5 t 2  2 (t 1) 2 76 I  2tdt  4 2 (t  2 2t   1)dt = 2  3 2 t  t   1  t 1  5 3    1 15 Baøi 18: 2 Tính tích phaân: x I   dx. 1 x 1 1 Giaûi x  1  t = 0
Ñaët t = x 1  t2 = x  1  2tdt = dx. Ñoåi caän  x = 2  t = 1 136
TT Luyện Thi Đại Học VĨNH VIỄN  2 1 t   1 2t 1 3 1 Vaäy t  t  2 2  I  dt  2 dt  2 t  t  2     dt 1 t t 1  t 1 0 0 0 1  3 2 t t  11
I  2    2t  2ln | t 1|   4ln2 .  3 2  3 0 Baøi 19: e Tính tích phaân: 1 3lnx.lnx I   dx . x 1 Giaûi Ñaët    2 3dx t 1 3lnx t  1 3lnx  2tdt = x x  e  t = 2 Ñoåi caän  x  1 t = 1 2  2 t 1 2 2tdt 2 2  5 3 t t  2 116 I  t     4 2  3 
t  t dt      3 9 9  5 3  1 135 1   1  
Baøi 20: ÑEÀ DÖÏ BÒ 2 2 4 Tính tích phaân: x  x 1 I   dx. 2 x  0 4 Giaûi 2 4 2 I = x  x 1  2 x 17  dx  x  4    dx 2  2 2  x  4  x  4 x  4 0 0 2  3 x 1  2 = dx   4x  ln 2 x  4 17 .  2  3 2  x  4 0 0 2 Tính: I dx 1 = 
. Ñaët x = 2tant  dx = 2(tan2x + 1)dt 2 x  0 4 x 0 2    4 2 4 Ñoåi caän: tan t 1 1  4   I 2 dt  dt    1 =  2  t 0 4 tan t 1 2 2 8 0    0 0 4 2  3 x 1  Vaäy I = 17 16  4x ln 2 x 4      17. =    ln2  3 2  8 8 3 0 137
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc – Baøi 21: 2 3 Tính tích phaân: dx I   . 2 5 x x  4 Giaûi 2 3 2 3 2 3 Tính tích phaân dx dx xdx I   . Ta coù I    2  2 2 2 5 x x  4 5 x x  4 5 x x  4 Ñaët xdx t  2 x  4  2 t  4  2 x  dt = 2 x  4 x  2 3  t = 4 Ñoåi caän  x  5  t = 3 4 dt 1 t 2 4 Vaäy  1  1 1  1 5 I   ln  ln  ln   ln . 2   t  4 4 t  2 3 4  3 5  4 3 3
Baøi 22: ÑEÀ DÖÏ BÒ 1 ln3 2x Tính tích phaân: e dx I   . x ln2 e  1 Giaûi ln5 2x e I   dx . Ñaët t = x
e 1  t2 = ex – 1  2tdt = exdx vaø ex = t2 + 1 x ln2 e  1 2 x ln2 ln5  2 2 t   1 .2tdt  3 t  Ñoåi caän: 20 I 2 t t 1 2         t  3 3 1   1 Baøi 23:  4 2 1 2sin x Tính tích phaân:  I   dx . 1 sin2x 0 Giaûi   4 4 cos2x 1 d1 sin2x 1   1 Ta coù I  dx   ln   1 sin2x 4  ln2. 1 sin2x 2 1 sin2x 2 0 2 0 0
Baøi 24: ÑEÀ DÖÏ BÒ 2 ln3 x Tính tích phaân: e dx I   .  3 x 0 e  1 138
TT Luyện Thi Đại Học VĨNH VIỄN Giaûi ln3 x x 0 ln3 e I  
dx . Ñaët  x    x t e 1 dt e dx ; Ñoåi caän:  3 t 2 4 x 0 e  1 4 4 Khi ñoù dt 2 I     2   1 3 t 2 2 t 2
Baøi 25: ÑEÀ DÖÏ BÒ 1  2
Tính tích phaân: I  6 1  3 5 cos x sinxcos xdx 0 Giaûi   2 2 I  6 1 3 5 cos x sinxcos xdx  6 1   3 3 2 cos x.cos x.sinx.cos xdx 0 0 Ñaët  6  3  6   3  5  2 t 1 cos x t 1 cos x 6t dt 3sinxcos xdx
 2t5dt = sinxcos2xdx vaø cos3x = 1 – t6 Ñoåi caän;  x 0 1 1 1 13 2 2 2t 12  I t. 6 1 t  5 2t dt  6 12 2t 2t        dt   7 t    t 0 1 7 13 91 0 0   0
Baøi 26: CAO ÑAÚNG KINH TEÁ TP. HCM  2
Tính tích phaân: I   xsin2xdx 0 Giaûi u  x  du  dx  cos2x dv  sin2xdx v    2    2 xcos2x 1 Vaäy: I = 2   sin2x 2    cos2xdx       2 0 2 4 2  2 0 4 0 139
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
Vaán ñeà 3: TÍNH TÍCH PHAÂN BAÈNG PHÖÔNG PHAÙP
TÍCH PHAÂN TÖØNG PHAÀN
A. PHÖÔNG PHAÙP GIAÛI b b Coâng thöùc: u(x).  v (x)dx  b u(x).v(x)  v(x).u  a  (x)dx a a b b Vieát goïn: b udv  uv  a  vdu  a a B. ÑEÀ THI
Baøi 1: ÑAÏI HOÏC KHOÁI B NAÊM 2011  3 Tính tích phaân: 1 xsin x I  dx.  2 0 cos x Giaûi    3 3 3 Ta coù: 1 xsin x 1 xsin x I  dx  dx  dx  2  2  2 0 cos x 0 cos x 0 cos x    3 3   3 xsin x xsin x tan x  dx  3  dx 0  2  . 2 0 cos x 0 cos x  3 xsinx Tính J = dx 
baèng phöông phaùp tích phaân töøng phaàn. 2 0 cos x Ñaët: u = x  du = dx dv = sin x dx, choïn v = 1 2 cos x cosx    3  x  1 3 2 1 Suy ra: J = 3  dx   dx cosx   =   0 cosx 3 cosx 0 0   3 3 1 cosx Tính K = dx  dx  
baèng phöông phaùp ñoåi bieán soá. 2 cosx 0 0 1  sin x
Ñaët t = sinx  dt = cosxdx. 140
TT Luyện Thi Đại Học VĨNH VIỄN 3 3 2     Suy ra: dt 1 1 t 2 1 2 3 K   ln  ln  2   1 t 2 1 t 2  2  3   0 0    1    2 2 3 ln    ln   2 3. 2 4  3     Vaäy I = 2 3    ln2  3 . 3
Baøi 2: ÑAÏI HOÏC KHOÁI B NAÊM 2009 3 Tính tích phaân: 3  ln x I   dx x  2 1 1 Giaûi dx 1 1 u  3  lnx  dv  ; du  dx  v   x  2 1 x x 1 3 3 3  lnx dx I     x 1 1 xx   1 1 3 3 3  ln3 3 1 dx 3  ln3 1 27     dx    3 3     ln x  ln x 1  3  ln 4 2 x x 1 1 1   4 4 16 1 1  
Baøi 3: ÑAÏI HOÏC KHOÁI D NAÊM 2008 2 Tính tích phaân: ln x I   dx . 3 1 x Giaûi 2 u  ln x Tính tích phaân: ln x I dx 1   dx . Ñaët:  dx  du  , choïn v   3 dv  x 2 1 x  2x  3 x 2 1 2 1 1 2 1 I 1 3 3 2ln2   ln x  dx =   ln2    ln2   . 2  3 2x 1 2 8 4x 1 8 16 16 1 2x
Baøi 4: ÑAÏI HOÏC KHOÁI D NAÊM 2007 e
Tính tích phaân: I   3 2 x ln xdx 1 Giaûi 141
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc – Tính tích phaân 4 Ñaët u = ln2x 2lnx x  du  dx; dv = x3dx  v  . x 4 4 e 4 e x e Ta coù: 1 e 1 I  2 .ln x  3 x lnxdx     3 x lnxdx 4 1 2 4 2 1 1 4 Ñaët u = lnx dx x  du  , dv = x3dx, choïn v  . Ta coù x 4 e e e 4 e 4 4 3 x 1 3 e 1 4 3e 1 x lnxdx  lnx  x dx   x    . 4 4 4 16 16 1 1 1 1 4 Vaäy 5e 1 I  32
Baøi 5: ÑAÏI HOÏC KHOÁI D NAÊM 2006 1
Tính tích phaân: I  (x   2x 2)e dx . 0 Giaûi Tính tích phaân. 1 u  x  2 1 I  (x   2x 2)e dx . Ñaët   du  2x dx, choïn v = e 2x dv e dx 2 0   1 1 2 1 2 1 1 I e 1 5 3e  (x  2x 2)e   2x e dx = 2x   1 e  2 0 2 2 4 4 0 0
Baøi 6: ÑEÀ DÖÏ BÒ 1 - ÑAÏI HOÏC KHOÁI D NAÊM 2006  2
Tính tích phaân: I = (x   1)sin2xdx 0 Giaûi u  x 1 Ñaët 1 
 du  dx, choïn v   cos2x dv  sin2xdx 2   2 x 1 1   I   2 cos2x  cos2xdx  1 0  2 2 4 0
Baøi 7: ÑEÀ DÖÏ BÒ 2 - ÑAÏI HOÏC KHOÁI D NAÊM 2006 142
TT Luyện Thi Đại Học VĨNH VIỄN 2
Tính tích phaân: I = (x   2)ln xdx 1 Giaûi   2 u lnx Ñaët 1 x  du dx, choïnv 2x dv   x  2     dx x 2 2  2 x  2 I =  x  5   2xlnx   2 dx  2ln2      2  2    4 1 1
Baøi 8: ÑAÏI HOÏC KHOÁI D NAÊM 2005  2
Tính tích phaân: I  2x    2 1 cos xdx . 0 Giaûi   2 2 2 1 cos2x
I  (2x 1)cos x.dx  (2x    1) dx 2 0 0   2 2 1 1  (2x 1)dx  (2x    1)cos2x.dx 2 2 0 0   2 2 2  
 Tính I  (2x 1)dx  x  x 2   1  0 4 2 0  2  Tính I  (2x  2  1)cos2x.dx . 0 u  2x 1 Ñaët 1 
 du  2dx choïn v  sin2x dv  cos2xdx 2    2 1 1 I  (2x  2 1)sin2x  sin2xdx  2 cos2x   2  1 2 0 2 0 0 2 1 1   1 I  I  I    1 2 . 2 2 8 4 2 143
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc – Baøi 9: 3
Tính tích phaân: I  ln 2 x   xdx . 2 Giaûi 3 I  ln 2 x   xdx 2 3 3 3 Ta coù I = ln 2
x  xdx  lnxx  1dx  lnx   lnx   1    dx 2 2 2  dx u  lnx  du = Ñaët  x dv  dx choïn v = x 3 3 3 3
I  lnxdx  xlnx  dx  1
xlnx  x  3ln3 3 2ln2    2 2 2 2 2  3ln3  2ln2 1 3 2 I  2 lnx  
1 dx  lnudu  ulnu  u2  2ln2    1 1 2 1 3 Vaäy I  ln 2
x  xdx  I  I  3ln3 2ln2 1 2ln2   1 2 1  I  3ln3  2 2
Baøi 10: ÑEÀ DÖÏ BÒ 1  4 Tính tích phaân: x I   dx . 1 cos2x 0 Giaûi   4 4 u  x  du  dx x 1 xdx I  dx    . Ñaët  du  1   2 cos2x 2 dv    choïn v  tan x 0 0 cos x  2 cos x   4 1 1 1   1 4 I  xtanx 
tanxdx  xtanx  ln cosx  4   ln2 2 2  2   0 0 8 4 0
Baøi 11: CÑ KINH TEÁ – KYÕ THUAÄT COÂNG NGHIEÄP I Tính tích phaân: lnx I  3 dx 1 (x  2 1) 144
TT Luyện Thi Đại Học VĨNH VIỄN Giaûi Ñaët u = lnx dx  du  x dv = (x + 1)-2dx, choïn 1 v   x 1 lnx 3 3 (x 1)  x 1 3 1 1  I    dx   ln3    dx x 1 1 1     x(x 1) 4 1  x x 1 3 = 1  x  1 3  ln3  ln   ln3    ln 4  x 1 1 4 2
Baøi 12: CAO ÑAÚNG KINH TEÁ ÑOÁI NGOAÏI 4 Tính tích phaân: ln 2x 1 I   dx (2x  3 0 1) Giaûi 3 1   Ñaët u = ln 2x 1 , dv=  2
(2x 1) dx  du = (2x 1)1dx, choïn v =   2 (2x 1) 1  1 2  I = (2x  4 2
1) ln 2x 1   ln3  0 3 3
Baøi 13: CAO ÑAÚNG KINH TEÁ TP. HCM  2
Tính tích phaân : I   xsin2xdx 0 Giaûi u  x  du  dx  cos2x
dv  sin2xdx, choïnv    2    2 Vaäy: I = xcos2x 2   1 sin2x2    cos2xdx       2 0 2 4 2  2 0 4 0
Vaán ñeà 4:
TÍNH TÍCH PHAÂN BAÈNG PHÖÔNG PHAÙP PHOÁI HÔÏP A.ÑEÀ THI
Baøi 1: ÑAÏI HOÏC KHOÁI A NAÊM 2010 1 2 x x Tính tích phaân : x (1 2e )  e I   dx 1 x 0 2e 145
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc – Giaûi 1 2 x (1 x 2e )  x 1 1 x e e I  dx  2 x dx   dx x   1 2e 1 x 0 0 0 2e 1 1 3 x 1 I  2 x dx   1  3 3 0 0 1 x e 1 1 d(1 x 2e ) 1 1 1 1 2e  I  dx x ln(1 2e ) ln 2  = =  1    x x 2 2 = 2 3 0 2e 1 0 2e 0   Vaäy I = 1 1 1 2e   ln  3 2  3 
Baøi 2: ÑAÏI HOÏC KHOÁI D NAÊM 2010 e Tính tích phaân:  3  I  2x   ln xdx  x  1 Giaûi e  3  e e 1 I  2x  lnxdx 2 xlnxdx      3 lnx. dx  x  x 1 1 1 e 2 Xeùt I dx x
 x ln xdx . Ñaët u  ln x  du  ; dv  xdx  v  1  x 2 1 e e  2 x  e 2 1 e 1  2 x  2 Do ñoù e 1 I  lnx xdx 1               2  2 2 2 2 4 1 1  1 e Xeùt I 1 2 =  ln x. dx . x 1 Ñaët t = lnx  dx dt 
. Vôùi x = 1  t = 0; x = e  t = 1 . x 1 1  2 t  2 Do ñoù 1 I e 2  tdt  2       . Vaäy  I  2 2 2 0   0
Baøi 3: ÑAÏI HOÏC KHOÁI A NAÊM 2009  2
Tính tích phaân I   3 cos x    2 1 cos xdx . 0 146
TT Luyện Thi Đại Học VĨNH VIỄN Giaûi   2 2 I  5 cos xdx    2 cos xdx 0 0
Ñaët t = sinx  dt = cosxdx; x = 0  t = 0,  x   t  1 2   2 2 1 2 2 5 I  cos xdx    2
1 sin x cosxdx   2 1 t  1  2 3 1 5  8 1 dt  t  t  t   3 5    15 0 0 0 0    2 2 1 1 1 I  cos xdx  2  1 cos2x   2 2  dx  x  sin2x    2 2  2  4 0 0 0 Vaäy 8  I  I  I   1 2 5 4
Baøi 4: CAO ÑAÚNG KHOÁI A, B, D NAÊM 2009 1 Tính tích phaân I    2x e   x x e dx 0 Giaûi 1 1 Ta coù  I  x e dx    x xe dx 0 0 1 1 1   I   x x 1 e dx   e  1 0 e 0 1  I   x 2 xe dx . x x
Ñaët u  x  du  dx; ñaët dv  e dx, choïn v  e 0 1 1 Suy ra I 1  x xe  x e dx  2
1 . Vaäy I  I  I  2  . 0  1 2 e 0
Baøi 5: ÑAÏI HOÏC SAØI GOØN KHOÁI A NAÊM 2007 1 Tính: 2x 1 I   dx 2 x  x  0 1 Giaûi 1 1 I = 2x 1 1 dx   2 dx 2  x  x  2 1 x  x  0 0 1 147
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc – 1 1 1 I 2x 1 2 dx 1 =  dx  ln x  x 1   ln3 ; I 2 2 =  x  x 1 0 2 0 0  1  3 x      2  4 Ñaët x + 1 3 3  tant  dx = 1 2 tan tdt 2 2 2  3 1 2 3 tan tdt I 2 2 2 =   3    2  6 3 1 tan t 6 4 I = 2 ln3  6 3
Baøi 6: CAO ÑAÚNG GTVT III KHOÁI A NAÊM 2007 2 9
Tính tích phaân : J   sin xdx 0 Giaûi  3
Ñaët t = x thì dx = 2tdt  J  2tsintdt 0 u  2t du  2dt Choïn :    dv  sin tdt  choïn v  cost     3
J = 2t cost3  2 costdt  2t cost3  2sint =    3 0  3 0 0 3 0
Baøi 7: ÑAÏI HOÏC KHOÁI D NAÊM 2005  2
Tính tích phaân I  2  sinx e   cosxcosxdx . 0 Giaûi     2 2 2 1 cos2x 2 sin x I 2 e dsinx     2 dx  sinx 2e 1  1    e  1 2  x  sin2x 2 0 0   2  2  0 0 148
TT Luyện Thi Đại Học VĨNH VIỄN
Baøi 8: ÑEÀ DÖÏ BÒ 2 2
Tính tích phaân: I   x sin xdx . 0 Giaûi 2  I  
x sin xdx . Ñaët t = x  t2 = x  2tdt = dx 0 Ñoåi caän x 0 2 t 0   2 du  2tdt  I u t
 2 2t sintdt . Ñaët      0 dv  sintdt v   cost   I   2
2(t cost)  4 t costdt  22   4 1I 0 0  Tính  I  1  tcostdt 0 u  t du  dt Ñaët    dv  costdt  choïn v  sin t   
I  tsint  sintdt  cost   1  2 . Vaäy I = 22 – 8 0 0 0
Baøi 9: ÑEÀ DÖÏ BÒ 1 1 2
Tính tích phaân: I   3 x x e dx 0 Giaûi 1 1 2 2 Tính I  3 x x e dx    2 x x e xdx 0 0 x 0 1 Ñaët t = x2 dt  dt = 2xdx   xdx . Ñoåi caän: 2 t 0 1 1  1  1 1 1 1 1 1 I  t te dt   t te  t e dt   t te  t e    2 2 0      2 2 0  0  0
Baøi 10: ÑEÀ DÖÏ BÒ 2 0
Tính tích phaân: I  x 2x e  3 x   1dx . 1 149
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc – Giaûi 0 0 0 Tính I  x 2x e  3 x 1dx  2x x.e .dx  3 x x     1dx 1 1 1 0 du    dx u x  Tính I   2x   1 xe dx . Ñaët    1  2x 2x dv  e dx choïn v  e 1  2 0 0 0 1 0 0 x 1 2x  1 2x 1 2x  3 1 I  uv  vdu  x.e  e dx  x.e  .e   1 1     2  2 1 2 2 4 4e 4 1    1 1 0  Tính I  3 x x  2  1dx 1 x 1 0 Ñaët  3 t x 1  3 t  x 1 2 3t dt  dx . Ñoåi caän: t 0 1 1 1 1 7 4  3t  3 1 .t.3t dt  3  6 3 t t 9 I2 t t        dt  3       7 4 28 0 0   0 Vaäy I = I 3 1 9 3 4 1 + I2 =     2 2 4e 4 28 4e 7
Baøi 11: CAO ÑAÚNG KYÕ THUAÄT CAO THAÉNG  4 Tính tích phaân: 1  sin2x dx 2 0 cos x Giaûi    4 4 4 I = 1  sin2x dx = 1 sin2x dx  dx 2  2  2 0 cos x 0 cos x 0 cos x  4 2 4 d(cos x)  tan x  dx  . 2 0 cos x 0   = 4  2 tan x ln(cos x) 4 = 1 + ln2 0 0 150
TT Luyện Thi Đại Học VĨNH VIỄN
Vaán ñeà 5:
ÖÙNG DUÏNG CUÛA TÍCH PHAÂN
A. PHÖÔNG PHAÙP GIAÛI TÍNH DIEÄN TÍCH
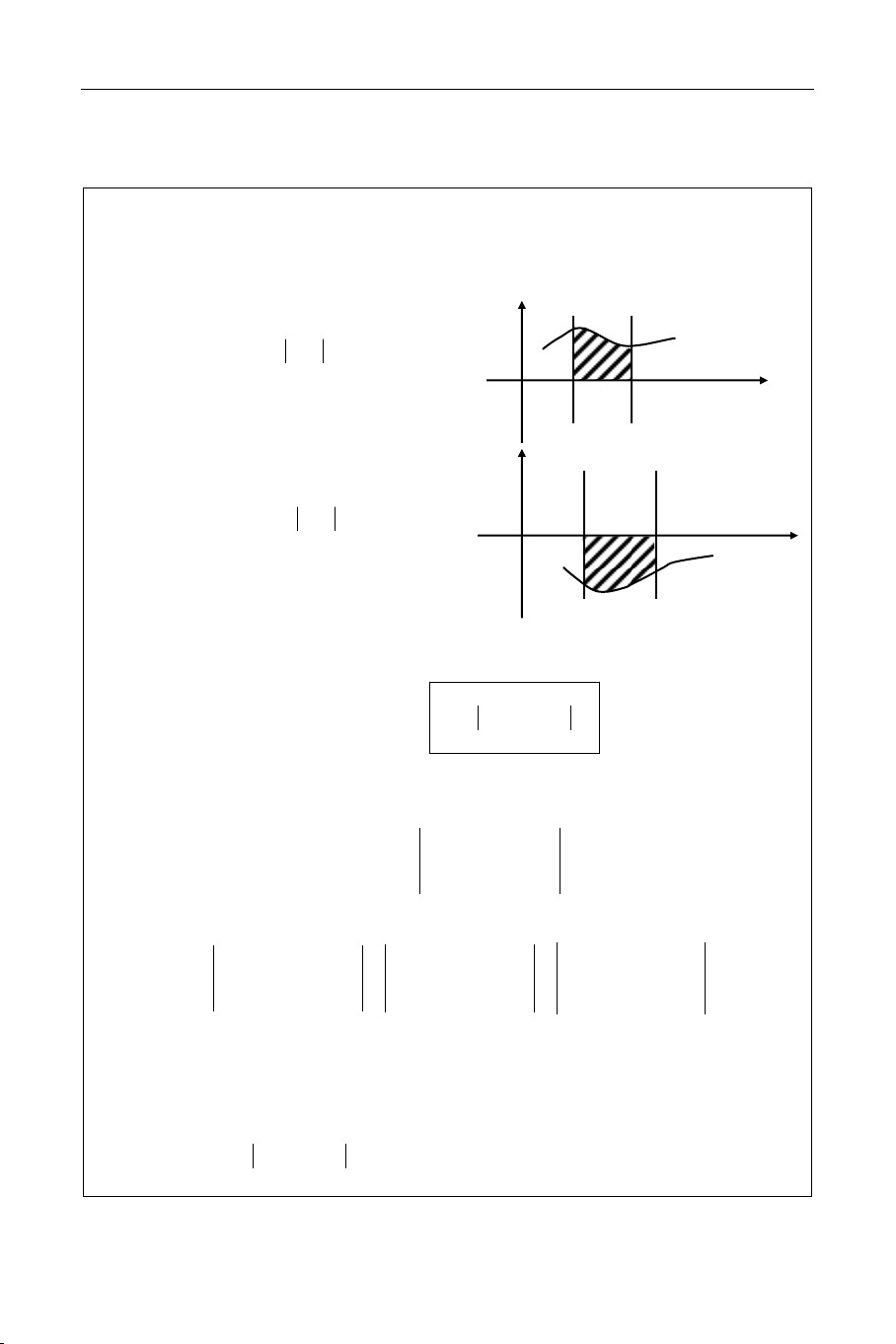
Baøi toaùn 1: Cho haøm soá y = f(x) lieân tuïc vaø khoâng aâm treân ñoaïn [a, b]. Dieän tích
hình phaúng giôùi haïn bôûi ñoà thò cuûa haøm soá y = f(x), truïc hoaønh vaø hai ñöôøng thaúng x = a, x = b laø: y b b y = f(x) S  f(x)dx    f(x) dx a a 0
Töø baøi toaùn 1 suy ra neáu f(x) khoâng x = a x = b
döông treân ñoaïn [a, b] y b b x = a x = b S  f(x)dx    f(x) dx a a 0 S y = f(x)
Baøi toaùn 2: (Toång quaùt)
Cho hai haøm soá y1 = f(x), y2 = g(x) lieân tuïc treân ñoaïn [a, b] vaø coù ñoà thò laàn löôït
laø (C1), (C2). Dieän tích hình phaúng giôùi haïn bôûi (C1), (C2) vaø hai ñöôøng x = a, b
x = b ñöôïc xaùc ñònh bôûi coâng thöùc: S  f(x)   g(x) dx (*) a
* Phöông phaùp giaûi (*):
 Giaûi phöông trình: f(x) = g(x) (1) b
 Neáu (1) voâ nghieäm thì: S  (f(x)   g(x))dx a
 Neáu (1) coù nghieäm thuoäc [a, b] giaû söû laø ,  (  ) thì   b
S  (f(x)  g(x)dx  (f(x)  g(x)dx  (f(x)     g(x)dx a   Baøi toaùn 3: Cho ( 1 C ): 1 x  f(y), ( 2
C ): x2  g(y), f(y), g(y) lieân tuïc treân ñoaïn [a, b].
Dieän tích hình phaúng S ñöôïc giôùi haïn bôûi (C1); (C2) vaø hai ñöôøng thaúng y = a,
y = b ñöôïc xaùc ñònh bôûi coâng thöùc: b S  f(y)   g(y) dy a 151
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –
THEÅ TÍCH CAÙC VAÄT THEÅ
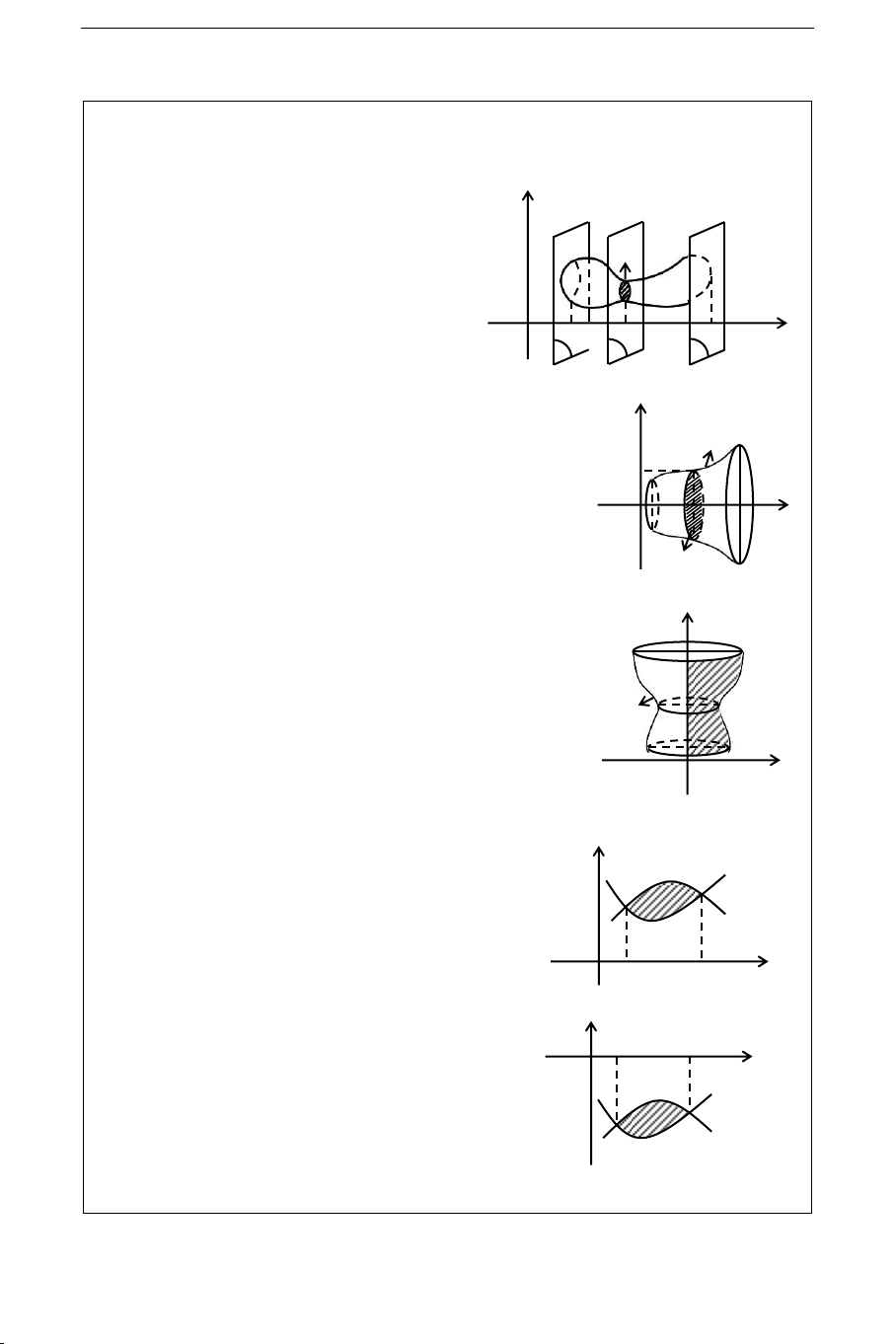
I. COÂNG THÖÙC THEÅ TÍCH
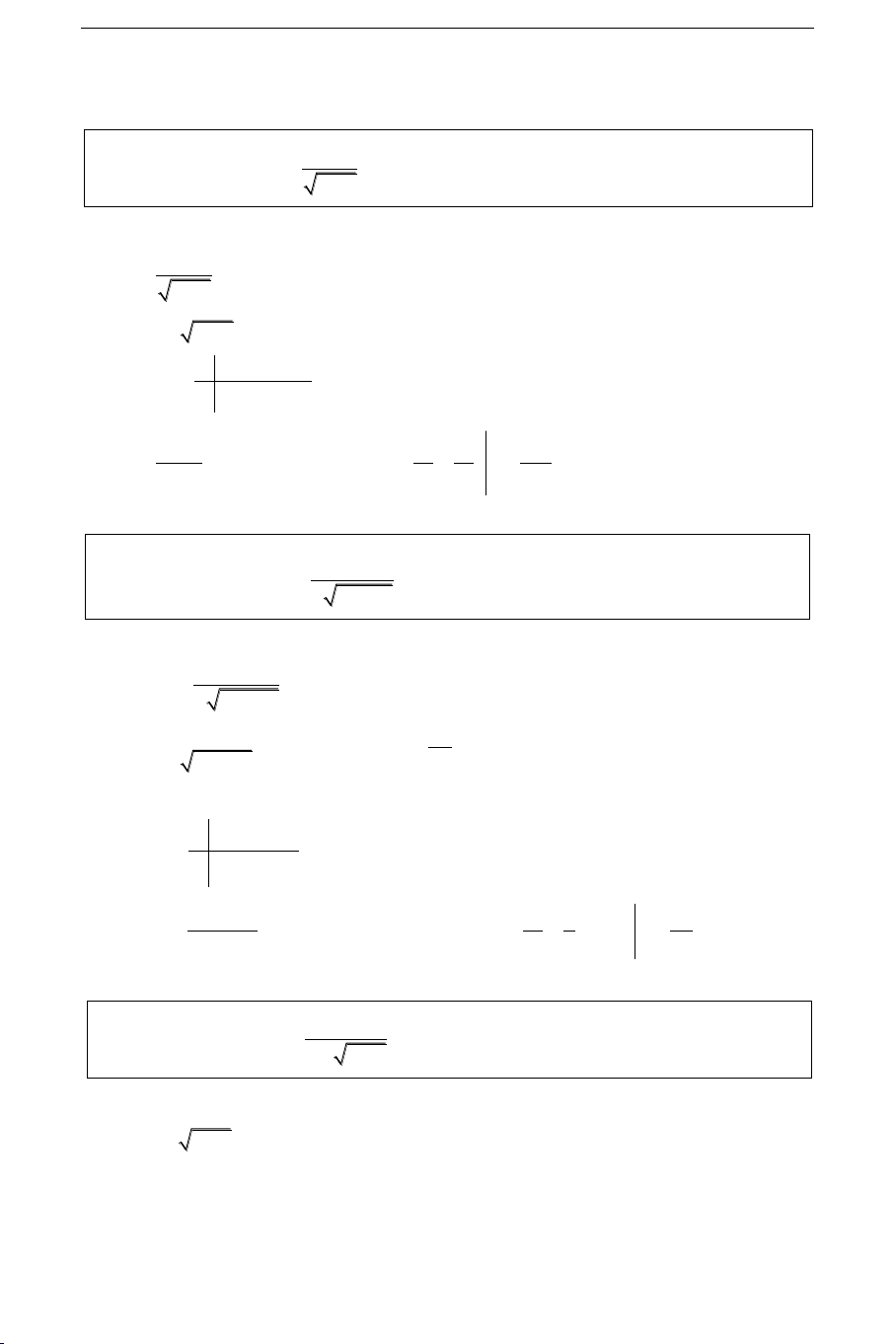
Giaû söû vaät theå T ñöôïc xaùc ñònh bôûi 2 maët y phaúng  ( ) vaø  ( ) song song vôùi nhau. Ta
choïn truïc Ox sao cho noù vuoâng goùc vôùi S(x)
caùc maët phaúng ( vaø (). Ta coù Ox  ()
= A, Ox  () = B. Giaû söû maët phaúng a x b x
( ()  Ox, () Ox  C, () caét vaät theå T O A C B  
coù thieát dieän laø S(x).  b Khi ñoù V  S(x)dx y y = f(x) a II. BAØI TOAÙN y a x
Baøi toaùn 1: Giaû söû hình phaúng giôùi haïn bôûi caùc b O x
ñöôøng y = f(x), x = a, x = b vaø y = 0 quay quanh Ox.
Hình troøn S(x) coù baùn kính R = y:   2 S(x) y S(x) b V    2 y dx y a b
Baøi toaùn 2: Theå tích do hình phaúng: x = g(y), x = 0, x
y = a, y = b quay quanh truïc Oy: x = g(y) a b V   2 x dy O x a
Baøi toaùn 3: Tính theå tích vaät theå do hình phaúng
giôùi haïn hai ñöôøng caét nhau quay quanh Ox: y f(x) = y1 y  f(x), y  g(x) 1 2 y2  1 y  0 x  [a, b] g(x) = y2 b V   2 (y   2 2 1 y )dx O a b x a
Baøi toaùn 4: Tính theå tích vaät theå do hình phaúng y x
giôùi haïn hai ñöôøng caét nhau quay quanh Ox. a b O y  f(x),y  g(x) 1 2 f(x) = y1 1 y  y2  0 x  [a,b] b g(x) = y2 V   2 (y   2 1 y2)dx a 152
TT Luyện Thi Đại Học VĨNH VIỄN B. ÑEÀ THI
Baøi 1: CAO ÑAÚNG KHOÁI A, B, D NAÊM 2008
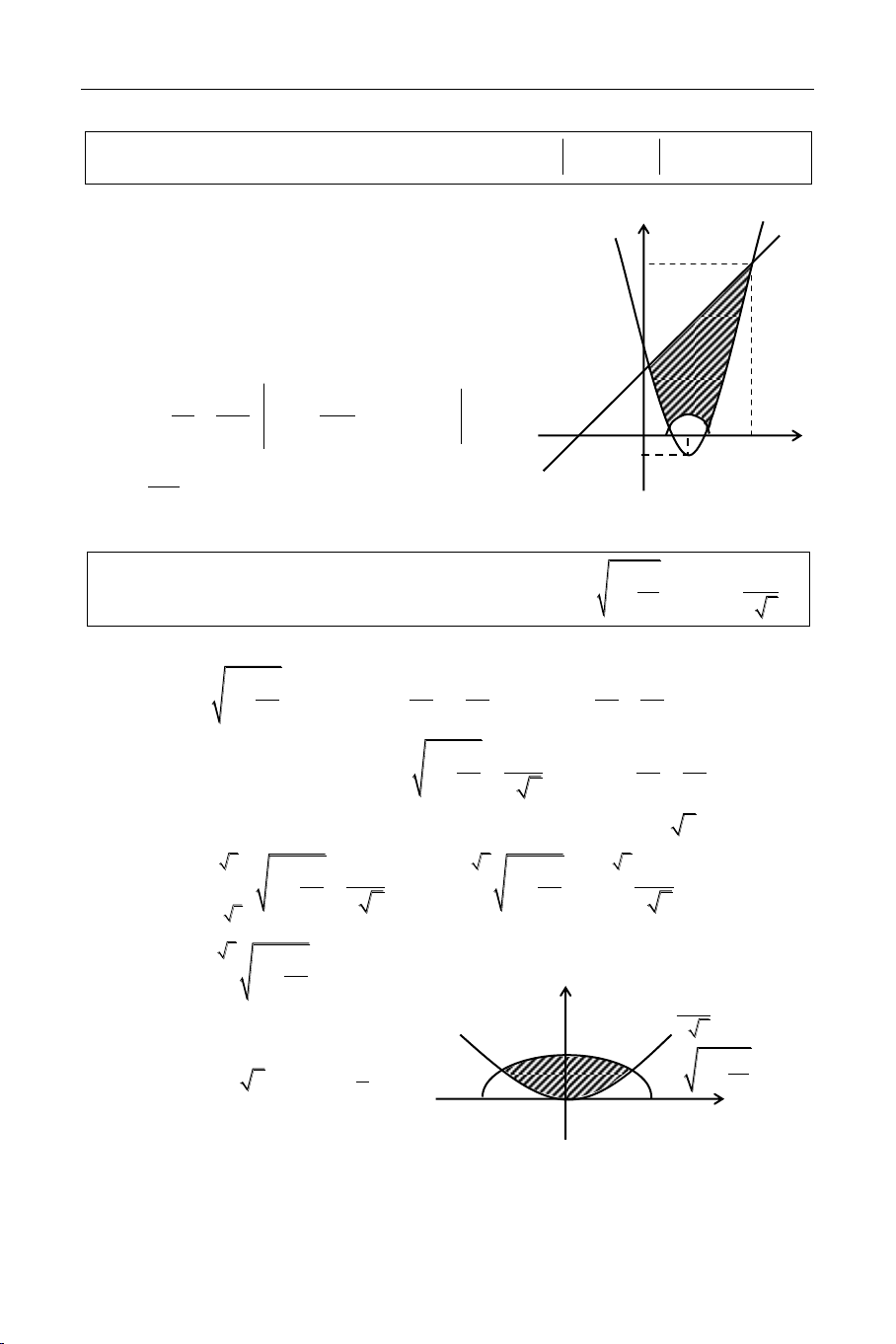
Tính dieän tích hình phaúng giôùi haïn bôûi parabol (P): x = x2 + 4x vaø ñöôøng thaúng d: y = x. Giaûi
Phöông trình hoaønh ñoä giao ñieåm cuûa (P) vaø d:  2
x  4x  x  x  0 hayx  3 3 3  3 2 x 3x  3 9 S  3 x  3x dx  ( 3 x  3x)dx         (ñvdt) 3 2  0 2 0 0  
Baøi 2: ÑAÏI HOÏC KHOÁI A NAÊM 2007
Tính dieän tích hình phaúng giôùi haïn bôûi caùc ñöôøng: y = (e + 1)x, y = (1 + ex)x Giaûi
Phöông trình hoaønh ñoä giao ñieåm cuûa hai ñöôøng ñaõ cho laø:
(e + 1)x = (1 + ex)x  (ex  e)x = 0  x = 0 hoaëc x = 1 1 1 1
Dieän tích cuûa hình phaúng caàn tìm laø: S  dx  e xdx   x x   xe dx xe ex 0 0 0 1 1 2 1 1 ex e 1 1 Ta coù: e xdx   x , xe dx  x xe  x e dx  e  x e    1 2 2 0  0 0 0 0 0 Vaäy e S  1(ñvdt). 2
Baøi 3: ÑAÏI HOÏC KHOÁI B NAÊM 2007
Cho hình phaúng (H) giôùi haïn bôûi caùc ñöôøng: y = xlnx, y = 0, x = e.
Tính theå tích cuûa khoái troøn xoay taïo thaønh khi quay hình (H) quanh truïc Ox. Giaûi
Phöông trình hoaønh ñoä giao ñieåm cuûa caùc ñöôøng y = xlnx vaø y = 0 laø: xlnx = 0  x = 1
Theå tích khoái troøn xoay taïo thaønh khi quay hình H quanh truïc hoaønh laø: e e V   2 y dx    2 (xlnx) dx 1 1 3 Ñaët u = ln2x, dv = x2dx 2lnx x  du  dx, v  .Ta coù: x 3 e e 3 e 3 e 2 x 2 e 2 (xlnx) dx  2 ln x  2 x lnxdx      2 x lnxdx 3 3 3 3 1 1 1 1 153
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc – 3 Ñaët u = lnx, dv = x2dx dx x  du  , choïnv  . Ta coù: x 3 e e e 3 e 3 3 3 2 x 1 2 e x 2e 1 x lnxdx  lnx  x dx      3 3 3 9 9 1 1 1 1 3 Vaäy (5e  2) V  (ñvtt). 27
Baøi 4: ÑEÀ DÖÏ BÒ 2 - ÑAÏI HOÏC KHOÁI A NAÊM 2006
Tính dieän tích hình phaúng giôùi haïn bôûi paraol y = x2 – x + 3 vaø ñöôøng thaúng d: y = 2x + 1. Giaûi
Phöông trình hoaønh ñoä giao ñieåm cuûa parabol vaø d:
x2 – x + 3 = 2x + 1  x2 – 3x + 2 = 0  x = 1  x = 2 2 2 Ta coù S  2
(x  x  3)  (2x 1)dx  2 x  3x    2 dx 1 1 2  3 2 x 3x  2 1  ( 2 x  3x  2)dx     2x    (ñvdt) 3 2  1 6 1  
Baøi 5: ÑEÀ DÖÏ BÒ 1
Tính theå tích vaät theå troøn xoay sinh ra trong pheùp quay xung quanh truïc Ox,
cuûa hình phaúng giôùi haïn bôûi truïc Ox vaø ñöôøng y = x sinx (0 x ) Giaûi        V =    2 2 f x    dx   x.sin xdx   
x1 cos2xdx =  xdx  x.cos2xdx 2   2 0 0 0   0 0    2 2  Tính : I x  1 = xdx    . Tính : I xcos2xdx 2 2 2 =  0 0 0 du  dx u  x Ñaët     1 dv  cos2xdx choïn v   sin2x  2   I x 1  x 1  2 = sin2x  sin2xdx  sin2x  cos2x     0 2 0 2  2 4  0  2  3 V =    0  (ñvtt) 2 2  4 154
TT Luyện Thi Đại Học VĨNH VIỄN Baøi 6:
Tính dieän tích hình phaúng giôùi haïn bôûi caùc ñöôøng:  2
y x  4x  3 vaø y = x + 3 . Giaûi 5 3 y  S  x 3  2 x 4x 3      dx  2    2 x  4x  3 dx    8 0 1 5 3 S   2 x  5xdx  2  2 x  4x    3dx 0 1 3  3 2 x 5x  5   3 x  3 y = x + 3 S      2  2 2x  3x 1  3 2  0  3      1 1 O1 3 5 x 1 109 S  (ñvdt) 6 Baøi 7: 2 2
Tính dieän tích cuûa hình phaúng giôùi haïn bôûi caùc ñöôøng: x x y  4  vaø y = 4 4 2 Giaûi 2 2 2 2 2 Ta coù x x x x y y  4   2 y  4    2 y  4    1 (E) 4 4 4 16 4 2 2 2 4
Phöông trình hoaønh ñoä giao ñieåm: x x x x 4    4   4 4 2 4 32  4 2 2 2
x  8x 128  0  x  8  x  1
 6 (loaïi)  x =  2 2 2 2  2 2  2 2 2 2 2 2  Neân S =  x x x x 4   dx  2 4  dx  dx   4 4 2     4 4 2  2 2    0 0  2 2 2 Tính x I  4  1  dx 4 y 0 y = 2 x
Ñaët x = 4sint  dx = 4costdt 4 2 2   x 2 2 t = y = 2 4 x  Ñoåi caän   4   4 x  0  4 O 4 x t  0 155
Höôùng daãn giaûi CDBT töø caùc ÑTQG Toaùn hoïc –   4 4  1 1 I  2 8cos tdt  41 cos2t      dt  4 t  4 sin2t      2  2  0 0 0 2 2 2 3 x x 2 2 4 I  dx   2  4 2 12 2 0 3 0 Vaäy  4 S 2        ñvdt .  3 
Baøi 8: CAO ÑAÚNG KYÕ THUAÄT CAO THAÉNG
Tính dieän tích hình phaúng giôùi haïn bôûi caùc ñöôøng
(P1): y = x2  2x vaø (P2) : y = x2 + 4x. Giaûi
Phöông trình hoaønh ñoä giao ñieåm cuûa (P1) vaø (P2) laø: x2  2x =  x2 + 4x  2x2 + 6x = 0
 2x(x  3) = 0  x = 0  x = 3. Dieän tích caàn tìm: 3 3 S  (( 2 x  4x)  2 (x  2x))dx  ( 2 2x    6x)dx 0 0 2 3 =   3 2  x   3x  = 9 (ñvdt)  3  0
Baøi 9: CAO ÑAÚNG KYÕ THUAÄT CAO THAÉNG
Tính dieän tích cuûa hình phaúng giôùi haïn bôûi caùc ñöôøng: y = 7 – 2x2, y = x2 + 4. Giaûi
Phöông trình hoaønh ñoä giao ñieåm 7 – 2x2 = x2 – 4
 3x2 = 3  x = 1 hoaëc x = 1 Dieän tích S caàn tìm 1 1 S  (7  2 2x  2 x  4)dx  (3  2 3x )dx   4 (ñvdt) 1   1 156