Phương pháp giải các dạng toán căn bậc hai, căn bậc ba

Tài liệu gồm 54 trang, tóm tắt kiến thức trọng tâm và hướng dẫn phương pháp giải các dạng toán căn bậc hai, căn bậc ba, giúp học sinh lớp 9 tham khảo khi học chương trình Toán 9 phần Đại số chương 1. Mời bạn đọc đón xem.

60 30 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Căn bậc hai. Căn bậc ba

Môn: Toán 9

Thông tin:

54 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
MỤC LỤC
PHẦN ĐẠI SỐ ........................................................................................................................... 2
Chương I. CĂN BẬC HAI, CĂN BẬC BA ............................................................................... 2
§1. CĂN BẬC HAI ................................................................................................................... 2
§2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨ
C
2
AA=
........................................ 2
§3. LIÊN HỆ GIỮA PHÉP NHÂN VÀ PHÉP KHAI PHƯƠNG .......................................... 10
§4. LIÊN HỆ GIỮA PHÉP CHIA VÀ PHÉP KHAI PHƯƠNG ............................................ 20
§6. §7. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI .................... 26
§8. RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI ............................................... 37
§9. CĂN BẬC BA .................................................................................................................. 50
PHẦN ĐẠI SỐ
Chương I. CĂN BẬC HAI, CĂN BẬC BA
§
1. CĂN BẬC HAI
§2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨ
C
2
AA=
A. TRỌNG
TÂM KIẾN THỨC
1. Căn bậ
c hai số học
Với số dương a, số
a
được gọi là căn bậc hai số học của a.
Số 0 cũng được gọi là căn bậc hai số học của 0.
Với
a0≥
, ta có:
2
x 0
a x
x a.
≥
= ⇔
=
Với hai số a và b không âm, ta có
a < b a b.⇔<
2. Căn th
ức bậc hai
Với A là một biểu thức đại số , người ta gọ
i
A
là căn thức bậc hai của A, còn A được gọi
là biểu thức lấy căn hay biểu thức dưới dấu căn.
A
xác định ( hay có nghĩa ) khi A lấy giá trị không âm.
Ta có
2
nÕu A 0
nÕu A < 0.
A
AA
A
≥
= =
−
B. CÁC D
ẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. TÌM CĂN BẬC HAI SỐ HỌC CỦA MỘT SỐ
Phương pháp giải
2
x 0
a x
x a.
≥
= ⇔
=
Ví dụ 1. Tìm căn bậc hai số học rồi tìm căn bậc hai của:
a) 121 b)
2
2
5

−


Gi
ải
a) Ta có
2
v× 11 0 vµ 11 121.121 11 ≥= =
Do đó s
ố 121 có hai căn bậc hai là 11 và -11.
b)
2
22
55

−=


vì
2
0
5
≥
và
22
22
.
55

= −


Do đó số
2
2
5

−


có hai căn bậc hai là
2
5
và
2
5
−
.
Ví dụ 2. Tính giá trị của biểu thức:
0,09 7. 0,36 3 2,25.+−
Giải
Ta có
0,09 7. 0,36 3 2,25+−
0,3 7.0,6 3.1,5 0,3 4,2 4,5 0=+ − =+−=
Ví dụ 3. Giá trị của biểu thức sau là số vô tỉ hay hữu tỉ:
99
1 - .18?
16 16



Gi
ải
9 9 25 9 5 3
1 - .18 - .18 .18 9 3.
16 16 16 16 4 4


= =−==




Vậy giá trị của biểu thức đã cho là một số hữu tỉ, hơn nữa còn là một số tự nhiên.
D
ạng 2. SO SÁNH CÁC CĂN BẬC HAI SỐ HỌC
Phương pháp giải
Dựa vào tính chất : Nếu
,0ab≥
thì
.ab a b<⇔ <
Ví dụ 1. Không dung máy tính hoặc bảng số , hãy so sánh 8 và
65.
Giải
Cách 1: Ta có
8 64=
. Vì
64 65<
nên
8 65<
.
Cách 2: Vì
( )
2
2
8 64; 65 65= =
Nên
( )
2
2
8 65<
, suy ra 8 <
65.
Cách giải này dựa vào tính chất: Nếu a, b > 0 và
22
ab<
thì a < b.
Như vậy, để so sánh hai số dương ta có thể so sánh các bình phương của chúng.
Ví dụ 2. Không dung máy tính hoặc bảng số , hãy so sánh
15 1−
và
10.
Giải
Ta có
15 1−
<
16 1−
= 4 – 1 = 3,
10
>
9
= 3.
V
ậy
15 1−
<
10.
Ví dụ 3. Với a < 0 thì số nào lớn hơn trong hai số
a−
và
2a−
?
Giải
Ta có -1 > -2 nên –a < -2a (vì a < 0 ).
Do đó
a−
<
2a−
.
D
ạng 3. GIẢI PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH
Phương pháp giải
0a ≥
•
2
khi x = xa a= ±
.
•
2
khi x = axa=
.
•
2
khi 0 x < axa<≤
.
Ví d
ụ 1. Giải phương trình:
2
3 0,75.x =
Giải
Ta có
22
3 0,75 0,25.xx= ⇔=
Do đó
0,25 0,5.x =±=±
Ví dụ 2. Giải phương trình:
2 3 12.x =
Giải
ĐKXĐ:
0.x ≥
Ta có :
2 3 12 3 6 3 36 12x xxx= ⇔ =⇔ = ⇔=
( thỏa mãn điều kiện).
Ví dụ 3. Tìm số x không âm, biết
1
5 10.
2
x <
Giải
Với
0x ≥
ta có :
1
5 10 5 20
2
xx<⇔ <
5 400 80.xx⇔ < ⇔<
Vậy
0 80.x≤<
Ví dụ 4. Tính tổng các giá trị của x thỏa mãn đẳng thức
2
25 13.x +=
Giải
Ta có :
2
25 13x +=
2
25 169x⇔+=
2
169 25x⇔= −
2
144x⇔=
12.x⇔=±
Vậy tổng các giá trị của x thỏa mãn đẳng thức đã cho là (-12) + 12 = 0.
D
ạng 4. TÌM ĐIỀU KIỆN ĐỂ
A
CÓ NGHĨA
Phương pháp giải
•
A
có nghĩa khi
0;A ≥
•
1
A
có nghĩa khi
0.A >
Ví d
ụ 1. Tìm x để căn thức
52x−
có nghĩa.
Giải
52x−
có nghĩa khi
5
52 0 2 5 .
2
x xx− ≥ ⇔− ≥− ⇔ ≤
Ví dụ
2. Tìm x để căn thức
2
1
44xx−+
có nghĩa.
Giải
2
1
44xx−+
có nghĩa khi
2
1
( 2)x −
có nghĩa.
Điều đó xảy ra khi
2
( 2) 0 2.xx− >⇔≠
Ví dụ 3. Với giá trị nào của x thì biểu thức
2
25 x−
có nghĩa?
Giải
2
25 x−
có nghĩa khi
2
25 0x−≥
2
25x⇔− ≥−
2
25x⇔≤
5x⇔≤
5 5.x⇔− ≤ ≤
Ví dụ 4. Tìm các giá trị của x để biểu thức
2
1
100x −
có nghĩa
Giải
2
1
100x −
có nghĩa khi
2
100 0x −>
2
100x⇔>
10x⇔>
10
10
x
x
>
⇔
<−
Ví d
ụ 5. Có bao nhiêu giá trị nguyên của x để biểu thức M =
42xx++ −
có nghĩa?
Giải
M có nghĩa khi
40 4
20 2
xx
xx
+ ≥ ≥−

⇔

−≥ ≤

Vì
xZ∈
nên
{ }
4; 3; 2; 1;0;1;2x∈−−−−
Vậy có 7 giá trị nguyên của x để biểu thức M có nghĩa
D
ạng 5. RÚT GỌN BIỂU THỨC DẠNG
2
A
Phương pháp giải
2
nÕu A 0
nÕu A < 0.
A
AA
A
≥
= =
−
Ví d
ụ 1. Rút gọn biểu thức
2
1
.
4
A xx= −+
Gi
ải
2
2
111
422
A xx x x

= −+ = − = −


N
ếu
1
2
x ≥
thì
1
2
Ax= −
N
ếu
1
2
x <
thì
1
2
Ax= −
Ví dụ 2. Rút gọn biểu thức
46
.Bx x= +
Giải
( ) ( )
22
46 2 3
Bx x x x=+= +
2 3 23
.xxxx=+=+
Nếu
0x ≥
thì
23
;Bx x= +
Nếu
0x <
thì
23
.Bx x= −
Ví dụ 3. Tính giá trị của biểu thức C =
3 22 6 42− −−
.
Giải
C =
( )
( )
22
3 22 6 42 2 1 2 2− −− = −− −
21 2 2 21(2 2)223.= − − − = −− − = −
Ví dụ 4. Tìm giá trị nhỏ nhất của biểu thức
2
4 4 1 3.D xx= − ++
Giải
2
4 4 13D xx= − ++
=
( )
2
21 32133xx− += −+≥
với mọi x
Vậy minD = 3 khi
1
2
x =
.
Ví dụ 5. Tìm x, biết
2
6 9 7 13.xx x− ++ =
Giải
Ta có
2
6 9 7 13xx x− ++ =
( )
2
3 7 13xx⇔ − +=
3 7 13 (1)xx⇔ −+ =
Nếu
3x ≥
thì
3 3.xx−=−
Khi đó (1) trở thành
3 7 13 8 16 2xx x x−+ = ⇔ = ⇔ =
( không thuộc khoảng đang xét )
Nếu
3x <
thì
33 .xx−=−
Khi đó (1) trở thành
5
3 7 13 6 10
3
xx x x−+ = ⇔ = ⇔=
( thuộc khoảng đang xét )
Vậy giá trị của x thỏa mãn đẳng thức đã cho là
5
3
x =
.
Ví dụ 6. Cho biểu thức:
2
3 10 25.Pxx x=− −+
a) Rút gọn biểu thức P;
b) Tính giá trị của P khi x = 2.
Giải
a)
2
3 10 25.Pxx x=− −+
( )
2
35xx=−−
3 5.xx= −−
• Nếu
5x ≥
thì P = 3x – ( x – 5 ) = 2x + 5;
• Nếu
5x <
thì P = 3x + ( x – 5 ) = 4x – 5.
b) Khi x = 2 < 5 thì giá trị của biểu thức là :
P = 4.2 – 5 = 3.
Lưu ý: Nếu bạn thay x = 2 vào biểu thức 2x + 5 để tính giá trị của P thì bạn sai lầm vì
biểu thức P = 2x + 5 khi
5x ≥
.
Ví dụ 7. Cho biểu thức:
2
2 2 1.Qxx x=− ++
a) Rút gọn biểu thức Q;
b) Tính các giá trị của x để Q = 7 .
Giải:
a)
22
2x 2x 1 2x ( 1) 2x 1Qx x x= − + += − + = − +
* N
ếu
1x ≥−
thì
2x ( 1) 1Q xx= −+=−
* N
ếu
1x <−
thì
2x ( 1) 3 1Q xx= ++= +
b) Ta ph
ải xét hai trường hợp:
*
7 17 8Qx x=⇔ −= ⇔ =
( Không thỏa mãn
1x≥−
)
*
7 3 17 2Qx x=⇔ += ⇔ =
( Không thỏa mãn
1x<−
).
Vậy
7Q =
khi
8x=
C. BÀI TẬ
P TỰ LUYỆN
1. Không dùng m
áy tính hoặc bảng số, hãy so sánh:
a)
26 3+
và
63
; b)
1
2
và
31
2
−
2. Tìm x, biết:
a)
2
5x 80=
b)
21x =
c)
3x 6≤
3.Tìm x để các căn thức bậc hai sau có nghĩa:
a)
2
9 x−
b)
2
2x 1x ++
c*)
2
4xx −
4.
Tìm x để các biểu thức sau có nghĩa:
a)
2
9 x−
b)
2
1
4x −
c)
1
23
x
xx
+
+−
5. Rút gọn các biểu thức sau:
a)
( )
2
3 10−
b)
9 45−
c)
2
3x 2x 1x− −+
6. Giải phương trình:
a)
2
10x 25 2x − +=
b)
2
3x 2x = −
c)
2
4x 12x 9 7x− +=+
7*. TÌm các giá trị của xsao cho
xx>
.
HƯ
ỚNG DẪN GIẢI – ĐÁP SỐ
1.
a)
26 3 63+>
b)
31 1
22
−
<
2.
a)
4x = ±
b)
1
4
x =
c)
0 12x≤≤
3. a)
9x <
b)
xR∈
c)
4x ≥
hoặc
0x ≤
4. a)
33x−≤ ≤
b) x > 2 hoặc x < -2
c)
0x ≥
và
9x ≠
5. a)
10 3−
b)
52−
c)
2x 1
4x 1
+
−
nếu
1
1
x
x
≥
<
6. a)
3x =
hoặc x = 7
b) x=
1
c)
4
10;
3
x

∈−


7.
xx>
(1). Điều kiện x > 0 . Khi đó
2
(1) xx⇔>
(do hai vế của (1) đều dương)
2
0xx⇔− >
(1 ) 0
00
01
10 1
xx
xx
x
xx
⇔ −>
>>

⇔ ⇔ ⇔<<

−> <

§3. LIÊN H
Ệ GIỮA PHÉP NHÂN VÀ PHÉP KHAI PHƯƠNG
A.
TRỌNG TÂM KIẾN THỨC
1. Đ
ịnh lí:
Với hai số a và b không âm, ta có:
..ab a b=
2. ÁP d
ụng
Muốn khai phương một tích của các số không âm, ta có thể khai phương từng thừa số
rồi nhân các kết quả với nhau.
Muốn nhân các căn bậc hai của các số không âm, ta có thể nhân các số dưới dấu căn rồi
khai phương kết quả đó.
3. Chú
ý:
Vói hai biểu thức A và B không âm
, ta có:
..AB A B=
và ngược lại
..A B AB=
. Đặc
biệt khi
0A ≥
, ta có:
( )
2
2
A AA= =
B. CÁC DẠ
NG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
D
ạng 1: KHAI PHƯƠNG MỘT TÍCH
Phương pháp giải:
Với
, 0ì . .a b th a b a b≥=
Ví dụ 1: Tính:
a)
12,1.160
b)
2500.4,9.0,9
Gi
ải:
a)
12,1.160 121. 16 11.4 44= = =
b)
2500.4,9.0,9 25.49.9 25. 49. 9 5.7.3 105= = = =
Ví dụ 2: Tính:
a)
22
41 40−
b)
81.6,25 2,25.81−
Giải:
a)
22
41 40 (41 40)(41 40) 1.81 1.9 9−= − += ==
81.6,25 2,25.81 81.(6,25 2,25) 81. 4 9.2 18− = −= ==
Ví dụ 3: Đẳng thức
(1 ) . 1xy x y−= −
đúng với những giá trị nào của x và y.
Giải:
Theo địnhlí khai phương một tích thì
(1 ) . 1xy x y−= −
khi
0 à 1-y 0 hay x 0 và 1xv y≥ ≥ ≥≤
.
Ví dụ 4: Cho cac biểu thức
( 1)( 3) à 1. 3M x x vN x x=−+ =− +
a) TÌm các giá trị của x để M có nghĩa;N có nghĩa.
b) V
ới giá trị nào của x thì M=N?
Giải:
M có nghĩa khi
( 1)( 3) 0.xx− +≥
Trường h
ợp 1:
10 1
1
30 3
xx
x
xx
−≥ ≥

⇔ ⇔≥

+ ≥ ≥−

Trường hợp 2:
10 1
3
30 3
xx
x
xx
−≤ ≤

⇔ ⇔ ≤−

+ ≤ ≤−

Vậy M có nghĩa khi
1x ≥
hoặc
3x ≤−
.
N có nghĩa khi
10 1
1
30 3
xx
x
xx
−≥ ≥

⇔ ⇔≥

+ ≥ ≥−

b) Đ
ể M và N đồng thời có nghĩa thì
1x ≥
Khi đó ta c
ó M = N theo định lí khai phương một tích.
D
ạng 2: NHÂN CÁC CĂN BẬC HAI
Phương pháp giải:
Với
, 0ì . .a b th a b a b≥=
Ví d
ụ 1: TÍnh:
a)
72. 50
b)
12,8. 0,2
Gi
ải:
a)
72. 50
72.50 36.100 6.10 60= = = =
b)
12,8. 0,2
12,8.0,2 128.0,02 64.0,04 8 .0,2 1,6= = = = =
Ví d
ụ 2: Tính:
a)
40. 20. 4,5
b)
2 12 1
..
3 25 2
Gi
ải:
a)
40. 20. 4,5
40.20.0,5 400.9 20.3 60= = = =
b)
2 12 1
..
3 25 2
2 12 1 4 2
..
3 25 2 25 5
= = =
Ví d
ụ 3: Thực hiện các phép tính:
a)
( )
20 45 5 . 5+−
b)
( )( )
12 3 27 3+−
c)
( )( )
5 31 51−+ −
Giải:
a)
( )
20 45 5 . 5+−
100 225 25 10 15 5 20= + − = + −=
b)
( )( )
12 3 27 3+−
324 36 81 9 18 6 9 3 18= − + − = −+−=
c)
( )
( )
5 31 51−+ −
5 5 15 3 5 1 4 15 3=−− ++−=− +
.
Ví dụ 4: Tính:
a)
( )
2
73+
b)
( )
2
82−
c)
( )( )
35 27 35 27−+
Gi
ải:
a)
( )
2
73+
( )
( )
22
7 2 7. 3 3 7 2 21 3 10 2 21= + + =+ += +
b)
( )
2
82−
( )
( )
22
8 2 8. 2 2 8 2 16 2 2= − + =− +=
c)
( )( )
35 27 35 27−+
( )
( )
22
5 3 2 7 25.3 4.7 47= − = −=
D
ạng 3: RÚT GỌN, TÍNH GIÁ TRỊ CỦA BIỂU THỨC:
Phương pháp giải:
* Áp dụng quy tắc khai phương một tích, quy tắc nhân các căn bậc hai, các hằng đẳng
thức để rút gọn.
Ví d
ụ 1: Rút gọn các biểu thức sau:
a)
3x 5x
.
5 27
với x > 0 b)
62
.( 2)xx−
với x > 2
Giải:
a)
2
3x 5x 3x 5x
..
5 27 5 27 9 3 3
x
xx
= = = =
(Vì x>0 )
b)
62
.( 2)xx−
6 23 3
. ( 2) . 2 ( 2)x x x x xx= − = −= −
(vì x > 2).
Ví dụ 2: Rút gọn các biểu thức sau:
a)
3
60
15x .
x
b)
2
16( 6x 9)x −+
Gi
ải:
a) ĐK:
0x ≠
.
32
30x
60
15x . 900 30
30
xx
x
x
= = =
−
nếu
0
0
x
x
>
<
b)
22
4( 3)
16( 6x 9) 16( 3) 4 3
4( 3)
x
x xx
x
−
− + = − = −=
−−
nếu
3
3
x
x
≥
<
Ví dụ 3: Rút gọn biểu thức
( )
2
25x 2 1M xx= −+
với 0 < x < 1.
Giải:
Ta có
( )
( )
2
2
25x 2 1 25 1 5 1M xx x x= − += − = −
.
Vì x > 0 nên
xx=
.
Vì 0 < x < 1 nên
1x <
. Do đó
11xx−=−
V
ậy
( )
5x 1Mx= −
Ví d
ụ 4: Tính giá trị của các biểu thức sau:
a)
4 23+
b)
8 2 15−
c)
9 45−
Gi
ải:
a)
( )
2
4 2 3 3 2. 3.1 1 3 1 3 1+ = + += + = +
b)
( )
2
8215 525.33 5 3 5 3− = − += − = −
c)
( )
2
9 4 5 5 2.2. 5 4 5 2 5 2− = − += − = −
Nhận xét: Phương pháp giải trong ví dụ này là biến đổi biểu thức lấy căn thành bình phương
của tổng hay hiệu hai số rồi áp dụng hằng đẳng thức
2
AA=
Ví dụ 5: Rút gọn các biểu thức sau:
a)
21xx+−
b)
22 1xx+− +
Gi
ải:
a)
( )
2
2 1 12 11 11 11xx x x x x+ − = −+ −+= −+ = −+
( ĐK:
x1≥
)
b)
( )
2
22 1 12 11 11 11x xx x x x+− + = +− ++= +− = +−
( ĐK
1x ≥−
)
Nếu
0x ≥
thì
11 11xx+−= +−
Nếu
0x <
thì
11 1 1xx+−=− +
D
ạng 4: BIẾN ĐỔI MỘT BIỂU THỨC VỀ DẠNG TÍCH
Phương pháp giải:
Dùng cách đặt nhân tử chung, nhóm các hạng tử, dùng các hằng đẳng thức,...
Ví d
ụ 1: Phân tích thành nhân tử:
a)
33−
b)
3x xy+
c
)
xy yx−
d)
x x xy y−− +
Gi
ải:
a)
( )
3 3 3 31−= −
b)
( )
33x xy x x y+= +
( ĐK
0; 0xy≥≥
)
c)
( )
x y y x xy x y−= −
( ĐK
0; 0xy≥≥
)
( )
( )
) 11d x x xy y x x y y− − + = −− −
( )
( )
1x xy=−−
( ĐK
0; 0xy≥≥
)
Ví dụ 2: Phân tích thành nhân tử:
a)
3
25xx−
b)
9x 6 xy y++
c)
33
xy+
d)
2
92 3xx−− −
Gi
ải:
a)
(
)
( )
( )
32
25 25 5 5x x xx xx x− = −= − +
ĐK:
0x ≥
b)
(
)
2
96 3x xy y x y+ += +
(ĐK:
,0xy≥
).
c)
( )( )
33
x y x y x xy y+=+ −+
(ĐK:
,0xy≥
).
d)
( )
2
92 3 3 32x x xx−− −= − +−
(ĐK:
3x ≥
).
Ví dụ 3. Rút gọn biểu thức:
( )
14 6 5 21+−
.
Giải
( )
( )
14 6 5 21 2 7 3 5 21+ −= + −
( )
( )
( )
2
7 3 10 2 7.3 7 3 7 3=+ −=+ −
( )( )
7 37 34=+ −=
.
Dạng 5: GIẢI PHƯƠNG TRÌNH
Phương pháp giải:
• Trước tiên tìm điều kiện để căn thức có nghĩa.
• Áp dụng quy tắc khai phương một tích, áp dụng các hằng đẳng thức
2
AA=
;
( )
2
AA=
(với
0A ≥
) đưa phương trình đã cho về phương trình đơn giản hơn.
• Có thể đưa về phương trình tích.
Ví d
ụ 1. Giải phương trình:
( )
2
25. 5 15.x +=
Gi
ải
Ta có
( )
2
25. 5 15x +=
53 2
5 5 15 5 3
5 3 8.
xx
xx
xx
+= =−

⇔ += ⇔+=⇔ ⇔

+=− =−

Ví dụ 2. Giải phương trình:
2
9 90 225 6.xx−+ =
Giải
Ta có:
2
9 90 225 6xx−+ =
( )
( )
2
2
9 10 25 6 9 5 6 3 5 6xx x x⇔ − + =⇔ − =⇔ −=
52 7
52
5 2 3.
xx
x
xx
−= =

⇔−=⇔ ⇔

−=− =

Ví dụ 3. Giải phương trình:
2
25 2 5.xx−= −
Giải
ĐK:
22
25 0 25
5.
50 5
xx
x
xx

−≥ ≥
⇔ ⇔≥

−≥ ≥

Khi đó
2
25 2 5xx−= −
( )( )
5 5 2 50xx x⇔ + − − −=
( )
5 52 0xx⇔ − +− =
( )
( )
5
50 50 50
54
1.
520 52
x TM
x xx
x
x
x
L
x

=
−= −= −=
⇔ ⇔⇔

+=
= −
+−= +=


Ví dụ 4. Giải phương trình:
11
5 9 45 25 125 6.
35
xx x−+ − = − +
Gi
ải
ĐK:
5.x ≥
Ta có
11
5 9 45 25 125 6
35
xx x−+ − = − +
( )
( )
11
5 9. 5 25 5 6
35
xx x⇔ −+ − = − +
5 5 56xxx⇔ −+ −= −+
56x⇔ −=
5 36x⇔−=
41x⇔=
(thỏa mãn điều kiện).
Ví dụ 5. Giải phương trình:
1
2.x
x
+=
Gi
ải
ĐK:
0.x >
Ta có:
1
2x
x
+=
( )
2
1 12
20 0 1 0
xx
xx
xx
+−
⇔ + −=⇔ =⇔ − =
10 1xx⇔ −= ⇔ =
(thỏa mãn điều kiện).
D
ạng 6: CHỨNG MINH BẤT ĐẲNG THỨC
Phương pháp giải
Có thể dùng các phương pháp sau:
• Với
0a ≥
;
0b ≥
thì
22
ab a b≤⇔ ≤
;
• Biến đổi tương đương.
Ví d
ụ 1: Không dùng máy tính hoặc bảng số, chứng minh rằng:
5 8 6 7.+<+
Giải
Ta có
5867+<+
( )
( )
22
58 67⇔+ <+
(vì hai vế đều dương)
5 2 40 8 6 2 42 7 13 2 40 13 2 42⇔++<++⇔+<+
40 42 40 42.⇔ < ⇔<
Bất đẳng thức cuối cùng hiển nhiên đúng nên bất đẳng thức đã cho là đúng.
Ví dụ 2: Không dùng máy tính hoặc bảng số, chứng minh rằng:
( )
3 2 2 3 1.+< +
Gi
ải
Ta có
( )
2
3 2 3 43 4 7 43+ =+ +=+
;
( ) ( ) ( )
2
2
2 31 2 31 23231 843.

+ = + = + +=+

Vì
7 43 8 43+ <+
nên
( ) ( )
2
2
32 2 31

+< +

.
Do đó
( )
32 2 31+< +
.
Ví dụ 3: Cho
0a >
, chứng minh rằng:
93aa+< +
.
Giải
Ta có
( )
2
99aa+=+
;
( )
2
3 6 9.a aa+=+ +
Do
0a >
nên
9 96aa a+<++
, do đó
( ) ( )
22
9 3.aa+< +
Vậy
9 3.aa+< +
Chú ý: Căn bậc hai của một tổng không bằng tổng các căn bậc hai.
Ví dụ 4. Cho
,, 0abc>
. Chứng minh rằng:
a)
2a b ab+≥
; b)
.a b c ab bc ca++≥ + +
Giải
a) Ta có
2a b ab+≥
20a b ab⇔+− ≥
( )
2
0ab⇔− ≥
(dấu
""=
xảy ra khi và chỉ khi
ab=
).
Bất đẳng thức cuối này đúng nên bất đẳng thức đã cho là đúng.
Lưu ý : Bất đẳng thức
2a b ab+≥
với
,0ab≥
gọi là bất đẳng thức Cô – si.
b) Ta có
,, 0abc≥
. Áp dụng bất đẳng thức Cô – si đối với hai số ta được:
2a b ab+≥
2b c bc+≥
2c a ca+≥
.
Công từng vế ba bất đẳng thức trên ta được
( )
( )
22a b c ab bc ca++ ≥ + +
.
Suy ra
a b c ab bc ca++≥ + +
(dấu
""=
xảy ra khi và chỉ khi
abc= =
).
Ví dụ 5: Cho
1
2
a ≥
, chứng minh rằng:
21aa−≤
.
Giải
Từ bất đẳng thức Cô – si
2a b ab+≥
suy ra
2
ab
ab
+
≤
.
Áp dụng bất đẳng thức này cho các số không âm
21a −
và 1 ta được:
( )
( )
2 11
21 21.1
2
a
aa a
−+
−= − ≤ =
.
Vậy
21aa−≤
(dấu
""=
xảy ra khi và chỉ khi
1a =
).
C. BÀI TẬP TỰ LUYỆN
1. Tính
a)
400.0,81
; b)
53
.
27 20
;
c)
( )
2
2
5 .3−
; d)
( ) ( )
22
2 5 .2 5−+
.
2.
Tính
a)
( )
( )
32xx−+
; b)
( )( )
xyxy−+
;
c)
25 49
33
33

−+


; d)
( )
( )
135135+− ++
.
3. Rút gọn các biểu thức sau:
a)
3 8 2 15+−
; b)
12 2xx−− −
.
4. Phân tích thành nhân tử
a)
5aa−
; b)
7a −
với
0a >
;
c)
44aa++
; d)
4 3 12xy x y−+−
.
5.
Giải phươn
g trình
a)
( )
2
49 1 2 35 0xx−+ −=
; b)
2
95 30xx−− +=
;
c)
21
13
xx
xx
−−
=
++
.
6
*
. Tìm
x
và
y
, biết
( )
13 2 2 3xy x y++ = +
.
7
*
.
Chứng minh rằng:
7362−<−
.
8.
Chứng minh bất đẳng thứ
c:
22
ab a b++
≥
với
,0ab≥
.
9
*
. Tính giá trị của biểu thức
7 13 7 13A =+ −−
.
HƯ
ỚNG DẪN GIẢI – ĐÁP SỐ
1. a) 18; b)
1
6
; c)
15
; d) 1.
2.
a)
6xx−−
; b)
xy−
; c)
1
; d)
23 1−
.
3. a)
5
; b)
21 3
1 2 3.
x khi x
x khi x
−− ≥
−− <
4.
a)
( )
5aa−
; b)
( )( )
77aa−+
;
c)
( )
2
2a +
; d)
( )
( )
34xy+−
.
5. a)
1
6x =
;
2
4x = −
; b)
1
3x = −
;
2
28x =
; c)
25x =
.
6
*
.
13 4 6xy x y++ = +
(ĐK:
,0xy≥
)
( )
(
)
( ) ( )
22
2
4 4 6 90 2 3 0xx yy x y⇔− ++− +=⇔ − + − =
( )
2
20x⇔ −=
và
( )
2
30y −=
4x⇔=
và
9y =
.
7
*
.
7362−<−
( )
( )
22
7263 72 63⇔+<+⇔ + < +
9 2 14 9 2 18 2 14 2 18⇔+ <+ ⇔ <
.
Bất đẳng thức cuối cùng đúng nên bất đẳng thức đã cho là đúng.
8.
Bình phương hai vế.
9
*
.
Tính
2
A
được
2
2A =
, suy ra
2A =
.
§4. LIÊN
HỆ GIỮA PHÉP CHIA VÀ PHÉP KHAI PHƯƠNG
A. TR
ỌNG TÂM KIẾN THỨC
1. Đ
ịnh lí
Với số
a
không âm và số
b
dương, ta có
aa
b
b
=
.
2. Áp dụn
g
Muốn khai phương một thương
a
b
, trong đó
0a ≥
và
0b ≥
, ta có thể lần lượt khai
phương số
a
và số
b
, rồi lấy kết quả thứ nhất chia cho kết quả thứ hai.
Muốn chia căn bậc hai của số
a
không âm cho căn bậc hai của số
b
dương, ta có thể
chia số
a
cho số
b
rồi khai phương kết quả đó.
3. Chú
ý
Với các biểu thức
0A ≥
và
0B >
, ta có
AA
B
B
=
.
B. CÁC DẠ
NG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: KHAI PHƯƠNG MỘT THƯƠNG
Phương pháp giải
Dựa vào quy tắc khai phương một thương:
Với
0a ≥
;
0b >
thì
aa
b
b
=
.
Ví d
ụ 1. Tính
a)
4 49
:
25 121
; b)
36
49
a−
với
0a <
.
Giải
a)
4 49 4 49 2 7 22
. ::
25 121 25 121 5 11 35
= = =
.
b)
36 36 36. 6
49 7
49 49
a a aa− − −−
= = =
.
Lưu ý: Vì
0a <
nên
a−
có nghĩa.
Ví dụ 2. Tính
a)
22
65 52
225
−
; b)
11 7
:1, 44 :1, 44
99
−
.
Giải
a)
( )( )
22
2
65 52 65 52
65 52 13.117
13.13.9 13.3 39
225 225 225
15 15 15
−+
−
= =
= = =
.
b)
11 7 11 7 144
:1, 44 :1, 44 :
9 9 9 9 100

−=−


4 144 4 144 2 12 5
:::
9 100 9 100 3 10 9
= = = =
.
Ví dụ 3. Đẳng thức
55
2
2
xx
y
y
−−
=
+
+
đúng với những giá trị nào của
x
và
y
?
Giải
Theo định lí khai phương một thương thì
55
2
2
xx
y
y
−−
=
+
+
khi
50x −≥
và
20y +>
hay
5x ≥
và
2y >−
.
D
ạng 2. CHIA CÁC CĂN BẬC HAI
Phương pháp giải
Dựa vào quy tắc chia các căn bậc hai:
Với
0a ≥
;
0b >
thì
aa
b
b
=
.
Ví d
ụ 1. Tính
a)
45 : 80
; b)
( )
5
35
2.3 : 2 .3
.
Giải
a)
45 9 3
45 : 80
80 16 4
= = =
.
b)
( )
55
5
35 2
35
2 .3
2.3 : 2 .3 2
2
2 .3
= = =
.
Ví dụ 2. Tính
a)
54: 2: 3
; b)
3 52
:
75 117
.
Giải
a)
54 : 2 : 3 54 : 2 : 3 27 :3 9 3= = = =
.
b)
3 52 3 52 1 4 1 2 3
: : ::
75 117 25 9 5 3 10
75 117
= =
= =
.
Ví dụ 3. Thực hiện các phép tính
a)
( )
45 125 20 : 5−+
; b)
( )
2 18 3 8 6 2 : 2+−
.
Giải
a)
( )
45 125 20 : 5 9 25 4 3 5 2 0− + = − + =−+=
.
b)
( )
2 18 3 8 6 2 : 2 2 9 3 4 6 2.3 3.2 6 6+ − = + −= + −=
.
Dạng 3. RÚT GỌN, TÍNH GIÁ TRỊ CỦA BIỂU THỨC
Phương pháp giải
• Tìm điều kiện của biến để căn thức có nghĩa.
• Áp dụng quy tắc khai phương môt thương hoặc quy tắc chia các căn bậc hai để rút gọn.
• Thay giá trị của biến vào biểu thức đã rút gọn ròi thực hiện các phép tính.
Ví d
ụ 1. Rút gọn biểu thức
16 12
12 8
33
33
−
−
.
Giải
( )
( )
12 4
16 12
4
84
12 8
331
33
39
33 1
33
−
−
= =
=
−
−
.
Ví dụ 2. Rút gọn rồi tính giá trị của biểu thức sau với
6x =
:
( )
22
165 124
.
369
Ax
−
=
.
Giải
( )
( )( )
22
165 124
165 124 165 124
..
369 369
Ax x
−
+−
= =
289.41 289 17
. ..
369 9 3
x xx= = =
.
Với
6x =
thì
17
.6 34
3
A = =
.
Ví dụ 3. Cho biểu thức
1
1
:
11
y
x
B
yx
+
+
=
−−
.
Rút gọn rồi tính giá trị của
B
với
5x =
;
10y =
.
Giải
1
1
:
11
y
x
B
yx
+
+
=
−−
. ĐK:
1x >
;
1y >
.
( )
( )
( )
( )
11
1
11
:
1
11
11
xx
y
xx
B
y
yx
yy
+−
+
+−
= = =
−
−−
−+
.
Với
5x =
;
10y =
thì
51 4 2
10 1 9 3
B
−
= = =
−
.
Ví dụ 4. Cho biểu thức
2
69
x xy y
C
x xy y
−+
=
++
với
0x >
,
0y >
.
Rút gọn rồi tính giá trị của
C
với
25x =
;
81y =
.
Giải
( )
( )
2
2
2
69 3
3
xy
xy
x xy y
C
x xy y x
y
xy
−
−
−+
= = =
++ +
+
.
Với
25x =
;
81y =
thì
25 81
59
41
5 3.9 32 8
25 3 81
C
−
−
= = = =
+
+
.
D
ạng 4. GIẢI PHƯƠNG TRÌNH
Phương pháp giải
• Tìm điều kiện để căn thức có nghĩa.
• Nếu hai vế không âm thì có thể bình phương hai vế để khử dấu căn.
Ví d
ụ 1. Giải phương trình
31
2
2
x
x
−
=
+
.
Giải
ĐKXĐ:
31x −
và
2x +
cùng dấu hoặc
1
3
x =
.
Trường hợp 1:
1
3 10
1
3
20
3
2
x
x
x
x
x
−>
>
⇔ ⇔>

+>
>−
.
Trường hợp 2:
1
3 10
2
3
20
2
x
x
x
x
x
−<
<
⇔ ⇔ <−

+<
<−
.
Vậy ĐKXĐ là
1
3
x ≥
hoặc
2x <−
.
Bình phương hai vế của phương trình ta được:
31
4
2
x
x
−
=
+
( )
3 14 2xx⇔ −= +
3 14 8xx⇔ −= +
9x = −
(thỏa mãn điều kiện).
Ví dụ 2. Giải phương trình
57
1
21
x
x
−
=
−
.
Giải
ĐKXĐ:
7
5 70
7
5
2 10
1
5
2
x
x
x
x
x
≥
−≥
⇔ ⇔≥

−>
>
.
Bình phương hai vế ta được:
57
1
21
x
x
−
=
−
5 72 1xx⇔ −= −
36x⇔=
2x⇔=
(thỏa mãn điều kiện).
C. BÀI TẬP TỰ LUYỆN
1.
Tính
a)
72 : 8
; b)
( )
28 7 112 : 7−+
.
2. Tính
a)
49 1
:3
88
; b)
54 : 6xx
; c)
1 32 56
.:
125 35 225
.
3.
Làm phép chia
32
12
:
2 3 31
aa
a aaa
−+
+ − +−
với
1a >
.
4.
Rút gọn biểu thức
a)
22
24
:
xx
yy
với
,0xy≠
;
b)
( )
( )
( )
2
2
2
27 1
3 50
2
12 2
82
x
x
x
x
−
+− −
−
với
12x<<
.
5. Cho
23
:
32
x =
, tính giá trị của biểu thức
65Mx= +
.
6
*
. Chứng minh đẳng thức
6 25 5 26
51 3 2
+−
=
+−
.
HƯỚNG DẪN GIẢI – ĐÁP SỐ
1. a) 3; b) 5.
2.
a)
7
5
; b)
3
; c)
6
35
.
3.
( )
2
1
2
a
a
−
+
.
4. a)
2
2
0
0
x khi x
x khi x
>
−<
; b)
4x
.
5.
2
3
x =
;
3M =
.
6
*
.
Mỗi vế đều bằng 1.
§6. §7. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
A. TR
ỌNG TÂM KIẾN THỨC
1. Đư
a thừa số ra ngoài dấu căn
Với hai biểu thức
,AB
mà
0B ≥
, ta có:
2
0
0
A B khi A
AB A B
A B khi A
≥
= =
−<
2. Đư
a thừa số vào trong dấu căn
2
A B AB=
, tức là:
• Nếu
0A ≥
;
0B ≥
thì
2
A B AB=
;
• Nếu
0A <
;
0B ≥
thì
2
A B AB= −
.
3. Khử mẫu
của biểu thức lấy căn.
Với các biểu thức
,AB
mà
.0AB≥
và
0B ≠
, ta có
A AB
BB
=
.
4. Tr
ục căn thức ở mẫu
Trường hợp 1: Với các biểu thức
,BC
mà
0B >
thì
C CB
B
B
=
.
Trường hợp 2: Với các biểu thức
,,ABC
mà
0A ≥
;
2
AB≠
thì
( )
2
C AB
C
AB
AB
±
=
−
±
.
Trường hợp 3: Với các biểu thức
,,ABC
mà
0A ≥
,
0B ≥
và
AB≠
thì
( )
CA B
C
AB
AB
±
=
−
±
.
Hai biểu thức
AB+
và
AB−
gọi là hai biểu thức liên hợp với nhau.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: ĐƯA THỪA SỐ RA NGOÀI DẤU CĂN
Phương pháp giải
• Biến đổi biểu thức lấy căn thành dạng tích trong đó có thừa số là bình phương của một
số hoặc một biểu thức.
• Khai phương thừa số này và viết kết quả ra ngoài dấu căn.
Ví d
ụ 1: Đưa thừa số ra ngoài dấu căn
a)
45
; b)
2400
; c)
147
; d)
1, 25
.
Giải
a)
45 9.5 3 5= =
;
b)
2400 400.6 20 6= =
;
c)
147 49.3 7 3= =
;
d)
1,25 0,25.5 0,5 5= =
.
Ví dụ 2: Đưa thừa số ra ngoài dấu căn
a)
50.6
; b)
14.21
; c)
32.45
; d)
125.27
.
Giải
a)
50.6 100.3 10 3= =
;
b)
14.21 7.7.2.3 7 6= =
;
c)
32.45 16.2.9.5 16.9.10 4.3. 10 12 10= = = =
;
d)
125.27 25.5.9.3 25.9.15 5.3 15 15 15= = = =
.
Ví dụ 3. Đưa thừa số ra ngoài dấu căn
a)
18x
; b)
2
75xy
; c)
32
605xy
.
Giải
a)
18 9.2 3 2x xx= =
(với
0x ≥
).
b)
22
75 25 .3 5 3xy x y x y= =
( )
0y ≥
53 0
5 3 0.
x y khi x
x y khi x
≥
−<
c)
32 2 2
605 121 . .5 11 5xy x y x xy x= =
( )
0x ≥
11 5 0
11 5 0.
xy x khi y
xy x khi y
≥
=
−<
Ví dụ
4. Đưa thừa số ra ngoài dấu căn
a)
( )
2
128 xy−
; b)
( )
2
150 4 4 1xx−+
; c)
32
6 12 8xx x−+−
.
Giải
a)
( )
( )
22
128 64 .2 8 2xy xy xy−= − =−
( )
( )
82
82 .
x y khi x y
y x khi x y
−≥
=
−<
b)
( )
( )
2
2
150 4 4 1 25.6 2 1xx x− += −
( )
( )
1
52 1 6
2
52 1 6
1
51 2 6 .
2
x khi x
x
x khi x
−≥
=−=
−<
c)
( ) ( ) ( )
32
32
6 12 8 2 2 . 2xx x x x x− + −= − = − −
( )
22xx=−−
(với
2x ≥
).
Dạng 2: ĐƯA THỪA SỐ VÀO TRONG DẤU CĂN
Phương pháp giải
• Nếu
0A ≥
thì ta nâng
A
lên lũy thừa bậc hai rồi viết kết quả vào trong dấu căn:
2
A B AB=
(với
0A ≥
;
0B ≥
).
• Nếu
0A <
thì ta coi
A
như là
( )
A−−
. Ta nâng
( )
A−
lên lũy thừa bậc hai rồi viết kết
quả vào trong dấu căn. Còn dấu
""−
vẫn để đằng trước dấu căn:
2
A B AB= −
(với
0A <
;
0B ≥
).
Ví d
ụ 1. Đưa thừa số vào trong dấu căn
a)
35
; b)
56
; c)
2
35
7
.
Giải
a)
2
3 5 3 .5 45= =
;
b)
2
5 6 5 .6 150= =
;
c)
2
2 2 20
35 .35
77 7

= =


.
Ví dụ 2. Đưa thừa số vào trong dấu căn:
a)
1
4
8
−
; b)
0,06 250−
.
a)
2
11
4 42
88
−=− =−
b)
( )
2
0,06 250 0,06 .250 0,9−=− =−
Ví
dụ 3. Đưa thừa số vào trong dấu căn
a)
xx
b)
x
y
y
c)
xy
yx
.
Giải
a)
( )
23
.0xxxxxx= = ≥
b) ĐK:
. 0; 0xy y≥≠
Xét trường hợp
0x ≥
,y > 0, ta có
2
xx
y y xy
yy
= =
Xét trường hợp x < 0; y < 0,ta có
2
xx
y y xy
yy
=−=−
c) ĐK: xy > 0, ta có
2
2
xyxyx
yxyxy
= =
Ví dụ
4. Đưa thừa số vào trong dấu căn:
a)
3
x
x
−
với x > 0 b)
1
x
x
−
−
với x < 0
Giải
a) Ta có
2
33
3xx x
xx
−=− =−
với x > 0
b) Ta có
2
11
()xx x
xx
−−

− =−− =−


với x < 0
Ví dụ 5. Chỉ ra chỗ sai trong các biến đổi sau:
a)
2
33
77
x
x =
b)
2
.
yy
xy y x y xy
xx
= =
Gi
ải
a) Bi
ến đổ
i
2
33
77
x
x =
chỉ đúng khi
0x ≥
Nếu x < 0 thì
2
33
77
x
x = −
b) Biến đổi
2
.
yy
xy y x y xy
xx
= =
chỉ đúng khi x > 0
Nếu x < 0 thì
2
.
yy
xy y x y xy
xx
=−=−
D
ạng 3. KHỬ MẪU CỦA BIỂU THỨC LẤY CĂN
Phương pháp giải
Vận dụng công thức
( )
. 0; 0
A AB
AB B
BB
= ≥≠
. Cụ thể gồm các bước sau :
- Biến đổi mẫu thành bình phương của một số hoặc một biểu thức ( nếu cần );
- Khai phương mẫu và đưa ra ngoài dấu căn.
Ví dụ 1. Khử mẫu của biểu thức lấy căn
5
72
Giải
Ta có
5 5.2 10 1
. 10
72 72.2 144 12
= = =
Nh
ận xét : Nếu bạn nhân cả tử và mẫu của phân số
5
72
với 72 thì vẫn ra kết quả nhưng biến đổi
phức tạp hơn :
2
5 5.72 360 6 1
. 10 . 10
72 72.72 72 72 12
= = = =
V
ậy tìm thừa số phụ như nào cho hợp lý ?
Trước hết bạn phân tích mẫu số ra thừa số nguyên tố: 72 = 2
3
.3
2
. Bạn thấy ngay thừa số phụ
laf2, lúc đó số mũ của các thừa số nguyên tố đều chẵn.
Ví dụ 2. Khử mẫu của biểu thức lấy căn
a)
11
27x
b)
3
3
5
x
y
Gi
ải
a)
2
11 11.3 33 1
33
27 27 .3x 81 9
xx
x
x x xx
= = =
(ĐK: x > 0)
b)
3 3 42
3 3 .5 15 1
15
5 5 .5 25 5
x x y xy
xy
y yy y y
= = =
( ĐK:
0; 0xy y≥≠
)
Ví dụ 3. Khử mẫu của biểu thức lấy căn
a)
32
1
3 31xxx+ ++
b)
23
11
xx
−
Gi
ải
a)
( )
( )
( )
3 42
32
1 1 11
1
3 31
1 11
x
x
xxx
x xx
+
= = = +
+ ++
+ ++
(ĐK: x > -1 )
b)
( )
23 3 4 2
1 1 1 .( 1) 1
.1
x xx
xx
xx x x x
−−
−= = = −
( ĐK:
1x ≥
hoặc x < 0 )’
D
ạng 4. TRỤC CĂN THỨC Ở MẪU
Phương pháp giải
Cách 1: Rút gọn biểu thức ( nếu có thể ):
+ Phân tích tử số thành tích có thừa số là căn thức ở mẫu.
+
Chia c
ả tử và mẫu cho thừa số chung.
Cách 2: Nhân cả tử và mẫu với biểu thức liên hợp của mẫu để làm mất dấu căn ở mẫu.
Ví dụ 1. Trục căn thức ở mẫu
a)
33
53
+
b)
22
21
+
+
Gi
ải
a) Ta có
3 3 3.( 3 1) ( 3 1)
5
53 53
+ ++
= =
b)
Ta có
2 2 2.( 2 1)
2
21 21
++
= =
++
Ví dụ 2. Trục căn thức ở mẫu
a)
3
7
b)
2
31−
c)
3
15 4+
Gi
ải
a)
3 3. 7 3. 7
7
7 7. 7
= =
b)
2 2.( 3 1) 2.( 3 1)
31
31
3 1 ( 3 1).( 3 1)
++
= =
= +
−
− −+
c)
3 3.( 15 4) 3.( 15 4)
3.(4 15)
15 16
15 4 ( 15 4).( 15 4)
−−
= = =
−
−
+ −+
Ví dụ 3. Trục căn thức ở mẫu
a)
53 35
53 35
−
+
b)
2
123−+
Gi
ải
a)
2
5 3 3 5 (5 3 3 5) 75 45 30 15
75 45
53 35 (53 35).(53 35)
30.(4 15)
4 15
30
− − +
−
= =
−
+ +−
−
= =
−
b)
2
2 2 (1 2 3) 2 (1 2 3) 2 (1 2 3)
1 2 3 (1 2 3)(1 2 3) (1 2 ) 3 (1 2 2 2 3
2 (1 2 3) 3 2 1
2
22
−− −− −−
= = =
−+ −+ −− − − − +−
−− +−
= =
−
Ví dụ 4. Trục căn thức ở mẫu.
a)
1
1
a
a
−
+
với
0; 1aa≥≠
b)
1
1ab+−
với a > 0; b > 0;
1
4
ab =
Gi
ải
a)
2
1 (1 ) 1 2
1
1 (1 )(1 )
a a aa
a
a aa
− − −+
= =
−
+ +−
b)
1 1.( 1) ( 1)
1 ( 1)( 1) 2 1
ab ab
ab ab ab ab ab
++ ++
= =
+− +− ++ ++ −
11
1
21
4
ab ab
ab
ab
++ ++
= =
+
++ −
D
ạng 5. SO SÁNH HAI SỐ
Phương pháp giải
Thực hiện các phép biến dổi đơn giản biểu thức chứa căn bận hai rồi so sánh hai kết
quả.
Chẳng hạn:
- Đưa thừa số vào trong dấu căn rồi dùng tính chất:
Nếu A > B > 0 thì
AB>
- Đư
a thừa số ra ngoài dấu căn rồi dùng tính chất:
Nếu A,B,C > 0 thì A > B
AC BC⇔>
Ví d
ụ 1. Không dùng máy tính hoặc bảng số , hãy so sánh :
a)
56
và
73
b)
2
32
3
và
1
51
5
Gi
ải
a) Ta có
5 6 25.6 150= =
;
7 3 49.3 147= =
Vì
150 147>
nên
56 73>
.
b) Ta có
28
3 2 9. 24
33
= =
16
5 1 25. 30
55
= =
Vì
24 30<
nên
21
32 51
35
<
Ví dụ
2. Không dùng máy tính hoặc bảng số , hãy so sánh :
a)
5
2
4
và
2
7
3
b)
3 11−
và
2 23−
Giải
a) Ta có
5 25 25 1
2 .2 3
4 16 8 8
= = =
2 4 28 1
7 .7 3
3 9 99
= = =
Vì
11
33
89
>
nên
52
27
43
>
b) Ta có
3 11 9.11 99−=− =−
2 23 4.23 92−=− =−
Vì
99 92− <−
nên
3 11 2 23− <−
Ví d
ụ 3. Sắp xếp theo thứ tự tăng dần
a)
22
6 3,7 2,15 ,9 1
59
b)
21
71, 12, 21, 5 3
32
−−
Gi
ải
a) Ta có
6 3 36.3 108;7 2 49.2 98;= = = =
2 2 2 11
15 225. 90;9 1 81. 99
5 5 99
= = = =
Vì
90 98 99 108<<<
nên
22
15 7 2 9 1 6 3
59
<< <
b)
Ta có
2 4 16 1
12 .12 5 ;
3 9 33
= = =
1 1 21 1
21 .21 5 ;
2 4 44
= = =
5 3 25.3 75.−=− =−
Vì
11
75 71 5 5
43
− <− < <
nên
12
5 3 71 21 12.
23
−< < <
D
ạng 6. RÚT GỌN BIỂU THỨC
Phương pháp giải
Thực hiện các phép biến đổi đơn giản biểu thức chứa căn bậ hai rồi thu gọn các căn thức đồng
dạng hoặc rút gọn các thừa số chung ở tử và mẫu.
Ví dụ 1. Rút gọn các biểu thức sau :
a)
1
200 50 4
8
−+
b)
( )
3 72 4,5 12,5++
Gi
ải
a)
11
200 50 4 10 2 5 2 4. . 2 6 2.
84
−+ = −+ =
b)
( )
3 72 4,5 12,5 216 13,5 37,5++ = + +
27 75 3 5
66 66
6 6 56
22 22
=+−=+−=
.
Ví dụ 2. Rút gọn các biểu thức sau :
a)
23
12
32

−


; b)
21 1
42
9 2 18
++
Gi
ải
a)
23 1 1
12 1
2 6 6 46 66 26
32 3 2


− = − =−=−




b)
21 1 4 1 1
4 2 2 2 2 22
9 2 18 3 2 6
++=++=
.
Ví dụ 3. Rút gọn các biểu thức sau :
1
97 5 3
ab
P ab ab
b a ab
= +−−
với a,b > 0
Giải
1
97 5 3
ab
P ab ab
b a ab
= +−−
7 5 1 75
3 3.P ab ab ab ab ab ab
b a ab b a

=+−− =−


Ví d
ụ 4. Rút gọn các biểu thức
341
52 62 65
B =++
−++
Gi
ải
3 4 1 3( 5 2) 4( 6 2) ( 6 5)
52 62 65
52 62 65
B
+ −−
=++= + +
− −−
−++
( 5 2) ( 6 2) 6 5 2 6B =++−+−=
Nhận xét: Phương pháp giải này ví dụ này là trục căn thức ở mẫu rồi làm các phép cộng,trừ.
Nếu quy đồng mẫu thì rất phức tạp.
Ví dụ 5. Cho a > b > 0, chứng minh rằng
( )
22
2
4
82
2
6
75 15
a ab b
ab
b
a b ab
−+
=
−
Gi
ải
Ta có
2 2 22 2
44
2
2
8( 2 ) 8( ) .
75 75 .
2( ) 2 2 2 .3 2
. . . 6.
5 3 5 9 15
ab a ab b ab a b b
a b ab a b abb
ab a b b b
b
a b ab
−+ −
=
−−
−
= = =
−
Ta th
ấy vế trái đúng bằng vế phải.
C. BÀI TẬ
P TỰ LUYỆN
1. Đưa thừa số ra ngoài dấu căn :
a)
3
75a
; b)
52
98a ( 6 9).bb−+
2. Rút gọn biểu thức :
a)
2 125 5 45 6 20;−+
b)
2 75 4 27 12.−+
3. So sánh các số sau:
a)
37
và
2 15
; b)
45−
và
53−
4.
Khử mẫu của biểu thức lấy c
ăn
a)
3
80
b)
2
75
5.
Trục căn thức ở mẫ
u
a)
2
2
aa
a
−
−
b)
13
23 5−
c)
2
123
−
−+
6.
Trục căn thức ở mẫ
u
a)
8
53−
b)
1
52 25−
c)
57
57
−
+
7.
Tính
a)
2
1
23


−

b)
111 1
...
1 2 2 3 3 4 99 100
++++
+++ +
8. Cho
75 12
147 48
x
+
=
−
. chứng minh rằng
3x
là một số nguyên.
9. Biến đổi
26
10 4 3+
về dạng
3ab+
. tính tích
.ab
10. Tìm các cặp số nguyên dương
(; )xy
trong đó
xy<
sao cho
539xy+=
HƯ
ỚNG DẪN GIẢI – ĐÁP SỐ
1. a)
5a 3a ( 0);a ≥
b)
2
2
7 ( 3) 2
7 (3 ) 2
ab a
a ba
−
−
2. a)
75
; b) 0
3. a)
3 7 2 15>
; b)
45 53− <−
4. a)
1
15
20
b)
1
6
15
5. a)
a
b)
(2 3 5)−+
c)
35 6−
6. a)
2( 5 3)−+
b)
52 25
30
+
c)
35 6−
7. a)
5 26+
b) tr
ục căn thức pử mẫu của mỗi số hạng rồi tính tổng được
100 1 9−=
8. tính
x
được
7
3
x =
, do đó
37xZ= ∈
9*.
26 13
5 23
10 43 5 23
= = −
++
V
ậy
5; 2.ab= = −
do đó
. 5.( 2) 10ab= −=−
10*.
539 49.11 7. 11= =
7. 11 11 6. 11 2. 11 5. 11 3. 11 4. 11=+=+=+
7. 11 7. 11 36.11 4.11 25.11 9.11 16.11=+=+=+
11 396 44 275 99 176xy+= + = + = +
Bài toán có
ba đáp số: (11;396); (44;275) ; (99 ; 176)
§8. RÚT
GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
A. TRỌNG TÂM KIẾN THỨC
Để rút gọn biểu thức có chứa căn thức bậc hai, ta có thế:
- Thực hiện các phép biến đổi đơn giản các căn thức bậc hai nhằm làm xuất hiện
các căn thức đồng dạng.
- Phối hợp thực hiện các phép tính với các biểu thức có dạng phân thức mà tử và
mẫu có chứa căn thức bậc hai theo quy tắc thực hiện các phép tính về phân thức
đại số.
nếu
nếu
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
D
ẠNG 1. RÚT GỌN BIỂU THỨC CHỈ CÓ CỘNG, TRỪ ĂN THỨC
Phương pháp giải
Đưa thừa số ra ngoài hoặc vào trong dấu căn, khử mẫu của biểu thức lấy căn rồi dùng
công thức:
()mAnApAq mnp Aq− + += −+ +
trong đó
0A ≥
Ví d
ụ 1. Rút gọn các biểu thức sau:
a)
20 80 45;−+
b)
18 50 98−+
Gi
ải
a)
Ta có
5 20 80 45 2 5 4 5 3 5−+= −+=
b) Ta có
18 50 98 3 2 5 2 7 2 5 2−+=−+=
Ví dụ 2: Rút gọn các biểu thức sau:
a)
11
4,5 72 5
22
−+
b)
25 3 98
42 10 12
623
−−
Giaỉ
a)
1 1 9.2 1 5
4,5 72 5 .6
2 2
2 2 2.2 2 2
35
2 32 2 2
22
− += − +
= −+ =
b)
25 3 98
42 10 12
623
517
42. 6 10. 6 12. 6
623
356 56 286 26.
−−
= −−
= −− =
Ví d
ụ 3: Rút gọn biểu thức
M =
3 33 3
2 16 7 25 3 36x xy xy y xy+−
với
0; 0xy≥≥
Giải
Ta có M =
3 33 3
2 16 7 25 3 36
8 35 18 25
x xy xy y xy
xy xy xy xy xy xy xy xy
+−
=+−=
Ví dụ 4: Rút gọn biểu thức N =
33
11
22
+ −−
Giaỉ
Ta có: N =
33
11
22
+ −−
=
( )
22
2 3 2 3 4 23 4 23
22 4 4
11
( 3 1) ( 3 1)
22
1
3 1) ( 3 1) 1
2
+−+ −
−= −
= +− −

= +− −=

Ví dụ
5. Biến đổi biểu thức
1
54
aa
b b ab
−−
về dạng
xyz
ab
abc

++


, trong đó
, 0; , ,ab xyz Z>∈
Tính tổng
xyz++
Gi
ải
Ta có
1 5 4 1 54 1
54
aa
ab ab ab ab
b b ab a b ab a b ab

− − = − − = −−


V
ậy
5; 4; 1.xy z= =−=−
do đó
0xyz++=
D
ạng 2 : RÚT GỌN BIỂU THỨC CÓ CHỨA CÁC PHÉP CỘNG, TRỪ , NHÂN,
CHIA CĂN THỨC DƯỚI DẠNG PHÂN THỨC ĐẠI SỐ
Phương pháp giải
- Xác định đieèu kiện để biểu thức có nghĩa gồm: điều kiện để biểu thức lấy căn không
âm và điều kiện để mẫu thức khác 0.
- Vận dụng các quy tắc của phép tính về phân thức đại số, kết hợp với các phép tính về
căn thức để đưa biểu thức đã cho về dạng đơn giản nhất.
Ví dụ 1. Rút gọn biểu thức
y
x
P
xy x y xy
= −
−−
Giải
Điều kiện:
0; 0; .x y xy>>≠
khi đó ta có:
()()()
y
x yx
P
xyx yyx xyyx
−
=−=
−− −
=
( )
( )
()
yxyx
yx
xy y x xy
−+
+
=
−
Ví d
ụ 2. Rút gọn biểu thức
3:
3
xy
x
P
y x xy

= −


+

Giải
Điều kiện:
0; 0.xy>>
khi đó ta có:
3 ( 3)
9
3: . .
3
xy x y x x y
x xy
P
y
y x xy y xy

−+
−
=−= =


+

Ví dụ 3. Rút gọn biểu thức
:( )
xx yy
P xy x y
xy

−
= +−


−

Giải
( )
( )
( )
( )
2
( )( )
:( )
1
2.
.
x y x xy y
P x
y x y
xy
P x xy y
xy
xy
xy
P
xy
xyxy

− ++
= +
−


−

=++
−
+
+
= =
−
−−
Ví d
ụ 4: rút gọn biểu thức
1
1:
11
xx
P
x x xx

+
= +

++ −

Gi
ải
Điều kiện:
0; 1xx≥≠
. Khi đó ta có:
2
11
.
11
21 1
.
11
( 1) ( 1).( 1)
.
11
1
x x x xx
P
xx x
x x xx
P
xx x
x x xx
P
xx x
Px

+ ++ −
=

++ +

++ −
=
++ +
+ − ++
=
++ +
= −
Ví d
ụ 5. Rút gọn biểu thức
12 3 1 22
.
1
11
x xx
P
xx
xx x

−−

= +− −


−
+−


Gi
ải
Điều kiện
0; 1xx>≠
. Khi đó ta có
2
( 1) 2 ( 1) 3 1 2 2
.
( 1)( 1)
2 1 2 2 3 1 2( 1)
.
( 1)( 1)
3 ( 1) 2( 1) 6
.
( 1)( 1)
x xx x x
P
x
xx
xx xxx x
P
x
xx
xx x
P
x
xx x
− + ++ − −
=
+−
− ++ + + − −
=
+−
+−
= =
+−
D
ạng 3. RÚT GỌN RỒI TÍNH GIÁ TRỊ CỦA BIỂU THỨC HOẶC RÚT GỌN RỒI
TÌM GIÁ TRỊ CỦA BIỂU THỨC ĐỂ BIỂU THỨC CÓ MỘT GIÁ TRỊ NÀO ĐÓ
Phương pháp giải
Trước hết tìm điều kiện để biểu thức có nghĩa rồi rút gọn biểu thức. sau đó thay giá trị
của biến vào biểu thức đã được rút gọn rồi thực hiện các phép tính
Hoặc có thể phải sử dụng kết quả rút gọn, lập phương trình hoặc bất phương trình rồi
giải ra để tìm giá trị của biến
Ví dụ 1. Cho biểu thức
1 2 25
4
22
xxx
P
x
xx
−−
=−−
−
+−
a
) Rút gọn P.
b) Tính giá trị của P vớ
i
2
23
x =
−
Gi
ả
i
a) Điều kiện:
0; 4xx≥≠
. Khi đó ta có:
( 1)( 2) 2 ( 2) (2 5 )
( 2)( 2)
3 22 4 25
( 2)( 2)
2
( 2)( 2)
( 2)
( 2)( 2) 2
x x xx x
P
xx
xx xx x
P
xx
xx
P
xx
xx x
P
xx x
− −− +−−
=
+−
− +− − −+
=
+−
−−
=
+−
−+
= =
+−−
b) Ta có
2
2
2(2 3) (31) 31
23
xx= = + = +⇒ =+
−
Do đó
2
31 31 (31) 423
(2 3)
22
2 ( 3 1) 1 3
P
+ + ++
= = = = =−+
−−
−+ −
Ví dụ 2. Cho biểu thức
2
2 24
:
1 ( 1)
21
xx x
P
xx
xx

+−
= −

−−
−+

a
) Rút gọn P
b) Tính giá trị của P, biế
t
54x −=
Gi
ải
a) Điều kiện:
0; 1.xx>≠
Khi đó ta có:
P =
( )
( )
( )
( )
2
2
2 2
1
1
.
4
1
1
xx
x
x
x
x
x

−
−
+
+
−
−
−
P
=
( )
( )
( )
( )
( )
( )
2
2
2 1 2 1
( 1)
.
4
11
xx xx
x
x
xx
+ −− − +
−
−+
P
=
( )
( )
( ) ( )
2
2
2 2
( 1)
.
4
11
xx xx
x
x
xx
+ −−− −
−
−+
P
=
( ) ( )
( )
2
2
2
( 1) 1
2
.
4
11
xx
x
x
xx
−+
−+
P
=
1
2
x
x
+
b) Ta có
54 9
| 5| 4
54 1
xx
x
xx
−= =

−=⇔ ⇔

−=− =

V
ới x = 9, ta có P =
91 4 2
63
29
+
= =
V
ới x = 1, không thỏa mãn điều kiện đã nêu nên biểu thức P không có giá trị.
Ví dụ 3. Cho biểu thức P =
2
2
.
22
xy x y
x
xy
x yxy

+
−


−
−−

a) Rút gọn P
b) Tính giá trị của P, biế
t
4
9
x
y
=
Gi
ải
a) Điều kiện:
0 ; 0 ; x y xy≥≥≠
. Khi đó ta có:
P =
2
2
.
2( )
xy x y
x
xy
xy xy

+
−

−
−−


P
=
2
4( )
2
.
2( )( )
xy x y
x
xyxyxy
−+
−+ −
P
=
42
2
.
2( )( )
xy x xy y
x
xyxyxy
−− −
−+ −
P
=
(2 )
2
.
2( )( )
x xy y
x
xyxyxy
−− +
−+ −
P
=
2
()
2
.
2( )( )
xy
x
xyxyxy
−−
−+ −
=
x
xy
−
+
b) Ta có
4
9
x
y
=
9
4
x
y⇒=
Do đó P =
2
35
5
9
22
4
x xx
xx x
xx
− − −−
= = =
+
+
Ví dụ 4. Cho
1 2 21
:
4
2 44 2
P
x
x xx x

=−−


−
+ ++ −

a) Rút gọn P
b) Tìm x để P =
1
2
−
Gi
ải
a) Điều kiện:
0 ; 4xx≥≠
. Khi đó ta có:
P =
2
1 2 21
:
4
2 ( 2) 2
x
xx x


−−


−
++ −


P
=
2
2 2 2 ( 2)
:
4
( 2)
xx
x
x
+− − +
−
+
P
=
2
( 2)( 2) 2
.
( 2) 2
xxx x
x xx
−+−
=
+− +
b) T
a có P =
1
2
−
21
2
2
x
x
−
⇔=−
+
24 2xx⇔ −= +
6x⇔=
36x⇔=
(thỏa mãn điều kiện)
Ví dụ 5. Cho biểu thức
P =
1 1 33
:
3 9 33
xx
x xx x x x x

−

+−


+ − ++


a
) Rút gọn P
b) Tìm x để
1P
Giải
a) Điều kiện:
0 ; 9xx≥≠
. Khi đó ta có:
P =
( 3) 3 3 3
:
( 3)( 3) ( 3)
xx x x
xx x xx
−+ − +
−+ +
P
=
3 3 ( 3)
.
( 3)( 3) 3 3
x x xx
xx x x x
−+ +
− + −+
P =
1
3x −
b) Đ
ể
1P
11
1 10
33xx
⇔ >⇔ −>
−−
13
0
3
x
x
−+
⇔>
−
4
0
3
x
x
−
⇔<
−
40
30
x
x
−>
⇔
−<
hoặc
40
30
x
x
−<
−>
⇔
9 16 x
(thỏa mãn điều kiện)
Dạng 4. RÚT GỌN BIỂU THỨC RỒI CHỨNG MINH BIỂU THỨC CÓ MỘT TÍNH CHẤT
NÀO ĐÓ HOẶC TÌM GIÁ TRỊ NHỎ NHẤT, GIÁ TRỊ LỚN NHẤT CỦA MỘT BIỂU
THỨC
Phương pháp giải
Sau đó rút gọn biểu thức, biến đổi kết quả ( nếu cần) rồi lập luận đi đến điều kiện phải
Ví dụ 1. Chứng minh rằng giá trị của biểu thức sau là hằng số với mọi giá trị thích hợp của
x và y :
A =
2
2
.
()
x y xy yx
x
xy y xy x x y

−−
+


− −−

Gi
ải
a) Điều kiện:
0 ; 0 ; x y xy≥≥≠
. Khi đó ta có:
A =
2
2 ()
.
()()()
xy xyxy
x
yxy xyx xy

−−
+


− −−

A =
2
2 ()
.
()()
x xy y xy x y
xyxy xy
−+ −
−−
A =
2
2
()()
.
()()
xy xyxy
xyxy xy
−−
−−
A =
1
Vậy giá trị của biểu thức A luôn là hằng số với mọi giá trị thích hợp x và y.
Ví dụ 2. Cho biểu thức
B =
2 11
1 11
xx
xx x x x
+−
+−
+ −+ +
a
) Rút gọn B.
b) Ch
ứng minh rằng B luôn luôn có giá trị không âm với mọi giá trị thích hợp của x.
Giải
a) Điều kiện
0 x≥
. Khi đó ta có:
B =
2 ( 1)( 1) ( 1)
( 1)( 1)
x x x xx
x xx
++ − + − − +
+ −+
B =
21 1
( 1)( 1)
x x xx
x xx
+ + −− + −
+ −+
B =
( 1)( 1)
xx
x xx
+
+ −+
B =
( 1)
( 1)( 1)
xx
x xx
+
+ −+
B =
1
x
xx−+
b) Ta cos
0 x≥
nên
0x ≥
2
13
1( )
24
xx x x− += − +
với mọi x.
Do đó B =
0
1
x
xx
≥
−+
với mọi
0x ≥
.
Ví dụ 3. Cho biểu thức C =
12
:1
1
11
x
x
x xx x x


−−


+
− −+ −


a
) Rút gọn C.
b) Chứng minh rằng C luôn luôn có giá trị âm với mọi giá trị thích hợp của x.
Gi
ải
a) Điều kiện
0 ; 1xx>≠
. Khi đó ta có:
C =
12 1
:
1
1 ( 1)( 1)
xx
x
x xx

−−
−

+
− −+

C =
1 2 ( 1)
.
( 1)(x 1) 1
xx
x xx
+− − +
−+ −+
C =
( 1)( 1) ( 1)
.
( 1)(x 1) 1
xx x
x xx
− + −+
−+ −+
C =
( 1)
1
x
xx
−+
−+
b) Ta có
0 ; 1xx≥≠
nên
( 1) 0x− +<
:
2
13
1 0.
24
xx x

− += − + >


Do đó C =
( 1)
0
1
x
xx
−+
−+
với mọi giá trị thích hợp của x.
Ví dụ 4. Cho biểu thức D =
1 61
2:
23(23)(1) 1
x xx
x xx x

−+
−+


− −+ +

.
a) Rút gọn D.
b) Chứng minh rằng
3
2
D <
Giải
a) Điều kiệ
n:
9
0 ; .
4
xx≥≠
Khi đó ta có:
D =
2(2 3) ( 1) 6 1 (2 3)
:
23 (23)(1)
x x x xx
x xx
− − − ++ −
− −+
D =
4 6 16 1 2 3
:
23 (23)(1)
x x x xx
x xx
− − + ++ −
− −+
D =
3 5 (2 3)( 1)
.
2 323 1
x xx
x xx
− −+
− ++
D =
3 5 (2 3)( 1)
.
2 3 (2 1)( 1)
x xx
x xx
− −+
− ++
D =
35
21
x
x
−
+
b) Xét hi
ệ
u
3 5 6 10 6 3 13
0
21 2(21) 2
2
(2 1
3
2
)
3
D
x xx
x xx
−= −
− −− − −
= <
+
=
++
Vậy
3
2
D <
Nh
ận xét: Về mặt phương pháp, muốn chứng minh
3
2
D <
ta chứng minh
3
0
2
D −<
Ví dụ 5. Cho biểu thức P =
11 4
:2 .
1
11
x
x
xx

−

+−


−
−−


a
) Rút gọn P.
b) Tìm giá trị lớn nhất của P
Giải
a) Điều kiện:
0 ; 1xx≥≠
. Khi đó ta có:
P =
( 1) 1 2.( 1) ( 4)
:
( 1)( 1) 1
x xx
xx x
++ −− −
−+ −
P
=
21
.
( 1)( 1) 2
xx
xx x
+−
−+ +
P =
1
1x +
.
b) Ta có P =
11
1
1
1x
≤=
+
vì
0x ≥
Do đó maxP = 1 đạt được khi
00xx=⇔=
Ví d
ụ 6. Cho biểu thức Q =
3 3 14 3
.
92
33
xx x
x
xx

−+ −
+−

−
+−

a
) Rút gọn Q.
b) Tìm giá trị nhỏ nhất của Q
Gi
ải
a) Điều kiện:
0 ; 9xx≥≠
. Khi đó ta có:
Q =
22
( 3) 3) 14 3
.
2
( 3)( 3)
xx x
xx
−+++ −
+−
Q =
x696914 3
.
2
( 3)( 3)
x xx x
xx
− +++ ++ −
+−
Q =
2 32 3
.
2
( 3)( 3)
xx
xx
+−
+−
Q =
16
3
x
x
+
+
b) Ta có Q =
16
3
x
x
+
+
=
9 25 25
3
33
x
x
xx
−+
= −+
++
25
36
3
x
x
= ++ −
+
25
2 ( 3). 6
3
x
x
≥+ −
+
(bất đẳng thức cô si)
> 10 – 6 = 4
Dấu “ = “ xảy ra khi và chỉ khi
25
3
3
x
x
+=
+
2
( 3) 25
35
x
x
⇔ +=
⇔ +=
2
( 3) 25
35
4
x
x
x
⇔ +=
⇔ +=
⇔=
4x⇔=
(thỏa mãn điều kiện)
Vậy minQ = 4 khi x = 4
D
ạng 5. CHỨNG MINH ĐẲNG THỨC
Phương pháp giải
Ví d
ụ 1. Chứng minh đẳng thức sau với
0 ; 0 x y và x y≥≥ ≠
:
4
:
x y xy x y
x
xy
xy x xy

+−
−=


−
−+

Gi
ải
Xét vế trái T :
T =
4
:
x y xy x y
xy
xy x

+−
−


−
−

T =
2
( )4
.
( )( )
x y xy
x
xyxy xy

+−


−+ −

T =
24
.
( )( )
x xy y xy
x
xyxy xy

+ +−


−+ −

T =
2
()
.
( )( )
xy
x
xyxy xy

−


−+ −

T =
x
xy+
Ta th
ấy vế trái đúng bằng vế phải nên đẳng thức đã cho là đúng.
Ví dụ 2. Chứng minh đẳng thức sau với
0 ; 0 x y và x y≥≥ ≠
:
2
: (x y) 1
xx yy y
xy
xy xy

+
− −=−


++

Gi
ải
Xét vế trái T :
T =
: (x y)
xx yy
xy
xy

+
−−


+

T =
( )( )
1
.
x y x xy y
xy
xy
xy

+ −+
−


−
+

T =
2
()
( )( )
xy
x yx y
−
+−
T =
xy
xy
−
+
Xét v
ế phải P :
P =
2xy y xy
xy xy
+− −
=
++
Rõ ràng T =
P , suy ra điều phải chứng minh.
C. BÀI TẬP TỰ LUYỆN
1. Rút gọn các biểu thức sau :
a)
23 1
6 3 4 12
32 6
+−+
;
b)
33
6 325 236 29a a ab a+− −
với
, 0ab>
.
2. Biến đổi biểu thức
11
11
xx
xx
+−
−
−+
về dạng
2
2
1
1
m
x
x
−
−
, trong đó
1x >
.
Tính giá trị của m.
3. Rút gọn rồi tính giá trị của biểu thức P với x = 0,36 :
P =
36
.
9
33
xx
x
xx
−−
−
+−
4. Ch
ứng minh đẳng thức sau với
0; 0;x y xy≥≥≠
:
1
4
:
xyxy y
x
xy
x y x yy y

+− −
−=


−
− +−

5. Cho bi
ểu thức P =
1 11
.
11
x
x
xx x x

−

+−


−+ +


a
) Rút gọn P.
b) Tìm các giá trị nguyên của x để P có giá trị nguyên.
6*. Cho biểu thức P =
6 36
:
36
6 2( 3)(x 2 3)
x x xx x
x
xx x x

−−
−

−
+ −− +

.
a) Rút gọn P.
b) Với giá trị nào của x thì P có giá trị lớn nhất ? Gía trị lớn nhất đó là bao nhiêu?
7*. Cho biểu thức P =
2 3 3 2 15 11
3 1 x 2 3)
xx x
xx x
+− −
+−
+ − +−
a
) Rút gọn P.
b) Tìm giá trị nhỏ nhất của P.
HƯỚNG DẪN GIẢI – ĐÁP SỐ
1. a) 2
√
6 b)
( )
35 4ab−
2. Khử mẫu của biểu thức lấy căn ta được
2
2
2
1
1
x
x
−
−
, suy ra m = 2.
3. P =
3
3
x
x
−
+
với điều kiện x ≥ 0 ; x ≠ 9. Khi đó x = 0,36, ta có P =
2
3
−
.
4. Rút gọn vế trái được
4
14
.
xy
x
xy xy
y
=
−−
.
5. a) P =
2
( 0);
x
x
x
−
>
b)
[ ]
1; 4x∈
.
6.
a)
6
x2 3x−+
với điều kiện
0; 9; 6xxx>≠≠
b) P =
2
66
3
2
( 1) 2x
≤=
−+
( vì
2
( 1) 0x −≥
).
Suy ra maxP = 3 đạt được khi x = 1.
7. a) P =
52
( 0; 1)
3
x
xx
x
−
≥≠
+
.
b) P =
5 15 17 17
5
33
x
xx
+−
= −
++
17
5
3
P ≥−
( vì
√
𝑥 ≥ 0 ).
2
3
P ≥−
( dấu bằng xảy ra khi x = 0).
Vậy minP =
2
3
−
, đạt được khi x = 0.
§
9. CĂN BẬC BA
A. TRỌNG TÂM KIẾN THỨC
1. Khái niệm căn bậc ba.
Căn bậc ba của một số a là số x sao cho x
3
= a.
3
3
ax x a=⇔=
.
Như vậy,
( )
3
3
3
3
a aa= =
Nhận xét :
- Căn bậc ba của một số dương là số dương ;
- Căn bậc ba của một số âm là một số âm ;
- Căn bậc ba của số 0 là số 0 ;
2. Tính chất
•
33
ab ab<⇔ <
;
•
3 33
.ab a b=
;
•
3
3
3
aa
b
b
=
( với
0b ≠
).
B. CÁC D
ẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. TÌM CĂN BẬC BA CỦA MỘT SỐ
Phương pháp giải
3
.aa=
Ví d
ụ 1. Hãy tìm :
a)
3
216
b)
3
729
c)
3
331
.
Giải
a)
3
3
3
216 6 6= =
b)
3
3
3
729 9 9= =
c)
3
3
3
331 11 11= =
Ví dụ 2. Hãy tìm :
a)
3
343−
b)
3
1000−
c)
3
1728−
.
3
3
3
23 4625<=
Gi
ải
𝑎)
3
3
3
343 7 7− =−=−
b)
3
3
3
1000 10 10− =−=−
c)
3
3
3
1728 12 12− =−=−
Ví d
ụ 2. Hãy tìm :
a)
3
8
27
b)
3
125
512
−
c)
3
0,064−
Gi
ải
a)
3
8
27
=
3
3
22
33

=


b)
3
125
512
−
=
3 33
3 27.12 1 324 1 343 1 7 1 6−= −< −= −=
c)
3
0,064−
=
( )
3
3
0,4 0,4−=−
.
Dạng 2. SO SÁNH
Phương pháp giải
• Đưa các thừa số vào trong dấu căn :
3
3
3
a b ab=
.
•
33
ab⇔<
Ví dụ 1. So sánh
a) 7 và
3
345
b)
3
2 6
và
3
32
Gi
ải
a)
33
7 343 345= <
;
b)
3
3
3
3
22 86 .6 4= =
3
3
3
3
33 42 .2 5= =
48 54<
nên
3
3
26 32<
Ví d
ụ 2. So sánh
a)
3
2
18
3
và
3
3
12
4
b)
3
130 1+
và
3
3 12 1−
Giải
a) Ta có
3
2
18
3
=
3
3
33
2 16 1
.18 5
3 33

= =


3
3
12
4
=
3
3
33
3 81 1
.12 5
4 16 16

= =


Vì
11
55
3 16
>
nên
3
2
18
3
>
3
3
12
4
b) Ta có
3
130 1+
>
3
125 1 5 1 6+=+=
;
3
3 12 1−
=
3 33
3 27.12 1 324 1 343 1 7 1 6−= −< −= −=
;
Vậy
3
130 1+
>
3
3 12 1−
.
Ví dụ 3. Cho a < 0 , hỏi số nào lớn hơn trong hai số
3
2a
và
3
3a
Gi
ải
Ta có 2 < 3 nên
23aa>
( vì
0a <
).
Do đó
3
2a
>
3
3a
.
Dạng 3. THỰC HIỆN CÁC PHÉP TÍNH
Phương pháp giải
Ví d
ụ 1. Rút gọn các biểu thức
a)
33 3
8 27 64+− +−
; b)
33 3
54 16 128−− +
Gi
ải
a) Ta có
33 3
8 27 64+− +−
( ) ( )
2 3 4 5= +− +− =−
b) Ta có
33 3
54 16 128−− +
=
3 33
33
3333
3
3 .2 ( 2) .2 4 .2 3 2 2 2 4 2 9 2.−− + = + + =
Ví dụ 2. Tính
a)
33 3 3
16. 13.5 120 : 15−
; b)
3 33
( 2 1)( 4 2 1).+ −+
Giải
a)
33 3 3
16. 13.5 120 : 15−
=
33
16.13.5 120 :15+
=
33
216 8−
6–2 4= =
6–2 4= =
b)
3 33
( 2 1)( 4 2 1).+ −+
=
3333
3
842421−++−+
2 1 3= +=
Nhận xét: Để tính tích trên có thể sử dụng hằng đẳng thức :
(a + b)(a
2
–ab + b
2
) = a
3
+ b
3
Ta có
33
3 33 3
(2 1)(4 2 1) (2) 1 21 3.+ − + = + = +=
Ví dụ 3. Tính
a)
3
3 33
( 5 1) 3 5( 5 1)+− +
; b)
3
3 3
3
3
(4 3) 62(2 1)−+ −
Giải
a) Ta có
3
3 33
( 5 1) 3 5( 5 1)+− +
=
33 33
5 3 25 3 5 1 3 25 3 5 6.+ + +− − =
b) Ta có
3
3 3
3 3 3
3 33
(4 3) 62(2 1) 4 332 316 2 64 62− + − =− + −+ −
=
33 33
6 64 62 2 64 62 2−+−+−=
.
Ví dụ 4. Tính A =
33
52 52+− −
.
Giải
Để tính giá trị của A, ta tính A
3
sau đó suy ra A.
Bạn nên nhớ hằng đẳng thức (a - b)
3
= a
3
-b
3
– 3ab(a – b).
Ta có
3
A =
(
33
52 52+− −
)
3
3
A =
( ) ( )
( )( ) ( ) ( )
3 33
52 52 3 52 52 52 52

+− −− + − +− −


3
43AA= −
3
3 – 4 0AA+=
2
( 1)( 4) 0A AA⇔ − ++ =
10A⇔ −=
( vì
2
40AA++>
)
Vậy
1A =
Ví dụ 4. Rút gọn biểu thức.
a)
3
3
1 3 ( 1)x xx++ +
; b)
2
3
3
1
1
x
xx
+
−+
Gi
ải
a) Ta có
3
3
1 3 ( 1)x xx++ +
=
3
3
( 1) 1xx+=+
.
b)
2
3
3
1
1
x
xx
+
−+
=
2
3
33
3
2
3
3
( 1)( 1)
1.
1
x xx
x
xx
+ −+
= +
−+
Dạng 4. GIẢI PHƯƠNG TRÌNH
• Nếu x
= a thì x =
3
3
Ví d
ụ 1. Giải phương trình
a)
3
731x +−=
; b)
2
3
1 20x− +=
.
Giải
a) Ta có
33
7 3 1 7 4 7 64 57x xx x+−=⇔ +=⇔+= ⇔=
.
b) Ta có
2 2 22
33
1 2 0 1 2 1 8 9 3.x x x xx−+=⇔−=−⇔−=−⇔=⇔=±
Ví dụ
1. Giải phương trình
a)
3 33
1000 64 27 15xxx−−=
; b)
3
33xx−+=
.
Gi
ải
a) Ta có
3 33
1000 64 27 15xxx−−=
333
3
3
10 4 3 15
3 15
5
125.
xxx
x
x
x
⇔ −−=
⇔=
⇔=
⇔=
| 1/54
| | Tải xuống

Có thể bạn quan tâm:

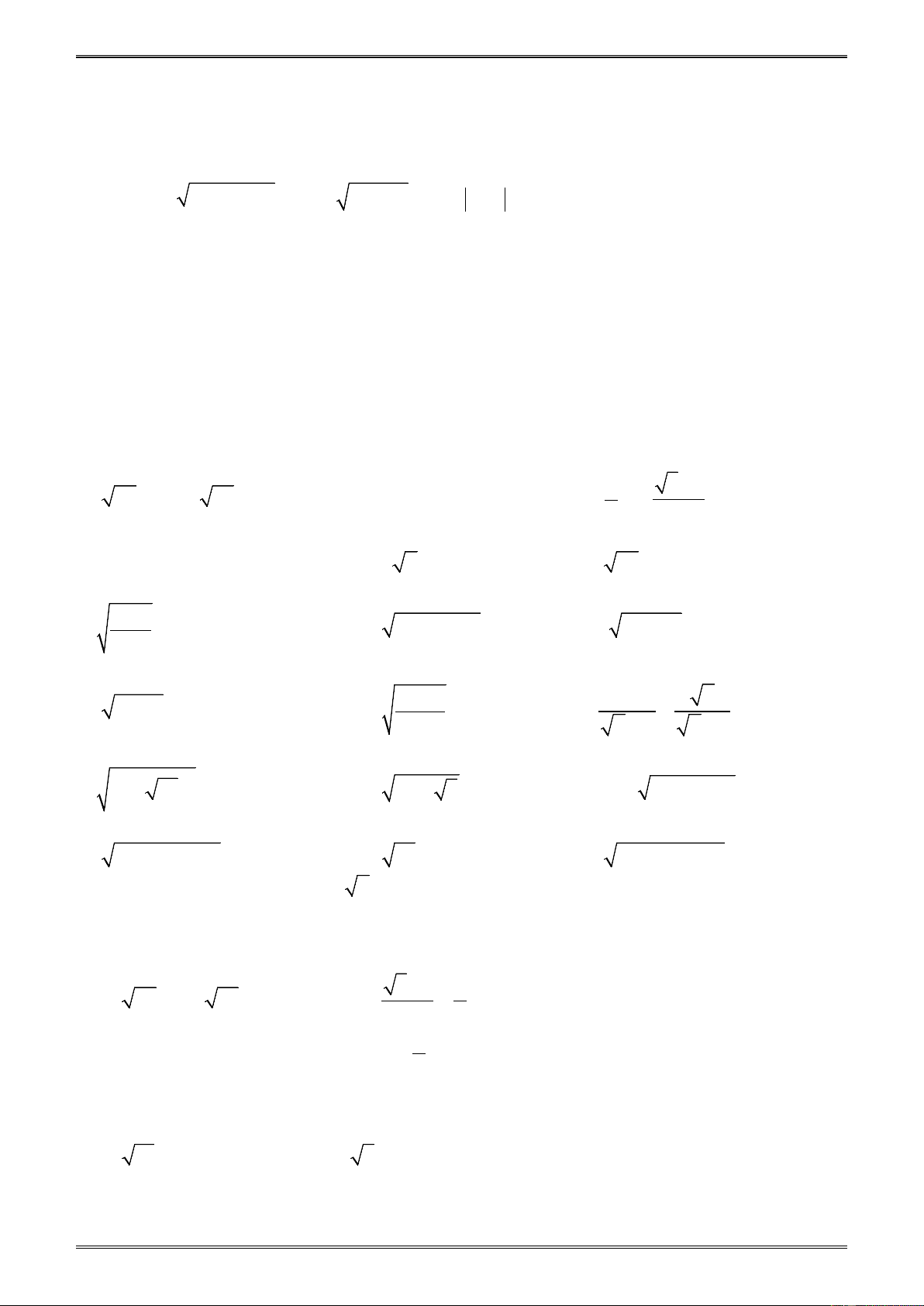
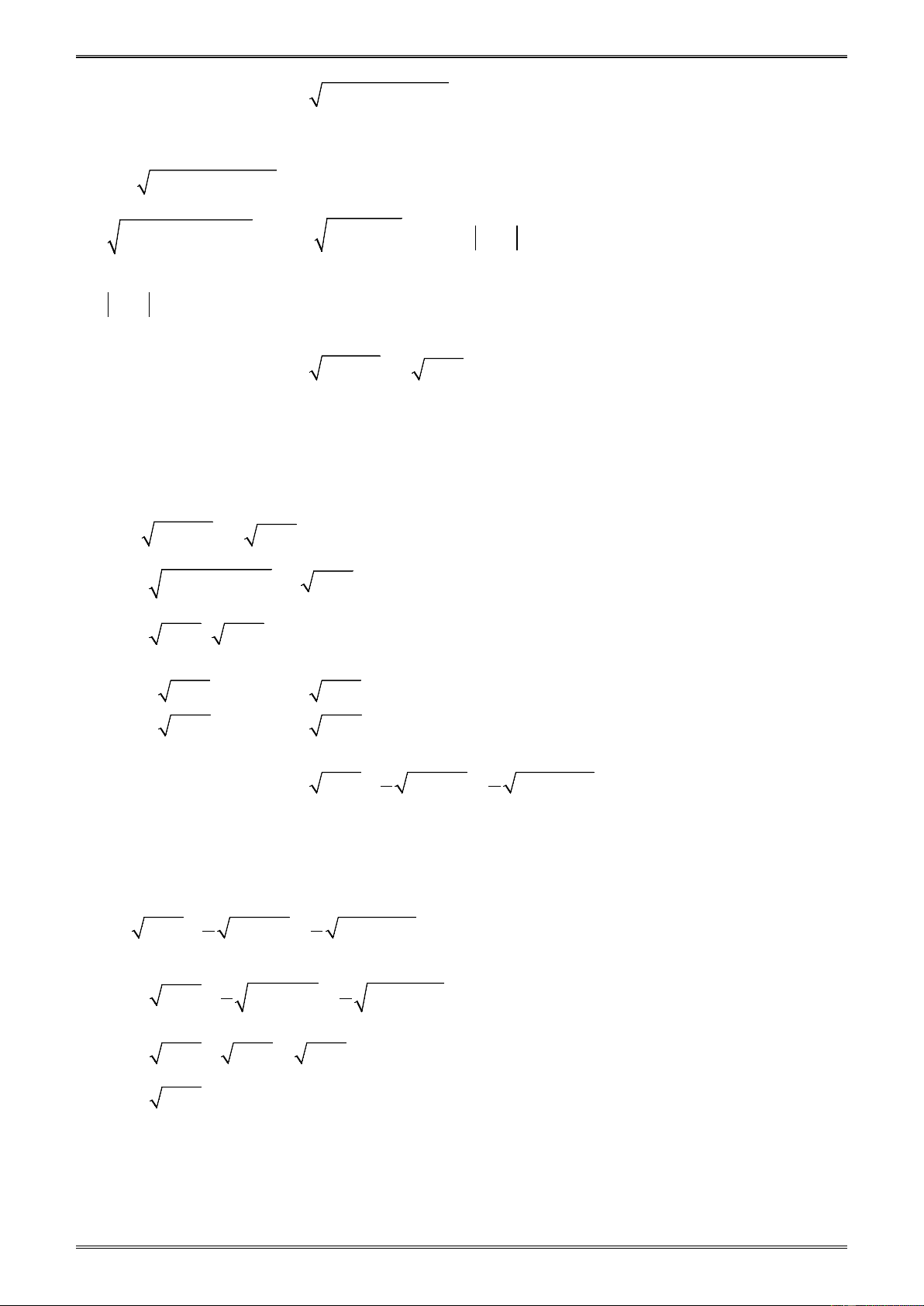
Preview text:

MỤC LỤC
PHẦN ĐẠI SỐ ........................................................................................................................... 2
Chương I. CĂN BẬC HAI, CĂN BẬC BA ............................................................................... 2
§1. CĂN BẬC HAI ................................................................................................................... 2
§2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC 2
A = A ........................................ 2
§3. LIÊN HỆ GIỮA PHÉP NHÂN VÀ PHÉP KHAI PHƯƠNG .......................................... 10
§4. LIÊN HỆ GIỮA PHÉP CHIA VÀ PHÉP KHAI PHƯƠNG ............................................ 20
§6. §7. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI .................... 26
§8. RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI ............................................... 37
§9. CĂN BẬC BA .................................................................................................................. 50 PHẦN ĐẠI SỐ
Chương I. CĂN BẬC HAI, CĂN BẬC BA §1. CĂN BẬC HAI
§2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC 2 A = A
A. TRỌNG TÂM KIẾN THỨC
1. Căn bậc hai số học
Với số dương a, số a được gọi là căn bậc hai số học của a.
Số 0 cũng được gọi là căn bậc hai số học của 0. Với a ≥ 0 , ta có: x 0 ≥ a = x ⇔  2 x = a.
Với hai số a và b không âm, ta có a < b ⇔ a < b.
2. Căn thức bậc hai
Với A là một biểu thức đại số , người ta gọi
A là căn thức bậc hai của A, còn A được gọi
là biểu thức lấy căn hay biểu thức dưới dấu căn.
A xác định ( hay có nghĩa ) khi A lấy giá trị không âm. A nÕu A ≥ 0 Ta có 2
A = A = −A nÕu A < 0.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. TÌM CĂN BẬC HAI SỐ HỌC CỦA MỘT SỐ Phương pháp giải
Dựa vào định nghĩa căn bậc hai số học của một số không âm: x 0 ≥ a = x ⇔  2 x = a.
Ví dụ 1. Tìm căn bậc hai số học rồi tìm căn bậc hai của: 2  2  a) 121 b) −    5  Giải a) Ta có 2
121 = 11 v× 11 ≥ 0 vµ 11 = 121.
Do đó số 121 có hai căn bậc hai là 11 và -11. 2  2  2 2 2 2  2   2  b) − =   vì ≥ 0 và = − .      5  5 5  5   5  2 Do đó số  2  2 2 − 
 có hai căn bậc hai là và − .  5  5 5
Ví dụ 2. Tính giá trị của biểu thức: 0, 09 + 7. 0,36 − 3 2, 25. Giải
Ta có 0, 09 + 7. 0,36 − 3 2, 25
= 0,3 + 7.0, 6 − 3.1,5 = 0,3 + 4, 2 − 4,5 = 0  9 9 
Ví dụ 3. Giá trị của biểu thức sau là số vô tỉ hay hữu tỉ:  1 - .18 ? 16 16   Giải  9 9   25 9   5 3   1 - .18 =  - .18 = − .18 = 9 = 3.   16 16 16 16      4 4 
Vậy giá trị của biểu thức đã cho là một số hữu tỉ, hơn nữa còn là một số tự nhiên.
Dạng 2. SO SÁNH CÁC CĂN BẬC HAI SỐ HỌC Phương pháp giải
Dựa vào tính chất : Nếu a,b ≥ 0 thì a < b ⇔ a < b.
Ví dụ 1. Không dung máy tính hoặc bảng số , hãy so sánh 8 và 65. Giải
Cách 1: Ta có 8 = 64 . Vì 64 < 65 nên 8 < 65 . Cách 2: Vì = ( )2 2 8 64; 65 = 65 Nên < ( )2 2 8 65 , suy ra 8 < 65.
Cách giải này dựa vào tính chất: Nếu a, b > 0 và 2 2
a < b thì a < b.
Như vậy, để so sánh hai số dương ta có thể so sánh các bình phương của chúng.
Ví dụ 2. Không dung máy tính hoặc bảng số , hãy so sánh 15 −1 và 10. Giải
Ta có 15 −1 < 16 −1 = 4 – 1 = 3, 10 > 9 = 3. Vậy 15 −1 < 10.
Ví dụ 3. Với a < 0 thì số nào lớn hơn trong hai số −a và 2 − a ? Giải
Ta có -1 > -2 nên –a < -2a (vì a < 0 ). Do đó −a < 2 − a .
Dạng 3. GIẢI PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH Phương pháp giải Với a ≥ 0 : • 2
x = a khi x = ± a . • 2
x = a khi x = a . • 2
x < a khi 0 ≤ x < a .
Ví dụ 1. Giải phương trình: 2 3x = 0, 75. Giải Ta có 2 2
3x = 0, 75 ⇔ x = 0, 25.
Do đó x = ± 0,25 = 0, ± 5.
Ví dụ 2. Giải phương trình: 2 3x = 12. Giải ĐKXĐ: x ≥ 0. Ta có : 2 3x = 12 ⇔
3x = 6 ⇔ 3x = 36 ⇔ x = 12 ( thỏa mãn điều kiện). 1
Ví dụ 3. Tìm số x không âm, biết 5x < 10. 2 Giải 1 Với x ≥ 0 ta có : 5x < 10 ⇔ 5x < 20 2
⇔ 5x < 400 ⇔ x < 80.
Vậy 0 ≤ x < 80.
Ví dụ 4. Tính tổng các giá trị của x thỏa mãn đẳng thức 2 x + 25 = 13. Giải Ta có : 2 x + 25 = 13 2 ⇔ x + 25 = 169 2 ⇔ x = 169 − 25 2 ⇔ x = 144 ⇔ x = 12. ±
Vậy tổng các giá trị của x thỏa mãn đẳng thức đã cho là (-12) + 12 = 0.
Dạng 4. TÌM ĐIỀU KIỆN ĐỂ A CÓ NGHĨA Phương pháp giải •
A có nghĩa khi A ≥ 0; •
1 có nghĩa khi A > 0. A
Ví dụ 1. Tìm x để căn thức 5 − 2x có nghĩa. Giải
5 − 2x có nghĩa khi 5 5 − 2x ≥ 0 ⇔ 2 − x ≥ 5 − ⇔ x ≤ . 2 1
Ví dụ 2. Tìm x để căn thức có nghĩa. 2 x − 4x + 4 Giải 1 1 có nghĩa khi có nghĩa. 2 x − 4x + 4 2 (x − 2) Điều đó xảy ra khi 2
(x − 2) > 0 ⇔ x ≠ 2.
Ví dụ 3. Với giá trị nào của x thì biểu thức 2 25 − x có nghĩa? Giải 2
25 − x có nghĩa khi 2 25 − x ≥ 0 2 ⇔ −x ≥ 25 − 2 ⇔ x ≤ 25 ⇔ x ≤ 5 ⇔ 5 − ≤ x ≤ 5. 1
Ví dụ 4. Tìm các giá trị của x để biểu thức có nghĩa 2 x −100 Giải 1 có nghĩa khi 2 x −100 > 0 2 x −100 2 ⇔ x > 100 ⇔ x > 10 x > 10 ⇔ x < 10 −
Ví dụ 5. Có bao nhiêu giá trị nguyên của x để biểu thức M = x + 4 + 2 − x có nghĩa? Giải x + 4 ≥ 0 x ≥ 4 − M có nghĩa khi  ⇔  2 − x ≥ 0
x ≤ 2 Vì x ∈ Z nên x ∈{ 4; − 3 − ; 2; − 1 − ;0;1; } 2
Vậy có 7 giá trị nguyên của x để biểu thức M có nghĩa
Dạng 5. RÚT GỌN BIỂU THỨC DẠNG 2 A Phương pháp giải
Vận dụng hằng đẳng thức: A nÕu A ≥ 0 2
A = A = −A nÕu A < 0. 1
Ví dụ 1. Rút gọn biểu thức 2 A = x − x + . 4 Giải 2 1  1  1 2 A = x − x + = x − = x −   4  2  2 1 1 Nếu x ≥ thì A = x − 2 2 1 1 Nếu x < thì A = − x 2 2
Ví dụ 2. Rút gọn biểu thức 4 6 B = x + x . Giải = + = ( )2 + ( )2 4 6 2 3 B x x x x 2 3 2 3
= x + x = x + x . Nếu x ≥ 0 thì 2 3
B = x + x ; Nếu x < 0 thì 2 3
B = x − x .
Ví dụ 3. Tính giá trị của biểu thức C = 3 − 2 2 − 6 − 4 2 . Giải 2 2
C = 3 − 2 2 − 6 − 4 2 = ( 2 − ) 1 − (2 − 2)
= 2 −1 − 2 − 2 = 2 −1− (2 − 2) = 2 2 − 3.
Ví dụ 4. Tìm giá trị nhỏ nhất của biểu thức 2
D = 4x − 4x +1 + 3. Giải 2
D = 4x − 4x +1 + 3 = ( x − )2 2 1
+ 3 = 2x −1 + 3 ≥ 3 với mọi x 1 Vậy minD = 3 khi x = . 2
Ví dụ 5. Tìm x, biết 2
x − 6x + 9 + 7x = 13. Giải Ta có 2
x − 6x + 9 + 7x = 13 ⇔ (x − )2 3
+ 7x = 13
⇔ x − 3 + 7x = 13 (1)
Nếu x ≥ 3 thì x − 3 = x − 3. Khi đó (1) trở thành
x − 3 + 7x = 13 ⇔ 8x = 16 ⇔ x = 2 ( không thuộc khoảng đang xét )
Nếu x < 3 thì x − 3 = 3 − .
x Khi đó (1) trở thành 5
3 − x + 7x = 13 ⇔ 6x = 10 ⇔ x =
( thuộc khoảng đang xét ) 3
Vậy giá trị của x thỏa mãn đẳng thức đã cho là 5 x = . 3
Ví dụ 6. Cho biểu thức: 2
P = 3x − x −10x + 25. a) Rút gọn biểu thức P;
b) Tính giá trị của P khi x = 2. Giải a) 2
P = 3x − x −10x + 25.
= x − (x − )2 3 5
= 3x − x − 5 .
• Nếu x ≥ 5 thì P = 3x – ( x – 5 ) = 2x + 5;
• Nếu x < 5 thì P = 3x + ( x – 5 ) = 4x – 5.
b) Khi x = 2 < 5 thì giá trị của biểu thức là : P = 4.2 – 5 = 3.
Lưu ý: Nếu bạn thay x = 2 vào biểu thức 2x + 5 để tính giá trị của P thì bạn sai lầm vì
biểu thức P = 2x + 5 khi x ≥ 5 .
Ví dụ 7. Cho biểu thức: 2
Q = 2x − x + 2x +1. a) Rút gọn biểu thức Q;
b) Tính các giá trị của x để Q = 7 . Giải: a) 2 2 Q = 2x −
x + 2x +1 = 2x − (x +1) = 2x − x +1 * Nếu x ≥ 1
− thì Q = 2x − (x +1) = x −1 * Nếu x < 1
− thì Q = 2x + (x +1) = 3x +1
b) Ta phải xét hai trường hợp:
* Q = 7 ⇔ x −1 = 7 ⇔ x = 8 ( Không thỏa mãn x ≥ −1)
* Q = 7 ⇔ 3x +1 = 7 ⇔ x = 2 ( Không thỏa mãn x < −1).
Vậy Q = 7 khi x = 8
C. BÀI TẬP TỰ LUYỆN
1. Không dùng máy tính hoặc bảng số, hãy so sánh: 1 3 −1 a) 26 + 3 và 63 ; b) và 2 2 2. Tìm x, biết: a) 2 5x = 80 b) 2 x = 1 c) 3x ≤ 6
3.Tìm x để các căn thức bậc hai sau có nghĩa: 2 a) b) 2 x + 2x +1 c*) 2 x − 4x 9 − x
4. Tìm x để các biểu thức sau có nghĩa: 1 1 x a) 2 9 − x b) c) + 2 x − 4 x + 2 x − 3
5. Rút gọn các biểu thức sau: a) ( − )2 3 10 b) 9 − 4 5 c) 2 3x − x − 2x +1
6. Giải phương trình: a) 2 x −10x + 25 = 2 b) 2 x = 3x − 2 c) 2 4x −12x + 9 = x + 7
7*. TÌm các giá trị của xsao cho x > x .
HƯỚNG DẪN GIẢI – ĐÁP SỐ 3 −1 1 1. a) 26 + 3 > 63 b) < 2 2 1 2. a) x = 4 ± b) x = c) 0 ≤ x ≤ 12 4 3. a) x < 9 b) x ∈ R
c) x ≥ 4 hoặc x ≤ 0 4. a) 3 − ≤ x ≤ 3 b) x > 2 hoặc x < -2
c) x ≥ 0 và x ≠ 9  2x +1 x ≥ 1 5. a) 10 − 3 b) 5 − 2 c)  4x − nếu 1 x < 1  4 
6. a) x = 3 hoặc x = 7 b) x=1 c) x ∈ 10  ;−   3 
7. x > x
(1). Điều kiện x > 0 . Khi đó 2 (1) ⇔ x > x
(do hai vế của (1) đều dương) 2
⇔ x − x > 0
⇔ x(1− x)>0 x > 0 x > 0 ⇔  ⇔  ⇔ 0 < x < 1 1  − x > 0 x < 1
§3. LIÊN HỆ GIỮA PHÉP NHÂN VÀ PHÉP KHAI PHƯƠNG
A. TRỌNG TÂM KIẾN THỨC 1. Định lí:
Với hai số a và b không âm, ta có: . a b = a. b 2. ÁP dụng
Muốn khai phương một tích của các số không âm, ta có thể khai phương từng thừa số
rồi nhân các kết quả với nhau.
Muốn nhân các căn bậc hai của các số không âm, ta có thể nhân các số dưới dấu căn rồi
khai phương kết quả đó. 3. Chú ý:
Vói hai biểu thức A và B không âm, ta có: . A B =
A. B và ngược lại A. B = . A B . Đặc
biệt khi A ≥ 0 , ta có: ( )2 2 A = A = A
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: KHAI PHƯƠNG MỘT TÍCH Phương pháp giải:
Dựa vào quy tắc khai phương một tích:
Với a,b ≥ 0 thì .
a b = a. b Ví dụ 1: Tính: a) 12,1.160 b) 2500.4,9.0,9 Giải:
a) 12,1.160 = 121. 16 =11.4 = 44 b) 2500.4,9.0,9 = 25.49.9 = 25. 49. 9 = 5.7.3 = 105 Ví dụ 2: Tính: a) 2 2 41 − 40 b) 81.6, 25 − 2, 25.81 Giải: a) 2 2 41 − 40 =
(41 − 40)(41 + 40) = 1.81 = 1.9 = 9
81.6, 25 − 2, 25.81 = 81.(6, 25 − 2, 25) = 81. 4 = 9.2 = 18
Ví dụ 3: Đẳng thức x(1− y) = x. 1− y đúng với những giá trị nào của x và y. Giải:
Theo địnhlí khai phương một tích thì x(1− y) =
x. 1− y khi x ≥ 0 à
v 1-y ≥ 0 hay x ≥ 0 và y ≤1 .
Ví dụ 4: Cho cac biểu thức M = (x −1)(x + 3) à v N = x −1. x + 3
a) TÌm các giá trị của x để M có nghĩa;N có nghĩa.
b) Với giá trị nào của x thì M=N? Giải:
M có nghĩa khi (x −1)(x + 3) ≥ 0.  − ≥  ≥ Trườ x 1 0 x 1 ng hợp 1:  ⇔  ⇔ x ≥1 x + 3 ≥0 x ≥ − 3  − ≤  ≤ Trườ x 1 0 x 1 ng hợp 2:  ⇔  ⇔ x ≤ − 3 x + 3 ≤0 x ≤ − 3
Vậy M có nghĩa khi x ≥ 1 hoặc x ≤ 3 − .  − ≥  ≥ N có nghĩa khi x 1 0 x 1  ⇔  ⇔ x ≥1 x + 3 ≥0 x ≥ − 3
b) Để M và N đồng thời có nghĩa thì x ≥1
Khi đó ta có M = N theo định lí khai phương một tích.
Dạng 2: NHÂN CÁC CĂN BẬC HAI Phương pháp giải:
Dựa vào quy tắc nhân các căn bậc hai :
Với a,b ≥ 0 thì a. b = a.b Ví dụ 1: TÍnh: a) 72. 50 b) 12,8. 0, 2 Giải:
a) 72. 50 = 72.50 = 36.100 = 6.10 = 60
b) 12,8. 0, 2 = 12,8.0, 2 = 128.0, 02 = 64.0, 04 = 8 .0, 2 = 1, 6 Ví dụ 2: Tính: 2 12 1 a) 40. 20. 4,5 b) . . 3 25 2 Giải: a) 40. 20. 4,5 = 40.20.0,5 = 400.9 = 20.3 = 60 2 12 1 2 12 1 4 2 b) . . = . . = = 3 25 2 3 25 2 25 5
Ví dụ 3: Thực hiện các phép tính: a) ( 20 + 45 − 5). 5 b) ( 12 + 3)( 27 − 3) c) ( 5 − 3 + ) 1 ( 5 − ) 1 Giải:
a) ( 20 + 45 − 5). 5 = 100 + 225 − 25 =10 +15 − 5 = 20
b) ( 12 + 3)( 27 − 3) = 324 − 36 + 81 − 9 = 18 − 6 + 9 − 3 = 18 c) ( 5 − 3 + ) 1 ( 5 − )
1 = 5 − 5 − 15 + 3 + 5 −1 = 4 − 15 + 3 . Ví dụ 4: Tính: a) ( + )2 7 3 b) ( − )2 8 2 c) (3 5 − 2 7 )(3 5 + 2 7 ) Giải: 2 2 a) ( + )2 7 3
= ( 7) + 2 7. 3 + ( 3) = 7 + 2 21 + 3 =10 + 2 21 2 2 b) ( − )2 8 2
= ( 8) − 2 8. 2 + ( 2) = 8− 2 16 + 2 = 2 2 2
c) (3 5 − 2 7 )(3 5 + 2 7 ) = (5 3) − (2 7 ) = 25.3 − 4.7 = 47
Dạng 3: RÚT GỌN, TÍNH GIÁ TRỊ CỦA BIỂU THỨC: Phương pháp giải:
*Trước hết tìm điều kiện của biến để biểu thức có nghĩa (nếu cần)
* Áp dụng quy tắc khai phương một tích, quy tắc nhân các căn bậc hai, các hằng đẳng thức để rút gọn.
* Thay giá trị của biến vào biểu thức đã rút gọn rồi thực hiện các phép tính.
Ví dụ 1: Rút gọn các biểu thức sau: 3x 5x a) . với x > 0 b) 6 2
x .(x − 2) với x > 2 5 27 Giải: 2 3x 5x 3x 5x x x x a) . = . = = = (Vì x>0 ) 5 27 5 27 9 3 3 b) 6 2 x .(x − 2) 6 2 3 3
= x . (x − 2) = x . x − 2 = x (x − 2) (vì x > 2).
Ví dụ 2: Rút gọn các biểu thức sau: 60 a) 3 15x . b) 2 16(x − 6x + 9) x Giải: a) ĐK: x ≠ 0 . 60 30  x x > 0 3 2 15x .
= 900x = 30 x =  nếu x  30 − x x < 0 4(x − 3) x ≥ 3 b) 2 2
16(x − 6x + 9) = 16(x − 3) = 4 x − 3 =  nếu  4 − (x − 3) x < 3
Ví dụ 3: Rút gọn biểu thức 2 M =
25x ( x − 2 x + ) 1 với 0 < x < 1. Giải: Ta có M =
(x− x + ) = ( x − )2 2 25x 2 1 25 1 = 5 x −1 .
Vì x > 0 nên x = x .
Vì 0 < x < 1 nên x < 1. Do đó x −1 = 1− x
Vậy M = 5x (1− x )
Ví dụ 4: Tính giá trị của các biểu thức sau: a) 4 + 2 3 b) 8 − 2 15 c) 9 − 4 5 Giải: a) + = + + = ( + )2 4 2 3 3 2. 3.1 1 3 1 = 3 +1 b) − = − + = ( − )2 8 2 15 5 2 5. 3 3 5 3 = 5 − 3 c) − = − + = ( − )2 9 4 5 5 2.2. 5 4 5 2 = 5 − 2
Nhận xét: Phương pháp giải trong ví dụ này là biến đổi biểu thức lấy căn thành bình phương
của tổng hay hiệu hai số rồi áp dụng hằng đẳng thức 2 A = A
Ví dụ 5: Rút gọn các biểu thức sau: a) x + 2 x −1
b) x + 2 − 2 x +1 Giải: a) x + x − = x − +
x − + = ( x − + )2 2 1 1 2 1 1 1 1
= x −1 +1 ( ĐK: x ≥1) b) x + − x + = x + −
x + + = ( x + − )2 2 2 1 1 2 1 1 1 1
= x +1 −1 ( ĐK x ≥ 1 − ) Nếu x ≥ 0 thì x +1 −1 = x +1 −1 Nếu x < 0 thì
x +1 −1 = 1 − x +1
Dạng 4: BIẾN ĐỔI MỘT BIỂU THỨC VỀ DẠNG TÍCH Phương pháp giải:
Dùng cách đặt nhân tử chung, nhóm các hạng tử, dùng các hằng đẳng thức,...
Ví dụ 1: Phân tích thành nhân tử: a) 3 − 3 b) x + 3 xy c) x y − y x d) x − x − xy + y Giải: a) 3 − 3 = 3 ( 3 − ) 1 b) x + 3 xy =
x ( x + 3 y ) ( ĐK x ≥ 0; y ≥ 0 ) c) x y − y x =
xy ( x − y ) ( ĐK x ≥ 0; y ≥ 0 )
d ) x − x − xy + y = x ( x − ) 1 − y ( y − ) 1 = ( x − )
1 ( x − y ) ( ĐK x ≥ 0; y ≥ 0 )
Ví dụ 2: Phân tích thành nhân tử: a) 3 x − 25 x b) 9x + 6 xy + y c) 3 3 x + y d) 2
x − 9 − 2 x − 3 Giải: a) 3 x − x = x ( 2 25
x − 25 ) = x ( x − 5)( x + 5) ĐK: x ≥ 0 b) x + xy + y = ( x + y )2 9 6 3
(ĐK: x, y ≥ 0 ). c) 3 3 x +
y = ( x + y )( x − xy + y) (ĐK: x, y ≥ 0 ). d) 2
x − 9 − 2 x − 3 =
x − 3 ( x + 3 − 2) (ĐK: x ≥ 3).
Ví dụ 3. Rút gọn biểu thức: ( 14 + 6 ) 5 − 21 . Giải
( 14 + 6) 5− 21 = 2( 7 + 3) 5− 21 = ( + ) − = ( + ) ( − )2 7 3 10 2 7.3 7 3 7 3 = ( 7 + 3)( 7 − 3) = 4.
Dạng 5: GIẢI PHƯƠNG TRÌNH Phương pháp giải:
• Trước tiên tìm điều kiện để căn thức có nghĩa.
• Áp dụng quy tắc khai phương một tích, áp dụng các hằng đẳng thức 2 A = A ; ( )2 A
= A (với A ≥ 0 ) đưa phương trình đã cho về phương trình đơn giản hơn.
• Có thể đưa về phương trình tích.
Ví dụ 1. Giải phương trình: (x + )2 25. 5 = 15. Giải Ta có (x + )2 25. 5 = 15 x + 5 = 3 x = 2 −
⇔ 5 x + 5 = 15 ⇔ x + 5 = 3 ⇔ ⇔   x + 5 = 3 − x = 8. −
Ví dụ 2. Giải phương trình: 2
9x − 90x + 225 = 6. Giải Ta có: 2
9x − 90x + 225 = 6 ⇔
(x − x + ) = ⇔ (x − )2 2 9 10 25 6 9 5 = 6 ⇔ 3 x − 5 = 6 x − 5 = 2 x = 7 ⇔ x − 5 = 2 ⇔ ⇔   x − 5 = 2 − x = 3.
Ví dụ 3. Giải phương trình: 2
x − 25 = 2 x − 5. Giải 2 2  − ≥  ≥ ĐK: x 25 0 x 25  ⇔  ⇔ x ≥ 5. x − 5 ≥ 0 x ≥ 5 Khi đó 2
x − 25 = 2 x − 5
⇔ (x + 5)(x − 5) − 2 x − 5 = 0
⇔ x − 5 ( x + 5 − 2) = 0  x − 5 = 0  x − 5 = 0
x − 5 = 0 x = 5(TM ) ⇔  ⇔  ⇔    + − =  + = x + 5 = 4 x 5 2 0 x 5 2 x = 1 −  (L).
Ví dụ 4. Giải phương trình: 1 1 x − 5 + 9x − 45 = 25x −125 + 6. 3 5 Giải ĐK: x ≥ 5. 1 1 Ta có x − 5 + 9x − 45 = 25x −125 + 6 3 5 1 ⇔ x − + (x − ) 1 5 9. 5 = 25( x − 5) + 6 3 5
⇔ x − 5 + x − 5 = x − 5 + 6 ⇔ x − 5 = 6 ⇔ x − 5 = 36
⇔ x = 41 (thỏa mãn điều kiện).
Ví dụ 5. Giải phương trình: 1 x + = 2. x Giải ĐK: x > 0. 1 Ta có: x + = 2 x x + − x ⇔ x + − = ⇔ = ⇔ ( x − )2 1 1 2 2 0 0 1 = 0 x x
⇔ x −1 = 0 ⇔ x = 1 (thỏa mãn điều kiện).
Dạng 6: CHỨNG MINH BẤT ĐẲNG THỨC Phương pháp giải
Có thể dùng các phương pháp sau:
• Với a ≥ 0 ; b ≥ 0 thì 2 2
a ≤ b ⇔ a ≤ b ;
• Biến đổi tương đương.
Ví dụ 1: Không dùng máy tính hoặc bảng số, chứng minh rằng: 5 + 8 < 6 + 7. Giải Ta có 5 + 8 < 6 + 7 ⇔ ( + )2 < ( + )2 5 8 6 7
(vì hai vế đều dương)
⇔ 5 + 2 40 + 8 < 6 + 2 42 + 7 ⇔ 13 + 2 40 < 13 + 2 42
⇔ 40 < 42 ⇔ 40 < 42.
Bất đẳng thức cuối cùng hiển nhiên đúng nên bất đẳng thức đã cho là đúng.
Ví dụ 2: Không dùng máy tính hoặc bảng số, chứng minh rằng: 3 + 2 < 2 ( 3 + ) 1 . Giải Ta có ( + )2 3 2 = 3 + 4 3 + 4 = 7 + 4 3 ;   ( + ) 2 =  ( + )2 2 3 1 2 3 1 = 2(3+ 2 3 + ) 1 = 8 + 4 3. 2
Vì 7 + 4 3 < 8 + 4 3 nên ( 3 + 2) <  2 ( 3 +  ) 2 1  . Do đó 3 + 2 < 2 ( 3 + ) 1 .
Ví dụ 3: Cho a > 0 , chứng minh rằng: a + 9 < a + 3 . Giải Ta có ( a + )2 9 = a + 9 ; ( a + )2 3 = a + 6 a + 9. 2 2
Do a > 0 nên a + 9 < a + 9 + 6 a , do đó ( a + 9 ) < ( a + 3) .
Vậy a + 9 < a + 3.
Chú ý: Căn bậc hai của một tổng không bằng tổng các căn bậc hai.
Ví dụ 4. Cho a,b,c > 0 . Chứng minh rằng:
a) a + b ≥ 2 ab ;
b) a + b + c ≥
ab + bc + ca. Giải
a) Ta có a + b ≥ 2 ab
⇔ a + b − 2 ab ≥ 0
⇔ ( a − b)2 ≥ 0 (dấu " = " xảy ra khi và chỉ khi a = b).
Bất đẳng thức cuối này đúng nên bất đẳng thức đã cho là đúng.
Lưu ý : Bất đẳng thức a + b ≥ 2 ab với a,b ≥ 0 gọi là bất đẳng thức Cô – si.
b) Ta có a,b, c ≥ 0 . Áp dụng bất đẳng thức Cô – si đối với hai số ta được:
a + b ≥ 2 ab
b + c ≥ 2 bc
c + a ≥ 2 ca .
Công từng vế ba bất đẳng thức trên ta được
2(a + b + c) ≥ 2( ab + bc + ca ).
Suy ra a + b + c ≥
ab + bc + ca (dấu " = " xảy ra khi và chỉ khi a = b = c ). 1
Ví dụ 5: Cho a ≥
, chứng minh rằng: 2a −1 ≤ a . 2 Giải a + b
Từ bất đẳng thức Cô – si a + b ≥ 2 ab suy ra ab ≤ . 2
Áp dụng bất đẳng thức này cho các số không âm 2a −1 và 1 ta được: − +
a − = ( a − ) (2a )1 1 2 1 2 1 .1 ≤ = a . 2
Vậy 2a −1 ≤ a (dấu " = " xảy ra khi và chỉ khi a = 1).
C. BÀI TẬP TỰ LUYỆN 1. Tính 5 3 a) 400.0,81 ; b) . ; 27 20 2 2 c) (− )2 2 5 .3 ; d) (2 − 5) .(2 + 5) . 2. Tính
a) ( x − 3)( x + 2) ;
b) ( x − y )( x + y ) ;  25 49  c)  − + 3  3 ; d) (1+ 3 − 5)(1+ 3 + 5) . 3 3  
3. Rút gọn các biểu thức sau: a) 3 + 8 − 2 15 ;
b) x −1 − 2 x − 2 .
4. Phân tích thành nhân tử a) a − 5 a ;
b) a − 7 với a > 0 ;
c) a + 4 a + 4 ;
d) xy − 4 x + 3 y −12 .
5. Giải phương trình a) ( 2
49 1 − 2x + x ) − 35 = 0 ; b) 2
x − 9 − 5 x + 3 = 0 ; x − 2 x −1 c) = . x +1 x + 3
6*. Tìm x và y , biết x + y +13 = 2(2 x + 3 y ). 7* − < − . Chứng minh rằng: 7 3 6 2 . a + b a + b
8. Chứng minh bất đẳng thức: ≥
với a,b ≥ 0 . 2 2
9*. Tính giá trị của biểu thức A = 7 + 13 − 7 − 13 .
HƯỚNG DẪN GIẢI – ĐÁP SỐ 1 1. a) 18; b) ; c) 15 ; d) 1. 6 2. a) x − x − 6 ; b) x − y ; c) 1 ; d) 2 3 −1.
 x − 2 −1 khi x ≥ 3 3. a) 5 ;
b) 1− x−2 khi x < 3. 
4. a) a ( a − 5) ;
b) ( a − 7 )( a + 7 ) ; c) ( a + )2 2 ;
d) ( x + 3)( y − 4) . 5. a) x = 6 ; x = 4 − ; b) x = 3
− ; x = 28; c) x = 25. 1 2 1 2 6* + + = + . x y 13 4 x
6 y (ĐK: x, y ≥ 0 )
⇔ (x − x + ) + ( y − y + ) = ⇔ ( x − )2 +( y − )2 2 4 4 6 9 0 2 3 = 0 ⇔ ( x − )2 2 = 0 và ( y − )2 3
= 0 ⇔ x = 4 và y = 9.
7*. 7 − 3 < 6 − 2 ⇔ + < + ⇔ ( + )2 < ( + )2 7 2 6 3 7 2 6 3
⇔ 9 + 2 14 < 9 + 2 18 ⇔ 2 14 < 2 18 .
Bất đẳng thức cuối cùng đúng nên bất đẳng thức đã cho là đúng.
8. Bình phương hai vế. 9*. Tính 2 A được 2
A = 2 , suy ra A = 2 .
§4. LIÊN HỆ GIỮA PHÉP CHIA VÀ PHÉP KHAI PHƯƠNG
A. TRỌNG TÂM KIẾN THỨC 1. Định lí
Với số a không âm và số b dương, ta có a a = . b b 2. Áp dụng
Muốn khai phương một thương a , trong đó a ≥ 0 và b ≥ 0 , ta có thể lần lượt khai b
phương số a và số b , rồi lấy kết quả thứ nhất chia cho kết quả thứ hai.
Muốn chia căn bậc hai của số a không âm cho căn bậc hai của số b dương, ta có thể
chia số a cho số b rồi khai phương kết quả đó. 3. Chú ý
Với các biểu thức A ≥ 0 và B > 0 , ta có A A = . B B
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: KHAI PHƯƠNG MỘT THƯƠNG Phương pháp giải
Dựa vào quy tắc khai phương một thương: a a
Với a ≥ 0 ; b > 0 thì = . b b Ví dụ 1. Tính 4 49 36 − a a) : ; b) với a < 0 . 25 121 49 Giải 4 49 4 49 2 7 22 a) . = : = : = . 25 121 25 121 5 11 35 36 − a 36 − a 36. −a 6 −a b) = = = . 49 49 49 7
Lưu ý: Vì a < 0 nên −a có nghĩa. Ví dụ 2. Tính 2 2 65 − 52 11 7 a) ; b) :1, 44 − :1, 44 . 225 9 9 Giải 2 2 65 − 52 (65−52)(65+ 52) 13.117 13.13.9 13.3 39 a) = = = = = . 2 225 225 225 15 15 15 11 7 11 7  144 b) :1, 44 − :1, 44 = − :   9 9  9 9  100 4 144 4 144 2 12 5 = : = : = : = . 9 100 9 100 3 10 9 x − 5 x − 5
Ví dụ 3. Đẳng thức =
đúng với những giá trị nào của x và y ? y + 2 y + 2 Giải
Theo định lí khai phương một thương thì x − 5 x − 5 = y + 2 y + 2
khi x − 5 ≥ 0 và y + 2 > 0 hay x ≥ 5 và y > 2 − .
Dạng 2. CHIA CÁC CĂN BẬC HAI Phương pháp giải
Dựa vào quy tắc chia các căn bậc hai: a a
Với a ≥ 0 ; b > 0 thì = . b b Ví dụ 1. Tính a) 45 : 80 ; b) ( )5 3 5 2.3 : 2 .3 . Giải 45 9 3 a) 45 : 80 = = = . 80 16 4 2 .3 b) (2.3) 5 5 5 3 5 2 : 2 .3 = = 2 = 2. 3 5 2 .3 Ví dụ 2. Tính 3 52 a) 54 : 2 : 3 ; b) : . 75 117 Giải a) 54 : 2 : 3 = 54 : 2 : 3 = 27 : 3 = 9 = 3 . 3 52 3 52 1 4 1 2 3 b) : = : = : = : = . 75 117 75 117 25 9 5 3 10
Ví dụ 3. Thực hiện các phép tính a) ( 45 − 125 + 20 ) : 5 ;
b) (2 18 + 3 8 − 6 2 ) : 2 . Giải
a) ( 45 − 125 + 20 ) : 5 = 9 − 25 + 4 = 3 − 5 + 2 = 0 .
b) (2 18 + 3 8 − 6 2 ) : 2 = 2 9 + 3 4 − 6 = 2.3 + 3.2 − 6 = 6 .
Dạng 3. RÚT GỌN, TÍNH GIÁ TRỊ CỦA BIỂU THỨC Phương pháp giải
• Tìm điều kiện của biến để căn thức có nghĩa.
• Áp dụng quy tắc khai phương môt thương hoặc quy tắc chia các căn bậc hai để rút gọn.
• Thay giá trị của biến vào biểu thức đã rút gọn ròi thực hiện các phép tính. 16 12 3 − 3
Ví dụ 1. Rút gọn biểu thức . 12 8 3 − 3 Giải 12 − 3 ( 4 16 12 3 − ) 1 3 3 = = = . 3 − 3 3 (3 − ) 4 3 9 8 4 12 8 1
Ví dụ 2. Rút gọn rồi tính giá trị của biểu thức sau với x = 6 : ( 2 2 165 −124 ) A = .x . 369 Giải ( 2 2 165 −124 ) (165+124)(165−124) A = .x = .x 369 369 289.41 289 17 = .x = .x = .x . 369 9 3 17
Với x = 6 thì A = .6 = 34 . 3 x +1 y +1
Ví dụ 3. Cho biểu thức B = : . y −1 x −1
Rút gọn rồi tính giá trị của B với x = 5; y = 10 . Giải x +1 y +1 B = :
. ĐK: x >1; y >1. y −1 x −1 + − x + 1 + ( x )1( x y )1 1 x −1 B = : = = . y −1 x −1
( y − )1( y + )1 y−1 5 −1 4 2
Với x = 5; y = 10 thì B = = = . 10 −1 9 3
x − 2 xy + y
Ví dụ 4. Cho biểu thức C =
với x > 0 , y > 0 .
x + 6 xy + 9 y
Rút gọn rồi tính giá trị của C với x = 25; y = 81. Giải − 2 + ( x − y)2 x − y x xy y C = = = .
x + 6 xy + 9 y ( + )2 x +3 3 y x y
Với x = 25 ; y = 81 thì 25 − 81 5 − 9 4 1 C = = = = . 25 + 3 81 5 + 3.9 32 8
Dạng 4. GIẢI PHƯƠNG TRÌNH Phương pháp giải
• Tìm điều kiện để căn thức có nghĩa.
• Nếu hai vế không âm thì có thể bình phương hai vế để khử dấu căn. x −
Ví dụ 1. Giải phương trình 3 1 = 2 . x + 2 Giải ĐKXĐ: 1
3x −1 và x + 2 cùng dấu hoặc x = . 3  1  − >  > Trườ 3x 1 0 x 1 ng hợp 1:  ⇔  3 ⇔ x > . x + 2 > 0 3 x > 2 −  1  − <  < Trườ 3x 1 0 x ng hợp 2:  ⇔  3 ⇔ x < 2 − . x + 2 < 0 x < 2 − Vậy ĐKXĐ là 1 x ≥ hoặc x < 2 − . 3
Bình phương hai vế của phương trình ta được: 3x −1 = 4 x + 2
⇔ 3x −1 = 4(x + 2)
⇔ 3x −1 = 4x + 8 x = 9
− (thỏa mãn điều kiện). x −
Ví dụ 2. Giải phương trình 5 7 =1. 2x −1 Giải  7 x ≥  − ≥  ĐKXĐ: 5x 7 0  5 7  ⇔  ⇔ x ≥ . 2x −1 > 0 1 5 x >  2
Bình phương hai vế ta được: 5x − 7 =1 2x −1
⇔ 5x − 7 = 2x −1 ⇔ 3x = 6
⇔ x = 2 (thỏa mãn điều kiện).
C. BÀI TẬP TỰ LUYỆN 1. Tính a) 72 : 8 ; b) ( 28 − 7 + 112 ) : 7 . 2. Tính 49 1 1 32 56 a) : 3 ; b) 54x : 6x ; c) . : . 8 8 125 35 225 3. Làm phép chia a −1 a + 2 : với a > 1. 3 2 a + 2
a − 3a + 3a −1
4. Rút gọn biểu thức 2 2 x x a) :
với x, y ≠ 0 ; 2 4 y y 27 ( x − )2 2 1 3 50x b) + − (x − 2)
với 1 < x < 2 . 12 2 8( x − 2)2 2 3 5. Cho x = :
, tính giá trị của biểu thức M = 6x + 5 . 3 2
6*. Chứng minh đẳng thức 6 + 2 5 5 − 2 6 = . 5 +1 3 − 2
HƯỚNG DẪN GIẢI – ĐÁP SỐ 1. a) 3; b) 5. 7 6 2. a) ; b) 3 ; c) . 5 35 (a − )2 1 3. a + . 2 2 x khi x > 0 4. a)  ; b) 4x . 2 −x khi x < 0  2 5. x = ; M = 3 . 3
6*. Mỗi vế đều bằng 1.
§6. §7. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
A. TRỌNG TÂM KIẾN THỨC
1. Đưa thừa số ra ngoài dấu căn Với hai biểu thức ,
A B mà B ≥ 0 , ta có: A B khi A ≥ 0  2 A B = A
B = −A B khi A < 0 
2. Đưa thừa số vào trong dấu căn 2 A B =
A B , tức là:
• Nếu A ≥ 0 ; B ≥ 0 thì 2 A B = A B ;
• Nếu A < 0 ; B ≥ 0 thì 2 A B = − A B .
3. Khử mẫu của biểu thức lấy căn. Với các biểu thức , A B mà .
A B ≥ 0 và B ≠ 0 , ta có A AB = . B B
4. Trục căn thức ở mẫu
Trường hợp 1: Với các biểu thức B,C mà B > 0 thì C C B = . B B
Trường hợp 2: Với các biểu thức ,
A B,C mà A ≥ 0 ; 2 A ≠ B thì
C ( A ± B C ) = . 2 A ± B A − B
Trường hợp 3: Với các biểu thức ,
A B,C mà A ≥ 0 , B ≥ 0 và A ≠ B thì
C ( A ± B C ) = . A ± B A − B
Hai biểu thức A + B và A − B gọi là hai biểu thức liên hợp với nhau.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: ĐƯA THỪA SỐ RA NGOÀI DẤU CĂN Phương pháp giải
• Biến đổi biểu thức lấy căn thành dạng tích trong đó có thừa số là bình phương của một
số hoặc một biểu thức.
• Khai phương thừa số này và viết kết quả ra ngoài dấu căn.
Ví dụ 1: Đưa thừa số ra ngoài dấu căn a) 45 ; b) 2400 ; c) 147 ; d) 1, 25 . Giải a) 45 = 9.5 = 3 5 ; b) 2400 = 400.6 = 20 6 ; c) 147 = 49.3 = 7 3 ; d) 1, 25 = 0, 25.5 = 0,5 5 .
Ví dụ 2: Đưa thừa số ra ngoài dấu căn a) 50.6 ; b) 14.21 ; c) 32.45 ; d) 125.27 . Giải a) 50.6 = 100.3 = 10 3 ; b) 14.21 = 7.7.2.3 = 7 6 ;
c) 32.45 = 16.2.9.5 = 16.9.10 = 4.3. 10 = 12 10 ; d) 125.27 = 25.5.9.3 = 25.9.15 = 5.3 15 = 15 15 .
Ví dụ 3. Đưa thừa số ra ngoài dấu căn a) 18x ; b) 2 75x y ; c) 3 2 605x y . Giải
a) 18x = 9.2x = 3 2x (với x ≥ 0 ). b) 2 2 75x y =
25x .3y = 5 x 3y ( y ≥ 0) 5
x 3y khi x ≥ 0    5
− x 3y khi x < 0.  c) 3 2 2 2
605x y = 121x .y .5x = 11x y 5x (x ≥ 0) 11
xy 5x khi y ≥ 0  =  11
− xy 5x khi y < 0. 
Ví dụ 4. Đưa thừa số ra ngoài dấu căn a) ( − )2 128 x y ; b) ( 2
150 4x − 4x + ) 1 ; c) 3 2
x − 6x +12x − 8 . Giải 2 2
a) 128( x − y) = 64( x − y) .2 = 8 x − y 2 8
 (x − y) 2 khi x ≥ y
= 8(y−x) 2 khi x< .y b) ( x − x + ) = ( x − )2 2 150 4 4 1 25.6 2 1  ( x − ) 1 5 2 1 6 khi x ≥  2
= 5 2x −1 6 =  ( − x) 1 5 1 2 6 khi x < .  2 3 2 c) 3 2
x − 6x +12x − 8 = ( x − 2) = ( x − 2) .( x − 2)
= (x − 2) x − 2 (với x ≥ 2 ).
Dạng 2: ĐƯA THỪA SỐ VÀO TRONG DẤU CĂN Phương pháp giải
• Nếu A ≥ 0 thì ta nâng A lên lũy thừa bậc hai rồi viết kết quả vào trong dấu căn: 2 A B =
A B (với A ≥ 0 ; B ≥ 0 ).
• Nếu A < 0 thì ta coi A như là −(−A) . Ta nâng (−A) lên lũy thừa bậc hai rồi viết kết
quả vào trong dấu căn. Còn dấu "− " vẫn để đằng trước dấu căn: 2
A B = − A B (với A < 0 ; B ≥ 0 ).
Ví dụ 1. Đưa thừa số vào trong dấu căn 2 a) 3 5 ; b) 5 6 ; c) 35 . 7 Giải a) 2 3 5 = 3 .5 = 45 ; b) 2 5 6 = 5 .6 = 150 ; 2 2  2  20 c) 35 = .35 =   . 7  7  7
Ví dụ 2. Đưa thừa số vào trong dấu căn: 1 a) 4 − ; b) 0 − ,06 250 . 8 1 1 a) 2 4 − = − 4 = − 2 8 8 b) − = − ( )2 0, 06 250 0, 06 .250 = − 0,9
Ví dụ 3. Đưa thừa số vào trong dấu căn x x y a) x x b) y c) . y y x Giải a) 2 3 x x = x .x =
x ( x ≥ 0) b) ĐK: .
x y ≥ 0; y ≠ 0 Xét trườ x x
ng hợp x ≥ 0 ,y > 0, ta có 2 y = y = xy y y Xét trườ x x
ng hợp x < 0; y < 0,ta có 2 y = − y = − xy y y 2 x y x y x c) ĐK: xy > 0, ta có = = 2 y x y x y
Ví dụ 4. Đưa thừa số vào trong dấu căn: 3 1 − a) −x với x > 0 b) −x với x < 0 x x Giải 3 3 a) Ta có 2 −x = − x
= − 3x với x > 0 x x 1 −  1 −  b) Ta có 2 −x = − (−x) = −x   với x < 0 xx
Ví dụ 5. Chỉ ra chỗ sai trong các biến đổi sau: 2 3 3x y y a) x = b) 2 xy = y x . = y xy 7 7 x x Giải 2 3 3x a) Biến đổi x =
chỉ đúng khi x ≥ 0 7 7 2 3 3x Nếu x < 0 thì x = − 7 7 y y b) Biến đổi 2 xy
= y x . = y xy chỉ đúng khi x > 0 x x y y Nếu x < 0 thì 2 xy
= −y x . = −y xy x x
Dạng 3. KHỬ MẪU CỦA BIỂU THỨC LẤY CĂN Phương pháp giải A AB Vận dụng công thức =
( .AB ≥ 0;B ≠ 0) . Cụ thể gồm các bước sau : B B -
Biến đổi mẫu thành bình phương của một số hoặc một biểu thức ( nếu cần ); -
Khai phương mẫu và đưa ra ngoài dấu căn.
Ví dụ 1. Khử mẫu của biểu thức lấy căn 5 72 Giải 5 5.2 10 1 Ta có = = = . 10 72 72.2 144 12 5
Nhận xét : Nếu bạn nhân cả tử và mẫu của phân số
với 72 thì vẫn ra kết quả nhưng biến đổi 72 5 5.72 360 6 1 phức tạp hơn : = = = . 10 = . 10 2 72 72.72 72 72 12
Vậy tìm thừa số phụ như nào cho hợp lý ?
Trước hết bạn phân tích mẫu số ra thừa số nguyên tố: 72 = 23.32. Bạn thấy ngay thừa số phụ
laf2, lúc đó số mũ của các thừa số nguyên tố đều chẵn.
Ví dụ 2. Khử mẫu của biểu thức lấy căn 11 3x a) b) 27x 3 5 y Giải 11 11.3x 33x 1 a) = = = 33x (ĐK: x > 0) 2 27x 27 .3 x x 81x 9x 3x 3 .5 x y 15xy 1 b) = = =
15xy ( ĐK: xy ≥ 0; y ≠ 0 ) 3 3 4 2 5 y 5 y .5 y 25 y 5 y
Ví dụ 3. Khử mẫu của biểu thức lấy căn 1 1 1 a) b) − 3 2
x + 3x + 3x +1 2 3 x x Giải 1 1 x +1 1 a) = = = x +1 (ĐK: x > -1 ) 3 2
x + 3x + 3x +1 (x + )3 1 (x + )4 1 (x + )2 1 1 1 x −1 . x (x −1) 1 b) − = = = .
x x −1 ( ĐK: x ≥ 1 hoặc x < 0 )’ 2 3 3 4 2 ( ) x x x x x
Dạng 4. TRỤC CĂN THỨC Ở MẪU Phương pháp giải
Cách 1: Rút gọn biểu thức ( nếu có thể ):
+ Phân tích tử số thành tích có thừa số là căn thức ở mẫu.
+ Chia cả tử và mẫu cho thừa số chung.
Cách 2: Nhân cả tử và mẫu với biểu thức liên hợp của mẫu để làm mất dấu căn ở mẫu.
Ví dụ 1. Trục căn thức ở mẫu 3 + 3 2 + 2 a) b) 5 3 2 +1 Giải 3 + 3 3.( 3 +1) ( 3 +1) a) Ta có = = 5 3 5 3 5 2 + 2 2.( 2 +1) b) Ta có = = 2 2 +1 2 +1
Ví dụ 2. Trục căn thức ở mẫu 3 2 3 a) b) c) 7 3 −1 15 + 4 Giải 3 3. 7 3. 7 a) = = 7 7. 7 7 2 2.( 3 +1) 2.( 3 +1) b) = = = 3 +1 3 −1 ( 3 −1).( 3 +1) 3 −1 3 3.( 15 − 4) 3.( 15 − 4) c) = = = 3.(4 − 15) 15 + 4 ( 15 − 4).( 15 + 4) 15 −16
Ví dụ 3. Trục căn thức ở mẫu 5 3 − 3 5 2 a) b) 5 3 + 3 5 1− 2 + 3 Giải 2 5 3 − 3 5 (5 3 − 3 5) 75 + 45 − 30 15 = = 5 3 + 3 5 (5 3 + 3 5).(5 3 − 3 5) 75 − 45 a) 30.(4 − 15) = = 4 − 15 30 2 2(1 − 2 − 3) 2(1 − 2 − 3) 2(1 − 2 − 3) = = = 2 1 − 2 + 3 (1 − 2 + 3)(1 − 2 − 3) (1 − 2) − 3 (1 − 2 2 + 2 − 3 b) 2(1 − 2 − 3) 3 + 2 −1 = = 2 − 2 2
Ví dụ 4. Trục căn thức ở mẫu. 1 − a 1 1 a)
với a ≥ 0; a ≠ 1 b)
với a > 0; b > 0; ab = 1 + a a + b −1 4 Giải 2 1 − a (1 − a ) 1 − 2 a + a a) = = 1 + a
(1 + a )(1 − a ) 1 − a 1 1.( a + b +1) ( a + b +1) b) = = a + b −1
( a + b −1)( a + b +1)
a + b + 2 ab −1 a + b +1 a + b +1 = = 1 a + b a + b + 2 −1 4
Dạng 5. SO SÁNH HAI SỐ Phương pháp giải
Thực hiện các phép biến dổi đơn giản biểu thức chứa căn bận hai rồi so sánh hai kết quả. Chẳng hạn: -
Đưa thừa số vào trong dấu căn rồi dùng tính chất:
Nếu A > B > 0 thì A > B -
Đưa thừa số ra ngoài dấu căn rồi dùng tính chất:
Nếu A,B,C > 0 thì A > B ⇔ A C > B C
Ví dụ 1. Không dùng máy tính hoặc bảng số , hãy so sánh : 2 1 a) 5 6 và 7 3 b) 3 2 và 5 1 3 5 Giải a) Ta có 5 6 = 25.6 = 150 ; 7 3 = 49.3 = 147 Vì
150 > 147 nên 5 6 > 7 3 . 2 8 b) Ta có 3 2 = 9. = 24 3 3 1 6 5 1 = 25. = 30 5 5 2 1 Vì 24 < 30 nên 3 2 < 5 1 3 5
Ví dụ 2. Không dùng máy tính hoặc bảng số , hãy so sánh : 5 2 a) 2 và 7 b) 3 − 11 và 2 − 23 4 3 Giải 5 25 25 1 a) Ta có 2 = .2 = = 3 4 16 8 8 2 4 28 1 7 = .7 = = 3 3 9 9 9 1 1 5 2 Vì 3 > 3 nên 2 > 7 8 9 4 3 b) Ta có 3 − 11 = − 9.11 = − 99 2 − 23 = − 4.23 = − 92 Vì − 99 < − 92 nên 3 − 11 < 2 − 23
Ví dụ 3. Sắp xếp theo thứ tự tăng dần 2 2 2 1 a) 6 3, 7 2,15 ,9 1 b) − 71, 12, 21, 5 − 3 5 9 3 2 Giải
a) Ta có 6 3 = 36.3 = 108;7 2 = 49.2 = 98; 2 2 2 11 15 = 225. = 90;9 1 = 81. = 99 5 5 9 9 2 2
Vì 90 < 98 < 99 < 108 nên 15 < 7 2 < 9 1 < 6 3 5 9 2 4 16 1 b) Ta có 12 = .12 = = 5 ; 3 9 3 3 1 1 21 1 21 = .21 = = 5 ; 2 4 4 4 5 − 3 = − 25.3 = − 75. 1 1 1 2 Vì − 75 < − 71 < 5 < 5 nên 5 − 3 < 71 < 21 < 12. 4 3 2 3
Dạng 6. RÚT GỌN BIỂU THỨC Phương pháp giải
Thực hiện các phép biến đổi đơn giản biểu thức chứa căn bậ hai rồi thu gọn các căn thức đồng
dạng hoặc rút gọn các thừa số chung ở tử và mẫu.
Ví dụ 1. Rút gọn các biểu thức sau : 1 a) 200 − 50 + 4 b) 3 ( 72 + 4,5 + 12,5) 8 Giải 1 1 a) 200 − 50 + 4
= 10 2 − 5 2 + 4. . 2 = 6 2. 8 4 b)
3 ( 72 + 4,5 + 12,5) = 216 + 13,5 + 37,5 27 75 3 5 = 6 6 + − = 6 6 + 6 − 6 = 5 6 . 2 2 2 2
Ví dụ 2. Rút gọn các biểu thức sau :  2 3  2 1 1 a) 12 −  ; b) 4 + 2 + 3 2   9 2 18
Giải  2 3  1 1  a) 12 −  = 12 6 − 6 = 4 6 − 6 6 = 2 − 6   3 2    3 2  2 1 1 4 1 1 b) 4 + 2 + = 2 + 2 + 2 = 2 2 . 9 2 18 3 2 6
Ví dụ 3. Rút gọn các biểu thức sau : a b 1 P = 9ab + 7 − 5 − 3ab với a,b > 0 b a ab Giải a b 1 P = 9ab + 7 − 5 − 3ab b a ab 7 5 1  7 5  P = 3 ab + ab − ab − 3 . ab ab = − ab   b a abb a
Ví dụ 4. Rút gọn các biểu thức 3 4 1 B = + + 5 − 2 6 + 2 6 + 5 Giải 3 4 1 3( 5 + 2) 4( 6 − 2) ( 6 − 5) B = + + = + + 5 − 2 6 + 2 6 + 5 5 − 2 6 − 2 6 − 5
B = ( 5 + 2) + ( 6 − 2) + 6 − 5 = 2 6
Nhận xét: Phương pháp giải này ví dụ này là trục căn thức ở mẫu rồi làm các phép cộng,trừ.
Nếu quy đồng mẫu thì rất phức tạp. 8( 2 2 2
a − 2ab + b a b ) 2
Ví dụ 5. Cho a > b > 0, chứng minh rằng = 6b 4 a − b 75a b 15 Giải Ta có 2 2 2 2 2 a b
8(a − 2ab + b ) a b
8(a − b) .b = 4 4 a − b 75a b a − b 75a . b b 2
a b 2(a − b) 2b 2 2 .3 b 2 = . . = . = 6b. 2 a − b 5a b 3 5 9 15
Ta thấy vế trái đúng bằng vế phải.
C. BÀI TẬP TỰ LUYỆN
1. Đưa thừa số ra ngoài dấu căn : a) 3 75a ; b) 5 2
98a (b − 6b + 9).
2. Rút gọn biểu thức :
a) 2 125 − 5 45 + 6 20; b) 2 75 − 4 27 + 12.
3. So sánh các số sau: a) 3 7 và 2 15 ; b) 4 − 5 và 5 − 3
4. Khử mẫu của biểu thức lấy căn 3 2 a) b) 80 75
5. Trục căn thức ở mẫu a − 2 a 13 − 2 a) b) c) a − 2 2 3 − 5 1 − 2 + 3
6. Trục căn thức ở mẫu 8 1 5 − 7 a) b) c) 5 − 3 5 2 − 2 5 5 + 7 7. Tính 2  1  a)    2 − 3  1 1 1 1 b) + + + ...+ 1 + 2 2 + 3 3 + 4 99 + 100 75 + 12 8. Cho x =
. chứng minh rằng 3x là một số nguyên. 147 − 48 26 9. Biến đổi
về dạng a + b 3 . tính tích . a b 10 + 4 3
10. Tìm các cặp số nguyên dương ( ;
x y) trong đó x < y sao cho x + y = 539
HƯỚNG DẪN GIẢI – ĐÁP SỐ 2
7a (b −3) 2a nếu
1. a) 5a 3a (a ≥ 0); b)  2
7a (3 − b) 2a nếu 2. a) 7 5 ; b) 0
3. a) 3 7 > 2 15 ; b) 4 − 5 < 5 − 3 1 1 4. a) 15 b) 6 20 15 5. a) a b) −(2 3 + 5) c) 35 − 6 5 2 + 2 5 6. a) 2 − ( 5 + 3) b) c) 35 − 6 30 7. a) 5 + 2 6
b) trục căn thức pử mẫu của mỗi số hạng rồi tính tổng được 100 − 1 = 9 7
8. tính x được x =
, do đó 3x = 7 ∈ Z 3 26 13 9*. = = 5 − 2 3 10 + 4 3 5 + 2 3
Vậy a = 5;b = 2 − . do đó . a b = 5.( 2) − = 10 − 10*. 539 = 49.11 = 7. 11
7. 11 = 11 + 6. 11 = 2. 11 + 5. 11 = 3. 11 + 4. 11 7. 11 = 7. 11 + 36.11 = 4.11 + 25.11 = 9.11 + 16.11 x +
y = 11 + 396 = 44 + 275 = 99 + 176
Bài toán có ba đáp số: (11;396); (44;275) ; (99 ; 176)
§8. RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
A. TRỌNG TÂM KIẾN THỨC
Để rút gọn biểu thức có chứa căn thức bậc hai, ta có thế: -
Thực hiện các phép biến đổi đơn giản các căn thức bậc hai nhằm làm xuất hiện
các căn thức đồng dạng. -
Phối hợp thực hiện các phép tính với các biểu thức có dạng phân thức mà tử và
mẫu có chứa căn thức bậc hai theo quy tắc thực hiện các phép tính về phân thức đại số.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
DẠNG 1. RÚT GỌN BIỂU THỨC CHỈ CÓ CỘNG, TRỪ ĂN THỨC Phương pháp giải
Đưa thừa số ra ngoài hoặc vào trong dấu căn, khử mẫu của biểu thức lấy căn rồi dùng công thức:
m A − n A + p A + q = (m − n + p) A + q trong đó A ≥ 0
Ví dụ 1. Rút gọn các biểu thức sau: a) 20 − 80 + 45; b) 18 − 50 + 98 Giải a) Ta có
20 − 80 + 45 = 2 5 − 4 5 + 3 5 = 5 b) Ta có
18 − 50 + 98 = 3 2 − 5 2 + 7 2 = 5 2
Ví dụ 2: Rút gọn các biểu thức sau: 1 1 25 3 98 a) 4,5 − 72 + 5 b) 42 −10 −12 2 2 6 2 3 Giaỉ 1 1 9.2 1 5 4,5 − 72 + 5 = − .6 2 + 2 a) 2 2 2.2 2 2 3 5 = 2 − 3 2 + 2 = 2 2 2 25 3 98 42 −10 −12 6 2 3 5 1 7 b) = 42. 6 −10. 6 −12. 6 6 2 3 = 35 6 − 5 6 − 28 6 = 2 6.
Ví dụ 3: Rút gọn biểu thức M = 3 3 3 3
2x 16xy + 7 25x y − 3y 36x y với x ≥ 0; y ≥ 0 Giải 3 3 3 3
2x 16xy + 7 25x y − 3y 36x y
Ta có M = =8xy xy +35xy xy −18xy xy = 25xy xy 3 3
Ví dụ 4: Rút gọn biểu thức N = 1+ − 1− 2 2 Giaỉ 3 3 Ta có: N = 1 + − 1− 2 2 2 + 3 2 − 3 4 + 2 3 4 − 2 3 − = − 2 2 4 4 1 1 = 2 2 = ( 3 +1) − ( 3 −1) 2 2 1
= ( 3 +1))−( 3 −1) =1 2  a a 1  x y z
Ví dụ 5. Biến đổi biểu thức 5 − 4 − về dạng + + ab   , trong đó b b aba b c
a,b > 0; x, y, z ∈ Z
Tính tổng x + y + z Giải a a 1 5 4 1  5 4 1  Ta có 5 − 4 − = ab − ab − ab = − − ab   b b ab a b aba b ab
Vậy x = 5; y = 4 − ; z = 1
− . do đó x + y + z = 0
Dạng 2 : RÚT GỌN BIỂU THỨC CÓ CHỨA CÁC PHÉP CỘNG, TRỪ , NHÂN,
CHIA CĂN THỨC DƯỚI DẠNG PHÂN THỨC ĐẠI SỐ Phương pháp giải
- Xác định đieèu kiện để biểu thức có nghĩa gồm: điều kiện để biểu thức lấy căn không
âm và điều kiện để mẫu thức khác 0.
- Vận dụng các quy tắc của phép tính về phân thức đại số, kết hợp với các phép tính về
căn thức để đưa biểu thức đã cho về dạng đơn giản nhất. y x
Ví dụ 1. Rút gọn biểu thức P = − xy − x y − xy Giải
Điều kiện: x > 0; y > 0; x ≠ . y khi đó ta có: y x y − x P = − = x ( y − x ) y ( y − x ) xy ( y − x )
( y − x)( y + x) y + x = = xy ( y − x ) xyxxy
Ví dụ 2. Rút gọn biểu thức P =  − 3 :   y x + 3 xy   Giải
Điều kiện: x > 0; y > 0. khi đó ta có:  xxy x − 3 y
x ( x + 3 y ) x − 9 y P =  − 3 : = . = .   y x + 3 xy y xy y    x x − y y
Ví dụ 3. Rút gọn biểu thức P = 
+ xy  : (x − y)   x − y   Giải
 ( x − y)(x + xy + y)  P = 
+ xy  : (x − y)   x − y   P = ( x + xy + y ) 1 2 . x − y ( x + y)2 x + y P = ( = x −
y )( x − y ) . x − yxx +1
Ví dụ 4: rút gọn biểu thức P = 1+  : x + x +1 x x −1   Giải
Điều kiện: x ≥ 0; x ≠ 1. Khi đó ta có:
x + x +1+ x x x −1 P =  . x + x +1 x +1  
x + 2 x +1 x x −1 P = . x + x +1 x +1 2 ( x +1) ( x −1).(x + x +1) P = . x + x +1 x +1 P = x −1  x −1 2 x 3 x −1   2 2 
Ví dụ 5. Rút gọn biểu thức P =  + − . −   x +1 x −1 1− x    x x Giải
Điều kiện x > 0; x ≠ 1. Khi đó ta có 2
( x −1) + 2 x ( x +1) + 3 x −1 2 x − 2 P = . ( x +1)( x −1) x
x − 2 x +1 + 2x + 2 x + 3 x −1 2( x −1) P = . ( x +1)( x −1) x 3 x ( x +1) 2( x −1) 6 P = . = ( x +1)( x −1) x x
Dạng 3. RÚT GỌN RỒI TÍNH GIÁ TRỊ CỦA BIỂU THỨC HOẶC RÚT GỌN RỒI
TÌM GIÁ TRỊ CỦA BIỂU THỨC ĐỂ BIỂU THỨC CÓ MỘT GIÁ TRỊ NÀO ĐÓ Phương pháp giải
Trước hết tìm điều kiện để biểu thức có nghĩa rồi rút gọn biểu thức. sau đó thay giá trị
của biến vào biểu thức đã được rút gọn rồi thực hiện các phép tính
Hoặc có thể phải sử dụng kết quả rút gọn, lập phương trình hoặc bất phương trình rồi
giải ra để tìm giá trị của biến x −1 2 x 2 − 5 x
Ví dụ 1. Cho biểu thức P = − − x + 2 x − 2 4 − x a) Rút gọn P. 2
b) Tính giá trị của P với x = 2− 3 Giải
a) Điều kiện: x ≥ 0; x ≠ 4 . Khi đó ta có:
( x −1)( x − 2) − 2 x ( x + 2) − (2 − 5 x ) P =
( x + 2)( x − 2)
x − 3 x + 2 − 2x − 4 x − 2 + 5 x P =
( x + 2)( x − 2) −x − 2 x
P = ( x + 2)( x − 2) − x( x + 2) x P = =
( x + 2)( x − 2) 2 − x 2 b) Ta có 2 x =
= 2(2 + 3) = ( 3 +1) ⇒ x = 3 +1 2 − 3 2 Do đó 3 +1 3 +1 ( 3 +1) 4 + 2 3 P = = = = = −(2 + 3) 2 − ( 3 +1) 1 − 3 2 − 2 − x + 2 x − 2  4x P =  −  :
Ví dụ 2. Cho biểu thức 2 x −1 x − 2 x +1 (x −1)   a) Rút gọn P
b) Tính giá trị của P, biết x − 5 = 4 Giải
a) Điều kiện: x > 0; x ≠ 1. Khi đó ta có:   x + 2
x − 2  ( x −  )2 1 P =  −  ( x − ) . 1 ( x + ) 1 ( x −  )2 4 1 x 
( x +2)( x − )1−( x −2)( x + ) 2 1 (x −1) P = ( − ) . 2 ( + ) 4 1 1 x x x
(x+ x−2)−(x− x −2) 2 (x −1) P = ( − ) . 2 ( + ) 4 1 1 x x x ( x −1) ( x + x )2 2 1 2 P = ( − ) . 2 ( + ) 4 1 1 x x x x +1 P = 2 xx − 5 = 4 x = 9
b) Ta có | x − 5 |= 4 ⇔ ⇔   x − 5 = 4 − x = 1 9 +1 4 2 Với x = 9, ta có P = = = 2 9 6 3
Với x = 1, không thỏa mãn điều kiện đã nêu nên biểu thức P không có giá trị.  2 xy x + y  2 x
Ví dụ 3. Cho biểu thức P =  − .  x y  − 2 x − 2 y x − y   a) Rút gọn P x 4 b)
Tính giá trị của P, biết = y 9 Giải a)
Điều kiện: x ≥ 0 ; y ≥ 0 ; x ≠ y . Khi đó ta có: 2 xy x + y  2 x P =  − .
x − y 2( x − y)   x − y  2 4 xy − ( x + y ) 2 x P = . 2( x − y )( x + y ) x − y
4 xy − x − 2 xy − y 2 x P = . 2( x − y )( x + y ) x − y
−(x − 2 xy + y) 2 x P = . 2( x − y )( x + y ) x − y 2 −( x − y) 2 x − x P = . = 2( x − y )( x + y ) x − y x + y x 4 x b) Ta có = 9 ⇒ y = y 9 4 − − − − Do đó P = x x x 2 = = = 3 5 9 5 + x + x x x x 2 2 4  1 2   2 1 
Ví dụ 4. Cho P = − : −    
x + 2 x + 4 x + 4  x − 4 x − 2  a) Rút gọn P 1 b) Tìm x để P = − 2 Giải a)
Điều kiện: x ≥ 0 ; x ≠ 4 . Khi đó ta có:  1 2   2 1  P =  −  : −   2
x + 2 ( x + 2)   x − 4 x − 2 
x + 2 − 2 2 − ( x + 2) P = : 2 ( x + 2) x − 4 x
( x − 2)( x + 2) 2 − x P = . = 2 ( x + 2) − x 2 + x 1 − x b) Ta có P = − 2 1 ⇔ = − 2 2 + x 2 ⇔ 2 x − 4 = x + 2 ⇔ x = 6
⇔ x = 36 (thỏa mãn điều kiện)
Ví dụ 5. Cho biểu thức  1 1   x 3 x − 3  P = + :    − 
x + 3 x x − 9 x x + 3 x + 3 x   a) Rút gọn P b) Tìm x để P  1 Giải a)
Điều kiện: x ≥ 0 ; x ≠ 9. Khi đó ta có: x ( x − 3) + 3 x − 3 x + 3 P = :
x ( x − 3)( x + 3) x ( x + 3) x − 3 x + 3 x ( x + 3) P = .
x ( x − 3)( x + 3) x − 3 x + 3 1 P = x − 3 1 1 b) Để P  1 ⇔ > 1 ⇔ −1 > 0 x − 3 x − 3 1 − x + 3 ⇔ > 0 x − 3 x − 4 ⇔ < 0 x − 3  x − 4 > 0  x − 4 < 0 ⇔  hoặc  ⇔ 9  x  16 (thỏa mãn điều kiện)  x − 3 < 0  x − 3 > 0
Dạng 4. RÚT GỌN BIỂU THỨC RỒI CHỨNG MINH BIỂU THỨC CÓ MỘT TÍNH CHẤT
NÀO ĐÓ HOẶC TÌM GIÁ TRỊ NHỎ NHẤT, GIÁ TRỊ LỚN NHẤT CỦA MỘT BIỂU THỨC
Phương pháp giải
Trước tiên tìm điều kiện để biểu thức có nghĩa.
Sau đó rút gọn biểu thức, biến đổi kết quả ( nếu cần) rồi lập luận đi đến điều kiện phải
chứng minh hoặc đến điều phải tìm.
Ví dụ 1. Chứng minh rằng giá trị của biểu thức sau là hằng số với mọi giá trị thích hợp của x và y :  x 2 x −
y x y − y x A =  + .   2 xy − y xy − x ( x − y )   Giải a)
Điều kiện: x ≥ 0 ; y ≥ 0 ; x ≠ y . Khi đó ta có: x 2 x − y
xy( x − y) A =  + .   2 y ( x − y )
x ( y − x ) ( x − y )  
x − 2 xy + y xy ( x − y ) A = . 2 xy ( x − y ) ( x − y ) 2 ( x − y ) xy ( x − y ) A = . 2 xy ( x − y ) ( x − y ) A = 1
Vậy giá trị của biểu thức A luôn là hằng số với mọi giá trị thích hợp x và y.
Ví dụ 2. Cho biểu thức x + 2 x −1 1 B = + − x x +1 x − x +1 x +1 a) Rút gọn B. b)
Chứng minh rằng B luôn luôn có giá trị không âm với mọi giá trị thích hợp của x. Giải a) Điều kiện x ≥ 0 . Khi đó ta có:
x + 2 + ( x −1)( x +1) − (x − x +1) B = ( x +1)(x − x +1)
x + 2 + x −1 − x + x −1 B = ( x +1)(x − x +1) x + x
B = ( x +1)(x − x +1) x ( x +1)
B = ( x +1)(x − x +1) x B = x − x +1 b) Ta cos x ≥ 0 nên x ≥ 0 1 3 2
x − x +1 = ( x − ) +  x với mọi x. 2 4 Do đó B = x
≥ 0 với mọi x ≥ 0 . x − x +1  1 2   x
Ví dụ 3. Cho biểu thức C = − :    −1
x −1 x x − x + x −1 x +1   a) Rút gọn C. b)
Chứng minh rằng C luôn luôn có giá trị âm với mọi giá trị thích hợp của x. Giải a)
Điều kiện x > 0 ; x ≠ 1. Khi đó ta có:  1 2  x − x −1 C =  −  :
x −1 ( x −1)( x +1) x +1  x +1− 2 −(x +1) C = .
( x −1)(x+1) x − x +1 ( x −1)( x +1) −(x +1) C = . ( x −1)(x+1) x − x +1 −( x +1) C = x − x +1 b)
Ta có x ≥ 0 ; x ≠ 1 nên −( x +1) < 0 : 2  1  3 x − x +1 = x − + > 0.    2  4 − +
Do đó C = ( x 1)  0 với mọi giá trị thích hợp của x. x − x +1  x −1   6 x +1 x
Ví dụ 4. Cho biểu thức D =  2 −  :  +  . 2 x − 3
(2 x − 3)( x +1) x +1     a) Rút gọn D. 3 b)
Chứng minh rằng D < 2 Giải 9 a)
Điều kiện: x ≥ 0 ; x ≠ . Khi đó ta có: 4
2(2 x − 3) − ( x −1) 6 x +1 + x (2 x − 3) D = : 2 x − 3
(2 x − 3)( x +1) 4 x − 6 −
x +1 6 x +1 + 2x − 3 x D = : 2 x − 3
(2 x − 3)( x +1)
3 x − 5 (2 x − 3)( x +1) D = . 2 x − 3 2x + 3 x +1
3 x − 5 (2 x − 3)( x +1) D = .
2 x − 3 (2 x +1)( x +1) 3 x − 5 D = 2 x +1 3 3 x − 5 3
6 x −10 − 6 x − 3 13 − b) Xét hiệu D − = − = = < 0 2 2 x +1 2 2(2 x +1) 2(2 x +1) 3 Vậy D < 2 3
Nhận xét: Về mặt phương pháp, muốn chứng minh D < ta chứng minh 2 3 D − < 0 2  1 1   x − 4 
Ví dụ 5. Cho biểu thức P = + :    2 − .
x −1 x −1 x −1   a) Rút gọn P. b)
Tìm giá trị lớn nhất của P Giải a)
Điều kiện: x ≥ 0 ; x ≠ 1 . Khi đó ta có: ( x +1) +1
2.( x −1) − ( x − 4) P = : ( x −1)( x +1) x −1 x + 2 x −1 P = . ( x −1)( x +1) x + 2 1 P = . x +1 1 1 b) Ta có P = ≤ = 1 vì x ≥ 0 x +1 1
Do đó maxP = 1 đạt được khi x = 0 ⇔ x = 0  x − 3 x + 3 14  x − 3
Ví dụ 6. Cho biểu thức Q =  + − . x + 3 x − 3 x − 9 2   a) Rút gọn Q. b)
Tìm giá trị nhỏ nhất của Q Giải a)
Điều kiện: x ≥ 0 ; x ≠ 9. Khi đó ta có: 2 2 ( x − 3) + x + 3) +14 x − 3 Q = .
( x + 3)( x − 3) 2
x− 6 x + 9 + x + 6 x + 9 +14 x − 3 Q = .
( x + 3)( x − 3) 2 2x + 32 x − 3 Q = .
( x + 3)( x − 3) 2 x +16 Q = x + 3 x +16 x − 9 + 25 25 b) Ta có Q = = = x − 3 + x + 3 x + 3 x + 3 25 = x + 3 + − 6 x + 3 25 ≥ 2 ( x + 3).
− 6 (bất đẳng thức cô si) x + 3 > 10 – 6 = 4 25
Dấu “ = “ xảy ra khi và chỉ khi x + 3 = x +3 2 ⇔ ( x + 3) = 25 ⇔ x + 3 = 5 2 ⇔ ( x + 3) = 25 ⇔ x + 3 = 5
⇔ x = 4 (thỏa mãn điều kiện) ⇔ x = 4 Vậy minQ = 4 khi x = 4
Dạng 5. CHỨNG MINH ĐẲNG THỨC Phương pháp giải
Biến đổi vế này thành vế kia hoặc biến đổi cả hai vế cùng bằng một biểu thức thứ ba.
Ví dụ 1. Chứng minh đẳng thức sau với x ≥ 0 ; y ≥ 0 và x ≠ y :
x + y 4 xy x − y x  −  : =   x − y x − y x x + y   Giải Xét vế trái T :
x + y 4 xy x − y T =  −  :   x − y x − y x   2
 ( x + y) − 4 xy x T =  .   ( x − y )( x + y ) x − y  
x + 2 xy + y − 4 xy x T =  .   ( x − y )( x + y ) x − y   2  ( x − y )  x T =  .   ( x − y )( x + y ) x − y   x T = x + y
Ta thấy vế trái đúng bằng vế phải nên đẳng thức đã cho là đúng.
Ví dụ 2. Chứng minh đẳng thức sau với x ≥ 0 ; y ≥ 0 và x ≠ y :  x x + y y  2 y
− xy  : (x− y) =1−   x + y x + y   Giải Xét vế trái T :  x x + y y  T =  − xy  : (x− y)   x + y  
 ( x + y)(x − xy + y)  1 T =  − xy .   x + y x − y   2 ( x − y )
T = ( x + y)( x − y) x − y T = x + y Xét vế phải P : x + y − 2 y x − y P = = x + y x + y
Rõ ràng T = P , suy ra điều phải chứng minh. C. BÀI TẬP TỰ LUYỆN 1.
Rút gọn các biểu thức sau : 2 3 1 a) 6 + 3 − 4 +12 ; 3 2 6 b) 3 3
6 a + 3 25a − 2 36ab − 2 9a với a, b > 0 . x +1 x −1 m 2. Biến đổi biểu thức − về dạng 2
x −1 , trong đó x > 1. x −1 x +1 2 x −1 Tính giá trị của m. 3.
Rút gọn rồi tính giá trị của biểu thức P với x = 0,36 : x 3 6 x P = − − . x + 3 3 − x x − 9 4.
Chứng minh đẳng thức sau với x ≥ 0; y ≥ 0; x ≠ y :  x + y x − y y −1 4 x  −  : =   x − y x + y y − y x − y    1  x −1 1  5.
Cho biểu thức P = x +   − . 
x x − x +1 x +1   a) Rút gọn P. b)
Tìm các giá trị nguyên của x để P có giá trị nguyên.  x x − 6  x x − 36 x
6*. Cho biểu thức P =  −  : . x − 36 x + 6 x
2( x − 3)(x− 2 x + 3)   a) Rút gọn P. b)
Với giá trị nào của x thì P có giá trị lớn nhất ? Gía trị lớn nhất đó là bao nhiêu? 2 x + 3 3 x − 2 15 x −11
7*. Cho biểu thức P = + − x + 3 x −1 x+ 2 x − 3) a) Rút gọn P. b)
Tìm giá trị nhỏ nhất của P.
HƯỚNG DẪN GIẢI – ĐÁP SỐ 1. a) 2√6 b) 3(5a − 4b) 2 2.
Khử mẫu của biểu thức lấy căn ta được 2 x −1 , suy ra m = 2. 2 x −1 x − 3 3. P =
với điều kiện x ≥ 0 ; x ≠ 9. Khi đó x = 0,36, ta có P = 2 − . x + 3 3 4 xy 1 4 x 4.
Rút gọn vế trái được . = . x − y y x − y x − 2 5. a) P = (x > 0); b) x ∈[1;4]. x 6 6. a)
với điều kiện x > 0; x ≠ 9; x ≠ 6 x− 2 x + 3 6 6 b) P = ≤ = 3 ( vì 2 ( x −1) ≥ 0 ). 2 ( x −1) + 2 2
Suy ra maxP = 3 đạt được khi x = 1. 5 x − 2 7. a) P =
(x ≥ 0; x ≠ 1) . x + 3 5 x +15 −17 17 b) P = = 5 − x + 3 x + 3 17 P ≥ 5 − ( vì √𝑥 ≥ 0 ). 3 2 P ≥ −
( dấu bằng xảy ra khi x = 0). 3 2
Vậy minP = − , đạt được khi x = 0. 3 §9. CĂN BẬC BA
A. TRỌNG TÂM KIẾN THỨC 1.
Khái niệm căn bậc ba.
Căn bậc ba của một số a là số x sao cho x3 = a. 3 3
a = x ⇔ x = a .
Như vậy, ( 3 a )3 3 3 = a = a Nhận xét : -
Căn bậc ba của một số dương là số dương ; -
Căn bậc ba của một số âm là một số âm ; -
Căn bậc ba của số 0 là số 0 ; 2. Tính chất • 3 3 a < b ⇔ a < b ; • 3 3 3 ab = a. b ; 3 • a a 3 = ( với b ≠ 0 ). 3 b b
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. TÌM CĂN BẬC BA CỦA MỘT SỐ
Phương pháp giải
Dựa vào định nghĩa căn bậc ba của một số : 3 a = . a
Ví dụ 1. Hãy tìm : a) 3 216 b) 3 729 c) 3 331 . Giải a) 3 3 3 216 = 6 = 6 b) 3 3 3 729 = 9 = 9 c) 3 3 3 331 = 11 = 11
Ví dụ 2. Hãy tìm : a) 3 343 − b) 3 1000 − c) 3 1728 − . 3 3 3 2 6 < 3 2 = 4 5 Giải 𝑎) 3 3 3 343 − = 7 − = 7 − b) 3 3 3 1000 − = 10 − = 10 − c) 3 3 3 1728 − = 12 − = 12 −
Ví dụ 2. Hãy tìm : 8 125 a) 3 b) 3 − c) 3 0 − ,064 27 512 Giải 3 8  2  2 a) 3 = 3 =   27  3  3 125 b) 3 − = 3 3 3 3 27.12 −1 = 324 −1 < 343 −1 = 7 −1 = 6 512 c) 3 0 − ,064 = (− )3 3 0, 4 = 0, − 4 . Dạng 2. SO SÁNH
Phương pháp giải
• Đưa các thừa số vào trong dấu căn : 3 3 3 a b = a b .
• So sánh hai số trong dấu căn : a < b 3 3 ⇔ a < b . Ví dụ 1. So sánh a) 7 và 3 345 b) 3 2 6 và 3 3 2 Giải a) 3 3 7 = 343 < 345 ; b) 3 3 3 3 2 6 = 2 .6 = 8 4 3 3 3 3 3 2 = 3 .2 = 54 48 < 54 nên 3 3 2 6 < 3 2 Ví dụ 2. So sánh 2 3 a) 3 18 và 3 12 b) 3 130 +1 và 3 3 12 −1 3 4 Giải 3 2  2  16 1 a) Ta có 3 18 = 3 3 3 .18 = = 5   3  3  3 3 3 3  3  81 1 3 12 = 3 3 3 .12 = = 5   4  4  16 16 1 1 2 3 Vì 5 > 5 nên 3 18 > 3 12 3 16 3 4
b) Ta có 3 130 +1 > 3 125 +1 = 5 +1 = 6 ; 3 3 12 −1= 3 3 3 3 27.12 −1 = 324 −1 < 343 −1 = 7 −1 = 6 ; Vậy 3 130 +1 > 3 3 12 −1.
Ví dụ 3. Cho a < 0 , hỏi số nào lớn hơn trong hai số 3 2a và 3 3a Giải
Ta có 2 < 3 nên 2a > 3a ( vì a < 0 ).
Do đó 3 2a > 3 3a .
Dạng 3. THỰC HIỆN CÁC PHÉP TÍNH Phương pháp giải
Vận dụng định nghĩa căn bậc hai của một số, các tính chất nhân các căn bậc ba, chia các căn bậc ba.
Ví dụ 1. Rút gọn các biểu thức a) 3 3 3 8 + 27 − + 64 − ; b) 3 3 3 54 − 16 − + 128 Giải a) Ta có 3 3 3 8 + 27 − + 64 − = 2 + ( 3 − ) + ( 4 − ) = 5 − b) Ta có 3 3 3 54 − 16 − + 128 = 3 3 3 3 3 3 3 3 3 3 3 .2 − ( 2)
− .2 + 4 .2 = 3 2 + 2 2 + 4 2 = 9 2. Ví dụ 2. Tính a) 3 3 3 3 16. 13.5 − 120 : 15 ; b) 3 3 3 ( 2 +1)( 4 − 2 +1). Giải a) 3 3 3 3 16. 13.5 − 120 : 15 = 3 3 16.13.5 + 120 :15 = 3 3 216 − 8 = 6 – 2 = 4 = 6 – 2 = 4 b) 3 3 3 ( 2 +1)( 4 − 2 +1). = 3 3 3 3 3 8 − 4 + 2 + 4 − 2 + 1 = 2 + 1 = 3
Nhận xét: Để tính tích trên có thể sử dụng hằng đẳng thức :
(a + b)(a2 –ab + b2) = a3 + b3 Ta có 3 3 3 3 3 3
( 2 +1)( 4 − 2 +1) = ( 2) +1 = 2 +1 = 3. Ví dụ 3. Tính a) 3 3 3 3 ( 5 +1) − 3 5( 5 +1) ; b) 3 3 3 3 3 ( 4 − 3) + 6 2( 2 −1) Giải a) Ta có 3 3 3 3 ( 5 +1) − 3 5( 5 +1) = 3 3 3 3
5 + 3 25 + 3 5 +1 − 3 25 − 3 5 = 6. b) Ta có 3 3 3 3 3 3 3 3 3
( 4 − 3) + 6 2( 2 −1) = 4 − 3 32 + 3 16 − 2 + 6 4 − 6 2 = 3 3 3 3
6 − 6 4 + 6 2 − 2 + 6 4 − 6 2 = 2 . Ví dụ 4. Tính A = 3 3 5 + 2 − 5 − 2 . Giải
Để tính giá trị của A, ta tính A3 sau đó suy ra A.
Bạn nên nhớ hằng đẳng thức (a - b)3 = a3 -b3 – 3ab(a – b). Ta có 3 A = ( 3 3 5 + 2 − 5 − 2 )3   3 A = ( + ) −( − ) 3 − ( + )( − ) 3 ( + ) 3 5 2 5 2 3 5 2 5 2 5 2 − ( 5 − 2)     3 A = 4 − 3A  3 A + 3A – 4 = 0 2
⇔ (A −1)(A + A + 4) = 0 ⇔ A −1 = 0 ( vì 2
A + A + 4 > 0 ) Vậy A = 1
Ví dụ 4. Rút gọn biểu thức. x +1 a) 3
3 x +1+ 3x(x +1) ; b) 3 2 3 x − x +1 Giải a) Ta có 3
3 x +1+ 3x(x +1) = 3
3 (x +1) = x +1. x +1 3 3 2 3 ( x +1)( x − x +1) b) = 3 = x +1. 3 2 3 x − x +1 3 2 3 x − x +1
Dạng 4. GIẢI PHƯƠNG TRÌNH
• Nếu x3 = a thì x = √3𝑎 • Nếu x3 = b thì x = b3
Ví dụ 1. Giải phương trình a) 3 x + 7 − 3 = 1 ; b) 3 2 1 − x + 2 = 0 . Giải a) Ta có 3 3 x + 7 − 3 = 1 ⇔
x + 7 = 4 ⇔ x + 7 = 64 ⇔ x = 57 . b) Ta có 3 2 3 2 2 2
1 − x + 2 = 0 ⇔ 1 − x = 2 − ⇔ 1− x = 8
− ⇔ x = 9 ⇔ x = 3. ±
Ví dụ 1. Giải phương trình a) 3 3 3
1000x − 64x − 27x = 15 ;
b) 3 x − 3 + 3 = x . Giải a) Ta có 3 3 3
1000x − 64x − 27x = 15 3 3 3
⇔ 10 x − 4 x − 3 x = 15 3 ⇔ 3 x = 15 3 ⇔ x = 5 ⇔ x = 125.
Document Outline

  • PHẦN ĐẠI SỐ
  • Chương I. CĂN BẬC HAI, CĂN BẬC BA
    • §1. CĂN BẬC HAI
    • §2. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
      • A. TRỌNG TÂM KIẾN THỨC
    • §3. LIÊN HỆ GIỮA PHÉP NHÂN VÀ PHÉP KHAI PHƯƠNG
    • §4. LIÊN HỆ GIỮA PHÉP CHIA VÀ PHÉP KHAI PHƯƠNG
    • §6. §7. BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
    • §8. RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
    • §9. CĂN BẬC BA