Phương Pháp Giải Hình 9 Ôn Chương Hệ Thức Lượng Trong Tam Giác Vuông

ÔN TẬP CHƯƠNG I
A. KIẾN THỨC TRỌNG TÂM
Xem lại phần kiến thức trọng tâm của các bài đã học
▪ Hệ thức liên hệ giữa cạnh và đường cao trong tam giác.
▪ Tỉ số lượng giác của góc nhọn.
▪ Hệ thức liên hệ giữa cạnh và góc trong tam giác.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: So sánh các tỉ số lượng giác
Ví dụ 1. Sắp xếp theo thứ tự tăng dần cos 72 , sin 65 , sin10 , cot 25 , sin 40 . Lời giải Ta có sin 65 = cos 25 ;  sin10 = cos80 ;  sin 40 = cos50 .
Vì cos80  cos 72  cos50  cos 25  cot 25 nên
sin10  cos 72  sin 40  sin 75  cot 25 . Ví dụ 2. So sánh
a) sin 55 ; cos 55 ; tan 55 .
b) cot 20 ; sin 20 ; cos 20 . Lời giải
So sánh tương tự Ví dụ 1.
a) cos 55  sin 55  tan 55 ;
b) sin 20  cos 20  cot 20 .
Ví dụ 3. Cho 0  45   . Chứng minh rằng a) sin  cos . b) tan  cot . Lời giải
a) Do 0    45 nên 90 −  45 suy ra   90 − . Do đó
sin  sin (90 − ) = cos .
b) Tương tự câu a)   90 − nên tan  tan (90 − ) = cot .
Ví dụ 4. Cho tam giác ABC vuông tại A có ˆ ˆ
B  C . Hãy sắp xếp theo thứ tự tăng dần sin B ,
cos B , tan B , sin C , cos C , cot C . Lời giải Ta có ˆ ˆ
B + C = 90 nên sin C = cos B ; cos C = sin B ; tan B = cot C
Lại có B  C nên cos B  cos C . sin B Mà tan B =  sin B . cos B Trang 1
Vậy sin C = cos B  cos C = sin B  tan B = cot C .
Dạng 2: Rút gọn và tính giá trị của biểu thức lượng giác
Ví dụ 5. Rút gọn các biểu thức a) 2 2 2
sin  cot  − cos  +1. b) (  −  )2 −(  +  )2 tan cot tan cot . c) 4 4 2 2
sin  − cos  − cos  − 3sin  . Lời giải 2 cos  a) 2 2 2 2 2 2 2
sin  cot  − cos  +1 = sin  
− cos  +1 = cos  − cos  +1 =1 . 2 sin  b) 2 2
(tan − cot ) − (tan + cot ) 2 2 =  −     +  − ( 2 2 tan 2 tan cot cot
tan  + 2 tan cot + cot  ) = 4 −  tan cot = 4 − . c) 4 4 2 2  −  −  −  = ( 2 2  −  )( 2 2  +  ) 2 2 sin cos cos 3sin sin cos sin cos − cos  − 3sin  = ( 2 2  −  ) 2 2 −  −  = − ( 2 2 1 sin cos cos 3sin 2 sin  + cos  ) = 2 − .
Ví dụ 6. Tính giá trị của biểu thức a)    2 sin 30 cos 60 tan 45 4cos 30 + − + . b) 2  2  2 cos 30 cot 60 tan 30 − + −1. 2  2 cot 45 − cos 45 c) . 2 2sin 60 Lời giải 2   a)    2  1 1 3
sin 30 + cos 60 − tan 45 + 4 cos 30 = + −1+ 4   = 3. 2 2  2    2 2 2       b) 2  2  2  3 3 3 3 1
cos 30 − cot 60 + tan 30 −1 =   −   +   −1 = −1 = −  . 2   3   3  4 4       2  2  1−   2  2 cot 45 − cos 45 2   1 c) = = . 2  2 2sin 60   3 3 2  2  
Ví dụ 7. Tính giá trị của biểu thức a) 2  2  2  2 cos 33 cos 41 cos 49 cos 57 + + + . b) 2  2  2  2  2  2 sin 35 sin 39 sin 43 sin 47 sin 51 sin 55 + + + + + . Lời giải Trang 2 a) 2  2  2  2  ( 2  2  ) ( 2  2 cos 33 cos 41 cos 49 cos 57 cos 33 cos 57 cos 41 cos 49 + + + = + + + ) ( 2  2  ) ( 2  2 cos 33 sin 33 cos 41 sin 41 = + + + ) =1+1= 2. b) 2  2  2  2  2  2 sin 35 sin 39 sin 43 sin 47 sin 51 sin 55 + + + + + ( 2  2  ) ( 2  2  ) ( 2  2 sin 35 sin 55 sin 39 sin 51 sin 43 sin 47 = + + + + + ) ( 2  2  ) ( 2  2  ) ( 2  2 sin 35 cos 35 sin 39 cos 39 sin 43 cos 43 = + + + + + ) =1+1+1=3
Dạng 3: Tính độ dài đoạn thẳng, tính số đo góc
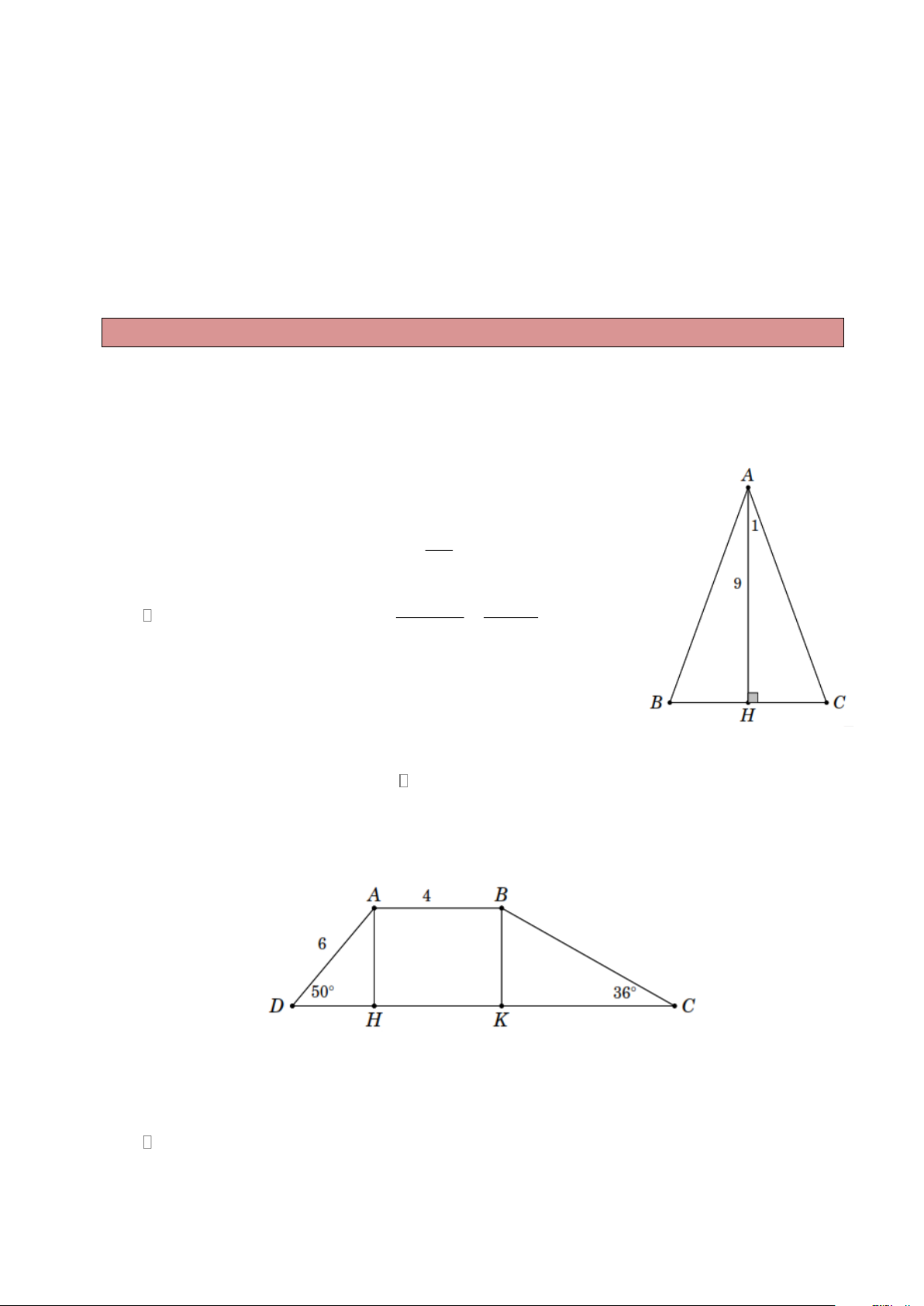
Ví dụ 8. Cho tam giác ABC cân tại A , đường cao AH . Biết ˆA 44 =
; AH = 9cm . Tính chu vi tam giác ABC . Lời giải
Do tam giác ABC cân đỉnh A , AH là đường cao nên AH cũng là
đường phân giác, đường trung tuyến. BC Do đó BAH CAH 22 = = và HB = HC = . 2 AH 9
Xét AHC vuông tại H , ta có AC = =  9,7  (cm) cos HAC cos 22 và HC
AH cot HAC 9 cot 22 =  =   3,6(cm).
Do đó chu vi tam giác ABC là 2(9,7 + 3,6)  26,6(cm) .
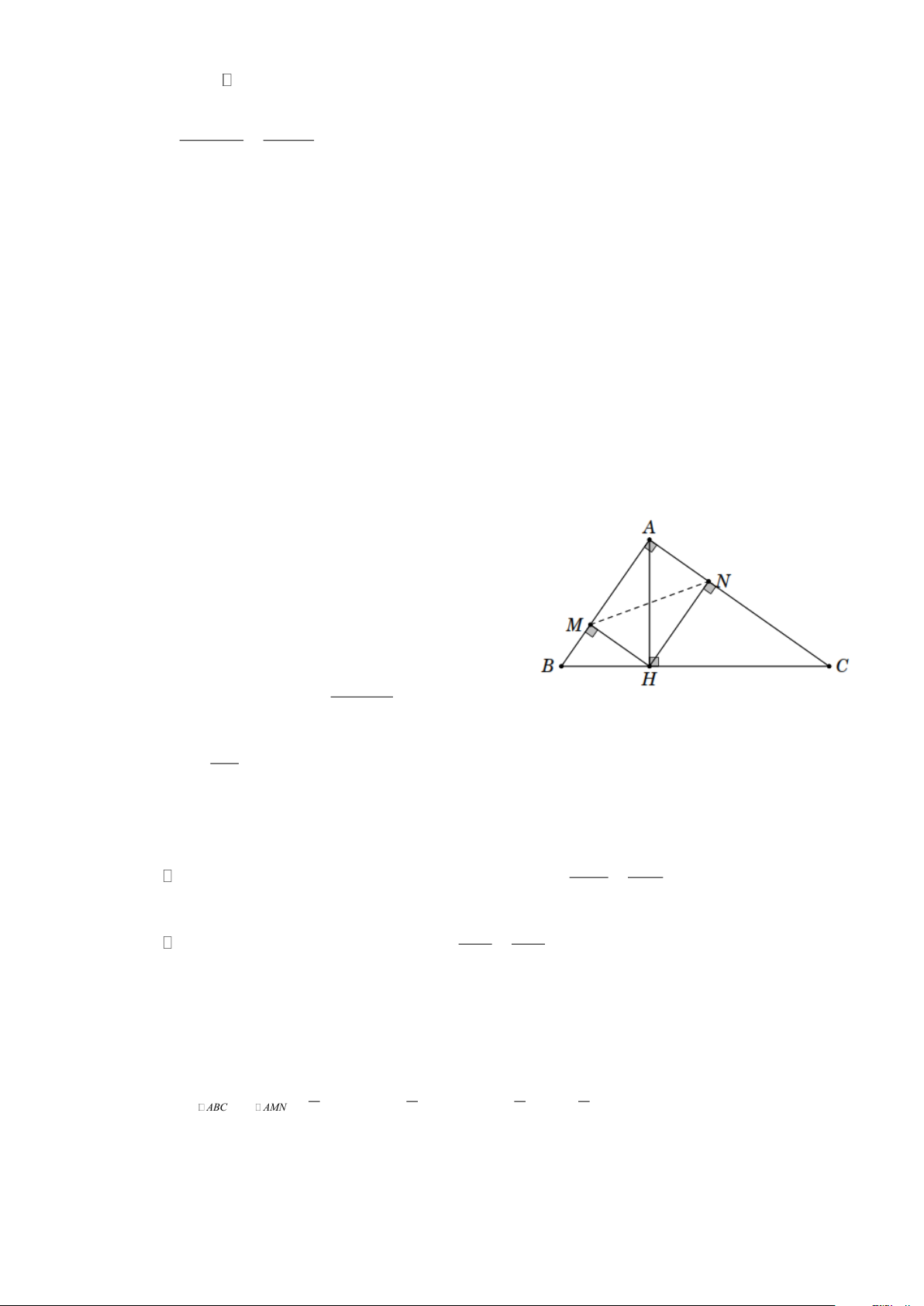
Ví dụ 9. Cho hình thang ABCD ( AB CD ), ˆ C 36 = ; ˆ D 50 =
. Biết AB = 4cm , AD = 6cm . Tính chu vi hình thang. Lời giải
Vẽ AH ⊥ CD và BK ⊥ CD , dễ thấy AHKB là hình chữ nhật.
Do đó AH = BK và AB = HK .
Xét ADH vuông tại H , ta có DH AD cos ADH 6 cos50 =  =   4,6(cm) . Trang 3
Tương tự, xét BKC vuông tại K , ta có KC BK cot BCK 4,6 cot 36 =  =   6, ( 3 cm) BK 4,6 và BC = =  7, .  ( 8 cm) sin KCB sin 36
Ta có DC = DH + HK + KC = 3,9 + 4 + 6,3  14, 2(cm) .
Do đó chu vi của hình thang là 4 + 7,8 +14, 2 + 614, 2  ( 32 cm) .
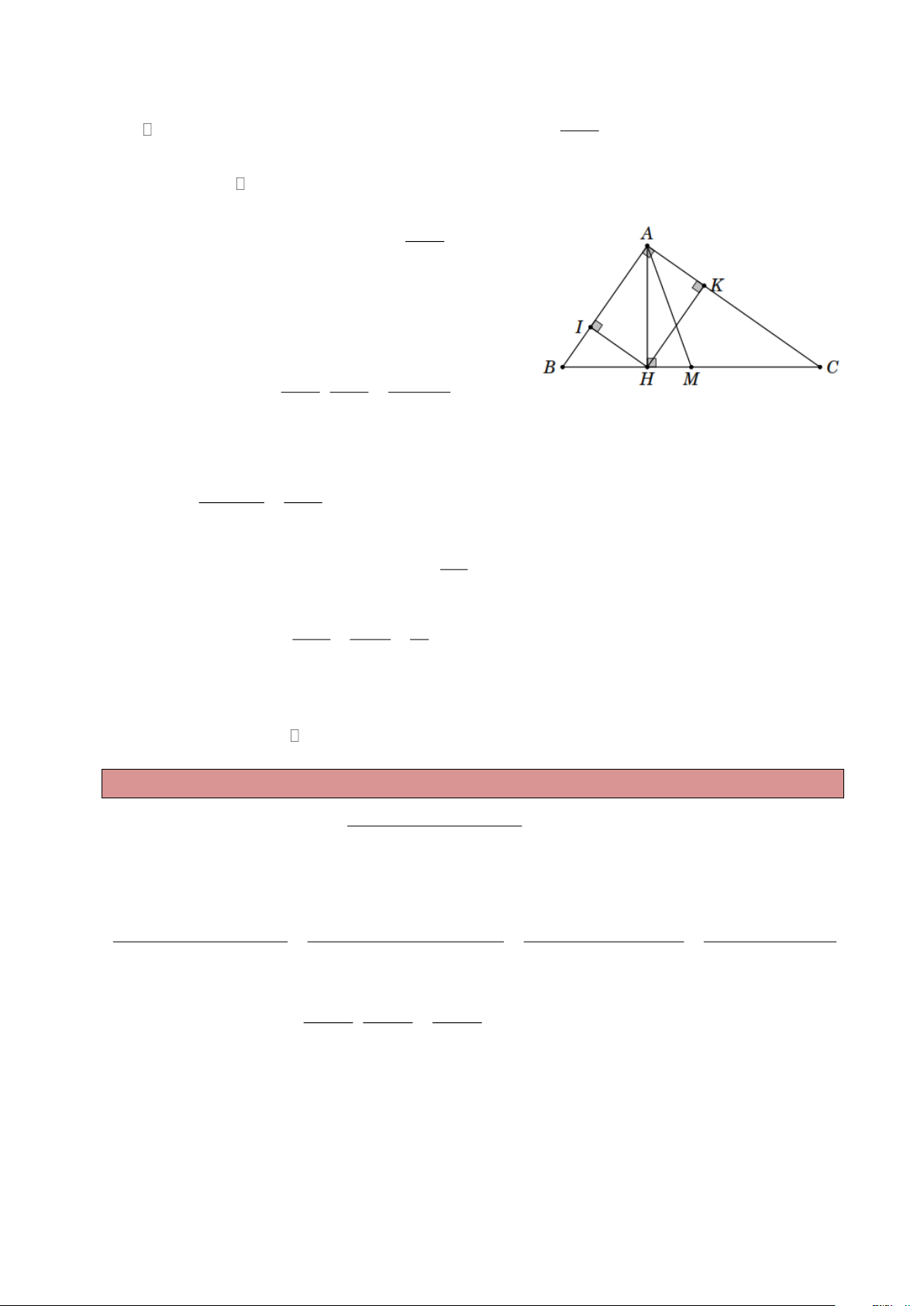
Ví dụ 10. Cho tam giác ABC vuông tại A , đường cao AH . Vẽ HM ⊥ AB ; HN ⊥ AC . Biết
AB = 3cm ; AC = 4cm .
a) Tính độ dài MN .
b) Tính số đo các góc của tam giác AMN .
c) Tính diện tích tứ giác BMNC . Lời giải
a) Áp dụng định lí Py-ta-go trong tam giác vuông ABC , ta có 2 2 2 2 2
BC = AB + AC = 3 + 4 = 25 suy ra BC = ( 5 cm) .
Theo hệ thức lượng trong tam giác vuông ABC , ta có AB  AC
AH  BC = AB  AC  AH = BC 3 4 suy ra AH = = 2, ( 4 cm) . 5
Dễ thấy AMHN là hình chữ nhật nên MN = AH nên MN = 2, 4cm . 2 2 AH 2, 4
b) Xét ABH vuông tại H , ta có 2
AH = AM  AB  AM = = =1,4 ( 4 cm) . AB 4 AN 1, 44
Ta xét AMN vuông tại A , ta có tan AMN = =
 tan 3652 . Do đó AMN = 3652 . AM 1,92
Mà ANM = 90 = AMN = 90 − 3652 = 53 8   .
c) Gọi S là diện tích tứ giác BMNC . 1 1 1 1 Ta có S = S − S
=  AB  AC −  AM  AN = 3 4 − 1,921,44  4, . ABC AMN ( 2 6 cm ) 2 2 2 2
Vậy diện tích tứ giác BMNC là 2 4, 6cm .
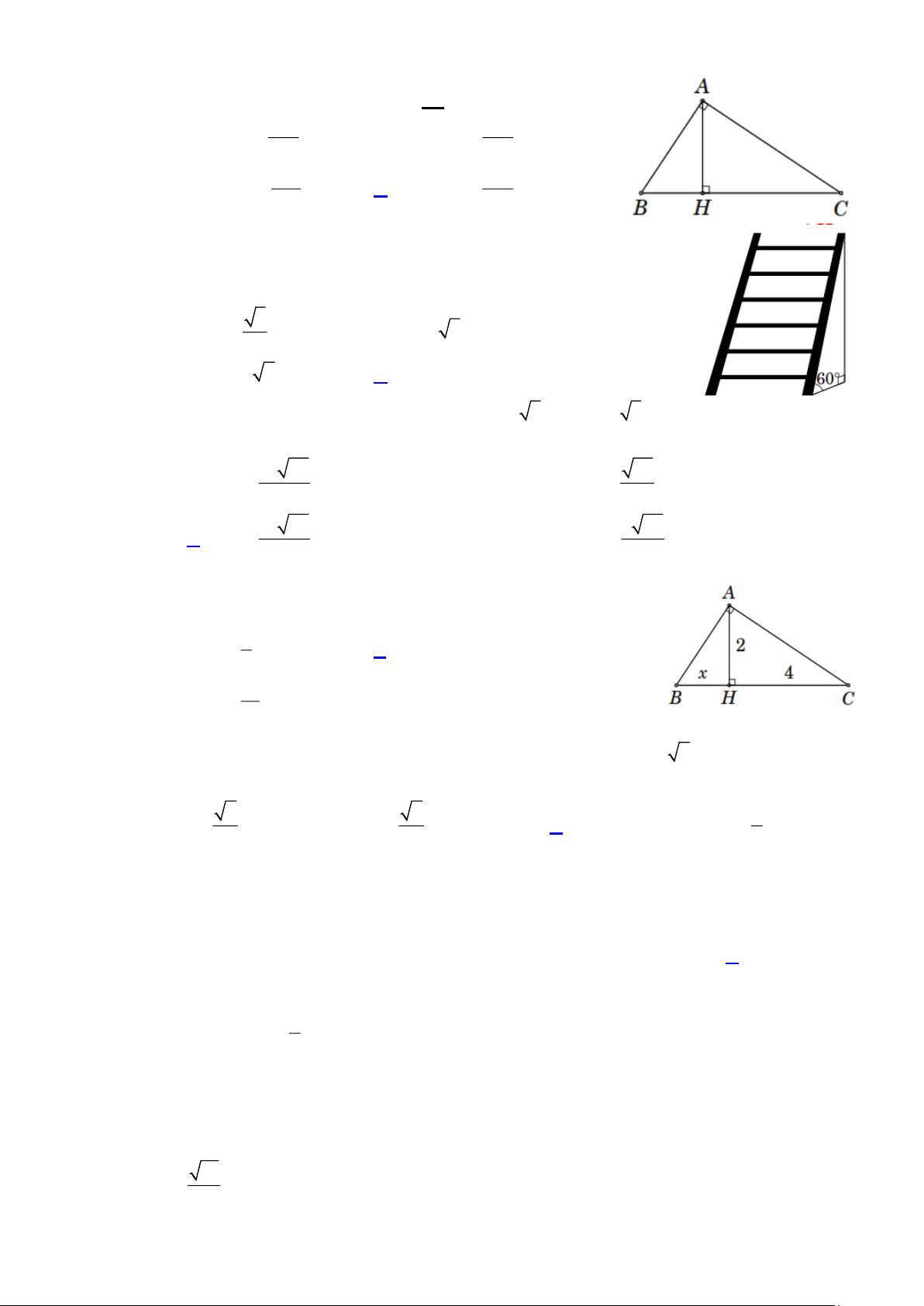
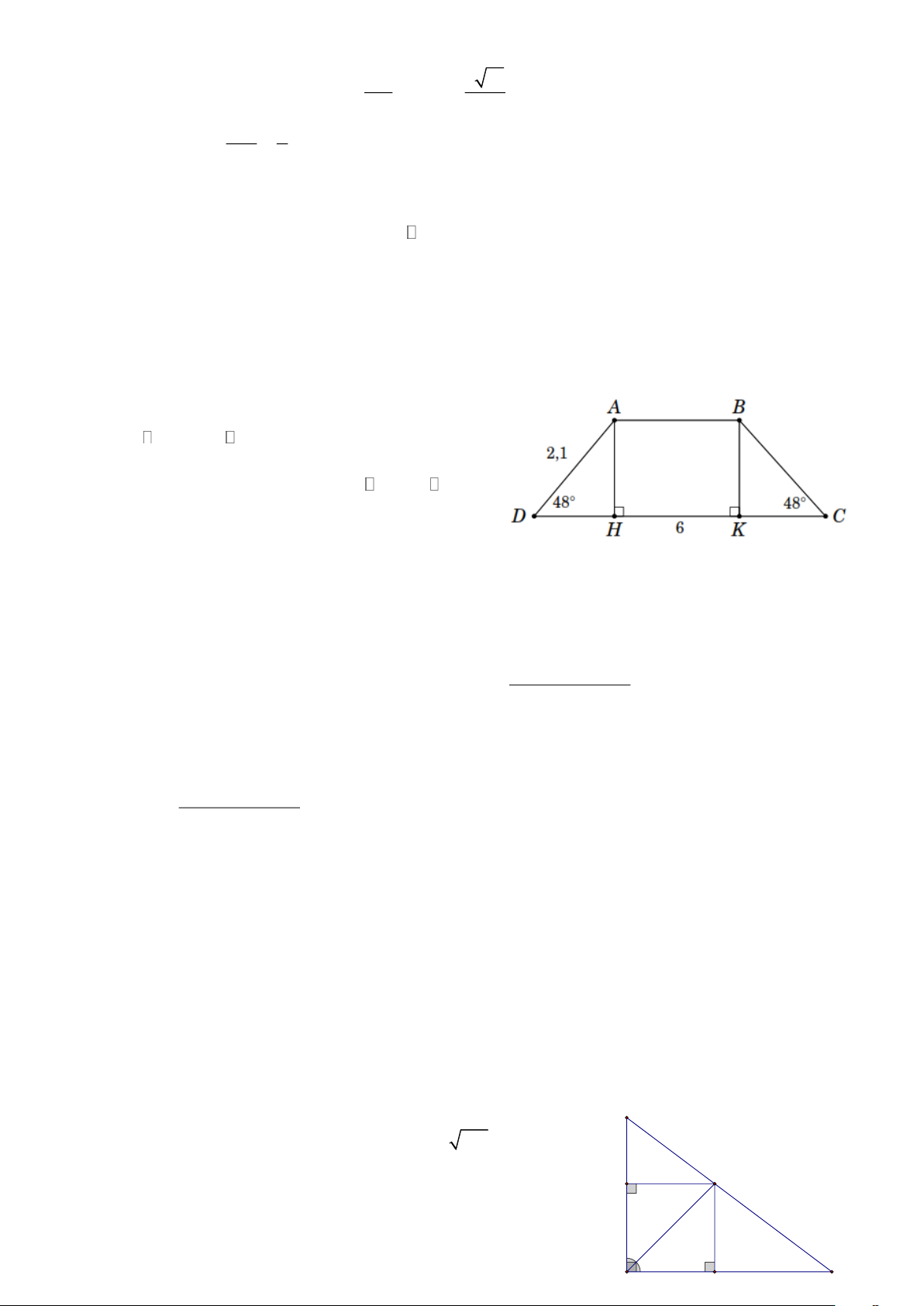
Ví dụ 11. Cho tam giác ABC vuông tại A , BC = 4cm . Vẽ đường cao AH ; vẽ HI ⊥ AB ,
HK ⊥ AC . Tìm giá trị lớn nhất của diện tích tứ giác AIHK . Trang 4 Lời giải 2 AH
Xét ABH vuông tại H , ta có 2
AH = AI  AB suy ra AI = . AB
Tương tự, ta xét ACH vuông tại H , ta có 2 AH 2
AH = AK  AC suy ra AK = . AC
Gọi S là diện tích của tứ giác AIHK .
Do tứ giác AIHK là hình chữ nhật nên 2 2 4 AH AH AH
S = AI  AK =  = . AB AC AB  AC
Mặt khác theo hệ thức lượng trong tam giác vuông ABC ta có AB  AC = AH  BC . 4 3 AH AH Khi đó S = = . AH  BC BC BC
Gọi M là trung điểm của BC , ta có AM = = ( 2 cm) . 2 3 3 3 AH AM 2
Mà AH  AM nên S =   = ( 2 2 cm ) . BC BC 4
Dấu đẳng thức xảy khi AH = AM hay tam giác ABC vuông cân tại A . Vậy 2
max S = 2cm khi ABC là tam giác vuông cân đỉnh A .
Dạng 4: Chứng minh hệ thức giữa các tỉ số lượng giác 2 2 4 cos  − sin  + sin 
Ví dụ 12. Chứng minh hệ thức 4 = cot . 2 2 4 sin  − cos  + cos  Lời giải 2 2  −  +  cos  − sin  ( 2 1− sin  ) 2  −   cos  ( 2 2 2 4 2 2 2 1− sin cos sin sin cos sin cos  ) = = = 2 2 4 2 2 sin  − cos  + cos  sin  − cos  ( 2 1− cos  ) 2 2 2 2 sin  − cos  sin  sin  ( 2 −cos  ) 2 2 4 cos  cos  cos  4 =  = = cot  . 2 2 4 sin  sin  sin 
Ví dụ 13. Chứng minh các đẳng thức sau a) 2
(1− cos )(1+ cos ) = sin  ; b) 2 2 sin  +1+ cos  = 2 ; c) 4 4 2 2
sin  + cos  + 2sin  cos  = 1; d) 2 3
sin − sin cos  = sin  . Lời giải Trang 5 a) 2 2
(1− cos )(1+ cos ) = 1− cos  = sin  ; b) 2 2 2 2
sin  +1+ cos  = sin  + cos  +1 = 1+1 = 2 ; c)  +  +   = (  +  )2 4 4 2 2 2 2 2 sin cos 2sin cos sin cos =1 =1; d) 2  −   =  ( 2 −  ) 2 3 sin sin cos sin 1 cos
= sin sin  = sin  . C. BÀI TẬP VẬN DỤNG I. PHẦN TRẮC NGHIỆM
Câu 1: Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm và BC = 13 cm. Giá trị của sin C bằng 5 1 12 5 A. . B. . C. . D. . 12 13 13 13
Câu 2: Cho tam giác ABC vuông tại A . Khẳng định nào sau đây đúng? AB AC AB AC A. cos B = . B. cos B = . C. cos B = . D. cos B = . BC AB AC BC
Câu 3: Cho tam giác ABC vuông tại A . Hệ thức nào sau đây đúng? AB AB AB AB A. sin B = . B. sin B = . C. tan B = . D. cos B = . BC AC AC AC
Câu 4: Khẳng định nào sau đây sai? A. cos 35 sin 40  . B. sin 35 cos 40  . C. sin 35 sin 40  . D. cos35 cos 40  .
Câu 5: Cho tam giác ABC vuông tại A , đường cao AH . Hệ thức nào đây sai? A. 2
AC = BC.HC . B. 2 AH = A . B AC . 1 1 1 C. = + . D. 2 AH = . HB HC . 2 2 2 AH AB AC
Câu 6: Cho ABC vuông tại ,
A đường cao AH. Biết BH = 3, 2cm; BC = 5cm thì độ đài AB bằng A. 8 cm. B. 16 cm. C. 1,8 cm. D. 4 cm.
Câu 7: Cho tam giác ABC vuông tại A , ACB 30 =
, cạnh AB = 5 cm. Độ dài cạnh AC là 5 5 2 A. 10 cm. B. cm. C. 5 3 cm. D. cm. 3 2 1
Câu 8: Cho tam giác ABC vuông tại C. Biết sin B = , khi đó tan A bằng 3 2 2 1 A. . B. 3 . C. 2 2 . D. . 3 2 2
Câu 9: Cho ABC cân tại A , BAC 120 =
, BC = 12 cm. Tính độ dài đường cao AH . A. AH = 3 cm. B. AH = 2 3 cm. C. AH = 4 3 cm. D. AH = 6 cm. Trang 6
Câu 10: Cho tam giác ABC vuông tại A , đường cao AH (hình
bên). Đẳng thức nào sau đây là sai? AH BH A. sin B = . B. tan BAH = . AB AH HC AH C. cosC = . D. cot HAC = . AC AC
Câu 11: Một cái thang dài 4 cm đặt dựa vào tường, biết góc
giữa thang và mặt đất là 60 . Khoảng cách d từ chân thang đến
tường bằng bao nhiêu? 3 A. d = m . B. d = 2 3 m . 2 C. d = 2 2 m . D. d = 2 m .
Câu 12: Cho tam giác ABC vuông tại A và AB = 2 5a , AC = 5 3a . Kẻ
AK vuông góc với BC , với K nằm trên cạnh BC . Tính AK theo a . 19 57 95 A. AK = a . B. AK = a . 10 2 10 57 5 57 C. AK = a . D. AK = a . 19 19
Câu 13: Cho tam giác ABC vuông tại A , đường cao AH . Biết
AH = 2 , HC = 4 . Đặt BH = x (hình bên). Tính x . 1 A. x = . B. x = 1 . 2 16 C. x = . D. x = 4 . 3
Câu 14: Cho xOy 45 =
. Trên tia Oy lấy hai điểm A , B sao cho AB = 2 cm. Tính độ dài hình
chiếu vuông góc của đoạn thẳng AB trên Ox . 2 2 1 A. cm. B. cm. C. 1 cm. D. cm. 2 4 2
Câu 15: Cho tam giác ABC vuông tại A , đường cao AH và đường trung tuyến AM (
H , M  BC ). Biết chu vi của tam giác là 72 cm và AM − AH = 7 cm. Tính diện tích S của tam giác ABC .
A. S = 48 cm 2 .
B. S = 108 cm 2 .
C. S = 148 cm 2 .
D. S = 144 cm 2 . II. PHẦN TỰ LUẬN 1
Bài 1. Cho biết cos = . 4 a) Tính sin .
b) Chứng minh rằng tan = 4sin . Lời giải 15 a) sin = . 4 Trang 7 sin sin b) tan = = = 4sin . cos 1 4
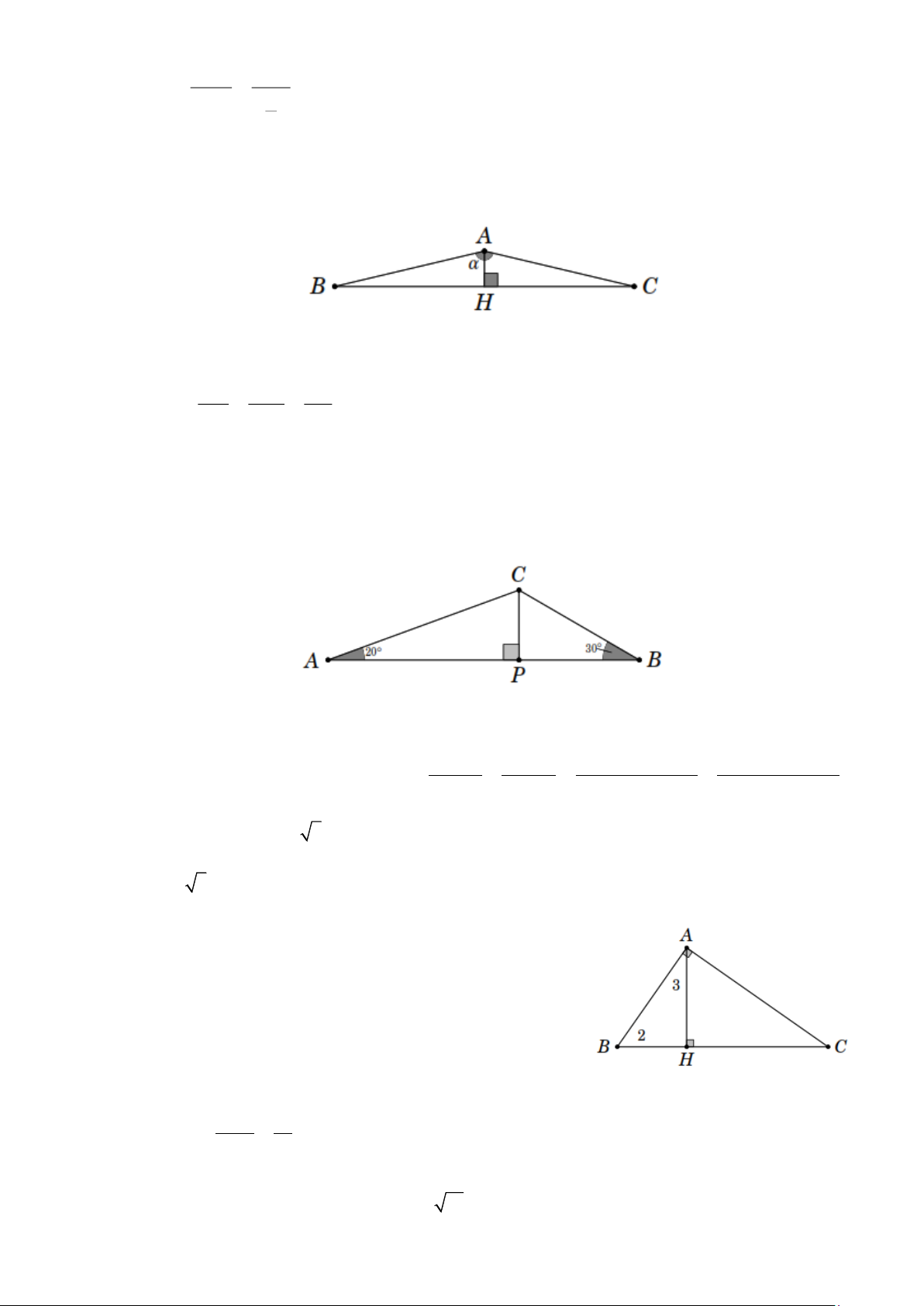
Bài 2. Xem hình bên và tính góc tạo bởi hai mái nhà AB và AC , biết rằng mỗi máy nhà dài 2,34m và cao 0,8m. Lời giải AH 0,8 40 cos BAH = = =
 BAH  70  BAC = 2BAH = 2.70 =140 . AB 2,34 117
Bài 3. Tam giác ABC có ˆA 20 = , ˆB 30 =
, AB = 6 cm. Đường vuông góc kẻ từ C đến AB cắt
AB tại P (hình vẽ bên). Hãy tìm a) AP , BP ; b) CP . Lời giải PA PB PA + PB 6
a) Ta có CP = A .
P tan 20 = P . B tan 30  = = = . tan 30 tan 20 tan 30 + tan 20 tan 30 + tan 20
Do đó PA = 6.tan 30 = 2 3 (cm) ; PB = 6.tan 20  2,18(cm).
b) CP = 2 3.tan 20  1, 26(cm) .
Bài 4. Tính độ dài các cạnh và số đo các góc nhọn của tam
giác ABC vuông tại A trong hình bên Lời giải 2 2 AH 3 ▪ HC = = = 4,5. HB 2
▪ BC = BH + HC = 2 + 4,5 = 6,5 . ▪ 2
BA = BH.BC = 2.6,5 = 13  BA = 13 . Trang 8 117 3 13 ▪ 2
CA = CH.CB = 4,5.6,5 =  AC = . 4 2 AH 3 ▪ tan B = =  B  59 1  9' . BH 2 ▪ C = 90 − 59 19  ' = 30 41  ' .
Bài 5. Cho hình thang cân ABCD ( AB CD ). Biết AD = 2,1cm ; CD = 6,0cm và ˆ D 48 = .
a) Tính độ dài AB .
b) Tính diện tích hình thang ABCD . Lời giải
a) Kẻ các đường cao AH ⊥ CD và BK ⊥ CD .
Dễ thấy ABKH là hình chữ nhật nên AB = HK .
Xét AHD và BKC , do giả thiết suy ra
AD = BC và ADH = BCK nên AHD = BKC .
Do đó DH = KC và HK = DC − 2DH .
Xét tam giác vuông AHD ta có DH AB cos ADH 2,1 cos 48 =  =  1,4(cm) .
Suy ra AB = 6,0 − 21, 4  3, 2(cm) .
(AB +CD) AH
b) Gọi S là diện tích hình thang ABCD . Khi đó S = . 2
Xét tam giác vuông ADH ta có AH AB sin ADH 2,1 sin 48 =  =  1,5 ( 6 cm) . (3,2+6,0)1,56 Nên S =  7,8 ( 2 8 cm ) . 2
Bài 6. Cho tam giác ABC vuông tại A , AB = 6 cm, AC = 8 cm.
a) Tính BC , ˆB , ˆ C ;
b) Phân giác của ˆA cắt BC tại D . Tính BD , CD .
c) Từ D kẻ DE và DF lần lượt vuông góc với AB , AC . Tứ giác AEDF là hình gì? Tính chu vi
và diện tích của tứ giác AEDF ? Lời giải
a) Theo định lý Py-ta-go, ta có B 2 2 2 2 2
BC = AB + AC = 6 + 8 = 100  BC = 100 = 10(cm) . D
Theo tỉ số lượng giác của góc nhọn trong tam giác ABC vuông E tại A Trang 9 C A F AC 8 4 tan B = = =  B  53 . AB 6 3
Do đó C = 90 − B = 90 − 53 = 37.
b) Theo tính chất đường phân giác trong tam giác ta có DB AB DB DC DB + DC BC 10 5 =  = = = = = . DC AC AB AC AB + AC 6 + 8 14 7 5 5
 DB = AB =   ( ) 5 5
6 4,3 cm ; DC = AC = 8 = 5,7(cm) . 7 7 7 7
c) Tứ giác AEDF có A = E = F = 90 nên là hình chữ nhật. Mặt khác DE = DF (tính chất tia
phân giác của một góc) nên AEDF là hình vuông.
Theo hệ thức liên hệ giữa cạnh và góc trong BED vuông tại E, ta có
DE = DB sin B = 4,3sin 53  3, 43(cm) .
Chu vi của hình vuông AEDF : 43, 43 = 13,72(cm).
Diện tích hình vuông AEDF : S = ( )2 = ( 2 3, 43 11,7649 cm ) . B AC
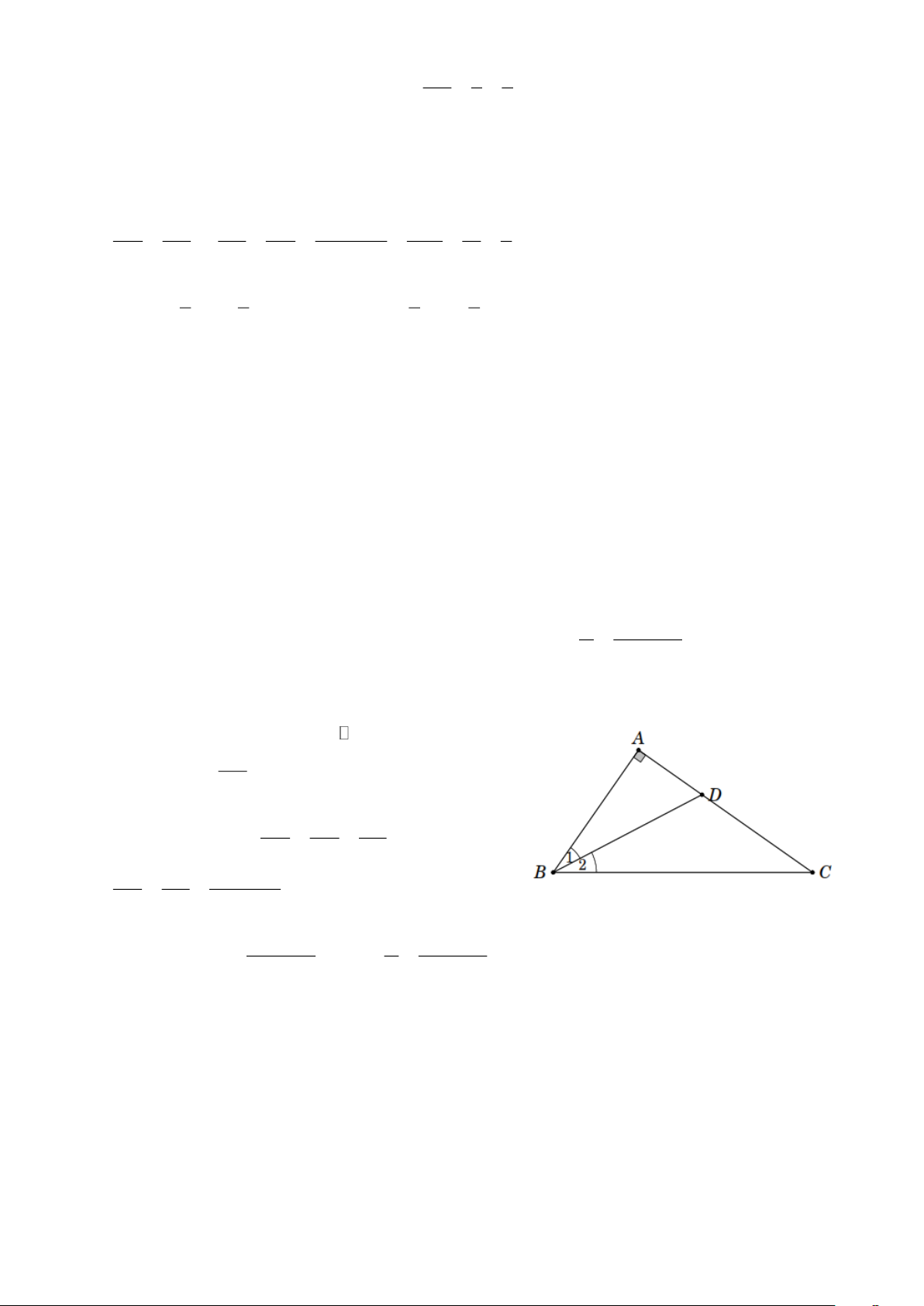
Bài 8. Cho tam giác ABC vuông tại A . Chứng minh rằng tan = . 2 AB + BC Lời giải
Vẽ đường phân giác BD . Xét ABD vuông tại A , ta AD có tan ABD = . AB AD AB AB Mặt khác = = suy ra DC DC BC AD CD AD + CD = = . AB BC AB + BC AC B AC Do đó tan ABD = hay tan = . AB + BC 2 AB + BC --- HẾT --- Trang 10