Phương pháp giải hình học 9 hình cầu- diện tích mặt cầu (có đáp án và lời giải chi tiết)
Tổng hợp Phương pháp giải hình học 9 hình cầu- diện tích mặt cầu (có đáp án và lời giải chi tiết) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.
Chủ đề: Chương 4: Hình trụ - Hình nón - Hình cầu
Môn: Toán 9
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
Bài 3. HÌNH CẦU – DIỆN TÍCH MẶT CẦU
VÀ THỂ TÍCH HÌNH CẦU
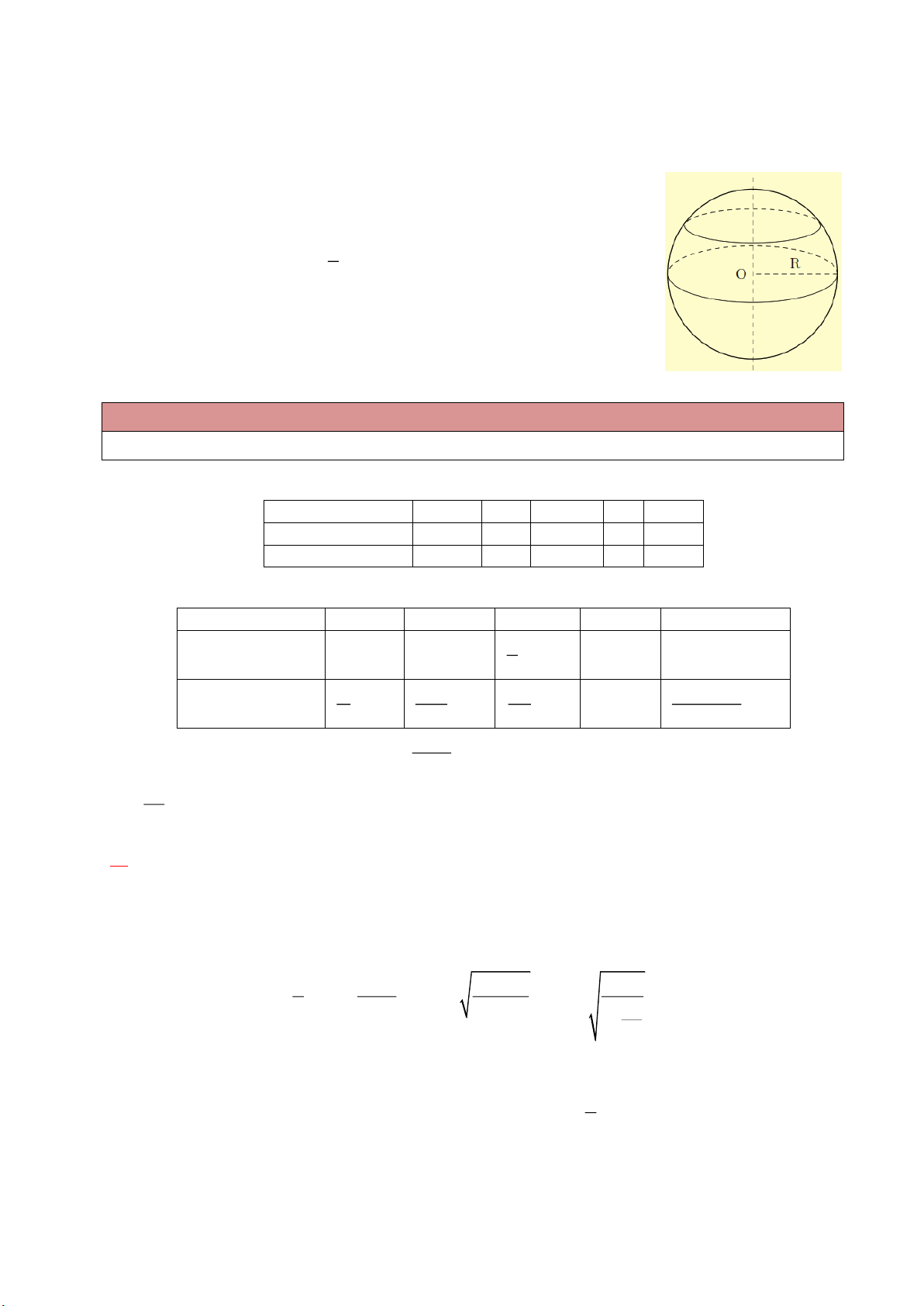
A. KIẾN THỨC TRỌNG TÂM Diện tích mặt cầu: 2
S 4 R hay 2 S d .
Với R là bán kính và d là đường kính của mặt cầu. 4 Thể tích hình cầu: 3 V R . 3
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tính diện tích mặt cầu, thể tích hình cầu và các đại lượng liên quan
Áp dụng công thức tính diện tích mặt cầu, thể tích hình cầu để giải bài toán.
Ví dụ 1. Hãy điền vào các ô trống trong bảng sau:
Bán kính mặt cầu 0,5mm 2cm 0,75dm 3m 50km Diện tích mặt cầu Thể tích hình cầu Lời giải Bán kính mặt cầu 0,5mm 2cm 0,75dm 3m 50km 9 Diện tích mặt cầu 2 mm 2 16 cm 2 dm 2 36 m 2 10000 km 4 32 9 500000 Thể tích hình cầu 3 mm 3 cm 3 dm 3 36 m 3 km 6 3 16 3 4312
Ví dụ 2. Thể tích của một hình cầu là
cm 3 . Thì bán kính của hình cầu là bao nhiêu? (Lấy 3 22 ). 7 A. 7 cm. B. 8 cm. C. 9 cm. D. 10 cm. Lời giải
Áp dụng công thức tính thể tích hình cầu và biến đổi ta được 4 4312 4312 3 4312 3 3 V R . R R 7 cm. 3 3 3 3 4 22 4 7
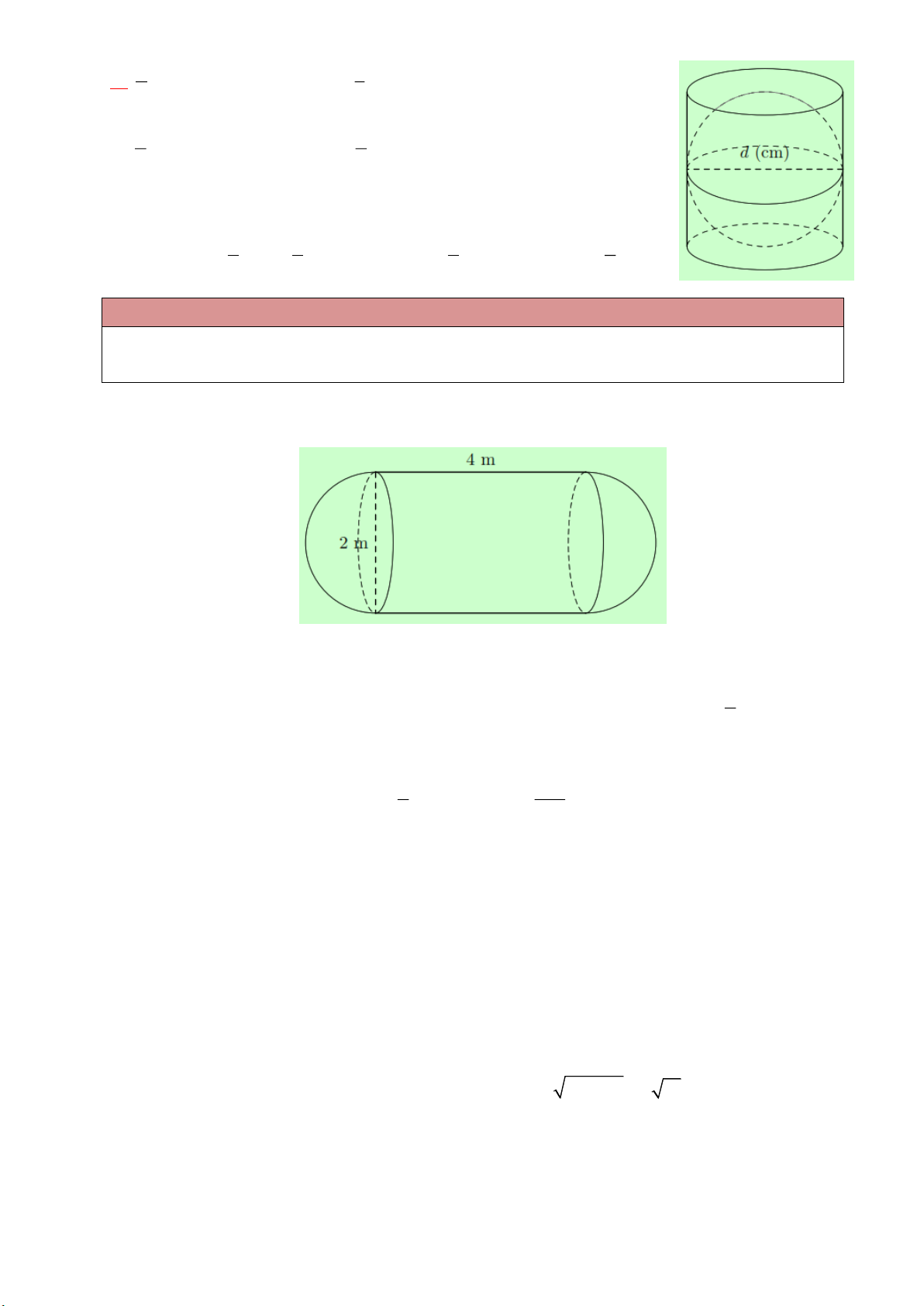
Ví dụ 3. Một hình cầu đặt vừa khít vào bên trong một hình trụ như hình vẽ (chiều cao của hình trụ 2
bằng độ dài đường kính của hình cầu) thì thể tích của nó bằng
thể tích hình trụ. Nếu đường kính 3
của hình cầu là d thì thể tích của hình trụ là Trang 1 1 1 A. 3 d . B. 3 d . 4 3 2 3 C. 3 d . D. 3 d . 3 4 Lời giải 4 1 2 1 Ta có 3 3 V
R d . Mà V V 3 V d . hình caàu hình caàu hình truï hình truï 3 6 3 4
Dạng 2: Dạng toán tổng hợp
Vận dụng linh hoạt các kiến thức đã được học kết hợp với các công thức và lý thuyết về
hình cầu để giải bài tập.
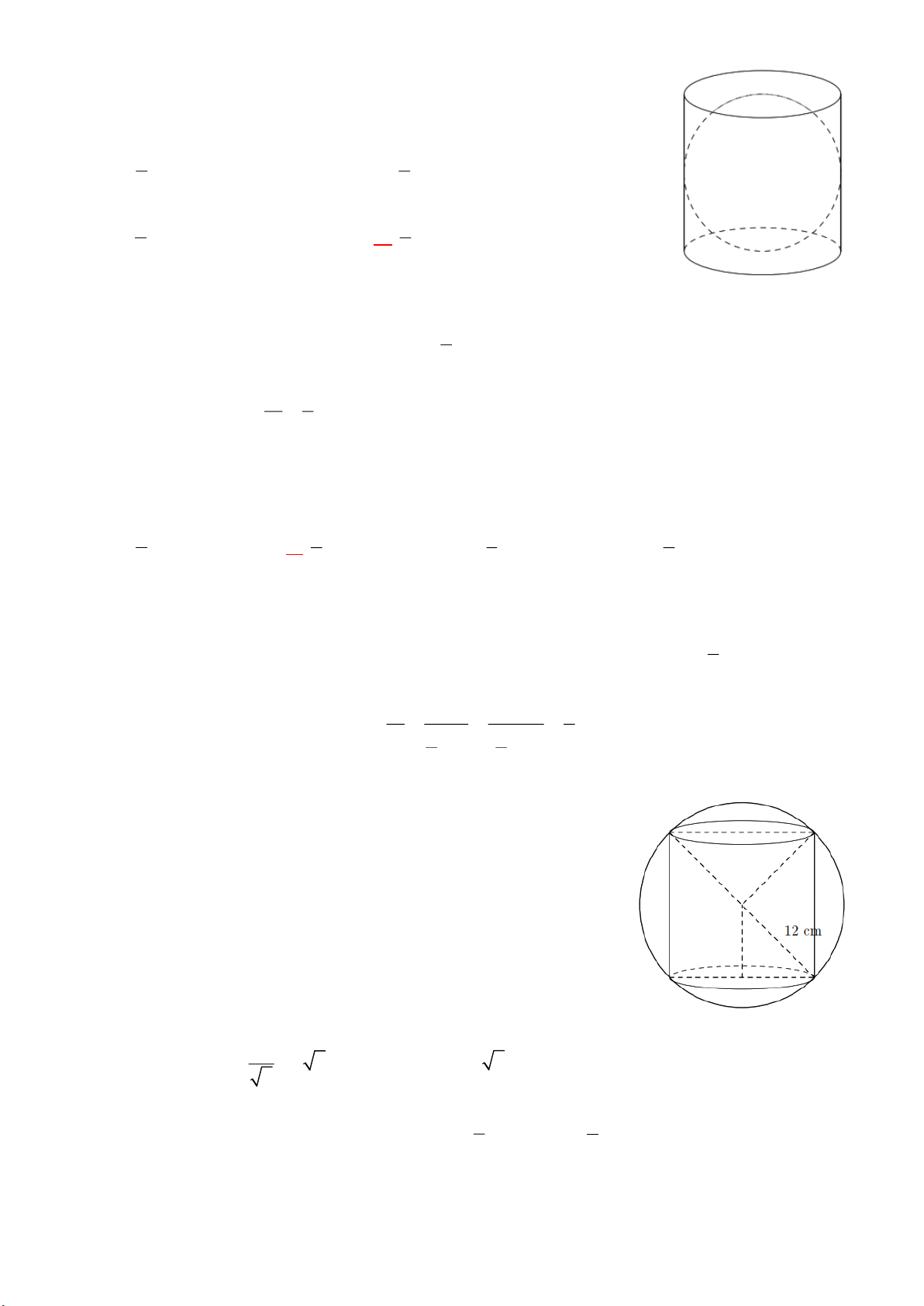
Ví dụ 4. Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ. Tính thể tích của bồn chứa
theo các kích thước như hình vẽ. Lời giải 4
Áp dụng công thức tính thể tích cho hình trụ 2
V r h và thể tích hình cầu 3 V R và kết hợp 3 lại ta có: 4 16 3 2 V 1 1 4 m 3 . 3 3
C. BÀI TẬP VẬN DỤNG
Bài 1. Một hình nón có bán kính đáy bằng 3 cm và có diện tích xung quanh bằng diện tích của mặt
cầu có bán kính 3 cm. Tính chiều cao của hình nón. Lời giải
Áp dụng công thức tính diện tích xung quanh hình nón S
rl 3l . xq
Áp dụng công thức tính diện tích mặt cầu 2
S 4 R 36 . c Từ giả thuyết S
S ta được 3l 36 2 2
l 12 h 12 3 3 15 cm. xq c Trang 2
Bài 2. Một cái hộp hình trụ được làm ra sao cho một quả bóng hình cầu
đặt vừa khít vào hộp đó như hình vẽ. Tỉ số thể tích của hình cầu và hình trụ là 3 4 A. . B. . 4 3 3 2 C. . D. . 2 3 Lời giải 4
Nhận thấy R R r và h 2r . Nên 3 V r và c t c 3 V 2 2 3
V r h 2 c r . t V 3 t
Bài 3. Chiều cao của một hình trụ gấp 3 lần bán kính đáy của nó. Tỉ số của thể tích hình trụ này và
thể tích của hình cầu có bán kính bằng bán kính đáy của hình trụ là 4 9 3 4 A. . B. . C. . D. . 3 4 1 9 Lời giải 4
Áp dụng công thức tính thể tích cho hình trụ 2
V r h và thể tích hình cầu 3 V R . 3 2 2 V
r h r 3r 9 t . V 4 4 3 3 4 c r r 3 3
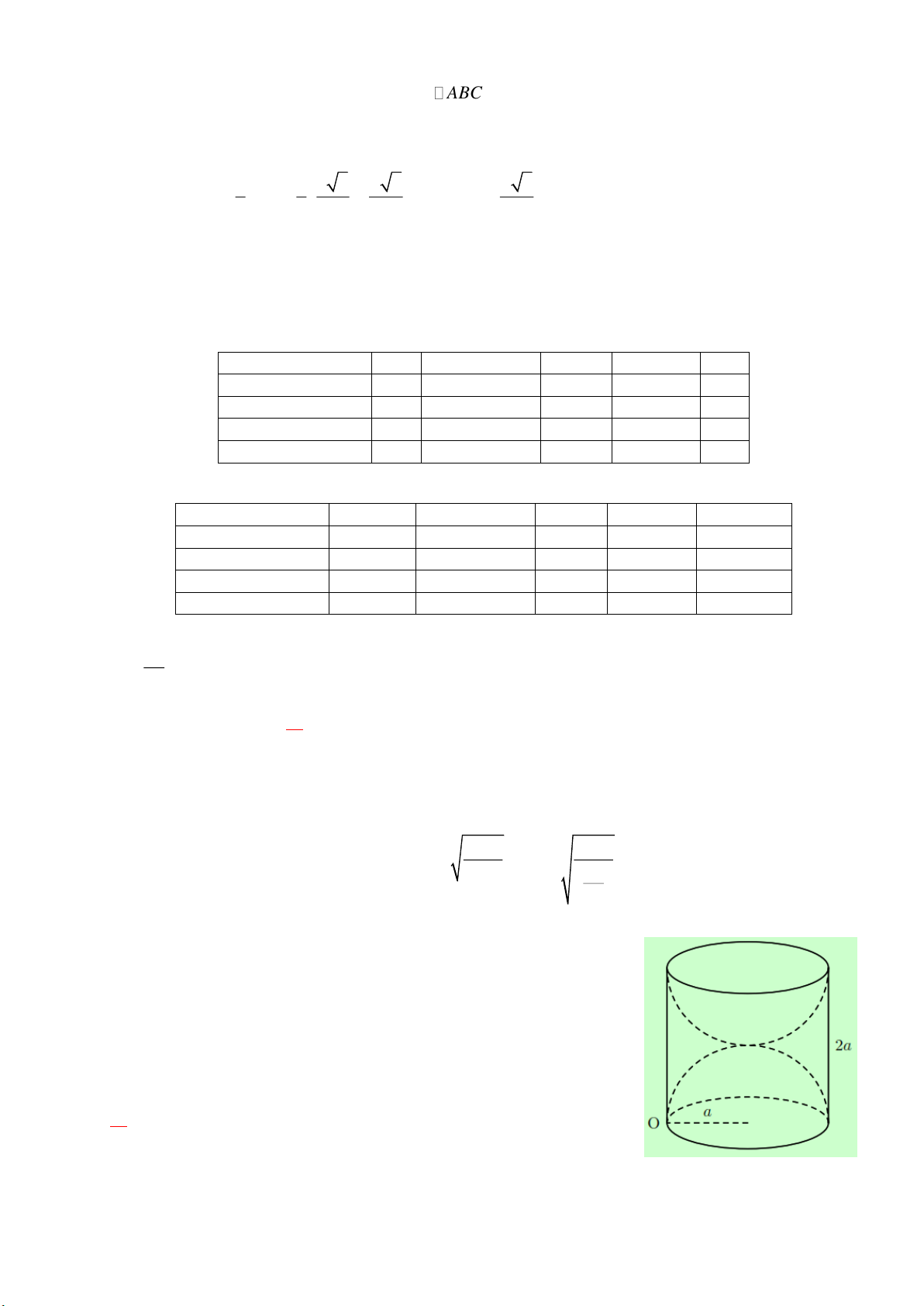
Bài 4. Một hình trụ được “đặt khít” vào bên trong một hình cầu bán
kính r 12 cm như hình vẽ. Tính:
a) Diện tích xung quanh của hình trụ, biết chiều cao của hình trụ
bằng đường kính đáy của nó.
b) Thể tích của hình cầu. c) Diện tích mặt cầu. Lời giải r a) Nhận thấy: r
6 2 cm, với h 2r 12 2 cm S 2 rh 288 cm 2 . t t xq 2 4 4
b) Áp dụng công thức tính thể tích hình cầu 3 V R 3 V 12 2304 cm 3 . 3 3
c) Áp dụng công thức tính diện tích mặt cầu 2
S 4 R 2
S 4 12 576 cm 2 . Trang 3
Bài 5. Cho tam giác đều ABC có cạnh AB 8 cm, đường cao AH . Khi đó diện tích mặt cầu được
tạo thành khi quay nửa đường tròn nội tiếp ABC một vòng quanh AH . Lời giải 2 1 1 8 3 4 3 4 3 Nhận thấy: r AH S 4 67,02 cm 2 nt 3 3 2 3 3
D. BÀI TẬP VỀ NHÀ
Bài 6. Các loại bóng cho trong bảng đều có dạng hình cầu. Hãy điền vào các ô trống ở bảng sau
(làm tròn kết quả đến chữ số thập phân thứ hai, đơn vị: mm): Loại bóng
Gôn Khúc côn cầu Ten-nít Bóng bàn Bi-a Đường kính 42,7 65 40 61 Độ dài đường tròn 230 Diện tích Thể tích Lời giải Loại bóng Gôn
Khúc côn cầu Ten-nít Bóng bàn Bi-a Đường kính 42,7 73,2 65 40 61 Độ dài đường tròn 134,15 230 204,2 125,66 191,64 Diện tích 1432 4210 3318 1256,64 2922,47 Thể tích 40764,51 205460 143790 33510,32 118846,77
Bài 7. Diện tích của một mặt cầu là 2464 m 2 thì đường kính của mặt cầu là bao nhiêu? (Lấy 22 ). 7 A. 28 cm. B. 28 mét. C. 38 mét. D. 30 mét. Lời giải
Áp dụng công thức tính diện tích mặt cầu và biến đổi ta được 2464 2464 2
S d 2464 d d 28 mét. 22 7
(Đơn vị của diện tích mặt cầu là m 2 ).
Bài 8. Một khối gỗ dạng hình trụ đứng, bán kính đường tròn đáy là a
(cm), chiều cao là 2a (cm). Người ta khoét rỗng hai nửa hình cầu
như hình vẽ. Diện tích toàn bộ của khối gỗ là A. 2 4 a cm 2 . B. 2 6 a cm 2 . C. 2 8 a cm 2 . D. 2 10 a cm 2 . Lời giải Trang 4
Nhận thấy: S S
S . Với S 2 R h 2 a 2a 2 4 a và 2 2
S 4 R 4 a . tb xqt c xqt c
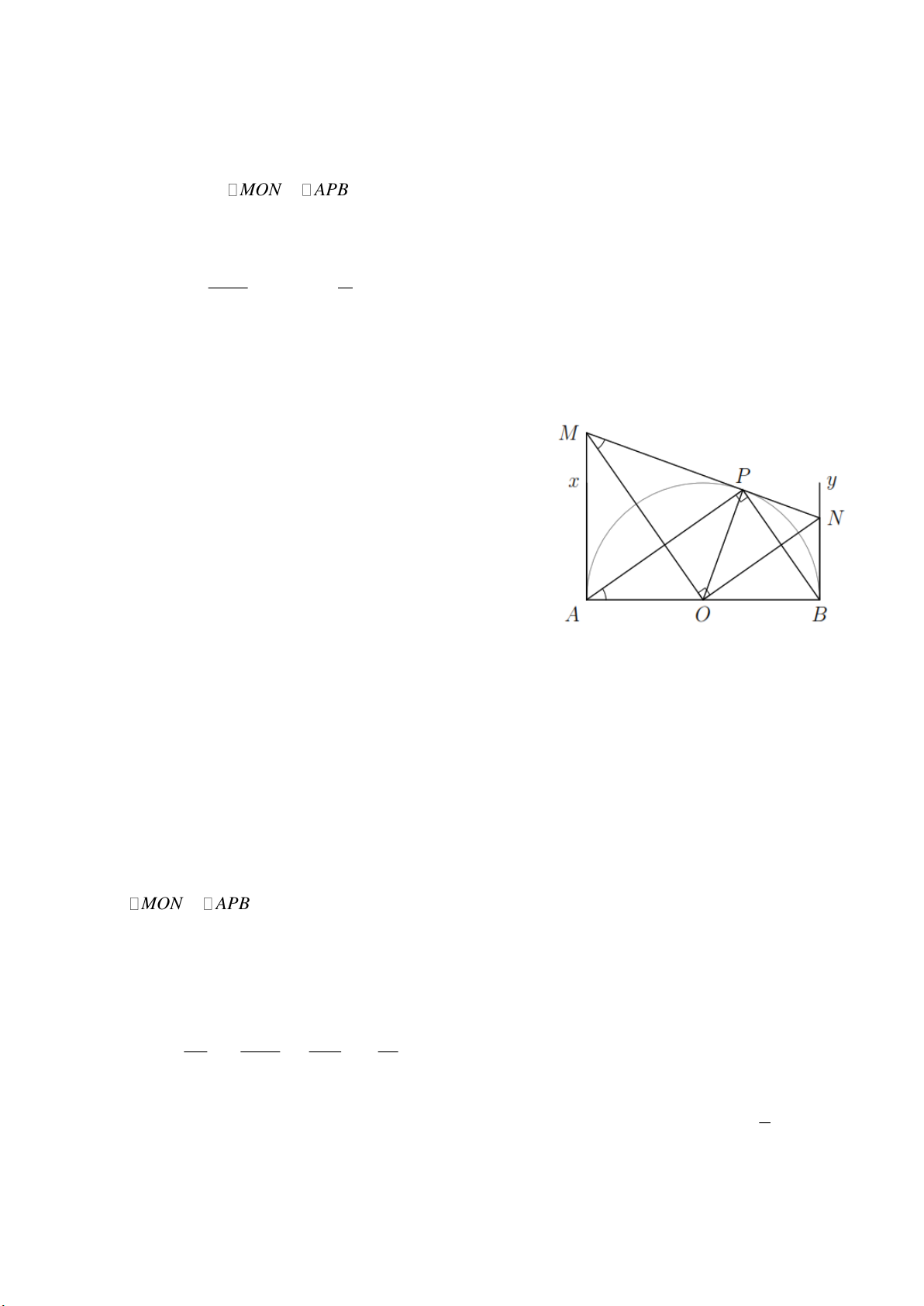
Câu 8. Cho nửa đường tròn tâm O , đường kính AB 2R , Ax và By là hai tiếp tuyến với nửa mặt
đường tròn tại A và B . Lấy trên Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N .
a) Chứng minh MON ∽ APB . b) Chứng minh 2
AM BN R . S R
c) Tính tỉ số MON khi AM . S 2 APB
d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra. Lời giải a) Ta có: - Góc APB 90
(góc nội tiếp chắn nửa đường tròn).
- Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OM là tia phân giác của AOP và ON là tia phân giác của góc BOP .
Mà AOP và BOP là 2 góc kề bù OM ON MON 90 .
- Xét tứ giác AMPO có MPO MAO 90 .
OMP và PAO cùng chắn cung OP OMP PAO . MON APB 90 .
BAP OMN
MON ∽ APB (g.g). b) 2 2
AM BN MP NP OP R . c) 2
AM BN R BN 2R . 2 5R S MN 25 MN MON . 2 S AB 16 APB 4
d) Nửa hình tròn APB quay quanh AB là hình cầu đường kính AB AO R 3 V R . 3 --- HẾT --- Trang 5