Phương pháp giải hình học 9 hình trụ (có đáp án và lời giải chi tiết)
Tổng hợp Phương pháp giải hình học 9 hình trụ (có đáp án và lời giải chi tiết) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.
Chủ đề: Chương 4: Hình trụ - Hình nón - Hình cầu
Môn: Toán 9
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
Chương 4 Bài 1. HÌNH TRỤ.
DIỆN TÍCH XUNG QUANH VÀ THỂ TÍCH CỦA HÌNH TRỤ
A. KIẾN THỨC TRỌNG TÂM
Diện tích xung quanh S 2 R . h xq Diện tích đáy 2 S R . Diện tích toàn phần 2
S 2 Rh 2 R . tp Thể tích khối trụ 2 V R . h
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tính chiều cao, bán kính đáy, diện tích xung quanh, diện tích toàn phần, thể tích
Áp dụng công thức tính diện tích xung quanh, diện tích đáy, diện tích toàn phần, thể tích để làm.
Ví dụ 1. Điền đầy đủ các kết quả vào bảng sau Bán kính Chiều cao
Chu vi đáy Diện tích đáy Diện tích xung Thể tích Hình đáy (cm) (cm) (cm) (cm 2 ) quanh (cm 2 ) (cm 3 ) 2 20 10 8 16 8 Lời giải Ta có bảng sau Bán kính
Chiều cao Chu vi đáy Diện tích đáy Diện tích xung Thể tích Hình đáy (cm) (cm) (cm) (cm 2 ) quanh (cm 2 ) (cm 3 ) 2 20 4 4 80 80 10 8 20 100 160 800 16 8 16 128 256
Ví dụ 2. Một hình trụ có bán kính đáy là 13 cm, diện tích xung quanh bằng 527 cm 2 . Khi đó,
chiều cao của hình trụ là A. 27, 958 cm. B. 17, 958 cm. C. 6, 451 cm. D. 28, 958 cm. Lời giải Sxq 527 Ta có S
2 Rh h 6,451 cm. xq 2 R 2 13
Ví dụ 3. Chiều cao của một hình trụ bằng bán kính của đường tròn đáy. Diện tích xung quanh của
hình trụ là 314 cm 2 . Tính
a) Bán kính của đường tròn đáy. Trang 1
b) Thể tích của khối trụ. (Làm tròn kết quả đến chữ số thập phân thứ hai). Lời giải
Theo giả thiết R h . Sxq 314 Ta có 2 S
2 Rh 2 h h 7,07 cm. xq 2 2 Ta có 2 3 3 3
V R h h 7, 07 1110, 22 cm .
Ví dụ 4. Một hình trụ có bán kính đáy đường tròn đáy là 16 cm, chiều cao là 9 cm. Tính
a) Diện tích xung quanh của hình trụ.
b) Thể tích của hình trụ. (Lấy 3,142 làm tròn kết quả đến hàng đơn vị). Lời giải a) Ta có 2 S
2 Rl 23,142169 983 cm . xq b) Ta có 2 2 3
V R h 3,142 16 9 7239 cm .
Ví dụ 5. Cho hình chữ nhật ABCD có AB 4, BC 2 . Quay hình chữ nhật đó quanh AB thì được
hình trụ có thể tích V ; quay quanh BC thì được hình trụ có thể tích V . Trong các đẳng thức dưới 1 2
đây đẳng thức nào đúng? A. V V . B. V 2V .
C. V 2V . D. V 3V . 1 2 1 2 2 1 2 1 Lời giải Ta thấy rằng,
Khi quay hình chữ nhật quanh AB thì h AB 4 , R BC 2 và 2 2
V R h 2 4 16 . 1
Khi quay hình chữ nhật quanh BC thì h BC 2 , R AB 4 và 2 2
V R h 4 2 32 . Suy 2 ra V 2V . 2 1
Ví dụ 6. Một vật thể có thể dáng hình trụ, bán kính đường tròn
đáy và độ dài của nó đều bằng 2r (cm). Người ta khoan một lỗ
cũng có dạng hình trụ như hình vẽ có bán kính đáy và độ sâu đều
bằng r (cm). Thể tích phần vật thể còn lại tính theo cm 3 là A. 3 4 r . B. 3 7 r . C. 3 8 r . D. 3 9 r . Lời giải
Gọi V là thể tích khối trụ bán kính đáy 2r và V là thể tích khối trụ bán kính đáy r . Khi đó 1 2 3
V (2r) 2r 8 r . Trang 2 2 3
V r r r . 1
Thể tích phần vật thể còn lại là 3 3 3
V V 8 r r 7 r . 1
Dạng 2: Dạng toán tổng hợp
Vận dụng linh hoạt các kiến thức đã học và kết hợp với công thức lý thuyết về hình trụ để giải bài tập.
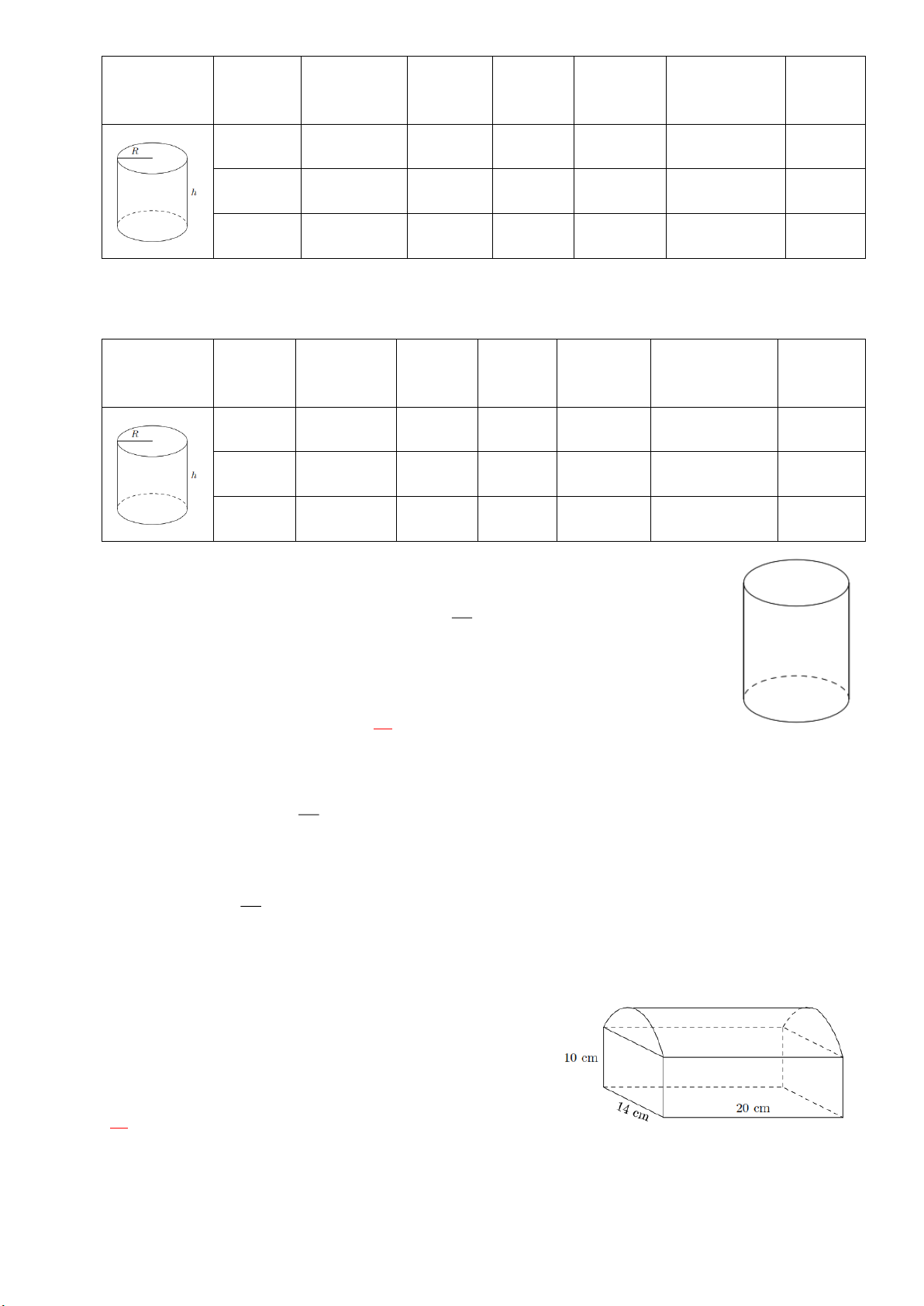
Ví dụ 7. Cho hình vẽ là một mẫu pho mát được cắt ra từ một khối pho
mát dạng hình trụ (có các kích thước như hình sau). Khối lượng của mẫu
pho mát là (khối lượng riêng của pho mát là 3 g/cm 3 ). A. 100 g. B. 100 g. C. 800 g. D. 800 g. Lời giải 2 10 15 100
Ta có V S h 8 q 360 3 100
m V D 3 100 . 3
Ví dụ 8. Một hình trụ có bán kính đáy là 3 cm, chiều cao 4 cm được đặt đứng trên mặt bàn. Một
phần của hình trụ bị cắt rời theo các bán kính OA , OB và theo chiều dài
thẳng đứng từ trên xuống dưới với AOB 30 .
a) Tính thể tích của phần bị cắt.
b) Tính thể tích của phần còn lại.
c) Diện tích toàn phần của hình trụ sau khi đã bị cắt. Lời giải 2 3 30 a) Ta có 3
V S h 4 3 cm . 1 q 360 b) Ta thấy 2 3
V V V 3 4 3 33 cm . 2 1 930 33
c) Diện tích phần còn lại của hai đáy là 2 2 9 cm . 360 2 R 30 Diện tích xung quanh là 2 2 Rh
2Rh 22 24 cm . 180 33 1 Diện tích toàn phần là 2
22 24 38 24 cm . 2 2
C. BÀI TẬP VẬN DỤNG
Bài 1. Điền đầy đủ các kết quả vào ô trống của bảng sau Trang 3 Đường Chu vi Diện tích Diện tích Bán kính Chiều Thể tích Hình kính đáy đáy đáy (cm) đáy (cm 2 xung quanh cao (cm) (cm 3 ) (cm) (cm) ) (cm 2 ) 20 8 12 2 10 1000 Lời giải Ta có Bán Đường Chiều Chu vi Diện tích Diện tích Thể tích Hình kính đáy kính đáy cao đáy đáy (cm 2 xung quanh (cm 3 ) (cm) (cm) (cm) (cm) ) (cm 2 ) 20 40 8 40 400 320 3200 6 12 2 12 100 24 72 10 20 3,183 20 100 199, 99 1000
Bài 2. Một cái trụ lăn có dạng hình trụ như hình bên. Đường kính của đường tròn
đáy là 42 cm, chiều dài trục lăn là 2 m. Sau khi lăn trọn 10 vòng thì trụ lăn tạo 22
trên mặt sân mặt phẳng một diện tích là . 7 A. 24600 cm 2 . B. 58200 cm 2 . C. 528 m 2 . D. 264000 cm 2 . Lời giải Bán kính của đáy là 42 R
21 cm và chiều cao h 200 cm. Do đó diện tích xung quanh của cái 2 trụ lăn một vòng là 22 2 S
2 R l 2 21 200 26400 cm . xq 7
Sau khi trụ lăn được 10 vòng thì diện tích là 264000 cm 2 .
Bài 3. Một vật thể hình học có hình vẽ như hình bên.
Phần trên là một nửa hình trụ, phần dưới là một hình hộp
chữ nhật. Với các kích thước cho như hình vẽ. Thể tích
của vật thể hình học này là A. 4340 cm 3 . B. 4760 cm 3 . C. 5880 cm 3 . D. 8 cm 3 . Lời giải Trang 4
Thể tích của hình hộp chữ nhật là 3
V 14 20 10 2800 cm . 1 1 22
Thể tích nữa hình trụ là 2 3 V 7 20 1540 cm . 2 2 7
Thể tích của vật thể là 3
V V V 4340 cm . 1 2 --- HẾT --- Trang 5