

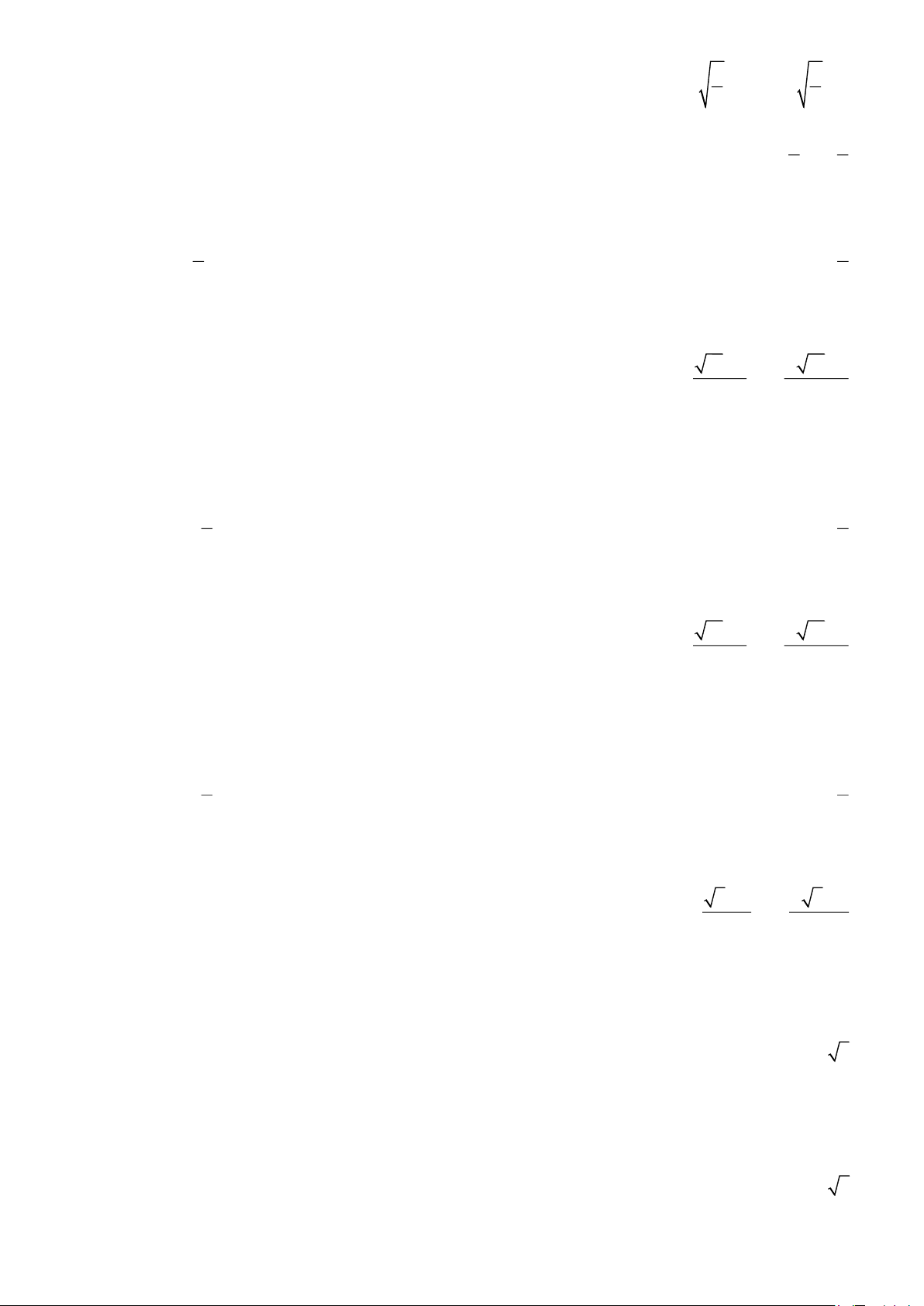







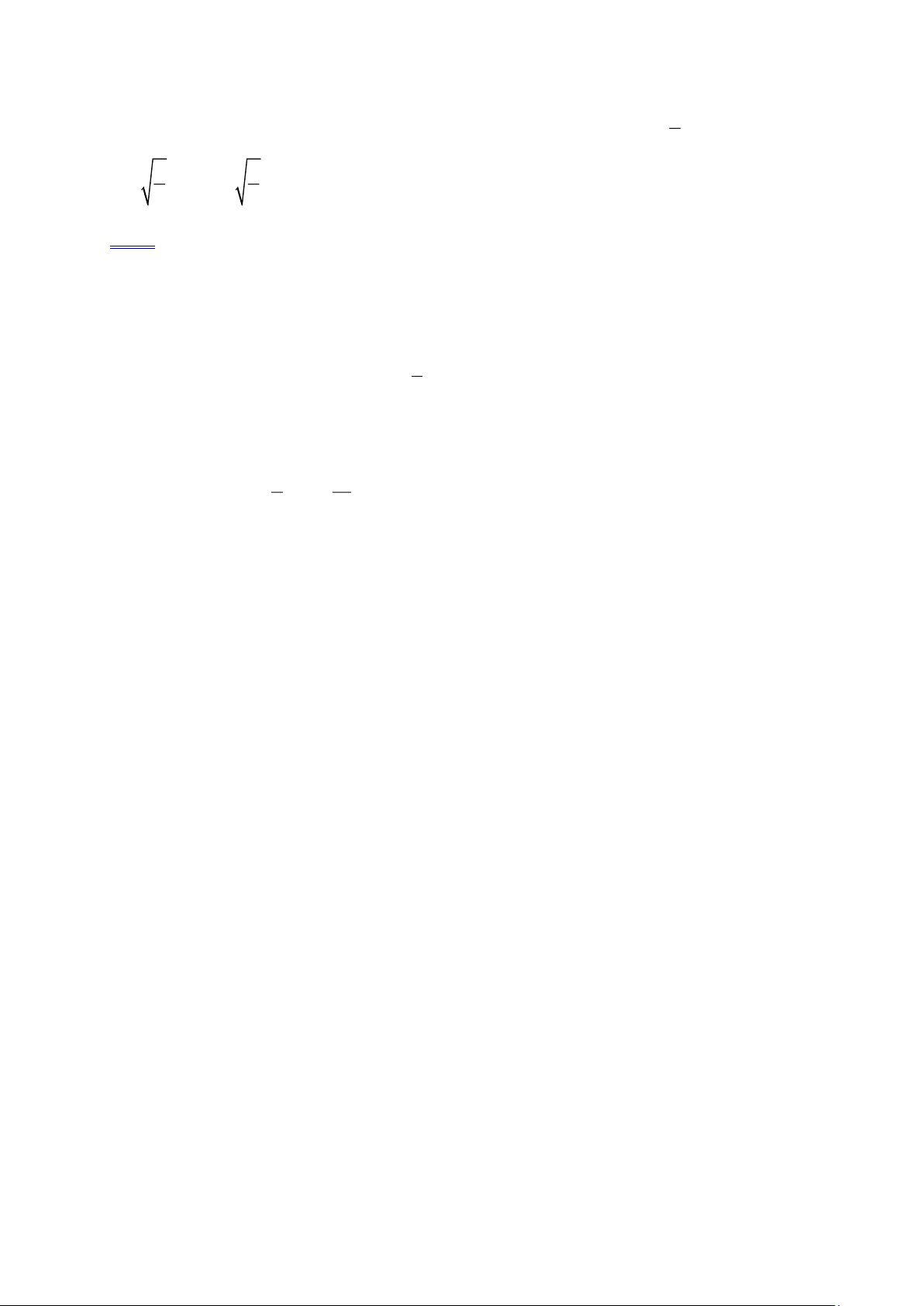
Preview text:
Bài 3. PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
A. KIẾN THỨC TRỌNG TÂM
▪ Phương trình bậc hai một ẩn (hay còn gọi là phương trình bậc hai) là phương trình có dạng: 2
ax + bx + c = 0 (a 0) trong đó a,b, c là những số thực cho trước được gọi là hệ số, x là ẩn số.
▪ Chú ý: Giải phương trình bậc hai một ẩn là đi tìm tập nghiệm của phương trình bậc hai một ẩn đó.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Nhận dạng và tìm hệ số của phương trình bậc hai một ẩn
▪ Đưa phương trình đã cho về dạng 2
ax + bx + c = 0 , từ đó đưa ra kết luận về dạng
phương trình và các hệ số.
▪ Lưu ý: Phương trình bậc hai có hệ số a khác 0.
Ví dụ 1. Đưa các phương trình sau về dạng 2
ax + bx + c = 0 và chỉ rõ các hệ số a,b, c . a) 2 3 − x = 0 . ĐS: 2
−x + 3 = 0 , với a = 1
− ,b = 0,c = 3 . . b) 2
x − x = 3x +1. ĐS: 2
x − 4x −1 = 0 , với a = 1,b = −4, c = −1. c) 2
3x − 4x = 2x + 2 . ĐS: 2
3x − (4 + 2) x − 2 = 0 , với a = 3,b = 4 − − 2,c = 2 − . d) 2
(x −1) = 3(x +1) . ĐS: 2
x − 5x − 2 = 0 , với a = 1,b = −5,c = −2 .
Ví dụ 2. Đưa các phương trình sau về dạng 2
ax + bx + c = 0 và chỉ rõ các hệ số a,b, c . a) 2
3x − x = 0 . ĐS: 2
−x + 3x = 0 , với a = 1
− ,b = 3,c = 0 . b) 2
x − 3x = 2x − 3. ĐS: 2
x − 5x + 3 = 0 , với a = 1,b = 5 − ,c = 3. c) 2 2
3x − 4x = 2x − 2 . ĐS: ( − ) 2 3
2 x − 4x + 2 = 0 , với a = 3 − 2,b = 4 − ,c = 2 . d) 2
(x +1) = 2(x −1) . ĐS: 2
x + 3 = 0 , với a = 1,b = 0,c = 3 .
Ví dụ 3. Phương trình nào sau dây đưa được về phương trình bậc 2 ? Xác định hệ số a của phương
trình đó ( m là hằng số) a) 2
1+ mx = x . ĐS: 2
x − mx −1 = 0; a = 1. b) 2
1+ mx = m .
ĐS: Không đưa được về phương trình bậc 2 . c) 2 2 2
m x − 4mx = − 2x +1. ĐS: ( 2 m + ) 2 2
2 x − 4mx −1 = 0, a = m + 2 . d) 2 2
m(x −1) = mx −1.
ĐS: Không đưa được về phương trình bậc 2 .
Ví dụ 4. Phương trình nào sau dây đưa được về phương trình bậc 2 ? Xác định hệ số a của phương
trình đó ( m là hằng số) Trang 1 a) 2
x = x − m . ĐS: 2
x − x − m = 0, a = 1. b) 2
m = m − mx .
ĐS: Không đưa được về phương trình bậc 2 . c) 2 2 2
(m −1)x − mx = −3x . ĐS: 2 2 2
(m + 2)x − mx = 0, a = m + 2 . d) 2
m(x −1) = x(1+ mx) .
ĐS: Không đưa được về phương trình bậc 2 .
Dạng 2: Sử dụng các phép biến đổi, giải phương trình bậc hai một ẩn cho trước
▪ Cách 1: Đưa phương trình đã cho về dạng tích.
▪ Cách 2: Đưa phương trình đã cho về phương trình mà vế trái của phương trình đó là bình
phương, còn vế phải là một hằng số.
Ví dụ 5. Giải các phương trình sau: a) 2
x − 2x = 0 .
ĐS: x = 0; x = 2 . 2 b) 2
3x = 2x .
ĐS: x = 0; x = . 3 c) 2
−3x +12 = 0 .
ĐS: x = −2; x = 2 . d) 2
x − 3x + 2 = 0 .
ĐS: x = 1; x = 2 .
Ví dụ 6. Giải các phương trình sau: a) 2
x − 3x = 0 .
ĐS: x = 0; x = 3. b) 2 x = 2x .
ĐS: x = 0; x = 2 . c) 2 x − 2 = 0 .
ĐS: x = − 2; x = 2 . d) 2
x + x − 2 = 0 .
ĐS: x = 1; x = −2 .
Ví dụ 7. Giải các phương trình sau: a) 2 (x +1) = 4 .
ĐS: x = 1; x = −3. b) 2
x + 2x = 3.
ĐS: x = 1; x = −3. 3 3 c) 2
2x + 4x − 7 = 0 . ĐS: x = −1; x = − −1. 2 2 1 5 d) 2
4x + 8x − 5 = 0 .
ĐS: x = ; x = − . 2 2
Ví dụ 8. Giải các phương trình sau: a) 2 (x − 2) = 9 .
ĐS: x = −1; x = 5. b) 2
x − 4x = 5 .
ĐS: x = −1; x = 5. Trang 2 3 3 c) 2
2x − 8x + 5 = 0 . ĐS: x = + 2; x = − + 2 . 2 2 1 9 d) 2
4x −16x − 9 = 0 .
ĐS: x = − ; x = . 2 2
Ví dụ 9. Giải các phương trình sau: 1 a) 2 1
x − x + = 0 . ĐS: x = . 4 2 b) 2
x − x = 2 .
ĐS: x = −1; x = 2 . 11 +1 − 11 +1 c) 2
2x − 2x − 5 = 0 . ĐS: x = ; x = . 2 2 d) 2
x − x +1 = 0 . ĐS: PT vô nghiệm.
Ví dụ 10. Giải các phương trình sau 1 a) 2 9
x − 3x + = 0 . ĐS: x = . 4 2 b) 2
x − 3x − 4 = 0 .
ĐS: x = −1; x = 2 . 11 +1 − 11 +1 c) 2
2x − 6x + 3 = 0 . ĐS: x = ; x = . 2 2 d) 2
x − 3x + 3 = 0 . ĐS: PT vô nghiệm.
Ví dụ 11. Giải các phương trình sau 3 a) 2 9
x − 3x + = 0 . ĐS: x = . 4 2 b) 2
x − 3x − 4 = 0 .
ĐS: x = −1; x = 4 . 3 + 3 − 3 + 3 c) 2
2x − 6x + 3 = 0 . ĐS: x = ; x = . 2 2 d) 2
x − 3x + 3 = 0 . ĐS: PT vô nghiệm.
Ví dụ 12. Tìm giá trị của tham số m để phương trình sau có nghiệm bằng 1 a) 2 2
x + m = 4x .
ĐS: m = 3 . b) 2 2
x − (m + 3)x + m = 0 .
ĐS: m = 2, m = −1.
Ví dụ 13. Với giá nào của m thì phương trình sau có nghiệm bằng 1 a) 2 2
x − m + 4 = 0 .
ĐS: m = 5 . Trang 3 b) 2
m + 4mx − 5 = 0 = 0 .
ĐS: m = 1, m = −5 . C. BÀI TẬP VẬN DỤNG
Bài 1. Đưa các phương trình sau về dạng 2
ax + bx + c = 0 và tính tổng T = a + b + c a) 2
25 − 4x = 0 . ĐS: T = 21. b) 2 x − 4x = 5 − x + 2 . ĐS: T = 0 . c) 2
(x −1) − 3x + 4 = 0 . ĐS: T = 1. d) 2
x(x − 3) = 2x − 2x .
ĐS: T = − 2 .
Bài 2. Giải các phương trình sau 3 a) 2 4x − 9 = 0 . ĐS: x = . 2 b) 2
x − 2 2x = 0 .
ĐS: x = 0; x = 2 2 . c) 2
x − 2 2x = 2 . ĐS: x = 2 . d) 2
x − 8x + 5 = 0 . ĐS: PT vô nghiệm.
Bài 3. Giải các phương trình sau a) 2
x + 2x = 0 .
ĐS: x = 0, x = −2 . b) 2 x − 5 = 0 .
ĐS: x = 5 . c) 2
x + 2x − 8 = 0 .
ĐS: x = 2, x = −4 . 7 d) 2
2x + 4x − 5 = 0 . ĐS: x = − −1. 2
Bài 4. Với giá nào của m thì phương trình sau có nghiệm là 1 − 2 a) 2 2
4x − 25m = 0. ĐS: m = . 5 b) 2 2
x − 3mx + 3m = 0 .
ĐS: Không tìm được m . Trang 4 HƯỚNG DẪN GIẢI
Ví dụ 1. Đưa các phương trình sau về dạng 2
ax + bx + c = 0 và chỉ rõ các hệ số a,b, c . a) 2 3 − x = 0 . b) 2
x − x = 3x +1. c) 2
3x − 4x = 2x + 2 . d) 2
(x −1) = 3(x +1) . Lời giải. a) Biến đổi PT 2 3 − x = 0 thành 2
−x + 3 = 0 , với a = 1
− ,b = 0,c = 3 . b) Biến đổi PT 2
x − x = 3x +1 thành 2
x − 4x −1 = 0 , với a = 1,b = −4, c = −1. c) Biến đổi PT 2
3x − 4x = 2x + 2 thành 2
3x − (4 + 2) x − 2 = 0 , với a = 3,b = 4 − − 2,c = 2 − . d) Biến đổi PT 2
(x −1) = 3(x +1) thành 2
x − 5x − 2 = 0 , với a = 1,b = −5,c = −2 .
Ví dụ 2. Đưa các phương trình sau về dạng 2
ax + bx + c = 0 và chỉ rõ các hệ số a,b, c . a) 2 3x − x = 0 . b) 2
x − 3x = 2x − 3. c) 2 2
3x − 4x = 2x − 2 . d) 2
(x +1) = 2(x −1) . Lời giải. a) Biến đổi PT 2
3x − x = 0 thành 2
−x + 3x = 0 , với a = 1
− ,b = 3,c = 0 . b) Biến đổi PT 2
x − 3x = 2x − 3 thành 2
x − 5x + 3 = 0 , với a = 1,b = 5 − ,c = 3. c) Biến đổi PT 2 2
3x − 4x = 2x − 2 thành ( − ) 2 3
2 x − 4x + 2 = 0 , với a = 3 − 2,b = 4 − ,c = 2 . d) Biến đổi PT 2
(x +1) = 2(x −1) thành 2
x + 3 = 0 , với a = 1,b = 0,c = 3 .
Ví dụ 3. Phương trình nào sau dây đưa được về phương trình bậc 2 ? Xác định hệ số a của
phương trình đó ( m là hằng số) a) 2 1+ mx = x . b) 2 1+ mx = m . c) 2 2 2
m x − 4mx = − 2x +1. d) 2 2
m(x −1) = mx −1. Lời giải. a) Biến đổi 2
1+ mx = x thành 2
x − mx −1 = 0; a = 1. b) 2
1+ mx = m không đưa được về phương trình bậc 2 . c) Biến đổi 2 2 2
m x − 4mx = − 2x +1 thành ( 2 m + ) 2 2
2 x − 4mx −1 = 0, a = m + 2 . d) 2 2
m(x −1) = mx −1 không đưa được về phương trình bậc 2 . Trang 5
Ví dụ 4. Phương trình nào sau dây đưa được về phương trình bậc 2 ? Xác định hệ số a của
phương trình đó ( m là hằng số) a) 2
x = x − m . b) 2
m = m − mx . c) 2 2 2
(m −1)x − mx = −3x . d) 2
m(x −1) = x(1+ mx) . Lời giải. a) 2 2
x = x − m x − x − m = 0, a = 1. b) 2
m = m − mx không đưa được về phương trình bậc 2 . c) 2 2 2 2 2 2
(m −1)x − mx = 3
− x (m + 2)x − mx = 0, a = m + 2 . d) 2
m(x −1) = x(1+ mx) không đưa được về phương trình bậc 2 .
Ví dụ 5. Giải các phương trình sau: a) 2 x − 2x = 0 . b) 2 3x = 2x . c) 2 −3x +12 = 0 . d) 2
x − 3x + 2 = 0 . Lời giải. a) Biến đổi 2
x − 2x = 0 thành x(x − 2) = 0 x = 0 hoặc x − 2 = 0 , từ đó tìm được x = 0; x = 2 . b) Biến đổi 2
3x = 2x thành x( 3x − 2) = 0 x = o hoặc 3x − 2 = 0 , từ đó tìm được 2 x = 0; x = . 3 c) Biến đổi 2
−3x +12 = 0 . thành 3
− (x + 2)(x − 2) = 0 hoặc đưa về 2
x = 4, từ đó tìm được
x = −2; x = 2 . d) Biến đổi 2
x − 3x + 2 = 0 thành (x −1)(x − 2) = 0 x −1 = 0 hoặc x − 2 = 0 , từ đó tìm được = 1; x = 2.
Ví dụ 6. Giải các phương trình sau: a) 2 x − 3x = 0 . b) 2
x = 2x . c) 2 x − 2 = 0 . d) 2
x + x − 2 = 0 . Lời giải. a) Biến đổi 2
x − 3x = 0 thành x(x − 3) = 0 , từ đó tìm được x = 0; x = 3. b) Biến đổi 2
x = 2x thành x(x − 2) = 0 , từ đó tìm được x = 0; x = 2 . c) Biến đổi 2
x − 2 = 0 thành (x + 2)(x − 2) = 0 , từ đó tìm được x = − 2; x = 2 . Trang 6 d) Biến đổi 2
x + x − 2 = 0 thành (x −1)(x + 2) = 0 , từ đó tìm được x = 1; x = −2 .
Ví dụ 7. Giải các phương trình sau: a) 2 (x +1) = 4 . b) 2 x + 2x = 3. c) 2
2x + 4x − 7 = 0 . d) 2
4x + 8x − 5 = 0 . Lời giải. x =1 a) Ta có PT 2
(x +1) = 4 x +1 = 2 x = 3. − x =1 b) Biến đổi 2
x + 2x = 3 ta được 2 (x +1) = 4 x = 3. −
Cách khác: đưa PT về dạng tích (x −1)(x + 3) = 0 . c) Biến đổi 2
2x + 4x − 7 = 0 ta được 2 2 9
2x + 4x − 7 = 0 (x +1) = , từ đó tìm được 2 3 3 x = −1; x = − −1. 2 2 5 9 1 5 d) Biến đổi PT 2
4x + 8x − 5 = 0 thành 2 2 x + 2x =
(x +1) = , từ đó tìm được x = ; x = − . 4 4 2 2
Ví dụ 8. Giải các phương trình sau: a) 2 (x − 2) = 9 . b) 2 x − 4x = 5 . c) 2
2x − 8x + 5 = 0 . d) 2
4x −16x − 9 = 0 . Lời giải. x = 1 − a) Ta có PT 2
(x − 2) = 9 x − 2 = 3 x = 5. x = 1 − b) Biến đổi 2
x − 4x = 5 ta được 2 (x − 2) = 9 x = 5.
Cách khác: đưa PT về dạng tích (x +1)(x − 5) = 0 . c) Biến đổi 2
2x − 8x + 5 = 0 ta được 2 2 3
2x − 8x + 5 = 0 (x − 2) = , từ đó tìm được 2 3 3 x = + 2; x = − + 2 . 2 2 Trang 7 9 25 d) Biến đổi PT 2
4x −16x − 9 = 0 thành 2 2 x − 4x = (x − 2) = , từ đó tìm được 4 4 1 9 x = − ; x = . 2 2
Ví dụ 9. Giải các phương trình sau: a) 2 1 x − x + = 0 . b) 2 x − x = 2 . 4 c) 2
2x − 2x − 5 = 0 . d) 2
x − x +1 = 0 . Lời giải. 2 1 1 1 1 a) Ta có PT 2 1 x − x + = 0 2
x − 2 x + = 0 x − = 0
, từ đó tìm được x = . 4 2 4 2 2 2 1 9 1 9 b) Biến đổi 2
x − x = 2 thành 2 x − x + = x − =
, từ đó tìm được x = −1; x = 2 . 4 4 2 4
Cách khác: chuyển vế đưa PT về dạng tích (x +1)(x − 2) = 0 . 2 5 1 11
c) Biến đổi PT đã cho 2
2x − 2x − 5 = 0 thành 2 x − x = x − = , từ đó tìm được 2 2 4 11 +1 − 11 +1 x = ; x = . 2 2 2 1 3
d) Biến đổi PT đã cho 2
x − x +1 = 0 thành x − = − PT vô nghiệm. 2 4
Ví dụ 10. Giải các phương trình sau a) 2 9
x − 3x + = 0 . b) 2
x − 3x − 4 = 0 . 4 c) 2
2x − 6x + 3 = 0 . d) 2
x − 3x + 3 = 0 . Lời giải. 2 1 1 1 1 a) Ta có PT 2 9 x − 3x + = 0 2
x − 2 x + = 0 x − = 0
, từ đó tìm được x = . 4 2 4 2 2 2 1 9 1 9 b) Biến đổi 2
x − 3x − 4 = 0 thành 2 x − x + = x − =
, từ đó tìm được x = −1; x = 2 . 4 4 2 4
Cách khác: chuyển vế đưa PT về dạng tích (x +1)(x − 2) = 0 . Trang 8 2 5 1 11
c) Biến đổi PT đã cho 2
2x − 6x + 3 = 0 thành 2 x − x = x − = , từ đó tìm được 2 2 4 11 +1 − 11 +1 x = ; x = . 2 2 2 1 3
d) Biến đổi PT đã cho 2
x − 3x + 3 = 0 thành x − = − PT vô nghiệm. 2 4
Ví dụ 11. Giải các phương trình sau a) 2 9
x − 3x + = 0 . b) 2
x − 3x − 4 = 0 . 4 c) 2
2x − 6x + 3 = 0 . d) 2
x − 3x + 3 = 0 . Lời giải. 2 3 9 3 3 a) Ta có PT 2 9 x − 3x + = 0 2
x − 2 x + = 0 x − = 0
, từ đó tìm được x = . 4 2 4 2 2 2 9 25 3 25 b) Biến đổi 2
x − 3x − 4 = 0 thành 2 x − 3x + = x − =
, từ đó tìm được x = −1; x = 4 . 4 4 2 4
Cách khác: chuyển vế đưa PT về dạng tích (x +1)(x − 4) = 0 . 2 3 3 3
c) Biến đổi PT đã cho 2
2x − 6x + 3 = 0 thành 2
x − 3x = − x − = , từ đó tìm được 2 2 4 3 + 3 − 3 + 3 x = ; x = . 2 2 2 3 3
d) Biến đổi PT đã cho 2
x − 3x + 3 = 0 thành x − = − PT vô nghiệm. 2 4
Ví dụ 12. Tìm giá trị của tham số m để phương trình sau có nghiệm bằng 1 a) 2 2
x + m = 4x . b) 2 2
x − (m + 3)x + m = 0 . Lời giải.
a) PT có nghiệm là 2
1 1+ m = 4 , từ đó tìm được m = 3 .
b) PT có nghiệm là 2
1 1− (m + 3) + m = 0 , biến đổi thành (m − 2)(m +1) = 0 suyra m = 2, m = −1.
Ví dụ 13. Với giá nào của m thì phương trình sau có nghiệm bằng 1 a) 2 2
x − m + 4 = 0 . b) 2
m + 4mx − 5 = 0 = 0 . Lời giải.
a) PT có nghiệm là 2
1 1− m + 4 = 0 , từ đó tìm được m = 5 . Trang 9
b) PT có nghiệm là 2
1 m + 4m − 5 = 0 = 0 , biến đổi thành (m −1)(m + 5) = 0 suyra m = 1, m = −5 . Bài 1.
Đưa các phương trình sau về dạng 2
ax + bx + c = 0 và tính tổng T = a + b + c a) 2 25 − 4x = 0 . b) 2 x − 4x = 5 − x + 2 . c) 2
(x −1) − 3x + 4 = 0 . d) 2
x(x − 3) = 2x − 2x . Lời giải. a) Phương trình 2
25 − 4x = 0 trở thành 2 4
− x + 25 = 0 a = −4;b = 0;c = 25. Từ đó tìm được T = 21. b) Phương trình 2 x − 4x = 5
− x + 2 trở thành 2
x + x − 2 = 0 T = 0 c) Phương trình 2
(x −1) − 3x + 4 = 0 trở thành 2
x − 5x + 5 = 0 T = 1. d) Phương trình 2
x(x − 3) = 2x − 2x trở thành ( − ) 2 1
2 x − x = 0 T = − 2 . Bài 2.
Giải các phương trình sau a) 2 4x − 9 = 0 . b) 2
x − 2 2x = 0 . c) 2
x − 2 2x = 2 . d) 2
x − 8x + 5 = 0 . Lời giải. a) Biến đổi 2 4x − 9 = 0 thành 2 9 3 x = x = . 4 2 b) Biến đổi 2
x − 2 2x = 0 thành x(x − 2 2) = 0 x = 0; x = 2 2 . c) Biến đổi 2
x − 2 2x = 2 thành (x − )2 2 = 0 x = 2 . d) Biến đổi 2
x − 8x + 5 = 0 thành x −
x + = − (x − )2 2 2 2 3 2 = 3 − PT vô nghiệm. Bài 3.
Giải các phương trình sau a) 2 x + 2x = 0 . b) 2 x − 5 = 0 . c) 2
x + 2x − 8 = 0 . d) 2
2x + 4x − 5 = 0 . Lời giải. a) Biến đổi 2
x + 2x = 0 thành x(x + 2) = 0 x = 0, x = −2 . b) Biến đổi 2 x − 5 = 0 thành 2
x = 5 x = 5 . c) Biến đổi 2
x + 2x − 8 = 0 thành (x − 2)(x + 4) = 0 x = 2, x = 4 − . Trang 10
Cách khác: Biến đổi thành 2
(x +1) = 9 kết quả. d) Biến đổi 2
2x + 4x − 5 = 0 thành 2 2 7
2(x + 2x) = 5 (x +1) = . Từ đó tìm được 2 7 7 x = −1, x = − −1. 2 2 Bài 4.
Với giá nào của m thì phương trình sau có nghiệm là 1 − a) 2 2 4x − 25m = 0. b) 2 2
x − 3mx + 3m = 0 . Lời giải. a) Điều kiện 2 2
4 − 25m = 0 m = . 5 b) Điều kiện 2
1+ 3m + 3m = 0 . 2 1 1
Biến đổi thành m + = −
PT vô nghiệm. Không tìm được m . 2 12 --- HẾT --- Trang 11



