


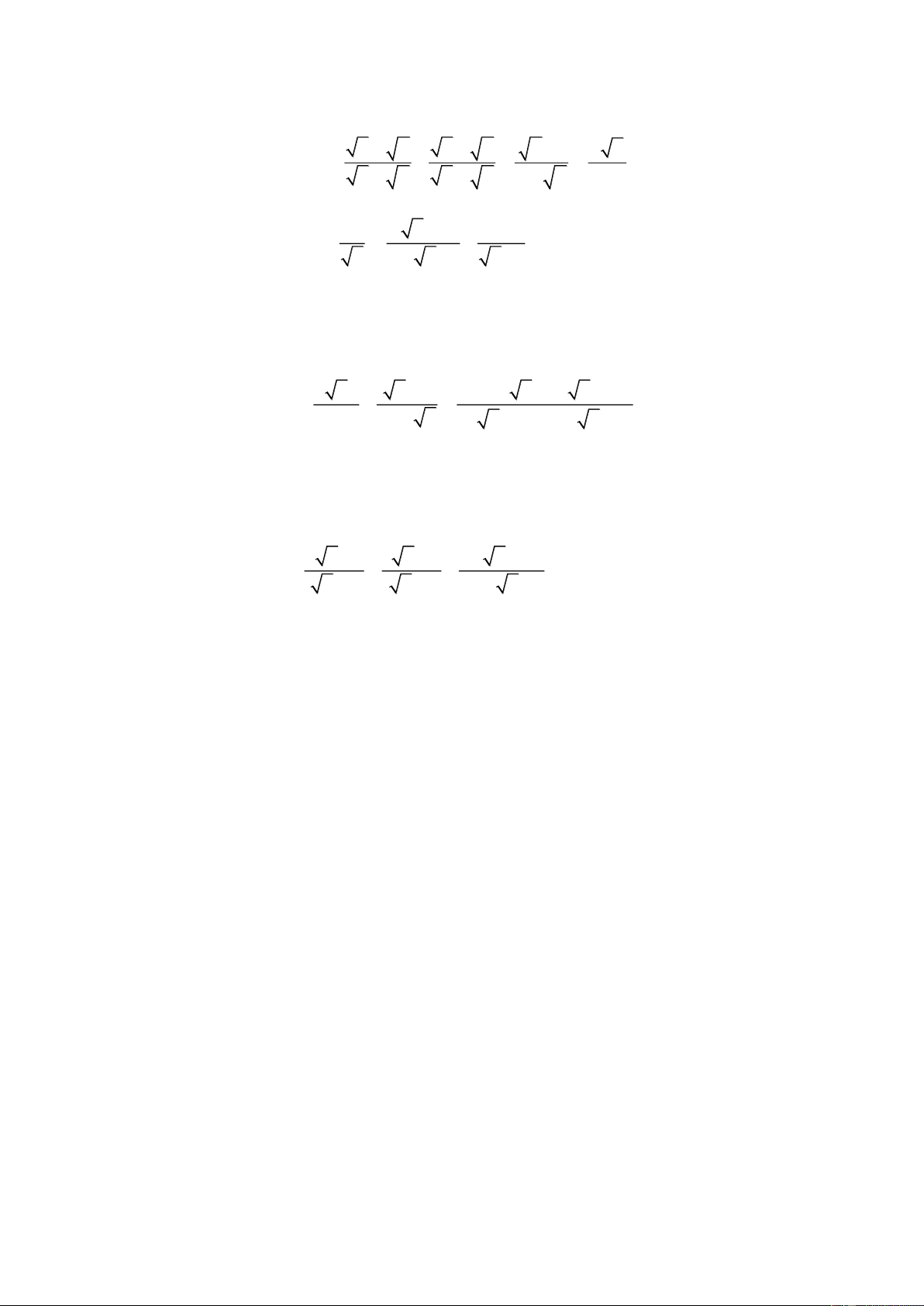
Preview text:
Bài 8. RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI
A. KIẾN THỨC TRỌNG TÂM
Để rút gọn biểu thức chứa căn thức bậc hai, ta có thể thực hiện theo các bước như sau
Bước 1: Đặt điều kiện thích hợp cho ẩn để biểu thức có nghĩa (thường thì đề bài cho sẵn hoặc
có thể tìm sau khi tìm được mẫu thức chung).
Bước 2: Phân tích các mẫu thức thành nhân tử để tìm mẫu thức chung.
Bước 3: Quy đồng mẫu thức rồi thực hiện phép tính tương tự như đối với phân thức đại số.
Bước 4: Rút gọn tử thức và phân tích tử thức thành nhân tử (nếu có).
Bước 5: Chia tử và mẫu cho nhân tử chung (nếu có) để rút gọn.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Rút gọn biểu thức chỉ chứa cộng, trừ căn thức
Đưa thừa số ra ngoài hoặc vào trong dấu căn hoặc khử mẫu của biểu thức lấy căn rồi rút
gọn các hạng tử đồng dạng.
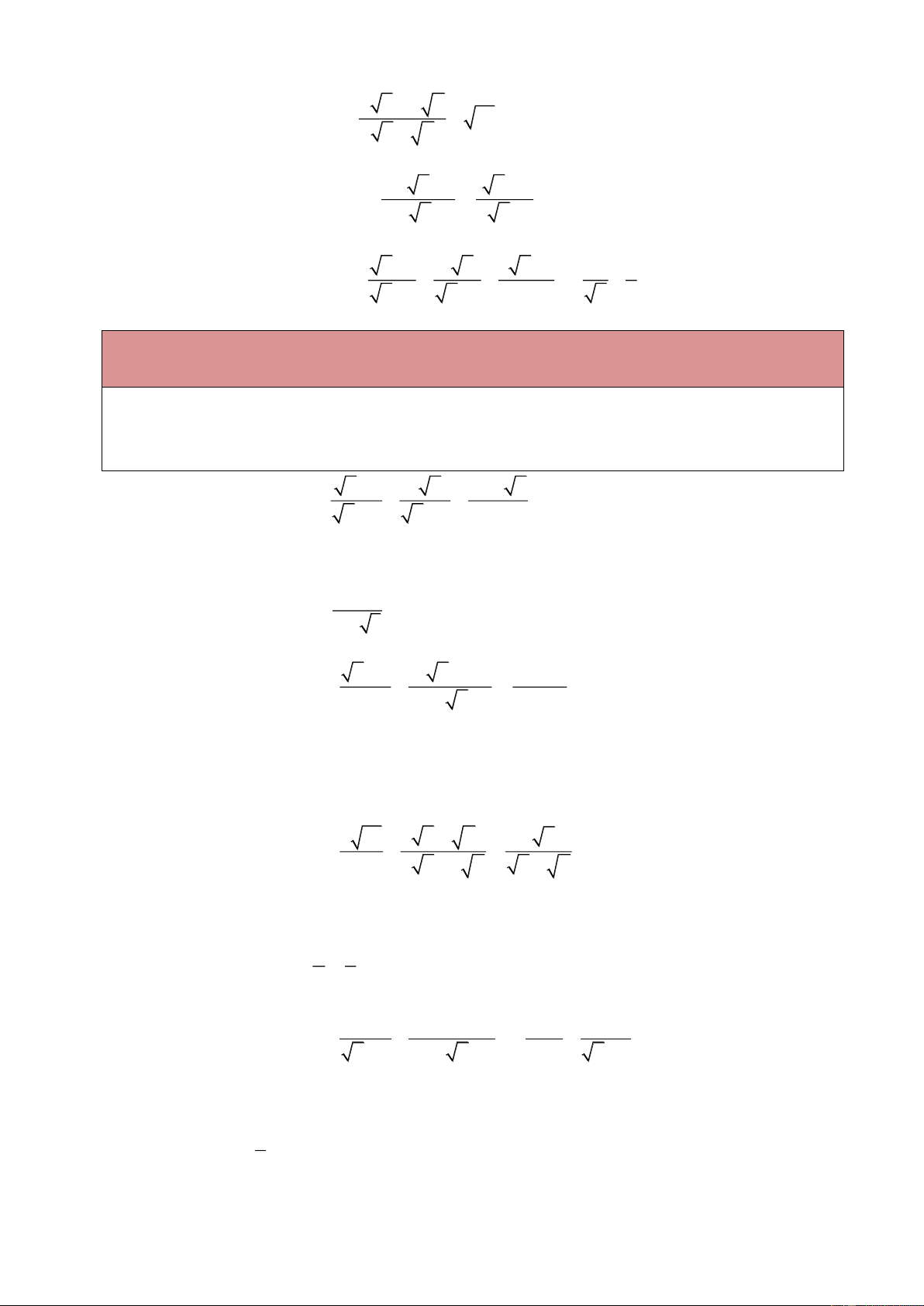
Ví dụ 1. Rút gọn các biểu thức sau: a) 20 80 45 ; b) 18 50 98 .
Ví dụ 2. Rút gọn các biểu thức sau: 1 1 25 3 98 a) 4,5 72 5 ; b) 40 10 12 . 2 2 6 2 3
Ví dụ 3. Rút gọn biểu thức 3 3 3 3
M 2x 16xy 7 25x y 3y 36x y với x 0 , y 0 . 3 3
Ví dụ 4. Rút gọn biểu thức N 1 1 . 2 2 b a 1 x y z
Ví dụ 5. Biến đổi biểu thức 5 4 về dạng ab
, trong đó a,b 0 ; a b ab a b ab
x, y, z
. Tính tổng x y z .
Dạng 2: Rút gọn biểu thức có chứa các phép toán cộng, trừ, nhân, chia căn thức dưới dạng
phân thức đại số
Xem phần kiến thức trọng tâm. y x
Ví dụ 6. Rút gọn biểu thức P . xy x y xy x xy
Ví dụ 7. Rút gọn biểu thức P 3 : . y x 3 xy Trang 1 x x y y
Ví dụ 8. Rút gọn biểu thức P
xy : (x y) . x y x x 1
Ví dụ 9. Rút gọn biểu thức P 1 : . x x 1 x x 1 x 1 2 x 3 x 1 2 2
Ví dụ 10. Rút gọn biểu thức P . x 1 x 1 1 x x x
Dạng 3: Rút gọn rồi tính giá trị của biểu thức hoặc rút gọn rồi tìm giá trị của biến để biểu
thức thỏa điều kiện nào đó.
Bước 1: Tìm điều kiện để biểu thức có nghĩa rồi rút gọn.
Bước 2: Thay giá trị của biến (thỏa điều kiện) vào biểu thức đã được rút gọn rồi thực hiện phép tính. x 1 2 x 2 5 x
Ví dụ 11. Cho biểu thức P . x 2 x 2 4 x a) Rút gọn P . 2
b) Tính giá trị của P với x . 2 3 x 2 x 2 4x
Ví dụ 12. Cho biểu thức P : . 2 x 1 x 2 x 1 (x 1) a) Rút gọn P .
b) Tính giá trị của P , biết | x 5 | 4 . 2 xy x y 2 x
Ví dụ 13. Cho biểu thức P . x y 2 x 2 y x y a) Rút gọn P . x 4
b) Tính giá trị của P , biết . y 9 1 2 2 1
Ví dụ 14. Cho biểu thức P : .
x 2 x 4 x 4 x 4 x 2 a) Rút gọn P . 1
b) Tìm x để P . 2 Trang 2 1 3 x 3 x 3
Ví dụ 15. Cho biểu thức P : .
x 3 x x 9 x x 3 x 3 x a) Rút gọn P .
b) Tìm x để P 1 .
Dạng 4: Rút gọn biểu thức rồi chứng minh biểu thức có một tính chất khác hoặc tìm
GTLN, GTNN của biểu thức
Bước 1: Tìm điều kiện để biểu thức có nghĩa (nếu có).
Bước 2: Rút gọn biểu thức.
Bước 3: Dựa vào yêu cầu bài toán để biến đổi biểu thức đã rút gọn và đi đến điều phải
chứng minh hoặc điều phải tìm. Lưu ý A Phân số hay phân thức
là số nguyên khi và chỉ khi B là ước của A. B
Nếu A M thì biểu thức A có giá trị lớn nhất là M.
Nếu B m thì biểu thức B có giá trị nhỏ nhất là m .
Biểu thức C không âm với mọi giá trị của biến khi và chỉ khi C 0 với mọi giá trị của
biến. Trường hợp biểu thức dương hoặc âm hoặc không dương thì làm tương tự
Ví dụ 16. Chứng minh rằng giá trị của biểu thức sau là hằng số với mọi giá trị của x và y : x 2 x
y x y y x A xy y xy x
x y 2 x 2 x 1 1
Ví dụ 17. Cho biểu thức B . x x 1 x x 1 x 1 a) Rút gọn B .
b) Chứng minh rằng B luôn luôn có giá trị không âm với mọi giá trị thích hợp của x . 1 2 x
Ví dụ 18. Cho biểu thức C : 1 .
x 1 x x x x 1 x 1 a) Rút gọn C .
b) Chứng minh rằng C luôn luôn có giá trị âm với mọi giá trị thích hợp của x . x 1 6 x 1 x
Ví dụ 19. Cho biểu thức D 2 : . 2 x 3
2 x 3 x 1 x 1 a) Rút gọn D . Trang 3 3
b) Chứng minh rằng D . 2 1 1 x 4
Ví dụ 20. Cho biểu thức P : 2 .
x 1 x 1 x 1 a) Rút gọn P .
b) Tìm giá trị lớn nhất của P . x 3 x 3 14 x 3
Ví dụ 21. Cho biểu thức Q . x 3 x 3 9 x 2 a) Rút gọn Q .
b) Tìm giá trị nhỏ nhất của Q .
Dạng 5: Chứng minh đẳng thức
Biến đổi vế này thành vế kia hoặc biến đổi cả hai vế cùng bằng một biểu thức thức ba.
Ví dụ 22. Chứng minh đẳng thức sau với x 0 , y 0 và x y .
x y 4 xy x y x : . x y x y x x y
Ví dụ 23. Chứng minh đẳng thức sau với x 0 , y 0 và x y . x x y y 2 y
xy : (x y) 1 . x y x y
C. BÀI TẬP VẬN DỤNG
Bài 1. Rút gọn các biểu thức sau: 2 3 1 a) 6 3 4 12 ; 3 2 6 b) 3 2
6 a 3 25a 2 36ab 2 9a với a, b 0 . x 1 x 1 m
Bài 2. Biến đổi biểu thức về dạng 2
x 1 , trong đó x 1. Tính giá trị của x 1 x 1 2 x 1 m .
Bài 3. Rút gọn rồi tính giá trị của biểu thức P với x 0, 36 : x 3 6 x P . x 3 3 x x 9 Trang 4
Bài 4. Chứng minh đẳng thức sau với x 0 , y 0 , y 1 , x y : x y x y y 1 4 x . x y x y y y x y 1 x 1 1
Bài 5. Cho biểu thức P x .
x x x 1 x 1 a) Rút gọn P .
b) Tìm các giá trị nguyên của x để P có giá trị nguyên. x x 6 x x 36 x
Bài 6. Cho biểu thức P . x 36 x 6 x
2 x 3x 2 x 3 a) Rút gọn P .
b) Với giá trị nào của x thì P có giá trị lớn nhất? Giá trị lớn nhất đó là bao nhiêu? 2 x 3 3 x 2 15 x 11
Bài 7. Cho biểu thức P . x 3 x 1 x 2 x 3 a) Rút gọn P .
b) Tìm giá trị nhỏ nhất của P . --- HẾT --- Trang 5




