




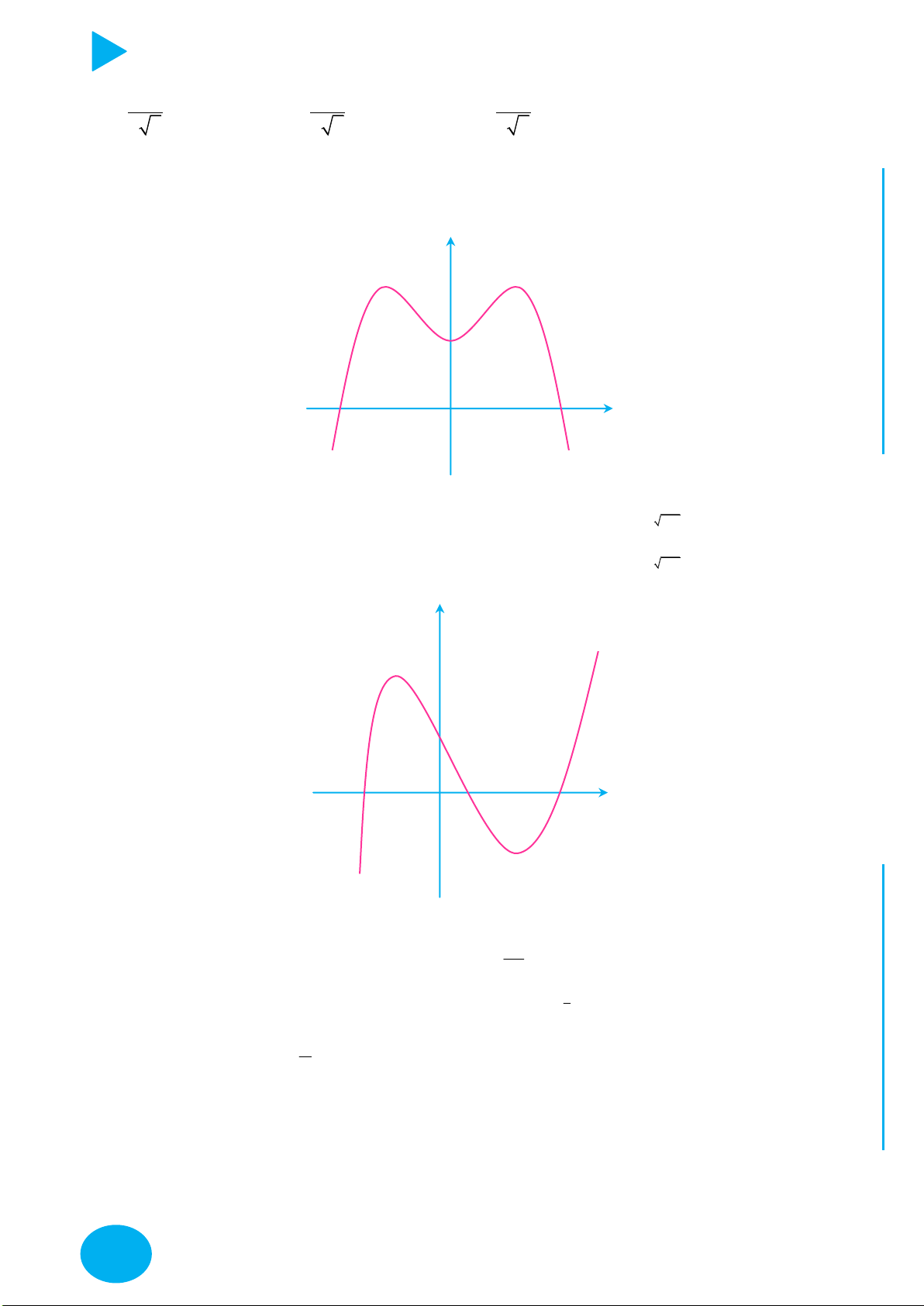




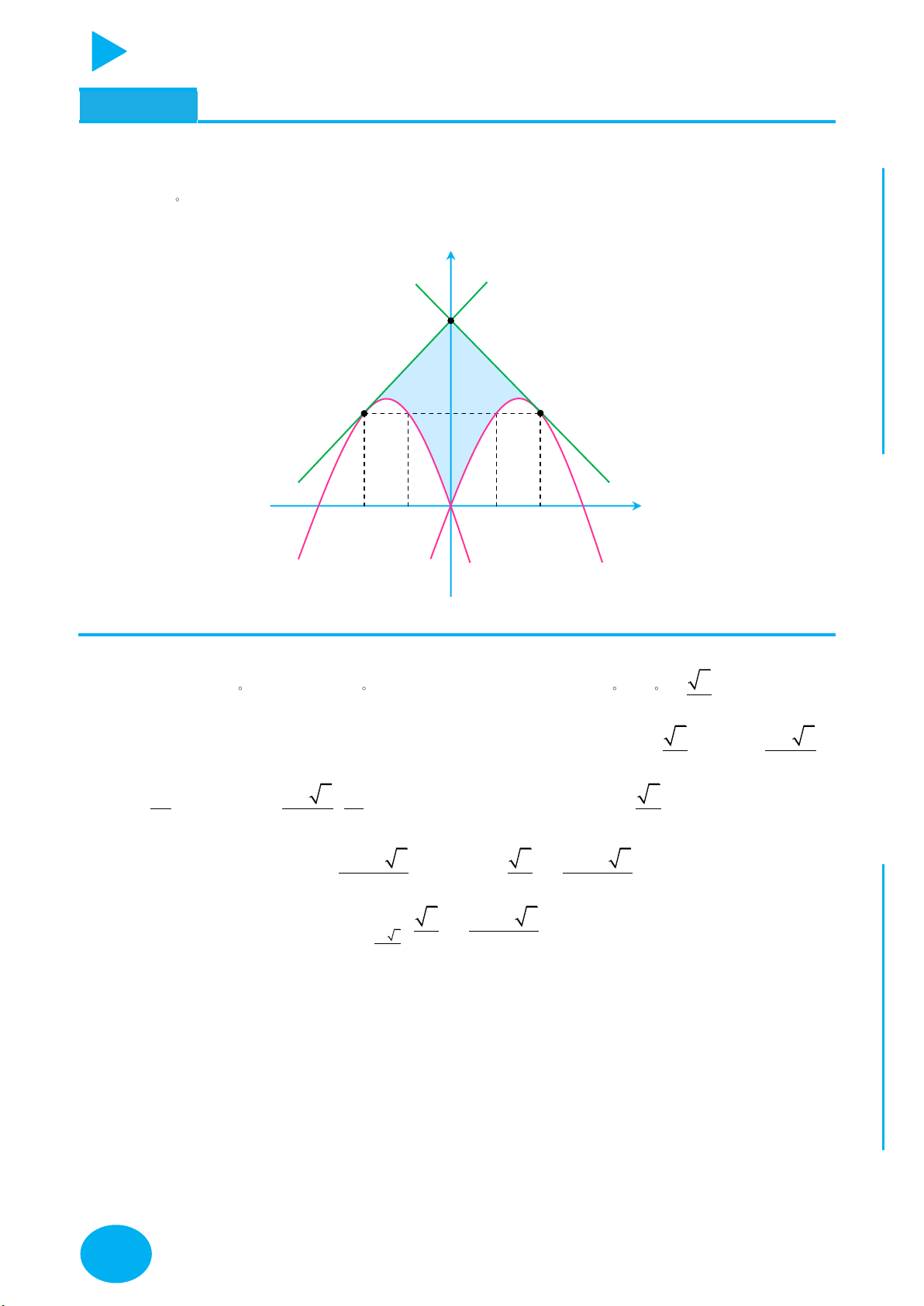
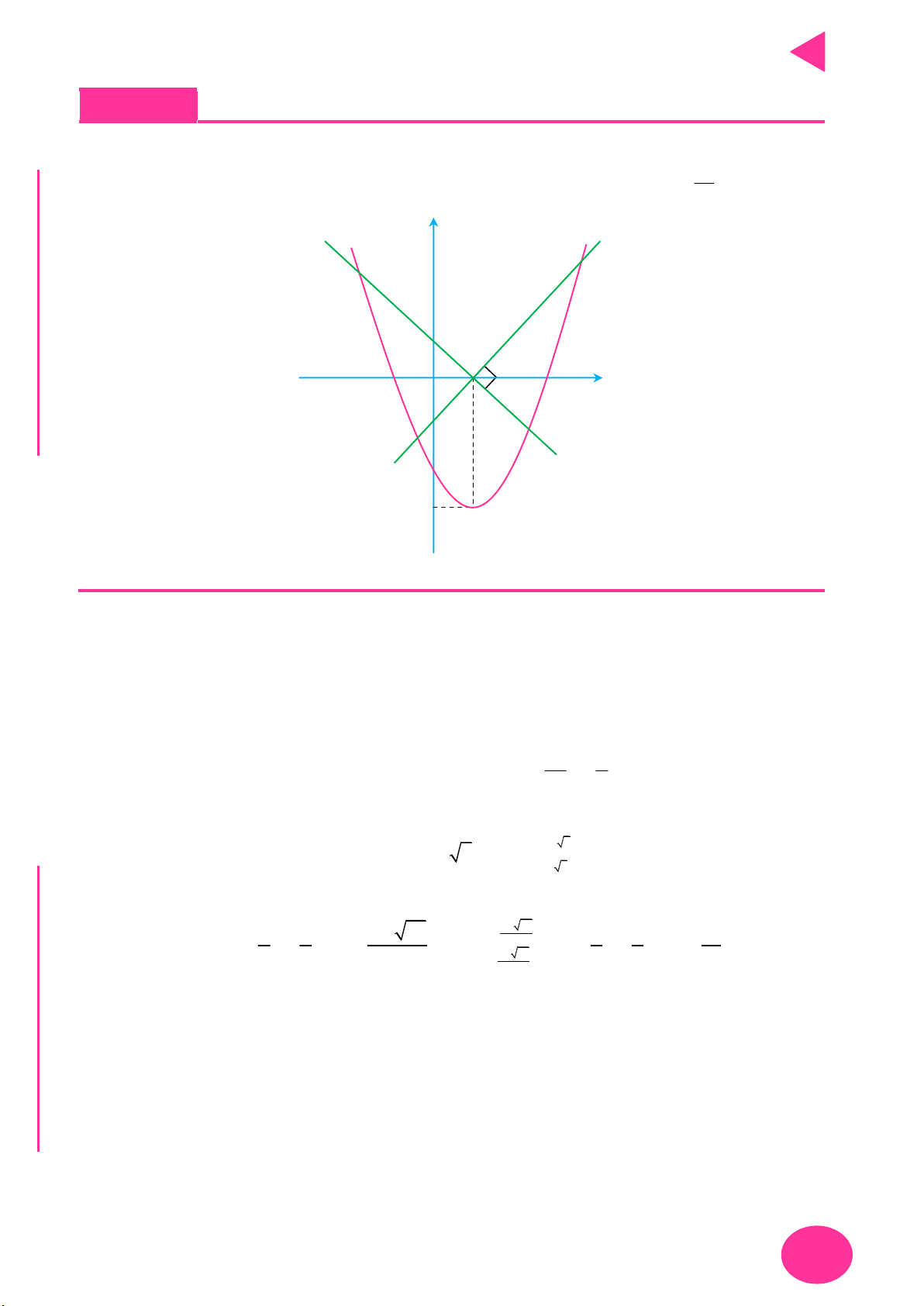



Preview text:
CHINH PHỤC OLYMPIC TOÁN NGUYỄN NAM TRUNG NGUYỄN MINH TUẤN NGUYỄN QUANG PHÁT NGUYỄN THỊ KIM ANH NGUYỄN TIẾN DŨNG MA TRUNG HIẾU PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ OMATHS Blog của Fanpage Phone Contact lovetoan.wordpress.com 0343763310 tuangenk@gmail.com
TẠP CHÍ VÀ TƯ LIỆU TOÁN HỌC
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
TẠP CHÍ VÀ TƯ LIỆU TOÁN HỌC C
CHINH PHỤC OLYMPIC TOÁN LỜI GIỚI THIỆU
Với kỳ thi THPT Quốc Gia hiện nay, các bài toán luôn có một chỗ đứng nhất định và ngày
càng biến hóa ra thành nhiều dạng, điều này làm cho nhiều bạn học sinh tỏ ra vô cùng lúng C
túng khi đối mặt với các dạng toán này, một phần chưa có phương pháp làm và đồng thời Ọ
cũng chưa được tiếp xúc nhiều với dạng bài tập này. Với tư cách là những người đã trải qua H
kỳ thi THPT Quốc Gia và nhiều kỳ thi thử khác bọn mình quyết định viết nên cuốn ebook N
này nhằm gửi tới cho các sĩ tử ôn thi THPT Quốc Gia năm nay có thể tổng ôn tập lại và tiếp
xúc với nhiều bài toán hơn để chuẩn bị cho kỳ thi THPT Quốc Gia đang đến rất gần. Các
bài toán trong ebook này chủ yếu được trích từ các đề thi thử của các trường, một số bọn
mình tự sáng tác, một số sưu tầm từ các thầy cô trên mạng. Xin gửi lời cảm ơn tới TOÁ
1. Thầy Nguyễn Đăng Ái – Thuận Thành Bắ c Ninh ỆU
2. Thầy Đào Văn Tiến – THPT A Nghĩa Hưng LI 3. Thầy Đỗ Văn Đức
4. Anh Phạm Minh Tuấn – ĐH Bách Khoa Đà Nẵng TƯ
5. Anh Nguyễn Quang Huy – ĐH Sư phạm Thái Nguyên À
6. Bạn Ngô Nguyên Quỳnh – ĐH Sư Phạm Quy Nhơn V 7. Thầy Nguyễn Chiến
C8. ỌBạn Tạ Công Hoàng – THPT Chuyên Lê Khiết
Đã giúp mình đồng thời viết ra những tài liệu hay để bọn mình tham khảo. Thay mặt nhóm HtáCc giả gồm P CHÍ
Ọ Nguyễn Minh Tuấn – ĐH FPT Hà Nội TẠ
H Nguyễn Thị Kim Anh – THPT Chuyên Nguyễn Trãi
Nguyễn Quang Phát – THPT Chuyên Nguyễn Trãi Nguyễn Nam Trung
Nguyễn Tiến Dũng – THPT Đô Lương 3 – Nghệ An
Ma Trung Hiếu – THPT Trịnh Hoài Đức
Cảm ơn mọi người đã theo dõi fanpage. Chúc các bạn có một mùa thi thành công!
Mọi ý kiến đóng góp vui lòng gửi về địa chỉ
NGUYỄN MINH TUẤN – K14 ĐẠI HỌC FPT
EMAIL: tuangenk@gmail.com
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
Tạp chí và tư liệu toán học I. LÝ THUYẾT.
Trước khi vào các bài toán cụ thể chúng ta cần nắm chắc các kiến thức sau.
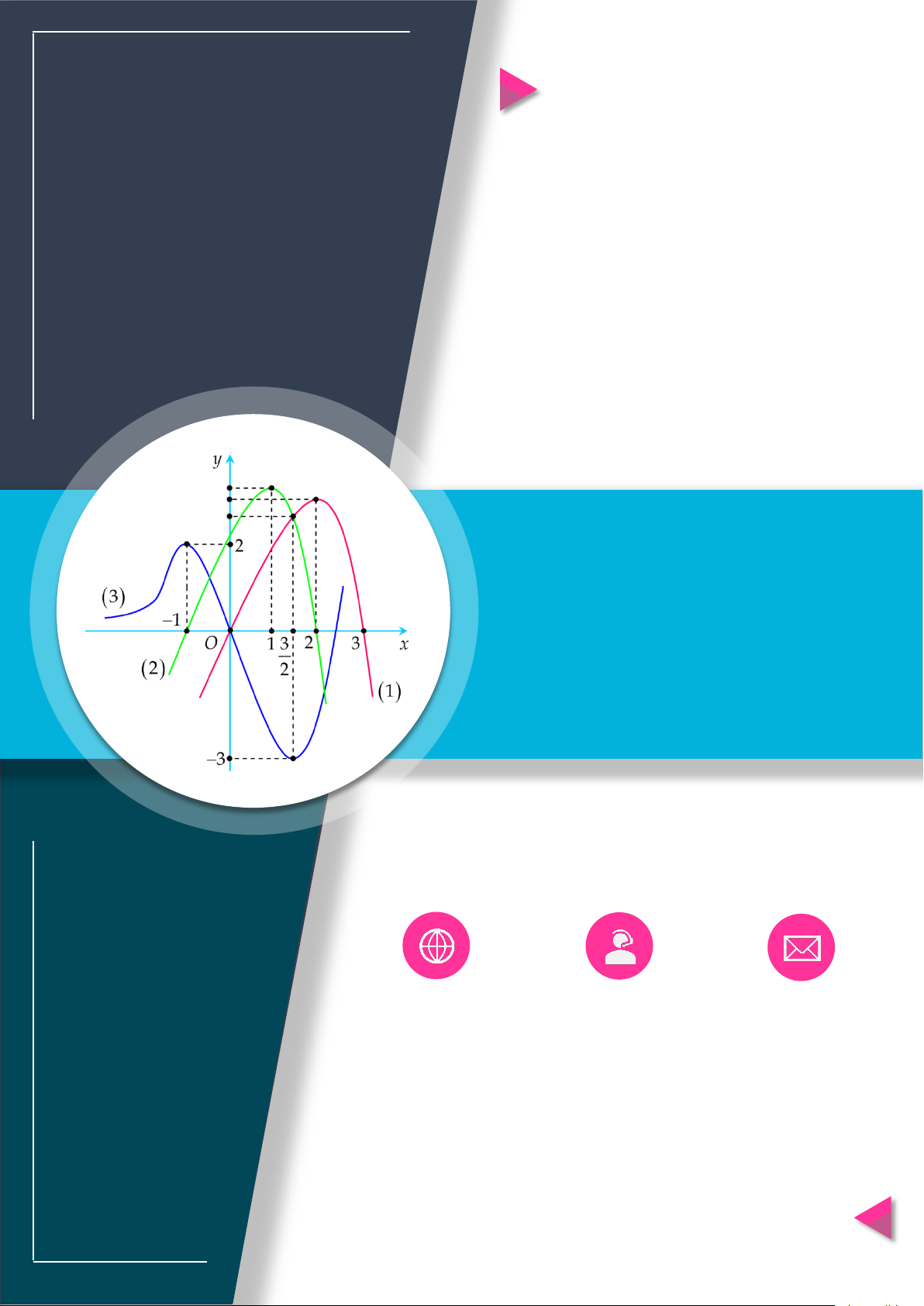
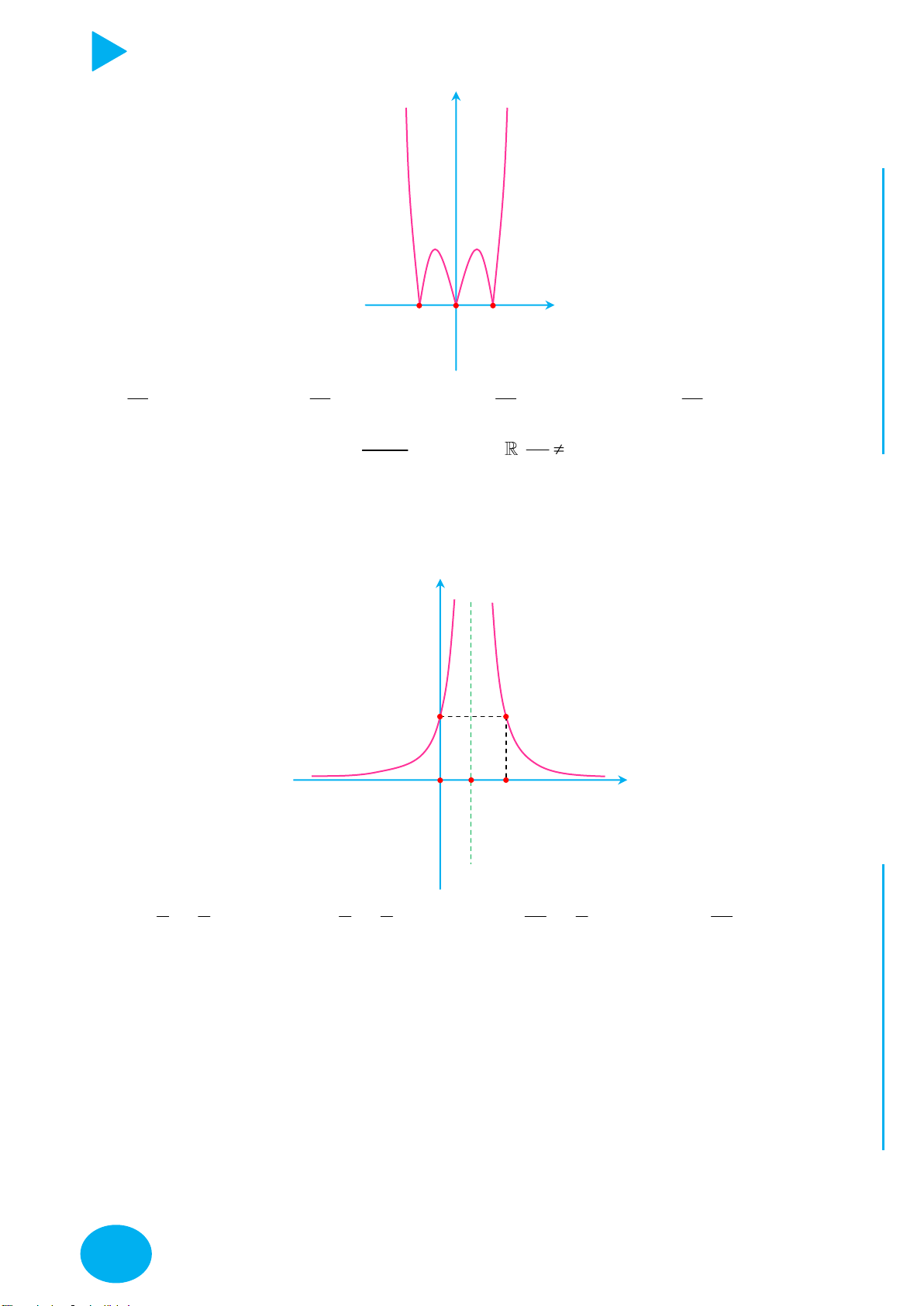
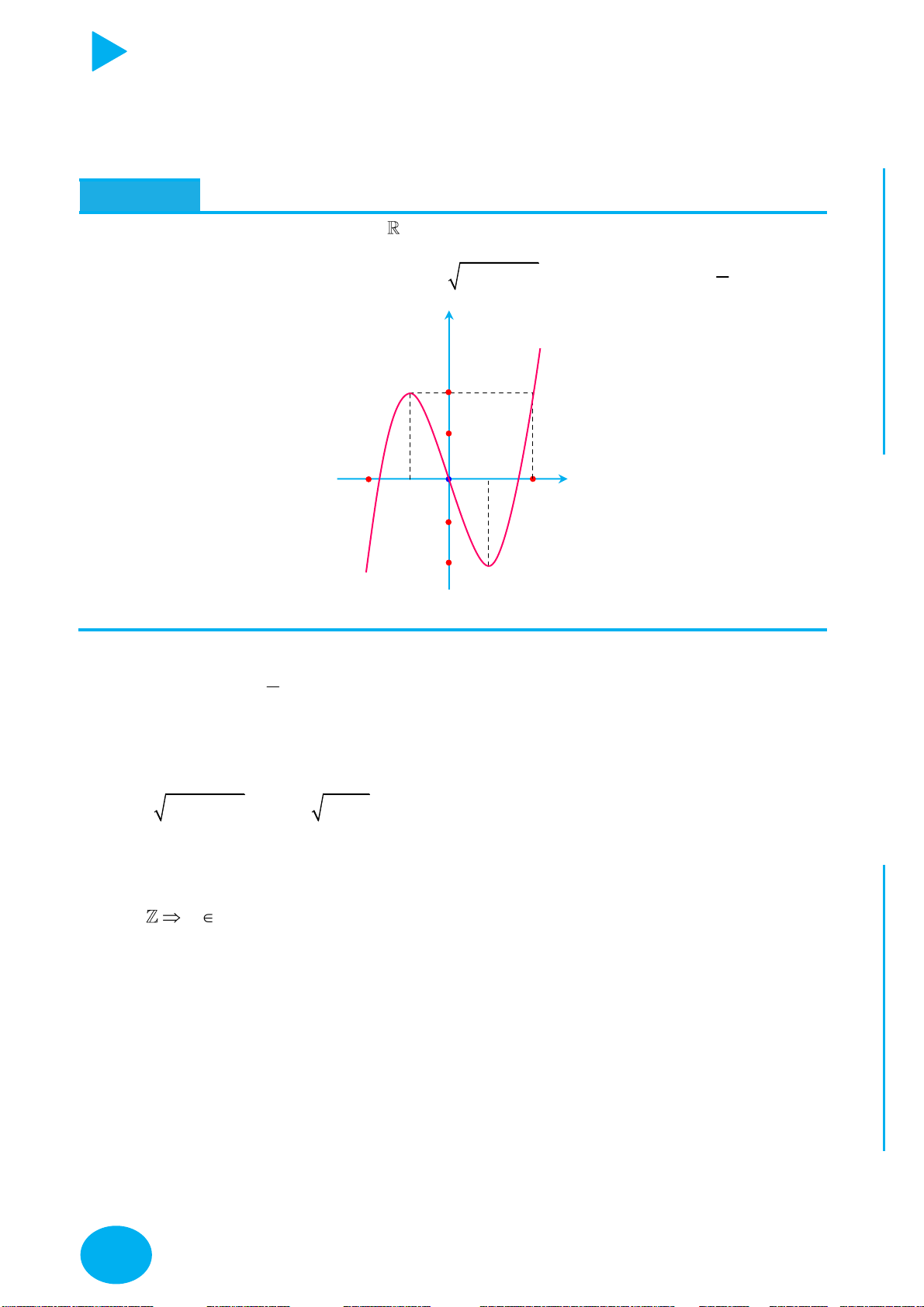
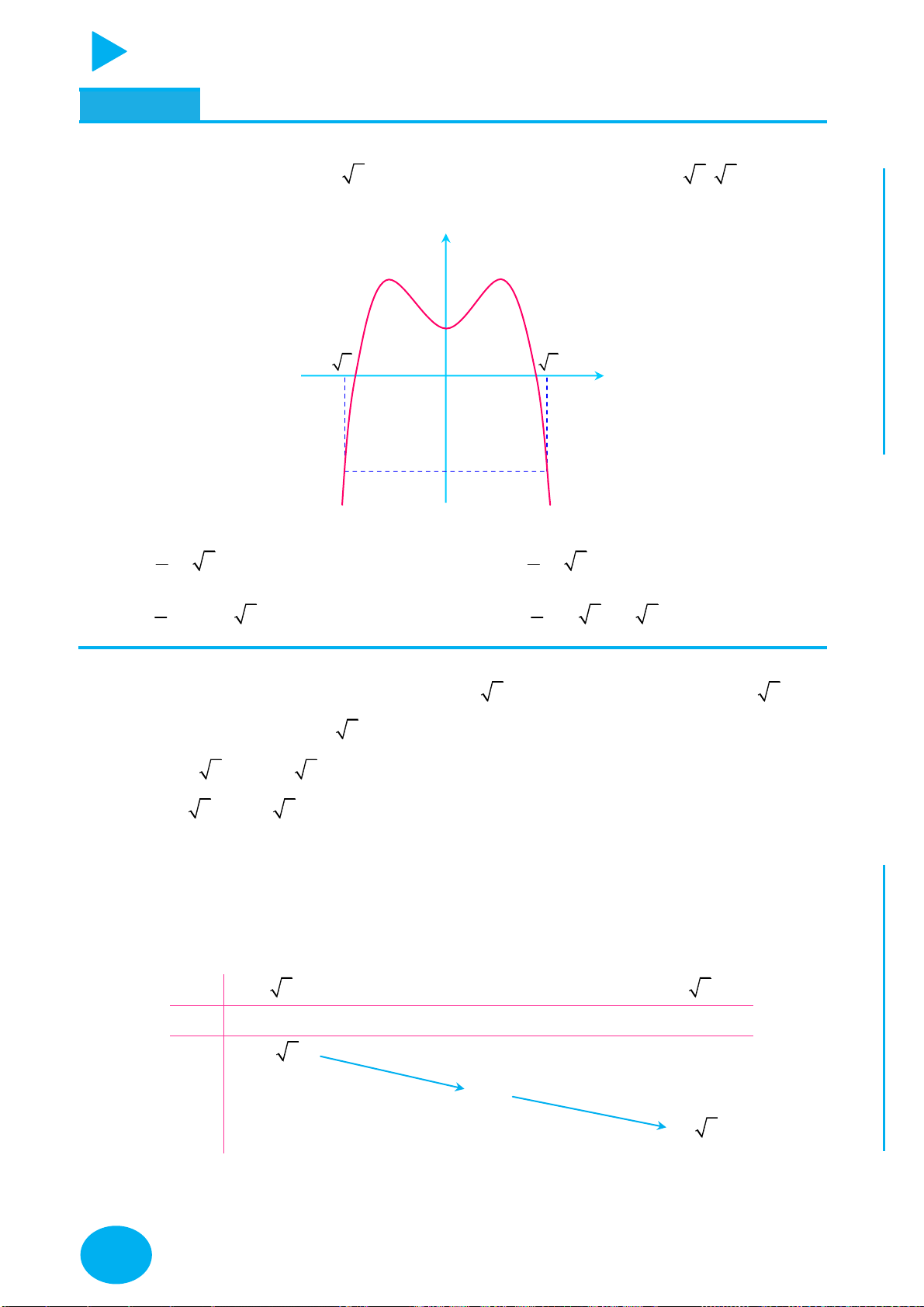
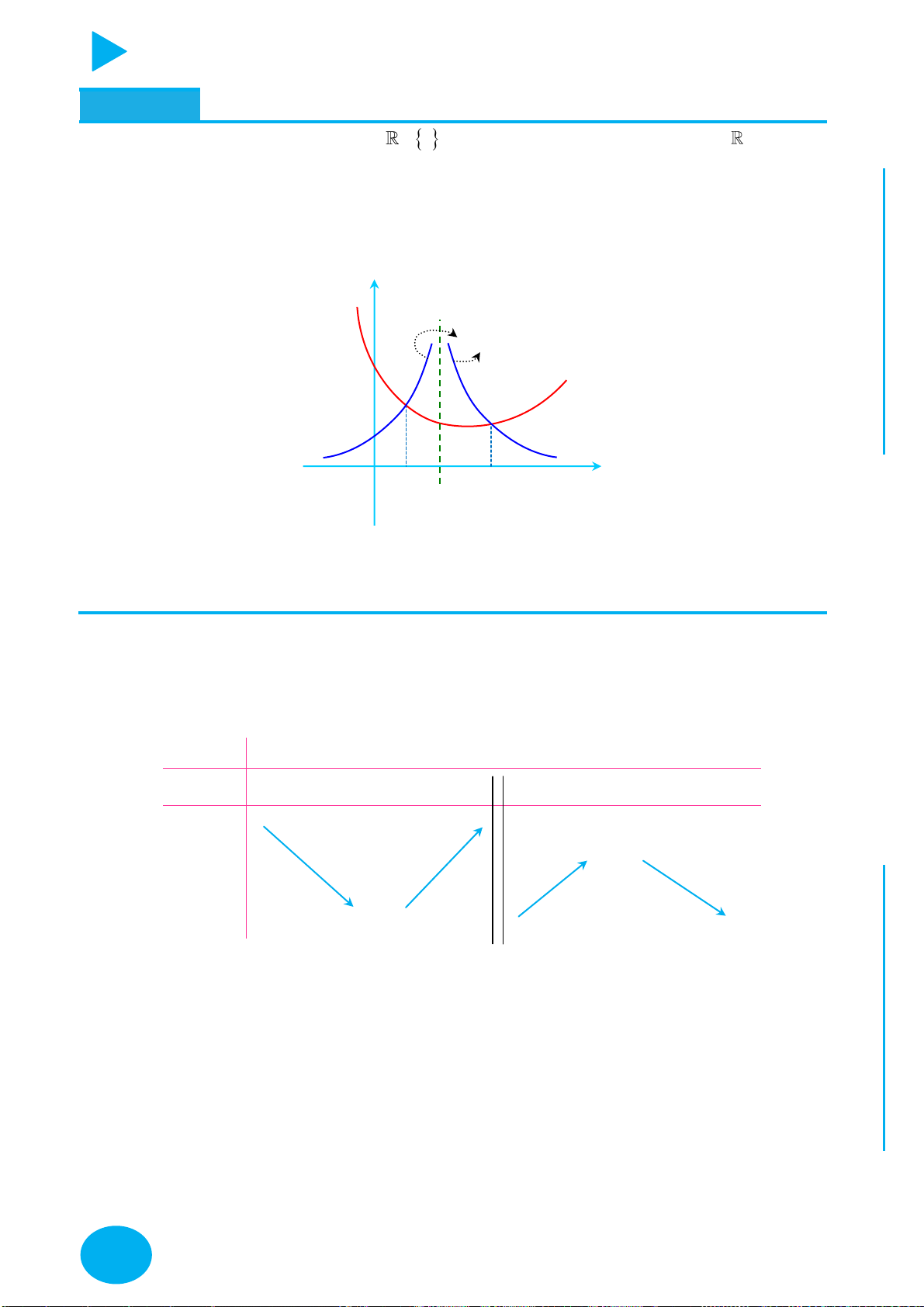
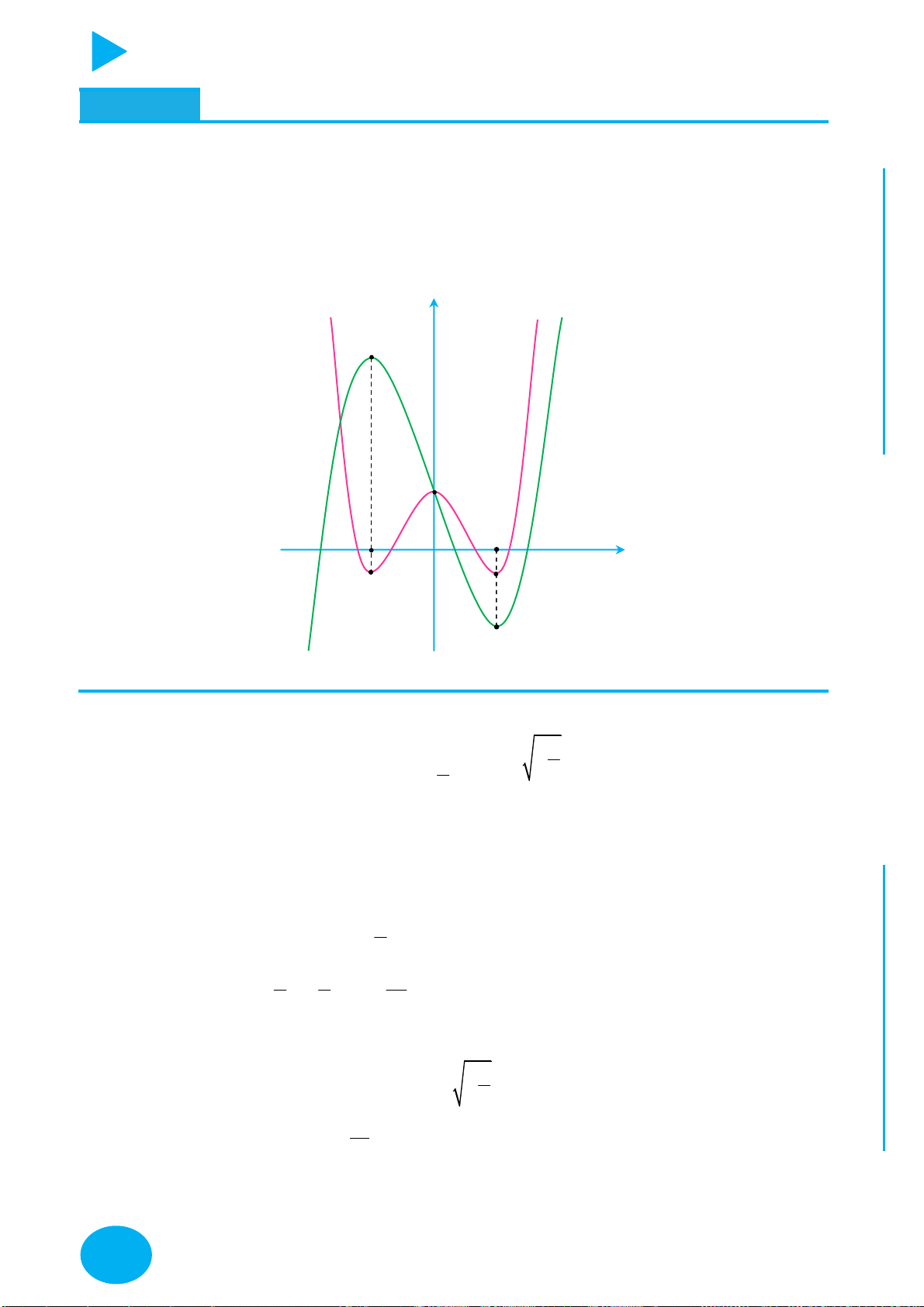
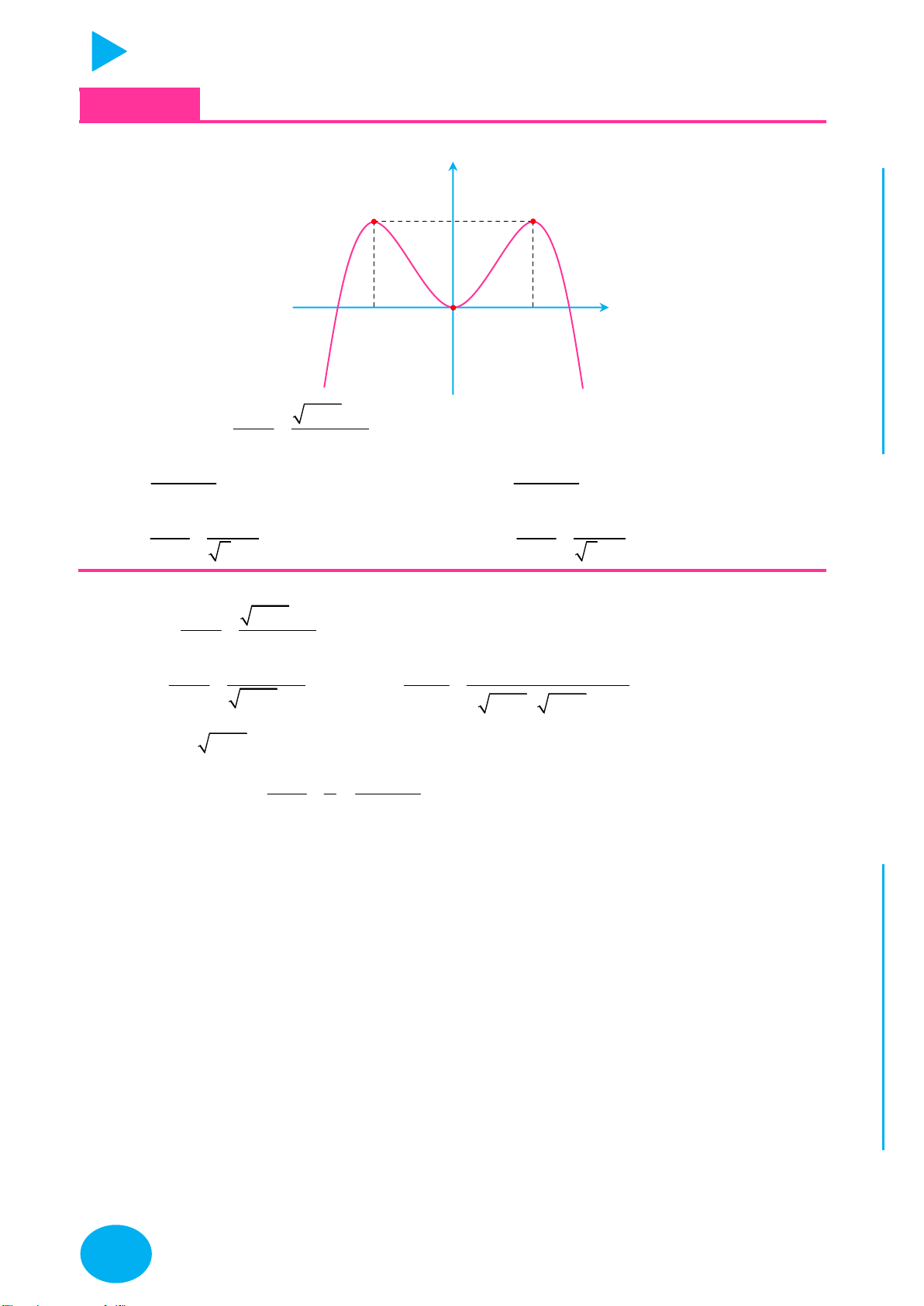
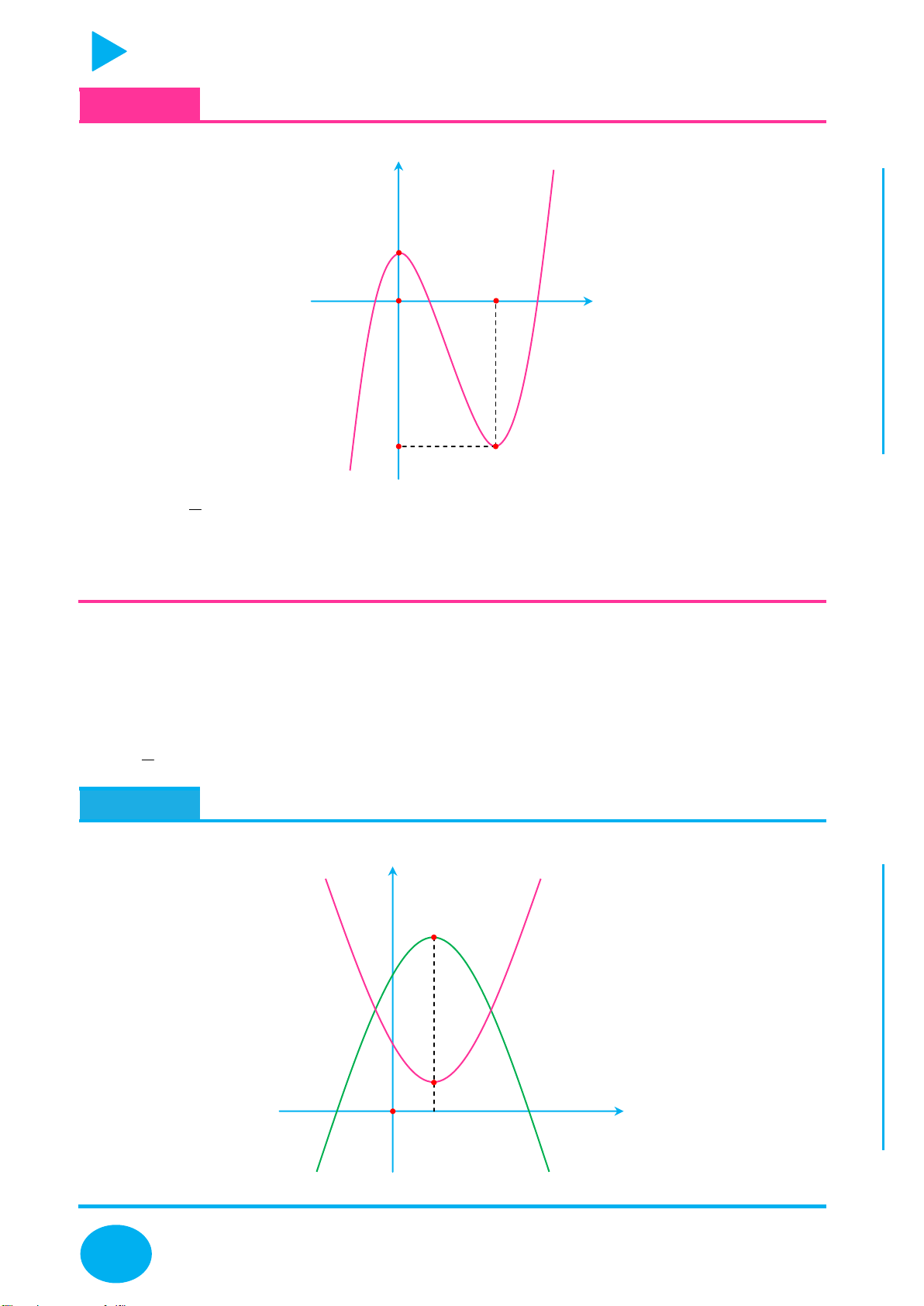
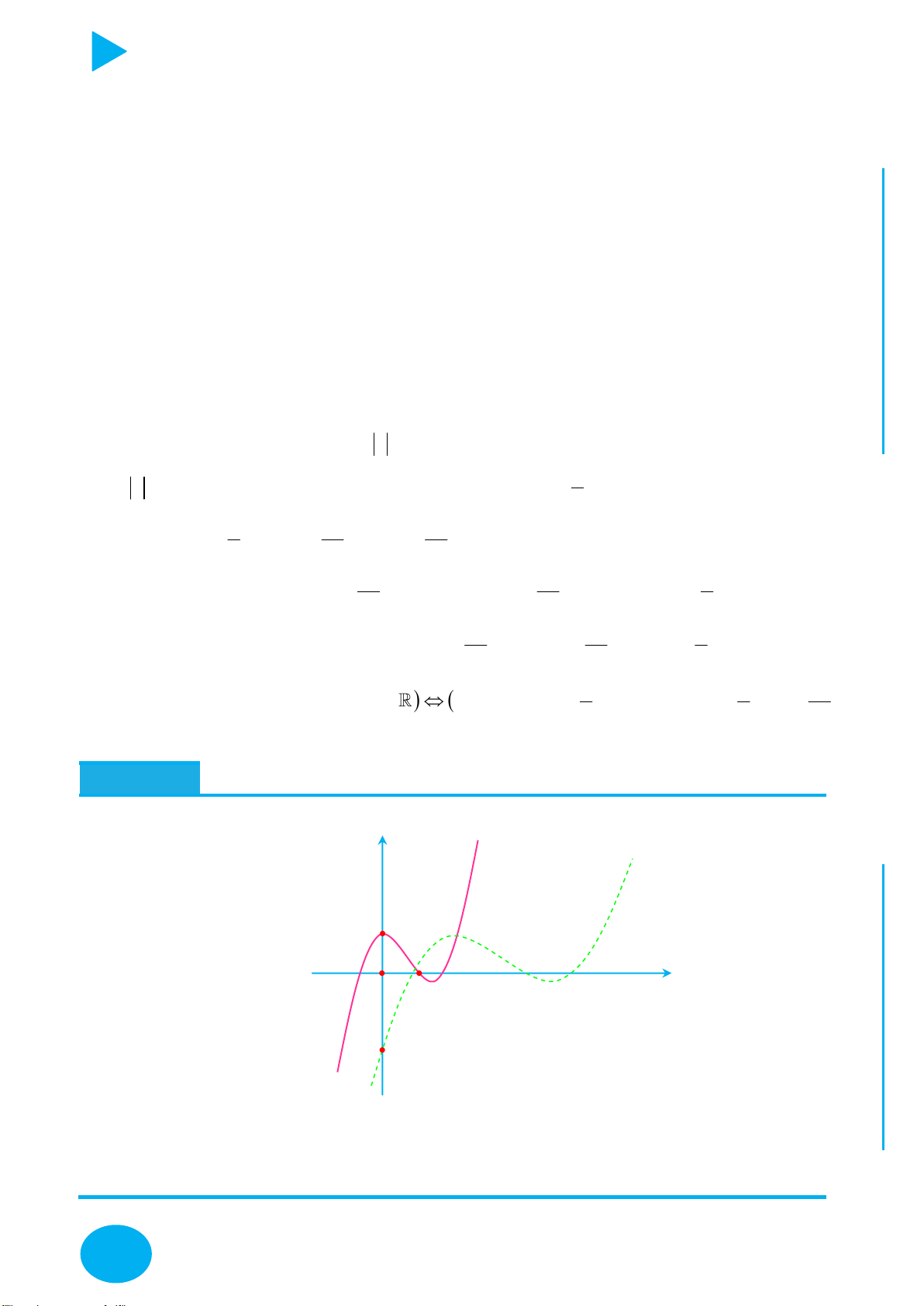
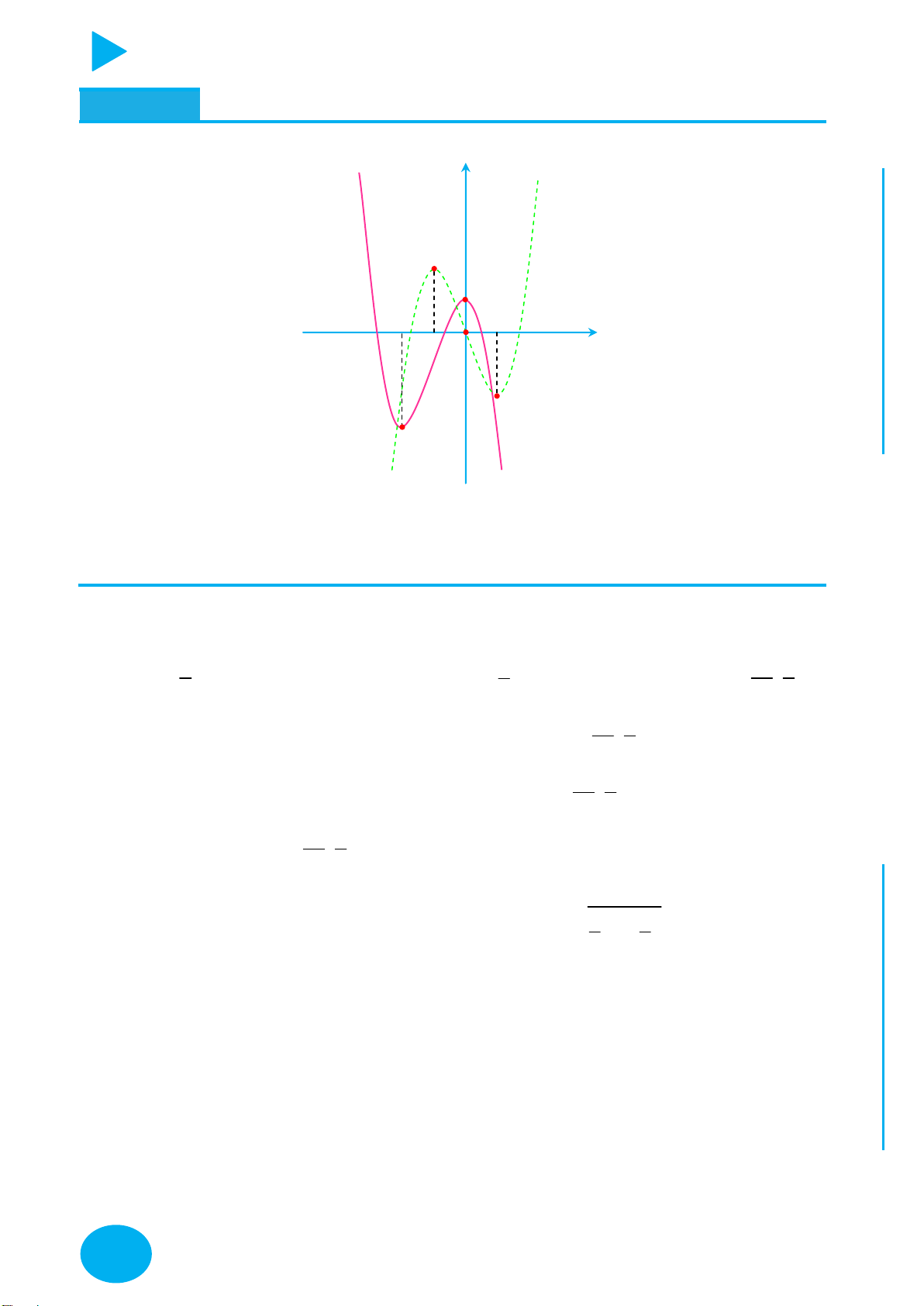
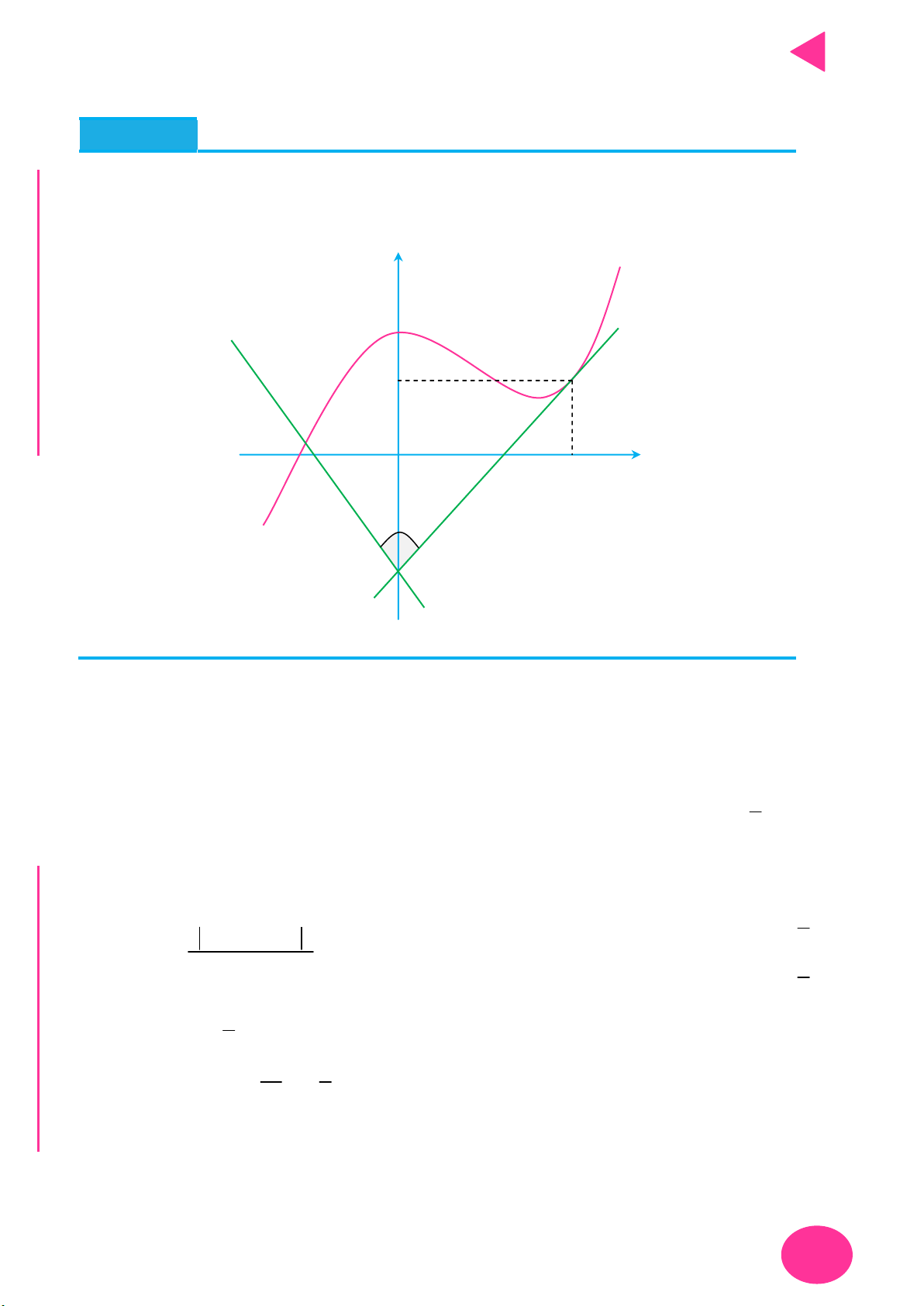
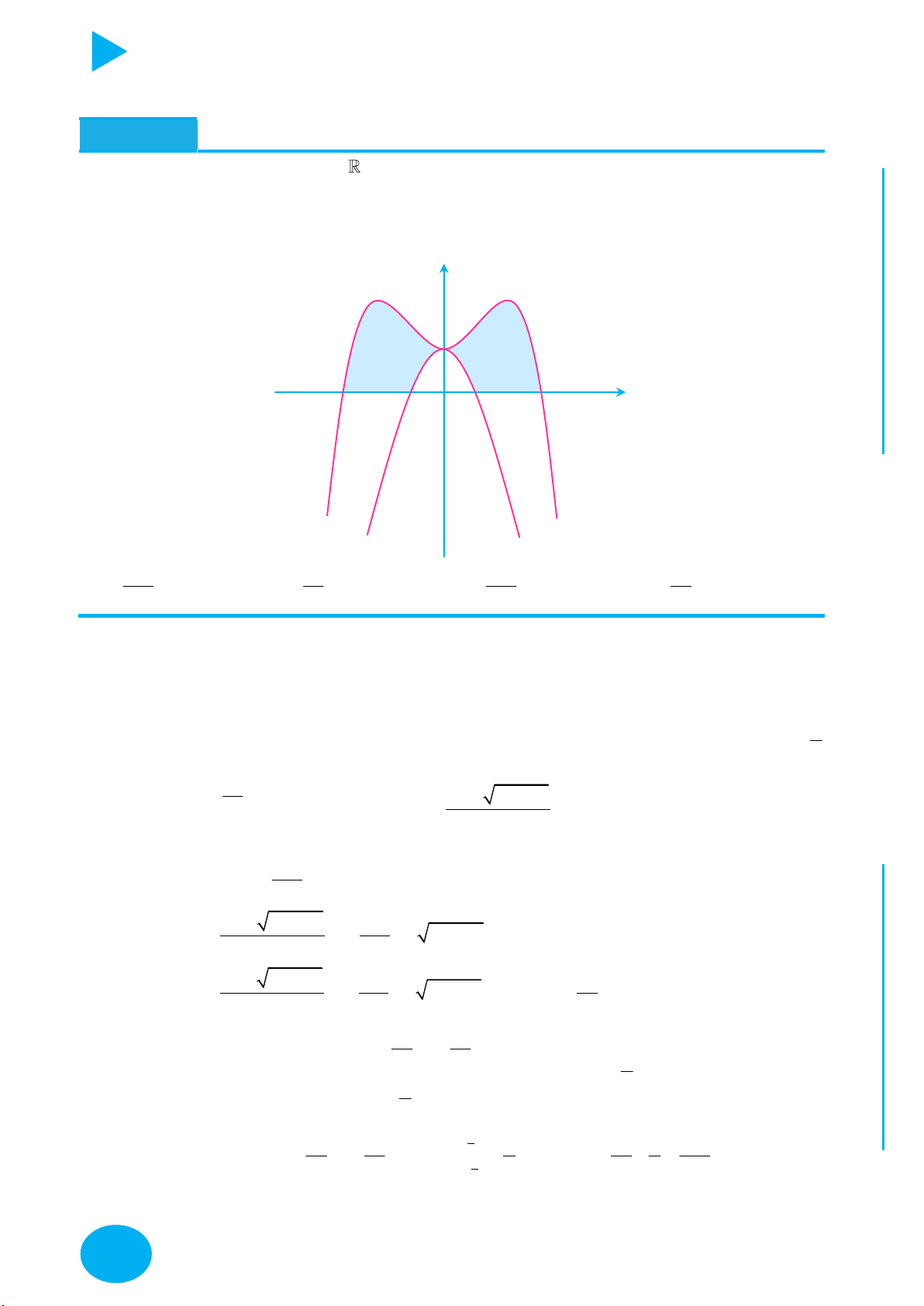
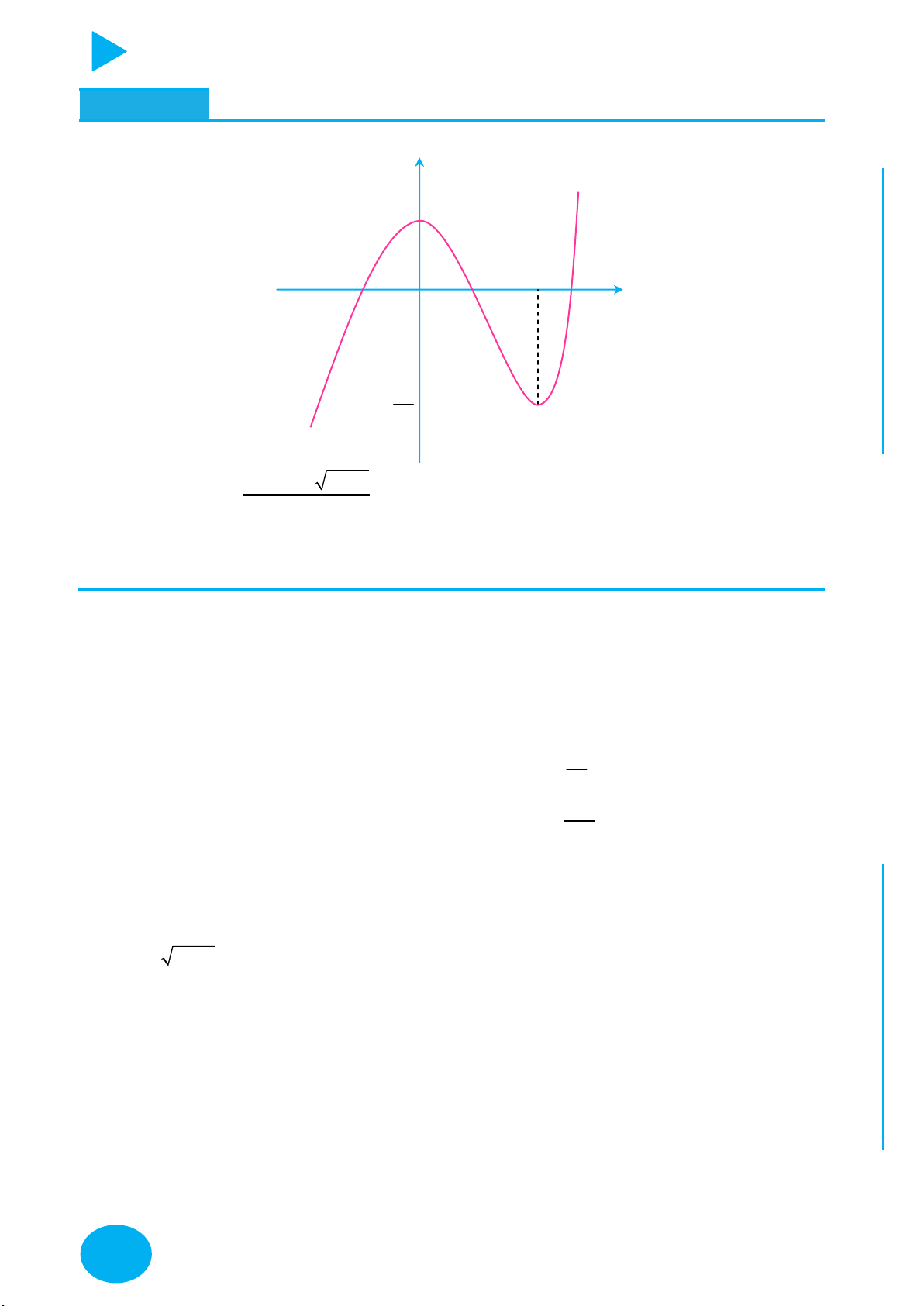
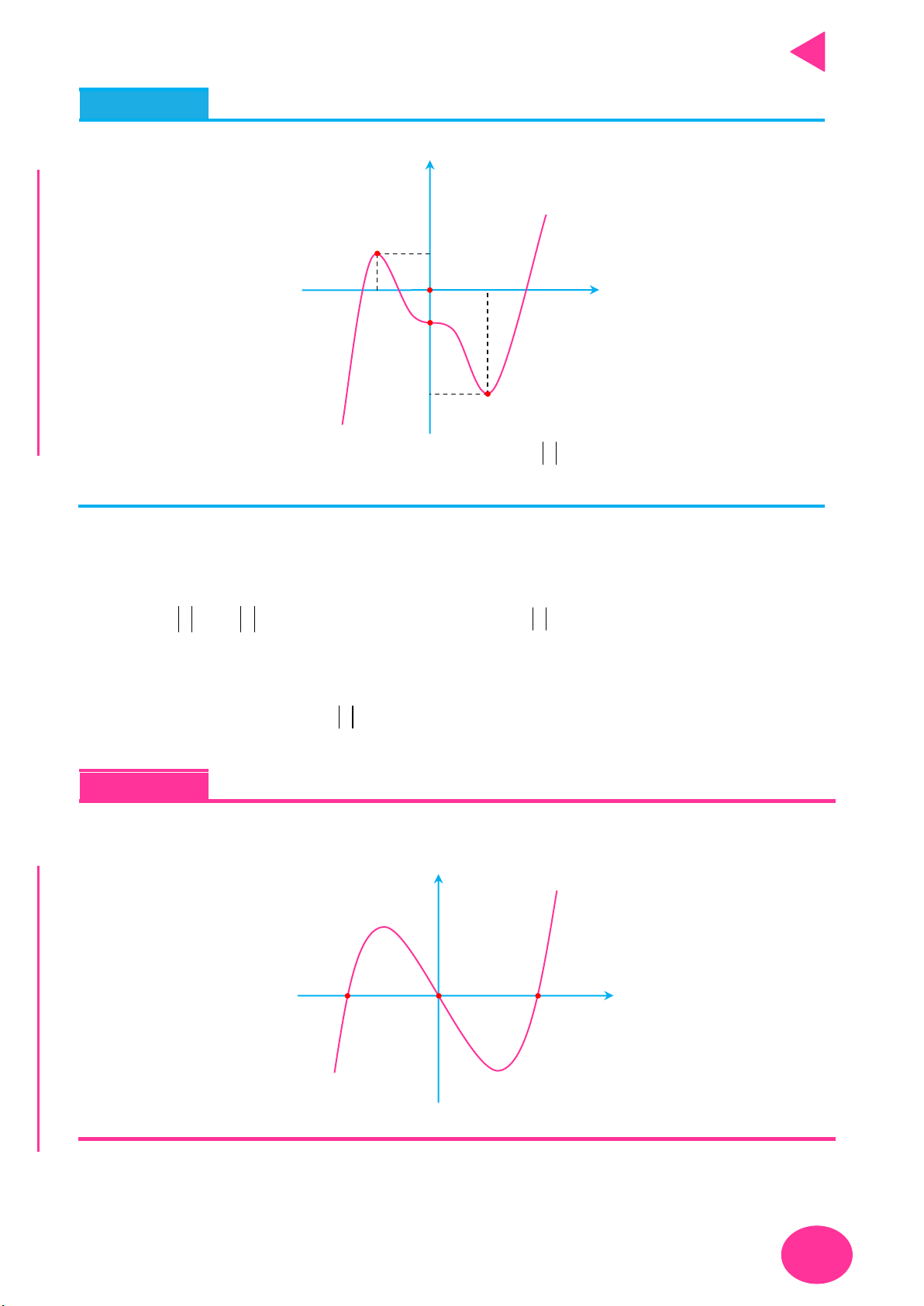
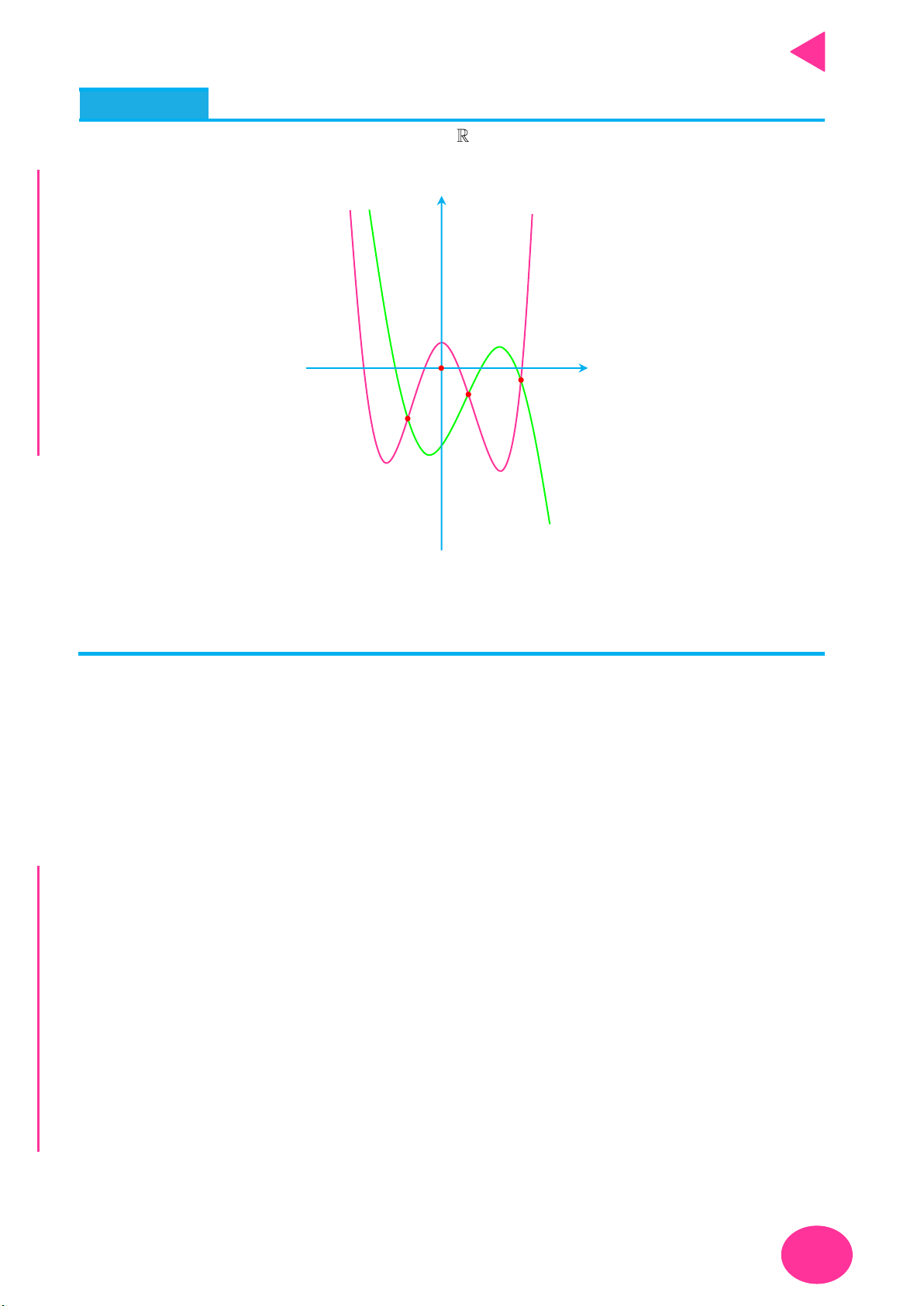
Cách vẽ và tịnh tiến đồ thị đặc biệt – Thầy Nguyễn Chiến ĐỒ THỊ CÁCH VẼ
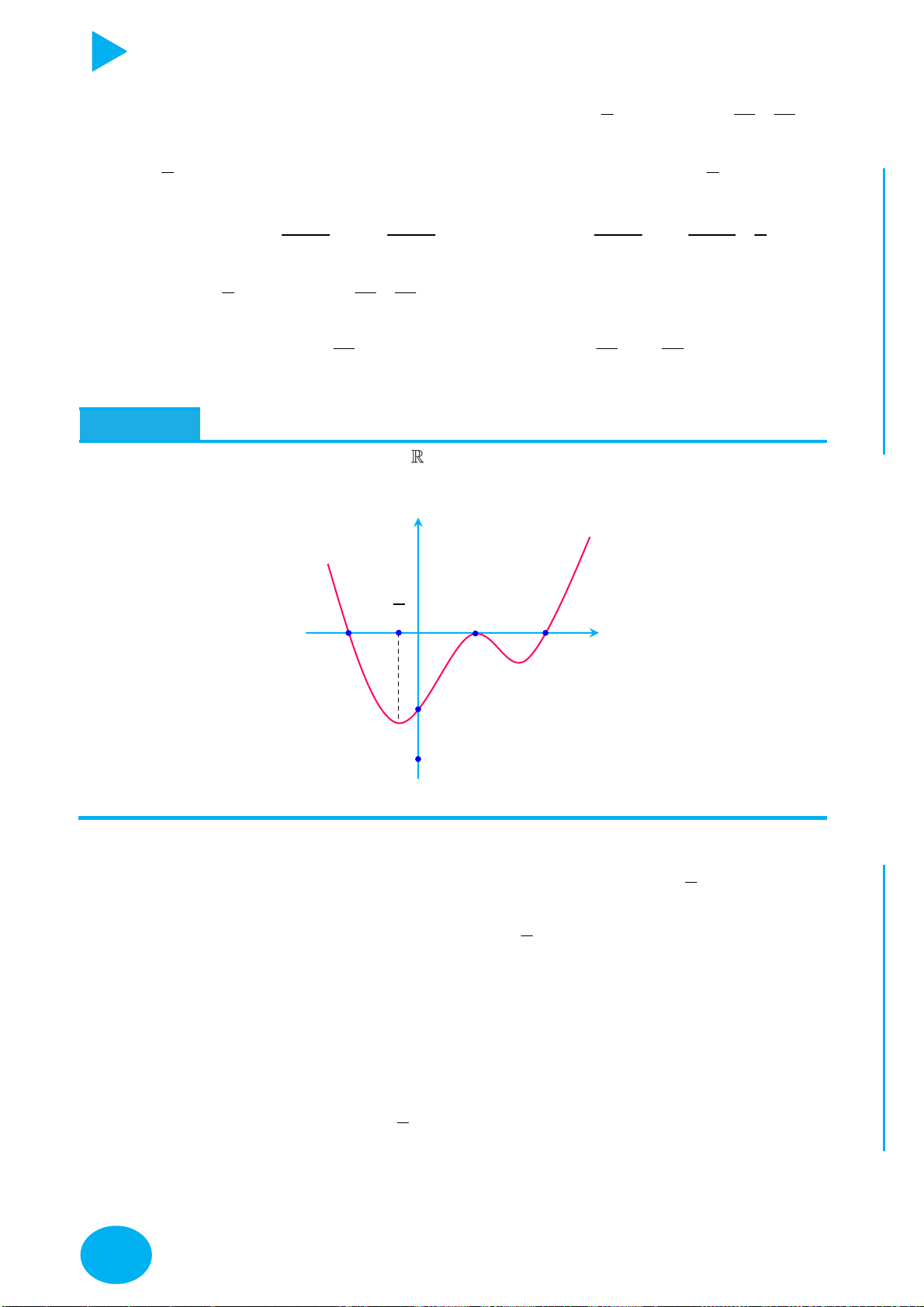
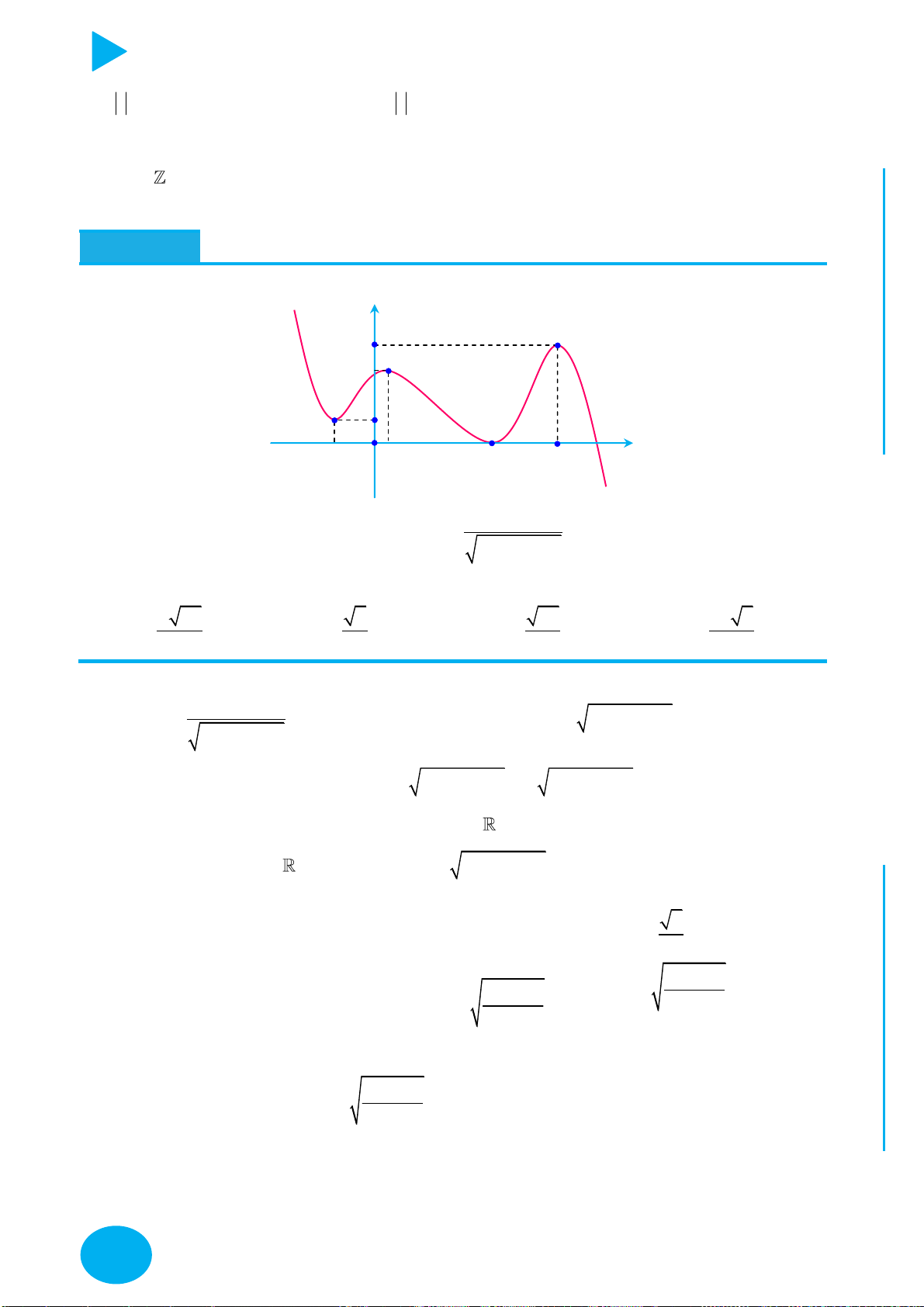
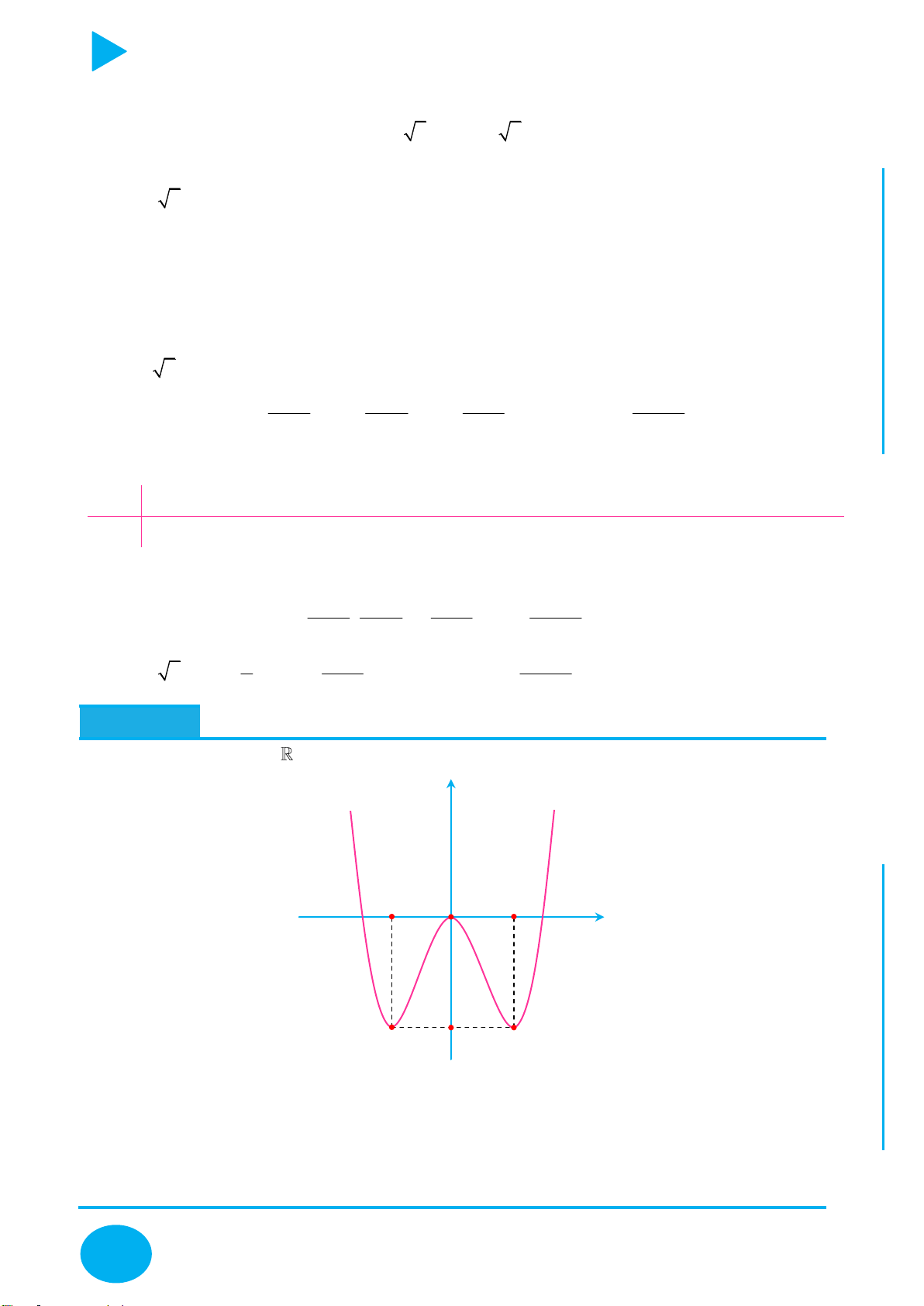
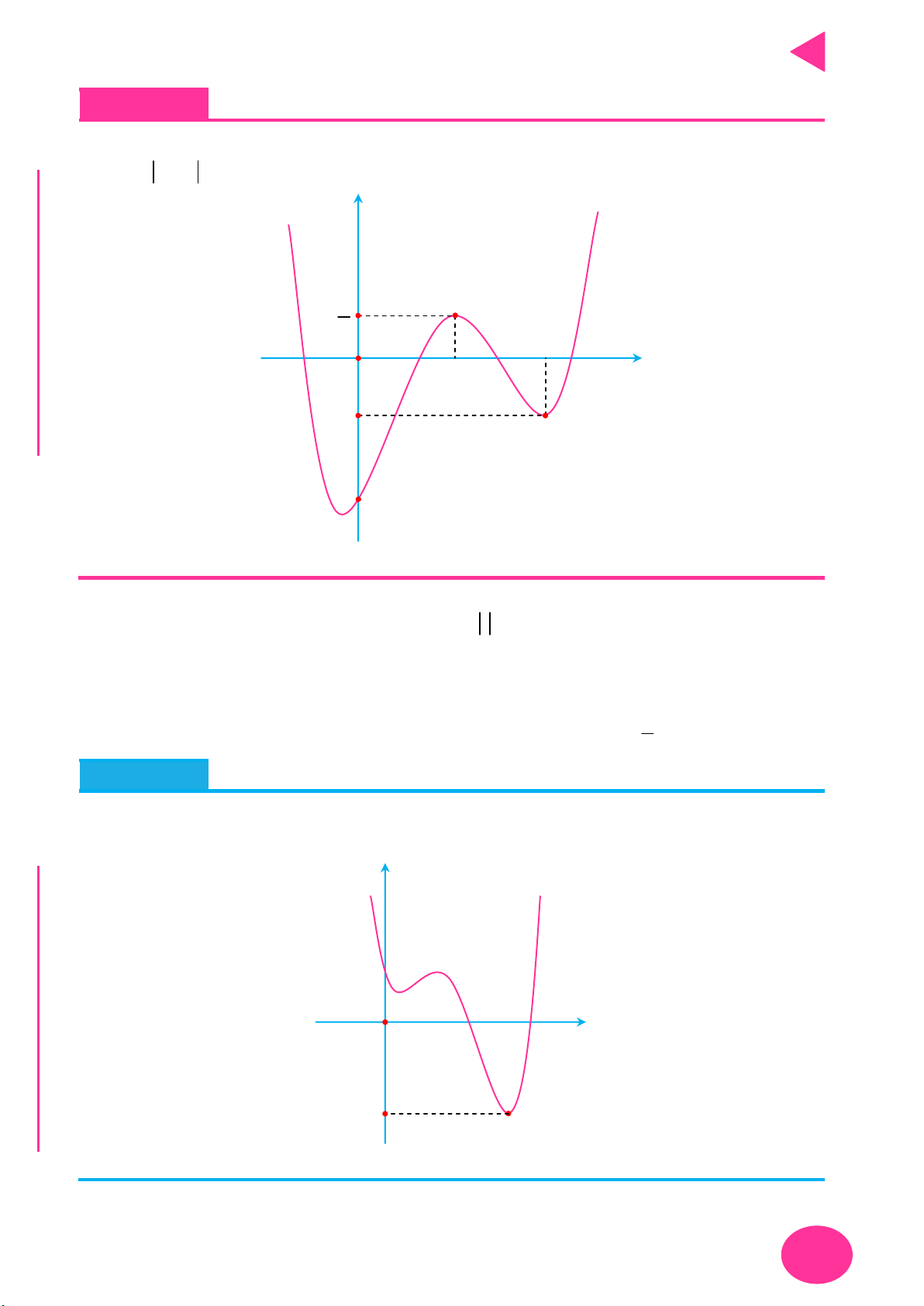
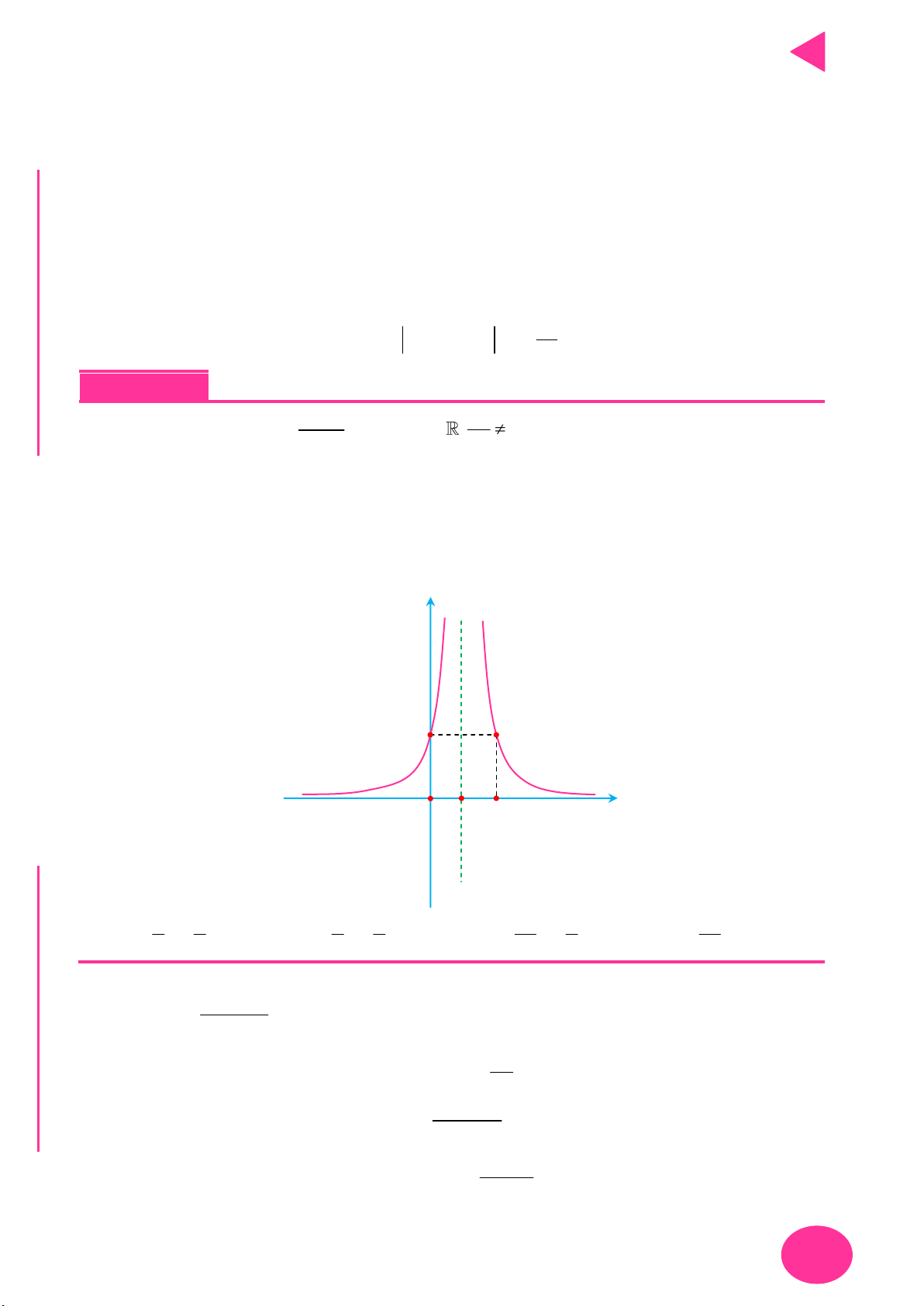
y f x
Lấy đối xứng đồ thị y f x qua trục Oy .
y f x
Lấy đối xứng đồ thị y f x qua trục Ox .
+ Giữ nguyên phần đồ thị bên phải Oy của đồ thị y f x .
y f x
+ Bỏ phần đồ thị bên trái Oy của y f x , lấy đối xứng phần đồ thị
được giữ qua Oy .
+ Giữ nguyên phần đồ thị phía trên Ox của đồ thị y f x .
y f x y f x OÁN
+ Bỏ phần đồ thị phía dưới Ox của
, lấy đối xứng phần đồ T
thị bị bỏ qua Ox . C
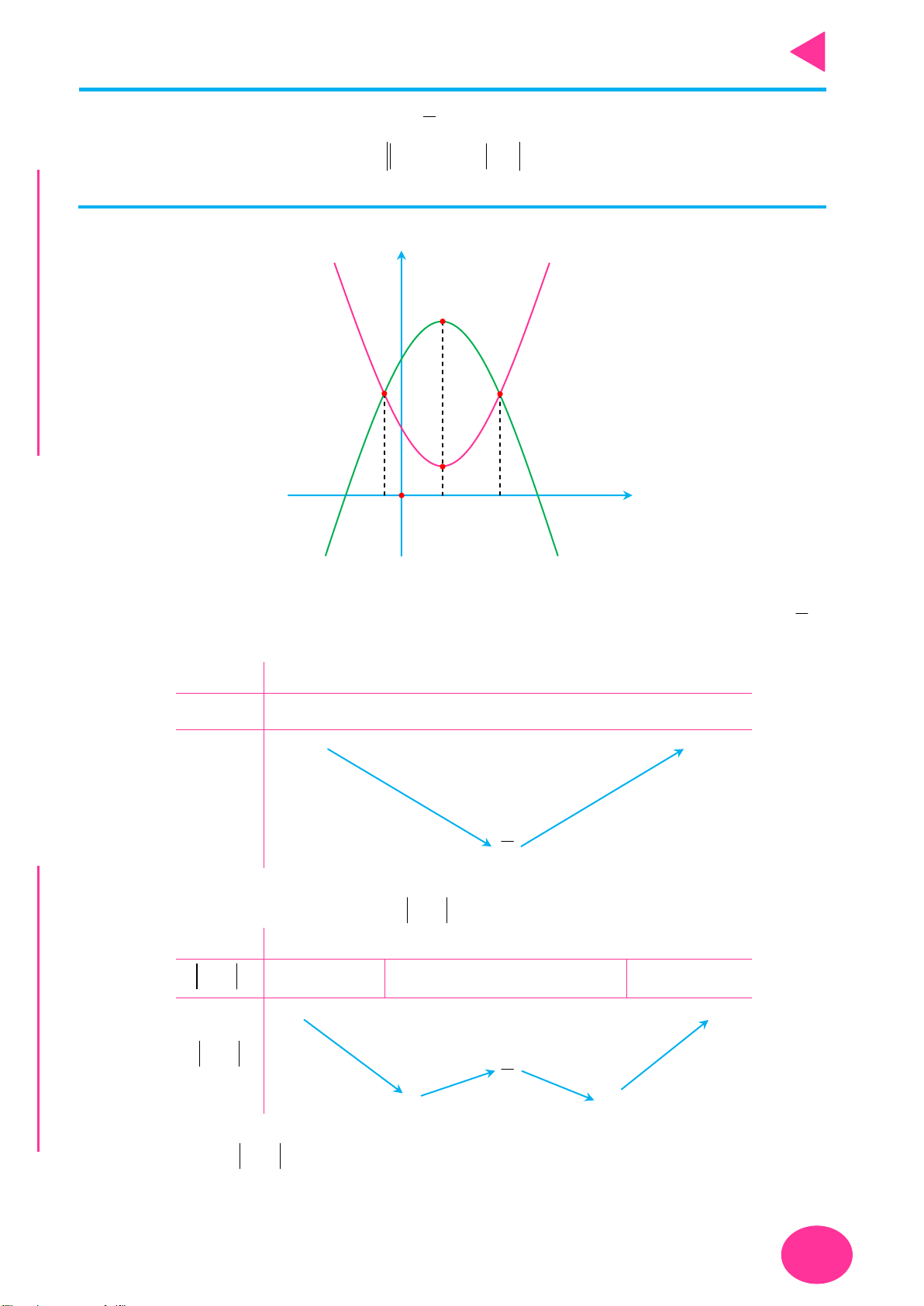
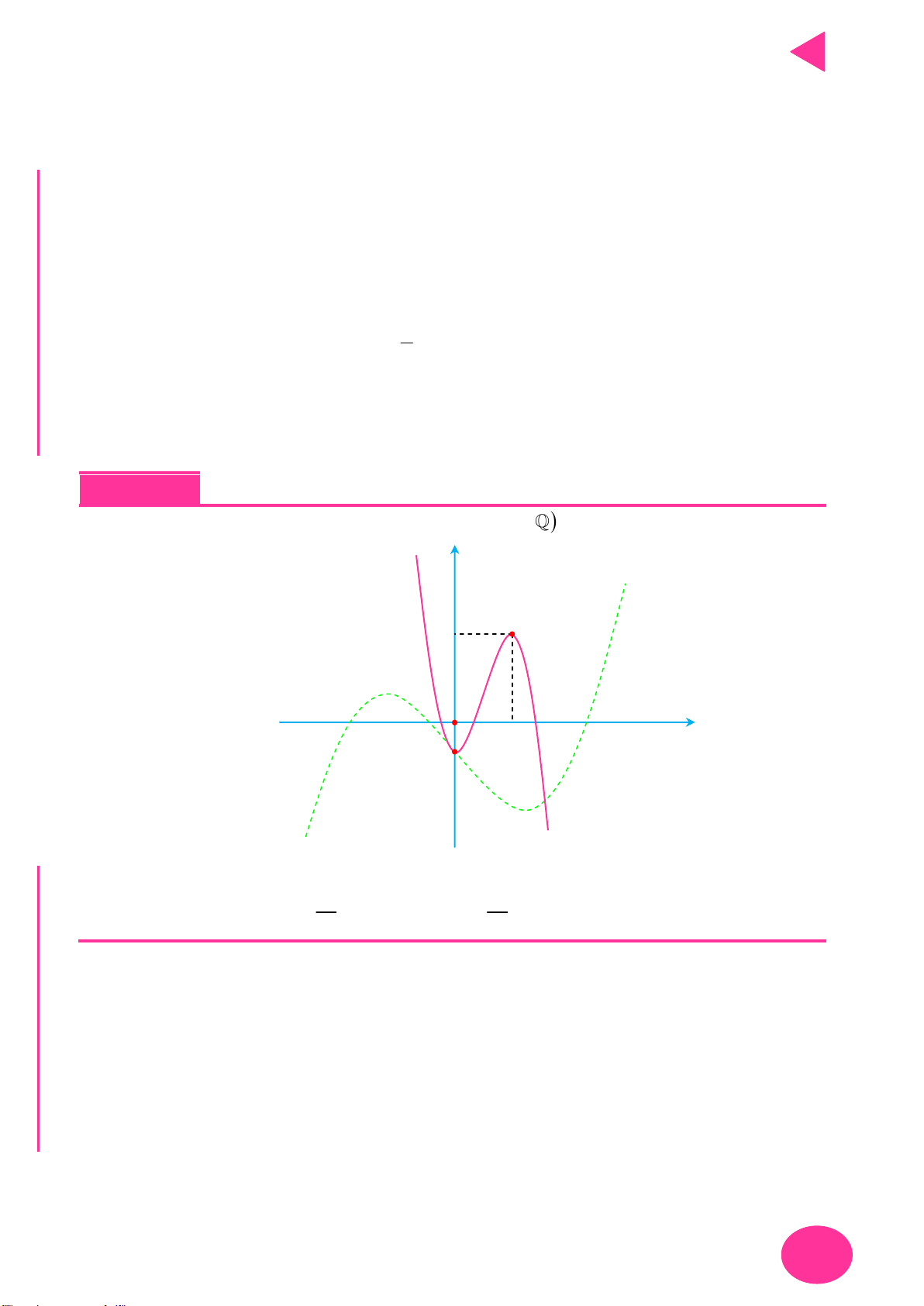
Thực hiện liên hoàn biến đổi đồ thị y f x thành đồ thị y f x ,
y f x YMPI
sau đó biến đổi đồ thị y f x thành đồ thị y f x . OL
+ Giữ nguyên phần đồ thị trên miền u x 0 của đồ thị y f x . C
y ux .vx với Ụ y
+ Bỏ phần đồ thị trên miền u x 0 của
f x , lấy đối xứng phần
C : y ux.vx đồ thị bị bỏ qua Ox.
y f x m với NH PH
Dịch chuyển đồ thị lên trên m đơn vị m 0 CHI
y f x m với
Dịch chuyển đồ thị xuống dưới m đơn vị. m 0
y f x n với
Dịch chuyển đồ thị sang trái n đơn vị. n 0
y f x n với
Dịch chuyển đồ thị sang phải n đơn vị. n 0
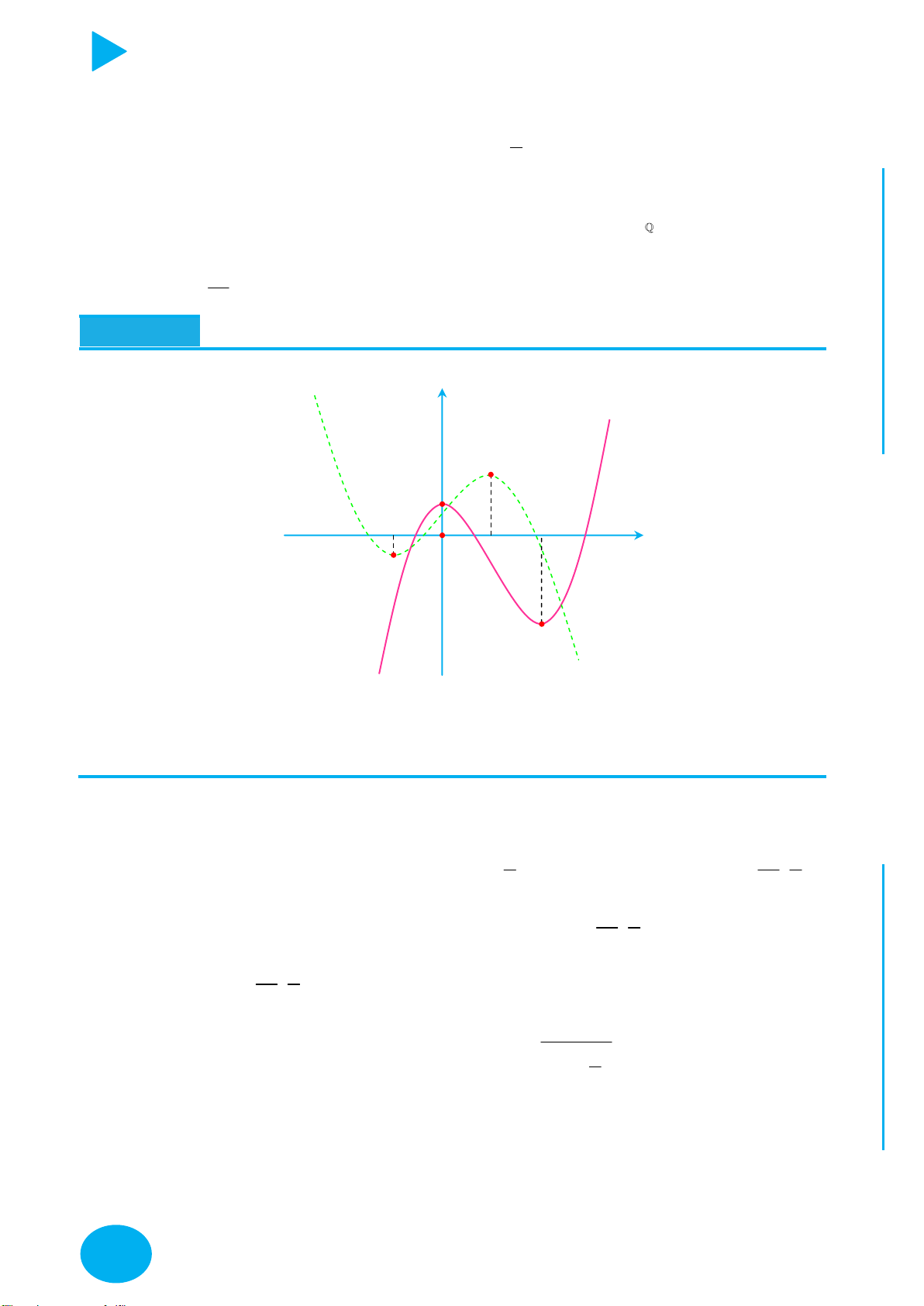
y f px với p 1 Co đồ thị theo chiều ngang hệ số p .
y f px với 1
Giãn đồ thị theo chiều ngang hệ số . 0 p 1 p
y qf x với q 1 Giãn đồ thị theo chiều dọc hệ số q . 1
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA 1
y qf x với q 1 Co đồ thị theo chiều dọc hệ số . q
Vẽ y f x trước sau đó tịnh tiến đồ thị lên trên hoặc xuống dưới
y f x m tùy theo m .
Tịnh tiến đồ thị qua trái, phải tùy theo m sau đó lấy đối xứng qua
y f x m
trục Ox (Giữ nguyên phần trên Ox , bỏ phần dưới Ox , lấy đối xứng
phần bị bỏ qua Ox ).
Tịnh tiến đồ thị qua trái, phải tùy theo m sau đó lấy đối xứng qua
y f x m
trục Oy (Giữ nguyên phần bên phải Oy , bỏ phần bên trái Oy , lấy
đối xứng phần được giữ nguyên qua Oy ).
Vẽ y f x trước sau đó tịnh tiến đồ thị sang trái hoặc phải tùy
y f x m theo m . C Ọ H
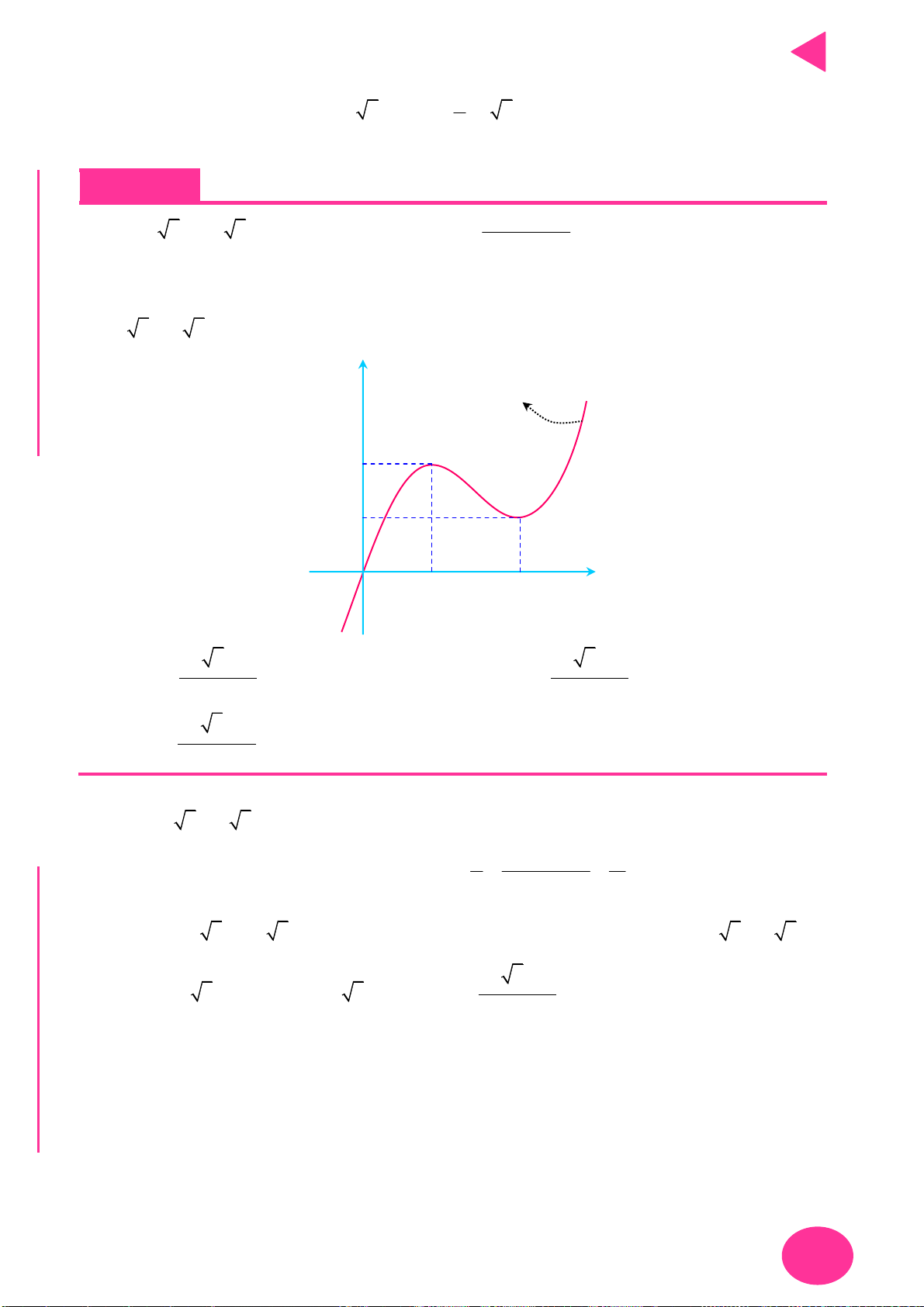
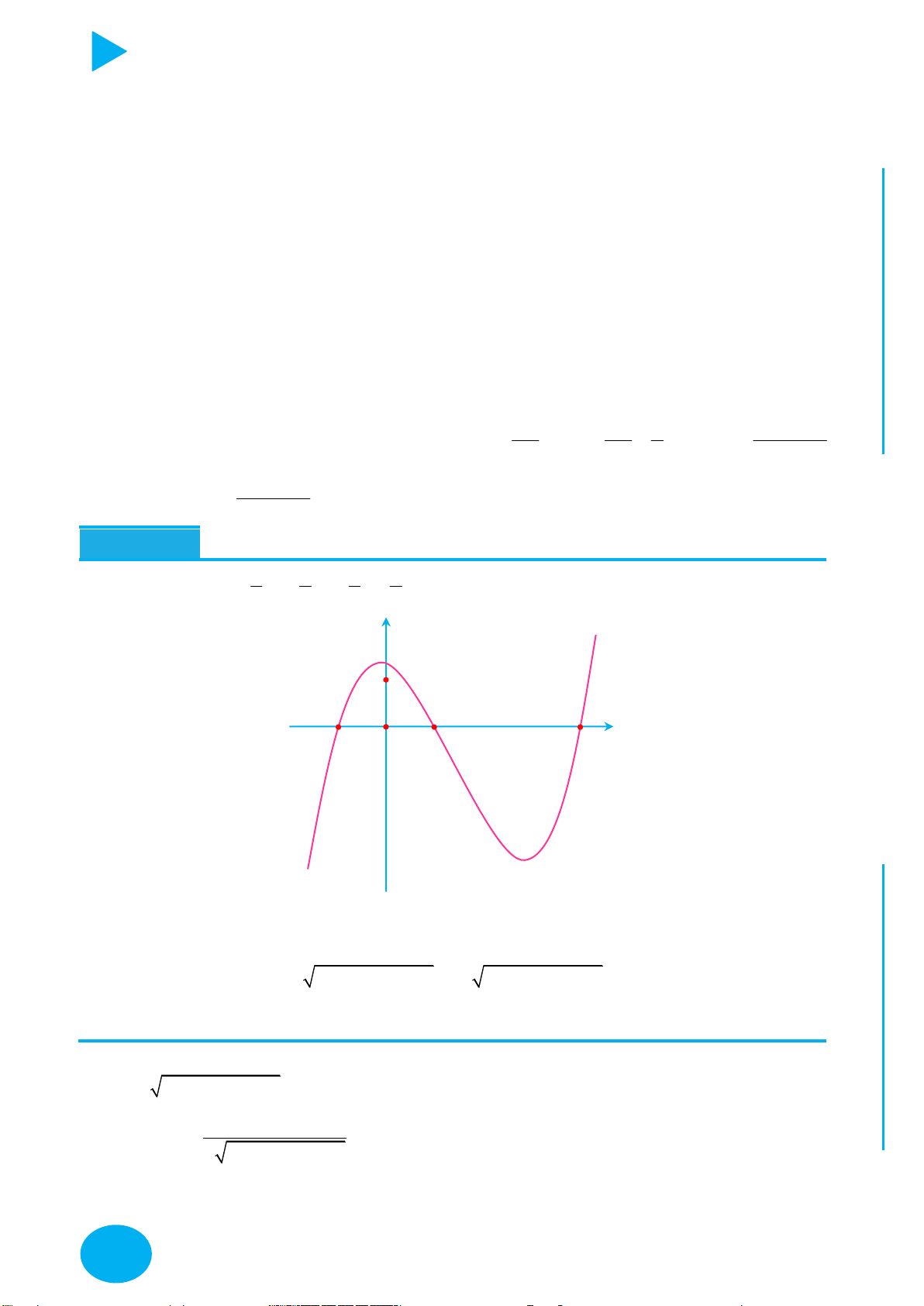
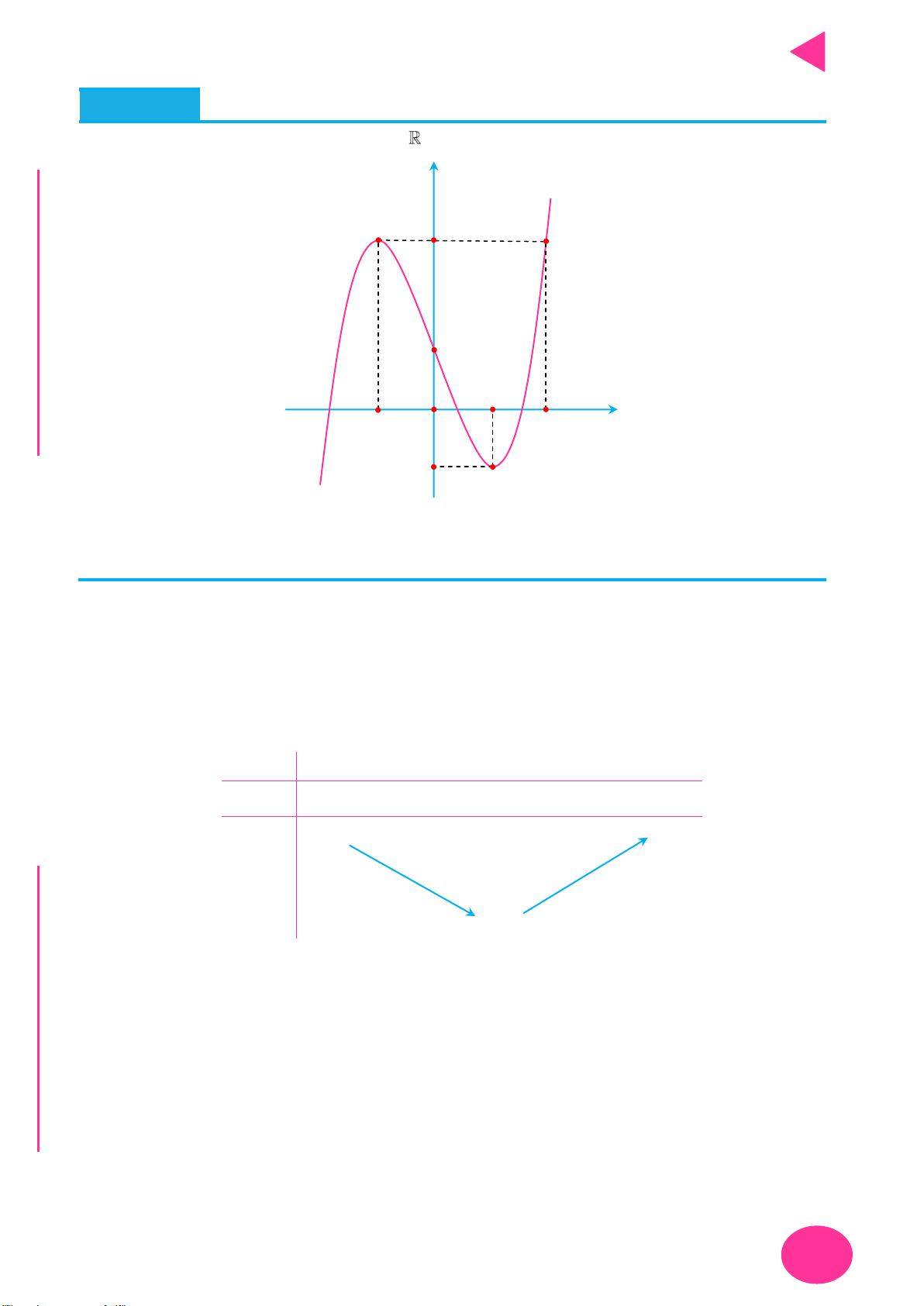
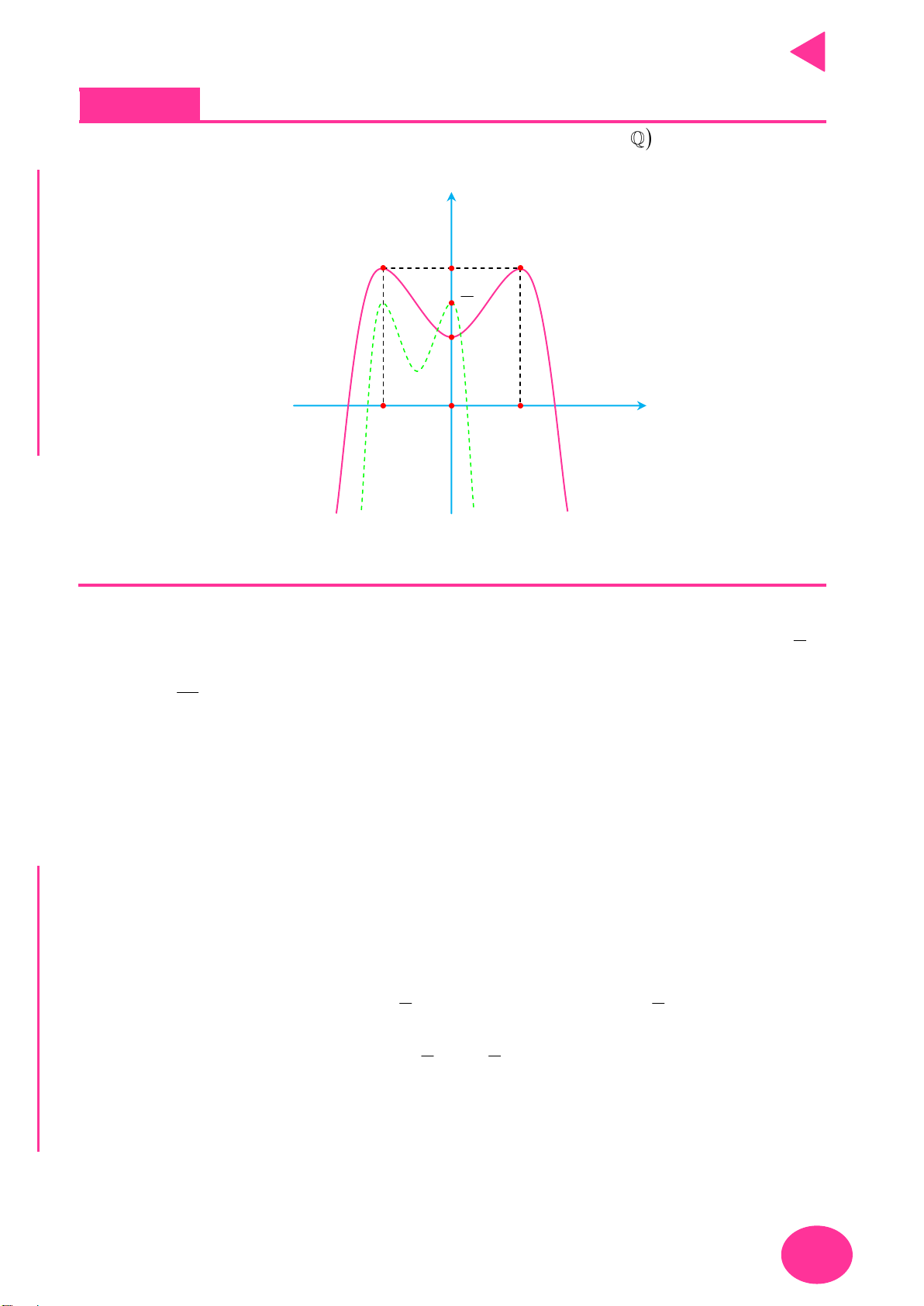
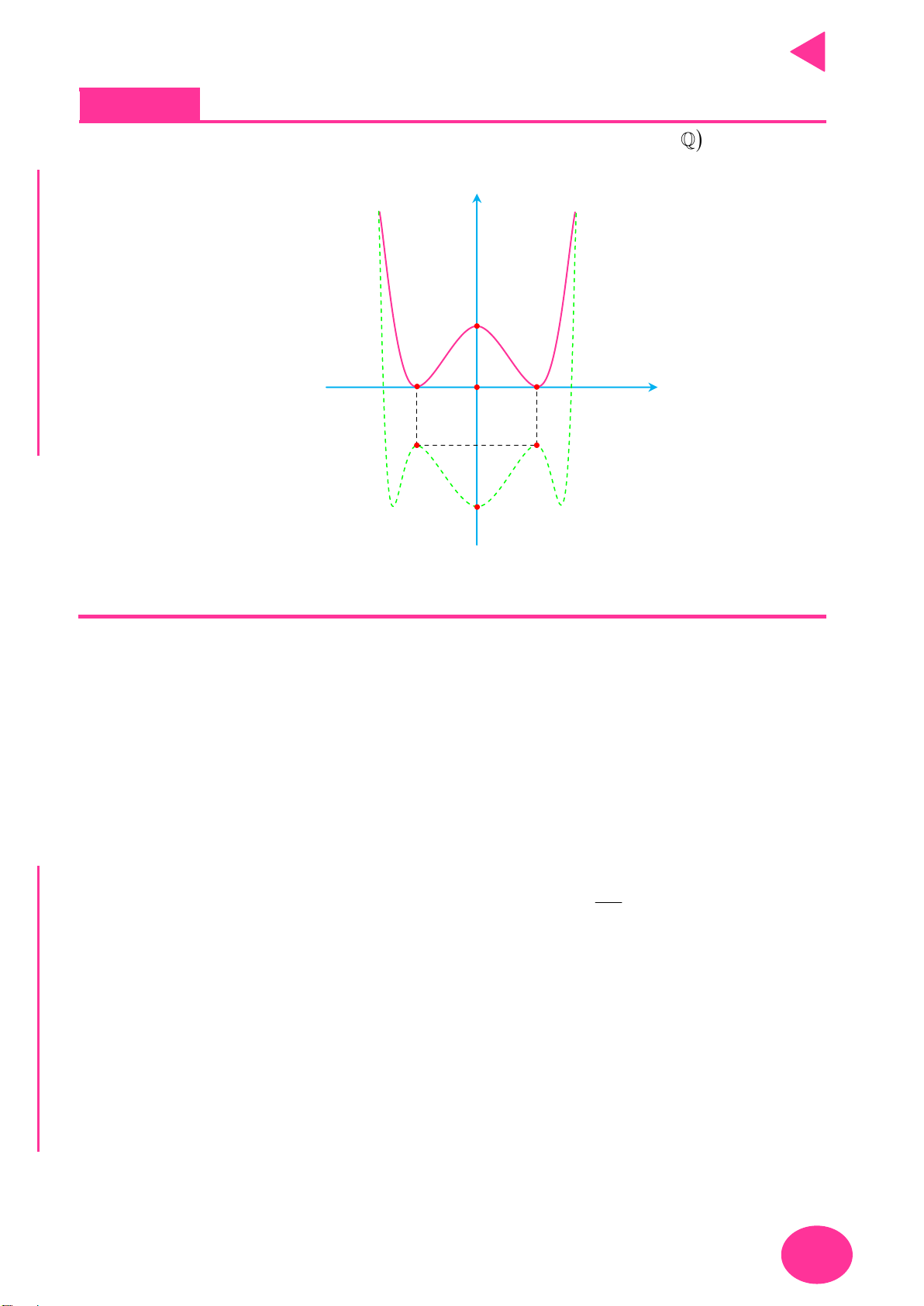
Số điểm cực trị của hàm trị tuyệt đối – Thầy Nguyễn Chiến. N
Gọi m là số điểm cực trị của hàm số y f x và k là số giao điểm giữa đồ thị
y f x với trục Ox . TOÁ U
Số điểm cực trị của đồ thị hàm số y f x là m k . IỆL
Gọi m là số điểm cực trị có hoành độ dương của hàm số của hàm số y f x . TƯ
số điểm cực trị của đồ thị hàm số y f x là 2n 1. VÀ y f x n
Bài toán chứa tham số: Cho hình vẽ đồ thị hàm số
có 1 điểm cực trị. Tìm giá trị
của tham số m để hàm số y f x k f m có n2 điểm cực trị. CHÍ P
+ Khi tịnh tiến sang trái hoặc sang phải đơn vị thì số điểm cực trị hàm số y f x k vẫn
ẠT bằng số điểm cực trị hàm số y f x.
+ Để tìm số giao điểm y f x f m với trục Ox ta chuyển về dạng tìm số giao điểm của
đồ thị y f x và đường thẳng y f m .
Lưu ý: số giao điểm này không tính giao tại điểm cực trị của hàm y f x .
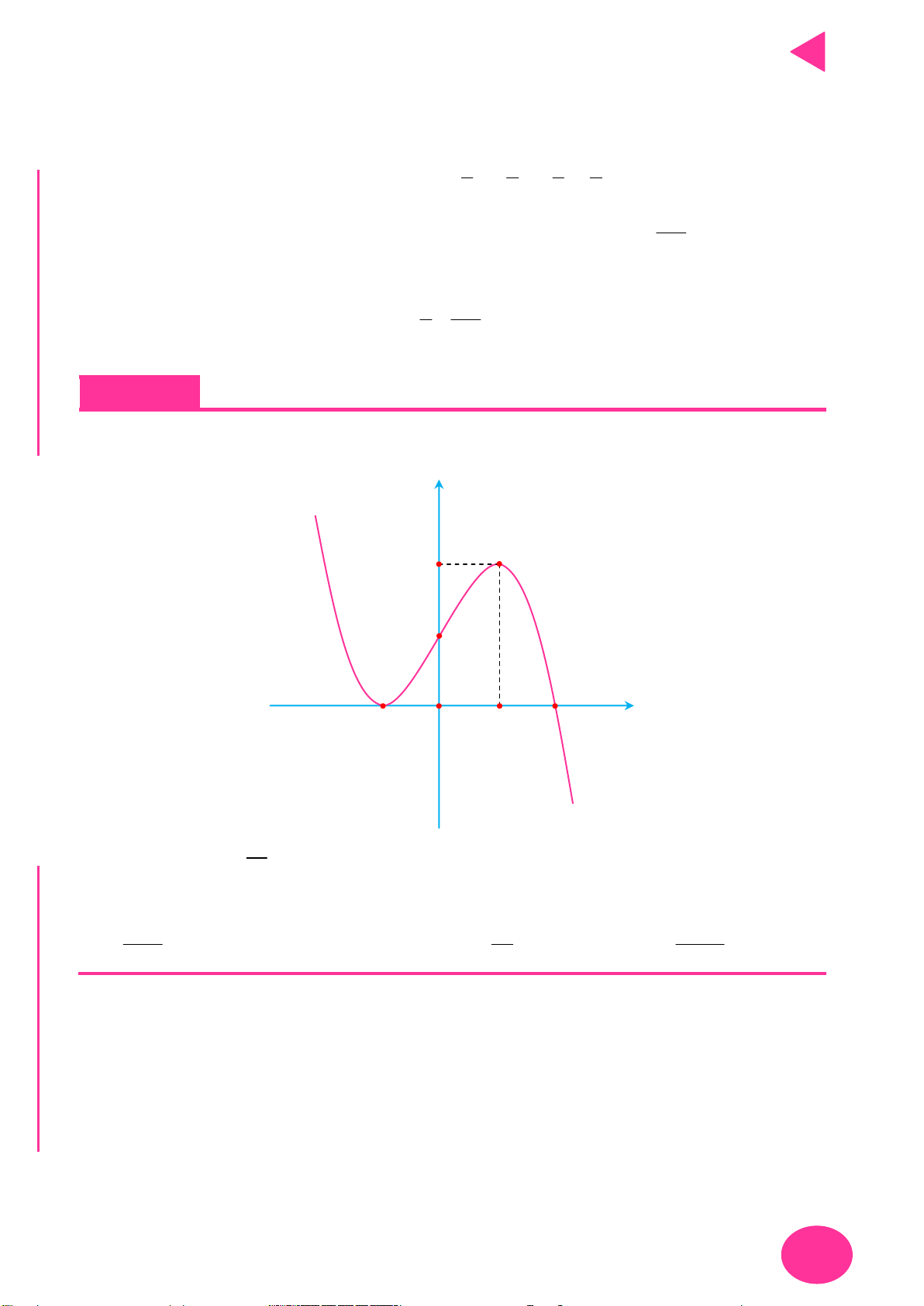
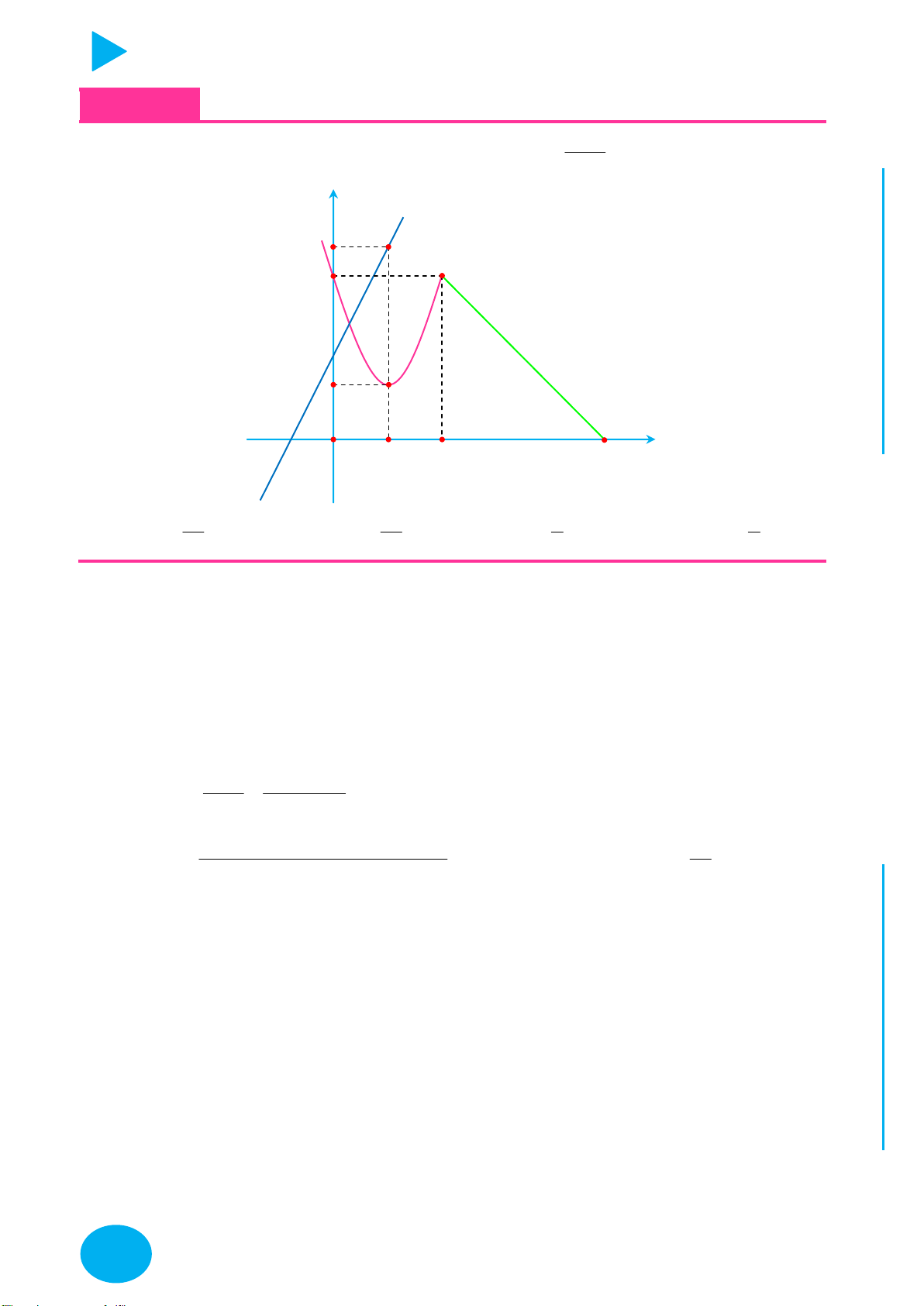
Phương pháp giải toán đồ thị tìm khoảng đồng biến và nghịch biến
Đây là dạng toán vô cùng đơn giản, cách làm bài nào cũng như bài nào, ta sẽ có 3 bước là
đạo hàm Tìm nghiệm Lập bảng biến thiên!
Khi vào ví dụ cụ thể ta sẽ hiểu được mấu chốt của bài toán này
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 2
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
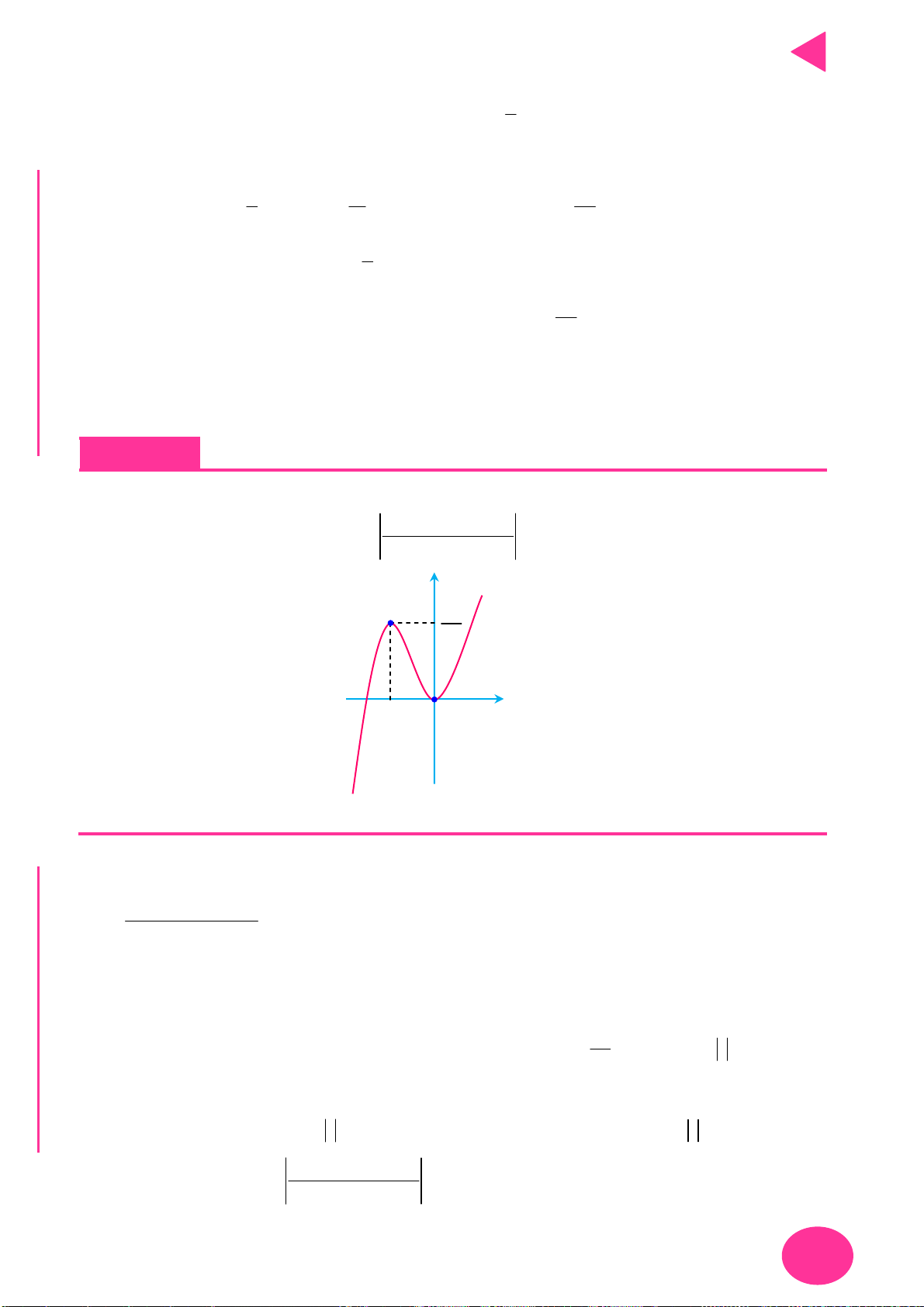
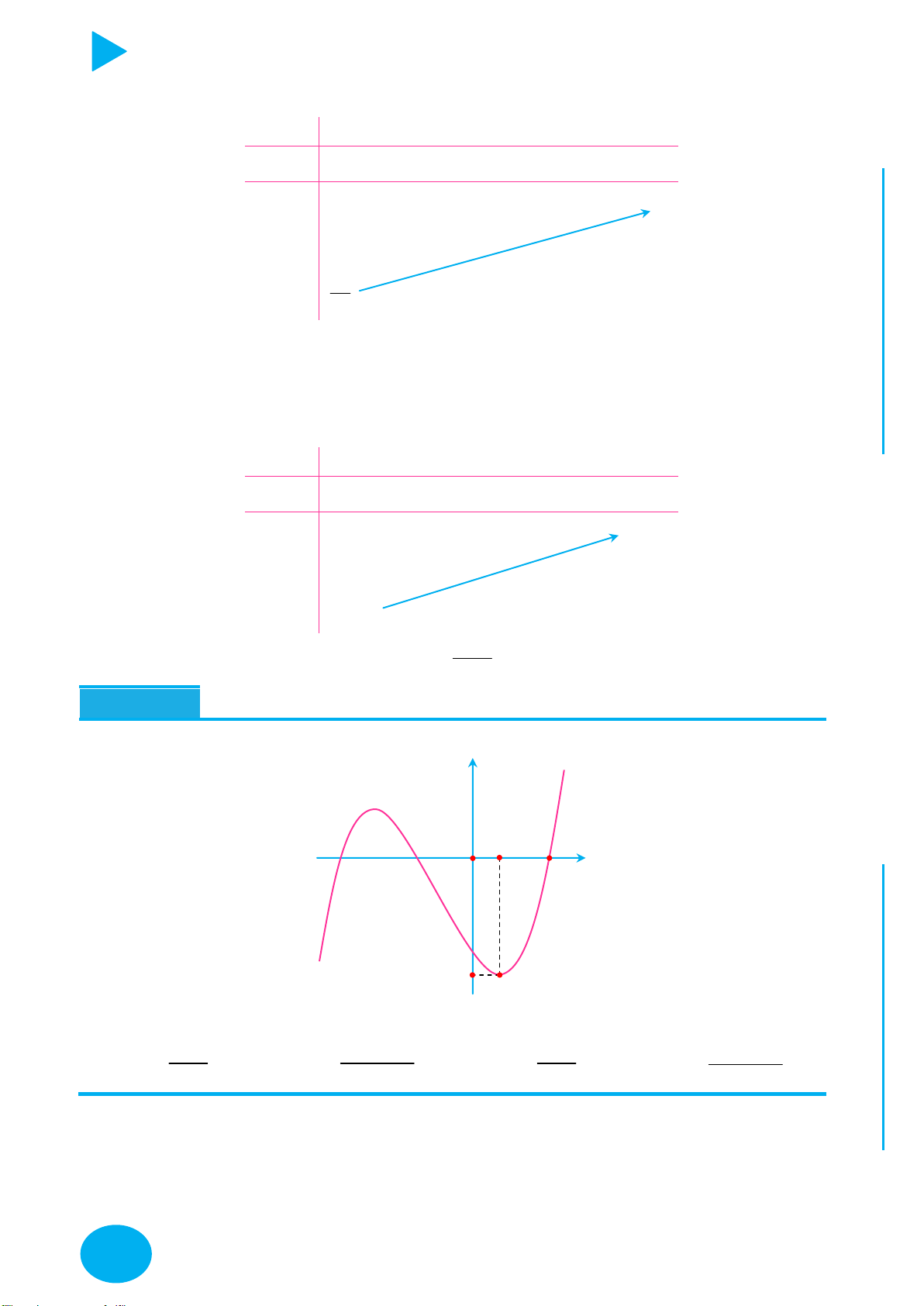
Phương pháp giải toán đồ thị chứa tham số.
Ở đây ta sẽ xét dạng toán f ux f m trong đó ux là bất kì hàm gì đó liên quan tới
x và f m là hàm theo biến m và đề bài yêu cầu tìm giá trị của m để thỏa mãn điều kiện gì
đó. Khi đó ta làm như sau:
Bước 1. Chặn giá trị x, ux , f ux
Bước 2. Đặt t ux, lập bảng biến thiên cho hàm f t
Bước 3. Từ bảng biến thiên suy ra điều kiện của hàm f m , từ đó suy ra điều kiện của m
Với những bạn nào cảm thấy khó hiểu thì có thể tham khảo các làm sau của bạn Sơn
Hoàng. Link https://www.youtube.com/channel/UCiduEKtcZZO8Yei-XBUq9lQ
Ví dụ đơn giản để hiểu, ta có thể lấy một đề bài kiểu như sau
Cho hàm số f x liên tục trên
có đồ thị như hình vẽ, hỏi có bao nhiêu giá trị nguyên của tham
số m đề phương trình f 2 x 2 4
m 1 có 2 nghiệm phân biệt. OÁN u 2 4 x 0;2 T
Vậy ở đây ta sẽ làm theo 3 bước trên, dễ thấy
, chuyển bài toán về tìm C
giá trị nguyên của tham số M để phương trình f u M có 2 nghiệm phân biệt, đây là bài toán cơ bản! YMPI OL C Ụ NH PH CHI 3
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA ĐỀ BÀI
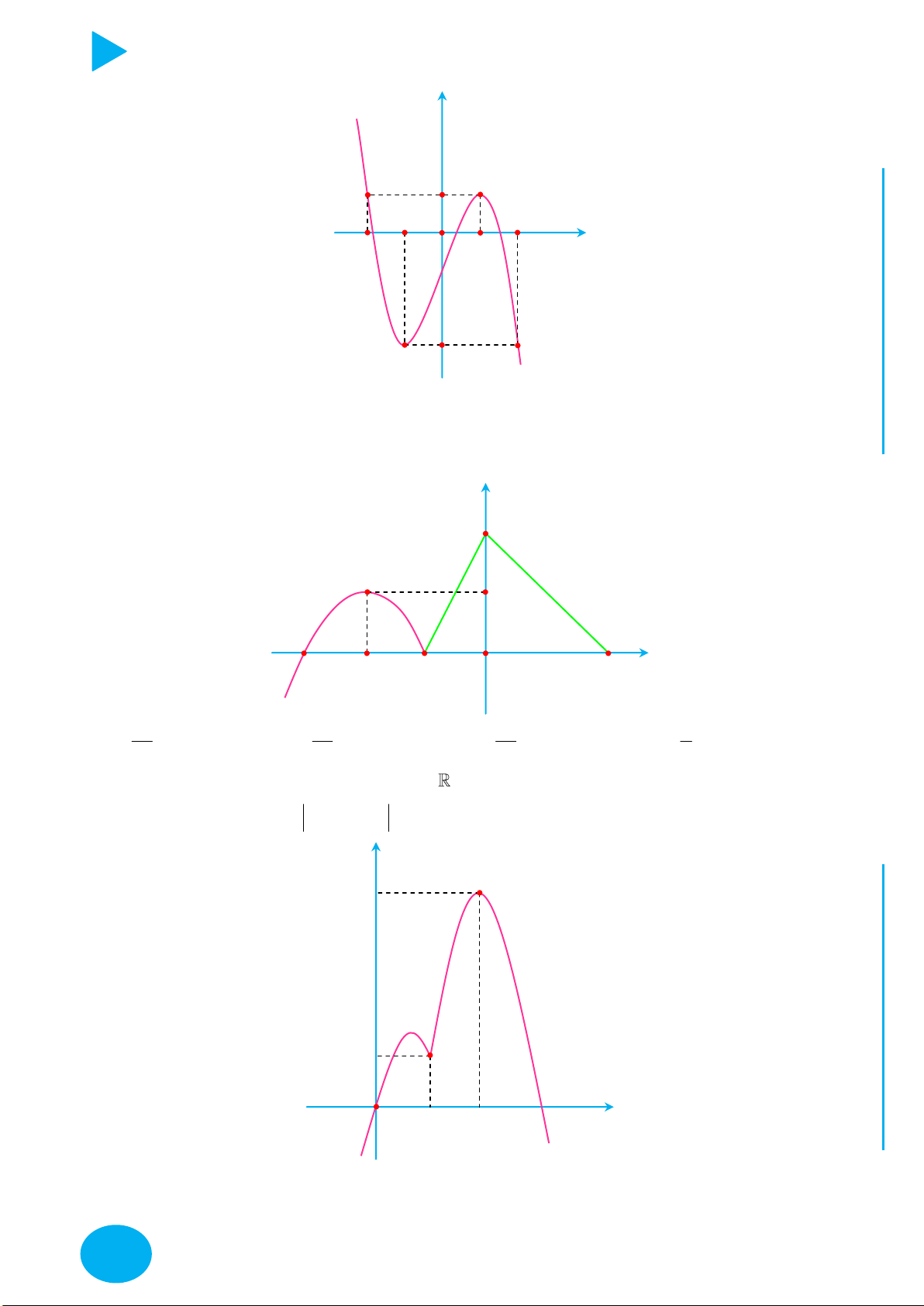
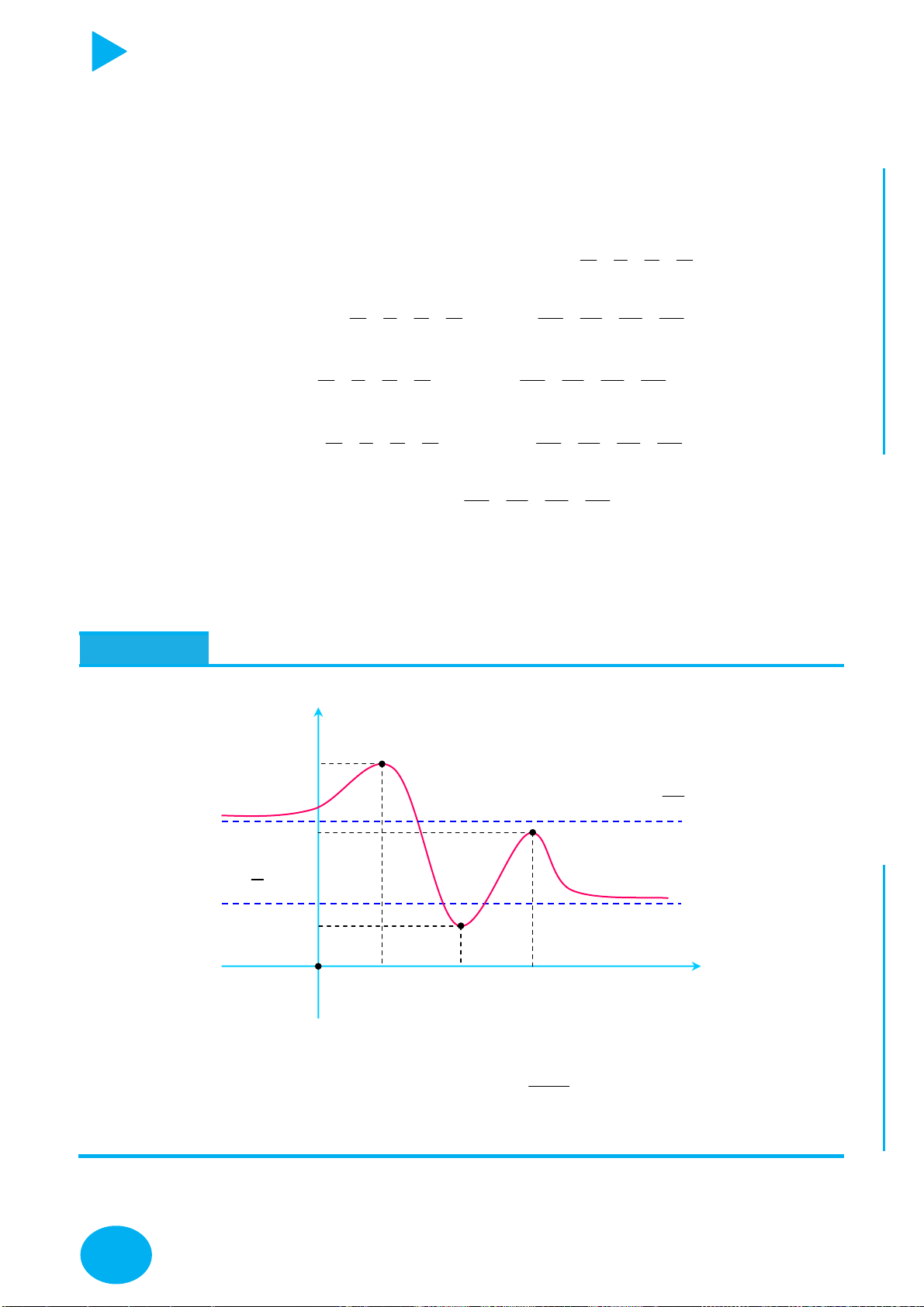
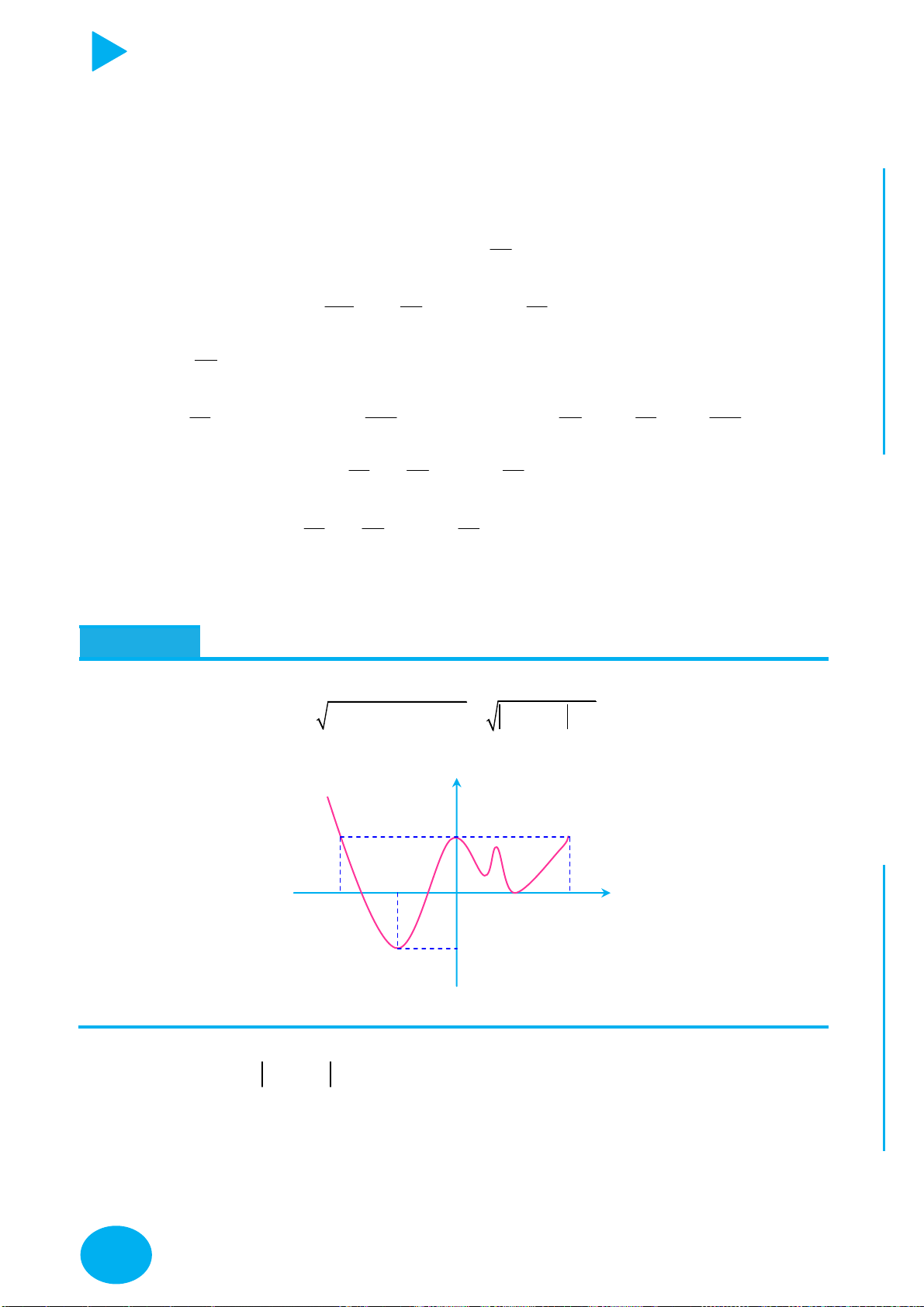
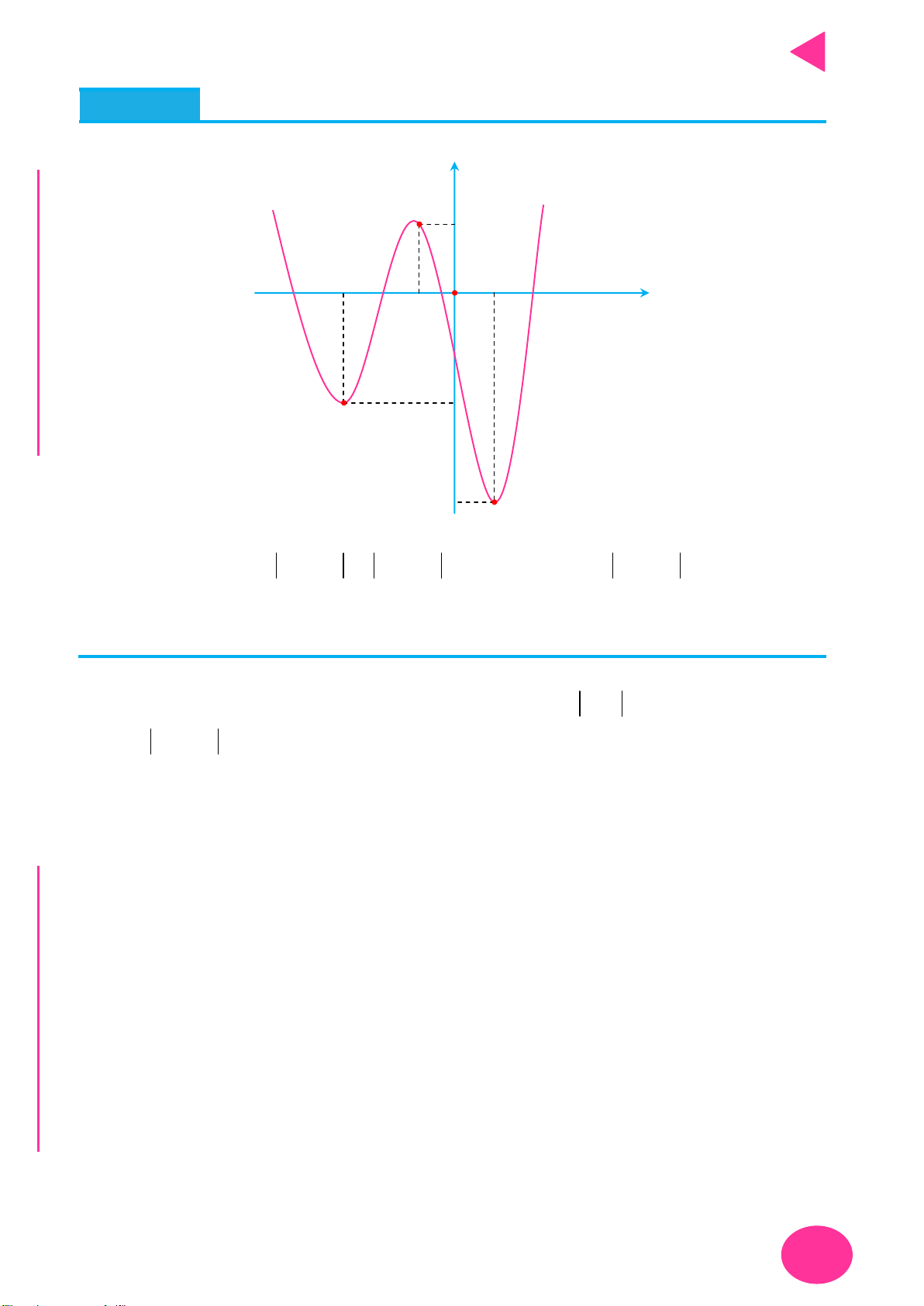
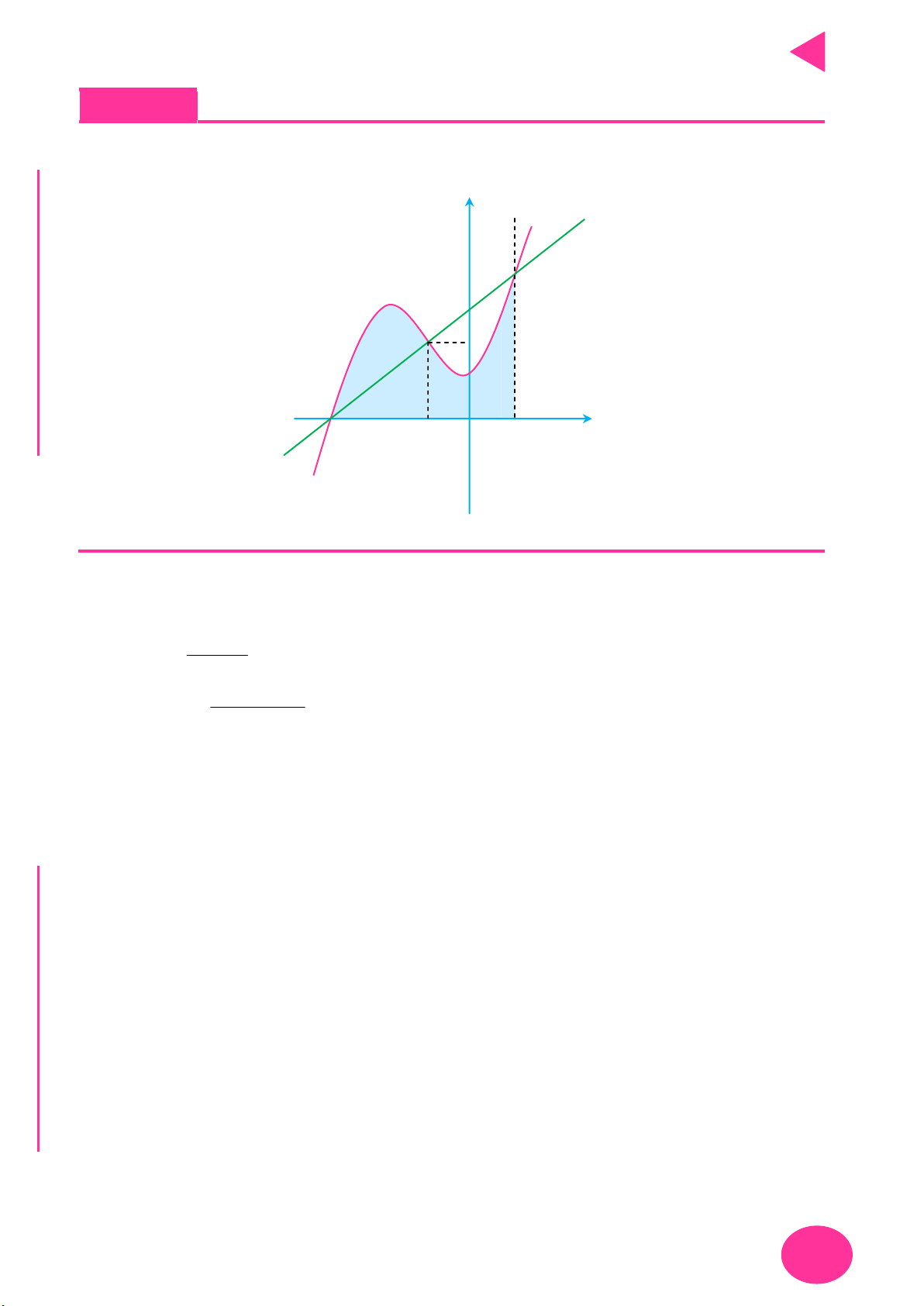
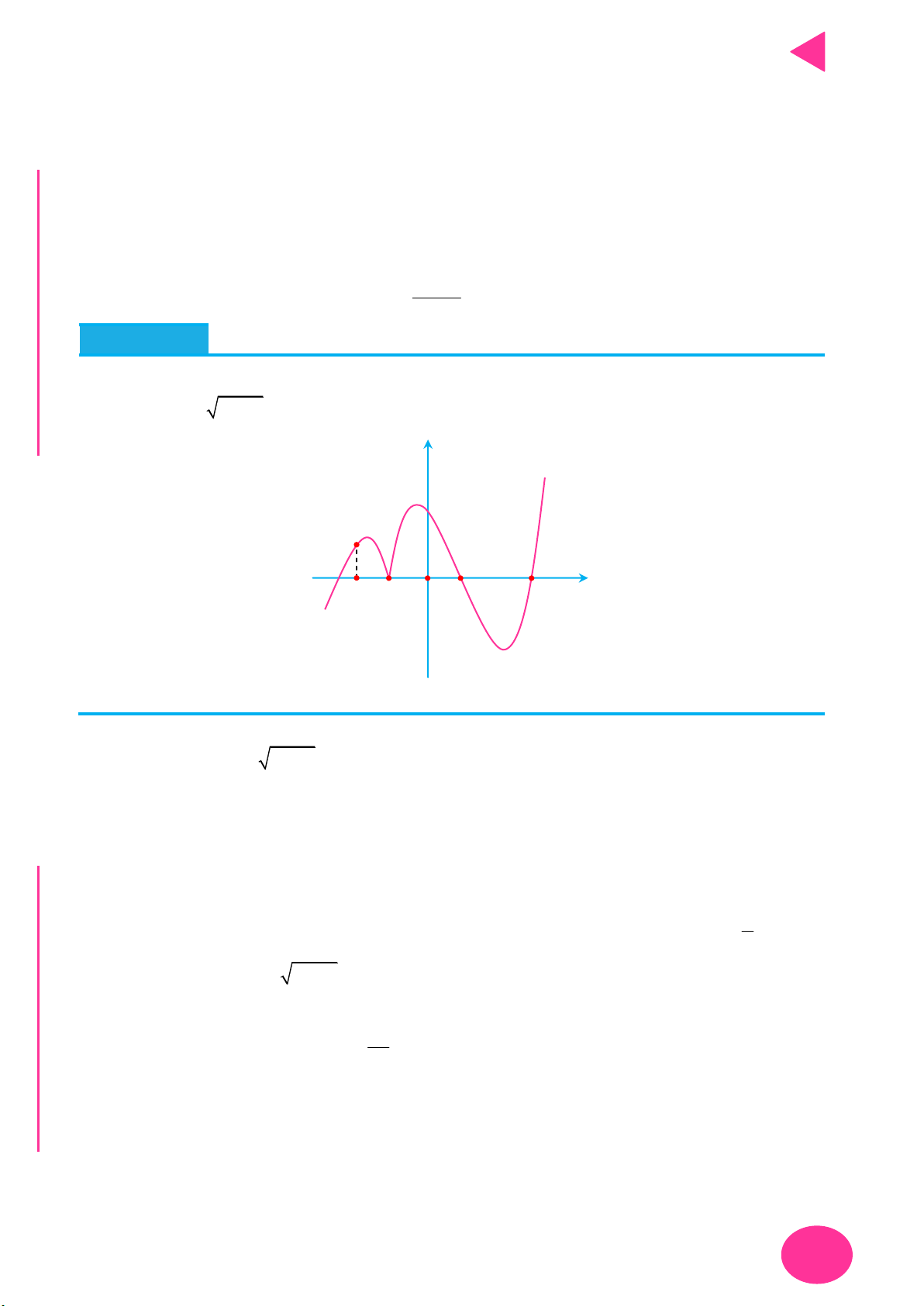
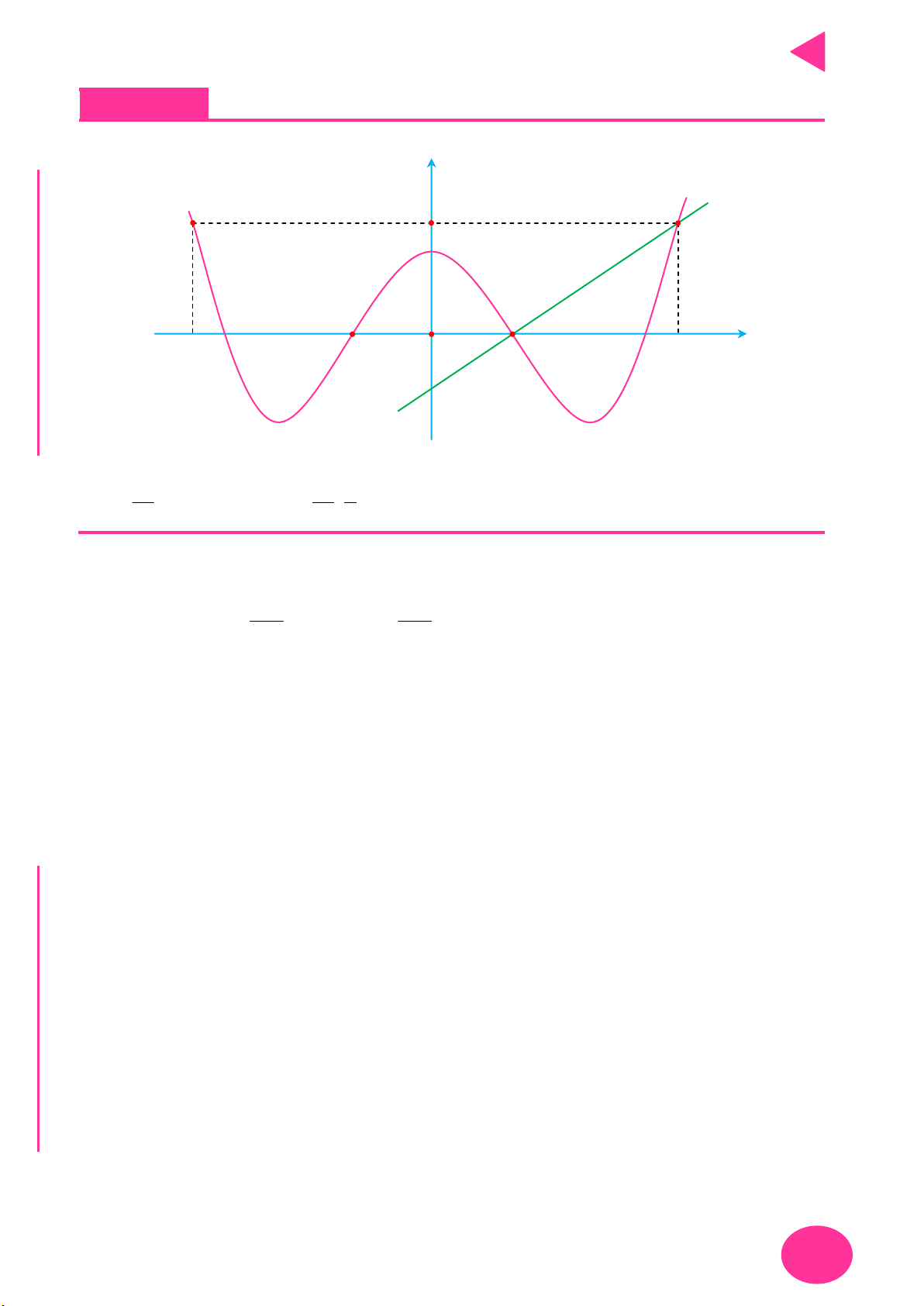
Câu 1. Cho hàm số y f x liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của tham số m để phương trình f 2 f cosx m có nghiệm x ; . 2 y 2 1 2 1 x 1 O 2 1 C 2 Ọ H A. 5. B. 3. C. 2. D. 4. N
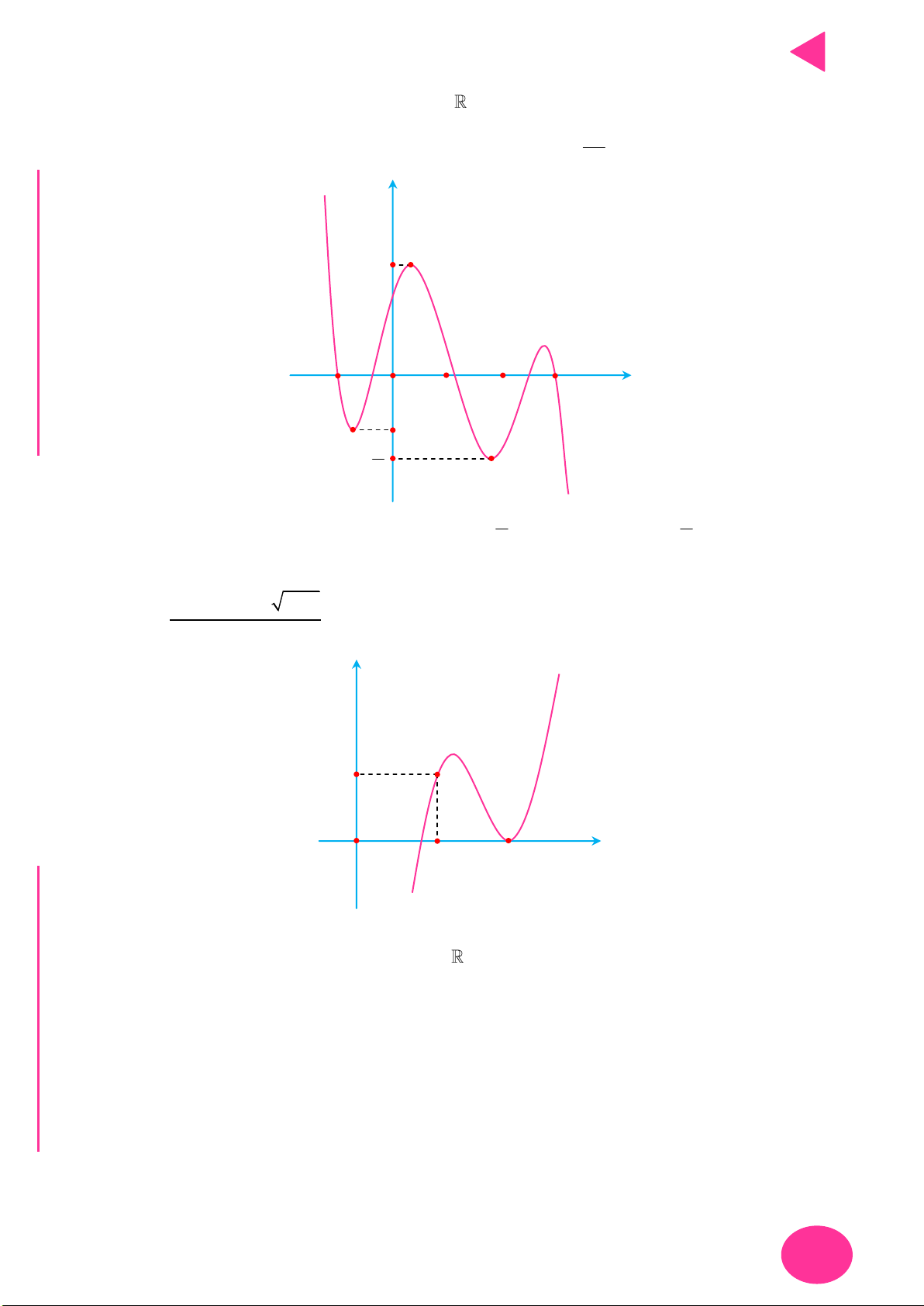
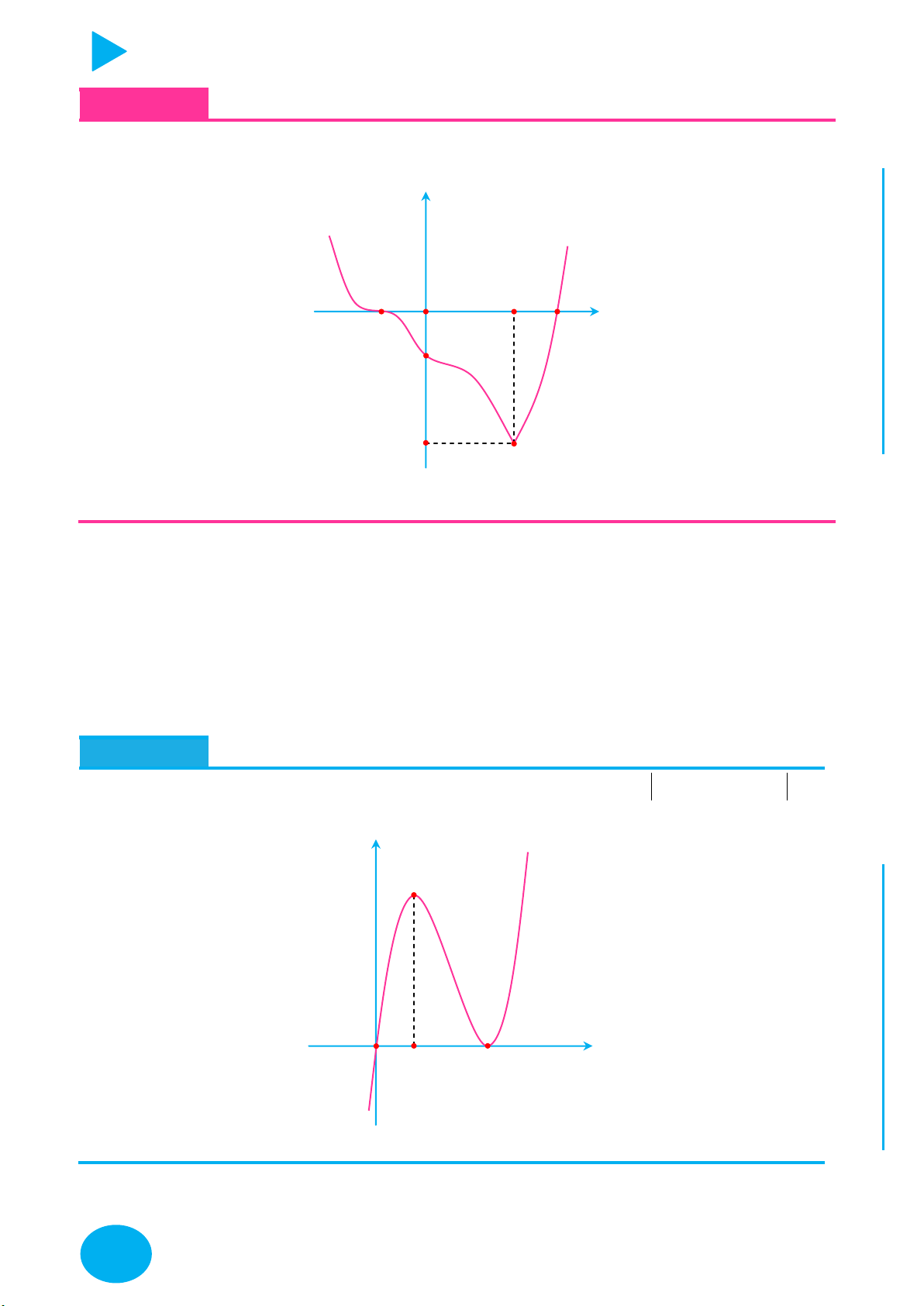
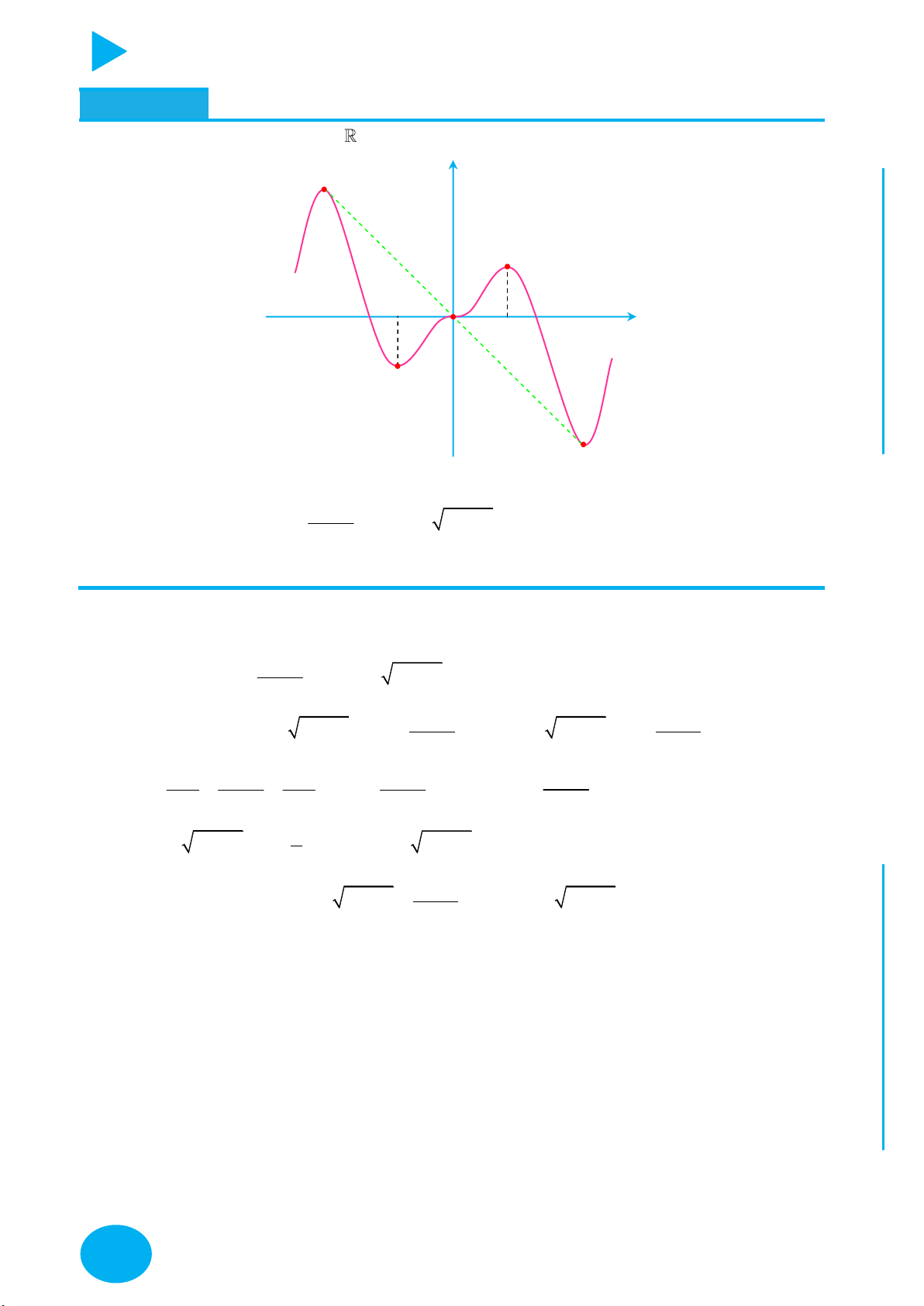
Câu 2. Cho hàm số f x liên tục trên
và có đồ thị như hình vẽ dưới đây: y TOÁ 3 U IỆL TƯ 1 VÀ 2 1 O 2 x CHÍ P 1 ẠT
Số các giá trị nguyên của tham số m không vượt quá 5 để phương trình f x 2 m
1 0 có hai nghiệm phân biệt là 8 A. 5. B. 4. C. 7. D. 6.
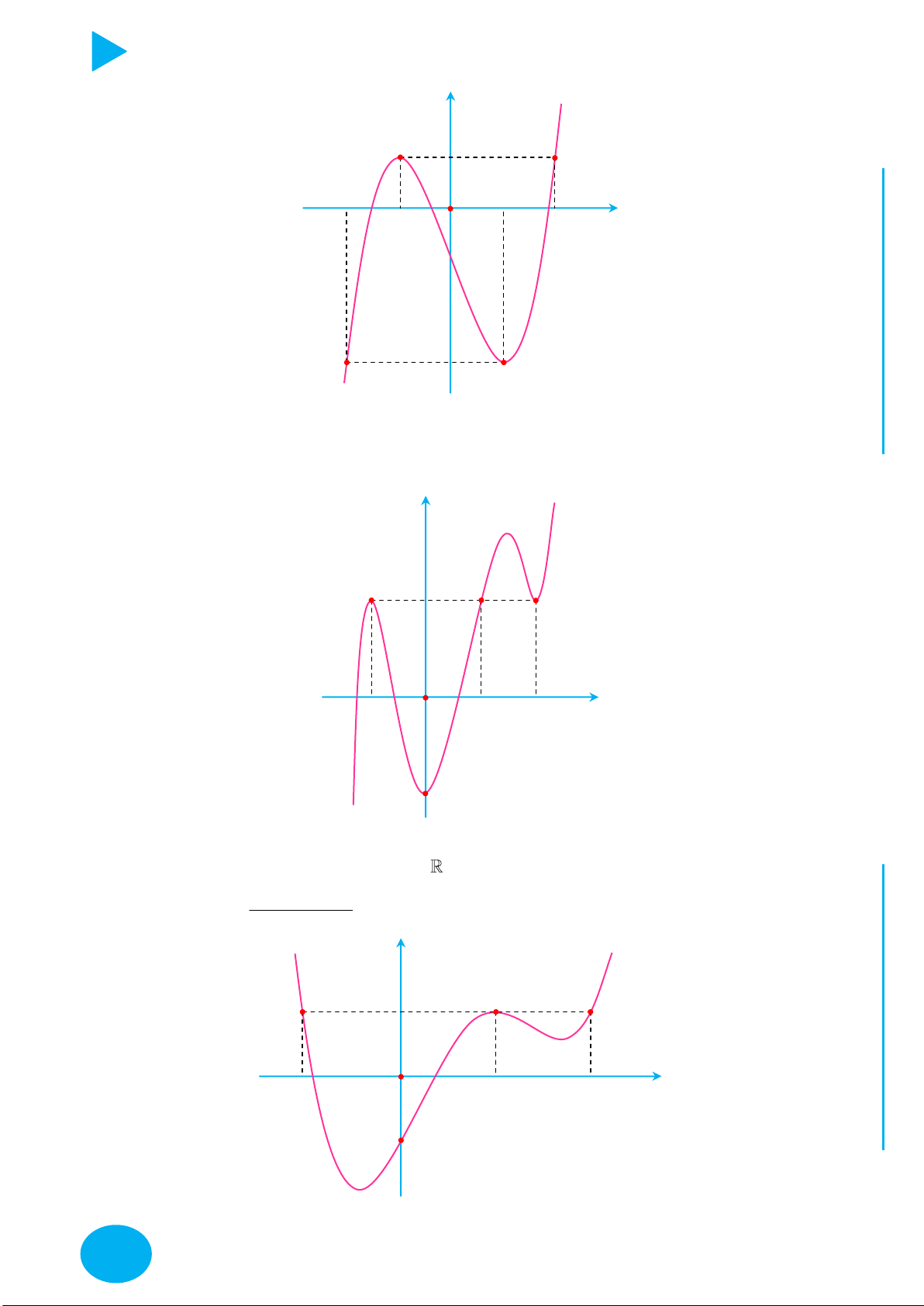
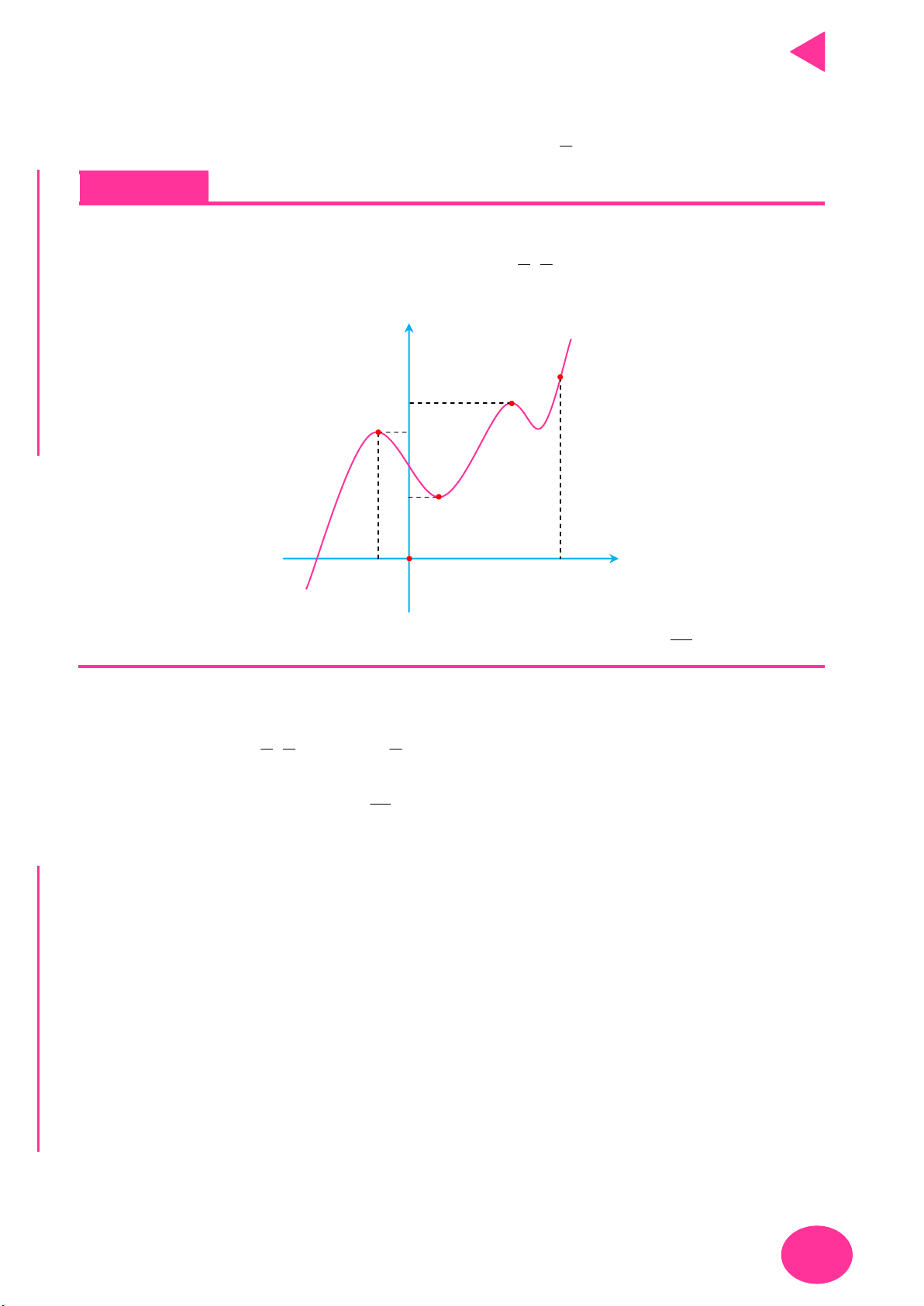
Câu 3. Cho hàm số f x liên tục trên 0; 5 và có đồ thị như hình vẽ dưới. 4
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 4 3 2 1 O 1 2 3 5 x
Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình m 2 2019
f x f x 1 3x 10 2x
Nghiệm đúng với mọi x 0; 5? A. 2014 B. 2015 C. 2016 D. 2017 OÁN
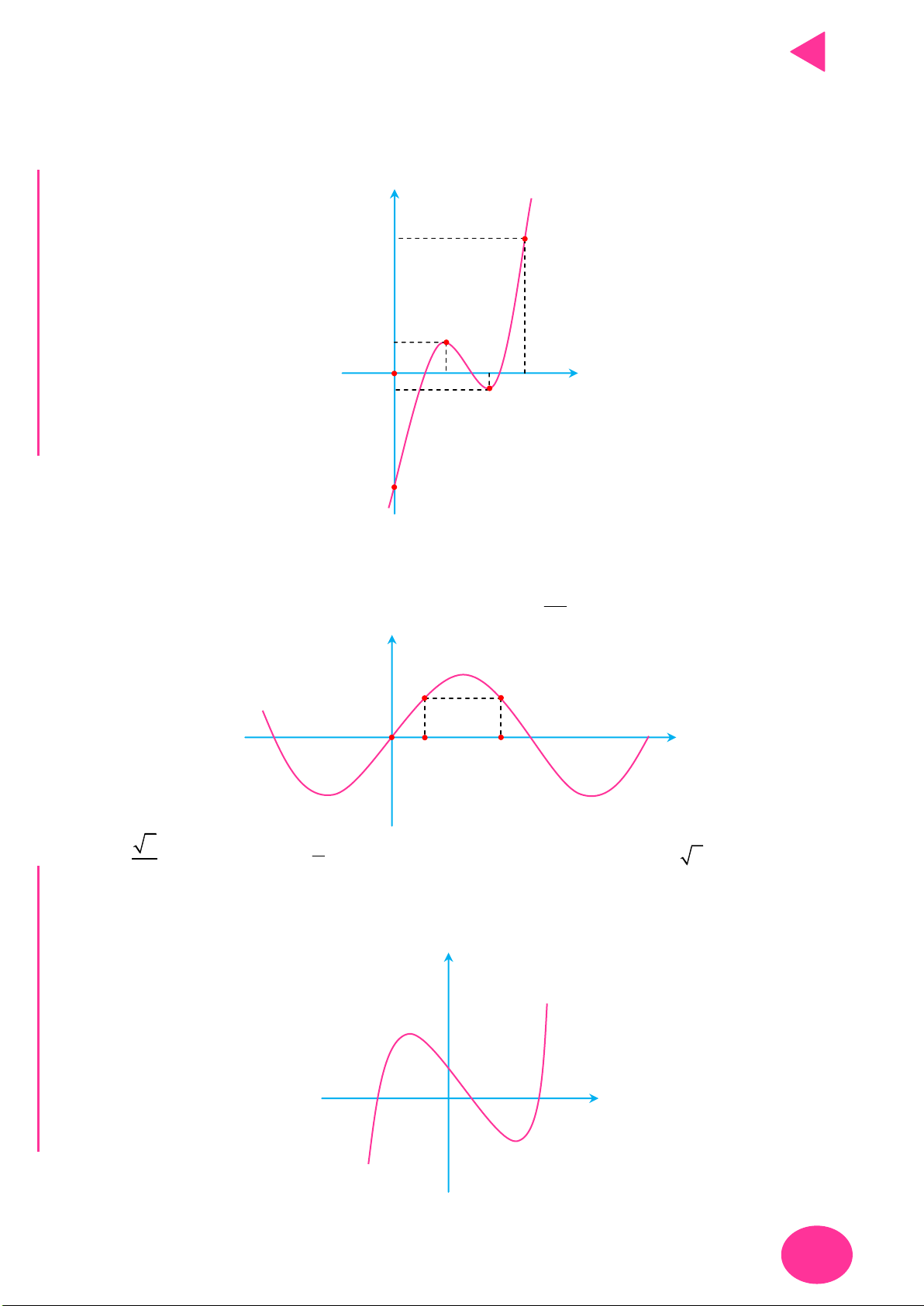
Câu 4. Cho hàm số f x liên tục trên và có đồ thị như hình vẽ. T y C 1 O 1 2 x YMPI OL C Ụ 2 NH PH 3 CHI 4
Tổng tất cả các giá trị của tham số m để bất phương trình f x 2 x f x 2 9.6 4 .9 m
5m fx .4
Đúng với mọi x là? A. 10. B. 4. C. 5 D. 9
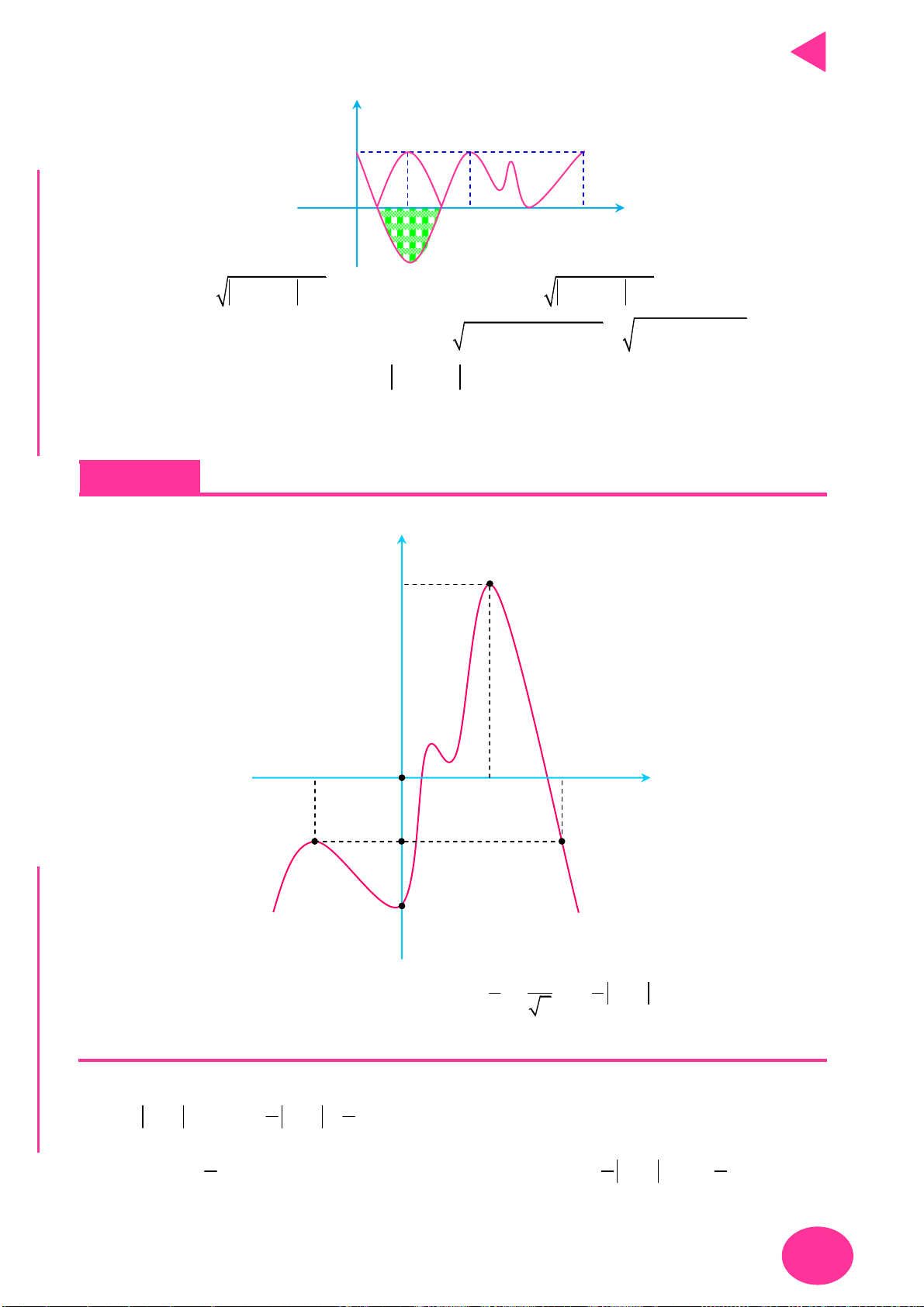
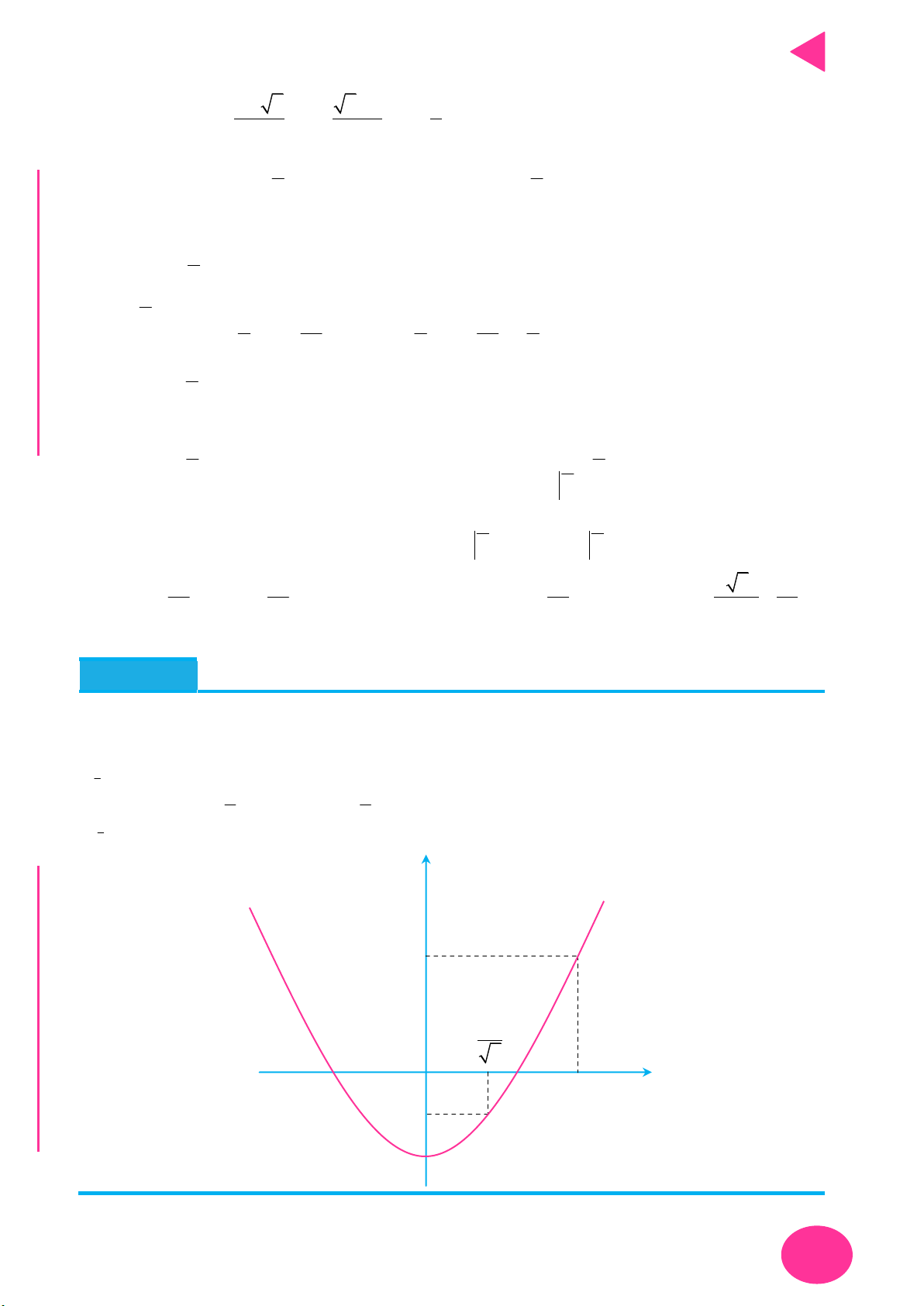
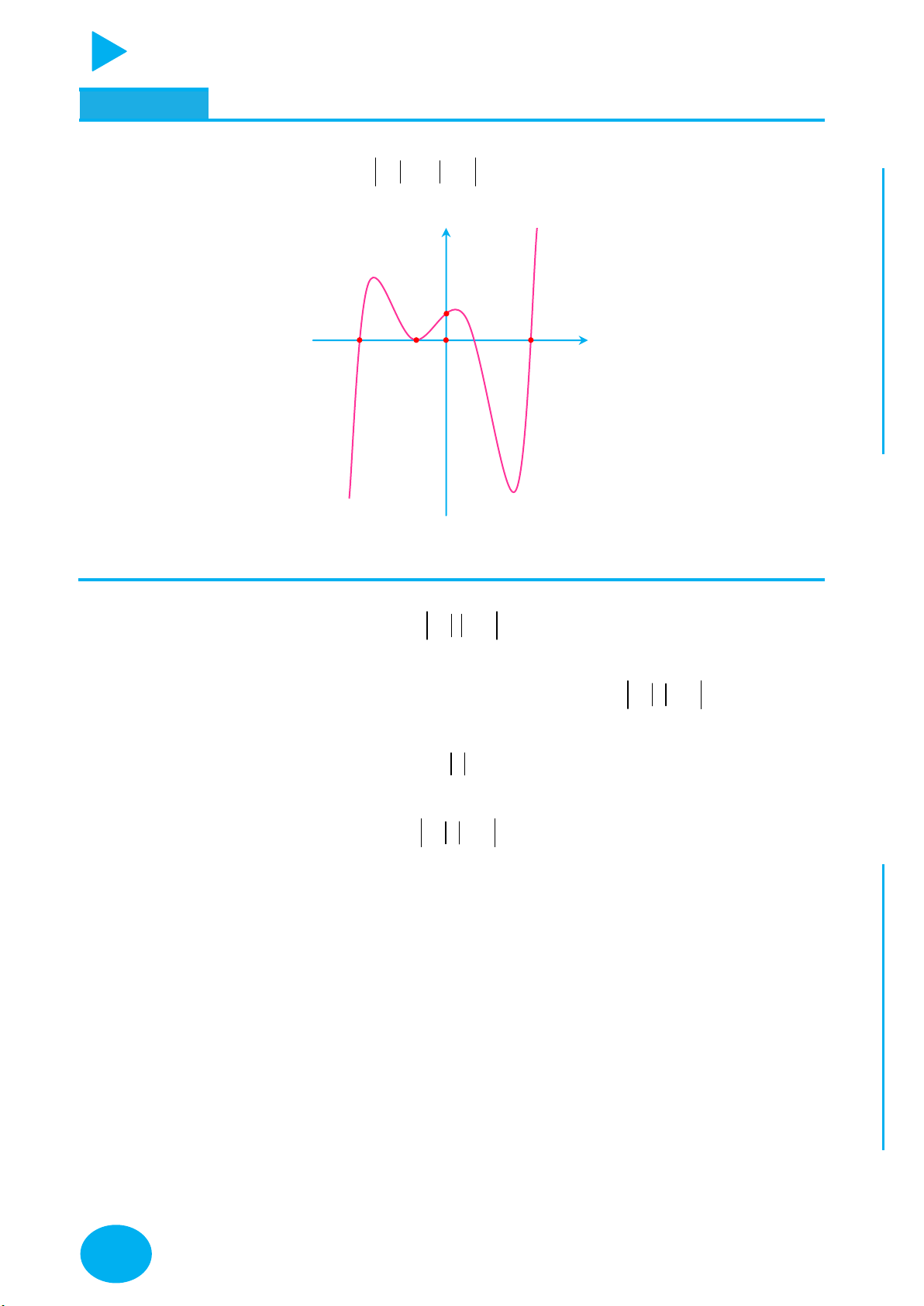
Câu 5. Cho hàm số y f x có đồ thị hàm số y f x như hình vẽ bên. Xét hàm số
g x f x 3 2
2x 4x 3m 6 5 với m là số thực. Để g x 0 x 5; 5 thì điều kiện của m là 5
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y f 'x 2 5 O 5 x B 13 A
A. m 2 f 5
B. m 2 f 5 3 3 2 m 2 f 0
m f 5 C C. 2 5 D. 4 5 3 3 Ọ H f x
Câu 6. Cho 0 a 1 b 1 a và hàm số y g x có đạo hàm trên 2 N
f x 1 0; y f x TOÁ
. Biết đồ thị hàm số
như hình vẽ dưới. Khẳng định nào sau đây đúng với U
mọi x a 1; b 1 IỆL y
y f x TƯ VÀ n CHÍ P m ẠT O a b x f b 1 f a 1
A. g x
B. g x m n f b 1 10 g x
C. g x D. 0 m
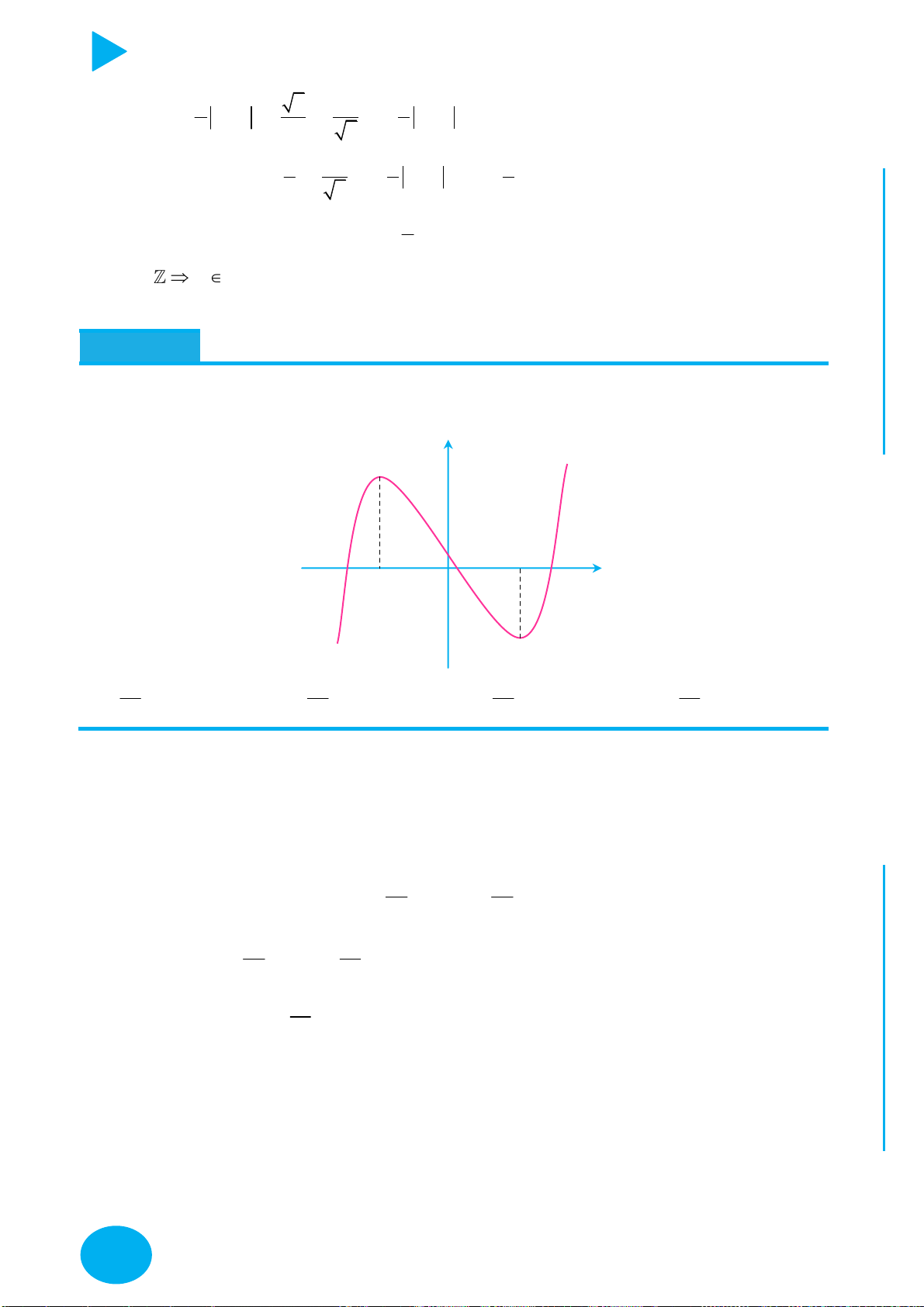
Câu 7. Cho hàm số f x có đạo hàm f 'x . Hàm số y f 'x liên tục trên tập số thực
và có đồ thị như hình vẽ. Số nghiệm thuộc đoạn 1; 4 của phương trình f x f 0 là? 6
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 1 O 1 2 4 x A. 4. B. 3. C. 2. D. 1.
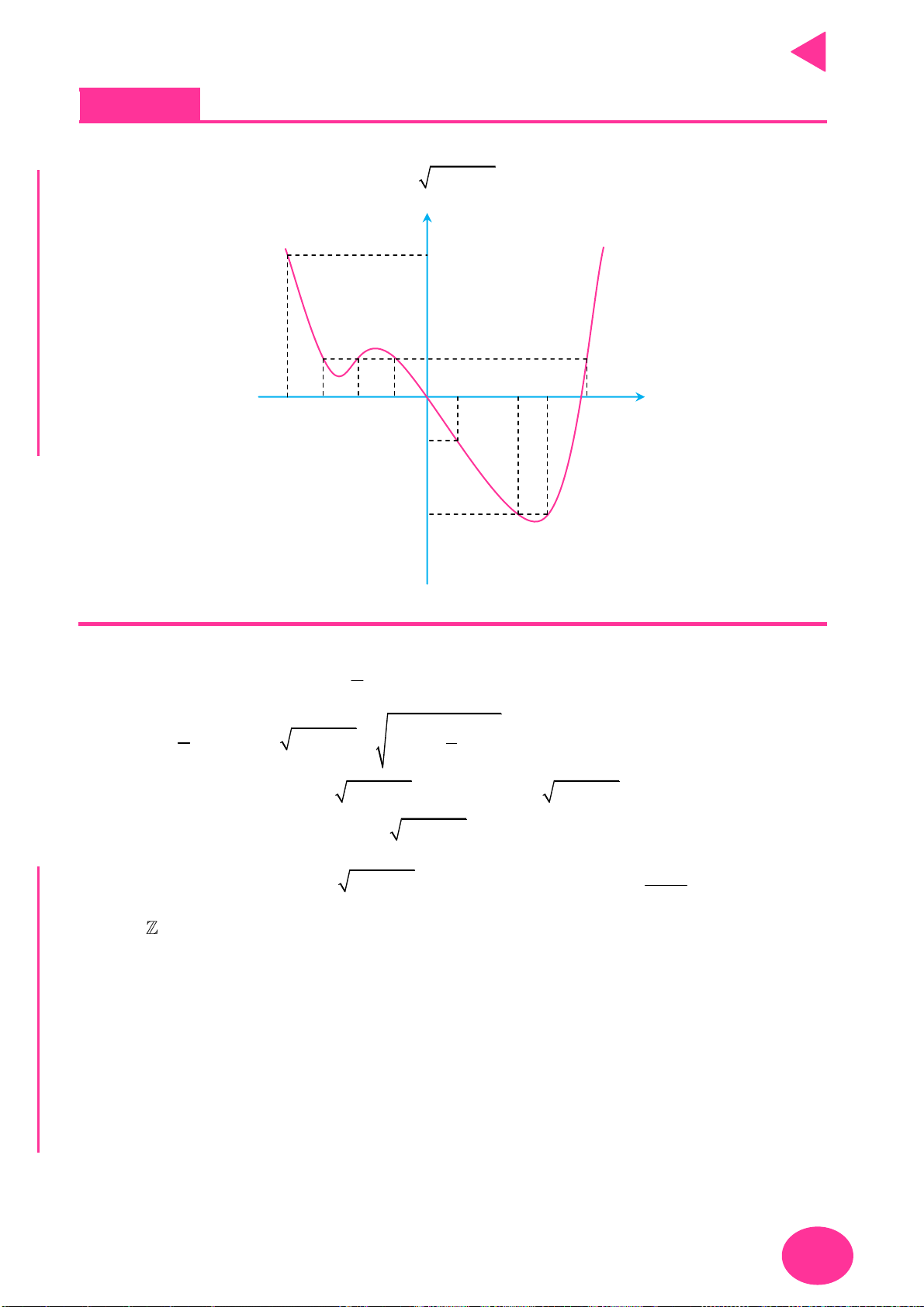
Câu 8. Cho đồ thị của hàm số f x ,F x , f 'x 1 như hình vẽ. Tính giá trị của tích phân
f 0 f 1.5 3 sin x.cos xdx ?
f '1F1.5 y 2 OÁNT 3 C 1 O 1 3 2 3 x 2 YMPI 2 1 OL C Ụ 3 A. 0 B. 1 C. 3 D. 4 NH PH
Câu 9. Cho hàm số f x có đạo hàm trên \
b và hàm số g x có đạo hàm trên . Biết
đồ thị của hai hàm số y f 'x , y g 'x như hình vẽ dưới. Đặt h x f x g x và CHI S 2 2 2 2
hx b
h b x 1 2hc hc
với a,b,c là các số thực đã biết. Khẳng định
đúng với mọi x 0 là? y
y f x
y gx O a b c x
A. S h c ; h a c
B. S h c 7
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
C. S h c ; h a b
D. S h a ; h c
Câu 10. Cho hàm số f x liên tục và xác định trên
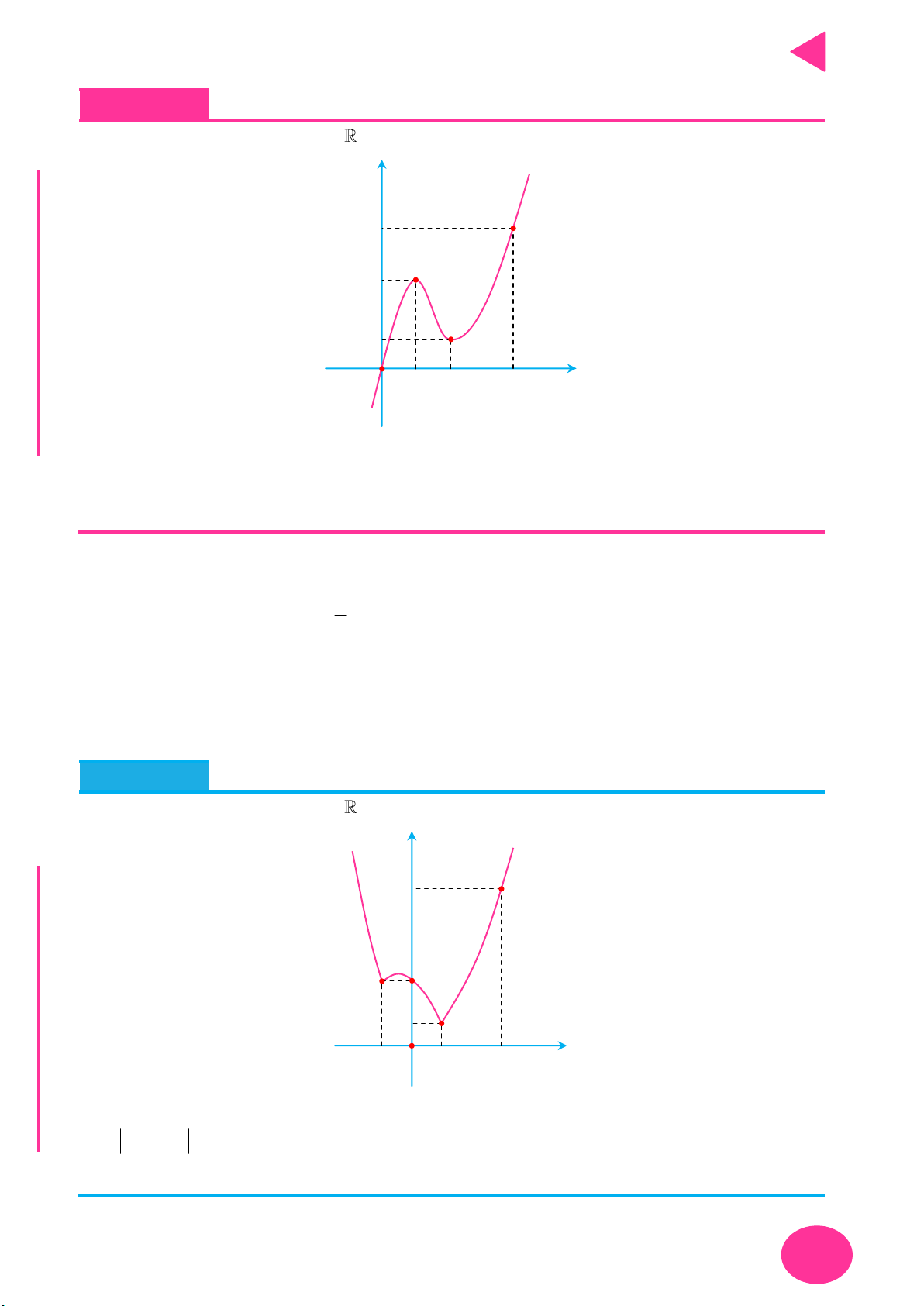
và có đồ thị f 'x như hình vẽ. Tìm
số điểm cực trị của hàm số 2 y f x x ? y O x 1 4 C A. 10 B. 11 C. 12 D. 13 Ọ
Câu 11. Cho hàm số f x có đạo hàm và xác định trên tập số thực và có đồ thị như hình H m 20; 20 N
vẽ dưới. Tính tổng tất cả các giá trị nguyên của tham số để hàm số
y f x m có 5 điểm cực trị? TOÁ x 2 U y IỆL TƯ 3 VÀ CHÍ 3 P Ạ O 1 x T 2 A. 210 B. 212 C. 211 D. 209
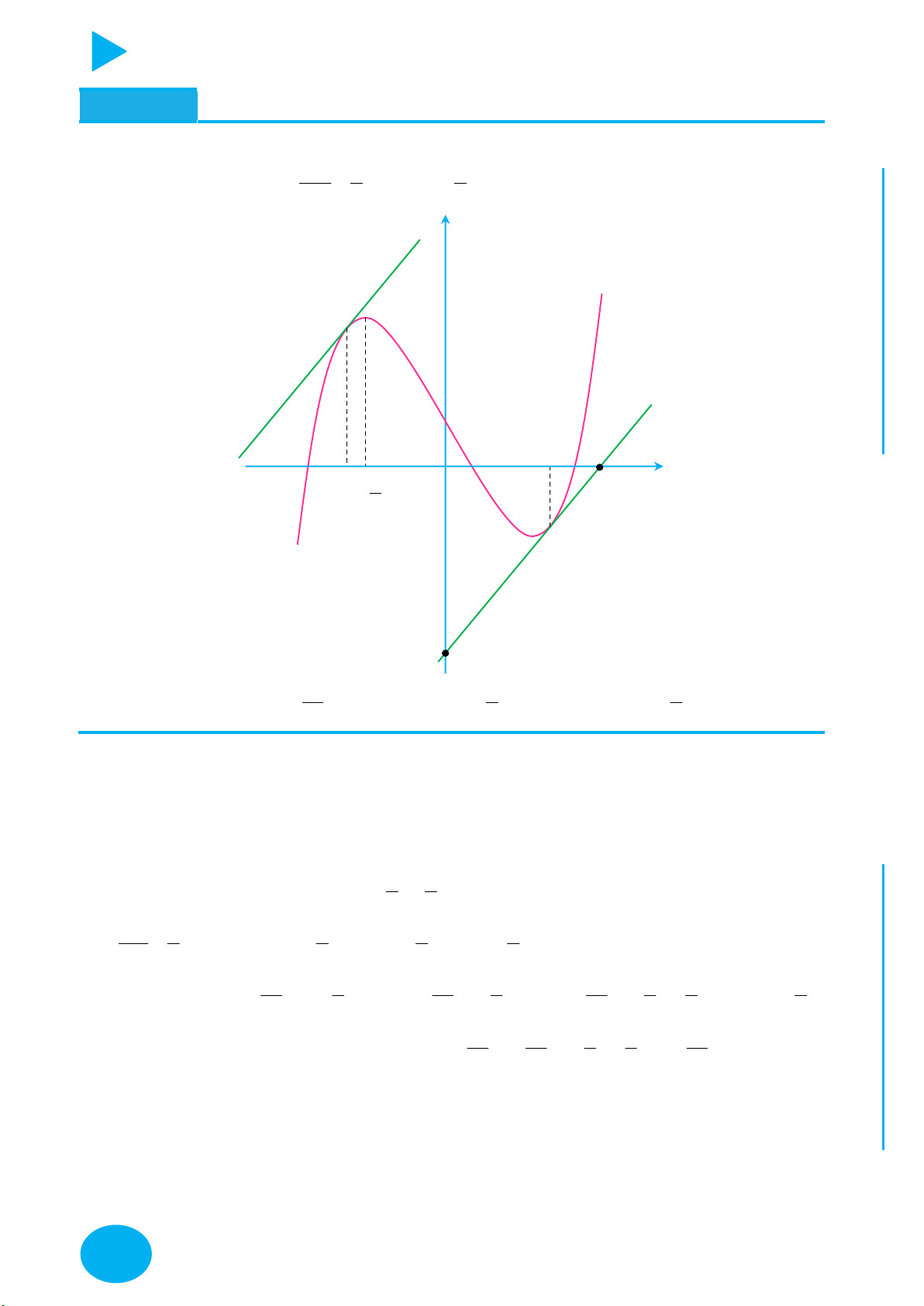
Câu 12. Cho hàm số bậc ba f x và g x f 2
mx nx pm,n, p có đồ thị như hình
dưới, trong đó đường nét liền là đồ thị hàm f x , đồ thị hàm nét đứt là đồ thị hàm g x ,
đường x 1 là trục đối xứng hàm g x . Giá trị của biểu thức P n mm pp 2n 2 bằng bao nhiêu? 8
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y g x f x 2 O 1 2 x 2 1 2 A. 6 B. 24 C. 12 D. 16
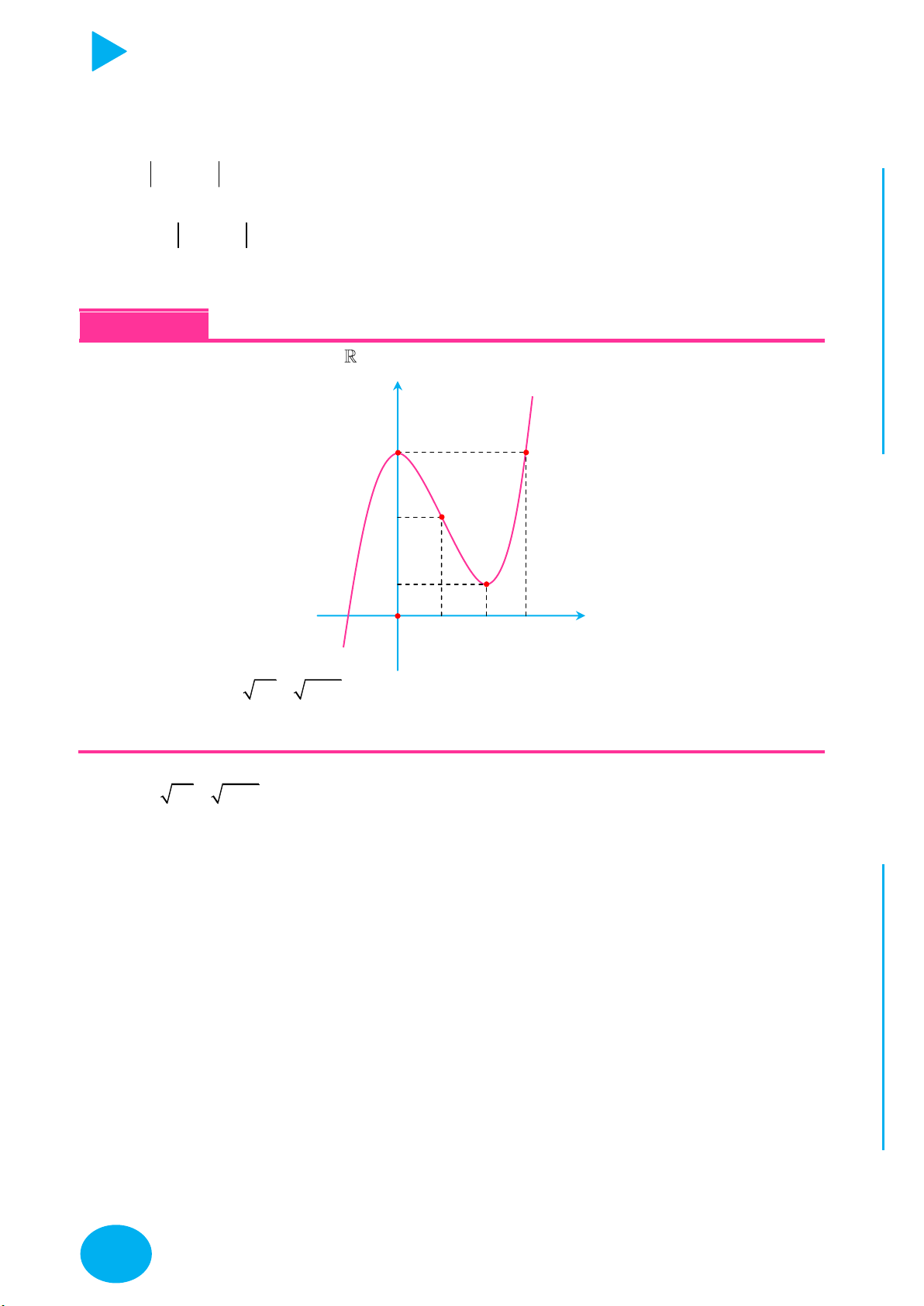
Câu 13. Giả sử hàm số y f x có đạo hàm là hàm số y f 'x có đồ thị được cho như
hình vẽ dưới đây và f 0 f 1 2 f 2 f 4 f 3. Tìm giá trị nhỏ nhất m của hàm số
y f x trên 0; 4 . y OÁNT C O 4 x YMPI 2 OL C Ụ
A. m f 4.
B. m f 0.
C. m f 2.
D. m f 1. Câu 14. Cho hàm số
f x có đồ thị như hình vẽ đồng thời 4 2 2 NH PH
f x 1 f x 2x2x 1 x 1* Biết rằng f x ax bx c ; gx mx nx p
và f x g 2 x 1 CHI
Tìm giá trị nhỏ nhất của hàm số g x y 11 O x 1 2 A. 1 B. 1 C. 2 D. 4 2 4 9
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Câu 15. Cho hai hàm số y f x , y g x có đạo hàm là f x , gx . Đồ thị hàm số
y f x và gx được cho như hình vẽ bên dưới. y f 'x g'x O 2 6 x
Biết rằng f 0 f 6 g 0 g 6 . Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
h x f x g x trên đoạn 0;6 lần lượt là:
A. h 2 , h 6.
B. h 6 , h 2.
C. h 0 , h 2.
D. h 2 , h 0.
Câu 16. Cho 2 hàm số f x , g x có đồ thị như hình vẽ bên dưới. Biết rằng x 1, x 6 C Ọ
đều là các điểm cực trị của 2 hàm số f x , g x đồng thời f 1 g 6 , 2 f 6 g 1 3 và H
2 f 5x 16 3g5x 9 1* N
.Gọi M,m lần lượt là giá trị nhỏ nhất của biểu thức
S f x f x gx 2 2 1
g x g x . Tính tổng P M m ? TOÁ y U IỆL g x TƯ VÀ f x CHÍ P O 1 6 x ẠT 27 23 9 11 A. B. C. D. 4 4 2 2
Câu 17. Cho hàm số y f x có đạo hàm trên
và có đồ thị là đường cong trong hình vẽ
dưới đây. Đặt g x f f x 1 . Tìm số nghiệm của phương trình g'x 0 . 10
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 1 3 1 1 2 x 2 3 A. 8. B. 10. C. 9. D. 6.
Câu 18. Biết rằng đồ thị hàm số bậc 4 : y f x được cho như hình vẽ bên. Tìm số giao 2
điểm của đồ thị hàm số y g x f x
f x. f x và trục Ox . y OÁNT C YMPI OL O x C Ụ A. 4. B. 0. C. 2. D. 4.
Câu 19. Cho hàm số f x có đồ thị như hình vẽ NH PH y CHI 5 y 17 5 3 y 32 1 O x
Giá trị nguyên nhỏ nhất của tham số m để phương trình sau có nghiệm là bao nhiêu? 3 f x 2 f x f x 1 2 7 5 e
ln f x ?
f x m 11
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA A. 3 B. 4 C. 5 D. 6
Câu 20. Cho hàm số f x liên tục trên R và có đồ thị như hình vẽ. Có bao nhiêu giá trị
3sin x cos x 1
nguyên của tham số m để phương trình f f 2 m 4m 4 có nghiệm? 2 cosx sinx 4 y 16
y f x 3 x 4 O A. 4. B. 5. C. Vô số D. 3. C f x Ọ
Câu 21. Cho hàm số liên tục và có đồ thị như hình vẽ. H y N 4 TOÁ U 1 IỆ x L O 3 6 TƯ 3 4m VÀ m
Các giá trị của tham số m để phương trình 2
f x 3 có 3 nghiệm phân biệt 2
2 f x 5 CHÍ là: P Ạ T A. m 37 .
B. m 3 . C. m 37 .
D. m 3 3 . 2 2 2 2 Câu 22. Cho hàm số 4 3 2 y f x ax bx
cx dx e với (a,b,c, d, e ). Biết hàm số
y f x có đồ thị như hình vẽ, đạt cực trị tại điểm O0;0 và cắt truc hoành tại A3;0.
Có bao nhiêu giá trị nguyên của m trên 5; 5 để phương trình f 2
x 2x m e có bốn nghiệm phân biệt. y 1 3 O 1 2 x A. 0. B. 2. C. 5. D. 7. 12
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
Câu 23. Cho hàm số f x liên tục và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên m
của tham số m để phương trình f 2 sin x
f có đúng 12 nghiệm phân biệt thuộc 2
đoạn ; 2 ? y 3 2 x O 2 27 16 A. 4. B. 5. C. 3. D. 2.
Câu 24. Cho đồ thị hàm số là nguyên hàm của f x có dạng F x 3 ax 2
bx 5x d . Tính
diện tích tạo bởi f x và trục hoành? y OÁNT C 4 4 O YMPI x OL C Ụ 80 20 50 70 A. . B. . C. . D. . 3 3 3 3 NH PH
Câu 25. Cho hàm số y f x liên tục trên đoạn 2; 2 và có đồ thị trên đoạn 2; 2 như 2 3 f
x 2 f x 9 f x 2 3 CHI
hình vẽ dưới. Hỏi phương trình có bao nhiêu nghiệm
thực trên đoạn 2; 3? y
y f x 1 1 2 O 1 2 x 1 A. 1 B. 2 C. 3 D. 4
Câu 26. Cho hàm số f x có đồ thị như hình vẽ dưới 13
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y 6 2 4 O 2 x 2 C 4 Ọ H 1 4 N
Có bao nhiêu giá trị nguyên của tham số m để f sin sin x m có nghiệm? 3 3 3 TOÁ A. 2 B. 3 C. 4 D. 5 U
Câu 27. Cho đồ thị hàm số là nguyên hàm của f x có dạng F x 3 ax 2
bx 5x d . Tính
IỆL diện tích tạo bởi f x và trục hoành? TƯ y VÀ CHÍ P 4 Ạ 4 O x T 80 20 50 70 A. . B. . C. . D. . 3 3 3 3
Câu 28. Cho hàm số f x xác định, liên tục trên R và có đồ thị như hình vẽ. Có bao nhiêu
giá trị nguyên của m để phương trình f x 2 2 3 4 6
9x m 3 có nghiệm. 14
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 3 1 O 1 3 4 4 3 2 1 5 x 1 5 A. 13 B. 14 C. 15 D. 16
Câu 29. Cho hai đồ thị
C : y f x x ax b 1
4 2 và đồ thị hàm số 3 2 OÁN
C : y g x x mx nx p C 2
như hình vẽ. Gọi B, D là hai điểm cực trị của 1 , A và T C C
C lần lượt là hai điểm cực đại và cực tiểu của 2 , (A và C đối xứng nhau qua điểm
U Oy . Biết hoành độ A và B bằng nhau, hoành độ của C và D bằng nhau. Có bao nhiêu YMPI
giá trị nguyên của a để AB 3 ? y OL C A Ụ NH PH CHI I x x 1 2 O x B D C A. 2 B. 5 C. 6 D. 7
Câu 30. Cho hàm số f x liên tục trên
có đồ thị như hình vẽ. 15
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y 1 1 O x
Có bao nhiêu giá trị nguyên của n để phương trình f 2
16 cos x 6sin 2x 8 f nn 1 có nghiệm x ? A. 10 B. 4 C. 8 D. 6 C Ọ
Câu 31. Cho 2 số x, y thỏa mãn 2 x 2
5y 1 4xy và hàm số bậc 3 y f x có đồ thị như H
2x 3y 3 N
hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P f . x 4y 4 TOÁ Tích M.m ? U y IỆL TƯ VÀ 2 CHÍ 1 P Ạ 1 O x T 2 1436 1436 1438 1436 A. B. C. D. 1333 1331 1331 1335
Câu 32. Cho f x là một đa thức hệ số thực có đồ thị hàm số y f 'x như hình vẽ bên
dưới . Hàm số g x m x 2 1
m 3 m thỏa mãn tính chất : mọi tam giác có độ dài
là ba cạnh là a, b,c thì có các số g a , g b , g c là ba cạnh của một tam giác. Khẳng định 2
nào sau đây đúng về hàm số y f mx m 1 mx 1 e 16
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y
y f 'x O 1 4 x 4
A. Hàm số đồng biến trên khoảng ; 1 3 1
B. Hàm số nghịch biến trên khoảng ;0 3
C. Hàm số nghịch biến trên khoảng 1; 2 và đồng biến trên khoảng 4; 9
D. Hàm số nghịch biến trên khoảng 1; 4 và đồng biến trên khoảng 4; 9 OÁNT
Câu 33. Cho f x liên tục trên
và có đồ thị hàm số y f x như hình vẽ C y YMPI OL C Ụ 2 O 2 x NH PH CHI 4
Bất phương trình sau nghiệm đúng với mọi x 1; 2 khi và chỉ khi :
f xm f x 3 4
m 5 f x 2 5m
A. f 1 m 1 f 2
B. f 2 m 1 f 1
C. f 2 m 1 f 1
D. f 2 m 1 f 1
Câu 34. Cho hàm số f x 3 ax 2
bx cx d a,b,c,d có đồ thị như hình vẽ : 17
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y
y f x 4 O 1 3 4 x CỌ H
Phương trình f f f f x 0có tất cả bao nhiêu nghiệm thực phân biệt N A. 12 B. 40 C. 41 D. 16 TOÁ 1 4 1 4
Câu 35. Cho hàm số f x 3 x 2
x x có đồ thị như hình vẽ. U 3 3 3 3 IỆ y L TƯ 1 VÀ 1 O 1 4 x CHÍ P ẠT
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình sau đây có 4 nghiệm
phân biệt thuộc đoạn 0;2 f 2 x x 2 2019 15 30 16
m 15x 30x 16 m 0 A. 1513 B. 1512 C. 1515 D. 1514
Câu 36. Cho hàm số y f x có đạo hàm f 'x . Hàm số y f 'x liên tục trên tập số thực
và có đồ thị như hình vẽ. 18
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 4 2 1 O 1 2 x 13
Biết rằng f 1
, f 2 6 . Tổng các giá trị lớn nhất và nhỏ nhất của hàm số 4 g x 3
f x 3 f x trên 1;2 bằng? 1573 37 14245 OÁN A. B. 198 C. D. T 64 4 64 C
Câu 37. Cho hàm số f x có đồ thị như hình vẽ. y YMPI OL C 1 3 Ụ O x NH PH 4 CHI
Bất phương trình x 3 x f e
m e 2019 có nghiệm x0;1 khi và chỉ khi 4 f e
A. m 4 B. m C. m 2 D. m 1011 3e 2019 1011 3e 2019
Câu 38. Cho hàm số y f x . Hàm số y f 'x có đồ thị như hình vẽ y 1 1 O 1 x 19
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA f x x 3 2 Bất phương trình
m đúng với mọi x 0;1 khi và chỉ khi 36 x 1 f 1 9 f 1 9 A. m B. m 36 36 f 1 1 f 1 1 C. m D. m 36 3 2 36 3 2
Câu 39. Cho hàm số y f x có đạo hàm trên
và có đồ thị như hình vẽ. y 3 C 1 Ọ H 1 x N 1 O 2 TOÁ 1 U IỆ 3 L
Đặt hàm số y g x f 2x x 1 m . Tìm m để max gx 10 . 0; 1 TƯ
A. m 13
B. m 3
C. m 12
D. m 1 f x VÀ
Câu 40. Cho hàm số f x , g x có đồ thị như hình vẽ. Đặt h x . Tính h '2 gx y CHÍ g x P Ạ 7 T 6 f x 2 O 2 4 10 x
A. h 4 ' 2
B. h 4 ' 2
C. h 2 ' 2
D. h 2 ' 2 49 49 7 7
Câu 41. Hình vẽ là đồ thị y f x . 20
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 3 O 1 x 3 6
Tập hợp tất cả các giá trị của m để phương trình 2 2
f x 1 f x 1 3 f x 1 2 m f x 1 2 f x 1 1
Có nghiệm trên 4; 2 là đoạn a; b . Khi đó 2a 3b bằng? OÁNT A. 4 B. 5 C. 6 D. 7 C
Câu 42. Cho hàm số y 3 ax 2
3bx 2cx d a 0 có đồ thị như hình vẽ. y YMPI OL C 1 Ụ 2 x O NH PH CHI 3 a Hàm số y 4
x a b 3
x b c 2 3
x d 2cx d 2019 nghịch biến trên khoảng nào 4 sau đây ?
A. ;0 B. 0; 2 C. 1; 2
D. 2;
Câu 43. Cho hai hàm đa thức y f x , y g x có đồ thị là hai đường cong ở hình vẽ bên. 21
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y A
y f x
y g x B O x
Biết rằng đồ thị hàm số y f x có đúng một điểm cực trị là A , đồ thị hàm số y g x có
đúng một điểm cực trị là B và AB 7 . Có bao nhiêu giá trị nguyên của tham số m thuộc 4 C Ọ
khoảng 5; 5 để hàm số y f x g x m có đúng 5 điểm cực trị? H A. 1 B. 3 C. 4 D. 6 N
Câu 44. Cho hàm số y f x liên tục trên
và hàm số y f 'x có đồ thị như hình vẽ TOÁ y U IỆL TƯ 2 3 4 x O VÀ CHÍ P ẠT
f xm f x m m
Bất phương trình f x 2 5
2 27 nghiệm đúng với x2;3 27
A. f 3 m f 3 1
B. f 2 1 m f 3
C. f 2 2 m f 3
D. f 3 m f 2 2
Câu 45. Cho hàm số y f x liên tục trên
và có đồ thị như hình bên dưới: 22
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 2 1 O x 1 2
Biết rằng trục hoành là tiệm cận ngang của đồ thị. Tìm tất cả các giá trị thực của tham số m để phương trình 2log4 2 4m f x
có hai nghiệm dương phân biệt.
A. 0 m 2.
B. 0 m 1.
C. 1 m
D. m 0. y
Câu 46. Cho hàm số f x có đạo hàm liên tục trên R và có đồ thị của
f 'x như hình vẽ bên dưới. y OÁNT C
y f 'x YMPI 1 O 5 x OL C Ụ b 3 NH PH
Để hàm số y f 2x 6x 3 đồng biến với mọi x m m R thì m asin trong đó c CHI b a b c * , , ,c 2b S 2a 3b c
và là phân số tối giản). Tổng bằng c A. 7 B. 9. C. 2. D. 5.
Câu 47. Cho hàm số 3 2 f x x
bx cx d và g x f mx n có đồ thị như hình vẽ : y f x g x 1 x O 1 2 23
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Hàm số f x đồng biến trên khoảng có độ dài bằng k , hàm số g x đồng biến trên
khoảng có độ dài bằng 2k . Giá trị biểu thức 2m n là A. 3 B. 0 C. 1 D. 5
Câu 48. Cho hàm số bậc ba f x và g x f mx n ,m;n có đồ thị hàm số như hình vẽ : y g x 3 O x 2 1 C Ọ H f x N
Hàm số g x nghịch biến trên khoảng có độ dài bằng 5. Giá trị biểu thức 3m 2n là TOÁ 16 U A. 5 B. 13 C. D. 4 5 5
IỆL Câu 49. Cho hai hàm số f x và gx có đồ thị như hình vẽ y TƯ g x f x VÀ CHÍ P 1 2 x ẠT O 1
Biết rằng hai hàm số y f 2x 1 và y 3g ax b có cùng khoảng đồng biến. Giá trị
biểu thức a 2b là A. 3 B. 4 C. 2 D. 6
Câu 50. Cho hàm số 4 2 f x ax
bx c và gx f mx n p ,m;n; p có đồ thị như hình vẽ 24
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 2 3 f x 2 1 O 1 x g x
Giá trị biểu thức m n 2p là A. 4 B. 2 C. 5 D. 6
Câu 51. Cho hai hàm số f x và g x có đồ thị như hình vẽ: y OÁNT C f x g x YMPI OL 2 1 x C 1 O Ụ NH PH CHI
Biết rằng hai hàm số y 3 f 3x 1 và y 2 f ax b có cùng khoảng đồng biến. Giá trị
biểu thức 2a b là A. 5 B. 2 C. 4 D. 6 Câu 52. Cho hàm số 4 2 f x ax
bx c và g x f 2
mx nx p q,m;n; p;q có đồ thị như hình vẽ: 25
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y 1 f x x 1 O 1 1 g x 2
Giá trị của biểu thức m 2n 3p 4q là C Ọ A. 4 B. 2 C. 8 D. 6 H
Câu 53. Cho hàm số y f x liên tục trên
và có đồ thị như hình vẽ. Tập hợp tất cả các N
giá trị thực của tham số m để phương trình f 4 x m có nghiệm thuộc nửa khoảng TOÁ 2; 3 là U IỆ y L 3 TƯ VÀ CHÍ P 1 ẠT 2 1 O 2 x 1
A. 1; 3 B.
1; f 2 C.
1; f 2
D. 1; 3
Câu 54. Cho hàm số y f x liên tục trên
có đồ thị như hình vẽ. Phương trình
f 2 f x 0 có tất cả bao nhiêu nghiệm thực phân biệt ? 26
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 1 1 2 2 O 1 x 3 A. 4 B. 5 C. 6 D. 7
Câu 55. Cho hàm số f x . Đồ thị hàm số f 'x trên 3; 2như hình vẽ (phần cong là 1 phần của Parabol 2
y ax bx c ). Biết f 3 0 . Giá trị của f 1 f 1 bằng bao nhiêu? y 2 OÁNT C 1 YMPI 3 2 1 O 2 x OL C Ụ 23 31 35 9 A. B. C. D. 6 6 3 2
Câu 56. Cho hàm số y f x lên tục trên
và có f 0 0 và có đồ thị hàm số y f 'x NH PH
như hình vẽ. Hàm số y f x 3 3
x đồng biến trên khoảng nào? CHI y 4 1 O 1 2 x
A. 2;
B. ; 2 C. 0; 2 D. 1; 3 27
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Câu 57. Cho hàm số y f x liên tục trên
có đồ thị như hình vẽ. Gọi M và m tương 3
ứng là GTLN và GTNN của hàm số y f 1 cos x trên 0;
. Giá trị của M m bằng : 2 y 2 1 O 1 2 3 x 1 3 C 2 Ọ H 1 3 A. 2 B. 1 C. D. N 2 2
Câu 58. Cho hàm số bậc ba 3 2 f x ax
bx cx d có đồ thị như hình vẽ. Hỏi đồ thị hàm TOÁ
2x 3x 2. x U 1
số g x
có bao nhiêu đường tiệm cận IỆ x. 2
f x f x L y TƯ VÀ CHÍ 1 P ẠT O 1 2 x A. 3 B. 4 C. 5 D. 6
Câu 59. Cho hàm số y f x lên tục trên
có đồ thị như hình vẽ dưới. Phương trình
f f x 1 0 có tất cả bao nhiêu nghiệm thực phân biệt? 28
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 1 2 1 x 1 O 2 3 A. 4 B. 5 C. 6 D. 7
Câu 60. Cho hàm số y f x có đồ thị hàm số y f 'x 1 như hình vẽ. Hỏi đồ thị hàm số f x 2 ( ) 4x y
đạt cực tiểu tại điểm nào y OÁNT C 2 YMPI OL C 1 O Ụ 1 2 x NH PH 2 CHI
A. x 1
B. x 0
C. x 1
D. x 2
Câu 61. Cho hàm số y f x lên tục trên
. Hàm số y f 'x có đồ thị như hình vẽ. Hàm x số g x f x 2019 2018 1
đồng biến trên khoảng nào dưới đây 2018 y 1 1 O 1 2 x 1 29
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA A. 2; 3 B. 0; 1
C. 1; 0 D. 1; 2
Câu 62. Cho hàm số y f x có đồ thị như hình vẽ. Tổng các giá trị nguyên của tham số
m để phương trình f f x 1 m có 3 nghiệm phân biệt bằng y 14 2 O 2 1 1 3 x C 13 Ọ H N A. 15 B. 14 C. 13 D. 11
Câu 63. Cho 2 điểm A, B thuộc đồ thị hàm số y sin x trên 0; , các điểm C, D thuộc TOÁ U
trục Ox sao cho tứ giác ABCD là hình chữ nhật là CD 2 . Độ dài cạnh BC là? 3 IỆ y L TƯ A B VÀ x O D C CHÍ P ẠT 2 1 A. B. C. 1 D. 2 2 2
Câu 64. Cho hàm số f x 4 mx 3 nx 2
px qx r r 0 có nghiệm. Hàm số y f 'x có
đồ thị như hình vẽ dưới. Số nghiệm của phương trình f x r là? y x1 x0 O x 30
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ A. 2. B. 4. C. 3. D. 1. 4
Câu 65. Cho f x như hình vẽ. Biết f ' x dx
60 . Giá trị của f 2 f 2 là ? 1 y 3 O x 2 10 A. . B. 31 . C. 12 . D. 32 . 3 3 3 3
Câu 66. Cho f x liên tục trên
có đồ thị hàm số như sau. Tìm số điểm cực trị của g x 2 x
1 f tdt 2019 y OÁNT f x C YMPI OL C Ụ 3 1 O 2 x NH PH A. 1 B. 3 C. 5 D. 7 CHI
Câu 67. Cho đồ thị hàm g x hàm bậc 4 như hình vẽ, biết g x f x f 1 x và 2 x
f 0 g0 . Tính tích phân xf ' dx ? 2 0 y O 1 x 31
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA A. 1 B. 1 C. 5 D. 1 10 5
Câu 68. Cho đồ thị hàm số là nguyên hàm của f x có dạng F x 3 ax 2
bx 5x d . Tính
diện tích tạo bởi f x và trục hoành ? y 4 4 O x 80 20 50 70 A. . B. . C. . D. . C 3 3 3 3 Ọ f ' x S ,S H
Câu 69. Cho đồ thị hàm số
như hình vẽ. Biết diện tích 2 hình 1 2 lần lượt là 3,2, 1 1 N
f 1 5 . Tính giá trị của tích phân x x e f x dx
e f 'xdx ? 0 0 TOÁ y U IỆL TƯ 2 2 O 1 x VÀ 3 CHÍ P
A. e 3.
B. 2e 2.
C. 4e 3.
D. 5e 3. ẠT 9
Câu 70. Cho đồ thị hàm số bậc 3 f x như hình vẽ. Biết S , a b 3 và f '0 1 . Tính 4
I 2a f xdx ba y f x S b O a x 32
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ 5 7 7 5 A. B. C. D. 6 6 12 12
Câu 71. Cho hàm số f x có đạo hàm đến cấp 2 liên tục trên 1; 4 thỏa mãn và có đồ thị
như hình vẽ dưới đây. Tính giá trị của tích phân I
f ' xx 1x 5 5dx ? 1 y 2 1 3 4 O 1 2 5 x 1 A. 4 B. 5 C. 6 D. 7
Câu 72. Cho đồ thị hàm số f x như hình vẽ. Biết S S S S 2 4 3
1 (hình vẽ chỉ mang tính
chất tương đối). Tính I
2 5f 55x 4x2 f 2x 4x dx 0 y OÁNT C YMPI OL S3 C Ụ 5 S S 2 4 S 4 O 2 3 x 1 NH PH CHI 23 6 A. 0 B. 1 C. D. 5 5
Câu 73. Cho hàm số f x có đạo hàm cấp hai f ''x liên tục trên và đồ thị hàm số
f x như hình vẽ bên dưới. Biết rằng hàm số f x đạt cực đại tại điểm x 1 . Đường
thẳng trong hình vẽ là tiếp tuyến của đồ thị hàm số f x tại điểm có hoành độ x 2 . x x e 1
Tính giá trị của tích phân I ln3 e f '' dx ? 0 2 33
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y
y f x O 1 2 x CỌ 3 H N A. 0 B. 1 C. 6 D. 7 TOÁ U Vted.vn IỆ 4 2 L
Câu 74. Cho đồ thị hàm số f x như hình vẽ. Biết
f x23m dx f x 1 12. 2 TƯ Giá trị của m là ? y VÀ 1 CHÍ P ẠT O 2 x A. 4. B. 0. C. 1. D. 2.
Câu 75. Cho đồ thị hàm số f x như hình vẽ, biết f '1 2 . Tính giá trị của biểu thức tích 2
phân f 'x ? 2 y 2 O 2 x 34
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ 64 25 14 A. . B. C. . D. 2. 3 3 3 3 3 3
Câu 76. Cho đồ thị của hàm số f x như hình vẽ bên dưới. Tính giá trị của biểu thức tích 3 phân I 2
x f 'xdx ? 0 y 3 O 3 x A. 1 B. 0 C. 3 D. 4 x2
Câu 77. Cho đồ thị hàm số f x 2 như hình vẽ. Đồ thị hàm số y f 2t 2dt cắt trục OÁNT x4 C
Ox tại nhiều nhất mấy điểm phân biệt ? y YMPI OL C Ụ NH PH 3 O 1 4 x CHI A. 0 B. 1 C. 3 D. 4 11
Câu 78. Cho đồ thị hàm số f 'x trên đoạn 4;
(lần lượt là các đoạn thẳng và nửa 2 0 1 6
parabol ). Tính giá trị S
f '2x 3dx f '2x 2dx cos .
x f '5sin x 3dx ? 3 1 0 2 35
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y 5 4 2 O 3 11 x 2 1 149 154 109 A. . B. . C. . D. . 2 6 4 3
Câu 79. Cho hàm số f x 4 ax 3 bx 2 cx
dx 4 .a Đồ thị của f 'x như hình vẽ. Tính
2 f ' x .f x 2 f ' x dx tích phân ? C 1 Ọ y H N TOÁ U IỆL O x 10 10 TƯ 2 2 VÀ A. 2. B. 1. C. 0. D. 3. CHÍ
Câu 80. Cho đồ thị hàm số f 'x như hình vẽ. Tính tổng bình phương các nghiệm của P Ạ
phương trình F x 0 , với F x là nguyên hàm của f x . Biết x 1 đều là nghiệm của T
của f x 0 và F x 0 .? y 1 O 1 x A. 0 B. 10. C. 12. D. 17. 36
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
Câu 81. Cho đồ thị hàm số f x trên đoạn 3; 13 như hình vẽ. Có bao nhiêu giá trị m m f x
nguyên không âm để phương trình e
f x 2 f mdx có 1 nghiệm duy nhất. 0 y 4 3 O 3 9 13 x A. 15. B. 12. C. 13. D. 17.
Câu 82. Cho đồ thị hàm số f 'x và g 'x như hình vẽ. Đặt h x f x g x . Biết
g 3 g4 3 f 3 f 4 , hỏi mệnh đề nào sau đây đúng? OÁN y T C YMPI g'x OL 1 C Ụ 1 3 O 4 x NH PH CHI f 'x
A. h x đạt min là h 1 , h 1 0
B. h x đạt min là h 1 , h 1 0
C. h x đạt max là h 1 , h 1 0
D. h x đạt max là h 1 , h 1 0
Câu 83. Cho đồ thị hàm số f 'x như hình vẽ. Khẳng định nào sau đây là đúng vể biểu thức
9 S f 0 cos f 0 f 1 cos f 1 . 2 37
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y 6 4 3 1 O 1 x 1 C A. Không xác định B. nhỏ hơn 0. C. bằng 0. D. lớn hơn 0. Ọ x H
Câu 84. Cho đồ thị hàm số f x như hình vẽ. Tìm m để f x xdx sin cos mx có nhiều N
nghiệm nhất có thể trên đoạn ; ? TOÁ y U IỆ 4 L TƯ VÀ 2 CHÍ 1 O 1 x P ẠT 4
A. 0 m 4 .
B. 0 m 4
C. m 0 .
D. 4 m 0 .
Câu 85. Cho đồ thị hàm số f x như hình vẽ, đồ thị hàm số f 'x và tiếp tuyến của f x 2 tạo với nhau một góc 0
45 . Tính giá trị của tích phân
f ' x f 'x dx ? 0 38
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 3 f x f ''x 1 O 2 x 0 45 3 A. 4. B. 3. C. 1. D. 2.
Câu 86. Cho đồ thị hàm số f 'x liên tục trên đoạn 3;3 như hình vẽ. Đặt hàm số 2 OÁN
g x f x 2 2 x . Biết
gxmmdx 0m thuộc đoạn 1;1. Khẳng định nào dưới T 2 C đây là đúng ? y f 'x YMPI OL C 3 Ụ O 1 3 NH PH 3 x 1 CHI 3
A. 4g 1 m 4g 3.
B. 3g 1 m 3g 3.
C. 2g 1 m 2g 3.
D. g 1 m g 3.
Câu 87. Cho đồ thị hàm số f 'x như hình vẽ. Gọi giá trị lớn nhất và giá trị nhỏ nhất và 2
giá trị nhỏ nhất của hàm số g x f x x 1 là a và b trên đoạn 1;3 . Biết 0.5 3 0.5
xf 'xdx
c và f 'xdx
d . Tính giá trị của tích phân f xdx ? 1 1 1 39
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y 10 1 1 0,5 O 4 x 1 1 1 1
A. a b d .
B. a b 2d . C 2 8 2 4 Ọ 1 H
C. a b d 1 .
D. a b 2 . d 8 2 N 1 2 TOÁ
Câu 88. Cho hàm số bậc 4 có đồ thị f 'x như hình vẽ. Biết f 0 0 ,
f 'x dx . Tính 6 U 1 1 IỆL 2
giá trị của tích phân sin f x
. f 'x. f xdx ? TƯ 1 y VÀ CHÍ P ẠT O 1 5 1 x 1 5 2 2 2 3 1 A. . 3 2 2 B. . 2 3 1 1 C. . D. . 12 2 2
Câu 89. Hàm số f x có dạng f x 2
ax ba 0 . Đồ thị hàm số f x được cho như
hình vẽ. Gọi diện tích hình tạo bởi f f x và f x là S. Tính giá trị của biểu thức tích 11 a 3 1 1
phân a x 1 x 1 x 1 x 1dx ? a a 1 1 a 40
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y m 3 6 O 2 x m 5 A. S. B. aS . C. 2 a .S D. 2 S . f ' x f 'x 2
Câu 90. Cho đồ thị hàm số f 'x như hình vẽ. Biết F x . Phương
f x f x dx OÁN
trình f x 4.F x 4 0 có tổng các nghiệm là bao nhiêu, biết F 3 0 ? T y C f x YMPI OL C Ụ 1 O 1 3 x NH PH CHI A. 15. B. 8. C. 20. D. 17.
Câu 91. Anh Tuấn có một con diều hình con cá chim. Con diều này được giới hạn bởi 2 Parabol P : x 3x 2 P : x 3x d d 1 2 , 2
và 2 tiếp tuyến 1 , 2 đối xứng qua trục tung sao cho
BAC 120 (hình vẽ). Tính chính xác diện tích của con diều (làm tròn đến 2 chữ số thập phân). 41
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y A B 2 C d2 d1 3 2 1 O 1 2 3 x P P2 1 A. 3, 81 B. 3, 82 C. 4, 31 D. 4, 32 C
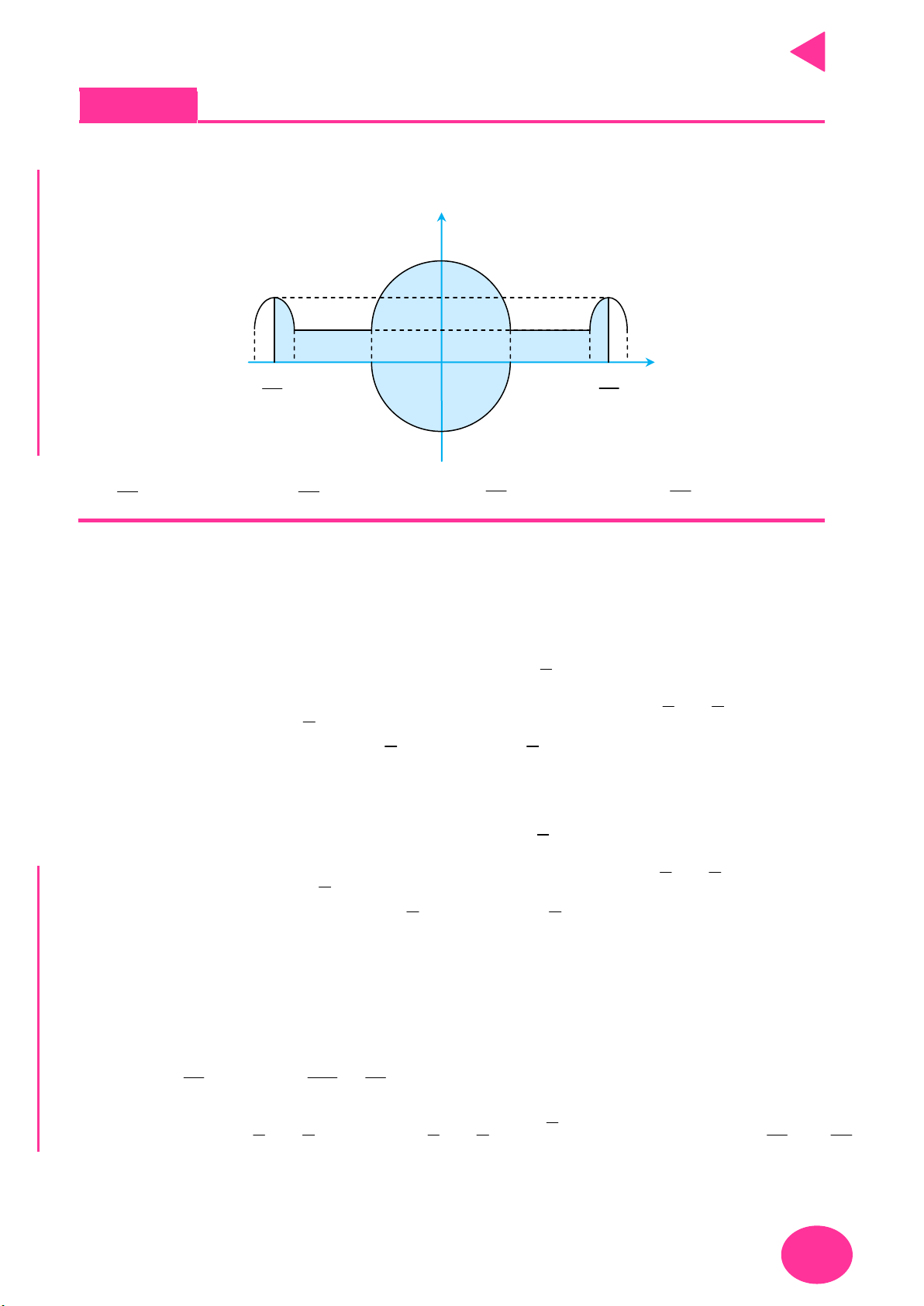
Câu 92. Cho thiết diện mặt cắt một chiếc đĩa bay của người ngoài hành tính như hình vẽ Ọ H
(phần tô đậm). Cho biết các đường cong trong hình vẽ đều là một phần của các Parabol. N
Tính diện tích thiết diện đó. y TOÁ 2, 5 P1 U IỆL P P4 3 2 TƯ 1 11 5 2 O 2 5 11 6 x VÀ 2 2 CHÍ 1, 5 P2 P Ạ 55 59 55 59 T A. B. C. D. 6 6 3 3
Câu 93. Cho hàm số f x liên tục trên
có dạng f x 4 ax 2
bx 1 . Biết đồ thị hàm số
f "x tiếp xúc đồ thị hàm số f x tại 1 điệm trên trục tung. Gọi x f x 1 là nghiệm của , x f " x x , x 0 x 3x 2 là nghiệm của 1 2 . Biết 1
2 , tính diện tích phần tô đậm (hình vẽ). 42
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y x x x x 1 2 O 2 1 x f x f 'x 152 73 152 73 A. B. C. D. 15 15 45 45
Câu 94. Cho diện tích phần tô đậm bằng a, f '1 b . Biết 2 f 1 f 1 f 3 và f x là
một hàm bậc 3, tính f '1 f '3 theo a và b y f x OÁNT f ''x C A YMPI OL C Ụ 3 1 O 1 x NH PH CHI A. 2b a
B. b a C. b
D. b a
Câu 95. Cho đồ thị hàm số là đa thức bậc 3 f x như hình vẽ. Biết d d 1 và 2 là tiếp tuyến OA 1 1
của f x tại x 1 và x 1; và f 2 0
. Tính f x f'xdx OB 4 5 1 43
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y d2 1 1 2 O B x 3 CỌ d1 H A N 7 7 7 TOÁ A. 1 B. C. D. 10 9 8 U
Câu 96. Cho đồ thị hàm số 2 f x
ax bx c như hình vẽ, d là đồ thị hàm số f 'x . Gọi IỆ 1 L S S ,S d , d f x 1
2 là các diện tích tạo bởi 1 2 với đồ thị hàm số
. Tính gần đúng tỉ số 1 TƯ S2 y VÀ CHÍ P ẠT 1 1 O 3 x d2 4 A. 1, 35 B. 1, 36 C. 1, 37 D. 1, 38
Câu 97. Cho đồ thị hàm số f x và f 'x như hình vẽ. Diện tích tạo bởi f 'x và f x gần nhất ? 44
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 2 O 3 x 5 A. 23. B. 65. C. 50. D. 43.
Câu 98. Hàm số f x có dạng 2 f x
ax b . Đồ thị hàm số f f x được cho như hình
vẽ. Gọi diện tích hình tạo bởi f f x và f x là S, t , t f f x 1
2 là hoành độ giao điểm và 2 2 2 2
f x t .t 0 t t 2 t t 9 1 2 sao cho 1 2 1 2 . Tính S ? y OÁNT C 5 /3 YMPI 43 /27 OL C Ụ O x NH PH CHI 50 42 32 65 A. . B. . C. . D. . 203 305 405 203
Câu 99. Cho đồ thị hàm số f x . S ,S 1
2 là diện tích hình phẳng được giới hạn như hình vẽ. 1
x 2sin x 11cosx 5 3sin x cosx 1
Tính giá trị lớn nhất của .f dx ? 2 x x x x x 2 cos sin 4 2 cos sin 4 0 45
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y 9 S 1 11 O 1 13 x S 4 2 2
A. S S S S S S 1 2 B. 1 C. 2 D. 1 2 3
Câu 100. Cho đồ thị f 'x như hình vẽ. Diện tích 2 hình tạo bởi f 'x và trục hoành là 4 C 9 5 , f 1 3
f ' x . f x dx Ọ
, . Tính giá trị của tích phân ? 8 4 H 1 y N TOÁ U 9 IỆL 8 TƯ 1 O 1 4 x VÀ 5 4 CHÍ P ẠT A. 0 B. 1 C. 3 D. 4
Câu 101. Cho đồ thị hàm số f x như hình vẽ. y 2 2 O 2 6 x 15 4 46
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ 2
x 8x n m
Để hàm số h x
có số tiệm cận đứng là lớn nhất là n ( với m,n nguyên
f f x m
dương). Tính giá trị nhỏ nhất của S = 2 2 m n A. 14 B. 74 C. 50 D. 3
Câu 102. Cho f x , f ' x và d là tiếp tuyến của f x dưới hình vẽ. Hàm số f x có dạng 3 2
mx nx p . Tính 43n 45p y d 26 5 OÁN O 1 x 6 T 5 C f x f ''x YMPI 285 A. B. 450 C. 201 D. 182 OL 3 C
Câu 103. Cho đồ thị hàm số f 'x như hình vẽ. Tổng các giá trị nguyên của m 3; 20 để Ụ
hàm số g x f x m có 4 cực trị. Biết tử số của f x có hệ số tự do dương. y x 1 NH PH CHI O x y 2 13 A. 64 B. 58 C. 75 D. 88
Câu 104. Cho 3 hàm số y f x , y g x , y h x . Đồ thị của 3 hàm số
y f x , y gx , y hx có đồ thị như hình vẽ dưới, trong đó đường đậm hơn là đồ 47
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
thị của hàm số y f x . Hàm số k x f x g x 3 7 5 1 h 4x đồng biến trên 2 khoảng nào dưới đây y
y g'x 10
y f 'x 5 O 3 4 8 x
y h'x C Ọ 15 1 3 3 H A. ;0. B. ; . C. ;1. D. ; . 4 4 8 8 N
Câu 105. Cho hình vẽ của đồ thị các hàm số
a ; b ; c
y x y x y x có đồ thị như hình bên. TOÁ
Khi đó hãy tìm tổng của giá trị nhỏ nhất và giá trị lớn nhất của biểu thức U
3a 2b a c2 2 IỆ T ? L 2 2
a 5c 4ac y TƯ c x VÀ 2m b x CHÍ m P Ạ 0, 5 a x T O x A. 31 B. 32 C. 33 D. 34
Câu 106. Hình vẽ bên là đồ thị của hai hàm số y log x y f x a và
. Đồ thị của chúng
đối xứng với nhau qua đường thẳng y x 1 .Tính f loga 2018 48
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y y log x a O 1 x
y f x y x 1 a
A. f log 2018 1 f a B. a 1 log 2018 1 2018 2018a a
C. f log 2018 1 f a D. a 1 log 2018 1 2018 2018a
Câu 107. Cho hàm số y f x có đồ thị như hình vẽ có bao nhiêu số nguyên m để bất
phương trình mx 2 m 2
5 x 2m 1 f x 0 có nghiệm đúng với mọi x2;2. OÁN y T C YMPI OL C 2 1 O 1 3 x Ụ NH PH A. 0. B. 1. C. 2. D. 3. CHI
Câu 108. Cho hàm số y f x có đồ thị như hình vẽ. Tìm tất cả giá trị thực của tham số m
để bất phương trình f x 2 2
x 4x m có nghiệm đúng với mọi x 1;3 y O 2 x 3 A. m 3. B. m 10. 49
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA C. m 2. D. m 5.
Câu 109. Cho hàm số f x có đồ thị như hình vẽ bên dưới. Để đồ thị của hàm số 2 h x
f x f x m có số điểm cực trị ít nhất thì giá trị nhỏ nhất của tham số m là m0 . Tìm mệnh đề đúng? y O 1 3 x CỌ H A. m 0; 1 . m 1;0 . m ; 1 . m 1; . 0 B. 0 C. 0 D. 0 N
Câu 110. Cho hàm số f x có đồ thị như hình vẽ bên dưới. Gọi M, m lần lượt là giá trị lớn TOÁ 3 7
nhất và giá trị nhỏ nhất của hàm số y f 2
x 2x trên
; . Tìm khẳng định sai trong U 2 2
IỆL các khẳng định sau? y TƯ VÀ 5 4 CHÍ P ẠT 2 1 O 5 x M
A. M m 7.
B. Mm 10.
C. M m 3. D. 2. m
Câu 111. Cho hàm số y f x liên tục trên R và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của m để phương trình f x 2 1 m 0 có 8 nghiệm phân biệt trong khoảng 5;5 50
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 1 3 1 O 3 x A. 0. B. 1. C. 2. D. 3.
Câu 112. Cho hàm số y f x có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để
phương trình f x m m có 4 nghiệm phân biệt là? y OÁNT C 3 YMPI 4 x OL O C Ụ 1 NH PH 3 CHI A. 0. B. 1. C. 2. D. Vô số
Câu 113. Cho hàm số y f x có đồ thị như hình vẽ. f x f x
Tìm số điểm cực trị của hàm số y 2 3 51
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y O x 1 A. 3. B. 4. C. 5. D. 6.
Câu 114. Cho đồ thị hàm số y f x xác định và có đạo hàm trên . Hàm số y f x có 2
đồ thị như hình vẽ. Số nghiệm nhiều nhất của phương trình f x m (m là tham số thực) C Ọ là? H y N TOÁ U IỆL x TƯ 2 O 1 3 VÀ CHÍ A. 2. B. 3. C. 4. D. 5. P
Câu 115. Cho hàm số y f x có đồ thị như hình vẽ. Số nghiệm thực của phương trình ẠT
f f cos x 0 trong đoạn 0;2019 là y 1 x 1 O 1 A. 642. B. 1002. C. 1003. D. 643.
Câu 116. Cho hàm số y f x liên tục trên
và có đồ thị như hình vẽ. Số giá trị nguyên
của tham số m để phương trình 2
f cos x m 2018 f cos x m 2019 0 có đúng 6
nghiệm thuộc 0; 2 là? 52
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 3 1 O x 1 1 1 A. 5. B. 3. C. 2. D. 1.
Câu 117. Cho hàm số y f x có đồ thị như hình vẽ y 1 OÁN 1 x T O C 1 1 YMPI OL 3 C Ụ
Có bao nhiêu giá trị nguyên của m để phương trình f x 1 m có 4 nghiệm phân biệt A. 2. B. 1. C. 3. D. 4. 3 2 NH PH
Câu 118. Cho hàm số y f x có đạo hàm tại x R, hàm số f 'x x ax bx c có đồ
thị như hình vẽ. Số điểm cực trị của hàm số y f f 'x là? CHI y 1 O 1 x A. 7. B. 11. C. 9. D. 8.
Câu 119. Cho hàm số 3 2 y f x ax
bx cx d a,b,c , a 0 có đồ thị C . Biết
rằng đồ thị C tiếp xúc với đường thẳng y 9 tại điểm có hoành độ dương và đồ thị 53
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
hàm số y f x cho bởi hình vẽ bên. Phần nguyên của giá trị diện tích hình phẳng giới
hạn bởi đồ thị C và trục hoành là? y 1 O 1 3 x 4 C Ọ A. 2 B. 27 C. 29 D. 35 H
Câu 120. Cho hàm số 3 2 y f x ax
bx cx d a,b,c , a 0 có đồ thị C . Biết rằng N
đồ thị C tiếp xúc với đường thẳng y 2 tại điểm có hoành độ dương và đồ thị hàm số 3 TOÁ
y f x 3a 2b c d U
cho bởi hình vẽ bên. Giá trị là? IỆ y L 4 TƯ VÀ CHÍ P 2 O 2 x ẠT A. 0. B. 2 C. 3. D. 4
Câu 121. Cho hàm số y f x 4 ax 2
bx c a 0 có đồ thị C , đồ thị hàm số y f x 3 8 3
như hình vẽ bên. Biết đồ thị hàm số y f x đạt cực tiểu tại điểm ; . Đồ thị 3 9
hàm số y f x tiếp xúc với trục Ox tại 2 điểm. Diện tích S của hình phẳng giới hạn bởi
đồ thị C và trục hoành là? 54
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 1 O 1 x 7 8 14 16 A. B. C. D. 15 15 15 15 ax b d
Câu 122. Cho hàm số y f x
a, b,c, d ,
0 có đồ thị C , đồ thị hàm số cx d c
y f x như hình vẽ bên. Biết đồ thị hàm số y f x cắt trục tung tại điểm có tung độ OÁN
bằng 3. Phương trình tiếp tuyến của C tại giao điểm của C với trục hoành có dạng ? T C y YMPI OL C Ụ 2 NH PH O 1 2 x CHI 1 3 1 3 1 3 1 A. y x B. y x C. y x D. y x 2 2 2 2 2 2 2 2
Câu 123. Cho hàm số y f x có đồ thị như hình vẽ và cắt trục hoành tại 5 điểm như hình
vẽ sao cho điểm C là tâm đối xứng của đồ thị. 55
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y 6, 2 2,8 O C x 2,8 6, 2 CỌ H
Xét các cặp số a; b với a, b và a b sao cho đồ thị hàm số N
gx f x a f x b TOÁ
Cắt trục hoành có đúng 3 cặp giao điểm đối xứng nhau qua điểm C. Tổng các giá trị a U nhận được? IỆ A. 15 B. 6 C. 12 D. 10 L
Nhóm toán VD – VDC TƯ
Câu 124. Cho hai hàm số y f x , y g x liên tục trên
có đồ thị được cho như hình VÀ g 2 m 5
vẽ bên dưới. Số giá trị nguyên của tham số m để bất phương trình f x có 2 x 4x 10 CHÍ P
nghiệm x 1; 4 là? ẠT y y g x 2 f x 30 O 2 4 x 1 11 2 O 3 7 15 x 3 32 2 A. 7 B. 8 C. 6 D. 5
Thầy Nguyễn Đăng Ái
Câu 125. Cho hàm số y f x xác định và liên tục trên
, hàm số g x 2 2x 3 và
đường thẳng d có đồ thị như hình vẽ dưới. 56
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y g x f x B O 1 x 9 A 4 d
Biết rằng A là điểm chung của 2 đồ thị f x , g x , x g x A
1 , điểm B thuộc đồ thị và x 9 y f x f ' x B
, đường thẳng d là tiếp tuyến của đồ thị hàm số
. Tính A 4 OÁN A. 1 B. 3 C. 5 D. 2 T 2 2 C
Câu 126. Cho hàm số 5 4 3 2 y ax bx cx
dx ex f có đồ thị f x như hình vẽ y YMPI 2 OL C Ụ y x 1 NH PH 3 O 1 3 x CHI
Hỏi hàm số y g x f x 2 1 2
2x 1 đồng biến trên khoảng nào sau đây? 3 1 1 A. ; 1 B. ;
C. 1; 0 D. 1; 3 2 2 2
Câu 127. Cho hàm số f x liên tục trên
có đồ thị như hình vẽ: 57
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y 1 O x 1
Có bao nhiêu giá trị nguyên của m 1; 2019 sao cho phương trình 2x f f m m 1 0 có nghiệm 2 2 1 x C Ọ A. 2018 B. 2019 C. 1 D. 2 H f x N
Câu 128. Cho hàm số liên tục trên
có đồ thị như hình vẽ: y TOÁ U 5 IỆL 3 TƯ VÀ 1 CHÍ O 1 2 4 x P Ạ T
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
gx f 4 x 4 2 sin
cos x . Tổng M m bằng A. 3 B. 4 C. 5 D. 6
Câu 129. Cho hàm số f x liên tục trên
có đồ thị như hình vẽ: 58
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ y 7 3 1 O 1 3 x
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y f x 3 f x 2 2 3
2 5 trên đoạn 1;3 . Tích M.m bằng A. 2 B. 3 C. 54 D. 55
Câu 130. Cho hàm số f x liên tục trên
có đồ thị như hình vẽ: y OÁN 5 T C 3 YMPI OL C 1 Ụ O 1 2 3 x NH PH
Ký hiệu g x f 2 2x 1 x m . Tìm m để max gx 2 min gx 0; 1 0; 1 CHI
A. m 4
B. m 3
C. 0 m 5
D. m 2
Câu 131. Cho hàm số y f x , y g x liên tục trên
có đồ thị hàm số y f x là
đường cong nét đậm và y gx là đường cong nét mảnh như hình vẽ. 59
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y g'x O C x B A f 'x
Gọi ba giao điểm A, B,C của đồ thị y f x , y gx trên hình vẽ lần lượt có hoành độ C Ọ
a,b,c . Giá trị nhỏ nhất trên đoạn bằng H
A. h 0
B. h a
C. h b
D. h c N
Câu 132. Cho hàm số f x liên tục trên
có đồ thị như hình vẽ: TOÁ y U IỆL 5 TƯ VÀ 3 CHÍ P 1 ẠT O 1 2 3 x
Ký hiệu g x f 3 x 2
x x 2 3m , với m là tham số thực. Giá trị nhỏ nhất của biểu thức P 2
m 3max g x 4min g x m 0;1 0;1 A. 105 B. 102 C. 50 D. 4
Câu 133. Cho hàm số y f x có đồ thị như hình vẽ y f x 4 O 1 x 60
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
Có bao nhiêu giá trị nguyên của m với m 1;5 để bất phương trình
f m m 1 f 5 x nghiệm đúng với mọi x1;4 A. 2 B. 1 C. 4 D. 3
Câu 134. Trên parabol y 2
x 1P lấy hai điểm A1;2.B3;10 gọi M là điểm di động
trên cung AB của P , M khác A, B . y B 10 M A 2 OÁNT O D E F x C
Gọi S1 là diện tích hình phẳng giới hạn bởi và , gọi là diện tích hình phẳng giới hạn bởi và
Gọi là tọa độ điểm khi đạt giá trị nhỏ nhất. Tính 2 x 2 y YMPI 0 0 OL A. 29 B. 11 C. 7 D. 5 C
Câu 135. Cho hàm số liên tục trên đoạn 1;9 và có đồ thị là đường cong trong hình vẽ Ụ dưới đây y NH PH 2 CHI O x 1 4
Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình
f x f x2 f x f x 2 16.3 2 8 .4
m 3m fx .6
Nghiệm đúng với mọi giá trị x 1;9? A. 22 B. 31 C. 5 D. 6 61
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Câu 136. Cho hai hàm số f x và g x có đồ thị các đạo hàm cho như hình vẽ với f 'x
(màu xanh) và g 'x (màu hồng) có đồ thị như hình vẽ. y 4 3 2 1, 5 2 1, 5 1 O 1 x C Ọ
Hỏi hàm số h x f x 1 g 2x đồng biến trên khoảng nào sau đây? H 1 1 5 N
A. 1; 0 B. 0; C. 1; D. 2; 2 2 2 TOÁ
Câu 137. Cho hai hàm số f x và g x có đồ thị biểu diễn đạo hàm f x và gx như U
hình vẽ. Biết rằng hàm số y f x g x 2 đồng biến trên khoảng ; và giá trị lớn
IỆL nhất của biểu thức 8; phương trình tiếp tuyến với đồ thị y gx tại điểm có TƯ hoành độ x 11 y 3x 2
y f x 1 là
và phương trình tiếp tuyến với đồ thị hàm số tại VÀ
điểm có hoành độ x 9 y ax f 9 2 là
1 Giá trị của bằng y CHÍ f 'x P Ạ g'x T O 1 3 21 x 2 A. 13 B. 28 C. 26 D. 22
Thầy Nguyễn Đăng Ái 62
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
TUYỂN TẬP MỘT SỐ BÀI TOÁN ĐỒ THỊ VẬN DỤNG
CAO ÔN THI THPT QG 2019 Bài toán 1
Cho hàm số y f x liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của tham số m để phương trình f 2 f cosx m có nghiệm x ; . 2 y 2 1 2 1 x 1 O 2 1 OÁNT 2 C A. 5. B. 3. C. 2. D. 4. YMPI Lời giải OL
Đặt t cos x , do x ;
nên suy ra t 1;0. C 2 Ụ
Trên khoảng 1; 0 hàm số nghịch biến nên suy ra
Với t 1;0 thì f 0 f t f 1 hay 0 f t 2. NH PH
Đặt u 2 f cos x thì u 2 f t ,u 0; 2. Khi đó bài toán trở thành: CHI
Tìm m để phương trình f u m có nghiệm u 0; 2.
Quan sát đồ thị ta thấy rằng với u 0; 2 thì f u 2; 2 2 m 2.
Vì m m 2; 1;0;
1 . Vậy có 4 giá trị của . m Chọn ý D. 63
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 2
Cho hàm số f x liên tục trên
và có đồ thị như hình vẽ dưới đây: y 3 1 2 1 O 2 x 1
Số các giá trị nguyên của tham số m không vượt quá 5 để phương trình C 2 x m 1 Ọ f
0 có hai nghiệm phân biệt là 8 H N A. 5. B. 4. C. 7. D. 6. Lời giải TOÁ Đặt x t
,t 0. Phương trình đã cho trở thành: U 2 2 IỆ m 1 m 1 L f t
0 f t ,t 0 . 8 8 TƯ
Quan sát đồ thị đã cho của hàm số y f x ta thấy rằng VÀ
Phương trình trên có hai nghiệm phân biệt khi và chỉ khi 2 m 1 1 1 7 2
m 9 3 m 3 CHÍ 8 P Ạ
Mà m m2; 1;0;1; 2 . T
Vậy có tất cả 5 giá trị nguyên của m . Chọn ý A.
Nhận xét. Không khó để nhận ra phương pháp bài này giống với bài toán 1, gồm 3 bước như ở lý
thuyết mình đã nêu, các bạn chú ý làm theo nhé!
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 64
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 3
Cho hàm số f x liên tục trên 0; 5 và có đồ thị như hình vẽ dưới. y 4 3 2 1 O 1 2 3 5 x
Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình m 2 2019
f x f x 1 3x 10 2x OÁNT
Nghiệm đúng với mọi x 0; 5? C A. 2014 B. 2015 C. 2016 D. 2017 Lời giải YMPI
Để bất phương trình đúng với mọi x 0; 5 thì ta cần có OL C 3x 10 2x Ụ 2019 m max 0;5 2
f x f x 2 1
Theo Cauchy – Schwarz ta có NH PH
3x 10 2x 3 x 2 5 x 3 2x 5 x 5 CHI
Dấu ”=” xảy ra khi x 3 . Nhìn vào đồ thị ta thấy rằng f x 1 dấu ”=” xảy ra khi và chỉ
khi x 3 x 1 x 5 . 3x 10 2x 5 Ta có 5 m 2014 2
f x f x 2 1
f x f x 1 Chọn ý A. 65
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 4
Cho hàm số f x liên tục trên và có đồ thị như hình vẽ. y 1 O 1 2 x 2 3 4 C Ọ H N
Tổng tất cả các giá trị của tham số m để bất phương trình TOÁ f x 2 x f x 2 9.6 4 .9 m
5m fx .4 U IỆ
Đúng với mọi x là? L A. 10. B. 4. C. 5 D. 9 TƯ Lời giải VÀ
Đặt t f x . Quan sát đồ thị ta thấy f x
2 x t 2
Bất phương trình đã cho được viết lại như sau CHÍ t 2t P
9.6t 4 2t .9t 2
m 5m t 3
.4 ,t 2 9
4 2t 3 2 Ạ m 5m T 2 2 3 t t 2 3 2
Xét hàm số g t 9 4 t 2 2 3 t 3 3 2t t 2 3 2 3
Có g 't 9. .ln 2t. 24 t .ln 0,t 2 2 2 2 2 2
Từ đó suy ra max g t g 2 4 ;2
Yêu cầu bài toán tương đương với 2
m 5m 4 1 m 4
Vì m m 1; 2; 3;
4 nên tổng tất cả các giá trị của tham số m là 10. Chọn ý A.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 66
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 5
Cho hàm số y f x có đồ thị hàm số y f x như hình vẽ bên. Xét hàm số
g x f x 3 2
2x 4x 3m 6 5 với m là số thực. Để g x 0 x 5; 5 thì điều kiện của m là y f 'x 2 5 O 5 x B 13 A OÁNT
A. m 2 f 5
B. m 2 f 5 3 3 C 2 2 C. m f 0 2 5 D. m f 5 4 5 3 3 YMPI Lời giải OL 3 3 C
Ta có g x 0 g x 2 f x 2x 4x 3m 6 5 0 3m 2 f x 2x 4x 6 5 Ụ
Đặt h x f x 3 2
2x 4x 6 5 . Ta có hx f x 2 2 6x 4 .
h 5 2 f 56.5 4 0 NH PH
h 5 2 f 56.54 0 CHI
Suy ra h0 2 f 0 0 4 0
h1 2 f 16.14 0
h1 2 f 1 6.1 4 0
Từ đó ta có bảng biến thiên x 5 0 5 h 0 h 5 h h 0 h 5 67
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Từ bảng biến thiên ta có 3m h 5 m 2 f 5 . 3 Chọn ý A. Bài toán 6 f x
Cho 0 a 1 b 1 a và hàm số y g x
có đạo hàm trên 0; . Biết
f x 2 1
đồ thị hàm số y f x như hình vẽ dưới. Khẳng định nào sau đây đúng với mọi
x a 1; b 1 y
y f x n C Ọ H m N TOÁ O a b x U IỆ L f b 1 f a 1 g x g x TƯ A. B. m n VÀ f b 1 10 g x
C. g x D. 0 m CHÍ P Lời giải Ạ
x a 1; b 1 2 T Ta có
x 1 a;b
, dựa vào đồ thị ta có
m f x 2 n 1 1 1 1 n f
x 12 m
Mặt khác 0 a 1 b 1 a dựa vào đồ thị ta thấy f x đồng biến trên a 1; b 1 f b 1
nên ta có f a 1 f x f b 1 gx m Chọn ý C.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 68
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 7
Cho hàm số f x có đạo hàm f 'x . Hàm số y f 'x liên tục trên tập số thực và có
đồ thị như hình vẽ. Số nghiệm thuộc đoạn 1; 4 của phương trình f x f 0 là? y 1 O 1 2 4 x A. 4. B. 3. C. 2. D. 1. Lời giải
Từ đồ thị của hàm số f x ta có bảng biến thiên của hàm số (đa thức nội suy): x 1 1 2 4 y ' OÁN
0 0 0 0 T y
f 1 C
f 4 YMPI
f 2 OL
f 1 C Ụ
Mặt khác quan sát hình vẽ ta thấy: 1 2
f 'x dx f 'x dx f 1 f 0 f 1 f 2 f 2 f 0 0 1 NH PH
Vậy trong đoạn 1; 4 phương trình f x f 0 có 1 nghiệm. CHI Chọn ý B. 69
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 8
Cho đồ thị của hàm số f x ,F x , f 'x 1 như hình vẽ. Tính giá trị của tích phân
f 0 f 1.5 3 sin x.cos xdx ?
f '1F1.5 y 2 3 1 O 1 3 2 3 x 2 2 C 1 Ọ H N 3 A. 0 B. 1 C. 3 D. 4 TOÁ U Lời giải
IỆL Đồ thị hàm số 1 cực đại khi x 2 nên 2 là đồ thị của đạo hàm hàm số 1 . TƯ
Chuyển dịch đồ thị hàm số 3 sang phải 1 đơn vị ta thấy có cắt trục Ox tại x 1 , đồng
thời tại đó đồ thị hàm số 2 cực đại 3 là đồ thị của đạo hàm 2 . VÀ
Suy ra đồ thị hàm số 1 , 2 , 3 lần lượt là đồ thị hàm số F x , f x , f 'x 1 . CHÍ
f 0 f 1.5 P
Ta có f 0 f 1.5 f '1 F 1.5 3
sin x.cos xdx 0 ẠT
f '1F1.5 Chọn ý A.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 70
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 9
Cho hàm số f x có đạo hàm trên \
b và hàm số g x có đạo hàm trên . Biết đồ
thị của hai hàm số y f 'x , y g 'x như hình vẽ dưới. Đặt h x f x g x và S 2 2 2 2
hx b
h b x 1 2hc hc
với a,b,c là các số thực đã biết. Khẳng
định đúng với mọi x 0 là? y
y f x
y gx O a b c x OÁN
A. S h c ; h a c
B. S h c T C
C. S h c ; h a b
D. S h a ; h c Lời giải YMPI x a OL
Từ đồ thị đã cho ta suy ra h'x f 'x g'x ; h'x 0 f 'x g'x x c C Ụ
Lập bảng biến thiên ta có x
a b c
h'x 0 + + 0 NH PH CHI h c h x h a 2
Lại có 2 2 2 S h b x h c h b x
h x b hc Chọn ý B. 71
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 10
Cho hàm số f x liên tục và xác định trên
và có đồ thị f 'x như hình vẽ. Tìm số
điểm cực trị của hàm số 2 y f x x ? y O x 1 4 C A. 10 B. 11 C. 12 D. 13 Ọ H Lời giải N
Ta có y x f 2 ' 2 1 ' x x, 2
x x m có nghiệm khi và chỉ khi m 1 . 4 TOÁ
Dựa vào đồ thị ta thấy đồ thị hàm f 'x cắt trục hoành tại 5 điểm trong đó 1 điểm có U
IỆL hoành độ nhỏ hơn 1và có một tiệm cận. 4 TƯ
Khi đó ứng với mỗi giao điểm có hoành độ lớn hơn 1 và 1 điểm không xác định thì 4 VÀ
y ' 0 có 2 nghiệm Từ đây dễ dàng suy ra hàm 2 y
f x x có 11 cực trị! CHÍ Chọn ý B. P ẠT
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 72
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 11
Cho hàm số f x có đạo hàm và xác định trên tập số thực và có đồ thị như hình vẽ
dưới. Tính tổng tất cả các giá trị nguyên của tham số m 20; 20 để hàm số
y f x m có 5 điểm cực trị? x 2 y 3 3 O 1 x 2 OÁNT C A. 210 B. 212 C. 211 D. 209 Lời giải YMPI
Chúng ta có thể tính nhanh theo công thức là hàm số y f x m có 5 điểm cực trị khi OL y f x C và chỉ khi hàm số
mcó 2 điểm cực trị dương và hàm số phải liên tục tại x 0 0 . Ụ
Dựa vào đồ thị của hàm số ta suy ra 1 m 0 m 1
m20,19,18,...,3,1, 0 2 m 0 m 2 NH PH
Suy ra tổng S các giá trị nguyên m : S 210. CHI Chọn ý A. 73
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 12
Cho hàm số bậc ba f x và g x f 2
mx nx pm,n, p có đồ thị như hình dưới,
trong đó đường nét liền là đồ thị hàm f x , đồ thị hàm nét đứt là đồ thị hàm g x ,
đường x 1 là trục đối xứng hàm g x . Giá trị của biểu thức 2
P n mm pp 2n bằng bao nhiêu? y g x f x 2 O 1 2 x C Ọ 2 1 H 2 N TOÁ U A. 6 B. 24 C. 12 D. 16 IỆ L Lời giải 3 2 2 TƯ
Ta có f x ax bx cx d f 'x 3ax 2bx c . Hàm số đạt cực trị tại x 0; x 2 và VÀ
đồ thị đi qua điểm 1;0 ,0; 2 nên ta có f '0 0 a 1 CHÍ f '2 0 b 3 P
f x 3 x 2 3x 2 Ạ f 1 0 c 0 T f 0 d 2 2 3 2
Ta có g x 2
mx nx p 2
3 mx nx p 2 . Hệ số tự do bằng 3 p 2 3p 2 . Đồ thị
hàm số g x đi qua điểm 0;0 nên 3 p 2
3p 2 0 p 1 . Đồ thị hàm số 2 g x
f mx nx p có trục đối xứng x 1 nên đồ thị hàm số 2 2 1 n 1
y mx nx p cũng có trục đối xứng x
m n . 2 2m 2
Đồ thị hàm số g x đi qua điểm 2; 2 nên m n 1 g 2 0
g x 2m 13 32m 12 2 2
m n 1 2
Do đồ thị có hướng quay lên trên nên ta suy ra m 0 m n p 1
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 74
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Chọn ý C. Bài toán 13
Giả sử hàm số y f x có đạo hàm là hàm số y f 'x có đồ thị được cho như hình vẽ
dưới đây và f 0 f 1 2 f 2 f 4 f 3. Tìm giá trị nhỏ nhất m của hàm số
y f x trên 0; 4 . y O 4 x 2
A. m f 4.
B. m f 0.
C. m f 2.
D. m f 1. Lời giải
Quan sát đồ thị hàm số y f 'x ta thấy: OÁNT
Trên khoảng 0;2 thì f 'x 0. C
Trên khoảng 2; 4 thì f 'x 0. Bảng biến thiên: YMPI OL x 0 1 2 3 4 C
f 'x Ụ f 2
f x f 1 f 3 NH PH
f 0 f 4 CHI
Từ bảng biến thiên ta nhận thấy GTNN của hàm số đạt được bằng f 0 hoặc f 4.
Ta lại có f 0 f 1 2 f 2 f 4 f 3 f 0 f 4 2 f 2 f 1 f 3
f 2 f 1
f 2 f 3
0 (do f 2 f 1 , f 2 f 3).
Do vậy f 0 f 4 0 f 0 f 4 .
Vậy m f 4. Chọn ý A. 75
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 14
Cho hàm số f x có đồ thị như hình vẽ đồng thời f x 1 f x 2x 2x 1x 1* Biết rằng 4 2 f x ax
bx c ; 2 g x
mx nx p và f x g 2 x 1
Tìm giá trị nhỏ nhất của hàm số g x y 11 O x 1 2 CỌH N A. 1 B. 1 C. 2 D. 4 2 4 TOÁ Lời giải U IỆ
Từ * ta thay x 0 f 1 f 0 L a b 0
x 0 y 1 c 1 x y f x 4 x 2 2, 11 x TƯ Ta có và 1 c 1 VÀ 2 Mặt khác 4 x 2
x g 2
x m 2
x n 2 1 1 1
x 1 p 4 mx 2 mx m 2 2
nx n p CHÍ m 1 m 1 1 P
2 n 1 n 1 gx 2
x x; g'x 2x 1; g'x 0 x Ạ 2 T 1 n p p 0
Vậy giá trị nhỏ nhất g x 1 4 Chọn ý B.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 76
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 15
Cho hai hàm số y f x , y g x có đạo hàm là f x , gx . Đồ thị hàm số y f x
và gx được cho như hình vẽ bên dưới. y f 'x g'x O 2 6 x
Biết rằng f 0 f 6 g 0 g 6 . Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
h x f x g x trên đoạn 0;6 lần lượt là:
A. h 2 , h 6.
B. h 6 , h 2.
C. h 0 , h 2.
D. h 2 , h 0. Lời giải OÁNT
Có h 'x f 'x g 'x C
Từ đồ thị đã cho ta có bảng biến thiên của hàm số h x trên 0; 6 x 0 2 6 YMPI h'x 0 OL C h 0 h 6 Ụ h x h 2 NH PH
Do đó min h x h 2 0;6 CHI
Giả thiết ta có f 0 g 0 f 6 g 6 h 0 h 6
Vậy nên max h x h 6 0;6 Chọn ý B. 77
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 16
Cho 2 hàm số f x , g x có đồ thị như hình vẽ bên dưới. Biết rằng x 1, x 6 đều là
các điểm cực trị của 2 hàm số f x , g x đồng thời f 1 g 6 , 2 f 6 g 1 3 và
2 f 5x 16 3g5x 9 1* .Gọi M,m lần lượt là giá trị nhỏ nhất của biểu thức
S f x f x gx 2 2 1
g x g x . Tính tổng P M m ? y g x f x C O 1 6 x Ọ H N 27 23 9 11 A. B. C. D. 4 4 2 2 TOÁ Lời giải U IỆ
Lần lượt thay x 2, x 3 vào * đồng thời kết hợp điều kiện ban đầu ta có hệ phương L
2 f 1 3g6 1 TƯ f 1 g 6 1
2 f 6 3g 1 1 trình VÀ 5
2 f 6 4g1 4
f 6 , g1 2
f 4g6 2 2 1 4 CHÍ P
Từ giả thiết kết hợp đồ thị ta nhận thấy rằng g x nghịch biến trên 1; 6 và f x đồng Ạ T 5 biến trên 1;6
gx 1;2, f x
1; .để đơn giản ta đặt u f x,y gx 2 Ta có S 2 u uy 2 2
y u y f u; y. Coi đây là 1 hàm số theo ẩn u ta có y f u y u y u u 2 1 ' ; 2 2 1 0 2 5 35
Ta có f 1; y 2 2
1 2y y y 1 y y 2; f ; y 2 y 4y 2 4 5 f
; y f 1; y 0,y 1;2 2 3 2y 1 5 3 2y 1 5 Xét y 1; u 1; và y ; 2 u 1; 2 2 2 2 2 2 3 5
Với y 1; 1khảo sát hàm số f u; y theo biến u 1; 2 2
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 78
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ 5 35 23 f u y f y y y 2 f u; y f ; y y 4y u 2 ; 1;
2 1 ,và u 2 4 4 3 5 Với y ; 2 2
. Lập bảng biến thiên cho hàm số f u; y theo biến u 1; ta có 2 2 2 y y y y f u y f y y y y y u 2 1 2 1 ; 2 1 2 1 8 2 1 7 ; 2 2 2 2 4 5 35 23 Và f u y f y y y u ; ; 2 4 2 4 4 23 23 27
Từ 1 và 2 max S M
,min S m 1 P M m 1 4 4 4 Chọn ý A. Bài toán 17
Cho hàm số y f x có đạo hàm trên và có đồ thị là đường cong trong hình vẽ dưới
đây. Đặt g x f f x 1 . Tìm số nghiệm của phương trình g'x 0 . y OÁNT C 1 3 1 YMPI 1 2 x OL C Ụ 2 3 NH PH A. 8. B. 10. C. 9. D. 6. CHI Lời giải
Quan sát đồ thị hàm số trên thì hàm số y f x có ba điểm cực trị x 1 , x 1 và 3
x a1 a 2 . Do đó, f 'x 0 có ba nghiệm x 1 , x 1 và x a1 a 2 . 3
Ta có g 'x f 'x f ' f x 1
f 'x 0
Xét g 'x 0
f ' f x 1 0
Phương trình 1 có ba nghiệm x 1 , x 1 và x a (1 a 2) 3 79
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
f x1 1 f x 2 3 3
Phương trình 2 f x 1 1 f x 2
f x1 a
f x a 1
Theo đồ thị, ta thấy f x 2 có hai nghiệm phân biệt và f x 2 cũng có hai nghiệm 3 phân biệt.
Đặt b a 1 . Do 1 a 2 nên 2 b 3
Xét phương trình f x b ( 2 b 3 ). Đường thẳng y b cắt đồ thị hàm số y f x tại
hai điểm phân biệt nên phương trình (5) có hai nghiệm phân biệt.
Xét thấy các nghiệm của phương trình 1 , 3 , 4 và 5 là các nghiệm phân biệt. Vậy C Ọ
phương trình g 'x 0 có 9 nghiệm phân biệt. H N Chọn ý C. Bài toán 18 TOÁ y f x U
Biết rằng đồ thị hàm số bậc 4 :
được cho như hình vẽ bên. Tìm số giao điểm IỆ 2 L
của đồ thị hàm số y g x f x
f x. f x và trục Ox . y TƯ VÀ CHÍ P ẠT O x A. 4. B. 0. C. 2. D. 4. Lời giải 2
Số giao điểm của đồ thị hàm số y g x f x
f x. f x và trục Ox bằng số 2 2
nghiệm của phương trình: f x
f x. f x 0 f x
f x. f x.
Giả sử đồ thị hàm số 4 3 2 y f x ax bx
cx dx e , a,b ,c, d, e ; a 0,b 0 cắt trục
hoành Ox tại 4 điểm phân biệt x x x x 1 , 2 , 3 , 4 .
Đặt A x x B x x C x x D x x 1 ,
2 , 3 , 4 ta có:
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 80
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
f x ax x x x x x x x . a ABCD 1 2 3 4 . 2
TH1: Nếu x x i
g x f x i i 0 i với
1,2,3, 4 thì .
Do đó x x i g x i ,
1,2,3, 4 không phải nghiệm của phương trình 0 .
TH2: Nếu x x i i với
1,2,3, 4 thì ta viết lại 1 1 1 1
f x aBCD ACD ABD ABC f x . A B C D
f x f x 1 1 1 1
f x 1 1 1 1 2 2 2 2 A B C D A B C D 2
f x 1 1 1 1 . f x 1 1 1 1 . 2 2 2 2 A B C D A B C D 1 1 1 1 2 2 2 1 1 1 1
Suy ra, f x. f x f x. f x. . 2 2 2 2 A B C D A B C D 2 1 1 1 1
Khi đó g x f x
f x. f x 2 f x . 0 x x i
i 1, 2, 3, 4 2 2 2 2 A B C D OÁN
Từ đó suy ra phương trình g x 0 vô nghiệm. T C
Vậy đồ thị hàm số y g x không cắt trục hoành. Chọn ý B. YMPI Bài toán 19 OL
Cho hàm số f x có đồ thị như hình vẽ C Ụ y 5 NH PH y 17 5 CHI 3 y 32 1 O x
Giá trị nguyên nhỏ nhất của tham số m để phương trình sau có nghiệm là bao nhiêu? 3 f x 2 f x f x 1 2 7 5 e
ln f x ?
f x m A. 3 B. 4 C. 5 D. 6 Lời giải
Quan sát đồ thị ta thấy rằng 1 f x 5 , đặt t f x , giả thiết trở thành 81
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA 3 t 2 2t 7t5 1 e ln t m t
Xét: g t 3 t 2
t t g t 2 2 7 5, '
3t 4t 7
0 t 1 g 1 g t g 5 1 g t 145 1 1 26
Mặt khác h t t , h't 1
0 t 1;5 2 ht 2 t t 5 3 2 t t t 1
Vậy hàm ut 2 7 5 e ln t
đồng biến với x 1; 5 t 26
Để phương trình đầu có nghiệm thì e ln 2 m 145 e ln 5
Vậy giá trị nguyên nhỏ nhất của m là 4. Chọn ý B. Bài toán 20 C Ọ
Cho hàm số f x liên tục trên R và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên H
3sin x cos x 1 2 N
của tham số m để phương trình f
f m 4m 4 có nghiệm? 2 cosx sinx 4 y TOÁ U 16
y f x IỆ 3 L TƯ x 4 O VÀ CHÍ P Ạ A. 4. B. 5. C. Vô số D. 3. T Lời giải
Vì 1 sin x 1; 1 cos x 1 nên 2 cos x sin x 3 2 cos x sin x 4 0
3sin x cos x 1 Đặt
t 3sin x cos x 1 t 2 cosx sin x 4
2 cos x sin x 4
cos x2t 1 sin xt 3 4t 1 2 2 2
Phương trình trên có nghiệm khi 2t 1 t 3 4t 1 2 t t 2 t t 2
t t 9 5 10 10 16 8 1 11 2 9 0
t 1 0 t 1 11
Từ đồ thị hàm số ta thấy hàm số f x đồng biến trên (0;1)
Nên phương trình f x f t với t 0;1 có nghiệm duy nhất khi x t x 0
3sin x cos x 1
Do đó phương trình f f 2 m m 4 có nghiệm 2 cosx sinx 4
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 82
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ t 2
m 4m 4 có nghiệm với 0 t 1
m m m 2 2 0 4 4 1
2 1 3 m 1
Mà m nên m 3; 2;
1 . Vậy có 3 giá trị của m thỏa mãn yêu cầu. Chọn ý C. Bài toán 21
Cho hàm số f x liên tục và có đồ thị như hình vẽ. y 4 1 x O 3 6 3 4m m
Các giá trị của tham số m để phương trình 2
f x 3 có 3 nghiệm phân 2 OÁN
2 f x 5 T C biệt là: A. m 37 .
B. m 3 . C. m 37 .
D. m 3 3 . YMPI 2 2 2 2 OL Lời giải C 3 4m m Ụ Ta biến đổi 2
f x 3 3
4m m 2
f x 3 2 2 f x 5 2
2 f x 5 3 3 m m 2
f x 2 8 2 2 5
2 f x 5. NH PH
Xét hàm số f t 3
t t f t 2 '
3t 1 0 t . CHI
f t đồng biến trên . Nên suy ra m 2 2
2 f x 5 m 5 0 m m 0 2 2 4m 5 0 2 2 4m 2 f x 5 2 4m 5 2 4m 5 f x f x 2 2
Do phương trình f x g m luôn có ít nhất một nghiệm nên để phương trình đã cho có 2 4m 5
3 nghiệm phân biệt thì f x
có một phương trình có 1 nghiệm và một 2
phương trình có 2 nghiệm. 83
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA 2 4m 5
Để ý rằng f x
có hai nghiệm khi m 5 và có một nghiệm khi m 5 . 2 2 2 5 m
f x 0 phương trình có 2 nghiệm. 2 2 4m 5
m 5 để phương trình có 3 nghiệm thì f x có hai nghiệm 2 2 2 4m 5 2
m 37 m 37 4 2 4 2 Vậy m 37 . 2 Chọn ý C. Bài toán 22 4 3 2 C
Cho hàm số y f x ax bx cx dx e với (a, b,c, d, e ) . Biết hàm số y f x Ọ H
có đồ thị như hình vẽ, đạt cực trị tại điểm O 0; 0 và cắt truc hoành tại A3; 0 . Có bao N
nhiêu giá trị nguyên của m trên 5; 5 để phương trình f 2
x 2x m e có bốn TOÁ nghiệm phân biệt. U y IỆL TƯ 1 3 VÀ O 1 2 x CHÍ P A. 0. B. 2. C. 5. D. 7. Ạ T Lời giải
Quan sát đồ thị f 'x như hình vẽ. Ta thấy rằng đây là hàm bậc 3 qua 0 không đổi dấu
và qua 3 đổi dấu 1 lần. Nên suy ra f x 2 '
k.x x 3 k 0 (vì lim f x nên k 0 ) x 1 1 3
Do f '2 1 4k 1 k
f 'x 3 x 2 x . 4 4 4 1 1 1 1
Suy ra f x 4 3 3
x x e x x 1 . e 16 4 4 4
Mà theo đề ta có phương trình 2 2 x x m f x
2x m e 2
x 2x m3 2 1 0 4
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 84
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ 2
x 2x m 0 1 2
x 2x m 4 0 2
Để phương trình f 2
x 2x m e có 4 nghiệm phân biệt thì phương trình (1) và (2) lần
1 m 0
lượt có 2 nghiệm phân biệt 1 m 3. 1 m 4 0 2 m Mà m
4;5 . Vậy có 2 giá trị nguyên m thoả mãn bài toán. m 5;5 Chọn ý B. Bài toán 23
Cho hàm số f x liên tục và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m
tham số m để phương trình f 2 sin x
f có đúng 12 nghiệm phân biệt thuộc 2
đoạn ; 2 ? y OÁNT 3 C 2 x O 2 YMPI 27 OL 16 C Ụ A. 4. B. 5. C. 3. D. 2. Lời giải NH PH m
Xét phương trình: f 2 sin x f (*) 2 CHI
Ta có đồ thị y sin x : y 1 x O 2 m 27 m 3 Nếu f m 3 2 16 2 2 x 3 x 3 * 2 sin sin
phương trình (*) có 6 nghiệm thuộc ;2 2 4 85
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA m 0 2 27 m 0 m 4 2 Nếu f 0 . 16 2 m 3 m 3 2 2 3
2 sin x x x 0; 1 1 2 Khi đó * ; 2
Phương trình * có 12 nghiệm thuộc 3
2 sin x x x ; 2 2 2 2 m 0 m m 0 2 Nếu f 0 2 m m 4 2 2 2 sin x 0 Khi đó *
Phương trình * có 7 nghiệm thuộc ;2 2 sin x 2 C Ọ m 0 H m m 0 2 Nếu f 0 N 2 m m 4 2 2 TOÁ
2 sin x x x 0 U Khi đó * 1 1
Phương trình * vô nghiệm. 2 sin x x x 2 2 2 IỆL 0 m 4 m m TƯ Suy ra . Mà 1;
2 . Vậy có tất cả 2 giá trị nguyên của m . m 3 VÀ Chọn ý D. Bài toán 24 CHÍ 3 2 P
Cho đồ thị hàm số là nguyên hàm của f x có dạng F x ax bx 5x d . Tính diện
ẠT tích tạo bởi f x và trục hoành? y 4 4 O x 80 20 50 70 A. . B. . C. . D. . 3 3 3 3 Lời giải
Đặt f x 3 ax 2
bx cx d f x 2
3ax 2bx c .
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 86
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
f x f x 3
ax b a 2 '
3 x c 2bx d c .
x 2 12a 4b c 0
Nhìn vào đồ thị ta có (1)
x 3 27a 6b c 0
f 'x có cực trị là -4 , gọi x0 là hoành độ của điểm cực trị thì b f ' x
0 6ax 2b 0 x 2 3 . a x 2bx c 5 0 0 0 và 3a 0 0 2 b 2 b b 3 . a 2b c 4 c 5 (2) 2 9a 3a 3a
Từ (1) a 2 b và c 4b 12a , thay vào (2) ta được 3 2 b 2 b 2 4
b a
b b b a c 24 4 12 5 4 8 5 . 3a 2b 5 15 5
f x f x 4 3 x 6 2 x x 24 ' 4
0 có nghiệm là x ,x 15 5 5 1 2 x2 4 3 6 24
Vậy diện tích cần tìm là x 2 x 4x 65, 4 OÁN 15 5 5 1 x T C Chọn ý B. YMPI Bài toán 25 OL
Cho hàm số y f x liên tục trên đoạn 2; 2 và có đồ thị trên đoạn 2; 2 như hình C 2 Ụ
vẽ dưới. Hỏi phương trình 3 f x 2 f x 9
f x 2 3 có bao nhiêu nghiệm thực trên đoạn 2; 3? y NH PH
y f x 1 CHI 1 2 O 1 2 x 1 A. 1 B. 2 C. 3 D. 4 Lời giải
Ta có đồ thị hàm y f x 2 như hình vẽ dưới ( phần trên trục Ox) 87
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA y 1 O 1 2 3 4 x Xét hàm số y
f x 2 3 trên đoạn 0;4 ta có y f x 2 3 2 , 2
Xét hàm số y f x trên đoạn 2;2 ta có 2
3 f x 2 f x 9 3 f x 1 8 2
f x 2 1 x 0
Suy ra VT VP dấu “=” xảy ra khi f x 1 x 2 Chọn ý B. C Bài toán 26 Ọ H
Cho hàm số f x có đồ thị như hình vẽ dưới N y TOÁ 6 U IỆL TƯ VÀ 2 4 CHÍ P O 2 x ẠT 2 4 1 4
Có bao nhiêu giá trị nguyên của tham số m để f sin sin x m có nghiệm? 3 3 3 A. 2 B. 3 C. 4 D. 5 Lời giải
Vì 0 sin x 1 0 sin x . 3 3
Trên đoạn 0; hàm số sin luôn tăng nên suy ra sin 0 sin sin x sin 3 3 3
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 88
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ 3 4 Hay 0 sin sin x sin sin x 0;2 3 2 3 3 1 4 4
Quan sát đồ thị ta thấy f sin sin x ; 2 3 3 3 3 4
Để phương trình đầu có nghiệm thì m 2 3
Mà m m 1;0;1;
2 . Vậy có 4 giá trị nguyên thoả mãn. Chọn ý C. Bài toán 27
Cho đồ thị hàm số là nguyên hàm của f x có dạng F x 3 ax 2
bx 5x d . Tính diện
tích tạo bởi f x và trục hoành? y OÁNT 4 4 O C x YMPI OL 80 20 50 70 C A. . B. . C. . D. . Ụ 3 3 3 3 Lời giải
Ta có F x 2
' 3ax 2bx 5 nên F '0 5 f 0 5 NH PH
Từ 2 điểm cực trị có hoành độ là -4 và 4 ta có thể vẽ đại khái đồ thị của f x như sau CHI f x 2 mx nx 5
x 4 16m 4n 5 0 5 5 Có m
f x 2 x 5 .
x 4 16m 4n 5 0 16 16 4 4 5 2 80
Suy ra f x x 5 . 16 3 4 4 80
Vậy diện tích cần tìm là . 3 Chọn ý A. 89
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 28
Cho hàm số f x xác định, liên tục trên R và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của m để phương trình f x 2 2 3 4 6
9x m 3 có nghiệm. y 3 1 O 1 3 4 4 3 2 1 5 x 1 CỌH 5 N TOÁ U A. 13 B. 14 C. 15 D. 16 IỆL Lời giải 2 2 TƯ
Điều kiện 6x 9x 0 0 x 3 VÀ 2 2 2 1
Với x 0; ta có 0 6x 9x 9 x 1 1 3 3 CHÍ P x 2 x x 2 0 4 6 9 4 3 3 4 6 9x 1
ẠT Dựa vào đồ thị ta suy ra f x 2 5 3 4 6 9x 1 m 3 Khi đó phương trình f x 2 2. 3 4 6
9x m 3 có nghiệm 5
1 7 m 5 2
Vì m nên m 7; 6; 5; 4; 2; 1;0;1; 2; 3; 4; 5
Vậy có 13 giá trị của m thỏa mãn. Chọn ý A.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 90
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 29 Cho hai đồ thị
C : y f x x ax b 1 4 2 và đồ thị hàm số
C : y g x x mx nx p C 2 3 2
như hình vẽ. Gọi B, D là hai điểm cực trị của 1 , A và
C lần lượt là hai điểm cực đại và cực tiểu của C2 , (A và C đối xứng nhau qua điểm
U Oy . Biết hoành độ A và B bằng nhau, hoành độ của C và D bằng nhau. Có bao nhiêu
giá trị nguyên của a để AB 3 ? y A I x x 1 2 OÁNT O x C B D YMPI C OL A. 2 B. 5 C. 6 D. 7 C Lời giải Ụ x 0 a
Ta có f 'x 3 4x
2ax; f 'x 0 a
x , vói a 0, 1 , 2 1 x 2 2 NH PH g x 2 '
3x 2mx n CHI Ta có x , x g' x 0 1
2 là nghiệm của phương trình
Vì điểm U 0; b là trung điểm của AC nên x x 0 m 0 1 2 n
Mặt khác x x 2
x x x n 2 3x , 2 1 2 1 1 2 1 , 3 n a a
Từ 1 ,2 ta suy ra n 3 3 2 2
Ngoài U 0; b C b p 2 nên suy ra a y 3
x nx p 3
2x p a p A 1 1 1 2 Ta có được 2
4 2 a y x ax b b B 1 1 4 91
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA 2 a a
Do đó AB 3 y y a B A 3 3,* 2 4 a Đặt t a 2
2t t 0 2 Từ 4 t 3 t 4 t 3 * 2 3
2t 3 0t 0
t 3t 2t t t 2 1 3 3 3 0 0 1
2t 2 2 a 0 Bài toán 30
Cho hàm số f x liên tục trên
có đồ thị như hình vẽ. y CỌH 1 N 1 TOÁ O x U IỆL TƯ
Có bao nhiêu giá trị nguyên của n để phương trình f 2
16 cos x 6sin 2x 8 f nn 1 có nghiệm x ? VÀ A. 10 B. 4 C. 8 D. 6 CHÍ Lời giải P Ạ
Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên . T Do đó f 2 x
x f nn 2 16 cos 6sin 2 8 1
16 cos x 6sin 2x 8 nn 1 1 cos 2x 16.
6sin 2x 8 nn 1 8cos2x 6sin 2x nn 1 2 2 2
Phương trình có nghiệm x 2 2 2
n n 2 8 6 1
n n 1 100
nn 1 10 2
n n 10 0 2 1 41 1 41 n n 10 0 n
nn 1 2 10
n n 10 0 2 2
Vì n n 3; 2; 1; 0; 1; 2
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 92
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 31
Cho 2 số x, y thỏa mãn 2 x 2
5y 1 4xy và hàm số bậc 3 y f x có đồ thị như hình
2x 3y 3
vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P f . Tích x 4y 4 M.m? y 2 1 1 O x 2 OÁNT C 1436 1436 1438 1436 A. B. C. D. 1333 1331 1331 1335 YMPI
Lời giải OL
Dễ thấy f x 3 x 3x . C Ụ 2
x 2y sin
x sin 2 cos Từ 2 x 2
y xy x y 2 5 1 4 2 y 1 ta đặt y cos y cos 2x 3y 3
2sin 2 cos 3cos 3 2 sin cos 3 NH PH Xét t x 4y 4 sin 2 cos
4 cos 4 sin 2 cos 4 CHI
Ta có t sin 2 cos 4 2 sin cos 3 t 2sin 1 2t cos 4t 3* 2 2 2 2
Phương trình * có nghiệm
t 2 2t 1 4t 3 2 t 11 718 1436 P f t 3 2
t 3t 2 t
M 2,m M.m . 11 1331 1331 93
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 32
Cho f x là một đa thức hệ số thực có đồ thị hàm số y f 'x như hình vẽ bên dưới .
Hàm số g x m x 2 1
m 3 m thỏa mãn tính chất : mọi tam giác có độ dài là
ba cạnh là a, b,c thì có các số g a , g b , g c là ba cạnh của một tam giác. Khẳng định 2
nào sau đây đúng về hàm số y f mx m 1 mx 1 e y
y f 'x O 1 4 x CỌHN TOÁ 4
A. Hàm số đồng biến trên khoảng ; 1 U 3 IỆL 1
B. Hàm số nghịch biến trên khoảng ;0 3 TƯ
C. Hàm số nghịch biến trên khoảng 1; 2 và đồng biến trên khoảng 4; 9 VÀ
D. Hàm số nghịch biến trên khoảng 1; 4 và đồng biến trên khoảng 4; 9 CHÍ Lời giải P
a,b,c 0 Ạ T
a b c 0
Ta có a, b,c là độ dài ba cạnh của một tam giác nên *
c b a 0
a c b 0
Ba số a , b , c , R là độ dài ba cạnh của một tam giác a 0 b 0 0 c 0 0
a b c 0 0
a b c 0 2 2
a b c 0
Áp dụng vào bài toán
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 94
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ 1 m 0
Từ giả thiết ta có 2
m 3 0 m 3 m 3 1m 2 m 3 0
Với m 3 thì hàm số mx y 1 e
đồng biến trên R 2 2
Xét hàm số y
f mx m 1
y' 2m mx m
1 . f ' mx m có 1
mx m 1 0
Ta có y ' 0 mx m 1 1 .
mx m 1 2
Do m 3 nên phương trình y ' 0 có 5 nghiệm phân biệt . 3 m 2 m 1 m 1 m x x x x 1 x 1 2 3 4 5 . m m m m 2
Bảng xét dấu đạo hàm của hàm số y
f mx m 1 như sau: x x x x x x 1 2 3 4 5 y ' 0 0 0 0 0 OÁNT 2
Suy ra hàm số h x f mx m 1 mx 1 e
đồng biến trên các khoảng C
3 m 2 m 1 m 1 m ; ; ; 1 ; ; m m m m YMPI 4 1 m 1 m OL
Với m 3 thì ; 1 ; 1 và (1;) ;
nên A đúng và B,C,D sai 3 m m C Ụ Bài toán 33
Cho f x liên tục trên
và có đồ thị hàm số y f x như hình vẽ y NH PH CHI 2 O 2 x 4
Bất phương trình sau nghiệm đúng với mọi x 1; 2 khi và chỉ khi :
f xm f x 3 4
m 5 f x 2 5m
A. f 1 m 1 f 2
B. f 2 m 1 f 1
C. f 2 m 1 f 1
D. f 2 m 1 f 1 95
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Lời giải
Từ đồ thị của hàm số suy ra bảng biến thiên x 1 2 f 'x f 1 f x f 2
Từ bảng biến thiên ta suy ra f 2 f x f 1 ,x 1; 2
f 2 m f x m f 1 m,x1;2
Đặt t f x m f 2 m t f 1 m,x 1; 2 3t 4t 5 2 3t 4t t 5t 2 0 1
Giả thiết tương đương C t Ọ 0
Xét phương trình 3t 4t 5t 2 0 H t 1 N
f 2 m 0
Dùng phương pháp xét dấu 1
0 t 1 f 2 m 1 f 1 f 1
m 1 TOÁ U Bài toán 34
IỆL Cho hàm số f x 3 ax 2
bx cx d a,b,c,d có đồ thị như hình vẽ : TƯ y
y f x VÀ CHÍ 4 P ẠT O 1 3 4 x
Phương trình f f f f x 0có tất cả bao nhiêu nghiệm thực phân biệt A. 12 B. 40 C. 41 D. 16 Lời giải
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 96
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ 2
Dựa vào đồ thị ta có f x ax x 3 đi qua điểm A1; 4
a a f x 3 x 2 4 4 1 6x 9x
x 0 f x 0 f f f f x 0 Phương trình vô nghiệm
x 4 f x 4 f f f f x 4 Phương trình vô nghiệm
Với x 0;4 đặt x 2 2 cost t 0;
f x t2 t2 t 3 2 2 cos 6 2 2 cos 9 2 2 cos
8cos t 6 cos t 2 2 cos 3t 1
Ta chứng minh được ' 2 cos3n f x
1 với f ' x f f f f f....
f f f f x 4
2 cos 3 t 1 2cos81t 1 81t 81t 2k 1
Có f f f f x 0 2cos81t 1 0 cos 0
k t 2 2 2 81 2k 1 Do t 0; 0
0 k 40 . Vậy có 41 giá trị 81 OÁN Bài toán 35 T 1 3 4 2 1 4 C
Cho hàm số f x x x x có đồ thị như hình vẽ. 3 3 3 3 y YMPI OL 1 C Ụ 1 O 1 4 x NH PH CHI
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình sau đây có 4 nghiệm
phân biệt thuộc đoạn 0; 2 f 2 x x 2 2019 15 30 16
m 15x 30x 16 m 0 A. 1513 B. 1512 C. 1515 D. 1514
Lời giải Đặt t 2
15x 30x 16, x 0;2 30 x 1
Ta cos t 'x
;t'x 0 x 1 2
2 15x 30x 16
Lập bảng biến thiên ta suy ra 1 t 4 97
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Với mỗi t 1; 4 cho ta 2 nghiệm x 0; 2
Khi đó phương trình đề cho trở thành
2019 f t mt 1 1 3 4 2 1 4 2019
t t t mt 1 3 3 3 3 m
673t 1t 1t 4 mt 1 t 1t 4 673
Xét g t t 1t 4 ,t 1; 4 , lập bảng biến thiên ta thấy phương trình đã cho có 4 9 m
nghiệm phân biệt thuộc đoạn 0;2
0 1514,25 m 0 4 673
Vậy có 1514 giá trị nguyên m Bài toán 36
Cho hàm số y f x có đạo hàm f 'x . Hàm số y f 'x liên tục trên tập số thực và có đồ thị như hình vẽ. C y Ọ H N 4 TOÁ U IỆ 2 L TƯ VÀ 1 O 1 2 x CHÍ P ẠT 13
Biết rằng f 1
, f 2 6 . Tổng các giá trị lớn nhất và nhỏ nhất của hàm số 4 g x 3
f x 3 f x trên 1;2 bằng? 1573 37 14245 A. B. 198 C. D. 64 4 64 Lời giải Bảng biến thiên
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 98
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ x 1 2 f 'x 0 0 6 f x 13 4
Ta có g x 2 '
3 f x f 'x 3 f 'x x 1
Xét trên đoạn 1; 2 có g'x 0 3 f 'x 2
f x 1 0 f 'x 0 x 2 Bảng biến thiên x 1 2 g'x 0 0 g 2 OÁNT g x C g 1 YMPI 1573
Suy ra min g x g 1 3
f 1 3 f 1 1;2 OL 64 C Bài toán 37 Ụ
Cho hàm số f x có đồ thị như hình vẽ. y NH PH CHI 1 3 O x 4
Bất phương trình x 3 x f e
m e 2019 có nghiệm x0;1 khi và chỉ khi 4 f e
A. m 4 B. m C. m 2 D. m 1011 3e 2019 1011 3e 2019
Lời giải Đặt x
e t t 0 . Ta đưa bất phương trình đã cho thành bất phương trình ẩn t. từ đó lập
luận để có phương trình ẩn t có nghiệm thuộc 1; e 99
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Ta chú ý rằng hàm số y f x với y f t có tính chất giống nhau nên từ đồ thị hàm số
đã cho ta suy ra tính chất hàm f t
Sử dụng phương pháp hàm số để tìm m sao cho bất phương trình có nghiệm
Bất phương trình m f x có nghiệm trong a; b khi m min f x a;b Cách giải
Xét bất phương trình x 3 x f e
m e 2019 * Đặt x
e t t 0 với x t 0 1 0;1
e ; e t 1; e f t
Ta được bất phương trình f t m3t 2019 m 1 3t 2019 f t
f ' t 3t 2019 3 f t
Ta xét hàm g t
trên t 1; e g'x 3t 2019 3t 20192 y f t y f x C Thấy đồ thị hàm số
có tính chất giống với đồ thị hàm số nên trên Ọ
khoảng đang xét f t 0 và đồ thị hàm số đi lên từ trái qua phải hay hàm số đồng biến H N
trên 1; e nên f 't 0
Từ đó g 't 0 với t 1; e hay hàm số g t đồng biến trên 1; e TOÁ U
Ta có bảng biến thiên của g t trên 1; e IỆL t 1 2 g't TƯ g e VÀ g t CHÍ P 2 Ạ 1011 T f t
Từ bảng biến thiên ta thấy để m
có nghiệm t 1; e thì m 2 3t 2019 1011
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 100
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 38
Cho hàm số y f x . Hàm số y f 'x có đồ thị như hình vẽ y 1 1 O 1 x f x x 3 2 Bất phương trình
m đúng với mọi x 0;1 khi và chỉ khi 36 x 1 f 1 9 f 1 9 A. m B. m 36 36 f 1 1 f 1 1 C. m D. m OÁN 36 3 2 36 3 2 T C Lời giải f x x 3 2 Đặt g x
. Cần chứng minh m g x ,x 0; 1 . Xét g x trên 0; 1 YMPI 36 x 1 OL f ' x 1
gx f x 1 , có g 'x 0 2 C 36 x 3 2 36
2 x 3 x 3 2 Ụ
Do f 'x 1, x 3 2 f 1 1 f 1 9 NH PH
Suy ra m lim g x x1 36 4 36 CHI 101
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 39
Cho hàm số y f x có đạo hàm trên
và có đồ thị như hình vẽ. y 3 1 1 x 1 O 2 1 C Ọ H
Đặt hàm số y g x f 3
2x x 1 m . Tìm m để max gx 10 . 0; 1 N
A. m 13
B. m 3
C. m 12
D. m 1 TOÁ
Lời giải U g' x 3
f 2x x 1 m 3 2 IỆ Ta có
' f '2x x 16x 1 L f ' 3
2x x 1 0 3
2x x 1 1 x a TƯ
g'x 0 2 6x 1 3 0VN
2x x 1 1 x 0 VÀ
Ta có bảng biến thiên như sau t CHÍ 0 a 1 P g't 0 ẠT g 0 g 1 g t g a
Vậy hàm số đạt giá trị lớn nhất tại x 0 hoặc x 1
Có g 0 f 1 m m 3; g 1 f 2 m m 3
Mà max g x 10 m 3 10 m 13 . 0;1
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 102
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 40 f x
Cho hàm số f x , g x có đồ thị như hình vẽ. Đặt h x . Tính h '2 gx y g x 7 6 f x 2 O 2 4 10 x
A. h 4 ' 2
B. h 4 ' 2
C. h 2 ' 2
D. h 2 ' 2 OÁN 49 49 7 7 T Lời giải C
Xét x ; 4. YMPI
Ta có đồ thị y g x là đường thẳng nên g x có dạng g x ax b và đồ thị y g x đi OL
qua hai điểm 0; 3 và 2;7 nên g x 2x 3 . C 2 Ụ
Ta có đồ thị y f x là parabol nên f x có dạng f x cx dx e và đồ thị y f x đi
qua điểm 0; 6 và có đỉnh là 2; 2 nên f x 2
x 4x 6 . 2 f x x 4x 6 NH PH Suy ra h x
khi x ; 4.
gx 2x 3 CHI
2x 42x 3 2 2x 4x 6
Ta có h 'x 2 mà
;4 nên h 4 ' 2 . 2x 32 49 103
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 41
Hình vẽ là đồ thị y f x . y 3 O 1 x 3 CỌ 6 H N
Tập hợp tất cả các giá trị của m để phương trình 2
f x f x f x m 2 1 1 3 1 2
f x 1 2 f x 1 1 TOÁ 4; 2 a;b 2a 3b U Có nghiệm trên
là đoạn . Khi đó bằng? IỆL A. 4 B. 5 C. 6 D. 7
Lời giải TƯ
Đặt h x 1, x 4; 2 h 3;1 3 f h 2 0 f h 3 VÀ
Đặt t f x 1 ,t 0; 3 CHÍ 2 2 Khi đó 3
t t m 2 3 2
t 2t 1 t 1 2 t mt 1 t 2 m P Ạ
Suy ra 0 2 m 3 1 m 2 2a 3b 4 . T
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 104
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 42 Cho hàm số y 3 ax 2
3bx 2cx d a 0 có đồ thị như hình vẽ. y 1 2 x O 3 a Hàm số y 4
x a b 3
x b c 2 3
x d 2cx d 2019 nghịch biến trên khoảng nào 4 OÁN sau đây ? T 2; C A. ;0 B. 0; 2 C. 1; 2 D. Lời giải 3 2 YMPI
Ta có y ' 3ax x 2 y ax 3ax d OL
Dựa vào đồ thị ta có y 0 1 d 1; y 2 3 4a d 3 a 1 C 3 2 Ụ
Suy ra y x 3x 1 b 1,c 0 y 1 4 x 2
3x x 2018 Hàm số nghịch biến trên khoảng 1;2 4 NH PH Bài toán 43 CHI
Cho hai hàm đa thức y f x , y g x có đồ thị là hai đường cong ở hình vẽ bên. y A
y f x
y g x B O x
Biết rằng đồ thị hàm số y f x có đúng một điểm cực trị là A , đồ thị hàm số y g x 105
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
có đúng một điểm cực trị là B và AB 7 . Có bao nhiêu giá trị nguyên của tham số m 4
thuộc khoảng 5; 5 để hàm số y f x g x m có đúng 5 điểm cực trị? A. 1 B. 3 C. 4 D. 6
Lời giải y A
y f x
y g x C B Ọ x x x H 1 O 0 2 x N
Ta đặt h x f x g x h x 0 có hai nghiệm x x 1 2 . TOÁ 7 U
Ta có hx f x gx hx 0 x x , x x x
h x f x g x 0 1 0 2 , 0 0 0 IỆ 4 L Bảng biến thiên x TƯ x 0 h'x 0 VÀ CHÍ P h x ẠT 7 4
Suy ra bảng biến thiên của hàm số y h x là: x x x x 1 0 2 h x ' 0 h x 7 4 0 0
Do đó hàm số y h x m cũng có ba điểm cực trị,
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 106
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
Vì số điểm cực trị hàm số y h x m bằng tổng số điểm cực trị của hàm số
y h x m và số nghiệm đơn và số nghiệm bội lẻ của phương trình hx m 0 , mà
hàm số y h x m cũng có ba điểm cực trị nên hàm số y h x m có đúng 5 điểm
cực trị khi phương trình h x m 0 có đúng hai nghiệm đơn (hoặc bội lẻ)
Dựa vào bảng biến thiên của hàm số y h x , phương trình h x m 0 có đúng hai 7 7
nghiệm đơn (hoặc bội lẻ) khi và chỉ khi m m 4 4 Vì m m 7 ,
và m 5; 5 nên m4; 3; 2 . 4 Bài toán 44
Cho hàm số y f x liên tục trên
và hàm số y f 'x có đồ thị như hình vẽ y 2 3 4 x OÁNT O C YMPI OL C Ụ NH PH
f xm f x m m
Bất phương trình f x 2 5
2 27 nghiệm đúng với x2;3 CHI 27
A. f 3 m f 3 1
B. f 2 1 m f 3
C. f 2 2 m f 3
D. f 3 m f 2 2 Lời giải
Ta có với x 2; 3 thì f 'x 0
Ta có f 3 f x f 2 ,x 2; 3 ; f 3 2m f x m f 2 m
Đặt t f x m f 3 m t f 2 m
f xm f x m m
Ta có f x 2 5 2 27 27
f xm f x 2 5
m 2 27 f x m 0 2t 5t 27t 2 0
Vế trái chỉ có 2 nghiệm t 0;t 2 107
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
f 3 m 0
Ta có 0 t 2
f 2 2 m f 3
f 2 m 2 Bài toán 45
Cho hàm số y f x liên tục trên
và có đồ thị như hình bên dưới: y 2 1 O x 1 C 2 Ọ H N
Biết rằng trục hoành là tiệm cận ngang của đồ thị. Tìm tất cả các giá trị thực của tham số
m để phương trình 2log4 2 4m f x
có hai nghiệm dương phân biệt. TOÁ
A. 0 m 2.
B. 0 m 1.
C. 1 m
D. m 0. U IỆ
Lời giải L Ta có 2log4 2 4m f x 2 1 2 m f x TƯ
Phương trình (*) có hai nghiệm dương phân biệt 2m1 2 2 m 0. VÀ Bài toán 46 f x
y f ' x CHÍ
Cho hàm số có đạo hàm liên tục trên R và có đồ thị của hàm số như hình P vẽ bên dưới. ẠT y
y f 'x 1 O 5 x b
Để hàm số y f 3
2x 6x 3 đồng biến với mọi x m m R thì m asin trong đó c b a b c * , , ,c 2b S 2a 3b c
và là phân số tối giản). Tổng bằng c A. 7 B. 9. C. 2. D. 5.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 108
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Lời giải
Đặt g x f 3
2x 6x 3 , ta có y g x 2
x f 3 ' ' 6 6.
2x 6x 3 2 x 1 0 2 x 1 0 3 f '2x 6x 3 3 0
2x 6x 3 5
Hàm số đồng biến khi và chỉ khi g 'x 0 2 x 1 0 2 x 1 0 3 3 f ' 2x 6x 3 0 2x 6x 3 5 2 x 1 0 2 x 1 0 3
2x 6x 3 3 5
2x 6x 2 0
x ;1,53 1;0,35 1;1,88 2 x 1 0 2 x 1 0 3
2x 6x 3 5 3
2x 6x 2 0 Xét phương trình 3
x 3x 1 . Với x 2 thì phương trình vô nghiệm. 1
Với x 2 . Đặt x 2 cost 3
8 cos t 6 cost 1 cos 3t ta được phương trình có 3 2 5 7
nghiệm x 2 cos ; x 2 cos ; x 2 cos
suy ra phương trình y ' 0 có 6 nghiệm OÁN 9 9 9 T 7 5 C
x 2 x 2 cos x 1 x 2 cos x 1 x 2 cos 1 ; 2 ; ; ; ; 9 3 4 9 5 6 9 7 5 YMPI
Vậy hàm số đồng biến trên các khoảng 2 cos ; 1 ; 2 cos ;1 ; 2 cos ; 9 9 9 OL 7 C
Hàm số đồng biến với mọi x mm m;
2 cos ; m 2 cos 2 sin Ụ 9 9 18
Vậy a 2; b 7; c 18 Bài toán 47 NH PH
Cho hàm số 3 2 f x x
bx cx d và g x f mx n có đồ thị như hình vẽ : CHI y f x g x 1 x O 1 2
Hàm số f x đồng biến trên khoảng có độ dài bằng k , hàm số g x đồng biến trên
khoảng có độ dài bằng 2k . Giá trị biểu thức 2m n là A. 3 B. 0 C. 1 D. 5 109
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Lời giải
Ta có f x 3 x 2
bx cx d f x 2
3x 2bx c
Hàm số đạt cực trị x 0 tại và đồ thị hàm số đi qua điểm 1;0 nên f 0 0 b 2 f 0
1 c 0 f x 3 x 2 2x 1 f 1 0 d 1
Hàm số f x đồng biến trên khoảng có độ dài bằng k , hàm số g x đồng biến trên
khoảng có độ dài bằng 2k suy ra m 1 2 3 2
Ta có g x mx n 2 mx n 1 . Hệ số tự do bằng 3 n 2
2n 1 Đồ thị hàm số g x
cắt trục tung tại điểm 0; 2 nên 3 n 2 n 3 n 2 2 1 2
2n 3 0 n 1
Vậy 2m n 0 C Ọ Bài toán 48 H
Cho hàm số bậc ba f x và g x f mx n ,m;n có đồ thị hàm số như hình vẽ : N y TOÁ U g x IỆ 3 L TƯ O x VÀ 2 1 CHÍ P ẠT f x
Hàm số g x nghịch biến trên khoảng có độ dài bằng 5. Giá trị biểu thức 3m 2n là 16 A. 5 B. 13 C. D. 4 5 5 Lời giải
Ta có f x 3 ax 2
bx cx d f x 2
3ax 2bx c
Hàm số đạt cực trị tại x 0; x 2 và đồ thị hàm số qua điểm 0; 1 ,2; 3 nên f 0 0 a 1 f 2 0 b 3 f x 3 2 x 3x 1 f 0 1 c 0 f 2 d 3 1
Hàm số f x đồng biến trên độ dài khoảng đồng biến bằng 2
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 110
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
Hàm số g x f mx n nghịch biến trên khoảng có độ dài bằng 5 nên g x f mx n
đồng biến trên khoảng có độ dài bằng 5 suy ra m 2 5 3 2
Ta có g x mx n 3mx n 3 2
1 .Hệ số tự do bằng : n 3n 1 Đồ thị hàm số n
cắt trục tung tại điểm 0; 1 nên 3 n 2 n 3 n 2 3 1 1
3n 2 0 n 1
Vậy m n 16 3 2 5 Bài toán 49
Cho hai hàm số f x và g x có đồ thị như hình vẽ y g x f x 1 2 x OÁN O 1 T C YMPI OL C
Biết rằng hai hàm số y f 2x 1 và y 3g ax b có cùng khoảng đồng biến.Giá trị Ụ
biểu thức a 2b là A. 3 B. 4 C. 2 D. 6 NH PH
Lời giải
Ta có hàm số f x nghịch biến trong khoảng 0; 2 nên hàm số f 2x đồng biến trong CHI 1 1 1
khoảng 1; 0 . Hàm số y f 2x 1 f 2 x
đồng biến trong khoảng ; 2 2 2 1 1
Để hàm số y 3g ax b có cũng đồng biến trong khoảng
; thì y gax b đồng 2 2 1 1 biến trong khoảng ; 2 2 1 1
Mà hàm số g x đồng biến trong khoảng 1; 1 a
2;b 0 a 2b 2 1 1 2 111
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 50 Cho hàm số 4 2 f x ax
bx c và g x f mx n p ,m;n; p có đồ thị như hình vẽ y 2 3 f x 2 1 O 1 x g x CỌH N
Giá trị biểu thức m n 2p là A. 4 B. 2 C. 5 D. 6 TOÁ Lời giải U IỆ 3 L
Ta có giá trị lớn nhất của hàm số f x là 2 và giá trị lớn nhất của của hàm số g x là 2 TƯ Suy ra p 1 2 VÀ
Đồ thị hàm số có 2 điểm cực đại là 1; 2 ,1; 2 và 1 điểm cực tiểu là 0; 1 nên
f 1 f CHÍ
1 0 a 1 P
f 1 f 1 2 b 2 f x 4 x 2 2x 1 ẠT f 0 1 c 1
Dựa vào đồ thị ta có hàm số y f x đồng biến trên khoảng 2k thì hàm số y g x đồng
biến trên khoảng k
Tương tự đối với hàm y f x nghịch biến trên khoảng 2h thì hàm số cũng nghịch biến
trên khoảng h . Suy ra m 2 4 2 1 1
Ta có g x mx n 2 mx n có hệ số tự do là 4 n 2 2n . 2 2 3 3
Đồ thị hàm số y g x đi qua điểm 0; ;
1; nên n 1 2 2
Vậy m n 2p 4 Chọn A
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 112
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 51
Cho hai hàm số f x và g x có đồ thị như hình vẽ: y f x g x 2 1 x 1 O
Biết rằng hai hàm số y 3 f 3x 1 và y 2 f ax b có cùng khoảng đồng biến. Giá trị
biểu thức 2a b là OÁNT A. 5 B. 2 C. 4 D. 6 C
Lời giải
Ta có hàm số f x đồng biến trong khoảng 2; 0 nên hàm số y f 3x đồng biến trong YMPI 2 1 1 1 OL khoảng
;0 . Hàm số y f 3x 1 f 3 x
đồng biến trong khoảng ; 3 3 3 C 3 Ụ 1 1
Suy ra hàm số y 3 f 3x 1 cũng đồng biến trong khoảng ; 3 3 1 1 NH PH
Để hàm số y 2g ax b cũng đồng biến trong khoảng
; thì hàm số y gax b 3 3 CHI 1 1
đồng biến trong khoảng ; 3 3 1 1
Mà hàm số g x nghịch biến trong khoảng 1; 1 nên a 3,b 0 1 1 3 3 113
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 52 Cho hàm số 4 2 f x ax
bx c và g x f 2
mx nx p q,m;n; p;q có đồ thị như hình vẽ: y 1 f x x 1 O 1 1 g x C Ọ H 2 N
Giá trị của biểu thức m 2n 3p 4q là TOÁ A. 4 B. 2 C. 8 D. 6 U IỆ Lời giải L
Ta có đồ thị hàm số có 2 điểm cực tiểu 1;0 , 1;0 và 1 điểm cực đại 0;1 nên TƯ
f 1 f 1 0 a 1 VÀ 4 2 f 0 1
b 2 f x x 2x 1 f
1 f 1 0 c 1 CHÍ P
Từ đồ thị ta thấy giá trị nhỏ nhất của là 0 và giá trị nhỏ nhất của là -2 ẠT Suy ra q 2
Đồ thị hàm số 2 g x
f mx nx p q nhận trục tung làm trục đối xứng thì đồ thị hàm n số 2
y mx nx p cũng nhận trục tung làm trục đối xứng 0 n 0 2m
Ta có khi hàm số f x đồng biến 1;0 và nghịch biến 0;1 thì hàm số g x lại nghịch
biến 1;0 và đồng biến 0;1 m 1 p 0
Hàm số đạt cực trị tại x 1 g1 0 2 1 f 1 p 0 p 1 p 2 4 2
Ta có g x 2
x p 2
2 x p 1 có hệ số tự do là 4 p 2
2p 1 . Đồ thị hàm số g x đi
qua điểm 0; 2 nên 4 p 2
2p 1 2 p 1
Suy ra p 1 m 2n 3p 4q 6
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 114
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 53
Cho hàm số y f x liên tục trên
và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị
thực của tham số m để phương trình f 4 x m có nghiệm thuộc nửa khoảng 2; 3 là y 3 1 2 1 O 2 x 1
A. 1; 3 B.
1; f 2 C. 1; f 2
D. 1; 3 OÁN T
Lời giải C
Một bài toán đồ thị hàm ẩn rất quen thuộc, có lẽ ta không cần bàn đến nó nhiều nữa ! x YMPI
Đặt 4 x t , ta có t '
, rõ ràng t ' 0 x 0 4 2 x OL C
Phương trình tương đương với f t m . Cần tìm m để phương trình này có nghiệm Ụ
t 1; 2. Tập giá trị của hàm số f xtrên 1;2 là 1;3. Bài toán 54 NH PH
Cho hàm số y f x liên tục trên
có đồ thị như hình vẽ. Phương trình f 2 f x CHI
0 có tất cả bao nhiêu nghiệm thực phân biệt ? y 1 1 2 2 O 1 x 3 A. 4 B. 5 C. 6 D. 7 Lời giải 115
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
x a2 a 1
2 f x a
f x a1
Ta có f x 0 x b 0 b 1 f 2 f x 0 2 f x b f x b 2
x c1 c 2 2 f x c f x c 3
a2;1 2 a3; 4 , do đó 1 có đúng 1 nghiệm.
b 0;1 2 b1;2 nên 2 có 1 nghiệm duy nhất.
c 1;2 2 c 0;1 nên 3 có 3 nghiệm phân biệt.
Vậy phương trình có 5 nghiệm. Bài toán 55
Cho hàm số f x . Đồ thị hàm số f 'x trên 3; 2 như hình vẽ (phần cong là 1 phần của Parabol 2
y ax bx c ). Biết f 3 0 . Giá trị của f 1 f 1 bằng bao nhiêu? y C 2 Ọ H N 1 TOÁ U 3 2 1 O 2 x IỆL 23 31 35 TƯ 9 A. B. C. D. 6 6 3 2 VÀ
Lời giải Parabol 2
y ax bx c có 2 nghiệm 3; 1 nên có dạng y ax 1x 3 CHÍ P
Vì Parabol đi qua điểm 2; 0 nên a 1 . ẠT 1
Để tính f 1 , ta xét : f 1 f 3
f 'xdx S S S 1
2 , trong đó 1 là diện tích tam giác 3 1
có 3 đỉnh tọa độ 1;0 , 0; 2 , 0;0 nên S .1.2 S 1 ;
là diện tích hình thang có các đỉnh 2 2 1 3
0;0 , 0;2 , 1;1 , 1;0nên S .2 1 . 2 2 2 5 4 31
Do đó f 1 f 1 f 1 f 1 2 f 1 2. . 2 3 6
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 116
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 56
Cho hàm số y f x lên tục trên
và có f 0 0 và có đồ thị hàm số y f 'x như
hình vẽ. Hàm số y f x 3 3
x đồng biến trên khoảng nào? y 4 1 O 1 2 x
A. 2;
B. ; 2 C. 0; 2 D. 1; 3 OÁN T Lời giải C
Xét hàm số g x f x 3 x
g x f x 2 3 , ' 3 ' 3x . x 0 YMPI 2
Vẽ đồ thị hàm số 2
y x trên cùng một trục tọa độ ta thấy g'x 0 f 'x x x 1 OL x C 2 Ụ
Từ đó ta có thể lập bảng biến thiên của hàm số g x , chú ý rằng g 0 3 f 0 0
Dựa vào bảng biến thiên ta thấy hàm số g x đồng biến và nhận giá trị dương trên 0; 2 NH PH
nên hàm số g x đồng biến trên 0; 2 . CHI
Chú ý. Bảng biến thiên các bạn tự lập nhé ! 117
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 57
Cho hàm số y f x liên tục trên
có đồ thị như hình vẽ. Gọi M và m tương ứng là 3
GTLN và GTNN của hàm số y f 1 cos x trên 0;
. Giá trị của M m bằng : 2 y 2 1 O 1 2 3 x C 1 Ọ 3 H 2 N 1 3 A. 2 B. 1 C. D. TOÁ 2 2 U
Lời giải IỆL 3
Đặt 1 cos 2x t , dễ thấy x 0;
thì cos x 1;1 , do đó t 1;3. 2 TƯ 3 3 1
Dựa vào đồ thị ta thấy max f t 2 và min f (t)
nên M m 2 . VÀ t [1;3] t [1;3] 2 2 2 Bài toán 58 CHÍ 3 2 P
Cho hàm số bậc ba f x ax bx cx d có đồ thị như hình vẽ. Hỏi đồ thị hàm số Ạ 2 T
x 3x 2. g x x 1
có bao nhiêu đường tiệm cận x. 2
f x f x y 1 O 1 2 x A. 3 B. 4 C. 5 D. 6 Lời giải
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 118
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
2x 3x2. x1 x1 x1x2
Ta có g x x. 2
f x f x
x. f x.
f x 1
Dựa vào đồ thị ta thấy f x 0 có 3 nghiệm x m 0;1 , x 2, với nghiệm x 2 là 2
nghiệm kép nên f x ax mx 2 .
Phương trình f x 1 có 3 nghiệm x 1, x n 1; 2 , x p 2; nên
f x 1 ax 1x nx p .
x 1 x 1 x 2 x 1
Do đó g x x. .
a x mx 22 . .
a x 1x nx p 2
a .x.x 2x mx nx p
Số tiệm cận đứng là 3, gồm các đường x 2, x n, x p (loại đường thẳng x 0 và
x mdo m 1).
Số tiệm cận ngang là 1, đó là đường y 0 .
Vậy có 4 đường tiệm cận Bài toán 59
Cho hàm số y f x lên tục trên
có đồ thị như hình vẽ dưới. OÁNT
Phương trình f f x 1 0 có tất cả bao nhiêu nghiệm thực phân biệt? C y YMPI 1 OL C 2 1 x Ụ 1 O 2 NH PH CHI 3 A. 4 B. 5 C. 6 D. 7
Lời giải
x a 2 a 1
Dựa vào đồ thị ta thấy f x 0 x b 1 b 0
x c 1 c 2
f x 1 a
f x a 1
Do đó phương trình f f x 1 0 f x 1 b f x b 1 f x 1 c
f x c 1
Phương trình f x a 1có a 11; 0 nên có 3 nghiệm phân biệt. 119
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Phương trình f x b 1có b 10; 1 nên có 3 nghiệm phân biệt.
Phương trình f x c 1 có c 12; 3 nên có đúng 1 nghiệm.
Vậy phương trình đã cho có 3+3+1=7 nghiệm. Chọn D. Bài toán 60
Cho hàm số y f x có đồ thị hàm số y f 'x 1 như hình vẽ. Hỏi đồ thị hàm số f x 2 ( ) 4x y
đạt cực tiểu tại điểm nào y 2 CỌH 1 O 1 2 x N TOÁ 2 U IỆ
A. x 1
B. x 0
C. x 1
D. x 2 L Lời giải TƯ
2 f x4x Xét f x
y 2( ( ) 4x) có y'
.ln 2 f 'x 4 VÀ
Hàm số đạt cực tiểu tại điểm x y o thì
' phải đổi dấu từ âm sang dương khi x đi qua điểm CHÍ
đó. Dựa vào đồ thị, ta thấy chỉ có điểm x 1 làm f 'x 2 đổi dấu từ âm sang dương P Ạ khi x đi qua. T
Vậy hàm đạt cực tiểu tại x 1 . Chọn C.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 120
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 61
Cho hàm số y f x lên tục trên
. Hàm số y f 'x có đồ thị như hình vẽ. Hàm số 2019 2018x g x f x 1
đồng biến trên khoảng nào dưới đây 2018 y 1 1 O 1 2 x 1 A. 2; 3 B. 0; 1
C. 1; 0 D. 1; 2
Lời giải OÁNT x 1 1 x 0
Ta có y ' f 'x 1 1 . Ta có y ' 0 f 'x 1 1 C x 1 2 x 3
Vậy hàm số đồng biến trên 1; 0 . YMPI Bài toán 62 OL C
Cho hàm số y f x có đồ thị như hình vẽ. Tổng các giá trị nguyên của tham số m để Ụ
phương trình f f x 1 m có 3 nghiệm phân biệt bằng y NH PH 14 CHI 2 O 2 1 1 3 x 13 A. 15 B. 14 C. 13 D. 11 Lời giải
Đặt f x 1 t , phương trình đã cho tương đương với f t m
Nếu phương trình f t m có nhiều hơn một nghiệm t (nghĩa là 1 m 2 ), giả sử 2 121
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
nghiệm trong số đó là t t 0; 3
1 và 2 , dựa vào đồ thị, ta thấy các nghiệm này đều thuộc ,
do đó t 1;t 11; 2 f x t 1 f x t 1 1 2
, nên các phương trình 1 và 2 đều có 3
nghiệm phân biệt . do đó phương trình f f x 1 m có ít nhất 6 nghiệm( loại ).
Vậy phương trình f t m có đúng 1 nghiệm, giả sử là nghiệm t0 . Phương trình tương
ứng với f x t 1 0
, phương trình này có 3 nghiệm phân biệt khi và chỉ khi
t 11;2 t 0;3 f t m 1 0
. Vậy cần tìm m để phương trình có đúng 1 nghiệm, 2,m 14
nghiệm đó thuộc 0; 3 . Điều này xảy ra khi và chỉ khi 13 m 1
Mà m m 3; 4;...;
13 12;11;...;
2 . Tổng các giá trị của m là 11 Bài toán 63
Cho 2 điểm A, B thuộc đồ thị hàm số y sin x trên 0; , các điểm C, D thuộc trục C Ọ
Ox sao cho tứ giác ABCDlà hình chữ nhật là CD 2 . Độ dài cạnh BC là? 3 H y N A B TOÁ U O x IỆ D C L TƯ VÀ 2 1 A. B. C. 1 D. 2 2 2 CHÍ P
Lời giải Ạ 2 T
Giả sử Dx ;0 C x ;0 x x 1 , 2 với 2 1 3 1 1
Ta có y y x x x x x y sin A B sin sin 1 2 1 2 . Do đó 1 BC= 6 A 6 2 2
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 122
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
Nào chúng ta cùng đổi chủ đề xíu trước khi quay lại đồ thị hàm số chương 1. Chủ đề tiếp
theo của chúng ta là đồ thị liên quan tới tích phân. Trong chủ đề này chúng mình sẽ giới
thiệu cho bạn đọc một số bài toán được 3 thành viên là Nguyễn Thị Kim Anh, Nguyễn
Quang Phát và Nguyễn Minh Tuấn sáng tác, để làm tốt được các bài này các bạn cần phải
nắm vững các kiến thức về diện tích hình phẳng, cực trị, đạo hàm v.v.. Nào chúng ta cùng
bắt đầu chủ đề này nhé! Bài toán 64
Cho hàm số f x 4 mx 3 nx 2
px qx r r 0 có nghiệm. Hàm số y f 'x có đồ thị
như hình vẽ dưới. Số nghiệm của phương trình f x r là? y x1 OÁN x0 O x T C YMPI A. 2. B. 4. C. 3. D. 1. OL Lời giải C Ụ
Xét hàm số g x f x 2r . Suy ra g x' f x'.
Dựa vào diện tích tích phân ta thấy 1 x 1 x
g' x dx g' x dx g x g 0 g x g x g x g 0 NH PH g x 1 1 0
1 0 . (1) 0 0 x CHI
Theo đề bài thì r 0 g 0 0 g x ' . Từ giả thiết nghiệm x’ của f x thuộc khoảng ;x g x' g x 0 nên 0 . (2)
Từ (1) và (2) suy ra phương trình f x r có 4 nghiệm. Chọn ý B. 123
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 65 4
Cho f x như hình vẽ. Biết f ' x dx
60 . Giá trị của f 2 f 2 là ? 1 y 3 O x 2 10 A. . B. 31 . C. 12 . D. 32 . 3 3 3 3 C Lời giải Ọ H
Phân tích : Một bài toán tìm dạng của hàm số ! N
Đồ thị hàm f x có cực trị tại x 0 và x 3 nên f 'x có dạng k. .
x x 3 . 4 4 TOÁ
f ' xdx 60 f 'x 60 f '4 f '1 60 28.k 2.k 60 k 2 . 1 U 1 IỆ 2 3 2 L
Nên f 'x 2. .
x x 3 f x x 3x r . 3 TƯ 2
Nhìn đồ thị, ta thấy x 0; y 2 r 2 f x 3 x 2 3x 2. 3 VÀ
Suy ra f f 32 2 2 . 3 CHÍ P Chọn ý D. ẠT
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 124
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 66
Cho f x liên tục trên
có đồ thị hàm số như sau. Tìm số điểm cực trị của gx 2 x
1 f tdt 2019 y f x 3 1 O 2 x A. 1 B. 3 C. 5 D. 7 Lời giải OÁNT x 0 C x 2 0 x 1 3 2 x 2 L
Có g x xf 2 ' 2
x 1 . Xét g'x 0 2 2 2 f x 1 0
x 1 1 x 0 YMPI 2 x 1 2 2 x 3 OL
Nhưng để g x đạt cực trị thì g 'x phải đổi dấu qua đạo hàm. Nhận thấy chỉ có duy C Ụ
nhất TH x 0 thỏa mãn. Chọn ý A. Bài toán 67 NH PH
Cho đồ thị hàm g x hàm bậc 4 như hình vẽ, biết g x f x f 1 x và f 0 g 0 . CHI 2 x
Tính tích phân xf ' dx ? 2 0 y O 1 x A. 1 B. 1 C. 5 D. 1 10 5 125
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Lời giải
Từ đồ thị ta suy ra g x 3
x x 3 1
x 1 x f x f 1 x 1 1
Từ * tích phân hai vế ta được f x dx
. Thay x 0 vào * ta được f 1 0 40 0 2 2 2 x x x 1
Tích phân từng phần được xf '
dx 2 x. f f dx = . 2 2 2 10 0 0 0 Chọn ý B. Bài toán 68
Cho đồ thị hàm số là nguyên hàm của f x có dạng F x 3 ax 2
bx 5x d . Tính diện
tích tạo bởi f x và trục hoành ? y CỌHN 4 4 O x TOÁ U IỆL 80 20 50 70 . . . . TƯ A. B. C. D. 3 3 3 3 VÀ Lời giải
Phân tích : Ý tưởng bài này cũng giống như ý tưởng bài trước. CHÍ
Ta có F x 2 '
3ax 2bx 5 nên F '0 5 f 0 5 P Ạ
Từ 2 điểm cực trị có hoành độ là -4 và 4 ta có thể vẽ đại khái đồ thị của f x như sau T f x 2 mx nx 5
x 4 16m 4n 5 0 5 5 Có m
f x 2 x 5 .
x 4 16m 4n 5 0 16 16 4 4 5 80 Suy ra f x 2 x 5 . 16 3 4 4 80
Vậy diện tích cần tìm là . 3 Chọn ý A.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 126
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 69
Cho đồ thị hàm số f 'x như hình vẽ. Biết diện tích 2 hình S ,S 1 2 lần lượt là 3,2, 1 1
f 1 5 . Tính giá trị của tích phân x x e f x dx
e f 'xdx ? 0 0 y 2 2 O 1 x 3
A. e 3.
B. 2e 2.
C. 4e 3.
D. 5e 3. Lời giải
Phân tích. Bài này quan trọng là biến đổi tích phân thôi nhé ! 1 1 1 x e f x dx x e f ' x dx x e f x x OÁN Ta có
e f 'xdx T 0 0 0 C 1
x 'dx x e f x
e f x 1 .e f 1 1. f 0 (1) 0 0 YMPI
Diện tích 2 hình S ,S 1 2 lần lượt là 3,2 nên OL 1 1 C
f 'xdx f x f 1 f 0 f 0 5 2 3 . 0 Ụ 0 Thay vào (1) ta được .
e f 1 f 0 5e 3 . 1 1 x x NH PH
Vậy e f x dx e f 'x dx 5e 3 . 0 0 CHI Chọn ý D 127
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 70 9
Cho đồ thị hàm số bậc 3 f x như hình vẽ. Biết S , a b 3 và f '0 1 . Tính 4
I 2a f xdx ba y f x S b O a x CỌ H A. 5 B. 7 C. 7 D. 5 N 6 6 12 12 Lời giải TOÁ
f x m x 2 a
x b m 3 x a 2 b x ab 2 a x 2 2 2 a b U Dễ thấy IỆL a 9 a 9 Ta có S 9
f xdx m x 2a bx 2ab a x a bdx b 3 2 2 2 4 4 b 4 TƯ a 4 x
2a b 3 2ab 2 a 9 x 2 x 2 a bx VÀ 4 3 2 4m b
Thay số, biến đổi, rút gọn, ta được CHÍ 4 3 2 2 3 4 P
a a b a b ab b 9 4a 3ab 2 2 a b 3 ab 4 b 27 4 6 4 Ạ 12 3 2 3 12 12m m T
a b4 27 27
m 1 f x 1 81
x a2 x b m m 3 3 1 2
f 'x 2x ax bx a . Mà f '0 1 3 1 2
a 2ab 1 2
a 2ab 3 2
a 2aa 3 3 a 1 b 2 3
f x 1 x x I 2a f xdx 2 2
1 x 2 x dx b a 5 1 2 1 2 3 3 3 12 Chọn ý D.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 128
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 71
Cho hàm số f x có đạo hàm đến cấp 2 liên tục trên 1; 4 thỏa mãn và có đồ thị như
hình vẽ dưới đây. Tính giá trị của tích phân I
f ' xx 1x 5 5dx ? 1 y 2 1 3 4 O 1 2 5 x 1 A. 4 B. 5 C. 6 D. 7 Lời giải
u x 1x 5
du 2x 6dx
Sử dụng tính chất nguyên hàm từng phần ta đặt v f ' x dx v f 'x OÁNT u 2x 6 du 2dx C
I 2x 5
6 f 'xdx . Đến đây đặt tiếp 1 v
f 'x dx v f x
I 2x 6 f x 5 2 f x dx 1 5 YMPI 1 OL
Đến đây ta sẽ tính 5 f xdx . Đặt A1;1,B2;2,C 3;1,D4;1 ,E5;1 đồng thời C 1 Ụ
M 1;0 ,N 2;0 ,P 3; 0 ,Q 4; 0 ,S 5; 0 .
Phương trình đường thẳng BC là y 3x 8 suy ra giao điểm của BC với trục 8 NH PH
hoành là điểm I ;0 . 3 CHI 4
Tọa độ giao điểm của DE với trục hoành là H ;0 5 3 Ta có
f xdx S S S S 5 . Vậy I 5 1 MABN BNI ICDH HSE 2 129
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 72
Cho đồ thị hàm số f x như hình vẽ. Biết S S S S 2 4 3
1 (hình vẽ chỉ mang tính chất
tương đối). Tính I
2 5f 55x 4x2 f 2x 4x dx 0 y S3 5 S S 2 4 S 4 O 2 3 x 1 CỌ H A. 0 B. 1 C. 23 D. 6 N 5 5 Lời giải TOÁ F x f x S S S S U
Gọi là họ nguyên hàm của . Ta có 2 4 3 1 IỆ 2 4 0 5 L
f xdx
f xdx
f xdx f x dx 0 5 4 2 TƯ
F 2 F 0 F 5 F 4 F 0 F 4 F 5 F 2 5 0 VÀ
F 5 F 5 2 F0F4
f xdx 2 f x dx 5 4
I 2 5 f 5 5x dx 2 4 x 2
2 f x 4x dx J K CHÍ Xét 0 0 P 5 5 Ạ
Đặt t 5 5x dt 5dx J
f tdt f t dt 5 T 5 4 0 Đặt u 2
x 4x dt 2x 2dx K 2
f tdt 2 f t dt 0 4
I J K 5 f tdt 0 2
f tdt 0 5 4 Chọn ý A.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 130
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 73
Cho hàm số f x có đạo hàm cấp hai f ''x liên tục trên
và đồ thị hàm số f x như
hình vẽ bên dưới. Biết rằng hàm số f x đạt cực đại tại điểm x 1 . Đường thẳng
trong hình vẽ là tiếp tuyến của đồ thị hàm số f x tại điểm có hoành độ x 2 . Tính giá x x e 1
trị của tích phân I ln3 e f '' dx ? 0 2 y
y f x OÁNT O 1 2 x C YMPI OL C 3 Ụ A. 0 B. 1 C. 6 D. 7 NH PH Vted.vn CHI Lời giải x 1 x e e dx Đặt t dt khi đó I
2f ' tdt 2 f '2 2 2 f '1 2 2 1
Ta có phương trình tiếp tuyến của hàm số y f '2x 2 f 2 đi qua điểm 0; 3 nên
có 3 2 f '2 f 2 2 f '2 f 2 3 .
Mặt khác do f '1 0 nên 0 f '2 f 2 f '2 f 2 f 2 3 I 6 Chọn ý C. 131
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 74 4 2
Cho đồ thị hàm số f x như hình vẽ. Biết
f x23mdx
f x 1 12 . 2 Giá trị của m là ? y 1 O 2 x A. 4. B. 0. C. 1. D. 2. Lời giải
Phân tích : Một bài toán lạ ! C Ọ
Ta thấy f x 2 1 với mọi x thuộc đoạn 2; 4 . H 4 N
f x 2 5 6
f x25dx 12 . 2 TOÁ 4 VP 2
f x 1 12 12 . Mà m 0 nên mdx 2m 0 m 0 . U 2 IỆL Chọn ý B. TƯ Bài toán 75
Cho đồ thị hàm số f x như hình vẽ, biết f '1 2 . Tính giá trị của biểu thức tích VÀ 2
phân f 'x ? CHÍ 2 P y ẠT 2 O 2 x 64 25 14 A. . B. C. . 3 3 3 3 3 3 D. 2. Lời giải
Phân tích : Một bài có sự xuất hiện của trị tuyệt đối !
Phương trình f x 0 có 3 nghiệm nên có thể viết dưới dạng :
kxx x k 3 2 2
x 4x . f x k 2 ' 3x 4
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 132
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ x 2 3
Ta có f 'x 0 k 2
3x 4 0 . x 2 3
f '1 2 k 2 k 2 f '0 8.
Đồ thị của f 'x có thể vẽ lại như sau y 2 O 2 x 3 3
Áp dụng công thức tính nhanh diện tích tạo bởi parabol và trục hoành OÁN 2 2 2 T 3 3 3 2 4 64 C Ta có
f 'x dx
f 'xdx f 'xdx .8. 3 3 3 3 2 2 2 3 3 3 YMPI Chọn ý A. OL Bài toán 76 C f x Ụ
Cho đồ thị của hàm số như hình vẽ bên dưới. Tính giá trị của biểu thức tích phân 3 I 2
x f 'xdx ? 0 NH PH y CHI 3 O 3 x A. 1 B. 0 C. 3 D. 4 Lời giải u 2 x du 2xdx
Ta có f 'x dx dv v f x 133
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA 3 3 3 3
I x f 'xdx x f x 3 2 2
2 f x.xdx 9.f 3
2 f x .xdx 2 f x.xdx 0 0 0 0 0 3 3 3
Vì đồ thị f x là hàm sỗ chẵn nên f x xdx
f x.x.dx
f xxdx 0 0 0 0 3 0 3
f xxdx f xxdx f xxdx f xxdx 0 3 3 3 0 3 3
Mà 2 f x.xdx
f x.x dx 0 I 0 . 0 3 Chọn ý B. Bài toán 77 x2
Cho đồ thị hàm số f x 2 như hình vẽ. Đồ thị hàm số y f 2t
2dt cắt trục Ox tại x4
C nhiều nhất mấy điểm phân biệt ? Ọ y H N TOÁ U IỆL TƯ 3 O 1 4 x VÀ CHÍ P Ạ A. 0 B. 1 C. 3 D. 4 T Lời giải x dx 1 1 Đặt 2
t 2 x 2tdt dx y f x
f x f x 2 . 2 2 2 x2
Đặt f x 2 k x 3x 1x 4 f x k x 1x 3x 6 .
f x f x 2 k 2
6x 20x 6 5 34 5 34 k x x . 3 3 x2
Nên đồ thị hàm số y f 2t
2dt có 2 cực trị nên cắt trục Ox nhiều nhất 3 điểm phân x4 biệt. Chọn ý C.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 134
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 78 11
Cho đồ thị hàm số f 'x trên đoạn 4;
(lần lượt là các đoạn thẳng và nửa parabol ). 2 0 1 6 Tính giá trị S
f '2x 3dx f '2x 2dx cos .
x f '5sin x 3dx ? 3 1 0 2 y 5 4 2 O 3 11 x 2 1 149 154 109 OÁN A. . B. . C. . D. . T 2 6 4 3 C Lời giải
Phân tích : Một bài toán cần áp dụng diện tích tích phân và sử dụng phương pháp đổi biến ! YMPI 3 x t 0 OL
Đặt 2x 3 t 2dx dt 2 . C
x 0 t 3 Ụ
x 1 m 4
Đặt 2x 2 m 2dx dm .
x 1 m 0 NH PH
x 0 n 3
Đặt 5 sin x 3 n 5 cos xdx dn .
x n 11 CHI 6 2 11 11 11 3 0 2 3 0 2 2
Nên S f 't dt
f 'mdm f 'ndn f 'xdx f 'xdx f 'xdx
f 'xdx . 0 4 3 0 4 3 4
Ta thấy rằng S chính là diện tích hình tạo bởi f 'x và trục Ox. 1
Diện tích hình tam giác là S .2.2 2. 1 2
Diện tích hình chữ nhật là S 2.2 4. 2 1 21
Diện tích hình thang là S .2 5.3 . 3 2 2 2 11 25
Diện tích nửa parabol là S . 3 .5 . 3 3 2 3 149
Diện tích hình tạo bởi f 'x và trục Ox là S S S S S . 1 2 3 4 6 135
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Chọn ý B. Bài toán 79
Cho hàm số f x 4 ax 3 bx 2
cx dx 4a . Đồ thị của f 'x như hình vẽ. Tính tích 2 2 phân
f ' x.f x f 'x dx ? 1 y O x 10 10 2 2 CỌ H A. 2. B. 1. C. 0. D. 3. N Lời giải TOÁ
Phân tích. Ta chỉ cần rút gọn tích phân và khai thác từ đồ thị là ra được bài toán ! U 10 10 2 5 IỆ
Nhìn đồ thị ta có f 'x axx x ax x . L 2 2 4 2 2 TƯ f 'x 2 5 dx x x
x 1x 1x 2x 2 . 4 1 1 VÀ
Ta có thể viết f x dưới dạng f x ax 1x 1x 2x 2 r .
a q x 4a r CHÍ
Nên r 0 f x ax 1x 1x 2x 2 f 1 0, f 2 0 . P 2 2 Ạ
f ' x.f x f 'x2dx 2
f 'x.f x'dx
f 'x.f x f '2.f 2 f '1.f 1 0 T 1 1 1 Chọn ý C.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 136
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 80
Cho đồ thị hàm số f 'x như hình vẽ. Tính tổng bình phương các nghiệm của phương
trình F x 0 , với F x là nguyên hàm của f x . Biết x 1 đều là nghiệm của của
f x 0 và F x 0 .? y 1 O 1 x A. 0 B. 10. C. 12. D. 17. OÁN Lời giải T C 3 x
Nhìn đồ thị ta có f 'x k x 1x 1
f x f 'x dx k
x c . 3 YMPI 4 2 OL x x
f 'x kx 1x 1
F x f x dx k
cx d . C 12 2 Ụ 3 1 f
k c c 2 1 0 1 0 3 k 3 3 x 2 1 Ta có F x
k x k k 4 2 NH PH 4 3 4 F 1 1 1 1 0 k
c.1 d d k 0 12 2 4 CHI x 1 4 2 x 1 F x x x 2 1 0 k
k k 0
T 1 1 5 5 12 12 2 3 4 x 5 x 5 Chọn ý C. 137
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 81
Cho đồ thị hàm số f x trên đoạn 3; 13 như hình vẽ. Có bao nhiêu giá trị m nguyên m f x
không âm để phương trình e
f x 2 f mdx có 1 nghiệm duy nhất. 0 y 4 3 O 3 9 13 x C Ọ A. 15. B. 12. C. 13. D. 17. H Lời giải N
Đặt ; t 2 ' t f x t g t e t g t e 1 . TOÁ
Vì f x 0 với mọi x nên t
e 1 0 với mọi x . U m IỆ 4 4 L
Nhìn đồ thị ta có 0 f x 4 1 g t e 6 1 f m dx e 6 . 0 TƯ
m f m 4 1 . e 6 VÀ
Để phương trình đã cho có nghiệm duy nhất thì .
m f m 0;12.f 12 m
0;1;2;3;4;5;6;7;8;9;10;11;1 2 CHÍ P
Suy ra có 13 giá trị của m. ẠT Chọn ý C.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 138
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 82
Cho đồ thị hàm số f 'x và g 'x như hình vẽ. Đặt h x f x g x . Biết
g 3 g4 3 f 3 f 4 , hỏi mệnh đề nào sau đây đúng? y g'x 1 1 3 O 4 x f 'x OÁN T
A. h x đạt min là h 1 , h 1 0
B. h x đạt min là h 1 , h 1 0 C
C. h x đạt max là h 1 , h 1 0
D. h x đạt max là h 1 , h 1 0 YMPI Lời giải OL
Xét h 'x f 'x g 'x . Dễ thấy h'3 h'1 h' 4 0 C Ụ
Dựa vào đò thị, thấy f 'x g 'x với x 1; 4 h 'x 0 với x 1; 4 Ta có bảng biến thiên x 3 1 4 NH PH h'x 0 0 0 CHI h x
h'x có cực tiểu là h1
Dựa vào tương quan các phần diện tích trên đồ thị, dễ thấy 4 1
1 g'xdx 1 g'xdx 5 g4 g1 2 g1 g 3 1 3
2g1 g4 g3 3 0 g1 0 1 1 4
1 f 'xdx 1 f 'xdx 2 f 1 f 3 5 f 4 f 1 3 1
2 f 1 f 3 f 4 3 0 f 1 0 2
Từ 1 và 2 h 1 f 1 g 1 0 139
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Chọn ý A. Bài toán 83
Cho đồ thị hàm số f 'x như hình vẽ. Khẳng định nào sau đây là đúng vể biểu thức
9 S f 0 cos f 0 f 1 cos f 1 . 2 y 6 4 C 3 1 Ọ O 1 x H N 1 TOÁ U A. Không xác định B. nhỏ hơn 0. C. bằng 0. D. lớn hơn 0. IỆ L Lời giải TƯ 3
Đặt g x f x 2
x 3x g 'x f 'x 3x 3 . 2 VÀ y CHÍ 6 P ẠT 4 3 1 O 1 x 1
Ta có đồ thị đạo hàm của hàm số g x như sau, ta thấy đường thẳng y 3x 3 đi qua 4
những điểm có hoành độ lần lượt là
;1;1 và g'x chuyển dấu qua điểm x 1 3 nên
x 1 là điểm cực đại.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 140
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ 0 1 9
Ta có g'x dx g'x dx g 1 f 0 g 1 g 1 g 0 g 1 f 0 f 1 2 1 1
Xét hàm số h x x cos x h'x 1 sin x . 9
Hàm số trên đồng biến với mọi x nên nó cũng đồng biến trên đoạn f 0 ; f 1 nên 2 f
f f f 9 0 cos 0 1 cos 1 2
S f
f f f 9 0 cos 0 1 cos 1 0 . 2 Chọn ý D. Bài toán 84 x
Cho đồ thị hàm số f x như hình vẽ. Tìm m để f x xdx sin cos mx có nhiều
nghiệm nhất có thể trên đoạn ; ? y OÁNT 4 C YMPI OL 2 C x Ụ 1 O 1 NH PH 4 CHI
A. 0 m 4 .
B. 0 m 4
C. m 0 .
D. 4 m 0 . Lời giải x
Ta có y f sin x cosxdx' f sin x cosx f f sin x cosx 1.
Ta phải tìm nghiệm của phương trình f sin x cos x 1 m .
Có g x sin x cos x cos x sinx g'x
0 cos x sin x x vì x ; 4 Mà g
2 ; g 1; g 1 . 4
Nên f cos x sin x f 2 ; f 1 vì hàm số f x nghịch biến trên đoạn 1; 2 .
Nên để phương trình đề bài cho có nhiều nghiệm nhất thì 0 m 4 . 141
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Chọn ý A. Bài toán 85
Cho đồ thị hàm số f x như hình vẽ, đồ thị hàm số f 'x và tiếp tuyến của f x 2 tạo với nhau một góc 0
45 . Tính giá trị của tích phân
f ' x f 'x dx ? 0 y 3 f x f ''x 1 2 C O x Ọ H 0 45 N 3 TOÁ U IỆL A. 4. B. 3. C. 1. D. 2. Lời giải TƯ
Phân tích : Bài toán có sử dụng công thức tính góc của 2 đường thẳng. VÀ Đặt 3 2 f x ax
bx cx d f x 2 '
3ax 2bx c . x f ' 0 0 c 0 CHÍ
Hàm số đạt cực trị tại 0 nên . P Ạ
Phương trình đường thẳng f ' x 6ax 2b có hệ số góc là 6a a a 1 6 3 . T 2
Phương trình tiếp tuyến tại điểm có hoành độ là 2 có hệ số góc là 12a 4b .
Vì đồ thị hàm số f ''x và tiếp tuyến của f x tạo với nhau một góc 0 45 nên 7
12a 4b 6a
12a 4b 6a 1 6a12a 4b b
3 17 8b 0 4 tan 45
1 6a12a 4b 12a 4b 6a 1
6a12a 4b 20 16b b 5 4
Trường hợp b 5 loại vì 6a nhỏ hơn 12a 4b . 4 1 7
Ta có hàm số f x 3 x 2 x . 2 4
Phương trình tiếp tuyến tại điểm có hoành độ x 2 là y x 2 3 x 1 . 2
f ' x f 'xdx
f '2 f '0 f 2 f 0 1 3 2 2 . 0
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 142
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Chọn ý D. Bài toán 86
Cho đồ thị hàm số f 'x liên tục trên đoạn 3; 3 như hình vẽ. Đặt hàm số 2
g x f x 2 2 x . Biết
gxmmdx
0 m thuộc đoạn 1;1. Khẳng định nào dưới 2 đây là đúng ? y f 'x 3 O 1 3 3 x 1 3 OÁNT C
A. 4g1 m 4g3.
B. 3g1 m 3g3. YMPI
C. 2g1 m 2g3.
D. g1 m g3. OL C Lời giải Ụ
Phân tích : Lại một bài chứa tham số nữa !
Ta có g 'x 2 f 'x 2x; g'x 0 f 'x x . NH PH CHI y f 'x 3 O 1 3 3 x 1 3 y x 143
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Ta thấy đường thẳng y x cắt đồ thị hàm số y f 'x tại những điểm có hoành độ
3; 3;1 , g'x đổi dấu tại x 1 nên là cực tiểu của hàm số gx . 3 3
Dựa vào đồ thị ta có g'xdx
2 f 'x2xdx 0
g3 g3 . 3 3
g1 gx g3 . 2 2 2 Ta có
gxmmdx 0
gxmdx mdx 4m . 2 2 2 2 2m
Đặt x m t dx dt
gx mdx
gtdt . 2 2m 2m 4g1
gxdx 4g3 g1 m g 3. 2m Chọn ý D. C Bài toán 87 Ọ H
Cho đồ thị hàm số f 'x như hình vẽ. Gọi giá trị lớn nhất và giá trị nhỏ nhất và giá trị N 2
nhỏ nhất của hàm số g x f x x 1 là a và b trên đoạn 1; 3 . Biết TOÁ 0.5 3 0.5
xf 'xdx
c và f 'xdx
d . Tính giá trị của tích phân f xdx ? U 1 1 1 IỆL y TƯ 10 VÀ CHÍ P ẠT 1 1 0,5 O 4 x A. 1 1 1
a b d 1 .
B. a b 2d . 2 8 2 4 C. 1
a b d 1 .
D. a b 2 . d 8 2 Lời giải
Phân tích : Tìm giá trị lớn nhất, nhỏ nhất của hàm hợp sau đó tìm mối quan hệ giữa a,b,c,d.
Ta có g 'x f 'x 2 x 1 .
Nhìn vào đồ thị ta thấy g 'x 0 có 3 nghiệm là 1; 0.5; 4.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 144
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ 0.5 3 Lại có
f 'x2x1dx
f 'x2x1 dx 1 0.5
g0.5 g1 g0,5 g3 g1 g3
Ta thấy g 'x đổi dấu tại x 0.5 trên đoạn 1;3 nên x 0.5 là cực đại của hàm số g x trên đoạn 1;3 . 1
Nên g 0.5 a; g 3 b f 0.5 a ; f 3 b 16 . 4 0.5 u x du dx Mà
xf 'xdx c . Đặt .
dv f 'x dx v f x 1 Ta có 0.5 0.5 c
xf xdx xf x 0.5
f xdx f
f I a 0.5 ' 0.5. 0.5 1 0.5 f 1 I . 1 4 1 1 3
Lại có f 'xdx d f 3 f 1 d f 1 b 16 d . 1 0.5 1 1 OÁN
I 0.5a
b 16 d a b d . T 4 2 8 C Chọn ý A. Bài toán 88 YMPI 1 2 OL
Cho hàm số bậc 4 có đồ thị f 'x như hình vẽ. Biết f 0 0 ,
f 'x dx . Tính giá 6 C 1 Ụ 1 2
trị của tích phân sin f x
. f 'x. f xdx ? 1 NH PH y CHI O 1 5 1 x 1 5 2 2 2 A. 3 1 . 2 2 B. 3 . 2 C. 3 1 . D. 1 . 12 2 2 Lời giải
Phân tích : Sử dụng phương pháp tích phân từng phần và đọc đồ thị để tìm ra đáp án nhé ! 145
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA 1 5 5 1 1
Đặt f 'x kx x x . 2 2 2
f x 1 k 3 x 2
x x f x 1 ' 4 6 2 2 k 4 x 3 2x 2
x 2x r. 4 4
Mà f 0 0 r 0 . 1
Nên f x k xx 1x 1x 2 . 4 1 2 1 1
Ta có f 'xdx f
f 1 f . 6 2 6 2 6 1 1 2
f x u Từ giả thiết sin f x
. f 'x. f xdx . Đặt f x sin
. f 'x.dx dv 1 1 1 2 1 2 C sin
f x. f 'x. f xdx f x.cos f x 2 cos f x f ' x dx 1 Ọ H 1 1 1 1 N
f x.cos f x 2 sin f x 2 1 1 TOÁ 1 1 f .cos f 1 3 1
f 1.cos f 1 sin f sin f 1 . U 2 2 2 12 2 IỆL Chọn ý C. TƯ Bài toán 89
Hàm số f x có dạng f x 2
ax ba 0. Đồ thị hàm số f x được cho như hình vẽ. VÀ
Gọi diện tích hình tạo bởi f f x và f x là S. Tính giá trị của biểu thức tích phân CHÍ 11 a P
3a x 1 1 1 x 1x 1 x 1 dx Ạ ? a a T 1 1 a y m 3 6 O 2 x m 5
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 146
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ A. S. B. aS . C. 2 a .S D. 2 S . Lời giải
Phân tích: Được phát triển lên từ bài toán tính diện tích. Bài toán đòi hỏi ta phải tìm được các
nghiệm của phương trình hoành độ giao điểm 2 đồ thị!
Phương trình hoành độ giao điểm của f x và f f x là
aax b2 2 b 2 ax b 3 4 a x 2 a b a 2 x 2 2 b a 0.1 .
Nhìn vào đồ thị ta thấy .1
a b 1 b 1 a .
Thay b vào (1) ta được 3 4 a x 2 a 3 a a 2 x a 2 a 3 . 2 2 2 a 0 * x 1 Đặt 2
x t . Ta thấy t 1 1 1
là nghiệm của phương trình (*) . x 1 2 Lại áp dụng Vi-et ta có 1 2 2 x 2 b a 3 a 1 2 2 a 2 1 1 1 3 a t .t 1 1 t 1 1 2 3 2 2 a a a a a a x 1 1 4 a OÁNT
Vì phương trình (*) có 4 nghiệm như trên nên C 11 a 3 4 a x 2 2a b a 2 2 x b a
3a x 1 1 x 1 x 1 1 x 1dx a a 1 YMPI 1 a OL 11 a C 3 1 1
Hay a x 1 x
1x 1 x 1 dx chính là diện tích S tạo bởi f f x và Ụ a a 1 1 a f x. NH PH Chọn ý A. CHI 147
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 90 f ' x f 'x 2
Cho đồ thị hàm số f 'x như hình vẽ. Biết F x . Phương trình
f x f x dx
f x 4.F x 4 0 có tổng các nghiệm là bao nhiêu, biết F 3 0 ? y f x 1 O 1 3 x CỌ H A. 15. B. 8. C. 20. D. 17. N Lời giải TOÁ
Phân tích. Việc rút gọn được tích phân kia là rất khó tuy nhiên khi tìm được rồi tìm ra đáp án là U
không khó và ta thấy bài toán khá là hay. IỆL
f ' x 4 f 'x 4 2
f ' x 4. f x 4 f 'x 42 Ta có dx d x 4 2 TƯ
f x 4 f x 4
f x 4 ' VÀ
f 'x 4 f ' x 4 d x 4 c .
f x 4 f x 4 CHÍ f ' 1 P
F 3 0 F 3
c 0 . Mà hàm số đạt cực trị tại x 1 nên f '1 0 c 0 . Ạ f 1 T
Nên f x 4.F x 4 f 'x 4 .
Vì f 'x 0 có 3 nghiệm phân biệt như hình vẽ đồ thị nên có dạng
f 'x k x 1x 1x 3 . x 3 f 'x 4 0
k x 4 1x 4 1x 4 3 0 x 5. x 7
Tổng các nghiệm là : 3 5 7 15 . Chọn ý A.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 148
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 91
Anh Tuấn có một con diều hình con cá chim. Con diều này được giới hạn bởi 2 Parabol
P : x 3x 2 P : x 3x d d 1 2 , 2
và 2 tiếp tuyến 1 , 2 đối xứng qua trục tung sao cho
BAC 120 (hình vẽ). Tính chính xác diện tích của con diều (làm tròn đến 2 chữ số thập phân). y A B 2 C d2 d1 3 2 1 O 1 2 3 x OÁNT P P2 1 C A. 3,81 B. 3,82 C. 4,31 D. 4,32 YMPI Lời giải OL C
Ta có BAC 120 BAO 60 hệ số góc của d 3 tan 90 60 1 là 3 Ụ d P x 2 3 9 3 x 3x ' x
1 tiếp xúc 1 tại B
B là nghiệm của phương trình 3 B 6 NH PH 9 3 13 3 y 13 B ; d y x a B điểm
có phương trình dạng 6 1 6 6 3 CHI 14 3 3 a d 3 14 y x 3 3 : 1 6 3 6 3 14 3 3 S S x x x dx ABOC 2 2 OAB 2 9 0 3 3 3,82 3 6 6 Chọn ý B. 149
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 92
Cho thiết diện mặt cắt một chiếc đĩa bay của người ngoài hành tính như hình vẽ (phần
tô đậm). Cho biết các đường cong trong hình vẽ đều là một phần của các Parabol. Tính
diện tích thiết diện đó. y 2, 5 P1 P P4 3 2 1 11 5 2 O 2 5 11 6 x 2 2 1, 5 P2 C 55 59 Ọ A. B. C. 55 D. 59 3 3 H 6 6 N Lời giải
Vì thiết diện là hình đối xứng qua trục tung, nên ta sẽ đi tính phần diện tích bên phải trục TOÁ
tung. Trước tiên, ta cần tìm phương trình của các Parabol. U
Xét Parabol P : y ax bx c 1 2 có IỆL a 3
x 2 y 1
4a 2b c 1 TƯ 8 3 5 5
4a 2b c 1 b 0 P : y x 1 2 VÀ
x 0 y 8 2 2 c 5 c 5 2 2 CHÍ 2 P
Xét Parabol P : y ax bx c 2 có ẠT a 3
x 2 y 0
4a 2b c 0 8 3 3 3
4a 2b c 0 b 0 P : y x 2 2
x 0 y 8 2 2 c 3 c 3 2 2
Xét Parabol P : y ax bx c 4 2 có
x 5 y 1
25a 5b c 1 a 4
x 6 y 1 36a 6b c 1
b 44 P : y 4x 44x 119 4 2 11 121 11 c x y a b c 119 2 2 2 4 2 2 3 5 2 2 3 2 3 11 S S 11 59 2 x dx x dx x x dx p 2. 1 4 44 119 1 .1 0 0 2 2 8 2 8 2 5 2 3
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 150
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Chọn ý D. Bài toán 93
Cho hàm số f x liên tục trên
có dạng f x 4 ax 2
bx 1 . Biết đồ thị hàm số f "x
tiếp xúc đồ thị hàm số f x tại 1 điệm trên trục tung. Gọi x f x x 1 là nghiệm của , 2
là nghiệm của f "x x , x 0 x 3x 1 2 . Biết 1
2 , tính diện tích phần tô đậm (hình vẽ). y x x x x 1 2 O 2 1 x f x f 'x OÁN T C A. 152 B. 73 C. 152 D. 73 15 15 45 45 Lời giải YMPI
Ta có f x 4 ax 2
bx f x 2 1 " 12ax 2b OL 4 2 2 C
Xét pt hoành độ giao điểm f x f "x ax bx 1 12ax 2b 0 . Vì f x cắt Oy tại Ụ
điểm 0;1 x 0 là nghiệm của phương trình hoành độ giao điểm b b 1 1 2 0 2 2 4 x NH PH
f x ax 1 1 1 16a 2 . Xét f x 2 0 x 2 x1 2 4a CHI
f "x 12ax 1 1
Xét f "x 0 2 x 2 x x 9x 2 . Xét 2 TH của pt 2 2 12a 1 2 TH 1: 1 1 16a 1 9. 1 16a 2 (loại) 4a 12a 1 1 16a 1 3 TH 2: 9.
1 16a 2 a 4a 12a 16 2
3 4 x f x x 1 2 16 2
và x 2; x 1 2 3
f "x 9 2 x 1 4 2 2 3 x 2 4 9 2 S 64 8 152 x
1dx 3 x 1 dx 2 2 16 2 4 15 9 45 3 Chọn ý C. 151
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 94
Cho diện tích phần tô đậm bằng a, f '1 b . Biết 2 f 1 f 1 f 3 và f x là một
hàm bậc 3, tính f '1 f '3 theo a và b y f x f ''x A 3 1 O 1 x CỌH N A. 2b a
B. b a C. b
D. b a Lời giải TOÁ f x dx a U
Nhận xét, diện tích phần tô đậm chính bằng 1 3 IỆL 1 3 1 2 TƯ Ta có
A là điểm đối xứng của f x f 1 f 1 f 3 VÀ 2
1 f x f "xdx 1 f "x f xdx 1 f xdx 1 f "xdx f '1 f ' 3 3 1 3 CHÍ 3 P
f '3 b a f '1 f '3 2b a ẠT Chọn ý A.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 152
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 95
Cho đồ thị hàm số là đa thức bậc 3 f x như hình vẽ. Biết d d 1 và 2 là tiếp tuyến của OA 1 1
f x tại x 1 và x 1; và f 2 0
. Tính f x f'xdx OB 4 5 1 y d2 1 1 2 O B x 3 OÁNT C d1 YMPI A OL C A. 1 B. 7 C. 7 D. 7 Ụ 10 9 8 Lời giải Ta có d d x f x d d 1 và 2 là tiếp tuyến tại x
1 và 1 của và 1 song song 2 NH PH
f '1 f '1 CHI
f 'x có dạng 2 f ' x ax b 2 4
Nhận thấy f x đạt cực trị tại x a b 0 1 3 9 OA 1 1 1 1 Có
tand ;Ox f '1 a b 2 1 OB 4 4 4 4 9 1 9 1 3 1 2
Từ 1 và 2 a
;b f 'x 2
x f x 3
x x (Vì f 2 0 ) 20 5 20 5 20 5 5 5
I 1 f x f x 1 3 3 9 2 1 1 dx x x x dx 7 ' 1 1 20 20 5 5 10 Chọn ý B. 153
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 96
Cho đồ thị hàm số 2 f x
ax bx c như hình vẽ, d f ' x S ,S 1 là đồ thị hàm số . Gọi 1 2 S
là các diện tích tạo bởi d , d f x 1 2 với đồ thị hàm số
. Tính gần đúng tỉ số 1 S2 y 1 1 O 3 x d2 CỌH 4 N A. 1,35 B. 1,36 C. 1,37 D. 1,38 TOÁ U Lời giải IỆ
Nhìn vào đồ thị, thấy f x nhận x 1 và x 3 là nghiệm và f 1 4 L
a b c 0 a 1 TƯ
9a 3b c 0 b 2 f x 2
x 2x 3 f 'x 2x 2 VÀ
a b c 4 c 3 1 1 CHÍ d d 1;0 d : y x 2 1 tại 2 2 2 P Ạ
Xét pt hoành độ giao điểm f x và f 'x T
x 2x 3 2x 2 x 2 5 S
x 4x 2 5 2 2 1 dx 1 2 5
Xét phương trình hoành độ giao điểm f x và d2 3 1 1 3 65 2 65 2 3 7 S x
2x 3 x x S 4 x x dx 1 1,37 2 3 65 2 2 4 2 2 S 4 2 Chọn ý C
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 154
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 97
Cho đồ thị hàm số f x và f 'x như hình vẽ. Diện tích tạo bởi f 'x và f x gần nhất ? y 2 O 3 x 5 A. 23. B. 65. C. 50. D. 43. Lời giải OÁNT
Phân tích: Bài toán đơn tuần là dùng kĩ thuật phân tích, biến đổi là nhiều. Dựa vào các dữ liệu C
của bài để suy ra được hàm từ đó tính được diện tích hình phẳng bằng tích phân.
Đặt f x 3 ax 2
bx cx d f x 2
3ax 2bx c . YMPI
f x f x 3
ax b a 2 '
3 x c 2bx d c . OL
x 2 12a 4b c 0 C
Nhìn vào đồ thị ta có . 1 Ụ
x 3 27a 6b c 0
Ta có f 'x có cực trị là -4 , gọi x0 là hoành độ của điểm cực trị thì b 2 NH PH f ' x
0 6ax 2b 0 x 3 . a x 2bx c 5 0 0 0 và 3a 0 0 2 2 CHI b b b 3 . a 2b c 4 c 5 2 2 9a 3a 3a
Từ 1 a 2 b và c 4b 12a , thay vào 2 ta được 3 2 b 2 b 2 4
b a
b b b a c 24 4 12 5 4 8 5 . 3a 2b 5 15 5
f x f x 4 3 x 6 2 x x 24 ' 4
0 có nghiệm là x ,x 15 5 5 1 2 x2 4 3 6 24
Vậy diện tích cần tìm là x 2 x 4x 65, 4 15 5 5 1 x Chọn ý B. 155
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 98
Hàm số f x có dạng 2 f x
ax b . Đồ thị hàm số f f x được cho như hình vẽ. Gọi
diện tích hình tạo bởi f f x và f x là S, t , t f f x 1
2 là hoành độ giao điểm và
f x t .t 0 2 2 2 2 t t 2 t t 9 1 2 sao cho 1 2 1 2 . Tính S ? y 5 /3 43 /27 CỌH O x N TOÁ 50 42 32 65 U A. . B. . C. . D. . 203 305 405 203 IỆ L Lời giải TƯ
Phương trình hoành độ giao điểm của f x và f f x là 2 VÀ a 2
ax b b 2 ax b 3 4 a x 2 a b a 2 x 2 2 b a 0 . 2 2 1 2b CHÍ t t 1 2 2 a a P Áp dụng Ta -let 2 Ạ 2 2 b T t .t 1 2 a 1 Theo giả thiết ta có 2 t 2 t 2 2
2 t t 9 a a 1 2 1 2
(do đồ thị hướng lên trên nên 0 ) 3 25 43 2
Nhìn vào đồ thị ta thấy a b b 9 27 3 1 2 2 1 1 2 2
Nên f x 2
x và f f x 2 x 3 3 3 3 3 3
Khi đó phương trình f f x f x 0 có 4 nghiệm là 1;1; 2; 2 Suy ra S 32 405 Chọn ý C.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 156
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 99
Cho đồ thị hàm số f x . S ,S 1
2 là diện tích hình phẳng được giới hạn như hình vẽ. Tính 1
x 2sin x 11cosx 5 3sin x cosx 1
giá trị lớn nhất của .f dx ? 2 x x x x x 2 cos sin 4 2 cos sin 4 0 y 9 S 1 11 O 1 13 x S 4 2 2
A. S S S S 1 2 B. 1 C. 2
D. S S OÁN 1 2 3 T C Lời giải
Phân tích: Bài toán có ý tưởng khác là hay về việc đổi biến, tuy nhiên cũng dễ nhầm lẫn trong việc YMPI
xác định khoảng giá trị của t. Bài toán còn là sự kết hợp giữa tích phân và tìm giá trị lớn nhất, nhỏ OL nhất. C
3sin x cos x 1
2 sin x 11cos x 5 x t 0 0 Ụ Đặt t
dx dt . Đổi biến
2 cos x sin x 4
2cosx sin x 42 x t 1 1 1
x 2sin x 11cosx 5 3sin x cosx 1 1 t Khi đó . f dx f t dt . 2 NH PH x x x x x 2 cos sin 4 2 cos sin 4 0 0 t
3sin x cos x 1 CHI Mặt khác ta lại có
t 3sin x cos x 1 t.2 cosx sin x 4
2 cos x sin x 4
3 t.sinx 1 2t.cos x 1 4t *
Để phương trình * có nghiệm thì
3sin x cos x 1 t 3sinxcosx1 t.2cosxsinx 4
2 cos x sin x 4 t2 t2 t2 2
t t 9 3 1 2 1 4 11 2 9 0 t 1 11 t1
Nhìn vào đồ thị ta thấy diện tích phần S f t dt
1 chính là giá trị lớn nhất của tích phân t0 Chọn ý B. 157
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 100
Cho đồ thị f 'x như hình vẽ. Diện tích 2 hình tạo bởi f 'x và trục hoành là 9 5 4
, , f 1 3 . Tính giá trị của tích phân f 'x.f xdx ? 8 4 1 y 9 8 1 O 1 4 x 5 4 CỌ H A. 0 B. 1 C. 3 D. 4 N Lời giải TOÁ
Phân tích: Một bài toán khá dễ thở nhá! U 4 2 2 f x f 4 f 2 4 4 1 IỆ
f ' x . f x dx
f x d f x 1 L Ta đặt 2 2 1 1 1 TƯ 1 9
f x
f f 9 f 15 ' 1 1 1 VÀ 8 1 8 8 Từ đồ thị suy ra
4 f 'x 5 5 7
f 4 f 1 f 4 CHÍ 4 4 4 1 P Ạ
f 2 f 2 4 1 29 T Thay vào 1 ta được . 2 128 Chọn ý B.
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton 158
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 101
Cho đồ thị hàm số f x như hình vẽ. y 2 2 O 2 6 x 15 4 2
x 8x n m
Để hàm số h x
có số tiệm cận đứng là lớn nhất là n ( với m,n nguyên
f f x m OÁN
dương). Tính giá trị nhỏ nhất của S = 2 2 m n T A. 14 B. 74 C. 50 D. 3 C Lời giải
f x m 2
f x 2 m YMPI
Để g x có số tiệm cận đứng thì f f x m 0 f x m 2 f x 2 m OL C
f x m 6
f x 6 m Ụ 6 m 2 15 m 5 2 m 4 NH PH
Để hàm số có số TCĐ là lớn nhất thì hoặc là 15 2 m m CHI 4 1 2 m 2
Có g 'x 2x 8 đồng biến trên 4, nên khi m 5 và đường thẳng y 7 giáp với
f x tại điểm có hoành độ lớn hơn 4 nên g x 0 với x thuộc 4; nên 2
x 8x n m 0 . Nên S 74 hoặc 50 S 50 min Chọn ý C. 159
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 102
Cho f x , f ' x và d là tiếp tuyến của f x dưới hình vẽ. Hàm số f x có dạng 3 2
mx nx p . Tính 43n 45p y d 26 5 O 1 x 6 C Ọ 5 f x H f ''x N 285 A. B. 450 C. 201 D. 182 TOÁ 3 U Lời giải
IỆL Phương trình f ''x là y' 6mx2n y m n x mn TƯ
Tiếp tuyến tại điểm có hoành độ là 1 là 3 2 1 p 26 1 VÀ
3m 2n m n p 5 5 Ta có 26 36 CHÍ m 2 n 5 5 P Ạ 18m 13 86m 39 T Tìm được n ; p 5 25 Chọn ý D. 160
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 103
Cho đồ thị hàm số f 'x như hình vẽ. Tổng các giá trị nguyên của m 3; 20 để hàm số
gx f x m có 4 cực trị. Biết tử số của f x có hệ số tự do dương. y x 1 O x y 2 13 A. 64 B. 58 C. 75 D. 88 OÁN T Lời giải C
Đặt h x f x mx h 'x f 'x m . Vì hệ số tự do của tử số của f x dương Và
mẫu có x 1 . Tức là f 0 0 . Ta thấy đường nét đứt giao với trục Oy và tại y 0 thì YMPI
điểm cực trị đó là cực đại x f x f M 0 0 M và
Đường đỏ tạo ra 3 điểm cực trị cho OL
g x nếu cắt trục Ox C Ụ
Trường hợp 1 : Cả 2 đường đỏ và vàng đều nằm trên Ox thì gx có 2 điểm cực trị.
Trường hợp 2 : Đường màu vàng cắt Ox tại 2 điểm khác cực trị của f 'x (hoặc 3 NH PH
điểm) có ít nhất 3 điểm cực trị và đường đỏ có 3 điểm cực trị (loại).
Trường hợp 3 : Đường màu vàng cắt Ox tại 4 điểm (loại) . CHI
Trường hợp 4 : Đường màu vàng cắt Ox tại 2 điểm là cực trị của f 'x ( hoặc không cắt điểm
nào) và để có 4 cực trị thì ta tịnh tiến đồ thị f 'x sao cho 13 m 2 . Khi đó tổng giá trị m là 75 Chọn ý C. 161
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 104
Cho 3 hàm số y f x , y g x , y h x . Đồ thị của 3 hàm số y f x , y gx
, y hx có đồ thị như hình vẽ dưới, trong đó đường đậm hơn là đồ thị của hàm số
y f x . Hàm số k x f x g x 3 7 5 1 h 4x
đồng biến trên khoảng nào 2 dưới đây y
y g'x 10
y f 'x 5 O C x Ọ 3 4 8 H N
y h'x TOÁ 15 1 3 3 U A. ;0. B. ; . C. ;1. D. ; . IỆ 4 4 8 8 L Lời giải TƯ
Ta cần giải bất phương trình k x f x 15 3 ' ' 7 2g' 2x 4h' 4x 0 2 2 VÀ
Không thể giải trực tiếp bất phương trình này. Quan sát các đồ thị của các hàm số
y f 'x , y g'x , y h'x CHÍ ta nhận thấy P
f 'x 10,x 3;8 ; g'x 5,x, h'x 5,x 3;8
ẠT Do đó f 'a2g'b4h'c102.54.50,a,c3;8,b 3 x 7 8 3
Vì vậy ta chỉ cần chọn 3 x 1 . 3 4x 8 8 2
Đối chiếu với đáp án ta chọn ý C. 162
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 105
Cho hình vẽ của đồ thị các hàm số
a ; b ; c
y x y x y x có đồ thị như hình bên. Khi đó
3a 2b a c2 2
hãy tìm tổng của giá trị nhỏ nhất và giá trị lớn nhất của biểu thức T ? 2 2
a 5c 4ac y c x 2m b x m 0, 5 a x O x A. 31 B. 32 C. 33 D. 34 Lời giải
Nhận thấy ngay khi x , ta có c b OÁN
2 c log 1 blog c b log 1 2 2 2 T
a 0.5 alog 1 C 2
a c b
Đến đây thay vào biểu thức ta được một hàm thuần nhất 2 biến rồi đặt 1 ẩn đưa về khảo YMPI sát hàm 1 biến! OL Bài toán 106 C Ụ
Hình vẽ bên là đồ thị của hai hàm số y log x y f x a và
. Đồ thị của chúng đối xứng
với nhau qua đường thẳng y x 1 .Tính f loga 2018 y NH PH y log x a CHI O 1 x
y f x y x 1 a
A. f log 2018 1 f a B. a 1 log 2018 1 2018 2018a a
C. f log 2018 1 f a D. a 1 log 2018 1 2018 2018a Lời giải 163
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Lời giải
Gọi b;c C : y log x; e; f C : y f x a . 1 2 Ta có hệ điều kiện
c f
b e 2
b c f e 2 b f 1 1
b e 1c f 0
b c e f c e 1 e 1 log f f a f a f x a a 1 e1 e1 1 1 e1 1 . Vậy f a a log 2018 1 1 log 2018 1 a 1 2018a Bài toán 107
Cho hàm số y f x có đồ thị như hình vẽ có bao nhiêu số nguyên m để bất phương trình mx 2 m 2
5 x 2m 1 f x 0 có nghiệm đúng với mọi x2;2. y CỌHN TOÁ 2 1 O 1 3 x U IỆL TƯ A. 0. B. 1. C. 2. D. 3. VÀ Lời giải Ta có g x 2 2
mx m 5 x 2m 1, rõ ràng gx xác định x 2;2. CHÍ P
Hàm số f x đổi dấu 1 lần trên2; 2 , tại điểm x 1 khi đó f x đổi dấu từ dương sang ẠT âm.
Vậy để f x.g x 0
x 2;2 thì gx 0
x 2;1 và gx 0 x 1;2 . m 1
Nhận thấy g x liên tục trên2; 2 nên g 1 2 0 m 2m 2m 1 0 . 1 m 2
Nếu m g x x 2 1
5 x 1, dễ thấy g x 0
x 2;1 và gx 0 x 1;2 .
Vậy m 1 thỏa mãn.
Ta không cần thử trường hợp m 1 vì đề bài nói m Z . 2 164
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 108
Cho hàm số y f x có đồ thị như hình vẽ. Tìm tất cả giá trị thực của tham số m để bất
phương trình f x 2 2
x 4x m có nghiệm đúng với mọi x 1;3 y O 2 x 3 A. m 3. B. m 10. C. m 2. D. m 5. Lời giải OÁNT
Bất phương trình đã cho tương đương với f x 2 2
x 4x m . C
Dựa vào đồ thị, ta thấy min f x 3, dấu bằng xảy ra khi x 2. 1;3 2 2 YMPI
Lại có x 4x x 2 4 4, dấu bằng xảy ra khi và chỉ khi x 2 . 2 OL
Vậy min 2 f x x 4x 2.3 4 10. 1;3 C Ụ
Do đó bất phương trình có nghiệm đúng với mọi x 1; 3 khi và chỉ khi m 10. Bài toán 109
Cho hàm số f x có đồ thị như hình vẽ bên dưới. Để đồ thị 2 h x
f x f x m có NH PH
số điểm cực trị ít nhất thì giá trị nhỏ nhất của tham số m là m0 . Tìm mệnh đề đúng? CHI y O 1 3 x A. m 0; 1 . m 1;0 . m ; 1 . m 1; . 0 B. 0 C. 0 D. 0 Lời giải 165
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Xét hàm g x 2
f x f x .
m Bằng việc khảo sát g x ,chỉ ra g x có 3 điểm cực trị, từ
đó h x muốn có 3 điểm cực trị thì g x x R m 1 0 . 4 Bài toán 110
Cho hàm số f x có đồ thị như hình vẽ bên dưới. Gọi M, m lần lượt là giá trị lớn nhất 3 7
và giá trị nhỏ nhất của hàm số y f 2
x 2x trên
; . Tìm khẳng định sai trong các 2 2 khẳng định sau? y 5 4 CỌ 2 H N 1 O 5 x TOÁ U IỆ M L
A. M m 7.
B. Mm 10.
C. M m 3. D. 2. m TƯ Lời giải
Một câu quá quen thuộc rồi phải không nào! VÀ 2 3 7 1
Đặt t x 2x, x ; t 1; . 2 2 4 CHÍ P 21
Từ đồ thị xét hàm y f t ,t 1;
, ta có m 2, M 5 Ạ 4 T Chọn A. 166
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 111
Cho hàm số y f x liên tục trên R và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của m để phương trình f x 2 1 m 0 có 8 nghiệm phân biệt trong khoảng 5; 5 y 1 3 1 O 3 x OÁNT A. 0. B. 1. C. 2. D. 3. C Lời giải
Đặt x 2 t, phương trình tương đương: f t 1 m1. YMPI
Phương trình có 8 nghiệm phân biệt thuộc 5; 5 khi và chỉ khi 1 có 8 nghiệm phân biệt OL C
thuộc 7; 3 . Ta thực hiện việc biến đổi ra đồ thị hàm số y f x 1 từ đồ thị hàm Ụ
số y f x như sau
Bước 1: Tạo ra đồ thị hàm số y f x 1 bằng cách lấy đối xứng qua trục tung NH PH
phần bên phải trục tung đồ thị hàm y f x rồi tịnh tiến lên trên 1 đơn vị: y f x 1 CHI
Bước 2: Tạo ra đồ thị hàm số
bằng cách lấy đối xứng phần dưới trục
hoành đồ thị hàm số bên trên, qua trục hoành.
Do đó đồ thị hàm số có 8 nghiệm thuộc 7; 3 thì m 1 . 167
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 112
Cho hàm số y f x có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để phương
trình f x m m có 4 nghiệm phân biệt là? y 3 4 x O 1 CỌ 3 H N A. 0. B. 1. C. 2. D. Vô số TOÁ Lời giải U
Đặt x m t, phương trình tương đương với f t m1
IỆL Nhận xét: Mỗi nghiệm của tở1 cho ta duy nhất 1 nghiệmx, do đó để phương trình có 4 TƯ
nghiệm phân biệt thì 1 có 4 nghiệm phân biệt f t m có hai nghiệm phân biệt VÀ
dương và không có nghiệm t 0 . Điều đó có nghĩa m 1 hoặc m 3 .Vì m Z m 1 . 4 CHÍ Bài toán 113 P Ạ
Cho hàm số y f x có đồ thị như hình vẽ. T f x f x
Tìm số điểm cực trị của hàm số y 2 3 y O x 1 A. 3. B. 4. C. 5. D. 6. Lời giải 168
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
Xét hàm số g x f x f x 2 3
g'x f 'x f x
2 .ln 2 f 'x f x 3 .ln 3;x . R f ' x 0 f x f 'x ' 0 1 0
Ta có g 'x f x 0 f x f x 2 ln 3 ln 3 2 .ln 2 3 .ln 3
f x log 2 2 3 ln 2 ln 2 3
Dựa vào đồ thị hàm số y f x , ta thấy:
Phương trình 1 có ba nghiệm phân biệt (vì hàm số y f x có 3 cực trị). ln 3
Phương trình 2 vô nghiệm vì đường thẳng y log 1 2
không cắt đồ thị hàm số. ln 2 3
Vậy phương trình g 'x 0 có ba nghiệm phân biệt hay hàm số đã cho có 3 cực trị. Bài toán 114
Cho đồ thị hàm số y f x xác định và có đạo hàm trên . Hàm số y f x có đồ thị
như hình vẽ. Số nghiệm nhiều nhất của phương trình 2
f x m (m là tham số thực) là? y OÁNT C x YMPI 2 O 1 3 OL C Ụ A. 2. B. 3. C. 4. D. 5. Lời giải NH PH
Dựa vào đồ thị hàm số y f x ta có bảng biến thiên của đồ thị hàm số y f x như sau: CHI x 2 0 1 3 f 'x 0 0 0 0 f 0 f x f 3 f 2 f 1
Từ bảng biến thiên ta thấy phương trình f x m có tối đa hai nghiệm dương, do đó phương trình 2
f x m có tối đa 4 nghiệm. Chọn C. 169
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 115
Cho hàm số y f x có đồ thị như hình vẽ. Số nghiệm thực của phương trình
f f cos x 0 trong đoạn 0;2019 là y 1 x 1 O 1 A. 642. B. 1002. C. 1003. D. 643. Lời giải C Ọ
x a x 1 H
Dựa vào đồ thị ta thấy
f x 0 x 0 . N
x b b 1 TOÁ
f cosx a x 1 U
Do đó f f cos x 0 f cos x 0 . IỆ L
f cos x b b 1 TƯ
Lại có, nếu x 1;1 thì f x 0;1. Suy ra vì cos x 1;1 nên f cos x 0;1.
Vậy nên loại các trường hợp f cos x a và f cos x .
b Chỉ còn f cosx 0. VÀ
cos x a x 1 loai CHÍ
Tiếp tục f cos x 0 cos x 0 . P cosx
b b 1 Ạ loai T 170
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 116
Cho hàm số y f x liên tục trên
và có đồ thị như hình vẽ. Số giá trị nguyên của
tham số m để phương trình 2
f cos x m 2018 f cos x m 2019 0 có đúng 6
nghiệm thuộc 0; 2 là? y 3 1 O x 1 1 1 A. 5. B. 3. C. 2. D. 1. OÁN Lời giải T
Phương trình đã cho tương đương với C f x f cos x 1
cos 1 f cosx m 2019 0
f cosx 2019 m YMPI 3 OL
Với f cos x
1 cos x 0 x ; C 2 2 Ụ
Do đó để phương trình đã cho có 6 nghiệm phân biệt thuộc0; 2 thì phương
trình f cos x 2019 m phải có 4 nghiệp phân biệt thuộc0; 2 , không tính cách nghiệm x NH PH làm cho cos 0 .
Đặt t cos x, f t 2019 m, theo yêu cầu bài toán có đúng 2 nghiệm phân CHI
biệt t 1;1\ 0 .
Từ đồ thị ta có phương trình có đúng 2 nghiệm khi
1 2019 m 1 2018 m 2020;m . Z
Vậy m 2018; 2019 171
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 117
Cho hàm số y f x có đồ thị như hình vẽ y 1 O 1 x 1 1 3 f x 1 m
Có bao nhiêu giá trị nguyên của m để phương trình có 4 nghiệm phân biệt C Ọ A. 2. B. 1. C. 3. D. 4. H Lời giải N
Đặt g x f x 1 , đồ thị hàm số y g x được xác định bằng cách tịnh tiến đồ thị hàm TOÁ
số y f x sang phải 1 đơn vị. U
Rõ ràng g x f x 1 , do đó đồ thị hàm số y f x 1 được xác định bằng cách giữ
IỆL nguyên phần bên phải trục tung của đồ thị hàm sốy gx và lấy đối xứng qua trục tung TƯ của phần đó f x 1 m 3 m 1. VÀ
Từ đó ta thấy phương trình
có 4 nghiệm phân biệt khi
Vậy có 3 giá trị nguyên m 2; 1; 0 CHÍ Bài toán 118 P Ạ y f x x R 3 2 f ' x x ax bx c T Cho hàm số
có đạo hàm tại , hàm số có đồ thị như
hình vẽ. Số điểm cực trị của hàm số y f f 'x là? y 1 O 1 x A. 7. B. 11. C. 9. D. 8. Lời giải 172
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ a 0
Đồ thị f 'x đi qua các điểm O 0;0 ; A1;0 ; B1;0 nên ta có b 1 c 0
Do đó f x 3
x x f x 2 ' " 3x 1.
Đặt g x f f 'x . 3
Ta có g x f f x
f f x
f x 3 x x 3 x x 2 ' ' ' ' ' . " 3x 1
xx x 3
x x 2 1 1 1 3x 1
Dễ thấy g x 0 có 7 nghiệm phân biệt, tất cả đều là nghiệm đơn nên hàm số có 7 điểm cực trị. Bài toán 119 Cho hàm số 3 2 y f x ax
bx cx d a,b,c , a 0 có đồ thị C . Biết rằng đồ
thị C tiếp xúc với đường thẳng y 9 tại điểm có hoành độ dương và đồ thị hàm số
y f x cho bởi hình vẽ bên. Phần nguyên của giá trị diện tích hình phẳng giới hạn
bởi đồ thị C và trục hoành là? OÁNT y C YMPI OL C Ụ 1 O 1 3 x NH PH CHI 4 A. 2 B. 27 C. 29 D. 35 Lời giải
Ta có f x 2
3ax 2bx c . Dựa vào đồ thị hàm số y f x ta thấy đồ thị hàm số a 1
3a 2b c 0 3
y f x đi qua 3 điểm 1;0 ,3;0 , 1; 4 ta có hệ: 27a 6b c 0 b 1
3a 2b c 4 c 3 1
Suy ra f x 2
x 2x 3 f x f xdx 2
x 2x 3dx 3 x 2 x 3x C . 3
Do C tiếp xúc với đường thẳng y 9 tại điểm có hoành độ x0 nên 173
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA x 1 f x 0 x 2x 3 0 x 0 x 3 0 2 0 0 0 , do . x 3 0 0 0 1 1
Từ đó suy ra f 3 9 .27 9 C 9 C 0 C :y 3 x 2 x 3x . 3 3
Xét phương trình hoành độ giao điểm của C và trục hoành: x 0 1 3 2
x x 3x 0 3 x 3 5 3 2 33 5 2 1
Diện tích hình phẳng cần tìm là S 3 x 2 x 3x dx 29.25 . 3 33 5 2 Bài toán 120 3 2
Cho hàm số y f x ax bx cx d a,b,c , a 0 có đồ thị C . Biết rằng đồ thị C Ọ
C tiếp xúc với đường thẳng y 2 tại điểm có hoành độ dương và đồ thị hàm số H 3 N
y f x cho bởi hình vẽ bên. Giá trị 3a 2b c d là? y TOÁ 4 U IỆL TƯ VÀ 2 O 2 x CHÍ P ẠT A. 0. B. 2 C. 3. D. 4 Lời giải
Ta có f x 2
3ax 2bx c . Đồ thị hàm y f x là hàm chẵn , suy ra b 0 . f c 4 0 4 Mà
1 f x 2 x 4 f 2 0 a 3 1
Ta có f x f x dx x 4 dx x 4x 2 3 C . 3
Do C tiếp xúc với đường thẳng y 13 tại điểm có hoành độ x nên 3 0 f x 0 x 4 0 x 2 x 0 x 2 0 2 0 0 , do 0 0 . 13 1 Suy ra f 2
C 1 C : y 3
x 4x 1 3a 2b c d 4 . 3 3 174
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 121
Cho hàm số y f x 4 ax 2
bx c a 0 có đồ thị C , đồ thị hàm số y f x như 3 8 3
hình vẽ bên. Biết đồ thị hàm số y f x đạt cực tiểu tại điểm ; . Đồ thị 3 9
hàm số y f x tiếp xúc với trục Ox tại 2 điểm. Diện tích S của hình phẳng giới hạn
bởi đồ thị C và trục hoành là? y 1 O 1 x OÁNT C 7 8 14 16 A. B. C. D. 15 15 15 15 YMPI Lời giải OL
Từ đồ thị hàm số y f x với a 0 ta dễ dàng có được đồ thị hàm số y f x như hình C vẽ dưới. Ụ y NH PH CHI 1 O 1 x 3 8 3
Ta có f x 3
4ax 2bx . Đồ thị hàm y f x qua 1;0 và ; nên ta có hệ : 3 9 f 1 0
4a 2b 0 a 1 3 8 3 3 3 3
f x 3 4x 4x f 8 3 4a 2b b 2 3 9 3 3 9 175
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Ta có: f x f x dx x xdx x x 3 4 4 4 2 C .
Do C tiếp xúc với đường thẳng Ox tại điểm có hoành độ x0 nên x 0 f x 0 4x 4x 0 y f x 0 3 0 0 0 . Đồ thị hàm số
tiếp xúc với trục Ox tại 2 x 1 0
điểm nên 2 điểm đó có hoành độ là 1 . Suy ra f C C y 4 x 2 1 0 1 : 2x 1 . x 1
Xét phương trình hoành độ giao điểm của C và trục hoành: 4 x 2 2x 1 0 . x 1 1 16
Diện tích hình phẳng cần tìm là: S 4 x 2 2x 1 dx . 15 1 Bài toán 122 ax b d Cho hàm số y f x
a, b,c, d ,
0 có đồ thị C , đồ thị hàm số cx d c
C y fx như hình vẽ bên. Biết đồ thị hàm số y f x cắt trục tung tại điểm có tung Ọ H
độ bằng 3. Phương trình tiếp tuyến của C tại giao điểm của C với trục hoành có N dạng ? TOÁ y U IỆL TƯ VÀ 2 CHÍ P Ạ O 1 2 x T 1 3 1 3 1 3 1 A. y x B. y x C. y x D. y x 2 2 2 2 2 2 2 2 Lời giải ad bc
Ta có f x
y f x . Từ đồ thị hàm số ta thấy : cx d2 d
Đồ thị y f x có tiệm cận đứng x 1
1 c d 1 . c ad bc 2
Đồ thị y f x qua điểm 2; 2
2 ad bc 2 2c d 2 2 2c d ad bc
Đồ thị y f x cắt trục tung tại y 2
2 ad bc 2 2d 3. 2 d 176
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ b
Mà đồ thị y f x cắt trục tung tại điểm có tung độ bằng 3
3 b 3d 4 . d c d a 1
ad bc 2 2c d2 b 3 x 3
Từ 1 , 2 , 3 , 4 ta có hệ
y f x . ad bc 2 d c 2 1 x 1 b d d 3 1 2 1
Đồ thị C giao với Ox tại 3;0 , f x f 3 . 2 x 1 2 1 1 3
Phương trình tiếp tuyến của C tại điểm 3;0 là : y x 3 y x . 2 2 2 Bài toán 123
Cho hàm số y f x có đồ thị như hình vẽ và cắt trục hoành tại 5 điểm như hình vẽ sao
cho điểm C là tâm đối xứng của đồ thị. y OÁN 6, 2 T C 2,8 YMPI OL C O C x Ụ 2,8 NH PH CHI 6, 2
Xét các cặp số a; b với a, b và a b sao cho đồ thị hàm số
gx f x a f x b
Cắt trục hoành có đúng 3 cặp giao điểm đối xứng nhau qua điểm C. Tổng các giá trị a nhận được? A. 15 B. 6 C. 12 D. 10
Nhóm toán VD – VDC Lời giải
Phương trình hoành độ giao điểm của đồ thị y g x với trục hoành là f x a
f x a
f x b 0 f x b 177
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Vì đồ thị hàm số y f x nhận điểm C làm tâm đối xứng nên để đồ thị hàm số y g x
cắt trục hoành có đúng 3 cặp giao điểm đối xứng với nhau qua điểm C khi và chỉ khi các
giao điểm của đồ thị hàm số y f x với đường thẳng y a, y b đối xứng với nhau qua
điểm C. Do đó a b 0 b a a 0 .
Quan sát đồ thị hàm số ta thấy f x a với a 0 có đúng 3 nghiệm phân biệt khi
2.8 a 6.2 mà a là số nguyên nên a3; 4; 5
Do đó tổng các giá trị a nhận được là T 3 4 5 12 Bài toán 124
Cho hai hàm số y f x , y g x liên tục trên
có đồ thị được cho như hình vẽ bên g 2 m 5
dưới. Số giá trị nguyên của tham số m để bất phương trình f x có 2 x 4x 10 x 1; 4 C nghiệm là? Ọ y H y N g x 2 f x TOÁ 30 U x IỆ O 2 4 L 1 11 2 O 3 7 15 x TƯ 3 32 2 VÀ CHÍ A. 7 B. 8 C. 6 D. 5 P Ạ
Thầy Nguyễn Đăng Ái T Lời giải Ta nhận thấy nhanh 2
x 4x 10 15 và f x 2 với x1;4 g 2 m 5 f x 2 2
x 4x 10 f x gm 5 có nghiệm x1;4 thì ta phải có 2
x 4x 10 điều kiện g 2 m 5 max 2
x 4x 10 f x 30 1;4 Nhận thấy 2 x x
f x 2 4 10
x 4x 10 . f x 15.2 30 với x1;4 Suy ra: 2
x 4x 10 f x 30 dấu “=” xảy ra khi x 1 Suy ra: g 2 m 5 max 2
x 4x 10 f x 30 1;4
Nhìn vào đồ thị hàm số y g x, ta có 7 2 m 5 15 12 2 m 20 g 2
m 5 30
m 0;1;2; 4 11 2 m 5 3 2 m 8 178
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ
Suy ra có tất cả 7 giá trị m nguyên thỏa mãn bài toán. Vậy ta chọn đáp án A Bài toán 125
Cho hàm số y f x xác định và liên tục trên
, hàm số g x 2
2x 3 và đường thẳng
d có đồ thị như hình vẽ dưới. y g x f x B O 1 x 9 A 4 d OÁN T C
Biết rằng A là điểm chung của 2 đồ thị f x , g x , x g x A
1 , điểm B thuộc đồ thị và x 9 y f x f ' x B
, đường thẳng d là tiếp tuyến của đồ thị hàm số
. Tính A 4 YMPI OL A. 1 B. 3 C. 5 D. 2 2 2 C Ụ Lời giải
Vì điểm A thuộc đồ thị hàm g x nên y 2 A 2.1 3 1 . 2 9 57 NH PH
Điểm B thuộc đồ thị hàm g x nên y B 2. 3 . 4 8 CHI
Đường thẳng tiếp tuyến có dạng y ax b đi qua 2 điểm A, B nên ta có hệ a 5 9 57 a b 2 4 8 .
a b 3 1 b 2
Mà hệ số góc của đường thẳng tiếp tuyến f x chính là f 'x f x A nên A 5 ' 2 179
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 126 Cho hàm số 5 4 3 2 y ax bx cx
dx ex f có đồ thị f x như hình vẽ y 2 y x 1 3 O 1 3 x 2
Hỏi hàm số y g x f 1 2x 2x 1 đồng biến trên khoảng nào sau đây? C Ọ 3 1 1 A. ;1 B. ;
C. 1; 0 D. 1; 3 H 2 2 2 N Lời giải
Ta có gx 2 f 1 2x 4x TOÁ U 1 t 1 t
Đặt t 1 2x x
2 f t 4
0 2 f t 21t 0 f t t 1 IỆ 2 2 L
Dựa vào hình vẽ thấy đường thẳng y x 1 ”nằm cao hơn” đồ thị f x khi 1 x 3 TƯ
Do đó, f t t 1 1 t 3 1 1 2x 3 1 x 0 VÀ Chọn ý C. CHÍ P ẠT 180
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 127
Cho hàm số f x liên tục trên
có đồ thị như hình vẽ: y 1 O x 1
Có bao nhiêu giá trị nguyên của m 1; 2019 sao cho phương trình 2x f f m m 1 0 có nghiệm 2 2 1 x OÁNT A. 2018 B. 2019 C. 1 D. 2 C Lời giải
Dựa vào đồ thị ta có f x f x nên hàm số f x là một hàm lẻ YMPI 2x OL f f m m 1 0 2 2 1 x C Ụ 2 2x f f 2 2x f m m 1 m m 1 f 2 2 1 x 1 x 2x 2x 2x 2x 2x 1 1 f NH PH Ta có 1;1 đồng biến 2 2 2x 1 x 2x x 1 2 x 1 CHI 1 Ta có: 2 m m 1
;0 f m 2
m 1 đồng biến 2 2 2x m m 1 m 2 1 m 1 1 2 x 1
Luôn đúng với m 1; 2019 Có 2019 giá trị nguyên m 181
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 128
Cho hàm số f x liên tục trên
có đồ thị như hình vẽ: y 5 3 1 O 1 2 4 x
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
C gx f 4x 4 2 sin
cos x . Tổng M m bằng Ọ H A. 3 B. 4 C. 5 D. 6 N Lời giải
Một bài toán rất quen thuộc phải không nào? TOÁ 4 4 1 2 U
Ta có 2 sin x cos x 2 1 sin 2x 1 2 cos 2x 1 2 4 sin x 4 cos x 2 IỆ 2 L
M max f t f 1 3 1;2 TƯ Ta có
m min f t f 2 1 1;2 VÀ
Vậy M m 4 CHÍ Bài toán 129 P Ạ
Cho hàm số f x liên tục trên
có đồ thị như hình vẽ: T y 7 3 1 O 1 3 x
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y f x 3 f x 2 2 3
2 5 trên đoạn 1;3 . Tích M.m bằng A. 2 B. 3 C. 54 D. 55 182
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Lời giải
Dựa vào đồ thị ta có max f x f 3 7;min f x f 1 0 2 13 1;3
Đặt t f x 2 t 0; 5
M max gt g5 55 3 2 0;5
Ta có : y f x
f x 3t 2 2 3 2 5
3t 5 g t
m min g t g2 1 0;5
Vậy M.m 55 Bài toán 130
Cho hàm số f x liên tục trên
có đồ thị như hình vẽ: y 5 3 OÁNT C 1 O 1 2 3 x YMPI OL
g x f 2 2x 1 x m
max gx 2 min gx C Ký hiệu . Tìm m để 0; 1 0; 1 Ụ
A. m 4
B. m 3
C. 0 m 5
D. m 2 Lời giải NH PH
Đặt t 2 2x 1 x t 1; 3
Để max g t 2 min g t g 3 2g 2 5 m 2 1 m m 3 CHI Chọn ý B. 183
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 131
Cho hàm số y f x , y g x liên tục trên
có đồ thị hàm số y f x là đường cong
nét đậm và y gx là đường cong nét mảnh như hình vẽ. y g'x O C x B A CỌ f 'x H N
Gọi ba giao điểm A, B,C của đồ thị y f x , y gx trên hình vẽ lần lượt có hoành TOÁ a b c U
độ , , . Giá trị nhỏ nhất trên đoạn bằng IỆ
A. h 0
B. h a
C. h b
D. h c L Lời giải TƯ
Ta có hx f x gx VÀ
Trên khoảng a, b thì đồ thị hàm số của f x nằm thấp hơn so với gx h x 0 x a;b CHÍ Suy ra với P
Trên khoảng b; c thì đồ thị hàm số của f x nằm cao hơn so với gx
ẠT Suy ra hx0với xb;c
Nên h x đạt cực tiểu tại x b a;c
Vậy min h x h b a;c Chọn ý C. 184
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 132
Cho hàm số f x liên tục trên
có đồ thị như hình vẽ: y 5 3 1 O 1 2 3 x
Ký hiệu g x f 3 x 2
x x 2 3m , với m là tham số thực. Giá trị nhỏ nhất của biểu thức P 2
m 3max g x 4min gx m 0;1 0;1 OÁN A. 105 B. 102 C. 50 D. 4 T C Lời giải Đặt 3 x 2
x x 2 t
x 0;1 t YMPI Do 2;3 OL
Ta có max g t g 3 5 3m;min g x g 2 1 3m 2;3 2;3 C 2 Ụ
Từ đó P m 22m 19 102 Vậy P 102 min Chọn ý B. NH PH Bài toán 133 CHI
Cho hàm số y f x có đồ thị như hình vẽ y f x 4 O 1 x
Có bao nhiêu giá trị nguyên của m với m 1; 5 để bất phương trình
f m m 1 f 5 x nghiệm đúng với mọi x1;4 A. 2 B. 1 C. 4 D. 3 Lời giải
Với m 1; 5 m m 1 1;6 5 f m m 1 nghịch biến 185
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA
Với x 1; 4 5 x 1;2 f 5 x nghịch biến
Bất phương trình f m m 1 f 5 x nghiệm đúng m m 1 min 5 x
m m 1 1 m 1
Vậy có 1 giá trị nguyên m thỏa mãn đề bài Chọn ý B. Bài toán 134 Trên parabol y 2
x 1P lấy hai điểm A1;2.B3;10 gọi M là điểm di động trên
cung AB của P , M khác A, B . y B 10 M C Ọ H N TOÁ A 2 U IỆL O D E F x TƯ
Gọi S1 là diện tích hình phẳng giới hạn bởi và , gọi là diện tích hình phẳng giới hạn bởi VÀ
và Gọi là tọa độ điểm khi đạt giá trị nhỏ nhất. Tính 2 x 2 y 0 0 CHÍ A. 29 B. 11 C. 7 D. 5 P Lời giải ẠT Gọi M 2
a; a 1P
Ta viết được phương trình đường thẳng
MA : y a 1x 1 2 và MB : y a 3x 3 10 a 3 3 13 1
Ta có S S a 1 x 1 2 a 3 x 3 10 x 1 dx a 4a 1 2
2 2 3 3 1 a 1 1
Ta có min S S
a 2 M 2;5 1 2 3 Vậy 2 x 2 y 29 0 0 Chọn ý A. 186
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 135
Cho hàm số liên tục trên đoạn 1; 9 và có đồ thị là đường cong trong hình vẽ dưới đây y 2 O x 1 4
Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình
f x f x2 f x f x 2 16.3 2 8 .4
m 3m fx .6 OÁN
Nghiệm đúng với mọi giá trị x 1;9? T C A. 22 B. 31 C. 5 D. 6 Lời giải YMPI
Từ đồ thị suy ra 4 f x 2 x 2;9 . Đặt t f x , t 4; 2 OL Ta tìm m sao cho t 2
t t t 2 16.3 2 8 .4 m t
3m.6 đúng với mọi t 4;2 C t 2 t 2 t Ụ
16.3 t 2t 8.4 m
3m.6 , t 4;2 16 t 2 2
t 2t 8. 2 m
m ,t 4;2 t 3 2 3 NH PH 16 Ta có
4 , t 4;2. Dấu bằng xảy ra khi t 2 . CHI 2t t 2 2 Mà 2
t 2t 8 0 ,t 4;2. Do đó t 2t 8.
0 , t 4;2. 3
Dấu bằng xảy ra khi t 2 . 16 t 2 2 Suy ra
t 2t 8.
,t 4;2. t 4 2 3 16 t 2 2 Vậy
t 2t 8. 2 m
m , t 4;2 2
m 3m 4 1 m 4 t 3 2 3
Kết quả m 1; 0; 1; 2; 3; 4 . 187
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA Bài toán 136
Cho hai hàm số f x và g x có đồ thị các đạo hàm cho như hình vẽ với f 'x (màu
xanh) và g 'x (màu hồng) có đồ thị như hình vẽ. y 4 3 2 1, 5 2 1, 5 1 O 1 x CỌH N
Hỏi hàm số h x f x 1 g 2x đồng biến trên khoảng nào sau đây? 1 1 5 1;0 0; 1; 2; TOÁ A. B. C. D. 2 2 2 U IỆ Lời giải L
Ta có h x f x 1 g 2x h'x f 'x 1 2g'2x TƯ
Dựa vào đồ thị ta thấy f 'x 2g 'x 0 x 2;0 x 1 2;0 VÀ
h'x f 'x 1 2g'2x 0 x 1;0 2x 2;0 CHÍ
Hàm số hx f x 1 g2x đồng biến trên khoảng 1;0 P Ạ T 188
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
PHƯƠNG PHÁP GIẢI TOÁN ĐỒ THỊ Bài toán 137
Cho hai hàm số f x và g x có đồ thị biểu diễn đạo hàm f x và gx như hình vẽ.
Biết rằng hàm số y f x g x 2 đồng biến trên khoảng ; và giá trị lớn nhất của
biểu thức 8 ; phương trình tiếp tuyến với đồ thị y g x tại điểm có hoành độ x 11 y 3x 2
y f x 1 là
và phương trình tiếp tuyến với đồ thị hàm số tại điểm có hoành độ x 9 y ax f 9 2 là
1 Giá trị của bằng y f 'x g'x O 1 3 21 x 2 OÁNT C A. 13 B. 28 C. 26 D. 22
Thầy Nguyễn Đăng Ái YMPI Lời giải OL
Ta có y f x gx 2 C Ụ
Đồ thị hàm số gx dịch sang trái 2 đơn vị so với trục tung sẽ được gx 2
Dựa vào đồ thị ta có f 1 g3 . Giả sử x
f x g x 2 0 là điểm thỏa mãn 0 0 Trên khoảng 1; x f x g x 2 0 thì
0 luôn nằm cao hơn so với 0 NH PH
Nên y 0 với x 1; x
max 8 x 1 8 x 9 0 . Từ 0 0 CHI
Hình vẽ tượng trưng y f 'x g'x O 1 3 9 21 x 2
Phương trình tiếp tuyến với đồ thị y g x tại điểm có hoành độ x 11 1 là 189
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
HƯỚNG TỚI KỲ THI THPT QUỐC GIA g 11 3
y g11x 11 g11 g11 35
Ta có f 9 g11 3
Phương trình tiếp tuyến với đồ thị hàm số y f x tại điểm có hoành độ x 9 2 là
a f 9 3
y f 9x 9 f 9
f 9 9 f 9 1 28 C Ọ H N TOÁ U IỆL TƯ VÀ CHÍ P ẠT THE END GAME 190
Điều ta biết là giọt nước, điều ta chưa biết là đại dương – Newton
TẠP CHÍ VÀ TƯ LIỆU TOÁN HỌC
MỌI NGƯỜI CÓ THỂ TÌM ĐỌC CUỐN “TẠI SAO NGUYÊN HÀM TÍCH
PHÂN LẠI KHÓ” CỦA CÙNG TÁC GIẢ
CHỊU TRÁCH NHIỆM NỘI DUNG VÀ THIẾT KẾ BÌA NGUYỄN MINH TUẤN
NHÓM CHINH PHỤC OLYMPIC TOÁN
Mọi ý kiến thắc mắc, góp ý vui lòng gửi về địa chỉ sau 0343763310 tuangenk@gmail.com Lovetoan.wordpress.com Đại học FPT Hà Nội




