Phương pháp tính diện tích tứ giác tam giác môn toán 9 (có đáp án và lời giải chi tiết)

Chuyên đề 5. TÍNH DIỆN TÍCH TAM GIÁC, DIỆN TÍCH TỨ GIÁC NHỜ SỬ DỤNG CÁC TỈ SỐ LƯỢNG GIÁC A. Đặt vấn đề Ta đã biế 1
t cách tính diện tích tam giác theo một công thức rất quen thuộc là S 
ah, trong đó a là độ dài 2
một cạnh của tam giác, h là chiều cao ứng với cạnh đó.
Bây giờ ta vận dụng các tỉ số lượng giác, các hệ thức về cạnh và góc trong tam giác vuông để xây dựng thêm
các công thức tính diện tích tam giác, tứ giác. B. Một số ví dụ
Ví dụ 1. Chứng minh rằng diện tích một tam giác bằng nửa tích hai cạnh nhân với sin của góc nhọn tạo bởi
các đường thẳng chứa hai cạnh ấy. Giải
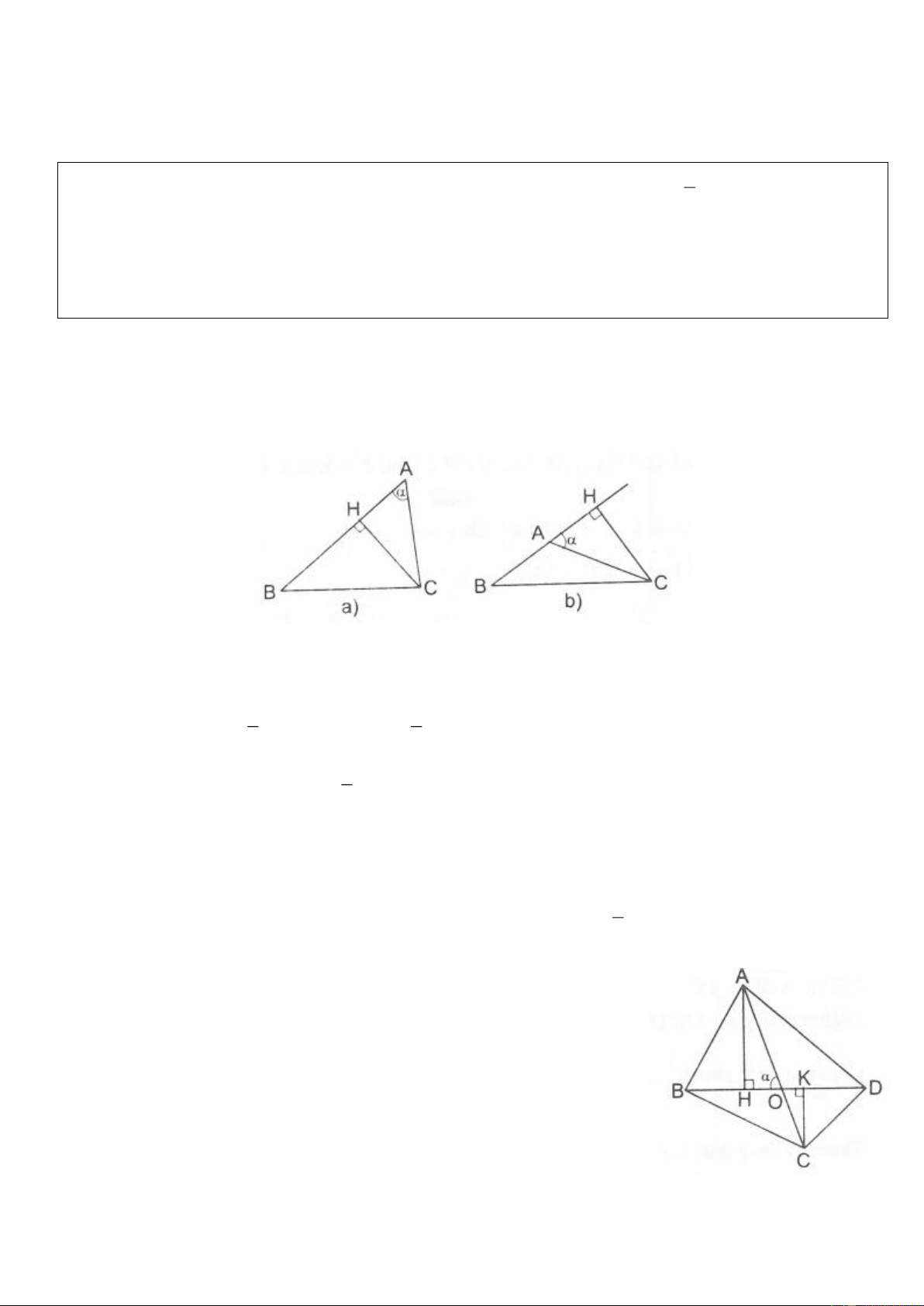
Gọi  là góc nhọn tạo bởi hai đường thẳng chứa hai cạnh AB, AC của tam giác ABC. Vẽ đường cao CH. Xét A
 CH vuông tại H có CH  A . C sin 1 1 Diện tích ABC  là S  .
AB CH . Do dó S  . AB AC.sin . 2 2 Lưu 1 ý: Nếu 0
  90 , ta có ngay S  . AB AC 2 Như vậy 0
sin 90  1, điều này sẽ học ở các lớp trên.
Ví dụ 2. Tứ giác ABCD có AC  , m BD  ,
n góc nhọn tạo bởi hai đường chéo bằng  . 1
Chứng minh rằng diện tích của tứ giác này được tính theo công thức S  mn sin . 2 Giải
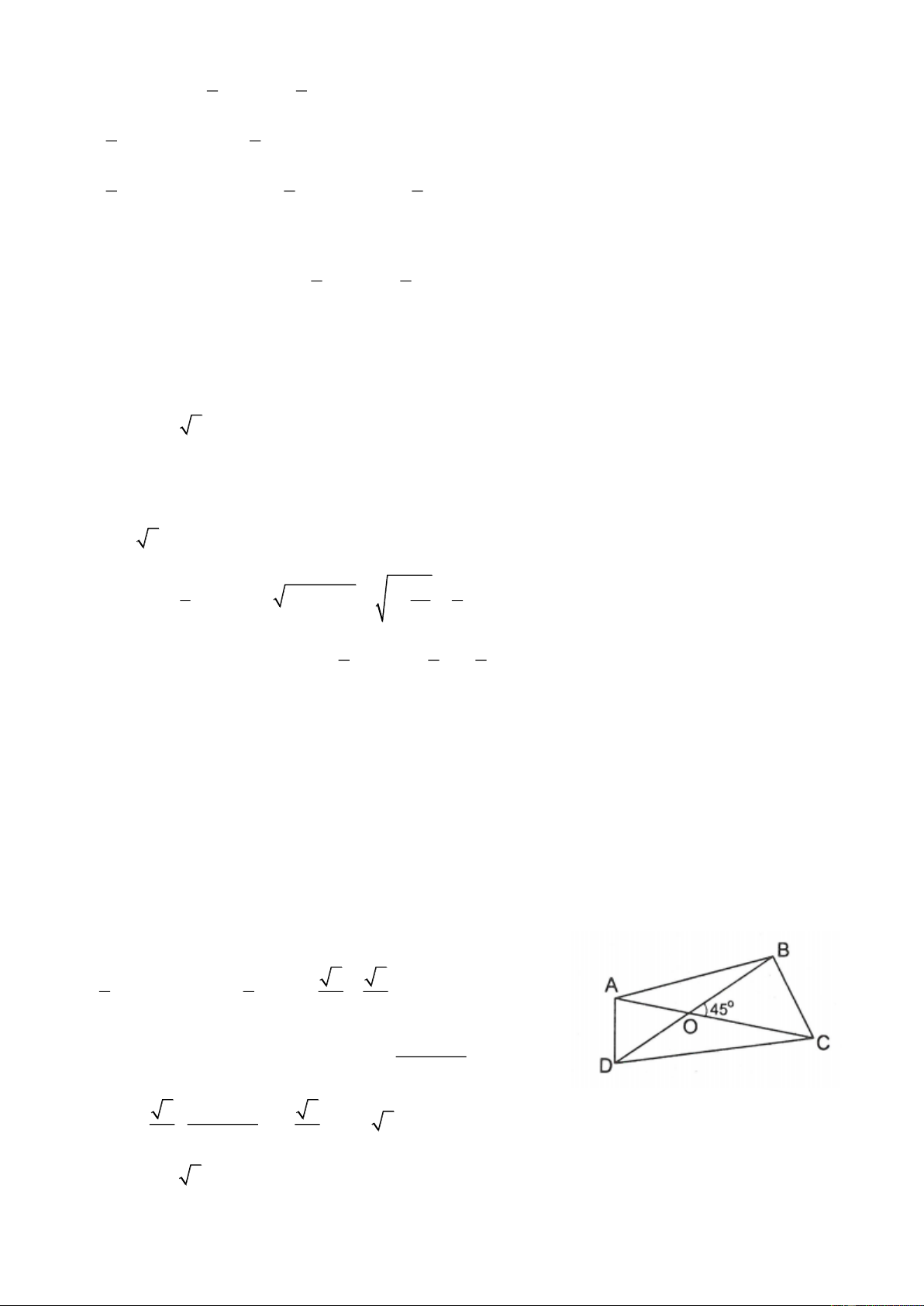
Gọi O là giao điểm của AC và BD. Giả sử BOC  .
Vẽ AH  BD, CK  . BD
Ta có AH  OAsin ;
CK  OC sin và OA OC  A . C
Diện tích tứ giác ABCD là: Trang 1 1 1 S  S  S  B . D AH  B . D CK ABD CBD 2 2 1 1
 BD(AH  CK)  BD(OAsin  OC sin) 2 2 1 1 1
 BDsin(OA  OC)  AC.BDsin  mnsin 2 2 2 Lưu ý: • Nế 1 1
u AC  BD ta có ngay S  AC.BD  mn 2 2
• Phương pháp tính diện tích của tứ giác trong ví dụ này là chia tứ giác thành hai tam giác không có điểm
trong chung, rồi tính diện tích của từng tam giác.
Ví dụ 3. Cho tam giác nhọn ABC. Gọi độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Tính diện tích tam giác
ABC biết a  4 2c ,
m b  5c ,
m c  7c . m Giải
Theo định lí côsin ta có: 2 2 2
a  b  c  2bc cos . A Do đó  2 2 2 4 2
 5  7  2.5.7.cos A 3 9 4 Suy ra 2 cos A 
 sin A  1 cos A  1  5 25 5 1 1 4
Vậy diện tích tam giác ABC là: S  bc sin A  .5.7. 14 2 cm  2 2 5
Nhận xét: Trong cách giải trên ta đã tìm cos A rồi suy ra sin .
A Ta cũng có thể vận dụng định lí côsin để
tìm cos B rồi suy ra sin B (hoặc tìm cosC rồi suy ra sin C)
Ví dụ 4. Tứ giác ABCD có AC  BD 12c .
m Góc nhọn giữa hai đường chéo là 45 .
 Tính diện tích lớn nhất của tứ giác đó. Giải
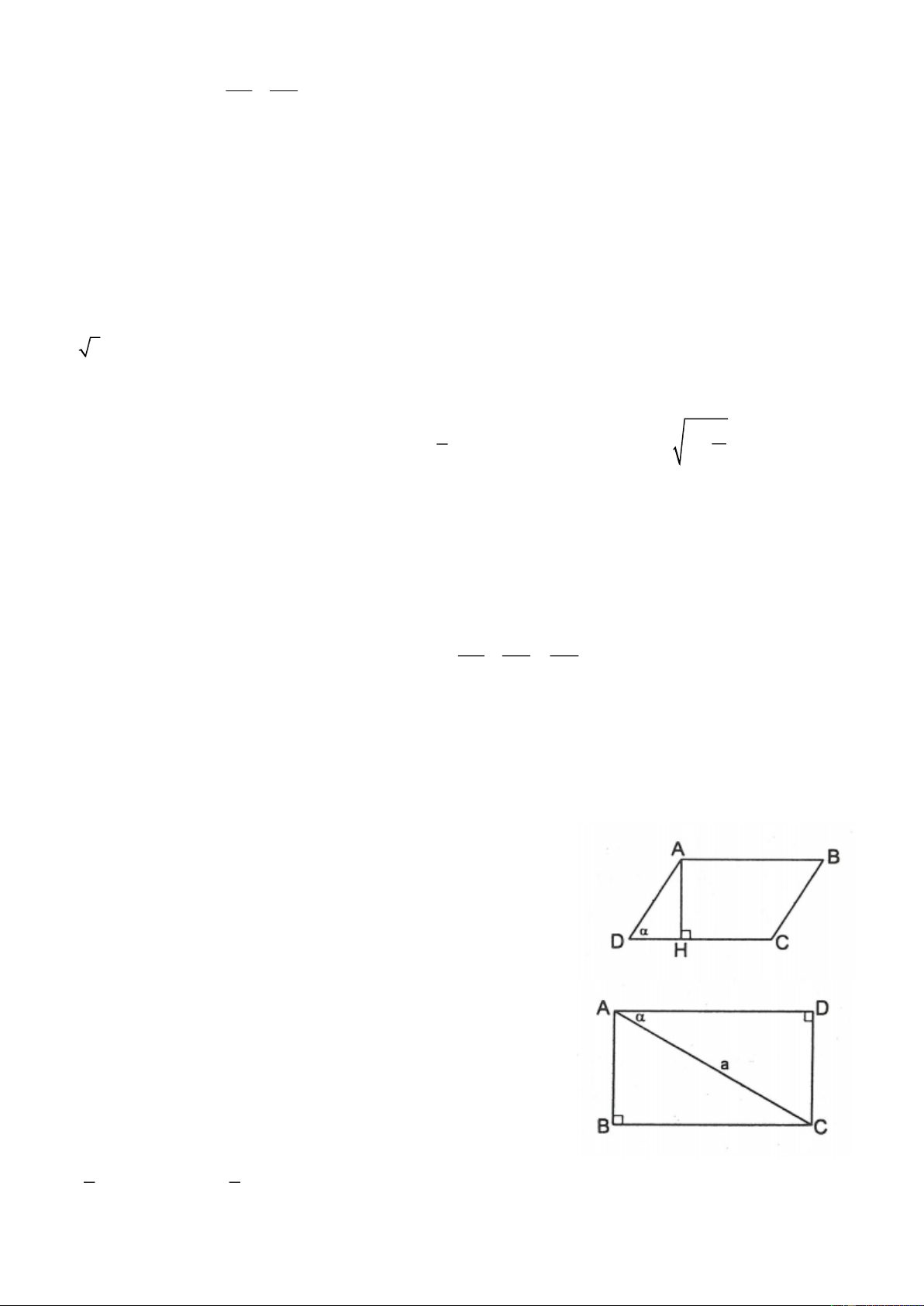
Gọi O là giao điểm của AC và BD. Giả sử AOD  45 . 
Diện tích tứ giác ABCD là: 1 1 2 2 S  AC. . BD sin 45  AC. . BD  .AC.BD 2 2 2 4 2
 AC  BD 
Theo bất đẳng thức Cô-si, ta có: AC.BD     2  2    Do đó 2 AC BD 2 2 S   .6  9 2    2 cm  4  2  4 Vậy 2
max S  9 2cm khi AC  BD  6c . m Trang 2
Ví dụ 5. Cho tam giác ABC, A  60 .
 Vẽ đường phân giác AD. 1 1 3 Chứng minh rằng:   AB AC AD Giải Ta có 1 1 1 0 S  . AB . AD sin 30  . AB . AD ABD 2 2 2 1 1 1 S  AC. . AD sin 30  AC. . AD . ACD 2 2 2 1 1 3 S  . AB AC.sin 60  . AB AC. ABC 2 2 2 1 1 1 1 1 3 Mặt khác S  S  S nên . AB . AD  AC. . AD  . AB AC. ABD ACD ABC 2 2 2 2 2 2
Do đó AD  AB  AC  A . B AC 3 AB  AC 3 1 1 3 Suy ra  hay   . AB.AC AD AB AC AD
Nhận xét: Phưong pháp giải trong ví dụ này dựa trên quan hệ tổng diện tích các tam giác ABD và tam giác
ACD bằng diện tích tam giác ABC.
Ví dụ 6. Tam giác ABC có mỗi cạnh đều nhỏ hơn 4cm. Chứng minh rằng tam giác này có diện tích nhỏ hơn 2 7cm Giải 3
Giả sử A  B  C, khi đó A  60 và sin A  2
Diện tích tam giác ABC là: 1 1 3 S  . AB AC.sin A  .4.4.
 4 3  6,92...  7  2 cm . 2 2 2
Nhận xét: Do vai trò các góc A, B, C của tam giác ABC là như nhau nên ta có thể giả sử A  B  C, từ đó 3 suy ra A  60 ,
 dẫn tới sin A  2
C. Bài tập vận dụng • Tính diện tích
5.1. Chứng minh rằng diện tích cùa hình bình hành bằng diện tích của hai cạnh kề nhân với sin của góc nhọn
tạo bởi hai đường thẳng chứa hai cạnh ấy. Trang 3
5.2. Cho hình chữ nhật ABCD, AC  a và BAC   0    45. Chứng minh rằng diện tích của hình 1 chữ nhật ABCD là 2 S  a sin 2 2 OA OB
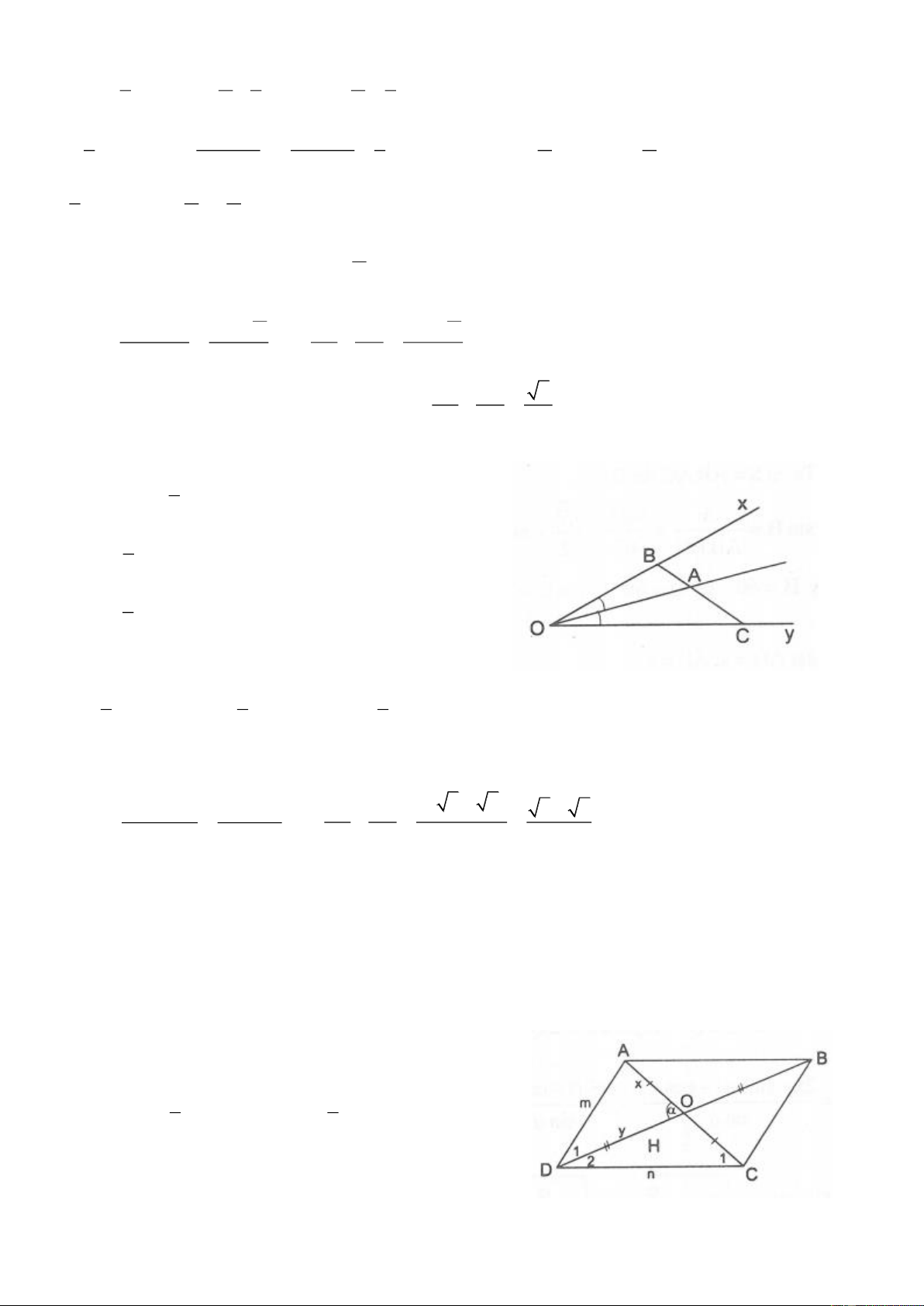
5.3. Cho góc nhọn xOy. Trên tia Ox lấy điểm A và C, trên tia Oy lấy điểm B và D sao cho  , m  . n OC OD S
Chứng minh rằng AOB  . m n SCOD
5.4. Tam giác nhọn ABC có BC  a, CA  , b AB  .
c Gọi diện tích tam giác ABC là S. Chứng minh rằng 2 2 2
b  c  a S 
. Áp dụng với a  39, b  40, c  41 và A  45 .  Tính S. 4 cot A
5.5. Cho góc xOy có số đo bằng 45 .
 Trên hai cạnh Ox và Oy lần lượt lấy hai điểm A và B sao cho
OA OB  8c .
m Tính diện tích lớn nhất của tam giác AOB. 1
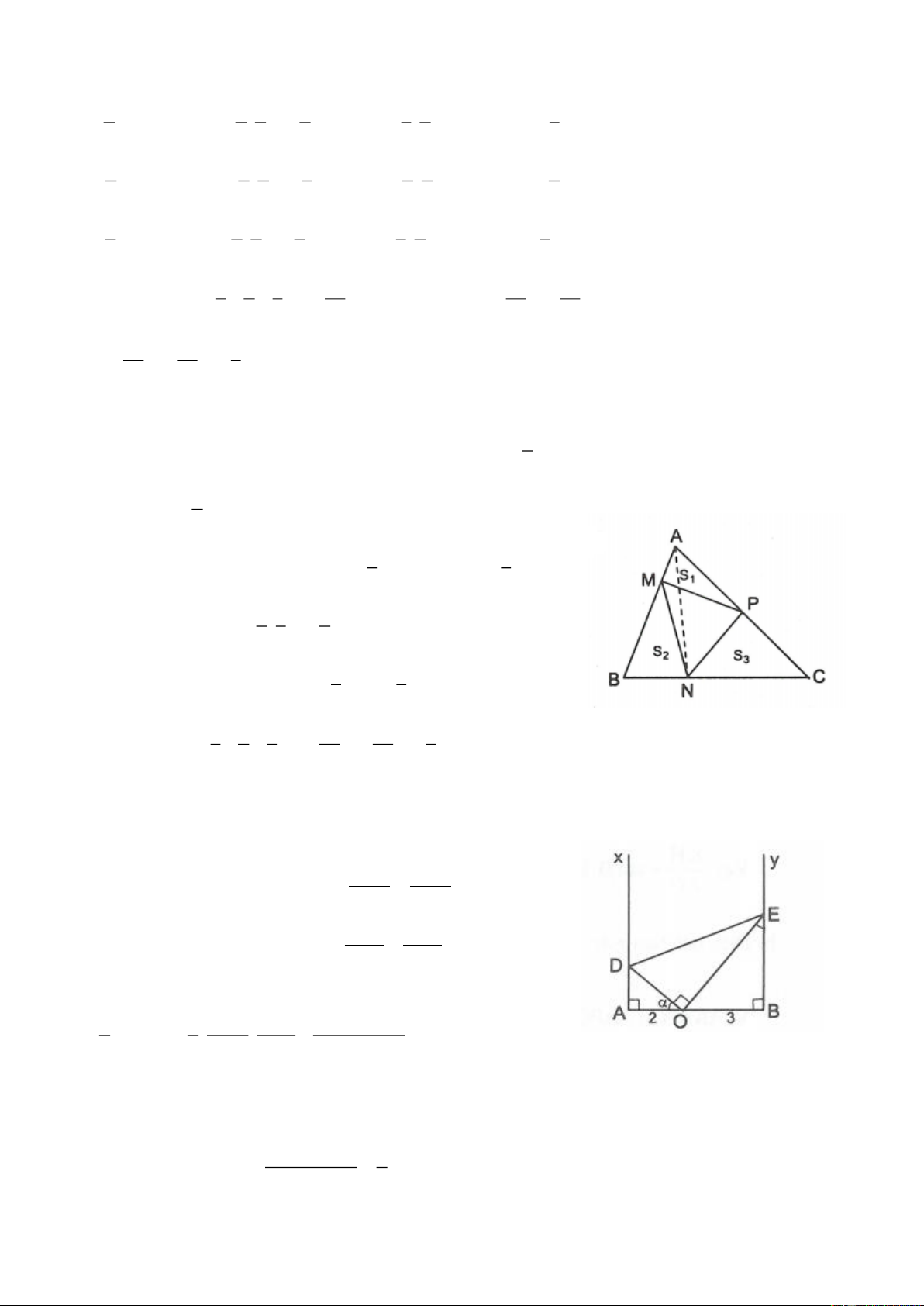
5.6. Cho tam giác nhọn ABC. Trên các cạnh AB, BC, CA lần lượt lấy các điểm M,N, P sao cho AM  AB, 4 1 1 BN  BC, CP  C .
A Chứng minh rằng diện tích tam giác MNP nhỏ hơn 1 diện tích tam giác ABC. 3 2 3
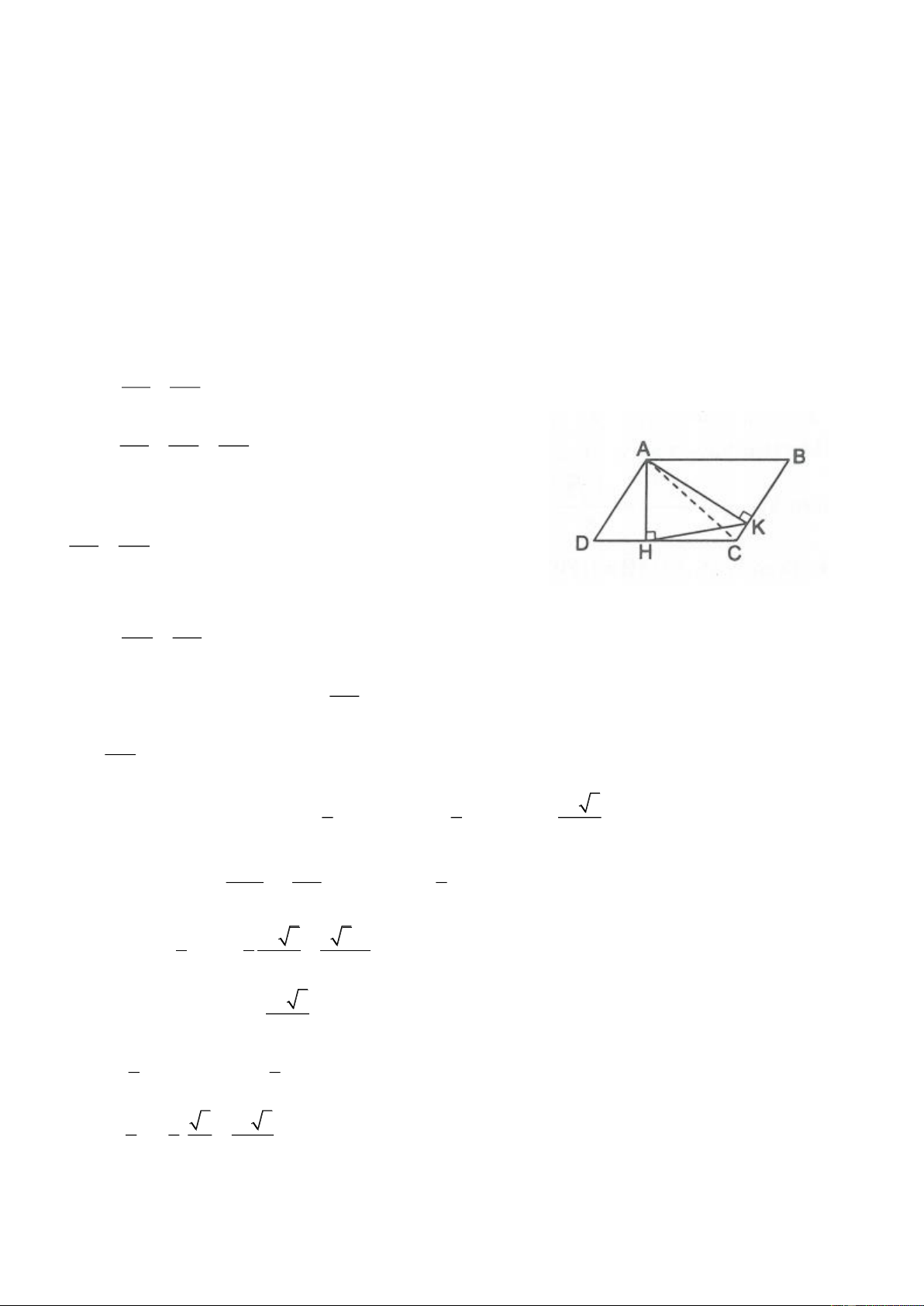
5.7. Cho đoạn thẳng AB  5c .
m Lấy điểm O nằm giữa A và B sao cho OA  2c .
m Trên một nửa mặt phẳng
bờ AB vẽ các tia Ax, By cùng vuông góc với AB. Một góc vuông đỉnh O có hai cạnh cắt các tia Ax, By lần
lượt tại D và E. Tính diện tích nhỏ nhất của tam giác DOE.
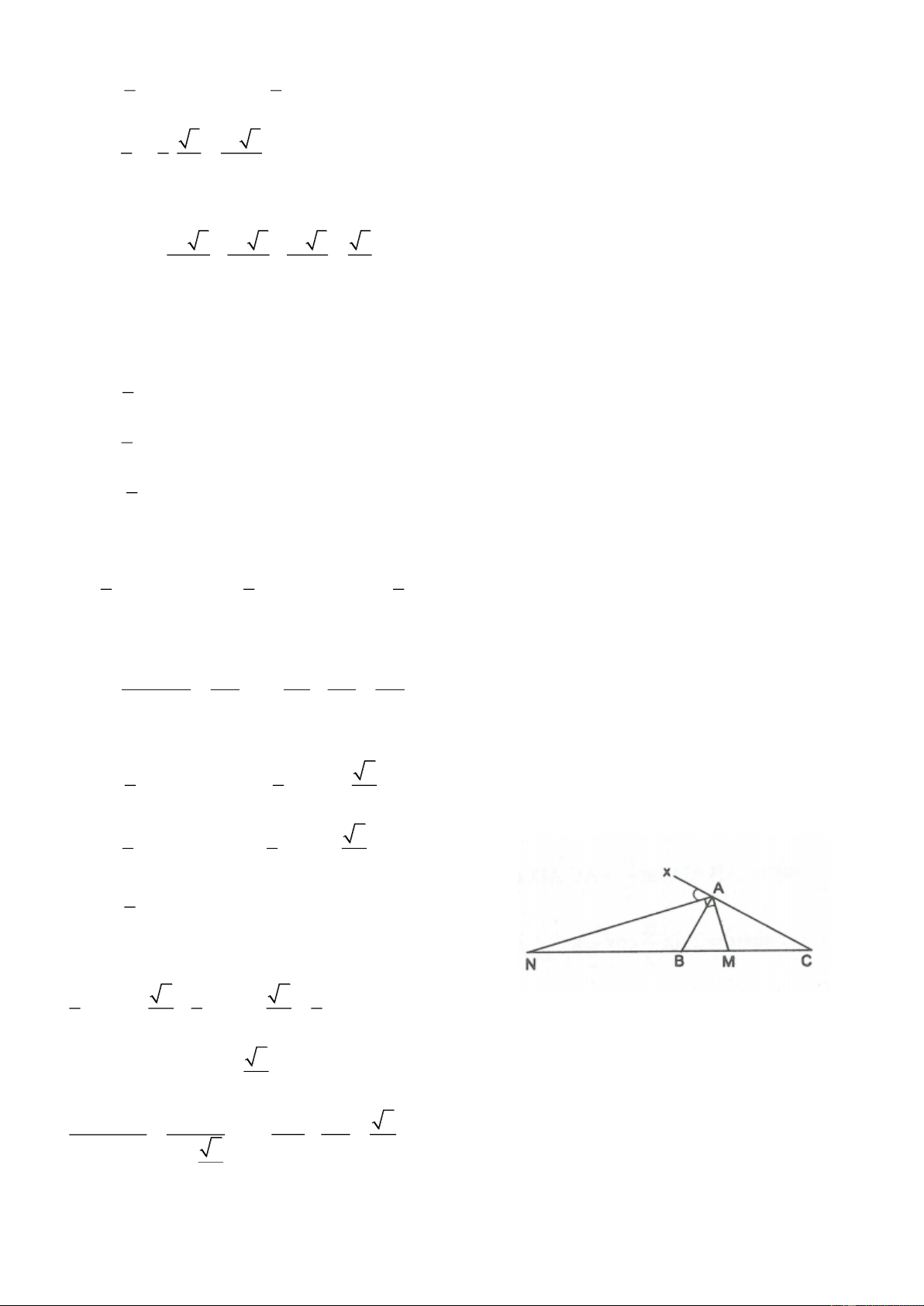
5.8. Cho hình bình hành ABCD, góc B nhọn. Gọi H và K lần lượt là hình chiếu của A trên các đường thẳng DC và BC.
a) Chứng minh rằng K  AH ABC 
, từ đó suy ra KH  AC.sin ; B
b) Cho AB  a, BC  b và B  60 .
 Tính diện tích A
 HK và tứ giác AKCH.
• Chứng minh các hệ thức
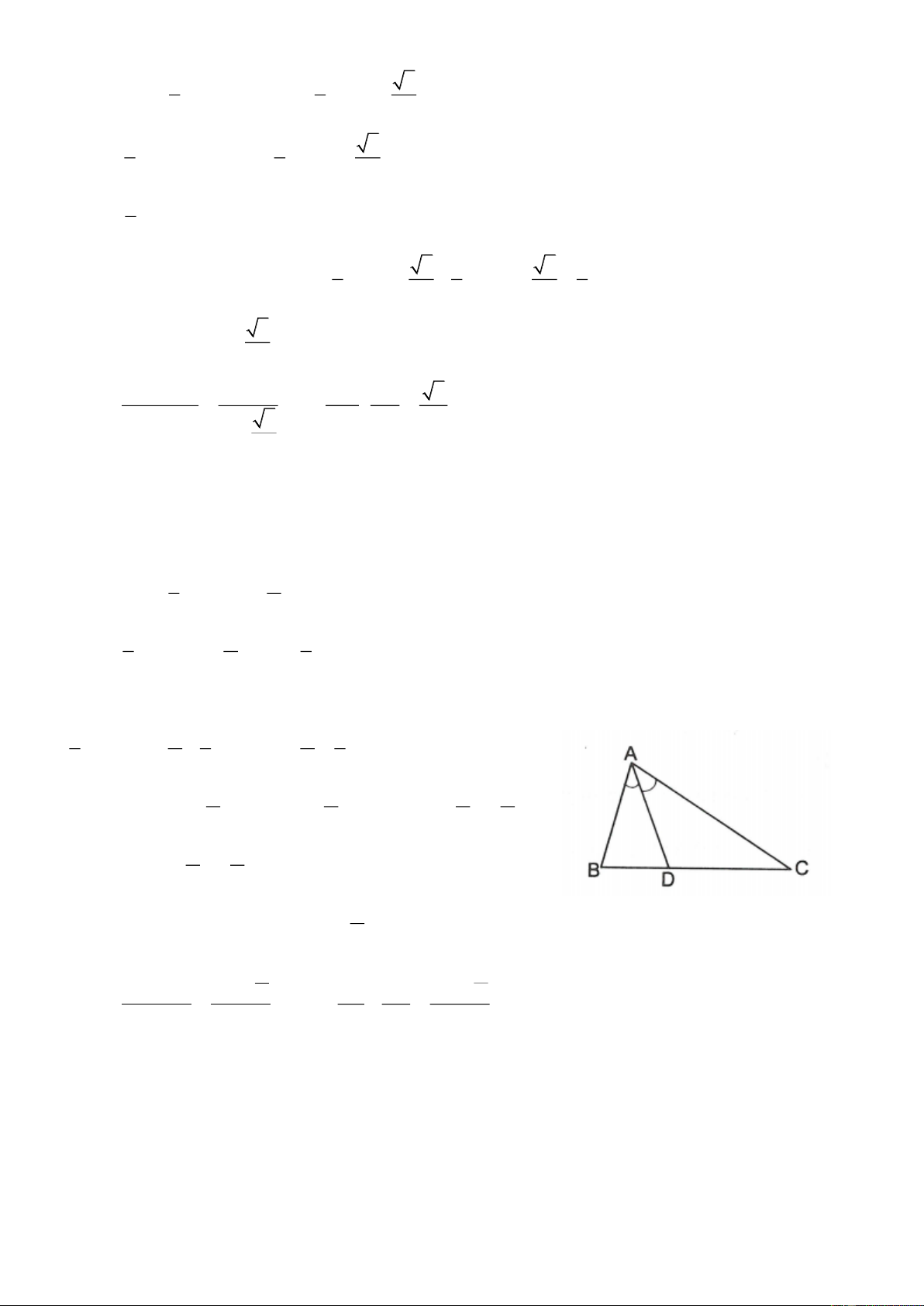
5.9. Cho tam giác ABC( AB  AC), A  60 .
 Đường phân giác ngoài tại đỉnh A cắt đường thẳng BC tại N. 1 1 1 Chứng minh rằng:   AB AC AN
5.10. Cho tam giác ABC vuông tại
A  AB  AC . Các đường phân giác trong và ngoài tại đỉnh A của tam
giác cắt đường thẳng BC tại M và N. Chứng minh rằng: 1 1 2 1 1 2 a)   b)   AM AN AB AM AN AC  2 cos 1 1 5.11. Cho tam giác 0
ABC, A    90 . Vẽ đường phân giác AD. Chứng minh rằng: 2   AB AC AD
5.12. Cho góc xOy có số đo bằng 30 .
 Trên tia phân giác của góc đó lấy điểm A sao choOA  a. Qua A vẽ
một đường thẳng cắt Ox và Oy theo thứ tự tại B và C. Trang 4 1 1 Tính giá trị của tổng  OB OC
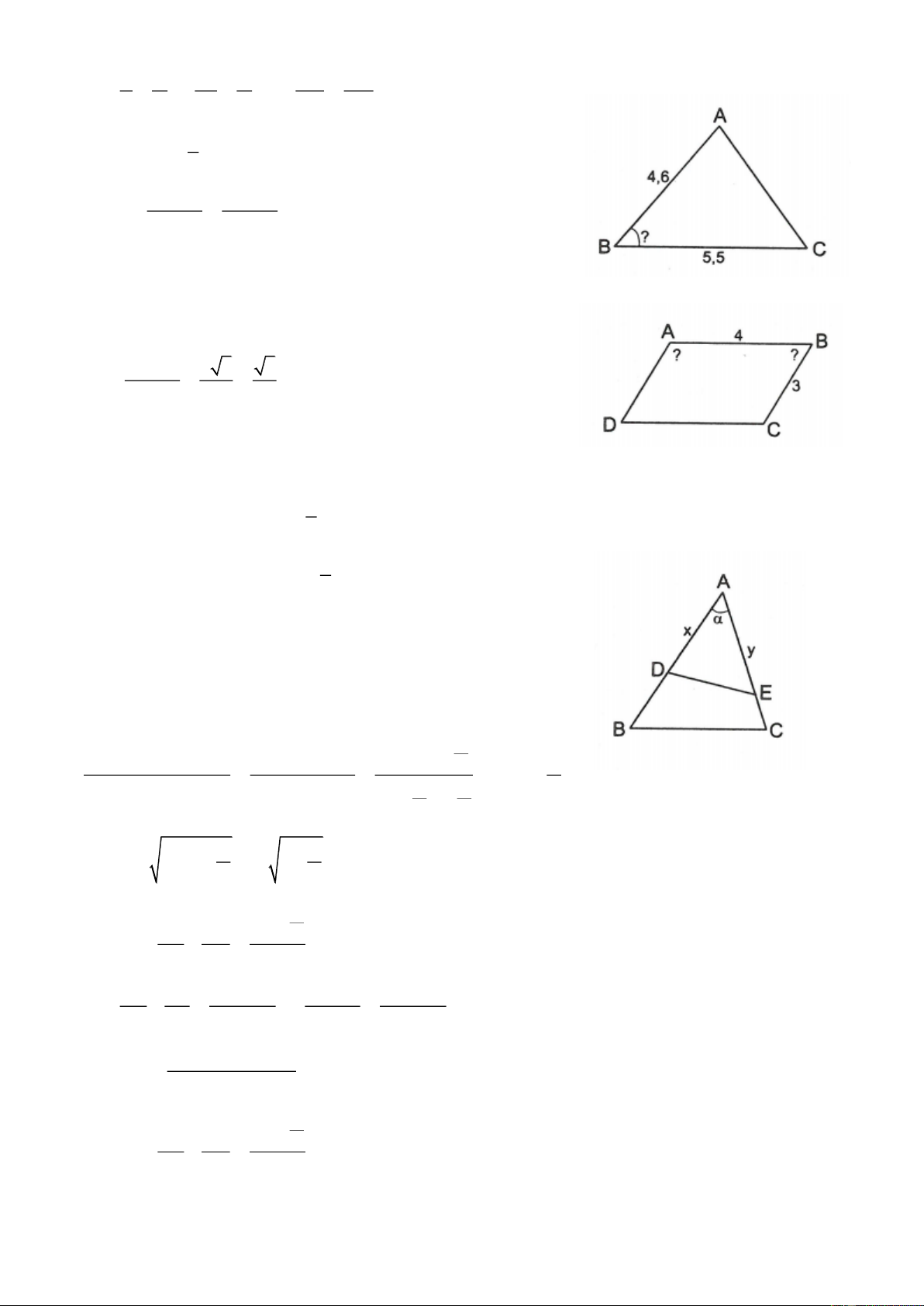
5.13. Cho hình bình hành ABCD, góc nhọn giữa hai đường chéo bằng góc nhọn của hình bình hành. Chứng
minh rằng độ dài hai đường chéo tỉ lệ với độ dài hai cạnh kề của hình bình hành.
• Tính số đo góc. Tính độ dài
5.14. Tam giác nhọn ABC có AB  4, 6c ;
m BC  5, 5cm và có diện tích là 2
9, 69cm . Tính số đo góc B (làm tròn đến độ).
5.15. Cho hình bình hành ABC , D B  90 .
 Biết AB  4c ,
m BC  3cm và diện tích của hình bình hành là 2
6 3cm . Tính số đo các góc của hình bình hành.
5.16. Cho tam giác ABC có diện tích 2
S  50cm , A    90 .
 Trên hai cạnh AB và AC lần lượt lấy các điểm 1 
D và E sao cho A
 DE nhọn, có diện tích là S  S. Chứng minh rằng DE 10 tan cm 1 2 2
5.17. Cho tam giác ABC, đường phân giác AD. Biết AB  4, 7c ,
m AC  5, 3cm và A  72 .
 Tính độ dài AD
(làm tròn đến hàng phần mười).
5.18. Cho tam giác ABC, AB  6c ,
m AC  12c , m A  120 .
 Vẽ đường phân giác AD. Tính độ dài AD.
5.19. Cho tam giác ABC, AB  5c ,
m BC  7c ,
m CA  8c .
m Vẽ đường phân giác AD. Tính độ dài AD. 1 1 1
5.20. Cho tam giác ABC, đường phân giác AD. Biết  
, tính số đo góc BAC. AB AC AD
HƯỚNG DẪN GIẢI-ĐÁP SỐ
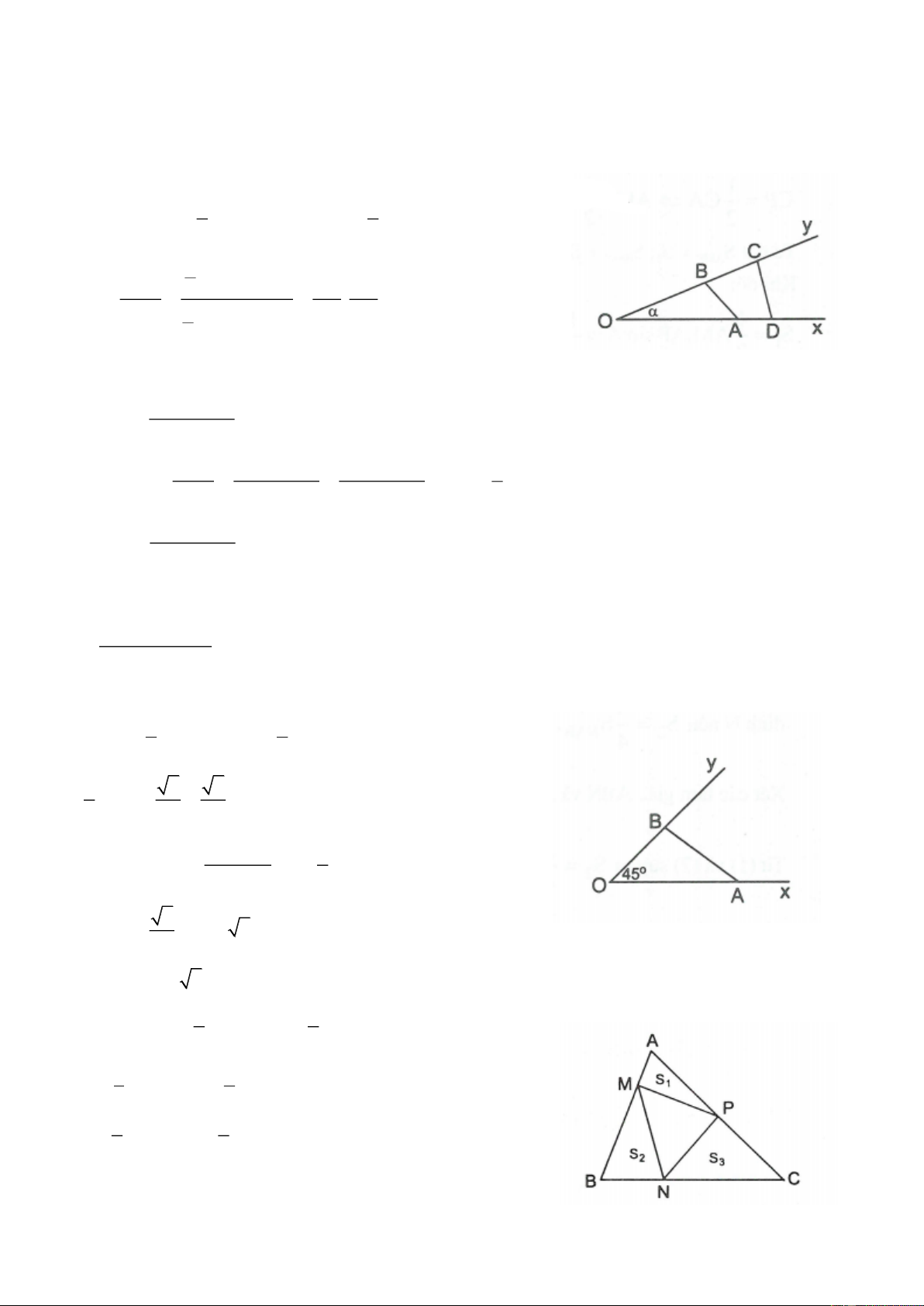
5.1. Xét hình bình hành ABC ,
D D    90 .  Vẽ đường cao AH.
Xét tam giác ADH vuông tại H, ta có: AH  A . D sin
Diện tích hình bình hành ABCD là: S  C . D AH  C . D A . D sin. Vậy S  A . D D . C sin. 5.2. Xét ABC  vuông tại B có
AB  AC cos  a cos; BC  AC sin   a sin 
Diện tích hình chữ nhật ABCD là: 2 S  A .
B BC  a cos. a sin   a sin  cos 1 1 2 2
 a .2sin cos  a sin 2 2 2 Trang 5 1 1 5.3. Tacó S  O . A OB sin ; S
 OC.ODsin. AOB 2 COD 2 1 O . A OB sin Do đó S OA OB AOB 2   .  . m n S 1 OC OD COD OC.OD sin  2 5.4. Vì ABC 
nhọn nên theo định lí côsin ta có 2 2 2
a  b  c  2bc cos A 2 2 2
b  c  a  cos A  2bc 2 2 2 2 2 2 cos A
b  c  a
b  c  a 1 Ta có cot A    (vì S  bc sin ) A sin A 2bc sin A 4S 2 2 2 2   Do đó b c a S  . 4 cot A
Áp dụng: Với a  39, b  40, c  41 và A  45 ta có: 2 2 2 40  41  39 S   440 (đvdt) 0 4 cot 45
5.5. Ta đặt diện tích tam giác AOB là S. 1 1 Ta có S  O . A OB sin O  O . A OB sin 45 2 2 1 2 2  . OA . OB  . OA OB 2 2 4 2 2      Nhưng OA OB 8 O . A OB   16      2   2  Do đó 2 S  .16  4 2  2
cm  khi OA  OB  4cm 4 Vậy 2
max S  4 2cm 1 3
5.6. Tacó AM  AB  BM  A ; B 4 4 1 2 BN  BC  CN  BC; 3 3 1 1 CP  CA  AP  C . A 2 2 Ta đặt S  S ; S  S ; S  S và S  S AMP 1 BMN 2 CNP 3 ABC Trang 6 Khi đó: 1 1 1 1 1 1 1 S 
AM .AP sin A  . A . B AC.sin A  . A . B AC.sin A  S 1 2 2 4 2 8 2 8 1 1 3 1 1 1 1 S 
BM .BN sin B  . A . B BC.sin B  . B . A BC.sin B  S 2 2 2 4 3 4 2 4 1 1 2 1 1 1 1 S 
CN.CP sin C  . . CB . . CA sin C  . . CB . CA sin C  S 3 2 2 3 2 3 2 3  1 1 1  17
Vậy S  S  S    S  S. Do đó 17 7 S  S  S  S 1 2 3    8 4 3  24 MNP 24 24 7 8 1 S  S  S  S. MNP 24 24 3
Cách giải khác: (không dùng tỉ số lượng giác) (h.5.10) 3
Vẽ đoạn thẳng AN. Xét các tam giác NMB và NAB có BM 
AB và chung chiều cao vẽ từ 4 4 đỉ 3 nh N nên S  S . 1 2   4 NAB 1 1
Xét các tam giác ABN và ABC có BN  BC nên S  S ABN 2 3 3 3 1 1
Từ (1) và (2) suy ra S  . S  S 2 4 3 4 1 1
Chứng minh tương tự ta được S  S; S  S 3 1 3 8   Do đó 1 1 1 7 8 1 S  S    S  S  S  S MNP    8 4 3  24 24 3
5.7. Ta có AOD  BEO (cùng phụ với BOE . )
Ta đặt AOD   thì BEO   OA 2 Xét A
 OD vuông tại O, ta có: OD   cos cos OB 3 Xét BEO 
vuông tại B, ta có: OE   sin  sin 
Diện tích tam giác DOE là: 1 1 2 3 6 S  O . D OE  . .  * 2 2 cos sin  2 sin  cos
Áp dụng bất đẳng thức 2 2
x  y  2xy ta được: 2 2
sin   cos   2 sin  cos hay 1 2sin o c s Thay vào (*) ta đươc: 6 6 S   2 sin  cos 1
(dấu “=” xảy ra khi sin   cos    45 )  Trang 7 Vậy 2
min S  6cm khi   45
Nhận xét: Việc đặt AOD   giúp ta tính được các cạnh góc vuông của DOE, từ đó tính được diện tích
của tam giác này theo các tỉ số lượng giác của góc  . Do đó việc tìm min S đưa về tìm max sin cos  đơn giản hơn.
5.8. a) Ta có AB / /CD mà AH  CD nên AH  A . B • A  DH và ABK 
có: H  K  90 ; 
D  B (hai góc đối của hình bình hành). Do đó A
 DH ∽ ABK (g.g). AD AH Suy ra  AB AK Do đó AK AH AH  
(vì AD  BC) AB AD BC • KA  H và ABC 
có KAH  B (cùng phụ với BAK ; ) AK  AH . AB BC Do đó KA  H ∽ ABC  (c.g.c). KH AK Suy ra  AC AB AK Xét ABK 
vuông tại K có sin B  AB KH Vậy
 sin B hay KH  A . C sin B AC 1 1 ab 3
b) Diện tích tam giác ABC là S  . AB BC.sin B  a . b sin 60  (đvdt). 2 2 4 2 S  AK  2 3 Vì S ∽ S nên KAH     sin B  KAH ABC S  AB  4 ABC 3 3 ab 3 3 3ab Suy ra S  S   (đvdt) KAH 4 ABC 4 4 16 ab 3 Ta có S  absin 60  (dvdt) ABCD 2 1 1 S  B . A BK.sin 60  .B . A BA   ABK  cos60 .sin60 2 2 2 1 1 3 a 3  . a . a .  (đvdt) 2 2 2 8 Trang 8 1 1 S  D . A DH .sin 60  .D . A DA   ADH  cos60 .sin60 2 2 2 1 1 3 b 3 2  b . .  (đvdt) 2 2 2 8 Mặt khác S  S  S  S AKCH ABCD ABK ADH 2 2 ab 3 a 3 b 3 3 Nên S    
ab  a  b (đvdt) AKCH  2 2 4  2 8 8 8
5.9. Ta có NAx  NAB   0 0   0 180 60 : 2  60 1 S
 AN.AC.sin 60 ANC 2 1 S  AN. . AB sin 60 ANB 2 1 S  . AB AC.sin 60 ABC 2 Vì S  S  S ANC ANB ABC 1 1 1 nên
AN.AC.sin 60  AN.A . B sin 60  A . B AC.sin 60 2 2 2
Do đó AN  AC  AB  A . B AC AC  AB 1 1 1 1 Suy ra  hay   A . B AC AN AB AC AN
5.10. a) AM, AN là hai đường phân giác của hai góc kề bù nên AM  AN. 1 1 2 0 S  . AB AM .sin 45  . AB AM . ; ABM 2 2 2 1 1 2 0 S  . AB AN.sin 45  . AB AN. ; ABN 2 2 2 1 S
 AM.AN (vì A
 MN vuông tại A). AMN 2 Mặt khác, S  S  S nên: ABM ABN AMN 1 2 1 2 1 . AB AM .  . AB AN.  AM .AN 2 2 2 2 2
Do đó AB  AM  AN  2 .  AM .AN. 2 AM  AN 1  1 1 2 hay +  ; AM .AN 2 AM AN AB . AB 2
b) Góc nhọn tạo bởi hai đường thẳng AN, AC là 45 .  Trang 9 1 1 2 Ta có S
 AC.AN.sin 45  AC.AN. ; ANC 2 2 2 1 1 2 S
 AC.AM .sin 45  AC.AM . ; AMC 2 2 2 1 S
 AM .AN (vì A
 MN vuông tại A). AMN 2 1 2 1 2 1 Mặt khác, S  S  S nên AC.AN.  AC.AM .  AM .AN. ANC AMC AMN 2 2 2 2 2
Do đó AC  AN  AM  2 .  AM .AN 2 AN  AM 1 1 1 2 Suy ra  hay -  AM .AN 2 AM AN AC AC. 2 5.11.
• Trường hợp góc A nhọn Ra đặt A   1  Ta có S  A . B A . D sin ABD 2 2 1  1 S  AC.A . D sin ; S  A . B AC.sin  ACD 2 2 ABC 2 Mặt khác, S  S  S nên ABD ACD ABC 1  1  1 A . B A . D sin  AC.A . D sin  A . B AC.sin  2 2 2 2 2     Suy ra A . B A . D sin  AC.A . D sin  A . B AC.2.sin cos 2 2 2 2   (vì sin   2sin cos ) 2 2 
Do đó AD  AB  AC  . AB AC.2.cos 2   2.cos 2.cos AB  AC 1 1 Suy ra 2  dẫn tới 2   A . B AC AD AB AC AD
• Trường hợp góc A tù
Ta đặt BAC   thì BAx  180 .
Khi đó BAx là góc nhọn. Ta có S  S  S ABD ACD ABC Trang 10   Do đó 1 1 1 A . B A . D sin  AC.A . D sin  A .
B AC.sin 180   2 2 2 2 2 1 180   180   1        . AB AC.2.sin cos  . AB AC.2.sin 90  cos 90      2 2 2 2  2   2  1   . AB AC.2.cos sin 2 2 2 
Suy ra AD  AB  AC   . AB AC.2.cos 2   2.cos  2.cos Do đó AB AC 2  1 1 hay 2   A . B AC AD AB AC AD 1 1 2
Nhận xét: Nếu A  90 thì ta chứng minh được  
, vẫn phù hợp với kết luận của bài toán. AB AC AD 5.12. 1 Ta có 0 S  . OA . OB sin15 AOB 2 1 0 S  O . A OC.sin15 AOC 2 1 0 S  O . B OC.sin 30 BOC 2 Mặt khác, S  S  S AOB AOC BOC 1 1 1 nên O . A O . B sin15  O . A OC.sin15  O .
B OC.2 sin15 cos15 2 2 2
Do đó OAOB  OC  2O . B OC cos15 .  2  6  2 1 1  OB  OC 2 cos15 6  2 Suy ra  hay    O . B OC OA OB OC .4 a 2a
5.13. Gọi O là giao điểm hai đường chéo.
Ta đặt OC  OA  x, OD  OB  y, AD  , m CD  . n
Giả sử AOD  ADC    90 .  Xét O
 CD có AOD là góc ngoài nên
D  C  A D O   2 1
Mặt khác D  C  A C D
 . Suy ra C  D 2 1 1 1 1 1 Ta có S  .
m y sin D ; S  . n x sin C ADO 1 DCO 1 2 2 Mặt khác S  S nên . m y  . n . x ADO DCO Trang 11 Do đó x m 2x m    AC AD hay  y n 2 y n BD DC 1
5.14. Ta có S  . AB BC sin B 2 2S 2.9, 69 0  sin B    sin 50 A . B BC 4, 6.5,5 Vậy B  50 . 
5.15. Ta có S  A . B A . C sin B S 6 3 3 sin B     sin 60 . AB BC 4.3 2
Vậy B  60  D  60 ;
 A  C 120 . 
5.16. Ta đặt AD  x, AE  . y Khi đó 1 diện tích A
 DE là S  . x y sin ; 1 2 1 2 S  S  25cm 1 2 Ta có 2 2 2
DE  x  y  2xy cos Mặt khác 2 2
x  y  2xy (dấu “=” xảy ra khi x  y). Do đó 2
DE  2xy  2xy cos  2xy 1 cos   xy      S     2 100.2sin 2 sin 1 cos 4 1 cos  1 2    100 tan sin sin   2 2sin cos 2 2   Vậy DE  100 tan 10 tan 2 2  2 cos 1 A 5.17. Ta có 2   (bài 5.11) AB AC AD 0 0 Do đó 1 1 2 cos 36 10 2 cos 36     4, 7 5,3 AD 4, 7.5,3 AD 0 4, 7.5, 3.2.cos 36 Suy ra AD   4,0cm 10  2 cos 1 A 5.18. Ta có 2   AB AC AD Trang 12 0 Do đó 1 1 2 cos 60 1 1    
 AD  4cm 6 12 AD 4 AD
5.19. Vì cạnh CA là cạnh lớn nhất nên góc B là góc lớn nhất trong . ABC  Ta thấy 2 2 2
AC  AB  BC (vì 2 2 2
8  5  7 ) nên góc B là góc nhọn, do dó ABC  là tam giác nhọn.
Theo định lí côsin ta có: 2 2 2 2 2 2
BC  AB  AC  2bc cos A  7  5  8  2.5.8cos A Do đó 1 0 cos A   A  60 2 0 1 A 2 cos 30 Ta có:   AB AC AD 3 2. 1 1 13 3 40 3 2       AD  cm 5 8 AD 40 AD 13  2 cos 1 1
5.20. Ta đặt BAC  . Ta có 2   AB AC AD 1 1 1 Mặt khác   AB AC AD  2 cos 1   1 Suy ra 2  . Do đó 0 2 cos 1 cos   cos 60 AD AD 2 2 2  Do đó 0 0  cos 60    120 2 Trang 13