Question 1: Given the folllowing distribution. X 10 20 30 40 P(x) 0.2 0.3 0.4 0.1
The expected and variance values of X (respectively) are a/ 24 and 84 b/ 25 and 9.165 c/ 30 and 85 d/ 100 and 93.33 ANS: A
Question 2: Given the folllowing distribution. X 10 20 30 40 P(x) 0.2 0.3 0.4 0.1
Suppose that Z = -2X + 3. Then the expected and variance values of Z respectively are a/ - 45 and 336 b/ - 45 and 339 c/ - 45 and 168 d/ 100 and 93.33
E(Z) = E(-2X +3) = E(-2X) +E(3) = -2E(X) + 3 = -2*24 + 3 = -45?
Var(Z) = Var(-2X +3) = Var(-2X) + Var(3) = 4*Var(X) + 0 = 4*84 = 336 ANS: A
Question: Given a random variable X (number of products sold
in a day) with a probability distribution table: X 10 20 30 40 P(x) 0.2 0.3 0.4 0.1
What is the average amount sold in a day, knowing that the selling price
of a product is 100 thousand VND per day? a/100*24 thousand VND per day. b/ c/ d/
Question 3: Ten percent of the items produced by a machine are
defective. Out of 15 items chosen at random, what is the
probability that exactly/ 3 items will be defective? a/ 0.129 b/ 0.456 c/ 0.871 d/ 0.237
X~B(15; 0.1), where X be the number of defective items in ….
Question: Ten percent of the items produced by a machine are
defective. Out of 150 items chosen at random. The average number of defective iterms is X~B(150; 0.1), a/15 = 150*0.1 b/ c/ d/
Question 4: X is a normally distributed random variable with a
mean of 5 and a variance of 4. The probability that X is greater than 10.52 is a/ 0.0029 b/ 0.0838 c/ 0.4971 d/ 0.9971 ANS: A X~N(5;4)
Hint: P(X>10.52) = 1- P(X<10.52) = X 5 10.52 5 1 P 1 P Z 2.76 1 0.9971 2 2 2 Given that X~N( ; )
a/ Form #1: Determine P(X< a) =? Explain: X a X a X a We have X a a P X a P P Z Then (Based on Table 1) X Z ~ N 0,1 where .
b/ Form #2: P(X>a) = 1- P(Xc/ Form#3: P(a Form #1 Chapter 6
Question 1: How will the confidence interval be affected
if the confidence level increases from 95% to 97% for the same sample data? s s ; x z ; x z x ; E x E 1 2 2 2 n n z P Z z 1 2 is determined by 2 2 (table 1)
Example: x_tb = 5; E1 = 1- (confidence interval (4; 6)
x_tb = 5; E1 = 2- (confidence interval (3; 7) wider/larger a/ b/ c/ d/
Question 2: A company has a new process for manufacturing
large artificial sapphires. In a trial run, 37 sapphires are
produced. The mean weight for these 37 gems is 6.75 carats,
and the standard deviation is 0.33 carat.
A 95% confidence interval for the for the distribution of all mean weight
sapphires produced by the new process is s s ; x z ; x z x ; E x E 1 2 2 2 n n a/ (6.64; 6.86) carats. b/ (5.54; 5.86) carats. c/ (3.34; 6.86) carats. d/ (6.64; 7.86) carats.
Question 3: The quality control manager at a factory manufacturing light bulbs is
interested to estimate the average life of a large shipment of light bulbs. The population
standard deviation is known to be 100 hours. A random sample of 50 light bulbs gave a
sample average life of 350 hours. A 95% confidence interval estimate of the true average
life of light bulbs in the shipment is ; x z ; x z x ; E x E 1 2 2 2 n n a/ (322.28; 377.72) hours. b/ c/ d/
Question 4: Consider a random sample size of 31, with sample
mean of 45.2 and sample standard deviation of 5.3. W ith 95%
confidence level, the margin of error is (s) E z2 n a/ 1.87 b/ 0.17 c/ 0.95 d/ 2.45 Question 5:
A survey of 100 Americans reports that 65% of them own a car.
With a 95% confidence level, what is the margin of error for
confidence interval in this example? p(1 p) p(1 p) p ;p p z ; p z 1 2 2 2 n n p(1 p) E z The margin of error, 2 n z P Z z 1 Where 2 is determined by 2 2 a/0.093 b/ 0.052 c/ 0.087 d/0.012 Question 6:
In a random sample of 50 intramural basketball players at a
large university, the average points per game was 8 points,
with a standard deviation of 2.5 points and a 95% confidence level.
Which of the following statements about the mean points
scored by all intramural basketball payers is correct? a/ (7.3; 8.7) points b/ (7.7; 8.4) points. c/ (5.5; 10.5) points. d/ (7.6; 8.4) points. Question 7:
A university planner is interested in determining the
percentage of spring semester students who will attend
summer school. She takes a pilot sample of 160 spring
semester students discovering that 56 will return to summer school.
Using the results of the pilot study with a 95% confidence level, p(1 p) p(1 p) p ;p p z ; p z 1 2 2 2 n n The margin of error, p(1 p) 0.35* 0.65 E z 1.96 0.074 7.4% 2 n 160
How large of a sample would have to be taken to provide
a margin of error of 3% or less? a/ 972 b/ c/ d/ Question 8:
A random sample of 49 lunch customers was taken at a
restaurant. The average amount of time the customers in the
sample stayed in the restaurant was 45 minutes with a standard deviation of 14 minutes.
With a 95% level of confidence, how large of a sample would
have to be taken to provide a margin of error of 2.5 minutes or less? (s) E z The margin of error: 2 n a/121 b/ c/ d/
Question: Assume that test scores from the college entrance exam are
normally distributed with a mean of 4.5 and a standard deviation of 1.
What is the test score (x0) so that 98.5% of candidates have test scores below that score (x0)? Sol: X~N(4.5; 1^2) P(X x ) 0.985 0 X 4.5 x 4.5 0 P( ) 0.985 1 1 x 4.5 0 P Z 0.985 1 x 4.5 0 2.17 x 2.17 4.5 6.67 0 1 Chapter 7:
Question 10: A company manufactures ball bearings for precision machines. The
average diameter of a certain type of ball bearing should be 6.0 mm. To check that the
average diameter is correct, the company formulates a statistical test. What should be used for the hypotheses? H : 6.0 0 H : 6.0 a/ a H : 6.0 0 H : 6.0 b/ a H : 6.0 0 H : 6.0 c/ a H : 6.0 0 H : 6.0 d/ a
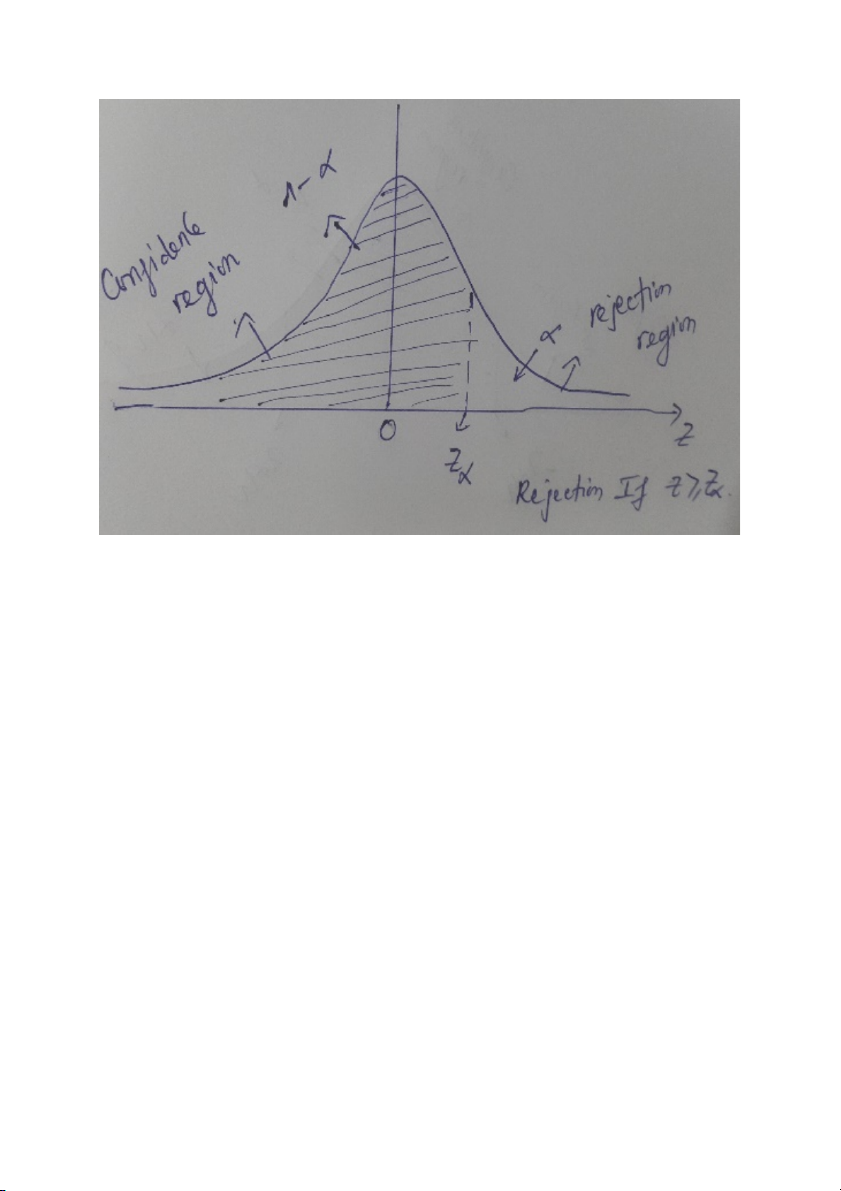
Question 11: Given the following information below. H : p 0.42 0 The hypotheses: H : p 0.42 a and the test statistic is 0.
Refer to the above information, at the level of signifcance of 5%, the correct conclusion is
Z(alpha) = 1.64, the test statistic Z = 0
- do not reject H0 (we tend to accept H0)
a/ the proportion of the population is not greater than 42%.
b/ the proportion of the population is greater 42%.
c/ the proportion of the population equals to 42%.
d/ Not enough information given to answer this question.
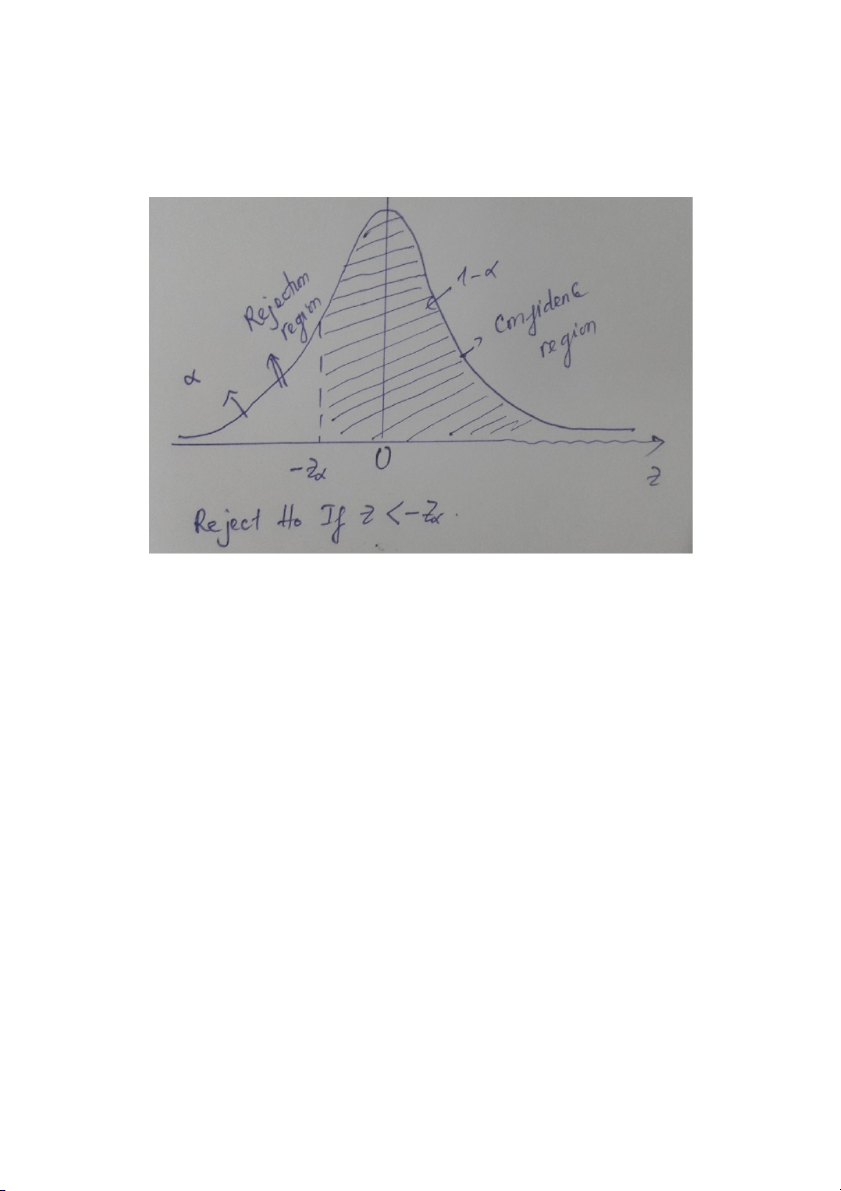
Question : In a test of H : 100 against H : 100, 0 a the sample data
yielded the test statistic Z = 2.17. At 5% level of significance, your
conclusion about the population mean is Z= 2.17; Z(alpha) = 1.64
Do not reject H0 ( we tend to accept H0).
a/ significantly greater than or equal to 100.
b/ significantly less than or equal 100.
c/ Not enough information given to answer this question. d/ significantly equal to 100. Chapter 8
Question . Given the following ANOVA table. Source of Sum of Degrees of Mean Variation Squares Freedom Square F Between groups 36 2 ---- ? Error (Within Groups) 240 __-----_ ----- Total ------ 42
Refer to the above table, the test statistic (F) is a/ 3 b/ 2 c/ 10 d/ 13
Question : Given the following ANOVA table. Source of Sum Degrees Mean Variation of of Squares Squares Freedom F Between groups 1,500 2 750 5 Within groups 4500 --- 150 Total 6,000 32
Refer to the above table, the null hypothesis is to be tested at the 5% level of significance,
The null hypothesis is to be tested at the 5% level of significance, your conclusion is
a/ one mean is different from the others. b/ c/ d/
The critical value F(k-1; n-k) = F(2; 30) at the level of significance of 5% is 3.32.
Since F= 5 > the critical value F(k-1; n-k) = F(2; 30) = 3.32, therefore reject H0.