Slide bài giảng Chương 1: Ma trận Ma trận nghịch đảo | Môn đại số tuyến tính
En là ma trận đơn vị cấp 𝑛 . Nếu có ma trận vuông 𝐵 cấp n sao cho 𝐴𝐵 = 𝐵𝐴 = 𝐸Hãy chứng minh ma trận 𝐴 =1 0 0 2 là ma trận khả nghịch và thì ta nói 𝐴 là ma trận khả nghịch và 𝐵 được gọi là ma trận nghịch đảo của ma trận 𝐴.Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem !
Môn: đại số tuyến tính ( UEH ) 31 tài liệu
Trường: Đại học Kinh tế Thành phố Hồ Chí Minh 1.7 K tài liệu
Tác giả:
Preview text:
lOMoAR cPSD| 49519085 12/2/2021 ảo 01/12/2021 1 1 lOMoAR cPSD| 49519085 12/2/2021 3 lOMoAR cPSD| 49519085 12/2/2021
Tìm nghịch đảo của ma trận 4 Định lý lOMoAR cPSD| 49519085 12/2/2021 | | 𝑨𝟏𝒏 ⋯ 𝑨𝒏𝒏 Với 𝐴 = −1 |𝑀 | 5 lOMoAR cPSD| 49519085 12/2/2021
Tìm nghịch đảo của ma trận
Tìm nghịch đảo của ma trận 6 7 lOMoAR cPSD| 49519085 12/2/2021
Tìm nghịch đảo của ma trận 8 9 lOMoAR cPSD| 49519085 12/2/2021 11 lOMoAR cPSD| 49519085 12/2/2021 và và 12 13 lOMoAR cPSD| 49519085 12/2/2021
Phương pháp khử Gauss-Jordan
• Sử dụng phép biến đổi sơ cấp
• Bước 1: Viết ma trận đơn vj 𝐸 cùng cấp với ma
trận A bên cạnh phía bên phải ma trận A được
ký hiệu ma trận mới [𝐴|𝐸]
• Bước 2: Dùng các phép biến đổi sơ cấp biến
đổi khối ma trận [𝐴|𝐸] thành khối ma trận
𝐸 𝐵 . Khi đó 𝐵 là nghịc đảo của ma trận 𝐴 14 Ví dụ 15 lOMoAR cPSD| 49519085 12/2/2021
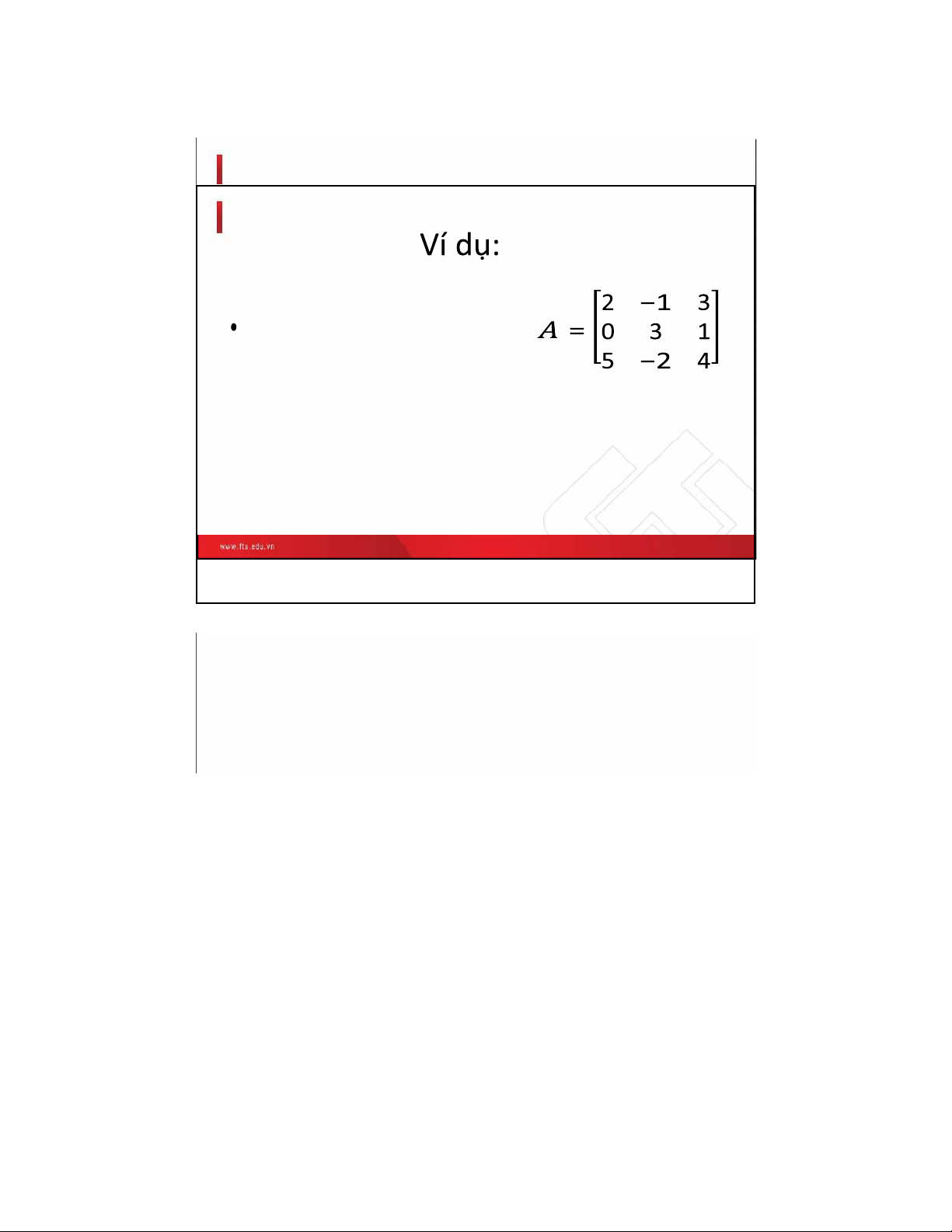
Ví dụ: Tìm nghịch đảo của ma trận 16 lOMoAR cPSD| 49519085 12/2/2021 17