

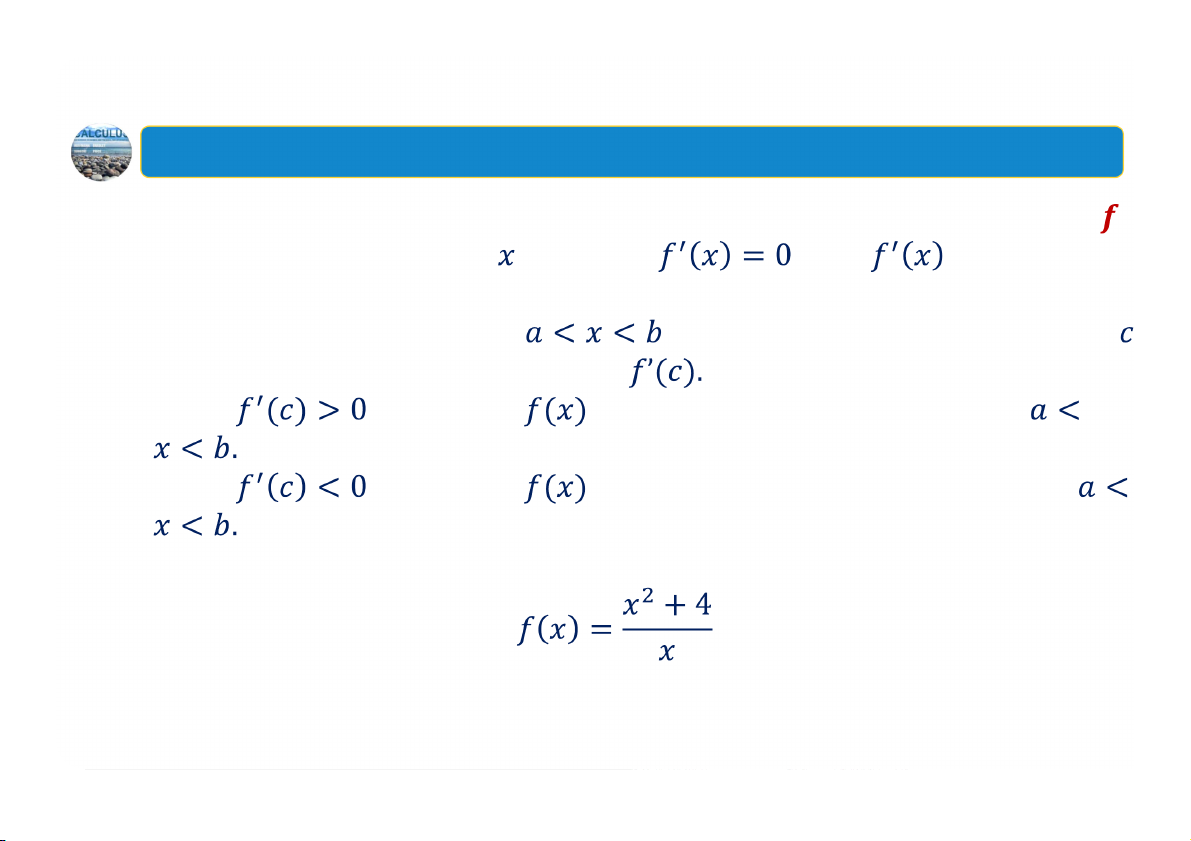








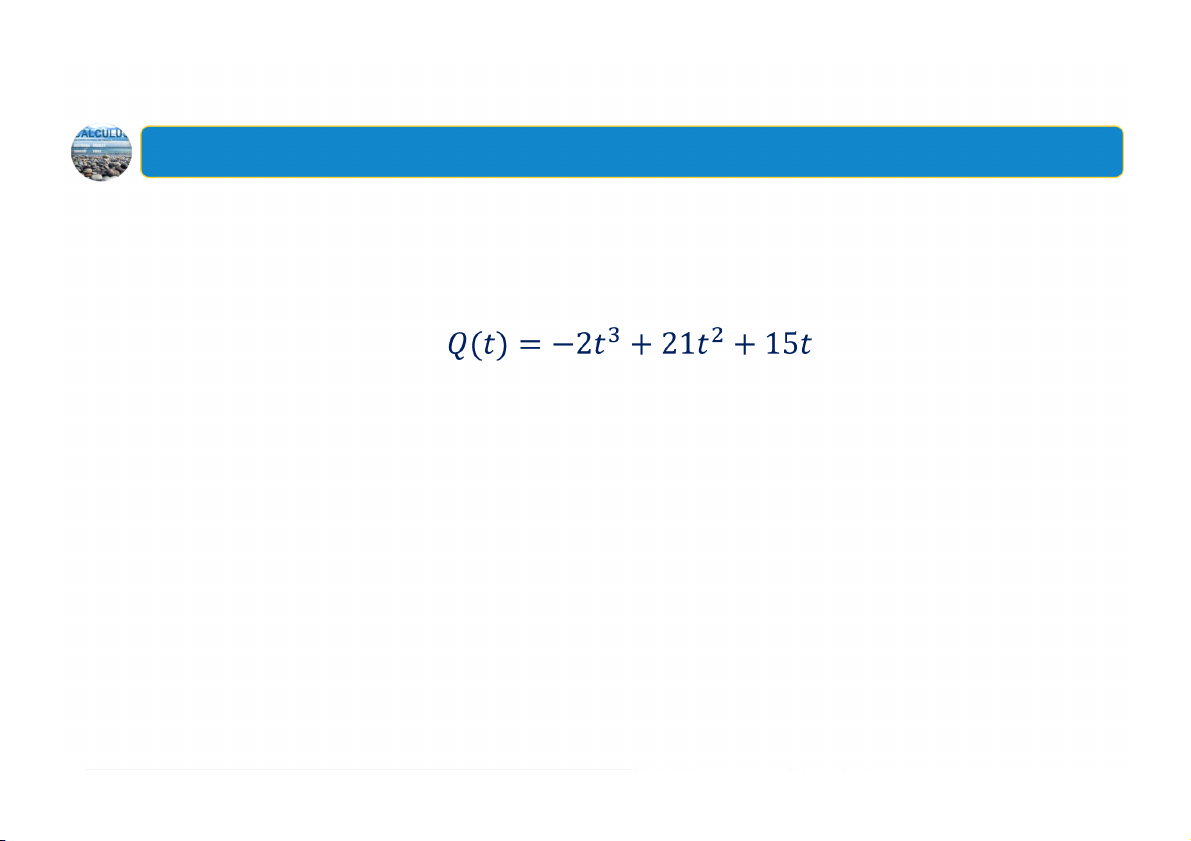





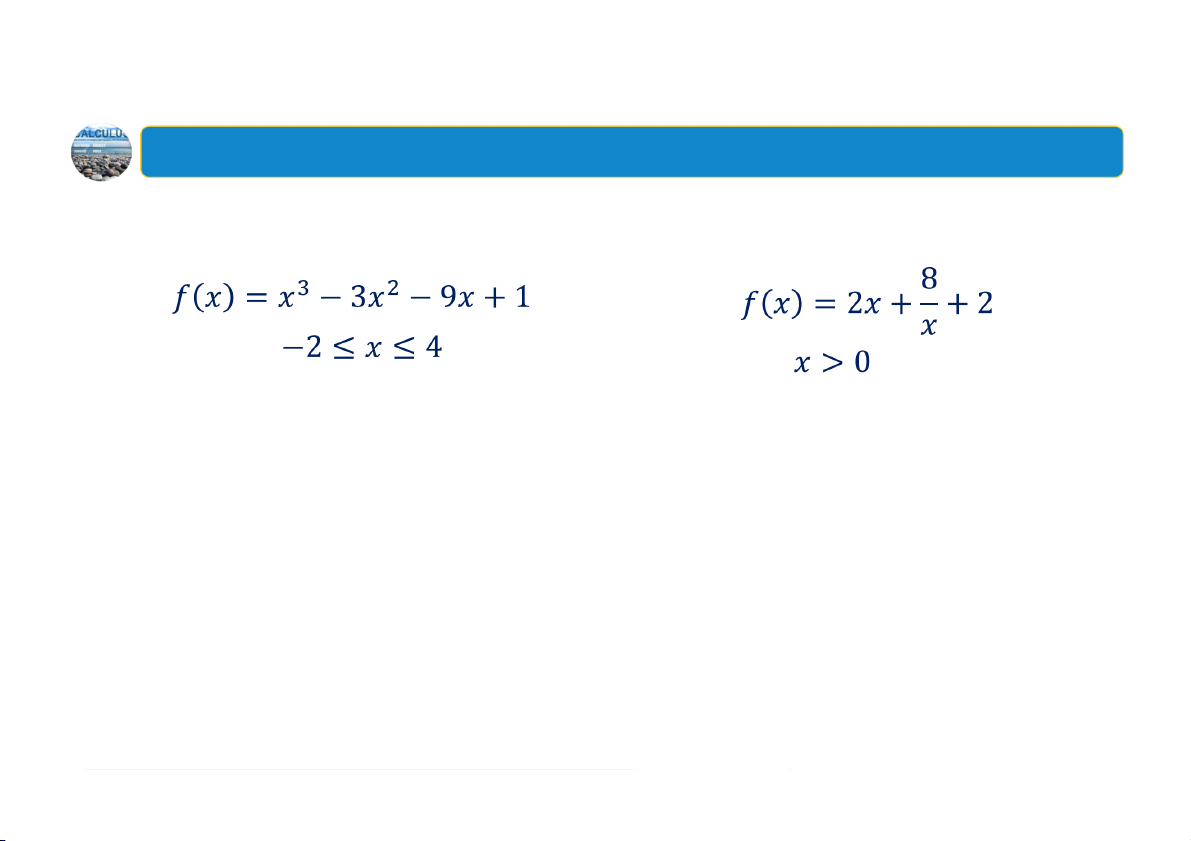
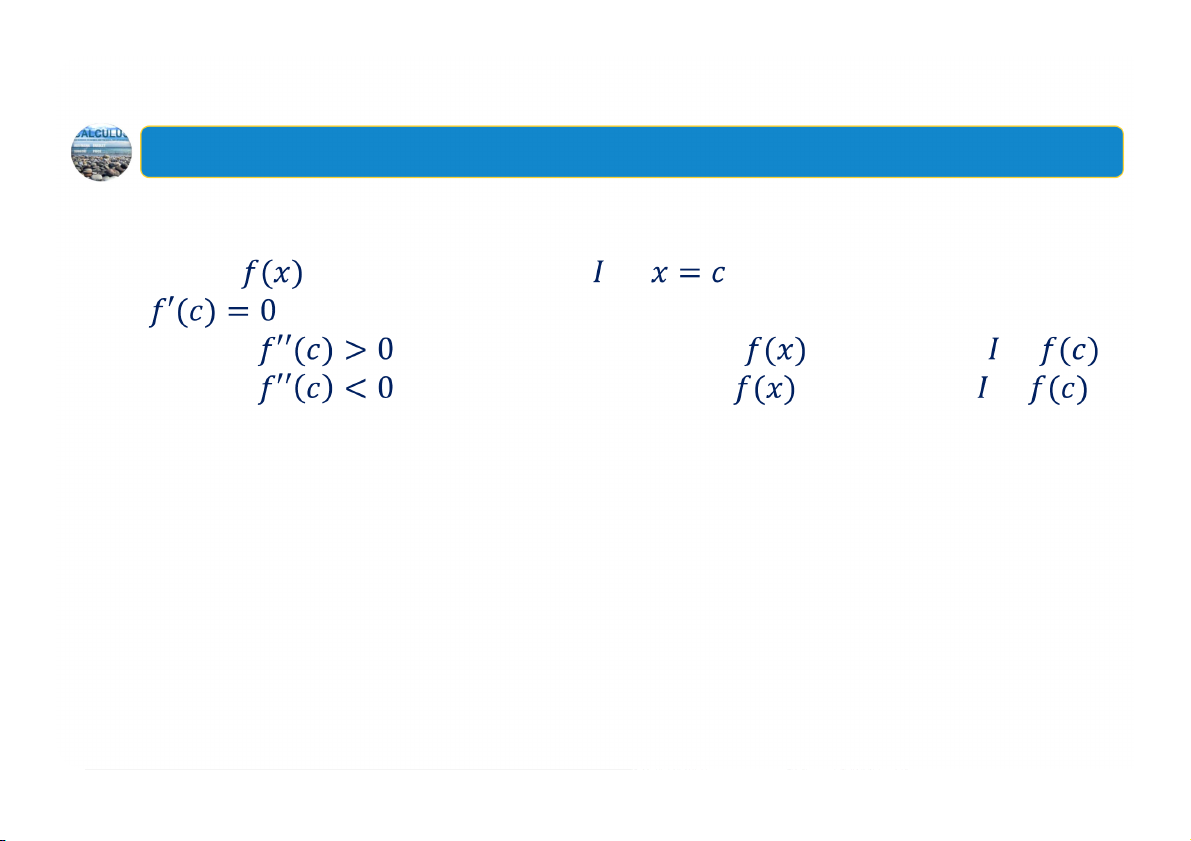







Preview text:
KHOA TOÁN KINH TẾ BỘ MÔN TOÁN CƠ BẢN Bài giảng TOÁN CHO CÁC NHÀ KINH TẾ
Chương 3: MỘT SỐ ỨNG DỤNG CỦA ĐẠO HÀM Mục tiêu chương 3 Mục tiêu:
Giới thiệu các khái niệm hàm tăng, hàm giảm, cực trị tương đối,
tính lõm và điểm uốn, bài toán tối ưu hoá, phân tích cận biên, độ co dãn của cầu.
Đề cập các ứng dụng của đạo hàm trong phân tích kinh doanh, kinh
tế và các bài toán khoa học xã hội. Nội dung:
1. Hàm tăng và hàm giảm; Cực trị tương đối
2. Tính lõm và điểm uốn
3. Vẽ đồ thị của hàm số
4. Tối ưu hoá; Độ co giãn của cầu
5. Các bài toán tối ưu hoá ứng dụng khác 2 KHOA TOÁN KINH TẾ BỘ MÔN TOÁN CƠ BẢN Bài giảng TOÁN CHO CÁC NHÀ KINH TẾ
Chương 3: MỘT SỐ ỨNG DỤNG CỦA ĐẠO HÀM
Bài 1: Hàm tăng và hàm giảm; cực trị tương đối Mục tiêu bài học
Tìm hiểu về hàm tăng và hàm giảm
Tìm các điểm tới hạn và cực trị tương đối.
Sử dụng đạo hàm cấp một để tìm cực trị tương đối và vẽ đồ thị của một hàm số 4 1. Hàm tăng và hàm giảm Định nghĩa
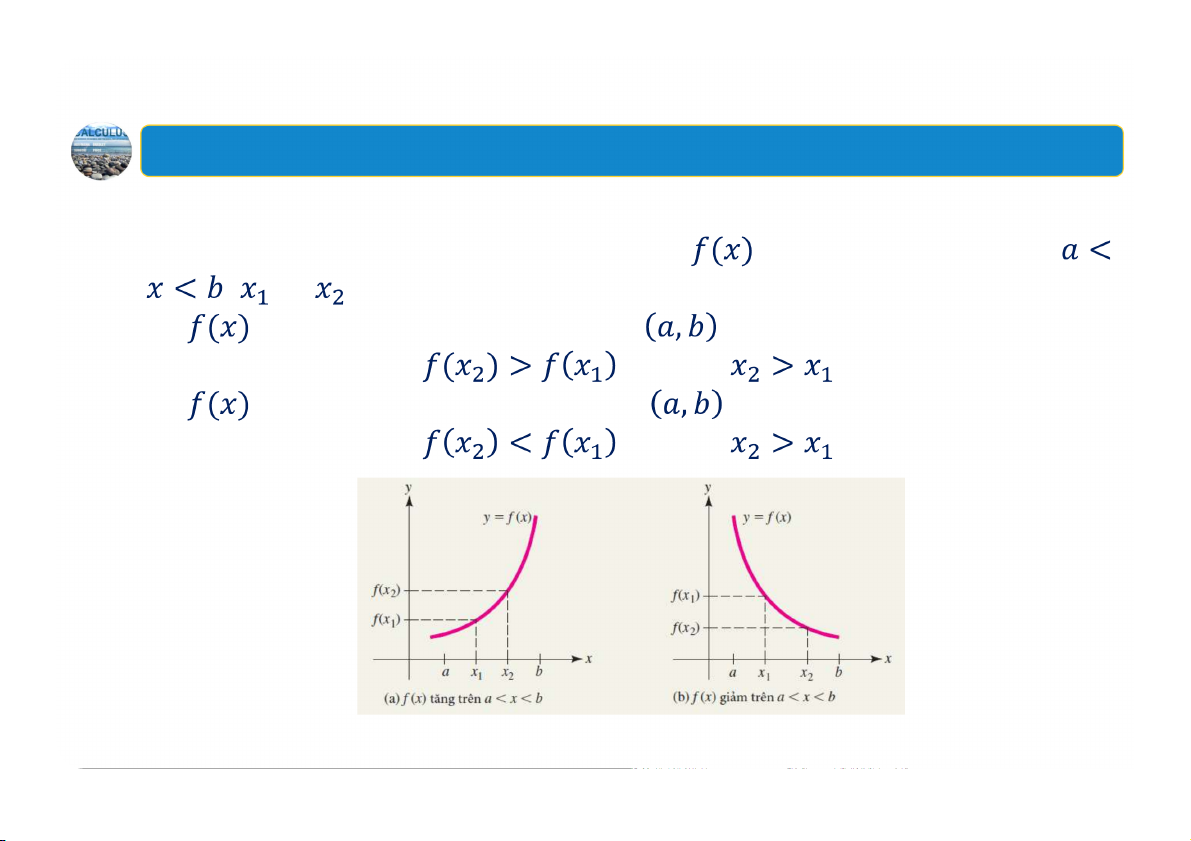
Hàm tăng và hàm giảm. Giả sử hàm số xác định trên khoảng , và
là hai số bất kỳ trên khoảng này. Khi đó
được gọi là tăng trên khoảng nếu: với mọi .
được gọi là giảm trên khoảng nếu: với mọi . 5 1. Hàm tăng và hàm giảm Minh họa
Đạo hàm của các hàm số tăng và giảm 6 1. Hàm tăng và hàm giảm
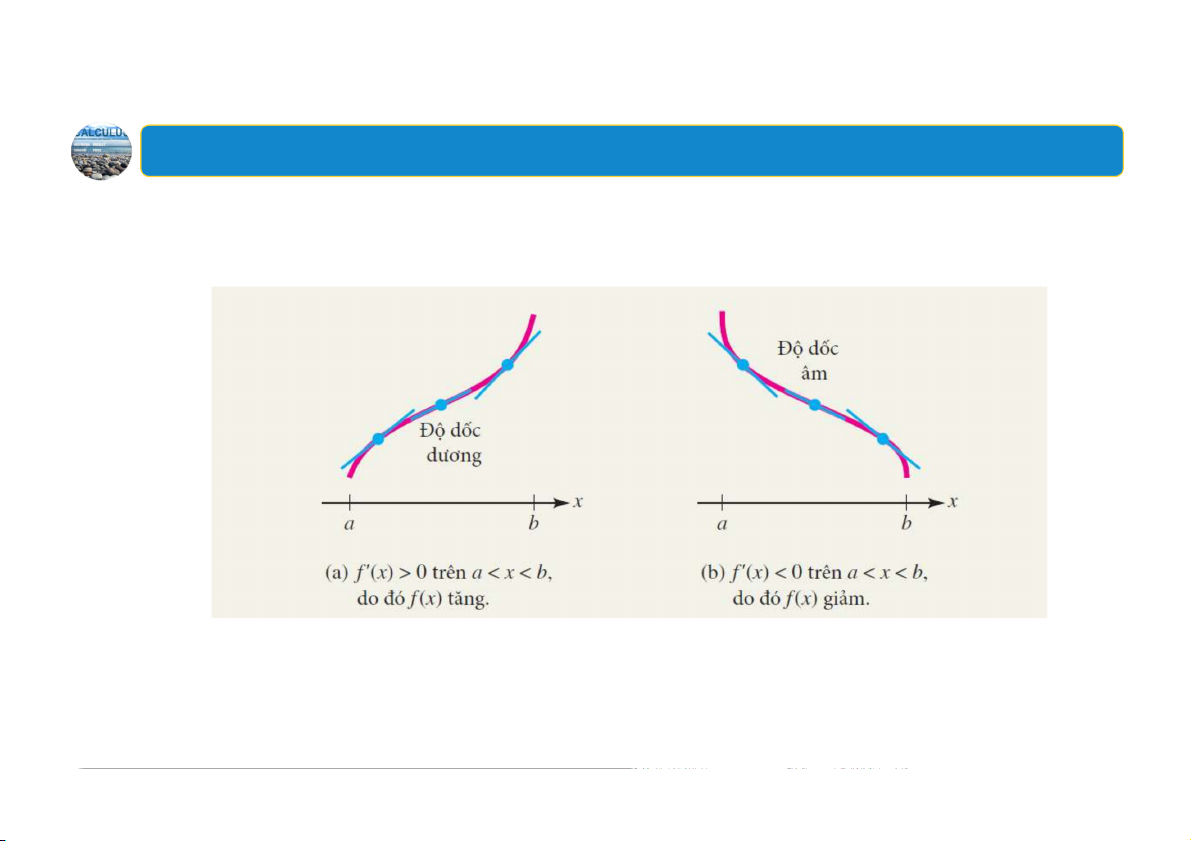
Quy trình sử dụng đạo hàm để tìm các khoảng tăng, giảm của hàm số .
Bước 1. Tìm tất cả giá trị của thỏa mãn hoặc không liên
tục. Các giá trị này chia trục số thành các khoảng rời nhau.
Bước 2. Trong mỗi khoảng con
được xác định ở Bước 1, chọn số
bất kỳ trong khoảng đó và tính Khi đó: Nếu thì hàm số
tăng (đồ thị đi lên) trên khoảng Nếu thì hàm số
giảm (đồ thị đi xuống) trên khoảng
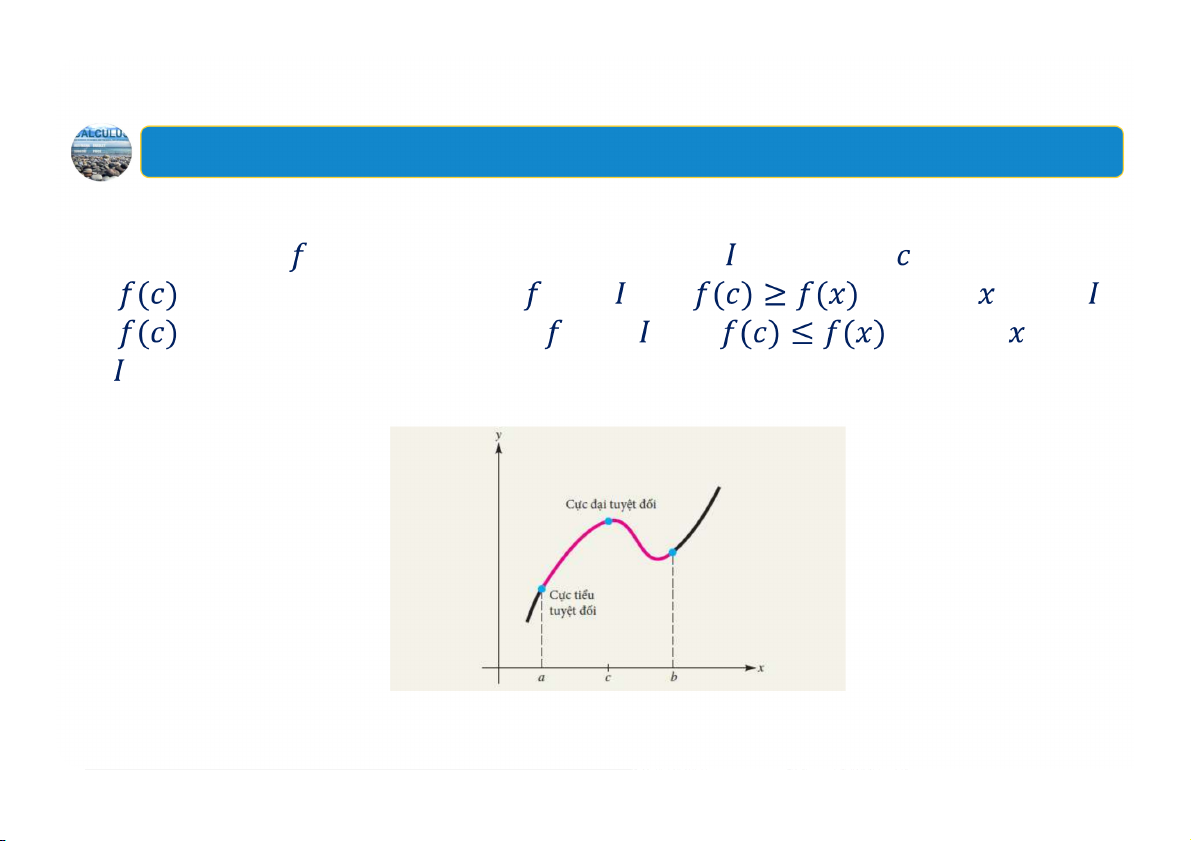
Ví dụ: Tìm các khoảng tăng, giảm của hàm số: 7 2. Cực trị tương đối Định nghĩa Hàm số
được gọi là có một cực đại tương đối tại nếu
với mọi thuộc một khoảng chứa c Hàm số
được gọi là có một cực tiểu tương đối tại nếu
với mọi thuộc một khoảng chứa c .
Cực đại tương đối và cực tiểu tương đối của được gọi là cực trị tương đối của nó.
Một số trong miền xác định của hàm
được gọi là một số tới hạn nếu hoặc
không tồn tại, điểm tương ứng trên đồ thị của
được gọi là một điểm tới hạn của
Lưu ý: Cực trị tương đối chỉ có thể xảy ra tại các điểm tới hạn, nhưng
không phải tất cả các điểm tới hạn đều tương ứng với cực trị tương đối. 8 2. Cực trị tương đối Minh họa Ba điểm tới hạn ở đó . 9 2. Cực trị tương đối Minh họa Ba điểm tới hạn ở đó không xác định. 10 2. Cực trị tương đối
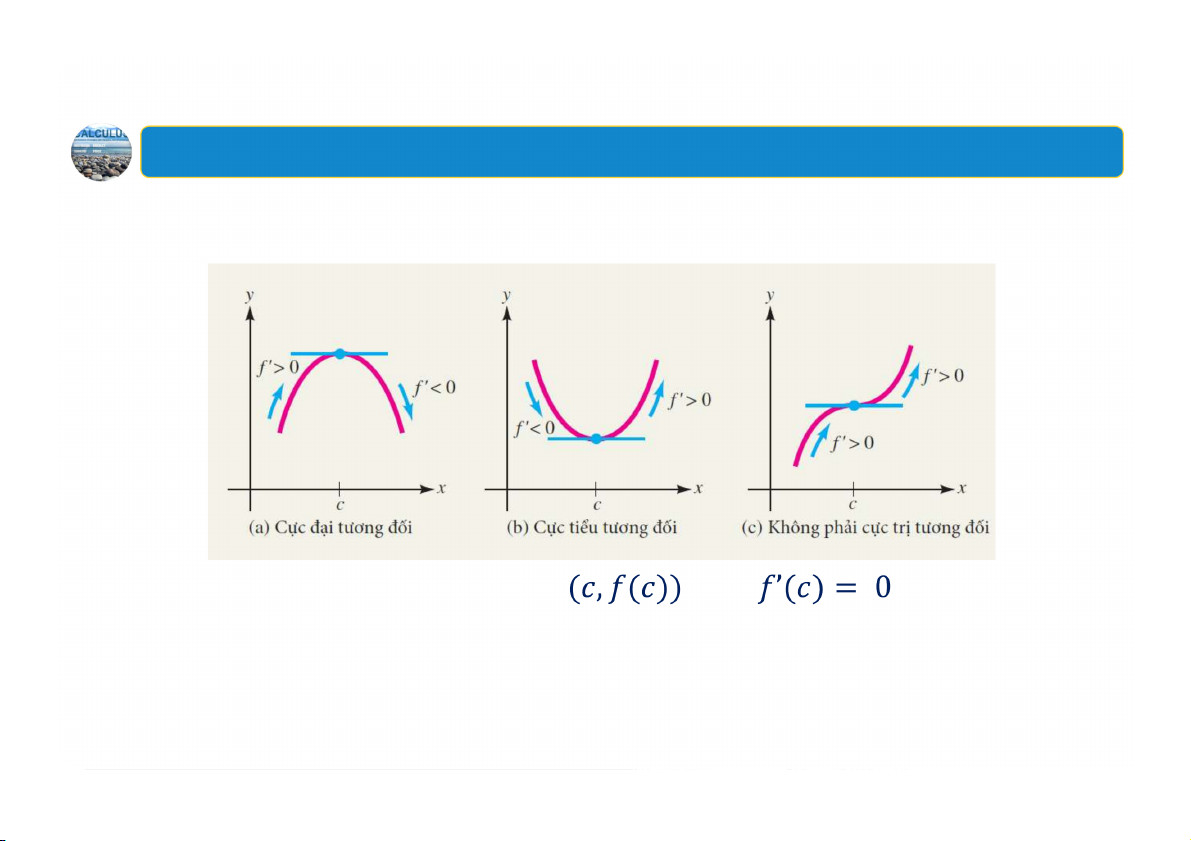
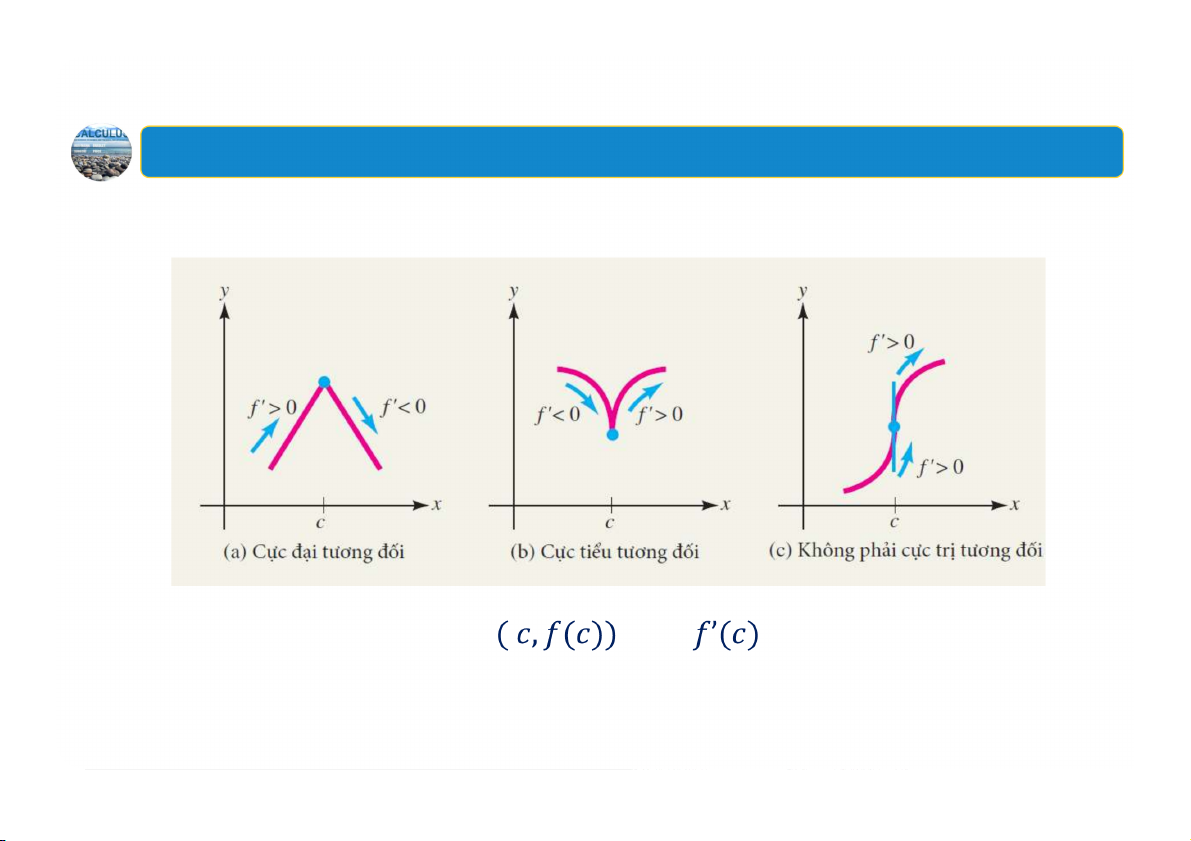
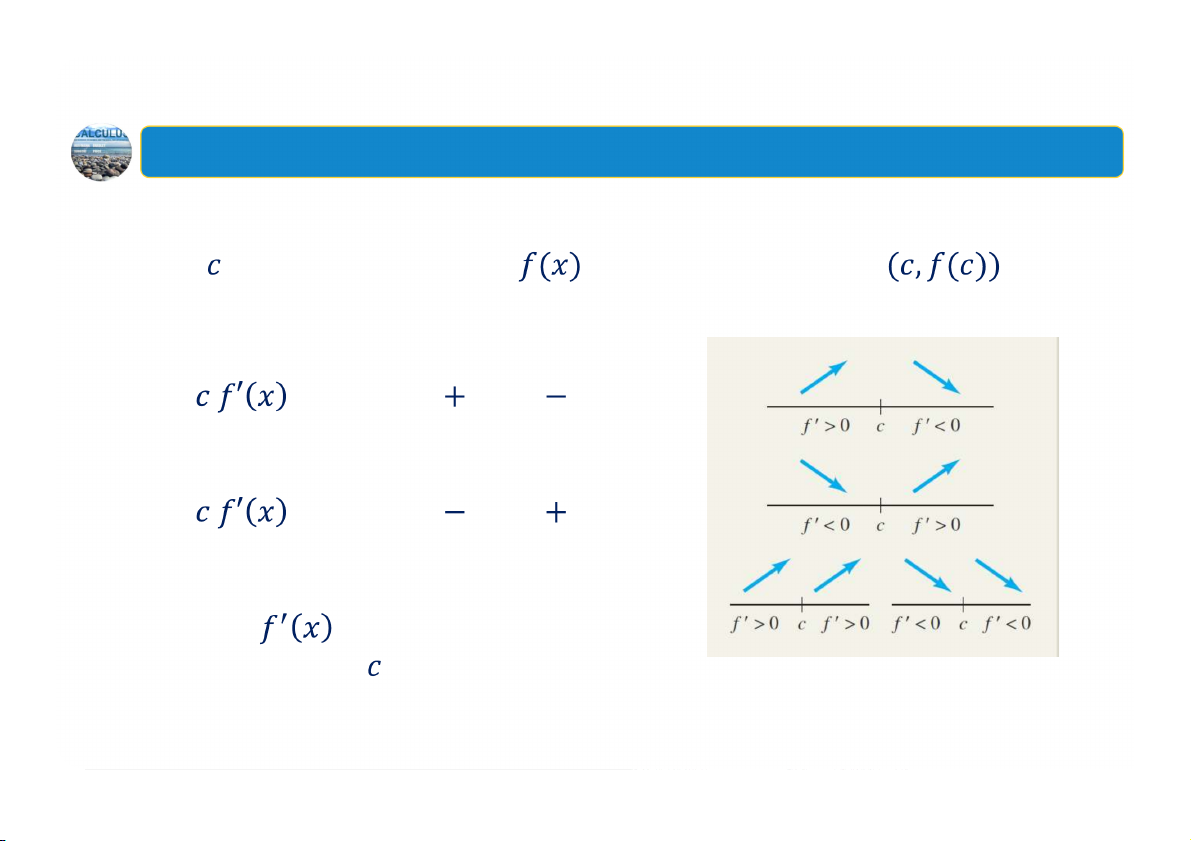
Kiểm tra cực trị tương đối bằng đạo hàm cấp một
Cho là một số tới hạn của
. Khi đó, điểm tới hạn là:
một cực đại tương đối nếu qua đổi dấu từ sang
một cực tiểu tương đối nếu qua đổi dấu từ sang
Không phải là cực trị tương đối nếu có cùng một dấu ở cả hai phía của 11 2. Cực trị tương đối
Ví dụ: Tìm các số tới hạn của
Ví dụ: Doanh thu từ việc bán một hàm số
số áo cho mùa hè mới sau tuần
kể từ khi được đưa ra thị trường
và phân loại các điểm tới hạn.
được cho bởi công thức:
triệu đô-la. Thời điểm nào doanh
thu đạt tối đa? Doanh thu tối đa bằng bao nhiêu. 12
3. Phác họa đồ thị của hàm số
Quy trình phác họa đồ thị của hàm liên tục trên miền xác
định sử dụng đạo hàm
Bước 1. Tìm miền xác định của . Bước 2. Tính
tìm các số tới hạn của và xác định các khoảng tăng, giảm của
trong miền xác định của nó.
Bước 3. Biểu diễn các điểm tới hạn
trên mặt phẳng tọa độ với hình "chóp mũ“
nếu nó là cực đại tương đối và hình "đáy cốc"
nếu nó là cực tiểu tương đối, tìm các giao điểm với các
trục tọa độ và một số điểm đặc biệt khác.
Bước 4. Phác họa đồ thị của là một đường cong trơn nối các điểm tới
hạn, sao cho đồ thị đi lên nếu , đi xuống nếu
và có tiếp tuyến nằm ngang tại các điểm mà . 13
3. Phác họa đồ thị của hàm số
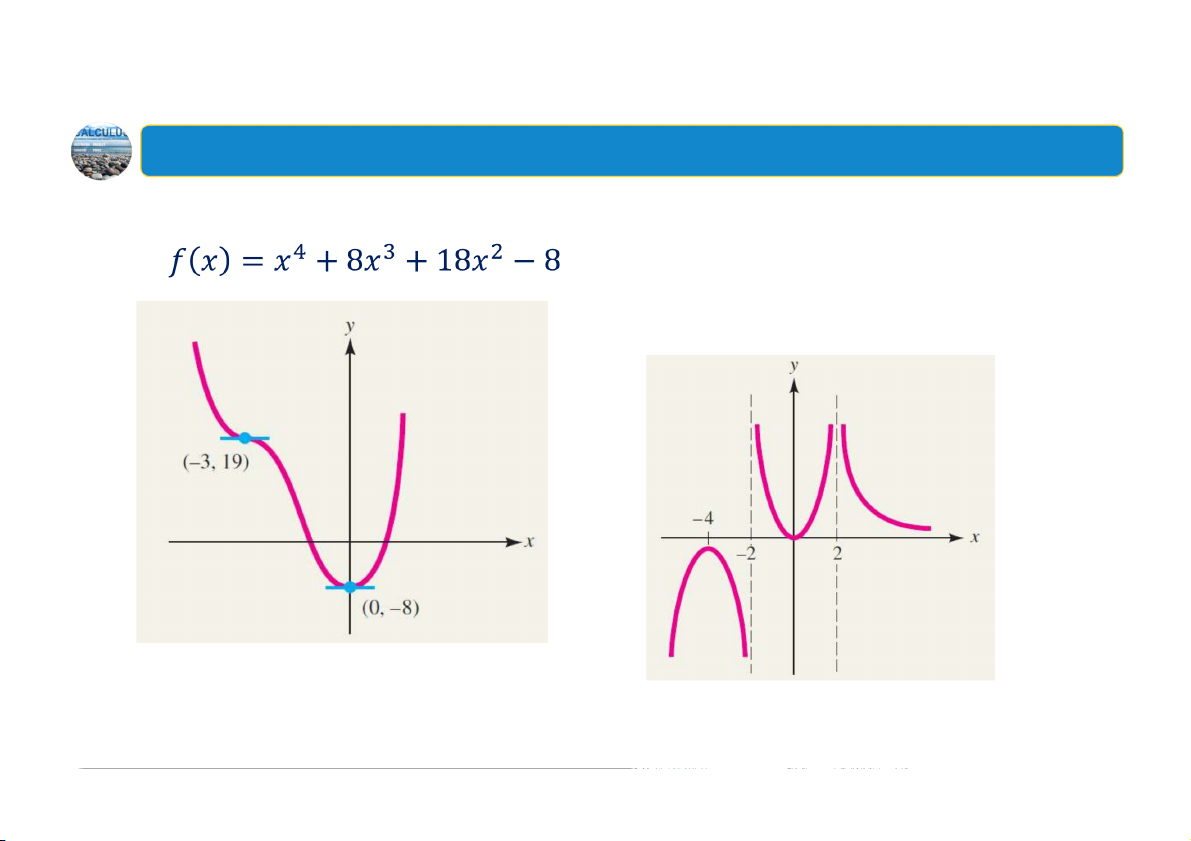
Ví dụ: Vẽ đồ thị của hàm số
Ví dụ thực hành từ đồ thị Dựa
vào đồ thị hàm số, hãy tìm các
khoảng mà đạo hàm của hàm số đã
cho có giá trị dương? giá trị âm? 14 KHOA TOÁN KINH TẾ BỘ MÔN TOÁN CƠ BẢN Bài giảng TOÁN CHO CÁC NHÀ KINH TẾ
Chương 3: MỘT SỐ ỨNG DỤNG CỦA ĐẠO HÀM
Bài 2: Tính lõm và Điểm uốn Mục tiêu bài học
Tìm hiểu về tính lõm.
Sử dụng dấu của đạo hàm cấp hai để tìm các khoảng lõm Tìm các điểm uốn.
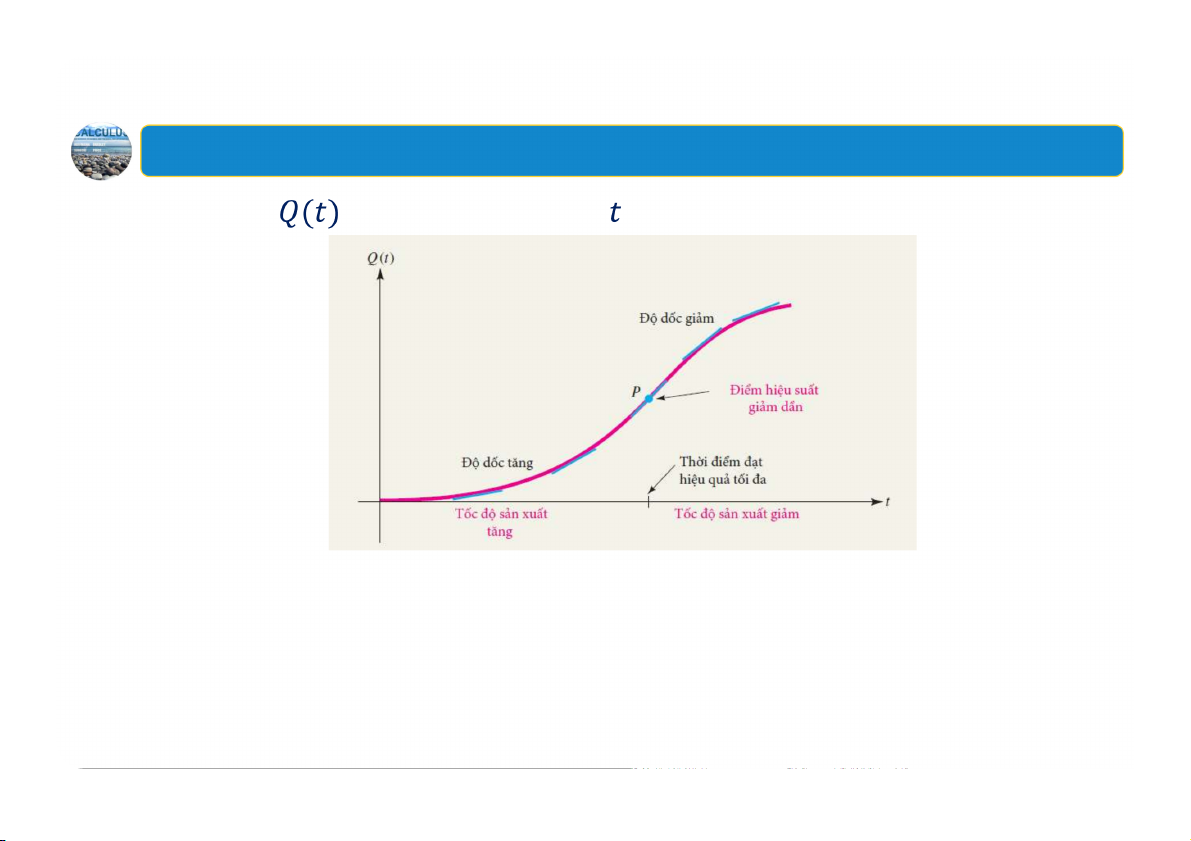
Sử dụng đạo hàm cấp hai để kiểm tra cực trị tương đối. 16 Ví dụ dẫn nhập Sản lượng
của lao động trong giờ làm việc.
Điểm P được gọi là điểm hiệu suất giảm dần.
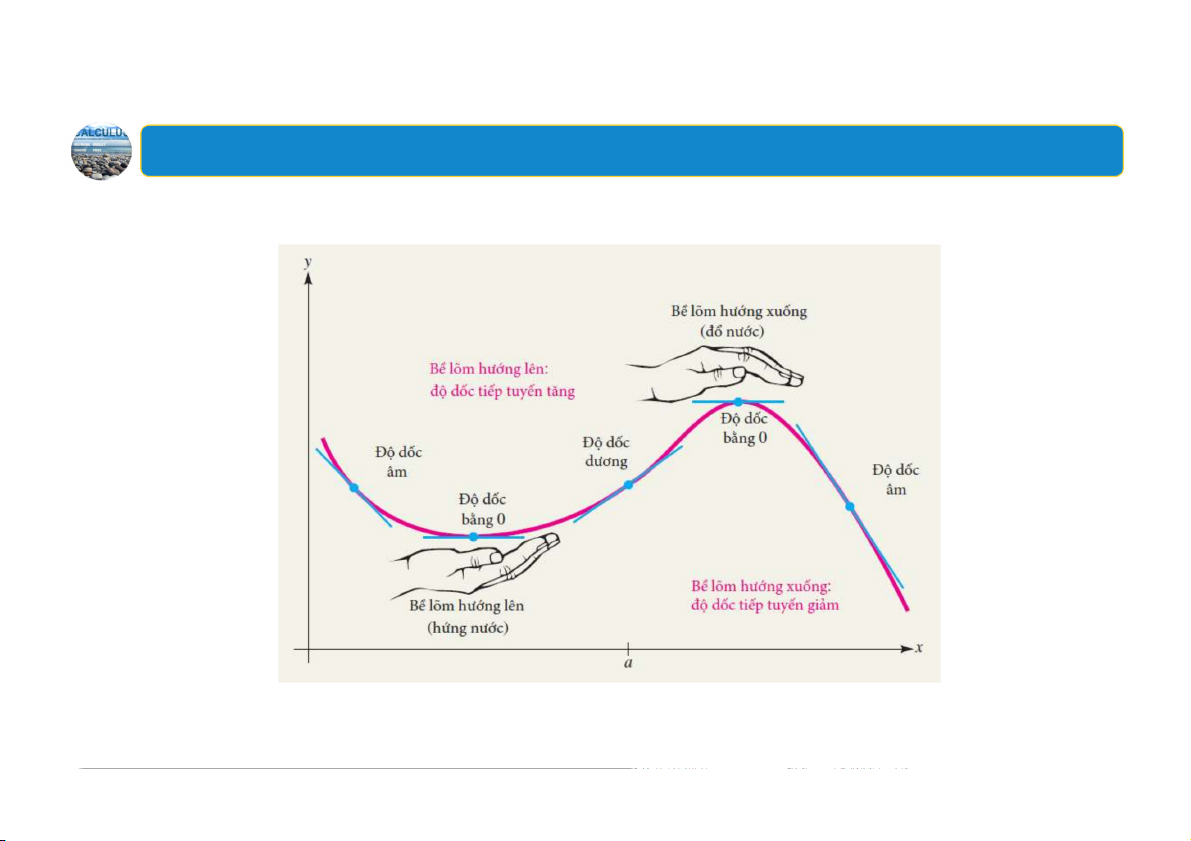
Sự tăng hay giảm của độ dốc tiếp tuyến với một đường cong cho trước
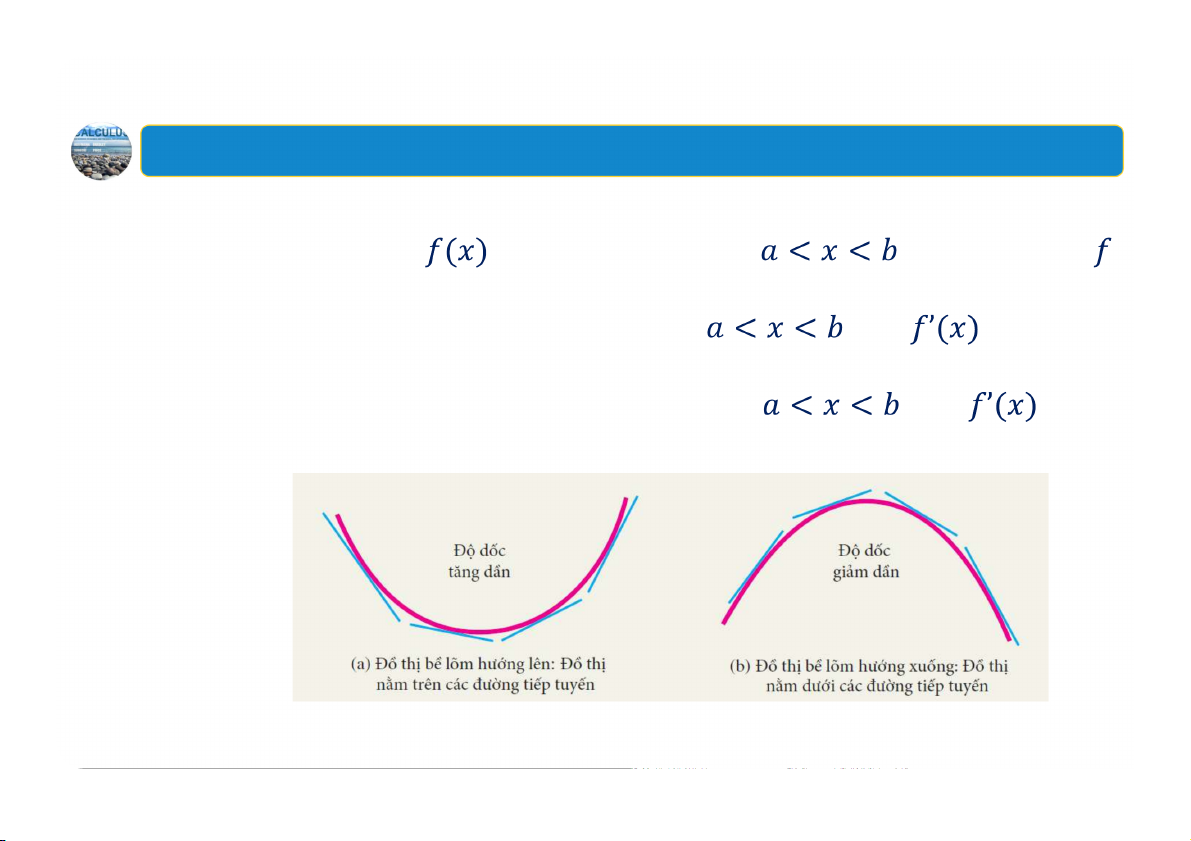
được mô tả bằng một thuật ngữ mang đặc tính của đồ thị là tính lõm. 17 1. Tính lõm Định nghĩa Tính lõm. Nếu hàm khả vi trên khoảng thì đồ thị của được gọi là:
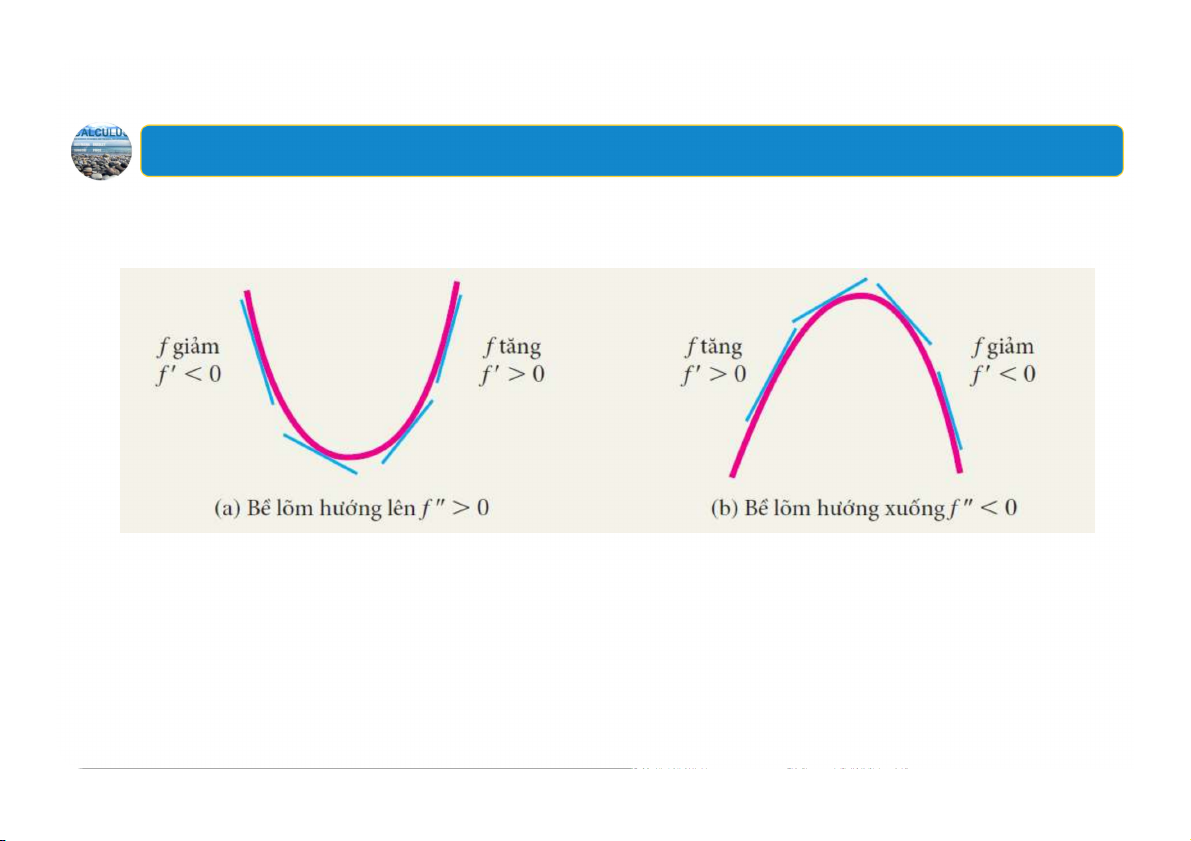
có bề lõm hướng lên trên khoảng nếu tăng trên khoảng đó
có bề lõm hướng xuống trên khoảng nếu giảm trên khoảng đó 18 1. Tính lõm
Minh họa tính lõm và độ dốc của tiếp tuyến 19 1. Tính lõm
Sử dụng đạo hàm cấp hai để xác định các khoảng lõm của đồ thị hàm
Bước 1. Tìm tất cả các giá trị của sao cho hoặc không
tồn tại và các giá trị này tạo thành các khoảng rời trên trục số.
Bước 2. Trên mỗi khoảng
tìm được trong bước 1, chọn một số bất kỳ và tính Khi đó: Nếu thì đồ thị của
có bề lõm hướng lên trong khoảng . Nếu thì đồ thị của
có bề lõm hướng xuống trong khoảng . 20 1. Tính lõm
Sử dụng đạo hàm cấp hai để xác định các khoảng lõm của đồ thị hàm
Bước 1. Tìm tất cả các giá trị của sao cho hoặc
không tồn tại và các giá trị này tạo thành các khoảng rời trên trục số.
Bước 2. Trên mỗi khoảng
tìm được trong bước 1, chọn một số bất kỳ và tính Khi đó: Nếu thì đồ thị của
có bề lõm hướng lên trong khoảng . Nếu thì đồ thị của
có bề lõm hướng xuống trong khoảng .
Ví dụ: Tìm các khoảng lõm của hàm số: 21 1. Tính lõm
Chú ý: Cần phân biệt giữa tính lõm với "hướng" của đồ thị. 22 2. Điểm uốn Định nghĩa
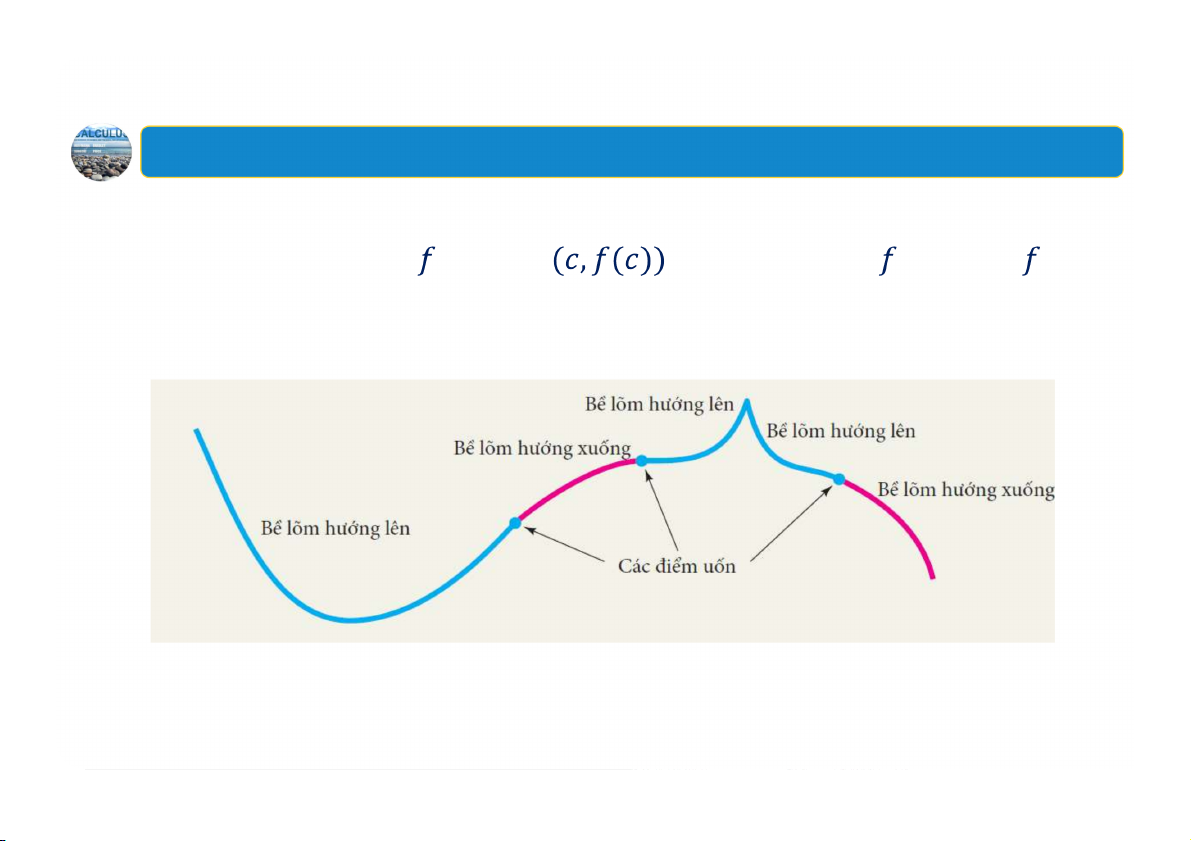
Điểm uốn của hàm là điểm
trên đồ thị của mà ở đó liên
tục và thay đổi tính lõm. Minh họa 23 2. Điểm uốn
Sử dụng đạo hàm cấp hai để
Ví dụ: Trong mỗi trường hợp, hãy
xác định các điểm uốn của đồ
tìm tất cả các điểm uốn của hàm số thị hàm cho trước. Bước 1. Tính và tìm tất a)
cả các điểm thuộc miền xác b) định của sao cho hoặc không tồn tại.
Bước 2. Với mỗi số tìm được trong Bước 1, nếu qua mà đổi dấu thì là một điểm uốn của . 24
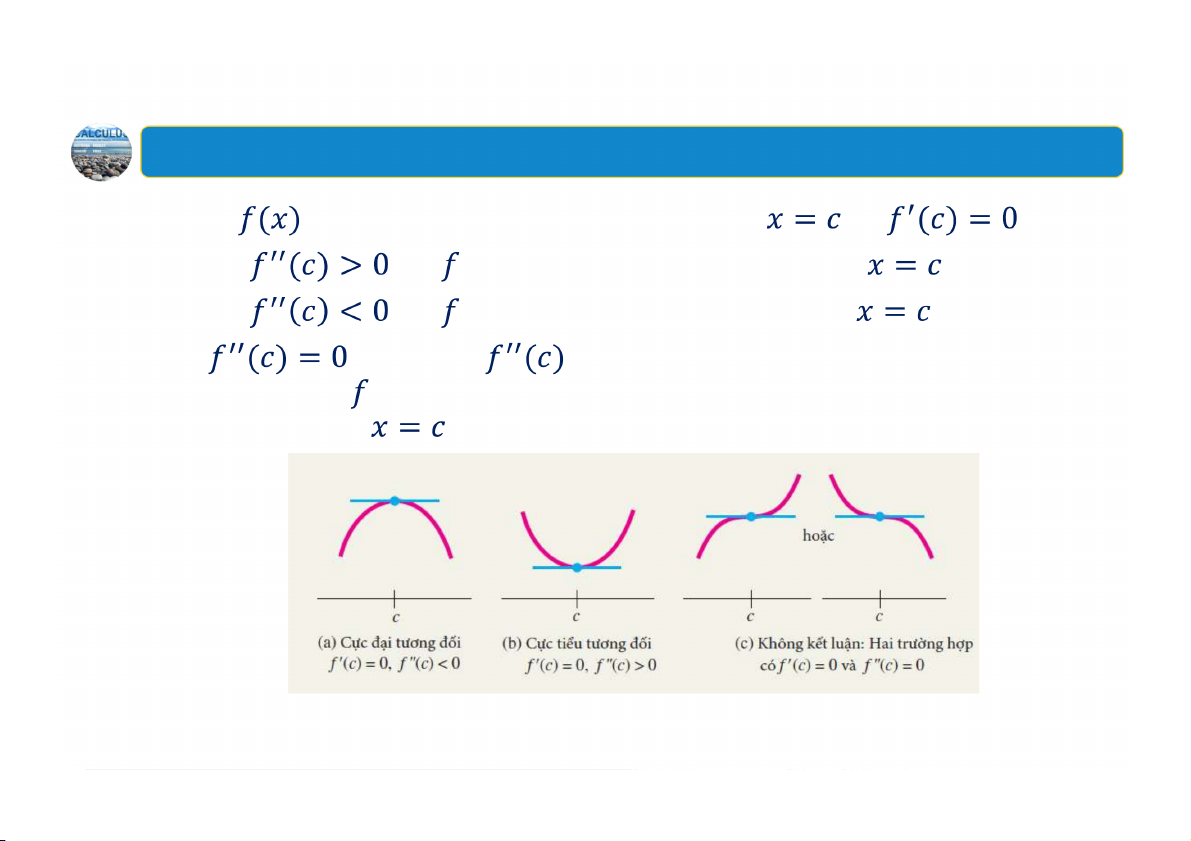
3. Sử dụng đạo hàm cấp hai để kiểm tra cực trị Giả sử
tồn tại trên một khoảng mở chứa và . Nếu
thì có một cực tiểu tương đối tại . Nếu
thì có một cực đại tương đối tại . Nếu hoặc nếu
không tồn tại thì chưa kết luận được về
cực trị. Khi đó, có thể đạt cực đại, cực tiểu hoặc có thể không đạt cực trị tương đối tại . 25
3. Sử dụng đạo hàm cấp hai để kiểm tra cực trị
Ví dụ: Tìm các điểm tới hạn của
Ví dụ: Tốc độ lan truyền tin đồn hàm số
trong một cộng đồng người tỷ lệ
đồng thời với số người đã nghe tin
và sử dụng đạo hàm cấp hai để đồn và số người chưa nghe.
phân loại các điểm tới hạn là
Chứng tỏ rằng tin đồn sẽ lan
cực đại tương đối hay cực tiểu
truyền nhanh nhất khi một nửa số tương đối.
người trong cộng đồng đã nghe tin đồn.
(Tỷ lệ đồng thời: Tốc độ lan truyền tin đồn số người đã nghe tin đồn số người chưa nghe) 26
Ví dụ : Hiệu suất của sản xuất giảm dần
Ví dụ: Một nghiên cứu về hiệu quả của ca sáng ở một nhà máy (7 giờ
sáng đến 12 giờ trưa) cho thấy trung bình một công nhân đến làm việc
lúc 7 giờ sẽ sản xuất được Q đơn vị sản phẩm trong t giờ sau, với
a) Thời điểm nào trong ca làm việc sáng, sản xuất của công nhân đạt tới
điểm hiệu suất giảm dần?
b) Thời điểm nào trong ca làm việc sáng, công nhân làm việc kém hiệu quả nhất? 27 KHOA TOÁN KINH TẾ BỘ MÔN TOÁN CƠ BẢN Bài giảng TOÁN CHO CÁC NHÀ KINH TẾ
Chương 3: MỘT SỐ ỨNG DỤNG CỦA ĐẠO HÀM
Bài 3: Vẽ đồ thị hàm số Mục tiêu bài học
Xác định các đường tiệm cận đứng và tiệm cận ngang của đồ thị
Thảo luận và áp dụng một quy trình chung để vẽ đồ thị hàm số 29
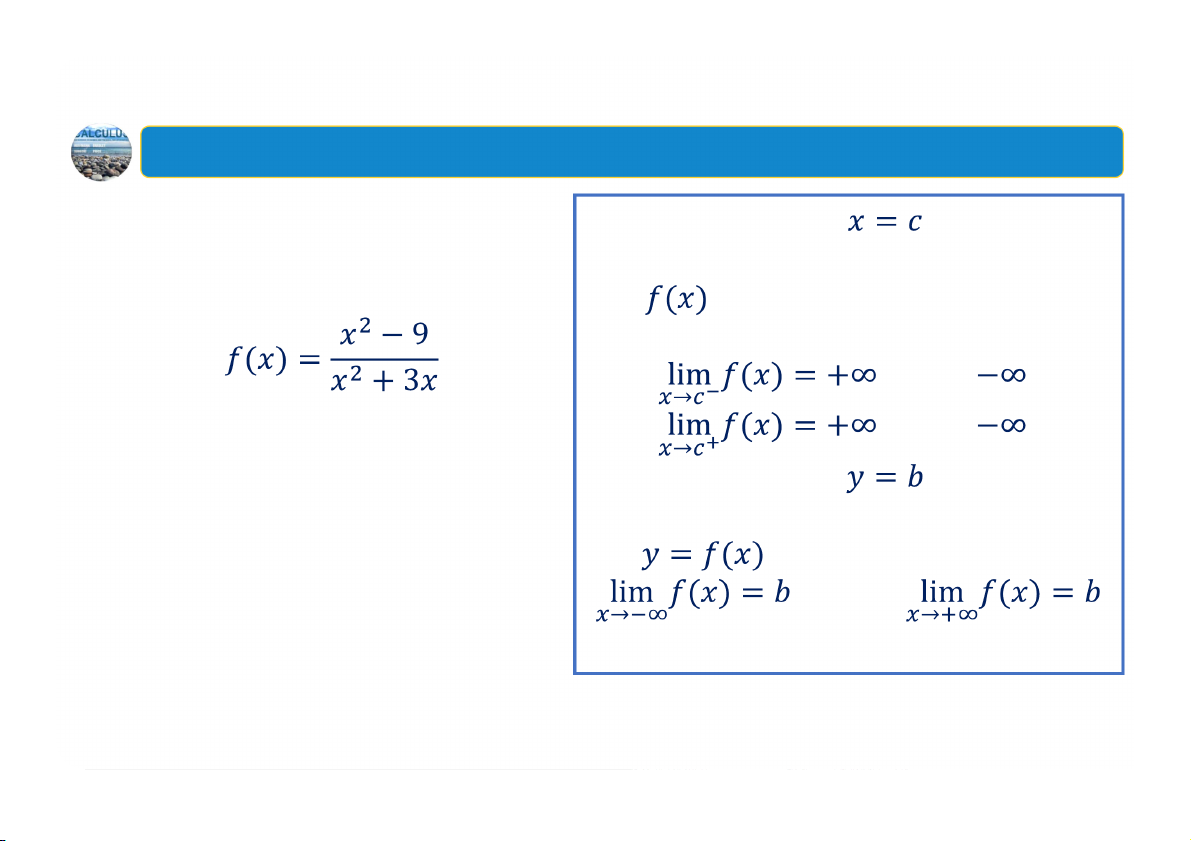
1. Tiệm cận đứng, tiệm cận ngang
Ví dụ: Tìm tất cả các tiệm Đường thẳng được gọi là
cận đứng và tiệm cận ngang
một tiệm cận đứng của đồ thị hàm
của đồ thị hàm số sau số
nếu một trong các điều kiện sau thỏa mãn: (hoặc ) (hoặc ) Đường thẳng được gọi là
một tiệm cận ngang của đồ thị hàm số nếu: hoặc 30
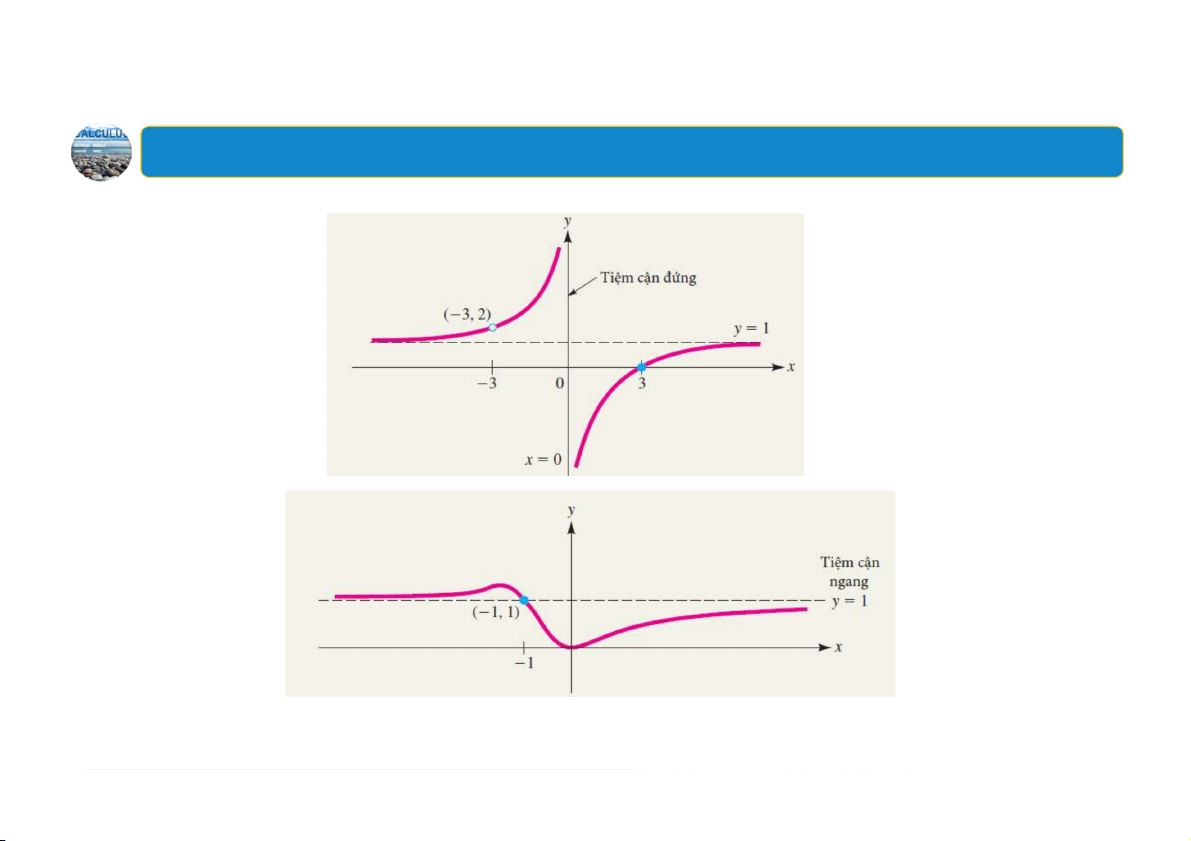
1. Tiệm cận đứng, tiệm cận ngang Minh họa 31 2. Vẽ đồ thị hàm số
Quy trình chung để vẽ đồ thị của hàm số
Bước 1. Tìm miền xác định của .
Bước 2. Tìm và định vị các hệ số chặn.
Bước 3. Tìm tất cả các tiệm cận đứng và tiệm cận ngang của đồ thị và vẽ
chúng trên cùng một hệ trục tọa độ. Bước 4. Tính
và xác định các số tới hạn, các khoảng tăng, giảm của
Bước 5. Tìm tọa độ các điểm cực trị tương đối của hàm số. Vẽ một chóp mũ
tại điểm cực đại tương đối và một đáy cốc tại điểm cực tiểu tương đối. Bước 6. Tính
và tìm các khoảng lõm và điểm uốn của đồ thị hàm số. Vẽ
tại vị trí điểm uốn một "đường xoắn" để định dạng của đồ thị tại những điểm gần điểm uốn.
Bước 7. Vẽ đồ thị hàm số. 32 2. Vẽ đồ thị hàm số
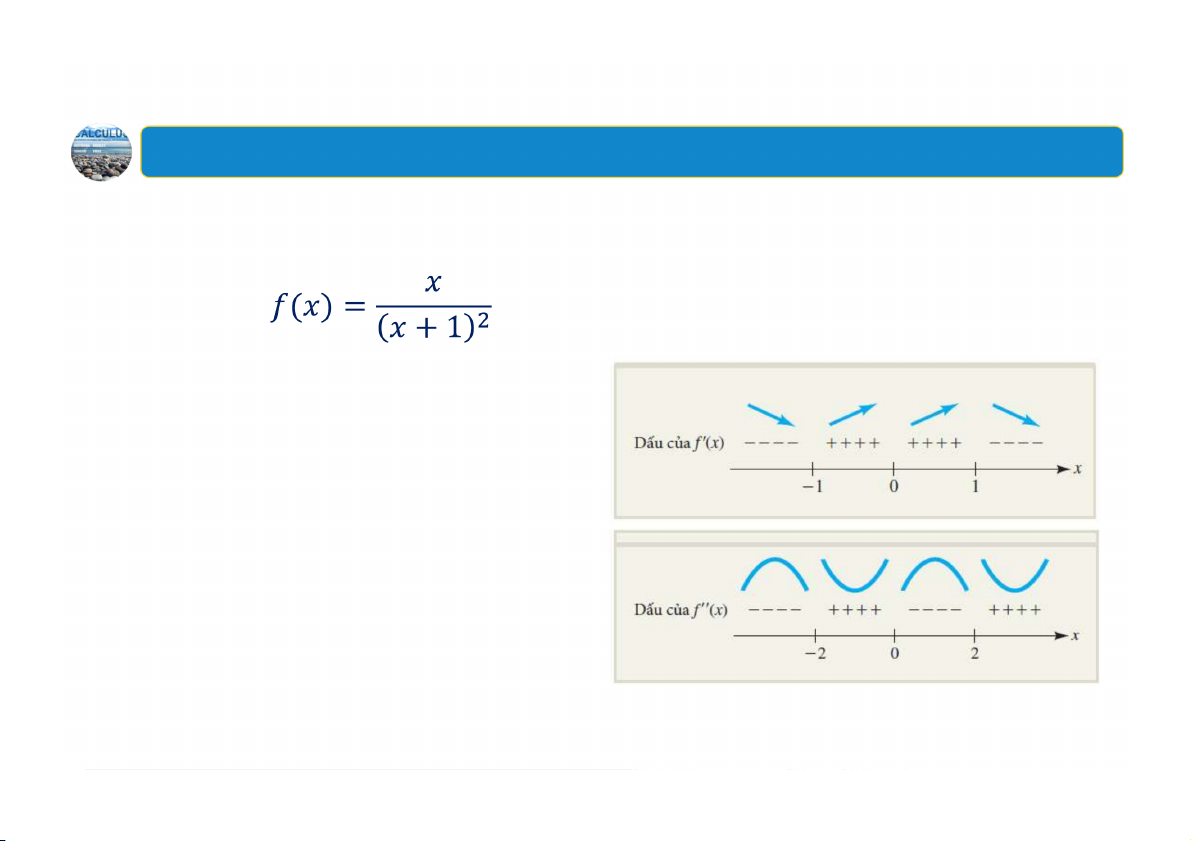
Ví dụ: Vẽ đồ thị của hàm số sau
Ví dụ: Dựa theo sơ đồ mô tả các
khoảng tăng, giảm và tính lõm,
hãy vẽ phác đồ thị của một hàm số có các đặc trưng đó 33 KHOA TOÁN KINH TẾ BỘ MÔN TOÁN CƠ BẢN Bài giảng TOÁN CHO CÁC NHÀ KINH TẾ
Chương 3: MỘT SỐ ỨNG DỤNG CỦA ĐẠO HÀM
Bài 4: Tối ưu hóa; Độ co giãn của cầu Mục tiêu bài học
Sử dụng định lý giá trị cực trị để tìm cực trị tuyệt đối
Tìm cực trị tuyệt đối trong các bài toán ứng dụng
Nghiên cứu các nguyên lý tối ưu hóa trong kinh tế học.
Định nghĩa và xem xét độ co giãn của cầu theo giá. 35 1. Cực trị tuyệt đối Định nghĩa
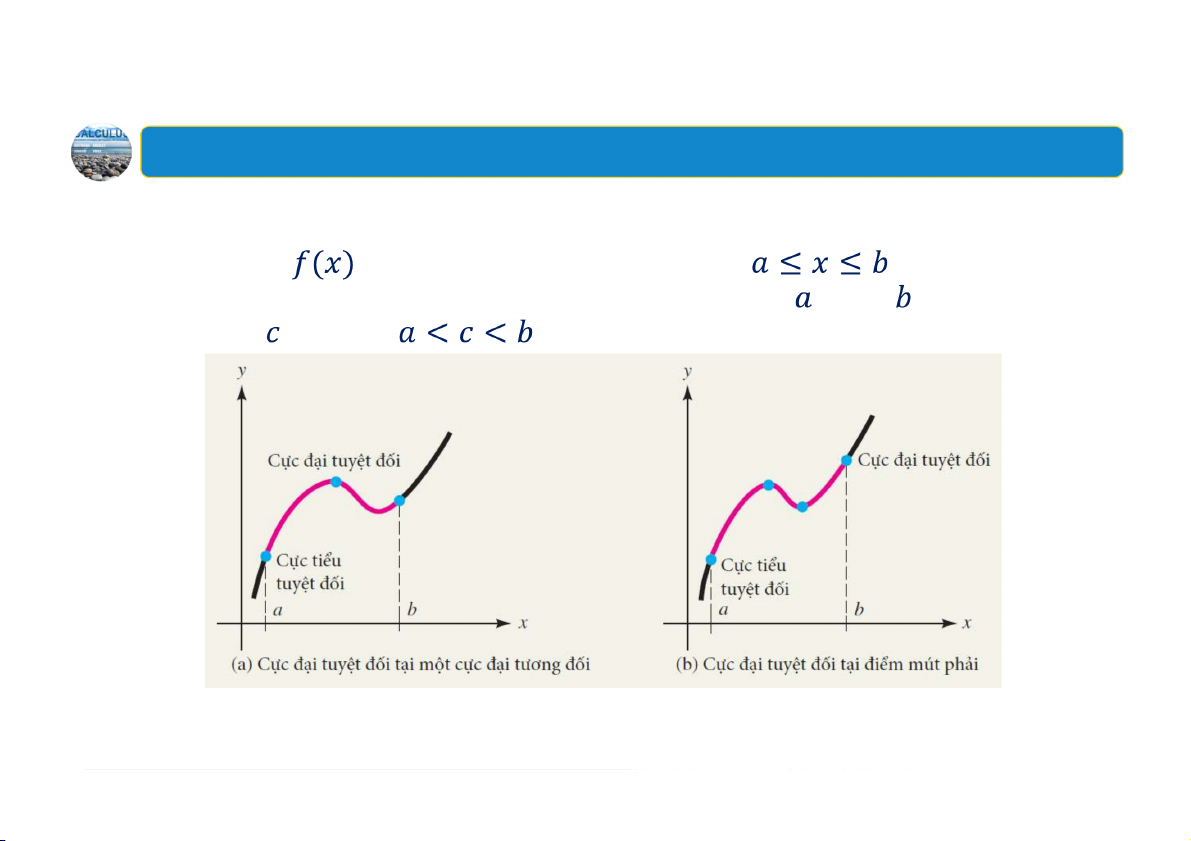
Giả sử hàm số xác định trên một khoảng mở chứa điểm . Khi đó:
là cực đại tuyệt đối của trên nếu với mọi thuộc
là cực tiểu tuyệt đối của trên nếu với mọi thuộc
Cực đại tuyệt đối và cực tiểu tuyệt đối được gọi chung là các cực trị tuyệt đối. 36 1. Cực trị tuyệt đối
Tính chất giá trị cực biên Một hàm
liên tục trên khoảng đóng đạt các cực trị
tuyệt đối trên đoạn này, hoặc tại một điểm mút ( hoặc ), hoặc tại một số tới hạn sao cho . 37 1. Cực trị tuyệt đối
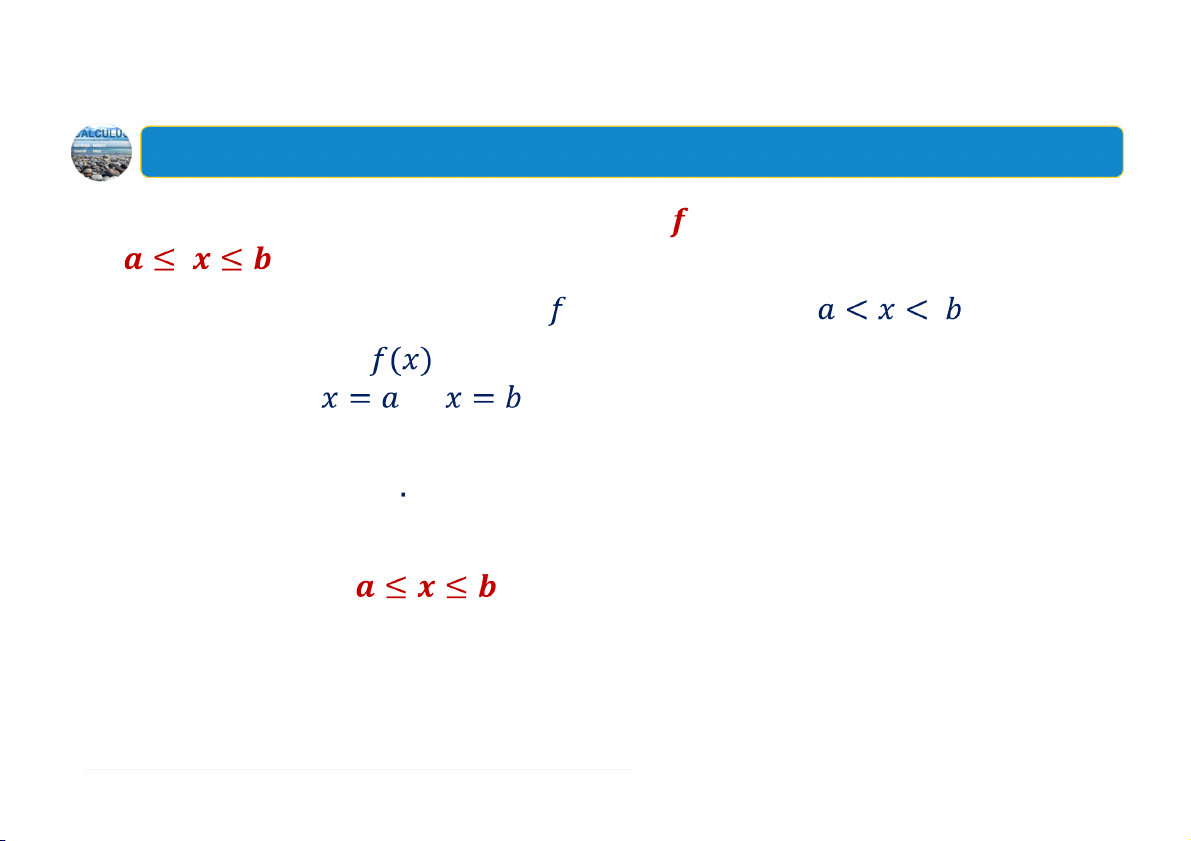
Thủ tục tìm cực trị tuyệt đối của hàm liên tục trên khoảng đóng
1. Tìm tất cả các số tới hạn của trong khoảng mở . 2. Tính giá trị của
tại các số tới hạn tìm được trong bước 1 và tại các đầu mút và .
3. Tìm giá trị lớn nhất và giá trị nhỏ nhất trong các giá trị tìm được trong bước 2 và kết luận
Tìm cực trị tuyệt đối của hàm liên tục trên một khoảng không phải là khoảng đóng :
Sử dụng đạo hàm cấp một để xác định các khoảng tăng, giảm, sau đó
vẽ phác thảo đồ thị của hàm số. Dựa vào đồ thị ta đưa ra kết luận. 38 1. Cực trị tuyệt đối
Ví dụ: Tìm cực đại tuyệt đối và
Ví dụ: Tìm cực đại tuyệt đối và cực
cực tiểu tuyệt đối của hàm số:
tiểu tuyệt đối (nếu có) của hàm số: trên đoạn . trên khoảng . 39 1. Cực trị tuyệt đối
Kiểm tra cực trị tuyệt đối bằng đạo hàm cấp hai. Giả sử liên tục trên khoảng và
là số tới hạn duy nhất và . Khi đó Nếu
thì cực tiểu tuyệt đối của trên khoảng là . Nếu
thì cực đại tuyệt đối của trên khoảng là . 40
Ví dụ: Tối đa hóa lợi nhuận và tối thiểu hóa chi phí bình quân
Một loại sản phẩm khi sản xuất
nghìn đơn vị được bán với mức giá
đô-la mỗi đơn vị và tổng chi phí là nghìn đô.
a) Xác định mức sản xuất
để tối đa hóa lợi nhuận và tìm mức lợi nhuận tối đa. b) Tìm
để tối thiểu hóa chi phí bình quân ? Tìm mức chi
phí bình quân tối thiểu đó.
c) Xác định mức sản xuất
để chi phí bình quân bằng chi phí cận biên . 41
2. Hai nguyên lý tổng quát của phân tích cận biên
Tiêu chuẩn phân tích cận biên cho lợi nhuận tối đa: Lợi nhuận
đạt tối đa ở mức sản xuất sao cho
doanhthucậnbiên bằngvớichiphícậnbiênvà tốc độ thay đổi của
chi phí cận biên lớn hơn tốc độ thay đổi của doanh thu cận biên, nghĩa là: ) và
Tiêu chuẩn phân tích cận biên cho chi phí bình quân tối thiểu:
Chi phí bình quân đạt tối thiểu ở mức sản xuất sao cho chiphíbình
quânbằngvớichiphícậnbiên, nghĩa là khi 42
3. Bài toán tối ưu ứng dụng
Bài toán tối ưu trong thực tế:
Biểu thức hàm số chưa được cho trước.
Cần thu thập thông tin, sau đó lập mô hình toán học phù hợp
Ta cần kết hợp kỹ thuật xây dựng mô hình ở chương 1 với các kỹ
thuật giải bài toán tối ưu hóa. 43
3. Bài toán tối ưu ứng dụng
Các bước giải các bài toán tối ưu hóa ứng dụng
Bước 1. Xác định đại lượng cần tối ưu hóa, gán tên cho tất cả các biến số quan tâm.
Bước 2. Biểu diễn quan hệ giữa các biến dưới dạng các phương trình hoặc bất phương trình.
Bước 3. Biểu diễn đại lượng cần tối ưu hóa theo một biến duy nhất dưới dạng hàm số .
Bước 4. Giải bài toán tìm cực trị hàm số .
Bước 5. Diễn giải kết quả thu được theo các đại lượng kinh tế, hình
học hoặc vật lý thích hợp. 44
3. Bài toán tối ưu ứng dụng Ví dụ
Mateo sở hữu một công ty nhỏ làm
áo thun lưu niệm. Anh ấy có thể sản
xuất áo thun với chi phí $2 mỗi
chiếc. Áo đang được bán với giá $5
mỗi chiếc, và ở mức giá này, du
khách sẽ mua 4,000 chiếc một
tháng. Mateo dự định nâng giá bán
áo lên và ước tính rằng với mỗi lần
tăng giá áo thêm $1 thì số áo bán
được mỗi tháng sẽ giảm đi 400
chiếc. Hỏi Mateo nên bán mỗi chiếc
áo với giá bằng bao nhiêu để tối đa hóa lợi nhuận? 45
3. Bài toán tối ưu ứng dụng
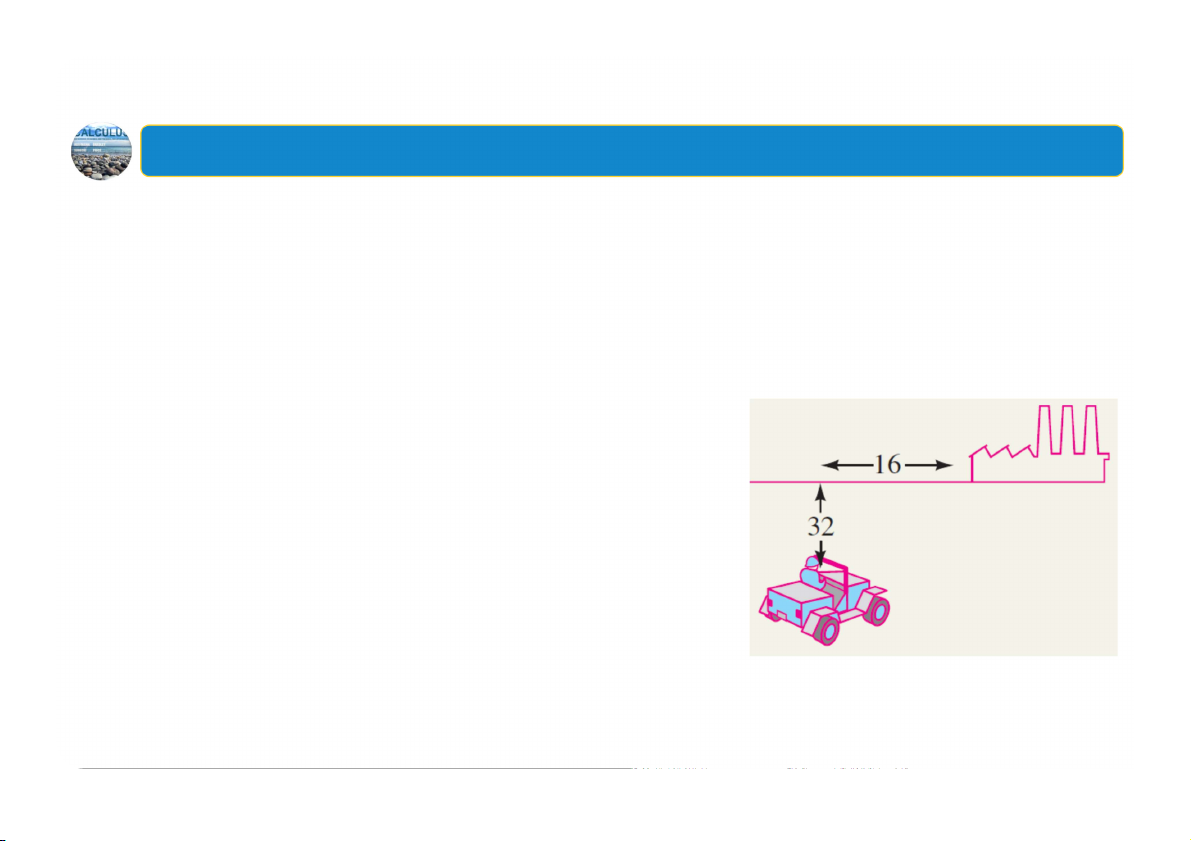
Ví dụ: Câu chuyện gián điệp
Vào lúc giữa trưa, chàng điệp viên lái một chiếc xe jeep băng qua sa mạc đầy
cát ở công quốc Alta Loma nhỏ bé. Anh ấy cách một con đường trải nhựa đúng
32 km tính tới điểm gần nhất. Dọc con đường này 16 km là một nhà máy điện
bỏ hoang, nơi mà một nhóm gián điệp thù địch đang giam giữ cấp trên của
anh, mật danh “N”. Nếu anh ấy không tới cùng tiền chuộc lúc 12:50 trưa, nhóm
người xấu dọa sẽ giết N.
Chiếc xe jeep có thể di chuyển với tốc độ 48 km
/ giờ trên cát và với tốc độ 80 km / giờ trên
đường trải nhựa. Liệu chàng điệp viên có đến
đúng giờ không, hay đây sẽ là sự kết thúc của
N? [Gợi ý: Mục tiêu là giảm thiểu thời gian, tức
là khoảng cách chia cho tốc độ.] 46
3. Bài toán tối ưu ứng dụng: Quản lý hàng tồn kho
Quản lý hàng tồn kho là một điều quan trọng cần phải tính đến trong kinh doanh.
Tổng chi phí = chi phí lưu kho + chi phí đặt hàng + chi phí mua hàng
Nếu mỗi lô hàng có số lượng lớn chi phí đặt hàng sẽ thấp, trong khi chi phí lưu kho sẽ cao.
Nếu mỗi lô hàng có số lượng nhỏ thì chi phí đặt hàng sẽ cao nhưng chi phí lưu kho sẽ thấp. 47
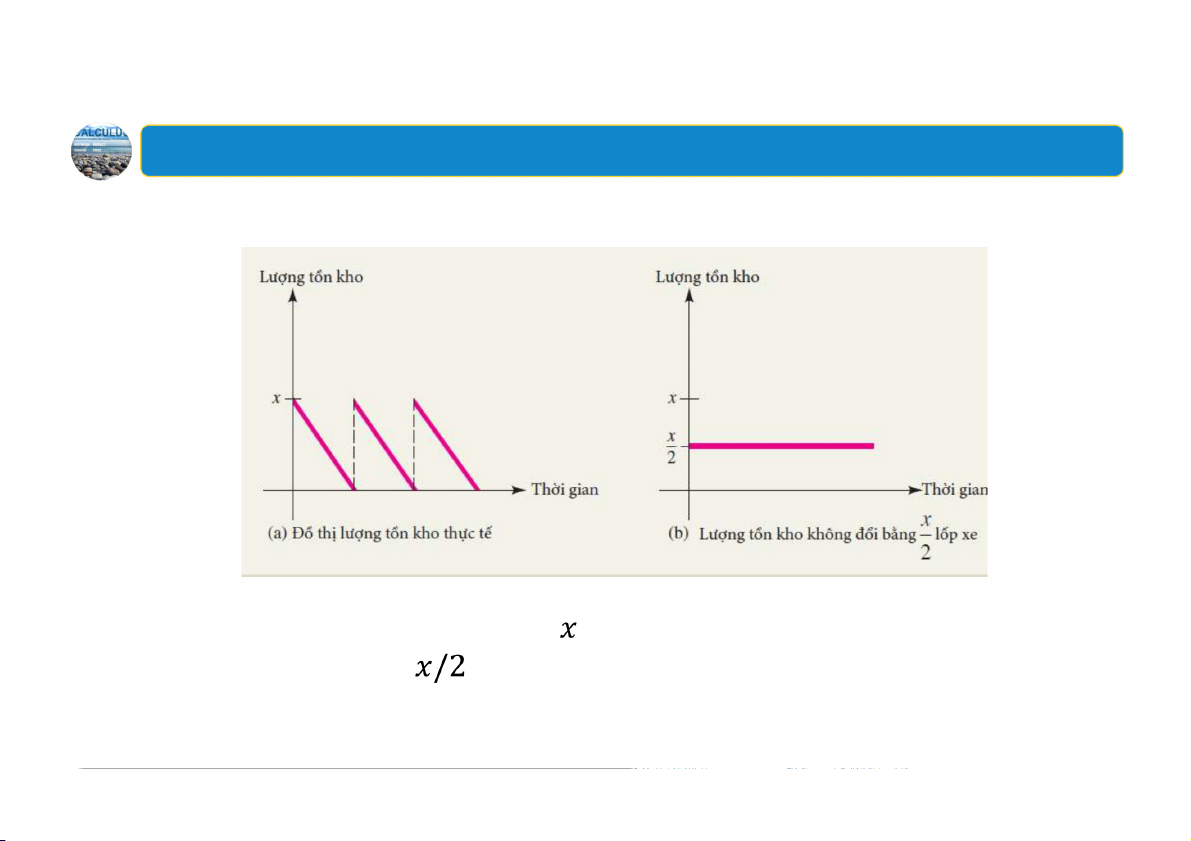
3. Bài toán tối ưu ứng dụng: Quản lý hàng tồn kho Minh họa
Gọi số hàng tồn kho ban đầu là thì tổng chi phí lưu kho hàng năm bằng chi phí lưu giữ
số hàng trong toàn bộ năm đó. 48
3. Bài toán tối ưu ứng dụng: Quản lý hàng tồn kho
Gọi số hàng tồn kho ban đầu là
Ví dụ: Sheldon Evans, giám đốc của
thì tổng chi phí lưu kho hàng
một công ty sản xuất xe đạp, mua
năm bằng chi phí lưu giữ
6,000 lốp xe một năm từ một nhà
phân phối. Mỗi lốp xe có giá là $21,
số hàng trong toàn bộ năm đó.
phí đặt hàng là $20 mỗi lô và chi
phí lưu kho là 96 cent mỗi lốp mỗi
năm. Giả sử rằng lốp xe được sử
dụng với tốc độ không đổi trong
suốt cả năm và mỗi lô hàng đến
ngay khi lô hàng trước được sử
dụng hết. Hỏi Sheldon nên đặt bao
nhiêu lốp xe mỗi lô hàng để tối thiểu hóa tổng chi phí? 49
4. Độ co giãn của cầu theo giá Định nghĩa Nếu
đơn vị của một loại hàng hóa được bán trên thị trường với mức giá , với
là một hàm khả vi thì độ co giãn của cầu theo giá
được tính theo công thức:
và được giải thích như sau:
Tốc độ phần trăm giảm của lượng cầu
gây ra bởi 1% tăng lên của mức giá 50
4. Độ co giãn của cầu theo giá
Ví dụ : Giả sử lượng cầu và giá
của một loại hàng hóa liên hệ với
nhau bởi phương trình tuyến tính (với ).
a. Biểu diễn độ co giãn của cầu như một hàm của .
b. Tính độ co giãn của cầu theo giá khi . Giải thích kết quả tính được.
c. Tính độ co giãn của cầu theo giá khi . Giải thích kết quả tính được.
d. Với mức giá nào thì độ co giãn của cầu bằng 1? Nêu ý nghĩa kinh tế của mức giá này? 51
4. Độ co giãn của cầu theo giá
Các mức của độ co giãn cầu
Ví dụ: Giả sử hàm cầu đối
Cầu co giãn. Phần trăm giảm với 1 loại hàng hóa là:
của lượng cầu lớn hơn phần trăm tăng lên của giá. (với ). Cầu không co giãn. Phần
a. Tìm mức giá tại đó cầu
trăm giảm của lượng cầu nhỏ
là co giãn, không co giãn, và
hơn phần trăm tăng lên của co giãn đơn vị. giá.
b. Giải thích ý nghĩa kết
quả tìm được trong phần (a).
Cầu co giãn đơn vị. Phần
trăm thay đổi của giá và của
lượng cầu (xấp xỉ) bằng nhau. 52 THANK YOU! 53




