Tài liệu Toán 9 chủ đề căn thức bậc hai và hằng đẳng thức

Tài liệu gồm 25 trang, bao gồm kiến thức cần nhớ, các dạng toán và bài tập chủ đề căn thức bậc hai và hằng đẳng thức  trong chương trình môn Toán 9, có đáp án và lời giải chi tiết. Mời bạn đọc đón xem.

31 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Căn bậc hai. Căn bậc ba

Môn: Toán 9

Thông tin:

25 trang 6 tháng trước

Tác giả:

Profile Hà Việt Anh
1
CĂN THỨC BẬC HAI VÀ HẰNG ĐẢNG THỨC
2
AA=
A. Tóm tắt lý thuyết
1. Căn thức bậc hai
a. Định nghĩa: Với
A
là một biểu thức đại số thì
A
được gọi là căn thức bậc hai của
A
và
A
gọi là biểu thức lấy căn hay là biểu thức dưới dấu căn
b.
A
có nghĩa (hay xác định) khi
1
0A
A
≥⇒
có nghĩa khi
0A >
Ví dụ:
3
x
có nghĩa khi
2. Hằng đẳng thức:
( )
( )
2
,0
,0
AA
AA
AA
≥
= =
−<
Ví dụ 1:
22
12 12 12; ( 7) 7 7= = − =−=
Ví dụ 2: Rút gọn biểu thức sau:
2
( 2)x −
với
2x ≥
Lời giải
Ta có:
2
( 2) 2 2x xx− =−=−
vì
2
x ≥
B. Bài tập và các dạng toán
Dạng 1: Tìm điều kiện để biểu thức chứa căn có nghĩa
Cách giải: Chú ý rằng
A
có nghĩa khi và chỉ khi
0A ≥
+)
A
có nghĩa khi
0A ≥
+)
1
A
có nghĩa khi
0A
>
+)
0AB AB+⇒+≥
có nghĩa khi
0AB+≥
+)
1
A
có nghĩa khi
0A >
+)
AB−
có nghĩa khi
0AB−≥
+)
2
1
A
có nghĩa khi
0A ≠
+)
1
AB−
có nghĩa khi
0
0
A
AB
≥
⇔
−≠
+)
1
AB+
có nghĩa khi
0
0
A
AB
≥
⇔
+≠
2
+)
. .0AB AB⇒≥
có nghĩa khi
0
0
0
0
A
B
A
B
≥
≥
⇔
≤
≤
+)
A
B
có nghĩa
0
0
0
0
A
B
A
B
≥
>
⇔
≤
<
+)
1
.
AB
có nghĩa
0
0
0
0
0
A
B
AB
A
B
>
>
>⇔
<
<
+)
2
( 0)x n n x nn≤ ⇔− ≤ ≤ ≥
+)
2
( 0)
xn
xn n
xn
≥
≥⇔ ≥
≤−
Bài 1: Tìm x để các căn thức sau có nghĩa
a.
3x−
b.
2 10x −
c.
34
x−−
d.
3 15x +
e.
1
5
2
x +
f.
2
89xx−−
Lời giải
a) Ta có:
3x−
có nghĩa
0x⇔≤
b) Ta có:
2 10x −
có nghĩa
2 10 0 5xx⇔ − ≥⇔≥
c) Ta có:
34x−−
có nghĩa
4
3 40
3
xx
−
⇔− − ≥ ⇔ ≤
d) Ta có:
3 15x +
có nghĩa
3 15 0 5xx⇔ + ≥ ⇔ ≥−
e) Ta có:
1
5
2
x +
có nghĩa
11
50
2 10
xx
−
⇔ +≥⇔≥
f) Ta có:
2
89xx−−
có nghĩa
( )( )
2
9
8 90 1 9 0
1
x
xx x x
x
≥
⇔ − −≥⇔ + − ≥⇔
≤−
Chú ý: Với a là số dương, ta có:
22
22
xa
xa
xa
x a axa
≥
≥⇔
≤−
≤ ⇔− ≤ ≤
3
Bài 2: Với giá trị nào của x thì mỗi biểu thức sau có nghĩa
a.
( 2)xx+
b.
2
5 38xx−−
c.
2
2 45
xx++
d.
2
4 x−
e.
2
21xx−+ −
Lời giải
a) Ta có:
( 2)xx+
có nghĩa khi
2
( 2) 0
0
x
xx
x
≤−
+ ≥⇔
≥
x
-2
0
x
-
│
-
0
+
2x +
-
0
+
│
+
( )
2
xx+
+
-
+
b) Ta có:
2
5 38xx−−
có nghĩa khi
2
1
5 3 8 0 ( 1)(5 8) 0
8
5
x
xx x x
x
≤−
− −≥⇔ + − ≥⇔
≥
c) Ta có:
2
2 45
xx++
có nghĩa khi
22
2 4 5 0 2( 1) 3 0xx x+ +≥⇔ + +≥
. Vậy biểu thức luôn có
nghĩa
d) Ta có:
2
4 x−
có nghĩa khi
22
4 0 42 2xx x− ≥⇔ ≤⇔−≤≤
e) Ta có:
2
21xx−+ −
có nghĩa khi
2
( 1) 0 1 0 1x xx
− + ≥ ⇔ −= ⇔ =
Bài 3: Với giá trị nào của x thì mỗi biểu thức sau có nghĩa:
a.
4
23x +
b.
2
1x
−
+
c.
1
32x−
d.
2
2
x
e.
2
2
x
x
x
+−
−
f.
2
2
x
x
x
+−
+
g.
2
2
4
x
x
x
+−
−
h.
3
3xx
x
+ +−
Lời giải
a) Ta có:
4
23x +
có nghĩa
43
0 2 30
23 2
xx
x
−
⇔ ≥⇔ +>⇔>
+
4
b) Ta có:
2
1x
−
+
có nghĩa
2
0 10 1
1
xx
x
−
⇔ ≥⇔+<⇔<−
+
c) Ta có:
1
32x−
có nghĩa
13
0 32 0
32 2
xx
x
⇔ ≥⇔− >⇔<
−
d) Ta có:
2
2
x
có nghĩa
2
00xx⇔ >⇔≠
e) Ta có:
2
2
x
x
x
+−
−
có nghĩa
20 2
2
20 2
xx
x
xx
−≥ ≥

⇔ ⇔ ⇔>

−≠ ≠

f) Ta có:
2
2
x
x
x
+−
+
có nghĩa
20 2
2
20 2
xx
x
xx
−≥ ≥

⇔ ⇔ ⇔≥

+≠ =−

g) Ta có:
2
2
4
x
x
x
+−
−
có nghĩa
2
2
2
x
x
x
≥
⇔ ⇔>
≠±
k) Ta có:
3
3xx
x
+ +−
có nghĩa
2
3
3
0
30
0
x
x
x
x
x
x
+
+>

⇔⇔


−≥
≤
(vô lý).
Vậy không có giá trị nào của x làm biểu thức có nghĩa.
Dạng 2: Tính giá trị của biểu thức
Cách giải: Sử dụng hằng đẳng thức:
( )
( )
2
,0
,0
AA
AA
AA
≥
= =
−<
Bài 1: Tính giá trị của các biểu thức sau
a.
49
144. . 0,01
64
A
−
= −
b.
( )
2
0,25 15 2,25 : 169
B

= −− +


c.
( )
2
0,04 1, 2 121 81C

= −− +


d.
( ) ( )
22
22
75: 3 4 3 5 3D = +− − − −
Lời giải
a) Ta có:
( )
2
2
2
49 7
144. . 0,01 12 . . 0,1 1, 05
64 8
A
−

=−= =


b) Ta có:
( )
( )
( )
2 22
22
0,25 15 2, 25 : 169 0,5 15 1,5 : 13 1B

= −− + = − + =−


5
c) Ta có:
( )
2
0,04 1, 2 121 81 90CC

= −− + ⇒=


d) Ta có:
( ) (
)
22
22
75: 3 4 3 5 3 3DD= +− − − − ⇒ =
Bài 2: Tính giá trị của các biểu thức sau
a.
6 4 2 22 12 2− +−
b.
2
( 3 2) 2−+
c.
2
3 5 (1 5 )−−
d.
17 12 2 9 4 2− ++
e.
6 25 6 25
+ +−
f.
3 22 6 42+ +−
g.
24 8 5 9 4 5+ +−
h.
41 12 5 41 12 5− −+
Lời giải
a) Ta có:
22
6 4 2 22 12 2 (2 2) (3 2 2) 2 2− + − = − + −=
b) Ta có:
2
(32) 2 32 23− +=−+=
c) Ta có:
2
35 (1 5) 35 1 5 35 1 5 35 (5 1) 25 1− − = −− = −− = − − = +
d) Ta có:
22
17122 9 42 (3 22) (22 1) 4− ++ = − + +=
e) Ta có:
22
6 25 6 25 (5 1) (5 1) 25+ +− = ++ −=
f) Ta có:
22
3 22 6 42 (2 1) (2 2) 3+ +− = ++ − =
g) Ta có:
2
24 8 5 9 4 5 4(6 2 5) ( 5 2) 2 5 1 5 2 3 5+ + − = + + − = ++ − =
h) Ta có:
( ) ( )
22
41 12 5 41 12 5 6 5 6 5 2 5− −+ =− −+ =−
Bài 3: Thực hiện các phép tính sau
a)
(
)
3 2.5 2 6A =−+
b)
22
4 23 4 23
31 1 3
B

−+
= −


−+

c)
5 9 29 12 5C = −− −
d)
13 30 2 9 4 2D = + ++
Lời giải
6
a) Ta có:
( ) ( )( )
32.526 32321A =− + =− +=
b) Ta có:
( ) ( )
22 2 2
22
4 2 3 4 2 3 ( 3 1) ( 3 1)
3 1 3 1 43
31 1 3 31 31
B

−+ − +
= − = − = −− +=−



−+ − −

c) Ta có:
2
5 9 29 12 5 5 9 20 12 5 9 5 9 (2 5 3)C
= −− − = −− − += −− +
d) Ta có:
2
13 30 2 9 4 2 13 30 2 (2 2 1) 13 30 2 (2 2 1) 13 30 3 2 2+++=++ +=+++=++
22
13 30 ( 2 1) 13 30( 2 1) 43 30 2 25 2.5.3 2 18 (5 3 2) 5 3 2= + + = + += + = + + = + =+
Bài 4: Rút gọn các biểu thức sau
a)
( )
2
4 15 15A =−+
b)
( )
( )
22
2 3 13B = − +−
c)
49 12 5 49 12 5C =− −+
d)
29 12 5 29 12 5
D
=+ −−
Lời giải
a) Ta có:
( ) ( )
2
4 15 15 4 15 15 4 4 15A =− +=−+=>
b) Ta có:
( )
( )
22
23 13 23131B = − + − = − ++ =
c) Ta có:
( )
( )
22
49 12 5 49 12 5 2 3 5 2 3 5 4CC= − − + = − − + ⇒=
d) Ta có:
( ) ( )
22
29 12 5 29 12 5 3 2 5 3 2 5 6DD= + − − = + − − ⇒=
Bài 5: Chứng minh rằng
a)
( )
2
11 6 2 3 2+=+
b)
11 6 2 11 6 2 6+ +− =
c)
( )
2
8 27 7 1−=−
d)
8 27 8 27 2− −+ =−
Lời giải
a) Ta có:
( )
2
11 6 2 9 2.3 2 2 3 2VT VP= + =+ += + = ⇒
đpcm
7
b) Ta có:
11 6 2 11 6 2 2 3 2 3 6VT VP= + + − = ++ −== ⇒
đpcm
c) Ta có:
( )
2
8 27 7 27 1 7 1− = − += − ⇒
đpcm
d) Ta có:
( ) ( )
22
8 27 8 27 7 1 7 1 2
VT VP= − − + = − − + =−= ⇒
Dạng 3: Rút gọn các biểu thức chứa biến
Cách giải: Sử dụng hằng đẳng thức:
( )
( )
2
,0
,0
AA
AA
AA
≥
= =
−<
Bài 1: Rút gọn các biểu thức sau
a)
2
64 2 ( 0)A a aa
= +≥
b)
2
5 25 25 ( 0)B a aa= −<
c)
42
16 6aa+
(với a bất kỳ) d)
63
39 6aa−
(với a bất kỳ )
e)
22
69 69Eaa aa= + ++ − +
(với a bất kỳ )
Lời giải
a) Ta có:
2
64 2 ( 0) 8 2 10 10
a aa a a a A a+ ≥ = + = ⇒=
b) Ta có:
2
5 25 25 ( 0) 5. 5 25 50 50a aa a a a B a− < = − =− ⇒=−
c) Ta có:
42 22 2 2
16 6 4 6 10 10aa a a aC a+= += ⇒=
(với a bất kỳ )
d) Ta có:
63 33
396336aa aa−= −
(với a bất kỳ )
+)
33 3 3 3
0 3. 3 6 3.( 3 ) 6 15a aa a a a<⇒ −=−−=−
+)
3 3 33 3
03.36963a a aaaa≥⇒ −=−=
e. (khó)
22
69 69Aa a a a= + ++ − +
với a bất kỳ
22
69 69 3 3Aa a a a a a= + ++ − += ++ −
+) Nếu
3 3 3 33 2a a a a aa<⇒ + + − =−−+− =−
+) Nếu
3
aa−≤ ≤
thì
3 3 33 6aaa a+ + − =++− =
+) Nếu
3a >
thì
3 3 3 32a a aa a+ + − = ++−=
8
Bài 2: Rút gọn các biểu thức sau
a)
( )
( )
( )
69 3
4 0; 9
9
xx x
A x xx
x
++ −
= − ≤≠
−
b)
2
9 12 4 2
32 3
xx
Bx
x
++ −

= ≠

+

Lời giải
a) Ta có:
( ) (
)
(
)( )
(
)
( )
2
33
4 3 10 9
33
xx
Ax A x x
xx
+−
= − ⇒ = − ≤≠
−+
b) Ta có:
2
2
1
32
3
9 12 4
32 32
2
1
3
x
x
xx
B
xx
x
−

>

+
++

= = =
++
−

−<


Bài 3: Thực hiện các phép tính
a)
( )
( )
( )
10 25 5
5 0 25
25
xx x
Ax x
x
−+ +
= − ≤≠
−
b)
2
4 41 1
21 2
xx
Bx
x
−+

= ≠

−

Lời giải
a) Ta có:
( )
4 5 0 25Ax x= + ≤≠
b) Ta có:
2
1
1
2
4 41
21
1
1
2
x
xx
B
x
x

>

−+

= =
−

−<


Bài 4: Rút gọn các biểu thức sau
a)
21 21(1 2)Aa a a a a= + −+ − − ≤ ≤
b)
2
4 4 4( 2)Bxx x x=− −+ ≥
c)
2
44
( 2)
2
xx
Cx
x
++
= ≠
+
d)
2
10 25
21
5
xx
Dx
x
−+
= −−
−
e)
( 6 9)( 3)
4 (0 9)
9
xx x
Ex x
x
++ −
= − ≤≠
−
Lời giải
a) Ta có:
21 21(1 2) 11 11Aa a a a a a a= + −+ − − ≤ ≤ = −++ −−
Với
1 2 1 1 0; 1 1 0aa a≤ ≤ ⇒ −+> −−≤
, ta được:
9
11 11 11 11 2Aa a a a= −++ −− = −+− −+=
b) Ta có:
2
4 4 4( 2) 4 2 4 ( 2) 3 2B x x x x xx x x x= − − + ≥ = −−= − − = +
c) Ta có:
2
2
44
( 2)
22
x
xx
Cx
xx
+
++
= ≠=
++
- Nếu
2x <−
thì
1A = −
- Nếu
2x >−
thì
1A =
d) Ta có:
2
5
10 25
21 21
55
x
xx
Dx x
xx
−
−+
= −− = −−
−−
+) Nếu
5 0 5 2 11 2
x x Ax x− ≤ ⇔ ≤ ⇒ = −+=
+) Nếu
5 22x Ax≥⇒ = −
e) Ta có:
(
)( )
( )
69 3
4 09
9
xx x
Ex x
x
++ −
= − ≤≠
−
( )( ) ( ) ( )
( )( )
( )
( )
2
69 3 3 3
4 4 3 10 9
9
33
xx x x x
Ex x x x
x
xx
++ − + −
⇒ = − = − = − ≤≠
−
−+
Bài 5:
Cho biểu thức:
22 22
21 21Ax x x x= + −− − −
a. Với giá trị nào của x thì A có nghĩa
b. Tính A nếu
2x ≥
Lời giải
a) Ta có:
2 2 2 2 2 2 2 22 2
2 1 2 1 ( 1 1) ( 1 1) 1 1 1 1Ax x x x x x x x= + −− − − = −+ − −− = −++ −−
A có nghĩa
22
1
10 1
1
x
xx
x
≤−
⇔ −≥ ⇔ ≥⇔
≥
b) Ta có:
22 2 2
221111110x xx x x≥ ⇒ ≥ ⇔ −≥⇒ −≥⇒ −−≥
22 2
11 11 2 1Ax x x⇒ = −++ −−= −
10
Bài 6:
Cho ba số dương
,,xyz
thỏa mãn:
1xy yz zx++=
Tính:
22 22 2 2
2 22
(1 )(1 ) (1 )(1 ) (1 )(1 )
111
yz zx xy
Ax y z
xyz
++ ++ ++
=++
+++
Lời giải
Ta có:
22 2 2
1 ( ) ( )( );1 ( )( );1 ( )( )
y xy yz zx y x y y z z y z z x x x z x y
+= ++ +=+ + +=+ + +=+ +
( ) ( ) ( )2( )2A x y z y z x z x y xy yz zx⇒= ++ ++ + = + + =
Vậy
2A
=
.
Dạng 4: giải phương trình
Cách giải: Chú ý một số cách biến đổi tương đương liên quan đến căn thức bậc hai
1)
2
0B
AB
AB
≥
= ⇔
=
2
2 2 22
1
10 1
11
0( )
1 ( 1) 1 2 1
1( / )
x
xx
xx
x loai
x x xx x
x tm
≥
−≥ ≥

− = −⇔ ⇔ ⇔
=

−=− −=−+

=
2)
2
A B AB=⇔=
3)
0( 0)A hayB
AB
AB
≥≥
= ⇔
=
4)
22
A B AB A B= ⇔ = ⇔=±
5)
22
AB A B= ⇔=±
Ví dụ:
22
0 1( )
1
( 1)
1
1
2
vn
xx
xx
xx
x
=
−=
−=⇔ ⇔
−=−
=
(thỏa mãn)
7)
0B
AB
AB
AB
≥
= ⇔
=
= −
11
Ví dụ:
2
0
20
1
1
11
(/ )
2
22
2
2
42
1
1
()
2
6
2
x
x
x tm
xx
xx x x x
x loai
xx
≥
≥
=
+=
++ = ⇔ + = ⇔ ⇔


−

=
+=−
8)
AB
AB
AB
=
= ⇔
= −
Ví dụ:
31 3 1
31 3
31 3 1
xx x
xx
xx x
+= + =

+= +⇔ ⇔

+=−− =−

9)
0
0
0
A
AB
B
=
+=⇔
=
Ví dụ:
2
5
5 25 0 5
5
5
x
xx x
x
x
= −
++ − =⇔ ⇔=−
=
= −
10)
0
0
0
A
AB
B
=
+=⇔
=
Bài 1: Giải các phương trình sau
a.
2
2 42 2xx x− += −
b.
2 12xx
+ −=
c.
2
2 2 12 1xx x− += −
d.
4 42
xx
+ −=
Lời giải
a) Ta có:
( )
2
2
22
2
2 20
1
2 42 2 2
2 44 8 4
2422
x
x
xx x x
xx xx
xx x
−≥
≥
− += −⇔ ⇔ ⇒=

− += − +
− += −
b) Cách 1: Ta có:
( ) ( )
2
2
40
212 212214 2
414
x
xx xx x x x
xx
−≥
+ −= ⇔ + −= ⇔ −=−⇔ ⇒ =
−= −
Cách 2: Ta có
2 1 2 11 2 2xx x x+ −= ⇔ −+ = ⇒ =
c) Ta có:
( )
2
2
2
2 10
2 2 12 1 1
2 2121
x
xx x x
xx x
−≥
− += −⇔ ⇒ =
− += +
12
d) Ta có: Điều kiện
40
4
4 40
x
x
xx
−≥
⇔≥
+ −≥
( )
( )
2
2
4 4 2 4 4 4 0 4 2. 4.2 4 4 4 2 2 4xx xx x x x x+ − =⇔+ −−=⇔ − + − +=⇔ −− = ⇒=
Bài 2: Giải các phương trình sau
a.
2
32 1xx x− += −
b.
22
4 4 4 12 9xx x x
− += − +
Lời giải
a) Ta có:
2
2
10
1
32 1
3
32 1
x
x
xx x
x
xx x
−≥
=
− + = −⇔ ⇔
=
− +=−
b) Ta có:
22
1
4 4 4 12 9 2 2 3
5
3
x
xx x x x x
x
=
− += − +⇔−= −⇒
=
Bài 3: Giải các phương trình sau
a.
2
( 3) 3xx−=−
b.
2
4 20 25 2 5xx x− ++=
c.
2
(3 2 ) 4x−=
d.
2 1 2( 1)xx x
+ −= ≥
Lời giải
a) Ta có:
2
( 3) 3 3 3 3 0 3
x x x xx x− =−⇔ −=−⇔−<⇔<
b) Ta có:
22
5
4 20 252 5 (52) 52 52 52 52 0
2
xx x x x x x x x− ++=⇔ − =−⇔− =−⇔−≥⇔≤
c) Ta có:
2
3 2 4 1, 5
(32) 4 32 4
3 2 4 3, 5
xx
xx
xx
−= =−

− =⇔− =⇔ ⇔

−=− =−

d) Ta có:
2
2 1 2( 1) 1 2 1 1 2 ( 1 1) 2 1 1 2xx x x x x x+ −= ≥ ⇔ −+ −+= ⇔ −− = ⇔ −− =
13
1 9 10
1 1( )
x
xx
x loai
−=
⇔ ⇔ −= ⇔ =
−=−
Bài 4: Giải các phương trình sau
a.
22
2 1 6 91xx xx− ++ − + =
b.
2
2 3 43xx−= −
13
c.
2
11xx−=−
Lời giải
a) Ta có:
2 2 22
2 1 6 9 1 ( 1) ( 3) 1 1 3 1(1)xx xx x x x x− ++ − + =⇔ − + − =⇔ −+ + =
+) Với
3
1 1 0; 3 0 (1) 1 3 1 ( )
2
x x x x x x loai<⇒−< −<⇒ ⇔−+−=⇔=
+) Với
1 3 1 0; 3 0 (1) 1 3 1 0 1( )x x x x x x loai≤≤⇒−≥ −≤⇒ ⇔−+−=⇔ =−
+) Với
5
3 1 0; 3 0 (1) 1 3 1 ( )
2
x x x x x x loai>⇒−> −>⇒ ⇔−+−=⇔ =
Vậy phương trình vô nghiệm
b) Ta có:
2
2
3
4 30
4
2 3 43
0( )
2 34 3
2( )
x
x
xx
x loai
xx
x tm
≥
−≥
−= −⇔ ⇔

=
−= −
=
c) Ta có:
{ }
2
2 22
1
1
10
1 1 1; 2
1
1 ( 1)
(/ )
2
x
x
x
xx x
x
xx
tm
x
≥
≤−
−≥
− = − ⇔ ⇔ ⇒ ∈± ±

= ±
−= −
= ±
Bài 5: Giải các phương trình sau
a.
22
21 1xx x− += −
b.
2
33
xx−=−
c.
22
4 4 40x xx−+ + +=
d. (Khó).
22 2
3 18 28 4 24 45 5 6x x x x xx− + + − + =−− +
Lời giải
a) Ta có:
14
2
2 2 22 2
2
2
10
2 1 1 ( 1) 1 1 1
11
1 ( 1)
x
xx x x x x x
xx
xx
−≥
− += −⇔ − = −⇔ − = −⇔
−= −
−=− −
{ }
2
2
1
1
1
1; 2
0( )
0
1( / )
( 1)( 2) 0
2( / )
x
x
x
x
x loai
xx
x tm
xx
x tm
≥
≤−
≥
⇔ ⇔ ⇒∈ −
=
−=


=
− +=
= −
b) Ta có:
2
2
2
3 3 ( 3)( 3) ( 3) 0
33
3 ( 3) ( 3)( 3) ( 3) 0
xx xx x
xx
x x xx x

−=− − + − − =
−=− ⇔ ⇔

−=− − − + + − =


30 3
310 1 3
30 3
310 1 3
xx
xx
xx
xx

−= =

+ −= =−

⇔⇔

−= =


+ + = =−−

c) Ta có:
2
22
2
2
40
4 4 40
22
4 40
2
x
x
x xx
xx
xx
x
=
−=

−+ + +=⇔ ⇔
=−⇔ =−

+ +=
= −
d. (Khó)
Ta có:
22 2
3 18 28 4 24 45 5 6x x x x xx− + + − + =−− +
22 2
3( 3) 1 4( 3) 9 4 ( 3) (1)xx x⇔ −++ −+=−−
Ta có:
( )
1 4; 4VT VP≥≤
Vậy phương trình có nghiệm khi hai vế đều bằng 4
2
( 3) 0 3xx⇔ − =⇔=
Vậy
3x =
.
Dạng 5: Tìm GTLN, GTNN của biểu thức
Cách giải: Áp dụng bất đẳng thức:
A B AB+ ≥+
Dấu “=” xảy ra
.0AB⇔≥
Bài 1: Tìm GTNN của các biểu thức sau
15
a)
22
21 21
Ax x x x
= + ++ − +
b)
2 1 32Bx x= −+−
c)
22
4 4 1 4 12 9C xx x x
= − ++ − +
d)
22
49 42 9 49 42 9xx xx
− ++ + +
Lời giải
a) Ta có:
22
21 21 1 1A x x x x Ax x= + ++ − +⇔ = ++ −
Cách 1:
+) Nếu
1 1 1 2 2(1)x Ax x x<− ⇒ =− − − + =− >
+) Nếu
1 1 1 1 2(2)x Ax x−≤ ≤⇒ = +− +=
+) Nếu
1 1 1 2 2(3)x Ax x x>⇒ = ++ −= >
Từ (1)(2)(3)
21 1MinA x⇒ = ⇔− ≤ ≤
Cách 2: Áp dụng bất đẳng thức
A B AB+ ≥+
1 1 1 1 11 2Ax x x x x x
= ++ −= ++− ≥ ++− =
Vậy
2 ( 1)(1 ) 0 1 1MinA x x x= ⇔ + − ≥ ⇔− ≤ ≤
b) Ta có:
13
2 1 32 2
22
B x x MinB x= −+− ⇒ = ⇔ ≤ ≤
c) Ta có:
22
4 4 1 4 12 9 2 1 32 (2 1)(32) 2C xx x x x x x x= −++ −+=−+−≥−+−=
13
(2 1)(3 2 ) 0
22
xx x⇔ − − ≥⇔ ≤≤
d) Ta có:
33
6
77
min
Dx
−
=⇔ ≤≤
16
BÀI TẬP TRẮC NGHIỆM
Câu 1: Khẳng định nào sau đây sai
a.
3x
xác định khi
0x ≥
b.
9x
−
xác định khi
0x ≤
c.
5
3
x −
xác định khi
5x ≥
d.
4
9x
−
−
xác định khi
7x >
Lời giải
Chọn đáp án D
Giải thích:
A)
3x
xác định
30 0xx⇔ ≥⇔≥
B)
9
x−
xác định
90 0xx⇔− ≥ ⇔ ≤
C)
5
3
x −
xác định
5
0 50 5
3
x
xx
−
⇔ ≥⇔−≥⇔≥
D)
4
9x
−
−
xác định
4
0 70 7
7
xx
x
−
⇔ >⇔−<⇔<
−
Câu 2: Điền vào chỗ (…) để được khẳng định đúng
a) Điều kiện xác định của
2
3xy
là… b) Điều kiện xác định của
54x−
là…
c) Điều kiện xác định của
2
81x −
là… d) Điều kiện xác định của
2
51
4
y
x
−
là…
Lời giải
17
A) Điều kiện xác định của
2
3xy
là:
0x ≤
B) Điều kiện xác định của
54x−
là:
5
4
x ≤
C) Điều kiện xác định của
2
81
x
−
là:
9x ≤−
hoặc
9x ≥
D) Điều kiện xác định của
2
51
4
y
x
−
là:
1
5
y ≥
và
0x ≠
Câu 3: Điều kiện xác định của
2
3
1a
a
+
là:
a)
0a
≥
b)
0a ≤
c)
0a >
d)
1a >−
Lời giải
Chọn đáp án C
Điều kiện xác định của
2
3
1a
a
+
là
2
3
3
1
0 00
a
aa
a
+
≥⇔ >⇔>
(vì
2
10a
+>
)
Câu 4: Biểu thức
( )
(
) ( )
22
2
6 . 1 3 23 1. 3
− − − −−
có giá trị đúng là số nào ?
a)
3
b)
3−
c)
23
d)
23−
Lời giải
Chọn đáp án B
Giải thích: Ta có
( )
( ) ( ) ( )
22
2
6 . 1 3 23 1. 3 6.1 3 323 1− − − − −=− − − −
(do
31>
và
23 1>
)
63 6 63 3 3= −− +=−
Câu 5:
9 45 5−−
có kết quả rút gọn là số nào ?
a)
2
b)
1
18
c)
2 10−
d)
2 10
Lời giải
Chọn đáp án B
Giải thích: Ta có
(
)
2
945 5 25 525 5 5252
− −= − −=−−=−−=−
(do
25<
)
Câu 6: Rút gọn
19 6 10 26 8 10− +−
ta được số nào ?
a)
1−
b)
1
c)
2 10−
d)
2 10
Lời giải
Chọn đáp án B
Giải thích: Ta có
(
)
( )
22
19 6 10 26 8 10 3 10 10 4 3 10 10 4− + − =− + −=− + −
10 3 4 10 1= −+− =−
Câu 7: Nếu
3
2
x >
thì phương trình
2
9 12 4 5 3xx x−+ =−
có nghiệm là số nào?
a)
1, 6x =
b)
1, 7x =
c)
1, 8x =
d)
1, 9x =
Lời giải
Chọn đáp án A
Giải thích: Ta có
( )
2
2
912 4 53 32 53 32 53xx x x x x x− + =−⇔ − =−⇔− =−
Vì
3
3 2 0,
2
xx> ⇒ −<
nên ta có:
8
32 53 2 353 1,6
5
x x x xx− =−⇔−=−⇔==
(thỏa mãn).
Câu 8: Với điều kiện
2
,
10
x <
phương trình
2
4 4 10 10 3 2 10xx x− +=−
có nghiệm là số
nào?
a)
1
2 10
x =
b)
1
10
x =
19
c)
1
10
x = −
d) Một kết quả khác
Lời giải
Chọn đáp án B
Giải thích: Ta có
( )
2
2
4 4 10 10 3 2 10 2 10 3 2 10 2 10 3 2 10xx x x x x x−+=−⇔− =−⇔−=−
Vì
21
2 10 0 2 10 3 2 10 2 10 3 2 10
10 10
x x x x x xx
−
<⇒−>⇒− =− ⇔−=− ⇔=
(thỏa mãn)
Câu 9: Giá trị của biểu thức
2
4 4 12 5A aa a= − ++ +
bằng số nào khi
3
2
a =
a)
6
b)
8
c)
10
d)
12
Lời giải
Chọn đáp án C
Giải thích: Ta có
( )
2
2
4 4125 21 252125A aa a a a a a= −+++= − ++= −++
Khi
3 33
2. 1 2. 5 3 1 3 5 2 3 5 10
2 22
aA= ⇒ = −+ +=−++=++=
.
Câu 10: Trong các kết luận sau, kết luận nào sai
a) Biểu thức
2
4yx= +
luôn có nghĩa với mọi giá trị của
x
b) Biểu thức
2
9yx= −
luôn có nghĩa với mọi giá trị của
x
c) Biểu thức
2
1
2 22 1
y
x
=
−+
luôn có nghĩa với mọi giá trị của
1
2
x ≠
d) Biểu thức
3
3
3
x
yx
x
−
= ++
+
có nghĩa khi
33x−≤ ≤
Lời giải
Chọn đáp án D
Giải thích:
A)
2
4yx= +
có nghĩa khi
2
40
x +≥
(luôn đúng)
20
B)
2
9yx= −
có nghĩa khi
22
9 0 9 33 3xx x x− ≥ ⇔ ≤ ⇔ ≤ ⇔− ≤ ≤
C)
( )
2
2
11
2 22 1
21
y
x
x
= =
−+
−
có nghĩa khi
1
2 10
2
xx−≠ ⇔ ≠
D)
3
3
3
x
yx
x
−
= ++
+
có nghĩa khi
30
3
3
0
3
x
x
x
x
+≥
⇔≥
−
≥
+
BÀI TẬP VỀ NHÀ
Bài 1: Với mỗi giá trị nào của
x
thì mỗi căn thức sau có nghĩa
a)
2
35x −
b)
3x−
c)
1
32x−
d)
2
2x
+
e)
2
3
1x +
f)
21x −
g)
2
21xx−+ −
h)
1x−+
i)
2
3x−−
Hướng dẫn giải
a)
2
35x −
có nghĩa khi
25
035035
35 3
x xx
x
>⇔ −>⇔ >⇔>
−
b)
3x−
có nghĩa khi
30 0xx− ≥⇔≤
c)
1
32x−
có nghĩa khi
1 33
032032
32 2 2
x x xx
x
>⇔− >⇔> ⇔ >⇔<
−
d)
2
2x +
có nghĩa khi
2
20x +≥
(luôn đúng)
e) Do
2
2
30
3
,
1
110
xR
x
x
>
∀∈ ⇒
+
+≥>
có nghĩa với mọi
xR∈
f)
21x −
có nghĩa khi
1
2 10 2 1
2
x xx−≥ ⇔ ≥⇔ ≥
g) Ta có:
( )
( )
2
22
2 1 2 1 1 0,x x x x x xR− + −=− − + =− − ≤ ∀∈
, nên
2
21xx−+ −
có nghĩa khi
( )
2
10 1xx− − =⇔=
21
h) Ta có
10 10, 1x x xR x+≥⇔−+≤ ∀∈ ⇒−+
có nghĩa khi
10 1
xx
−+=⇔=−
i) Ta có
( )
22
33xx− −=− +
, do
( )
22
330 3 0
xx+ ≥ > ⇒− + <
Do đó không tồn tại
x
để
2
3
x−−
có nghĩa.
Bài 2: Tính
a)
49. 144 256 : 64
A
= +
b)
22
72: 2 .36.3 225B = −
Hướng dẫn giải
a) Ta có:
49. 144 256 : 64 86AA= + ⇒=
b) Ta có:
22
72: 2 .36.3 225 13
BB= − ⇒=−
Bài 3: Tính giá trị của biểu thức
a)
22
(2 5) (2 2 5)A =−+ −
b)
22
( 7 2 2) (3 2 2)B = − +−
c)
11 6 2 11 6 2C
=+ −−
d)
17 12 2 17 12 2D =+ +−
Hướng dẫn giải
a) Ta có:
22
(2 5) (2 2 5) 2 2 2AA= − + − ⇒= −
b) Ta có:
22
( 7 2 2) (3 2 2) 3 7BB= − + − ⇒=−
c) Ta có:
1162 1162 22CC= + − − ⇒=
d) Ta có:
17 12 2 17 12 2 6DD= + + − ⇒=
Bài 4: Rút gọn các biểu thức sau
a)
2
64 2A aa= +
b)
63
39 6B aa
= −
c)
( )
( )
( )
2
0
xy
C x y xy
xy
=−>
−
d)
2
2
96
25
xx
D
y
−+
=
e)
( )
( )
42
3
8 4 21
22 1
E xx x
x
= −+
−
f)
( )
22
2
5 14 4
21
F a aa
a
= −+
−
Hướng dẫn giải
a) Ta có:
( )
( )
2
10 0
64 2
60
Aa
A aa
A aa
= ≥
= +⇒
=−<
22
b) Ta có:
( )
(
)
3
63
3
15 0
39 6
30
B aa
B aa
B aa
=−<
= −⇒
= ≥
c) Biểu thức có nghĩa khi
0;xy x y≥≠
Ta có:
( )
( )
( )
( )
( )
2
.
xy x y
xy
xy
C xy xy
xy
xy
xy x y
>
=− =−=
−
−
−<
d) Biểu thức có nghĩa khi
0y
≠
Ta có:
( )
22
2
22
3
96 3 3
25 25 5 3
x
xx x x
D
y y yy
−

−+ − −
= = = =


30 30
3
00
5
30 30
3
00
5
xx
x
khi hoac
yy
y
xx
x
khi hoac
yy
y
−≥ −≤

−

><

=
−≥ −≤

−

<>

e) Ta có:
( )
( )
( )
( )
( )
( )
2
2
42 2 2
33 3
8 4 2 1 . 2. 2 . 2 1 .2 . 2 1 . 2
22 1 22 1 22 1
E xx x x x xx
xx x
= − += − = −
−− −
2
2
2
1
32
32
2
.2 1
1
21
32
2
x khi x
x
x
x
x khi x
>
= −=
−
−<
f) Ta có:
( )
( )
( )
2
22 42 4 2
2222
5 14 4 5 14 4 5 2 1 .5 2 1
21 21 21 21
F a aa a aa aa aa
aaaa
= −+ = −+ = − = −
−−−−
2
2
1
10
2
1
10
2
a khi a
a khi a
>
=
−<
Bài 5: Rút gọn các biểu thức sau
a)
22
69 69(3 3)Aa a a a a= + + + − + −≤ ≤
b)
21 21(1 2)
Ba a a a a= + −+ − − ≤ ≤
Hướng dẫn giải
a) Ta có:
22
69 69(3 3) 3 3 33 6Aa a a a a a a a a= + ++ − + −≤ ≤ = + + − =++− =
b) Ta có:
21 21(1 2)2Ba a a a a= + −+ − − ≤ ≤ =
23
Bài 6: Giải các phương trình sau
a)
2
x xx+=
b)
2
11xx−=−
c)
22
21 1xx x− += −
d)
2
4 41 1
xx x− +=−
e)
42
21 1xx x
− +=−
f)
2
1 10xx−+ +=
g)
2
1 10
xx− + +=
Hướng dẫn giải
a) Ta có:
2
22
0
0
0
0
x
x
x xx x
x
x xx
≥
≥
+=⇔ ⇔ ⇔=

=
+=
b) Ta có:
( )
( )
2
2
2
10
1
1
11 1
2 10
0; 1
11
x
x
x
xx x
xx
xx
xx
−≥
≥
≥

− = −⇔ ⇔ ⇔ ⇔ =

−=
= =
−=−
c) Ta có:
( )
( )
2
22 2 2
2 1 1 1 1 1 1*xx x x x x x− += −⇔ − = −⇔ − = −
Cách 1:
( )
( )
( )( )
2
2
22
22
22
1
1
10 1
1
0
10
*
11 0
2
1
1 20
11 2 0
2
x
x
xx
x
x
xx
x x xx
x
x
xx
x x xx
x
≥
≥

−≥ ≥
=

=
−=
⇔ ⇔ ⇔ ⇔⇔

−= − − =

=
=


− +=
−=− + − =



=
( )
*
Nhận xét: Ở cách này ta dùng phương pháp:
0B
AB
AB
AB
≥
= ⇔
=
= −
Cách 2:
( )
2
10
*
11
x
xx
−≥
⇔
−= −
hoặc
( )
2
10
*
11
x
xx
−<
⇔
−=−
Giải 2 trường hợp ra ta nhận được kết quả giống cách 1.
( )
*
Nhận xét: Ở cách này ta dùng phương pháp:
0A
AB
AB
≥
= ⇔
=
hoặc
0A
AB
AB
<
= ⇔
= −
d) Ta có:
( )
2
2
10
4 41 1 21 1 21 1
21 1
2 11
x
xx x x x x x
xx
xx
−≥
− += −⇔ − = −⇔ − = −⇔
−= −
−=−
(vô nghiệm)
24
e) Ta có:
(
)
2
42 2 2
2
2
10
21 1 1 1 1 1 1
11
11
x
xx x x x x x x
xx
xx
−≥
− += −⇔ − = −⇔ − = −⇔ ⇔ =
−= −
−=−
f) Ta có:
2
2
1
10
1 10 1
1
10
x
x
xx x
x
x
= ±
−=
−+ +=⇔ ⇔ ⇔ =−

= −
+=
g) Ta có:
2
2
1
10
1 10 1
1
10
x
x
xx x
x
x
= ±
−=
− + += ⇔ ⇔ ⇔ =−

= −
+=
Bài 7: Giải các phương trình sau
a)
2
6 94xx x− +=−
b)
22
2 1 4 43xx xx−++ −+=
c)
22223 2138235x xx x−+ −+ + + − =
d)
22
9 6 90x xx−+ − +=
Hướng dẫn giải
a) Cách 1:
2
22
40
7
6 94
2
69(4)
x
xx x x
xx x
−≥
− +=−⇔ ⇔=
− += −
Cách 2:
2
7
6 94 34
2
x x x x xx− +=−⇔ −=−⇒=
b)
22
2 1 4 43 1 23xx xx x x−++ −+=⇔−+−=
+ Nếu
12x<<
, ta được:
12 3 13xx−+ − = ⇔ =
(vô nghiệm)
+ Nếu
2
x >
, ta được:
1 23 3xx x−+ − = ⇔ =
+ Nếu
1x <
, ta được:
12 3 0xx x−+−=⇔ =
Vậy
0x =
hoặc
3x =
c) Ta có:
3
22223 2138235 231 2345
2
x xx x x x x−+ −+ + + − =⇔ −++ −+ =⇒=
d) Ta có:
( )
2
22
2
90
9 6 90 3
30
x
x xx x
x
−=
−+ − +=⇒ ⇒=
−=
Bài 8:
Tìm các số thực x, y, z thỏa mãn đẳng thức:
82 14 26 3xyz x y z+ ++= −+ − + −
25
Hướng dẫn giải
Cách 1: Ta có:
2 22
82 14 26 3 ( 11) ( 22) ( 33) 0
2; 6; 12
xyz x y z x y z
xyz
+++= −+ −+ −⇔ −− + −− + −− =
⇔= = =
Cách 2:
Ta có:
( 1)12 1; 2( 2)44 2; 6( 3)96 3xx x y y y z z z= −+≥ − += − +≥ − += − +≥ −
Vậy:
2; 6; 12xyz= = =
.
| 1/25
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

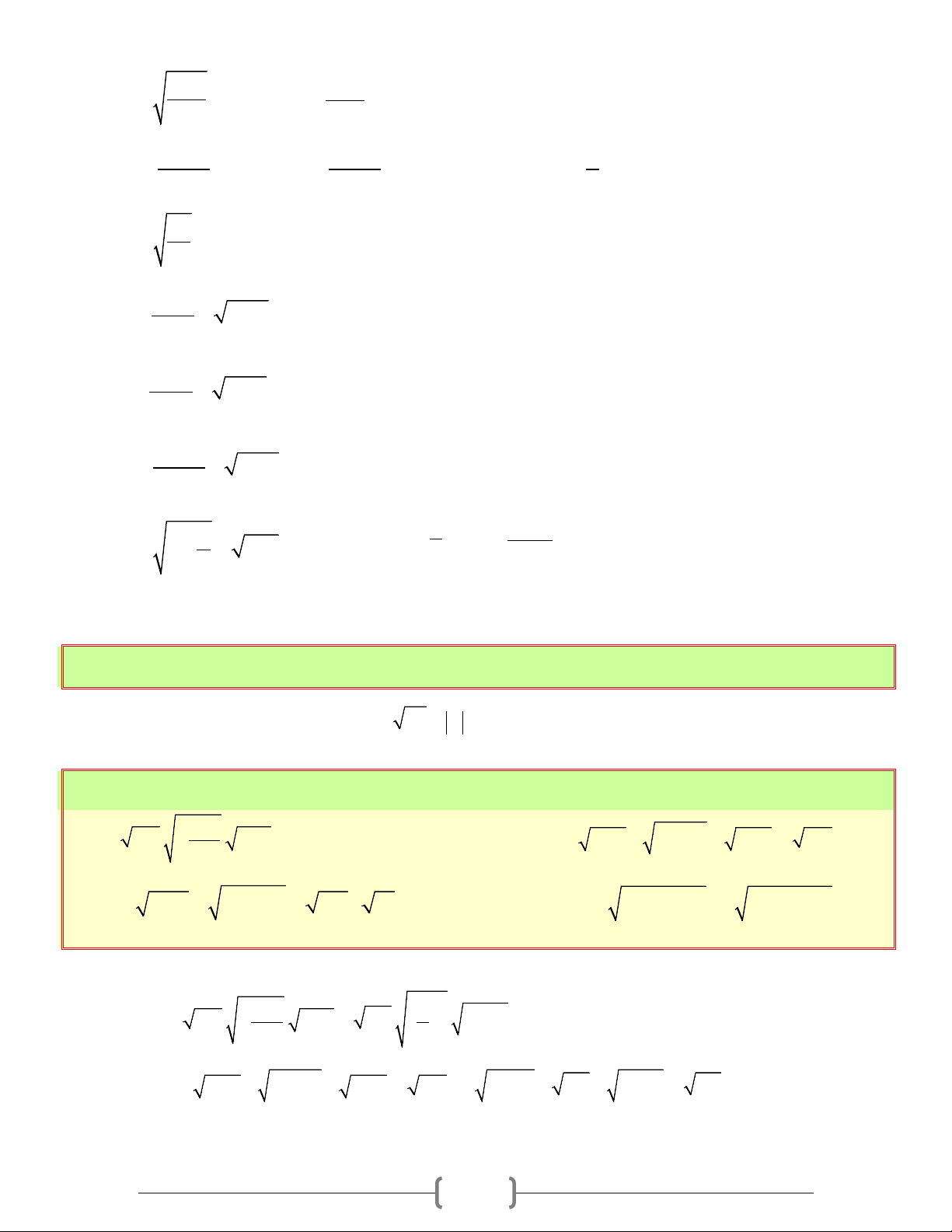
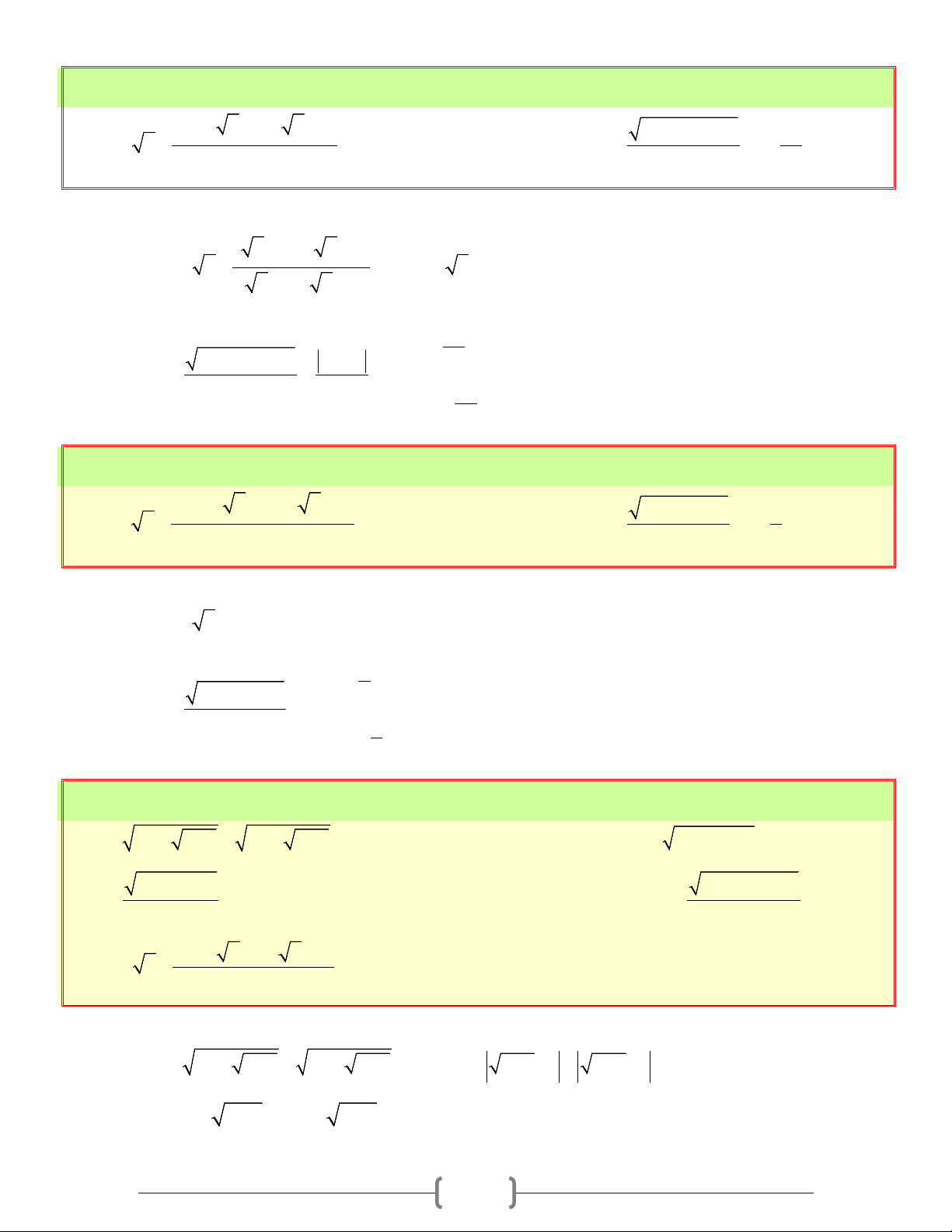
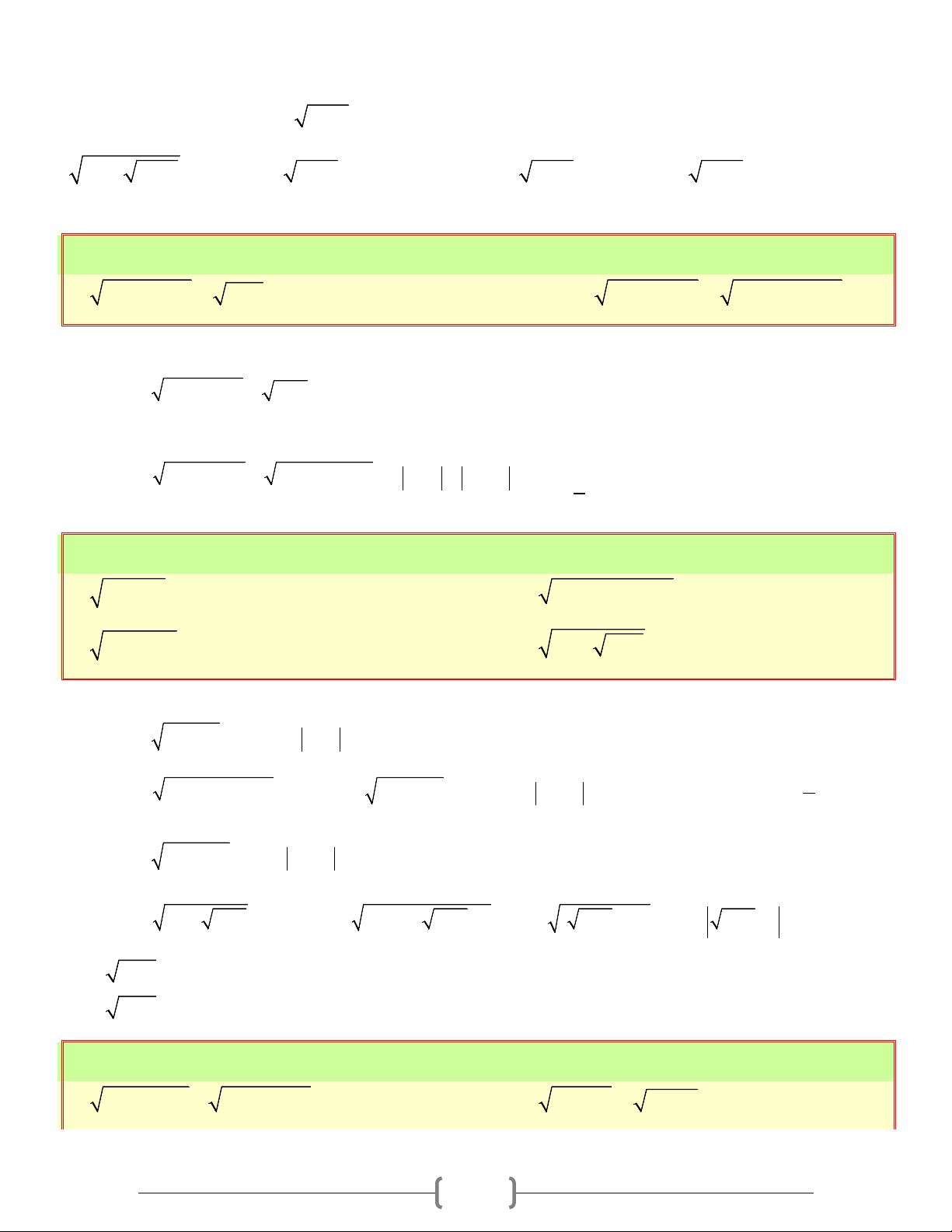
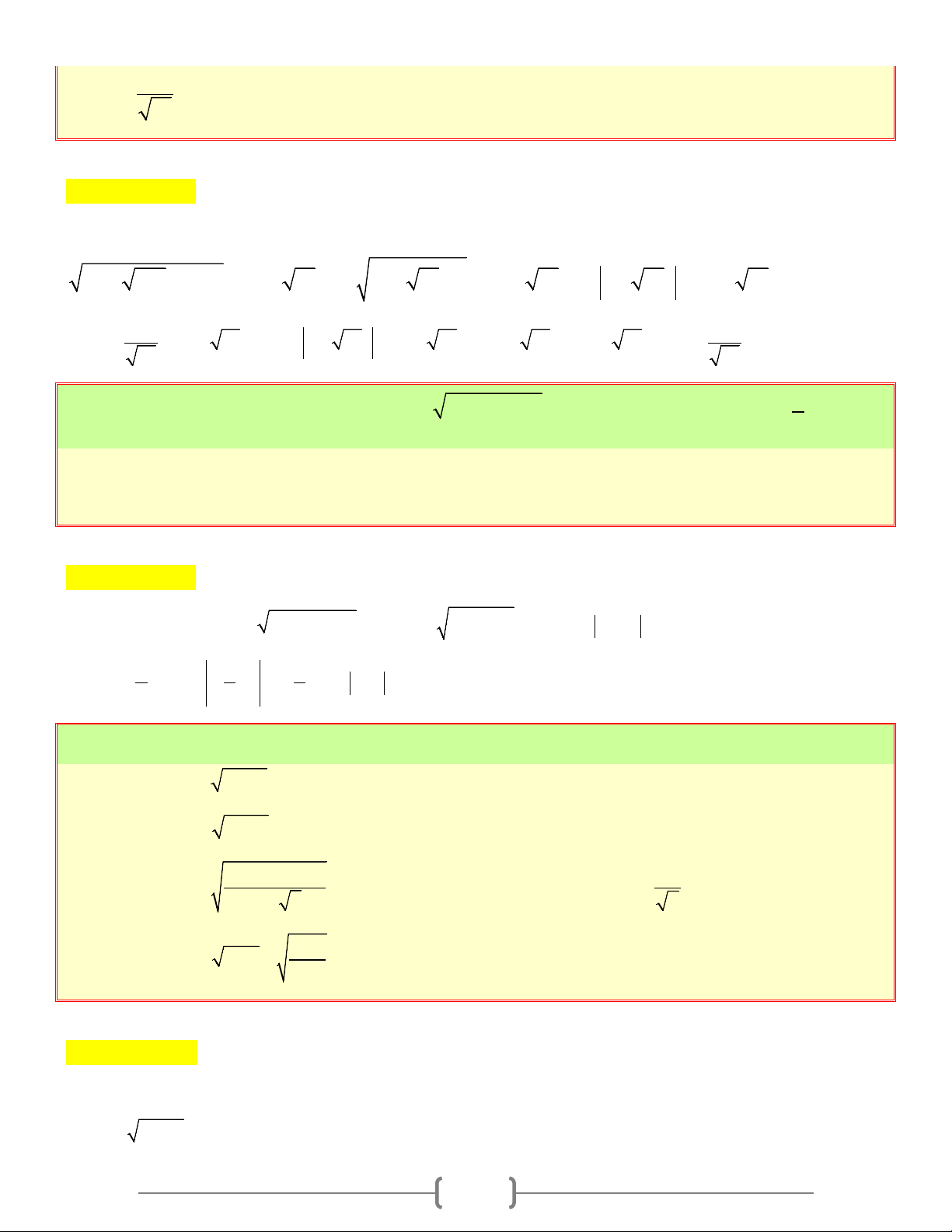
CĂN THỨC BẬC HAI VÀ HẰNG ĐẢNG THỨC 2 A = A A. Tóm tắt lý thuyết 1. Căn thức bậc hai
a. Định nghĩa: Với A là một biểu thức đại số thì A được gọi là căn thức bậc hai của A và
A gọi là biểu thức lấy căn hay là biểu thức dưới dấu căn
b. A có nghĩa (hay xác định) khi 1 A ≥ 0 ⇒
có nghĩa khi A > 0 A
Ví dụ: 3x có nghĩa khi 3x ≥ 0 ⇔ x ≥ 0  , A ( A ≥  0)
2. Hằng đẳng thức: 2 A = A =  − , A  (A < 0) Ví dụ 1: 2 2 12 = 12 =12; ( 7 − ) = 7 − = 7
Ví dụ 2: Rút gọn biểu thức sau: 2
(x − 2) với x ≥ 2 Lời giải Ta có: 2
(x − 2) = x − 2 = x − 2 vì x ≥ 2
B. Bài tập và các dạng toán
Dạng 1: Tìm điều kiện để biểu thức chứa căn có nghĩa
Cách giải: Chú ý rằng A có nghĩa khi và chỉ khi A ≥ 0 1
+) A có nghĩa khi A ≥ 0
+) A có nghĩa khi A > 0 1
+) A + B ⇒ A + B ≥ 0 có nghĩa khi A + B ≥ 0 +)
có nghĩa khi A > 0 A 1
+) A − B có nghĩa khi A − B ≥ 0 +)
có nghĩa khi A ≠ 0 2 A 1 A ≥ 0 +) có nghĩa khi ⇔  A − B
 A − B ≠ 0 1 A ≥ 0 +) có nghĩa khi ⇔  A + B
 A + B ≠ 0 1 A ≥ 0  A ≥ 0  B ≥ 0 B > 0 +) . A B ⇒ .
A B ≥ 0 có nghĩa khi ⇔  +) A có nghĩa ⇔ A ≤ 0   BA ≤ 0   B ≤ 0 B < 0 A > 0  B > 0
+) 1 có nghĩa AB > 0 ⇔ . A B A < 0  B < 0 +) 2
x ≤ n ⇔ − n ≤ x ≤ n(n ≥ 0)  ≥ +) x n 2 x ≥ n ⇔  (n ≥ 0)
x ≤ − n
Bài 1: Tìm x để các căn thức sau có nghĩa a. 3 − x b. 2x −10 c. 3 − x − 4 1 d. 3x +15 e. 5x + x − x − 2 f. 2 8 9 Lời giải a) Ta có: 3
− x có nghĩa ⇔ x ≤ 0
b) Ta có: 2x −10 có nghĩa ⇔ 2x −10 ≥ 0 ⇔ x ≥ 5 4 c) Ta có: 3 − x − 4 có nghĩa 3x 4 0 x − ⇔ − − ≥ ⇔ ≤ 3
d) Ta có: 3x +15 có nghĩa ⇔ 3x +15 ≥ 0 ⇔ x ≥ 5 − 1 1 1 e) Ta có: 5x + 5x 0 x − ⇔ + ≥ ⇔ ≥ 2 có nghĩa 2 10  ≥ f) Ta có: x 9 2
x −8x − 9 có nghĩa 2
⇔ x −8x − 9 ≥ 0 ⇔ (x + )
1 (x −9) ≥ 0 ⇔  x ≤ 1 −  x ≥ a 2 2 x ≥ a ⇔
Chú ý: Với a là số dương, ta có:   x ≤ −a  2 2
x ≤ a ⇔ −a ≤ x ≤ a 2
Bài 2: Với giá trị nào của x thì mỗi biểu thức sau có nghĩa a. x(x + 2) b. 2 5x − 3x −8 c. 2 2x + 4x + 5 d. 2 4 − x e. 2
−x + 2x −1 Lời giải a) Ta có: x ≤ −
x(x + 2) có nghĩa khi 2
x(x + 2) ≥ 0 ⇔  x ≥ 0 x -2 0 x - │ - 0 + x + 2 - 0 + │ + x(x + 2) + - + x ≤ 1 − b) Ta có: 2
5x − 3x −8 có nghĩa khi 2 5x 3x 8 0 (x 1)(5x 8) 0  − − ≥ ⇔ + − ≥ ⇔ 8 x ≥  5 c) Ta có: 2
2x + 4x + 5 có nghĩa khi 2 2
2x + 4x + 5 ≥ 0 ⇔ 2(x +1) + 3 ≥ 0 . Vậy biểu thức luôn có nghĩa d) Ta có: 2
4 − x có nghĩa khi 2 2
4 − x ≥ 0 ⇔ x ≤ 4 ⇔ 2 − ≤ x ≤ 2 e) Ta có: 2
−x + 2x −1 có nghĩa khi 2
−(x +1) ≥ 0 ⇔ x −1 = 0 ⇔ x =1
Bài 3: Với giá trị nào của x thì mỗi biểu thức sau có nghĩa: 4 2 − 1 a. 2x+3 b. x+1 c. 3− 2x 2 x x d. + x − + x − 2 2 x e. 2 f. x − 2 x + 2 x 3 g. + x − 2 x + + 3 − x 2 h. x − 4 x Lời giải 4 4 3 − a) Ta có: ⇔
≥ 0 ⇔ 2x + 3 > 0 ⇔ x > 2x + 3 có nghĩa 2x + 3 2 3 2 − 2 − b) Ta có: ⇔
≥ 0 ⇔ x +1< 0 ⇔ x < 1 − x +1 có nghĩa x +1 1 1 3 c) Ta có: có nghĩa ⇔
≥ 0 ⇔ 3− 2x > 0 ⇔ x < 3− 2x 3x − 2 2 2 d) Ta có: ⇔ > ⇔ ≠ 2 x x x có nghĩa 2 0 0 xx − 2 ≥ 0 x ≥ 2 e) Ta có:
+ x − 2 có nghĩa ⇔  ⇔  ⇔ x > 2 x − 2 x − 2 ≠ 0 x ≠ 2 xx − 2 ≥ 0 x ≥ 2 f) Ta có:
+ x − 2 có nghĩa ⇔  ⇔  ⇔ x ≥ 2 x + 2 x + 2 ≠ 0 x = 2 − xx ≥ 2 g) Ta có: + x − 2 ⇔  ⇔ x > 2 2 có nghĩa x − 4 x ≠ 2 ± 3 2  3  x + 3 k) Ta có: x + + 3 − xx + > 0  ⇔  ⇔ x có nghĩa xx (vô lý).  3 − x ≥ 0 x ≤ 0
Vậy không có giá trị nào của x làm biểu thức có nghĩa.
Dạng 2: Tính giá trị của biểu thức  , A ( A ≥  0)
Cách giải: Sử dụng hằng đẳng thức: 2 A = A =  − , A  (A < 0)
Bài 1: Tính giá trị của các biểu thức sau a. 49 A − = 144. − . 0,01 b. B  ( )2 0,25 15 2,25  = − − +  : 169 64   c. C  ( )2 0,04 1,2 121 = − − +  81 d. D = + (− )2 − (− )2 2 2 75: 3 4 3 5 − 3   Lời giải 2 a) Ta có: 49  7 A − 144. . 0,01 12 .  = − = . (0, )2 2 1 =   1,05 64  8  b) Ta có: B  =  − (− )2   +  =  ( )2 − + ( )2 2  2 0,25 15 2,25 : 169 0,5 15 1,5  : 13 = 1 −     4 c) Ta có: C  ( )2 0,04 1,2 121 = − − +  81 ⇒ C = 90   d) Ta có: D = + (− )2 − (− )2 2 2 75: 3 4 3 5 − 3 ⇒ D = 3
Bài 2: Tính giá trị của các biểu thức sau a. 6 − 4 2 + 22 −12 2 b. 2 ( 3 − 2) + 2 c. 2 3 5 − (1− 5) d. 17 −12 2 + 9 + 4 2 e. 6 + 2 5 + 6 − 2 5 f. 3+ 2 2 + 6 − 4 2
g. 24 + 8 5 + 9 − 4 5 h. 41−12 5 − 41+12 5 Lời giải a) Ta có: 2 2
6 − 4 2 + 22 −12 2 = (2 − 2) + (3 2 − 2) = 2 2 b) Ta có: 2
( 3 − 2) + 2 = 3 − 2 + 2 = 3 c) Ta có: 2
3 5 − (1− 5) = 3 5 − 1− 5 = 3 5 − 1− 5 = 3 5 − ( 5 −1) = 2 5 +1 d) Ta có: 2 2
17 −12 2 + 9 + 4 2 = (3− 2 2) + (2 2 +1) = 4 e) Ta có: 2 2
6 + 2 5 + 6 − 2 5 = ( 5 +1) + ( 5 −1) = 2 5 f) Ta có: 2 2
3+ 2 2 + 6 − 4 2 = ( 2 +1) + (2 − 2) = 3 g) Ta có: 2
24 + 8 5 + 9 − 4 5 = 4(6 + 2 5) + ( 5 − 2) = 2 5 +1 + 5 − 2 = 3 5 2 2
h) Ta có: 41−12 5 − 41+12 5 = (6 − 5) − (6 + 5) = 2 − 5
Bài 3: Thực hiện các phép tính sau 2 2  −   +  a) 4 2 3 4 2 3
A = ( 3 − 2). 5+ 2 6 b) B =   −    3 1   1 3  − +     c) C = 5 − 9 − 29 −12 5
d) D = 13+ 30 2 + 9 + 4 2 Lời giải 5
a) Ta có: A = ( 3 − 2). 5+ 2 6 = ( 3 − 2)( 3 + 2) =1 2 2 2 2 2 2  −   +   −   +  b) Ta có: 4 2 3 4 2 3 ( 3 1) ( 3 1) B =   −   =   −   =     ( 3− )1−( 3+ )1= 4− 3 3 −1 1+ 3 3 −1 3 −        1  c) Ta có: 2 C = 5 − 9 − 29 −12 5 = 5 − 9 − 20 −12 5 + 9 = 5 − 9 − (2 5 + 3) d) Ta có: 2
13+ 30 2 + 9 + 4 2 = 13+ 30 2 + (2 2 +1) = 13+ 30 2 + (2 2 +1) = 13+ 30 3+ 2 2 2 2
= 13+ 30 ( 2 +1) = 13+ 30( 2 +1) = 43+ 30 2 = 25 + 2.5.3 2 +18 = (5 + 3 2) = 5 + 3 2
Bài 4: Rút gọn các biểu thức sau a) 2 2 A = ( − )2 4 15 + 15
b) B = (2− 3) + (1− 3)
c) C = 49 −12 5 − 49 +12 5
d) D = 29 +12 5 − 29 −12 5 Lời giải a) Ta có: A = ( − )2 4
15 + 15 = 4 − 15 + 15 = 4(4 > 15)
b) Ta có: B = ( − )2 + ( − )2 2 3 1 3 = 2 − 3 + 1+ 3 =1 c) Ta có: C = − − + = ( − )2 − ( + )2 49 12 5 49 12 5 2 3 5 2 3 5 ⇒ C = 4 d) Ta có: D = + − − = ( + )2 − ( − )2 29 12 5 29 12 5 3 2 5 3 2 5 ⇒ D = 6
Bài 5: Chứng minh rằng a) + = ( + )2 11 6 2 3 2 b) 11+ 6 2 + 11− 6 2 = 6 c) − = ( − )2 8 2 7 7 1 d) 8− 2 7 − 8+ 2 7 = 2 − Lời giải a) Ta có: VT = + = + + = ( + )2 11 6 2 9 2.3 2 2 3 2 = VP ⇒ đpcm 6
b) Ta có: VT = 11+ 6 2 + 11− 6 2 = 2 + 3 + 2 −3 = 6 =VP ⇒ đpcm c) Ta có: − = − + = ( − ) 2 8 2 7 7 2 7 1 7 1 ⇒ đpcm d) Ta có: 2 2
VT = 8 − 2 7 − 8 + 2 7 = ( 7 − ) 1 − ( 7 + )1 = 2 − = VP ⇒
Dạng 3: Rút gọn các biểu thức chứa biến  , A ( A ≥  0)
Cách giải: Sử dụng hằng đẳng thức: 2 A = A =  − , A  (A < 0)
Bài 1: Rút gọn các biểu thức sau a) 2
A = 64a + 2a(a ≥ 0) b) 2
B = 5 25a − 25a(a < 0) c) 4 2
16a + 6a (với a bất kỳ) d) 6 3
3 9a − 6a (với a bất kỳ ) e) 2 2
E = a + 6a + 9 + a − 6a + 9 (với a bất kỳ ) Lời giải a) Ta có: 2
64a + 2a(a ≥ 0) = 8a + 2a =10a ⇒ A =10a b) Ta có: 2
5 25a − 25a(a < 0) = 5. 5a − 25a = 50 − a ⇒ B = 50 − a c) Ta có: 4 2 2 2 2 2
16a + 6a = 4a + 6a =10a ⇒ C =10a (với a bất kỳ ) d) Ta có: 6 3 3 3
3 9a − 6a = 3 3a − 6a (với a bất kỳ ) +) 3 3 3 3 3
a < 0 ⇒ 3. 3a − 6a = 3.( 3
− a ) − 6a = 15 − a +) 3 3 3 3 3
a ≥ 0 ⇒ 3. 3a − 6a = 9a − 6a = 3a e. (khó) 2 2
A = a + 6a + 9 + a − 6a + 9 với a bất kỳ 2 2
A = a + 6a + 9 + a − 6a + 9 = a + 3 + a − 3
+) Nếu a < 3 ⇒ a + 3 + a − 3 = −a − 3+ 3− a = 2 − a +) Nếu 3
− ≤ a ≤ a thì a + 3 + a − 3 = a + 3 + 3 − a = 6
+) Nếu a > 3 thì a + 3 + a − 3 = a + 3+ a − 3 = 2a 7
Bài 2: Rút gọn các biểu thức sau
(x+6 x +9)( x −3) 2 a) + +  − A = 4 x − (0 ≤ ;xx ≠ 9) b) 9x 12x 4 2 Bx  = ≠ x − 9 3x 2 3  +   Lời giải ( x + )2 3 ( x −3)
a) Ta có: A = 4 x − ( ⇒ A = x − ≤ x ≠ x − 3)( x +3) 3( )1(0 9)   2 − 1   x  > 2  + + + b) Ta có: 9x 12x 4 3x 2   3 B  = = = 3x 2 3x 2  + +   2 − 1 − x  <   3    
Bài 3: Thực hiện các phép tính
(x−10 x +25)( x +5) 2 a) − + A = 5 x − (0 ≤ x ≠ 25) b) 4x 4x 1  1 Bx  = ≠ x − 25 2x 1 2  −   Lời giải
a) Ta có: A = 4 x + 5(0 ≤ x ≠ 25)   1 1   x  > 2  b) Ta có: 4x − 4x +1  2 B  = =  2x −1   1  1 x  − <  2   
Bài 4: Rút gọn các biểu thức sau
a) A = a + 2 a −1 + a − 2 a −1(1≤ a ≤ 2) b) 2
B = 4x − x − 4x + 4(x ≥ 2) 2 2 c) x + 4x + 4 C − + = (x ≠ 2) d) x 10x 25 D = 2x −1− x + 2 x − 5 e)
(x + 6 x + 9)( x − 3) E = 4 x − (0 ≤ x ≠ 9) x − 9 Lời giải
a) Ta có: A = a + 2 a −1 + a − 2 a −1(1≤ a ≤ 2) = a −1 +1 + a −1 −1
Với 1≤ a ≤ 2 ⇒ a −1 +1 > 0; a −1 −1≤ 0, ta được: 8
A = a −1 +1 + a −1 −1 = a −1 +1− a −1 +1 = 2 b) Ta có: 2
B = 4x − x − 4x + 4(x ≥ 2) = 4x − x − 2 = 4x − (x − 2) = 3x + 2 2 + + + c) Ta có: x 4x 4 x 2 C = (x ≠ 2) = x + 2 x + 2 - Nếu x < 2 − thì A = 1 − - Nếu x > 2 − thì A =1 2 − + − d) Ta có: x 10x 25 x 5 D = 2x −1− = 2x −1− x − 5 x − 5
+) Nếu x − 5 ≤ 0 ⇔ x ≤ 5 ⇒ A = 2x −1+1 = 2x
+) Nếu x ≥ 5 ⇒ A = 2x − 2
(x+6 x +9)( x −3)
e) Ta có: E = 4 x − (0 ≤ x ≠ 9) x − 9
(x+ x + )( x − ) ( x + )2 6 9 3 3 ( x −3) ⇒ E = 4 x − = 4 x − = x − ≤ x ≠ x − 9 (
x − 3)( x +3) 3( )1(0 9) Bài 5: Cho biểu thức: 2 2 2 2
A = x + 2 x −1 − x − 2 x −1
a. Với giá trị nào của x thì A có nghĩa
b. Tính A nếu x ≥ 2 Lời giải a) Ta có: 2 2 2 2 2 2 2 2 2 2
A = x + 2 x −1 − x − 2 x −1 = ( x −1 +1) − ( x −1 −1) = x −1 +1 + x −1 −1  ≤ − A có nghĩa x 1 2 2
⇔ x −1≥ 0 ⇔ x ≥1 ⇔  x ≥1 b) Ta có: 2 2 2 2
x ≥ 2 ⇒ x ≥ 2 ⇔ x −1≥1⇒ x −1 ≥1⇒ x −1 −1≥ 0 2 2 2
⇒ A = x −1 +1+ x −1 −1 = 2 x −1 9 Bài 6:
Cho ba số dương x, y, z thỏa mãn: xy + yz + zx =1 2 2 2 2 2 2 Tính: (1+ y )(1+ z ) (1+ z )(1+ x ) (1+ x )(1+ y ) A = x + y + z 2 2 2 1+ x 1+ y 1+ z Lời giải Ta có: 2 2 2 2
1+ y = (xy + yz + zx) + y = (x + y)(y + z);1+ z = (y + z)(z + x);1+ x = (x + z)(x + y)
⇒ A = x(y + z) + y(z + x) + z(x + y) = 2(xy + yz + zx) = 2 Vậy A = 2 .
Dạng 4: giải phương trình
Cách giải: Chú ý một số cách biến đổi tương đương liên quan đến căn thức bậc hai B ≥ 0 1) A = B ⇔  2 A = Bx ≥1 x −1≥ 0 x ≥1 2 1 x x 1  − = − ⇔  ⇔ 
⇔ x = 0(loai) 2 2 2 2 1
 − x = (x −1) 1
 − x = x − 2x +1 
x =1(t / m) 2) 2
A = B ⇔ A = B
A ≥ 0(hayB ≥ 0) 3) A = B ⇔  A = B 4) 2 2
A = B ⇔ A = B ⇔ A = ±B 5) 2 2
A = B ⇔ A = ±B 0 =1(vn)  − = Ví dụ: x 1 x 2 2 (x 1) x  − = ⇔ ⇔  1 (thỏa mãn) x −1 = −xx =  2 B ≥ 0 7) A B
= ⇔ A = B  A = −B 10 2x ≥ 0 x ≥ 0  1  1 1 1  x + = 2x
x = (t / m) Ví dụ: 2
x + x + = 2x ⇔ x + = 2x ⇔   2 ⇔   2 4 2    1  1 −  x + = 2 − xx = (loai)   2   6  = 8) A B A = B ⇔  A = −B  + = +  = Ví dụ: 3x 1 x 3 x 1
3x +1 = x + 3 ⇔ ⇔  3x 1 x 3  + = − − x = 1 −  = 9) A 0
A + B = 0 ⇔  B = 0 x = 5 − Ví dụ: 2 x 5 x 25 0  + + −
= ⇔ x = 5 ⇔ x = 5 −  x = 5 −  = 10) A 0
A + B = 0 ⇔  B = 0
Bài 1: Giải các phương trình sau a. 2
x − 2x + 4 = 2x − 2
b. x + 2 x −1 = 2 c. 2
2x − 2x +1 = 2x −1
d. x + 4 x − 4 = 2 Lời giải 2x − 2 ≥ 0  x ≥1 a) Ta có: 2
x − 2x + 4 = 2x − 2 ⇔  ⇔  ⇒ x = 2 2
x − 2x + 4 =  (2x − 2)2 2 2
x − 2x + 4 = 4x −8x + 4 4 − x ≥ 0 b) Cách 1: Ta có: 2 x 2 x 1 2 x 2 x 1 2 2 x 1 4 x  + − = ⇔ + − = ⇔ − = − ⇔  ⇒ x = 4  ( x − ) 1 = (4 − x) 2 2
Cách 2: Ta có x + 2 x −1 = 2 ⇔ x −1 +1 = 2 ⇒ x = 2 2x −1≥ 0 c) Ta có: 2
2x 2x 1 2x 1  − + = − ⇔  ⇒ x =
2x − 2x +1 =  (2x + ) 1 2 2 1 11 x − 4 ≥ 0 d) Ta có: Điều kiện  ⇔ x ≥ 4
x + 4 x − 4 ≥ 0 x + x − = ⇔ x +
x − − = ⇔ (x − ) + x − + = ⇔ ( x − − )2 2 4 4 2 4 4 4 0 4 2. 4.2 4 4 4 2 = 2 ⇒ x = 4
Bài 2: Giải các phương trình sau a. 2
x − 3x + 2 = x −1 b. 2 2
x − 4x + 4 = 4x −12x + 9 Lời giải x −1≥ 0  = a) Ta có: x 1 2
x − 3x + 2 = x −1 ⇔  ⇔ 2
x − 3x + 2 = x −1  x = 3 x =1 b) Ta có: 2 2 x 4x 4 4x 12x 9 x 2 2x 3  − + = − + ⇔ − = − ⇒ 5 x =  3
Bài 3: Giải các phương trình sau a. 2
(x − 3) = 3− x b. 2
4x − 20x + 25 + 2x = 5 c. 2 (3− 2x) = 4
d. x + 2 x −1 = 2(x ≥1) Lời giải a) Ta có: 2
(x − 3) = 3− x ⇔ x − 3 = 3− x ⇔ x − 3 < 0 ⇔ x < 3 b) Ta có: 2 2 5
4x − 20x + 25 + 2x = 5 ⇔ (5 − 2x) = 5 − 2x ⇔ 5 − 2x = 5 − 2x ⇔ 5 − 2x ≥ 0 ⇔ x ≤ 2  − =  = − c) Ta có: 3 2x 4 x 1,5 2
(3− 2x) = 4 ⇔ 3− 2x = 4 ⇔ ⇔  3 2x 4  − = − x = 3, − 5 d) Ta có: 2
x + 2 x −1 = 2(x ≥1) ⇔ x −1+ 2 x −1 +1 = 2 ⇔ ( x −1 −1) = 2 ⇔ x −1 −1 = 2  x −1 = 3 ⇔ 
⇔ x −1 = 9 ⇔ x =10  x −1 = 1( − loai)
Bài 4: Giải các phương trình sau a. 2 2
x − 2x +1 + x − 6x + 9 =1 b. 2
2x − 3 = 4x − 3 12 c. 2 1− x = x −1 Lời giải a) Ta có: 2 2 2 2
x − 2x +1 + x − 6x + 9 =1 ⇔ (x −1) + (x − 3) =1 ⇔ x −1 + x + 3 =1(1) 3
+) Với x <1⇒ x −1< 0; x − 3 < 0 ⇒ (1) ⇔ 1− x + 3− x =1 ⇔ x = (loai) 2
+) Với 1≤ x ≤ 3 ⇒ x −1≥ 0; x − 3 ≤ 0 ⇒ (1) ⇔ x −1+ 3− x =1 ⇔ 0x = 1( − loai) 5
+) Với x > 3 ⇒ x −1 > 0; x − 3 > 0 ⇒ (1) ⇔ x −1+ x − 3 =1 ⇔ x = (loai) 2
Vậy phương trình vô nghiệm  3 x ≥ 4x 3 0  − ≥ b) Ta có:  4 2
2x − 3 = 4x − 3 ⇔  ⇔  2
2x − 3 = 4x − 3 x = 0(loai) 
x = 2(tm) x ≥1  x −1≥ 0  x ≤ 1 − c) Ta có: 2
1− x = x −1 ⇔  ⇔  ⇒ x ∈ 1; ± ± 2 2 2 2 { }
x −1 = (x −1) x = 1 ±  (t / m)  x = ± 2
Bài 5: Giải các phương trình sau a. 2 2
x − 2x +1 = x −1 b. 2
x − 3 = x − 3 c. 2 2
x − 4 + x + 4x + 4 = 0 2 d. (Khó). 2 2
3x −18x + 28 + 4x − 24x + 45 = 5 − − x + 6x Lời giải a) Ta có: 13 2 x −1≥ 0  2 2 2 2 2 2
x − 2x +1 = x −1 ⇔ (x −1) = x −1 ⇔ x −1 = x −1 ⇔ x −1= x −1  2 
x −1 = −(x −1) x ≥1 2 x ≥1   x ≤ 1 −   2
⇔ x − x = 0
⇔ x = 0(loai) ⇒ x∈{1;− } 2 
(x −1)(x + 2) = 0
x =1(t / m)  x = 2( −  t / m) b) Ta có: 2 x − = x −  x − x + − x − = 2 3 3 ( 3)( 3) ( 3) 0
x − 3 = x − 3 ⇔  ⇔  2
x − 3 = −(x − 3)
(x − 3)(x + 3) + (x − 3) = 0 x − 3 = 0 x = 3   x + 3 −1 = 0 x =1− 3 ⇔ ⇔   x − 3 = 0 x = 3 x 3 1 0  + + = x = 1 − −   3 x = 2 2  − = c) Ta có: x 4 0 2 2 x 4 x 4x 4 0  − + + + = ⇔  ⇔ x = 2 − ⇔ x = 2 − 2
x + 4x + 4 = 0  x = 2 − d. (Khó) Ta có: 2 2 2
3x −18x + 28 + 4x − 24x + 45 = 5
− − x + 6x 2 2 2
⇔ 3(x − 3) +1 + 4(x − 3) + 9 = 4 − (x − 3) (1) Ta có: VT ( ) 1 ≥ 4;VP ≤ 4
Vậy phương trình có nghiệm khi hai vế đều bằng 4 2
⇔ (x − 3) = 0 ⇔ x = 3 Vậy x = 3.
Dạng 5: Tìm GTLN, GTNN của biểu thức
Cách giải: Áp dụng bất đẳng thức: A + B ≥ A+ B Dấu “=” xảy ra ⇔ . A B ≥ 0
Bài 1: Tìm GTNN của các biểu thức sau 14 a) 2 2
A = x + 2x +1 + x − 2x +1
b) B = 2x −1 + 3− 2x c) 2 2
C = 4x − 4x +1 + 4x −12x + 9 d) 2 2
49x − 42x + 9 + 49x + 42x + 9 Lời giải a) Ta có: 2 2
A = x + 2x +1 + x − 2x +1 ⇔ A = x +1 + x −1 Cách 1: +) Nếu x < 1
− ⇒ A = −x −1− x +1 = 2 − x > 2(1) +) Nếu 1
− ≤ x ≤1⇒ A = x +1− x +1 = 2(2)
+) Nếu x >1⇒ A = x +1+ x −1 = 2x > 2(3)
Từ (1)(2)(3) ⇒ MinA = 2 ⇔ 1 − ≤ x ≤1
Cách 2: Áp dụng bất đẳng thức A + B ≥ A + B
A = x +1 + x −1 = x +1 + 1− x ≥ x +1+1− x = 2
Vậy MinA = 2 ⇔ (x +1)(1− x) ≥ 0 ⇔ 1 − ≤ x ≤1 b) Ta có: 1 3
B = 2x −1 + 3− 2x ⇒ MinB = 2 ⇔ ≤ x ≤ 2 2 c) Ta có: 2 2
C = 4x − 4x +1 + 4x −12x + 9 = 2x −1 + 3− 2x ≥ (2x −1) + (3− 2x) = 2 1 3
⇔ (2x −1)(3− 2x) ≥ 0 ⇔ ≤ x ≤ 2 2 d) Ta có: 3 − 3 D = ⇔ ≤ x ≤ min 6 7 7 15
BÀI TẬP TRẮC NGHIỆM
Câu 1: Khẳng định nào sau đây sai
a. 3x xác định khi x ≥ 0 b. 9
− x xác định khi x ≤ 0 x − 5 4 − c.
xác định khi x ≥ 5 d.
xác định khi x > 7 3 x − 9 Lời giải Chọn đáp án D Giải thích:
A) 3x xác định ⇔ 3x ≥ 0 ⇔ x ≥ 0 B) 9
− x xác định ⇔ 9
− x ≥ 0 ⇔ x ≤ 0 x − 5 x − 5 C) xác định ⇔
≥ 0 ⇔ x − 5 ≥ 0 ⇔ x ≥ 5 3 3 4 − 4 − D) ⇔
> 0 ⇔ x − 7 < 0 ⇔ x < 7 x xác định − 9 x − 7
Câu 2: Điền vào chỗ (…) để được khẳng định đúng
a) Điều kiện xác định của 2 3xy là…
b) Điều kiện xác định của 5 − 4x là… 5y −1
c) Điều kiện xác định của 2 x −81 là…
d) Điều kiện xác định của 2 là… 4x Lời giải 16
A) Điều kiện xác định của 2
3xy là: x ≤ 0 5
B) Điều kiện xác định của 5 − 4x là: x ≤ 4
C) Điều kiện xác định của 2
x −81 là: x ≤ 9 − hoặc x ≥ 9 5y −1 1
D) Điều kiện xác định của y ≥ 2 là: và x ≠ 0 4x 5 2 a +1
Câu 3: Điều kiện xác định của 3 a là: a) a ≥ 0 b) a ≤ 0 c) a > 0 d) a > 1 − Lời giải Chọn đáp án C 2 a +1 2 a +1
Điều kiện xác định của 3
≥ 0 ⇔ a > 0 ⇔ a > 0 3 a là 3 a (vì 2 a +1 > 0) 2 2
Câu 4: Biểu thức (− )2
6 . (1− 3) − (2 3 − )1 . 3
− có giá trị đúng là số nào ? a) 3 b) 3 − c) 2 3 d) 2 − 3 Lời giải Chọn đáp án B 2 2
Giải thích: Ta có (− )2
6 . (1− 3) − (2 3 − )1 . 3 − = 6
− .1− 3 − 3(2 3 − )1 (do 3 >1 và
2 3 >1) = 6 3 − 6 − 6 3 + 3 = 3 −
Câu 5: 9 − 4 5 − 5 có kết quả rút gọn là số nào ? a) 2 b) 1 17 c) 2 − 10 d) 2 10 Lời giải Chọn đáp án B
Giải thích: Ta có − − = ( − )2 9 4 5 5 2
5 − 5 = 2 − 5 − 5 = 5 − 2 − 5 = 2 − (do 2 < 5 )
Câu 6: Rút gọn 19 − 6 10 + 26 −8 10 ta được số nào ? a) 1 − b) 1 c) 2 − 10 d) 2 10 Lời giải Chọn đáp án B 2 2
Giải thích: Ta có 19 − 6 10 + 26 −8 10 = (3− 10) + ( 10 − 4) = 3− 10 + 10 − 4 = 10 − 3+ 4 − 10 = 1 − 3
Câu 7: Nếu x > thì phương trình 2
9 −12x + 4x = 5 − 3x có nghiệm là số nào? 2 a) x =1,6 b) x =1,7 c) x =1,8 d) x =1,9 Lời giải Chọn đáp án A
Giải thích: Ta có
− x + x = − x ⇔ ( − x)2 2 9 12 4 5 3 3 2
= 5 − 3x ⇔ 3− 2x = 5 − 3x 3
Vì x > ⇒ 3x − 2 < 0, nên ta có: 8
− x = − x ⇔ x − = − x ⇔ x = = (thỏa mãn). 2 3 2 5 3 2 3 5 3 1,6 5
Câu 8: Với điều kiện 2 x < , phương trình 2
4 − 4 10x +10x = 3− 2 10x có nghiệm là số 10 nào? 1 1 a) x = b) x = 2 10 10 18 1 c) x = − d) Một kết quả khác 10 Lời giải Chọn đáp án B
Giải thích: Ta có − x + x = − x ⇔ ( − x)2 2 4 4 10 10 3 2 10 2 10
= 3− 2 10x ⇔ 2 − 10x = 3− 2 10x Vì 2 1 x 2 10x 0 2 10x 3 2 10x 2 10x 3 2 10x x − < ⇒ − > ⇒ − = − ⇔ − = − ⇔ = (thỏa mãn) 10 10
Câu 9: Giá trị của biểu thức 2
A = 4a − 4a +1 + 2a + 5 bằng số nào khi 3 a = 2 a) 6 b) 8 c) 10 d) 12 Lời giải Chọn đáp án C
Giải thích: Ta có A = a − a + + a + = ( a − )2 2 4 4 1 2 5
2 1 + 2a + 5 = 2a −1 + 2a + 5 Khi 3 3 3
a = ⇒ A = 2. −1 + 2. + 5 = 3−1 + 3+ 5 = 2 + 3+ 5 =10 . 2 2 2
Câu 10: Trong các kết luận sau, kết luận nào sai a) Biểu thức 2
y = x + 4 luôn có nghĩa với mọi giá trị của x b) Biểu thức 2
y = 9 − x luôn có nghĩa với mọi giá trị của x c) Biểu thức 1 y =
luôn có nghĩa với mọi giá trị của 1 x ≠ 2 2x − 2 2 +1 2 d) Biểu thức x −3 y = x + 3 + có nghĩa khi 3 − ≤ x ≤ 3 x + 3 Lời giải Chọn đáp án D Giải thích: A) 2
y = x + 4 có nghĩa khi 2
x + 4 ≥ 0 (luôn đúng) 19 B) 2
y = 9 − x có nghĩa khi 2 2
9 − x ≥ 0 ⇔ x ≤ 9 ⇔ x ≤ 3 ⇔ 3 − ≤ x ≤ 3 C) 1 1 y = = có nghĩa khi 1
2x −1 ≠ 0 ⇔ x ≠ 2 2x − 2 2 +1 ( 2x− )2 1 2 x + 3 ≥ 0 D) x −3 y = x + 3 +
có nghĩa khi  x −3 ⇔ x ≥ 3 x + 3 ≥  0  x + 3 BÀI TẬP VỀ NHÀ
Bài 1: Với mỗi giá trị nào của x thì mỗi căn thức sau có nghĩa a) 2 b) 3 − x c) 1 3x − 5 3− 2x d) 2 x + 2 3 e) f) 2x −1 2 x +1 g) 2 −x + 2x −1 h) − x +1 i) 2 −x − 3 Hướng dẫn giải a) 2 có nghĩa khi 2 5
> 0 ⇔ 3x − 5 > 0 ⇔ 3x > 5 ⇔ x > 3x − 5 3x − 5 3 b) 3 − x có nghĩa khi 3
− x ≥ 0 ⇔ x ≤ 0 c) 1 có nghĩa khi 1 3 3
> 0 ⇔ 3− 2x > 0 ⇔ 3 > 2x ⇔ > x ⇔ x < 3− 2x 3− 2x 2 2 d) 2 x + 2 có nghĩa khi 2
x + 2 ≥ 0 (luôn đúng) 3  > 0 e) Do 3  , x ∀ ∈ R ⇒
có nghĩa với mọi x∈ R 2 2 x +1≥1 > 0 x +1
f) 2x −1 có nghĩa khi 1
2x −1≥ 0 ⇔ 2x ≥1 ⇔ x ≥ 2
g) Ta có: −x + x − = −(x − x + ) = −(x − )2 2 2 2 1 2 1 1 ≤ 0, x ∀ ∈ R , nên 2
−x + 2x −1 có nghĩa khi −(x − )2 1 = 0 ⇔ x =1 20
h) Ta có x +1 ≥ 0 ⇔ − x +1 ≤ 0, x
∀ ∈ R ⇒ − x +1 có nghĩa khi − x +1 = 0 ⇔ x = 1 − i) Ta có 2 −x − = −( 2 3 x + 3), do 2 x + ≥ > ⇒ −( 2 3 3 0 x + 3) < 0
Do đó không tồn tại x để 2 −x − 3 có nghĩa. Bài 2: Tính
a) A = 49. 144 + 256 : 64 b) 2 2
B = 72 : 2 .36.3 − 225 Hướng dẫn giải
a) Ta có: A = 49. 144 + 256 : 64 ⇒ A = 86 b) Ta có: 2 2
B = 72 : 2 .36.3 − 225 ⇒ B = 13 −
Bài 3: Tính giá trị của biểu thức a) 2 2
A = (2 − 5) + (2 2 − 5) b) 2 2
B = ( 7 − 2 2) + (3− 2 2)
c) C = 11+ 6 2 − 11− 6 2
d) D = 17 +12 2 + 17 −12 2 Hướng dẫn giải a) Ta có: 2 2
A = (2 − 5) + (2 2 − 5) ⇒ A = 2 2 − 2 b) Ta có: 2 2
B = ( 7 − 2 2) + (3− 2 2) ⇒ B = 3− 7
c) Ta có: C = 11+ 6 2 − 11− 6 2 ⇒ C = 2 2
d) Ta có: D = 17 +12 2 + 17 −12 2 ⇒ D = 6
Bài 4: Rút gọn các biểu thức sau a) 2
A = 64a + 2a b) 6 3
B = 3 9a − 6a 2 c) − + = ( − ) xy C x y xy > 0 d) 9 6x x D = 2 ( ) (x − y) 2 25y e) 3 4 E = 8x ( 2 4x − 2x + ) 2 2 2 ( f) F =
5a (1− 4a + 4a ) x − ) 1 2 2 1 2a −1 Hướng dẫn giải
A =10(a ≥ 0) a) Ta có: 2
A = 64a + 2a ⇒  A = 6 − a  (a < 0) 21 3 B = 15 − a (a < 0) b) Ta có: 6 3
B = 3 9a − 6a ⇒  3 B = 3a  (a ≥ 0)
c) Biểu thức có nghĩa khi xy ≥ 0; x ≠ y xy xy
xy (x > y)
Ta có: C = (x − y) = x − y . =  2 ( ) (x − y)
x − y − xy  (x < y)
d) Biểu thức có nghĩa khi y ≠ 0 9 − 6x + x (x −3)2 2 2 Ta có:  x − 3  x − 3 D = = = = 2 2 25y 25y  5y    3yx −3 x − 3 ≥ 0 x − 3 ≤ 0  khi hoac 5y  y > 0  y < 0 =  3− xx − 3 ≥ 0 x − 3 ≤ 0  khi hoac  5yy 0  < y > 0 e) Ta có: 3 E =
8x (4x − 2x + ) 3 1 = . 2.(2x )2 2 4 2 2 3 2 ( − = − x − ) ( x − ) .(2x ) 1
( x − ).2x . 2x 1. 2 2 2 1 2 2 1 2 2 1  2 1 > 2 3 2x khi x 3 2x  2 = . 2x −1 =  2x −1  2 1 3 − 2x khi x <  2 f) Ta có: 2 F =
5a (1− 4a + 4a ) 2 =
5a (1− 4a + 4a ) 2 = 5a (2a − )2 2 2 4 2 4 2 2 1 = .5a 2a −1 2a −1 2a −1 2a −1 2a −1  2 1 10a khi a >  2 =   2 1 10 − a khi a <  2
Bài 5: Rút gọn các biểu thức sau a) 2 2
A = a + 6a + 9 + a − 6a + 9( 3 − ≤ a ≤ 3)
b) B = a + 2 a −1 + a − 2 a −1(1≤ a ≤ 2) Hướng dẫn giải a) Ta có: 2 2
A = a + 6a + 9 + a − 6a + 9( 3
− ≤ a ≤ 3) = a + 3 + a − 3 = a + 3+ 3− a = 6
b) Ta có: B = a + 2 a −1 + a − 2 a −1(1≤ a ≤ 2) = 2 22
Bài 6: Giải các phương trình sau a) 2
x + x = x b) 2 1− x = x −1 c) 2 2
x − 2x +1 = x −1 d) 2
4x − 4x +1 = x −1 e) 4 2 x 2
− x +1 = x −1 f) 2
x −1 + x +1 = 0 g) 2
1− x + x +1 = 0 Hướng dẫn giải x ≥ 0  ≥ a) Ta có: x 0 2
x + x = x ⇔  ⇔  ⇔ x = 0 2 2
x + x = xx = 0 x −1≥ 0  x ≥1  ≥ b) Ta có: x 1 2
1− x = x −1 ⇔  ⇔  ⇔  ⇔ x = 1  − x =  (x − ) 1 2 2 1 2x  ( x − ) 1 = 0 x = 0; x =1
c) Ta có: x − x + = x − ⇔ (x − )2 2 2 2 2 2 1 1
1 = x −1 ⇔ x −1 = x −1(*) 2  2 2 2 x ≥1 x −1≥ 0 x ≥1 x ≥1     Cách 1: ( x = x = *) 0 1 2 2
⇔ x −1= x −1⇔ x − x = 0
⇔ x(x − ) 1 = 0 ⇔ ⇔     x =1  x = 2 2 2 
x −1 = 1− x
x + x − 2 = 0  ( x − ) 1 (x + 2) = 0   x = 2 B ≥ 0
(*) Nhận xét: Ở cách này ta dùng phương pháp: A B
= ⇔ A = B  A = −B  − ≥  − < Cách 2: ( ) x 1 0 x 1 0 * ⇔  hoặc (*) ⇔  2
x −1 = x −1 2
x −1 =1− x
Giải 2 trường hợp ra ta nhận được kết quả giống cách 1. ( A ≥ A <
*) Nhận xét: Ở cách này ta dùng phương pháp: 0 A = B ⇔  hoặc 0 A = B ⇔  A = BA = −Bx −1≥ 0
d) Ta có: 4x 4x 1 x 1 (2x )2 2 1 x 1 2x 1 x 1  − + = − ⇔ − = − ⇔
− = − ⇔ 2x −1= x −1 (vô nghiệm) 
2x −1 =1− x 23 x −1≥ 0 e) Ta có:  x 2
− x +1 = x −1 ⇔ (x − )2 4 2 2 2 2
1 = x −1 ⇔ x −1 = x −1 ⇔ x −1= x −1⇔ x =1  2 
x −1 =1− x 2  − =  = ± f) Ta có: x 1 0 x 1 2
x −1 + x +1 = 0 ⇔  ⇔  ⇔ x = 1 − x +1 = 0 x = 1 − 2  − =  = ± g) Ta có: 1 x 0 x 1 2
1− x + x +1 = 0 ⇔  ⇔  ⇔ x = 1 − x +1 = 0 x = 1 −
Bài 7: Giải các phương trình sau a) 2
x − 6x + 9 = 4 − x b) 2 2
x − 2x +1 + x − 4x + 4 = 3
c) 2x − 2 + 2 2x − 3 + 2x +13+ 8 2x − 3 = 5 d) 2 2
x − 9 + x − 6x + 9 = 0 Hướng dẫn giải 4 − x ≥ 0 a) Cách 1: 2 7
x − 6x + 9 = 4 − x ⇔  ⇔ x = 2 2
x − 6x + 9 = (4 − x) 2 Cách 2: 2 7
x − 6x + 9 = 4 − x ⇔ x − 3 = 4 − x ⇒ x = 2 b) 2 2
x − 2x +1 + x − 4x + 4 = 3 ⇔ x −1 + x − 2 = 3
+ Nếu 1< x < 2, ta được: x −1+ 2 − x = 3 ⇔1= 3 (vô nghiệm)
+ Nếu x > 2 , ta được: x −1+ x − 2 = 3 ⇔ x = 3
+ Nếu x <1, ta được: 1− x + 2 − x = 3 ⇔ x = 0
Vậy x = 0 hoặc x = 3 c) Ta có: 3
2x − 2 + 2 2x − 3 + 2x +13+ 8 2x − 3 = 5 ⇔ 2x − 3 +1 + 2x − 3 + 4 = 5 ⇒ x = 2  2 x − 9 = 0 d) Ta có: 2 2 x 9 x 6x 9 0  − + − + = ⇒  ⇒ x = 3  (x − 3)2 = 0  Bài 8:
Tìm các số thực x, y, z thỏa mãn đẳng thức: x + y + z + 8 = 2 x −1 + 4 y − 2 + 6 z − 3 24 Hướng dẫn giải Cách 1: Ta có: 2 2 2
x + y + z + 8 = 2 x −1 + 4 y − 2 + 6 z − 3 ⇔ ( x −1 −1) + ( y − 2 − 2) + ( z − 3 − 3) = 0
⇔ x = 2; y = 6; z =12 Cách 2:
Ta có: x = (x −1) +1≥ 2 x −1; y + 2 = (y − 2) + 4 ≥ 4 y − 2; z + 6 = (z − 3) + 9 ≥ 6 z − 3
Vậy: x = 2; y = 6; z =12 . 25