Tài liệu Toán 9 chủ đề liên hệ giữa phép chia và phép khai phương

Tài liệu gồm 14 trang, bao gồm kiến thức cần nhớ, các dạng toán và bài tập chủ đề liên hệ giữa phép chia và phép khai phương trong chương trình môn Toán 9, có đáp án và lời giải chi tiết. Mời bạn đọc đón xem.

41 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Căn bậc hai. Căn bậc ba

Môn: Toán 9

Thông tin:

14 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1
LIÊN HỆ GIỮA PHÉP CHIA VÀ PHÉP KHAI PHƯƠNG
A. Tóm tắt lý thuyết
1. Định lý: Với
0, 0AB≥>
thì
AA
B
B
=
2. Quy tắc khai phương một thương: Muốn khai phương
A
B
(với
0, 0AB≥>
), ta khai phương
A
, khai phương
B
, rồi lấy thương của hai kết quả
Ta có:
( 0; 0)
AA
AB
B
B
= ≥>
3. Quy tắc chia các căn bậc hai: Muốn chia căn bậc hai của số
0A ≥
cho căn bậc hai của số
, ta có thể chia
A
cho
B
rồi khai phương kết quả đó
( )
0; 0
AA
AB
B
B
= ≥>
B. Bài tập và các dạng toán
Dạng 1: Thực hiện phép tính
Cách giải: Áp dụng công thức khai phương một thương
Bài 1: Tính
a)
9
1
16
b)
12,5
0,5
c)
25
64
d)
230
2,3
Lời giải
a) Ta có:
9 25 25 5
1
16 16 4
16
= = =
b) Ta có:
12,5 12,5
25 5
0,5
0,5
= = =
c) Ta có:
25 25 5
64 8
64
= =
d) Ta có:
230 230
100 10
2,3
2,3
= = =
Bài 2: Tính
2
a)
1 16
7:7
77

−+



b)
36 12 5 : 6
−
c)
14
3:3
33

−+



d)
3 5: 2−
Lời giải
a) Ta có:
1 16 1 16 1 4
7: 7 7.
77 7
77 7

−+ = −+ =



b) Ta có:
36 12 5 : 6 6 2 5 5 1− =−=−
c) Ta có:
14 2
3:3
33 3

−+ =



d) Ta có:
6 25 5 1
3 5: 2 2. 3 5:2
22
−−
− = −= =
Bài 3: Tính
a)
(
)
12 75 27 : 15A
= ++
b)
( )
12 50 8 200 7 450 : 10B = −+
Lời giải
a) Ta có:
( )
12 75 27 4 9 2 3 5
12 75 27 : 15 5 5 5 2 5
15 15 15 5 5
5 55
A
= + + = + + = ++ = ++ = +=
b) Ta có:
( )
12 50 8 200 7 450 : 10 12 5 8 20 7 45 12 5 16 5 21 5 17 5B = − + =−+ =−+=
Bài 4: Tính
a)
( )
27 12 2 6 : 3 3A = −+
b)
( )
2
12 2 18 .
2
B = −
c)
1 21 2
: 72
1 21 2
C

−+
= −


+−

d)
1 1 22
.
32 321 2
D
−

= −

− +−

Lời giải
a) Cách 1:
( )
27 12 2 6 1 27 1 12 2 6 1 1 2
27 12 2 6 :3 3 .3 .2 . 2
3 3 3 3 33 3 3 3
33 33 33
A = − + = − + = − + =−+
12
2
33
= +
3
Cách 2:
( )
( )
31 2 2
33 23 23.2 1 22
27 12 2 6 : 3 3
3
33 33
A
+
−+ +
= −+ = = =
b) Ta có:
( )
( )
( )
2
2 2 12 18
12 2 18 . 12 2 18 . 2 6 2 9 6 6
2 22
2
B = − = − =− =−=−
c) Ta có:
( ) ( )
( )
( )
22
12 12
1 2 1 2 22.2 42 4 2
: 72 : 72 : 72
12 6 3
1 2 1 2 72
1 21 2
C
− −+

−+ −
=−= ====


−
+−
−+

d) Ta có:
( )
42 2 1
1 1 22 422
. . 42
34
32 3212 12 21
D
−
−−

=−===

−
− +− − −

Bài 5: Tính
a)
23 23+−−
b)
35 35 2+ −− −
c)
6,5 12 6,5 12 2 6++ −+
Lời giải
a) Ta có:
22
31 31
( 3 1) ( 3 1)
4 23 4 23 2
2
22
2 2 2 22
+−
+−
+−
− = − =−==
b) Ta có:
22
(51) (51) 51 51
35 35 2 2 0
22
2
+ − +− +
+−−−= − −= =
c) Ta có:
6,5 12 6,5 12 2 6 4 6++ −+=
Bài 6:
Cho biểu thức
2
1
44
.2 1
x
x
A
xx x
++
=
−−
. Tính giá trị của
A
, biết
( 10 6). 4 15x =−+
Lời giải
Ta có:
1
( 10 6)( 10 10)(4 15) ( 10 6)( 10 6) 4 2
2
xA=−−+=−+==⇒=
Vậy
1
2
A =
4
Dạng 2: Rút gọn biểu thức
Cách giải: Áp dụng quy tắc khai phương một thương
Bài 1: Rút gọn
a)
10 15
8 12
A
−
=
−
b)
6 15
35 14
B
−
=
−
c)
55
10 2
C
+
=
+
d)
15 5 5 2 5
3 1 25 4
D
−−
= +
−−
Lời giải
a) Ta có:
10 15 5. 2 5. 3 5
2
8 12 4. 2 4. 3
AA
−−
= = ⇒=
−−
b) Ta có:
6 15 3 21
7
35 14 7
B
− −−
= = =
−
c) Ta có:
5 5 5 10
2
10 2 2
C
+
= = =
+
d) Ta có:
15 5 5 2 5 5( 3 1) 5( 5 2) 5 3 5
5
22
3 1 2 5 4 3 1 2( 5 2)
D
−− − −
= + = + =+=
−−− −
Bài 2: Rút gọn các biểu thức
a)
2
24
5
P xy
xy
=
với
0; 0xy<≠
b)
( )
2
36 4
144
a
Q
−
=
với
4a <
c)
(
)
33
:
H a b ab ab ab= +−
d)
( )
2
2
96
3
xx
E
x
−+
=
−
với
3x >
e)
( )
( )
2
xy
F xy
xy
= −
−
với
0xy<<
f)
(
)
( )
4
2
2
1
2
2
2
x
x
T
x
x
−
−
= +
−
−
với
2x <
Lời giải
a) Ta có:
(
)
( )
22
2
24 2 2
5 55
0; 0 5
xy xy
P xy x y x x
x y x y xy
= < ≠ = = =−=−
−
b) Ta có:
( )
( )
2
36 4
64 4
4
4
144 12 2 2
a
aa
a
Qa
−
−−
−
= = = = <
c) Ta có:
5
(
)
3 3 3 3 22
: : ::H a b ab ab ab a b ab ab ab ab ab a b ab a b ab= + − = + − = + − =+−
d) Ta có:
( )
( )
( )
( )
( )
( )
( )
( )
2
22
2
22 2 2
3
33
96
11
33 3 3
3
x
xx
xx
E
x
x
x xx

−−
−−
−+

= = > = = = =
−− − −
e) Ta có:
( )
( )
( )
2
.
xy
xy
F xy xy
xy
xy
=−=−
−
−
Vì
( ) ( )
( )
xy
xy xy xy F xy xy
xy
<⇒− =− − ⇒ = − =−
−−
f) Ta có:
( )
( )
( )
( )
( )
42
22
22
2
2
21 2
11
2 2 23
2 22 2 2
2
xx x
xx
xx x
T
x xx x x
x
x
− − ++ −
−−
−− −
= + = += =
− −−
<
−−
−
Bài 3: Rút gọn các biểu thức rồi tính
a)
11
:
11
ab
A
ba
−−
=
++
tại
7,25; 3,25ab= =
b)
2
15 8 15 16B aa=−+
tại
358
53
15
a =+=
c)
22
( 6) 36
( 5)
55
xx
Cx
xx
−−
=−<
−−
tại
4
x =
d)
32
5
5 125 ( 0)
5
xx
Dx x
x
+
=−+ ≥
+
tại
5
x =
e)
22 22
21 21Ea a a a
= + −− − −
tại
5a =
Lời giải
a) Ta có:
(
)
( 1)( 1) 1 5
7,25, 3,25
13
( 1)( 1)
aa a
A ab
b
bb
−+ −
= = = = =
−
−+
b) Ta có:
2 2 22
88
15 8 15 16 15.( ) 8. . 15 16 8 8 16 16 4
15 15
B aa= − += − += −+= =
c) Do
22 2
( 6) ( 36) 2 12
5 5 0 5 5 16
55
x x xx
x x x xC
xx
−+− −
<⇒−>⇒− =−⇒ = = =−
−−
d) Ta có:
32
05x xx≥⇒ +
và
5x +
. Vậy D luôn xác định
6
32 2
5 .5
5 125 5 125 5 125 6 5 5( 0) 5
55
x x xx
Dx x x x x x D
xx
++
=−+ =−+ =−+=− ≥⇒=
++
e) Ta có:
22 22 2 2 2 2
21 21(1)211(1)211Ea a a a a a a a
= + −− − − = − + −+− − − −+
2 2 2 22 2 2 2
( 11) ( 11) 11 11 (5) 11 (5) 11a a aa= −+ − −− = −+− −−= −+− −−
41 41 21 21 2
= +− −= +− −=
7
Dạng 3: Giải phương trình
Cách giải: Khi giải phương trình chứa căn thức, luôn cần chú ý đến các điều kiện đi kèm.
+)
2
0
B
AB
AB
≥
= ⇔
=
+)
0( 0)B hoacA
AB
AB
≥≥
= ⇔
=
Bài 1: Giải các phương trình sau
a)
2 50 0x −=
b)
3 3 12 27x −= +
c)
2
3 12 0x −=
d)
2
20 0
5
x
−=
e)
( )
2
39x −=
d)
2
4 4 16xx+ +=
Lời giải
a) Ta có:
2 50 0 2 2. 25 0 5 0 5x x xx− =⇔ − =⇔−=⇔ =
b) Ta có:
( )
3 3 12 27 3 1 2 3 3 3 1 5 6x x xx− = + ⇔ − = + ⇔ −= ⇔ =
c) Ta có:
2 2 22
3 12 0 3 12 3 2 3 2 2x x x xx
−=⇔=⇔=⇔=⇔=±
d) Ta có:
2
2
20 0 5. 20 100 10 10
5
x
xx− =⇔ = = = ⇔=±
e) Ta có:
( )
2
33 6
3 9 33
33 0
xx
xx
xx
−= =

− =⇔−=⇔ ⇔

−=− =

f) Ta có:
( )
2
2
5
2 16
2
4 416 21 6 216
21 6 7
2
x
x
xx x x
x
x
=
+=
+ +=⇔ + =⇔ +=⇔ ⇔
+=− −
=
Bài 2: Giải các phương trình sau
a)
1 3 13xx+ +=
b)
2
6 93 6xx x+ += −
c)
2 35 1xx+ −= +
d)
57
4
3
x
x
+
=
+
Lời giải
8
a) Điều kiện:
2
0( )
1
(1) 3 1 3 1 (3 1) 3 1 9 ( 1) 0
1( )
3
x loai
x x x x x xx
x tm
=
≥ ⇒ ⇔ −= +⇔ − = +⇔ − = ⇔
=
b)
22
3 60
6936 (3)36 336
33 6
3 36
x
xx x x x x x
xx
xx
−≥
+ += −⇔ + = −⇔ += −⇔
+= −
+=− +
2
9
()
2
3
()
4
x
x tm
x loai
≥
=
⇔
=
c) Điều kiện:
3 50
5
10
3
x
x
x
−≥
⇔≥
+≥
2
2 35 1 2 35 1 35 135 21
x x xx xx xxx
+ −= +⇔+ −=+⇔ −=−⇔ −= − +
2( )
( 3)( 2) 0
3( )
x tm
xx
x tm
=
⇔− −=⇔
=
d) Điều kiện:
7
5 70
5
30 3
57 7
03
35
5 70 7
5
30
3
x
x
xx
x
x
x
x
x
x
x
−
≥
+≥
+ > >−
+−

≥ ⇔ ⇔ ⇔ ≤ <−
+
+≤ −

≤
+<
<−
Ta có:
57 57 41
4 16
3 3 11
xx
x
xx
++ −
=⇔ = ⇔=
++
(thỏa mãn)
9
BÀI TẬP TRẮC NGHIỆM
Câu 1: Khẳng định nào sau đây là sai ?
a.
31
3
27
=
b.
15 1
7
735
=
c.
480000
4
300
=
d.
5
35
12
2
2 .6
=
Lời giải
Chọn đáp án C
Giải thích:
A.
3 3 11
27 9 3
27
= = =
B.
15 15 1 1
735 49 7
735
= = =
C.
480000 480000
1600 40
300
300
= = =
D.
5 5 55
2
35 35
35
12 12 2 .6
22
2 .6 2 .6
2 .6
= = = =
Câu 2: Tính
1,69.1,38 1,69.0,74M = −
a.
1, 04M =
b.
1, 64M =
c.
2,08M =
d.
2,14M =
Lời giải
Chọn đáp án A
Giải thích:
Ta có:
( )
1,69.1,38 1,69.0,74 1,69 1,38 0,74 1,69.0,64 1,3.0,8 1,04M
= − = −= = =
Câu 3: Tính
2
125 100
400
N
−
=
a.
15
2
N =
b.
1
15
N =
c.
5
4
N =
d. Một kết quả khác
Lời giải
Chọn đáp án D
Giải thích:
10
Ta có:
( )( )
2
22
125 100 125 100
125 100 225.25 15.5 15
400 20 20 20 4
N
+−
−
= = = = =
Câu 4: Biểu thức rút gọn của số
62
2
361
là số nào?
a.
26
19
b.
27
19
c.
28
19
d.
29
19
Lời giải
Chọn đáp án C
Giải thích:
Ta có:
2
2
62 784 28 28
2
361 361 19 19
= = =
Câu 5: Mỗi khẳng định sau đúng hay sai
a.
0,01 0,0001=
b.
0,5 0, 25−=−
c.
39 7
<
và
39 6>
d.
( )
( )
4 13 .2 3 4 13 2 3xx− < − ⇔<
Lời giải
Chọn đáp án B
Giải thích:
Do
0, 25−
không tồn tại
Câu 6: Thực hiện các phép tính và rút gọn
5, 29
17,64
ta được số nào
a.
23
42
b.
23
48
c.
23
52
d.
23
58
Lời giải
Chọn đáp án A
Giải thích:
11
Ta có:
2
5,29 529 23 23
1764 42 42
17,64

= = =


Câu 7: Biểu thức
( )
4
44
3
.
2
3
yy
x
y
z
−+
+
−
+
có giá trị bằng số nào khi
2x
=
và
16
y =
a.
1
3
b.
1
3
−
c.
1
5
d.
1
5
−
Lời giải
Chọn đáp án D
Giải thích:
Ta có:
( )
( )
( )
( )
( )
( )
2
4 42
2
22
44
3 33
. ..
2 22
3 43
23
y
yy
yy
x xx
y yy
z xx
yx
−
−−
−+
+ ++
= = =
− −−
+ ++
−+
Thay
16, 2yx= =
vào biểu thức
(
)
( )
2
23
y
yx
−
−+
, ta được:
(
)
( )
( )
16 2
42
1
2 4 .5 5
2 16 2 3
−
−
−
= =
−
−+
.
Câu 8: Phương trình
5 125 80 245x +=−
có nghiệm là số nào
a.
1
3
b.
1
3
−
c.
1
5
d.
1
5
−
Lời giải
Chọn đáp án D
Giải thích:
Ta có:
( ) ( )
5 125 80 245 5 25. 5 16. 5 49. 5 5 25 5 16 49xx x+=−⇔+=−⇔+= −
5 47 3 35 8xx⇔ + = − =−⇔ =−− =−
.
Câu 9: Tìm
x
biết:
2
4 4 15xx+ +=
a.
2x =
hoặc
3x = −
b.
2x = −
hoặc
3x =
c.
1x =
hoặc
4x = −
d.
4x =
hoặc
1x = −
12
Lời giải
Chọn đáp án A
Giải thích:
Ta có:
( )
2
2
2 15 2
4 415 21 5 215
21 5 3
xx
xx x x
xx
+= =

+ +=⇔ + =⇔ +=⇔ ⇔

+=− =−

Câu 10: Tìm
x
biết:
( ) ( )
3 13 .3 2. 3 13x− >−
Để tìm
x
, bạn Tâm đã làm như sau:
( )
(
)
3 13 .3 2. 3 13x− >−
Bước 1:
( )
2 3 13
3
3 13
x
−
⇔>
−
Bước 2:
32x⇔>
Bước 3:
2
2
x⇔>
Theo em bạn Tâm làm đúng hay sai, nếu sai thì sai ở bước nào?
A. Các bước đều dúng B. Các bước đều sai
C. Sai từ bước 2 C. Sai từ bước 3
Lời giải
Chọn đáp án B
Giải thích:
Ta có:
( ) ( )
( )
3 13 .3 2. 3 13 *x− >−
Vì
( )
( )
2 3 13
2
3 13 3 13 0 * 3
3
3 13
xx
−
< ⇒− <⇒ ⇔ < ⇔ <
−
Bạn Tâm đã làm sai từ bước 1 vì khi chia hai vế của bất đẳng thức cho một số âm, bạn Tâm
đã không đổi chiều của bất đẳng thức đó.
13
BÀI TẬP VỀ NHÀ
Bài 1: Thực hiện phép tính
a)
1,6. 250 19,6 : 4,9A = +
b)
324
1 .2 .5
479
B =
Lời giải
a) Ta có:
1,6. 250 19,6 : 4,9 22A =+=
b) Ta có:
3 2 4 14
1 .2 .5
479 3
B = =
Bài 2: Thực hiện phép tính
a)
( )
20 300 15 675 5 75 : 15A = −+
b)
( )
325 117 2 208 : 13
B = −+
Lời giải
a) Ta có:
( )
20 300 15 675 5 75 : 15 0A
= −+ =
b) Ta có:
( )
325 117 2 208 : 13 10B = −+ =
Bài 3: Rút gọn các biểu thức sau
a)
23 9
( 0; 0; )
4
25 3
u uv v
A uvuv
u uv v
+−
= ≥≥≠
−+
b)
2
5
( 5)
2 55
x
Bx
xx
+
= ≠−
++
c)
( )
33
48
16
0, 2 0; 0C xy x y
xy
= ≠≠
d)
( )
( )
2
4
21
1
1
1
yy
x
D
y
x
−+
−
=
−
−
Lời giải
a) Ta có:
2 3 9( )(23)23
( 0; 0; )
4
25 3 ( )(23)23
uuvv uvuv uv
A uvuv
uuvv uvuv uv
+− − + +
= ≥≥≠ = =
−+ − − −
b) Ta có:
2
5
( 5)
2 55
x
Bx
xx
+
= ≠−
++
c) Ta có:
( )
33 33
48 24
16 4
0, 2 0; 0 0, 2 . 0,8
x
C xy x y xy
xy xy y
= ≠ ≠= =
14
d) Ta có:
( )
( )
(
)
( )
22
42
21 1
1
11
.
1
11
11
yy y
y
xx
D
x
yy
xx
−+ −
−
−−
= = =
−
−−
−−
.
Bài 4: Rút gọn các biểu thức sau
a)
( )
2
2
2 22
2
2
xx
Ax
x
−+
= ≠±
−
b)
2
5
( 5)
2 55
x
Bx
xx
+
= ≠−
++
Lời giải
a) Ta có:
( )
( )
(
)(
)
2
2
2
2
2 22 2
2
2
2
22
x
xx x
A xA
x
x
xx
−
−+ −
= ≠± ⇒ = =
−
+
−+
b) Ta có:
( )
2
2
5 51
( 5)
2 55 5
5
xx
Bx
xx x
x
++
= ≠− = =
++ +
+
Bài 5: Giải các phương trình sau
a)
2 50 0
x −=
b)
3 3 12 27x += +
c)
2
6 216 0x −=
d)
( )
2
7
567 0x
x
= ≠
Hướng dẫn
a) Ta có:
2 50 0 2 50 2 5 2 5x x xx
−=⇔=⇔=⇔=
b) Ta có:
( )
( )
3 3 12 27 3 1 3 4 9 1 5 4x x xx+ = + ⇔ + = + ⇔ += ⇔ =
c) Ta có:
2 22 2
216
6 216 0 6 216 6 6
6
x x x xx− =⇔ = ⇔= ⇔=⇔=±
d) Ta có:
22
2
7 7 11
567
81 3
567
x xx
x
= ⇔= ⇔= ⇔=±
Bài 6:
Giải phương trình sau:
2
25 9 2 5 3tt−= −
Hướng dẫn
Ta có:
22
1
()
5
25 9 2 5 3 25 9 4(5 3)
3
()
5
t loai
ttt t
t tm
=
−= −⇔ −= − ⇔
=
| 1/14
| | Tải xuống

Có thể bạn quan tâm:

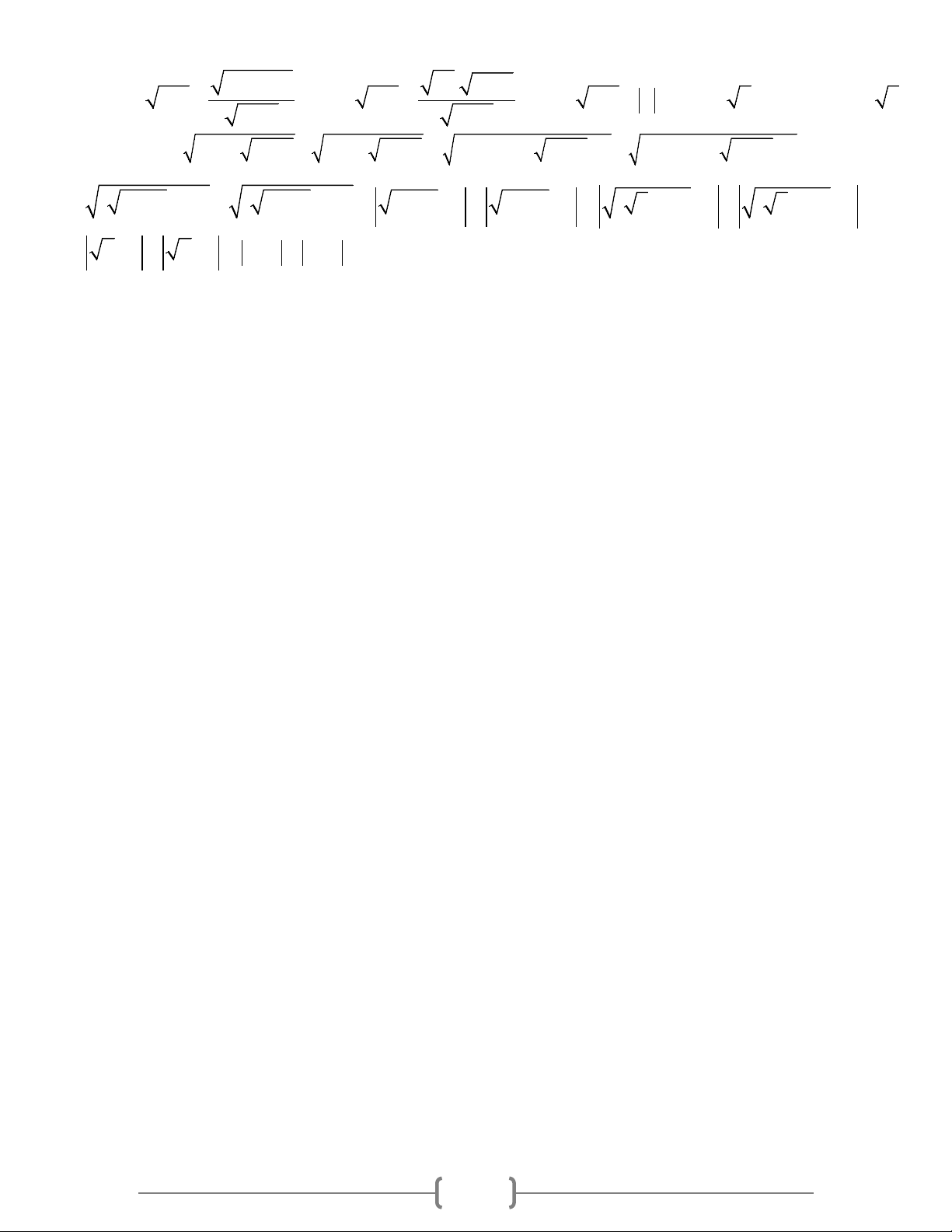
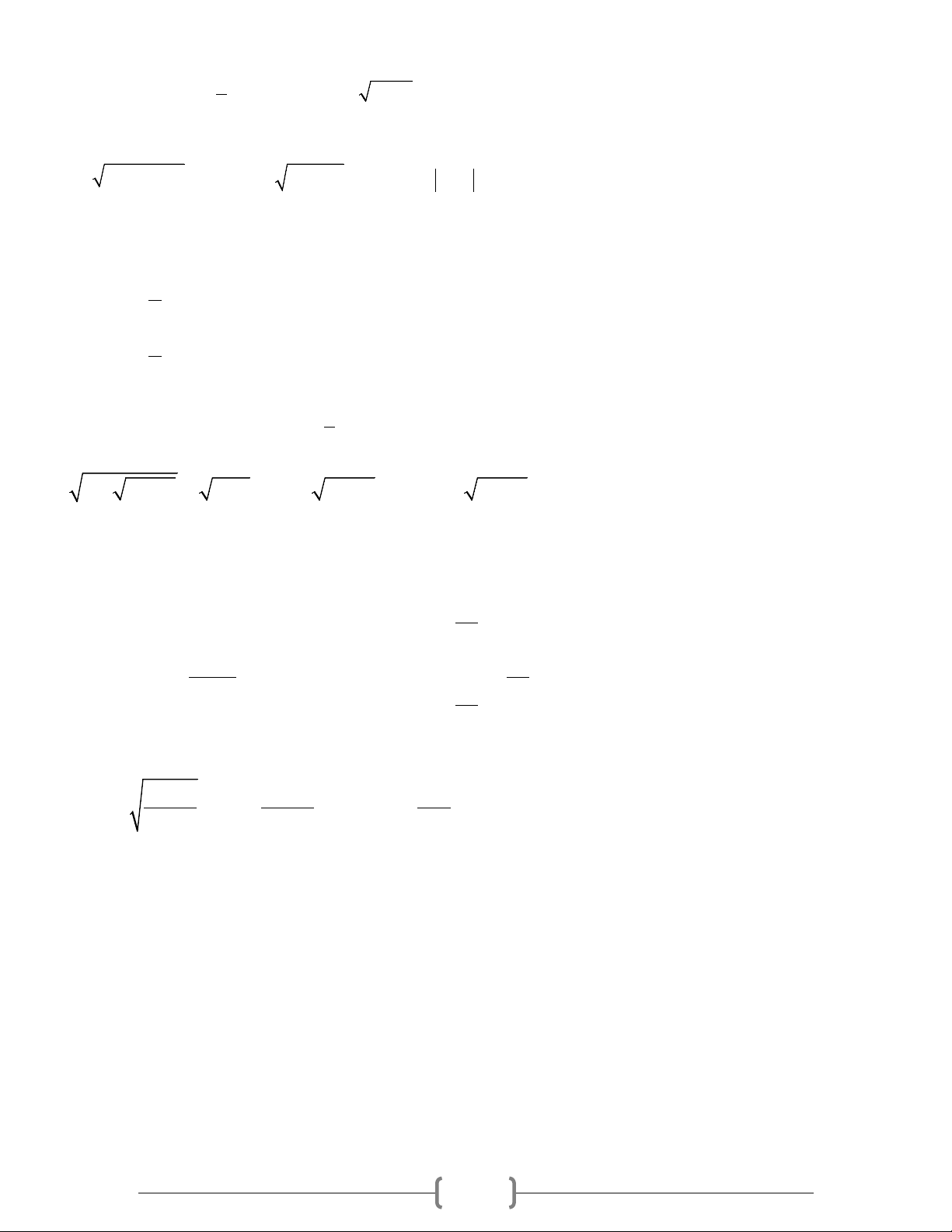
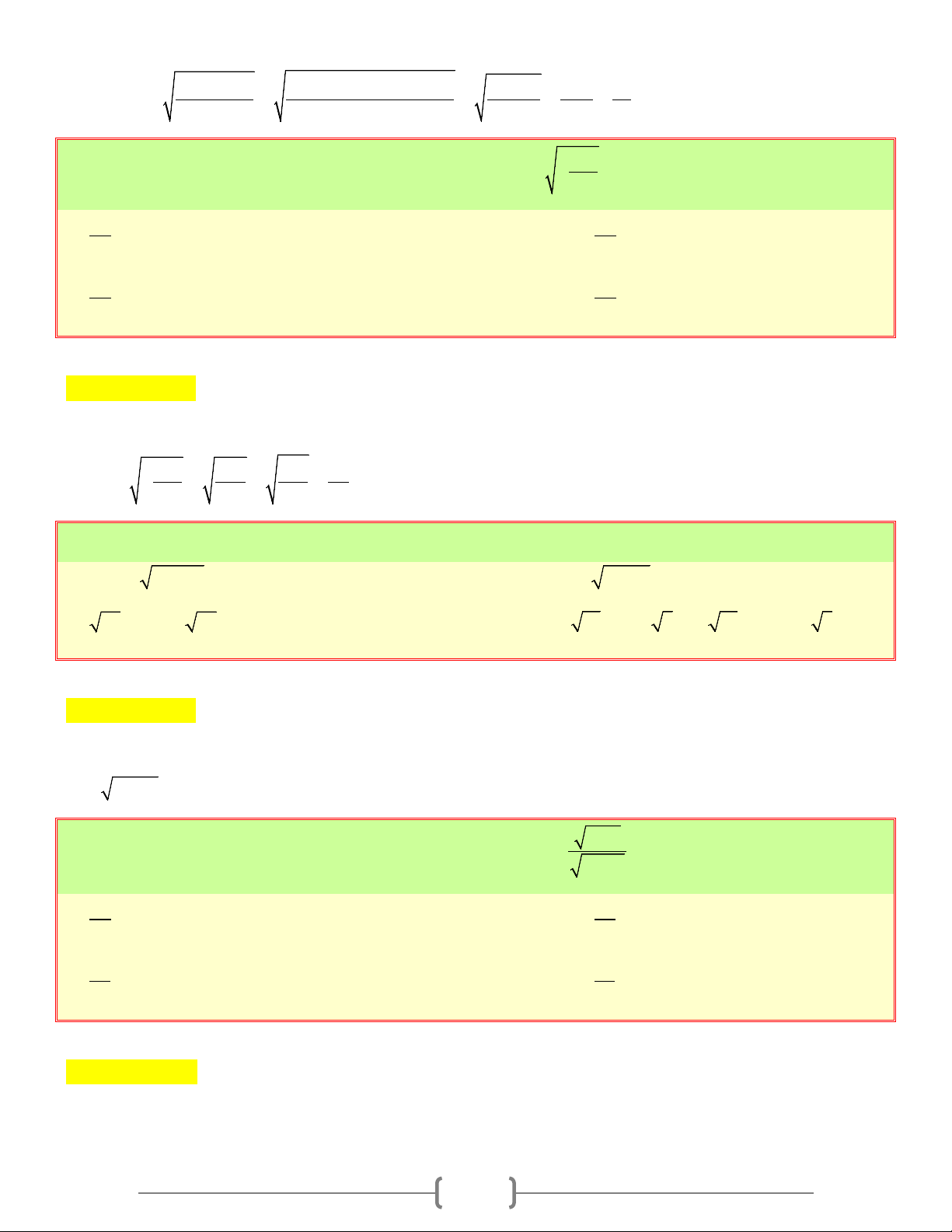
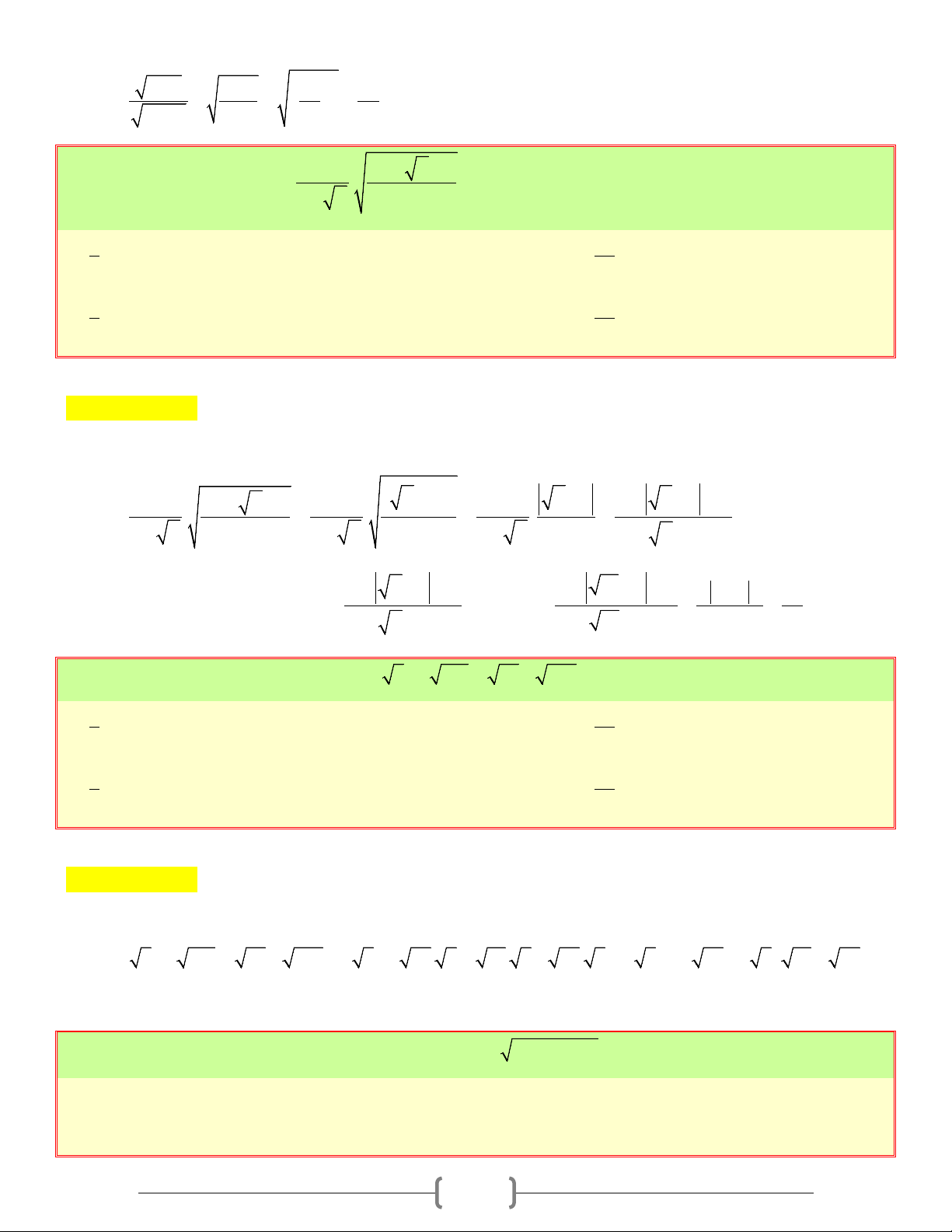
Preview text:

LIÊN HỆ GIỮA PHÉP CHIA VÀ PHÉP KHAI PHƯƠNG
A. Tóm tắt lý thuyết
1. Định lý: Với A ≥ 0, B > 0 thì A A = B B
2. Quy tắc khai phương một thương: Muốn khai phương A (với A ≥ 0, B > 0 ), ta khai phương B
A , khai phương B , rồi lấy thương của hai kết quả A A Ta có: =
(A ≥ 0; B > 0) B B
3. Quy tắc chia các căn bậc hai: Muốn chia căn bậc hai của số A ≥ 0 cho căn bậc hai của số
B > 0 , ta có thể chia A cho B rồi khai phương kết quả đó A A =
( A ≥ 0;B > 0) B B
B. Bài tập và các dạng toán
Dạng 1: Thực hiện phép tính
Cách giải: Áp dụng công thức khai phương một thương Bài 1: Tính a) 9 1 b) 12,5 16 0,5 c) 25 d) 230 64 2,3 Lời giải 9 25 25 5 12,5 12,5 a) Ta có: 1 = = = b) Ta có: = = 25 = 5 16 16 16 4 0,5 0,5 25 25 5 230 230 c) Ta có: = = d) Ta có: = = 100 =10 64 64 8 2,3 2,3 Bài 2: Tính 1  1 16  a)  − + 7  : 7  b) 36 −12 5 : 6 7 7     1 4  c)  − + 3  : 3  d) 3− 5 : 2 3 3    Lời giải     a) Ta có: 1 16 1 16 1 4  − + 7  : 7 =  − + 7 . =  7 7   7 7      7 7
b) Ta có: 36 −12 5 : 6 = 6 − 2 5 = 5 −1   c) Ta có: 1 4 2  − + 3  : 3 =  3 3  3   d) Ta có: 6 − 2 5 5 −1 3− 5 : 2 = 2. 3− 5 : 2 = = 2 2 Bài 3: Tính
a) A = ( 12 + 75 + 27): 15
b) B = (12 50 −8 200 +7 450): 10 Lời giải a) Ta có: A = ( + + ) 12 75 27 4 9 2 3 5 12 75 27 : 15 = + + = + 5 + = + 5 + = + 5 = 2 5 15 15 15 5 5 5 5 5
b) Ta có: B = (12 50 −8 200 +7 450): 10 =12 5 −8 20 +7 45 =12 5 −16 5 + 21 5 =17 5 Bài 4: Tính
a) A = ( 27 − 12 + 2 6):3 3 b) B = ( − ) 2 12 2 18 . 2  − +  c) 1 2 1 2 C   =  −  : 72  d) 1 1 2 2 D − = −  . 1 2 1 2  + −    3 − 2 3 + 2  1− 2 Lời giải
a) Cách 1: A = ( − + ) 27 12 2 6 1 27 1 12 2 6 1 1 2 27 12 2 6 :3 3 = − + = − + = .3− .2 + . 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 2 = + 2 3 3 2 3 1+ − + 2 2 Cách 2: A = ( − + ) 3 3 2 3 2 3. 2 ( ) 1+2 2 27 12 2 6 :3 3 = = = 3 3 3 3 3 b) Ta có: B = ( − ) 2 =( − ) 2 12 18 12 2 18 . 12 2 18 . = − = − = − 2 ( ) 2 6 2 9 6 6 2 2 2 2 1− 2 1+ 2  ( − )2 −( + )2 1 2 1 2 c) Ta có: 2 − 2.2 4 2 4 2 C =  −  : 72 = = = = =  1+ 2 1− 2  (1− 2)(1+ 2) : 72 : 72 1− 2 72 6 3   4 2 1 1 2 2 4 2 2 ( 2 − − − )1 d) Ta có: D = − . = . = =   4 2  3 − 2 3 + 2  1− 2 3− 4 1− 2 2 −1 Bài 5: Tính a) 2 + 3 − 2 − 3 b) 3+ 5 − 3− 5 − 2 c) 6,5+ 12 + 6,5− 12 + 2 6 Lời giải 2 2 + − 3 +1 3 − + − 1 a) Ta có: 4 2 3 4 2 3 ( 3 1) ( 3 1) 2 − = − = − = = 2 2 2 2 2 2 2 2 2 2 b) Ta có: ( 5 +1) ( 5 −1) 5 +1− 5 +1 3+ 5 − 3− 5 − 2 = − − 2 = = 0 2 2 2
c) Ta có: 6,5+ 12 + 6,5− 12 + 2 6 = 4 6 Bài 6: 1 4x + 4 + Cho biểu thức x A =
. Tính giá trị của A , biết x = ( 10 − 6). 4 + 15 2
x. 2x − x −1 Lời giải Ta có: 1
x = ( 10 − 6)( 10 − 10)(4 + 15) = ( 10 − 6)( 10 + 6) = 4 = 2 ⇒ A = 2 Vậy 1 A = 2 3
Dạng 2: Rút gọn biểu thức
Cách giải: Áp dụng quy tắc khai phương một thương Bài 1: Rút gọn a) 10 15 A − = b) 6 15 B − = 8 − 12 35 − 14 c) 5 5 C + = d) 15 5 5 2 5 D − − = + 10 + 2 3 −1 2 5 − 4 Lời giải a) Ta có: 10 − 15 5. 2 − 5. 3 5 A = = ⇒ A = 8 − 12 4. 2 − 4. 3 2 b) Ta có: 6 15 3 21 B − − − = = = 35 − 14 7 7 c) Ta có: 5 5 5 10 C + = = = 10 + 2 2 2 d) Ta có: 15 5 5 2 5 5( 3 1) 5( 5 2) 5 3 5 D − − − − = + = + = 5 + = 3 −1 2 5 − 4 3 −1 2( 5 − 2) 2 2
Bài 2: Rút gọn các biểu thức 36(a − 4)2 a) 2 5 P = xy
với x < 0; y ≠ 0 b) Q = với a < 4 2 4 x y 144 2 c) 9 − 6x + x H = ( 3 3
a b + ab − ab): ab d) E = x > ( với 3 x − 3)2 (x − )4 2 e) xy 1 x − 2
F = ( x − y) x < y < f) T = + x < ( với 0 với 2 x − y)2
(2− x)2 x − 2 Lời giải 2 2 a) Ta có: 2 5 xy 5 xy 5 P = xy
x < 0; y ≠ 0 = =
x = −x = − 5 2 4 ( ) 2 2 ( ) x y x y −xy 36(a − 4)2 b) Ta có: 6 a − 4 a − 4 4 − a Q = = = = (a < 4) 144 12 2 2 c) Ta có: 4 H = ( 3 3
a b + ab − ab) 3 3 2 2
: ab = a b : ab + ab : ab − ab : ab = a + b − ab = a + b − ab 9 − 6x + x (3− x) −  ( x − 3) 2 2  (x −3)2 2 d) Ta có: E = = x > 3 = = = 1 =1 2 2 ( ) (x −3) (x −3) (x −3)2 (x −3)2
e) Ta có: F = (x − y) xy xy = x − y . 2 ( ) (x − y) x − y
Vì < ⇒ − = −( − ) ⇒ = ( − ) xy x y x y x y F x y −( − ) = − xy x y (x − )4 2 2 2 2 2 1 x − 2 x −1
x − 2 − x − 2x +1 + x − 2 f) Ta có: − T = + x < 2 2x 3 = + = = 2 ( ) ( ) ( ) (2− x) x − 2 2 − x x − 2 x − 2 x − 2
Bài 3: Rút gọn các biểu thức rồi tính a) a −1 b −1 A = :
tại a = 7,25;b = 3,25 b +1 a +1 b) 2
B = 15a −8a 15 +16 tại 3 5 8 a = + = 5 3 15 2 2 c) (x − 6) x −36 C = −
(x < 5) tại x = 4 5 − x x −5 3 2 d) x + 5x
D = 5x − 125 +
(x ≥ 0) tại x = 5 x + 5 e) 2 2 2 2
E = a + 2 a −1 − a − 2 a −1 tại a = 5 Lời giải a) Ta có: ( a −1)( a +1) a −1 5 A = =
= (a = 7,25,b = 3,25) ( b −1)( b +1) b −1 3 b) Ta có: 2 8 2 8 2 2
B = 15a −8a 15 +16 = 15.( ) −8.
. 15 +16 = 8 −8 +16 = 16 = 4 15 15 2 2 2 c) Do
(x − 6) + (x − 36) 2x −12
< 5 ⇒ 5 − > 0 ⇒ 5 − = 5 x x x x − x ⇒ C = = = 16 − 5 − x 5 − x d) Ta có: 3 2
x ≥ 0 ⇒ x + 5x và x + 5 . Vậy D luôn xác định 5 3 2 2 x + 5x x . x + 5 D = 5x − 125 + = 5x − 125 +
= 5x − 125 + x = 6x − 5 5(x ≥ 0) ⇒ D = 5 x + 5 x + 5 e) Ta có: 2 2 2 2 2 2 2 2
E = a + 2 a −1 − a − 2 a −1 = (a −1) + 2 a −1 +1 − (a −1) − 2 a −1 +1 2 2 2 2 2 2 2 2
= ( a −1 +1) − ( a −1 −1) = a −1 +1 − a −1 −1 = ( 5) −1 +1 − ( 5) −1 −1
= 4 +1 − 4 −1 = 2 +1 − 2 −1 = 2 6
Dạng 3: Giải phương trình
Cách giải: Khi giải phương trình chứa căn thức, luôn cần chú ý đến các điều kiện đi kèm. B ≥ 0 +) A = B ⇔  2 A = B  ≥ ≥ +) B 0(hoacA 0) A = B ⇔  A = B
Bài 1: Giải các phương trình sau a) 2x − 50 = 0 b) 3x − 3 = 12 + 27 2 c) x 2 3x − 12 = 0 d) − 20 = 0 5 e) (x − )2 3 = 9 d) 2 4x + 4x +1 = 6 Lời giải
a) Ta có: 2x − 50 = 0 ⇔ 2x − 2. 25 = 0 ⇔ x −5 = 0 ⇔ x = 5
b) Ta có: 3x − 3 = 12 + 27 ⇔ 3(x − )
1 = 2 3 + 3 3 ⇔ x −1 = 5 ⇔ x = 6 c) Ta có: 2 2 2 2
3x − 12 = 0 ⇔ 3x = 12 ⇔ 3x = 2 3 ⇔ x = 2 ⇔ x = ± 2 2 d) Ta có: x 2
− 20 = 0 ⇔ x = 5. 20 = 100 =10 ⇔ x = ± 10 5  − =  = e) Ta có: (x − )2 x 3 3 x 6
3 = 9 ⇔ x − 3 = 3 ⇔ ⇔  x 3 3  − = − x = 0  5 x =  + = 
f) Ta có: x + x + = ⇔ ( x + )2 2x 1 6 2 2 4 4 1 6
2 1 = 6 ⇔ 2x +1 = 6 ⇔ ⇔   2x +1 = 6 −  7 x − =  2
Bài 2: Giải các phương trình sau
a) 1+ 3x +1 = 3x b) 2
x + 6x + 9 = 3x − 6 c) 5x + 7
2 + 3x − 5 = x +1 d) = 4 x + 3 Lời giải 7  = a) Điều kiện: 1 x 0(loai) 2
x ≥ ⇒ (1) ⇔ 3x −1 = 3x +1 ⇔ (3x −1) = 3x +1 ⇔ 9x(x −1) = 0 ⇔ 3  x =1(tm) 3  x − 6 ≥ 0 b) 2 2
x 6x 9 3x 6 (x 3) 3x 6 x 3 3x 6  + + = − ⇔ + = − ⇔ + =
− ⇔ x + 3 = 3x − 6  x + 3 = 3 − x + 6 x ≥ 2  9  x = (tm) ⇔   2   3  x = (loai)   4  − ≥
c) Điều kiện: 3x 5 0 5  ⇔ x ≥ x +1≥ 0 3 2
2 + 3x − 5 = x +1 ⇔ 2 + 3x − 5 = x +1 ⇔ 3x − 5 = x −1 ⇔ 3x − 5 = x − 2x +1 x = 2(tm)
⇔ (x − 3)(x − 2) = 0 ⇔  x = 3(tm)  7 −  5  + 7 ≥ 0 x x ≥  5   5x + 7 x + 3 > 0  x > 3 − d) Điều kiện: 7 − ≥ 0 ⇔ ⇔ ⇔ ≤ +   x < 3 − x 3 5  x + 7 ≤ 0  7 − 5    x ≤ x + 3 < 0  5  x < 3 − 5x + 7 5x + 7 4 − 1 Ta có: = 4 ⇔ =16 ⇔ x = x (thỏa mãn) + 3 x + 3 11 8
BÀI TẬP TRẮC NGHIỆM
Câu 1: Khẳng định nào sau đây là sai ? a. 3 1 = b. 15 1 = 27 3 735 7 5 c. 480000 = 4 d. 12 = 2 300 3 5 2 .6 Lời giải Chọn đáp án C Giải thích: A. 3 3 1 1 = = = B. 15 15 1 1 = = = 27 27 9 3 735 735 49 7 5 5 5 5 C. 480000 480000 = = 1600 = 40 D. 12 12 2 .6 2 = = = 2 = 2 300 300 3 5 3 5 3 5 2 .6 2 .6 2 .6
Câu 2: Tính M = 1,69.1,38−1,69.0,74 a. M =1,04 b. M =1,64 c. M = 2,08 d. M = 2,14 Lời giải Chọn đáp án A Giải thích:
Ta có: M = 1,69.1,38−1,69.0,74 = 1,69(1,38−0,74) = 1,69.0,64 =1,3.0,8 =1,04 2 Câu 3: Tính 125 100 N − = 400 a. 15 N = b. 1 N = 2 15 c. 5 N = d. Một kết quả khác 4 Lời giải Chọn đáp án D Giải thích: 9 2 125 −100 (125+100)(125−100) Ta có: 225.25 15.5 15 N = = = = = 2 2 400 20 20 20 4
Câu 4: Biểu thức rút gọn của số 62 2 là số nào? 361 a. 26 b. 27 19 19 c. 28 d. 29 19 19 Lời giải Chọn đáp án C Giải thích: 2 Ta có: 62 784 28 28 2 = = = 2 361 361 19 19
Câu 5: Mỗi khẳng định sau đúng hay sai a. 0,01= 0,0001 b. 0, − 5 = 0, − 25 c. 39 < 7 và 39 > 6
d. (4− 13).2x < 3(4− 13) ⇔ 2x < 3 Lời giải Chọn đáp án B Giải thích: Do 0, − 25 không tồn tại
Câu 6: Thực hiện các phép tính và rút gọn 5,29 ta được số nào 17,64 a. 23 b. 23 42 48 c. 23 d. 23 52 58 Lời giải Chọn đáp án A Giải thích: 10 2 Ta có: 5,29 529  23  23 = = = 17,64 1764  42   42
Câu 7: Biểu thức x +3 y − 4 y + 4 .
có giá trị bằng số nào khi x = 2 và y =16 2 − y (z +3)4 a. 1 b. 1 − 3 3 c. 1 d. 1 − 5 5 Lời giải Chọn đáp án D Giải thích: x + 3 y 4 y 4 x + 3 ( y −2)2 + y − 2 y − − + 2 Ta có: x 3 . = . = . = 2 − y (z +3)4 2 − y (x + 4)4
2 − y (x + 3)2 (2− y )(x +3) y − 2 16 − 2 Thay 4 − 2 −
y =16, x = 2 vào biểu thức 1 ( , ta được: = = . 2 − y )(x +3) (2− 16)(2+3) (2−4).5 5
Câu 8: Phương trình 5x + 125 = 80 − 245 có nghiệm là số nào a. 1 b. 1 − 3 3 c. 1 d. 1 − 5 5 Lời giải Chọn đáp án D Giải thích:
Ta có: 5x + 125 = 80 − 245 ⇔ 5x + 25. 5 = 16. 5 − 49. 5 ⇔ 5 (x + 25) = 5( 16 − 49) ⇔ x + 5 = 4 − 7 = 3 − ⇔ x = 3 − − 5 = 8 − .
Câu 9: Tìm x biết: 2 4x + 4x +1 = 5
a. x = 2 hoặc x = 3 − b. x = 2 − hoặc x = 3
c. x =1 hoặc x = 4 −
d. x = 4 hoặc x = 1 − 11 Lời giải Chọn đáp án A Giải thích: Ta có:  x + = x =
4x + 4x +1 = 5 ⇔ (2x + )2 2 1 5 2 2 1 = 5 ⇔ 2x +1 = 5 ⇔ ⇔  2x 1 5  + = − x = 3 −
Câu 10: Tìm x biết: (3− 13).3x > 2.(3− 13)
Để tìm x , bạn Tâm đã làm như sau: (3− 13).3x > 2.(3− 13) 2 (3− 13) Bước 1: ⇔ 3x > 3− 13
Bước 2: ⇔ 3x > 2 Bước 3: 2 ⇔ x > 2
Theo em bạn Tâm làm đúng hay sai, nếu sai thì sai ở bước nào? A. Các bước đều dúng B. Các bước đều sai C. Sai từ bước 2 C. Sai từ bước 3 Lời giải Chọn đáp án B Giải thích:
Ta có: (3− 13).3x > 2.(3− 13)(*) 2 (3− 13) Vì < ⇒ − < ⇒ ( ) 2 3 13 3 13 0 * ⇔ 3x < ⇔ x < 3− 13 3
Bạn Tâm đã làm sai từ bước 1 vì khi chia hai vế của bất đẳng thức cho một số âm, bạn Tâm
đã không đổi chiều của bất đẳng thức đó. 12 BÀI TẬP VỀ NHÀ
Bài 1: Thực hiện phép tính 3 2 4
a) A = 1,6. 250 + 19,6 : 4,9 b) B = 1 .2 .5 4 7 9 Lời giải
a) Ta có: A = 1,6. 250 + 19,6 : 4,9 = 22 b) Ta có: 3 2 4 14 B = 1 .2 .5 = 4 7 9 3
Bài 2: Thực hiện phép tính
a) A = (20 300 −15 675 +5 75): 15
b) B = ( 325 − 117 + 2 208): 13 Lời giải
a) Ta có: A = (20 300 −15 675 +5 75): 15 = 0
b) Ta có: B = ( 325 − 117 + 2 208): 13 =10
Bài 3: Rút gọn các biểu thức sau a)
2u + uv − 3v 9 x + 5 A =
(u ≥ 0;v ≥ 0;u ≠ v) b) B = (x ≠ − 5)
2u − 5 uv + 3v 4 2 x + 2x 5 + 5 1 ( y − 2 y x + − )21 c) 16 3 3 C = 0,2x y
x ≠ 0; y ≠ 0 d) D = 4 8 ( ) x y y −1 (x − )4 1 Lời giải a) Ta có:
2u + uv − 3v 9
( u − v)(2 u + 3 v) 2 u + 3 = ( ≥ 0; ≥ 0; ≠ ) v A u v u v = =
2u − 5 uv + 3v 4
( u − v)(2 u − 3 v) 2 u − 3 v b) Ta có: x + 5 B = (x ≠ − 5) 2 x + 2x 5 + 5 c) Ta có: 3 3 16 = ( ≠ ≠ ) 3 3 4 0,2 0; 0 = 0,2 . = 0,8 x C x y x y x y 4 8 2 4 x y x y y 13
x −1 ( y − 2 y + )2 1
x −1 ( y − )2 1 d) Ta có: y −1 D = = . = . y −1 (x − )4 1 y −1 (x − )2 1 x −1
Bài 4: Rút gọn các biểu thức sau 2 a) x − 2x 2 + 2 + A = x ≠ ± 2 b) x 5 B = (x ≠ − 5) 2 ( ) x − 2 2 x + 2x 5 + 5 Lời giải x x (x− − + 2 2 2 2 )2 2 a) Ta có: x − 2 A = x ≠ 2 ± ⇒ A = = 2 ( ) x − 2
(x− 2)(x+ 2) x+ 2 b) Ta có: x + 5 x + 5 1 B = (x ≠ − 5) = = 2 x + 2x 5 + 5 (x )2 x+ + 5 5
Bài 5: Giải các phương trình sau a) 2x − 50 = 0 b) 3x + 3 = 12 + 27 c) 7 2 6x − 216 = 0 d) = 567 x ≠ 0 2 ( ) x Hướng dẫn
a) Ta có: 2x − 50 = 0 ⇔ 2x = 50 ⇔ 2x = 5 2 ⇔ x = 5
b) Ta có: 3x + 3 = 12 + 27 ⇔ 3(x + )
1 = 3 ( 4 + 9) ⇔ x +1= 5 ⇔ x = 4 c) Ta có: 2 2 2 216 2
6x − 216 = 0 ⇔ 6x = 216 ⇔ x =
⇔ x = 6 ⇔ x = 6 ± 6 d) Ta có: 7 2 7 2 1 1 = 567 ⇔ x = ⇔ x = ⇔ x = ± 2 x 567 81 3 Bài 6: Giải phương trình sau: 2
25t − 9 = 2 5t − 3 Hướng dẫn  1 t = (loai)  Ta có: 2 2 5
25t − 9 = 2 5t − 3 ⇔ 25t − 9 = 4(5t − 3) ⇔   3 t = (tm)  5 14