Tài liệu Toán 9 chủ đề liên hệ giữa phép nhân và phép khai phương

Tài liệu gồm 19 trang, bao gồm kiến thức cần nhớ, các dạng toán và bài tập chủ đề liên hệ giữa phép nhân và phép khai phương trong chương trình môn Toán 9, có đáp án và lời giải chi tiết. Mời bạn đọc đón xem.

49 25 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Căn bậc hai. Căn bậc ba

Môn: Toán 9

Thông tin:

19 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1
LIÊN HỆ GIỮA PHÉP NHÂN VÀ PHÉP KHAI PHƯƠNG
A. Tóm tắt lý thuyết
1. Định lý: Với hai số
,0ab≥
, ta có:
..ab a b=
Chú ý: Định lí trên còn có thể mở rộng cho tích của nhiều số không âm
2. Quy tắc khai phương một tích
Với
0, 0,
AB≥≥
ta có:
.AB A B=
Mở rộng: Với
12
0, 0,..., 0
n
AA A≥≥ ≥
ta có:
12 1 2
.... . ...
nn
AA A A A A
=
3. Quy tắc nhân các căn bậc hai
Với hai biểu thức
0, 0,AB≥≥
ta có:
Chú ý: Với
0A ≥
, ta có:
( )
2
2
A A AA= = =
B. Bài tập và các dạng toán
Dạng 1: Tính giá trị biểu thức
Cách giải: Áp dụng công thức khai phương một tích
Bài 1: Tính
a.
25.144
b.
52.13
c.
45.80
d.
7. 28
Lời giải
a) Ta có:
25.144 5.12 60= =
b) Ta có:
2
52.13 52.13 4.13.13 4. 13 26= = = =
c) Ta có:
2
45.80 5.9.5.16 5 . 9. 16 60= = =
d) Ta có:
22
7. 28 7.28 7.7.4 7 . 2 14= = = =
Bài 2: Tính
a.
2 50
24 . 6
33

+−



b.
3 5. 2+
c.
34
3 5 . 12
43

−+



d.
3 5. 8−
2
Lời giải
a) Ta có:
2 50 2 50
24 . 6 .6 .6 24.6 0
33 3 3

+− = + − =



b) Ta có:
( )
2
3 5. 2 3.2 2 5 5 1 5 1+ = + = +=+
c) Ta có:
34
3 5 . 12 7
43

−+ =



d) Ta có:
( )
3 5. 8 2 5 1−=−
Bài 3: Tính
a.
55.77.35
b.
11
. 2. 125.
85
c.
2 1. 2 1−+
d.
2
2 2.( 3 2) (1 2 2) 2 6− ++ −
Lời giải
a) Ta có:
55.77.35 5.11.7.11.5.7 5.7.11 385= = =
b) Ta có:
1 1 1 1 2.125 25 5
. 2. 125. .2.125.
8 5 8 5 8.5 4 2
= = = =
c) Ta có:
2 1. 2 1 ( 2 1).( 2 1) 2 1 1
− += − + = −=
d) Ta có:
2
22.(3 2) (122) 26 26 42 142 8 26 9−++ −=−+++−=
Bài 4: Tính
a)
3 5 23.3 5 23A =++ −+
b)
48.222.222B =+ ++ −+
c)
( )
12 3 15 4 135 3C =+−
d)
2 40 12 2 75 3 5 48D = −−
Lời giải
a) Ta có:
22
3 5 23.3 5 23 3 (5 23) 9 (5 23)A = + + − + = − + = −+
2
9 5 23 4 23 (3 1) 3 1=−−=−= −=−
b) Ta có:
3
22
4 8.2 2 2.2 2 2 4 4.2.2 (2 2) 4 22.2 2B =+ ++ −+ =+ − + =+ −
2.(2 2)(2 2) 2.2 2B⇒= + − = =
c) Ta có:
2
( 12 3 15 4 135) 3 36 3 9.5 4 9 .5 6 9 5 36 5 6 27 5
+ − =+ − =+− =−
d) Ta có:
2 40 12 2 75 3 5 48 2 40 12 2 5 3 3 20 3 2 80 3 2 5 3 6 5 3C
= −− = −− = −−
853 253 653 53(8 2 6) 0
C⇒ = − − = −− =
Bài 5: Tính
a)
(4 15)( 10 6) 4 15A =+ −−
b)
(3 5) 3 5 (3 5) 3 5B =− + ++ −
c)
23.223.2223.2223C =+ ++ +++ −++
Lời giải
a) Ta có:
(4 15)( 10 6) 4 15 ( 10 6) 4 15. 4 15. 4 15A =+ −−=−+ + −
( 10 6) 4 15. (4 15)(4 15) 10 6. ( 10 6)(4 15)=− + + −= − − +
10 6. 4 10 150 4 6 90 10 6. 10 6 ( 10 6)( 10 6) 4 2= − + − − = − += − + ==
b) Ta có:
(35)35(35)35 35.35.35(35)35B =− + ++ − = − − + ++ −
(
)
35.3535 352(35 35) 2(35.2 35.2)=− + − ++ = − ++ = − ++
22
2 ( 6 2 5 6 2 5 ) 2 ( ( 5 1) ( 5 1) 2 ( 5 1 5 1) 2 10= − + + = − + + = −+ + =
c) Ta có:
23.223.2223.2223C =+ ++ +++ −++
23.223.223C⇒= + + + − +
22
23.(2(23)) 23.231C⇒= + − + = + − =
4
Dạng 2: Rút gọn biểu thức
Cách giải: Áp dụng công thức khai phương của một tích
Bài 6: Rút gọn
a)
10 15
8 12
A
−
=
−
b)
6 15
35 14
B
−
=
−
c)
55
10 2
C
+
=
+
d)
15 5 5 2 5
3 1 25 4
D
−−
= +
−−
Lời giải
a) Ta có:
10 15 5. 2 5. 3 5
2
8 12 4. 2 4. 3
AA
−−
= = ⇒=
−−
b) Ta có:
6 15 3 21
7
35 14 7
B
− −−
= = =
−
c) Ta có:
5 5 5 10
2
10 2 2
C
+
= = =
+
d) Ta có:
15 5 5 2 5 5( 3 1) 5( 5 2) 5 3 5
5
22
3 1 2 5 4 3 1 2( 5 2)
D
−− − −
= + = + =+=
−−− −
Bài 7: Rút gọn các biểu thức sau
a)
6 14
2 3 28
B
+
=
+
b)
23684
234
C
++++
=
++
c)
3 8 2 12 20
3 18 2 27 45
D
−+
=
−+
Lời giải
a) Ta có:
6 14 2. 3 2. 7 2 1
2
23 28 23 4.7 2
B
++
= = = =
++
b) Ta có:
23684 234468
21
234 234
C
++++ +++++
= = = +
++ ++
c) Ta có:
3 8 2 12 20 3.2 2 2.2 3 2 5 2(3 2 2 3 5) 2
3
3 18 2 27 45 3.3 2 2.3 3 3 5 3(3 2 2 3 5)
D
− + − + −+
= = = =
−+−+−+
5
Bài 8: Rút gọn biểu thức sau:
2 15 2 10 6 3
2521036
A
− +−
=
− −+
Lời giải
Ta có:
( )
( )
( ) ( )
2532 332
2 15 2 10 6 3 2 5.3 2 5.2 3.2 3
2 5 2 10 3 6 2 5 2 5.2 3 3.2
2512 312
A
−− −
− +− − + −
= = =
− −+ − −+
−− −
32
12
A
−
⇒=
−
Bài 9: Rút gọn các biểu thức sau:
a)
( )
23
.0
38
tt
At
−
= ≤
b)
( )
6
4
28
0
7
y
By
y
= <
c)
( )
22
1. 1 1C xx xx x=−− +−≥
d)
4 24 2
4. 4D x xx x= +− ++
Lời giải
a) Ta có:
( )
2
23 2 3
.. 0
38 3 8 42
tt t t t t
At
− −− −

= = = = ≤


b) Ta có:
( )
6
4
28
02
7
y
B y By
y
= < ⇒=−
a) Ta có:
(
)
2
2 2 22
1. 1 1 1C xx xx x x
= − − + −= − − =
a) Ta có:
4242 4242 4 22
4. 4 (4)(4)(4)()42xxxx xxxxx x+− ++ = +− ++ = + − = =
Bài 10: Rút gọn các biểu thức sau:
a)
( )
0; 0; 0
2
xy yx
A x y xy
x xy y
+
= ≥≥ ≠
++
b)
( 0; 0; )
2
xy yx
B x y xy
x xy y
−
= ≥≥≠
−+
c)
3 21 1
( 0; )
4
44 1
aa
aa
aa
−−
≥≠
−+
d)
4 44
( 0; 4)
22
aa a
D aa
aa
++ −
= + ≥≠
+−
Lời giải
6
a) Ta có:
( )
( )
2
2
xy x y
x y y x xy
AA
x xy y x y
xy
+
+
= = ⇒=
++ +
+
b) Ta có:
2
x y y x xy
B
x xy y x y
−
= =
−+ −
c) Ta có:
2
3 2 1 (2 1)(1 ) 1
441 (21) 21
aa a a a
aa a a
−− − − −
= =
−+ − −
d) Ta có:
( ) ( )( )
2
2 22
4 44
0
2 22 2
a aa
aa a
D
a aa a
+ −+
++ −
= += − =
+ −+ −
7
Dạng 3: Giải phương trình
Cách giải: Khi giải phương trình chứa căn thức, luôn cần chú ý đến các điều kiện đi kèm.
+)
2
0
B
AB
AB
≥
= ⇔
=
+)
0( 0)
B hoac A
AB
AB
≥≥
= ⇔
=
Bài 1: Giải các phương trình sau
a)
2
2 42 2xx x− += −
b)
2
2 23xx x−=−
c)
2
43xx x− ++=−
d)
2
32 9 0
xx+− −=
Lời giải
a) Ta có:
( )
2
2
2
2 20
2 20
2 42 2 2
2
2422
x
x
xx x x
x
xx x
−≥
−≥
− += −⇔ ⇔ ⇒=

=
− += −
b) Ta có:
2
2
2
2
23 0
2 23 2
3
2 23
20
x
x
xx x x
xx x
xx
−≥
≤
− = − ⇔ ⇔ ⇒=−

−=−
+−=
c) Ta có:
( )
2
2
2
30
30
1
43
43
5
2
x
x
x
xx x x
xx x
x
−≥
−≥

=
− ++=−⇔ ⇔ ⇒∈∅

− ++= −
=
d) Cách 1: Ta có
( )
( )
( )
2
2
3
30
32 9 0 3
11
34 9
4
x tm
x
xx x
xx
x loai
=
−≥
+− −=⇔ ⇔ ⇒=
−
−= −
=
Cách 2: Với
( )
( )
2
3 9 3. 3 3 1 2 3 0 3x x x x x x x tm≥⇒ −= − +⇒ − − + =⇒=
Bài 2: Giải các phương trình sau
a.
2
9.(2 3 ) 6x−=
b.
2
4 9 22 3xx−= +
c.
10( 3) 20x −=
d.
2
6 93 6xx x+ += −
Lời giải
8
a) Ta có:
2
4
9.(23) 6 323 6 23 2
3
0
x
x xx
x
=
− =⇔−=⇔−=⇔
=
b) Ta có:
2
4 9223 (23)(23)223 23.23223x x xx xxxx
−= +⇔ − + = +⇔ − += +
3
2 30
2
2 3.( 2 3 2) 0
7
2 30
2
x
x
xx
x
x
−
=

+=
⇔ + −− =⇔ ⇔

−=

=
c) Ta có:
10( 3) 20 10( 3) 20 5( )x x x tm− = ⇔ − = ⇔=
(điều kiện
3x ≥
)
d) Ta có:
2
2
3 60
9
()
(3)36 336
33 6
2
3 36 3
()
4
x
x
x tm
x xxx
xx
xx
x loai
≥
−≥
=
⇔ + = −⇔ += −⇔ ⇔
+= −


+=− +
=
Bài 3: Giải phương trình ẩn y
a)
1
4 20 5 9 45 4
3
yy y− + −− − =
b)
11
2 9 27 25 75 49 147 20
57
yyy−− −− − =
Lời giải
a) Điều kiện
5y
≥
Ta có:
1
4 20 5 9 45 4 2 5 4 9
3
yy y y y− + −− − =⇔ −=⇔ =
(thỏa mãn)
b) Điều kiện
3y ≥
Ta có:
( ) ( ) ( )
11 1 1
2 9 27 25 75 49 147 20 2 9 3 25 3 49 3 20
57 5 7
yyy y x x− − − − − = ⇔ −− −− −=
( )
(
)
( )
11
2 9 3 25 3 49 3 20 6 3 3 3 20 4 3 20
57
y y y yyy y
− − − − − = ⇔ −− −− −= ⇔ −=
3 5 28yy⇔ −=⇔=
(thỏa mãn)
Bài 4: Giải các phương trình sau
a)
2
4 9 22 3xx−= +
b)
97
75
75
x
x
x
−
= +
+
Lời giải
9
a) Ta có:
22
22
33
49223 49812
22
4 9 8 12 4 8 21 0
xx
x x xx
x x xx
−−

≥≥

−= +⇔ −= + ⇔ ⇔


−= + − − =

3
2
7
73
7
2
;
3
22
2
3
2
2
x
x
S
x
x
x
≥−
=
−

⇔ ⇔ ⇒=
=

−

=
−
=
b) Điều kiện
5
7 50
7
xx
−
+>⇔>
Ta có:
( )
2
97
75 97 75 75 6
75
x
x x x xx
x
−
= +⇔ −= + = +⇔ =
+
(thỏa mãn)
10
Dạng 4: Chứng minh đẳng thức
Cách giải: Áp dụng bất đẳng thức Côsi cho các số không âm, ta có:
+)
2
ab
ab
+
≥
, dấu “=” xảy ra khi và chỉ khi
ab=
+)
3
3
abc
abc
++
≥
Bài 1: Cho các số không âm
,,abc
. Chứng minh
a)
2
ab
ab
+
≥
(BĐT Cauchy) b)
ab a b+< +
c)
1
2
ab a b++ ≥ +
d)
a b c ab bc ca++≥ + +
Lời giải
a) Do
0
2
,, 0
0
ab
abc
ab
+
≥
≥⇒
≥
Bình phương hai vế của bất đẳng thức ta được:
( )
2
22 22 22
2
2 2 24
00
2 44 4
a b a ab b a ab b a ab b ab
ab ab ab
+ ++ ++ ++−

≥ ⇔ ≥ ⇔ − ≥⇔ ≥


(
)
2
22
2
00
44
ab
a ab b
−
−+
⇔ ≥⇔ ≥
(bất đẳng thức đúng)
b) Bình phương hai vế của bất đẳng thức ta được:
( )
( )
22
2 02ab a b abab ab ab+ < + ⇔+<++ ⇔<
(bất đẳng thức đúng)
c) Ta có:
( ) ( )
22
11
0 1 10
22
ab a b ab a b a b++ ≥ + ⇔++ − − ≥⇔ − + − ≥
(bất đẳng thức
đúng)
d) Ta có:
2222 2 2 0
a b c ab bc ca a b c ab bc ca++≥ + + ⇔ + + − − − ≥
(
) ( )
( )
( )
( )
( )
222
2 2 20 0a abbb bccc caa ab bc ca⇔ − ++− ++− +≥⇔ − + − + − ≥
(đúng)
11
Bài 2: Cho các số không âm
,,abc
. Chứng minh rằng:
a)
22
ab a b++
≥
b)
(
)
2
2
2
2
1
a
aR
a
+
≥ ∀∈
+
c)
2
ab
ba
+≥
d)
( )
11
4ab
ab

+ +≥


e)
6
ab bc ca
cab
+++
++≥
Lời giải
a) Bình phương hai vế ta được:
22
22
2
2 2 2 4 44
ab a b ab ab ab ab ab
a b ab

+ + + ++ +
≥ ⇔≥ ⇔≥ ⇔+≥



(bất đẳng thức
đúng)
b) Ta có:
( )
2
2
22
11
2
11
a
a
aa
++
+
=
++
Áp dụng bất đẳng thức Cauchy cho hai số không âm
2
1a +
và
1
, ta có:
(
)
2 2 22
1 1 2 1 .1 2 2 1
a a aa
++≥ + ⇔ + ≥ +
Như vậy
22
22
22 1
2
11
aa
aa
++
≥=
++
(đpcm)
c) Áp dụng bất đẳng thức Cauchy cho hai số không âm
a
b
và
b
a
, ta có:
2. 2
a b ab
b a ba
+≥ =
d) Ta có:
( )
11
1 12 224
ab ab
ab
ab ba ba

+ + =+++=++≥+=


(đpcm)
e) Ta có:
2226
ab bc ca a c b c a b
c a b ca cb ba
+++
 
+ + =+++++≥++=
 
 
(đpcm)
12
BÀI TẬP TRẮC NGHIỆM
Câu 1: Tính
22
117,5 26,5 1440
P = −−
a)
108P =
b)
110P =
c)
120P =
d)
135P =
Lời giải
Chọn đáp án A
Giải thích:
Ta có:
( )( )
22
117,5 26,5 1440 117,5 26,5 117,5 26,5 1440 144.91 144.10P = − −= + − −= −
( )
144. 91 10 144.81 12.9 108
= −= = =
Câu 2: Phép tính nào sai
a)
13,5. 150 45
=
b)
4,8. 30 12
=
c)
7,2. 80 36=
d)
0,05. 500 5=
Lời giải
Chọn đáp án C
Giải thích:
A)
13,5. 150 13,5.150 135.15 15.9.15 15.3 45= = = = =
B)
4,8. 30 4,8.30 144 12= = =
C)
7,2. 80 7, 2.80 72.8 8.9.8 8.3 24= = = = =
D)
0,05. 500 0,05.500 5.5 5= = =
Câu 3: Phép tính
(
)
2
3 22 3 22− ++
cho kết quả là số nào
a)
3
a)
4
a)
5
a)
6
Lời giải
Chọn đáp án B
Giải thích:
Ta có:
13
(
)
(
)
(
)
(
)
(
)
2
22
2
22
3 22 3 22 2 22 1 2 22 1 2 1 2 1 2 1 2 1

− + + = − +− + + = − − + = −− +


(
) (
)
( )
2
2
2
21 21 21 21 2 4

= −− + = −− − =− =

Câu 4: Biểu thức
( )
( )
( )
2
344 1 2
x x x xy y− −++ +
có giá trị bằng số nào nếu thay
9; 4xy= =
a)
60
a)
65
a)
70
a)
75
Lời giải
Chọn đáp án D
Giải thích:
Ta có:
(
)
(
)(
)
( )
(
)
( )
22
22
344 1 2 32 1 3.2 1.
x x x xyy x xy x xy
− − + + +=− − + =− − +
( )
3. 2 1
x xy= −+
Thay
9x =
và
4y =
vào biểu thức
( )
3. 2 1x xy= −+
, ta được:
( )
( )( )
3. 2 9 1 9 4 3. 6 1 3 2 3.5.5 75= − + = − += =
Câu 5: Rút gọn
( ) ( )
2
25 5 2 1 25 25− ++ −
sẽ được số nào
a)
2
a)
4
a)
4−
a)
6
Lời giải
Chọn đáp án D
Giải thích:
Ta có:
( ) ( ) ( )
22
25 5 2 1 25 25 25.5 45 1 45 25 25 10 45 1 45 20 25 6−++ −= − ++ + −=− ++ +−=
Câu 6: Rút gọn
236816
234
E
++++
=
++
ta được:
a)
15E = +
b)
13E = −
c)
51−
d)
12E = +
14
Lời giải
Chọn đáp án D
Giải thích:
Ta có:
( )
( )
234 468
236816 236844
234 234 234
E
+++++
++++ +++++
= = =
++ ++ ++
( )( )
23412
12
234
E
++ +
⇒= =+
++
Câu 7: Trong các kết luận sau đây, kết luận nào sai
a)
3 5 15+>
b)
36 28+>+
c)
1 3 52−<−
d)
2 7 5 3 10−>−
Lời giải
Chọn đáp án B
Giải thích: Ta có
A)
( )
2
3 5 15 3 5 15 8 2 15 15+ > ⇔ + > ⇔+ >
, lại có
2 15 7,>
đúng vì
( )
2
2
2 15 7>
B)
( )
( )
22
3 6 2 8 3 6 2 8 9 2 18 10 2 16 18+>+⇔ + > + ⇔+ >+ =
( )
2
2
2 18 9 2 18 9 72 81⇔ >⇔ > ⇔ >
(sai)
C)
1 3 52−<−
, đúng vì
1 30
520
−<
−>
D)
2 7 5 3 10 2 7 8 10 28 74 16 10 16 10 74 28 46 8 10 23−>− ⇔ >− ⇔>− ⇔ >−=⇔ >
640 529⇔>
(đúng)
Câu 8: Nếu
15xx
− +=
thì
x
là số nào?
a)
3x =
b)
4x =
c)
6x =
d)
8
x =
Lời giải
Chọn đáp án D
Giải thích:
15
Ta có:
15 5 1
xx x x− +=⇔−= +
(
5
x −
phải là số không âm)
( )
( )
( )
( )
2
2
22
8
5 1 10 25 1 11 24 0
3
x tm
x x xx x xx
x loai
=
⇔− = + ⇔− +=+⇔− +=⇔
=
Câu 9: Điều kiện để
2
4 4 16xx++ −
có nghĩa là
a)
4
x = −
b)
4x =
c)
4
x = −
hoặc
4x ≥
d)
4x ≤
Lời giải
Chọn đáp án C
Giải thích:
Ta có:
( )( )
2
44 1644 4 4x x x xx
++ − = ++ − +
Để
2
4 4 16xx++ −
có nghĩa thì
( )( )
4
40 4
40
4
40
4
4 40
4
4
40
40
x
xx
x
x
x
x
xx
x
x
x
x
≥−
+ ≤ ≥−

+≥
= −


−≤
⇔ ⇔⇔
≤−

+ −≥
≥

≥
+≥
−≥
16
BÀI TẬP VỀ NHÀ
Bài 1: Tính
a)
32.200
A =
b)
5. 125
B
=
c)
(
)
(
)
9 2 14 9 2 14
C
=+−
d)
22
117,5 26,5 1440D = −−
Lời giải
a) Ta có:
2 22 2
32.200 4.8.2.10 2 .4 .10 2.4.10 80AA= = = = ⇒=
b) Ta có:
22
5. 125 5.5.25 5 .5 5.5 25BB= = = = ⇒=
c) Ta có:
( )
(
)
( )
2
2
9 2 14 9 2 14 9 2 14 81 56 25 5C = + − = − = −= =
d) Ta có:
( )( )
22
117,5 26,5 1440 117,5 26,5 117,5 26,5 1440 144.91 144.10D = − −= − + −= −
( )
144. 91 10 144.81 12.9 108= −= = =
Bài 2: Thực hiện phép tính
a)
2 8 12 5 27
18 48 30 162
A
−+
= −
−+
b)
3 23 2 2
( 2 3)
3 21
B
++
= + −+
+
Lời giải
a) Ta có:
2 8 12 5 27 6 6 6
36 2
18 48 30 162
A
− +− −
= − = −=
−+
b) Ta có:
3 23 2 2
( 2 3) 2
3 21
++
+ −+=
+
Bài 3: Rút gọn các biểu thức
a)
33
( , 0; )
uv u v
A uv u v
uv
uv
−+
= − ≥≠
−
+
b)
2
2
2 22
( 2)
2
xx
Bx
x
−+
= ≠±
−
Lời giải
a) Ta có:
33
( , 0; )
u v u v uv
A uv u v
uv
uv uv
−+ −
= − ≥ ≠=
−
+−
b) Ta có:
2
2
2 22 2
( 2)
2
2
xx x
Bx
x
x
−+−
= = ≠±
−
+
17
Bài 4: Rút gọn biểu thức
a)
(
)
2
xx yy
A xy
xy
+
= −−
+
b)
21
21
xx
B
xx
−+
=
++
c)
( )
( )
2
4
21
1
.
1
1
yy
x
C
y
x
−+
−
=
−
−
Lời giải
a) Ta có
( )
(
)
(
)
(
)
( )
( )
( )
33
2
22
x y x y x xy y
xx yy
A x y x y xy x y xy
xy xy xy
+ + −+
+
= − − = − +− = − +−
++ +
( )
2x xy y x y xy xy
=− +− +− =
b) Ta có
( )
( )
2
2
1
1
21
21 1
1
x
x
xx
B
xx x
x
−
−
−+
= = =
++ +
+
c) Ta có
( )
( )
( )
( )
( )
( )
2 42
4 42
21 1 1
1
1 11
. ..
1
1 11
1 11
yy y y
y
x xx
C
x
y yy
x xx
−+ − −
−
− −−
= = = =
−
− −−
− −−
Bài 5: So sánh các số sau
a)
72−
và
1
b)
85+
và
76
+
c)
2005 2007+
và
2 2006
d)
23 23++−
và
21+
Lời giải
a) Ta có:
( )
2
2
7 2 9 2 14
11
−=−
=
Xét
( )
22
9 2 14 1 8 2 14 8 2 .14 64 56 0 : 64 56do− −=− = − = − > >
Do đó
7 21
−>
b)
( )
( )
2
2
8 5 13 2 40
7 6 13 2 42
+=+
+=+
18
Xét
( )
(
)
( )
13 2 40 13 2 42 2 40 2 42 0 40 42 8 5 7 6+ −+ = − < < ⇒+<+
c) Ta có:
( )
( )
2
2
2005 2007 4012 2 2005.2007
2 2006 4.2006 8024
+=+
= =
Xét
( )
( )( )
22
4012 2 2005.2007 8024 2 2006 1 2006 1 2.2006 2 2006 1 2. 2006 0+ − = − + − = −− <
(vì
22
2006 1 2006−<
)
Do đó
2005 2007 2 2006+<
d) Ta có:
(
)
( )
( )
2
2
2
2
23 23 2322 3 236
21 323
+ + − =+ + − +− =
+=+
Xét
( )
6 3 22 3 22 0 2 3 2 3 2 1− + =− >⇒ + + − > +
Bài 6: Giải các phương trình sau
a)
2
25 9 2 5 3tt−= −
b)
3
2
21
t
t
−
=
+
c)
2
2 6 1( 1)x xx− +=− ≥
d)
1
5 4 20 9 45 3
5
tt t−+ − − − =
Lời giải
a) Ta có:
( )
( )
22
1
()
5
25 9 2 5 3 25 9 4 5 3
3
5
t loai
ttt t
t tm
=
−= −⇔ −= − ⇒
=
b) Ta có:
3
2 3221 3 4(21)
21
t
t t t tt
t
−
=⇒ −= +⇔ −= + ⇒=∅
+
c) Ta có:
2 22
5
2 6 1( 1) 2 6 ( 1) ( )
3
x x x x x x tm−+=−≥⇔−+=−⇔=
d) Ta có:
1 12 105
5 4 20 9 45 3 5 3
5 5 16
tt t t t−+ − − − = ⇔ − =⇒=
19
Bài 7:
Cho biểu thức
2
42
2
( 3 2) 6
x
A
xx
−
=
+− −
. Rút gọn rồi tìm giá trị của x để A có GTLN, tìm
GTLN đó
Lời giải
Ta có:
2
22 2 2
21
( 2)
( 2) 3( 2) 3
x
Ax
xx x x
−
= = ≠±
−+ − +
Vì
2
3 3,xx+ ≥∀
nên
2
11 1
axA= 0
x 33 3
Mx≤ ⇒ ⇔=
+
.
Bài 8: So sánh các số sau
a)
35+
và
22 6+
b)
23 4+
và
3 2 10+
c)
18
và
15. 17
Lời giải
a) Ta có:
2
(3 5) 14 6 5 14 180;(2 2 6) 14 4 12 14 192 3 5 2 2 6+ = + = + + = + = + ⇒+ < +
b)
22
(2 3 4) 12 16 3 16 28 16 3 28 256.3;(3 2 10) 28 36.20+ =+ +=+ =+ + =+
23 4 32 10
⇒+>+
c)
Cách 1:
22
18 324;( 15. 15) 255 18 15. 17= = ⇒>
Cách 2:
22
15. 17 16 1. 17 1 16 1 16 16 18= − −= −< = <
.
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

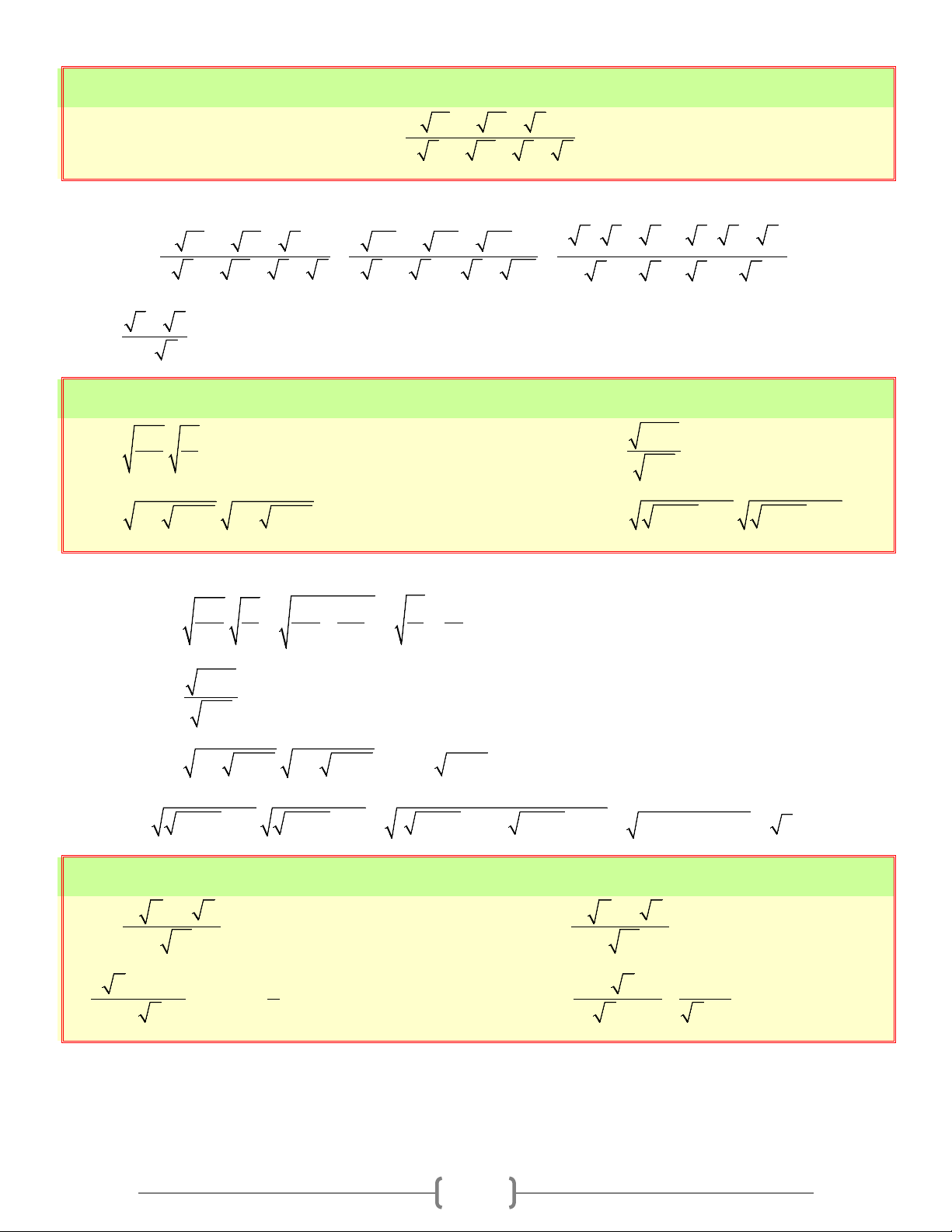
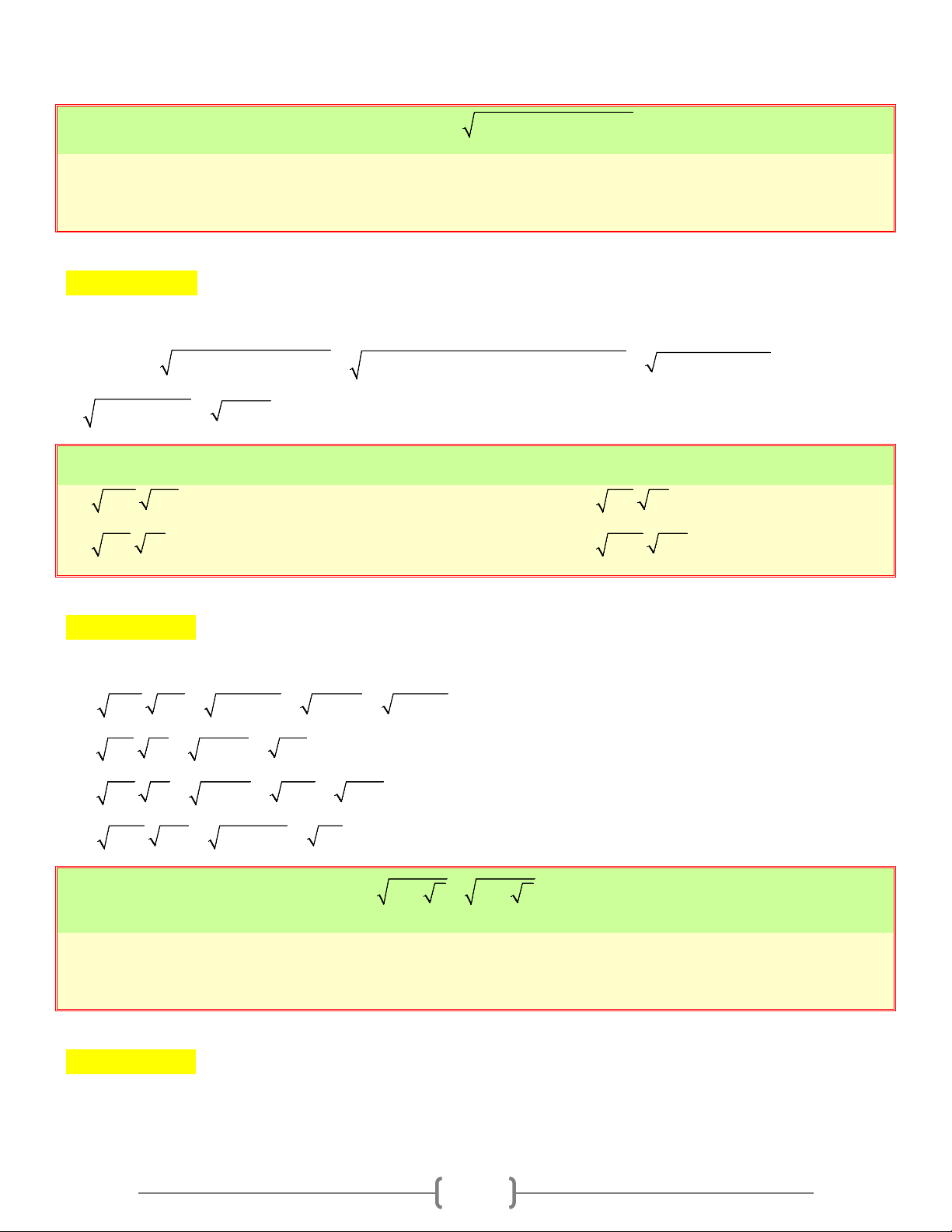
LIÊN HỆ GIỮA PHÉP NHÂN VÀ PHÉP KHAI PHƯƠNG A. Tóm tắt lý thuyết
1. Định lý: Với hai số a,b ≥ 0 , ta có: .
a b = a. b
Chú ý: Định lí trên còn có thể mở rộng cho tích của nhiều số không âm
2. Quy tắc khai phương một tích
Với A ≥ 0, B ≥ 0, ta có: AB = A. B
Mở rộng: Với A ≥ 0, A ≥ 0,..., A ≥ n 0 1 2
ta có: A A ....A = A A A n . ... 1 2 1 2 n
3. Quy tắc nhân các căn bậc hai
Với hai biểu thức A ≥ 0, B ≥ 0, ta có: A. B = . A B
Chú ý: Với A ≥ 0, ta có: ( )2 2
A = A = A = A
B. Bài tập và các dạng toán
Dạng 1: Tính giá trị biểu thức
Cách giải: Áp dụng công thức khai phương một tích Bài 1: Tính a. 25.144 b. 52.13 c. 45.80 d. 7. 28 Lời giải a) Ta có: 25.144 = 5.12 = 60 b) Ta có: 2
52.13 = 52.13 = 4.13.13 = 4. 13 = 26 c) Ta có: 2
45.80 = 5.9.5.16 = 5 . 9. 16 = 60 d) Ta có: 2 2
7. 28 = 7.28 = 7.7.4 = 7 . 2 =14 Bài 2: Tính  2 50  a.  + − 24 . 6  + 3 3  b. 3 5. 2    3 4  c.  − 3 + 5 . 12  d. 3− 5. 8 4 3    1 Lời giải  2 50  2 50 a) Ta có:  + − 24 . 6 = .6 + .6 − 24.6 = 0  3 3  3 3   b) Ta có: + = + = ( + )2 3 5. 2 3.2 2 5 5 1 = 5 +1   c) Ta có: 3 4  − 3 + 5 . 12 = 7  4 3   
d) Ta có: 3− 5. 8 = 2( 5 − )1 Bài 3: Tính 1 1 a. 55.77.35 b. . 2. 125. 8 5 c. 2 −1. 2 +1 d. 2
2 2.( 3 − 2) + (1+ 2 2) − 2 6 Lời giải
a) Ta có: 55.77.35 = 5.11.7.11.5.7 = 5.7.11 = 385 1 1 1 1 2.125 25 5 b) Ta có: . 2. 125. = .2.125. = = = 8 5 8 5 8.5 4 2 c) Ta có: 2 −1.
2 +1 = ( 2 −1).( 2 +1) = 2 −1 =1 d) Ta có: 2
2 2.( 3 − 2) + (1+ 2 2) − 2 6 = 2 6 − 4 2 +1+ 4 2 + 8 − 2 6 = 9 Bài 4: Tính
a) A = 3+ 5+ 2 3 . 3− 5+ 2 3
b) B = 4 + 8. 2 + 2 + 2 . 2 − 2 + 2
c) C = ( 12 +3 15 −4 135) 3
d) D = 2 40 12 − 2 75 −3 5 48 Lời giải a) Ta có: 2 2
A = 3+ 5 + 2 3 . 3− 5 + 2 3 = 3 − ( 5 + 2 3) = 9 − (5 + 2 3) 2
= 9 − 5 − 2 3 = 4 − 2 3 = ( 3 −1) = 3 −1 b) Ta có: 2 2 2
B = 4 + 8. 2 + 2 + 2 . 2 − 2 + 2 = 4 + 4. 2. 2 − ( 2 + 2 ) = 4 + 2 2. 2 − 2
⇒ B = 2.(2 + 2)(2 − 2) = 2.2 = 2 c) Ta có: 2
( 12 + 3 15 − 4 135) 3 = 36 + 3 9.5 − 4 9 .5 = 6 + 9 5 − 36 5 = 6 − 27 5 d) Ta có:
C = 2 40 12 − 2 75 − 3 5 48 = 2 40 12 − 2 5 3 − 3 20 3 = 2 80 3 − 2 5 3 − 6 5 3
⇒ C = 8 5 3 − 2 5 3 − 6 5 3 = 5 3(8 − 2 − 6) = 0 Bài 5: Tính
a) A = (4 + 15)( 10 − 6) 4 − 15
b) B = (3− 5) 3+ 5 + (3+ 5) 3− 5
c) C = 2 + 3. 2 + 2 + 3 . 2 + 2 + 2 + 3 . 2 − 2 + 2 + 3 Lời giải
a) Ta có: A = (4 + 15)( 10 − 6) 4 − 15 = ( 10 − 6) 4 + 15. 4 + 15. 4 − 15
= ( 10 − 6) 4 + 15. (4 + 15)(4 − 15) = 10 − 6. ( 10 − 6)(4 + 15) =
10 − 6. 4 10 + 150 − 4 6 − 90 =
10 − 6. 10 + 6 = ( 10 − 6)( 10 + 6) = 4 = 2
b) Ta có: B = (3− 5) 3+ 5 + (3+ 5) 3− 5 = 3− 5. 3− 5. 3+ 5 + (3+ 5) 3− 5
= 3− 5. 3+ 5 ( 3− 5 + 3+ 5 ) = 2( 3− 5 + 3+ 5) = 2( 3− 5. 2 + 3+ 5. 2) 2 2
= 2( 6 − 2 5 + 6 + 2 5 ) = 2( ( 5 −1) + ( 5 +1) = 2( 5 −1+ 5 +1) = 2 10
c) Ta có: C = 2 + 3. 2 + 2 + 3 . 2 + 2 + 2 + 3 . 2 − 2 + 2 + 3
⇒ C = 2 + 3. 2 + 2 + 3 . 2 − 2 + 3 2 2
⇒ C = 2 + 3.( 2 − ( 2 + 3 ) ) = 2 + 3. 2 − 3 =1 3
Dạng 2: Rút gọn biểu thức
Cách giải: Áp dụng công thức khai phương của một tích
Bài 6: Rút gọn a) 10 15 A − = b) 6 15 B − = 8 − 12 35 − 14 c) 5 5 C + = d) 15 5 5 2 5 D − − = + 10 + 2 3 −1 2 5 − 4 Lời giải a) Ta có: 10 − 15 5. 2 − 5. 3 5 A = = ⇒ A = 8 − 12 4. 2 − 4. 3 2 b) Ta có: 6 15 3 21 B − − − = = = 35 − 14 7 7 c) Ta có: 5 5 5 10 C + = = = 10 + 2 2 2 d) Ta có: 15 5 5 2 5 5( 3 1) 5( 5 2) 5 3 5 D − − − − = + = + = 5 + = 3 −1 2 5 − 4 3 −1 2( 5 − 2) 2 2
Bài 7: Rút gọn các biểu thức sau a) 6 14 B + = b) 2 3 6 8 4 C + + + + = 2 3 + 28 2 + 3 + 4 c) 3 8 2 12 20 D − + = 3 18 − 2 27 + 45 Lời giải a) Ta có: 6 14 2. 3 2. 7 2 1 B + + = = = = 2 3 + 28 2 3 + 4. 7 2 2 b) Ta có: 2 3 6 8 4 2 3 4 4 6 8 C + + + + + + + + + = = = 2 +1 2 + 3 + 4 2 + 3 + 4 c) Ta có: 3 8 2 12 20 3.2 2 2.2 3 2 5 2(3 2 2 3 5) 2 D − + − + − + = = = =
3 18 − 2 27 + 45 3.3 2 − 2.3 3 + 3 5 3(3 2 − 2 3 + 5) 3 4
Bài 8: Rút gọn biểu thức sau: 2 15 2 10 6 3 A − + − = 2 5 − 2 10 − 3 + 6 Lời giải 2 5 ( 3 − 2)− 3( 3 − − + − − + − 2 2 15 2 10 6 3 2 5.3 2 5.2 3.2 3 ) Ta có: A = = =
2 5 − 2 10 − 3 + 6 2 5 − 2 5.2 − 3 + 3.2 2 5 (1− 2)− 3(1− 2) 3 2 A − ⇒ = 1− 2
Bài 9: Rút gọn các biểu thức sau: 6 a) 2 − t 3 28y = . t A (t ≤ 0) b) B = ( y < 0) 3 8 4 7y c) 2 2
C = x − x −1. x + x −1 (x ≥ ) 1 d) 4 2 4 2 D =
x + 4 − x . x + 4 + x Lời giải 2 a) Ta có: 2 − t 3t 2 − t  3 −  − = . = . t t t A = = (t ≤   0) 3 8 3  8  4 2 6 b) Ta có: 28y B =
( y < 0) ⇒ B = 2 − y 4 7y
a) Ta có: C = x − x −
x + x − = x − ( x − )2 2 2 2 2 1. 1 1 =1 a) Ta có: 4 2 4 2 4 2 4 2 4 2 2
x + 4 − x . x + 4 + x = ( x + 4 − x )( x + 4 + x ) = (x + 4) − (x ) = 4 = 2
Bài 10: Rút gọn các biểu thức sau: a) x y + y x x y − y x A =
(x ≥ 0; y ≥ 0;xy ≠ 0) b) B =
(x ≥ 0; y ≥ 0; x ≠ y)
x + 2 xy + y
x − 2 xy + y
c) 3 a − 2a −1 1 + + −
(a ≥ 0;a ≠ ) d) a 4 a 4 4 a D = +
(a ≥ 0;a ≠ 4) 4a − 4 a +1 4 a + 2 a − 2 Lời giải 5 x y ( x + + y x y y x ) a) Ta có: xy A = = ⇒ = x + xy + y ( ) A 2 2 x + + y x y b) Ta có: x y − y x xy B = =
x − 2 xy + y x − y
c) Ta có: 3 a − 2a −1 (2 a −1)(1− a) 1− a = = 2 4a − 4 a +1 (2 a −1) 2 a −1 a a a ( a + )2 2 ( a −2)( a + + + − 2 4 4 4 ) d) Ta có: D = + = − = 0 a + 2 a − 2 a + 2 a − 2 6
Dạng 3: Giải phương trình
Cách giải: Khi giải phương trình chứa căn thức, luôn cần chú ý đến các điều kiện đi kèm. B ≥ 0 +) A = B ⇔  2 A = B  ≥ ≥ +) B 0(hoac A 0) A = B ⇔  A = B
Bài 1: Giải các phương trình sau a) 2
x − 2x + 4 = 2x − 2 b) 2
x − 2x = 2 − 3x c) 2
−x + x + 4 = x − 3 d) 2
x + 3 − 2 x − 9 = 0 Lời giải 2x − 2 ≥ 0   − ≥ a) Ta có: 2x 2 0 2
x − 2x + 4 = 2x − 2 ⇔  ⇔  ⇒ x =
x − 2x + 4 =  (2x − 2) 2 2 2 x = 2  2 2 − 3x ≥ 0 x ≤ b) Ta có: 2
x − 2x = 2 − 3x ⇔  ⇔  3 ⇒ x = 2 − 2
x − 2x = 2 − 3x  2
x + x − 2 = 0 x − 3 ≥ 0 x − 3 ≥ 0  c) Ta có: 2  x =1
−x + x + 4 = x − 3 ⇔  ⇔  ⇒ x ∈∅  x x 4  (x 3)2 2  − + + = −  5 x =  2 x = 3  − ≥ (tm) x 3 0 d) Cách 1: Ta có 2 x 3 2 x 9 0   + − − = ⇔  ⇔ ⇒ = x − =  ( − x 3 2 x − )  11 3 4 9 x = (loai)  4 Cách 2: Với 2
x ≥ 3 ⇒ x − 9 = x − 3. x + 3 ⇒ x − 3 (1− 2 x +3) = 0 ⇒ x = 3(tm)
Bài 2: Giải các phương trình sau a. 2 9.(2 − 3x) = 6 b. 2
4x − 9 = 2 2x + 3
c. 10(x −3) = 20 d. 2
x + 6x + 9 = 3x − 6 Lời giải 7  4 a) Ta có: x = 2 9.(2 3x) 6 3 2 3x 6 2 3x 2  − = ⇔ − = ⇔ − = ⇔ 3  x = 0 b) Ta có: 2
4x − 9 = 2 2x + 3 ⇔ (2x − 3)(2x + 3) = 2 2x + 3 ⇔ 2x − 3. 2x + 3 = 2 2x + 3  3 − 2 + 3 = 0 x x =   2
⇔ 2x + 3.( 2x − 3 − 2) = 0 ⇔  ⇔   2x −3 = 0  7 x =  2
c) Ta có: 10(x −3) = 20 ⇔10(x −3) = 20 ⇔ x = 5(tm) (điều kiện x ≥ 3) x ≥ 2 3  x − 6 ≥ 0  9   d) Ta có: 2 x = (tm)
⇔ (x + 3) = 3x − 6 ⇔ x + 3 = 3x − 6 ⇔ x + 3 = 3x − 6 ⇔   2   x 3 3x 6  + = − +  3  x = (loai)   4
Bài 3: Giải phương trình ẩn y a) 1
4y − 20 + y − 5 − 9y − 45 = 4 b) 1 1 2 9y − 27 − 25y − 75 − 49y −147 = 20 3 5 7 Lời giải
a) Điều kiện y ≥ 5 1
Ta có: 4y − 20 + y − 5 −
9y − 45 = 4 ⇔ 2 y − 5 = 4 ⇔ y = 9 (thỏa mãn) 3
b) Điều kiện y ≥ 3 Ta có: 1 1 y − − y − − y − = ⇔ ( y − ) 1 − (x − ) 1 2 9 27 25 75 49 147 20 2 9 3 25 3 − 49(x −3) = 20 5 7 5 7 ( y − ) 1 − ( y − ) 1 2 9 3 25 3 −
49( y −3) = 20 ⇔ 6 y −3 − y −3 − y −3 = 20 ⇔ 4 y −3 = 20 5 7
⇔ y − 3 = 5 ⇔ y = 28 (thỏa mãn)
Bài 4: Giải các phương trình sau a) − 2 x
4x − 9 = 2 2x + 3 b) 9 7 = 7x + 5 7x + 5 Lời giải 8  3 −  3 x ≥ x − ≥ a) Ta có: 2 2
4x − 9 = 2 2x + 3 ⇔ 4x − 9 = 8x +12 ⇔  2 ⇔  2  2  2
4x − 9 = 8x +12
4x −8x − 21 = 0  3 x ≥ −  2  7  x =  7  2 7 3 − ⇔  x = ⇔  ⇒ S =  ;    2  3 − 2 2  x  =  3 −  2 x =   2 b) Điều kiện 5 7x 5 0 x − + > ⇔ > 7
Ta có: x − = x + ⇔ x − = ( x + )2 9 7 7 5 9 7 7
5 = 7x + 5 ⇔ x = 6 (thỏa mãn) 7x + 5 9
Dạng 4: Chứng minh đẳng thức
Cách giải: Áp dụng bất đẳng thức Côsi cho các số không âm, ta có:
+) a + b ≥ ab , dấu “=” xảy ra khi và chỉ khi a = b 2
+) a + b + c 3 ≥ abc 3
Bài 1: Cho các số không âm a,b,c . Chứng minh
a) a + b ≥ ab (BĐT Cauchy)
b) a + b < a + b 2 c) 1
a + b + ≥ a + b
d) a + b + c ≥ ab + bc + ca 2 Lời giải a + b  ≥ a) Do 0
a,b,c ≥ 0 ⇒  2  ab ≥ 0
Bình phương hai vế của bất đẳng thức ta được: 2
a + b  ≥ ( ) 2 2 2 2 2 2 2
a + 2ab + b
a + 2ab + b
a + 2ab + b − 4 ⇔ ≥ ⇔ − ≥ 0 ab ab ab ab ⇔ ≥   0  2  4 4 4
a − ab + b (a −b)2 2 2 2 ⇔ ≥ 0 ⇔
≥ 0 (bất đẳng thức đúng) 4 4
b) Bình phương hai vế của bất đẳng thức ta được:
( a+b)2 <( a + b)2 ⇔ a+b< a+b+2 ab ⇔ 0< 2 ab (bất đẳng thức đúng)
c) Ta có: a + b + ≥ a + b ⇔ a + b + − a − b ≥ ⇔ ( a − )2 +( b − )2 1 1 0 1 1 ≥ 0 (bất đẳng thức 2 2 đúng)
d) Ta có: a +b + c ≥ ab + bc + ca ⇔ 2a + 2b + 2c − 2 ab − 2 bc − 2 ca ≥ 0
⇔ (a − ab +b)+(b − bc + c)+(c − ca + a) ≥ ⇔ ( a − b)2 +( b − c)2 +( c − a )2 2 2 2 0 ≥ 0 (đúng) 10
Bài 2: Cho các số không âm a,b,c . Chứng minh rằng: 2 a) a + b a + b a + ≥ b) 2 ≥ 2( a ∀ ∈ R) 2 2 2 a +1 c) a b + ≥ 2 d) (a b) 1 1  + + ≥   4 b aa b
e) a + b b + c c + a + + ≥ 6 c a b Lời giải
a) Bình phương hai vế ta được: 2 2
a + b   a + b
a + b a + b + 2 ab
a + b 2 ab   ≥   ⇔ ≥ ⇔ ≥
⇔ a + b ≥ 2 ab  (bất đẳng thức 2   2  2 4 4 4     đúng) a + 2 ( 2 2 a + ) 1 +1 b) Ta có: = 2 2 a +1 a +1
Áp dụng bất đẳng thức Cauchy cho hai số không âm 2 a +1 và 1, ta có: 2 a + + ≥ ( 2a + ) 2 2 1 1 2
1 .1 ⇔ a + 2 ≥ 2 a +1 2 2
Như vậy a + 2 2 a +1 ≥ = 2 (đpcm) 2 2 a +1 a +1
c) Áp dụng bất đẳng thức Cauchy cho hai số không âm a và b , ta có: b a a b
+ ≥ 2 a . b = 2 b a b a d) Ta có: ( ) 1 1  + + =1 a b + + +1 = 2 a b a b + + ≥ 2 + 2 =   4 (đpcm)  a b b a b a
e) Ta có: a + b b + c c + a a c   b c   a b  + + = + + + + + ≥ 2 + 2 + 2 =       6 (đpcm) c a b
c a   c b   b a  11
BÀI TẬP TRẮC NGHIỆM Câu 1: Tính 2 2
P = 117,5 − 26,5 −1440 a) P =108 b) P =110 c) P =120 d) P =135 Lời giải Chọn đáp án A Giải thích: Ta có: 2 2
P = 117,5 − 26,5 −1440 = (117,5 + 26,5)(117,5 − 26,5) −1440 = 144.91−144.10
= 144.(91−10) = 144.81 =12.9 =108
Câu 2: Phép tính nào sai a) 13,5. 150 = 45 b) 4,8. 30 =12 c) 7,2. 80 = 36 d) 0,05. 500 = 5 Lời giải Chọn đáp án C Giải thích:
A) 13,5. 150 = 13,5.150 = 135.15 = 15.9.15 =15.3 = 45 B) 4,8. 30 = 4,8.30 = 144 =12
C) 7,2. 80 = 7,2.80 = 72.8 = 8.9.8 = 8.3 = 24
D) 0,05. 500 = 0,05.500 = 5.5 = 5
Câu 3: Phép tính ( − + + )2 3 2 2
3 2 2 cho kết quả là số nào a) 3 a) 4 a) 5 a) 6 Lời giải Chọn đáp án B Giải thích: Ta có: 12 ( )2 ( )2 ( )2 ( ) 22 3 2 2 3 2 2 2 2 2 1 2 2 2 1 2 1 2 1  − + + = − + − + + = − − + =  ( 2−1− 2+1)2   =  − −  ( + ) 2 =  ( − − − )2 =(− )2 2 1 2 1 2 1 2 1 2 = 4
Câu 4: Biểu thức (− )2
3 (4x − 4 x + )
1 (x + 2 xy + y) có giá trị bằng số nào nếu thay x = 9; y = 4 a) 60 a) 65 a) 70 a) 75 Lời giải Chọn đáp án D Giải thích:
Ta có: (− ) ( x − x + )(x + xy + y) = (− ) ( x − )2 ( x + y)2 2 2 3 4 4 1 2 3 2 1 = 3
− . 2 x −1 . x + y
= 3. 2 x −1 ( x + y )
Thay x = 9 và y = 4 vào biểu thức = 3. 2 x −1 ( x + y), ta được:
= 3. 2 9 −1 ( 9 + 4) = 3.(6− ) 1 (3+ 2) = 3.5.5 = 75 Câu 5: Rút gọn ( − )+( + )2 2 5 5 2
1 2 5 − 25 sẽ được số nào a) 2 a) 4 a) 4 − a) 6 Lời giải Chọn đáp án D Giải thích: Ta có: ( − )+( + )2 − = − + + + ( )2 2 5 5 2 1 2 5 25 2 5. 5 4 5 1 4 5
2 5 − 25 =10 − 4 5 +1+ 4 5 + 20 − 25 = 6 Câu 6: Rút gọn 2 3 6 8 16 E + + + + = ta được: 2 + 3 + 4 a) E =1+ 5 b) E =1− 3 c) 5 −1 d) E =1+ 2 13 Lời giải Chọn đáp án D Giải thích: ( 2 + 3+ 4)+( 4 + 6 + + + + + + + + + + 8 2 3 6 8 16 2 3 6 8 4 4 ) Ta có: E = = = 2 + 3 + 4 2 + 3 + 4 2 + 3 + 4 ( 2 + 3+ 4)(1+ 2) ⇒ E = = 1+ 2 2 + 3 + 4
Câu 7: Trong các kết luận sau đây, kết luận nào sai a) 3 + 5 > 15 b) 3 + 6 > 2 + 8 c) 1− 3 < 5 − 2 d) 2 7 −5 > 3− 10 Lời giải Chọn đáp án B
Giải thích: Ta có A) + > ⇔ ( + )2 3 5 15 3
5 >15 ⇔ 8 + 2 15 >15 , lại có 2 15 > 7, đúng vì ( )2 2 2 15 > 7 B) + > + ⇔ ( + )2 > ( + )2 3 6 2 8 3 6 2
8 ⇔ 9 + 2 18 >10 + 2 16 =18 ⇔ > ⇔ ( )2 2 2 18 9
2 18 > 9 ⇔ 72 > 81 (sai)  − <
C) 1− 3 < 5 − 2, đúng vì 1 3 0   5 − 2 > 0
D) 2 7 −5 > 3− 10 ⇔ 2 7 > 8− 10 ⇔ 28 > 74 −16 10 ⇔16 10 > 74 − 28 = 46 ⇔ 8 10 > 23 ⇔ 640 > 529 (đúng)
Câu 8: Nếu x − x +1 = 5 thì x là số nào? a) x = 3 b) x = 4 c) x = 6 d) x = 8 Lời giải Chọn đáp án D Giải thích: 14
Ta có: x − x +1 = 5 ⇔ x −5 = x +1 ( x −5 phải là số không âm)  ⇔ ( x = tm
x − 5) = ( x +1)2 8 2 ( ) 2 2
⇔ x −10x + 25 = x +1 ⇔ x −11x + 24 = 0 ⇔  x = 3  (loai)
Câu 9: Điều kiện để 2
4 x + 4 + x −16 có nghĩa là a) x = 4 − b) x = 4 c) x = 4 − hoặc x ≥ 4 d) x ≤ 4 Lời giải Chọn đáp án C Giải thích: Ta có: 2
4 x + 4 + x −16 = 4 x + 4 + (x − 4)(x + 4) x ≥ 4 − x+4 ≤ 0   x ≥ 4 − x + 4 ≥ 0 Để   x = 4 − 2
4 x + 4 + x −16 có nghĩa thì (
⇔  − ≤ ⇔  ≤ − ⇔  x +  )(x − ) x 4 0 x 4 4 4 ≥ 0    x ≥ 4 x + 4 ≥ 0 x ≥ 4   x − 4 ≥ 0 15 BÀI TẬP VỀ NHÀ Bài 1: Tính a) A = 32.200 b) B = 5. 125
c) C = (9+ 2 14)(9−2 14) d) 2 2
D = 117,5 − 26,5 −1440 Lời giải a) Ta có: 2 2 2 2
A = 32.200 = 4.8.2.10 = 2 .4 .10 = 2.4.10 ⇒ A = 80 b) Ta có: 2 2
B = 5. 125 = 5.5.25 = 5 .5 = 5.5 ⇒ B = 25 c) Ta có: C = ( + )( − ) = −( )2 2 9 2 14 9 2 14 9 2 14 = 81− 56 = 25 = 5 d) Ta có: 2 2
D = 117,5 − 26,5 −1440 = (117,5 − 26,5)(117,5 + 26,5) −1440 = 144.91−144.10
= 144.(91−10) = 144.81 =12.9 =108
Bài 2: Thực hiện phép tính a) 2 8 12 5 27 A − + = − b) 3 2 3 2 2 B + + = + − ( 2 + 3) 18 − 48 30 + 162 3 2 +1 Lời giải a) Ta có: 2 8 12 5 27 6 6 6 A − + − − = − = − = 18 − 48 30 + 162 3 6 2 b) Ta có: 3+ 2 3 2 + 2 + − ( 2 + 3) = 2 3 2 +1
Bài 3: Rút gọn các biểu thức 3 3 2 a) u − v u + v A − + = −
(u,v ≥ 0;u ≠ v) b) x 2x 2 2 B = (x ≠ ± 2) u + v u − v 2 x − 2 Lời giải 3 3 a) Ta có: u − v u + v − = − ( , ≥ 0; ≠ ) uv A u v u v = u + v u − v u − v 2 b) Ta có:
x − 2x 2 + 2 x − 2 B = = (x ≠ ± 2) 2 x − 2 x + 2 16
Bài 4: Rút gọn biểu thức a) + = − ( − )2 x x y y A x y b) x − 2 x +1 B = x + y x + 2 x +1 1 (y−2 y x + − )2 1 c) C = . y −1 (x − )4 1 Lời giải a) Ta có 3 3 =
− ( − )2 ( x) +( y ) = − (
x + y x − xy + + y x x y y A x y
x + y − 2 xy ) ( )( ) =
− (x + y − 2 xy ) x + y x + y x + y
= x − xy + y − (x + y − 2 xy ) = xy x 2 x 1 ( x − )21 x − − + 1 b) Ta có B = = = x + 2 x +1 ( x )2 x + + 1 1 x −1
(y−2 y + )21 x−1 ( y − )41 x−1 ( y − )21 c) Ta có y −1 C = . = . = . = y −1 (x − )4 1 y −1 (x − )4 1 y −1 (x − )2 1 x −1
Bài 5: So sánh các số sau a) 7 − 2 và 1 b) 8 + 5 và 7 + 6 c) 2005 + 2007 và 2 2006 d) 2 + 3 + 2 − 3 và 2 +1 Lời giải ( 7 − 2)2 a) Ta có: = 9 − 2 14  2 1  =1 Xét 2 2
9 − 2 14 −1 = 8 − 2 14 = 8 − 2 .14 = 64 − 56 > 0(do : 64 > 56) Do đó 7 − 2 >1 ( 8+ 5  )2 =13+2 40 b) ( 7 + 6  )2 =13+2 42 17
Xét (13+ 2 40)−(13+ 2 42) = 2 40 −2 42 < 0(40 < 42) ⇒ 8 + 5 < 7 + 6 ( 2005+ 2007  )2 = 4012+2 2005.2007 c) Ta có: (2 2006  )2 = 4.2006=8024 Xét ( + )− = ( − )( + ) 2 2
4012 2 2005.2007 8024 2 2006 1 2006 1 − 2.2006 = 2 2006 −1 − 2. 2006 < 0 (vì 2 2 2006 −1< 2006 )
Do đó 2005 + 2007 < 2 2006
( 2+ 3 + 2− 3)2 =2+ 3+2 2 −( 3)2 2 + 2 − 3 =  6 d) Ta có:  ( 2 +  )2 1 = 3+ 2 3
Xét 6 −(3+ 2 2) = 3−2 2 > 0 ⇒ 2+ 3 + 2− 3 > 2 +1
Bài 6: Giải các phương trình sau a) − 2 t
25t − 9 = 2 5t − 3 b) 3 = 2 2t +1 c) 2 2
− x + 6 = x −1(x ≥1) d) 1
t − 5 + 4t − 20 − 9t − 45 = 3 5 Lời giải  1 t = (loai)  a) Ta có: 2 2 t − = t − ⇔ t − = ( t − ) 5 25 9 2 5 3 25 9 4 5 3 ⇒   3 t = (tm)  5
b) Ta có: t −3 = 2 ⇒ t −3 = 2 2t +1 ⇔ t −3 = 4(2t +1) ⇒ t = ∅ 2t +1 c) Ta có: 2 2 2 5 2
− x + 6 = x −1(x ≥1) ⇔ 2
− x + 6 = (x −1) ⇔ x = (tm) 3 d) Ta có: 1 12 105
t − 5 + 4t − 20 − 9t − 45 = 3 ⇔
t − 5 = 3 ⇒ t = 5 5 16 18 Bài 7: 2 Cho biểu thức x − 2 A =
. Rút gọn rồi tìm giá trị của x để A có GTLN, tìm 4 2
x + ( 3 − 2)x − 6 GTLN đó Lời giải 2 Ta có: x − 2 1 A = = (x ≠ ± 2 ) 2 2 2 2
x (x − 2) + 3(x − 2) x + 3 Vì 2 x + 3 ≥ 3 x ∀ , nên 1 1 1 ≤ ⇒ a M xA= ⇔ x = 0 . 2 x + 3 3 3
Bài 8: So sánh các số sau a) 3+ 5 và 2 2 + 6 b) 2 3 + 4 và 3 2 + 10 c) 18 và 15. 17 Lời giải a) Ta có: 2
(3+ 5) =14 + 6 5 =14 + 180;(2 2 + 6) =14 + 4 12 =14 + 192 ⇒ 3+ 5 < 2 2 + 6 b) 2 2
(2 3 + 4) =12 +16 3 +16 = 28 +16 3 = 28 + 256.3;(3 2 + 10) = 28 + 36.20 ⇒ 2 3 + 4 > 3 2 + 10 c) Cách 1: 2 2
18 = 324;( 15. 15) = 255 ⇒18 > 15. 17 Cách 2: 2 2
15. 17 = 16 −1. 17 −1 = 16 −1 < 16 =16 <18 . 19