Tài liệu Toán 9 chủ đề một số hệ thức về cạnh và góc trong tam giác vuông

MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG A. Tóm tắt lý thuyết 1. Cho A
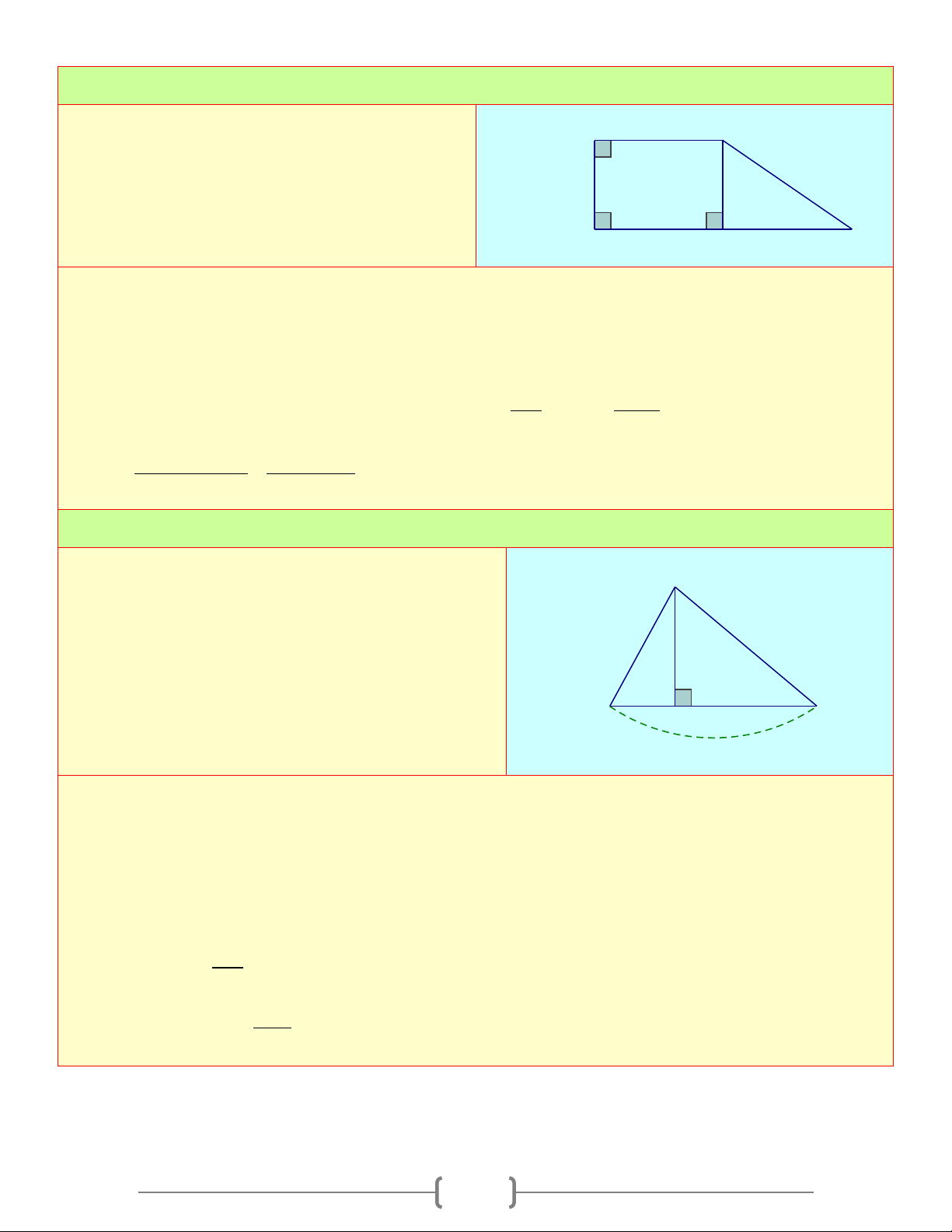
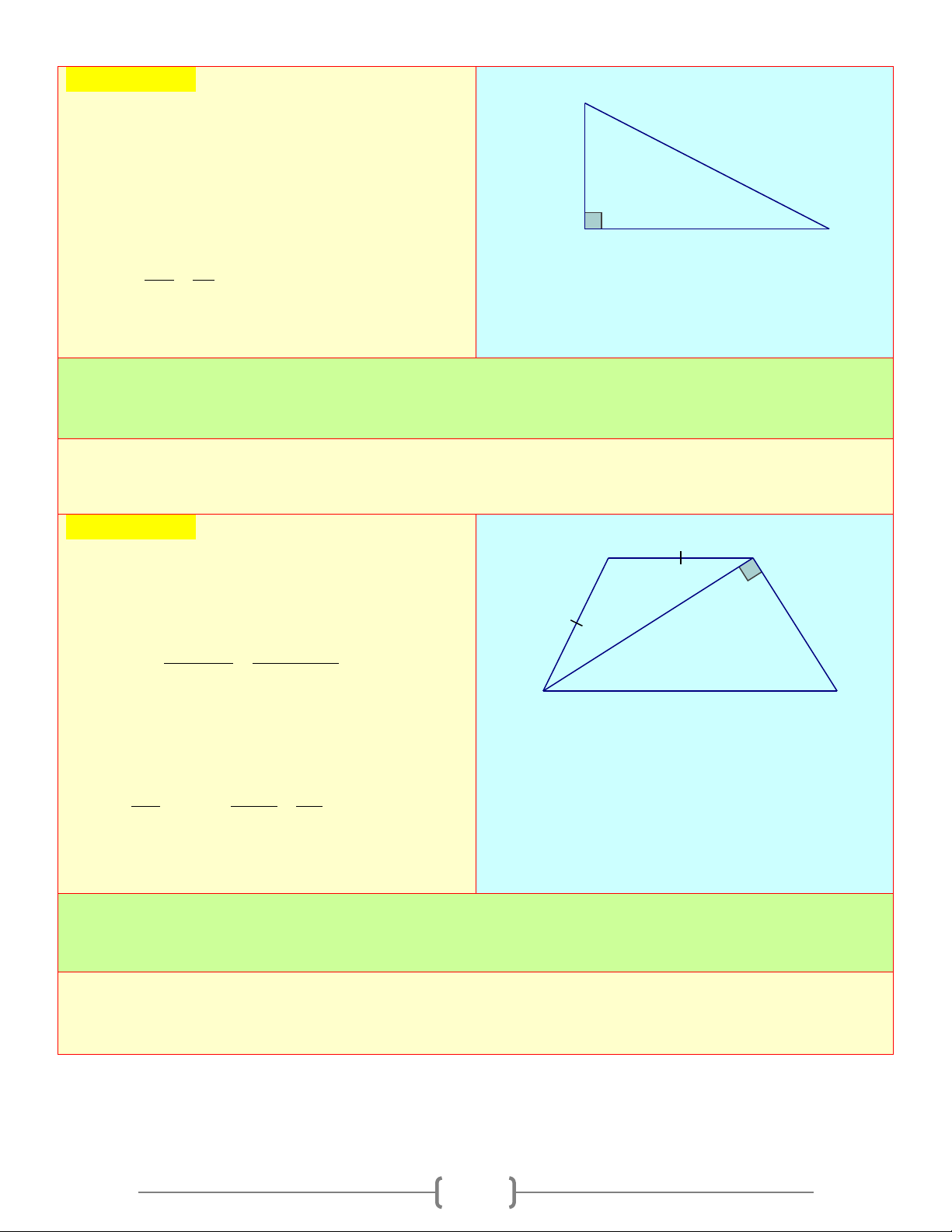
∆ BC vuông tại A , có BC = a, AB = c, AC = b, ta có: A + =  =  b . a sinB . a cosC + =  =  b . c tanB . c cosC c b + =  =  c . a sinC . a cosB B a + =  =  c . b tanC . b cotB C 2. Giải tam giác vuông
Trong một tam giác vuông, nếu biết trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh
và không kể góc vuông) thì ta sẽ tìm được tất cả các yếu tố còn lại của tam giác vuông đó.
(Bài toán này gọi là bài toán: Giải tam giác vuông)
B. Bài tập và các dạng toán
Dạng 1: Giải tam giác vuông
Cách giải: Để giải tam giác vuông ta dùng hệ thức giữa cạnh và các góc trong tam giác vuông
- Chú ý: Các bài toán về giải tam giác vuông bao gồm:
+) Gải tam giác vuông khi biết độ dài 1 cạnh và số đo 1 góc nhọn
+) Giải tam giác vuông khi biết độ dài 2 cạnh Bài 1: Cho tam giác A
∆ BC vuông tại A . Gọi BC = a A
AC = b, AB = c . Giải tam giác A ∆ BC , biết a) b = (cm)  0 10 ;C = 30 c b b) =  0 a 20c , m B = 35 B a C c) a =15c , m b =10cm Lời giải a) Sử dụng tỉ số   cosC, sinC 20 3 10 3 ⇒ = =  0 a (cm);c (cm); B = 60 3 3 1 b) Ta có: 0 0
b = 20.sin35 ≈11,47(cm);c = 20.cos35 ≈16,38(cm) c) Ta có: =  10 = ⇒  0 ≈  0
c 5 5(cm);SinB
B 41,8 ,C = 48,2 15 d) Ta có: =  12 = ⇒  0 ≈  0 a 193(cm),tanB
B 59,7 ,C ≈ 30,3 . 7 Bài 2: Cho tam giác A
∆ BC vuông tại A . Gọi A
BC = a, AC = b, AB = c . Giải A ∆ BC , biết: a) =  0 c 3,8c ; m B = 51 c b b) =  0 a 11c , m C = 60 B a C Lời giải a) Xét tam giác A
∆ BC vuông tại A . Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông, ta có:  AB 0 3,8 cosB = ⇔ cos51 = ⇒ BC = 6c ; m AC = 4,6cm AC BC b) Ta có:  0 = ⇒  0 0 C 60
B = 30 ⇒ AB = sin60 .11 = 8,6c ; m AC = 4,3cm 2
Dạng 2: Tính cạnh và góc của tam giác
Cách giải: Làm xuất hiện tam giác vuông để áp dụng các hệ thức trên bằng cách kẻ thêm đường cao. Bài 1: Cho tam giác A ∆ BC có  0 =  0 B 38 ,C = 30 , A
BC =11cm . Gọi N là chân đường vuông góc
hạ từ A xuống cạnh BC . Hãy tính
a) Độ dài đoạn thẳng AN 38° 30°
b) Độ dài đoạn thẳng AC B N C Lời giải
a) Cách 1: Sử dụng các tỉ số lượng giác trong các tam giác vuông NAB và NAC , ta có:
BN.tanB = NC.tanC
Chú ý: BN + NC = BC ⇒ BN ≈ 4,67c ;
m AN ≈ 3,65cm
Cách 2: Gợi ý: Kẻ CH ⊥ AB = H
b) Xét tam giác ANC vuông, có AN AC =
⇒ AC ≈ 7,3cm SinC Bài 2: Cho tam giác A
∆ BC có BC =11cm , H  0 =  0
B 38 ,C = 30 . Gọi N là chân đường vuông A
góc hạ từ A xuống cạnh BC . Hãy tính
a) Độ dài đoạn thẳng AN 38° 30°
b) Độ dài cạnh AC B N C
c) Tính diện tích tam giác ABC 11 Lời giải
Kẻ BH ⊥ AC ⇒ B
∆ HC vuông tại ⇒  0 =  0 0 0 H
HBC 60 ; HBA = 60 − 38 = 22 Do đó 1 1
BH = BC = .11 = 5,5(cm) (trong tam giác vuông cạnh đối diện với góc 0 30 bằng nửa 2 2 cạnh huyền) 3
a) Tam giác BHA vuông tại H , cạnh huyền BA và cạnh BH = 5,5cm kề với  0 0 BH 5,5
B = 22 ⇒ cos22 = ⇒ AB = ≈ 5,932 cm 0 ( ) AB cos22 Kẻ AN ⊥ BC
Trong tam giác vuông ABN vuông tại N có AN đối diện với góc 0 38 nên 0 38 AN sin = AB 0 0 ⇒ AN = A . B si 38 n = 5,932.si 38 n ≈ 3,652(cm)
b) Tam giác ANC vuông tại  0 AN 3,652
N,C = 30 ⇒ AC = ≈ = 7,304 cm 0 ( ) si 3 n 0 0,5 c) Ta có: 1 1 S = AN BC = = cm . ABC . .3,652.11 20,086( 2 ) 2 2 Bài 3:
Cho tam giác ABC có  0 B = 60 ,  0
C = 50 , AC = 35cm . A
Tính diện tích tam giác ABC 60° 50° B H C Lời giải
Xét tam giác ABC , có:  +  +  0 = ⇒  0 A B C 180 A = 70
Vẽ đường cao AH (H ∈ BC) Ta có:  AH = ⇒ =  0 SinC
AH sinC.AC = si 5
n 0 .AC = 26,8(cm) AC  26,8 26,8 SinB = ⇒ AB = = 38,5(cm) 0 AB Sin60
Xét tam giác ABH vuông tại H , có: BH =15,8(cm) ⇒ CH = 22,7(cm) ⇒ BC ≈ 38,5(cm) 1 1 2 S = BC AH = = cm ABC . . .26,8.38,5 510( ) 2 2 4 Bài 4:
Cho tứ giác ABCD , có:  =  0 =  0 A D 90 ,C = 40 A 4 B AB = 4c , m AD = 3c . m S = ABCD ? 3 30° D H C Lời giải
Kẻ BH ⊥ CD(H ∈CD), ta có tứ giác ABHD là hình chữ nhật (tứ giác có 3 góc vuông) ⇒ BH = 3c , m DH = 4cm
Xét tam giác BHC vuông tại BH H , có:  0 3 tanC = tan40 = ⇒ HC = = 3,58(cm) HC 0,839
(AB + CD).AD (4 + 7,58).3 2 S = = = cm ABCD 17,37( ) 2 2 Bài 5:
Cho tam giác ABC , đường cao AH (H ∈ BC) , A  0
B = 42 , AB =12c , m BC = 22c .
m Tính các cạnh và 1 2
các góc của tam giác ABC . 12 42° B H C 22 Lời giải
Xét tam giác ABH vuông tại H , có:  0 = ⇒  0 B 42 A = 48 1
Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông, ta có: =  0 AH A .
B sinB =12.sin42 = 8cm =  BH A .
B cosB = 8,916(cm) ⇒ HC =13(cm) Ta lại có:  AH = = ⇒  0 = ⇒  0 = ⇒  0 tanC 0,614 C 31 30' A 58 30' BAC =106 30' 2 HC =  . AH
AH AC sinC ⇒ AC =  =15,350(cm) sinC 5 Bài 6:
Cho tam giác ABC , đường cao AH = 5(cm), A  0 =  0
B 70 ,C = 35 . Tính các cạnh của A ∆ BC 5 35° 70° C H B Lời giải Tam giác AH AHB vuông tại ⇒ =  5 H AH A . B sinB ⇒ AB = = ≈ 5,32 cm 0 ( )  sinB sin70 Tam giác AH 5 AHC vuông tại ⇒ =  H
AH AC.sinC ⇒ AC = = ≈ 8,72 cm 0 ( )  sinC si 35 n Ta lại có: =  0
BH AH.cotB = AH.cot70 ≈ 5.0,3640 ≈1,82(cm) =  0
CH AH.cotC = AH.cot35 ≈ 5.1,4281 ≈ 7,14(cm)
Vậy BC = BH + HC =1,82 + 7,14 = 8,96(cm) Bài 7:
Cho tam giác ABC , có AB =16c , m AC =14cm A  0 B = 60 a) Tính BC b) Tính S ABC 14 16 60° C H B Lời giải 6
a) Trong tam giác vuông AHB , ta có: =  0 BH A .
B cosB =16.cos60 =16.0,5 = 8(cm)
Trong hai tam giác vuông AHB và AHC , theo định lý pytago ta có: 2 2 2 2 2 2 2 2 2 2
AH = AB − HB ; AH = AC − HC ⇒ AB − HB = AC − HC Hay 2 2 2 2 2
16 −8 =14 − HC ⇒ HC = 4 ⇒ HC = 2(cm)
Vậy BC = BH + HC = 8+ 2 =10(cm) b) Cách 1: Ta có 1 =  1 0 S BA BC sinB = sin ≈ cm ABC . . .16.10. 60 69,28( 2 ) 2 2
Cách 2: Trong tam giác vuông AHB , ta có: =  0 AH AB sinB = sin ≈ ( 2 . 16. 60 69,28 cm ). Bài 8:
Cho hình bình hành ABCD , có:  0 A = 45 , B C
AB = BD =18(cm) a) Tính AB b) Tính S 45 ° ABCD A H D Lời giải
a) Xét tam giác ABD , có AB = AD nên tam giác ABD cân tại B
Kẻ BH ⊥ AD ⇒ H là trung điểm của AD
Xét tam giác AHB vuông tại H . Áp dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông ta có:  =  0 BH A .
B sinA = 45 = 9 2(cm) 
⇒ AD = 2AH =18 2(cm)  =  AH A . B cosA = 9 2  (cm) b) 1 2 S = S = AD BH = cm ABCD 2. ABD 2. . . 342( ) 2 7 Bài 9: Cho A
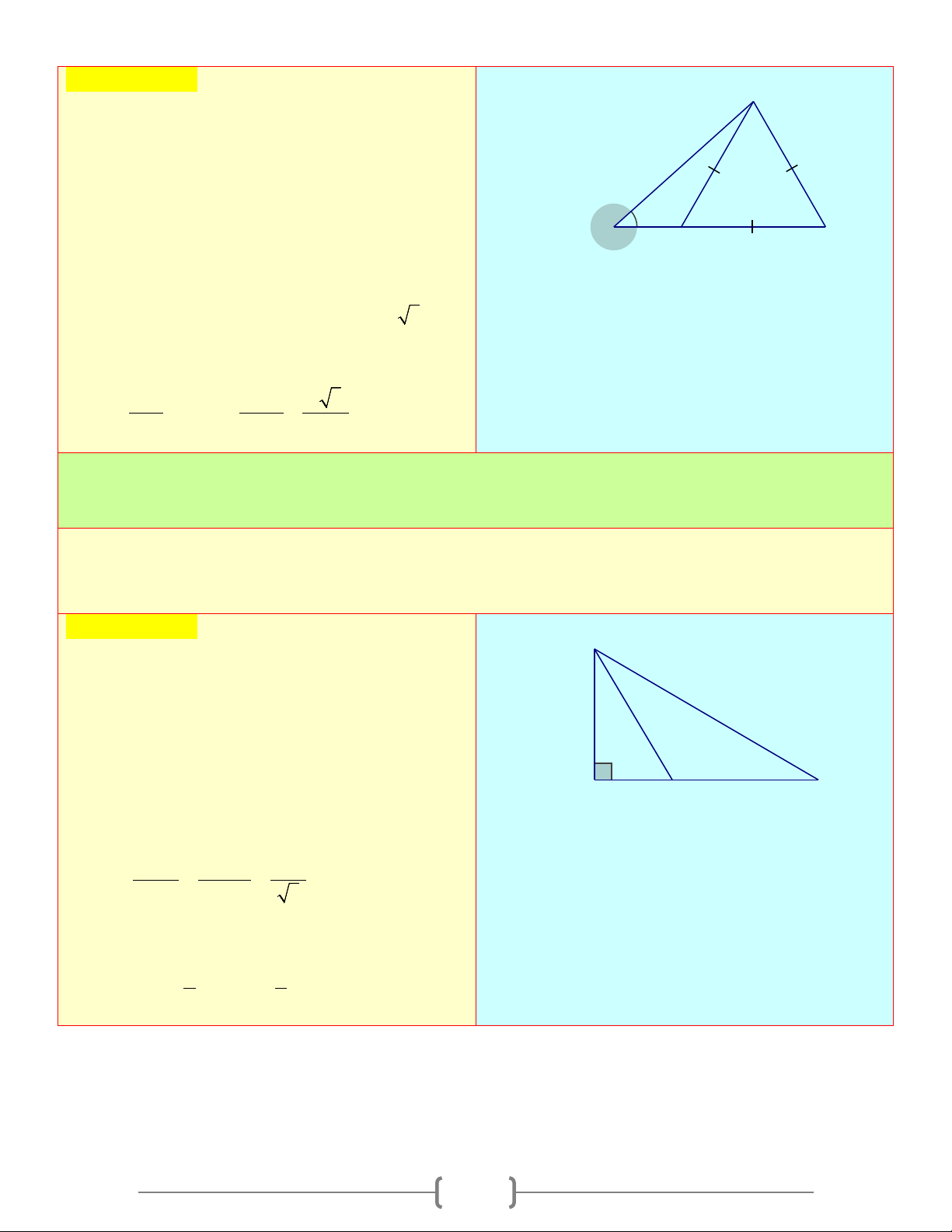
∆ BC cân tại A có  0
A = 30 , đường trung A
tuyến BM . Tính góc 
CBM (làm tròn kết quả 1 2 đến độ) M O 1 B H C Lời giải
Vẽ đường cao AH của A
∆ BC cắt BM tại O Do A
∆ BC cân tại A nên AH cũnglà đường trung tuyến, đồng thời là đường phân giác của A
⇒ O là trọng tâm A ∆ BC và  =  0 A A =15 1 2 Trong BH A
∆ HB vuông tại H ta có:  tanA = 1 1 ( ) AH Trong OH OHB ∆
vuông tại H ta có:  tanB = 2 1 ( ) BH
Nhân (1) và (2) vế theo vế ta được:   BH OH OH 1 tanA .tanB = . = = (vì 1 1 O là trọng tâm) AH BH AH 3 ⇒  1 1 1 = = = = ⇒  0 tanB 1,2442 B = 51 . 1  0 1 3.tanA 3.t 15 an 3.0.2679 1 8
Dạng 3: Toán ứng dụng thực tế
Cách giải: Dùng hệ thức giữa cạnh và góc trong tam giác vuông để giải quyết tình huống trong thực tế Bài 1:
Một cột đèn có bóng trên mặt đất dài 7,5cm. Các
tia nắng mặt trời tạo với mặt đất một góc xấp xỉ 0
42 . Tính chiều cao của cột đèn? B 42° A 7,2cm C Lời giải
Gọi chiều cao của cột đèn là AB , bóng của cột đèn trên mặt đất là AC
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác ABC vuông tại A , ta tính được: AB ≈ 6,75cm Bài 2:
Một cột đèn điện AB cao 6m có bóng in trên mặt
đất là AC dài 3,5m. Hãy tính 
BCA (làm tròn đến
phút) mà tia nắng mặt trời tạo với mặt đất B 6 A 3,5 C 9 Lời giải
Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông ABC , ta có:  6 = ⇒  tanC C = ... 3,5 Bài 3:
Một cầu trượt trong công viên có độ dốc là 0 28 B
và có độ cao là 2,1cm . Tính độ dài của mặt cầu 2,1
trượt (làm tròn đến chữ số thập phân thứ nhất) 28° A C Lời giải
Ta có độ dài cầu trượt là: 2,1 ≈ 4,5m 0 Sin28 10
Dạng 4: Toán tổng hợp
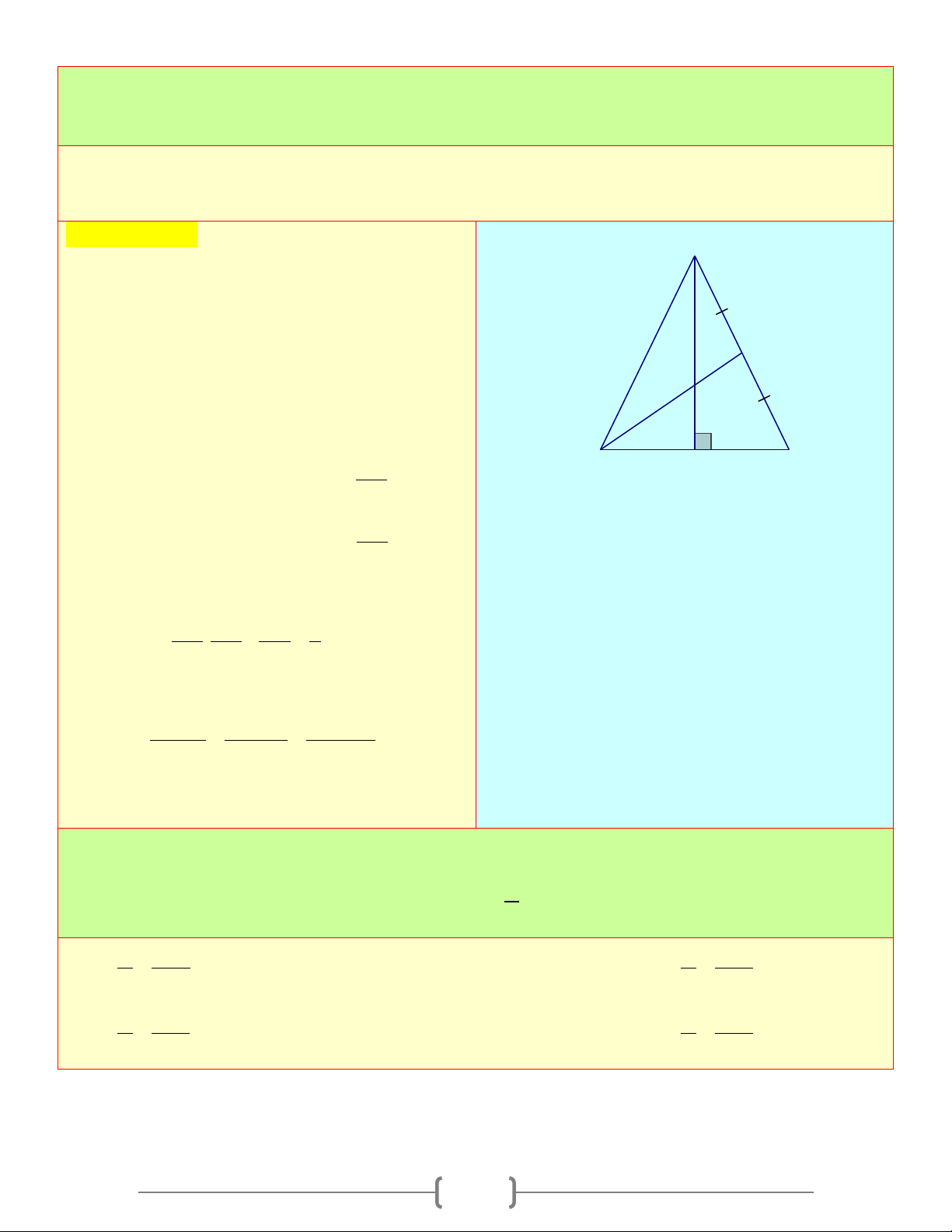
Cách giải: Vận dụng linh hoạt một số hệ thức giữa cạnh và góc trong một tam giác vuông để giải toán. Bài 1:
Cho tam giác ABC vuông tại A , có: AC > AB B
và đường cao AH . Gọi D, E lần lượt là hình D H
chiếu của H trên AB, AC
a. Chứng minh rằng A .
D AB = AE.AC và tam
giác ABC đồng dạng tam giác AED A E C b. Cho BH = 2c , m CH = 4,5cm
- Tính độ dài đoạn thẳng DE
- Tính số đo góc ABC (làm tròn đến độ)
- Tính diện tích tam giác ADE Lời giải
a) Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông AHC và AHB , ta có: 2
AE.AC = AH = A . D AB ⇒ A ∆ BC# A ∆ ED( . c g.c)
b) Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông ABC , ta có: AH = 3cm ⇒ DE = 3cm
+) Xét tam giác AHB vuông tại H , có:  AH = ⇒  0 27 tanABC ABC ≈ 56 ⇒ S = cm ADE ( 2) HB 13 Bài 2:
Cho hình chữ nhật ABCD . Qua B kẻ đường B C
thẳng vuông góc với đường chéo AC tại H .
Gọi E, F,G theo thứ tự là trung điểm của F G
AH, BH,CD a. Chứng minh tứ giác H EFCG là hình bình E hành A D b. Chứng minh  0 BEG = 90 11 c. Cho biết =  0 BH 4c ; m BAC = 30 . Tính S S ABCD , EFCG Lời giải
a) Xét tam giác ABH , có EF là đường trung bình của tam giác
⇒ EF / / AB ⇒ EF / /CG ⇒ ◊EFCG là hình bình hành.
b. Xét tam giác BEC , có: BH ⊥ EC;FE ⊥ BC ⇒ F là trực tâm của tam giác BEC ⊥ ⇒ ⊥ ⇒  0 CF BE EG BE BEG = 90
c) Xét tam giác vuông ABH vuông tại H , có:  BH 4 = ⇒ = = 8 ; BH BH sinA BA cm tanA = ⇒ AH = = 6,9 cm 0 ( )  0 ( ) BA si 30 n AB ta 30 n + Xét BC A
∆ BC vuông tại B , có 0 0 tan30 = ⇒ BC = 8.t 30 an = 4,6(cm) AB +) 2 S = AB BC = = cm ABCD . 8.4,6 36,8( ) 12
BÀI TẬP TRẮC NGHIỆM
Câu 1: Giải tam giác ABC vuông tại A. Cho biết =  0 AB 14c , m C = 30 a) = =  0 AC 15c , m BC 26c , m B = 60 b) = =  0 AC 12 3c , m BC 14 3c , m B = 60 c) = =  0 AC 14 3c , m BC 28c , m B = 60 d) 14 3 = =  0 AC c , m BC 14c , m B = 60 3 Chọn đáp án C B Giải thích:
Ta có ABC vuông tại ⇒  +  0 A B C = 90 14 Mà  0 = ⇒  0 C 30 B = 60 30° + =  0 AC A .
B tanB =14.tan60 ⇒ AC =14 3 (cm) A C +  AB AB AB cosB = ⇒ BC = = = 28(cm) BC  cosB 0,5 Vậy  0
B = 60 ; AC =14 3 (cm); BC = 28(cm)
Câu 2: Giải tam giác ABC vuông tại B . Cho biết =  0 AC 15c ,
m A = 52 (làm tròn kết quả đến chữ
số thập phân thứ nhất) a)  0
C = 38 , AB = 8,4c ,
m BC =10,5cm b)  0
C = 38 , AB = 9,2c , m BC =11,8cm c)  0
C = 38 , AB = 9,8c ,
m BC =12,4cm d) Một kết quả khác Chọn đáp án B A Giải thích: 52°
Ta có ABC vuông tại ⇒  +  0 B A C = 90 15cm Mà  0 = ⇒  0 A 52 C = 38 + =  0
AB AC.sinC =15.si 38 n ≈ 9,2cm B C + =  0
BC AC.sinA =15.sin52 ≈11,8cm
Câu 3: Giải tam giác ABC vuông tại A. Cho biết AB = 7 2c ,
m AC =11cm (cạnh làm tròn đến
chữ số thập phân thứ hai, góc làm tròn đến chữ số thập phân thứ hai, góc làm tròn đến độ) a)  0 =  0
B 48 ,C = 42 , BC =14,08cm b)  0 =  0
B 51 ,C = 39 , BC =14,08cm c)  0 =  0
B 53 ,C = 37 , BC =16,09cm d) A, B, C đều sai 13 Chọn đáp án A B Giải thích: Ta có:  AC 11 = = = ⇒  0 tanB 1,1145 B = 48 AB 7 2 7 2 Lại có:  +  0 = ⇒  0 B C 90 C = 42 A 11 C
Áp dụng định lí Pytago vào tam giác vuông ABC , ta có:
BC = AB + AC = ( )2 2 2 2 2 7 2 +11 = 219
⇒ BC = 219 ≈14,80(cm) .
Câu 4: Giải tam giác MNP có  0 =  0
N 70 ; P = 38 , đường cao MI = 8cm . Diện tích MN ∆ P bằng?
(làm tròn kết quả đến chữ số thập phân thứ hai) a) 2 42,65cm b) 2 48,08cm c) 2 51,54cm d) 2 52,68cm Chọn đáp án D M Giải thích: Ta có: =  0
NI MI.cotN = 8.cot70 = 2,91(cm) 8 + =  0 1
PI MI.cotP = 8.cot38 = 8. = 10,26(cm) 0,78 70° 38°
⇒ NP = NI + IP = 2,91+10,26 =13,17(cm) N I P 1 ⇒ S = = cm MNP .8.13,17 52,68( 2 ) 2
Câu 5: Giải tam giác ABC có AB =12c , m AC =12c ,
m BC = 20cm. Tính các góc của tam giác
ABC (làm tròn đến độ) a)  0 =  0 =  0
A 80 ; B 62 ;C = 38 b)  0 =  0 =  0
A 90 ; B 53 ;C = 37 c)  0 =  0 =  0
A 90 ; B 58 ;C = 32 d) Một kết quả khác 14 Chọn đáp án B B Giải thích: 2 2 2 2 20
Ta có AB + AC =12 +16 =  400 ( ) 1  12 2 2 BC = 20 = 400  (2) ⇒ A
∆ BC vuông tại A A 16 C ⇒  AC 16 = = = ⇒  0 sinA 0,8 B = 53 BC 20 Ta có:  0 = −  0 0 0
C 90 B = 90 − 53 = 37 .
Câu 6: Cho hình thang ABCD sao cho = = =  0 AB AD 10c , m BC 14c ,
m A =120 , BC vuông góc với
đường chéo BD . Chu vi của ABCD bằng
a) 48cm b) 54cm
c) 62cm d) 68cm Chọn đáp án C A 10cm B Giải thích: 120° 1 Ta có: A
∆ BD cân tại A( AB = AD =10cm) 14cm ⇒  =  0 −  0 0 180 A 180 −120 1 0 B D = = = 30 1 1 1 2 2 2 ⇒  =  0 D B = 30 (so le trong) 2 1 D C B
∆ CD vuông tại B , có:  BC BC 14 sinD = ⇒ CD = = = 28 cm 2 ( ) CD  sinD 0,5 2 Do đó P
= AB + BC + CD + DA = cm ABCD 62( )
Câu 7: Hình vẽ cho biết A
∆ BC là tam giác đều cạnh 8cm và  0
AMB = 42 . Tính AM (làm tròn
kết quả đến chữ số thập phân thứ hai)
a) AM =10,34cm b) AM =10,83cm
c) AM =11,05cm d) AM =12,43cm 15 Chọn đáp án A A Giải thích:
Vẽ đường cao AH (H ∈ BC) 8cm Do A
∆ BC đều nên AH cũng là đường trung 42°
tuyến ⇒ HB = HC = 4cm M B C Từ A
∆ BH vuông tại H, ta có: 2 2 2 2 2
AH = AB − BH = 8 − 4 = 48 ⇒ AH = 4 3 (cm) Từ A
∆ HM vuông tại H , ta có:  AH AH 4 3 sinM = ⇒ AM = = ≈10,34(cm) AM  sinM 0,669
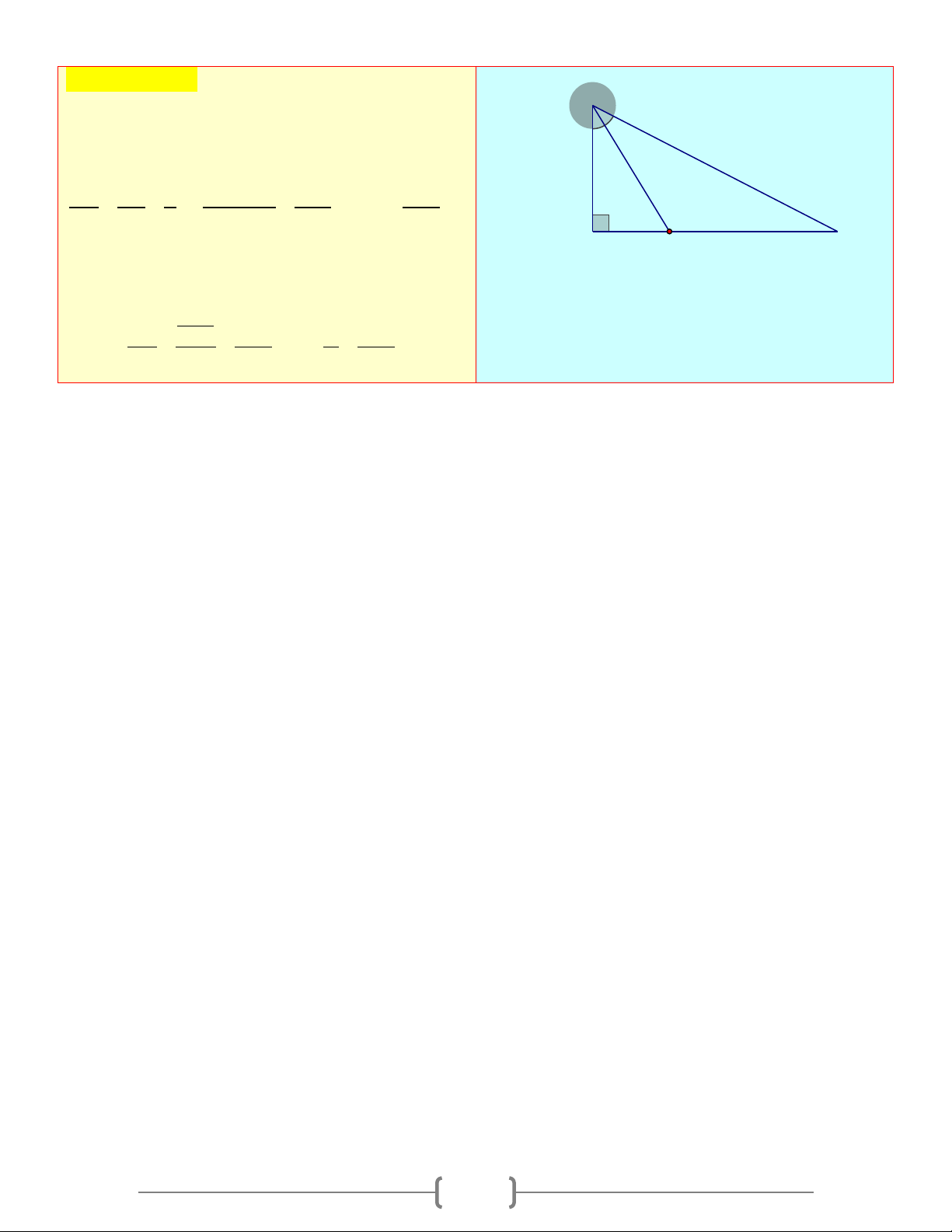
Câu 8: Với hình vẽ đã cho. Tính diện tích tam giác OMN (làm tròn kết quả đến chữ số hàng đơn vị) a) 2 S = cm b) 2 S = cm OMN 8 OMN 7 c) 2 S = cm d) 2 S = cm OMN 11 OMN 9 Chọn đáp án D O Giải thích: OP ∆
N vuông tại P nên ta có: 9cm + =  0
OP ON.sinN = 9.si 38 n ≈ 5,54(cm) 60° 38° + =  0
NP ON.cosN = 9.cos38 ≈ 7,09(cm) P M N OP ∆
M vuông tại P nên ta có: + OP 5,54 5,54 MP = = = = 3,2 cm 0 ( )  tanM tan60 3
Ta có: MN = NP − MP = 7,09 −3,2 = 3,89(cm) Do đó 1 1 S = OP MN = ≈ cm OMN . .5,554.3,89 11( 2 ) 2 2 16 Câu 9: Cho A
∆ BC cân tại A có  0
A = 30 , đường trung tuyến BM . Tính số đo  CBM (làm tròn kết quả đến độ) a) 0 45 b) 0 51 c) 0 58 d) 0 60 Chọn đáp án D A Giải thích: 1 2
Vẽ đường cao AH của A
∆ BC cắt BM tại O Do A
∆ BC cân tại A nên AH cũng là đường M
trung tuyến, đường phân giác O
⇒ O là trọng tâm của A ∆ BC và  =  0 A A =15 1 2 1 BH B H C A
∆ BH vuông tại H , ta có  tanA = 1 1 ( ) AH OH OHB ∆
vuông tại H , ta có  tanB = 2 1 ( ) BH
Nhân (1) và (2) vế với vế, ta được:   BH OH OH 1 tanA .tanB = . = = (O là trọng tâm 1 1 AH BH AH 2 của A ∆ BC ) ⇒  1 1 1 tanB = = = =1,2442 1  0 3.tanA 3.t 15 an 3.0,2679 1 ⇒  0 0 B = 51 12' ≈ 51 1 Câu 10: Cho A
∆ BC vuông tại A có AB = c, AC = b, BC = a . Tia phân giác của B cắt AC tại D .  Tính B tan 2   a) B a + b tan = b) B b tan = 2 b − c 2 a − c   c) B b tan = d) B b tan = 2 a + c 2 a − c 17 Chọn đáp án D B Giải thích: 2 1
Ta có: BD là phân giác của B , ta có: c a AD AB c AD c bc = = ⇒ = ⇒ AD = DC BC a
DC + AD c + a a + c  b AC A D C A
∆ BD vuông tại A , ta có: bc   AD a + c b B b tanB = = = ⇒ tan = . 1 AB c a + c 2 a + c 18 BÀI TẬP VỀ NHÀ Bài 1:
Cho tam giác ABC vuông tại A , có B
BC = a, AC = b, AB = c . Hãy giải tam giác ABC , biết: a) =  0 b 5,4c ; m C = 30 A C b) =  0 c 10c ; m C = 45 Lời giải
a) Xét tam giác ABC vuông tại AB AB A , có:  0 = ⇒ = ⇒ ⇒ ⇒  tanC t 30 an AB BC B AC 5
b) Xét tam giác ABC vuôn tại AB A , có:  0 3 = ⇒ = ⇒ ⇒ ⇒  tanC tan45 AC AB B AC AC Bài 2:
Cho tam giác ABC vuông tại A , có B
BC = a, AC = b, AB = c . Hãy giải tam giác ABC , biết: a) a =15c , m b =10cm A C b) b =12c , m c = 7cm Lời giải
a) Dùng định lý pytago tính được AB ⇒  ⇒  B C
b) Dùng định lý pytago tính được BC ⇒  ⇒  B C Bài 3:
Cho tam giác ABC có  0 =  0
B 60 ;C = 50 ; AC = 35 B Tính S ABC 60° H 50° A 35 C Lời giải 19
- Kẻ đường cao AH (H ∈ BC) 2 ⇒ S = cm ABC 509,08 Bài 4:
Cho tứ giác ABCD có  =  0 =  0 A D 90 ;C = 30 A 4cm B AB = 4c , m AD = 3c . m Tính S ABCD 3cm 30° D H C Lời giải
- Kẻ BH ⊥ CD = H
- Chú ý diện tích đa giác ABCD bằng tổng diện tích hai đa giác ABHD và BHC Bài 5:
Cho tam giác ABC vuông tại A , có đường
cao AH, HB = 9c , m HC =16cm
a) Tính AB, AC, AH
b) Gọi D và E lần lượt là hình chiếu vuông
góc của H trên AB và AC . Tứ giác ADHE là hình gì?
c) Tính chu vi và diện tích của tứ giác ADHE
d) Tính chu vi và diện tích tứ giác BDEC Lời giải
a) HB = 9, HC =16 ⇒ AH ⇒ AB ⇒ AC
b) Tứ giác ADHE là hình chữ nhật vì có ba góc vuông
c) - Tính AD dựa vào tam giác AHD vuông tại D
- Tính HD dựa vào tam giác vuông AHD +) P = AD + DH ADHE ( ).2 +) S = AD DH ADHE . 20 d) P
= BD + DE + EC + BC S = S − S BDEC ; BDEC ABC ADE Bài 6:
Cho tam giác ABC vuông tại A , biết B AB = 3c , m BC = 5cm E
a) Giải tam giác ABC (số đo góc làm tròn 5 đến độ) F 3
b) Từ B kẻ đường thẳng vuông góc với BC , D A 4 C
đường thẳng này cắt đường thẳng AC tại D .
Tính độ dài các đoạn thẳng AD, BD
c) Gọi E, F lần lượt là hình chiếu của A trên
BC và BD . Chứng minh B ∆ EF# B ∆ DC Lời giải
a) Dùng định lý pytago tính được AC = 4cm
⇒ các góc của tam giác ABC
b) Xét tam giác vuông BCD vuông tại B , tính được AD
- Dùng định lý Pytago vào tam giác vuông ABD tính được BD
c) Chứng minh được B ∆ EF# B ∆ DC (cgc) Bài 7:
Cho tam giác ABC vuông tại A , biết C =  0 AB 21c ,
m C = 40 . Tính độ dài đường phân 40° giác BD của 
ABC , với D nằm trên cạnh AC D A 21 B Lời giải  0
ABD = 25 . Áp dụng tỉ số lượng giác trong tam giác vuông ABD ta có: 21 BD = ≈ 21,19 cm 0 ( ) cos25 21