Thông tin
Quiz

Tài liệu tự học nguyên hàm, tích phân và ứng dụng – Nguyễn Trọng Toán 12

Tài liệu tự học nguyên hàm, tích phân và ứng dụng – Nguyễn Trọng Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề:

Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn:

Toán 12 3.8 K tài liệu

Thông tin:

80 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Tài liệu tự học nguyên hàm, tích phân và ứng dụng – Nguyễn Trọng Toán 12

87 44 lượt tải Tải xuống

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

B1: NGUYÊN HÀM

_ . 

-Phương pháp:

_ Sử dụng bảng nguyên hàm





 

u u x



.

dx x C



.

du u C



. Vi phân

 

ddax b x



.

x x C











 





.

u u C











 





.

 

d ( )

a x b x ax b C





    





.

 

ln 0

x C x

  



.

 

ln 0

u C u x

  



.

 

ln 0

ax b C a

ax b a

   





.

cos d sinx x x C



.

cos d sinu u u C



.

cos( )d sin( )ax b x ax b C

   



.

sin d cosx x x C  



.

sin d cosu u u C  



.

sin( )d cos( )ax b x ax b C

    



.

d tan

cos

x x C





Với





.

d tan

cos

u u C





Với

 

u x k





.

 

tan

cos

ax b C

ax b a

  





.

d cot

sin

x x C

  



Với





.

d cot

sin

u u C

  



Với

 

u x k





.

 

cot

sin

ax b C

ax b a



  





.

e x e C



.

e u e C



.

ax b ax b

e x e C







.

a x C





 

01a

.

a u C





 

01a

.

.ln

px q px q

a x a C







 

01a

_ 

Cho

( ) (x) Cf x dx F



. Tìm

()fx

hoặc

F( )x

. Nhấn shift

( ( )) ( )

F X f X





. Nhấn phím Calc nhập X = 2.5

. Nếu kết quả bằng 0 (gần bằng 0 ) thì đó là đáp án cần chọn

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

_

Câu 1. Tất cả nguyên hàm của hàm số

 





là

ln 2 3

xC

. B.

 

ln 2 3

xC

ln 2 3xC

. D.

ln 2 3

ln2

xC



CA

   

1 1 1 1

d d d 2 3 ln 2 3

2 3 2 2 3 2

f x x x x x C

     



  



 Dùng máy tính cầm tay:

( ln(| 2 3 |)) |

2 2 3

dx x

CALC X = -2

Trong kết quả A và C nếu cho X =

2 thì đều cho kết quả là 0. Vậy khi có trị

tuyệt đối thì cho X một giá trị cho biểu

thức trong trị tuyệt đối âm.

Câu 2. Nếu

 

d4f x x x x C  



thì hàm số

 

bằng

 

f x x Cx  

. B.

 

12 2f x x x C  

 

12 2f x x x

. D.

 

f x x



CC

Ta có:

   

 

3 2 2

d 4 12 2f x f x x x x C x x



     





 Dùng máy tính cầm tay tương tự câu 1

Câu 3. Cho hàm số

 

có

 





với mọi

x 

và

 

11f 

. Khi đó giá trị của

 

bằng

ln 2

. B.

ln3

. C.

ln 2 1

. D.

ln3 1



CD

Ta có:

   

'df x x f x C



nên

 

d ln 2 1

2 1 2

f x x x C

   





Mặt khác theo đề ra ta có:

 

11f 

ln 2.1 1 1 1

CC     

nên

 

ln 2 1 1

f x x  

Do vậy

 

5 ln 2.5 1 1 ln9 1 ln3 1

f       



  :

     

       

5 1 1

f x dx f f

f f f x dx f x dx







    





  : Sử dụng chức

năng tính tích phân:

- Tính

x 



và lưu vào A

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

- Tìm phương án có giá trị bằng 1 + A

- Là giá trị rất nhỏ gần đến 0 nên thỏa mãn.



_ (10 câu NB; 10 câu TH)

(10 câu)

Câu 1. Tìm nguyên hàm của hàm số

 

f x x



 

3f x dx x C

  



. B.

 

f x dx x C  



 

3f x dx x C

  



. D.

 

f x dx x C  



Câu 2. Trong các khẳng định sau, khẳng định nào sai?

cos2 d sin2

x x x C



. B.

x x C









d lnx x C





. D.

x x C









Câu 3. Họ nguyên hàm của hàm số

 

3 sinf x x x

là:

cosx x C

. B.

6 cosx x C

cosx x C

. D.

6 cosx x C

Câu 4. Tất cả nguyên hàm của hàm số

 





là.

ln 2 3

xC

. B.

 

ln 2 3

xC

ln 2 3xC

. D.

ln 2 3

ln2

xC

Câu 5. Giả sử các biểu thức sau đều có nghĩa công thức nào sau đây sai?

tan

cos

dx x C





. B.

e dx e C



Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

lnxdx c





. D.

sin cosxdx x C  



Câu 6. Họ nguyên hàm của hàm số

 

22x

f x e x

là

 

F x C  

. B.

 

23x

F x e x C  

 

F x e x C  

. D.

 

F x e C  

Câu 7. Nguyên hàm của hàm số

 

32f x x x  

là hàm số nào trong các hàm số sau?

 

33F x x x C  

. B.

 

F x x x C   

 

F x x C   

. D.

 

F x x C   

Câu 8. Họ nguyên hàm của hàm số

( ) e (3 e )





là

( ) 3e

F x C  

. B.

( ) 3e

F x x C  

( ) 3e e lne

x x x

F x C  

. D.

( ) 3e

F x x C  

Câu 9. Họ nguyên hàm của hàm số

 

e cos

f x x

là

e sin

xC

. B.

e sin







e sin

x x C





. D.

e sin

xC

Câu 10. Nguyên hàm của hàm số

f x x

là:

2 ln3

F x C

. B.

ln3

F x C

. D.

3 .ln3

F x C

2. : (10 câu)

Câu 11. Tìm nguyên hàm

 

của hàm số

 

sin cosf x x x

thoả mãn











 

cos sin 3F x x x  

. B.

 

cos sin 3F x x x   

 

cos sin 1F x x x   

. D.

 

cos sin 1F x x x   

Câu 12. Tìm nguyên hàm

cos2

sin cos



 

cos sinF x x x C   

. B.

 

cos sinF x x x C  

 

cot tanF x x x C  

. D.

 

cot tanF x x x C   

Câu 13. Cho

 

là một nguyên hàm của hàm số

( ) 4 2

f x e x

thỏa mãn

 

01F 

. Tìm

 

43  

F x e x

. B.

 

21  

F x e x

 

21  

F x e x

. D.

 

21  

F x e x

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Câu 14. Cho hàm số

 

y F x

là một nguyên hàm của hàm số

yx

. Biểu thức

 

25F



bằng

125

. B.

625

. C.

. D.

Câu 15. Biết

 

là một nguyên hàm của hàm số

 





và

 

01F

. Tính

 

1 ln2 1F

. B.

 

1 ln2 1

F

. C.

 

10F

. D.

 

1 ln 2 2F

Câu 16. Biết

 

là một nguyên hàm của hàm số

 

f x x

thoả mãn

 

00F 

. Ta có

 

bằng

ln2





. B.

ln2





. C.

 

1 2 1 ln 2



. D.

x 

Câu 17. Cho

 

là một nguyên hàm của hàm số

 





. Biết

 

12F 

. Giá trị của

 

là

 

2 ln3 2.

F 

 

2 ln3 2.F 

 

2 ln3 2.

F 

 

2 2ln3 2.F 

Câu 18. Nguyên hàm

 

của hàm số

 

sin

f x x



thỏa mãn











là

cot



  

. B.

cot





. C.

cot 1xx  

. D.

cot





Câu 19. Tìm nguyên hàm

của hàm số

sin 2f x x



thỏa mãn



cos( 2 ) 1

()



. B.

cos( 2 ) 1

()



cos( 2 )

( ) 1



. D.

cos( 2 ) 1

()



Câu 20. Tìm

 

là một nguyên hàm của hàm số

 

f x e

trên

 

; 

, biết

 

02F 

 

ln 1F x x x  

. B.

 

F x e x  

 

F x x

  

. D.

 

F x e x  



1.D

2.D

3.C

4.A

5.C

6.A

7.C

8.D

9.D

10.A

11.D

12.D

13.B

14.B

15.D

16.A

17.A

18.A

19.B

20.D



Câu 1. Tìm nguyên hàm của hàm số

 

f x x



 

3f x dx x C

  



. B.

 

f x dx x C  



 

3f x dx x C

  



. D.

 

f x dx x C  





CD

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Ta có:

 

f x dx x dx x dx dx x C



      





   

Câu 2. Trong các khẳng định sau, khẳng định nào sai?

cos2 d sin2

x x x C



. B.

x x C









d lnx x C





. D.

x x C











CD

Câu 3. Họ nguyên hàm của hàm số

 

3 sinf x x x

là:

cosx x C

. B.

6 cosx x C

. C.

cosx x C

. D.

6 cosx x C



CC

Ta có

 

3 sin d cosx x x x x C   



Câu 4. Tất cả nguyên hàm của hàm số

 





là

ln 2 3

xC

. B.

 

ln 2 3

xC

ln 2 3xC

. D.

ln 2 3

ln2

xC



Chn A

 

d d ln 2 3

2 3 2

f x x x x C

   





Câu 5. Giả sử các biểu thức sau đều có nghĩa công thức nào sau đây sai?

tan

cos

dx x C





. B.

e dx e C



lnxdx c





. D.

sin cosxdx x C  





CC

Theo bảng nguyên hàm ta chọn câu sai là

lnxdx c





Câu 6. Họ nguyên hàm của hàm số

 

22x

f x e x

là

 

F x C  

. B.

 

23x

F x e x C  

 

F x e x C  

. D.

 

F x e C  



CA

Ta có

   

 

F x f x x e x x C     



Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Vậy

 

F x C  

Câu 7. Nguyên hàm của hàm số

 

32f x x x  

là hàm số nào trong các hàm số sau?

 

33F x x x C  

. B.

 

F x x x C   

 

F x x C   

. D.

 

F x x C   



Chn C

Ta có:

 

( ) 3 2 2

F x f x dx x x dx x C       



Câu 8. Họ nguyên hàm của hàm số

( ) e (3 e )





là

( ) 3e

F x C  

. B.

( ) 3e

F x x C  

( ) 3e e lne

x x x

F x C  

. D.

( ) 3e

F x x C  



Chn D

 

e (3 e )d 3e 1 d 3e

x x x x

x x x C



     



Câu 9. Họ nguyên hàm của hàm số

 

e cos

f x x

là

e sin

xC

. B.

e sin







e sin

x x C





. D.

e sin

xC



Chn D

Ta có:

 

e cos d e sin

x x x C   



Câu 10. Nguyên hàm của hàm số

f x x

là:

2 ln3

F x C

. B.

ln3

F x C

. D.

3 .ln3

F x C



CA

Ta có:

2 ln3

f x dx x dx C

Câu 11. Tìm nguyên hàm

 

của hàm số

 

sin cosf x x x

thoả mãn











 

cos sin 3F x x x  

. B.

 

cos sin 3F x x x   

 

cos sin 1F x x x   

. D.

 

cos sin 1F x x x   



Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

CD

Có

cos d sinu u u C



;

sin d cosu u u C  



nên

   

sin cos cos sinf x dx x x dx x x C     



cos sin .

π π π

F C C



     





2 2 2

Mà



  







. Do đó

 

cos sinF x x x   1

Câu 12. Tìm nguyên hàm

cos2

sin cos



 

cos sinF x x x C   

. B.

 

cos sinF x x x C  

 

cot tanF x x x C  

. D.

 

cot tanF x x x C   



CD

Ta có:

2 2 2 2 2 2

cos2 cos sin 1 1

d d d cot tan

sin cos sin cos sin cos

x x x

x x x x x C

x x x x x x





      





  

Câu 13. Cho

 

là một nguyên hàm của hàm số

( ) 4 2

f x e x

thỏa mãn

 

01F 

. Tìm

 

43  

F x e x

. B.

 

21  

F x e x

 

21  

F x e x

. D.

 

21  

F x e x

 

CB

Ta có:

 

2 2 2

4 2 2

F x e x dx e x C    



 

2.0 2

0 2. 0 2F e C C    

. Mà

 

0 1 2 1 1F C C      

Do đó:

 

F x e x  

Câu 14. Cho hàm số

()y F x

là một nguyên hàm của hàm số

yx

. Biểu thức

'(25)F

bằng:

125

. B.

625

. C.

. D.



CB

Ta có:

 

được gọi là nguyên hàm của

 

trên

nếu

'( ) ( ),F x f x x K  

Mà

()y F x

là một nguyên hàm của hàm số

yx

nên

'( )F x x

Vậy

'(25) 25 625F 

Câu 15. Biết

 

là một nguyên hàm của hàm số

 





và

 

01F

. Tính

 

1 ln2 1F

. B.

 

1 ln2 1

F

. C.

 

10F

. D.

 

1 ln2 2F



CB

 

ln 1



    



  

f x dx dx x c

Vì

 

là một nguyên hàm của hàm số

 

nên

 

ln 1

  F x x c

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 

0 1 ln1 1 1

     F c c

Do đó

 

ln 1 1

  F x x

Vậy

 

1 ln 1 1 1 ln2 1

    F

Câu 16. Biết

 

là một nguyên hàm của hàm số

 

f x x

thoả mãn

 

00F 

. Ta có

 

bằng

ln2





. B.

ln2





. C.

 

1 2 1 ln 2



. D.

x 



CA

Ta có:

 

2 2 d

ln2

x x x C   



. Do đó.

Theo giả thiết

 

0 0 0 0

ln2 ln2

F C C       

Vậy

 

2 1 2 1

ln2 ln2 ln2

F x x x



    

Câu 17. Cho hàm số

 

có

 





với mọi

x 

và

 

12f 

. Khi đó giá trị của

 

bằng

 

2 ln3 2

F 

. B.

 

2 ln3 2F 

. C.

 

2 2ln3 2F 

. D.

 

2 ln3 2

F 



CD

Ta có:

   

'df x x f x C



nên

 

d 2 1

1 1 1

d ln 2 1

2 1 2 2 1 2

f x x x C



    





Mặt khác theo đề ra ta có:

 

12f 

ln 2.1 1 2 2

CC     

nên

 

ln 2 1 2

f x x  

Do vậy

 

2 ln 2.2 1 2 ln3 2

f     

Câu 18. Nguyên hàm

 

của hàm số

 

sin

f x x



thỏa mãn











là

cot



  

. B.

cot





. C.

cot 1xx  

. D.

cot







CA

Ta có

( ) 2 cot

sin

F x x dx x x C



    







1 cot 1

4 4 4 16

F C C

   

   

         

   

   

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Vậy F(x) =

cot



  

Câu 19. Tìm nguyên hàm

của hàm số

sin 2f x x



thỏa mãn



cos( 2 ) 1

()



. B.

cos( 2 ) 1

()



cos( 2 )

( ) 1



. D.

cos( 2 ) 1

()





Chn B

cos 2

sin 2 d C

F x x x



Vậy

cos( 2 ) 1

()



Câu 20. Tìm

 

là một nguyên hàm của hàm số

 

f x e

trên

 

; 

, biết

 

02F 

 

ln 1F x x x  

. B.

 

F x e x  

. C.

 

F x x

  

. D.

 

F x e x  



CD

Ta có:

   

 

d 1 d

x e x eF x f x xC     



Theo bài:

 

0 2 0 2 1 2 1F e C C C         

Vậy

 

F x e x  

_ 

_

-Phương pháp:

_ . Chọn

 





. Trong đó

 



là hàm số mà ta chọn thích hợp.

. Tính vi phân hai vế:

 

'dt x dx





. Biểu thị:

   

( ) ' ( )f x dx g x x dx g t dt









. Khi đó:

( ) ( ) ( )I f x dx g t dt G t C   



_Casio: Cho

( ) (x) Cf x dx F



. Tìm

()fx

hoặc

F( )x

. Nhấn shift

( ( )) ( )

F X f X





. Nhấn phím Calc nhập

2.5 X 

. Nếu kết quả bằng 0 (gần bằng 0 ) thì đó là đáp án cần chọn

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

_

Câu 1. Tìm nguyên hàm của hàm số

sin

()

1 3cos





( )d ln 1 3cos

f x x x C  



. B.

( )d ln 1 3cosf x x x C  



( )d 3ln 1 3cosf x x x C  



. D.

( )d ln 1 3cos

f x x x C



  





C D

 Đặt

1 3cos 3sint x dt xdx    

1 1 1 1

( )d ln | | ln 1 3cos

3 3 3

f x x dt t C x C



       





 Dù

Câu 2. Tính nguyên hàm

ln 1







(ln 1)

I x C  

. B.

ln 1I x C  

(ln 1)

I x C  

. D.

2 ln 1I x C  



C D

 Đặt

ln 1 ln 1 2t x t x tdt dx

      

d 2 2 2 ln 1

ln 1

I x dt t C x C

      







 

Câu 3. Tìm họ nguyên hàm của hàm số

 

.1f x x x

 

( 1)

F x x C   

. B.

 

( 1)

F x x C  

 

( 1)

F x x C  

. D.

 

( 1)

F x x C  



C D

 Đặt

2 3 2 2

1 1 3 2t x t x t dt xdx      

2 3 4 2

3 3 3

. 1 ( 1)

2 8 8

x x dx t dt t C x C      





 

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

_ (10 câu NB; 10 câu TH)

(10 câu)

Câu 1. Tìm



có kết quả là.

ln ln xC

. B.



. C.

 

ln 1



xC

Câu 2. Nguyên hàm

x



bằng.

2 2ln| 1|x x C  

. B.

2 xC

2ln | 1|xC

. D.

2 2ln| 1|x x C  

Câu 3. Cho hàm số

 

2dF x x x x



. Biết

 

F 

, tính

 

. B.

. C.

. D.

Câu 4. Biết

()Fx

là một nguyên hàm của hàm số

 

fx

và

 

F 

. Giá trị







là:



. B.

2e 1

. C.



. D.



Câu 5. Tính nguyên hàm











2ln 2 3xC

. B.

ln 2 3

xC

. C.

ln 2 3xC

. D.

 

ln 2 3

xC

Câu 6. Xét

 

43I x x dx



. Bằng cách đặt

43ux

, khẳng định nào sau đây đúng?

I u du



. B.

I u du



. C.

I u du



. D.

I u du



Câu 7. Họ nguyên hàm của hàm số

 

4f x x x

là:

 

xC

. B.

24 xC

. C.

 

xC

. D.

 

24xC

Câu 8. Nguyên hàm

 







bằng:

33 1













. B.

11 1

























. D.

11 1













Câu 9. Nguyên hàm của hàm số

( ) sin . cosf x x x

là:

cos

sin

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

sin

sin cos

x x C

Câu 10. Nguyên hàm

 

của hàm số

 

sin 2 .cos 2f x x x

thỏa











là:

 

1 1 4

sin 2 sin 2

6 10 15

F x x x  

. B.

 

1 1 1

sin 2 sin 2

6 10 15

F x x x  

 

1 1 1

sin 2 sin 2

6 10 15

F x x x  

. D.

 

1 1 1

sin 2 sin 2

6 10 15

F x x x  

2. : (10 câu)

Câu 11. Nếu

 

F x x









thì.

 

F x C







. B.

 

ln 2 3

F x x x C   

 

23F x x x C   

. D.

 

F x x x C   

Câu 12. Cho

là nguyên hàm của hàm số

ln x

. Tính

   

e1FF

. B.

. C.

. D.

Câu 13. Hàm số nào sau đây là một nguyên hàm của hàm số

 





 

1F x x

. B.

 

41F x x

. C.

 

21F x x

. D.

 





Câu 14. Nguyên hàm của hàm số

 

y f x





là:

lnI x x C  

. B.

 

ln 1

I e e C   

lnI x x C  

 

1 ln 1

I e e C    

Câu 15. Một nguyên hàm của hàm số

1y x x

là:





x

. B.





x

. C.





x

. D.





x

Câu 16. Tìm nguyên hàm







ln 1

I x e C    

. B.

ln 1

I x e C   

ln 1

I x e C   

. D.

ln 1

I x e C   

Câu 17. Cho

     

6 8 7

2 3 2 d 3 2 3 2x x x A x B x C     



với



và

C

. Giá trị của biểu

thức

12 7AB

bằng:

252

. B.

241

252

. C.

. D.

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Câu 18. Tìm họ nguyên hàm của hàm số:

 

3sin 2cos

3cos 2sin

f x x









 

d ln 3sin 2cosf x x x x C  



. B.

   

d ln 3cos 2sinf x x x x C   



 

d ln 3cos 2sinf x x x x C  



. D.

 

d ln 3cos 2sinf x x x x C    



Câu 19. Khi tính nguyên hàm







, bằng cách đặt

1ux

ta được nguyên hàm nào?

 

2 4 duu



. B.

 

3duu



. C.

 

2 4 du u u



. D.

 

4duu



Câu 20. Kết quả của phép tính

2. 1







bằng:





. B.





 

ln 2 1

e e C



  

. D.







1.D

2.D

3.A

4.B

5.C

6.D

7.A

8.A

9.D

10.C

11.C

12.A

13.B

14.D

15.B

16.D

17.D

18.B

19.A

20.A



Câu 1. Tìm



có kết quả là.

ln ln xC

. B.



. C.

 

ln 1



xC



CD

Ta có

ln ln

d ln dln

  



x x x C

Câu 2. Nguyên hàm

x



bằng.

2 2ln| 1|x x C  

. B.

2 xC

2ln | 1|xC

. D.

2 2ln| 1|x x C  



CD

Đặt

d 2 dtx t x t x t    

d 2 d 2 2ln 1 2 2ln | 1|

t t t t C x x C



         









Câu 3. Cho hàm số

 

2dF x x x x



. Biết

 

F 

, tính

 

. B.

. C.

. D.



CA

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Ta có:

 

2dF x x x x



 

2d 2

xx  







xC  

Mà

 

F 

C  

2C  

Vậy

 

7 9 2 7F   

Câu 4. Biết

()Fx

là một nguyên hàm của hàm số

 

fx

và

 

F 

. Giá trị







là



. B.

2e 1

. C.



. D.



Li gii

CB

Ta có:

   

d e d e

F x f x x x C   



Theo giả thiết:

 

FC  

. Vậy









Câu 5. Tính nguyên hàm











2ln 2 3xC

. B.

ln 2 3

xC

. C.

ln 2 3xC

. D.

 

ln 2 3

xC



CB

Ta có:

 

1 1 1 1

d d 2 3 ln 2 3

2 3 2 2 3 2

x x x C

   

    

   



   



Câu 6. Xét

 

43I x x dx



. Bằng cách đặt

43ux

, khẳng định nào sau đây đúng.

I u du



. B.

I u du



. C.

I u du



. D.

I u du



 

C C

Ta có

4 3 3

4 3 16

u x du x dx x dx     

; Suy ra:

 

3 4 5

I x x dx u du  



Câu 7. Họ nguyên hàm của hàm số

 

4f x x x

là:

 

xC

. B.

24 xC

. C.

 

xC

. D.

 

24xC



CA

Ta có

4dx x x



 

4 d 4

xx  



   

4 d 4

xx  



 

xC  

 

xC  

Câu 8. Nguyên hàm

 







bằng.

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

33 1













. B.

11 1

























. D.

11 1















CA

Biến đổi

 









 















Đặt









 





Do đó

I t t



tC

33 1













Câu 9. Nguyên hàm của hàm số

( ) sin . cosf x x x

là:

cos

sin

sin cos

x x C



CC

Sử dụng casio: đạo hàm của đáp án tại 3 trừ hàm dưới dấu tích phân tại 3 bằng 0 thì chọn đáp

án.

Câu 10. Nguyên hàm

 

của hàm số

 

sin 2 .cos 2f x x x

thỏa











là

 

1 1 4

sin 2 sin 2

6 10 15

F x x x  

. B.

 

1 1 1

sin 2 sin 2

6 10 15

F x x x  

 

1 1 1

sin 2 sin 2

6 10 15

F x x x  

. D.

 

1 1 1

sin 2 sin 2

6 10 15

F x x x  

 

C D

Đặt

sin2tx

d 2.cos2 dt x x

d cos2 d

t x x

Ta có:

 

sin 2 .cos 2 dF x x x x



 

. 1 d

t t t



 

t t t



6 10

t t C  

sin 2 sin 2

6 10

x x C  











sin sin 0

6 2 10 2



   

C  

Vậy

 

1 1 1

sin 2 sin 2

6 10 15

F x x x  

Câu 11. Nếu

 

F x x









thì:

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 

F x C







. B.

 

ln 2 3

F x x x C   

 

23F x x x C   

. D.

 

F x x x C   



CC

Đặt

   

2 2 2

2 3 2 3 2 d 2 1 d 1 d dt x x t x x t t x x x x t t            

Do đó

 

F x t C x x C



       





Câu 12. Cho

là nguyên hàm của hàm số

ln x

. Tính

e1FF

. B.

. C.

. D.

 

C A

Đặt

t x dt

ln ln

x t x

x t t C C F x C

Câu 13. Hàm số nào sau đây là một nguyên hàm của hàm số

 





 

1F x x

. B.

 

41F x x

. C.

 

21F x x

. D.

 







CB

Ta có:

 

d 4 4 1

1 2 1

F x x x C



    





Họ nguyên hàm của hàm số đã cho là

d 4 1

x x C

  





, nên hàm số đã cho có một

nguyên hàm là hàm

 

41F x x

Câu 14. Nguyên hàm của hàm số

 

y f x





là:

lnI x x C  

. B.

 

ln 1

I e e C   

lnI x x C  

 

1 ln 1

I e e C    



CD

I x e x







Đặt

1 1 d d

x x x

t e e t t e x      

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Ta có

d 1 d ln

I t t t t C





     







Trở lại biến cũ ta được

 

1 ln 1

I e e C    

Câu 15. Một nguyên hàm của hàm số

1y x x

là:





x

. B.





x

. C.





x

. D.





x



CB

Đặt

2 2 2

11t x t x tdt xdx      





x x dx t dt C C



      



Câu 16. Tìm nguyên hàm







ln 1

I x e C    

. B.

ln 1

I x e C   

ln 1

I x e C   

. D.

ln 1

I x e C   



CD

 

dx e dx







Đặt

t e dt e dx  

 

e dx dt

t t t t



   









  

ln ln 1t t C   

ln ln 1

e e C   

ln 1

x e C   

Câu 17. Cho

     

6 8 7

2 3 2 d 3 2 3 2x x x A x B x C     



với



và

C

. Giá trị của biểu

thức

12 7AB

bằng:

252

. B.

241

252

. C.

. D.

 

C D

Đặt

32tx





tx

Ta có:





 

+2 d

t t t



9 8 9 7

C  

   

. 3 2 . 3 2

36 63

x x C    

Suy ra

A 

B 

1 4 7

12. 7.

36 63 9



Câu 18. Tìm họ nguyên hàm của hàm số:

 

3sin 2cos

3cos 2sin

f x x









 

d ln 3sin 2cosf x x x x C  



. B.

   

d ln 3cos 2sinf x x x x C   



Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 

d ln 3cos 2sinf x x x x C  



. D.

 

d ln 3cos 2sinf x x x x C    





C B

Ta có:

 

d 3cos 2sin

dx ln 3cos 2sin

3cos 2sin

f x x x C



     





Câu 19. Khi tính nguyên hàm







, bằng cách đặt

1ux

ta được nguyên hàm nào?

 

2 4 duu



. B.

 

3duu



. C.

 

2 4 du u u



. D.

 

4duu





CA

Đặt

1ux

0u 

nên

1ux

d 2 d

x u u













Khi đó







.2 d







 

2 4 duu



Câu 20. Kết quả của phép tính

2. 1







bằng:





. B.





 

ln 2 1

e e C



  

. D.





Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

_  3. 

-Phương pháp:

_ Định lý. Cho hai hàm số

và

liên tục trên đoạn

 

;ab

và có đạo hàm liên tục

trên đoạn

 

;ab

Khi đó:

d d .u v uv v u



 

_  Để tính nguyên hàm

 

df x x



bằng từng phần ta làm như sau:

Bước 1. Chọn

, uv

sao cho

 

ddf x x u v

(chú ý

 

d ' dv v x x

Sau đó tính

dvv



và

d '.du u x

Bước 2. Thay vào công thức

 

và tính

dvu



Chú ý : Cần phải lựa chọn

và

hợp lí sao cho ta dễ dàng tìm được

và tích phân

dvu



dễ tính hơn

duv



. Ta thường gặp các dạng sau:

⍟Dạng 1.

 

sin

cos

I P x x











, trong đó

 

là đa thức.

Với dạng này, ta đặt

 

sin

cos

u P x





















⍟ Dạng 2.

 

ax b

I P x e x







, trong đó

 

là đa thức.

Với dạng này, ta đặt

 

ax b

u P x

v e x















⍟ Dạng 3.

   

ln dI P x mx n x



, trong đó

 

là đa thức.

Với dạng này, ta đặt

 

u mx n

v P x x















_ Casio: Cho

( ) (x) Cf x dx F



. Tìm

()fx

hoặc

F( )x

. Nhấn shift

( ( )) ( )

f X F X





. Nhấn phím Calc nhập

2.5 X 

. Nếu kết quả bằng

(gần bằng

) thì đó là đáp án cần chọn .

Nguyên tắc chung để đặt u và dv : Tìm được

dễ dàng và

.v du



tính được.

Nhấn mạnh: Thứ tự ưu tiên khi chọn đặt

:  (hàm

lôgarit, hàm đa thức, hàm lượng giác, hàm mũ).

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

_

Câu 1. Họ nguyên hàm của hàm số

 

cos2f x x x

là:

sin2 cos2

x x x

C

. B.

cos2

sin2

x x C

cos2

sin2

x x C

. D.

sin2 cos2

x x x

C



CA

cos2 dI x x x



Đặt

d cos2 d

sin 2

v x x























Khi đó

1 1 1 1

sin2 sin2 d sin2 cos2

2 2 2 4

I x x x x x x x C    





 

Câu 2. Họ nguyên hàm của hàm số

 

ln2f x x x

là:

ln2









. B.

ln2

x x C

 

ln2 1

xC

. D.

ln2

x x C



C A

 Đặt

ln2

v x x





























   

2 2 2

d .ln 2 . d

ln2 ln 2

2 4 2 2

F x f x x x x

x x x

x C x C

  



     









 

Câu 3. Tìm nguyên hàm của hàm số

 

f x x

F x x C

. B.

F x x C

. D.

F x x C



C A

Ta có:

 

F x x dx



Đặt



 

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 

2 2 2

1 1 1 1

e e d e

2 2 2 2

x x x

du x

dv e dx

F x x x x C

























     







_Bà (10 câu NB; 10 câu TH)

(10 câu)

Câu 1. Nguyên hàm của hàm số

 

sinf x x x

là:

– cos sinx x x C

. B.

sin cosx x x C

cos sinx x x C

. D.

cos sinx x x C

Câu 2. Kết quả của

I xe x



là:

I e e C  

. B.

I e xe C  

I e C

. D.

I xe e C  

Câu 3. Tính

( ) sin 2F x x xdx



. Chọn kết quả ?

( ) (2 cos2 sin2 )

F x x x x C  

. B.

( ) (2 cos2 sin2 )

F x x x x C   

( ) (2 cos2 sin2 )

F x x x x C   

. D.

( ) (2 cos2 sin2 )

F x x x x C  

Câu 4. Nguyên hàm của hàm số

   

f x x

là

xC

. B.

 

xC

. C.

 

xC

. D.

xC

Câu 5. Họ các nguyên hàm của

 

lnf x x x

là:

ln .

x x C

ln .

x x x C

ln .

x x C

ln .

x x x C

Câu 6. Tìm nguyên hàm của hàm số

   

ln 2f x x x

   

d ln 2

x x x

f x x x C



   



. B.

   

d ln 2

x x x

f x x x C



   



   

d ln 2

x x x

f x x x C



   



. D.

   

d ln 2

x x x

f x x x C



   



Câu 7. Cho hàm số

sin 2 dy x x x



. Chọn mệnh đề đúng trong các mệnh đề sau:

6 12













. B.













6 12













. D.

6 24













Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Câu 8. Gọi

 

là một nguyên hàm của hàm số

 

f x x





. Tính

 

biết

 

01F 

   

1 e 2

F x x



  

. B.

   

1 e 1

F x x



   

   

1 e 2

F x x



   

. D.

   

1 e 1

F x x



  

Câu 9. Tìm họ nguyên hàm

 

của hàm số

 

f x x

   

2e 2

F x x C  

. B.

   

F x x C  

 

F x x C



  





. D.

 

F x x C



  





Câu 10. Cho

()Fx

là một nguyên hàm của hàm số

   

5 1 e

f x x

và

 

03F 

. Tính

 

1 e 2F 

. B.

 

1 11e 3F 

. C.

 

1 e 3F 

. D.

 

1 e 7F 

2. : (10 câu)

Câu 11. Kết quả của

ln dxx



là:

ln x x x C

. B.

ln x x C

. C.

ln x x x C

. D.

ln x x x

Câu 12. Tìm nguyên hàm của hàm số

 

lnf x x x

   

d 3ln 2

  



f x x x x C

. B.

   

d 3ln 2

  



f x x x x C

   

d 3ln 2

  



f x x x x C

. D.

   

d 3ln 1

  



f x x x x C

Câu 13. Biết

cos2 d sin 2 cos2x x x ax x b x C  



với

là các số hữu tỉ. Tính tích

ab 

. B.

ab 

. C.

ab 

. D.

ab 

Câu 14. Biết

 

2 2 2

d , .

x x x

xe x axe be C a b   



Tính tích

ab 

. B.

ab 

. C.

ab 

. D.

ab 

Câu 15. Biết

 

3 1 d

I x e x a be   



với

,ab

là các số nguyên. Tính

.S a b

8S 

. B.

10S 

. C.

12S 

. D.

16S 

Câu 16. Ta có

 

x e x x mx n e C   



khi đó

.mn

bằng.

. B.

4

. C.

. D.

Câu 17. Nguyên hàm của hàm 2018

 

f x x

là:

 

( ) e 2

F x x C  

. B.

( ) e

F x x C



  





( ) 2e

F x x C



  





. D.

 

( ) 2e 2

F x x C  

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Câu 18. Cho

 

F x ax bx c  

là một nguyên hàm của hàm số

 

2018 3 1 e

f x x x  

trên khoảng

 

; 

. Tính

24T a b c  

1011T 

. B.

3035T 

. C.

1007T 

. D.

5053T 

Câu 19. Biết

   

3 . d 2

x e x e x n C



    



, với

,mn

. Khi đó tổng

S m n

có giá trị

bằng

. B.

. C.

. D.

Câu 20. Tìm nguyên hàm



sin dxx

   



sin d 2 cos 2sinx x x x C

. B.

  



sin d cosx x x C





sin d cosx x x C

. D.





sin d cos

x x x C



1.A

2.D

3.C

4.A

5.C

6.D

7.C

8.C

9.D

10.D

11.C

12.B

13.B

14.B

15.C

16.B

17.B

18.B

19.B

20.A



Câu 1. Nguyên hàm của hàm số

 

sinf x x x

là

– cos sinx x x C

. B.

sin cosx x x C

cos sinx x x C

. D.

cos sinx x x C



Cn A

Ta có:

sin dx x x



Đặt

d sin d

v x x











cos













Vậy

sinx xdx



cos cosx x xdx  



cos sinx x x C   

Câu 2. Kết quả của

I xe x



là

I e e C  

. B.

I e xe C  

I e C

. D.

I xe e C  

 

C D

Cách 1: Sử dụng tích phân từng phần ta có

d d d .

x x x x x x

I xe x x e xe e x xe e C      

  

Cách 2: Ta có

 

x x x x x x

I xe e C e xe e xe



      

Câu 3. Tính

( ) sin 2F x x xdx



. Chọn kết quả ?

( ) (2 cos2 sin2 )

F x x x x C  

. B.

( ) (2 cos2 sin2 )

F x x x x C   

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

( ) (2 cos2 sin2 )

F x x x x C   

. D.

( ) (2 cos2 sin2 )

F x x x x C  



CC

Đặt

sin 2

dux

v x x

























, ta được

( ) cos2 cos2

dF x x x x x  



cos2 sin2

x x x C   

(2 cos2 sin2 )

x x x C   

Câu 4. Nguyên hàm của hàm số

   

f x x

là

xC

. B.

 

xC

. C.

 

xC

. D.

xC

 

CA

Xét

         

d 1 e d 1 de 1 e e d 1 e e e

x x x x x x x

f x x x x x x x x C x C            

   

Câu 5. Họ các nguyên hàm của

 

lnf x x x

là:

ln .

x x C

ln .

x x x C

ln .

x x C

ln .

x x x C



CC

Đặt

xdx dv





























. Suy ra

1 1 1

ln d ln d ln .

2 2 2 4

x x x x x x x x x C    



Câu 6. Tìm nguyên hàm của hàm số

   

ln 2f x x x

   

d ln 2

x x x

f x x x C



   



. B.

   

d ln 2

x x x

f x x x C



   



   

d ln 2

x x x

f x x x C



   



. D.

   

d ln 2

x x x

f x x x C



   





CD

Đối với nguyên hàm dạng

   

ln dP x Q x x







ta đặt

 

u Q x

v P x x



















để tính theo phương pháp

nguyên hàm từng phần.

Câu 7. Cho hàm số

sin 2 dy x x x



. Chọn mệnh đề đúng trong các mệnh đề sau:

6 12













. B.













. C.

6 12













. D.

6 24













 

CC

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

sin2 d sin2 ; sin 2.

6 6 6 12

y x x x y x x y

   

   



    

   

   



Câu 8. Gọi

 

là một nguyên hàm của hàm số

 

f x x





. Tính

 

biết

 

01F 

   

1 e 2

F x x



  

. B.

   

1 e 1

F x x



   

   

1 e 2

F x x



   

. D.

   

1 e 1

F x x



  



CC

Đặt

d e d e

u x u x

v x v











  



Do đó

e d e e d

x x x

x x x x

  

  



 

e e ;

x C F x C



    

 

01F 

e 1 2CC



     

. Vậy

   

1 e 2

F x x



   

Câu 9. Tìm họ nguyên hàm

 

của hàm số

 

f x x

   

2e 2

F x x C  

. B.

   

F x x C  

 

F x x C



  





. D.

 

F x x C



  





 

CD

Đặt



























   

dF x f x x



e e d

xx



1 1 1

e . e

2 2 2

xC  



  





Câu 10. Cho

()Fx

là một nguyên hàm của hàm số

   

5 1 e

f x x

và

 

03F 

. Tính

 

1 e 2F 

. B.

 

1 11e 3F 

. C.

 

1 e 3F 

. D.

 

1 e 7F 



CD

Ta có

   

5 1 e d

F x x x



Đặt

d e d











d 5d













   

5 1 e 5e d

F x x x  



 

5 1 e 5e

xC   

 

5 4 e

xC  

Mặt khác

 

03F 

43C   

7C

   

5 4 e 7

F x x   

Vậy

 

1 e 7F 

Câu 11. Kết quả của

ln dxx



là

ln x x x C

. B.

ln x x C

. C.

ln x x x C

. D.

ln x x x

 

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

CC

Đặt

d dx

dv=dx





















ln dx lnx . dx lnx     



x x x x x C

Câu 12. Tìm nguyên hàm của hàm số

 

lnf x x x

   

d 3ln 2

  



f x x x x C

. B.

   

d 3ln 2

  



f x x x x C

   

d 3ln 2

  



f x x x x C

. D.

   

d 3ln 1

  



f x x x x C



CB

 

d ln .d



I f x x x x x

Đặt:

d d 2 d d

    t x t x t t x

2 2 2

2 ln .d 4 ln .d  



I t t t t t t

Đặt:





























v t t t

 

3 2 3 3 3

1 1 1 1 2

2 ln d 2 ln 3ln 1

3 3 3 9 9

   

        

   

   



I t t t t t t t C t t C

 

3ln 1

  x x C

 

3ln 2

  x x C

Câu 13. Biết

cos2 d sin 2 cos2x x x ax x b x C  



với

là các số hữu tỉ. Tính tích

ab 

. B.

ab 

. C.

ab 

. D.

ab 



CB

Đặt

d cos2 d

sin 2

v x x























Khi đó

cos2 d sin2 sin2 d

x x x x x x x



sin2 cos2

x x x C  

a

b 

Vậy

ab 

Câu 14. Biết

 

2 2 2

d , .

x x x

xe x axe be C a b   



Tính tích

ab 

. B.

ab 

. C.

ab 

. D.

ab 

 

C B

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Đặt

v e x























Suy ra:

2 2 2

x x x

xe x xe e x



xe e C  

Vậy:

1 1 1

; .

2 4 8

a b ab     

Câu 15. Biết

 

3 1 d

I x e x a be   



với

,ab

là các số nguyên. Tính

.S a b

8S 

. B.

10S 

. C.

12S 

. D.

16S 

Li gii

Chn C

 

3 1 d

I x e x



Đặt

3 1 d 3d

d e dx 2e

u x u x

  















Ta có:

 

2 2 2

2 3 1 6 d 10 2 12 10 2 12 12 14 2

x x x

I x e e x e e e e e           



Vậy

12ab

Câu 16. Ta có

 

x e x x mx n e C   



khi đó

.mn

bằng.

. B.

4

. C.

. D.

Li gii

Chn B

Đặt

d 2 d

u x x

v e x





















. d 2 d

x x x

x e x x e xe x  



Đặt

2 d 2d

u x u x

v e x v e













2 d 2 2 d 2 2

x x x x x

xe x xe e x xe e C     



 

. d 2 2

x e x x x e C    



Khi đó

.4mn

Câu 17. Nguyên hàm của hàm 2018

 

f x x

là:

 

( ) e 2

F x x C  

. B.

( ) e

F x x C



  





( ) 2e

F x x C



  





. D.

 

( ) 2e 2

F x x C  



CB

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Đặt

d e d























Khi đó:

 

2 2 2 2 2 2

1 1 1 1 1 1

.e d .e e d .e e e

2 2 2 4 2 2

x x x x x x

F x x x x x x C x C



        







Câu 18. Cho

 

F x ax bx c  

là một nguyên hàm của hàm số

 

2018 3 1 e

f x x x  

trên khoảng

 

; 

. Tính

24T a b c  

1011T 

. B.

3035T 

. C.

1007T 

. D.

5053T 

 

C B

Vì

 

F x ax bx c  

là một nguyên hàm của hàm số

 

2018 3 1 e

f x x x  

trên

khoảng

 

; 

nên ta có:

 

F x f x





, với mọi

 

;x  

 

   

2 2 2 2

2 2 2 2 e 2018 3 1 e

ax x b a c b x x       

, với mọi

 

;x  

2 2018

2 2 3







   





  



1009

2021

2023









  











Vậy

24T a b c  

2021 2023

1009 2. 4.

   

    

   

   

3035

Câu 19. Biết

   

3 . d 2

x e x e x n C



    



, với

,mn

. Khi đó tổng

S m n

có giá trị

bằng:

. B.

. C.

. D.



CB

Đặt

v e x



























Khi đó

   

2 2 2

3 . d 3 d

x x x

x e x e x e x

  

    



 

e x e C



    

   

. 2 6 1 2 7

e x C e x C



        

4; 7mn  

65mn  

Câu 20. Tìm nguyên hàm

sin dxx



sin d 2cos 2sinx x x x C   



. B.

sin d cosx x x C  



sin d cosx x x C



. D.

sin d cos

x x x C





 

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

C A

Đặt

tx

, ta có

sin 2 sinxdx t tdt



Đặt

sin

dv tdt











ta có

cos

du dt

v tdt











2 sin 2 cos 2cos 2 cos 2sin 2 cos 2sint tdt t t tdt t t t C x x x C          



B2: 

_ . 

-Phương pháp:

_ Cho hàm số

liên tục trên đoạn

[ ; ].ab

Giả sử hàm số

()u u x

có đạo hàm liên tục

trên đoạn

[ ; ]ab

và

( ) .ux





Giả sử có thể viết

( ) ( ( )) '( ), [ ; ],f x g u x u x x a b

với

liên tục trên đoạn

[ ; ].



Khi đó, ta có

()

( ) ( ( )) ( ) ( ) .

a a u a

I f x dx g u x u x dx g u du  

  

_ Để tính tích phân:

 

I g x dx



ta thực hiện các bước:

. Bước 1. Biến đổi để chọn phép đặt

 

t u x

()dt u x dx





. Bước 2. Thực hiện phép đổi cận:

 Với

xa

thì

 

t u a

 Với

xb

thì

 

t u b

. (Nhớ : )

. Bước 3. Đưa về dạng

()

I f t dt



đơn giản và dễ tính hơn.

_ch phân





Có

 

()t f x

Có

()

ax b

t ax b

Có

()fx

()t f x

Có

và x

lntx

hoặc biểu thức chứa

ln x

Có

e dx

te

hoặc biểu thức chứa

Có

sin xdx

costx

Có

cosxdx

sint xdx

Có

cos

tantx

Có

sin

cottx

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

_Bài 

Câu 1. Tính tích phân

(1 )I x x dx



I 

. B.

I 

. C.

I 

. D.

I 



C B

 Đặt

12t x dt xdx   

 Đổi cận:

01xt  

;

12xt  

 Nên

2 10 10

I dt  





 Để tính giá trị 1 tích phân xác định bằng máy tính

570ES.

. Bước 1. Sử dụng lệnh để màn hình máy tính cầm

tay hiện:

. Bước 2. Nhập hàm số f(x)

. Bước 3. Nhập cận

. Bước 4. Ấn phím =

Câu 2. Tính tích phân

21I x x dx



bằng cách đặt

1ux

, mệnh đề nào dưới đây đúng?

2I udu



. B.

I udu



. C.

I udu



. D.

I udu





CC

 Đặt

12u x du xdx   

 Đổi cận

10xu  

;

23xu  

 Nên

I udu





+ Tính tích phân I bằng MTCT.

+ Tính tích phân từng đáp án A, B, C, D.

+ Đối chiếu kết quả, chọn đáp án C.

Câu 3. Tính tích phân

cos .sin dI x x x











. B.





. C.

0I 

. D.

I 



CC

 Đặt

cos sin sint x dt xdx dt xdx      

 Đổi cận: với

01xt  

;

với

1xt



   

 Vậy

 

4 4 4

I t dt t dt



      





 Sử dụng máy tính, tính tích phân hàm lượng giác

phải chuyển về đơn vị radian.

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

(10 câu NB; 10 câu TH)

(10 câu)

Câu 1. Tính tích phân

( 2) (2 1)dI x x x x   



chọn cách đổi biến hợp lí nhất.

( ) dt x x x

. B.

21tx

( ) (2 1)t x x x  

. D.

2t x x  

Câu 2. Tính tích phân

5 3 4 2

1(5 3 )I x x x x dx   



chọn cách đổi biến hợp lí nhất.

( )dt x x x

. B.

53t x x

. C.

1t x x  

. D.

dt x x x

Câu 3. Tính tích phân









chọn cách đổi biến hợp lí nhất.





. B.

43t x x

. C.







2t x x  

Câu 4. Tính tích phân

ln d

I x x





chọn cách đổi biến hợp lí nhất.



. B.

lntx

. D.



Câu 5. Tính tích phân

(2x 1)d

I e x







chọn cách đổi biến hợp lí nhất.

31t x x  

. B.

21tx

. C.

t x x

. D.

(2 1)

t e x





Câu 6. Tính tích phân

3 (3 1)d

I x x







chọn cách đổi biến hợp lí nhất.

3t x x

. B.

3t x x

. C.

t x x

. D.

3 (3x 1)





Câu 7. Tính tích phân

sin cos dI x x x







chọn cách đổi biến hợp lí nhất.

sintx

. B.

sintx

. C.

costx

. D.

sin .cost x x

Câu 8. Tính tích phân

cos .sin dI x x x







chọn cách đổi biến hợp lí nhất.

ost c x

. B.

sintx

. C.

costx

. D.

os .sint c x x

Câu 9. Tính tích phân

tan . d

cos

I x x







chọn cách đổi biến hợp lí nhất.

tantx

. B.

tantx

. C.

costx

. D.

costx

Câu 10. Tính tích phân

cot .

sin

I x dx







chọn cách đổi biến hợp lí nhất.

cottx

. B.

sintx

. C.

cottx

. D.

sintx

 (10 câu)

Câu 11. Tích phân

x 





. Khi đó

ab

bằng:

A. 6. B. 8. C. 9. D. 10.

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Câu 12. Cho tích phân

1dxx



, với cách đặt

1tx

thì tích phân đã cho bằng với tích phân nào

sau đây?

3dtt



. B.

dtt



. C.

3dtt



. D.

3dtt



Câu 13. Cho







,với cách đặt

1tx

thì tích phân đã cho bằng với tích phân nào sau

đây?

dtt



. B.



. C.

dtt



. D.



Câu 14. Tích phân

cos .sinx x dx





bằng



. B.

. C.



. D.

Câu 15. Cho

là hàm số liên tục thỏa

 

d7f x x 



. Tính

 

cos . sin dI x f x x







. B.

. C.

. D.

Câu 16. Cho

( )d 2018f x x 



. Tính tích phân

 

(2 ) (4 2 ) dI f x f x x  



0I 

. B.

2018I 

. C.

4036I 

. D.

1009I 

Câu 17. Cho tích phân

 

d 32.I f x x



Tính tích phân

 

2 d .J f x x



32.J 

64.J 

8.J 

16.J 

Câu 18. Cho

I xe x







.Biếtrằng

ae b





. Khiđó,

ab

bằng:

. B.

. C.

. D.

Câu 19. Với cách đổi biến

1 3lnux

thì tích phân

1 3ln

xx



trở thành:

 

uu



. B.

 

uu



. C.

 

2 1 duu



. D.





Câu 20. Tính tích phân

1 3ln







bằng cách đặt

1 3lntx

, mệnh đề nào dưới đây sai?

It

. B.

I t t



. C.

I t t



. D.

I 



1.D

2.C

3.D

4.B

5.C

6.C

7.B

8.C

9.B

10.C

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

11.D

12.D

13.A

14.B

15.D

16.B

17.A

18.C

19.B

20.B



Câu 11. Tích phân

x 





khi đó

ab

bằng

A. 6. B. 8. C. 9. D. 10.



CD

Đặt

32t x dt xdx   

Đổi cận

03xt  

;

27xt  

Nên

2 2 3





Câu 12. Cho tích phân

1dxx



, với cách đặt

1tx

thì tích phân đã cho bằng với tích phân nào

sau đây?

3dtt



. B.

dtt



. C.

3dtt



. D.

3dtt





CD

Đặt

1 (1 ) 3tt x t x dx       

Đổi cận

01xt  

;

10xt  

Nên

.3 3I t t dt t dt  



Câu 13. Cho

I dx







,với cách đặt

1tx

thì tích phân đã cho bằng với tích phân nào sau

đây?

dtt



. B.



. C.

dtt



. D.





CD

Đặt

2 2 2

11t x t x tdt xdx      

Đổi cận

01xt  

;

12xt  

Nên

I dt dt





Câu 14. Tích phân

cos .sinx x dx





bằng



. B.

. C.



. D.



CB

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Đặt

cos sin .t x tdt x dx   

Đổi cận:

01xt  

1xt



   

Khi đó:

I t dt







Câu 15. Cho

là hàm số liên tục thỏa

 

d7f x x 



. Tính

 

cos . sin dI x f x x







. B.

. C.

. D.



CD

Đặt

sin cos .t x dt x dx  

Đổi cận

00xt  

;



  

Khi đó:

( ) 7I f t dt



Câu 16. Cho

( )d 2018f x x 



. Tính tích phân

 

(2 ) (4 2 ) dI f x f x x  



0I 

. B.

2018I 

. C.

4036I 

. D.

1009I 



CB

Ta có

(2 )d ( )dt

f x x f t





2 0 4

0 4 0

(4 2 )d ( )dt ( )dt

f x x f t f t



   

  

Suy ra

 

2 4 4

0 0 0

(2 ) (4 2 ) d ( )dt ( )d 2018I f x f x x f t f x x     

  

Câu 17. Cho tích phân

 

d 32.I f x x



Tính tích phân

 

2 d .J f x x



32.J 

64.J 

8.J 

16.J 



CD

Đặt

2 d 2d d .

t x t x x    

Đổi cận:

0 0; 2 4.x t x t     

     

2 4 4

0 0 0

1 1 1

2 d d d 16.

2 2 2

J f x x f t t f t t I    

  

Câu 18. Cho

I xe x







. Biết rằng

ae b





. Khi đó,

ab

bằng:

. B.

. C.

. D.



Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

CC

Đặt

1 d 2 dt x t x x    

Đổi cận:

0 1; 1 0.x t x t     

1 1 1

e dt e d

2 2 2



   



Câu 19. Với cách đổi biến

1 3lnux

thì tích phân

1 3ln

xx



trở thành:

 

uu



. B.

 

uu



. C.

 

2 1 duu



. D.







CB

Đặt

1 3ln 1 3ln d .du

u x u x x

      

Đổi cận:

x e u

  





  



Khi đó

 

. . . 1 .

u.3 3 9

I dt u du



  



Câu 20. Tính tích phân

1 3ln







bằng cách đặt

1 3lntx

, mệnh đề nào dưới đây sai?

It

. B.

I t t



. C.

I t t



. D.

I 



CC

Đặt

1 3ln 1 3ln d .d

t x t x x t

      

Đổi cận:

x e t

  





  



Khi đó

2 2 14

. . . t .

3 3 9

I t dt dt  



_ 2. 2

_  Để tính tích phân:

 

I f x x



, mà biểu thức dưới dấu tích phân có dạng

ax

: đặt

| |sin ; ;

x a t t





  





xa

: đặt

; ; \{0}

sin 2 2





  





xa

tan ; ;

x a t t





  









hoặc





: đặt

.cos2x a t

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

_

Câu 1. Tính tích phân sau:

1I x dx





. B. 1. C. 0 D.







CA

 Đặt

sinxt

ta có

cos .dx tdt

Đổi cận:

0 0; 1

x t x t



     

Vậy

0 0 0

1 |cos |cos cosI x dx t tdt tdt



   

  

1 cos2











 . Bước 1. Sử dụng lệnh để màn

hình máy tính cầm tay hiện:

. Bước 2. Nhập hàm số f(x)

. Bước 3. Nhập cận

. Bước 4. Ấn phím =

Câu 2. Tính tích phân sau:









. B.



. C.



. D.







CA

 Đặt

tan ,xt

ta có

 

1 tandx t dt

Đổi cận:



  







  





Vậy

I dt t



   







 . Bước 1. Sử dụng lệnh để màn

hình máy tính cầm tay hiện

. Bước 2. Nhập hàm số f(x)

. Bước 3. Nhập cận

. Bước 4. Ấn phím =

Câu 3. Khi đổi biến

5 tantx 

thì tích phân







trở thành tích phân nào sau đây?

5dt.I







dt.







5tdt.I







dt.









C B

Đặt

5 tant 5(1 tan t)dtx dx   

Đổi cận.



  

;

00xt  

trở thành





+ Tính tích phân I bằng mt.

+ Tính tích phân từng đáp án A,B,C,D.

+ Đối chiếu kết quả, chọn đáp án C.

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

   

4 4 4

0 0 0

5 1 tan t dt 5 1 tan dt

5dt

5tan t 5 5(tan 1) 5

  







  

(10 câu NB; 10 câu TH)

(10 câu)

Câu 1. Tính tích phân







chọn cách đổi biến hợp lí nhất:

3tx

. B.

3 tanxt

. C.

3sintx

. D.

3xt

Câu 2. Tính tích phân







chọn cách đổi biến hợp lí nhất:

16tx

. B.

4sintx

. C.

4tanxt

. D.

4xt

Câu 3. Tính tích phân







chọn cách đổi biến hợp lí nhất:

25tx

. B.

5xt

. C.

5sintx

. D.

5tanxt

Câu 4. Tính tích phân







chọn cách đổi biến hợp lí nhất:

7tx

. B.

7 tanxt

. C.

7sintx

. D.

7xt

Câu 5. Tính tích phân







chọn cách đổi biến hợp lí nhất:

4tx

. B.

4tanxt

. C.

4sintx

. D.

4xt

Câu 6. Tính tích phân

4 d ,I x x



chọn cách đổi biến hợp lí nhất:

2tanxt

. B.

4tx

. C.

2sinxt

. D.

2sintx

Câu 7. Tính tích phân

9dI x x



chọn cách đổi biến hợp lí nhất:

3cosxt

. B.

9tx

. C.

3tanxt

. D.

3tantx

Câu 8. Tính tích phân

25 dI x x



chọn cách đổi biến hợp lí nhất:

25tx

. B.

5cosxt

. C.

5tanxt

. D.

5tantx

Câu 9. Tích phân

16 dxx



chọn cách đổi biến hợp lí nhất:

16tx

. B.

4tanxt

. C.

4sintx

4cosxt

Câu 10. Tích phân

3dxx



chọn cách đổi biến hợp lí nhất:

3tx

2cosxt

3 tanxt

3tantx

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 (10 câu)

Câu 11. Đổi biến số

4sinxt

của tích phân

16 x dx



ta được:

16 cos dI t t







. B.

 

8 1 cos2 dI t t







16 sin dI t t







. D.

 

8 1 cos2 dI t t







Câu 12. Tích phân

1dxx



bằng:

sin t.dx







. B.

sin t.dt





. C.

cos t.dt







. D.

cos t.dt





Câu 13. Đổi biến

2sinxt

tích phân

x



trở thành:

tdt





. B.





. C.





. D.





Câu 14. Khi đổi biến

3tanxt

thì tích phân







trở thành tích phân nào sau đây?

3dt









3dt





3dt





Câu 15. Tích phân

x



bằng:





. B.





. C.







. D.







Câu 16. Tích phân

ax



với

0a 

bằng:





. B.





. C.





. D.





Câu 17. Tích phân: I =

a x dx



với a > 0 bằng:



. B.



. C.



. D.



Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Câu 18. Tích phân: I =

9 x dx



bằng:



. B.



. C.



. D.



Câu 19. Tích phân: I =

16 x dx



bằng:



. B.



. C.



. D.



Câu 20. Tích phân: I =

25 x dx



bằng:



. B.



. C.



. D.





1.B

2.C

3.D

4.B

5.B

6.C

7.A

8.B

9.D

10.B

11.B

12.C

13.A

14.B

15.A

16.A

17.B

18.C

19.B

20.B



Câu 11. Đổi biến số

4sinxt

của tích phân

16 x dx



ta được:

16 cos dI t t







. B.

 

8 1 cos2 dI t t







16 sin dI t t







. D.

 

8 1 cos2 dI t t









CB

Đặt

4sinxt

ta có

4cos .dx tdt

Đổi cận:

0 0; 8

x t x t



     

Vậy :

0 0 0

1 16 | cos |cos 16 cos 8 (1 cos2 ) .I x dx t tdt tdt t dt





     

   

Câu 12. Tích phân

1dxx



bằng

sin t.dx







. B.

sin t.dt





. C.

cos t.dt







. D.

cos t.dt







CD

Đặt

sinxt

ta có

cos .dx tdt

Đổi cận:

0 0; 1

x t x t



     

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Vậy

0 0 0

1 | cos |cos cos .I x dx t tdt tdt



   

  

Câu 13. Đổi biến

nt2six 

tích phân

x



trở thành:

tdt





. B.





. C.





. D.







CB

Đặt

2sinxt

ta có

2cos .dx tdt

Đổi cận:

0 0; 1

x t x t



     

Vậy:

0 0 0

2cos

4 4 4sin

dx t

I dx dt dt



  



  

Câu 14. Khi đổi biến

3tanxt

thì tích phân







trở thành tích phân nào sau đây?

3dt









3dt





3dt







CB

Đặt

 

3tant, t ; d 3 1 tan t dt





     





Đổi cận:

0 t 0x   

;



  

Suy ra:

 

.3 1 tan t dt dt

9 9tan t 3



  





Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

B3: 

_ Dạng 1.

 

sin

cos d

f x ax x













_

Câu 1. Tính tích phân





I xe dx

Ie

. B.

Ie

. C.

Ie

. D.

32I e e



CA

Đặt













u x du dx

dv e dx v e

 

2 2 2

x x x x

I xe dx xe e dx e e e

e e e e e

     

    





- Tính tích phân

- Lưu kết quả bằng biến A

- Kiểm tra các đáp án: A đúng

Câu 2. Tính tích phân

( 2)

I x e dx







. B.





. C.





. D.







CB



 Tính tích phân:

-Phương pháp:

Đặt:

   

sin sin

cos d cos d

ax ax

u f x du f x dx

ax ax

dv ax x v ax x







   







   





   



   

   





Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 Đặt

du dx

dv e dx























(chọn

0C 

)

1 1 5 3

( 2)

2 2 4

I x e e dx



    



- Lưu kết quả bằng biến B

- Kiểm tra các đáp án: B đúng

Câu 3. Tích phân

 

3 2 cos dx x x







bằng:





. B.





. C.





. D.







CB

 Đặt

 

3 2 cos dI x x x







. Ta có:

  

3 2 1 cos2 d

x x x



  



     

3 2 d 3 2 cos2 d

x x x x x I I





     







 

3 2 dI x x



  









  





 

3 2 cos2 dI x x x







. Dùng tích phân từng phần

Đặt

d 3d

d cos2 d

sin 2

v x x























Khi đó

 

3 2 sin2 sin 2 d

I x x x x



  



 

0 cos2 0



  

Vậy

1 3 3

2 2 4

   



   







 Tinh tích phân:

- Lưu kết quả bằng biến C

Kiểm tra các đáp án: B đúng

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

(10 câu NB; 10 câu TH)

(10 câu)

Câu 1. Cho tích phân

 

1 sin 2 d .I x x x







Tìm đẳng thức đúng?

 

1 cos2 cos2 dI x x x x



   



. B.

 

1 cos2 cos2 d

I x x x x



   



 

1 cos2 cos2 d

I x x x x



   



. D.

 

1 cos2 cos2 dI x x x x



   



Câu 2. Tính tích phân

 

2 1 cosI x xdx











. B.





. C.





. D.





Câu 3. Giá trị của

cos2I x xdx







là:



. B.



. C.



. D.



Câu 4. Tính tích phân

 

2 sin3x xdx







bằng:

. B.

. C.

. D.

Câu 5. Tính tích phân

 

1 sinI x xdx







bằng:





. B.





. C.





. D.





Câu 6. Tính tích phân

I (2x 1)sin3xdx









Câu 7. Tính tích phân

I x(1 sin2x)dx







32 4





32 4





32 4





32 4





Câu 8. Tính tích phân

I (2x 1)e dx



Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

ee

. B.

1ee

ee

1ee

Câu 9. Tính tích phân

 

I x 1 e dx



e

e

e

Câu 10. Tính tích phân

 

2x x

I e x e dx









 (10 câu)

Câu 11. Tính tích phân

I (x 1)e dx



25e

23e

21e

24e 

Câu 12. Tính tích phân

 

I x e x dx  



e 

4 10

e 

4 14

e 

4 14

e 

Câu 13. Cho

 

I x e dx



. Đặt

dv e dx











. Chọn khẳng định đúng.

3 1 2

I e e dx  



. B.

3 1 2

I e e dx  



. C.

I e e dx



. D.

I e e dx



Câu 14. Biết tích phân

 

x e dx a be  



với

,.ab

Tìm tổng a+b.

1.ab

. B.

25.ab

. C.

43.a b e  

. D.

1ab  

Câu 15. Cho biết tích phân

(2 ln )

a e b e c

I x x x dx



  



với

,,abc

là các ước nguyên của 4.

Tính tổng:

abc

A. 4. B. 1. C. 3. D. 2.

Câu 16. Cho

 

1 '( ) x 2x f x d



và

2 (1) (0) 1ff

. Tính

( ) x ?f x d 



1I 

. B.

1I 

. C.

2I 

. D.

2I 

Câu 17. Cho

 

2 1 '( ) x 3x f x d



và

3 (1) (0) 1ff

. Tính

( ) x ?f x d 



1I 

. B.

I 

. C.

1I 

. D.

I 

Câu 18. Tính

sin dJ x x x



Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

π

. B.

. C.

. D.

Câu 19. Biết

( 2020) . .

x e dx a e b  



Với

,ab

. Tính

T a b

1T 

. B.

2T 

. C.

3T 

. D.

4T 

Câu 20. Tính

I x x



eI 

. B.

eI 

. C.

3e 2eI 

. D.

eI 



1.C

2.B

3.D

4.D

5.A

6.B

7.A

8.C

9.D

10.A

11.B

12.C

13.B

14.A

15.D

16.A

17.A

18.B

19.A

20.A

_ D.

_

Câu 1. Cho

ln dI x x x



.eab





với

c

. Tính

T a b c  

. B.

. C.

. D.



C D

Ta có:

v x x











nên

















ln dI x x x



ln d

x x x





















Vậy

T a b c  

6





_ Dạng 2. :

( )ln( )f x ax dx







-Phương pháp:

Đặt:

ln( )

()

u ax

dv f x dx

v f x dx

























Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Câu 2. Tính tích phân

   

1 ln 3 dI x x x  



10ln2

. B.

10ln2



. C.

10ln2



. D.

10ln2





 C D

Đặt

 

ln 3

v x x

































 

ln 3 d

I x x x x





   









35 1 9 9 3 3

ln2

2 2 3 3

dx dx

   

  





 

35 1 9

ln2 3 9ln2 1 3ln2

2 2 2



     





10ln2





Quy trình bm máy.

 Bấm máy tính:

 Lưu kết quả:

 Kiểm tra kết quả:

Câu 3. Biết

 

2 ln 1 d .lnx x x a b



, với

,ab

là số nguyên tố. Tính

67ab

. B.

. C.

. D.



C D

 Xét

 

2 ln 1 dI x x x



6

Đặt

 

ln 1

d 2 d

v x x

  

























Ta có:

 

1 ln 1 d

I x x x



   





 

3ln3 1 dxx  



3ln3 3ln3



   





Vậy

3a 

3b 

6 7 39ab  



 _Quy trình bm máy.

Ta có

.ln ln

a b b

c 1.

c 2.

a a A

A b b e  

c 3. Bm Shift + FACT

Vy

3a 

3b 

6 7 39ab  

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 (10 câu NB; 10 câu TH)

(10 câu)

Câu 1. Tính tích phân

( 2)ln

I x xdx



I 

. B.





. C.





. D.





Câu 2. Nếu đặt

 

dv x dx











thì tích phân

 

2 1 ln

I x xdx



trở thành:

 

I x x x dx   



. B.

 

ln 1

I x x x dx  



I x x xdx



. D.

 

ln 1

I x x x x dx   



Câu 3. Tính tích phân

ln(x 1)J x dx



ln3

J 

. B.

ln3

J 

. C.

ln3

J 

. D.

ln3

J 

Câu 4. Biết rằng

 

ln 1 d ln3 ln2x x a b c   



với

là các số nguyên. Tính

S a b c  

0S 

. B.

1S 

. C.

2S 

. D.

2S 

Câu 5. Biết

 

2 ln 1 d .lnx x x a b



, với

,ab

là số nguyên tố. Tính

ab

. B.

. C.

. D.

Câu 6. Tính tích phân

   

1 ln 3 dI x x x  



10ln2

. B.

10ln2



. C.

10ln2



. D.

10ln2



Câu 7. Biết

 

2 ln 1 d .lnx x x a b



, với

,ab

là số nguyên tố. Tính

34ab

. B.

. C.

. D.

Câu 8. Biết

ln( 1) ln2x dx a b  



với

,ab

là các số nguyên. Khi đó,

ab

bằng

Câu 9. Tính

 

ln3 ln2

I dx a b

  





Tính

3T a b

1T 

. B.

5T 

. C.

3T 

. D.

4T 

Câu 10. Tích Phân

ln( )



I x x dx

là :

3ln3

. B.

2ln 2

. C.

3ln3 2

. D.

2 3ln3

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 (10 câu)

Câu 11. Tích phân





I dx

bằng:

 

1 ln2



 

1 ln2



 

ln2 1



 

1 ln2



Câu 12. Tích phân

(2 1)ln



K x xdx

bằng:

3ln2

K

K

3ln2K

2ln2

K

Câu 13. Cho

ln d

x x x







với

,ab

. Tổng

ab

bằng

. B.

. C.

. D.

Câu 14. Biết

ln d

I x x x ae b  



với

là các số hữu tỉ. Giá trị của

 

9 ab

bằng

. B.

. C.

. D.

Câu 15. Biết

 

2 ln 1 dx lnx x a b



, với

,ab

là số nguyên tố. Tính

67ab

. B.

. C.

. D.

Câu 16. Biết

(4 1)lnxdx ln2 b.xa  



, với

,ab

. Tính

2ab

. B.

. C.

. D.

Câu 17. Cho tích phân

d ln2

I x a

  



với

là số thực,

và

là các số nguyên dương, đồng

thời

là phân số tối giản. Tính giá trị của biểu thức

23P a b c  

6P 

. B.

6P 

. C.

5P 

. D.

4P 

Câu 18. Cho

 

ln d ln5 ln 2x x x a b c   



với

là các số nguyên. Tính

2S a b c  

23S 

. B.

20S 

. C.

17S 

. D.

11S 

Câu 19. Cho

 

ln 1

d ln2

x x a



  





với

là các số nguyên dương và là phân số tối giản.

Tính giá trị của biểu thức





S 

. B.

S 

. C.

S 

. D.

S 

Câu 20. Cho

1ab  

. Tích phân

 

ln 1 d

I x x



bằng biểu thức nào sau đây?

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

   

1 ln 1

I x x a b    

. B.

   

1 ln 1

I x x b a    

 





. D.

 

ln 1 d

I x x x

  







1.C

2.D

3.C

4.A

5.D

6.D

7.B

8.B

9.D

10.C

11.A

12.D

13.A

14.A

15.D

16.D

17.D

18.B

19.B

20.B

_ .

_

Câu 1. Tính tích phân

cos . d

I x e x











. B.





. C.





. D.







C D



cos . d

I x e x







Đặt:

sin

u cosx du xdx

dv dx v

  











. sin . 1 sin . (*)

x x x

I cosx e x e dx x e dx





    



sin . d

J x e x







Đặt:

sin

u x du cosxdx

dv dx v















 Tính:

Kiểm tra các đáp án:

_ Dạng 3.

sin









e dx

cosax





-Phương pháp:

Đặt:

sin

cos

ac ax

du dx

a ax

dv e dx











































Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

sin . cos . cos .

(2*)

x x x

J x e x e dx e x e dx





   





Thay (2*) vào (*) ta có:







Câu 2. Tính tích phân

sin . d

I x e x









-e 2







. B.

-e 2





. C.

-e 1







. D.

-e 1







C D



sin . d

I x e x









Đặt:

sin

u x du cosxdx

dv dx v











  



sin . cos . e (*)

I x e x e dx J







     



cos . d

J x e x









Đặt:

sin

u cosx du xdx

dv dx v



  







  



s . sin .

1 (2*)

J co x e x e dx





  





Thay (2*) vào (*) ta có:











 Tính:

Kiểm tra các đáp án:

Câu 3.

sinx

.sin 2I e xdx







. B.

. C.

1

. D.

2

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020



C B



inx

I e x xdx

2 .sin cos







Đặt

u x du xdx

dv e xdx v e

sin sin

sin cos

cos















  

  



I xe e xdx

sin sin

sin

2sin .cos

2 2 2



 Tính:



Câu 1. Tính tích phân

e cos2

I xdx













. B.







. C.







. D.







Câu 2. Tính tích phân

e cos2

Idx x















. B.







. C.







. D.







Câu 3. Tính tích phân

e sin

xI dx







2Ie





. B.

1Ie





. C.

3Ie





. D.





Câu 4. Tính tích phân

e sin 2

I xdx













. B.







. C.







. D.







Câu 5. Tính tích phân

e sin3

I xdx













. B.







. C.







. D.







Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Câu 6. Tính tích phân

e cos

I xdx







3 3 1 3

()

10 2 6 10



  

. B.

3 3 1 3

()

10 2 6 10



  

3 3 1 3

()

10 2 6 10



  

. D.

3 3 1 3

()

10 2 6 10



  

Câu 7. Tính tích phân

e sin

Idx x















. B.









. C.







. D.







Câu 8. Tính tích phân

e sin

I xdx







( 3 2) 1







. B.

( 3 2) 1







. C.

( 3 2) 1







. D.

( 3 2) 1







Câu 9. Tính tích phân

e cos

xI dx













. B.







. C.







. D.







Câu 10. Tính tích phân

e sin

xI dx













. B.







. C.







. D.









1.A

2.A

3.B

4.C

5.D

6.B

7.A

8.D

9.A

10.B

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

B4: 

_ . Ứng dụng của tích phân tính 

_ Dạng 1. Ứng dụng của tích phân tính diện tích hình phẳng

-Phương pháp:

 Diện tích hình phẳng giới hạn bởi đồ thị hàm số

()y f x

liên tục trên đoạn

 

;ab

, trục

hoành và hai đường thẳng

xa

xb

được xác định:

()

S f x dx



 Diện tích hình phẳng giới hạn bởi đồ thị hàm số

()y f x

()y g x

liên tục trên đoạn

 

;ab

và hai đường thẳng

xa

xb

được xác định:

( ) ( )

S f x g x dx



Chú ý:

- Nếu trên đoạn

[ ; ]ab

, hàm số

()fx

không đổi dấu thì:

( ) ( )

f x dx f x dx



- Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối

- Diện tích của hình phẳng giới hạn bởi các đường

()x g y

()x h y

và hai đường thẳng

yc

yd

được xác định:

( ) ( )

S g y h y dy























()

y f x

 ()y f x

()

S f x dx























( ) : ( )

()

C y f x

()C

( ) ( )

S f x f x dx



Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

y = -

y =

_

Câu 1.

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số

2yx

và

.yx

. C.

. D.



C A

 Phương trình hoành độ giao điểm của hai đồ thị

là:

2 2 0 .

x x x x





      







Diện tích của hình phẳng cần tìm là

2 ( 2)

3 2 2

S x x dx x x dx





       



    









  Trên

 

1;2

hàm số

( ) 2y f x x x    

không đổi dấu nên

( ) ( ) .f x dx f x dx







 

- Nhập biểu thức

2x x dx



  



vào màn hình

bằng cách bấm lần lượt các phím sau:

- Khi đó trên màn hình xuất hiện

Câu 2. Gọi

là diện tích của hình phẳng giới hạn bởi các đường

ln x



0y 

1x 

ex 

. Mệnh

đề nào dưới đây đúng?







. B.





. C.











. D.















C B

 Ta có





Vì

ln ln

[1;e], ln 0 0 d

x x S x

      





 Xét dấu của hàm số

ln x



trên đoạn

[1;e]

Câu 3. Tính diện tích hình phẳng giới hạn bởi các đường

và trục hoành như hình

vẽ.

. B.

. C.

. D.



C D

 Dựa vào đồ thị ta có:

Diện tích hình phẳng cần tìm là



  

- Nhập biểu thức

x dx x dx



  







vào màn

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

1 4 1 4

3 3 3 6 3

1 8 7 11

3 3 6 6

S x dx x dx x x



       





   



hình (thao tác tương tự câu 1).

- Khi đó trên màn hình xuất hiện

 (10 câu NB; 10 câu TH)

(10 câu)

Câu 1. Diện tích phần hình phẳng tô đen trong hình vẽ bên dưới được tính theo công thức nào dưới

đây?

 

( ) ( ) df x g x x





. B.

 

( ) ( )g x f x dx





   

( ) ( ) d g( ) ( ) df x g x x x f x x



  



. D.

   

( ) ( ) ( ) ( )g x f x dx f x g x dx



  



Câu 2. Diện tích hình phẳng giới hạn bởi hai đường

11 6y x x  

và

6yx

là

. B.

. C.

. D.

Câu 3. Diện tích hình phẳng giới hạn bởi

; 0; 1; 2y x y x x   

bằng

. B.

. C.

. D.

Câu 4. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

 

2 2 4 dx x x







. B.

 

2 2 4 dx x x







Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 

2 2 4 dx x x



  



. D.

 

2 2 4 dx x x



  



Câu 5. Tính diện tích

của hình phẳng (phần gạch sọc) giới hạn bởi hai đồ thị hàm số

   

;2f x x g x x  

trong hình sau

S 

. B.

S 

. C.

S 

. D.

S 

Câu 6. Tính diện tích

của hình phẳng

()H

giới hạn bởi các đường cong

12y x x  

và

yx

937

S 

. B.

343

S 

. C.

793

S 

. D.

397

S 

Câu 7. Gọi

là diện tích hình phẳng giới hạn bởi đồ thị hàm số

 







và các trục tọa độ.

Khi đó giá trị của

bằng

2ln2 1S 

. B.

ln2 1S

. C.

ln2 1S

. D.

2ln2 1S 

Câu 8. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

 

4 3 dx x x  



. B.

 

2 11 dx x x  



 

2 11 dx x x



. D.

 

4 3 dx x x



Câu 9. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

 

3dx x x







. B.

 

3dx x x







Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 

5 2 dx x x



  



. D.

 

5 2 dx x x







Câu 10. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

 

2 3 1 dx x x



  



. B.

 

2 2 3 dx x x x



  



 

2 3 1 dx x x







. D.

 

2 2 3 dx x x x



   



 (10 câu)

Câu 11. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

 

5 9 7 dx x x x  



. B.

 

5 9 7 dx x x x   



 

9 9 dx x x x   



. D.

 

9 9 dx x x x  



Câu 12. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

 

5 8 dxx





. B.

 

2 5 2 dx x x







Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 

5 8 dxx







. D.

 

2 5 2 dx x x



  



Câu 13. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số

yx

và

yx

1S

. B.

2S

. C.

S

. D.

S

Câu 14. Tính diện tích

của hình phẳng giới hạn bởi các đường

2y x x

0y 

10x 

10x 

2000

S 

. B.

2008S 

. C.

2000S 

. D.

2008

S 

Câu 15. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

 

2 2 4 dx x x







. B.

 

2 2 dxx







 

2 2 dxx





. D.

 

2 2 4 dx x x



  



Câu 16. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số

4y x x

và trục

. B.

. C.

. D.

Câu 17. Cho hình phẳng (H) được giới hạn bởi đồ thị hàm số

ye

, trục

,Ox Oy

và đường thẳng

. Tính

hình phẳng trên.

1e 

. B.

 

e 

. C.

. D.

 

e 

Câu 18. Tính diện tích hình phẳng giới hạn bởi hai đồ thị

 

: y 8 7

P x x   

 







3,455

. B.

9 8ln2

. C.

3 ln4

. D.

161

4ln3 8ln2



Câu 19. Tính diện tích

của hình phẳng giới hạn bởi các đường

2y x x

0y 

10x 

10x 

2000

S 

. B.

 2008S

. C.

2000S 

. D.

2008

S 

Câu 20. Cho đồ thị hàm số

()y f x

. Diện tích hình phẳng (phần tô đậm trong hình) là

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

( ) ( )S f x dx f x dx







()S f x dx







( ) ( )S f x dx f x dx







( ) ( )S f x dx f x dx









1.C

2.D

3.A

4.C

5.B

6.A

7.A

8.A

9.B

10.C

11.C

12.D

13.C

14.D

15.D

16.D

17.B

18.B

19.D

20.D



Câu 1. Diện tích phần hình phẳng tô đen trong hình vẽ bên dưới được tính theo công thức nào dưới

đây?

 

( ) ( ) df x g x x





. B.

 

( ) ( )g x f x dx





   

( ) ( ) d g( ) ( ) df x g x x x f x x



  



. D.

   

( ) ( ) ( ) ( )g x f x dx f x g x dx



  





CC

Từ đồ thị hai hàm số

()y f x

và

()y g x

ta có diện tích phần hình phẳng tô đen trong hình vẽ

bên dưới được tính là:

   

( ) ( )

( ) ( ) ( ) ( )

( ) ( ) ( ) ( ) .

S f x g x dx

f x g x dx f x g x dx

f x g x dx g x f x dx





   





Câu 2. Diện tích hình phẳng giới hạn bởi hai đường

11 6y x x  

và

6yx

là

. B.

. C.

. D.



Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

CD

Phương trình hoành độ giao điểm của hai đồ thị là:

11 6 6x x x  

















Diện tích của hình phẳng là :

   

3 2 3 2

6 11 6 6 11 6S x x x dx x x x dx       



3 2 3 2

11 11

2 6 2 6

4 2 4 2

x x x x x x

   

       

   

   

1 1 1

4 4 2

  

Câu 3. Diện tích hình phẳng giới hạn bởi

; 0; 1; 2y x y x x   

bằng

. B.

. C.

. D.



CA

Diện tích của hình phẳng là

S x dx x dx   



Câu 4. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

 

2 2 4 dx x x







. B.

 

2 2 4 dx x x







 

2 2 4 dx x x



  



. D.

 

2 2 4 dx x x



  





CC

Từ đồ thị ta thấy

3 2 1x x x    

 

1;2x  

Vậy diện tích phần hình phẳng gạch chéo trong hình vẽ là

   

3 2 1 dS x x x x





     





 

2 2 4 dx x x



   



Câu 5. Tính diện tích

của hình phẳng (phần gạch sọc) giới hạn bởi hai đồ thị hàm số

   

;2f x x g x x  

trong hình sau

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

S 

. B.

S 

. C.

S 

. D.

S 



CB

   

2 10

2 2 2

3 2 3

S x x dx x x dx x x



         







Câu 6. Tính diện tích

của hình phẳng

()H

giới hạn bởi các đường cong

12y x x  

và

yx

937

S 

. B.

343

S 

. C.

793

S 

. D.

397

S 



CA

Xét phương trình hoành độ giao điểm 2 đường cong:

3 2 2

12 ( 12) 0 3

x x x x x x x







          







Diện tích cần tìm là:

4 0 4

3 2 3 2 3 2

3 3 0

12 d 12 d 12 dS x x x x x x x x x x x x



        

  

   

4 3 4 3

3 2 3 2 2 2

12 d 12 d 6 6

4 3 4 3

x x x x

x x x x x x x x x x



   

           

   

   



99 160 937

4 3 12



  

Câu 7. Gọi

là diện tích hình phẳng giới hạn bởi đồ thị hàm số

 







và các trục tọa độ.

Khi đó giá trị của

bằng

2ln2 1S 

. B.

ln2 1S

. C.

ln2 1S

. D.

2ln2 1S 



CA

 







 

cắt trục

,Ox Oy

lần lượt tại

   

1;0 , 0; 1AB

Gọi

 

là hình phẳng giới hạn bởi các đường

, 0, 0



  



y y x

Suy ra









1 dx













(do





không đổi dấu với

 

0;1x

)

2ln 1xx    



2ln 2 1

. Vậy

2ln2 1S 

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Câu 8. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

 

4 3 dx x x  



. B.

 

2 11 dx x x  



 

2 11 dx x x



. D.

 

4 3 dx x x





CA

Ta thấy:

 

1;3x

3 4 7x x x    

nên

 

3 4 7 dS x x x x



     





 

4 3 dx x x   



Câu 9. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

 

3dx x x







. B.

 

3dx x x







 

5 2 dx x x



  



. D.

 

5 2 dx x x









C B

Ta thấy:

 

3;0x  

1 4 1x x x   

nên

 

1 4 1 dS x x x x





    





 

3dx x x



  



Câu 10. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 

2 3 1 dx x x



  



. B.

 

2 2 3 dx x x x



  



 

2 3 1 dx x x







. D.

 

2 2 3 dx x x x



   





C C

Ta thấy:



  





3 2 2

2 2 1 2x x x x x     

nên

   

3 2 2

2 2 1 2 dS x x x x x x



      





 

2 3 1 dx x x  



Câu 11. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

 

5 9 7 dx x x x  



. B.

 

5 9 7 dx x x x   



 

9 9 dx x x x   



. D.

 

9 9 dx x x x  





CC

Ta thấy:

 

1;3x

2 3 2

2 9 8 3 1x x x x     

nên

   

2 3 2

2 9 8 3 1 dS x x x x x



      





 

9 9 dx x x x    



Câu 12. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 

5 8 dxx





. B.

 

2 5 2 dx x x







 

5 8 dxx







. D.

 

2 5 2 dx x x



  





CD

Ta thấy:



   





5 5 3x x x    

nên

   

5 5 3 dS x x x x





     





 

2 5 2 dx x x



   



Câu 13. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số

yx

và

yx

1S

. B.

2S

. C.

S

. D.

S



CC

Xét phương trình hoành độ giao điểm

xx



0xx



 

10xx

















Diện tích hình phẳng giới hạn bởi đồ thị các hàm số

yx

và

yx

là:

dS x x x









Ta được

S x x x



  





dS x x x



  



   

5 3 5 3

ddx x x x x x



  



6 4 6 4

1 1 1 1 1

6 4 6 4 6

x x x x



   

   

   

   

Câu 14. Tính diện tích

của hình phẳng giới hạn bởi các đường

2y x x

0y 

10x 

10x 

2000

S 

. B.

2008S 

. C.

2000S 

. D.

2008

S 



CD

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Cách 1: Phương trình hoành độ giao điểm của hai đường

 

:2C y x x

và

 

:0dy

là:





  







Bảng xét dấu:

Diện tích cần tìm:

     

10 0 2 10

2 2 2 2

10 10 0 2

2 d 2 d 2 d 2 dS x x x x x x x x x x x x



       

   

0 2 10

3 3 3

2 2 2

10 0 2

3 3 3

x x x



     

     

     

     

1300 4 704 2008

3 3 3 3

   

Cách 2: Dùng MTCT Casio fx 580VN X

Câu 15. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

 

2 2 4 dx x x







. B.

 

2 2 dxx







 

2 2 dxx





. D.

 

2 2 4 dx x x



  





CD

Từ đồ thị hai hàm số

3yx  

và

21y x x  

ta có

3 2 1x x x    

 

1;2x  

Diện tích hình phẳng gạch chéo trong hình vẽ là

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

     

2 2 2

3 2 1 d 2 2 4 dS x x x x x x x





         





Câu 16. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số

4y x x

và trục

. B.

. C.

. D.



CD

Gọi

là diện tích hình phẳng giới hạn bởi đồ thị hàm số

4y x x

và trục

Xét phương trình





  







Ta có

2 2 2

4 (4 ) (2 )

S x x dx x x dx x      



Câu 17. Cho hình phẳng (H) được giới hạn bởi đồ thị hàm số

ye

, trục

,Ox Oy

và đường thẳng

. Tính

hình phẳng trên.

1e 

. B.

 

e 

. C.

. D.

 

e 



CB

Ta có:

2 2 4

S e dx e e

Câu 18. Tính diện tích hình phẳng giới hạn bởi hai đồ thị

 

: y 8 7

P x x   

 







3,455

. B.

9 8ln2

. C.

3 ln4

. D.

161

4ln3 8ln2





CB

Phương trình hoành độ giao điểm

 



   



 

7 4 0x x x   















Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Diện tích hình phẳng là

 

8 7 d

S x x x



   





 

8 7 d

x x x



   





 

8 7 d

x x x





   









 

1 8 7



     







4ln 3 4 7

x x x x



      





9 8ln2

Câu 19. Tính diện tích

của hình phẳng giới hạn bởi các đường

2y x x

0y 

10x 

10x 

2000

S 

. B.

 2008S

. C.

2000S 

. D.

2008

S 



CD

Phương trình hoành độ giao điểm của hai đường

 

:2C y x x

và

 

:0dy

là:





  







Bảng xét dấu:

Diện tích cần tìm:

     

10 0 2 10

2 2 2 2

10 10 0 2

2 d 2 d 2 d 2 dS x x x x x x x x x x x x



       

   

0 2 10

3 3 3

2 2 2

10 0 2

3 3 3

x x x



     

     

     

     

1300 4 704 2008

3 3 3 3

   

Cách 2: Dùng MTCT Casio fx 580VN X

Câu 20. Cho đồ thị hàm số

()y f x

. Diện tích hình phẳng (phần tô đậm trong hình) là

( ) ( )S f x dx f x dx







()S f x dx







Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

( ) ( )S f x dx f x dx







( ) ( )S f x dx f x dx









CD

[-2;0], f( ) 0; [0;1], f( ) 0x x x x     

nên ta có:

( ) ( )S f x dx f x dx







_ Dạng 2. 

_ Dạng 2. Ứng dụng của tích phân tính thể tích

-Phương pháp:

1. Bài toán1: Tính thể tích vật thể tròn xoay sinh bởi miền

 

giới hạn bởi

 

y f x

;

0y 

và

, x a x b

khi quay quanh trục

 áp dụng công thức:

V y dx







2. Bài toán 2: Tính thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi:

 

y f x

;

 

y g x

quay quanh trục



+ Giải phương trình:

   

f x g x

có nghiệm

, x a x b

+ Khi đó thể tích cần tìm :

   

V f x g x dx







3. Bài toán3: Tính thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi:

 

x g y

;

;y a y b

*  áp dụng công thức:

xdV y







4. Bài toán 4: Tính thể tích vật thể tròn xoay do hình phẳng giới hạn

bởi

   

: ; x f y x g y

và

, y a y b

* Ph

Áp dụng công thức:

( ) ( )

f y gV y dy







5. Bài toán 5: Tính thể tích vật thể tròn xoay sinh bởi miền

 

giới hạn bởi một đường cong

 

kín.

* 

1/ Khi

 

quay quanh trục

Chia đường cong

 

thành 2 cung:

 

y f x

và

 

y f x

với

 

;x a b

và

   

; f x f x

cùng dấu. Khi đó thể tích cần tính:

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

_

Câu 1. Cho hàm số

()y f x

liên tục trên đoạn





;ab

. Gọi

là hình phẳng giới hạn bởi đồ thị hàm số

()y f x

, trục hoành và hai đường thẳng

, ( )x a x b a b  

. Thể tích khối tròn xoay tạo thành

khi quay

quanh trục hoành được tính theo công thức

()

V f x dx







. B.

()

V f x dx







. C.

()

V f x dx







. D.

2 ( )

V f x dx









Cn B



[a; ]xb

ta có

()

V f x dx









 Học thuộc công thức.

Câu 2. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng

1x 

và

3x 

, biết rằng khi cắt vật

thể bởi mặt phẳng vuông góc với trục

tại điểm có hoành độ

(

13x

) thì được thiết diện

là một hình chữ nhật có độ dài hai cạnh là

và

32x 

32 2 15.V 

124





124

V 

. D.

(32 2 15) .V







C C

 Diện tích thiết diện là:

( ) 3 . 3 2S x x x



Thể tích vật thể là:

124

3 . 3 2

V x x dx  





 Ta nhập biểu thức

3 . 3 2x x dx



như sau:

y3Q(s3Q(dp2R1E3=

+ Màn hình hiển thị:

Chọn C

Câu 3. Gọi

là diện tích hình phẳng

 

giới hạn bởi các đường

 

y f x

, trục hoành và hai đường

thẳng

1x 

2x 

(như hình vẽ bên dưới). Đặt

 

da f x x







 

db f x x



, mệnh đề nào sau

đây đúng?

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

S b a

S b a

S b a  

S b a  



C A

 Ta có:

     

2 0 2

1 1 0

d d dS f x x f x x f x x



  

  

   

ddf x x f x x a b



     





 Dựa vào đồ thị ta thấy

()fx

là hàm đồng

biến trên nên ta có thể chọn một hàm đồng

biến trên để thay thế, ví dụ chọn

( ) xfx

suy ra

a x x



  



xd 2bx



Vậy

Sxx







Lại thấy

ba

, chọn A

(10 câu NB; 10 câu TH)

(10 câu)

Câu 1. Gọi

 

là hình phẳng giới hạn bởi các đường:

sinyx

;

0x 

;





. Quay

 

xung

quanh trục

ta được khối tròn xoay có thể tích là:



. B.



. C.



. D.



Câu 2. Cho hình

 

giới hạn bởi

sinyx

0,xx





và

0y 

. Thể tích khối tròn xoay khi

quay

 

quanh trục

bằng:



. B.



. C.



. D.



Câu 3. Gọi

 

là hình phẳng giới hạn bởi các đường

ln ,y x x

trục

, 1,Ox x x e

. Tính thể tích

khối tròn xoay được tạo thành khi quay hình phẳng

 

quanh trục

 





. B.

 





. C.

 





. D.

 





Câu 4. Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol

 

:P y x

và đường

thẳng

:2d y x

quay quanh trục

bằng:

4x dx x dx







. B.

 

2x x dx







. C.

4x dx x dx







. D.

 

2x x dx







Câu 5. Tính thể tích vật thể tròn xoay do hình phẳng giới hạn bởi

lnyx

, trục

và đường thẳng

quay xung quanh trục

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

2ln2 1

. B.

2 ln2



. C.

2 ln2



. D.

2ln2 1

Câu 6. Cho hình phẳng

giới hạn với đường cong

1yx

, trục hoành và các đường thẳng

0, 1xx

. Khối tròn xoay tạo thành khi quay

quanh trục hoành có thể tích

bằng bao

nhiêu?









V 

2V 

Câu 7. Cho hình phẳng

giới hạn bởi đường cong

2 sinyx

, trục hoành và các đường thẳng

0x 





. Khối tròn xoay tạo thành khi quay

quay quanh trục hoành có thể tích

bằng

bao nhiêu?





. B.

 

21V





. C.





. D.

 

21V





Câu 8. Cho hình phẳng

 

giới hạn bởi các đường

3yx

0y 

0x 

2x 

. Gọi

là thể

tích của khối tròn xoay được tạo thành khi quay

 

xung quanh trục

. Mệnh đề nào dưới

đây đúng?

 

3V x dx







. B.

 

3V x dx







. C.

 

3V x dx



. D.

 

3V x dx



Câu 9. Cho hình phẳng

 

giới hạn bởi các đường thẳng

2, 0, 1, 2y x y x x    

. Gọi

là thể

tích của khối tròn xoay được tạo thành khi quay

 

xung quanh trục

. Mệnh đề nào dưới

đây đúng?

 

2dV x x







. B.

 

2dV x x



. C.

 

2dV x x







. D.

 

2dV x x



Câu 10. Viết công thức tính thể tích

của khối tròn xoay được tạo ra khi quay hình thang cong, giới

hạn bởi đồ thị hàm số

 

y f x

, trục

và hai đường thẳng

 

,x a x b a b  

, xung quanh

trục

 

V f x dx







. B.

 

V f x dx



. C.

 

V f x dx







. D.

 

V f x dx



 (10 câu)

Câu 11. Cho hàm số

 

y f x

liên tục trên đoạn

 

;ab

. Gọi

là hình phẳng giới hạn bởi đồ thị hàm

số

 

y f x

, trục hoành và hai đường thẳng

xa

xb

 

ab

. Thể tích khối tròn xoay tạo

thành khi quay

quanh trục hoành được tính theo công thức

 

V f x x







. B.

 

V f x x







. C.

 

V f x x







. D.

 

V f x x







Câu 12. Kí hiệu

 

là hình phẳng giới hạn bởi đồ thị hàm số

2( 1) ,

y x e

trục tung và trục hoành.

Tính thể tích

của khối tròn xoay thu được khi quay hình

 

xung quanh trục

42Ve

. B.

 

42Ve





. C.

5Ve

. D.

 

5Ve





Câu 13. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

3 , 0y x x y  

. B.



. C.



. D.



Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Câu 14. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

2, 2y x x y    



. B.

3564



. C.

3654



. D.

729

Câu 15. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

2,y x y x

1536

. B.

256

. C.

1536

. D.

265

Câu 16. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

, 0, 1y x y x  



. B.



. C.



. D.



Câu 17. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục tung hình phẳng giới hạn

bởi đồ thị của các hàm số

2 3; 1; 2; 0y x y y x    



. B.



. C.



. D.

206

Câu 18. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

9, 0, 1, 3xy y x x   



. B.



. C.



. D.

Câu 19. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

 

cos , 0, 0,y x y x x



   

 





. B.

 

sin2 2





. C.

sin2 2



. D.





Câu 20. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

cos , 0, 0,y x y x x



   



. B.



. C.



. D.





1.A

2.D

3.D

4.A

5.C

6.A

7.B

8.A

9.A

10.A

11.A

12.D

13.C

14.A

15.B

16.D

17.C

18.A

19.B

20.C



Câu 1. Gọi

 

là hình phẳng giới hạn bởi các đường:

sinyx

;

0x 

;





. Quay

 

xung

quanh trục

ta được khối tròn xoay có thể tích là



. B.



. C.



. D.





CA

Thể tích khối tròn xoay là

 

sin .d 1 2 .d sin2

cV x x x x x x





  





     







Câu 2. Cho hình

 

giới hạn bởi

sinyx

0,xx





và

0y 

. Thể tích khối tròn xoay khi

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

quay

 

quanh trục

bằng



. B.



. C.



. D.





CD

Thể tích khối tròn xoay

 

quanh trục

là:

 

0 0 0

1 cos2 1

sin 1 cos2 sin2 .

2 2 2 2 2 2

V xdx dx x dx x x



  

   

  





       





  

Câu 3. Gọi

 

là hình phẳng giới hạn bởi các đường

ln ,y x x

trục

, 1,Ox x x e

. Tính thể tích

khối tròn xoay được tạo thành khi quay hình phẳng

 

quanh trục

 





. B.

 





. C.

 





. D.

 





Li gii

Chn D

Ta có

V x xdx







Đặt

du xdx

dv x





























. Suy ra

ln ln

V x x x xdx













Đặt

du dx

dv x





























Suy ra

2 2 2

1 1 1

ln ln

2 2 2

V x x x x xdx





   

  



   



   





2 2 2 2

1 1 1

1 1 1 e 1

ln ln

2 2 4 4

e e e

x x x x x







     

   



     



     



Câu 4. Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol

 

:P y x

và đường

thẳng

:2d y x

quay quanh trục

bằng

4x dx x dx







. B.

 

2x x dx







. C.

4x dx x dx







. D.

 

2x x dx









CA

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Phương trình hoành độ giao điểm của

 

và

là

2xx













Thể tích của khối tròn xoay là

 

2dx x x













4x d dx x x







Câu 5. Tính thể tích vật thể tròn xoay do hình phẳng giới hạn bởi

lnyx

, trục

và đường thẳng

quay xung quanh trục

2ln2 1

. B.

2 ln2



. C.

2 ln2



. D.

2ln2 1



CC

Giao của đồ thị hàm số

lnyx

với trục

có hoành độ là nghiệm của phương trình

ln 0 1xx

Gọi

là thể tích vật thể cần tìm, ta có:

ln ln 2 ln2V xdx x x dx

    

Câu 6. Cho hình phẳng

giới hạn với đường cong

1yx

, trục hoành và các đường thẳng

0, 1xx

. Khối tròn xoay tạo thành khi quay

quanh trục hoành có thể tích

bằng bao

nhiêu?









V 

2V 



CA

Thể tích khối tròn xoay được tính theo công thức:





 

1 d 1 d

V x x x x x



  



      







Câu 7. Cho hình phẳng

giới hạn bởi đường cong

2 sinyx

, trục hoành và các đường thẳng

0x 





. Khối tròn xoay tạo thành khi quay

quay quanh trục hoành có thể tích

bằng

bao nhiêu?





. B.

 

21V





. C.





. D.

 

21V





i 

Chn B

Ta có phương trình

2 sin 0x

vô nghiệm nên:

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

 

2 sin d 2 sin dV x x x x



   



   

2 cos 2 1xx



  

   

Câu 8. Cho hình phẳng

 

giới hạn bởi các đường

3yx

0y 

0x 

2x 

. Gọi

là thể

tích của khối tròn xoay được tạo thành khi quay

 

xung quanh trục

. Mệnh đề nào dưới

đây đúng?

 

3V x dx







. B.

 

3V x dx







. C.

 

3V x dx



. D.

 

3V x dx





C A

Thể tích của khối tròn xoay được tạo thành khi quay

 

xung quanh trục

là:

 

3V x dx







Câu 9. Cho hình phẳng

 

giới hạn bởi các đường thẳng

2, 0, 1, 2y x y x x    

. Gọi

là thể

tích của khối tròn xoay được tạo thành khi quay

 

xung quanh trục

. Mệnh đề nào dưới

đây đúng?

 

2dV x x







. B.

 

2dV x x



. C.

 

2dV x x







. D.

 

2dV x x





C A

Ta có:

 

2dV x x







Câu 10. Viết công thức tính thể tích

của khối tròn xoay được tạo ra khi quay hình thang cong, giới

hạn bởi đồ thị hàm số

 

y f x

, trục

và hai đường thẳng

 

,x a x b a b  

, xung quanh

trục

 

V f x dx







. B.

 

V f x dx



. C.

 

V f x dx







. D.

 

V f x dx





CA

Câu 11. Cho hàm số

 

y f x

liên tục trên đoạn

 

;ab

. Gọi

là hình phẳng giới hạn bởi đồ thị hàm

số

 

y f x

, trục hoành và hai đường thẳng

xa

xb

 

ab

. Thể tích khối tròn xoay tạo

thành khi quay

quanh trục hoành được tính theo công thức

 

V f x x







. B.

 

V f x x







. C.

 

V f x x







. D.

 

V f x x









C A

Theo công thức tính thể tích vật tròn xoay khi quay hình

 

quanh trục hoành ta có

 

V f x x







Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Câu 12. Kí hiệu

 

là hình phẳng giới hạn bởi đồ thị hàm số

2( 1) ,

y x e

trục tung và trục hoành.

Tính thể tích

của khối tròn xoay thu được khi quay hình

 

xung quanh trục

42Ve

. B.

 

42Ve





. C.

5Ve

. D.

 

5Ve







CD

Phương trình hoành độ giao điểm

 

2 1 0 1

x e x   

Thể tích của khối tròn xoay thu được khi quay hình

 

xung quanh trục

là:

   

2 1 4 1

V x e dx x e dx





   





. Đặt

 

du x dx

dv e dx





















       

2 2 2

4 1 4 2 1 4 1 4 1

2 2 2

x x x

e e e

V x x dx x x e dx

   

        



Gọi

 

I x e dx



. Đặt

u x du dx

dv e dx v

   







  





 

2 2 2

4 1 4 2 2 3

I x dx e e e

        

          



Vậy

 

   

4 1 2 3 5

V x I e e

    

        

Câu 13. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

3 , 0y x x y  

. B.



. C.



. D.





C C

Ta có:





  







Thể tích:

 

dV x x x



  



Câu 14. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

2, 2y x x y    



. B.

3564



. C.

3654



. D.

729



Ch A

Ta có:





    







Thể tích:

 

3 2 2

2 2 .

dV x x x



     



Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Câu 15. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

2,y x y x

1536

. B.

256

. C.

1536

. D.

265



C B

Ta có:













. Thể tích:

256

dV x x x



  



Câu 16. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

, 0, 1y x y x  



. B.



. C.



. D.





C D

Ta có:

00xx  

. Thể tích:

dV x x







Câu 17. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục tung hình phẳng giới hạn

bởi đồ thị của các hàm số

2 3; 1; 2; 0y x y y x    



. B.



. C.



. D.

206



C C

Ta có:

y x x



    

nên thể tích của khối tròn xoay được tạo thành là:

3 3 3 9

2 2 4 2 4

y y y

V y y y

   







    







Câu 18. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

9, 0, 1, 3xy y x x   



. B.



. C.



. D.



C A

Ta có:

9xy y

  

Thể tích:

54 .dVx







Câu 19. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

 

cos , 0, 0,y x y x x



   

 





. B.

 

sin2 2





. C.

sin2 2



. D.







C B

Tài liệu tự học dành cho HS Lớp KHXH

Fb: ThayTrongDGl

i li

ệ

u bi

n so

ạ

n v

u t

ầ



Ôn thi QG Lớp KHXH

New 2020

Thể tích:

   

 

sin2 2

cos 1 cos 2

ddV x x x x





  



    







Câu 20. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn

bởi đồ thị của các hàm số

cos , 0, 0,y x y x x



   



. B.



. C.



. D.





C C

Thể tích:

   

0 0 0

cos 1 cos2 3 4cos2 cos4

4 8 8

d d dV x x x x x x x





  



       

  

Bấm Tải xuống để xem toàn bộ.

| 1/80

| | Tải xuống

Preview text:

Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH B I 1: NGUYÊN HÀM
_ Dạng 1. Định nghĩa, tính chất và nguyên hàm cơ bản
-Phương pháp: _ S
ử dụng bảng nguyên hàm Hàm sơ cấp
Hàm số hợp u  u  x Thường gặp
. dx  x  C 
. du  u  C  . . Vi phân ax b 1 d  dx a  1   1    . x  u
. x dx   C 
. u du   C   1 1  1  1   a x b 1 dx (ax ) b       C      1    1 a 1 . . dx 1 .
 ln ax  b  C  a  0 dx  du ax  b a ln x  C  x  0  ln u  C 
ux  0 x u . cos d
x x  sin x  C  . cos d
u u  sin u  C  1
. cos(ax  )d b x  sin(ax  ) b  C  a . sin        1 d x x cos x C . sin d u u cos u C 
. sin(ax  )
b dx   cos(ax  ) b  C  a 1 1 dx 1 .
dx  tan x  C  .
du  tan u  C  .
 tan ax  b  C  co 2 2 s x 2 cos u
cos ax  b a Với Với   x   k u  x   k 2 2 . 1 dx 1  .
du   cot u  C  . 
cot ax  b  C  1 2 sin u 2
sin ax  b a
dx   cot x  C  . 2 sin x
Với u  x  k
Với x  k x . d x
e x  e  C  . u d u
e u  e  C  axb 1 axb . e dx  e  C  a x a u a pxq 1  pxq . x a dx   C  . u a du   C  . a dx  a  C  ln a ln a . p ln a 0  a   0  a   0  a   1 1 1 _
Dùng máy tính cầm tay Cho f (x)dx F  (x)  C 
. Tìm f (x) hoặc F(x) d . Nhấn shift (F(X ))  f (X ) x X dx 
. Nhấn phím Calc nhập X = 2.5
. Nếu kết quả bằng 0 (gần bằng 0 ) thì đó là đáp án cần chọn 1
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
_Bài tập minh họa: Câu 1.
Tất cả nguyên hàm của hàm số f x 1  là 2x  3 1 1 A.
ln 2x  3  C . B.
ln 2x  3  C . 2 2 1
C. ln 2x  3  C . D.
ln 2x  3  C . ln 2 Lời giải
PP nhanh trắc nghiệm Chọn A
 Dùng máy tính cầm tay: d 1 1 f  x 1 1 1 x  x     x   1 d d d 2 3 
ln 2x  3  C . ( ln(| 2x 3 |)) | 2x  3 2 2x  3 2 dx 2 x X 2x 3 CALC X = -2
Lưu ý: Trong kết quả A và C nếu cho X =
2 thì đều cho kết quả là 0. Vậy khi có trị
tuyệt đối thì cho X một giá trị cho biểu
thức trong trị tuyệt đối âm. Câu 2. Nếu f  x 3 2
dx  4x  x  C thì hàm số f  x bằng x
A. f  x 3 4  x   Cx .
B. f  x 2
12x  2x  C . 3 x
C. f  x 2 12x  2x .
D. f  x 3 4  x  . 3 Lời giải
PP nhanh trắc nghiệm Chọn C
 Dùng máy tính cầm tay tương tự câu 1  
Ta có: f  x   f
 x x   3 2
x  x  C  2 d 4 12x  2x 1 Câu 3.
Cho hàm số f  x có f x 1 '  x  và f  
1  1. Khi đó giá trị của f 5 bằng 2x  với mọi 1 2 A. ln 2 . B. ln 3 . C. ln 2 1. D. ln 3 1. Lời giải
PP nhanh trắc nghiệm Chọn D  Tư duy : Ta có: f '
 xdx  f xC nên 5 f 
 xdx  f 5 f  1 1 f  x 1 1  dx  ln 2x 1  C  . 2x 1 2 5 5
 f 5  f   1  f 
 xdx 1 f   x
Mặt khác theo đề ra ta có: dx 1 1 f   1  1 1 
ln 2.11  C  1  C  1 nên
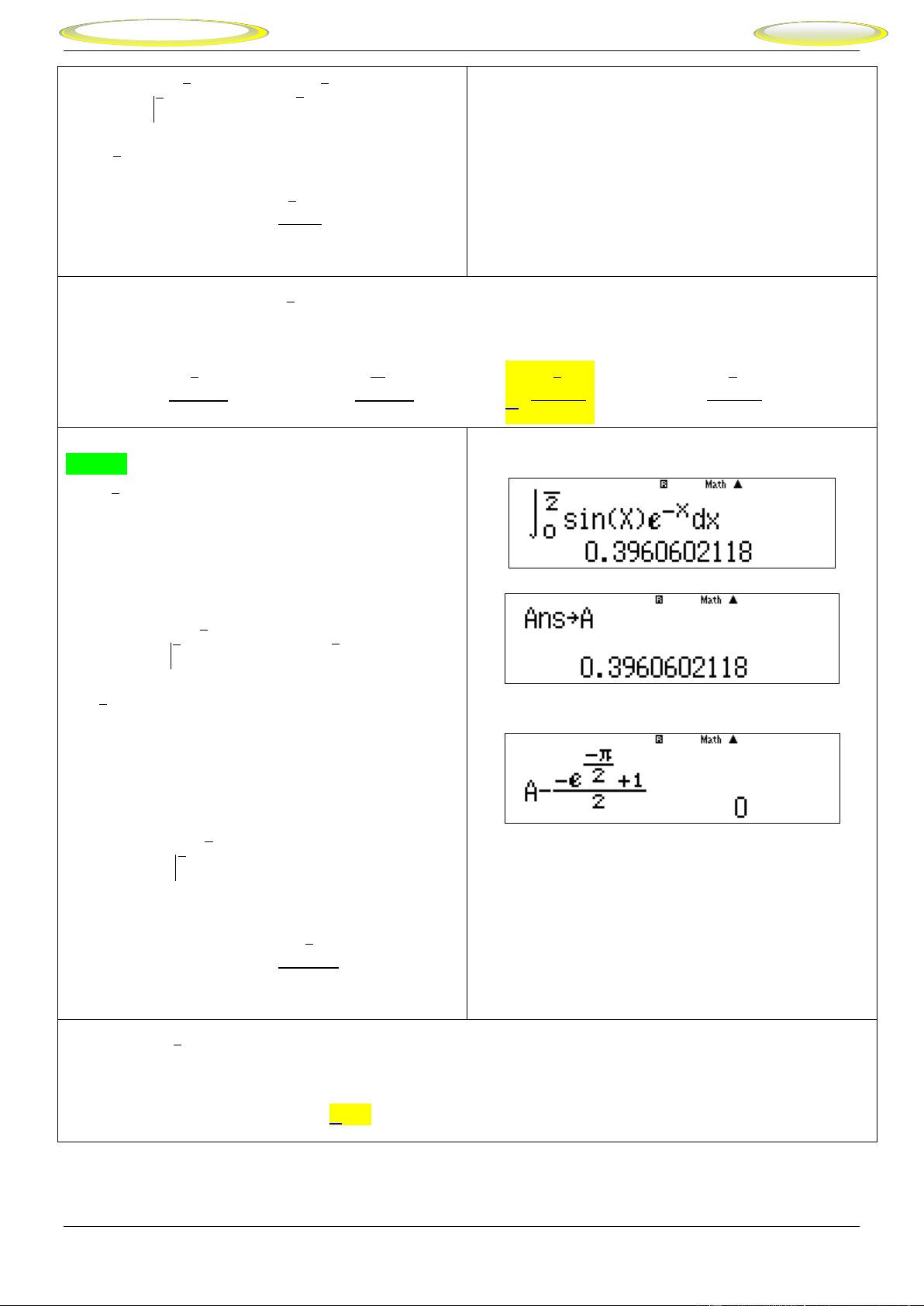
 Quy trình bấm máy : Sử dụng chức 2 năng tính tích phân: 5 f  x 1  ln 2x 1 1 1 2 - Tính dx  và lưu vào A 2x 1 1 Do vậy f   1 1 5  ln 2.5 1 1  ln 9 1  ln 3 1. 2 2 2
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
- Tìm phương án có giá trị bằng 1 + A A. D.
- Là giá trị rất nhỏ gần đến 0 nên thỏa mãn. Chọn D
_Bài tập áp dụng: (10 câu NB; 10 câu TH)
1. Nhận biết: (10 câu) 1 Câu 1.
Tìm nguyên hàm của hàm số f  x 3  x  . x 1 x A. f  x 2 dx  3x   C . B. f  x 4 dx 
 ln x  C . 2 x 4 1 x C. f  x 2 dx  3x   C . D. f  x 4 dx 
 ln x  C . 2 x 4 Câu 2.
Trong các khẳng định sau, khẳng định nào sai? 1 e 1 x  A. cos 2 d x x  sin 2x  C  . B. e x dx   C  2 e 1 1 e 1 x  C.
dx  ln x  C  . D. e x dx   C  x x 1 Câu 3.
Họ nguyên hàm của hàm số f  x 2
 3x  sin x là: A. 3
x  cos x  C .
B. 6x  cos x  C . C. 3
x  cos x  C .
D. 6x  cos x  C . Câu 4.
Tất cả nguyên hàm của hàm số f x 1  2x là. 3 1 1 A.
ln 2x  3  C . B.
ln 2x  3  C . 2 2 1
C. ln 2x  3  C . D.
ln 2x  3  C . ln 2 Câu 5.
Giả sử các biểu thức sau đều có nghĩa công thức nào sau đây sai? 1 A.
dx  tan x  C  . B. x x
e dx  e  C  . 2 cos x 3
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 1 C. lnxdx   c  .
D. sinxdx   cos x  C  . x Câu 6.
Họ nguyên hàm của hàm số f  x 2 x 2
 e  x là x e x
A. F  x 2 3    C .
B. F  x 2 x 3
 e  x  C . 2 3 x C.   2  2 x F x e  2x  C .
D. F  x 3 2 x  e   C . 3 Câu 7.
Nguyên hàm của hàm số f  x 3
 x  3x  2 là hàm số nào trong các hàm số sau? x
A. F  x 2
 3x  3x  C .
B. F  x 4 2 
 3x  2x  C . 3 x x x x
C. F  x 4 2 3    2x  C .
D. F  x 4 2    2x  C . 4 2 4 2 Câu 8.
Họ nguyên hàm của hàm số ( ) ex (3 e x f x    ) là x 1
A. F(x)  3e   C . B. ( )  3ex F x  x  C . ex C.
( )  3ex  ex ln ex F x  C . D. ( )  3ex F x  x  C . Câu 9.
Họ nguyên hàm của hàm số    ex f x  cos x là 1 
A. ex  sin x  C . B. x 1 e  sin x  C x  . 1 C. x 1 e
x   sin x  C .
D. ex  sin x  C .
Câu 10. Nguyên hàm của hàm số 3x f x x là: 2 3x x 3x A. F x C . B. F x 1 C . 2 ln 3 ln 3 2 x 2 x C. F x 3x C . D. F x 3 . x ln 3 C . 2 2
2. Thông hiểu: (10 câu)   
Câu 11. Tìm nguyên hàm F  x của hàm số f  x  sin x  cos x thoả mãn F  2   .  2 
A. F  x  cos x  sin x  3 .
B. F  x   cos x  sin x  3 .
C. F  x   cos x  sin x 1.
D. F  x   cos x  sin x 1. cos 2x
Câu 12. Tìm nguyên hàm dx  2 2 sin x cos x
A. F  x   cos x  sin x  C .
B. F  x  cos x  sin x  C .
C. F  x  cot x  tan x  C .
D. F  x   cot x  tan x  C .
Câu 13. Cho F  x là một nguyên hàm của hàm số 2 ( )  4 x f x e
 2x thỏa mãn F 0  1. Tìm F x .
A. F  x 2 x 2
 4e  x  3 .
B. F  x 2 x 2
 2e  x 1.
C. F  x 2 x 2
 2e  x 1.
D. F  x 2 x 2
 2e  x 1. 4
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
Câu 14. Cho hàm số y  F  x là một nguyên hàm của hàm số 2
y  x . Biểu thức F25 bằng A. 125 . B. 625 . C. 5 . D. 25 . x
Câu 15. Biết F  x là một nguyên hàm của hàm số f  x 
và F 0  1. Tính F   1 . 2 x  1 A. F   1  ln 2  1. B. F   1 1  ln 2 1 . C. F   1  0 . D. F   1  ln 2  2 . 2
Câu 16. Biết F  x là một nguyên hàm của hàm số    2  2x f x x
thoả mãn F 0  0 . Ta có F  x bằng 2x 1 1 2x A. 2 x  . B. 2 x  . C. 1 2x    1 ln 2 . D. 2 2x x  1. ln 2 ln 2
Câu 17. Cho F  x là một nguyên hàm của hàm số f  x 1  . Biết F  
1  2 . Giá trị của F 2 là 2x 1 A. F   1 2  ln 3  2.
B. F 2  ln 3  2. C. F   1 2 
ln 3  2. D. F 2  2 ln 3  2. 2 2 1   
Câu 18. Nguyên hàm F  x của hàm số f  x  2x  thỏa mãn F  1    là 2 sin x  4  2  2  2  A. 2
cot x  x  . B. 2 cot x  x  . C. 2
cot x  x 1. D. 2 cot x  x  . 16 16 16 
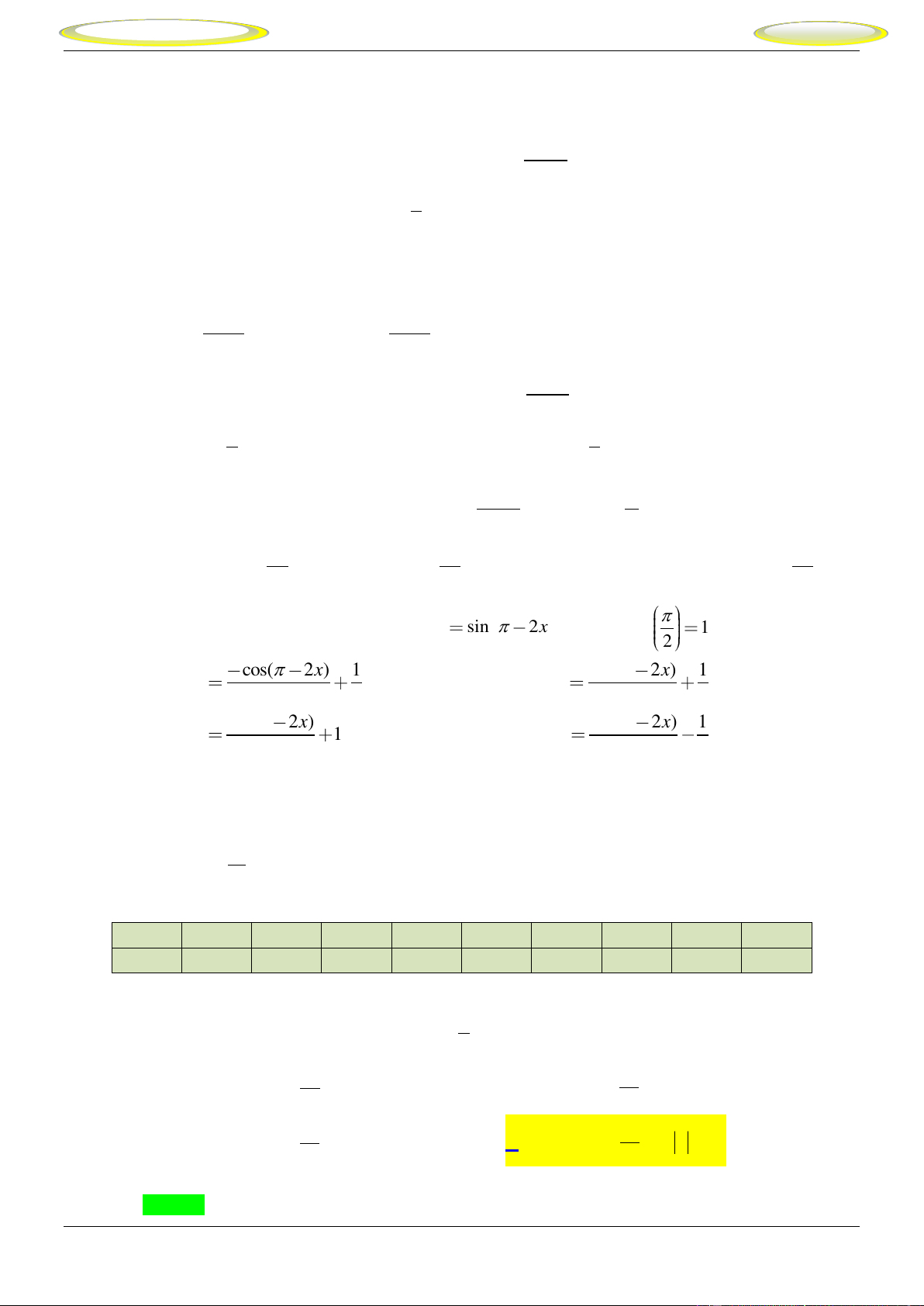
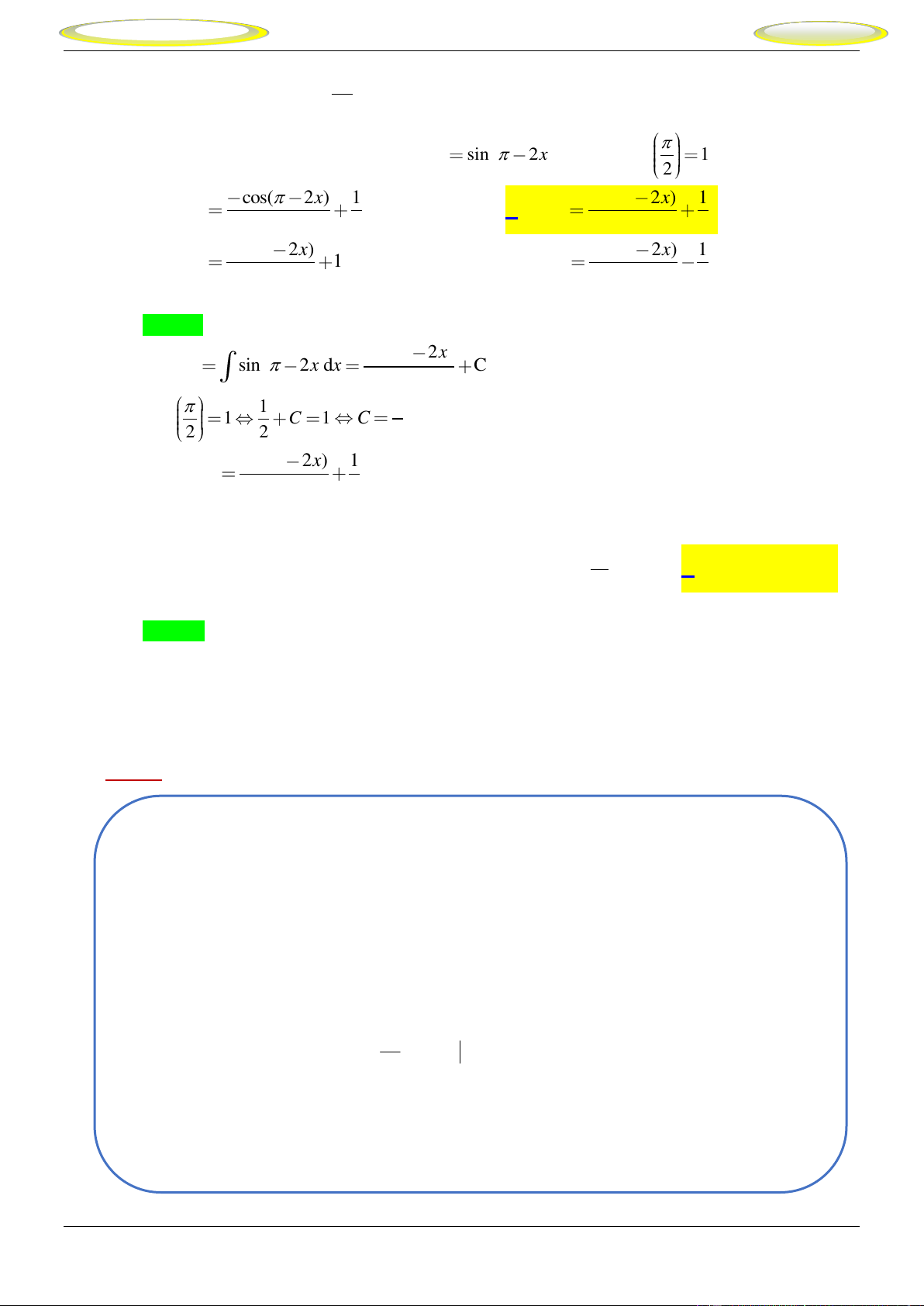
Câu 19. Tìm nguyên hàm F x của hàm số f x sin 
2x thỏa mãn F 1. 2 cos( 2x) 1 cos( 2x) 1 A. F(x) . B. F(x) . 2 2 2 2 cos( 2x) cos( 2x) 1 C. F(x) 1. D. F(x) . 2 2 2
Câu 20. Tìm F  x là một nguyên hàm của hàm số   x
f x  e 1 trên  ;
  , biết F 0  2 .
A. F  x  ln x  x 1 . B.   x
F x  e  x 1 .
C. F  x 1   x 1. D.   x
F x  e  x 1. x e Bảng đáp án 1.D 2.D 3.C 4.A 5.C 6.A 7.C 8.D 9.D 10.A 11.D 12.D 13.B 14.B 15.D 16.A 17.A 18.A 19.B 20.D Hướng dẫn giải 1 Câu 1.
Tìm nguyên hàm của hàm số f x 3  x  . x 1 x A. f  x 2 dx  3x   C . B. f  x 4 dx 
 ln x  C . 2 x 4 1 x C. f  x 2 dx  3x   C . D. f  x 4 dx 
 ln x  C . 2 x 4 Lời giải Chọn D 5
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH  1  1 x Ta có: f  x 4 3 3 dx  x  dx  x dx  dx   ln x  C     .  x  x 4 Câu 2.
Trong các khẳng định sau, khẳng định nào sai? 1 e 1 x  A. cos 2 d x x  sin 2x  C  . B. e x dx   C  . 2 e 1 1 e 1 x  C.
dx  ln x  C  . D. e x dx   C  . x x 1 Lời giải Chọn D Câu 3.
Họ nguyên hàm của hàm số f  x 2
 3x  sin x là: A. 3
x  cos x  C .
B. 6x  cos x  C . C. 3
x  cos x  C .
D. 6x  cos x  C . Lời giải Chọn C Ta có  2 x  x 3 3 sin
dx  x  cos x  C . Câu 4.
Tất cả nguyên hàm của hàm số f x 1  là 2x  3 1 1 A.
ln 2x  3  C . B.
ln 2x  3  C . 2 2 1
C. ln 2x  3  C . D.
ln 2x  3  C . ln 2 Lời giải Chọn A f  x 1 1 dx  dx 
ln 2x  3  C  . 2x  3 2 Câu 5.
Giả sử các biểu thức sau đều có nghĩa công thức nào sau đây sai? 1 A.
dx  tan x  C  . B. x x
e dx  e  C  . 2 cos x 1 C. lnxdx   c  .
D. sinxdx   cos x  C  . x Lời giải Chọn C
Theo bảng nguyên hàm ta chọn câu sai là 1 lnxdx   c  . x Câu 6.
Họ nguyên hàm của hàm số f  x 2 x 2
 e  x là x e x
A. F  x 2 3    C .
B. F  x 2 x 3
 e  x  C . 2 3 x C.   2  2 x F x e  2x  C .
D. F  x 3 2 x  e   C . 3 Lời giải Chọn A x e x
Ta có F  x  f
 x x   x e  x  2 3 2 2 d dx    C . 2 3 6
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH x Vậy   2 3 e x F x    C . 2 3 Câu 7.
Nguyên hàm của hàm số f  x 3
 x  3x  2 là hàm số nào trong các hàm số sau? x
A. F  x 2
 3x  3x  C .
B. F  x 4 2 
 3x  2x  C . 3 x x x x
C. F  x 4 2 3    2x  C .
D. F  x 4 2    2x  C . 4 2 4 2 Lời giải Chọn C x 3x Ta có: F(x)  f
 xdx  x 3x2 4 2 3 dx    2x  C . 4 2 Câu 8.
Họ nguyên hàm của hàm số ( ) ex (3 e x f x    ) là x 1
A. F(x)  3e   C . B. ( )  3ex F x  x  C . ex C.
( )  3ex  ex ln ex F x  C . D. ( )  3ex F x  x  C . Lời giải Chọn D
ex (3  ex )d  
3ex  1d  3ex x x  x  C . Câu 9.
Họ nguyên hàm của hàm số    ex f x  cos x là 1
A. ex  sin x  C . B. x 1
e   sin x  C . x 1 C. x 1 e
x   sin x  C .
D. ex  sin x  C . Lời giải Chọn D
Ta có: ex  cos d  ex x x
 sin x  C .
Câu 10. Nguyên hàm của hàm số 3x f x x là: 2 3x x 3x A. F x C . B. F x 1 C . 2 ln 3 ln 3 2 x 2 x C. F x 3x C . D. F x 3 .
x ln 3 C . 2 2 Lời giải Chọn A 2 x x 3x Ta có: f x dx x 3 dx C . 2 ln 3   
Câu 11. Tìm nguyên hàm F  x của hàm số f  x  sin x  cos x thoả mãn F  2    2 
A. F  x  cos x  sin x  3 .
B. F  x   cos x  sin x  3 .
C. F  x   cos x  sin x 1.
D. F  x   cos x  sin x 1. Lời giải 7
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH Chọn D Có cos d
u u  sin u  C  ; sin d
u u   cos u  C  nên f
 xdx  sin xcos xdx  cos xsin xC  π  π π    F
 cos  sin  C  1 C.   F   C   
. Do đó F  x  cos x  sin x 1.  2  2 2 Mà 2 1  2  cos 2x
Câu 12. Tìm nguyên hàm dx  2 2 sin x cos x
A. F  x   cos x  sin x  C .
B. F  x  cos x  sin x  C
C. F  x  cot x  tan x  C .
D. F  x   cot x  tan x  C . Lời giải Chọn D 2 2 cos 2x cos x  sin x  1 1  Ta có: dx  dx  
dx   cot x  tan x  C     2 2 2 2 2 2 sin x cos x sin x cos x
 sin x cos x 
Câu 13. Cho F  x là một nguyên hàm của hàm số 2 ( )  4 x f x e
 2x thỏa mãn F 0  1. Tìm F x .
A. F  x 2 x 2
 4e  x  3 .
B. F  x 2 x 2
 2e  x 1.
C. F  x 2 x 2
 2e  x 1.
D. F  x 2 x 2
 2e  x 1. Lời giải Chọn B
Ta có: F  x   2x e  x 2 x 2 4 2 dx  2e  x  C . F   2.0 2 0  2.e
 0  C  2  C . Mà F 0  1  2  C  1  C  1  .
Do đó: F  x 2 x 2
 2e  x 1.
Câu 14. Cho hàm số y  F (x) là một nguyên hàm của hàm số 2
y  x . Biểu thức F '(25) bằng: A. 125 . B. 625 . C. 5 . D. 25 . Lời giải Chọn B
Ta có: F  x được gọi là nguyên hàm của f  x trên K nếu F '(x)  f (x), x   K
Mà y  F (x) là một nguyên hàm của hàm số 2 y  x nên 2
F '(x)  x Vậy 2
F '(25)  25  625 . x
Câu 15. Biết F  x là một nguyên hàm của hàm số f  x 
và F 0  1. Tính F   1 . 2 x  1 A. F   1  ln 2  1. B. F   1 1  ln 2 1 . C. F   1  0 . D. F   1  ln 2  2 . 2 Lời giải Chọn B  2      1 1 1    ln   d x x f x dx dx
 2x 1 c. 2 2  x  1 2 x  1 2 1
Vì F  x là một nguyên hàm của hàm số f  x nên F  x  ln  2 x   1  c . 2 8
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH F   1 0  1 
ln1 c  1  c  1. 2
Do đó F x 1  ln  2 x   1 1. 2 Vậy F   1 1  ln  1 2 1   1 1  ln 2 1. 2 2
Câu 16. Biết F  x là một nguyên hàm của hàm số    2  2x f x x
thoả mãn F 0  0 . Ta có F  x bằng 2x 1 1 2x A. 2 x  . B. 2 x  . C. 1 2x    1 ln 2 . D. 2 2x x  1. ln 2 ln 2 Lời giải Chọn A x 2x
Ta có: 2x  2  2 dx  x   C . Do đó. ln 2
Theo giả thiết F 0 0 2 1 2  0  0 
 C  0  C   . ln 2 ln 2 x x  Vậy 2 1 2 1 F  x 2 2  x    x  . ln 2 ln 2 ln 2
Câu 17. Cho hàm số f  x có f  x 1 '  x  và f  
1  2 . Khi đó giá trị của f 2 2x  với mọi 1 1 2 bằng A. F   1 2  ln 3  2 .
B. F 2  ln 3  2 .
C. F 2  2 ln 3  2 . D. F   1 2  ln 3  2 . 2 2 Lời giải Chọn D 1 1 d 2x 1 1 Ta có: f '
 xdx  f xC nên f x    dx 
 ln 2x 1  C   2x 1 2 2x 1 2
Mặt khác theo đề ra ta có: f   1  1 2 
ln 2.11  C  2  C  2 nên f  x 1  ln 2x 1  2 2 2 Do vậy f   1 1 2  ln 2.2 1  2  ln 3  2 . 2 2 1   
Câu 18. Nguyên hàm F  x của hàm số f  x  2x  thỏa mãn F  1    là 2 sin x  4  2  2  2  A. 2
cot x  x  . B. 2 cot x  x  . C. 2
cot x  x 1. D. 2 cot x  x  . 16 16 16 Lời giải Chọn A  1  Ta có 2 F (x)  2x 
dx  x  cot x  C   2  sin x  2 2         F  1    cot  C  1   C        4   4  4 16 9
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 2  Vậy F(x) = 2
cot x  x  16 
Câu 19. Tìm nguyên hàm F x của hàm số f x sin 
2x thỏa mãn F 1. 2 cos( 2x) 1 cos( 2x) 1 A. F(x) . B. F(x) . 2 2 2 2 cos( 2x) cos( 2x) 1 C. F(x) 1. D. F(x) . 2 2 2 Lời giải Chọn B cos  2x + F x sin  2x dx C 2  1 1 + F 1 C 1 C 2 2 2  Vậy cos( 2x) 1 F(x) 2 2
Câu 20. Tìm F  x là một nguyên hàm của hàm số   x
f x  e 1 trên  ;
  , biết F 0  2 .
A. F  x  ln x  x 1 . B.   x
F x  e  x 1 . C. F  x 1 
 x 1. D.   x
F x  e  x 1. x e Lời giải Chọn D
Ta có: F  x  f
 xd   x  1d x x e
x  e  x  C . Theo bài: F   0
0  2  e  0  C  2  1 C  2  C  1 . Vậy   x
F x  e  x 1.
_ Dạng 2. Đổi biến
-Phương pháp:
_ . Chọn t    x . Trong đó   x là hàm số mà ta chọn thích hợp.
. Tính vi phân hai vế: dt   'xdx .     
. Biểu thị: f (x)dx g  x '
  xdx g(t)dt .
. Khi đó: I  f (x)dx  g(t)dt  G(t)  C  
_Casio: Cho f (x)dx F  (x)  C 
. Tìm f (x) hoặc F(x)  d _Bài tập minh h  ọa: . Nhấn shift (F(X ))  f (X ) x X dx 
. Nhấn phím Calc nhập X  2.5
. Nếu kết quả bằng 0 (gần bằng 0 ) thì đó là đáp án cần chọn 10
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
_Bài tập minh họa: x Câu 1.
Tìm nguyên hàm của hàm số sin f (x)  . 1 3cos x 1 A.
f (x) dx  ln 1 3cos x  C  . B.
f (x) dx  ln 1 3cos x  C  . 3 1  C.
f (x) dx  3ln 1 3cos x  C  . D.
f (x) dx 
ln 1 3cos x  C  . 3 Lời giải
PP nhanh trắc nghiệm Chọn D
 Dùng máy tính cầm tay
 Đặt t  1 3cos x  dt  3  sin xdx 1 1 1 1 
f (x) dx  
dt   ln | t | C  
ln 1 3cos x  C   3 t 3 3 1 Câu 2.
Tính nguyên hàm I  dx  . x ln x 1 2 A. 3 I 
(ln x 1)  C .
B. I  ln x 1  C . 3 1 C. 2 I 
(ln x 1)  C .
D. I  2 ln x 1  C . 2 Lời giải
PP nhanh trắc nghiệm Chọn D
 Dùng máy tính cầm tay  Đặt 2 1
t  ln x 1  t  ln x 1  2tdt  dx x 1 I 
dx  2 dt  2t  C  2 ln x 1  C   x ln x 1 Câu 3.
Tìm họ nguyên hàm của hàm số f  x 3 2  . x x 1 ? 4 3 4 8
A. F  x 2 3
  (x 1)  C .
B. F  x 2 3
 (x 1)  C . 8 3 3 3 4 3
C. F  x 2 4
 (x 1)  C .
D. F  x 2 3
 (x 1)  C . 8 8 Lời giải
PP nhanh trắc nghiệm Chọn D
 Dùng máy tính cầm tay.  3 Đặt 2 3 2 2 t 
x 1  t  x 1  3t dt  2xdx 4 3 3 3 3 2 3 4 2 3 . x x 1dx 
t dt  t  C  (x 1)  C   2 8 8 11
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
_Bài tập áp dụng: (10 câu NB; 10 câu TH)
1. Nhận biết: (10 câu) ln Câu 1. Tìm d
 x x có kết quả là. x 2 x 2 x 1
A. ln ln x  C . B. ln  C . C. ln x   1  C . D. 2
ln x  C . 2 2 2 1 Câu 2. Nguyên hàm dx  bằng. 1 x
A. 2 x  2ln | x 1| C  .
B. 2 x  C .
C. 2ln | x 1| C  .
D. 2 x  2ln | x 1 | C  . Câu 3.
Cho hàm số F x 2  x x  2dx  . Biết F   2 2 
, tính F  7. 3 23 40 A. 7 . B. 11. C. . D. . 6 3   Câu 4.
Biết F(x) là một nguyên hàm của hàm số   2 e x f x  và F   3 0  . Giá trị 1 F   là: 2  2  1 1 1 1 A. e  2 . B. 2e 1. C. e 1 . D. e  . 2 2 2 2  1  Câu 5. Tính nguyên hàm dx   .  2x  3  1 1
A. 2 ln 2x  3  C . B.
ln 2x  3  C .
C. ln 2x  3  C . D. ln 2x   3  C . 2 2 Câu 6.
Xét I  x  x   5 3 4 4
3 dx . Bằng cách đặt 4
u  4x  3 , khẳng định nào sau đây đúng? 1 1 1 A. 5 I  u du  . B. 5 I  u du  . C. 5 I  u du  . D. 5 I  u du  . 4 12 16 Câu 7.
Họ nguyên hàm của hàm số f  x 2 3
 x 4  x là: 2 1 A. 4 x 3 3  C . B. 3
2 4  x  C . C. 4 x 3 3  C . D.   3 3 2 4 x  C . 9 9  x  210 Câu 8. Nguyên hàm   bằng: x   dx 12 1 11 11 1  x  2  1  x  2  A.    C    C 33  x 1  .
B. 11 x 1  . 11 11 1  x  2  1  x  2  C.    C     C 3  x 1  .
D. 11 x 1  . Câu 9. Nguyên hàm của hàm số 3 f (x)
sin x. cos x là: 1 1 3 3 A. cos x C B. sin x C 4 4 12
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 1 1 4 4 C. sin x C D. sin x cosx C 4 4   
Câu 10. Nguyên hàm F  x của hàm số f  x 2 3  sin 2 .
x cos 2x thỏa F  0   là:  4  1 1 4 1 1 1
A. F  x 3 5  sin 2x  sin 2x  .
B. F  x 3 5  sin 2x  sin 2x  . 6 10 15 6 10 15 1 1 1 1 1 1
C. F  x 3 5  sin 2x  sin 2x  .
D. F  x 3 5  sin 2x  sin 2x  . 6 10 15 6 10 15
2. Thông hiểu: (10 câu) x 1
Câu 11. Nếu F  x    dx  thì. 2 x  2x  3 x 1 1
A. F  x  ln  C .
B. F  x  ln  2
x  2x  3  C . 2 x  2x  3 2 1
C. F  x 2
 x  2x  3  C .
D. F  x 2 
x  2x  3  C . 2
Câu 12. Cho F x là nguyên hàm của hàm số ln x f x
. Tính F e  F   1 . x 1 1 A. I . B. I 1. C. I . D. I e . 2 e
Câu 13. Hàm số nào sau đây là một nguyên hàm của hàm số f  x 2  ? x 1
A. F  x  x 1.
B. F  x  4 x 1.
C. F  x  2 x 1 .
D. F  x 1  . x 1 x e
Câu 14. Nguyên hàm của hàm số y  f  x 2  là: x e 1
A. I  x  ln x  C . B. x   ln  x I e e   1  C .
C. I  x  ln x  C . D. x  1 ln  x I e e   1  C .
Câu 15. Một nguyên hàm của hàm số 2
y  x 1 x là: 1 1 2 2 x 2 3 x
A.  1 x 6 2 .
B.  1 x 3 2 . C.  2 1 x  . D.  2 1 x  . 3 3 2 2 dx
Câu 16. Tìm nguyên hàm I   . 1 x  e A.    ln 1 x I x
 e  C . B.   ln 1 x I x
 e  C . C.   ln 1 x I x
 e  C . D.   ln 1 x I x
 e  C . 6 8 7 Câu 17. Cho 2x
 3x2 dx  A3x2  B3x2 C với A , B  và C . Giá trị của biểu
thức 12A  7B bằng: 23 241 52 7 A. . B. . C. . D. . 252 252 9 9 13
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH x  x
Câu 18. Tìm họ nguyên hàm của hàm số: f  x 3sin 2cos  dx  .
3cos x  2sin x A. f
 xdx  ln 3sin x 2cos x C . B. f
 xdx  ln 3cos x  2sin x C . C. f
 xdx  ln 3cos x  2sin x C . D. f
 xdx  ln 3
 cos x  2sin x  C . x  3
Câu 19. Khi tính nguyên hàm dx 
, bằng cách đặt u  x 1 ta được nguyên hàm nào? x  1 A.   2
2 u  4du . B.  2 u   3du. C. u   2 2
u  4du . D.  2
u  4du . dx
Câu 20. Kết quả của phép tính  bằng: x e 2. x e  1 1 x e 1 x e 1 A. ln  C ln  C 3 x e  . B. 2 x e  . 2 1 x e 1
C. ln  x  2 x e e   1  C . D. ln  C . 3 x e  2 Bảng đáp án 1.D 2.D 3.A 4.B 5.C 6.D 7.A 8.A 9.D 10.C 11.C 12.A 13.B 14.D 15.B 16.D 17.D 18.B 19.A 20.A Hướng dẫn giải ln Câu 1. Tìm d
 x x có kết quả là. x 2 x 2 x 1
A. ln ln x  C . B. ln  C . C. ln x   1  C . D. 2 ln x  C . 2 2 2 Lời giải Chọn D 2 ln x ln x Ta có dx  ln d x ln x     C . x 2 1 Câu 2. Nguyên hàm dx  bằng. 1 x
A. 2 x  2ln | x 1| C  .
B. 2 x  C .
C. 2ln | x 1| C  .
D. 2 x  2ln | x 1 | C  . Lời giải Chọn D Đặt 2
x  t  x  t  dx  2tdt . 2t  2  dt  2 
dt  2t  2 ln 1 t  C  2 x  2 ln | x 1| C    . 1 t  1 t  Câu 3.
Cho hàm số F x 2  x x  2dx  . Biết F   2 2 
, tính F  7. 3 23 40 A. 7 . B. 11. C. . D. . 6 3 Lời giải Chọn A 14
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 1 1
Ta có: F  x 2  x x  2dx  2  x  2d 
 2x 2   x 23 2  C 2 3 Mà F   2 2  8 2
  C   C  2  3 3 3
Vậy F  7  92  7 .   Câu 4.
Biết F(x) là một nguyên hàm của hàm số   2 e x f x  và F   3 0  . Giá trị 1 F   là 2  2  1 1 1 1 A. e  2 . B. 2e 1. C. e 1 . D. e  . 2 2 2 2 Lời giải Chọn B x 1 Ta có:       2 2 d  e d  e x F x f x x x  C  . 2  
Theo giả thiết: F   3 0   C 1. Vậy 1 F  2e 1   . 2  2   1  Câu 5. Tính nguyên hàm dx   .  2x  3  1 1
A. 2 ln 2x  3  C . B.
ln 2x  3  C .
C. ln 2x  3  C . D. ln 2x   3  C . 2 2 Lời giải Chọn B  1  1  1  1 Ta có: dx  d   
 2x  3  ln 2x  3  C .  2x  3  2  2x  3  2 Câu 6.
Xét I  x  x   5 3 4 4
3 dx . Bằng cách đặt 4
u  4x  3 , khẳng định nào sau đây đúng. 1 1 1 A. 5 I  u du  . B. 5 I  u du  . C. 5 I  u du  . D. 5 I  u du  . 4 12 16 Lời giải Chọn C du 1 Ta có 4 3 3
u  4x  3  du  16x dx  x dx 
; Suy ra: I  x  4x 35 3 4 5 dx  u du  . 16 16 Câu 7.
Họ nguyên hàm của hàm số f  x 2 3
 x 4  x là: 2 1 A. 4 x 3 3  C . B. 3
2 4  x  C . C. 4 x 3 3  C . D.   3 3 2 4 x  C . 9 9 Lời giải Chọn A 1 1 1 1 2 Ta có 2 3 x 4  x dx  3  4  x d   3 4  x    3 4  x  d 3 2
4  x   . 4  x 3 3 2  C 3 3 3 3 2  4 x 3 3  C . 9  x  210 Câu 8. Nguyên hàm   bằng. x   dx 12 1 15
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 11 11 1  x  2  1  x  2  A.    C    C 33  x 1  .
B. 11 x 1  . 11 11 1  x  2  1  x  2  C.    C     C 3  x 1  .
D. 11 x 1  . Lời giải Chọn A  10 x  210  x  2  dx
Biến đổi I    =   . . 2 x   dx 12 1
 x 1   x   1  Đặt x 2 3 t   dt  dx . x 1  x  2 1 11 1  x  2  Do đó 1 1 10 I  t dt  = 11 t  C =    C 3 33 33  x 1  . Câu 9. Nguyên hàm của hàm số 3 f (x)
sin x. cos x là: 1 1 3 3 A. cos x C B. sin x C 4 4 1 1 4 4 C. sin x C D. sin x cosx C 4 4 Lời giải Chọn C
Sử dụng casio: đạo hàm của đáp án tại 3 trừ hàm dưới dấu tích phân tại 3 bằng 0 thì chọn đáp án.   
Câu 10. Nguyên hàm F  x của hàm số f  x 2 3  sin 2 .
x cos 2x thỏa F  0   là  4  1 1 4 1 1 1
A. F  x 3 5  sin 2x  sin 2x  .
B. F  x 3 5  sin 2x  sin 2x  . 6 10 15 6 10 15 1 1 1 1 1 1
C. F  x 3 5  sin 2x  sin 2x  .
D. F  x 3 5  sin 2x  sin 2x  . 6 10 15 6 10 15 Lời giải Chọn D
Đặt t  sin 2x  dt  1 2.cos 2 d x x  dt  cos 2 d x x . 2 Ta có: 1 1 1 1 F  x 2 3  sin 2 . x cos 2 d x x  2  t .   2
1 t dt   2 4
t  t dt 3 5  t  t  C 2 2 6 10 1 1 3 5  sin 2x  sin 2x  C . 6 10    1  1  F  0   3 5  sin  sin  C  1 0  C   .  4  6 2 10 2 15
Vậy F x 1 1 1 3 5  sin 2x  sin 2x  . 6 10 15 x 1
Câu 11. Nếu F  x    dx  thì: 2 x  2x  3 16
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH x 1 1
A. F  x  ln  C .
B. F  x  ln  2
x  2x  3  C . 2 x  2x  3 2 1
C. F  x 2
 x  2x  3  C .
D. F  x 2 
x  2x  3  C . 2 Lời giải Chọn C Đặt 2 2 2
t  x  2x  3  t  x  2x  3  2 d
t t  2 x  
1 dx  x   1 dx  d t t . x 1 dx tdt
Do đó F  x   2  
 t  C  x  2x  3  C   . 2  2  3 t x x
Câu 12. Cho F x là nguyên hàm của hàm số ln x f x . Tính F e F 1 x 1 1 A. I . B. I 1. C. I . D. I e . 2 e Lời giải Chọn A Đặt dx t ln x dt . x 2 2 ln x t ln x 1 dx d t t C C F x C F e F 1 . x 2 2 2
Câu 13. Hàm số nào sau đây là một nguyên hàm của hàm số f  x 2  ? x 1
A. F  x  x 1.
B. F  x  4 x 1.
C. F  x  2 x 1 .
D. F  x 1  . x 1 Lời giải Chọn B 2 d x 1
Ta có: F  x    dx  4
 4 x 1  C   . x 1 2 x 1 2
Họ nguyên hàm của hàm số đã cho là
dx  4 x 1  C 
, nên hàm số đã cho có một x 1
nguyên hàm là hàm F  x  4 x 1 . x e
Câu 14. Nguyên hàm của hàm số y  f  x 2  là: x e 1
A. I  x  ln x  C . B. x   ln  x I e e   1  C .
C. I  x  ln x  C . D. x  1 ln  x I e e   1  C . Lời giải Chọn D 2 x x e e I  d x x  e dx   . x e 1 x e 1 Đặt x  1 x   1 d x t e e t
t  e dx . 17
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH t 1  1  Ta có I  dt  1
dt  t  ln t  C    . 1  t 
Trở lại biến cũ ta được x  1 ln  x I e e   1  C .
Câu 15. Một nguyên hàm của hàm số 2
y  x 1 x là: 1 1 2 2 x 2 3 x
A.  1 x 6 2 .
B.  1 x 3 2 . C.  2 1 x  . D.  2 1 x  . 3 3 2 2 Lời giải Chọn B Đặt 2 2 2 t 
x 1  t  x 1  tdt  xdx .  t  x 13 2 3 2 2
 x x 1dx  t dt   C   C   . 3 3 dx
Câu 16. Tìm nguyên hàm I   . 1 x  e A.    ln 1 x I x
 e  C . B.   ln 1 x I x
 e  C . C.   ln 1 x I x
 e  C . D.   ln 1 x I x  e  C . Lời giải Chọn D x dx e dx I     . 1 x x  e e 1 x  e  Đặt x x
t  e  dt  e dx . x e dx dt 1 1  I       
  ln t  ln t 1  C  ln x  ln x e e 1  C x e 1 x  e  t 1 t   t t 1   ln x x
e 1  C . 6 8 7 Câu 17. Cho 2x
 3x2 dx  A3x2  B3x2 C với A , B  và C . Giá trị của biểu
thức 12A  7B bằng: 23 241 52 7 A. . B. . C. . D. . 252 252 9 9 Lời giải Chọn D  Đặt t t  3x  2 2  x  1  dt  dx . 3 3 2 t  2 2 8 7 2 t 4 t 1 8 4 7 Ta có: 6 .t dt    7 6
t +2t dt  .  .  C  .3x  2 
.3x  2  C . 3 3 9 9 8 9 7 36 63 1 4 1 4 7 Suy ra A  , B  , 12.  7.  . 36 63 36 63 9 x  x
Câu 18. Tìm họ nguyên hàm của hàm số: f  x 3sin 2cos  dx  .
3cos x  2sin x A. f
 xdx  ln 3sin x 2cos x C . B. f
 xdx  ln 3cos x  2sin x C . 18
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH C. f
 xdx  ln 3cos x  2sin x C . D. f
 xdx  ln 3
 cos x  2sin x  C . Lời giải Chọn B
d 3cos x  2sin x Ta có: f  x   dx    ln 
3cos x  2sin xC .
3cos x  2sin x x  3
Câu 19. Khi tính nguyên hàm dx 
, bằng cách đặt u  x 1 ta được nguyên hàm nào? x  1 A.   2
2 u  4du . B.  2 u   3du. C. u   2 2
u  4du . D.  2 u  4du . Lời giải Chọn A
dx  2udu
Đặt u  x 1 , u  0 nên 2
u  x 1   . 2 x  u 1  2   Khi đó x 3 u 1 3 dx   .2udu     2
2 u  4du . x 1 u dx
Câu 20. Kết quả của phép tính  bằng: x e 2. x e  1 1 x e 1 x e 1 A. ln  C ln  C 3 x e  . B. 2 x e  . 2 1 x e 1
C. ln  x  2 x e e   1  C . D. ln  C . 3 x e  2 19
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
_ Dạng 3. Từng Phần -Phương pháp:
_ Định lý. Cho hai hàm số u và v liên tục trên đoạn a;b và có đạo hàm liên tục
trên đoạn a;b. Khi đó: d u v  uv  d v . u   *
_ Tự luận. Để tính nguyên hàm f xdx 
bằng từng phần ta làm như sau:
Bước 1. Chọn u, v sao cho f  xdx  udv (chú ý dv  v'xdx ).
Sau đó tính v  dv
 và du u'.dx.
Bước 2. Thay vào công thức * và tính vdu  .
Chú ý : Cần phải lựa chọn u và dv hợp lí sao cho ta dễ dàng tìm được v và tích phân vdu
 dễ tính hơn udv
 . Ta thường gặp các dạng sau:  x  
, trong đó P  x là đa thức. ⍟Dạng 1. I P
 x sin dx   cos x u   Px  Với dạng này, ta đặt .  sin x  dv  dx     cos x
⍟ Dạng 2.     axb I P x e
dx , trong đó P  x là đa thức. u
  Px
Với dạng này, ta đặt  . axb
dv  e dx
⍟ Dạng 3. I  P
 xlnmx  ndx, trong đó Px là đa thức. u   ln  mx  n
Với dạng này, ta đặt  . dv  P  x dx
_ Casio: Cho f (x)dx  F(x)  C 
. Tìm f (x) hoặc F(x) d . Nhấn shift ( f (X ))  F(X ) x X dx 
. Nhấn phím Calc nhập X  2.5
. Nếu kết quả bằng 0 (gần bằng 0 ) thì đó là đáp án cần chọn .
Nguyên tắc chung để đặt u và dv : Tìm được v dễ dàng và . v du  tính được.
Nhấn mạnh: Thứ tự ưu tiên khi chọn đặt u : “Nhất lô, nhì đa, tam lượng, tứ mũ” (hàm
lôgarit, hàm đa thức, hàm lượng giác, hàm mũ). 20
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
_Bài tập minh họa: Câu 1.
Họ nguyên hàm của hàm số f  x  x cos 2x là: x sin 2x cos 2x cos 2x A.   C .
B. x sin 2x   C . 2 4 2 cos 2x x sin 2x cos 2x
C. x sin 2x   C . D.   C . 2 2 4 Lời giải
PP nhanh trắc nghiệm Chọn A
 Máy tính cầm tay. I  x cos 2 d x x  . du  dx u   x  Đặt    1 . dv  cos 2 d x x v  sin 2x  2 Khi đó 1 1 1 1 I  x sin 2x  sin 2 d x x  x sin 2x  cos 2x  C  . 2 2 2 4 Câu 2.
Họ nguyên hàm của hàm số f  x  x ln 2x là: 2 x  1  2 x A. ln 2x   C   . B. 2 x ln 2x   C . 2  2  2 2 x 2 x C.
ln2x  1C . D. 2
ln 2x  x  C . 2 2 Lời giải
PP nhanh trắc nghiệm Chọn A
 Máy tính cầm tay  1 du  u   ln 2x   x Đặt    . 2 dv  d x x x v   2       2 2 x 1 x F x f x dx  .ln 2x  . dx  2 x 2 . 2 2 2 x x x  1   ln 2x   C  ln 2x   C   2 4 2  2  Câu 3.
Tìm nguyên hàm của hàm số   2  .e x f x x . 1 x 1 A. F x e2 x C . B. e2 2 x F x x 2 C . 2 2 1 x 1 C. F x e2 2 x C . D. e2x F x x 2 C . 2 2 Lời giải
PP nhanh trắc nghiệm Chọn A
 Máy tính cầm tay Ta có:   2  .e x F x x dx  . Đặt 21
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH du  dx u   x     1 2 x 2 dv  e dx v  e x  2    F x 1 x 1 x 1 x 1 2 2 2  e x  e dx  e x   C    2 2 2  2 
_Bài tập áp dụng: (10 câu NB; 10 câu TH)
1. Nhận biết: (10 câu) Câu 1.
Nguyên hàm của hàm số f  x  x sin x là:
A. –x cos x  sin x  C .
B. x sin x  cos x  C .
C. x cos x  sin x  C .
D. x cos x  sin x  C . Câu 2. Kết quả của x
I  xe dx  là: 2 x A. x x I 
e  e  C . B. x x
I  e  xe  C . 2 2 x C. x I 
e  C . D. x x
I  xe  e  C . 2 Câu 3.
Tính F (x)  x sin 2xdx 
. Chọn kết quả đúng? 1 1
A. F(x) 
(2x cos 2x  sin 2x)  C .
B. F(x)   (2x cos 2x  sin 2 )
x  C . 4 4 1 1
C. F(x)   (2x cos 2x  sin 2x)  C .
D. F(x) 
(2x cos 2x  sin 2 )
x  C . 4 4 Câu 4.
Nguyên hàm của hàm số       1 ex f x x là A. ex x  C .
B.   2 ex x  C . C.    1 ex x  C . D. 2 ex x  C . Câu 5.
Họ các nguyên hàm của f  x  x ln x là: 2 x 1 1 A. 2 ln x 
x  C. B. 2 2 x ln x  x  . C 2 4 2 2 x 1 1 C. 2 ln x 
x  C.
D. x ln x  x  C. 2 4 2 Câu 6.
Tìm nguyên hàm của hàm số f  x  x ln  x  2 . 2 2 x x  4x 2 2 x  4 x  4x A. f
 xdx  lnx2  C . B. f
 xdx  ln  x  2   C . 2 2 2 2 2 2 x x  4x 2 2 x  4 x  4x C. f
 xdx  lnx2  C . D. f
 xdx  ln  x  2   C . 2 4 2 4 Câu 7.
Cho hàm số y  x sin 2 d x x 
. Chọn mệnh đề đúng trong các mệnh đề sau:     3     3 A. y    . B. y    .  6  12  6  6         C. y    . D. y    .  6  12  6  24 22
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH Câu 8.
Gọi F  x là một nguyên hàm của hàm số   e x f x x  
. Tính F  x biết F 0  1. A.    1e x F x x     2 . B.    1e x F x x     1. C.    1e x F x x      2 . D.    1e x F x x    1. Câu 9.
Tìm họ nguyên hàm F  x của hàm số   2  .e x f x x . 1 A.   2  2e x F x
x  2C . B.   2  e x F x
x 2C . 2   1   x 1 x 1
C. F  x 2  2e x   C   .
D. F  x 2  e x   C   .  2  2  2 
Câu 10. Cho F (x) là một nguyên hàm của hàm số    5    1 ex f x x
và F 0 3. Tính F   1 . A. F   1  e  2 . B. F   1  11e  3 . C. F   1  e  3 . D. F   1  e  7 .
2. Thông hiểu: (10 câu)
Câu 11. Kết quả của ln d x x  là:
A. x ln x  x  C .
B. x ln x  C .
C. x ln x  x  C .
D. x ln x  x .
Câu 12. Tìm nguyên hàm của hàm số f  x  x ln x . 3 2 3 1 A.   2 d  3ln 2  f x x x x C . B.   2 d  3ln 2  f x x x x C . 9 9 3 2 3 2 C.   2 d  3ln 2  f x x x x C . D.   2 d  3ln  1  f x x x x C . 3 9
Câu 13. Biết x cos 2 d
x x  ax sin 2x  b cos 2x  C 
với a , b là các số hữu tỉ. Tính tích ab ? 1 1 1 1
A. ab   . B. ab  . C. ab  .
D. ab   . 4 8 4 8 Câu 14. Biết 2 x 2 x 2 d x xe x  axe
 be  C a, b 
. Tính tích ab . 1 1 1 1 A. ab  .
B. ab   . C. ab  .
D. ab   . 4 8 8 4 2 x
Câu 15. Biết I  3x   2
1 e dx  a  be với a,b là các số nguyên. Tính S  a  . b 0
A. S  8 .
B. S  10 .
C. S  12 .
D. S  16 . Câu 16. Ta có 2 x    2 . d    x x e x x mx
n e  C khi đó . m n bằng. A. 0 . B. 4 . C. 5 . D. 4 .
Câu 17. Nguyên hàm của hàm 2018   2  .e x f x x là: 1 1   x 1 A. 2 ( )  e x F x
x 2C . B. 2 F (x)  e x   C   . 2 2  2    x 1 C. 2 F (x)  2e x   C   . D. 2 ( )  2e x F x
x  2C .  2  23
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH Câu 18. Cho
    2    2ex F x ax bx c
là một nguyên hàm của hàm số     2    2 2018 3 1 e x f x x x trên khoảng  ;
  . Tính T  a  2b  4c .
A. T  1011. B. T  3035  .
C. T  1007 . D. T  5053  .  x 1
Câu 19. Biết   3 2 2 . d  x x e x   e
2x  n  C, với , m n  . Khi đó tổng 2 2
S  m  n có giá trị m bằng A. 5 . B. 65 . C. 41 . D. 10 .
Câu 20. Tìm nguyên hàm sin xdx . A. x x   x  x  sin d 2cos 2sin C . B. x x   x  sin d cos C . C. x x  x  sin d cos C . D. x x  x   1 sin d cos C . 2 x Bảng đáp án 1.A 2.D 3.C 4.A 5.C 6.D 7.C 8.C 9.D 10.D 11.C 12.B 13.B 14.B 15.C 16.B 17.B 18.B 19.B 20.A Hướng dẫn giải Câu 1.
Nguyên hàm của hàm số f  x  x sin x là
A. –x cos x  sin x  C .
B. x sin x  cos x  C .
C. x cos x  sin x  C .
D. x cos x  sin x  C . Lời giải Chọn A Ta có: x sin d x x  . u   x du  dx Đặt    . dv  sin d x x
v  cos x Vậy x sin xdx 
 x cos x  cos xdx 
 xcos x  sin x  C . Câu 2. Kết quả của x
I  xe dx  là 2 x A. x x I 
e  e  C . B. x x
I  e  xe  C . 2 2 x C. x I 
e  C . D. x x
I  xe  e  C . 2 Lời giải Chọn D
Cách 1: Sử dụng tích phân từng phần ta có x  d  d x x x   d x x I xe x x e xe
e x  xe  e  C.    
Cách 2: Ta có    x x    x x x x I xe e C
 e  xe  e  xe . Câu 3.
Tính F (x)  x sin 2xdx 
. Chọn kết quả đúng? 1 1
A. F(x) 
(2x cos 2x  sin 2x)  C .
B. F(x)   (2x cos 2x  sin 2 )
x  C . 4 4 24
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 1 1
C. F(x)   (2x cos 2x  sin 2x)  C .
D. F(x) 
(2x cos 2x  sin 2 ) x  C . 4 4 Lời giải Chọn C du  dx u   x  Đặt    1 , ta được dv  sin 2 d x x v   cos 2x  2 1 1 F (x)   x cos 2x  cos 2 d x x  1 1
  xcos 2x  sin 2x  1
C   (2x cos 2x  sin 2 )
x  C . 2 2 2 4 4 Câu 4.
Nguyên hàm của hàm số       1 ex f x x là A. ex x  C .
B.   2 ex x  C . C.    1 ex x  C . D. 2 ex x  C . Lời giải Chọn A
Xét   d    
1 exd     1 dex     1 ex  exd      1 ex  ex   ex f x x x x x x x x C x  C . Câu 5.
Họ các nguyên hàm của f  x  x ln x là: 2 x 1 1 2 x 1 1 A. 2 ln x 
x  C. B. 2 2 x ln x  x  . C C. 2 ln x 
x  C. D. x ln x  x  C. 2 4 2 2 4 2 Lời giải: Chọn C  1 v  x2 xdx  dv  2 1 1 x 1 Đặ 2 t    . Suy ra 2 2 x ln d x x  x ln x  d x x  ln x  x  C.   ln x  u  1 2 2 2 4 du   x Câu 6.
Tìm nguyên hàm của hàm số f  x  x ln  x  2 . 2 2 x x  4x 2 2 x  4 x  4x A. f
 xdx  lnx2  C . B. f
 xdx  ln  x  2   C . 2 2 2 2 2 2 x x  4x 2 2 x  4 x  4x C. f
 xdx  lnx2  C . D. f
 xdx  ln  x  2   C . 2 4 2 4 Lời giải Chọn D u
  ln Qx   
Đối với nguyên hàm dạng P
 xln Q
  x dx  ta đặt 
để tính theo phương pháp dv  P  xdx nguyên hàm từng phần. Câu 7.
Cho hàm số y  x sin 2 d x x 
. Chọn mệnh đề đúng trong các mệnh đề sau:     3     3         A. y    . B. y    . C. y  . D. y  .      6  12  6  6  6  12  6  24 Lời giải Chọn C 25
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH         y  x sin 2 d
x x  y  x sin 2x ; y  sin 2.       .  6  6  6  12 Câu 8.
Gọi F  x là một nguyên hàm của hàm số   e x f x x  
. Tính F  x biết F 0  1. A.    1e x F x x     2 . B.    1e x F x x     1. C.    1e x F x x      2 . D.    1e x F x x    1. Lời giải Chọn C u   x du  dx Đặt    .
dv  exdx
v  ex Do đó  
exd   ex  ex x x x dx  
  e x  e x x
 C  F  ; x C  . F 0  1 0 e  
 C 1  C  2 . Vậy    1e x F x x      2 . Câu 9.
Tìm họ nguyên hàm F  x của hàm số   2  .e x f x x . 1 A.   2  2e x F x
x  2C . B.   2  e x F x
x 2C . 2   1   x 1 x 1
C. F  x 2  2e x   C   .
D. F  x 2  e x   C   .  2  2  2  Lời giải Chọn D du  dx u   x  Đặt    1 2
v  e xdx 2 v  e x  2 1 1 1   x 1 x 1 1 x 1
F  x  f  xdx 2 2  e  e x x dx  2 2  e  . e x x  C 2  e x   C   . 2 2 2 2 2 2  2 
Câu 10. Cho F (x) là một nguyên hàm của hàm số
   5  1ex f x x
và F 0  3. Tính F   1 . A. F   1  e  2 . B. F   1  11e  3 . C. F   1  e  3 . D. F   1  e  7 . Lời giải Chọn D Ta có    5    1 ex F x x dx . u  5x 1 du  5dx Đặt    .
dv  exdx  v  ex    5   1 ex  5ex F x x dx   5   1 ex  5ex x
 C  5  4ex x  C .
Mặt khác F 0  3  4
  C  3  C  7 .
    5  4ex F x x  7 . Vậy F   1  e  7 .
Câu 11. Kết quả của ln d x x  là
A. x ln x  x  C .
B. x ln x  C .
C. x ln x  x  C .
D. x ln x  x . Lời giải 26
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH Chọn C  1 u  ln x du  dx Đặt 1    x  ln d
x x  x ln x  . d
x x  x ln x  x    C . dv=dx  x v  x
Câu 12. Tìm nguyên hàm của hàm số f  x  x ln x . 3 2 3 1 A.   2 d  3ln 2  f x x x x C . B.   2 d  3ln 2  f x x x x C . 9 9 3 2 3 2 C.   2 d  3ln 2  f x x x x C . D.   2 d  3ln  1  f x x x x C . 3 9 Lời giải Chọn B
I   f xdx  x ln . x d  x . Đặt: 1 t  x  dt  dx  2 d t t  dx 2 2 2
 I  2 t ln t .dt  4 t ln t.d   t . 2 x  1 du  d   t u ln t  Đặt:    t . 2 3
dv  t dt v  t  3  1 1   1 1  2 3 2 3 3 3  I  2 t ln t  t dt  2
t ln t  t  C  
t 3ln t   1      C  3 3   3 9  9 3 2 3 1 2
 x 3ln x   1  C 2
 x 3ln x  2  C . 9 9
Câu 13. Biết x cos 2 d
x x  ax sin 2x  b cos 2x  C 
với a , b là các số hữu tỉ. Tính tích ab ? 1 1 1 1
A. ab   . B. ab  . C. ab  . D. ab   . 4 8 4 8 Lời giải Chọn B du  dx u   x  Đặt    1 d v  cos 2 d x x v  sin 2x  2 Khi đó 1 1 x cos 2 d x x  x sin 2x  sin 2 d x x   1 1
 xsin 2x  cos 2x  C 2 2 2 4 1  1 a  , b  . 2 4 Vậy 1 ab  . 8 Câu 14. Biết 2 x 2 x 2 d x xe x  axe
 be  C a, b 
. Tính tích ab . 1 1 1 1 A. ab  .
B. ab   . C. ab  . D. ab   . 4 8 8 4 Lời giải Chọn B 27
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH du  dx u   x  Đặt    1 2 x 2 dv  e d x x v  e  2 1 x 1 x 1 x 1 Suy ra: 2 2 2 d x xe x  xe  e dx   2 2 x
 xe  e  C 2 2 2 4 Vậy: 1 1 1 a  ; b  
 ab   . 2 4 8 2 x
Câu 15. Biết I  3x   2
1 e dx  a  be với a,b là các số nguyên. Tính S  a  . b 0
A. S  8 .
B. S  10 .
C. S  12 . D. S  16 . Lời giải Chọn C 2 x I  3x    2 1 e dx . 0 u   3x 1 du  3dx   Đặt   x  x . 2 2
dv  e dx v  2e 2 2 x 2 x x
Ta có: I  23x   2 2 2 1 e
 6e dx 10e  2 12e
10e  2 12e 12 14  2e  . 0 0 0
Vậy a  b 12 . Câu 16. Ta có 2 x    2 . d    x x e x x mx
n e  C khi đó . m n bằng. A. 0 . B. 4 . C. 5 . D. 4 . Lời giải Chọn B 2 u   x du  2 d x x Đặt    . d x v  e d x x v  e 2 x 2  . d x   2 x x e x x e xe dx   . u   2x du  2dx Đặt    . d x v  e d x x v  e
 2 xd  2 x  2 xd  2 x  2 x xe x xe e x xe e  C   . 2 x     2 . d  2  2 x x e x x x e  C . Khi đó . m n  4  .
Câu 17. Nguyên hàm của hàm 2018   2  .e x f x x là: 1 1   x 1 A. 2 ( )  e x F x
x 2C . B. 2 F (x)  e x   C   . 2 2  2    x 1 C. 2 F (x)  2e x   C   . D. 2 ( )  2e x F x
x  2C .  2  Lời giải Chọn B 28
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH du  dx u   x  Đặt    1 . 2 x 2 dv  e dx v  e x  2  
Khi đó: F  x x 1 x 1 x 1 x 1 x 1 x 1 2 2 2 2 2 2  . x e dx  . x e  e dx  . x e  e  C  e x   C     . 2 2 2 4 2  2  Câu 18. Cho
    2    2ex F x ax bx c
là một nguyên hàm của hàm số     2    2 2018 3 1 e x f x x x trên khoảng  ;
  . Tính T  a  2b  4c .
A. T  1011. B. T  3035  .
C. T  1007 . D. T  5053  . Lời giải Chọn B Vì
    2    2ex F x ax bx c
là một nguyên hàm của hàm số     2    2 2018 3 1 e x f x x x trên khoảng   ;
  nên ta có: F x  f x , với mọi x ;   .   2   
   2x   2    2 2 2 2 2 e 2018 3 1 e x ax x b a c b x x
, với mọi x  ;   .     a 1009 2a  2018     2021
2b  2a  3   b    .  2  2  c  b 1   2023 c    4     Vậy 2021 2023
T  a  2b  4c  1009  2.   4.       3035  .  2   4   x 1
Câu 19. Biết   3 2 2 . d  x x e x   e
2x  n  C, với , m n  . Khi đó tổng 2 2
S  m  n có giá trị m bằng: A. 5 . B. 65 . C. 41 . D. 10 . Lời giải Chọn B du  dx u   x  3  Đặt     1 2 x 2  dv  e d x x v   e  2 Khi đó     1  x 1 x 1  x 1 2 2 3 . d    3 2  x x e x e x  e dx  2   .  3 2  x e x  e  C 2 2 2 4 1  x 1 2   .2  6   2 1  x e x
 C   e 2x  7C  m  4;n  7 4 4 2 2
 m  n  65.
Câu 20. Tìm nguyên hàm sin xdx  .
A. sin xdx  2
 cos x  2sin x  C  .
B. sin xdx   cos x  C  . 1
C. sin xdx  cos x  C  .
D. sin xdx  cos x  C  . 2 x Lời giải 29
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH Chọn A
Đặt t  x , ta có sin xdx  2t sin tdt   . u   2t du  2dt Đặt  ta có  .
dv  sin tdt
v   costdt 2t sin tdt  2
 t cost  2costdt   2t cost  2sin t  C  2 
x cos x  2 sin x  C   .
B I 2: TÍCH PHÂN ĐỔI BIẾN SỐ
_ Dạng 1. Đổi biến số dạng 1 -
Phương pháp: _
Định lí. Cho hàm số f liên tục trên đoạn [ ;
a b]. Giả sử hàm số u  u(x) có đạo hàm liên tục trên đoạn [ ;
a b] và   u(x)  . Giả sử có thể viết f (x)  g(u(x))u '(x), x [ ; a ] b ,
với g liên tục trên đoạn [;  ]. Khi đó, ta có b b u (b) ' I 
f (x)dx  g(u(x))u (x)dx  g(u)d . u    a a u (a) b
_Phương pháp. Để tính tích phân: I  g
 xdx ta thực hiện các bước: a
. Bước 1. Biến đổi để chọn phép đặt t  u  x  dt  u (  x)dx
. Bước 2. Thực hiện phép đổi cận:
 Với x  a thì t  u a .
 Với x  b thì t  u b . (Nhớ : đổi biến phải đổi cận) u (b)
. Bước 3. Đưa về dạng I  f (t)dt 
đơn giản và dễ tính hơn. u (a)
_Dấu hiệu nhận biết và cách tính tích phân Dấu hiệu Có thể đặt Có f  x t  f (x) Có (  )n ax b
t  ax  b Có f (x) a
t  f (x) dx Có và ln x
t  ln x hoặc biểu thức chứa ln x x Có x e dx x
t  e hoặc biểu thức chứa x e Có sin xdx t  cos x Có cos xdx t  sin xdx dx Có t  tan x 2 cos x dx Có t  cot x 2 sin x 30
Fb: T hayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
_Bài tập minh họa: 1 Câu 1. Tính tích phân 2 4
I  x(1 x ) dx  : 0 16 31 1 1 A. I  . B. I  . C. I  . D. I   . 5 10 10 10 Lời giải
PP nhanh trắc nghiệm Chọn B
 Để tính giá trị 1 tích phân xác định bằng máy tính  Đặt 2
t  1 x  dt  2xdx . 570ES.
 Đổi cận: x  0  t 1;
. Bước 1. Sử dụng lệnh để màn hình máy tính cầm
x  1 t  2 tay hiện: 2 4 5 t t 2 31  Nên I  dt    . 2 10 1 10 1
. Bước 2. Nhập hàm số f(x)
. Bước 3. Nhập cận
. Bước 4. Ấn phím = 2 Câu 2. Tính tích phân 2
I  2x x 1dx  bằng cách đặt 2
u  x 1, mệnh đề nào dưới đây đúng? 1 3 2 3 2 1 A. I  2 udu  . B. I  udu  . C. I  udu  . D. I  udu  . 2 0 1 0 1 Lời giải
PP nhanh trắc nghiệm Chọn C
+ Tính tích phân I bằng MTCT.  Đặt 2
u  x 1 du  2xdx .
+ Tính tích phân từng đáp án A, B, C, D.
 Đổi cận x 1 u  0 ; x  2  u  3
+ Đối chiếu kết quả, chọn đáp án C. 3  Nên I  udu  . 0  Câu 3. Tính tích phân 3 I  cos . x sin d x x  . 0 1 1 A. 4 I    . B. 4 I    . C. I  0 . D. I   . 4 4 Lời giải
PP nhanh trắc nghiệm Chọn C
 Sử dụng máy tính, tính tích phân hàm lượng giác
 Đặt t  cos x  dt  sin xdx  d
 t  sin xdx
phải chuyển về đơn vị radian.
 Đổi cận: với x  0  t 1;
với x    t  1  . 1  t 1 1  3 3  4 1 1 4 4
 Vậy I   t dt  t dt     0   . 4 4 4 1 1  1  31
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
_Bài tập áp dụng: (10 câu NB; 10 câu TH)
1. Nhận biết: (10 câu) 1 Câu 1. Tính tích phân 2 5 I 
(x  x  2) (2x 1)dx 
chọn cách đổi biến hợp lí nhất. 0 A. 2 5
t  (x  x) dx .
B. t  2x 1. C. 2 5
t  (x  x) (2x 1) . D. 2
t  x  x  2 . 1 Câu 2. Tính tích phân 5 3 4 2 I 
x  x 1(5x  3x )dx 
chọn cách đổi biến hợp lí nhất. 0 A. 5 3
t  (x  x )dx . B. 4 2
t  5x  3x . C. 5 3 t  x  x 1 . D. 5 3 t 
x  x dx . 3 2 1 4x  3x Câu 3.
Tính tích phân I  dx 
chọn cách đổi biến hợp lí nhất. 4 3 0 x  x  2 1 3 2 4x  3x A. t  . B. 3 2
t  4x  3x . C. t  . D. 4 3
t  x  x  2 . 4 3 x  x  2 4 3 x  x  2 e 1 Câu 4. Tính tích phân 5 I  ln d x x 
chọn cách đổi biến hợp lí nhất. 1 x 1 dx A. t  .
B. t  ln x . C. 5 t  ln x . D. t  . x x 1 2 Câu 5. Tính tích phân x  x I  e (2x 1)dx 
chọn cách đổi biến hợp lí nhất. 0 2 A. 2
t  x  3x 1 .
B. t  2x 1. C. 2
t  x  x . D. x  x t  e (2x 1) . 3  1 x x Câu 6. Tính tích phân 2 I  3 (3x 1)dx 
chọn cách đổi biến hợp lí nhất. 0 3 A. 3 2
t  x  3x . B. 2
t  3x  x . C. 3
t  x  x . D. x  x 2 t  3 (3x 1) .  Câu 7. Tính tích phân 6 2 I  sin x cos d x x 
chọn cách đổi biến hợp lí nhất. 0 A. 6 t  sin x .
B. t  sin x .
C. t  cos x . D. 6 t  sin . x cos x .  Câu 8. Tính tích phân 6 2 I  cos . x sin d x x 
chọn cách đổi biến hợp lí nhất. 0 A. 6 t  os c x .
B. t  sin x .
C. t  cos x . D. 6 t  o c s . x sin x .  1 Câu 9. Tính tích phân 6 4 I  tan . x dx 
chọn cách đổi biến hợp lí nhất. 2 0 cos x A. 6 t  tan x .
B. t  tan x .
C. t  cos x . D. 2 t  cos x .  1
Câu 10. Tính tích phân 6 4 I  cot . x dx  
chọn cách đổi biến hợp lí nhất. 2 sin x 6 A. 6
t  cot x .
B. t  sin x .
C. t  cot x . D. 2
t  sin x .
2. Thông hiểu: (10 câu) 2 x 1 a Câu 11. Tích phân dx   ln
. Khi đó a  b bằng: 2 x  3 2 b 0 A. 6. B. 8. C. 9. D. 10. 32
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 1
Câu 12. Cho tích phân 3 1 xdx  , với cách đặt 3
t  1 x thì tích phân đã cho bằng với tích phân nào 0 sau đây? 1 1 1 1 A. 3 d t t  . B. 3 t dt  . C. 2 3 t dt  . D. 3 3 t dt  . 0 0 0 0 1 x
Câu 13. Cho I  dx  ,với cách đặt 2 t 
x 1 thì tích phân đã cho bằng với tích phân nào sau 2  0 x 1 đây? 2 2 1 2 2 A. tdt  . B. 2 t dt  . C. 2 t dt  . D. dt  . 2 0 0 0 1  Câu 14. Tích phân 2 cos . x sin x dx  bằng 0 3 2 2 3 A.  . B. . C.  . D. . 2 3 3 2  1 2
Câu 15. Cho f là hàm số liên tục thỏa f
 xdx  7 . Tính I  cos .xf 
sin xdx . 0 0 A. 1. B. 9 . C. 3 . D. 7 . 4 2 Câu 16. Cho
f (x)dx  2018 
. Tính tích phân I   f (2x)  f (4  2x)dx 0 0 A. I  0 . B. I  2018 . C. I  4036 . D. I  1009 . 4 2
Câu 17. Cho tích phân I  f
 xdx  32. Tính tích phân J  f
 2xd .x 0 0 A. J  32. B. J  64. C. J  8. D. J  16. 1  2 ae b Câu 18. Cho 1 x I  xe dx  .Biếtrằng I 
. Khiđó, a  b bằng: 2 0 A. 1. B. 0 . C. 2 . D. 4 . e ln x
Câu 19. Với cách đổi biến u  1 3ln x thì tích phân dx  trở thành: x 1 3ln x 1 2 2 2 2 2 2 2 2 u 1 A.  2u   1du . B.  2u   1du . C. 2  2 u   1du. D. du  . 3 9 9 u 1 1 1 1 e 1 3ln x
Câu 20. Tính tích phân I  dx 
bằng cách đặt t  1 3ln x , mệnh đề nào dưới đây sai? x 1 2 2 2 2 2 2 14 A. 3 I  t . B. I  tdt  . C. 2 I  t dt  . D. I  . 9 1 3 3 9 1 1 Bảng đáp án 1.D 2.C 3.D 4.B 5.C 6.C 7.B 8.C 9.B 10.C 33
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 11.D 12.D 13.A 14.B 15.D 16.B 17.A 18.C 19.B 20.B
Hướng dẫn giải( phần TH) 2 x 1 a Câu 11. Tích phân dx   ln
khi đó a  b bằng 2 x  3 2 b 0 A. 6. B. 8. C. 9. D. 10. Lời giải Chọn D Đặt 2
t  x  3  dt  2xdx .
Đổi cận x  0  t  3 ; x  2  t  7 7 dt 1 7 Nên I   ln  2t 2 3 3 1
Câu 12. Cho tích phân 3 1 xdx  , với cách đặt 3
t  1 x thì tích phân đã cho bằng với tích phân nào 0 sau đây? 1 1 1 1 A. 3 d t t  . B. 3 t dt  . C. 2 3 t dt  . D. 3 3 t dt  . 0 0 0 0 Lời giải Chọn D Đặt 3 3 2
t  1 x  t  (1 x)  3t  dx .
Đổi cận x  0  t 1; x 1 t  0 0 1 Nên 2 3
I   t.3t dt  3t dt   1 0 1 x
Câu 13. Cho I  dx  ,với cách đặt 2 t 
x 1 thì tích phân đã cho bằng với tích phân nào sau 2  0 x 1 đây? 2 2 1 2 2 A. tdt  . B. 2 t dt  . C. 2 t dt  . D. dt  . 2 0 0 0 1 Lời giải Chọn D Đặt 2 2 2 t 
x 1  t  x 1  tdt  xdx .
Đổi cận x  0  t 1; x 1 t  2 2 2 t Nên I  dt  dt   . t 1 1  Câu 14. Tích phân 2 cos . x sin x dx  bằng 0 3 2 2 3 A.  . B. . C.  . D. . 2 3 3 2 Lời giải Chọn B 34
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
Đặt t  cos x  t  dt  sin . x dx .
Đổi cận: x  0  t 1, x    t  1  . 1 Khi đó: 2 2 I  t dt   . 3 1   1 2
Câu 15. Cho f là hàm số liên tục thỏa f
 xdx  7 . Tính I  cos .xf 
sin xdx . 0 0 A. 1. B. 9 . C. 3 . D. 7 . Lời giải Chọn D
Đặt t  sin x  dt  cos . x dx 
Đổi cận x  0  t  0 ; x   t 1 2 1
Khi đó: I  f (t) dt  7  . 0 4 2 Câu 16. Cho
f (x)dx  2018 
. Tính tích phân I   f (2x)  f (4  2x)dx . 0 0 A. I  0 . B. I  2018 . C. I  4036 . D. I  1009 . Lời giải Chọn B 2 4 2 xt 1 Ta có
f (2x)dx  f (t)dt   . 2 0 0 2 0 4 42 xt 1 1
f (4  2x)dx   f (t)dt  f (t)dt    2 2 0 4 0 2 4 4
Suy ra I   f (2x)  f (4  2x)dx  f (t)dt  f (x)dx 2018   . 0 0 0 4 2
Câu 17. Cho tích phân I  f
 xdx  32. Tính tích phân J  f
 2xd .x 0 0 A. J  32. B. J  64. C. J  8. D. J  16. Lời giải Chọn D Đặt dt
t  2x  dt  2dx   d . x 2
Đổi cận: x  0  t  0; x  2  t  4. 2 4 4 J  f   x 1 x  f  t 1 t  f  t 1 2 d d dt  I  16. 2 2 2 0 0 0 1  2 ae b Câu 18. Cho 1 x I  xe dx  . Biết rằng I 
. Khi đó, a  b bằng: 2 0 A. 1. B. 0 . C. 2 . D. 4 . Lời giải 35
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH Chọn C Đặt 2
t  1 x  dt  2  d x x .
Đổi cận: x  0  t 1; x 1 t  0. 0 1 1 e  t 1 t 1 I   e dt  e dt    . 2 2 2 1 0 e ln x
Câu 19. Với cách đổi biến u  1 3ln x thì tích phân dx  trở thành: x 1 3ln x 1 2 2 2 2 2 2 2 2 u 1 A.  2u   1du . B.  2u   1du . C. 2  2 u   1du. D. du  . 3 9 9 u 1 1 1 1 Lời giải Chọn B Đặt 1 2u 2
u  1 3ln x  u  1 3ln x  dx  .du x 3
x 1 u 1 Đổi cận: 
x  e  u  2  2 2 u   2 1 Khi đó 2u 2 I  . .dt  .  2 u    1.du u .3 3 9 1 1 e 1 3ln x
Câu 20. Tính tích phân I  dx 
bằng cách đặt t  1 3ln x , mệnh đề nào dưới đây sai? x 1 2 2 2 2 2 2 14 A. 3 I  t . B. I  tdt  . C. 2 I  t dt  . D. I  . 9 1 3 3 9 1 1 Lời giải Chọn C Đặt 1 2t 2
t  1 3ln x  t  1 3ln x  dx  .dt x 3
x 1 t 1 Đổi cận:  .
x  e  t  2 2 2 Khi đó 2t 2 14 2 I  t. .dt  . t .dt    . 3 3 9 1 1
_ Dạng 2. Đổi biến số dạng 2 b _ Ph
ương pháp: Để tính tích phân: I  f
 xdx , mà biểu thức dưới dấu tích phân có dạng a     1. 2 2
a  x : đặt x |
 a | sin t; t   ;    2 2       : đặt | a |    2. 2 2 x a x ; t ; \ {0}   sin t  2 2      3. 2 2
x  a : x  a tan t; t   ;    2 2  a  x  4.
hoặc a x : đặt x  . a cos 2t a  x a  x 36
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
_Bài tập minh họa: 1 Câu 1. Tính tích phân sau: 2 I  1 x dx  . 0   A. . B. 1. C. 0 D.  . 4 4 Lời giải
PP nhanh trắc nghiệm Chọn A
 . Bước 1. Sử dụng lệnh để màn
 Đặt x  sin t ta có dx  costdt.
hình máy tính cầm tay hiện: 
Đổi cận: x  0  t  0; x 1 t  . 2 Vậy   1 2 2  1 cos2t 
. Bước 2. Nhập hàm số f(x) 2 2 I 
1 x dx  | cos t |cos tdt  cos tdt    2  dt  .  0 2 4
. Bước 3. Nhập cận 0 0 0
. Bước 4. Ấn phím = 1 dx Câu 2.
Tính tích phân sau: I   . 2 1 x 0     3 A. . B. . C. . D.  . 4 12 6 6 4 Lời giải
PP nhanh trắc nghiệm Chọn A
 . Bước 1. Sử dụng lệnh để màn
 Đặt x  tan t, ta có dx   2
1 tan t  dt .
hình máy tính cầm tay hiện
x  0  t  0  Đổi cận:   .
x  1  t   4 
. Bước 2. Nhập hàm số f(x) 1 4   Vậy dx 4 I 
 dt  t |  .  
. Bước 3. Nhập cận 2 0 1 x 4 0 0
. Bước 4. Ấn phím = 5 dx Câu 3.
Khi đổi biến x  5 tant thì tích phân I  
trở thành tích phân nào sau đây? 2 x  5 0     4 4 5 6 6 1 A. I  5dt.  B. I  dt.  C. I  5tdt.  D. I  dt.  5 t 0 0 0 0 Lời giải
PP nhanh trắc nghiệm Chọn B  Đặt 2
x  5 tan t  dx  5(1 tan t)dt
+ Tính tích phân I bằng mt. Đổi cận.
+ Tính tích phân từng đáp án A,B,C,D. 
+ Đối chiếu kết quả, chọn đáp án C.
x  5  t 
; x  0  t  0 4 I trở thành 37
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH    5  2 1 tan t dt 5  2 4 4 1 tan t  4 dt 5dt   .    2 2 5 tan t  5 5(tan t 1) 5 0 0 0
_Bài tập áp dụng: (10 câu NB; 10 câu TH)
1. Nhận biết:(10 câu) 1 dx Câu 1.
Tính tích phân I  
chọn cách đổi biến hợp lí nhất: 2 x  3 0 A. 2 t  x  3 .
B. x  3 tan t .
C. t  3 sin x . D. 2 x  t  3 . 4 dx Câu 2.
Tính tích phân I  
chọn cách đổi biến hợp lí nhất: 2 x 16 0 A. 2 t  x 16 .
B. t  4sin x .
C. x  4 tan t . D. 2 x  t  4 . 5 dx Câu 3.
Tính tích phân I  
chọn cách đổi biến hợp lí nhất: 2 x  25 0 A. 2 t  x  25. B. 2 x  t  5 .
C. t  5sin x .
D. x  5 tan t . 7 dx Câu 4.
Tính tích phân I  
chọn cách đổi biến hợp lí nhất: 2 x  7 0 A. 2 t  x  7 .
B. x  7 tan t .
C. t  7sin x . D. 2 x  t  7 . 2 dx Câu 5.
Tính tích phân I  
chọn cách đổi biến hợp lí nhất: 2 4  x 0 A. 2 t  4  x .
B. x  4 tan t .
C. t  4sin x . D. 2 x  t  4 . 2 Câu 6. Tính tích phân 2 I  4  x dx, 
chọn cách đổi biến hợp lí nhất: 0
A. x  2 tan t . B. 2 t  4  x .
C. x  2sin t .
D. t  2sin x . 3 Câu 7. Tính tích phân 2 I  9  x dx 
chọn cách đổi biến hợp lí nhất: 0
A. x  3cos t . B. 2 t  9  x .
C. x  3tan t .
D. t  3tan x . 5 Câu 8. Tính tích phân 2 I  25  x dx 
chọn cách đổi biến hợp lí nhất: 0 A. 2
t  25  x .
B. x  5cos t .
C. x  5 tan t .
D. t  5 tan x . 4 Câu 9. Tích phân 2 16  x dx 
chọn cách đổi biến hợp lí nhất: 0 A. 2
t  16  x .
B. x  4 tan t .
C. t  4sin x .
D. x  4cost . 3 Câu 10. Tích phân 2 3  x dx 
chọn cách đổi biến hợp lí nhất: 0 A. 2 t  3  x
B. x  2 cost
C. x  3 tan t
D. t  3tan x 38
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
2. Thông hiểu: (10 câu) 8
Câu 11. Đổi biến số x  4sin t của tích phân 2 16  x dx  ta được: 0   4 4 A. 2 I  1  6 cos d t t  .
B. I  8 1 cos 2tdt . 0 0   4 4 C. 2 I  16 sin d t t  .
D. I  8 1 cos 2tdt . 0 0 1 Câu 12. Tích phân 2 1 x dx  bằng: 0     2 2 2 2 A. 2  sin t.dx  . B. 2 sin t.dt  . C. 2  cos t.dt  . D. 2 cos t.dt  . 0 0 0 0 1 dx
Câu 13. Đổi biến x  2sin t tích phân  trở thành: 2  0 4 x     6 6 6 1 3 A. tdt  . B. dt  . C. dt  . D. dt  t 0 0 0 0 3 dx
Câu 14. Khi đổi biến x  3tan t thì tích phân I  
trở thành tích phân nào sau đây? 2 x  9 0     4 4 1 4 4 A. 3dt  B. dt  C. 3dt  D. 3dt  3 0 0 0 0 3 5 dx
Câu 15. Tích phân  bằng: 9 2 3  x 5 25     4 3 4 5 4 3 4 5 A. dt  . B. dt  . C.  dt  . D.  dt  . 5  3  5  3  6 6 6 6 a 2 dx
Câu 16. Tích phân 
với a  0 bằng: 2 2  0 a x     4 3 6 12 A. dt  . B. dt  . C. dt  . D. dt  . 0 0 0 0 a
Câu 17. Tích phân: I = 2 2 a  x dx 
với a > 0 bằng: 0 4 a  4 a  4 a  4 a  A. . B. . C. . D. . 8 16 4 32 39
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 3
Câu 18. Tích phân: I = 2 9  x dx  bằng: 0 81 81 4 81  81 A. . B. . C. . D. . 8 4 16 32 4
Câu 19. Tích phân: I = 2 16  x dx  bằng: 0 A. 32 . B. 64 . C. 16 . D. 8 . 5
Câu 20. Tích phân: I = 2 25  x dx  bằng: 0 A. 32 . B. 64 . C. 16 . D. 8 . Bảng đáp án 1.B 2.C 3.D 4.B 5.B 6.C 7.A 8.B 9.D 10.B 11.B 12.C 13.A 14.B 15.A 16.A 17.B 18.C 19.B 20.B
Hướng dẫn giải( phần TH) 8
Câu 11. Đổi biến số x  4sin t của tích phân 2 16  x dx  ta được: 0   4 4 A. 2 I  1  6 cos d t t  .
B. I  8 1 cos 2tdt . 0 0   4 4 C. 2 I  16 sin d t t  .
D. I  8 1 cos 2tdt . 0 0 Lời giải Chọn B
Đặt x  4sin t ta có dx  4costdt. 
Đổi cận: x  0  t  0; x  8  t  . 4   8 4 4  Vậy : 2 2 4 I 
1 x dx  16 | cos t |cos tdt  16 cos tdt  8 (1 cos 2t)dt.     0 0 0 0 1 Câu 12. Tích phân 2 1 x dx  bằng 0     2 2 2 2 A. 2  sin t.dx  . B. 2 sin t.dt  . C. 2  cos t.dt  . D. 2 cos t.dt  . 0 0 0 0 Lời giải Chọn D
Đặt x  sin t ta có dx  costdt. 
Đổi cận: x  0  t  0; x 1 t  . 2 40
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH   1 2 2 Vậy 2 2 I 
1 x dx  | cos t |cos tdt  cos tdt.    0 0 0 1 dx
Câu 13. Đổi biến x  2s n i t tích phân  trở thành: 2  0 4 x     6 6 6 1 3 A. tdt  . B. dt  . C. dt  . D. dt  t 0 0 0 0 Lời giải Chọn B
Đặt x  2sin t ta có dx  2costdt. 
Đổi cận: x  0  t  0; x 1 t  . 6   1 6 6 Vậy: dx 2 cos t I  dx  dt  dt    2 2   0 4 x 0 4 4sin t 0 3 dx
Câu 14. Khi đổi biến x  3tan t thì tích phân I  
trở thành tích phân nào sau đây? 2 x  9 0     4 4 1 4 4 A. 3dt  B. dt  C. 3dt  D. 3dt  3 0 0 0 0 Lời giải Chọn B     Đặt x     x     2 3 tan t, t ; d 3 1 tan t dt  2 2  
Đổi cận: x  0  t  0 ; x  3  t  . 4   4 4 1 1 Suy ra: I  .3   2 1 tan t dt  dt  . 2  9  9 tan t 3 0 0 41
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
B I 3: TÍCH PHÂN TỪNG PHẦN sin ax     _ Dạng 1. f
 x cosax dx   .  ax e    - Phương pháp: u
  f x
du  f 'x dx         Đặt: sin ax sin ax       
dv  cos ax dx v  cos ax dx      .    ax    ax e e       
_Bài tập minh họa: 2 Câu 1.
Tính tích phân   x I xe dx . 1 A. 2 I  e . B. 2 I  e .
C. I  e . D. 2
I  3e  2e . Lời giải
PP nhanh trắc nghiệm Chọn A - Tính tích phân u  x du  dx Đặt    dv  x e dx v  x e 2 2 x x 2 x 2 x 2
I  xe dx  xe
 e dx  2e  e  e   1 1
- Lưu kết quả bằng biến A 1 1 . 2
 2e  e   2 e  e 2  e
- Kiểm tra các đáp án: A đúng 1 Câu 2. Tính tích phân 2  (  2) x I x e dx  . 0 2 5  3e 2 5  3e 2 5  3e 2 5  3e A. I  . B. I  . C. I  . D. I  . 4 4 4 4 Lời giải
PP nhanh trắc nghiệm Chọn B  Tính tích phân: 42
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH du  dx u   x  2   Đặt    1 (chọn C  0 ) 2 x 2 x dv  e dx v  e  2 1 1 2 1  e x 1 x 5 3 2 2
 I  (x  2) e  e dx   .
- Lưu kết quả bằng biến B 2 2 4 0 0
- Kiểm tra các đáp án: B đúng  Câu 3.
Tích phân 3x  2 2
cos x dx bằng: 0 3 3 1 1 A. 2   . B. 2   . C. 2   . D. 2   . 4 4 4 4 Lời giải
PP nhanh trắc nghiệm Chọn B  Tinh tích phân: 
 Đặt I  3x  2 2
cos x dx . Ta có: 0  1
 3x  21cos2xdx 2 0   1   
x   x   x   1 3 2 d 3
2 cos 2x dx   I  I . 1 2 
- Lưu kết quả bằng biến C 2 2 0 0     3  3 I  3x  2 dx   2 2 x  2x    2   . 1    2  2 0 0  I 
3x  2 cos 2x dx 
. Dùng tích phân từng phần 2   0 du  3dx
Kiểm tra các đáp án: B đúng u   3x  2  Đặt    1 .
dv  cos 2x dx v  sin 2x  2 Khi đó   1 3 I 
3x  2 sin 2x  sin 2x dx  2   2 2 0 0  3
 0  cos 2x  0 . 4 0   Vậy 1 3 3 2 2 I    2      . 2  2  4 43
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
_Bài tập áp dụng: (10 câu NB; 10 câu TH)
1. Nhận biết:(10 câu)  4 Câu 1.
Cho tích phân I   x    1 sin 2 d x .
x Tìm đẳng thức đúng? 0    1
A. I    x   4 1 cos2x  cos2 d x x  .
B. I    x   4 4 1 cos2x  cos2 d x x  . 2 0 0 0     1 1
C. I    x   4 4 1 cos2x  cos2 d x x  .
D. I    x   4 4 1 cos2x  cos2 d x x  . 2 2 0 0 0 0  2 Câu 2.
Tính tích phân I  2x    1 cos xdx . 0 A.   2 . B.   3 . C.  1 . D.   4 .  4 Câu 3.
Giá trị của I  x cos 2xdx  là: 0   1  1  1 A. . B. + . C. - . D. - . 8 8 4 4 4 8 4  6 Câu 4.
Tính tích phân 2  xsin3xdx bằng: 0 4 7 8 5 A. . B. . C. . D. . 9 9 9 9  2 Câu 5.
Tính tích phân I   2 x  
1sin xdx bằng: 0  
A. I   1. B. I  1.
C. I  1 . D. I  1 . 2 2  2 Câu 6.
Tính tích phân I  (2x 1) sin 3xdx 0 5 5 5 5 A. B.  C. D.  9 9 8 8  4 Câu 7.
Tính tích phân I  x(1 sin 2x)dx  4 0 2  1 2  2  2   1  3  3  A. 32 4 B. 32 4 C. 32 4 D. 32 4 2 Câu 8. Tính tích phân x I  (2x 1)e dx  8 1 44
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH A. 2 e  e . B. 2 e  e 1. C. 2 e  e D. 2 e  e 1. 1 Câu 9.
Tính tích phân I  x    3x 1 e dx 0 2 4  e 3 4  e 3 4  2e 3 4  e A. B. C. D. 9 9 9 9 1
Câu 10. Tính tích phân I   2x e  x x e dx 0 1 1 1 1 A. 2  B. 3  C. 1  D. 4  e e e e
2. Thông hiểu: (10 câu) 1
Câu 11. Tính tích phân 2 x I  (x 1)e dx  0 A. 2e  5 B. 2e  3 C. 2e 1 D. 2e  4 1
Câu 12. Tính tích phân I  x   2x 3 e
 x 1dx 0 1 1 1 1 1 1 1 1 A. 2 e  . B. 2 e  C. 2 e  D. 2 e  4 8 4 10 4 14 4 14 1 u  2x 1
Câu 13. Cho  2   1 x I x e dx . Đặt 
. Chọn khẳng định đúng. x dv  e dx 0 1 1 1 1 A.  3 1 2 x I e e dx  . B.  3 1 2 x I e e dx  . C.  3  2 x I e e dx  . D.  3  2 x I e e dx  . 0 0 0 0 1
Câu 14. Biết tích phân    3 x x
e dx  a  be với ,
a b  . Tìm tổng a+b. 0
A. a  b  1. .
B. a  b  25. .
C. a  b  4  3 . e .
D. a  b  1  . e 4 2 . a e  . b e  c
Câu 15. Cho biết tích phân 2
I  x(2x  ln x)dx   với a, ,
b c là các ước nguyên của 4. 4 1
Tính tổng: a  b  c A. 4. B. 1. C. 3. D. 2. 1 1
Câu 16. Cho x   1 f '(x) x
d  2 và 2 f (1)  f (0)  1. Tính f (x) x d  ?  0 0 A. I  1  . B. I  1. C. I  2  .
D. I  2 . 1 1
Câu 17. Cho 2x   1 f '(x) x
d  3 và 3 f (1)  f (0)  1 . Tính f (x) x d  ?  0 0 1 1 A. I  1  . B. I   . C. I  1. D. I  . 2 2 π
Câu 18. Tính J  x sin x dx  . 0 45
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH π π A. π . B. π . C. . D. . 4 2 1
Câu 19. Biết (  2020) x x e dx  . a e  . b  Với , a b 
. Tính T  a  b 0 A. T  1. B. T  2 . C. T  3. D. T  4 . 2 Câu 20. Tính  ex I x dx  . 1 A. 2 I  e . B. 2 I   e . C. 2 I  3e  2 e . D. I  e . Bảng đáp án 1.C 2.B 3.D 4.D 5.A 6.B 7.A 8.C 9.D 10.A 11.B 12.C 13.B 14.A 15.D 16.A 17.A 18.B 19.A 20.A _ Dạng 2. 
_ Dạng 2. : f (x) ln(ax)dx 
_Bài tập minh họa: 
-Phương pháp:  dx    du u ax  Đặt: ln( )   x 
dv  f (x)dx
v  f (x)dx   e 2 .e a  b Câu 1. Cho I  x ln d x x  
với a , b , c 
. Tính T  a  b  c . c 1 A. 5 . B. 3 . C. 4 . D. 6 . Lời giải
PP nhanh trắc nghiệm Chọn D   1 du  dx u   ln x  x Ta có:  nên  . dv  d x x 2 x v   2 e e 2 e x 1 2 e  1 I  x ln d x x   ln x  d x x   . 2 2 4 1 1 1 a  1   b   1 . c  4 
Vậy T  a  b  c  6 . 46
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 5 Câu 2.
Tính tích phân I  x  
1 ln  x  3dx ? 4 19 19 19 A. 10ln 2 . B. 10ln 2  . C. 10ln 2 . D. 10ln 2  . 4 4 4 Lời giải
PP nhanh trắc nghiệm  Chọn D
Quy trình bấm máy.  1
 Bấm máy tính:     x   du dx u ln 3   Đặt x 3    .
dv  x 1 1 2
v  x  x  2 1 2  5 x  x 
Lưu kết quả: 1  5 2 I  x  x    x   2 ln 3  dx   2  4 x  3 4 5 2 5 35 1 x  9  9 x  3  3  ln 2  dx  dx   2 2 x  3 x  3 4 4
 Kiểm tra kết quả: 35 1  9   ln 2   3 9ln 2    1 3ln 2 2 2  2  19 10ln 2  . 4 2 Câu 3. Biết 2x ln  x   1 dx  . a ln b , với * a, b 
, b là số nguyên tố. Tính 6a  7b . 0 A. 33 . B. 25 . C. 42 . D. 39 . Lời giải
PP nhanh trắc nghiệm Chọn D
 _Quy trình bấm máy. 2
Ta có .ln  ln a a b b
 Xét I  2x ln  x    1 dx  6 . Bước 1. 0   1
u  ln  x   1 du  dx Đặt    x 1 . dv  2 d x x 2
v  x 1 Ta có:
Bước 2.  ln a a A A
b  b  e     2 x  I x 1 ln  x   2 2 1 2 1  dx  0 x 1 0 2 2 2    x 3ln 3   x    1 dx  3ln 3    x  3ln3.  2 
Bước 3. Bấm Shift + FACT 0 0
Vậy a  3, b  3  6a  7b  39 .
Vậy a  3, b  3  6a  7b  39 . 47
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
_Bài tập áp dụng: (10 câu NB; 10 câu TH)
1. Nhận biết:(10 câu) e Câu 1.
Tính tích phân I  (x  2) ln xdx  : 1 1 2 e  2 2 e 1 2 e 1 A. I  . B. I  . C. I  . D. I  . 2 2 4 4  u  ln x e Câu 2. Nếu đặt 
thì tích phân I  2x   
1 ln xdx trở thành: dv  2x    1 dx 1 e e e e A. I   2
x  x   x    1 dx . B. 2
I  x ln x   x    1 dx . 1 1 1 1 e e e e C. 2
I  x ln x  xdx  . D. I   2
x  xln x   x    1 dx . 1 1 1 1 2 Câu 3.
Tính tích phân J  x ln(x1) dx  . 0 4 5 3 3 A. J  ln 3 . B. J  ln 3. C. J  ln 3 . D. J  ln 3 . 3 3 2 4 2 Câu 4. Biết rằng ln
 x 1dx  aln3bln2c với a , b , c là các số nguyên. Tính S  abc. 1 A. S  0 . B. S  1. C. S  2 . D. S  2  . 2 Câu 5. Biết 2x ln  x   1 dx  . a ln b , với * a, b 
, b là số nguyên tố. Tính a  b . 0 A. 33 . B. 25 . C. 42 . D. 6 . 5 Câu 6.
Tính tích phân I  x  
1 ln  x  3dx ? 4 19 19 19 A. 10ln 2 . B. 10ln 2  . C. 10ln 2 . D. 10ln 2  . 4 4 4 2 Câu 7. Biết 2x ln 
1 xdx  .alnb , với * a, b 
, b là số nguyên tố. Tính 3a  4b . 0 A. 42 . B. 21 . C. 12 . D. 32 . 3 Câu 8.
Biết ln(x 1)dx  a ln 2  b 
với a,b là các số nguyên. Khi đó, a  b bằng 2 A. 0. B. 1. C. 3. D. 2. 2 ln x Câu 9. Tính I        . Tính T a 3b . x   dx a ln 3 b ln 2 2 1 1 A. T  1. B. T  5 . C. T  3. D. T  4 . 3
Câu 10. Tích Phân 2
I  ln(x  x) 
dx là : 2 A. 3ln 3 . B. 2 ln 2 . C. 3ln 3  2 . D. 2  3ln 3 . 48
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
2. Thông hiểu: (10 câu) 2 ln
Câu 11. Tích phân   x I dx bằng: 2 x 1 1 1 1 1 A. 1ln2 . B. 1ln2 . C. ln 2   1 . D. 1 ln 2 . 2 2 2 4 2
Câu 12. Tích phân K  (2x 1) ln  xdx bằng: 1 1 1 1
A. K  3ln 2  . B. K  .
C. K  3ln 2 .
D. K  2ln 2  . 2 2 2 e 3 a e 1 Câu 13. Cho 3 x ln d x x   với , a b 
. Tổng a  b bằng b 1 A. 20 . B. 10 . C. 17 . D. 12 . e Câu 14. Biết 2 3 I  x ln d
x x  ae  b 
với a , b là các số hữu tỉ. Giá trị của 9 a  b bằng 1 A. 3 . B. 10 . C. 9 . D. 6 . 2
Câu 15. Biết 2x ln 
x  1dx  alnb, với * a, b 
, b là số nguyên tố. Tính 6a  7b . 0 A. 33 . B. 25 . C. 42 . D. 39 . 2
Câu 16. Biết (4x 1) lnx dx  a ln 2  b.  , với , a b 
. Tính 2a  b . 0 A. 5 . B. 8 . C. 13 . D. 10 . 2 ln x b
Câu 17. Cho tích phân I  dx   a ln 2 
với a là số thực, b và c là các số nguyên dương, đồng 2 x c 1 b
thời là phân số tối giản. Tính giá trị của biểu thức P  2a  3b  c . c A. P  6 . B. P  6  . C. P  5 . D. P  4 . 5 Câu 18. Cho ln
  2x  xdx  aln5bln2c với a , b , c là các số nguyên. Tính S  a2bc. 2 A. S  23 . B. S  20 . C. S  17 . D. S 11 . 2 x  ln x a 1
Câu 19. Cho I     
với a , b , m là các số nguyên dương và là phân số tối giản. x   dx ln 2 2 1 b c 1 
Tính giá trị của biểu thức a b S  . c 2 5 1 1 A. S  . B. S  . C. S  . D. S  . 3 6 2 3 b
Câu 20. Cho a  b  1
 . Tích phân I  ln x   
1 dx bằng biểu thức nào sau đây? a 49
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH b b
A. I   x   1 ln  x   1  a  b .
B. I   x   1 ln  x   1 b  a . a a b 1 b b x C. I   .
D. I  x ln  x   1  dx  . x   1 a x 1 a a Bảng đáp án 1.C 2.D 3.C 4.A 5.D 6.D 7.B 8.B 9.D 10.C 11.A 12.D 13.A 14.A 15.D 16.D 17.D 18.B 19.B 20.B _ Dạng 3.  sin ax
_ Dạng 3. e .  ax  dx  cosax
-Phương pháp:   a os c ax   sin ax    du dx u        asin ax Đặt:  cos ax     1 ax ax dv  e dx v  e   a
_Bài tập minh họa:  2 Câu 1.
Tính tích phân  cos . x I x e dx  . 0     2 e  2 2 e  2 2 e 1 2 e 1 A. . B. . C. . D. . 2 2 2 2 Lời giải
PP nhanh trắc nghiệm Chọn D  Tính:  2   cos . x I x e dx  0 u   cosx
du  sin xdx Đặt:    dv  exdx v  ex    2 2 x 2  .  sin . x  1   sin . x I cosx e x e dx x e dx (*)   0 0 0  2  Kiểm tra các đáp án: sin . x J x e dx  0 u   sin x du  cosxdx Đặt:    dv  exdx v  ex 50
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH    2  2 x 2 x 2  sin .  cos .   cos . x J x e x e dx e x e dx   0 0 0  2  e  I (2*)  2 e 1
Thay (2*) vào (*) ta có: I  2  2 Câu 2.
Tính tích phân  sin . x I x e dx  . 0        2 -e  2 2 -e  2 2 -e 1 2 -e 1 A. . B. . C. . D. . 2 2 2 2 Lời giải
PP nhanh trắc nghiệm Chọn D  Tính:  2
  sin . x I x e dx  0 u   sin x du  cosxdx Đặt:   
dv  exdx
v  ex   2   x  2 x 2 I   sin . x e  cos . x e dx  e J (*)  0 0  2  Kiểm tra các đáp án: cos . x J x e dx  0 u   cosx
du  sin xdx Đặt:   
dv  exdx v  ex   2  x  2   s .  sin . x J co x e x e dx  0 0 1 I (2*)   2 e 1
Thay (2*) vào (*) ta có: I  2  2 Câu 3. sinx I  e .sin 2xdx  0 A. 1. B. 2 . C. 1  . D. 2 . 51
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH Lời giải
PP nhanh trắc nghiệm Chọn B  Tính:  2  sinx I  2 e .sin x cos xdx  . 0 u  sin x
du  cos xdx Đặt  sin x   sin x dv  e cos xdx v  e   2  I  sin x 2sin xe 2  0  sinx e .cos xdx 0   2e  sin x 2e 2  0 2
_Bài tập áp dụng:  4 Câu 1.
Tính tích phân  ex I cos2xdx  : 0     4 e 1 4 e  2 4 e  3 4 e  4 A. I  . B. I  . C. I  . D. I  . 5 5 5 5  4 Câu 2.
Tính tích phân  ex I cos2 d x x  : 0         4 1 2e 4 2  2e 4 3  2e 4 4  2e A. I  . B. I  . C. I  . D. I  . 3 3 3 3  2 Câu 3.
Tính tích phân I  ex sin xdx  . 0     1 A. 2 I  e  2 . B. 2 I  e 1. C. 2 I  e  3 . D. 2 I  e  . 2  4 Câu 4.
Tính tích phân  ex I sin 2xdx  . 0     4 e  3 4 e 1 4 e  2 4 e  4 A. I  . B. I  . C. I  . D. I  . 5 5 5 5  6 Câu 5.
Tính tích phân  ex I sin 3xdx  0     6 e 1 6 e 1 6 e 1 6 e 1 A. I  . B. I  . C. I  . D. I  . 7 8 9 10 52
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH  6 Câu 6. Tính tích phân 3  e x I cosxdx  0   3 3 1 3 3 3 1 3 A. 2 I  (  )e  . B. 2 I  (  )e  . 10 2 6 10 10 2 6 10   3 3 1 3 3 3 1 3 C. 2 I  (  )e  . D. 2 I  (  )e  . 10 2 6 10 10 2 6 10  4 Câu 7.
Tính tích phân  ex I sin d x x  0       4 1 2e 4 1 2e 4 1 2e 4 1 2e A. I  . B. I  . C. I  . D. I  . 2 2 2 2  3 x Câu 8. Tính tích phân 2 I  e sin xdx  0     6 ( 3  2)e 1 6 ( 3  2)e 1 6 ( 3  2)e 1 6 ( 3  2)e 1 A. I  . B. I  . C. I  . D. I  . 2 3 4 5  4 Câu 9. Tính tích phân x 2 I  e cos xdx  0     4 3e  3 4 3e  2 4 3e  4 4 3e 1 A. I  . B. I  . C. I  . D. I  . 5 5 5 5  4
Câu 10. Tính tích phân x 2 I  e sin xdx  0     4 2e 1 4 2e  2 4 2e  3 4 2e  4 A. I  . B. I  . C. I  . D. I  5 5 5 5 Bảng đáp án 1.A 2.A 3.B 4.C 5.D 6.B 7.A 8.D 9.A 10.B 53
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
B I 4: ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
_ Dạng 1. Ứng dụng của tích phân tính diện tích hình phẳng
_ Dạng 1. Ứng dụng của tích phân tính diện tích hình phẳng
-Phương pháp:
 Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f (x) liên tục trên đoạn a;b , trục b hoà
nh và hai đường thẳng x  a , x  b được xác định: S  f (x) dx  . a y
y  f (x)
y  f (x) b  y  0  S
f ( x) dx 
(H)x  a a  O a c c c b x 1 2 3  x  b 
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f (x) , y  g(x) liên tục trên đoạn a;b b và hai đường thẳng     x a , x
b được xác định: S f (x) g(x) dx  a y
(C ) : y  f (x) 1 1 (C ) 1 
(C ) : y  f (x) 2 2
(H)x a (C ) 2  x  b b   a c O c 1 b x 2  S
f ( x)
f ( x) dx 1 2 a Chú ý: b b - Nế u trên đoạn [ ;
a b] , hàm số f (x) không đổi dấu thì:
f (x) dx  f (x)dx   . a a - Nắ
m vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối
- Diện tích của hình phẳng giới hạn bởi các đường x  g( y) , x  h( y) và hai đường thẳng y  c , d
y  d được xác định: S 
g( y)  h( y) dy  . c 54
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
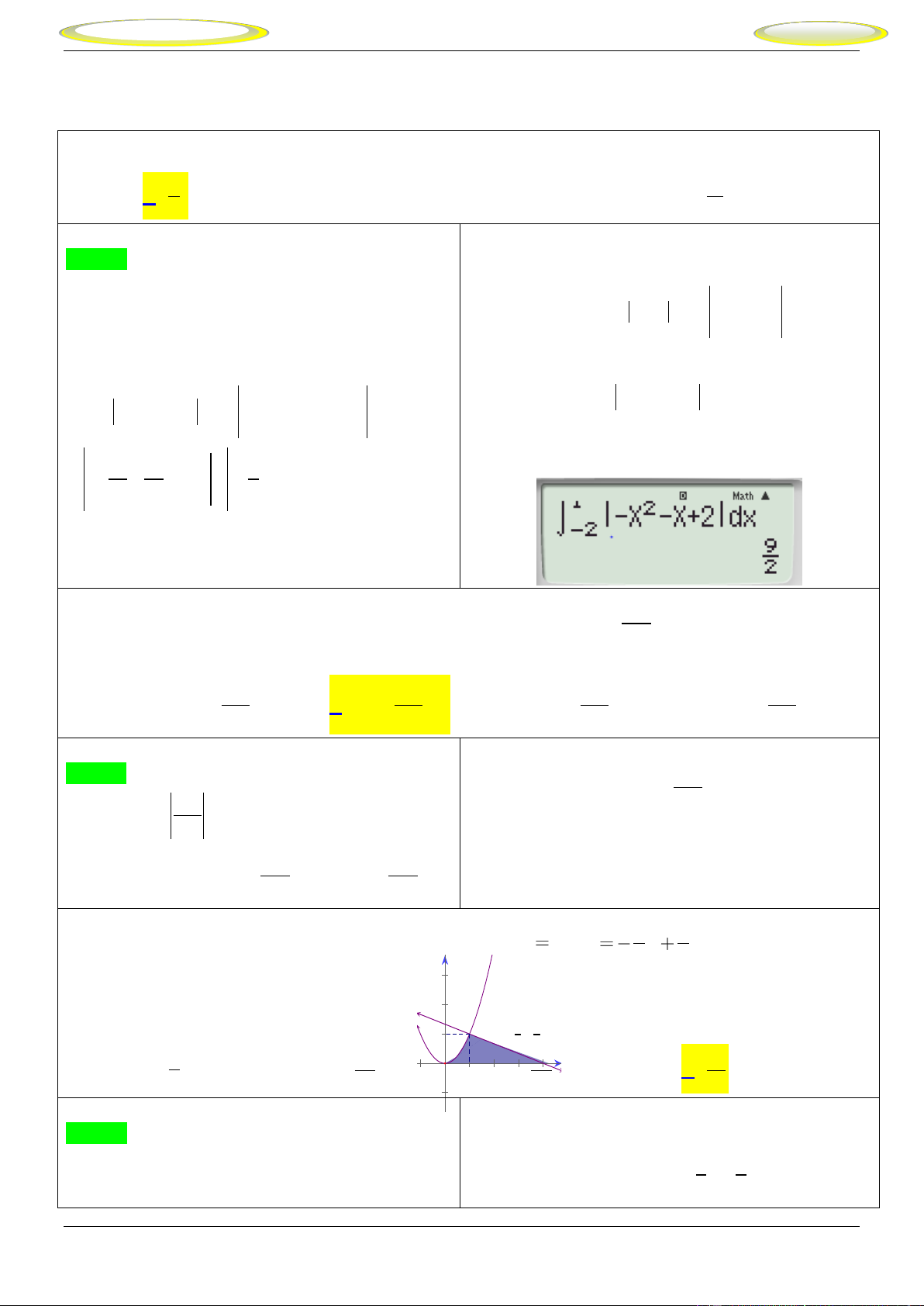
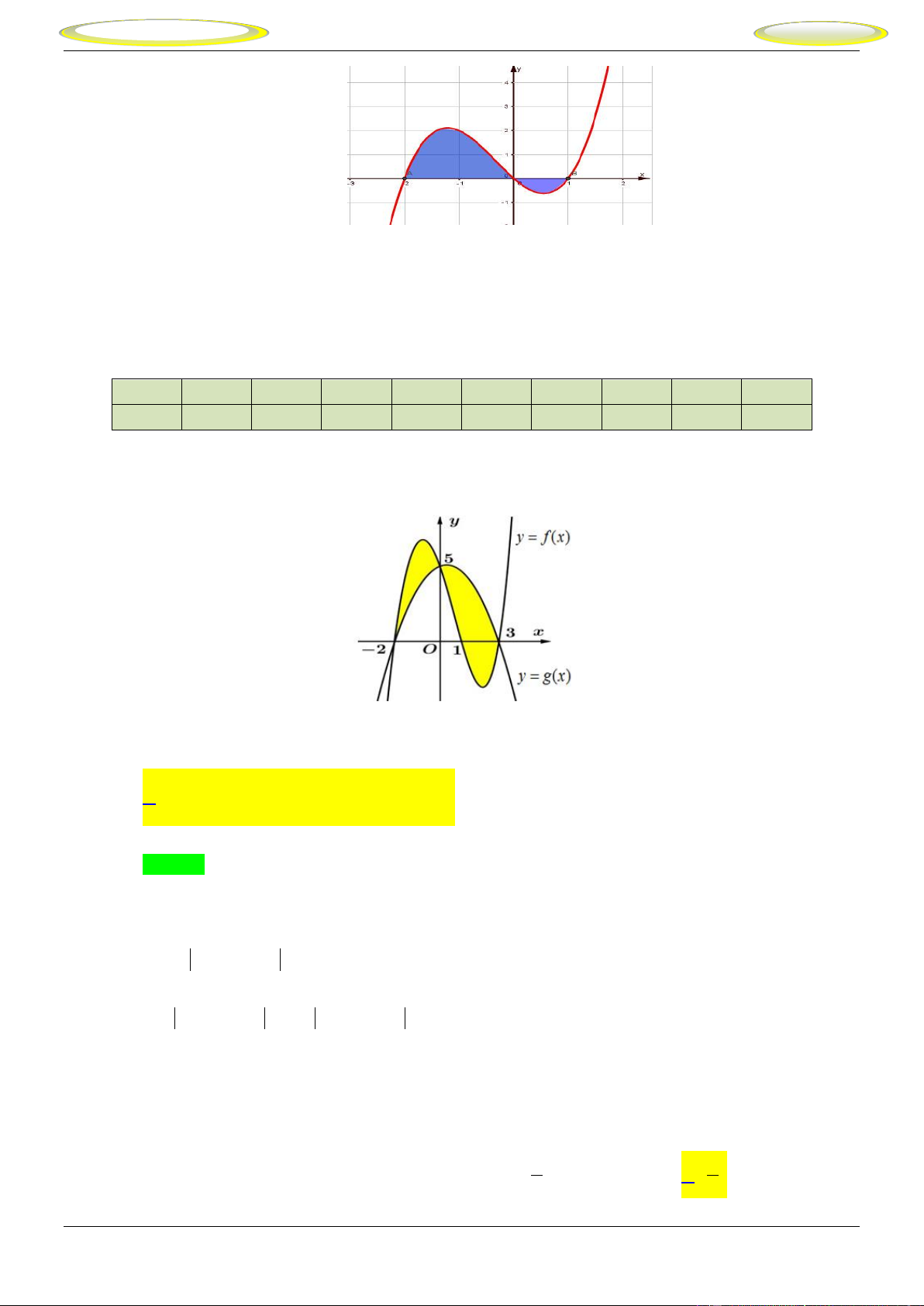
_Bài tập minh họa: Câu 1.
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  2  x và y  . x 9 11 A. . B. 7 . C. 5 . D. . 2 2 Lời giải
PP nhanh trắc nghiệm Chọn A
  Trên  1  ;2 hàm số 2
y  f (x)  x  x  2
 Phương trình hoành độ giao điểm của hai đồ thị 1 1 x  2  không đổi dấu nên
f (x) dx  f (x)dx .   là: 2 2
2  x  x  x  x  2  0  .  x 1 2  2  
Diện tích của hình phẳng cần tìm là
Quy trình bấm máy. 1 1 1 - Nhập biểu thức 2
x  x  2 dx  vào màn hình 2 2 S 
x  x  2 dx  (x  x  2)dx   2  2  2 
bằng cách bấm lần lượt các phím sau: 1 3 2  x x  9 
- Khi đó trên màn hình xuất hiện     2x  .  3 2  2 2  ln x Câu 2.
Gọi S là diện tích của hình phẳng giới hạn bởi các đường y 
, y  0 , x  1, x  e . Mệnh 2 x
đề nào dưới đây đúng? e e 2 e 2 ln x e ln x  ln x  ln x A. S   dx  . B. S  dx  . C. S  dx
  . D. S     dx   . 2 x 2 x 2  x  2  x  1 1 1 1 Lời giải
PP nhanh trắc nghiệm Chọn B  ln x
Xét dấu của hàm số y  trên đoạn [1;e] . e ln x 2 x  Ta có S  dx  . 2 x 1 e ln x ln x Vì x
 [1;e], ln x  0   0  S  dx  . 2 2 x x 1 1 4 Câu 3.
Tính diện tích hình phẳng giới hạn bởi các đường 2 y x , y x và trục hoành như hình y 3 3 vẽ. y = x2 2 1 4 1 y = - x+ 3 3 x 7 56 39 11 A. . B. . O C. 4 1 . D. 3 3 2 6 Lời giải
PP nhanh trắc nghiệm Chọn D
  Quy trình bấm máy.
 Dựa vào đồ thị ta có: 1 4  1 4  2
Diện tích hình phẳng cần tìm là
- Nhập biểu thức x dx   x  dx   vào màn    3 3  0 1 55
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 4 1 4 1
hình (thao tác tương tự câu 1). 2  1 4  1  x 4  2 3 S  x dx   x  dx  x        x 
- Khi đó trên màn hình xuất hiện 3 3  3  6 3  0 1 0 1 1 8 7 11     . 3 3 6 6
_Bài tập áp dụng: (10 câu NB; 10 câu TH)
1. Nhận biết:(10 câu) Câu 1.
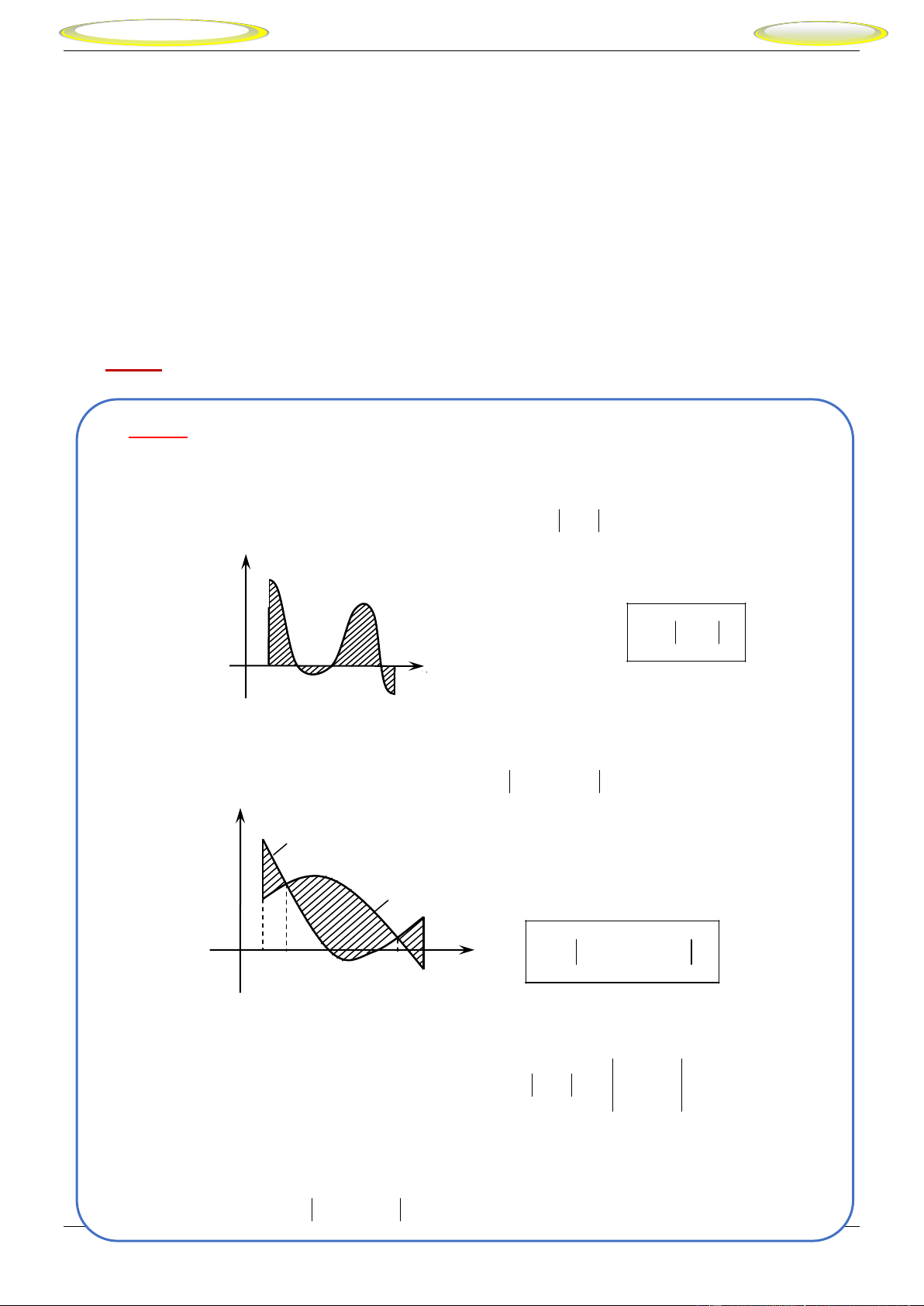
Diện tích phần hình phẳng tô đen trong hình vẽ bên dưới được tính theo công thức nào dưới đây? 3 3
A.   f (x)  g(x)dx .
B.  g(x)  f (x)dx . 2  2  0 3 0 3
C.   f (x)  g(x)dx  g(x)  f (x)dx .
D.  g(x)  f (x)dx   f (x)  g(x)dx . 2  0 2  0 Câu 2.
Diện tích hình phẳng giới hạn bởi hai đường 3
y  x 11x  6 và 2 y  6x là 1 1 A. 52 . B. 14 . C. . D. . 4 2 Câu 3.
Diện tích hình phẳng giới hạn bởi 2
y  x ; y  0; x  1; x  2 bằng 7 4 8 A. . B. . C. . D. 1. 3 3 3 Câu 4.
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 2 2 A.   2
2x  2x  4dx . B.   2
2x  2x  4dx . 1  1  56
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 2 2 C.   2 2
 x  2x  4dx . D.   2 2
 x  2x  4dx . 1  1  Câu 5.
Tính diện tích S của hình phẳng (phần gạch sọc) giới hạn bởi hai đồ thị hàm số
f  x  x; g  x  x  2 trong hình sau y 2 O 2 4 x 7 10 11 7 A. S  . B. S  . C. S  . D. S  . 3 3 3 3 Câu 6.
Tính diện tích S của hình phẳng (H ) giới hạn bởi các đường cong 3
y  x 12x và 2 y  x . 937 343 793 397 A. S  . B. S  . C. S  . D. S  . 12 12 4 4 x  Câu 7.
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số H  1 : y  và các trục tọa độ. x 1
Khi đó giá trị của S bằng
A. S  2ln 2 1.
B. S  ln 2 1.
C. S  ln 2 1.
D. S  2ln 2 1. Câu 8.
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 3 3 A.  2
x  4x  3dx . B.  2
x  2x 1  1 dx . 1 1 3 3 C.  2 x  2x    11 dx . D.  2
x  4x  3dx . 1 1 Câu 9.
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 0 0 A.   2
x  3xdx . B.   2
x  3xdx . 3  3  57
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 0 0 C.   2
x  5x  2dx . D.   2
x  5x  2dx . 3  3 
Câu 10. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 1 1 A.  3 2 2  x  3x   1dx . B.   3 2
2x  x  2x  3dx . 1  1  2 2 1 1 C.  3 2 2x  3x   1dx. D.   3 2 2
 x  x  2x  3dx . 1  1  2 2
2. Thông hiểu: (10 câu)
Câu 11. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 3 3 A.  3 2
x  5x  9x  7dx . B.  3 2
x  5x  9x  7dx . 1 1 3 3 C.  3 2
x  x  9x  9dx . D.  3 2
x  x  9x  9dx . 1 1
Câu 12. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 1  1  2 2
A.  5x 8dx . B.   2
2x  5x  2dx . 2 2  58
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 1  1  2 2
C.  5x 8dx . D.   2 2
 x  5x  2dx . 2 2 
Câu 13. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 3 y  x và 5 y  x ? 1 1 A. S  1. B. S  2 . C. S  . D. S  . 6 3
Câu 14. Tính diện tích S của hình phẳng giới hạn bởi các đường 2
y  x  2x , y  0 , x  10
 , x 10 . 2000 2008 A. S  .
B. S  2008 .
C. S  2000 . D. S  . 3 3
Câu 15. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 2 2 A.   2
2x  2x  4dx . B.   2
 x  2dx . 1  1  2 2
C.  2x  2dx . D.   2 2
 x  2x  4dx . 1  1 
Câu 16. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  4x  x và trục Ox . 34 31 32 A. 11. B. . C. . D. . 3 3 3
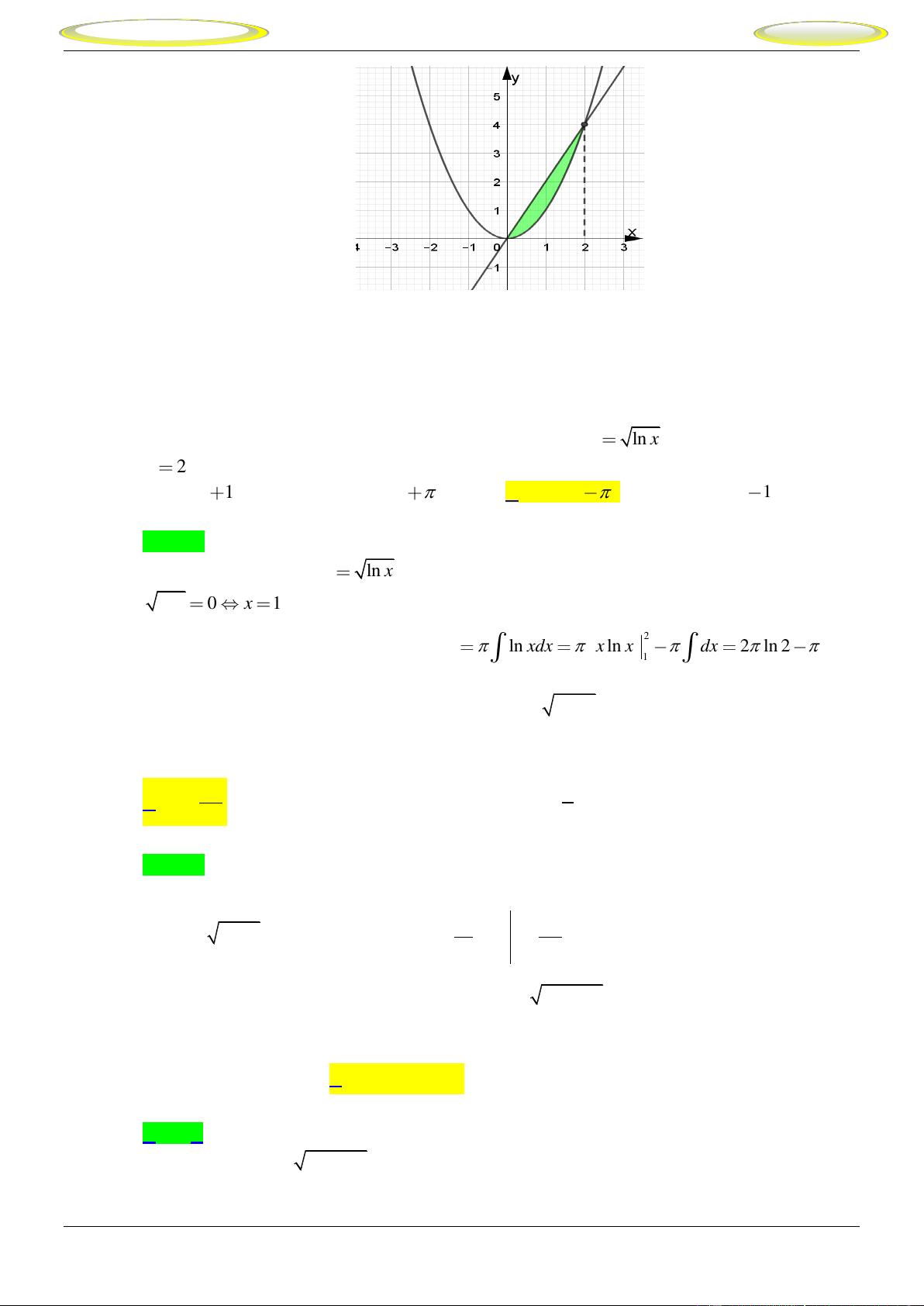
Câu 17. Cho hình phẳng (H) được giới hạn bởi đồ thị hàm số 2 x
y  e , trục Ox,Oy và đường thẳng
x 2 . Tính S hình phẳng trên. 1 1 1 A. 4 e 1. B.  4e  1. C. 4 e . D.  4e  1. 2 2 2 1 x 
Câu 18. Tính diện tích hình phẳng giới hạn bởi hai đồ thị  P : y    2
x  8x  7 , H  7 : y  3 3  . x 161 A. 3, 455 . B. 9  8ln 2 . C. 3  ln 4 . D.  4ln38ln 2 . 9
Câu 19. Tính diện tích S của hình phẳng giới hạn bởi các đường 2
y  x  2x , y  0 , x  10
 , x 10 . 2000 2008 A. S  . B. S  2008. C. S  2000 . D. S  . 3 3
Câu 20. Cho đồ thị hàm số y  f (x) . Diện tích hình phẳng (phần tô đậm trong hình) là 59
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 0 1 1 A. S 
f (x)dx  f (x)dx   B. S  f (x)dx  2  0 2  2  1 0 1 C. S 
f (x)dx  f (x)dx   D. S 
f (x)dx  f (x)dx   0 0 2  0 Bảng đáp án 1.C 2.D 3.A 4.C 5.B 6.A 7.A 8.A 9.B 10.C 11.C 12.D 13.C 14.D 15.D 16.D 17.B 18.B 19.D 20.D
Hướng dẫn giải( phần TH) Câu 1.
Diện tích phần hình phẳng tô đen trong hình vẽ bên dưới được tính theo công thức nào dưới đây? 3 3
A.   f (x)  g(x)dx .
B.  g(x)  f (x)dx . 2  2  0 3 0 3
C.   f (x)  g(x)dx  g(x)  f (x)dx .
D.  g(x)  f (x)dx   f (x)  g(x)dx . 2  0 2  0 Lời giải Chọn C
Từ đồ thị hai hàm số y  f (x) và y  g(x) ta có diện tích phần hình phẳng tô đen trong hình vẽ
bên dưới được tính là: 3 S 
f (x)  g(x) dx 2 0 3 
f (x)  g(x) dx 
f (x)  g(x) dx   2  0 0 3
   f (x) g(x)dx  g(x) f (x)d .x 2  0 Câu 2.
Diện tích hình phẳng giới hạn bởi hai đường 3
y  x 11x  6 và 2 y  6x là 1 1 A. 52 . B. 14 . C. . D. . 4 2 Lời giải 60
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH Chọn D  x 1
Phương trình hoành độ giao điểm của hai đồ thị là  : 3 2
x 11x  6  6x  x  2  . x  3 2 3
Diện tích của hình phẳng là : S   3 2
x  6x 11x  6 dx   3 2
x  6x 11x  6 dx 1 2 2 3 4 4  x 11   x 11  1 1 1 3 2 3 2
   2x  x 6x    2x  x 6x    .  4 2   4 2  4 4 2 1 2 Câu 3.
Diện tích hình phẳng giới hạn bởi 2
y  x ; y  0; x  1; x  2 bằng 7 4 8 A. . B. . C. . D. 1. 3 3 3 Lời giải Chọn A 2 2 2 3
Diện tích của hình phẳng là x 7 2 2 S 
x dx  x dx     . 3 3 1 1 1 Câu 4.
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 2 2 A.   2
2x  2x  4dx . B.   2
2x  2x  4dx . 1  1  2 2 C.   2 2
 x  2x  4dx . D.   2 2
 x  2x  4dx . 1  1  Lời giải Chọn C
Từ đồ thị ta thấy 2 2
x  3  x  2x 1, x   1  ;2 .
Vậy diện tích phần hình phẳng gạch chéo trong hình vẽ là 2 2 S     2 x  3   2 x  2x  2  1dx 
  2x  2x  4dx . 1 1 Câu 5.
Tính diện tích S của hình phẳng (phần gạch sọc) giới hạn bởi hai đồ thị hàm số
f  x  x; g  x  x  2 trong hình sau 61
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH y 2 O 2 4 x 7 10 11 7 A. S  . B. S  . C. S  . D. S  . 3 3 3 3 Lời giải Chọn B 4 4 4 3      x  S x x  2dx  x   x  2 2 2 10 2 dx   x   2x   . 3 2 3   0 0 2 Câu 6.
Tính diện tích S của hình phẳng (H ) giới hạn bởi các đường cong 3
y  x 12x và 2 y  x . 937 343 793 397 A. S  . B. S  . C. S  . D. S  . 12 12 4 4 Lời giải Chọn A
Xét phương trình hoành độ giao điểm 2 đường cong: x  0  3 2 2
x 12x  x  x(x  x 12)  0  x  3   . x  4  4 0 4 Diện tích cần tìm là: 3 2 3 2 3 2 S 
x  x 12x dx 
x  x 12x dx 
x  x 12x dx    3  3  0 0 4 0    x x   x x  
x  x 12x 4
dx  x  x 12x 4 3 4 3 3 2 3 2 2 2 dx   
 6x      6x  4 3 4 3     3  0 3  0 99  160  937    . 4 3 12 x  Câu 7.
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số H  1 : y  và các trục tọa độ. x 1
Khi đó giá trị của S bằng
A. S  2ln 2 1.
B. S  ln 2 1.
C. S  ln 2 1.
D. S  2ln 2 1. Lời giải Chọn A H x 1 : y 
,  H  cắt trục O ,
x Oy lần lượt tại A1;0, B 0;   1 . x 1 x 
Gọi  K  là hình phẳng giới hạn bởi các đường 1 y 
, y  0, x  0 x 1 1  1 1  2  x 1 Suy ra  dx  x S  1 dx   (do
không đổi dấu với x  0;  1 ) x 1  x 1  x 1 0 0 1
 x  2ln 1 x  
  2ln 2 1. Vậy S  2ln 2 1. 0 62
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH Câu 8.
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 3 3 A.  2
x  4x  3dx . B.  2
x  2x 1  1 dx . 1 1 3 3 C.  2 x  2x    11 dx . D.  2
x  4x  3dx . 1 1 Lời giải Chọn A Ta thấy: x  1;  3 : 2
x  3x  4  7  x nên 3 3 S    2  2
x  3x  4 7  xdx 
 x  4x 3dx . 1 1 Câu 9.
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 0 0 A.   2
x  3xdx . B.   2
x  3xdx . 3  3  0 0 C.   2
x  5x  2dx . D.   2
x  5x  2dx . 3  3  Lời giải Chọn B Ta thấy: x   3  ;0 : 2
x 1  x  4x 1 nên 0 0 S  
 x 1 2x 4x 2  1dx 
  x 3xdx. 3  3 
Câu 10. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 63
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 1 1 A.  3 2 2  x  3x   1dx . B.   3 2
2x  x  2x  3dx . 1  1  2 2 1 1 C.  3 2 2x  3x   1dx. D.   3 2 2
 x  x  2x  3dx . 1  1  2 2 Lời giải Chọn C   Ta thấy: 1 x    ;1   : 3 2 2
2x  2x  x 1  x  x  2 nên  2  3 3 S    3 2  3 2
2x  2x  x   1   2
x  x  2 dx 
 2x 3x   1dx. 1 1
Câu 11. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 3 3 A.  3 2
x  5x  9x  7dx . B.  3 2
x  5x  9x  7dx . 1 1 3 3 C.  3 2
x  x  9x  9dx . D.  3 2
x  x  9x  9dx . 1 1 Lời giải Chọn C Ta thấy: x  1;  3 : 2 3 2 2
 x  9x 8  x 3x 1 nên 3 3 S     2 2
 x  9x 8  3 2 x  3x  3 2  1dx 
 x  x 9x 9dx . 1 1
Câu 12. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 64
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 1  1  2 2
A.  5x 8dx . B.   2
2x  5x  2dx . 2 2  1  1  2 2
C.  5x 8dx . D.   2 2
 x  5x  2dx . 2 2  Lời giải Chọn D   Ta thấy: 1 x   2;     : 2 2
x 5x 5  x 3 nên  2  1  1  2 2 S    2  2
x  5x  5  2 x  3 dx     2
 x  5x  2dx . 2  2 
Câu 13. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 3 y  x và 5 y  x ? 1 1 A. S  1. B. S  2 . C. S  . D. S  . 6 3 Lời giải Chọn C x  1 
Xét phương trình hoành độ giao điểm  5 3 x  x  5 3
x  x  0  3 x  2 x   1  0  x  0  . x 1 
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 3 y  x và 5 y  x là: 1 5 3 S 
x  x dx  . 1 
Cách 1: Bấm máy tính 1 Ta được 1 5 3 S 
x  x dx   . 6 1 
Cách 2: Giải tự luận 1 0 1 0 1  1 1   1 1  1 5 3 S 
x  x dx     5 3
x  x dx   5 3
x  x dx = 6 4 6 4 x  x  x  x      .  6 4   6 4  6 1  1  0 1  0
Câu 14. Tính diện tích S của hình phẳng giới hạn bởi các đường 2
y  x  2x , y  0 , x  10
 , x 10 . 2000 2008 A. S  .
B. S  2008 .
C. S  2000 . D. S  . 3 3 Lời giải Chọn D 65
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
Cách 1: Phương trình hoành độ giao điểm của hai đường C  2
: y  x  2x và d  : y  0 là: x  0 2
x  2x  0   . x  2 Bảng xét dấu: Diện tích cần tìm: 10 0 S 
x  2x dx  
 x 2x 2
dx  x  2x 10 2 2 2 dx    2
x  2xdx 1  0 1  0 0 2 0 2 10 3 3 3  x   x   x  1300 4 704 2008 2 2 2
   x    x    x      .  3   3   3  3 3 3 3 1  0 0 2
Cách 2: Dùng MTCT Casio fx 580VN X .
Câu 15. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 2 2 A.   2
2x  2x  4dx . B.   2
 x  2dx . 1  1  2 2
C.  2x  2dx . D.   2 2
 x  2x  4dx . 1  1  Lời giải Chọn D
Từ đồ thị hai hàm số 2
y  x  3 và 2
y  x  2x 1 ta có 2 2
x  3  x  2x 1, x   1  ;2 .
Diện tích hình phẳng gạch chéo trong hình vẽ là 66
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 2 S  
 x 3x 2x  2 2 2 1  dx     2 2
 x  2x  4dx . 1  1 
Câu 16. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  4x  x và trục Ox . 34 31 32 A. 11. B. . C. . D. . 3 3 3 Lời giải Chọn D
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  4x  x và trục Ox . x  0 Xét phương trình 2
4x  x  0   . x  4 4 4 4 3 x 32 Ta có 2 2 2 S 
4x  x dx  (4x  x )dx  (2x  )    . 3 3 0 0 0
Câu 17. Cho hình phẳng (H) được giới hạn bởi đồ thị hàm số 2 x
y  e , trục Ox,Oy và đường thẳng
x 2 . Tính S hình phẳng trên. 1 1 1 A. 4 e 1. B.  4e  1. C. 4 e . D.  4e  1. 2 2 2 Lời giải Chọn B 2 2 2x 1 2x 1 4 Ta có: S e dx e e 1 . 0 2 2 0 1 x 
Câu 18. Tính diện tích hình phẳng giới hạn bởi hai đồ thị  P : y    2
x  8x  7 , H  7 : y  3 3  . x 161 A. 3, 455 . B. 9  8ln 2 . C. 3  ln 4 . D.  4ln38ln 2 . 9 Lời giải Chọn B x  0 1 x  7
Phương trình hoành độ giao điểm   2 
x  8x  7  2
 x  7 x  4x  0  x  4 . 3 3     x  x  7  67
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 7  7 
Diện tích hình phẳng là x 7 1 x 7 1 S   
 2x 8x7 dx   
 2x 8x7 dx 3  x 3 3  x 3 4 4 7  x  7 1     4 1     2
x  8x  7 dx   1    
x 8x7 7 2   3  x 3   3  x 3  4 4 7 3  1  x  2
 x  4ln 3 x    4x  7x  98ln 2. 3   3  4
Câu 19. Tính diện tích S của hình phẳng giới hạn bởi các đường 2
y  x  2x , y  0 , x  10
 , x 10 . 2000 2008 A. S  . B. S  2008. C. S  2000 . D. S  . 3 3 Lời giải Chọn D
Phương trình hoành độ giao điểm của hai đường C 2
: y  x  2x và d  : y  0 là: x  0 2
x  2x  0   . x  2 Bảng xét dấu: Diện tích cần tìm: 10 0 S 
x  2x dx  
 x 2x 2
dx  x  2x 10 2 2 2 dx    2
x  2xdx 1  0 1  0 0 2 0 2 10 3 3 3  x   x   x  1300 4 704 2008 2 2 2
   x    x    x      .  3   3   3  3 3 3 3 1  0 0 2
Cách 2: Dùng MTCT Casio fx 580VN X
Câu 20. Cho đồ thị hàm số y  f (x) . Diện tích hình phẳng (phần tô đậm trong hình) là 0 1 1 A. S 
f (x)dx  f (x)dx   B. S  f (x)dx  2  0 2  68
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 2  1 0 1 C. S 
f (x)dx  f (x)dx   D. S 
f (x)dx  f (x)dx   0 0 2  0 Lời giải Chọn D 0 1 x
 [-2;0], f(x)  0; x  [0;1], f( )
x  0 nên ta có: S 
f (x)dx  f (x)dx   2  0
_ Dạng 2. Ứng dụng của tích phân tính thể tích
_ Dạng 2. Ứng dụng của tích phân tính thể tích
-Phương pháp: 
1. Bài toán1: Tính thể tích vật thể tròn xoay sinh bởi miền  D giới hạn bởi y f  x ;
y  0 và x  a, x  b khi quay quanh trục Ox . b
* Phương pháp giải: áp dụng công thức: 2 V   y dx  a
2. Bài toán 2: Tính thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi: y  f  x ;
y  g  x quay quanh trục Ox .
* Phương pháp giải:
+ Giải phương trình: f  x  g  x có nghiệm   x a, x b b
+ Khi đó thể tích cần tìm : 2 V   f  x 2
 g xdx a
3. Bài toán3: Tính thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi:  x
g  y ; y  ; a y  b b
* Ph ương pháp giải: áp dụng công thức: 2 V   x dy  a
4. Bài toán 4: Tính thể tích vật thể tròn xoay do hình phẳng giới hạn
bởi: x  f  y; x  g  y và   . y , a y b
* Ph ương pháp giải: b Áp dụng công thức: 2 2 V  
f ( y)  g ( y) dy  a
5. Bài toán 5: Tính thể tích vật thể tròn xoay sinh bởi miền  D giới hạn bởi một đường cong C kín.
* Phương pháp giải: 69
1/ Khi  D quay quanh trục Ox :
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Chia đường cong C  thành 2 cung: y  f x và y  f x
với x a;b và 2 2   1 1   f x ; f
x cùng dấu. Khi đó thể tích cần tính: 1   2   Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 70
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
_Bài tập minh họa: Câu 1.
Cho hàm số y  f (x) liên tục trên đoạn a;b 
 . Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
y  f (x) , trục hoành và hai đường thẳng x  ,
a x  b (a  )
b . Thể tích khối tròn xoay tạo thành
khi quay D quanh trục hoành được tính theo công thức b b b b A. 2 2 V   f (x)dx  . B. 2 V   f (x)dx  . C. 2 V   f (x)dx  . D. 2 V  2 f (x)dx  . a a a a Lời giải
PP nhanh trắc nghiệm Chọn B
 Học thuộc công thức. b  x  [a; ] b ta có 2 V   f (x)dx  a Câu 2.
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x  1 và x  3, biết rằng khi cắt vật
thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (1 x  3 ) thì được thiết diện
là một hình chữ nhật có độ dài hai cạnh là 3x và 2 3x  2 . 124
A. V  32  2 15. B. V  . 3 124 C. V  .
D. V  (32  2 15). 3 Lời giải
PP nhanh trắc nghiệm Chọn C 3
 Ta nhập biểu thức 2 3 .
x 3x  2dx  như sau:
 Diện tích thiết diện là: 2 S(x)  3 . x 3x  2 1  3 124 y3Q(s3Q(dp2R1E3= Thể tích vật thể là: 2 V  3 .
x 3x  2dx   . + Màn hình hiển thị 3 : 1 Chọn C Câu 3.
Gọi S là diện tích hình phẳng H  giới hạn bởi các đường y  f  x , trục hoành và hai đường 0 2 thẳng x  1
 , x  2 (như hình vẽ bên dưới). Đặt a  f
 xdx ,b  f
 xdx , mệnh đề nào sau 1  0 đây đúng? 71
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
A. S  b  a
B. S  b  a
C. S  b   a
D. S  b   a Lời giải
PP nhanh trắc nghiệm Chọn A
 Dựa vào đồ thị ta thấy f (x) là hàm đồng  Ta có:
biến trên nên ta có thể chọn một hàm đồng 2 0 2
biến trên để thay thế, ví dụ chọn f (x)  x , S  f
 x dx  f
 x dx  f  x dx 1  1  0 suy ra 0 2 0 2   1 f
 xdx  f
 xdx  a b . a  d x x   
, b  xdx  2  , 1  0 2 1  0 2 Vậy 5 S  x dx   2 1  Lại thấy 5 b  a  , chọn A 2
_Bài tập áp dụng: (10 câu NB; 10 câu TH)
1. Nhận biết:(10 câu) Câu 1.
Gọi H  là hình phẳng giới hạn bởi các đường: y  sin x ; Ox ; x  0 ; x   . Quay H  xung
quanh trục Ox ta được khối tròn xoay có thể tích là: 2   A. . B. . C.  . D. 2  . 2 2 Câu 2.
Cho hình  H  giới hạn bởi y  sin x , x  0, x   và y  0 . Thể tích khối tròn xoay khi
quay H  quanh trục Ox bằng:  2  2  A. . B. 2 . C. . D. . 2 4 2 Câu 3.
Gọi  H  là hình phẳng giới hạn bởi các đường y  x ln , x trục O ,
x x  1, x  e . Tính thể tích
khối tròn xoay được tạo thành khi quay hình phẳng  H  quanh trục Ox .   2e   1   2 e   1  e   1  e   1 A. . B. . C. . D. . 4 3 3 4 Câu 4.
Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol  P 2
: y  x và đường
thẳng d : y  2x quay quanh trục Ox bằng: 2 2 2 2 2 2 2 A. 2 4
 4x dx  x dx   . B.   2
x  2x dx . C. 2 4
 4x dx  x dx   . D.   2
x  2x dx . 0 0 0 0 0 0 Câu 5.
Tính thể tích vật thể tròn xoay do hình phẳng giới hạn bởi y
ln x , trục Ox và đường thẳng x
2 quay xung quanh trục Ox . 72
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH A. 2ln 2 1 . B. 2 ln 2  .
C. 2 ln 2  . D. 2 ln 2 1. Câu 6.
Cho hình phẳng D giới hạn với đường cong 2 y 
x 1 , trục hoành và các đường thẳng
x  0, x  1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 4 4 A. V 
B. V  2 C. V 
D. V  2 3 3 Câu 7.
Cho hình phẳng D giới hạn bởi đường cong y  2  sin x , trục hoành và các đường thẳng
x  0 , x   . Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng bao nhiêu? A. 2 V  2 .
B. V  2    1 .
C. V  2 .
D. V  2   1 . Câu 8.
Cho hình phẳng H  giới hạn bởi các đường 2
y  x  3 , y  0 , x  0 , x  2 . Gọi V là thể
tích của khối tròn xoay được tạo thành khi quay H  xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2
A. V    2
x  3 dx . B. V    2
x  3 dx . C. V   2
x  3 dx . D. V   2 x  3 dx . 0 0 0 0 Câu 9.
Cho hình phẳng H  giới hạn bởi các đường thẳng 2
y  x  2, y  0, x  1, x  2 . Gọi V là thể
tích của khối tròn xoay được tạo thành khi quay H  xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2
A. V    2
x  2 dx . B. V   2
x  2 dx . C. V    2
x  2dx . D. V   2 x  2dx . 1 1 1 1
Câu 10. Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới
hạn bởi đồ thị hàm số y  f  x , trục Ox và hai đường thẳng x  a, x  ba  b , xung quanh trục Ox . b b b b A. 2 V   f
 xdx . B. 2 V  f
 xdx . C. V  f
 xdx . D. V  f  xdx . a a a a
2. Thông hiểu: (10 câu)
Câu 11. Cho hàm số y  f  x liên tục trên đoạn a ;b . Gọi D là hình phẳng giới hạn bởi đồ thị hàm
số y  f  x , trục hoành và hai đường thẳng x  a , x  b a  b . Thể tích khối tròn xoay tạo
thành khi quay D quanh trục hoành được tính theo công thức b b b b A. 2 V   f
 xdx. B. 2 V  2 f
 xdx. C. 2 2 V   f
 xdx. D. 2 V   f  xdx. a a a a
Câu 12. Kí hiệu  H  là hình phẳng giới hạn bởi đồ thị hàm số  2( 1) x y x
e , trục tung và trục hoành.
Tính thể tích V của khối tròn xoay thu được khi quay hình H  xung quanh trục Ox .
A. V  4  2e .
B. V  4  2e . C. 2 V  e  5 . D. V   2 e  5 .
Câu 13. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số 2
y  3x  x , y  0 . 16 16 81 16 A. . B.  . C.  . D. 15 15 10 15 . 73
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
Câu 14. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số 3 2
y  x  x  2, y  2 . 12 3564 3654 729 A.  . B.  . C.  . D. . 35 35 35 35
Câu 15. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số 2 3
y  2x , y  x . 1536 256 1536 265 A. π . B. π . C. . D. . 35 35 35 35
Câu 16. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số 3
y  x , y  0, x  1.  4   A. . B. . C. . D. . 4 7 2 7
Câu 17. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục tung hình phẳng giới hạn
bởi đồ thị của các hàm số 2
y  2x  3; y  1; y  2; x  0 .  9 206 A. 8 . B. . C. . D. . 2 4 15
Câu 18. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số xy  9, y  0, x 1, x  3. A. 54 . B. 6 . C. 12 . D. 6 .
Câu 19. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số y   x 1 cos
, y  0, x  0, x   .    2  sin 2  2 sin 2  2   2 A. . B. . C. . D. . 8 4 4 8
Câu 20. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số 2 y  cos ,
x y  0, x  0, x   . 2  3 2 3  A. . B. . C. . D. . 2 8 8 2 Bảng đáp án 1.A 2.D 3.D 4.A 5.C 6.A 7.B 8.A 9.A 10.A 11.A 12.D 13.C 14.A 15.B 16.D 17.C 18.A 19.B 20.C Hướng dẫn giải Câu 1.
Gọi H  là hình phẳng giới hạn bởi các đường: y  sin x ; Ox ; x  0 ; x   . Quay H  xung
quanh trục Ox ta được khối tròn xoay có thể tích là 2   A. . B. . C.  . D. 2  . 2 2 Lời giải Chọn A      
Thể tích khối tròn xoay là V     sin . x dx   1c so2x 2 1 2 .dx  x  sin 2x    . 2 2  2  0 2 0 0 Câu 2.
Cho hình  H  giới hạn bởi y  sin x , x  0, x   và y  0 . Thể tích khối tròn xoay khi 74
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
quay H  quanh trục Ox bằng  2  2  A. . B. 2 . C. . D. . 2 4 2 Lời giải Chọn D
Thể tích khối tròn xoay  H  quanh trục Ox là:     1 cos2x      
V   sin xdx   dx    1cos2x 2 1 2 dx  x  sin2x  .    . 2 2 2  2  2 2 0 0 0 0 Câu 3.
Gọi  H  là hình phẳng giới hạn bởi các đường y  x ln , x trục O ,
x x  1, x  e . Tính thể tích
khối tròn xoay được tạo thành khi quay hình phẳng  H  quanh trục Ox .   2e   1   2 e   1  e   1  e   1 A. . B. . C. . D. . 4 3 3 4 Lời giải Chọn D e Ta có 2 V   x ln xdx  Ox 1  2 du  ln xdx 2 e u   ln x  e     Đặ x 1 t    . Suy ra 2 2 V    x ln x  x ln xdx    . dv  x 1 Ox     2  2 v  x  1 1   2  1 du  dx u   ln x  Đặ x t    . dv  x 1 2 v  x  2 e e  1 1 1 e      Suy ra 2 2 2 V    x ln x  x ln x  xdx   Ox      2 2 2       1 1 1  e e e 2  1   1   1    e 1 2 2 2 2    x ln x  x ln x  x             . 2 2 4           4  1 1 1 Câu 4.
Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol  P 2
: y  x và đường
thẳng d : y  2x quay quanh trục Ox bằng 2 2 2 2 2 2 2 A. 2 4
 4x dx  x dx   . B.   2
x  2x dx . C. 2 4
 4x dx  x dx   . D.   2
x  2x dx . 0 0 0 0 0 0 Lời giải Chọn A 75
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH x 
Phương trình hoành độ giao điểm của  P và d  0  là 2 x 2x  . x  2 2 2 2 2 2 
Thể tích của khối tròn xoay là  
 2x  2x dx 2 4       4x dx x dx   0 0 0 Câu 5.
Tính thể tích vật thể tròn xoay do hình phẳng giới hạn bởi y
ln x , trục Ox và đường thẳng x
2 quay xung quanh trục Ox . A. 2ln 2 1 . B. 2 ln 2  .
C. 2 ln 2  . D. 2 ln 2 1. Lời giải Chọn C
Giao của đồ thị hàm số y
ln x với trục Ox có hoành độ là nghiệm của phương trình ln x 0 x 1. 2 2 Gọi 2
V là thể tích vật thể cần tìm, ta có: V
 ln xdx  x ln x  dx 2 ln 2  1 1 1 Câu 6.
Cho hình phẳng D giới hạn với đường cong 2 y 
x 1 , trục hoành và các đường thẳng
x  0, x  1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 4 4 A. V 
B. V  2 C. V 
D. V  2 3 3 Lời giải Chọn A
Thể tích khối tròn xoay được tính theo công thức:      x  V x 1 1 1 1
dx   x   3 2 4 2 2 1 dx     x  .  3  3 0 0 0 Câu 7.
Cho hình phẳng D giới hạn bởi đường cong y  2  sin x , trục hoành và các đường thẳng
x  0 , x   . Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng bao nhiêu? A. 2 V  2 .
B. V  2    1 .
C. V  2 .
D. V  2   1 . Lời giải Chọn B
Ta có phương trình 2  sin x  0 vô nghiệm nên: 76
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH   
V    2  sin x 2dx   2  sin xdx   2x cos x  2    1 . 0 0 0 Câu 8.
Cho hình phẳng H  giới hạn bởi các đường 2
y  x  3 , y  0 , x  0 , x  2 . Gọi V là thể
tích của khối tròn xoay được tạo thành khi quay H  xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2
A. V    2
x  3 dx . B. V    2
x  3 dx . C. V   2
x  3 dx . D. V   2 x  3 dx . 0 0 0 0 Lời giải Chọn A
Thể tích của khối tròn xoay được tạo thành khi quay H  xung quanh trục Ox là: 2
V   x  32 2 dx . 0 Câu 9.
Cho hình phẳng H  giới hạn bởi các đường thẳng 2
y  x  2, y  0, x  1, x  2 . Gọi V là thể
tích của khối tròn xoay được tạo thành khi quay H  xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2
A. V    2
x  2 dx . B. V   2
x  2 dx . C. V    2
x  2dx . D. V   2 x  2dx . 1 1 1 1 Lời giải Chọn A 2 2
Ta có: V    2 x  2 dx . 1
Câu 10. Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới
hạn bởi đồ thị hàm số y  f  x , trục Ox và hai đường thẳng x  a, x  ba  b , xung quanh trục Ox . b b b b A. 2 V   f
 xdx . B. 2 V  f
 xdx . C. V  f
 xdx . D. V  f  xdx . a a a a Lời giải Chọn A
Câu 11. Cho hàm số y  f  x liên tục trên đoạn a ;b . Gọi D là hình phẳng giới hạn bởi đồ thị hàm
số y  f  x , trục hoành và hai đường thẳng x  a , x  b a  b . Thể tích khối tròn xoay tạo
thành khi quay D quanh trục hoành được tính theo công thức b b b b A. 2 V   f
 xdx. B. 2 V  2 f
 xdx. C. 2 2 V   f
 xdx. D. 2 V   f  xdx . a a a a Lời giải Chọn A
Theo công thức tính thể tích vật tròn xoay khi quay hình H  quanh trục hoành ta có b 2 V   f  xdx. a 77
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
Câu 12. Kí hiệu  H  là hình phẳng giới hạn bởi đồ thị hàm số  2( 1) x y x
e , trục tung và trục hoành.
Tính thể tích V của khối tròn xoay thu được khi quay hình H  xung quanh trục Ox
A. V  4  2e .
B. V  4  2e . C. 2 V  e  5 . D. V   2 e  5 . Lời giải Chọn D
Phương trình hoành độ giao điểm 2   1 x x
e  0  x  1
Thể tích của khối tròn xoay thu được khi quay hình H  xung quanh trục Ox là:
du  2 x 1 dx 1 1 u
  x  2      1  2     2 1 x   4   2 2 1 x V x e dx x e dx   . Đặt   2 x  e 2 x     0 0 dv e dx v  2 1 1 2 x 1 2 x 2 x 1 e e e
V  4 x  2 1  4 2x   1
dx  4  x  2 1  4 x     2 1 x e dx 2 2 2 0 0 0 0 u
  x 1 du  dx 1  Gọi      2 1 x I x e dx . Đặt 2 x  1 e 2 x
dv  e dx  v  0  2 1 2 x 1 x e e
 I  4 x   2 1 2 x 2 2 1  4
dx  2   e
 2 e   3 e  1 0 2 2 0 0 1 2 x Vậy e
V  4  x  2 1  I  2     2
3   e     2 e  5 1  2 0
Câu 13. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số 2
y  3x  x , y  0 . 16 16 81 16 A. . B.  . C.  . D. 15 15 10 15 . Lời giải Chọn C x  0 Ta có: 2
3x  x  0   x  3 3 2
Thể tích: V    2 x  x  81 3 dx  . 10 0
Câu 14. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số 3 2
y  x  x  2, y  2 . 12 3564 3654 729 A.  . B.  . C.  . D. . 35 35 35 35 Lời giải Chọn A x  0 Ta có: 3 2
x  x  2  2   x  1 1 2
Thể tích: V     3 2
x  x   2 12 2  2 dx  . 35 0 78
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH
Câu 15. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số 2 3
y  2x , y  x . 1536 256 1536 265 A. π . B. π . C. . D. . 35 35 35 35 Lời giải Chọn B x  0 2 256 Ta có: 2 3 2x  x   . Thể tích: 6 4 V  
x  4x dx  .  x  2 35 0
Câu 16. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số 3
y  x , y  0, x  1.  4   A. . B. . C. . D. . 4 7 2 7 Lời giải Chọn D 1 1 Ta có: 3
x  0  x  0 . Thể tích: 6
V   x dx  .  7 0
Câu 17. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục tung hình phẳng giới hạn
bởi đồ thị của các hàm số 2
y  2x  3; y  1; y  2; x  0 .  9 206 A. 8 . B. . C. . D. . 2 4 15 Lời giải Chọn C y  3 Ta có: 2
y  2x  3  x  
nên thể tích của khối tròn xoay được tạo thành là: 2 2 2 2 2 2  y  3   y  3   y 3  9 V     dy   dy         y    . 2    2   4 2  4 1 1 1
Câu 18. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số xy  9, y  0, x 1, x  3. A. 54 . B. 6 . C. 12 . D. 6 . Lời giải Chọn A 3 9 81
Ta có: xy  9  y  Thể tích: V   dx  54.  x 2 x 1
Câu 19. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số y   x 1 cos
, y  0, x  0, x   .    2  sin 2  2 sin 2  2   2 A. . B. . C. . D. . 8 4 4 8 Lời giải Chọn B 79
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt ! Ôn thi QG Lớp KHXH New 2020
Tài liệu tự học dành cho HS Lớp KHXH 1 1     sin 2  2 Thể tích: 2 V   cos 
 xdx  1   cos   2 x    dx    2 4 0 0
Câu 20. Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới hạn
bởi đồ thị của các hàm số 2 y  cos ,
x y  0, x  0, x   . 2  3 2 3  A. . B. . C. . D. . 2 8 8 2 Lời giải Chọn C 1 1    2    Thể tích: 4 V   d x x    x2 dx    x  x 3 cos 1 cos 2 3 4 cos 2 cos 4 dx      4 8 8 0 0 0 80
Fb: ThayTrongDGl Tài liệu biên soạn và sưu tầm Chúc các em học tốt !